浙江省绍兴县鲁迅中学2014届高考数学适应性考试 文 新人教A版
【2014绍兴一模】浙江省绍兴市2014届高三教学质量调测数学文试题 Word版含答案

2014年绍兴市高三教学质量调测数学(文)一、选择题1. 已知集合},20|{},1|{≤≤=≤=x x N x x M 则=N MA.]0,(-∞B. ]1,0[C. ]2,1[D. ]2,0[ 2. 已知i 为虚数单位,若,)2)(1(i a i i +=-+则实数a 的值为 A.1-B.1C.3-D.3 3. 某程序框图如图所示,则该程序运行后输出的值为 A.23 B.47 C.95D.1914. ”“0=ϕ是为奇函数”的“函数)sin()(ϕ+=x x f A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5. 从集合}5,4,3,2,1{=A 中任取3个数,这3个数的和能被3A.51 B.103 C.52 D.21 6. 若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥+-≥++≥-,012,01,02y x y x x 则x y 3-的最大值为A. 6-B.3-C.2-D.1-7. 在四棱锥ABCD V -中,ABCD 为正方形,侧棱均相等,Q P ,分别为棱VD VB ,的中点,则下列结论错误..的是 A.直线ABCD PQ 平面// B.直线VBD AC 平面⊥ C.平面VAC APQ 平面⊥D.平面VAB APQ 平面⊥8. 如图,双曲线)0,0(12222>>=-b a by a x 的左、右焦点分别为,,21F F 过点2F 作倾斜角为 60的直线交双曲线于点,P 设2PF 的中点为.M 若|,|||22M F OF =则该双曲线的离心率为A.212+ B.213+C.12+D.13+9. 已知点B A ,分别在直线3,1==x x 上,O 为坐标原点,且 4.||=-当||+取到最小值时,OB OA ⋅的值为 A.0B.2C.3D.610. 已知函数,1)1()(22++-=x k x x f 若存在],4,2[],1,[21++∈+∈k k x k k x 使得),()(21x f x f =则实数k 的取值范围为 A.]5,5[-B.]3,1[]1,3[ --11C. ]2,1[]1,2[ --D. ]3,2[]2,3[ --二、填空题 11.已知,33cos =θ则θ2cos =_____________. 12.已知函数⎩⎨⎧≥+-<=1,31,2)(2x x x x f x ,则))2((f f =____________. 13.已知等差数列},{n a 若,6732=++a a a 则=+71a a _____________. 14.已知),3,1(),1,2(-==若)(λ-⊥,则实数λ的值为___________. 15.某几何体的三视图如图所示,则该几何体的体积为______________.16.若直线03=++m my x 被圆)0(222>=+r r y x 所截得的最短弦长为8,则r =______________.17.D C ,两点在PAB ∆的边AB 上,,BD AC =若90=∠CPD 1022=+PB PA ,则CD AB +2的最大值是______________.三、解答题18.在ABC ∆中,角C B A ,,所对的边分别是c b a ,,,已知.3,1π==C c(Ⅰ)若,33sin =B 求b 的值; (Ⅱ)若ABC ∆的面积为,63求C B A sin sin sin +的值。
浙江省绍兴县鲁迅中学2014届高考理综(化学部分)适应性考试新人教版

浙江省鲁迅中学2014届高三普通高等学校招生5月适应性考试理综试题理科综合能力测试本试题卷分选择题和非选择题两部分。
全卷共页,选择题部分1至6页,非选择题部分7至14页。
满分300分,考试时间150分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(120分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
选择题部分共20小题,每小题6分,共120分。
可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 K 39 Cl 35.5 Fe 56 I 127一、选择题(本题共17题。
在每小题给出的四个选项中,只有一项符合题目要求的。
)7.下列说法不正确的是A.2011年诺贝尔化学奖授予以色列科学家达尼埃尔·谢赫特曼,以表彰他发现了准晶体。
化学式为Al63Cu24Fe13的准晶体可与稀硝酸发生反应。
B.分光光度计可用于分析溶液颜色与反应物(或生成物)浓度的关系,从而确定化学反应速率。
C.绿色化学的核心是应用化学原理对环境污染进行治理。
D.在即将到来的新能源时代,核能、太阳能、氢能将成为主要能源。
8.下列说法正确的是A. 用纸上层析法分离和检验墨水的成分,为了看到色斑,只有有色离子的检验才可以用纸层析法。
B.容量瓶、量筒、滴定管上都具体标明使用温度,容量瓶有标线无“0”刻度,量筒、滴定管都有“0”刻度;使用时容量瓶水洗后不用润洗,量筒、滴定管水洗后还需润洗C.溴水中加入苯,溴水褪色了是因为溴与苯发生了取代反应,溴水中通入乙烯,溴水褪色了是因为溴与乙烯发生了加成反应D.物质的分离提纯方法之一为“筛分”:如胶体—渗析法分离提纯;浊液—过滤分离,本质上就是依据所分离粒子的直径大小选择具有合适孔径的“筛子”。
2014届浙江数学(文)高考模拟卷八

2014届浙江高三数学(文)高考模拟卷八命题学校:台州一中、建人高复、绍兴二中 2014.2.5考生须知:1、全卷分试卷I 、II ,试卷共4页,有五大题,满分150分。
考试时间120分钟。
2、本卷答案必须做在答卷I 、II 的相应位置上,做在试卷上无效。
3、请用蓝、黑墨水笔或圆珠笔将姓名、准考证号分别填写在答卷I 、II 的相应位置上,用2B 铅笔将答卷I 的准考证号和学科名称所对应的方框内涂黑。
参考公式:球的表面积公式 S =4πR 2球的体积公式 V =43πR 3 其中R 表示球的半径 锥体的体积公式 V =13Sh 其中S 表示锥体的底面积,h 表示锥体的高柱体的体积公式 V =Sh其中S 表示柱体的底面积,h 表示柱体的高 台体的体积公式 V =13h (S 1S 2) 其中S 1,S 2分别表示台体的上、下底面积, h 表示台体的高如果事件A ,B 互斥,那么 P (A +B )=P (A )+P (B )选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合{}1-==x y x M ,{})2(log 2x y x N -==,则=)(N M C R ( ▲ )(A ) [1,2) (B )),2[)1,(+∞-∞ (C ) [0,1] (D ) ),2[)0,(+∞-∞ (2)设复数z 满足iz=2-i (i 为虚数单位),则z= ( ▲ ) (A ) -1-2i (B ) 1-2i (C )1+2i (D )-1+2i (3)在ABC ∆中,“23sin =A ”是“3π=A ”的( ▲ ) (A) 充分而不必要条件 (B)必要而不充分条件(C) 充分必要条件 (D )既不充分也不必要条件(4)已知m,n 是两条不同直线,βα,是两个不同平面,以下命题正确的是( ▲ ) (A )若,,//αα⊂n m 则n m // (B) 若,,n m m ⊥=βα 则α⊥n (C )若,//,//ααn m 则n m // (D) 若n m m =⊂βαβα ,,//则n m //(5)阅读右面的程序框图,则输出的S 等于( ▲ )(A )40 (B)38 (C)32 (D)20(6)已知函数),0(21ln )(>-+=x xx x f 则函数)(x f 的零点个数是( ▲ ) (A )0 (B)1 (C)2 (D)3(7)一空间几何体的三视图如图所示,该几何体的体积为12π+853,则正视图中x 的值为( ▲ )(A ) 5 (B)4 (C)3 (D)2(8)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a cos A =b sin B ,则sin A cos A +cos 2B =( ▲ )(A)21-(B)21(C)-1 (D)1 (9)已知双曲线()0,012222>>=-b a by a x 的右焦点为F,若过点F 且倾斜角为060的直线与双曲线右支有且仅有一个交点,则此双曲线的离心率的取值范围是( ▲ )(A)()2,1 (B)(]2,1 (C)[)+∞,2 (D)()+∞,2(10)若函数3)3()(ax x a x f --=在区间[0,1]上的最小值等于-3,则实数a 的取值范围是( ▲ )(A ) ),23[+∞-(B) ]12,23[- (C) )13,23[- (D) ]12,2(- 非选择题部分(共100分)二、 填空题:本大题共7小题,每小题4分,共28分. (11)数列{}n a 中,,0,262==a a 且数列⎭⎬⎫⎩⎨⎧+11n a 是等差数列,则4a =________. (12)某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是_______. (13)依次写出函数f(x)的值,f(1)=1,f(2),f(3),…,规则如下:如果f(x)-2为自然数,则写f(x+1)= f(x)-2,否则写f(x+1)= f(x)+3,则f(2012)=__________ .(14)在平面直角坐标系xOy 中,已知圆x 2+y 2=4上有且只有四个点到直线12x -5y +c =0的距离为1,则实数c 的取值范围是________.(15)已知),4,2(),1,(==k 若k4≤的一随机整数,则ABC ∆是直角三角形的概率是________.(16)若实数x,y 满足不等式组⎪⎩⎪⎨⎧≤++≤≤-0202k y x x y x ,(其中k 为常数),若y x z 3+=的最大值为5,则k 的值等于___________. (17) 设函数f (x )的定义域为D ,若存在非零实数l 使得对于任意x ∈M (M ⊆D ),有x +l ∈D ,且f (x +l )≥f (x ),则称f (x )为M 上的l 高调函数.如果定义域为[-1,+∞)的函数f (x )=2x 为[-1,+∞)上的m 高调函数,那么实数m 的取值范围是________.三、解答题:本大题共5小题,共72分。
浙江省2014届高考数学模拟卷(提优卷)试题(三)文 新人教A版

2014年浙江省高考模拟冲刺卷(提优卷)数学 (文科)测试卷(三)本试题卷分选择题和非选择题两部分。
满分150分, 考试时间120分钟。
参考公式:球的表面积公式 柱体的体积公式 S=4πR2 V=Sh球的体积公式 其中S 表示柱体的底面积,h 表示柱体的高 V=34πR3 台体的体积公式其中R 表示球的半径 V=31h(S1+21SS +S2)锥体的体积公式 其中S1, S2分别表示台体的上、下底面积, V=31Sh h 表示台体的高其中S 表示锥体的底面积,h 表示锥体的高 如果事件A ,B 互斥,那么 P(A+B)=P(A)+P(B)选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x|4≤x2≤16},B =[a ,b],若A ⊆B ,则实数a -b 的取值范围是( ) A. (-∞,-2] B. [)+∞-,2 C. (-∞,2] D. [)+∞,22.“函数y=sin(x +φ)为偶函数” 是“φ=2π” 的A.充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3.某校150名教职工中,有老年人20个,中年人50个,青年人80个,从中抽取20个作为样本.①采用随机抽样法:抽签取出30个样本;②采用系统抽样法:将教工编号为00,01,…,149,然后平均分组抽取30个样本; ③采用分层抽样法:从老年人,中年人,青年人中抽取30个样本. 下列说法中正确的是( )[来源:学_科_网Z_X_X_K]A .无论采用哪种方法,这150个教工中每一个被抽到的概率都相等B .①②两种抽样方法,这150个教工中每一个被抽到的概率都相等;③并非如此C .①③两种抽样方法,这150个教工中每一个被抽到的概率都相等;②并非如此D .采用不同的抽样方法,这150个教工中每一个被抽到的概率是各不相同的4.已知函数()⎩⎨⎧>≤+=1,lg 1,92x x x x x f ,记()()x f x f =1,()()()x f f x f 12=,()()()x f f x f 23=, ,则()=102014f ( )A .lg109B .2C .1D .105.一个正三棱柱的三视图如图所示,这个三棱柱的侧(左)视图的面积为36则这个三棱柱的体积为 ( )A .12B .16C .8 3D .12 36.执行如图所示的程序框图,如果输入的N 是4, 那么输出的p 是( )A .6B .24C .120D .7207.观察下列各式:a +b =1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a8+b8=( ) A .28 B .47 C .76 D .1238.如图所示,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,则它的涂漆面数为2的概率( )A. 8125B. 27125C. 36125D. 541259.已知△ABC 外接圆的半径为1,圆心为O ,且OA BA CA 2=+,||||OA AB =,则BC CA ⋅的值是( )(A) 3 (B) 2 (C) 2- (D) 3-10.设双曲线22221(0,0)x y a b a b -=>>的右焦点为F ,过点F 作与x 轴垂直的直线l 交两渐近线于A 、B 两点,且与双曲线在第一象限的交点为P ,设O 为坐标原点,若(,)OP OA OB R λμλμ=+∈,81=λμ,则该双曲线的离心率为( )A .322B .2C .233 D .2非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分.11.设i 是虚数单位,则复数(1-i)2-i i2124-+20144i -= .12.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知()22cos -=+C B ,bsin ⎝ ⎛⎭⎪⎫π4+C =a+ csin ⎝ ⎛⎭⎪⎫π4+B ,则C= .13.已知PA 垂直于正方形ABCD 所在平面,连接PB 、PC 、PD 、AC 、BD,则下列垂直关系中正确的序号是 . ①平面PAB ⊥平面PBC ②平面PAB ⊥平面PAD ③平面PAB ⊥平面PCD14.已知函数f(x)=eax -x 1-,其中a≠0.若对一切x ∈R ,f(x)≥0恒成立,则a 的取值集合 .15.已知x ,y 满足⎩⎪⎨⎪⎧y -2≤0,x +3≥0,x -y -1≤0,则46--+x y x 的取值范围是 .16.已知定义在R 上的函数f(x),g(x)满足()()x g x f =ax ,且f ′(x)g(x)+ f(x)·g ′(x) <0,()()11g f +()()11--g f =310,若有穷数列 {()()n g n f }(n∈N *)的前n 项和等于8140,则n 等于 .17.已知()⎪⎪⎭⎫ ⎝⎛+βαα2sin sin ,1A ,()⎪⎪⎭⎫ ⎝⎛--1,22sin sin βααB ,且0=⋅OB OA ,0sin ≠β 0cos sin =-βαk ,则k = .三、解答题:本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.18.(本小题满分14分)设函数()xx x x f cos sin 223sin +⎪⎭⎫⎝⎛-=π求函数()f x 的周期和单调递增区间;设A,B,C 为∆ABC 的三个内角,若AB=1,3()22C f =,932=AC , 求sinB 的值.19.(本小题满分14分)已知正项数列{}n a 满足:231=a , 1323n n n a a a +=+ (1)求通项na ;(2)若数列{}n b 满足⎪⎭⎫⎝⎛-=⋅nn n a b 2113,求数列{}n b 的前n 和.20.(本小题满分14分)已知四棱锥P —GBCD 中(如图),PG ⊥平面GBCD ,GD ∥BC ,GD=43BC ,且BG ⊥GC ,GB=GC=2,E 是BC 的中点,PG=4(Ⅰ)求异面直线GE 与PC 所成角的余弦值;(Ⅱ)若F 点是棱PC 上一点,且0=⋅GC DF ,CF k PF =,求k 的值.21.(本小题满分15分)已知函数()x x ln =ϕ(Ⅰ)若曲线()()1-+=x ax x g ϕ在点()()2,2g 处的切线与直线013=-+y x 平行,求a 的值;(Ⅱ)记()()()xa ax x x f 122+-+=ϕ,a ∈R ,且0a ≥.求函数()f x 的单调递增区间.22.(本小题满分15分)已知椭圆C :x2a2+y2b2=1()0>>b a 的离心率为33,左焦点为F(-1,0),(1) 设A ,B 分别为椭圆的左、右顶点,过点F 且斜率为k 的直线L 与椭圆C 交于M ,N 两点,若7=⋅+⋅MB AN NB AM ,求直线L 的方程;(2)椭圆C 上是否存在三点P ,E ,G ,使得S △OPE =S △OPG =S △OEG =62?2014年浙江省高考模拟冲刺卷(提优卷) 数学 (文科)(三)参考答案1.[答案]A[解析]集合A 是不等式4≤x2≤16的解集,由题意,集合A =[2,4],因为A ⊆B ,故a ≤2,b ≥4,故a -b ≤2-4=-2,即a -b 的取值范围是(-∞,-2].[中国教&育%出@版 2.[答案] B[解析]φ=2π时,y=sin(x +φ)=x cos 为偶函数;若y=sin(x +φ)为偶函数,则k=ϕZk ∈+,2ππ;选B.3.[答案] A[解析] 三个抽样方法, 每一个被抽到的概率都等于5115030=.4.[答案]D[解析]∵10>1,∴()101f =f(10)=lg10=1≤1,∴()102f =f(f(10))=f(1)=12+9=10,()103f =f(f(f(10)))= f(10)=lg10=1, ,()=102014f 10,故选D.5.[答案]D[解析]设此三棱柱底面边长为a ,高为h ,则由图示知32a =23,∴a =4, 侧视图面积为23×h =63,∴h =3. 这个三棱柱的体积为34×42×h =12 3. 6.[答案]B[解析]k =1时,p =1; k =2时,p =1×2=2; k =3时,p =2×3=6; k =4时,p =6×4=24. 7.[答案]B[解析]由于a +b =1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,通过观察发现,从第三项起,等式右边的常数分别为其前两项等式右边的常数的和.因此,a6+b6=11+7=18,a7+b7=18+11=29,a8+b8=29+18=47,故选B. 8.[答案]C[解析] 涂漆面数为2的小正方体每条棱上有3个, 12条棱共36个,所以涂漆面数为3的概率为36125.故选C.9.[答案]D[解析]由OA BA CA 2=+易得△ABC 是直角三角形,且A 为直角,又||||OA AB =, 故C=30°.由此AC =2BC =,BC CA⋅31500-=.10.[答案] D[解析] 双曲线的渐近线为:y =b x a ±,设焦点F (c ,0),则A (c ,bc a ),B (c ,-bca ),P (c ,2b a ),因为OP OA OB λμ=+所以,(c ,2b a )=(()c λμ+,()bca λμ-),所以,λμ+=1,λμ-=b c ,解得:,22c b c bc c λμ+-==,又由81=λμ,得:814222=-c b c , 解得:2122=c a ,所以,e =2,选D. 11.[答案] 44i -[解析] (1-i)2-i i 2124-+20144i -=-2i -)21)(21()21)(24(i i i i +-+++4=-2i -54284-++i i +4=-2i -2i+4=4-4i.12.[答案] 8π.[解析]由已知()22cos -=+C B 得43π=+C B ,所以A =π4,由bsin ⎝ ⎛⎭⎪⎫π4+C -csin ⎝ ⎛⎭⎪⎫π4+B =a ,应用正弦定理,得sinBsin ⎝ ⎛⎭⎪⎫π4+C -sinCsin ⎝ ⎛⎭⎪⎫π4+B =sinA , sinB ⎝⎛⎭⎪⎫22sinC +22cosC -sinC ⎝ ⎛⎭⎪⎫22sinB +22cosB =22.整理得sinBcosC -cosBsinC =1,即sin(B -C)=1, 由于0<B ,C<34π,从而B -C =π2,又43π=+C B ,故8π=C .13. [答案]①②[解析]易证BC ⊥平面PAB, 则平面PAB ⊥平面PBC; 又AD ∥BC, 故AD ⊥平面PAB, 则平面PAD ⊥平面PAB, 因此①②正确.14.[答案] {1}[解析]若a <0,则对一切x >0,f(x)=eax -x-1<0, 这与题设矛盾.又a ≠0,故a >0.而f ′(x)=aeax -1,令f ′(x)=0得x =1a ln 1a.当x <1a ln 1a 时,f ′(x)<0,f(x)单调递减;当x >1a ln 1a 时,f ′(x)>0,f(x)单调递增.故当x =1a ln 1a ,f(x)取最小值f ⎝ ⎛⎭⎪⎫1a ln 1a =1a -1a ln 1a-1.于是对一切x ∈R ,f(x)≥0恒成立,当且仅当1a -1a ln 1a-1≥0. ①令g(t)=t -tlnt-1,则g ′(t)=-lnt.当0<t <1时,g ′(t)>0,g(t)单调递增;当t >1时,g ′(t)<0,g(t)单调递减. 故当t =1时,g(t)取最大值g(1)=1-1=0.因此,当且仅当1a=1,即a =1时,①式成立.综上所述,a 的取值集合为{1}.15. [答案]⎥⎦⎤⎢⎣⎡713,1[解析] 由题意绘出可行性区域如图所示,46--+x y x =y -2x -4+1求y -2x -4的取值范围,即求可行域内任一点与点(4,2)连线的斜率k 的取值范围,由图像可得y -2x -4∈⎣⎢⎡⎦⎥⎤0,67,46--+x y x ⎥⎦⎤⎢⎣⎡∈713,1. 16.[答案]4[解析] 由()()()'x g x f = f ′(x)g(x)+ f(x)·g ′(x) <0,即axln a<0,故0<a<1. 由()()11g f +()()11--g f =310,得a +1a=310,解得a =31,所以有穷数列{()()n g n f }(n ∈N*)是等比数列,其前n 项和Sn==-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-31131131n8140,得n =4.17.[答案] 2±[解析] 由已知有0)2sin(sin 2)2sin(sin =++--βααβαα, 即)2sin(1)2sin(1sin 2βαβαα++-=,故αβαβαβαβαsin )]2sin()2[sin()2sin()2sin(2++-=+⋅-,即βαβαβα2cos sin 2)2sin()2sin(22⋅=+⋅-,βααβ2cos sin 22cos 4cos 2⋅=-∴ αβαβααβ222222sin sin 2sin 2cos sin cos 2cos ⋅-=⋅=-∴,即αββ222sin sin 22sin ⋅=, 因为0sin ≠β,所以有αβ22sin cos 2=,于是k =2cos sin ±=βα.18. [解析] ()x x x x f cos sin 223sin +⎪⎭⎫ ⎝⎛-=π=⎪⎭⎫ ⎝⎛+32sin πx (I )函数()f x 的周期为π.令222,232k x k k Zπππππ-≤+≤+∈,则5,1212k x k k Z ππππ-≤≤+∈∴函数f(x)的单调递增区间为5[,]().1212k k k Z ππππ-+∈(II)由已知()sin()3C f C π+==22, 因为40,333C C ππππ<<∴<+<所以233C ππ+=,3C π=,∴sinC =. 在∆ABC 中,由正弦定理,sin sin AC ABB C =,得 sinB=31.19.[解析](1)∵()1n n a f a +=,∴1323n n n a a a +=+,即11123n n a a +=+,∴()11122133n n n a a =+-=,则32n a n =.(2) ⎪⎭⎫⎝⎛-=⋅nn n a b 2113,∴n b =⎪⎭⎫ ⎝⎛-n n 2112∴n S =n b b b ++21=()n 242+++ ⎪⎭⎫ ⎝⎛++++--12223221n n2123(1)(1)222n n n n -=+-++++令21231222n n n T -=++++则23112322222n n nT =++++,两式相减得23111111112(1)22222222n n n n n n nT -=+++++-=--,124(1)22n n n n T ∴=--21242nn n S n n -+∴=+-+. 20.[解析](Ⅰ)在平面ABCD 内,过C 点作CH//EG 交AD 于H ,连结PH ,则∠PCH (或其补角)就是异面直线GE 与PC 所成的角. 在△PCH 中,18,20,2===PH PC CH由余弦定理得,cos ∠PCH=1010∴异面直线GE 与PC 所成角的余弦值为1010.(Ⅱ)在平面GBCD 内,过D 作DM ⊥GC ,M 为垂足,连结MF ,又因为DF ⊥GC∴GC ⊥平面MFD , ∴GC ⊥FM由平面PGC ⊥平面ABCD ,∴FM ⊥平面ABCD ∴FM//PG由0=⋅GC DF 得GM ⊥MD ,∴GM=GD ·cos45°=2332123===MC GM FC PF ,∴3-=k .21.[解析](Ⅰ)()()1-+=x a x x g ϕ =1ln -+x a x (0x >),()21x ax x g -='(0x >), 因为曲线()()1-+=x ax x g ϕ在点()()2,2g 处的切线与直线013=-+y x 平行,()34212-=-='ag ,解得14=a .(Ⅱ)因为21(1)1(1)(1)()(1)ax a x ax x f x ax a x x x -++--'=+-+==(1)当0a =时,1()x f x x -'=.令1()0x f x x -'=>解得01x << (2)0a >时 令(1)(1)0ax x x --=,解得1x a =或1x =. (ⅰ)当11a >即01a <<时, 由1)10ax x x -->((),及0x >得1)10ax x -->((). 解得01x <<,或1x a >; (ⅱ)当11a =即1a =时,因为0x >,2221(1)()0x x x f x x x -+-'==≥恒成立. (ⅲ)当11a <即1a >时,由1)10ax x x -->((),及0x >得1)10ax x -->((). 解得10x a <<,或1x >.综上所述,当0a =时,函数()f x 的递增区间是(0, 1); 当01a <<时,函数()f x 的递增区间是(0, 1),1(, )a +∞;当1a =时,函数()f x 的递增区间是(0, )+∞;当1a >时,函数()f x 的递增区间是1(0, )a ,(1, )+∞. 22.[解析](1)由题意:椭圆的方程为x23+y22=1. 设点M(x1,y1),N(x2,y2),由F(-1,0)得直线MN 的方程为y =k(x +1).由方程组⎩⎪⎨⎪⎧y =k (x +1),x23+y22=1,消去y ,整理得(2+3k2)x2+6k2x +3k2-6=0,可得x1+x2=-6k22+3k2,x1x2=3k2-62+3k2. 因为A(-3,0),B(3,0), 所以MB AN NB AM ⋅+⋅=(x1+3,y1)·(3-x2,-y2)+(x2+3,y2)·(3-x1,-y1)=6-2x1x2-2y1y2=6-2x1x2-2k2(x1+1)(x2+1)=6-(2+2k2)x1x2-2k2(x1+x2)-2k2=6+2k2+122+3k2. 由已知得6+2k2+122+3k2=7,解得k =±10. 故所求直线L 的方程为:()110+=x y 和()110+-=x y(2) 假设存在P(u ,v),E(x1,y1),G(x2,y2)满足S △OPE =S △OPG =S △OEG =62. 不妨设E(x1,y1),G(x2,y2)两点确定的直线为 l ,(ⅰ)当直线l 的斜率不存在时, E , G 两点关于x 轴对称,所以x2=x1,y2=-y1,因为 E (x1,y1)在椭圆上,所以x213+y212=1.① 又因为S △OEG =62, 所以|x1|·|y1|=62,② 由①、②得|x1|=62,|y1|=1, 此时x21+x22=3,y21+y22=2.(ⅱ)当直线l 的斜率存在时,设直线l 的方程为y =kx +m ,由题意知m ≠0,将其代入x23+y22=1得 (2+3k2)x2+6kmx +3(m2-2)=0,其中Δ=36k2m2-12(2+3k2)(m2-2)>0,即3k2+2>m2,(★)又x1+x2=-6km 2+3k2,x1x2=3(m2-2)2+3k2,所以|EG|=1+k2·(x1+x2)2-4x1x2=1+k2·263k2+2-m22+3k2. 因为点O 到直线l 的距离为d =|m|1+k2, 所以S △OEG =12|EG|·d =121+k2·263k2+2-m22+3k2·|m|1+k2=6|m|3k2+2-m22+3k2. 又S △OEG =62, 整理得3k2+2=2m2,且符合(★)式.此时x21+x22=(x1+x2)2-2x1x2=⎝ ⎛⎭⎪⎫-6km 2+3k22-2×3(m2-2)2+3k2=3, y21+y22=23(3-x21)+23(3-x22)=4-23(x21+x22)=2. 综上所述,x21+x22=3,y21+y22=2,结论成立.同理可得:u2+x21=3,u2+x22=3,v2+y21=2,v2+y22=2, 解得u2=x21=x22=32;v2=y21=y22=1. 因此u ,x1,x2只能从±62中选取,v ,y1,y2只能从±1中选取. 因此P 、E 、G 只能在⎝ ⎛⎭⎪⎫±62,±1这四点中选取三个不同点, 而这三点的两两连线中必有一条过原点,与S △OPE =S △OPG =S △OEG =62矛盾, 所以椭圆C 上不存在满足条件的三点P 、E 、G.。
中学高三数学适应性考试试题文新人教A版.doc

浙江省绍兴县鲁迅中学 适应性考试(文科)数学试卷考生须知:1. 本科考试分试题卷和答题卷,考生须在答题卷上作答.答题前,请在答题卷的密封 线内填写学校、班级、考号、姓名 ;2. 本试题卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,全卷满分 150分,考试时间120分钟.参考公式:如果事件A, B 互斥,那么P(A+ B)= P(A)+ P(B)・ 如果事件A, B 相互独立,那么 P(A ・B)= P(A)・P(B)・ —n43球的表面积公式2S =4HR ,其中R 表示球的半共50分)岭分,在每小题给岀的四个选项中 开始2、 3、集合M={ x | yx 1}B 1 {x| 2x },贝If Cu M 1 x 1} 设全集U=R, A. {X| 1C ・ y I X 1 或 X 1} 执行右边的程序框图,则输出的 A. 20 B ・ 30 C ・ 42已知某几何体的三视图如右图所示,则该兀何体的体祓是GD3!D.T>S S=S+5n=n+2T-T+n输出T结束A.2B.161C.12 D.118(第3题)7T4、已知等差 数列 a1满足 a2 34 4 , 83 项的和Sio a 5 10 ,则它的前A. 85B. 135C. 95D. 23球的体积公式V柱体的体积公式 锥体的体积公式台体的体积公式R ,其中R 表示球的半径.3-Sh,其中S 表示柱体的底面积,h 表示柱体的高.Sh,其中S 表示锥体的底面积, h 表示锥体的高. 3 1h SSS 其中S,S2分别表示台体的上、下底面积, I I讥Q 叶I 戈一第I 韻选释题 一、选择题(乐夭题共>10小题,每小题 一项是符合题目要求的)15等于■5、要得到函数y sin (2x )的图象,只要将函数y sin 2x的图象4C.向右平移 单位 D •向左平移 a P Y单位 £u a6、已知m , n 是两,条不同的直笔, ,则na 厂 & A.若m || n=, m c.若 丄,单位 8:为三个不同的平面, B .若m || n,;+ D ・・=^m ||则下列怨正确的気P (%卩 a PII ; IIb 满足ab ) b 匹则向量a , b 的夹角为_开A.1( f 0)f(x)A.c.9、双 10、 二、 1213、 )U (1(0 x 1)f (x) f( x) 1 的b ( i曲线 PF- 2B .2 X 2 a F1A. 54【一 +已知 f(x) 值范围是(A. 1,2y2 b ,直 1, 1qU (0,1) 2」 1 0,121(a 0,b 0)1+B . x 22 卜 a(k f(x 1)(x0),)B. 1,0第II 卷 +的左右焦点为F I ,F 2 , P 是双曲线上一点,满足 0),0^ 2y a 相切,则双曲线的离心率为3 [-) f (x) X 恰有D. 53(+oC3个不同的零点, )则实数 a 的取2, 0,(非选扌 —0分) 填空题(玉越姿7小题,每小题4分,共28分) 1 -<则复数 l一 - 设为虚数单位,已知1X 4|的虚部为 4x 2y 的最大值 = + + 用分层抽样的方法从某学校的高中学生中抽取一个容量为 抽20人,高三年级抽10人,已知该校高二年级共有 为 人; 45的样本, 其中高一年级 300人,则该校高中学生总人数=2a 十 2 一1(11匸 N ,n -2)》n,若存在实数为等差数列,则|BM | 2|CN |,则AM AN 的取值范围是・ |BC | |CD |A三、解答题(本大题共5小题,共72分,•解答应给出文字说明,证明过程或演算步骤7T7T18・U 本题椭分创-分力设a,b,c 分别是 ABC 内角A,B,C 所对边长,并且 2sin判断{ABp 的形状19.(植漏分 14分):差数列 a n 的首项为ai,公差d 1,前n 项和为S,其中3i 1,1,2,3洱,5 t =—(I )若存在n N ,使S 5成立,求a 的值;n1(n)是否存在a ,使S a 对任意大于1的正整数n 均成立?若存在,求出a 的值;1nn1ai =5,a2, AD仁点M ,N 分别是BC, CD 边上的动点,且2sin A sin% B) si 呜 B) (I )求角A 的值; (n)若2a cos B b cn则cos2x 的值为16、数列20.(本题满分14分)如图,菱形ABCD所在平面与平面四边形ABEF所在平面互相垂△ ABE是等腰直角三角形, AB AE 2,FA FE, AEF 45(1)线段CD的中点为P ,线段AE的中点为M ,求证:PM 〃平面BCE ;(2)求直线CF与平面BC匡所成角的正弦值=・21.(本题满分15分)已知a R,函数f(x) ax In x , x 0,e否则,说明理由.数的底数为常数),(1)当a 1时,求f(x)的单调区间与极值;F(2)是否存在实数a ,使得f (x)的最小值为3•若存在,求出a的值,若不存在,说明理由。
浙江省绍兴县鲁迅中学2014届高三高考适应性考试 英语 Word版含答案

绝密★考试结束前鲁迅中学2014年普通高等学校招生适应性考试英语(姓名准考证号本试题卷分选择题和非选择题两部分。
满分120分,考试时间120分钟。
选择题部分(共80分)第一部分英语知识运用(共两节,满分30分)第一节:单项填空(共20小题;每小题0.5分,满分10分)从A、B、和D四个选项中,选出可以填入空白处的最佳选项。
1.--–So you gave her your phone?---______. She said she’d return it to me when she could afford her own.A. My pleasureB. Not exactlyC. No wonderD. All right2.The word ―ungelievable‖ based on Chinese, which has become a big hit online very quickly,____a message that Chinese can also serve as an addition to English vocabulary.A. deliversB. simplifiesC. declaresD. clarifies3. He ____to go to Beijing today, but he postponed the trip when he heard that there would be a downpour at noon.A. was intendingB. would intendC. had intendedD. intended4. On the bank of the river, we found him _____on a bench, with his eyes _____on a kite in the sky.A. seated; fixingB. sitting; fixingC. seated; being fixedD. sitting; fixed5. In order to put an end to poverty, the World Bank has switched its ______to providing technical assistance and long-term loans to developing countries.A. concernB. processC. struggleD. focus6. The machine has been used many years. It’s no wonder that it doesn’t work well________.A. regularlyB. constantlyC. occasionallyD. frequently7. People in these countries demand equal treatment for all, ____race, religion or sex.A. in defence ofB. regardless ofC. instead ofD. in support of8. Eric didn’t feel at ____ease in the party, because he was afraid of losing ____lose.A. the; aB. an; /C. /; theD. /; /9. To my surprise, at yesterday’s meeting he again _________the plan that didn’t sound reasonable.A. cheered upB. settled downC. brought upD. put up10. John worked hard at his lessons and gained _____to a famous university last year.A. permissionB. admissionC. agreementD. freedom11. _________by the beauty of nature, the girl from London decided to spend another two days on the farm.A. AttractingB. AttractedC. To be attractedD. Having attracted12. I haven’t had a phone in the house for three weeks now, and it’s several days ____I used a phone box last time.A. asB. whenC. ifD. since13. ____cleaning the yard and making up the beds for the old, we also read newspapers for themand had chats with them.A. Except forB. Rather thanC. Apart fromD. Instead of14. He didn’t put the things ____they belonged, for ____he got his punishment.A. which; thatB. what; thisC. that; whoseD. where; which15. We should consider the students’request ______the school library provide more books on popular science.A. thatB. whenC. whichD. where16. Drinking water , having a healthy snack and taking exercise are all positive ways to ____you when you are working on a tight schedule.A. relieveB. refreshC. liberateD. comfort17. It was from only a few supplies that she had bought in the village _____the hostess cooked such a nice dinner.A. whereB. thatC. whenD. which18. --- Jack wasn’t saying anything, but the teacher smiled at him ____he is all right now.---What a lucky dog! He ________himself badly.A. should injureB. might injureC. should have injuredD. could have injured19. When you get involved in sports, a lot of racial____are broken down because players developed friendship quickly.A. barriersB. threatsC. approachesD. hardships20. ---Where on earth did you get the book?---_________A. What did you say?B. I beg your pardon?C. Say it again!D. I didn’t get it on earth.第二节:完形填空(共20小题)阅读下面短文,从短文后各题所给的四个选项(A、B、C和D)中,选出可以填入空白处的最佳选项。
2014届浙江数学(文)高考模拟卷二

是否开始S =1n =1n =n +1S =S +(-1)n +1n 2输出S 结束第(4)题2014届浙江高三数学(文)高考模拟卷二试卷来源:嘉兴一中、绍兴一中、慈溪实验高级中学 2014.1.27考生须知:1、全卷分试卷I 、II ,试卷共4页,有五大题,满分150分。
考试时间120分钟。
2、本卷答案必须做在答卷I 、II 的相应位置上,做在试卷上无效。
3、请用蓝、黑墨水笔或圆珠笔将姓名、准考证号分别填写在答卷I 、II 的相应位置上,用2B 铅笔将答卷I 的准考证号和学科名称所对应的方框内涂黑。
参考公式:如果事件A , B 互斥, 那么 棱柱的体积公式P (A +B )=P (A )+P (B )V =Sh如果事件A , B 相互独立, 那么 其中S 表示棱柱的底面积, h 表示棱柱的高 P (A ·B )=P (A )·P (B )棱锥的体积公式如果事件A 在一次试验中发生的概率是p , 那么n V =31Sh次独立重复试验中事件A 恰好发生k 次的概率其中S 表示棱锥的底面积, h 表示棱锥的高 P n (k )=C k n p k (1-p )n -k (k = 0,1,2,…, n ) 球的表面积公式棱台的体积公式S = 4πR 2)2211(31S S S S h V ++=球的体积公式其中S 1, S 2分别表示棱台的上.下底面积, h 表示棱台 V =34πR 3的高 其中R 表示球的半径选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合M ={0,1,2,3}, N ={x |12<2x <4},则集合M ∩(C R N )等于( ▲ )A .{0,1,2}B .{2,3}C .∅D .{0,1,2,3}2.设i 是虚数单位,若复数10()3a a R i-∈-是纯虚数,则a 的值为( ▲ ) A .3-B. 1- C.1D.3 3.已知))(sin()(R x x f ∈+=ϕϕ,则“2πϕ=”是“)(x f 是偶函数”的( ▲ ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件4.如右图所示的算法流程图中输出的最后一个数为10-,则判断框中的条件是( ▲ )A . 4?n < B. 4?n ≥ C. 5?n ≥ D.5?n < 5.若函数()(01)xxf x ka a a a -=->≠且在(-∞,+∞)上既是奇函数又是增函数,则函数()log ()a g x x k =+的图象是(▲)第(6)题A B C D 6.函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( ▲ ) A.2,3π-B.2,6π-C.4,6π-D.4,3π7. 设a 是空间中的一条直线,α是空间中的一个平面,则下列说法正确的是( ▲ )A . 过a 一定存在平面β,使得αβ//B . 过a 一定不存在平面β,使得αβ⊥C . 在平面α内一定存在直线b ,使得b a ⊥D . 在平面α内一定不存在直线b ,使得b a // 8. 有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( ▲ ) A .13B .12C .23D .349.设双曲线)0,0(12222>>=-b a by a x 的左、右焦点分别为21,F F ,离心率为e ,过2F 的直线与双曲线的右支交于B A ,两点,若AB F 1∆是以A 为直角顶点的等腰直角三角形,则=2e ( ▲ )A. B.224- 10.是定义在R 上的奇函数,若()0.30.333a f =⋅,)log (.log 33ππf b =系是( ▲ )A .c a b >>B .c b a >>C .b c a >>D .a c b >>非选择题部分(共100分)二.填空题:本大题共7小题,每小题4分,共28分11.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中不低于70分的学生数是 ▲ . 12.一个多面体的直观图及三视图如图所示(其中M 、N 分别是AF 、BC 的中点),则多面体F —MNB 的体积= ▲ .13.若实数,x y 满足不等式组2,24,0,x y x y x y +≥⎧⎪-≤⎨⎪-≥⎩则x y z 1+=的最小值是 ▲ .14.从1到100的正整数中删去所有2的倍数及3的倍数后,剩下数有 ▲ 个.15.设1x 、2x 是关于x 的方程220x mx m m ++-=的两个不相等的实数根,那么过两 点211(,)A x x ,222(,)B x x 的直线与圆22(1)(1)1x y -+-=的位置关系是 ▲ .(相交、 相离、相切 )16.向量d c b a ,,,满足: 1=||a ,2=||b ,b 在a 上的投影为21,0=-⋅-)()(c b c a ,1=-||c d ,则||||d c +的最大值是 ▲ .17.定义:关于x 的两个不等式()0f x <和()0g x <的解集分别为(,)a b 和11(,)b a ,则称这两个不等式为对偶不等式.如果不等式2cos 220x θ-+<与不等式224s i n 210x x θ++<为对偶不等式,且(0,)θπ∈,则θ= ▲ . 三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤 18.在ABC ∆中,角,,A B C 所对的边分别为,,a b c 且满足sin cos .c A a C = (Ⅰ)求角C 的大小; (Ⅱcos()4A B π-+的最大值,并求取得最大值时角,A B 的大小.19.设等差数列{}n a 的前n 项和为n S ,公比是正数的等比数列{}n b 的前n 项和为n T ,已知1122331,3,815a b a b T S ==+=-= (Ⅰ)求{},{}n n a b 的通项公式.(Ⅱ)若数列{}n c 满足112211(1)(2)1()n n n n a c a c a c a c n n n n N *--++++=+++∈ 求数列{}n c 的前n 项和n W .20. (本题满分14分)如图,四棱锥P -ABCD ,P A ⊥底面ABCD ,AB ∥CD ,AB ⊥AD ,AB =AD =12CD =2,P A =2,E ,F 分别是PC ,PD 的中点. (Ⅰ) 证明:EF ∥平面P AB ;(Ⅱ) 求直线AC 与平面ABEF 所成角的正弦值.21.已知函数x xe x f =)(()x ∈R .(Ⅰ)求函数()x f 的单调区间;(Ⅱ)若()3f x kx k '≥-对一切[)1,x ∈-+∞恒成立,求正实数k 的取值范围.22.设动点(),P x y ()0x ≥到定点1,02F ⎛⎫⎪⎝⎭的距离比到y 轴的距离大12.记点P 的轨迹为曲线C . (Ⅰ)求点P 的轨迹方程;(Ⅱ)设圆M 过()1,0A ,且圆心M 在P 的轨迹上,BD 是圆M在y 轴的截得的弦,当M运动时弦长BD 是否为定值?说明理由;(Ⅲ)过1,02F ⎛⎫⎪⎝⎭作互相垂直的两直线交曲线C 于G 、H 、R 、S ,求四边形GRHS 面积的最小值.AB CD PEF(第20题图)2014届浙江数学(文)高考模拟卷二参考答案二、填空题11. 60012.三分之八13.1214.33 15. 无解 16. 23+ 17.三、解答题18..(1)由正弦定理得:sin sin sin cos A C A C =,因为0A π<<故sin 0A >; 从而sin cos cosC 0C C =≠又,所以tan 1C =,则4C π= ----------4分(2)由(1)知34B A π=-,于是 cos()cos()4cos 2sin()6A B A A A A A πππ-+=--=+=+3110,46612A A ππππ<<∴<+< ,从而62A ππ+=即3A π=时,2sin()6A π+取最大值2cos()4A B π-+的最大值为2,此时5,312A B ππ==19. ⑴ 设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q 111,3a b == 由 228a b +=,得 138d q ++= ① 由 3315T S -= 得 23(1)(33)15q q d ++-+= ② 化简①② 23735q d q q d +=⎧∴⎨+-=⎩消去d 得24120q q +-= 2q ∴=或6q =-0q > 2q ∴= 则 1d =n a n ∴= 132n n b -=⋅ (7分)⑵n a n =12323c c c ∴+++…(1)(2)1n nc n n n +=+++ ①当2n ≥时,12323c c c +++…1(1)(1)(1)1n n c n n n -+-=-++ ②由①-②得3(1)n nc n n =+33n c n ∴=+ (2)n ≥又由⑴得17c =337n n c +⎧∴=⎨⎩ (2)(1)n n ≥= {}n a ∴的前n 项和7912n w =+++…33n ++2633391()122n n nn +++=+⋅=+ (14分)20.(Ⅰ) 因为E ,F 分别是PC ,PD 的中点,所以EF ∥CD ,———————————2分 又因为CD ∥AB , 所以EF ∥AB , ————————————4分又因为EF ⊄平面P AB所以EF ∥平面P AB . ………… 6分(Ⅱ) 取线段P A 中点M ,连结EM ,则EM ∥AC ,故AC 与面ABEF 所成角的大小等于ME 与面ABEF 所成角的大小.——————— 8分作MH ⊥AF ,垂足为H ,连结EH .—————9分 因为P A ⊥平面ABCD ,所以P A ⊥AB , 又因为AB ⊥AD ,所以AB ⊥平面P AD , 又因为EF ∥AB , 所以EF ⊥平面P AD .因为MH ⊂平面P AD ,所以EF ⊥MH , 所以MH ⊥平面ABEF ,所以∠MEH 是ME 与面ABEF 所成的角.—————12分在直角△EHM 中,EM =12ACMHsin ∠MEH.———13分所以AC 与平面ABEF. ………… 14分21.解:(Ⅰ)xe x xf )1()(+=', …………………2分当(),1x ∈-∞-时,()0f x '<;当()1,x ∈-+∞时,()0f x '>,所以()f x 的单调递增区间为()1,-+∞,单调递减区间为(),1-∞-.………5分(Ⅱ)由已知条件可知,原不等式等价于(1)xx e +(31)k x ≥-,当113x -≤≤时,0k > ,(31)0k x ∴-≤, 而(1)0xx e +≥,此时不等式显然成立;………………………7分A BCDP EF(第20题图)MH当13x >时,(1)31xx e k x +≤-. ………………8分设()g x =(1)1()(31)3x x e x x +>-,2'2(325)().(31)x x x e g x x +-=-………………9分 '()0g x =令得53x =-或1x =, …………………………10分当1,1)3x ∈(时,'()0g x <,()g x 单调递减,…………11分当,)x ∈+∞(1时,'()0g x >,()g x 单调递增,……………12分 故当1x =时,()g x 有最小值e ,………………………13分 即得0k e <≤. …………………15分 22.(Ⅰ) 由题意知,所求动点(),P x y 为以1,02F ⎛⎫⎪⎝⎭为焦点,直线1:2l x =-为准线的抛物线,方程为22y x =.(Ⅱ)因为圆心M 在抛物线22y x =上,可设圆心2(,)2a M a,半径r =圆的方程为222222()()(1)22a a x y a a -+-=-+,令0x =,得(0,1)B a +,(0,1)D a -+,所以||2BD =,所以弦长||BD 为定值.(Ⅲ)设过F 的直线方程为1()2y k x =-,11(,)G x y ,22(,)H x y ,由21()22y k x y x ⎧=-⎪⎨⎪=⎩得2222(2)04k k x k x -++=,由韦达定理得12221x x k +=+,1214x x =,所以||GH222k +,同理2||22RS k =+.所以四边形GRHS 的面积()22221212222282T k k k k ⎛⎫⎛⎫=++=++≥ ⎪ ⎪⎝⎭⎝⎭, 即四边形GRHS 面积的最小值为8.。
2014届浙江数学(文)高考模拟卷七

俯视图(第7题图) 2014届浙江高三数学(文)高考模拟卷七命题学校:鲁迅中学、温州一中、杭州外国语学校选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合S ={x |3<x ≤6},T ={x |x 2-4x -5≤0},则S ∪T =( ▲ )A .[-1,6]B .(3,5]C .(-∞,-1)∪(6,+∞)D .(-∞,3]∪(5,+∞) 2.已知i 是虚数单位,则 (3-i) (2+i)=( ▲ )A .5+iB .5-iC .7+iD .7-i3.已知a ,b ∈R ,则“b ≥0”是“a 2+b ≥0”的( ▲ )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.若函数y =sin 2x 的图象向左平移π4个单位得到y =f (x )的图象,则( ▲ ) A .f (x )=cos 2x B .f (x )=sin 2x C .f (x )=-cos 2x D .f (x )=-sin 2x 5.已知α,β,γ是三个不同的平面,α∩γ=m ,β∩γ=n .( ▲ )A .若m ⊥n ,则α⊥βB .若α⊥β,则m ⊥nC .若m ∥n ,则α∥βD .若α∥β,则m ∥n6.从1,2,3,4这四个数字中依次取(不放回)两个数a ,b ,使得a 2≥4b 的概率是( ▲ )A .31B .512 C .21D .7127.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( ▲ )A .10 cm 3B .20 cm 3C .30 cm 3D .40 cm 38.若正数x ,y 满足x 2+3xy -1=0,则x +y 的最小值是( ▲ )A .32 B .322 C .33 D .3329.如图,F 1,F 2是双曲线C 1:1322=-y x 与椭圆C 2的公共 焦点,点A 是C 1,C 2在第一象限的公共点.若|F 1F 2|=|F 1A |,则C 2的离心率是 A .31 B .32 C .51D .5210.设a ,b 为单位向量,若向量c 满足|c -(a +b )|=|a -b |,则|c |的最大值是A .1 BC .2D .(第13题图)非选择题部分(共100分)二、 填空题:本大题共7小题,每小题4分,共28分.11.某篮球运动员在5场比赛中得分的茎叶图如图所示,则这位球员得分的平均数等于________. 12.已知a ,b ∈R ,若4a =23-2b,则a +b =________.13.若某程序框图如图所示,则该程序运行后输出的值等于________.14.设z =x -2y ,其中实数x ,y 满足⎪⎩⎪⎨⎧≤≤-≥+,4,42,2y y x y x 则z 的最大值等于________.15.已知点O (0,0),A (2,0),B (-4,0),点C 在直线l :y =-x 上. 若CO 是∠ACB 的平分线,则点C 的坐标为________.16.设A (1,0),B (0,1),直线l :y =ax ,圆C :(x -a )2+y 2=1.若圆C 既与线段AB 又与直线l 有公共点,则实数a 的取值范围是________.17.已知t >-1,当x ∈[-t ,t +2]时,函数y =(x -4)|x |的最小值为-4, 则t 的取值范围是________.三、 解答题: 本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分) 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2a cos C +c =2b .(Ⅰ) 求角A 的大小;(Ⅱ) 若a 2=3bc ,求tan B 的值.19.(本题满分14分) 已知等差数列{a n }的首项a 1=2,a 7=4a 3,前n 项和为S n .(I) 求a n 及S n ; (Ⅱ) 设b n =44n n S a n--,n ∈N *,求b n 的最大值.20.(本题满分15分) 如图,在直三棱柱ABC -A 1B 1C 1中,0 9 1 2 5 6 2 3A 1B 1C 1DBAC(第20题图)∠BAC=90°,AB=AC=AA1.(Ⅰ) 求证:AB1⊥平面A1BC1;(Ⅱ) 若D为B1C1的中点,求AD与平面A1BC1所成的角.21.(本题满分15分) 已知m∈R,设函数f(x)=x3-3(m+1)x2+12mx+1.(Ⅰ) 若f(x)在(0,3)上无极值点,求m的值;(Ⅱ) 若存在x0∈(0,3),使得f(x0)是f(x)在[0,3]上的最值,求m的取值范围.22.(本题满分14分) 已知抛物线C:y=x2.过点M(1,2)的直线B两点.抛物线C在点A处的切线与在点B(Ⅰ) 若直线l的斜率为1,求|AB|;(Ⅱ) 求△P AB面积的最小值.(第22题图)2014届浙江高三数学(文)高考模拟卷七参考答案一、选择题: 本题考查基本知识和基本运算。
浙江省绍兴县鲁迅中学高三高考适应性考试 语文 Word版含答案.pdf

鲁迅中学2014年普通高等学校招生适应性考试 语 文 姓名 准考证号 全卷共8页,满分150分,考试时间150分钟。
请考生按照规定用笔,将所有试题的答案涂、写在答题纸上。
注意事项: 1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.答题不能答在试题卷上。
选择题必须使用2B铅笔填涂;非选择题必须使用黑色字迹的签字笔或钢笔书写,字体要工整,笔迹要清楚。
一、语言文字运用(共24分,其中选择题每小题3分) A.确凿(záo) 剽悍(piāo) 好莱坞(wù) 潜力股(qiǎn) B.朴刀(pǔ) 畏葸(xǐ) 供销社(gng) 入场券(quàn) C.反刍(zhōu) 道行(héng) 盖然性(gài) 瓦楞纸(léng) D.髌骨(bìn) 画片(piàn) 揩油(kāi) 重创(chuāng) A.一晃神,一转眼,我们就这样垂垂老去 。
雨淋过天气,疲倦的人心,记忆里的童话早已慢慢地融化。
跟着时间走,忘了自己的来路,散了自己的执意。
B.群众路线教育实践活动所取得的成效就证明,反对“四风”、把八项规定变成“铁八条”,关键正在于从小处抓严、抓实。
因此,培育和践行核心价值观,也须及时检视细枝未节,防范小积弊拖成大问题。
C.过去三年,直播前绝对保密的短片,现场提问嘉宾举起的哭脸牌,问政嘉宾接踵而至的麻辣点评和市民代表随手按动的表诀器,让不少官员坐立不安。
D.惟其如此,方能让人们真切体悟到真善美就在身边,逐步涵养传递爱与善的自觉,激发见贤思齐、明德惟磬的正能量。
A.住房问题牵扯面广,如何理清政府和市场的边界、如何看待住房在经济社会中的作用等都是需要破解的方向性问题。
B.该镇距县城不远不近,没有优势,没有特色,再怎么想发展,面临的局面却总是让人不尴不尬,无论是目标招商还是外出引资,总是底气不足。
浙江省绍兴市2014届高三数学教学质量调测文试题(绍兴一模)新人教A版
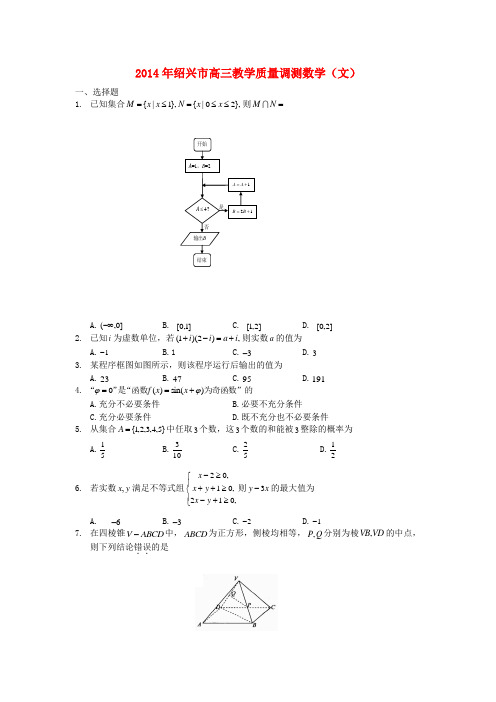
2014年绍兴市高三教学质量调测数学(文)一、选择题1. 已知集合},20|{},1|{≤≤=≤=x x N x x M 则=N MA.]0,(-∞B. ]1,0[C. ]2,1[D. ]2,0[ 2. 已知i 为虚数单位,若,)2)(1(i a i i +=-+则实数a 的值为 A.1- B.1 C.3- D.3 3. 某程序框图如图所示,则该程序运行后输出的值为A.23B.47C.95D.1914. ”“0=ϕ是为奇函数”的“函数)sin()(ϕ+=x x fA.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5. 从集合}5,4,3,2,1{=A 中任取3个数,这3个数的和能被3整除的概率为A.51B.103 C.52 D.21 6. 若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥+-≥++≥-,012,01,02y x y x x 则x y 3-的最大值为A. 6-B.3-C.2-D.1-7. 在四棱锥ABCD V -中,ABCD 为正方形,侧棱均相等,Q P ,分别为棱VD VB ,的中点,则下列结论错误..的是11A.直线ABCD PQ 平面//B.直线V BD AC 平面⊥C.平面VAC APQ 平面⊥D.平面VAB APQ 平面⊥8. 如图,双曲线)0,0(12222>>=-b a by a x 的左、右焦点分别为,,21F F 过点2F 作倾斜角为 60的直线交双曲线于点,P 设2PF 的中点为.M 若|,|||22M F OF =则该双曲线的离心率为A.212+ B.213+C.12+D.13+9. 已知点B A ,分别在直线3,1==x x 上,O 为坐标原点,且 4.||=-OB OA 当||OB OA +取到最小值时,OB OA ⋅的值为 A.0B.2C.3D.610. 已知函数,1)1()(22++-=x k x x f 若存在],4,2[],1,[21++∈+∈k k x k k x 使得),()(21x f x f =则实数k 的取值范围为 A.]5,5[-B.]3,1[]1,3[ --C. ]2,1[]1,2[ --D. ]3,2[]2,3[ --二、填空题 11.已知,33cos =θ则θ2cos =_____________. 12.已知函数⎩⎨⎧≥+-<=1,31,2)(2x x x x f x ,则))2((f f =____________. 13.已知等差数列},{n a 若,6732=++a a a 则=+71a a _____________. 14.已知),3,1(),1,2(-==b a 若)(b a a λ-⊥,则实数λ的值为___________. 15.某几何体的三视图如图所示,则该几何体的体积为______________.16.若直线03=++m my x 被圆)0(222>=+r r y x 所截得的最短弦长为8,则r =______________.17.D C ,两点在PAB ∆的边AB 上,,BD AC =若90=∠CPD 1022=+PB PA ,则CD AB +2的最大值是______________.三、解答题18.在ABC ∆中,角C B A ,,所对的边分别是c b a ,,,已知.3,1π==C c(Ⅰ)若,33sin =B 求b 的值; (Ⅱ)若ABC ∆的面积为,63求CB A sin sin sin +的值。
中学高三数学适应性考试试题文新人教A版
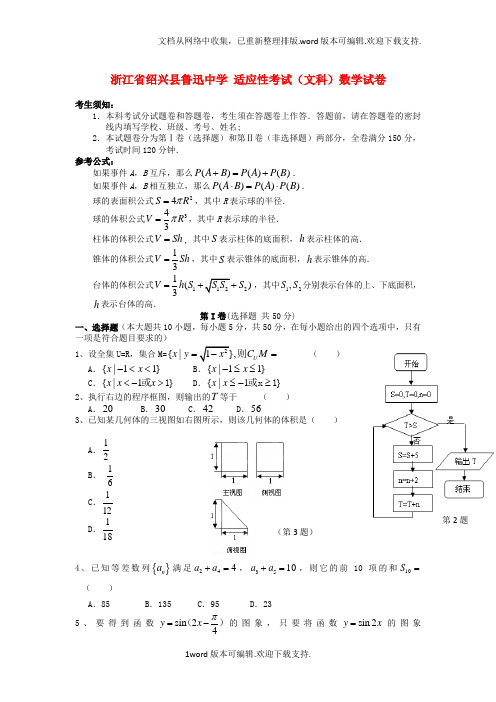
浙江省绍兴县鲁迅中学 适应性考试(文科)数学试卷考生须知:1.本科考试分试题卷和答题卷,考生须在答题卷上作答.答题前,请在答题卷的密封线内填写学校、班级、考号、姓名;2.本试题卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟.参考公式:如果事件A ,B 互斥,那么()()()P A B P A P B +=+.如果事件A ,B 相互独立,那么()()()P A B P A P B ⋅=⋅. 球的表面积公式24S R π=,其中R 表示球的半径.球的体积公式343V R π=,其中R 表示球的半径. 柱体的体积公式V Sh =,其中S 表示柱体的底面积,h 表示柱体的高.锥体的体积公式13V Sh =,其中S 表示锥体的底面积,h 表示锥体的高.台体的体积公式11221()3V h S S S S =++,其中12,S S 分别表示台体的上、下底面积,h 表示台体的高.第I 卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、设全集U=R ,集合M=2{|1},U x y x C M =-=则 ( ) A .{|11}x x -<< B .{|11}x x -≤≤ C .{|1}x x x <->或1D .{|1}x x ≤-≥或x 12、执行右边的程序框图,则输出的T 等于 ( ) A .20 B .30 C .42 D .563、已知某几何体的三视图如右图所示,则该几何体的体积是( )A .21B . 61C .121D .1814、已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S = ( ) A .85B .135C .95D .235、要得到函数sin24y x π=-()的图象,只要将函数sin 2y x =的图象(第3题)第2题( )A .向左平移4π单位 B .向右平移4π单位 C .向右平移8π单位 D .向左平移8π单位6、已知m ,n 是两条不同的直线,α,β,γ为三个不同的平面,则下列命题正确的是( ) A .若m ∥n ,m ⊂α,则n ∥α; B .若m ∥n ,m ⊂α,n ⊂β,则α∥β; C .若α⊥γ,α⊥β,则β∥γ; D .若m ∥n ,m ⊥α,n ⊥β,则α∥β.7、若非零向量,=且0)2(=•+b b a ,则向量,的夹角为 ( )A .π32B .6πC .3πD .π658、函数⎩⎨⎧≤<+-<≤---=)10(1)01(1)(x x x x x f ,则1)()(->--x f x f 的解集为( ) A .()(),11,-∞-+∞ B .(]11,0,12⎡⎫--⎪⎢⎣⎭ C .()(),01,-∞+∞ D .()11,0,12⎡⎤--⎢⎥⎣⎦9、双曲线22221(0,0)x y a b a b-=>>的左右焦点为12,F F ,P 是双曲线上一点,满足212PF F F =,直线1PF 与圆222x y a +=相切,则双曲线的离心率为( )A .54 B C D .5310、已知⎩⎨⎧≥-<+--=),0)(1(),0(2)(2x x f x a x x x f x x f y -=)(恰有3个不同的零点,则实数a 的取值范围是( )A .[)1,-+∞B .[)1,0-C .[)2,-+∞D .()0,+∞第Ⅱ卷(非选择题,共100分)二、填空题(本大题共7小题,每小题4分,共28分) 11、设为虚数单位,则复数34ii+的虚部为 ; 12、已知1311x y x y ≤+≤⎧⎨-≤-≤⎩, 则42x y +的最大值是 ;13、用分层抽样的方法从某学校的高中学生中抽取一个容量为45的样本,其中高一年级抽20人, 高三年级抽10人,已知该校高二年级共有300人,则该校高中学生总人数为 人; 14、若正实数,a b 满足2=ab ,则)1)(21(b a ++的最小值为 ;15、已知3sin 44x π⎛⎫-=⎪⎝⎭,且,24x ππ⎛⎫∈-- ⎪⎝⎭,则cos2x 的值为 ; 16、数列{}n a 中,)2,(122,511≥∈-+==*-n N n a a a n n n ,若存在实数λ,使得数列⎭⎬⎫⎩⎨⎧+n n a 2λ为等差数列,则λ= ; 17、在长方形ABCD 中,2,1AB AD ==,点,M N 分别是,BC CD 边上的动点,且||2||||||BM CN BC CD =,则AM AN ⋅的取值范围是 . 三、解答题(本大题共5小题,共72分,.解答应给出文字说明,证明过程或演算步骤) 18.(本题满分14分)设,,a b c 分别是ABC ∆内角,,A B C 所对边长,并且22sin sin() sin() sin 33A B B B ππ=+-+(Ⅰ)求角A 的值;(Ⅱ)若c b B a +=cos 2,判断ABC ∆的形状19.(本题满分14分)等差数列{}n a 的首项为1a ,公差1d =-,前n 项和为n S ,其中{}11,1,2,3,4,5a ∈-.(Ⅰ)若存在n N +∈,使5n S =-成立,求1a 的值;(Ⅱ)是否存在1a ,使n n S a <对任意大于1的正整数n 均成立?若存在,求出1a 的值;否则,说明理由.20.(本题满分14分)如图,菱形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直,△ABE 是等腰直角三角形,2,,45AB AE FA FE AEF ︒===∠=,045=∠ABC(1)线段CD 的中点为P ,线段AE 的中点为M ,求证://PM BCE 平面;(2)求直线CF 与平面BCE 所成角的正弦值.21.(本题满分15分)已知R a ∈,函数x ax x f ln )(-=,(]e x ,0∈,(其中e 是自然对数的底数为常数),(1)当1=a 时,求)(x f 的单调区间与极值;(2)是否存在实数a ,使得)(x f 的最小值为3. 若存在,求出a 的值,若不存在,说明理由。
【数学】浙江省嵊州中学2014届高三上学期第一次模拟考试(文)9

浙江省嵊州中学2014届高三上学期第一次模拟考试(文)一•选择题(本小题共10小题,每小题5分,共50分)1.设集合 M =「x |x 2 x — 2 :: 0,x R,^ = \xl0 :x<2},贝U M 一 N 二()A.(-1,2)B. 0,1 ]C.(0,1)D. -2,112. 若“ -1 ::: x ::: 2 ”是“ x :: m ”的充分不必要条件,则( )Am_-1Bm_-1Cm_2Dm_2x3. 已知1 - yi 其中x,y 是实数,i 是虚数单位,则x yi 为()1 + iA 2 iB 2-iC 1 2iD 1-2i4. 等差数列 g n ?中,a 5= 4,则 log 2(2a 2a2 2a^ 2a0^ ()f(x)的图象x 2y _3乞0*X +3y -3色0,若当且仅当在点(3,0)处, OM ON 取得最大值,则a 的取值范围是( )111 1A . (0, )B . (;) C . (0) D .(;)A10B 20C 40D 2 log 2 55.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是(A . f (x ) nx?B f(x)二凶xx_xe —ef (x)xZxe +e1 s in x cosx D . f (x):1 +sin x — cosx6.设a = ( 3,4),a_b ,且b 在x 轴上的投影为2, 则b =(A . (2, IC七,-1 )3D . (-2,-)27.已知函数nf (x)二 sin(2x为了得到函数 g(x) =cos2x 的图象,则只要将函数A .向右平移 C .向左平移个单位长度6 it个单位长度6B .向右平移 D .向左平移'个单位长度12 个单位长度128.已知O 为坐标原点,点 M 的坐标为(a,1)(a 0), 点N(x,y)的坐标x 、y 满足不等式t3 3 2 29. 若函数f (x ) =sin 2(x )与y =sin2x • acos2x 的图像的对称轴相同,则a 的值 6为( ) A.3 B. - 310. 在 ABC 中,已知 AB ・ AC = 9 ,sinB=cosAsinC,S ABC =6,P 为线段 AB 上的点,CA CB=x + yCA CB二.填空题(本小题共6题,每小题4分,共24分)11. 若曲线y=kx+lnx 在点(1,k )处的切线平行于x 轴,则k= _____________2: 1 I 「12. 若:;三(0,)且 cos 二 1 sin ( 2 ) ,贝U tan 二二 ______________. 2 2213. 已知 向量a =(2,1),b =(1,k ),且a 与b 的夹角为锐角,则实数k 的取值范围是 _______14. 等比数列 玄,的前n 项和为S n ,已知3,2S 2,3S 3成等差数列,则 玄?的公比 为 ____________ .15. 在 ABC 中,B=60°,AC= 3,则 AB 2 BC 的最大值为 _________________ . 16. 已知数列:a n *的前n 项和为S n , a n - 0,a n a m = 3m n , m, n N ■,满足 12^1 S n 1000成立的n 的集合为 ______________ .三.解答题:(6题共76分,最后两题20分)17. (本小题共13分)在 ABC 中,a,b,c 分别是角代B,C 的对边,且cosB b cosC 2a c(1) 求角B 的大小; (2)若 b 13,a <=4,求 ABC 的面积.18. (本小题共14分)在等差数列*春中,a i =3,其前n 项和为S n ,等比数列D.且CP ,则xy 的最大值为(的各项均为正数,b =1,公比为q,且b2 S^12,q 2.b2(1)求a n 与b n;⑵设T n二aQ ~2b2 •……a n b n,求人的值.19. (本小题共14分)已知数列:a n /的各项排成如图所示的三角形数阵,数阵中每一行的第一个数ai,a2,a4,a7,…构成等差数列"b^f, S n是ej的前n项和, 且bj = c =1,S s -15ffia2 a y«4 兔a7a10(i)若数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知a9=16,求a50的值;11 1(II)设T n=丄+丄+…+丄,当m迂[―1,1】时,对任意n E N J 不等式S n 舟S n 七S2nt2-2mt-8 T n恒成立,求t的取值范围.3 n「3 220. (本小题共15分)已知函数心)=厂x +x忸+曲灯),的图象过点.al nx(xX1)(-1,2),且在点(-1, f(-1))处的切线与直线x-5y"=0垂直.(1)求实数b,c的值;⑵求f(x)在[-1,e](e为自然对数的底数)上的最大值;⑶对任意给定的正实数a ,曲线y二f(x)上是否存在两点P, Q,使得△ POC是以O为直角顶点的直角三角形,且此三角形斜边的中点在y轴上?21. (19, 20班同学不做。
浙江省绍兴一中2014届高三数学下学期回头考试卷 文 新人教A版

浙江省绍兴一中2014届高三数学下学期回头考试卷 文 新人教A 版本试题卷分选择题和非选择题两部分。
满分150分, 考试时间120分钟。
第Ⅰ卷选择题部分(共50分)一、选择题: 本大题共10小题, 每小题5分,共50分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
1.已知i 为虚数单位,则21ii=-( ) A .1i + B .1i -+ C . 1i - D . 1i --2.已知⎩⎨⎧≤+>=0)1(02)(x x f x x f x ,则)1(-f =( )A .0B .1C . 2D . 43.设函数()2xf x =,则下列结论中正确的是( )A. (1)(2)(f f f -<<B. ((1)(2)f f f <-<C. (2)((1)f f f <<-D. (1)((2)f f f -<<4.已知某四棱锥的三视图(单位:cm )如图所示,则该四棱锥的体积是( ) A3B 3C 3D 35.已知不重合的直线m 、和平面βα、,且βα⊂⊥l m ,,给出下列命题:①若α∥β,则l m ⊥;②若α⊥β,则l m //; ③若l m ⊥,则α∥β;④若l m //,则αβ⊥.其中正确命题的个数是( ) A .1 B .2 C .3 D .46.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若1cos ,3,sin 3A b c C ==则=( )A BC .13 D 7.已知平面上不共线的四点O ,A 、B 、C ,若540,||AB OA OB OC BC-+==则( )A .2B .3C .4D .58.设()x f 是定义在R 上的奇函数,且当0≥x 时,()2x x f =.若对任意的[]2,+∈a a x , 不等式()()x fa x f 2≥+恒成立,则实数a 的取值范围是 ( )正视图俯视图第11题A .0≤aB .2≥a C .2≤a D .0≥a9.已知双曲线)0(12222>>=-a b by a x 的两条渐近线为21,l l ,过右焦点F 作垂直1l 的直线交21,l l 于B A ,两点。
浙江省绍兴一中2014届高三数学考前模拟试卷 文 新人教A版

第3题图绍兴一中 高考模拟卷数学(文科) 2014-05-26本试题卷分选择题和非选择题两部分.全卷共4页, 选择题部分1至2页, 非选择题部分3至4页.满分150分, 考试时间120分钟.请考生按规定用笔将所有试题的答案写在答题纸上. 参考公式:柱体的体积公式 V Sh =,其中S 表示底面积,h 表示柱体的高.锥体的体积公式 13V Sh =,其中S 表示锥体的底面积,h 表示锥体的高. 球的表面积公式 24S R π=,球的体积公式 343V R =,其中R 表示球的半径.第Ⅰ卷(选择题部分 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知复数21iz i=-,则z z ⋅的值为( )A .0BC .2D .2-2.已知集合{A x y ==,{2,0}x B y y x ==>时,A B =( )A .{3}x x ≥-B .{13}x x <≤C .{1}x x >D .∅3.若某程序框图如图所示,则该程序运行后输出的值是( )A .4B .5C .6D .74.已知x a α:≥ ,11x β-<: .若α是β的必要非充分条件,则实数a 的取值范围是( ) A .0a ≥B .0a ≤C .2a ≥D .2a ≤5.设,a b 表示两条不同的直线,,αβ表示两个不同的平面( ) A .若α∥,,,a b βαβ⊂⊂则a ∥b B .若α⊥,a β∥β,则a α⊥ C .若,,a a b a α⊥⊥∥,β则b ∥β D .若α⊥,,,a b βαβ⊥⊥则a b ⊥6.已知函数()f x 是定义在R 上的偶函数, 且在区间[0,)+∞单调递增. 若实数a 满足212(log )(log )2(1)f a f f a ≤+, 则a 的最小值是( )A .32B .1C .12 D .27.函数sin(),0,02y x πωϕωϕ=+><<()在一个周期内的图象如图所示,(,0)6A π-,B 在y 轴上,C 为图象上的最低点,E 为该函数图象的一个对称中心,B 与D 关于点E 对称,CD 在x 轴上的投影为π12,则ω,φ的值为( )A .ω=2,φ=π3B .ω=2,φ=π6C .ω=12,φ=π3D .ω=12,φ=π68.已知约束条件对应的平面区域D 如图所示,其中123,,l l l 对应的直线方程分别为:112233,,y k x b y k x b y k x b =+=+=+,若目标函数z kx y =-+仅.在点(,)A m n 处取到最大值,则有( )A .12k k k << B. 13k k k << C. 13k k k ≤≤ D. 1k k<或3k k >9.已知1F,2F 是双曲线22221(0,0)x y a b a b-=>>的左,右焦点,若双曲线右支上存在一点P 与点1F 关于直线bxy a=-对称,则该双曲线的离心率为( ) A .2B . D . 2 10.已知二次函数2y ax =(0a >),点(12)P -,。
浙江省绍兴县鲁迅中学2014届高考文综(历史部分)适应性考试新人教版

鲁迅中学2014年普通高等学校招生适应性考试文科综合能力本试题卷分选择题和非选择题两部分,满分300分,考试时间150分钟。
选择题部分(共140分)一、选择题部分共35小题,每小题4分,共140分。
在每题给出的四个选项中,只有一项是符合题目要求的。
12.历史学家何炳松曾说:“(路德)忽悟自救之道端在‘信’字。
所谓信即吾人与上帝发生亲密关系之意。
”类似可以评述A.庄子 B.董仲舒 C.朱熹 D.王阳明13.“其大者为都督府,以其首领为都督、刺史,皆得世袭。
虽贡赋版籍,多不上户部然声教所暨,皆边州都督、都护所领,著于令式。
”这一制度的创立时间应在A.公元前3世纪 B.公元7世纪 C.公元14世纪 D.公元17世纪晚期14.《秦律》规定“有买及卖也,各婴其价(挂上价格标签);小物不能各一钱者,勿婴”,从事手工业和为官府出售产品的人“受钱必辄入其钱缿(陶制容钱器)中,令市者见其入,不从令者赀(罚)一甲”。
从中可以获悉秦朝①已有管理市场交易的法律②所有商品须明码标价③市场交易受到一定监督④政府对经济生活全面控制A.①③B.②④C.①②③D.②③④15.“自晚唐五代以来,词的内容上多以闲愁别恨的婉约词为主流。
然而,的横空出世,打破了这道数百年的樊篱,他以壮美的风格和阔大的意境,抒发自我的真实性情和独特的人生感受,自成一家,成就了宋词的另一座高峰”。
上述材料划线处应填入的是A.李煜B.柳永C.苏轼 D.辛弃疾16.加拿大历史学家哈罗德•伊尼斯在其所著的《全球通史》中指出:“梭伦寻求善世的真理。
他相信,违背公正必然要扰乱公众的生活。
个人对自己的行为负责。
于是,权威的根基就被摧毁了。
”梭伦改革中摧毁“权威的根基”的主要措施是A.颁布"解负令"废除债务奴隶制B.根据公民财产多少授予政治权力C.实行一系措施促进工商业的发展D.组成"四百人会议"作为常设机构17.中国纺织业源远流长,下列叙述正确的是A.汉代,中国最早出现了人工育蚕和丝织技术B.唐代,中国丝织品远销地中海地区,始有“丝国”之誉C.明清,手工工场和雇佣劳动关系在纺织业普遍出现D.民国,纺织业成为当时中国最大的新式工业之一18.历史上的某一经济政策建立在这样的信念上:即一国的国力基于通过贸易的顺差所能获得的财富。
2014届新课程高三第二次适应性测试数学(文)试题版含答案

文科数学试题(二)命题解析设计思路:主要考查平面向量数量积基本运算,容易题。
4.解:22log sinlog cos88ππ+=1sin 24223log (sincos )log 882πππ==-.答案:B.设计思路:主要考查三角函数与对数求值,中档题。
5. 解:∵a 、b 、c 成等比数列,∴b 2=ac 。
又a 2-c 2=ac -bc ,∴b 2+c 2-a 2=bc 。
在△ABC 中,由余弦定理得:cos A =bc a c b 2222-+=bc bc 2=21,∴∠A =60°。
由正弦定理得sin B =aAb sin ,∵b 2=ac ,∠A =60°,∴2123sin sin 60sin 60c ac b B b ===︒︒答案:C.设计思路:主要考查余弦定理,正弦定理及其应用,中档题。
6. 解:21(2)1(),.(2)2(1)f f x f x ''==--答案:B.设计思路:主要考查导数知识,容易题。
7. 解:设公差为d ,2242844443696245454(2)(4)4,33(2)18 2.29a a a a a d a d a d a a a a a d da a a a a d d=⋅⇒=-⋅+⇒=+++====+++答案:A.设计思路:主要考查等差数列与等比数列基本计算,中档题。
8.解:设xOB β∠=,则43sin ,cos 55ββ==-,则413sin sin()sin()()3525παπαβ=-=-=⨯--⨯=D 。
答案:D.设计思路:主要考查三角函数概念和求值,中档题。
9.解:设等差数列)}1({log 2-n a 的公差为d .由,8log 2log )2(log 29,322231+=+==d a a 得即d =1.所以2log (1)1(1)1,n a n n -=+-⨯=即.12+=n n a 得10a =210+1.答案:A.设计思路:主要考查数列与对数知识,考查综合应用知识能力,中高档题。
浙江绍兴鲁迅中学高三适应性考试数学文

7 8 9 8 7 2 8 8 1 082 6 乙甲绍兴鲁迅中学2010学年高考适应性考试数学试题(文科)一、选择题(每小题5分,共50分.每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知集合{}{}221,,20R A y y x x B x x x =+=+-∈=>,则下列正确的是( ) A .{}2A B y y =>I B .{}1,A B y y =>I C .{}21A B y y ⋃=-<<D .{}21A B y y y ⋃=<>-或2.“双曲线C 的方程为12222=-b y a x ()00>>b a ,”是“双曲线C 的渐近线方程为x aby ±=”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件3.在复平面内,复数2334ii-+-所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限4.已知等差数列}{n a 的前n 项和为n S ,若854,18S a a 则-=等于 ( )5.某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过50 kg 按0.53元/kg 收费,超过50 kg 的部分 按0.85元/kg 收费.相应收费系统的流程图如右图所示, 则①处应填 ( ) A .0.85y x =B .500.53(50)0.85y x =⨯+-⨯C .0.53y x =D .500.530.85y x =⨯+6.已知6||=,3||=,12-=⋅b a ,则向量a 在向量bA .4-B .4C .2-D .27.甲乙两位同学在高三的5次月考中数学成绩统计如茎叶图所示,若甲乙两人的平均成绩分别是x x 乙甲,,则下列正确的是( ) A .x x >乙甲;乙比甲成绩稳定 B .x x >乙甲;甲比乙成绩稳定C .x x <乙甲;乙比甲成绩稳定D .x x <乙甲;甲比乙成绩稳定8.设α、β是两个不同的平面,a 、b 是两条不同的直线,给出下列4个命题,其中正确命题是( )A .若a ∥α,b ∥α,则a ∥bB .若a ∥α,b ∥β,a ∥b ,则α∥β;C .若a ⊥α,b ⊥β,a ⊥b ,则α⊥β;D .若a 、b 在平面α内的射影互相垂直,则a ⊥b .9.函数⎪⎩⎪⎨⎧≤≤+<≤-+=)380(),sin(2)02(,1πϕωx x x kx y 的图象如下图,则( )A .6,21,21πϕω===k B .3,21,21πϕω===kC .6,2,21πϕω==-=kD .3,2,2πϕω==-=k10.已知椭圆的中心在坐标原点,焦点在x 轴上,以其两个焦点和短轴的两个端点为顶点的四边形是一个面积为4的正方形,设P 为该椭圆上的动点,C 、D 的坐标分别是())2,0,2,0-,则PC ·PD 的最大值为( ) A .4B .22C .3D .22+2二、填空题(本大题共有7小题,每小题4分,共28分.) 11.已知函数⎩⎨⎧+-+=,2,2)(x x x f 00>≤x x 则不等式()1f x ≥的解集为__________. 12.x 、y 满足约束条件:225040y x y x y ≥⎧⎪+-≥⎨⎪+-≤⎩,则1|5|2z x y =+-的最小值是 .13.下面为某一立体的三视图,则该立体的体积为14.抛掷甲、乙两枚质地均匀且四面上分别标有1,2,3,4的正四面体,其底面落于桌面,记所得的数字分别为x ,y ,则x y为整数的概率是 .15.若曲线C :22224540x y ax ay a ++-+-=上所有的点均在第二象限内,则a 的取值范围为__________________.16.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过2000元的部分不必纳税,超过2000元的部分为全月应纳税所得额.此项税款按下表分段累进计算:某人一月份应交纳此项税款135元,则他的当月工资、薪金的税后所得是 元.17.设函数2()3f x x ax a =-++,()2g x ax a =-.若存在0R x ∈,使得0()0f x <与0()0g x <同时成立,则实数a 的取值范围是 .三、解答题(本大题共有5小题,共72分.解答应写出文字说明、证明过程或演算步骤) 18.(本小题满分14分)如图,过原点且倾斜角为α的直线交单位圆于点34,55A ⎛⎫⎪⎝⎭,C 是单位圆与x 轴正半轴的交点,B 是单位圆上第二象限的点,且AOB ∆为正三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
鲁迅中学2014年普通高等学校招生适应性考试数 学(文科)本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页,非选择题部分3至4页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分 (共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
参考公式: 球的表面积公式 柱体的体积公式 S =4πR 2 V =Sh 球的体积公式 其中S 表示柱体的底面积,h 表示柱体的高V =34πR 3 台体的体积公式其中R 表示球的半径 V =31h (S 1+21S S +S 2) 锥体的体积公式其中S 1, S 2分别表示台体的上、下底面积,V =31Sh h 表示台体的高 其中S 表示锥体的底面积,h 表示锥体的高 如果事件A ,B 互斥,那么P (A +B )=P (A )+P (B )选择题部分(共50分)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求. 1.设全集R U =,集合}31|{},20|{≤≤=≤≤=y y B x x A ,则B A C U ⋂)(=A. (]3,2B.(]()+∞∞-,21,C.[)2,1D.()[)+∞∞-,10, 2.同时抛掷两枚质地均匀的骰子,则出现向上面的点数之和不小于8的概率是A .31B .125C .21D .127 3.已知11xi yi=-+,其中,,x y R i ∈为虚数单位,则=+yi xA . 1+2iB . 1-2iC .2+iD .2-i4.对于函数y =f (x ),x ∈R ,“y =|f (x )|的图象关于y 轴对称”是“y =f (x )是奇函数”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.设,,αβγ是三个互不重合的平面,m ,n 是两条不重合的直线,则下列命题中正确的是A .若,,a αββγγ⊥⊥⊥则B .若//,,//,//m m m αββαβ⊄则C .若,,//m m αβαβ⊥⊥则D .若//,//,,m a n a m n ββ⊥⊥则6.将函数x y 2sin =的图象向左平移4π个单位,所得图象对应函数的一个单调递增区间是A. ]2,0[πB. ],2[ππC. ]43,4[ππD. ]4,4[ππ- 7.已知点P (3,3),Q (3,-3),O 为坐标原点,动点M (x , y )满足||12||12OP OM OQ OM ⎧⋅≤⎪⎨⋅≤⎪⎩,则点M所构成的平面区域的面积是(A )12 (B )16(C )32(D )649. 设双曲线2222:1(0)x y C a b a b-=>>的右焦点为F ,左右顶点分别为12,A A ,过F 且与双曲线C 的一条渐近线平行的直线l 与另一条渐近线相交于P ,若P 恰好在以12A A 为直径的圆上,则双曲线的离心率为 A . 2B . 22C . 3D .3210.已知正实数a ,b 满足12=+b a ,则ab b a 1422++的最小值为 A .27B .4C .36161D .217非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分,把答案填在题中横线上.11. 为了了解某学校2000名高中男生的身体发育情况,抽查了该校100名高中男生的体重情况.根据所得数据画出样本的频率分布直方图,据此估计该校高中男生体重在70~78kg 的人数为_______人;12.若3sin cos 0αα+=,则21cos sin 2αα+的值为_13.执行如图所示的程序框图,则输出的k 值是 .14. 某几何体的三视图如图所示,根据图中标出的数据,则这个几何体的体积为 _ .15.对于正项数列{}n a ,定义nn na a a a nH +⋯+++=32132为{}n a 的“给力”值,现知数列{}n a 的“给力”值为1n H n=,则数列{}n a 的通项公式为n a = . 16.锐角ABC ∆的三边c b a ,,和面积S 满足条件22()4c a b S k--=,又角C 既不是ABC ∆的最大角也不是ABC ∆的最小角,则实数k 的取值范围是 .17.已知点)0,3(-A 和圆O :922=+y x ,AB 是圆O 的直径,M 和N 是AB 的三等分点,P(异于B A ,)是圆O 上的动点,AB PD ⊥于D ,)0(>=λλED PE ,直线PA 与BE 交于C ,则当=λ 时,||||CN CM +为定值.三、解答题: 本大题共5小题, 共72分.解答应写出文字说明、 证明过程或演算步骤. 18. (本题满分14分)已知函数()21)cos sin 3(cos +-=x x x x f ωωω的周期为π2. (Ⅰ)求ω的值;(Ⅱ)在△ABC 中,角A ,B ,C 的对边分别是,,a b c ,且满足a c A b 32cos 2-=,求)(B f 的值.否是俯视图19.(本题满分14分)设公比大于零的等比数列{}n a 的前n 项和为n S ,且11=a ,245S S =,数列{}n b 的前n 项和为n T ,满足11=b ,n n b n T 2=,*∈N n .(Ⅰ)求数列{}n a 、{}n b 的通项公式;(Ⅱ)设))(1(λ-+=n n n nb S C ,若数列{}n C 是单调递减数列,求实数λ的取值范围.20.(本题满分14分) 在正ABC∆中,点PF E ,,分别是BCAC AB 、、边上的点,且21::::===PB CP FA CF EB AE ,将AEF ∆沿EF 折起到EF A 1∆的位置,使二面角B EF A --1成直二面角,连结P A B A 11、(如图)(Ⅰ)求证:BEP E A 平面⊥1;(Ⅱ)求直线E A 1与平面BP A 1所成角的大小.21.(本题满分15分)已知函数()ax x x f +=331,()a x x g --=2 (a ∈R). (Ⅰ)若函数()()x g x f x F -=)(在[)+∞∈,1x 上单调递增,求a 的最小值;(Ⅱ)若函数()()x g x f x G +=)(的图象与x 轴有且只有一个交点,求a 的取值范围.ACBEF PA 1FEPC22.(本题满分15分)已知抛物线22(0)y px p =>的焦点为F ,点P 是抛物线上的一点,且其纵坐标为4,4PF =.(Ⅰ)求抛物线的方程;(Ⅱ)设点1122(,),(,)(0,1,2)i A x y B x y y i ≤=是抛物线上的两点,APB ∠的角平分线与x 轴垂直,求PAB ∆的面积最大时直线AB 的方程.参考答案(文)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
10:【解析】因为812221≤⇒≥+=ab ab b a ,当且仅当212==b a 时取等号.又因为ab ab ab b a ab b a 141)2(21422+=+⋅≥++.令ab t =,所以t t t f 14)(+=在]81,0(单调递减,所以217)81()(min ==f t f .此时212==b a .二、 填空题: 本大题共7小题, 每小题4分, 共28分。
15. 1=2n a n-16. 1,1) 17. 81=λ17:【解析】设),(00y x P ,则)11,(00y x E λ+,)3(3:00++=x x y y PA …① )3(311:00--+=x x y y BE λ…② 由①②得)9()9)(1(220202--+=x x y y λ, 将20209xy -=代入,得119922=++λy x .由1199=+-λ,得到81=λ. 三、解答题: 本大题共5小题, 共72分。
解答应写出文字说明、 证明过程或演算步骤。
18.【解析】:(Ⅰ)()2122cos 12sin 2321cos cos sin 32++-=+-=x x x x x x f ωωωωω x x ωω2cos 212sin 23-=⎪⎭⎫ ⎝⎛-=62sin πωx 21=∴ω(Ⅱ)解法(一)a c A b 32cos 2-=a c bca cb b 3222222-=-+⋅⇒ 整理得ac b c a 3222=-+,故232cos 222=-+=ac b c a B 6,0ππ=∴<<B B 00sin )6sin()(==-=∴πB B f解法(二)a c A b 32cos 2-=A C A B sin 3sin 2cos sin 2-=⇒A B A A B sin 3)sin(2cos sin 2-+=⇒0sin 3cos sin 2=-⇒A B A 0)3cos 2(sin =-⇒B A0sin ,0≠∴<<A A π 23cos =∴B 又6,0ππ=∴<<B B 00sin )6sin()(==-=∴πB B f19. 【解析】:(Ⅰ)由245S S =,,0>q 得 12,2-==n n a q又11)1(11212+-=⇒⎪⎩⎪⎨⎧-==---n n b b b n T b n T n n n n nn ()1>n , 则得)1(23142132111232211+=⋅⋅⋅--⋅-⋅+-=⋅⋅⋅⋅-----n n n n n n n n b b b b b b b b n n n n n n 所以)1(2+=n n b n ,当1=n 时也满足.(Ⅱ)12-=n n T ,所以)12(2λ-+=n C nn ,使数列{}n C 是单调递减数列, 则0)1224(21<-+-+=-+λn n C C nn n 对*∈N n 都成立, 即max )1224(01224+-+>⇒<-+-+n n n n λλ, nn n n n n n 232)2)(1(21224++=++=+-+, 当1=n 或2时,,31)1224(max =+-+n n 所以31>λ. 20.【解析】:不妨设正三角形ABC 的边长为3(1)取BE 中点D ,连接DF .AE :EB=CF :FA=1:2∴AF=AD=2而∠A=60°,∴△ADF 是正三角形,又AE=DE=1,∴EF ⊥AD 在图2中,A 1E ⊥EF ,BE ⊥EF , ∴∠A 1EB 为二面角A 1-EF-B 的平面角.由题设条件知此二面角为直二面角,A 1E ⊥BE ,又BE∩EF=E∴A 1E ⊥平面BEF , 即A 1E ⊥平面BEP ……6分 (2)在图中,A 1E 不垂直A 1B ,∴A 1E 不是平面A 1BP 的垂线,又A 1E ⊥平面BEP , ∴A 1E ⊥BE .设Q BP G A G BP A于交,连结于平面⊥EG21.【解析】:(1)()()a x ax x x g x f x F +++=-=233)(,a x x x F ++=2)(2' 因函数()()x g x f x F -=)(在[)+∞∈,1x 上单调递增,所以02)(2'≥++=a x x x F 在[)+∞∈,1x 恒成立,即3-≥a ,a 的最小值为.3- ----------5分A 1 FE PC B Q G(2)()()a ax x x x g x f x G -+-=+=2331)( ∵ ()x G '= a x x +-22,∴△= a 44-= ()a -14 . ① 若1≥a ,则△≤0, ∴()x G '≥0在R 上恒成立,∴G (x )在R 上单调递增 . ∵G (0)0<-=a ,()023>=a G , ∴当1≥a 时,函数G (x )的图象与x 轴有且只有一个交点. ----------9分 ② 若a <1,则△>0,∴()x G '= 0有两个不相等的实数根,不妨设为x 1,x 2,(x 1<x 2). ∴x 1+x 2 = 2,x 1x 2 = a .当x 变化时,()()x G x G ,'的取值情况如下表:∵02121=+-a x x , ----------12分∴1212x x a +-=.∴()a ax x x x G -+-=12131131 =12112131231x x ax x x -++- ()131231x a x -+= ()[]2331211-+=a x x同理()2x G ()[]2331222-+=a x x .∴()()()[]()[]23239122212121-+⋅-+=⋅a x a x x x x G x G()()()()()[]2222122121292391-++-+=a x x a x x x x ()()[](){}22122122922391-+-+-+=a x x x x a a a ()33942+-=a a a . 令G (x 1)G (x 2)>0, 解得a >0. 而当10<<a 时,()()023,00>=<-=a G a G ,故当10<<a 时, 函数f (x )的图象与x 轴有且只有一个交点. 综上所述,a 的取值范围是()+∞,0. ------------------15分22.【解析】(1)设0(,4)P x ,因为4PF =,由抛物线的定义得042px +=,又2042px =,所以08x p =,因此842pp +=,解得4p =,从而抛物线的方程为28y x =. (2)由(1)知点P 的坐标为(2,4)P ,因为APB ∠的角平分线与x 轴垂直,所以可知,PA PB的倾斜角互补,即,PA PB 的斜率互为相反数设直线PA 的斜率为k ,则:4(2)PA y k x -=-,由题意0k ≠,把42y x k k =+-代入抛物线方程得2832160y y k k--+=,该方程的解为4、1y , 由韦达定理得184y k +=,即184y k =-,同理284y k=--,所以2121222121218188AB y y y y k y y x x y y --====--+-, 设:AB y x b =-+,把x y b =-+代入抛物线方程得2880y y b +-=, 由题意64320b ∆=+>,且1280y y b =-≥,从而20b -<≤又128y y +=-,所以12AB y -=,点P 到AB的距离d =,因此PAB S ∆=2(0,2]b t +=∈,则232(2)(1236)1664()b b b t t t f t +⋅-+=-+=,2()33264(38)(8)f t t t t t '=--=-- 由(0,2]t ∈知()0f t '>,所以()f t 在(0,2]t ∈上为增函数,因此max ()(2)72f t f ==, 即PAB ∆面积的最大值为24PAB S ∆==.PAB ∆的面积取最大值时0b =,所以直线AB 的方程为0x y +=.。
