《数学建模入门》练习题北京石油化工学院
数学建模题目及答案

09级数模试题1. 把四只脚的连线呈长方形的椅子往不平的地面上一放,通常只有三只脚着地,放不稳,然后稍微挪动几次,就可以使四只脚同时着地,放稳了。
试作合理的假设并建立数学模型说明这个现象。
(15分)解:对于此题,如果不用任何假设很难证明,结果很可能是否定的。
因此对这个问题我们假设 :(1)地面为连续曲面(2)长方形桌的四条腿长度相同(3)相对于地面的弯曲程度而言,方桌的腿是足够长的(4)方桌的腿只要有一点接触地面就算着地。
那么,总可以让桌子的三条腿是同时接触到地面。
现在,我们来证明:如果上述假设条件成立,那么答案是肯定的。
以长方桌的中心为坐标原点作直角坐标系如图所示,方桌的四条腿分别在A 、B 、C 、D 处,A 、B,C 、D的初始位置在与x 轴平行,再假设有一条在x 轴上的线ab,则ab 也与A 、B ,C 、D 平行。
当方桌绕中心0旋转时,对角线 ab 与x 轴的夹角记为θ。
容易看出,当四条腿尚未全部着地时,腿到地面的距离是不确定的。
为消除这一不确定性,令 ()f θ为A 、B 离地距离之和,()g θ为C 、D 离地距离之和,它们的值由θ唯一确定。
由假设(1),()f θ,()g θ均为θ的连续函数。
又由假设(3),三条腿总能同时着地, 故()f θ()g θ=0必成立(∀θ)。
不妨设(0)0f =,(0)0g >g (若(0)g 也为0,则初始时刻已四条腿着地,不必再旋转),于是问题归结为:已知()f θ,()g θ均为θ的连续函数,(0)0f =,(0)0g >且对任意θ有00()()0f g θθ=,求证存在某一0θ,使00()()0f g θθ=。
证明:当θ=π时,AB 与CD 互换位置,故()0f π>,()0g π=。
作()()()h f g θθθ=-,显然,()h θ也是θ的连续函数,(0)(0)(0)0h f g =-<而()()()0h f g πππ=->,由连续函数的取零值定理,存在0θ,00θπ<<,使得0()0h θ=,即00()()f g θθ=。
数学建模试卷及参考答案

数学建模 试卷及参考答案一.概念题(共3小题,每小题5分,本大题共15分)1、一般情况下,建立数学模型要经过哪些步骤?(5分)答:数学建模的一般步骤包括:模型准备、模型假设、模型构成、模型求解、模型分析、模型检验、模型应用。
2、学习数学建模应注意培养哪几个能力?(5分)答:观察力、联想力、洞察力、计算机应用能力。
3、人工神经网络方法有什么特点?(5分)答:(1)可处理非线性;(2)并行结构.;(3)具有学习和记忆能力;(4)对数据的可容性大;(5)神经网络可以用大规模集成电路来实现。
二、模型求证题(共2小题,每小题10分,本大题共20分)1、 某人早8:00从山下旅店出发,沿一条路径上山,下午5:00到达山顶并留宿.次日早8:00沿同一路径下山,下午5:00回到旅店.证明:这人必在2天中同一时刻经过路途中某一地点(15分) 证明:记出发时刻为t=a,到达目的时刻为t=b,从旅店到山顶的路程为s.设某人上山路径的运动方程为f(t), 下山运动方程为g(t),t 是一天内时刻变量,则f(t),g(t)在[a,b]是连续函数。
作辅助函数F(t)=f(t)-g(t),它也是连续的,则由f(a)=0,f(b)>0和g(a)>0,g(b)=0,可知F (a )<0, F(b)>0,由介值定理知存在t0属于(a,b)使F(t0)=0, 即f(t0)=g(t0) 。
2、三名商人各带一个随从乘船过河,一只小船只能容纳二人,由他们自己划行,随从们秘约,在河的任一岸,一旦随从的人数比商人多,就杀人越货,但是如何乘船渡河的大权掌握在商人们手中,商人们怎样才能安全渡河呢?(15分)解:模型构成记第k 次渡河前此岸的商人数为k x ,随从数为k y ,k=1,2,........,k x ,k y =0,1,2,3。
将二维向量k s =(k x ,k y )定义为状态。
安全渡河条件下的状态集合称为允许状态集合,记做S 。
北京石油化工学院大一高等数学上册期末考试卷及答案

北京石油化工学院大一高等数学上册期末考试卷及答案一、单选题1、曲线2x y = ,1=x ,0=y 所围成的图形绕y 轴旋转所得旋转体体积=V ( ).A 、⎰104dx x π B 、⎰10ydy π C 、⎰-10)1(dy y π D 、⎰-104)1(dx x π 【答案】A2、下列各组函数中,是相同函数的是( ).(A) ()f x x =和()g x =()211x f x x -=-和1y x =+ (C) ()f x x =和()22(sin cos )g x x x x =+ (D) ()2ln f x x =和()2ln g x x =【答案】C3、下列定积分为零的是( ).(A )424arctan 1x dx x ππ-+⎰ (B )44arcsin x x dx ππ-⎰ (C )112x x e e dx --+⎰ (D )()121sin x x x dx -+⎰ 【答案】A4、曲线ln y x x =的平行于直线10x y -+=的切线方程为( ).(A )1y x =- (B )(1)y x =-+ (C )()()ln 11y x x =-- (D )y x =【答案】A5、曲线 23-+=x x y 在点)0,1(处的切线方程是( )A 、 )1(2-=x yB 、)1(4-=x yC 、14-=x yD 、)1(3-=x y【答案】B6、设函数()y f x =在点0x 处可导,且()f x '>0, 曲线则()y f x =在点()()00,x f x 处的切线的倾斜角为{ }. (A) 0 (B)2π (C) 锐角 (D) 钝角 【答案】C7、设 a ﹥0,则=-⎰dx x a a 022( ). A 、2a B 、22a π C 、241a 0 D 、241a π 【答案】D 8、下列各微分式正确的是( ).A 、)(2x d xdx =B 、)2(sin 2cos x d xdx =C 、)5(x d dx --=D 、22)()(dx x d =【答案】C9、211f dx x x⎛⎫' ⎪⎝⎭⎰的结果是( ). (A )1f C x ⎛⎫-+ ⎪⎝⎭ (B )1f C x ⎛⎫--+ ⎪⎝⎭ (C )1f C x ⎛⎫+ ⎪⎝⎭ (D )1f C x ⎛⎫-+ ⎪⎝⎭【答案】D10、方程( )是一阶线性微分方程.A 、0ln 2=+'xy y x B 、0=+'y e y x C 、0sin )1(2=-'+y y y x D 、0)6(2=-+'dy x y dx y x【答案】B11、方程( )是一阶线性微分方程.A 、0ln 2=+'xy y x B 、0=+'y e y x C 、0sin )1(2=-'+y y y x D 、0)6(2=-+'dy x y dx y x【答案】B12、方程( )是一阶线性微分方程.A 、0ln 2=+'xy y x B 、0=+'y e y x C 、0sin )1(2=-'+y y y x D 、0)6(2=-+'dy x y dx y x【答案】B二、填空题1、求抛物线2x y = 与 22x y -=所围成的平面图形的面积.【答案】38; 2、不定积分ln x xdx =⎰______________________.【答案】2211ln 24x x x c -+ 3、=⎰-113cos xdx x ;【答案】04、=⎰-113cos xdx x ;【答案】05、微分方程 023=+'-''y y y 的通解是 .【答案】x x e C e C 221+.三、解答题(难度:中等)1、求方程y xy y x =+'2 满足初始条件4)21(=y 的特解. 【答案】x e xy 122-= ; 2、求曲线22y x =和直线4y x =-所围图形的面积.【答案】18S =3、求微分方程6130y y y '''++=的通解.【答案】特征方程:2312613032(cos 2sin 2)x r r r i y e C x C x -++=⇒=-±=+4、求方程y xy y x =+'2 满足初始条件4)21(=y 的特解. 【答案】xe x y 122-= ;5、求由曲线 22x y -= 和直线 0=+y x 所围成的平面图形的面积. 【答案】29;6、求不定积分⎰+dx x x ln 21; 【答案】C x ++ln 22 ;7、求由曲线21,y x =+ 直线0,0y x ==和1x =所围成的平面图形的面积, 以及此图形绕y 轴旋转所得旋转体的体积. 【答案】12210013(1)()22S x dx x x =+=+=⎰ 112242005210(1)(21)228()5315V x dx x x dx x x x ππππ=+=++=++=⎰⎰8、求 x x y arccos 12-= 的导数; 【答案】1arccos12---x x x ;。
《数学建模》课程第一章自测练习及解答提示

《数学建模》课程第一章自测练习及解答提示一、填空题:1.设年利率为0.05,则10年后20万元的现值按照复利计算应为 . 解:根据现值计算公式:10)05.01(20)1(+=+=n R S Q 2783.1221201011≈=(万元) 应该填写:12.2783万元.2.设年利率为0.05,则20万元10年后的终值按照复利计算应为 . 解:根据终值计算公式:10)05.01(20)1(+=+=n R P S =5779.322021910=(万元) 应该填写:32.57793.所谓数学建模的五步建模法是指下列五个基本步骤,按一般顺序可以写出为 .解:应该填写:问题分析,模型假设,模型建立,模型求解,模型分析.4.设某种商品的需求量函数是,1200)(25)(+-=t p t Q 而供给量函数是3600)1(35)(--=t p t G ,其中)(t p 为该商品的价格函数,那麽该商品的均衡价格是 .解: 由商品的均衡价格公式:80352536001200)(=++=++=c a d b t p 应该填写:80.5.一家服装店经营的某种服装平均每天卖出110件,进货一次的批发手续费为200元,存储费用为每件0.01元/天,店主不希望出现缺货现象,则最优进货周期与最优进货量分别为 .解:根据经济订购批量公式:1911001.020022*≈⨯⨯==R c c T s b 209701.011020022*≈⨯⨯==s b c R c Q 应该填写:.2097,19**=≈Q T二、分析判断题1. 从下面不太明确的叙述中确定要研究的问题,需要哪些数据资料(至少列举3个),要做些甚麽建模的具体的前期工作(至少列举3个) ,建立何种数学模型:一座高层办公楼有四部电梯,早晨上班时间非常拥挤,该如何解决.解:(1)要研究的问题:如何设置四部电梯的停靠方式,使之发挥最大效益.(2)所需资料为:每天早晨乘电梯的总人数、各层上、下电梯的人数、电梯的速度、楼层的高度、层数等.(3)要做的具体建模前期工作:观察和统计所需资料,一般讲,需要统计一周内每天的相关资料.(4)可以建立概率统计模型,亦可在适当的假设下建立确定性模型.2.一条公路交通不太拥挤,以至人们养成“冲过”马路的习惯,不愿意走临近的“斑马线”.交管部门不允许任意横穿马路,为方便行人,准备在一些特殊地点增设“斑马线”,以便让行人可以穿越马路.那末“选择设置斑马线的地点”这一问题应该考虑哪些因素?试至少列出3种.解:(1)车流的密度(2)车的行驶速度(3)道路的宽度(4)行人穿越马路的速度(5)设置斑马线地点的两侧视野等.3.怎样解决下面的实际问题.包括需要哪些数据资料,要作些什么观察、试验以及建立什么样的数学模型等.(1)估计一个人体内血液的总量.(2)为保险公司制定人寿保险计划(不同年龄的人应缴纳的金额和公司赔偿的金额).(3)估计一批日光灯管的寿命.(4)确定火箭发射至最高点所需的时间.(5)决定十字路口黄灯亮的时间长度.(6)为汽车租赁公司制订车辆维修、更新和出租计划.(7)一高层办公楼有4部电梯,早晨上班时间非常拥挤,试制订合理的运行计划解:(1)注射一定量的葡萄糖,采集一定容量的血样,测量注射前后葡萄糖含量的变化,即可估计人体的血液总量.注意采集和测量的时间要选择恰当,使血液中的葡萄糖含量充分均匀,又基本上未被人体吸收.(2)调查不同年龄的人的死亡率,并估计其在未来一定时期的变化,还应考虑银行存款利率和物价指数,保险金与赔偿金之比大体上应略高于死亡率.(3)从一批灯管中取一定容量的样本,测得其平均寿命,可作为该批灯管寿命的估计值.为衡量估计的精度,需要从样本寿命确定该批灯管寿命的概率分布,即可得到估计值的置信区间.还可试验用提高电压的办法加速寿命测试,以缩短测量时间.(4)根据牛顿第二定律建立火箭向上发射后的运动方程,初速已知,若不考虑空气阻力,很容易算出到达最高点(即速度为零)时间;若考虑空气阻力,不妨设其与火箭速度(或速度的平方)成正比,并有试验及拟合方法确定阻力系数,再解方程得到结果.(5)司机看到黄灯后停车要有一定的刹车距离S1,设通过十字路口的距离为S2,汽车行驶速度为v,则黄灯的时间长度t应使距停车线S1之内的汽车能通过路口,即t (S1+S2)/v.S1可由试验得到,或按照牛顿第二定律解运动方程,进一步可考察不同车重、不同路面及司机反应灵敏程度等因素的影响.(6)根据资料和经验确定维修费用随着车龄和行驶里程的增加而增加的关系,再考虑维修和更新费用,可以以一年为一个时段,结合租金决定应该维修或更新.(7)统计在各层上班的人数,通过数据或计算确定电梯运行时间,以等待的人数与时间乘积为目标,建立优化模型,确定每部电梯运行的楼层(有的从大厅直接运行到高层).4.为了培养想象力、洞察力,考察对象时除了从正面分析外,还常常需要从侧面或反面思考,试尽可能迅速地回答下列的问题:(1)某甲早8:00从山下旅馆出发,沿一条路径上山,下午5:00到达山顶并留宿.次日早8:00沿同一路径下山,下午5:00回到旅馆.某乙说,甲必在2天中的同一时刻经过路径中的同一地点.为什么?(2)甲乙两站之间有电车相通,每隔10分钟甲乙两站相互发一趟车,但发车时刻不一定相同,甲乙之间有一中间站丙,某人每天在随机的时刻到达丙站,并搭乘最先经过丙站的那趟车,结果发现100天中约有90天到达甲站,约有10天到达乙站.问开往甲乙两站的电车经过丙站的时刻表是如何安排的?(3)某人住T 市在他乡工作,每天下班后乘火车于6:00抵达T 市车站,他的妻子驾车准时到车站接他回家.一日他提前下班搭乘早一班火车于5:30抵T 市车站,随即步行回家,他的妻子像往常一样驾车前往,在半路上遇到他,即接他回家,此时发现比往常提前10分钟.问他步行了多长时间.解:(1)设想有两个人一人上山,一人下山,同一天同时出发,沿同一路径,必定相遇.(2)不妨设从甲站到乙站经过丙站的时刻表是:8:00,8:10,8:20,…,那么从乙站到甲站经过丙站的时刻表应该是:8:09,8:19,8:29,….(3)步行了25分钟.设想他的妻子驾车遇到他后,先带他去车站,再回家,汽车多行驶了10分钟,于是带他去车站这段路程汽车跑了5分钟,而到车站的时间是6:00,所以妻子驾车遇到他的时刻是5:55.三、计算题1.下面是众所周知的智力游戏:人带猫、鸡、米过河,船除需要人划之外,至多能载猫、鸡、米三者之一,而当人不在场时猫要吃鸡、鸡要吃米.试设计一个安全过河方案,并使渡河次数尽量地少.解:人、猫、鸡、米分别记为i =1, 2, 3, 4,当i 在此岸时记x i =1,否则记x i =0,则此岸的状态可用s =(x 1, x 2, x 3, x 4)表示.记s 的反状态为s '=(1-x 1, 1-x 2, 1-x 3, 1-x 4),允许状态集合为S ={(1, 1, 1, 1),(1, 1, 1, 0),(1, 1, 0, 1),(1, 0, 1, 1)(1, 0, 1, 0)及它们的5个反状态}.决策为乘船方案,记作d =(u 1, u 2, u 3, u 4),当i 在船上时记u i =1,否则记u i =0,允许决策集合为D ={(1, 1, 0, 0),(1, 0, 1, 0),(1, 0, 0, 1),(1, 0, 0, 0)}.记第k 次渡河前的状态为s k ,第k 次渡河的决策为d k ,则状态转移律为s k +1=s k +(-1)k d k ,设计安全过河方案归结为求决策序列d 1, d 2, …, d n ∈D ,使状态s n ∈S 按状态转移律由初始状态s 1=(1, 1, 1, 1)经n 步到达s n +1=(0, 0, 0, 0).一个可行方案如下:2.假定人口的增长服从这样的规律:时间t 的人口为x (t ),t 到t +∆t 时间内人口的增长与x m - x (t )成正比 (其中x m 为最大容量).试建立模型并求解.作出解的图形并与指数增长模型、阻滞增长模型的结果进行比较.解 )(d d x x r t x m -=,r 为比例系数,0)0(x x =, 解为rt m m x x x t x ---=e )()(0,如图1中粗实线所示.当t 充分大时,它与Logistic 模型相近. 图13.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗?比如洁银牙膏50g 装的每支1.50元,120g 装的每支3.00元,二者单位重量的价格比是1.2:1.试用比例x x方法构造模型解释这个现象.(1)分析商品价格c 与商品重量w 的关系.价格由生产成本、包装成本和其它成本决定,这些成本中有的与重量w 成正比,有的与表面积成正比,还有与w 无关的因素.(2)给出单位重量价格c 与w 的关系,画出它的简图,说明w 越大c 越小,但是随着w 的增加c 减小的程度变小.解释实际意义是什么? 解:(1)生产成本主要与重量w 成正比,包装成本主要与表面积s 成正比,其它成本也包含与w 和s 成正比的部分,上述三种成本中都含有与w 和s 无关的成分.又因为形状一定时一般有s ∝w 2/3,故商品的价格可表为C = αw +β w 2/3+γ(α,β,γ为大于0的常数).(2)单位重量价格131--++==w w w C c γβα,其 图2 简图如图2所示.显然c 是w 的减函数,说明大包装商品比小包装商品便宜;曲线是下凸的,4.用宽w 的布条缠绕直径d的圆形管道,要求布条 不重叠,问布条与管道轴线的夹角α应多大(如图3). 若知道管道长度,需用多长布条(可考虑两端的影响). 如果管道是其它形状呢?解:将管道展开如图4,可得απcos d w =,若d 一 图3 定,0→w ,2πα→;d w π→,0→α.若管道长度为l ,不考虑两端的影响时布条长度显然为w dl π,若考虑两 端的影响,则应加上απsin dw .对于其它形状管道,只需将d π 改为相应的周长即可.5.建立不允许缺货的生产销售存贮模型.设生产速率为常数k ,销售速率为常数r ,k >r .在每一生产周期T 内,开 图4 始的一段时间(0<t <T 0)一边生产一边销售,后来的一段时间(T 0<t <T )只销售不生产,画出贮存量)(t q 的图形.设每次生产准备费为1c ,单位时间每件产品贮存费为2c ,以总费用最小为目标确定最优生产周期.讨论k 》r 和k ≈ r 的情况. 解: 贮存量)(t q 的图形如图5.单位时间总费用 KT r k r c T c T c 2)()(21-+=, 使)(T c 达到最小值的最优周期)(221r k r c k c T -=*. 图5 当k 》r 时,rc c T 212=*,相当 于不考虑生产的情况.当k ≈ r 时,∞→*T ,因为0产量被销量抵消,无法形成贮存量.四、综合应用题1.试建立方桌问题在四条腿脚呈长方形情形时的数学模型,以说明方桌能否在地面上放稳的问题.( 提示:要求按照五步建模法进行建模工作,本题至少应给出前四个步骤.) 解:问题分析所谓方桌可否在地面上放稳,可视为其四个桌脚可否同时着地,从而可将问题归结为桌脚与地面的距离是否同时为零,故构造这个距离函数是建模的关键,而证明四个距离函数同时为零这个命题是建模的最终目的.模型假设(1) 四条桌腿同长,视四个桌脚为四个几何点,四脚的连线呈长方形;(2) 地面的高度是连续变化的,即将地面看作数学上的连续曲面;(3)模型建立 如图6,以长方形的两条对角线的交点为原点建立平面直角坐标系,且不妨设A ,C 两桌脚开始时位于横轴上,则问题与旋转角度θ有关.注意到假设3,设A ,B 两个桌脚与地面距离之和为0)(≥θf ,另外两个桌脚与地面距离之 和为,0)(≥θg 则)(,θθf ∀与)(θg 中至少有一个为零,当 图6 0=θ时不妨假设0)(,0)(>=θθg f .又由假设2,以上两个函数均为旋转角度的连续函数,于是有命题:已知,0)0(,0)0(,0)()()(),(>==∀g f g f g f 且,的连续函数,对是θθθθθθ则0θ∃,使得.0)()(00==θθg f上述命题即为所建立的数学模型.模型求解将桌子旋转0180)(π,则A 、B 两点与D 、C 两点恰好交换位置.由假设便有,)(,0)(ππg f >.0=又由前述假设,.0)0(,0)0(>=g f令),()()(θθθg f h -=则有.0)(,0)0(><πh h 由于)(),(θθg f 的连续性知)(θh 也是连续函数.依据连续函数的基本性质(零点定理),必至少存在一个角度0θ,,00πθ<<使得0)(0=θh ,即).()(00θθg f =又根据θθθ∀=,0)()(g f 成立,故有.0)()(00==θθg f 模型分析由于本问题结论简单,符合实际,故分析过程从略.2.试建立确定情形下允许缺货的存储问题的数学模型.提示: 所谓的确定情形下的存储模型是指文字教材第一章提到过的不允许缺货的存储模型;所谓允许缺货是在不允许缺货模型假设条件下,再考虑因缺货造成的损失建立相应的模型.(要求按照五步建模法进行建模工作,本题应给出五个步骤.)解: 问题分析由题设,只须在不允许缺货模型条件下,考虑因缺货造成的损失即可.而缺货损失按天计算与下列因素有关:货物总需求量、缺货量、缺货时刻、每单位的缺货费用等. 模型假设 (1)每次定货费为C 1,每天每单位货物的存储费为C 2 (2)每天货物的需求量为r 单位.(3) 每T 天定货Q 单位,所定货物可在瞬间到达.(4)允许缺货,每天每单位货的缺货费为C 3缺货时,存储量q 视为负值,则)(t q 的图形变为,Q rt q +-=如图7所示.模型建立 图7 货物在1T t =时售完,则必有一段时间缺货.又在T t =时下一次定货量Q 到达,于是有1rT Q = (1)在一个定货周期内的总费用包括定货费1C 、存储费Q T C dt t q C T 102221)(1⎰=和缺货费.)(13dt t q C T T ⎰其中21)(2)()(11T T r dt Q rt dt t q TT T T -=-=⎰⎰ 其中用到了(1)式.于是总费用应为2/)(2/213121T T r C QT C C C -++= (2) 则由(1)式解出r Q T /1=并代入(2)式可得r Q rT C r Q C C C 2/)(2/23221-++= (3)每天的平均总费用便是rT Q rT C rT Q C T C T C Q T C 2/)(2///),(23221-++== (4)(4)式即为所求的数学模型.模型求解对(4)式分别求总费用对定货周期和定货量的偏导数,并令其为零解得0)()(22322322221=-+----=∂∂Q rT T C Q rT rT C rT Q C T C T C0)(32=--=∂∂Q rT rTC rT Q C Q C 由3230C C rT C Q Q C +=⇒=∂∂,代入0=∂∂TC 便可解出 32321*33221*2;2C C C C r C Q C C C rC C T +=+=. (5) (5)式就是在允许缺货情形下,最佳定货周期与最佳定货量公式.模型分析当3C 远远超过2C 时,(5)式就转化为不允许缺货模型中的相应结论,这也说明所建模型是合理的,结论也是正确的.。
(完整版)数学建模模拟试题及答案

数学建模模拟试题及答案一、填空题(每题 5 分,共 20 分)1.一个连通图能够一笔画出的充分必要条件是.2. 设银行的年利率为 0.2,则五年后的一百万元相当于现在的万元.3. 在夏季博览会上,商人预测每天冰淇淋销量N 将和下列因素有关:(1) 参加展览会的人数n; (2)气温T 超过10o C;(3)冰淇淋的售价p .由此建立的冰淇淋销量的比例模型应为 .4. 如图一是一个邮路,邮递员从邮局 A 出发走遍所有 A长方形街路后再返回邮局 .若每个小长方形街路的边长横向均为 1km,纵向均为 2km,则他至少要走 km .二、分析判断题(每题 10 分,共 20 分)1. 有一大堆油腻的盘子和一盆热的洗涤剂水。
为尽量图一多洗干净盘子,有哪些因素应予以考虑?试至少列出四种。
2. 某种疾病每年新发生 1000 例,患者中有一半当年可治愈 .若 2000 年底时有1200 个病人,到 2005 年将会出现什么结果?有人说,无论多少年过去,患者人数只是趋向 2000 人,但不会达到 2000 人,试判断这个说法的正确性 .三、计算题(每题 20 分,共 40 分)1. 某工厂计划用两种原材料A, B 生产甲、乙两种产品,两种原材料的最高供应量依次为 22 和 20 个单位;每单位产品甲需用两种原材料依次为 1 、1 个单位,产值为 3 (百元);乙的需要量依次为 3、1 个单位,产值为 9 (百元);又根据市场预测,产品乙的市场需求量最多为 6 个单位,而甲、乙两种产品的需求比不超过 5: 2,试建立线性规划模型以求一个生产方案,使得总产值达到最大,并由此回答:(1) 最优生产方案是否具有可选择余地?若有请至少给出两个,否则说明理由 .(2) 原材料的利用情况 .2. 两个水厂A1 , A2将自来水供应三个小区B1 , B2 , B3 , 每天各水厂的供应量与各小区的需求量以及各水厂调运到各小区的供水单价见下表 .试安排供水方案,使总供水费最小?四、 综合应用题(本题 20 分)某水库建有 10 个泄洪闸,现在水库的水位已经超过安全线,上游河水还在不断地流入 水库.为了防洪,须调节泄洪速度 .经测算,若打开一个泄洪闸, 30 个小时水位降至安全线, 若打开两个泄洪闸, 10 个小时水位降落至安全线 .现在,抗洪指挥部要求在 3 个小时内将水 位降至安全线以下,问至少要同时打开几个闸门?试组建数学模型给予解决 .注:本题要求按照五步建模法给出全过程 .小区 单价/元水厂A1A供应量 / t170B34B11 07 1B26数学建模 06 春试题模拟试题参考解答一、填空题(每题 5 分,共 20 分)1. 奇数顶点个数是 0 或 2;2. 约 40.1876 ;3. N = Kn(T10) / p, (T > 10 0 C), K 是比例常数; 4. 42.二、分析判断题(每题 10 分,共 20 分)1. 解: 问题与盘子、水和温度等因素直接相关,故有相关因素:盘子的油腻程度,盘子的温度,盘子的尺寸大小;洗涤剂水的温度、浓度; 刷洗地点 的温度等.注:列出的因素不足四个,每缺一个扣 2.5 分。
《数学建模》练习题库及答案.doc

一、名词解释1.Table命令的使用格式;2.Solve命令的使用格式;3.Do命令的使用格式;4.Plot命令的使用格式;5.ListPlot命令的使用格式;6.Reduce命令的使用格式;7.Expand命令的使用格式;8.FindRoot命令的使用格式;9.Switch命令的使用格式;lO.ConstrainedMin命令的使用格式;11 .Factor命令的特点与几种使用格式。
12.Clear命令的特点与使用格式二、计算题1. 1959年8月4日是星期几,这一天与2001年12月4日之间共有多少天?2.求我国北京市的地理经纬度。
3.北美地区有几个国家?写出它们的名字。
4.求解递归关系式a” = 3% _2a”_2,ao =1,4 = 2。
5.求斐波那契(Fibonacci)数列Fibonacci[n]从n=l至【Jn = 50的值。
6.分别以0.1、0.01、0.001为误差上限,将J方化成近似分数。
7 .求下列矩阵的特征值与对应的特征向量:13•求解方程7% -和"—张+ 1X 14.求1+ 28+38+...+n 8的简洁表达式。
15.求Pell 方程.r 2 -234y 2 -1的最小正整数解。
16.将16进制的数字20转化为10进制的数字。
17.求下列矩阵的行列逆矩阵与转置矩‘1 2 3、A= 2 3 1、3 1 2,8.求多项式 f=( X1 + X2 +X3 + X4 + X5严中 Xi 3 x 23 X35 X42 X55 的系数。
9•求208素因子分解。
10. 用Lindo 求解下列整数线性规划问题。
max / = 20 兀 1 +10%兀1 +兀2 +兀3 = 30y, + y 2 + = 2020x l +10% = 30X 2 + 20y 2 = 25 x 3 + 15y 3s.tA 20兀i +10% <20*30 + 10*2030兀2+20y2 <30*30 + 20*20 25兀3+15儿 <25*30 + 15*20 x t , y j > 0,integers11. 求中国香港的地理经纬度。
数学建模第一次培训习题解答1

数学建模第一次作业院系:机电学院通信工程姓名:严宏海学号:20101003032数学建模习题11用给定的多项式,如y=x3-6x2+5x-3,产生一组数据(xi,yi,i=1,2,…,n),再在yi上添加随机干扰(可用rand产生(0,1)均匀分布随机数,或用rands产生N(0,1)分布随机数),然后用xi和添加了随机干扰的yi作的3次多项式拟合,与原系数比较。
分别作1、2、4、6次多项式拟合,比较结果,体会欠拟合、过拟合现象。
解:程序如下:x=1:0.5:10;y=x.^3-6*x.^2+5*x-3;y0=y+rand;f1=polyfit(x,y0,1)%输出多项式系数y1=polyval(f1,x);%计算各x点的拟合值plot(x,y,'+',x,y1)grid ontitle('一次拟合曲线');figure(2);f2=polyfit(x,y0,2)%2次多项式拟合y2=polyval(f2,x);plot(x,y,'+',x,y2);grid ontitle('二次拟合曲线');figure(3);f4=polyfit(x,y0,4)%4次多项式拟合y3=polyval(f4,x);plot(x,y,'+',x,y3)grid ontitle('四次拟合曲线');figure(4);f6=polyfit(x,y0,6)%6次多项式拟合y4=polyval(f6,x);plot(x,y,'+',x,y4)grid ontitle('六次拟合曲线');运行结果如下:依次为各个拟合曲线的系数(按降幂排列)f1 =43.2000 -149.0663f2 = 10.5000 -72.3000 89.8087f4 =0.0000 1.0000 -6.0000 5.0000 -2.5913f6 = 0.0000 -0.0000 0.0000 1.0000 -6.0000 5.0000-2.4199运行后,比较拟合后多项式和原式的系数,发现四次多项式系数与原系数比较接近,四次多项式的四次项系数很小。
数学建模模拟试题及参考答案

《数学建模》模拟试题一、(02')人带着猫、鸡、米过河,船除希望要人计划之外,至多能载猫、鸡、米三者之一,而当人不在场时猫要吃鸡、鸡要吃米,设计一个安全过河方案,并使渡河次数尽量地少。
二、(02')雨滴的速度v 与空气密度ρ、粘滞系数μ和重力加速度g 有关,其中粘滞系数的定义是:运动物体在六题中受的摩擦力与速度梯度和接触面积的乘积成正比,比例系数为粘滞系数,用量纲分析方法给出速度v 的表达式。
三、(03')要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学,模型讨论是否跑都越快,淋雨量越少。
将人体简化成一个长方体,高m a 5.1=(颈部以下),宽m b 5.0=厚m c 2.0=,设跑步距离,1000m d =跑步最大速度s m v m /5=,雨速s m u /4= ,降雨量h cm w /2=,记跑步速度为v ,按以下步骤进行讨论;(1)不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量(2)雨从迎面吹来,雨线与跑步方向在同一铅直平面内,且与人体的夹角为θ,如图1建立总淋雨量与速度v 及参数θ,,,,,,w u d c b a 之间的关系,问速度v 多大,总淋雨量最少,计算030,0==θθ时的总淋雨量。
(3))雨从背面吹来,雨线方向与跑步方向在同一铅直平面内,且与人体的夹角为∂,如图2建立总淋雨量与速度v 及参数∂,,,,,,w u d c b a 之间的关系,问速度v 多大,总淋雨量最少,计算030=θ时的总淋雨量。
四、(03')建立铅球掷远模型,不考虑阻力,设铅球初速度为v ,出手高度为h 出手角度为α(与地面夹角),建立投掷距离与α,,h v 的关系式,并在h v ,一定的条件下求最佳出手角度。
参考答案一、人、猫、鸡、米分别记为4,3,2,1=i ,当i 在此岸时记1=i x ,否则记0=i x ,则此岸的状态可用()4321,,,x x x x s =表示。
培养学生数学建模能力的测试题

培养学生数学建模能力的测试题数学建模是培养学生综合能力的重要途径之一。
通过数学建模,学生可以运用所学的数学知识和技巧,解决实际问题,提升分析和解决问题的能力。
本文将给出一道测试题,帮助读者了解如何培养学生的数学建模能力。
【测试题】假设有一辆以恒定速度行驶的列车,始发站与终点站之间的距离为300公里。
已知该列车在该段线路上的行驶时间为3小时。
请问,在行驶的过程中,该列车距离始发站多少公里时速度达到最大值?【解析】解决这道测试题需要学生将问题抽象化,利用已知条件和数学模型进行分析和计算。
首先,我们假设列车始发站到达终点站所需的时间为t,列车的速度为v,该段线路的长度为d。
根据已知条件,我们可以列出以下方程:(1) v = d/t(2) t = 3小时(3) d = 300公里将已知条件带入方程(1),可以得到:v = 300公里/3小时=> v = 100公里/小时这说明列车的速度是恒定的,为每小时100公里。
接下来,我们需要确定列车距离始发站多少公里时速度达到最大值。
假设列车行驶了x公里时,速度达到最大值。
根据常识,列车在始发站时速度为0,随着行驶的进行,速度逐渐增加,直到达到某一值后保持恒定。
列车行驶了x公里时,所花费的时间为t1,行驶了d-x公里时,所花费的时间为t2。
根据已知条件,可列出以下方程:(4) t1 + t2 = t(5) v = x/t1(6) v = (d-x)/t2将已知条件带入方程(4),可以得到:t1 + t2 = 3小时根据方程(5)和方程(6),我们可以得到:x/t1 = (d-x)/t2将方程(5)中的t1转化为t-t2,再带入方程(6),可以得到:x/(t-t2) = (d-x)/t2接下来,我们将方程中的分式进行通分和简化,得到:x*t2 = (d-x)*(t-t2)再展开并整理方程:x*t2 = d*t - d*t2 - x*t + x*t2合并同类项并整理方程:2*x*t2 - x*t = d*t - d*t2=> x*t = (d*t - d*t2)/(2*t2 - t)最后,我们将已知条件代入方程,得到:x = (300公里*3小时 - 300公里*t2)/(2*t2 - 3小时)通过解方程,可以求得列车距离始发站多少公里时速度达到最大值。
数学建模试题(带答案)三

数学建模试题(带答案)实验03 简单的优化模型(2学时)(第3章简单的优化模型)1. 生猪的出售时机p63~65目标函数(生猪出售纯利润,元):Q(t) = ( 8 – g t )( 80 + rt ) – 4t–640其中,t≥0为第几天出售,g为每天价格降低值(常数,元/公斤),r为每天生猪体重增加值(常数,公斤)。
求t使Q(t)最大。
1.1(求解)模型求解p63(1) 图解法绘制目标函数Q(t) = ( 8 – g t )( 80 + rt ) – 4t–640的图形(0 ≤t≤ 20)。
其中,g=0.1, r=2。
从图形上可看出曲线Q(t)的最大值。
(2) 代数法对目标函数Q(t) = ( 8 – g t )( 80 + rt ) – 4t–640用MATLAB求t使Q(t)最大。
其中,r, g是待定参数。
(先对Q(t)进行符号函数求导,对导函数进行符号代数方程求解)然后将代入g=0.1, r=2,计算最大值时的t和Q(t)。
要求:①编写程序绘制题(1)图形。
②编程求解题(2).③对照教材p63相关内容。
相关的MATLAB函数见提示。
★要求①的程序和运行结果:★要求②的程序和运行结果:syms g t r ;Q=(8-g.*t).*(80+r.*t)-4.*t-640;q=diff(Q,t);q=solve(q);g=0.1;r=2;tm=eval(q)Q=(8-g.*tm).*(80+r.*tm)-4.*tm-6401.2(编程)模型解的的敏感性分析p63~64对1.1中(2)所求得的符号表达式t(r,g),分别对g和r进行敏感性分析。
(1) 取g=0.1,对t(r)在r=1.5:0.1:3上求r与t的关系数据,绘制r与t的关系图形(见教材p65)。
(2) 取r=2,对t(g)在g=0.06:0.01:0.15上求g与t的关系数据,绘制g与t 的关系图形(见教材p65)。
要求:分别编写(1)和(2)的程序,调试运行。
数学建模基础练习一及参考答案

数学建模基础练习一及参考答案练习1 matlab练习一、矩阵及数组操作1.利用基本矩阵产生3×3和15×8的单位矩阵、全1矩阵、全0矩阵、均匀分布随机矩阵([-1,1]之间)、正态分布矩阵(均值为1,方差为4),然后将正态分布矩阵中大于1的元素变为1,将小于1的元素变为0。
2.利用fix及rand函数生成[0,10]上的均匀分布的10×10的整数随机矩阵a,然后统计a中大于等于5的元素个数。
3.在给定的矩阵中删除含有整行内容全为0的行,删除整列内容全为0的列。
4.随机生成10阶的矩阵,要求元素值介于0~1000之间,并统计元素中奇数的个数、素数的个数。
二、绘图5.在同一图形窗口画出下列两条曲线图像,要求改变线型和标记y1=2x+5;y2=x^2-3x+1,并且用legend标注。
6.画出下列函数的曲面及等高线z=sinxcosyexp(-sqrt(x^2+y^2)). 7.在同一个图形中绘制一行三列的子图,分别画出向量x=[1 5 8 10 12 5 3]的三维饼图、柱状图、条形图。
三、程序设计8.编写程序计算(x在[-8,8],间隔0.5)先新建的,在那上输好,保存,在命令窗口代数;9.用两种方法求数列前15项的和。
10.编写程序产生20个两位随机整数,输出其中小于平均数的偶数。
11.试找出100以内的所有素数。
12.当时,四、数据处理与拟合初步1随机产生由10个两位随机数的行向量A,将A中元素按降序排列为B,再将B重排为A。
14.通过测量得到一组数据t 1 2 3 4 5 6 7 8 9 10 y 842 362 754 368 169 038 034 016 012 005 分别采用y=c1+c2e^(-t)和y=d1+d2te^(-t)进行拟合,并画出散点及两条拟合曲线对比拟合效果。
15.计算下列定积分16.(1)微分方程组当t=0时,x1(0)=1,x2(0)=-0.5,求微分方程t在[0,25]上的解,并画出相空间轨道图像。
《数学建模入门》练习题北京石油化工学院

《数学建模入门》练习题练习题1:发现新大陆!发现新大陆!人人都能做到,可是最终哥伦布做到了。
为什么哥伦布能做到呢?(参考答案:有兴趣、能想到、去做了、坚持到底。
)答:哥伦布对待有想别人所不敢想,做别人所不敢做的这种能力。
练习题2:棋盘问题有一种棋盘有64个方格,去掉对角的两个格后剩下62个格(如下图),给你31块骨牌,每块是两个格的大小。
问能否用这些骨牌盖住这62个方格?答:不能。
对剪掉对角格以后的棋盘进行黑白涂色(相邻的涂不同的颜色,就好像国际象棋棋盘一样).这样,由于剪掉的两格恰好是同色的(你可以自己验证下),因此剩下的黑格和白格不等,但是每个骨牌必然同时覆盖一黑一白两个格子(相邻的嘛...),因此无法完全覆盖练习题3:硬币游戏如果你和你的对手准备依次轮流地将硬币放在一个长方形桌子上,使得这些硬币不重叠。
最后放上硬币的人为胜者,在开始时你有权决定先放还是后放。
为了能赢得这场比赛,你决定先放还是后放呢?答:首先将硬币放在长方形桌子的中心,然后根据对手所放的硬币,找一桌子中心为对称中心的位置,直至对方没有地方放硬币为止,由长方形的对称性,只有中心不存在对称位置,故先放者必定会赢。
练习题4:高速问题一个人从A 地出发,以每小时30公里的速度到达B 地,问他从B 地回到A 地的速度要达到多少?才能使得往返路程的平均速度达到每小时60公里?答:模型假设:设AB 相距S,B 到A 的速度为v,往返平均速度为v’ 模型建立:A 到 B 的时间为t1=s/30,B 到 A 的时间为t2=s/v 往返总时间为t1+t2=s/30+s/v 平均速度为v’=2s/t1+t2=2s/(s/30+s/v)模型求解:令v’=60,分析得,只有v 趋于无穷大时,才能使v’的极限值等于60 练习题5:登山问题某人上午八点从山下的营地出发,沿着一条山间小路登山,下午五点到达山顶;次日上午八点又从山顶开始下山(沿同一条小路)返回,下午五点又到达了山下的营地。
数学建模习题及答案课后习题

第一部分课后习题1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。
学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:(1)按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者。
(2)2.1节中的Q值方法。
(3)d’Hondt方法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,其商数如下表:将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A,B,C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位。
你能解释这种方法的道理吗。
如果委员会从10人增至15人,用以上3种方法再分配名额。
将3种方法两次分配的结果列表比较。
(4)你能提出其他的方法吗。
用你的方法分配上面的名额。
2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。
比如洁银牙膏50g装的每支1.50元,120g装的3.00元,二者单位重量的价格比是1.2:1。
试用比例方法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。
价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。
(2)给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w 的增加c减少的程度变小。
解释实际意义是什么。
3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数4.用宽w的布条缠绕直径d的圆形管道,要求布条不重叠,问布条与管道轴线的夹角 应多大(如图)。
若知道管道长度,需用多长布条(可考虑两端的影响)。
如果管道是其他形状呢。
5. 用已知尺寸的矩形板材加工半径一定的圆盘,给出几种简便、有效的排列方法,使加工出尽可能多的圆盘。
数学建模关于石油习题

10)炼油厂将A 、B 、C 三种原料加工成甲乙丙三种汽油。
一桶原油加工成汽油的费用为4元,每天至多能加工汽油14,000桶。
原油的买入价、买入量、辛烷值、硫含量,及汽油的卖出价、需求量、辛烷值、硫含量由下表给出。
问如何安排生产计划,在满足需求的条件下使利润最大?一般来说,作广告可以增加销售,估计一天向一种汽油投入一元广告费,可以使这种汽油日销量增加10桶。
问如何安排生产计划和广告计划使利润最大?间最大化?问题分析求解:A 种原油加工的汽油桶数分别为131211x x xB 种原油加工的汽油桶数分别为232221x x xC 种原油加工的汽油桶数分别为333231x x x依题意知,目标函数为总利润,记为f ,约束条件为买入量、需求量的限制,加工能力的限制以及辛烷值、硫含量的要求。
可得: 111213212223313233max 2111312111413121f x x x x x x x x x =++++++++S.T. 每天至多加工汽油总量为14 000桶11121321222331323314000x x x x x x x x x ++++++++≤;ABC 的买入量都小于50001112135000x x x ++≤,2122235000x x x ++≤,3132335000x x x ++≤;甲乙丙三种日需求总量分别为3000、2000、10003000312111=++x x x ,2000322212=++x x x ,1000332313=++x x x ;甲乙丙的辛烷值有要求112131112131126810()x x x x x x ++≥++, 12223212223212688()x x x x x x ++≥++, 13233313233312686()x x x x x x ++≥++;甲乙丙的硫含量有要求1121311121310.5 2.0 3.0 1.0()x x x x x x ++≤++, 1222321222320.5 2.0 3.0 2.0()x x x x x x ++≤++, 1323331323330.5 2.0 3.0 1.0()x x x x x x ++≤++;加工汽油量为非负数0,0,0,0,0,0,0,0,0333231232221131211≥≥≥≥≥≥≥≥≥x x x x x x x x x运行如下程序:c=[-21,-11,-1,-31,-21,-11,-41,-31,-21];a=[1,1,1,0,0,0,0,0,0; 0,0,0,1,1,1,0,0,0; 0,0,0,0,0,0,1,1,1; -2,0,0,-4,0,0,2,0,0; 0,-4,0,0,2,0,0,0,0; 0,0,-6,0,0,0,0,0,-2; -0.5,0,0,1,0,0,2,0,0; 0,-1.5,0,0,0,0,0,1,0; 0,0,-2.5,0,0,-1,0,0,0; 1,1,1,1,1,1,1,1,1]b=[5000;5000;5000;0;0;0;0;0;0;14000]; l=[0 0 0 0 0 0 0 0 0] aeq=[1,0,0,1,0,0,1,0,0; 0,1,0,0,1,0,0,1,0; 0,0,1,0,0,1,0,0,1;];beq=[3000;2000;1000];[x,r]=linprog(c,a,b,aeq,beq,l,[]) 运行结果是x = 1.0e+003 *[ 2.4000,0.8000,0.0000,0.0000,0.0000,0.0000,0.6000,1.2000 1.0000] r = -1.4200e+005[x,fval,exitflag,output,lambda]=linprog(c,a1,b1,[],[],v1,[],[]) f=c*x输出结果为: x = 1.0e+003 * 2.4000 0.8000 0.8000 0.0000 0.0000 0.0000 0.6000 1.2000 0.2000f = -1.2600e+005每天的生产计划为 :A 原油中用2400桶生产甲汽油,800桶生产乙,800桶生产丙。
2020知到答案数学建模基础-校内完整网课章节测试答案

2020知到答案数学建模基础-校内完整网课章节测试答案1例如:绪论单元测试1、判断题:对于现实世界的一个特定对象,为了一个特定目的,根据特有的内在规律,做出一些必要的简化假设,运用适当的数学工具,得到的一个数学结构.选项:A:对B:错答案: 【对】2、判断题:建立数学模型简称为数学建模或建模.选项:A:错答案: 【对】3、判断题:建立数学模型时,模型假设作的越简单越好. 选项:A:对B:错答案: 【错】4、判断题:建立数学模型时,模型假设作的越详细越好. 选项:A:错B:对答案: 【错】5、单选题:数学建模的一般步骤中,第二步是()。
选项:A:模型准备B:模型构成C:模型假设D:模型检验E:模型应用F:模型分析G:模型求解答案: 【模型假设】6、单选题:建立数学模型时,模型假设作的越()越好. 选项:A:复杂B:简单C:合理答案: 【合理】7、单选题:全国大学生数学建模竞赛创办于()年。
选项:A:1992B:2000C:1995D:1990答案: 【1992】8、多选题:以下对数学模型表述正确的是()。
选项:A:数学模型的主要研究方法是演绎推理B:数学模型是对于现实世界的一个特定对象,根据特有的内在规律,做出一些必要的简化假设运用适当的数学工具得到的一个数学结构.C:数学模型是通过抽象、简化的过程,使用数学语言对实际现象的一个近似刻画、以便于人们更深刻地认识所研究的对象.D:数学模型是研究对象的共性和一般规律答案: 【数学模型是对于现实世界的一个特定对象,根据特有的内在规律,做出一些必要的简化假设运用适当的数学工具得到的一个数学结构.; 数学模型是通过抽象、简化的过程,使用数学语言对实际现象的一个近似刻画、以便于人们更深刻地认识所研究的对象.】9、多选题:属于数学建模的方法的是()选项:A:机理分析法B:构造分析法C:数值分析法D:直观分析法答案: 【机理分析法;构造分析法;数值分析法;直观分析法】10、多选题:以下哪些问题可以用数学建模的方法研究()选项:A:养老保险问题B:新技术的传播问题C:合理投资问题D:传染病的流行问题答案: 【养老保险问题;新技术的传播问题;合理投资问题;传染病的流行问题】第一章单元测试1、判断题:选项:A:错B:对答案: 【对】2、判断题:选项:A:错B:对答案: 【对】3、单选题:若线性规划问题的可行域有界,则问题的最优解一定在可行域的()达到。
数学建模第一次作业

数学建模第一次作业14-15(2)数学建模第一次作业注意事项:提交时间截至3月27日课前,请将电子文档发送至邮箱sxjm@。
这两个主题位于word文档中,文档和电子邮件标题以“学生编号+姓名”命名。
请注意提交时间(顺序会影响给分结果)。
一、 Ppt思考题(1)~(4)由学生编号最后两位数的剩余部分除以4确定;二、(必做题)本文档里的题目1~5,由学号的后两位除以5的余数来确定;三、(选题目)对“生猪降价1%”的理解p?0.65?(1?1%),请根据PPT课件上的流程给出相应的结果(包括图形和灵敏度分析)。
t1.油污清洗一处石油泄漏污染了200英里的太平洋海岸线,所属石油公司被责令在14天内将其清除,预期则要被处以10000美元/天的罚款。
当地的清洁队每周可以清理5英里的海岸线,耗资500美元/天,额外雇佣清洁队则要付每支清洁队18000美元的费用和500美元/天的清洁费用.(1). 为了最大限度地减少公司的总开支,应该雇佣多少额外的清洁团队?采用五步法,计算清洁成本。
(2). 讨论清洁团队每周清洁海岸线长度的敏感性。
考虑额外的清洁队和公司的总开支的最佳数量分别。
(3).讨论罚金数额的灵敏性。
分别考虑公司用来清理漏油的总天数和公司的总支出。
(4).石油公司认为罚金过高而提出上诉。
假设处以罚金的唯一目的是为了促使石油公司及时清理泄漏的石油,那么罚金的数额是否过高?*(5). (可选标题)即使一开始就采取了遏制措施,海浪仍然会导致石油污染以每天0.5英里的速度沿着海岸线扩散,最终导致200多海里的清理。
请分析扩散速度对公司总支出的影响。
2报刊价格问题一家拥有8万订户的当地日报计划提高订阅价格。
目前的价格是每周1.50美元,估计每上涨10美分,就会损失5000名订户。
(1)采取五个步骤找到利润最大化的认购价格(2)对(1)中所得结论讨论损失5000订户这一参数的灵敏性。
分别假设这个参数值为3000,4000、5000、6000或7000来计算最佳认购价格(3)设n=5000为提高定价10美分而损失的订户数,求最优订阅价格p作为n的函数关系。
常见数学建模练习题目及解答

=
3
−
x2
+
x3
+
d
− 4
−
d
+ 4
=
0
x1
+
d
− 5
−
d
+ 5
=
2.4
x2
+
d
− 6
−
d
+ 6
=3
model: sets: level/1..3/:p,z,goal; variable/1..3/:x; s_con_num/1..6/:g,dplus,dminus; s_con(s_con_num,variable):c; obj(level,s_con_num)/1 1,2 2,2 3,2 4,3 5,3 6/:wplus,wminus; endsets data: ctr=?; goal=? ? 0; g=9000 3 3 0 2.4 3; c=500 500 1000 100 -1 1 0 0 -1 1 100 0 1 0; wplus=1 1 1 1 0 0; wminus=0 0 0 0 1 1; enddata min=@sum(level:p*z);
⎨ ⎪⎩
y
2
'
=
−
y2 x
− (1 −
1 4x
2
)
y1
y1=dsolve('x^2*D2y+x*Dy+(x^2-1/4)*y','y(pi/2)=2,Dy(pi/2)=-2/pi',' x'); subplot(1,3,1) ezplot(y1,[pi/2,pi]) f=@(x,y) [y(2);-y(2)/x-(1-0.25./x.^2)*y(1)]; [x,y2]=ode45(f,[pi/2,pi],[2,-2/pi]) subplot(1,3,2) plot(x,y2(:,1)) y3=subs(y1,'x',x); subplot(1,3,3) plot(x,y3)
中国石油大学 建模作业

数学规划上机实践作业一1 首先练习一下书中线性规划案例。
2 某企业和用户签定了设备交货合同,已知该企业各季度的生产能力、每台设备的生产成本和每季度末的交货量见下表,若生产出的设备当季度不交货,每台设备每季度需要支付保管费0.1万元,试问在遵守合同的条件下,企业应如何安排生产计划,才能使年消耗费用最低?变量定义:设第i 季度生产i x 台,4,3,2,1=i ;模型假设:,①每个季度都交货交满②第四季度交货后无设备剩余;目标函数:5.12*1.0*)252015(5.11*1.0*)2015(11*1.0*)15(*124123312211x x x x x x x x x x z +---++++--+++-+=约束条件: 151≥x ,202520151234=---+++x x x x ,0201512≥--+x x ,025*******≥---++x x x ,,3502≤≤x ,3003≤≤x 2004≤≤x 。
Lingo程序:model:min=12*x1+(x1-15)*0.1+11*x2+(x2+x1-15-20)*0.1+x3*11.5+(x3+x2+x1-1 5-20-25)*0.1+x4*12.5;x2+x1>=35;x3+x2+x1>=60;x4+x3+x2+x1=80;x1>=15;x2<=35;x3<=30;x4<=20;@gin(x1);@gin(x2);@gin(x3);@gin(x4);End程序运行结果:Global optimal solution found.Objective value: 913.5000Objective bound: 913.5000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX1 15.00000 12.30000X2 35.00000 11.20000X3 30.00000 11.60000X4 0.000000 12.50000Row Slack or Surplus Dual Price1 913.5000 -1.0000002 0.000000 0.0000003 15.00000 0.0000004 20.00000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 20.00000 0.000000建模结果:第一季度生产15台,第二季度生产35台,第三季度生产30台,第四季度生产0台,最小值913.5万元。
数学建模作业题
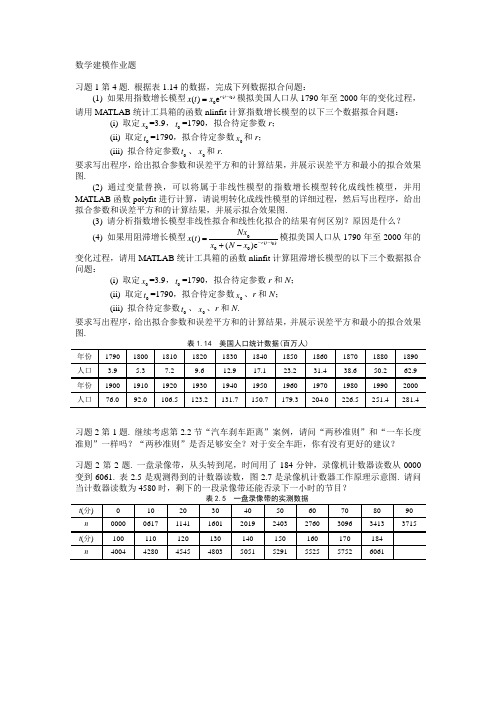
数学建模作业题习题1第4题. 根据表1.14的数据,完成下列数据拟合问题:(1) 如果用指数增长模型0()0()e r t t x t x -=模拟美国人口从1790年至2000年的变化过程,请用MATLAB 统计工具箱的函数nlinfit 计算指数增长模型的以下三个数据拟合问题:(i) 取定0x =3.9,0t =1790,拟合待定参数r ;(ii) 取定0t =1790,拟合待定参数0x 和r ; (iii) 拟合待定参数0t 、0x 和r .要求写出程序,给出拟合参数和误差平方和的计算结果,并展示误差平方和最小的拟合效果图.(2) 通过变量替换,可以将属于非线性模型的指数增长模型转化成线性模型,并用MATLAB 函数polyfit 进行计算,请说明转化成线性模型的详细过程,然后写出程序,给出拟合参数和误差平方和的计算结果,并展示拟合效果图.(3) 请分析指数增长模型非线性拟合和线性化拟合的结果有何区别?原因是什么?(4) 如果用阻滞增长模型00()00()()e r t t Nx x t x N x --=+-模拟美国人口从1790年至2000年的变化过程,请用MATLAB 统计工具箱的函数nlinfit 计算阻滞增长模型的以下三个数据拟合问题:(i) 取定0x =3.9,0t =1790,拟合待定参数r 和N ; (ii) 取定0t =1790,拟合待定参数0x 、r 和N ;(iii) 拟合待定参数0t 、0x 、r 和N .要求写出程序,给出拟合参数和误差平方和的计算结果,并展示误差平方和最小的拟合效果图.习题2第1题. 继续考虑第2.2节“汽车刹车距离”案例,请问“两秒准则”和“一车长度准则”一样吗?“两秒准则”是否足够安全?对于安全车距,你有没有更好的建议?习题2第2题. 一盘录像带,从头转到尾,时间用了184分钟,录像机计数器读数从0000变到6061. 表2.5是观测得到的计数器读数,图2.7是录像机计数器工作原理示意图. 请问当计数器读数为4580时,剩下的一段录像带还能否录下一小时的节目?习题3第4题. 某成功人士向学院捐献20万元设立优秀本科生奖学金,学院领导打算将这笔捐款以整存整取一年定期的形式存入银行,第二年一到期就支取,取出一部分作为当年的奖学金,剩下的继续以整存整取一年定期的形式存入银行……请你研究这个问题,并向学院领导写一份报告.习题3第5题. 有一位老人60岁时将养老金10万元以整存零取方式(指本金一次存入,分次支取本金的一种储蓄)存入,从第一个月开始每月支取1000元,银行每月初按月利率0.3%把上月结余额孳生的利息自动存入养老金. 请你计算老人多少岁时将把养老金用完?如果想用到80岁,问60岁时应存入多少钱?习题4第3题. 继续考虑第3.4.2小节“酵母培养物的增长”案例,建立微分方程模型,模拟酵母培养物的增长.习题6第2题. 13名儿童参加了一项睡眠时间(分钟)与年龄(岁)关系的调查,表6.18中的睡眠时间是根据连续3天记录的每天睡眠时间的平均值得到的. 请建立和求解回归模型,解释得到的结果,给出10岁儿童的平均睡眠时间及预测区间.习题6第3题. 水的沸点与大气压强有密切关系,表6.19中包含了17次试验中所测得的水的沸点(华氏温度)和大气压强(水银英寸),请建立回归模型估计沸点和压强之间的关系,并给出当沸点为201.5F 时压强的预测值及预测区间.习题7第2题. 某配件厂为装配线生产若干种部件. 每次轮换生产不同的部件时,因更换设备要付生产准备费(与生产数量无关). 同一部件的产量大于需求时,因积压资金、占用仓库要付库存费. 今已知某一部件的日需求量100件,生产准备费5000元,库存费每日每件1元. 如果生产能力远大于需求,并且不允许出现缺货,请制定最优生产计划.习题7第3题. 某商场把销售所剩的空纸皮箱压缩并打成包准备回收,每天能产生5包,在商场后院存放的费用是每包每天10元. 另一家公司负责将这些纸包运送到回收站,要收取固定费用1000元租装卸车,外加运输费每包100元. 请制定运送纸包到回收站的最优策略.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数学建模入门》练习题练习题1:发现新大陆!发现新大陆!人人都能做到,可是最终哥伦布做到了。
为什么哥伦布能做到呢?(参考答案:有兴趣、能想到、去做了、坚持到底。
)答:哥伦布对待有想别人所不敢想,做别人所不敢做的这种能力。
练习题2:棋盘问题有一种棋盘有64个方格,去掉对角的两个格后剩下62个格(如下图),给你31块骨牌,每块是两个格的大小。
问能否用这些骨牌盖住这62个方格?答:不能。
对剪掉对角格以后的棋盘进行黑白涂色(相邻的涂不同的颜色,就好像国际象棋棋盘一样).这样,由于剪掉的两格恰好是同色的(你可以自己验证下),因此剩下的黑格和白格不等,但是每个骨牌必然同时覆盖一黑一白两个格子(相邻的嘛...),因此无法完全覆盖练习题3:硬币游戏如果你和你的对手准备依次轮流地将硬币放在一个长方形桌子上,使得这些硬币不重叠。
最后放上硬币的人为胜者,在开始时你有权决定先放还是后放。
为了能赢得这场比赛,你决定先放还是后放呢?答:首先将硬币放在长方形桌子的中心,然后根据对手所放的硬币,找一桌子中心为对称中心的位置,直至对方没有地方放硬币为止,由长方形的对称性,只有中心不存在对称位置,故先放者必定会赢。
练习题4:高速问题一个人从A 地出发,以每小时30公里的速度到达B 地,问他从B 地回到A 地的速度要达到多少?才能使得往返路程的平均速度达到每小时60公里?答:模型假设:设 AB 相距 S,B 到 A 的速度为 v,往返平均速度为v’ 模型建立:A 到 B 的时间为 t1=s/30,B 到 A 的时间为 t2=s/v 往返总时间为t1+t2=s/30+s/v 平均速度为v’=2s/t1+t2=2s/(s/30+s/v)模型求解:令v’=60,分析得,只有 v 趋于无穷大时,才能使v’的极限值等于 60 练习题5:登山问题某人上午八点从山下的营地出发,沿着一条山间小路登山,下午五点到达山顶;次日上午八点又从山顶开始下山(沿同一条小路)返回,下午五点又到达了山下的营地。
问:是否能找到一个地点来回时刻是相同的?答:假如我们换一种想法,把第二天的返回改成另一个人在同一时间由山顶开始下山,并且也在下午五点到达山下,这样,只要两人在途中相遇,该地点就是上山下山来回时刻相同的地点。
练习题6:兄弟三人戴帽子问题解放前,在一个村子里住着聪明的三兄弟,他们除恶杀了财主的儿子,犯了人命案。
县太爷有意想免他们一死,决意出一个难题测测他们是否真的聪明,如果他们能在一个时辰内回答出来,就免他们一死,否则就被处死。
题目如下:兄弟三人站成一路纵队(老三选择了站在最前面,他后面是老二,老大站在了最后面 ),并分别被蒙住了眼睛,县太爷说我这里有两顶黑帽子和三顶红帽子,接着分别给他们头上各带了一顶帽子,然后又分别把被蒙住的眼睛解开。
此时,老大只可以看见老三和老二头上的帽子,老二只可以看见老三头上的帽子,老三看不见帽子。
只有一个时辰的时间,看谁能说出自己头上帽子的颜色,第一句声音有效。
现在开始! (县太爷有多少种带帽子的方案,那一种最难?你能回答吗?) 答:(1)7种。
(2)首先肯定是老大猜,因为他能看到老二老三的帽子颜色,如果老二老三帽子都是黑的,那么老大马上就能判断自己帽子是红的,这就是1红2黑的3种中的一种情况。
共1种,这种情况最简单。
但是万一老大猜不出来呢?那就是老二老三帽子要么1黑1红, 要么2红,这个时候,该让老二猜了,如果老二看到老三的帽子是黑的,他马上就可以猜到自己帽子是红的。
(因为老大不能猜出来,则肯定老二老三的帽子1红1黑或2红)如果让老二猜,并且猜出来,这是较难的戴帽方法,包括2红1黑3种中的一种,1红2黑3种中的一种。
共2种,这2种较难。
但是万一老二也猜不出来呢?那就是老三的帽子是红的,老二不能猜出来,老三要经过老大老二都不能猜出来分析来判断自己的帽子是红的。
包括3红情况下的1种,2红1黑3种情况下中的2种,1红2黑3种情况中的一种,共4种。
这4种是最难的。
练习题7:做出空间图形做出由曲面222y x z +=与2226y x z --=相交的空间曲线和所围成的立体的图形。
练习题8:π之事,知多少?关于圆周率π的事,你们知道多少?答:实际上π=C/2R , 式中圆的周长 C 是可以用圆内接正多边形的周长 Pn 来近似代替的, 当圆内接正 n 边行的边数不断地成倍增大时,它的周长 Pn 就不断地增大,并且越来越接近 圆的周长 C ,于是 Pn/2R 的值就越来越接近 C/2R 的值。
练习题9:身高和年龄的关系你不认为“身高和年龄之间有关系吗?”请你们三个人分别按照每人从出生到现在每年的身高和对应的年龄记录下来(在你本人的宝宝成长纪念册中),制成表(注明:男生、女生,籍贯),然后分别找到它们之间的关系,用数学(函数和图形)的方法表示出来。
答:年龄身高(赵天乐)身高(陈广芮)身高(王静)1 70 75 732 82 83 843 93 92 934 97 95 965 100 99 996 108 105 1017 116 112 1058 120 119 1099 134 129 11810 138 135 12311 141 139 13412 145 144 13913 148 146 14214 153 151 14715 157 156 15216 158 158 15417 159 159 15518 160 160 15619 162 161 15720 164 163 158籍贯黑龙江北京江苏由图意得y=35.377ln(x)+67.59练习题10:过三峡大坝请你说明船舶是如何从上游通过长江三峡大坝去下游的,又是如何从下游通过长江三峡大坝去上游的。
换句话说,船舶是如何通过长江三峡大坝的。
答:上下游各有一个闸门,中间形成一个闭合河道 AB 上游到下游,打开上游的闸门,使得 AB 段与上游的水位一样,船舶驶入,后关上上游闸门,打开下游闸门,使得 AB 段与下游水位一样,驶出,进入下游。
下游到上游,关闭闸门顺序相反。
练习题11:你如何解释?首都博物馆里有一个展品是一个出土的石盒子容器(见下图),它的外侧表面的石刻画中,有一个佛的头像是一个方形的洞,这如何解释呢?答:仔细看那几个佛像的头部,好像和身体并不是一体雕刻成的,也就是说头部是单独雕刻然后安装上去的,那么这个洞就是安装佛头用的,现在这个佛头丢失了,就露出了这个洞。
如果把其它几个佛像(特别是头部后面带圆圈的那几个佛像)的头也去悼,后面很可能也会有洞。
练习题12:海盗分金币有五个海盗在海上抢得了100枚金币,上岸后他们要分赃。
他们五个人排了个顺序,第一个人先制定一个分配方案,如果第一个人的方案被通过并执行,此次分金币的事结束,如果第一个人的方案被否决,把第一个人杀掉。
100枚金币由其余的四个人分,再由第二个人制定一个分配方案,依次类推,直到金币被分完。
请你替第一个人制定一个合适的分配方案。
(注:分配方案被通过是指同意的人数大于反对的人数,否则方案被否决。
)答:假设对这五个海盗编号为1,2,3,4,5如果只剩下4,5两个海盗,那么不论4号如何分配,5号都可以说不同意,那么4号的下场是死,5号的结果是获得金币。
因此如果还剩下3,4,5三个海盗。
那么不论3号如何分配,4号只能同意,因为保命要紧(他们都是理智的),这样3号可以提出的分配原则是(100,0,0)。
不论5号是否同意,3,4号都会赞成。
最终少数服从多数,结果便是3号得100金币,4,5号没有金币。
如果还剩下2,3,4,5四个海盗,2号可以提出的分配原则是(98,0,1,1),这样3号肯定不同意,但是4,5号却会同意,因为与前面的方案相比,4号和5号都能获得一个金币,这总比没有金币强,因此4,5号也一定会同意,这样一来,结果便是2号得98个金币,3号没有金币,4号和5号一人一个金币。
如果是1,2,3,4,5五个海盗,1号可以提出得分配原则是(97,0,1,0,2)或者是(97,0,1,2,0)这样2号肯定不同意,3号不得不同意,因为3号不同意,那么等到下一轮他就没有金币了。
至于4号和5号,只要给其中一个人两个金币,那么他(4或者5)便得到了比前一个方案更多的甜头。
那么他们中的一个必然同意,而另一个必然反对,最后是三个人同意,两个人反对,使得此方案通过,因此最终的分配方法是(97,0,1,2,0)或者是(97,0,1,0,2)。
练习题13:学会管理工作你的公司需要确定五名员工值一个月(30天)的班,每天只需要安排这五名员工中的二名值班。
请你们安排一个公平、合理、科学的值班表。
答:30天可以分成6组,每5天一组,这样循环值班。
每轮值班情况如下:将5个人假设为 A,B,C,D,E。
注:员工顺序可以调换,但是还是每5天保证2天班。
这样每个员工在五天内都可以值两天班,这样公平,合理又科学。
练习题14:身高和鞋码的关系你不认为“身高和鞋码之间有关系吗?”请把你们三个班同学的身高和对应的鞋码记录下来,制成表(男生、女生分开),然后分别找到它们之间的关系,用数学(函数和图形)的方法表示出来。
答:如下所示:函数:男生身高与鞋码关系女生身高与鞋码的关系对数 (男生身高与鞋码的关系) 对数 (女生身高与鞋码的关系) 根据我们的观察,我们认为鞋码和身高之间是一种简单的对数函数的关系,即鞋码与身高满足: f(x)=m*lnx+n 其中 f(x)表示鞋码(号),x 表示身高(cm),m 与n 是两个参数。
从我们三个的数据计算可得,m=44.95,n=-188.87。
因此可得,鞋码与身高的函数关系为: y=44.95*lnx-188.87 以上的函数是对于男生而言的,对于女生,由数据可知女生的鞋码普遍比男生小2—3 码,因此女生的函数关系为y=44.95*lnx-190.87练习题15:近几年北京市空气质量好多了!你不认为“近几年北京市空气质量好多了吗?”请你们寻找近几年北京市空气质量的数据,并用得到的数据找出年份和对应的蓝天数之间的关系,用数学模型的方法表示出来。
再用你们建立的数学模型预测今年、明年北京市空气质量(主要指蓝天数)。
再用你们建立的数学模型预测一下,到那年北京市空气质量全达标(主要指蓝天数等于全年的天数)。
答:数据如下:错误!链接无效。
直接由图得出在一定范围内,对应的年份与蓝天数的关系:蓝天数 y 与年份 x 的关系为:y = 2E-29e0.0356x练习题16:为什么要更改名字?我校为了庆祝建校30周年,在校园内立了几个雕塑,其中一个(见下图)刚立时名字叫“麦比乌斯环”,可是过了一段时间后就把名字改了,为什么要更改名字呢?答:麦比乌斯环有三个特征:一、麦比乌斯环只存在一个面。
