南海区八年级2018——2018学年度第一学期期末考试试题

合集下载

佛山市2018年八年级数学上学期期末试卷合集10套word文档含答案

＝八年级数学上学期期末考试试题一、选择题（本大题共 8 小题，每小题 2 分，共 16 分.在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项填写第 3 页相应答题栏内，在卷Ⅰ上答题无效）1.在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是A .B .C .D .2.在－0.101001， 7 ， 1 ，－，0.2121121112…中，无理数的个数是 4 2A ．1 个B ．2 个C ．3 个D ．4 个3.下列调查中，适宜采用普查方式的是A ．了解一批圆珠笔的寿命B ．检查一枚用于发射卫星的运载火箭的各零部件C ．考察人们保护海洋的意识D ．了解全国九年级学生的身高现状4.下列四组数据中，“不能”作为直角三角形的三边长的是A ．3，4，6B ．5，12，13C ．6，8，10D ． 2 ， 2 ，25.若点 A （﹣3，y 1），B （2，y 2），C （3，y 3）是函数 y=﹣x+2 图象上的点，则A ．y 2＜y 3＜y 1B ．y 1＜y 2＜y 3C ．y 1＜y 3＜y 2D ．y 1＞y 2＞y 3 6.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB 的示意图，请你根据所学的图形的全等这一章的知识，说明画出∠A′O′B′=∠AOB 的依据是A ．SASB ．ASAC ．SSSD ．AASBA（第 6 题）（第 7 题）（第 8 题）7.如图，直线 y=﹣x+c 与直线 y=ax+b 的交点坐标为（3，﹣1），关于 x 的不等式﹣x+c≥ax+b 的解集为A ．x≥﹣1B ．x≤﹣1C ．x≥3D ．x≤38.如图，正方形格中的每个小正方形边长都是 1．已知 A 、B 是两格点，若△ABC 为等腰三角形，且 △SABC 1.5，则满足条件的格点 C 有A ．1 个B ．2 个C ．3 个D ．4 个，二、填空题（本大题共 10 小题，每小题 2 分，共 20 分．请将答案填写第 3 页相应答题栏内，在卷Ⅰ上答题无效）9. 81 的算术平方根是 ▲ ．10.某市在一次扶贫助残活动中，共捐款 3185800 元，将 3185800 用科学记数法表示为 ▲ （精确到万位）． 11.己知点 P 的坐标为（2，-3），若点 Q 与点 P 关于 y 轴对称，则点 Q 的坐标为 ▲ . 12.某市决定从桂花、菊花、杜鹃花中随机选取一种作为市花，选到杜鹃花的概率是 ▲ . 13.等腰三角形两边长分别为 4 和 8，则这个等腰三角形的周长为 ▲ ． 14.如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形 A ，B ，C ，D 的面积和是 49cm 2，则其中最大的正方形 S 的边长为 ▲ cm ．（第 14 题）（第 16 题） 15.若点 A 的坐标（x ，y ）满足条件（x ﹣3）2+|y+2|=0，则点 A 在第 ▲ 象限． 16. 如图，在等边△ABC 中，D 、E 分别是 AB 、AC 上的点，且 AD=CE ，则∠BCD+∠CBE = ▲ 度． 17.已知直线 a ∥b ，且 a 与 b 之间的距离为 4，点 A 到直线 a 的距离为 2，点 B 到直线 b 的距离为 3 AB= 2 30 ．试在直线 a 上找一点 M ，在直线 b 上找一点 N ，满足 MN ⊥a 且 AM+MN+NB 的长度和最短，则此时 AM+NB=▲ ． 18.如图，点 A 、B 的坐标分别为（0，3）、（4，6），点 P 为 x 轴上的一个动点，若点 B 关于直线 AP 的对称点 B′ 恰好落在坐标轴上，则点 B′ 的坐标为 ▲ ．（第 17 题）（第 18 题）2016-2017 学年度第一学期期末调研测试八年级数学答题卷卷Ⅱ-20三题号一二192021222324252627总分得分一、选择题答题栏(每小题2分，共16分)题号12345678选项二、填空题答题栏(每小题2分，共20分)9.10.11.12.13.14.15.16.17.18.三、解答题（本大题共有9小题，共64分，解答时在试卷相应的位置上写出必要的文字说明、证明过程或演算步骤．)19．（本小题满分5分）计算：|3﹣π|+(4)+(7-1)+3-64.20．（本小题满分6分）求下面各式中的x：⑴2x2=50；⑵(x+1)3=—8．21.（本小题满分7分）“春节”是我国的传统佳节，民间历来有吃“汤圆”的习俗．某食品厂为了解市民对去年销量较好的肉馅（A）、豆沙馅(B)、菜馅(C)、三丁馅(D)四种不同口味汤圆的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚根据以上信息回答：⑴本次参加抽样调查的居民人数是__________人;⑵将图①②补充完整；(直接补填在图中)⑶求图②中表示“A”的圆心角的度数；⑷若居民区有8000人，请估计爱吃D汤圆的人数．不完整）．请22.（本小题满分7分）已知：如图：AB∥CD，AB=CD，AD、BC相交于点O，BE∥CF，BE、CF分别交AD于点E、F，求证：⑴OA=OD；⑵BE=CF．23.(本小题满分7分)已知：如图,方格纸中格点A，B的坐标分别为(﹣1，3),(﹣3，2)．⑴请在方格内画出平面直角坐标系；⑵已知点A与点C关于y轴对称，点B与点D关于x轴对称，请描出点C、D的位置，并求出直线CD的函数表达式．24.（本小题满分7分）已知：如图，在△ABC中，∠ACB=90o,AC=BC,,D是AB的中点，点E在AC上，点F在BC上，且AE=CF.⑴求证：DE=DF,DE⊥DF;⑵若AC=2,，求四边形DECF面积.AECDFB25.（本小题满分8分）某学校利用寒假组织340名师生进行社会实践活动，带有行李170件，计划租用甲、乙两种型号的汽车10辆．经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李．⑴请你帮助学校设计所有可行的租车方案；⑵如果甲车的租金为每辆2000元，乙车的租金为每辆1800元，问哪种可行方案使租车费用最省？26.（本小题满分8分）如图1，在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，试判断BC和AC、AD之间的数量关系．小明发现，利用轴对称做一个变化，在B C上截取CA′=CA，连接DA′，得到一对全等的三角形，从而将问题解决（如图2）．请回答：．．．．．．．．．．⑴BC和AC、AD之间的数量关系并证明.⑵参考上述思考问题的方法，解决下列问题：如图3，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9．求AB的长．27.（本小题满分9分）一辆快车和一辆慢车分别从甲、乙两地同时出发匀速相向而行，快车到达乙地后，原路原速返回甲地．图1表示两车行驶过程中离甲地的路程y（km）与行驶时间x（h）的函数图象．⑴直接写出快慢两车的速度；⑵在行驶过程中，慢车出发多长时间，两车相遇？⑶若两车之间的距离为s km，在图2的直角坐标系中画出s（km）与x（h）的函数图象．在△ABO 与△CDO 中， ⎨∠AOB = ∠DOC ，⎪ A B = CD在△EBA 和△FCD 中， ⎨∠AEB = ∠DFC ，⎪ A B = CD数学上学期期末考试试题答案一、选择题 ACBA DCDB二、填空题9. 9 10. 3.19×106 11.（-2,-3） 12. 1 3 13. 20 14.7 15.四 16. 60 17. 8 18.（﹣4，0）、（0，﹣2）、（0，8）三、解答题19．解：原式=π -3+4+1-4…………………4 分 =π -2． …………………5 分20．解：（1）原方程可化为：x 2=25…………………1 分开方得：x=5 或 x=﹣5； …………………3 分（2）开立方得：x+1=—2， …………………2 分解得：x=—3． …………………3 分21. 解：(1)本次参加抽样调查的居民的人数是：60÷10%=600(人); …………………1 分(2) 如图所示…………………4 分(一个 1 分)(3)360°×30%=108°.图②中表示“A”的圆心角的度数 108° (5)(4)8000×40%=3200(人)．即爱吃 D 汤圆的人数约为 3200 人.…………7 分22.证明：（1）∵AB∥CD，∴∠A=∠D，⎧∠A = ∠D⎪⎩∴△ABO≌△CDO，分∴AO=CO； …………………3 分（2）∵AB∥CD，∴∠A=∠D，∵BE∥CF，∴∠BEO=∠CFO，∴∠AEB=∠DFC，⎧∠A = ∠D⎪⎩ （第 22 题）∴△ABE≌△DCF（AAS ）．∴EB=CF． (7)23. 解：（1）如图所示；…………………2 分分k = ⎩- 3k + b = -2 2 ABC ;…………………6 分 △+S = = ⎩16x + 20(10 - x) ≥ 170 （2）如图所示，由图可知，C （1，3），D （﹣3，﹣2），作图 C 、D 点…………………4 分设直线 CD 的解析式为 y=kx+b （k≠0），⎧ ⎧k + b = 3 ⎪ 则 ⎨ ，解得 ⎨ ⎪b = ⎪⎩5 4 74，故直线 CD 的解析式为 y = 5 7 x + ．………7 分 4 424.⑴∵AC=BC,∠ACB=90o , ∴∠A=∠B=45o∵CD 是 AB 边中线∴AD=CD, ∠DCB=45o∴∠A=∠DCB又∵AE=CF ∴△AED≌△CFD ∴DE=DF, ∠ADE=∠CDF, …………………3 分 ∵AC=BC,CD 是 AB 边中线 ∴CD⊥AB ∴∠CDA=90o ∴∠EDF=90o ∴DE⊥DF. …………………5 分 ⑵由⑴得△AED≌△CFD∴四边形 DECF 面积=S CED CFD S △CED +S △AED △=S ACD1S又∵AC=2, ∴△ABC 面积=2∴四边形 DECF 面积=1. …………………7 分25.解：（1）设甲车租 x 辆，则乙车租（10－x ）辆，根据题意，得⎧40x + 30(10 - x) ≥ 340 ⎨解之得 4 ≤ x ≤ 7.5…………………2 分∵x 是整数∴x＝4、5、6、7∴所有可行的租车方案共有四种：①甲车 4 辆、乙车 6 辆；②甲车 5 辆、乙车 5 辆；③甲车 6 辆、乙车 4 辆；④甲车 7 辆、乙车 3 辆．…………………4 分（2）设租车的总费用为 y 元，则 y ＝2000x ＋1800（10－x ），即 y ＝200x ＋18000……6 分在△ADC 和△A′DC 中， ⎨∠ACD = ∠A 'CD ， ⎪CD = CD 在△AEC 和△ADC 中， ⎨∠DAC = ∠EAC ， ⎪ A C = AC ∵k＝200＞0，∴y 随 x 的增大而增大∵x＝4、5、6、7∴x＝4 时，y 有最小值为 18800 元，即租用甲车 4 辆、乙车 6 辆，费用最省．………8 分26. 解：（1）BC=AC+AD ；………………1 分证明：∵CD 平分∠ACB， ∴∠ACD=∠A′CD，⎧CA ' = CA ⎪ ⎩∴△ADC≌△A′DC（SAS ）；………………2 分∴DA′=DA，∠CA′D=∠A=60°，∵∠ACB=90°，∴∠B=90°﹣∠A=30°，∵∠CA′D=∠B+∠BDA′，∴∠BDA′=30°=∠B，∴DA′=BA′， ∴BA′=AD，∴BC=CA′+BA′=AC+AD；………………4 分⑵如图，在 AB 上截取 AE=AD ，连接 CE ，如图 3 所示：∵AC 平分∠BAD，∴∠DAC=∠EAC．⎧CA ' = CA ⎪ ⎩∴△ADC≌△AEC（SAS ），………………5 分∴AE=AD=9，CE=CD=10=BC ，过点 C 作 CF⊥AB 于点 F ，∴EF=BF，设 EF=BF=x ．在 Rt△CFB 中，∠CFB=90°，由勾股定理得 CF 2=CB 2﹣BF 2=102﹣x 2，在 Rt△CFA 中，∠CFA=90°，由勾股定理得 CF 2=AC 2﹣AF 2=172﹣(9+x)2．∴102﹣x 2=172﹣(9+x)2，解得：x=6，………………7 分∴AB=AE+EF+FB=9+6+6=21，∴AB 的长为 21．………………8 分27. 解：（1）由题意，得，A 、B 两地距离之间的距离为 2250km ，2250=10k ， ⎨ ， ⎨ 2 20k + b = 0 30k + b = 0 1 1⎩ ⎩ 解得：k=225， ⎨⎧k = -225 ， ⎨ 2 ⎩b = 4500 ⎩b = 2250快车的速度为：2250÷10=225km/h，慢车的速度为：2250÷30=75km/h； ………………2 分（2）设 OA 的解析式为 y=kx ，AB 的解析式为 y 1=k 1x+b 1，CD 的解析式为 y 2=k 2x+b 2，由题意，得⎧10k + b = 2250 ⎧b = 22501 12 2， 1 12⎧k = -75，∴y=225x，y 1=﹣225x+4500，y 2=﹣75x+2250 ………………5 分当 225x=﹣75x+2250 时，x=7.5．当﹣225x+4500=﹣75x+2250 时，解得：x=15．答：慢车出发 7.5 小时或 15 小时时，两车相遇；………………7 分（3）由题意，得7.5 小时时两车相遇，10 时时，两车相距 2.5（225+75）=750km ，15 时时两车相遇，20 时时两车相距 750km ，20 时时两车相距为 0，由这些关键点画出图象即可．……………9 分八年级数学上学期期末考试试题一、选择题（本大题共10小题，每小题3分，共30分）1．若一个三角形的两边长分别为3和7，则第三边长可能是（）A．6B．3C．2D．112．要使分式x+1有意义，则x的取值应满足（x-2）A．x=-1B．x≠-1C．x=2D．x≠23．下列运算正确的是（）A．m6÷m2=m3B．(x+1)2=x2+14．下列图形中不是轴对称图形的是（）C．(3m2)3=9m6D．2a3⋅a4=2a7A．B．C．D．5．已知一个多边形的内角和是1080°，则这个多边形的边数是（）A．6B．7C．8D．96．把多项式x2+ax+b分解因式得(x+1)(x-3)，则a，b的值分别是（）A．a=2，b=3B．a=-2，b=-3A D C．a=-2，b=3D．a=2，b=-3E△7．如图，在AFD和△CEB中，点A、E、F、C在同一直线上，∠B=∠D，FAD=BC，AD∥BC，若AE=6，则CF=（）B第7题图C A．4B．8C．3D．68．用换元法解方程2x2-24x x2-1-=3时，设=y，则原方程可化为（）x x2-1xA．y114y4--3=0B．2y--3=0C．2y--3=0D．--3=0xkb1 24y4y y2yB A9．如图，已知AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若A P=4，则AD=（）A．8B．6C．4D．2CPD10．如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，第9题图则∠B的度数为（）A．45°B．40°C．36°D．30°二、填空题（本大题共6小题，每小题4分，共24分）11．分解因式：a2-4b2=．AB D第10题图C12．分式方程23=的解为．x-3xA△13．如图，在ABC中，AB=AC，AD⊥BC于点D，若AB=6，CD=4，则△ABC的周长是．△14．如图，在ABC中，∠A=40°，点O是∠ABC和∠ACB角平分线的交点，则∠BOC=．115．计算：(-3)2016⋅(-)2017=．3B D第13题图AC16．若113+=，ab=2，那么a-b的值为．a b2O三、解答题（一）（本大题共3小题，每小题6分，共18分）B C 17．化简：(x+5)(x-1)+(x-2)2．第14题图1a218．先化简，再求值：(1+)⋅a a2-1，其中a=2017．△19．如图，已知在Rt ABC中，∠C=90°，∠CAB的平分线交BC于点E，EF⊥AB于点F．求证：AC=AF．AFC E第19题图B四、解答题（二）（本大题共3小题，每小题7分，共21分）20．已知：x=1-2，y=1+2，求x2+y2-xy-2x+2y的值．21．如图，在等边三角形ABC中，点D，E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．（1）求∠F的度数；（2）若CD=2，求DF的长．AEB DC F第21题图22．“新鲜水果店”在批发市场用3000元购进一批葡萄进行销售，前两天以高于进价40%的价格共卖出150千克．因出现高温天气，葡萄不易保鲜，为减少损失，第三天该店老板果断地将剩余葡萄以低于进价20%的价格全部售出，前后一共获利750元．求该水果店老板购进葡萄多少千克？五、解答题（三）（本大题共3小题，每小题9分，共27分）△23．如图，已知ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM⊥AE于点M，连结BE．（1）请判断线段AD、BE之间的数量关系，并说明理由；CE（2）求证：AM=CM+BE．MDA B第23题图24．阅读下列材料：对于任意的正实数a，b，总有a+b≥2ab成立（当且仅当a=b时，等号成立），这个不等式称为“基本不等式”．利用“基本不等式”可求一些代数式的最小值．例如：若x>0，求式子x+1x的最小值．解：∵x>0，∴x+11≥2x⋅=21=2，x x∴x+1x的最小值为2．解答下列问题：9x2-2x+5（1）若x>0，求x+的最小值；（2）已知x>1，求的最小值．x x-125．如图①，点A、B分别在射线OM，ON上，且∠MON为钝角，现以线段OA、OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP和△OBQ，点C、D分别是OA、OB的中点，且四边形CODE是平行四边形．（△1）求证：PCE≌△EDQ；（△2）如图②，延长PC，QD交于点R．若∠MON=150°，求证：A BR为等边三角形．MAC EPO DB NQ第25题图①R MA P CEO D B N第25题图②Q18．解：原式= a + 1 ⋅ a = a + 1 ⋅ ∴CE=EF，------------------------------------------------------------------------- 2分⎧CE = FE ，----------------------------------------------------------------------- 4分⎩ AE = AE 数学上学期期末考试试题答案一、选择题（本大题共 10 小题，每小题 3 分，共 30 分）1．A ；2．D ；3．D ；4．B ；5．C ；6．B ；7．D ；8．C ；9．A ；10．C ．二、填空题（本大题共 6 小题，每小题 4 分，共 24 分）11． (a + 2b )(a - 2b ) ；12． x = 9 ；13．20；14．110°；15． - 1 ；16． ± 1 ．3三、解答题（一）（本大题共 3 小题，每小题 6 分，共 18 分）17．解：原式 = x 2 + 4x - 5 + x 2 - 4x + 4 ------------------------------------4 分= 2x 2 - 1 ．-------------------------------------------------------6 分2a a 2 - 1------------------------------------------------------1分a 2 a (a + 1)(a -1) ---------------------------------------------2分= a ，----------------------------------------------------------4分 a -1当 a = 2017 时，原式= 2017 = 2017 ．------------------------------------6分2017 - 1201619．证明：∵AE 是∠BAC 的平分线，EC⊥AC，EF⊥A B ，AFCEB第 19 题图在Rt△ACE 与Rt△AFE 中，⎨∴Rt△ACE≌Rt△AFE（HL ）, ------------------------------------------------5分∴AC =AF ．------------------------------------------------------------------------6 分四、解答题（二）（本大题共 3 小题，每小题 7 分，共 21 分）20．解：∵ x = 1 - 2 ， y = 1 + 2 ，∴ x - y = (1 - 2) - (1 + 2) = -2 2 ，---------------------------------------1分x ⋅ y = (1 - 2) (1 + 2) = -1 ，-----------------------------------------------2分∴ x 2 + y 2 - xy - 2 x + 2 y = ( x - y)2 + 2 x y - xy - 2( x - y) ----------------4分= ( x - y)2 + xy - 2( x - y) -------------------------5分MC∴∠CD M=45°，-----------------------------------------------------------------------5分∴x+9≥2x⋅----------------------------------------------------------------------2分=(-22)2-1-2⨯(-22)------------------------6分=42+7．------------------------------------------7分△21．解：（1）∵ABC是等边三角形，∴∠B=60°，-----------------------1分∵DE∥AB，∴∠EDC=∠B=60°，------------------------------------------------2分∵EF⊥DE，∴∠DEF=90°，A∴∠F=90°﹣∠EDC=30°．----------------------------------------------------------3分（2）∵∠ACB=60°，∠EDC=60°，∴∠DE C=60°，E∴△EDC是等边三角形，-----------------------------------------------------------4分B D F ∴ED=DC=2，--------------------------------------------------------------------------5分第21题图∵∠DEF=90°，∠F=30°，∴DF=2DE=4．------------------------------------------------------------------------7分22．解：设水果店老板购进葡萄x千克，根据题意得：---------------------1分30003000⨯40%⨯150-⨯20%⨯(x-150)=750x x-------------------------------3分解得：x=200，-----------------------------------------------------------------------5分经检验x=200是原方程的解，-----------------------------------------------------6分答：该水果店老板购进葡萄200千克．------------------------------------------7分五、解答题（三）（本大题共3小题，每小题9分，共27分）23．（1）解：AD=BE，理由如下：-----------------------------------------------1分∵△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，∴AC=BC,CD=CE，∠ACB-∠DCB=∠DCE-∠DCB，即∠ACD=∠BCE，-------------------------------------------------------------------2分C∴△ACD≌△BCE，------------------------------------------------------------------3分E∴AD=BE．----------------------------------------------------------------------------4分（△2）证明：∵DCE为等腰直角三角形，∠DCE=90°，DA第23题图∵CM⊥AE，∴∠DC M=45°，------------------------------------------------------6分∴∠CD M=∠DC M=45°，------------------------------------------------------------7分∴CM=DM，---------------------------------------------------------------------------8分∵A M=AD+DM，AD=BE，∴A M=CM+BE．----------------------------------------------------------------------9分24．解：（1）∵x>0，9x xB∴ x - 2 x + 5 = x - 2 x + 1 + 4x 2 - 2 x + 5 ⎨∠PCE = ∠EDQ ， ⎪CE = DQ = 2 9 = 6 ，------------------------------------------------------------------3 分∴ x + 9 的最小值为 6．----------------------------------------------------4 分x（2）∵ x > 1 ，∴ x - 1 > 0 ，2 2 x - 1 x - 1 =( x - 1)2 + 4 -----------------------------------------------5 分x - 1= ( x - 1) +4 x - 1--------------------------------------------6 分≥ 2 ( x - 1)(4) ------------------------------------------7 分 x - 1= 2 4 = 4 ，-----------------------------------------------8 分∴ 的最小值为 4．--------------------------------------------9 分 x - 1△25．（1）证明：∵OAP 是等腰直角三角形，且点C 是OA 的中点，∴ P △C A 和△PCO 都是等腰直角三角形， M∴ PC = AC = OC ，∠PCO =90°，ACE同理： QD = OD = BD ，∠QDO=90°，-------------------------------1分∵四边形CODE 是平行四边形，∴ CE = OD ， ED = OC ，P O第 25 题图①DQBN∴ED=PC，QD=CE ，----------------------------------------------------2分∵CE ∥ON ，DE ∥OM ，∴∠ACE=∠AOD，∠BDE =∠AOD，∴∠ACE=∠BDE，∴∠OCE=∠ODE，-------------------------------------------------------3分∴∠OCE+∠PCO =∠ODE+∠QDO，即∠PC E=∠EDQ，-------------------------------------------------------4分M在△PCE 与△EDQ 中，R⎧PC = ED ⎪⎩ACPOEDB N第 25 题图②∴△PCE≌△EDQ．------------------------------------------------------5分（2）连结RO ，-----------------------------------------------------------6分∵ OAP 和 OBQ 均为等腰直角三角形，点C 、D 分别是OA 、OB 的中点△∴PR 与QR 分别是OA ，OB 的垂直平分线，∴AR=OR=BR ，-----------------------------------------------------------7分Q∴∠ARC=∠ORC，∠OR D=∠BR D，--------------------------------8分∵∠RCO=∠RDO=90°，∠COD=150°，∴∠CRD=30°，∴∠ARB=60°，∴△ARB是等边三角形．-----------------------------------------------9分7.不等式组⎨的解集在数轴上可表示为()x≤5A.1000B. C. D.八年级数学上学期期末考试试题一、选择题（本大题共12小题，每小题3分，满分36分；在每小题给出的四个选项中，其中只有一是正确的，多选或漏选均不得分.）1.要使分式2x+1A．x≠1有意义，则x的取值范围是()B．x＞1C．x＜1D．x≠-12.下列各式中，正确的是()A.9＝±3B.-9＝－3C．-9＝3D．±9=±33.已知a＜b，则下列结论不一定正确的是()A．2a<3a B．a+2<b+2 C.若c＞0，则4.下列根式中，不能与3合并的是()b a> D.-3a>-3bc cA.11B. C.3323 D.125.下列各式中属于最简分式的是()2x21A． B.a+b C. D.x2x+16.下列命题中,为真命题的是()2x-2x-1A.对顶角相等C.若a2=b2,则a=bB.同位角相等D.同旁内角相等,两直线平行⎧x>-2⎩8.如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E，已知∠BAE=10°，则∠C的度数为()AA.30ºB.40°C.50ºD.60°DB E C第8题图9．甲队修路1000m与乙队修路800m所用天数相同，已知甲队比乙队每天多修20m，设甲队每天修路x m．依题意，下面所列方程正确的是()800100080010008001000800====x x-20x x+20x-20x x+20xA．x≤-1.10.若二次根式3x+1在实数范围内有意义，则x的取值范围是()11B．x≥-C．x≠-D．x≥033311.不等式(1－a)x﹥2变形后得到x<21-a成立，则a的取值()A.a>0 C.a<0 C.a>1 D.a<112．如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=42°，则∠P的度数为()A．44°B．66°C．96°D．92°二、填空题（本大题共6小题，每小题3分，满分18分）第12题图13.16的算术平方根是__.14．不等式2x+6＞3x+4的正整数解是__.15．H7N9禽流感病毒的直径大约是0.000000078米，用科学记数法表示为__.16.设2=m，3=n，则150=(结果用m，n表示).△17．如图，ABC中，AC=6，BC=4，AB的垂直平分线DE交AB于点D，交边AC于点E，则BCE的周长为△__.18.如图，在△ABC中，AC=BC，D是BC边上一点，连接AD，若AB=AD=DC，则∠B=__.三、解答题（本大题共8小题，满分66分，解答应写出必要的文字说明，演算步骤或推理过程）第171题图119.（本题满分6分）计算：(3)0+()-1+2⨯3-(-3)228第18题图20.（本题满分6分）计算：(3-2)2+(5+3)(5-3)21.（本题满分8分）解方程：3x2-=1 x-11-x22.（本题满分8分）如图，已知△ABC.（△1）用尺规作图的方法分别作出ABC的角平分线BE和CF,且BE和CF交于点O.（保留作图痕迹，不要求写出作法）；（2）在（1）中，如果∠ABC=40°,，∠ACB=60°，求∠BOC的度数.AB C1a2-123.（本题满分8分）先化简，再求值：(1+)÷，其中a=3.a a224.(本题满分10分△)如图，在ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N，（△1）若CMN的周长为21cm，求AB的长；（2）若∠MCN=50°，求∠ACB的度数.CD EA M N第24题图B25.（本题满分10分）某班为了奖励在学校体育运动会中表现突出的同学，班主任派生活委员小明到文具店为获奖的同学买奖品，小明发现，如果买1本笔记本和3支钢笔，则需要19元；如果买2本笔记本和5支钢笔，则需要33元.（1）求购买每本笔记本和每支钢笔各多少元？（2）班主任给小明的班费只有110元，要奖励24名同学每人一件奖品，则小明至少要购买多少本笔记本？26.（本题满分10分）如图①，在△ABC中，AC=BC，点D为BC的中点，DE⊥AB，垂足为点E，过点B作BG∥AC交DE 的延长线于点G.（1）求证：DB=BG；（2）当∠ACB=90°时，如图②，连接AD、CG，求证：AD⊥CG。

2018秋南海区8年级期末统考

（1）至于夏水襄陵，沿溯阻绝。
_______________________________________________________________________________________________
（2）虽乘奔御风，不以疾也。
_______________________________________________________________________________________________
佛山精品课堂教研中心出品
绝密★启用前
2018-2019（上）八年级语文期末考试
考试时间：120 分钟；满分：130 分；命题人：南海区
题号得分
基础
阅读
作文
名著阅读
总分
一、基础（24 分）
1.根据课文默写古诗文。（10 分）
（1）征蓬出汉塞，__________________。（马致远《天净沙·秋思》）（1 分）
（5）请把《黄鹤楼》默写完整。（4 分）
昔人已乘黄鹤去，此地空余黄鹤楼。__________________，__________________。
__________________，__________________。日暮相关何处是？烟波江上使人愁。
2.根据拼音写出相应的词语。（4 分）
（1）无疑，这张脸平淡无奇，障碍重重，没法弥补，不是传播智慧的庙堂，而是 jìn gù（
D.作者写景，采用的是大笔点染的手法，把七百里三峡万千气象尽收笔底。
《经典咏流传》是央视推出的中国首档大型原创诗词文化类音乐节目，用“和诗以歌”的形式让传统经典诗词与新时代流行元素相结合，使传统文化焕发出独特的魅力。袁行霈指出，我们的目的就是激活经典，让经典的生命力绵延下去。据了解，《百部经典》已确定了四批书目，共 54 种。书目上起先秦，下至辛亥革命，突破了传统的经、史、子、集四部分类法，力求做到广纳百家、百花齐放，不仅选入哲学、文学、历史等著作，还选择一些科技类、艺术类等著作，充分展现了中华传统文化的广泛性和多样性。（1）请用简明的语言概括以上内容，不超过 30 字。 _______________________________________________________________________________________________ _______________________________________________________________________________________________ （2）以“经典”开头，用一种修辞手法来描写你心中的经典。 _______________________________________________________________________________________________ _______________________________________________________________________________________________

┃精选3套试卷┃2018届佛山市八年级上学期物理期末达标测试试题

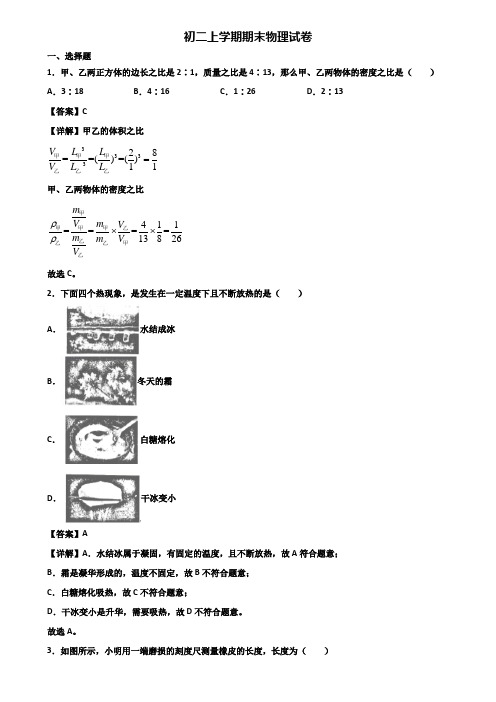
初二上学期期末物理试卷一、选择题1．甲、乙两正方体的边长之比是2∶1，质量之比是4∶13，那么甲、乙两物体的密度之比是（） A ．3∶18B ．4∶16C ．1∶26D ．2∶13【答案】C【详解】甲乙的体积之比 333328==()=()11V L L V L L =甲甲甲乙乙乙甲、乙两物体的密度之比411====13826m V m V m m V V ρρ⨯⨯甲甲甲甲乙乙乙乙甲乙故选C 。

2．下面四个热现象，是发生在一定温度下且不断放热的是（）A ．水结成冰B ．冬天的霜C ．白糖熔化D ．干冰变小【答案】A【详解】A ．水结冰属于凝固，有固定的温度，且不断放热，故A 符合题意；B ．霜是凝华形成的，温度不固定，故B 不符合题意；C ．白糖熔化吸热，故C 不符合题意；D ．干冰变小是升华，需要吸热，故D 不符合题意。

故选A 。

3．如图所示，小明用一端磨损的刻度尺测量橡皮的长度，长度为（）A．3.15cmB．3.150cmC．2.15cmD．2.150cm【答案】C【分析】（1）刻度尺的最小刻度值为相邻的刻度线表示的长度；（2）起始端没从0开始，把1.00cm处当作“0”刻度，读出末端刻度值，减去1.00cm即为物体长度，注意刻度尺要估读到分度值的下一位．【详解】(1)图示刻度尺1cm又分为10个小刻度，故最小刻度值为1mm；(2)图中起始端刻度值为1.00cm，末端刻度值为3.15cm，物体长度为3.15cm−1.00cm=2.15cm.【点睛】刻度尺是初中物理中基本的测量工具，使用前要观察它的量程和分度值，使用时刻度要紧贴被测物体，读数时视线与刻度垂直，估读到分度值的下一位．4．下列实验中，测量多组数据是为了减小实验误差的是（）A．探究并联电路中电压的规律B．测量小灯泡的电功率C．伏安法测电阻D．探究电流与电压和电阻的关系【答案】C【详解】AD．探究并联电路中电压的规律、探究电流与电压和电阻的关系两个实验中测量多组数据是为了得到普遍规律，使结论更可靠，故AD不符合题意；B．测量小灯泡的电功率实验中，测量多组数据是为了探究不同电压下的小灯泡的电功率，寻找一定的规律，故B不符合题意；C．伏安法测电阻实验中测量多组数据是为了使测量值更准确，减小误差，故C符合题意；故选C。

2018年广东省佛山市南海区八年级上学期物理期末考

（选填“变大”、“变小”或“不变”）．
15. 完成下列光现象作图： (1) 如下图所示的是一条经水面折射后的光线，在图中画出入射光线的大致方向并标出入射角；
(2) 在如下图所示的方框中填入合适的透镜；
(3) 如下图所示，用一平面将与水平面成角的阳光竖直照射到深井来，请你在图中画出反射光线、平面镜的位置，并标出反射角的度数．
(1) 用图甲所示的装置测出凸透镜的焦距为
．
(2) 图乙是某次实验时观察到的清晰的像的情景图，生活中的
（选填“放大
镜”、“投影仪”或“照相机”）是利用这一原理制成的。保持凸透镜不动，把蜡烛向左移动
一段距离，要想在光屏上再次得到清晰的像，应该把光屏向
（选填
“左”或“右”）移动一段距离，像
（选填“变大”、“变小”或“不
2018年广东省佛山市南海区八年级上学期物理期末考试
1. 对于声音的产生，下列说法中正确的是（
）
A．只有固体的振动才能发声
B．声音是由物体的振动产生的
C．物体不振动也能发声
D．振动停止后，发声体仍能发声
2. 如图是探究光的反射规律的实验装置，下列描述中不合理的是（
）
A．可沿折叠的白色硬纸板应垂直放置于平面镜上 B．为研究反射角与入射角间的关系，应多次改变入射光与法线间的夹角 C．为研究反射光线、入射光线和法线的位置关系，应绕前后折转入射光所在的光屏 D．如果让入射光沿着的方向射向镜面，会发现反射光沿着方向射出，这表明在光的反射现象中，光路是可逆的
16. 完成下列问题：
(1) 如图所示，用刻度尺测量木块的长度，测量值为
．
(2) 如图所示，秒表的读数为
．
(3) 小张做“测食用油密度”的实验，先用调节好的天平测出烧杯和食用油的总质量为，然后

佛山市南海区八年级上学期期末物理试卷

佛山市南海区八年级上学期期末物理试卷姓名:________ 班级:________ 成绩:________一、选择题 (共7题；共14分)1. （2分）(2016·咸宁) 下列事例中说法正确的是（）A . “窃窃私语”指说话时声音的响度较小B . 减速进站的火车其惯性逐渐滅小C . 磕到碗边上的鸡蛋破了，是因为碗给鸡蛋的力大于鸡蛋给碗的力D . 注射器能把药水吸上来，说明注射器对药水有吸引力2. （2分）下列实例中，为了加快蒸发的是（）A . 用地膜覆盖农田B . 给盛有饮料的瓶子加盖C . 把湿衣服晾在通风向阳处D . 把新鲜的樱桃装入保鲜盒3. （2分）如图所示的是某种物质发生物态变化过程中温度——时间图像。

该物态变化过程可能是（）A . 水的凝固过程B . 海波的凝固过程C . 玻璃的凝固过程D . 蜡的凝固过程4. （2分） (2018八上·福田期末) 下列关于光的知识应用的说法，不正确的是（）A . 照相机照相是利用了“凸透镜能成正立、缩小的实像”的规律B . 用光沿直线传播知识可以解释“小孔为什么可以成像”C . 近视眼镜利用了“凹透镜对光的发散作用”的特点D . 使用投影仪时，利用了“凸透镜能成倒立、放大的实像”的规律5. （2分）甲、乙两列火车，以甲车为参照物，得出乙车向东运动的结论。

若以地面为参照物，甲车的运动情况是（）A . 一定向东运动B . 一定向西运动C . 一定静止不动D . 向东、向西运动或静止均有可能6. （2分）(2020·遵化模拟) 我国的古诗词文化有几千年的灿烂历史，很多名句蕴含着丰富的物理知识，下列诗句从物理学的角度解释错误的是（）A . “池水映明月，潭清疑水浅”句中“水浅”是由于光的反射造成的B . “大漠孤烟直，长河落日圆”，诗人看到的“落日”是光线经过大气发生折射而成的像C . “绿树浓荫夏日长，楼台倒影入池塘”句中“浓荫”是光的直线传播形成的D . “朝辞白帝彩云间，千里江陵一日还”句中的“彩云”是由于光的色散形成的7. （2分）(2017·祁阳模拟) 下列有关厨房里的物理知识，说法不正确的是（）A . 洗碗时，油花飘在水面上，说明油的密度比水小B . 在水中下饺子，饺子不会被煮焦；在油中煎饺子，饺子被煎焦，说明油的沸点比水高C . 厨刀刀口磨得很锋利是为了增大压力D . 拧开醋瓶盖，醋味扑鼻，说明分子在做无规则的运动二、填空题 (共7题；共14分)8. （2分）(2017·齐齐哈尔) 同学们使用的中性笔，在使用的过程中笔管里的墨水质量________（选填“变大”“变小”或“不变”），写字时的笔相当于________（选填“省力”“费力”或“等臂”）杠杆．9. （4分） (2016八·酒泉月考) 在下列数字后面填上适当的单位（符号表示）：一桶食用油的体积是5________；一瓶矿泉水的体积为500________；一拃的长度约为20________；物理课本的长度是26________．10. （1分）下表是一些物质的熔点和沸点（1个标准大气压），根据下表，在我国各个地区都能测量气温的是________温度计．水水银酒精乙醚熔点/C0﹣39﹣117﹣114沸点/C100357783511. （2分） (2016八上·惠来期中) 温度计是根据________制成的，如图所示温度计的读数是________．12. （1分） (2017八上·蚌埠期末) 近视患者可以通过佩戴角膜塑形镜来改变角膜的几何形态，使原来成像在视网膜________（选填“前方”或“后方”）的近视眼有效降低、甚至消除近视度数．13. （2分） (2015八上·江苏月考) 我国许多地区遭遇了严重的雾霾天气，其中“雾”的形成是水蒸气________形成的，而造成“霾”的主要元凶之一就是PM2.5等可吸入颗粒物，它们与雾气结合在一起，让天空瞬间变得阴沉灰暗．大气中PM2.5指直径小于或等于2.5微米的颗粒物，2.5微米合________米，它还将通过呼吸道进入人体血液，危害人体的健康．14. （2分）一瓶标有“550mL”字样的纯净水，水的质量是________ g，小明喝了半瓶水，则剩余半瓶水的密度是________ kg/m3 ，已知水的密度是1g/cm3 ．三、作图题 (共2题；共10分)15. （5分） (2018九下·东台月考) 在图中入射光线AO在水和空气的界面同时发生了反射和折射，请画出折射光线大致方向.16. （5分） (2017八上·广东月考) 如图所示，请你完成图中两条光线的光路图．四、实验题 (共3题；共14分)17. （4分） (2017八下·大丰期中) 阅读下面短文，回答问题纳米陶瓷纳米陶瓷作为高新材料应用广泛．贴于“神舟七号”飞船外表面的“太空”纳米陶瓷，具有永久、稳定的防静电性能，且有耐磨、耐腐蚀、耐高温、防渗透等特点，采用氧化锆材料精制而成的纳米陶瓷刀，具有金属刀无法比拟的优点：刀刃锋利，能切割钢铁等物质，能削出如纸一样薄的肉片；硬度高，其耐磨性是金属刀的60倍；完全无磁性；不生锈变色，健康环保；可耐各种酸碱有机物的腐蚀；为全致密材料，无孔隙，不玷污，易清洁，纳米陶瓷充分体现新世纪、新材料的绿色环保概念，是高新技术为现代人奉献的又一杰作．（1）“神舟七号”飞船发射升空过程中，与空气摩擦呈炽热状态时，飞船舱不至于被烧毁的原因之一是飞船外表面的陶瓷具有________的特点．（2）纳米（nm）是1m的十亿分之一，糖分子的直径约为1 nm=________m．（3）纳米陶瓷刀的耐磨性好，是因为它的________高．（4）如图所示是陶瓷纳米刀、合金钢刀、普通菜刀磨损程度随磨损时间变化的曲线，其中能反映纳米陶瓷刀特点的是曲线________（填表示曲线的字母）.18. （6分） (2017八上·灌南期末) 某同学利用图示装置来研究凸透镜成像．（1）实验前，应调整烛焰、凸透镜和光屏三者的中心在________；（2）如图1所示，当凸透镜位于光具座上A处时，恰好在光屏上成清晰的像，成的是________（选填“正立”或“倒立”）的像．蜡烛燃烧一段时间后，烛焰的像将位于光屏中心的________方；（3）在保持（2）中蜡烛和光屏位置不变的情况下，将凸透镜向右移到B处（图中未标出），光屏上再次成清晰的像，成的是________（选填“放大”、“缩小”或“等大”）的像；（4）在上述探究活动中，若已知蜡烛与光屏间的距离为L0，与凸透镜第一次所在位置A间的距离为L，如图2所示，则该透镜焦距f________L（选填“＞”、“＜”或“=”），透镜先后两次所在位置A、B之间的距离S=________（用L0、L表示）19. （4分）(2016·河池) 南丹县盛产锡矿，素有“锡都”之称，刘洋同学捡到一小块锡矿石，想测出矿石的密度，做了如下实验：（1）他将天平放于水平桌面上，移动游码至标尺左端零刻度处，发现指针指在分度盘中央的右侧，则应将平衡螺母向________（选填“左”或“右”）调节，使天平横梁平衡．（2）刘洋用天平称出矿石的质量，平衡时右盘中的砝码和游码在标尺上的位置如图甲所示，则矿石的质量为________ g．（3）他用细线绑住矿石放入盛有20cm3水的量筒中，静止时液面如图乙所示，矿石的体积为________ cm3，矿石的密度为________ kg/m3．五、计算题 (共2题；共20分)20. （5分） (2016八上·井陉矿期中) 蝙蝠在飞行时会发出超声波，这些声波碰到墙壁时会反射回来，根据回声到来的方位和时间，蝙蝠可以确定墙壁的位置．若一只蝙蝠在发出超声波0.3s后接收到了回声．忽略蝙蝠从发射声波到接收到回声的这段时间内飞行的距离．求：蝙蝠与墙壁之间的距离．（此时声音的传播速度为340m/s）21. （15分）(2017·苏州模拟) 在新农村建设中很多楼房顶上装有如图1所示的太阳能热水器，图2是内部水箱的结构示意图．S1是自动温控开关，当水温低于20℃时闭合，辅助加热电阻R开始加热；当水温高60℃时断开，辅助加热电阻R停止加热．A、B是水箱中两个相同的实心圆柱体，密度为1.8×103kg/m3 ，悬挂在水箱顶部的压力传感开关S2上．当S2受到竖直向下的拉力达到16N才闭合，电动水泵M开始向水箱注水；当拉力小于等于10N时，S2断开，电动水泵M停止注水．求：（1）若水箱内有100kg的水，夜晚在辅助加热系统作用下，水温升高了20℃，水吸收的热量．[C水=4.2×103J/（kg•℃）]（2）A、B的体积均为500cm3，A、B的总重力．（3）正常情况下水箱中的水面最高时，A受到的浮力．（开关S2下的细绳和A、B间的细绳质量与体积均忽略不计．）六、综合能力题 (共3题；共13分)22. （3分） (2015八上·霞浦期末) 如图所示是甲乙两种固体的熔化实验图象，固体甲是________（晶体或非晶体），固体甲第2分钟的是________状态，由图象可知甲乙两种固体的区别是________．23. （6分） (2017八上·黑龙江期中) 小明同学利用如图所示装置进行“探究平面镜成像的特点”的实验：（1）小明选用玻璃板而不选用平面镜，是因为________.（2）实验时，小明在玻璃板前放一支点燃的蜡烛甲，还要在玻璃板后面放一支未点燃的蜡烛乙，对这两只蜡烛的要求是________.（3）小明在寻找蜡烛甲的像的位置时，眼睛应在玻璃板放有蜡烛________（选填“甲”或“乙”）的一侧观察.（4）如果小明在寻找蜡烛甲的像的位置时，无论怎样沿桌面移动蜡烛乙，都不能使它与蜡烛甲的像重合，可能的原因是________.（5）在玻璃板的同一侧，小明同学通过玻璃板看到了蜡烛甲的两个像.形成两个像的原因是________；解决这一问题的办法是________.24. （4分）(2014·铁岭) 顺顺放学回家，妈妈正在看电视，他隔着门就听到李好主持的“一站到底”节目，这是根据声音的________来判断的；顺顺告诉妈妈，辽宁观众能看到江苏电视台的节目，是因为电视信号能通过________波传送过来；为了不打扰顺顺的学习，妈妈减小电视音量，这是在________处减弱噪声；电视屏幕上丰富的色彩是由红、________、蓝三种色光组成的．参考答案一、选择题 (共7题；共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、二、填空题 (共7题；共14分)8-1、9-1、10-1、11-1、12-1、13-1、14-1、三、作图题 (共2题；共10分)15-1、16-1、四、实验题 (共3题；共14分) 17-1、17-2、17-3、17-4、18-1、18-2、18-3、18-4、19-1、19-2、19-3、五、计算题 (共2题；共20分)20-1、21-1、21-2、21-3、六、综合能力题 (共3题；共13分)22-1、23-1、23-2、23-3、23-4、23-5、24-1、。

∥3套精选试卷∥2018年佛山市八年级上学期物理期末质量检测试题

初二上学期期末物理试卷一、选择题1．一个质量为0.25kg的玻璃瓶，盛满水时称得质量是1.5kg，若盛满某液体时称得质量是1.75kg，那么这种液体的密度是A．1.0×103 kg/m3B．1.16×10 3 kg/m3C．1.75×103kg/m3D．1.2×103kg/m3【答案】D【详解】m水=1.5kg﹣0.25kg=1.25kg，V水===1.25×10﹣1m1=V瓶=V液m液=1.75kg﹣0.25kg=1.5kg，ρ液===1.2×101kg/m1．故选D．2．如图所示的光现象中，由于光的反射形成的是（）A．墙上“孔雀”B．缸中“游鱼”C．镜中“演员”D．林中“光线”【答案】C【详解】A．墙上“孔雀”属于影子，是光在同种均匀介质中沿直线传播形成的，故A不符合题意；B．缸中“游鱼”是光透过水和玻璃缸时发生了折射的缘故，故B不符合题意；C．镜中“演员”属于平面镜成像，是光的反射现象，故C符合题意；D．林中“光线”，说明了光在同种均匀介质中沿直线传播，故D不符合题意，故选C。

3．下列关于声现象的说法中，正确的是：A．声音可以在固体中传播B．声音在真空中的传播速度为340sC．敲锣时锣面振动的幅度越大，音调越高D．只要物体振动，我们就能听到声音【答案】A【详解】A．声音的传播需要介质，在固体液体气体中都可以传播，A符合题意；B．声音的传播需要介质，真空中不能传声，B不符合题意；C．物体振动时，振动的幅度越大，响度越大，C不符合题意；D．物体振动能产生声音，但需要经过介质传播进入耳朵，且频率在人耳能听见的范围，我们才能听见声音，D部不符合题意。

4．宠物狗狗正前方竖立着一面镜子，它正在欣赏镜中的自己(如图所示)，假设狗狗不动，把平面镜沿MN 截成两半，并分别向两侧平移一段距离(两块镜面仍然在原镜面平面内)，则狗狗的头部通过左、右两面镜子（）A．都不能成像B．各成半个像，合起来成一个完整的像C．都成完整的像，且两个像在不同位置D．都成完整的像，且两个像在同一位置【答案】D【详解】AB．平面镜所成的像，像和物体形状、大小相同，与平面镜的大小无关，半个平面镜仍能成完整像，故AB错误；CD．平面镜左右两部分都能成完整的像，像与宠物狗关于镜面对称，所以两个像的位置是相同，故C错误，D正确．5．夏天，盛一盆水，在盆里放入两块高出水面的砖头，砖头上搁一只篮子，再把装有剩饭剩菜的碗放入篮子，用纱布袋罩好，就做成一个“简易冰箱”如图，篮子里的饭菜放置大半天也不会变质，以上“简易冰箱”的工作原理是（）A．液化放热B．蒸发吸热C．凝固放热D．升华吸热【答案】B【详解】试题分析：把一个纱布袋罩在篮子上，并使口袋边缘浸入水里，这样增大了液体的表面积，加快水的蒸发，使食物温度降低，防止变质，故应选B．6．如图所示是温度计测液体温度时的示意图，其中正确的是（）A．B．C．D．【答案】B【详解】使用温度计测量液体温度时，要使温度计的玻璃泡与被测液体充分接触，不要接触容器底或容器壁。

广东省佛山市南海区2018-2019年八年级上学期期末考试数学试题(解析版)

广东省佛山市南海区2018-2019年八年级上学期期末考试数学试题（解析版）广东省佛山市南海区2018-2019学年八年级上学期期末考试数学试题一、选择题（本大题共10小题，共30.0分）1.下列实数是无理数的是A. B. C. D.【答案】B【解析】解：是整数，属于有理数；B.是无理数；C.是有限小数，即分数，属于有理数；D.是分数，属于有理数；故选：B．无理数就是无限不循环小数理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称即有限小数和无限循环小数是有理数，而无限不循环小数是无理数由此即可判定选择项．此题主要考查了无理数的定义，其中初中范围内学习的无理数有：，等；开方开不尽的数；以及像，等有这样规律的数．2.下列各点中位于第四象限的点是A. B. C. D.【答案】C【解析】解：第四象限的点的坐标的符号特点为，观察各选项只有C符合条件，故选C．应先判断点在第四象限内点的坐标的符号特点，进而找相应坐标．本题主要考查了平面直角坐标系中各象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限；第二象限；第三象限；第四象限．3.以下列各组数据为三角形的三边，能构成直角三角形的是A. 1cm，2cm，3cmB. 2cm，2cm，2cmC. 4cm，2cm，2cmD. ，，1cm【答案】D【解析】解：A、，故不能构成直角三角形；B、，故不能构成直角三角形；C、，故不能构成直角三角形；D、，故能构成直角三角形；故选：D．由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可本题考查勾股定理的逆定理的应用判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可勾股定理的逆定理：若三角形三边满足，那么这个三角形是直角三角形．4.已知是方程的解，则k的值为1 / 11A. B. 3 C. 5 D.【答案】B【解析】解：把代入方程得：，解得：，故选：B．把x与y的值代入方程计算即可求出k的值．此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．5.下列根式是最简二次根式的是B. C. D.【答案】D【解析】解：A．，不符合题意；B.，不符合题意；C.，不符合题意；D.是最简二次根式，符合题意；故选：D．判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．本题考查最简二次根式的定义根据最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．6.如图，三角形是直角三角形，四边形是正方形，已知正方形A的面积是64，正方形B的面积是100，则半圆C的面积是A. 36B.C.D.【答案】B【解析】解：正方形A的面积是64，正方形B的面积是100，，，由勾股定理得，，半圆C的面积，故选：B．根据正方形的性质分别求出DE，EF，根据勾股定理求出DF，根据圆的面积公式计算．本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么．7.下列说法错误的是A. 5是25的算术平方根B. 1的立方根是C. 没有平方根D. 0的平方根与算术平方根都是0【答案】B【解析】解：是25的算术平方根，此选项说法正确；B.1的立方根是1，此选项说法错误；广东省佛山市南海区2018-2019年八年级上学期期末考试数学试题（解析版） 3 / 11C . 没有平方根，此选项说法正确；D .0的平方根与算术平方根都是0，此选项说法正确；故选：B ．根据算术平方根和平方根及立方根的定义逐一求解可得．本题主要考查立方根、平方根与算术平方根，解题的关键是熟练掌握算术平方根和平方根及立方根的定义．8.根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择A. 甲B. 乙C. 丙D. 丁【答案】A【解析】解：甲丙乙丁，从甲和丙中选择一人参加比赛，甲乙丙丁，选择甲参赛，故选：A ．首先比较平均数，平均数相同时选择方差较小的运动员参加．此题考查了平均数和方差，正确理解方差与平均数的意义是解题关键．9. 已知点，则点P 到y 轴的距离为A. 4B.C. 3D. 【答案】A【解析】解：点，点P 到y 轴的距离为：4．故选：A ．利用点的横坐标得出点P 到y 轴的距离．此题主要考查了点的坐标，正确理解点的横纵坐标的意义是解题关键．10. 一次函数的大致图象如图所示，关于该次函数，下列说法错误的是A.B. y 随x 的增大而增大C. 该函数有最小值D. 函数图象经过第一、三、四象限【答案】C【解析】解：观察图象知：y 随x 的增大而增大，且交与y 轴负半轴，函数图象经过第一、三、四象限，，解得：，该函数没有最小值，故选：C．根据一次函数的增减性确定有关k的不等式组，求解即可．本题考查了一次函数的图象与系数的关系，解题的关键是了解系数对函数图象的影响，难度不大．二、填空题（本大题共6小题，共24.0分）11.计算：______．【答案】4【解析】解：，，故答案为4．根据算术平方根的概念去解即可算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．12.已知点与点关于x轴对称，则______．【答案】【解析】解：点与点关于x轴对称，，，则，故答案为：．根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得a与b的值，再代入计算即可．此题主要考查了关于x轴对称点的坐标特点，关键是掌握点的坐标的变化规律．13.已知数据，，3，，2，3，1，，这组数据的众数是______．【答案】【解析】解：数据出现了4次，最多，众数为，故答案为：．根据众数的定义进行解答即可．此题考查了众数的知识，众数是一组数据中出现次数最多的数，众数可能不唯一．14.已知，则______．【答案】1【解析】解：，，则原式，故答案为：1．由已知等式得出，代入到原式计算可得．本题主要考查代数式的求值，解题的关键是掌握整体代入思想的运用．广东省佛山市南海区2018-2019年八年级上学期期末考试数学试题（解析版） 5 / 1115. 如图，在平面直角坐标系内，一次函数与正比例函数的图象相交于点A ，且与x 轴交于点B ，点A 的纵坐标为2，则根据图象可得二元一次方程组的解是______．【答案】【解析】解：当时，，解得，则，所以二元一次方程组的解是．故答案为．先利用直线的解析式确定A 点坐标，然后根据方程组的解就是两个相应的一次函数图象的交点坐标求解．本题考查了一次函数与二元一次方程组：方程组的解就是两个相应的一次函数图象的交点坐标．16. 如图是一个“螺旋形”图案，该图案是由一连串直角三角形演化而成的，其中，，则的面积为______．【答案】【解析】解：，，，，，，，，的面积，故答案为：．根据勾股定理求出各斜边的长，然后根据三角形的面积公式即可得到结论．此题主要考查的是勾股定理的运用，三角形的面积，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键三、解答题（本大题共9小题，共66.0分） 17. 计算：【答案】解：原式．【解析】先根据二次根式的乘除法则运算，然后化简后合并即可．本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．18.如图，已知，若，，求的度数．【答案】解：，，又，．【解析】依据平行线的性质，即可得到，再根据三角形外角性质，即可得到的度数．本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等．19.在直角坐标系内的位置如图．请在这个坐标系内画出，使与关于x轴对称；求线段的长度．【答案】解：如图所示：，即为所求；线段的长度为：．【解析】直接利用关于x轴对称点的性质得出对应点位置即可；利用勾股定理进而得出答案．此题主要考查了轴对称变换以及勾股定理，正确得出对应点位置是解题关键．20.某商场计划购进A、B两种新型节能台灯共100盏，已知A型台灯的进价是元盏，B型台灯每台进价比A型台灯贵20元，若商场预计进货款为3500元，则这两种台灯各购进多少盏？广东省佛山市南海区2018-2019年八年级上学期期末考试数学试题（解析版） 7 / 11【答案】解：设该商场购进A 型台灯x 台，B 型台灯y 台，依题意，得：，解得：．答：该商场购进A 型台灯75台，B 型台灯25台．【解析】设该商场购进A 型台灯x 台，B 型台灯y 台，根据总价单价数量结合用3500元共购进A 、B 两种新型节能台灯共100盏，即可得出关于x ，y 的二元一次方程组，解之即可得出结论．本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．21. 如图所示，中．若：：：3：4，求的度数；若，，，求BC 边上的高．【答案】解：设，，，由题意得，，解得，所以，，，，，，是直角三角形，边上的高．【解析】根据比例设，，，然后利用三角形的内角和等于列出方程，再求出k ，从而得到即可；根据勾股定理的逆定理得出是直角三角形，进而解答即可．此题考查勾股定理问题，关键是根据勾股定理和其逆定理解答．22. 为了解某校八年级体育科目训练情况，从八年级学生中随机抽取了部分学生进行了一次体育科目测试把测试结果分为四个等级：A 级：优秀；B 级：良好；C 级：及格；D 级：不及格，并将测试结果绘成了如下两幅不完整的统计图请根据统计图中的信息解答下列问题：图1中的度数是______，并把图2条形统计图补充完整．抽取的这部分的学生的体育科目测试结果的中位数是在______级；依次将优秀、良好、及格、不及格记为90分、80分、70分、50分，请计算抽取的这部分学生体育的平均成绩．【答案】C【解析】解：本次抽查的学生有：人，的度数是：，C级学生有：人，补全的条形统计图如右图所示，故答案为：；由统计图可得，抽取的这部分的学生的体育科目测试结果的中位数是在C级，故答案为：C；分，答：抽取的这部分学生体育的平均成绩是72分．根据统计图中的数据可以计算出本次抽查的学生数，从而可以求得的度数和C 级的学生数，从而可以将条形统计图补充完整；根据中补充完整的条形统计图和中位数的定义可以解答本题；根据题意和统计图中的数据可以计算出抽取的这部分学生体育的平均成绩．本题考查条形统计图、扇形统计图、中位数、加权平均数，解答本题的关键是明确题意，利用数形结合的思想解答．23.某游泳馆普通票价30元张，暑假为了促销，新推出一种优惠卡：售价300元张，每次凭卡另收15元暑假普通票正常出售，优惠卡仅限暑假使用，不限次数设游泳x次时，所需总费用为y元．分别写出选择优惠卡、普通票消费时，y与x之间的函数关系式；在同一坐标系中，若两种消费方式对应的函数图象如图所示，请求出点A、B的坐标；【答案】解：由题意可得，选择优惠卡时，y与x的函数关系式为：，当选择普通票时，y与x的函数关系式为：；将代入，得，即点A的坐标为，令，得，则，即点B的坐标为，由上可得，点A的坐标为，点B的坐标为．【解析】根据题意可以分别写出选择优惠卡、普通票消费时，y与x之间的函数关系式；根据题意可知，点A的坐标就是选择优惠卡时对应的函数解析式与y轴的交点，点B 的坐标就是两个函数交点的坐标，本题得以解决．本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．24.图是我们常见的基本图形，我们可以称之为“8”字形“8”字形有一个重要的性质如下：广东省佛山市南海区2018-2019年八年级上学期期末考试数学试题（解析版）9 / 11利用这个性质并结合你所学的知识解决以下问题：如图，，，直接写出的度数为______；如图，若BN 、DN 分别是、的角平分线，BN 与DN 交于点N 、且，，求的度数；如图，若AM 、BN 、CM 、DN 分别是、、和的角平分线，AM 与CM 、BN 交于点M 、G ，DN 与BN 、CM 交于点N 、H ，且，求的度数．【答案】【解析】解：，，，，故答案为：．如图2，、DN 分别是、的角平分线，，，又，，两式相减可得，，，即，又，，；如图3，、DN 分别是、的角平分线，，，又，，两式相减可得，，，即，同理可得，，又，，．依据，，，即可得到的度数；依据BN、DN分别是、的角平分线，即可得到，，再根据8字形即可得到，，两式相减可得，，进而得到的度数；根据中的方法可得，，再根据，可得，进而得到．本题考查了三角形的内角和定理，角平分线的定义的综合运用注意利用对顶角相等和三角形内角和定理求出角的关系是解题的关键，要注意整体思想的利用．25.如图，已知直线：和直线：，过点作轴，交直线于点A，若点P是x轴上的一个动点，过点P作平行于y轴的直线，分别与、交于点C、D，连接AD、BC．直接写出线段______；当P的坐标是时，求直线BC的解析式；若的面积与的面积相等，求点P的坐标．【答案】【解析】解：轴且点A在直线上，将代入，得即点轴，将代入，得，故点C的坐标为设直线BC的解析式为：，将点C，点B代入得，解得故直线BC的解析式为：由题意得，当时，设点P的坐标为广东省佛山市南海区2018-2019年八年级上学期期末考试数学试题（解析版），解得或．点P的坐标为或轴且点A在直线上，点B的坐标为所以求出点A的坐标即可求AB 因轴于点P，点，点C在直线上，即可以求出点C的坐标，即可用待定系数法求直线BC的解析式因的面积与的面积相等，即时两三角形的面积相等，设点，则有，即可求出点P的坐标此题主要考查的是一次函数的图象及用待定系数法求直线的解析式，但要注意到三角形的边长与一次函数y值的区别．11 / 11。

南海区2018-2019学度初二(上)年末数学试题(含解析)

南海区2018-2019学度初二(上)年末数学试题(含解析)八年级数学试卷试卷说明:本试卷分第一卷〔选择题〕和第二卷〔非选择题〕两部分，共4页，总分值120分，考试时间100分钟。

答题前，学生务必将自己的姓名和学校、班级、学号等填写在答题卷上；答案必须写在答题卷各题目指定区域内的相应位置上；考试结束后，只需将答题卷交回。

第一卷〔选择题〕【一】选择题〔本大题共10小题，每题3分，共30分，在每题给出的四个选项中，只有一项正确〕1、9的平方根是()、A 、3B 、－3C 、±3D 、±32、将以下长度的三根木棒首尾顺次连接，能组成直角三角形的是〔〕、A 、1、2、3B 、2、3、4C 、3、4、5D 、4、5、6 3、以下说法：①实数与数轴上的点一一对应；②2a 没有平方根；③任何实数的立方根有且只有一个；④平方根与立方根相同的数是0和1.其中正确的有〔〕 A 、1个B 、2个C 、3个D 、4个4、以下各组图形，可以经过平移变换由一个图形得到另一个图形的是〔〕、ABCD5、假设一个多边形的内角和等于720°，那么这个多边形的边数是〔〕、 A 、5B 、6C 、7D 、86、为筹备本班元旦联欢晚会，在准备工作中，班长对全班同学爱吃什么水果作了民意调查，再决定最终买哪种水果，下面的调查数据中，他最关注的是〔〕 A 、中位数B 、平均数C 、加权平均数D 、众数7、如图，棋子“车”的坐标为〔-2，3〕，棋子“马”的坐标为〔1，3〕，那么棋子“炮”的坐标为〔〕、 A 、〔3，1〕B 、〔2，2〕C 、〔3，2〕D 、〔-2，2〕8、以下一次函数中，y 的值随着x 值的增大而减小的是()、A 、y ＝xB 、y ＝－xC 、y ＝x ＋1D 、y ＝x －19、如下图，两张等宽的纸条交叉重叠在一起，那么重叠部分ABCD 一定是〔〕、 A 、菱形B 、矩形C 、正方形D 、梯形 10、一水池蓄水20m 3，打开阀门后每小时流出5m 3，放水后池内剩下的水的立方数Q 〔m 3〕与放水时间t 〔时〕的函数关系用图表示为〔〕ABCD第二卷〔非选择题〕【二】填空题〔本大题共5小题，每题3分，共15分，将答案填写在题中横线上〕 11、比较大小：2332〔填“＞”、“＜”、或“=”〕、12、写出一个你所学过的既是轴对称又是中心对称图形的四边形：、13、如图，是用形状、大小完全相同的等腰梯形密铺成的图案，那么这个图案中的等腰梯形（第9题图）（第7题图）的底角〔指锐角〕是度、14、如图，假设直线l 1：32-=x y 与l 2：3+-=x y 相交于点P ，那么根据图象可得，二元一次方程组⎩⎨⎧=+=-332y x y x 的解是、 15、如图，在直角坐标平面内的△ABC 中，点A 的坐标为〔0，2〕，点C 的坐标为〔5，5〕，要使以A 、B 、C 、D 为顶点的四边形是平行四边形，且点D 坐标在第一象限，那么点D 的坐标是、【三】解答题〔本大题共10小题，共75分。

★试卷3套精选★佛山市2018届八年级上学期数学期末达标检测试题

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．如图，在平面直角坐标系中，O 为坐标原点，点N 在x 轴正半轴上，点1A ，2A ，3A ……在射线ON 上，点1B ，2B ，3B ……在射线OM 上，30MON ∠=，112A B A ∠，223A B A ∠，334A B A ∠……均为等边三角形，依此类推，若11OA =，则点2020B 的横坐标是（）A ．201723⨯B ．201823⨯C ．201923⨯D ．202023⨯【答案】B 【分析】根据等边三角形的性质和30MON ∠=以及外角的性质，可求得1290OB A ∠=︒，可求得2122OA OA ==，122B A =由勾股定理得13OB =，再结合30的直角三角形的性质，可得点1B 横坐1333322-==⨯，利用中位线性质，以此类推，可得2B 的横坐标为032⨯，3B 的横坐标为132⨯……，所以n B 的横坐标为232n -⨯，即得2020B ．【详解】30MON ∠=，112A B A ∆为等边三角形，由三角形外角的性质，1290OB A ∴∠=︒，2122OA OA ==11OA =，由勾股定理得13OB ∴=1B 的纵坐标为32，由30的直角三角形的性质，可得1B ∴13333222-==⨯，以此类推2B 的横坐标为032⨯，3B 的横坐标为132⨯……，所以n B 的横坐标为232n -⨯，2020B ∴横坐标为201823⨯．故选：B ．【点睛】考查了图形的规律，等边三角形的性质，30的直角三角形的性质，外角性质，勾股定理，熟练掌握这些性质内容，综合应用能力很关键，以及类比推理的思想比较重要．2．下列能作为多边形内角和的是（）A．312340︒B．211200︒C．200220︒D．222120︒【答案】D【分析】用以上数字分别除以180，判断商是否为整数，即可得出答案.【详解】A：312340°÷180°≈1735.2，故A错误；B：211200°÷180°≈1173.3，故B错误；C：200220°÷180°≈1112.3，故C错误；D：222120°÷180°=1234，故D正确；故答案选择D.【点睛】本题考查的是多边形的内角和公式：(n-2)×180°，其中n为多边形的边数.3．如图，在4×4方格中，以AB为一边，第三个顶点也在格点上的等腰三角形可以作出()A．7个B．6个C．4个D．3个【答案】A【分析】分别以A、B为圆心，AB长为半径画弧，圆弧经过的格点即为第三个顶点的位置，作AB的垂直平分线，如果经过格点，则这样的点也满足条件，由上述作法即可求得答案.【详解】如图所示，分别以A、B为圆心，AB长为半径画弧，则圆弧经过的格点C1、C2、C3、C4、C5、C6、C7即为第三个顶点的位置；作线段AB的垂直平分线，垂直平分线未经过格点，故以AB为一边，第三个顶点也在格点上的等腰三角形可以作出7个，故选A．【点睛】本题考查了等腰三角形的判定，关键是根据题意画出符合条件的等腰三角形．4．如图所示在ABC ∆中，AB 边上的高线画法正确的是( )A ．B ．C ．D ．【答案】B【分析】直接利用高线的概念得出答案．【详解】在ABC ∆中，AB 边上的高线画法正确的是B ，故选B ．【点睛】此题主要考查了三角形高线的作法，正确把握相关定义是解题关键．5．若长度分别为,3,5a 的三条线段能组成一个三角形，则a 的值可以是（）A ．1B ．2C ．3D ．8【答案】C【分析】根据三角形三边关系可得5﹣3＜a ＜5+3，解不等式即可求解．【详解】由三角形三边关系定理得：5﹣3＜a ＜5+3，即2＜a ＜8，由此可得，符合条件的只有选项C ，故选C ．【点睛】本题考查了三角形三边关系，能根据三角形的三边关系定理得出5﹣3＜a ＜5+3是解此题的关键，注意：三角形的两边之和大于第三边，三角形的两边之差小于第三边．6．如图，∠ACB=900，AC=BC ，BE ⊥CE ，AD ⊥CE 于D ，AD=2.5cm ，DE=1.7cm ，则BE=（）A ．1cmB ．0.8cmC ．4.2cmD ．1.5cm 【答案】B【详解】解：90ACB ∠=，90BCE ACE ∴∠+∠=，∵BE ⊥CE ，AD ⊥CE ，90E ADC ∴∠=∠=，90CAD ACE ∠+∠=，∴∠BCE=∠CAD ，在△ACD 和△CBE 中，90BCE CAD E ADC AC BC ∠=∠⎧⎪∠=∠=⎨⎪=⎩， ∴△ACD ≌△CBE(AAS)，∴AD=CE=2.5cm ，BE=CD ，∵CD=CE−DE=2.5−1.7=0.8cm ，∴BE=0.8cm.故选B.7．如图，“士”所在位置的坐标为()12--，，“相”所在位置的坐标为()22-，，那么“炮”所在位置的坐标为（）A ．()21-，B ．()31-，C ．()21-，D ．()31-，【答案】B 【分析】由士和相的坐标推得坐标原点所在的位置，即可得出“炮“所在的位置坐标．【详解】解：根据“士”所在位置的坐标为（−1，−2），“相”所在位置的坐标为（2，−2）可建立如图所示坐标系，∴“炮”所在位置为（−3，1），故选：B ．本题考查了坐标确定位置的知识，解答本题的关键是要建立合适的坐标系．8．已知a ，b ，c 是△ABC 的三条边，满足下列条件的△ABC 中，不是直角三角形的是（） A ．222b c a =-B ．∠A ：∠B ：∠C=3：4：5C ．∠C=∠A-∠BD ．a ：b ：c=5：12：13【答案】B【分析】解答此题时根据直角三角形的判定方法，当一个角是直角时，或两边的平方和等于第三条边的平方，也可得出它是直角三角形，分别判定即可．【详解】解：A 、∵b 2=c 2-a 2，∴c 2=b 2+a 2，∴△ABC 是直角三角形故本选项不符合题意；B 、∵∠A+∠B+∠C=180°，∠A ：∠B ：∠C=3：4：5，∴最大角∠C=512×180°=75°，此三角形不是直角三角形，本选项符合题意； C 、∵∠C=∠A-∠B ，∴∠C+∠B=∠A ，∴∠A=90°，∴△ABC 是直角三角形，故本选项不符合题意；D 、∵a ：b ：c=12：13：5，∴a 2+c 2=b 2，∴△ABC 是直角三角形，故本选项不符合题意；故选：B ．【点睛】本题考查了直角三角形的判定方法、勾股定理的逆定理和三角形的内角和定理，能理解勾股定理的逆定理的内容是解此题的关键．9．若ABC ∆≌DEF ∆，则根据图中提供的信息，可得出x 的值为（）A ．30B ．27C ．35D ．40【分析】在△ABC 中利用三角形内角和可求得∠A=70°，则可得∠A 和∠D 对应，则EF=BC ，可得到答案．【详解】∵∠B=50°，∠C=60°，∴∠A=70°，∵△ABC ≌△DEF ，∴∠A 和∠D 对应，∴EF=BC=30，∴x=30，故选：A ．【点睛】本题主要考查全等三角形的性质，掌握全等三角形的对应边、对应角相等是解题的关键．10．如图，A 和B 两地在一条河的两岸，现要在河上造一座桥MN ，使从A 到B 的路径AMNB 最短的是（假定河的两岸是平行直线，桥要与河岸垂直）（）A ．B ．C ．D ．【答案】D【分析】过A 作河岸的垂线AH ，在直线AH 上取点I ，使AI 等于河宽，连接BI 即可得出N ，作出MN ⊥a 即可得到M ，连接AM 即可．【详解】解：根据河的两岸是平行直线，桥要与河岸垂直可知，只要AM ＋BN 最短就符合题意，即过A 作河岸a 的垂线AH ，垂足为H ，在直线AH 上取点I ，使AI 等于河宽．连结IB 交河岸b 于N ，作MN 垂直于河岸交河岸a 于M 点，连接AM ．故选D ．【点睛】本题考查了最短路线问题以及三角形三边关系定理的应用，关键是找出M 、N 的位置．二、填空题11．如图，在Rt ABC △中，90C ∠=︒，边AB 的垂直平分线DE 交BC 于点D ，AD 平分BAC ∠，则B ∠=_______︒．【答案】30【分析】根据垂直平分线的性质和角平分线的定义得出EAD B CAD ∠=∠=∠，然后利用直角三角形两锐角互余即可求出答案．【详解】DE 垂直平分AB ，∴AD BD = ，EAD B ∴∠=∠．∵AD 平分BAC ∠，EAD CAD ∴∠=∠，EAD B CAD ∴∠=∠=∠．90C ∠=︒，90BAC B ∴∠+∠=︒，390B ∴∠=︒ ，30B ∴∠=︒．故答案为：1．【点睛】本题主要考查垂直平分线的性质，角平分线的定义和直角三角形两锐角互余，掌握垂直平分线的性质和角平分线的定义是解题的关键．12．已知 12,3a b ab -=-=22222a b ab a b ab +-++ 的值等于______． 23 ()()223,a b a b ab --+ 代入求值即可. 详解：12,3a b ab -=-=原式()()223,a b a b ab =--+()(221223,3=--+⨯ 221,=+2 3.=2 3.点睛：考查二次根式的化简求值，对所求式子进行变形是解题的关键.13．实数94的平方根是____________．【答案】32± 【分析】直接利用平方根的定义计算即可．【详解】∵±32的平方是94，∴94的平方根是±32．故答案为±32．【点睛】本题考查了平方根的定义：如果一个数的平方等于a ，这个数就叫做a 的平方根，也叫做a 的二次方根．注意：一个正数有两个平方根，这两个平方根互为相反数，零的平方根是零，负数没有平方根． 14．已知：23x =，45y =，则22x y -=__________. 【答案】35【分析】将45y =转化为()224225y y y ===，再把22x y -转化为222x y ，则问题可解【详解】解：∵()224225y y y ===22232=25x x y y -= 【点睛】本题考查了同底数幂的除法和幂的乘方的逆运算，解答关键是将不同底数的幂运算转化成同底数幂进行计算.15．若27m a a a ⋅=，则m 的值为_________．【答案】1【分析】根据同底数幂相乘，底数不变，指数相加即可列出方程，求出m 的值．【详解】解：∵27m a a a ⋅=∴27m a a +=∴27m +=解得：m=1故答案为：1．【点睛】此题考查的是幂的运算性质，掌握同底数幂相乘，底数不变，指数相加是解决此题的关键．16．若3a 2﹣a ﹣2＝0，则5+2a ﹣6a 2＝_____．【答案】1【分析】先观察3a 2﹣a ﹣2＝0，找出与代数式5+2a ﹣6a 2之间的内在联系后，代入求值．【详解】解:∵3a 2﹣a ﹣2＝0，∴3a 2﹣a ＝2，∴5+2a ﹣6a 2＝5﹣2（3a 2﹣a ）＝5﹣2×2＝1．故答案为：1．【点睛】本题考查了整体代入法求代数式的值，以及添括号法则.添括号法则：添括号时，如果括号前面是正号，括到括号里的各项都不变号，如果括号前面是负号，括号括号里的各项都改变符号．17．如图，等腰直角三角形 ABC 中，∠BAC=90°，AB=AC ，点 M ，N 在边 BC 上，且∠MAN=45°．若 BM=1， CN=3，则 MN的长为．【答案】10．【分析】过点C 作CE ⊥BC ，垂足为点C ，截取CE ，使CE=BM ．连接AE 、EN ．通过证明△ABM ≌△ACE （SAS ）推知全等三角形的对应边AM=AE 、对应角∠BAM=∠CAE ；然后由等腰直角三角形的性质和∠MAN=45°得到∠MAN=∠EAN=45°，所以△MAN ≌△EAN （SAS ），故全等三角形的对应边MN=EN ；最后由勾股定理得到EN 2=EC 2+NC 2即MN 2=BM 2+NC 2．【详解】解：如图，过点C 作CE ⊥BC ，垂足为点C ，截取CE ，使CE=BM ．连接AE 、EN ．∵AB=AC ，∠BAC=90°，∴∠B=∠ACB=45°．∵CE ⊥BC ，∴∠ACE=∠B=45°．在△ABM 和△ACE 中，AB AC B ACE BM CE =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△ACE （SAS ）．∴AM=AE ，∠BAM=∠CAE ．∵∠BAC=90°，∠MAN=45°，∴∠BAM+∠CAN=45°．于是，由∠BAM=∠CAE ，得∠MAN=∠EAN=45°．在△MAN 和△EAN 中，AM AE MAN EAN AN AN =⎧⎪∠=∠⎨⎪=⎩∴△MAN ≌△EAN （SAS ）．∴MN=EN ．在Rt △ENC 中，由勾股定理，得EN 2=EC 2+NC 2．∴MN 2=BM 2+NC 2．∵BM=2，CN=3，∴MN 2=22+32，∴MN=10考点：2．正方形的性质；2．全等三角形的判定与性质．三、解答题18．如图，在每个小正方形的边长均为1的方格纸中有线段AB ，其中点A 、B 均在小正方形的顶点上．（1）在方格纸中画出以BC 为底的钝角等腰三角形ABC ，且点C 在小正方形的顶点上；（2）将（1）中的△ABC 绕点C 逆时针旋转90°得到△DEC （点A 的对应点是点D ，点B 的对应点是点E ），画出△CDE ；（3）在（2）的条件下，连接BE ，请直接写出△BCE 的面积．【答案】 (1)详见解析;(2)详见解析;(3)1【分析】（1）依据BC 为等腰三角形的底边，AB 的长为5，即可得到点C 的位置，进而得出钝角等腰三角形ABC ；（2）依据△ABC 绕点C 逆时针旋转90°，即可得到△DEC ；（3）连接BE ，运用割补法即可得出△BCE 的面积．【详解】（1）如图所示，等腰三角形ABC即为所求；（2）如图所示，△DEC即为所求；（3）如图，连接BE，△BCE的面积为8×12-12×4×8×2-12×4×12=96-32-24=1．【点睛】此题考查作图-旋转，等腰三角形的性质，解题关键在于根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．19．太原市积极开展“举全市之力，创建文明城市”活动，为2020年进人全国文明城市行列莫定基础．某小区物业对面积为3600平方米的区域进行了绿化，整项工程由甲、乙两个林队先后接力完成，甲园林队每天绿化200平方米，乙园林队每天绿化160平方米，两队共用21天．求甲乙两个园林队在这项绿化工程中分别工作了多少天．【答案】甲园林队工作了6天，乙园林队工作了15天．【解析】设甲园林队工作了x天，乙园林队工作了y天，根据题意列出二元一次方程组即可求解．【详解】设甲园林队工作了x天，乙园林队工作了y天，根据题意得21 2001603600x yx y+=⎧⎨+=⎩解，得615 xy=⎧⎨=⎩，答：甲园林队工作了6天，乙园林队工作了15天．【点睛】此题主要考查二元一次方程的应用，解题的关键是根据题意找到等量关系列方程．20．制文中学2019年秋季在政大商场购进了A、B两种品牌的冰鞋，购买A品牌冰鞋花费了8000元，购买B品牌冰鞋花费了6000元，且购买A品牌冰鞋的数量是购买B品牌冰鞋数量的2倍，已知购买一双B品牌冰鞋比购买一双A品牌冰鞋多花100元．（1）求购买一双A品牌，一双B品牌的冰鞋各需多少元？（2）为开展好“冰雪进校园”活动，制文中学决定再次购买两种品牌冰鞋共50双，如果这所中学这次购买A、B两种品牌冰鞋的总费用不超过13100元，那么制文中学最多购买多少双B品牌冰鞋？【答案】（1）购买一双A 品牌、一双B 品牌冰鞋各需200元、300元；（2）制文中学最多购买B 品牌冰鞋31双【分析】(1)设购买一双A 品牌冰鞋需x 元,则购买一双B 品牌冰鞋需要(x+100)元,根据题意列出方程即可解出．(2)设购买B 品牌冰鞋a 双,则购买A 品牌冰鞋(50－a)双,根据题意列出不等式解出范围即可．【详解】解(1)：设购买一双A 品牌冰鞋需x 元,则购买一双B 品牌冰鞋需要(x+100)元,根据题意得, 800060002100x x =⨯+ 解得, x=200经检验x=200是原分式方程的解∴x+100=300答：购买一双A 品牌、一双B 品牌冰鞋各需200元、300元．(2)解：设购买B 品牌冰鞋a 双,则购买A 品牌冰鞋(50－a)双根据题意得,300a+200(50－a )≤13100解得, a ≤31∵ a 取整数∴ a=31答：制文中学最多购买B 品牌冰鞋31双．【点睛】本题考查分式方程的应用、不等式的应用,关键在于理解题意找到等量关系．21．如图所示，已知ABC ∆中，90B ∠=︒，16AB cm =，20AC cm =，P 、Q 是ABC ∆的边上的两个动点，其中点P 从点A 开始沿A B →方向运动，且速度为每秒1cm ，点Q 从点B 开始沿B C A →→方向运动，且速度为每秒2cm ，它们同时出发，设出发的时间为ts ．（1）则BC =____________cm ；（2）当t 为何值时，点P 在边AC 的垂直平分线上？此时CQ =_________?（3）当点Q 在边CA 上运动时，直接写出使BCQ ∆成为等腰三角形的运动时间．【答案】（1）11；（1）t=11.5s 时，13 cm ；（3）11s 或11s 或13.1s【分析】（1）由勾股定理即可得出结论；（1）由线段垂直平分线的性质得到PC= PA=t ，则PB=16-t ．在Rt △BPC 中，由勾股定理可求得t 的值，判断出此时，点Q 在边AC 上，根据CQ=1t-BC 计算即可；（3）用t 分别表示出BQ 和CQ ，利用等腰三角形的性质可分BQ=BC 、CQ=BC 和BQ=CQ 三种情况，分别得到关于t 的方程，可求得t 的值．【详解】（1）在Rt △ABC 中，BC 2222212016AC AB =-=-=(cm)．故答案为：11；（1）如图，点P 在边AC 的垂直平分线上时，连接PC ，∴PC= PA=t ，PB=16-t ．在Rt △BPC 中，222BC BP CP +=，即2221216)t t +-=（，解得：t=252． ∵Q 从B 到C 所需的时间为11÷1=6(s)，252＞6， ∴此时，点Q 在边AC 上，CQ=25212132⨯-=(cm)；（3）分三种情况讨论：①当CQ=BQ 时，如图1所示，则∠C=∠CBQ ．∵∠ABC=90°，∴∠CBQ+∠ABQ=90°，∠A+∠C=90°，∴∠A=∠ABQ ，∴BQ=AQ ，∴CQ=AQ=10，∴BC+CQ=11，∴t=11÷1=11(s)．②当CQ=BC 时，如图1所示，则BC+CQ=14，∴t=14÷1=11(s)．③当BC=BQ 时，如图3所示，过B 点作BE ⊥AC 于点E ，则BE 121648205AB BC AC ⋅⨯===， ∴CE 2222483612()55BC BE =-=-==7.1． ∵BC=BQ ，BE ⊥CQ ，∴CQ=1CE=14.4，∴BC+CQ=16.4，∴t=16.4÷1=13.1(s)．综上所述：当t 为11s 或11s 或13.1s 时，△BCQ 为等腰三角形．【点睛】本题考查了勾股定理、等腰三角形的性质、方程思想及分类讨论思想等知识．用时间t 表示出相应线段的长，化“动”为“静”是解决这类问题的一般思路，注意方程思想的应用．22．先化简，再求2241()2442x x x x x x -+⋅--++的值，其中x=1．【答案】12x -，2．【解析】试题分析：原式括号中两项通分并利用同分母分式的加法法则计算，约分得到最简结果，把x 的值代入计算即可求出值．试题解析：原式=2(2)241(2)2x x x x x -+-⋅-+=2(2)(2)1(2)2x x x x +-⋅-+=12x - 当x=2时，原式=2．考点：分式的化简求值．23．（1）问题背景：如图1，在四边形ABCD 中，AB ＝AD ，∠BAD ＝120°，∠B ＝∠ADC ＝90°．E ，F 分别是BC ，CD 上的点，且∠EAF ＝60°，请探究图中线段BE ，EF ，FD 之间的数量关系是什么？小明探究此问题的方法是：延长FD 到点G ，使DG ＝BE ，连结AG ．先证明△ABE ≌△ADG ，得AE ＝AG ；再由条件可得∠EAF ＝∠GAF ，证明△AEF ≌△AGF ，进而可得线段BE ，EF ，FD 之间的数量关系是．（2）拓展应用：如图2，在四边形ABCD 中，AB ＝AD ，∠B+∠D ＝180°．E ，F 分别是BC ，CD 上的点，且∠EAF ＝12∠BAD ．问（1）中的线段BE ，EF ，FD 之间的数量关系是否还成立？若成立，请给出证明；若不成立，请说明理由．【答案】（1）EF ＝BE+DF ；（2）结论EF ＝BE+DF 仍然成立；证明见解析．【分析】（1）延长FD 到点G ．使DG=BE ．连结AG ，即可证明△ABE ≌△ADG ，可得AE=AG ，再证明△AEF ≌△AGF ，可得EF=FG ，即可解题；（2）延长FD 到点G ．使DG=BE ．连结AG ，即可证明△ABE ≌△ADG ，可得AE=AG ，再证明△AEF ≌△AGF ，可得EF=FG ，即可解题．【详解】（1）EF ＝BE+DF ，理由如下：在△ABE 和△ADG 中，90DG BE B ADG AB AD ︒=⎧⎪∠=∠=⎨⎪=⎩，∴△ABE ≌△ADG （SAS ），∴AE ＝AG ，∠BAE ＝∠DAG ，∵∠EAF ＝12∠BAD ， ∴∠GAF ＝∠DAG+∠DAF ＝∠BAE+∠DAF ＝∠BAD ﹣∠EAF ＝∠EAF ，∴∠EAF ＝∠GAF ，在△AEF 和△GAF 中，AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△AGF （SAS ），∴EF ＝FG ，∵FG ＝DG+DF ＝BE+DF ，∴EF ＝BE+DF ；故答案为：EF ＝BE+DF ．（2）结论EF ＝BE+DF 仍然成立；理由：延长FD 到点G ．使DG ＝BE ．连结AG ，如图2，∵∠B+∠ADC ＝180°，∠ADC+∠ADG ＝180°，∴∠B ＝∠ADG ，在△ABE 和△ADG 中，DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ADG （SAS ），∴AE ＝AG ，∠BAE ＝∠DAG ，∵∠EAF ＝12∠BAD ， ∴∠GAF ＝∠DAG+∠DAF ＝∠BAE+∠DAF ＝∠BAD ﹣∠EAF ＝∠EAF ，∴∠EAF ＝∠GAF ，在△AEF 和△GAF 中，AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△AGF （SAS ），∴EF ＝FG ，∵FG ＝DG+DF ＝BE+DF ，∴EF ＝BE+DF ．【点睛】本题是四边形综合题，考查了全等三角形的判定和性质，直角三角形的性质，添加恰当辅助线构造全等三角形是解题的关键．24．四边形ADBC 是由等边ABC ∆和顶角为120°的等腰三角形ABD ∆拼成，将一个60°角顶点放在点D 处，60°角两边分别交直线,BC AC 于,M N ，交直线AB 于,F E 两点．（1）当,E F 都在线段AB 上时，探究,,BM AN MN 之间的数量关系，并证明你的结论；（2）当E 在边BA 的延长线上时，求证：BM AN MN -=．【答案】（1）BM+AN=MN ，证明见解析；（2）见解析；【分析】（1）把△DBM 绕点D 逆时针旋转120°得到△DAQ ，根据旋转的性质可得DM=DQ ，AQ=BM ，∠ADQ=∠BDM ，然后求出∠QDN=∠MDN ，利用“边角边”证明△MND 和△QND 全等，根据全等三角形对应边相等可得MN=QN ，再根据AQ+AN=QN 整理即可得证；（2）把△DAN 绕点D 顺时针旋转120°得到△DBP ，根据旋转的性质可得DN=DP ，AN=BP ，根据∠DAN=∠DBP=90°可知点P 在BM 上，然后求出∠MDP=60°，然后利用“边角边”证明△MND 和△MPD 全等，根据全等三角形对应边相等可得MN=MP ，从而得证；【详解】（1）证明：∵四边形ADBC 是由等边ABC ∆和顶角为120°的等腰三角形ABD ∆拼成， ∴∠CAD=∠CBD=60°+30°=90°把△DBM 绕点D 逆时针旋转120°得到△DAQ ，则DM=DQ ，AQ=BM ，∠ADQ=∠BDM ，∠CBD=∠QAD =90°∴∠CAD+∠QAD =180°∴N 、A 、Q 三点共线∵∠QDN=∠ADQ+∠ADN=∠BDM+∠ADN=∠ABD-∠MDN=120°-60°=60°，∴∠QDN=∠MDN=60°，∵在△MND 和△QND 中，DM DQ QDN MDN DN DN =⎧⎪∠=∠⎨⎪=⎩∴MN=QN ，∵QN=AQ+AN=BM+AN ，∴BM+AN=MN ；（2）MN+AN=BM ．理由如下：如图，把△DAN 绕点D 顺时针旋转120°得到△DBP ，则DN=DP ，AN=BP ，∵∠DAN=∠DBP=90°，∴点P 在BM 上，∵∠MDP=∠ADB-∠ADM-∠BDP=120°-∠ADM-∠ADN=120°-∠MDN=120°-60°=60°，∴∠MDP=∠MDN=60°，∵在△MND 和△MPD 中，DN DP MDP MDN DM DM =⎧⎪∠=∠⎨⎪=⎩∴△MND ≌△MPD （SAS ），∴MN=MP ，∵BM=MP+BP ，∴MN+AN=BM ；∴MN=BM -AN ；【点睛】本题考查了全等三角形的判定与性质及等腰三角形的性质，根据等边三角形的性质，旋转变换的性质作辅助线构造全等三角形是解题的关键25．如图，在平面直角坐标系中，A(﹣3，2)，B(﹣4，﹣3)，C(﹣1，﹣1)．（1）在图中作出ABC 关于y 轴对称的111A B C △；（2）写出点111,,A B C 的坐标（直接写答案）；（3）在y 轴上画出点P ，使PB+PC 最小．【答案】（1）图见解析；（2）111(3,2),(4,3),(1,1)A B C --；（3）图见解析．【分析】（1）先根据轴对称的性质分别描出点111,,A B C ，再顺次连接即可得；（2）根据点坐标关于y 轴对称的变化规律即可得；（3）先根据轴对称的性质可得1PB PC PB PC +=+，再根据两点之间线段最短即可得．【详解】（1）先根据轴对称的性质分别描出点111,,A B C ，再顺次连接即可得到111A B C △，如图所示：（2）点坐标关于y 轴对称的变化规律：横坐标变为相反数，纵坐标不变3,24,3(),(),()1,1A B C -----1113,24,(),(),(3)1,1A B C ∴--；（3）由轴对称的性质得：1PB PB =则1PB PC PB PC +=+由两点之间线段最短得：当1,,C P B 三点共线时，1PB PC +取得最小值，最小值为1CB如图，连接1CB ，与y 轴的交点P 即为所求．【点睛】本题考查了画轴对称图形、点坐标关于y 轴对称的变化规律、两点之间线段最短，熟练掌握轴对称的性质是解题关键．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．若等腰三角形的周长为18 cm ，其中一边长为8 cm ，则该等腰三角形的底边长为（） A ．8 cmB ．2 cm 或8 cmC ．5cmD ．8 cm 或5 cm 【答案】B【分析】由于长为8cm 的边可能是腰，也可能是底边，故应分两种情况讨论．【详解】解：由题意知，可分两种情况：①当腰长为8cm 时，则另一腰长也为8cm ，底边长为18-8×2=2（cm ），∵8-2<8<8+2即6<8<10，∴可以组成三角形∴当腰长为8cm 时，底边长为2cm ；②当底边长为8cm 时，腰长为(18-8)÷2=5（cm ），∵5-5<8<5+5，即0<8<10，∴可以组成三角形∴底边长可以是8cm ．故选B ．【点睛】本题考查了等腰三角形的性质和三角形的三边关系．已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点也是解题的关键．2．已知两数x ，y 之和是10，且x 比y 的2倍大3，则下列所列方程组正确的值是（） A ．1023x y y x +=⎧⎨=+⎩ B ．1023x y y x +=⎧⎨=-⎩ C ．1023x y x y +=⎧⎨=+⎩ D ．1023x y x y +=⎧⎨=-⎩【答案】C【分析】根据x ，y 之和是10，列出方程10x y +=，再由x 比y 的2倍大3，列出方程23x y =+，最后写成方程组形式即可解题．【详解】根据题意列出方程组，得：1023x y x y +=⎧⎨=+⎩故选C ．【点睛】本题考查由实际问题抽象出二元一次方程组的知识，是重要考点，找到等量关系，掌握相关知识是解题关键．3．如图，AC ∥BD ，AD 与BC 相交于O ，∠A ＝45°，∠B ＝30°，那么∠AOB 等于（）A ．75°B ．60°C ．45°D ．30°【答案】A 【详解】解：三角形的外角等于与它不相邻的两个内角和,由题,∵AC ∥BD ，∴∠C=∠B=30°, ∵∠AOB 是△AOC 的一个外角,∴∠AOB=∠C+∠A= 45°+30°=75°，选A ．【点睛】本题考查平行线的性质和三角形的外角．4．老大爷背了一背鸡鸭到市场出售，单价是每只鸡100元，每只鸭80元，他出售完收入了660元，那么这背鸡鸭只数可能的方案有（）A ．4种B ．3种C ．2种D ．1种【答案】C【分析】设有鸡x 只，有鸭y 只，根据收入共660元列方程，然后根据鸡鸭只数是正整数分析求解．【详解】设有鸡x 只，鸭y 只，根据题意，得 10080660x y +=，整理，得：5433x y +=， ∴3354x y -=， ∵x 、y 必须是正整数， ∴3354x -≥，且335x -必须是偶数，即x 为奇数， ∴2905x ≤≤，且x 为奇数，则x =1，3，5，当1x =时，7y =，符合题意；当3x =时，184y =，不是整数，不符合题意，舍去．当5x =时，2y =，符合题意．所以，这背鸡鸭只数可能的方案有2种．故选：C．【点睛】本题综合考查了二元一次方程的应用，能够根据不等式求得未知数的取值范围，从而分析得到所有的情况．5．如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为()A．4B．8C．6D．10【答案】B【详解】解：设AG与BF交点为O，∵AB=AF，AG平分∠BAD，AO=AO，∴可证△ABO≌△AFO，∴BO=FO=3，∠AOB=∠AOF=90º，AB=5，∴AO=4，∵AF∥BE，∴可证△AOF≌△EOB，AO=EO，∴AE=2AO=8，故选B．【点睛】本题考查角平分线的作图原理和平行四边形的性质．6．点P（﹣2，3）关于y轴对称点的坐标在第（）象限A．第一象限B．第二象限C．第三象限D．第四象限【答案】A【解析】∵点P（-2，3）在第二象限，∴点P关于y轴的对称点在第一象限.故选A.7．下列命题是假命题的是（）A．如果a∥b，b∥c，那么a∥c；B．锐角三角形中最大的角一定大于或等于60°；C．两条直线被第三条直线所截，内错角相等；D．三角形三个内角和等于180°．【答案】C【分析】根据平行线的性质和判定和三角形的内角对每一个选项进行判断即可．【详解】解：A、如果a∥b，b∥c，那么a∥c，是真命题，不符合题意，本选项错误；B、锐角三角形中最大的角一定大于或等于60°，是真命题，不符合题意，本选项错误；C、两条直线被第三条直线所截，若这两条直线平行，则内错角相等，故是假命题，符合题意，本选项正确；D、三角形三个内角和等于180°，真命题，不符合题意，本选项错误；故选：C．【点睛】本题考查了真假命题的判断，掌握平行线的性质和判定和三角形内角问题是解题关键．8．如图，从标有数字1,2,3.4的四个小正方形中拿走一个，成为一个轴对称图形，则应该拿走的小正方形的标号是（）A．1 B．2 C．3 D．4【答案】B【分析】根据轴对称图形的概念，逐一判断选项，即可得到答案.【详解】∵拿走数字1的小正方形，不是轴对称图形，∴A错误；∵拿走数字2的小正方形，可得轴对称图形，∴B正确；∵拿走数字3的小正方形，不是轴对称图形，∴C错误；∵拿走数字4的小正方形，不是轴对称图形，∴D错误；故选B.【点睛】本题主要考查轴对称图形的概念，掌握轴对称图形的概念，是解题的关键.9．如图，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与A对应，则角α的大小为（）A．30°B．60°C．90°D．120°【答案】C【详解】分析：先根据题意确定旋转中心，然后根据旋转中心即可确定旋转角的大小．详解：如图，连接A′A，BB′，分别A′A，BB′作的中垂线，相交于点O.显然，旋转角为90°，故选C ．点睛：考查了旋转的性质，解题的关键是能够根据题意确定旋转中心，难度不大．先找到这个旋转图形的两对对应点，连接对应两点，然后就会出现两条线段，分别作这两条线段的中垂线，两条中垂线的交点就是旋转中心.10．一次函数21y x =-+的图象与y 轴的交点坐标是( )A ．(-2，0)B ．(12，0)C ．(0，2)D ．(0，1)【答案】D【分析】令x=0，代入函数解析式，求得y 的值，即可得到答案．【详解】令x=0，代入21y x =-+得：2011y =-⨯+=，∴一次函数21y x =-+的图象与y 轴的交点坐标是：(0，1)．故选D ．【点睛】本题主要考查一次函数图象与y 轴的交点坐标，掌握直线与y 轴的交点坐标的特征，是解题的关键．二、填空题11．如图，如果你从P 点向西直走25米后，向左转，转动的角度为=40α°，再走25米，再向左转40度，如此重复，最终你又回到点P ，则你一共走了__________米．【答案】1．【分析】根据题意转动的角度为=40α°，结合图我们可以知道，最后形成的正多边形的一个外角是40°，利用多边形的外角和可求出是正几边形，即可求得一共走了多少米．【详解】解：360°÷40=9（边）9×25=1（米）故答案为：1【点睛】本题主要考查的是正多边形的性质以及多边形的外角和公式，掌握以上两个知识点是解题的关键． 12．当x 为______时，分式2361x x -+的值为1．【答案】2．【分析】先根据分式的值为零的条件确定分子为零分母不为零，再求解方程和不等式即得．【详解】解：∵分式2361x x -+的值为1 ∴236010x x -=⎧⎨+≠⎩∴2x =．故答案为：2．【点睛】本题考查分式的定义，正确抓住分式值为零的条件是解题关键．13．如图所示，在Rt △ABC 中，∠A=30°，∠B=90°，AB=12，D 是斜边AC 的中点，P 是AB 上一动点，则PC +PD 的最小值为_____．【答案】12【分析】作C 关于AB 的对称点E ，连接ED ，易求∠ACE=60°，则AC=AE ，且△ACE 为等边三角形，CP+PD=DP+PE 为E 与直线AC 之间的连接线段，其最小值为E 到AC 的距离=AB=12，所以最小值为12.【详解】作C 关于AB 的对称点E ，连接ED ，∵∠B=90°，∠A=30°，∴∠ACB=60°，∵AC=AE ，∴△ACE 为等边三角形，∴CP+PD=DP+PE为E与直线AC之间的连接线段，∴最小值为C'到AC的距离=AB=12，故答案为12【点睛】本题考查的是最短线路问题及等边三角形的性质，熟知两点之间线段最短的知识是解答此题的关键．14．新定义：[a，b]为一次函数y ax b=+(a≠0，,a、b为实数)的“关联数”．若“关联数”为[3，m-2] 的一次函数是正比例函数，则点(1-m，1+m)在第_____象限．【答案】二．【分析】根据新定义列出一次函数解析式，再根据正比例函数的定义确定m的值，进而确定坐标、确定象限.【详解】解：∵“关联数”为[3，m﹣2]的一次函数是正比例函数，∴y＝3x+m﹣2是正比例函数，∴m﹣2＝0，解得：m＝2，则1﹣m＝﹣1，1+m＝3，故点（1﹣m，1+m）在第二象限．故答案为：二．【点睛】本题属于新定义和正比例函数的定义，解答的关键运用新定义和正比例函数的概念确定m的值.15．已知13xy=⎧⎨=⎩是二元一次方程组71mx nynx my+=⎧⎨-=⎩的解，则2m+n的值为_____．【答案】1【解析】解：由题意可得：3731m nn m+=⎧⎨-=⎩①②，①－②得：4m+2n=6，故2m＋n =1．故答案为1．16．已知∠AOB＝60°，OC是∠AOB的平分线，点D为OC上一点，过D作直线DE⊥OA，垂足为点E，且直线DE交OB于点F，如图所示．若DE＝2，则DF＝_____．【答案】1．【分析】过点D作DM⊥OB，垂足为M，则DM=DE=2，在Rt△OEF中，利用三角形内角和定理可求出。

┃精选3套试卷┃2018届佛山市八年级上学期物理期末监测试题

初二上学期期末物理试卷一、选择题1．小付在探究电荷间作用力的大小与哪些因素有关。

如图，他将一个带电球体M 放在绝缘支架上，用绝缘丝线将带电小球N 先后悬挂在横杆上的P 1、P 2和P 3处，当小球N 静止时，观察丝线与竖直方向的夹角：小球N 挂在P 1时，丝线与竖直方向的夹角最大；小球N 挂在P 3时，丝线与竖直方向的夹角最小，则小付所探究问题的自变量是（）A ．电荷量的大小B ．电荷间作用力大小C ．夹角大小D ．电荷间距离大小【答案】D 【详解】由题意可知，随着小球N 距离带电球体 M 的距离在增大，发现小球在竖直方向上偏转的角度在减小，即其受到的作用力在减小，由此可以提出问题“电荷间的作用力大小与电荷间的距离有什么关系？”，则小付所探究问题的自变量是电荷间距离大小。

故选D 。

2．某运动物体在前一半路程内运动的平均速度为20m/s ，后一半路程内运动的平均速度为30m/s ，则该物体在整个运动过程中的平均速度为A ．10m/sB ．24m/sC ．25m/sD ．50m/s 【答案】B【解析】设该物体通过的整个路程为s ，则前一半路程2s s =前，20m /s v =前．后一半路程2s s =后，30m /s v =后，由速度公式v s t=可知，平均速度2230/20/v 24/30/20/22v v s s s m s m s m s s s s s t t v v m s m s v v v v 后前前后后后前前后前后前⨯⨯======+++++．故B 正确为答案． 3．如图，让一束太阳光照射三棱镜，射出的光射到竖直放置的白屏上．以下说法正确的是（）A ．如果在白屏与棱镜之间竖直放一块红色玻璃，则白屏上其他颜色的光消失，只留下红色B ．如果在白屏与棱镜之间竖直放一块蓝色玻璃，则白屏上蓝色光消失，留下其他颜色的光C．如果把一张红纸贴在白屏上，则在红纸上看到彩色光带D．如果把一张绿纸贴在白屏上，则在绿纸上看到除绿光外的其他颜色的光【答案】A【详解】白光通过三棱镜分解为七种单色光．如果在白屏与棱镜之间竖直放一块红色玻璃，红色玻璃纸透过红光，则白屏上其他颜色的光消失，只留下红色，故A正确为答案．B．如果在白屏与棱镜之间竖直放一块蓝色玻璃，则白屏上只有蓝色光，其他颜色的光消失，故B错误．C．如果把一张红纸贴在白屏上，红纸只反射红光，则在红纸上看不到其他彩色光带，C错误．D．如果把一张绿纸贴在白屏上，则在绿纸上只看到绿光，所以D错误．4．疫情期间，手持式电子测温仪最为常见，如图甲是某款电子测温仪，图乙是它内部的原理图，其中电源电压保持不变，R是热敏电阻，用于靠近人体测温，定值电阻R0为保护电阻；在测人的体温时，当被测温者体温较高时，显示仪的示数也会变大。

南海区2018—2019学年度第一学期期末教学质量检测八年级语文答案示例与评分标准 20190130

南海区2018－2019学年第一学期期末敏学质量检测八年级语文答案示例与评分标准【全卷参考答案及评分标准说明】1．主观题答案只要意思相同或相近即可酌情给分；如果考生的答案与下面参考答案说法不一致，但符合题目要求且言之成理，也应该酌情给分。

2．主观题答案语言表述不准确（如有错别字，重复的不计）的酌情扣分，但扣分不得超过该小题的分值。

3．附加题从严给分。

题号分值参考答案及评分说明一24分1 10 本题共5小题，每句1分，每句错、漏、多1字扣0．5分，扣完小题分为止（1） 1 归雁入胡天（2） 1 白头搔更短（3） 2 黑云压城城欲摧甲光向日金鳞开（4） 2 经纶世务者窥谷忘反（5） 4 黄鹤一去不复返白云千载空悠悠晴川历历汉阳树芳草萋萋鹦鹉洲2 4 （1）禁锢（2）跋涉（3）诚惶诚恐（4）摩肩接踵每小题错一字，该小题不得分，每小题1分3 3 C（“跌宕起伏”应改为“抑扬顿挫”）4 3 A5 4 （1）激活经典传承传播中华传统文化，绵延经典的生命力。

（2）示例：经典是一座深山，神秘而又充满诱惑力，等待你前往探索。

二46分（一) 106 3 （1）同“缺”，空隙、缺口（2）肃杀，凄寒（3）延长7 4 （1）到夏天江水漫上山陵的时候，上行和下行的航道都被阻断，不能通航。

（或到了夏天，江水漫上两岸的丘陵的时候，顺流而下和逆流而上的船只都被阻隔了）（关键词：“沿”、“溯”每个1分）（2）即使骑着骏马（或飞奔的马），驾着疾风，也不如坐船快。

（关键词：“虽”，“奔”每个1分）8 3 B（二）99 3 C（A固定的／经常B背，背着／凭借C交换、更替D来／凭借）10 3 夫人好学／虽死犹存／不学者虽存／调之行尸走肉耳11 3 示例：①学无常师，负笈不远险阻。

②削荆为笔，刻树汁为墨。

③夜则映星望月而读，暗则缕麻蒿以自照。

④观书有合意者，题其衣裳，以记其事，（每一点1分，不超本题总得分）1【参考译文】任末十四岁，学习没有固定的老师，背着书箱不怕路途遥远，危险困阻，常常说人如果不学习，那么凭什么成功呢。

南海实验区八年级第一学期期末考试物理试卷

广东南海实验区八年级第一学期期末考试物理试卷一、选择题（每题 3 分，共 30 分，从每题的四个选项中选出一个符合题目要求的答案）1、在城市道路常如同图 1 所示的标牌，它表示的意思是（）A．鼓号乐队不可以进入B．严禁鸣笛，保持沉静C．道路曲折，行车注意安全D．乐器商铺的标记2．你的街坊搞装饰十分喧华，搅乱你的学习和生活，以下举措中哪一个是无效的（）A．赶忙将门窗关紧B．用棉花塞住耳朵C．将窗翻开让空气加速流通D．将棉被挂在窗户上3．在平时生活中，常用“响彻云霄”来形容人说话的状况（）A．音调B．响度C．音色D．都有可能4．“女高音歌唱家”和“男低音歌唱家”这里的“高”与“低”指的是（）A．音调B．响度C．音色D．都有可能5．以下现象中属于光的反射的是（）A．在颐和园内昆明湖的水中可看到十七孔桥的倒影B．注满水的游泳池，池底看起来变浅了C．人在阳光下，地面上出现影子D．筷子斜插入水中，水下的部分看起来上折了7．站在平面镜前的人向平面镜走近时，下边说法中正确的选项是（）A 他的像变大B．他的像变小C．他的像不变D．不可以确立，要看距离的远近8．植树时．要想判断这行树直不直，采纳的方法是：人站在第一棵树前方，假如后边的树都被第一棵树挡住，说明这行树栽直了，其原因是（）A．光的直线流传B．光的折射现象 C ．光的反射现象D．光的漫反射现象6．以下连线哪一组是有错误的（）9．小明用照相机为同学摄影，在底片上获得的是（）A 正立、减小的虚像B．正立、减小的实像C．倒立、减小的虚像D．倒立、减小的实像10．雨后天晴的夜晚，为了不踩到地上的积水，以下判断正确的选项是（）A．迎着月光走，地上暗处是积水B．迎着月光走，地上光明处是积水C．背着月光走，地上光明是积水D．迎着月光走，背着月光走，地上暗处都是积水二、填空题（每空 1 分，共 12 分）1．如图这是由于2 所示，笛子发出的声是由消逝了。

振动惹起的，锣发声的时候，用手按住锣面．锣声就消逝了，2．乐器可以分为：打击乐器，，，三种主要乐器。

广东省佛山市南海区2018-2019学年八年级上学期期末考试物理试题(word无答案)

广东省佛山市南海区2018-2019学年八年级上学期期末考试物理试题(word无答案)一、单选题(★) 1 . 对于声音的产生，下列说法正确的是A．只有固体的振动才能发声B．声音是由物体的振动产生的C．物体不振动也能发声D．振动停止后，发声体仍能发声(★) 2 . 图为探究光的反射规律的实验装置，下列描述中不合理的是A．可沿ON折叠的白色硬纸板应垂直放置于平面镜上B．为研究反射角与入射角间的关系，应多次改变光线AO与ON间的夹角C．为研究入射光线、反射光线和法线的位置关系，应绕ON前后折转入射光线所在的光屏E D．如果让光线沿着FO的方向射向镜面，会发现反射光线沿着OA方向射出，这表明光路是可逆的(★) 3 . 如图光现象中，由光的直线传播形成的是A．水面“折”笔B．彩虹C．树荫下圆形光斑D．白塔在水中的倒影(★★) 4 . 如图所示的四种现象中，其物态变化属于升华的是A．吉林冬天树上的“雾凇”B．水蒸气在凉玻璃上形成水珠C．冬季，堆在户外的“雪人”没熔化却变小D．晾晒的湿衣服逐渐变干(★) 5 . 如图为航天员王亚平太空授课的情景，图中水球相当于一个透镜，假设水球的焦距为f，此时王亚平到水球的距离40cm，则下列说法正确的是A ．f ＜20cmB ．40cm ＞f ＞20cmC ．水球相当于一个凹透镜D ．王亚平的像是虚像(★) 6 . 一汽车在公路上做匀速直线运动，如图正确表示汽车通过的路程与时间的关系是A ．B ．C ．D ．(★) 7 . 某研究性学习课题小组在老师的指导下，完成“水的体积随温度变化”的研究，得到如图所示的图象。

根据这个图象，可得到水的温度从8℃降到2℃的过程中有关水的变化的一些信息，下列说法中①水遵从热胀冷缩的规律 ②水的体积先变小后变大③水的密度先变小后变大④水在4℃时密度最大A ．只有①正确B ．②③正确C ．②④正确D ．①③正确二、填空题(★) 8 . 许多男生在变声期后，说话时声带的振动频率比以前低，因而声音的_____会降低。

2018-2019学年广东省佛山市南海区八年级(上)期末物理试卷

2018-2019学年广东省佛山市南海区八年级（上）期末物理试卷一、单选题（本大题7小题，每小题3分，共21分）1．（3分）对于声音的产生，下列说法正确的是（）A．只有固体的振动才能发声B．声音是由物体的振动产生的C．物体不振动也能发声D．振动停止后，发声体仍能发声2．（3分）图为探究光的反射规律的实验装置，下列描述中不合理的是（）A．可沿ON折叠的白色硬纸板应垂直放置于平面镜上B．为研究反射角与入射角间的关系，应多次改变光线AO与ON间的夹角C．为研究入射光线、反射光线和法线的位置关系，应绕ON前后折转入射光线所在的光屏ED．如果让光线沿着FO的方向射向镜面，会发现反射光线沿着OA方向射出，这表明光路是可逆的3．（3分）如图光现象中，由光的直线传播形成的是（）A．水面“折”笔B．彩虹C．树荫下圆形光斑D．白塔在水中的倒影4．（3分）如图所示的四种现象中，其物态变化属于升华的是（）A．吉林冬天树上的“雾凇”B．水蒸气在凉玻璃上形成水珠C．冬季，堆在户外的“雪人”没熔化却变小D．晾晒的湿衣服逐渐变干5．（3分）如图为航天员王亚平太空授课的情景，图中水球相当于一个透镜，假设水球的焦距为f，此时王亚平到水球的距离40cm，则下列说法正确的是（）A．f＜20cm B．40cm＞f＞20cmC．水球相当于一个凹透镜D．王亚平的像是虚像6．（3分）一汽车在公路上做匀速直线运动，如图正确表示汽车通过的路程与时间的关系是（）A．B．C．D．7．（3分）某研究性学习课题小组在老师的指导下，完成“水的体积随温度变化”的研究，得到如图所示的图象。

根据这个图象，可得到水的温度从8℃降到2℃的过程中有关水的变化的一些信息，下列说法中（）①水遵从热胀冷缩的规律②水的体积先变小后变大③水的密度先变小后变大④水在4℃时密度最大A．只有①正确B．②③正确C．②④正确D．①③正确二、填空题（本大题共7小题，共21分）8．（3分）许多男生在变声期后，说话时声带的振动频率比以前低，因而声音的会降低。

广东省佛山市南海区八年级上学期期末考试数学试题解析版

广东省佛山市南海区八年级上学期期末考试数学试题一、选择题（本大题共10小题，共30.0分）1.下列实数是无理数的是A. B. C. D.【答案】B【解析】解：是整数，属于有理数；B.是无理数；C.是有限小数，即分数，属于有理数；D.是分数，属于有理数；故选：B．无理数就是无限不循环小数理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称即有限小数和无限循环小数是有理数，而无限不循环小数是无理数由此即可判定选择项．此题主要考查了无理数的定义，其中初中范围内学习的无理数有：，等；开方开不尽的数；以及像，等有这样规律的数．2.下列各点中位于第四象限的点是A. B. C. D.【答案】C【解析】解：第四象限的点的坐标的符号特点为，观察各选项只有C符合条件，故选C．应先判断点在第四象限内点的坐标的符号特点，进而找相应坐标．本题主要考查了平面直角坐标系中各象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限；第二象限；第三象限；第四象限．3.以下列各组数据为三角形的三边，能构成直角三角形的是A. 1cm，2cm，3cmB. 2cm，2cm，2cmC. 4cm，2cm，2cmD. ，，1cm【答案】D【解析】解：A、，故不能构成直角三角形；B、，故不能构成直角三角形；C、，故不能构成直角三角形；D、，故能构成直角三角形；故选：D．由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可本题考查勾股定理的逆定理的应用判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可勾股定理的逆定理：若三角形三边满足，那么这个三角形是直角三角形．4.已知是方程的解，则k的值为A. B. 3 C. 5 D.【答案】B【解析】解：把代入方程得：，解得：，故选：B．把x与y的值代入方程计算即可求出k的值．此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．5.下列根式是最简二次根式的是B. C. D.【答案】D【解析】解：A．，不符合题意；B.，不符合题意；C.，不符合题意；D.是最简二次根式，符合题意；故选：D．判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．本题考查最简二次根式的定义根据最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．6.如图，三角形是直角三角形，四边形是正方形，已知正方形A的面积是64，正方形B的面积是100，则半圆C的面积是A. 36B.C.D.【答案】B【解析】解：正方形A的面积是64，正方形B的面积是100，，，由勾股定理得，，半圆C的面积，故选：B．根据正方形的性质分别求出DE，EF，根据勾股定理求出DF，根据圆的面积公式计算．本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么．7.下列说法错误的是A. 5是25的算术平方根B. 1的立方根是C. 没有平方根D. 0的平方根与算术平方根都是0【答案】B【解析】解：是25的算术平方根，此选项说法正确；B.1的立方根是1，此选项说法错误；C.没有平方根，此选项说法正确；D.0的平方根与算术平方根都是0，此选项说法正确；故选：B．根据算术平方根和平方根及立方根的定义逐一求解可得．本题主要考查立方根、平方根与算术平方根，解题的关键是熟练掌握算术平方根和平方根及立方根的定义．8.根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择A. 甲B. 乙C. 丙D. 丁【答案】A【解析】解：甲丙乙丁，从甲和丙中选择一人参加比赛，，甲乙丙丁选择甲参赛，故选：A．首先比较平均数，平均数相同时选择方差较小的运动员参加．此题考查了平均数和方差，正确理解方差与平均数的意义是解题关键．9.已知点，则点P到y轴的距离为A. 4B.C. 3D.【答案】A【解析】解：点，点P到y轴的距离为：4．故选：A．利用点的横坐标得出点P到y轴的距离．此题主要考查了点的坐标，正确理解点的横纵坐标的意义是解题关键．10.一次函数的大致图象如图所示，关于该次函数，下列说法错误的是A.B. y随x的增大而增大C. 该函数有最小值D. 函数图象经过第一、三、四象限【答案】C【解析】解：观察图象知：y随x的增大而增大，且交与y轴负半轴，函数图象经过第一、三、四象限，，解得：，该函数没有最小值，故选：C．根据一次函数的增减性确定有关k的不等式组，求解即可．本题考查了一次函数的图象与系数的关系，解题的关键是了解系数对函数图象的影响，难度不大．二、填空题（本大题共6小题，共24.0分）11.计算：______．【答案】4【解析】解：，，故答案为4．根据算术平方根的概念去解即可算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．12.已知点与点关于x轴对称，则______．【答案】【解析】解：点与点关于x轴对称，，，则，故答案为：．根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得a与b的值，再代入计算即可．此题主要考查了关于x轴对称点的坐标特点，关键是掌握点的坐标的变化规律．13.已知数据，，3，，2，3，1，，这组数据的众数是______．【答案】【解析】解：数据出现了4次，最多，众数为，故答案为：．根据众数的定义进行解答即可．此题考查了众数的知识，众数是一组数据中出现次数最多的数，众数可能不唯一．14.已知，则______．【答案】1【解析】解：，，则原式，故答案为：1．由已知等式得出，代入到原式计算可得．本题主要考查代数式的求值，解题的关键是掌握整体代入思想的运用．15.如图，在平面直角坐标系内，一次函数与正比例函数的图象相交于点A，且与x轴交于点B，点A的纵坐标为2，则根据图象可得二元一次方程组的解是______．【答案】【解析】解：当时，，解得，则，所以二元一次方程组的解是．故答案为．先利用直线的解析式确定A点坐标，然后根据方程组的解就是两个相应的一次函数图象的交点坐标求解．本题考查了一次函数与二元一次方程组：方程组的解就是两个相应的一次函数图象的交点坐标．16.如图是一个“螺旋形”图案，该图案是由一连串直角三角形演化而成的，其中，，则的面积为______．【答案】【解析】解：，，，，，，，，的面积，故答案为：．根据勾股定理求出各斜边的长，然后根据三角形的面积公式即可得到结论．此题主要考查的是勾股定理的运用，三角形的面积，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键三、解答题（本大题共9小题，共66.0分）17.计算：【答案】解：原式．【解析】先根据二次根式的乘除法则运算，然后化简后合并即可．本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．18.如图，已知，若，，求的度数．【答案】解：，，又，．【解析】依据平行线的性质，即可得到，再根据三角形外角性质，即可得到的度数．本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等．19.在直角坐标系内的位置如图．请在这个坐标系内画出，使与关于x轴对称；求线段的长度．【答案】解：如图所示：，即为所求；线段的长度为：．【解析】直接利用关于x轴对称点的性质得出对应点位置即可；利用勾股定理进而得出答案．此题主要考查了轴对称变换以及勾股定理，正确得出对应点位置是解题关键．20.某商场计划购进A、B两种新型节能台灯共100盏，已知A型台灯的进价是元盏，B型台灯每台进价比A型台灯贵20元，若商场预计进货款为3500元，则这两种台灯各购进多少盏？【答案】解：设该商场购进A型台灯x台，B型台灯y台，依题意，得：，解得：．答：该商场购进A型台灯75台，B型台灯25台．【解析】设该商场购进A型台灯x台，B型台灯y台，根据总价单价数量结合用3500元共购进A、B两种新型节能台灯共100盏，即可得出关于x，y的二元一次方程组，解之即可得出结论．本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．21.如图所示，中．若：：：3：4，求的度数；若，，，求BC边上的高．【答案】解：设，，，由题意得，，解得，所以，，，，，，是直角三角形，边上的高．【解析】根据比例设，，，然后利用三角形的内角和等于列出方程，再求出k，从而得到即可；根据勾股定理的逆定理得出是直角三角形，进而解答即可．此题考查勾股定理问题，关键是根据勾股定理和其逆定理解答．22.为了解某校八年级体育科目训练情况，从八年级学生中随机抽取了部分学生进行了一次体育科目测试把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格，并将测试结果绘成了如下两幅不完整的统计图请根据统计图中的信息解答下列问题：图1中的度数是______，并把图2条形统计图补充完整．抽取的这部分的学生的体育科目测试结果的中位数是在______级；依次将优秀、良好、及格、不及格记为90分、80分、70分、50分，请计算抽取的这部分学生体育的平均成绩．【答案】C【解析】解：本次抽查的学生有：人，的度数是：，C级学生有：人，补全的条形统计图如右图所示，故答案为：；由统计图可得，抽取的这部分的学生的体育科目测试结果的中位数是在C级，故答案为：C；分，答：抽取的这部分学生体育的平均成绩是72分．根据统计图中的数据可以计算出本次抽查的学生数，从而可以求得的度数和C 级的学生数，从而可以将条形统计图补充完整；根据中补充完整的条形统计图和中位数的定义可以解答本题；根据题意和统计图中的数据可以计算出抽取的这部分学生体育的平均成绩．本题考查条形统计图、扇形统计图、中位数、加权平均数，解答本题的关键是明确题意，利用数形结合的思想解答．23.某游泳馆普通票价30元张，暑假为了促销，新推出一种优惠卡：售价300元张，每次凭卡另收15元暑假普通票正常出售，优惠卡仅限暑假使用，不限次数设游泳x次时，所需总费用为y元．分别写出选择优惠卡、普通票消费时，y与x之间的函数关系式；在同一坐标系中，若两种消费方式对应的函数图象如图所示，请求出点A、B的坐标；【答案】解：由题意可得，选择优惠卡时，y与x的函数关系式为：，当选择普通票时，y与x的函数关系式为：；将代入，得，即点A的坐标为，令，得，则，即点B的坐标为，由上可得，点A的坐标为，点B的坐标为．【解析】根据题意可以分别写出选择优惠卡、普通票消费时，y与x之间的函数关系式；根据题意可知，点A的坐标就是选择优惠卡时对应的函数解析式与y轴的交点，点B 的坐标就是两个函数交点的坐标，本题得以解决．本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．24.图是我们常见的基本图形，我们可以称之为“8”字形“8”字形有一个重要的性质如下：利用这个性质并结合你所学的知识解决以下问题：如图，，，直接写出的度数为______；如图，若BN、DN分别是、的角平分线，BN与DN交于点N、且，，求的度数；如图，若AM、BN、CM、DN分别是、、和的角平分线，AM与CM、BN交于点M、G，DN与BN、CM交于点N、H，且，求的度数．【答案】【解析】解：，，，，故答案为：．如图2，、DN分别是、的角平分线，，，又，，两式相减可得，，，即，又，，；如图3，、DN分别是、的角平分线，，，又，，两式相减可得，，，即，同理可得，，又，，．依据，，，即可得到的度数；依据BN、DN分别是、的角平分线，即可得到，，再根据8字形即可得到，，两式相减可得，，进而得到的度数；根据中的方法可得，，再根据，可得，进而得到．本题考查了三角形的内角和定理，角平分线的定义的综合运用注意利用对顶角相等和三角形内角和定理求出角的关系是解题的关键，要注意整体思想的利用．25.如图，已知直线：和直线：，过点作轴，交直线于点A，若点P是x轴上的一个动点，过点P作平行于y轴的直线，分别与、交于点C、D，连接AD、BC．直接写出线段______；当P的坐标是时，求直线BC的解析式；若的面积与的面积相等，求点P的坐标．【答案】【解析】解：轴且点A在直线上，将代入，得即点轴，将代入，得，故点C的坐标为设直线BC的解析式为：，将点C，点B代入得，解得故直线BC的解析式为：由题意得，当时，设点P的坐标为，解得或．点P的坐标为或轴且点A在直线上，点B的坐标为所以求出点A的坐标即可求AB 因轴于点P，点，点C在直线上，即可以求出点C的坐标，即可用待定系数法求直线BC的解析式因的面积与的面积相等，即时两三角形的面积相等，设点，则有，即可求出点P的坐标此题主要考查的是一次函数的图象及用待定系数法求直线的解析式，但要注意到三角形的边长与一次函数y值的区别．。

┃精选3套试卷┃2018届佛山市八年级上学期数学期末监测试题

八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．若一组数据2，3，，5，7的众数为7，则这组数据的中位数为( )A ．2B ．3C ．5D ．7【答案】C【解析】试题解析：∵这组数据的众数为7，∴x=7，则这组数据按照从小到大的顺序排列为：2，3，1，7，7，中位数为：1．故选C ．考点：众数；中位数.2．下列图形中，是轴对称图形的是（）． A ． B ． C ． D ．【答案】A【分析】轴对称图形的定义：图形沿某一条直线折叠后，直线两旁的部分重合，则这个图形是轴对称图形；根据轴对称图形定义，逐个判断，即可得到答案．【详解】四个选项中，A 是轴对称图形，其他三个不是轴对称图形；故选：A ．【点睛】本题考查了轴对称图形的知识；解题的关键是熟练掌握轴对称图形的定义，即可完成求解． 3．两人在直线跑道上同起点、同终点、同方向匀速跑步400米，先到终点的人原地休息．已知甲先出发2秒，在跑步过程中，甲、乙两人之间的距离y （米）与乙出发的时间t （秒）之间的关系如图所示给出以下结论：①8a =；②72b =；③98c =．其中正确的是（）A ．②③B ．①②③C ．①②D ．①③【答案】B 【分析】易得乙出发时，两人相距8m ，除以时间2即为甲的速度；由于出现两人距离为0的情况，那么乙的速度较快．乙80s 跑完总路程400可得乙的速度，进而求得80s 时两人相距的距离可得b 的值，同法求得两人距离为0时，相应的时间，让两人相距的距离除以甲的速度，减2即为c 的值．【详解】由函数图象可知，甲的速度为824÷=（米/秒），乙的速度为400805÷=（米/秒），8(54)8∴÷-=（秒），8a ∴=，故①正确；5804(802)400328b =⨯-⨯+=-72=（米）故②正确；4004298c =÷-=（秒）故③正确；∴正确的是①②③．故选B ．【点睛】本题考查了一次函数的应用，得到甲乙两人的速度是解决本题的突破点，得到相应行程的关系式是解决本题的关键．4．估计10+1的值应在（）A ．3和4之间B ．4和5之间C ．5和6之间D ．6和7之间【答案】B【解析】解：∵3104<<，∴41015<+<．故选B ．点睛：此题主要考查了估算无理数的大小，正确得出10 的取值范围是解题关键．5．点P （﹣3，﹣4）位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】根据第三象限内点的横坐标小于零，纵坐标小于零，可得：点P （﹣3，﹣4）位于第三象限. 故选C.6．如图，矩形纸片ABCD 中，已知AD =8，折叠纸片使AB 边与对角线AC重合，点B 落在点F 处，折痕为AE ，且EF=3，则AB 的长为( )A ．3B ．4C ．5D ．6【答案】D 【解析】试题分析：先根据矩形的特点求出BC 的长，再由翻折变换的性质得出△CEF 是直角三角形，利用勾股定理即可求出CF 的长，再在△ABC 中利用勾股定理即可求出AB 的长．解：∵四边形ABCD 是矩形，AD=8，∴BC=8，∵△AEF 是△AEB 翻折而成，∴BE=EF=3，AB=AF ，△CEF 是直角三角形，∴CE=8﹣3=5，在Rt △CEF 中，CF===4，设AB=x ，在Rt △ABC 中，AC 2=AB 2+BC 2，即（x+4）2=x 2+82，解得x=6，故选D ．考点：翻折变换（折叠问题）；勾股定理．7．如图，BM 是ABC ∆的角平分线，D 是BC 边上的一点，连接AD ，使AD DC =，且130BAD ∠=︒，则AMB ∠的度数是（）A ．20︒B ．22.5︒C ．25︒D ．30【答案】C 【分析】根据∠AMB ＝∠MBC ＋∠C ，想办法求出∠MBC ＋∠C 即可．【详解】解：∵DA ＝DC ，∴∠DAC ＝∠C ，∵∠ADB ＝∠C ＋∠DAC ，∴∠ADB ＝2∠C ，∵MB 平分∠ABC ，∴∠ABM ＝∠DBM ，∵∠BAD ＝130°，∴∠ABD ＋∠ADB ＝50°，∴2∠DBM ＋2∠C ＝50°，∴∠MBC ＋∠C ＝25°，∴∠AMB ＝∠MBC ＋∠C ＝25°，故选：C ．【点睛】本题考查三角形内角和定理、三角形的外角的性质、等腰三角形的性质，角平分线的定义等知识，解题的关键是灵活运用所学知识解决问题．8．已知ABC ∆的三边长分别为a b c 、、，且()()()M a b c a b c a b c =+++---那么( )A ．0M >B ．0M ≥C ．0M =D ．0M <【答案】D【分析】根据三角形的三边关系即可求解.【详解】∵ABC ∆的三边长分别为a b c 、、∴a b c ++＞0，a b c +-＞0，a b c --＜0∴()()()M a b c a b c a b c =+++---＜0故选D.【点睛】此题主要考查三角形的三边关系的应用，解题的关键是熟知两边之和大于第三边.9．如图，已知ABC ∆，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF CA =；连接DE 、EF 、FD ，得DEF ∆.若ABC ∆的面积为k ，则DEF ∆的面积为( )A ．10kB ．15kC ．18kD ．20k【答案】C 【分析】如图所示：连接AE 、CD,要求△DEF 的面积，可以分三部分来计算，利用高一定时，三角形的面积与高对应的底成正比的关系进行计算；利用已知△ABC 的面积k 计算与它同高的三角形的面积，然后把所求各个面积相加即可得出答案．【详解】如图所示：连接AE 、CD∵BD ＝AB∴S △ABC ＝S △BCD ＝k则S △ACD ＝2 k∵AF ＝3AC∴FC ＝4AC∴S △FCD ＝4S △ACD ＝4×2k ＝8k同理求得：S △ACE ＝2S △ABC ＝2kS △FCE ＝4S △ACE ＝4×2k ＝8kS △DCE ＝2S △BCD ＝2×k ＝2k∴S △DEF ＝S △FCD ＋S △FCE ＋S △DCE ＝8k ＋8k ＋2k ＝18 k故选：C【点睛】本题主要考查三角形的面积与底的正比关系的知识点：当高相同时，三角形的面积与高对应的底成正比的关系，掌握这一知识点是解题的关键．10．从边长为a 的正方形内去掉-一个边长为b 的小正方形(如图1)，然后将剩余部分剪拼成一个矩形（如图2），上述操作所能验证的等式是（）A ．()2222a b a ab b -=-+B ．()()22a b a b a b -=+-C ．()2222a b a ab b +=++D ．()2a ab a a b +=+ 【答案】B 【分析】分别求出从边长为a 的正方形内去掉一个边长为b 的小正方形后剩余部分的面积和拼成的矩形的面积，根据面积相等即可得出算式，即可选出选项．【详解】解：∵从边长为a 的正方形内去掉一个边长为b 的小正方形，剩余部分的面积是：22a b -，拼成的矩形的面积是：()()a b a b +-，∴根据剩余部分的面积相等得：()()22a b a b a b -=+-，故选：B ．二、填空题11．一次函数的图象经过点(0,2)-，且函数y 的值随自变量x 的增大而增大，请写出一个符合条件的一次函数表达式_________________.【答案】y=x-2【分析】设y=kx+b ，根据一次函数的图象经过点(0,2)-，且函数y 的值随自变量x 的增大而增大，可得：b=-2，且k>0，即可得到答案.【详解】设y=kx+b ，∵一次函数的图象经过点(0,2)-，且函数y 的值随自变量x 的增大而增大，∴b=-2，且k>0，∴符合条件的一次函数表达式可以是：y=x-2（答案不唯一）.故答案是：y=x-2【点睛】本题主要考查待定系数法求一次函数解析式以及一次函数的性质，掌握一次函数的系数的意义，是解题的关键.12．已知长为a 、宽为b 的长方形的周长为16，面积为15，则22a b ab +=__________．【答案】1【分析】根据长方形的周长公式和面积公式可得2（a+b ）=16，ab=15，从而求出a+b=8，然后将多项式因式分解，最后代入求值即可．【详解】解：∵长为a 、宽为b 的长方形的周长为16，面积为15∴2（a+b ）=16，ab=15∴a+b=8∴()22158120a b ab ab a b +=+=⨯= 故答案为：1．【点睛】此题考查的是长方形的周长公式、面积公式和因式分解，掌握长方形的周长公式、面积公式和用提公因式法因式分解是解决此题的关键．13．如图，AB ＝AC ，∠C ＝36°，AC 的垂直平分线MN 交BC 于点D ，则∠DAB ＝_____．【答案】72°【解析】根据等腰三角形的性质得到∠B ＝∠C ＝36°，由线段垂直平分线的性质得到CD ＝AD ，得到∠CAD ＝∠C ＝36°，根据外角的性质得到∠ADB ＝∠C+∠CAD ＝72°，根据三角形的内角和即可得到结论．【详解】解：∵AB ＝AC ，∠C ＝36°，∴∠B ＝∠C ＝36°，∵AC的垂直平分线MN交BC于点D，∴CD＝AD，∴∠CAD＝∠C＝36°，∴∠ADB＝∠C+∠CAD＝72°，∴∠DAB＝180°﹣∠ADB﹣∠B＝72°，故答案为72°【点睛】本题考查了等腰三角形的性质，线段垂直平分线的性质，熟练掌握等腰三角形的性质是解题的关键．14．分解因式：（1）3a2-6a+3=________；（2）x2+7x+10 = _______．【答案】3（a-1）2(x+2)(x+5)【分析】（1）原式提取公因式，再利用完全平方公式分解即可；（2）原式利用十字相乘法分解即可．【详解】解：（1）3a2-6a+3=3（a2-2a+1）=3（a-1）2(2)x2+7x+10 =(x+2)(x+5)故答案为：3（a-1）2；（x+2）（x+5）【点睛】此题考查了提公因式法，公式法及十字相乘法分解因式，熟练掌握因式分解的方法是解本题的关键．15．小明同学在计算一个多边形(每个内角小于180°)的内角和时，由于粗心少算一个内角，结果得到的和是2020°，则少算了这个内角的度数为_________．【答案】140°【分析】n边形的内角和是（n−2）•180°，少计算了一个内角，结果得2020°，则内角和是（n−2）•180°与2020°的差一定小于180度，并且大于0度．因而可以解方程（n−2）•180°≥2020°，多边形的边数n一定是最小的整数值，从而求出多边形的边数，内角和，进而求出少计算的内角．【详解】设多边形的边数是n，依题意有（n−2）•180°≥2020°，解得：n≥1329，则多边形的边数n＝14；多边形的内角和是（14−2）•180＝2160°；则未计算的内角的大小为2160°−2020°＝140°．故答案为：140°．【点睛】本题主要考查了多边形的内角和定理，正确确定多边形的边数是解题的关键．16．碳纳米管的硬度与金刚石相当，却拥有良好的柔韧性，可以拉伸，我国某物理所研究组已研制出直径为0.5纳米的碳纳米管，已知1纳米0.000000001=米，则0.5纳米用科学记数法表示为_____________米．【答案】5×1−1【分析】0.5纳米＝0.5×0.000000001米＝0.0000000005米．小于1的正数也可以利用科学记数法表示，一般形式为a ×1−n ，在本题中a 为5，n 为5前面0的个数．【详解】解：0.5纳米＝0.5×0.000 000 001米＝0.000 000 000 5米＝5×1−1米．故答案为：5×1−1．【点睛】用科学记数法表示较小的数，一般形式为a ×1−n ，其中1≤|a|＜1，n 为由原数左边起第一个不为零的数字前面的0的个数．注意应先把0.5纳米转化为用米表示的数．17．在等腰ABC ∆中，若40A ∠=，则B ∠=__________度．【答案】40°或70°或100°．【分析】分为两种情况：（1）当∠A 是底角，①AB=BC ，根据等腰三角形的性质求出∠A=∠C=40°，根据三角形的内角和定理即可求出∠B ；②AC=BC ，根据等腰三角形的性质得到∠A=∠B=40°；（2）当∠A 是顶角时，AB=AC ，根据等腰三角形的性质和三角形的内角和定理即可求出∠B ．【详解】（1）当∠A 是底角，①AB=BC ，∴∠A=∠C=40°，∴∠B=180°-∠A-∠C=100°；②AC=BC ，∴∠A=∠B=40°；（2）当∠A 是顶角时，AB=AC ，∴∠B=∠C=12（180°-∠A ）=70°；故答案为：40°或70°或100°．【点睛】本题主要考查对等腰三角形的性质，三角形的内角和定理等知识点的理解和掌握，能进行分类讨论，并求出各种情况的时∠B 的度数是解此题的关键．三、解答题18．如图，在平面直角坐标系中，直线AB 分别交x 轴、y 轴于点()0A a ，点，()0B b ，，且a b 、满足24420a a a b -++-=，点P 在直线AB 的左侧，且45APB ∠=．（1）求a b 、的值；（2）若点P 在x 轴上，求点P 的坐标；（3）若ABP ∆为直角三角形，求点P 的坐标．【答案】（1）a ＝2，b ＝1；（2）P （1，0）；（3）P （﹣1，2）或（﹣2，﹣2）．【分析】（1）将244a a -+利用完全平方公式变形得到（a-2）2+|2a-b|＝0，即可求出a 、b 的值；（2）由b 的值得到OB=1，根据45APB ∠=得到OP=OB=1，即可得到点P 的坐标；（3）由45APB ∠=可分两种情况求使ABP ∆为直角三角形，当∠ABP ＝90°时，当∠BAP ＝90°时，利用等腰三角形的性质证明三角形全等，由此得到点P 的坐标.【详解】（1）∵a 2-1a+1+|2a-b|＝0，∴（a-2）2+|2a-b|＝0，∴a ＝2，b ＝1．（2）由（1）知，b ＝1，∴B （0，1）．∴OB ＝1．∵点P 在直线 AB 的左侧，且在 x 轴上，∠APB ＝15°∴OP ＝OB ＝1，∴P （1，0）．（3）由（1）知 a ＝﹣2，b ＝1，∴A （2,0），B （0,1）∴OA ＝2，OB ＝1，∵△ABP 是直角三角形，且∠APB ＝15°，∴只有∠ABP ＝90°或∠BAP ＝90°，如图，①当∠ABP＝90°时，∵∠BAP＝15°，∴∠APB＝∠BAP＝15°.∴AB＝PB .过点P 作PC⊥OB 于C，∴∠BPC+∠CBP＝90°，∵∠CBP+∠ABO＝90 °，∴∠ABO＝∠BPC .在△AOB 和△BCP 中，AOB BCP90ABO BPCAB PB︒⎧∠=∠=⎪∠=∠⎨⎪=⎩，∴△AOB≌△BCP(AAS) .∴PC＝OB＝1，BC＝OA＝2 .∴OC＝OB﹣BC＝2.∴P(-1，2)②当∠BAP＝90°时，过点P'作P'D⊥OA于D，同①的方法得，△ADP'≌△BOA.∴DP'＝OA＝2，AD＝OB＝1.∴OD＝AD﹣OA＝2.∴P'（﹣2，-2）.即：满足条件的点P（﹣1，2）或（﹣2，﹣2）.【点睛】此题考查等腰直角三角形的性质，完全平方公式，三角形全等的判定及性质，分类讨论直角三角形形成的点的坐标.19．已知120MAN ∠=︒，AC 平分MAN ∠，点,B D 分别在,AN AM 上．（1）如图1，若CD AM ⊥于点D ，CB AN ⊥于点B ．①利用等腰三角形“三线合一”，将ADC ∆补成一个等边三角形，可得,AC AD 的数量关系为________． ②请问：AC 是否等于AB AD +呢？如果是，请予以证明．（2）如图2，若180ABC ADC ∠+∠=︒，则（1）中的结论是否仍然成立？若成立，请予以证明；若不成立，请说明理由．【答案】（1）①12AD AC =（或2AC AD =），理由见解析；②AD AB AC +=，理由见解析；（2）仍成立，理由见解析【分析】（1）①由题意利用角平分线的性质以及含30角的直角三角形性质进行分析即可；②根据题意利用①的结论进行等量代换求解即可；（2）根据题意过点C 分别作,AM AN 的垂线，垂足分别为,E F ，进而利用全等三角形判定得出()CED CFB AAS ∆≅∆，以此进行分析即可．【详解】解：（1）①12AD AC =（或2AC AD =） AC 平分,120MAN MAN ∠∠=︒，60CAD ∴∠=︒，又90ADC ∠=︒，30ACD ∴∠=︒利用等腰三角形“三线合一”，将ADC ∆补成一个等边三角形，可知12AD AC = ②AD AB AC += 证明：由①知，12AD AC =同理，AC 平分,120MAN MAN ∠∠=︒，60CAB ∴∠=︒，又90ABC ∠=︒，30ACB ∴∠=︒,12AB AC = AD AB AC ∴+=（2）仍成立证明：过点C 分别作,AM AN 的垂线，垂足分别为,E FAC 平分,MAN ∠CE CF ∴=，180,180ABC ADC ADC CDE ∠+∠=︒∠+∠=︒CDE ABC ∴∠=∠又90CED CFB ∠=∠=︒()CED CFB AAS ∴∆≅∆ED FB ∴=AD AB AE ED AF FB AE AF ∴+=-++=+由（1）中②知AE AF AC +=AD AB AC ∴+=．【点睛】本题考查等腰三角形性质以及全等三角形判定，熟练掌握角平分线的性质以及含30角的直角三角形性质和全等三角形判定定理是解题的关键．20．如图，E ，F 分别是等边三角形ABC 的边AB ，AC 上的点，且BE ＝AF ，CE ，BF 交于点P.（1）求证：BF ＝CE ；（2）求∠BPC 的度数．【答案】（1）见解析；（2）见解析．【分析】（1）先根据等边三角形和已知条件证明△ABF ≌△BCE ，然后根据全等三角形的性质证明即可；（2）先证明∠ABF=∠BCE ，再运用等量代换说明∠BCE+∠FBC=60°，最后根据三角形内角和定理即可解答．【详解】（1）证明：∵△ABC 是等边三角形,A EBC AB BC ∴∠=∠=在△ABF 和△BCE 中AF BE A EBC AB BC =⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△BCE∴BF=CE ；（2）∵△ABF ≌△BCE∴∠ABF=∠BCE∵∠ABF+∠FBC=60°∴∠BCE+∠FBC=60°∴∠BPC=180°-（∠BCE+∠FBC ）=180°-60°=120°．【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质以及三角形内角和定理，灵活应用相关知识成为解答本题的关键．21．如图在等腰三角形△ABC 中，AC=BC ，D 、E 分别为AB 、BC 上一点，∠CDE=∠A ．（1）如图①，若BC=BD ，求证：CD=DE ；（2）如图②，过点C 作CH ⊥DE ，垂足为H ，若CD=BD ，EH=1，求DE ﹣BE 的值．【答案】（1）证明见解析（1）1【解析】试题分析：（1）先根据条件得出∠ACD=∠BDE ，BD=AC ，再根据ASA 判定△ADC ≌△BED ，即可得到CD=DE ；（1）先根据条件得出∠DCB=∠CDE ，进而得到CE=DE ，再在DE 上取点F ，使得FD=BE ，进而判定△CDF ≌△DBE （SAS ），得出CF=DE=CE ，再根据CH ⊥EF ，运用三线合一即可得到FH=HE ，最后得出DE ﹣BE=DE ﹣DF=EF=1HE=1．试题解析：（1）∵AC=BC ，∠CDE=∠A ，∴∠A=∠B=∠CDE ，∴∠ACD=∠BDE ，又∵BC=BD ，∴BD=AC ，在△ADC 和△BED 中，，∴△ADC≌△BED（ASA），∴CD=DE；（1）∵CD=BD，∴∠B=∠DCB，又∵∠CDE=∠B，∴∠DCB=∠CDE，∴CE=DE，如图，在DE上取点F，使得FD=BE，在△CDF和△DBE中，，∴△CDF≌△DBE（SAS），∴CF=DE=CE，又∵CH⊥EF，∴FH=HE，∴DE﹣BE=DE﹣DF=EF=1HE=1．22．已知：如图，一次函数y=34x+3的图象分别与x轴、y轴相交于点A、B，且与经过点C(2，0)的一次函数y=kx+b的图象相交于点D，点D的横坐标为4，直线CD与y轴相交于点E．(1)直线CD的函数表达式为______；(直接写出结果)(2)在x轴上求一点P使△PAD为等腰三角形，直接写出所有满足条件的点P的坐标．(3)若点Q为线段DE上的一个动点，连接BQ．点Q是否存在某个位置，将△BQD沿着直线BQ翻折，使得点D恰好落在直线AB下方的y轴上？若存在，求点Q的坐标；若不存在，请说明理由．【答案】(1)y=3x-6；(2)点P的坐标为(94，0)或(6，0)或(-14，0)或(12，0)；(3)存在，点Q的坐标为(187，117)【分析】(1)求出D的坐标，即可求解；(2)分PA=PD、当PA=AD、DP=AD三种情况，分别求解即可；(3)利用BD=BD′，DQ=D′Q，即可求解．【详解】解：(1)将点D的横坐标为4代入一次函数y=34x+3表达式，解得：y=6，即点D的坐标为(4，6)，将点C、D的坐标代入一次函数表达式y=kx+b得：64 02,k bk b=+⎧⎨=+⎩解得：36, kb=⎧⎨=-⎩故答案为y=3x-6；(2)①当PA=PD时，点B是AD的中点，故：过点B且垂直于AD的直线方程为：y=-43x+3，令y=0，则x=94，即点P的坐标为(94，0)；②当PA=AD时，=10，故点P的坐标为(6，0)或(-14，0)；③当DP=AD时，同理可得：点P的坐标为(12，0)；故点P的坐标为(94，0)或(6，0)或(-14，0)或(12，0)；(3)设翻转后点D落在y轴上的点为D′，设点Q的坐标为(x，3x-6)，则：BD=BD′，DQ=D′Q，=5，故点D′的坐标为(0，-2)，DQ2=D′Q2，即：x2+(3x-6+2)2=(x-4)2+(3x-6-6)2，解得：x=187，故点Q的坐标为(187，117)．【点睛】本题考查的是一次函数的综合运用，涉及到图象翻折、勾股定理运用等知识点，其中(2)要分类讨论，避免遗漏．23．节能又环保的油电混合动力汽车，既可以用油做动力行驶，也可以用电做动力行驶，某品牌油电混合动力汽车从甲地行驶到乙地，若完全用油做动力行驶，则费用为80元；若完全用电做动力行驶，则费用为30元，已知汽车行驶中每千米用油费用比用电费用多0.5元．(1)求：汽车行驶中每千米用电费用是多少元？甲、乙两地的距离是多少千米？(2)若汽车从甲地到乙地采用油电混合动力行驶，且所需费用不超过50元，则至少需要用电行驶多少千米？【答案】(1)每千米用电费用是0.3元，甲、乙两地的距离是100千米；(2)至少需要用电行驶60千米．【分析】(1)根据从甲地行驶到乙地的路程相等列出分式方程解答即可；(2)根据所需费用不超过50元列出不等式解答即可．【详解】解：(1)设汽车行驶中每千米用电费用是x元，则每千米用油费用为(x+0.5)元，可得：8030x0.5x=+，解得：x=0.3，经检验x=0.3是原方程的解，∴汽车行驶中每千米用电费用是0.3元，甲、乙两地的距离是30÷0.3=100千米；至少需要用电行驶60千米．(2)汽车行驶中每千米用油费用为0.3+0.5=0.8元，设汽车用电行驶ykm，可得：0.3y+0.8(100-y)≤50，解得：y≥60，所以至少需要用电行驶60千米．【点睛】本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：(1)找准等量关系，正确列出分式方程；(2)根据各数量间的关系，正确列出一元一次不等式．24．（列二元一次方程组求解）班长安排小明购买运动会的奖品，下面对话是小明买回奖品时与班长的对话情境：小明说：“买了两种不同的笔记本共50本，单价分别是5元和9元，我给了400元，现在找回88元．”班长说：“你肯定搞错了．”小明说：“我把自己口袋里的18元一起当作找回的钱款了．”班长说：“这就对啦！”请根据上面的信息，求两种笔记本各买了多少本？【答案】两种笔记本各买30本，20本【分析】分析题目中给出的条件，设两种笔记本各买x本、y本，列出方程组解答即可．【详解】解：设两种笔记本各买x本、y本，根据题意得50594008818x y x y +=⎧⎨+=-+⎩ 解得3020x y =⎧⎨=⎩ 答：两种笔记本各买30本，20本．【点睛】本题主要考查二元一次方程组的应用，根据题意列出方程组是解题的关键．25．分解因式：2363x x -+．【答案】23(1)x -【分析】先提取公因式3，再根据完全平方公式进行二次分解，即可得到答案.【详解】解：原式=3（x 1-1x+1）=3（x-1）1．【点睛】本题考查了提公因式法，公式法分解因式，提取公因式后利用完全平方公式进行二次分解，注意分解要彻底．八年级上学期期末数学试卷一、选择题（每题只有一个答案正确）1．化简－5a·(2a 2－ab)，结果正确的是( )A ．－10a 3－5abB ．－10a 3－5a 2bC ．－10a 2＋5a 2bD ．－10a 3＋5a 2b 【答案】D【解析】试题分析：根据单项式乘以多项式的计算法则进行计算，原式=32105a a b -+，故选D ． 2．二次三项式212x mx --（m 是整数），在整数范围内可分为两个一次因式的积，则m 的所有可能值有（）个A ．4B ．5C ．6D ．8 【答案】C【分析】根据十字相乘法的分解方法和特点可知：m -的值应该是12-的两个因数的和，即11,11,4,4,1,1,---即得m 的所有可能值的个数．【详解】121122634-=-⨯=-⨯=-⨯，m ∴- 的可能值为：112,26,34,112,26,34,-+-+-+---故m 的可能值为：11,11,4,4,1,1,--- 共6个，故选：C ．【点睛】考查了十字相乘法分解因式，对常数项的不同分解是解本题的关键，注意所求结果是值的个数．3．在2、0.3•、227-中，无理数的个数有（） A ．1个B ．2个C ．3个D ．4个【答案】A【分析】根据无理数的三种形式，①开方开不尽的数，②无限不循环小数，③含有π的数，结合题意判断即可．【详解】解：在实数2、•0.3、227-2是无理数； •0.3循环小数，是有理数；227-是分数，是有理数；，是整数，是有理数；所以无理数共1个．故选：A ．【点睛】此题考查了无理数的概念，解答本题的关键是掌握无理数的定义，属于基础题，要熟练掌握无理数的三种形式，难度一般．4．已知21x y =⎧⎨=⎩是方程2x －ay ＝5的一个解，则2a 的值为（） A ．14B ．4C ．25D ．1 【答案】D【分析】把x 与y 的值代入方程计算求出a 的值，代入原式计算即可求出值．【详解】把21x y =⎧⎨=⎩代入方程得：4﹣a ＝5，解得：a ＝﹣1，则22=(1)a -＝1，故选：D ．【点睛】此题考查了二元一次方程的解，方程的即为能使方程左右两边相等的未知数的值．5．石墨烯目前是世界上最稀薄却也是最坚硬的纳米材料，同时还是导电性最好的材料，其理论厚度仅0.00000000034米，将这个数用科学计算法表示为（）A ．90.3410-⨯B ．93.410-⨯C ．103.410-⨯D ．113.410-⨯ 【答案】C【分析】根据科学记数法的表示形式对数值进行表示即可．【详解】解：0.00000000034=103.410-⨯，故选：C ．【点睛】本题考查了科学记数法，掌握科学记数法的表示形式是解题关键．6．在下列长度的四根木棒中，能与4cm ，9cm 长的两根木棒钉成一个三角形的是（） A ．3cmB ．8cmC ．13cmD ．16cm 【答案】B【分析】首先设第三根木棒长为xcm ，根据三角形的三边关系定理可得9−4＜x ＜9＋4，计算出x 的取值范围，然后可确定答案．【详解】设第三根木棒长为xcm ，由题意得：9−4＜x ＜9＋4，5＜x ＜13，故选B ．【点睛】此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边．三角形的两边差小于第三边． 7．8的平方根为（）A ．2B ．-2C ．22±D ．22【答案】C【解析】直接根据平方根的定义求解即可．【详解】解：∵2(22)8±=，∴8的平方根为22±，故答案为：C ．【点睛】本题考查了平方根的概念，牢记平方根的概念是解题的关键．8．如图，已知数轴上点P 表示的数为1-，点A 表示的数为1，过点A 作直线l 垂直于PA ，在l 上取点B ，使1AB =，以点P 为圆心，以PB 为半径作弧，弧与数轴的交点C 所表示的数为（）A 5B 51C 51D ．51【答案】B 【分析】由数轴上点P 表示的数为1-，点A 表示的数为1，得PA=2，根据勾股定理得5PB ，进而即可得到答案．【详解】∵数轴上点P 表示的数为1-，点A 表示的数为1，∴PA=2，又∵l ⊥PA ，1AB =，∴225PB PA AB +∵5∴数轴上点C 51．【点睛】本题主要考查数轴上点表示的数与勾股定理，掌握数轴上两点之间的距离求法，是解题的关键． 9．若x 2+mxy+4y 2是一个完全平方式，那么m 的值是（）A ．±4B ．﹣2C ．±2D ．4 【答案】A【分析】先根据两平方项确定出这两个数，再根据完全平方公式的乘积二倍项即可确定m 的值．【详解】∵x 2+mxy+1y 2＝x 2+mxy+（2y ）2，∴mxy ＝±2x×2y ，解得：m ＝±1．故选：A ．【点睛】本题主要考查了完全平方式，根据平方项确定出这两个数是解题的关键．10．已知点M 到x 轴的距离为3，到y 轴距离为2，且在第四象限内，则点M 的坐标为（） A ．（2，3）B ．（2，-3）C ．（3，-2）D ．不能确定【答案】B【分析】根据第四象限内的点的坐标第四象限（+，-），可得答案．【详解】解：M 到x 轴的距离为3，到y 轴距离为2，且在第四象限内，则点M 的坐标为（2，-3），故选：B ．【点睛】本题考查了点的坐标，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．二、填空题11．直线21y x =-沿x 轴向右平移3个单位长度后与两坐标轴所围成的三角形面积等于______________．【答案】12.25【分析】根据“平移k 不变，b 值加减”可以求得新直线方程；根据新直线方程可以求得它与坐标轴的交点坐标，所以由三角形的面积公式可以求得该直线与两坐标轴围成的三角形的面积．【详解】解：平移后解析式为：2(3)127,y x x =--=-当x=0时，7y =-，当y=0时，72x =， ∴平移后得到的直线与两坐标轴围成的三角形的面积为：17712.25.22⨯⨯= 故答案是：12.25．本题考查了一次函数图象与几何变换．直线平移变换的规律：上下移动，上加下减；左右移动，左加右减，掌握其中变与不变的规律是解决直线平移变换的关键．12．已知△ABC为等边三角形，BD为△ABC的高，延长BC至E，使CE=CD=1，连接DE，则BE=___________，∠BDE=_________ ．【答案】1120°【分析】根据等腰三角形和10度角所对直角边等于斜边的一半，得到BC的长，进而得到BE的长，根据三角形外角性质求出∠E=∠CDE=10°，进而得出∠BDE的度数．【详解】∵△ABC为等边三角形，∴∠ABC=∠ACB=60°，AB=BC．∵BD为高线，∴∠BDC=90°，∠DBC12∠ABC=10°，∴BC=2DC=2，∴BE=BC+CE=2+1=1．∵CD=CE，∴∠E=∠CDE．∵∠E+∠CDE=∠ACB=60°，∴∠E=∠CDE=10°，∴∠BDE=∠BDC+∠CDE=120°．故答案为：1，120°．【点睛】本题考查了等边三角形性质，含10度角的直角三角形的性质，等腰三角形性质，三角形的外角性质等知识点的应用，关键是求出BD的长．13．已知：如图，在长方形ABCD中，AB＝4，AD＝1．延长BC到点E，使CE＝2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为__秒时，△ABP和△DCE全等．【答案】1或2【分析】分两种情况进行讨论，根据题意得出BP=2t=2或AP=11-2t=2即可求得结果．【详解】因为AB＝CD，若∠ABP＝∠DCE＝90°，BP＝CE＝2，根据SAS证得△ABP≌△DCE，因为AB＝CD，若∠BAP＝∠DCE＝90°，AP＝CE＝2，根据SAS证得△BAP≌△DCE，由题意得：AP＝11﹣2t＝2，解得t＝2．所以，当t的值为1或2秒时．△ABP和△DCE全等．故答案为：1或2．【点睛】本题考查了全等三角形的判定，要注意分类讨论．14．等腰三角形的一个角是50°，则它的顶角等于°．【答案】50°或80°【分析】等腰三角形一内角为50°，没说明是顶角还是底角，所以有两种情况．【详解】（1）当50°为顶角，顶角度数即为50°；（2）当50°为底角时，顶角=18025080︒-⨯︒=︒．故答案为：50°或80︒.考点：等腰三角形的性质．15．若多项式241x mx++是一个完全平方式，则m的值为______．【答案】±1【分析】先根据两平方项确定出这两个数，再根据完全平方公式的乘积二倍项即可确定m的值．【详解】∵1x2+mx+1=（2x）2+mx+12，∴mx=±2×2x×1，解得m=±1．故答案为：±1．【点睛】考查了完全平方式，解题的关键是熟记完全平方公式，并根据平方项确定出这两个数．16．某班数学兴趣小组对不等式组3xx a>⎧⎨≤⎩，讨论得到以下结论：①若a＝5，则不等式组的解集为3<x≤5；②若a＝2，则不等式组无解；③若不等式组无解，则a的取值范围为a<3；④若不等式组只有两个整数解，则a的值可以为5.1,其中，正确的结论的序号是____．【答案】①，②，④.【解析】（1）把a＝5代入不等式组，解不等式组的解集与选项解集对照即可解答；（2）把a＝2代入不等式组，解不等式组，根据大大小小无解从而确定改选项正确；（3）根据不等式组无解，确定a的取值范围为a≤3；（4）根据不等式组只有两个整数解，可知这两个整数解为：x=3,x=4，所以x的取值范围是：3<x≤5.1. 【详解】解：①a=5,则不等式组的解集为3<x≤5，所以①正确；②a=2,x的取值范围是x>3和x≤2,无解，所以②正确；④若a=5.1则，x的取值范围是：3<x≤5.1,整数解为：x=4,x=5，共有两个解．故答案为①，②，④.【点睛】本题考查一元一次不等式的解法、整数解及解集判定，解题关键是熟练掌握同大取大、同小取小、大小小大中间找、大大小小找不到.17．若代数式1x-在实数范围内有意义，则x的取值范围是_______．【答案】1x≥【解析】先根据二次根式有意义的条件列出关于x的不等式，求出x的取值范围即可．解：∵1x-在实数范围内有意义，∴x-1≥2，解得x≥1．故答案为x≥1．本题考查的是二次根式有意义的条件，即被开方数大于等于2．三、解答题18．如图，车高4m（AC＝4m），货车卸货时后面支架AB弯折落在地面A1处，经过测量A1C＝2m，求弯折点B与地面的距离．【答案】弯折点B与地面的距离为32米【分析】设BC＝xm，则AB＝A1B＝（4﹣x）m，在Rt△A1BC中利用勾股定理列出方程22+x2＝（4﹣x）2即可求解．【详解】由题意得，AB＝A1B，∠BCA＝90°，设BC＝xm，则AB＝A1B＝（4﹣x）m，在Rt△A1BC中，A1C2+BC2＝A1B2，即：22+x2＝（4﹣x）2，解得：x＝32，答：弯折点B与地面的距离为32米．【点睛】本题考查勾股定理，解题的关键是掌握勾股定理的应用.。

∥3套精选试卷∥2018年佛山市八年级上学期物理期末综合测试试题

初二上学期期末物理试卷一、选择题1．一个放大镜的焦距为8cm，张大爷用此放大镜来观察药品使用说明书上较小的文字时，放大镜与药品使用说明书之间的距离应A．小于8cm B．等于8cm C．大于8cm D．在8cm和16cm之间【答案】A【详解】放大镜实际上是一个凸透镜，凸透镜的焦距是8cm，张大爷用此放大镜来观察药品使用说明书上较小的文字时，放大镜与药品使用说明书之间的距离应小于凸透镜的一倍焦距，即小于8cm。

故选A。

2．下列做法属于在传播途径中控制噪声的是（）A．汽车进入市区后禁止鸣喇叭B．图书馆里不能大声喧哗C．飞机旁的工作人员带上耳罩D．高速公路两侧安装透明板墙【答案】D【详解】本题涉及的知识是防治噪声的途径．“汽车进入市区后禁止鸣喇叭”和“图书馆里不能大声喧哗”是在声源处减弱噪声，“飞机旁的工作人员带上耳罩”是在人耳处减弱噪声，“高速公路两侧安装透明板墙” 是在传播过程中减弱噪声．故D符合题意．3．下列各种声学现象中，分析正确的是A．抽出罩内空气，听到闹钟的声音变小，说明发声体的振动变小了B．穿越公园的公路设置“隔音蛟龙”，是在声源处减弱噪声C．正在发声的音叉轻触悬挂的乒乓球，球被多次弹开，说明发声体在振动D．鸟鸣声和流水声在空气中传播速度一定不同【答案】C【详解】A．抽出罩内空气，听到闹钟的声音变小，说明声音传播需要介质，真空不能传声，不能说明发声体的振动变小了，故A错误；B．道路两旁建隔音墙是在传播过程中减弱噪声，故B错误；C．发声的音叉靠近乒乓球，球多次被弹开，说明发声体在振动，故C正确；D．鸟鸣声和流水声虽然声源不同，但都是在空气中传播，若空气的温度相同，则声音的传播速度相同，故D错误。

4．下表搜集的是在标准大气压下一些物质的相关信息，下列说法中错误的是：（）介质水水银酒精乙醚凝固点/℃0 -39 -117 -114沸点/℃100 357 78 35A ．从室温逐渐降低温度，这几种物质中最先凝固的是酒精B ．将乙醚抹在皮肤上，乙醚会沸腾C ．将装有酒精的试管放入装有水的烧杯中，加热烧杯中的水，酒精会比水先沸腾D ．能够装入1kg 酒精的烧杯肯定能装下1kg 的水【答案】A【详解】A ．凝固点为晶体固态和液态的分界点，图中水的凝固点最高，所以室温逐渐降低时，这几种物质中最先凝固的是水，故A 错误，符合题意；B ．乙醚的沸点是35℃，而人体的正常体温在36℃37℃范围内，已超过乙醚的沸点，所以将乙醚抹在皮肤上，乙醚会沸腾。