六年级奥数题:立体图形(B)
小学奥数几何专题--立体图形(六年级)竞赛测试.doc

小学奥数几何专题--立体图形(六年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】如图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?【答案】600【解析】我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10106600.【题文】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)【答案】120【解析】原正方体的表面积是44696(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边评卷人得分长是1厘米的正方形.从而,它的表面积是:9646120平方厘米.【题文】在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【答案】15000【解析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:5050615000(平方厘米).【题文】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为厘米,那么最后得到的立体图形的表面积是多少平方厘米?【答案】【解析】我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2228(平方厘米);左右方向、前后方向:22416(平方厘米),1144(平方厘米),41(平方厘米),4(平方厘米),这个立体图形的表面积为:41(平方厘米).【题文】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?【答案】18【解析】锯一次增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数2增加的面数.原正方体表面积:1166(平方米),一共锯了(21)(31)(41)6次,6112618(平方米).【题文】一个表面积为的长方体如图切成27个小长方体,这27个小长方体表面积的和是多少平方厘米?【答案】168平方厘米【解析】每一刀增加两个切面,增加的表面积等于与切面平行的两个表面积,所以每个方向切两刀后,表面积增加到原来的3倍,即表面积的和为.【题文】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?【答案】54【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【题文】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?⑴当 b2h时,如何打包?⑵当 b2h时,如何打包?⑶当 b2h时,如何打包?【答案】如解析图【解析】图2和图3正面的面积相同,侧面面积正面周长长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h6b,图3的周长是12h4b.两者的周长之差为2(b2h).当b2h时,图2和图3周长相等,可随意打包;当b2h时,按图2打包;当b2h时,按图3打包.【题文】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?【答案】1034【解析】考虑所有的包装方法,因为6123,所以一共有两种拼接方式:第一种按长宽高116拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高123拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.【题文】如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.【答案】214【解析】我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:(平方分米);侧面:(平方分米),(平方分米).这个立体图形的表面积为:(平方分米).【题文】如图,棱长分别为厘米、厘米、厘米、厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是多少平方厘米?【答案】194平方厘米【解析】 (法1)四个正方体的表面积之和为:(平方厘米),重叠部分的面积为:(平方厘米),所以,所得到的多面体的表面积为:(平方厘米).(法2)三视图法.从前后面观察到的面积为平方厘米,从左右两个面观察到的面积为平方厘米,从上下能观察到的面积为平方厘米.表面积为(平方厘米).【题文】把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.【答案】54【解析】从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面个左面个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的面积为:10平方厘米.因此,这个立体图形的总表面积为:(平方厘米).上下面左右面前后面【题文】用棱长是1厘米的立方块拼成如图所示的立体图形,问该图形的表面积是多少平方厘米?【答案】46平方厘米【解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于个小正方形的面积,所以该图形表面积为46平方厘米.【题文】有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.【答案】56【解析】(平方米).【题文】棱长是厘米(为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为,此时的最小值是多少?【答案】5【解析】切割成棱长是1厘米的小正方体共有个,由于其中至少有一面是红色的小正方体与没有红色面的个数之比为,而,所以小正方体的总数是25的倍数,即是25的倍数,那么是5的倍数.当时,要使得至少有一面的小正方体有65个,可以将原正方体的正面、上面和下面涂色,此时至少一面涂红色的小正方体有个,表面没有红色的小正方体有个,个数比恰好是,符合题意.因此,的最小值是5.【题文】有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?【答案】74【解析】要使大正方体的表面上白色部分最多,相当于要使大正方体表面上黑色部分最少,那么就要使得黑色小正方体尽量不露出来.在整个大正方体中,没有露在表面的小正方体有(个),用黑色的;在面上但不在边上的小正方体有(个),其中个用黑色.这样,在表面的个的正方形中,有22个是黑色,(个)是白色,所以在大正方体的表面上白色部分最多可以是74平方厘米.【题文】三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个?【答案】307【解析】每个长方体的棱长和是厘米,所以,每个长方体长、宽、高的和是厘米.因为,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,所以,每个长方体的长、宽、高分别是9厘米、8厘米、7厘米.要求切割后只有一个面涂色的小正方体最少有多少个,则需每一个长方体按题意涂色时,应让切割后只有一个面涂色的小正方体最少.所以,涂一面的长方体应涂一个面,有个;涂两面的长方体,若两面不相邻,应涂两个面,有个;若两面相邻,应涂一个面和一个面,此时有个,所以涂两面的最少有105个;涂三面的长方体,若三面不两两相邻,应涂两个面、一个面,有个;若三面两两相邻,有个,所以涂三面的最少有146个.那么切割后只有一个面涂色的小正方体最少有个.【题文】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?【答案】108【解析】设小正方体的棱长为1,考虑两种不同的情况,一种是长方体的长、宽、高中有一个是1的情况,另一种是长方体的长、宽、高都大于1的情况.当长方体的长、宽、高中有一个是1时,分割后只有一层小正方体,其中有两个面涂上红色的小正方体是去掉最外层一圈的小正方体后剩下的那些.因为有两个面涂上红色的小正方体恰好是100块,设,那么分成的小正方体个数为,为了使小正方体的个数尽量少,应使最小,而两数之积一定,差越小积越小,所以当时它们的和最小,此时共有个小正方体.当长方体的长、宽、高都大于1时,有两个面涂上红色的小正方体是去掉8个顶点所在的小正方体后12条棱上剩余的小正方体,因为有两个面涂上红色的小正方体恰好是100块,所以长方体的长、宽、高之和是.由于三个数的和一定,差越大积越小,为了使小正方体的个数尽量少,应该令,此时共有个小正方体.因为,所以至少要把这个大长方体分割成108个小正方体.【题文】把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?【答案】22【解析】一个面最多有5个方格可染成红色(见左下图).因为染有5个红色方格的面不能相邻,可以相对,所以至多有两个面可以染成5个红色方格.其余四个面中,每个面的四个角上的方格不能再染成红色,至多能染4个红色方格(见上中图).因为染有4个红色方格的面也不能相邻,可以相对,所以至多有两个面可以染成4个红色方格.最后剩下两个相对的面,每个面最多可以染2个红色方格(见右上图).所以,红色方格最多有(个).(另解)事实上上述的解法并不严密,“如果最初的假设并没有两个相对的有5个红色方格的面,是否其他的四个面上可以出现更多的红色方格呢?”这种解法回避了这个问题,如果我们从约束染色方格数的本质原因入手,可严格说明是红色方格数的最大值.对于同一个平面上的格网,如果按照国际象棋棋盘的方式染色,那么至少有一半的格子可以染成红色.但是现在需要染色的是一个正方体的表面,因此在分析问题时应该兼顾棱、角等面与面相交的地方:⑴⑵⑶⑴如图,每个角上三个方向的3个方格必须染成不同的三种颜色,所以8个角上最多只能有8个方格染成红色.⑵如图,阴影部分是首尾相接由个方格组成的环,这9个方格中只能有个方格能染成同一种颜色(如果有5个方格染同一种颜色,必然出现相邻,可以用抽屉原理反证之:先去掉一个白格,剩下的然后两两相邻的分成四个抽屉,必然有一个抽屉中有两个红色方格),像这样的环,在正方体表面最多能找到不重叠的两道(关于正方体中心对称的两道),涉及的个方格中最多能有个可染成红色.⑶剩下个方格,分布在条棱上,这个格子中只能有个能染成红色.综上所述,能被染成红色的方格最多能有个格子能染成红色,第一种解法中已经给出个红方格的染色方法,所以个格子染成红色是最多的情况.【题文】一个长、宽、高分别为厘米、厘米、厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?【答案】1107【解析】本题的关键是确定三次切下的正方体的棱长.由于,为了方便起见.我们先考虑长、宽、高分别为厘米、厘米、厘米的长方体.因为,容易知道第一次切下的正方体棱长应该是厘米,第二次切时,切下棱长为厘米的正方体符合要求.第三次切时,切下棱长为厘米的正方体符合要求.那么对于原长方体来说,三次切下的正方体的棱长分别是12厘米、9厘米和6厘米,所以剩下的体积应是:(立方厘米).【题文】有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标的为黑色,图中共有黑色积木多少块?【答案】17【解析】分层来看,如下图(切面平行于纸面)共有黑色积木17块.【题文】有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?【答案】216【解析】第一层如下图,第二层、第三层依次比上面一层每格都多1(见下图).上面的9个数之和是27,由对称性知,上面、前面、右面的所有数之和都是27.同理,下面的9个数之和是45,下面、左面、后面的所有数之和都是45.所以六个面上所有数之和是.【题文】如图所示,一个的立方体,在一个方向上开有的孔,在另一个方向上开有的孔,在第三个方向上开有的孔,剩余部分的体积是多少?表面积为多少?【答案】100;204【解析】求体积:开了的孔,挖去,开了的孔,挖去;开了的孔,挖去,剩余部分的体积是:.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:.求表面积:表面积可以看成外部和内部两部分.外部的表面积为,内部的面积可以分为前后、左右、上下三个方向,面积分别为、、,所以总的表面积为.(另解)运用类似于三视图的方法,记录每一方向上的不同位置上的裸露正方形个数:前后方向:上下方向:左右方向:总表面积为.总结:“切片法”:全面打洞(例如本题,五层一样),挖块成线(例如本题,在前一层的基础上,一条线一条线地挖),这里体现的思想方法是:化整为零,有序思考!【题文】如图,原来的大正方体是由个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?【答案】72【解析】对于这一类从立体图形中间挖掉一部分后再求体积(或小正方体数l【题文】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方体中相对的两面打通,右图就是抽空的状态.右图中剩下的小正方体有多少个?【答案】73【解析】解法一:(用“容斥原理”来解)由正面图形抽出的小正方体有个,由侧面图形抽出的小正方体有个,由底面图形抽出的小正方体有个,正面图形和侧面图形重合抽出的小正方体有个,正面图形和底面图形重合抽出的小正方体有个,底面图形和侧面图形重合抽出的小正方体有个,三个面的图形共同重合抽出的小正方体有4个.根据容斥原理,,所以共抽出了52个小正方体.,所以右图中剩下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个,必须知道是哪4块,这是最让人头疼的事.但你可以先构造空的两个方向上共同部分的模型,再由第三个方向来穿过“花墙”.这里,化虚为实的思想方法很重要.解法二:(用“切片法”来解)可以从上到下切五层,得:⑴从上到下五层,如图:⑵或者,从右到左五片,如图:请注意这里的挖空的技巧是:先认一种方向.比如:从上到下的每一层,首先都应该有第一层的空四块的情况,即——如果挖第二层:第(1)步,把中间这些位置的四块挖走如图:第(2)步,把从右向左的两块成线地挖走.(请注意挖通的效果就是成线挖去),如图:第(3)步,把从前向后的一块(请注意跟第二层有关的只是一块!)挖成线!如图:【题文】右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的多少倍.【答案】16【解析】本题中的两个图都是立体图形的平面展开图,将它们还原成立体图形,可得到如下两图:其中左图是以⑴⑵⑶⑷为平面展开图的立体图形,是一个四个面都是正三角形的正四面体,右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形,是一个不规则图形,底面是⑾,四个侧面是⑺⑻⑼⑽,两个斜面是⑸⑹.对于这两个立体图形的体积,可以采用套模法来求,也就是对于这种我们不熟悉的立体图形,用一些我们熟悉的基本立体图形来套,看看它们与基本立体图形相比,缺少了哪些部分.由于左图四个面都是正三角形,右图底面是正方形,侧面是等腰直角三角形,想到都用正方体来套.对于左图来说,相当于由一个正方体切去4个角后得到(如下左图,切去、、、);而对于右图来说,相当于由一个正方体切去2个角后得到(如下右图,切去、).假设左图中的立方体的棱长为,右图中的立方体的棱长为,则以⑴⑵⑶⑷为平面展开图的立体图形的体积为:,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为.由于右图中的立方体的棱长即是题中正方形⑾的边长,而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长,通过将等腰直角三角形⑺分成4个相同的小等腰直角三角形可以得到右图中的立方体的棱长是左图中的立方体的棱长的2倍,即.那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为:,也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍.【题文】图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴图⑵【答案】20【解析】首先,我们把展开图折成立体图形,见下列示意图:图⑴图⑵对于这类题目,一般采用“套模法”,即用一个我们熟悉的基本立体图形来套,这样做基于两点考虑,一是如果有类似的模型,可以直接应用其计算公式;二是如果可以补上一块或者放到某个模型里面,那么可以从这个模型入手.我们把图⑴中的立体图形切成两半,再转一转,正好放进去!我们看到图⑴与图⑶的图形位置的微妙关系:图⑶图⑷由图⑷可见,图⑴这个立体的体积与图⑶这个被切去了8个角后的立体图形的体积相等.假设立方体的1条边的长度是1,那么一个角的体积是,所以切掉8个角后的体积是.再看图⑵中的正四面体,这个正四面体的棱长与图⑶中的每一条实线线段相等,所以应该用边长为的立方体来套.如果把图⑵的立体图形放入边长为的立方体里的话是可以放进去的.这是切去了四个角后的图形,从上面的分析可知一个角的体积为,所以图⑵的体积是:,那么前者的体积是后者的倍.【题文】如图,用高都是米,底面半径分别为米、米和米的个圆柱组成一个物体.问这个物体的表面积是多少平方米?(取)【答案】32.97【解析】从上面看到图形是右上图,所以上下底面积和为(立方米),侧面积为(立方米),所以该物体的表面积是(立方米).【题文】有一个圆柱体的零件,高厘米,底面直径是厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是厘米,孔深厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【答案】307.72【解析】涂漆的面积等于大圆柱表面积与小圆柱侧面积之和,为(平方厘米).【题文】圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是多少立方厘米.(结果用表示)【答案】立方厘米或立方厘米【解析】当圆柱的高是12厘米时体积为(立方厘米)当圆柱的高是12厘米时体积为(立方厘米).所以圆柱体的体积为立方厘米或立方厘米.【题文】如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.()【答案】100.48【解析】圆的直径为:(米),而油桶的高为2个直径长,即为:,故体积为立方米.【题文】如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?()【答案】2056【解析】做成的圆柱体的侧面是由中间的长方形卷成的,可见这个长方形的长与旁边的圆的周长相等,则剪下的长方形的长,即圆柱体底面圆的周长为:(厘米),原来的长方形的面积为:(平方厘米).【题文】把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少平方厘米.原来的圆柱体的体积是多少立方厘米?【答案】25.12【解析】沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少的部分为减掉的2厘米圆柱体的侧面积,所以原来圆柱体的底面周长为厘米,底面半径为厘米,所以原来的圆柱体的体积是(立方厘米).【题文】一个圆柱体的体积是立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? ()【答案】16【解析】从图中可以看出,拼成的长方体的底面积与原来圆柱体的底面积相同,长方体的前后两个侧面面积与原来圆柱体的侧面面积相等,所以增加的表面积就是长方体左右两个侧面的面积.(法1)这两个侧面都是长方形,且长等于原来圆柱体的高,宽等于圆柱体底面半径.可知,圆柱体的高为(厘米),所以增加的表面积为(平方厘米);(法2)根据长方体的体积公式推导.增加的两个面是长方体的侧面,侧面面积与长方体的长的乘积就是长方体的体积.由于长方体的体积与圆柱体的体积相等,为立方厘米,而拼成的长方体的长等于圆柱体底面周长的一半,为厘米,所以侧面长方形的面积为平方厘米,所以增加的表面积为平方厘米.【题文】一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是多少立方厘米.(取)【答案】100.48【解析】由于瓶子倒立过来后其中水的体积不变,所以空气部分的体积也不变,从图中可以看出,瓶中的水构成高为厘米的圆柱,空气部分构成高为厘米的圆柱,瓶子的容积为这两部分之和,所以瓶。
小学六年级奥数教案—13立体图形.

小学六年级奥数教案—13立体图形本教程共30讲立体图形(一)我们学过的立体图形有长方体、正方体、圆柱体、圆锥体等。
这一讲将通过长方体、正方体及其组合图形,讲解有关的计数问题。
例1左下图中共有多少个面?多少条棱?分析与解:如右上图所示,可以分前、后、左、右、上、下六个方向看这个立体图形。
前、后看各有1个面,左面看有1个面,右面看有2个面,上面看有2个面,下面看有1个面。
所以共有1+1+1+2+2+1= 8(个)面。
前后方向的棱有6条,左右方向的棱有6条,上下方向的棱也有6条,所以共有棱6+6+6=18(条)。
例2右图是由18个边长为1厘米的小正方体拼成的,求它的表面积。
分析与解:如果一面一面去数,那么虽然可以得到答案,但太麻烦,而且容易出错。
仔细观察会发现,这个立体的上面与下面、左面与右面、前面与后面的面积分别相等。
如上图所示,可求得表面积为(9+7+8)×2=48(厘米2)。
例3右图是由22个小正方体组成的立体图形,其中共有多少个大大小小的正方体?由两个小正方体组成的长方体有多少个?分析与解:正方体只可能有两种:由1个小正方体构成的正方体,有22个;由8个小正方体构成的2×2×2的正方体,有4个。
所以共有正方体 22+4=26(个)。
由两个小正方体组成的长方体,根据摆放的方向可分为下图所示的上下位、左右位、前后位三种,其中上下位有13个,左右位有13个,前后位有14个,共有13+13+14=40(个)。
例4有一个棱长为5厘米的正方体木块,从它的每个面看都有一个穿透的完全相同的孔(见下页左上图),求这个立体图形的表面积。
分析与解:由于正方体中间被穿了孔,表面积不好计算。
我们可以将这个立体图形看成由8个棱长为2厘米的正方体和12个棱长为1厘米的立方体粘合而成。
如右上图所示,八个棱长为2厘米的正方体分别在8个顶角,12个棱长1厘米的正方体分别在12条棱的中间。
由于每个小正方体都有2个面分别粘接两个较大正方体,相对于不粘接,减少了表面积4厘米2,所以总的表面积为(2×2×6)×8+(1×1×6)×12-4×12=216(厘米2)。
小学六年级奥数 立体几何——表面积与体积
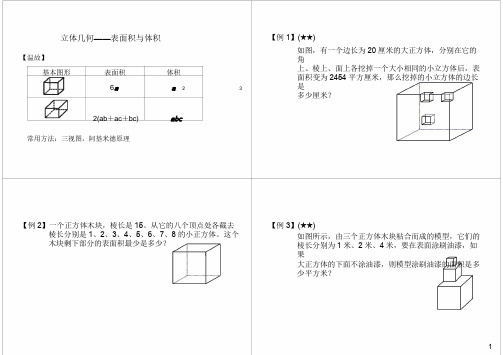
立体几何——表面积与体积【例1】(★★)【温故】基本图形表面积体积6a a2 3 如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?2(ab+ac+bc)abc 常用方法:三视图,阿基米德原理【例2】一个正方体木块,棱长是15。
从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体。
这个木块剩下部分的表面积最少是多少?【例3】(★★)如图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?1【例4】(★★★)【例5】(★★★)小明用若干个大小相同的正方体木块堆成一个几何体,这个几何体从正面看如下图左,从上面看如下图右。
那么这个几何体至少用了_____块木块。
有大、中、小三个正方形水池,它们的内边长分别是6米、3米、2米。
把两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米。
如果将这两堆碎石都沉没在大水池的水里,大水池的水面升高了多少厘米?【例6】(★★★★★)【例7】(★★)如图,有一个棱长为10厘米的正方体铁块,现已在每两个对面的中央钻一个边长为4厘米的正方形孔(边平行于正方体的棱),且穿透。
另有一长方体容器,从内部量,长、宽、高分别为15厘米、12厘米、9厘米,内部有水,水深3 厘米。
若将正方体铁块平放入长方体容器中,则铁块在水下部分的体积为___立方厘米。
图是4×5×6长方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小正方体各有多少块?2【知新】【例8】(★★★)基本图形表面积体积2πR2+2πRhπR2h 如图,用高都是 1米,底面半径分别为 1.5米、 1米和. 。
多少平方米?( π取 3.14)1 3 πR2h 0.51111.5【例9】(★★★)(”希望杯”一试六年级)如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水升。
六年级奥数之 立体图形

六年级奥数之立体图形(圆柱和圆锥)2013.3.201.把一个棱长为6厘米的正方体削成一个最大的圆锥,求削取得体积是多少?2.一个圆锥体的容器,高15厘米,底面半径比高少7厘米,容器装满水后,将其中的水又倒入高20厘米,底面半径5厘米的圆柱体容器中,水面距离圆柱体容器上端几厘米?3.把一段圆柱体木料沿着底面直径往下切成两块,得到两个半圆柱,已知圆柱体木料的底面周长是25.12厘米,高是15厘米,求半圆柱的表面积和体积。
4.将一张长12.56厘米,宽9.42厘米的长方形纸卷成一个圆柱体,圆柱体体积最大是多少?5.在一个圆柱形水桶里,放进一根半径是5厘米的圆钢,把圆钢完全放入水里,桶里水面就上升9厘米,这时如果把水中的圆钢往上提,使它露出水面9厘米,那么桶里水就会下降8厘米,求圆钢的体积。
6把一个圆柱沿着半径切成若干块拼成一个近似长方体,它高8厘米,比圆柱的表面积增加了96平方厘米,那么这个圆柱的体积是多少立方厘米?思考与练习:1.一个圆柱高6厘米,如果截取2厘米,表面积就会减少12.56平方厘米,原来圆柱的表面积是多少平方厘米?2.有A/B两个圆柱形的容器,最初在A容器里装有2升水,B容器是空的。
现在往两个容器里以每分钟0.4升的流量注水,4分钟后,两个容器的水面高度相等,如果B容器的底面半径是5厘米,求A容器的底面直径。
3.一个圆锥与一个圆柱的底面积相等。
已知圆锥与圆柱的体积比是1:6,圆锥的高是4.8厘米,圆柱的高是多少厘米?4.如下图,有一张长方形的铁皮,现在要把它做成一个圆柱,求这个圆柱的表面积。
(长16.56厘米)5.在一个直径是20厘米的圆柱形的容器里,放入一个底面半径为3厘米圆锥形铁块,体块已经被淹没,这是水面上升0.3厘米,求铁块的高。
6一个圆柱形的杯子内盛有水,水面高2.5厘米,内侧底面积为72平方厘米,在这个杯中放入一个棱长6厘米的铁块,水面没有淹没铁块,这是水高几厘米?7.一个圆柱高10厘米,如果高减少3厘米,则表面积减少94.2平方厘米,原来圆柱的表面积是多少平方厘米?8.把一个底面周长12.56厘米,高6厘米的圆柱形钢材,熔铸成一个圆锥,它的底面积是16平方厘米,圆锥高几厘米?9.一个圆柱底面直径增加2厘米,它侧面积增加62。
最新小学奥数之立体几何问题

立体图形⑴ 立体图形的表面积和体积公式长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED BA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?改.又是多少?【例 2】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)练习:在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?(锯一次增加两个面)练习.一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.表面积最小:互相重合的面最多时表面积最小【例 5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?体积:例1. 如图11-6,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?例2. 某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条如图11-9所示在三个方向上加固.所用尼龙编织条的长分别为365厘米、405厘米、485厘米.若每个尼龙条加固时接头处都重叠5厘米,则这个长方体包装箱的体积是多少立方米?⑵不规则立体图形的表面积整体观照法例1. 如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.例2. 如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.例3.把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.例4.用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?例5.下图是由18个边长为1厘米的小正方体拼成的,求它的表面积。
六年级奥数-第五讲.几何-立体部分.教师版

六年级奥数-第五讲.几何-立体部分.教师版work Information Technology Company.2020YEAR第五讲 几何——立体部分教学目标:对于小学几何而言,立体图形的表面积和体积计算,既可以很好地考查学生的空间想象能力,又可以具体考查学生在公式应用中处理相关数据的能力,所以,很多重要考试都很重视对立体图形的考查.知识点拨:一、长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED CBA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形.如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥例题精讲:【例 1】如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?【例 2】【解析】我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10⨯10⨯6=600.【例 3】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)【解析】原正方体的表面积是4⨯4⨯6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4⨯6=120平方厘米.【巩固】在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【解析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:50⨯50⨯6=15000(平方厘米).【例 4】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 5】【解析】我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2⨯2⨯2=8(平方厘米);左右方向、前后方向:2⨯2⨯4=16(平方厘米),1⨯1⨯4=4(平方厘米),12⨯12⨯4=1(平方厘米),1 4⨯14⨯4=14(平方厘米),这个立体图形的表面积为:816++4+1+14=1294(平方厘米).【例 6】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?【解析】锯一次增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数⨯2=增加的面数.原正方体表面积:1⨯1⨯6=6(平方米),一共锯了(2-1)+(3-1)+(4-1)=6次,6+1⨯1⨯2⨯6=18(平方米).【巩固】(2008年走美六年级初赛)一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.【解析】每一刀增加两个切面,增加的表面积等于与切面平行的两个表面积,所以每个方向切两刀后,表面积增加到原来的3倍,即表面积的和为2563168(cm)⨯=.【例 7】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少【例 8】【例 9】25块积木【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个333⨯⨯的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【例 10】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?【例 11】⑴当b=2h时,如何打包?⑵当b<2h时,如何打包?⑶当b>2h时,如何打包?【解析】图2和图3正面的面积相同,侧面面积=正面周长⨯长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h+6b,图3的周长是12h+4b.两者的周长之差为2(b-2h).当b=2h时,图2和图3周长相等,可随意打包;当b<2h时,按图2打包;当b>2h 时,按图3打包.图3图2图1hba【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?【解析】考虑所有的包装方法,因为6=1⨯2⨯3,所以一共有两种拼接方式:第一种按长宽高1⨯1⨯6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1⨯2⨯3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.【例 12】如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.【解析】我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:⨯⨯=(平方分米),44464⨯⨯=(平方分米).这个⨯⨯=(平方分米);侧面:55410055250立体图形的表面积为:5010064214++=(平方分米).【例 13】(2008年“希望杯”五年级第2试)如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.【解析】(法1)四个正方体的表面积之和为:2222+++⨯=⨯=(平方厘米),(1235)6396234重叠部分的面积为:22222222213(221)(321)(321)39141440⨯+⨯+++++++=+++=(平方厘米),所以,所得到的多面体的表面积为:23440194-=(平方厘米).(法2)三视图法.从前后面观察到的面积为222++=平方厘米,从左右两个面观察53238到的面积为225334=平方厘米.+=平方厘米,从上下能观察到的面积为2525表面积为()++⨯=(平方厘米).3834252194【例 14】把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.【解析】从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面2+个左面2+个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的面积为:10平方厘米.因此,这个立体图形的总表面积为:(9810)254++⨯=(平方厘米).上下面左右面前后面【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米【解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(977)246++⨯=个小正方形的面积,所以该图形表面积为46平方厘米.【例 15】有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.【解析】44(1234)456⨯++++⨯=(平方米).【例 16】棱长是m厘米(m为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12,此时m的最小值是多少?【例 17】【解析】 切割成棱长是1厘米的小正方体共有3m 个,由于其中至少有一面是红色的小正方体与没有红色面的个数之比为13:12,而131225+=,所以小正方体的总数是25的倍数,即3m 是25的倍数,那么m 是5的倍数.当5m =时,要使得至少有一面的小正方体有65个,可以将原正方体的正面、上面和下面涂色,此时至少一面涂红色的小正方体有5554265⨯+⨯⨯=个,表面没有红色的小正方体有1256560-=个,个数比恰好是13:12,符合题意.因此,m 的最小值是5.【例 18】 有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?【例 19】【解析】 要使大正方体的表面上白色部分最多,相当于要使大正方体表面上黑色部分最少,那么就要使得黑色小正方体尽量不露出来.在整个大正方体中,没有露在表面的小正方体有3(42)8-=(个),用黑色的;在面上但不在边上的小正方体有2(42)624-⨯=(个),其中30822-=个用黑色.这样,在表面的44696⨯⨯=个11⨯的正方形中,有22个是黑色,962274-=(个)是白色,所以在大正方体的表面上白色部分最多可以是74平方厘米.【例 20】 三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个?【例 21】【解析】 每个长方体的棱长和是288396÷=厘米,所以,每个长方体长、宽、高的和是96424÷=厘米.因为,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,所以,每个长方体的长、宽、高分别是9厘米、8厘米、7厘米.要求切割后只有一个面涂色的小正方体最少有多少个,则需每一个长方体按题意涂色时,应让切割后只有一个面涂色的小正方体最少.所以,涂一面的长方体应涂一个87⨯面,有8756⨯=个;涂两面的长方体,若两面不相邻,应涂两个87⨯面,有872112⨯⨯=个;若两面相邻,应涂一个87⨯面和一个97⨯面,此时有()7892105⨯+-=个,所以涂两面的最少有105个;涂三面的长方体,若三面不两两相邻,应涂两个87⨯面、一个97⨯面,有()78894147⨯++-=个;若三面两两相邻,有()()()()()()718171918191146-⨯-+-⨯-+-⨯-=个,所以涂三面的最少有146个.那么切割后只有一个面涂色的小正方体最少有56105146307++=个.【例 22】 把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?【例 23】【解析】 设小正方体的棱长为1,考虑两种不同的情况,一种是长方体的长、宽、高中有一个是1的情况,另一种是长方体的长、宽、高都大于1的情况.当长方体的长、宽、高中有一个是1时,分割后只有一层小正方体,其中有两个面涂上红色的小正方体是去掉最外层一圈的小正方体后剩下的那些.因为有两个面涂上红色的小正方体恰好是100块,设100a b =⨯,那么分成的小正方体个数为()()()()221242104a b ab a b a b +⨯+⨯=+++=++,为了使小正方体的个数尽量少,应使()a b +最小,而两数之积一定,差越小积越小,所以当10a b ==时它们的和最小,此时共有()()102102144+⨯+=个小正方体.当长方体的长、宽、高都大于1时,有两个面涂上红色的小正方体是去掉8个顶点所在的小正方体后12条棱上剩余的小正方体,因为有两个面涂上红色的小正方体恰好是100块,所以长方体的长、宽、高之和是10042331÷+⨯=.由于三个数的和一定,差越大积越小,为了使小正方体的个数尽量少,应该令312227=++,此时共有2227108⨯⨯=个小正方体.因为108144<,所以至少要把这个大长方体分割成108个小正方体.【例 24】 把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?【例 25】【解析】 一个面最多有5个方格可染成红色(见左下图).因为染有5个红色方格的面不能相邻,可以相对,所以至多有两个面可以染成5个红色方格.红红红红红红红红红红红其余四个面中,每个面的四个角上的方格不能再染成红色,至多能染4个红色方格(见上中图).因为染有4个红色方格的面也不能相邻,可以相对,所以至多有两个面可以染成4个红色方格.最后剩下两个相对的面,每个面最多可以染2个红色方格(见右上图).所以,红色方格最多有52422222⨯+⨯+⨯=(个).(另解)事实上上述的解法并不严密,“如果最初的假设并没有两个相对的有5个红色方格的面,是否其他的四个面上可以出现更多的红色方格呢?”这种解法回避了这个问题,如果我们从约束染色方格数的本质原因入手,可严格说明22是红色方格数的最大值.对于同一个平面上的格网,如果按照国际象棋棋盘的方式染色,那么至少有一半的格子可以染成红色.但是现在需要染色的是一个正方体的表面,因此在分析问题时应该兼顾棱、角等面与面相交的地方:⑴⑵⑶⑴如图,每个角上三个方向的3个方格必须染成不同的三种颜色,所以8个角上最多只能有8个方格染成红色.⑵如图,阴影部分是首尾相接由9个方格组成的环,这9个方格中只能有4个方格能染成同一种颜色(如果有5个方格染同一种颜色,必然出现相邻,可以用抽屉原理反证之:先去掉一个白格,剩下的然后两两相邻的分成四个抽屉,必然有一个抽屉中有两个红色方格),像这样的环,在正方体表面最多能找到不重叠的两道(关于正方体中心对称的两道),涉及的18个方格中最多能有8个可染成红色.⑶剩下633839212⨯⨯-⨯-⨯=个方格,分布在6条棱上,这12个格子中只能有6个能染成红色.综上所述,能被染成红色的方格最多能有88622++=个格子能染成红色,第一种解法中已经给出22个红方格的染色方法,所以22个格子染成红色是最多的情况.【例 26】一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?【例 27】【解析】本题的关键是确定三次切下的正方体的棱长.由于21:15:127:5:4=,为了方便起见.我们先考虑长、宽、高分别为7厘米、5厘米、4厘米的长方体.因为754>>,容易知道第一次切下的正方体棱长应该是4厘米,第二次切时,切下棱长为3厘米的正方体符合要求.第三次切时,切下棱长为2厘米的正方体符合要求.那么对于原长方体来说,三次切下的正方体的棱长分别是12厘米、9厘米和6厘米,所以剩下的体积应是:()333⨯⨯-++=(立方厘米).2115121296110712129996663121263912【例 28】 有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标A 的为黑色,图中共有黑色积木多少块? 【例 29】A【解析】 分层来看,如下图(切面平行于纸面)共有黑色积木17块.【巩固】这个图形,是否能够由112⨯⨯的长方体搭构而成?【解析】 每一个112⨯⨯的长方体无论怎么放,都包含了一个黑色正方体和一个白色正方体,而黑色积木有17块,白色积木有15块,所以该图形不能够由112⨯⨯的长方体搭构而成.【巩固】有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少33223323322323111111【解析】 第一层如下图,第二层、第三层依次比上面一层每格都多1(见下图).765434565第三层654323454第二层第一层343212345上面的9个数之和是27,由对称性知,上面、前面、右面的所有数之和都是27.同理,下面的9个数之和是45,下面、左面、后面的所有数之和都是45.所以六个面上所有数之和是(2745)3216+⨯=.【例 30】 (05年武汉明心杯数学挑战赛)如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?【解析】 求体积:开了315⨯⨯的孔,挖去31515⨯⨯=,开了115⨯⨯的孔, 挖去11514⨯⨯-=;开了215⨯⨯的孔, 挖去215(22)6⨯⨯-+=,剩余部分的体积是:555(1546)100⨯⨯-++=.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:22412100⨯+=. 求表面积:表面积可以看成外部和内部两部分.外部的表面积为55612138⨯⨯-=,内部的面积可以分为前后、左右、上下三个方向,面积分别为()22515121320⨯⨯+⨯-⨯-⨯=、()2153513132⨯⨯+⨯-⨯-=、()2151511214⨯⨯+⨯-⨯-=,所以总的表面积为138203214204+++=.(另解)运用类似于三视图的方法,记录每一方向上的不同位置上的裸露正方形个数:前后方向:32上下方向:30左右方向:40总表面积为()2323040204⨯++=.【总结】“切片法”:全面打洞(例如本题,五层一样),挖块成线(例如本题,在前一层的基础上,一条线一条线地挖),这里体现的思想方法是:化整为零,有序思考!【巩固】(2008年香港保良局第12届小学数学世界邀请赛)如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?第8题【解析】对于这一类从立体图形中间挖掉一部分后再求体积(或小正方体数目)的题目一般可以采用“切片法”来做,所谓“切片法”,就是把整个立体图形切成一片一片的(或一层一层的),然后分别计算每一片或每一层的体积或小正方体数目,最后再把它们相加.采用切片法,俯视第一层到第五层的图形依次如下,其中黑色部分表示挖除掉的部分.第1层第2层第3层第4层第5层从图中可以看出,第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个,所以总共还剩下22111162272++++=(个)小正方体.【巩固】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方体中相对的两面打通,右图就是抽空的状态.右图中剩下的小正方体有多少个【解析】解法一:(用“容斥原理”来解)由正面图形抽出的小正方体有5525⨯=个,由侧面图形抽出的小正方体有5525⨯=个,正面图形和⨯=个,由底面图形抽出的小正方体有4520侧面图形重合抽出的小正方体有1221228⨯+⨯+⨯=个,正面图形和底面图形重合抽出的小正方体有13227⨯+⨯=个,底面图形和侧面图形重合抽出的小正方体有⨯+⨯+⨯=个,三个面的图形共同重合抽出的小正方体有4个.根据容斥原理,1211227-=,所以右图中剩++---+=,所以共抽出了52个小正方体.1255273252520877452下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个,必须知道是哪4块,这是最让人头疼的事.但你可以先构造空的两个方向上共同部分的模型,再由第三个方向来穿过“花墙”.这里,化虚为实的思想方法很重要.解法二:(用“切片法”来解)可以从上到下切五层,得:⑴从上到下五层,如图:⑵或者,从右到左五片,如图:请注意这里的挖空的技巧是:先认一种方向.比如:从上到下的每一层,首先都应该有第一层的空四块的情况,即——如果挖第二层:第(1)步,把中间这些位置的四块挖走如图:第(2)步,把从右向左的两块成线地挖走.(请注意挖通的效果就是成线挖去),如图:第(3)步,把从前向后的一块(请注意跟第二层有关的只是一块!)挖成线!如图:【例 31】(2009年迎春杯高年级组复赛)右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的倍.⑷⑶⑵⑴⑾⑽⑼⑻⑺⑹⑸【解析】本题中的两个图都是立体图形的平面展开图,将它们还原成立体图形,可得到如下两图:其中左图是以⑴⑵⑶⑷为平面展开图的立体图形,是一个四个面都是正三角形的正四面体,右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形,是一个不规则图形,底面是⑾,四个侧面是⑺⑻⑼⑽,两个斜面是⑸⑹.对于这两个立体图形的体积,可以采用套模法来求,也就是对于这种我们不熟悉的立体图形,用一些我们熟悉的基本立体图形来套,看看它们与基本立体图形相比,缺少了哪些部分.由于左图四个面都是正三角形,右图底面是正方形,侧面是等腰直角三角形,想到都用正方体来套.对于左图来说,相当于由一个正方体切去4个角后得到(如下左图,切去1ABDA 、1CBDC 、111D AC D 、111B AC B );而对于右图来说,相当于由一个正方体切去2个角后得到(如下右图,切去1BACB 、1DACD ).D 1C 1B 1A 1D CBAABCDA 1B 1C 1D 1假设左图中的立方体的棱长为a ,右图中的立方体的棱长为b ,则以⑴⑵⑶⑷为平面展开图的立体图形的体积为:3231114233a a a a -⨯⨯⨯=,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为3231122233b b b b -⨯⨯⨯=. 由于右图中的立方体的棱长即是题中正方形⑾的边长,而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长,通过将等腰直角三角形⑺分成4个相同的小等腰直角三角形可以得到右图中的立方体的棱长是左图中的立方体的棱长的2倍,即2b a =.那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为:()33331212::21:163333a b a a =⨯=,也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍.【例 32】 图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?【例 33】图⑴图⑵【解析】首先,我们把展开图折成立体图形,见下列示意图:图⑴图⑵对于这类题目,一般采用“套模法”,即用一个我们熟悉的基本立体图形来套,这样做基于两点考虑,一是如果有类似的模型,可以直接应用其计算公式;二是如果可以补上一块或者放到某个模型里面,那么可以从这个模型入手.我们把图⑴中的立体图形切成两半,再转一转,正好放进去!我们看到图⑴与图⑶的图形位置的微妙关系:1和图3一致!60°图⑶图⑷由图⑷可见,图⑴这个立体的体积与图⑶这个被切去了8个角后的立体图形的体积相等.假设立方体的1条边的长度是1,那么一个角的体积是1111112222348⨯⨯⨯⨯=,所以切掉8个角后的体积是1518486-⨯=.再看图⑵中的正四面体,这个正四面体的棱长与图⑶中的每一条实线线段相等,所以应该用边长为12的立方体来套.如果把图⑵的立体图形放入边长为12的立方体里的话是可以放进去的.12这是切去了四个角后的图形,从上面的分析可知一个角的体积为148,所以图⑵的体积是:1111142224824⨯⨯-⨯=,那么前者的体积是后者的5120624÷=倍.【例 34】 如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.5【解析】 从上面看到图形是右上图,所以上下底面积和为22 3.14 1.514.13⨯⨯=(立方米),侧面积为2 3.14(0.51 1.5)118.84⨯⨯++⨯=(立方米),所以该物体的表面积是14.1318.8432.97+=(立方米).【例 35】 有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【例 36】【解析】 涂漆的面积等于大圆柱表面积与小圆柱侧面积之和,为266π10π()24π560π18π20π98π307.722⨯+⨯⨯+⨯=++==(平方厘米).【例 37】 (第四届希望杯2试试题)圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米.(结果用π表示)【解析】 当圆柱的高是12厘米时体积为210300π()122ππ⨯⨯=(立方厘米)。
六年级奥数-第五讲[1].几何-立体部分.教师版
![六年级奥数-第五讲[1].几何-立体部分.教师版](https://img.taocdn.com/s3/m/c06f770cb52acfc789ebc9b0.png)
第五讲 几何——立体部分一、长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED CBA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥例题精讲:【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?【解析】 我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10⨯10⨯6=600.【例 2】 右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l 厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、【巩固】在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【解析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:50⨯50⨯6=15000(平方厘米).【例3】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【解析】我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2⨯2⨯2=8(平方厘米);左右方向、前后方向:2⨯2⨯4=16(平方厘米),1⨯1⨯4=4(平方厘米),12⨯12⨯4=1(平方厘米),1 4⨯14⨯4=14(平方厘米),这个立体图形的表面积为:816++4+1+14=1294(平方厘米).【例4】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?【解析】锯一次增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数⨯2=增加的面数.原正方体表面积:1⨯1⨯6=6(平方米),一共锯了(2-1)+(3-1)+(4-1)=6次,6+1⨯1⨯2⨯6=18(平方米).【巩固】(2008年走美六年级初赛)一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.【解析】每一刀增加两个切面,增加的表面积等于与切面平行的两个表面积,所以每个方向切两刀后,表面积增加到原来的3倍,即表面积的和为2563168(cm)⨯=.【例5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?25块积木【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个333⨯⨯的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【例6】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?⑴当b=2h时,如何打包?⑵当b<2h时,如何打包?⑶当b>2h时,如何打包?【解析】图2和图3正面的面积相同,侧面面积=正面周长⨯长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h+6b,图3的周长是12h+4b.两者的周长之差为2(b-2h).当b=2h时,图2和图3周长相等,可随意打包;当b<2h时,按图2打包;当b>2h时,按图3打包.图3图2图1hba【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?【解析】考虑所有的包装方法,因为6=1⨯2⨯3,所以一共有两种拼接方式:第一种按长宽高1⨯1⨯6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1⨯2⨯3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.【例7】如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.【解析】我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:55250⨯⨯=(平方分米);侧面:554100⨯⨯=(平方分米),44464⨯⨯=(平方分米).这个立体图形的表面积为:5010064214++=(平方分米).【例8】(2008年“希望杯”五年级第2试)如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.【解析】(法1)四个正方体的表面积之和为:2222+++⨯=⨯=(平方厘米),(1235)6396234重叠部分的面积为:22222222213(221)(321)(321)39141440⨯+⨯+++++++=+++=(平方厘米),所以,所得到的多面体的表面积为:23440194-=(平方厘米).(法2)三视图法.从前后面观察到的面积为22253238++=平方厘米,从左右两个面观察到的面积为22=平方厘米.+=平方厘米,从上下能观察到的面积为25255334表面积为()++⨯=(平方厘米).3834252194【例9】把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.【解析】从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面2+个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的+个左面2面积为:10平方厘米.因此,这个立体图形的总表面积为:(9810)254++⨯=(平方厘米).上下面左右面前后面【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?【解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(977)246++⨯=个小正方形的面积,所以该图形表面积为46平方厘米.【例10】有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.【解析】44(1234)456⨯++++⨯=(平方米).【例 11】 棱长是m 厘米(m 为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12,此时m 的最小值是多少?【解析】 切割成棱长是1厘米的小正方体共有3m 个,由于其中至少有一面是红色的小正方体与没有红色面的个数之比为13:12,而131225+=,所以小正方体的总数是25的倍数,即3m 是25的倍数,那么m 是5的倍数.当5m =时,要使得至少有一面的小正方体有65个,可以将原正方体的正面、上面和下面涂色,此时至少一面涂红色的小正方体有5554265⨯+⨯⨯=个,表面没有红色的小正方体有 1256560-=个,个数比恰好是13:12,符合题意.因此,m 的最小值是5.【例 12】 有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?【解析】 要使大正方体的表面上白色部分最多,相当于要使大正方体表面上黑色部分最少,那么就要使得黑色小正方体尽量不露出来.在整个大正方体中,没有露在表面的小正方体有3(42)8-=(个),用黑色的;在面上但不在边上的小正方体有2(42)624-⨯=(个),其中30822-=个用黑色.这样,在表面的44696⨯⨯=个11⨯的正方形中,有22个是黑色,962274-=(个)是白色,所以在大正方体的表面上白色部分最多可以是74平方厘米.【例 13】 三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个?【解析】 每个长方体的棱长和是288396÷=厘米,所以,每个长方体长、宽、高的和是96424÷=厘米.因为,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,所以,每个长方体的长、宽、高分别是9厘米、8厘米、7厘米.要求切割后只有一个面涂色的小正方体最少有多少个,则需每一个长方体按题意涂色时,应让切割后只有一个面涂色的小正方体最少.所以,涂一面的长方体应涂一个87⨯面,有8756⨯=个; 涂两面的长方体,若两面不相邻,应涂两个87⨯面,有872112⨯⨯=个;若两面相邻,应涂一个87⨯面和一个97⨯面,此时有()7892105⨯+-=个,所以涂两面的最少有105个;涂三面的长方体,若三面不两两相邻,应涂两个87⨯面、一个97⨯面,有()78894147⨯++-=个;若三面两两相邻,有()()()()()()718171918191146-⨯-+-⨯-+-⨯-=个,所以涂三面的最少有146个.那么切割后只有一个面涂色的小正方体最少有56105146307++=个.【例 14】 把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?【解析】 设小正方体的棱长为1,考虑两种不同的情况,一种是长方体的长、宽、高中有一个是1的情况,另一种是长方体的长、宽、高都大于1的情况.当长方体的长、宽、高中有一个是1时,分割后只有一层小正方体,其中有两个面涂上红色的小正方体是去掉最外层一圈的小正方体后剩下的那些.因为有两个面涂上红色的小正方体恰好是100块,设100a b =⨯,那么分成的小正方体个数为()()()()221242104a b ab a b a b +⨯+⨯=+++=++,为了使小正方体的个数尽量少,应使()a b +最小,而两数之积一定,差越小积越小,所以当10a b ==时它们的和最小,此时共有 ()()102102144+⨯+=个小正方体.当长方体的长、宽、高都大于1时,有两个面涂上红色的小正方体是去掉8个顶点所在的小正方体后12条棱上剩余的小正方体,因为有两个面涂上红色的小正方体恰好是100块,所以长方体的长、宽、高之和是10042331÷+⨯=.由于三个数的和一定,差越大积越小,为了使小正方体的个数尽量少,应该令312227=++,此时共有2227108⨯⨯=个小正方体. 因为108144<,所以至少要把这个大长方体分割成108个小正方体.【例 15】 把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?【解析】 一个面最多有5个方格可染成红色(见左下图).因为染有5个红色方格的面不能相邻,可以相对,所以至多有两个面可以染成5个红色方格.红红红红红红红红红红红其余四个面中,每个面的四个角上的方格不能再染成红色,至多能染4个红色方格(见上中图).因为染有4个红色方格的面也不能相邻,可以相对,所以至多有两个面可以染成4个红色方格.最后剩下两个相对的面,每个面最多可以染2个红色方格(见右上图).所以,红色方格最多有52422222⨯+⨯+⨯=(个).(另解)事实上上述的解法并不严密,“如果最初的假设并没有两个相对的有5个红色方格的面,是否其他的四个面上可以出现更多的红色方格呢?”这种解法回避了这个问题,如果我们从约束染色方格数的本质原因入手,可严格说明22是红色方格数的最大值.对于同一个平面上的格网,如果按照国际象棋棋盘的方式染色,那么至少有一半的格子可以染成红色.但是现在需要染色的是一个正方体的表面,因此在分析问题时应该兼顾棱、角等面与面相交的地方:⑴ ⑵ ⑶ ⑴如图,每个角上三个方向的3个方格必须染成不同的三种颜色,所以8个角上最多只能有8个方格染成红色. ⑵如图,阴影部分是首尾相接由9个方格组成的环,这9个方格中只能有4个方格能染成同一种颜色(如果有5个方格染同一种颜色,必然出现相邻,可以用抽屉原理反证之:先去掉一个白格,剩下的然后两两相邻的分成四个抽屉,必然有一个抽屉中有两个红色方格),像这样的环,在正方体表面最多能找到不重叠的两道(关于正方体中心对称的两道),涉及的18个方格中最多能有8个可染成红色. ⑶剩下633839212⨯⨯-⨯-⨯=个方格,分布在6条棱上,这12个格子中只能有6个能染成红色. 综上所述,能被染成红色的方格最多能有88622++=个格子能染成红色,第一种解法中已经给出22个红方格的染色方法,所以22个格子染成红色是最多的情况.【例 16】 一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?【解析】 本题的关键是确定三次切下的正方体的棱长.由于21:15:127:5:4=,为了方便起见.我们先考虑长、宽、高分别为7厘米、5厘米、4厘米的长方体.因为754>>,容易知道第一次切下的正方体棱长应该是4厘米,第二次切时,切下棱长为3厘米的正方体符合要求.第三次切时,切下棱长为2厘米的正方体符合要求.那么对于原长方体来说,三次切下的正方体的棱长分别是12厘米、9厘米和6厘米,所以剩下的体积应是:()33321151212961107⨯⨯-++=(立方厘米).12129996663121263912【例 17】 有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标A 的为黑色,图中共有黑色积木多少块?A【解析】 分层来看,如下图(切面平行于纸面)共有黑色积木17块.【巩固】这个图形,是否能够由112⨯⨯的长方体搭构而成? 【解析】 每一个112⨯⨯的长方体无论怎么放,都包含了一个黑色正方体和一个白色正方体,而黑色积木有17块,白色积木有15块,所以该图形不能够由112⨯⨯的长方体搭构而成.【巩固】有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?33223323322323111111【解析】 第一层如下图,第二层、第三层依次比上面一层每格都多1(见下图).765434565第三层654323454第二层第一层343212345上面的9个数之和是27,由对称性知,上面、前面、右面的所有数之和都是27.同理,下面的9个数之和是45,下面、左面、后面的所有数之和都是45.所以六个面上所有数之和是(2745)3216+⨯=.【例 18】 (05年武汉明心杯数学挑战赛)如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?【解析】 求体积:开了315⨯⨯的孔,挖去31515⨯⨯=,开了115⨯⨯的孔, 挖去11514⨯⨯-=;开了215⨯⨯的孔, 挖去215(22)6⨯⨯-+=,剩余部分的体积是:555(1546)100⨯⨯-++=.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:22412100⨯+=. 求表面积:表面积可以看成外部和内部两部分.外部的表面积为55612138⨯⨯-=,内部的面积可以分为前 后、左右、上下三个方向,面积分别为()22515121320⨯⨯+⨯-⨯-⨯=、 ()2153513132⨯⨯+⨯-⨯-=、()2151511214⨯⨯+⨯-⨯-=,所以总的表面积为 138203214204+++=.(另解)运用类似于三视图的方法,记录每一方向上的不同位置上的裸露正方形个数: 前后方向:32上下方向:30 左右方向:40总表面积为()2323040204⨯++=.【总结】“切片法”:全面打洞(例如本题,五层一样),挖块成线(例如本题,在前一层的基础上,一条线一条线地挖),这里体现的思想方法是:化整为零,有序思考!【巩固】(2008年香港保良局第12届小学数学世界邀请赛)如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?第8题【解析】对于这一类从立体图形中间挖掉一部分后再求体积(或小正方体数目)的题目一般可以采用“切片法”来做,所谓“切片法”,就是把整个立体图形切成一片一片的(或一层一层的),然后分别计算每一片或每一层的体积或小正方体数目,最后再把它们相加.采用切片法,俯视第一层到第五层的图形依次如下,其中黑色部分表示挖除掉的部分.第1层第2层第3层第4层第5层从图中可以看出,第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个,所以总共还剩下22111162272++++=(个)小正方体.【巩固】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方【解析】解法一:(用“容斥原理”来解)5525⨯=个,由侧面图形抽出的小正方体有5525⨯=个,由底面图形抽出的小正方体有4520⨯=个,正面图形和侧面图形重合抽出的小正方体有1221228⨯+⨯+⨯=个,正面图形和底面图形重合抽出的小正方体有13227⨯+⨯=个,底面图形和侧面图形重合抽出的小正方体有1211227⨯+⨯+⨯=个,三个面的图形共同重合抽出的小正方体有4个.根据容斥原理,252520877452++---+=,所以共抽出了52个小正方体.1255273-=,所以右图中剩下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个,必须知道是哪4块,这是最让人头疼的事.但你可以先构造空的两个方向上共同部分的模型,再由第三个方向来穿过“花墙”.这里,化虚为实的思想方法很重要.解法二:(用“切片法”来解)可以从上到下切五层,得:⑴从上到下五层,如图:⑵或者,从右到左五片,如图:请注意这里的挖空的技巧是:先认一种方向.比如:从上到下的每一层,首先都应该有第一层的空四块的情况,即——如果挖第二层:第(1)步,把中间这些位置的四块挖走如图:第(2)步,把从右向左的两块成线地挖走.(请注意挖通的效果就是成线挖去),如图:第(3)步,把从前向后的一块(请注意跟第二层有关的只是一块!)挖成线!如图:【例19】(2009年迎春杯高年级组复赛)右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的倍.⑷⑶⑵⑴⑾⑽⑼⑻⑺⑹⑸【解析】本题中的两个图都是立体图形的平面展开图,将它们还原成立体图形,可得到如下两图:其中左图是以⑴⑵⑶⑷为平面展开图的立体图形,是一个四个面都是正三角形的正四面体,右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形,是一个不规则图形,底面是⑾,四个侧面是⑺⑻⑼⑽,两个斜面是⑸⑹.对于这两个立体图形的体积,可以采用套模法来求,也就是对于这种我们不熟悉的立体图形,用一些我们熟悉的基本立体图形来套,看看它们与基本立体图形相比,缺少了哪些部分.由于左图四个面都是正三角形,右图底面是正方形,侧面是等腰直角三角形,想到都用正方体来套. 对于左图来说,相当于由一个正方体切去4个角后得到(如下左图,切去1ABDA 、1CBDC 、111D AC D 、111B AC B );而对于右图来说,相当于由一个正方体切去2个角后得到(如下右图,切去1BACB 、1DACD ).D 1C 1B 1A 1D CBAAB CDA 1B 1C 1D 1假设左图中的立方体的棱长为a ,右图中的立方体的棱长为b ,则以⑴⑵⑶⑷为平面展开图的立体图形的体积为:3231114233a a a a -⨯⨯⨯=,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为3231122233b b b b -⨯⨯⨯=.由于右图中的立方体的棱长即是题中正方形⑾的边长,而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长,通过将等腰直角三角形⑺分成4个相同的小等腰直角三角形可以得到右图中的立方体的棱长是左图中的立方体的棱长的2倍,即2b a =.那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为:()33331212::21:163333a b a a =⨯=,也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍.【例 20】 图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴ 图⑵【解析】 首先,我们把展开图折成立体图形,见下列示意图:图⑴ 图⑵对于这类题目,一般采用“套模法”,即用一个我们熟悉的基本立体图形来套,这样做基于两点考虑,一是如果有类似的模型,可以直接应用其计算公式;二是如果可以补上一块或者放到某个模型里面,那么可以从这个模型入手.我们把图⑴中的立体图形切成两半,再转一转,正好放进去!我们看到图⑴与图⑶的图形位置的微妙关系:1和图3一致!60°图⑶ 图⑷ 由图⑷可见,图⑴这个立体的体积与图⑶这个被切去了8个角后的立体图形的体积相等.假设立方体的1条边的长度是1,那么一个角的体积是1111112222348⨯⨯⨯⨯=,所以切掉8个角后的体积是1518486-⨯=.再看图⑵中的正四面体,这个正四面体的棱长与图⑶中的每一条实线线段相等,所以应该用边长为12的立方体来套.如果把图⑵的立体图形放入边长为12的立方体里的话是可以放进去的.12这是切去了四个角后的图形,从上面的分析可知一个角的体积为148,所以图⑵的体积是:1111142224824⨯⨯-⨯=,那么前者的体积是后者的5120624÷=倍.【例 21】 如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.5【解析】 从上面看到图形是右上图,所以上下底面积和为22 3.14 1.514.13⨯⨯=(立方米),侧面积为2 3.14(0.51 1.5)118.84⨯⨯++⨯=(立方米),所以该物体的表面积是14.1318.8432.97+=(立方米).【例 22】 有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【解析】 涂漆的面积等于大圆柱表面积与小圆柱侧面积之和,为266π10π()24π560π18π20π98π307.722⨯+⨯⨯+⨯=++==(平方厘米).【例 23】 (第四届希望杯2试试题)圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米.(结果用π表示)【解析】 当圆柱的高是12厘米时体积为210300π()122ππ⨯⨯=(立方厘米)当圆柱的高是12厘米时体积为212360π()102ππ⨯⨯=(立方厘米).所以圆柱体的体积为300π立方厘米或360π立方厘米.【例 24】 如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14=)【解析】 圆的直径为:()16.561 3.144÷+=(米),而油桶的高为2个直径长,即为:428(m)⨯=,故体积为100.48立方米.【巩固】如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?(π 3.14=)【解析】 做成的圆柱体的侧面是由中间的长方形卷成的,可见这个长方形的长与旁边的圆的周长相等,则剪下的长方形的长,即圆柱体底面圆的周长为:2π1062.8⨯⨯=(厘米),原来的长方形的面积为:10462.81022056⨯+⨯⨯=()()(平方厘米).【例 25】 把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?【解析】 沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少的部分为减掉的2厘米圆柱体的侧面积,所以原来圆柱体的底面周长为12.562 6.28÷=厘米,底面半径为6.28 3.1421÷÷=厘米,所以原来的圆柱体的体积是2π188π25.12⨯⨯==(立方厘米).【例 26】 一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? (π 3.14=)【解析】 从图中可以看出,拼成的长方体的底面积与原来圆柱体的底面积相同,长方体的前后两个侧面面积与原来圆柱体的侧面面积相等,所以增加的表面积就是长方体左右两个侧面的面积. (法1)这两个侧面都是长方形,且长等于原来圆柱体的高,宽等于圆柱体底面半径.可知,圆柱体的高为()250.24 3.1424÷⨯=(厘米),所以增加的表面积为24216⨯⨯=(平方厘米);(法2)根据长方体的体积公式推导.增加的两个面是长方体的侧面,侧面面积与长方体的长的乘积就是长方体的体积.由于长方体的体积与圆柱体的体积相等,为50.24立方厘米,而拼成的长方体的长等于圆柱体底面周长的一半,为3.142 6.28⨯=厘米,所以侧面长方形的面积为50.24 6.288÷=平方厘米,所以增加的表面积为8216⨯=平方厘米.【例 27】 (2008年”希望杯”五年级第2试)一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是_______ 立方厘米.(π取3.14)(单位:厘米)【解析】 由于瓶子倒立过来后其中水的体积不变,所以空气部分的体积也不变,从图中可以看出,瓶中的水构成高为6厘米的圆柱,空气部分构成高为1082-=厘米的圆柱,瓶子的容积为这两部分之和,所以瓶子的容积为:24π()(62) 3.1432100.482⨯⨯+=⨯=(立方厘米).【巩固】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米;瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?。
六年级奥数题:立体图形(B)

六年级奥数题:⽴体图形(B)⼗三、⽴体图形(2)1. _____________ 右图表⽰的长⽅体(单位:⽶),长和宽都是3⽶,体积是24⽴⽅⽶.这个长⽅体的表⾯积是平⽅⽶.r332. ________________ 把两个相同的正⽅体拼在⼀起成⼀个长⽅体,这个长⽅体的表⾯积是两个正⽅体表⾯积之和的分之_」3. ⼀个长6分⽶、宽4分⽶、⾼2分⽶的⽊箱.⽤三根铁丝捆起来(如右图), 打结处要⽤1分⽶铁丝.这根铁丝总长⾄少为_______ 分⽶.4. ⼀个长⽅体的底⾯、侧⾯和前⾯的⾯积分别是12平⽅厘⽶、8平⽅厘⽶和6平⽅厘⽶.那么它的体积是.5. ________________________________________________ 如图,从长为13厘⽶,宽为9厘⽶的长⽅形硬纸板的四⾓去掉2厘⽶的正⽅形,然后,沿虚线折叠成长⽅体容器?这个容器的体积是__________________________________ ⽴⽅厘⽶?6. 将⾼都是1⽶,底⾯半径分别为1.5⽶、1⽶和0.5⽶的三个圆柱组成⼀个物体.这个物体的表⾯积是13rL9____ 年级⼀、填空题____ 班姓名__________ 得分______3.14)7. 把⼀个长、宽、⾼分别是7厘⽶、6厘⽶、5厘⽶的长⽅体,截成两个长⽅体,使这两个长⽅体的表⾯积之和最⼤?这时表⾯积之和是__________ 平⽅厘⽶?8. ⼀个圆柱形玻璃杯中盛有⽔,⽔⾯⾼2.5厘⽶,玻璃内侧的底⾯积是72平⽅厘⽶,在这个杯中放进棱长6厘⽶的正⽅体的铁块后,⽔⾯没有淹没铁块,这时⽔⾯⾼厘⽶?9. 正⽅体的每⼀条棱长是⼀个⼀位数;表⾯的每个正⽅形⾯积是⼀个两位数整个表⾯积是⼀个三位数.⽽且若将正⽅形⾯积的两位数中两个数码调过来恰好是三位数的⼗位上与个位上的数码.这个正⽅形的体积是10. 如图所⽰,剪⼀块硬纸⽚可以做成⼀个多⾯体的纸模型线粘)?这个多⾯体的⾯数、顶点数和棱数的总和是.⼆、解答题11. 在底⾯边长为60厘⽶的正⽅形的⼀个长⽅体的容器⾥,直⽴着⼀个长1 ⽶,底⾯为正⽅形,边长15厘⽶的四棱柱铁棍.这时容器⾥的⽔半⽶深,现在把铁棍轻轻地向正上⽅提起24厘⽶,露出⽔⾯的四棱柱铁棍浸湿部分长多少厘⽶?12. ⼀个长、宽和⾼分别为21厘⽶、15厘⽶和12厘⽶的长⽅体,现从它的上⾯尽可能⼤地切下⼀个正⽅体,然后从剩余的部分再尽可能⼤地切下⼀个正⽅体,最后再从第⼆次剩余的部分尽可能⼤地切下⼀个正⽅体,剩下的体积是多少⽴⽅厘⽶?13. 如图是⼀个⽴体图形的侧⾯展开图,求它的全⾯积和体积(沿虚线折,沿实14. 现有⼀个长,宽,⾼都为1cm的正⽅体,⼀个长,宽,为1cm,⾼为2cm的长⽅体,三个长,宽为1cm,⾼为3cm 的长⽅体.下列图是把这五个⽴体图形合并成某⼀⽴体图形时,从上⾯,前⾯,侧⾯所看到的图形?试利⽤下⾯三个图形把合并成的⽴体图形如(例)的样⼦画出来,并求出其表⾯积.rlj' n上⾯所看到的图形----------------------------- 答案 ----------------------------------------------1. 50.长⽅体的底⾯积为3X 3=9(⽶2),故其⾼为24 9 2⼻(⽶),从⽽其表⾯积 22 2 为3 3 32- 3 2- 2 50(⽶) 332.六分之五.设⼀个正⽅体的⼀个⾯积为 1,则两个正⽅体表⾯积为1X 6X 2=12.⽽将两5个正⽅体拼成⼀个长⽅体之后,这个长⽅体的表⾯积是10,它是12的-.6 3. 43.铁丝总长等于长⽅体长的2倍,宽的4倍与⾼的6倍之和,再加上三个打结处所⽤铁丝长,即(6 X 2+2X 6+4X 4)+1 X 3=43(分⽶)4. 24平⽅厘⽶.设长⽅体的长宽⾼分别为x, y, z 厘⽶,体积为V ⽴⽅厘⽶,则xy =12, yz=8, xz=6,将上⾯三式相乘,有x 2y 2z 2 12 8 6 576,故xyz 24,即V 24.5. 90.长⽅体容器的长为13-2 X 2=9(厘⽶),宽为9-2 X 2=5(厘⽶),⾼为2厘⽶,故体积9X 5X 2=90(⽴⽅厘⽶). 6.32.97平⽅⽶.侧前⾯所看到的图形侧⾯所看到的图形六年级奥数题:⽴体图形(B)这个物体的表⾯积是⼤圆柱的表⾯积加上中、⼩圆柱的侧⾯积,故它的表⾯积为:1.52 2 2 1.5 1 2 1 1 2 0.5 1 10.5 32.97(平⽅⽶).7. 298.把⼀个长⽅体截成两个长⽅体,只截⼀次,增加两个横截⾯,由题意应增加⾯积为7X 6=42(平⽅厘⽶)的横截⾯,其表⾯之和最⼤,最⼤⾯积为(7 X 6+7X 5+6 X 5)X 2+7X 6X 2=298(平⽅厘⽶).8. 5.⽔的体积为72 X 2.5=180( cm2),放⼊铁块后可以将⽔看作是底⾯积为72-6 X 6=36(cm i)的柱体,所以它的⾼为180-36=5(cm)9. 343.根据正⽅体的每⼀条棱长是⼀个⼀位数,表⾯积的每个正⽅形⾯积是⼀个两位数,整个表⾯积是⼀个三位数”的条件,可以判断正⽅体的棱长有5,6,7,8,9 这五种可能性.由下表的数据及条件:将正⽅形⾯积的两位数中两个数码调过来恰好是三位数的⼗位数上与个位数上的数码”可知这个正⽅体的棱长是7.棱长56789正⽅形⾯积2536496481全⾯积125216294384486因此,这个长⽅体的体积是7X 7X 7=343.10. 74.这个多⾯体的⾯数可以直接数出是20,⽽棱数为实线条数⼗2+虚线条数” 等于34- 2+19=36.顶点数⼆棱数-⾯数+2(欧拉定理)是36-20+2=18,所以这个多⾯体的⾯数、顶点数和棱数的总和是20+18+36=74.11. ⽔的体积为602 152 50 168750⽴⽅厘⽶.当将铁棍提起后,铁棍下⽅⽔的体积为60224 86400 (⽴⽅厘⽶),所以浸湿部分长为168750 86400 602 15224.4 (厘⽶).12.第⼀次切下的尽可能⼤的正⽅体的棱长是12321921六年级奥数题:⽴体图形(B )9厘⽶,体积为1231728(⽴⽅厘⽶)这时剩余⽴体底⾯形状如图(1),其⾼是12厘⽶.这样第⼆次切下的尽可能⼤的正⽅体棱长为9厘⽶,其体积是93929 (⽴⽅厘⽶).第⼆次切割后,剩下的⽴体可以看作是由两部分组成的:⼀部分的底⾯形状如图(2),⾼为12厘⽶,另⼀部分底⾯形状如图3,⾼是3厘⽶.显然,第三次切下的尽可能⼤的正⽅体棱长为6厘⽶,其体积为63 216 (⽴⽅厘⽶).所以,剩下的体积为21 X 15X 12-1728-729-216=1107(⽴⽅厘⽶). ⽴体图形的形状如右图所⽰?从上⾯和下⾯看到的形状⾯积都是 9 cm 2,共cm 2; 从两个侧⾯看到的形状⾯积都为 7 cm 2,共14 cm 2;从前⾯和后⾯看到的形状⾯积都为 6 cm 2,共12 cm 2. 隐藏着的⾯积有2 cm 2.⼀共有 18+16+12+2=46(sm 2).径为10厘⽶,⾼为8厘⽶.它的全⾯积为:12 3.14 10 8 2 10 8 1 2 3.14 102 44157 125.6 160 442.6 (平⽅厘⽶).它的体积为:- 43.14 102 8628(⽴⽅厘⽶).13.这个⽴体图形是⼀个圆柱的四分之⼀(如图),圆柱的底⾯半 14.8”7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十三、立体图形(2)
年级 班 姓名 得分 一、填空题
1.右图表示的长方体(单位:米),长和宽都是3米,体积是24立方米.这个长方体的表面积是 平方米.
2.把两个相同的正方体拼在一起成一个长方体,这个长方体的表面积是两个正方体表面积之和的 分之 .
3.一个长6分米、宽4分米、高2分米的木箱.用三根铁丝捆起来(如右图),打结处要用1分米铁丝.这根铁丝总长至少为 分米.
4.一个长方体的底面、侧面和前面的面积分别是12平方厘米、8平方厘米和6平方厘米.那么它的体积是 .
5.如图,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉2厘米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是 立方厘米.
6.将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.这个物体的表面积是 .(14.3=π)
7.把一个长、宽、高分别是7厘米、6厘米、5厘米的长方体,截成两个长方体,使这两个长方体的表面积之和最大.这时表面积之和是平方厘米.
8.一个圆柱形玻璃杯中盛有水,水面高2.5厘米,玻璃内侧的底面积是72平方厘米,在这个杯中放进棱长6厘米的正方体的铁块后,水面没有淹没铁块,这时水面高厘米.
9.正方体的每一条棱长是一个一位数;表面的每个正方形面积是一个两位数,整个表面积是一个三位数.而且若将正方形面积的两位数中两个数码调过来恰好是三位数的十位上与个位上的数码.这个正方形的体积是 .
10.如图所示,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘).这个多面体的面数、顶点数和棱数的总和是 .
二、解答题
11.在底面边长为60厘米的正方形的一个长方体的容器里,直立着一个长1米,底面为正方形,边长15厘米的四棱柱铁棍.这时容器里的水半米深,现在把铁棍轻轻地向正上方提起24厘米,露出水面的四棱柱铁棍浸湿部分长多少厘米?
12.一个长、宽和高分别为21厘米、15厘米和12厘米的长方体,现从它的上面尽可能大地切下一个正方体,然后从剩余的部分再尽可能大地切下一个正方体,最后再从第二次剩余的部分尽可能大地切下一个正方体,剩下的体积是多少立方厘米?
13.如图是一个立体图形的侧面展开图,求它的全面积和体积.
14.现有一个长,宽,高都为1cm的正方体,一个长,宽,为1cm,高为2cm的长
方体,三个长,宽为1cm ,高为3cm 的长方体.下列图是把这五个立体图形合并成某一立体图形时,从上面,前面,侧面所看到的图形.试利用下面三个图形把合并成的立体图形如(例)的样子画出来,并求出其表面积.
———————————————答 案——————————————————————
1. 50.
长方体的底面积为3×3=9(米2),故其高为3
2
2924=÷(米),从而其表面积
为5023223322333=⨯⎪⎭⎫ ⎝
⎛
⨯+⨯+⨯(米2)
2. 六分之五.
设一个正方体的一个面积为1,则两个正方体表面积为1×6×2=12.而将两
个正方体拼成一个长方体之后,这个长方体的表面积是10,它是12的6
5
.
3. 43.
铁丝总长等于长方体长的2倍,宽的4倍与高的6倍之和,再加上三个打结处所用铁丝长,即(6×2+2×6+4×4)+1×3=43(分米)
4. 24平方厘米.
设长方体的长宽高分别为x ,y ,z 厘米,体积为V 立方厘米,则xy =12, yz=8, xz=6,将上面三式相乘,有5766812222=⨯⨯=z y x ,故24=xyz ,即24=V .
5. 90.
长方体容器的长为13-2×2=9(厘米),宽为9-2×2=5(厘米),高为2厘米,故体积9×5×2=90(立方厘米).
6. 32.97平方米.
前面所看
到的图形
这个物体的表面积是大圆柱的表面积加上中、小圆柱的侧面积,故它的表面积为:
97.325.1015.0211215.1225.12≈=⨯⨯+⨯⨯+⨯⨯+⨯⨯πππππ(平方米).
7. 298.
把一个长方体截成两个长方体,只截一次,增加两个横截面,由题意应增加面积为7×6=42(平方厘米)的横截面,其表面之和最大,最大面积为(7×6+7×5+6×5)×2+7×6×2=298(平方厘米).
8. 5.
水的体积为72×2.5=180(cm 2),放入铁块后可以将水看作是底面积为72-6
×6=36(cm 2
)的柱体,所以它的高为180÷36=5(cm )
9. 343.
根据“正方体的每一条棱长是一个一位数,表面积的每个正方形面积是一个两位数,整个表面积是一个三位数”的条件,可以判断正方体的棱长有5,6,7,8,9这五种可能性.
由下表的数据及条件: “将正方形面积的两位数中两个数码调过来恰好是三位数的十位数上与个位数上的数码”可知这个正方体的棱长是7.
因此,这个长方体的体积是7×7×7=343.
10. 74.
这个多面体的面数可以直接数出是20,而棱数为“实线条数÷2+虚线条数”,等于34÷2+19=36.顶点数=棱数-面数+2(欧拉定理)是36-20+2=18,所以这个多面体的面数、顶点数和棱数的总和是20+18+36=74.
11. 水的体积为()16875050156022=⨯-立方厘米.当将铁棍提起后,铁棍下方水的体积为8640024602=⨯(立方厘米),所以浸湿部分长为
()()4.2415608640016875022=-⨯-(厘米).
12. 第一次切下的尽可能大的正方体的棱长是12
3
15
21
3
6
3
9
( 2 )
厘米,体积为1728123=(立方厘米)
这时剩余立体底面形状如图(1),其高是12厘米.这样第二次切下的尽可能大的正方体棱长为9厘米,其体积是92993=(立方厘米). 第二次切割后,剩下的立体可以看作是由两部分组成的:一部分的底面形状如图(2),高为12厘米,另一部分底面形状如图3,高是3厘米.显然,第三次切下的尽可能大的正方体棱长为6厘米,其体积为21663=(立方厘米).
所以,剩下的体积为21×15×12-1728-729-216=1107(立方厘米).
13. 这个立体图形是一个圆柱的四分之一(如图),圆柱的底面半径为10厘米,高为8厘米. 它的全面积为:
810281014.324
1
1014.34122⨯⨯+⨯⨯⨯⨯+⨯⨯⨯
6.4421606.125157=++=(平方厘米).
它的体积为:62881014.34
1
2=⨯⨯⨯(立方厘米).
14. 立体图形的形状如右图所示.
从上面和下面看到的形状面积都是9 cm 2,共cm 2; 从两个侧面看到的形状面积都为7 cm 2,共14 cm 2; 从前面和后面看到的形状面积都为6 cm 2,共12 cm 2
隐藏着的面积有2 cm 2.
一共有18+16+12+2=46(cm 2).
9
( 3 )
9。
