8函数的连续性
《函数的连续》课件

闭区间上连续函数的零点定理
如果闭区间上的连续函数在区间两端取值异号,则函数在该区间内至少有一个零点。
03
函数连续性的应用
利用连续性求极限
总结词
利用连续性求极限是函数连续性应用的重要方面之一。
详细描述
在数学分析中,许多函数的极限可以通过利用函数的连续性来求解。例如,利用函数在某点的连续性 ,可以推导出该点的极限值。此外,连续函数的极限定理也是利用连续性求极限的重要工具。
二次函数
二次函数在定义域内也是连续的 。例如,函数$f(x) = x^2$在全 体实数域$mathbf{R}$上是连续 的。
分段函数的连续性
• 分段函数:分段函数在各段定义域的交界处可能不连 续,但在整个定义域内是连续的。例如,函数$f(x) = \begin{cases} x^2, & x \geq 0 \ x, & x < 0 \end{cases}$在全体实数域$\mathbf{R}$上是连续的 ,但在$x=0$处不连续。
函数连续性的性质
Байду номын сангаас
如果内层函数和外层函数都在 某点连续,则复合函数在该点
也连续。
02
反函数的连续性
01
复合函数的连续性
反函数存在的前提下,如果原函 数在某点连续,则反函数在该点
也连续。
02
函数连续性的判定
函数在某点连续的判定
函数在某点连续的定义
如果函数在某一点的极限值等于该点的函数值,则函数在该点连续。
无穷函数的连续性
• 无穷函数:无穷函数在无穷处的值可能不定义,因此不连续。 例如,函数$f(x) = \frac{1}{x}$在$x=0$处不连续。
第一章 习题 1-8 函数的连续性与间断点
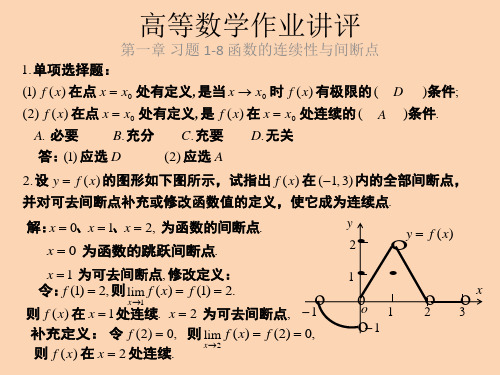
lim
( x 1)( x 1) ( x 1)( x 2 )
x 1
lim
x 1 x2
x 1
2.
所以 x 1 为函数的第一类可去间
断点 . 补充定义: f (1) 2 .
在 x 2 处 , 因为 lim
x 1
2
x 2
x 3x 2
2
所以 x 2 为函数的第二类无穷间
解: f ( 0 ) lim
x 0
x0 x0; x0 在 x 0 处连续?
1 x
sin x 1 .
1 f ( 0 ) lim x sin 1 1 . x x 0
欲使 f ( x ) 在 x 0 处连续 , 应 f ( 0 ) f ( 0 ) f ( 0 ).
( 第 4 题的函数图形 )
5 . 下列函数在指出点处间
断 , 说明这些间断点属于哪 义使它连续:
一类?如是可去间断
点 , 则补充或改变函数的定
(1) y
x 1
2
x 3x 2
2
,
x 1, x 2 ;
x 1
2
解: 在 x 1 处 , 因为 lim
x 1
x 3x 2
f ( x ) 在 x 1 处不连续 .
在 x 3 处
f ( 3 ) lim
x
x 3
x
1;
f ( x ) 在 x 3 处右连续 .
f ( 3 ) lim
x3
在 x 3处
x x
.
1-8 函数的连续性与间断点 (高等数学)

§1.8 函数的连续性与间断点教学内容:一.函数连续的概念定义 增量:设变量u 从它的一个初值1u 变到终值2u ,终值与初值的差21-u u 称为变量u 的增量,记为∆u ,即21∆=-u u u .定义 在某一点处的连续性:(1)设函数()y f x =在点0x 的某邻域内有定义,如果当自变量x 有增量x ∆时,函数相应的有增量y ∆, 若0lim 0x y ∆→∆=,则称函数()y f x =在点0x 处连续,0x 为()f x 的连续点.(2)设函数()y f x =在点0x 的某邻域内有定义,若00lim ()()x x f x f x →=,则称()y f x =在点0x 处连续.(3)设函数()y f x =在点0x 的某邻域有定义,如果对于任意正数ε,总存在正数δ,使得当x 满足不等式0x x δ-<时,有0()()f x f x ε-<,则称函数()y f x =在点0x 处连续.定义 函数在区间上的连续性:如果函数()f x 在开区间(,)a b 内每一点都连续,则称()f x 在(,)a b 内连续;如果函数()f x 在开区间(,)a b 内每一点都连续,且在左端点x a =处右连续,在右端点x b =处左连续,则称()f x 在闭区间a b [,]上连续,并称a b [,]是()f x 的连续区间.注 (1) ()f x 在左端点x a =右连续是指满足lim ()();x a f x f a +→=(2) ()f x 在右端点x b =左连续是指满足lim ()()x b f x f b -→=.定理:函数()f x 在点0x 处连续的充分必要条件是函数()f x 在点0x 处既左连续又右连续.二.函数的间断点定义函数间断点:如果函数()f x 在点0x 处不连续,则称函数()f x 在点0x 处间断,点0x 称为()f x 的间断点.第一类间断点 ()f x 在点0x 的左右极限00()f x -和00()f x +都存在的间断点为第一类间断点. 它包含两种类型:可去间断点与跳跃间断点.第二类间断点 称00()f x -和00()f x +中至少有一个不存在的间断点为第二类间断点.。
数学知识点:函数的连续性_知识点总结

数学知识点:函数的连续性_知识点总结
(1)如果函数y=f(x)在点x=x0处及其附近有定义,并且满足,则称函数y=f(x)在点x=x0处连续;否则称y=f(x)在点x=x0处不连续,或间断点。
(2)如果函数f(x)在某一开区间(a,b)内每一点处都连续,就说函数f(x)在开区间(a,b)内连续,对于闭区间[a,b]上的函数f(x),高考语文,如果在开区间(a,b)内连续,在左端点x=a处有,在右端点x=b处有,就说函数f(x)在闭区间[a,b]上连续。
3、如果f(x)是闭区间[a,b]上的连续函数,那么在闭区间[a,b]上f(x)一定有最大值和最小值。
函数的连续性的特点:
(1)f(x)在x0处有定义;
(2)f(x)在x0处的极限存在;
(3)f(x)在点x0处的极限等于函数值。
三大特点,缺一不可。
常用结论:
如果f(x)是闭区间[a,b]上的连续函数,那么在闭区间[a,b]上f(x)一定有最大值和最小值。
1-8函数的间断点与连续性

⎧∆x可正可负,但不为0 ⎨ ⎩ ∆y可正可负,但可为0
例:y = c
⇒ ∆y = 0
3
从几 何 上 看: ( 图 )
y = f ( x)
lijuan
y
f ( x0 + ∆x)
当 ∆ x → 0时 ,
∆y
f ( x0 )
∆y → 0
o
∆x x 0 x0 + ∆x
x
4
例:设函数y = x ,当x0 = 2, ∆x = 0.01时,函数的
x →0
在该点连续
2 lim f ( x ) = lim x =0 − −
x →0
� o
∴ 函数在 x = 0处不连续,为可去间断点。
x
可改变定义,令:f (0) = 0,则可在x = 0处连续
17
⎧ x2 x <1 例、讨论函数f ( x) = ⎨ 的连续性 ⎩ln x + 1 x > 1
lijuan
lijuan
⎧ tan x = 0 ⇒ x = kπ (k = 0, ±1, ±2,...) 解: ⎨ ⎩ tan x → ∞ ⇒ x = kπ + π
x (1)当x = 0时,lim x → 0 tan x
2 = 1, 但在x = 0处无定义,
∴ x = 0为可去间断点, 补充定义:f (0) = 1
5
反之:曲线在x0处不连续,如图: 则当∆x → 0时, ∆y → 0
lijuan
y
∆y
o
x0
x0 + ∆x
x
6
连续性的定义:
lijuan
设函数y = f ( x)在x0的某邻域内有定义,若在x0处, 当∆x = x − x0 → 0时, 相应的∆y = f ( x0 + ∆x) − f ( x0 ) → 0,
高等数学(8)函数的连续性与间断点

⾼等数学(8)函数的连续性与间断点⼀、函数的连续性增量变量u:初值u1 -> 终值u2增量Δu: Δu = u2-u1正的增量Δu:u1变到u2时是增⼤的负的增量Δu:u1变到u2时是减⼩的函数的增量即:当因变量增量随⾃变量增量趋于0,称为连续。
单侧连续·左连续:如果limx->x0- f(x)存在且等于f(x0) 即f(x0-) = f(x0)·右连续:如果limx->x0+f(x)存在且等于f(x0) 即f(x0+) = f(x0)·定理函数f(x)在x0处连续=函数f(x)在x0处既左连续⼜右连续连续函数定义:在区间上每⼀点都连续的函数,叫做在该区间上的连续函数或者说函数在该区间上连续注1 如果区间包括端点,那么函数在右端点处左连续,在左端点处右连续注2 连续函数的图形是⼀条连续⽽不间断的曲线例题例证明函数y = sinx 在区间(-∞,+∞)内连续⼆、函数的间断点第⼀类间断点(左右极限都存在)跳跃间断点·如果f(x)在x0处左右极限都存在·但f(x0-0)≠f(x0+0)则称点x0为函数f(x)的跳跃间断点讨论f(x) = { -x,x<=0 1+x,x>0} 在x=0处的连续性可去间断点·如果f(x)在x0处极限存在·但limx->x0 f(x) = A ≠f(x0) 或在点x0处⽆定义则称点x0为函数f(x)的可去间断点注意·注1:可去间断点只要改变或者补充间断处函数的定义,则可使其变为连续点·注2:跳跃间断点与可去间断点统称为第⼀类间断点第⼆类间断点·如果f(x)在x0处左右极限⾄少有⼀个不存在·则称x0为函数f(x)的第⼆类间断点例题1讨论f(x) = { 1/x (x>0 x(x<=0 ) 在x=0处的连续性四、章⼩结·函数在⼀点连续必须满⾜的三个条件;1.在这⼀点有定义2.在这⼀点极限是存在的3.极限存在的情况下还要等于在这⼀点的函数值·区间上的连续函数;函数在区间上的任意⼀点都连续,我们就说函数在区间上是连续的·间断点的分类与判别;间断点{第⼀类间断点:可去型,跳跃型 (左右极限都存在第⼆类间断点:⽆穷型, 振荡型 (⾄少有⼀个极限不存在}。
1.8 函数的连续性与间断点(1)

对 x 1:
lim f ( x) lim(1 x) 2,
x 1
x 1
lim f ( x) lim cos x 0
x 1
x1
2
x 1是其跳跃间断点。
16
对 x 1: f (1 0) 0, f (1 0) 0, f (1) 0 f ( x)在x 1点连续。
注 由定义1.8.1知,函数 f(x)在x0点处连续,需满足 以下条件:
(1) f ( x)在U( x0 )内有定义 x0 Df
(2) lim f ( x)存在 x xo
f ( x0 ), f ( x0 )都存在且相等
(3) lim x x0
f (x)
f ( x0 )
若三者有一不满足,则x0为f ( x)的间断点。 7
2. 间断点的分类 定义1.8.5 设点 x0 是函数 f ( x ) 的间断点, (1)如果 f-( x0)与 f+( x0)都存在,则称点x0是函 数 f (x)的第一类间断点; (2)凡不是第一类间断点的任何间断点称为第 二类间断点。 下面举例说明:
lim y 0
x 0
那么就称函数 y = f(x)在 x0 点处连续。
对该定义进行分析,可得与此等价的另外一 种定义:
2
定义1.8.2 设函数 y = f (x)在x0的某邻域内有定
义,如果
lim
x x0
f (x)
f ( x0 )
那么就称函数 y = f (x) 在 x0 点处连续。
x1
x1 2x 2
x 1为f (x)的无穷间断点。
注 找间断点时,不可先将函数表达式变形,
否则失去x 0为间断点。 15ຫໍສະໝຸດ 例7讨论f ( x)
§1.8 函数的连续性与间断点

.
解 f (1 0) 2, f (1 0) 2,
2
lim f ( x) 2 f ((11)), 2 x1
y2 x 1
x 1 为函数的第一类 间断点.
O1
x
且是可去间断点(removable discontinuity).
则
f (x)
2
x,
1 x,
所以,函数在点x 1不连续.
y
但 lim x2 1 limx 1 2
x1 x 1 x1
2
如补充定义:令 f (1) 2,
1
则 所给函数在x 1处连续. O 1
x
所以x 1称为函数的可去间断点.
23
例
函数f
(
x)
x, 1 x,
x 0, x 0,
12
sin x
设
f
(
x)
x a
b
x
sin
1 x
x0 x 0 问a, b为何值时, x0
(1) lim f ( x)存在; (2) f ( x)在x 0处连续. x0
解 因为 lim f ( x) 1, lim f ( x) b, 所以
x0
x0
(1) 要lim f ( x)存在,必需且只需
left);
若 lim x x0 0
f (x)
f ( x0 ) f ( x0 0)
f ( x0 ),
则称f ( x)在点x0处右连续(continuity from the
right).y
y
左连续
右连续
O
数学《函数的连续性》讲义

第四章函数的连续性1. 教学框架与内容教学目标①掌握函数连续性概念.②掌握连续函数的局部性质和闭区间上连续函数的整体性质.③掌握初等函数的连续性.教学内容①函数在一点和在区间上连续的定义,可去间断点,跳跃间断点,第二类间断点等间断点的分类.②连续函数的局部保号性,局部有界性,四则运算;闭区间上连续函数的最大最小值定理,有界性定理,介值性定理,反函数的连续性,一致连续性.③初等函数的连续性.2. 重点和难点①用较高的分析方法、技巧证明函数的连续性.②一致连续性和非一致连续性的特征, 如何判别函数是否一致连续.③用初等函数的连续性计算极限.3. 研究性学习选题● 连续函数介值性的应用,特别是方程根的问题, 举例说明应用.● 一致连续性的判定通过自学和小组讨论,写出对函数一致连续性的理解.4. 综合性选题,写学习笔记■ 函数极限性质、连续函数局部性质、连续函数整体性质的内在联系.5. 评价方法◎课后作业,计20分.◎研究性学习布置的两个选题合计30分.●闭区间上连续函数的性质(计15分)● 一致连续性(计15分)◎学习笔记计20分.◎小测验(第三章与第四章) 计30分§1 连续函数概念一、函数在一点的连续性回顾函数在一点的极限0lim ()x x f x A →=,可以有三种情况:1) 0()f x 无定义,如000sin()limx x x x x x →--.2) 0()f x 存在但0()f x A ≠,如00()1xx x f x x x x ≠⎧=⎨+=⎩.3) 0()f x A =,如()1f x x =+, 00lim ()()x x f x f x →=.从图形上看,函数3)的图像为一条连绵不断的曲线,这种函数我们就称为连续函数.下面我们就给出这种函数的定义.定义1 设函数f 在某0()U x 内有定义,若00lim ()()x x f x f x →=,则称f 在0x 处连续.例 1 1) ()21f x x =+在2x =处连续.2) 1sin 0()00x x f x xx ⎧≠⎪=⎨⎪=⎩在0x =处连续.结论1 若f 在0x 处连续, 则f 在0x 处存在极限(0()f x ).注 1 若要f 在0x 处连续,不仅要求f 在0x 处存在极限,而且要求极限就是函数值0()f x .而以前我们讨论函数f 在0x 处的极限,其与f 在0x 处是否有定义或f 在0x 处的值为多少均无关.定义2(εδ-) 设f 在某0(,')U x δ内有定义,若任0ε>,0δ∃>(')δδ<,使得对任意0(,)x U x δ∈, 有0()()f x f x ε-<,则称f 在0x 处连续.记0x x x ∆=-,称为x 自变量在0x 处的增量(或称作改变量,可正也可负),相应地, 函数y 在00()y f x =处的函数值增量,记为0000()()()()y y y f x f x f x x f x ∆=-=-=+∆-.定义3 f 在0x 处连续0lim 0x y ∆→⇔∆=.注 2 ()f x 在0x 处连续00lim ()()(lim )x x x x f x f x f x →→⇔==.由此可见,f 在0x 处连续0lim x x →⇔与对应法则f 可交换次序,又由左右极限,f 在0x 处连续00lim ()()x x f x f x →⇔=;0lim ()lim ()()x x x x f x f x f x +-→→⇔==;0lim ()()x x f x f x +→⇔=且00lim ()()x x f x f x -→=.(⇔f 在0x 处右、左连续).定义4 设函数f 在0()U x +(或0()U x -)内有定义,若00lim ()()x x f x f x +→=(或00lim ()()x x f x f x -→=).则称f 在0x 处右(左)连续.结论2 f 在0x 处连续⇔f 在0x 处右、左连续.例2 已知2,0,(),0,,0,x x f x A x x B x +>⎧⎪==⎨⎪-<⎩讨论()f x 在0x =处的连续性及左右连续性.二、间断点及其分类定义5 设函数f 在某00()U x 内有定义,若f 在0x 处无定义或f 在0x 处有定义但不连续,则称点0x 为f 的间断点或不连续点.若f 在0x 处不连续,则对极限必有如下情形:1) 0lim ()x x f x A →=,而f 在0x 处无定义或有定义,但00lim ()()x x f x A f x →=≠.2) 左右极限都存在但不相等,称0|lim ()lim ()|x x x x f x f x α+-→→=-为f 在0x 处的跳跃度.3) 左右极限至少有一个不存在.下面我们对间断点进行分类.1、第一类间断点------函数在此点的左右极限均存在1) 可去间断点 若00lim ()lim ()x x x x f x f x A -→+→== (此时0lim ()x x f x A →=存在,0()A f x ≠或0()f x 无意义),则称0x 为f 的可去间断点.例3 1) 1,0,()0,0,x f x x ≠⎧=⎨=⎩在0x =处.2) sin ()xf x x=在0x =处.对可去间断点,其最大的特征是0lim ()x x f x A →=存在,因而可重新定义f 在0x 处的函数值,使新的函数f 在0x 处连续.例4 对sin ()x f x x =, 定义sin ,0,()1,0,xx f x x x ⎧≠⎪=⎨⎪=⎩ 则()f x 在0x =处的连续.2) 跳跃间断点 若f 的左右极限都存在但不相等,则称0x 为f 的跳跃间断点. 例5 (1)()[]f x x =,在x n =处,跳跃度为1,在R 上任一点处都是右连续的.(2) 函数 1,0()0,01,0x x f x x x x +>⎧⎪==⎨⎪-<⎩在0x =处间断,为跳跃间断点.2、第二类间断点-----f 在此点处至少有一单侧极限不存在 例6 Dirichlet 函数()D x 在R 上任一点处间断且都是第二类间断.例7 1) 求2(1)()(1)x x f x x x -=-的间断点类型.2) 举例定义在R 上且在1x =,2x =处间断的函数.思考 有无在R 上定义但仅在1x =,2x =处连续的函数?3) 考察,;(),,x x f x x x ⎧=⎨-⎩为有理数为无理数的间断点.例8 设函数f 是区间I 上的单调函数,证明: 若0x I ∈为f 的间断点, 则0x 必为f 的第一类间断点. (单调函数的间断点必为第一类间断点)三、区间上的连续函数若函数f 是区间I 上的每一点都连续,则称f 为I 上的连续函数,而对于闭区间的端点,函数在此点连续,是指在该点的左(右)连续,如f 在[,]a b 上连续df ⇔在(,)a b 上连续且在x a =,x b =处分别是右、左连续的.例9()f x =1,1x =-处分别是右、左连续的,在(1,1)x ∈-上连续,从而()f x =[1,1]-上连续.分段连续 若f 是[,]a b 上仅有有限个第一类间断点,则称f 在[,]a b 上分段连续.例10 []y x =在任一个有限区间上分段函数.例11 证明: Riemann 函数1,(,),()0,0,1p x p q q q R x x ⎧=⎪=⎨⎪=⎩既约或无理数,在(0,1)内任何无理点均连续,但在任何有理点均不连续.例12 确定,,a b c 的值,使2111,0()0011x ax bx c x x f x x x -≤-⎧⎪++<≠⎪=⎨=⎪⎪≥⎩在R 上连续.练习 设f 为R 上的连续函数, 常数0>c . 记,();()(),();,().c f x c F x f x f x c c f x c -<-⎧⎪=≤⎨⎪>⎩若若若 证明: F 在R 上连续 (一般称F 为f 的截断函数) .习 题1. 用定义证明下列函数在其定义域上连续.2)1x2. 指出下列函数的间断点并说明类型.1)1ln x2) sin x x 3) [sin ]x 4) 112121xx -+5) sgn(sin )x 6) []x x 7) 1arctan x8) 1x e -3. 确定,,a b c 的值,使()f x 连续, 其中21101()0011x ax bx c x f x x x -≤-⎧⎪++<<⎪=⎨=⎪⎪≥⎩.4. 如何补充定义使函数f 连续.1) 24()2x f x x -=- 2) 3tan sin ()x xf x x -=5. 若f 在0x 处连续, 则||f 在0x 处连续. 反之呢? 又2f 呢?6. 若偶函数()f x 在x a =处连续,则f 在x a =-处也连续.(0)a ≠.7. 构造满足下列条件的R 上定义的函数1) 仅在1,2x =处不连续的函数; 2) 仅在1,2x =处连续的函数; 3) 仅在1()x n N n=∈处间断的函数. 8. 若对任何0ε>,f 在[,]a b εε+-上连续,则f 在(,)a b 上连续.9. 设()sin f x x =,,0,(),0,x x g x x x ππ-≤⎧=⎨+>⎩, 求证: (())f g x 在0x =处连续,而g 在0x =处间断.10. 设f 为R 上的单调函数,定义)0()(+=x f x g .证明:g 在R 上每一点都右连续.§2 连续函数性质一、连续函数的局部性质若函数f 在0x 处连续,则f 在0x 处有极限且极限等于函数值,由函数极限性质,有(复习极限性质,然后估计那些性质会减少或有什么不同) 定理 (局部有界性) 若函数f 在0x 处连续,则f 在0()U x 内有界.定理 (局部保号性) 若函数f 在0x 处连续,且0()0f x >(或0<),则对任何正数00()r f x <<(或00()r f x <<-), 存在0()U x , 使得对一切0()x U x ∈有()f x r >(或()f x r <-).注 1 一般可取01()2r f x =. 定理 (四则运算) 若函数f 和g 在0x 处连续,则f g +、f g ⋅、fg0(()0)g x ≠均 在0x 处连续.例1 1) ()f x c =,()f x x =连续,从而 多项式函数 1110()n n n n P x a x a x a x a --=++⋅⋅⋅++, 有理函数()()P x Q x (P 、Q 为多项式) 在其定义域上连续. 2) sin x 、cos x 连续,从而tan x 、cot x 在其定义域上连续.定理 (复合函数连续性) 若函数f 在0x 处连续,g 在00()u f x =连续,则复合函数g f 在0x 处连续.注 2 定理4可简写成 00lim (())(lim ())((lim ))(())x x x x x x g f x g f x g f x g f x →→→===.注 3 由上章变量代换法则定理,当内层函数f 0x x →时极限为a 而0()a f x ≠ 或()f x 在0x 无意义(即0x 为f 的可去间断点),又外层函数g 在u a =连续, 仍有上述定理结论成立,即 0lim (())(lim ())x x x x g f x g f x →→=.例2 1) 21limsin(1)x x →-; 2) x3) 0x →; 4) 0lim x x x a →, (0,1)a a >≠.二、反函数的连续性定理 若函数f 在[,]a b 上严格单调且连续,则反函数1f -在其定义域[(),()]f a f b (或[(),()]f b f a )上连续.例 3 由sin y x =在[,]22ππ-上严格单调且连续,则其反函数sin y arc x =在[1,1]-上连续. 类似地可证1ny x =,q py x =在[0,]+∞上连续.思考 反函数在其定义域上连续能否推出函数本身连续? 三、有限闭区间上连续函数的性质 (整体性质)设f 为闭区间[,]a b 上的连续函数,下面我们讨论f 在[,]a b 上的整体性质. 1、最值性定义1 设f 为定义在数集D 上的函数,若存在0x D ∈,使得对一切x D ∈,有0()()f x f x ≥(或0()()f x f x ≤) ,则称f 在D 上有最小(大)值, 0()f x 称为f 在D 上有最小(大)值, 而0x 相应地称为最小(大)值点.注4 一般而言,函数在其定义域上未必有最大值、最小值(即使f 在D 上有界),如 ()f x x =,(0,1)x ∈,-----上下确界存在.又如1,(0,1),()2,0,1.x g x x x ⎧∈⎪=⎨⎪=⎩ 在[0,1]上无最大、最小值.定理 (最值定理) 若函数f 在闭区间上[,]a b 上的连续,则f 在[,]a b 上存在最大值和最小值,即存在01,[,]x x a b ∈,使得10()()()f x f x f x ≤≤ [,]x a b ∀∈.推论 (有界性定理) 若函数f 在闭区间上[,]a b 上的连续,则f 在[,]a b 上有界. [分析 注4中两个例子为什么无界?]练习 举例说明最值定理的条件仅是充分的,易见最值点存在也未必唯一.在中学二次函数2y ax bx c =++常遇到方程20ax bx c ++=根的问题,一般找一个值0>,一个值0<(作图解释) .这实际上就是应用了连续函数的介值性. 2、介值性定理(介值性定理) 若函数f 在闭区间[,]a b 上连续且()()f a f b ≠,若μ为介于()f a 与()f b 之间的任一实数(()()f a f b μ<<,或()()f b f a μ<<) ,则至少存在一点(,)a b ξ∈,使得()f ξμ=.推论 (根的存在性定理) 若函数f 在闭区间[,]a b 上连续,且()f a 与()f b 异号, 则至少存在一点(,)a b ξ∈,使得()0f ξ=. 注 5 介值性定理与根的存在性定理是等价的.注 6 由介值性定理,若f 在[,]a b 上的连续,()()f a f b <,则f 在[,]a b 上能取到 区间[(),()]f a f b 之间的一切值,则([,])[(),()]f a b f a f b ⊃.特别地,若f 在[,]a b 上的最大值M 、最小值m ,则([,])[,]f a b m M =.结论 若f 是闭区间I 上连续且不恒为常数,则值域()f I 亦为一个闭区间.例4 证明: 方程cos x x x =在0到2π之间有实根.例5 证明: 若0r >,n 为正整数,则存在唯一正数0x 使得0n x r =(0x 称为r 的n 次正根,记作0x =).例6 设f 在[,]a b 上的连续,([,])[,]f a b a b ⊂,证明:存在0[,]x a b ∈,使得0()f x x =.注 对上述问题的根的存在性,一般可构造函数使得函数在适当区间上连续, 且在端点处的值异号,而对唯一性,一般可利用函数严格单调性说明. 练习 若f 在[0,2]a 上的连续,(0)(2)f f a =,证明: 存在点0[0,]x a ∈, 使00()()f x f x a =+.3、一致连续性----整体性质 1) 连续性定义中δ对0x 的依赖性 例7 考察函数1()f x x=在(0,1]上的连续性.例8 考察函数1()f x x=在[1,)+∞上的连续性.2) 一致连续性定义定义 设f 定义在区间I 上的函数,若对任给的0ε>,存在()0δδε=>,使得对任何',''x x I ∈,只要'''x x δ-<,就有(')('')f x f x ε-<,则称函数f 定义在I 上一致连续.注 7 若固定0''x x =,则易见f 在I 上一致连续,则f 在I 上必连续(一致连续性 定义中存在的δ与0x I ∈的选择无关).注 8 直观上说,f 在I 上一致连续⇔不论两点',''x x 在I 中什么位置,只要'''x x δ-<,就有(')('')f x f x ε-<.例9 1) 验证函数()f x ax b =+ (0)a ≠在R 上一致连续.2) 验证函数1()sin f x x=在(,1)c (01)c <<上一致连续.思考 c 能否等于0?注 9 用定义确定一致连续性时,关键是确定δ的存在,我们一般从(')('')f x f x - 入手,放大此式,除因子'''x x -外,其余不含',''x x , 再解出'''x x -. 例10 验证()ln f x x =在[1,)+∞上一致连续.例11 若函数f 在有限区间(,)a b 上一致连续,则f 在(,)a b 上必有界.3) 一致连续性的否定f 在I 上不一致连续012121200,,,, :()()x x I x x f x f x εδδε⇔∃>∀∃∈-<-≥.例12 1) 证明函数1()sin f x x=在(0,1)内非一致连续. 2) 证明函数1()f x x=在(0,1)内非一致连续. 3) 验证函数2()f x x =在[1,)+∞上非一致连续.4) Lipschitz 连续与一致连续性定义 设函数f 定义在区间I 上,若存在0L >,使得在I 上12,x x I ∀∈, 有1212()()f x f x L x x -≤-,则称f 在I 上Lipschitz 连续(或称f 在I 上满足Lipschitz 条件),而L 称为Lipschitz 常数.定理 若函数f 在区间I 上Lipschitz 连续,则f 在I 上一致连续.例13 ()sin f x x =在R 上一致连续,()f x =[,)a +∞ (0)a >上一致连续.思考 a 能否等于0? 如果能, 0a =时怎么处理? 5) 一致连续函数的判定定理 (一致连续性) 函数f 在闭区间[,]a b 上连续,则f 在[,]a b 上一致连续. 例14 f 在(,)a b 上一致连续⇔f 在(,)a b 上连续且(0),(0)f a f b ++存在. 由此说明1()f x x=在(0,1)内非一致连续.思考 上述结论对无穷区间是否成立? 即设()f x 在[,)a +∞上的连续函数,则f 在[,)a +∞上一致连续⇔lim ()x f x →∞存在且为有限值?例15 f 在I 上一致连续{},{},0()()0n n n n n n x y I x y f x f y ⇔∀⊂-→⇒-→.6) 一致连续函数的性质定理 若f 、g 在区间I 上一致连续,则||f 、f g +仍为一致连续.又若I 为有限区间,则f g ⋅也是一致连续.例16 当I [,)a =+∞,举例说明乘积f g ⋅在I 上未必一致连续.思考* 一致连续函数的复合是否仍然一致连续?例17* 设区间1I 的右端点为1c I ∈,区间2I 的左端点也为2c I ∈,用一致连续性定义证明:若f 在1I 、2I 上分别一致连续,则f 在12I I I =一致连续.特别地,若f 在[,]a c 、[,]c b 上连续,则f 在[,]a b 上一致连续(而这是显然的,关键在于1I 、2I 可能为无限区间) , 由此可得()f x =[0,)+∞上必一致连续.思考 若f 在[,)a c 、[,]c b 上连续,是否仍然有f 在[,]a b 上(一致)连续?习 题1. 求极限: 1) x x x tan )(lim 4-→ππ; 2) 1121lim 21+--++→x x x x x2. 设f ,g 在区间I 上连续, 记()max{(),()}, ()min{(),()}F x f x g x G x f x g x == 证明: F 和G 也都在I 上连续.3. 设0≠x 时, )()(x g x f ≡, 而)0()0(g f ≠. 证明: f 与g 两者中至多有一个在0=x 连续.4. 设f ,g 在点0x 连续, 证明:1) 若)()(00x g x f >, 则存在);(0δx U , 使在其内有)()(x g x f >; 2) 若在某)(00x U 内有)()(x g x f >, 则)()(00x g x f ≥.5. 证明:若f 在[,]a b 上连续,且对任何[,]x a b ∈,()0f x ≠,则f 在[,]a b 上 恒正或恒负.6. 证明: 方程sin x a x b =+(,0)a b >在(0,]a b +内至少一个实根. 7. 设f 在],[b a 上连续,12,,...,[,]n x x x a b ∈.证明:存在],[b a ∈ξ,使得121()[()()()]n f f x f x f x nξ=++⋅⋅⋅+8.设f 为],[b a 上的增函数,其值域为)](),([b f a f .证明: f 在],[b a 上连续. 9. 证明: 奇次多项式必有实根,而偶次多项式必有最大值或最小值.10.设f 在),[+∞a 上连续, 且)(lim x f x +∞→存在, 证明: f 在),[+∞a 上有界, 又f 在),[+∞a 上必有最大值或最小值吗?11. 证明: 2()f x x =在[,]a b (,)a b R ∀∈上一致连续,而在(,)-∞+∞上不一致连续.12. 证明: ()f x =[1,)+∞上一致连续. 13.证明: x x f cos )(=在),0[+∞上一致连续. 14.证明: x x f =)(在),0[+∞上一致连续.§3 初等函数的连续定理 基本初等函数在其定义域上连续. 定理 任何初等函数在其定义域上连续.例1 求()ln(2)f x x =-的连续区间和间断点.例2 利用函数的连续性求下列极限1) 20ln(1)lim cos x x x →+ 2) 0lim x +→3) sec tan 0lim(1tan )x x x x ⋅→+ 4) sin x →∞习 题1. 求下列极限:1) )1ln(15cos lim 20x x x e x x -+++→;2) )(lim x x x x x -+++∞→;3) )111111(lim 0xx x x x x x +--+++→; 4) 1lim++++∞→x xx x x ;5) x x x cot 0)sin 1(lim +→.习题课一、连续性概念 设f 在某0x 的某邻域内有定义f 在0x 处连续d⇔0ε∀>,0δ∃> ,0x x δ-<,0()()f x f x ε-<.0lim ()()x x f x f x →⇔=.000(0)(0)()f x f x f x ⇔+=-=.(其中000(0)lim (),(0)lim ()x x x x f x f x f x f x +-→→+=-=).⇔f 在0x 处左、右连续.00{}(),n n x U x x x ⇔∀⊂→,有0()()n f x f x →.f 在,a b 〈〉处连续⇔f 在(,)a b 上连续,而在端点处,若端点属于,a b 〈〉,则要求相应的单侧连续性二、连续函数的性质 1. 局部性质1) 若f 在0x 处连续,则f 在0x 处局部有界.2) 若f 在0x 处连续,0()f x c <,则00,(,):()<x U x f x c δδ∃>∀∈. 3) 若f 、g 在0x 处连续,则f g +、f g ⋅、fg0(()0)g x ≠在0x 处连续. 4) 若()f x 在0x x =连续,()g u 在0()u f x =连续,则(())g f x 在0x x =处连续. 2. 闭区间上连续函数性质1) 若f 在[,]a b 上连续,则f 在[,]a b 上有界.2) 若f 在[,]a b 上连续,则f 在[,]a b 上有最大值和最小值.3) 若f 在[,]a b 上连续,12,[,]x x a b ∈,12x x <,12()()f x f x ≠,则对任何12((),())c f x f x ∈或21((),())c f x f x ∈,必存在(,)a b ξ∈,使得()f c ξ=.4) 若f 在[,]a b 上的连续,且()()0f a f b ⋅<, 则方程()0f x =必在(,)a b 上 至少有一个根.5) 设f 在[,]a b 上严格递增(或减) 连续函数,则其反函数在其定义域[(),()]f a f b (或[(),()]f b f a )上连续.6) f 在[,]a b 上连续f ⇔在[,]a b 上一致连续 7) 任何初等函数在其定义域上都是连续的. 三、一致连续函数的性质f 在I 上一致连续1212120,0,,,:()()dx x I x x f x f x εδδε⇔∀>∃>∀∈-<-<.1、判定1) 必要条件 若f 在有限区间I 上一致连续, 则f 在I 上有界连续.(证明:1、用极限方法 2、用延拓)2) 充分条件 若f 在I 上Lipschitz 连续,则f 在I 上一致连续. 3) 充要条件a) f 在I 上一致连续{},{},0()()0n n n n n n x y I x y f x f y ⇔⊂-→⇒-→ b) f 在(,)a b 上一致连续⇔f 在(,)a b 上连续且(0),(0)f a f b ++存在且都为有限值c) 12,], [,I a b I b c =<=> (,a c 可为∞)f 在12,I I 上一致连续⇔f 在12I I I =上一致连续2、性质1) 若f 、g 在I 上一致连续,则f g +、f 在I 上一致连续. 此时, 若f 、g 还是有界的(或I 为有限区间), 则f g ⋅在I 上一致连续. 2) 设f 在(,)a +∞上连续,且lim (),(0)x f x f a →+∞+存在,则f 在(,)a +∞上一致连续,但反之未必. 3) f 在(,)-∞+∞上…4) 若f 在I 上一致连续,J I ⊂,则f 在J 上一致连续. 5) 若f 在(,)a b 上单调有界连续,则f 在(,)a b 上一致连续.3、一致连续的否定四、间断点的分类若单调函数具有介值性,则其必连续. (单调函数仅有第一类间断点)五、一些例子例1 若对任意0ε>,f 在[,]a b εε+-上连续,能否推出f 在(,)a b 上连续, 一致连续呢?例2 若f 在0x 处连续,则2||,f f 在0x 也连续,又若2||,f f 都在I 上连续, 则f 在I 上是否连续?思考 若3f 在I 上连续,则f 在I 上是否连续?例3 举出定义在[0,1]分别符合下列要求的函数1) 只在11,23和14不连续的函数,2) 只在11,23和14连续的函数,3) 只在1n(1,2,3,)n =⋅⋅⋅上间断的函数,4) 只在0x =右连续,而在其它点不连续的函数.例4 讨论复合函数g f 与f g 的连续性, 设1)21)(,sgn )(x x g x x f +==; 2) x x x g x x f )1()(,sgn )(2-==.例5 设f 、g 在区间I 上连续,记()max{(),()}F x f x g x =,()min{(),()}G x f x g x =证明:,F G 也都在I 上连续.例6 设f 在区间[,]a b 上连续,记()max{(),}F x f t a t x =≤≤,()min{(),}G x f t a t x =≤≤证明:,F G 也都在[,]a b 上连续.例7 若f 在[,]a b 上连续且对任何[,]x a b ∈,()0f x ≠, 则f 在[,]a b 上恒正 或恒负.例8 若f 在[,]a b 上连续且对任何[,]x a b ∈,()0f x ≠,则存在0c >, 使得 f 在[,]a b 上()0f x c ≥>或()0f x c ≤-<.例9 若f 在(,)a b 上连续,lim ()lim ()0x a x bf x f x +-→→⋅<,则存在(,)a b ξ∈,使得 ()0f ξ=.(或lim (), lim ()x a x bf x f x +-→→=+∞=-∞)例10 若f 在(,)a b 上连续,a c d b <<<,()()k f c f d =+,则1) 存在(,)a b ξ∈,使2()k f ξ=,2) 存在(,)a b ξ∈,使()()()()m n f mf c nf d ξ+=+ (,0)m n >.例11 若f 在[,]a b 上连续,12n a x x x b <<<⋅⋅⋅<<,则1) 1[,]n x x ξ∃∈,使11()[()()]n f f x f x nξ=+⋅⋅⋅+, 2) 1[,]n x x ξ∃∈,使11()()()n n f f x f x ξλλ=+⋅⋅⋅+.其中 12,,0n λλλ⋅⋅⋅≥ 满足121n λλλ++⋅⋅⋅+=,例12 设f 在[0,1]上连续,(0)(1)f f =,证明:对任何正数n ,存在[0,1]ξ∈,使得 1()()f f nξξ=+.例13 设f 在[,]a b 上单调递增,值域为[(),()]f a f b ,求证:f 在[,]a b 上连续.例14 设f 在区间I 上连续,证明1) 若对任何的有理数r I ∈有()0f r =,则在I 上()0f x =,2) 若对任意两个有理数12,r r 且12r r <,有12()()f r f r <,则f 为严格增函数.例15 f 在[0,)+∞上连续,满足0()f x x ≤≤,[0,)x ∈+∞,设10a ≥, 1()n n a f a +=,1,2,3,n =⋅⋅⋅,证明1) {}n a 为收敛数列; 2) 设lim n n a t →∞=,则有()f t t =; 3) 若条件改为0()f x x <<,(0,]x ∈+∞,则0t =.例16 设f 在0x =处连续,且对任何,x y R ∈有()()()f x y f x f y +=+ 证明: 1) f 在R 上连续; 2) ()(1)f x f x =⋅.例17 设f 在R 上连续且lim (),lim ()x x f x A f x B →-∞→+∞==,求证:()f x 在R 上 一致连续.例18 设f 在R 上连续有渐近线y kx b =+,求证:()f x 在R 上一致连续.例19 设f 在R 上连续, g 在R 上一致连续且lim ()()0x f x g x →∞-=,求证: ()f x 在R 上一致连续.。
函数的一致连续性

函数的一致连续性函数的一致连续性是指在定义域内的每一个点上,函数值的变化都可以通过自变量的微小变化来控制,即函数在整个定义域上的变化都是连续的。
一致连续性是连续性的一种更强的性质,它要求函数在整个定义域上都保持连续性,而不仅仅是在某个点或某个区间上连续。
在数学分析中,一致连续性是一个重要的性质,它可以帮助我们更好地理解函数的性质和行为。
一、函数的连续性在介绍函数的一致连续性之前,首先需要了解函数的连续性。
函数的连续性是指函数在某一点或某一区间上没有间断或跳跃,即函数在这些点上的极限存在且与函数在该点的取值相等。
如果函数在定义域内的每一个点上都是连续的,那么我们称这个函数在整个定义域上是连续的。
二、一致连续性的定义函数的一致连续性是指对于任意给定的ε>0,存在一个δ>0,使得当函数的自变量之间的距离小于δ时,函数值之间的距离小于ε。
换句话说,对于任意给定的ε>0,存在一个δ>0,使得当|x-y|<δ时,|f(x)-f(y)|<ε对于所有的x,y∈D都成立。
这就是函数的一致连续性的定义。
三、一致连续性与局部连续性的区别函数的一致连续性与局部连续性是两个不同的概念。
局部连续性是指函数在某一点附近连续,而一致连续性要求函数在整个定义域上都连续。
局部连续性只要求函数在某一点附近连续,对于不同的点可以有不同的δ,而一致连续性要求对于整个定义域上的任意ε,都存在一个δ,使得函数在整个定义域上都满足ε-δ的条件。
四、一致连续性的性质1. 一致连续性是连续性的更强的性质,具有更好的连续性和稳定性。
2. 一致连续性可以保证函数在整个定义域上的变化都是连续的,而不仅仅是在某个点或某个区间上连续。
3. 一致连续性可以帮助我们更好地理解函数的性质和行为,对于分析函数的性质和性质具有重要的作用。
五、一致连续性的应用1. 在实际问题中,一致连续性可以帮助我们更好地分析函数的性质和行为,从而更好地解决实际问题。
函数的连续性

第八讲 函数的连续性一、 函数的连续性客观世界许多现象都是连续变化的;比如时间的变化是连续的;所谓连续就是不间断;1、 函数连续的定义1引例:观察函数图像 y =x 2,y =1x ,y ={2x ,x ≤0x +1,x >0,y ={1,x ≠00,x =02 定义:设函数yfx 在点x 0 的某一个邻域内有定义若)()(lim 00x f x f x x =→ 则称函数yfx 在点x 0 处连续否则称函数fx 在点x 0不连续,点x 0为函数fx 的不连续点或间断点注 ① 0lim 0=∆→∆y x )()(lim 00x f x f x x =→ ②函数在点x 0连续的几何意义:函数的图形在x 0不断开;连续的实质是当自变量变化不大时,函数值变化也不大;2、左右连续性如果)()(lim 00x f x f x x =-→ 则称yfx 在点0x 处左连续 如果)()(lim 00x f x f x x =+→ 则称yfx 在点0x 处右连续 左右连续与连续的关系3、 函数在区间上的连续性在区间上每一点都连续的函数 叫做在该区间上的连续函数如果区间包括端点 那么函数在右端点连续是指左连续 在左端点连续是指右连续连续函数举例1 如果fx 是多项式函数 则函数fx 在区间 内是连续的2 函数y sin x 在区间 内是连续的二、函数的间断点的分类通常把间断点分成两类如果x 0是函数fx 的间断点左极限fx 00及右极限fx 00都存在 那么x 0称为函数fx 的第一类间断点其中左、右极限相等者称为可去间断点 不相等者称为跳跃间断点不是第一类间断点的任何间断点 称为第二类间断点例1 正切函数y tan x 在2 π=x 处没有定义 点2π=x 是函数tan x 的无穷间断点 例2 函数x y 1sin =在点x 0没有定义 所以点x 0是函数x1sin 的振荡间断点 例3 函数112--=x x y 在x 1没有定义点x 1是函数的可去间断点 例4 设函数⎪⎩⎪⎨⎧>+=<-=010 00 1)(x x x x x x f函数fx 的图形在x 0处产生跳跃现象 我们称x 0为函数fx 的跳跃间断点三、初等函数的连续性定理1 设函数fx 和gx 在点x 0连续 则函数 fxgx fxgx)()(x g x f 当0)(0≠x g 时在点x 0也连续 例1 sin x 和cos x 都在区间 内连续故tan x 和cot x 在它们的定义域内是连续的 定理2 设函数yfgx 由函数yfu 与函数ugx 复合而成 若函数ugx 在点x 0连续 函数yfu在点u 0gx 0连续 则复合函数yfx 在点x 0也连续例4 讨论函数xy 1sin =的连续性 解 函数x y 1sin =是由y sin u 及x u 1=复合而成的 sin u 当<u <时是连续的 x1当<x <0和0<x <时是连续的 函数x1sin 在无限区间 0和0 内是连续的 结论 基本初等函数在它们的定义域内都是连续的如果fx 是初等函数 且x 0是fx 的定义区间内的点则0lim x x →fxfx 0 例5 求201lim x x -→ 例6 求x x sin ln lim 2π→四、闭区间上连续函数的性质定理1最大值和最小值定理在闭区间上连续的函数在该区间上一定能取得它的最大值和最小值注意如果函数在开区间内连续或函数在闭区间上有间断点那么函数在该区间上就不一定有最大值或最小值定理2有界性定理在闭区间上连续的函数一定在该区间上有界零点如果x0使fx00 则x0称为函数fx的零点定理3零点定理设函数fx在闭区间a b上连续且fa与fb异号那么在开区间a b内至少有一点使f0例1 证明方程x 34x 210在区间0 1内至少有一个根定理4介值定理设函数fx在闭区间a b上连续且fafb那么对于fa与fb之间的任意一个数C在开区间a b内至少有一点使得fC推论在闭区间上连续的函数必取得介于最大值M与最小值m之间的任何值。
1-8函数的连续性

但反之不成立.
1, x 0 例 f ( x) x0 1,
在 x0 0 不连续
但 | f ( x ) | 、 f 2 ( x ) 在 x0 0 连续
o x
x 0称 为 函 数 的 无 穷 间 断 点 .
1 例4 讨论函数 f ( x ) sin 在 x 0处的连续性. x
解 当x 0时f ( x )在 1与 1
之间变动无限多次 ,
y sin
1 x
x 0称 为 函 数 的 振 荡 间 断 点 .
第一类间断点: 左、右极限都存在的间断点.
练习
证明函数y cos x在区间 ( , )内连续.
二 函数的间断点
函数 f ( x )在点 x0处连续必须满足的三个条件 :
(1) f ( x )在点x 0处有定义;
( 2) lim f ( x )存在;
x x0
( 3) lim f ( x ) f ( x 0 ).
x x0
x x0
且 0 f ( x ) f ( x0 ) f ( x ) f ( x0 )
lim f ( x ) f ( x0 )
x x0
lim f 2 ( x ) lim f ( x ) lim f ( x ) f 2 ( x0 ) x x0 x x0 x x0
sin x , x0 f ( x) x . 1 , x0
解:1)
lim f ( x ) f (0), x 0是连续点.
x 0
2) lim f ( x ) lim sin x lim siபைடு நூலகம் x 1
函数的连续性

一、函数的连续性 二、函数的间断点
三、闭区间上连续函数的性质
首页
上页
返回
下页
结束
铃
一、函数的连续性
变量的增量
设函数y=f(x)在点x0的某一个邻域U(x0)内有定义 在邻域U(x0)内 若自变量x从初值x0变到终值x1 则称Dx=x1-x0为自变量x的增量 称Dy=f(x0+Dx)-f(x0)为函数y的增量
二、函数的间断点
y
y
f (x)在 x0 处无定义
O
x
0
x0
x
0
x0
y
f (x)在 x0 处无极限
O
x
0
x0
y
lim
xx0
f (x)
f
(x0 )
O
x
0
x0
二、函数的间断点
•间断点的定义
设函数 f(x)在点x0的某去心邻域内有定义 在此前提 下 如果函数 f(x)有下列三种情形之一
(1)在x0没有定义
这是因为 函数P(x)在(- +)内任意一点 x0处有定 义 并且
lim
x x0
P(
x)
=
P(x0
)
注: 如果区间包括端点 那么函数在右端点连续是指左连续
在左端点连续是指右连续
下页
连续函数
在区间上每一点都连续的函数 叫做在该区间上的 连续函数 或者说函数在该区间上连续
并且
f(0)=1>0 f(1)=-2<0
根据零点定理 在(0 1)内至少有一点x 使得 f(x)=0
即
x 3-4x 2+1=0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( 2) lim f ( x) = a 存在 ; ( x → x0 时, f ( x ) 有极限 )
x → x0
(3) a = f ( x0 ) . (极限值等于函数在点 x0 处的函数值)
1.函数间断点的定义
定义
∧
若函数 f (x) 在 U ( x0 ) 内有定义, 且在点 x0 处 满足下述三个条件中的任何一个, 则称函数 f (x) 在点 x0 处间断, 点 x0 称为函数 f (x) 的一个间断点: (1) f (x) 在 x0 处无定义.
对半开闭区间和无穷区间可类似定义连续性
一般地, 如果函数 f (x) 在区间 I 上连续, 则记为 f (x) ∈C( I ) .
二. 函数的间断点
通常将函数的不连续点叫做 函数的间断点.
函数 f (x ) 在点 x0 处连续, 应该满足以下三点: (1) f (x) 在 U(x0) 内有定义; (包括在点 x0 处有定义)
定义
若 x0 为函数 f (x) 的一个间断点, 且 ,
+ x → x0
lim f ( x) 与 lim f ( x) 存在 , 则称 x0 为函数
− x → x0
f (x) 的第一类间断点.
(2) 第二类间断点
定义
凡不属于第一类的间断点, 称为函数的第二类间断点. .
即左右极限至少有一个不存在的点. 即左右极限至少有一个不存在的点
故 x = 0 为函数的第二类间断点.
看看该函数的图形.
y
1
1 y = sin x
O
−1
x
1 称 x = 0 为 f (x) = sin 的振荡型间断点 . x
无穷型间断点 第 二 类 间 型间断点 断 点 间断点
无穷
函 数 的 间 断 点
第二类间断点
无穷 振荡 其它 跳跃 可去
第一类间断点
内容小结
3.连续性概念的增量形式
定义
在某过程中, 变量 u 的终值 u2 与它的 初值 u1 的差 u2 − u1, 称为变量 u 在 u1处的 增量, 记为 ∆u = u2-u1.
∆u 是一个整体记号, 它可以取正值、负值或零.
设函数 f (x) 在 U(x0) 内有定义, x∈U(x0) , 则称 ∆x = x − x0 为自变量 x 在 x0 点处的增量. 此时, x = x0 + ∆x , 相应地, 函数在点 x0 点处 有增量 ∆ y ∆y = f (x) − f (x0 ) = f (x0 + ∆ x) − f (x0 )
在点 连续的等价形式
在点
左连续 间断的类型
右连续
第一类间断点
第二类间断点
可去间断点 左右极限都存在 跳跃间断点 无穷间断点 左右极限至少有一 个不存在
∆x = x − x0
∀ε > 0, 若 ∃ δ > 0, 当 | x − x0 | < δ 时, 有 | f (x) −f (x0) | < ε
∆y = f (x) − f (x0 )
成立, 则称函数 f (x) 在点 x0 处是连续的.
函数的连续性是通过极限定义的, 当然可以 运用《 ε − δ 》语言描述它.
O x0 y y = f (x) ∆y ∆x x x
连续性概念的增量形式
定义
设 f (x) 在 U(x0) 内有定义. 若
∆x →0
lim ∆y = 0
(∆x = x − x0 )
则称 f (x) 在点 x0 处连续.
自变量的增量趋于零时, 函数的增量也趋于零.
4.函数的左、右连续性
定义 设函数 f (x) 在 [x0, x0+δ ) 内有定义. 若
例8
1 讨论函数 f ( x ) = 在 x = 0 处的连续性. x
1 y= x
1 y 解 Q f ( x) = 在 x = 0 无定义, x
∴
x = 0为函数的间断点,
O
1 又 lim± f ( x ) = lim± = ±∞, x →0 x →0 x
x
1 故 x = 0为函数 f ( x) = 的第二类间断点. x
第八节 函数的连续性与间断点
一、连续函数的概念 二、 函数的间断点
一、连续函数的概念
极限形式 增量形式
1.函数连续性的定义 (极限形式)
是整个邻域 可减弱:x0 为聚点 定义
设 f (x) 在 U(x0) 内有定义, 若
x→ x0
lim f ( x) = f ( x0 )
则称函数 f (x) 在点 x0 处是连续的.
x→x0
lim f ( x) = f ( x0 )
⇐⇒
x→x
lim f (x) = lim f (x) = f (x 0) + −
0
x→x0
函数在点 x0 连续, 等价于它在点 x0 既 左连续又右连续.
例2
讨论 y = | x |, x∈(−∞,+∞) 在点 x = 0 处 的连续性. y
解
Q lim | x |= 0
函数的连续性是一个局部性的概念, 是逐点定义的.
函数 f (x ) 在点 x0 处连续, 应该满足以下三点: (1) f (x) 在 U(x0) 内有定义;(包括在点 x0 处有定义)
(2) lim f ( x) = a 存在;( x → x0 时, f ( x ) 有极限 )
x → x0
(3) a = f ( x0 ) . (极限值等于函数在点 x0 处的函数值)
x →0
x →0
x →0
lim− sgn x = lim− (−1) = −1
sgn x|x=0=sgn 0 = 0 故符号函数 y = sgn x 在点 x = 0 处不连续.
x2, 例4 讨论函数 f (x) =
x ≤1,
x + 1, x >1,
在 x = 1 处的连续性. 解
x →1
Q f (1) = x
(2) lim f ( x ) = a 不存在 .
x → x0
(3) lim f ( x ) = a 但 a ≠ f(x 0 ) .
x → x0
求函数间断点的途径: 求函数间断点的途径:
(1) f (x)在 x0 处无定义, 但 f (x) 在 U( x0 ) 内有定义. (2) lim f ( x) 与 lim f ( x) 中至少有一个不存在.
进一步分析该间断点的特点.
这个间断点的特点是该处的左、右极限存 在且相等, 即极限存在, 经过补充定义间断点 处函数值后, 可得到一个新的连续函数 , 故将 这种间断点称为可去间断点.
补 充 定 义 f * (x) =
f (x) ,
x→x0
x ≠ x0
lim f (x) , x = x0
第 一 类 间 断 点 间断点 跳跃型间断点
例7
x −1 讨论 f ( x ) = 在 x = 1 处的连续性. x −1
2
解 Q函数在 x =1 无定义,
y P(1,2) 1 O 1 x
∴ x =1 为函数的间断点.
x2 −1 而 lim = lim( x + 1) = 2 x →1 x − 1 x →1
故 x =1 为函数的第一类间断点.
x→x0
lim f ( x) = f ( x0 ) +
则称 f (x) 在 x0 点处右连续. . 设函数 f (x) 在 (x0– δ , x0 ] 内有定义. 若
x→ x0
lim f ( x) = f ( x0 ) −
则称 f (x) 在 x0 点处左连续. 其中, δ > 0 为任意常数.
定理
x →1
2
x =1
= 1,
x→1
lim f ( x) = lim x 2 = 1 − −
lim f ( x) = lim( x + 1) = 2 + +
x→1
∴ 函数 f (x) 在点 x = 1 处不连续. 但由于
x →1
lim f ( x) = 1 = f 1 处是左连续的.
+ x → x0 − x → x0
∧
(3) xlim f ( x) 与 xlim f ( x) 存在, 但不相等. →x →x
+ 0 − 0
(4) lim+ f ( x) = lim− f ( x) = a, 但 a ≠ f (x0 ).
x → x0 x → x0
2.函数间断点的分类 (1) 第一类间断点
这算定义吗?
例6
讨论函数 f (x)=
x +1 1 2 sinx y
x>0
x=0
x<0
在 x = 0 处的连续性. y=x+1
1 1 2
由图可知, 函数在 点 x0 处间断.
y = f (x)
x O 将左、右极限存在但不相等的间断点, y 跳跃型间断点 = sinx 称为函数的跳跃型间断点 跳跃型间断点.
由于 lim f ( x) = ∞ 所以称它为无穷间断点.
x →0
例9
1 讨论函数 f ( x ) = sin 在 x = 0 处的连续性 . x
1 解 Q f ( x ) = sin 在 x = 0 处无定义, x
∴ x = 0 为函数的间断点 .
1 又 lim f ( x ) = lim sin 不存在, x→0 x→0 x
5.函数在区间上的连续性
定义
设函数 f (x) 在开区间 (a, b) 内有定义. 若 ∀ x0∈(a, b), f (x) 在点 x0 处连续, 则称 f (x) 在开区间 (a, b) 内连续, 记为 f (x)∈C( (a, b) ).
