北京建筑工程学院水力学第05章
北航水力学课件s5 第五章粘性流体的动力学

截面平均 hw h dQ hw dQ hw Q w
( Z1
p1
) Q
112
2g
Q (Z2
p2
) Q
222
2g
Q hw Q
p1 112 p2 222 z1 z2 hw12 2g 2g
恒定总流(粘性流体)的伯努利方程
第三节 恒定总流(粘性流体)的伯努利方程 5.3.1 渐变流及其过流断面上动压强的分布
实际流体流动中: 一种是流线图形变化剧烈,流线曲率较大,流线间的夹角较大等,这种流 动叫做突变流动。如,管道大拐弯处的流动等。突变流动的动水压强分布 比较复杂,难以推导总流能量方程。 另一种,流线图形变化极其缓慢;流线曲率很小,几乎呈直线;流线 间的夹角很小,几乎是平行的,这种流动叫做渐变流动。 渐变流中的过流断面可以看做是平面。 恒定渐变流在同一过流断面上动压强的分布近似地符合静压强分布 规律。
注意:两断面间的某些流动可以是急变流。
l
总水头线
H1
hw
v 2g
p
2
hw12
测压管水头线
H2
位置水头线
z
水平基准线
H 2 H1 hw1 2 J l l
水力坡度
表示单位重量液体在单位长度流程上水头损失
伯努利方程
z1
p1
112
2g
z2
p2
2 22
2g
hw
5.3.3
恒定总流的伯努利方程的应用
恒定总流的伯努利方程的适用条件: (1)流体是不可压缩的; (2)流动是恒定的; (3)作用于流体上的质量力只有重力; (4)所取得两个过水断面都必须位于均匀流或渐变流段,但两断面之 间不必都是渐变流动。这样建立能量方程时,保证可以在断面上简单 积分,从而得到总流的伯努利方程。 (5)所取得两个过水断面没有流量汇入或流量分出,亦没有能量的输 入或输出。否则要分别建立相应的方程。(后面讨论) 。
北工大水力学课件4

----------(4-2)
2、区分恒定流和非恒定流的欧拉运动微分方程 、 加速度表示式展开, 加速度表示式展开,欧拉运动微分方程写为
∂u ∂u ∂u 1 ∂p ∂ux = +ux x +uy x +uz x ρ ∂x ∂t ∂x ∂y ∂z ∂uy ∂uy ∂uy 1 ∂p ∂uy fy − = +ux +uy +uz ∂x ∂y ∂z ρ ∂y ∂t 1 ∂p ∂uz ∂uz ∂uz ∂uz fz − = +ux +uy +uz ρ ∂z ∂t ∂x ∂y ∂z ∂ux ∂uy ∂uz 当恒定流时 = = =0 ∂t ∂t ∂t 1 ∂p ∂u ∂u ∂u fx − = ux x +uy x +uz x ρ ∂x ∂x ∂y ∂z ∂uy ∂uy ∂uy 1 ∂p fy − = ux +uy +uz ρ ∂y ∂x ∂y ∂z ∂uz ∂uz ∂uz 1 ∂p fz − = ux +uy +uz ρ ∂z ∂x ∂y ∂z fx −
u(x, y, z,t) t=0 = u0 (x, y, z)
p(x, y, z,t) t=0 = p0(x, y, z)
边界条件:一般包括固体边界和自由表面等处的运动要素情况。 边界条件:一般包括固体边界和自由表面等处的运动要素情况。 固体边界: 固体边界: 自由表面: 自由表面:
u(x, y, z,t) n = 0 p(x, y, z,t) Γ = pa (x, y, z,t)
根据牛顿第二定律
1 ∂p 1 ∂p dux (p− dx)dydz −( p + dx)dyd + fxρdxdydz = ρdxdydz 2 ∂x 2 ∂x dt
北工大水力学课件5

2、作用在一平面上M点的表面应力
表面应力 pn 在x、y、z三个轴向都有三个分量: 与平面成法向的压应力pzz,即动压强; 与平面成切向的切应力τzx,和τzy。
3、通过任一点在三个互相垂直的作用面上的表面应力。
共有九个分量 三个是压应力px、py、pz。 六个是切应力τxy、τxz、τyx、τyz、τzx、τzy。 压应力和切应力的第一个下标,表示作用面的法线方向,即表示应力的作用面与那 一个轴相垂直; 另两个下标,表示应力的作用方向,即表示应力作用方向与那一个轴相平行。
3
τ
Γ3
=0
例5-1:圆管中的层流运动 (哈根-泊肃叶流动)的流量与压降的关系(哈根-泊肃叶定 律,或简称泊肃叶定律) 自习
5-1 实际流体的运动微分方程—纳维-斯托克斯方程
例5-1:圆管中的层流运动 (哈根-泊肃叶流动)的流量与压降的关系(哈根-泊肃叶定 律,或简称泊肃叶定律) 设实际流体在很长的水平圆管内作有压恒定(层流)运动,如图5-3所示。已知管径为dl 速度 ux=u(y , z) , uy=0, uz=0 。试用 N-S方程求解过流断面上的速度分布和通过的流量以 及断面平均通度。 解;由连续性方程和N-S方程可得 微分方程:
px= p − 2 µ
p y= p − 2 µ
∂u x ∂x ∂u y
∂y ∂u pz= p − 2 µ z ∂z
------(5-5)
5-1 实际流体的运动微分方程—纳维-斯托克斯方程
3、实际流体中任一点的应力状态讨论
(1)理想流体,μ=0,
px =py =pz =p
。
(2)实际流体的均匀直线流中ux=a(不为零的常数),uy=O,uz=0和固体边壁处ux = uy = uz= 0。
北京建筑工程学院水力学考研试题题库选择题一

10.1.3 强化训练题库1、恒定流是()。
A.流动随时间按一定规律变化的流动B.流场中任意空间点的运动要素不随时间变化的流动C.各过流断面的速度分布相同的流动D.各过流断面的压强相同的流动2、一元流动是指()。
A.均匀流B.速度分布按直线变化的流动C.运动参数随一个空间坐标和时间变化的流动D.流线为直线的流动。
3、在恒定流条件下()。
A.流线和迹线正交B.流线和迹线重合C.流线是平行直线D.迹线是平行直线。
4、恒定流条件下流场内()。
A.,B.,C.,D.不一定。
5、非恒定流条件下流场内()。
A.,B.,C.,D.,6、在恒定流条件下()。
A.流线形状不变B.流线形状不断变化C.流线是平行直线D.迹线是平行直线。
7、理想流体的运动方程式与实际流体的运动方程式的差别在于()。
A.后者考虑了加速度B.后者考虑了质量力C.后者考虑了压力D.后者考虑了粘性。
8、如图10.1-11,等直径管考虑损失,A-A断面为过流断面,B-B断面为水平面1、2、3、4各点的物理量有()关系。
A.B.p3=p4C.p1=p2D.9、条件同上,各点的物理量有()关系。
A.B.p3=p4C.p1=p2D.10、总流能量方程中表示()。
A.单位重量流体具有的机械能B.单位质量流体具有的机械能C.单位体积流体具有的机械能D.通过过流断面流体的总机械能。
11、水平放置的渐扩管如图10.1-12所示,如忽略水头损失,断面形心点的压强有()关系。
A.p1>p2B.p1=p2C.p1<P2D.不定。
12、粘性流体总水头线沿程的变化是()。
A.沿程下降B.沿程上升C.保持水平D.前三种情况都有可能。
13、粘性流体测压管水头线的沿程变化是()。
A.沿程下降B.沿程上升C.保持水平D.前三种情况都有可能。
14、如图10.1-13所示垂直下泄恒定流水管,出口流速v=6m/s,管径不变,上游断面1—1高于出口断面2-2,高差为4m,水头损失不计。
大学_《工程流体力学(水力学)》第二版(禹华谦)课后答案

《工程流体力学(水力学)》第二版(禹华谦)课后答案《工程流体力学(水力学)》第二版(禹华谦)内容介绍目录绪言1 流体及其主要物理性质1.1 流体的概念1.2 流体的密度和重度1.3 流体的压缩性和膨胀性1.4 流体的粘性1.5 液体的表面性质1.6 汽化压强1.7 思考题1.8 习题2 流体静力学2.1 作用在流体上的力2.2 流体静压强及其特性2.3 流体平衡微分方程2.4 流体静力学基本方程2.5 流体静压强的度量与测量2.6 流体静压强的传递和分布2.7 流体的相对平衡2.8 静止流体作用在平面上的总压力2.9 静止流体作用在曲面上的总压力2.10 思考题2.11 习题3 流体动力学基础3.1 描述流体流动的方法3.2 流体流动的基本概念3.3 连续性方程3.4 理想流体的运动微分方程(欧拉运动微分方程) 3.5 伯努利方程3.6 伯努利方程的应用3.7 动量方程3.8 动量矩方程3.9 思考题3.10 习题4 相似原理与量纲分析4.1 流动相似的基本概念4.2 相似准则4.3 近似相似4.4 量纲分析的基本概念4.5 量纲分析法4.6 思考题4.7 习题5 流动阻力与水头损失5.1 流动阻力产生的.原因及分类5.2 粘性流体的两种流动状态5.3 均匀流沿程水头损失与切应力的关系 5.4 粘性流体的层流流动5.5 粘性流体的紊流流动5.6 紊流沿程阻力系数的计算5.7 局部水头损失5.8 思考题5.9 习题6 管路水力计算6.1 概述6.2 简单管路6.3 管路水力计算的三类问题6.4 自流管路6.5 串联管路6.6 并联管路6.7 分支管路6.8 沿程均匀泄流及装卸油鹤管6.9 有压管路中的水击6.10 思考题6.11 习题附录附录I 常见流体的密度和粘度附录Ⅱ Dg80~Dg300的管路内水力坡度i值表附录Ⅲ国际单位与工程单位对照表附录Ⅳ压强单位的换算参考文献《工程流体力学(水力学)》第二版(禹华谦)作品目录内容提要本书在论述工程流体力学基本理论的基础上,针对油料管理工作的实际需要,详细介绍了管路水力计算的常用方法并编写了相应的计算机语言程序。
水力学-第五章 明渠均匀流ppt课件

2019/12/18
长安大学
30
5.4 明渠均匀流的水力计算
3.确定断面尺寸 根据工程要求或者地形条件,选定b或者h,求对应的h或者b
2019/12/18
长安大学
31
5.4 明渠均匀流的水力计算
3.确定断面尺寸 根据工程要求或者地形条件,选定b或者h,求对应的h或者b
已知渠道的设计流量Q,底坡i,水深h,边坡系数m和粗糙系数n,求底宽b。 这一类问题的计算方法,与前一类求h的方法类似,也是采用试算—图解法。 例4.某灌溉渠道上有一渡槽,拟采用混凝土 (用刮泥刀做平)预制构件拼接成矩形断面, 根据渡槽两端渠道尺寸及渠底高,初步拟定 渡槽的底坡i为1/1000,水深h为3.5m,设计 流量Q为31m3/s。试计算渠道底宽b。
2019/12/18
长安大学
8
5.1明渠均匀流的水力特性和基本公式
明渠均匀流的计算公式
明渠均匀流的基本计算公式为谢才公式:
v C RJ C Ri
C
1
1
R6
n
v
1
21
R3i2
n
Q
vA
1
R
21
3i2
A
n
W C R v , K AC R Q
i
i
2019/12/18
长安大学
2019/12/18
长安大学
32
5.4 明渠均匀流的水力计算
3.确定断面尺寸 根据工程要求或者地形条件,选定b或者h,求对应的h或者b
解:由表5.3,对于刮泥刀做平的混凝土预制构 件,n=0.013。
9
5.2 水力最优断面
Q
北京建筑工程学院水力学课程教学大纲

2、流体静力学(1)流体静压强静压强概念及其性质,流体平衡微分方程,重力场中流体静压强的分布,压强的计算标准和度量单位及测量压强的仪器*(2)液体的相对平衡(3)静水总压力作用于平面壁上的静水总压力和作用于曲面壁上的静水总压力。
(4)阿基米德原理本部分的重点是使学生掌握点压强与总压力的计算方法。
3、流体运动学与动力学基础(1)描述流体运动的两种方法及欧拉法的基本概念。
(2)流体力学基本方程。
*欧拉运动微分方程,连续性方程,恒定元流的能量方程(伯诺里方程),恒定总流的能量方程(伯诺里方程),*恒定气流的能量方程(伯诺里方程),恒定总流的动量方程。
*(3)理论流体力学初步流体微团运动的分析,几种简单的平面无旋流动,势流叠加原理及圆柱绕流,理想流体运动微分方程及其积分,黏性流体与动微分方程。
本部分的重点是使学生具有灵活运用连续性方程、伯诺里方程和动量方程流体动力学三大方程求解实际问题的能力;难点是理解欧拉法及其基本概念、明确伯诺里方程断面平均的意义,掌握动量方程的投影关系及流动有势的含义。
4、相似原理与量纲分析(1)量纲分析的意义与量纲和谐原理(2)量纲分析原理雷列法与π定理法(3)流动相似概念及流动相似条件相似准则及模型实验。
本部分的重点是量纲分析法及模型实验的基本内容、原理和基础理论。
5、流动阻力与水头损失(1)流动阻力与水头损失的两种形式。
(2)雷诺实验及流体流动的两种形态。
(3)均匀流动基本方程及圆管中的层流运动。
*(4)紊流理论初步。
(5)非圆管的沿程损失及管道的局部损失本部分的重点是使学生掌握层流与紊流概念及其流态判别方法,圆管层流的运动规律,沿程水头损失及局部水头损失的计算方法,沿程阻力系数的变化规律以及影响因素。
6、不可压缩流体的管道流动(1)孔口与管嘴出流(2)简单管路与串并联管路(3)管网计算基础(4)有压管路的水击本部分的重点是使学生掌握有压管流的水力计算,复杂管路系统中各管段与总系统间水头损失、流量以及阻抗的关系,并联支管的流量分配。
水力学第五讲

H1
铰o
α
h
H2
合成后闸板压强分布为: 例2: 合成后闸板压强分布为: P =ρg(H1-H2) g 2 = 29.40kN/m
F
H1
o
α h H2
闸板上静水总压力: 闸板上静水总压力: P = pA = 41.45kN 对铰O取矩: 对铰O取矩:
F ×1 = P ×
0 . 5h sin α
= 29 . 31 kN
闸板提升力: 闸板提升力: F = 29.31 kN
2. 曲面壁静水总压力 曲面壁
(1) 水平分力 Fpx = pcAx=γhcAx 水平分力: (2) 铅垂分力 Pz =ρgV 铅垂分力: (3) 合力 P = PX + PZ 合力:
2 2
z
P (4) 合力方向 a = arctan 合力方向: P
1.7.2静水总压力的铅垂分力 1.7.2静水总压力的铅垂分力
d Pz = d P sin α Pz = Pz =
∫ dP
A
z
=
∫ dP
sin α
sin α
∫ γh d A
Q d A sin α = d A z ∴ Pz = γ V =
∫ hdA
Az
表明: 表明:作用于曲面上静水总 压力P的铅垂分力 压力 的铅垂分力Pz 等于 的铅垂分力
x
(5) 水平分力和 压力体绘制
Pz
P
X
Pz
Px
1.7 作用于曲面上的静水总压力
研究范围:两向曲面, 研究范围:两向曲面,柱状曲面 例如,隧洞的进口、弧形闸门。 例如,隧洞的进口、弧形闸门。
图 隧洞进口和弧形工作门
1.7 作用于曲面上的静水总压力
北京建筑工程学院水力学考研试题题库选择题三

复习题6-1 (2008年真题)理想流体的基本特征是()。
A.黏性系数是常数 B. 不可压缩C. 无黏性D. 符合符合牛顿内摩擦定律6-2水的动力粘性系数随温度的升高()。
A.增大 B.减小C.不变 D.不定6-3 流体运动粘度ν的单位是()。
A.m2/s B.N/mC. kg/mD. N·s/m6-4当水受的压强增加时,水的密度()。
A.减小 B.加大C.不变 D.不确定6-5气体体积不变,温度从0℃上升到100℃时,气体绝对压强变为原来的()。
A.0.5倍 B.1.56倍C.1.37 D.2倍6-6如图,平板与固体壁面间间距为1mm,流体的动力粘滞系数为0.1Pa·s,以50N的力拖动,速度为1m/s,平板的面积是()。
A.1m2 B.0.5 m2C.5 m2 D.2m26-7牛顿流体是指()。
A.可压缩流体 B.不可压缩流体C.满足牛顿内摩擦定律的流体 D.满足牛顿第二定律的流体6-8静止液体中存在()。
A.压应力 B.压应力和拉应力C.压应力和切应力 D.压应力、拉应力和切应力。
6-9 (2008年真题)根据静水压强的特性,静止液体中同一点各方向的压强()。
A.数值相等 B.数值不等C.仅水平方向数值相等 D.铅直方向数值最大6-10金属压力表的读值是()。
A.绝对压强 B.相对压强C.绝对压强加当地大气压 D.相对压强加当地大气压。
6-11 某点的真空压强为65000Pa,当地大气压为0.1MPa,该点的绝对压强为()。
A.65000Pa B.55000PaC.35000Pa D. 165000Pa。
6-12绝对压强p aBs与相对压强p、真空度p v、当地大气压p a之间的关系是()。
A.p= p a -p aBs B.p=p aBs+p aC.p v=p a-p aBs D.p=p v+p a。
6-13在密闭容器上装有U形水银测压计,其中1、2、3点位于同一水平面上,2管中为气体,其压强关系为()。
北工大水力学课件1

§1— 1
工程流体力学的任务及其发展简史
§1—2
1-2-1
连续介质假设·流体的主要物理性质
连续介质假设:
一、流体微观特点:
流体(fluid)由许多不连续(continue)的、相隔一定距离的分子(molecule)所组成, 而分子则由更小的原子所组成; 所有物体的分子和原子都处在永不停息的不规则运动之中,相互间经常碰撞、掺和, 进行动量(momentum)、热量/能量 (heat/energy)、质量的交换。 流体的微观结构和运动,在空间和时 间上都是不连续的,呈现着离散性、不均 匀性和随机性。 工程流体力学主要是研究流体的宏观 (机械)运动。有两种研究方法。 一种是从分子和原子微观运动出发的统 计平均方法。 二是把流体看成质点连续地充满流体所 占有的空间的的连续介质方法。
§1—2 连续介质假设·流体的主要物理性质
若以表示单位面积上的切力,即切应力(shear stess),则为
τ =µ
称流体(牛顿)内摩擦定律。
流体质点(fluid particle):又称“流体微团”。含有足够的分子,可作为连续介质基 本单质假设·流体的主要物理性质
特征体积(characteristic volume) ∆V′ :是使平均密度具有确定的数值,并表征其中 足够多分子的统计平均值即液体的宏观密度时的体积。
F=-Ma
式中 F—惯性力,国际单位制中为N,工程单位制中为 公斤力, 1 kgf = 9.8 N; M—质量,国际单位制中为 kg,工程单位制中为 公斤力·秒2/米, 1(公斤力·秒2/米)= 9.8 千克; a—加速度,m/s2;负号表示惯性力的方向与加速度方向相反。
§1—2
连续介质假设·流体的主要物理性质
§1—2
北京建筑工程学院考研水力学习题4
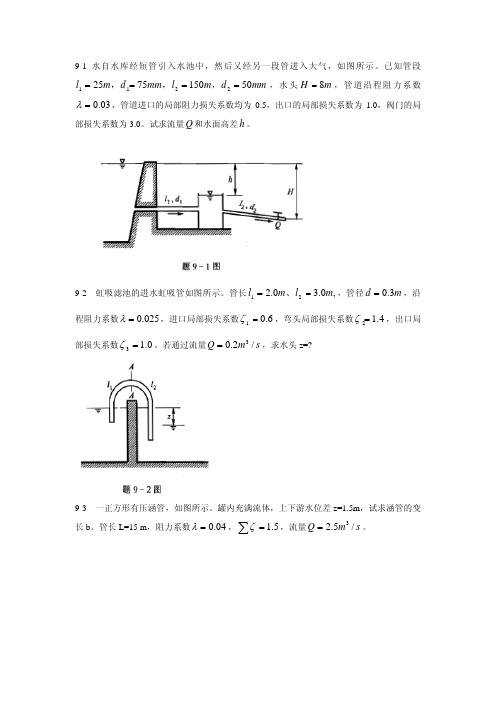
9-1水自水库经短管引入水池中,然后又经另一段管进入大气,如图所示。
已知管段mm d m l mm d m l 5015075252211====,,,,水头m H 8=,管道沿程阻力系数03.0=λ,管道进口的局部阻力损失系数均为0.5,出口的局部损失系数为1.0,阀门的局部损失系数为3.0。
试求流量Q 和水面高差h 。
9-2 虹吸滤池的进水虹吸管如图所示。
管长,0.30.221m l m l ==、,管径m d 3.0=,沿程阻力系数025.0=λ,进口局部损失系数6.01=ζ,弯头局部损失系数4.12=ζ,出口局部损失系数0.13=ζ。
若通过流量s m Q /2.03=,求水头z=?9-3 一正方形有压涵管,如图所示。
罐内充满流体,上下游水位差z=1.5m ,试求涵管的变长b 。
管长L=15 m ,阻力系数04.0=λ,∑=5.1ζ,流量s m Q /5.23=。
9-7有一先串联后并联的管道系统如图所示。
一直分流点A 前的干管流量s m Q /16.03=,各支管管长分别为m l m l m l m l 9008007006004321====、、、,各支管管径分别为mm d mm d mm d mm d 3502503002004321====、、、,粗糙系数均为012.0=n 。
求支管内流量以及分流点A 与汇流点B 之间的水头损失(按湍流粗糙区计算)。
9-17 压力钢管的直径m D 2.1=,管壁厚度mm 15=δ,水的弹性模量Pa E 31003.2×=,管长m l 2000=,管末端阀门的关闭时间T ,分别为2 s 及6 s ,是判断各产生何种水击。
设管内恒定流时的流速s m v /5.10=。
试求直接水击压强值,并估算间接水击压强值。
10-3 某梯形断面渠道内的流动,流量s m Q /203=,渠道底宽m b 0.5=,水深m h 5.20=,边坡系数m =1.0,粗糙系数n =0.025,试求渠道底坡i 。
工程流体力学基础(第2版)第5章

的量纲也相应地分为基本量纲和导出量纲。基本量纲是不能从别的量 纲推导出来的,而导出量纲是可以从别的量纲推导出来的。但哪些量 纲作为基本量纲并没有一定的标准,只是一个习惯和方便的问题。
上一页 下一页 返回
第 4 节 量纲分析
上一页 下一页 返回
第 2 节 动力相似准则
• 本节导出的牛顿数、弗劳德数、雷诺数、欧拉数、柯西数、马赫数、 韦伯数、斯特劳哈尔数统称为流体动力学相似准则数。
上一页
返回
第 3 节 相似模型试验
• 对于模型试验设计,如果在原型与模型之间严格满足相似律,则两个 流动就是相似的,模型试验的结果,按照相似律完全可以反映出原型 的流动情况。在相似律中,几何相似是由加工来完成的,运动相似可 以由动力相似反映出来,那么动力相似律能否完全满足呢?
• 流体力学中常取长度 L 、时间 T 和质量 M 为基本量纲;在与温度有 关的流体力学问题中,还要增加温度的量纲 Θ 为基本量纲。由基本 量纲组成的单位称为导出量纲,任一物理量 N 的量纲表示为 dim N 。
• 力学中的基本量纲一般定为三个,关于三个基本量纲的选取有一定的 要求,即要求基本量纲必须具有独立性,其中任何一个都不能从其余 的基本量纲导出。例如长度、时间和速度三个显然是不成的,因为速 度可以由长度和时间导出,不是独立的。
上一页 下一页 返回
第 3 节 相似模型试验
• 另外还可采用自模化的特性和稳定性来简化模型设计。例如,在有压 黏性管流中,当雷诺数大到一定数值后,管内流体的紊乱程度及速度 剖面几乎不再变化,阻力系数与雷诺数无关,此时雷诺准则已失去作 用,流动进入自动模化区,此时不必考虑模型的雷诺数与原型的雷诺 数是否相等,只要模型与原型所处同一模化区即可。
清华大学水力学(1)第五章教案

第五章 有旋流动和有势流动本章首先从运动学的角度对有旋流动的流场特性作进一步的讨论和分析,然后从动力学的角度介绍在质量力有势,流体为理想正压流体的条件下,有关涡通量的保持性定理。
论述势流理论的基本内容,引出不可压流体平面流动的流函数概念,重点讨论不可压流体平面无旋流动的速度势函数与流函数的关系以及求解势流问题的奇点叠加方法。
§5—1 有旋流动的运动学性质z 有旋流动与有势流动的判别就在于流速场的旋度是否为零。
对于有旋流动,将流速场的旋度称为涡量,它是流体微团旋转角速度矢量的两倍,ωG G G 2=×∇=Ωu . z 正象流线是流速场的矢量线一样,定义涡线是涡量场的矢量线。
涡线的微分方程为: 0d =×Ωl G G , 即 ),,,(d ),,,(d ),,,(d t z y x z t z y x y t z y x x z y x Ω=Ω=Ω.z 对应于流速场中流管、流量的概念可以建立涡量场中的涡管、涡通量概念。
涡管的涡通量又称为涡管强度I . z 斯托克斯公式 ∫∫∫⋅=⋅×∇A Ll u A n u G G G G d d )( 表明了速度环量与涡通量之间的关系。
其中n G 为曲面A 的法向,A 周界L 的正向与n G成右手系。
z 由于 ,所以涡量场是无源(管形)场。
这表明在同一时刻,穿过同一涡管的各断面的涡通量都是相同的。
换句话说,同一时刻,一根涡管对应一个涡管强度。
这是个纯运动学范畴的定理。
表明涡管不能在流体中产生与消失,要么成环形,要么两端位于流场的自由面或固体边界。
0)(≡×∇⋅∇=Ω⋅∇u G G z 封闭流体线上的速度环量对于时间的变化率等于此封闭流体线上的加速度环量。
记 ∫⋅=L l u ΓG G d ,则 ∫⋅=L l t u t ΓG G d d d d d . 注意这里的L 是由确定的流体质点组成的一条封闭线,是一个系统,在流动中会改变位置和形状。
北京建筑工程学院考研水力学习题3

2-1 设水管上安装一复式水银测压计,如图所示。
试问测压管中1-2-3-4水平液面上的压强1p 、2p 、3p 、4p 中哪个最大?哪个最小?哪个相等?2-3 设有一盛水的密闭容器,如图所示。
已知容器内点A 的相对压强为Pa 4109.4×。
如在该点左侧器壁上安装一玻璃测压管,已知水的密度3/1000m kg =ρ,试问需要多长的玻璃测压管?如在该点右侧器壁上安装一水银压差计,已知水银密度33/106.13m kg Hg ×=ρ,m h 2.01=,试问水银柱高度差2h 是多大值?2-5 设有一盛空气的密闭容器,在其两侧各接一测压装置,如图所示。
已知m h 3.01=。
试求容器内空气的绝对压强值和相对压强值,以及水银真空计左右两肢水银液面的高差2h 。
(空气质量略去不计)2-25 设有一水平底边矩形铅垂金属闸门,它由三根水平横梁和平板所组成,如图所示。
已知阀门宽度m b 3=,闸门前水深m H 2=。
试根据横梁负荷相等的条件布置闸门三根横梁的位置(321y y y 、、)。
2-36 比重计系由带有刻度的空心圆玻璃管和充以铅丸的玻璃圆球组成,如图所示。
已知管外径m d 025.0=,球外径m D 03.0=,比重计重量N G 49.0=。
如果比重计浸入某液体内的浸没深度m h 10.0=,试求该液体的密度ρ。
2-37 设有一外径为R 、内径为r 的空心圆球,由密度为1ρ的材料制成。
现要求把球完全淹没在水中,能在任何高度处平衡,试求该球的内、外径之比。
水的密度为ρ、球体体积334R V π=。
3-9 已知水平圆管过流断面上的液流速度分布为⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−=20max 1r r u u , max u 为管轴处最大流速、0r 为圆管半径,r 为点流速u 距管轴的径距。
试求断面平均流速v 。
3-13 送风管的断面面积为25050cm ×,通过d c b a 、、、四个送风口向室内输送空气,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、汇流或分流,有能量输入或输出的伯努利方 程 五、 总水头线测压管水头线 以图形方式来表示沿管路全线总水头和测压 管水头的大小,称为总水头线和测压管水头 线。
水头线的特点 四根有能量意义的线:总水头线,测压 管水头线,水流轴线(管轴线)和基准面 线。 这四根线的相互铅直距离,反映了全线 各断面的各种水头值。 ※水流轴线到基准线之间的铅直距离, 就是断面的位置水头。
2 2 2
⎫ ⎪ ⎬ ⎪ ⎭
Q=
πd d
4
2 2 1 2
2 g ⋅ Δh 4 4 d1 − d 2
Q=μ
πd d
2 1
2 2
4
2 g Δh 4 4 d1 − d 2
μ 流量系数
与毕托管的问题相类似,这里的 Δh 也是要讨论的,例如水银为测量介质, 测量水流量时的情况。
Q=μ
πd d
2 1
2 2
4
2 g ⋅ 12.6 ⋅ Δh 4 4 d1 − d 2
2 1 2 2 2
恒定不可压缩实际流体 总流的伯努利方程
二、总流伯努力方程的应用条件和应用方法 条件: 1恒定 2连续 3质量力只有重力 4计算断面为均匀流或渐变流断面 5计算断面间没有流量流入流出,没有能量 输入输出 步骤: 1分析流动 2选计算断面# 3基准面 4压强表示统一 5全面分析损失 6列方程、求解
对其进行积分,得到总流的伯努力方程
2 1 2 2
2 A2 1 u1 dA1 A1 1 2
总流的能量方程
2 1 2 2
p1 u p2 u ′ z1 + + = z2 + + + hw ρ g 2g ρ g 2g
* 过流断面的压强分布
2 p2 L
p z+ =C ρg
Z2
mg
dA 1 p1
α
Z1
p1 α1 v p2 α v z1 + + = z2 + + + hw ρ g 2g ρ g 2g
′ hw
表示两断面间单位重量流体损失的 机械能。
其他各项的意义与理想流体的完全相同
水力坡度的概念
dh dH J= =− dl dl
只可为正
' w
p d (z + ) dH p ρg Jp = − =− dl dl
可正可负
§5-3 实际流体总流的伯努力方程 一、实际流体总流的伯努力方程
p1 u p2 u ′ z1 + + = z2 + + + hw ρ g 2g ρ g 2g
能量方程问题的一般步骤是:
分析流动 划分计算断面 选择基准面 压强统一表示 分析损失 列出方程 解方程
三、文丘里管:
已知 d1,d2 ,△h求Q
⎧ p1 α v p2 α v + = z2 + + ⎪ z1 + ρ g 2g ρ g 2g ⎨ ⎪v A = v A ⎩ 1 1 2 2
2 1 1
v2 − β 1 v1 ) 2
ρ Q( β 2v2 x − β 1v1 x ) = ∑ Fx
标量形式
ρ Q( β 2v2 y − β 1v1 y ) = ∑ Fy
ρ Q( β 2v2 z − β 1v1 z ) = ∑ Fz
求解问题的过程: 1、划分控制体:a均匀流渐变流断面,b 跨越发生力的区域,c尽可能多的已知量 2、建坐标系: a惯性坐标系,b尽可能 多的力和速度与坐标轴平行或垂直 3、全面分析控制体内流体所受的力:重 力,流体压力,固体边界力(不知道,设 一个)
第五章
§5-1 N-S
实际流体动力学基础
方程
∂u x ∂u x ∂u x ∂u x 1 ∂p μ 2 fx − + ∇ ux = + ux + uy + uz ∂t ∂x ∂y ∂z ρ ∂x ρ ∂u y ∂u y ∂u y ∂u y 1 ∂p μ 2 fy − + ∇ uy = + ux + uy + uz ∂t ∂x ∂y ∂z ρ ∂y ρ ∂uz ∂uz ∂uz ∂uz 1 ∂p μ 2 + ∇ uz = + ux + uy + uz fz − ∂t ∂x ∂y ∂z ρ ∂z ρ
§5-2 实际流体元流的伯努力方程 一、实际流体元流的伯努力方程
p1 u p2 u ′ z1 + + = z2 + + + hw ρ g 2g ρ g 2g
实际流体考虑能量损失时,两断面间的机械 能是不守恒的
2 1 2 2
′ hw
表示两断面间单位重量流体损失 的机械能。
二、实际流体元流伯努利方程的 物理意义和几何意义
※测压管水头线到水流轴线之间的铅直 距离,就是断面的压强水头。 ※总水头线到测压管水头线之间的铅直距 离,就是断面流速水头。 ※总水头线总是沿程下降的,测压管水头可 升
要解决作用力,特别是流体与固体之间的作 用力,要用动量方程。
#控制断面与控制体:
4、求解控制断面的各参数,“Q,v,p (P)一个都不能少” 5、列方程,注意各力和速度的正负 号,分解关系。 6、解方程 7、讨论力的方向,“谁对谁的力,指向 哪里?”
我们将流段占有的空间称为控制体,是根据 问题的需要所选择的固定的空间体积。控制 体的整个表面称为控制面。控制体可以是有 限体积,也可以无限小。控制体欧拉法所采 用的概念。 #控制断面:流出或流入控制体流动的过流 断面,可人为选取。
冲量定理
矢量形式
∑ F idt = d ( ∑ m u )
∑ F = ρ Q( β
