电偶极子散射截面的计算
冉绍尔汤森效应验证和测量气体原子散射截面与电子能量的关系
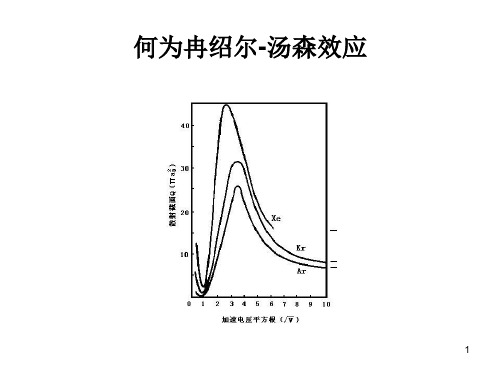
散射截面用以表示A粒子与B粒子发生相互作用而离开入 射束的概率
3
测量原理
冉绍尔-汤森效应实验仪
4
• 测量气体原子总散射截面的原理图
5
• 灯丝被加热,电子自阴极逸出,设阴极电流为Ik,电子在 加速电压的作用下,有一部分电子在到达栅极之前,被屏 极接收,形成电流Is1;有一部分穿越屏极上的矩形孔,形 成电流I0,由于屏极上的矩形孔与板极P之间是一个等势 空间,所以电子穿越矩形孔后就以恒速运动,受到气体原 子散射的电子则到达屏极,形成散射电流Is2;而未受到散 射的电子则到达板极P,形成透射电流Ip
9
• 用测量所得数据作图,分别得到Ea- Is曲线、Ea-Ip曲线、 Ea- Is*曲线、 Ea- Ip*曲线、Ea-f曲线。与交流观察的现象吻 合,各个电流与加速电压的关 系基本成正比例,而Ea-Ip 曲线存在拐角,验证了在交流观察时看到的明显的凹陷。 同时得到的Ea-f曲线,f数值可以低至0.02左右,可视为 f<<1,故关系式(总有效散射截面) Q=-(1/L)*ln[(Ip/Is)*( Is*/ Ip*)]在实验处理时完全可以采用。
10
作出散射几率与电子能量平方根的关系图
Pห้องสมุดไป่ตู้s
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.5
1.0
1.5
2.0
2.5
3.0
3.5
(eV)1/2
11
曲线分析: 有效散射截面与电子的运动速度密切相关。电子能量
降到约6.5eV时,散射截面达到极大值;进一步降低电子 能量,散射截面急剧变小,当电子能量低至约0.9eV,散 射截面出现极小值,此时,气体原子呈现所谓的“透明” 现象,即电子经过原子气体时,几乎不与原子发生碰撞而 径直透过;再降低电子的能量,散射截面将迅速增大。
电偶极子散射截面的计算

电偶极子散射截面的计算电偶极子散射截面的计算是重点研究的内容之一。
一般情况下,电偶极子散射截面是以一定体积的原子的能量、级联的激发阶梯、碰撞入射能量、旋转模型以及谱线的宽度等参数来计算的。
一、空穴模型空穴模型是根据电子可能性场中电偶极子(EPP )散射中原子间力学作用考虑电偶极子能散射的一种模型,其基本思想是用空穴力学去替换传统电子散射中势能,以求取更精确的散射截面。
它可以准确地处理电子可能性场下大能量差跨度的散射,也可以处理二倍态的各向异性,对空穴极化效应的影响等的散射进行运算。
二、交换空穴模式交换空穴模式(Exchange Hole Model)是一种二体系统的小栗(Krylov)方法,它最初由前俄罗斯科学家小栗设计的。
该模型采用第二量子力学的理论,利用磁化中空来模拟电偶极子衰减效应,用有限噪声能量来描述谱线的宽度。
交换空穴模式比起空穴模型具有更高的精度,可以更精确地计算出电子可能性场中原子间力学作用的空穴散射截面。
三、轨道混合模型轨道混合模型(Orbital Mixing Model)是模拟电子可能性场中截面参数的一种有效途径。
该模型以实际原子的电子轨道和旋转模态为基础建立,将电偶极子散射定义为一种混合状态,它在计算上表现得比空穴模型更加精确,能够正确拟合出分部散射截面。
四、低能量模型低能量模型是在空穴模型基础上改进的一个模型,它使用更简单的数值方法和计算机编程技术来计算低能量的电偶极子散射截面,可以得到更准确的数值解。
低能量模型的描述范围会比空穴模型更广,可以纳入碰撞动能效应,较之前模型,低能量模型可以比较准确地准确描述低能散射截面。
总之,电偶极子散射截面的计算需要采用恰当的模型,根据不同的实验条件来确定最有效的原子间力学作用的计算方案,空穴模型、交换空穴模型、轨道混合模型和低能量模型等模型都可以在电偶极子散射的研究中发挥重要作用,从各个方面都重要地影响到最终的散射截面计算结果。
第七讲 散射 一、散射截面

(6) (7)
令
r
将(6)式写成 ˆ2 2 2 L k 2 0 2 r r
在 r 的情形下,此方程简化为
2 2 k 0 2 r
(8 )
此方程类似一维波动方程,我们知道: 对于一维势垒或势阱的散射情况
ds θ
Z
散射角:入射粒子受靶粒子势场的作用,其运动方向偏离入射方向的角度。
弹性散射:若在散射过程中,入射粒子和靶粒子的内部状态都不发生变化,则称
弹性散射,否则称为非弹性散射。
入射粒子流密度N :单位时间内通过与入射粒子运动方向垂直的单位面积的入 射粒子数,用于描述入射粒子流强度的物理量,故又称为 入射粒子流强度。 散射截面:
ikx
ik r ( r , , ) f ( , ) e
ikr e ( r , , )f( , ) 因此, 2 r ikr e ( r , , )f( , ) 2 r
2 代表由散射中心向外传播的球面散射波, 2 代表向散射中心会聚的球面波,
2
之和。
ikx 2 e | | 为方便起见,取入射平面波 的系数A=1,这表明 1 1 ,入射粒子束单
(10)
散射波的几率流密度
* i * 2 2 2 J | f ( , ) | (11) r 2 2 2 r 2 r r
1 i (l ) l 2
(3-13)
将此结果代入(3-11)式
i 2 l l 0 l
( 2 l 1 ) eP (cos ) 2 ikf ( ) ( 2 l 1 ) P (cos )
低RCS宽带磁电偶极子贴片天线设计

低RCS宽带磁电偶极子贴片天线设计张晨;曹祥玉;高军;李思佳;黄河【摘要】该文设计了一种低雷达散射截面(RCS)的宽带磁电偶极子贴片天线,其中印刷在介质板上的金属贴片为电偶极子,3个金属过孔连接辐射贴片与金属地板构成磁偶极子。
整个天线采用“T”型渐变馈电结构同时激励电偶极子与磁偶极子,天线的频带范围为7.81~13.65 GHz,覆盖了整个X波段。
实测和仿真结果表明,通过在磁电偶极子贴片天线底面采用开槽技术并优化开槽的形状、大小、位置等变量,在天线工作频带范围内实现了RCS的减缩,最大缩减量达到了17.9 dB,同时天线保持了增益稳定不变,E面、H面方向图一致的特性。
%A low Radar Cross Section (RCS) and broadband Magneto-Electric (ME) dipole patch antenna from 7.81 GHz to 13.65 GHz covering the whole X band is designed and fabricated. Metal patches printed on the substrate form the electric dipoles, three metallic vias connected to the radiation patches and the metal ground account for the magnetic dipole radiation. The whole antenna is connected with a T-shaped feed structure which excites electric and magnetic dipoles simultaneously. Numericaland experimental results incident that the RCS of the ME dipole patch antenna can be reduced inthe whole bandwidth which the largest value is up to 17.9 dB by cutting slots on the ground and optimizing the size, shape, position of the slots. Also, the antenna shows advanced performances such as stable gain and almost consistent pattern in E and H plane.【期刊名称】《电子与信息学报》【年(卷),期】2016(038)004【总页数】5页(P1012-1016)【关键词】磁电偶极子天线;宽频带;开槽技术;低RCS;一致性【作者】张晨;曹祥玉;高军;李思佳;黄河【作者单位】空军工程大学信息与导航学院西安 710077;空军工程大学信息与导航学院西安 710077;空军工程大学信息与导航学院西安 710077;空军工程大学信息与导航学院西安 710077;西安通信学院西安 710106【正文语种】中文【中图分类】TN821 引言微带贴片天线以其低剖面、易共形等优点在战场通信、监视及其它作战平台上得到了广泛应用,但由于带宽窄,不能用于宽频天线系统,且E面、H面方向图差异较大,不易于组成天线阵[1,2]。
经典库仑散射公式的简便推导

经典库仑散射公式的简便推导
库仑散射(即转折散射)是指粒子在遇到重物粒时所发生的散射现象。
库仑散射公式是用来计算粒子散射强度的一种常用方法。
经典库仑散射公式是由爱因斯坦和费曼在1906年推导出来的。
它可以用来描述小粒子(如电子)在遇到重物粒(如原子核)时的散射情况。
经典库仑散射公式的一般形式是:
dΩ/dΩ = (r_e^2)/(4E^2) [ 1 + cos^2(θ) ]
其中,r_e是电子的质量半径,E是粒子的能量,θ是散射角。
该公式表明,粒子散射的强度与其质量半径的平方成正比,与能量的平方成反比。
此外,散射角θ与cos^2(θ)成正比,这意味着粒子在正前方散射时强度最大。
库仑散射公式是经典物理学中的一个重要公式,在原子核物理学、电子学、化学等领域有广泛的应用。
7.4 电偶极子 电偶层

dS cos θ r
则有: 则有:
2
面元dS对a点 面元 对 点
所张的立体角 dΩ
d U = kτ d Ω
9
如果从a点看到电偶层元 如果从 点看到电偶层元 带正电面,则 d Ω 取正值, 带正电面, 取正值, 反之取负值。 反之取负值。 整个电偶层在a点的电势为: 整个电偶层在 点的电势为: 点的电势为
5
v 1 q i 2 4 π ε 0 ( x + r0 2) v 2 xr0 q 2 2 2 i 4 π ε 0 ( x − r0 4)
v 1 q v r0 v E+ = (y j − i ) 3 4π ε0 r 2 v 1 q v r0 v E− = − (y j + i ) 3 4π ε0 r 2 v v v v 1 qr i 0 E = E+ + E− = − 3 4π ε0 r v qr0 i 1 =− 2 4π ε0 2 r0 3/ 2 (y + ) v4
第四节 电偶极子 电偶层
一、电偶极子的电场 二、电偶层
1
一、电偶极子的电场
电偶极子的极轴 L r 的方向由负 极轴 L 的方向由负电荷指 电荷。 向正电荷。 电偶极矩(电矩) 电偶极矩(电矩)
电偶极子的电势和电场 r
−q
r v p = qL
−
v p +q
r L
+
设电偶极子的电场中任意一点a到正负点电荷的距 设电偶极子的电场中任意一点 到正负点电荷的距 离分别为: 离分别为:1 和 r2 。 r 点电荷电势 的计算公式: 的计算公式:
σ dS
该偶元可看成电偶极子, 该偶元可看成电偶极子,其电 矩大小为: 矩大小为:
高压电场的电阻与电场电容

电容器的电容等 于电量与电压的 比值,C=Q/U
电容的定义式为 C=εS/4πkd,其 中ε为介电常数, S为极板面积,d 为极板间距
电容的计算方法 包括平行板电容 器的电容计算和 电容器串联、并 联的电容计算
存储电荷:电容在高压电场中能够 存储大量电荷,起到缓冲和平衡电 场的作用。
过滤噪声:电容可以吸收电场中的 噪声,降低电路中的干扰和噪声, 提高信号质量。
静电计法:利用 静电计的偏转角 度来测量电场强 度,但需要注意 校准和温度等因
素的影响。
磁感应法:利用 磁场的变化来间 接测量电场强度, 但需要考虑到磁 场干扰和测量误
差等因素。
添加 标题
测量原理:通过测量电场中电荷的运动行为,推导出电场的分布和强度
添加 标题
实验设备:电场测量仪、高压电源、测量电极等
XX,a click to unlimited possibilities
汇报人:XX
01
02
03
04
05
06
电阻:导体对 电流的阻碍作
用
计算公式: R=ρl/S,其中ρ 为导体电阻率, l为导体长度, S为导体横截面
积
影响因素:温 度、材料、长 度、横截面积
单位:欧姆 (Ω)
电介质极化:在高压 电场下,电介质中的 分子发生极化,形成 偶极子,阻碍电流流 动
添加标题
添加标题
添加标题
添加标题
稳定电压:电容的储能特性可以吸 收电压波动,减小电压变化对电路 的影响,提高电路的稳定性。
传递能量:在某些情况下,电容可 以通过充放电过程传递能量,实现 电场能量的储存和释放。
电容是存储电荷的物理量,其大小与电极间距离、电极面积等有关。 电容具有隔直通交的特性,即直流电流不能通过电容,而交流电流可以。 电容具有滤波、耦合、旁路等作用,广泛应用于电子电路中。 电容的单位是法拉,用字母F表示。
6-高等电磁场理论-电磁散射

第6章
电磁散射
散射矩阵与散射截面
理想导电圆柱对平面波的散射 理想导电圆柱对柱面波的散射 理想导电球对平面波的散射 理想导电球对球面波的散射
an H (ka) ( j ) J n (ka) 0
J n (ka ) an ( j ) (2) H n (ka )
n
故得到
★ 讨论: ① 远区散射场
J n (ka ) (2) E ( j ) H n (k )e jn (2) H n (ka ) n
xLeabharlann es 1 (2) e jkz cos an H n (k sin )e jn k 0sin n
ei es 边界条件: ( )
a
0
an
§6.3 理想导电圆柱对柱面波的散射
问题:如图所示,一半径为a 的无限长理想
导体圆柱沿z 轴放置,附近放置一根无限长 的线电流 I,计算导体圆柱的散射场。 1. 无限长线源的场 位于 ( 0 ,0 ) 的无限长的线源的位函数满足方程
e
jkx
a
0
(Ei E S )
a
0
a
n
(2) an H n (ka )e jn 0
★ 平面波→基本柱面波函数展开 r (ex cos ey sin ) ez z jk r , 平面波: e k k (ex cos k ey sin k ) ez kz
物理光学第3讲-第三节光在金属表面的反射和透射_光的散射

对于稀薄气体介质,设频率为 的光波 E A exp it 入射到气体 介质内,使介质内的束缚电子做受迫振动,由于磁场对电子的 作用远小于电场力,则电子受迫振动方程为
12
第四节 光的吸收、色散和散射
对于固体和液体、压缩气体,周围分子在光场作用下计划所 产生的影响不可以忽略,可以证明这时作用在电子上的电场 E’为 P
E E 3 0
Nq 2 0m Nq 2 3m 0
2 0 2
类似推导得到
n2 1
或者
n2 1 Nq 2 2 2 n 2 3 0 m 0 2
利用光波作用于物质中分子、原子所导致的电偶极子振荡解释散射现象。当光 波射入介质中时,会激发起介质中电子做受迫振动而发出次级电磁波,对于均 匀介质,这些次波叠加使光波沿着反射和折射定律方向传播,不发生散射。当 介质非均匀时,介质内有悬浮微粒而由入射波激发起的次波的振幅和相位不完
全相同,则次波干涉的结果使在非透射方向上不能完全抵消而造成散射光。
~ n1 i 记复折射率为 n
~ ~ k kn kn1 i
0
2、在共振频率附近的选择吸收区,即当入射光频率处于 0
的吸收带附近时,折射率n表示式中的 项不能忽略,此时n是复 数,即 ~ n1 i ~ 2 n2 1 2 i 2n2 2 n n
1 2 s s i s
~ rp
t an t an
2
1
2
~ i p ~ 1 2 r e ~ p 1 2
钠原子光电离2p→kl(ks,kd)散射截面理论计算

[
]
(
)
确求解, 因此许多近似方法被提出来, 微扰法便是其 中 的 一 种。 根 据 多 体 微 扰 理 论 中 的 当微扰为 (H ) R a l e i h S c h r ö d i n e r展开式, y g g c +V e x t 时, 系统的波函数表示为:
✷ 收稿日期: 2 0 0 1 0 8 0 9 基金项目: 国家自然科学基金资助项目 (批准号: ) 1 9 9 7 4 0 2 8 作者简介: 冯一兵 ( , 男, 四川师范大学物理系副教授, 主要研究方向为原子和分子碰撞。 1 9 6 6 -)
摘要:用多体微扰理论研究和计算了钠原子2 ( 光电离截面, 计算结果与实验结果相符合。 k l k s, k d) p→ 关键词: 多体微扰理论; 光电离; 散射截面 中图分类号: O 5 6 2 . 4 文献标识码: A
1 引言
光子与原子的相互作用是原子物理学中最重要 的研究领域之一, 光电离过程则是这一领域最活跃 的研究方向。正是因为光电离过程中显示了电子的 关联相互作用, 从事理论和实验的物理学家们对其 产生了极大的兴趣。在理论和实验中, 光电离过程 的研究主要集中在对离化电子的散射截面和角分布 进行测定和计算。 光电离过程中的散射截面和共振结构是理论物 理学家研究的重点。研究的内容从单光电离过程到 复杂的光电离过程。研究的对象从最先的闭壳层原 子到现在的开壳层原子。实验方法由早期的电子光 谱方法发展到激光光谱和同步辐射方法。在理论计 算方面, 最早是用简单的 H a r t r e e F o c k 和偶极子计 算方法, 后来发展到 R 矩阵方法、 交换相移近似方 法 (R ) 、 组态相互作用方法和多体微扰理论方 P A E 法 (M B P T
第3章---- 静电场及其边值问题的解法--2

ˆ r
P 0
介质内表面(r=a)的束缚电荷面密度:
r 1 Q P n ˆ P r ˆ S 2 r 4a
ˆ : 介质表面外法线方向; n
介质外表面(r=b)的束缚电荷面密度:
r 1 Q P n ˆ P r ˆ S 2 r 4b
介质中的电场强度为
D
(与未加介质板前相同)
U ˆ Ed x r 0 9d
D
D
(是未加介质板前场强的1/9)
电磁场
第3章 静电场及其边值问题的解法
(2) 介质中的极化强度
8 s ˆ P 0 xe Ed 0 ( r 1) Ed x 9 P 0 v 上 P n ˆ上 s 下 P n ˆ下 s 8 s 9 8 s 9 8 s ˆx ˆ x 9 8 s ˆ ( x ˆ) x 9
——已知源电荷分布,求空间场分布
(r) P (r) n ˆ S
(r) P (r) v
右式又可写为积分形式
q P dS
S
由此可见,任一块介质内部体分布的束缚电荷与介质块的表
面束缚电荷是等值异性的。
电磁场
第3章 静电场及其边值问题的解法
1. 极化强度矢量
P
为了计算电介质内所有电偶极子产生的宏观电场 , 我们用极
称为束缚电荷(或极化电荷);
☆ 介质中的场强为自由电荷与束缚电荷产生的场强的叠加;
电磁场
第3章 静电场及其边值问题的解法
实际上,介质极化现象是逐渐形成的。当外加电场Ea 加到介质中 以后,介质中出现的电偶极子产生二次电场Es,这种二次电场 Es 又
影响外加电场,从而导致介质极化发生改变,使二次电场又发生变
《材料分析测试方法》课程笔记

《材料分析测试方法》课程笔记第一章:x射线的物理学基础一、x射线的性质1. x射线的定义与产生x射线是一种波长位于紫外线和γ射线之间的电磁波,其波长范围大约在0.01纳米到10纳米之间。
x射线的产生通常是通过x射线管,其中高速运动的电子撞击金属靶材(如铜或钨)时,由于突然减速,电子会将部分动能转换为x 射线。
2. x射线的特点(1)穿透能力:x射线的穿透能力远强于可见光,能够穿透大多数非金属物质,但会被重金属等高原子序数物质吸收。
(2)电离作用:x射线能够电离物质,从原子或分子中移除电子,导致形成带电的离子。
(3)荧光效应:x射线能够激发某些物质发光,这种现象称为荧光效应。
(4)生物效应:x射线对生物组织具有损害作用,可以破坏细胞结构,因此在使用时需要谨慎。
二、x射线谱1. x射线谱的分类x射线谱主要包括两种类型:连续谱和特征谱。
2. 连续谱连续谱是由高速电子撞击靶材时产生的,它包含了从低能量到高能量的一系列波长。
连续谱的强度随波长的增加而减小,其峰值波长与加速电子的电压有关。
3. 特征谱特征谱是由靶材原子的内层电子跃迁到外层轨道时释放的特定能量的光子形成的。
每种元素都有其特定的特征谱线,这些谱线对应于元素原子内电子能级的特定差异。
三、x射线与物质的相互作用1. 吸收x射线在穿透物质时,其强度会随着穿透深度的增加而减弱,这是因为物质中的原子吸收了部分x射线能量。
吸收系数与物质的种类、密度和x射线的波长有关。
2. 散射(1)弹性散射(康普顿散射):x射线光子与物质中的自由电子发生碰撞后,光子的能量和方向发生改变,但波长不变。
(2)非弹性散射(瑞利散射):x射线光子与物质中的原子或分子相互作用,能量部分转化为物质的内能,导致光子的能量降低,波长变长。
3. 荧光当x射线光子的能量足够高时,可以激发物质中的原子或分子,使其电子跃迁到更高能级,随后返回基态时释放出能量,通常以可见光的形式。
4. 产生电子对在x射线能量非常高时(大于1.022 MeV),x射线光子在物质中可以转化为一个正电子和一个负电子。
计算电偶极子电场的电势和电场强度

E 2 0
dr r
dE
P
x
R
—点电荷的场!
11.3 高斯定理
描述电场的两种方法:电力线和电通量。
一、电场线
(1)曲线上各点的切线方向都与该点处的场强方向一致
(2)电场线密度
dN E dS
EP
Q
EQ
dS
dN
P
电场线的性质:
电场线起自于正电荷或无穷远,止于负电荷 或无穷远 ,没有电荷处不中断; 对于静电场不可能出现单一绕向的闭合电力线。 两条电场线不会相交,不能相切。
11.1 电力和电荷
一、电力
(1)质子与电子之间电力比引力强 39个数量级 (2)长程力,存在于原子内部和宇宙天体之间 (3)吸引与排斥两种形式 (4)电力比磁力要强的多
二、电荷
(1)电荷的正负性
(2)电荷的量子性 电子电荷(元电荷)
e 1.60217733 10 C
层子模型(quark理论)与分数电荷 (3)电荷的守恒性 (4)电荷运动不变性,即具有相对论不变性
把曲面分成许多个面积元每一面 元处视为匀强电场
非匀强电场
dΦ E dS
对整个曲面积分,即得:
dS
enE
Φ dΦ
E dS
S
讨论: 1.
dΦ E dS 的正、负取决于面元
的法线方向与电场强 度方向的关系
E
dS
如图所示: 若面元法向相反:
dq r
dV
Q
P
E
(Q )
dE
•体电荷分布
•面电荷分布
•线电荷分布
4 0 r dq dq dV dV ds dq dq ds ds dq d l dq dl dl
分子间的相互作用

BRAND PLANING
风暴石 欢迎学化物理方向的同学讨论交流
2011-3-1
分子的相互作用
分子的电性质
1.
电偶极矩
2.极化
3.相对介电常数
分子间的相互作用
1.
偶极作用
2.排斥力和总作用力
气体和液体
1.
气体分子作用
2.液-气界面
3.冷凝
01 品牌介绍
02 产品展示
01
电偶极矩
02
气体分子的相 互作用
气体分子的相互作用通过分子束来研究。分子束是指一束在真空管 道中平行前进的狭窄分子流,这束分子被引导撞击其他分子,发生 的散射与分子间相互作用有关可供研究。
分子束实验的最重要的实验信息来源于向一个特定方向撞击的入射 分子流中的分子碎片。分子碎片被散射为一个锥形的速率由dI表 示。
1
电场
点电荷产生的电场
E=q/4πε0 r2
偶极子产生的电场 E=μ/2πε0 r3
多级子产生的电场随 距离增加而减弱的速 度比点电荷快。
2
偶极-偶极作用
两个极性分子间相互作
用的势能是一个复杂的
函数,与两个分子的取
向有关。两个自由转动
的偶极子之间相互作用
的势能为零,然而它们
共有的势能与相对取向
• 总吸引力
若分子间无氢键,则转动的分子所具有的总 吸引力的能量为三种范德瓦尔斯力之和。分 子间的吸引能量一般近似表示为
V=-C6/r6,C6是与分子本身有关的系数。 若有三分子相互作用,色散能近似由 Axilrod-Teller公式表达:
V=-C6/r6AB-C6/r6BCC6/r6CA+C’/(rABrBCrCA)3
中高能区电子与分子散射总截面的计算

(1.DepartmentofTechnologyandPhysics,ZhengzhouInstituteofLightIndustry,Zhengzhou450003,P.R.China; 2.DepartmentofPhysicsandInformationEngineering,HenanNormalUniversity,Xinxiang453002,P.R.China)
b(XnYm )E nb(X)+ mb(Y)
(5)
σZ E20(ヘα-1)
(6)
α 为分子的极化率(以α30 为单位);b(X)为原子高 能时的渐进行为参数。Grzegorz把分子的特征参数 考虑进去,对于卤代甲烷计算,结果较好。我们看一
下实验上测量 TCS与分子特征参数的关系。 我们根据实验测量结果可知分子的 TCS与分
具体算法是采用hartee2fock原子波函但众所周知bon2bethe理论在我们所考虑的能量范围内明显高估了总截面特别是对于弹性部及其参数算得的总截面高于实验值甚至在10kev时仍高于实验值13所以我们可以把它看作一种能量相关的渐进行为假定入射电子的能量足够高可以用一级bro根据此思想最近给出了公式13为靶分子的电子总数为分子的极化率以kev为单位此理论是无法成立的所以误差较大分子13kev时有40的偏差直到10kev以上结果与bo近似的渐进行为符合的较好
第21卷第2期 2004年4月
原子与分子物理学报
JOURNALOFATOMICAND MOLECULARPHYSICS
文章编号:1000-0364(2004)02-0187-04
Vol.21,№.2 Apr.,2004
中高能区电子与分子散射总截面的计算✷
商继敏1,王如梅1,孙金锋2,刘玉芳2
用FDTD方法计算电磁波在各向异性介质中的散射

论证本文方法的可用性 ,首先计算了各项异性等离子体球壳的雷
达散射截面 ,具体参数如下各项异性等离子体的复介电系数为 :
5 - i 0
ε= i 5 0 ε0 , 等离子体球壳的内半径 r1 = 0. 05m , 外半径
0 0 7
图 1 双站雷达散射截面随散射角的变化
r2 = 0. 1m ,计算结果如图 1 所示 。图 1 给出了用球矢量波函数[4]
Vol. 26 ,No. 1 Feb. 2006
用 FDTD 方法计算电磁波在各向异性介质中的散射
吴跃丽1 ,耿友林2
(1. 杭州电子科技大学理学院 ,浙江 杭州 310018 ;2. 杭州电子科技大学电子信息学院 ,浙江 杭州 310018)
摘要 :由于各向异性等离子体介质中的介质参数是张量形式 ,而在各向同性介质中为标量形式 ,故 在研究各向异性等离子体与电磁波的相互作用与分析各向同性媒质的方法就不同 。采用线性插 值的方法给出各向异性等离子体介质中的 FDTD 离散式 ,编写了程序并进行了数值计算 ,给出与解 析方法比较结果 ,两者符合的很好 ,并给出等离子体球的电磁散射的若干算例 。结果可应用于等 离子体的电波传播 、天线等领域 。 关键词 :时域有限差分方法 ;各向异性介质 ;等离子体 中图分类号 :TN011 文献标识码 :A 文章编号 :1001 - 9146 (2006) 01 - 0074 - 03
n + 1/ 2 i + 1/ 2 ,j
,k
+
+
v12 Ey|
n i + 1/ 2
,j
,k
(5)
+
k13·
99HXy|
n + 1/ 2 i + 1/ 2 ,j ,k
SERS(表面增强拉曼散射)理论

SERS 的物理类模型物理类模型致力于阐释金属表面局域场的增强,它的主要代表包括表面电磁增强模型和镜像场模型。
1、表面电磁增强模型(Electromagnetic Enhancemant Model ,简记为EM )表面电磁增强模型[5~7]又可称为表面等离子体共振模型,它认为一个吸附在金属表面的分子的诱发偶极矩是通过金属椭球由入射场和散射场共同产生的。
对于椭球比光波波长小的情况,在频率与偶极表面等离子体共振时,散射场比入射场大,这可以看作是椭球外部空间的场密度的影响。
因此拉曼散射场会与金属颗粒的强散射场引起的金属颗粒表面的等离子体振荡发生共振,这种共振的结果使振荡分子产生了非常大的能量。
如图2-1所示,把一个可以看成经典电偶极子的分子放在球形金属颗粒外的r ' 处,以频率为ω0的平面波照射,分子偶极子会产生频率为ω的拉曼散射,其偶极矩为:),(),(00ωαωr E r P P •'=' (2-1)这里的α'是分子的拉曼极化率而P E 包括两部分:),(),(),(000ωωωr E r E r E LM i P '+'=' (2-2)其中i E 是入射场的场强,LM E 是用Lorenz-Mie 理论计算获得的散射场场强。
在观察点r 处与拉曼散射相关的电场由下式给出),(),(),(ωωωr E r E r E sc dip R +=(2-3)图2-1 纳米颗粒表面增强散射示意图其中,dip E 是球形颗粒不存在时振荡偶极子P 发射的场,sc E 是由球形颗粒产生的必须满足频率ω的边值问题的散射场。
拉曼散射的强度R I 是远场振幅R E 的平方:2/)ex p(),(lim r ikr r E I R kr R ω ∞→=,增强因子G 定义为0R R I I G =,其中0R I 是在金属球形颗粒不存在时的拉曼强度。
那么在小颗粒的限制下,增强因子可由下式给出:[]230333033303)(3)1/()1/()(3i n n r g a r i r g a g a r i i n n g a i G ⋅+'+'-'+'-⋅+=(2-4) 这里的i 指入射场在r '处的偏振态,也就是()i E r E i 00,='ω,r r n ''=/ ,g和g 0是表达式()()21+-εε在ω和ω0处的值,其中ε是胶体颗粒与周围物质的复合介电函数的比值。
