09靖江二模
2022年江苏省泰州靖江市中考二模英语试题

2022年江苏省泰州靖江市中考二模英语试题学校:___________姓名:___________班级:___________考号:___________一、单项选择1.—I heard that you volunteered for the 2022 Beijing Winter Olympics.—Yeah. I felt really ________ to help so many people and it was enjoyable.A.suitable B.proud C.stressed D.tired2.— We can always find something good in a bad ________ if we look for it.— It’s so true. Let’s make full use of what comes.A.situation B.direction C.instruction D.competition 3.Helen could _________control her excitement when her dog came back on the tenth day after being missing.A.mainly B.hardly C.successfully D.exactly 4.The whole society should ________ doctors, nurses and volunteers for their contributions. A.prepare B.praise C.promise D.present 5.—Andy, when can we start to discuss the case given to you last week?—I’ll be ready to discuss it ________ you have time.A.before B.until C.unless D.whenever 6.— Have you heard of the music Kiss the Rain?— Yes. It ________ every Saturday evening by my daughter when she was young.A.is played B.plays C.has played D.was played 7.—Could you teach me how to show the health code (健康码) on my smart phone?—_________.A.Don’t mention it B.It doesn’t matter C.It’s a pity D.Sure, I’ll be glad to8.—These days I am preparing for the exam, learning cooking and decorating my new house at the same time. I’m tired out!—Well, just as the saying goes, “_________.” You’d better not do many things at one time. A.Don’t burn the candle at both sides B.Many hands make light work C.Actions speak louder than words D.A friend in need is a friend indeed 9.—I can’t help wondering _________.—It rained so heavily that we had no choice but to stay at home.A.what was the weather like B.why the trip was cancelledC.when you stayed at home D.how do you make a decision 10.What can we learn about from the sign?A.We can’t enter this building.B.We should stop entering this building.C.We should wear masks before entering this building.D.We should enter this building after the special period.二、完形填空Sitting in the classroom, I felt nervous.Our teacher pointed at the blackboard and gave us instructions. Looking around, I watched as my classmates lowered their heads and started writing. I felt __11__ —I couldn’t read the board, for I couldn’t see clearly. It didn’t __12__ at primary school because my teachers always read aloud what they were writing. But now, I was expected to read by myself.Mum took me to a(n) __13__. He told me that I had a terrible eyesight problem. I was __14__ blind.However, though there were a lot of difficulties, I __15__ to reach the age of 13! As a kid living on a farm, I was always __16__ objects. I could only see the outlines(轮廓) of things and differences between different shades. I was given reading glasses but they didn’t help much.I was __17__ to let my poor eyesight stop me moving forward, I continued doing everything I loved, including milking the cows. Over the years, I’ve __18__ lovely familyholidays, but sometimes felt my families __19__ me too much. __20__ I was excited when I heard about a travel company that takes those who are blind or have poor eyesight on adventures(冒险) by themselves. Uncertain, I booked myself onto a trip to the __21__. It was amazing to enjoy places, such as the beach and seaside theme parks, with __22__ just like me. And the guides were good at __23__ us through all the way while making sure we had a fun and __24__ time. Since then, I’ve travelled with them a lot. While we can’t see the views like others, our __25__ takes us to amazing places. I don’t want people to feel sorry for me. I’m so lucky to have a wonderful family and lots of adventures.Life is of great value—you don’t need sight to “see” that.11.A.relaxed B.helpless C.surprised D.confident 12.A.mean B.change C.work D.matter 13.A.doctor B.teacher C.engineer D.singer 14.A.completely B.finally C.hopefully D.nearly 15.A.managed B.decided C.expected D.liked 16.A.caring about B.taking on C.knocking over D.putting down 17.A.ready B.happy C.sorry D.unwilling 18.A.missed B.enjoyed C.hated D.avoided 19.A.asked B.hurt C.protected D.trusted 20.A.Because B.So C.But D.Though 21.A.museum B.coast C.village D.countryside 22.A.classmates B.relatives C.tourists D.families 23.A.supporting B.punishing C.accepting D.treating 24.A.silent B.short C.simple D.safe 25.A.education B.agreement C.imagination D.blindness三、阅读单选AMadrid Poetry (诗歌) CompetitionMadrid Poetry Day is celebrated in October every year. This year, the Poetry Centre is holding a poetry competition to celebrate the festival! The competition is open to all the poets aged 18 and over from all over the world, and they will be divided into two groups: Open Group (open to all the poets aged 18 and over whose mother language is English) ESL Group (open to all the poets aged 18 and over who can write in English as a second language)The winners of each group will receive €1,000. So come on! Just get your poems ready. RULES:All the poems must be works that haven't come out yet.The poems will not be returned, so please keep a copy of each poem.The poem(s) must be written in English and created by the poet himself/herself.The poems can be written on any proper subject. No subject against laws.The competition begins on 3 June and ends on 28 November.To enter the competition, please visit the Centre Shop on our website and pay €5 for each poem. Once the payment is made, please email the poem(s) to poetrycomp@center. Madrid Remember to mark Open or ESL in the top right-hand corner of the document (文档) to show which group to enter before emailing your poem(s).********************************************************************.We really hope to receive your poem(s)!26.The poetry competition is held to _________.A.celebrate Madrid Poetry Day B.teach us how to write poemsC.introduce Madrid Poetry Day D.collect poems all around the world 27.Madrid Poetry Competition will last _________.A.about four months B.about six monthsC.about three months D.over seven months28.If one wants to enter the Madrid Poetry Competition, he/she has to ________.A.be good at Chinese B.pay €1,000 firstC.write poems in English D.be over 16 years old29.If a Chinese wants to take part in the competition, his/her document should be like________.A.B.C.D.How many tests do you have to take at school for a day? How do you usually prepare for them or are you really able to prepare for each of them well? Understanding how your brain works can be very helpful for you.Our memory is in fact made up of three parts—sensory memory, short-term memory and long-term memory. Sensory memory takes in information from our five senses and stays for only a few seconds. Short-term memory is where we store the new information that we have just taken in. However, the information also won’t stay there very long if we don’t keep doing something to that information. In other words, we turn it into long-term memory, which includes everything from all our best friends’ birthdays to our favourite poems. When studying, either for tests or other purposes, you are trying to turn the information from the books into long-term memory.Remember that our brain works better when we are interested in a subject, already have basic knowledge about it, and know that we are going to need it for future use. So helpful methods include speaking out the ideas loud in your own words or draw a picture of the information. Also, remember that our brain can deal with limited information at one time, so filling your brain with materials for several tests in one night isn’t a good idea.30.In which part of a magazine can you read this passage?A.Art.B.Sports.C.History.D.Science. 31.Lucy did badly in the History test. Which is the best advice according to the passage? A.You’d better turn what’s written on books into your long-term memory.B.To do well on the tests, you must build up your short-term memory.C.Being good at short-term memory is helpful for learning history.D.Remember to use your sensory memory as it’s the first step in learning.32.How does the writer organize Paragraph 3?A.By telling stories.B.By explaining the reasons.C.By making questions.D.By comparing differences. 33.What is the main idea of this passage?A.The best way to prepare for several tests at a time.B.Different parts of the brain work in different ways.C.Better use of the brain leads to better learning results.D.How the brain turns sensory memory into long-term memory.Little Hands, a raccoon (浣熊) without parents, was just a few weeks old when it was found all alone on the side of the road. It was early June, and all the wildlife rescue centers (救助中心) in the area were already full. Then Nikki Robinson decided to take it home.While Robinson was busy with her work, her mom, Linda, was retired at home. So after Robinson made it clear that she wouldn’t have grandchildren soon, Linda became Little Hands’ mom. “The first time my mom bottle-fed it and it looked up at her, her heart was greatly warmed,” Robinson said. “She treated it very sweetly early on because it liked to be touched a lot. So she created a strong connection with it, even knowing it would go back to the wild some day.”Little Hands grew up strong, and by the end of the summer, it struck out on its own. But Little Hands kept coming back and remained friendly with the whole family and it was very kind and sweet with them. “My mom has a bench where she sits outside, and it would come up and climb onto the bench and sit beside her,” Robinson said. “It snuggled (依偎) up to my mom, and then it would have its food and run off. ”Since Little Hands left the house, Linda has taken in many raccoon babies that have no parents. And each year, the raccoons she releases (释放) into the wild continue coming back. “Every day, she sits outside and waits, and even when they’re grown up, they’ll visit her and she just loves it,” Robinson said.Because of Linda, the little raccoons are able to live out their lives in the wild, but justlike her human children, they know they can always come home to Mom for a snack and a hug.34.What caused Robinson to take Little Hands home?A.She wanted to keep a pet.B.She found it had nowhere else to go.C.She noticed it was badly hurt.D.She wanted it to play with her mom.35.What can we learn about from Paragraph 2?A.Linda failed to take good care of Little Hands.B.Little Hands finally found its mom in the wild.C.Little Hands was afraid of going back to nature.D.Linda had a close relationship with Little Hands.36.What does the writer mean by saying “it struck out on its own”?A.Little Hands completely lived on its own.B.Little Hands went to the rescue center by himself.C.Little Hands began to live in the wild alone.D.Little Hands went away with other raccoons.37.Why does Linda always stay outside?A.To wait for the raccoons’ visits.B.To enjoy the beauty of nature.C.To play with her grandchildren.D.To teach the raccoons survival skills. 38.What’s the best title for the passage?A.How to get on with wild animals B.An interesting but dangerous jobC.A woman and her special children D.How to help animals live well in the wildI love taking exercise with my husband Chris. In general, we do our own exercise separately first, but then we really enjoy spending 30—40 minutes doing something we both like together. I also train with my family—my brother, his wife and sometimes our cousins will come to our house to train together. It’s like family fun time! A little bit of competition also makes us exercise harder.As you know, laziness is contagious. This is also true for the love of sport. If you can get your partner to join you in sport, you two will be able to encourage each other on those days when the other doesn’t want to move. If you set yourself a challenge and add competition tothe mix, I’m sure that the exercising will be much more fun. Time will fly by and you’ll want to do it again.This is why I wanted to learn Chris’s favourite sport—climbing. Not only would we have more things to do together, but also it would be a great challenge for me. In turn, I have introduced Chris to two of my favourite activities: horse riding and motorbiking. Now he also loves them, which means we have even more chances to have fun together. Influenced by our example, my brother and his wife now do sport together too. This is what it’s all about at the end of the day: quality time with your partner.What if you don’t have a partner? Well, I’m sure you have a friend who would love to exercise with you. Or, if you have young children, why not do that in the backyard with another parent while they play? You just need some music. The important thing is to have a plan and to make the time to do it. It will be much more fun than doing it on your own. 39.How does the writer exercise with her husband?A.They exercise together all the time.B.They start with separate exercise. C.They exercise for half an hour each time.D.They always do the same exercise. 40.The underlined word “contagious” in the second paragraph probably means _________. A.可发现的B.可质疑的C.可传染的D.可避免的41.What happens when the writer does exercise with the family?A.Everyone relaxes after work.B.Everyone gets more active. C.Everyone is crazy about competition.D.Everyone feels time is slowing down. 42.How does the writer find climbing?A.It requires hard work to learn.B.It makes her less confident.C.It’s not so hard as she expected.D.It’s more suitable for men.43.What is the writer trying to do in the last paragraph?A.To look for help.B.To express thanks.C.To make a promise.D.To give encouragement.四、阅读回答问题阅读下面的短文,并根据短文后的要求答题(每题答案不超过6个词)。
专题4 整式及其运算(分层精练)(解析版)

专题4 整式及其运算一、基础过关练1.(2022·重庆大渡口·中考二模)下列各式中,不是..整式的是( ) A .1xB .x -yC .6xy D .4x【答案】A【分析】利用整式的定义逐项判断即可得出答案.【详解】解:A.1x既不是单项式,又不是多项式,不是整式,故本选项符合题意;B.x -y ,是多项式,是整式,故本选项不符合题意;C.6xy,是单项式,是整式,故本选项不符合题意; D.4x ,是单项式,是整式,故本选项不符合题意; 故选A .【点睛】本题考查整式的定义,整式为单项式和多项式的统称,是有理式的一部分,在有理式中可以包含加,减,乘,除、乘方五种运算,但在整式中除数不能含有字母. A .339a a a ⋅= B .()3328a a −=−C .()31024a a a ÷−=D .()()2224a a a −+−−=+【答案】B【分析】分别根据同底数幂的乘法法则,积的乘方运算法则,同底数幂的除法法则、幂的乘方法则以及平方差公式逐一判断即可. 【详解】A. 33336a a a a +⋅==,故本选项错误; B. 3333(2)(2)8a a a −=−=−,故本选项符合题意; C. 102310234()a a a a −⨯÷−=−=−,故本选项错误; D. 222(2)(2)()24a a a a −+−−=−−=−,故本选项错误; 故选:B .【点睛】本题主要考查了同底数幂的乘法法则,积的乘方运算法则,同底数幂的除法法则、幂的乘方法则以及平方差公式,熟记相关运算法则是解答本题的关键. 3.(2022·内蒙古赤峰·一模)下列代数式中,互为同类项的是( ) A .22a b −与23abB .2218x y 与2292x y +C .()n a b +与()3a b +D .2xy −与2y x【答案】D【分析】根据同类项的定义逐项进行判断即可.【详解】A.22a b −与23ab 相同字母的指数不同,因此不是同类项,故A 错误; B.2292x y +是多项式,所以2218x y 与2292x y +不是同类项,故B 错误;C.()n a b +与3()a b +是多项式,且含有的字母也不同,因此它们不是同类项,故C 错误;D.−xy 2与y 2x 含有的字母相同,相同字母的指数也相同,因此它们是同类项,故D 正确. 故选:D .【点睛】本题主要考查了同类项的定义,熟练掌握同类项的定义,含有字母相同,相同字母的指数也相同的单项式为同类项,是解题的关键. 4.(2022·安徽·模拟预测)下列说法正确的是( ) A .32x −的项是3x ,2 B .222x y xy x +−是二次三项式 C .23x y 与24yx −是同类项 D .单项式23x y π−的系数是3−【答案】C【分析】根据单项式与多项式的特点及性质即可求解. 【详解】A.32x −的项是3x ,-2,故A 错误; B.222x y xy x +−是三次三项式,故B 错误; C.23x y 与24yx −是同类项,故C 正确; D.单项式23πx y −的系数是3π−,故D 错误. 故选:C .【点睛】此题主要考查单项式与多项式的定义,解题的关键是熟知单项式与多项式的特点及性质.5.(2022·云南·中考真题)按一定规律排列的单项式:x ,3x 2,5x 3,7x 4,9x 5,……,第n 个单项式是( ) A .(2n -1)n x B .(2n +1)n x C .(n -1)n x D .(n +1)n x【答案】A【分析】系数的绝对值均为奇数,可用(2n -1)表示;字母和字母的指数可用xn 表示. 【详解】解:依题意,得第n 项为(2n -1)xn , 故选:A .【点睛】本题考查的是单项式,根据题意找出规律是解答此题的关键.6.(2022·陕西·中考真题)计算:()2323x x y ⋅−=( )A .336x yB .236x y −C .336x y −D .3318x y【答案】C【分析】利用单项式乘单项式的法则进行计算即可.【详解】解:()()23233323236x x y x x y x y ⋅−=⨯−⨯=−⋅⨯.故选:C .【点睛】本题考查了单项式乘单项式的运算,正确地计算能力是解决问题的关键. 7.(2022·湖北武汉·中考真题)计算()342a 的结果是( )A .122aB .128aC .76aD .78a【答案】B【分析】直接运用幂的乘方、积的乘方计算即可. 【详解】解:()()()4134233228a a a ==.故答案为B .【点睛】本题主要考查了幂的乘方、积的乘方的运算,灵活运用相关运算法则成为解答本题的关键.8.(2022·四川眉山·中考真题)下列运算中,正确的是( ) A .3515x x x ⋅= B .235x y xy +=C .22(2)4x x −=−D .()2242235610x x y x x y ⋅−=−【答案】D【分析】根据同底数幂的乘法法则,合并同类项,完全平方公式,单项式乘多项式的法则分析选项即可知道答案.【详解】解:A. 根据同底数幂的乘法法则可知:358⋅=x x x ,故选项计算错误,不符合题意;B. 2x 和3y 不是同类项,不能合并,故选项计算错误,不符合题意;C. 根据完全平方公式可得:22(2)44−=+−x x x ,故选项计算错误,不符合题意;D. ()2242235610x x y x x y ⋅−=−,根据单项式乘多项式的法则可知选项计算正确,符合题意; 故选:D【点睛】本题考查同底数幂的乘法法则,合并同类项,完全平方公式,单项式乘多项式的法则.9.(2022·山东聊城·中考真题)下列运算正确的是( ) A .()22233xy x y −=B .2243474x x x +=+C .()2323131t t t t t −+=−+D .()()43341a a −÷−=−【答案】D【分析】A 选项根据积的乘方等于乘方的积即可判断;B 选项合并同类型:字母和字母的指数比不变,系数相加;C 选项利用乘方的分配律;D 选项先用幂的乘方化简,在运用整式的除法法则.【详解】解:A 、原式229x y =,不合题意; B 、原式27x =,不合题意; C 、原式323t t t =−+,不合题意; D 、原式=-1,符合题意; 故选:D .【点睛】本题考查积的乘方、幂的乘方、合并同类型、乘法分配律、整式的除法,掌握相应的运算法则是解题的关键,其中每一项的符号是易错点. 10.(2022·山东济宁·中考真题)下列各式运算正确的是( ) A .3()3x y x y −−=−+ B .326x x x ⋅= C .0( 3.14)1π−= D .()235x x =【答案】C【分析】利用去括号的法则,幂的运算法则和零指数幂的意义对每个选项进行判断即可. 【详解】A :3()33x y x y −−=−+,故选项A 不正确; B :325x x x ?,故选项B 不正确;C :0( 3.14)1π−=,故选项C 正确;D :()236x x =,故选项D 不正确;故选:C .【点睛】本题考查了去括号法则,幂的运算法则和零指数幂的意义,正确利用上述法则对每个选项做出判断是解题的关键.11.(2022·上海市青浦区教育局二模)下列关于代数式的说法中,正确的有( ) ①单项式20222−系数是2,次数是2022次;②多项式21x x+9式;④对于实数a 2a a =±. A .1个 B .2个 C .3个 D .4个【答案】B【分析】根据单项式的系数,次数,多项式的次数,二次根式的定义,二次根式的性质逐个分析判断即可.【详解】解:①单项式20222−系数是20222−,次数是0次,故①不正确; ②多项式21x x +1x =+中2x x不能约分,故②不正确;③93=是二次根式,故③正确; ④对于实数a ,2a a a ==±,故④正确; 故选B .【点睛】本题考查了单项式的系数,次数,多项式的次数,二次根式的定义,二次根式的性质,掌握以上知识是解题的关键.单项式中,所有字母的指数和叫单项式的次数,数字因数叫单项式的系数,单项式中所有字母的指数的和叫做它的次数,通常系数不为0, 多项式的每一项都有次数,其中次数最高的项的次数,就是这个多项式的次数,一个多项式的项数就是合并同类项后用“+”或“-”号之间的多项式个数,次数就是次数和最高的那一项的次数; 一个多项式中,次数最高的项的次数,叫做这个多项式的次数;多项式的项数就是多项式中包含的单项式的个数.形如()0a a ≥的代数式是二次根式.菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为( )A .15B .13C .11D .9【答案】C【分析】根据第①个图案中菱形的个数:1;第②个图案中菱形的个数:123+=;第③个图案中菱形的个数:1225+⨯=;…第n 个图案中菱形的个数:()121n +−,算出第⑥个图案中菱形个数即可.【详解】解:∵第①个图案中菱形的个数:1; 第②个图案中菱形的个数:123+=; 第③个图案中菱形的个数:1225+⨯=; …第n 个图案中菱形的个数:()121n +−,∴则第⑥个图案中菱形的个数为:()126111+⨯−=,故C 正确. 故选:C .【点睛】本题主要考查的是图案的变化,解题的关键是根据已知图案归纳出图案个数的变化规律.13.(2022·黑龙江牡丹江·中考真题)观察下列数据:12,25−,310,417−,526,…,则第12个数是( ) A .12143B .12143−C .12145D .12145−【答案】D【分析】仔细观察给出的一列数字,从而可发现,分子等于其项数,分母为其所处的项数的平方加1,根据规律解题即可.【详解】解:12,25−,310,417−,526,…,根据规律可得第n 个数是12(1)1n nn +−+,∴第12个数是12145−, 故选:D .【点睛】本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.a b 【答案】4【分析】根据单项式次数的定义进行解答即可. 【详解】解:单项式22a b 的次数为224+=. 故答案为:4.【点睛】本题主要考查了单项式的次数,熟练掌握单项式中所有字母的指数和叫做这个单项式的次数,是解题的关键.15.(2022·甘肃武威·中考真题)计算:323a a ⋅=_____________. 【答案】53a【分析】根据单项式的乘法直接计算即可求解. 【详解】解:原式=323a a ⋅=53a . 故答案为:53a .【点睛】本题考查了单项式的乘法,正确的计算是解题的关键.16.(2022·青海·海东市教育研究室一模)若单项式222m x y 与单项式2413n x y +是同类项,则m nm n−=+_______. 【答案】-3【分析】根据同类项的概念,转化为关于m 、n 的一元一次方程,可求出m 、n 的值,代入代数式中即可得到答案.【详解】∵单项式222m x y 与单项式2413n x y +是同类项,∴2224m n =⎧⎨=+⎩解得12m n =⎧⎨=−⎩ ∴m n m n −+=()()1212−−+−=-3. 故答案为:-3.【点睛】本题考查了同类项的概念,所含字母相同,且所含字母的指数也相同的项叫做同类项,要注意同类项与字母的顺序无关.n 图中共有木料______根.【答案】()21n n +【分析】第一个图形有1根木料,第二个图形有2(21)122⨯++=根木料,第三个图形有3(31)1232⨯+++=根木料,第四个图形有4(41)12342⨯++++=根木料,以此类推,得到第n 个图形有()21n n +根木料.【详解】解:∵第一个图形有1(11)12⨯+=根木料, 第二个图形有2(21)122⨯++=根木料, 第三个图形有3(31)1232⨯+++=根木料, 第四个图形有4(41)12342⨯++++=木料, ∴第n 个图形有()11232n n n +++++=L 根木料, 故答案为:()21n n +.【点睛】本题考查了图形的变化类问题,仔细观察,分析,归纳并发现其中的规律是解本题的关键.18.(2022·广西·中考真题)先化简,再求值()2x y x y xy xy x +−+−÷,其中11,2x y ==. 【答案】x 2-2y ,0【分析】首先运用平方差公式计算,再运用单项式乘以多项式计算,最后合并同类项,即可化简,然后把x 、y 值代入计算即可.【详解】解:()()()22x y x y xy xy x +−+−÷=x 2-y 2+y 2-2y =x 2-2y当x =1,y =12时,原式=12-2×12=0.【点睛】本题考查整式化简求值,熟练掌握整式混合运算法则是解题的关键. 19.(2022·浙江丽水·中考真题)先化简,再求值:(1)(1)(2)x x x x +−++,其中2x =. 【答案】12x + ;2 【分析】先利用平方差公式,单项式与多项式乘法化简,然后代入12x =即可求解. 【详解】(1)(1)(2)x x x x +−++ 2212x x x =−++12x =+当12x =时, 原式12x =+11222=+⨯=. 【点睛】本题考查了整式的化简求值,正确地把代数式化简是解题的关键.二、能力提升练20.(2022·云南昆明·三模)按一定规律排列的代数式:2,2468−−,,,x x x x ,……,第n 个单项式是( )A .()2221nn nx−−B .()12221n n n x −−−C .()1221nn nx −− D .()12221n n nx −−− 【答案】B【分析】不难看出奇数项为正,偶数项为负,分母为x 2n -2,分子的指数为由1开始的自然数,据此即可求解.【详解】解:∵2=1222x−,∴按一定规律排列的代数式为:1222x−,22222x ⨯−−,32322x ⨯−,42422x ⨯−−,52522x ⨯−,…,∴第n 个单项式是(-1)n -1222n n x−,故选:B .【点睛】本题考查单项式的规律,根据所给单项式的系数与次数的特点,确定单项式的规律是解题的关键.21.(2022·山东威海·中考真题)由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为()A.(43)3B.(43)7C.(43)6D.(34)6【答案】C【分析】根据题意得出A、O、G在同一直线上,B、O、H在同一直线上,确定与△AOB位似的三角形为△GOH,利用锐角三角函数找出相应规律得出OG=6233x⎛⎫⎪⎪⎝⎭,再由相似三角形的性质求解即可.【详解】解:∵∠AOB=∠BOC=∠COD=…=∠LOM=30°∴∠AOG=180°,∠BOH=180°,∴A、O、G在同一直线上,B、O、H在同一直线上,∴与△AOB位似的三角形为△GOH,设OA=x,则OB=12323cos3033OA xx⎛⎫== ⎪⎪︒⎝⎭,∴OC=2423cos3033OB xx⎛⎫== ⎪⎪︒⎝⎭,∴OD=38323cos3093OC xx⎛⎫== ⎪⎪︒⎝⎭,…∴OG=6233x⎛⎫⎪⎪⎝⎭,∴6233OG OA ⎛⎫= ⎪ ⎪⎝⎭, ∴12623433GOH AOBS S ⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭n n , ∵1AOB S =n , ∴643GOHS ⎛⎫= ⎪⎝⎭n , 故选:C .【点睛】题目主要考查利用锐角三角函数解三角形,找规律问题,相似三角形的性质等,理解题意,找出相应边的比值规律是解题关键.22.(2022·湖北恩施·中考真题)观察下列一组数:2,12,7,…,它们按一定规律排列,第n 个数记为n a ,且满足21112n n n a a a +++=.则4a =________,2022a =________. 【答案】1513032【分析】由题意推导可得an =23(1)1n −+,即可求解.【详解】解:由题意可得:a 1=2=21,a 2=1224=,a 3=27,∵243112a a a +=, ∴2+41a =7, ∴a 4=12510=, ∵354112a a a +=, ∴a 5=213, 同理可求a 6=12816=,L∴an =23(1)1n −+,∴a 2022=2160643032=, 故答案为:15,13032.【点睛】本题考查了数字的变化类,找出数字的变化规律是解题的关键.23.(2022·湖南岳阳·中考真题)已知2210a a −+=,求代数式()()()4111a a a a −++−+的值. 【答案】-2【分析】先化简所求的式子,再结合已知求解即可.【详解】解:()()()4111a a a a −++−+22411a a a =−+−+224a a =−()222a a =−, ∵2210a a −+=,∴221a a −=−,∴原式()212=⨯−=−.【点睛】本题考查代数式的运算,熟练掌握单项式乘多项式,平方差公式是解题的关键. 24.(2022·湖北襄阳·中考真题)先化简,再求值:(a +2b )2+(a +2b )(a -2b )+2a (b -a ),其中a 32b 32 【答案】6,6ab【分析】直接利用完全平方公式、平方差公式化简,进而合并同类项,再把已知数据代入得出答案.【详解】解:原式=2222244422a b ab a b ab a +++−+−6ab =; Q a =3-2,b =3+2,∴原式()()63232=−+ 6=【点睛】此题主要考查了二次根式的混合运算与整式的混合运算——化简求值,正确掌握整式的混合运算法则是解题关键.是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.(1)我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)公式①:()a b c d ad bd cd ++=++公式②:()()a b c d ac ad bc bd ++=+++公式③:()2222a b a ab b −=−+公式④:()2222a b a ab b +=++图1对应公式______,图2对应公式______,图3对应公式______,图4对应公式______;(2)《几何原本》中记载了一种利用几何图形证明平方差公式()()22a b a b a b +−=−的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)(3)如图6,在等腰直角三角形ABC 中,90BAC ∠=︒,D 为BC 的中点,E 为边AC 上任意一点(不与端点重合),过点E 作EG BC ⊥于点G ,作EH AD ⊥F 点H 过点B 作BF //AC 交EG 的延长线于点F .记△BFG 与△CEG 的面积之和为1S ,△ABD 与△AEH 的面积之和为2S .①若E 为边AC 的中点,则12S S 的值为_______; ②若E 不为边AC 的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由. 【答案】(1)①,②,④,③(2)证明见解析(3)①2②结论仍成立,理由见解析【分析】(1)观察图形,根据面积计算方法即可快速判断;(2)根据面积关系:矩形AKHD 面积=矩形AKLC 面积+矩形CLHD 面积=矩形DBFG 面积+矩形CLHD 面积=正方形BCEF 面积-正方形LEGH 面积,即可证明;(3)①由题意可得△ABD ,△AEH ,△CEG ,△BFG 都是等腰直角三角形,四边形DGEH 是正方形,设BD =a ,从而用含a 的代数式表示出S 1、S 2进行计算即可;②由题意可得△ABD ,△AEH ,△CEG ,△BFG 都是等腰直角三角形,四边形DGEH 是矩形,设BD =a ,DG =b ,从而用含a 、b 的代数式表示出S 1、S 2进行计算即可.(1)解:图1对应公式①,图2对应公式②,图3对应公式④,图4对应公式③;故答案为:①,②,④,③;(2)解:由图可知,矩形BCEF 和矩形EG HL 都是正方形,且AK =DB =a -b ,∴()AKLC DBFG S a a b S −==矩形矩形,∵AKHD AKLC CLHD S S S =+矩形矩形矩形,∴22AKHD DBFG CLHD BCEF LEGH a S S S S S b ==−=+−矩形矩形矩形正方形正方形,又∵()()AKHD S a b a b =+−矩形,∴()()22a b a b a b +−=−;(3)解:①由题意可得:△ABD ,△AEH ,△CEG ,△BFG 都是等腰直角三角形,四边形DGEH 是正方形,设BD a =,∴AD BD a ==,12AH HE DG a ===,12EG CG a ==,32FG BG a ==, ∴222113115()22224BFG CEG S S S a a a ⎛⎫=+=⨯+⨯= ⎪⎝⎭△△,222211152228ABD AEHS S S a a a ⎛⎫=+=+⨯= ⎪⎝⎭△△, ∴122S S =; 故答案为:2;②成立,证明如下:由题意可得:△ABD ,△AEH ,△CEG ,△BFG 都是等腰直角三角形,四边形DGEH 是矩形,设BD a =,DG b =,∴AD BD a ==,AH HE DG b ===,EG CG a b ==−,FG BG a b ==+,∴()2222111()22BFG CEG S S S a b a b a b =+=++−=+△△, ()22222111222ABD AEH S S S a b a b =+=+=+△△, ∴122S S =仍成立. 【点睛】本题主要考查了公式的几何验证方法,矩形和正方形的判定与性质,掌握数形结合思想,观察图形,通过图形面积解决问题是解题的关键.。
高二常考的三角函数的试题整理

高二常考的三角函数的试题整理经典数学题【例一】1.(2009·江苏常州一模)已知角α是第三象限角,则角-α的终边在第________象限. 2.(2010·连云港模拟)与610°角终边相同的角表示为______________.1sin 2θ3.(2010·浙江潮州月考)已知2<1,则θ所在象限为第________象限.π3π4.(2010·南通模拟)已知角θ的终边经过点P(-4cos α,3cos α)(<α<,则sin θ+cos θ=________.22ππ-且sin θ+cos θ=a,其中a∈(0,1),则关于tan θ的值,以下四个答案中,可能正5.(2010·福州调研)已知θ∈22111确的是________(填序号).①-3 ②3或③- ④-3或-3336.(2009·江西九江模拟)若角α的终边与直线y=3x重合且sin α<0,又P(m,n)是角α终边上一点,且|OP|10,则m-n=________.|sin α||cos α|7.(2010·山东济南月考)已知角α的终边落在直线y=-3x (x<0)上,则=________.sin αcos α8.(2010·南京模拟)某时钟的秒针端点A到中心点O的距离为5 cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合.将A、B两点间的距离d(cm)表示成t(s)的函数,则d=________,其中t∈[0,60].π49.(2010·泰州模拟)若0”,“<”或“=”填空).2π210.(2010·镇江模拟)已知角θ的终边上一点P(3,m),且sin θm,求cos θ与tan θ的值.411.(2010·江苏南京模拟)在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合:31(1)sin α;(2)cos α.2212.(2010·佳木斯模拟)角α终边上的点P与A(a,2a)关于x轴对称(a≠0),角β终边上的点Q与A关于直线y=x对称,求sin α·cos α+sinβ·cosβ+tan α·tan β的值.同角三角函数的基本关系及诱导公式1.(2010·南通模拟)cos(-174-sin(-174π)的值为___________________________.2.(2010·江苏镇江一模)设tan(5π+α)=m,则sin(α-3π)+cos(π-α)sin(-α)-cos(π+α)的值为__________.3.(2009·辽宁沈阳四校联考)已知sin α+cos αsin α-cos α=2,则sin αcos α=________.4.(2008·浙江理,8)若cos α+2sin α=-,则tan α=__________.5.(2008·四川理,5)设0≤α<2π,若sin α3cos α,则α的取值范围是____________.6.(2010·吉林长春调研)若sin α+cos α=tan α0<α<π2,则α的取值范围是__________. 7.(2009·苏州二模)sin21°+sin22°+sin23°+…+sin289°=________.8.(2010·浙江嘉兴月考)已知f(x)= 1-xπ1+xα∈(2,π),则f(cos α)+f(-cos α)=________.9.(2009·北京)若sin θ=-45tan θ>0,则cos θ=____________________________________.10.(2010·泰州模拟)化简:(1)1-cos4α-sin4α1-cosα-sinα2sin(π4x)+6cos(π; 4-x).11.(2010·盐城模拟)已知sin22α+sin 2αcos α-cos 2α=1,α∈(0,π2),求sin α、tan α的值.12.(2009·福建宁德模拟)已知0<α<π52sin αcos α-cos α+12cos α-sin α=-5,试求1-tan α和差倍角的三角函数1.(2010·山东青岛模拟)cos 43°cos 77°+sin 43°·cos 167°的值为________. 2.(2010·南京模拟)已知α、β均为锐角,且cos(α+β)=sin(α-β),则tan α=________.3.(2009·湖北四校联考)在△ABC中,3sin A+4cos B=6,4sin B+3cos A=1,则∠C的大小为________.4.(2009·湖南长沙调研)在锐角△ABC中,设x=sin A·sin B,y=cos A·cos B,则x,y的大小关系是________.5.(2009·广东韶关模拟)已知tan α=2,则sin 2α-cos 2α1+cosα________.6.(2010·无锡模拟)1+tan x1-tan x2 010,则1cos 2x+tan 2x的值为________.7.(2010·苏州调研)若锐角α、β满足(1+3tan α)·(13tan β)=4,则α+β=________. 8.(2009·江苏南通二模)已知sin αcos β=12,则cos αsin β的取值范围是____________.9.(2010·苏、锡、常、镇四市调研)若tan(α+β)=2π1π5,tan(β-4)=4,则tan(α+4=________.10.(2008·广东)已知函数f(x)=Asin(x+φ) (A>0,0<φ<π) (x∈R)的最大值是1,其图象经过点Mπ13,2. (1)求f(x)的解析式;(2)已知α、β∈0,π2,且f(α)=3125,f(β)=13,求f(α-β)的值.11.(2010·宿迁模拟)已知向量a=(cos α,sin α),b=(cos β,sin β),|a-b|=41313(1)求cos(α-β)的值;(2)若0<α<π2,-π42β<0,且sin β=-5,求sin α的值.三角函数的图象与性质1.(2009·大连一模)y=sin(2x+π6)的最小正周期是_____________________________.2.(2010·扬州模拟)y=2-cos__________,此时x=________.3π3.(2010·盐城模拟)函数y=tan(x)的定义域是________________.4.(2009·牡丹江调研)已知函数y=2cos x(0≤x≤1 000π)的图象和直线y=2围成一个封闭的平面图形,则这个封闭图形的面积是________5.(2010·江苏盐城月考)已知函数y=tan ωx在(-,内是减函数,则ω的取值范围是________________.7.(2009·浙江宁波检测)定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周8.(2010·连云港模拟)sin 2,cos 1,tan 2的大小顺序是________________.9.(2008·全国Ⅱ理)若动直线x=a与函数f(x)=sin x和g(x)=cos x的图象分别交于M、N两点,则|MN|的最大值为_______.11.(2008·陕西)已知函数f(x)=2sincos+3cos.12.(2010·山东济宁第一次月考)设a=sin2b. ,cos x+sin x,b=(4sin x,cos x-sin x),f(x)=a·4(1)求函数f(x)的解析式(3)设集合A=x6x≤3,B={x||f(x)-m|<2},若A⊆B,求实数m的取值范围.三角函数的`最值及应用1.(2010·连云港模拟)函数y3sin(2x)-cos 2x的最小值为________.2.(2010·泰州模拟)若函数y=2cos ωx在区间[0,上递减,且有最小值1,则ω的值可以是________.3.(2010·湖北黄石调研)设函数f(x)=2sin(+.若对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为____.4.(09·湖南株州模拟)函数y=sin 2x按向量a平移后,所得函数的解析式是y=cos 2x+1,则模最小的一个向量a=__.5.(2009·广东惠州二模)函数y=Asin(ωx+φ)(ω>0,|φ|<在同一单调区间内的x=x29291小值-________________________.2a+b,ab≤0,6.(2010·广西南宁检测)定义运算a*b=a则函数f(x)=(sin x)*(cos x)的最小值为________., ab>0,b7.(2010·苏州调研)一半径为10的水轮,水轮的圆心距水面7,已知水轮每分钟旋转4圈,水轮上点P到水面距离y与时间x(s)满足函数关系y=Asin(ω+φ)+7(A>0,ω>0),则A=________,ω=________. 8.(2009·徐州二模)函数y=(sin x-a)2+1,当sin x=a时有最小值,当sin x=1时有最大值,则a的取值范围是_______. 9.(2009·江苏)函数y=Asin(ωx+φ)(A、ω、φ为常数,A>0,ω>0)在闭区间[-π,0]上的图象如图所示,则ω=10.(2010·镇江模拟)已知函数f(x)=cos(2ωx+2φ) (A>0,ω>0,0<φ<),且y=f(x)的最大值为2,其图象上相邻两对称轴间的距离为2,并过点(1,2).(1)求φ;(2)计算f(1)+f(2)+…+f(2 008).11.( 10·辽宁瓦房店月考)如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b. (1)求这段时间的最大温差; (2)写出这段曲线的函数解析式.12.(2010·吉林延吉模拟)如图,在一个奥运场馆建设现场,现准备把一个半径为3 m的球形工件吊起平放到6 m高的平台上,工地上有一个吊臂长DF=12 m的吊车,吊车底座FG高1.5 m.当物件与吊臂接触后,钢索CD的长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触.求物件能被吊车吊起的最大高度,并判断能否将该球形工件吊到平台上?解三角形1.(2010·江苏靖江调研)在△ABC中,若(a+b+c)(b+c-a)=3bc,则A=________.2.(2010·宿迁模拟)在△ABC中,已知acos A=bcos B,则△ABC的形状为____________. 3.(2010·江苏淮阴模拟)如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为____________. 4.(2010·浙江绍兴模拟)△ABC中,a,b,c分别为∠A,∠B,∠C的对边,如果a,b,c成等差数列,∠B=30°,△ABC的面积为,那么b=__________.25b,A=2B,则cos B=________. 26.(2010·南通模拟)一船以每小时15 km的速度向东航行,船在A处看到一个灯塔M在北偏东60°方向,行驶4 h后,船到达B处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为________km.7.(2009·福建泉州二模)如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6 000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是________________(结果保留根号).8.(2009·江西宜泰模拟)线段AB外有一点C,∠ABC=60°,AB=200 km,汽车以80 km/h的速度由A向B行驶,同时摩托车以50 km/h的速度由B向C行驶,则运动开始____ h后,两车的距离最小. 9.(2009·广东改编)已知△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若a=c=6+2,且∠A=75°,则b=________.10.(2009·安徽)在△ABC中,C-A=sin B=23(1)求sin A的值;(2)设AC=6,求△ABC的面积.11.(2009·山东泰安第二次月考)在海岸A处,发现北偏东45°方向,距A处3-1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以103海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.5.(2008·四川,7)△ABC的三内角A、B、C的对边边长分别为a、b、c.若a=三角函数的综合应用1.(2009·济宁期末)已知a=(cos 2α,sin α),b=(1,2sin α-1),α∈π),若a·b=,则25πtan(α+的值为________.2.(2008·江苏)若AB=2,AC2BC,则S△ABC的最大值是________.3.(2009·肇庆期末)定义运算a*b=a2-ab-b2,则sin=________.4.(2009·广州第二次联考)已知a,b,x,y∈R,a2+b2=4,ax+by=6,则x2+y2的最小值为________.5.(2010·宿州模拟)若函数f(x)=sin(x+α)-2cos(x-α)是偶函数,则cos2α=________.6.(2010·泰州调研)函数f(x)=(sin2x+(cos2x+)的最小值是________. 2 009sinx2 009cosx7.(2009·福建文)已知锐角△ABC的面积为33,BC=4,CA=3,则角C的大小为________.8.(2010·苏南四市模拟)俗话说“一石激起千层浪”,小时候在水上打“水漂”的游戏一定不会忘记吧.现在一个圆形2π波浪实验水池的中心已有两个振动源,在t秒内,它们引发的水面波动可分别由函数y1=sin t和y2=sin(t+来描3述,当这两个振动源同时开始工作时,要使原本平静的水面保持平静,则需再增加一个振动源(假设不计其他因素,则水面波动由几个函数的和表达),请你写出这个新增振动源的函数解析式______________. 9.(2010·南通模拟)2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos 2θ的值等于____________.经典数学题【例二】知识考点:本节知识的考查一般以填空题和选择题的形式出现,主要考查锐角三角函数的意义,即运用sina、cosa、tana、cota准确表示出直角三角形中两边的比(a为锐角),考查锐角三角函数的增减性,特殊角的三角函数值以及互为余角、同角三角函数间的关系。
实验09 探究二力平衡的条件-备战2020年中考物理必考实验精解精练(解析版)

实验09 探究二力平衡的条件探究课题:探究二力平衡的条件实验装置实验原理小车受到几个力的作用, 小车处于静止状态或匀速直线运动状态, 那么这几个力相互平衡探究过程1如图甲所示, 改变两端托盘中砝码的质量, 使其质量不同或相同, 从而改变力的大小, 放手后观察小车的运动状态;2.如图乙所示, 将右边托盘上的砝码放到左边托盘上, 从而使两个力的方向不同,放手后观察小车的运动状态;3.让小车在水平桌面上处于静止状态, 将小车扭转一个角度, 如图丙所示, 使两细线不在同一直线上, 放手后观察小车的运动状态;4.如图丁所示, 两个力分别作用在两个小车上, 也就是说两个力作用在不同物体上, 放手后观察此时小车所处的状态;5.记录数据;记录表格实验结论二力平衡的条件: 作用在同一物体上的两个力大小相等、方向相反、作用在同一直线上。
满分归纳——考点方向器材作用1.本实验中选用了小车而不选用木块, 理由是: 因为小车有轮子, 滚动摩擦小于滑动摩擦,为了减小摩擦力的影响注意事项1.定滑轮有什么作用:答:改变拉力的方向2.如何探究两个力在同一直线上:把纸板转动一个角度,然后松手,观察小车的运动状态3.把纸板转动一个角度的目的是:探究两个是否作用在同一直线上4.如何探究两个力作用在同一物体上?将纸板从中间剪开,观察纸板是否还处于平衡状态5.选择静止状态的原因:匀速运动状态不好控制6.进行多次实验的目的:得出普遍规律,避免偶然性7.在探究究二力平衡问题时,什么因素影响实验结果?答:摩擦力1.(2019•铜仁市)小明在探究“二力平衡”条件的实验中,设计了如图所示的两种实验方案。
(1)通过实验比较,小明发现采用方案乙,实验效果更好,原因是。
(2)该实验装置中,木板两端的定滑轮的作用是。
(3)保持两盘中砝码质量相等,把小车在水平桌面上扭转一个角度,放手后观察到小车转动,最后恢复到静止状态。
这个实验现象说明:作用在同一物体上的两个力,大小相等,方向相反,并且,这两个力才能彼此平衡。
初一数学上册教案2.3 整式的化简求值(教师版)

个性化教学辅导教案——进门测评分_____1.★★(2017•桂林二模)若﹣x3y a与x b y是同类项,则a+b的值为()A.5B.4C.3D.2【考点】34:同类项.【分析】依据同类项的定义可得到a、b的值,然后再代入计算即可.【解答】解:依据同类项的定义可知a=1,b=3,∴a+b=4.故选:B.【点评】本题主要考查的是同类项的定义,熟练掌握同类项的定义是解题的关键.2.★★(2016秋•巫溪县期末)下列各组代数式中,是同类项的是()A.﹣3p2与2p3B.2xy与2ab C.a3b2与a2b3D.﹣5mn与10mn【考点】同类项.【分析】本题是对同类项定义的考查,同类项的定义是所含有的字母相同,并且相同字母的指数也相同的项叫同类项,所以只要判断所含有的字母是否相同,相同字母的指数是否相同即可.【解答】解:A,不是,因为字母不同且字母的指数不同;1.★★(2016•靖江市二模)已知m﹣n=100,x+y=﹣1,则代数式(n+x)﹣(m﹣y)的值是()A.﹣99B.﹣101C.99D.101【考点】整式的加减—化简求值.【专题】计算题;整式.【分析】原式去括号整理后,将已知等式代入计算即可求出值.【解答】解:∵m﹣n=100,x+y=﹣1,∴原式=n+x﹣m+y=﹣(m﹣n)+(x+y)=﹣100﹣1=﹣101,故选B【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.2.★★★(2016秋•大悟县期中)已知:x﹣2y=﹣3,则5(x﹣2y)2﹣3(x﹣2y)+40的值是()A.5B.94C.45D.﹣4【考点】整式的加减—化简求值.【专题】计算题;整式.【分析】把x﹣2y的值代入原式计算即可得到结果.【解答】解:当x﹣2y=﹣3时,原式=45+9+40=94,故选B【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.3.★★★(2016秋•天门校级期中)若|a﹣2|+(b+3)2=0,则式子(a+5b)﹣(3b﹣2a)﹣1的值为()A.﹣11B.﹣1C.11D.1【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【专题】计算题;整式.【分析】利用非负数的性质求出a与b的值,原式去括号合并后代入计算即可求出值.【解答】解:原式=a+5b﹣3b+2a﹣1=3a+2b﹣1,∵|a﹣2|+(b+3)2=0,∴a=2,b=﹣3,则原式=6﹣6﹣1=﹣1,故选B【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.4.★★★(2016秋•卢龙县期末)先化简,再求值:x﹣(2x﹣y2)+(﹣x+y2),其中x=﹣,y=﹣.【考点】整式的加减—化简求值.【分析】本题应先对代数式进行去括号,合并同类项,然后进行移项,将整式化为最简式,最后把x、y的值代入即可解出整式的值.【解答】解:原式=x﹣2x+y2﹣x+y2=y2﹣3x,当,时,原式=1.【点评】本题考查的是代数式的化简,学生容易在去括号时单项式的符号出现错误.5.★★★★(2017春•海宁市校级月考)(1)化简:(4x+2y)﹣2(x﹣y)(2)先化简再求值:﹣(a2﹣6ab+9)+2(a2+4ab+4.5),其中a=6,b=﹣.【考点】整式的加减—化简求值.【专题】计算题;整式.【分析】(1)原式去括号合并即可得到结果;(2)原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.【解答】解:(1)原式=2x+y﹣2x+2y=3y;(2)原式=﹣a2+6ab﹣9+2a2+8ab+9=a2+14ab,当a=6,b=﹣时,原式=36﹣56=﹣20.【点评】此题考查了整式的加减﹣化简求值,熟练掌握去括号法则与合并同类项法则是解本题的关键.知识点一:整式的加减—化简求值给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.例题:1.★★当x=﹣3时,代数式5x﹣[3x﹣2(2x﹣3)]的值为()A.12B.﹣12C.﹣21D.﹣24【考点】45:整式的加减—化简求值.【分析】先把代数式去括号,再合并同类项,化为最简,最后代入计算.【解答】解:5x﹣[3x﹣2(2x﹣3)],=5x﹣(3x﹣4x+6),=5x﹣3x+4x﹣6,=6x﹣6,当x=﹣3时,原式=6×(﹣3)﹣6=﹣18﹣6=﹣24.故选D.【点评】本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.2.★★若x,y互为相反数,则2x﹣3y﹣(3x﹣2y)的值为()A.0B.1C.﹣1D.随x,y的不同而不同【考点】45:整式的加减—化简求值;14:相反数.【专题】11 :计算题.【分析】原式去括号合并得到最简结果,由x与y互为相反数得到x+y=0,代入计算即可求出值.【解答】解:根据题意得:x+y=0,则原式=2x﹣3y﹣3x+2y=﹣x﹣y=﹣(x+y)=0.故选A.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.3.★★(2016秋•回民区校级期中)(2x2y﹣4xy2)﹣(﹣3xy2+x2y),其中x=﹣1,y=2.【考点】45:整式的加减—化简求值.【分析】先去括号,合并同类项,化到最简,再代数求值即可.【解答】解:(2x2y﹣4xy2)﹣(﹣3xy2+x2y),=2x2﹣4xy2+3xy2﹣x2=x2﹣xy2,当x=﹣1,y=2时,原式=(﹣1)2﹣(﹣1)×22=1+4=5.【点评】对于此类求值问题一般先化简再求值.4.★★★(2015秋•重庆校级期中)先化简,再求值:已知:|m+3|+|n﹣|=0,求代数式2m2n﹣[3mn2﹣2(2mn2﹣m2n)]的值.【考点】整式的加减—化简求值;非负数的性质:绝对值.【专题】计算题.【分析】原式去括号合并得到最简结果,利用非负数的性质求出m与n的值,代入计算即可求出值.【解答】解:∵|m+3|+|n﹣|=0,∴m=﹣3,n=,则原式=2m2n﹣3mn2+4mn2﹣2m2n=mn2=﹣.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.5.★★★(2016秋•江阴市期中)已知:A=2a2+3ab﹣2a﹣1,B=﹣a2+ab+1(1)当a=﹣1,b=2时,求4A﹣(3A﹣2B)的值;(2)若(1)中的代数式的值与a的取值无关,求b的值.【考点】45:整式的加减—化简求值.【专题】11 :计算题.【分析】(1)把A与B代入原式计算得到最简结果,将a与b的值代入计算即可求出值;(2)把(1)结果变形,根据结果与a的值无关求出b的值即可.【解答】解:(1)∵A=2a2+3ab﹣2a﹣1,B=﹣a2+ab+1,∴原式=4A﹣3A+2B=A+2B=5ab﹣2a+1,当a=﹣1,b=2时,原式=﹣7;(2)原式=5ab﹣2a+1=(5b﹣2)a+1,由结果与a的取值无关,得到b=.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.1.★★当a=5时,()﹣(﹣2a+1)的值()A.4B.﹣4C.﹣14D.1【考点】45:整式的加减—化简求值.【分析】去括号,合并同类项,代入求出即可.【解答】解:(a2﹣a)﹣(a2﹣2a+1)=a2﹣a﹣a2+2a﹣1=a﹣1,当a=5时,原式=5﹣1=4,故选A.【点评】本题考查了整式的加减的应用,主要考查学生的化简能力和计算能力.2.★★(2015秋•廊坊期末)若(a+1)2+|b﹣2|=0,化简a(x2y+xy2)﹣b(x2y﹣xy2)的结果为()A.3x2y B.﹣3x2y+xy2C.﹣3x2y+3xy2D.3x2y﹣xy2【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【专题】计算题.【分析】利用非负数的性质求出a与b的值,代入原式,去括号合并即可得到结果.【解答】解:∵(a+1)2+|b﹣2|=0,∴a+1=0,b﹣2=0,即a=﹣1,b=2,则原式=﹣(x2y+xy2)﹣2(x2y﹣xy2)=﹣x2y﹣xy2﹣2x2y+2xy2=﹣3x2y+xy2.故选B【点评】此题考查了整式的加减﹣化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.3.★★★(2016秋•濮阳期中)已知整式6x﹣l的值是2,y2的值是4,则(5x2y+5xy﹣7x)﹣(4x2y+5xy﹣7x)=()A.﹣B.C.﹣或﹣D.2或﹣【考点】整式的加减—化简求值.【专题】计算题;整式.【分析】原式去括号合并得到最简结果,求出x与y的值,代入计算即可求出值.【解答】解:由题意得:x=,y=2或﹣2,原式=5x2y+5xy﹣7x﹣4x2y﹣5xy+7x=x2y,当x=,y=2时,原式=;当x=,y=﹣2时,原式=﹣,故选C【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.4.★★(2016秋•河源校级期末)先化简再求值:(1)2x3y﹣y3x﹣xy+3yx3+2xy3﹣2xy,其中x=1,y=2.(2)(2x2﹣2y2)﹣3(x2y2+x)+3(x2y2+y),其中x=﹣1,y=2.(3)(2x2﹣2y2)﹣3(x2y2+x2)+3(x2y2+y2),其中x=﹣1,y=2.(4)﹣9y+6x2+3(y﹣x2),其中x=2,y=﹣1;【考点】45:整式的加减—化简求值.【专题】11 :计算题;512:整式.【分析】原式合并同类项得到最简结果,把x与y的值代入计算即可求出值.【解答】解:(1)原式=5x3y+xy3﹣3xy,当x=1,y=2时,原式=10+8﹣6=12.(2)原式=2x2﹣2y2﹣3x2y2﹣3x+3x2y2+3y=2x2﹣2y2﹣3x+3y,当x=﹣1,y=2时,原式=2﹣8+3+6=3.(3)原式=2x2﹣2y2﹣3x2y2﹣3x2+3x2y2+3y2=﹣x2+y2,当x=﹣1,y=2时,原式=﹣1+4=3;(4)原式=﹣9y+6x2+3y﹣2x2=﹣6y+4x2,当x=2,y=﹣1时,原式=﹣6×(﹣1)+4×22=6+16=22;【点评】此题考查了整式的加减﹣化简求值,熟练掌握合并同类项法则是解本题的关键.5.★★★(2015秋•绍兴校级期中)化简或求值:(1)先化简,再求值:(2x2+x)﹣[4x2﹣(3x2﹣x)],其中x=﹣.(2)3x2y﹣[2xy﹣2(xy﹣x2y+2xy)],其中x=﹣1,y=2.(3)5a2﹣[a2﹣(2a﹣5a2)﹣2(a2﹣3a)],其中a=4.(4)6ab﹣2(﹣3b+2a)+3(﹣2ab﹣5a),其中a=﹣1,b=1.【考点】整式的加减—化简求值;整式的加减.【解答】解:(1)(2x2+x)﹣[4x2﹣(3x2﹣x)]=2x2+x﹣[4x2﹣3x2+x]=2x2+x﹣4x2+3x2﹣x=x2,当x=﹣时,原式=(﹣)2=.(2)原式=3x2y﹣2xy+2xy﹣3x2y+4xy=4xy,当x=﹣1,y=2时,原式=4×(﹣1)×2=﹣8.(3)原式=5a2﹣a2+2a﹣5a2+2a2﹣6a=a2﹣4a,当a=4时,原式=16﹣16=0.(4)原式=6ab+6b﹣4a﹣6ab﹣15a=6b﹣19a,当a=﹣1,b=1时,原式=6×1﹣19×(﹣1)=25.【点评】本题考查了整式的加减和求值,有理数的混合运算的应用,能正确运用法则进行计算和化简是解此题的关键,注意:运算顺序.6.★★★(2015秋•建湖县期中)先化简,再求值:(1)2xy﹣(4xy﹣8x2y2)+2(3xy﹣5x2y2);其中x、y满足(x﹣1)2+|y+2|=0.(2)已知|a+2|+(b﹣2015)2+|7c+42|=0,化简并求代数式﹣3b﹣2c﹣[﹣5a+3(c﹣b)]的值.(3)若(a﹣1)2+|b+2|=0,求多项式a2﹣3ab+b2﹣2a2+2ab﹣b2的值.【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【专题】计算题.【分析】原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.【解答】解:(1)原式=2xy﹣2xy+4x2y2+6xy﹣10x2y2=6xy﹣6x2y2,由题意得:x=1,y=﹣2,则原式=6×1×(﹣2)﹣6×1×(﹣2)2=﹣36.(2)原式=﹣3b﹣2c+5a﹣3c+3b=5a﹣5c,∵|a+2|+(b﹣2015)2+|7c+42|=0,∴a=﹣2,b=2015,c=﹣6,则原式=﹣10+30=20.(3)∵(a﹣1)2+|b+2|=0,∴a=1,b=﹣2,则原式=﹣a2﹣ab=﹣1+2=1.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.7.★★★(2015秋•宣威市校级期中)先化简,再求值.(1)2(2x2﹣3x﹣1)﹣3(3x2﹣4x+1)﹣4(4x2+3x﹣3),其中x=﹣2,y=﹣3.(2)3x2y﹣[2xy2﹣2(xy﹣x2y)]+3xy2,其中x=3,y=﹣.【考点】整式的加减—化简求值.【分析】(1)先去括号,然后合并同类项,最后代入计算即可.(2)先去括号,然后合并同类项,最后代入计算即可.【解答】解:(1)原式=4x2﹣6x﹣2﹣9x2+12x﹣3﹣16x2﹣12x+12=﹣21x2﹣6x+7,当x=﹣2时,原式=﹣21×4+12+7=﹣65.(2)原式=3x2y﹣2xy2+2xy﹣3x2y+3xy2=xy2+2xy,当x=3,y=﹣时,原式=3×﹣2=﹣.【点评】本题考查整式的加减﹣化简求值,熟练掌握去括号法则、合并同类项法则是解题的关键,属于中考常考题型.8.★★★(2016秋•西城区校级期中)已知﹣x﹣m y2与x5y4﹣n是同类项,求(m﹣2n)2﹣5(m+n)﹣2(2n﹣m)2+m+n的值.【考点】45:整式的加减—化简求值;34:同类项.【专题】11 :计算题.【分析】利用同类项的定义求出m与n的值,原式合并后,把m与n的值代入计算即可求出值.【解答】解:∵﹣x﹣m y2与x5y4﹣n是同类项,∴﹣m=5,4﹣n=2,即m=﹣5,n=2,原式=﹣(m﹣2n)2﹣4(m+n),将m=﹣5,n=2代入上式,得原式=﹣69.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.9.★★★(2016秋•永定区期中)已知代数式A=x2+xy+2y﹣,B=2x2﹣2xy+x﹣1(1)求2A﹣B;(2)当x=﹣1,y=﹣2时,求2A﹣B的值;(3)若2A﹣B的值与x的取值无关,求y的值.【考点】45:整式的加减—化简求值.【专题】11 :计算题;512:整式.【分析】(1)把A与B代入2A﹣B中,去括号合并即可得到结果;(2)把x与y的值代入2A﹣B计算即可得到结果;(3)由2A﹣B与x取值无关,确定出y的值即可.【解答】解:(1)2A﹣B=2(x2+xy+2y﹣)﹣(2x2﹣2xy+x﹣1)=4xy+4y﹣x;(2)当x=﹣1,y=﹣2时,2A﹣B=4xy+4y﹣x=4×(﹣1)×(﹣2)+4×(﹣2)﹣(﹣1)=1;(3)由(1)可知2A﹣B=4xy+4y﹣x=(4y﹣1)x+4y若2A﹣B的值与x的取值无关,则4y﹣1=0,解得:y=﹣.【点评】此题考查了有理数的减法,熟练掌握运算法则是解本题的关键.10.★★★(2016秋•宜兴市校级期中)已知:A=3a2﹣4ab,B=a2+2ab.(1)求A﹣2B;(2)若|a+1|+(2﹣b)2=0,求A﹣2B的值.【考点】45:整式的加减—化简求值;16:非负数的性质:绝对值;1F:非负数的性质:偶次方.【分析】(1)根据整式的加减,可得答案;(2)根据非负数的和为零,可得a,b的值,根据代数式求值,可得答案.【解答】解:(1)A﹣2B=(3a2﹣4ab)﹣2(a2+2ab)=3a2﹣4ab﹣2a2﹣4ab=a2﹣8ab;(2)由|a+1|+(2﹣b)2=0,得a=﹣1,b=2.A﹣2B=a2﹣8ab=1+16=17.【点评】本题考查了整式的加减,(1)多项式加减多项式,要先加括号,再去括号,合并同类项,(2)利用了非负数的性质.【规律方法】1.整式化简求值时需注意:①有括号的一般先去括号,合并同类项,化简后再求值.②含有非负数等式时,一般利用非负数(绝对值、偶次方)的性质先求出未知数的值,再代入求值.③在整式混合运算时,能正确根据整式的运算法则进行化简.——出门测评分_____1.★★当x=2时,(x2﹣x)﹣2(x2﹣x﹣1)的值等于()A.4B.﹣4C.1D.0【考点】45:整式的加减—化简求值.【专题】11 :计算题;512:整式.【分析】原式去括号合并得到最简结果,把x的值代入计算即可求出值.(3)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=1,y=﹣1.(4)3(2x2﹣xy)﹣2(3x2﹣2xy),其中x=﹣2,y=﹣3.(5)5abc﹣2a2b﹣[3abc+2(ab2﹣a2b)],其中a=﹣,b=﹣1,c=3【考点】整式的加减—化简求值.【分析】(1)先合并同类项,得出最简整式,代入x的值即可得出答案;(2)先合并同类项,得出最简整式,代入x、y的值即可得出答案;【解答】解:(1)原式=2x2+4x+5,当x=﹣2时,原式=2×(﹣2)2+4×(﹣2)+5=5;(2)原式=a2﹣6a﹣7﹣3a2+9a﹣12=﹣2a2+3a﹣19;当a=﹣1时,原式=-2-3+19=14(3)原式=2x2y+2xy﹣3x2y+3xy﹣4x2y=﹣5x2y+5xy,当x=1,y=﹣1时,原式=﹣5×12×(﹣1)+5×1×(﹣1)=0.(4)3(2x2﹣xy)﹣2(3x2﹣2xy)=6x2﹣3xy﹣6x2+4xy=xy,当x=﹣2,y=﹣3时,原式=(﹣2)×(﹣3)=6.(5)5abc﹣2a2b﹣[3abc+2(ab2﹣a2b)]=5abc﹣2a2b﹣[3abc+2ab2﹣2a2b]=5abc﹣2a2b﹣3abc﹣2ab2+2a2b=2abc﹣2ab2,当a=﹣,b=﹣1,c=3时,原式=2×(﹣)×(﹣1)×3﹣2×(﹣)×(﹣1)2=4;【点评】本题考查了整式的加减及化简求值的知识,化简求值是课程标准中所规定的一个基本内容,它涉及对运算的理解以及运算技能的掌握两个方面,也是一个常考的题材.5.★★★(2016秋•相城区期中)已知A=x﹣2y,B=﹣x﹣4y+1(1)求2(A+B)﹣(2A﹣B)的值(结果用x,y表示);(2)若|x+|+y2=0,求(1)中代数式的值.【考点】45:整式的加减—化简求值.【专题】11 :计算题;512:整式.【分析】(1)原式去括号整理后,将A与B代入计算即可求出值;(2)利用非负数的性质求出x与y的值,代入计算即可求出值.【解答】解:(1)原式=2A+2B﹣2A+B=3B=3(﹣x﹣4y+1)=﹣3x﹣12y+3;(2)∵|x+|+y2=0,∴x=﹣,y=0,则原式=+3=.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.6.★★★(2016秋•蔚县期中)已知A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,按要求完成下列各小题.(1)若A+B的结果中不存在含x的一次项,求a的值;(2)当a=﹣2时,求A﹣3B的结果.【考点】45:整式的加减—化简求值.【专题】11 :计算题;512:整式.【分析】(1)把A与B代入A+B中,去括号合并得到最简结果,由结果中不含x的一次项求出a的值即可;(2)把A与B代入A﹣3B中,去括号合并得到最简结果,将a的值代入计算即可求出值.【解答】解:(1)∵A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,∴A+B=2x2﹣6ax+3﹣7x2﹣8x﹣1=﹣5x2﹣(6a+8)x+2,由A+B结果中不含x的一次项,得到6a+8=0,解得:a=﹣;(2)∵A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,a=﹣2,∴A﹣3B=2x2﹣6ax+3+21x2+24x+3=23x2+(24﹣6a)x+6=23x2+36x+6.【点评】此题考查了整式的加减﹣化简求值,熟练掌握去括号法则与合并同类项法则是解本题的关键.——课后作业1.★★如果a,b互为相反数,那么(5a2﹣10a)﹣5(a2+2b﹣3)的值为()A.﹣10B.5C.15D.﹣15【考点】45:整式的加减—化简求值;14:相反数.【专题】11 :计算题.【分析】原式去括号合并后,根据a,b互为相反数得到a+b=0,代入计算即可求出值.【解答】解:由a,b互为相反数,得到a+b=0,则原式=5a2﹣10a﹣5a2﹣10b+15=﹣10(a+b)+15=15.故选C.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.2.★★已知a﹣b=4,c+d=3,则(b+c)﹣(a﹣d)的值为()A.﹣1B.1C.﹣5D.15【考点】45:整式的加减—化简求值.【专题】11 :计算题.【分析】已知等式相减后代入原式计算即可得到结果.【解答】解:由a﹣b=4,c+d=3,得到(c+d)﹣(a﹣b)=﹣1,即c+d﹣a+b=﹣1,整理得:(b+c)﹣(a﹣d)=﹣1,故答案为:﹣1.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.3.★★★若x2﹣2x=2,2x2﹣4x+3的值为()A.7B.﹣2C.5D.﹣3【考点】整式的加减—化简求值.【分析】将2x2﹣4x+3变形为:2(x2﹣2x)+3,再将x2﹣2x=2代入可得出答案.【解答】解:由题意得:2x2﹣4x+3=2(x2﹣2x)+3,由x2﹣2x=2,故可得:2x2﹣4x+3=7.故选A.【点评】本题考查整式的加减,化简求值是各地常考的考点,同学们要注意此类题目的=10(x﹣2y),当x=﹣1,y=2时,原式=10×(﹣1﹣2×2)=﹣50;(4)x2+(2xy﹣3y2)﹣2(x2+yx﹣2y2)=x2+2xy﹣3y2﹣2x2﹣2yx+y2,=﹣xx2+y2,把x=﹣1,y=2代入﹣x2+y2=﹣(﹣1)2+22=3;当a=,b=﹣时,原式=3ab(a+b)=0.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.6.★★★(2016秋•西陵区校级期中)先化简再求值:(1)(2x2﹣3xy﹣5x﹣1)﹣6(﹣x2+xy﹣1),其中x、y满足(x+2)2+|y﹣|=0.(2)若|3x+6|+(3﹣y)2=0,求多项式3y2﹣x2+(2x﹣y)﹣(x2+3y2)的值.【考点】45:整式的加减—化简求值;16:非负数的性质:绝对值;1F:非负数的性质:偶次方.【专题】11 :计算题;512:整式.【分析】原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.【解答】解:(1)原式=2x2﹣3xy﹣5x﹣1+6x2﹣6xy+6=8x2﹣9xy﹣5x+5,由(x+2)2+|y﹣|=0,得x=﹣2,y=.当x=﹣2,y=时,原式=32+12+10+5=59.(2)∵|3x+6|+(3﹣y)2=0,∴3x+6=0,3﹣y=0,解得:x=﹣2,y=3,则原式=3y2﹣x2+2x﹣y﹣x2﹣3y2=﹣2x2+2x﹣y=﹣8﹣4﹣3=﹣15.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.7.★★★(2016秋•敦煌市校级期中)先化简,再求值5a2+3b2+2(a2﹣b2)﹣(5a2﹣3b2),其a为最大的负整数,b为2的倒数.【考点】45:整式的加减—化简求值;12:有理数;17:倒数.【分析】根据去括号、合并同类项,可化简整式,根据代数式求值,可得答案.【解答】解:由a为最大的负整数,b为2的倒数,得a=﹣1,b=.5a2+3b2+2(a2﹣b2)﹣(5a2﹣3b2)=5a2+3b2+2a2﹣2b2﹣5a2+3b2=2a2﹣2b2当a=﹣1,b=时,原式=2×(﹣1)2﹣2×()2=2﹣=.【点评】本题考查了整式的化简求值,去括号、合并同类项是解题关键.8.★★★(2016秋•宝应县期中)已知A=4a2﹣6b,B=2a2+a﹣1.(1)求A﹣2B;(2)若a+3b=5,求A﹣2B的值.【考点】45:整式的加减—化简求值.【分析】根据题意列出代数式,根据去括号法则、合并同类项法则把原式化简即可.【解答】解:(1)求A﹣2B=(4a2﹣6b)﹣2(2a2+a﹣1)=4a2﹣6b﹣4a2﹣2a+2=﹣6b﹣2a+2;(2)当a+3b=5时,A﹣2B=﹣(a+3b)+2=﹣3.【点评】本题考查的是整式的化简求值,掌握整式的加减混合运算法则是解题的9.★★★(2016秋•牡丹江期中)已知4|x+2|+(y﹣5)2=0,A=3x2﹣2xy+y2,B=x2+xy ﹣5y2,求A﹣3B的值.【考点】45:整式的加减—化简求值;16:非负数的性质:绝对值;1F:非负数的性质:偶次方.【分析】先求出x与y的值,然后化简A﹣3B,最后代入求值即可.百度文库花文定制教案21。
2023年江苏省中考生物第一轮复习卷:4绿色植物

2023年江苏省中考生物第一轮复习卷:4绿色植物一.选择题(共21小题)1.(2022•苏州)2022年4月,苏州树山梨花文化旅游节举行了以“寻梦江南,云赏黎里”为主题的线上发布会,如图为树山梨花美景。
下列有关叙述错误的是()A.梨树属于种子植物B.梨的种子外有果皮包被C.梨的受精方式是双受精D.梨花最主要的结构是花瓣2.(2022•泰州)菜农在移栽茄子幼苗时,根部往往带上许多泥土。
“带土”的生物学意义是()A.防止倒伏B.便于运输C.保存营养D.保护根尖3.(2022•苏州)《国家油仓储管理办法》中明确规定:在常规储存条件下,小麦储存年限一般不超过5年,稻谷、玉米不超过3年。
超过规定年限后,即便种子完好,也不再作为粮食出售,主要原因是()A.种子呼吸作用消耗了大量有机物B.种子进入了休眠期从而无法播种C.种子的胚已经死亡无法正常萌发D.种子完全腐烂发霉不能继续食用4.(2022•宿迁)日常生活中,人们通常将蔬菜和水果放入冰箱进行低温冷藏,其主要自的是()A.抑制呼吸作用B.促进气体流动C.促进呼吸作用D.有利于消耗有机物5.(2022•宿迁)“山上种满树,等于修水库”,绿色植物在生物圈水循环中具有重要的作用。
关于生物圈水循环的描述,不正确的是()A.植物的蒸腾作用能提高大气湿度,增加降水B.植物的气孔很小,因此通过气孔散失的水分很少C.森林中的枯枝落叶能吸纳大量雨水,也使雨水更多地渗入地下,补充地下水D.在植物体内,水能往高处流,主要是因为蒸腾作用产生一种将水分向上运输的拉力6.(2022•泰州)农业谚语中常常包含着一定的生物学原理。
下列对相应谚语的解释,错误的是()A.“有收无收在于水”——植物的各项生命活动离不开水B.“收多收少在于肥”——无机盐是植物生长不可缺少的物质C.“大树底下好乘凉”——凉爽感主要来自于枝叶的遮光作用D.“无心插柳柳成荫”——柳树可用扦插的方式进行营养繁殖7.(2022•盐城)东台西瓜广受市民的喜爱,下列措施中有利于提高西瓜产量的是()①过量浇水②适当延长光照时间③提高夜间氧气浓度④适当提高二氧化碳浓度A.①②B.①③C.②④D.③④8.(2022•连云港)图是某同学建构的绿色植物光合作用概念图。
相似三角形的判定与性质九年级数学上学期期末考试真题汇编(苏科版)

专题12 相似三角形的判定与性质一.选择题(共4小题)1.(2021秋•徐州期末)如图,在△ABC 中,若EF ∥BC ,AE BE=23,EF =4,则BC 的长为( )A .6B .8C .10D .12【分析】先利用比例的性质得到AEAB=25,再证明△AEF ∽△ABC ,然后利用相似比得到BC =52EF . 【解答】解:∵AE BE=23,∴AE AB=25,∵EF ∥BC , ∴△AEF ∽△ABC , ∴EF BC=AE AB=25,∴BC =52EF =52×4=10. 故选:C .【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;同时灵活运用相似三角形的性质进行几何计算.2.(2021秋•鼓楼区校级期末)如图,在△ABC 中,∠BAC =45°,BD 、CE 分别是AC 、AB 边上的高,连接DE ,若DE =2,则BC 的长为( )A .√5B .32√2C .52D .2√2【分析】根据等腰直角三角形的性质得到AD AB=√22,AE AC =√22,进而得到AD AB =AE AC,得到△ADE ∽△ABC ,根据相似三角形的性质列出比例式,计算即可. 【解答】解:在R t △ADB 中,∠BAC =45°, 则AD AB=√22, 同理:AE AC=√22, ∴AD AB=AE AC,∵∠DAE =∠BAC , ∴△ADE ∽△ABC , ∴DE BC=AD AB=√22, ∵DE =2, ∴BC =2√2, 故选:D .【点评】本题考查的是相似三角形的判定与性质、等腰直角三角形的性质,证明△ADE ∽△ABC 是解题的关键.3.(2021秋•如皋市期末)如图,网格中的每个小正方形边长为1,点A ,B 都在小正方形的顶点上,线段AB 与网格线MN 交于点C ,则AC 的长为( )A .32B .43C .54D .65【分析】先利用勾股定理求出AB 的长,再利用A 字模型相似三角形证明△ANC ∽△ADB ,然后利用相似三角形的性质进行计算即可解答. 【解答】解:如图:由题意得:AB =√AD 2+BD 2=√42+32=5, CN ∥BD ,∴∠ANC =∠ADB ,∠ACN =∠ABD , ∴△ANC ∽△ADB , ∴AN AD =AC AB,∴14=AC 5,∴AC =54, 故选:C .【点评】本题考查了勾股定理,相似三角形的判定与性质,熟练掌握A 字模型相似三角形是解题的关键.4.(2021秋•鼓楼区校级期末)如图,D ,E 分别是△ABC 的边AB ,AC 上的点,AD AB=13,DE ∥BC ,若△ADE 的面积为6,则△ABC 的面积等于( )A .12B .18C .24D .54【分析】利用DE ∥BC 判定△ADE ∽△ABC ,再利用相似三角形的面积比等于相似比的平方,列出关系式即可求得结论. 【解答】解:∵DE ∥BC , ∴△ADE ∽△ABC . ∴S △ADE S △ABC=(AD AB)2.∵AD AB=13,∴S △ADE S △ABC=19.∴S △ABC =9S △ADE =54. 故选:D .【点评】本题主要考查了相似三角形的判定与性质,利用相似三角形的判定方法得出△ADE ∽△ABC 是解题的关键. 二.填空题(共4小题)5.(2021秋•兴化市期末)如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,E 是CD 的中点.则△DEO 与△BCD 的面积的比等于 1:4 .【分析】由平行四边形ABCD 的对角线AC ,BD 相交于点O ,可得O 是BD 中点,已知条件中有E 是CD 的中点,则OE 是△BCD 的中位线,所以OE ∥BC ,OE =12BC ,则△DEO ∽△BCD ,根据相似三角形面积的比等于相似比的平方可以求出△DEO 与△BCD 的面积的比.【解答】解:∵四边形ABCD 是平行四边形,且对角线AC 、BD 交于点O , ∴O 是BD 的中点, ∵E 是CD 的中点, ∴OE ∥BC ,OE =12BC , ∴OE BC=12,∵△DEO ∽△BCD , ∴S △DEO S △BCD=(OE BC)2=(12)2=14,∴△DEO 与△BCD 的面积的比等于1:4, 故答案为:1:4.【点评】此题考查平行四边形的性质、三角形中位线定理、相似三角形的判定与性质等知识,根据三角形中位线定理证明OE ∥BC 是解题的关键.6.(2021秋•建邺区期末)如图,在边长为1的正方形网格中,A 、B 、C 、D 为格点,连接AB 、CD 相交于点E ,则AE 的长为6√25.【分析】根据题意可得AB =3√2,AC ∥BD ,所以△AEC ∽△BED ,进而可以解决问题. 【解答】解:根据题意可知:AB =3√2,AC ∥BD ,AC =2,BD =3, ∴△AEC ∽△BED , ∴AE BE=AC BD,∴3√2−AE=23,解得AE =6√25. 故答案为:6√25. 【点评】本题考查的是相似三角形的判定和性质、正方形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.7.(2021秋•崇川区期末)在我国古代数学专著《九章算术》中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何?”其大意为:如图,R t △ABC 的两条直角边AC ,BC 的长分别为5步和12步,则它的内接正方形CDEF 的边长为6017步.【分析】利用A 字模型相似三角形证明△ADE ∽△ACB ,然后利用相似三角形的性质解答即可.【解答】解:∵四边形CDEF 是正方形, ∴DE ∥CF ,DE =DC ,∴∠ADE =∠C ,∠AED =∠B , ∴△ADE ∽△ACB , ∴AD AC =DE CB, ∴5−DC5=DE 12,∴5−DE 5=DE 12,∴DE =6017,∴正方形CDEF 的边长为:6017步,故答案为:6017.【点评】本题考查了数学常识,正方形的性质,相似三角形的判定与性质,熟练掌握A 字模型相似三角形是解题是关键.8.(2022春•工业园区校级期末)如图,平行四边形ABCD 中,点E 为BC 边上的一点,AE 和BD 相交于点P ,已知△ABF 的面积等于12,△BEF 的面积等于8,则四边CDFE 形的面积是 22 .【分析】利用三角形面积公式得到AF :FE =3:2,再根据平行四边形的性质得到AD ∥BE ,S △ABD =S △CBD ,则可判断△AFD ∽△EFB ,利用相似的性质可计算出S △AFD =18,所以S △ABD =S △CBD =30,然后用△BCD 的面积减去△BEF 的面积得到四边形CDFE 的面积.【解答】解:∵△ABF 的面积等于12,△BEF 的面积等于8, 即S △ABF :S △BEF =12:8=3:2, ∴AF :FE =3:2,∵四边形ABCD 为平行四边形, ∴AD ∥BE ,S △ABD =S △CBD , ∴△AFD ∽△EFB , ∴S △AFD S △BEF=(AF EF)2=(32)2=94,∴S △AFD =94×8=18,∴S △ABD =S △CBD =12+18=30, ∴四边形CDFE 的面积=30﹣8=22. 故答案为:22.【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形,灵活运用相似三角形的性质表示线段之间的关系;也考查了平行四边形的性质. 三.解答题(共4小题)9.(2022春•工业园区校级期末)在△ABC 中,AB =AC ,∠BAC =36°,BD 是△ABC 的角平分线.(1)找出图中的相似三角形,并证明; (2)求出BC AB的值.【分析】(1)由AB =AC ,∠BAC =36°,得∠ABC =∠C =12(180°﹣36°)=72°,由BD 是△ABC 的角平分线求得∠DBC =36°,则∠DBC =∠BAC ,而∠C 是△BDC 和△ABC 的公共角,即可证明△BDC ∽△ABC ;(2)先证明AD =BD ,BD =BC ,则AD =BC ,设AD =BC =x ,AC =AB =a ,由△BDC ∽△ABC 得DC BC=BC AC,所以BC 2=AC •(AC ﹣AD ),可列方程x 2=a (a ﹣x ),解方程求得符合题意的x 的值为√5−12a ,即可求出BC AB的值.【解答】(1)△BDC ∽△ABC . 证明:AB =AC ,∠BAC =36°,∴∠ABC =∠C =12(180°﹣36°)=72°, ∵BD 是△ABC 的角平分线, ∴∠DBC =∠DBA =12∠ABC =12×72°=36°, ∴∠DBC =∠BAC , ∵∠C =∠C , ∴△BDC ∽△ABC .(2)解:∵∠DBA =∠BAC , ∴AD =BD ,∵∠BDC =∠DBA +∠A =36°+36°=72°, ∴∠BDC =∠C , ∴BD =BC ,∴AD =BC ,设AD =BC =x ,AC =AB =a , ∵△BDC ∽△ABC , ∴DC BC=BC AC,∴BC 2=AC •(AC ﹣AD ), ∴x 2=a (a ﹣x ), 解得x 1=√5−12a ,x 2=−√5−12a (不符合题意,舍去), ∴BC =√5−12a , ∴BC AB=√5−12a a=√5−12. 【点评】此题考查等腰三角形的判定与性质、相似三角形的判定与性质、三角形内角和定理及其推论、一元二次方程的解法等知识,证明图中的两个等腰三角形相似是解题的关键.10.(2021秋•赣榆区期末)如图,在R t △ABC 中,∠ACB =90°,以斜边AB 上一点O 为圆心,OB 为半径作⊙O ,交AC 于点E ,交AB 于点D ,且∠BEC =∠BDE . (1)求证:AC 是⊙O 的切线; (2)连接OC 交BE 于点F ,若CE AE=25,求OF CF的值.【分析】(1)连接OE ,通过证明∠CBE =∠OEB 得OE ∥BC ,从而得OE ⊥AC ,再结合OE 是半径即可得出结论;(2)由OE ∥BC ,得△AOE ∽△ABC ,进而得出OE BC=57,再由OE ∥BC ,得△OEF ∽△CBF ,即可推出结果. 【解答】(1)证明:连接OE ,∵OB =OE , ∴∠OBE =∠OEB , ∵∠ACB =90°, ∴∠CBE +∠BEC =90°, ∵BD 是直径, ∴∠BED =90°, ∴∠DBE +∠BDE =90°, ∴∠CBE =∠DBE , ∴∠CBE =∠OEB , ∴OE ∥BC ,∴∠OEA =∠ACB =90°, ∴OE ⊥AC , 又∵OE 是半径, ∴AC 是⊙O 的切线; (2)解:∵OE ∥BC , ∴△AOE ∽△ABC , ∴OE BC =AE AC ,∵CE AE =25, ∴AE AC =57, ∴OE BC=57,∵OE ∥BC , ∴△OEF ∽△CBF , ∴OF CF=OE BC=57.【点评】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.11.(2022春•太仓市期末)如图,在△ABC 中,BC 的垂直平分线分别交BC ,AC 于点D ,E ,BE 交AD 于点F ,AB =AD . (1)求证:△BFD ∽△CAB ; (2)求证:AF =DF ; (3)EF FB的值等于13.(直接写出结果,无需解答过程)【分析】(1)由垂直平分线的性质得出BE =CE ,进而得出∠C =∠EBD ,由等腰三角形的性质得出∠FDB =∠ABD ,即可证明△BFD ∽△CAB ; (2)由DE 垂直平分BC ,得出BD BC=12,由相似三角形的性质得出FD AB=BD BC=12,进而得出FD =12AB ,由AB =AD ,得出FD =12AD ,即可得出AF =FD ; (3)过点C 作CH ∥AD ,交BE 的延长线于点H ,由DE 垂直平分BC ,得出BD BC =12,证明△BDF ∽△BCH ,得出DF HC=BF BH=BD BC=12,由AF =FD ,即可得出AFHC=12,再证明△AFE ∽△CHE ,得出FEEH=AF HC=12,进而得出FEFH=13,由BFBH=12,得出FH =FB ,即可得出EFFB=13.【解答】(1)证明:∵DE 垂直平分BC , ∴BE =CE , ∴∠C =∠EBD , ∵AB =AD , ∴∠FDB =∠ABD , ∴△BFD ∽△CAB ;(2)证明:∵DE 垂直平分BC , ∴BD BC=12,∵△BFD ∽△CAB , ∴FD AB=BD BC=12,∴FD =12AB , ∵AB =AD , ∴FD =12AD , ∴AF =FD ;(3)解:如图,过点C 作CH ∥AD ,交BE 的延长线于点H ,∵DE 垂直平分BC , ∴BD BC=12,∵CH ∥AD ,∴∠BDF =∠BCH ,∠BFD =∠BHC , ∴△BDF ∽△BCH , ∴DF HC=BF BH=BD BC=12,∵AF =FD , ∴AF HC=12,∵AD ∥HC ,∴∠FAE =∠HCE ,∠AFE =∠CHE , ∴△AFE ∽△CHE , ∴FE EH =AF HC =12,∴FE FH =13, ∵BF BH=12,∴FH =FB , ∴EF FB=13,故答案为:13.【点评】本题考查了线段的垂直平分线的性质,相似三角形的判定与性质,熟练掌握线段垂直平分线的性质,等腰三角形的性质,相似三角形的判定与性质是解决问题的关键.12.(2021秋•阜宁县期末)已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E 是AC的中点,ED与AB的延长线相交于点F.(1)求证:DE为⊙O的切线;(2)求证:AB•DF=AC•BF.【分析】(1)连AD,OD,根据直径所对的圆周角为直角知∠ADB=∠ADC=90°,再根据E是AC的中点,得EA=ED,根据OD=OA,利用等边对等角,可知∠ODE=90°,从而证明结论;(2)首先证明△ABD∽△CBA,得ABAC=BDAD,再证明△FDB∽△FAD,得BDAD=BFDF,等量代换即可.【解答】证明:(1)连AD,OD,∵AB为⊙O的直径,∴∠ADB=∠ADC=90°,∵E是AC的中点,∴EA=ED,∴∠EDA=∠EAD,∵OD=OA,∴∠ODA=∠OAD,∴∠EDO=∠EAO,∵AB⊥AC∴∠EAO=90°,∴∠EDO =90°, ∴DE 为⊙O 的切线;(2)∵∠BAC =∠ADC =90°, ∴∠C =∠BAD , ∵∠ABD =∠CBA , ∴△ABD ∽△CBA , ∴AB AC=BD AD,∵∠FDB +∠BDO =∠BDO +∠ADO =90°, ∴∠FDB =∠ADO =∠OAD , ∵∠F =∠F , ∴△FDB ∽△FAD , ∴BD AD =BF DF ,∴AB AC=BF DF,∴AB •DF =AC •BF .【点评】本题主要考查了圆周角定理,切线的判定与性质,相似三角形的判定与性质,证明△FDB ∽△FAD 是解题的关键.一.选择题(共4小题)1.(2022•泰州二模)如图,平行四边形ABCD 中,E 是BC 上的一点,且AB =BE ,AE 、DC 的延长线相交于点F ,S △ABE :S 四边形AECD =3:7,若AD =5cm ,则CF 的长为( )A .1cmB .1.2cmC .3cmD .2cm【分析】连接AC ,根据S △ABE :S ▱ABCD =3:10,得S △ABE :S △ABC =3:5,则BE :BC =3:5,求出CE 的长,再说明CE =CF ,进而得出答案. 【解答】解:连接AC ,∵S△ABE:S四边形AECD=3:7,∴S△ABE:S▱ABCD=3:10,∴S△ABE:S△ABC=3:5,∴BE:BC=3:5,∵AD=5cm,∴AD=BC=5cm,∴BE=3cm,∴CF=2cm,∵AB=BE,∴∠BAE=∠BEA,∵AB∥CD,∴∠BAE=∠F,∵∠BEA=∠CEF,∴∠CEF=∠F,∴CF=CE=2cm,故选:D.【点评】本题主要考查了平行四边形的性质,平行线的性质,等腰三角形的判定与性质等知识,求出BE的长是解题的关键.2.(2022秋•惠山区期中)如图,已知▱ABCD中,点E是DC边的中点,连结BD、BE、AE,AE交BD于点F,则下列结论正确的是()A.BD=2DF B.AF=2BFC.S△ABF=2S△DEF D.S△ADF=S△BEF【分析】根据平行四边形的性质得DE∥AB,则△DEF∽△BAF,可判断AC错误,根据条件无法说明B成立,由△ADE与△BED同底等高,则S△ADE=S△BED,可知D正确.【解答】解:∵点E是DC边的中点,∴DE=12 DC,∵四边形ABCD 是平行四边形, ∴DC =AB , ∴DE =12AB , ∵DE ∥AB , ∴△DEF ∽△BAF , ∴DE AB =DF BF =12,∴DF BD=13,即BD =3DF , 故A 错误;根据条件无法说明B 成立, ∵DE ∥AB , ∴△DEF ∽△BAF , ∴S △DEF S △ABF=(DE AB)2=14,即S △ABF =4S △DEF , 故C 错误;∵△ADE 与△BED 同底等高, ∴S △ADE =S △BED , ∴S △ADF =S △BEF , 故D 正确; 故选:D .【点评】本题主要考查是相似三角形的判定与性质,平行四边形的性质等知识,熟练掌握相似三角形的性质是解题的关键.3.(2022春•新吴区期中)如图,四边形ABCD 是平行四边形,点E 为AB 边中点,点F 为对角线BD 上一点,且FB =2DF ,连接DE 、EF 、EC ,则S △DEF :S △CED =( )A .1:4B .1:3C .1:6D .2:5【分析】根据四边形ABCD 是平行四边形,点E 为AB 边中点,可得S △ADE =S △BDE =14S平行四边形ABCD,根据FB =2DF ,可得S △BDE =3S △DEF ,进而可得结果.【解答】解:∵四边形ABCD 是平行四边形,点E 为AB 边中点, ∴S △ADE =S △BDE =14S 平行四边形ABCD , ∵FB =2DF , ∴S △DEF =13S △BDE =112S 平行四边形ABCD , ∵S △CDE =12S 平行四边形ABCD ,∴S △DEF :S △CDE =112S 平行四边形ABCD :12S 平行四边形ABCD =1:6.故选:C .【点评】本题考查平行四边形的性质,掌握平行四边形的性质是解题的关键. 4.(2022秋•锡山区校级月考)如图,正方形ABCD 的边长为6,点E 是BC 的中点,连接AE 与对角线BD 交于点G ,连接CG 并延长,交AB 于点F ,连接DE 交CF 于点H ,连接AH .以下结论:①∠DEC =∠AEB ;②CF ⊥DE ;③AF =BF ;④CH HF=23,⑤HG =4√55,其中正确结论的个数是( )A .2B .3C .4D .5【分析】由四边形ABCD 是边长为6的正方形,点E 是BC 的中点,得DC =AB =6,∠DCE =∠ABE =90°,CE =BE =3,即可证明△DCE ≌△ABE ,得∠DEC =∠AEB ,可判断①正确;由∠ABG =∠CBG =45°,AB =CB ,BG =BG ,证明△ABG ≌△CBG ,得∠BAE =∠BCF =∠CDE ,则∠DHF =∠DCF +∠CDE =∠DCF +∠BCF =90°,即可证明CF ⊥DE ,可判断②正确;由∠BCF =∠BAE ,CB =AB ,∠CBF =∠ABE ,证明△CBF ≌△ABE ,得BF =BE =3,所以AF =BF =3,可判断③正确;根据勾股定理求得CF =AE =DE =√62+32=3√5,则12×3√5CH =12×6×3=S △CDE ,求得CH =6√55,则HF =9√55,所以CH HF =23,可判断④正确;由△BFG ∽△DCG ,得FG CG=BFDC =12,则FG =13×3√5=√5,所以HG =3√5−6√55−√5=4√55,可判断⑤正确,于是得到问题的答案. 【解答】解:∵四边形ABCD 是边长为6的正方形,点E 是BC 的中点, ∴DC =AB =6,∠DCE =∠ABE =90°,CE =BE =3, ∴△DCE ≌△ABE (SAS ), ∴∠DEC =∠AEB , 故①正确;∵AB =AD ,∠BAD =90°, ∴∠ABD =∠ADB =45°, 同理∠CBD =∠CDB =45°, ∴∠ABG =∠CBG =45°, ∵AB =CB ,BG =BG , ∴△ABG ≌△CBG (SAS ), ∴∠BAE =∠BCF =∠CDE ,∴∠DHF =∠DCF +∠CDE =∠DCF +∠BCF =∠BCD =90°, ∴CF ⊥DE , 故②正确;∵∠BCF =∠BAE ,CB =AB ,∠CBF =∠ABE , ∴△CBF ≌△ABE (AAS ), ∴BF =BE =3, ∴AF =BF =3, 故③正确;∵S △CDE =12DE •CH =12DC •CE ,CF =AE =DE =√62+32=3√5, ∴12×3√5CH =12×6×3,∴CH =6√55, ∴HF =3√5−6√55=9√55, ∴CH HF=6√559√55=23,故④正确; ∵BF ∥CD , ∴△BFG ∽△DCG , ∴FG CG=BF DC=36=12,∴FG=11+2CF=13×3√5=√5,∴HG=3√5−6√55−√5=4√55,故⑤正确,故选:D.【点评】此题重点考查正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识,证明△DCE≌△ABE及△CBF ≌△ABE是解题的关键.二.填空题(共4小题)5.(2022•靖江市二模)如图,AB⊥BC,AB=5,点E、F分别是线段AB、射线BC上的动点,以EF为斜边向上作等腰R t△DEF,∠D=90°,连接AD,则AD的最小值为5√22.【分析】连接BD并延长,利用四点共圆的判定定理得到B,E,D,F四点共圆,再利用等腰直角三角形的性质和圆周角定理得到∠DBF=∠DEF=45°,得到点D的轨迹,【解答】解:连接BD并延长,如图,∵AB⊥BC,∴∠ABC=90°,∠EDF=90°,∴∠ABC+∠EDF=180°,∴B,E,D,F四点共圆,∵△DEF为等腰直角三角形,∴∠DEF=∠DFE=45°,∴∠DBF=∠DEF=45°,∴∠DBF =∠DBE =45°,∴点D 的轨迹为∠ABC 的平分线上, ∵垂线段最短,∴当AD ⊥BD 时,AD 取最小值, ∴AD 的最小值为√22AB =5√22,故答案为:5√22.【点评】本题主要考查了直角三角形的性质,等腰直角三角形的性质,四点共圆的判定 圆周角定理,点的轨迹,垂线段的性质,利用已知条件求得点D 的轨迹是解题的关键. 6.(2022秋•梁溪区校级期中)如图,在△ABC 中,D 在AC 边上,AD :DC =1:2,O 是BD 的中点,连接AO 并延长交BC 于E ,则OE :OA = 1:2 ,S △BOE :S △BCD = 1:8 .【分析】过点D 作DF ∥AE ,交CE 于点F ,根据已知可得CD CA=23,再证明A 字模型相似三角形△CDF ∽△CAE ,从而利用相似三角形的性质可得AE =32DF ,CF EF=2,然后根据线段中点的定义可得BO =12BD ,再证明A 字模型相似三角形△BEO ∽△BFD ,从而利用相似三角形的性质可得OE =12DF ,BF =2BE ,S △BOE S △BDF=(12)2=14,进而可得OE AE=13,CF =BF ,最后进行计算即可解答.【解答】解:过点D 作DF ∥AE ,交CE 于点F ,∵AD :DC =1:2, ∴CD CA=23,∵DF ∥AE ,∴∠CDF =∠CAE ,∠CFD =∠CEA ,∴△CDF ∽△CAE , ∴CD CA=DF EA=CF CE=23,∴AE =32DF ,CF EF=2,∴CF =2EF , ∵O 是BD 的中点, ∴BO =OD =12BD , ∵OE ∥DF ,∴∠BOE =∠BDF ,∠BEO =∠BFD , ∴△BEO ∽△BFD , ∴BO BD=OE DF=BE BF=12,∴OE =12DF ,BF =2BE ,S △BOE S △BDF=(12)2=14,∴OE AE=12DF 32DF =13,∴OE :OA =1:2,∵CF =2EF ,BF =2BE =2EF , ∴CF =BF ,∴△BDF 的面积=△CDF 的面积, ∴S △BOE :S △BCD =1:8, 故答案为:1:2,1:8.【点评】本题考查了相似三角形的判定与性质,三角形的面积,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.7.(2022秋•崇川区校级月考)如图,在R t △ABC 中,∠ABC =90°,AB =6,BC =8,点O 为△BC 的内心,连接OA ,OC ,过点O 作OD ∥BC 交AC 于点D ,则OD 的长为53.【分析】过点O 作OE ⊥AC 于E ,OF ⊥BC 于F ,OH ⊥AB 于H ,连接AO ,BO ,由面积法可求OE =OF =OH =1,可证四边形OFBH 是矩形,可得BF =OH =1,由“AAS ”可证△COE ≌△COF ,可得CE =CF =3,由勾股定理可求解.【解答】解:如图,过点O 作OE ⊥AC 于E ,OF ⊥BC 于F ,OH ⊥AB 于H ,连接AO ,BO ,∵点O 为R t △ABC 的内心,OE ⊥AC ,OF ⊥BC ,OH ⊥AB ,∴OE =OH =OF ,∵∠ABC =90°,AB =3,BC =4,∴AC =√AB 2+BC 2=5,∵S △ABC =S △ABO +S △BCO +S △ACO ,∴12×3×4=12×3×OH +12×4×OF +12×5×OE , ∴OE =OF =OH =1,∵OE ⊥AC ,OF ⊥BC ,OH ⊥AB ,∴四边形OFBH 是矩形,∴BF =OH =1,∴CF =3,∵点O 为R t △ABC 的内心,∴∠OCF =∠OCE ,∵∠CEO =∠CFO =90°,在△COE 和△COF 中,{∠OCE =∠OCF∠CEO =∠CFO OC =OC,∴△COE ≌△COF (AAS ),∴CE =CF =3,∵OD ∥BC ,∴∠DOC =∠OCF =∠OCE ,∴OD =DC ,∵OD 2=DE 2+OE 2,∴CD 2=(3﹣CD )2+1,∴CD =53,∴OD =53.故答案为:53.【点评】本题考查了三角形的内切圆和内心,考查了三角形的内心的性质,全等三角形判定和性质,矩形的判定和性质,勾股定理等知识,添加恰当辅助线构造全等三角形是本题的关键.8.(2022秋•惠山区校级月考)如图,矩形ABCD 中,点E 在BC 上,AE ⊥DE ,点F 为AE 延长线上一点,满足EF =AE ,连接DF 交BC 于点G ,若AB =4,BE =2,则GC = 3 .【分析】由余角的性质可得∠BAE =∠DEC ,根据相似三角形的性质可求EC =4,由等腰三角形的性质和平行线的性质可证EG =DG ,由勾股定理可求解.【解答】解:∵AE ⊥DE ,∴∠AED =90°=∠B =∠C ,∴∠AEB +∠DEC =∠AEB +∠,∴∠BAE =∠DEC ,∴△ABE ∽△ECD ,∴AB EC =BE CD , ∴4EC =24,∴EC =8,∵AE =EF ,∠AED =90°,∴AD =DF ,∵∠AED =90°,∴∠ADE =∠FDE ,∵AD ∥BC ,∴∠ADE =∠DEC =∠FDE ,∴DG =EG ,∵DG 2=DC 2+GC 2,∴(8﹣GC )2=16+GC 2,∴GC =3.故答案为:3.【点评】本题考查了相似三角形的判定和性质,矩形的性质,等腰三角形的判定和性质,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.三.解答题(共4小题)9.(2022秋•高邮市期中)如图,点P 在△ABC 的外部,连结AP 、BP ,在△ABC 的外部分别作∠1=∠BAC ,∠2=∠ABP ,连结PQ .(1)求证:AC •AP =AB •AQ ;(2)判断∠PQA 与∠ACB 的数量关系,并说明理由.【分析】(1)由∠1=∠BAC ,得∠1+∠PAC =∠BAC +∠PAC ,则∠CAQ =∠BAP ,而∠2=∠ABP ,即可根据“两角分别相等的两个三角形相似”证明△CAQ ∽△BAP ,则AC AB =AQ AP ,所以AC •AP =AB •AQ ;(2)由AC •AP =AB •AQ ,变形为AP AB =AQ AC ,而∠1=∠BAC ,即可由“两边成比例且夹角相等的两个三角形相似”证明△APQ ∽△ABC ,得∠PQA =∠ACB .【解答】(1)证明:∵∠1=∠BAC ,∴∠1+∠PAC =∠BAC +∠PAC ,∴∠CAQ =∠BAP ,∵∠2=∠ABP ,∴△CAQ ∽△BAP ,∴AC AB =AQ AP ,∴AC •AP =AB •AQ .(2)解:∠PQA =∠ACB ,理由:∵AC •AP =AB •AQ ,∴AP AB =AQ AC ,∵∠1=∠BAC ,∴△APQ ∽△ABC ,∴∠PQA =∠ACB .【点评】此题重点考查相似三角形的判定与性质、等式的性质等知识,找到相似三角形的对应边和对应角并且证明△CAQ ∽△BAP 及△APQ ∽△ABC 是解题的关键.10.(2022秋•苏州期中)如图,R t △ABC 中∠BCA =90°,AE 2=AD •AC ,点D 在AC 边上,以CD 为直径画⊙O 与AB 交于点E .(1)求证:AB 是⊙O 的切线;(2)若AD =DO =1,求BE 的长度.【分析】(1)连接OE ,则∠OEC =∠ACE ,再证明△ADE ∽△AEC ,得∠AED =∠ACE ,则∠AED =∠OEC ,所以∠OEA =∠AED +∠OED =∠OEC +∠OED =90°,即可证明AB 是⊙O 的切线;(2)由AD =DO =OC =1,得AC =3,则AE 2=AD •AC =3,所以AE =√3,再证明△AOE ∽△ABC ,求得BC =√3,即可根据切线长定理求得BE =BC =√3.【解答】(1)证明:连接OE ,则OE =OD =OC ,∴∠OEC =∠ACE ,∵AE 2=AD •AC ,∴AE AC =AD AE ,∵∠A =∠A ,∴△ADE ∽△AEC ,∴∠AED =∠ACE ,∴∠AED =∠OEC ,∵CD 是⊙O 的直径,∴∠OEA =∠AED +∠OED =∠OEC +∠OED =∠CED =90°,∵AB 经过⊙O 的半径OE 的外端,且AB ⊥OE ,∴AB 是⊙O 的切线.(2)解:∵AD =DO =OC =OE =1,∴AC =3,∴AE 2=AD •AC =1×3=3,∴AE =√3,∵∠OEA =∠BCA =90°,∠A =∠A ,∴△AOE ∽△ABC ,∴OE BC =AE AC ,∴BC =AC⋅OE AE =3×1√3=√3, ∵OC 是⊙O 的半径,且CB ⊥OC ,∴BC 是⊙O 的切线,∴BE =BC =√3,∴BE 的长度是√3.【点评】此题重点考查圆的切线的判定、切线长定理、直角所对的圆周角等于90°、等腰三角形的性质、相似三角形的判定与性质等知识,正确地作出所需要的辅助线是解题的关键.11.(2022秋•惠山区校级期中)如图,在R t △ABC 中,∠C =90°,点O 在AB 上,以点O 为圆心,OA 长为半径的圆与AC 、AB 分别交于点D 、E ,且∠CBD =∠A .(1)判断直线BD 与⊙O 的位置关系,并说明理由;(2)若AD :AO =5:3,BC =3,求BD 的长.【分析】(1)连接OD ,先利用角间关系说明∠ODB =90°,再利用切线的判定方法得结论;(2)连接DE ,先说明△ADE ∽△BCD ,再利用相似三角形的性质得结论.【解答】解:(1)BD 是⊙O 的切线.理由:连接OD .∵点D 在⊙O 上,∴OD =OA ,∴∠A =∠ADO .∵∠C =90°,∴∠A +∠CBD +∠DBA =90°.∵∠CBD =∠A ,∴2∠A +∠DBA =90°.∵∠DOB =∠A +∠ADO =2∠A ,∠DOB +∠DBA +∠ODB =180°,∴∠ODB =90°.∵点D 在⊙O 上,∴BD 是⊙O 的切线.(2)连接DE .∵AE 是⊙O 的直径,∴AE =2AO ,∠ADE =90°=∠C .又∵∠CBD =∠A ,∴△ADE ∽△BCD .∴AD AE =BC BD .∵AD :AO =5:3,∴AD :AE =5:6.∴BC :BD =5:6,∵BC =3,∴BD =185.【点评】本题考查了圆的切线和相似三角形,掌握圆的切线的判定方法和三角形的判定与性质是解决本题的关键.12.(2022•崇川区一模)矩形ABCD 中,AB <BC ,AB =6,E 是射线CD 上一点,点C 关于BE 的对称点F 恰好落在射线DA 上.(1)如图,当点E 在边CD 上时,若BC =10,DF 的长为 2 ;若AF •DF =9时,求DF 的长;(2)作∠ABF 的平分线交射线DA 于点M ,当MF BC =12时,求DF 的长.【分析】(1)①利用轴对称的性质和勾股定理求得AF ,则DF =AD ﹣AF ;②利用已知条件和相似三角形的平行于性质求得CE ,EF ,再利用勾股定理即可求得结论;(2)利用分类讨论的思想方法分点F 在AD 边上或点F 在边DA 的延长线上两种情况解答:①点F 在AD 边上时,过点M 作MN ⊥BF 于点N ,利用相似三角形的判定与性质,全等三角形的判定与性质和勾股定理解答即可;②点F 在边DA 的延长线上,利用①中方法解答即可.【解答】解:(1)当点E 在边CD 上时,∵点C 关于BE 的对称点F 恰好落在射线DA 上,∴BF =BC =10.∴AF =√BF 2−AB 2=√102−62=8.∴DF =AD ﹣AF =10﹣8=2.故答案为:2;∵四边形ABCD 是矩形,∴∠A =∠D =90°,∴∠AFB +∠DFE =90°,∠DEF +∠DFE =90°,∴∠AFB =∠DEF .∴△FAB ∽△EDF ,∴AF DE =AB DF .∴AF •DF =AB •DE .∵AF •DF =9,AB =6,∴DE =32.∴CE =CD ﹣DE =92.∵点C 关于BE 的对称点F 恰好落在射线DA 上,∴EF =CE =92.∴DF =√EF 2−DE 2=3√2;(2)①点F 在AD 边上时,过点M 作MN ⊥BF 于点N ,如图,∵BM 平分∠ABF ,MA ⊥AB ,MN ⊥BF ,∴MA =MN .∵∠A =∠MNF =90°,∠AFB =∠NFM ,∴△FAB ∽△FNM ,∴MN AB =MF BF . ∵MF BC =12,BF =BC , ∴NM AB =MF BF =12. ∵AB =6,∴MN =3.在R t △ABM 和R t △NBM 中,{BM =BM AM =MN, ∴R t △ABM ≌R t △NBM (HL ).∴BN =AB =6.设MF =x ,则BF =BC =2x ,∴FN =2x ﹣6,在R t △MNF 中,∵MN 2+FN 2=MF 2,∴32+(2x ﹣6)2=x 2,解得:x =5或x =3(舍去),∴BC =2x =10,∴AD =BC =10.∴DF =AD ﹣AM ﹣MF =2;②点F 在边DA 的延长线时,过点M 作MN ⊥BF 于点N ,如图,同①可得:AM =MN =3,BN =AB =6,BC =AD =10.∵BF =BC =10,∴FN =BF ﹣BN =10﹣6=4.∴MF =√FN 2+MN 2=√42+32=5,∴DF =AD +AM +MF =18.综上,当MF BC =12时,DF 的长为2或18. 【点评】本题主要考查了矩形的性质,轴对称的性质,勾股定理,相似三角形的判定与性质,全等三角形的判定与性质,角平分线的性质,利用分类讨论的思想方法解答是解题的关键.。
考向09 绿色植物的光合作用-备战2023年中考生物一轮复习考点微专题(解析版)

考向09 绿色植物的光合作用1.(2022•济宁)如图为将天丝葵放置在黑暗处一昼夜后,光合作用探究实验的部分步骤。
下列说法错误的是()A.步骤b是为了溶解叶片中的叶绿素B.步骤d遮光部分变成蓝色,说明光合作用的产物为淀粉C.光合作用的实质是制造有机物,储存能量D.暗处理的作用是通过呼吸作用消耗尽叶片中的原有淀粉【答案】B【解析】A、步骤b酒精能溶解叶绿素,而且酒精是易燃、易挥发的物质,直接加热容易引起燃烧发生危险。
使用水对酒精进行加热,起到控温作用,以免酒精燃烧发生危险,A正确。
B、步骤d中,叶片遮光部分缺乏光没有进行光合作用制造淀粉,因此滴加碘液后叶片不变蓝色,还是黄白色;叶片见光部分能进行光合作用制造淀粉,因此滴加碘液后叶片后变蓝色,B错误。
C、光合作用的物质转变是:是把无机物合成有机物,放出氧气;能量转变:把光能转变成化学能储存在合成的有机物中,所以光合作用的实质是制造有机物,储存能量,C正确。
D、步骤a暗处理的作用是通过呼吸作用消耗叶片中原有的淀粉,确保后续的淀粉是实验时光合作用产生的,D正确。
故选:B。
2.(2022•眉山)在夏季晴朗的一天,分别于早晨、中午、傍晚、深夜四个时间段在同一株绿色植物上摘下生长部位、生长期及长势大小相同的四片绿叶,经酒精脱色处理后,分别滴加等量的碘液进行染色处理。
其中染色最深的应该是哪个时间段摘取的叶片()A.早晨B.中午C.傍晚D.深夜【答案】C【解析】植物在白天主要进行光合作用,晚上进行呼吸作用。
光合作用是制造有机物,呼吸作用是消耗有机物。
傍晚植物进行了一天的光合作用,积累了大量的有机物(淀粉),所以滴上碘液,颜色最深;深夜植物进行呼吸作用,消耗了一些有机物(淀粉),所以滴上碘液,颜色不会很深。
故选:C。
1、实验:绿叶在光下制造淀粉。
①步骤:暗处理——部分遮光——照光——摘下叶片,去下纸片——酒精脱色——滴加碘液——显色;②暗处理的目的是耗尽叶片中原有的淀粉;酒精可以溶解叶绿素,脱色后叶片呈黄白色;加碘检验的结果是叶片的见光部分变蓝(因为绿叶在光下产生了淀粉),遮光部分不变蓝(没有产生淀粉)。
2023年江苏省中考生物第一轮复习卷:5人体消化系统

2023年江苏省中考生物第一轮复习卷:5人体消化系统一.选择题(共19小题)1.(2022•无锡)“补钙新观念,吸收是关键”。
小萌同学的妈妈一直给她吃钙片,医生却说小萌缺钙,建议小萌在补钙的同时还要适当晒太阳并补充()A.维生素A B.维生素B1 C.维生素C D.维生素D 2.(2022•无锡)人体消化和吸收营养物质的主要场所是()A.小肠B.胃C.口腔D.大肠3.(2022•泰州)如图表示某营养物质在人体消化道内的含量变化曲线,据此判断该物质的消化场所及消化后的最终产物是()A.口腔和胃葡萄糖B.胃和小肠氨基酸C.胃和大肠氨基酸D.小肠和大肠脂肪酸4.(2022•常州)缺铁性贫血患者应多吃()A.含钙丰富的食物B.含铁和蛋白质丰富的食物C.含碘丰富的食物D.含维生素C丰富的食物5.(2022•连云港)小肠是人体消化食物和吸收营养物质的主要器官。
关于小肠适于吸收功能的结构特点的叙述,错误的是()A.小肠内表面有许多皱襞和绒毛B.小肠绒毛壁由一层细胞构成C.肠液内多种消化酶将蛋白质初步分解D.小肠绒毛中有毛细血管和毛细淋巴管6.(2022•泰州模拟)小肠是人体消化和吸收营养物质的主要场所,下列结构与小肠吸收功能无关的是()A.小肠内表面有许多皱襞B.小肠绒毛内有毛细血管C.小肠壁上有许多分泌消化液的肠腺D.小肠是消化道最长的部分,有5﹣7米7.(2022•建湖县三模)如图为心脏、器官、血管之间的关系示意图,其中①②代表血管,A代表器官,下列叙述正确的是()A.血液从心脏流向①,①为动脉,动脉中均流动脉血B.血液经②流回心脏,②为静脉,静脉中均流静脉血C.若A表示小肠,②比①内流含营养物质增多的静脉血D.若A表示肾脏,则与①相比,②内流所有代谢废物和氧气均减少的静脉血8.(2022•苏州模拟)下列疾病中,与激素无关的是()A.佝偻病B.巨人症C.侏儒症D.呆小症9.(2022•靖江市二模)在盛有等量鲜牛肉的四支试管中,分别加入等量配置的消化液,充分振荡后置于37℃的温水中观察。
萧山区2009年中小学生车辆模型比赛获奖名单

附件:
萧山区2009年中小学生车辆模型比赛获奖名单一、团体
(一)小学组
(二)初中组
(三)高中组
二、个人
(一)小学组
1.1/32雷速登追逐赛
(1)男子组
(2)女子组
2. 1/18(1/20)遥控车绕标计时赛(1)1/18遥控车绕标计时赛
①男子组
②女子组
(2)1/20遥控车绕标计时赛①男子组
②女子组
3.小白龙星际飚车王轨道赛(1)男子组
(2)女子组
4.“捷豹”电动两用赛车制作与竞速赛(1)男子组
(2)女子组
5. 1/10无线电遥控电动房车竞速赛
(二)初中组
1.“漫步者”智能小车竞赛车(1)男子组
(2女子组
2. 1/18(1/20)遥控车绕标计时赛(1)1/18遥控车绕标计时赛
①男子组
②女子组
(2) 1/20遥控车绕标计时赛①男子组
②女子组
3.1/32雷速登追逐赛
(1)男子组
(2)女子组
4.小白龙星际飚车王轨道赛(1)男子组
(2)女子组
5. 1/10无线电遥控电动房车竞速赛
(三)高中组
1.“漫步者”智能小车竞赛车(1)男子组
(2)女子组
2.“1/18遥控车绕标计时赛
(1)男子组
(2)女子组
3. 1/32雷速登追逐赛(1)男子组
(2)女子组
4. 小白龙星际飚车王轨道赛(1)男子组
(2)女子组。
第1章《一元二次方程》知识讲练(学生版)

2023-2024学年苏科版数学九年级上册章节知识讲练知识点1:一元二次方程的有关概念1.一元二次方程的概念:通过化简后,只,并且未知数的的,叫做一元二次方程.2.一元二次方程的一般式:3.一元二次方程的解:使叫做一元二次方程的解,也叫做细节剖析:判断一个方程是否为一元二次方程时,首先观察其是否是,否则一定一元二次方程;其次再将整式方程整理化简使方程的,看是否具备另两个条件:①一个;②未知数的最高次数为对有关一元二次方程定义的题目,要充分考虑定义的三个特点,不要忽视二次项系数不为0.知识点2:一元二次方程的解法1.基本思想一元二次方程 2.基本解法细节剖析:解一元二次方程时,根据方程特点,灵活选择解题方法,先考虑能否用知识点3:一元二次方程根的判别式及根与系数的关系一元二次方程中,叫做一元二次方程的根的判别式,通常用“”来表示,即(1)当△>0时,一元二次方程有 的实数根;(2)当△=0时,一元二次方程有 的实数根;(3)当△<0时,一元二次方程 实数根.如果一元二次方程的两个实数根是, 那么,. 注意它的使用条件为a ≠0, Δ≥0.细节剖析:1.一元二次方程的根的判别式正反都成立.利用其可以解决以下问题:(1)不解方程判定方程根的情况; (2)根据参系数的性质确定根的范围; (3)解与根有关的证明题.−−−→降次)0(02≠=++a c bx ax ac b 42-)0(02≠=++a c bx ax ∆ac b 42-=∆)0(02≠=++a c bx ax 21x x ,a b x x -=+21ac x x =212. 一元二次方程根与系数的应用很多:(1)已知方程的一根,不解方程求另一根及参数系数;(2)已知方程,求含有两根对称式的代数式的值及有关未知数系数;(3)已知方程两根,求作以方程两根或其代数式为根的一元二次方程.知识点4:列一元二次方程解应用题1.列方程解实际问题的三个重要环节:一是审题;二是把握问题中的三是的合理性.2.利用方程解决实际问题的关键是寻找等量关系.3.解决应用题的一般步骤:审 (审题目,分清等);设 (设,有时会用 );列 (根据题目中的, );解 (解方程,注意分式方程需检验,将所求量表示清晰);验 (检验方程的解能否保证实际问题有意义);答 (写出答案,切忌答非所问).数字问题、平均变化率问题、利息问题、利润(销售)问题、形积问题等.细节剖析:列方程解应用题就是先把实际问题抽象为,然后由数学问题的解决而获得对的解决.一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2022秋•江都区期末)如图,在长为28米、宽为10米的矩形空地上修建如图所示的道路(图中的阴影部分)余下部分铺设草坪,要使得草坪的面积为243平方米,则可列方程为()A.28×10﹣28x﹣10x=243 B.(28﹣x)(10﹣x)+x2=243C.(28﹣x)(10﹣x)=243 D.2(28﹣x+10﹣x)=2432.(2分)(2023•锡山区校级四模)若关于x的方程x2﹣x﹣m=0有实数根,则实数m的取值范围是()A.B.C.D.3.(2分)(2023•雨花台区校级模拟)方程(x+1)(x﹣2)+1=0的根的情况,下列结论中正确的是()A.两个正根B.两个负根C.一个正根,一个负根D.无实数根4.(2分)(2023•无锡)2020年﹣2022年无锡居民人均可支配收入由5.76万元增长至6.58万元,设人均可支配收入的平均增长率为x,下列方程正确的是()A.5.76(1+x)2B.5.76(1+x2C.5.76(1+2x x25.(2分)(2023•海门市二模)《九章算术》是我国古代数学名著,记载着“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意思是:一根笔直生长的竹子,高一丈(一丈=10尺),因虫害有病,一阵风吹来将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,求折断处离地面的高度是多少尺?设折断处离地面的高度为x尺,则可列方程为()A.x2+32=(10﹣x)2B.x2+32=102C.x2+(10﹣x)2=32D.(10﹣x)2+32=x26.(2分)(2023•海门市二模)若实数a,b,c满足a﹣b2﹣2=0,2a2﹣4b2﹣c=0,则c的最小值是()A.6 B.7 C.8 D.97.(2分)(2023•秦淮区二模)下列一元二次方程(a为常数,且a>0),有两个异号的实数根的是()A.(x﹣1)2+a=0 B.(x﹣1)(x﹣a)=0C.a(x+1)2=0 D.x2﹣x﹣a=08.(2分)(2023•武进区校级模拟)若关于x的一元二次方程(k﹣2)x2+x+k2﹣4=0有一个根是0,则k的值是()A.﹣2 B.2 C.0 D.﹣2或29.(2分)(2022秋•江阴市期末)已知关于x的一元二次方程x2+10x+2a+6=0,其中一根是另一根的4倍,则a的值为()A.或5 B.或﹣5 C.D.510.(2分)(2023春•扬州月考)已知一元二次方程a(x+m)2+n=0(a≠0)的两根分别为﹣3,1,则方程a(x+m﹣2)2+n=0(a≠0)的两根分别为()A.1,5 B.﹣1,3 C.﹣3,1 D.﹣1,5二.填空题(共10小题,满分20分,每小题2分)11.(2分)(2023•高邮市模拟)设x1、x2是方程x2+mx﹣2=0的两个根,且x1+x2=2x1x2,则m=.12.(2分)(2023•淮安模拟)已知关于x的方程x2﹣(2m﹣1)x+m2=0的两实数根为x1,x2,若(x1+1)(x2+1)=3,则m的值为.13.(2分)(2023•邗江区二模)《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云阔不及长一十二步,问长及阔各几步”.意思是:一块矩形田地的面积为864平方步,只知道它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为.14.(2分)(2023•海陵区校级二模)对于实数a,b,定义运算“*”:,例如4*2,因为4>2,所以4*2=42﹣4×2=8.若a,b是一元二次方程x2﹣2x﹣3=0的两个根,则a*b =.15.(2分)(2022秋•靖江市期末)已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2,且x1+x2+x1x2=1,则m的值为.16.(2分)(2023•建邺区二模)设x1,x2是关于x的方程x2+6x+m=0的两个根,且x1=2x2,则m=.17.(2分)(2022秋•宿城区期末)如果一元二次方程的两根相差1,那么该方程成为“差1方程”.例如x2+x =0是“差1方程”.若关于x的方程ax2+bx+1=0(a,b是常数,a>0)是“差1方程”设t=10a﹣b2,t的最大值为.18.(2分)(2023•靖江市模拟)已知x、y为实数,且满足x2﹣xy+y2=2,记W=x2+xy+y2的最大值为M,最小值为m,则M+m=.19.(2分)(2020秋•常州期中)如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的有(填序号)①方程x2﹣x﹣2=0是倍根方程;②若(x﹣2)(mx+n)=0是倍根方程:则4m2+5mn+n2=0;③若p,q满足pq=2,则关于x的方程px2+3x+q=0是倍根方程;④若方程以ax2+bx+c=0是倍根方程,则必有2b2=9ac.20.(2分)(2019秋•滨湖区期末)已知关于x的方程a(x+m)2+b=0(a、b、m为常数,a≠0)的解是x1=2,x2=﹣1,那么方程a(x+m+2)2+b=0的解.三.解答题(共8小题,满分60分)21.(6分)(2023春•仪征市期末)解方程:(1);(2)x2+3x﹣2=0.(用配方法)22.(6分)(2023•姜堰区二模)如图,用总长48m的篱笆依墙(墙足够长)围成如图所示的①②③三块矩形区域,且三块区域面积相等.(1)的值为;的值为;(2)当矩形ABCD的面积为108m2时,求BC的长.23.(8分)(2023•姜堰区一模)某草莓采摘园收费信息如下表:成人票儿童票带出草莓价格不超过10人超过10人20元/人30元/斤30元/人每增加1人,人均票价下降1元,但不低于儿童票价.(1)某社团共32人去该采摘园进行综合实践活动,购买了10张儿童票,其余均为成人票,总费用不超过1240元,求本次活动他们最多共带出草莓多少斤?(2)某公司员工(均为成人)在该草莓采摘园组织团建活动,共支付票价391元,求这次参加团建的共多少人?24.(8分)(2023春•仪征市期末)端午节前夕,某超市从厂家分两次购进蛋黄粽子、红豆粽子,两次进货时,两种粽子的进价不变.第一次购进蛋黄粽子60袋和红豆粽子90袋,总费用为4800元;第二次购进蛋黄粽子40袋和红豆粽子80袋,总费用为3600元.(1)求蛋黄粽子、红豆粽子每袋的进价各是多少元?(2)当蛋黄粽子销售价为每袋70元时,每天可售出20袋,为了促销,该超市决定对蛋黄粽子进行降价销售,经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当蛋黄粽子每袋的销售价为多少元时,每天售出蛋黄粽子所获得的利润为220元?25.(8分)(2023•广陵区校级一模)已知关于x的方程x2﹣(k+1)x+2k﹣2=0.(1)求证:无论k取何值,此方程总有实数根;(2)若等腰△ABC的三边a,b,c中a=3,另两边b、c恰好是这个方程的两个根,求k值.26.(8分)(2023•海陵区一模)2022年北京冬奥会吉祥物“冰墩墩”意喻敦厚、健康、活泼、可爱,象征着冬奥会运动员强壮的身体、坚韧的意志和鼓舞人心的奥林匹克精神.随着北京冬奥会开幕日的临近,某特许零售店“冰墩墩”的销售日益火爆.据调查“冰墩墩”每盒进价8元,售价12元.(1)商店老板计划首月销售330盒,经过首月试销售,老板发现单盒“冰墩墩”售价每增长1元,月销量就将减少20盒.若老板希望“冰墩墩”月销量不低于270盒,则每盒售价最高为多少元?(2)实际销售时,售价比(1)中的最高售价减少了2a元,月销量比(1)中最低销量270盒增加了60a 盒,于是月销售利润达到了1650元,求a的值.27.(8分)(2023•滨海县模拟)某服装销售商用48000元购进了一批时尚新款服装,通过网络平台进行销售,由于行情较好,第二次又用100000元购进了同种服装,第二次购进数量是第一次购进数量的2倍,每件的进价多了10元.(1)该销售商第一次购进了这种服装多少件,每件进价多少元?(2)该销售商卖出第一批服装后,统计发现:若按每件300元销售,每天平均能卖出80件,销售价每降低10元,则多卖出20件.依此行情,卖第二批服装时,让利促销,并使一天的利润恰好为3600元,销售价应为多少?28.(8分)(2022秋•灌南县校级月考)某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同(1)求每次下降的百分率;(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?。
关于2009年全国高中数学联赛(江苏赛区)靖江市获奖结果...

7
陈思佳
泰州市靖江高级中学
4
李钰
泰州市靖江高级中学
省三等奖(17人)
序号
姓名
学校
序号
姓名
学校
1
宋有成
泰州市靖江高级中学
10
肖艺
泰州市靖江高级中学
2
张时耘
泰州市靖江高级中学
11
张梦圆
泰州市靖江高级中学
3
吴凯
泰州市靖江高级中学
12
杨溢
泰州市靖江高级中学
4
王靖
泰州市靖江高级中学
13
盛达
泰州市靖江第一中学
江苏省靖江高级中学
6
纪鹏
靖江市刘国钧中学
14
薛亚军
江苏省靖江高级中学
7
杨磊
靖江市刘国钧中学
15
范文超
江苏省靖江高级中学
8
唐伟
靖江市第一中学
16
刘松
江苏省靖江高级中学
靖江市一等奖(30人)
序号
姓名
学校
序号
姓名
学校
1
蒋帅
靖江市第一中学
16
刘聪
靖江市刘国钧中学
2
马盈秋
靖江市第一中学
17
孙嘉
靖江市刘国钧中学
靖江市刘国钧中学
19
朱琦
靖江市斜桥中学
39
曹莉
靖江市刘国钧中学
20
杨蓝澜
靖江市斜桥中学
40
刘国兴
靖江市刘国钧中学
靖江市教育局教研室
二〇〇九年十二月二十五日
29
洪亮
靖江市第一中学
15
方栋
2023年江苏省泰州市靖江市中考二模英语试题(含答案)

2023年初中适应性调研测试(二)九年级英语(考试时间:100分钟满分:120分)请注意:1. 本卷分选择题和非选择题两个部分。
2. 所有试题的答案均填写在答题卡上,答案写在试卷上无效。
第一部分选择题(65分)一、选择题从下列每题所给的选项中选择一个最佳答案。
(本题共10小题;每小题1分,满分10分)1. Please mind your ________, Linda. It's not polite to make a loud noise at the dinner table.A. methodsB. materialsC. mysteriesD. manners2. —Mr. Li, can you ________ what "Grain in Ear (Mang zhong)" is?—Sure. It is the ninth of the 24 solar terms (节气). It means the farmer is getting back to the busy field work.A. experienceB. explainC. expectD. explore3. ________ antibiotics (抗生素) is very useful, it's never a good idea to take it too often.A. AlthoughB. AsC. WheneverD. Until4. "Peter, ________ your lessons instead of watching TV. The final exam is coming soon." said Mum.A. come overB. fall overC. go overD. knock over5. —How exciting! The 19th Asian Games ________ in Hangzhou in September 2023.—Yes, I can't wait to watch the Games.A. holdsB. is holdingC. was heldD. will be held6. Kunqu Opera is one of the oldest Chinese opera forms. ________, fewer young people want to learn or enjoy it.A. SadlyB. SimplyC. SpeciallyD. Certainly7. There are many old sayings requiring us to be ________, such as "The early bird catches the worm" and "Practice makes perfect".A. generousB. modestC. hard-workingD. organized8. V olunteering is a great contribution to our world ________ a chance for us to learn and grow.A. as well asB. as good asC. as far asD. as soon as9. What can we know from the picture on the right?A. The man wants to close the door.B. The man knows how to open the door.C. The man is pulling the door open hard.D. The man opens the door in a wrong way.10. —One cannot achieve anything by sitting around and talking about it.—________. That's why Johnson couldn't get into college.A. I agreeB. Not exactlyC. Nothing muchD. It all depends二、完形填空阅读下面短文,从每题所给的选项中选出可以填入空白处的最佳选项。
重难点02“四点共圆”模型(原卷版)-【暑假自学课】2024年新九年级数学暑假精品课(苏科版)

重难点02“四点共圆”模型1.识别几何模型。
2.利用“四点共圆”模型解决问题一.填空题(共3小题)1.(2021秋•南京期中)如图,在⊙O的内接五边形ABCDE中,∠C=100°,BC=CD,则∠A+∠D =°.2.(2022•靖江市二模)如图,AB⊥BC,AB=5,点E、F分别是线段AB、射线BC上的动点,以EF为斜边向上作等腰Rt△DEF,∠D=90°,连接AD,则AD的最小值为.3.(2022秋•大丰区期中)如图,△ABC中,AD⊥BC,∠B=45°,∠C=30°.以AD为弦的圆分别交AB、AC于E、F两点.点G在AC边上,且满足∠EDG=120°.若CD=4+2,则△DEG的面积的最小值是.二.解答题(共7小题)4.(2022秋•宿城区期中)如图,BD,CE是△ABC的高,BD,CE相交于点F,M是BC的中点,⊙O是△ABC的外接圆.(1)点B,C,D,E是否在以点M为圆心的同一个圆上?请说明理由.(2)若AB=8,CF=6,求△ABC外接圆的半径长.5.(兴化市校级期中)已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.(1)线段AF与BE有何关系.说明理由;(2)延长AF、BC交于点H,则B、D、G、H这四个点是否在同一个圆上.说明理由.6.(2022秋•建湖县期中)如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.(1)若∠DAE=75°,则∠DAC=°;(2)过点D作DE⊥AB于E,判断AB、AE、AC之间的数量关系并证明;(3)若AB=6、AE=2,求BD2﹣AD2的值.7.(2023•淮安区一模)综合与实践“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.提出问题:如图1,在线段AC同侧有两点B,D,连接AD,AB,BC,CD,如果∠B=∠D,那么A,B,C,D四点在同一个圆上.探究展示:如图2,作经过点A,C,D的⊙O,在劣弧AC上取一点E(不与A,C重合),连接AE,CE,则∠AEC+∠D=180°(依据1)∵∠B=∠D∴∠AEC+∠B=180°∴点A,B,C,E四点在同一个圆上(对角互补的四边形四个顶点共圆)∴点B,D在点A,C,E所确定的⊙O上(依据2)∴点A,B,C,D四点在同一个圆上反思归纳:(1)上述探究过程中的“依据1”、“依据2”分别是指什么?依据1:;依据2:.(2)如图3,在四边形ABCD中,∠1=∠2,∠3=45°,则∠4的度数为.拓展探究:(3)如图4,已知△ABC是等腰三角形,AB=AC,点D在BC上(不与BC的中点重合),连接AD.作点C关于AD的对称点E,连接EB并延长交AD的延长线于F,连接AE,DE.①求证:A,D,B,E四点共圆;②若AB=2,AD•AF的值是否会发生变化,若不变化,求出其值;若变化,请说明理由.8.(2022秋•靖江市期末)小明在学习了《圆周角定理及其推论》后,有这样的学习体会:在Rt△ABC中,∠C=90°,当AB长度不变时,则点C在以AB为直径的圆上运动(不与A、B重合).[探索发现]小明继续探究,在Rt△ABC中,∠C=90°,AB长度不变.作∠A与∠B的角平分线交于点F,小明计算后发现∠AFB的度数为定值,小明猜想点F也在一个圆上运动.请你计算∠AFB的度数,并简要说明小明猜想的圆的特征.[拓展应用]在[探索发现]的条件下,若AB=2,求出△AFB面积的最大值.[灵活运用]在等边△ABC中,AB=2,点D、点E分别在BC和AC边上,且BD=CE,连接AD、BE交于点F,试求出△ABF周长的最大值.9.(2022秋•鼓楼区期中)以下是“四点共圆”的几个结论,你能证明并运用它们吗?Ⅰ.若两个直角三角形有公共斜边,则这两个三角形的4个顶点共圆(图1、2);Ⅱ.若四边形的一组对角互补,则这个四边形的4个顶点共圆(图3);Ⅲ.若线段同侧两点与线段两端,点连线的夹角相等,则这两点和线段两端点共圆(图4).(1)在图1、2中,取AC的中点O,根据得OA=OB=OC=OD,即A,B,C,D共圆;(2)在图3中,画⊙O经过点A,B,D(图5).假设点C落在⊙O外,BC交⊙O于点E,连接DE,可得=180°,所以∠BED=,得出矛盾;同理点C也不会落在⊙O内,即A,B,C,D共圆.结论Ⅲ同理可证.(3)利用四点共圆证明锐角三角形的三条高交于一点.已知:如图6,锐角三角形ABC的高BD,CE相交于点H,射线AH交BC于点F.求证:AF是△ABC的高.(补全以下证明框图,并在图上作必要标注)(4)如图7,点P是△ABC外部一点,过P作直线AB,BC,CA的垂线,垂足分别为E,F,D,且点D,E,F在同一条直线上.求证:点P在△ABC的外接圆上.10.(2022秋•仪征市期中)【问题提出】苏科版九年级(上册)教材在探究圆内接四边形对角的数量关系时提出了两个问题:1.如图(1),在⊙O的内接四边形ABCD中,BD是⊙O的直径.∠A与∠C、∠ABC与∠ADC有怎样的数量关系?2.如图(2),若圆心O不在⊙O的内接四边形ABCD的对角线上,问题(1)中发现的结论是否仍然成立?(1)小明发现问题1中的∠A与∠C、∠ABC与∠ADC都满足互补关系,请帮助他完善问题1的证明:∵BD是⊙O的直径,∴,∴∠A+∠C=180°,∵四边形内角和等于360°,∴.(2)请回答问题2,并说明理由;【深入探究】如图(3),⊙O的内接四边形ABCD恰有一个内切圆⊙I,切点分别是点E、F、G、H,连接GH,EF.(3)直接写出四边形ABCD边满足的数量关系;(4)探究EF、GH满足的位置关系;(5)如图(4),若∠C=90°,BC=3,CD=2,请直接写出图中阴影部分的面积.一.选择题(共3小题)1.(2022•思明区二模)如图,四边形ABCD是⊙O的内接四边形,点E为边CD上任意一点(不与点C,点D重合),连接BE,若∠A=60°,则∠BED的度数可以是()A.110°B.115°C.120°D.125°2.(2023•泾阳县模拟)刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.如图,已知⊙O的半径为2,则⊙O的内接正六边形ABCDEF的面积为()A.6B.C.D.3.(2023•蜀山区校级模拟)如图,△ABC中,∠BAC=60°,AD平分∠BAC,∠BDC=120°,连接BD,CD并延长分别交AC,AB于点E和点F,若DE=6,,则BD的长为()A.10B.12C.15D.16二.填空题(共2小题)4.(2023•银川校级二模)如图,在直径为AB的⊙O中,点C,D在圆上,AC=CD,若∠CAD=28°,则∠DAB的度数为.5.(2023•海曙区校级一模)如图,在等腰三角形纸片ABC中,AB=AC,将该纸片翻折,使得点C落在边AB的F处,折痕为DE,D,E分别在边BC,AC上,∠AFD=∠DEF,若DE=4,BD=9,则DF=,△ABC的面积为.三.解答题(共7小题)6.(2022秋•南关区校级期末)【问题情境】如图①,在四边形ABCD中,∠B=∠D=90°,求证:A、B、C、D四点共圆.小吉同学的作法如下:连结AC,取AC的中点O,连结OB、OD,请你帮助小吉补全余下的证明过程;【问题解决】如图②,在正方形ABCD中,AB=2,点E是边CD的中点,点F是边BC上的一个动点,连结AE,AF,作EP⊥AF于点P.(1)如图②,当点P恰好落在正方形ABCD对角线BD上时,线段AP的长度为;(2)如图③,过点P分别作PM⊥AB于点M,PN⊥BC于点N,连结MN,则MN的最小值为.7.(2023•萍乡模拟)如图,点A,B,C在⊙O上,且∠ABC=120°,请仅用无刻度的直尺,按照下列要求作图.(保留作图痕迹,不写作法)(1)在图(1)中,AB>BC,作一个度数为30°的圆周角;(2)在图(2)中,AB=BC,作一个顶点均在⊙O上的等边三角形.8.(2022•芜湖一模)如图,在正方形ABCD中,P是边BC上的一个动点(不与点B,C重合),作点B 关于直线AP的对称点E,连接AE,再连接DE并延长交射线AP于点F,连接BF和CF.(1)若∠BAP=α,则∠AED=(用含α的式子直接填空);(2)求证:点F在正方形ABCD的外接圆上;(3)求证:AF﹣CF=BF.9.(2021秋•鹿城区校级期中)如图,△ABC内接于⊙O,CD⊥AB,CB=10cm,CD=8cm,AB=14cm.(1)∠A度数.(直接写出答案)(2)求的长度.(3)P是⊙O上一点(不与A,B,C重合),连结BP.①若BP垂直△ABC的某一边,求BP的长.②将点A绕点P逆时针旋转90°后得到A′,若A′恰好落在CD上,则CA'的长度为.(直接写出答案)10.(2021秋•永泰县期中)如图,在Rt△ABC中,∠BAC=90°,∠ABC=40°,将△ABC绕A点顺时针旋转得到△ADE,使D点落在BC边上.(1)求∠BAD的度数;(2)求证:A,D,B,E四点共圆.11.(2022秋•新华区校级期末)如图△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC,PD=3.(1)求证:P A是⊙O的切线;(2)求⊙O的直径;(3)当点B在CD下方运动时,直接写出△ABC内心的运动路线长是.12.(2021秋•固始县月考)阅读材料并完成相应任务:婆罗摩笈多是一位印度数学家与天文学家,他的一些数学成就在世界数学史上有较高的地位.其中就包括他提出的婆罗摩笈多定理(也称布拉美古塔定理).婆罗摩笈多定理:若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边.下面对该定理进行证明.已知:如图(1),四边形ABCD内接于⊙O,对角线AC⊥BD于点P,PM⊥BC于点M,延长MP交AD于点N.求证:AN=ND.证明:∵AC⊥BD,PM⊥BC,∴∠BPM+∠PBM=90°,∠PCB+∠PBC=90°,∴∠BPM=∠PCB.……任务:(1)请完成该证明的剩余部分;(2)请利用婆罗摩笈多定理完成如下问题:如图(2),已知Rt△ABC中,∠BAC=90°,AB=AC=4,BC,AC分别交⊙O于点D,E,连接AD,BE交于点P.过点P作MN∥BC,分别交DE,AB于点M,N.若AD⊥BE,求NP的长.。
靖江外国语学校九年级历史二模试卷

靖江外国语学校2012~2013学年九年级历史第二次模拟试卷(满分:50分时间:60分钟考试形式:闭卷)第一部分选择题(共20分)一、选择题(本题20小题,每题1分,共20分。
每题只有一个选项符合题意。
)1. 2013年2月底,国民党荣誉主席连战二次破冰大陆,两岸关系更清澈安心。
八年前访问团成员谒见黄帝陵时激动地说:“……每天都有回家的感觉。
我们的根就在这里呀。
”是因为()A.黄帝教人农耕,是农业生产创始人 B.黄帝是中华民族的人文始祖C.黄帝独自打败了蚩尤 D.黄帝建立我国第一个奴隶制国家2.中华大地人杰地灵,自古以来人才辈出。
“祸兮福之所倚,福兮祸之所伏”的名言出自下列哪位历史人物?()A.孔子B.孟子 C.庄子 D.老子3.泰州市的行政区划中有区、县和县级市,这些“区”、“县”、“县级市”都是县级行政单位。
秦朝统一后,在地方上全面推行的是()A.分封制B.郡县制C.县制 D.行省制4.“构成中国内聚性(注:模块内的联系)的又一重要因素是……存在着一种可追溯到数千年前、最古老的商朝的书面语”。
这里的“商朝的书面语”具体是指()A.青铜器 B.甲骨文 C.小篆 D.隶书5. 明朝时,一位家境殷实的人家家庭生活中可能存在的场景有()①书房的桌上摆着曹雪芹的《红楼梦》②客厅墙上挂着隶书撰写的书法作品③书架上摆着活字印刷的《史记》④书房的墙上挂着孔子的画像⑤几位孩子伏案写八股文A.①②③④⑤B.②③④⑤C.①③④⑤D. ①②③④6.2012年省区GDP统计表明,排在前三位的是广东、江苏、山东,南方省份在全国经济比重中占据优势地位。
中国历史上经济重心从黄河流域向长江流域转移,自魏晋南北朝开始到南宋最终完成,下列叙述与经济重心南移有关的是()①南朝四百八十寺,多少楼台烟雨中②忆昔开元全盛日,小邑犹藏万家室③苏湖熟,天下足④国家根本(税收),仰给东南A.①②B. ②③C. ①③D. ③④7.下列著名的航海活动中,未使用指南针的是()A.哥伦布发现新大陆 B.鉴真东渡日本 C.郑和下西洋 D.麦哲伦环球航行8.如果把中国由完整主权的封建国家转变为半殖民地半封建化的过程看作是一个物体从山崖上坠下的过程,你认为《辛丑条约》的签订使中国所处的位置是() A.崖边 B.崖底 C.悬崖的上半部 D.悬崖的下半部9.与1842年的《南京条约》相比,1895年中日《马关条约》反映了帝国主义阶段列强侵华的新特点,这主要体现在 ( )A.割地赔款 B.开埠通商 C.协定关税 D.设立工厂10.时政漫画常以特有的艺术形式反映某一时期复杂的政治形势。
江苏省靖江市外国语学校2011届中考英语二模试题_冀教版

靖江外国语学校2010~2011学年度九年级英语二模试卷(考试时间:120分钟,满分120分)第Ⅰ卷(选择题;共70分)一、单项选择(共15小题;每小题1分,共15分)从A、B、C、D四个选项中选出一个最佳选项,填在题前括号。
1. I have to walk _____ dog every evening, because my aunt is on ____ holiday.A. a; theB. the; theC. a; 不填D. the; 不填2. Is there __________ in the f itting room? No, _________ is in.A. somebody, nobodyB. somebody, anybodyC. anybody, nobodyD. nobody, nobody3. You worry too much at times . What's the underlined part of the sentence?A. objectB. adverbialC. predicativeD. attributive4. You’d better stay at home while they .A. are leavingB. leaveC. are awayD. are left5. None of you have been to Beijing, ?A. haven’t youB. do youC. have youD. don’t you6. How happy we were each other !A.to seeB. seeingC. sawD. have seen7. I hear he the song in English wellA. singsB. singC. to singD. singing8. All of the plans are very good. I really don’t know __________.A. which to talkB. which to talk aboutC. to talk about whichD. I asked you for help9. Jane is going to get married ?A. Who do you thinkB. Do you think whoC. To whom do you thinkD. Does who you think10. The woman is older than she .A . looks B. looks at C. is looking D. is looked at11. The police ______ the man to see if he had a gun .A. searched B .searched for C .looked D. looked for12 ---Did you have a good time in Thailand last week? ---_____, it was too hot.A. Not reallyB.Yeah, why notC. Oh, greatD.You are right.13. I don’t think math _______.A.easily to be learnedB.easily to learnC.easy to be learnedD.easy to learn14. This kind of music is often by old people.A. listening toB. listened toC. listeningD. listened15. Just like weather, life ____________ be beautiful all the time.A. mustn’tB. needn’tC. can’tD. wouldn’t二、完形填空从每小题所给的四个选项中,选出最佳答案填空(共15题,每小题1分,满分15分)Terry was a middle-aged businessman.He was unsuccessful in career and often complained that he had been fooled by others. One day he told his wife he was 16 disappointed (失望的)with the city that he had to leave.So his family moved to another city.It was Saturday 17 . When Terry and his wife were busy putting their things in their new home,the lights suddenly 18 and they were forced to stop work.Terry was sorry to have 19 to bring along some candles.Just then he heard light 20 on his door.“Who is it?”he wondered.Terry knew 21 else in the new city, and this was the moment he especially hated to be 22 .He opened the door impatiently. At the door was a little 23 , shyly asking,“Sir, do you have 24 ?I`m your neighbor.”“N o.”answered Terry angr ily.He shut the door 25 .After a while the door was knocked again.He opened it and found the same little girl outside.But this time she was 26 two candles radiating(放光)red light.she said,“My grandma told me the 27 neighbor downstairs might need candles.She sent me here to give you these”At that moment Terry suddenly realized what 28 his failure in life. It was his indifference(冷漠)and unkindness to other people.The person who had fooled him in life was actually nobody else 29 himself, for his eyes had been covered by his 30 mind.16. A.very B.so C.such D.rather17. A.morning B.afternoon C.noon D.evening18. A.went down B.went out C.went by D.went on19. A .wanted B.decided C.forgotten D.remembered20. A.knocks B.calls C.strikes D.sounds21. A.everybody B.anybody C.somebody D.nobody22. A.troubled B.followed C.liked D.1earned23. A.boy B.girl C.postman D.shopper24. A.candies B.toys C.lights D.candles25. A.easily B.worriedly C.happily D.heavily26. A.bringing B.seeing C.holding D.drawing27. A.poor B.kind C.new D.young28. A.made B.caused C.developed D.stopped29. A.besides B.except C.but D.than30. A.open B.right C.warm D.cold三、阅读理解从每小题所给的四个选项中选出最佳答案。
2024年江苏省泰州市靖江市中考二模数学试题

2024年江苏省泰州市靖江市中考二模数学试题一、单选题1.下列计算正确的是( )A .()22--=-B .()22+-=C .()22-+=-D .()22++=- 2.下列四个展开图中,可以折叠成一个无盖的正方体纸盒的是( )A .B .C .D . 3)A B C D 4.四个实数:1,2,3,x 的极差等于这4个数之和,则这四个数的中位数是( ) A .1.5 B .2.5 C .2 D .35.下列函数中,函数值y 随自变量x 增大而减小的是( )A .21y x =+B .21y x =-+C .6y x =D .1y x =-+ 6.如图,矩形ABCD 中,9AB =,12BC =,点F 在CD 上,且6CF =,E 是BC 边上的一动点,M 、N 分别是AE 、EF 上的点,13AM AE =,13FN EF =,则在点E 从B 向C 运动的过程中,线段MN 所扫过的图形面积是( )A .8B .10C .12D .14二、填空题7.当x =时,分式23x x-的值为0. 8.我国首个国家级陆相页岩油示范区——吉庆油田作业区,2024年一季度页岩油产量达215000吨,创历史新高.将数字215000用科学记数法表示为.9.若实数m ,n 是方程:2640x x ++=的两个根,则m n +=.10.在一个不透明的布袋中装有红色、白色玻璃球共50个,除颜色外其他完全相同.小明每次从中任意摸出一个球,记下颜色后将球放回并搅匀,通过多次重复试验,算得摸到红色球的频率为30%,则估计该布袋中红色球有个.11.用反证法证明,“在△ABC 中,∠A 、∠B 对边是a 、b ,若∠A >∠B ,则a >b .”第一步应假设.12.已知54a =,56b =,59c =,则a ,b ,c 之间满足的等量关系是.13.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径2r cm =,扇形的圆心角120θ=o ,则该圆锥的母线长l 为cm .14.若2244243M x xy y x y =-++-+,则M 的最小值为.15.若点(),P a b 在直线29y x =-+上,点P 到x 轴的距离与到y 轴的距离之和为6,则a 的值为.16.已知,如图AB DE ∥,点C 在BD 上,2BC CD =,AC DE =,ACB E ∠=∠,若6AB =,则AC =.三、解答题17.(1)计算:()10202434si 13n 60π-⎛⎫++- ⎪⎭+⎝; (2)解不等式组:()32252123x x x x ⎧+≥+⎪⎨--<⎪⎩18.小晗家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?(2)若任意按下其中的两个开关,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表加以说明.19.为了解某校七~九年级学生的视力情况,该校数学兴趣小组收集有关数据,并进行整理分析.【收集数据】(1)数学兴趣小组设计了以下三种调查方案:方案一:随机抽取300名女生进行调查;方案二:分别从三个年级各随机抽取100名学生进行调查;方案三:从初一年级随机抽取8个班级共300名学生进行调查.其中抽取的样本具有代表性的方案是;【整理数据】(2)抽查了部分学生进行视力检测.根据检测结果,制成下面不完整的统计图表.抽取的学生视力情况频数表则m=;【分析数据】(3)兴趣小组在分析数据时发现,这次抽样调查的平均数和中位数是一样的.有同学就提出:在生活中知道一组数据的平均数,则这个平均数也就处于这组数据的中游水平.你认为他的说法对吗?请说明理由.四、填空题20.在某市组织的农机推广活动中,甲、乙两人分别操控A ,B 两种型号的收割机参加水稻收割比赛.已知乙每小时收割的亩数比甲少40%,若两人各收割6亩水稻,则乙比甲多用0.4小时完成任务.求甲、乙两人分别操控A ,B 两种型号的收割机每小时各能收割多少亩水稻?五、解答题21.如图,在正方形ABCD 中,点E 为BC 边上一点.(1)请用直尺与圆规在CD 边上画一点F ,使得AF 恰是DFE ∠的平分线(保留作图痕迹,不写作法);(2)在(1)的条件下,若30EAB ∠=︒,3AB =AEF S V 的值.22.如图,已知()1,A A n y -,()1,B B n y +,(),C C n y 三点在反比例函数()0,0k y k x x=>>的图像上,且1n >.(1)当3n =时,请比较A B y y +与2C y 的大小关系,并说明理由;(2)若2A C y y -=,1C B y y -=,求该函数的表达式.23.如图,O e 是ABC V 的外接圆,90ACB ∠=︒.D 是O e 上一点,连接CD ,与AB 交于点F ,点E 在DC 的延长线上.(1)结合以上信息,从①AE 与O e 相切;②AC EC =;③AD AE =这三个信息中,选择两个作为条件,剩余的一个作为结论构成一个命题.试写出你所构造的命题,判断命题是否正确,并说明理由;你选择的条件是,;结论是.(只要填写序号)(2)在(1)的条件下,若AE 3CD =,求O e 的直径.24.如图,二次函数()230y ax bx a =++≠的图像与x 轴交于点()1,0A -,()3,0B 两点,P为抛物线顶点,D 为对称轴l 左侧图像上一动点,连接PD ,过点D 作DE l ⊥交l 于点E ,过点P 作PF PD ⊥交抛物线于点F ,过点F 作FG l ⊥于点G .(1)求抛物线的表达式;(2)证明:随着D 点的变化,始终存在1FG DE ⋅=.25.消防云梯车中的数学是消防云梯车的实物图,主要由车身、伸展臂、延展臂、支撑臂与救援转台组成,且在作业过程中,车身、救援转台与地面始终平行,延展臂可绕、在同一平面内,为车轮圆心,均距离,支撑臂互相垂直时,救援转台上的消防员方可开展救援工作,问题解决:26.图算法是根据几何原理,将某一已知函数关系式中的各变量,分别编成有刻度的直线(或曲线),并把它们按一定的规律排列在一起的一种图形,可以用来解函数式中的未知量,这样的图形叫诺模图.设有两只电阻,16R =千欧,24R =千欧,问并联后的总电阻值R 是多少千欧?我们可以利用公式求得R 的值,也可以设计一种图算法(如图1)直接得出结果:我们先来画出一个120︒的角,再画一条角平分线,在角的两边及角平分线上用同样的单位长度进行刻度,这样就制好了一张算图.我们只要把角的两边刻着6和4的两点连成一条直线,这条直线与角平分线的交点的刻度值就是并联后的总电阻值R .(1)①16R =千欧,24R =千欧,计算R =千欧;②如图1,已知120AOB ∠=︒,OC 是AOB ∠的角平分线,1OA R =,2OB R =,OC R =.用你所学的几何知识说明:12111R R R =+;(2)如图2,已知90AOB ∠=︒,OC 是AOB ∠的角平分线,1OA R =,2OB R =,OC R =.此时关系式可以写成12111m R R R ⋅=+,其中0m ≠的常数,求m 的值; (3)如图3,若AO B α∠=,(2)中其余条件不变,请探索1R ,2R ,R 之间的关系.(用含α的代数式表示)。
2023年中考数学【填空题】讲练必考重点10 解三角形

【填空题】必考重点10 解三角形解三角形是指已知三角形的部分边和角,求出三角形中其他未知的边和角。
通常利用勾股定理、相似三角形的性质或者锐角三角函数的边角关系进行求解,是江苏省各地市中考的必考点,考查形式多样,既有选择题、填空题,也会考查解答题,选择和填空考查时,难度中等或者偏难,综合题考查时难度中等。
接此类题目时,要善于运用勾股定理、相似三角形的对应边成比例的性质求三角形的边长,能够运用锐角三角函数的基本知识进行边角互化,从而解出三角形。
【2022·江苏南通·中考母题】如图,B 为地面上一点,测得B 到树底部C 的距离为10m ,在B 处放置1m 高的测角仪BD ,测得树顶A 的仰角为60︒,则树高AC 为___________m (结果保留根号).【考点分析】本题考查了解直角三角形,解直角三角形的应用—仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.【思路分析】在Rt ADE △中,利用tan 10∠===AE AE ADE DE AE =1m 即为AC 的长.【2022·江苏常州·中考母题】如图,在四边形ABCD 中,90A ABC ∠=∠=︒,DB 平分ADC ∠.若1AD =,3CD =,则sin ABD ∠=______.【考点分析】本题考查了锐角三角函数、矩形、等腰三角形形、勾股定理、平行线的性质,解题的关键是构造直角三角形求解.【思路分析】过点D 作BC 的垂线交于E ,证明出四边形ABED 为矩形,BCD △为等腰三角形,由勾股定理算出DE BD【2022·江苏南通·中考母题】如图,点O 是正方形ABCD 的中心,AB =Rt BEF △中,90,︒∠=BEF EF 过点D ,,BE BF 分别交,AD CD 于点G ,M ,连接,,OE OM EM .若1,tan 3=∠=BG DF ABG ,则OEM △的周长为___________.【考点分析】本题主要考查了正方形的性质,解直角三角形,勾股定理,全等三角形的判定和性质,等腰三角形的判定和性质,直角三角形斜边中线的性质以及三角形中位线定理,综合性较强,能够作出合适的辅助线,构造出全等三角形是解题的关键.【思路分析】连接BD ,则BD 过正方形ABCD 的中心点O ,作FH ⊥CD 于点H ,解直角三角形可得BG=AG =13AB ,然后证明△ABG ≌△HFD (AAS ),可得DH =AG =13AB =13CD ,BC =HF ,进而可证△BCM ≌△FHM (AAS ),得到MH =MC =13CD ,BM =FM ,然后根据等腰三角形三线合一求出DF =FM ,则BG =DF =FM =BM =出OM 、EM 和OE 即可解决问题.【2022·江苏无锡·中考母题】△ABC 是边长为5的等边三角形,△DCE 是边长为3的等边三角形,直线BD 与直线AE 交于点F .如图,若点D 在△ABC 内,∠DBC =20°,则∠BAF =________°;现将△DCE 绕点C 旋转1周,在这个旋转过程中,线段AF 长度的最小值是________.【考点分析】本题考查了旋转的性质,等边三角形的性质,圆周角定理,切线的性质,解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件.【思路分析】利用SAS 证明△BDC ≌△AEC ,得到∠DBC=∠EAC =20°,据此可求得∠BAF 的度数;利用全等三角形的性质可求得∠AFB =60°,推出A 、B 、C 、F 四个点在同一个圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,此时线段AF 长度有最小值,据此求解即可.1.(2022·江苏无锡·模拟预测)如图,在平面直角坐标系中,矩形ABCD 的边4AB =,6BC =,若不改变矩形ABCD A 在x 轴的正半轴上左右移动时,矩形的另一个顶点D 始终在y 轴的正半轴上随之上下移动,当点A 移动到某一位置时,点C 到点O 的距离有最大值,则此时点A 的横坐标为______ .2.(2022·江苏·阳山中学一模)在Rt ABC △中,90C ∠=︒,有一个锐角为60°,AB =4,若点P 在线段AB上(不与点A 、B 重合),且30PCB ∠=︒,则CP 的长为______.3.(2022·江苏·无锡市天一实验学校三模)如图,平面内几条线段满足10AB BC ==.AB 、CD 的交点为E ,现测得AD BC ⊥,AD DE =,3tan 4DAE ∠=,则CD 的长度为___________.4.(2022·江苏苏州·二模)如图,在ABC 中,90ACB ∠=︒,5AB =,4BC =.将ABC 绕点A 旋转得AB C ''△,连接B C ',B ′B ,则B CB '△面积的最大值为________.5.(2022·江苏镇江·二模)如图,在等腰直角△ABC 中,90ACB ∠=︒,点D 在△ABC 内部,连接BD 、CD ,将△BDC 绕点C 逆时针旋转90°得到△AEC ,点M 在边AE 上,若=90BDC ∠︒,24AC CD ==,则线段BM 的最小值为______.6.(2022·江苏苏州·一模)如图,在Rt ABC △中,90ACB ∠=︒,30ABC ∠=︒,2AC =,点P 是边AB 上的一动点.A B C ABC ''△△≌,将A B C ''△绕点C 按逆时针方向旋转,点E 是边A C '的中点,则PE 长度的最小值为______.7.(2022·江苏·宜兴市实验中学二模)如图,在Rt ABC △中,90C ∠=︒,4AC BC ==.矩形DEFG 的顶点D 、E 、F 分别在边BC 、AC 、AB 上,若3tan 4DEC ∠=,则当EC =______时,矩形DEFG 面积的最大值=______.8.(2022·江苏南通·二模)某校航模小组打算制作模型飞机,设计了如图所示的模型飞机机翼图纸,图纸中AB CD ∥,均与水平方向垂直.根据图中数据,机翼外缘CD 的长为______cm .(结果取整数,参考sin 270.45︒≈,cos270.89︒≈,tan 270.51︒≈)9.(2022·江苏·靖江市教师发展中心二模)如图,AB BC ⊥,5AB =,点E 、F 分别是线段AB 、射线BC 上的动点,以EF 为斜边向上作等腰Rt DEF △,90D ∠=︒,连接AD ,则AD 的最小值为______.10.(2022·江苏泰州·二模)如图,在等边ABC 外侧作直线AD ,点C 关于直线AD 的对称点为M ,连接CM ,BM .其中BM 交直线AD 于点E .若60120CAD <∠<︒︒,当3BE =,4ME =时,则等边ABC 的边长为______.11.(2022·江苏·无锡市河埒中学二模)如图,已知正方形ABCD 的边长为4,P 是CD 边上的一点,连接BP ,以BP 为一边在正方形内部作45PBQ ∠=︒,过点A 作AE BP ∥,交BQ 的延长线于点E ,则BP BE ⋅=______.12.(2022·江苏宿迁·二模)如图,在ABC 中,21530AC A B =∠=︒∠=︒,,,则ABC 的面积为_______.13.(2022·江苏常州·二模)如图,在Rt ABC 中,90ACB ∠=︒,3sin 5B =.D 是边BC 的中点,点E 在AB 边上,将BDE △沿直线DE 翻折,使点B 落在同一平面内点F 处,线段FD 交边AB 于点G ,若FD AB ⊥时,则AE BE=______.14.(2022·江苏南京·一模)如图Rt △ABC 中,∠BAC =90°,AB =2,AC =4,点P 为BC 上任意一点,连接P A ,以P A ,PC 为邻边作平行四边形P AQC ,连接PQ ,则PQ 的最小值为 _____.15.(2022·江苏常州·模拟预测)如图,正方形ABCD 的边长是3.BP CQ =,连接AQ 、DP 交于点O ,并分别与边CD 、BC 交于点F 、E ,连接AE ,下列到结论:①DF CE =;②2OQ OA OF =⋅;③AOD OECF S S ∆=四边形;④222AO OE BC +=;⑤当1BP =时,1an 136t OAE ∠=,其中正确结论是:__.16.(2022·江苏·无锡市天一实验学校二模)如图,将两块三角板OAB (∠OAB =45°)和三角板OCD (∠OCD =30°)放置在矩形BCEF 中,直角顶点O 重合,点A 、D 在EF 边上,AB =6.(1)若点O 到BC ,则点O 到EF 的距离为_________;(2)若BC =3AD ,则△OCD 外接圆的半径为_________.17.(2022·江苏·苏州草桥中学一模)如图,将Rt ACB 绕斜边AB 的中点O 旋转一定的角度得到Rt FAE ,已知3AC =,2BC =,则cos CAE ∠=________.18.(2022·江苏徐州·二模)如图,在等边三角形ABC 中,2AB =,点D ,E ,F 分别是边BC ,AB ,AC 边上的动点,则DEF 周长的最小值是______.19.(2022·江苏南通·一模)如图,△ABC 中,90ACB ∠=,3sin 5B =,将△ABC 绕顶点C 逆时针旋转,得△DCE ,点D ,点E 分别与点A ,点B 对应,边CE , DE 与边AB 相交,交点分别为点F ,点G ,若32AF BF =,则EG BC的值为_________.20.(2022·江苏无锡·一模)如图,在四边形ABCD 中,AD CD ==6CB AB ==,90BAD BCD ∠=∠=︒,点E 在对角线BD 上运动,⊙O 为△DCE 的外接圆,当⊙O 与AD 相切时,⊙O 的半径为__________;当⊙O 与四边形ABCD 的其它边相切时,其半径为__________.21.(2022·江苏无锡·一模)如图,Rt △ABC 中,∠ACB =90°,AC =3,BC =4,D 是BC 的中点,连接AD ,过点C 作CF ⊥AD 交AB 于F ,则△ABD 的面积为______,BF =______.22.(2022·江苏无锡·一模)一个含30度角的三角板和一个含45度角的三角板按如图所示的方式拼接在一起,经测量发现,AC =CE AB 中点O ,连接OF .∠FCE 在∠ACB 内部绕点C 任意转动(包括边界),则CE 在运动过程中扫过的面积为____;在旋转过程中,线段OF 的长度最小时,两块三角板重叠部分的周长为____.23.(2022·江苏·靖江市实验学校一模)在△ABC 中,∠BAC =120°,D 为BC 的中点,AE =6,把AD 绕点A 逆时针旋转120°,得到AF ,若CF =7,∠ACF =∠AEC ,则AC =________.24.(2022·江苏连云港·一模)如图,在矩形ABCD 和Rt BEF △中,6,5,4AB BC BE BF ====,将BEF △绕着点B 顺时针旋转,连接,CE AF ,当BCE ∠最大时,ABF △的面积为___________.25.(2022·江苏·常州市武进区前黄实验学校一模)如图,矩形ABCD中,3AB=,4BC=,点E是矩形ABCD对角线AC上的动点,连接DE,过点E作EF DE⊥交BC所在直线与点F,以DE、EF为边作矩形DEFG,当92DEFGS=矩形时,则AE长为______.【填空题】必考重点10 解三角形解三角形是指已知三角形的部分边和角,求出三角形中其他未知的边和角。
专题11.1 角度计算的综合题(专项拔高卷)学生版-2024-2025学年八年级数学上册真题汇编章节

2024-2025学年人教版数学八年级上册同步专题热点难点专项练习专题11.1 角度计算的综合题(专项拔高卷)考试时间:90分钟试卷满分:120分难度:0.40姓名:___________班级:___________考号:___________题号一二三总分得分评卷人得分一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2023春•遵义期末)如图,∠ABC=50°,点D,E分别在射线BA,BC上,将三角形BED沿着DE 折叠,若点B恰好落在射线DA的B′处,则∠BEB′的度数是()A.50°B.80°C.100°D.130°2.(2分)(2023春•大荔县期末)如图,若点A在y轴上,点B在x轴上,∠OAB的平分线交△OAB外角∠OBD的平分线于点C,则∠C的度数是()A.30°B.45°C.50°D.60°3.(2分)(2023春•高青县期末)如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为()A.40°B.41°C.42°D.43°4.(2分)(2023春•鼓楼区校级期末)如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC,②∠ACB=∠ADB,③∠ADC+∠ABD=90°,④∠ADB=45°﹣∠CDB,其中正确的结论有()A.1个B.2个C.3个D.4个5.(2分)(2023春•鼓楼区校级期末)如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的角平分线BF所在直线与射线AE相交于点G,若∠ABC=3∠C,且∠G=20°,则∠DFB的度数为()A.50°B.55°C.60°D.65°6.(2分)(2023春•渠县校级期末)如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=20°,则∠BDC的度数为()A.70°B.65°C.60°D.40°7.(2分)(2023•大连一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AC上一点,将△ABD 沿线段BD翻折,使得点A落在A'处,若∠A'BC=28°,则∠CBD=()A.15°B.16°C.18°D.20°8.(2分)(2022秋•武昌区期末)如图,在△ABC中,∠ABC=60°,∠ACB=80°,点D在△ABC外,连接AD,BD,CD,若∠DBA=20°,∠ACD=30°,则∠BAD的度数是()A.20°B.25°C.30°D.35°9.(2分)(2018秋•玉州区期中)如图,已知△ABC的内角∠A=α,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;……以此类推得到∠A2018,则∠A2018的度数是()A.B.C.D.90°+10.(2分)(2022秋•黄骅市校级期中)在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为()A.60°B.10°C.45°D.10°或60°评卷人得分二.填空题(共10小题,满分20分,每小题2分)11.(2分)(2023春•宣化区期末)如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为.12.(2分)(2022秋•葫芦岛期末)在△ABC中,∠ACB=50°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=3:5,则∠BEC的度数为.13.(2分)(2023春•鹤壁期末)如图,在△ABC中,AD是BAC的平分线,EF∥AD,交BC于E、AB于F、CA 的延长线于G,∠B=30°,∠C=70°,则∠G的度数为.14.(2分)(2023•靖江市二模)如图,∠ABD,∠ACD的角平分线交于点P,若∠A=70°,∠D=10°,则∠P的度数为.15.(2分)(2023春•新民市期末)如图,将一张三角形纸片ABC的一角折叠,使得点A落在四边形BCDE 的外部A'的位置,且A'与点C在直线AB的异侧,折痕为DE,已知∠C=90°,∠A=30°.若保持△A′DE的一边与BC平行,则∠ADE的度数.16.(2分)(2023春•明水县期中)如图,已知∠A=ɑ,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线相交于点A1,得∠A1;若∠A1BC的平分线与∠A1CD的平分线相交于点A2,得∠A2…∠A2015BC的平分线与∠A2015CD的平分线相交于点A2016,得∠A2016,则∠A2016=.(用含ɑ的式子表示)17.(2分)(2022秋•潍坊期末)如图,AB和CD相交于点O,∠C=∠COA,∠BDC=∠BOD,AP,DP分别平分∠CAO和∠BDC,若∠C+∠P+∠B=165°,则∠C的度数是.18.(2分)(2021秋•武昌区期末)如图,在△ABC中,∠ACB=2α,CD平分∠ACB,∠CAD=30°﹣α,∠BAD=30°,则∠BDC=.(用含α的式子表示)19.(2分)(2021秋•西华县期中)如图,∠BCD是△ABC的一个外角,∠B=50°,∠BCD=110°,CE平分∠ACB,则∠BEC=.20.(2分)(2019秋•临安区期中)如图,△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC、BC的延长线于E、H、F、G,已知下列四个式子:(1)∠1=(∠2+∠3);(2)∠1=2(∠3﹣∠2);(3)∠4=(∠3﹣∠2);(4)∠4=∠1.其中有两个式子是正确的,它们是和.评卷人得分三.解答题(共8小题,满分80分)21.(6分)(2023春•江北区期末)如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD 交BC的延长线于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B,∠ACB的数量关系,并证明.22.(10分)(2023春•郯城县期中)已知AB∥CD,直线MN交AB、CD交于点M、N.(1)如图1所示,点E在线段MN上,设∠MBE=15°,∠MND=70°,则∠MEB=.(2)如图2所示,点E在线段MN上,∠1=∠2,DF平分∠EDC,交BE的延长线于点F,试找出∠AEN、∠1、∠3之间的数量关系,并证明;(提示:不能使用“三角形内角和是180°”).(3)如图3所示,点B、C、D在同一条直线上,∠ABC与∠ACD的角平分线交于点P,请直接写出∠A 与∠P的数量关系:.23.(10分)(2022秋•邢台期末)材料阅读:如图①所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”.解决问题:(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下两个问题:Ⅰ.如图②,把一块三角尺DEF放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点B,C,若∠A=40°,则∠ABD+∠ACD=°.Ⅱ.如图③,BD平分∠ABP,CD平分∠ACP,若∠A=40°,∠BPC=130°,求∠BDC的度数.24.(8分)(2023春•永川区期末)如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.(1)请你判断BF与CD的位置关系,并说明理由;(2)求∠3的度数.25.(10分)(2023春•虹口区期末)△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.(1)如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数.26.(12分)(2023春•巨野县期末)将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C.(1)如图①,若∠A=40°时,点D在△ABC内,则∠ABC+∠ACB=度,∠DBC+∠DCB=度,∠ABD+∠ACD=度;(2)如图②,改变直角三角板DEF的位置,使点D在△ABC内,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论.(3)如图③,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.27.(12分)(2022秋•榆次区校级期末)探究与发现:如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,(1)观察“规形图”,直接写出∠BDC与∠A、∠B、∠C之间的关系:;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=42°,则∠ABX+∠ACX=°;②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=140°,则∠DCE=°;③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=142°,∠BG1C=70°,则∠A=°.28.(12分)(2021秋•阿鲁科尔沁旗期末)在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如图1,若∠A=80°,求∠BPC的度数;(2)如图2.作△ABC外角∠MBC,∠NCB的平分线,相交于点Q.试探索∠BQC与∠A之间的数量关系;(3)如图3,在图2中延长线段BP,QC.交于点E,若在△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.。
专题06 四点共圆(专项训练)(老师版)
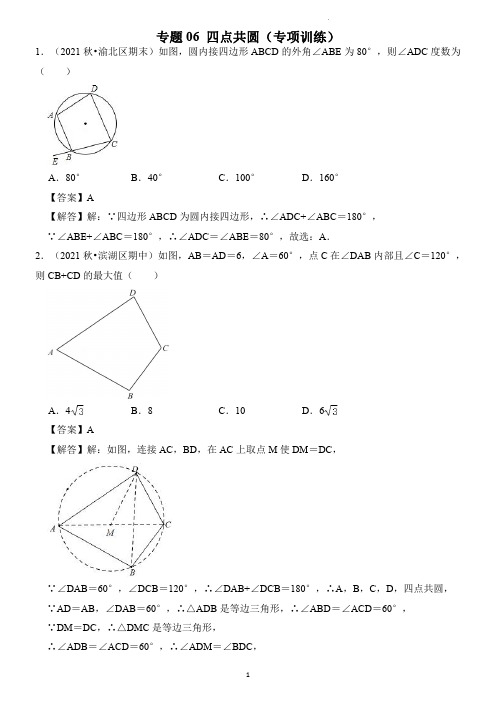
专题06四点共圆(专项训练)1.(2021秋•渝北区期末)如图,圆内接四边形ABCD的外角∠ABE为80°,则∠ADC度数为()A.80°B.40°C.100°D.160°【答案】A【解答】解:∵四边形ABCD为圆内接四边形,∴∠ADC+∠ABC=180°,∵∠ABE+∠ABC=180°,∴∠ADC=∠ABE=80°,故选:A.2.(2021秋•滨湖区期中)如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值()A.4B.8C.10D.6【答案】A【解答】解:如图,连接AC,BD,在AC上取点M使DM=DC,∵∠DAB=60°,∠DCB=120°,∴∠DAB+∠DCB=180°,∴A,B,C,D,四点共圆,∵AD=AB,∠DAB=60°,∴△ADB是等边三角形,∴∠ABD=∠ACD=60°,∵DM=DC,∴△DMC是等边三角形,∴∠ADB=∠ACD=60°,∴∠ADM=∠BDC,∵AD=BD,∴△ADM≌△BDC(SAS),∴AM=BC,∴AC=AM+MC=BC+CD,∵四边形ABCD的周长为AD+AB+CD+BC=AD+AB+AC,且AD=AB=6,∴当AC最大时,四边形ABCD的周长最大,则CB+CD最大,此时C点在的中点处,∴∠CAB=30°,∴AC的最大值=AB×cos30°=4,∴CB+CD最大值为AC=4,故选:A.3.(2022•靖江市二模)如图,AB⊥BC,AB=5,点E、F分别是线段AB、射线BC上的动点,以EF为斜边向上作等腰Rt△DEF,∠D=90°,连接AD,则AD的最小值为.【答案】【解答】解:连接BD并延长,如图,∵AB⊥BC,∴∠ABC=90°,∠EDF=90°,∴∠ABC+∠EDF=180°,∴B,E,D,F四点共圆,∵△DEF为等腰直角三角形,∴∠DEF=∠DFE=45°,∴∠DBF=∠DEF=45°,∴∠DBF=∠DBE=45°,∴点D的轨迹为∠ABC的平分线上,∵垂线段最短,∴当AD⊥BD时,AD取最小值,∴AD的最小值为AB=,故答案为:.4.如图,△ABC和△BCD均为直角三角形,∠BAC=∠BDC=90°,AB=2,连接AD.若∠ADB=30°,则AC的长为.【答案】【解答】解:∵∠BAC=∠BDC=90°,∴A,B,C,D四点共圆,∵∠ADB=30°,AB=2,∴∠ACB=∠ADB=30°,∴BC=2AB=4,∴AC=.故答案为:.5.如图,在四边形ABCD中,BD=6,∠BAD=∠BCD=90°,则四边形ABCD面积的最大值为.【答案】18【解答】解:∵∠BAD=∠BCD=90°,∴A,C两点在以BD为直径的圆上,∴当AB=AD,CB=CD时,四边形ABCD面积最大,∵BD=6,∴AB=AD=CB=CD=3,∴四边形BCD的面积为3××=18.故答案为:18.6.如图,在△ABC和△ACD中,∠ABC=∠ADC=45°,AC=6,则AD的最大值为.【答案】6【解答】解:∵∠ABC=∠ADC=45°,∴A,C,D,B四点共圆,如图,作⊙O经过A,C,D,B四点,当AD(D′)为直径时,AD有最大值,∵∠ADC=45°,∴∠AOC=90°,∵OA=OC,∴△AOC是等腰直角三角形,∵AC=6,∴AO=6×=3,∴AD′=2AO=6,即AD的最大值为6.故答案为:6.7.如图,△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,点E,F分别为AB,AC边上的点,且∠EDF=90°,连接EF,则∠DEF的度数为.【答案】45°【解答】解:如图,连接AD,∵△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,∴∠ADC=90°,AD=CD,∠BAD=∠C=45°,而∠EDF=90°,∴∠ADE=∠CDF,在△ADE和△CDF中,,∴△ADE≌△CDF(ASA),∴DE=DF,而∠EDF=90°,∴∠DEF=∠DFE=45°.故答案为:45°.8.(2022秋•萧山区月考)如图,以C为公共顶点的Rt△ABC和Rt△CED中,∠ACB=∠CDE =90°,∠A=∠DCE=30°,且点D在线段AB上,则∠ABE=30°,若AC=10,CD=9,则BE=.【答案】【解答】解:∵∠ACB=∠CDE=90°,∠A=∠DCE=30°,∴∠DBC=∠DEC=60°,∴B、C、D、E四点共圆,∴∠DBE=∠DCE=30°,∴∠ABE=30°,设BC=x,则AB=2x,在Rt△ABC中,由勾股定理得AB2=AC2+BC2,∵AC=10,∴(2x)2=102+x2,解得:x=,∴BC=,设DE=a,则CE=2a,在Rt△CED中,由勾股定理得CE2=DE2+CD2,∵CD=9,∴(2a)2=a2+92,解得:a=,∴DE=,CE=,∵∠ABC=60°,∠ABE=30°,∴∠CBE=∠ABC+∠ABE=90°,在Rt△CBE中,由勾股定理得=.9.(2021秋•宽城区期末)【问题原型】如图①,在⊙O中,弦BC所对的圆心角∠BOC=90°,点A在优弧BC上运动(点A不与点B、C重合),连结AB、AC.(1)在点A运动过程中,∠A的度数是否发生变化?请通过计算说明理由.(2)若BC=2,求弦AC的最大值.【问题拓展】如图②,在△ABC中,BC=4,∠A=60°.若M、N分别是AB、BC的中点,则线段MN的最大值为.【解答】解:【问题原型】(1)∠A的度数不发生变化,理由如下:∵,∠BOC=90°,∴;(2)当AC为⊙O的直径时,AC最大,在Rt△BOC中,∠BOC=90°,根据勾股定理,得OB2+OC2=BC2,∵OB=OC,∴,∴,即AC的最大值为;【问题拓展】如图,画△ABC的外接圆⊙O,连接OB,OC,ON,则ON⊥BC,∠BON=60°,BN=BC=2,∴OB=,∵M、N分别是AB、BC的中点,∴MN是△ABC的中位线,∴MN=AC,∴AC为直径时,AC最大,此时AC=2OB=,∴MN最大值为,故答案为:.10.(2022秋•仪征市期中)【问题提出】苏科版九年级(上册)教材在探究圆内接四边形对角的数量关系时提出了两个问题:1.如图(1),在⊙O的内接四边形ABCD中,BD是⊙O的直径.∠A与∠C、∠ABC与∠ADC有怎样的数量关系?2.如图(2),若圆心O不在⊙O的内接四边形ABCD的对角线上,问题(1)中发现的结论是否仍然成立?(1)小明发现问题1中的∠A与∠C、∠ABC与∠ADC都满足互补关系,请帮助他完善问题1的证明:∵BD是⊙O的直径,∴,∴∠A+∠C=180°,∵四边形内角和等于360°,∴.(2)请回答问题2,并说明理由;【深入探究】如图(3),⊙O的内接四边形ABCD恰有一个内切圆⊙I,切点分别是点E、F、G、H,连接GH,EF.(3)直接写出四边形ABCD边满足的数量关系;(4)探究EF、GH满足的位置关系;(5)如图(4),若∠C=90°,BC=3,CD=2,请直接写出图中阴影部分的面积.【解答】解:【问题提出】(1)∵BD是⊙O的直径,∴∠A=∠C=90°,∴∠A+∠C=180°,∵四边形内角和等于360°,∴∠ABC+∠ADC=180°;故答案为:∠A=∠C=90°,∠ABC+∠ADC=180°;(2)成立,理由如下:连接AC、BD,∵∠DAC=∠CBD,∠ACD=∠ABD,∴∠DAC+∠ACD=∠DBC+∠ABD=∠ABC,∵∠DAC+∠ACD+∠ADC=180°,∴∠ABC+∠ADC=180°;同理,∠BAD+∠BCD=180°;【深入探究】(3)AD+BC=AB+CD,理由如下:连接AI、BI、CI、DI,∵圆I是四边形ABCD的内切圆,∴AG=AE,DE=DH,CH=CF,BF=BG,∴AD+BC=AE+ED+BF+CF=AG+DH+BG+CH=AB+CD,即AD+BC=AB+CD,故答案为:AD+BC=AB+CD;(4)EF⊥GH,理由如下:连接EH、IH、IG、IF、GF,∵四边形ABCD是圆O的内接四边形,∴∠B+∠D=180°,∵BG⊥IG,IF⊥BF,∴∠BGI=∠IFB=90°,∴∠B+∠GIF=180°,∴∠GIF=∠D,∵GI=IF,∴∠GFI=90°﹣∠GIF,∵ED=DH,∴∠DEH=90°﹣∠D,∴∠GFI=∠DEH,∵=,∴∠GFE=∠GHE,∴∠GHE=∠GFI+∠IFE,∵IF=IE,∴∠IFE=∠IEF,∴∠FEH+∠EHG=∠FEH+∠IEF+∠DEH=∠EID=90°,∴EF⊥GH;(5)连接BD,∵∠C=90°,∴∠A=90°,∵ABCD是圆O的内接圆,∴BD是圆O的直径,连接IF、IH,∵I是四边形ABCD的内切圆圆心,∴∠ADI=∠IDH,∠ABI=∠FBI,∵IH⊥CD,IF⊥BC,∴∠BIF=90°﹣∠IBF,∠DIH=90°﹣∠IDH,∴∠BIF+∠DIH=180°﹣(∠IBF+∠IDH)=180°﹣(∠ADC+∠ABC),∵∠ABC+∠ADC=180°,∴∠BIF+∠DIH=90°,∵IF⊥FC,IH⊥CD,∠C=90°,IH=IF,∴四边形IHCF是正方形,∴∠HIF=90°,∴I点在BD上,=3×2=6,∵BC=3,CD=2,∴S四边形ABCD∵∠DIH+∠IDH=90°,∠IBF+∠IDH=90°,∴∠DIH=∠IBF,∵∠IHD=∠IFB=90°,∴△DHI∽△IFB,∴=,即=,解得IH=,∴S⊙I=π,∴阴影部分的面积=6﹣π.10.(2022•遵义)综合与实践“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.提出问题:如图1,在线段AC同侧有两点B,D,连接AD,AB,BC,CD,如果∠B=∠D,那么A,B,C,D四点在同一个圆上.探究展示:如图2,作经过点A,C,D的⊙O,在劣弧AC上取一点E(不与A,C重合),连接AE,CE,则∠AEC+∠D=180°(依据1)∵∠B=∠D∴∠AEC+∠B=180°∴点A,B,C,E四点在同一个圆上(对角互补的四边形四个顶点共圆)∴点B,D在点A,C,E所确定的⊙O上(依据2)∴点A,B,C,D四点在同一个圆上反思归纳:(1)上述探究过程中的“依据1”、“依据2”分别是指什么?依据1:;依据2:.(2)如图3,在四边形ABCD中,∠1=∠2,∠3=45°,则∠4的度数为.拓展探究:(3)如图4,已知△ABC是等腰三角形,AB=AC,点D在BC上(不与BC的中点重合),连接AD.作点C关于AD的对称点E,连接EB并延长交AD的延长线于F,连接AE,DE.①求证:A,D,B,E四点共圆;②若AB=2,AD•AF的值是否会发生变化,若不变化,求出其值;若变化,请说明理由.【解答】(1)解:依据1:圆内接四边形对角互补;依据2:过不在同一直线上的三个点有且只有一个圆,故答案为:圆内接四边形对角互补;过不在同一直线上的三个点有且只有一个圆;(2)解:∵∠1=∠2,∴点A,B,C,D四点在同一个圆上,∴∠3=∠4,∵∠3=45°,∴∠4=45°,故答案为:45°;(3)①证明:∵AB=AC,∴∠ABC=∠ACB,∵点E与点C关于AD的对称,∴AE=AC,DE=DC,∴∠AEC=∠ACE,∠DEC=∠DCE,∴∠AED=∠ACB,∴∠AED=∠ABC,∴A,D,B,E四点共圆;②解:AD•AF的值不会发生变化,理由如下:如图4,连接CF,∵点E与点C关于AD的对称,∴FE=FC,∴∠FEC=∠FCE,∴∠FED=∠FCD,∵A,D,B,E四点共圆,∴∠FED=∠BAF,∴∠BAF=∠FCD,∴A,B,F,C四点共圆,∴∠AFB=∠ACB=∠ABC,∵∠BAD=∠FAB,∴△ABD∽△AFB,∴=,∴AD•AF=AB2=8.11.如图,在△ABC中,以AB为直径作⊙O交AC于点D,交BC于点E,CE=BE,过点E作EF⊥AC于点F,FE的延长线交AB的延长线于点G,连接DE.(1)求证:FG是⊙O的切线;(2)求证:EG2=AG•BG;(3)若BG=1,EG=,求sin∠CDE的值.【解答】(1)证明:连接OE,∵CE=BE,OA=BO,∴OE是△ABC的中位线,∴OE∥AC,∵EF⊥AC,∴OE⊥EF,∵E点在圆O上,∴FG是⊙O的切线;(2)证明:∵OE⊥GF,∴∠OEG=90°,∴OG2=OE2+EG2,∵EG2=OG2﹣OE2=(OG+OE)(OG﹣OE),∵EO=BO=OA,∴EG2=(OG+OA)(OG﹣OB)=AG•BG;(3)解:连接AE,过E点作EM⊥AB交于点M,∵EG2=AG•BG,BG=1,EG=,∴AG=2,∴AB=1,∵AB是直径,∴∠AEB=90°,∵∠OEG=90°,∴∠AEO=∠BEB,∵AO=OE,∴∠EAO=∠OEA,∴∠BEG=∠EAO,∴△AEG∽△EBG,∴==,设EB=x,则AE=x,在Rt△ABE中,1=x2+2x2,解得x=,∴BE=,AE=,∵AE•BE=AB•EM,∴EM=,∵A、B、E、D四点共圆,∴∠CDE=∠ABE,∴sin∠CDE=sin∠EBM===.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省靖江高级中学2009届高三3月月考语文试卷2009、3一、语言文字运用(15分)1.下列各组词语中加点的字,读音都不相同的一组是(3分)A.择.菜/择.业炮.烙/炮.制模.型/模.棱两可B.窥伺./伺.候扎.堆/包扎.契.合/锲.而不舍C.提挈./堆砌.玄.理/船舷.朔.风/横槊.赋诗D.眩.晕/炫.耀庇.佑/毗.邻对峙./有恃.无恐2.下列各句中,加点的成语使用恰当的一句是(3分)A.在繁忙而紧张的高三学习中,父母见微知著....的关怀,老师循循善诱的教导,使同学们倍受感动和鼓舞。
B..东风城里的人,对外来人员的所有问题都微笑着不予回答,但看得出来,这里的居民安.之若素...,或许神七发射本就是他们平静生活的一部分。
C.有消息称,国际恐怖组织在遭到国际社会强烈谴责和连续打击后,正准备重整旗鼓....,进一步在世界制造更多的恐怖活动。
D.国际社会应加强协作,决不能让被劫的先进武器装备落到恐怖分子手中,否则,恐怖分子将如虎添翼....,很难对付。
3.我国拟于2009年1月1日实行燃油税费改革。
阅读下列“燃油税费改革前后部分轿车开支对照表”,概括说明燃油税费改革前后轿车开支变化的情况。
(5分)答:_▲___▲__4.某中学开展校园广播“温馨提示语”征集活动,在一些主要时段用富有学生特色的话语,配上动听的音乐播放,让校园时时充满关爱和温情。
请从起床、晨读、午餐、放学三个时段中任选两个,各拟一段温馨提示语。
注意简明连贯,亲切生动,符合时段特点和校园环境氛围。
(4分)(1)_▲__▲(2)_▲__▲二、文言文阅读(19分)阅读下面文言文,完成5——8题。
阅读下面的文字,完成5~8题。
景延广,字航川,陕州人也。
父建善射,尝教延广曰:“射不入铁,不如不发。
”由是延广以挽强见称。
事梁邵王友诲,友诲谋反被幽,延广亡去。
后从王彦章战中都,彦章败,延广身被.数创,仅以身免。
明宗时,朱守殷以汴州反,晋高祖为六军副使,主诛从守殷反者。
延广为汴州军校当诛。
高祖惜其才,阴纵之使亡,后录以为客将。
高祖即位,以为侍卫步军都指挥使,领果州团练使,从领宁江军节度使。
天福四年,出镇义成,又徙保义,复召为侍卫马步军都虞侯,徙镇河阳三城,迁马步军都指挥使,领天平。
高祖崩,出帝立,延广有力。
颇伐其功。
初,出帝立,晋大臣议告契丹,致表称臣,延广独不肯,但致书称孙而已,大臣皆知其不可而不能夺.。
契丹果怒,数以责晋,延广谓契丹使者乔莹曰:“先皇帝北朝所立,今卫子中国自册,可以为孙,而不可为臣。
且晋有横磨大剑十万口,翁要战则来,他日不禁孙子,取笑天下。
”莹知其言必起两国之争,惧后无以取信也,因请载.于纸,以备遗忘。
延广敕吏具载以授莹,莹藏其书衣领中以归,具以延广语告契丹,契丹益怒。
明年春,契丹入寇,延广从出帝北征为御营使,相拒澶、魏之间。
先锋石公霸遇虏于戚城,高行周、符彦卿兵少不能救,驰骑促延广益兵,延广按兵不动。
三将被围数重,帝自御军救之,三将得出,皆泣诉。
然延广方握亲兵,恃功恣横,诸将皆由其节度,帝亦不能制也。
契丹尝呼晋人日:“景延广唤我来,何不速战?”是时。
诸将皆力战,而延广未尝见敌。
契丹已去。
延广独闭壁不敢出。
自延广一言而契丹与晋交恶,凡号令征伐一出延广,晋大臣皆不得与,故契丹凡所书檄,未尝不以延广为言。
契丹去,出帝还京师,乃出延广为河南尹,留守西京。
延广居洛阳,郁郁不得志。
见晋日削,度必不能支.契丹,乃为长夜之饮,大治第宅,园置伎乐,惟意所为。
后帝亦追悔,遣供奉官张晖奉表称臣以求和,德光报曰:“使桑维翰、景延广来,而割镇、定与我,乃可和。
”晋知其不可,乃止。
契丹至中渡,延广屯河阳,闻杜重威降。
乃还。
德光犯京师,行至相州,遣骑兵数千杂晋军渡河趋洛,以取延广,戒曰:“延广南奔吴,西走蜀,必追而取之。
”而延广顾虑其家,未能引决.虏骑奄至,乃与从事阎丕驰骑见德光于封丘,并丕见锁。
延广曰:“丕,臣从事也,以职相随,何罪而见锁?”丕乃得释。
德光责延广曰:”南北失欢,皆因尔也。
”召乔莹质其前言,延广初不服,莹从衣领中出所藏书,延广乃服。
遂叱而锁之。
将送之北行,至陈桥,止民家。
夜分,延广伺守者殆。
引手扼吭而死,时年五十六。
(节选自欧阳修《新五代史》卷二十九)5.对下列句子中加点的词的解释.不正确的一项是(3分)A.延广身被.数创被:蒙受,遭受B.大臣皆知其不可而不能夺.夺:争夺,抢夺C.因请载.于纸载:记载,记录D.度必不能支.契丹支:支撑,对付6.以下各组句子中,分别表明景延广“有勇”和“无谋”的一组是(3分)A.由是延广以挽强见称。
友诲谋反被幽,延广亡去。
B.延广身被数创。
延广按兵不动。
C.翁要战则来。
延广敕吏具载以授莹。
D.以职相随,何罪而见锁。
延广伺守者殆,引手扼吭而死。
7.下列对原文有关内容的分析和概括,不正确...的一项是(3分)A.景延广在父亲的指导下练就一身武艺,辗转数主,终于遇到了赏识他的晋高祖,从此身兼数职,大权在握,渐渐骄狂起来。
B.新皇帝继位时许多大臣认为应该像晋高祖石敬瑭在世时那样向契丹称臣,景延广却极力反对,觉得称孙就可以,表现了景延广的民族气节。
C.耶律德光对景延广说:“南北失欢,皆因尔也。
”这话其实是一个幌子,真正的原因是契丹对后晋一直蠢蠢欲动,而景延广“可以为孙,而不可为臣”的话只是引发战争的一个导火索而已。
D.景延广活着的时候没有完全打败契丹,也曾消沉过,但最后的果断自杀也算对得起他那句“晋有横磨大剑十万口”的话。
8.将文言文阅读材料中画线的句子翻译成现代汉语。
(10分)(1)具以延广语告契丹,契丹益怒。
(4分)译文:_▲___▲__(2)诸将皆由其节度,帝亦不能制也。
(3分)译文:_▲___▲__(3)以职相随,何罪而见锁? (3分)译文:_▲___▲__三、古诗鉴赏(10分)9.阅读下面这首宋诗,然后回答问题。
泊公安县陆游秦关蜀道何辽哉!公安渡头今始回。
无穷江水与天接,不断海风吹月来。
船窗帘卷萤火闹,沙渚露下萍花开。
少年许国忽衰老,心折舵楼长笛哀。
[注]①陆游经公安入蜀已辗转八年,今回京“廷对”停泊公安。
(1)首联中“辽”和“回”互相照应,请简要说明这两个字在表情达意上的作用。
(3分)____▲____________________▲______________(2)颔联与颈联的景物层次分明,互为一体,请从写景角度分析其表达特点及作用。
(4分)____▲___________________▲______________(3)尾联表达了作者怎样的情感?(3分)____▲____________________▲______________四、名句名篇默写(8分)10.补写下列名句名篇中的空缺部分。
(8分)•(1)▲,不如登高之博见也。
(荀子《劝学》)(2)___________▲____,蓝田日暖玉生烟。
(李商隐《锦瑟》)•(3)西当太白有鸟道,________▲ _________,地崩山摧壮士死, ___▲___________ 。
(李白《蜀道难》)•(4)香远益清,亭亭净植,________▲_____(周敦颐《爱莲说》)•(5)无丝竹之乱耳, __▲(刘禹锡《陋室铭》)• (6)曾子曰:“士不可以不弘毅, __▲。
仁以为己任,不亦重乎? ▲,不亦远乎?”(《论语·泰伯第八》)五、现代文阅读必考题:文学类文本阅读。
(23分)阅读下面的作品,完成11~14题。
回望雁门王海英①初见雁门关,是一次不期而遇,那是一个深秋的上午。
②(甲)秋风瑟瑟荒草萋萋,深秋的勾注山,一派滚滚无边的黄褐,远远近近薄薄的初雪花花点点。
关城渐近,小北门上“雁门关”三个大字迎风而立,木镌“三边冲要无双地,九塞尊崇第一关”的楹联,静静地偎依在门两侧。
空空荡荡的门洞内是光滑安静的青石板路,路上两道深深的车辙分外醒目。
③登上关楼,顿觉山风强劲。
放眼望去,一节节残缺的长城,像一根根苍老的肋骨,虽历尽千年风霜,依然兀自挺立着,不卑不亢、处乱不惊地勾画着山势的雄浑险峻。
没有了滚滚狼烟的烽火台,如一个个古埙在风中呜呜地吹响。
关楼下曾经鼓角争鸣的关城早已荡然无存。
这一切留给今人的除了空灵的凭吊和怀古的幽思还能有什么呢?④告别关楼,回望雁门,此时的雁门关更像一位慈祥的老人,淡淡的秋阳下,它谦恭地退于历史一隅,聆听着来来往往的脚步声,用洞明世事的目光穿越岁月的迷雾。
这让我充满了莫名的感动,我感到我与雁门关之间还有许多未尽之意。
⑤再一次拜访雁门关,是次年的初秋。
一路行来,导游把雁门关的历史、文化都讲了个遍,尤其强调了它的军事地位。
翻看史书,雁门关几乎就是一部战争史,从先秦开始,这里一直是兵家必争之地,大大小小的战争就发生过200多次。
史载,赵国名将李牧大破匈奴十余万骑;唐初李世民全歼突厥二十万众……连汉军,亦是“十万汉军零落尽”,这是怎样的一种悲壮场面啊。
唐朝诗人常建有句写雁门关的诗:“城下有寡妻,哀哀哭枯骨。
”古往今来,战争给民众带来的只能是流离失所、家破人亡和心灵创伤。
导游的讲解让我有了一种难以言说的痛,我似乎看见,前边有千万个灵魂,他们在秋天明媚的阳光里冷冷地注视着我们,我们对雁门关的热情,焐不暖他们千年的冰凉记忆。
⑥在李牧祠,导游还历数了李牧之后的李广、薛仁贵、杨业等有着赫赫战功的守关名将,他说雁门关是刚烈的英雄的。
是啊,古往今来,雁门关演绎了多少波澜壮阔的历史画卷,造就了多少名垂千古的英雄人物,但这刚烈和英雄的背后有多少悲伤的眼泪和惨痛的教训啊,这是千百年来雁门关无法言说的心痛。
⑦第二次告别雁门,耳边战争的脚步声似乎刚刚远去,但我们仍能感受到它那似怨似艾的苍凉之音,那是一代代封建王朝覆灭的绝响。
第二次回望雁门,我向雁门深深作揖,壮美与惨烈已然远逝,我们用真诚打磨它的锈蚀,总能闻到岁月的芬芳。
⑧又见雁门关,是一个盛夏的下午。
(乙)轻风吹拂,小草欢快地跳动着,阳光慢慢扫过土黄色的城门,抚摩着沧桑剥露出的深深裂纹。
重新走进阅尽沧桑的城门,又一次与那两道车辙相遇。
⑨依然光滑宁静,依然淳古苍茫,没有忧虑,只有纯正的安详。
那一刻,我知道它要向我倾诉什么。
我久久地凝视,久久地倾听。
⑩终于,耳边传来了环佩叮当声和琵琶呤唱声,是她——美丽的汉家女王昭君走过来了。
公元前33年一个云淡风轻的日子,窈窕俊美的昭君,毅然出关走向大漠。
碾着昭君的车辙,先后十几位中原公主从雁门出塞,使辽阔荒凉的塞北大漠一次次唱响民族融合之曲。
⑾接着进入眼帘的是满栽着各色货物的车队和马队,他们从雁门关出出进进,使中原和北方少数民族之间的物资、技术得以流通,雁门古道成为了”丝绸之路”衰落后第一条陆上国际贸易商路。
⑿站在两道深深的车辙之间,我感觉到了生命的充实和浑厚。
雁门古道用有限的时空实现了对无限生命境界的苦苦追寻和辉煌展现。
