方波分解为多次正弦波之和
方波信号的分解与合成

方波信号的分解与合成方波信号是一种在电子技术中常见的信号类型,它被广泛应用于数字电路、通信系统和控制系统中。
方波信号被描述为周期性的,其波形为高电平和低电平两种状态的交替出现。
本文将介绍方波信号的分解与合成。
一、方波信号的分解方波信号可以看作是由多个正弦波信号组成的。
根据傅里叶级数定理,任何一个周期信号都可以表示成一系列正弦波的叠加。
因此,我们可以将方波信号分解成一系列正弦波信号的叠加。
具体来说,我们可以通过傅里叶级数公式将方波信号分解为无限个正弦波信号的叠加:f(t) = (4/π) * [sin(ωt) + (1/3)sin(3ωt) + (1/5)sin(5ωt) + ...]其中,ω是正弦波的角频率,由周期T计算得到:ω = 2π/T。
式中的系数表示了每个正弦波信号的幅值。
显然,随着正弦波频率的增加,其幅值逐渐减小,因此只需要保留前几项即可近似表示方波信号。
二、方波信号的合成与分解相反,我们也可以将多个正弦波信号合成成一个方波信号。
这可以通过将多个正弦波信号的叠加,利用傅里叶变换得到一个方波信号的过程实现。
具体来说,我们可以将多个正弦波信号的幅值和相位进行适当的调整,使它们的叠加形成一个方波信号。
这个过程可以通过傅里叶变换实现,傅里叶变换将多个正弦波信号的叠加转换为频域上的一个复杂函数,然后再通过反向变换回到时域上得到方波信号。
三、应用方波信号的分解和合成在许多领域中都有广泛的应用。
在数字电路中,方波信号可以用于实现各种逻辑门和计数器。
在通信系统中,方波信号可以用于数字调制和解调。
在控制系统中,方波信号可以用于实现各种控制算法和控制器。
总结:本文介绍了方波信号的分解和合成。
方波信号可以看作是由多个正弦波信号组成的,可以通过傅里叶级数定理进行分解。
同时,我们也可以将多个正弦波信号合成成一个方波信号,利用傅里叶变换实现。
方波信号在数字电路、通信系统和控制系统中有广泛的应用。
电路、信号与系统(2)实验指导书

描述线性时不变离散系统的差分方程为
编写求解上述方程的通用程序。
[建模]
将方程变形可得(用MATLAB语言表示)
a(1)*y(n)= b(1)*u(n)+…+ b(nb)*u(n-nb+1)- a(2)*y(n-1)-…- a(na)*y(n-na+1)
令us== [u(n),…, u(n-nb+1)]; ys=[y(n-1),…, y(n-na+1)]
x(n)={2,1,-1,3,1,4,3,7}(其中加下划线的元素为第0个采样点)在MATLAB中表示为:
n=[-3,-2,-1,0,1,2,3,4]; x=[2,1,-1,3,1,4,3,7];
当不需要采样位置信息或这个信息是多余的时候,可以只用x向量来表示。
(一)离散信号的MATLAB表述
[问题]
实验一连续时间信号与系统分析
一、实验目的
1、了解连续时间信号的特点;
2、掌握连续时间信号的MATLAB描述;
3、掌握连续LTI系统单位冲激响应的求解方法;
4、掌握连续LTI系统的零状态响应的求解方法。
二、实验内容
严格说来,只有用符号推理的方法才能分析连续系统,用数值方法是不能表示连续信号的,因为它给出的是各个样点的数据。只有当样本点取得很密时才可看成连续信号。所谓很密,是相对于信号变化的快慢而言的。以下均假定相对于采样点密度而言,信号变化足够慢。
elseif lu<lh nh=0; nu=lh-lu;
else nu=0; nh=0;
end
dt=0.1;
lt=lmax;
u=[zeros(1, lt), uls, zeros(1, nu), zeros(1, lt)];
方波信号合成与分解

方波信号合成与分解在信号处理领域中,方波信号是一种非常常见的信号类型。
它的特点是在一个周期内,信号的幅值会在两个固定的值之间来回变化。
方波信号的合成和分解是信号处理中的基本操作之一,本文将对这两个操作进行详细介绍。
一、方波信号的合成方波信号的合成是指将多个不同频率的正弦波信号叠加在一起,得到一个具有方波形状的信号。
这个过程可以用傅里叶级数展开来描述。
傅里叶级数是一种将周期信号分解成一系列正弦波的方法,它可以将一个周期为T的信号f(t)表示为以下形式的级数:f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt))其中,a0是信号的直流分量,an和bn是信号的交流分量,ω是角频率,n是正整数。
对于方波信号,它的傅里叶级数可以表示为:f(t) = (4/π) * Σ(sin((2n-1)ωt)/(2n-1))其中,ω是角频率,n是正整数。
这个式子的意思是,将一系列正弦波信号按照一定的权重相加,就可以得到一个方波信号。
这个权重是由sin((2n-1)ωt)/(2n-1)这个函数决定的,它的图像如下所示:图1:sin((2n-1)ωt)/(2n-1)的图像可以看到,当n越大时,这个函数的周期越短,振幅越小。
因此,只需要取前几项的和,就可以得到一个近似的方波信号。
二、方波信号的分解方波信号的分解是指将一个方波信号分解成多个不同频率的正弦波信号的和。
这个过程可以用傅里叶变换来描述。
傅里叶变换是一种将时域信号转换成频域信号的方法,它可以将一个信号f(t)表示为以下形式的积分:F(ω) = ∫f(t)*e^(-jωt)dt其中,F(ω)是信号在频域上的表示,e^(-jωt)是复指数函数,j是虚数单位。
对于方波信号,它的傅里叶变换可以表示为:F(ω) = (2/π) * Σ(1/n * sin(nω/2))这个式子的意思是,将一个方波信号在频域上表示为一系列正弦波信号的和,其中每个正弦波信号的频率是nω/2,振幅是1/n。
方波信号的傅里叶级数展开

方波信号的傅里叶级数展开方波信号是一种特殊的周期信号,在每个周期内信号值交替地取正弦波的最大值和最小值。
它可以用傅里叶级数展开来表示,下面我将详细介绍关于方波信号的傅里叶级数展开的相关内容。
傅里叶级数是一种将一个周期性函数分解为一系列正弦和余弦函数的无穷级数的表示方法。
对于一个周期为T的函数f(t),其傅里叶级数表示为:f(t) = a0/2 + Σ(an*cos(nωt) + bn*sin(nωt))其中,a0/2表示直流分量,an和bn分别表示正弦和余弦分量的系数,ω为角频率,等于2π/T。
对于方波信号,其周期为T,即一个周期内正弦波的最大值和最小值的持续时间。
方波信号可以表示为一个由无限多个正弦波组成的傅里叶级数。
在方波信号的傅里叶级数展开中,直流分量a0/2表示方波的平均值,等于正弦波最大值和最小值的平均值。
对于幅值为A,周期为T的方波信号,其直流分量a0/2等于A/2。
正弦和余弦分量的系数an和bn可以通过积分计算得到。
由于方波信号在一个周期内的正弦和余弦分量只有在0到T/2的时间段内有贡献,所以对an和bn的计算可以将积分区间限制在0到T/2。
根据傅里叶级数的定义,an和bn的计算公式为:an = (2/T) * ∫[0,T/2] (f(t)*cos(nωt) dt)bn = (2/T) * ∫[0,T/2] (f(t)*sin(nωt) dt)其中,f(t)为方波信号。
对于方波信号,可以将其正弦和余弦分量表示为:an = (2/T) * ∫[0,T/2] (A*cos(nωt) dt)= (2/T) * (A/nω) * [sin(nωt)] from 0 to T/2= (2/T) * (A/nω) * sin(nωT/2)bn = (2/T) * ∫[0,T/2] (A*sin(nωt) dt)= (2/T) * (-A/nω) * [cos(nωt)] from 0 to T/2= (2/T) * (-A/nω) * [cos(nωT/2) - 1]根据傅里叶级数展开的定义,方波信号可以表示为:f(t) = A/2 + Σ[(2A/(nπ)) * sin(nωt)] from n = 1 to ∞其中,A为方波信号的幅值,T为方波信号的周期。
信号与系统实验指导书(matlab软件仿真)

信号与系统实验指导书(MATLAB仿真)目录实验一MATLAB 基本应用 (2)实验二信号的时域表示 (7)实验三连续信号卷积 (11)实验四典型周期信号的频谱表示 (18)实验五傅立叶变换性质研究 (23)实验六离散信号分析 (26)实验七离散系统的Z域分析 (29)Matlab相关符号及函数说明 (37)实验一MATLAB 基本应用一、实验目的:学习MATLAB的基本用法,了解 MATLAB 的目录结构和基本功能以及MATLAB在信号与系统中的应用。
二、实验内容:例一已知x的取值范围,画出y=sin(x)的图型。
参考程序:x=0:0.05:4*pi;y=sin(x);plot(y)例二计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围,x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围,用subplot函数绘图。
参考程序:x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表示1、指数信号:指数信号Ae at在MATLAB中可用exp函数表示,其调用形式为:y=A*exp(a*t) (例取A=1,a=-0.4)参考程序:A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;注:grid on是一个函数,表示在画图的时候添加网格线。
方波信号的傅里叶级数

方波信号的傅里叶级数
方波信号是一种典型的周期信号,其波形为一段时间内等幅的正弦波,然后突然反向等幅的负正弦波,如此往复。
方波信号的傅里叶级数是
将其分解为一系列正弦波的和,是信号处理中重要的基础理论之一。
傅里叶级数的基本思想是将一个周期信号分解为一系列正弦波的和,
这些正弦波的频率是原始信号频率的整数倍。
对于方波信号,其周期
为T,可以表示为:
f(t) = A/2 + Σ(A/nπ)sin(nπt/T)
其中A为方波信号的幅值,n为正整数,表示正弦波的次数。
这个式
子可以理解为,方波信号可以分解为一系列正弦波的和,每个正弦波
的振幅和频率都不同,但都是原始信号频率的整数倍。
傅里叶级数的计算可以通过复杂的积分公式来完成,但是在实际应用中,通常使用离散傅里叶变换(DFT)来计算。
DFT是一种将时域信
号转换为频域信号的算法,可以将一个N点的离散信号转换为N个频率分量的复数值。
对于方波信号,可以通过DFT算法计算出其傅里叶
级数的系数,从而得到每个正弦波的振幅和频率。
傅里叶级数的应用非常广泛,例如在音频和图像处理中,可以使用傅
里叶级数将信号转换为频域信号,从而实现滤波、降噪、压缩等处理。
此外,在通信系统中,傅里叶级数也被广泛应用于信号调制和解调中。
总之,方波信号的傅里叶级数是将其分解为一系列正弦波的和,是信
号处理中重要的基础理论之一。
通过傅里叶级数的计算,可以得到每
个正弦波的振幅和频率,从而实现各种信号处理和调制解调等应用。
方波信号的分解与合成

实验四方波信号的分解与合成任何电信号都是由各种不同频率、幅度和初相的正弦波迭加而成的。
1822年法国数学家傅里叶在研究热传导理论时提出并证明了将周期函数展开为正弦级数的原理。
奠定了傅里叶级数的理论基础、揭示了周期信号的本质,即任何周期信号(正弦信号除外)都可以看作是由无数不同频率、不同幅度的正弦波信号叠加而成的,就像物质都是由分子或者原子构成一样。
周期信号的基本单元信号是正弦谐波信号。
一、实验目的1、通过对周期方波信号进行分解,验证周期信号可以展开成正弦无穷级数的基本原理,了解周期方波信号的组成原理。
2、测量各次谐波的频率与幅度,分析方波信号的频谱。
3、观察基波与不同谐波合成时的变化规律。
4、通过方波信号合成的实验,了解数字通信中利用窄带通信系统传输数字信号(方波信号)的本质原理。
二、实验原理1、一般周期信号的正弦傅里叶级数按照傅里叶级数原理,任何周期信号在满足狄利克雷条件时都可以展开成如式2-3-1所示的无穷级数oO QO A O0f(t)=」亠二a n cos( n'」t)亠二b n si n(n0A n cos (n '」t n)(2-4-1)2 n =1 n T 2 nT其中A n Cos(n f^ n)称为周期信号的n谐波分量,n次谐波的频率为周期信号频率的n倍,每一次的谐波的幅度随谐波次数的增加依次递减。
当n二0时的谐波分量为ao(直流分量)。
当n =1时的谐波分量为Acos『t「1)(一次谐波或基2波分量直流分量)。
2、一般周期信号的有限次谐波合成及其方均误差按照傅里叶级数的基本原理可知,周期信号的无穷级数展开中,各次谐波的频率按照基波信号的频率的整数倍依次递增,幅度值确随做谐波次数的增加依次递减,趋近于零。
因此,从信号能量分布的角度来讲,周期信号的能量主要分布在频率较低的有限次谐波分量上。
此原理在通信技术当中得到广泛应用,是通信技术的理论基础。
周期信号可以用其有限次谐波的合成来近似表示,当合成的谐波次数越多时,近似程度越高,可以用方均误差来定义这种近似程度,设傅里叶级数前有限项(N项)和为a NS N(t) - - v [a n cos n1.b n sinn'.4] ( 2-4-2)2 n吕用S N(t)近似表示f (t)所引起的误差函数为;N (t)二f (t) - S N(t) ( 2-4-3)1 T方均误差可以定义为E N二;N(t) N(t)dt ( 2-4-4) 通常,随着合成的谐波次数的增加,方均误差逐渐减小,可见合成波形与原波形之间的偏差越来越小。
方波的合成与分解

方波的合成与分解
方波的合成与分解
方波(Square Wave)是在数学中最基本的一种波形,可用来表示信号的频率和幅度,它是由一系列的正弦波组成的离散波形。
它可以用于声音的合成,也可以用于将复杂的信号分解成简单的信号,从而提取信号中的特征。
方波的合成是一个经典的信号处理问题,它的基本思想是通过一系列的正弦波和余弦波的叠加,来实现对方波的合成。
在这种方波合成的过程中,幅度的变化可以用正弦波和余弦波来表示,而频率的变化可以用不同的正弦波和余弦波的叠加来表示。
采用此方波合成的方式,可以产生任何复杂的波形,从而用来模拟复杂的信号。
方波的分解是指将一个复杂信号分解为若干个基本单元的过程,其中每个基本单元可以用一个方波来表示。
这是一种经典的信号处理问题,它可以用来提取信号中的特征。
方波的分解的基本思想是,通过拆分一个复杂信号,将其分解成一系列不同频率、不同幅度的方波信号,从而提取信号中的特征。
方波的合成与分解是在数学和信号处理方面最基本的概念,它们可以用来模拟复杂的信号,以及提取信号中的特征。
它们也可以应用到声音合成和信号分析中,为我们提供了一种有效的方法。
方波的合成与分解

方波的合成与分解方波是一种特殊的波形,它的波形呈现出一种矩形的形状,即在一个周期内,波形的上升和下降都是突然的,没有任何渐变的过程。
方波在电子工程、通信工程、信号处理等领域中都有着广泛的应用。
在本文中,我们将探讨方波的合成与分解。
一、方波的合成方波的合成是指将多个正弦波按照一定的比例相加,得到一个近似于方波的波形。
这个过程也被称为傅里叶级数展开。
傅里叶级数展开的基本思想是,任何一个周期函数都可以表示为一系列正弦函数的叠加。
具体来说,我们可以将一个周期为T的方波表示为以下形式:f(t) = A0 + Σ(Ak*cos(kωt) + Bk*sin(kωt))其中,A0是直流分量,Ak和Bk是傅里叶系数,k是正整数,ω是角频率,ω=2π/T。
傅里叶级数展开的过程可以通过傅里叶变换来实现。
傅里叶变换是一种将时域信号转换为频域信号的方法,它可以将一个周期函数分解为一系列正弦函数的叠加。
具体来说,我们可以将一个周期为T 的函数f(t)表示为以下形式:f(t) = Σ(c(k)*exp(jkωt))其中,c(k)是傅里叶系数,k是正整数,ω是角频率,ω=2π/T,j 是虚数单位。
通过傅里叶变换,我们可以得到一个函数的频谱,即它在不同频率下的振幅和相位。
对于一个方波来说,它的频谱是一个包含无限多个正弦函数的级数,每个正弦函数的频率是原始方波频率的整数倍。
在实际应用中,我们通常只需要考虑前几个傅里叶系数即可。
例如,对于一个周期为T的方波,我们可以只考虑前n个傅里叶系数,即:f(t) ≈ A0 + Σ(Ak*cos(kωt) + Bk*sin(kωt)) (k=1,2,...,n)这样,我们就可以用有限个正弦函数的叠加来近似表示一个方波了。
二、方波的分解方波的分解是指将一个方波分解为多个正弦波的叠加。
这个过程也被称为傅里叶级数分解。
傅里叶级数分解的基本思想是,一个周期函数可以表示为一系列正弦函数的叠加,而每个正弦函数的频率是原始函数频率的整数倍。
1将方波分解为多次正弦谐波之和
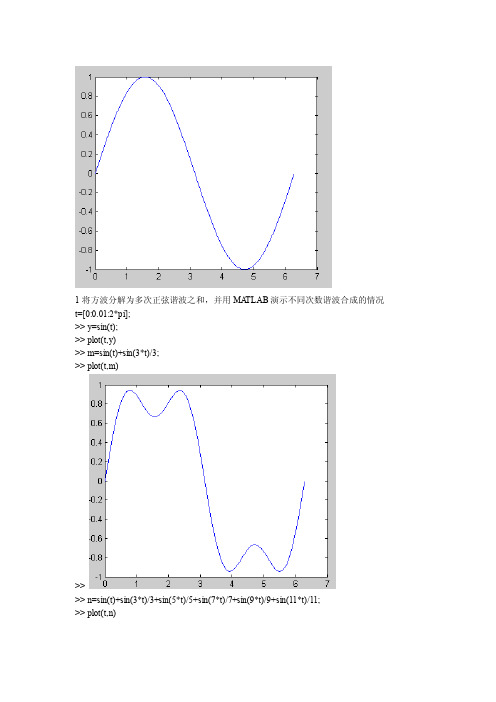
1将方波分解为多次正弦谐波之和,并用MA TLAB演示不同次数谐波合成的情况t=[0:0.01:2*pi];>> y=sin(t);>> plot(t,y)>> m=sin(t)+sin(3*t)/3;>> plot(t,m)>>>> n=sin(t)+sin(3*t)/3+sin(5*t)/5+sin(7*t)/7+sin(9*t)/9+sin(11*t)/11;>> plot(t,n)2.利用MA TLAB实现一些常用周期信号的频谱3.非周期信号(方波)的频谱分析;重点分析方波高度、宽度跟其频谱的关系。
,tf=10;N=input('取时间分隔的点数N=');dt=10/N;t=[1:N]*dt;f=[ones(1,N/2),zeros(1,N/2)];wf=input('需求的频谱的宽度wf=');nf=input('需求的频谱的点数nf=');w1=linspace(0,wf,nf);dw=wf/(nf-1);f1=f*exp(-j*t'*w1)*dt;w=[-fliplr(w1),w1(2:nf)];F=[fliplr(f1),f1(2:nf)];subplot(1,2,1),plot(t,f,'linewidth',1.5),gridaxis([-6,6,-6,6])subplot(1,2,2),plot(w,abs(F),'linewidth',1.5),gridaxis([-60,60,-6,6])4利用MA TLAB计算幅度为1,宽度为5s的矩形脉冲信号通过理想低通滤波器的响应,观察分析滤波器取不同截止频率时的结果。
w2f=input('理想低通滤波器的带宽(1/秒)=');n2=find((w>-w2f)&(w<w2f));w2=w(n2);y2=F(n2);figure(1),subplot(1,2,1),plot(w2,abs(y2),'linewidth',1.5),gridy3=y2*exp(j*w2'*t)/pi*dw;subplot(1,2,2),plot(t,f,t,y3,'linewidth',1.5),grid。
方波由正弦波叠加的公式

方波由正弦波叠加的公式
方波可以通过将多个正弦波叠加而成。
这种叠加的公式可以用于生
成方波信号,其中包含了许多不同频率的正弦波。
方波信号是一种矩形波形,其周期为T,可以表示为:
f(t) = (4/π) * [ sin(ωt) + (1/3) * sin(3ωt) + (1/5) * sin(5ωt) + ...]
其中,ω为2π/T,是正弦波的角频率。
方波信号中的每一个正弦波
分量的频率都是原始方波频率的倍数。
上述公式中,第一个正弦波项sin(ωt) 的系数为1,第二个正弦波项sin(3ωt) 的系数为1/3,第三个正弦波项sin(5ωt) 的系数为1/5,以此类推,每个正弦波项的系数为1/n,其中n为奇数。
通过这种方式,我们可以使用不同频率的正弦波叠加,有效地逼近
一个方波信号。
当我们添加足够多的正弦波项,并且系数按照递减的
比例来选择时,逼近效果会越来越好。
然而,这种叠加方式也有其局限性。
频率的选择受到采样率的限制,如果采样率不足够高,会造成信号失真。
另外,由于方波信号具有垂
直和水平跳变,因此在实际应用中,这种叠加公式也可能需要进行额
外的加工和处理,以满足特定需求。
总结而言,方波由正弦波叠加的公式可以通过将不同频率的正弦波
按一定比例相加而得。
这种方法可以用于逼近方波信号,但在实际应
用中需要考虑到采样率和信号处理等因素。
傅里叶变换 正弦波 分解 方波

傅里叶变换正弦波分解方波傅里叶变换是一种非常重要的数学工具,可以将一个信号分解成不同频率的正弦波的叠加。
而其中一种特殊的信号,方波,可以通过傅里叶变换来进行分解和理解。
正弦波是一个周期性的波形,具有不同的频率和振幅。
傅里叶变换可以将任意一个周期性的信号分解成多个正弦波。
这是因为正弦波具有唯一的频率,可以表示任意周期性信号的一个重要组成部分。
通过傅里叶变换,我们可以知道一个信号包含哪些频率的正弦波,以及每个正弦波的振幅。
方波是一种非常特殊的波形,它在每个周期内都有两个不同的振幅值。
在傅里叶变换中,方波可以看作是多个正弦波的叠加。
具体地说,一个方波信号可以拆解成一个基频为f的正弦波和其奇数倍频的正弦波的叠加。
这是因为方波信号的周期性导致其可以用不同频率的正弦波分解。
通过傅里叶变换分解方波信号,我们可以得到其包含的不同频率的正弦波,并且可以知道每个正弦波的振幅。
这种分解和分析的方法非常有意义。
首先,我们可以了解方波信号的频率组成成分,进一步理解信号的特性和波动规律。
其次,我们可以根据每个正弦波的振幅来合成原始的方波信号。
这种合成是通过将不同频率的正弦波按照其振幅进行叠加而实现的。
通过合成,我们可以得到与原始方波信号非常相似的近似信号。
这种信号合成的方法在通信、音频处理和图像处理等领域中非常实用。
在实际应用中,傅里叶变换和方波信号的分解是非常有指导意义的。
首先,当我们需要分析一个信号的频率特性时,可以通过傅里叶变换将其分解成不同频率的正弦波,从而获得有关信号频率特性的重要信息。
其次,当我们需要合成一个复杂的周期性信号时,可以根据傅里叶变换的结果,通过合成不同频率和振幅的正弦波来重建原始信号。
这种技术在信号处理、音频合成和图像合成等领域中得到了广泛应用。
综上所述,傅里叶变换是一个非常有用的工具,可以将一个信号拆解成不同频率的正弦波。
方波信号作为一种特殊的周期性信号,可以通过傅里叶变换来进行分解和合成。
通过这种分解和合成的方法,我们可以了解信号的频率特性,并且可以进行信号的重建和合成。
方波分解为多次正弦波之和

目录1 技术要求 (1)2 基本原理 (1)3 建立模型描述 (2)4 模块功能分析或源程序代码 (2)5 调试过程及结论 (4)5.1调试过程 (4)5.2 结论 (5)6 心得体会 (7)7参考文献 (8)方波分解为多次正弦波之和的设计1 技术要求已知某一周期性方波,用matlab仿真软件演示谐波合成情况,讨论参数对分解和合成波形的影响。
2 基本原理根据三角傅里叶级数:(1)(2)(3)对于任何一个周期为T的周期信号f(t),都可以求出它在上述各函数中的分量,从而将此函数在区间(t1,t1+T)内表示为(4)这就是函数f(t)在上述区间内的三角傅里叶级数表达式。
方波函数表达式:(5)先把这个函数展开为三角级数,为此就要求出分量系数a和b。
(6)(7)(8)因此,该非周期性方波在区间(0,T )内可以表示为(9)3 建立模型描述4 模块功能分析或源程序代码figure(1) ts=0.0001;t=0:ts:4*pi;%t 的取值范围为0到4*pi ,间隔0.0001取一个点 f=1/ts; N=length(t);y1=square(0.32*pi*t);%产生一个方波 plot(t,y1);title('产生一个方波');pause hold on figure(2)利用Matlab 画出方波波形 根据公式(9)令=1分别作出各次谐波的波形 分别作出不同次谐波叠加后的波形 将各波形图叠加作图 与方波比较 得出结论:方波可以分解为多次正弦波之和y2=4/pi*sin(t);%频率为1(f=1/2*pi)的正弦基波%plot(t,y2);title('正弦基波')subplot 322y3=4/pi*(sin(3*t)/3);%三次谐波plot(t,y3);title('三次谐波')subplot 323y4=4/pi*(sin(5*t)/5);%五次谐波plot(t,y4);title('五次谐波')subplot 324y5=4/pi*(sin(7*t)/7);%七次谐波plot(t,y5);title('七次谐波')subplot 325y6=4/pi*(sin(9*t)/9);%九次谐波plot(t,y6);title('九次谐波');pausefigure(3)subplot 221y7=4/pi*(sin(t)+sin(3*t)/3);%将前两次谐波叠加plot(t,y7);title('前两次谐波叠加')subplot 222y8=4/pi*(sin(t)+sin(3*t)/3+sin(5*t)/5);%将前三次谐波叠加plot(t,y8);title('前三次谐波叠加')y9=4/pi*(sin(t)+sin(3*t)/3+sin(5*t)/5+sin(7*t)/7+sin(9*t)/t);%将前五次谐波叠加plot(t,y9);title('前五次谐波叠加')%重新定义y,把各次波形数据存为一个三维数组y=zeros(10,max(size(t)));x=zeros(size(t));for k=1:2:15x=x+4/pi*(sin(k*t)/k);y((k+1)/2,:)=x;end%将各波形叠合绘出pause,figure(4),plot(t,y(1:9,:)),title('各波形叠合')5 调试过程及结论5.1调试过程在调试过程中,编写方波时由于当时没有注意方波扫描的精确度,将ts的数值选取的过于大了而导致方波的波形出现了大的失真,经过反复几次的调试后终于得出了一个比较理想的方波图形。
实验一 方波分解为多次正弦波之和的设计

实验一 方波分解为多次正弦波之和的设计一、实验目的1、了解信号分解与正交函数集;2、了解三角函数的正交性;3、了解基波与谐波的概念与关系;二、实验原理1、信号分解与正交函数集信号通常以时间函数表示,所以信号的分量及其分解指的就是函数的分量及其分解。
可利用与矢量分解相类比的方法来来研究如何将一信号分解为其分量。
与矢量用另一矢量上的分量表示原矢量类似。
在一定的时间区间()12,t t 内,若用函数2()f t 中的122()c f t 来近似的表示原函数1()f t ,将存在一误差函数()t ε∆,且有:1122()()t f c f t ε∆=- (1)在矢量近似中最佳系数选择的依据,是使得误差矢量的长度的平方最小;而12c 的选择,则是要求使误差函数的方均值最小。
误差函数的方均值为:222121()1()()t t t t t dt t εε∆∆=-⎰ (2) 此值最小时有:2221212211()()()t t c f t f t dt f t dt t t =⎰⎰ (3) 系数12c 是在最小方均误差的意义上代表二函数1()f t 、2()f t 的相关联的程度的度量。
当120c =时,由式(3)可知,此时有:2121()()0t f t f t dt t =⎰ (4)如果满足这一条件,则称1()f t 与2()f t 在区间12(,)t t 内正交。
此时1()f t 与2()f t 就构成一个正交函数集。
1()f t 与2()f t 两函数正交时,1()f t 在2()f t 中的分量122()c f t 为零。
一个函数可以在另一个函数中具有分量,则和矢量的情况类似,可以将一代表信号的函数表示为该函数在一正交函数集中的分量的加权和。
在区间12(,)t t 内互相正交的n 个函数123()()()()n g t g t g t g t 、、、...、组成一个n 维的正交信号空间。
此函数集中的函数之间,在区间12(,)t t 内具有如下关系:212()tm m t g t dt k =⎰ (5) 21()()0t l m t g t g t dt l m =≠⎰ (6) 其中m k 为一常数。
方波的基波分量

方波的基波分量方波是一种矩形波形,可以用一系列的正弦波相加的傅里叶级数表示。
在这个傅里叶级数中,有一个特殊的频率,称为方波的基波分量。
这个基波分量具有非常重要的物理意义,因为它描述了方波中最重要的振动。
下面我们将对方波的基波分量进行详细的介绍。
步骤一:了解方波的基本特性方波是一种以矩形波形为基础的波形。
它的周期是T,它的频率是f=1/T。
通常情况下,我们用以下公式来表示一个周期为T的方波:f(t) = a, -T/2 <= t < 0= b, 0 <= t < T/2其中a和b是方波的两个不同的振幅。
在理论上,我们可以将方波中的任何一个周期都表示为一系列正弦波的加和。
事实上,这就是傅里叶级数的定义。
步骤二:理解傅里叶级数的概念傅里叶级数是一种将周期函数分解为无限个谐波的方法。
在这个级数中,每个谐波都有一个特定的频率,同时还有一个对应的振幅。
在数学上,傅里叶级数可以表示为以下形式:f(t) = a/2 + Σ(cn*cos(2πnft) + dn*sin(2πnft))其中,a/2是常数项,cn和dn是分别对应着正弦波和余弦波的系数,n是一个整数,f是方波的频率。
步骤三:计算方波的基波分量在方波的傅里叶级数中,最重要的分量是基波分量。
基波分量就是代表着方波最基本的振动模式的分量,它的频率就是方波的频率f。
我们可以用以下公式来计算方波的基波分量:cn = (4/π)*sin(πn/2), n=1, 2, 3,...dn = 0, n=1, 2, 3,...其中,cn表示正弦波的系数,dn表示余弦波的系数,n表示谐波的顺序。
可以看出,基波分量的系数cn只有在n是奇数时才存在,而且其系数随着n的增大而迅速减小。
这反映了基波分量在整个谐波级数中占有非常重要的地位。
步骤四:应用基波分量方波的基波分量在实际应用中发挥着重要的作用。
例如,在音频系统中,声波的振动就可以通过一系列的基波分量来表示。
方波变正弦波原理

方波,就是由一定频率的正弦波经过逐级函数逼近变换得到的信号波形。
方波包含了无限多个正弦波成分,而正弦波是最基本的信号波形之一。
本文将介绍方波变正弦波的原理。
第一段:方波的定义和特点方波由一连串的正弦波成分组成,每个成分周期相同,且幅值递减,直至趋近于零。
方波的特点是波形为等宽的矩形脉冲,光谱密集且频率响应快速。
但是方波包含的成分较多,因此在实用中很难直接使用。
第二段:方波变换的目的和原理方波变换的目的是通过逐层函数逼近,将方波变换成为更加简单的信号波形。
变换的原理是基于傅里叶级数的思想,即每个周期可以表示为一系列正弦波的叠加。
通过对频率、幅值、相位等参数的处理,将方波的成分转换为更容易处理的正弦波成分。
第三段:低通滤波器的作用方波变正弦波的过程中,利用了低通滤波器的作用,它可以消除较高频率的成分,并保留较低频率的成分。
低通滤波器的作用是在频率域中将高频截止,使得信号中的高频成分得到压制,从而实现了信号的降噪和谐波滤除。
第四段:正弦波的特点和应用正弦波是具有周期性和平滑变化的信号波形,它具有一致性、可恢复性、高灵敏性和完美的谐波特性。
正弦波在信号处理中有着广泛应用,例如在通信、功率电子、控制系统和音频处理等领域,都有正弦波的应用。
第五段:方波变正弦波的应用方波变正弦波是将复杂的波形转换成为简单的波形的过程,它可以被广泛应用于音频处理、图像处理、模拟信号处理、数字信号处理等领域。
通过方波变换,可以将信号的噪声、失真降至最小,从而提高信号的质量和可靠性。
总结:方波变正弦波原理是通过逐层逼近,将复杂的信号波形转化为简单的信号波形,其关键在于低通滤波器的作用,实现信号的降噪和谐波滤除。
正弦波作为一种最基本的信号波形,具有广泛的应用领域,而方波变正弦波也在信号处理中有着重要的应用。
实验五、方波信号合成和分解

实验五、方波信号合成和分解实验五、方波信号的合成与分解一、实验目的1、观测1KHz Vpp =3V 方波信号的频谱,并与其傅利叶级数各项的频率与系数作比较;2、观测基波和其谐波的合成。
二、实验原理任何确定性的电信号都可以表示为随时间变化的某种物理量,比如:电压)(t u 和电流)(t i 等。
主要表现在随着时间t 的变化,信号波形幅值的大小、持续时间的长短、变化速率的快慢、波动的速度及重复周期的大小等变化,信号的这一特性称为信号的时间特性。
信号还可以分解为一直流分量和许多不同频率的正弦分量之和。
主要表现在各频率正弦分量所占比重的大小不同,主要频率分量所占有的频率范围也不同等,信号的这一特性称为信号的频率特性。
无论是信号的时间特性,还是信号的频率特性,都包含了信号的全部信息量。
根据周期信号的富里叶级数展开式可知,任何非正弦周期信号,只要满足狄里赫利条件都可以分解为一直流分量和由基波及各次谐波(基波的整数倍)分量的叠加。
例如一个周期的方波信号)(t f 可以分解为++++=t t t t E t f 11117sin 715sin 513sin 31sin 4)(ωωωωπ 如图5-1(a)所示。
同样,由基波及各次谐波分量也可以叠加出来一个周期方波信号,如图5-1(b)所示。
至于叠加出来的信号与原信号的误差,则取决于富里叶级数的项数。
(a) 方波信号的分解 (b) 方波信号的合成图 5-1 方波信号的分解与合成分解方法是,将输出信号加到一个滤波器组,其中每一个单元滤波器中心频率等于信号的各次谐波频率,在滤波器输出端得到分开来的基频信号和各次谐波信号。
图5.1 1KHz带通滤波图5.2 3KHz带通滤波图5.3 5KHz带通滤波图5.4 7KHz带通滤波图5.5 9KHz带通滤波将所得到的基波和各次谐波分量送到一个加法器输入端进行重新合成,合成后的波形从加法器输出端得到。
图5.6 方波合成三、实验设备和元件:1.实验主板;2.方波信号合成与分解模块;3.跳线若干。
方波的傅里叶分解与合成
方波的傅里叶分解与合成【实验目的】1.用RLC 串联谐振方法将方波分解成基波和各次谐波,并测量它们的振幅与相位关系。
2.将一组振幅与相位可调正弦波由加法器合成方波。
3.了解傅里叶分析的物理含义和分析方法。
【实验仪器】FD-FLY-A 型傅里叶分解与合成,示波器,电阻箱,电容箱,电感。
【实验原理】1.数学基础任何具有周期为T 的波函数f(t)都可以表示为三角函数所构成的级数之和,即:∑∞=++=10)sin cos (21)(n n n t n b t n a a t f ωω其中:T 为周期,ω为角频率。
ω=Tπ2;第一项20a 为直流分量。
所谓周期性函数的傅里叶分解就是将周期性函数展开成直流分量、基波和所有n阶谐波的迭加。
如图1所示的方法可以写成:⎪⎩⎪⎨⎧<≤-<≤-=)02()20()(t TT t h ht f此方波为奇函数,它没有常数项。
数学上可以证明此方波可表示为:)7sin 715sin 513sin 31(sin 4)(ΛΛ++++=t t t t ht f ωωωωπ=∑∞=--1])12sin[()121(4n t n n hωπ同样,对于如图2所示的三角波也可以表示为:)434()44()21(24)(T t T Tt T T th t T h t f <≤<≤-⎪⎩⎪⎨⎧-= )7sin 715sin 513sin 31(sin 8)(2222ΛΛ+-+-=t t t t h t f ωωωωπ=∑∞=----1212)12sin()12(1)1(8n n t n n hωπ2.周期性波形傅里叶分解的选频电路我们用RLC 串联谐振电路作为选频电路,对方波或三角波进行频谱分解。
在示波器上显示这些被分解的波形,测量它们的相对振幅。
我们还可以用一参考正弦波与被分解出的波形构成李萨如图形,确定基波与各次谐波的初相位关系。
本仪器具有1KH z的方波和三角波供做傅里叶分解实验,方波和三角波的输出阻抗低,可以保证顺利地完成分解实验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录
1 技术要求 (1)
2 基本原理 (1)
3 建立模型描述 (2)
4 模块功能分析或源程序代码 (2)
5 调试过程及结论 (4)
5.1调试过程 (4)
5.2 结论 (5)
6 心得体会 (7)
7参考文献 (8)
方波分解为多次正弦波之和的设计
1 技术要求
已知某一周期性方波,用matlab仿真软件演示谐波合成情况,讨论参数对分解和合成波形的影响。
2 基本原理
根据三角傅里叶级数:
(1)
(2)
(3)对于任何一个周期为T的周期信号f(t),都可以求出它在上述各函数中的分量,从而将此函数在区间(t1,t1+T)表示为
(4)
这就是函数f(t)在上述区间的三角傅里叶级数表达式。
方波函数表达式:
(5)
先把这个函数展开为三角级数,为此就要求出分量系数a和b。
(6)(7)
(8)因此,该非周期性方波在区间(0,T)可以表示为
(9)
3 建立模型描述
4 模块功能分析或源程序代码
figure(1)
ts=0.0001;
t=0:ts:4*pi;%t的取值围为0到4*pi,间隔0.0001取一个点
f=1/ts;
N=length(t);
y1=square(0.32*pi*t);%产生一个方波
plot(t,y1);
title('产生一个方波');pause
利用Matlab画出方波波形
根据公式(9)令=1
分别作出各次谐波的波形
分别作出不同次谐波叠加后的波形
将各波形图叠加作图
与方波比较
得出结论:方波可以分解为多次正弦波之和
hold on
figure(2)
subplot 321
y2=4/pi*sin(t);%频率为1(f=1/2*pi)的正弦基波%
plot(t,y2);
title('正弦基波')
subplot 322
y3=4/pi*(sin(3*t)/3);%三次谐波
plot(t,y3);
title('三次谐波')
subplot 323
y4=4/pi*(sin(5*t)/5);%五次谐波
plot(t,y4);
title('五次谐波')
subplot 324
y5=4/pi*(sin(7*t)/7);%七次谐波
plot(t,y5);
title('七次谐波')
subplot 325
y6=4/pi*(sin(9*t)/9);%九次谐波
plot(t,y6);
title('九次谐波');pause
figure(3)
subplot 221
y7=4/pi*(sin(t)+sin(3*t)/3);%将前两次谐波叠加
plot(t,y7);
title('前两次谐波叠加')
subplot 222
y8=4/pi*(sin(t)+sin(3*t)/3+sin(5*t)/5);%将前三次谐波叠加
plot(t,y8);
title('前三次谐波叠加')
subplot 223
y9=4/pi*(sin(t)+sin(3*t)/3+sin(5*t)/5+sin(7*t)/7+sin(9*t)/t);%将前五次谐波叠加
plot(t,y9);
title('前五次谐波叠加')
%重新定义y,把各次波形数据存为一个三维数组
y=zeros(10,max(size(t)));x=zeros(size(t));
for k=1:2:15
x=x+4/pi*(sin(k*t)/k);y((k+1)/2,:)=x;
end
%将各波形叠合绘出
pause,figure(4),plot(t,y(1:9,:)),
title('各波形叠合')
5 调试过程及结论
5.1调试过程
在调试过程中,编写方波时由于当时没有注意方波扫描的精确度,将ts的数值选取的过于大了而导致方波的波形出现了大的失真,经过反复几次的调试后终于得出了一个比较理想的方波图形。
由于在设计之初是要将方波与后来要形成的多次正弦波叠加后的波形放到一起,所以对于方波周期的选取以及方波振幅的确定也尝试了好多次。
最终才将这两个数值确定下来。
本事课程设计的目的是要证明方波能够分解为多次正弦波之和,所以程序的设计目的在于体现分解的过程以及最后n次谐波叠加后所形成的波形是否为方波。
根据上述公式9得出的方波表达式,令=1后分别画出y=4/pi*sin(t)的正弦基波、y=4/pi*(sin(3*t)/3)的三次谐波、y=4/pi*(sin(5*t)/5)的五次谐波、y=4/pi*(sin(7*t)/7)的七次谐波以及y=4/pi*(sin(9*t)/9)的九次谐波,为了能够充分的
显示风波分解为多次正弦波之和的过程,又分别作出了前两、三、五次谐波叠加的波形。
最后为了能够完美的证明方波分解为多次正弦波之和,利用了一个for循环语句画出了经过前n次谐波叠加后的波形(其中令n=15),并且与之前程序最开始画出的方波波形相互叠加。
由于经过三角级数傅里叶分解得到的方波表达式是一个非周期性函数,故只有当无限次谐波叠加后才能形成正真的方波,所以本次的实验是存在一定的误差的,本想在程序中作出其误差的图形表示以及计算出不同次数的方波叠加形成的方波所造成的误差,但由于知识以及能力有限,经过多次尝试无果后放弃了计算误差这部分项目。
造成了一定的遗憾。
5.2 结论
经过此次的实验,充分的证明了方波能够分解为多次正弦波之和,叠加次数越多误差越小越接近方波真实的波形。
所得波形如下所示:
图5-1 方波波形
图5-2 各次谐波波形
图5-3 叠加后的波形
图5-4 前n次叠加后的波形
6 心得体会
通过此次的课程设计可以知道利用Matlab所得出的结果与利用理论知识通过计算得出的结果是一样的,方波,正弦波,以及正弦波叠加后的波形都能够利用程序编写出来的,并且通过利用Matlab所得出的波形能够很清晰的表达出各个波形的物理意义。
Matlab是一款非常强大非常实用的软件,利用Matlab我们不仅能够证明许多数学上的问题,而且许多我们通过理论知识所无法计算的问题都能够解决,比如说我们这次的课程设计,通过人工计算我们能够得出方波的公式,但是这个公式却是一个非周期性的,我们无法准确的算出方波的波形。
但是利用Matlab却是能够做到。
通过利用Matlab进行仿真,仅仅用一个循环语句就能够让我们的波形无限的接近方波的真实波形,而且我们还能利用Matlab 计算出不同次正弦波叠加后所产生的误差并且通过图形模式表示出来以及我们还可以通过建立一个三维坐标模型将方波分解为多次正弦波之和的趋势表示出来,使我们更加直观的了解方波是如何分解为多次正弦波之和的。
这次的课程设计让我真的很难忘,经过两个多星期的努力,终于顺利完成了课程设计。
开始做课程设计不知道从何入手,困难很多,经过查阅资料,和同学讨论,终于了解了许多。
在做课程设计的过程中,我学会了很多,最主要的是我对Matlab的运用更加熟练了,同时对信号这门课的知识又弄懂了不少,增加了对信号课程的学习兴趣。
课程设计是每个大学生必须面临的一项综合素质的考验,如果说在我们的学习阶段是一个知识的积累过程,那么现在的课程设计就是对过去所学的知识的综合应用,是对理论进行深化和重新认识的实践活动。
在这期间,我们有艰辛的付出,当然也有丰收的喜悦。
首先,学习能力和解决问题的信心都得到了提高。
通过这次课程设计,我不仅对理论有了更深一步的认识,还培养了自学能力和解决问题的能力,更重要的是,培养了克服困难的勇气和信心。
7参考文献
[1]吴大正.信号与线性系统分析(第四版).:高等教育.2010
[2]卫国.MATLAB程序设计教程(第二版).:中国水利水电.2010
[3]梁虹,梁洁,跃斌.信号与线性系统分析及MATLAB实现.:电子工业.2002
[4]利竹,王华.MATLAB 电子仿真与应用[M].:国防工业,2001.
[5]怀,高西全.MATLAB 及在电子信息课程中的应用[M].:电子工业,2003.。
