【新人教版七年级数学上册单元测试及答案】第4章单元测试及答案2
第四章《几何图形初步》单元测试卷(A)2022-2023学年人教版七年级数学上册(含答案)
人教版七年级数学上册第四章《几何图形初步》单元测试卷(A)一、单选题(本题共10小题,每小题5分,共50分)1.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是()A.B.C.D.2.点A、B、C三点在同一直线上,且线段AB=4cm,BC=2cm,若点M为AC的中点,那么线段BM的长为()A.1cm B.3cm C.1cm或3cm D.无法确定3.如果一个角是50°,那么它的余角的度数是()A.40°B.50°C.100°D.130°4.用一个平面去截一个正方体,截出截面不可能是()A.三角形B.五边形C.六边形D.七边形5.平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,若平面上不同的n个点最多可确定28条直线,则n的值是()A.6B.7C.8D.96.如图,将甲,乙两把尺子拼在一起,两端重合,如果甲尺经校定是直的,那么乙尺不是直的,判断依据是()A.两点之间直线最短B.经过一点有且只有一条直线C.经过两点有且只有一条直线D.线段可以向两个方向延长7.用直尺和圆规作∠HDG=∠AOB的过程,弧∠是()A.以D为圆心,以DN为半径画弧B.以D为圆心,以EF为半径画弧C.以M为圆心,以DN为半径画弧D.以M为圆心,以EF为半径画弧8.如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第二次将点A向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点A n,如果点A n与原点的距离不小于20,那么n的最小值是()A.12B.13C.14D.159.如图,已知A,B(B在A的左侧)是数轴上的两点,点A对应的数为4,且AB=6,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左运动,在点P的运动过程中,M,N始终为AP,BP的中点,设运动时间为t(t>0)秒,则下列结论中正确的有()∠B对应的数是2;∠点P到达点B时,t=3;∠BP=2时,t=2;∠在点P的运动过程中,线段MN的长度不变.A.∠∠∠B.∠∠∠C.∠∠D.∠∠10.已知A,B,C三点在同一条直线上,M,N分别为线段AB,BC的中点.且AB=80,BC=60,则MN的长为()A.10B.70C.10或70D.30或70二、填空题(本题共5小题,每小题5分,共25分)11.数轴上点P与原点距离为3,点Q与点P的距离为3,则点Q所表示的数为12.如图,P是直线a外一点,点A,B,C,D为直线a上的点PA=5,PB=4,PC=2,PD=7,根据所给数据写出点P到直线a的距离l的取值范围是。
人教版数学七年级上册《几何图形初步》单元综合检测卷(带答案)

人教版数学七年级上学期第四章单元测试考试时间:100分钟;总分:120分一、单选题(每小题3分,共30分)1.(2019·四川初一期中)有以下五种立体图形:①正方体;②三棱柱;③四棱柱;④长方体;⑤圆柱.其中有六个面的立体图形是( )A .4B .3C .2D .12.(2019·西安交通大学附属中学初一月考)用如图所示的图形,旋转一周所形成的几何体是( )A .B .C .D .3.(2019·河北初二期中)一副三角板按如图方式摆放,已知∠1=5∠2,则∠1的度数是( )A .15°B .18°C .72°D .75°4.(2019·山西初三)如图,点O 是直线AB 上的一点,AOC 40∠=,OM 平分BOC ∠,则BOM ∠等于( )A .60B .65C .70D .755.(2019·贵州省织金县第六中学初一期中)将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创“相对的字是( )A.文B.明C.城D.市6.(2019·福建聚龙外国语学校初二月考)下列说法正确的是( )A.延长线段AB和延长线段BA的含义相同B.射线AB的长度为12cmC.经过两点可以画一条直线,并且只能画一条直线D.延长直线AB7.(2019·济宁高新区第五中学初一期末)下面说法错误的是( )A.两点确定一条直线B.射线AB也可以写作射线BAC.等角的余角相等D.同角的补角相等8.(2019·广东正德中学初一月考)下列说法正确的有()①长方体、正方体都是棱柱;②圆锥和圆柱的底面都是圆;③若直棱柱的底面边长相等,则它的各个侧面的面积相等;④棱锥底面的边数与侧棱数相等;⑤直棱柱的上、下底面是形状、大小相同的多边形,侧面都是长方形.A.2个B.3个C.4个D.5个9.(2018·河北省保定市第十七中学初一期末)已知线段AB=6cm,线段BC=8cm,则线段AC 的长度为( ) A.14cm B.2cm C.14cm或2cm D.不能确定10.(2019·山东初一期中)如图,在正方形网格中,∠1+∠2+∠3=( )A.90°B.120°C.135°D.150°二、填空题(每小题4分,共24分)11.(2019·河北初一期中)如图,直线AB和CD相交于点O,OE是∠DOB的平分线,若∠AOC=76°,则∠EOB=_______.12.(2019·重庆市第一一0中学校初一期中)三条直线两两相交,它们的交点个数是________个。
人教版七年级上册数学《第四章几何图形初步》单元测试题(含解析)

人教版七年级上册数学《第四章几何图形初步》单元测试题(含解析)一.选择题(共10小题)1.如图所示的四种物体中,哪种物体最接近于圆柱()A.B.C.D.2.下列几何体的截面分别是()A.圆、平行四边形、三角形、圆B.圆、长方形、三角形、圆C.圆、长方形、长方形、三角形D.圆、长方形、三角形、三角形3.如图是我国南海地区图,图中的点分别代表三亚市,永兴岛,黄岩岛,渚碧礁,弹丸礁和曾母暗沙,该地区图上两个点之间距离最短的是()A.三亚﹣﹣永兴岛B.永兴岛﹣﹣黄岩岛C.黄岩岛﹣﹣弹丸礁D.渚碧礁﹣﹣曾母暗山4.如图,图中共有线段()第 1 页共31 页A.7条B.8条C.9条D.10条5.如图,C为线段AB上一点,D为线段BC的中点,AB=20,AD=14,则AC的长为()A.10B.8C.7D.66.如图,∠AOB是平角,∠AOC=50°,∠BOD=60°,OM平分∠BOD,ON平分∠AOC,则∠MON的度数是()A.135°B.155°C.125°D.145°7.将长方形纸片按如图所示的方式折叠,BC、BD为折痕.若∠ABC=25°,则∠DBE的度数为()A.50°B.65°C.45°D.60°8.将一块长为a米,宽为b米的矩形空地建成一个矩形花园,要求在花园中修两条入口宽均为x米的小道,其中一条小道两边分别经过矩形一组对角顶点,剩余的地方种植花草,现有从左至右三种设计方案如图所示,种植花草的面积分别为S1,S2和S3,则它们的大小关系为()第 2 页共31 页A.S3<S1<S2B.S1<S2<S3C.S2<S1<S3D.S1=S2=S39.下列七个图形中是正方体的平面展开图的有()A.1个B.2个C.3个D.4个10.如图是一个棱长为1的正方体的展开图,点A,B,C是展开后小正方形的顶点,连接AB,BC,则∠ABC的大小是()A.60°B.50°C.45°D.30°二.填空题(共8小题)11.下面的几何体中,属于柱体的有个.12.如图,是正方体的一个平面展开图,在这个正方体中,与“爱”字所在面相对的面上的汉字是第 3 页共31 页13.如果线段AB=10,点C、D在直线AB上,BC=6,D是AC的中点,则A、D 两点间的距离是.14.已知线段MN=16cm,点P为任意一点,那么线段MP与NP和的最小值是cm.15.如图,若∠3:∠2=2:5,且∠2﹣∠1=12°,∠3等于.16.如图,点B、O、D在同一直线上,且OB平分∠AOC,若∠COD=150°,则∠AOC的度数是.17.如图,一纸片沿直线AB折成的V字形图案,已知图中∠1=62°,则∠2的度数=.18.如图,A、O、B在一直线上,∠1=∠2,则与∠1互补的角是.若∠1=28°32′35″,则∠1的补角=.三.解答题(共7小题)19.太阳可以近似地看成球体,已知太阳的半经为6.96×108m,太阳的体积大约是多少?(球的体积的计算公式是V=πr3,π取3.14)第 4 页共31 页20.已知一个长方体的长为1cm,宽为1cm,高为2cm,请求出:(1)长方体有条棱,个面;(2)长方体所有棱长的和;(3)长方体的表面积.21.如图所示,若剪下来折叠能拼成一个正方体盒子,请你想象一下,能否在空格中填上适当的数,使相对的两个面上的数互为相反数?22.如图,点B、C把线段MN分成三部分,其比是MB:BC:CN=2:3:4,P 是MN的中点,且MN=18cm,求PC的长.23.如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.(1)若∠AOE=32°,求∠BOC的度数;(2)若OD是∠AOC的角平分线,求∠AOE的度数.24.以直线AB上点O为端点作射线OC,使∠BOC=60°,将直角△DOE的直角顶点放在点O处.(1)如图1,若直角△DOE的边OD放在射线OB上,则∠COE=;(2)如图2,将直角△DOE绕点O按逆时针方向转动,使得OE平分∠AOC,说第 5 页共31 页明OD所在射线是∠BOC的平分线;(3)如图3,将直角△DOE绕点O按逆时针方向转动,使得∠COD=∠AOE.求∠BOD的度数.25.探索性问题:已知A,B在数轴上分别表示m,n.(1)填表:(2)若A,B两点的距离为d,则d与m,n有何数量关系.(3)在数轴上整数点P到4和﹣5的距离之和为9,求出满足条件的所有这些整数的和.第 6 页共31 页2018年秋人教版七年级上册数学《第四章几何图形初步》单元测试题参考答案与试题解析一.选择题(共10小题)1.如图所示的四种物体中,哪种物体最接近于圆柱()A.B.C.D.【解答】解:最接近圆柱的是生日蛋糕.故选:A.2.下列几何体的截面分别是()A.圆、平行四边形、三角形、圆B.圆、长方形、三角形、圆C.圆、长方形、长方形、三角形D.圆、长方形、三角形、三角形【解答】解:当截面平行于圆柱底面截取圆柱时得到截面图形是圆,截面截取经过四个顶点的截面时可以截得长方形,当截面垂直圆锥的底面时,截面图形是三角形,当截面平行于圆锥的底面时,截面图形是圆.所以这几个几何体的截面分别是:圆、长方形、三角形、圆,故选:B.3.如图是我国南海地区图,图中的点分别代表三亚市,永兴岛,黄岩岛,渚碧礁,弹丸礁和曾母暗沙,该地区图上两个点之间距离最短的是()第7 页共31 页A.三亚﹣﹣永兴岛B.永兴岛﹣﹣黄岩岛C.黄岩岛﹣﹣弹丸礁D.渚碧礁﹣﹣曾母暗山【解答】解:由图可得,三亚﹣﹣永兴岛两个点之间距离最短,故选:A.4.如图,图中共有线段()A.7条B.8条C.9条D.10条【解答】解:线段由AD,AE,DE,AB,AC,BD,EC,BC,故选:B.5.如图,C为线段AB上一点,D为线段BC的中点,AB=20,AD=14,则AC的长为()A.10B.8C.7D.6【解答】解:∵AB=20,AD=14,∴BD=AB﹣AD=20﹣14=6,∵D为线段BC的中点,∴BC=2BD=12,∴AC=AB﹣BC=20﹣12=8.第8 页共31 页6.如图,∠AOB是平角,∠AOC=50°,∠BOD=60°,OM平分∠BOD,ON平分∠AOC,则∠MON的度数是()A.135°B.155°C.125°D.145°【解答】解:∵∠AOC+∠COD+∠BOD=180°,∴∠COD=180°﹣∠AOC﹣∠COD=70°,∵OM、ON分别是∠AOC、∠BOD的平分线,∴∠MOC=∠AOC=25°,∠DON=∠BOD=30°,∴∠MON=∠MOC+∠COD+∠DON=125°,故选:C.7.将长方形纸片按如图所示的方式折叠,BC、BD为折痕.若∠ABC=25°,则∠DBE的度数为()A.50°B.65°C.45°D.60°【解答】解:∵一张长方形纸片沿BC、BD折叠,∴∠ABC=∠A′BC,∠EBD=∠E′BD,而∠ABC+∠A′BC+∠EBD+∠E′BD=180°,∴∠A′BC+∠E′BD=180°×=90°,即∠ABC+∠DBE=90°,∵∠ABC=25°,∴∠DBE=65°.第9 页共31 页8.将一块长为a米,宽为b米的矩形空地建成一个矩形花园,要求在花园中修两条入口宽均为x米的小道,其中一条小道两边分别经过矩形一组对角顶点,剩余的地方种植花草,现有从左至右三种设计方案如图所示,种植花草的面积分别为S1,S2和S3,则它们的大小关系为()A.S3<S1<S2B.S1<S2<S3C.S2<S1<S3D.S1=S2=S3【解答】解:∵矩形的长为a米,宽为b米,小路的宽为x米,∴S1=ab﹣(a+b)x+S4;S2=ab﹣(a+b)x+S5;S3=ab﹣(a+b)x+S6.∵S4=x•x=x2,S5=x•sin60°•x•sin60°=x2,S6=x•sin60°•=x2,∴S2<S1<S3.故选:C.9.下列七个图形中是正方体的平面展开图的有()A.1个B.2个C.3个D.4个【解答】解:由题可得,是正方体的平面展开图的有:故选:B.第10 页共31 页10.如图是一个棱长为1的正方体的展开图,点A,B,C是展开后小正方形的顶点,连接AB,BC,则∠ABC的大小是()A.60°B.50°C.45°D.30°【解答】解:连接AC.根据勾股定理可以得到:AC=BC=,AB=,∵()2+()2=()2,即AC2+BC2=AB2,∴△ABC是等腰直角三角形.∴∠ABC=45°.故选:C.二.填空题(共8小题)11.下面的几何体中,属于柱体的有4个.【解答】解:柱体分为圆柱和棱柱,所以柱体有圆柱、正方体、六棱柱,三棱柱共4个.故答案为:4.12.如图,是正方体的一个平面展开图,在这个正方体中,与“爱”字所在面相对的面上的汉字是中【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,第11 页共31 页“我”与“城”是相对面,“北”与“三”是相对面,“爱”与“中”是相对面.故答案为:中.13.如果线段AB=10,点C、D在直线AB上,BC=6,D是AC的中点,则A、D 两点间的距离是2或8.【解答】解:①如图1所示,∵AB=10,BC=6,∴AC=AB﹣BC=10﹣6=4,∵D是线段AC的中点,∴AD=AC=×4=2;②如图2所示,∵AB=10,BC=6,∴AC=AB+BC=10+6=16,∵D是线段AC的中点,∴AD=AC=×16=8.故答案为:2或8.14.已知线段MN=16cm,点P为任意一点,那么线段MP与NP和的最小值是16 cm.【解答】解:如图所示:所以线段MP与NP和的最小值是16cm,故答案为;1615.如图,若∠3:∠2=2:5,且∠2﹣∠1=12°,∠3等于32°.第12 页共31 页【解答】解:∵∠3:∠2=2:5,设∠3=2x,∠2=5x,∵∠1+∠2+∠3=180°,∠2﹣∠1=12°,可得:5x﹣12°+5x+2x=180°,解得:x=16,所以∠3=2×16°=32°,故答案为:32°16.如图,点B、O、D在同一直线上,且OB平分∠AOC,若∠COD=150°,则∠AOC的度数是60°.【解答】解:∵点B、O、D在同一直线上,∠COD=150°,∴∠COB=180°﹣150°=30°,∵OB平分∠AOC,∴∠AOC=2×30°=60°,故答案为:60°.17.如图,一纸片沿直线AB折成的V字形图案,已知图中∠1=62°,则∠2的度数=56°.【解答】解:由折叠可得出2∠1+∠2=180°,∵∠1=62°,第13 页共31 页∴∠2=180°﹣2×62°=56°,故答案为56°.18.如图,A、O、B在一直线上,∠1=∠2,则与∠1互补的角是∠AOD.若∠1=28°32′35″,则∠1的补角=151°27′25″.【解答】解:∵∠1=∠2,∴与∠1互补的角是∠AOD,∵∠1=28°32′35″,∴∠1的补角=151°27′25″,故答案为:∠AOD;151°27′25″三.解答题(共7小题)19.太阳可以近似地看成球体,已知太阳的半经为6.96×108m,太阳的体积大约是多少?(球的体积的计算公式是V=πr3,π取3.14)【解答】解:当r=6.96×108时,V=πr3≈×3.14×(6.96×108)3≈1.41×1027m3,答:太阳的体积大约是1.41×1027m3.20.已知一个长方体的长为1cm,宽为1cm,高为2cm,请求出:(1)长方体有12条棱,6个面;(2)长方体所有棱长的和;(3)长方体的表面积.【解答】解:(1)长方体有12条棱,6个面;第14 页共31 页故答案为:12,6;(2)(1+1+2)×4=4×4=16(cm).故长方体所有棱长的和是16cm;(3)(1×1+1×2+1×2)×2=(1+2+2)×2=5×2=10(cm2).故长方体的表面积是10cm2.21.如图所示,若剪下来折叠能拼成一个正方体盒子,请你想象一下,能否在空格中填上适当的数,使相对的两个面上的数互为相反数?【解答】解:依题意得:A=﹣2,B=﹣3,C=﹣4.22.如图,点B、C把线段MN分成三部分,其比是MB:BC:CN=2:3:4,P 是MN的中点,且MN=18cm,求PC的长.【解答】解:设MB=2x,则BC=3x,CN=4x,因为P是MN中点,所以MP=MN=×(2x+3x+4x)=x=9.解得x=2,∴PC=MC﹣MP=2x+3x﹣x=0.5x=1.23.如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.(1)若∠AOE=32°,求∠BOC的度数;(2)若OD是∠AOC的角平分线,求∠AOE的度数.第15 页共31 页【解答】解:(1)∠AOD=∠DOE﹣∠AOE=90°﹣32°=58°∠BOD=∠AOB﹣∠AOD=180°﹣58°=122°又OC平分∠BOD所以:∠BOC=∠BOD=×122°=61°(2)因为OC平分∠BOD,OD平分∠AOC 所以∠BOC=∠DOC=∠AOD又∠BOC+∠DOC+∠AOD=180°所以∠AOD=×180°=60°所以∠AOE=∠DOE﹣∠AOD=90°﹣60°=30°24.以直线AB上点O为端点作射线OC,使∠BOC=60°,将直角△DOE的直角顶点放在点O处.(1)如图1,若直角△DOE的边OD放在射线OB上,则∠COE=30°;(2)如图2,将直角△DOE绕点O按逆时针方向转动,使得OE平分∠AOC,说明OD所在射线是∠BOC的平分线;(3)如图3,将直角△DOE绕点O按逆时针方向转动,使得∠COD=∠AOE.求∠BOD的度数.【解答】解:(1)∵∠BOE=∠COE+∠COB=90°,又∵∠COB=60°,∴∠COE=30°,第16 页共31 页故答案为:30°;(2)∵OE平分∠AOC,∴∠COE=∠AOE=COA,∵∠EOD=90°,∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,∴∠COD=∠DOB,∴OD所在射线是∠BOC的平分线;(3)设∠COD=x°,则∠AOE=5x°,∵∠DOE=90°,∠BOC=60°,∴6x=30或5x+90﹣x=120∴x=5或7.5,即∠COD=5°或7.5°∴∠BOD=65°或52.5°.25.探索性问题:已知A,B在数轴上分别表示m,n.(1)填表:(2)若A,B两点的距离为d,则d与m,n有何数量关系.(3)在数轴上整数点P到4和﹣5的距离之和为9,求出满足条件的所有这些整数的和.【解答】解:(1)5﹣2=3;0﹣(﹣4)=4;6﹣(﹣6)=12;﹣4﹣(﹣5)=1;2﹣(﹣90)=92;﹣2.5﹣(﹣4.5)=2;故答案为:3,4,12,1,92,2;(2)∵数轴上两点间的距离d等于表示两点数之差的绝对值,第17 页共31 页∴d=|m﹣n|.(3)设整数点P表示的数为x,∵点P到4和﹣5的距离之和为9,∴|x﹣4|+|x﹣(﹣5)|=9,即x﹣4+x+5=9,﹣(x﹣4)+x+5=9(﹣5和4两点间所有的整数点均成立),x ﹣4﹣(x+5)=9(舍去)或﹣(x﹣4)﹣(x+5)=9,解得x=﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2,3,4;∴有这些整数的和为4+3+2+1+0﹣1﹣2﹣3﹣4﹣5=﹣5.第18 页共31 页人教版七年级上册数学第四章几何图形初步单元测试题(含答案)一、选择题1.角是指()A. 由两条线段组成的图形B. 由两条射线组成的图形C. 由两条直线组成的图形D. 有公共端点的两条射线组成的图形2.如果一个角的补角是150°,那么这个角的余角的度数是()A. 30°B. 60°C. 90°D. 120°3.下列说法正确的是()A. 经过两点有且只有一条线段B. 经过两点有且只有一条直线C. 经过两点有且只有一条射线D. 经过两点有无数条直线4.如图,四条线段中,最短和最长的一条分别是()A. acB. bdC. adD. bc5.如图,B在线段AC上,且BC=2AB,D,E分别是AB,BC的中点.则下列结论:①AB= AC;②B是AE的中点;③EC=2BD;④DE=AB.其中正确的有()A. 1个B. 2个C. 3个D. 4个6.已知∠α=70°,则∠α的补角为()A. 120°B. 110°C. 70°D. 20°7.下列语句中,正确的是().A. 比直角大的角钝角;B. 比平角小的角是钝角C. 钝角的平分线把钝角分为两个锐角;D. 钝角与锐角的差是锐角8.如图,已知AD平分∠BAE,若∠BAD=62°,则∠CAE的度数是()第19 页共31 页A. 55°B. 56°C. 58°D. 62°9.如图,下列关系式中与图不符合的式子是()A. AD-CD=AB+BCB. AC-BC=AD-BDC. AC-BC=AC+BDD. AD-AC=BD-BC10.如图是一个正方体的平面展开图,当把它拆成一个正方体,与空白面相对的字应该是()A. 北B. 京C. 欢D. 迎二、填空题11.已知线段AB=8 cm,在直线AB上画线段BC,使它等于3 cm,则线段AC=________.12.若∠α=32°22′,则∠α的余角的度数为________.13.已知一个角的补角等于155°,则这个角的余角等于________14.八棱柱有________个顶点,________条棱,________个面.15.和互补,且-=50°,求和的度数. ________、 ________16.34.42°=________(用度、分、秒表示).17.一个角的补角加上10°后,等于这个角的余角的3倍,则这个角=________ °.18.用一个平面去截长方体,截面________是平行四边形(填“可能”或“不可能”).19.一条直线上有A、B、C三个点,AB=7cm,BC=4cm,则AC=________ .20.已知线段AB=1996,P、Q是线段AB上的两个点,线段AQ=1200,线段BP=1050,则线段PQ=________.三、解答题21.已知∠BOC=120°,∠AOB=70°,求∠AOC的大小。
人教版数学七年级上册第4章 几何图形初步单元测试(含答案)

七年级上册第4章单元测试一.选择题(共10小题)1.一个角的余角是44°,这个角的补角是()A.134°B.136°C.156°D.146°2.下列图形能折叠成正方体的是()A .B .C .D .3.下面各图是圆柱的展开图的是()A .B .C .D .4.甲、乙两个城市,乙城市位于甲城市北偏东50°方向,距离为80km,那么甲城市位于乙城市()A.南偏东50°方向,距离为80kmB.南偏西50°方向,距离为80kmC.南偏东40°方向,距离为80km第1页(共12页)D.南偏西40°方向,距离为80km5.有一个正六面体骰子放在桌面上,将骰子如图所示顺时针方向滚动,每滚动90°算一次,则滚动第2020次后,骰子朝下一面的数字是()A.5B.4C.3D.26.下列各角中,()是钝角.A .周角B .平角C.平角D .平角7.小明家在学校的南偏西50°方向上,则学校在小明家()上.A.南偏西50°B.西偏南50°C.北偏东50°D.北偏东40°8.下列度分秒运算中,正确的是()A.48°39′+67°31′=115°10′B.90°﹣70°39′=20°21′C.21°17′×5=185°5′D.180°÷7=25°43′(精确到分)9.一个圆柱体切拼成一个近似长方体后()A.表面积不变,体积变大B.表面积变大,体积不变C.表面积变小,体积不变D.表面积不变,体积不变10.下列语句中,正确的个数是()第2页(共12页)①直线AB和直线BA是两条直线;②射线AB和射线BA是两条射线;③若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余;④一个角的余角比这个角的补角小;⑤一条射线就是一个周角;⑥两点之间,线段最短.A.1个B.2个C.3个D.4个二.填空题(共5小题)11.已知,∠A=46°28',则∠A 的余角=.12.一个长方体的高是10cm,它的底面是边长为4cm的正方形,如果底面正方形的边长增加acm,则它的体积增加了cm3.13.已知如图,C是线段AB上的一点,N是线段BC的中点,若AB=10,AC=6,则AN=.14.已知线段AB=8cm.在直线AB上画线段AC=5cm,则BC的长是cm.15.如图,将长方形ABCD纸片按如图所示的方式折叠,EF,EG为折痕,点A落在A',点B落在B',点A',B',E在同一直线上,则∠FEG=度.三.解答题(共5小题)16.如图,CD是Rt△ABC斜边上的高,请找出图中各对互余的角.第3页(共12页)17.如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:(1)图中到小明家距离相同的是哪些地方?(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.18.如图,已知线段AB=12 cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.(1)若点C恰好是AB的中点,则DE =cm;(2)若AC=4 cm,求DE的长;(3)试说明无论AC取何值(不超过12 cm),DE的长不变.第4页(共12页)19.如图,已知射线OB平分∠AOC,∠AOC的余角比∠BOC小42°.(1)求∠AOB的度数:(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数.(3)在(2)的条件下,画∠AOD的角平分线OE,则∠BOE=.20.如图,平面上有四个点A,B,C,D.(1)根据下列语句画图:Ⅰ、画射线DC;Ⅱ、画直线AC与线段BD相交于点F ;(2)图中以F为顶点的角中,请写出∠AFB的补角.第5页(共12页)参考答案一.选择题(共10小题)1.解:∵一个角的余角是44°,∴这个角的度数是:90°﹣44°=46°,∴这个角的补角是:180°﹣46°=134°.故选:A.2.解:A、能折叠成正方体,故此选项符合题意;B、出现了“凹”字格,不能折叠成正方体,故此选项不符合题意;C、折叠后有两个面重合,不能折叠成正方体,故此选项不符合题意;D、出现了“田”字格,不能折成正方体,故此选项不符合题意.故选:A.3.解:由图可知,该圆柱底面直径为6,高为4,所以该圆柱的底面周长(圆柱侧面展开得到的长方形的长)为:6×3.14=18.84,故选:C.4.解:如图:第6页(共12页)∵乙城市位于甲城市北偏东50°方向,距离为80km,∴甲城市位于乙城市南偏西50°方向,距离为80km,故选:B.5.解:观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,∵2020÷4=505,∴滚动第2020次后与第一个相同,∴朝下的数字是3的对面4,故选:B.6.解:平角=180°,钝角大于90°而小于180°,平角=×180°=120°,是钝角.故选:B.7.解:∵小明家在学校的南偏西50°方向上,∴学校在小明家北偏东50°方向上.故选:C.8.解:48°39'+67°31'=115°70'=116°10',故A选项错误;90°﹣70°39'=19°21',故B选项错误;21°17'×5=105°85'=106°25',故C选项错误;180°÷7=25°43',故D选项正确.故选:D.9.根据立体图形的切拼方法可知:圆柱体切拼成一个长方体后,体积大小不变,表面积增加了两个以圆柱的高和第7页(共12页)底面半径为边长的长方形的面积,所以表面积变大了.故选:B.10.解:①直线AB和直线BA是一条直线,原来的说法是错误的;②射线AB和射线BA是两条射线是正确的;③互余是指的两个角的关系,原来的说法是错误的;④一个角的余角比这个角的补角小是正确的;⑤周角的特点是两条边重合成射线.但不能说成周角是一条射线,原来的说法是错误的;⑥两点之间,线段最短是正确的.故正确的个数是3个.故选:C.二.填空题(共5小题)11.解:∵∠A=46°28′,∴∠A的余角=90°﹣46°28′=43°32′.故答案为:43°32′.12.解:长方体原体积为:4×4×10=160cm3.底面边长增加acm后,边长为(4+a)cm,体积为:10(4+a)2=(10a2+80a+160)cm3.体积增加为:10a2+80a+160﹣160=10a2+80a.故答案为:(10a2+80a).13.解:∵AB=10,AC=6,∴CB=10﹣6=4,第8页(共12页)∵N是线段BC的中点,∴CN=2,∴AN=AC+CN=6+2=8.14.解:当C点在线段AB上时,BC=AB﹣AC=8﹣5=3(cm);当C点在线段BA的延长线上时,BC=AB+AC=8+5=13(cm).故BC的长为3或13cm.故答案为3或13.15.解:由折叠可得∠AEF=∠A'EF,∠BEG=∠B'EG,∵∠AEB=180°,∴∠FEG=∠A'EF+∠B'EG =∠AEB=90°,故答案为90.三.解答题(共5小题)16.解:∵CD⊥AB,∴△ABC,△BCD是直角三角形,又∵△ABC是直角三角形,∴∠A与∠B,∠A与∠ACD,∠B与∠BCD互余(直角三角形的两个锐角互余),又∵∠ACB=90°,∴∠ACD与∠BCD互余.∴图中互余的角有:∠A与∠B,∠A与∠ACD,∠B与∠BCD,∠ACD与∠BCD.17.解:(1)因为点C为OP的中点,第9页(共12页)所以OC=2km,因为OA=2km,所以可得出距小明家距离相同的是学校和公园;(2)由图可知,学校在小明家东偏北45°方向2km处,商场在小明家西偏北60°方向3.5km处,停车场在东偏南30°方向4km处.18.解:(1)∵点D,E分别是AC和BC的中点,∴DC =AC,CE =CB,∴DC+CE =(AC+CB)=6cm;故答案为:6.(2)∵AC=4cm,∴CD=2cm,∵AB=12cm,AC=4cm,∴BC=8cm,∴CE=4cm,DE=DC+CE=6cm;(3)∵点D,E分别是AC和BC的中点,∴DC =AC,CE =CB,∴DC+CE =(AC+CB),即DE =AB=6cm,故无论AC取何值(不超过12 cm),DE的长不变.第10页(共12页)19.解:(1)由射线OB平分∠AOC可得∠AOC=2∠BOC,设∠BOC=x,则∠AOC=2x,依题意列方程90°﹣2x=x﹣42°,解得:x=44°,即∠AOB=44°.(2)由(1)得,∠AOC=88°,①当射线OD在∠AOC内部时,∠AOD=22°,则∠COD=∠AOC﹣∠AOD=66°;②当射线OD在∠AOC外部时,∠AOD=22°则∠COD=∠AOC+∠AOD=110°;(3)∵OE平分∠AOD,∴∠AOE =,当射线OD在∠AOC内部时,∠BOE=∠AOB﹣∠AOE=44°﹣11°=33°;当射线OD在∠AOC外部时,∠BOE=∠AOB+∠AOE=44°+11°=55°.∴∠BOE度数为33°或55°.故答案为:33°或55°20.解:(1)作图如下:第11页(共12页)(2)∠AFB的补角为∠BFC,∠AFD.第12页(共12页)。
人教版七年级数学上册《第四章整式的加减》单元测试卷及答案

人教版七年级数学上册《第四章整式的加减》单元测试卷及答案一、整体代入法求值整体代入法求值,就是将一个复杂的表达式或方程看作一个整体,然后将其代入到另一个表达式或方程中进行求解的方法。
通过“比较各项系数”“拼拆各项构造整体”“比较各项系数”“拼拆各项构造整体”等方法“化繁为简”,将复杂的问题分解成若干个简单的问题,再逐一解决,最终汇聚成整体的答案。
一、 整体代入——比较各项系数1. 若代数式b a -2的值为1 ,则代数式b a 247-+ 的值为( ) .A. 7B. 8C. 9D. 102. 若a 、b 互为相反数,c 、d 互为倒数,则()=-+cd b a 3 .3. 已知代数式y x 2+的值是3 ,则代数式142-+y x 的值是 .4. 若6=+b a ,则=--b a 2218 ( ) .A. 6B. 6-C. 24-D. 125. 已知,0122=++a a 求3422-+a a 的值 . 6. 若72=-b a ,则b a 426+- 的值为 .7. 如果代数式b a -的值为4 ,那么代数式522--b a 的值为 . 8. 已知代数式y x -2的值是2- ,则代数式y x +-21 的值是 .二、 整体代入——拼拆各项构造整体1. 请回答下列各题:( 1 )化简:()().363252222y x xy xy y x --+ ( 2 )化简求值:已知,2,9==+ab b a 求()()⎪⎭⎫ ⎝⎛+--++-b ab a ab ab ab 2141025131532的值.2. 已知,12,5=-=+c b b a 则c b a -+2 的值为( ) . A. 17B. 7C. 17-D.7-3. 已知5=-b a ,2=+d c 则()()d a c b --+的值是( ) .A.3-B. 3C.7-D. 74. 已知3=-b a ,2=+dc 则()()d a c b --+ 的值为 .5. 已知,6,1422-=-=+bc b bc a 则22b a+ 的值是 ,bc b a 3222+-的值是6. 已知,5,14=-=+ab b a 求()()[]a b ab a b ab 65876+--++ 的值 .三、 整体代入——比较各项系数1. 代数式22++x x 的值为0 ,则代数式3222-+x x 的值为( ) . A. 6 B. 7 C. 6- D. 7-2. 解答下列问题:( 1 )若代数式7322++x x 的值为 8 ,那么代数式2025962++x x 的值为( 2 )若5,7==+xy y x .则代数式xy y x +--228的值为 ( 3 )若,5,162244=-=+xy y x y x 则()()()422244253y xy xy y x y x----- 的值是多 少?3. 若代数式y x 32-的值是1 ,那么代数式846+-x y 的值是 .4. 已知a ,b 互为相反数, c ,d 互为倒数, x 的绝对值为2 .求()()20252cd x cd b a x -+++-的值 .5. 已知a 与b 互为相反数,c 与d 互为倒数, m 的值为6-,求m cd mba +-+的值 . 6. 若代数式5322++x x 的值是 8 ,则代数式7642-+x x 的值是( ) . A. 1- B. 1 C. 9- D. 9 7. 若1-=-n m ,则()n m n m 222+-- 的值是 .四、 整体代入——拼拆各项构造整体1. 若32-=+mn m,1832=-mn n 则224n mn m -+ 的值为 .2. 已知2,522-==+ab b a ,求代数式()()222222353242b b ab ab ab a ++---+的值.3. 已知:1,4-==-mn n m .求:()()()mn n m m n mn n m mn ++--+-++-4223322的值 . 4. 已知(),07535172=-++-+y x y x 求=+y x 32 .5. 已知,62,1422-=-=+bc b bc a 则=-+bc b a 54322 ( ) .A. 18B. 18-C. 20D. 86. 已知2-=-+a c b ,则()()=-++⎪⎭⎫ ⎝⎛+-+--a c b c b a c b c b a a 2223132323232 参考答案一、 整体代入——比较各项系数【解答】()b a b a -+=-+227247把12=-b a 代入上式得:927=+=∴原式. 答案:C【解答】b a 、 互为相反数,d c 、互为倒数.,1,0==+∴cd b a(),3303-=-=-+∴cd b a 答案:3-【知识点】倒数的定义1. 【解答】由题意可知:,32=+y x 原式().516122=-=-+=y x【解答】,6=+b a(),612182182218=-=+-=--∴b a b a 答案:A 2. 【解答】,0122=++a a ()550512234222=-=-++=-+∴a a a a3. 【解答】()b a b a 226426--=+-,其中,72=-b a 所以原式8726-=⨯-=4. 【解答】,4=-b a ()35425252=-⨯=--=--b a b a5. 【解答】22-=-y x()()3212121=--=--=+-∴y x y x二、 整体代入——拼拆各项构造整体1.【解答】(1)原式222222913361510xy y x y x xy xy y x +=+-+=(2)原式b ab a ab ab ab 24252210---++-=(),255822524210b a ab ba ab +--=--⎪⎭⎫ ⎝⎛+-+-=其中.2,9==+ab b a.5206511618922558-=--=⨯-⨯-=∴原式 2.【解答】12,5=-=+c b b a()()171252=+=-++=-+∴c b b a c b a .答案:A3.【解答】2,5=+=-d c b a()()325-=+-=++-=+-+=∴d c b a d a c b 原式.答案:A4.【解答】,d a c b +-+=原式()()132-=-=--+=+-+=b a d c ba d c5.【解答】()();86142222=-+=-++=+bc b bc a b a()()();346282322222=--=--+=+-bc bbc abc b a答案:8;346.【解答】()34228=++=++=ab b a a b ab 原式三、整体代入——比较各项系数1. 【解答】2,0222-=+=++x x x x 即()734322-=--=-+=x x 原式.答案:D2. 【解答】(1)87322=++x x,1322=+∴x x则原式(),20282025320253232=+=++=x x(2),5,7==+xy y x()xy y x ++-=∴28原式151485728-=+-=+⨯-=(3)()()()422244253y xy xy y xyx -----()()115165,16,3225322442244422244=-=∴=-=+∴--+=+-+--=原式xy y x y x xy y x y x y xy xy y x y x3. 【解答】,132=-y x()6828322=+-=+--=∴y x 原式【解答】b a , 互为相反数,d c ,互为倒数,x 的绝对值为2,2,1,0±===+∴x cd b a当2=x 时,原式()();11241210220252=--=-+⨯+-=当2-=x 时,原式()()()();51241210220252=-+=-+-⨯+--= 所以()()20252cd x cd b a x -+++-的值为1或5.【解答】b a , 互为相反数0=+∴b ad c , 互为倒数1=∴cd.5610610=+-=-+-=+-+m cd mba 4. 【解答】由题意可知:85322=++x x,3322=+∴x x().1732276422-=-+=-+∴x x x x 答案:A5. 【解答】1-=-n m()()()()()3121222222=-⨯--=---=+-=n m n m nm n m四、整体代入——拼拆各项构造整体1. 【解答】方法一:,183,322=--=+mn n mn m∴将这两个等式的两边相减得:(),183322--=--+mn n mn m,21322-=+-+∴mn n mn m ,21422-=-+∴n mn m方法二:原式(),332222mn n mn m n mn mn m --+=-++= 将183,322=--=+mn n mn m 代入 得原式21183-=--=2.【解答】原式,691524822222b b ab a b ab a +-+--+=(),137,71372222ab b a b ab a ++-=-+-=当2,522-==+ab b a 时 原式612635-=--=.3. 【解答】原式,4223322mn n m m n mn n m mn ---+--++-=(),36336n m mn nm mn -+-=-+-=把1,4-==-mn n m 代入得:原式18126=+=.4. 【解答】 已知条件17-+y x 和()27535-+y x 都是非负数,且(),07535172=-++-+y x y x .3932,5127535170753517=+∴⎩⎨⎧==∴⎩⎨⎧=+=+∴=-+=-+∴y x y x y x y x y x y x5. 【解答】bc b a 54322-+()()182414324322=-⨯=-++=bc b bc a6. 【解答】原式().382323222=⨯=--=c b a。
人教版七年级上册数学第四章《几何图形》单元测试卷(Word版,含答案)
人教版七年级上册数学第四章《几何图形》单元测试卷(满分100分,时间90分钟)一、选择题(本大题共十小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是正确的.)1.下列说法不正确的是()A.用一个平面去截一个正方体可能截得五边形B.五棱柱有10个顶点C.沿直角三角形某条边所在的直线旋转一周,所得的几何体为圆柱D.将折起的扇子打开,属于“线动成面”的现象2.下列图形中,经过折叠不能围成一个正方体的是()A.B.C.D.3.图1是一个正六面体,把它按图2中所示方法切割,可以得到一个正六边形的截面,则下列展开图中正确画出所有的切割线的是()A.B.C.D.4.已知∠1=27°18′,∠2=27.18°,∠3=27.3°,则下列说法正确的是()A.∠1=∠3B.∠1=∠2C.∠1<∠2D.∠2=∠35.如图是顺义区地图的一部分,小明家在怡馨家园小区,小宇家在小明家的北偏东约15°方向上,则小宇家可能住在()A.裕龙花园三区B.双兴南区C.石园北区D.万科四季花城6.一个正方体的展开图如图所示,将它折成正方体后,数字“0”的对面是()A.数B.5 C.1 D.学7.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于()A.65°B.50°C.40°D.25°8.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形,其中作法错误的为()A.B.C.D.9.如图所示,一艘船从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC的余角是()A.15°B.30°C.45°D.75°10.某乡镇的4个村庄A,B,C,D恰好位于正方形的4个顶点上,为了解决农民出行难问题,镇政府决定修建连接各村庄的道路系统,使得每两个村庄都有直达的公路,设计人员给出了如下四个设计方案(实线表示连接的道路)在上述四个方案中最短的道路系统是方案()A.一B.二C.三D.四二、填空题(本大题共10小题,每小题2分,共20分)11.有一正角锥的底面为正三角形.如果这个正角锥其中两个面的周长分别为27,15,则此正角锥所有边的长度和为.12.有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是.13.如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13,9,3的对面的数分别是a,b,c,则a2+b2+c2﹣ab﹣ac﹣bc的值为.14.用一根长28分米的木条截开后刚好能搭一个长方体的架子,这个长方体的长、宽、高的长度都是整数分米,且都不相等,那么这个长方体的体积等于立方分米.15.经过A,B两点的直线上有一点C,AB=10,CB=6,D和E分别是AB,BC的中点,则DE 的长是.16.上午8:30钟表的时针和分针构成角的度数是.17.下列几何体属于柱体的有个.18.平面内不同的两点确定一条直线,不同的三点最多确定三条直线,平面内不同的七个点最多可确定条直线.19.用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②圆柱;③圆锥;④正三棱柱(写出所有正确结果的序号).20.已知一个圆柱的侧面展开图是如图所示的矩形,长为6π,宽为4π,那么这个圆柱底面圆的半径为.三、解答题(21 ~23题每题7分,25题8分,26题8分,27题8分)21.如图,点C在线段AB上,AC=6cm,MB=10cm,点M,N分别为AC,BC的中点.(1)求线段BC,MN的长;(2)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M,N分别是线段AC,BC的中点,求MN的长度.22.如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,已知正方体相对两个面上的代数式的值相等.求a+的值.。
人教版数学七年级上册第四单元测试试卷(含答案)

人教版数学7年级上册第4单元·时间:120分钟满分:120分班级__________姓名__________得分__________一、选择题(共12小题,满分36分,每小题3分)1.(3分)(2022秋•榕城区校级月考)圆柱的截面不可能是( )A.梯形B.长方形C.正方形D.椭圆2.(3分)(2022秋•南岗区校级月考)如果长方体的长、宽、高都扩大3倍,则它的体积扩大( )倍.A.3B.9C.6D.273.(3分)(2022秋•南岗区校级月考)一个长方体的棱长之和是180厘米,相交于一个顶点的三条棱的长度和是( )A.45厘米B.30厘米C.90厘米D.60厘米4.(3分)(2022秋•南岗区校级月考)一个长方体水箱,从里面量长5分米,宽和高都是2分米,现在往这个水箱倒入15升水,水箱( )A.倒满了B.还没倒满C.溢出来了D.无法确定5.(3分)(2022秋•和平区校级月考)如图,AB=12cm,C为AB的中点,点D在线段AC上且AD:CB=1:3,则DB的长是( )A.8cm B.10cm C.12cm6.(3分)(2022秋•天桥区校级月考)用纸片和小棒做成下面的小旗,快速旋转小棒,所形成的图形正确顺序是( )A.①②③④B.③④①②C.①③②④D.④②①③7.(3分)(2021秋•萨尔图区校级期末)甲、乙两人要从学校回家,他们分别选择了①、②两条路线,比较一下,所走的路程是( )A .①条长B .②条长C .一样长D .无法确定8.(3分)(2022秋•聊城月考)下列各选项中的图形绕虚线旋转一周后,得到的几何体是圆柱的是( )A .B .C .D .9.(3分)(2021秋•乌当区期末)如图,点O 在直线AB 上,射线OD 是∠AOC的平分线,若∠COB =40°,则∠DOC 的度数是( )A .20°B .45°C .60°D .70°10.(3分)(2021秋•萨尔图区校级期末)一个圆锥的体积是12立方厘米,底面积是4平方厘米,高是( )厘米.A .3B .6C .9D .1211.(3分)(2022春•东营期末)如图,OC 平分∠AOB ,OD 平分∠BOC ,下列各式正确的是( )A .∠COD =12∠AOBB .∠BOD =12∠AODC .∠BOC =23∠AOD D .∠AOD =23∠AOB 12.(3分)(2022•南京模拟)如图,已知B ,C 是线段AD 上任意两点,E是AB 的中点,F 是CD 的中点,下列结论不正确的是( )A.AC=CD B.AB=2AECD D.BC=EF﹣AE﹣FDC.CF=12二、填空题(共6小题,满分18分,每小题3分)13.(3分)(2021秋•栾城区期末)如图,∠AOB=∠COD=90°,则∠AOC ∠BOD(选填“>”、“=”或“<”).14.(3分)(2022秋•新城区校级月考)如图,将一个装了一半水的密闭圆柱形玻璃杯水平放置时,水面的形状是 .15.(3分)(2022秋•柳江区月考)如图,把6个形状、大小完全相同的长方形如图摆放,面积共是12平方单位,则阴影部分的面积是 平方单位.16.(3分)(2021秋•萨尔图区校级期末)一个体积是60立方厘米的圆柱,削成一个最大的圆锥体,这个圆锥的体积是 cm3.17.(3分)(2022春•沂水县期中)如图,AB与CD相交于点O,OE是∠AOC 的平分线,且OA恰好平分∠EOD,则∠AOC= 度.18.(3分)(2022春•岚山区期末)如图,将一张宽度相等的纸条折叠,折叠后的一边与原边的夹角是140°,则∠α的度数是 .三、解答题(共7小题,满分66分)19.(9分)(2022秋•新城区校级月考)已知一个直棱柱,它有27条棱,其中一条侧棱长为20,底面各边长都为5.(1)这是几棱柱?(2)它有多少个面?多少个顶点?(3)这个棱柱的所有侧面的面积之和是多少?20.(9分)(2022秋•昭阳区校级月考)如图,经测量,B处在A处的南偏西56°的方向,C处在A处的南偏东17°方向,C处在B处的北偏东78°方向,求∠C的度数.21.(9分)(2022秋•高州市校级月考)如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它有多少条棱?它有多少个顶点?它的所有侧面的面积之和是多少?22.(9分)(2021秋•萨尔图区校级期末)求阴影部分的面积.23.(10分)(2022秋•萍乡月考)如图所示是一个多面体的展开图形,每个面(外表面)都标注了字母,请你根据要求回答问题:(1)这个多面体是什么常见几何体;(2)如果B 在前面,C 在左面,那么哪一面在上面.24.(10分)(2022•丰顺县校级开学)如图1,把一张长10cm 、宽6cm 的长方形纸板分成两个相同的直角三角形(圆锥的体积公式为V 圆锥=13πr 2ℎ,π取3.14).(1)甲三角形(如图2)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?(2)乙三角形(如图3)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?25.(10分)(2022春•钢城区期末)如图,点C 是线段AB 上的一点,点M是线段AC 的中点,点N 是线段BC 的中点.(1)如果AB =14cm ,AM =5cm ,求BC 的长;(2)如果MN =8cm ,求AB 的长.参考答案一、选择题(共12小题,满分36分,每小题3分)1.A2.D3.A4.B5.B6.B7.C8.C9.D10.C11.C12.A二、填空题(共6小题,满分18分,每小题3分)13.=14.长方形15.816.2017.12018.70°三、解答题(共7小题,满分66分)19.【解答】解:(1)∵此直棱柱有27条棱,∴由27÷3=9,可知此棱柱是九棱柱;(2)这个九棱柱有11个面,有18个顶点;(3)这个棱柱的所有侧面的面积之和是5×9×20=900.20.【解答】解:由题意得:∠ABC=78°﹣56°=22°,∠BAC=56°+17°=73°,∴∠C=180°﹣∠ABC﹣∠BAC=180°﹣22°﹣73°=85°,∴∠C 的度数为85°.21.【解答】解:如图,它有7个面,15条棱,10个顶点,所有侧面的面积之和为:5×12×5=300(cm 3).答:它有7个面,15条棱,10个顶点,它的所有侧面的面积之和是300cm 3.22.【解答】解:阴影部分的面积为:90°360°×π×(42)2=π(cm 2).23.【解答】解:(1)根据多面体的展开图形可知,多面体是长方体;(2)根据长方体及其表面展开图的特点可知,面“B ”与面“D ”相对,面“E ”与面“A ”相对,面“C ”与面“F ”相对,如果B 在前面,C 在左面,则E 在下面,A 在上面.24.【解答】解:(1)甲三角形旋转一周可以形成一个圆锥,它的体积是 13×3.14×62×10=376.8(cm 3).(2)乙三角形旋转一周可以形成一个圆柱,里面被挖去一个圆锥,它的体积是 3.14×62×10―13×3.14×62×10=753.6(cm 3).25.【解答】解:(1)∵点M 是线段AC 的中点,AM =5cm ,∴AC =2AM =10cm ,∵AB =14cm ,∴BC =AB ﹣AC =14﹣10=4cm ;(2)∵点M 是线段AC 的中点,点N 是线段BC 的中点,∴NC =12BC ,CM =12AC ,∴MN =NC +CM =12(BC +AC )=12AB ,∵MN =8cm ,∴12AB =8,∴AB =16cm .。
2022-2023学年人教版七年级数学上册《第4章几何图形初步》单元达标测试题(附答案)
2022-2023学年人教版七年级数学上册《第4章几何图形初步》单元达标测试题(附答案)一.选择题(共8小题,满分32分)1.下列四个几何体中,是棱柱的是()A.B.C.D.2.已知∠α=35°40′,则∠α的补角的度数为()A.55°60′B.55°20′C.144°60′D.144°20′3.下列日常现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③利用圆规可以比较两条线段的大小;④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.其中,可以用“两点确定一条直线”来解释的现象是()A.①④B.②③C.①②④D.①③④4.将一副常规的三角尺如图放置,则图中∠ACB的度数是()A.75°B.95°C.15°D.120°5.如图,若∠1=32°,则∠2的度数是()A.32°B.58°C.48°D.68°6.如图,若∠AOB=∠COD=∠EOF=90°,且∠DOF=45°,∠AOE=30°,求∠BOC 的度数为()A.15°B.20°C.25°D.30°7.若∠1与∠2互为余角,∠1与∠3互为补角,则下列结论:①∠3﹣∠2=90°;②∠3+∠2=270°﹣2∠1;③∠3﹣∠1=2∠2;④∠3<∠1+∠2.其中正确的是()A.①B.①②C.①②③D.①②③④8.如图,∠AOB与∠COB的度数分别记为m,n(m>n),OM,ON分别是∠COB,∠AOC 的平分线,则∠MON的度数为()A.B.C.D.二.填空题(共8小题,满分32分)9.如图,已知线段AB长度为x,CD长度为y,则图中所有线段的长度和为.10.点A,B,C是同一直线上的三个点,若AB=7cm,BC=5cm,则AC=cm.11.(1)钟表上的时间是3时30分,此时时针与分针所成的夹角是度.(2)计算:24°24′=°.(3)一个角是40°,则它的补角是度.12.如图是一个底面各边都相等的六棱柱,它的底面边长为2cm,高为5cm.这个棱柱共有条棱,个面,侧面积是cm2.13.在平整的地面上,有若干个完全相同的棱长为2cm的小正方体堆成一个几何体,如图所示:这个几何体露出的表面积是cm2.14.如图,将一个三角板60°角的顶点与另一个三角的直角顶点重合,∠1=28°,∠2=°.15.如图,已知点O是直线AB上的一点,∠COE=120°,∠AOF=∠AOE.(1)当∠BOE=15°时,∠COA的度数为;(2)当∠FOE比∠BOE的余角大40°,∠COF的度数为.16.某天卢老师在数学课上,利用多媒体展示如下内容:如图,C为直线AB上一点,∠DCE 为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各学习小组经过讨论后得到以下结论:①∠ACF与∠BCH互余;②∠HCG=45°;③∠ECF与∠GCH互补;④∠ACF﹣∠BCG=45°.聪明的你认为哪些结论是正确的,请写出正确结论的序号.三.解答题(共7小题,满分56分)17.如图所示的是一个正方体的平面展开图,若将该展开图折叠成正方体后,相对面上的两个数字互为相反数,求2x+y﹣z的值.18.如图是一个食品包装盒的表面展开图.(1)该包装盒的几何体名称是;(2)根据图中所标尺寸,用a,b表示这个几何体的表面积S,并计算当a=1,b=4时,S的值.19.如图,C为线段AD上一点,点B为CD的中点,且AD=9cm,BD=2cm.(1)图中共有条线段.(2)求AC的长.(3)若点E在直线AD上,且EA=3cm,求BE的长.20.如图,点C在线段AB上,点M,N分别为AC,BC的中点.(1)若AC=6cm,MB=10cm,求线段MN的长;(2)若C为线段AB上任一点,满足AC=2acm,MB=bcm,其它条件不变,你能猜想MN的长度吗?并说明理由;(3)若C在线段AB的延长线上,且满足AC=xcm,BC=ycm,M,N分别是线段AC,BC的中点,请画出图形,并用含x,y的式子表示MN的长度.21.如图1,∠AOC和∠BOD都是直角.(1)如果∠DOC=35°,则∠AOB=;(2)找出图1中一组相等的锐角为:;(3)若∠DOC变小,∠AOB将;(填变大、变小、或不变)(4)在图2中,利用能够画直角的工具在图2上再画一个与∠BOC相等的角.22.直观想象,逻辑推理已知点O为直线AB上一点.(1)如图1,过点O作射线OC,使∠AOC:∠BOC=3:2,求∠AOC与∠BOC的度数;(2)如图2,射线OC为∠AOB内部任意一条射线,射线OD、OE分别是∠AOC、∠BOC 的角平分线,求∠DOE的度数,并写出简要的推理过程;(3)写出图2中所有互余的角和互补的角.23.如图,∠AOB=m°,OC是∠AOB内的一条射线,OD、OE分别平分∠BOC、∠AOC.(1)若∠BOC=90°,∠AOC=30°,求∠DOE的度数;(2)试用含m的代数式表示∠DOE;(3)在图中,将OC反向延长,得到OP,OM、ON分别平分∠BOP、∠AOP.请将图补充完整,并用含m的代数式表示∠MON.参考答案一.选择题(共8小题,满分32分)1.解:选项A中的几何体是圆柱,因此选项A不符合题意;选项B中的几何体是三棱柱,因此选项B符合题意;选项C中的几何体是三棱锥,因此选项C不符合题意;选项D中的几何体是四棱台,因此选项D不符合题意;故选:B.2.解:∵∠α=35°40′,∴∠α的补角的度数为180°﹣35°40′=144°20′.故选:D.3.解:①④可以用“两点确定一条直线”来解释;②可以用“两点之间线段最短”来解释;③根据“作一条线段等于已知线段”的方法进行解释;故选:A.4.解:由题意得:∠ACD=45°,∠BCD=30°,则∠ACB=∠ACD﹣∠BCD=15°.故选:C.5.解:由图可得∠1+∠2+90°=180°,∵∠1=32°,∴∠2=58°.故选:B.6.解:∵∠COD=90°,∠DOF=45°,∴∠COF=45°,∵∠EOF=90°,∴∠EOC=45°,∵∠AOB=90°,∴∠AOE+∠BOC=45°,∵∠AOE=30°,∴∠BOC=15°,故选:A.7.解:根据题意得:(1)∠1+∠2=90°,(2)∠1+∠3=180°,∴(2)﹣(1)得,∠3﹣∠2=90°,∴①正确;(1)+(2)得,∠1+∠2+∠1+∠3=270°,∴∠3+∠2=270°﹣2∠1,∴②正确;(2)﹣(1)×2得,∠3﹣∠1=2∠2,∴③正确;∵(1)∠1+∠2=90°,(2)∠1+∠3=180°,∴2(∠1+∠2)=180°,∴∠3=180°﹣∠1=2(∠1+∠2)﹣∠1=∠1+2∠2,∴∠3>∠1+∠2,∴④错误;故选:C.8.解:∵∠AOC=∠AOB+∠BOC=m+n,∵射线ON平分∠AOC,∴∠CON=∠AOC=(m+n),∵OM平分∠BOC,∴∠COM=∠BOC=n,∴∠MON=∠CON﹣∠COM=(m+n)﹣n=m;故选:A.二.填空题(共8小题,满分32分)9.解:∵线段AB长度为x,∴AB=AC+CD+DB=x,又∵CD长度为y,∴AD+CB=x+y,∴图中所有线段的长度和为:AB+AC+CD+DB+AD+CB=x+x+x+y=3x+y,故答案为:3x+y.10.解:①当点C在线段AB的延长线上时,AC=AB+BC=7+5=12cm.②当点C在线段AB上时.AC=AB﹣BC=7﹣5=2cm.故答案为:12或2.11.解:(1)3点30分时,时针与分针的较小夹角是2.5个大格,一个大格的度数是30°,所以30°×2.5=75°;故答案为:75;(2)24°24′=24.4°.故答案为:24.4;(3)由补角的性质,得40°角的补角是180°﹣40°=140°,故答案为:140.12.解:六棱柱有18条棱,8个面,侧面积是2×6×5=60cm2.故答案为:18,8,60.13.解:∵几何体露出的小正方体的面一共有32个,∴这个几何体露出的表面积为32×4=128(cm2),故答案为:128.14.解:∵∠BAC=60°,∠1=28°,∴∠EAC=∠BAC﹣∠1=32°,∵∠DAE=90°,∴∠2=∠DAE﹣∠EAC=58°.故答案为:58.15.解:(1)∵∠BOE=15°,∠COE=120°,∴∠COA=180°﹣120°﹣15°=45°.故答案为:45°.(2)由题意得,∠FOE=90°﹣∠BOE+40°=130°﹣∠BOE.∵∠AOF=∠AOE,∴180°﹣∠BOF=.∴180°﹣(∠EOF+∠BOE)=60°﹣.∴180°﹣130°=60°﹣.∴∠BOE=30°.∴∠EOF=90°﹣30°+40°=100°.∴∠COF=∠COE﹣∠EOF=120°﹣100°=20°.故答案为:20°.16.解:∵CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,∴∠ACF=∠FCD=∠ACD,∠DCH=∠HCB=∠DCB,∠BCG=∠ECG=∠BCE,∵∠ACB=180°,∠DCE=90°,∴∠FCH=90°,∠HCG=45°,∠FCG=135°∴∠ACF+∠BCH=90°,故①②正确,∵∠ECF=∠DCE+∠FCD=90°+∠FCD,∠FCD+∠DCH=90°,∴∠ECF+∠DCH=180°,∵∠HCG≠∠DCH,∴∠ECF与∠GCH不互补,故③错误,∵∠ACD﹣∠BCE=180°﹣∠DCB﹣∠BCE=90°,∴∠ACF﹣∠BCG=45°.故④正确.故答案为:①②④.三.解答题(共7小题,满分56分)17.解:由题意得:2与y,3与z,x与﹣2分别是相对面上的两个数,所以y=﹣2,z=﹣3,x=2,则2x+y﹣z=4﹣2+3=5.18.解:(1)由展开图知,该包装盒的几何体为长方体,故答案为:长方体;(2)由题知,S=2×2a×a+2×2a×b+2×a×b=4a2+6ab,当a=1,b=4时,S=4+6×4=28.19.解:(1)以A为端点的线段为:AC,AB,AD;以C为端点的线段为:CB,CD;以B为端点的线段为:BD;共有3+2+1=6(条);故答案为:6.(2)∵点B为CD的中点,BD=2cm.∴CD=2BD=2×2=4(cm),∴AC=AD﹣CD=9﹣4=5(cm),答:AC的长是5cm.(3)AB=AC+BC=7cm,EA=3cm,当点E在线段AD上时,BE=AB﹣AE=7﹣3=4(cm),当点E在线段DA的延长线上时,BE=AB+AE=7+3=10(cm),答:BE的长是4或10cm.20.解:(1)∵M是AC的中点,∴MC=AC=3cm,∴BC=MB﹣MC=7cm,又∵N为BC的中点,∴CN=BC=3.5cm,∴MN=MC+NC=6.5cm;(2)∵点M、N分别是AC、BC的中点,AC=2acm,MB=bcm,∴AM=AC=a cm,AC+CB=(a+b)cm,∴CM=AC,CN=BC,∴MN=CM+CN=AC+BC=(AC+BC)=(a+b)cm,即线段MN的长是(a+b)cm;(3)如图:MN=(x﹣y)cm,理由是:∵点M、N分别是AC、BC的中点,AC﹣CB=(x﹣y)cm,∴CM=AC,CN=BC,∴MN=CM﹣CN=AC﹣BC=(AC﹣BC)=(x﹣y)cm,即线段MN的长是(x﹣y)cm.21.解:(1)∵∠AOC=∠DOB=90°,∠DOC=35°,∴∠COB=∠BOD﹣∠DOC=90°﹣35°=55°,∴∠AOB=∠AOC+∠COB=90°+55°=145°;故答案为:145°;(2)∵∠AOC=∠DOB=90°,∴∠AOD+∠COD=∠BOC+∠COD=90°,∴∠AOD=∠BOC;故答案为:∠AOD=∠BOC;(3)∵∠AOD+∠DOC+∠DOC+∠BOC=∠AOB+∠COD=∠AOC+∠BOD=180°,∴∠AOB=180°﹣∠DOC,∴∠DOC逐渐变小,∠AOB逐渐变大;故答案为:变大;(4)利用三角板画∠AOC=∠BOD=90°,则∠AOD=∠BOC,理由如下:∵∠AOC=∠DOB=90°,∴∠AOD+∠COD=∠BOC+∠COD=90°,∴∠AOD=∠BOC.22.解:(1)设∠AOC=3x,∠BOC=2x,∵∠AOC+∠BOC=180°,∴3x+2x=180°,∴x=36°,∴∠AOC=3×36°=108°,∠BOC=2×36°=72°;(2)∵OD、OE分别是∠AOC、∠BOC的角平分线,∴∠DOC=∠AOD=,∠COE=∠BOE=∠BOC,∵∠AOC+∠BOC=180°,∠DOE=∠DOC+∠COE,∴∠DOE====90°;(3)互余的角有,∠DOC与∠COE,∠AOD与∠COE,∠BOE与∠COD,∠BOE与∠AOD;互补的角有,∠AOD与∠BOD,∠AOC与∠BOC,∠AOE与∠BOE.23.解:(1)∵OD、OE分别平分∠BOC、∠AOC,∴∠DOE==60°;(2)由(1)知,∠DOE===;(3)补充图形如下:∵∠AOB=m°,∴∠BOP+∠AOP=360°﹣∠AOB=360°﹣m°,∵OM、ON分别平分∠BOP、∠AOP,∴∠MON=∠MOP+∠NOP==.。
人教版七年级数学上册《第四章》单元测试题及答案

人教版七年级数学上册《第四章》单元测试题及答案人教版七年级数学上册第四章单元测试题及答案一、选择题(每小题3分,共30分)1.下列说法正确的是()A.①②2.(2013•浙江温州中考)下列各图中,经过折叠能围成一个立方体的是(C)3.在直线l上顺次取A、B、C三点,使得AB=5㎝,BC=3㎝,如果O是线段AC的中点,那么线段OB的长度是(C)4.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段架设;④把弯曲的公路改直,就能缩短路程.其中可用“两点之间,线段最短”来解释的现象有(B)5.如图所示,从A地到达B地,最短的路线是(A)6.(2013•云南昭通中考)如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是(B)7.如图所示的立体图形从上面看到的图形是(D)8.如果∠1与∠2互为补角,且∠1∠2,那么∠2的余角是(。
)C.(∠1-∠2)9.若∠=40.4°,∠=40°4′,则∠与∠的关系是(。
)D.以上都不对10.下列叙述正确的是()B.110°和90°的角互为补角二、填空题(每小题3分,共24分)11.(2013•山东枣庄中考)从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为12.12.(2012•山东菏泽中考)已知线段AB=8cm,在直线AB上画线段BC,使它等于3cm,则线段AC=5cm.13.若一个角的补角是这个角的余角的3倍,则这个角的度数是多少?答案:设这个角的度数为x,则它的补角为90-x,余角为180-x。
根据题意,有90-x=3(180-x),解得x=30.因此,这个角的度数为30°。
14.已知直线上有A、B、C三点,其中AB=3cm,BC=5cm,则AC的长度是多少?答案:根据三角形两边之和大于第三边的性质,知ACBC-AB=2cm。
新人教版初中数学七年级数学上册第四单元《几何图形初步》测试卷(答案解析)(2)

一、选择题1.下列说法错误的是( )A .若直棱柱的底面边长都相等,则它的各个侧面面积相等B .n 棱柱有n 个面,n 个顶点C .长方体,正方体都是四棱柱D .三棱柱的底面是三角形2.如图,点C 是线段AB 的中点,点D 是线段CB 上任意一点,则下列表示线段关系的式子不正确的是( )A .AB=2ACB .AC+CD+DB=ABC .CD=AD-12ABD .AD=12(CD+AB ) 3.一副三角板按如图方式摆放,且1∠的度数比2∠的度数小20︒,则2∠的度数为( )A .35︒B .40︒C .45︒D .55︒4.下列语句正确的有( )(1)线段AB 就是A 、B 两点间的距离;(2)画射线10AB cm =;(3)A ,B 两点之间的所有连线中,最短的是线段AB ;(4)在直线上取A ,B ,C 三点,若5AB cm =,2BC cm =,则7AC cm =. A .1个 B .2个 C .3个 D .4个5.如图,已知线段12AB =,延长线段AB 至点C ,使得12BC AB =,点D 是线段AC 的中点,则线段BD 的长是( ).A .3B .4C .5D .66.如图,AD 是△ABC 的角平分线,点O 在AD 上,且OE ⊥BC 于点E ,∠BAC=60°,∠C=80°,则∠EOD 的度数为( )A.20°B.30°C.10°D.15°7.如图,长度为12cm的线段AB的中点为M,C为线段MB上一点,且MC:CB=1:2,则线段AC的长度为()A.8cm B.6cm C.4cm D.2cm8.如图,点A、B、C是直线l上的三个定点,点B是线段AC的三等分点,AB=BC+4m,其中m为大于0的常数,若点D是直线l上的一动点,M、N分别是AD、CD的中点,则MN与BC的数量关系是()A.MN=2BC B.MN=BC C.2MN=3BC D.不确定9.一根直木棒长10厘米,棒上有刻度如图,若把它作为尺子,只测量一次,能测量的长度共有()A.7种B.6种C.5种D.4种10.如图,图中射线、线段、直线的条数分别为()A.5,5,1 B.3,3,2C.1,3,2 D.8,4,111.下列事实可以用“经过两点有且只有一条直线”来说明的是()A.从王庄到李庄走直线最近B.在正常情况下,射击时要保证瞄准的一只眼睛在准星和缺口确定的直线上,才能射中目标C.向远方延伸的铁路给我们一条直线的印象D.数轴是一条特殊的直线12.下列说法不正确的是()A.两条直线相交,只有一个交点B.两点之间,线段最短C.两点确定一条直线D.过平面上的任意三点,一定能作三条直线二、填空题13.如图,记以点A为端点的射线条数为x,以点D为其中一个端点的线段的条数为y, 的值为________.则x y14.看图填空.(1)AC=AD-_______=AB+_______,(2)BC+CD=_______=_______-AB,(3)AD=AC+___.15.用一个平面截三棱柱,最多可以截得________边形;用一个平面截四棱柱,最多可以截得________边形;用一个平面截五棱柱,最多可以截得________边形.试根据以上结论,猜测用一个平面去截n棱柱,最多可以截得________边形.16.科学知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面的这两个情景,请你做出判断.情景一:如图,从教学楼到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所.学数学知识来说明这个问题:_______________________________________________.情景二:农民兴修水利,开挖水渠,先在两端立桩拉线,然后沿线开挖,请你说出其中的道理:_______________________________________________________________________________ _.你赞同以上哪种做法,你认为应用科学知识为人类服务时应注意什么?17.魏老师去农贸市场买菜时发现,若把10千克的菜放在秤上,则指针盘上的指针转了180︒,第二天魏老师请同学们回答以下两个问题:(1)若把0.5千克的菜放在秤上,则指针转过________度;(2)若指针转了243︒,则这些菜共有________千克.18.将下列几何体分类,柱体有:______(填序号).19.如图,将一副三角板叠放一起,使直角的顶点重合于点O,则∠AOD +∠COB的度数为___________度.20.若1∠与2∠互补,2∠的余角是36︒,则1∠的度数是________.三、解答题21.射线OA ,OB ,OC ,OD ,OE 有公共端点O .(1)若OA 与OE 在同一直线上,如图(1),试写出图中小于平角的角.(2)如图(2),若108AOC ︒∠=,(072)COE n n ︒∠=<<,OB 平分AOE ∠,OD平分COE ∠,求BOD ∠的度数.22.P 是线段AB 上任一点,12AB cm =,C D 、两点分别从P B 、同时向A 点运动,且C 点的运动速度为2/cm s ,D 点的运动速度为3/cm s ,运动的时间为t s .(1)若8AP cm =,①运动1s 后,求CD 的长;②当D 在线段PB 上运动时,试说明2AC CD =;(2)如果2t s =时,1CD cm =,试探索AP 的值.23.如图是一个去掉盖子的长方体礼品盒的展开图(单位:cm ).从A ,B 两题中任选一题作答.A .该长方体礼品盒的容积为______3cm .B .如果把这个去掉盖子的礼品盒沿某些棱重新剪开,可以得到周长最大的展开图,则周长最大为____cm .24.如图,已知∠AOB=90°,∠EOF=60°,OE 平分∠AOB ,OF 平分∠BOC ,求∠AOC 和∠COB 的度数.25.如图,以直线AB 上一点O 为端点作射线OC ,使70AOC ∠=︒,在同一个平面内将一个直角三角板的直角顶点放在点O 处.(注:90DOE ∠=︒)(1)如图1,如果直角三角板DOE 的一边OD 放在射线OA 上,那么COE ∠的度数为______;(2)如图2,将直角三角板DOE 绕点O 按顺时针方向转动到某个位置,如果OC 恰好平分AOE ∠,求COD ∠的度数;(3)如图3,将直角三角板DOE 绕点O 任意转动,如果OD 始终在AOC ∠的内部,请直接用等式表示AOD ∠和COE ∠之间的数量关系.26.如图所示,长度为12cm 的线段AB 的中点为点M ,点C 将线段MB 分成:1:2MC CB =,求线段AC 的长度.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】A 、若直棱柱的底面边长都相等,则它的各个侧面面积相等,说法正确;B 、n 棱柱有n+2个面,n 个顶点,故原题说法错误;C 、长方体,正方体都是四棱柱,说法正确;D 、三棱柱的底面是三角形,说法正确;故选B .2.D解析:D【解析】解:A 、由点C 是线段AB 的中点,则AB=2AC ,正确,不符合题意;B 、AC+CD+DB=AB ,正确,不符合题意;C 、由点C 是线段AB 的中点,则AC=12AB ,CD=AD-AC=AD-12AB ,正确,不符合题意;D 、AD=AC+CD=12AB+CD ,不正确,符合题意.故选D . 3.D解析:D【分析】根据题意结合图形列出方程组,解方程组即可.【详解】解:由题意得,1290,2120∠+∠︒⎧⎨∠-∠︒⎩==,解得135,255.∠︒⎧⎨∠︒⎩==. 故选:D .【点睛】本题考查的是余角和补角的概念和性质,两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.4.A解析:A【分析】根据两点之间距离的定义可以判断A 、C ,根据射线的定义可以判断B ,据题意画图可以判断D .【详解】∵线段AB 的长度是A 、 B 两点间的距离,∴(1)错误;∵射线没有长度,∴(2)错误;∵两点之间,线段最短∴(3)正确;∵在直线上取A ,B ,C 三点,使得AB=5cm ,BC=2cm ,当C 在B 的右侧时,如图,AC=5+2=7cm当C 在B 的左侧时,如图,AC=5-2=3cm ,综上可得AC=3cm 或7cm ,∴(4)错误;正确的只有1个,故选:A .【点睛】本题考查了线段与射线的定义,线段的和差,熟记基本定义,以及两点之间线段最短是解题的关键.5.A解析:A【分析】根据题意可知BC=6,所以AC=18,由于D 是AC 中点,可得AD=9,从BD=AB-AD 就可求出线段BD 的长.【详解】由题意可知12AB =,且12BC AB =, 所以6BC =,18AC =.因为点D 是线段AC 的中点, 所以1118922AD AC ==⨯=, 所以1293BD AB AD =-=-=.故选A .【点睛】本题考查了两点间的距离以及中点的性质,根据图形能正确表达线段之间的和差关系是解决本题的关键.6.A解析:A【分析】首先根据三角形的内角和定理求得∠B ,再根据角平分线的定义求得∠BAD ,再根据三角形的一个外角等于和它不相邻的两个内角和求得∠ADC ,最后根据直角三角形的两个锐角互余即可求解.【详解】∵∠BAC=60°,∠C=80°,∴∠B=180°-∠BAC-∠C=40°,又∵AD 是∠BAC 的角平分线,∴∠BAD=12∠BAC=30°, ∴∠ADE=∠B+∠BAD=70°,又∵OE ⊥BC ,∴∠EOD=90°-∠ODE=90°-70°=20°.故选:A .【点睛】本题考查了三角形的内角和定理及其推论、角平分线的定义等知识,此类题要首先明确解题思路,再利用相关知识解答.7.A解析:A【分析】先根据点M 是AB 中点求出AM=BM=6cm ,再根据MC :CB=1:2求出MC 即可得到答案.【详解】∵点M 是AB 中点,∴AM=BM=6cm ,∵MC :CB=1:2,∴MC=2cm ,∴AC=AM+MC=6cm+2cm=8cm ,故选:A.【点睛】此题考查线段的中点性质,线段的和差计算,正确理解图形中线段之间的数量关系是解题的关键.8.C解析:C【分析】可用特殊值法,设坐标轴上的点A 为0,C 为12m ,求出B 的值,得出BC 的长度,设D 为x ,则M 为2x ,N 为122m x ,即可求出MN 的长度为6m ,可算出MN 与BC 的关系. 【详解】设坐标轴上的点A 为0,C 为12m ,∵AB =BC+4m ,∴B 为8m ,∴BC =4m ,设D 为x ,则M 为2x ,N 为122m x , ∴MN 为6m ,∴2MN =3BC ,故选:C .【点睛】本题考查了两点间的距离,解题关键是注意特殊值法的运用及方程思想的运用. 9.B解析:B【分析】根据棒上标的数字,找出这根木棒被2、7两点分成的线段的条数即可.【详解】如图,∵线段AD 被B 、C 两点分成AB 、AC 、AD 、BC 、BD 、CD 六条的线段∴能量的长度有:2、3、5、7、8、10,共6个,故选B .【点睛】本题考查的实质是找出已知图形上线段的条数.10.D解析:D【分析】直线没有端点,射线有一个端点,线段有两个端点.【详解】以A 点为端点的射线有2条,以B 为端点的射线有3条,以C 为端点的射线有2条,以D 为端点射线有1条,合计射线8条.线段:AB ,BC ,AC ,BD ,合计4条.直线:AC ,合计1条故本题 D.【点睛】直线没有端点,射线有一个端点,线段有两个端点.11.B解析:B【分析】根据两点确定一条直线进而得出答案.【详解】在正常情况下,射击时要保证瞄准的一只眼在准星和缺口确定的直线上,才能射中目标,这说明了两点确定一条直线的道理.故选B.【点睛】此题主要考查了直线的性质,利用实际问题与数学知识联系得出是解题关键. 12.D解析:D【解析】【分析】根据直线公理、线段公理进行逐一分析判断.【详解】A. 根据直线公理“两点确定一条直线”,则两条直线相交,只有一个交点,故该选项正确;B.两点之间,线段最短,是线段公理,故该选项正确;C. 两点确定一条直线,是直线公理,故该选项正确;D. 当三点共线时,则只能确定一条直线,故该选项错误.故选 D.【点睛】此题考查直线、射线、线段,直线的性质:两点确定一条直线,线段的性质:两点之间线段最短,解题关键在于掌握各性质定义.二、填空题13.【分析】先根据射线和线段的定义求出xy 的值再代入求解即可【详解】以点为端点的射线有射线AC 和射线AB 共两条故点为其中一个端点的线段有线段ADODBDCD 共四条故将代入中原式故答案为:【点睛】本题考查解析:2-【分析】先根据射线和线段的定义求出x ,y 的值,再代入求解即可.【详解】以点A 为端点的射线有射线AC 和射线AB ,共两条,故2x =点D 为其中一个端点的线段有线段AD 、OD 、BD 、CD ,共四条,故4y =将2x =,4y =代入x y -中原式242=-=-故答案为:2-.【点睛】本题考查了代数式的运算,掌握射线和线段的定义是解题的关键.14.CDBCBDADCD 【分析】根据线段之间的和差关系进行解答即可得答案【详解】(1)AC=AD-CD=AB+BC (2)BC+CD=BD=AD-AB (3)AD=AC+CD 故答案为:CD ;BC ;BD ;AD解析:CD BC BD AD CD【分析】根据线段之间的和差关系进行解答即可得答案.【详解】(1)AC=AD-CD=AB+BC,(2)BC+CD=BD=AD-AB,(3)AD=AC+CD,故答案为:CD;BC;BD;AD;CD【点睛】本题主要考查线段之间的和差关系,灵活运用线段的和、差、倍、分转化线段之间的数量关系是解题关键.15.五六七【分析】三棱柱有五个面用平面去截三棱柱时最多与五个面相交得五边形因此最多可以截得五边形;四棱柱有六个面用平面去截三棱柱时最多与六个面相交得六边形因此最多可以截得六边;五棱柱有七个面用平面去截三n .解析:五,六,七,2【分析】三棱柱有五个面,用平面去截三棱柱时最多与五个面相交得五边形.因此最多可以截得五边形;四棱柱有六个面,用平面去截三棱柱时最多与六个面相交得六边形.因此最多可以截得六边;五棱柱有七个面,用平面去截三棱柱时最多与七个面相交得七边形.因此最多可以截得七边形;n棱柱有n+2个面,用平面去截三棱柱时最多与n+2个面相交得n+2边形.因此最多可以截得n+2边形.【详解】用一个平面去截三棱柱最多可以截得5边形,用一个平面去截四棱柱最多可以截得6边形,用一个平面去截五棱柱最多可以截得7边形,试根据以上结论,用一个平面去截n棱柱,最多可以截得n+2边形.故答案为五;六;七; n+2.【点睛】此题考查截一个几何体,解题关键在于熟练掌握常见几何体的截面图形.16.情景一:两点之间线段最短;情景二:两点确定一条直线;赞同第二种应用科学知识为人类服务时应注意保护周边的环境等(合理即可)【解析】【分析】学校和图书馆两根立桩之间的路线可看做是一条线段接下来根据根据线解析:情景一:两点之间,线段最短;情景二:两点确定一条直线;赞同第二种,应用科学知识为人类服务时,应注意保护周边的环境等.(合理即可)【解析】【分析】学校和图书馆、两根立桩之间的路线可看做是一条线段,接下来,根据根据线段的性质来分析得出即可.【详解】第一个情景是根据两点之间线段最短的原理来做的,第二个是两点确定一条直线;我赞同第二种做法.我们利用科学的同时,必须注意保护我们周围赖以生存的生态环境.故答案为:两点之间线段最短;两点确定一条直线;我赞同第二种做法.我们利用科学的同时,必须注意保护我们周围赖以生存的生态环境.【点睛】此题考查两点之间线段最短的应用,两点确定一条直线,掌握线段的性质是解题的关键. 17.135【分析】(1)算出秤上放1千克菜转过的角度为多少乘以05即可;(2)让243°除以1千克菜转过的角度即可【详解】解:(1)=18°05×18°=9°05千克的菜放在秤上指针转过9°;(2)24解析:13.5【分析】(1)算出秤上放1千克菜转过的角度为多少,乘以0.5即可;(2)让243°除以1千克菜转过的角度即可.【详解】解:(1)18010=18°,0.5×18°=9°,0.5千克的菜放在秤上,指针转过9°;(2)243°÷18°=13.5(千克),答:共有菜13.5千克.故答案为9,13.5【点睛】本题考查了角度计算的应用,解决本题的关键是得到秤上放1千克菜转过的角度为多少.18.(1)(2)(3)【分析】解这类题首先要明确柱体的概念和定义然后根据图示进行解答【详解】柱体分为圆柱和棱柱所以柱体有:(1)(2)(3)故答案为(1)(2)(3)【点睛】此题主要考查了认识立体图形几解析:(1)(2)(3)【分析】解这类题首先要明确柱体的概念和定义,然后根据图示进行解答.【详解】柱体分为圆柱和棱柱,所以柱体有:(1)(2)(3).故答案为(1)(2)(3).【点睛】此题主要考查了认识立体图形,几何体的分类,一般分为柱体、锥体和球,注意球和圆的区别,球是立体图形,圆是平面图形.19.180【分析】根据角度的关系∠AOD+∠COB=∠COD+∠AOB据此即可求解【详解】∠AOD+∠COB=∠COD+∠AOC+∠COB=∠COD+∠AOB=90°+90°=180°故答案是:180【解析:180【分析】根据角度的关系∠AOD+∠COB=∠COD+∠AOB ,据此即可求解.【详解】∠AOD+∠COB=∠COD+∠AOC+∠COB =∠COD+∠AOB=90°+90°=180°.故答案是:180.【点睛】本题考查了三角板中角度的计算,正确把∠AOD+∠COB 转化成∠COD+∠AOB 是解决本题的关键.20.【分析】首先根据∠1与∠2互补可得∠1+∠2=180°再表示出∠1的余角90°-(180°-∠2)即可得到结论【详解】∵的余角是∴∵与互补∴故答案为126°【点睛】本题考查了余角和补角关键是掌握余角解析:126︒【分析】首先根据∠1与∠2互补可得∠1+∠2=180°,再表示出∠1的余角90°-(180°-∠2),即可得到结论.【详解】∵2∠的余角是36︒,∴2903654︒︒︒∠=-=.∵1∠与2∠互补,∴118054126︒︒︒∠=-=.故答案为126°.【点睛】本题考查了余角和补角,关键是掌握余角和补角的定义.三、解答题21.(1)AOD ∠,AOC ∠,AOB ∠,∠BOE ,BOD ∠,BOC ∠,COE ∠,COD ∠,DOE ∠;(2)54︒【分析】(1)根据角的定义即可解决;(2)利用角平分线的性质即可得出∠BOD=12∠AOC+12∠COE ,进而求出即可. 【详解】(1)题图(1)中小于平角的角有AOD ∠,AOC ∠,AOB ∠,∠BOE ,BOD ∠,BOC ∠,COE ∠,COD ∠,DOE ∠.(2)因为OB 平分AOE ∠,OD 平分COE ∠,108AOC ︒∠=,(072)COE n n ︒∠=<<,所以1111()2222BOD BOE DOE AOE COE AOE COE AOC ∠=∠-∠=∠-∠=∠-∠=∠. 因为108AOC ∠=︒,所以54BOD ∠=︒【点睛】 本题考查了角的平分线的定义和角的有关计算,本题中将所有锐角的和转化成与∠AOE 、∠BOD 和∠BOD 的关系是解题的关键,22.(1)①3cm ;②见解析;(2)9AP =或11cm.【分析】(1)①先求出PB 、CP 与DB 的长度,然后利用CD=CP+PB-DP 即可求出答案;②用t 表示出AC 、DP 、CD 的长度即可求证AC=2CD ;(2)t=2时,求出CP 、DB 的长度,由于没有说明点D 再C 点的左边还是右边,故需要分情况讨论.【详解】解:(1)①由题意可知:212,313CP cm DB cm =⨯==⨯=,∵8,12AP cm AB cm ==,∴4PB AB AP cm =-=,∴2433CD CP PB DB cm =+-=+-=;②∵8,12AP AB ==,∴4,82BP AC t ==-,∴43DP t =-,∴2434CD DP CP t t t =+=+-=-,∴2AC CD =;(2)当2t =时,224,326CP cm DB cm =⨯==⨯=,当点D 在C 的右边时,如图所示:由于1CD cm =,∴7CB CD DB cm =+=,∴5AC AB CB cm =-=,∴9AP AC CP cm =+=,当点D 在C 的左边时,如图所示:∴6AD AB DB cm =-=,∴11AP AD CD CP cm =++=,综上所述,9AP =或11cm.【点睛】本题考查的知识点是线段的简单计算以及线段中动点的有关计算.此题的难点在于根据题目画出各线段.23.A:800;B:146【分析】A:根据题意可以得到长方体的长为16宽为10高为5,即可求出体积.B:依据题意展开,计算即可.【详解】解:A:根据题意 高为20-15=5 宽为15-5=10 长为 26-10=16V=16×10×5=800B:依据题意展开如图周长=5×2+16×6+10×4=146【点睛】此题主要考查了立体图形体积计算及最大展开周长,注意最大展开周长一定是最长棱长最多的.24.120°,30°【分析】先根据角平分线,求得∠BOE 的度数,再根据角的和差关系,求得BOF ∠的度数,最后根据角平分线,求得BOC ∠、AOC ∠的度数.【详解】∵OE 平分∠AOB ,∠AOB=90°∴∠BOE=∠AOB =45°又∵∠EOF=60°∴∠BOF=∠EOF -∠BOE= 15°又∵OF 平分∠BOC∴∠BOC=2∠BOF=30°∴∠AOC=∠AOB +∠BOC=120°故∠AOC=120°,∠COB=30°.【点睛】本题主要考查了角平分线的定义,根据角的和差关系进行计算是解题的关键.注意:也可以根据AOC ∠的度数是EOF ∠度数的2倍进行求解.25.(1)20︒;(2)20︒;(3)20COE AOD ∠-∠=︒或20COE AOD ∠=︒+∠.【分析】(1)如图1,如果直角三角板DOE 的一边OD 放在射线OA 上,则∠COE =20°; (2)由角平分线可得70COE AOC ∠=∠=︒,再利用角的和差进行计算即可; (3)分别用∠COE 及∠AOD 的式子表达∠COD ,进行列式即可.【详解】解:(1)∵90DOE ∠=︒,70AOC ∠=︒∴907020COE DOE AOC =∠-∠=︒-︒=︒∠故答案为:20︒(2)∵OC 平分AOE ∠,70AOC ∠=︒,∴70COE AOC ∠=∠=︒,∵90DOE ∠=︒,∴907020COD DOE COE ∠=∠-∠=︒-︒=︒.(3)∵90COD DOE COE COE =∠-∠=︒-∠∠,70COD AOC AOD AOD =∠-∠=︒-∠∠∴9070COE AOD ︒-∠=︒-∠∴20COE AOD ∠-∠=︒或20COE AOD ∠=︒+∠.故答案为:20COE AOD ∠-∠=︒或20COE AOD ∠=︒+∠.【点睛】本题考查了角的和差关系,准确表达出角的和差关系是解题的关键.26.8cm【解析】【分析】设MC =xcm ,由MC :CB =1:2得到CB =2xcm ,则MB =3x ,根据M 点是线段AB 的中点,AB =12cm ,得到AM =MB 12=AB 12=⨯12=3x ,可求出x 的值,又AC =AM +MC =4x ,即可得到AC 的长.【详解】设MC =xcm ,则CB =2xcm ,∴MB =3x .∵M 点是线段AB 的中点,AB =12cm ,∴AM =MB 12=AB 12=⨯12=3x , ∴x =2,而AC =AM +MC ,∴AC =3x +x =4x =4×2=8(cm ).故线段AC 的长度为8㎝.【点睛】本题考查了两点间的距离:两点的连线段的长叫两点间的距离.也考查了方程思想的运用.。
人教版七年级上册数学《几何图形初步》单元检测卷带答案

人教版数学七年级上学期第四章单元测试考试时间:100分钟;满分:100分第Ⅰ卷(选择题)一.选择题(共10小题,满分30分,每小题3分)1.(2018秋•密云区期末)下列四个几何体中,是三棱柱的为()A.B.C.D.2.(2017秋•宿州期末)雨滴滴下来形成雨丝属于下列哪个选项的实际应用()A.点动成线B.线动成面C.面动成体D.以上都不对3.(2018秋•竞秀区期末)”在山区建设公路时,时常要打通一条隧道,就能缩短路程”其中蕴含的数学道理是()A.两点之间,线段最短B.两点确定一条直线C.过一点,有无数条直线D.连接两点之间的线段的长度是两点间的距离4.(2019春•文登区期末)下列说法正确的是()A.延长直线ABB.延长射线ABC.反向延长射线ABD.延长线段AB到点C,使AC=BC5.(2018秋•榆林期末)如图,右边的平面图形绕虚线l旋转一周,可以得到左边图形的是()A.B.C.D.6.(2018秋•临沧期末)如图,下列说法中不正确的是()A.∠1与∠AOB是同一个角B.∠AOC也可以用∠O表示C.∠β=∠BOC D.图中有三个角7.(2019春•红河州期末)点A,B,C在同一直线上,已知AB=3cm,BC=1cm,则线段AC的长是()A.2cm B.3cm C.4cm D.2cm或4cm8.(2019春•岱岳区期末)如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC﹣DB,②CD AB,③CD=AD﹣BC,④BD=2AD﹣AB.其中正确的等式编号是()A.①②③④B.①②③C.②③④D.②③9.(2019春•开福区校级期末)嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km(最小圆的半径是1km),下列关于小艇A,B的位置描述,正确的是()A.小艇A在游船的北偏东60°方向上,且与游船的距离是3kmB.游船在小艇A的南偏西60°方向上,且与小艇A的距离是3kmC.小艇B在游船的北偏西30°方向上;且与游船的距离是2kmD.游船在小艇B的南偏东60°方向上,且与小艇B的距离是2km10.(2018秋•嘉祥县期末)观察下列图形,并阅读相关文字那么20条直线相交,最多交点的个数是()A.190 B.210 C.380 D.420第Ⅱ卷(非选择题)二.填空题(共6小题,满分24分,每小题4分)11.(2018秋•番禺区期末)如图,将甲,乙两个尺子拼在一起,两端重合.若甲尺经校订是直的,那么乙尺就一定不是直的;用数学知识解释这种生活现象为.12.(2019春•莱州市期末)如图,把一条绳子折成3折,用剪刀从中剪断,得到几条绳子.13.(2019春•浦东新区期末)计算:48°59′+67°31′﹣21°12′=.14.(2019春•浦东新区期末)在直线MN上取A、B两点,使AB=10cm,再在线段AB上取一点C,使AC =2cm,P、Q分别是AB、AC的中点,则PQ=cm.15.(2018秋•福田区校级期末)当时间为3点30分时,时钟上时针与分针所成夹角的度数是.16.(2018秋•孝义市期末)已知∠AOB=60°,以点O为端点作射线OC,使∠BOC=20°,再作∠AOC的平分线OD,则∠AOD的度数为.评卷人得分三.解答题(共6小题,满分46分)17.(6分)(2018秋•龙岩期末)根据语句画出图形:如图,已知A、B、C三点.①画线段AB;②画射线AC;③画直线BC;④取AB的中点P,连接PC.18.(6分)(2018秋•天心区校级期末)角度计算题:如图,已知O为AD上一点,∠AOB与∠AOC互补,ON平分∠AOB,OM平分∠AOC,若是∠MON=42°,求∠AOB与∠AOC的度数.19.(8分)(2018秋•宁德期末)图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.(1)这个三棱柱有条棱,有个面;(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开条棱,需剪开棱的棱长的和的最大值为cm.20.(8分)(2018秋•龙泉驿区期末)如图,已知∠AOB内部有三条射线,其中OE平分角∠BOC,OF平分∠AOC.(1)如图1,若∠AOB=120°,∠AOC=50°,求∠EOF的度数;(2)如图2,若∠AOB=α,∠AOC=β,求∠EOF的度数.21.(8分)(2018秋•绍兴期末)如图①点C在线段AB上,点M、N分别是AC、BC的中点,且满足AC =a,BC=b.(1)若a=4 cm,b=6 cm,求线段MN的长;(2)若点C为线段AB上任意一点,其它条件不变,你能猜想MN的长度吗?直接写出你的猜想结果;(3)若点C在线段AB的延长线上,其它条件不变,你能猜想MN的长度吗?请在图②中画出图形,写出你的猜想并说明理由.22.(10分)(2018秋•永新县期末)如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一直角边OM在射线OB上,另一直角边ON在直线AB的下方,(1)将图①中的三角板绕点O逆时针方向旋转至图②,使边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON大小;(2)将图①中的三角板绕点O逆时针方向旋转至图③.①如果ON恰好是∠AOC的角平分线,则∠AOM﹣∠NOC的度数为;②如果ON始终在∠AOC的内部,∠AOM﹣∠NOC的度数不会变化,请猜测出∠AOM﹣∠NOC的度数并说明理由.参考答案一.选择题(共10小题,满分30分,每小题3分)1.(2018秋•密云区期末)下列四个几何体中,是三棱柱的为()A.B.C.D.【解析】解:A、该几何体为四棱柱,不符合题意;B、该几何体为四棱锥,不符合题意;C、该几何体为圆柱,不符合题意;D、该几何体为三棱柱,符合题意;故选:D.【点睛】考查了认识立体图形的知识,解题的关键是能够认识各个几何体,难度不大.2.(2017秋•宿州期末)雨滴滴下来形成雨丝属于下列哪个选项的实际应用()A.点动成线B.线动成面C.面动成体D.以上都不对【解析】解:雨滴滴下来形成雨丝属于点动成线,故选:A.【点睛】此题考查点、线、面、体,关键是根据点动成线解答.3.(2018秋•竞秀区期末)”在山区建设公路时,时常要打通一条隧道,就能缩短路程”其中蕴含的数学道理是()A.两点之间,线段最短B.两点确定一条直线C.过一点,有无数条直线D.连接两点之间的线段的长度是两点间的距离【解析】解:由线段的性质可知,”在山区建设公路时,时常要打通一条隧道,就能缩短路程”这其中蕴含的数学道理是:两点之间,线段最短.故选:A.【点睛】本题考查的是线段的性质,即两点之间线段最短.4.(2019春•文登区期末)下列说法正确的是()A.延长直线ABB.延长射线ABC.反向延长射线ABD.延长线段AB到点C,使AC=BC【解析】解:A.延长直线AB,说法错误;B.延长射线AB,说法错误;C.反向延长射线AB,说法正确;D.延长线段AB到点C,则AC>BC,故本选项错误;故选:C.【点睛】本题主要考查了直线、射线、线段的概念,注意用两个字母表示射线时,端点的字母放在前边.5.(2018秋•榆林期末)如图,右边的平面图形绕虚线l旋转一周,可以得到左边图形的是()A.B.C.D.【解析】解:由图可知,只有D选项图形绕直线l旋转一周得到如图所示立体图形,故选:D.【点睛】本题考查了点、线、面、体,熟悉常见图形的旋转得到立体图形是解题的关键.6.(2018秋•临沧期末)如图,下列说法中不正确的是()A.∠1与∠AOB是同一个角B.∠AOC也可以用∠O表示C.∠β=∠BOC D.图中有三个角【解析】解:A、∠1与∠AOB是同一个角,说法正确;B、∠AOC也可用∠O来表示,说法错误;C、∠β与∠BOC是同一个角,说法正确;D、图中共有三个角:∠AOB,∠AOC,∠BOC,说法正确;故选:B.【点睛】此题主要考查了角的概念,关键是掌握角的表示方法.7.(2019春•红河州期末)点A,B,C在同一直线上,已知AB=3cm,BC=1cm,则线段AC的长是()A.2cm B.3cm C.4cm D.2cm或4cm【解析】解:本题有两种情形:(1)当点C在线段AB上时,如图,AC=AB﹣BC,又∵AB=3cm,BC=1cm,∴AC=3﹣1=2cm;(2)当点C在线段AB的延长线上时,如图,AC=AB+BC,又∵AB=3cm,BC=1cm,∴AC=3+1=4cm.故线段AC=2cm或4cm.故选:D.【点睛】考查了两点间的距离,在未画图类问题中,正确画图很重要,本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.8.(2019春•岱岳区期末)如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC﹣DB,②CD AB,③CD=AD﹣BC,④BD=2AD﹣AB.其中正确的等式编号是()A.①②③④B.①②③C.②③④D.②③【解析】解:①点C是AB的中点,AC=CB.②点C是AB的中点,∴,又∵点D是BC的中点,∴CD.故②正确;③点C是AB的中点,AC=CB.CD=AD﹣AC=AD﹣BC,故③正确;④2AD﹣AB=2AC+2CD﹣AB=2CD=BC,故④错误.故正确的有①②③.故选:B.【点睛】此题考查的是两点间的距离的计算,掌握线段中点的概念和性质、灵活运用数形结合思想是解题的关键.9.(2019春•开福区校级期末)嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km(最小圆的半径是1km),下列关于小艇A,B的位置描述,正确的是()A.小艇A在游船的北偏东60°方向上,且与游船的距离是3kmB.游船在小艇A的南偏西60°方向上,且与小艇A的距离是3kmC.小艇B在游船的北偏西30°方向上;且与游船的距离是2kmD.游船在小艇B的南偏东60°方向上,且与小艇B的距离是2km【解析】解:A、小艇A在游船的北偏东30°,且距游船3km,故本选项不符合题意;B、游船在小艇A的南偏西30°方向上,且与小艇A的距离是3km,故本选项不符合题意;C、小艇B在游船的北偏西60°,且距游船2km,故本选项不符合题意;D、游船在小艇B的南偏东60°方向上,且与小艇B的距离是2km,故本选项符合题意.故选:D.【点睛】本题考查了方向角.熟练掌握平面内特殊位置的点的坐标特征.理解方向角的表示方法.10.(2018秋•嘉祥县期末)观察下列图形,并阅读相关文字那么20条直线相交,最多交点的个数是()A.190 B.210 C.380 D.420【解析】解:设直线有n条,交点有m个.有以下规律:直线n条交点m个2 13 1+24 1+2+3…n m=1+2+3+…+(n﹣1),20条直线相交有190个.故选:A.【点睛】此题主要考查了相交线,关键是找出直线条数与交点个数的计算公式.二.填空题(共6小题,满分24分,每小题4分)11.(2018秋•番禺区期末)如图,将甲,乙两个尺子拼在一起,两端重合.若甲尺经校订是直的,那么乙尺就一定不是直的;用数学知识解释这种生活现象为两点确定一条直线.【解析】解:∵甲尺是直的,两尺拼在一起两端重合,∴甲尺经校订是直的,那么乙尺就一定不是直的,用数学知识解释这种生活现象为:两点确定一条直线.故答案为:两点确定一条直线.【点睛】本题考查的是直线的性质,熟知两点确定一条直线是解答此题的关键.12.(2019春•莱州市期末)如图,把一条绳子折成3折,用剪刀从中剪断,得到几条绳子4.【解析】解:如图折成3折,有两个拐点,而不是折叠三次,故能得到4条绳子.【点睛】解题的关键是看清图中折的方式,从而作出判断.注意结合图形解题的思想.13.(2019春•浦东新区期末)计算:48°59′+67°31′﹣21°12′=95°18′.【解析】解:48°59′+67°31′﹣21°12′=116°30′﹣21°12′=95°18′.故答案为:95°18′【点睛】本题主要考查了度、分、秒的四则混合运算,是角度计算中的一个难点,注意以60为进制即可,难度适中.14.(2019春•浦东新区期末)在直线MN上取A、B两点,使AB=10cm,再在线段AB上取一点C,使AC =2cm,P、Q分别是AB、AC的中点,则PQ=4cm.【解析】解:如图,∵AB=10cm,P为AB的中点∴AP=PB=5cm∵AC=2cm,∴CP=3cm∵Q为AC的中点∴QC=AQ=1cm∴PQ=QC+CP=1+3=4cm故答案为:4【点睛】此题主要考查两点间的距离(线段长度)计算,此类题目,通常利用图形结合进行解题.15.(2018秋•福田区校级期末)当时间为3点30分时,时钟上时针与分针所成夹角的度数是75°.【解析】解:时针从数3开始30分转了30×0.5°=15°,分针从数字12开始30分转了30×6°=180°,所以3点30分,时针与分针所成夹角的度数=180°﹣90°﹣15°=75°.故答案为:75°.【点睛】本题考查了钟面角:钟面被分成12大格,每大格30°;分针每分钟转6°,时针每分钟转0.5°.16.(2018秋•孝义市期末)已知∠AOB=60°,以点O为端点作射线OC,使∠BOC=20°,再作∠AOC 的平分线OD,则∠AOD的度数为20°或40°.【解析】解:(1)当OC在∠AOB的内部时,如图1所示:∵∠BOC=20°,∠AOB=60°,∠AOB=∠AOC+∠BOC,∴∠AOC=60°﹣20°=40°,又∵OD是∠AOC的平分线,∴∠AOD=∠COD20°;(2)当OC在∠AOB的外部时,如图2所示:∵∠AOC=∠AOB+∠BOC,∠AOB=60°,∠BOC=20°,∴AOC=80°,又∵OD是∠AOC的平分线,∴∠AOD=∠COD40°;综合所述∠AOD的度数有两个,故答案为20°或40°.【点睛】本题综合了角平分线定义和角的和差知识,重点掌握角的计算,难点是用分类计算角的大小,易掉角的外部这一种情况.三.解答题(共6小题,满分46分)17.(6分)(2018秋•龙岩期末)根据语句画出图形:如图,已知A、B、C三点.①画线段AB;②画射线AC;③画直线BC;④取AB的中点P,连接PC.【解析】解:如图.【点睛】本题考查了直线、射线、线段,正确区分直线、线段、射线是解题关键.18.(6分)(2018秋•天心区校级期末)角度计算题:如图,已知O为AD上一点,∠AOB与∠AOC互补,ON平分∠AOB,OM平分∠AOC,若是∠MON=42°,求∠AOB与∠AOC的度数.【解析】解:设∠AOB=x°,因为∠AOC与∠AOB互补,则∠AOC=180°﹣x°.由题意,得42.∴180﹣x﹣x=84,∴﹣2x=﹣96,解得x=48,故∠AOB=48°,∠AOC=132°.【点睛】本题考查补角的定义,角平分线的定义,及角的运算.在图形中,找补角关系时,除了借助图形外,还需考虑等量关系即有没有相等的角.19.(8分)(2018秋•宁德期末)图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.(1)这个三棱柱有9条棱,有5个面;(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开5条棱,需剪开棱的棱长的和的最大值为31cm.【解析】解:(1)这个三棱柱有条9棱,有个5面;故答案为:9,5;(2)如图;(3)由图形可知:没有剪开的棱的条数是4条,则至少需要剪开的棱的条数是:9﹣4=5(条).故至少需要剪开的棱的条数是5条.需剪开棱的棱长的和的最大值为:7×3+5×2=31(cm).故答案为:5,31.【点睛】本题主要考查的是认识立体图形,明确n棱柱有n个侧面,2个底面,3n条棱,2n个顶点;能够数出三棱柱没有剪开的棱的条数是解答此题的关键.20.(8分)(2018秋•龙泉驿区期末)如图,已知∠AOB内部有三条射线,其中OE平分角∠BOC,OF平分∠AOC.(1)如图1,若∠AOB=120°,∠AOC=50°,求∠EOF的度数;(2)如图2,若∠AOB=α,∠AOC=β,求∠EOF的度数.【解析】解:(1)∵OF平分∠AOC,∴∠COF∠AOC30°=15°,∵∠BOC=∠AOB﹣∠AOC=120°﹣30°=90°,OE平分∠BOC,∴∠EOC∠BOC=45°,∴∠EOF=∠COF+∠EOC=60°;(2)∵OF平分∠AOC,∴∠COF∠AOC,同理,∠EOC∠BOC,∴∠EOF=∠COF+∠EOC∠AOC∠BOC(∠AOC+∠BOC)∠AOBα.【点睛】本题考查了角平分线的性质,以及角度的计算,正确理解角平分线的定义是关键.21.(8分)(2018秋•绍兴期末)如图①点C在线段AB上,点M、N分别是AC、BC的中点,且满足AC =a,BC=b.(1)若a=4 cm,b=6 cm,求线段MN的长;(2)若点C为线段AB上任意一点,其它条件不变,你能猜想MN的长度吗?直接写出你的猜想结果;(3)若点C在线段AB的延长线上,其它条件不变,你能猜想MN的长度吗?请在图②中画出图形,写出你的猜想并说明理由.【解析】解:(1)∵M、N分别是AC、BC的中点,∴MC AC,CN BC,∴MN=MC+CNAC BC4 6=5cm,所以MN的长为5cm.(2)同(1),MN AC CB(AC+CB)(a+b).(3)图如右,MN(a﹣b).理由:由图知MN=MC﹣NCAC BCa b(a﹣b).【点睛】本题主要考查线段中点的定义,线段的中点把线段分成两条相等的线段.22.(10分)(2018秋•永新县期末)如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一直角边OM在射线OB上,另一直角边ON在直线AB的下方,(1)将图①中的三角板绕点O逆时针方向旋转至图②,使边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON大小;(2)将图①中的三角板绕点O逆时针方向旋转至图③.①如果ON恰好是∠AOC的角平分线,则∠AOM﹣∠NOC的度数为30°;②如果ON始终在∠AOC的内部,∠AOM﹣∠NOC的度数不会变化,请猜测出∠AOM﹣∠NOC的度数并说明理由.【解析】解:(1)∵OM平分∠BOC,∠BOC=120°,∴∠BOM=∠MON=60°,∵∠MON=90°,∴∠BON=∠MON﹣∠BOM=90°﹣60°=30°;(2)①∠AOM﹣∠NOC=30°;故答案为:30°②∠AOM﹣∠NOC=30°,理由如下:∵∠AOM=∠MON﹣∠AON=90°﹣∠AON,∠NOC=∠AOC﹣∠AON=60°﹣∠AON,∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.【点睛】本题考查了角平分线的定义,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.。
2019-2020学年人教版初中数学七年级(上)《第4章几何图形初步》单元测试卷解析版

2019学年人教版初中数学七年级(上)《第4章几何图形初步》单元测试卷一.选择题(共10小题)1.下列表述能确定一个地点的位置的是()A.北偏西45°B.东北方向C.距学校200m D.学校正南1000m2.下列图形中表示北偏东60°的射线是()A.B.C.D.3.如图,是某住宅小区平面图,点B是某小区“菜鸟驿站”的位置,其余各点为居民楼,图中各条线为小区内的小路,从居民楼点A到“菜鸟驿站”点B的最短路径是()A.A﹣C﹣G﹣E﹣B B.A﹣C﹣E﹣B C.A﹣D﹣G﹣E﹣B D.A﹣F﹣E﹣B4.如图线段AB和线段CD,在平面内找一点P,使得它到四端点的距离和P A+PB+PC+PD最小,则点P()A.线段AB的中点B.线段CD的中点C.线段AB和线段CD的交点D.线段AD和线段BC的交点5.如图,下列关于图中线段之间的关系一定正确的是()A.x=2x+2b﹣c B.c﹣b=2a﹣2b C.x+b=2a+c﹣b D.x+2a=3c+2b6.如图,AB⊥AC,AD⊥BC垂足分别为A,D,图中互余的角共有()A.2对B.3对C.4对D.5对7.如果∠α和∠β互补,且∠α<∠β,则下列表示∠α的余角的式子中①90°﹣∠α;②∠β﹣90°③(∠α+∠β)④(∠β﹣∠α)其中正确的有()A.1个B.2个C.3个D.4个8.如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=40°,射线OM平分∠BOC,ON平分∠AOC,则∠MON的度数为()A.45°B.65°C.50°D.25°9.如图,矩形纸片ABCD,M为AD边的中点将纸片沿BM、CM折叠,使A点落在A1处,D点落在D1处,若∠1=30°,则∠BMC=()A.75°B.150°C.120°D.105°10.如图,图1和图2中,两个剪刀张开的角度α和β的大小关系为()A.α>βB.α<βC.α=βD.不能确定二.填空题(共6小题)11.矩形长和宽分别为8cm、6cm,以其中一边所在直线为轴旋转一周,得到的几何体的底面积是.12.如图是一个正方体的展开图,将它折叠成正方体后,字母B的对面是.(用图中字母表示)13.如图,已知A、B、C三点在同一直线上,AB=24m,BC=AB,E是AC的中点,D是AB的中点,则DE的长.14.点A、B、C在直线l上,AB=4cm,BC=6cm,点E是AB中点,点F是BC的中点,EF=.15.将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕.若∠ABE=30°,则∠DBC为度.16.如图将一副三角板的直角顶点重合,摆放在桌面上,若∠AOC=110°,则∠BOD=°.三.解答题(共7小题)17.做大小两个长方体纸盒,尺寸如下(单位:cm)(1)做这两个纸盒共用料多少平方厘来?(2)做大纸盒比做小纸盒多用料多少平方厘米?(3)若a=6,b=5,c=3,则大纸盒的体积是多少cm3?18.邮递员骑摩托车从邮局出发在一条东西向的道路上送快递,他先向西骑行2千米到达A村,继续向西骑行3千米到达B村,然后向东骑行9千米到达C村,最后回到邮局.(1)规定郎局为原点,向东为正方向,1千米为1个单位长度,画出数轴并在数轴上标出A、B、C三个村子的位置;(2)求C村到A村的距离;(3)若摩托车每10千米需用1.5升汽油邮递员从邮局出发到最后回到邮局时,一共用了多少升汽油?19.如图,圆柱的高为15cm,全面积(也称表面积)为200π平方厘米,则圆柱底面半径为多少?20.一个六棱柱模型如所示,它的底面边长都是6cm,侧棱长4cm,观察这个模型,回答下列问题:(1)这个六棱柱的几个面分别是什么形状?哪些面的形状、大小完全相同?(2)这个六棱柱的所有侧面的面积之和是多少?21.已知∠AOB=108°,∠BOC=22°,射线OD、OE分别是∠AOB和∠BOC的平分线,求∠DOE的度数.22.数形结合(1)如图已知线段AB=10cm,点N在AB上,NB=2cm,M是AB的中点,那么线段MN的长为多少?(2)如图所示,射线OA的方向是北偏东15.8°,射线OB的方向是北偏西40°30',若∠AOC=∠AOB,则射线OC的方向是北偏东多少度?23.如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一直角边OM在射线OB上,另一直角边ON在直线AB的下方,(1)将图①中的三角板绕点O逆时针方向旋转至图②,使边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON大小;(2)将图①中的三角板绕点O逆时针方向旋转至图③.①如果ON恰好是∠AOC的角平分线,则∠AOM﹣∠NOC的度数为;②如果ON始终在∠AOC的内部,∠AOM﹣∠NOC的度数不会变化,请猜测出∠AOM﹣∠NOC的度数并说明理由.2019学年人教版初中数学七年级(上)《第4章几何图形初步》单元测试卷参考答案与试题解析一.选择题(共10小题)1.【解答】解:确定一个地点的位置需要两个条件:方向和距离,符合条件的只有D选项.故选:D.2.【解答】解:北偏东60°就是从北向东偏60°,即从上往右偏60°,故选:A.3.【解答】解:由题意可得BE是必须经过的路段,∴由两点之间线段最短,可得点A到点E的最短路径A﹣F﹣E,∴从居民楼点A到“菜鸟驿站”点B的最短路径是A﹣F﹣E﹣B,故选:D.4.【解答】解:线段AB和线段CD,在平面内找一点P,使得它到四端点的距离和P A+PB+PC+PD最小,则点P 是线段AD和线段BC的交点,故选:D.5.【解答】解:∵x﹣c+2b=2a,∴x+2a=2x+2b﹣c,故选项A错误;∵2a﹣2b=x﹣c,故选项B错误;∵x+b=2a+c﹣b,故选项C正确;∵2a﹣2b=x﹣c,∴﹣x+2a=﹣c+2b,故选项D错误,故选:C.6.【解答】解:在Rt△ABC中,∵AD⊥BC于D,∴∠B+∠C=90°,∠B+∠BAD=90°,∠BAD+∠CAD=90°,∠CAD+∠C=90°,则互余的角共有4个.故选:C.7.【解答】解:∵∠α和∠β互补,∴∠α+∠β=180°,∴∠α=180°﹣∠β,于是有:∠α的余角为:90°﹣∠α,故①正确,∠α的余角为:90°﹣∠α=90°﹣(180°﹣∠β)=∠β﹣90°,故②正确,∠α的余角为:90°﹣∠α=∠α+∠β﹣∠α=∠β﹣∠α,故④正确,而(∠α+∠β)=90°,而∠α不一定是直角,因此③不正确,因此正确的有①②④,故选:C.8.【解答】解:∵∠AOB=90°,且∠AOC=40°,∴∠COB=∠AOB+∠AOC=90°+40°=130°,∵OM平分∠BOC,∴∠BOM=∠BOC=65°,∴∠AOM=∠AOB﹣∠BOM=25°,∵ON平分∠AOC,∴∠AON=∠AOC=20°,∴∠MON=∠AOM+∠AON=45°.∴∠MON的度数是45°.故选:A.9.【解答】解:∵∠1=30°,∠AMA1+∠1+∠DMD1=180°,∴∠AMA1+∠DMD1=180°﹣30°=150°.∴∠BMA1+∠CMD1=75°.∴∠BMC=∠BMA1+∠CMD1+∠1=105°.故选:D.10.【解答】解:由图可得,两个剪刀张开的角度α和β的大小关系为α=β,故选:C.二.填空题(共6小题)11.【解答】解:当把矩形8cm的一边所在直线为轴旋转一周,那么圆柱的底面半径为6cm,高和母线长都为8cm,∴圆柱的侧面积为π×6×2×8=96π(cm2),两个底面的面积为π×62×2=72π(cm2),∴圆柱体的表面积为168πcm2;当把矩形6cm的一边所在直线为轴旋转一周,那么圆柱的底面半径为8cm,高和母线长都为6cm,∴圆柱的侧面积为π×8×2×6=96π(cm2),两个底面的面积为π×82×2=128π(cm2),∴圆柱体的表面积为224πcm2;故得到的几何体的底面积是168πcm2或224πcm2.故答案为:168πcm2或224πcm2.12.【解答】解:正方体的平面展开图中,相对的面一定相隔一个正方形,字母B的对面是“D”.故答案为:D.13.【解答】解:∵AB=24cm,BC=AB,∴BC=9,∴AC=AB+BC=33,∵E是AC的中点,D是AB的中点,∴AE=AC=,AD=AB=12,∴DE=AE﹣AD=.故答案为:.14.【解答】解:如图,∵AB=4cm,BC=6cm,点E是AB中点,点F是BC的中点,∴BE=AB=2cm,BF=BC=3cm,①点B在A、C之间时,EF=BE+BF=2+3=5cm;②点A在B、C之间时,EF=BF﹣BE=3﹣2=1cm.∴EF的长等于5cm或1cm.故答案为:5cm或1cm.15.【解答】解:∵BD、BE为折痕,∴BD、BE分别平分∠CBC′、∠ABA′∴∠A′BE=∠ABE=30°,∠DBC=∠DBC′∵∠A′BE+∠ABE+∠DBC+∠DBC′=180°∴∠ABE+∠DBC=90°∴∠DBC=60°.故答案为60°16.【解答】解:∵∠AOB=∠COD=90°,∴∠AOD=∠AOC﹣∠COD=110°﹣90°=20°,∴∠BOD=∠AOB﹣∠AOD=90°﹣20°=70°.故答案为:70.三.解答题(共7小题)17.【解答】解:(1)做这两个纸盒共用料(单位:cm2)(2ab+2bc+2ac)+(20ab+16ac+10bc),=2ab+2bc+2ac+20ab+16ac+10bc,=22ab+12bc+18ac;(2)做大纸盒比做小纸盒多用料(单位:cm2),(20ab+16ac+10bc)﹣(2ab+2bc+2ac)=20ab+10bc+16ac﹣2ab﹣2bc﹣2ac=18ab+8bc+14ac;(3)大纸盒的体积V=4a×2.5b×2c=20abc,当a=6,b=5,c=3时V=20×6×5×3=1800cm3.18.【解答】解:(1)A、B、C三个村庄的位置如图所示:(2)4﹣(﹣2)=6,答:C村离A村有6km;(3)2+3+9+4=18,18÷100×1.5=27(升).答:一共用了27升汽油.19.【解答】解:设圆柱的底面半径为rcm,由题意得,πr2×2+2πr×15=200π,解得,r=5,或r=﹣20(舍去)答:圆柱的底面半径为5cm.20.【解答】解:(1)这个六棱柱由8个面,其中2个底面是大小和形状相同的正六边形,6个侧面是长为6cm,宽为4cm的长方形;(2)其侧面积为:6×4×6=144cm2,答:这个六棱柱的所有侧面的面积之和为144cm2.21.【解答】解:(1)当OC在∠AOB的内部时,如图1所示:∵OE是∠BOC的平分线,∴∠BOE=∠COE=,又∵∠BOC=22°,∴∠COE=11°,∵OD是∠AOB的平分线,∴∠AOD=∠BOD=,又∵∠AOB=108°,∴∠BOD=54°,又∵∠BOC+∠COD=∠BOD,∵∠COD=54°﹣22°=32°,又∵∠DOE=∠DOC+COE,∴∠DOE=32°+11°=43°;(2)当OC在∠AOB的外部时,如图2所示:∵OE是∠BOC的平分线,∴∠BOE=∠COE=,又∵∠BOC=22°,∴∠BOE=11°,∵OD是∠AOB的平分线,∴∠AOD=∠BOD=,又∵∠AOB=108°,∴∠BOD=54°,又∵∠DOE=∠BOD+∠BOE,∴∠DOE=54°+11°=65°;综合所述,∠DOE的度数为43°或65°.22.【解答】解:(1)∵AB=10cm,M是AB的中点,∴MA=MB=AB=5cm,∵NB=2cm,∴MN=5﹣2=3cm,答:线段MN的长度为3cm.(2)如图,由题意得,∠DOA=15.8°,∠DOB=40°30'=40.5°,∴∠AOB=15.8°+40.5°=56.3°=∠AOC,∴∠DOC=∠DOA+∠AOC=15.8°+56.3°=72.1°,答:射线OC的方向是北偏东72.1度.23.【解答】解:(1)∵OM平分∠BOC,∠BOC=120°,∴∠BOM=∠MON=60°,∵∠MON=90°,∴∠BON=∠MON﹣∠BOM=90°﹣60°=30°;(2)①∠AOM﹣∠NOC=30°;故答案为:30°②∠AOM﹣∠NOC=30°,理由如下:∵∠AOM=∠MON﹣∠AON=90°﹣∠AON,∠NOC=∠AOC﹣∠AON=60°﹣∠AON,∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.。
2020年人教版七年级数学上册《第4章几何图形初步》单元测试卷(解析版)
2020年人教版七年级数学上册《第4章几何图形初步》单元测试卷一.选择题(共10小题)1.一个棱柱有10个面,那么它的棱数是()A.16B.20C.22D.242.如图所示的圆台中,可由下列图中的()图形绕虚线旋转而成.A.B.C.D.3.一个长方体音箱,长是宽的2倍,宽和高相等,它的体积是54000cm2,则这个音箱的长是()A.30cm B.60cm C.300cm D.600cm4.下面图形中,平面图形是()A.B.C.D.5.如图是一个几何体的展开图,这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱6.下列各图中,经过折叠能围成一个正方体的是()A.B.C.D.7.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“我”字的一面相对面上的字是()A.国B.厉C.害D.了8.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是()A.B.C.D.9.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG 是()A.以点C为圆心,OD为半径的弧B.以点C为圆心,DM为半径的弧C.以点E为圆心,OD为半径的弧D.以点E为圆心,DM为半径的弧10.如图,依据尺规作图的痕迹,计算∠α=()A.56°B.68°C.28°D.34°二.填空题(共8小题)11.一个直棱柱有八个面,所有侧棱长的和为24cm,则每条侧棱的长是cm.12.如图,将长方形ABCD绕CD边旋转一周,得到的几何体是.13.一个五棱柱的面数为个,棱数为条,顶点数为个.14.若两正方体所有棱长之和为48,表面积之和为72,则体积之和为.15.已知甲乙两圆的周长之比是3:4,那么甲乙两圆的直径之比是.16.如图所示,是一个立体图形的展开图,这立体图形是.17.用一张边长是10cm的正方形铁皮围成一个圆柱体,这个圆柱的侧面积是cm2.18.如图,在△ABC,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E、F为圆心,大于EF 的长为半径画弧,两弧相交于点G;③作射线AG交BC边与点D.则∠ADB的度数为.三.解答题(共8小题)19.打谷场上,有一个近似于圆锥的小麦堆,测得底面直径是12米,高是底面半径的,(1)求这堆小麦的体积是多少立方米?(π取3.14)(2)在某仓库有一些相同的圆柱形有盖平顶粮仓,每个粮仓的高为1.1米,侧面积为π,求该粮仓的底面积是多少平方米?(结果保留π)(3)在(2)的条件下,若将打谷场上的这堆小麦全部装入仓库的圆柱形的粮仓内,至少需要多少个这样的粮仓?20.在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,形成的几何体的体积是多少?(结果用π表示)21.三棱柱有9条棱、6个顶点、5个面,三棱锥有6条棱、4个顶点、4个面;四棱柱有12条棱、8个顶点、6个面,四棱锥有8条棱、5个顶点、5个面等等,问能否组成一个有24条棱,10个面,15个顶点的多面体?请简要说明.22.棱长为a的正方体,摆放成如图所示的形状,动手试一试,并回答下列问题:(1)如果这一物体摆放了如图所示的上下三层,由几个正方体构成?(2)如图形所示物体的表面积是多少?23.如图,点C是线段AB的中点.(1)尺规作图:延长AB到D,使BD=AB(不写作法,保留作图痕迹).(2)若AC=2cm,求AD的长.24.如图,已知△ABC中,∠B>90°,请用尺规作出AB边的高线CD(请留作图痕迹,不写作法)25.如图,已知∠AOB=60°,∠AOD是∠AOB的补角.(1)在∠AOB的外部画出它的余角∠AOC,并用直尺和圆规作出∠AOD的平分线OE;(不写作法,保留作图痕迹)(2)在完成画图和作图后所得的图形中,与∠EOD互余的角有.26.如图,AD是Rt△ABC斜边BC上的高.(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;(3)在(2)的条件下,连结DE、DH.求证:ED⊥HD.2020年人教版七年级数学上册《第4章几何图形初步》单元测试卷参考答案与试题解析一.选择题(共10小题)1.一个棱柱有10个面,那么它的棱数是()A.16B.20C.22D.24【分析】根据八棱柱的定义可知,一个棱柱有10个面,那么这个棱柱是八棱柱,即可得出答案.【解答】解:一个棱柱有10个面,那么这个棱柱是八棱柱,它的棱数为3×8=24;故选:D.【点评】本题考查了棱柱的特征:n棱柱有(n+2)个面,有3n条棱;熟记棱柱的特征是解题的关键.2.如图所示的圆台中,可由下列图中的()图形绕虚线旋转而成.A.B.C.D.【分析】根据面动成体的原理即可解.【解答】解:圆台是梯形绕直角腰旋转而成.故选:A.【点评】考查了点、线、面、体,解决本题的关键是掌握各种面动成体的特征.3.一个长方体音箱,长是宽的2倍,宽和高相等,它的体积是54000cm2,则这个音箱的长是()A.30cm B.60cm C.300cm D.600cm【分析】根据立方根的定义和长方体的体积公式解答.【解答】解:设长方体的宽为xcm,则高是xcm,长是2xcm,根据题意,得2x3=54000,x3=27000,x=30,所以这个音箱的长是60cm.故选:B.【点评】本题考查了立方根的定义和长方体的体积公式,解题的关键掌握立方根的定义.4.下面图形中,平面图形是()A.B.C.D.【分析】根据平面图形和立体图形是区别即可解答.【解答】解:选项A是圆锥,选项B是圆柱,选项C是四棱柱,选项D是三角形,三角形是平面图形.故选:D.【点评】本题考查了平面图形和立体图形的认识,掌握定义是解题的关键.5.如图是一个几何体的展开图,这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱【分析】根据四棱柱的展开图解答.【解答】解:由图可知,这个几何体是四棱柱.故选:D.【点评】本题考查了展开图折叠成几何体,熟记四棱柱的展开图的形状是解题的关键.6.下列各图中,经过折叠能围成一个正方体的是()A.B.C.D.【分析】由平面图形的折叠及正方体的展开图解题.【解答】解:A、是“田”字格,故不能折叠成一个正方体;B、是“凹”字格,故不能折叠成一个正方体;C、折叠后有两个面重合,缺少一个面,所以也不能折叠成一个正方体;D、可以折叠成一个正方体.故选:D.【点评】本题考查了展开图折叠成几何体.注意只要有“田”、“凹”字格的展开图都不是正方体的表面展开图.7.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“我”字的一面相对面上的字是()A.国B.厉C.害D.了【分析】利用正方体及其表面展开图的特点解题.【解答】解:这是一个正方体的平面展开图,共有六个面,其中有“我”字的一面相对面上的字是国.故选:A.【点评】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.8.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是()A.B.C.D.【分析】A、根据作法无法判定PQ⊥l;B、以P为圆心大于P到直线l的距离为半径画弧,交直线l,于两点,再以两点为圆心,大于它们的长为半径画弧,得出其交点,进而作出判断;C、根据直径所对的圆周角等于90°作出判断;D、根据全等三角形的判定和性质即可作出判断.【解答】解:根据分析可知,选项B、C、D都能够得到PQ⊥l于点Q;选项A不能够得到PQ⊥l于点Q.故选:A.【点评】此题主要考查了过直线外以及过直线上一点作已知直线的垂线,熟练掌握基本作图方法是解题关键.9.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG 是()A.以点C为圆心,OD为半径的弧B.以点C为圆心,DM为半径的弧C.以点E为圆心,OD为半径的弧D.以点E为圆心,DM为半径的弧【分析】运用作一个角等于已知角可得答案.【解答】解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.故选:D.【点评】本题主要考查了作图﹣基本作图,解题的关键是熟习作一个角等于已知角的方法.10.如图,依据尺规作图的痕迹,计算∠α=()A.56°B.68°C.28°D.34°【分析】先根据矩形的性质得出AD∥BC,故可得出∠DAC的度数,由角平分线的定义求出∠EAF的度数,再由EF是线段AC的垂直平分线得出∠AEF的度数,根据三角形内角和定理得出∠AFE的度数,进而可得出结论.【解答】解:∵四边形ABCD是矩形,∴AD∥BC,∴∠DAC=∠ACB=68°.∵由作法可知,AF是∠DAC的平分线,∴∠EAF=∠DAC=34°.∵由作法可知,EF是线段AC的垂直平分线,∴∠AEF=90°,∴∠AFE=90°﹣34°=56°,∴∠α=56°.故选:A.【点评】本题考查的是作图﹣基本作图,熟知角平分线及线段垂直平分线的作法是解答此题的关键.二.填空题(共8小题)11.一个直棱柱有八个面,所有侧棱长的和为24cm,则每条侧棱的长是4cm.【分析】先根据这个棱柱有8个面,求出这个棱柱是6棱柱,有6条侧棱,再根据所有侧棱的和为24cm,即可得出答案.【解答】解:∵这个棱柱有八个面,∴这个棱柱是6棱柱,有6条侧棱,∵所有侧棱的和为24cm,∴每条侧棱长为24÷6=4(cm);故答案为:4【点评】本题考查了立体图形,主要利用了棱柱面的个数与棱数的关系,是一道基础题.12.如图,将长方形ABCD绕CD边旋转一周,得到的几何体是圆柱.【分析】根据面动成体可得长方形ABCD绕CD边旋转可得答案.【解答】解:将长方形ABCD绕CD边旋转一周,得到的几何体是圆柱,故答案为:圆柱.【点评】此题主要考查了点线面体,是基础题,熟悉常见几何体的形成是解题的关键.13.一个五棱柱的面数为7个,棱数为15条,顶点数为10个.【分析】根据五棱柱的形状可得答案.【解答】解:一个五棱柱的面数为7个,棱数为15条,顶点数为10个.故答案为:7,15,10.【点评】此题主要考查了认识立体图形,关键是掌握五棱柱的形状.14.若两正方体所有棱长之和为48,表面积之和为72,则体积之和为40.【分析】根据正方体的棱有12条,设其中一个正方体的棱长为x,则另一个为4﹣x,根据正方体的表面积公式列方程解答即可.【解答】解:设其中一个正方体的棱长为x,则另一个为4﹣x,根据题意得,6x2+6(4﹣x)2=72,解得,,故这两个正方体的棱长分别为2+,2﹣,体积之和为:=(2++2﹣)[﹣(2+)(2﹣)+]=40.故答案为:40【点评】此题考查正方体的表面积公式的灵活应用,根据正方体一个面的面积求出正方体的棱长是解决此类问题的关键.15.已知甲乙两圆的周长之比是3:4,那么甲乙两圆的直径之比是3:4.【分析】根据圆的周长公式C=πd或C=2πr,圆的周长和半径(直径)成正比例,已知两个圆的周长之比是3:4,两个圆的直径的比也是3:4;由此解答.【解答】解:∵甲乙两圆的周长之比是3:4,∴甲乙两圆的直径之比是3:4.故答案为:3:4.【点评】考查了认识平面图形,此题主要根据圆的周长计算方法进行判断,两个圆的周长之比等于两个圆的半径(直径)的比.16.如图所示,是一个立体图形的展开图,这立体图形是圆锥.【分析】根据圆锥表面展开图的特点解题.【解答】解:如图所示,是一个立体图形的展开图,这个立体图形是圆锥.故答案为:圆锥.【点评】本题考查圆锥表面展开图,记住圆锥的表面展开图的特征是解题的关键.17.用一张边长是10cm的正方形铁皮围成一个圆柱体,这个圆柱的侧面积是100cm2.【分析】易得此几何体为圆柱,那么侧面积=底面周长×高,依此即可求解.【解答】解:10×10=100(cm2).答:这个圆柱的侧面积是100cm2.故答案:100.【点评】考查了展开图折叠成几何体,本题难点是确定几何体的形状,关键是找到等量关系里相应的量.18.如图,在△ABC,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E、F为圆心,大于EF 的长为半径画弧,两弧相交于点G;③作射线AG交BC边与点D.则∠ADB的度数为115°.【分析】利用角平分线的作法可得出答案.【解答】解:∵根据作法可得AG是∠CAB的角平分线,∴∠DAC=∠CAB=×50°=25°,∴∠ADB=∠DAC+∠ACD=25°+90°=115°故答案为:115°.【点评】本题主要考查了基本作图,解的关键是熟记角平分线的作法.三.解答题(共8小题)19.打谷场上,有一个近似于圆锥的小麦堆,测得底面直径是12米,高是底面半径的,(1)求这堆小麦的体积是多少立方米?(π取3.14)(2)在某仓库有一些相同的圆柱形有盖平顶粮仓,每个粮仓的高为1.1米,侧面积为π,求该粮仓的底面积是多少平方米?(结果保留π)(3)在(2)的条件下,若将打谷场上的这堆小麦全部装入仓库的圆柱形的粮仓内,至少需要多少个这样的粮仓?【分析】(1)根据圆锥的体积公式解答即可;(2)根据圆柱的侧面积公式即可求出r,再根据圆的面积公式解答即可;(3)求出一个圆柱形的粮仓的体积,然后用麦的体积去除以一个圆柱形的粮仓的体积即可解答.【解答】解(1)(米),V=≈24×3.14=75.36(立方米),麦这堆小麦的体积是75.36立方米;(2),(米),(平方米),所以该粮仓的底面积是4π平方米;(3)(立方米),,所以至少需要6个这样的粮仓.【点评】本题主要考查了圆柱和圆锥的体积公式、圆柱的侧面积公式,熟练掌握公式是解答本题的关键.20.在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,形成的几何体的体积是多少?(结果用π表示)【分析】圆柱体的体积=底面积×高,注意底面半径和高互换得圆柱体的两种情况.【解答】解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.故形成的几何体的体积是36πcm3或48πcm3.【点评】本题考查圆柱体的体积的求法,注意分情况讨论.21.三棱柱有9条棱、6个顶点、5个面,三棱锥有6条棱、4个顶点、4个面;四棱柱有12条棱、8个顶点、6个面,四棱锥有8条棱、5个顶点、5个面等等,问能否组成一个有24条棱,10个面,15个顶点的多面体?请简要说明.【分析】简单多面体的顶点数V、面数F及棱数E间的关系为:V+F﹣E=2.这个公式叫欧拉公式.依此即可求解.【解答】解:∵10+15﹣24=1,不符合欧拉公式V+F﹣E=2,∴不能组成一个有24条棱,10个面,15个顶点的多面体.【点评】考查了欧拉公式,公式描述了简单多面体顶点数、面数、棱数特有的规律.解题的关键是熟练掌握欧拉公式.22.棱长为a的正方体,摆放成如图所示的形状,动手试一试,并回答下列问题:(1)如果这一物体摆放了如图所示的上下三层,由几个正方体构成?(2)如图形所示物体的表面积是多少?【分析】(1)分别数出各层正方体的个数,再相加即可求解;(2)每个方向上均有6个等面积的小正方形,求出1个正方形面积,再乘36即可求解.【解答】解:(1)第一层1个,第一层3个,第一层6个,1+3+6=10(个).答:由10个正方体构成;(2)每个正方形面积为a2,左面:6小正方形,前面:6小正方形,右面:6小正方形,后面:6小正方形,上面:6小正方形,下面:6小正方形.物体的表面积为:6×6a2=36a2(平方单位).答:如图形所示物体的表面积是36a2平方单位.【点评】本题考查了立体图形的有关知识,关键是要注意立体图形的各个面,及每个面的正方形的个数.23.如图,点C是线段AB的中点.(1)尺规作图:延长AB到D,使BD=AB(不写作法,保留作图痕迹).(2)若AC=2cm,求AD的长.【分析】(1)在AB的延长线上截取BD=AB即可;(2)根据中点的定义先求出AB,再求出AD的长.【解答】解:(1)如图所示:(2)∵点C是线段AB的中点,AC=2cm,∴AB=4cm,∵BD=AB,∴AD=8cm.【点评】本题考查了作图﹣基本作图:作一条线段等于已知线段,线段中点的定义等知识,作出点D是解题的关键.24.如图,已知△ABC中,∠B>90°,请用尺规作出AB边的高线CD(请留作图痕迹,不写作法)【分析】延长AB,以点C为圆心,大于点C到直线AB的距离的长为半径画弧,交AB 的延长线于点M和点N,再作线段MN的垂直平分线CD即可.【解答】解:延长AB,以点C为圆心,大于点C到直线AB的距离的长为半径画弧,交AB的延长线于点M和点N,再作线段MN的垂直平分线CD,如下图所示:【点评】本题考查作图﹣基本作图,掌握作垂直平分线的基本步骤为解题关键.25.如图,已知∠AOB=60°,∠AOD是∠AOB的补角.(1)在∠AOB的外部画出它的余角∠AOC,并用直尺和圆规作出∠AOD的平分线OE;(不写作法,保留作图痕迹)(2)在完成画图和作图后所得的图形中,与∠EOD互余的角有∠COE、∠AOC.【分析】(1)按要求作图;(2)根据∠AOB=60°,分别计算各角的度数,可作解答.【解答】解:(1)如图所示:(2)∵OC⊥BD,∴∠BOC=∠COD=90°,∵∠AOB=60°,∴∠AOC=30°,∠AOD=120°,∵OE平分∠AOD,∴∠AOE=∠DOE=60°,∴与∠EOD互余的角有:∠COE、∠AOC.故答案为:∠COE、∠AOC.【点评】本题考查了角平分线的定义、余角以及角的计算,还考查了基本作图﹣角平分线、过直线上一点作已知直线的垂线;注意基本作图时要认真、准确.26.如图,AD是Rt△ABC斜边BC上的高.(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;(3)在(2)的条件下,连结DE、DH.求证:ED⊥HD.【分析】(1)利用尺规作∠C的平分线即可解决问题;(2)结论:FH=HC.只要证明∠HCF=∠HFC即可;(3)只要证明△EAD∽△HCD,可得∠ADE=∠CDH,推出∠EDH=∠ADC=90°即可;【解答】解:(1)如图所示:(2)结论:FH=HC.理由:∵FH∥BC,∴∠HFC=∠FCB,∵∠FCB=∠FCH,∴∠FCH=∠HFC,∴FH=HC.(3)∵AD是Rt△ABC斜边BC上的高,∴∠ADC=∠BAC=90°,∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,∴∠B=∠CAD,∵∠AEF=∠B+∠ECB,∠AFE=∠CAD+∠ACF,∠ACF=∠ECB,∴∠AEF=∠AFE,∴AE=AF,∵FH∥CD,∴=,∵AF=AE,CH=FH,∴=,∴=,∵∠BAD=∠DCH,∴△EAD∽△HCD,∴∠ADE=∠CDH,∴∠EDH=∠ADC=90°,∴ED⊥DH.【点评】本题考查作图﹣基本作图,等腰三角形的判定和性质、相似三角形的判定和性质、平行线分线段成比例定理等知识,本题综合性比较强,属于中考常考题型.。
七年级上册数学《几何图形初步》单元综合测试题含答案
3.如图,若CB=4,DB=7,且D是AC的中点,则AC的长为()
A.3B.6C.9D.11
4.下列图形中不是正方体的平面展开图的是()
A B.
C. D.
5.钟表在2点半时,其时针和分针所成的角是()
A.60°B.75°C.105°D.120°
6.将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是()
(1)特殊情况,探索结论:
①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小:
∠AOB的度数
60°
90°
120°
∠MON的度数
②探索发现:无论∠AOB的度数是多少,∠MON与∠AOB的数量关系是不变的,请你直接写出结论:
∠MON∠AOB.
(2)特例启发,解答题目:
如图2,如果∠AOB=α,请你求∠MON的大小(用α表示).
【答案】C
【解析】
【分析】
根据六棱柱侧面积的面积公式,代入数据即可得出结论.
【详解】六棱柱的侧面积为:4×5×6=120(cm2).
故选C.
【点睛】本题考查了几何体的表(侧)面积,熟练掌握“几何体的侧面积的求法”是解题的关键.
二.填空题
13.一个棱柱有20个顶点,每条侧棱长6cm,底面每条边长是2m,则所有侧棱长是_____.
D、∠α与∠β不互余,∠α和∠β互补,故本选项错误;
故选:C.
【点睛】本题考查的知识点是对顶角、余角和补角.解题关键是熟记“互余的两个角的和等于90°”.
7.下列说法正确的有()句.
①两条射线组成的图形叫做角;
②同角的补角相等;
③若AC=BC,则C为线段AB的中点;
④线段AB就是点A与点B之间的距离;
新人教版初中数学七年级数学上册第四单元《几何图形初步》测试题(含答案解析)

一、选择题1.如图,已知直线上顺次三个点A 、B 、C ,已知AB =10cm ,BC =4cm .D 是AC 的中点,M 是AB 的中点,那么MD =( )cmA .4B .3C .2D .1 2.一个角的补角比这个角的余角3倍还多10°,则这个角的度数为( )A .140°B .130°C .50°D .40°3.如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是A .美B .丽C .云D .南 4.计算:135333030306︒︒''''⨯-÷的值为( )A .335355︒'''B .363355︒'''C .63533︒'''D .53533︒''' 5.已知:∠AOC =90°,∠AOB :∠AOC =2:3,则∠BOC 的度数是( )A .30°B .60°C .30°或60°D .30°或150°6.平面内有两两相交的七条直线,若最多有m 个交点,最少有n 个交点,则m+n 等于( ) A .16B .22C .20D .187.如图,一副三角尺按不同的位置摆放,摆放位置中αβ∠=∠的图形的个数是( )A .1B .2C .3D .48.若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )A .∠A >∠B >∠CB .∠B >∠A >∠CC .∠A >∠C >∠BD .∠C >∠A >∠B9.已知线段AB =6cm ,反向延长线段AB 到C ,使BC =83AB ,D 是BC 的中点,则线段AD的长为____cm A .2 B .3 C .5D .610.已知线段AB=8cm ,在直线AB 上画BC ,使BC=2cm ,则线段AC 的长度是( ) A .6cmB .10cmC .4cm 或10cmD .6cm 或10cm11.由A 站到G 站的某次列车,运行途中停靠的车站依次是A 站——B 站—C 站——D 站——E 站——F 站——G 站,那么要为这次列车制作的火车票有( ) A .6种B .12种C .21种D .42种12.下列说法不正确的是()A.两条直线相交,只有一个交点B.两点之间,线段最短C.两点确定一条直线D.过平面上的任意三点,一定能作三条直线二、填空题13.硬币在桌面上快速地转动时,看上去象球,这说明了_________________.14.如图,共有_________条直线,_________条射线,_________条线段.15.同一条直线上有三点A,B,C,且线段BC=3AB,点D是BC的中点,CD=3,则线段AC的长为______.16.已知一个角的补角是它余角的3倍,则这个角的度数为_____.17.下面的图形是某些几何体的表面展开图,写出这些几何体的名称.18.把一条长为20厘米的线段分成三段,如果中间一段长为8厘米,那么第一段中点到第三段中点间的距离等于________厘米.19.如图是一个正方体盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得折成正方体后相对面上的两个数互为相反数,则填入正方形中A,B,C内的三个数依次为__,___,___.20.如图,上午6:30时,时针和分针所夹锐角的度数是_____.三、解答题21.已知:如图,在∠AOB的内部从O点引3条射线OC,OD,OE,图中共有多少个角?若在∠AOB的内部,从O点引出4条,5条,6条,…,n条不同的射线,可以分别得到多少个不同的角?22.如图,将一个长方形沿它的长或宽所在的直线旋转一周,回答下列问题:(1)得到什么几何体?(2)长方形的长和宽分别为6cm 和4cm ,分别绕它的长和宽所在直线旋转一周,得到不同的几何体,它们的体积分别为多少?(结果保留π)23.如图,C 是线段AB 上一点,M 是AC 的中点,N 是BC 的中点.(1)若1AM =,4BC =,求MN 的长度. (2)若6AB =,求MN 的长度. 24.将一副三角尺叠放在一起:(1)如图①,若∠1=4∠2,请计算出∠CAE 的度数; (2)如图②,若∠ACE =2∠BCD ,请求出∠ACD 的度数. 25.[阅读理解]射线OC 是AOB ∠内部的一条射线,若1,2COA BOC ∠=∠则我们称射线OC 是射线OA 的伴随线.例如,如图1,60 20AOB AOC COD BOD ∠=∠=∠=∠=,,则12AOC BOC ∠=∠,称射线OC 是射线OA 的伴随线:同时,由于12BOD AOD ∠=∠,称射线OD 是射线OB 的伴随线. [知识运用](1)如图2,120AOB ∠=,射线OM 是射线OA 的伴随线,则AOM ∠= ,若AOB ∠的度数是α,射线ON 是射线OB 的伴随线,射线OC 是AOB ∠的平分线,则NOC ∠的度数是 .(用含α的代数式表示)(2)如图,如180AOB ∠=,射线OC 与射线OA 重合,并绕点O 以每秒3的速度逆时针旋转,射线OD 与射线OB 重合,并绕点O 以每秒5的速度顺时针旋转,当射线OD 与射线OA 重合时,运动停止,现在两射线同时开始旋转.①是否存在某个时刻t (秒),使得COD ∠的度数是20,若存在,求出t 的值,若不存在,请说明理由;②当t 为多少秒时,射线OC OD OA 、、中恰好有一条射线是其余两条射线的伴随线. 26.如图,已知40AOB ∠=︒,3BOC AOB ∠=∠,OD 平分AOC ∠,求BOD ∠的度数.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】由AB =10cm ,BC =4cm .于是得到AC =AB +BC =14cm ,根据线段中点的定义由D 是AC 的中点,得到AD ,根据线段的和差得到MD =AD ﹣AM ,于是得到结论. 【详解】解:∵AB =10cm ,BC =4cm ,∴AC=AB+BC=14cm,∵D是AC的中点,∴AD=1AC=7cm;2∵M是AB的中点,∴AM=1AB=5cm,2∴DM=AD﹣AM=2cm.故选:C.【点睛】此题主要考查了两点之间的距离,线段的和差、线段的中点的定义,利用线段差及中点性质是解题的关键.2.C解析:C【分析】根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°,列出方程,然后解方程即可.【详解】设这个角为α,则它的余角为90°-α,补角为180°-α,根据题意得,180°-α=3(90°-α)+10°,180°-α=270°-3α+10°,解得α=50°.故选C.【点睛】本题考查了互为余角与补角的性质,表示出这个角的余角与补角然后列出方程是解题的关键.3.D解析:D【分析】如图,根据正方体展开图的11种特征,属于正方体展开图的“1-4-1”型,折成正方体后,“建”与“南”相对,“设”与“丽”相对,“美”与“云”相对.【详解】如图,根据正方体展开图的特征,折成正方体后,“建”与“南”相对,“设”与“丽”相对,“美”与“云”相对.故选D .4.B解析:B 【分析】先进行度、分、秒的乘法除法计算,再算减法. 【详解】135333030306︒︒''''⨯-÷4139555︒︒''''=- 386415055︒︒''''-''='''363355︒=. 故选:B . 【点睛】本题考查了度、分、秒的四则混合运算,是角度计算中的一个难点,注意以60为进制即可.5.D解析:D 【分析】根据两角的比和两角的和即可求得两个角的度数. 【详解】由∠AOC =90°,∠AOB :∠AOC =2:3,可得 当B 在∠AOC 内侧时,可以知道∠AOB 23=⨯90°=60°,∠BOC =30°; 当B 在∠AOC 外侧时,∠BOC =150°. 故选:D . 【点睛】本题考查了三角形中角的求法,解题的关键是分两种情况讨论.6.B解析:B 【分析】由题意可得7条直线相交于一点时交点最少,任意两直线相交都产生一个交点时交点最多,由此可得出m ,n 的值,进而可得答案. 【详解】解:根据题意可得:7条直线相交于一点时交点最少,此时交点为1个,即n =1; 任意两直线相交都产生一个交点时,交点最多,此时交点为:7×(7﹣1)÷2=21,即m =21;则m +n =21+1=22. 故选:B . 【点睛】本题考查了直线的交点问题,注意掌握直线相交于一点时交点最少,任意n条直线两两相交时交点最多为12n(n﹣1)个.7.C解析:C【分析】根据直角三角板可得第一个图形∠β=45°,进而可得∠α=45°;根据余角和补角的性质可得第二个图形、第四个图形中∠α=∠β,第三个图形∠α和∠β互补.【详解】根据角的和差关系可得第一个图形∠α=∠β=45°,根据等角的补角相等可得第二个图形∠α=∠β,第三个图形∠α+∠β=180°,不相等,根据同角的余角相等可得第四个图形∠α=∠β,因此∠α=∠β的图形个数共有3个,故选:C.【点睛】此题主要考查了余角和补角,关键是掌握余角和补角的性质:等角的补角相等.等角的余角相等.8.C解析:C【分析】根据度分秒之间的换算,先把∠C的度数化成度、分、秒的形式,再根据角的大小比较的法则进行比较,即可得出答案.【详解】解:∵∠C=20.25°=20°15′,∴∠A>∠C>∠B,故选:C.【点睛】此题考查了角的大小比较,先把∠C的度数化成度、分、秒的形式,再进行比较是本题的关键.9.A解析:A【分析】由BC=83AB可求出BC的长,根据中点的定义可求出BD的长,利用线段的和差关系求出AD的长即可.【详解】∵BC=83AB,AB=6cm,∴BC=6×83=16cm,∵D是BC的中点,∴BD=12BC=8cm,∵反向延长线段AB到C,∴AD=BD-AB=8-6=2cm,故选A.【点睛】本题考查了比较线段的长短,理解线段中点的概念,利用中点的性质转化线段之间的倍分关系是解题关键.10.D解析:D【分析】由点C在直线AB上,分别讨论点C在线段AB上和在线段AB的延长线上两种情况,根据线段的和差关系求出AC的长即可.【详解】∵点C在直线AB上,AB=8,BC=2,∴当点C在线段AB上时,AC=AB-BC=8-2=6cm,当点C在线段AB的延长线上时,AC=AB+BC=8+2=10cm,∴AC的长度是6cm或10cm.故选D.【点睛】本题考查线段的和与差,注意点C在直线AB上,要分几种情况讨论是解题关键.11.C解析:C【解析】【分析】从A出发要经过6个车站,所以要制作6种车票,从B出发要经过5个车站,所以要制作5种车票,从C出发要经过4个车站,所以要制作4种车票,从D出发要经过3个车站,所以要制作3种车票,从E出发要经过2个车站,所以要制作2种车票,从F出发要经过1个车站,所以要制作1种车票,把车票数相加即可得解.【详解】共需制作的车票数为:6+5+4+3+2+1=21(种).故选C.【点睛】本题从A站出发,逐站求解即可得到所有可能的情况,不要遗漏.12.D解析:D【解析】【分析】根据直线公理、线段公理进行逐一分析判断.【详解】A. 根据直线公理“两点确定一条直线”,则两条直线相交,只有一个交点,故该选项正确;B.两点之间,线段最短,是线段公理,故该选项正确;C. 两点确定一条直线,是直线公理,故该选项正确;D. 当三点共线时,则只能确定一条直线,故该选项错误.故选 D.【点睛】此题考查直线、射线、线段,直线的性质:两点确定一条直线,线段的性质:两点之间线段最短,解题关键在于掌握各性质定义.二、填空题13.面动成体【分析】本题是面动成体的原理在现实中的具体表现根据面动成体原理解答即可【详解】硬币在桌面上快速地转动时看上去象球这说明了面动成体故答案为面动成体【点睛】本题考查了点线面体掌握面动成体原理是解解析:面动成体【分析】本题是面动成体的原理在现实中的具体表现,根据面动成体原理解答即可.【详解】硬币在桌面上快速地转动时,看上去象球,这说明了面动成体,故答案为面动成体.【点睛】本题考查了点、线、面、体,掌握面动成体原理是解题的关键.14.63【解析】【分析】根据线段射线和直线的特点:线段有两个端点有限长可以测量;射线有一个端点无限长;直线无端点无限长;进行解答即可【详解】因为线段有两个端点射线只有一个端点所以由图可以看出:图中有1条解析:6 3【解析】【分析】根据线段、射线和直线的特点:线段有两个端点,有限长,可以测量;射线有一个端点,无限长;直线无端点,无限长;进行解答即可.【详解】因为线段有两个端点,射线只有一个端点,所以由图可以看出:图中有1条直线,3条线段,有6条射线.故此题答案为:1,6,3.【点睛】此题主要考查直线、线段和射线的特点,此类型的题,在数时,应做到有顺序,做到不遗漏、不重复.15.4或8【分析】分点C在AB的延长线上与点C在BA的延长线上两种情况画出图形分别利用线段中点的定义和已知条件求出BC和AB再利用线段的和差计算即可【详解】解:(1)当点C在AB的延长线上时如图1∵点D解析:4或8【分析】分点C在AB的延长线上与点C在BA的延长线上两种情况,画出图形,分别利用线段中点的定义和已知条件求出BC和AB,再利用线段的和差计算即可.【详解】解:(1)当点C在AB的延长线上时,如图1,∵点D是线段BC的中点,CD=3,∴BC=2CD=6,∵BC=3AB,∴AB=13BC=13×6=2,∴AC=AB+BC=2+6=8;(2)当点C在BA的延长线时,如图2,∵点D是线段BC的中点,CD=3,∴BC=2CD=6,∵BC=3AB,∴AB=13BC=13×6=2,∴AC=BC-AB=6-2=4.故答案为:4或8.【点睛】本题考查了线段中点的定义、两点间的距离和线段的和差等知识,正确分类、画出图形、熟练掌握线段中点的概念和线段的和差计算是解题的关键.16.45°【分析】根据互为余角的和等于90°互为补角的和等于180°用这个角表示出它的余角与补角然后列方程求解即可【详解】设这个角为α则它的余角为90°﹣α补角为180°﹣α根据题意得180°-α=3(解析:45°【分析】根据互为余角的和等于90°,互为补角的和等于180°用这个角表示出它的余角与补角,然后列方程求解即可.【详解】设这个角为α,则它的余角为90°﹣α,补角为180°﹣α,根据题意得,180°-α=3(90°-α),解得α=45°.故答案为:45°.【点睛】本题考查了余角与补角,能分别用这个角表示出它的余角与补角是解题的关键.17.正方体四棱锥三棱柱【解析】【分析】根据常见的几何体的展开图进行判断【详解】根据几何体的平面展开图的特征可知:①是正方体的展开图;②是四棱锥的展开图;③是三棱柱的展开图;故答案为:正方体四棱锥三棱柱;解析:正方体四棱锥三棱柱【解析】【分析】根据常见的几何体的展开图进行判断.【详解】根据几何体的平面展开图的特征可知:①是正方体的展开图;②是四棱锥的展开图;③是三棱柱的展开图;故答案为:正方体,四棱锥,三棱柱;【点睛】此题考查几何体的展开图,解题关键在于掌握其展开图.18.14【解析】【分析】先求出两边线段的长度之和第一段中点到第三段中点之间的距离等于两边线段的一半与中间线段的和【详解】根据题意第一段与第三段长度之和=20-8=12cm所以第一段中点到第三段中点之间的解析:14【解析】【分析】先求出两边线段的长度之和,第一段中点到第三段中点之间的距离等于两边线段的一半与中间线段的和.【详解】根据题意,第一段与第三段长度之和=20-8=12cm,所以第一段中点到第三段中点之间的距离=12÷2+8=6+8=14cm.【点睛】能正确找出“第一段中点到第三段中点之间的距离等于两边线段的一半与中间线段的和”是解本题的关键.19.02【分析】利用正方体及其表面展开图的特点解题【详解】解:由于只有符号不同的两个数互为相反数由正方体的展开图解题得填入正方形中内的三个数依次为102故答案为102【点睛】本题主要考查互为相反数的概念解析:0 2【分析】利用正方体及其表面展开图的特点解题.【详解】解:由于只有符号不同的两个数互为相反数,由正方体的展开图解题得填入正方形中A,B,C内的三个数依次为1,0,2.故答案为1,0,2【点睛】本题主要考查互为相反数的概念,只有符号不同的两个数互为相反数.解题时勿忘记正方体展开图的各种情形.20.15°【分析】计算钟面上时针与分针所成角的度数一般先从钟面上找出某一时刻分针与时针所处的位置确定其夹角再根据表面上每一格30°的规律计算出分针与时针的夹角的度数【详解】∵时针12小时转一圈每分钟转动解析:15°【分析】计算钟面上时针与分针所成角的度数,一般先从钟面上找出某一时刻分针与时针所处的位置,确定其夹角,再根据表面上每一格30°的规律,计算出分针与时针的夹角的度数.【详解】∵时针12小时转一圈,每分钟转动的角度为:360°÷12÷60=0.5°,∴时针1小时转动30°,∴6:30时,分针指向刻度6,时针和分针所夹锐角的度数是30°×12=15°.故答案是:15°.【点睛】考查了钟面角,解题时注意,分针60分钟转一圈,每分钟转动的角度为:360°÷60=6°;时针12小时转一圈,每分钟转动的角度为:360°÷12÷60=0.5°.三、解答题21.角的个数分别为10,15,21,28,…,(2)(1)2n n++.【分析】1、在锐角∠AOB的内部以O为顶点作3条射线,由此你能得到以O为顶点的射线共有多少条吗?2、根据以一条射线为边,以其余n+1条射线为另一边可作n+1个角,相信你能求得5条射线共多少个锐角;3、由于任意两射线所得的角都多计一次,所以当在∠AOB 的内部从O 点引3条射线共有1452⨯⨯个角; 4、结合作3条射线得到的角的个数,可以推出以O 为顶点共有n 条射线时,得到的角的个数为(1)(2)2n n ++,继而将n=5、6、7代入即可. 【详解】 解:顺时针数,与射线OA 构成的角有4个,与射线OC 构成的角有3个,与射线OD 构成的角有2个,与射线OE 构成的角有1个,故共有角4+3+2+1=10(个). 类似地,引4条射线有角5+4+3+2+1=15(个),引5条射线有角6+5+4+3+2+1=21(个),引6条射线有角7+6+5+4+3+2+1=28(个),…,以此类推,引n 条射线有角(n +1)+n +(n -1)+…+2+1=(1)(2)2n n ++ (个) . 【点睛】本题中,根据以点O 为顶点的射线有n+2条,再求这n+2条射线可形成的角的个数.要求同学们能够准确利用题目中的已知信息,灵活运用所学知识进行解答.本题还可以采用顺序枚举法进行解答,按一定顺序,把所有元素一一列举出来,要做到不重不漏,适合元素(射线)个数较少情况,如果图中有n 条射线这时无法逐一列举,可用规律归纳法.22.(1)圆柱;(2)它们的体积分别为3144cm π,396cm π【分析】(1)矩形旋转一周得到圆柱;(2)绕长旋转得到的圆柱的底面半径为4cm ,高为6cm ,绕宽旋转得到圆柱底面半径为6cm ,高为4cm ,从而可以计算出体积.【详解】解:(1)圆柱(2) 绕宽旋转得到圆柱底面半径为6cm ,高为4cm , 21V r h π=264π=⨯⨯144π=绕长旋转得到的圆柱的底面半径为4cm ,高为6cm ,2246V π=⨯⨯96π=∴它们的体积分别为3144cm π,396cm π【点睛】本题主要考查的是圆柱的体积,熟记圆柱的体积公式是解题的关键.23.(1)3;(2)3.【分析】(1)由中点可得CN 和MC 的长,再由 MN=MC+CN 可求得MN 的长;(2)由已知可得AB 的长是NM 的2倍,已知AB 的长,可求得MN 的长度.【详解】解:(1)∵N 是BC 的中点,M 是AC 的中点,1AM =,4BC =,∴2CN =,1AM CM ==,∴3MN MC CN =+=.(2)∵M 是AC 的中点,N 是BC 的中点,6AB =, ∴132NM MC CN AB =+==. 【点睛】本题主要考查了两点间的距离,利用中点性质转化线段之间的倍分关系,在不同情况下灵活选用它的不同表示方法,有利于解题的简洁性.24.(1)∠CAE =18°;(2)∠ACD =120°.【分析】(1)由题意根据∠BAC =90°列出关于∠1、∠2的方程求解即可得到∠2的度数,再根据同角的余角相等求出∠CAE =∠2,从而得解;(2)根据∠ACB 和∠DCE 的度数列出等式求出∠ACE ﹣∠BCD =30°,再结合已知条件求出∠BCD ,然后由∠ACD =∠ACB+∠BCD 并代入数据计算即可得解.【详解】解:(1)∵∠BAC =90°,∴∠1+∠2=90°,∵∠1=4∠2,∴4∠2+∠2=90°,∴∠2=18°,又∵∠DAE =90°,∴∠1+∠CAE =∠2+∠1=90°,∴∠CAE =∠2=18°;(2)∵∠ACE+∠BCE =90°,∠BCD+∠BCE =60°,∴∠ACE ﹣∠BCD =30°,又∠ACE =2∠BCD ,∴2∠BCD ﹣∠BCD =30°,∠BCD =30°,∴∠ACD =∠ACB+∠BCD =90°+30°=120°.【点睛】本题考查三角形的外角性质,三角形的内角和定理,准确识图理清图中各角度之间的关系是解题的关键.25.(1)40︒,16α;(2)①存在,当20t =秒或25秒时,∠COD 的度数是20︒;②当907t =,36019,1807,30时,OC 、OD 、OA 中恰好有一条射线是其余两条射线的伴随线.【分析】(1)根据伴随线定义即可求解;(2)①利用分类讨论思想,分相遇之前和之后进行列式计算即可;②利用分类讨论思想,分相遇之前和之后四个图形进行计算即可.【详解】(1)∵120AOB ∠=,射线OM 是射线OA 的伴随线, 根据题意,12AOM BOM ∠=∠,则111204033AOM AOB ∠=∠=⨯︒=︒; ∵AOB ∠的度数是α,射线ON 是射线OB 的伴随线,射线OC 是AOB ∠的平分线, ∴111233BON AON AOB α∠=∠=∠=,1122BOC AOB α∠=∠=, ∴111236NOC BOC BON ααα∠=∠-∠=-=; 故答案为:40︒,16α; (2)射线OD 与OA 重合时,180365t ==(秒), ①当∠COD 的度数是20°时,有两种可能: 若在相遇之前,则1805320t t --=,∴20t =;若在相遇之后,则5318020t t +-=,∴25t =;所以,综上所述,当20t =秒或25秒时,∠COD 的度数是20°;②相遇之前:(i )如图1,OC 是OA 的伴随线时,则12AOC COD ∠=∠, 即()13180532t t t =--, ∴907t =; (ii )如图2,OC 是OD 的伴随线时, 则12COD AOC ∠=∠, 即11805332t t t --=⨯, ∴36019t =; 相遇之后: (iii )如图3,OD 是OC 的伴随线时, 则12COD AOD ∠=∠, 即()153********t t t +-=-, ∴1807t =; (iv )如图4,OD 是OA 的伴随线时,则12AOD COD ∠=∠, 即()118053t 5t 1802t -=+-, ∴30t =;所以,综上所述,当907t =,36019,1807,30时,OC 、OD 、OA 中恰好有一条射线是其余两条射线的伴随线.【点睛】本题是几何变换综合题,考查了角的计算,考查了动点问题,解题的关键是理解题意,学会用分类讨论的思想思考问题.26.40°【分析】根据3BOC AOB ∠=∠,40AOB ∠=︒求出120BOC ∠=︒,得到∠AOC 的度数,利用OD 平分AOC ∠,求出∠AOD 的度数,即可求出BOD ∠的度数.【详解】解:∵3BOC AOB ∠=∠,40AOB ∠=︒,∴120BOC ∠=︒.∵AOC AOB BOC ∠=∠+∠,40120=︒+︒,160=︒,又∵OD 平分AOC ∠, ∴1802AOD AOC ∠=∠=︒, ∴BOD AOD AOB ∠=∠-∠,8040=︒-︒, 40=︒.【点睛】此题考查角度的和差计算,会看图明确各角之间的大小关系,注意角平分线的运用.。
(常考题)人教版初中数学七年级数学上册第四单元《几何图形初步》测试卷(答案解析)(2)

一、选择题1.如图所示的四个几何体中,从正面、上面、左面看得到的平面图形都相同的有( )A .1个B .2个C .3个D .4个2.如图,点C 是线段AB 的中点,点D 是线段CB 上任意一点,则下列表示线段关系的式子不正确的是( )A .AB=2ACB .AC+CD+DB=ABC .CD=AD-12AB D .AD=12(CD+AB ) 3.如图,O 是直线AC 上一点,OB 是一条射线,OD 平分∠AOB ,OE 在∠BOC 内,且∠DOE =60°,∠BOE =13∠EOC ,则下列四个结论正确的个数有( ) ①∠BOD =30°;②射线OE 平分∠AOC ;③图中与∠BOE 互余的角有2个;④图中互补的角有6对.A .1个B .2个C .3个D .4个4.如图,点O 在直线AB 上,射线OC ,OD 在直线AB 的同侧,∠AOD =40°,∠BOC =50°,OM ,ON 分别平分∠BOC 和∠AOD ,则∠MON 的度数为( )A .135°B .140°C .152°D .45°5.如图.已知//AB CD .直线EF 分别交,AB CD 于点,,E F EG 平分BEF ∠.若1 50∠=︒.则2∠的度数为( )A.50︒B.65︒C.60︒D.70︒6.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为A.圆锥,正方体,三棱锥,圆柱B.圆锥,正方体,四棱锥,圆柱C.圆锥,正方体,四棱柱,圆柱D.圆锥,正方体,三棱柱,圆柱7.如果∠1的余角是∠2,并且∠1=2∠2,则∠1的补角为()A.30°B.60°C.120°D.150°8.如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是()A.85°B.105°C.125°D.160°9.若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有()A.∠A>∠B>∠C B.∠B>∠A>∠C C.∠A>∠C>∠B D.∠C>∠A>∠B 10.对于线段的中点,有以下几种说法:①若AM=MB,则M是AB的中点;②若AM=MB=12AB,则M是AB的中点;③若AM=12AB,则M是AB的中点;④若A,M,B在一条直线上,且AM=MB,则M是AB的中点.其中正确的是()A.①④B.②④C.①②④D.①②③④11.用一个平面去截一个圆锥,截面的形状不可能是()A.B.C.D.12.用一个平面去截正方体,所得截面是三角形,留下较大的几何体一定有()A.7个面B.15条棱C.7个顶点D.10个顶点二、填空题13.从起始站A 市坐火车到终点站G 市中途共停靠5次,各站点到A 市距离如下: 站点B C D E F G 到A 市距离(千米)4458051135149518252270若火车车票的价格由路程决定,则沿途总共有不同的票价____种. 14.如图,点C 是线段AB 的中点,点D ,E 分别在线段AB 上,且ADDB =23,AE EB=2,则CDCE的值为____.15.如图,若AOB ∠是直角,OM 平分AOC ∠,ON 平分COB ∠,则MON ∠=________.16.用一个平面分别截棱柱、圆锥,都能截出的一个图形是________.17.把棱长为1cm 的四个正方体拼接成一个长方体,则在所得长方体中,表面积最大等于________2cm .18.把一条长为20厘米的线段分成三段,如果中间一段长为8厘米,那么第一段中点到第三段中点间的距离等于________厘米.19.乘火车从A 站出发,沿途经过3个车站方可到达B 站,那么在A ,B 两站之间需要安排不同的车票________种.20.如图,小颖从家到超市共有4条路可走,小颖应选择第________条路才能使路程最短,用数学知识解释为________________.三、解答题21.把一副三角板的直角顶点O 重叠在一起.(1)问题发现:如图①,当OB 平分∠COD 时,∠AOD+∠BOC 的度数是 ; (2)拓展探究:如图②,当OB 不平分∠COD 时,∠AOD+∠BOC 的度数是多少? (3)问题解决:当∠BOC 的余角的4倍等于∠AOD 时,求∠BOC 的度数.22.如图,射线ON ,OE ,OS ,OW 分别表示以点O 为中心的北,东,南,西四个方向,点A 在点O 的北偏东45︒方向,点B 在点O 的北偏西30方向.(1)画出射线OB ,若BOC ∠与AOB ∠互余,请在图(1)或备用图中画出BOC ∠; (2)若OP 是AOC ∠的平分线,直接写出AOP ∠的度数.(不需要计算过程) 23.已知长方形纸片ABCD ,点E 在边AB 上,点F ,G 在边CD 上,连接EF ,EG .将BEG ∠对折,点B 落在直线BG 上的点B '处,得折痕EM ;将AEF ∠对折,点A 落在直线EF 上的点A '处,得折痕EN .(1)如图(1),若点F 与点G 重合,求MEN ∠的度数;(2)如图(2),若点G 在点F 的右侧,且30FEG ︒∠=,求MEN ∠的度数; (3)若MEN α∠=,请直接用含α的式子表示FEG ∠的大小. 24.如图,平面上有四个点A 、B 、C 、D ,根据下列语句画图.(1)画直线AB 、CD 交于E 点; (2)画线段AC 、BD 交于点F ; (3)连接E 、F 交BC 于点G ; (4)连接AD ,并将其反向延长;(5)作射线BC .25.如图,以直线AB 上一点O 为端点作射线OC ,使70AOC ∠=︒,在同一个平面内将一个直角三角板的直角顶点放在点O 处.(注:90DOE ∠=︒)(1)如图1,如果直角三角板DOE 的一边OD 放在射线OA 上,那么COE ∠的度数为______;(2)如图2,将直角三角板DOE 绕点O 按顺时针方向转动到某个位置,如果OC 恰好平分AOE ∠,求COD ∠的度数;(3)如图3,将直角三角板DOE 绕点O 任意转动,如果OD 始终在AOC ∠的内部,请直接用等式表示AOD ∠和COE ∠之间的数量关系.26.如图,一个五棱柱的盒子(有盖),有一只蚂蚁在A 处发现一只虫子在D 处,立刻赶去捕捉,你知道它怎样去的吗?请在图中画出它的爬行路线,如果虫子正沿着DI 方向爬行,蚂蚁预想在点I 处将它捕捉,应沿着什么方向?请在图中画出它的爬行路线.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】分别找出每个图形从三个方向看所得到的图形即可得到答案.【详解】解:①正方体从上面、正面、左侧三个不同方向看到的形状都是正方形,故此选项正确;②球从上面、正面、左侧三个不同方向看到的形状都是圆,故此选项正确;③圆锥,从左边看是三角形,从正面看是三角形,从上面看是圆,故此选项错误;④圆柱从左面和正面看都是矩形,从上边看是圆,故此选项错误;故选B.【点睛】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.2.D解析:D【解析】解:A、由点C是线段AB的中点,则AB=2AC,正确,不符合题意;B、AC+CD+DB=AB,正确,不符合题意;C、由点C是线段AB的中点,则AC=12AB,CD=AD-AC=AD-12AB,正确,不符合题意;D、AD=AC+CD=12AB+CD,不正确,符合题意.故选D.3.D解析:D【分析】根据题意首先计算出∠AOD的度数,再计算出∠AOE、∠EOC、∠BOE、∠BOD的度数,然后再分析即可.【详解】解:由题意设∠BOE=x,∠EOC=3x,∵∠DOE=60°,OD平分∠AOB,∴∠AOD=∠BOD =60°-x,根据题意得:2(60°-x)+4x=180°,解得x=30°,∴∠EOC=∠AOE=90°,∠BOE=30°,∴∠BOD=∠AOD=30°,故①正确;∵∠BOD=∠AOD=30°,∴射线OE平分∠AOC,故②正确;∵∠BOE=30°,∠AOB=60°,∠DOE=60°,∴∠AOB+∠BOE=90°,∠BOE+∠DOE=90°,∴图中与∠BOE互余的角有2个,故③正确;∵∠AOE=∠EOC=90°,∴∠AOE+∠EOC=180°,∵∠EOC=90°,∠DOB=30°,∠BOE=30°,∠AOD=30°,∴∠COD+∠AOD=180°,∠COD+∠BOD=180°,∠COD+∠BOE=180°,∠COB+∠AOB=180°,∠COB+∠DOE=180°,∴图中互补的角有6对,故④正确,正确的有4个,故选:D.【点睛】本题主要考查角平分线以及补角和余角,解答的关键是正确计算出图中各角的度数.4.A解析:A【分析】根据题意各种角的关系直接可求出题目要求的角度.【详解】因为∠AOD=40°,∠BOC=50°,所以∠COD=90°,又因为OM,ON分别平分∠BOC和∠AOD,所以∠N OD+∠M OC=45°,则∠MON=∠N OD+∠M OC+∠COD=135°.【点睛】本题考查了角平分线的知识,掌握角平分线的性质是解决此题的关键.5.B解析:B【分析】根据平行线的性质和角平分线性质可求.【详解】解:∵AB∥CD,∴∠1+∠BEF=180°,∠2=∠BEG,∴∠BEF=180°-50°=130°,又∵EG平分∠BEF,∠BEF=65°,∴∠BEG=12∴∠2=65°.故选:B.【点睛】此题考查平行线的性质,角平分线的性质,解题关键在于掌握两直线平行,内错角相等和同旁内角互补这两个性质.6.D解析:D【分析】根据常见的几何体的展开图进行判断,即可得出结果.【详解】根据几何体的平面展开图,则从左到右,其对应的几何体名称分别为:圆锥,正方体,三棱锥,圆柱;故选:D【点睛】本题考查了常见几何体的展开图;熟记常见几何体的平面展开图的特征,是解决此类问题的关键.7.C解析:C【分析】根据∠1的余角是∠2,并且∠1=2∠2求出∠1,再求∠1的补角.【详解】∵∠1的余角是∠2,∴∠1+∠2=90°,∵∠1=2∠2,∴2∠2+∠2=90°,∴∠2=30°,∴∠1=60°,∴∠1的补角为180°﹣60°=120°.故选:C.【点睛】本题考查了余角和补角,熟记概念并理清余角和补角的关系求解更简便.8.C解析:C【分析】首先求得AB与正东方向的夹角的度数,即可求解.【详解】根据题意得:∠BAC=(90°﹣70°)+15°+90°=125°,故选:C.【点睛】本题考查了方向角,正确理解方向角的定义是关键.9.C解析:C【分析】根据度分秒之间的换算,先把∠C的度数化成度、分、秒的形式,再根据角的大小比较的法则进行比较,即可得出答案.【详解】解:∵∠C=20.25°=20°15′,∴∠A>∠C>∠B,故选:C.【点睛】此题考查了角的大小比较,先把∠C的度数化成度、分、秒的形式,再进行比较是本题的关键.10.B解析:B【分析】根据线段中点的定义和性质,可得答案.【详解】若AM=MB,M不在线段AB上时,则M不是AB的中点,故①错误,若AM=MB=12AB,则M是AB的中点,故②正确;若AM=12AB,M不在线段AB上时,则M不是AB的中点,故③错误;若A,M,B在一条直线上,且AM=MB,则M是AB的中点,故④正确;故正确的是:②④故选B.【点睛】本题考查了线段中点的定义和性质,线段上到线段两端点距离相等的点是线段的中点.11.D解析:D【解析】【分析】圆锥是由圆和扇形围成的几何体,圆锥的底面是圆,侧面是曲面,截一个几何体,截面的形状既与被截的几何体有关,还与截面的角度和方向有关,据此对所给选项一一进行判断.【详解】圆锥的轴截面是B,平行于底面的截面是C,当截面与轴截面斜交时截面是A;无论如何截,截面都不可能是D.故选D.【点睛】此题考查截一个几何体,解题关键是掌握圆锥的特点进行求解.12.A解析:A【解析】【分析】用一个平面截正方体,若所得的截面是一个三角形,此时剩下的较大的几何体一定比正方体多了一个面,如果过三个面截得的截面是三角形,那么就能多出3条棱和两个顶点,如果过3个顶点截得的截面是三角形,那么就能多出0条棱和两个顶点.【详解】用一个平面截正方体,若所得的截面是一个三角形,此时剩下的较大的几何体一定比正方体多了一个面,如果过三个面截得的截面是三角形,那么就能多出3条棱和两个顶点,如果过3个顶点截得的截面是三角形,那么就能多出0条棱和两个顶点.故选:A.【点睛】此题考查截一个几何体,解题关键在于掌握立体图形.二、填空题13.14【分析】画出图形后分别求出BCCDDEEFFG的大小可得AB=FGBC=DECD=EF然后根据票价是由路程决定再分别求出从ABCDEF出发的情况相加即可【详解】解:①从A分别到BCDEFG共6种解析:14【分析】画出图形后分别求出BC、CD、DE、EF、FG的大小,可得AB=FG,BC=DE,CD=EF,然后根据票价是由路程决定,再分别求出从A、B、C、D、E、F出发的情况,相加即可.【详解】解:①从A分别到B、C、D、E、F、G共6种票价,如图:BC=805﹣445=360,CD=1135﹣805=330,DE=1495﹣1135=360,EF=1825﹣1495=330,FG=2270﹣1825=445,即AB=FG,BC=DE,CD=EF,②∵BC=360,BD=690,BE=1050,BF=1380,BG=1825=AF,∴从B出发的有4种票价,有BC、BD、BE、BF,4种;③∵CD=330,CE=690=BD,CF=1020,CG=1465,∴从C出发的(除去路程相同的)有3种票价,有CD,CF,CG,3种;④∵DE=360=BC,DF=690=BD,DG=1135=AD,∴从D出发的(除去路程相同的)有0种票价;⑤∵EF=330=CD,EG=775,∴从E出发的(除去路程相同的)有1种票价,有EG,1种;⑥∵FG=445=AB,∴从F出发的(除去路程相同的)有0种票价;∴6+4+3+0+1+0=14.故答案为:14.【点睛】本题考查了线段知识的实际应用,正确理解题意、不重不漏的求出所有情况是解此题的关键,这是一道比较容易出错的题目,求解时注意分类全面.14.【分析】由线段中点的定义可得AC=BC=AB根据线段的和差关系及==2可得出CDCE与AB的关系进而可得答案【详解】∵点C是线段AB的中点∴AC=BC=AB∵==2BD=AB-ADAE=AB-BE∴解析:3 5【分析】由线段中点的定义可得AC=BC=12AB,根据线段的和差关系及ADDB=23,AEEB=2,可得出CD、CE与AB的关系,进而可得答案.【详解】∵点C是线段AB的中点,∴AC=BC=12AB,∵ADDB =23,AEEB=2,BD=AB-AD,AE=AB-BE,∴AD=25AB,BE=13AB,∵CD=AC-AD,CE=BC-BE,∴CD=12AB-25AB=110AB,CE=12AB-13AB=16AB,∴CDCE=11016ABAB=35,故答案为3 5【点睛】本题主要考查中点的定义及线段之间的和差关系,灵活运用线段的和、差、倍、分转化线段之间的数量关系是解题关键.15.45°【分析】结合图形根据角的和差以及角平分线的定义找到∠MON与∠AOB的关系即可求出∠MON的度数【详解】解:∵OM平分∠AOCON平分∠BOC∴∠MOC=∠AOC∠NOC=∠BOC∴∠MON=解析:45°【分析】结合图形,根据角的和差,以及角平分线的定义,找到∠MON与∠AOB的关系,即可求出∠MON的度数.【详解】解:∵OM平分∠AOC,ON平分∠BOC,∴∠MOC=12∠AOC,∠NOC=12∠BOC,∴∠MON=∠MOC-∠NOC=12(∠AOC-∠BOC)=12(∠AOB+∠B0C-∠BOC)=12∠AOB=45°.故选答案为45°.【点睛】本题考查了角的计算,属于基础题,此类问题,注意结合图形,运用角的和差和角平分线的定义求解.16.三角形【分析】分析用一个平面分别去截圆锥棱柱分别能够得到哪些截面图形然后从分别得到的截面图形中找出都有的图形即可【详解】用一个平面去截棱柱可以得到三角形长方形;用一个平面去截圆锥可以得到圆三角形等故解析:三角形【分析】分析用一个平面分别去截圆锥、棱柱,分别能够得到哪些截面图形,然后从分别得到的截面图形中找出都有的图形即可.【详解】用一个平面去截棱柱可以得到三角形、长方形;用一个平面去截圆锥可以得到圆、三角形等.故用一个平面分别去截分别截棱柱、圆锥,都能截出的一个截面是三角形.故答案为三角形.【点睛】此题考查几何体的截面图形,熟练掌握常见几何体的截面图形是解题的关键.17.【分析】棱长为1cm的正方体拼的表面积是6要使拼接成的长方体表面积最大则重合的面要最少当四个正方体排成一列时面积最大重合的有6个面【详解】解:当四个正方体排成一列时面积最大重合的有6个面根据以上分析解析:18【分析】棱长为1cm的正方体拼的表面积是6,要使拼接成的长方体表面积最大则重合的面要最少,当四个正方体排成一列时,面积最大.重合的有6个面.【详解】解:当四个正方体排成一列时,面积最大.重合的有6个面.根据以上分析表面积最大的为:4×(4×1)+2×(1×1)=18.故答案为18.【点睛】本题的考查了长方体表面积的计算,关键是要分析出什么情况下表面积最大.18.14【解析】【分析】先求出两边线段的长度之和第一段中点到第三段中点之间的距离等于两边线段的一半与中间线段的和【详解】根据题意第一段与第三段长度之和=20-8=12cm所以第一段中点到第三段中点之间的解析:14【解析】【分析】先求出两边线段的长度之和,第一段中点到第三段中点之间的距离等于两边线段的一半与中间线段的和.【详解】根据题意,第一段与第三段长度之和=20-8=12cm,所以第一段中点到第三段中点之间的距离=12÷2+8=6+8=14cm.【点睛】能正确找出“第一段中点到第三段中点之间的距离等于两边线段的一半与中间线段的和”是解本题的关键.19.20【解析】【分析】本题需先求出AB之间共有多少条线段根据线段的条数即可求出车票的种数【详解】设点CDE是线段AB上的三个点根据题意可得:图中共用=10条线段∵A到B与B到A车票不同∴从A到B的车票解析:20【解析】【分析】本题需先求出A、B之间共有多少条线段,根据线段的条数即可求出车票的种数.【详解】设点C、D、E是线段AB上的三个点,根据题意可得:图中共用()5152-⨯=10条线段∵A到B与B到A车票不同.∴从A到B的车票共有10×2=20种故答案为20.【点睛】本题主要考查了如何求线段的条数的问题,在解题时要注意线段的条数与车票种数的联系与区别.20.②两点之间线段最短【分析】结合两点之间线段最短以及图形信息即可解答本题【详解】根据题意可把家与超市看作两个点结合两点之间线段最短即可得出第②条为最短距离即数学知识为两点之间线段最短【点睛】本题考查两解析:② 两点之间,线段最短【分析】结合“两点之间线段最短”以及图形信息即可解答本题.【详解】根据题意,可把家与超市看作两个点,结合“两点之间线段最短”即可得出第②条为最短距离,即数学知识为“两点之间线段最短”.【点睛】本题考查两点之间的最短距离,熟练掌握“两点之间线段最短”的性质是解题关键.三、解答题21.(1)180°;(2)180°;(3)60°.【解析】试题分析:(1)先根据OB平分∠COD得出∠BOC及∠AOC的度数,进而可得出结论;(2)根据直角三角板的性质得出∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°进而可得出结论;(3)根据(1)、(2)的结论可知∠AOD+∠BOC=180°,故可得出∠AOD=180°﹣∠BOC,根据∠BOC的余角的4倍等于∠AOD即可得出结论.解:(1)∵OB平分∠COD,∴∠BOC=∠BOD=45°.∵∠AOC+∠BOC=45°,∴∠AOC=45°,∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°.故答案为180°;(2)∵∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,∴∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=90°+90°=180°;(3)∵由(1)、(2)得,∠AOD+∠BOC=180°,∴∠AOD=180°﹣∠BOC.∵∠AOD=4(90°﹣∠BOC),∴180°﹣∠BOC=4(90°﹣∠BOC),∴∠BOC=60°.考点:余角和补角;角平分线的定义.22.(1)见解析;(2)45 或30.【分析】(1)根据题意作出图形即可;(2)根据角平分线的定义即可得到结论.【详解】(1)如图所示,BOC ∠与BOC '∠即为所求.(2)AOP ∠的度数为45︒或30︒.∵∠AON=45°,∠BON=30°,∴∠AOB=75°,∵∠BOC 与∠AOB 互余,∴∠BOC=∠BOC′=15°,∴∠AOC=90°,∠AOC=60°,∵OP 是∠AOC 的角平分线,∴∠AOP=45°或30°.【点睛】本题主要考查了方向角的定义,余角的定义,作出图形,正确掌握方向角的定义是解题关键.23.(1)90︒;(2)105︒;(3)若点G 在点F 的右侧,2180FEG α︒∠=-;若点G 在点F 的左侧,1802FEG α︒∠=-【分析】(1)由题意根据角平分线的定义,平角的定义,角的和差定义计算即可.(2)由题意根据∠MEN=∠NEF+∠FEG+∠MEG ,求出∠NEF+∠MEG 即可解决问题. (3)根据题意分点G 在点F 的右侧以及点G 在点F 的左侧两种情形分别求解即可.【详解】解:(1)因为EN 平分AEF ∠,EM 平分BEF ∠, 所以12NEF AEF ∠=∠,12MEF BEF ∠=∠, 所以1111()2222MEN NEF MEF AEF BEF AEF BEF AEB ∠=∠+∠=∠+∠=∠+∠=∠. 因为180AEB ︒∠=, 所以1180902MEN ︒︒∠=⨯=.(2)因为EN 平分AEF ∠,EM 平分BEG ∠, 所以12NEF AEF ∠=∠,12MEG BEG ∠=∠, 所以1111()()2222NEF MEG AEF BEG AEF BEG AEB FEG ∠+∠=∠+∠=∠+∠=∠-∠. 因为180AEB ︒∠=,30FEG ︒∠=,所以()118030752NEF MEG ︒︒︒∠+∠=-=, 所以7530105MEN NEF FEG MEG ︒︒︒∠=∠+∠+∠=+=.(3)因为EN 平分AEF ∠,EM 平分BEG ∠,所以12NEF AEF AEN ∠=∠=∠,12MEG BEG BEM ∠=∠=∠, 若点G 在点F 的右侧,MEN NEF FEG MEG α∠=∠+∠+∠=, ()()(180)2180FEG NEF MEG AEN BEM ααααα︒︒∠=-∠+∠=-∠+∠=-=--;若点G 在点F 的左侧,MEN NEF MEG FEG α∠=∠+∠-∠=1801802FEG NEF MEG AEN BEM ααααα︒︒∠=∠+∠-=∠+∠-=--=-.【点睛】本题考查角的计算,翻折变换,角平分线的定义,角的和差定义等知识,解题的关键是学会用分类讨论的思想思考问题.24.见解析.【分析】(1)连接AB 、CD 并向两方无限延长即可得到直线AB 、CD ;交点处标点E ;(2)连接AC 、BD 可得线段AC 、BD ,交点处标点F ;(3)连接AD 并从D 向A 方向延长即可;(4)连接BC ,并且以B 为端点向BC 方向延长.【详解】解:所求如图所示:.本题考查的是直线、射线、线段的定义及性质,解答此题的关键是熟知以下知识,即直线向两方无限延伸;射线向一方无限延伸;线段有两个端点画出图形即可.25.(1)20︒;(2)20︒;(3)20COE AOD ∠-∠=︒或20COE AOD ∠=︒+∠.【分析】(1)如图1,如果直角三角板DOE 的一边OD 放在射线OA 上,则∠COE =20°; (2)由角平分线可得70COE AOC ∠=∠=︒,再利用角的和差进行计算即可; (3)分别用∠COE 及∠AOD 的式子表达∠COD ,进行列式即可.【详解】解:(1)∵90DOE ∠=︒,70AOC ∠=︒∴907020COE DOE AOC =∠-∠=︒-︒=︒∠故答案为:20︒(2)∵OC 平分AOE ∠,70AOC ∠=︒,∴70COE AOC ∠=∠=︒,∵90DOE ∠=︒,∴907020COD DOE COE ∠=∠-∠=︒-︒=︒.(3)∵90COD DOE COE COE =∠-∠=︒-∠∠,70COD AOC AOD AOD =∠-∠=︒-∠∠∴9070COE AOD ︒-∠=︒-∠∴20COE AOD ∠-∠=︒或20COE AOD ∠=︒+∠.故答案为:20COE AOD ∠-∠=︒或20COE AOD ∠=︒+∠.【点睛】本题考查了角的和差关系,准确表达出角的和差关系是解题的关键.26.第一问:如图沿线段AD 爬行;第二问取线段E J 的中点M ,连结AM 和MI ,此路线为蚂蚁爬行的路线.【分析】根据两点之间线段最短,结合图形得出蚂蚁爬行的路线.【详解】解:第一问:如图沿线段AD 爬行;第二问取线段E J 的中点M ,连结AM 和MI ,此路线为蚂蚁爬行的路线.理由都是:两点之间线段最短.本题考查了几何体的展开图与两点之间线段最短,利用展开图的性质得出答案是解题的关键.。
数学七年级上册《几何图形初步》单元测试题含答案

【答案】C
【解析】
【分析】
本题应考虑到A、B、C三点之间的位置关系的多种可能,即当点C在线段AB上时和当点C在线段AB的延长线上时.
【详解】(1)当点C在线段AB上时,则MN= AC+ BC= AB=5;
(2)当点C在线段AB的延长线上时,则MN= AC- BC=7-2=5.
人教版数学七年级上学期
第四章单元测试
满分:100分 时间:90分钟
一.选择题
1.下列说法正确的是( )
A.直线BA与直线AB是同一条直线B.延长直线AB
C.射线BA与射线AB是同一条射线D.直线AB 长为2cm
2.如图,将一副三角尺按不同的位置摆放,下列摆放方式中 与 互余的是()
A.图①B.图②C.图③D.图④
25.(1)下面四个图分别由六个相同的正方形拼接而成,其中不能折(从A、B、C、D选择)的是_________.
(2)用斜二侧画法补画图1的图形,使之成为长方体的直观图(虚线表示被遮住的线段;只要在已有图形基础上画出长方体,不必写画法步骤).
(3)在这一长方体中,从同一个顶点出发的三个面的面积之比是5:7:2,其中最大的比最小的面积大60cm2,求这个长方体的表面积.
详解:∵180°-60°30′=119°30′, ∴60°30′的补角为119°30′.
点睛:本题主要考查的是角的计算问题,属于基础题型.明确度、分、秒之间的进率关系是解题的关键.
12.如图,点C在线段AB上,D是线段AC的中点,若CB=2,CD=3CB,则线段AB的长_____.
A. 100°B. 115°C. 65°D. 130°
9.已知∠A=55°34′,则∠A的余角等于( )
2024-2025学年人教新版七年级上册数学《第4章 整式的加减》单元测试卷(有答案)

2024-2025学年人教新版七年级上册数学《第4章整式的加减》单元测试卷一.选择题(共8小题,满分24分)1.代数式x2+5,﹣1,x2﹣8x+2,π,,中,整式有()A.3个B.4个C.5个D.6个2.已知﹣2x6y与5x2m y n是同类项,则()A.m=2,n=1B.m=3,n=1C.m=,n=1D.m=3,n=03.下列计算正确的是()A.5a﹣2a=3B.2a2+6a2=8a4C.x2y﹣2xy2=﹣xy2D.3mn﹣2mn=mn4.在等式1﹣a2+2ab﹣b2=1﹣()中,括号里应填()A.a2﹣2ab+b2B.a2﹣2ab﹣b2C.﹣a2﹣2ab+b2D.﹣a2+2ab﹣b25.若a<0,则|a﹣(﹣a)|等于()A.﹣a B.0C.2a D.﹣2a6.如图是小明完成的线上作业,他的得分是()判断题(每小题2分,共10分)①1是单项式.(×)②非负有理数不包括零.(×)③绝对值不相等的两个数的和一定不为零.(√)④单项式﹣a的系数与次数都是1.(√)⑤将34.945精确到十分位为34.95.(×)A.4分B.6分C.8分D.10分7.在下列各整式中,次数为5的是()A.8x3y B.m+n2+q2C.52c3D.x2y38.若代数式2(mx2+x﹣1)﹣(x2﹣nx+1)的值与x的取值无关,则m2023n2025的值为()A.﹣4B.4C.D.二.填空题(共8小题,满分24分)9.有一道题:﹣3x(﹣2x2+3x﹣1)=6x3﹣9x2+□,“□”的地方被墨水弄污了,你认为“□”内应填写.10.已知关于x的整式x3﹣x2+x a﹣2x﹣2bx中不含有x的一次项和二次项,则a+b=.11.若关于x,y,z的单项式﹣mx3y n与单项式的次数相同,系数互为倒数,则该单项式是.12.多项式x2+x+1的次数是.13.若2a m+1b2与﹣3a3b n是同类项,则m+n的值为.14.若一个四位自然数M各个数位上的数字均不为0,且前两位数字之和为5,后两位数字之和为8,则称M为“幸福数”.把四位数M的前两位数字和后两位数字整体交换得到新的四位自然数N.规定.例如:M=2344,∵2+3=5,4+4=8,∴2344是“幸福数”,则.若P是最大的“幸福数”,则F(P)=;若S是“幸福数”,且F(S)恰好能被8整除,则所有满足题意的S的值共有个.15.如果a2﹣3a﹣7=0,那么代数式(a﹣1)2+a(a﹣4)﹣2的值为.16.设x、y互为相反数,且xy≠0.m的绝对值为8,则的值为.三.解答题(共6小题,满分52分)17.已知单项式﹣3xy2的系数和次数分别是a,b,求ab+a b的值.18.已知A=3x2+xy+y,B=2x2﹣xy+2y.(1)化简2A﹣3B.(2)当x=2,y=﹣3,求2A﹣3B的值.19.【问题呈现】(1)已知代数式mx﹣y﹣3x+4y﹣1的值与x的值无关,求m的值;【类比应用】(2)将7张长为a,宽为b的小长方形纸片(如图①),按如图②的方式不重叠地放在长方形ABCD 内,未被覆盖的两部分的面积分别记为S1,S2,当AB的长度变化时,S1﹣S2的值始终不变,求a与b 的数量关系.20.已知多项式A=(m﹣3)2﹣(2﹣m)(2+m)+6m.(1)化简多项式A;(2)若m2﹣4=5,求多项式A的值.21.类比同类项的概念,我们规定:所含字母相同,并且相同字母的指数之差的绝对值等于0或1的项是“强同类项”,例如:﹣x3y4与2x4y3是“强同类项”.(1)给出下列四个单项式:①5x2y5,②﹣x5y5,③4x4y4,④﹣2x3y6.其中与x4y5是“强同类项”的是(填写序号);(2)若x3y4z m﹣2与﹣2x2y3z6是“强同类项”,求m的值;(3)若C为关于x、y的多项式,C=(n﹣5)x5y6+3x4y5﹣7x4y n,当C的任意两项都是“强同类项”,求n的值;(4)已知2a2b s、3a t b4均为关于a,b的单项式,其中s=|x﹣1|+k,t=2k,如果2a2b s、3a t b4是“强同类项”,那么x的最大值是,最小值是.22.定义:若非零实数a,b,c满足,则称c是a和b的“协调数”.如4是3和6的“协调数”.(1)问:是不是﹣2和﹣3的“协调数”?(2)若2m是p和q的“协调数”,用m,q的代数式表示q.参考答案与试题解析一.选择题(共8小题,满分24分)1.B2.B3.D4.A5.D6.B7.D8.A二.填空题(共8小题,满分24分)9.3x.10.1.11.﹣3x3y2.12.2.13.4.14.30,3.15.13.16.16或﹣16.三.解答题(共6小题,满分52分)17.﹣36.18.解:(1)2A﹣3B=2(3x2+xy+y)﹣3(2x2﹣xy+2y)=6x2+2xy+2y﹣6x2+3xy﹣6y=5xy﹣4y;(2)当x=2,y=﹣3时,2A﹣3B=5xy﹣4y=5×2×(﹣3)﹣4×(﹣3)=﹣18.19.(1)3;(2)a﹣2b=0.20.(1)2m2+5;(2)23.21.(1)②③④;(2)m=7,8,9;(3)n=5或n=6;(4),.22.(1)是;(2).。
人教版七年级数学上册《第4章几何图形初步》单元测试含答案解析

《第4章几何图形初步》一、选择题1.分别从正面、左面和上面这三个方向看下面的四个几何体,得到如图所示的平面图形,那么这个几何体是()A.B.C.D.2.从左面看图中四个几何体,得到的图形是四边形的几何体共有()A.1个B.2个C.3个D.4个3.如图,四个图形是由立体图形展开得到的,相应的立体图形顺次是()A.正方体、圆柱、三棱柱、圆锥B.正方体、圆锥、三棱柱、圆柱C.正方体、圆柱、三棱锥、圆锥D.正方体、圆柱、四棱柱、圆锥4.如图,对于直线AB,线段CD,射线EF,其中能相交的图是()A.B.C. D.5.下面等式成立的是()A.83.5°=83°50′B.37°12′36″=37.48°C.24°24′24″=24.44° D.41.25°=41°15′6.下列语句:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;③不在同一直线上的四个点可画6条直线;④如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.其中错误的有()A.1个B.2个C.3个D.4个7.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是()A.25° B.35° C.45° D.55°8.如图,∠1+∠2等于()A.60° B.90° C.110°D.180°9.C是线段AB上一点,D是BC的中点,若AB=12cm,AC=2cm,则BD的长为()A.3cm B.4cm C.5cm D.6cm10.甲乙两人各用一张正方形的纸片ABCD折出一个45°的角(如图),两人做法如下:甲:将纸片沿对角线AC折叠,使B点落在D点上,则∠1=45°;乙:将纸片沿AM、AN折叠,分别使B、D落在对角线AC上的一点P,则∠MAN=45°.对于两人的做法,下列判断正确的是()A.甲乙都对 B.甲对乙错 C.甲错乙对 D.甲乙都错二、填空题11.如图,各图中的阴影部分绕着直线l旋转360°,所形成的立体图形分别是.12.如图,以图中A,B,C,D,E为端点的线段共有条.13.如图所示:把两块完全相同的直角三角板的直角顶点重合,如果∠AOD=128°,那么∠BOC= .14.如图,直线AB,CD相交于点0,OE平分∠AOD,若∠BOC=80°,则∠AOE= °.15.如图是某几何体的平面展开图,则这个几何体是.16.如图绕着中心最小旋转能与自身重合.17.如图所示,一艘船从A点出发,沿东北方向航行至B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC等于度.18.一个圆绕着它的直径只要旋转180度,就形成一个球体;半圆绕着直径旋转度,就可以形成一个球体.19.已知∠A=40°,则它的补角等于.20.两条直线相交有个交点,三条直线相交最多有个交点,最少有个交点.三、解答题(21、22、26、27小题各12分,23、24、25题各14分,共90分)21.如图,若CB=4cm,DB=7cm,且D是AC的中点,求线段DC和AB的长度.22.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.23.已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.(1)求∠MON的大小;(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?24.如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.(1)求x的值.(2)求正方体的上面和底面的数字和.25.如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD 的度数.26.如图,已知C是AB的中点,D是AC的中点,E是BC的中点.(1)若DE=9cm,求AB的长;(2)若CE=5cm,求DB的长.27.一个角的余角比它的补角的还少20°,求这个角.《第4章几何图形初步》参考答案与试题解析一、选择题1.分别从正面、左面和上面这三个方向看下面的四个几何体,得到如图所示的平面图形,那么这个几何体是()A.B.C.D.【考点】由三视图判断几何体.【分析】由主视图和左视图可得此几何体为柱体,根据俯视图是三角形可判断出此几何体为三棱柱.【解答】解:∵主视图和左视图都是长方形,∴此几何体为柱体,∵俯视图是一个三角形,∴此几何体为三棱柱.故选C.【点评】本题主要考查了由三视图判断几何体,由主视图和左视图可得几何体是柱体,锥体还是球体,由俯视图可确定几何体的具体形状.2.从左面看图中四个几何体,得到的图形是四边形的几何体共有()A.1个B.2个C.3个D.4个【考点】简单几何体的三视图.【分析】四个几何体的左视图:圆柱是矩形,圆锥是等腰三角形,球是圆,正方体是正方形,由此可确定答案.【解答】解:因为圆柱的左视图是矩形,圆锥的左视图是等腰三角形,球的左视图是圆,正方体的左视图是正方形,所以,左视图是四边形的几何体是圆柱和正方体;故选B.【点评】本题主要考查三视图的左视图的知识;考查了学生的空间想象能力,属于基础题.3.如图,四个图形是由立体图形展开得到的,相应的立体图形顺次是()A.正方体、圆柱、三棱柱、圆锥B.正方体、圆锥、三棱柱、圆柱C.正方体、圆柱、三棱锥、圆锥D.正方体、圆柱、四棱柱、圆锥【考点】几何体的展开图.【分析】根据正方体、圆锥、三棱柱、圆柱及其表面展开图的特点解题.【解答】解:观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱、圆锥.故选A.【点评】可根据所给图形判断具体形状,也可根据所给几何体的面数进行判断.4.如图,对于直线AB,线段CD,射线EF,其中能相交的图是()A.B.C. D.【考点】直线、射线、线段.【分析】根据直线、射线、线段的定义对各选项分析判断利用排除法求解.【解答】解:A、直线AB与线段CD不能相交,故本选项错误;B、直线AB与射线EF能够相交,故本选项正确;C、射线EF与线段CD不能相交,故本选项错误;D、直线AB与射线EF不能相交,故本选项错误.故选B.【点评】本题考查了直线、射线、线段,熟记定义并准确识图是解题的关键.5.下面等式成立的是()A.83.5°=83°50′B.37°12′36″=37.48°C.24°24′24″=24.44° D.41.25°=41°15′【考点】度分秒的换算.【专题】计算题.【分析】进行度、分、秒的加法、减法计算,注意以60为进制.【解答】解:A、83.5°=83°50′,错误;B、37°12′=37.48°,错误;C、24°24′24″=24.44°,错误;D、41.25°=41°15′,正确.故选D.【点评】此类题是进行度、分、秒的加法、减法计算,相对比较简单,注意以60为进制即可.6.下列语句:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;③不在同一直线上的四个点可画6条直线;④如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.其中错误的有()A.1个B.2个C.3个D.4个【考点】垂线;直线、射线、线段;对顶角、邻补角.【分析】根据垂线的性质可得①错误;根据对顶角的性质可得②正确;根据两点确定一条直线可得③错误;根据邻补角互补可得④正确.【解答】解:①一条直线有且只有一条垂线,说法错误;②不相等的两个角一定不是对顶角,说法正确;③不在同一直线上的四个点可画6条直线,说法错误,应为4或6条;④如果两个角是邻补角,那么这两个角的平分线组成的图形是直角,说法正确.故选:B.【点评】此题主要考查了垂线、邻补角、对顶角,关键是熟练掌握课本知识.7.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是()A.25° B.35° C.45° D.55°【考点】角平分线的定义;对顶角、邻补角.【专题】计算题.【分析】根据角平分线的定义求出∠AOC的度数,再根据对顶角相等即可求解.【解答】解:∵OA平分∠EOC,∠EOC=110°,∴∠AOC=∠COE=55°,∴∠BOD=∠AOC=55°.故选D.【点评】本题主要考查了角平分线的定义以及对顶角相等的性质,认准图形是解题的关键.8.如图,∠1+∠2等于()A.60° B.90° C.110°D.180°【考点】余角和补角.【专题】计算题.【分析】根据平角的定义得到∠1+90°+∠2=180°,即有∠1+∠2=90°.【解答】解:∵∠1+90°+∠2=180°,∴∠1+∠2=90°.故选B.【点评】本题考查了平角的定义:180°的角叫平角.9.C是线段AB上一点,D是BC的中点,若AB=12cm,AC=2cm,则BD的长为()A.3cm B.4cm C.5cm D.6cm【考点】两点间的距离.【分析】先求出BC,再根据线段中点的定义解答.【解答】解:∵AB=12cm,AC=2cm,∴BC=AB﹣AC=12﹣2=10cm.∵D是BC的中点,∴BD=BC=×10=5cm.故选C.【点评】本题考查了两点间的距离,主要利用了线段中点的定义,熟记概念是解题的关键,作出图形更形象直观.10.甲乙两人各用一张正方形的纸片ABCD折出一个45°的角(如图),两人做法如下:甲:将纸片沿对角线AC折叠,使B点落在D点上,则∠1=45°;乙:将纸片沿AM、AN折叠,分别使B、D落在对角线AC上的一点P,则∠MAN=45°.对于两人的做法,下列判断正确的是()A.甲乙都对 B.甲对乙错 C.甲错乙对 D.甲乙都错【考点】翻折变换(折叠问题).【分析】甲沿正方形的对角线进行折叠,根据正方形对角线的性质,可得∠1=45°,故甲的做法是正确的;乙进行折叠后,可得两对等角,而四个角的和为90°,故∠MAN=45°是正确的,这样答案可得.【解答】解:∵AC为正方形的对角线,∴∠1=×90°=45°;∵AM、AN为折痕,∴∠2=∠3,4=∠5,又∵∠DAB=90°,∴∠3+∠4=×90°=45°.∴二者的做法都对.故选A.【点评】本题考查了图形的翻折问题;解答此类问题的关键是找着重合的角,结合直角进行求解.二、填空题11.如图,各图中的阴影部分绕着直线l旋转360°,所形成的立体图形分别是圆柱;圆锥;球.【考点】点、线、面、体.【分析】三角形旋转可得圆锥,长方形旋转得圆柱,半圆旋转得球,结合这些规律直接连线即可.【解答】解:根据分析可得:各图中的阴影图形绕着直线l旋转360°,各能形成圆柱、圆锥、球.故答案为:圆柱、圆锥、球.【点评】本题考查面动成体的知识,难度不大,熟记常见平面图形旋转可得到什么立体图形是解决本题的关键.12.如图,以图中A,B,C,D,E为端点的线段共有10 条.【考点】直线、射线、线段.【分析】分别写出各个线段即可得出答案.【解答】解:图中的线段有:线段AB,线段AC,线段AD,线段AE,线段BC,线段BD,线段BE,线段CD,线段CE,线段DE,线段共10条.故答案为:10.【点评】本题考查了直线上点与线段的数量关系,同学们可以记住公式:线段数=.13.如图所示:把两块完全相同的直角三角板的直角顶点重合,如果∠AOD=128°,那么∠BOC= 52°.【考点】角的计算.【专题】计算题.【分析】根据题意得到∠AOB=∠COD=90°,再计算∠BOD=∠AOD﹣90°=38°,然后根据∠BOC=∠COD ﹣∠BOD进行计算即可.【解答】解:∵∠AOB=∠COD=90°,而∠AOD=128°,∴∠BOD=∠AOD﹣90°=38°,∴∠BOC=∠COD﹣∠BOD=90°﹣38°=52°.故答案为52°.【点评】本题考查了角的计算:1直角=90°;1平角=180°.14.如图,直线AB,CD相交于点0,OE平分∠AOD,若∠BOC=80°,则∠AOE= 40 °.【考点】对顶角、邻补角;角平分线的定义.【分析】根据对顶角相等可得∠AOD=80°,再根据角平分线的性质可得∠AOE的度数.【解答】解:∵∠BOC=80°,∴∠AOD=80°,∵OE平分∠AOD,∴∠AOE=80°÷2=40°,故答案为:40.【点评】此题主要考查了角平分线定义,以及对顶角性质,关键是掌握对顶角相等,角平分线平分角.15.如图是某几何体的平面展开图,则这个几何体是三棱柱.【考点】几何体的展开图.【分析】侧面为三个长方形,底边为三角形,故原几何体为三棱柱.【解答】解:由几何体展开图可知,该几何体是三棱柱,故答案为:三棱柱.【点评】本题考查的是三棱柱的展开图,对三棱柱有充分的理解是解题的关键.16.如图绕着中心最小旋转90°能与自身重合.【考点】旋转对称图形.【分析】该图形被平分成四部分,因而每部分被分成的圆心角是90°,并且圆具有旋转不变性,因而旋转90°的整数倍,就可以与自身重合.【解答】解:该图形围绕自己的旋转中心,最少顺时针旋转360°÷4=90°后,能与其自身重合.【点评】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.17.如图所示,一艘船从A点出发,沿东北方向航行至B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC等于60 度.【考点】方向角.【分析】根据南北方向是平行的得出∠ABF=45°,再和∠CBF相加即可得出答案.【解答】解:∵AE∥BF,∴∠ABF=∁EAB=45°,∴∠ABC=∠ABF+∠CBF=45°+15°=60°,故答案为:60.【点评】本题考查了方向角和角的有关计算的应用,主要考查学生的计算能力.18.一个圆绕着它的直径只要旋转180度,就形成一个球体;半圆绕着直径旋转360 度,就可以形成一个球体.【考点】点、线、面、体.【分析】一个半圆围绕直径旋转一周,根据面动成体的原理即可解.【解答】解:半圆绕它的直径旋转360度形成球.【点评】本题考查了平面图形与立体图形的联系,培养学生的观察能力和空间想象能力.19.已知∠A=40°,则它的补角等于140°.【考点】余角和补角.【专题】计算题.【分析】根据补角的和等于180°计算即可.【解答】解:∵∠A=40°,∴它的补角=180°﹣40°=140°.故答案为:140°.【点评】本题考查了补角的知识,熟记互为补角的两个角的和等于180°是解题的关键.20.两条直线相交有 1 个交点,三条直线相交最多有 3 个交点,最少有 1 个交点.【考点】直线、射线、线段.【分析】解析:两条直线相交有且只有1个交点;三条直线两两相交且不交于一点时,有3个交点;当三条直线交于同一点时,有1个交点.【解答】解:两条直线相交有1个交点,三条直线相交最多有3个交点,最少有1个交点.故答案为:1;3;1.【点评】本题考查了直线、射线、线段,主要利用了相交线的交点,是基础题.三、解答题(21、22、26、27小题各12分,23、24、25题各14分,共90分)21.如图,若CB=4cm,DB=7cm,且D是AC的中点,求线段DC和AB的长度.【考点】两点间的距离.【分析】根据线段的和差,CB、DB的长,可得DC的长,根据线段中点的性质,可得AD与DC的关系,根据线段的和差,可得答案.【解答】解:DC=DB﹣CB=7﹣4=3(cm);D是AC的中点,AD=DC=3(cm),AB=AD+DB=3+7=10(cm).【点评】本题考查了两点间的距离,线段的和差,线段中点的性质是解题关键.22.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.【考点】对顶角、邻补角;角平分线的定义.【专题】计算题.【分析】由已知∠FOC=90°,∠1=40°结合平角的定义,可得∠3的度数,又因为∠3与∠AOD互为邻补角,可求出∠AOD的度数,又由OE平分∠AOD可求出∠2.【解答】解:∵∠FOC=90°,∠1=40°,AB为直线,∴∠3+∠FOC+∠1=180°,∴∠3=180°﹣90°﹣40°=50°.∠3与∠AOD互补,∴∠AOD=180°﹣∠3=130°,∵OE平分∠AOD,∴∠2=∠AOD=65°.【点评】本题主要考查邻补角的概念以及角平分线的定义.23.已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.(1)求∠MON的大小;(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?【考点】角的计算;角平分线的定义.【专题】计算题.【分析】(1)根据∠AOB是直角,∠AOC=40°,可得∠AOB+∠AOC=90°+40°=130°,再利用OM是∠BOC的平分线,ON是∠AOC的平分线,即可求得答案.(2)根据∠MON=∠MOC﹣∠NOC,又利用∠AOB是直角,不改变,可得.【解答】解:(1)∵∠AOB是直角,∠AOC=40°,∴∠AOB+∠AOC=90°+40°=130°,∵OM是∠BOC的平分线,ON是∠AOC的平分线,∴,.∴∠MON=∠MOC﹣∠NOC=65°﹣20°=45°,(2)当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.∵=,又∠AOB是直角,不改变,∴.【点评】此题主要考查角的计算和角平分线的定义等知识点的理解和掌握,难度不大,属于基础题.24.如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.(1)求x的值.(2)求正方体的上面和底面的数字和.【考点】专题:正方体相对两个面上的文字.【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,然后列出方程求解即可;(2)确定出上面和底面上的两个数字3和1,然后相加即可.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“A”与“﹣2”是相对面,“3”与“1”是相对面,“x”与“3x﹣2”是相对面,(1)∵正方体的左面与右面标注的式子相等,∴x=3x﹣2,解得x=1;(2)∵标注了A字母的是正方体的正面,左面与右面标注的式子相等,∴上面和底面上的两个数字3和1,∴3+1=4.【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.25.如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD 的度数.【考点】角的计算;翻折变换(折叠问题).【分析】根据翻折变换的性质可得∠ABC=∠A′BC,再根据角平分线的定义可得∠A′BD=∠EBD,再根据平角等于180°列式计算即可得解.【解答】解:由翻折的性质得,∠ABC=∠A′BC,∵BD平分∠A′BE,∴∠A′B D=∠EBD,∵∠ABC+∠A′BC+∠A′BD+∠EBD=180°,∴∠A′BC+∠A′BD=90°,即∠CBD=90°.【点评】本题考查了角的计算,主要利用了翻折变换的性质,角平分线的定义,熟记概念与性质是解题的关键.26.如图,已知C是AB的中点,D是AC的中点,E是BC的中点.(1)若DE=9cm,求AB的长;(2)若CE=5cm,求DB的长.【考点】比较线段的长短.【专题】计算题.【分析】(1)根据中点的概念,可以证明:AB=2DE,故AB的长可求;(2)由CE的长先求得BC的长,再根据C是AB的中点,D是AC的中点求得CD的长,最后即可求得BD的长.【解答】解:(1)∵D是AC的中点,E是BC的中点,∴AC=2CD,BC=2CE,∴AB=AC+BC=2DE=18cm;(2)∵E是BC的中点,∴BC=2CE=10cm,∵C是AB的中点,D是AC的中点,∴DC=AC=BC=5cm,∴DB=DC+CB=10+5=15cm.【点评】考查了线段的中点的概念.利用中点性质转化线段之间的倍分关系是解题的关键,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.27.一个角的余角比它的补角的还少20°,求这个角.【考点】余角和补角.【专题】计算题.【分析】首先根据余角与补角的定义,设这个角为x,则它的余角为(90°﹣x),补角为(180°﹣x),再根据题中给出的等量关系列方程即可求解.【解答】解:设这个角为x,则它的余角为(90°﹣x),补角为(180°﹣x),根据题意可,得90°﹣x=(180°﹣x)﹣20°,解得x=75°.故答案为75°.【点评】此题综合考查余角与补角,属于基础题中较难的题,解答此类题一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式和方程求解.。
人教版数学七年级上册《几何图形初步》单元检测卷附答案
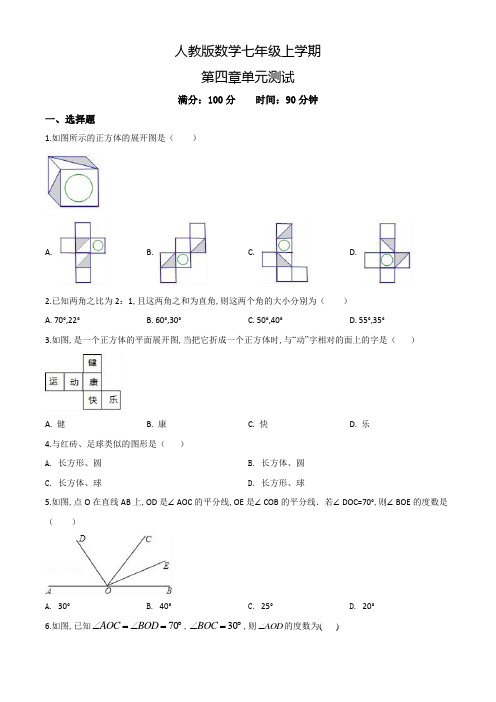
故选D.
【点睛】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
4.与红砖、足球类似的图形是( )
A.长方形、圆B.长方体、圆
C.长方体、球D.长方形、球
16.天上一颗颗闪烁的星星给我们以“_____”的形象;中国武术中有“枪扎一条线,棍扫一大片”的说法,这句话给我们以“_____”的形象;宾馆里旋转的大门给我们以“_____”的形象.
17.定义:两个直角三角形,若一个三角形的两条直角边分别与另一个三角形的两条直角边相等,我们就说这两个直角三角形是“同胞直角三角形”.如图,在边长为10的正方形中有两个直角三角形,当直角三角形①和直角三角形②是同胞直角三角形时,a的值是_____.
9.A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cmB.9cmC.1cm或9cmD. 以上答案都不对
二、填空题
10.如图,有一个长方形纸片,减去相邻的两个角,使∠ABC=90°,如果∠1=152°,那么∠2=_____________°.
11.一个长方体形状的粉笔盒展开如图所示,相对的两个面上的数字之和等于6,则a+b+c=_____.
(1)数一下每一个多面体具有的顶点数 、棱数 和面数 .并且把结果记入表中.
多面体
顶点数
面数
棱数
正四面体
4
4
6
正方体
正八面体
正十二面体
正ห้องสมุดไป่ตู้十面体
12
20
30
(2)观察表中数据,猜想多面体的顶点数 、棱数 和面数 之间的关系.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(第6题)(第7题) 第4章单元测试题2检测时间:45分钟,满分:100分班级学号姓名得分一、填空题:(每空2分,共46分)1.正方体有______条棱,_____个顶点,个面.2.圆柱的侧面展开图是一个,圆锥的侧面展开图是一个,棱柱的侧面展开图是一个。
3.请同学们手拿一枚硬币,将其立在桌面上用力一转,它形成的是一个体,由此说明________________.4.如图,该图中不同的线段共有_______条.5.讲台上放着一个圆锥和一个正方体(如图)请说明下面的三幅图分别是从哪个方向看到的。
(1)从面看到的平面图形;(2)从面看到的平面图形;(3)从面看到的平面图形。
6.已知,如图,∠1=∠2,∠3=∠4,∠AOF=︒=∠9021AOB.(1)射线OD是∠AOC的__________;(2)∠AOC的补角是____________;(3)_______________是∠AOC的余角;(4)∠DOC的余角是____________;(5)∠COF的补角____________.7.直线AB与CD相交于E点,∠1=∠2,EF平分∠AED,且∠1=50°,则∠AEC=,∠CEF = .8.北京时间2点30分,钟面上的时针和分针的夹角为度。
9.用一副三角板可以画的角共有__________个锐角, ________个钝角.10.如图,折叠围成一个正方体时,数字会在与数字2所在的平面相对的平面上。
二、选择题:(每小题3分,共18分)11.平面上有五个点,其中只有三点共线。
经过这些点可以作直线的条数是()(第13题) A .6条 B.8条 C.10条 D.12条12.下列图形中,图中共有8个角的是 ( )A . B. C. D.13.把一张报纸的一角斜折过去,使A 点落在E 点处,BC 为折痕,BD 是∠EBM 的平分线,则∠CBD = ()A.85°B.80°C.75°D.90° 14.如图,AB=16 cm ,C 是AB 上一点,且AC=10 cm ,D 是AC 的中点,E 是BC 的中点,则线段DE 的长度为( )A .6 cm B.8 cm C.10 cmD.12cm 15.如图,能用∠1,∠ACB ,∠C 三种方法表示同一个角的是( )16. 下图中是正方体的展开图的共有 ( )A .1个 B.2个 C.3个 D.4个三、解答题:(第17题8分,第18 题8分、第19题6分,第20题6分,第21题8分,共36分)17.如图,已知AOB 是一条直线,∠1=∠2,∠3=∠4,OF ⊥AB 。
则(1)∠AOC 的补角是 ;(2) 是∠AOC 的余角;(3)∠DOC 的余角是 ;(4)∠COF 的补角是18.如图,有一个几何体,请画出从不同方向看它的平面图形(1)从正面看:(2)从左面看(3)从上面看19. 读下列语句,并按照这些语句画出图形;(1) 在直线l上取三点A、B、C,在直线l外取一点P,画线段AP;画直线PC;画射线BP;(2)射线OP的端点是直线m与直线n的交点,且点P不在直线m、n上;(3)直线a、b相交于点C,直线b、c相交于点A,直线a、c相交于点B;(4)在三角形ABC中,D、E分别为边AC、BC上的点,延长线段AB,反向延长线段ED相交于F。
20.如图,直线AB与CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=65°。
求:(1)∠BOE的度数;(2)∠AOC的度数。
21.如图,在下面的横线上填上适当的角;(1)∠AOC=∠ +∠;(2)∠AOB=∠-∠;或∠AOB=∠-∠;(3)若∠AOC=∠BOD,则∠AOB ∠COD(填“>”、“<”或“=”);(4)若∠AOB=∠COD,则∠AOC ∠BOD(填“>”、“<”或“=”)。
答案:《图形的认识初步》一、1.12,8,6; 2.长方形,扇形,长方形; 3.球体,面动成体; 4.10; 5.正,左,上;6.(1)平分线, (2)∠BOC, (3) ∠3或∠4, (4) ∠DOF ,(5) ∠AOE;7.80,130; 8.105°; 9.5, 5; 10.5.二、 11.B; 12. A; 13. D;14.B; 15. C;16.B.三、 17.(1)∠BOC(2)∠3和∠4(3)∠DOF,(4) ∠AOE。
18. 略(注意阴影). 19.略. 20.(1)65°(2)25 °21.(1)AOB,BOC;(2)AOC,BOC;AOD,BOD(3)=(4)=如何学好初中数学经典介绍浅谈如何学好初中数学数学是必考科目之一,故从初一开始就要认真地学习数学。
那么,怎样才能学好数学呢,现介绍几种方法以供参考:一、课内重视听讲,课后及时复习。
新知识的接受,数学能力的培养主要在课堂上进行,所以要特点重视课内的学习效率,寻求正确的学习方法。
上课时要紧跟老师的思路,积极展开思维预测下面的步骤,比较自己的解题思路与教师所讲有哪些不同。
特别要抓住基础知识和基本技能的学习,课后要及时复习不留疑点。
首先要在做各种习题之前将老师所讲的知识点回忆一遍,正确掌握各类公式的推理过程,庆尽量回忆而不采用不清楚立即翻书之举。
认真独立完成作业,勤于思考,从某种意义上讲,应不造成不懂即问的学习作风,对于有些题目由于自己的思路不清,一时难以解出,应让自己冷静下来认真分析题目,尽量自己解决。
在每个阶段的学习中要进行整理和归纳总结,把知识的点、线、面结合起来交织成知识网络,纳入自己的知识体系。
二、适当多做题,养成良好的解题习惯。
要想学好数学,多做题目是难免的,熟悉掌握各种题型的解题思路。
刚开始要从基础题入手,以课本上的习题为准,反复练习打好基础,再找一些课外的习题,以帮助开拓思路,提高自己的分析、解决能力,掌握一般的解题规律。
对于一些易错题,可备有错题集,写出自己的解题思路和正确的解题过程两者一起比较找出自己的错误所在,以便及时更正。
在平时要养成良好的解题习惯。
让自己的精力高度集中,使大脑兴奋,思维敏捷,能够进入最佳状态,在考试中能运用自如。
实践证明:越到关键时候,你所表现的解题习惯与平时练习无异。
如果平时解题时随便、粗心、大意等,往往在大考中充分暴露,故在平时养成良好的解题习惯是非常重要的。
三、调整心态,正确对待考试。
首先,应把主要精力放在基础知识、基本技能、基本方法这三个方面上,因为每次考试占绝大部分的也是基础性的题目,而对于那些难题及综合性较强的题目作为调剂,认真思考,尽量让自己理出头绪,做完题后要总结归纳。
调整好自己的心态,使自己在任何时候镇静,思路有条不紊,克服浮躁的情绪。
特别是对自己要有信心,永远鼓励自己,除了自己,谁也不能把我****,要有自己不垮,谁也不能打垮我的自豪感。
在考试前要做好准备,练练常规题,把自己的思路展开,切忌考前去在保证正确率的前提下提高解题速度。
对于一些容易的基础题要有十二分把握拿全分;对于一些难题,也要尽量拿分,考试中要学会尝试得分,使自己的水平正常甚至超常发挥。
由此可见,要把数学学好就得找到适合自己的学习方法,了解数学学科的特点,使自己进入数学的广阔天地中去。
如何提高解数学题的能力任何学问都包括知识和能力两个方面,在数学方面,能力比具体的知识要重要的多。
当然,我们也不能过分强调能力,而忽视知识的学习,我们应当在学习一定数量知识的同时,还应该学会一些解决问题的能力。
能力是什么,心理学中是这样定义的:能力是指直接影响人的活动效率,使活动顺利完成的个性心理特征。
在数学里,我认为,能力就是解决问题的才智。
一、怎样才能提高自己的解题能力首先是模仿。
解题是一种本领,就像游泳、滑雪、弹钢琴一样,开始只能靠模仿才能够学到它。
其次是实践。
如果你不亲自下水游泳,你就永远也学不会游泳,因此,要想获得解题能力,就必须要做习题,并且要多做习题。
再次,要提高自己的解题能力,光靠模仿是不够的,你必须要动脑筋。
例如,对于课本的定理的证明,例题的解法、证法能读懂听懂还不够,你必须明白人家是怎样想出那个解题方法的,为什么要那样解题,有没有其它的解题途径,我认为这才是最重要的东西。
如果你真正领会了人家的解题思路,那么在此基础上你就有所创新,就能够提高你的解题能力。
二、学习数学应注意培养什么样的能力1运算能力。
2空间想象能力。
3逻辑思维能力。
4将实际问题抽象为数学问题的能力。
5形数结合互相转化的能力。
6观察、实验、比较、猜想、归纳问题的能力。
7研究、探讨问题的能力和创新能力。
三、提高数学解题能力的关键是什么?灵活应用数学思想方法是提高解题能力的关键,我们的先辈数学家们,已经为我们创造出了很多的数学思想方法,我们应该很好地体会它,理解它,并且要灵活地应用它。
对于初中数学主要是以下四类数学思想(所谓思想就是指导我们实践的理论方法,这里主要指想法或方法):1转化思想。
2方程思想。
3形数结合思想。
4函数思想。
5.整体思想6分类讨论思想.7统计思想。
只要我们能够深入地理解上述思想方法,并能灵活地应用到具体的解题实践中,就能极大地提高你的解题能力。
提高你的分类讨论能力分类讨论是中学数学中一种重要的思想方法,在每年的中考中都会涉及到有关分类讨论方面的试题,而许多同学在解答过程中经常会出现漏解、讨论不完整的现象。
临近中考,将同学中出现的部分漏解现象进行分析,希望能帮助同学们提高分类讨论的能力。
概念不清,导致漏解对所学知识概念不清,领会不够深刻,导致答题不完整。
例:已知(a-3)x>6,求x的取值范围。
分析:根据不等式的性质“不等式的两边同乘或同除以不为零的负数,不等号的方向要改变”,而此题中(a-3)的符号并未确定,所以要分类讨论(a-3)的正负问题。
例:若y2+(k+2)y+16是完全平方式,求k。
分析:完全平方式中有两种情况:(a?b)2=a2?2ab+b2,而同学们往往容易忽略k+2=-8这一解。
思维固定,导致漏解在日常解题过程中,许多同学往往受平时学习中习惯性思维的影响,导致解题不全面。
例:若等腰三解形腰上的高等于腰长的一半、求底角。
分析:据题意,由于等腰三解形既不可能是锐角等腰三解形也可能是钝角等腰三角形,所以腰上的高可能在三角形内部,也可能在外部。
而同学们受习惯思维影响,大都忽略了高在三角形外的一种可能。
例:若直角三角形三条边分别为3、4、c,求c的值。
分析:此题中的c并不一定是代表斜边,也可能是直角边,而有些同学错误地将其与勾股定理中的c混淆起来,认为c一定是斜边,导致漏解。
例:圆O的半径为5cm,两条互相平行的弦长分别为6cm、8cm,求两条弦之间的距离。
分析:两条弦在圆中的位置关系可能在圆心的同侧或者在圆心的两侧,因此在解答时不能依据自己的习惯进行思考。
