聚类分析
聚类分析

聚类分析(一)聚类分析基本概念(1)有若干个变量(或指标),例3-1的2个变量是样本均值和样本标准差;例3-2的变量是对式样、图案、颜色、材料的态度;例3-3的变量是销售增长、销售利润和新客户销售额;例3-4的变量是出生率、死亡率和婴儿死亡率;…。
这些变量称为自变量或聚类变量。
(2)有若干次观测,每次观测值由若干个数值组成,每次观测值称为1个个体或1个样品:例3-1其观测次数共有4次(甲、乙、丙、丁),其观测值都是2个值组成:第1次观测(第1个样品)是向量,第2次观测(第2个样品)是,……。
例3-2有5次观测(5位顾客),每人4项指标;例3-3、3-4、3-5,的变量各有50、97、39次观测值;而例3-6将许多次原始观测整理为协方差阵,并未提供原始观测数据。
(3)要求分类(或分组):例3-3、3-4要求把观测值分为3类,而例3-1和例3-2则不限定观测值分为几类;例3-1、3-2、3-3、3-4要求按观测值分类,而例3-5,3-6要求按变量分类。
因为是把大量的样品变为少量的类,通常这种分类称为聚类。
(二)聚类原理1)聚类原则选定观测值(点)间距离,类间距离,按照距离最近两类合并在一起的原则合并。
(也有用相似远离)。
常用聚类方法分为:(1)系统聚类MINITAB译为观测值聚类(得到谱系图或树状图)(2)动态聚类MINITAB译为K均值聚类。
可由统计>多变量>观测值聚类,统计>多变量>K均值聚类分别进入。
2)常用点间距离(距离度量)有时先把数据标准化再聚类以免单位影响,例如x1观测值3,2,1,0,-1;x2取值30,20,10,0,-10。
X1均值1,样本标准差;将x1观测值减去平均值1,除以,得到,,,,;,,,,是3,2,1,0,-1的标准化。
X2标准化后也得到,,,,。
标准化后的数与单位无关。
系统聚类从“统计>多变量>观测值聚类”进入观测值聚类框;点间距离,类间距离根据情况选取。
聚类分析

聚类分析聚类分析又称群分析,它是研究(样品或指标)分类问题的一种多元统计方法,所谓类,通俗地说,就是指相似元素的集合。
聚类分析内容非常丰富,按照分类对象的不同可分为样品分类(Q-型聚类分析)和指标或变量分类(R-型聚类分析);按照分类方法可分为系统聚类法和快速聚类法。
1. 系统聚类分析先将n 个样品各自看成一类,然后规定样品之间的“距离”和类与类之间的距离。
选择距离最近的两类合并成一个新类,计算新类和其它类(各当前类)的距离,再将距离最近的两类合并。
这样,每次合并减少一类,直至所有的样品都归成一类为止。
系统聚类法直观易懂。
1.1系统聚类法的基本步骤:第一,计算n 个样品两两间的距离 ,记作D= 。
第二,构造n 个类,每个类只包含一个样品。
第三,合并距离最近的两类为一新类。
第四,计算新类与各当前类的距离。
第五,重复步骤3、4,合并距离最近的两类为新类,直到所有的类并为一类为止。
第六,画聚类谱系图。
第七,确定类的个数和类。
1.2 系统聚类方法:1.2.1最短距离法1.2.2最长距离法1.2.3中间距离法1.2.4重心法1.2.5类平均法1.2.6离差平方和法(Ward 法)上述6种方法归类的基本步骤一致,只是类与类之间的距离有不同的定义。
最常用的就是最短距离法。
1.3 最短距离法以下用ij d 表示样品i X 与j X 之间距离,用ij D 表示类i G 与j G 之间的距离。
定义类i G 与j G 之间的距离为两类最近样品的距离,即ij G G G G ij d D j J i i ∈∈=,min设类p G 与q G 合并成一个新类记为r G ,则任一类k G 与r G 的距离是:ij G X G X kr d D j j i i ∈∈=,min ⎭⎬⎫⎩⎨⎧=∈∈∈∈ij G X G X ij G X G X d d q j k i p j k i ,,min ,min min {}kq kp D D ,min = 最短距离法聚类的步骤如下:ij d {}ij d(1)定义样品之间距离,计算样品两两距离,得一距离阵记为)0(D ,开始每个样品自成一类,显然这时ij ij d D =。
什么是聚类分析,它有哪些应用?

什么是聚类分析,它有哪些应用?
一、聚类分析的实现方式
聚类分析的实现方式有很多种,如下面几种:
1. 基于距离的聚类:
这种方法将数据点之间的距离作为相似性的度量,然后将距离最近的数据点聚在一起,并逐渐地将距离较远的数据点加入到不同的簇中。
2. 基于密度的聚类:
这种方法通过计算数据点的密度来确定簇边界,而不是使用距离来度量相似性。
将密度较高的数据点聚集在一起,而将密度较低的数据点单独作为一个簇。
3. 基于层次的聚类:
这种方法将数据点逐层进行聚合,每一层都是由多个子层组成的。
聚类过程一直持续到所有数据点都被分配到一个簇中,或者簇的数量达到预设的值。
二、聚类分析的应用领域
聚类分析作为一种重要的数据挖掘技术,在多个领域中都有着广泛的应用,下面介绍一些主要应用领域:
1. 市场细分:
聚类分析可以帮助企业将市场分割成不同的细分市场,然后根据每个细分市场的特点定制相应的市场策略。
2. 生物分类:
聚类分析在生物学领域中应用非常广泛,例如,可以用于分类分子或组分、成本分析以及微生物学等方面。
3. 网络流量分析:
聚类分析可以帮助网络管理员对网络流量进行分类,以便更好地了解网络中流动的数据类型,从而更好地优化网络性能。
4. 风险评估:
聚类分析可以用于对风险进行分类和评估,例如,可以将客户分类成高风险、中风险和低风险客户,以快速响应某些意外事件。
结论
聚类分析是一种非常有用的技术,可以用于许多不同的领域。
以上只是聚类分析的一些基本理解和应用,随着技术的不断发展,聚类分析在未来也将有着更广泛的应用。
聚类分析
C
E
A
F B
重心距离
D
4.中间距离法(Median clustering )
如果类与类之间的距离既不采用两类之间最近的距离,也 不采用两类之间最远的距离,而是采用两者之间的距离, 则称为中间距离法.当两类 G p 和 Gq 合并成新类 Gr Gp Gq 时, Gr 与任一类 Gk 的距离如何决定呢? Gkq 、 G pq 为边作三角形,可设 Gkq Gkp ,按最短 以Gkp、 距离法核算类间距离;若 Gkq Gkp ,按最远距离法核 算类间距离;若 Gkq Gkp 取其中线,由初等几何知这 个中线的平方等于任一类 Gk 与 Gr 间的距离。计算公式 如下: 1 2 1 2 1 2 2 Gkr Gkp Gkq G pq 2 2 4
得到新矩阵
G6 G1 G 2 G 5 G 6 0 D1 G1 13.12 0 G 2 24.06 11.67 0 G 5 2.21 12.80 23.54 0
合并类6和类5,得到新类7
类7与剩余的1、2之间的距离分别为:
d(5,6)1=min(d51,d61)=min(12.80,13.12)=12.80 d(5,6)2=min(d52,d62)=min(23.54,24.06)=23.54
0 2.20 3.51
因此将3.4合并为一类,为类6,替代了3、4两类 类6与剩余的1、2、5之间的距离分别为:
d(3,4)1=min(d31,d41)=min(13.80,13.12)=13.12 d(3,4)2=min(d32,d42)=min(24.63,24.06)=24.06 d(3,4)5=min(d35,d45)=min(3.51,2.21)=2.21
聚类分析

聚类分析也是一种分类技术。
与多元分析的其他方法相比,该方法较为粗糙,理论上还不完善,但应用方面取得了很大成功。
与回归分析、判别分析一起被称为多元分析的三大方法。
聚类的目的。
根据已知数据,计算各观察个体或变量之间亲疏关系的统计量(距离或相关系数)。
根据某种准则(最短距离法、最长距离法、中间距离法、重心法),使同一类内的差别较小,而类与类之间的差别较大,最终将观察个体或变量分为若干类。
聚类分析又叫群分析、点群分析或者簇分析,是直接比较各事物之间的性质,将性质相近的归为一类,将性质差别较大的归入不同的类。
1、聚类分析聚类分析也称群分析、点群分析。
例如,我们可以根据各个银行网点的储蓄量、人力资源状况、营业面积、特色功能、网点级别、所处功能区域等因素情况,将网点分为几个等级,再比较各银行之间不同等级网点数量对比状况。
1、基本思想:我们所研究的样品(网点)或指标(变量)之间存在程度不同的相似性(亲疏关系——以样品间距离衡量)。
于是根据一批样品的多个观测指标,具体找出一些能够度量样品或指标之间相似程度的统计量,以这些统计量为划分类型的依据。
把一些相似程度较大的样品(或指标)聚合为一类,把另外一些彼此之间相似程度较大的样品(或指标)又聚合为另一类,直到把所有的样品(或指标)聚合完毕,这就是分类的基本思想。
在聚类分析中,通常我们将根据分类对象的不同分为Q型聚类分析和R型聚类分析两大类。
R型聚类分析是对变量进行分类处理,Q型聚类分析是对样本进行分类处理。
R型聚类分析的主要作用是:1、不但可以了解个别变量之间的关系的亲疏程度,而且可以了解各个变量组合之间的亲疏程度。
2、根据变量的分类结果以及它们之间的关系,可以选择主要变量进行回归分析或Q型聚类分析。
Q型聚类分析的优点是:1、可以综合利用多个变量的信息对样本进行分类;2、分类结果是直观的,聚类谱系图非常清楚地表现其数值分类结果;3、聚类分析所得到的结果比传统分类方法更细致、全面、合理。
聚类分析原理及步骤

聚类分析原理及步骤
一,聚类分析概述
聚类分析是一种常用的数据挖掘方法,它将具有相似特征的样本归为
一类,根据彼此间的相似性(相似度)将样本准确地分组为多个类簇,其中
每个类簇都具有一定的相似性。
聚类分析是半监督学习(semi-supervised learning)的一种,半监督学习的核心思想是使用未标记的数据,即在训
练样本中搜集的数据,以及有限的标记数据,来学习模型。
聚类分析是实际应用中最为常用的数据挖掘算法之一,因为它可以根
据历史或当前的数据状况,帮助组织做出决策,如商业分析,市场分析,
决策支持,客户分类,医学诊断,质量控制等等,都可以使用它。
二,聚类分析原理
聚类分析的本质是用其中一种相似性度量方法将客户的属性连接起来,从而将客户分组,划分出几个客户类型,这样就可以进行客户分类、客户
细分、客户关系管理等,更好地实现客户管理。
聚类分析的原理是建立在相似性和距离等度量概念之上:通过对比一
组数据中不同对象之间的距离或相似性,从而将它们分成不同的类簇,类
簇之间的距离越近,则它们之间的相似性越大;类簇之间的距离越远,则
它们之间的相似性越小。
聚类分析的原理分为两类,一类是基于距离的聚类。
聚类分析(共8张PPT)
聚类分析
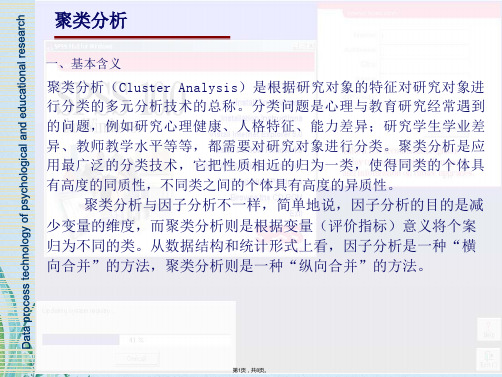
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
第十二章 聚类分析

第十二章聚类分析聚类分析(CLUSTER)是将样本或变量进行分类的一种方法。
通常用相似性指标“距离”和“相似系数”来衡量研究对象的联系紧密程度,从而进行合理分类。
“距离”常用来对样本分类,即把每一个样本看作是m维空间(若样本被m个变量所描述)的一个点,把距离较近的点归为一类,距离较远的点归为不同的类。
“相似系数”用来对变量分类,将变量间相似系数较大的归为一类,较小的归为不同类。
第一节距离和相似系数一、距离1、“欧几里得”距离A和B两点由m个变量所描述,其坐标分别是(x1,x2,…,x m)和(y1,y2,…,y m),那么d(A,B)=例如:某次收视率调查中的部分数据如表1,则1号被访者和2号被访者的Array“距离”为:d(A,B)=表1:原始数据-上述测量的距离存在问题:(1)同一个变量单位不同会导致不同的距离;(2)不同变量的度量不一致,无法判断变量值大小和变量的重要程度,从而无法判断距离的意义。
因而需要对原始数据进行标准化。
表2:标准化数据2、SPSS 聚类分析中提供的距离(1)欧式距离(EUCLID ),等于 (2)欧式距离的平方(SEUCLID ),等于变量差2+变量差2+……(3)曼哈顿距离(BLOCK ),等于变量差的绝对值之和(4)切比雪夫距离(CHEBYCHEV ),等于变量差中绝对值最大者(5)幂距离POWER(p,r),等于变量差的绝对值的p 次方之和,再求r 方根。
2、相似系数(1)变量间的相关系数即皮尔逊相关系数; …(2)变量间的夹角余弦,即将两变量分别看成n 维空间的向量时的夹角余弦值。
相关系数一般针对定距变量,对于定类变量特别是二项变量也可引入虚拟变量后计算相关系数。
例1:假定5个样本(人)具有如下指标:(1)请对个体进行分类;(2)对变量进行分类。
表3:五个人的六种身体特征指标解:变量中包含定距和定类变量,可以全部变成虚拟变量(也可将后四个虚拟),令X 1= ;X 2= ;X 3= ; ; X 4= ;X 5= ;X 6= ,表3可转化为表4:(1)根据两个个体共同特征的多少来对个体分类,以欧式距离的平方来进行聚类,个体之间的距离越小越相似,可求得: d 2(1,2)=(0-1)2+(0-1)2+(0-1)2+(1-0)2+(0-0)2+(1-0)2=5; d 2(1,3)=(0-0)2+(0-1)2+(0-0)2+(1-1)2+(0-0)2+(1-0)2=2; d 2(1,4)=(0-0)2+(0-0)2+(0-1)2+(1-0)2+(0-0)2+(1-1)2=2;d 2(1,5)=(0-1)2+(0-1)2+(0-1)2+(1-0)2+(0-1)2+(1-0)2=6;同理计算其他距离,得到下表:表5:5个体间距离1,身高≥170 0,身高<170 1,体重≥130 ^1,双眼皮 0,单眼皮1,高鼻梁 0,低鼻梁1,用左手 0,用右手1,女 0,男根据距离大小,判断相似程度。
《多元统计分析》第四章 聚类分析

G1
G2
G3
G4
G5
G1
0
G2
1
0
G3
5
4
0
G4
7
6
2
0
G5
10
9
5
3
0
G6=G1∪G2={1,2}。
6
G6
G3
G4
G5
G6
0
G3
4
0
G4
6
2
0
G5
9
5
3
0
G7=G3∪G4={6,8}。
x1:食品
x5:交通和通讯
x2:衣着
x6:娱乐教育文化服务
x3:家庭设备用品及服务 x7:居住
x4:医疗保健
x8:杂项商品和服务
分别用最短距离法、重心法和Ward方法对各地区作聚类分析。为同等
地对待每一变量,在作聚类前,先对各变量作标准化变换。
18
地区 北京 天津 河北 山西 内蒙古 辽宁 吉林 黑龙江 上海 江苏 浙江 安徽 福建 江西 山东
类与类之间的距离定义为两类最远样品间的距离,即
DKL
max
iGK , jGL
dij
最长距离法与最短距离法的并类步骤完全相同,只是递推公式不同。
10
最长距离法的递推公式
DMJ maxDKJ , DLJ
11
最长距离法容易被异常值严重地扭曲。
12
3.类平均法
有两种定义。
xi*
xi
xi sii
聚类分析详解

聚类分析应注意的问题
(1)所选择的变量应符合聚类的要求
如果希望依照学校的科研情况对高校进行分类,那么可以 选择参加科研的人数、年投入经费、立项课题数、支出经 费、科研成果数、获奖数等变量,而不应选择诸如在校学 生人数、校园面积、年用水量等变量。因为它们不符合聚 类的要求,分类的结果也就无法真实地反映科研分类的情 况。
以上我们对例6.3.1采用了多种系统聚类法进行聚类,其结果 都是相同的,原因是该例只有很少几个样品,此时聚类的过 程不易有什么变化。一般来说,只要聚类的样品数目不是太 少,各种聚类方法所产生的聚类结果一般是不同的,甚至会 有大的差异。从下面例子中可以看到这一点。
动态聚类法(快速聚类)
聚类分析工具及案例分析
SPSS IBM SPSS Modeler(以前叫Clementine,商业化软件) SAS(SAS Enterprise Miner) 商业数学软件MATLAB 数据挖掘软件WEKA(免费的,非商业化) IBM DB2 Intelligent Miner 其他(如DBMiner、See5等)
详细步奏和实例
最长距离法的聚类步奏
最长距离法与最短距离法的并类步骤完全相同,只 是类间距离的递推公式有所不同。
递推公式:
D M J m a x D K J,D L J
最长距离法容易被异常值严重地扭曲,一个有效的 方法是将这些异常值单独拿出来后再进行聚类。
三、中间距离法
类与类之间的距离既不取两类最近样品间的距离,也不取两 类最远样品间的距离,而是取介于两者中间的距离。
二是计算样品或变量的相似系数,用相似系数来描述样品 或变量之间的亲疏程度。
聚类分析特点
聚类分析是一种建立分类的多元统计分析方法,它能将一 批样本(或变量)数据根据其诸多特征,按照在性质上的 亲疏程度在没有先验知识的情况下进行自动分类,产生多 个分类结果。类内部的个体在特征上具有相似性,不同类 间个体特征的差异性较大。
《多元统计分析》第四章 聚类分析

类与类之间的距离定义为两类最远样品间的距离,即
DKL
max
iGK , jGL
dij
最长距离法与最短距离法的并类步骤完全相同,只是递推公式不同。
10
最长距离法的递推公式
DMJ maxDKJ , DLJ
11
最长距离法容易被异常值严重地扭曲。
12
3.类平均法
有两种定义。
记G1={1},G2={2},G3={6},G4={8},G5={11},样品间采用绝对值 距离。
G1
G2
G3
G4
G5
G1
0
G2
1
0
G3
5
4
0
G4
7
6
2
0
G5
10
9
5
3
0
G6=G1∪G2={1,2}。
6
G6
G3
G4
G5
G6
0
G3
4
0
G4
6
2
0
G5
9
5
3
0
G7=G3∪G4={6,8}。
xi*
xi
xi sii
,
i 1, 2,, p
其中 xi 和sii分别为xi的样本均值和样本方差。
4
绝对值距离
v
p
d x, y xi yi
i 1
v 常被形象地称作“城市街区”距离,
当我们对某城市(需考虑彼此之间
路程)的位置点进行聚类时,使用
绝对值距离一般是合适的。
5
马氏距离
3
《多元统计分析》
4.2 距离Байду номын сангаас相似系数
聚类分析

聚类分析聚类分析作为一种数据分析的方法,在许多领域中都得到了广泛应用。
它是一种无监督学习的技术,通过对数据进行分组或分类,寻找其中的内在结构和规律。
聚类分析的目的是将相似的数据点分配到同一组,而不同组之间的数据点则具有较大的差异性。
聚类分析可以用于各种各样的问题,比如市场细分、社交网络分析、客户行为分析等。
它可以帮助我们理解数据之间的相似性和差异性,发现潜在特征和趋势,并指导我们做出更好的决策。
聚类分析的基本思想是通过计算数据之间的相似度或距离,将相似的数据点归为一类。
常用的相似度度量方法有欧氏距离、曼哈顿距离、余弦相似度等。
根据具体应用的需求,我们可以选择不同的相似度度量方法。
聚类分析有许多不同的算法,常见的有K均值算法、层次聚类算法、DBSCAN算法等。
不同的算法适用于不同类型的数据和问题。
其中,K均值算法是最常用的一种算法,它通过迭代的方式找到数据点的最佳分组。
K均值算法是一种迭代算法,首先随机选择k个初始中心点,然后将所有的数据点根据与中心点的距离归类。
然后,计算每个类别的均值点,并将均值点作为新的中心点。
不断迭代这个过程,直到中心点的位置不再变化,或达到设定的迭代次数。
聚类分析的结果可以通过可视化的方式呈现出来,比如散点图、热力图等。
通过观察这些可视化结果,我们可以快速地了解数据的分布和聚类的效果。
聚类分析还可以与其他数据分析技术结合起来,以获得更深入的洞察。
比如,我们可以在进行聚类分析的同时,应用主成分分析(PCA)降维技术,以提高聚类的效果和可解释性。
最后,聚类分析也存在一些限制和挑战。
首先,聚类分析是一种无监督学习方法,对数据的预处理和特征选择十分关键。
其次,选择合适的聚类算法和参数也需要一定的经验和领域知识。
此外,聚类分析对于异常值和噪声敏感,在处理这些问题时需要额外的注意。
总而言之,聚类分析作为一种无监督学习方法,可以帮助我们理解数据之间的相似性和差异性,发现内在的结构和规律。
第十章--聚类分析

p
当q=2,即为欧式距离
当q=∞,有 dij () max xik x jk 1 k p (Chebychev)距离 , 称为切比雪夫
k 1
各指标同等对待(权数相同),不能反映各指标变
异程度上的差异 距离的大小与各指标的观测单位有关,有时会出现 不合理结果 没有考虑指标之间的相关性
50
51
将所有省份聚为3类,统计它们各个指数的 均值、标准差、最大值和最小值
52
2、利用裁判打分数据进行聚类分析。
性格、学习成绩、课余爱好等方面有许多共同之处,而关系比较疏远的同学在
这些方面有较大的差异性。为了研究家庭情况、性格、学习成绩、课余爱好等 是否会成为划分学生小群体的主要决定因素,可以从有关这些方面的数据入手,
进行客观分组,然后比较所得的分组是否与实际相吻合。对学生的客观分组就
可采用聚类分析方法。
第二,个体间的差异程度。衡量个体间的相似程度通常可采用简单相关系数或
等级相关系数。个体间的差异程度通常通过某种距离来测度。
为定义个体间的距离应先将每个样本数据看成k维空间的一个点,通常,点与 点之间的距离越小,意味着他们越“亲密”,越有可能聚成一类,点与点之间 的距离越大,意味着他们越“疏远”,越有可能分别属于不同的类。
Q型聚类:对样本进行聚类,使具有相似特征的样本聚集在一起,差异性
大的样本分离开来。
R型聚类:对变量进行聚类,使具有相似性的变量聚集在一起,差异性大 的变量分离开来,可在相似变量中选择少数具有代表性的变量参与其他分 析,实现减少变量个数,达到变量降维的目的。
凝聚方式聚类:其过程是,首先,每个个体自成一类;然后,按照某种方法 度量所有个体间的亲疏程度,并将其中最“亲密”的个体聚成一小类,形成 n-1个类;接下来,再次度量剩余个体和小类间的亲疏程度,并将当前最亲密 的个体或小类再聚到一类;重复上述过程,直到所有个体聚成一个大类为止。 这种聚类方式对n个个体通过n-1步可凝聚成一大类。
聚类分析——精选推荐

1聚类分析内涵1.1聚类分析定义聚类分析(Cluster Analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术. 也叫分类分析(classification analysis)或数值分类(numerical taxonomy),它是研究(样品或指标)分类问题的一种多元统计方法,所谓类,通俗地说,就是指相似元素的集合。
聚类分析有关变量类型:定类变量,定量(离散和连续)变量聚类分析的原则是同一类中的个体有较大的相似性,不同类中的个体差异很大。
1.2聚类分析分类聚类分析的功能是建立一种分类方法,它将一批样品或变量,按照它们在性质上的亲疏、相似程度进行分类.聚类分析的内容十分丰富,按其聚类的方法可分为以下几种:(1)系统聚类法:开始每个对象自成一类,然后每次将最相似的两类合并,合并后重新计算新类与其他类的距离或相近性测度.这一过程一直继续直到所有对象归为一类为止.并类的过程可用一张谱系聚类图描述.(2)调优法(动态聚类法):首先对n个对象初步分类,然后根据分类的损失函数尽可能小的原则对其进行调整,直到分类合理为止.(3)最优分割法(有序样品聚类法):开始将所有样品看成一类,然后根据某种最优准则将它们分割为二类、三类,一直分割到所需的K类为止.这种方法适用于有序样品的分类问题,也称为有序样品的聚类法.(4)模糊聚类法:利用模糊集理论来处理分类问题,它对经济领域中具有模糊特征的两态数据或多态数据具有明显的分类效果.(5)图论聚类法:利用图论中最小支撑树的概念来处理分类问题,创造了独具风格的方法.(6)聚类预报法:利用聚类方法处理预报问题,在多元统计分析中,可用来作预报的方法很多,如回归分析和判别分析.但对一些异常数据,如气象中的灾害性天气的预报,使用回归分析或判别分析处理的效果都不好,而聚类预报弥补了这一不足,这是一个值得重视的方法。
聚类分析根据分类对象的不同又分为R型和Q型两大类,R型是对变量(指标)进行分类,Q 型是对样品进行分类。
聚类分析

聚类分析(一)聚类分析基本概念(1)有若干个变量(或指标),例3-1的2个变量是样本均值和样本标准差;例3-2的变量是对式样、图案、颜色、材料的态度;例3-3的变量是销售增长、销售利润和新客户销售额;例3-4的变量是出生率、死亡率和婴儿死亡率;…。
这些变量称为自变量或聚类变量。
(2)有若干次观测,每次观测值由若干个数值组成,每次观测值称为1个个体或1个样品:例3-1其观测次数共有4次(甲、乙、丙、丁),其观测值都是2个值组成:第1次观测(第1个有5次观测(53-6将(31(也有用相(2>K均值聚230,20,10,0 1.26502,0.63251,0.00000,-0.63251,-1.26502;1.26502,0.63251,0.00000,-0.63251,-1.26502是3,2,1,0,-1的标准化。
X2标准化后也得到1.26502,0.63251,0.00000,-0.63251,-1.26502。
标准化后的数与单位无关。
系统聚类从“统计>多变量>观测值聚类”进入观测值聚类框;点间距离,类间距离根据情况选取。
动态聚类从“统计>多变量>K均值聚类”进入K均值聚类框;点间距离固定为Euclidean,类间距离固定为质心法,无需再选取。
(1)欧氏距离欧氏(Euclidean )距离定义为:ij d =,(,1,)i j n = (3-2)欧氏距离是聚类分析中使用最广泛的距离,上式也称为简单欧氏距离。
另一种常用的形式是平方欧氏距离,即取上式的平方,记为2ij d 。
平方欧氏距离的优点是,因为不再计算平方根,不仅理论上简单,而且提高了计算机的运算速度。
(2)Pearson 距离1,,)n , (3-3)其中k V 个变量的方差。
这个距离考虑到了各个变量的不同标准差,但未考虑各变量间可能存在的相关。
(3,)n (3-4)平方绝对值距离是对上式取平方。
(4当变量之间不相关时效果较好,如果变量i j i j (3-5)有时为了避免开平方,称-1i j i j (X -X )'S (X -X )为平方马氏距离。
《多元统计分析》第三章聚类分析

图像处理
聚类分析可用于图像分割、目 标检测等任务,提高图像处理 的效率和准确性。
社交网络
通过聚类分析,可以发现社交 网络中的社区结构,揭示用户 之间的关联和互动模式。
聚类分析的常用方法
K-均值聚类
一种迭代算法,通过最小化每个簇内对象与簇质 心的距离之和来实现聚类。需要预先指定簇的数 量K。
DBSCAN
感谢聆听
聚类结果的优化方法
层次聚类法
通过不断合并或分裂簇来优化聚类结果,可以灵活处理不同形状 和大小的簇,但计算复杂度较高。
基于密度的聚类法
通过寻找被低密度区域分隔的高密度区域来形成簇,可以发现任意 形状的簇,但对参数敏感。
基于网格的聚类法
将数据空间划分为网格单元,然后在网格单元上进行聚类,处理速 度较快,但聚类精度受网格粒度影响。
一种基于密度的聚类方法,通过寻找被低密度区 域分隔的高密度区域来实现聚类。可以识别任意 形状的簇,且对噪声数据具有较强的鲁棒性。
层次聚类
通过计算对象之间的距离,逐步将数据集构建成 一个层次结构的聚类树。可以分为凝聚法和分裂 法两种。
谱聚类
利用图论中的谱理论进行聚类分析,将数据集中 的对象表示为图中的节点,节点之间的相似度表 示为边的权重。通过求解图的拉普拉斯矩阵的特 征向量来实现聚类。
药物发现
通过对化合物库进行聚类分析,研究人员可以发现具有相 似化学结构和生物活性的化合物,从而加速新药的发现和 开发过程。
生物信息学
在基因表达谱、蛋白质互作网络等生物信息学研究中,聚 类分析可以帮助研究人员发现基因或蛋白质之间的功能模 块和调控网络。
在社交网络中的应用案例
社区发现
聚类分析可用于识别社交网络中的社区结构,即具有相似兴趣、行为或属性的用户群体。 这有助于社交网络运营商为用户提供更加个性化的推荐和服务。
聚类分析ppt课件

第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
聚类分析

聚类分析:是将样品置入聚类空间,通 过比较样品间的类似程度,即样品间的 距离进行聚类的。 聚类分析是基于多变量数据,对n个样品 进行分类的一种方法。这种方法是将那 些相似的样品归为一类,不同的样品分 别归到各自不同的类别中。聚类分析是 以样品的分类为基本目的的。
聚类分析的分类
1、基于相同率的聚类分析 2、基于相关系数的聚类分析 3、基于主因子的聚类分析 4、基于主成分的聚类分析 5、基于距离的聚类分析
ຫໍສະໝຸດ 小组实验步骤
一:讨论选定实验题目 二:选定问卷调查法; 三:进行问卷设计; 四:发放问卷; 五:录入数据; 六:数据分析; 七:得出结论; 八:小结。
聚类分析的实验
首先我们确定需要的调查的相关内容: 调查对象:瑞京公寓周边餐厅 调查目的:对瑞京公寓周边餐厅进行聚类 分类得出同学们选择餐厅的情况,对其 进行分类。帮助同学们更有效的选择餐 厅。 调查方式:问卷调查
基于相关系数的聚类分析
课本所讲的例子是对某教育局对所属六所中学 根据七项指标A~G进行教学评估,每项指标评 分范围为1~10分。
通过公式:y= ∑(yi -y)(xi-x) (∑σ:西格玛 Sigma ) √ ∑ (yi -y)2 ∑(xi-x)2 计算出六所学校每两所间的相关系数。 再将相关的系数进行聚类分析。 最后根据相关系数及其有关的平均数可作出聚 类分析的树状图。
我们的问卷
我们发放问卷总数40份,废卷4份,有效 问卷36份。
我们将36份问卷的数据一一录入到电脑 中,再利用spss软件对数据进行相关的 聚类分析。 利用公式: 计算出瑞京周边的6间餐厅的相关系数, 对其进行聚类分析。
树状图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
Ex1 m1 x1 m1
E
x2
m2
x1
m1
Exn
mn
x1
m1
Ex1 m1 x2 m2 Ex2 m2 x2 m2
Ex1 m1 xn mn
汉明距离:
Dh ( Xi ,
X
j
)
1 2
n
n k 1
xik
x jk
式中, xik、xjk分别表示Xi和Xj的第k个分量。
两个模式向量的各分量取值均不同:Dh(Xi, Xj)=n; 全相同: Dh(Xi, Xj)=0
5)角度相似性函数
S(Xi
,
X
j
)
XiT X j ||X i|| || X
集出现不同聚类结果的现象。
5
x2 (mm )
x2 (mm )
5
4 c(0.1,4)
3
2
1 a(0,1)
0
d(0.4,5)
b(0.5,0) 12
(b)
5 c(1,4)
4
d(4,5)
3
2
1 a(0,1)
b(5,0)
0
1
23 4
(a)
5 x1 (mm )
x2 (cm)
3 x1 (cm)
3 2 1 c(1,0.4)
模式分类,需视情况作适当选择。
11
2 聚类准则
聚类准则:根据相似性测度确定的,衡量模式之间是否相似的标 准。即把不同模式聚为一类还是归为不同类的准则。
确定聚类准则的两种方式: 1) 阈值准则:根据规定的距离阈值进行分类的准则。 2) 函数准则:利用聚类准则函数进行分类的准则。
聚类准则函数:在聚类分析中,表示模式类间相似或差异性 的函数。
结果:Z1=X1;Z2=X6;
x1
Z3=X7 。
⑤ 聚类
21
四 层次聚类法
(Hierarchical Clustering Method) (系统聚类法、分级聚类法)
思路:每个样本先自成一类, 然后按距离准则逐步合并,减少类数。
1 算法描述
① N个初始模式样本自成一类,即建立N 类:
G1(0), G2 (0), ,GN (0)
0 12
a(0,0.1)
d(4,0.5)
3
4
(c)
b(5,0) 5
x1 (mm )
B)解决方法:使特征数据标准化,使其与变量的单位无关。6
2) 马氏距离(Maharanobis) 平方表达式:D2 ( X M )T C 1( X M )
式中,X:模式向量; M:均值向量; C:该类模式总体的协方差矩阵。
S j 集的样本的均值向量,
N j 为 S j中样本数目。
J代表了分属于c个聚类类别的全部模式样本与其相应类别模 式均值之间的误差平方和。
适用范围: 适用于各类样本密集且数目相差不多,而不同类间的样本又
明显分开的情况。 13
例1:
x2
2
1
M2
3
x2
1
M1
M3
O (a)
x1
O
2
M2 M1
x1
3) 算法特点 A)局限性:很大程度上依赖于第一个聚类中心的位置选择、待
分类模式样本的排列次序、距离阈值T的大小以及样本分布 的几何性质等。
B)优点:计算简单。(一种虽粗糙但快速的方法)
17
4)算法讨论
用先验知识指导阈值T 和起始点Z1的选择,可获得合理的 聚类结果。否则只能选择不同的初值重复试探,并对聚类结果 进行验算,根据一定的评价标准,得出合理的聚类结果。
欧氏距离定义为:
D(X1, X2) X1 X2 ( X1 X2 )T ( X1 X2 )
(x11 x21)2 (x1n x2n )2
距离越小,越相似。
( D_Distance )
注意:
A)各特征向量对应的维上应当是相同的物理量;
注意物理量的单位。
某些维上物理量采用的单位发生变化,会导致对同样的点
若D21 T ,定义一新的聚类中心Z2 = X2 ; 否则 X2 ∈以Z1为中心的聚类。
16
③ 假设已有聚类中心Z1、Z2,计算 D31 X3 Z1 和 D32 X3 Z2 , 若 D31 T 且 D32 T ,则建立第三个聚类中心Z3 = X3; 否则X3∈离Z1和Z2中最近者(最近邻的聚类中心)。 ……依此类推,直到将所有的N个样本都进行分类。
j
||
是模式向量Xi,Xj之间夹角的余弦。
10
6)Tanimoto测度
用于0,1二值特征的情况,
S(Xi, X j)
XiT
Xi
XiT
X
T j
Xj Xj
XiT
Xj
Xi
,
X
中共有的特征数目
j
X
和
i
X
中占有的特征数目的总数
j
相似性测度函数的共同点都涉及到把两个相比较的向量Xi,Xj 的分量值组合起来,但怎样组合并无普遍有效的方法,对具体的
x1
m1
对n维向量:X
,
M
xn
m n
C E X M X M T
x1 m1
E{x2
m2
x1
m1
x2 m2
xn mn
( M_Mean ) ( C_covariance)
错误分类 15
三、 基于距离阈值的聚类算法
1 近邻聚类法
1) 问题:有N个待分类的模式X1, X 2, , X N ,要求按距离阈
值T分类到以 Z1, Z2, 为聚类中心的模式类中。 (T_threshold )
2) 算法描述 ① 任取样本Xi 作为第一个聚类中心的初始值,如令Z1 = X1 。 ② 计算样本X2 到Z1 的欧氏距离 D21 X2 Z1 ,
④ 在所有最小距离中选出最大距离,如该最大值达到 Z1 Z2 的一定分数比值( 阈值T ) 以上,则相应的样本点取为新的聚类 中心,返回③;否则,寻找聚类中心的工作结束。
例k =2时
若max{min(Di1, Di2),i 1,2,...,N} Z1 Z2 , 0 1
则Z3存在。(θ:用试探法取为一固定分数,如1/2。) ⑤ 重复步骤③④,直到没有新的聚类中心出现为止。
(b)
类内误差平方和很 小,类间距离很远。 可得到最好的结果。
1 类长轴两端距离中心很 远,J值较大,结果不易令 人满意。
14
例2:另一种情况 有时可能把样本数目多的一类分拆为二,造成错误聚类。 原因:这样分开,J值会更小。
x2
1
M1
2
M2
x2
1
M1
2
M2
O (a)
正确分类
x1 O
x1
(b)
注意:聚类分析是否有效,与模式特征向量的分布形式有很大关 系。选取的特征向量是否合适非常关键。 例:酱油与可乐。
3
二、 相似性测度和聚类准则
1 相似性测度 相似性测度:衡量模式之间相似性的一种尺度。如:距离。
y1
复习:已知向量
Y
y2
,则:
y3
y1
YY
T
n
D1( X i , X j ) xik x jk
x2
Xj 欧氏
k 1
称为“街坊”距离 (“City block”distance)。 X i
当k=2时:图示
D1( Xi , X j ) xi1 x j1 xi2 x j2
街坊
x1 9
4)汉明(Hamming)距离
设Xi、Xj 为n维二值(1或-1)模式样本向量,则
① 选任意一模式样本做为第一聚类中心Z1。 ② 选择离Z1距离最远的样本作为第二聚类中心Z2。 ③ 逐个计算各模式样本与已确定的所有聚类中心之间的距离, 并选出其中的最小距离。例当聚类中心数k=2时,计算
Di1 Xi Z1
Di2 Xi Z2
min( Di1 , Di2 ),i=1,…,N(N个最小距离) 19
(G_Group)
计算各类之间(即各样本间)的距离,得一N×N维距离矩阵
D(0)。“0”表示初始状态。
22
②假设已求得距离矩阵D(n)(n为逐次聚类合并的次数),找出 D(n)中的最小元素,将其对应的两类合并为一类。由此建立新的 分类:
G1(n 1), G2 (n 1),
③计算合并后新类别之间的距离,得D(n+1)。
它应是模式样本集{X }和模式类别 S j , j 1,2, , c 的函数。
可使聚类分析转化为寻找准则函数极值的最优化问题。一种常用 的指标是误差平方之和。
12
聚类准则函数:
c
J
2
X Mj
j 1 X S j
式中:c为聚类类别的数目,
M j
1 Nj
X 为属于
XS j
DX H , X K :H类中的某个样本XH和K类中的某个样本XK之间
的欧氏距离。 DHK:H类中所有样本与K类中所有样本之间的最小距离。
H
K
24
如果K类由I和J两类合并而成,则
