z i g z a g 压 缩 算 法 ( 2 0 2 0 )
通信网络基础(李建东盛敏)课后习题答案

通信⽹络基础(李建东盛敏)课后习题答案1.1答:通信⽹络由⼦⽹和终端构成(物理传输链路和链路的汇聚点),常⽤的通信⽹络有A TM ⽹络,X.25分组数据⽹络,PSTN ,ISDN ,移动通信⽹等。
1.2答:通信链路包括接⼊链路和⽹络链路。
接⼊链路有:(1)Modem 链路,利⽤PSTN 电话线路,在⽤户和⽹络侧分别添加Modem 设备来实现数据传输,速率为300b/s和56kb/s ;(2)xDSL 链路,通过数字技术,对PSTN 端局到⽤户终端之间的⽤户线路进⾏改造⽽成的数字⽤户线DSL ,x 表⽰不同的传输⽅案;(3)ISDN ,利⽤PSTN 实现数据传输,提供两个基本信道:B 信道(64kb/s ),D 信道(16kb/s 或64kb/s );(4)数字蜂窝移动通信链路,⼗⼏kb/s ~2Mb/s ;(5)以太⽹,双绞线峰值速率10Mb/s,100Mb/s 。
⽹络链路有:(1)X.25提供48kb/s ,56kb/s 或64kb/s 的传输速率,采⽤分组交换,以虚电路形式向⽤户提供传输链路;(2)帧中继,吞吐量⼤,速率为64kb/s ,2.048Mb/s ;(3)SDH (同步数字系列),具有标准化的结构等级STM-N ;(4)光波分复⽤WDM ,在⼀根光纤中能同时传输多个波长的光信号。
1.3答:分组交换⽹中,将消息分成许多较短的,格式化的分组进⾏传输和交换,每⼀个分组由若⼲⽐特组成⼀个⽐特串,每个分组都包括⼀个附加的分组头,分组头指明该分组的⽬的节点及其它⽹络控制信息。
每个⽹络节点采⽤存储转发的⽅式来实现分组的交换。
1.4答:虚电路是分组传输中两种基本的选择路由的⽅式之⼀。
在⼀个会话过程开始时,确定⼀条源节点到⽬的节点的逻辑通路,在实际分组传输时才占⽤物理链路,⽆分组传输时不占⽤物理链路,此时物理链路可⽤于其它⽤户分组的传输。
会话过程中的所有分组都沿此逻辑通道进⾏。
⽽传统电话交换⽹PSTN 中物理链路始终存在,⽆论有⽆数据传输。
GB T 17747.2-1999 天然气压缩因子的计算 第2部分:用摩尔组成进行计算

0 a 镇6 MP MP<p 5 a 25 <30 2K <T 5 K 2 MJ m- 0 ・ ' <4 MJ ' <H, 8 " m-
注 2 将本条中的高位发热量和相对密度换算为我国石油气体标准参 比条件下 的高位发热量和相对密度 , : 则高位 发热1 范围为 79 -4. " , 2. 19 MJ '相对密度范围为 050 -. , 1 5 3 m- . -080 5 0
天然气中各组分 的摩尔分数应在 以下范围以内:
— 第3 部分: 用物性值进行计算。
附录 A、 附录B 附录C 附录D是标准的附录。附录E 附录 F 附录G是提示的附录。 、 、 、 、
中华 人 民共 和 国国 家标 准
天然气压缩因子的计算 第2 部分: 用摩尔组成进行计算
N t a gs ac a o o o rsi fco- rl -C l l in cmpes n tr au a ut f o a P r 2C l l inபைடு நூலகம்ig lr o p sin a s at a u t u n m a- m oio a l i : c ao s o c t n ys
似法是否会使计算结果变差.
摩尔分数大于 000 .0 0 5的所有组分都必须在计算中考虑。痕量组分( C 等) 如 M; 应按表 1中指定 的赋值组分处理。所有组分的摩尔分数之和为 1 . 1 士000 0 ,
如果已知体积分数组成, 则应将其换算成摩尔分数组成, 具体换算方法见 G / 102 B T 6 0 1
c / 1772 99 S T 4 .-19 7
绝对压力:
热力学温度 :
0 a -1 MP MP <p 2 a <
2 3 6 K镇T蕊3 8 3 K
化工原理课后习题答案上下册(钟理版)

第一章 流体流动习题解答1-1 已知甲城市的大气压为760mmHg ,乙城市的大气压为750mmHg 。
某反应器在甲地操作时要求其真空表读数为600mmHg ,若把该反应器放在乙地操作时,要维持与甲地操作相同的绝对压,真空表的读数应为多少,分别用mmHg 和Pa 表示。
[590mmHg, 7.86×104Pa]解:P (甲绝对)=760-600=160mmHg 750-160=590mmHg=7.86×104Pa1-2用水银压强计如图测量容器内水面上方压力P 0,测压点位于水面以下0.2m 处,测压点与U 形管内水银界面的垂直距离为0.3m ,水银压强计的读数R =300mm ,试求 (1)容器内压强P 0为多少?(2)若容器内表压增加一倍,压差计的读数R 为多少?习题1-2 附图[(1) 3.51×104N ⋅m -2 (表压); (2)0.554m] 解:1. 根据静压强分布规律 P A =P 0+g ρHP B =ρ,gR因等高面就是等压面,故P A = P BP 0=ρ,gR -ρgH =13600×9.81×0.3-1000×9.81(0.2+0.3)=3.51×104N/㎡ (表压) 2. 设P 0加倍后,压差计的读数增为R ,=R +△R ,容器内水面与水银分界面的垂直距离相应增为H ,=H +2R∆。
同理, ''''''02R p gR gH gR g R gH gρρρρρρ∆=-=+∆--000p g g p p 0.254m g g 10009.81g g 136009.812R H R ρρρρρρ⨯∆⨯⨯,,,4,,-(-)- 3.5110====---220.30.2540.554m R R R ∆,=+=+=1-3单杯式水银压强计如图的液杯直径D =100mm ,细管直径d =8mm 。
流体静力学基本方程
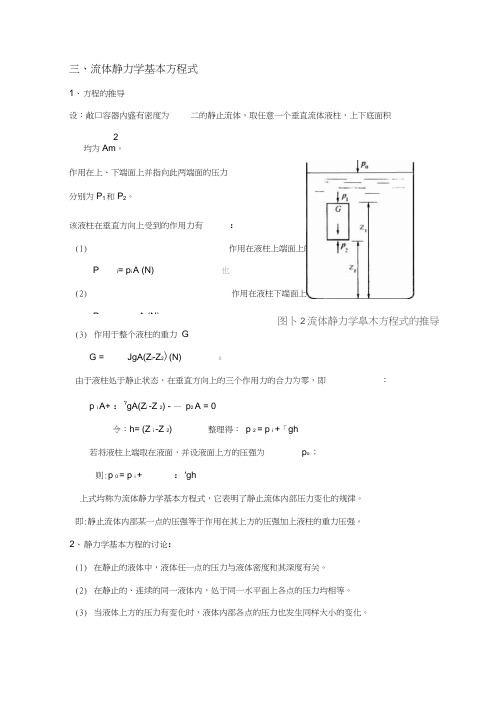
图卜2流体静力学皐木方程式的推导(3) 作用于整个液柱的重力 GG = JgA(Z i -Z 2)(N) 0由于液柱处于静止状态,在垂直方向上的三个作用力的合力为零,即 :p i A+ :?gA(Z i -Z 2) - — p 2 A = 0令:h= (Z i -Z 2) 整理得: p 2 = p i +「gh若将液柱上端取在液面,并设液面上方的压强为p o ; 则:p 0 = p i + :'gh上式均称为流体静力学基本方程式,它表明了静止流体内部压力变化的规律。
即:静止流体内部某一点的压强等于作用在其上方的压强加上液柱的重力压强。
2、 静力学基本方程的讨论:(1) 在静止的液体中,液体任一点的压力与液体密度和其深度有关。
(2) 在静止的、连续的同一液体内,处于同一水平面上各点的压力均相等。
(3) 当液体上方的压力有变化时,液体内部各点的压力也发生同样大小的变化。
三、流体静力学基本方程式1、 方程的推导设:敞口容器内盛有密度为 二的静止流体,取任意一个垂直流体液柱,上下底面积2均为Am 。
作用在上、下端面上并指向此两端面的压力分别为P 1和P 2。
该液柱在垂直方向上受到的作用力有: (1) 作用在液柱上端面上的总压力 P iPi = p i A (N) 也 (2) 作用在液柱下端面上的总压力 P 2P = p A (N)压强差的也大小可利用一定高度的液体柱来表示。
p P (5) 整理得:z 1g1二z 2g 也为静力学基本方程P g (6) 方程是以不可压缩流体推导出来的,对于可压缩性的气体,只适用于压强变 化不大的情况。
3、静力学基本方程的应用(1)测量流体的压差或压力①U 管压差计U 管压差计的结构如图。
对指示液的要求:指示液要与被测流体不互溶,不起 A化学作用,且其密度:7指应大于被测流体的密度:、。
通常采用的指示液有:水、油、四氯化碳或汞等。
I测压差:设流体作用在两支管口的压力为 p 1和P 2,且P i > P 2 , A-B 截面为等压面 即:P A 二P B 根据流体静力学基本方程式分别对 U 管左侧和U 管右侧进行计算整理得: P i - P 2 =:〔'指一'Rg讨论: (a )压差(p i -P 2)只与指示液的读数 R 及指示液冋被测流体的密度差有关。
热力学第一定律的统计解释[1]
![热力学第一定律的统计解释[1]](https://img.taocdn.com/s3/m/501084abdd3383c4bb4cd27d.png)
仍
为碰 撞 前 的几 率分 布 函 数
△
所 以 每一 个 分 子 发 生 一 次 碰撞 可 获 得 的动 能 增量 △
c 。·
为
(9 )
一合
m
[
Z 。 ‘V + V
” 一V )
2
Z
一〕
。
-
Zm
o ( V 若 V V e p s o) +
系 统 在 △ t 时 间 内获 得 的总 动能 增 量 为 △E k 一 e k v , , △ dN
,
N
保 持不 变 仅仅 是 由 于 系 统 内 单粒子 态能 级 。; 3 正是 ( ) 式 中的 第 一 项 艺 N 滋
。
;
,
。;
的 改 变 而 使 整 个 系 统 的 内能 发 生 了变 化
。
。
这
4 3 4 4
.
。
在无 功情 况 下
,
系 统 内 能 的改 变 在 数 值 上 等 于 系 统 与 外 界 交 换 的热 量
N。
;
。
综 上 所述
,
方程 d u
,
一
艺N
d 。; +
艺
。;
dN
;
表示 热力 学 第 一 定 律
i 其 中乙 N 奴
一
参
dA
(2 ) 3
(24 )
万
F 马l L 自F . Q J se r , ew 厂亡 J L J‘ 门 r 勺曰 」刁 盈」
。;
d N ; 一d。
考
文
献
陈仁 烈
王云程
·
《 计物 理 引 论》 统
-
流体力学第二章一压强规律及平面压力

作用在平面上的总水压力 是平行分布力的合力
P dp hdA
A
y sindA sin ydA
A
A
1.静水总压力的大小
ydA 受压面A对OX轴的静矩
A
ydA yc A(面积距定理)
A
P dp hdA y sindA sin ydA
A
A
A
P sinyc A hc A pc A
的大小与作用面的方位无关。
➢ 静压强 p 与作用方向无关,仅
取决于作用点的空间位置;流体是 连续介质 ,因此:p= p(x,y,z)。
➢ 静止流体的静压强 p = p(x, y, z),是空间点的连续函数。
2.2 流体平衡微分方程
在静止流体内部任取一点O’,该点的压强为p=p(x,y,z)
两个受压面abcd和a’b’c’d’中心点M,N 的压强:
解:pabs p0 γwh 78 9.81.5
92.7kN/m2
p0
pr pabs pat 92.7 98
5.3kN/m2
h
pv pr 5.3kN/m2
c
hv
pv
w
0.54m水柱
情 况 同 上 例 , 试 问 当点C 相 对 压 强 p为 8.k4N/m2时 , C点 在 自 由 面 下 的 淹 没 深 度 h为 多 少 ?
p po gh
(p p0 h)
2.3.2 帕斯卡原理(巴斯加原理)
根据流体静力学基本方程 p p0 h 可知,液面压强p0与液 柱所具有的重量 h 无关,如果液面压强p0增大(或减小) △p,则液体内任意点的压强都将同时增大(或减小)同样 大小的△p。
因此可得出结论:静止流体内任一点的压强变化,会等值 传递到流体的其他各点。这就是帕斯卡原理,或称静压传 递原理。
数值分析习题

习题11. 填空题(1) 为便于算法在计算机上实现,必须将一个数学问题分解为 _________ 的 _______ 运算; (2) 在数值计算中为避免损失有效数字,尽量避免两个 _________ 数作减法运算;为避免误差的扩大,也尽量避免分母的绝对值 ______________ 分子的绝对值;(3) 误差有四大来源,数值分析主要处理其中的 __________ 和 ___________ ; (4) 有效数字越多•相对误差越_________ ;2. 用例1.4的算法计算価•迭代3次•计算结果保留4位有效数字.3. 推导开平方运算的误差限公式,并说明什么情况下结果误差不大于自变量误差.4. 以下各数都是对准确值进行四舍五入得到的近似数,指出它们的有效数位、误差限和相对误差限.斗=0.3040, x 2 =5.1x10% 兀=400,些=°・°°3346, x 5 = 0.875x 1Q-55. 证明1.2.3之定理1. 1.6. 若钢珠的的直径d 的相对误差为1.0%,则它的体积卩的相对误差将为多少。
(假定钢珠为 标准的球形)7. 若跑道长的测量有0.欣的误差,对400m 成绩为60s 的运动员的成绩将会带来多大的误差和相对误差.8. 为使J 亦的近似数相对误差小于0. 05%,试问该保留几位有效数字.9. 一个园柱体的工件•直径d 为10・25±0・25mm.高力为40. 00± 1.00mm •则它的体枳卩的近 似值、误差和相对误差为多少.10证明对一元函数运算有并求出/(x) = tanx,x = 1.57时的k 值,从而说明/(x) = tanx 在人任彳时是病态问题.11. 定义多元函数运算s =》g,其中工q =1,£(舌)“,r-l求出w(S)的表达式,并说明q 全为正数时,计算是稳定的,q 有正有负时,误差难以控制.12. 下列各式应如何改进•使计算更准确:其中"(4) y = ^p'+q 2 - P, (p>O,q>O,p»q)习题21. 填空题(1) Gauss 消元法求解线性方程组的的过程中若主元素为零会发生 _______________ 主元素的绝对值太小会发生 ___________ ;(2) Gauss 消元法求解线性方程组的计算工作量以乘除法次数计大约为 ___________ .平方根法求解对称正定线性方程组的计算工作量以乘除法次数计大约为 __________ ;(3) 直接£〃分解法解线性方程组时的计算量以乘除法计为 __________ ,追赶法解对角占优的三对角方程组肘的计算量以乘除法计为 _____________ ;⑷ ;)阀二——•114= ------- ・——;t 0(5) A =yt > 1 p{A) _________ , cond 2(A) = _________I"丿(6) A = b 9c > b > a > 0 p{A) _______________ , cond ?(A) = ________4. 用Gauss —Jordan 消元法求:(卜l 《l)f 1 1 -1)T(1)八1 2 -2 ,b =1一2 1 1 丿丄2 6、3(1)心10 -7 0 ,b = 7< 5 -1 5丿r4 3 2 r3 4 3 21(2) A =•—2 3 4 3 -1<1 2 3 4;r0 2 0 1、2 232-2 (2) A =b =4-3 01-76 1 -6-56 ,(i) y =⑵y =1l — x(心1)2・用Gauss 消元法求解下列方程组Ax = b3.用列主元消元法解下列方程组Ax = b.2 1 0 J -1 o>5. 用直接厶U 分解方法求1题中两个矩阵的厶(/分解,并求解此二方程组.6. 用平方根法解方程组Ax = b<3 2 1、‘4、2 2 1 ,b = 3J 1 1丿O7.用追赶法解三对角方程组Ax = b2 -1一1 2 0-I0 0 0T0 A = 0 一1 2 -1 0 ,b = 00 0 -1 2 -1<0 0 0 -1 2丿©8. 证明:(1) 单位下三角阵的逆仍是单位下三角阵. (2) 两个单位下三角阵的乘积仍是单位下三角阵. 9. 由厶=却冴・・£[「(见(2. 18)式),证明:10 •证明向量范数有下列等价性质: (1)14^14^14⑶|HL<H 2<^Kii. 求下列矩阵的||州删2,lkt“(q ).81 3、(2) A= 1 10 2、3 26,12. 求 cond 2 (A)1 A = 1-13)2丿'13. 证明:⑴若A 是正交矩阵,即A rA = /f 则cond 2(A) = l ; (2)若A 是对称正定阵,心是A 的最大特征值,人是最小特征值,则cond 2(A )=习题31. 填空题:(1) 当A 具有严格对角线优势或具有对角优势且 ____________ 时,线性方程组Ax=b 用Jacobi 迭代法和Gauss —Seidel 迭代法均收敛; (2) 当线性方程组的系数矩阵力对称正定时, ___________ 迭代法收敛. (3) 线性方程组迭代法收敛的充分必要条件是迭代矩阵的 _________ 小于1; S0R 法收敛的必要条件是 ______________ ;(4) 用迭代法求解线性方程组,若⑷,q _______________ 时不收敛,g 接近 _______ 时收 敛较快,g 接近 _______ 时收敛较慢;(5)(1 \\A= ?,$= _________ : Bs = _______ ; Q(坊)= _______ ; °(块)= ___ ・2. 用Jacobi 迭代法和Gauss —Seidel 迭代法求解方程组V 1 0、'3 ''-81 1 丫和‘1、 (1)1 2 1= -5 ; (2)1-5 1 x 2 = 16W 1 2,宀< 1 1 -仏丿6各分量第三位稳定即可停止.3•庄SOR 法解方程组,取60 = 0.9 ,与取CO = 1 (即Gauss-Seidel 法)作比较.(32 1]/ \<-5> -5 7 3 £ = 13 2 \ -5 7 /<X 3>4・下面是一些方程组的系数阵,试判断它们对Jacobi 迭代法,Gauss-Seidel 迭代法的收 敛性"5 2 1(\ 2) 1 3 2 ; ⑵…13 21 1 2\ / (1)flOO 99、99 9J(2) COS0A --sin& COS0 y6•设‘1 a 宀A= a 1 a ,d 为实数;⑴a 1;(1) 若q 正定,a 的取值范围;(2) 若Jacobi 迭代法收敛,a 的取值范围.习题41. 填空题:(1) 毎法主要用于求一般矩阵的 __________________ 特征值,Jacobi 旅转法用于求对称矩阵的 ______ 待征值;(2) 古典的Jacobi 法是选择 ______________ 的一对 _____________ 元素将其消为零; (3) Q?方法用于求 ___________ 矩阵的全部特征值,庾黑法加上原点平移用于一个近似特征值的 _________ 和求出对应的 ______________ ■2. 用嫁法求矩阵•〔6 2 1'-4 14 0、⑴ 2 3 1, (2)-5 13 0,1 1 1、-1 0 2 丿按模最大的特征值和对应的特征向量,精确到小数三位.-11 11 1 '3.已知: A= 11 9 -2< 1—2 13>"-2 1 0 0'21 2、1 -2 10 1 2 1 ;(4)1 -2 1-2 1 2\、01 -2;10 -1 I —1 -1 _i -r -1 -15 -1 -1 10;5.方程组a\\ 如、 / 、 丙=*<U2\ “22丿 1兀丿如证明用Jacobi 迭代法收敛的充要条件是:5 -1取t =15,作原点平移的幕法,求按模最大特征值.‘4 1 4、4.A= I 10 1、4 1 10,用反無法加原点平移求最接近12的特征值与相应的特征向量,迭代三次.5.若A的特征值为人,易,…,九,r是一实数,证明:人―『是〃的特征值,且特征向量不变.6.已知x =(3,2,l)7求平面反射阵H使y = Hx=(0,*,0)‘,即使x的1, 3两个分量化零.5 3 2、7.A= 3 3 1<2 1 6丿试用Jacobi 转法求作一次症转,消去最大的非对角元,写出旋转矩阵,求出〃角和结果./ r 0(3x2)、8.设已知2是人的特征值,相应的特征向量为(4卫2,6)丁,证明几也是丁的特征值,相应的特征向量为(坷,《2,偽,0,0『.9.证明定理4. 5.10.证明(4. 21)中的A,.和£+1相似.习题51.填空題(1)用二分法求方程x3+x-l = 0在[0,1]内的根,迭代一次后,根的存在区间为___________ ,迭代两次后根的存在区间为_____________ ;(2)设/(x)可微,则求方程x = /(%)根的Newton迭代格式为______________________ ;(3)(p(x) = x + C(x2-5),若要使迭代格式x k+} =(p(x k)局部收敛到a = >/5 ,则C取值范围为_____________ ;(4)用迭代格式x k+l=x k-AJ\x k )求解方程f(x) = x3-x2-x-\ = 0的根,要使迭代序列{忑}是二阶收敛,则心二;2 1(5)迭代格式兀+|=二忑+斗收敛于根a二_______________ ,此迭代格式是__________ 阶收3 x k敛的.2.证明Newton迭代格式(5. 10)满足3.方程/一9十+ 18尢一6 = 0, xe[0,+oo)的根全正实根,试用逐次扫描法(出1),找出它的全部实根的存在区间,并用二分法求出最大实根,精确到0.01.4.用二分法求下列方程的根,精度£ = 0・001・仃)x-x+4=0(2) b+10x — 2 = 0 xe[0J]5.用迭代法求X3-2X-5= 0的正根,简略判断以下三种迭代格式:在x() = 2附近的收敛情况,并选择收敛的方法求此根.精度£ = 10_.6.方程= e~x(1)证明它在(0,1)区间有且只有一个实根;(2)证明x k+i = e~Xt,k = 0,1,---,在(0,1)区间内收敛;(3)用Newton迭代法求出此根,精确到5位有效数字.7.对方程X3-3X-1=0,分别用(1)Newton法(州=2); (2)割线法(观=2,召=1.9)求其根.精度f = 10~4.8.用迭代法求下列方程的最小正根(1) x5 -4x-2 = 0: (2) 2tanx—x = 0 ;(3) x = 2sinx9.设有方程3x2-e x=0(1)以力=1,找出根的全部存在区间;(2)验证在区间[0,1]上Newton法的区间收敛定理条件不成立;⑶ 验证取x() = 0.21 ,用Newton法不收敛;(4)用Newton下山法,取x()=0.21求出根的近似值,精度£ = 10_・10.分别用Jacobi法,Gauss—Seidel法求解非线性方程组\+2y-3=0<2x2 + y2-5 = 0在(1.5,0. 7)附近的根,精确到IO-4.11.分别用Newton法,简化Newton法求解非线性方程组sin x + cos y = 0<x+y = l在(0,1)附近的根,精确到10*.习题61.填空題(1)设J\x) = x5+x3+x + \ ,则 /[0,1]______________ , /[0,1,2]= _________________ /[0,1,2,3,4,习= ___________ : /[0,1,2,3,4,5,6] = ________________ .(2)设?o(x),/i(x),…,/”(%)是以节点0,1,2, •••,/?的Lagrange 插值基函数,则£儿(羽= _______________;£旳伙)= _______________ •;-() J-0(3)设/(0) = 0,/⑴=16,/(2) = 46,则/[0,1]= ____________ , /[0,1,2]= ____________ ,/(X)的二次Newton插值多项式为________________________ ・2.3-利用心在“畤能及壬处的值,求S哙的近似值,并估计误差.4.利用数据计算积分[千,当二时的兀的取值.5.试用Newton插值求经过点(一3,-1), (0,2), (3,-2), (6,10)的三次插值多项式.6.求满足Pg) = f(Xo),P(xJ = f(xJ及Pg = f(XQ)的次数不超过2次的插值多项式Pg,并给出其误差表达式.7.设比是互异节点,3 是Lagrange插值基函数(j =0,1,2,,证明(1)£<,(%)三1;(2)$>乂(力三十伙=0,1,2,…丿);(3)£(◎一x)k/丿(x)三0 仏=0,1,2,•••/).8 •设有如下数据试计算此表中函数的差分表,并分别利用Newton向前,向后插值公式求出它的插值多项式. 9.试构造一个三次Hermite插值多项式使其满足/(0) = 1,广(0) = 0.5, /(1) = 2,广⑴=0.510・已知函数/(X)的数据表分别用Newton向前插值公式和向后插值公式求x=0. 05, x二0. 42, X二0. 75的近似值.11.对函数f(x) = sinx进行分段线性插值,要求误差不超过0.5x10",问步长力应如何选取.12.设有数据用三转角插值法求满足下述条件的三次样条插值函数(1)570.25) = 1.0000 , 570.53) = 0.6868(2)S"(0.25) = —2 , S"(0.53) = 0.647913.证明定理6.6.习题81 •填空題⑴ “+1个点的插值型数值积分公式f 的代数精度至少是_____ ,最高不超过__________ .(2)梯形公式有______ 次代数精度,Simpson公式有______ 次代数精度.(3)求积公式打⑴川細(0)+ /(/?)]+ 加[八0)_/伽中的参数& =时,才能保证该求积公式的代数精度达到最高,最高代数精度为__________ •2.确定下列求积公式的求积系数和求积节点,使其代数精度尽量高,并指出其最高代数精度.(1)『/(X)厶a A)/(0) + AJ(//) + A2f(2h)f(f(x)dx q+ 2/(“) + 3/(x2)]⑶£ f(x)dx = A/(-D + AJ (-# + A J(4) jj Mdx a AJ(x{) + A2/(0) + AJ(l)⑸[/⑴厶« f(xj + f(x2)3.分别利用复化梯形公式,复化Simpson公式,复化Cotes公式计算下列积分(1)「一3 二8)Jo4 + x2(2)^yfxdx (n =10)(3)("=io)(4)(弘—抽讼・5二6)(5)P —Jx (/? =8)J() x4.用Romberg公式计算枳分(1) 丄(精度要求£ = 10一‘)⑵佃 + cos4xdx(精度要求£ = 10-5)5.分别取节点数为2, 3, 4利用Gauss—Legendre求积公式计算积分(1) 「一厶,(2) 「八心,(3) f-dxJ T I+ Q血Ji X6.利用Gauss型求积公式,分别取节点数2, 3, 4计算积分(1) £e~x yfxdx , (2) J e~x <1 + x2 dx7.用节点数为4的Gauss —Laguerre求积公式和Gauss—Hermite求积公式计算积分的近似值,并与准确值/=—作比较・28.分别用两点公式与三点公式求f(x)=一在x=l・0,x二1.2的导数值,并估计误差, (l + x)・其中/(x)的数据由下表给出习题91.填空題(1)解初值问题的Euler法是________ 阶方法,梯形方法是 _____ 阶方法,标准R-K方法是_____ 阶方法.(2)解初值问题#(x) = 20(x—y),y(O) = 1时,为保证计算的稳定性,若用经典的四阶R-K方法,步长0V/Y ________ ・采用Euler方法,步长力的取值范围为______ ,若采用Euler 梯形方法,步长力的取值范围为_______ 若采用Adams外推法,步长力的范围为________ ,若采用Adams内插法,步长方的取值范围为__________ .(3) __________________________________________ 求解初值问题Euler方法的局部截断误差为_____________________________________________ Euler梯形方法的局部截断误差为_____________ , Adams外推法的局部截断误差为_______________ Adams内插法的局部截断误差为_____________ .2.对初值问题1 ?/ = ----- -2y~0<x<l1 + JC.y(o)= oX试用Euler法取步长〃二0. 1和“二0.2计算其近似解,并与准确解y =—匚进行比较.1 + JC3.利用Euler预测一校正法和四阶经典R-K方法,取步长h=Q. 1,求解方程y f = x+y 0<x<\y(O) = 1并与准确解y(x) = -x-\ + 2e x进行比较.4.用待定系数法推导二步法公式>\+1 = y> + ~ (5齐+1 + 一Z-i)并证明它是三阶公式,求出它的局部截断误差.5.用Adams预测一校正法求解y = -y20 < X < 1.y(o)= 1并与准确解y(x)=—进行比较.1 + x6.用Euler中点公式计算y f = -y O< x< 2.5y(O) = 1取步长/?=0. 25,与准确解>'=比较,并说明中点公式是不稳定的.7.写出用经典的R-K方法及Adams预测一校正法解初值问题)/ = _8y + 7z< z,=兀2 + yzy(O) = l,z(O) = O的计算公式.8.写出用Euler方法及Euler预测一校正法解二阶常微分方程初值问題),/r + siny = 0y(O) = 1, V(O) = 0的计算公式.9.证明用单步法y1+i = X+呵兀+£, x+,x)解方程= -2ax的初值问题,可以给出准确解.。
ToII

t i o n wi t h f u n c t i o n l c a o mp u t e d t o mo g r a p h y p e r f u s i o n i ma g i n g i n
供、 受 者 肝 实 质血 流 动力 学 改 变 , 但 是 由于 研究 对
v a l u a t i o n a f t e r y t t r i u m- 9 0 r a d i o e mb o l i z a t i o n o f l i v e r ma l i g n a n c y
现状与进展I J J . 江西医药, 2 0 1 1 , 4 6 ( 7 ) : 6 7 0 .
象 、感兴 趣 区 的选取 和术 后 检查 时 间 不 同造成 肝 移植术后 H A P、 P V P结果 在 不 同 的 研 究 中存 在 较 大 的差异 。 以后 的研 究 主 要 是进 一 步 加 大 样 本量
p a t i e n t s w i t h c i r r h o t i c l i v e r d i s e a s e[ J J . H e p a t o b i l i a r y P a n c r e a t D i s I n t . 2 0 1 1 , 1 0 ( 1 ) : 4 3 . ( 1 1 ] Y a n g HF , D u Y, N i J X, e t a 1 . P e r f u s i o n c o mp u t e d t o m o g r a p h y e -
JPEG及JPEG2000

DCi-1
DCi
根据这个特点,JPEG算法使用了差分脉冲调制编码 (DPCM)技术,对相邻图像块之间量化DC系数的差 值进行编码 。∆DCi=DCi -DCi-1
(2)AC交流系数的编码 Z字形编排。对于量化后的二维数组,我们还要对其进行线 性化,然后再进行压缩加以传输。为保证低频分量先出现, 高频分量后出现,以增加行程中连续“0”的个数,63个AC系 数采用z字形排列。
新一代静态图像压缩标准---JPEG2000
1. JPEG2000概述 概述
虽然JPEG 标准是一个非常成功的标准,但在一些新的 应用如高清图像、数字图书馆、高精确彩色图像、多 媒体和因特网的应用、无线、医学图像等方面,JPEG 表现出不足,因此弥补JPEG对连续色调静止图像的无 损压缩和近无损压缩效率不高的缺陷,最终提出了 JPEG2000标准。 该标准采用了先进的压缩技术并在可伸缩压缩图像及 灵活性方面有许多先进的特征,其系统功能比JPEG 标 准优越,尤其JPEG2000 采用的是离散小波变换 (DWT)替代了JPEG 中采用的离散余弦变换DCT), 并采用了最新的编码算法来支持灵活性,这样许多应 用只需用单一码流提供。JPEG2000 可广泛应用于通信、 图像处理、信号处理、信息理论和多媒体等领域中。
尺寸分类(符号1 ) 0 1 2 3 4 5 6 7 8 9 10 11
码长 2 3 3 3 3 3 4 5 6 7 8 9 00 010 011 100 101 110 1110 11110 111110 1111110 11111110 111111110
码字
亮度DC系数表
行程/尺寸(符号1) 0/0(EOB) 0/1 0/2 0/3 0/4 0/5 0/6 0/7 0/8 0/9 0/A 1/1 1/2 …
美国ASME与TEMA标准管板计算方法比较(一)

S t A一 i 1 e iA ei c n D . p d A一1同时,OA o v A nx , p CD P
( 章) C 及欧共体标准(P Dsn 一 ls 7 UV i Pt Cu eg a ae r
1) 3也采用该方法。在 20 年, 3 02 这 个标准正式发
u日 餐S
() 2
布了 该计算方法, 这也是后来 AM S tn珊- S E i eo c
式中,一无因次量, C 圆板周边支承系数;
D . H 一2 基础, i1 v 中U X 1章的 . 更为详细的 资料参见
FOwi r 0) . l (02 发表的有关文章“CV 20 se e 2 IPT 2 0
Vnovr 1" acue R v 。 e 1
F V准规范
石油化工设计 Ptce i l e g eohmc Ds r a i n
20 ,1 ) 1 2 042( 2 一 6 4
编者按: 美国AM 和TM S E E A标准是国际上最具影响力的两大压力容器标准, 其中都有关于换热器管板等的设计方法。该
两标准在国内 外石化、 化工装置设计中 得到日 益广泛的应用。为此了解、 比较该两标准的理论基础及其差异对做好 国际、 国内 压力容器设计都显得十分重要。
宽度计算得到(SE AM 中的管板的 孔桥带效率产 ’
是基于最小的孔桥宽度计算得到的, 因而该值较
题。Gr e在 1 9 an d r 9 年时曾推荐过该值, 6 并被欧洲 的 一些国家标准采纳(S50C DP , B50, A )并运用了 O
近2 年。经圆平板极限载荷分析的修正, 0 对于简
TM 中, 最小值为0 2三角形排管) 的 EA .( 4 及
有关内 综合考虑了以 容, 下4 条: 1 管板开孔部分简化为当量均质的平板, ) 有
复变函数积分的几种计算方法

复变函数积分的几种计算方法
陈 静 , 贠书杰
(河南机电高等专科学校 , 河南 新乡 453000)
倡
摘要 :复变函数积分是复变函数的重要内容 。 文章对复变函数积分的计算方法进行归纳 , 以典型例题加以说 明 。 主要包括积分曲线的参数方程法 、 牛顿 - 莱布尼兹公式 、 柯西积分定理及公式 、 高阶导数公式 、 留数定理等 计算方法 。 关键词 : 复变函数 ; 复积分 ; 计算方法 中图分类号 : O174 . 55 文献标识码 : A 文章编号 : 1008 - 2093(2013)02 - 0021 - 03
5 利用重要结论求复积分
1)利用结论 ①
即在 D 内 f ( z )的积分与路径无关 。 例 3 计算积分 I =
2 2
∫ (e
C 2
2
其中 C 为 ( x - + 2 z ) dz ,
∮
C
1 n dz = ( z - z0 )
2 πi , n= 1 , 0, n≠ 1
1) + y = 1 的上半圆周 , 逆时针方向 。 2 解 :因为 e 和 2 z 在复平面上处处解析 , 则 I =
n k= 1
∮
∮
C
f ( z ) dz = 0 或
∮
C
f ( z ) dz =
钞∮
简单闭曲线 (互不包含也不相交 ) , C 及 C i 都是逆 时针 。 2 z - 1 dz 2 z - z 解 :被积函数有两个奇点 z = 0 , z = 1 均在 | z | = 2 例 5 计算积分
Ck
C2 ,… Cn , 是在 C 内部的 f ( z ) dz 。 其中 C1 ,
2
用牛顿 — 莱布尼茨公式求复积分时要注意 : (1) D 是单连通的 ; (2)积分值与具体的路径无关 , 仅与起点 、 终点有关 ; (3)原函数是初等函数 。
GBZT 160.16-2004工作场所空气有毒物质测定 镍及其化合物

前言为贯彻执行‘工业企业设计卫生标准“(G B Z1)和‘工作场所有害因素职业接触限值“(G B Z2),特制定本标准㊂本标准是为工作场所有害因素职业接触限值配套的监测方法,用于监测工作场所空气中镍及其化合物[包括金属镍(N i c k e l)㊁氧化镍(N i c k e l o x i d e)和硝酸镍(N i c k e l n i t r i d e)等]的浓度㊂本标准是总结㊁归纳和改进了原有的标准方法后提出㊂这次修订将同类化合物的同种监测方法和不同种监测方法归并为一个标准方法,并增加了长时间采样和个体采样方法㊂本标准从2004年12月1日起实施㊂同时代替G B/T16103 1995㊁G B/T17087 1997㊂本标准首次发布于1995年,本次是第一次修订㊂本标准由全国职业卫生标准委员会提出㊂本标准由中华人民共和国卫生部批准㊂本标准起草单位:四川省疾病预防控制中心㊁安徽省职业病防治研究所㊂本标准主要起草人:林葆华和陈绯㊂工作场所空气有毒物质测定镍及其化合物1范围本标准规定了监测工作场所空气中镍及其化合物浓度的方法㊂本标准适用于工作场所空气中镍及其化合物浓度的测定㊂2规范性引用文件下列文件中的条款,通过本标准的引用而成为本标准的条款㊂凡是注日期的引用文件,其随后所有的修改单(不包括勘误的内容)或修订版均不适用于本标准,然而,鼓励根据本标准达成协议的各方研究是否可使用这些文件的最新版本㊂凡是不注日期的引用文件,其最新版本适用于本标准㊂G B Z159工作场所空气中有害物质监测的采样规范3火焰原子吸收光谱法3.1原理空气中气溶胶态的镍及其化合物用微孔滤膜采集,消解后,在232.0n m波长下,用乙炔 空气火焰原子吸收光谱法测定㊂3.2仪器3.2.1微孔滤膜,孔径0.8μm㊂3.2.2采样夹,滤料直径为40m m㊂3.2.3小型塑料采样夹,滤料直径为25m m㊂3.2.4空气采样器,流量0~3L/m i n和0~10L/m i n㊂3.2.5烧杯,50m l㊂3.2.6电热板或电砂浴㊂3.2.7具塞刻度试管,10m l㊂3.2.8原子吸收分光光度计,配备乙炔 空气火焰燃烧器和镍空心阴极灯㊂3.3试剂实验用水为去离子水,用酸为优级纯㊂3.3.1硝酸,ρ20=1.42g/m l㊂3.3.2高氯酸,ρ20=1.67g/m l㊂3.3.3消化液:高氯酸ʒ硝酸=1ʒ9㊂3.3.4硝酸溶液,1%(v/v)㊂3.3.5标准溶液:称取0.1000g金属镍粉(光谱纯),加入少量硝酸,加热溶解并蒸发至近干,用硝酸溶液定量转移入100m l容量瓶中,并稀释至刻度㊂此溶液为1.0m g/m l标准贮备液㊂临用前,用硝酸溶液稀释成10.0μg/m l镍标准溶液㊂或用国家认可的标准溶液配制㊂3.4样品的采集㊁运输和保存现场采样按照G B Z159执行㊂3.4.1短时间采样:在采样点,将装好微孔滤膜的采样夹,以5L/m i n流量采集15m i n空气样品㊂3.4.2长时间采样:在采样点,将装好微孔滤膜的小型塑料采样夹,以1L/m i n流量采集2~8h空气样1品㊂3.4.3 个体采样:将装好微孔滤膜的小型塑料采样夹佩戴在采样对象的前胸上部,进气口尽量接近呼吸带,以1L /m i n 流量采集2~8h 空气样品㊂3.4.4 样品空白:将装好微孔滤膜的采样夹带至采样点,除不连接空气采样器采集空气样品外,其余操作同样品㊂采样后,将滤膜的接尘面朝里对折2次,放入清洁的容器内运输和保存㊂在室温下,样品可长期保存㊂3.5 分析步骤3.5.1 样品处理:将采过样的滤膜放入烧杯中,加入5m l 消化液,置于电热板上缓缓加热消解,保持温度在200ħ左右㊂至溶液基本挥干时为止㊂若消解不完全,可再加少量消化液继续消解至完全㊂用硝酸溶液溶解残液,并定量转移入具塞刻度试管中,加至10.0m l ,摇匀,供测定㊂若样品液中待测物的浓度超过测定范围,可用硝酸溶液稀释后测定,计算时乘以稀释倍数㊂3.5.2 标准曲线的绘制:取6只具塞刻度试管,分别加入0.0㊁1.0㊁2.0㊁3.0㊁4.0㊁5.0m l 镍标准溶液,各加硝酸溶液至10.0m l ,配成0.0㊁1.0㊁2.0㊁3.0㊁4.0㊁5.0μg /m l 镍标准系列㊂将原子吸收分光光度计调节至最佳操作条件,在232.0n m 波长下,用乙炔 空气火焰分别测定标准系列,每个浓度重复测定3次,以吸光度均值对镍浓度(μg /m l )绘制标准曲线㊂3.5.3 样品测定:用测定标准系列的操作条件测定样品和样品空白溶液,测得样品吸光度值后,由标准曲线得镍浓度(μg /m l )㊂3.6 计算3.6.1 按式(1)将采样体积换算成标准采样体积:V o =Vˑ293273+t ˑP 101.3(1)………………………………………………式中:V o 标准采样体积,L ;V 采样体积,L ;t 采样点的温度,ħ;P 采样点的大气压,k P a㊂3.6.2 按式(2)计算空气中镍的浓度:C =10c V o (2)…………………………………………………………式中:C 空气中镍的浓度,m g /m 3;10 样品溶液的体积,m l;c 测得样品溶液中镍的浓度(减去样品空白),μg /m l ;V o 标准采样体积,L ㊂3.6.3 时间加权平均接触浓度按G B Z159规定计算㊂3.7 说明3.7.1 本法的检出限为0.1μg /m l ;最低检出浓度为0.013m g /m 3(以采集75L 空气样品计)㊂测定范围为0.1~5.0μg /m l ;平均相对标准偏差为2.6%㊂3.7.2 本法的平均采样效率>99%㊂3.7.3 样品中含有100μg /m l 铝㊁钙㊁镉㊁镍㊁铬㊁铁㊁锰㊁铅㊁锡不干扰测定㊂样品溶液中如有白色沉淀,可离心或放置过夜后取上清液测定㊂3.7.4 本法可采用微波消解法㊂2G B Z /T 160.16 2004。
材料力学知识点总结
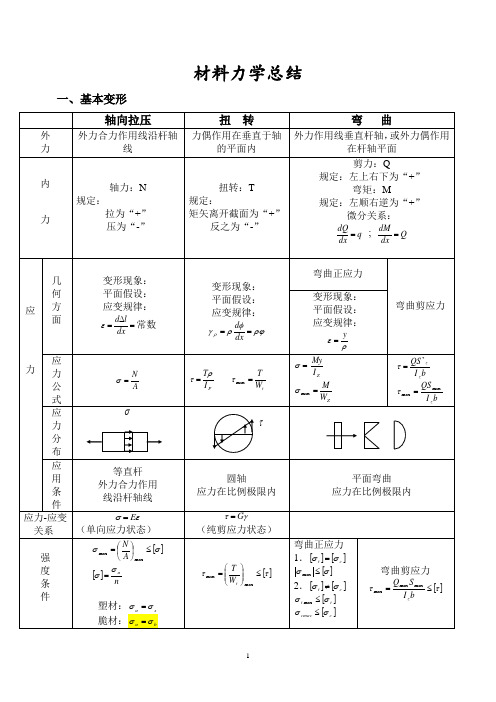
变形现象:
平面假设:
应变规律:
d dx
T IP
max
T Wt
弯曲正应力
变形现象: 平面假设: 应变规律:
y
My IZ
max
M WZ
弯曲剪应力
QS * z Izb
max
QS max Izb
圆轴 应力在比例极限内
平面弯曲 应力在比例极限内
G
(纯剪应力状态)
max
T Wt
max
断口特征:断口成光滑区和粗糙区。
循环特征 r min ;
max
平均应力
m
max
2
min
;
应力幅度
max
min 2
材料疲劳极限:材料经无限次应力循环而不发生疲劳破坏的应力极限值——N=107: 1
条件疲劳极限:(有色金属)无水平渐近线:N=(5-7)107 对应的 1
构件疲劳极限:考虑各种因素
2r 2t
(3)矩形截面杆扭转剪应力: max
T ; b 2 h
T Gb 3 h
2
三、截面几何性质
(1)平行移轴公式: I Z I ZC a 2 A;
I YZ I ZcYc abA
(2)组合截面:
n
Ai yci
1.形
心: yc
i 1 n
;
Ai
i 1
n
Ai z ci
zc
i 1 n
Ai
i 1
2.静 矩: S Z Ai yci ; S y Ai zci
3. 惯性矩: I Z (I Z )i ; I y (I y )i
四、应力分析:
(1)二向应力状态(解析法、图解法)
流体输配管网第三版第三章

皮肌炎图片——皮肌炎的症状表现
• 皮肌炎是一种引起皮肤、肌肉 、心、肺、肾等多脏器严重损害 的,全身性疾病,而且不少患者 同时伴有恶性肿瘤。它的1症状表 现如下:
• 1、早期皮肌炎患者,还往往伴 有全身不适症状,如-全身肌肉酸 痛,软弱无力,上楼梯时感觉两 腿费力;举手梳理头发时,举高 手臂很吃力;抬头转头缓慢而费 力。
– 在并联立管的阻力平衡时应计算重力作用
19
3.1.2 闭式液体管网水力计算
液体管网与气体管网水力计算的区别:
■ 主要目的、基本原理和方法相同 ■ 液体与气体的物性参数有显著的差别 ■ 液体与气体管网的工作参数有一定区别 ■ 水力计算使用的计算公式和技术数据不同
◆ 液体管网水力计算的基本公式
■ 沿程阻力:
为了排气,系统的供水干管必须有0.5~1.0%向膨胀水 箱方向上坡度,散热器支管的坡度一般取1%。在重力 循环系统中,水的流速较低,空气能逆着水流方向, 经过供水干管聚集到系统的最高处,通过膨胀水箱排 除。
8
(1)并联管路的水力特征
9
(1)并联管路的水力特征
重力循环双管热水采暖系统的作用压头
第一层: 环路a-S1-b-热源-a
Rm
6.25 108
G2 d5
Pa / m
1 2 lg k 2.51
3.7d Re
0.11 k 68 0.25 d Re
■ k的取值:
■局部阻力 p 2
2
20
液体管网水力计算的主要任务和方法
任务(1) :已知管网各管段的流量和循环动力, 确定各管段的管径。
方法:压损平均法。预先求出管段的平均比摩阻, 作为选择管径的控制参数。
PaS2b g(h1 h2 )(h g ) Pb热源a
化工原理(上)主要知识点

化工原理(上)各章主要知识点绪论三个传递:动量传递、热量传递和质量传递三大守恒定律:质量守恒定律——物料衡算;能量守恒定律——能量衡算;动量守恒定律——动量衡算第一章 流动流体第一节 流体静止的基本方程一、密度1. 气体密度:RTpMV m ==ρ2. 液体均相混合物密度:nm aa a ρρρρn 22111+++= (m ρ—混合液体的密度,a —各组分质量分数,n ρ—各组分密度) 3. 气体混合物密度:n n m ρϕρϕρϕρ+++= 2211(m ρ—混合气体的密度,ϕ—各组分体积分数)4. 压力或温度改变时,密度随之改变很小的流体成为不可压缩流体(液体);若有显着的改变则称为可压缩流体(气体)。
二、.压力表示方法1、常见压力单位及其换算关系:2、压力的两种基准表示:绝压(以绝对真空为基准)、表压(真空度)(以当地大气压为基准,由压力表或真空表测出) 表压 = 绝压—当地大气压 真空度 = 当地大气压—绝压 三、流体静力学方程1、静止流体内部任一点的压力,称为该点的经压力,其特点为: (1)从各方向作用于某点上的静压力相等;(2)静压力的方向垂直于任一通过该点的作用平面;(3)在重力场中,同一水平面面上各点的静压力相等,高度不同的水平面的经压力岁位置的高低而变化。
2、流体静力学方程(适用于重力场中静止的、连续的不可压缩流体)p z gp=ρ(容器内盛液体,上部与大气相通,g p ρ/—静压头,“头”—液位高度,p z —位压头 或位头)上式表明:静止流体内部某一水平面上的压力与其位置及流体密度有关,所在位置与低则压力愈大。
四、流体静力学方程的应用 1、U 形管压差计指示液要与被测流体不互溶,且其密度比被测流体的大。
测量液体:)()(12021z z g gR p p -+-=-ρρρ 测量气体:gR p p 021ρ=-2、双液体U 形管压差计 gR p p )(1221ρρ-=-第二节 流体流动的基本方程一、基本概念1、体积流量(流量s V ):流体单位时间内流过管路任意流量截面(管路横截面)的体积。
复变函数积分方法总结

复变函数积分⽅法总结复变函数积分⽅法总结经营教育乐享[选取⽇期]复变函数积分⽅法总结数学本就灵活多变,各类函数的排列组合会衍⽣多式多样的函数新形势,同时也具有本来原函数的性质,也会有多类型的可积函数类型,也就会有相应的积分函数求解⽅法。
就复变函数:z=x+iy i2=-1 ,x,y分别称为z的实部和虚部,记作x=Re(z),y=Im(z)。
arg z=θ? θ?称为主值-π<θ?≤π,Arg=argz+2kπ。
利⽤直⾓坐标和极坐标的关系式x=rcosθ,y=rsinθ,故z= rcosθ+i rsinθ;利⽤欧拉公式e iθ=cosθ+isinθ。
z=re iθ。
1.定义法求积分:定义:设函数w=f(z)定义在区域D内,C为区域D内起点为A终点为B 的⼀条光滑的有向曲线,把曲线C任意分成n个弧段,设分点为A=z0,z1,…,z k-1,z k,…,z n=B,在每个弧段z k-1 z k(k=1,2…n)上任取⼀点?k并作和式S n=?(z k-z k-1)=??z k记?z k= z k- z k-1,弧段z k-1 z k的长度={?S k}(k=1,2…,n),当0时,不论对c的分发即?k的取法如何,S n 有唯⼀的极限,则称该极限值为函数f(z)沿曲线C的积分为:=??z k设C负⽅向(即B到A的积分记作).当C为闭曲线时,f(z)的积分记作(C圆周正⽅向为逆时针⽅向)例题:计算积分,其中C表⽰a到b的任⼀曲线。
(1)解:当C为闭合曲线时,=0.∵f(z)=1 S n=?(z k-z k-1)=b-a∴=b-a,即=b-a.(2)当C为闭曲线时,=0. f(z)=2z;沿C连续,则积分存在,设?k=z k-1,则∑1= ()(z k-z k-1)有可设?k=z k,则∑2= ()(z k-z k-1)因为S n的极限存在,且应与∑1及∑2极限相等。
所以S n= (∑1+∑2)==b2-a2∴=b2-a21.2 定义衍⽣1:参数法:f(z)=u(x,y)+iv(x,y), z=x+iy带⼊得:= - vdy + i+ udy再设z(t)=x(t)+iy(t) (≤t≤)=参数⽅程书写:z=z0+(z1-z0)t(0≤t≤1);z=z0+re iθ,(0≤θ≤2π) 例题1:积分路线是原点到3+i的直线段解:参数⽅程z=(3+i)t=′=(3+i)3=6+i例题2:沿曲线y=x2计算()解:参数⽅程或z=t+it2 (0≤t≤1)=()=(1+i)+ 2i]=-+i1.3定义衍⽣2 重要积分结果:z=z0+ re iθ,(0≤θ≤2π)由参数法可得:=dθ=dθ()=例题1:例题2:解:=0 解=2πi2.柯西积分定理法:2.1柯西-古萨特定理:若f(z)dz在单连通区域B内解析,则对B内的任意⼀条封闭曲线有:=02.2定理2:当f为单连通B内的解析函数是积分与路线⽆关,仅由积分路线的起点z0与终点z1来确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
JPEG图像压缩
1算法思【现场实操追-女生资-源】想:
JPEG算法主要负责定制静态图像的编码方法,其核心是DCT变换,经过DC【扣】T变换将时域图像转换为频率域的图像,变换后的矩阵中左上角的系数【1】比较大,而右下角的系数比较小,基本接近于0。
根据这个特性,【О】经过量化以及编码过程,我们可以去除图像中的空间冗余,以达到【⒈】压缩的效果。
并且根据人眼对亮度以及色度的敏感度的不同,对亮度以【6】及色度进行不同程度的压缩,从而在保证图像品质的条件下得到【⒐】更高的压缩率。
2算法【⒌】流程
3主要【2】步骤
(1)【б】? 颜色转换
JPEG采用的是YCrCb颜色空间,而BMP采用的是RGB颜色空间,要想对BMP图片进行压缩,首先需要进行颜色空间的转换。
YCrCb颜色空间中,Y代表亮度,U代表饱和度,V代表色度。
U,V也可以通称为色度。
Y?=?0.299R+0.587G+0.114B
U=?-0.1687R-0.3313G+0.5B+128
V=?0.5R=0.418G-0.0813B+128
一般来说,U和V应该是一个有符号的数字,?但这里通过加上128,使其变为8位的无符号整数,从而方便数据的存储和计算。
(2)? 采样
JPEG图片中,通常采用两种采样方式:YUV411和YUV422,它们所代表的意义是Y,U,V三个分量的数据取样比例一般是4:1:1或者4:2:2。
这样的采样方式,虽然损失了一定的精度但也在人眼不太察觉到的范围内减小了数据的存储量。
?YUV4:1:1
4:1:1的色度抽样,是在水平方向上对色度进行4:1抽样。
对于低端用户和消费类产品这仍然是可以接受的。
对非压缩的8比特量化的视频来说,每个由4个水平方向相邻的像素组成的宏像素需要占用6字节内存(亮度4个字节,两个色度各1个字节)。
下面的四个像素为:?[Y0 U0 V0] [Y1 U1 V1] [Y2 U2 V2] [Y3 U3V3] 存放的码流为:?Y0 U0 Y1 Y2 V2 Y3
映射出像素点为:[Y0 U0 V2][Y1 U0 V2] [Y2 U0 V2] [Y3 U0 V2] YUV 4:2:2
每个色差信道的抽样率是亮度信道的一半,所以水平方向的色度抽样率只是4:4:4的一半。
对非压缩的8比特量化的图像来说,每个由两个水平方向相邻的像素组成的宏像素需要占用4字节内存(亮度2个字节,两个色度各1个字节)。
下面的四个像素为:?[Y0 U0V0] [Y1 U1 V1]?[Y2 U2 V2] [Y3 U3 V3] 存放的码流为:?Y0 U0 Y1V1?Y2 U2 Y3 V3
映射出像素点为:[Y0 U0 V1] [Y1 U0V1] [Y2 U2 V3] [Y3 U2 V3] (3)?分块
源图象中每点的3个分量是交替出现的,先要把这3个分量分开,存放到3张表中去。
然后由左及右,由上到下依次读取8x8的子块,存放在长度为64的表中,即可以进行DCT变换。
如果原始图片的长宽不是8的倍数,?都需要先补成8的倍数,?使其可以进行一块块的处理。
编码时,程序从源数据中读取一个8x8的数据块后,进行DCT变换,量化,编码,然后再读取、处理下一个8*8的数据块。
?图像的数据值必须减去128,是因为DCT公式所接受的数字范围是-128到127之间。
(4)? DCT变换
DCT(离散余弦变换)是将图像从空间域转换到频率域中,是一种无损的变换方式,可以去除图像中的空间冗余。
在JPEG中,分别对8x8的分块进行变换,其变换方程为:
当u=0,v=0时:
当u,v不为0时:
其中,N=64,而u,v=1,2.N-1。
其变换后的8x8数组中的每个数字为原8x8数组中的每个数字经过一定的组合而成,最终变换后的数组的左上角表示原图片的低频部分,右下角表示图片的高频部分,经过反变换可以变换回原图片。
(5)? Zigzag扫描
?DCT?将一个?8x8?的数组变换成另一个?8x8?的数组.?但是内存里所有数据都是线形存放的,?如果我们一行行的存放这?64?个数字,?每行的结尾的点和下行开始的点就没有什么关系。
JPEG算法按如下方式扫描存储数据,数列里的相邻点在图片上也是相邻的了。
(6)量化
量化阶段需要两个8*8量化矩阵数据,一个是专门处理亮度的频率系数,另一个则是针对色度的频率系数,将频率系数除以量化矩阵的值之后取整,即完成了量化过程。
当频率系数经过量化之后,将频率系数由浮点数转变为整数,这才便于执行最后的编码。
不难发现,经过量化阶段之后,所有的数据只保留了整数近似值,也就再度损失了一些数据内容。
在JPEG 算法中,由于对亮度和色度的精度要求不同,分别对亮度和色度采用不同的量化表。
前者细量化,后者粗量化。
(6)?编码
DC系数编码
DC系数即直流分量系数,是对8x8模块进行DCT变换后的第一个分量,其具有以下两个特点:
a.系数的数值比较大;
b.相邻的8*8图像块的DC系数值变化不大;
根据这两个特点,DC系数一般采用差分脉冲调制编码DPCM,即:取同一个图像分量中每个DC值与前一个DC值的差值来进行编码。
AC系数编码
量化之后的AC系数的特点是,63个系数中含有很多值为0的系数,因此,可以采用行程编码RLC来更进一步降低数据的传输量。
在JPEG编码中,假设RLC编码之后得到了一个(M,N)的数据对,其中M是两个非零AC系数之间连续的0的个数(即,行程长度),N是下一个非零的AC系数的值。
采用这样的方式进行表示,是因为AC系数当中有大量的0,而采用
Zigzag扫描也会使得AC系数中有很多连续的0的存在,如此一来,使用RLC编码会大大降低数据的传输量。
对于AC系数,有两个符号。
符号1为行程和尺寸。
(0,0)和(15,0)是两个比较特殊的情况。
(0,0)表示块结束标志(EOB),(15,0)表示ZRL,当行程长度超过15时,用增加ZRL的个数来解决,所以最多有三个ZRL(3×16+15=63)。
符号2为幅度值(Amplitude)。
在得到DC系数的中间格式和AC系数的中间格式(借助VLI编码表)之后,为进一步压缩图象数据,有必要对两者的第一个字节进行熵编码。
JPEG基本系统规定采用Huffman编码。
Huffman编码时DC系数与AC系数分别采用不同的Huffman编码表,对于亮度和色度也采用不同的Huffman编码表。
因此,需要4张Huffman编码表才能完成熵编码的工作。
具体的Huffman编码采用查表的方式来高效地完成。
然而,在JPEG标准中没有定义缺省的Huffman表,用户可以根据实际应用自由选择,也可以使用JPEG标准推荐的Huffman表。
或者预先定义一个通用的Huffman表,也可以针对一副特定的图像,在压缩编码前通过搜集其统计特征来计算Huffman表的值。
这个算法的java代码放在thrift的org.apache.thrift.protocol.TCompactProtocol类里,数据传输的时候用做数字的压缩,以减少数据的传输量。
在聊这个算法之前,我们得先补补课,聊聊二进制补码相关的东东。
把8 * 8的DCT系数矩阵排列成1*64的向量,沿Z字形路径可以有效积累连续0的个数,提高编码压缩效率。
DC系数和低频的AC系数被排在
向量的前部
游程编码的原理:用一个符号值或串长代替具有相同值的连续符号,使符号长度少于原始数据长度。
Cb?=?-0.1687R-0.3313G+0.5B+128
double temp = preData[posy + y][posx + x];
IDCT(priv-component_infos[cY], priv-Y+64*2, 16);
% log(abs(dctfre)*5+1) 修正DCT系数以便频谱观察
只处理每对数右边的那个数据,对其进行VLI编码:?查找上面的VLI 编码表格,可以发现,57在第6组当中,因此,可以将其写成(0,6),57的形式,该形式,称之为AC系数的中间格式。
?ByteArrayOutputStream out = new ByteArrayOutputStream();。
