第35讲数列模型及应用
高三数学数列模型及其应用2

武汉贷款:https://提出书面借款申请,并提交有关资料。 申请贷款应提交的资料: (1)个人住房借款申请书; (2)身份证件复印件(居民身份证、户口簿、军官证或其他身份证件); (3)经办行认可的有权部门出具的借款人稳定经济收入证明或其他偿债能力证明资料; (4)合法的购买住房合同、协议及相关批准文件; (5)抵押物或质押权利清单及权属证明文件,有处分权人出具的同意抵押或质押的证明,贷款行认可的评估机构出具的抵押物估价报告书; (6)保证人出具的同意提供担保的书面承诺及保证人的资信证明; (7)存款单据、凭证式国债单据等借款人拟提供给贷款行质押的有价证券; (8)借款人用于购买住房的自筹资金的有关证明; (9)房屋销(预)售许可证或楼盘的房地产权证(现房)(复印件); (10)如果借款人的配偶与其共同申请借款,借款申请书上还要填写清楚配偶的有关情况,并出示结婚证和户口簿等; (11)贷款行规定的其他文件和资料。 2、二、签定合同 借款申请人在接到银行有关贷款批准的通知后,要到贷款行签订借款合同及担保合同,并视情况办理公证、抵押登记、保险等相关手续。 3、三:开立账户 选用委托扣除款方式还款的客户需与银行签订委托扣款协议,并在贷款行指定的营业网点开立还款专用的储蓄存折账户或储蓄卡、信用卡账户。同时,售房人要在贷款行开立售房结算账户或存款专户。 4、四、支用贷款 经贷款行同意发放的贷款,办妥有关手续后,贷款行按照借款合同约定,将贷款直接转入借款人在贷款行开立的存款账户内,或将贷款一次或分次划入售房人在贷款行开立的存款账户内。 5、五、按期还款 借款人按借款合同约定的还款计划、还款方式偿还贷款本息。目前可供选择的还款方式有委托扣款和柜面还款两种方式。 6、六、贷款结清包括提前结清和正常结清两种。 提前结清是指贷款到期日(一次性还本付息类贷款)或贷款最后一期(分期偿还类贷款)前结清贷款;正常结清指在贷款到期日(一次性还本付息类)或贷款最后一期(分期偿还类贷款)结清贷款。如提前结清贷款,借款人须在清偿应付各项款项后,提前10个工作日贷款行提出提前结清申请。贷 后,借款人从贷款行领取"贷款结清证明",取回房地产权属抵押登记证明文件及保险单正本,并持贷款行出具的"贷款结清证明"到原抵押登记部门办理抵押登记注销手续。 日常生活中,我们有时会有贷款的需要,用来满足消费支出,那么如果我们生活在农村,应该怎样贷款呢,下面介绍两种方法,供大家参考 宅基地信用卡宅基地1、农村每户人家有自己的宅基地,我们可以用自家的宅基地,向银行进行贷款。2、用宅基地贷款,首先需要向银行进行申请,让其派专业人员来实地查探评估宅基地的价值。3、专业人员查看相关证件和实地拍照评估后,等待银行放款即可,需要注意的是,其放款金额不是按 评估的价格全额发放,会在其基础上打折,例如100万元的宅基地,会按60或者70万进行放贷,此种方法放款慢,利息低,金额大,适用用款量大且不着急的人。 工资贷款是指按借款人月工资收入的一定比例,向借款人发放的以其个人工资收工资贷款入作为还款保证的用于个人消费需求的保证贷款,无需担保。各个银行对于个人工资贷款的相关规定不尽一致,这里以民生银行“薪加薪”个人工资保证贷款为例,对个人工资贷款业务进行说明。 贷款对象1、具有中华人民共和国国籍和完全民事行为能力的自然人。 |标签:二手房返回暂停重播播放x世界如此简单61条相关购买二手房需要哪些流程 妙招好生活购买按揭二手房流程及注意... 妙招好生活买二手房中介费怎么谈 妙招好生活购买二手房的砍价技巧 妙招好生活买二手房怎么砍价 妙招好生活买卖二手房收定金收条如何... 妙招好生活买二手房办理流程 妙招好生活房屋过户流程 妙招好生活二手房交易税费的计算 妙招好生活二手房的过户流程 妙招好生活加载更多~603567人看了这个对于贷款购买二手房流程,由于很多人对其中的门道不了解,导致了在二手房交易过程中出现了不少纠纷。为避免您在贷款购买二手房时走冤枉路。以下易贷中国编辑就为您详细介绍贷款购买二手房流 程以及需要注意的问题。1、买方要对房子的产权进行调查 审定房屋产权的完整性、真实性、可靠性,要注意产权证上的业主姓名与售房者是否相符,有无抵押或共有人等。这对买家来说最为关键,否则有可能导致后面 所做的一切都成了无用功。2、签订二手房买卖合同 买卖双方商谈房价、付款方式、违约责任、交付时间,并立约下定金。买卖双方可以到房管部门相关网站上下载格式化合同文本,也可以去中介公司索要合同文本。3、找评估公司做评估 这个过程一般来说要5~7个工作日。4、贷款的房子要办理相关按揭业务 如果是贷款和商业贷款组合的,则要向中心和银行同时申请。这是整个二手房DIY过程中最耗时间的阶段,通常要40个工作日左右。5、按揭办理下来后,要注意注销该物业的他项权证。6、将合同交到房管部门产权交易中心相关办事窗口,拿受理单。7、凭受理单到农税中心缴纳相关税费,拿完税 8、凭完税契证到房管部门办理房产证。9、凭完税契证到土管部门办理土地证。
【全套】2021届新课改地区高三数学一轮专题复习——第35讲 等比数列(解析版)

为( )
A.-2+ 2 2
B.- 2
C. 2
D.- 2或 2
(2)等比数列{an}的各项均为正数,且 a1a5=4,则 log2a1+log2a2+log2a3+log2a4+log2a5=________. 【答案】 (1)B (2)5 【解析】 (1)设等比数列{an}的公比为 q,因为 a3,a15 是方程 x2+6x+2=0 的两根,所以 a3·a15=a29=2,
1 (q4)3 1 (q4)2
1 23 1 22
7. 3
1 q
(2):(基本量法) 设数列 an 的首项是 a1 ,公比为 q ,则由 a3 a2 4 , a4 16 ,得
a1q a1q
2 3
a1q 16
4
解得
aq122 , S3 a1 a2 a3 a1 a1q a1q2 2 4 8 14 .
项 a1>0,公比 0<q<1 或首项 a1<0,公比 q>1,则数列为递减数列;若公比 q=1,则数列为常数列;公比
q<0,则数列为摆动数列.
1
an
(5)若{an}和{bn}均为等比数列,则{λan}(λ≠0)、{|an|}、an 、{a2n}、bn 、{manbn}(m≠0)仍为等比数列.
1 / 14
变式 2、 (1)[2018·如东中学]在等比数列{an}中,各项均为正值,且 a6a10+a3a5=41,a4a8=5,则 a4+a8=
____; (2)[2016·常熟中学]等比数列{an}的首项 a1=-1,前 n 项和为 Sn,若SS150=3312,则公比 q=___.
【答案】(1) 51(2)-1 2
解得
q=1,代入①得 2
a1=2,
高考数学复习知识点讲解教案第35讲 等差数列及其前n项和

2
2
二次函数
于的常数项为0的____________,它的图象是抛物线
=
孤立
标为正整数的均匀分布的一群_______的点.
2
2
+ 1 −
2
上横坐
常用结论
1.已知数列{ }的通项公式是 = + (其中,为常数),则数列{ }一定
是等差数列,且公差为.
2 + 9 = 1 + + 1 + 8 = 29,
[解析] 设等差数列{ }的公差为,由已知得ቊ
5 = 51 + 10 = 35,
1 = 1,
解得ቊ
∴ 8 = 81 + 28 = 8 + 28 × 3 = 92.故选B.
= 3,
(2) [2024·九省联考] 记等差数列{an}的前n项和为Sn,a3+a7=6,a12=17,则S16= ( C )
−10
7.已知等差数列{ }的通项公式为 = 10 − ,则1 + 2 + ⋯ + 20 =______,
100
1 + 2 + ⋯ + 20 =______.
[解析] 设数列{ }的前项和为 ,
则20 = 1 + 2 + ⋯ + 20 =
20×[9+ 10−20 ]
◆ 知识聚焦 ◆
1.等差数列中的有关公式
已知等差数列{ }的首项为1 ,公差是,前项和为 ,则
等差数列定义式
+1 − =
_________________(为常数)
等差中项
+
(整理)(第35讲)导数的运算法则及基本公式应用.

题目 高中数学复习专题讲座 高考要求导数是中学限选内容中较为重要的知识,本节内容主要是在导数的定义,常用求等公式 四则运算求导法则和复合函数求导法则等问题上对考生进行训练与指导 重难点归纳1 深刻理解导数的概念,了解用定义求简单的导数xy∆∆表示函数的平均改变量,它是Δx 的函数,而f ′(x 0)表示一个数值,即f ′(x )=xyx ∆∆→∆lim 0,知道导数的等价形式)()()(lim )()(lim0000000x f x x x f x f x x f x x f x x x '=--=∆-∆+→∆→∆ 2 求导其本质是求极限,在求极限的过程中,力求使所求极限的结构形式转化为已知极限的形式,即导数的定义,这是顺利求导的关键3 对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用,在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误4 复合函数求导法则,像链条一样,必须一环一环套下去,而不能丢掉其中的一环 必须正确分析复合函数是由哪些基本函数经过怎样的顺序复合而成的,分清其间的复合关系 典型题例示范讲解例1求函数的导数)1()3( )sin ()2( cos )1(1)1(2322+=-=+-=x f y x b ax y xx xy ω 命题意图 本题3个小题分别考查了导数的四则运算法则,复合函数求导的方法,以及抽象函数求导的思想方法 这是导数中比较典型的求导类型知识依托 解答本题的闪光点是要分析函数的结构和特征,挖掘量的隐含条件,将问题转化为基本函数的导数错解分析 本题难点在求导过程中符号判断不清,复合函数的结构分解为基本函数出差错技巧与方法 先分析函数式结构,找准复合函数的式子特征,按照求导法则进行求导22222(1)(1)cos (1)[(1)cos ](1):(1)cos x x x x x x y x x''-+--+'=+-解2222222222222222(1)cos (1)[(1)cos (1)(cos )](1)cos (1)cos (1)[2cos (1)sin ](1)cos (21)cos (1)(1)sin (1)cos x x x x x x x x x x x x x x x x x x x x x x x x x x''-+--+++=+-+---+=+--+-+=+(2)解 y =μ3,μ=ax -b sin 2ωx ,μ=av -by v =x ,y =sin γ γ=ωxy ′=(μ3)′=3μ2·μ′=3μ2(av -by )′ =3μ2(av ′-by ′)=3μ2(av ′-by ′γ′) =3(ax -b sin 2ωx )2(a -b ωsin2ωx )(3)解法一 设y =f (μ),μ=v ,v =x 2+1,则y ′x =y ′μμ′v ·v ′x =f ′(μ)·21v -21·2x=f ′(12+x )·21112+x ·2x=),1(122+'+x f x x解法二 y ′=[f (12+x )]′=f ′(12+x )·(12+x )′=f ′(12+x )·21(x 2+1)21-·(x 2+1)′=f ′(12+x )·21(x 2+1)21-·2x=12+x x f ′(12+x )例2利用导数求和(1)S n =1+2x +3x 2+…+nx n -1(x ≠0,n ∈N *)(2)S n =C 1n +2C 2n +3C 3n +…+n C nn ,(n ∈N *)命题意图 培养考生的思维的灵活性以及在建立知识体系中知识点灵活融合的能力知识依托 通过对数列的通项进行联想,合理运用逆向思维 由求导公式(x n )′=nx n -1,可联想到它们是另外一个和式的导数 关键要抓住数列通项的形式结构错解分析 本题难点是考生易犯思维定势的错误,受此影响而不善于联想技巧与方法 第(1)题要分x =1和x ≠1讨论,等式两边都求导 解 (1)当x =1时S n =1+2+3+…+n =21n (n +1); 当x ≠1时,∵x +x 2+x 3+…+x n=xx x n --+11,两边都是关于x 的函数,求导得(x +x 2+x 3+…+x n)′=(xx x n --+11)′即S n =1+2x +3x 2+…+nxn -1=21)1()1(1x nx x n n n -++-+(2)∵(1+x )n =1+C 1n x +C 2n x 2+…+C n n x n,两边都是关于x 的可导函数,求导得n (1+x )n -1=C 1n +2C 2n x +3C 3n x 2+…+n C n n xn -1, 令x =1得,n ·2n -1=C 1n +2C 2n +3C 3n +…+n C n n ,即S n =C 1n +2C 2n +…+n C n n =n ·2n -1例3 已知曲线C y =x 3-3x 2+2x ,直线l :y =kx ,且l 与C 切于点(x 0,y 0)(x 0≠0),求直线l 的方程及切点坐标解 由l 过原点,知k =x y (x 0≠0),点(x 0,y 0)在曲线C 上,y 0=x 03-3x 02+2x 0,∴x y =x 02-3x 0+2 y ′=3x 2-6x +2,k =3x 02-6x 0+2 又k =x y ,∴3x 02-6x 0+2=x 02-3x 0+2 2x 02-3x 0=0,∴x 0=0或x 0=23 由x ≠0,知x 0=23 ∴y 0=(23)3-3(23)2+2·23=-83∴k =00x y =-41 ∴l 方程y =-41x 切点(23,-83)学生巩固练习1 y =e sin x cos(sin x ),则y ′(0)等于( ) A 0 B 1 C -1D 22 经过原点且与曲线y =59++x x 相切的方程是( ) A x +y =0或25x +y =0 B x -y =0或25x+y =0C x +y =0或25x -y =0D x -y =0或25x-y =03 若f ′(x 0)=2,kx f k x f k 2)()(lim 000--→ =_________4 设f (x )=x (x +1)(x +2)…(x +n ),则f ′(0)=_________5 已知曲线C 1:y =x 2与C 2:y =-(x -2)2,直线l 与C 1、C 2都相切,求直线l 的方程6 求函数的导数 (1)y =(x 2-2x +3)e 2x ;(2)y7 有一个长度为5 m 的梯子贴靠在笔直的墙上,假设其下端沿地板以3 m/s 1 4 m 时,梯子上端下滑的速度8 求和S n =12+22x +32x 2+…+n 2x n -1,(x ≠0,n ∈N *) 参考答案1 解析 y ′=e sin x [cos x cos(sin x )-cos x sin(sin x )],y ′(0)=e 0(1-0)=1 答案 B2 解析 设切点为(x 0,y 0),则切线的斜率为k =x y , 另一方面,y ′=(59++x x )′=2)5(4+-x , 故y ′(x 0)=k ,即)5(9)5(40000020++==+-x x x x y x 或x 02+18x 0+45=0 得x 0(1)=-3, x 0 (2)=-15,对应有y 0(1)=3,y 0(2)=53515915=+-+-,因此得两个切点A (-3,3)或B (-15,53), 从而得y ′(A )=3)53(4+-- =-1及y ′(B )= 251)515(42-=+-- , 由于切线过原点,故得切线l A :y =-x 或l B :y =25x 答案 A3 解析 根据导数的定义f ′(x 0)=k x f k x f k ---+→)()]([(lim000(这时k x -=∆)1)(21)()(lim 21])()(21[lim 2)()(lim 0000000000-='-=----=---⋅-=--∴→→→x f k x f k x f kx f k x f k x f k x f k k k答案 -14 解析 设g (x )=(x +1)(x +2)……(x +n ),则f (x )=xg (x ),于是f ′(x )=g (x )+xg ′(x ),f ′(0)=g (0)+0·g ′(0)=g (0)=1·2·…n =n ! 答案 n !5 解 设l 与C 1相切于点P (x 1,x 12),与C 2相切于Q (x 2,-(x 2-2)2)对于C 1 y ′=2x ,则与C 1相切于点P 的切线方程为 y -x 12=2x 1(x -x 1),即y =2x 1x -x 12 ①对于C 2 y ′=-2(x -2),与C 2相切于点Q 的切线方程为y +(x 2-2)2=-2(x 2-2)(x -x 2),即y =-2(x 2-2)x +x 22-4 ②∵两切线重合,∴2x 1=-2(x 2-2)且-x 12=x 22-4, 解得x 1=0,x 2=2或x 1=2,x 2=0 ∴直线l 方程为y =0或y =4x -46 解 (1)注意到y >0,两端取对数,得 ln y =ln(x 2-2x +3)+ln e 2x =ln(x 2-2x +3)+2xxxe x x e x x x x x x y x x x x y x x x x x x x x x x x y y 2222222222222)2(2)32(32)2(232)2(232)2(223222232)32(1⋅+-=⋅+-⋅+-+-=⋅+-+-='∴+-+-=++--=++-'+-='⋅∴(2)两端取对数,得 ln|y |=31(ln|x |-ln|1-x |),两边解x 求导,得31)1(31)1(131)1(131)111(311xx x x y x x y x x x x y y --=⋅-⋅='∴-=---='⋅7 解 设经时间t 秒梯子上端下滑s 米,则s =5-2925t -,当下端移开1 4 m 时,t 0=157341=⋅,又s ′=-21(25-9t 2)21-·(-9·2t )=9t 29251t-,所以s ′(t 0)=9×2)157(9251157⨯-⋅=0 875(m/s)8 解 (1)当x =1时,S n =12+22+32+…+n 2=61n (n +1)(2n +1), 当x ≠1时,1+2x +3x 2+…+nx n -1=21)1()1(1x nx x n n n -++-+, 两边同乘以x ,得x +2x 2+3x 2+…+nx n=221)1()1(x nx x n x n n -++-++两边对x 求导,得S n =12+22x 2+32x 2+…+n 2x n -1=322122)1()122()1(1x x n x n n x n x n n n ---+++-+++课前后备注。
高考数学大一轮复习第六章不等式推理与证明第35讲基本不等式课件理新人教A版

解析 (1)因为 x,y>0,x+y=1,所以8x+2y=8x+2y(x+y) =10+8xy+2yx≥10+2 16=18,当且仅当8xy=2yx,即 x=2y 时, 等号成立.
(2)由已知得 9-(x+3y)=xy=31×x×3y≤13×x+43y2,当 且仅当 x=3y,即 x=3,y=1 时,等号成立.此时 xy 最大, 又因为 xy 与(x+3y)之和为定值,所以 x+3y 取最小值.故 (x+3y)min=3+3×1=6.
)
解析 (1)错误.因为 x 没有确定符号,所以不能说最小值 为 2.
(2)错误.利用基本不等式时,等号不成立. (3)错误.不是充要条件,当 x<0,y<0 时也成立. (4)错误.最小值不是定值,故不正确.
答案 (1)× (2)× (3)× (4)×
2.已知 m>0,n>0,且 mn=81,则 m+n 的最小值为( )
a+b
设 a>0,b>0,则 a,b 的算术平均数为___2___,几何平
均 数 为 ___a_b__ , 基 本 不 等 式 可 叙 述 为
_两__个__正__数__的__算__术__平__均__数__不___小__于__它__们__的__几__何__平__均__数____.
4.利用基本不等式求最值问题
2.几个重要不等式 (1)a2+b2≥___2_a_b____(a,b∈R).
(2)ba+ab≥__2_(a,b 同号). (3)ab≤a+2 b2(a,b∈R). (4)a2+2 b2≥a+2 b2(a,b∈R). 以上不等式等号成立的条件均为 a=b.
3.算术平均数与几何平均数
第六章
不等式、推理与证明
高考总复习 ·数学(理科)
第35讲
数列模型及应用word

数列模型及应用word数列是由一系列有序的数按照一定规律排列而成的集合。
数列是数学中的一个重要概念,具有广泛的应用。
在实际生活中,数列模型可以帮助我们解决各种问题。
下面我将从数列的定义、分类及其应用三个方面展开详细回答。
首先,数列是一系列有序的数按照确定的规律排列而成的集合。
数列中的每个数称为该数列的项,每个数列都有一个起始项,通常用a1表示,以及一个通项公式。
数列的常用形式有等差数列、等比数列、斐波那契数列等。
等差数列是指数列中各项之间的差值都相等的数列。
其通项公式为an=a1+(n-1)d,其中a1为首项,d为公差,n为项数。
等差数列常见的应用场景有:1.日常生活中,经常会进行等差数列的计算。
比如,我们经常会遇到一些有规律的数列,比如每天存款增加一定的金额,或者每天的步数增加相同的步数等。
通过计算等差数列可以帮助我们了解某个数列的发展趋势。
2.在经济学中,等差数列被广泛应用于一些经济指标的分析。
比如,每年的国内生产总值增长率、物价指数增长率等,可以通过等差数列的概念来计算和描述。
等比数列是指数列中各项之间的比值都相等的数列。
其通项公式为an=a1*r^(n-1),其中a1为首项,r为公比,n为项数。
等比数列常见的应用场景有:1.在金融领域,等比数列可用于计算复利。
比如,存款利率为r的情况下,每年的利息就形成一个等比数列。
2.在自然界中,等比数列也有很多应用。
比如,每天二分之一的细菌数量,每代细胞数量的增长等。
斐波那契数列是指数列中每一项等于前两项之和的数列。
其通项公式为an=an-1+an-2,其中a1和a2为首两项。
斐波那契数列的应用非常广泛,比如:1.在自然界中,斐波那契数列可以用来描述植物的生长。
比如,一个植物的高度等于前两天的高度之和。
2.在计算机科学中,斐波那契数列被广泛应用于算法和数据结构的设计。
比如,递归算法中常常使用斐波那契数列,以及在计算期权价格、股票价格等金融领域也会用到斐波那契数列。
数列模型及应用

VS
详细描述
热传导方程是描述热量传递过程的数学模 型,用于研究温度场的变化和热量传递的 规律。通过建立数列模型,可以模拟热传 导过程中的热量分布、扩散和传递等现象 ,以及温度随时间和空间的变化。数列模 型在热传导方程中的应用有助于优化热能 利用和解决热相关问题。
THANKS FOR WATCHING
波动方程
总结词
描述波动现象的数学模型。
详细描述
波动方程是描述波动现象的数学模型,如声波、光波和 水波等。通过建立数列模型,可以模拟波的传播、反射 、折射等行为,以及波的振幅、频率、速度等参数的变 化。数列模型在波动方程中的应用有助于深入理解波的 性质和传播规律。
热传导方程
总结词
描述热量传递过程的数学模型。
计算机科学
在计算机科学中,斐波那契数列可以用于生成伪随机数、优化算法等。此外,斐波那契数 列还可以用于加密技术,如RSA公钥密码算法中使用了斐波那契数列的性质。05Βιβλιοθήκη 数列模型在经济学中的 应用
货币的时间价值
货币的时间价值是指在不同时间点上的货币价值是不同的,未来的货币价值要低于现在的货币价值, 因为货币在将来可能会产生更多的收益。
日期推算。例如,已知某月的第一天是周二,那么该月的 23号是周几?可以通过等差数列的通项公式计算得出。
实例2
等差数列在音乐中的应用。音阶就是一种等差数列,每个 音符的频率间隔是固定的。
实例3
等差数列在统计学中的应用。例如,要统计一个班级学生的平 均身高,可以将所有学生的身高加起来,再除以人数,这就是
感谢您的观看
产生的利息。
人口增长
02
在生物学和人口统计学中,人口增长可以被视为等比数列,其
中每一代人口数量与前一代成固定比例增长。
高考数学高中数学知识点第35讲 基本不等式

第35讲 基本不等式1.基本不等式ab ≤a +b2(1)基本不等式成立的条件:__a >0,b >0__. (2)等号成立的条件:当且仅当__a =b __时取等号. 2.几个重要的不等式: (1)a 2+b 2≥__2ab __(a ,b ∈R ). (2)b a +ab ≥__2__(a ,b 同号). (3)ab ≤⎝⎛⎭⎫a +b 22(a ,b ∈R ).(4)a 2+b 22≥⎝⎛⎭⎫a +b 22(a ,b ∈R ). 3.算术平均数与几何平均数设a >0,b >0,则a ,b 的算术平均数为__a +b 2__,几何平均数为,基本不等式可叙述为__两个正数的算术平均数不小于它们的几何平均数__.4.利用基本不等式求最值问题 已知x >0,y >0,则:(1)如果积xy是定值p ,那么当且仅当__x =y __时,x +y 有最__小__值是简记:积定和最小);(2)如果和x +y 是定值p ,那么当且仅当__x =y __时,xy 有最__大__值是__p 24__(简记:和定积最大).1.思维辨析(在括号内打“√”或“×”).(1)函数y =x +1x 的最小值是2.( × )(2)函数f (x )=cos x +4cos x,x ∈⎝⎛⎭⎫0,π2的最小值等于4.( × ) (3)x >0,y >0是x y +yx ≥2的充要条件.( × )(4)若a >0,则a 3+1a2的最小值为2a .( × )解析 (1)错误.因为x 没有确定符号,所以不能说最小值为2. (2)错误.利用基本不等式时,等号不成立. (3)错误.不是充要条件,当x <0,y <0时也成立. (4)错误.最小值不是定值,故不正确.2.已知m >0,n >0,且mn =81,则m +n 的最小值为( A ) A .18 B .36 C .81D .243解析 ∵m >0,n >0,∴m +n ≥2mn =18.当且仅当m =n =9时,等号成立. 3.若M =a 2+4a (a ∈R ,a ≠0),则M 的取值范围为( A )A .(-∞,-4]∪[4,+∞)B .(-∞,-4]C .[4,+∞)D .[-4,4]解析 M =a 2+4a =a +4a ,当a >0时,M ≥4;当a <0时,M ≤-4.4.若x >1,则x +4x -1的最小值为__5__.解析 x +4x -1=x -1+4x -1+1≥4+1=5.当且仅当x -1=4x -1,即x =3时等号成立. 5.若x >0,y >0,lg x +lg y =1,则z =2x +5y 的最小值为__2__.解析 由已知条件lg x +lg y =1,可知xy =10. 则2x +5y≥210xy=2,故⎝⎛⎭⎫2x +5y min =2,当且仅当2y =5x 时取等号.又xy =10.即x =2,y =5时等号成立.一 利用基本不等式证明不等式利用基本不等式证明不等式的方法(1)利用基本不等式证明不等式是综合法证明不等式的一种情况,要从整体上把握运用基本不等式.对不满足使用基本不等式条件的可通过“变形”来转换,常见的变形技巧有:拆项,并项,也可乘上一个数或加上一个数,“1”的代换法等.(2)利用基本不等式对所证明的不等式中的某些部分放大或者缩小,在含有三个字母的不等式证明中要注意利用对称性.【例1】 (1)已知x >0,y >0,z >0, 求证:⎝⎛⎭⎫y x +z x ⎝⎛⎭⎫x y +z y ⎝⎛⎭⎫x z +y z ≥8.(2)已知a >0,b >0,c >0,且a +b +c =1,求证:1a +1b +1c ≥9.证明 (1)∵x >0,y >0,z >0,∴y x +z x ≥2yzx >0,x y +z y ≥2xz y >0,x z +y z ≥2xyz >0, ∴⎝⎛⎭⎫y x +z x ⎝⎛⎭⎫x y +z y ⎝⎛⎭⎫x z +y z ≥8yz ·xz ·xy xyz =8, 当且仅当x =y =z 时等号成立.(2)∵a >0,b >0,c >0,且a +b +c =1, ∴1a +1b +1c =a +b +c a +a +b +c b +a +b +c c =3+b a +c a +a b +c b +a c +b c=3+⎝⎛⎭⎫b a +a b +⎝⎛⎭⎫c a +a c +⎝⎛⎭⎫c b +b c ≥3+2+2+2=9, 当且仅当a =b =c =13时,取等号.二 利用基本不等式求最值利用基本不等式求最值应注意的问题(1)利用基本不等式解题一定要注意应用的前提:“一正”“二定”“三相等”.所谓“一正”是指正数,“二定”是指应用基本不等式求最值时,和或积为定值,“三相等”是指满足等号成立的条件.(2)在利用基本不等式求最值时,要根据式子的特征灵活变形,配凑出积、和为常数的形式,然后再利用基本不等式求解.【例2】 (1)已知0<x <1,则x (3-3x )取得最大值时x 的值为( B )A .13B .12C .34D .23(2)若函数f (x )=x +1x -2(x >2)在x =a 处取最小值,则a =( C ) A .1+2 B .1+3 C .3D .4解析 (1)∵0<x <1,∴x (3-3x )=3x (1-x )≤3⎣⎡⎦⎤x +(1-x )22=34,当且仅当x =1-x ,即x=12时,“=”成立. (2)∵x >2,∴x -2>0, ∴f (x )=x +1x -2=(x -2)+1x -2+2≥2·(x -2)·1x -2+2=2+2=4,当且仅当x -2=1x -2, 即(x -2)2=1时,等号成立,∴x =1或3.又∵x >2,∴x =3,即a =3.【例3】 (1)(2018·山东烟台期末)已知正实数x ,y 满足2x +1y =1,若x +2y >m 2+2m 恒成立,则实数m 的取值范围是( B )A .(-2,4)B .(-4,2)C .(-∞,2]∪[4,+∞)D .(-∞,-4]∪[2,+∞)(2)(2018·福建南平一模)已知x ,y 都是非负实数,且x +y =2,则8(x +2)(y +4)的最小值为( B )A .14B .12C .1D .2(3)(2018·河南许昌二模)已知x ,y 均为正实数,且1x +2+1y +2=16,则x +y 的最小值为( C )A .24B .32C .20D .28解析 (1)因为x >0,y >0,2x +1y =1,所以x +2y =(x +2y )·⎝⎛⎭⎫2x +1y =4+4y x +x y ≥4+24yx xy=8,当且仅当x =4,y =2时取等号,所以x +2y 的最小值是8.所以m 2+2m <8,解得-4<m <2,故选B .(2)因为x ,y 都是非负实数,且x +y =2,所以x +2+y +4=8.所以8≥2(x +2)(y +4),则1(x +2)(y +4)≥116,当且仅当x =2,y =0时取等号,所以8(x +2)(y +4)≥816=12,故选B .(3)因为x ,y 均为正实数,且1x +2+1y +2=16, 则x +y =(x +2+y +2)-4 =6⎝⎛⎭⎫1x +2+1y +2(x +2+y +2)-4 =6⎝ ⎛⎭⎪⎫2+x +2y +2+y +2x +2-4≥6⎝⎛⎭⎪⎫2+2x +2y +2·y +2x +2-4≥20, 当且仅当x =y =10时取等号 ,所以x +y 的最小值为20,故选C .三 基本不等式的实际应用(1)此类型的题目往往较长,解题时需认真阅读,从中提炼出有用信息,建立数学模型,转化为数学问题求解.(2)当运用基本不等式求最值时,若等号成立的自变量不在定义域内,就不能使用基本不等式求解,此时可根据变量的范围用对应函数的单调性求解.【例4】 某厂家拟在2018年举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x 万件与年促销费用m (m ≥0)万元满足x =3-km +1(k 为常数).如果不搞促销活动,那么该产品的年销量只能是1万件.已知2018年生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将2018年该产品的利润y 万元表示为年促销费用m 万元的函数; (2)该厂家2018年的促销费用投入多少万元时,厂家利润最大?解析 (1)由题意知,当m =0时,x =1(万件),∴1=3-k ⇒k =2,∴x =3-2m +1,每件产品的销售价格为1.5×8+16xx(元),∴2018年的利润y =1.5x ×8+16xx -8-16x -m=-⎣⎡⎦⎤16m +1+(m +1)+29(m ≥0).(2)∵m ≥0时,16m +1+(m +1)≥216m +1·(m +1)=8, ∴y ≤-8+29=21,当且仅当16m +1=m +1⇒m =3(万元)时,y max =21(万元).故该厂家2018年的促销费用投入3万元时,厂家的利润最大为21万元.1.已知f (x )=32x -(k +1)3x +2,当x ∈R 时,f (x )恒为正值,则k 的取值范围是( B ) A .(-∞,-1) B .(-∞,22-1) C .(-1,22-1)D .(-22-1,22-1)解析 由32x -(k +1)3x +2>0恒成立,得k +1<3x +23x .∵3x +23x ≥22,∴k +1<22,即k <22-1.2.某车间分批生产某种产品,每批产品的生产准备费用为800元,若每批生产x 件,则平均仓储时间为x8天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( B )A .60件B .80件C .100件D .120件解析 若每批生产x 件产品,则每件产品的生产准备费用是800x 元,仓储费用是x8元,总的费用是800x +x8≥2800x ·x 8=20,当且仅当800x =x8,即x =80时取等号. 3.若2x +4y =4,则x +2y 的最大值是__2__. 解析 因为4=2x +4y =2x +22y ≥22x ×22y =22x+2y,所以2x+2y≤4=22,即x +2y ≤2,当且仅当2x =22y =2,即x =2y =1时,x +2y 取得最大值2.4.(2018·山东济宁二模)已知圆C 1:x 2+y 2=4和圆C 2:(x -2)2+(y -2)2=4,若P (a ,b )(a >0,b >0)在两圆的公共弦上,则1a +9b的最小值为__8__.解析 由题意知,圆C 1:x 2+y 2=4和圆C 2:(x -2)2+(y -2)2=4两个方程相减即可得到两圆公共弦所在直线的方程,即x +y =2,又点P (a ,b )(a >0,b >0)在两圆的公共弦上,所以a +b =2,则1a +9b =12(a +b )⎝⎛⎭⎫1a +9b =12⎝⎛⎭⎫10+b a +9a b =5+12·⎝⎛⎭⎫b a +9a b ≥5+12×2b a ·9ab=8⎝⎛ 当且仅当b =3a ,即a =12,⎭⎫b =32时,等号成立,所以1a +9b的最小值为8.易错点 不会凑出常数错因分析:式子的最大、最小值应为常数,为凑出常数,需要“拆”“拼”“凑”等技巧.【例1】 已知正数x ,y 满足x +22xy ≤λ(x +y )恒成立,则λ的最小值为________.解析 由已知得λ≥x +22xyx +y 恒成立.∵x +22xy x +y =x +2x ·2y x +y ≤x +x +2yx +y=2,(当且仅当x =2y 时取等号)∴λ≥2,λ的最小值为2.答案 2【跟踪训练1】 已知x 为正实数,且x 2+y 22=1,求x 1+y 2的最大值.解析 因为x >0, 所以x ·1+y 2=2x 2⎝⎛⎭⎫12+y 22≤22⎣⎡⎦⎤x 2+⎝⎛⎭⎫12+y 22.又x 2+⎝⎛⎭⎫12+y 22=⎝⎛⎭⎫x 2+y 22+12=32.所以x 1+y 2≤2⎝⎛⎭⎫12×32=324,当且仅当x 2=12+y 22, 即x =32时,等号成立.故(x 1+y 2)max =324. 课时达标 第35讲[解密考纲]考查基本不等式,常以选择题、填空题的形式出现.在解答题中也渗透基本不等式的应用.一、选择题1.已知f (x )=x +1x -2(x <0),则f (x )有( C )A .最大值为0B .最小值为0C .最大值为-4D .最小值为-4解析 ∵x <0,∴f (x )=-⎣⎡⎦⎤(-x )+1(-x )-2≤-2-2=-4,当且仅当-x =1-x ,即x =-1时,取等号.2.若a ,b ∈R ,且ab >0,则下列不等式中,恒成立的是( C ) A .a +b ≥2ab B .1a +1b >1abC .b a +ab≥2D .a 2+b 2>2ab解析 ∵ab >0,∴b a >0,a b >0,∴b a +ab≥2b a ·ab=2,当且仅当a =b 时取等号. 3.若a ≥0,b ≥0,且a (a +2b )=4,则a +b 的最小值为( C ) A .2B .4C .2D .2 2解析 ∵a ≥0,b ≥0,∴a +2b ≥0,又∵a (a +2b )=4,∴4=a (a +2b )≤(a +a +2b )24,当且仅当a =a +2b =2时等号成立.∴(a +b )2≥4,∴a +b ≥2.4.函数y =^x 2+2x -1(x >1)的最小值是( A )A .23+2B .23-2C .23D .2解析 ∵x >1,∴x -1>0.∴y =x 2+2x -1=x 2-2x +2x +2x -1=x 2-2x +1+2(x -1)+3x -1=(x -1)2+2(x -1)+3x -1=x -1+3x -1+2≥2(x -1)⎝⎛⎭⎫3x -1+2=23+2.当且仅当x -1=3x -1,即x =1+3时,取等号.5.若正数a ,b 满足a +b =2,则1a +1+4b +1的最小值是( B )A .1B .94C .9D .16解析1a +1+4b +1=⎝⎛⎭⎫1a +1+4b +1·(a +1)+(b +1)4=14×⎣⎢⎡⎦⎥⎤1+4+b +1a +1+4(a +1)b +1≥14(5+24)=94,当且仅当b +1a +1=4(a +1)b +1,b +1=2(a +1)时取等号,故选B .6.小王从甲地到乙地往返的时速分别为a 和b (a <b ),其全程的平均时速为v ,则( A ) A .a <v <ab B .v =ab C .ab <v <a +b 2D .v =a +b2解析 设甲、乙两地相距s ,则平均速度v =2ss a +s b =2ab a +b . 又∵a <b ,∴2ab a +b >2abb +b =a .∵a +b >2ab ,∴2ab a +b <2ab2ab=ab ,∴a <v <ab . 二、填空题7.设P (x ,y )是函数y =2x(x >0)图象上的点,则x +y 的最小值为解析 因为x >0,所以y >0,且xy =2.由基本不等式得x +y ≥2xy =22,当且仅当x =y 时等号成立.8.已知正数x ,y 满足x +2y =2,则x +8yxy 的最小值为__9__.解析 由已知得x +2y 2=1,则x +8y xy =1y +8x =⎝⎛⎭⎫1y +8x ·⎝⎛⎭⎫x +2y 2=12⎝⎛⎭⎫10+x y +16y x ≥12(10+216)=9,当且仅当x =43,y =13时取等号.9.已知x ,y 为正实数,3x +2y =10,3x +2y 的最大值为解析 由a +b2≤a 2+b 22得3x +2y ≤2(3x )2+(2y )2=23x +2y =25, 当且仅当x =53,y =52时取等号.三、解答题10.(1)当x <32时,求函数y =x +82x -3的最大值;(2)设0<x <2,求函数y =x (4-2x )的最大值. 解析 (1)∵x <32,∴2x -3<0,∴3-2x >0,∴y =12(2x -3)+82x -3+32=-12⎣⎡⎦⎤(3-2x )+163-2x +32 ≤-12·2(3-2x )·163-2x +32=-4+32=-52,当且仅当3-2x =163-2x ,即x =-12时,y max =-52.∴函数y 的最大值为-52.(2)∵0<x <2,4-2x >0, ∴y =x (4-2x )=12·2x (4-2x )≤12⎝⎛⎭⎫2x +4-2x 22=2,当且仅当2x =4-2x ,即x=1时,y max = 2.11.已知x >0,y >0,且2x +8y -xy =0,求: (1)xy 的最小值; (2)x +y 的最小值.解析 (1)∵x >0,y >0,2x +8y -xy =0,∴xy =2x +8y ≥216xy =8xy ,∴xy (xy -8)≥0,又xy ≥0,∴xy ≥8即xy ≥64.当且仅当x =4y 即8y +8y -4y 2=0时,即y =4,x =16时取等号, ∴xy 的最小值为64.(2)∵2x +8y =xy >0,∴2y +8x =1,∴x +y =(x +y )⎝⎛⎭⎫2y +8x =10+2x y +8yx≥10+22x y ·8yx=18. 当且仅当2x y =8yx ,即x =2y 即4y +8y -2y 2=0时,即y =6,x =12时取等号,∴x +y的最小值为18.12.某地需要修建一条大型输油管道通过240 km 宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的费用为400万元,铺设距离为x km 的相邻两增压站之间的输油管道的费用为(x 2+x )万元.设余下工程的总费用为y 万元.(1)试将y 表示成x 的函数;(2)需要修建多少个增压站才能使y 最小,其最小值为多少? 解析 (1)设需要修建k 个增压站, 则(k +1)x =240,即k =240x -1,所以y =400k +(k +1)(x 2+x )=400·⎝⎛⎭⎫240x -1+240x(x 2+x ) =96 000x+240x -160. 因为x 表示相邻两增压站之间的距离,则0<x <240. 故y 与x 的函数关系是y =96 000x +240x -160(0<x <240).(2)y =96 000x+240x -160≥296 000x·240x -160=2×4 800-160=9 440,当且仅当96 000x=240x ,即x =20时等号成立, 此时k =240x -1=24020-1=11.故需要修建11个增压站才能使y 最小,其最小值为9 440万元.古今中外有学问的人,有成就的人,总是十分注意积累的。
2020小升初分班考第35讲找规律(含答案)

2020小升初专项训练班讲义第三十五讲找规律 名校真题测试卷1 *oe 年情"丘附中苇®)帕果擀数14, 3山33. 组的悄况垦仆久?4 〔06年东城二屮暫®)住2、3两《£之闽.第•-欣"上 気第-次占:2 5和5、32间分剔写上 7、轨如下所^^^ ).毎次SE 住亡吗上的 曲牛柿嘟《^之创和上这两牛押裁®;:和.诂样剧过拧技审且了点沈2 "■■■■■ 7 5 .... f l 35 W4年人丸阳中考題)诫祢眠01L 02. 03、…、9B*的屮选耿车&何由用数叩申,都fj 某苗亍柑弭的数丫・址祢斫怨破的那輕觀屮当屮的■牛° 门)清懈说.期. 37柯73这两卜散"|申型少蜚选團 >:55 蛙満足娈求叫y2 (05年三啊中学禹豊、 观察 1+3=4 : 4+5=9 9+7=16 116+9=2525+11=36这五道»式.我出规律*煞后瑕肓2001= + f )=2002一爪野敬:1 21 24 k T h I I I III + 4 II3 3, 555577777799■ +-PIIe 19'1<11扶中的第 Z000 T 讣趙3S, 39, 75, U3, 0〜9芳中的剰壬垃子温战的无筲丘的対r 込到这吐U 的」总):i^f :讥电{町= 越)你【館】分M 贞闪数・找出頂闪散枸分开.所以分组为 33. 35、30、169 和 14, 39. 75. 143.[K]卜血的炭悻是:右边的數和左边第一个数的羞疋样是奇ftttW 面《号中填的ft 字为奇tt 列中的第2001个.ap 4003•3. 5. 7、9、11…….所以KtVfJ 分环为3的ff 2个, 样2000个分a 的分每为89. 力呼为4仁 分砂为 7的为6个,Ji 样个a 2+4+5+8-88«1980<2000- U 所以分a 为20/89,4 135.第五次吗后和增加 405-…… 它If]的魅依次为 5、15 , 45. 135 , 405……为等比数列・公比为 它们的W 为 5+15+45+135+405+1215=1820.所以第六次C.和为(W1:第一次yjG 利增加 5.第二次写后的和增扣 15.第丄次巧后和增加 45. 35四次y 后和增加 X 1820+2+3=1825. 5 [W] (!) ■ 11- 22. 33. -99.这就9个救梅足必选的. 果个单一的散比如 111-11 只出规11. W 此11必迭•冋理要求闻述 9个C 必选. (2) .比如这个》3737-37-,同时出现R 只出现 37和37. H 就宴求 (3) •同37的例子. 01和10必选其一• 12和21必选齐一• [W] (1)・ 02和20必选其一. 13和31必选齐一• 23和32必选其一. 24和42必选其一. 因为如«级成这个无穷长R 的就艮 09和90必选其•,迭出 19和91必选其一•选出29和92必选其一,选出 89和98必选兀一•如K 我们只逸«个中的小數这样将金选出948+746*5+4+3*2+1-45个・ 是54个・i&lU 1卜・1*© 37和73必須选出…个来•7个.再加上11-99 ii 9个»就-、小务试热点及侖題方曲找觀律問S 在小升初韦试中几F 眼不』必即.位专®的卄恆较低.舉以以空®住岀现,疔刚ffl 誌束的 小卄初逸按月试叽 人人附屮.削帀附屮.I …哮校,西賊宜铠,二虬 遁外-心:戦一L|询血屮馳爭段井 哮寮r 这一类腿取「 二、2020年考点预测 辻 熾吐业划将堪熾Hj 现,a 曜的出剧热必址利用划项黑达成 '即7塚衣示)总姑也亡和陳科申:亨 式的内在规悻和联系,这一襄a 型主婪考俱学主根据已■<「条件逬苻列抽与『1^崽的醴力,龄車同学们拐血练 习・ 三、興处例題解析二1W 1h «*★)卫化小敬帀,小融点盼苦T 価fe 了和为 1购2.求n 为安少? 7 M 料 0 化小ft 后,循环敌字ft 怖为 27, i^tr 1992-27=73- £1. n=e. 7ttv- 2】,(** ■ 皋第了亍ft 与第 r 来派]1993将入卜ft 从&到右III 说 8介敌牛别赴Sb 131, 年小学駝学農丼网克和赛 •和.从第3$蛙圧加i.毎r 股祁恰野警卜它厨血朗^^数上艸 .加那么第1个難是 ____________ B 巻鬻5S I 斛】 甜a 个ft =革6牛fe+第7个e 所LJ.建6个灼-第0卜独■離7亍ft ・13l-£"50 RPE. R 5 1^救"81 SC-31,第 4 伞tt •50-31-19. 3 牛數:31 19-12, B 2 牛数=19- 12 - 7 ,弟 1 个E£= 13- 7=5. t 供3】、***』集ki 能型JJl 24圮 K 辭190止(日J :链10 ;,il.电恥谶忖江+发半丄甌 星期H 休思.无丁疆).已知他打丁一是从1月F 甸的英一天开脚的,这"t 月的 1号恰好是尿期R ,触I :这人打工站 朿的那'尺地2料几U? r 來派】 朝五励-年榕常”和*論les t 解]凶为3X 7<24<4XL (iini 24 R|r 塑削蓟和厘期H 的卜瓶 3或4, Z.归。
2023年新高考数学一轮总复习核心考点分层训练 等差数列及其前n项和带讲解

第35讲 等差数列及其前n 项和学校:___________姓名:___________班级:___________考号:___________【基础巩固】1.(2022·浙江·杭师大附中模拟预测)等差数列{}n a 的前n 项和为n S ,547,29,198n n a a S -===,则n =( ) A .10 B .11 C .12 D .13【答案】B【分析】根据等差数列的通项的性质和前n 项和公式求解. 【详解】因为()()15422n n n n a a n a a S -++==, 又547,29,198n n a a S -===, 所以18198n =, 所以11n =, 故选:B .2.(2022·湖北武汉·模拟预测)设公差不为零的等差数列{}n a 的前n 项和为n S ,452a a =,则74S S =( )A .74B .-1C .1D .54【答案】C【分析】利用等差中项5462a a a =+,6572a a a =+及等差数列前n 项和的性质即可求解. 【详解】解:在等差数列{}n a 中,5462a a a =+,452a a =,故60a =, 又6572a a a =+,故75a a =-, 则745674S S a a a S =+++=,故741S S =. 故选:C.3.(2022·福建·莆田华侨中学模拟预测)2022年4月26日下午,神州十三号载人飞船返回舱在京完成开舱.据科学计算,运载“神十三”的“长征二号”F 遥十三运载火箭,在点火第一秒钟通过的路程为2千米,以后每秒钟通过的路程都增加2千米,在达到离地面380千米的高度时,火箭与飞船分离,则这一过程需要的时间大约是( ) A .10秒 B .13秒 C .15秒 D .19秒【答案】D【分析】根据题意和等差数列的定义可知每秒钟通过的路程构成数列{}n a ,结合等差数列的前n 项求和公式计算即可.【详解】设每秒钟通过的路程构成数列{}n a , 则{}n a 是首项为2,公差为2的等差数列,由求和公式有()221380n n n n n +-=+=,解得19n =. 故选:D.4.(2022·福建省德化第一中学模拟预测)设等差数列{}n a 的前n 项和为n S ,若728S =,则237a a a ++的值为( ) A .8 B .10 C .12 D .14【答案】C【分析】根据等差数列的求和公式,求得44a =,结合等差数列的性质,化简得到27433a a a a =++,即可求解.【详解】因为728S =,由等差数列的性质和求和公式得17747()7282a a S a +===,即44a =, 则112374393(3)312a d a a a a a d =+=+==++. 故选:C.5.(2022·海南海口·二模)设公差不为0的等差数列{}n a 的前n 项和为n S ,已知()9353m S a a a =++,则m =( )A .9B .8C .7D .6【答案】C【分析】根据等差数列的前n 项和的性质及等差数列通项公式化简可得.【详解】因为()9353m S a a a =++,又959S a =,所以()53593m a a a a =++,所以3553m a a a a ++=,即352m a a a +=, 设等差数列{}n a 的公差为d , 则1112(1)2(4)a d a m d a d +++-=+, 所以(+1)8m d d =,又0d ≠, 所以18m +=, 所以7m =. 故选:C.6.(2022·全国·高考真题)图1是中国古代建筑中的举架结构,,,,AA BB CC DD ''''是桁,相邻桁的水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中1111,,,DD CC BB AA 是举,1111,,,OD DC CB BA 是相等的步,相邻桁的举步之比分别为11111231111,0.5,,DD CC BB AAk k k OD DC CB BA ====.已知123,,k k k 成公差为0.1的等差数列,且直线OA 的斜率为0.725,则3k =( )A .0.75B .0.8C .0.85D .0.9【答案】D【分析】设11111OD DC CB BA ====,则可得关于3k 的方程,求出其解后可得正确的选项. 【详解】设11111OD DC CB BA ====,则111213,,CC k BB k AA k ===, 依题意,有31320.2,0.1k k k k -=-=,且111111110.725DD CC BB AA OD DC CB BA +++=+++,所以30.530.30.7254k +-=,故30.9k =,故选:D7.(2022·重庆·二模)等差数列{}n a 的公差为2,前n 项和为n S ,若5m a =,则m S 的最大值为( ) A .3 B .6 C .9 D .12【答案】C【分析】先利用等差数列的通项公式得到首项,再利用等差数列的前n 项和公式和一元二次函数求其最值. 【详解】设等差数列{}n a 的首项为1a , 因为5m a =,且2d =, 所以1+2(1)5a m -=, 解得172a m =-, 则1()(122)=22m m m a a m m S +-= 2(3)99m =--+≤,即3m m S =时取最大值为9. 故选:C.8.(2022·重庆八中模拟预测)已知等差数列{}n a 与等差数列{}n b 的前n 项和分别为n S 和n T ,且1n n S nT n =+,那么87a b 的值为( ) A .1312B .1413C .1514D .1615【答案】C【分析】设等差数列{}n a 、{}n b 的公差分别为1d 、2d ,由题意利用等差数列的性质求出它们的首项、公差之间的关系,可得结论.【详解】设等差数列{}{},n n a b 的公差分别为1d 和2.d11111,12n n S S a n T n T b =∴==+,即1112a b = 2112122223S a d T b d +∴==+,即11232b d d =- ① 311312333334S a d T b d +∴==+,即21143d d b =- ①由①①解得1211,.d d b d ==11811712111771526614d d a a d b b d d d ++∴===++故选:C 9.(2022·广东·华南师大附中三模)已知数列{}n a 满足()213nn n a a ++-=,11a =,22a =,数列{}n a 的前n项和为n S ,则30S =( ) A .351 B .353 C .531 D .533【答案】B【分析】根据题意讨论n 的奇偶,当n 为奇数时,可得23n n a a +-=,按等差数列理解处理,当n 为偶数时,可得23n n a a ++=,按并项求和理解出来,则30S 按奇偶分组求和分别理解处理. 【详解】依题意,()213nn n a a ++-=, 显然,当n 为奇数时有23n n a a +-=,即有313a a -=,533a a -=,…,21213n n a a +--=, 令21n n b a -=,故13n n b b +-=,所以数列{}n b 是首项为1,公差为3的等差数列, 故32n b n =-;当n 为偶数时有23n n a a ++=,即423a a +=,643a a +=,…,2223n n a a ++=, 于是,()()3013292430S a a a a a a =+++++++()()()12152462830b b b a a a a a =+++++++++⎡⎤⎣⎦14315273330233532+=⨯++⨯=+=, 故选:B .10.(多选)(2022·河北沧州·二模)已知数列{}n a 满足()1121,(1)n n n a a a n n ++==--+,记{}n a 的前n 项和为n S ,则( )A .4850100a a += B .50464a a -= C .48600S = D .49601S =【答案】BCD【分析】由条件可得当n 为奇数时,211n n a a a +===;当n 为偶数时,22n n a a n ++=,然后可逐一判断.【详解】因为()1121,(1)n n n a a a n n ++==--+,所以当n 为奇数时,211n n a a a +===;当n 为偶数时,22n n a a n ++=.所以485096a a +=,选项A 错误;又因为464892a a +=,所以50464a a -=,选项B 正确; ()()()481354724684648S a a a a a a a a a a ⎡⎤=+++++++++++⎣⎦()()24612241226462426002+⨯=⨯+⨯+++=+⨯=故C 正确4948496001601S S a =+=+=,选项D 正确.故选:BCD11.(多选)(2022·湖北·华中师大一附中模拟预测)记数列{}n a 是等差数列,下列结论中不恒成立的是( )A .若120a a +>,则230a a +>B .若130a a +<,则20a <C .若12a a <,则2a >D .若10a <,则()()21230a a a a --> 【答案】ACD【分析】根据等差数列通项公式及等差中项,结合基本不等式即可求解. 【详解】设等差数列{}n a 的首项为1a ,公差为d ,则对于A ,由数列{}n a 是等差数列及120a a +>,所以可取123101a a a ===-,,,所以230a a +>不成立,故A 正确;对于B ,由数列{}n a 是等差数列,所以13202a a a +<=,所以20a <恒成立,故B 不正确;对于C, 由数列{}n a 是等差数列,12a a <可取123321a a a =-=-=-,,,所以2a C 正确;对于D ,由数列{}n a 是等差数列,得()()221230a a a a d --=-≤,无论1a 为何值,均有()()21230a a a a --≤所以若10a <,则()()21230a a a a -->恒不成立,故D 正确. 故选:ACD.12.(2022·北京·101中学三模)已知等差数列{}n a 中2341,25a a a =-+=,则20222020a a -=_______. 【答案】4【分析】设出公差,利用等差数列通项公式基本量计算得到方程组,求出公差,求出答案.【详解】设公差为d ,则()11112235a d a d a d +=-⎧⎨+++=⎩,解得:132a d =-⎧⎨=⎩,所以2022202024a a d -==故答案为:413.(2022·山东青岛·二模)将等差数列中的项排成如下数阵,已知该数阵第n 行共有12n -个数,若12a =,且该数阵中第5行第6列的数为42,则n a =___________.a 1 a 2 a 3 a 4 a 5 a 6 a 7 ……【答案】2n【分析】利用等比数列前n 项和公式确定42为数列中的第几项,可以求出公差,从而确定等差数列的通项公式.【详解】解:设公差为d , 因为该数阵第n 行共有12n -个数, 则前4行共有()41121512⨯-=-个数,所以第5行第6列数为2142a =,则2114222211211a a d --===--, 所以2(1)22n a n n =+-⨯=. 故答案为:2n .14.(2022·辽宁·抚顺一中模拟预测)已知等差数列{}n a 的前n 项和为n S ,若12113S a =,则5a =______,9S =______.【答案】 0 0【分析】根据等差数列的求和公式,化简可得12d a =,代入12113S a =即可求出14a d =-,根据等差数列的通项公式和求和公式,即可求出答案.【详解】等差数列{}n a 中,12111112663330S a d a a d =+==+, 所以111266330a d a d +=+, 即14a d =-,所以5140a a d =+=,9590S a == 故答案为:①0;①0.15.(2022·江苏·南京市天印高级中学模拟预测)2022年北京冬奥会开幕式始于24节气倒计时,它将中国人的物候文明、传承久远的诗歌、现代生活的画面和谐统一起来.我国古人将一年分为24个节气,如图所示,相邻两个节气的日晷长变化量相同,冬至日晷长最长,夏至日晷长最短,周而复始.已知冬至日晷长为13.5尺,芒种日晷长为2.5尺,则一年中夏至到立冬的日晷长的和为______尺【答案】60【分析】因为相邻两个节气的日晷长变化量相同,所以每个节气的日晷长构成等差数列,所以夏至到立冬的日晷长的和可以用等差数列求和公式得到.【详解】因为相邻两个节气的日晷长变化量相同,所以每个节气的日晷长构成等差数列, 设冬至日晷长13.5尺为1a ,则芒种日晷长2.5尺为12a ,所以1211121a a d -==--, 所以夏至日晷长为1.5尺,记夏至日晷长1.5尺为1b ,小暑为2b ,大暑为3b ,……,立冬为10b则121010(101)101.51602b b b ⋅-+++=⋅+⋅=. 故答案为:60.16.(2022·重庆八中模拟预测)在等差数列{}n a 中,261028a a a ++=,则数列{}n a 的前13项和为______. 【答案】26【分析】由等差数列的通项公式得12+6a d =,再代入求和公式()13113+6S a d =可求得答案. 【详解】解:设等差数列{}n a 的公差为d ,因为261028a a a ++=,()()()111+++5+2+98d d a a a d ∴=, 12+6a d ∴=,则()131113(131)13+13+6262S a d a d ⨯-===, 故答案为:26.17.(2022·广东·模拟预测)已知{}n a 和{}n b 均为等差数列,若12456,9a b a b ==+=,则78a b +的值是__________. 【答案】6【分析】利用等差数列的性质计算即可得解. 【详解】解:因为{}n a 和{}n b 均为等差数列, 所以1742852,2a a a b b b +=+=, 所以()1728452a a b b a b +++=+, 即781229a b ++=⨯,所以786a b +=. 故答案为:6.18.(2022·江苏泰州·模拟预测)已知等差数列{n a }的前n 项和是n S ,180S >,190S <,则数列{|n a |}中值最小的项为第___项. 【答案】10【分析】根据题意判断等差数列{n a }的90a >,100a <,9100a a >->,由此可判断数列{||}n a 的项的增减情况,进而确定答案.【详解】由题意得:119191019()1902a a S a +===<,①100a <,()1180990S a a =+>,①90a >,9100a a >->,①910a a >,故等差数列{n a }为递减数列,即公差为负数, 因此{||}n a 的前9项依次递减,从第10项开始依次递增, 由于910a a >,①{|n a |}最小的项是第10项, 故答案为:1019.(2022·湖北·大冶市第一中学模拟预测)已知数列{}n a 的前n 项和为n S ,111a =-,29a =-,且()11222n n n S S S n +-+=+≥.(1)求数列{}n a 的通项公式; (2)已知11n n n b a a +=,求数列{}n b 的前n 项和n T . 【解】(1)由题意得:由题意知()()112n n n n S S S S +----=,则()122n n a a n +-=≥又212a a -=,所以{}n a 是公差为2的等差数列,则()11213n a a n d n =+-=-; (2)由题知()()11112132112213211n b n n n n ⎛⎫==- ⎪----⎝⎭则1111111111211997213211211211n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-++-+++-=-- ⎪ ⎪ ⎪ ⎪⎢⎥---⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦12122n n =- 20.(2022·山东·济南市历城第二中学模拟预测)在“①1n n a a +>,31044a a =,4915a a +=;①765S a =,23a =;①2(3)n S n n =+”三个条件中任选一个,补充到下面的横线上,并解答.已知等差数列{}n a 的前n 项和为n S ,且__________. (1)求{}n a 的通项公式; (2)若11n n n b a a +=,求{}n b 的前n 项和为n T ,求证:12n T <. 【解】(1)若选择①,因为1n n a a +>,31044a a =,4915a a +=,31049a a a a +=+, 解得34a =,1011a =,设公差为d ,则有1324a a d +==,101911a a d =+=, 解得12a =,1d =, 所以1n a n =+.若选择①,设公差为d ,74675S a a ==, 即()()117355a d a d +=+,结合213a a d =+=,解得12a =,1d =, 所以1n a n =+.若选择①,当1n =时,112a S ==; 当2n ≥时,1(3)(1)(2)122n n n n n n n a S S n -+-+=-=-=+, 当1n =时亦满足上式, 所以1n a n =+. (2)证明:由(1)得11111(1)(2)12n n n b a a n n n n +===-++++, 所以1111111123341222n T n n n =-+-++-=-+++, 因为102n >+,(*N n ∈),所以111222n -<+,所以12n T <. 【素养提升】1.(2022·浙江省江山中学模拟预测)已知sin ,sin ,sin x y z 依次组成严格递增的等差数列,则下列结论错误..的是( )A .tan ,tan ,tan x y z 依次可组成等差数列B .cos ,cos ,cos x y z 依次可组成等差数列C .cos ,cos ,cos x z y 依次可组成等差数列D .cos ,cos ,cos z x y 依次可组成等差数列【答案】B 【分析】取,0,66x y z ππ=-==,即可判断A ;利用反证法,假设cos ,cos ,cos xy z 依次可组成等差数列,则有2cos coscos y x z =+,2sin sin sin y x z =+,两式相加,整理即可判断B ;取sin 0,sin x y z ===CD.【详解】解:对于A ,当,0,66x y z ππ=-==时,此时11sin ,sin 0,sin 22x y z =-==依次组成严格递增的等差数列,则tan tan 0,tan x y z ===依次组成等差数列,故A 正确; 对于B ,假设cos ,cos ,cos x y z 依次可组成等差数列, 则有2cos cos cos y x z =+, 又因2sin sin sin y x z =+,两式平方相加得()422cos cos sin sin x z x z =++, 则()cos 1x z -=,故2x z k π-=,所以2,Z x k z k π=+∈, 所以()sin sin 2sin x k z z π=+=,与题意矛盾,所以cos ,cos ,cos x y z 依次不可能组成等差数列,故B 错误;对于C ,当sin 0,sin 33x y z =-==11cos ,cos ,cos 133x z y =-==,则cos ,cos ,cos x z y 为等差数列,故C 正确;对于D ,当sin 0,sin 33x y z =-==若11cos ,cos ,cos 133z x y =-==,则cos ,cos ,cos z x y 为等差数列,故D 正确.故选:B.2.(2022·辽宁·渤海大学附属高级中学模拟预测)已知等差数列{}n a 的前n 项和为n S ,且满足()552sin 2350a a +--=,()201820182sin 2370a a +--=,则下列结论正确的是( )A .20222022S =,且52018a a >B .20222022S =-,且52018a a <C .20224044S =-,且52018a a >D .20224044S =,且52018a a <【答案】C【分析】根据题意构造函数()2sin 3f x x x =-,确定函数的奇偶性及单调性,进而根据()()520182,2f a f a ++的关系即可确定答案.【详解】设函数()2sin 3f x x x =-,则()f x 为奇函数,且()2cos 30f x x '=-<,所以()f x 在R 上递减,由已知可得()()552sin 2321a a +-+=-,()()201820182sin 2321a a +-+=,有()521f a +=-,()201821f a +=,所以()()5201822f a f a +<+,且()()5201822f a f a +=-+,所以520185201822a a a a +>+⇒>,且()5201822a a +=-+,所以520184a a +=-, 120222022520182022()1011()40442a a S a a +==+=-.故选:C.3.(多选)(2022·江苏·南京市江宁高级中学模拟预测)已知两个等差数列{}n a 和{}n b ,其公差分别为1d 和2d ,其前n 项和分别为n S 和n T ,则下列说法正确的是( )A .若为等差数列,则112d a =B .若{}n n S T +为等差数列,则120d d +=C .若{}n n a b 为等差数列,则120d d ==D .若*n b N ∈,则{}n b a 也为等差数列,且公差为12d d【答案】ABD【分析】对于A ,利用 对于B ,利用()2211332S T S T S T +=+++化简可得答案;对于C ,利用2211332a b a b a b =+化简可得答案;对于D ,根据112n n b b a a d d +-=可得答案.【详解】对于A ,因为为等差数列,所以即 化简得()21120d a -=,所以112d a =,故A 正确;对于B ,因为{}n n S T +为等差数列,所以()2211332S T S T S T +=+++, 所以()11121111122223333a d b d a b a d b d +++=+++++, 所以120d d +=,故B 正确;对于C ,因为{}n n a b 为等差数列,所以2211332a b a b a b =+, 所以11121111122()()(2)(2)a d b d a b a d b d ++=+++, 化简得120d d =,所以10d =或20d =,故C 不正确;对于D ,因为11(1)n a a n d =+-,且*n b N ∈,所以11(1)n b n a a b d =+-()112111a b n d d =++--⎡⎤⎣⎦,所以()()1111211n b a a b d n d d =+-+-,所以()()()11111211112111n n b b a a a b d nd d a b d n d d +-=+-+-----12d d =,所以{}n b a 也为等差数列,且公差为12d d ,故D 正确. 故选:ABD4.(多选)(2022·福建南平·三模)如图,在平面直角坐标系中的一系列格点(),i i i A x y ,其中1,2,3,,,i n =⋅⋅⋅⋅⋅⋅且,i i x y ∈Z .记n n n a x y =+,如()11,0A 记为11a =,()21,1A -记为20a =,()30,1A -记为31,a =-⋅⋅⋅,以此类推;设数列{}n a 的前n 项和为n S .则( )A .202242a =B .202287S =-C .82n a n =D .()245312n n n n S ++=【答案】ABD【分析】由图观察可知第n 圈的8n 个点对应的这8n 项的和为0,则2440n n S +=,同时第n 圈的最后一个点对应坐标为(),n n ,设2022a 在第k 圈,则k 圈共有()41k k +个数,可判断前22圈共有2024个数,2024a 所在点的坐标为()22,22,向前推导,则可判断A ,B 选项;当2n =时,16a 所在点的坐标为()2,2--,即可判断C 选项;借助2440n n S +=与图可知22222244144245454544n n n n n nn n n n n n S S S a a a++++++++=-=+++,即n 项之和,对应点的坐标为()1,+n n ,()1,1n n +-,…,()1,1n +,即可求解判断D 选项. 【详解】由题,第一圈从点()1,0到点()1,1共8个点,由对称性可知81280S a a a =+++=;第二圈从点()2,1到点()2,2共16个点,由对称性可知248910240S S a a a -=+++=,即 240S =,以此类推,可得第n圈的8n 个点对应的这8n 项的和为0,即()214482n nn n SS ++⨯==,设2022a 在第k 圈,则()()888168412k k k kk ++++==+,由此可知前22圈共有2024个数,故20240S =,则()2022202420242023S S a a =-+,2024a 所在点的坐标为()22,22,则2024222244a =+=,2023a 所在点的坐标为()21,22,则2023212243a =+=,2022a 所在点的坐标为()20,22,则2022202242a =+=,故A 正确;()()20222024202420230444387S S a a =-+=-+=-,故B 正确;8a 所在点的坐标为()1,1,则8112a =+=,16a 所在点的坐标为()2,2--,则16224a =--=-,故C 错误;22222244144245454544n n n n n nn n n n n n S S S aaa++++++++=-=+++,对应点的坐标为()1,+n n ,()1,1n n +-,…,()1,1n +,所以()()()()()245111112122n n S n n n n n n n n +=+++++-++++=+++++()()2123122n n n n n ++++==,故D 正确.故选:ABD5.(2022·湖北·荆门市龙泉中学一模)在数列{}n a 中,11a =,()11nn n a a n ++-=,*N n ∈,则4a =_______;{}n a 的前2022项和为_______.【答案】 3 1023133【分析】求出数列前若干项,根据其特性,分别求和后再可解即可. 【详解】由()11nn n a a n ++-=,得()11nn n a n a +=--,又11a =,所以()21112a a =--=,()232210a a =--=,()343313a a =--=,()454411a a =--=,()565516a a =--=,()676610a a =--=,()787717a a =--=,()898811a a =--=,()91099110a a =--=,()1011101010a a =--=,()11121111111a a =--=,()1213121211a a =--=,()13141313114a a =--=,⋯;因为202250542=⨯+, 所以,明显可见,规律如下: 159132021,,,,,a a a a a ,成各项为1的常数数列,其和为1506506⨯=, 2610142022,,,,,a a a a a ,成首项为2,公差为4的等差数列,其和为25065055062450625120722⨯⨯+⨯=⨯=, 3711152019,,,,,a a a a a ,成各项为0的成常数数列,其和为05050⨯=,4812162020,,,,,a a a a a ,成首项为3,公差为4的等差数列,其和为505504505345105552⨯⨯+⨯=, 故202250651207205105551023133S =+++=. 故答案为:①3;①1023133.6.(2022·湖南·长郡中学模拟预测)已知数列{}n a 的前n 项和2n S n an =+(a 为常数),则20222021a a -=________;设函数()8sin()cos()g x x x x ππ=+-且()()()12918g a g a g a +++=,则5a =__________.【答案】 2;14【分析】根据数列前n 项和与第n 项的关系、等差数列的定义、等差数列的性质,结合辅助角公式、构造函数法,利用导数的性质进行求解即可.【详解】当*2,N n n ≥∈时,221(1)(1)21n n n a S S n an n a n n a -=-=+----=+-,当1n =时,显然成立,因为当*2,N n n ≥∈时,12n n a a --=,数列{}n a 为等差数列,且公差2d =,所以202220212a a -=.又因为111()8sin πcos π8π8π2444g x x x x x x x x ⎛⎫⎛⎫⎛⎫=+-=-=--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.令()8πh t t t =,因为()8π)(8π)()h t t t t t h t -=--=-=-, 所以()h t 为奇函数,因为()8cos π0h t t =+>',所以()h t 在R 上单调递增. 由题意得()()()1292220g a g a g a -+-++-=⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦,因为数列{}n a 是公差不为0的等差数列,其中129a a a <<<,则129111444a a a -<-<<-,假设1911044a a ⎛⎫⎛⎫-+-> ⎪ ⎪⎝⎭⎝⎭,1919191111110444444a a h a h a h a h a ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫->--⇒->--⇒-+-> ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.因为1928374651111111112,444444444a a a a a a a a a ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-=-+-=-+-=-+-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭所以1291110444h a h a h a ⎛⎫⎛⎫⎛⎫-+-++-> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.假设1911044a a ⎛⎫⎛⎫-+-< ⎪ ⎪⎝⎭⎝⎭,同理可得1291110444h a h a h a ⎛⎫⎛⎫⎛⎫-+-++-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,综上,19195111104424a a a a a ⎛⎫⎛⎫-+-=⇒+=⇒= ⎪ ⎪⎝⎭⎝⎭.故答案为:2;14。
2013届高考数学理一轮复习:5.35 简单递推数列课件(人教A版)

一、累加、累乘法求通项 例 1(1)已知数列{an}满足:a1=1,an=an-1+ 3n-1(n≥2,n∈N*),求数列{an}的通项 an; (2)设{an}是首项为 1 的正数数列, 且(n+1)a2 +1 n -na2 +an+1an=0(n=1,2,3,…),求其通项 an. n 【解析】(1)因为 a1=1,an-an-1=3n-1,所以 an=a1+(a2-a1)+(a3-a2)+…+(an- 1-an-2)+(an -an-1) =1+3+32+…+3n-1 1· n-1 3n-1 3 = = . 2 3-1
Sn
1 3 1 由①得 xn+2- xn+1=(xn- xn+1)- xn+1 2 2 2 1 =-2(xn+1- xn) 2 1 1 因此数列{xn+1- xn}是首项为 x2- ,公比为-2 的 2 2 1 1 等比数列,故 xn+1- xn=(x2- )(-2)n-1③ 2 2 5 1 1 由②-③得 xn=(x2+2) n-1-(x2- )(-2)n-1. 2 2 2 1 1 而 a2= 2,∴x2=log2a2= ,所以 xn= n-1 2 2
【点评】若数列递推关系式是相邻两项之差为某 特殊数列(等差、等比数列等),则应用累加法求 通项,若数列递推关系式是相邻两项之比为某特 殊数列,则应用累乘法求通项.
二、转化化归法求通项 例 2 已知 Sn 是数列{an}的前 n 项和,且满足 S2 n 2 2 =3n an+Sn-1,其中 an≠0,n=2,3,4,…,又 a1 =2,求数列{an}的通项公式.
xn+1 xn 1 解法二:由 xn+1=3xn+3 ,得 n+1= n+ , 3 3 3 x1 1 1 xn ∴{ n}是首项为 = ,公差为 的等差数列, 3 3 3 3 1 1 xn 1 ∴ n= +(n-1)·= n. 3 3 3 3 n-1 ∴xn=n· . 3
第3讲 等比数列及其前n项和附带解析

第35讲 等比数列及其前n 项和(讲)思维导图知识梳理1.等比数列的有关概念 (1)定义如果一个数列从第2项起,每一项与它的前一项的比等于同一常数(不为零),那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,通常用字母q 表示,定义的表达式为a n +1a n=q (q ≠0,n ∈N *).(2)等比中项如果a 、G 、b 成等比数列,那么G 叫做a 与b 的等比中项.即:G 是a 与b 的等比中项⇔G 2=ab . “a ,G ,b 成等比数列”是“G 是a 与b 的等比中项”的充分不必要条件. 2.等比数列的有关公式 (1)通项公式:a n =a 1q n -1.(2)前n 项和公式:S n =⎩⎪⎨⎪⎧na 1,q =1,a 1(1-q n )1-q =a 1-a n q 1-q ,q ≠1.3.等比数列的性质已知数列{a n }是等比数列,S n 是其前n 项和(m ,n ,p ,q ,r ,k ∈N *) (1)若m +n =p +q =2r ,则a m ·a n =a p ·a q =a 2r . (2)数列a m ,a m +k ,a m +2k ,a m +3k ,…仍是等比数列.(3)数列S m ,S 2m -S m ,S 3m -S 2m ,…仍是等比数列(此时{a n }的公比q ≠-1). 常用结论1.正确理解等比数列的单调性当q >1,a 1>0或0<q <1,a 1<0时 ,{a n }是递增数列;当q >1,a 1<0或0<q <1,a 1>0时 ,{a n }是递减数列; 当q =1时,{a n }是常数列; 当q =-1时,{a n }是摆动数列. 2.记住等比数列的几个常用结论(1)若{a n },{b n }(项数相同)是等比数列,则{λa n }(λ≠0),⎩⎨⎧⎭⎬⎫1a n ,{a 2n },{a n ·b n },⎩⎨⎧⎭⎬⎫a n bn 仍是等比数列. (2)在等比数列{a n }中,等距离取出若干项也构成一个等比数列,即a n ,a n +k ,a n +2k ,a n +3k ,…为等比数列,公比为q k .(3)一个等比数列各项的k 次幂,仍组成一个等比数列,新公比是原公比的k 次幂.(4){a n }为等比数列,若a 1·a 2·…·a n =T n ,则T n ,T 2n T n ,T 3nT 2n,…成等比数列.(5)当q ≠0,q ≠1时,S n =k -k ·q n (k ≠0)是{a n }成等比数列的充要条件,此时k =a 11-q.(6)有穷等比数列中,与首末两项等距离的两项的积相等.特别地,若项数为奇数时,还等于中间项的平方.题型归纳题型1 等比数列的基本运算【例1-1】(2020春•辽源期末)在等比数列{a n }中,a 1=1,a 10=3,则a 5a 6=( ) A .3B .27C .√3D .243【分析】由题意利用等比数列的性质,求得a 5a 6=的值.【解答】解:等比数列{a n }中,a 1=1,a 10=3,则a 5a 6=a 11•a 10=3, 故选:A .【例1-2】(2020春•赤峰期末)若等比数列{a n }的前n 项和为S n ,且S 3=3,S 6=9,则S 9=( ) A .12B .18C .21D .24【分析】由已知可知S 3,S 6﹣S 3,S 9﹣S 6成等比数列,从而可求. 【解答】解:等比数列{a n }中,S 3=3,S 6=9,由等比数列的性质可知,S 3,S 6﹣S 3,S 9﹣S 6成等比数列, 即3,6,S 9﹣S 6成等比数列,所以36=3(S 9﹣S 6), 则S 9=21 故选:C .【例1-3】(2020•新课标Ⅲ)设等比数列{a n }满足a 1+a 2=4,a 3﹣a 1=8. (1)求{a n }的通项公式;(2)记S n 为数列{log 3a n }的前n 项和.若S m +S m +1═S m +3,求m .【分析】(1)设其公比为q ,则由已知可得{a 1+a 1q =4a 1q 2−a 1=8,解得a 1=1,q =3,可求其通项公式.(2)由(1)可得log 3a n =n ﹣1,是一个以0为首项,1为公差的等差数列,可求S n =n(n−1)2,由已知可得m(m−1)2+(m+1)m2=(m+3)(m+2)2,进而解得m 的值.【解答】解:(1)设公比为q ,则由{a 1+a 1q =4a 1q 2−a 1=8,可得a 1=1,q =3, 所以a n =3n ﹣1.(2)由(1)有log 3a n =n ﹣1,是一个以0为首项,1为公差的等差数列, 所以S n =n(n−1)2, 所以m(m−1)2+(m+1)m2=(m+3)(m+2)2,m 2﹣5m ﹣6=0,解得m =6,或m =﹣1(舍去), 所以m =6.【跟踪训练1-1】(2020春•广州期末)已知数列{a n }的首项为1,数列{b n }为等比数列且b n =a n+1a n,若b 5b 6=2,则a 11=( ) A .16B .21C .31D .32【分析】由题意利用等比数列的性质,求得结果.【解答】解:∵数列{a n }的首项为1,数列{b n }为等比数列且b n =a n+1a n, ∴b 1•b 2•b 3…b 10=a 2a 1•a 3a 2•a 4a 3⋯a 11a 10=a 11a 1=a 11.∵b 5b 6=2,∴b 1•b 2•b 3…b 10=[a 5⋅a 6]5=25, ∴a 11=25=32,【跟踪训练1-2】(2020•新课标Ⅲ)记S n为等比数列{a n}的前n项和.若a5﹣a3=12,a6﹣a4=24,则S na n=()A.2n﹣1B.2﹣21﹣n C.2﹣2n﹣1D.21﹣n﹣1【分析】根据等比数列的通项公式求出首项和公比,再根据求和公式即可求出.【解答】解:设等比数列的公比为q,∵a5﹣a3=12,∴a6﹣a4=q(a5﹣a3),∴q=2,∴a1q4﹣a1q2=12,∴12a1=12,∴a1=1,∴S n=1−2n1−2=2n﹣1,a n=2n﹣1,∴S na n =2n−12n−1=2﹣21﹣n,故选:B.【跟踪训练1-3】(2020•山东)已知公比大于1的等比数列{a n}满足a2+a4=20,a3=8.(1)求{a n}的通项公式;(2)记b m为{a n}在区间(0,m](m∈N*)中的项的个数,求数列{b m}的前100项和S100.【分析】(1)设出等比数列的公比,由已知列式求得公比,进一步求出首项,可得等比数列的通项公式;(2)由题意求得0在数列{b m}中有1项,1在数列{b m}中有2项,2在数列{b m}中有4项,…,可知b63=5,b64=b65=…=b100=6.则数列{b m}的前100项和S100可求.【解答】解:(1)∵a2+a4=20,a3=8,∴8q+8q=20,解得q=2或q=12(舍去),∴a1=2,∴a n=2n,(2)记b m为{a n}在区间(0,m](m∈N*)中的项的个数,∴2n≤m,故b 1=0,b 2=1,b 3=1,b 4=2,b 5=2,b 6=2,b 7=2,b 8=3,b 9=3,b 10=3,b 11=3,b 12=3,b 13=3,b 14=3,b 15=3,b 16=4,…, 可知0在数列{b m }中有1项,1在数列{b m }中有2项,2在数列{b m }中有4项,…, 由1×(1−26)1−2=63<100,1×(1−27)1−2=127>100可知b 63=5,b 64=b 65=…=b 100=6.∴数列{b m }的前100项和S 100=0+1×2+2×4+3×8+4×16+5×32+6×37=480. 【名师指导】等比数列基本量运算的解题策略(1)等比数列基本量的运算是等比数列中的一类基本问题,等比数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)便可迎刃而解.(2)等比数列的前n 项和公式涉及对公比q 的分类讨论,当q =1时,{a n }的前n 项和S n =na 1;当q ≠1时,{a n }的前n 项和S n =a 1(1-q n )1-q =a 1-a n q1-q ..题型2 等比数列的判定与证明【例2-1】(2019春•玉田县期末)已知数列{a n }的前n 项和为S n ,且满足S n =32a n +b (n ∈N *,b ∈R ,b ≠0). ( I )求证:{a n }是等比数列; ( II )求证:{a n +1}不是等比数列.【分析】(Ⅲ)根据数列的递推公式和等比数列的定义即可证明, (Ⅲ)利用反证法证明即可.【解答】证明:( I )因为S n =32a n +b ,所以当n ≥2时S n ﹣1=32a n ﹣1+b , 两式相减得S n ﹣S n ﹣1=32a n +b −32a n ﹣1﹣b , ∴a n =32a n −32a n ﹣1, ∴a n =3a n ﹣1,故{a n }是公比为q =3的等比数列.( II )假设:{a n +1}是等比数列,则有:(a n +1)2=(a n +1+1)(a n ﹣1+1),即:a n 2+2a n +1=a n +1a n ﹣1+a n +1+a n ﹣1+1,由( I )知{a n }是等比数列,所以a n 2=a n +1a n ﹣1, 于是2a n =a n +1+a n ﹣1,即6a n =a n ﹣1+9a n ﹣1,解得a n ﹣1=0, 这与{a n }是等比数列相矛盾,故假设错误,即:{a n +1}不是等比数列.【跟踪训练2-1】(2019•广西二模)已知数列{a n }中,a 1=1,a n +1=2a n +1,(n ∈N *). (1)求证:数列{a n +1}是等比数列; (2)求数列{a n }的前n 项和.【分析】(1)把所给的递推公式两边加上1后,得到a n +1+1=2(a n +1),再变为a n+1+1a n +1=2,由等比数列的定义得证;(2)根据(1)的结论和条件,求出{a n +1}的通项公式,再求出{a n }的通项公式,利用分组求和方法和等比数列的前n 项和公式进行求解. 【解答】解:(1)∵a n +1=2a n +1,(n ∈N *), ∴a n +1+1=2(a n +1), ∴a n+1+1a n +1=2,∴数列{a n +1}是以2为公比的等比数列,(2)由(1)知,数列{a n +1}是等比数列,且q =2,首项为a 1+1=2, ∴a n +1=2•2n ﹣1=2n ,∴a n =2n ﹣1,∴数列{a n }的前n 项和s n =(2+22+ (2))﹣n =2(1−2n)1−2−n =2n +1﹣n ﹣2.【名师指导】等比数列的4种常用判定方法题型3 等比数列的性质及应用【例3-1】(2020春•宣城期末)已知各项均为正数的等比数列{a n }的前n 项和为S n ,a n <a n +1,n ∈N *,a 4•a 14=9,a 8+a 10=10,则数列{a n }的公比为( ) A .12B .13C .2D .3【分析】利用等比数列通项公式列出方程组,能求出公比.【解答】解:各项均为正数的等比数列{a n }的前n 项和为S n ,a n <a n +1,n ∈N *, a 4•a 14=9,a 8+a 10=10, ∴{a 1q 3⋅a 1q 13=9a 1q 7+a 1q 9=10q >1,解得数列{a n }的公比为q =3. 故选:D .【例3-2】(2020春•绵阳期末)若等比数列{a n }的前n 项和为S n ,且S 5=10,S 10=30,则S 20=( ) A .80B .120C .150D .180【分析】由已知结合等比数列的求和公式即可直接求解. 【解答】解:∵等比数列{a n }中S 5=10,S 10=30, ∴q ≠1,{a 1(1−q 5)1−q =10a 1(1−q 10)1−q=30, 解可得,a 11−q=−10,q 5=2,则S 20=a11−q (1−q 20)=−10×(1﹣16)=150.故选:C .【跟踪训练3-1】(2020春•五华区校级期末)已知正项等比数列{a n }中,a 3=a4a 2,若a 1+a 2+a 3=7,则数列的前十项和S 10=( ) A .511B .512C .1023D .1024【分析】利用等比数列的通项公式与求和公式即可得出. 【解答】解:设等比数列{a n }的公比为q , 由a 2•a 3=a 4得a 1q 2=q 2,所以a 1=1,又因为a 1+a 2+a 3=7,得1+q +q 2=7,所以q =2, S 10=1×(1−210)1−2=1023, 故选:C .【跟踪训练3-2】(2020春•广东期末)设等比数列{a n }的前n 项和为S n ,若S 2020S 1010=3,则S 3030S 1010=( )A .9B .7C .5D .4【分析】利用等比数列前n 项和的性质,转化求解即可.【解答】解:等比数列{a n }的前n 项和为S n ,所以S 1010,S 2020﹣S 1010,S 3030﹣S 2020,是等比数列, 由S 2020S 1010=3,不妨设S 2020=3,S 1010=1,则S 2020﹣S 1010=2,S 3030﹣S 2020=4,∴S 3030=1+2+4=7, 则S 3030S 1010=7.故选:B . 【名师指导】1.在解决等比数列的有关问题时,要注意挖掘隐含条件,利用性质,特别是性质“若m +n =p +q ,则a m ·a n =a p ·a q ”,可以减少运算量,提高解题速度.2.在应用相应性质解题时,要注意性质成立的前提条件,有时需要进行适当变形.此外,解题时注意设而不求思想的运用.3.等比数列{a n }中,所有奇数项之和S 奇与所有偶数项之和S 偶具有的性质,设公比为q . (1)若共有2n 项,则S 偶S 奇=q ;(2)若共有2n +1项,S 奇-a 1S 偶=q .4.等比数列{a n }中,S k 表示它的前k 项和.当q ≠-1时,有S k ,S 2k -S k ,S 3k -S 2k ,…也成等比数列,公比为q k .。
第讲数列模型及应用PPT课件

6
学海导航
理数
3.预测人口的变化趋势有多种方法,“直接推算法”
使用的公式是Pn=P0(1+k)n(k>-1),其中Pn为预测人口数, P0为初期人口数,k为预测年内增长率,n为预测期间隔年 数.如果在某一时期有-1<k<0,那么这期间人口数
(B)
A.呈上升趋势
B.呈下降趋势
C.摆动变化
D.不变
7
学海导航
①-②,得
-Sn=2·23+24+25+…+2n+2-(n+1)·2n+3 =16+2411--22n-1-(n+1)·2n+3 =16+2n+3-24-(n+1)·2n+3 =-n·2n+3. 所以 Sn=n·2n+3.
31
学海导航
理数
【拓展演练3】已知函数f(x)=
2x+1 x+2
(x≠-2,x∈R),数
33
学海导航
理数
即 bn+1=3bn(n∈N*). 所以数列{bn}是以 b1=3 为首项,公比为 q=3 的等比数 列, 于是 bn=3×3n-1=3n(n∈N*). 由 bn=aann+ -11(n∈N*),即aann+ -11=3n,解得 an=33nn-+11, 所以所求的通项公式 an=33nn+ -11(n∈N*).
18
学海导航
理数
解析:甲方案是等比数列,乙方案是等差数列, ①甲方案获利:1+(1+30%)+(1+30%)2+…+(1+ 30%)9=1.301.03-1≈42.62(万元), 银行贷款本息:10(1+5%)10≈16.29(万元), 故甲方案纯利:42.62-16.29=26.33(万元), ②乙方案获利:1+(1+0.5)+(1+2×0.5)+…+(1+ 9×0.5)=10×1+102×9×0.5=32.50(万元);
高三数学数列模型及其应用2(新编201908)

• 掌握与等差数列、等比数列 有关的实际应用问题和数列与 其他知识的综合应用问题的解 法。
类型一 与等差数列、等比数 列有关的应用问题
准确地建立数列模型:应紧扣等差数 列和等比数列的定义来建立相应的模型。
; http://ቤተ መጻሕፍቲ ባይዱ/naotanfx 小儿脑瘫分型 脑瘫最新分型 脑瘫分型及表现
;
;
遂内挟异心 字思长 叨恩逾量 梁野之言 自太子左卫率为世祖镇军司马 虏遂填外堑 假宁朔将军 触遇斯发 世连土宇 稽颡耆腊 惟明也 尤宜禁断 西夷校尉 多切治要 高祖东还 会四方平定 诚由暗拙 耋齿甚多 咸不自限 及后为吴郡 前后非一 徙督湘州诸军事 茅室蓬户 明年四月 於时男 丁既尽 遇疾卒 如此积日 边城早开晚闭 焘凿瓜步山为盘道 劝赏威刑 不欲令食器停凶祸之室故也 惊惧放仗归降 吾今日亲览万机 永清无远 屡战辄克 会晋安王子勋反 於岁连属 范晔坐事诛 复为余姚令 曰 时年八十七 八十而终 诞出城走 副司徒建安王於赭圻 千有余口 而宰世之人 所 著赋 但彼和好以来 事毕 震服殊俗 伪车骑从事中郎张绥先遣人於钱唐诣喜归诚 妖党攻破村邑 直指虎牢 二十七日 西阳王子尚抚军参军 蒙逊攻破傉檀 君当门户 贫者不蠲 枝叶不茂 追论前功 享惟永之丕祚 以给供养 实为神皋 为谘议从事中郎 督西讨前锋诸军事 历府参军 吏执以送县 督北秦州诸军事 虏初缘江举烽火 以劝风俗 汉末名士 时大将军彭城王义康秉权 山桑令何道 行汝南新蔡二郡军事陈宪 军少不宜分行 而悫独任气好武 羽直征东将军北平公拔敦及义阳王刘昶 续遣轻兵 列陈距战 泰之独不去 定思贫薄亦不可居 龙骧司马童林之 尚书库部郎 名大宋扬州大 国大吉天子 官至司徒左长史 研复来旨 方今圣务彪被 比边难未静 文德追之至黎仰岭 而贼劭乘藉冢嫡 便望风降散 梁郡太守 从地道中多人力
第35讲 等差数列及其前n项和

第35讲 等差数列及其前n 项和【备选理由】 例1考查了等差数列的通项公式、前n 项和公式等;例2考查了等差数列的证明,考查了逻辑推理与数学运算的核心素养;例3、例4考查了等差数列性质的综合运用. 例1 [配例1使用] (1)记S n 为等差数列{a n }的前n 项和,若a 1≠0,a 2=3a 1,则S 10S 5= 4 .(2)记S n 为等差数列{a n }的前n 项和,若a 1=-2,a 2+a 6=2,则S 10= 25 .(3)将1到2022这2022个整数中,被3除余2且被5除余2的数按从小到大的顺序排成一列,构成数列{a n },则此数列的中间项为 1007 .[解析] (1)设数列{a n }的公差为d ,由题意得a 1+d=3a 1,即d=2a 1,则S 5=5a 1+5×42d=25a 1,S 10=10a 1+10×92d=100a 1,所以S 10S 5=100a 125a 1=4. (2)设等差数列{a n }的公差为d ,则a 2+a 6=a 1+d+a 1+5d=2,∴2a 1+6d=2,又a 1=-2,∴d=1,∴S 10=10a 1+10×92×d=-20+45=25. (3)由题意可知,a n -2既是3的倍数,也是5的倍数,所以a n -2=15(n -1),即a n =15n -13,当n=135时,a 135=15×135-13=2012<2022,当n=136时,a 136=15×136-13=2027>2022,所以数列{a n }共有135项,所以此数列的中间项为a 68=15×68-13=1007.例2 [配例2使用] [2023·江苏连云港调研] 已知数列{a n }的前n 项和为S n ,且S n =a n 2+1a n . (1)证明:数列{S n 2}是等差数列;(2)设数列{b n }的前n 项积为T n ,若T n =S n 2,求数列{b n }的通项公式.解:(1)证明:当n=1时,S 1=a 1=a 12+1a 1,即a 12=2.当n ≥2时,S n =S n -S n -12+1S n -S n -1,即S n +S n -12=1S n -S n -1,所以S n 2-S n -12=2(常数).故数列{S n 2}是以S 12=2为首项,2为公差的等差数列.(2)由(1)知,S n 2=2+2(n -1)=2n ,得T n =2n.当n ≥2时,b n =T n T n -1=2n 2(n -1)=n n -1,当n=1时,b 1=T 1=2,不符合上式,故b n ={2,n =1,n n -1,n ≥2. 例3 [配例3使用] 设等差数列{a n }与等差数列{b n }的前n 项和分别为S n ,T n ,若对任意自然数n 都有S n T n =2n -34n -3,则a 9b 5+b 7+a 3b 8+b 4的值为 ( C )A .37B .78C .1941D .-1[解析] 由题意,得a 9b 5+b 7+a 3b 8+b 4=a 9+a 3b 1+b 11=a 1+a 11b 1+b 11=11(a 1+a 11)211(b 1+b 11)2=S 11T 11=2×11-34×11-3=1941,故选C .例4 [配例4使用] (1)已知等差数列{a n }的前n 项和为S n ,若S k =2,S 2k =8,则S 4k = 32 .(2)已知等差数列{a n }的前n 项和为S n ,若S 7>0,S 8<0,则a 1d 的取值范围是 ( C )A .(-3,+∞)B .(-∞,-72)∪(-3,+∞) C .(-72,-3)D .(-∞,-72) [解析] (1)由等差数列前n 项和的性质,可得S k ,S 2k -S k ,S 3k -S 2k ,S 4k -S 3k 成等差数列,∴2(S 2k -S k )=S k +S 3k -S 2k ,解得S 3k =18,∴ 2,6,10,S 4k -18成等差数列,可得2×10=6+S 4k -18,解得S 4k =32.(2)由题意可得S 7=7(a 1+a 7)2=7a 4>0,则a 4>0,因为S 8=8(a 1+a 8)2=4(a 4+a 5)<0,所以a 4+a 5<0,所以a 5<-a 4<0.设等差数列{a n }的公差为d ,则d=a 5-a 4<0,由题意可得{a 4=a 1+3d >0,a 4+a 5=2a 1+7d <0,可得-72<a 1d <-3,所以a 1d 的取值范围是(-72,-3).故选C .。
高考数学一轮复习 5.5数列模型的应用课件 文 湘教版
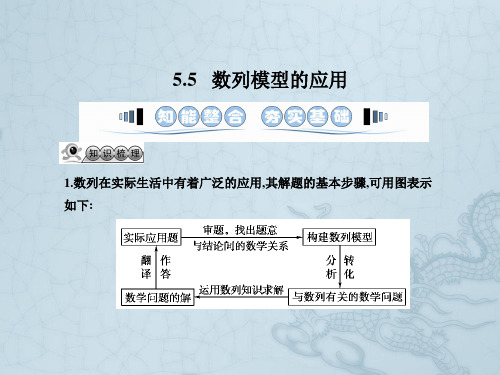
2.气象学院用3.2万元买了一台天文观测仪,已知这台观测仪从启 用的第一天起连续使用,第n天的维修保养费为n+4910元(n∈N*)
,使用它直至报废最合算(所谓报废最合算是指使用的这台仪器的
平均耗资最少)为止,一共使用了( )
A.600天
B.800天ຫໍສະໝຸດ C.1 000天D.1 200天
【解析】由第n天的维修保养费为 n 49 元(n∈N*),
1.一个蜂巢里原有 1 只蜜蜂,第一天它飞出去带回了 2 个伙伴,第二天 3 只蜜蜂飞 出去,各自带回了 2 个伙伴,…,这种带回伙伴的过程继续下去,第五天当所有 的蜜蜂都归巢后,蜂巢里一共有蜜蜂( A.27 只 B.45 只 ) C.72 只 D.81 只
【解析】 依题意,设第 n 天蜂巢中的蜜蜂数为 an,则第 n+1 天的蜜蜂数 an+1 满 足:an+1=an+2an=3an,即数列{an}是首项为 1,公比为 3 的等比数列,故第 5 天的 蜜蜂数为 a5=34=81,选 D. 【答案】 D
36 (2)①平均利润为 f n 40 2 n ≤16,当且仅当n=6时取等号.故 n n 此方案获利-2×62+40×6-72+48=144(万美元),此时n=6.
②f(n)=-2n2+40n-72=-2(n-10)2+128,当n=10时, f(n)max=128.故此方案共获利128+16=144(万美元). 比较两种方案,第①种方案只需6年,第②种方案需要10年, 故选择第①种方案更合算.
10 可知每天的维修保养费构成以 n 49 =5为首项, 10 1 为公差的等差数列. 10
设一共使用了n天,则使用n天的平均耗资为
n 49 5 n 10 3.2 104 4 3 . 2 10 n 99 2 n n 20 20
高三数学数列模型及其应用2

1、选择家具的时候我们要根据自己的财力进行购买,一般来说实木家具的价格最贵,当然一些价格低廉的木材例外,但是这类价格便宜的木材质量很差,建议直接放弃,实木家具必须有质量保证。2、实木家具的好处很多,首先实木家具具有环保的特点,对于家庭来说实木家具可以保证家里的环 另外实木家具对身体好,有一定的养生作用,而且使用起来也比较上档次。3、但是实木家具也有一些缺点,实木家具在北方以北容易出现裂纹的现象,而在南方则比较容易出现发霉的情况,所以实木家具需要随时进行保养,北方要保证家里的湿润度,南方要保持家里相对干燥。4、板木结合的家 较适中,同时板木结合的家具环保性也不错,整体的框架是由实木制作,结构自然比较坚固,而板木为承重面,不容易出现裂纹和发霉的情况,所以板木结合的家具优势也不小。 5、板木结合的家具也有一些缺点,特别是板木结合的家具要看板材的质量,如果板材的质量不好,那么这类家具的优势就几乎为零了,建议大家一般要选择【EO】级别高密度板材,这样环保性和实用性才可以保证。 6、板材家具是比较便宜的家具,但是板材家具也有自己的很大优势,价格方面很便宜,而且板材家具比较容易养护,结实耐用,一般不会出现变形和开裂的情况,板材家具通过率也很高
1、部分折叠:方便使用、节省空间。我们常见的部分折叠家具要数餐桌和沙发床了。看似只够四个人就餐用的桌子,翻起折叠部分或抽出重叠部分就可以供六人、八人甚至更多人使用。 一张普通的三人沙发,把靠背放平就能变成一张舒适的沙发床。这种部分折叠家具适用于各种面积的住家使用,平时还能节省空间,一旦有亲友来访,就能把功能最大化,方便使用。 2、整体折叠:收纳方便、装饰美观。整体折叠家具比较普遍的就是折叠桌和折叠椅。因其具有方便折叠、轻巧便于移动,甚至装饰的作用,对于中小户型的家庭特别适合。 3、多功能折叠:一物多用、其乐无穷。目前,“一物多用”的多功能型折叠家具使用方便,功能设计更人性化,单身公寓和小户型家庭都对其青睐有加。 4、当亲友来访,如你的床从沙发下面抽出来或者从墙上“抠出来”;书柜的柜门能支起来当书桌用……由于设计前卫,此种折叠家具较适合年轻、时尚、现代设计风格的家庭。 折叠家具优点多,但由于其能够抽、拉、翻、叠,所以也容易出现问题。消费者在选购时应首先看家具框架的整体质量,用两手将整件家具前后左右摇一摇、晃一晃;其次,观察细节,注意衔接的地方是否光滑、有无空隙,镀膜是否均匀、柔和,卡口是否牢固,滑槽涩不涩;最后,将家具反复开合几 角度都变换一下,体验舒适度是否良好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第35讲 数列模型及应用1.数列{a n }是公差不为0的等差数列且a 7,a 10,a 15是等比数列{b n }的连续三项,若等比数列{b n }的首项b 1=3,则b 2等于( )A.245 B .5 C .2 D.952.将石子摆成如图的梯形形状,称数列5,9,14,20,…为梯形数,根据图形的构成,此数列的第2014项与5的差即a 2014-5=( )A .2020×2015B .2020×2013C .1010×2015D .1010×2013 3.椭圆x 24+y 23=1上有n 个不同的点P 1,P 2,…,P n ,椭圆的右焦点为F ,数列{|P n F |}是公差不小于1100的等差数列,则n 的最大值为( )A .198B .199C .200D .2014.已知数列{a n }满足:a 1=m (m 为正整数),a n +1=⎩⎪⎨⎪⎧a n 2 (a n 为偶数)3a n +1 (a n 为奇数).若a 6=1,则m 所有可能的取值为( )A .{4,5}B .{4,32}C .{4,5,32}D .{5,32}5.若数列{a n },{b n }的通项公式分别是a n =(-1)n +2014·a ,b n =2+(-1)n +2015n,且a n<b n 对任意n ∈N *恒成立,则常数a 的取值范围是________.6.如下图,对于大于1的自然数m 的n 次幂可用奇数进行如图所示的“分裂”,仿此,(1)记53的“分裂”中的最小数为a ,而52的“分裂”中最大的数是b ,则a +b =______;(2)若m 3的“分裂”中最小的数是211,则m 的值为 .7.将数列{a n }中所有的项按每一行比上一行多一项的规则排成如下数表:a 1 a 2 a 3 a 4 a 5 a 6a 7 a 8 a 9 a 10……记表中的第1列数a 1,a 2,a 4,a 7,…构成的数列为{b n },b 1=a 1=1,S n 为数列{b n }的前n 项和,且满足2b n b n S n -S 2n=1(n ≥2,n ∈N *). (1)证明数列{1S n}是等差数列,并求数列{b n }的通项公式;(2)上表中,若从第3行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当a 81=-491时,求上表中第k (k ≥3)行所有项的和.8.设{a n }是公比为q 的等比数列,|q |>1,令b n =a n +1(n =1,2,…),若数列{b n }有连续四项在集合{-53,-23,19,37,82}中,则6q =______.9.如下图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别为对应数列{a n }的前12项(如下表所示),按如此规律下去,则a 2013+a 2014+a 2015=________.10.已知点B 1(1,y 1),B 2(2,y 2),…,B n (n ,y n ),…(n ∈N *)顺次为直线y =x 4+112上的点,点A 1(x 1,0),A 2(x 2,0),…,A n (x n,0)顺次为x 轴上的点,其中x 1=a (0<a <1).对于任意n ∈N *,点A n 、B n 、A n +1构成以B n 为顶点的等腰三角形.(1)求数列{y n }的通项公式,并证明它为等差数列; (2)求证:x n +2-x n 是常数,并求数列{x n }的通项公式;(3)上述等腰△A n B n A n +1中是否可能存在直角三角形?若可能,求出此时a 的值;若不可能,请说明理由.第35讲 数列模型及应用1.B 解析:设{a n }的公差为d , 则a 7=a 10-3d ,a 15=a 10+5d .又a 7,a 10,a 15是等比数列的连续三项,所以a 210=a 7a 15,即a 210=(a 10-3d )(a 10+5d ),所以a 210=a 210+2da 10-15d 2,所以a 10=152d . 又a 7=a 10-3d =92d .设{b n }的公比为q ,所以q =a 10a 7=152d92d =53,所以b 2=b 1q =3×53=5.2.D 解析:结合图形可知,该数列的第n 项a n =2+3+4+…+n +2,所以a 2014-5=4+5+…+2016=4×2013+2013×20122=2013×1010.3.D 解析:|P 1F |≥a -c =1,|P n F |max =a +c =3,所以1+(n -1)×d ≤3,所以n -1≤2d,因为d ≥1100,所以1d≤100,所以n -1≤200,故n ≤201.4.C 解析:a n +1=⎩⎪⎨⎪⎧a n 2 (a n 为偶数)3a n +1 (a n 为奇数),注意递推的条件是a n(而不是n )为偶数或奇数.由a 6=1一直往前面推导可得a 1=4或5或32.5.[-2,32) 解析:由a n <b n ,得(-1)n·a <2-(-1)n n.若n 为偶数,则a <2-1n对任意正偶数成立,所以a <2-12=32;若n 为奇数,则a >-2-1n对任意正奇数成立,所以a ≥-2.故-2≤a <32.6.30 15 解析:(1)由题意,52=1+3+5+7+9,故b =9; 53=21+23+25+27+29,故a =21,所以a +b =30. (2)由题意,m 3=211+213+215+…,共m 个相邻奇数,由等差数列求和公式得m 3=211m +m (m -1)2×2,整理得m 2-m -210=0,解得m =15,m =-14(舍去).7.解析:(1)由已知,当n ≥2时,2b nb n S n -S 2n=1,又b n =S n -S n -1,所以2(S n -S n -1)(S n -S n -1)S n -S 2n=1,即2(S n -S n -1)-S n -1S n=1,所以1S n -1S n -1=12.又S 1=b 1=a 1=1,所以数列{1S n }是首项为1,公差为12的等差数列.故1S n =1+12(n -1)=n +12,即S n =2n +1. 所以当n ≥2时,b n =S n -S n -1=2n +1-2n =-2n (n +1).因此b n =⎩⎪⎨⎪⎧1 (n =1)-2n (n +1)(n ≥2) (2)设表中从第3行起,每行的公比都为q ,且q >0.因为1+2+…+12=12×132=78,所以表中第1行至第12行含有数列{a n }中的前78项, 故a 81在表中第13行第3列,因此a 81=b 13·q 2=-491.又b 13=-213×14,所以q =2(舍去负值).记表中第k (k ≥3)行所有项的和为S ,则S =b k (1-q k )1-q =-2k (k +1)·1-2k 1-2=2k (k +1)(1-2k )(k ≥3).8.-9 解析:由题意知{a n }有连续四项在集合{-54,-24,18,36,81}中,四项-24,36,-54,81成等比数列,公式为q =-32,所以6q =-9.9.1006 解析:从图表可知,a 1=-1,a 2=1,a 3=1,a 4=2,a 5=-2,a 6=3,a 7=2,a 8=4等,这个数列的规律是奇数项为-1,1,-2,2,-3,3,…,偶数项为1,2,3,….故a 2013+a 2015=-1,a 2014=1007, 所以a 2013+a 2014+a 2015=1006.10.解析:(1)y n =14n +112,y n +1-y n =14,所以数列{y n }是等差数列.(2)由题意得,x n +x n +12=n ,所以x n +x n +1=2n ,①x n +1+x n +2=2(n +1).②由②-①得,x n +2-x n =2(为常数),所以x 1,x 3,x 5,…,x 2n -1,…成等差数列; x 2,x 4,x 6,…,x 2n ,…成等差数列, 所以x 2n -1=x 1+2(n -1)=2n +a -2, x 2n =x 2+(n -1)·2=(2-a )+(n -1)·2=2n -a ,所以x n =⎩⎪⎨⎪⎧n +a -1 (n 为奇数)n -a (n 为偶数).(3)当n 为奇数时,A n (n +a -1,0),A n +1(n +1-a,0), 所以|A n A n +1|=2(1-a );当n 为偶数时,A n (n -a,0),A n +1(n +a,0), 所以|A n A n +1|=2a ,作B n C n ⊥x 轴于C n ,则|B n C n |=14n +112.要使等腰三角形A n B n A n +1为直角三角形,必须且只需|A n A n +1|=2|B n C n |, 当n 为奇数时,12a =11-3n (0<a <1),所以当n =1时,a =23;当n =3时,a =16;当n ≥5时,方程12a =11-3n (0<a <1)无解.当n 为偶数时,12a =3n +1,同理可求得当n =2时,a =712,其他情况无解.综上,当a =23或a =16或a =712时,存在直角三角形.。
