信息论与编码实验程序与结果图(matlab)
信息论与编码实习报告

信息论与编码实习报告指导老师:姓名:班级:学号:实验一绘制二进制熵函数曲线一、内容用Matlab软件制作二进制熵函数曲线。
二、要求1.掌握Matlab绘图函数2.掌握、理解熵函数表达式及其性质三.Matlab程序及实验结果1.matlab程序:p=0.00001:0.001:1;h=-p.*log2(p)-(1-p).*log2(1-p);plot(p,h);title('二进制熵函数曲线');ylabel('H(P,1-P)')2.运行结果:结果分析:从图中可已看出当p=0.5即信源等概时熵取得最大值。
实验二一般信道容量迭代算法一、内容编程实现一般信道容量迭代算法。
伪代码见教材。
二、要求1.掌握一般信道容量迭代算法的原理2.掌握MA TLAB开发环境的使用(尤其是程序调试技巧),或者使用C语言完成程序设计三.Matlab程序及运行结果1.matlab程序:clc;clear all;N = input('输入信源符号X的个数N=');M = input('输入信源符号Y的个数M=');p_yx=zeros(N,M); %程序设计需要信道矩阵初始化为零fprintf('输入信道矩阵概率\n')for i=1:Nfor j=1:Mp_yx(i,j)=input('p_yx='); %输入信道矩阵概率if p_yx(i)<0error('不符合概率分布')endendEndfor i=1:N %各行概率累加求和s(i)=0;for j=1:Ms(i)=s(i)+p_yx(i,j);endendfor i=1:N %判断是否符合概率分布if (s(i)<=0.999999||s(i)>=1.000001)error('不符合概率分布')endendb=input('输入迭代精度:'); %输入迭代精度for i=1:Np(i)=1.0/N; %取初始概率为均匀分布endfor j=1:M %计算Q(j)Q(j)=0;for i=1:NQ(j)=Q(j)+p(i)*p_yx(i,j);endendfor i=1:N %计算F(i) f(i)=0;for j=1:Mif(p_yx(i,j)==0)f(i)=f(i)+0;elsef(i)=f(i)+p_yx(i,j)*log(p_yx(i,j)/Q(j));endendF(i)=exp(f(i));endx=0;for i=1:N %计算x x=x+p(i)*F(i);endIL=log2(x); %计算ILIU=log2(max(F)); %计算IUn=1;while((IU-IL)>=b) %迭代计算for i=1:Np(i)=p(i)*F(i)/x; %重新赋值p(i) endfor j=1:M %计算Q(j) Q(j)=0;for i=1:NQ(j)=Q(j)+p(i)*p_yx(i,j);endendfor i=1:N %计算F(i) f(i)=0;for j=1:Mif(p_yx(i,j)==0)f(i)=f(i)+0;elsef(i)=f(i)+p_yx(i,j)*log(p_yx(i,j)/Q(j));endEndF(i)=exp(f(i));endx=0;for i=1:N %计算xx=x+p(i)*F(i);endIL=log2(x); %计算ILIU=log2(max(F)); %计算IUn=n+1;endfprintf('信道矩阵为:\n');disp(p_yx);fprintf('迭代次数n=%d\n',n);fprintf('信道容量C=%f比特/符号',IL);2.运行结果为:若输入信道矩阵为:0.8500 0.15000.7500 0.2500则运行结果为:实验四线性分组码的信道编码和译码一、内容编程实现线性分组码(6,2)重复码的信道编码和译码。
信息论与编码实验2-实验报告

信息论与编码实验2-实验报告信息论与编码实验 2 实验报告一、实验目的本次信息论与编码实验 2 的主要目的是深入理解和应用信息论与编码的相关知识,通过实际操作和数据分析,进一步掌握信源编码和信道编码的原理及方法,提高对信息传输效率和可靠性的认识。
二、实验原理(一)信源编码信源编码的目的是减少信源输出符号序列中的冗余度,提高符号的平均信息量。
常见的信源编码方法有香农编码、哈夫曼编码等。
香农编码的基本思想是根据符号出现的概率来分配码字长度,概率越大,码字越短。
哈夫曼编码则通过构建一棵最优二叉树,为出现概率较高的符号分配较短的编码,从而实现平均码长的最小化。
(二)信道编码信道编码用于增加信息传输的可靠性,通过在发送的信息中添加冗余信息,使得在接收端能够检测和纠正传输过程中产生的错误。
常见的信道编码有线性分组码,如汉明码等。
三、实验内容与步骤(一)信源编码实验1、选取一组具有不同概率分布的信源符号,例如:A(02)、B (03)、C(01)、D(04)。
2、分别使用香农编码和哈夫曼编码对信源符号进行编码。
3、计算两种编码方法的平均码长,并与信源熵进行比较。
(二)信道编码实验1、选择一种线性分组码,如(7,4)汉明码。
2、生成一组随机的信息位。
3、对信息位进行编码,得到编码后的码字。
4、在码字中引入随机错误。
5、进行错误检测和纠正,并计算错误纠正的成功率。
四、实验结果与分析(一)信源编码结果1、香农编码的码字为:A(010)、B(001)、C(100)、D (000)。
平均码长为 22 比特,信源熵约为 184 比特,平均码长略大于信源熵。
2、哈夫曼编码的码字为:A(10)、B(01)、C(111)、D (00)。
平均码长为 19 比特,更接近信源熵,编码效率更高。
(二)信道编码结果在引入一定数量的错误后,(7,4)汉明码能够成功检测并纠正大部分错误,错误纠正成功率较高,表明其在提高信息传输可靠性方面具有较好的性能。
《信息论》实验指导书—-应用MATLAB软件实现

《信息论》实验指导书—-应用M A T L A B软件实现-CAL-FENGHAI.-(YICAI)-Company One1《信息与编码理论》上机实验指导书———————应用MATLAB软件实现UPC通信工程系前言本实验系列是采用MATLAB软件,主要针对《信息论基础》课程中的相关内容进行的实验。
MATLAB是一完整的并可扩展的计算机环境,是一种进行科学和工程计算的交互式程序语言。
它的基本数据单元是不需要制定维数的矩阵,它可直接用于表达数学的算式和技术概念,解决同样的数值计算问题,使用MATLAB要比使用Basic、Fortran和C语言等提高效率许多倍。
MATLAB还是一种有利的教学工具,在大学的线性代数课程以及其它领域的高一级课程的教学中,已称为标准的教学工具。
该指导书共安排了4个实验,现就一些情况作简要说明:各实验要求学生在MATLAB系统上尽量独立完成,弄懂。
实验内容紧扣课程教学内容的各主要基本概念,希望同学们在完成每个实验后,对所学的内容起到巩固和加深理解的作用。
每个实验做完后必须交一份实验报告。
恳请各位实验老师和同学在实验中提出宝贵意见,以利于以后改进提高。
目录实验一离散信源及其信息测度 (3)实验二离散信道及其容量 (6)实验三无失真信源编码 (8)实验四有噪信道编码 (10)附录部分常用MATLAB命令 (12)实验一 离散信源及其信息测度一、[实验目的]离散无记忆信源是一种最简单且最重要的信源,可以用完备的离散型概率空间来描述。
本实验通过计算给定的信源的熵,加深对信源及其扩展信源的熵的概念的理解。
二、[实验环境]windows XP,MATLAB三、[实验原理]信源输出的各消息的自信息量的数学期望为信源的信息熵,表达式如下 1()[()]()log ()qi i i H X E I xi p x p x ===-∑信源熵是信源的统计平均不确定性的描述,是概率函数()p x 的函数。
信息论编码实验一MATLAB的基本操作

实验一 MATLAB 的基本操作一、实验目的1、掌握Matlab 软件使用的基本方法;2、熟悉Matlab 的数据表示、基本运算方法;3、熟悉Matlab 绘图命令及基本绘图控制。
二、实验仪器与软件1、PC 机 1台2、MATLAB7.0环境三、实验原理MATLAB 环境是一种为数值计算、数据分析和图形显示服务的交互式的环境。
MATLAB 有3种窗口,即:命令窗口(The Command Window )、m-文件编辑窗口(The Edit Window )和图形窗口(The Figure Window ),而Simulink 另外又有Simulink 模型编辑窗口。
1、命令窗口(The Command Window )当MATLAB 启动后,出现的最大的窗口就是命令窗口。
用户可以在提示符“>>”后面输入交互的命令,这些命令就立即被执行。
在MATLAB 中,一连串命令可以放置在一个文件中,不必把它们直接在命令窗口内输入。
在命令窗口中输入该文件名,这一连串命令就被执行了。
因为这样的文件都是以“.m ”为后缀,所以称为m-文件。
2、m-文件编辑窗口(The Edit Window )我们可以用m-文件编辑窗口来产生新的m-文件,或者编辑已经存在的m-文件。
在MATLAB 主界面上选择菜单“File/New/M-file ”就打开了一个新的m-文件编辑窗口;选择菜单“File/Open ”就可以打开一个已经存在的m-文件,并且可以在这个窗口中编辑这个m-文件。
如,计算3[(12)34)]2+⨯-÷,只需在提示符“>>”后输入“((1+2)*3-4)/2^3”,然后按Enter 键。
该命令行涉及加、减、乘、除及幂运算符,MATLAB 运算的执行次序遵循的优先规则为:从左到右执行;幂运算具有最高的优先级,乘法和除法具有相同的次优先级,加法和减法有相同的最低优先级;使用括号可以改变前述优先次序,并由最内层括号向外执行。
信息论与编码实验报告

信息论与编码实验报告实验一:英文文本信息量的计算一、实验目的及要求a)实验目的1。
通过本实验熟悉MATLAB软件编程环境。
2.编写m文件,实现英文文本信息的统计,掌握信息和源熵的计算方法。
B)实验要求1。
了解m文件在MATLAB中的编辑和调试过程。
2.编写程序实现给定英文文本信息的统计。
3.英语本中字母不区分大小写,考虑空格的信息量,但不考虑标点符号的信息量4、建议英文文本采用txt格式二、实验步骤和操作结果记录a)实验步骤1、查找各个英文字母及空格出现的频率2、在matlab中读取给定的英文文章(该文章为txt格式)3、计算英文文章的长度4、统计在该文章中各个字母及空格出现的次数并放入数组n中5、计算各个字母和空格的信息量及整篇文章的信息量6、计算信源熵b)实验结果sumi=3.0516e+003;h=4.0324三、程序流程图(附件1)IV.程序列表和每个句子的注释(附件2)v.实验总结通过这次实验,我熟悉了MATLAB软件编程环境以及一些函数的功能和用法,掌握了信息熵和源熵的计算方法。
一附一:开始读取英文文章计算文章的长度嵌套的for循环语句假判断是否符合循环条件真如果没有其他选项,则确定单词是否大写。
输入相应的频率否elseif要确定它是否为小写,需要计算每个字母、空格和整篇文章的信息量判断是否为小写字母是计算源熵是非常困难的放入数组n中对应的位置放入数组n中对应的位置放入数组n中对应的位置结论附件二:wenzhang=textread('实验一:englishtext.txt','\');m=尺寸(文章);row=m(1,1);直线=m(1,2);n=零(1,27);fori=1:rowforj=1:line%读取英文文章%文章的长度如果double(wenzhang(i,j))>96&&double(wenzhang(i,j))<=122n(1,double(wenzhang(i,j))-96)=n(1,double(wenzhang(i,j))-96)+1;埃尔塞夫double(wenzhang(i,j))>64&&double(wenzhang(i,j))<=90n(1,双(文章(i,j))-64)=n(1,双(文章(i,j))-64)+1;埃尔塞夫double(wenzhang(i,j))==32n(1,27)=n(1,27)+1;endendend%统计各字母和空格出现的个数并存入n数组中。
信息论与编码实验报告

实验一:计算离散信源的熵一、实验设备:1、计算机2、软件:Matlab二、实验目的:1、熟悉离散信源的特点;2、学习仿真离散信源的方法3、学习离散信源平均信息量的计算方法4、熟悉 Matlab 编程;三、实验内容:1、写出计算自信息量的Matlab 程序2、写出计算离散信源平均信息量的Matlab 程序。
3、将程序在计算机上仿真实现,验证程序的正确性并完成习题。
四、求解:1、习题:A 地天气预报构成的信源空间为:()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡6/14/14/13/1x p X 大雨小雨多云晴 B 地信源空间为:17(),88Y p y ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦ 小雨晴 求各种天气的自信息量和此两个信源的熵。
2、程序代码:p1=[1/3,1/4,1/4,1/6];p2=[7/8,1/8];H1=0.0;H2=0.0;I=[];J=[];for i=1:4H1=H1+p1(i)*log2(1/p1(i));I(i)=log2(1/p1(i));enddisp('自信息I分别为:');Idisp('信息熵H1为:');H1for j=1:2H2=H2+p2(j)*log2(1/p2(j));J(j)=log2(1/p2(j));enddisp('自信息J分别为');Jdisp('信息熵H2为:');H23、运行结果:自信息量I分别为:I = 1.5850 2.0000 2.0000 2.5850信源熵H1为:H1 = 1.9591自信息量J分别为:J =0.1926 3.0000信源熵H2为:H2 =0.54364、分析:答案是:I =1.5850 2.0000 2.0000 2.5850 J =0.1926 3.0000H1 =1.9591; H2 =0.5436实验2:信道容量一、实验设备:1、计算机2、软件:Matlab二、实验目的:1、熟悉离散信源的特点;2、学习仿真离散信源的方法3、学习离散信源平均信息量的计算方法4、熟悉 Matlab 编程;三、实验内容:1、写出计算自信息量的Matlab 程序2、写出计算离散信源平均信息量的Matlab 程序。
信息论与编码实验报告
《信息论与编码》实验报告《信息论与编码》实验报告实验序号:02 实验项目名称:离散信道及其信道容量结论:1、当输入和输出符号个数相同,且都等于r 时,则此信道称为强对称信道或均匀信道;2、这类信道中总的错误概率为 p ,对称地平均分配给r-1个输出符号。
实验内容二:平均互信息I (X ;Y )是凸函数的论文一、 问题:由信源的概率分布P (Y )=对x 求和P (X )*P(Y|X)和平均互信息I(X;Y)=对x,y 求和p(x)*P(y|x)*logP(y|x)/P(y)可知,平均互信息只与信源的概率分布和信道的传递概率有关,但是它们之间有种什么关系?二、 证明定理一:平均互信息I(X;Y)是输入信源的概率分布P(x)的形函数(上凸函数)解: 根据上凸函数的定义来证明,先固定信道,即信道的传递概率P(y|x)是固定的。
那么平均互信息I(X;Y)将只是P(x)的函数,简写成I[P(x)]。
现选择输入信源X 的两种已知的概率分布P1(x)和P2(x)。
其对应的联合分布概率为P1(xy)=P1(x)P(y|x)和P2(xy)=P2(x)P(y|x),因而信道输出端的平均互信息分别为I[P1(x)]和I[P2(x)]。
再选择输入变量X 的另一种概率分布P(x),令01θ<<,和1θθ+=,而P(x)= 12()()P x P x θθ+,因而得其相应的平均互信息为I[P(x)]。
根据平均互信息的定义得1212,,,12[()][()][()](|)(|)(|)()log()log ()log ()()()x yx y x y I P x I P x I P x P y x P y x P y x P xy P xy P xy P y P y P y θθθθ+-=+-∑∑∑结论:平均互信息与信源的概率分布有关,有上可知,平均互信息是输入信源的概率分布P(x)的形凸函数。
定理二:平均互信息I(X;Y)是信道传递概率P(Y|X)的形凸函数(又称下凸函数)猜想:由平均互信息是输入信源的概率分布的形凸函数知,当固定某信道时,选择不同的信源(其概率分布不同)与信道连接,在信道输出端接收到每个符号后获得的信息量是不同的。
信息论与编码技术之实验

前两个是别人的,后两个是自己的,学术交流,抛砖引玉。
信息论与编码 实验报告样板实验室名称:S1-306实验一 二维随机变量信息熵的计算 教学实验报告[实验目的]掌握二变量多种信息量的计算方法。
[实验要求]1.熟悉二变量多种信息量的计算方法,设计实验的数据结构和算法;2.编写计算二维随机变量信息量的书面程序代码。
[实验内容]离散二维随机变换熵的计算说明:(1)利用random 函数和归一化方法构造一个二维离散随机变量(X ,Y );(2)分别计算X 与Y 的熵、联合熵、条件熵:H (X )、H (Y )、H (X,Y )H (X|Y )、I (X|Y );(3)对测试通过的程序进行规范和优化;(4)编写本次实验的实验报告。
[实验步骤]实验过程中涉及的各种熵的主要公式(或定义式):1、离散信源熵(平均不确定度/平均信息量/平均自信息量)()()()()log ()i i i i i i H X p x I x p x p x ==-∑∑2、在给定某个y j 条件下,x i 的条件自信息量为I(x i /y j ),X 集合的条件熵H (X/y j )为 ,,(/)(/)(/)Y X H(X/Y)()(/)()(/)(/)()(/)j i j i j ij j j i j i j j i ji j i j i jH X y p x y I x y p y H X y p y p x y I x y p x y I x y ===∑∑∑∑在给定条件下,集合的条件熵为:H(X/Y)=相应地,在给定X (即各个x i )的条件下,Y 集合的条件熵H(Y/X)定义为:,,(/)()(/)()log (/)i j j i i j j i i j i jH Y X p x y I y x p x y p y x ==-∑∑3、联合熵是联合符号集合 XY 上的每个元素对x i y j 的自信息量的概率加权统计平均值,表示X 和Y 同时发生的不确定度。
信息论与编码实验报告

信息论与编码实验报告一、实验目的信息论与编码是一门涉及信息的度量、传输和处理的学科,通过实验,旨在深入理解信息论的基本概念和编码原理,掌握常见的编码方法及其性能评估,提高对信息处理和通信系统的分析与设计能力。
二、实验原理(一)信息论基础信息熵是信息论中用于度量信息量的重要概念。
对于一个离散随机变量 X,其概率分布为 P(X) ={p(x1), p(x2),, p(xn)},则信息熵H(X) 的定义为:H(X) =∑p(xi)log2(p(xi))。
(二)编码原理1、无失真信源编码:通过去除信源中的冗余信息,实现用尽可能少的比特数来表示信源符号,常见的方法有香农编码、哈夫曼编码等。
2、有噪信道编码:为了提高信息在有噪声信道中传输的可靠性,通过添加冗余信息进行纠错编码,如线性分组码、卷积码等。
三、实验内容及步骤(一)信息熵的计算1、生成一个离散信源,例如信源符号集为{A, B, C, D},对应的概率分布为{02, 03, 01, 04}。
2、根据信息熵的定义,使用编程语言计算该信源的信息熵。
(二)香农编码1、按照香农编码的步骤,首先计算信源符号的概率,并根据概率计算每个符号的编码长度。
2、确定编码值,生成香农编码表。
(三)哈夫曼编码1、构建哈夫曼树,根据信源符号的概率确定树的结构。
2、为每个信源符号分配编码,生成哈夫曼编码表。
(四)线性分组码1、选择一种线性分组码,如(7, 4)汉明码。
2、生成编码矩阵,对输入信息进行编码。
3、在接收端进行纠错译码。
四、实验结果与分析(一)信息熵计算结果对于上述生成的离散信源,计算得到的信息熵约为 184 比特/符号。
这表明该信源存在一定的不确定性,需要一定的信息量来准确描述。
(二)香农编码结果香农编码表如下:|信源符号|概率|编码长度|编码值|||||||A|02|232|00||B|03|174|10||C|01|332|110||D|04|132|111|香农编码的平均码长较长,编码效率相对较低。
信息论实验报告(实验三、香农编码)
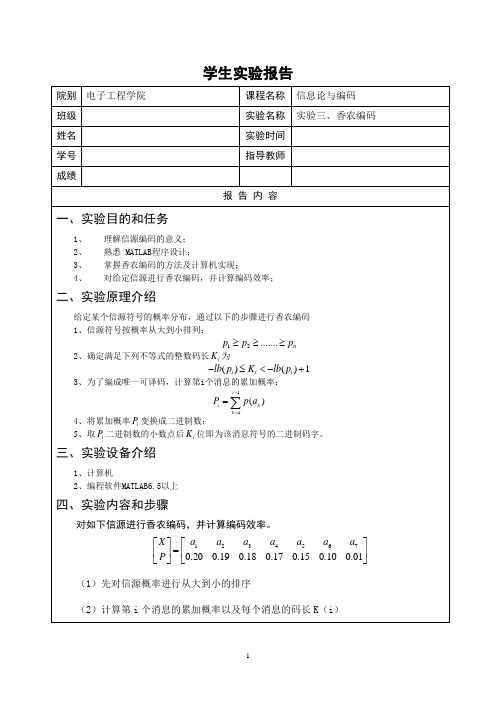
学生实验报告 院别 电子工程学院课程名称 信息论与编码 班级实验名称 实验三、香农编码 姓名实验时间 学号指导教师 成绩报 告 内 容 一、实验目的和任务1、理解信源编码的意义; 2、熟悉 MATLAB 程序设计; 3、掌握香农编码的方法及计算机实现; 4、 对给定信源进行香农编码,并计算编码效率;二、实验原理介绍给定某个信源符号的概率分布,通过以下的步骤进行香农编码1、信源符号按概率从大到小排列;12.......n p p p ≥≥≥2、确定满足下列不等式的整数码长i K 为()()1i i i lb p K lb p -≤<-+3、为了编成唯一可译码,计算第i 个消息的累加概率:4、将累加概率i P 变换成二进制数;5、取i P 二进制数的小数点后i K 位即为该消息符号的二进制码字。
三、实验设备介绍1、计算机2、编程软件MATLAB6.5以上四、实验内容和步骤对如下信源进行香农编码,并计算编码效率。
12345670.200.190.180.170.150.100.01X a a a a a a a P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)先对信源概率进行从大到小的排序(2)计算第i 个消息的累加概率以及每个消息的码长K (i )11()i i k k P p a -==∑(3)调用子函数将累加概率的十进制表示转换成二进制(4)取第i个累加概率二进制的小数点后的K(i)位,即为该消息符号的二进制码字。
五、实验数据记录六、实验结论与心得通过本次实验,加强了对matlab程序的学习,进一步提高了我的编程能力。
信息论与编码实验报告

实验报告课程名称:信息论与编码姓名:系:专业:年级:学号:指导教师:职称:年月日目录实验一信源熵值的计算 (1)实验二 Huffman信源编码 (5)实验三 Shannon编码 (9)实验四信道容量的迭代算法 (12)实验五率失真函数 (15)实验六差错控制方法 (20)实验七汉明编码 (22)实验一 信源熵值的计算一、 实验目的1 进一步熟悉信源熵值的计算 2熟悉 Matlab 编程二、实验原理熵(平均自信息)的计算公式∑∑=--==qi i i qi i i p p p p x H 1212log 1log )(MATLAB 实现:))(log *.(2x x sum HX -=;或者))((log *)(2i x i x h h -= 流程:第一步:打开一个名为“nan311”的TXT 文档,读入一篇英文文章存入一个数组temp ,为了程序准确性将所读内容转存到另一个数组S ,计算该数组中每个字母与空格的出现次数(遇到小写字母都将其转化为大写字母进行计数),每出现一次该字符的计数器+1;第二步:计算信源总大小计算出每个字母和空格出现的概率;最后,通过统计数据和信息熵公式计算出所求信源熵值(本程序中单位为奈特nat )。
程序流程图:三、实验内容1、写出计算自信息量的Matlab 程序2、已知:信源符号为英文字母(不区分大小写)和空格。
输入:一篇英文的信源文档。
输出:给出该信源文档的中各个字母与空格的概率分布,以及该信源的熵。
四、实验环境Microsoft Windows 7Matlab 6.5五、编码程序#include"stdio.h"#include <math.h>#include <string.h>#define N 1000int main(void){char s[N];int i,n=0;float num[27]={0};double result=0,p[27]={0};FILE *f;char *temp=new char[485];f=fopen("nan311.txt","r");while (!feof(f)) {fread(temp,1, 486, f);}fclose(f);s[0]=*temp;for(i=0;i<strlen(temp);i++){s[i]=temp[i];}for(i=0;i<strlen(s);i++){if(s[i]==' ')num[26]++;else if(s[i]>='a'&&s[i]<='z')num[s[i]-97]++;else if(s[i]>='A'&&s[i]<='Z')num[s[i]-65]++;}printf("文档中各个字母出现的频率:\n");for(i=0;i<26;i++){p[i]=num[i]/strlen(s);printf("%3c:%f\t",i+65,p[i]);n++;if(n==3){printf("\n");n=0;}}p[26]=num[26]/strlen(s);printf("空格:%f\t",p[26]);printf("\n");for(i=0;i<27;i++){if (p[i]!=0)result=result+p[i]*log(p[i]);}result=-result;printf("信息熵为:%f",result);printf("\n");return 0;}六、求解结果其中nan311.txt中的文档如下:There is no hate without fear. Hate is crystallized fear, fear’s dividend, fear objectivized. We hate what we fear and so where hate is, fear is lurking. Thus we hate what threatens our person, our vanity andour dreams and plans for ourselves. If we can isolate this element in what we hate we may be able to cease from hating.七、实验总结通过这次实验,我们懂得了不必运行程序时重新输入文档就可以对文档进行统计,既节省了时间而且也规避了一些输入错误。
信息论与编码matlab1

信息论实验报告姓名胡小辉班级电子信息工程0902 学号 **********1.实验目的1、掌握哈夫曼编码、费诺编码、汉明码原理;2、熟练掌握哈夫曼树的生成方法;3、学会利用matlab、C语言等实现Huffman编码、费诺编码以及hamming编码。
2.实验原理Huffman编码:哈夫曼树的定义:假设有n个权值,试构造一颗有n个叶子节点的二叉树,每个叶子带权值为wi,其中树带权路径最小的二叉树成为哈夫曼树或者最优二叉树;实现Huffman编码原理的步骤如下:1. 首先将信源符号集中的符号按概率大小从大到小排列。
2. 用0和1表示概率最小的两个符号。
可用0表示概率小的符号,也可用1表示概率小的符号,但整个编码需保持一致。
3. 将这两个概率最小的符号合并成一个符号,合并符号概率为最小概率之和,将合并后的符号与其余符号组成一个N-1的新信源符号集,称之为缩减符号集。
4. 对缩减符号集用步骤1,2操作5. 以此类推,直到只剩两个符号,将0和1分别赋予它们。
6. 根据以上步骤,得到0,1赋值,画出Huffman码树,并从最后一个合并符号回朔得到Huffmaan编码。
费诺编码:费诺编码的实现步骤:1、将信源消息符号按其出现的概率大小依次排列:。
2、将依次排列的信源符号按概率值分为两大组,使两个组的概率之和近似相同,并对各组赋予一个二进制码元“0”和“1”。
3、将每一大组的信源符号再分为两组,使划分后的两个组的概率之和近似相同,并对各组赋予一个二进制符号“0”和“1”。
4、如此重复,直至每个组只剩下一个信源符号为止。
5、信源符号所对应的码字即为费诺码。
hamming编码:若一致监督矩阵H 的列是由不全为0且互不相同的所有二进制m(m≥2的正整数)重组成,则由此H矩阵得到的线性分组码称为[2m-1,2m-1-m,3]汉明码。
我们通过(7,4)汉明码的例子来说明如何具体构造这种码。
设分组码(n,k)中,k = 4,为能纠正一位误码,要求r≥3。
实验1 Huffman编码生成器-matlab

1.计算机
2.Windows 2000或以上
3.MatLab
四、实验原理
Huffman编码算法
为使平均码长最短,必须使最后一步缩减信源有m个信源符号。如果第一步给概率最小的符号分配码元时,所取的符号数就不一定是m个。
对于m进制编码,若所有码字构成全树,可分离的码字数必为m+k(m-1),式中k为非负整数,即缩减次数。
% L为编码返回的平均码字长度,q为编码效率%
%*****************************************%
function [W,L,q]=huffman(P)
if (length(find(P<=0))~=0)
error('Not a prob.vector,negative component'); %判断是否符合概率分布条件
% H为信息熵%
%******************************%
function H=entropy(P,r)
if (length(find(P<=0))~=0)
error('Not a prob.vector,negative component'); %判断是否符合概率分布条件
end
s2='Huffman编码平均码字长度L:';
s3='Huffman编码的编码效率q:';
disp(s0);
disp(s1),disp(B),disp(W);
disp(s2),disp(L);
disp(s3),disp(q);
%函数说明:%
% H=entropy(P,r)为信息熵函数%
信息论与编码实验报告

信息论与编码实验报告,信息论与编码实验报告,姓名:xxxxx学号: xxxxxxxx专业:电子信息工程班级:电子信息xxxx班指导老师: xx实验一关于信源熵的实验一、实验目的1. 掌握离散信源熵的原理和计算方法。
2. 熟悉matlab 软件的基本操作,练习使用matlab 求解信源的信息熵。
3. 自学图像熵的相关概念,并应用所学知识,使用matlab 或其他开发工具求解图像熵。
4. 掌握Excel的绘图功能,使用Excel绘制散点图、直方图。
二、实验原理1. 离散信源相关的基本概念、原理和计算公式产生离散信息的信源称为离散信源。
离散信源只能产生有限种符号。
随机事件的自信息量I(xi)为其对应的随机变量xi 出现概率对数的负值。
即: I (xi )= -log2p ( xi)随机事件X 的平均不确定度(信源熵)H(X)为离散随机变量 xi 出现概率的数学期望,即:2.二元信源的信息熵设信源符号集X={0,1} ,每个符号发生的概率分别为p(0)= p,p(1)= q,p+ q =1,即信源的概率空间为 :则该二元信源的信源熵为:H( X) = - plogp–qlogq = - plogp –(1 - p)log(1- p) 即:H (p) = - plogp –(1 - p)log(1- p) 其中 0 ? p ?13. MATLAB二维绘图用matlab 中的命令plot( x , y) 就可以自动绘制出二维图来。
例1-2,在matlab 上绘制余弦曲线图,y = cos x ,其中 0 ? x ? 2>>x =0:0.1:2*pi; %生成横坐标向量,使其为 0,0.1,0.2,…,6.2>>y =cos(x ); %计算余弦向量>>plot(x ,y ) %绘制图形4. MATLAB求解离散信源熵求解信息熵过程:1) 输入一个离散信源,并检查该信源是否是完备集。
信息论与编码实验程序与结果图(matlab)
结果图信源熵实验程序:clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);I=-log2(p);plot(p,I,'k');title('I=-log2(p)函数图');xlabel('p');ylabel('I');clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);H=-p.*log2(p)-(1-p).*log2(1-p);plot(p,H,'k');title('H=-p.*log2(p)-(1-p).*log2(1-p)函数图');xlabel('p');ylabel('H');信道容量实验程序:clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);r=4c=log2(r)+(1-p).*log2(1-p)+p.*log2(p/(r-1));plot(p,c,'k');title('强对称信道容量数值模拟图');有噪信道编码--费诺不等式程序:结果图clc;close all;clear;r=3;p0=0.00001;pd=0.99999;N=2000;p=linspace(p0,pd,N);q=1-p;H=-p.*log2(p)-q.*log2(q);hold onHH=H+p.*log2(r-1)title('费诺不等式示意图');box onxlabel('PE');ylabel('H(X/Y)');plot(p,HH,'k:')hold onhold onfill([p,1],[HH,0],[0.6,0.6,0.6])stem((r-1)/r,1.59,'--.r')text(0.66,1.6,'最大值')香农编码程序:clc;clear all;close all;p=[0.2 0.19 0.18 0.17 0.15 0.1 0.01]; if sum(p)<1||sum(p)>1error('输入概率不符合概率分布')end[p index]=sort(p,'descend');n=length(p);pa=zeros(n,1);for ii=2:npa(ii)=pa(ii-1)+p(ii-1);endk=ceil(-log2(p));%码字长度计算c=cell(1,n);%生成元胞数组,用来存不同长度的码字for ii=1:nc{ii}='';tmp=pa(ii);for jj=1:k(ii)tmp=tmp*2;if tmp>=1tmp=tmp-1;%c{ii}{jj}='1';c{ii}=[char(c{ii}),'1']; else%c{ii}{jj}='0';c{ii}=[char(c{ii}),'0']; endendend c(index)=c;%换回原来的顺序codelength=zeros(1,n);%码长初始化for ii=1:nfprintf(['第',num2str(ii),'个消息对应为']);disp(c{ii});%显示码字codelength(ii)=length(c{ii});%endn_average=sum(codelength.*p) %平均码长fprintf('平均码长为');disp(n_average);H=-sum(p.*log2(p));fprintf('信源熵');disp(H);x=H/(n_average.*log2(2))fprintf('编码效率');disp(x);figureh=stem(1:n,codelength);%axis([0 n+1 0 n+1]);set(h,'MarkerFaceColor','blue','linewidth',2)实验结果结果图第1个消息对应为000第2个消息对应为001第3个消息对应为011第4个消息对应为100第5个消息对应为101第6个消息对应为1110第7个消息对应为1111110n_average = 3.1400平均码长为 3.1400信源熵 2.6087x =0.8308编码效率 0.8308费诺编码程序:endfor rr=2:2:needgroupnum*2index2=index_aftergroup(rr,:);for ii=index2(1):index2(2)c{ii}=[char(c{ii}),'1']; endendflag=0;index_p=[];for rr=1:needgroupnum*2indextmp=index_aftergroup(rr,:); if(indextmp(2)-indextmp(1)+1>1) flag=1;index_p=[index_p;indextmp]; endendjj=jj+1;endc(index)=c;codelength=zeros(1,N);for ii=1:Nfprintf(['第',num2str(ii),'个消息对应为']);disp(c{ii});codelength(ii)=length(c{ii}); endn_average=sum(codelength.*p)fprintf('平均码长为');disp(n_average);H=-sum(p.*log2(p));fprintf('信源熵');disp(H);x=H/(n_average.*log2(2))fprintf('编码效率');disp(x); figureh=stem(1:N,codelength);axis([0 N+1 0 N+1]);set(h,'MarkerFaceColor','blue','linewidth',2)endfunction index_aftergroup=func_group(p,index_p)index=index_p(1):index_p(2);n=length(index);p0=p(index);sump0=sum(p0);half_sump0=sump0/2;for ii=1:n-1tmpsum=sum(p0(1:ii));if abs(tmpsum-half_sump0)<=abs(tmpsum-half_sump0+p0(ii+1))index_aftergroup=[index(1) index(ii);index(ii+1) index(n)]; break;endendend实验结果结果图第1个消息对应为00第2个消息对应为010第3个消息对应为011第4个消息对应为10第5个消息对应为110第6个消息对应为1110第7个消息对应为1111n_average = 2.7400平均码长为 2.7400信源熵 2.6087x =0.9521编码效率 0.9521霍夫曼编码程序:clc;clear all;close all; A=[0.4 0.2 0.2 0.1 0.1]; A=sort(A,'descend');T=A;[m,n]=size(A);B=zeros(n,n-1);B(:,1)=T;r=B(n,1)+B(n-1,1);T(n-1)=r; T(n)=0;T=sort(T,'descend');t=n-1;for j=2:n-1B(1:t,j)=T(1:t);K=find(T==r);%B(n,j)=K(end);B(n,j)=K(1);r=(B(t-1,j)+B(t,j));T(t-1)=r;T(t)=0;T=sort(T,'descend');t=t-1;endB;ENDc1=sym('[1,0]');ENDc=ENDc1;t=3;d=1;for j=n-2:-1:1for i=1:t-2if i>1&&B(i,j)==B(i-1,j)d=d+1;elsed=1;endB(B(n,j+1),j+1)=-1;temp=B(:,j+1);x=find(temp==B(i,j));ENDc(i)=ENDc1(x(d));endy=B(n,j+1);ENDc(t-1)=[char(ENDc1(y)),'1']; ENDc(t)=[char(ENDc1(y)),'0'];t=t+1;ENDc1=ENDc;endA%排序后的原概率序列ENDc%编码结果for i=1:n[a,b]=size(char(ENDc(i)));L(i)=b;endavlen=sum(L.*A)%平均码长selen=(L-avlen).^2%?mselen=sum((selen).*A)%码长均方差H=-A*(log2(A'))%?P=H/avlen%?figure;subplot(2,1,1)h=stem(1:n,selen);%axis([0 n+1 0 max(selen)+0.1]);set(h,'MarkerFaceColor','blue','lin ewidth',2)xlabel('信源向上排');ylabel('方差值selen');hold onplot(0:n+1,mselen*ones(1,n+2),'r',' linewidth',2);hold offlegend('每个信源码长与平均码长的方差','码长均方差');A=[0.4 0.2 0.2 0.1 0.1];A=sort(A,'descend');T=A;[m,n]=size(A);B=zeros(n,n-1); B(:,1)=T;r=B(n,1)+B(n-1,1);T(n-1)=r;T(n)=0;T=sort(T,'descend');t=n-1;for j=2:n-1B(1:t,j)=T(1:t);K=find(T==r);B(n,j)=K(end);%B(n,j)=K(1);r=(B(t-1,j)+B(t,j));T(t-1)=r;T(t)=0;T=sort(T,'descend');t=t-1;endB;ENDc1=sym('[1,0]');ENDc=ENDc1;t=3;d=1;for j=n-2:-1:1for i=1:t-2if i>1&&B(i,j)==B(i-1,j)d=d+1;elsed=1;endB(B(n,j+1),j+1)=-1;temp=B(:,j+1);x=find(temp==B(i,j));ENDc(i)=ENDc1(x(d));endy=B(n,j+1);ENDc(t-1)=[char(ENDc1(y)),'1'];ENDc(t)=[char(ENDc1(y)),'0'];t=t+1;ENDc1=ENDc;endA%排序后的原概率序列ENDc%编码结果for i=1:n[a,b]=size(char(ENDc(i)));L(i)=b;endavlen=sum(L.*A)%平均码长selen=(L-avlen).^2%?mselen=sum((selen).*A)%码长均方差H=-A*(log2(A'))%?P=H/avlen%?subplot(2,1,2)h=stem(1:n,selen);%axis([0 n+1 0 max(selen)+0.1]);set(h,'MarkerFaceColor','blue','linewidth',2)xlabel('信源向下排');ylabel('方差值selen');hold onplot(0:n+1,mselen*ones(1,n+2),'r','linewidth',2);hold offlegend('每个码长与平均码长的方差','码长均方差');实验结果A = 0.4000 0.2000 0.20000.1000 0.1000ENDc =[ 11, 1, 0, 101, 100]avlen = 1.8000selen = 0.0400 0.6400 0.64001.4400 1.4400mselen =0.5600H =2.1219P =1.1788A =0.4000 0.2000 0.20000.1000 0.1000ENDc =[ 0, 10, 111, 1101, 1100]avlen =2.2000selen = 1.4400 0.0400 0.64003.2400 3.2400mselen =1.3600H =2.1219P =0.9645结果图。
信息论编码matlab实现

Im=imread('1.png');figure(1);imshow(Im),title('原图');%图像灰度化I=Im(:,:,3);Im=I;figure(2);imshow(Im),title('灰度图');Im=double(Im);[m,n]=size(Im);ImgSize=m*n;ImgLeavel = reshape(Im, 1, prod(size(Im)));i=unique(ImgLeavel);j=ImgLeavel;[Num,Leavel]=hist(j,i); %i是像素点的个数,j是像素值sort(Leavel);Leavel=fliplr(Leavel);for k=1:256p(k) = Num(k)/ImgSize; %求得概率endfigure(3);hist(p,100),title('灰度值统计');for k=1:255 %冒泡法排序得到P从大到小的排列for L=1:256-kif(p(L)<p(L+1))tmp=p(L);p(L)=p(L+1);p(L+1)=tmp;endendendCodeLength=ceil(-log2(p)); %计算码长AddP = zeros(size(p));AddP(1)=0; %计算累加概率for k=2:256AddP(k)=AddP(k-1)+p(k-1);endsheet=cell(5,256);for k=1:256x=dec(AddP(k),CodeLength(k)); %得到码表 sheet(1,k)={[x]};sheet(2,k)={Leavel(k)};sheet(3,k)={AddP(k)};sheet(4,k)={p(k)};sheet(5,k)={Num(k)};endsheet=sheet';global sheet;%编码Img=cell(m,n);for k1=1:mfor k2=1:npixel=Im(k1,k2);Img{k1,k2}=Code(pixel);endend%解码DeImg=zeros(m,n);for k1=1:mfor k2=1:nScode=Img{k1,k2};DeImg(k1,k2)=Decode(Scode);endendfigure(7),imshow(uint8(DeImg)),title('还原后的图像');function pix=Decode(Scode)global sheet;for k=1:256if(isequal(Scode,sheet{k,1}))pix=sheet{k,2};break;endendfunction record=dec(DecNum,length)count=0;tempnum=DecNum;record=zeros(1,length);while(length)count=count+1;%长度小于lengthif(count>length)length=0;endtempnum=tempnum*2;%小数转换为二进制,乘2取整if tempnum>1record(count)=1;tempnum=tempnum-1; elseif(tempnum==1)record(count)=1;length=0;elserecord(count)=0; endendfunction Scode=Code(pix) global sheet;Leavel=zeros(256,1);for k1=1:256Leavel(k1)=sheet{k1,2}; endLocation=find(Leavel==pix); Scode=sheet{Location,1};。
信息论与编码matlab仿真报告

MATLAB对香农编码的实现姓名:学号:院系:电子与信息工程学院摘要:通过对信息论与编码的课程学习使我们对通信系统中的信息编码方式和信息量的计算有了一个较为深入的认识,再结合计算机我们可以方便快捷的实现对各种编码的信息转换,这里我们给出了matlab中对香农编码的实现方式和C 语言代码。
关键词:main,for,printf正文:一在课程中我们清楚地知道了香农编码的方法和具体步骤:1)将信息源符号按照概率从大到小的顺序排列。
2)令p(a0)=0,用p a(aj)(j=i+1)表示第i个码字的累加概率;3)确定ki个码字的长度;4)将用二进制表示,并取小数点后ki位作为符号ai的编码。
二matlab对香农编码的实现代码:#include<stdio.h>#include<math.h>#define N 30main(){int i,j,q,x;int l[N];float t,sum[N],a[N],C[N],D[N];clrscr();printf("please input the xin yuan fu hao zong shu q:");scanf("%d",&q);printf("please input the q ge xin hao gai lv :\n");for(i=0;i<q;i++)scanf("%f",&a[i]);for(i=0;i<q-1;i++)for(j=0;j<q-1;j++){if(a[j]<a[j+1]){ t=a[j];a[j]=a[j+1];a[j+1]=t; }}printf("the new order as follow:\n");for(i=0;i<q;i++)printf("%f\n",a[i]);printf("the sum GaiLv and DuiShu as follows:\n");for(i=0;i<q;i++){sum[i]=0;for(j=0;j<i;j++)sum[i]=sum[i]+a[j];}for(i=0;i<q;i++)printf("%4f\n",sum[i]);for(i=0;i<q;i++){C[i]=-log10(a[i]);D[i]=3.322*C[i]; /* 换2为底数的对数*/printf("%4f\n",D[i]}printf("show us the ma chang l :\n");for(i=0;i<q;i++){ l[i]=ceil(D[i]); /* 取整*/x=ceil(D[i]);printf("%d\n",x);}printf("show us the binary-codes:\n");for(i=0;i<q;i++){ for(j=0;j<l[i];j++){if(2*sum[i]>=1){ printf("1");sum[i]=2*sum[i]-1; }else{ printf("0");sum[i]=2*sum[i]; }}printf("\n");}getch();}总结:通过对香农编码的仿真,我们意识到计算机在通信领域的应用将会大大的增加我们学习的效率和加深对课程的理解,从而更好的掌握所学的知识,更为灵活的应用与生活中的方方面面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结果图信源熵实验程序:clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);I=-log2(p);plot(p,I,'k');title('I=-log2(p)函数图');xlabel('p');ylabel('I');clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);H=-p.*log2(p)-(1-p).*log2(1-p);plot(p,H,'k');title('H=-p.*log2(p)-(1-p).*log2(1-p)函数图');xlabel('p');ylabel('H');信道容量实验程序:clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);r=4c=log2(r)+(1-p).*log2(1-p)+p.*log2(p/(r-1));plot(p,c,'k');title('强对称信道容量数值模拟图');有噪信道编码--费诺不等式程序:结果图clc;close all;clear;r=3;p0=0.00001;pd=0.99999;N=2000;p=linspace(p0,pd,N);q=1-p;H=-p.*log2(p)-q.*log2(q);hold onHH=H+p.*log2(r-1)title('费诺不等式示意图');box onxlabel('PE');ylabel('H(X/Y)');plot(p,HH,'k:')hold onhold onfill([p,1],[HH,0],[0.6,0.6,0.6])stem((r-1)/r,1.59,'--.r')text(0.66,1.6,'最大值')香农编码程序:clc;clear all;close all;p=[0.2 0.19 0.18 0.17 0.15 0.1 0.01]; if sum(p)<1||sum(p)>1error('输入概率不符合概率分布')end[p index]=sort(p,'descend');n=length(p);pa=zeros(n,1);for ii=2:npa(ii)=pa(ii-1)+p(ii-1);endk=ceil(-log2(p));%码字长度计算c=cell(1,n);%生成元胞数组,用来存不同长度的码字for ii=1:nc{ii}='';tmp=pa(ii);for jj=1:k(ii)tmp=tmp*2;if tmp>=1tmp=tmp-1;%c{ii}{jj}='1';c{ii}=[char(c{ii}),'1']; else%c{ii}{jj}='0';c{ii}=[char(c{ii}),'0']; endendend c(index)=c;%换回原来的顺序codelength=zeros(1,n);%码长初始化for ii=1:nfprintf(['第',num2str(ii),'个消息对应为']);disp(c{ii});%显示码字codelength(ii)=length(c{ii});%endn_average=sum(codelength.*p) %平均码长fprintf('平均码长为');disp(n_average);H=-sum(p.*log2(p));fprintf('信源熵');disp(H);x=H/(n_average.*log2(2))fprintf('编码效率');disp(x);figureh=stem(1:n,codelength);%axis([0 n+1 0 n+1]);set(h,'MarkerFaceColor','blue','linewidth',2)实验结果结果图第1个消息对应为000第2个消息对应为001第3个消息对应为011第4个消息对应为100第5个消息对应为101第6个消息对应为1110第7个消息对应为1111110n_average = 3.1400平均码长为 3.1400信源熵 2.6087x =0.8308编码效率 0.8308费诺编码程序:endfor rr=2:2:needgroupnum*2index2=index_aftergroup(rr,:);for ii=index2(1):index2(2)c{ii}=[char(c{ii}),'1']; endendflag=0;index_p=[];for rr=1:needgroupnum*2indextmp=index_aftergroup(rr,:); if(indextmp(2)-indextmp(1)+1>1) flag=1;index_p=[index_p;indextmp]; endendjj=jj+1;endc(index)=c;codelength=zeros(1,N);for ii=1:Nfprintf(['第',num2str(ii),'个消息对应为']);disp(c{ii});codelength(ii)=length(c{ii}); endn_average=sum(codelength.*p)fprintf('平均码长为');disp(n_average);H=-sum(p.*log2(p));fprintf('信源熵');disp(H);x=H/(n_average.*log2(2))fprintf('编码效率');disp(x); figureh=stem(1:N,codelength);axis([0 N+1 0 N+1]);set(h,'MarkerFaceColor','blue','linewidth',2)endfunction index_aftergroup=func_group(p,index_p)index=index_p(1):index_p(2);n=length(index);p0=p(index);sump0=sum(p0);half_sump0=sump0/2;for ii=1:n-1tmpsum=sum(p0(1:ii));if abs(tmpsum-half_sump0)<=abs(tmpsum-half_sump0+p0(ii+1))index_aftergroup=[index(1) index(ii);index(ii+1) index(n)]; break;endendend实验结果结果图第1个消息对应为00第2个消息对应为010第3个消息对应为011第4个消息对应为10第5个消息对应为110第6个消息对应为1110第7个消息对应为1111n_average = 2.7400平均码长为 2.7400信源熵 2.6087x =0.9521编码效率 0.9521霍夫曼编码程序:clc;clear all;close all; A=[0.4 0.2 0.2 0.1 0.1]; A=sort(A,'descend');T=A;[m,n]=size(A);B=zeros(n,n-1);B(:,1)=T;r=B(n,1)+B(n-1,1);T(n-1)=r; T(n)=0;T=sort(T,'descend');t=n-1;for j=2:n-1B(1:t,j)=T(1:t);K=find(T==r);%B(n,j)=K(end);B(n,j)=K(1);r=(B(t-1,j)+B(t,j));T(t-1)=r;T(t)=0;T=sort(T,'descend');t=t-1;endB;ENDc1=sym('[1,0]');ENDc=ENDc1;t=3;d=1;for j=n-2:-1:1for i=1:t-2if i>1&&B(i,j)==B(i-1,j)d=d+1;elsed=1;endB(B(n,j+1),j+1)=-1;temp=B(:,j+1);x=find(temp==B(i,j));ENDc(i)=ENDc1(x(d));endy=B(n,j+1);ENDc(t-1)=[char(ENDc1(y)),'1']; ENDc(t)=[char(ENDc1(y)),'0'];t=t+1;ENDc1=ENDc;endA%排序后的原概率序列ENDc%编码结果for i=1:n[a,b]=size(char(ENDc(i)));L(i)=b;endavlen=sum(L.*A)%平均码长selen=(L-avlen).^2%?mselen=sum((selen).*A)%码长均方差H=-A*(log2(A'))%?P=H/avlen%?figure;subplot(2,1,1)h=stem(1:n,selen);%axis([0 n+1 0 max(selen)+0.1]);set(h,'MarkerFaceColor','blue','lin ewidth',2)xlabel('信源向上排');ylabel('方差值selen');hold onplot(0:n+1,mselen*ones(1,n+2),'r',' linewidth',2);hold offlegend('每个信源码长与平均码长的方差','码长均方差');A=[0.4 0.2 0.2 0.1 0.1];A=sort(A,'descend');T=A;[m,n]=size(A);B=zeros(n,n-1); B(:,1)=T;r=B(n,1)+B(n-1,1);T(n-1)=r;T(n)=0;T=sort(T,'descend');t=n-1;for j=2:n-1B(1:t,j)=T(1:t);K=find(T==r);B(n,j)=K(end);%B(n,j)=K(1);r=(B(t-1,j)+B(t,j));T(t-1)=r;T(t)=0;T=sort(T,'descend');t=t-1;endB;ENDc1=sym('[1,0]');ENDc=ENDc1;t=3;d=1;for j=n-2:-1:1for i=1:t-2if i>1&&B(i,j)==B(i-1,j)d=d+1;elsed=1;endB(B(n,j+1),j+1)=-1;temp=B(:,j+1);x=find(temp==B(i,j));ENDc(i)=ENDc1(x(d));endy=B(n,j+1);ENDc(t-1)=[char(ENDc1(y)),'1'];ENDc(t)=[char(ENDc1(y)),'0'];t=t+1;ENDc1=ENDc;endA%排序后的原概率序列ENDc%编码结果for i=1:n[a,b]=size(char(ENDc(i)));L(i)=b;endavlen=sum(L.*A)%平均码长selen=(L-avlen).^2%?mselen=sum((selen).*A)%码长均方差H=-A*(log2(A'))%?P=H/avlen%?subplot(2,1,2)h=stem(1:n,selen);%axis([0 n+1 0 max(selen)+0.1]);set(h,'MarkerFaceColor','blue','linewidth',2)xlabel('信源向下排');ylabel('方差值selen');hold onplot(0:n+1,mselen*ones(1,n+2),'r','linewidth',2);hold offlegend('每个码长与平均码长的方差','码长均方差');实验结果A = 0.4000 0.2000 0.20000.1000 0.1000ENDc =[ 11, 1, 0, 101, 100]avlen = 1.8000selen = 0.0400 0.6400 0.64001.4400 1.4400mselen =0.5600H =2.1219P =1.1788A =0.4000 0.2000 0.20000.1000 0.1000ENDc =[ 0, 10, 111, 1101, 1100]avlen =2.2000selen = 1.4400 0.0400 0.64003.2400 3.2400mselen =1.3600H =2.1219P =0.9645结果图。
