第一章部分习题解答
离散数学第一章部分课后习题参考答案

第一章部分课后习题参考答案16 设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
(1)p∨(q∧r)0∨(0∧1) 0(2)(p?r)∧(﹁q∨s) (0?1)∧(1∨1) 0∧10.(3)(p∧q∧r)?(p∧q∧﹁r) (1∧1∧1)? (0∧0∧0)0(4)(r∧s)→(p∧q) (0∧1)→(1∧0) 0→0 117.判断下面一段论述是否为真:“是无理数。
并且,如果3是无理数,则也是无理数。
另外6能被2整除,6才能被4整除。
”答:p: 是无理数 1q: 3是无理数0r: 是无理数 1s:6能被2整除 1t: 6能被4整除0命题符号化为:p∧(q→r)∧(t→s)的真值为1,所以这一段的论述为真。
19.用真值表判断下列公式的类型:(4)(p→q) →(q→p)(5)(p∧r) (p∧q)(6)((p→q) ∧(q→r)) →(p→r)答:(4)p q p→q q p q→p (p→q)→(q→p)0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式(5)公式类型为可满足式(方法如上例)(6)公式类型为永真式(方法如上例)第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.(1) (p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答:(2)(p→(p∨q))∨(p→r)(p∨(p∨q))∨(p∨r)p∨p∨q∨r1所以公式类型为永真式(3)P q r p∨q p∧r (p∨q)→(p∧r)0 0 0 0 0 10 0 1 0 0 10 1 0 1 0 00 1 1 1 0 01 0 0 1 0 01 0 1 1 1 11 1 0 1 0 01 1 1 1 1 1所以公式类型为可满足式4.用等值演算法证明下面等值式:(2)(p→q)∧(p→r)(p→(q∧r))(4)(p∧q)∨(p∧q)(p∨q) ∧(p∧q)证明(2)(p→q)∧(p→r)(p∨q)∧(p∨r)p∨(q∧r))p→(q∧r)(4)(p∧q)∨(p∧q)(p∨(p∧q)) ∧(q∨(p∧q)(p∨p)∧(p∨q)∧(q∨p) ∧(q∨q)1∧(p∨q)∧(p∧q)∧1(p∨q)∧(p∧q)5.求下列公式的主析取范式与主合取范式,并求成真赋值(1)(p→q)→(q∨p)(2)(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)解:(1)主析取范式(p→q)→(q p)(p q)(q p)(p q)(q p)(p q)(q p)(q p)(p q)(p q)(p q)(p q)(p q)∑(0,2,3)主合取范式:(p→q)→(q p)(p q)(q p)(p q)(q p)(p(q p))(q(q p))1(p q)(p q) M1∏(1)(2) 主合取范式为:(p→q)q r(p q)q r(p q)q r0所以该式为矛盾式.主合取范式为∏(0,1,2,3,4,5,6,7)矛盾式的主析取范式为 0(3)主合取范式为:(p(q r))→(p q r)(p(q r))→(p q r)(p(q r))(p q r)(p(p q r))((q r))(p q r))1 11所以该式为永真式.永真式的主合取范式为 1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14. 在自然推理系统P中构造下面推理的证明:(2)前提:p q,(q r),r结论:p(4)前提:q p,q s,s t,t r结论:p q证明:(2)①(q r) 前提引入②q r ①置换③q r ②蕴含等值式④r 前提引入⑤q ③④拒取式⑥p q 前提引入⑦¬p(3)⑤⑥拒取式证明(4):①t r 前提引入②t ①化简律③q s 前提引入④s t 前提引入⑤q t ③④等价三段论⑥(q t)(t q) ⑤置换⑦(q t)⑥化简⑧q ②⑥假言推理⑨q p 前提引入⑩p ⑧⑨假言推理(11)p q ⑧⑩合取15在自然推理系统P中用附加前提法证明下面各推理:(1)前提:p(q r),s p,q结论:s r证明①s 附加前提引入②s p 前提引入③p ①②假言推理④p(q r) 前提引入⑤q r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理:(1)前提:p q,r q,r s结论:p证明:①p 结论的否定引入②p﹁q 前提引入③﹁q ①②假言推理④¬r q 前提引入⑤¬r ④化简律⑥r¬s 前提引入⑦r ⑥化简律⑧r﹁r ⑤⑦合取由于最后一步r﹁r 是矛盾式,所以推理正确.第四章部分课后习题参考答案3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值:(1) 对于任意x,均有2=(x+)(x).(2) 存在x,使得x+5=9.其中(a)个体域为自然数集合.(b)个体域为实数集合.解:F(x): 2=(x+)(x).G(x): x+5=9.(1)在两个个体域中都解释为,在(a)中为假命题,在(b)中为真命题。
计算机网络第一章习题解答

第一章概述1-01 计算机网络向用户可以提供那些服务?答:连通性和共享1-02 试简述分组交换的要点。
答:采用存储转发的分组交换技术,实质上是在计算机网络的通信过程中动态分配传输线路或信道带宽的一种策略。
它的工作机理是:首先将待发的数据报文划分成若干个大小有限的短数据块,在每个数据块前面加上一些控制信息(即首部),包括诸如数据收发的目的地址、源地址,数据块的序号等,形成一个个分组,然后各分组在交换网内采用“存储转发” 机制将数据从源端发送到目的端,到达目的端后再按照一定的方式方法进行组装成一个数据块。
分组交换网是由若干节点交换机和连接这些交换机的链路组成,每一结点就是一个小型计算机。
基于分组交换的数据通信是实现计算机与计算机之间或计算机与人之间的通信,其通信过程需要定义严格的协议。
分组交换网的主要优点:1、高效。
在分组传输的过程中动态分配传输带宽。
2、灵活。
每个结点均有智能,可根据情况决定路由和对数据做必要的处理。
3、迅速。
以分组作为传送单位,在每个结点存储转发,网络使用高速链路。
4、可靠。
完善的网络协议;分布式多路由的通信子网。
电路交换相比,分组交换的不足之处是:①每一分组在经过每一交换节点时都会产生一定的传输延时,考虑到节点处理分组的能力和分组排队等候处理的时间,以及每一分组经过的路由可能不等同,使得每一分组的传输延时长短不一。
因此,它不适用于一些实时、连续的应用场合,如电话话音、视频图像等数据的传输;②由于每一分组都额外附加一个头信息,从而降低了携带用户数据的通信容量;③分组交换网中的每一节点需要更多地参与对信息转换的处理,如在发送端需要将长报文划分为若干段分组,在接收端必须按序将每个分组组装起来,恢复出原报文数据等,从而降低了数据传输的效率。
1-03 试从多个方面比较电路交换、报文交换和分组交换的主要优缺点。
(教材11—15)1-04 为什么说因特网是自印刷术以来人类通信方面最大的变革?答:融合其他通信网络,在信息化过程中起核心作用,提供最好的连通性和信息共享,第一次提供了各种媒体形式的实时交互能力。
习题解答(第1章)

习题解答 第一章1.举例说明符合光传播基本定律的生活现象及各定律的应用。
答:(1)光的直线传播定律影子的形成;日蚀;月蚀;均可证明此定律。
应用:许多精密的测量,如大地测量(地形地貌测量),光学测量,天文测量。
(2)光的独立传播定律定律:不同光源发出的光在空间某点相遇时,彼此互不影响,各光束独立传播。
说明:各光束在一点交会,光的强度是各光束强度的简单叠加,离开交会点后,各光束仍按各自原来的方向传播。
2.已知真空中的光速c 3×108m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:v=c/n(1) 光在水中的速度:v=3×108/1.333=2.25×108 m/s (2) 光在冕牌玻璃中的速度:v=3×108/1.51=1.99×108 m/s (3) 光在火石玻璃中的速度:v=3×108/1.65=1.82×108 m/s (4) 光在加拿大树胶中的速度:v=3×108/1.526=1.97×108 m/s (5) 光在金刚石中的速度:v=3×108/2.417=1.24×108 m/s*背景资料:最初用于制造镜头的玻璃,就是普通窗户玻璃或酒瓶上的疙瘩,形状类似“冠”,皇冠玻璃或冕牌玻璃的名称由此而来。
那时候的玻璃极不均匀,多泡沫。
除了冕牌玻璃外还有另一种含铅量较多的燧石玻璃(也称火石玻璃)。
3.一物体经针孔相机在屏上成像的大小为60mm ,若将屏拉远50mm ,则像的大小变为70mm ,求屏到针孔的初始距离。
解:706050=+l l l =300mm4.一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:本题是关于全反射条件的问题。
《电子电路基础》习题解答第1章

第一章习题解答题1.1 电路如题图1.1所示,试判断图中二极管是导通还是截止,并求出AO两端的电压UAO。
设二极管是理想的。
解:分析:二极管在外加正偏电压时是导通,外加反偏电压时截止。
正偏时硅管的导通压降为0.6~0.8V 。
锗管的导通压降为0.2~0.3V 。
理想情况分析时正向导通压降为零,相当于短路;反偏时由于反向电流很小,理想情况下认为截止电阻无穷大,相当于开路。
分析二极管在电路中的工作状态的基本方法为“开路法”,即:先假设二极管所在支路断开,然后计算二极管的阳极(P 端)与阴极(N 端)的电位差。
若该电位差大于二极管的导通压降,该二极管处于正偏而导通,其二端的电压为二极管的导通压降;如果该电位差小于导通压降,该二极管处于反偏而截止。
如果电路中存在两个以上的二极管,由于每个二极管的开路时的电位差不等,以正向电压较大者优先导通,其二端电压为二极管导通压降,然后再用上述“开路法”法判断其余二极管的工作状态。
一般情况下,对于电路中有多个二极管的工作状态判断为:对于阴极(N 端)连在一起的电路,只有阳极(P 端)电位最高的处于导通状态;对于阳极(P 端)连在一起的二极管,只有阴极(N 端)电位最低的可能导通。
图(a )中,当假设二极管的VD 开路时,其阳极(P 端)电位P U 为-6V ,阴极(N 端)电位N U 为-12V 。
VD 处于正偏而导通,实际压降为二极管的导通压降。
理想情况为零,相当于短路。
所以V U AO 6-=;图(b )中,断开VD 时,阳极电位V U P 15-=,阴极的电位V U N 12-=, ∵ N PUU < ∴ VD 处于反偏而截止∴ VU AO 12-=; 图(c ),断开VD1,VD2时∵ V U P 01= V U N 121-= 11N P U U > V U P 152-= V U N 122-= 22N P U U<∴ VD1处于正偏导通,VD2处于反偏而截止V U AO 0=;或,∵ VD1,VD2的阴极连在一起∴ 阳极电位高的VD1就先导通,则A 点的电位V U AO 0=,而 A N P U UV U =<-=2215∴ VD2处于反偏而截止 图(d ),断开VD1、VD2,∵ V U P 121-= V U N 01= 11N P U U < V U P 122-= VU N 62-= 22N P U U <;∴ VD1、VD2均处于反偏而截止。
第一章 题解答 物理化学

第一章习题解答1.1 物质的体膨胀系数αV与等温压缩率κT的定义如下:试导出理想气体的、与压力、温度的关系解:对于理想气体:PV=nRT , V= nRT/P求偏导:1.2 气柜储存有121.6kPa,27℃的氯乙烯(C2H3Cl)气体300m3,若以每小时90kg的流量输往使用车间,试问储存的气体能用多少小时?解:将氯乙烯(M w=62.5g/mol)看成理想气体:PV=nRT , n= PV/RT n=121600⨯300/8.314⨯300.13 (mol)=14618.6molm=14618.6⨯62.5/1000(kg)=913.66 kgt=972.138/90(hr)=10.15hr1.3 0℃,101.325kPa的条件常称为气体的标准状况,试求甲烷在标准状况下的密度?解:将甲烷(M w=16g/mol)看成理想气体:PV=nRT , PV =mRT/ M w甲烷在标准状况下的密度为=m/V= PM w/RT=101.325⨯16/8.314⨯273.15(kg/m3)=0.714 kg/m31.4 一抽成真空的球形容器,质量为25.0000g。
充以4℃水之后,总质量为125.0000g。
若改充以25℃,13.33kPa的某碳氢化合物气体,则总质量为25.0163g。
试估算该气体的摩尔质量。
水的密度按1 g.cm-3计算。
(答案来源:)解:球形容器的体积为V=(125-25)g/1 g.cm-3=100 cm3将某碳氢化合物看成理想气体:PV=nRT , PV =mRT/ M wM w= mRT/ PV=(25.0163-25.0000)⨯8.314⨯300.15/(13330⨯100⨯10-6) M w =30.51(g/mol)1.5 两个容器均为V的玻璃球之间用细管连接,泡内密封着标准状况下的空气。
若将其中一个球加热到100℃,另一个球则维持0℃,忽略连接细管中的气体体积,试求该容器内空气的压力。
电路理论习题解答 第一章

1.5
u /V
内阻不为零
+ us
R0
I
+
u
RL
−
伏安关系曲线
−
I/A 0.15
0
1.5
u /V
注:这里的伏安关系曲线只能在第一象限,原因也是,一旦出了第一象限, u 和 I 的比值就 变为负的了,反推出的 RL 就变为负值了,与题意不符。
V
V
1.5V
1.5V
R 内阻为零时 内阻不为零时
R
1-9 附图是两种受控源和电阻 RL 组成的电路。现以 RL 上电压作为输出信号,1)求两电路的电 压增益(A,gmRL);2)试以受控源的性质,扼要地说明计算得到的结果。
1) 如果不用并联分压(在中学就掌握的东西),当然也可以用两个回路的 KVL 方程和顶部 节点的 KCL 方程,得出上面的 H(jω)的表达式,但是显然这样做是低效的。 2) 事实上,本课程的目的是希望学习者能够根据不同的题目,尽可能采用多种方法中的一 种最简单的方法去解决问题。因此, a) 只要没有要求,任意的逻辑完整的解题思路都是可取的; b) 学习者可以视自己的练习目的选择一种简单熟悉的方法、或者一种较为系统的方法、 或者多种方法来完成习题。
第一章习题答案 1-1 已知电路中某节点如图,I1=-1A,I2=4A,I4=-5A,I5=6A,用 KCL 定律建立方程并求解 I3 ( 4A )
图 1-1 解:由 KCL 定律:任一集中参数电路中的任一节点,在任一时刻,流入该节点的电流之和与 流出该节点的电流之和相同。 即: I1+I3+I4+I5=I2 =〉-1+(-5)+6+I3=4 =〉I3=4(A)
1 2
大学物理习题答案第一章

大学物理习题答案第一章-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN[习题解答]1-3 如题1-3图所示,汽车从A地出发,向北行驶60km到达B地,然后向东行驶60km到达C地,最后向东北行驶50km到达D地。
求汽车行驶的总路程和总位移。
解汽车行驶的总路程为;汽车的总位移的大小为∆r =位移的方向沿东北方向,与方向一致。
1-4 现有一矢量R是时间t的函数,问与在一般情况下是否相等为什么解与在一般情况下是不相等的。
因为前者是对矢量R的绝对值(大小或长度)求导,表示矢量R的大小随时间的变化率;而后者是对矢量R的大小和方向两者同时求导,再取绝对值,表示矢量R大小随时间的变化和矢量R方向随时间的变化两部分的绝对值。
如果矢量R方向不变只是大小变化,那么这两个表示式是相等的。
1-5 一质点沿直线L运动,其位置与时间的关系为r = 6t 2 -2t 3 ,r和t的单位分别是m和s。
求:(1)第二秒内的平均速度;(2)第三秒末和第四秒末的速度;(3)第三秒末和第四秒末的加速度。
解取直线L的正方向为x轴,以下所求得的速度和加速度,若为正值,表示该速度或加速度沿x轴的正方向,若为负值表示,该速度或加速度沿x轴的反方向。
(1)第二秒内的平均速度m⋅s-1;(2)第三秒末的速度因为,将t = 3 s 代入,就求得第三秒末的速度,为v3 = - 18 m⋅s-1;用同样的方法可以求得第四秒末的速度,为v4 = - 48 m⋅s-1;(3)第三秒末的加速度因为,将t = 3 s 代入,就求得第三秒末的加速度,为a3 = - 24 m⋅s-2;用同样的方法可以求得第四秒末的加速度,为v4 = - 36 m⋅s-2 .1-6 一质点作直线运动,速度和加速度的大小分别为和,试证明:(1) v d v = a d s;(2)当a为常量时,式v 2 = v02 + 2a (s-s0 )成立。
解(1);(2)对上式积分,等号左边为,等号右边为,于是得,即.1-7 质点沿直线运动,在经过时间t后它离该直线上某定点O的距离s满足关系式:s = (t-1)2 (t-2),s和t的单位分别是m和s。
电工部分习题解答(1,2,3)

第一章 习题解答1-1 在图1-39所示的电路中,若I 1=4A ,I 2=5A ,请计算I 3、U 2的值;若I 1=4A ,I 2=3A ,请计算I 3、U 2、U 1的值,判断哪些元件是电源?哪些是负载?并验证功率是否平衡。
解:对节点a 应用KCL 得 I 1+ I 3= I 2 即4+ I 3=5, 所以 I 3=1A 在右边的回路中,应用KVL 得6⨯I 2+20⨯I 3= U 2,所以U 2=50V 同理,若I 1=4A ,I 2=3A ,利用KCL 和KVL 得I 3= -1A ,U 2= -2V 在左边的回路中,应用KVL 得20⨯I 1+6⨯I 2= U 1,所以U 1=98V 。
U 1,U 2都是电源。
电源发出的功率:P 发=- U 1 I 1- U 2 I 3=-98⨯4-2=-394W 负载吸收的功率:P 吸=2021I +622I +2023I =394W 二者相等,整个电路功率平衡。
1-2 有一直流电压源,其额定功率P N =200W ,额定电压U N =50V ,内阻R o =0.5Ω,负载电阻R L 可以调节,其电路如图1-40所示。
试求:⑴额定工作状态下的电流及负载电阻R L 的大小;⑵开路状态下的电源端电压;⑶电源短路状态下的电流。
解:⑴A U P I N N N 450200===Ω===5.12450N N L I U R ⑵ =⨯+==0R I U U U N N S OC 50+4⨯0.5 = 52V ⑶ A R U I S SC 1045.0520===图1-39 习题1-1图 图1-40 习题1-2图1-9 求图1-44所示电路中电阻的电流及其两端的电压,并求图1-44a 中电压源的电流及图1-44 b 中电流源的电压,判断两图中的电压源和电流源分别起电源作用还是负载作用。
解:图1-44a 中,A I R 2=,V U R 2=,电压源的电流A I 2=。
电路基础第1章习题解答
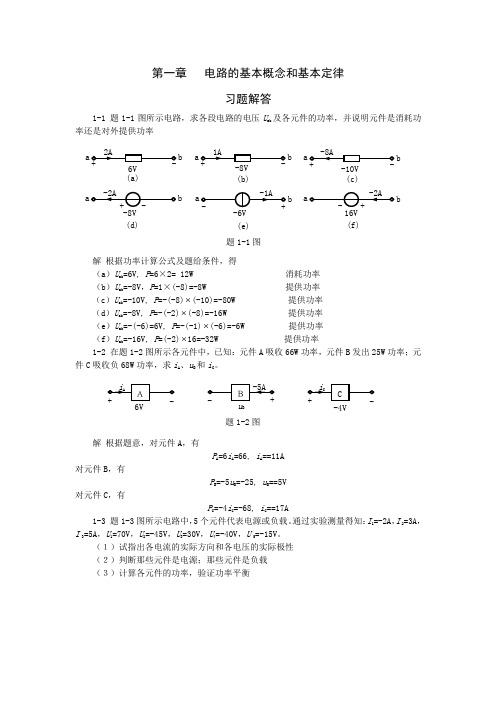
第一章 电路的基本概念和基本定律习题解答1-1 题1-1图所示电路,求各段电路的电压U ab 及各元件的功率,并说明元件是消耗功率还是对外提供功率解 根据功率计算公式及题给条件,得(a )U ab =6V, P =6×2= 12W 消耗功率(b )U ab =-8V ,P =1×(-8)=-8W 提供功率(c )U ab =-10V, P =-(-8)⨯(-10)=-80W 提供功率(d )U ab =-8V, P =-(-2)⨯(-8)=-16W 提供功率(e )U ab =-(-6)=6V, P =-(-1)⨯(-6)=-6W提供功率(f )U ab =-16V, P =(-2)⨯16=-32W 提供功率1-2 在题1-2图所示各元件中,已知:元件A吸收66W 功率,元件B 发出25W 功率;元件C 吸收负68W 功率,求i A 、u B 和i C 。
解 根据题意,对元件A ,有P A =6i A =66, i A ==11A对元件B ,有P B =-5u B =-25, u B ==5V对元件C ,有P C =-4i C =-68, i C ==17A1-3 题1-3图所示电路中,5个元件代表电源或负载。
通过实验测量得知:I 1=-2A ,I 2=3A ,I 3=5A ,U 1=70V ,U 2=-45V ,U 3=30V ,U 4=-40V ,U 5=-15V 。
(1)试指出各电流的实际方向和各电压的实际极性(2)判断那些元件是电源;那些元件是负载(3)计算各元件的功率,验证功率平衡(a) (b) (d) (e)(f) a 6V b a -8V b a -10V b (c) a -8V b a 16V b a -6V b 题1-1图 题1-2图 6V B -4V题1-3图U解(1)图中虚线箭头为各支路电流的实际方向。
、(2)按实际方向判断元件的状态:U 、I 关联者为负载,U 、I 非关联者为电源。
物理初二第一章练习题答案

物理初二第一章练习题答案1. 速度和加速度的关系根据物理学的基本概念,速度是物体运动的一个重要参量,而加速度则表示物体速度变化的快慢。
在初二的物理学习中,我们常常需要研究速度和加速度之间的关系。
以下是第一章练习题的答案:题目1:一个从静止开始的物体以恒定的加速度3 m/s²沿着一条直线运动,求它在5秒后的速度是多少?答案:根据物理学中的加速度公式v = u + at,其中v是末速度,u是初速度,a是加速度,t是时间。
给定初速度u=0,加速度a=3 m/s²,时间t=5秒。
代入公式计算可得v = 0 + 3 × 5 = 15 m/s。
题目2:一辆汽车在道路上以25 m/s的速度匀速行驶,经过10秒后它的位置是多少?答案:根据物理学中的位移公式s = ut,其中s是位移,u是速度,t 是时间。
给定速度u=25 m/s,时间t=10秒。
代入公式计算可得s = 25 ×10 = 250 m。
题目3:一个物体的速度从10 m/s增加到20 m/s,经过2秒的时间,求它的加速度是多少?答案:根据物理学中的加速度公式a = (v - u) / t,其中a是加速度,v是末速度,u是初速度,t是时间。
给定初速度u=10 m/s,末速度v=20 m/s,时间t=2秒。
代入公式计算可得a = (20 - 10) / 2 = 5 m/s²。
2. 动量守恒定律在物理学中,动量守恒定律是一个重要的原理,它指出在一个系统内,所有物体的总动量在没有外力作用的情况下保持不变。
以下是第一章练习题中涉及到动量守恒定律的答案:题目1:一辆质量为1000 kg的小轿车以20 m/s的速度向东行驶,和一辆质量为1500 kg的卡车以15 m/s的速度向东行驶发生碰撞,碰撞后两车结合在一起,求结合后的速度是多少?答案:根据动量守恒定律,碰撞前的总动量等于碰撞后的总动量。
小轿车的动量为mv1,卡车的动量为mv2,碰撞后的总动量为(m1 +m2)v。
01流体流动习题答案

第一章 流体流动习题解答1. 某设备上真空表的读数为×103 Pa ,试计算设备内的绝对压强与表压强。
已知该地区大气压强为×103 Pa 。
解:真空度=大气压-绝压3(98.713.3)10atm p p p Pa =-=-⨯绝压真空度表压=-真空度=310Pa ⨯2. 在本题附图所示的贮油罐中盛有密度为960 kg/m 3的油品,油面高于罐底9.6 m ,油面上方为常压。
在罐侧壁的下部有一直径为760 mm 的圆孔,其中心距罐底800 mm ,孔盖用14 mm 的钢制螺钉紧固。
若螺钉材料的工作应力取为×106 Pa ,问至少需要几个螺钉解:设通过圆孔中心的水平液面生的静压强为p ,则p 罐内液体作用于孔盖上的平均压强9609.81(9.60.8)82874p g z Pa ρ=∆=⨯⨯-=(表压)作用在孔盖外侧的是大气压a p ,故孔盖内外所受的压强差为82874p Pa ∆= 作用在孔盖上的净压力为2282575(0.76) 3.7644p p d N ππ=∆=⨯⨯=⨯410 每个螺钉能承受的最大力为:62332.23100.014 4.96104F N π=⨯⨯⨯=⨯钉p螺钉的个数为433.7610/4.96107.58⨯⨯=个所需的螺钉数量最少为8个3. 某流化床反应器上装有两个U 管压差计,如本题附图所示。
测得R 1=400 mm ,R 2=50 mm ,指示液为水银。
为防止水银蒸气向空间扩散,于右侧的U 管与大气连通的玻璃管内灌入一段水,其高度R 3=50mm 。
试求A 、B 两处的表压强。
解:U 管压差计连接管中是气体。
若以2,,g H O Hg ρρρ分别表示气体、水与水银的密度,因为g Hg ρρ=,故由气柱高度所产生的压强差可以忽略。
由此可以认为A C p p ≈,B D p p ≈。
由静力学基本方程式知232A C H O Hg p p gR gR ρρ≈=+ 10009.810.05136009.810.05=⨯⨯+⨯⨯7161Pa =(表压)417161136009.810.4 6.0510B D A Hg p p p gR Pa ρ≈=+=+⨯⨯=⨯4. 本题附图为远距离制量控制装置,用以测定分相槽内煤油和水的两相界面位置。
高等代数北大编 第1章习题参考答案

第一章 多项式一 、习题及参考解答1. 用)(x g 除)(x f ,求商)(x q 与余式)(x r : 1)123)(,13)(223+-=---=x x x g x x x x f ; 2)2)(,52)(24+-=+-=x x x g x x x f 。
解 1)由带余除法,可得92926)(,9731)(--=-=x x r x x q ; 2)同理可得75)(,1)(2+-=-+=x x r x x x q 。
2.q p m ,,适合什么条件时,有 1)q px x mx x ++-+32|1, 2)q px x mx x ++++242|1。
解 1)由假设,所得余式为0,即0)()1(2=-+++m q x m p ,所以当⎩⎨⎧=-=++0012m q m p 时有q px x mx x ++-+32|1。
2)类似可得⎩⎨⎧=--+=--010)2(22m p q m p m ,于是当0=m 时,代入(2)可得1+=q p ;而当022=--m p 时,代入(2)可得1=q 。
综上所诉,当⎩⎨⎧+==10q p m 或⎩⎨⎧=+=212m p q 时,皆有q px x mx x ++++242|1。
3.求()g x 除()f x 的商()q x 与余式:1)53()258,()3f x x x x g x x =--=+; 2)32(),()12f x x x x g x x i =--=-+。
解 1)432()261339109()327q x x x x x r x =-+-+=-;2)2()2(52)()98q x x ix i r x i=--+=-+。
4.把()f x 表示成0x x -的方幂和,即表成2010200()()...()n n c c x x c x x c x x +-+-++-+L 的形式:1)50(),1f x x x ==;2)420()23,2f x x x x =-+=-;3)4320()2(1)37,f x x ix i x x i x i =+-+-++=-。
数学物理方法习题解答(完整版)

数学物理方法习题解答一、复变函数部分习题解答第一章习题解答1、证明Re z 在z 平面上处处不可导。
证明:令Re z u iv =+。
Re z x =,,0u x v ∴==。
1ux∂=∂,0v y ∂=∂,u v x y ∂∂≠∂∂。
于是u 与v 在z 平面上处处不满足C -R 条件, 所以Re z 在z 平面上处处不可导。
2、试证()2f z z=仅在原点有导数。
证明:令()f z u iv =+。
()22222,0f z z x y u x y v ==+ ∴ =+=。
2,2u u x y x y ∂∂= =∂∂。
v vx y∂∂ ==0 ∂∂。
所以除原点以外,,u v 不满足C -R 条件。
而,,u u v vx y x y∂∂∂∂ , ∂∂∂∂在原点连续,且满足C -R 条件,所以()f z 在原点可微。
()0000x x y y u v v u f i i x x y y ====⎛⎫∂∂∂∂⎛⎫'=+=-= ⎪ ⎪∂∂∂∂⎝⎭⎝⎭。
或:()()()2*000lim lim lim 0z z x y z f z x i y z∆→∆→∆=∆=∆'==∆=∆-∆=∆。
22***0*00limlim lim()0z z z z z z zzz z z z z z z z z=∆→∆→∆→+∆+∆+∆∆==+−−→∆∆∆。
【当0,i z z re θ≠∆=,*2i z e z θ-∆=∆与趋向有关,则上式中**1z zz z∆∆==∆∆】3、设333322()z 0()z=00x y i x y f z x y ⎧+++≠⎪=+⎨⎪⎩,证明()z f 在原点满足C -R 条件,但不可微。
证明:令()()(),,f z u x y iv x y =+,则()33222222,=00x y x y u x y x y x y ⎧-+≠⎪=+⎨+⎪⎩, 33222222(,)=00x y x y v x y x y x y ⎧++≠⎪=+⎨+⎪⎩。
第一章 流体力学部分练习题及答案(2014)

11
农业设施设计基础
第一章 流体力学部分习题
为什么用下临界雷诺数,而不用上临界雷诺数作为层流与紊流的判别
准则? 答:上临界雷诺数不稳定,而下临界雷诺数较稳定,பைடு நூலகம்与水流的过水
断面形状有关。
当管流的直径由小变大时,其下临界雷诺数如何变化? 答:不变,下临界雷诺数只取决于水流边界形状,即水流的过水断面 形状。 两个不同管径的管道,通过不同粘滞性的液体,它们的临界雷诺数是 否相同? 答: 不一定。
Rec
d 4Q d
圆管中层流与紊流,其流速分布有什么不同? 答: 层流为抛物线分布,紊流为对数曲线分布。
8
农业设施设计基础
第一章 流体力学部分习题
如图所示,水流通过由两段等截面及一段变截面组成的管道,试问: (1)当阀门开度一定,上游水位保持不变,各段管中,是恒定流还是非 恒定流?是均匀流还是非均匀流? (2)当阀门开度一定,上游水位随时间下降,这时管中是恒定流还是非 恒定流? (3)恒定流情况下,当判别第II段管中是渐变流还是急变流时,与该段 管长有无关系?
(z1 - z 2)( g) 称 ,p 2
理想气体伯努力方程 。
p
u 2
2
中
u
2
势压
,
称全压,
p (z1 - z 2)( g)
u 2
2
称总压
3
农业设施设计基础
第一章 流体力学部分习题
判断题
有两个圆形管道,管径不同,输送的液体也不同,则流态判别数(雷
对
均匀流过流断面是一平面,渐变流过流断面近似平面。
对
孔口淹没出流时,孔口淹没越深,其出流的流速和流量就越大。 X “水一定由高处向低处流” X 平衡流体中任意点的静压强值只能由该点的坐标位置来决定,而与该 压强的作用方向无关。即作用于同一点上各方向的静压强大小相等。 √
应用光学习题(第一章部分课后习题)
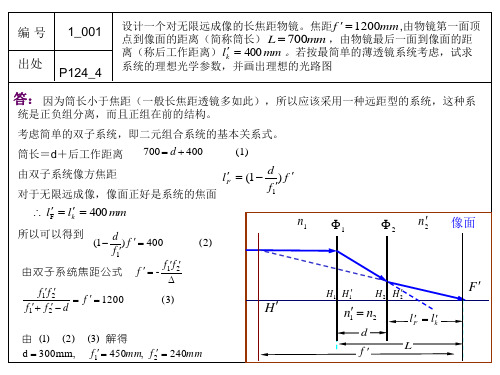
编号
出处
1_008
P125_13
答:(接上一页)
h1 d1 h1 d1 h2 h1 d1tgu1 n 1 h1 1 n 1 1 1
h1 d1 d2 d 2 h2 1 h3 h1 d1 d h h h 1 2 2 1 1 1 2 n 1 2 n 1 1 n2 n2 h1 2 1 n1 d1 d2 d 2 2 d1 h1 1 1 1 h1 1 1 n n n h n 1 2 2 1 1 d1 d2 d2 d1 d 2 h1 1 1 2 1 2 n 1 n n2 n1n1 1 2
答:由组合系统光焦度公式 1 h h h 1 1 2 2 3 3 h1 如果考虑平行光入射到 这个薄透镜系统, 即 tgu1 0,薄透镜系统处于空气中
n1 1 n n n 2 1 令 1 n3 n2 n 2 1 n3 光线在第二个子系统主 面上的高度 光线在第三个子系统主 面上的高度 而 由角度公式得, tgu1
f1 f 2
r1 n1 1.5 20 60m m n1 1.5 1 n1
n2 r2 1.5 ( 15 ) 132.35m m n2 n2 1.33 1.5
r2 n2 1.33 ( 15 ) 117.35m m n2 n2 1.33 1.5
答: 透镜的结构参数为: r1 20mm, r2 15mm
d 15mm
该透镜为双凸透镜
n1 1 n 2 n 1 .5 n1 n 1.33 2
第1章 部分习题解答

第一章 部分习题解答(数字信号处理(第二版),刘顺兰,版权归作者所有,未经许可,不得在互联网传播) 1.1 序列)(n x 示意如图T1-1,请用各延迟单位脉冲序列的幅度加权和表示。
)(n图T1-1解: )3(2)1(3)()3(2)(−+−+−+−=n n n n n x δδδδ1.3 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期。
(1)873cos()(ππ−=n A n x (2))313sin()(n A n x π=(3))6()(n j en x −=π(4) )18/sin()12/cos()(ππn n n x += 解 (a) 873cos()(ππ−=n A n x314722,7311===πωππω为有理数 所以该序列为周期序列,其周期143314=×=N (b ))313sin()(n A n x π=13631322,31322===ππωππω为有理数 所以该序列为周期序列,其周期613136=×=N (c ))6()(n j e n x −=πππωπω2122,133===为无理数 所以该序列为非周期序列。
1.12有一连续正弦信号)2cos(ϕπ+ft ,其中6,20πϕ==Hz f 。
(1) 求其周期0T ;(2) 在nT t =时刻对其采样,s T 02.0=,写出采样序列)(n x 的表达式; 求)(n x 的周期N 。
解: 6,20πϕ==Hz f(1)其周期ms s s f T 5005.020110====(2)s T 02.0=,)68.0cos()2cos()(ππϕπ+=+=n fnT n x(3)252,8.000==ωππω 则)(n x 的周期5225=×=N 1.13 今对三个正弦信号t t x πα2cos )(1=,t t x πα6cos )(2−=,t t x πα10cos )(3=进行理想采样,采样频率为π8=Ωs ,求三个采样输出序列,比较这三个结果,画出)(1t x α、)(2t x α、)(3t x α的波形及采样点位置并解释频谱混淆现象。
电路分析基础第四版课后习题第一章第二章第三章第四章答案
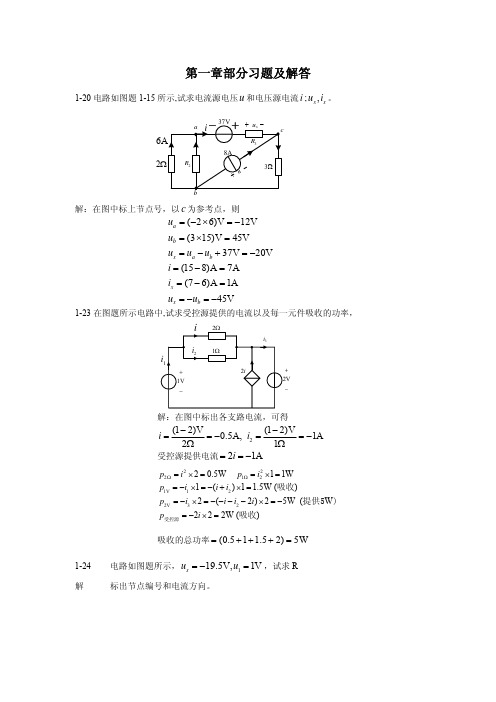
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ,列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示,试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向,
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
工程力学(一)习题集及部分解答指导

工程力学(一)习题集及部分解答指导第一章静力学基础一、判断题1-1.如物体相对于地面保持静止或匀速运动状态,则物体处于平衡。
()1-2.作用在同一刚体上的两个力,使物体处于平衡的必要和充分条件是:这两个力大小相等、方向相反、沿同一条直线。
()1-3.静力学公理中,二力平衡公理和加减平衡力系公理仅适用于刚体。
()1-4.二力构件是指两端用铰链连接并且指受两个力作用的构件。
()1-5.对刚体而言,力是滑移矢量,可沿其作用线移动。
()1-6.对非自由体的约束反力的方向总是与约束所能阻止的物体的运动趋势的方向相反。
()1-7.作用在同一刚体的五个力构成的力多边形自行封闭,则此刚体一定处于平衡状态。
()1-8.只要两个力偶的力偶矩相等,则此两力偶就是等效力偶。
()二、单项选择题1-1.刚体受三力作用而处于平衡状态,则此三力的作用线()。
A、必汇交于一点B、必互相平行C、必都为零D、必位于同一平面内1-2.力的可传性()。
A、适用于同一刚体B、适用于刚体和变形体C、适用于刚体系统D、既适用于单个刚体,又适用于刚体系统1-3.如果力FR是F1、F2二力的合力,且F1、F2不同向,用矢量方程表示为FR=F1+F2,则三力大小之间的关系为()。
A、必有FR=F1+F2B、不可能有FR=F1+F2C、必有FR>F1,FR>F2D、必有FR<F1,FR<F21-4.作用在刚体上的一个力偶,若使其在作用面内转移,其结果是()。
A、使刚体转动B、使刚体平移C、不改变对刚体的作用效果D、将改变力偶矩的大小三、计算题1-1.已知:F1=2000N,F2=150N,F3=200N,F4=100N,各力的方向如图1-1所示。
试求各力在某、y轴上的投影。
解题提示F某=+FcoαFy=+Finα注意:力的投影为代数量;式中:F某、Fy的“+”的选取由力F的指向来确定;α为力F与某轴所夹的锐角。
图1-11-2.铆接薄钢板在孔A、B、C、D处受四个力作用,孔间尺寸如图1-2所示。
机械制造技术基础(第2版)第一章课后习题标准答案

《机械制造技术基础》部分习题参考解答第一章绪论1-1 什么是生产过程、工艺过程和工艺规程?答:生产过程——从原材料(或半成品)进厂,一直到把成品制造出来的各有关劳动过程的总称为该工厂的过程。
工艺过程——在生产过程中,凡属直接改变生产对象的尺寸、形状、物理化学性能以及相对位置关系的过程。
工艺规程——记录在给定条件下最合理的工艺过程的相关内容、并用来指导生产的文件。
1-2 什么是工序、工位、工步和走刀?试举例说明。
答:工序——一个工人或一组工人,在一个工作地对同一工件或同时对几个工件所连续完成的那一部分工艺过程。
工位——在工件的一次安装中,工件相对于机床(或刀具)每占据一个确切位置中所完成的那一部分工艺过程。
工步——在加工表面、切削刀具和切削用量(仅指机床主轴转速和进给量)都不变的情况下所完成的那一部分工艺过程。
走刀——在一个工步中,如果要切掉的金属层很厚,可分几次切,每切削一次,就称为一次走刀。
比如车削一阶梯轴,在车床上完成的车外圆、端面等为一个工序,其中,n, f, a p不变的为一工步,切削小直径外圆表面因余量较大要分为几次走刀。
1-3 什么是安装?什么是装夹?它们有什么区别?答:安装——工件经一次装夹后所完成的那一部分工艺过程。
装夹——特指工件在机床夹具上的定位和夹紧的过程。
安装包括一次装夹和装夹之后所完成的切削加工的工艺过程;装夹仅指定位和夹紧。
1-4 单件生产、成批生产、大量生产各有哪些工艺特征?答:单件生产零件互换性较差、毛坯制造精度低、加工余量大;采用通用机床、通用夹具和刀具,找正装夹,对工人技术水平要求较高;生产效率低。
大量生产零件互换性好、毛坯精度高、加工余量小;采用高效专用机床、专用夹具和刀具,夹具定位装夹,操作工人技术水平要求不高,生产效率高。
成批生产的毛坯精度、互换性、所以夹具和刀具等介于上述两者之间,机床采用通用机床或者数控机床,生产效率介于两者之间。
1-5 试为某车床厂丝杠生产线确定生产类型,生产条件如下:加工零件:卧式车床丝杠(长为1617mm ,直径为40mm ,丝杠精度等级为8级,材料为Y40Mn );年产量:5000台车床;备品率:5%;废品率:0.5%。
第1章物质聚集状态习题

第一章 物质聚集状态 习 题解答(教材)1.计算在15℃和97 kPa 压力下,15 g 氮气所占有的体积。
解:330132.01097)15273(314.82515PV m nRT =⨯+⨯⨯==2.在20℃和97 kPa 压力下,0.842 g 某气体的体积是0.400 L ,这气体的摩尔质量是多少?解: RT m V M p =13386.52104.010********.8842.0M --⋅=⨯⨯⨯⨯⨯==molg pRT Vm3. 407℃时,2.96 g 氯化汞在 l .00 L 的真空器中蒸发,压力为60 kPa ,求氯化汞的摩尔质量和化学式。
解:由公式PRT Mρ=得,9.278100.110602933148842.0M 33=⨯⨯⨯⨯⨯=-.g ⋅mol -1,M(Hg)=200.59 g ⋅mol -1,25.35==Cl n又25.35131169≈-=x ,所以分子式为HgCl 24.在30℃和 102 kPa 压力下,用 47.0 g 铝和过量的稀硫酸反应可以得到多少升干燥的 氢气?如果上述氢气是在相同条件下的水面上收集的,它的体积是多少? (已知,30℃,液态水的饱和蒸气压为4. 24k kPa )[解:设p 为总压,即常压。
2Al+3H 2SO 4 ==== Al 2(SO 4 )3 + 3H 2 37 347 x 37 :3=47: x x=2.61mol333105.641010215.303314.861.222mPRT n VH H -⨯=⨯⨯⨯== 或)5.64(Lp 总 =O H p 2+P`P` = 102-4. 24k=97.76kPa T 一定,P`V`= P V LP PV V 3.6776.975.64102``=⨯==5,在100 kPa 和 100℃下,混合0.300 L 氢与 0.100 L 氧,然后使之爆炸。
如果爆炸后压力和温度不变,则混合气体的体积是多少? 解: H 2(g) + 1/2O 2(g) = H 2O(l) 0.3 0.10.2 0.1 V(H 2)=0.2L 混合气体的体积0.3L6.在25℃时,初始压力相同的5.0 L 氮和 15 L 氧压缩到体积为 10.0L 的真空容器中, 混合气体的总压力是 150 kPa 试求:(1)两种气体的初始压力;()混合气体中氮和氧的分 压;(3)如果把温度升到210℃,容器的总压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 一 章 部 分 习 题 解 答习题一4.用定义证明:若) ,2 ,1(0 =>n x n 且0lim ≥=∞→a x n n ,则a x n n =∞→lim。
证明:∵a x n n =∞→lim ,∴0>ε∀,∃+∈N N ,∍N n >时,恒有ε<-a x n 。
当0>a 时,aaax a x a x a x a x a x n n n n n n ε<-≤+-=+-=-,当0=a ,ε<=-n n x x 0综上可得a x n n =∞→lim。
5.证明 lim lim lim 212a x x a x n n n n n n ==⇔=∞→-∞→∞→。
证明:先证“⇒”, 若 lim a x n n =→∞,则0>ε∀,∃+∈N N ,∍N n >时,恒有ε<-a x n , ∵N n n n >>->122,∴ε<--a x n 12和ε<-a x n 2成立, ∴ lim lim 212a x x n n n n ==→∞-→∞。
再证“⇐”,若 lim lim 212a x x n n n n ==→∞-→∞, 则0>ε∀,∃+∈N N N 21,,∍1N n >时,恒有ε<--a x n 12; ∍2N n >时,恒有ε<-a x n 2,取) 2 ,12 ( max 21N N N -=,则当N n >时,恒有ε<-a x n ,故 lim a x n n =→∞。
综上可知, lim lim lim 212a x x a x n n n n n n ==⇔=∞→-∞→∞→。
6(2)证明)1( 0lim2>=∞→a an nn 。
证明:设h a +=1)0(>h ,∵n n n n n n n h C h C h C h a )()(1)1(221++++=+=nhh n n n hn n nh ++--+-++= 326)2)(1(2)1(136)2)(1(hn n n -->,∴332322)3(6)23(66)2)(1(hn hn nnhn n n n an n-<+-=--<,>ε∀,要使ε<-02nan ,即ε<-3)3(6hn ,只要363+ε>hn ,故取⎥⎦⎤⎢⎣⎡+ε=363h N , ∵0>ε∀,∃⎥⎦⎤⎢⎣⎡+ε=363h N ,∍当N n >时, 有ε<-<-32)3(60hn an n,∴)1( 0lim2>=∞→a an nn 。
习题二2.证明:(1)若a x n n =→∞lim ,b y n n =→∞lim ,且n n y x ≤,则b a ≤。
证明:用反证法。
假设b a >,根据数列极限的性质3, 必存在∃+∈N N ,∍N n >时,有n n y x >, 与已知条件n n y x ≤矛盾。
于是b a ≤。
(2)若a x n n =→∞lim ,且b a <(或b a >),则∃+∈N N ,∍b x N n n <⇒>(或b x n >)。
证明:若a x n n =∞→lim ,且b a <,取a b -=ε,则∃+∈N N ,∍N n >时, 恒有a b a x n -<-, 从而得b x a b a x n n <⇒-<-。
若a x n n =∞→lim ,且b a >时,同理可证。
3.证明:(1)若n n x q x ≤+1(10<<q , ,2 ,1=n ), 则0lim =→∞n n x 。
证明:∵n n x q x ≤+1( ,2 ,1=n )∴11210x q x q x q x n n n n ≤≤≤≤≤-+ , ∵0lim lim 11==∞→∞→n n n n q x x q (10<<q ),∴0lim 0lim 0lim 11=⇒=⇒=∞→+∞→+∞→n n n n n n x x x 。
(2)若0>n x ,且1lim1<=+∞→r x x nn n ,则0lim =→∞n n x 。
证明:∵1lim1<=+∞→r x x nn n ,由极限的保序性知,∃+∈N N ,∍N n >时,11<+nn x x ,∴当Nn >时,{}n x 单调减少。
又∵0>n x ,∴{}n x 有下界。
故由单调有界原理知,{}n x 必收敛,设A x n n =∞→lim 。
∵)(lim lim 11n nn n n n x x x x ⋅=+∞→+∞→,∴Ar A ⋅=,0)1(=⋅-A r ,∵1<r ,∴0)1(≠-r ,故0=A ,即0lim =→∞n n x 。
4.利用单调有界数列必有极限,证明下列数列的极限存在,并求出它们。
(2)1= x ,x x x ++=111,nn n x x x ++=+111( 2, 1, =n )解:∵1= x ,23111=++=x x x ,11<+nnx x ,∴2111<++=+nn n x x x ,即{}n x 有上界。
12x x >,假设) ,2 ,1(1 =>+k x x k k 成立,则有)11()11(1112kk k k k k x x x x x x ++-++=-++++kk k k x x x x +-+=++11110)1)(1(11>++-=++k k k k x x x x ,由数学归纳法知,) ,2 ,1(1 =>+n x x n n 成立,故{}n x 单调增加。
由单调有界原理知,{}n x 必有极限,设A x n n =→∞lim 。
∵nn n x x x ++=+1211,∴nn nn n n x x x →∞→∞+→∞++=lim 1lim 21lim 1,即AA A ++=121,012=--A A ,解得251±=A (负值应舍去),∴251lim +=→∞n n x 。
(3)设0>a ,01>x ,)(211nn n x a x x +=+( ,2 ,1=n )。
解:显然,0>n x ,∴{}n x 有下界。
∵a x a x x a x x nn nn n =⋅≥+=+)(211( ,2 ,1=n ), ∴1)1(2121≤+=+nnn x a x x ( ,3 ,2=n ),故{}2≥n x n 单调减少, 由单调有界原理知,{}n x 必有极限,设A x n n =→∞lim 。
∵)(21limlim 1nn n n n x a x x +=→∞+→∞,∴)(21Aa A A +=aA =⇒2,a A ±=(负值应舍去),故a x n n =→∞lim 。
(4)10<<n x ,且),2 ,1(41)1(1 =≥-+n x x n n证:∵1x 0n <<,∴{}n x 有界。
∵41)1(1≥-+n n x x ,110<-<n x ,∴)1(411n n x x -≥+,∵0)1(4)21()1(4441)1(41221≥--=-+-=--≥-+n n n nn n n n n x x x x x x x x x ,∴{}n x 单调增加。
由单调有界原理知,{}n x 必有极限,设A x n n =→∞lim 。
∵)1(41limlim 1n n n n x x -≥→∞+→∞,∴)1(41A A -≥,0412≤+-A A ,0)21(2≤-A ,21=A ,即21lim =∞→n n x 。
(6)) ,2 ,1(!==n n ax nn ,解:①当0=a 时,) ,2 ,1(0 ==n x n ,显然有0lim =→∞n n x 。
②当0≠a 时,∵11+=+n a x x nn ,而101limlim1<=+=∞→+∞→n a x x n nn n ,∴+∈∃N N ,N n >∍时,恒有11<+nn x x ,故当N n >时{}n x 单调减少。
又∵0>n x ,∴{}n x 有下界。
由单调有界原理知,{}n x 必收敛。
设A x n n =∞→lim ,则0≥A 。
∵n n x n a x 11+=+,∴nn n n n x n a x ∞→∞→+∞→⋅+=lim 1limlim 1,00=⋅=A A即0lim 0lim =⇒=∞→∞→n n n n x x 。
习题三7并作出函数的图象。
(2)][)(x x f =,在n x =(Z n ∈解:1)0(-=-n n f ,n n f =+)0(。
(3)][)(x x x f -=,在n x =(Z n ∈ 解:1)0(=-n f ,0)0(=+n f 。
习题四1. 用极限的定义证明:若A x f x x =→)(lim,而0>A ,则存在0>δ,使得当),(δ∈x N x 时,0)(>x f 。
x证明:∵A x f x x =→)(lim,∴取02>=εA ,0>δ∃,∍),(δ∈x N x 时,恒有2)(A A x f =ε<-,从而23)(22)(2A x f A A A x f A A <<⇒+<<-,∵0>A ,∴02)(>>A x f 。
2.求下列极限(9)xx nx 11lim-+→(N n ∈)解:设n x a +=1,则1-=n a x ,当0→x 时,1→a ,)1)(1(1lim11lim11lim2111++++--=--=-+--→→→a aa a a a a xx n n a na nxna aan n a 111lim211=++++=--→ 。
(7)1lim21--+++→x nx x x nx ;解:1)1()1()1(lim1lim2121--++-+-=--+++→→x x xx x nx x x nx nx1)1]()2()1([lim121--++-+-+=-→x x xx n x n n n x])2()1([lim 121-→++-+-+=n x x x n x n n2)1()1()2(21+=+-+-++++=n n n n n 。
(8)2)1()1(limxnx mx mn x +-+→(+∈N n m ,)解:2)1()1(limxnx mx nnx +-+→2221221])()()(1[)()()(1limxnx C nx C nx C mx C mx C mx C mmm m m nnn n n x +++-+++=→2)()(lim)(lim)()(lim222222022222220m n mn xx o n C mC xx o x n C mC x m n x m n x -=+-=+-=→→→。
