高中数学 1.1.1 柱、锥、台、球的结构特征素材 新人教A版必修2
人教A高中数学必修二1.1.1柱、锥、台、球的结构特征2

多面体
旋转体
顶点
面
轴
棱
课堂练习: 下列物体中,哪些具有多面体的形状,哪些具有旋 转体的形状?
问题3:视察下列多面体,它们共同的特点是什么?
C'
D'
之间的部分,这样的多面体叫做棱台.
2.分类:由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做
三棱台、四棱台、五棱台……
3.表示:棱台ABCD-A'B'C'D'
D’
C’
D
A’
B’
C
D’
D A’
A
B
A
C’ 上底面
侧棱
B’
C
侧面
下底面
B
顶点
课堂练习: 4.(P 9第2题)判断下列几何体是不是棱台,为什么?
C'
E'
D'
C'
A'
B'
A'
B'
A'
B'
D
E
D
C
C
C
A
B
A
B
A
B
1.定义: 有两个面互相平行,其余各面都是四边形,并且每相邻
两个四边形的公共边都互相平行,由这些面所围成的多 面体叫做棱柱。
E’ F’ A’
D’
2.分类: 棱柱的底面是三角形、四边形、五边
B’ C’
形……的棱柱分别叫做三棱柱、四棱柱、
S
顶点 2.分类: 底面是三角形、四边形、
高中数学人教a版必修二课件:1.1.1《柱、锥、台、球的结构特征》

1.1 空间几何体的结构
1.1.1 柱、锥、台、球的结构特征
本节课以学生探究为主,通过呈现大量的简单几何体图片说明空间几 何体分多面体和旋转体两种类型,运用影片演示棱柱、棱锥,动画演示棱 柱、棱锥的分类、棱柱的结构特征、微课讲解棱柱的结构特征 ,几何画 板演示从左到右拖动相互转化按钮演示由棱锥---棱台---棱柱的转化。几 何画板演示圆柱的形成过程,几何画板上下拖动上方的控制点演示圆柱、 圆锥、圆台的形成过程及它们之间的转化。动画演示球的形成。
有两个面互相平行,其余各面都是四边形, 每相邻两个四边形的公共边都互相平行, 由这些面围成的多面体叫做棱柱.
问题2:棱柱中两个互相平行的面叫做棱柱的 底面 ,其余各面叫做棱柱的
,相侧邻侧面面的公共边叫做棱柱的
,侧面侧与棱底面的公共顶点
叫做棱柱的 顶点 .你能指出下面棱柱的底面、侧面、侧棱、顶点吗?
何?
动画演示棱柱的结构特征
/edu/ppt/ppt_playVideo.actio n?mediaVo.resId=5424d3b25aa8a9cc1dd72060
动画演示棱柱的结构特征
/edu/ppt/ppt_playVideo.acti on?mediaVo.resId=5424d39b5aa8a9cc1dd7205e
讲解棱柱的结构特征
/edu/ppt/ppt_playVideo.action ?mediaVo.resId=5424d3b55aa8a9cc1dd72062
两底面是全等的多边形,各侧面都是平行四边形
棱锥的结构特征
什么叫棱锥1?
什么叫棱锥2?
/edu/ppt/ppt_playVide o.action?mediaVo.resId=55c2b1a6af508f009 9b1c24f
1.1.柱、锥、台、球的结构特征-人教A版必修二教案

1.1.柱、锥、台、球的结构特征-人教A版必修二教案一、柱体的结构特征柱体是一种线塑体,它具有以下结构特征:1.每个截面都是圆形,而且圆心在这个截面的中心;2.每个截面之间距离相等,所以从任意角度看上去,都是圆形。
柱体在物理世界中十分常见,例如水管、电线杆等。
由于其圆形结构,柱体具有抗弯和抗压的能力较强,因此被广泛使用。
二、锥体的结构特征锥体是一种线塑体,它具有以下结构特征:1.由一个圆锥顶点到底面任意一点的直线段为母线,锥体的结构由该直线段和底面围成;2.底面是个圆形。
锥体在构造物理学中有着广泛的应用,例如锥形漏斗、冰淇淋锥等。
锥体在制作过程中,需要注意底面的圆心和母线的长度,以确保最终产品符合需求。
三、台体的结构特征台体是一种线塑体,它具有以下结构特征:1.由一个圆台顶点到底面圆心的直线段为轴线,台体的结构由该直线段和上下两个圆台围成;2.上下两个圆台面积大小相等。
台体的结构在物理实验中被广泛使用,例如水流研究、电场模拟等。
在设计制作台体时,需注意两个圆台的形状和尺寸,以达到理想的实验效果。
四、球体的结构特征球体是一种线塑体,它具有以下结构特征:1.每个表面都是一个圆形,而且所有圆心都在同一点;2.所有体内点到同一点的距离相等。
球体在物理学、地理学、天文学等领域有着广泛的应用。
例如在天文观测中,我们所看到的星星通常是球体形状的天体。
制作球体时,通常需要注意表面的光滑度、圆心位置和直径等因素。
五、小结本文介绍了四种线塑体:柱体、锥体、台体和球体,以及它们的结构特征。
在物理世界中,这四种形态常常出现,有着广泛的应用。
熟悉这些塑体的结构特征,对于理解相关的物理现象和设计制作模型等都十分重要。
以上仅为基础知识的介绍,希望能够引起读者对这些形体结构的关注,进而领悟常见的物理现象和背后的原理。
高中数学人教版必修二:1.1.1柱、锥、台、球的结构特征

理解棱柱的定义
⑤棱柱两个互相平行的面以外的面 都是平行四边形吗? 答:是.
E′ F′ A′ B′
D′
C′
⑥为什么定义中要说“其余各面都 是四边形,并且相邻两个四边形的公共 边都互相平行,”而不简单的只说“其 余各面是平行四边形呢”?
答:满足“有两个面互相平行,其 余各面都是平行四边形的几何体”这样 说法的还有右图情况,如图所示.所以 定义中不能简单描述成“其余各面都是 平行四边形”.
答:满足“有两个面互相平行,其 余各面都是平行四边形的几何体”这样 说法的还有右图情况,如图所示.所以 定义中不能简单描述成“其余各面都是 平行四边形”.
2.棱锥的结构特征
观察下列几何体,有什么相同点?
1、棱锥的概念
有一个面是多边形,其余各面是有 一个公共顶点的三角形, 由这些面所围 成的几何体叫做棱锥。
上底面 侧棱 侧面 高 顶点 下底面
2.棱台的分类:
由三棱锥、四棱锥、五棱锥……截得的 棱台分别叫做三棱台、四棱台、五棱台…… 用顶点各底面各顶点的字母表示 3.棱台的表示:
棱台ABCD-A‘B’C‘D’
三棱台
四棱台
五棱台
辨析
判断:下列几何体是不是棱台,为什么?
(1)
(2)
棱柱、棱锥、棱台的结构特征比较
3、圆台与棱台统称为台体。
O'
底面 轴 侧面 母线
O
底面
判断题:
(1)在圆柱的上下底面上各取一点,这两点的连
线是圆柱的母线.
(
)
(2)圆台所有的轴截面是全等的等腰梯形.( )
(3)与圆锥的轴平行的截面是等腰三角形.( )
圆柱与棱柱统 称为柱体。
圆台与棱台统 称为台体。
人教A版高中数学必修2课件1.1.1柱、锥、台、球的结构特征课件

柱、锥、台、球的结构特征
【棱台的结构特征】
(2)棱台的分类 由三棱锥、四棱锥、五棱锥、…截得的棱台, 分别叫做三棱台、四棱台、五棱台、…
(3)棱台的表示法 用表示棱台的各顶点的字母表示,如上图所示的 棱台可表示为棱台ABCD-A′B′C′D′.
柱、锥、台、球的结构特征
【球的结构特征】 (1)球的有关概念 ①球的定义:以半圆的直径所在直 线为旋转轴,半圆面旋转一周形成 的旋转体叫做球体,简称球. ②各部分名称:半圆的半径叫做球 的半径;半圆的圆心叫做球心;半 圆的直径叫做球的直径. ③图示:
柱、锥、台、球的结构特征
【棱锥的结构特征】
棱锥的分类 按底面多边形的边数分类: 三棱锥(底面是三角形);四 棱锥(底面是四边形);五棱 锥(底面是五边形)· · · · · n棱锥 (底面是n边形); (3)棱锥的表示法 用表示顶点和底面各顶点的字 母表示,如上图所示的棱锥表 示为四棱锥S-ABCD.
柱、锥、台、球的结构特征
【典型例题】 【分析】 充分利用空间几何体的结构特征.
【解】 (1)不正确,当截面和底面平行 时,这种说法是正确的;当截面与底面 不平行时,这种说法是错误的. 对棱锥来说,截面截掉的部分是棱锥, 但当截面与底面不平行时,截面和底面 之间的部分不是棱台,如图(1);对圆锥 来说,只要截面和底面不平行,截面和 底面之间的部分既不是圆台,截掉的部 分也不是圆锥,如图(5).
台,故该几何体为圆台.
【点评】 根据圆柱、圆锥、圆台的结构特 征进行判断.
知识点—— 柱、锥、台、球 的结构特征
柱、锥、台、球的结构特征
【棱柱的结构特征】 (1)棱柱的有关概念 ①定义:一般地,有两个面互相平行,其余各 面都是四边形,并且每相邻两个四边形的公共 边都互相平行,由这些面所围成的多面体叫做 棱柱. ②各部分名称:棱柱中,两个互相平行的面叫 做棱柱的底面,简称底;其余各面叫做棱柱的 侧面;相邻侧面的公共边叫做棱柱的侧棱;侧 面与底面的公共顶点叫做棱柱的顶点. ③图示:
人教A版数学必修2 柱、锥、台、球的结构特征

分类:
三棱台 四棱台 五棱台 等
分类标准: 底面多边形的 边数
思考9:
用一个平行于棱锥底面的平面去截棱锥, 截面与底面的形状关系如何?
相似多边形
棱台的结构特征和表示:
结构特征: • 两个底面是相似多边形; • 侧面都是梯形; • 侧棱延长后交于一点.
表示:棱台ABC-A1B1C1
小结 : 1.棱柱:
棱锥的分类及表示
分类标准: 底面多边形的边数
三棱锥
棱锥S-ABC
四棱锥
棱锥S-ABCD
五棱锥
棱锥P-ABCDE
思考8: 观察并对比以下两个多面体.
思考II中多面体与I中四棱锥有何关系?
棱台的概念及分类:
棱锥被平行于棱锥
底面的平面所截后,
截面和底面之间的部 分叫做棱台.
(上底面、下底面、侧面、 侧棱、顶点 )
思考2:
为了研究方便,我们把棱柱中两个互相平行的 面叫做棱柱的底面,其余各面叫做棱柱的侧面, 相邻侧面的公共边叫做棱柱的侧棱,侧面与底面 的公共顶点叫做棱柱的顶点. 你能指出上面棱柱 的底面、侧面、侧棱、顶点吗?
顶点
侧面
侧棱
底面
棱柱的分类及表示
分类标准: 底面多边形的边数
D
三棱柱
四棱柱
五棱柱
棱柱ABC-A'B'C' 棱柱ABCD-A1B1C1D1 棱柱ABCDE-A'B'C'D'E'
• 第一个图中其余各面是几边形?第二个图中 其余各面是几边形?
• 第一个图中其余各面的公共边位置关系如何? 第二个图中有同样的特征吗?
棱柱的结构特征:
• 有两个面互相平行; • 其余各面都是四边形 ; • 每相邻两个四边形的公共边互相平行 。
新课标人教A版高中数学必修2知识点总结

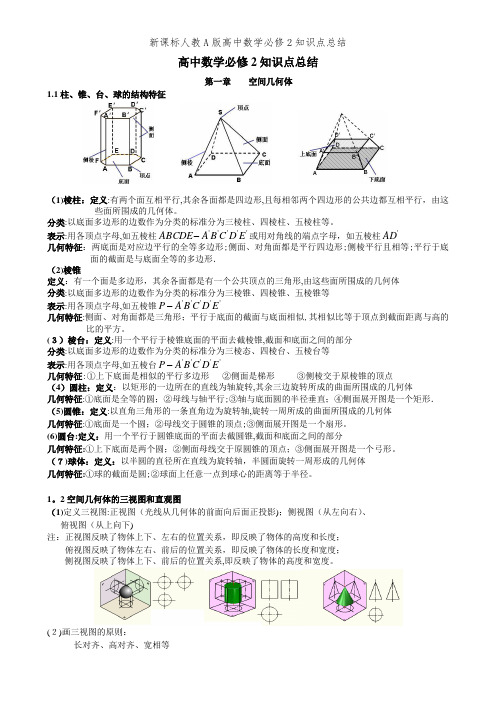
高中数学必修2知识点总结第一章 空间几何体1.1柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱'''''E D C B A ABCDE -或用对角线的端点字母,如五棱柱'AD几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
(2)棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体 分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分 分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如五棱台'''''E D C B A P -几何特征:①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
(5)圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体 几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
(6)圆台:定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
新课标人教A版高中数学必修2知识点总结
高中数学必修2知识点总结第一章 空间几何体1.1柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱'''''E D C B A ABCDE -或用对角线的端点字母,如五棱柱'AD几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.(2)棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体 分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分 分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如五棱台'''''E D C B A P -几何特征:①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形. (5)圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体 几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
(6)圆台:定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
高中必修二人教A版数学1.1.1-2 柱、锥、台、球及简单组合的结构特征

(2)常见的几种四棱柱之间的转化关系
判断正误(正确的打“√”,错误的打“×”) (1)棱柱的侧面都是平行四边形.(
√
)
(2) 用 一 个 平 面 去 截 棱 锥 , 底 面 和 截 面 之 间 的 部 分 叫 棱 台.(
×
)
√
(3)将棱台的各侧棱延长可交于一点.(
)
下列图形中是棱锥的是(
)
答案:C
探究点 2 棱锥、棱台的结构特征 下列关于棱锥、棱台的说法: ①棱台的侧面一定不会是平行四边形; ②棱锥的侧面只能是三角形; ③由四个面围成的封闭图形只能是三棱锥. 其中正确说法的序号是__________.
【解析】 边形;
①正确,棱台的侧面一定是梯形,而不是平行四
②正确,由棱锥的定义知棱锥的侧面只能是三角形; ③正确,由四个面围成的封闭图形只能是三棱锥.
解析:三棱锥的面最少,有 4 个.
答案:4
探究点 1 棱柱的结构特征 下列关于棱柱的说法:①所有的面都是平行四边形; ②每一个面都不会是三角形;③两底面平行,并且各侧棱也 平行.其中正确说法的序号是__________.
【解析】 ①错误,棱柱的底面不一定是平行四边形;
②错误,棱柱的底面可以是三角形; ③正确,由棱柱的定义易知.
【答案】 ①②③
判断棱锥、棱台形状的两个方法 (1)举反例法 结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构 特征的某些说法不正确. (2)直接法 棱锥 定底面 看侧棱 面即为底面 相交于一点 棱台 即为底面 延长后相交于一点 只有一个面是多边形,此 两个互相平行的面,
2.(1)棱台不具有的性质是( A.两底面相似 B.侧面都是梯形 C.侧棱长都相等 D.侧棱延长后相交于一点
1.1.柱、锥、台、球的结构特征-人教A版必修二教案

1.1.柱、锥、台、球的结构特征-人教A版必修二教案本文将介绍柱、锥、台、球这四种常见结构的特征和相关知识点,帮助读者更好地理解和掌握这些知识。
1. 柱的结构特征1.1 基本结构柱是一种直线向上延伸的立方体,底面为正方形或长方形,底面和顶面平行。
1.2 相关知识点•底面积和侧面积:柱的底面积为底面的面积,侧面积为侧面的面积,总面积等于底面积加上侧面积。
•体积:柱的体积等于底面积乘以高度。
•直径和半径:柱的底面为圆形时,可以用直径和半径来表示。
2. 锥的结构特征2.1 基本结构锥是一种底面为圆形的立体,顶点在圆心上方的一种立体图形。
2.2 相关知识点•底面积和侧面积:锥的底面积为底面的面积,侧面积为底面到顶点的直线段所包含的表面积,总面积等于底面积加上侧面积。
•体积:锥的体积等于底面积乘以高度再除以3。
•直径和半径:锥的底面为圆形时,可以用直径和半径来表示。
3. 台的结构特征3.1 基本结构台是一种上下底面均为平行四边形的立体,上下底面相等,侧面为梯形或矩形。
3.2 相关知识点•底面积和侧面积:台的底面积为下底面的面积,顶面积为上底面的面积,侧面积为侧面的面积,总面积等于底面面积加上顶面面积再加上侧面面积。
•体积:台的体积等于上下底面积之和再乘以高度再除以2。
4. 球的结构特征4.1 基本结构球是一种没有尖角、底面和顶面相等、关于任何一条直径对称的立体图形。
4.2 相关知识点•表面积:球的表面积等于4倍半径的平方。
•体积:球的体积等于4/3乘以半径的立方。
总结通过本文的介绍,我们了解了柱、锥、台、球这四种常见结构的特征和相关知识点。
掌握这些知识有助于更好地理解和应用于实际生活中。
高中数学人教A版必修二:1.1.1柱、锥、台、球的结构特征-课件

(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
思考:1.(2)(6)为什么不是棱柱?2.观察(3)(9)两个 的棱柱,分别有多少对平行平面?能作为棱柱的底面的有几对? 3.有两个面互相平行,其余各面都是平行四边形的几何体是棱柱 吗?
高中数学人教A版必修二:1.1.1柱、 锥、台 、球的 结构特 征-课件
高中数学人教A版必修二:1.1.1柱、 锥、台 、球的 结构特 征-课件
高中数学人教A版必修二:1.1.1柱、 锥、台 、球的 结构特 征-课件
练习:判断下列几个命题中的对错
(1)有两个面平行,其余各面都是平行四边行的几何体 叫棱柱 ( × ) (2) 有一个面是多边形,其余各面都是三角形的几何 体叫棱锥 ( × ) (3)两个面平行且相似,其余各面都是梯形的多面体是 棱台 ( × )
高中数学人教A版必修二:1.1.1柱、 锥、台 、球的 结构特 征-课件
探究二:同学们我们已经愉快的研究认 识了棱柱,那下面我们按研究棱柱的方 式研究棱锥的定义、分类及给出表示方 法吧!
高中数学人教A版必修二:1.1.1柱、 锥、台 、球的 结构特 征-课件
高中数学人教A版必修二:1.1.1柱、 锥、台 、球的 结构特 征-课件
的公共边都互相平行(侧棱),由这些面所围成的几何体
叫做棱柱。
E1
D1 C1
A1
B1
底面 侧面
E
DC
AB
侧棱 顶点
高中数学人教A版必修二:1.1.1柱、 锥、台 、球的 结构特 征-课件
高中数学人教A版必修二:1.1.1柱、 锥、台 、球的 结构特 征-课件
2、棱柱的分类:(法一)棱柱的底面可以是三角形、四 边形、五边形、 …… 我们把这样的棱柱分别叫做三棱 柱、四棱柱、五棱柱、……
高中数学人教A版必修二1.1.1 柱、锥、台、球的结构特征

有一个面是多边形,其余各面都是有 一个公共顶点的三角形,由这些面围 成的多面体叫做棱锥.
参照棱柱的说法,请你在图中找出棱 锥的底面、侧面、侧棱、和顶点。
顶点
侧面
底面
侧棱
练习3:下列多面体都是棱锥吗?如何命 名?
与圆柱和圆锥一样,圆台也有轴、底 面、侧面、母线,请你在图中找出来。
上底面
侧面
A
母线
轴
B
下底面
知识探究(八):球的结构特征
定义:以半圆的直 径所在直线为旋转 轴,半圆面旋转一 周形成的几何体.
半径 O
球心
球的表示方法:用表示球 心的字母表示,如:“球O”
知识小结
简单几何体的结构特征
柱体
锥体
台体
母线
底面
生活中的圆柱
知识探究(六):圆锥的结构特征
定义:以直角三角形的一条直角边所在 直线为旋转轴,其余两边旋转形成的面 所围成的旋转体叫做圆锥
母线
Hale Waihona Puke 顶点S轴侧面
A
O
B
底面
知识探究(七):圆台的结构特征
定义:用一个平行于圆锥底面的平面去截 圆锥,截面与底面之间的部分叫做圆台. 圆台可以由什么平面图形旋转而形成?
以矩形的一边所在 直线为旋转轴,其 余三边旋转形成的 面所围成的旋转体 叫做圆柱.
底面
旋转轴
A′
O′
A
O
侧面 母线
在圆柱的形成中,旋转轴叫做圆柱的轴,垂直于 轴的边旋转而成的圆面叫做圆柱的底面,平行于 轴的边旋转而成的曲面叫做圆柱的侧面,平行于 轴的边在旋转中的任何位置叫做圆柱侧面的母线.
1.1.1柱、锥、台、球的结构特征-人教A版高中数学必修二课件(共38张PPT)

(2)侧棱垂直于底的棱柱叫做直棱柱。 特别地,底面是正多边形的直棱柱叫做正棱柱。
棱柱集合、斜棱柱集合、直棱柱集合、 正棱柱集合之间存在怎样的包含关系?
棱柱
直棱柱 正棱柱
斜棱柱
2.棱柱的分类
(1)按侧棱与底面的关系分为: 侧棱不垂直于底的棱柱叫做斜棱柱. 侧棱垂直于底的棱柱叫做直棱柱. 其中,底面是正多边形的直棱柱叫做正棱柱.
第一章 空间几何体
1.1.1 柱、锥、台、球的结构特征
现代城市的建筑都是由各种各样的漂亮的几何体组成的.
我们的生活中离不开各种美妙的几何体
如果我们只考虑这些物体的形
状和大小,而不考虑其他因素,那 么由这些物体抽象出来的空间图形 叫做空间几何体.
一
⊙
、
多
面
√
体
和 旋
√
转
体
√
⊙ √
⊙
√
⊙
⊙
√
√
2,5,7,9,13,14,15,16的共同点: 1,3,4,6,8,10,11,12的共同点:
C'
总结: 棱柱的性质
1. 侧棱都互相平行且相等 ,侧面都是平行四边 形; 2. 平行于底面的截面与两个底面是 全等的多边形; 3. 过不相邻的两条侧棱的截面是 平行四边形.
三、 棱锥
1.棱锥的结构
一般地,有一个面是多边形,其余各面都是有一个公共顶
点的三角形,由这些面所围成的多面体叫做棱锥.
如图:
上底面
四、棱台
3.棱台的分类: 由三棱锥、四棱锥、五棱锥等截得的棱台分别 叫做三棱台、四棱台、五棱台.
O
4.棱台的表示方法: 棱台ABCD A' B 'C ' D '
高中数学 1.1.1柱、锥、台、球的结构特征(一) 新人教A版必修2

答:圆锥的母线长为40/3cm。
柱、锥、台体的关系
棱柱、棱锥、棱台之间有什么关系?圆柱、圆锥、 圆台之间呢?柱、锥、台体之间有什么关系?
上底扩大
上底缩小
柱
台
锥
体
上底扩大
体
上底缩小
体
球的结构特征
7、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转 一周形成的几何体叫做球体,简称球。
(1)半圆的半径叫做球的半径。
•
• A.(1)是棱台 B.(2)是圆台 • C.(3)是棱锥 D.(4)不是棱柱
作业精选 巩固提高
• 3.有下列四种说法: • ①圆柱是将矩形旋转一周所得的几何体; • ②以直角三角形的一直角边为旋转轴,旋转所得
的几何体是圆锥; • ③圆台的任意两条母线的延长线,可能相交也可
能不相交; • ④圆锥的底面是圆面,侧面是曲面;
作业精选 巩固提高
• 5.设圆锥的母线长为,高为,过圆锥的两条 母线作一个截面,则截面面积的最大值为
• _______4_3_l_2__________。
作业精选 巩固提高
• 6.以直角边为3 cm和4 cm的直角三角形绕 其直角边旋转而形成的圆锥,母线长为
____5__c_m_______.
知识小结
三棱柱
四棱柱
五棱柱
二、请同学们观察下面几何体,并总结它们的共同特点 ?
棱锥的定义
2.棱锥:有一个面是多边形,其余各面是有一 个公共顶点的三角形,由这些面所围成的几何 体叫做棱锥。
这个多边形面叫做棱锥的底面 有。公共顶点的各个三角形叫做棱 锥的侧面。
各侧面的公共顶点叫做棱锥 的顶点。
相邻侧面的公共边叫做棱锥 的侧棱 。
人教A版高中数学必修2:1.1.1 柱、锥、台、球的结构特征(1)

平面 ABC,AB⊥BC,AB=BC=1,PA= 3,则该三棱
锥外接球的表面积为( )
A.5π
B. 2π
C.20π
解析 (1)法一 由几何体的三视图
D.4π
可知空间几何体的直观图如图所示,
其中侧面 ABD⊥底面 BCD,另两个
侧面 ABC,ACD 为等边三角形,则
有表面积
S
表=2×12×2×1+2×
A.2+ 5
B.4+ 5 C.2+2 5 D.5
基础诊断
考点突破
课堂总结
解析 (1)由正视图与俯视图想象出其直观图,然后进行运算 求解.如图,该几何体是一个半球与一个半圆柱的组合体,球 的半径为 r,圆柱的底面半径为 r,高为 2r,则表面积 S=12× 4πr2+πr2+4r2+πr·2r=(5π+4)r2.又 S=16+20π, ∴(5π+4)r2=16+20π,∴r2=4,r=2,故选 B.
A.8-2π C.8-π2
B.8-π D.8-π4
基础诊断
考点突破
课堂总结
解析 (1)由三视图可知,这是一个三棱锥与半个圆柱的组合 体,其中半圆柱的底面半径为 1,高为 2,三棱锥的底面为一 个斜边长为 2 的等腰直角三角形,高为 1,所以该几何体的体 积 V=12π×12×2+13×12×1×2×1=π+13,选 A. (2)直观图为棱长为 2 的正方体割去两个底面半径为 1 的14圆柱, 所以该几何体的体积为 23-2×π×12×2×14=8-π. 答案 (1)A (2)B
基础诊断
考点突破
课堂总结
5.(2015·江苏卷)现有橡皮泥制作的底面半径为5,高为4的圆 锥和底面半径为2、高为8的圆柱各一个.若将它们重新制 作成总体积与高均保持不变,但底面半径相同的新的圆锥 和圆柱各一个,则新的底面半径为________. 解析 设新的底面半径为 r,由题意得13πr2·4+πr2·8=13π ×52×4+π×22×8,解得 r= 7. 答案 7
人教A版高中数学必修2:1.1.1 柱、锥、台、球的结构特征

• 1两底面互相
• 1.底面是
________;
________,各 • 2棱台是用一个
侧面均是三角形; 平行于
• 2.各侧面有一个 公共点.
________的平 面去截棱锥,底 面和截面之间的
课堂练习:
1. 下列几何体是棱柱的有( )
课堂练习:
2. 下面是几种常见的棱柱,如何在名称上区 分这些棱柱?
高中数学必修2
空间几何体 棱柱、棱锥、棱台的结构特征
酒泉市肃州中学 杨述苏
研究棱柱、棱锥、棱台的联系. 欧拉公式:
知识探究(一)空间几何体及其类型
问如题果:我观们察只空考间虑几物何体体的,形组状成和这大些小空,间而几不何考体虑的其每它个因面素, 有那什么么由特这点些?物你体能抽将象它出分来成的两空类间吗图?形说就一叫说做空间几何体.
E'
示例图 符号表示
A' B'
D' C'
F E
A B
D C
观察侧棱位置关系
观察底面 观察侧面
• 底面图形形状 • 两底面关系
结构特征
• 1.两底面 ________,其余 各面都是 ________;
• 2.侧棱____且相 等.
棱锥
S
D A
C B
棱台
P
A1 A
C1 B1
C
B
底面图形形状 • 底面图形形状 • 两底面关系
多面体欧拉公式:
D1 A1
D A
C1 B1
C B
D1
A1 D
A
C1
B1 C
B
F' E'
A' B'
C'
D'
A
F
ED
B
C
人教A版高中数学必修2:1.1.1 柱、锥、台、球的结构特征(7)

棱台的表示方法:“棱台ABCD—A'B'C'D'”
想一想,怎样给多面体分类呢?
答:可以按面数分类,多面体有几个面就 称为几面体。如:三棱锥是四面体,四棱柱 是六面体.
2、旋转体 一条平面曲线绕着它所在的平面内的一条
定直线旋转所形成的曲面叫作旋转面。
封闭的旋转面围成的几何体叫作旋转体。
O Rd
r Oˊ P
r R2 d2
例1 已知球的半径为10cm,一个截
面圆的面积是36 cm2,则球心到截面圆
圆心的距离是 8cm .
O Rd
r Oˊ P
练习: 1、下列命题是正确的是( A ) A 以直角三角形的一直角边所在的直线为轴 旋转所得的几何体为圆锥;
B 圆锥的侧面展开图为扇形,这个扇形所在 圆的半径等于圆锥底面圆的半径
1-3、棱台的概念
用一个平行于棱锥底面的平面去截棱锥,底面与 截面之间的部分叫作棱台。
上底面 侧棱
侧面
高
顶点
下底面
辨析
判断:下列几何体是不是棱台,为什么?
(1)
(2)
正棱台 用正棱锥截得的棱台叫作正棱台。 正棱台的侧面是全等的等腰梯形, 它的高叫作正棱台的斜高。
正棱锥
斜高 正四棱台
棱台的分类: 由三棱锥、四棱锥、五棱锥…截
底面
圆柱的表示方法:用表示它的轴的字母表
示,如:“圆柱OO'”
定义:以直角三角形的
一条直角边所在直线为
母
旋转轴,其余两边旋转
线
形成的曲面所围成的几
何体叫做圆锥。 A
顶点 S
轴
侧 面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.1 柱、锥、台、球的结构特征
备用习题
1.下列说法错误的是()
A.多面体至少有四个面
B.九棱柱有9条侧棱,9个侧面,侧面为平行四边形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
分析:多面体至少应有四个顶点组成(否则至多3个顶点,而3个顶点只围成一个平面图形),而四个顶点当然必须围成四个面,所以A正确;棱柱侧面为平行四边形,其侧棱和侧面的个数与底面多边形的边数相等,所以B正确;长方体、正方体都是棱柱,所以C正确;三棱柱的侧面是平行四边形,不是三角形,所以D错误.
答案:D
2.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为___________ cm.
分析:n棱柱有2n个顶点,由于此棱柱有10个顶点,那么此棱柱为五棱柱,又因棱柱的侧棱都相等,五条侧棱长的和为60 cm,可知每条侧棱长为12 cm.
答案:12
3.在本节我们学过的常见几何体中,如果用一个平面去截几何体,如果截面是三角形,那么这个几何体可能是___________.
分析:棱锥、棱柱、棱台、圆锥等几何体的截面都可以是三角形,因此本题答案是开放的,作答时要考虑周全.
答案:棱锥、棱柱、棱台、圆锥
4.如图25所示,有12个小正方体,每个正方体6个面上分别写着数字1、9、9、8、4、5,用这12个小正方体拼成一个长方体,那么图中看不见的那些小正方体的面有多少个?并求这些面上的数字和.
图25
分析:先求看得见的个数,再求看不见的面的个数,同样,先求这12个小正方体各个面上的数字的和,再减去看得见的数字的和.
解:这12个小正方体,共有面数6×12=72个,图中看得见的面共有3+4×4=19个,
故图中看不见的面有72-19=53个,
12个小正方体各个面的数字的和为(1+9+9+8+4+5)×12=432,
而图中看得见的数字的和为130,
所以看不见的那些小正方体的面上的数字的和为432-130=302,
即看不见的那些小正方体的面有53个,这些面上的数字和是302.
知识拓展
1.特殊的棱柱:侧棱不垂直于底面的棱柱称为斜棱柱;侧棱垂直于底面的棱柱叫做直棱柱;底面是正多边形的直棱柱是正棱柱;底面是平行四边形的四棱柱叫做平行六面体;侧棱垂直于底面的平行六面体叫做直平行六面体;底面是矩形的直平行六面体叫做长方体;棱长都相等的长方体叫做正方体.其中长方体对角线的平方等于同一顶点上三条棱的平方和.
2.特殊的棱锥:如果棱锥的底面为正多边形,且各侧面是全等的等腰三角形,那么这样的棱
锥称为正棱锥,正棱锥各侧面底边上的高均相等,叫做正棱锥的斜高;侧棱长等于底面边长的正三棱锥又称为正四面体.
3.特殊的棱台:由正棱锥截得的棱台叫做正棱台,正棱台的侧面是全等的等腰梯形,正棱台各侧面等腰梯形的高称为正棱台的斜高.
4.球心与球的截面圆心的连线垂直于截面.
5.规定:在多面体中,不在同一面上的两个顶点的连线叫做多面体的对角线,不在同一面上的两条侧棱称为多面体的不相邻侧棱,侧棱和底面多边形的边统称为棱.
精美句子
1、善思则能“从无字句处读书”。
读沙漠,读出了它坦荡豪放的胸怀;读太阳,读出了它普照万物的无私;读春雨,读出了它润物无声的柔情。
读大海,读出了它气势磅礴的豪情。
读石灰,读出了它粉身碎骨不变色的清白。
2、幸福幸福是“临行密密缝,意恐迟迟归”的牵挂;幸福是“春种一粒粟,秋收千颗子”的收获. 幸福是“采菊东篱下,悠然见南山”的闲适;幸福是“奇闻共欣赏,疑义相与析”的愉悦。
幸福是“随风潜入夜,润物细无声”的奉献;幸福是“夜来风雨声,花落知多少”的恬淡。
幸福是“零落成泥碾作尘,只有香如故”的圣洁。
幸福是“壮志饥餐胡虏肉,笑谈渴饮匈奴血”的豪壮。
幸福是“先天下之忧而忧,后天下之乐而乐”的胸怀。
幸福是“人生自古谁无死,留取丹心照汗青”的气节。
3、大自然的语言丰富多彩:从秋叶的飘零中,我们读出了季节的变换;从归雁的行列中,我读出了集体的力量;从冰雪的消融中,我们读出了春天的脚步;从穿石的滴水中,我们读出了坚持的可贵;从蜂蜜的浓香中,我们读出了勤劳的甜美。
4、成功与失败种子,如果害怕埋没,那它永远不能发芽。
鲜花,如果害怕凋谢,那它永远不能开放。
矿石,如果害怕焚烧(熔炉),那它永远不能成钢(炼成金子)。
蜡烛,如果害怕熄灭(燃烧),那它永远不能发光。
航船,如果害怕风浪,那它永远不能到达彼岸。
5、墙角的花,当你孤芳自赏时,天地便小了。
井底的蛙,当你自我欢唱时,视野便窄了。
笼中的鸟,当你安于供养时,自由便没了。
山中的石!当你背靠群峰时,意志就坚了。
水中的萍!当你随波逐流后,根基就没了。
空中的鸟!当你展翅蓝天中,宇宙就大了。
空中的雁!当你离开队伍时,危险就大了。
地下的煤!你燃烧自己后,贡献就大了
6、朋友是什么?
朋友是快乐日子里的一把吉它,尽情地为你弹奏生活的愉悦;朋友是忧伤日子里的一股春风,轻轻地为你拂去心中的愁云。
朋友是成功道路上的一位良师,热情的将你引向阳光的地带;朋友是失败苦闷中的一盏明灯,默默地为你驱赶心灵的阴霾。
7、一粒种子,可以无声无息地在泥土里腐烂掉,也可以长成参天的大树。
一块铀块,可以平庸无奇地在石头里沉睡下去,也可以产生惊天动地的力量。
一个人,可以碌碌无为地在世上厮混日子,也可以让生命发出耀眼的光芒。
8、青春是一首歌,她拨动着我们年轻的心弦;青春是一团火,她点燃了我们沸腾的热血;青春是一面旗帜,她召唤着我们勇敢前行;青春是一本教科书,她启迪着我们的智慧和心灵。
