修车时间(3)
铁路机车统计规则(二)

铁路机车统计规则(二)机车运用与检修指标第37条机车运用工作量指标及计算方法。
(一)机车走行公里:为运用机车实际走行或换算走行的公里。
1. 机车总走行公里:为沿线走行公里及换计走行公里之和。
2.本务机走行公里:为牵引列车的本务机车走行公里3.沿线走行公里:为本务、单机(含有动力附挂)、重联和补机走行公里之和。
4.辅助走行公里:为单机(含有动力附挂)、重联、补机及各种换算走行公里之和。
5.换算走行公里:为按机车台小时换算的走行公里。
调车工作每小时作业时间换算20公里;其他工作每小时换算5公里;有动力停留每小时换算4公里(内燃、电力运用机车的段内停留均按有动力停留统计)。
(二)牵引总重吨公里:为机车牵引列车(包括单机牵引车辆)完成的工作量。
计算方法:机车牵引总重吨公里=机车牵引总重×实际走行公里注:双机合并牵引及挂有补机、重联机车时,按附件二“重联、补机机车牵引能力比例表”分劈:3台机车牵引列车时不考虑机型,其总重吨公里本务机车按40%,其余两台各按30%分劈。
4台及以上机车牵引列车时,不分机型,平均分劈。
(三)机车自重吨公里:是指机车沿线走行产生的自重吨公里。
机车自重根据附件三“机车重量、长度及功率表”确定。
计算方法:机车自重吨公里=机车重量×沿线走行公里(四)通过总重吨公里:是指沿线上通过的总重吨公里。
计算方法:通过总重吨公里=机车自重吨公里+牵引总重吨公里(五)机车专调时间:指机车担当专用调车工作产生的调车时间,是根据司机报单记载的每次由实际工作开始至实际工作完了的时间。
包括专调机车在编组站、区段站以及运输方案规定的专调站调车时间和月间计划指定利用列车的本务机车在列车始发站及终到站兼作调车工作的实际作业时间。
(六)车辆公里:为车辆运行的公里。
计算方法:车辆公里=机车牵引车辆辆数×实际走行公里(七)载重吨公里:为机车牵引列车完成的货物运输量(包括单机牵引车辆完成的货物运输量)。
汽修工作制度怎么样

标题:汽修工作制度探究随着经济的不断发展,汽车已经成为人们生活中不可或缺的一部分。
而汽车产业的发展也带动了汽修行业的繁荣。
那么,汽修行业的工作制度是怎样的呢?本文将从工作时间、休息制度、工资待遇、职业发展等方面进行详细介绍。
一、工作时间汽修行业的工作时间通常为周一至周五,每天工作8小时,周末双休。
但在一些特殊的汽车维修店或4S店,可能会根据业务需要调整工作时间。
此外,由于汽车维修工作具有一定的紧急性,员工在工作中可能会遇到加班的情况。
但加班工资会按照相关法规进行支付。
二、休息制度汽修行业的休息制度一般为周末双休,国家法定节假日也会按照规定放假。
在一些企业中,员工还可以享受年假、婚假、产假等福利待遇。
此外,企业会为员工提供一定的休息时间和休息场所,以确保员工在紧张的工作之余得到充分的休息和放松。
三、工资待遇汽修行业的工资待遇与员工的技术水平、工作经验和所在地区等因素有关。
一般来说,初级汽修工的工资较低,随着技术水平的提高和经验的积累,工资待遇也会相应提高。
此外,企业会为员工提供五险一金等福利待遇,保障员工的基本生活需求。
四、职业发展汽修行业提供了丰富的职业发展机会。
员工可以通过不断提升自己的技术水平和综合素质,逐步晋升为高级汽修工、技术主管、店长等职位。
此外,企业还会为员工提供培训和学习机会,帮助员工不断提升自己的专业技能。
在行业内,员工还可以通过考取相关证书,进一步提升自己的职业地位。
五、企业文化汽修行业的企业文化氛围浓厚,员工之间团结协作,共同为企业的发展贡献力量。
企业会定期举办各类活动,如团建、庆典等,增强员工的凝聚力和向心力。
同时,企业注重员工个人成长,鼓励员工积极参与各类培训和学习,提升自己的综合素质。
六、总结汽修行业作为一个技术性较强的行业,其工作制度具有一定的特殊性。
员工在工作中需要具备较强的责任心和敬业精神,不断提升自己的技术水平和综合素质。
企业也会为员工提供良好的工作环境和福利待遇,帮助员工实现职业生涯的发展。
(好题)初中数学七年级数学下册第三单元《变量之间的关系》检测题(包含答案解析)

一、选择题1.为了更好地保护水资源,造福人类,某工厂计划建一个容积为200m3的污水处理池,池的底面积S(m2)与其深度h(m)满足关系式:S•h=200,则S关于h的函数图象大致是()A.B.C.D.2.已知圆柱的高为3 cm,当圆柱的底面半径r(cm)由小变大时,圆柱的体积V(cm3)随之变化,则V与r的关系式是 ( )A.V=πr2B.V=9πr2C.V=13πr2D.V=3πr23.用固定的速度向如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是A.B.C.D.4.在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是()x/kg012345y/cm2020.52121.52222.5A.x与y都是变量,且x是自变量,y是x的函数B.弹簧不挂重物时的长度为0 cmC.物体质量每增加1 kg,弹簧长度y增加0.5 cmD.所挂物体质量为7 kg时,弹簧长度为23.5 cm5.下列说法中正确的是 ( )A.变量 x , y 满足 x + 3y = 1 ,则 y 是 x 的函数B.变量 x , y 满足23y x=--,则 y 是 x 的函数C.变量 x , y 满足∣ y ∣= x ,则 y 是 x 的函数D.变量 x , y 满足 y2 = x ,则 y 是 x 的函数6.下列各图给出了变量x 与y 之间的对应关系,其中y 是x 的函数的是( )A .B .C .D .7.根据图示的程序计算变量y 的对应值,若输入变量x 的值为-1,则输出的结果为( )A .-2B .2C .-1D .08.油箱中存油20升,油从油箱中均匀流出,流速为0.2升/分钟,则油箱中剩余油量 Q(升)与流出时间t(分钟)的函数关系是( )A .Q =0.2tB .Q =20﹣0.2tC .t =0.2QD .t =20﹣0.2Q9.如图,在ABC △中,6BC ,AD 为BC 边上的高,A 点沿AD 所在的直线运动时,三角形的面积发生变化,当ABC △的面积为48时,AD 的长为( ).A .8B .16C .4D .2410.如图,在梯形ABCD 中,AD ∥BC ,∠ABC=60º,AB=DC=2,AD=1,R 、P 分别是BC 、CD 边上的动点(点R 、B 不重合,点P 、C 不重合),E 、F 分别是AP 、RP 的中点,设BR=x ,EF=y ,则下列图象中,能表示y 与x 的函数关系的图象大致是A.B.C.D.11.如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F,设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是A.B.C.D.12.某油箱容量为60 L的汽车,加满汽油后行驶了100 Km时,油箱中的汽油大约消耗了1,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解5析式和自变量取值范围分别是( )A .y=0.12x ,x >0B .y=60﹣0.12x ,x >0C .y=0.12x ,0≤x≤500D .y=60﹣0.12x ,0≤x≤500 二、填空题13.拖拉机工作时,油箱中的余油量Q (升)与工作时间t (时)的关系式为406Q t =-.当4t =时,Q =_________,从关系式可知道这台拖拉机最多可工作_________小时.14.如果一个三角形的底边固定,高发生变化时,面积也随之发生改变.现已知底边长为10,则高从3变化到10时,三角形的面积变化范围是____.15.如图,都是由边长为1的正方体叠成的图形。
汽修厂规章制度

汽修厂规章制度
第一条为了规范汽修厂的管理,保障员工和客户的安全,制定本规章制度。
第二条汽修厂的工作时间为每周一至周五上午8:00至下午5:00,中午12:00
至1:00为午休时间。
周六、周日为休息日。
第三条所有员工必须严格遵守工作纪律,不得擅自离岗,不得迟到早退,不
得私自使用公司设备。
第四条员工在工作期间必须穿着工作服,佩戴工牌,不得穿拖鞋、短裤等不
符合工作要求的服装。
第五条汽修厂内禁止吸烟、酗酒,禁止携带易燃易爆物品进入工作区域。
第六条员工必须严格遵守安全操作规程,使用工具和设备时必须佩戴防护用具,确保安全生产。
第七条汽修厂内禁止私自接受客户的私活,不得擅自调换零件,不得私自向
客户收取额外费用。
第八条汽修厂内禁止恶意竞争,不得诋毁竞争对手,不得利用不正当手段获
取客户。
第九条员工之间要相互尊重,不得进行言语或行为上的侮辱、挑衅,不得进
行人身攻击。
第十条对于违反本规章制度的员工,将按照公司规定给予相应的处罚,情节
严重者将予以开除。
第十一条汽修厂的规章制度如有变动,将提前通知员工,并进行相关培训。
以上为汽修厂规章制度,所有员工必须严格遵守,如有违反将受到相应的处罚。
车辆维修工作计划

车辆维修工作计划
一、维修对象及时间
1. 车牌号码:津12345号车
2. 计划维修时间:2021年5月15日上午9:00-中午12:00
二、维修内容
1. 油级及油量检查更换(检查机油级别及量,如需要更换新机油)
2. 变速箱油检查更换(检查变速箱油级别及量,如需要更换新变速箱油)
3. 悬挂系统检查(检查车轮、摇车臂、减震器等状况)
4. 刹车系统检查(检查刹车片、盘带使用情况)
5. 轮胎压力检查充气(检查并按需要充气)
6. 电池电量检查(使用电表检查电量)
7. 内外消毒养护(清洗车内车外,消毒即可养护表面)
三、责任人
1. 执行人:车间车间主任李
2. 监督人:车队长王
四、备注
1. 若发现其他问题及需要维修项目,经监督人同意后可增加对应项目
2. 维修结束后填写工时和耗材明细,盖章备案
以上就是为这辆车制定的"车辆维修工作计划"的初步内容,请检查修改完善。
(完整word版)2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组b卷)

2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B 卷)一、填空题(每小题10分,共80分)1.(10分)1111113352015201711111111123345201520162017---++⋯+=⨯⨯⨯⨯⨯⨯ . 2.(10分)甲、乙两车分别从A 、B 两地同时出发,相向而行,出发时甲乙两车的速度比为5:4.出发后不久,甲车发生爆胎,停车更换轮胎后继续前进,并且将速度提高20%,结果在出发后3小时,与乙车相遇在AB 两地中点,相遇后,乙车继续往前行驶,而甲车掉头行驶,当甲车回到A 地时,乙车恰好到达甲车爆胎的位置,那么甲车更换轮胎用了 分钟.3.(10分)在33⨯的网格中(每个格子是个11⨯的正方形)放两枚相同的棋子,每个格子中最多放一枚棋子,共有 种不同的摆放方法.(如果两种放法能够由旋转而重合,则把它们视为同一种摆放方法).4.(10分)小于1000的自然数中,有 个数的数字组成中最多有两个不同的数字. 5.(10分)如图,ABC ∆的面积为100平方厘米,ABD ∆的面积为72平方厘米.M 为CD 边的中点,90MHB ∠=︒,已知20AB =厘米,则MH 的长度为 厘米.6.(10分)一列数1a 、2a ⋯,n a ⋯,记()i S a 为i a 的所有数字之和,如(22)224S =+=,若12017a =,222a =,12()()n n n a S a S a --=+,那么2017a 等于 .7.(10分)一个两位数,其数字和是它的约数,数字差(较大数减去较小数)也是它的约数,这样的两位数的个数共有 个.8.(10分)如图,六边形的六个顶点分别标志为A ,B ,C ,D ,E ,F .开始的时候“华罗庚金杯赛”六个汉字分别位于A ,B ,C ,D ,E ,F 顶点处.将六个汉字在顶点处任意摆放,最终结果是每个顶点处仍各有一个汉字,每个字在开始位置的相邻顶点处,则不同的摆放方法共有种.二、解答下列各题(每小题10分,共40分)9.(10分)平面上有5条不同的直线,这5条直线共形成m个交点,则m有多少个不同的数值?10.(10分)求能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数.11.(10分)从1001,1002,1003,1004,1005,1006,1007,1008,1009中任意选出四个数,使它们的和为偶数,则共有多少种不同的选法.12.(10分)使3251nn++不为最简分数的三位数n之和等于多少.三、解答下列各题(每小题15分,共30分)13.(15分)一个正六边形被剖分成6个小三角形,如图,在这些小三角形的7个顶点处填上7个不同的整数,能否找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列,如果可以,请给出一种填法;如果不可以,请说明理由.14.(15分)77⨯的方格黑白染色,如果黑格比白格少的列的个数为m,黑格比白格多的行的个数为n,求m n+的最大值.2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B 卷)参考答案与试题解析一、填空题(每小题10分,共80分)1.(10分)1111113352015201711111111123345201520162017---++⋯+=⨯⨯⨯⨯⨯⨯ 2034144 . 【分析】观察一下,首先把分子的两个分数变换一下形式,变成两个分数的乘积,恰好能和分母约分,这样就把原来的繁杂的分数变成简单的整数加减运算.【解答】解:1111113352015201711111111123345201520162017---++⋯+⨯⨯⨯⨯⨯⨯ 31532017201513352015201711111111123345201520162017---⨯⨯⨯=++⋯+⨯⨯⨯⨯⨯⨯111122221335572015201711111111132354576201520172016⨯⨯⨯⨯⨯⨯⨯⨯=+++⋯+⨯⨯⨯⨯⨯⨯⨯⨯ 2(24682016)=⨯++++⋯+ (22016)2016222+=⨯⨯20181008=⨯ 2034144=【点评】本题考查了分数的拆项运算知识,本题突破点:把分子拆分成两个分数的乘积形式,从而和分母约分2.(10分)甲、乙两车分别从A 、B 两地同时出发,相向而行,出发时甲乙两车的速度比为5:4.出发后不久,甲车发生爆胎,停车更换轮胎后继续前进,并且将速度提高20%,结果在出发后3小时,与乙车相遇在AB 两地中点,相遇后,乙车继续往前行驶,而甲车掉头行驶,当甲车回到A 地时,乙车恰好到达甲车爆胎的位置,那么甲车更换轮胎用了 52 分钟.【分析】首先分析后半程冲中点到A的过程,求出两人的速度比就可知道路程比,找到爆胎位置.然后再根据原来的速度比求出正常行驶的时间减去爆胎前的时间.最后根据甲前后两次的速度比求出时间比做差即可.【解答】解:依题意可知:甲乙两车的后来速度比:5(120%):43:2+=,甲回来走3份乙走两份路程.得知甲车爆胎的位置是AC的13处.如果不爆胎的甲行驶的时间和速度成反比:设甲行驶的时间为x则有:4:5:3x=,125 x=甲在行驶AC的爆胎位置到中点的正常时间为:121248(1)53155⨯-==(小时);甲乙爆胎前后的速度比为:5:5(120%)5:6+=;路程一定时间和速度成反比:设爆胎后到中点的时间为y则有:86:5:5y=,43y=;修车时间为:121413353315-⨯-=(小时)13605215⨯=(分)故答案为:52分【点评】本题考查对比例应用题的理解和运用,关键是根据不变量判断正反比,找到甲原来不受影响的时间,再和后面的进行比较做差即可,问题解决.3.(10分)在33⨯的网格中(每个格子是个11⨯的正方形)放两枚相同的棋子,每个格子中最多放一枚棋子,共有10种不同的摆放方法.(如果两种放法能够由旋转而重合,则把它们视为同一种摆放方法).【分析】可以分情况讨论,四个顶点的位值一样,正中间的一个方格一个位值,剩下的四个方格位值相同,故可以分次三种情况分别计算不同的摆放方法.【解答】解:根据分析,份三种情况:①当正中间即E处放一颗棋子,然后另一颗棋子放在外围任意一个位置,除去对称性因素,有2种不同的摆放方法,即AE 、BE ;②当两颗棋子都不在正中间E 处时,而其中有一颗在顶点处时,有4种不同摆法,即AB 、AF 、AH 、AD ;③当两颗棋子都在顶点处时,有2种不同摆法,即AC 、AI ;④当两颗棋子都在除顶点和正中间之外的4个方格中,有2种不同摆法,即BD 、BH .综上,共有:242210+++=种不同摆放方法.【点评】本题考查了排列组合,突破点是:分情况讨论,根据不同的位置求出总的不同摆放方法.4.(10分)小于1000的自然数中,有 352 个数的数字组成中最多有两个不同的数字. 【分析】可以先求出有三个同数字的数的个数,再用总数1000减去后就是符合题意“数字组成中最多有两个不同的数字”的个数.【解答】解:根据分析,小于1000的自然数中,有三个不同数字的数有:998648⨯⨯=个, 则最多有两个不同数字的数有:1000648352-=个. 故答案是:352.【点评】本题考查了数的问题,突破点是:先求有三个不同数字的数的个数,用总数减去即可.5.(10分)如图,ABC ∆的面积为100平方厘米,ABD ∆的面积为72平方厘米.M 为CD 边的中点,90MHB ∠=︒,已知20AB =厘米,则MH 的长度为 8.6 厘米.【分析】可以利用面积公式分别求出ABC ∆、ABD ∆的高,而已知20AB =厘米,再利用MH 的中位线性质求出MH 的长度.【解答】解:根据分析,过D ,C 分别作DE AB ⊥交AB 于E ,CF AB ⊥交AB 于F ,如图:ABD ∆的面积11722022DE AB DE ==⨯⨯=⨯⨯,7.2DE ∴=厘米,ABC ∆的面积111002022CF AB CF ==⨯⨯=⨯⨯,10CF ∴=厘米;又11()(7.210)8.622MH DE CF =⨯+=⨯+=厘米.故答案是:8.6.【点评】本题考查了三角形面积,本题突破点是:利用三角形面积公式先求出高,再利用中位线的关系求出MH 的长.6.(10分)一列数1a 、2a ⋯,n a ⋯,记()i S a 为i a 的所有数字之和,如(22)224S =+=,若12017a =,222a =,12()()n n n a S a S a --=+,那么2017a 等于 10 .【分析】首先要分析清楚()i S a 的含义,即i a 是一个自然数,()i S a 表示i a 的数字和,再根据n a 的递推式列出数据并找出规律.【解答】解:()i S a 表示自然数i a 的数字和,又12()()n n n a S a S a --=+,在下表中列出1n =,2,3,4,⋯时的n a 和()n S a ,nn a ()n S a1 2017 102 22 43 145 4 9 9 5 14 56 14 57 10 1 866由上表可以得出:4289a a ==,428()()9S a S a ==;52914a a ==,529()()5S a S a ==;⋯可以得到规律:当4i 时,24i i a a +=,24()()i i S a S a +=, 201732014-=,2014248322÷=⋯,所以:20173222510a a a +===.【点评】本题重点是弄清楚()i S a 的含义,通过地推找到规律,再进行求解.7.(10分)一个两位数,其数字和是它的约数,数字差(较大数减去较小数)也是它的约数,这样的两位数的个数共有 19 个.【分析】首先看所有的10的倍数都是满足条件的,再找出尾数不为0的满足条件的数字即可,数字不多枚举法解决. 【解答】解:枚举法:(1)尾数为0的有:10,20,30,40,50,60,70,80,90. (2)尾数不为0 的有:12,21,24,36,42,45,48,54,63,84. 故答案为:19【点评】本题是考察因数和倍数的关系,同时关键是在枚举过程中按照顺序,可以是数字和也可以是首位数字的大小,问题解决.8.(10分)如图,六边形的六个顶点分别标志为A ,B ,C ,D ,E ,F .开始的时候“华罗庚金杯赛”六个汉字分别位于A ,B ,C ,D ,E ,F 顶点处.将六个汉字在顶点处任意摆放,最终结果是每个顶点处仍各有一个汉字,每个字在开始位置的相邻顶点处,则不同的摆放方法共有 4 种.【分析】显然,只有两种情况,分别讨论,相邻两个字互换,以及顺时针移动一个位值,或逆时针移动一个位值,最后可以求得总的不同的摆放方法. 【解答】解:根据分析,分两类情况:①按顺序移动一个位置,顺时针移动一个位置,有1种不同摆放方法,逆时针移动一个位置,有1种不同摆放方法;②相邻两个位置互换,则共有:2种不同的摆放方法.综上,共有:1124++=种不同摆放方法.故答案是:4.【点评】本题考查排列组合,突破点是:分情况讨论,相邻两个字互换,以及顺时针移动一个位值,或逆时针移动一个位值,最后求和.二、解答下列各题(每小题10分,共40分)9.(10分)平面上有5条不同的直线,这5条直线共形成m个交点,则m有多少个不同的数值?【分析】分情况讨论m的值,有5条直线平行、4条直线平行,三条直线平行,两条直线平行,0条直线平行,五条直线交于一点,四条直线共点,三条直线共点,分别求得m的数值.【解答】解:根据分析,①若5条直线互相平行,则形成的交点为0,故m为0;②若有4条直线互相平行,则交点个数4m=;③若有三条直线互相平行,则5m=,6,7;④若有两条直线互相平行,则5m=,6,7,8,9;⑤若没有直线平行,则1m=,5,6,7,8,9,10.综上,m的可能取值有:0、1、4、5、6、7、8、9、10共9种不同的数值.故答案是:9.【点评】本题考查了组合图形的计数,本题突破点是:分类讨论,确定m的取值的种类.10.(10分)求能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数.【分析】要使整数最大,且每一位数字都是奇数,必须保证整数的位数足够多,且含有尽量多的1;据此分析解答即可.【解答】解:要使整数最大,且每一位数字都是奇数,必须保证整数的位数足够多,且含有尽量多的1.根据能被7整除的数的特征可得,111111是每个数位均为1且能被7整除的最小数. 又有:20176336163357=⨯+=⨯+当有336个111111组成时,因为所有数字之和要是2017,首位数字只能是1,不能被7整除;当有335个111111组成时,前面还需要加上一个正整数,使得它各位数字之和等于7,且这个数最大.满足这个条件的最大整数是13111.说明:我们可以用以下方法,构造一个能被7整除且除了首位数之外,其余数字均为1的数列如下: 21,49021511+=, 7005111211+=, 56005116111+=, 7000611113111+=, 35000611141111+=, 7000041111111111+=, 7000041111111111+=,我们注意到,7000611113111+=是能被7整除且各位数字之和等于7 的最大正整数. 所以,各位数字和为 2017 的最大正整数1311111⋯,其中1的个数是335642014⨯+=,即201311311111⋯个.答:能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数是201311311111⋯个.【点评】本题关键是根据能被7整除的数的特征得到由数字“1”组成的最小数是111111;难点是寻找同时满足数字和是7的最大整数是13111.11.(10分)从1001,1002,1003,1004,1005,1006,1007,1008,1009中任意选出四个数,使它们的和为偶数,则共有多少种不同的选法.【分析】首先分析如果结果是偶数可以分为0,2,4个奇数,把每一种结果加起来即可. 【解答】解:依题意可知:根据四个数的结果是偶数.那么必定是0个奇数,2个奇数或者是4个奇数.在1001,1002,1003,1004,1005,1006,1007,1008,1009奇数的个数为5个,偶数的个数为4个.当0个奇数时有一种情况.当是2个奇数2个偶数时是225460C C=种.当选择4个奇数时有5种.605166++=(种)答:共有66种选择方法.【点评】本题考查对奇偶性的理解和综合运用,同时关键是分类中的排列组合.问题解决.12.(10分)使3251nn++不为最简分数的三位数n之和等于多少.【分析】3251nn++不为最简,表明(51,32)1n n a++=≠,根据辗转相除原理有1|(51)3(32)5a n n≠+⨯-+⨯即1|7a=≠,则a只能等于7,我们可以用51n+尝试来锁定答案,一次尝试可知511n+=或6或11或16或21,因为2137=⨯,所以5121n+=时7|51n+成立,此时n为最小值,且为4,其它值即可顺次找出,只需要将4递加7即可,题中让我们求的是符合条件的三位数,那么最小为102,最大为998,此后利用等差数列求和即可.【解答】解:3251nn++不为最简,表明(51,32)1n n a++=≠,根据辗转相除原理有1|(51)3(32)5a n n≠+⨯-+⨯即1|7a=≠,则a只能等于7,一次尝试可知511n+=或6或11或16或21,因为2137=⨯,所以5121n+=时7|51n+成立,此时n为最小值,且为4,将4递加7即可,符合条件的三位数,那么最小为102,最大为998,102109116998+++⋯+(102998)1292=+⨯÷70950=答:使3251nn++不为最简分数的三位数n之和等于70950.【点评】考查了辗转相除原理,等差数列求和公式,关键是得到符合条件的三位数,最小为102,最大为998.三、解答下列各题(每小题15分,共30分)13.(15分)一个正六边形被剖分成6个小三角形,如图,在这些小三角形的7个顶点处填上7个不同的整数,能否找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列,如果可以,请给出一种填法;如果不可以,请说明理由.【分析】首先分析最小数字的位置,可以放在圆心出也可以放在外边,两种情况分析即可.【解答】解:依题意可知:分两种情况讨论:假设将最小数放在中心位置,我们只能在外圈顺时针依次从小到达放数字.但是只能满足五个三角形,最后一个三角形无法满足条件.假设将最小的数字放在外圈,然后在周边顺时针依次从小到大放数字,如果想要五个三角形都满足条件,则中心位置必须放大数字,但这样的话,最后一个又不能满足条件.综上所述:不能找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列.【点评】本题是对凑数谜的理解和运用,关键问题是找最小数字的位置.问题解决.14.(15分)77⨯的方格黑白染色,如果黑格比白格少的列的个数为m,黑格比白格多的+的最大值.行的个数为n,求m n+的值最大.【分析】在m取最大值的条件下n尽量取最大值可使m n【解答】解:根据分析,1黑格和白格的行数7;1列数7,当7⨯=.然后,可以把21个m=时,可以设7列之中黑格个数为3,则黑格总数为:3721黑格在15-行之中每行放4个,第6行放1个,第7行不放.这样就有5行中黑格数量超过白格,所以5+=为最大.如下图1所示:m nn=,从而使得12当6m =时,可以设6列之中黑格个数均为3,其余一列黑格个数为7,这样黑格总数为36725⨯+=.然后,我们使得16-行黑格个数为4个,最后一行只有1个.这样就有6行中黑格数列超过白格,所以6n =,从而使得12m n +=,如图2所示:当5m 时,12m n +.综上,m n +的最大值为12.故答案是:12.【点评】本题考查了最大与最小,本题突破点是:在行数和列数的最小与最大的范围内,确定最大值.。
车修理活动方案

车修理活动方案一、背景介绍随着社会经济的发展,汽车已经成为人们生活中不可或缺的交通工具。
然而,随之而来的问题是汽车维修保养费用高昂,很多车主由于经济原因无法及时修理自己的车辆,导致车辆状况逐渐恶化。
为了帮助这些车主解决维修问题,我们计划举办车修理活动,提供免费或者低价的维修服务。
二、活动内容1.时间安排:–活动时间为每周末上午9点至下午5点。
2.地点选择:–在市中心或者人流密集的地区设立维修点,方便车主前来维修。
3.服务项目:–提供免费或者低价的基础维修服务,如更换机油、检查电瓶、轮胎充气等。
4.志愿者招募:–邀请专业汽修技师和爱心志愿者参与活动,确保维修质量和服务态度。
5.宣传推广:–通过社交媒体、宣传单张等途径宣传活动,吸引更多车主参与。
三、活动目标1.服务车主:–帮助有需求的车主解决车辆维修问题,提高道路交通安全。
2.社区互动:–增加社区居民的互动和交流机会,促进社区和谐发展。
3.公益宣传:–通过此类活动传递爱心公益理念,激励更多人积极参与社会公益事业。
四、活动准备1.活动资金:–寻找赞助商或者申请相关资助,确保活动经费充足。
2.场地准备:–选址、搭建帐篷、提供基础设施等。
3.物资准备:–根据活动需求准备维修工具,替换零件等。
4.志愿者培训:–为参与活动的志愿者进行相关培训,确保他们熟知活动流程和维修技巧。
五、活动执行1.活动流程:–到岗签到、车辆接待、检测维修、交车还车等步骤。
2.分工合作:–派遣志愿者分工协作,确保活动有序进行。
3.服务记录:–记录每个车主的服务内容和车辆情况,便于后续跟进。
六、活动评估1.满意度调查:–针对参与活动的车主进行满意度评价,收集意见和建议。
2.效果分析:–分析活动实施过程中的问题及改进措施,总结经验。
结语通过本次车修理活动,我们希望能够帮助更多有需要的车主,传递公益理念,促进社会和谐发展。
让我们共同努力,让爱心传递,让社区更加和谐美好!。
公司车辆维修通知

公司车辆维修通知
尊敬的全体员工:
为了确保公司车辆的正常运行和安全性,现对公司车辆维修进行
通知。
请各位员工务必认真阅读以下内容,并配合做好相关准备工作。
一、维修时间安排
根据公司安排,公司车辆的维修时间将安排在每周六的上午
9:00-12:00。
请各部门负责人提前通知相关驾驶员,确保车辆按时到
达维修点并按时完成维修。
二、维修内容
机油更换:所有公司车辆将进行机油更换,确保发动机正常运转。
轮胎检查:对车辆轮胎进行检查,确保胎压正常,磨损均匀。
刹车系统检修:对刹车系统进行检修,确保刹车灵敏可靠。
发动机检测:对发动机进行全面检测,确保动力系统正常。
灯光检查:对车辆灯光进行检查,确保夜间行驶安全。
三、维修注意事项
请驾驶员提前清理车辆内部物品,以便维修人员操作。
维修期间,请勿在车内吸烟或乱丢杂物,保持车内整洁。
维修结束后,请仔细核对维修单据,确保维修内容无误。
如发现其他问题,请及时向维修人员反映,以便及时处理。
四、维修后的检验
经过维修后,公司将安排专业人员对每辆车进行检验。
请各位驾驶员配合检验工作,并按要求完成相关手续。
五、感谢信
最后,感谢各位员工对公司车辆维护工作的支持与配合。
希望大家能够共同努力,确保公司车辆始终处于良好状态,为公司的发展贡献自己的一份力量。
祝工作顺利!
此致
敬礼
公司管理部敬上。
修程和周期

修程和周期第3条内燃机车应根据其构造特点、运用条件、实际技术状态和一定时期的生产技术水平来确定其检修修程和周期,以保证机车安全可靠地运用。
一、修程:分为大修、架修、定修三级,其中架修和定修为段修修程。
二、周期(公里或期限):各级修程的周期,应按非经该修程不足以恢复其基本技术状态的机车零部件在两次修程间保证安全运用的最短期限确定。
根据当前机车技术状态及生产技术水平,检修周期规定如下:客、货运机车:大修45~54万公里架修两架一大不少于17万公里定修不少于1.7万公里调车机车:大修4.5~6年架修两架一大不少于1年8个月定修不少于2个月架修周期包括新造或大修至架修、架修至架修和架修至大修间的公里或期限。
由于机车担当客、货运输任务不同,各地运用条件差异也较大,各铁路局应根据本规程的要求,结合具体情况,制定本局内燃机车各级修程的周期,并报铁道部核备。
检修周期确定后,在日常掌握中,定修公里或期限允许伸缩10%(但不得少于1.7万公里);架修公里或期限需要延长或缩短时由机务段鉴定,报铁路局审批;大修公里或期限需要延长或缩短时,经机务段鉴定,由铁路局审查,报铁道部(机务局)批准。
检修计划第4条内燃机车检修应按计划均衡地进行。
检修计划由机务段技术室负责会同检修、运用车间,根据机车的实际技术状态、走行公里或期限,以及检修、运用车间的生产安排进行编制。
机务段长应定期检查检修计划的执行情况。
一、定修计划:机车定修月度或旬(周)计划应在月或旬(周)开始前3~5天提出,经机务段长批准,报铁路分局后执行。
运用车间要于机车定修开工48小时前填好“机统一28”,并于24小时前交检修车间。
二、架修计划:机务段在每年度开始前85天编制出分季的年度架修计划报铁路局,铁路局平衡汇总后报铁道部备案。
每季度开始前45天编制出分月的季度架修计划报铁路局,铁路局审查、平衡批准后,于季度开始前30天下达到承修段,并通知到委修段。
委修段于月度开始前25天将架修机车不良状态书寄给承修段。
汽车维修店规章制度

汽车维修店规章制度一、工作时间规定:1.维修店正常工作时间为每周六至周日,上午9点至下午6点。
2.维修店在法定假日、节假日和特殊情况下,可根据实际情况调整工作时间。
3.维修店员工应准时上班,不得迟到早退,如需请假应提前向店长提出申请。
二、员工着装规定:1.维修店员工应穿着整洁的工作服,不得穿拖鞋、短裤等不符合工作要求的服装。
2.长发员工应将头发束起,避免影响工作。
三、工作要求:1.员工应具备相关汽车维修知识和技能,熟悉常见汽车故障及修理方法。
2.员工应各司其职,不得擅自调换工作岗位。
3.员工应认真对待每一位顾客,提供优质的服务。
4.员工应在工作期间保持工作场所整洁,不得随意乱放工具和零件。
5.员工应保持工作区域的安全,正确使用各种设备和工具。
6.员工不得私自接受顾客的私下车辆维修委托。
1.维修店员工应以顾客为中心,礼貌待客,耐心解答顾客的疑问。
2.维修店员工应及时将车辆维修情况反馈给顾客,并向顾客说明维修费用和所需时间。
3.维修店员工应严格按照顾客要求进行维修,不得擅自更换零件或增加维修费用。
4.维修店员工在工作过程中应注意车辆安全,避免损坏客户车辆。
5.维修店应当妥善保管客户车辆及其财物,防止丢失或损坏。
五、物品使用规定:1.维修店员工应妥善使用维修工具和设备,防止损坏。
2.维修店员工应当及时归还使用的工具和设备,禁止私自带离店面。
六、安全操作规定:1.维修店员工应严格遵守维修操作的规范,确保操作安全。
3.维修店员工不得私自调整车辆的相关部件,造成安全隐患。
七、违纪处分规定:1.维修店员工如违反工作时间、员工着装、工作要求等相关规定,将视情节轻重给予相应的处分。
2.严重违反规定的员工将被解除劳动合同,并承担相应的法律责任。
八、规章制度的修改:1.维修店规章制度如有修改,应提前通知员工,并征求员工的意见和建议。
以上为汽车维修店规章制度的主要内容,员工应严格遵守,以确保维修店的正常运营和顾客的满意度。
汽车维修电工的规章制度

汽车维修电工的规章制度第一条维修电工必须严格遵守公司制定的各项规章制度,服从管理,听从指挥,执行任务。
第二条维修电工工作时间为每天8小时,上午8:00-12:00,下午13:00-17:00,中午休息1小时。
第三条维修电工必须严格遵守安全操作规程,穿戴好相应的防护用具,做好安全防护工作,确保人身安全。
第四条维修电工必须具备相关岗位技能证书,经过公司培训合格后方可上岗工作。
第五条维修电工必须维护好所使用的工具和设备,做好日常维护保养工作,确保设备正常运转。
第六条维修电工必须按照公司制定的维修作业流程和标准操作程序进行操作,保证维修质量。
第七条维修电工必须严格按照工作计划和维修任务进行工作,不得擅自更改工作内容。
第八条维修电工在工作过程中如需请假,必须提前向上级领导请示,并经过批准方可请假。
第九条维修电工必须积极保持工作环境的整洁和卫生,不得在工作场所乱丢垃圾。
第十条维修电工必须遵守工作纪律,不得迟到早退,不能私自使用工作时间进行私事。
第十一条维修电工必须做好相关记录工作,包括工作内容、维修项目、维修结果等,确保工作的可追溯性。
第十二条维修电工必须服从公司管理部门的各项管理制度和工作安排,如有违反将受到相应的处罚。
第十三条维修电工接受公司安排的培训和评估,并配合公司开展相关工作。
第十四条维修电工有义务保护公司的商业秘密和客户信息,不得擅自泄露。
第十五条维修电工必须尊重公司领导和同事,保持良好的职业道德和团队合作精神。
第十六条维修电工要不断提升自身技能和知识水平,适应行业发展的需要。
第十七条维修电工如有疾病需要休息,必须提供相关医疗证明,经过公司批准才可休假。
第十八条维修电工在工作中发现安全隐患或问题时,应及时向上级领导报告,协助解决。
第十九条维修电工严禁酗酒、吸毒、晚归或其他违背公司规定的行为,否则将受到相应处理。
第二十条维修电工在工作中遇到困难和问题,应及时向上级领导请示和汇报,寻求解决方案。
第二十一条维修电工如需离职,必须提前一个月向公司提交书面辞职申请,并按照公司规定办理离职手续。
修车总结报告书范文模板(3篇)

第1篇一、报告封面报告名称:修车总结报告报告单位:(单位名称)报告人:(姓名)报告日期:(日期)二、报告目录一、前言二、实习目的与意义三、实习过程概述四、实习内容及心得体会五、实习成果与收获六、实习中存在的问题及改进措施七、实习总结与展望八、附录三、前言随着我国经济的快速发展,汽车行业得到了迅猛的崛起,汽车维修行业作为汽车产业链的重要组成部分,也日益受到重视。
本次实习,旨在通过对汽车维修技术的学习和实践,提高自身的专业技能,为今后从事汽车维修工作打下坚实基础。
四、实习目的与意义1. 通过实习,加深对汽车维修专业知识的理解,提高动手操作能力。
2. 熟悉汽车维修行业的工作流程和标准,为今后就业提供实际经验。
3. 培养团队合作精神,提高沟通协调能力。
4. 激发学习热情,为今后的职业发展奠定基础。
五、实习过程概述本次实习为期一个月,主要在(实习单位名称)进行。
实习期间,我们按照实习大纲的要求,进行了以下工作:1. 参观了实习单位,了解了汽车维修行业的发展现状和维修流程。
2. 在师傅的指导下,学习了汽车维修的基本知识和技能。
3. 参与了实际维修工作,提高了动手操作能力。
4. 通过与同事的交流,培养了团队合作精神。
六、实习内容及心得体会1. 汽车维修基础知识在实习过程中,我们学习了汽车维修的基本知识,包括汽车构造、汽车维修工具、汽车维修工艺等。
通过学习,我们对汽车维修有了更深入的了解。
2. 汽车维修技能在师傅的指导下,我们学习了汽车维修的技能,如发动机维修、底盘维修、车身维修、电气设备维修等。
通过实际操作,我们掌握了汽车维修的基本技能。
3. 团队合作在实习过程中,我们与同事共同完成了多个维修项目,培养了团队合作精神。
通过沟通协调,我们提高了工作效率。
4. 实习心得体会通过本次实习,我深刻认识到以下问题:(1)理论知识与实践操作相结合的重要性。
(2)汽车维修行业的发展前景。
(3)团队合作在汽车维修工作中的重要性。
汽车修理厂规章制度

汽车修理厂规章制度为了规范汽车修理厂的运营,保障员工和顾客的安全,维护良好的工作环境,制定以下规章制度:一、工作时间。
1.1 汽车修理厂的工作时间为每周一至周五,上午8:00至下午5:00,中午12:00至1:00为午休时间。
1.2 周末和法定节假日根据工作情况灵活安排,需提前向主管汇报。
二、员工着装。
2.1 所有员工必须穿着整洁工作服上班,不得穿拖鞋、短裤等不符合工作要求的服装。
2.2 需佩戴安全帽、护目镜等个人防护用品,并遵守相关安全操作规程。
三、工作流程。
3.1 所有维修工作必须按照标准操作流程进行,不得擅自改变或省略步骤。
3.2 对于需要使用特殊工具或设备的维修项目,必须经过相关培训并持有相应资质证书。
四、安全管理。
4.1 员工必须遵守安全操作规程,严禁在未经培训的情况下操作危险设备。
4.2 发现安全隐患或异常情况,应立即向主管报告并采取相应措施。
五、设备维护。
5.1 所有维修设备必须经过定期检查和维护,确保正常运行。
5.2 对于出现故障的设备,应立即停止使用并通知维修人员进行维修处理。
六、顾客服务。
6.1 对顾客要礼貌周到,提供专业的服务和建议。
6.2 对于维修项目,必须提供详细的维修方案和费用预估,不得出现隐瞒或虚假宣传。
七、违规处理。
7.1 对于违反规章制度的员工,将按照公司规定进行相应处理,包括警告、罚款、停职等。
7.2 对于严重违规行为,将按照公司规定进行解雇处理。
以上规章制度,由汽车修理厂全体员工必须严格遵守,违反者将受到相应的处罚。
同时,欢迎员工提出建议和意见,共同维护汽车修理厂的良好秩序和形象。
汽车修理厂规章制度

汽车修理厂规章制度
为了规范汽车修理厂的管理,保障修理工作的顺利进行,特制定以下规章制度:
一、工作时间。
1. 汽车修理厂的工作时间为每周一至周五,上午8:00至下午5:00,中午12:00至1:00为午休时间。
2. 如有特殊情况需要延长工作时间,必须提前向上级汇报并经批准。
二、安全生产。
1. 汽车修理厂必须严格遵守国家安全生产法律法规,加强安全生产教育和培训,确保员工的安全意识和技能。
2. 严禁在未经许可的情况下进行违章操作,如私接电线、乱拉乱接电源等行为。
三、环境保护。
1. 汽车修理厂必须合法排放废气和废水,严禁乱倾倒废弃物和
化学品。
2. 做好废旧机油、废旧电池等有害废弃物的分类收集和处理工作。
四、服务质量。
1. 修理厂必须保证修理质量,对每一辆车进行维修保养前必须
进行全面的检查和测试。
2. 对于客户的投诉和意见必须认真对待,及时处理并做好记录。
五、员工管理。
1. 员工必须遵守公司的规章制度,服从管理,不得擅自离岗或
私自接单。
2. 员工必须保持工作区域的整洁,保持个人形象,不得在工作
时间内私自聊天、打电话等影响工作的行为。
六、其他。
1. 严禁在工作场所吸烟,不得饮酒上班。
2. 严禁擅自调动设备,如需维修或更换设备,必须经过相关部
门的批准和操作。
以上规章制度必须严格执行,违反者将受到相应的处罚。
同时,汽车修理厂的管理者应当定期对规章制度进行检查和修订,以保证
其时效性和有效性。
2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B卷)

2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B 卷)一、填空题(每小题10分,共80分) 1.(10分)++…+= .2.(10分)甲、乙两车分别从A 、B 两地同时出发,相向而行,出发时甲乙两车的速度比为5:4.出发后不久,甲车发生爆胎,停车更换轮胎后继续前进,并且将速度提高20%,结果在出发后3小时,与乙车相遇在AB 两地中点,相遇后,乙车继续往前行驶,而甲车掉头行驶,当甲车回到A 地时,乙车恰好到达甲车爆胎的位置,那么甲车更换轮胎用了到达甲车爆胎的位置,那么甲车更换轮胎用了分钟. 3.(10分)在3×3的网格中(每个格子是个1×1的正方形)放两枚相同的棋子,每个格子中最多放一枚棋子,共有子,每个格子中最多放一枚棋子,共有种不同的摆放方法.(如果两种放法能够由旋转而重合,则把它们视为同一种摆放方法).4.(10分)小于1000的自然数中,有的自然数中,有 个数的数字组成中最多有两个不同的数字.5.(10分)如图,△ABC 的面积为100平方厘米,△ABD 的面积为72平方厘米.M 为CD 边的中点,∠MHB=90°,已知AB=20厘米,则MH 的长度为的长度为 厘米.6.(10分)一列数a 1、a 2…,a n …,记S (a i )为a i 的所有数字之和,如S (22)=2+2=4,若a 1=2017,a 2=22,a n =S (a n ﹣1)+S (a n ﹣2),那么a 2017等于等于 .7.(10分)一个两位数,其数字和是它的约数,数字差(较大数减去较小数)也是它的约数,这样的两位数的个数共有也是它的约数,这样的两位数的个数共有 个. 8.(10分)如图,六边形的六个顶点分别标志为A ,B ,C ,D ,E ,F .开始的时候“华罗庚金杯赛”六个汉字分别位于A ,B ,C ,D ,E ,F 顶点处.将六个汉字在顶点处任意摆放,最终结果是每个顶点处仍各有一个汉字,每个字在开始位置的相邻顶点处,则不同的摆放方法共有位置的相邻顶点处,则不同的摆放方法共有种.二、解答下列各题(每小题10分,共40分)9.(10分)平面上有5条不同的直线,这5条直线共形成m 个交点,则m 有多少个不同的数值?少个不同的数值?10.(10分)求能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数.整数.11.(10分)从1001,1002,1003,1004,1005,1006,1007,1008,1009中任意选出四个数,使它们的和为偶数,则共有多少种不同的选法.任意选出四个数,使它们的和为偶数,则共有多少种不同的选法.12.(10分)使不为最简分数的三位数n之和等于多少.三、解答下列各题(每小题15分,共30分)13.(15分)一个正六边形被剖分成6个小三角形,如图,在这些小三角形的7个顶点处填上7个不同的整数,能否找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列,如果可以,请给出一种填法;如果不可以,请说明理由.14.(15分)7×7的方格黑白染色,如果黑格比白格少的列的个数为m,黑格比的方格黑白染色,如果黑格比白格少的列的个数为白格多的行的个数为n,求m+n的最大值.2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B 卷)参考答案与试题解析一、填空题(每小题10分,共80分) 1.(10分)++…+= 2034144 .【分析】观察一下,首先把分子的两个分数变换一下形式,变成两个分数的乘积,恰好能和分母约分,这样就把原来的繁杂的分数变成简单的整数加减运算.【解答】解:===2×(2+4+6+8+…+2016) =2×=2018×1008 =2034144【点评】本题考查了分数的拆项运算知识,本题考查了分数的拆项运算知识,本题突破点:本题突破点:本题突破点:把分子拆分成两个分数把分子拆分成两个分数的乘积形式,从而和分母约分2.(10分)甲、乙两车分别从A 、B 两地同时出发,相向而行,出发时甲乙两车的速度比为5:4.出发后不久,甲车发生爆胎,停车更换轮胎后继续前进,并且将速度提高20%,结果在出发后3小时,与乙车相遇在AB 两地中点,相遇后,乙车继续往前行驶,而甲车掉头行驶,当甲车回到A 地时,乙车恰好到达甲车爆胎的位置,那么甲车更换轮胎用了到达甲车爆胎的位置,那么甲车更换轮胎用了 52 分钟.【分析】首先分析后半程冲中点到A 的过程,求出两人的速度比就可知道路程比,找到爆胎位置.然后再根据原来的速度比求出正常行驶的时间减去爆胎前的时间.最后根据甲前后两次的速度比求出时间比做差即可. 【解答】解:依题意可知:甲乙两车的后来速度比:5(1+20%):4=3:2,甲回来走3份乙走两份路程.得知甲车爆胎的位置是AC 的处.如果不爆胎的甲行驶的时间和速度成反比:设甲行驶的时间为x 则有:4:5=x :3,x=甲在行驶AC 的爆胎位置到中点的正常时间为:×==(小时);甲乙爆胎前后的速度比为:5:5(1+20%)=5:6;路程一定时间和速度成反比:设爆胎后到中点的时间为y 则有:6:5=:y ,y=; 修车时间为:3﹣×=(小时)=52(分)故答案为:52分【点评】本题考查对比例应用题的理解和运用,关键是根据不变量判断正反比,找到甲原来不受影响的时间,再和后面的进行比较做差即可,问题解决. 3.(10分)在3×3的网格中(每个格子是个1×1的正方形)放两枚相同的棋子,每个格子中最多放一枚棋子,共有子,每个格子中最多放一枚棋子,共有 10 种不同的摆放方法.(如果两种放法能够由旋转而重合,则把它们视为同一种摆放方法).【分析】可以分情况讨论,四个顶点的位值一样,正中间的一个方格一个位值,剩下的四个方格位值相同,故可以分次三种情况分别计算不同的摆放方法.【解答】解:根据分析,份三种情况:①当正中间即E处放一颗棋子,然后另一颗棋子放在外围任意一个位置,除去对称性因素,有2种不同的摆放方法,即AE、BE;②当两颗棋子都不在正中间E处时,而其中有一颗在顶点处时,有4种不同摆法,即AB、AF、AH、AD;③当两颗棋子都在顶点处时,有2种不同摆法,即AC、AI;④当两颗棋子都在除顶点和正中间之外的4个方格中,有2种不同摆法,即BD、BH.综上,共有:2+4+2+2=10种不同摆放方法.【点评】本题考查了排列组合,突破点是:分情况讨论,根据不同的位置求出总的不同摆放方法.4.(10分)小于1000的自然数中,有的自然数中,有 352 个数的数字组成中最多有两个不同的数字.【分析】可以先求出有三个同数字的数的个数,再用总数1000减去后就是符合题意“数字组成中最多有两个不同的数字”的个数.【解答】解:根据分析,小于1000的自然数中,有三个不同数字的数有:9×9×8=648个,则最多有两个不同数字的数有:1000﹣648=352个.故答案是:352.【点评】本题考查了数的问题,突破点是:先求有三个不同数字的数的个数,用总数减去即可.5.(10分)如图,△ABC的面积为100平方厘米,△ABD的面积为72平方厘米.M8.6 厘的长度为 为CD边的中点,∠MHB=90°,已知AB=20厘米,则MH的长度为米.【分析】可以利用面积公式分别求出△ABC、△ABD的高,而已知AB=20厘米,再利用MH的中位线性质求出MH的长度.【解答】解:根据分析,过D,C分别作DE⊥AB交AB于E,CF⊥AB交AB于F,如图:△ABD的面积=72=,∴DE=7.2厘米,△ABC的面积=100=,∴CF=10厘米;又∵MH==×(7.2+10)=8.6厘米.故答案是:8.6.【点评】本题考查了三角形面积,本题突破点是:利用三角形面积公式先求出高,再利用中位线的关系求出MH的长.6.(10分)一列数a1、a2…,a n…,记S(a i)为a i的所有数字之和,如S(22)=2+2=4,若a1=2017,a2=22,a n=S(a n﹣1)+S(a n﹣2),那么a2017等于等于10 .【分析】首先要分析清楚S(a i)的含义,即a i是一个自然数,S(a i)表示a i的数字和,再根据a n的递推式列出数据并找出规律.【解答】解:S(a i)表示自然数a i的数字和,又a n=S(a n﹣1)+S(a n﹣2),在下表中列出n=1,2,3,4,…时的a n和S(a n),n a n S(a n)1 2017 102 22 43 14 54 9 95 14 56 14 57 10 18 6 69 7 710 13 411 11 212 6 613 8 814 14 515 13 416 9 917 13 418 13 419 8 820 12 321 11 222 5 5 23 7 7 24 12 3 25 10 1 26 4 4 27 5 5 28 9 9 29 14 5 30 14 5 31 10 1 3266由上表可以得出:a 4=a 28=9,S (a 4)=S (a 28)=9; a 5=a 29=14,S (a 5)=S (a 29)=5; …可以得到规律:当i ≥4时,a i =a i +24,S (a i )=S (a i +24), 2017﹣3=2014,2014÷24=83…22, 所以:a 2017=a 3+22=a 25=10.【点评】本题重点是弄清楚S (a i )的含义,通过地推找到规律,再进行求解.7.(10分)一个两位数,其数字和是它的约数,数字差(较大数减去较小数)也是它的约数,这样的两位数的个数共有也是它的约数,这样的两位数的个数共有 19 个.【分析】首先看所有的10的倍数都是满足条件的,再找出尾数不为0的满足条件的数字即可,数字不多枚举法解决. 【解答】解:枚举法:(1)尾数为0的有:10,20,30,40,50,60,70,80,90. (2)尾数不为0 的有:12,21,24,36,42,45,48,54,63,84.故答案为:19【点评】本题是考察因数和倍数的关系,本题是考察因数和倍数的关系,同时关键是在枚举过程中按照顺序,同时关键是在枚举过程中按照顺序,同时关键是在枚举过程中按照顺序,可可以是数字和也可以是首位数字的大小,问题解决.8.(10分)如图,六边形的六个顶点分别标志为A ,B ,C ,D ,E ,F .开始的时候“华罗庚金杯赛”六个汉字分别位于A ,B ,C ,D ,E ,F 顶点处.将六个汉字在顶点处任意摆放,最终结果是每个顶点处仍各有一个汉字,每个字在开始位置的相邻顶点处,则不同的摆放方法共有位置的相邻顶点处,则不同的摆放方法共有 4 种.【分析】显然,只有两种情况,分别讨论,相邻两个字互换,以及顺时针移动一个位值,或逆时针移动一个位值,最后可以求得总的不同的摆放方法. 【解答】解:根据分析,分两类情况:①按顺序移动一个位置,①按顺序移动一个位置,顺时针移动一个位置,顺时针移动一个位置,顺时针移动一个位置,有有1种不同摆放方法,种不同摆放方法,逆时针移逆时针移动一个位置,有1种不同摆放方法;②相邻两个位置互换,则共有:2种不同的摆放方法. 综上,共有:1+1+2=4种不同摆放方法. 故答案是:4.【点评】本题考查排列组合,突破点是:分情况讨论,相邻两个字互换,以及顺时针移动一个位值,或逆时针移动一个位值,最后求和.二、解答下列各题(每小题10分,共40分)9.(10分)平面上有5条不同的直线,这5条直线共形成m 个交点,则m 有多少个不同的数值?【分析】分情况讨论m 的值,有5条直线平行、4条直线平行,三条直线平行,两条直线平行,0条直线平行,五条直线交于一点,四条直线共点,三条直线共点,分别求得m的数值.【解答】解:根据分析,①若5条直线互相平行,则形成的交点为0,故m为0;②若有4条直线互相平行,则交点个数m=4;③若有三条直线互相平行,则m=5,6,7;④若有两条直线互相平行,则m=5,6,7,8,9;⑤若没有直线平行,则m=1,5,6,7,8,9,10.综上,m的可能取值有:0、1、4、5、6、7、8、9、10共9种不同的数值.故答案是:9.【点评】本题考查了组合图形的计数,本题突破点是:分类讨论,确定m的取值的种类.10.(10分)求能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数.【分析】要使整数最大,且每一位数字都是奇数,必须保证整数的位数足够多,且含有尽量多的1;据此分析解答即可.【解答】解:要使整数最大,且每一位数字都是奇数,必须保证整数的位数足够多,且含有尽量多的1.根据能被7整除的数的特征可得,111111是每个数位均为1且能被7整除的最小数.又有:2017=6×336+1=6×335+7当有336个111111组成时,因为所有数字之和要是2017,首位数字只能是1,整除;不能被7整除;当有335个111111组成时,前面还需要加上一个正整数,使得它各位数字之和等于7,且这个数最大.满足这个条件的最大整数是13111.整除且除了首位数之外,其余数字其余数字我们可以用以下方法,构造一个能被构造一个能被7整除且除了首位数之外,说明:我们可以用以下方法,均为1的数列如下:21,490+21=511,700+511=1211,5600+511=6111,7000+6111=13111,35000+6111=41111,70000+41111=111111,70000+41111=111111,我们注意到,7000+6111=13111是能被7整除且各位数字之和等于7 的最大正整数.2017 的最大正整数13111…11,其中1的个数是335×所以,各位数字和为所以,各位数字和为6+4=2014,即.答:能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数是.【点评】本题关键是根据能被7整除的数的特征得到由数字“1”组成的最小数是111111;难点是寻找同时满足数字和是7的最大整数是13111.11.(10分)从1001,1002,1003,1004,1005,1006,1007,1008,1009中任意选出四个数,使它们的和为偶数,则共有多少种不同的选法.【分析】首先分析如果结果是偶数可以分为0,2,4个奇数,把每一种结果加起来即可.【解答】解:依题意可知:根据四个数的结果是偶数.那么必定是0个奇数,2个奇数或者是4个奇数. 在1001,1002,1003,1004,1005,1006,1007,1008,1009奇数的个数为5个,偶数的个数为4个.当0个奇数时有一种情况.当是2个奇数2个偶数时是=60种.当选择4个奇数时有5种.60+5+1=66(种)答:共有66种选择方法.【点评】本题考查对奇偶性的理解和综合运用,同时关键是分类中的排列组合.问题解决.12.(10分)使不为最简分数的三位数n之和等于多少.【分析】不为最简,表明(5n+1,3n+2)=a≠1,根据辗转相除原理有1≠a|(5n+1)×3﹣(3n+2)×5即=1≠a|7,则a只能等于7,我们可以用5n+1尝试来锁定答案,一次尝试可知5n+1=1或6或11或16或21,因为21=3×7,所以5n+1=21时7|5n+1成立,此时n为最小值,且为4,其它值即可顺次找出,只需要将4递加7即可,题中让我们求的是符合条件的三位数,那么最小为102,最大为998,此后利用等差数列求和即可.【解答】解:不为最简,表明(5n+1,3n+2)=a≠1,根据辗转相除原理有1≠a|(5n+1)×3﹣(3n+2)×5即=1≠a|7,则a只能等于7,一次尝试可知5n+1=1或6或11或16或21,因为21=3×7,所以5n+1=21时7|5n+1成立,此时n为最小值,且为4,将4递加7即可,符合条件的三位数,那么最小为102,最大为998,102+109+116+…+998=(102+998)×129÷2=70950 答:使不为最简分数的三位数n 之和等于70950.【点评】考查了辗转相除原理,考查了辗转相除原理,等差数列求和公式,等差数列求和公式,等差数列求和公式,关键是得到符合条件的三位关键是得到符合条件的三位数,最小为102,最大为998.三、解答下列各题(每小题15分,共30分)13.(15分)一个正六边形被剖分成6个小三角形,如图,在这些小三角形的7个顶点处填上7个不同的整数,能否找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列,如果可以,请给出一种填法;如果不可以,请说明理由.【分析】首先分析最小数字的位置,首先分析最小数字的位置,可以放在圆心出也可以放在外边,可以放在圆心出也可以放在外边,可以放在圆心出也可以放在外边,两种情况两种情况分析即可.【解答】解:依题意可知:分两种情况讨论:假设将最小数放在中心位置,我们只能在外圈顺时针依次从小到达放数字.但是只能满足五个三角形,最后一个三角形无法满足条件.假设将最小的数字放在外圈,然后在周边顺时针依次从小到大放数字,如果想要五个三角形都满足条件,则中心位置必须放大数字,但这样的话,最后一个又不能满足条件.综上所述:不能找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列.【点评】本题是对凑数谜的理解和运用,本题是对凑数谜的理解和运用,关键问题是找最小数字的位置.关键问题是找最小数字的位置.关键问题是找最小数字的位置.问题解问题解决.14.(15分)7×7的方格黑白染色,的方格黑白染色,如果黑格比白格少的列的个数为如果黑格比白格少的列的个数为m ,黑格比白格多的行的个数为n ,求m +n 的最大值.【分析】在m 取最大值的条件下n 尽量取最大值可使m +n 的值最大.【解答】解:根据分析,1≤黑格和白格的行数≤7;1≤列数≤7,当m=7时,可以设7列之中黑格个数为3,则黑格总数为:3×7=21.然后,可以把21个黑格在1﹣5行之中每行放4个,第6行放1个,第7行不放.这样就有5行中黑格数量超过白格,所以n=5,从而使得m +n=12为最大.如下图1所示:当m=6时,可以设6列之中黑格个数均为3,其余一列黑格个数为7,这样黑格总数为3×6+7=25.然后,我们使得1﹣6行黑格个数为4个,最后一行只有1个.这样就有6行中黑格数列超过白格,所以n=6,从而使得m +n=12,如图2所示:当m ≤5时,m +n ≤12.综上,m +n 的最大值为12.故答案是:12.【点评】本题考查了最大与最小,本题考查了最大与最小,本题突破点是:本题突破点是:本题突破点是:在行数和列数的最小与最大的在行数和列数的最小与最大的范围内,确定最大值.。
事故车维修时效标准
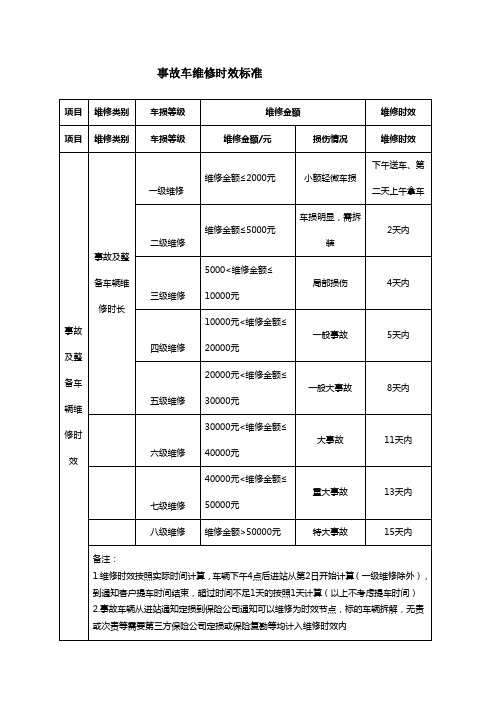
4天内
四级维修
10000元<维修金额≤20000元
一般事故
5天内
五级维修
20000元<维修金额≤30000元
一般大事故
8天内
六级维修
30000元<维修金额≤40000元
大事故
11天内
七级维修
40000元<维修金额≤50000元
重大事故
13天内
八级维修
维修金额>50000元
特大事故
15天内
备注:
4.特殊情况提前报备
注:
1、如各班组未在上述规定的时间内完成修理并交付使用(因公司问题引起的延迟交付不算),需承担公司跟甲方签约的维修超时赔付金,150元/辆/天的违约金直至修理完毕并交付使用,该笔费用从当事班组或个人的工时提成中扣除。
1.维修时效按照实际时间计算,车辆下午4点后进站从第2日开始计算(一级维修除外),到通知客户提车时间结束,超过时间不足1天的按照1天计算(以上不考虑提车时间)
2.事故车辆从进站通知定损到保险公司通知可以维修为时效节点,标的车辆拆解,无责或次责等需要第三方保险公司定损或保险复勘等均计入维修时效内
3.车辆整备维修按照车损等级对应的维修时效考核
事故车维修时效标准
项目
维修类别
车损等级
维修金额
维修时效
项目
维修类别
车损等级
维修金额/元
损伤情况
维修时效
事故及整备车辆维修时效
事故及整备车辆维修时长
一级维修维修金额≤2000元 Nhomakorabea小额轻微车损
下午送车、第二天上午拿车
二级维修
维修金额≤5000元
车损明显,需拆装
修程和周期

修程和周期第3条内燃机车应根据其构造特点、运用条件、实际技术状态和一定时期的生产技术水平来确定其检修修程和周期,以保证机车安全可靠地运用。
一、修程:分为大修、架修、定修三级,其中架修和定修为段修修程。
二、周期(公里或期限):各级修程的周期,应按非经该修程不足以恢复其基本技术状态的机车零部件在两次修程间保证安全运用的最短期限确定。
根据当前机车技术状态及生产技术水平,检修周期规定如下:客、货运机车:大修45~54万公里架修两架一大不少于17万公里定修不少于1.7万公里调车机车:大修4.5~6年架修两架一大不少于1年8个月定修不少于2个月架修周期包括新造或大修至架修、架修至架修和架修至大修间的公里或期限。
由于机车担当客、货运输任务不同,各地运用条件差异也较大,各铁路局应根据本规程的要求,结合具体情况,制定本局内燃机车各级修程的周期,并报铁道部核备。
检修周期确定后,在日常掌握中,定修公里或期限允许伸缩10%(但不得少于1.7万公里);架修公里或期限需要延长或缩短时由机务段鉴定,报铁路局审批;大修公里或期限需要延长或缩短时,经机务段鉴定,由铁路局审查,报铁道部(机务局)批准。
检修计划第4条内燃机车检修应按计划均衡地进行。
检修计划由机务段技术室负责会同检修、运用车间,根据机车的实际技术状态、走行公里或期限,以及检修、运用车间的生产安排进行编制。
机务段长应定期检查检修计划的执行情况。
一、定修计划:机车定修月度或旬(周)计划应在月或旬(周)开始前3~5天提出,经机务段长批准,报铁路分局后执行。
运用车间要于机车定修开工48小时前填好“机统一28”,并于24小时前交检修车间。
二、架修计划:机务段在每年度开始前85天编制出分季的年度架修计划报铁路局,铁路局平衡汇总后报铁道部备案。
每季度开始前45天编制出分月的季度架修计划报铁路局,铁路局审查、平衡批准后,于季度开始前30天下达到承修段,并通知到委修段。
委修段于月度开始前25天将架修机车不良状态书寄给承修段。
修理厂规章制度

修理厂规章制度为了规范修理厂的管理秩序,保障员工和顾客的权益,提高修理质量和效率,特制定以下规章制度:一、工作时间。
1. 修理厂的工作时间为每周一至周五,早上8:00至晚上6:00,周六早上8:00至下午2:00,周日休息。
2. 员工需严格遵守工作时间,不得迟到早退,如有特殊情况需请假,需提前向主管汇报并得到批准。
二、工作服装。
1. 员工需穿着整洁、统一的工作服上岗,不得穿着拖鞋、短裤等不符合工作要求的服装。
2. 需要进行机械操作的员工必须佩戴防护用具,确保人身安全。
三、工作纪律。
1. 员工需严格遵守工作纪律,不得在工作时间内进行私人活动,不得在工作岗位上吸烟、喧哗等影响工作的行为。
2. 不得擅自调动他人工具和设备,不得私自调整机械设备的参数和操作规程。
四、安全管理。
1. 严格遵守安全操作规程,不得违反操作规程进行维修和保养工作。
2. 发现设备故障或安全隐患,需立即向主管报告并采取相应措施,确保员工和顾客的安全。
五、服务规范。
1. 修理厂员工需以客户至上的态度为顾客提供优质的服务,不得对顾客进行不文明、不礼貌的行为。
2. 严禁向顾客提供虚假的维修信息和服务内容,确保维修质量和透明度。
六、违纪处罚。
1. 对于违反规章制度的员工,将给予相应的处罚,包括扣工资、警告、停职甚至解雇等处理。
2. 对于严重违纪的员工,将追究其法律责任。
以上规章制度为修理厂的基本管理制度,所有员工必须严格遵守,如有违反将受到相应的处罚。
希望各位员工共同遵守,共同维护修理厂的良好秩序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
59.5 38 123.5 49 20 16.5 173
合
计
1732
506
2238
201.5
119.5
217.5 337
164 501 149 34.5 38 130 218.5 47 9 252 392.5
物流中心2011年5月份车辆维修时间汇总表
单 位 汽 车 铲 车 合 计 备 注
矿粉车队 原煤车队 钢材调运车队 轧钢车队 炉料车队 一焦化车队 二焦化车队 一炼钢车队 二炼钢车队 一炼铁车队 二炼铁车队 188 354.5 182.5 44.5 24 43 43 27.5 6 207.5 188.5 0 14.5 188 369 182.5 44.5 107 128 156 40.5 16 226.5 351.5
83 85 113 13 10 19 163
合
计
1309
500.5
1809.5
物流中心2011年7月份车辆维修时间汇总表
单 位 汽 车 铲 车 合 计 备 注
矿粉车队 原煤车队 钢材调运车队 轧钢车队 炉料车队 一焦化车队 二焦化车队 一炼钢车队 二炼钢车队 一炼铁车队 二炼铁车队 275 471.5 279 43.5 48 56 101 38 69.5 159 191.5 8 18.5 283 490 279 43.5 107.5 94 224.5 87 89.5 175.5 364.5
208 353.5 204 58.5 8 4.5 41 20.5 17.5 216 217 1348.5
12.5
82.5 111 215.5 26.5 5 140.5 208 801.5
208 366 204 58.5 90.5 115.5 256.5 47 22.5 356.5 425 2150
物流中心2011年4月份车辆维修时间汇总表
159.5 131 179 12
21 53 110.5 27 7 60 177
34 71.5 122.5 44 13 167 400.5
合
计
871.5
462.5
1334
物流中心2011年3月份车辆维修时间汇总表
单
位
汽
车
铲
车
合
计
备
注
矿粉车队 原煤车队 钢材调运车队 轧钢车队 炉料车队 一焦化车队 二焦化车队 一炼钢车队 二炼钢车队 一炼铁车队 二炼铁车队 合 计
合
计
1564.5
632.5
2197
物流中心2011年2月份车辆维修时间汇总表
单 位 汽 车 铲
2 5
车
合
计
备
注
矿粉车队 原煤车队 钢材调运车队 轧钢车队 炉料车队 一焦化车队 二焦化车队 一炼钢车队 二炼钢车队 一炼铁车队 二炼铁车队
157.5 126 179 12 13 18.5 12 17 6 107 223.5
单 位 汽 车 铲
17 20
车
合
计
备
注
矿粉车队 原煤车队 钢材调运车队 轧钢车队 炉料车队 一焦化车队 二焦化车队 一炼钢车队 二炼钢车队 一炼铁车队 二炼铁车队
147 481 149 34.5 27 14.5 59 23 8 228.5 224
11 115.5 159.5 24 1 23.5 168.5
12.5 48 166 16.5 1 7 119.5
14.5 87 201 49.5 111.5 147.5 337
合
计
1351
377.5
1728.5
物流中心2011年1月份车辆维修时间汇总表
单 位 汽 车 铲 车 合 计 备 注
矿粉车队 原煤车队 钢材调运车队 轧钢车队 炉料车队 一焦化车队 二焦化车队 一炼钢车队 二炼钢车队 一炼铁车队 二炼铁车队 205.5 408 277 46 26.5 11.5 45 13 29 180.5 322.5 5 17.5 143.5 5 9 162.5 276.5 5.5 8 211 416 277 46 31.5 29 188.5 18 38 343 599
物流中心2011年8月份车辆维修时间汇总表
单 位 汽 车 铲
7
车
合
计
备
注
矿粉车队 原煤车队 钢材调运车队 轧钢车队 炉料车队 一焦化车队 二焦化车队 一炼钢车队 二炼钢车队 一炼铁车队 二炼铁车队
194.5 402 163 14 2 39 35 33 110.5 140.5 217.5
201.5 402 163 14
