2016学年北京市西城区鲁迅中学七年级(上)数学期中试卷带参考答案
2015-2016年西城区鲁迅中学七年级上期中数学试卷含解析

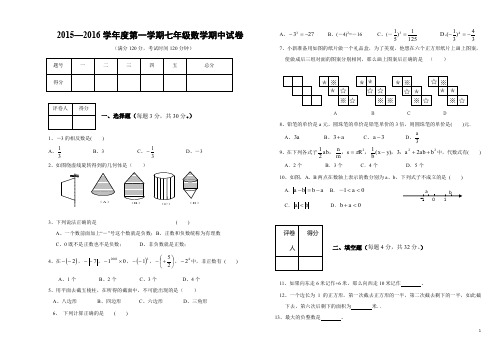
2015-2016学年北京市西城区鲁迅中学七年级(上)期中数学试卷一、选择题:在每小题的四个选项中,只有一项是符合题目要求的.(每小题3分,共30分.)1.﹣5的绝对值等于()A.﹣5 B. C.5 D.2.下列各式中,等号成立的是()A.|﹣a|=a B.﹣32=(﹣3)2C.﹣27=(﹣2)7D.﹣(﹣3)2=﹣(﹣2)33.光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是()A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km4.若>0,则一定有()A.a>0且b>0 B.a<0且b<0C.a,b同正或同负D.不确定5.已知关于x的方程2x+m=5的解是x=﹣1,则m的值为()A.3 B.7 C.﹣7 D.﹣36.下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b7.若﹣1<m<0,则m、m2、的大小关系是()A.m<m2<B.m2<m<C.<m<m2D.m<<m28.下列说法正确的个数有()①若|a|=|b|,则a=b;②若a≠b,则a2≠b2;③若a>b,则a2>b2;④a2>a.A.0个B.1个C.2个D.3个9.当式子(2x﹣1)2+2取最小值时,x等于()A.2 B.﹣2 C.0.5 D.﹣0.510.数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d﹣2a=10,则数轴上原点应是()A.A点 B.B点C.C点D.D点二、填空题:把答案填在题中横线上.(每题2分,共20分.)11.0的相反数为,的倒数为.12.数轴上与原点相距3个单位长度的点有个,它们表示的数各是.13.甲数x的与乙数y的的差可以表示为.14.单项式的系数是,次数是.15.m2﹣n4+3mn+2是次项式.16.m、n两数在数轴上的位置如图,请按从小到大的顺序排列m、n、﹣m、﹣n.17.已知:|x﹣2|+(y+3)2=0,则x2+y2=.18.若2a2m b4和﹣a6b n﹣2是同类项,则m=、n=.19.有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|﹣|c﹣b|﹣|b+a|=.20.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…(1)按此规律写出第6个单项式;(2)试猜想第n个单项式为.三、计算题.(每小题30分,共30分.)21.(1)﹣6﹣7﹣8(2)(3)﹣3x2y+2x2y+3xy2﹣2xy2(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)(5)解方程x+12=4x﹣15(6)解方程:y﹣=2﹣.四、解答题:(本大题共4小题,每小题5分,共20分.)22.求3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab的值,已知4|a﹣1|+8(b+3)2=0.23.已知﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,求a2﹣2a+1的值.24.(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,(1)试求x值;(2)求关于y方程n+|y|=x的解.25.已知:有理数a、b满足ab>0,当时,|y﹣4|=2,3a3z﹣1b与7ba5能够合并,求y ﹣2x+z的值.五、解答题26.(2007•湘潭)为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n27.(2015秋•西城区校级期中)如果a2+a﹣1=0,求a3+2a2+2的值.28.(2015秋•西城区校级期中)如图是一块在电脑屏幕上出现的长方形色块图,它是由6个不同颜色的正方形组成的,已知中间最小的正方形的边长是1cm,则这块长方形色块图的总面积是多少?2015-2016学年北京市西城区鲁迅中学七年级(上)期中数学试卷参考答案与试题解析一、选择题:在每小题的四个选项中,只有一项是符合题目要求的.(每小题3分,共30分.)1.﹣5的绝对值等于()A.﹣5 B. C.5 D.【考点】绝对值.【专题】常规题型.【分析】根据负数的绝对值等于它的相反数解答.【解答】解:﹣5的绝对值|﹣5|=5.故选C.【点评】本题考查了绝对值的性质,熟记一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0是解题的关键.2.下列各式中,等号成立的是()A.|﹣a|=a B.﹣32=(﹣3)2C.﹣27=(﹣2)7D.﹣(﹣3)2=﹣(﹣2)3【考点】有理数的乘方.【分析】根据绝对值的性质,有理数乘方的定义对各选项分析判断后利用排除法求解.【解答】解:A、只有a≥0时,|﹣a|=a成立,故本选项错误;B、﹣32=﹣9,(﹣3)2=9,故本选项错误;C、(﹣2)7=﹣27,故本选项正确;D、﹣(﹣3)2=﹣9,﹣(﹣2)3=8,﹣9≠8,故本选项错误.故选C.【点评】本题考查了有理数的乘方,负数的奇数次幂是负数,负数的偶数次幂是正数,要特别注意﹣32和(﹣2)2的区别.3.光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是()A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将9500 000 000 000km用科学记数法表示为:9.5×1012km.故选:B.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.若>0,则一定有()A.a>0且b>0 B.a<0且b<0C.a,b同正或同负D.不确定【考点】有理数的除法.【分析】根据有理数的除法运算法则,同号得正,异号得负解答.【解答】解:∵>0,∴a>0,b>0或a<0,b<0.故选C.【点评】本题考查了有理数的除法运算,熟记运算符合法则“同号得正,异号得负”是解题的关键.5.已知关于x的方程2x+m=5的解是x=﹣1,则m的值为()A.3 B.7 C.﹣7 D.﹣3【考点】一元一次方程的解.【分析】直接把x=﹣1代入2x+m=5可得关于m的方程,再解即可.【解答】解:把x=﹣1代入2x+m=5得:﹣2+m=5,m=7.故选:B.【点评】此题主要考查了一元一次方程的解,关键是掌握把方程的解代入原方程,等式左右两边相等.6.下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b【考点】合并同类项.【分析】本题考查同类项的概念,含有相同的字母,并且相同字母的指数相同,是同类项的两项可以合并,否则不能合并.合并同类项的法则是系数相加作为系数,字母和字母的指数不变.【解答】解:A、3a与b不是同类项,不能合并.错误;B、3a﹣a=2a.错误;C、2a3与3a2不是同类项,不能合并.错误;D、﹣a2b+2a2b=a2b.正确.故选D.【点评】同类项的概念是所含字母相同,相同字母的指数也相同的项是同类项;注意不是同类项的一定不能合并.7.若﹣1<m<0,则m、m2、的大小关系是()A.m<m2<B.m2<m<C.<m<m2D.m<<m2【考点】有理数大小比较.【分析】本题可采用取特殊值的方法.由于﹣1<m<0,可设m=﹣,然后代入m、m2、中分别计算,然后进行比较即可.【解答】解:根据分析,可设m为﹣,代入可得m=﹣,m2=,=﹣2.即可得.故选C.【点评】本题为简单的有理数比较大小的题目,将满足条件的数字代入即可.8.下列说法正确的个数有()①若|a|=|b|,则a=b;②若a≠b,则a2≠b2;③若a>b,则a2>b2;④a2>a.A.0个B.1个C.2个D.3个【考点】有理数大小比较.【分析】根据绝对值相等的两个数可能相等也可能是相反数可得①错误;根据乘方的计算可得②③④的正误,并且找出错误命题的反例.【解答】解:①若|a|=|b|,则a=b,说法错误,例如:|﹣1|=|1|,但是﹣1≠1;②若a≠b,则a2≠b2,说法正确;③若a>b,则a2>b2;说法错误,例如2>﹣4,但是a2<b2;④a2>a,说法错误,例如0.12<0.1.正确的有1个,故选:B.【点评】此题主要考查了有理数的比较大小,以及绝对值和乘方,关键是错误的命题要正确找出反例.9.当式子(2x﹣1)2+2取最小值时,x等于()A.2 B.﹣2 C.0.5 D.﹣0.5【考点】非负数的性质:偶次方.【分析】根据非负数的性质解答即可.【解答】解:∵(2x﹣1)2,≥0,∴2x﹣1=0时,式子(2x﹣1)2+2取最小值,∴x=0.5.故选:C.【点评】本题考查的是非负数的性质,掌握一个数的偶次方是非负数是解题的关键.10.数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d﹣2a=10,则数轴上原点应是()A.A点 B.B点C.C点D.D点【考点】数轴.【分析】直接利用数轴得出a=d﹣7,再代入已知关系式求出答案.【解答】解:由数轴可得:a=d﹣7,则d﹣2a=d﹣2(d﹣7)=14﹣d=10,解得:d=4.故数轴上原点应是4.故选:C.【点评】此题主要考查了数轴,根据题意得出a=d﹣7是解题关键.二、填空题:把答案填在题中横线上.(每题2分,共20分.)11.0的相反数为0,的倒数为﹣4.【考点】倒数;相反数.【分析】根据相反数、倒数,即可解答.【解答】解:0的相反数是0,﹣的倒数为﹣4,故答案为:0,﹣4.【点评】本题考查了相反数、倒数,解决本题的关键是熟记相反数、倒数的定义.12.数轴上与原点相距3个单位长度的点有2个,它们表示的数各是±3.【考点】数轴.【专题】探究型.【分析】设数轴上与原点相距3个单位长度的点所表示的数为a,再根据数轴上两点间的距离公式求出a的值即可得出结论.【解答】解:设数轴上与原点相距3个单位长度的点所表示的数为a,故|a|=3,解得a=±3.故答案为:2,±3.【点评】本题考查的是数轴的特点,即在数轴上到原点距离相等的点有两个,这两个数互为相反数.13.甲数x的与乙数y的的差可以表示为x﹣y.【考点】列代数式.【分析】被减式为x的,减式为y的,让它们相减即可.【解答】解:所求的关系式为:x﹣y.【点评】求两个式子的差的关键是找到被减式和减式.14.单项式的系数是,次数是3.【考点】单项式.【分析】根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.【解答】解:根据单项式系数、次数的定义可知:单项式的系数是,次数是1+2=3.【点评】确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.15.m2﹣n4+3mn+2是4次4项式.【考点】多项式.【分析】多项式中次数最高的项的次数叫做多项式的次数,多项式的每一项都是一个单项式,单项式的个数就是多项式的项数,进而可得出答案.【解答】解:多项式的最高次数项为:﹣n4,故次数为4;多项式有4个单项式组成,故项数是4.即m2﹣n4+3mn+2是4次4项式.故答案为:4、4.【点评】此题考查了多项式的知识,属于基础题,解答本题的关键是掌握多项式次数及项数的判断方法.16.m、n两数在数轴上的位置如图,请按从小到大的顺序排列m、n、﹣m、﹣n m<﹣n<n<﹣m..【考点】有理数大小比较;数轴.【专题】计算题.【分析】根据数轴表示数的方法得到m<0<n,且|m|>n,则﹣m>n,﹣n>m,即可得到m、n、﹣m、﹣n的大小关系.【解答】解:∵m<0<n,且|m|>n,∴﹣m>n,﹣n>m,∴m、n、﹣m、﹣n的大小关系为m<﹣n<n<﹣m.故答案为m<﹣n<n<﹣m.【点评】本题考查了有理数的大小比较:正数大于零,负数小于零;负数的绝对值越大,这个数反而越小.也考查了数轴.17.已知:|x﹣2|+(y+3)2=0,则x2+y2=13.【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:由题意得,x﹣2=0,y+3=0,解得,x=2,y=﹣3,则x2+y2=13,故答案为:13.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.18.若2a2m b4和﹣a6b n﹣2是同类项,则m=3、n=6.【考点】同类项.【分析】根据同类项的概念求解.【解答】解:∵2a2m b4和﹣a6b n﹣2是同类项,∴2m=6,n﹣2=4,解得:m=3,n=6.故答案为:3,6.【点评】本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.19.有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|﹣|c﹣b|﹣|b+a|=2b﹣2c.【考点】整式的加减;数轴;绝对值.【分析】根据数轴,可得出a+c、c﹣b、a+b的符号,再去绝对值即可.【解答】解:由数轴得,a<b<c,且|a|>|b|>|c|,∴a+c<0,c﹣b>0,b+a<0,∴原式=﹣a﹣c﹣c+b+b+a=2b﹣2c.故答案为2b﹣2c.【点评】本题考查了整式的加减,以及绝对值、数轴,掌握正数的绝对正等于本身,负数的绝对值等于它的相反数,0的绝对值是0是解题的关键.20.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…(1)按此规律写出第6个单项式﹣32x6y;(2)试猜想第n个单项式为(﹣1)n+12n﹣1x n y.【考点】单项式.【专题】规律型.【分析】(1)通过观察题意可得:6为偶数,单项式为负数.x的指数为6时,2的指数为5,由此可解出本题;(2)通过观察题意可得:n为偶数时,单项式为负数.x的指数为n时,2的指数为(n﹣1),由此可解出本题.【解答】解:(1)∵当n=1时,xy,当n=2时,﹣2x2y,当n=3时,4x3y,当n=4时,﹣8x4y,当n=5时,16x5y,∴第6个单项式是﹣26﹣1x6y,即﹣32x6y.故答案为:﹣32x6y.(2)∴n为偶数时,单项式为负数.x的指数为n时,2的指数为n﹣1,∴当n为奇数时的单项式为2n﹣1x n y,该单项式为(﹣1)n+12n﹣1x n y.故答案为:(﹣1)n+12n﹣1x n y.【点评】本题考查的是单项式,根据题意找出各式子的规律是解答此题的关键.三、计算题.(每小题30分,共30分.)21.(1)﹣6﹣7﹣8(2)(3)﹣3x2y+2x2y+3xy2﹣2xy2(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)(5)解方程x+12=4x﹣15(6)解方程:y﹣=2﹣.【考点】有理数的混合运算;解一元一次方程.【分析】(1)根据有理数的减法计算即可;(2)根据有理数的混合计算解答即可;(3)根据合并同类项进行计算即可;(4)根据整式的混合计算即可;(5)利用一元一次方程进行解答即可;(6)利用一元一次方程进行解答即可.【解答】解:(1)﹣6﹣7﹣8=﹣21;(2)=﹣1﹣=﹣1+=;(3)﹣3x2y+2x2y+3xy2﹣2xy2=﹣x2y+xy2;(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)=x﹣3+6x﹣3x2﹣4+6x+2x2=12x﹣7;(5)x+12=4x﹣154x﹣x=27,3x=27,x=9;(6)y﹣=2﹣,10y﹣5(y﹣1)=20﹣2(y+2)10y﹣5y+5=20﹣2y﹣47y=11y=【点评】此题考查有理数混合计算,关键是根据有理数的混合计算顺序、整式的混合计算和解方程计算解答.四、解答题:(本大题共4小题,每小题5分,共20分.)22.求3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab的值,已知4|a﹣1|+8(b+3)2=0.【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【分析】先求出a、b的值,再去小括号,去中括号,合并同类项,最后代入求出即可.【解答】解:∵4|a﹣1|+8(b+3)2=0,∴a﹣1=0,b+3=0,∴a=1,b=﹣3,∴3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab=3a2b﹣[2a2b﹣2ab+a2b﹣4a2]﹣ab=3a2b﹣2a2b+2ab﹣a2b+4a2﹣ab=ab+4a2=1×(﹣3)+4×12=1.【点评】本题考查了整式的加减和求值的应用,解此题的关键是能根据整式的加减法则进行化简,难度不是很大.23.已知﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,求a2﹣2a+1的值.【考点】多项式.【分析】根据多项式的次数为7,项数为3,可得出a的值,继而可得出代数式的值.【解答】解:∵﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,∴3+|a|=7,a﹣4≠0,解得:a=﹣4,故a2﹣2a+1=(a﹣1)2=25.【点评】本题考查了多项式的知识,用到的知识点为:多项式的次数由组成多项式的单项式的最高次数决定;组成多项式的单项式叫做多项式的项,有几项就是几项式.24.(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,(1)试求x值;(2)求关于y方程n+|y|=x的解.【考点】一元一次方程的定义;解一元一次方程.【分析】(1)根据二次项系数为零且一次项系数不为零是一元一次方程,可得n的值,根据解方程,可得方程的解;(2)根据互为相反数的绝对值相等,可得方程的解.【解答】解:(1)由(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,得4﹣n2=0且n﹣2≠0.解得n=﹣2.原方程等价于4x﹣8=0.解得x=2;(2)将n,x的值代入关于y方程n+|y|=x,得﹣2+|y|=2.化简,得|y|=4.解得y=4或y=﹣4.【点评】本题考查了一元一次方程的定义,利用二次项系数为零且一次项系数不为零是一元一次方程得出n的值是解题关键.25.已知:有理数a、b满足ab>0,当时,|y﹣4|=2,3a3z﹣1b与7ba5能够合并,求y﹣2x+z的值.【考点】代数式求值;绝对值;同类项.【分析】先根据ab>0可得出x的值,再由|y﹣4|=2求出y的值,3a3z﹣1b与7ba5能够合并求出z的值,代入代数式进行计算即可.【解答】解:∵ab>0,∴ab同号.当a>0,b>0时,x=2;当a<0,b<0时,x=﹣2.∵|y﹣4|=2,∴y=6或y=2;∵3a3z﹣1b与7ba5能够合并,∴3z﹣1=5,解得z=2.∴当x=2,y=6,z=2时,y﹣2x+z=6﹣4+2=4;当x=2,y=2,z=2时,y﹣2x+z=2﹣4+2=0;当x=﹣2,y=6,z=2时,y﹣2x+z=6+4+2=12;当x=﹣2,y=2,z=2时,y﹣2x+z=2+4+2=8.综上所述,代数式的值为4,0,12或8.【点评】本题考查的是代数式求值,在解答此题时要注意进行分类讨论.五、解答题26.(2007•湘潭)为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n【考点】规律型:图形的变化类.【专题】压轴题;规律型.【分析】观察给出的3个例图,注意火柴棒根数的变化是图②的火柴棒比图①的多6根,图③的火柴棒比图②的多6根,而图①的火柴棒的根数为2+6.【解答】解:第n条小鱼需要(2+6n)根,故选A.【点评】本题考查列代数式,本题的解答体现了由特殊到一般的数学方法(归纳法),先观察特例,找到火柴棒根数的变化规律,然后猜想第n条小鱼所需要的火柴棒的根数.27.(2015秋•西城区校级期中)如果a2+a﹣1=0,求a3+2a2+2的值.【考点】因式分解的应用.【分析】由已知条件得出a2+a=1,通过式子变形和因式分解得出a3+2a2=1,即可得出结果.【解答】解:∵a2+a﹣1=0,∴a2+a=1,∴a3+2a2=a3+a2+a2=a(a2+a)+a2=a+a2=1,∴a3+2a2+2=1+2=3.【点评】本题考查了因式分解的应用、等式变形、代数式的求值;熟练掌握因式分解和等式变形是解决问题的关键.28.(2015秋•西城区校级期中)如图是一块在电脑屏幕上出现的长方形色块图,它是由6个不同颜色的正方形组成的,已知中间最小的正方形的边长是1cm,则这块长方形色块图的总面积是多少?【考点】一元一次方程的应用.【专题】几何图形问题;方程思想.【分析】若设第二小的正方形的边长为xcm.则有两种不同的方法可以表示出长方形的长:根据正方形的边长相等,可得:第一种表示方法为x+x+(x+1);第二种表示方法为(x+2)+(x+3),即可列出方程.【解答】解:设第二小的正方形的边长为xcm,则有:x+x+(x+1)=(x+2)+(x+3),解之得:x=4,所以长方形的长为13cm,宽为11cm,面积=13×11=143cm2.【点评】注意要会由设第二小的正方形的边长,从两个不同的角度去表示长方形的长,从而列出方程.。
北京市西城区七年级(上)期中数学试卷(解析版)

北京市西城区七年级(上)期中数学试卷一.选择题1.如果零上5℃记作+5℃,那么零下5℃记作()A.﹣5 B.﹣10 C.﹣10℃D.﹣5℃2.据统计,2014年国庆黄金周期间,北京全市公园风景区共接待游客约13550000人次,将13550000用科学记数法表示应为()A.1355×104B.1.355×106C.0.1355×108D.1.355×1073.9的倒数是()A.9 B.C.﹣9 D.4.下列说法正确的是()A.整数包括正整数和负整数B.分数包括正分数和负分数C.正有理数和负有理数组成有理数集合D.0既是正整数也是负整数5.在﹣22,(﹣2)2,﹣(﹣2),﹣|0|中,负数的个数是()A.1个B.2个C.3个D.4个6.下面计算正确的是()A.3x2﹣x2=3 B.3a2+2a3=5a5C.3+x=3x D.﹣0.25ab+ba=07.下列去括号正确的是()A.﹣(2x+5)=﹣2x+5 B.C.D.8.已知2x3y2和﹣x3m y2是同类项,则式子4m﹣24的值是()A.20 B.﹣20 C.28 D.﹣289.若两个非零的有理数a、b,满足:|a|=a,|b|=﹣b,a+b<0,则在数轴上表示数a、b的点正确的是()A.B.C. D.10.如果y<0<x,则化简的结果为()A.0 B.﹣2 C.2 D.1二.填空题11.﹣3的倒数是,﹣2的相反数为.12.数轴上到原点的距离等于3个单位长度的点所表示的数为.13.某地某天早晨的气温是18℃,中午上升了4℃,夜间又下降了10℃,那么这天夜间的气温是℃.14.根据要求,取近似数:1.4149≈(精确到百分位);将用科学记数法的数还原:3.008×105= .15.单项式﹣的系数是,次数是.16.多项式5x3y﹣2x2y3﹣3xy+5的次数是.最高次项系数是,常数项是.17.某商品进价为a元,商店将价格提高30%作零售价销售,这时一件商品的售价为.18.任写一个与﹣a2b是同类项的单项式.19.已知(a﹣2)2+|b+3|=0,则a﹣b= .20.定义计算“☆”,对于两个有理数a,b,有a☆b=a+b﹣ab,例如:﹣3☆2=5.则(﹣2☆3)☆0=.三.解答题(21题6分,22题至29题每题5分)21.直接写出计算结果(1)﹣8﹣8= (2)﹣24×(﹣1)=(3)﹣3÷3×= (4)5+5÷(﹣5)=(5)3﹣(﹣1)2= (6)x2y﹣x2y= .22.+4+2.75+(﹣5)23.计算:(﹣28)÷(﹣6+4)+(﹣1)×5.24.﹣12﹣(1﹣0.5)××[2﹣(﹣3)2].25.(+﹣)÷(﹣)26.﹣(3a2b﹣4ab2).27.﹣3(a﹣5)28.先化简,再求值:﹣(x2+3x)+2(4x+x2),其中x=﹣2.29.已知x2﹣3x﹣1=0,求代数式2x﹣2[x﹣(2x2﹣3x+2)]﹣2x2的值.四.解答题(第30题4分,第31题5分)30.已知数a、b、c在数轴上的位置如图所示,化简|a|+|b|+|a+b|﹣|b﹣c|.31.按照规律填上所缺的单项式并回答问题:(1)a、﹣2a2、3a3、﹣4a4,,;(2)试写出第2007个单项式;第2008个单项式;(3)试写出第n个单项式.五.附加题(10分)32.定义:a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是=﹣1,﹣1的差倒数是=.已知a1=﹣,(1)a2是a1的差倒数,则a2= ;(2)a3是a2的差倒数,则a3= ;(3)a4是a3的差倒数,则a4= ,…依此类推,则a2013= .33.已知:a,b互为相反数,c,d互为倒数,x=3(a﹣1)﹣(a﹣2b),y=c2d+d2﹣(+c﹣2),求:﹣的值.参考答案与试题解析一.选择题1.如果零上5℃记作+5℃,那么零下5℃记作()A.﹣5 B.﹣10 C.﹣10℃D.﹣5℃【考点】正数和负数.【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.【解答】解:∵“正”和“负”相对,零上5℃记作+5℃,∴零下5℃记作﹣5℃.故选D.【点评】解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.2.据统计,2014年国庆黄金周期间,北京全市公园风景区共接待游客约13550000人次,将13550000用科学记数法表示应为()A.1355×104B.1.355×106C.0.1355×108D.1.355×107【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:13550000用科学记数法表示应为:1.355×107,故选:D.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.9的倒数是()A.9 B.C.﹣9 D.【考点】倒数.【分析】直接运用倒数的求法解答.【解答】解:∵9×=1,∴9的倒数是,故选:B.【点评】此题考查倒数的意义和求法:乘积是1的两个数互为倒数,是基础题目.4.下列说法正确的是()A.整数包括正整数和负整数B.分数包括正分数和负分数C.正有理数和负有理数组成有理数集合D.0既是正整数也是负整数【考点】有理数.【分析】根据有理数的分类,结合相关概念进行判断即可,整数包括正整数、负整数和0;分数包括正分数和负分数;有理数包括正有理数、负有理数和0;0不是正数也不是负数.【解答】解:整数包括正整数、负整数和0,所以A错误;分数包括正分数和负分数,所以B正确;有理数包括正有理数、负有理数和0,所以C错误;0不是正数也不是负数,所以D错误.故选B.【点评】此题主要考查有理数的概念,理解有理数的分类中各自的含义是解题的关键.5.在﹣22,(﹣2)2,﹣(﹣2),﹣|0|中,负数的个数是()A.1个B.2个C.3个D.4个【考点】正数和负数.【分析】根据小于零的数是负数,可得答案.【解答】解:﹣22是负数,故选:A.【点评】本题考查了正数和负数,注意﹣2的平方与2的平方的相反数之间的区别,负数的相反数是正数,负数的绝对值是它的相反数.6.下面计算正确的是()A.3x2﹣x2=3 B.3a2+2a3=5a5C.3+x=3x D.﹣0.25ab+ba=0【考点】整式的加减.【分析】先判断是否为同类项,若是同类项则按合并同类项的法则合并.【解答】解:A、3x2﹣x2=2x2≠3,故A错误;B、3a2与2a3不可相加,故B错误;C、3与x不可相加,故C错误;D、﹣0.25ab+ba=0,故D正确.故选:D.【点评】此题考查了合并同类项法则:系数相加减,字母与字母的指数不变.7.下列去括号正确的是()A.﹣(2x+5)=﹣2x+5 B.C.D.【考点】去括号与添括号.【专题】常规题型.【分析】去括号时,若括号前面是负号则括号里面的各项需变号,若括号前面是正号,则可以直接去括号.【解答】解:A、﹣(2x+5)=﹣2x﹣5,故本选项错误;B、﹣(4x﹣2)=﹣2x+1,故本选项错误;C、(2m﹣3n)=m﹣n,故本选项错误;D、﹣(m﹣2x)=﹣m+2x,故本选项正确.故选D.【点评】本题考查去括号的知识,难度不大,注意掌握去括号的法则是关键.8.已知2x3y2和﹣x3m y2是同类项,则式子4m﹣24的值是()A.20 B.﹣20 C.28 D.﹣28【考点】同类项.【专题】计算题.【分析】根据同类项相同字母的指数相同可得出m的值,继而可得出答案.【解答】解:由题意得:3m=3,解得m=1,∴4m﹣24=﹣20.故选B.【点评】本题考查同类项的知识,比较简单,注意掌握同类项的定义.9.若两个非零的有理数a、b,满足:|a|=a,|b|=﹣b,a+b<0,则在数轴上表示数a、b的点正确的是()A.B.C. D.【考点】数轴;绝对值.【分析】根据|a|=a得出a是正数,根据|b|=﹣b得出b是负数,根据a+b<0得出b的绝对值比a 大,在数轴上表示出来即可.【解答】解:∵两a、b是两个非零的有理数满足:|a|=a,|b|=﹣b,a+b<0,∴a>0,b<0,∵a+b<o,∴|b|>|a|,∴在数轴上表示为:故选B.【点评】本题考查了数轴,绝对值,有理数的加法法则等知识点,关键是确定出a>0,b<0,|b|>|a|.10.如果y<0<x,则化简的结果为()A.0 B.﹣2 C.2 D.1【考点】有理数的除法;绝对值;约分.【分析】先根据绝对值的性质去掉绝对值,再约分化简即可.【解答】解:∵y<0<x∴xy<0∴=+=1﹣1=0.故选A.【点评】此题主要考查绝对值的化简和分式的运算,准确分析去掉绝对值号是解题的关键.二.填空题11.﹣3的倒数是﹣,﹣2的相反数为2.【考点】倒数;相反数.【分析】根据乘积为1的两个数互为倒数,只有符号不同的两个数互为相反数,可得答案.【解答】解:﹣3的倒数是﹣,﹣2的相反数为 2,故答案为:﹣,2.【点评】本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.12.数轴上到原点的距离等于3个单位长度的点所表示的数为﹣3或3 .【考点】数轴.【分析】此题注意考虑两种情况:该点在原点的左侧,该点在原点的右侧.【解答】解:根据数轴的意义可知,在数轴上与原点的距离等于3个单位长度的点所表示的数是﹣3或3.故答案为:﹣3或3.【点评】主要考查了数轴,要注意数轴上距离某个点是一个定值的点有两个,左右各一个,不要漏掉一种情况.把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.13.某地某天早晨的气温是18℃,中午上升了4℃,夜间又下降了10℃,那么这天夜间的气温是12 ℃.【考点】有理数的加减混合运算.【专题】计算题.【分析】气温上升用加下降用减,列出算式后运用有理数的加减混合运算法则计算.【解答】解:根据题意列算式得:18+4﹣10=22﹣10=12.∴这天夜间的气温是12℃.故应填12.【点评】本题主要考查正负数在实际生活中的意义,所以学生在学这一部分时一定要联系实际,不能死学.14.根据要求,取近似数:1.4149≈ 1.41 (精确到百分位);将用科学记数法的数还原:3.008×105= 300800 .【考点】科学记数法与有效数字.【分析】把千分位上的数子4进行四舍五入即可;通过科学记数法换算成原数,正负符号不变,乘以几次幂就将小数点后移几位,不足的补0.【解答】1.4149≈1.41(精确到千分位);3.008×105=300800,故答案为1.415,300800.【点评】此题考查的是近似数和有效数字,将用科学记数法表示的数改为原数的原理,即科学记数法的逆推,解决本题的关键是熟记通过科学记数法换算成原数,正负符号不变,乘以几次幂就将小数点后移几位,不足的补0.15.单项式﹣的系数是﹣,次数是 3 .【考点】单项式.【分析】根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数,次数为1+2=3.【解答】解:单项式﹣的系数是﹣,次数是1+2=3.故答案为:﹣,3.【点评】考查了单项式,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.16.多项式5x3y﹣2x2y3﹣3xy+5的次数是 5 .最高次项系数是﹣2 ,常数项是+5 .【考点】多项式.【分析】根据多项式的概念及单项式的次数、系数的定义解答.【解答】解:多项式5x3y﹣2x2y3﹣3xy+5的次数是5.最高次项系数是﹣2,常数项是+5.故答案为:5,﹣2,+5.【点评】本题考查了多项式:几个单项式的和叫多项式.多项式中每个单项式都是多项式的项,这些单项式的最高次数,就是这个多项式的次数.17.某商品进价为a元,商店将价格提高30%作零售价销售,这时一件商品的售价为 1.3a .【考点】列代数式.【分析】此题的等量关系:进价×(1+提高率)=售价列出代数式即可.【解答】解:商品的售价为1.3a,故答案为:1.3a【点评】此题考查列代数式,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的数量关系进行解题.有关销售问题中的提高30%名词要理解透彻,正确应用.18.任写一个与﹣a2b是同类项的单项式a2b .【考点】同类项.【专题】开放型.【分析】根据同类项的定义(所含字母相同,相同字母的指数相同),即可解答.【解答】解:与﹣a2b是同类项的单项式是a2b(答案不唯一).故答案是:a2b.【点评】本题考查了同类项的定义,同类项定义中的两个“相同”:相同字母的指数相同,是易混点,因此成了中考的常考点.19.已知(a﹣2)2+|b+3|=0,则a﹣b= 5 .【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.【解答】解:根据题意得,a﹣2=0,b+3=0,解得a=2,b=﹣3,所以,a﹣b=2﹣(﹣3)=2+3=5.故答案为:5.【点评】本题考查了绝对值非负数,平方数非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.20.定义计算“☆”,对于两个有理数a,b,有a☆b=a+b﹣ab,例如:﹣3☆2=5.则(﹣2☆3)☆0= 7 .【考点】有理数的混合运算.【专题】新定义.【分析】根据题中的新定义化简所求式子,计算即可得到结果.【解答】解:根据题意得:(﹣2☆3)☆0=(﹣2+3+6)☆0=7☆0=7+0﹣0=7.故答案为:7【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.三.解答题(21题6分,22题至29题每题5分)21.直接写出计算结果(1)﹣8﹣8= ﹣16 (2)﹣24×(﹣1)= 44(3)﹣3÷3×= ﹣(4)5+5÷(﹣5)= 4(5)3﹣(﹣1)2= 2 (6)x2y﹣x2y= x2y .【考点】合并同类项;有理数的混合运算.【分析】(1)根据有理数的减法,可得答案;(2)有理数的乘法,可得答案;(3)有理数的乘除法,可得答案;(4)根据有理数的混合运算,可得答案;(5)根据有理数的混合运算,可得答案;(6)根据合并同类项系数相加字母及指数不变,可得答案.【解答】解:(1)﹣8﹣8=﹣16 (2)﹣24×(﹣1)=44(3)﹣3÷3×=﹣(4)5+5÷(﹣5)=4(5)3﹣(﹣1)2=2 (6)x2y﹣x2y=x2y,故答案为:﹣16,44,﹣,4,2, x2y.【点评】本题考查了合并同类项法则的应用,注意:合并同类项时,把同类项的系数相加作为结果的系数,字母和字母的指数不变.22.(﹣1.5)+4+2.75+(﹣5)【考点】有理数的加法.【分析】根据加法结合律,可得答案.【解答】解:原式=[(﹣1.5)+(﹣5)]+(4+2.75)=﹣7+7=0.【点评】本题考查了有理数的加法,利用结合律是解题关键,同号结合,同形结合,凑整结合,相反数结合.23.计算:(﹣28)÷(﹣6+4)+(﹣1)×5.【考点】有理数的混合运算.【专题】计算题.【分析】原式先计算乘除运算,再计算加减运算即可得到结果.【解答】解:原式=﹣28÷(﹣2)﹣5=14﹣5=9.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.24.﹣12﹣(1﹣0.5)××[2﹣(﹣3)2].【考点】有理数的混合运算.【专题】计算题;实数.【分析】原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.【解答】解:原式=﹣1﹣××(﹣7)=﹣1+=.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.25.(+﹣)÷(﹣)【考点】有理数的混合运算.【分析】根据有理数的除法和乘法分配律可以解答本题.【解答】解:( +﹣)÷(﹣)=(+﹣)×(﹣36)==(﹣18)+(﹣30)+21=﹣27.【点评】本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.26.(4a2b﹣5ab2)﹣(3a2b﹣4ab2).【考点】整式的加减.【专题】计算题.【分析】先去括号,然后合并同类项即可得出答案.【解答】解:原式=4a2b﹣5ab2﹣3a2b+4ab2=a2b﹣ab2.【点评】本题考查整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.27.(3a﹣2)﹣3(a﹣5)【考点】整式的加减.【专题】计算题.【分析】先去括号,然后合并同类项可得出答案.【解答】解:原式=3a﹣2﹣3a+15=13.【点评】本题考查整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.28.先化简,再求值:﹣(x2+3x)+2(4x+x2),其中x=﹣2.【考点】整式的加减—化简求值.【专题】计算题.【分析】原式去括号合并得到最简结果,将x的值代入计算即可求出值.【解答】解:原式=﹣x2﹣3x+8x+2x2=x2+5x,当x=﹣2时,原式=4﹣10=﹣6.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.29.已知x2﹣3x﹣1=0,求代数式2x﹣2[x﹣(2x2﹣3x+2)]﹣2x2的值.【考点】整式的加减—化简求值.【专题】计算题;整式.【分析】原式去括号合并得到最简结果,已知等式变形后代入计算即可求出值.【解答】解:原式=2x﹣2x+4x2﹣6x+4﹣2x2=2(x2﹣3x)+4,由x2﹣3x﹣1=0,得到x2﹣3x=1,则原式=2+4=6.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.四.解答题(第30题4分,第31题5分)30.已知数a、b、c在数轴上的位置如图所示,化简|a|+|b|+|a+b|﹣|b﹣c|.【考点】整式的加减;数轴;绝对值.【分析】根据数轴判断a、b、a+b、b﹣c与0的大小关系.【解答】解:由数轴可知:a<0,b>0,a+b<0,b﹣c<0,∴原式=﹣a+b﹣(a+b)+(b﹣c)=﹣a+b﹣a﹣b+b﹣c=﹣2a+b﹣c【点评】本题考查利用数轴比较数的大小关系,涉及绝对值的性质,整式加减等知识.31.按照规律填上所缺的单项式并回答问题:(1)a、﹣2a2、3a3、﹣4a4,5a5,﹣6a6;(2)试写出第2007个单项式2007a2007;第2008个单项式﹣2008a2008;(3)试写出第n个单项式(﹣1)n+1na n.【考点】单项式.【分析】(1)通过观察题意可得:每一项都是单项式,其中系数为n×(﹣1)n+1,字母是a,x的指数为n的值;(2)通过观察题意可得:每一项都是单项式,其中系数为n×(﹣1)n+1,字母是a,x的指数为n 的值;(3)通过观察题意可得:每一项都是单项式,其中系数为n×(﹣1)n+1,字母是a,x的指数为n 的值,即可得出答案.【解答】解:(1)a、﹣2a2、3a3、﹣4a4,5a5,﹣6a6;故答案为:5a5,﹣6a6;(2)第2007个单项式:2007a2007;第2008个单项式:﹣2008a2008;故答案为:2007a2007;﹣2008a2008;(3)第n个单项式的系数为:n×(﹣1)n+1,次数为n,故第n个单项式为:(﹣1)n+1na n.故答案为:(﹣1)n+1na n.【点评】此题考查了找规律的单项式题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.五.附加题(10分)32.定义:a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是=﹣1,﹣1的差倒数是=.已知a1=﹣,(1)a2是a1的差倒数,则a2= ;(2)a3是a2的差倒数,则a3= 4 ;(3)a4是a3的差倒数,则a4= ﹣,…依此类推,则a2013= 4 .【考点】规律型:数字的变化类;倒数.【分析】(1)根据定义由a2=可得;(2)由a3=可得;(3)由a4=可得a4,继而可知数列以﹣,,4三个数依次不断循环出现,据此可得答案.【解答】解:(1)根据题意,知a2===,故答案为:;(2)a3===4,故答案为:4;(3)a4===﹣,因此数列以﹣,,4三个数依次不断循环出现.∴2013÷3=671,∴a 2013=a 3=4, 故答案为:﹣,4.【点评】本题主要考查数字的变化规律;得到相应的数据及变化规律是解决本题的关键.33.已知:a ,b 互为相反数,c ,d 互为倒数,x=3(a ﹣1)﹣(a ﹣2b ),y=c 2d+d 2﹣(+c ﹣2),求:﹣的值.【考点】代数式求值.【分析】根据题意得a+b=0,cd=1,求得x ,y ,再代入求值即可. 【解答】解:∵a ,b 互为相反数,c ,d 互为倒数, ∴a+b=0,cd=1,∴x=3(a ﹣1)﹣(a ﹣2b )=3a ﹣3﹣a+2b=2a+2b ﹣3=2(a+b )﹣3=﹣3, y=c 2d+d 2﹣(+c ﹣2)=c 2d+d 2﹣d 2﹣c+2=2, 原式=﹣==;当x=﹣3,y=2时,原式==﹣.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.。
北京市XX中学2016-2017学年度七年级上数学期中试卷含答案

北京市XX 中学2016-2017学年度七年级数学期中测试 2016年11月一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的。
1、某市2013年元旦的最高气温为2℃,最低气温为-8℃,这天的最高气温比最低气温高( )A .-10℃B .-6℃C .6℃D .10℃2、地球与太阳之间的距离约为149600000千米,将149600000用科学记数法表示应为( ).A .5101496⨯B .71096.14⨯C .810496.1⨯D .9101496.0⨯ 3、下列式子中,正确的是 ( ) A .0<-21 B .54<76- C .89> 98 D .4->3- 4、下列式子的变形中,正确的是( )A . 由6+x =10得x =10+6B . 由3x +5=4x 得3x -4x =-5C . 由8x =4-3x 得8x -3x =4D . 由2(x -1)= 3得2x -1=3 5、下列各式中运算正确的是( )A . 43m m -=B . 220a b ab -=C . 33323a a a -=D . 2xy xy xy -=- 6、若0)3-(22=++y x ,则=yx( )A . -8B . -6C . 6D . 87、今年哥哥的年龄是妹妹年龄的2倍,四年前哥哥的年龄是妹妹年龄的3倍,如果设妹妹今年x 岁,可列方程为( )A .2x+4=3(x-4)B .2x-4=3(x-4)C .2x=3(x-4)D .2x-4=3x8、已知代数式-2.5x a+b y a-1与3x 2y 是同类项,则a-b 的值为( )A.2B.0C. 2-D.19、表示x 、y 两数的点在x 轴上的位置如图所示,则x y 1x -+-等于( )A .y -1B .x y 21-+C .x y 21--D .2x -y -110、如图,M N P R ,,,分别是数轴上四个整数所对应的点,其中有一点是原点,并且1MN NP PR ===.数a 对应的点在M 与N 之间,数b 对应的点在P 与R 之间,若3a b +=,则原点可能是( )A .M 或RB .N 或PC .M 或ND .P 或R二、填空题(本题共16分,每小题2分) 11、31-的倒数是 . 12、某商店上月收入为a 元,本月的收入比上月的2倍还多10元,本月的收入是 元.13、若关于x 的一元一次方程23=+x ax 的解是1=x ,则a = . 14、化简3()()2()m n m n m n ---+-的结果是 . 15、当x = 时,代数式534x +的值为2. 16、若代数式2x 2+3y +7的值为8,那么代数式6x 2+9y +8的值为 . 17、定义运算“∆”,对于两个有理数a ,b ,有a ∆b =ab -(a +b ),例如:-3∆2=516)23(23-=+-=+--⨯-,则[]4)1()1(∆-∆-m =___ __. 18、有一列式子,按一定规律排列成-2a 2,4a 5,-8a 10,16a 17,-32a 26,……,第n 个式子为 (n 为正整数).三、解答题(本题共40分,每小题4分)19、计算:(1)23-17-(-7)+(-16) (2) )32(176)211(652-÷⨯-⨯ (3) 2111()()941836-+÷- (4)-72 + 2 ⨯ (-3)2 + (-6) ÷ (-21)3ab x20、化简:(1)3x 2-y 2-3x 2-5y +x 2-5y +y 2 (2) 22123(2)33x y x y --+() 21、求abc c a c a abc b a b a 3431323212222-⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛----的值, 其中a = -1, b = -3, c = 1.22、解方程:(1)90.55.14--=-x x x (2)2(10)6x x x -+=(3)+221=132x x --四、解答题(本题共14分,其中23题4分,24、25每题5分)23、某日,司机小张作为志愿者在东西向的公路上免费接送游客。
北京市第七中学七年级(上)期中数学试卷(含答案解析)

北京市第七中学2015~2016学年度第一学期期中检测试卷初一数学 2015年11月试卷满分:100分 考试时间:100分钟一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.在2,0,1-,2-这四个数中,最小的数是( ).A . 2-B . 1-C .0 D . 1【答案】A 【解析】由题可知,2102-<-<<,最小的数是2-.2.北京时间21日晚间,法国电力公司(E D F )正式宣布,中国广核集团将在英国欣克利角核电项目中投资约58800000000元人民币,所投资的该工程被称为“地球上最昂贵的工程”.将数字58800000000用科学记数法表示为( ).A .858.810⨯B .95.8810⨯C .105.8810⨯D .110.58810⨯【答案】C【解析】58800000000用科学记数法表示为105.8810⨯.3.下列计算正确的是( ).A .(3)(5)8---=-B .239-=-C .()339-=-D .(3)(5)8-+-=+【答案】B【解析】A :(3)(5)352---=-+=,错误;B :239-=-,正确;C :()3327-=-,错误;D :(3)(5)8-+-=-,错误.4.下列各数是方程23515x x -=-的解的是( ).A .3x =B .4x =C .3x =-D .4x =-【答案】B【解析】移项:25153x x -=-+,合并同类项:312x -=-,化x 的系数为1:4x =.5.若21(2)02x y -++=,则2015()xy 的值为( ). A . 1 B . 1- C . 2015- D . 2015【答案】B 【解析】由题可知10220x y ⎧-=⎪⎨⎪+=⎩,解得122x y ⎧=⎪⎨⎪=-⎩, 2015201520151()(2)(1)12xy =-⨯=-=-.6.有理数23-,2(3)-,33-,13-按从小到大的顺序排列是( ). A .22313(3)33-<-<-<- B .322133(3)3-<-<-<- C .22313(3)33-<-<-<- D .232133(3)3-<-<-<-【答案】C【解析】239-=-,2(3)9-=,3327-=,∵99-=,1133-=, ∴193-<-,∴22313(3)33-<-<-<-.7. 在223ab 与232b a ,32x -与32y -,4abc 与cab ,3a 与34,23-与5,234a b c 与234a b 中,同类项有( ). A . 4组 B . 5组 C . 2组 D . 3组【答案】D【解析】由题可知,223ab 与232b a ,4abc 与cab ,23-与5共3组是同类项.8.有理数a ,b 在数轴上的对应点如图所示,则下面式子中正确的是( ).①0b a << ②b a < ③0ab > ④a b a b ->+A .①④B .①②C .②③D .③④【答案】A【解析】∵从数轴可知:0b a <<,b a >,∴①正确;②错误,∵0a >,0b <,∴0ab <,∴③错误;∵0b a <<,b a >,∴0a b ->,0a b +<,∴a b a b ->+,∴④正确;即正确的有①④.9. 若a ,b 互为相反数,且都不为零,则()1(1)a a b b+-+的值为( ). A . 0 B . 1- C . 1 D . 2-【答案】A【解析】a ,b 互为相反数,即0a b +=,1a b=-, 则()1(1)(01)(11)0a a b b+-+=-⨯-+=.10. 若“!”是一种数学运算符号,并且11=!,2212=⨯=!,33216=⨯⨯=!,44321=⨯⨯⨯!,L ,则100!98!的值为( ).A .5049B . 99!C . 9900D . 2!【答案】C 【解析】100!1009998972110099990098!98979621⨯⨯⨯⨯⨯⨯==⨯=⨯⨯⨯⨯⨯L L .二、填空题(本题共20分,每空2分)11.4-的倒数是__________. 【答案】14- 【解析】4-的倒数是14-.12. “m 与n 的平方差”用式子表示为__________.【答案】22m n -【解析】m 与n 的平方差是22m n -.13.若225m x y -是关于x 、y 的五次单项式,则m 为__________. 【答案】3【解析】由题可知,25m +=,即3m =.14.已知多项式22x y +的值是3,则多项式224x y ++的值是__________.【答案】7【解析】∵223x y +=,∴224347x y ++=+=.15.绝对值大于1而小于4的整数有__________.【答案】3±;2±【解析】∵124<±<,134<±<,∴绝对值大于1而小于4的整数有3±,2±.16.已知2x =是关于x 的方程1(2)3x k k x -+=+的解,则k 的值等于__________. 【答案】19【解析】由题可知21(22)3k k -+=+,即143k k +=, 解得19k =.17.已知轮船在静水中前进的速度是m 千米/时,水流的速度是2千米/时,则这轮船在逆水中航行的速度是__________千米/时;顺水中航行的速度是__________千米/时.【答案】2m -;2m +【解析】由题可知,在逆水中航行的速度是(2)2m m +-=-,顺水中航行的速度是2m +.18.根据规律填空: 134+=;1359++=;135716+++=;1357925++++=;L L1357999+++++⋅⋅⋅+=__________.1357999...(21)n +++++⋅⋅⋅++++=__________.【答案】250;2(1)n + 【解析】2231134()22++===;22511359()32+++===;2271135716()42++++===;22911357925()52+++++===;L ;229911357999()502++++++⋅⋅⋅+==; 222111357999...(21)()(1)2n n n +++++++⋅⋅⋅++++==+.三、计算题(本题共16分,每小题4分)19. 3011(10)(12)-+--- 【解析】原式30111012=--+4221=-21=.20.51(3)()(1)64-⨯-÷- 【解析】原式54365=-⨯⨯ 2=-.21.523()(12)1234+-⨯- 【解析】原式523(12)(12)(12)1234=⨯-+⨯--⨯- 589=--+139=-+4=-.22.()()420132163217⎛⎫---÷--- ⎪⎝⎭【解析】原式()1691617⎛⎫=--÷--- ⎪⎝⎭()7916116⎛⎫=--⨯--- ⎪⎝⎭971=-++1=-.四、解下列方程(本题共12分,每小题4分),23. 6745x x -=-【解析】移项:6475x x -=-合并同类项:22x =化x 的系数为1:1x =.24.13624x x -= 【解析】去分母:2243x x -=移项:2324x x -=合并同类项:24x -=化x 的系数为1:24x =-.25.21252x x x +--=- 【解析】去分母:2(2)20105(1)x x x +-=-- 去括号:24201055x x x +-=-+移项:21055420x x x -+=-+合并同类项:321x -=化x 的系数为1:7x =-.五、解答题(本题共5个小题,每小题4分,共20分)26. 合并同类项:223247a a a a -+-【解析】原式2(34)(27)a a =++--279a a =-.27. 化简:()()3322x y y x x ----【解析】原式3924x y y x x =--+-611x y =-.28.先化简,再求值.()2221142()2a b ab a b ---,其中1a =-,13b =. 【解析】原式22212222a b ab a b =--+ 2122ab =-, 当1a =-,13b =时 原式2112(1)()23=-⨯-⨯112(1)29=-⨯-⨯ 1229=+ 1318=.29.已知2320x x -+=,求代数式222(3)261x x x x --++的值.【解析】∵2320x x -+=,∴232x x -=-,22(3)2(2)x x --=--,即:2264x x -+=,222(3)261x x x x --++222(3)2(3)1x x x x =---+2(2)2(2)1=--⨯-+9=.30.有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数 记作负数, 称后的记录如下:1.5 3- 2 0.5- 1 2- 2-2.5-回答下列问题:(1)这8筐白菜中,最接近25千克的那筐白菜为__________千克;(2)以每筐25千克为标准,这8筐白菜总计超过多少千克或不足多少千克?(3)若白菜每千克售价2.6元,则出售这8筐白菜可卖多少元?【解析】(1)24.5千克,绝对值最小的数0.5-,因而是250.524.5-=千克.(2)258(1.5320.5122 2.5)⨯+-+-+---5.5=-,答:这8筐白菜总计不足5.5千克 .(3)由题意可得[825( 5.5)] 2.6505.7⨯+-⨯=元,答:出售这8筐白菜可卖505.7元.六、解答题(本题共2分)31. 阅读下面材料并解决有关问题: 我们知道: (0),0 (0), (0),x x x x x x >⎧⎪==⎨⎪-<⎩现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式, 如化简代数式||12x x ++-时,可令10x +=和20x -=,分别求得1x =-,2x =(称1-,2分别为1x +与|2|x -的零点值). 在实数范围内,零点值1x =-和2x =可将全体实数分成不重复且不遗漏的如下3种情况:(1)1x <-;(2)12x -<≤;(3)2x ≥. 从而化简代数式||12x x ++-可分以下3种情况: (1)当1x <-时,原式(1)(2)21x x x =-+--=-+; (2)当12x -<≤时,原式1(2)3x x =+--=; (3)当2x ≥时,原式1221x x x =++-=-.综上讨论,原式2 1 (1),3 (12),2 1 (2),x x x x x -+<-⎧⎪=-<⎨⎪-⎩≤≥ 通过以上阅读,请你解决以下问题:(1)化简代数式||24x x ++-.(2)求141x x --+的最大值.【解析】(1)①当2x <-时,原式2422x x x ---+=-+; ②当24x -<≤时,原式246x x =+-+=; ③当4x ≥时,原式2422x x x =++-=-.综上讨论,原式2 2 (2),6 (24),2 2 (4),x x x x x -+<-⎧⎪=-<⎨⎪-⎩≤≥.(2)①当1x <-时,原式14435x x x -+++=+;②当11x -<≤时,原式14453x x x =-+--=--; ③当1x ≥时,原式14435x x x =---=--. 综上讨论,原式3 5 (1),5 3 (11),3 5 (1),x x x x x x +<-⎧⎪=---<⎨⎪--⎩≤≥;最大值是2,此时1x =-.。
北京市西城区月坛中学2015-2016学年七年级数学上学期期中试题(含解析) 新人教版

北京市西城区月坛中学2015-2016学年七年级数学上学期期中试题一、选择题:认真是成功的保证(每小题3分,共计30分)1.﹣的相反数是()A.2 B.﹣2 C.D.﹣2.在﹣32,(﹣3)2,﹣(﹣3),﹣|﹣3|中,负数的个数是()A.l个B.2个C.3个D.4个3.有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是()A.a>b B.a<b C.ab>0 D.4.我国的陆地面积为9600000平方千米,9600000用科学记数法可表示为()A.96×105B.9.6×106C.0.96×107D.960×1045.下面各式中,与﹣2xy2是同类项的是()A.y2x B.4x2y C.﹣2ab2D.﹣5xy2z6.下列计算正确的是()A.2a+2b=4ab B.3x2﹣x2=2 C.5mn﹣5nm=0 D.a﹣a=a27.下列代数式书写规范的是()A.8x2y B.C.ax3 D.2m÷n8.对于多项式﹣x3﹣3x2+x﹣7,下列说法正确的是()A.最高次项是x3 B.二次项系数是3C.常数项是7 D.是三次四项式9.原产量是a吨,增产30%后的产量是()A.(1﹣30%)a B.(1+30%)a C.a+30% D.30%a10.如果x是最大的负整数,y是绝对值最小的整数,则﹣x2010+y的值是()A.﹣2008 B.﹣1 C.1 D.2008二、填空题:沉着冷静是成功的法宝(每题2分,共计20分)11.的绝对值是,的倒数是.12.单项式的系数是,次数是.13.多项式x2﹣3kxy﹣3y2+6xy﹣8不含xy项,则k= .14.如图是一数值转换机,若输入的x为﹣1,则输出的结果为.15.绝对值小于2的所有整数有.16.数轴上到原点的距离等于3个单位长度的点所表示的数为.17.如果多项式3x2+2xy n+y2是个三次多项式,那么n= .18.已知|a|=2,|b|=5,且ab<0,那么a+b的值为.19.如果有|x﹣3|+(y+4)2=0,则x= ,y x= .20.观察下列单项式:﹣x,3x2,﹣5x3,7x4按此规律,第n个单项式表示为.三、解答题:细心是成功的关键(每题4分,共计28分)21.把下面的有理数填在相应的大括号里:(★友情提示:将各数用逗号分开)15,,0,﹣30,0.15,﹣128,,+20,﹣2.6正数集合{ ﹜;负数集合﹛﹜;整数集合﹛﹜;非负数集合﹛﹜.22.计算:23﹣37+3﹣52.23.计算:(﹣+)÷(﹣)24.25.化简:3x2﹣3+x﹣2x2+5.26.计算:﹣x+(2x﹣2)﹣(3x+5)27.定义新运算,规定运算*是a*b=ab﹣a+b,求(﹣3)*4的值.四、综合应用(共计22分)28.画出数轴,在数轴上表示下列各数,并用“<”连接:﹣3.5,,﹣1,4,0,2.5.29.先化简,再求值:5(3a2b﹣ab2)﹣3(ab2+5a2b),其中a=,b=﹣.30.有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:回答下列问题:(1)这8筐白菜中最接近标准重量的这筐白菜重千克;(2)这8筐白菜一共重多少千克?31.已知有理数a,b,c在数轴上的位置如图所示,(1)用<,>,=填空:a+c 0,c﹣b 0,b+a 0,abc 0;(2)化简:|a+c|+|c﹣b|﹣|b+a|.五、附加题32.(2015秋•西城区校级期中)观察下列各式: =1﹣, =﹣, =﹣,…(1)请根据以上的式子填写下列各题:①= ;②= .(n是正整数)(2)由以上的几个式子及你找到的规律计算:.33.(2011•凉山州)我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等.(1)根据上面的规律,写出(a+b)5的展开式.(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.2015-2016学年北京市西城区月坛中学七年级(上)期中数学试卷参考答案与试题解析一、选择题:认真是成功的保证(每小题3分,共计30分)1.﹣的相反数是()A.2 B.﹣2 C.D.﹣【考点】相反数.【分析】根据只有符号不同的两个数叫做互为相反数解答.【解答】解:﹣的相反数是.故选C.【点评】本题考查了相反数的定义,是基础题,熟记概念是解题的关键.2.在﹣32,(﹣3)2,﹣(﹣3),﹣|﹣3|中,负数的个数是()A.l个B.2个C.3个D.4个【考点】正数和负数.【分析】先把各数化简,再根据负数的定义,即可解答.【解答】解:﹣32=﹣9,(﹣3)2=9,﹣(﹣3)=3,﹣|﹣3|=﹣3,﹣9,﹣3是负数,共2个.故选:B.【点评】本题考查了正数和负数,解决本题的关键是先把各数化简.3.有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是()A.a>b B.a<b C.ab>0 D.【考点】有理数大小比较;数轴;有理数的乘法;有理数的除法.【分析】根据数轴上的点表示数的特点:右边的数大于左边的数,再结合有理数的乘除法法则求得结果.【解答】解:由图可知:b<0,a>0,根据正数大于一切负数,所以a>b.故选:A.【点评】由于引进了数轴,我们把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.4.我国的陆地面积为9600000平方千米,9600000用科学记数法可表示为()A.96×105B.9.6×106C.0.96×107D.960×104【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将9600000用科学记数法表示为:9.6×106.故选:B.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.下面各式中,与﹣2xy2是同类项的是()A.y2x B.4x2y C.﹣2ab2D.﹣5xy2z【考点】同类项.【分析】同类项的定义是所含有的字母相同,并且相同字母的指数也相同的项叫同类项,所以只要判断所含有的字母是否相同,相同字母的指数是否相同即可.【解答】解:由同类项的定义可知,x的指数是1,y的指数是2.A、正确,因为x的指数是1,y的指数是2;B、不正确,因为x的指数是2,y的指数是1;C、不正确,因为其所含的字母不相同;D、不正确,因为其所含的字母不相同.故选A.【点评】判断两个项是不是同类项,只要两看,即一看所含有的字母是否相同,二看相同字母的指数是否相同.6.下列计算正确的是()A.2a+2b=4ab B.3x2﹣x2=2 C.5mn﹣5nm=0 D.a﹣a=a2【考点】合并同类项.【分析】根据同类项的概念及合并同类项的法则得出.【解答】解:A、字母不同,不是同类项,不能合并,错误;B、3x2﹣x2=2x2,错误;C、正确;D、a﹣a=0,错误.故选C.【点评】本题主要考查同类项的概念和合并同类项的法则.同类项的概念是所含字母相同,相同字母的指数也相同的项是同类项,不是同类项的一定不能合并.合并同类项的法则,即系数相加作为系数,字母和字母的指数不变.7.下列代数式书写规范的是()A.8x2y B.C.ax3 D.2m÷n【考点】代数式.【专题】分类讨论.【分析】根据代数式的书写要求判断各项即可得出正确答案.【解答】解:选项A正确,B正确的书写格式是b,C正确的书写格式是3ax,D正确的书写格式是.故选A.【点评】代数式的书写要求:(1)在代数式中出现的乘号,通常简写成“•”或者省略不写;(2)数字与字母相乘时,数字要写在字母的前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.8.对于多项式﹣x3﹣3x2+x﹣7,下列说法正确的是()A.最高次项是x3 B.二次项系数是3C.常数项是7 D.是三次四项式【考点】多项式.【分析】根据几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数进行分析即可.【解答】解:多项式﹣x3﹣3x2+x﹣7最高次项是﹣x3,二次项系数是﹣3,常数项是﹣7,是三次四项式,故选:D.【点评】此题主要考查了多项式,题目比较基础,关键是掌握和多项式有关的定义.9.原产量是a吨,增产30%后的产量是()A.(1﹣30%)a B.(1+30%)a C.a+30% D.30%a【考点】列代数式.【分析】原产量a吨,增产30%之后的产量为a+a×30%,再进行化简即可.【解答】解:由题意得,增产30%之后的产量为a+a×30%=(1+30%)a吨.故选:B.【点评】本题考查了根据实际问题列代数式,列代数式要分清语言叙述中关键词语的意义,理清它们之间的数量关系.10.如果x是最大的负整数,y是绝对值最小的整数,则﹣x2010+y的值是()A.﹣2008 B.﹣1 C.1 D.2008【考点】代数式求值;有理数.【分析】先求出x、y的值,再代入求出即可.【解答】解:∵x是最大的负整数,y是绝对值最小的整数,∴x=﹣1,y=0,∴﹣x2010+y=﹣(﹣1)2010=0=﹣1.故选B.【点评】本题考查了求代数式的值,有理数的应用,能根据题意求出x、y的值是解此题的关键.二、填空题:沉着冷静是成功的法宝(每题2分,共计20分)11.的绝对值是,的倒数是.【考点】倒数;绝对值.【分析】根据绝对值、倒数,即可解答.【解答】解:﹣的绝对值为,1的倒数为.故答案为:,.【点评】本题考查了绝对值、倒数,解决本题的关键是熟记绝对值、倒数的定义.12.单项式的系数是﹣,次数是 3 .【考点】单项式.【分析】单项式中的数字因数叫做单项式的系数,一个单项式中所有字母的指数的和叫做单项式的次数.【解答】解:单项式的系数是﹣,次数是3.故答案为:﹣;3.【点评】本题考查了单项式的知识,解答本题的关键是掌握单项式次数及系数的定义.13.多项式x2﹣3kxy﹣3y2+6xy﹣8不含xy项,则k= 2 .【考点】多项式.【专题】方程思想.【分析】先将原多项式合并同类项,再令xy项的系数为0,然后解关于k的方程即可求出k.【解答】解:原式=x2+(﹣3k+6)xy﹣3y2﹣8,因为不含xy项,故﹣3k+6=0,解得:k=2.故答案为:2.【点评】本题考查了合并同类项法则及对多项式“项”的概念的理解,题目设计巧妙,有利于培养学生灵活运用知识的能力.14.如图是一数值转换机,若输入的x为﹣1,则输出的结果为9 .【考点】有理数的混合运算.【专题】图表型.【分析】根据运算规则:先﹣2,再×(﹣3),进行计算即可求解.【解答】解:(﹣1﹣2)×(﹣3)=(﹣3)×(﹣3)=9.故答案为:9.【点评】此题主要考察根据运算规则列式计算,读懂题中的运算规则,并准确代入求值是解题的关键.15.绝对值小于2的所有整数有0,1,﹣1 .【考点】有理数大小比较;绝对值.【分析】根据绝对值的性质即可得出结论.【解答】解:∵|x|<2,且x为整数,∴﹣2<x<2,∴x=0,±1.故答案为:0,1,﹣1.【点评】本题考查的是有理数的大小比较,熟知绝对值的性质是解答此题的关键.16.数轴上到原点的距离等于3个单位长度的点所表示的数为﹣3或3 .【考点】数轴.【分析】此题注意考虑两种情况:该点在原点的左侧,该点在原点的右侧.【解答】解:根据数轴的意义可知,在数轴上与原点的距离等于3个单位长度的点所表示的数是﹣3或3.故答案为:﹣3或3.【点评】主要考查了数轴,要注意数轴上距离某个点是一个定值的点有两个,左右各一个,不要漏掉一种情况.把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.17.如果多项式3x2+2xy n+y2是个三次多项式,那么n= 2 .【考点】多项式.【分析】根据多项式次数的定义求得n的值.【解答】解:该多项式共有三项:3x2、2xy n、y2,其中3x2、y2是二次项,2xy n是三次项,根据单项式的次数的定义,1+n=3,解得n=2.故答案为:2.【点评】此题考查了多项式的次数:多项式里次数最高项的次数,叫做这个多项式的次数.18.已知|a|=2,|b|=5,且ab<0,那么a+b的值为3或﹣3 .【考点】有理数的乘法;绝对值;有理数的加法.【专题】计算题.【分析】根据题意可得a和b异号,分情况讨论①a>0,b<0;②a<0,b>0.【解答】解:①a>0,b<0,则a=2,b=﹣5,a+b=﹣3;②a<0,b>0,则a=﹣2,b=5,a+b=3.故填3或﹣3.【点评】本题考查有理数的加法,注意讨论a和b的取值范围得出a和b的值是关键.19.如果有|x﹣3|+(y+4)2=0,则x= ﹣3 ,y x= ﹣64 .【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:由题意得,x﹣3=0,y+4=0,解得,x=3,y=﹣4,则y x=﹣64,故答案为:﹣3;﹣64.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.20.观察下列单项式:﹣x,3x2,﹣5x3,7x4按此规律,第n个单项式表示为(﹣1)n(2n﹣1)x n.【考点】单项式.【专题】规律型.【分析】根据题意可得,单项式的系数为:(﹣1)n(2n﹣1),次数为n,据此写出第n个单项式.【解答】解:第n个单项式为:(﹣1)n(2n﹣1)x n.故答案为:(﹣1)n(2n﹣1)x n.【点评】本题考查了单项式的知识,数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式.三、解答题:细心是成功的关键(每题4分,共计28分)21.把下面的有理数填在相应的大括号里:(★友情提示:将各数用逗号分开)15,,0,﹣30,0.15,﹣128,,+20,﹣2.6正数集合{ 15,0.15,,+20 ﹜;负数集合﹛﹣,﹣30,﹣128,﹣2.6 ﹜;整数集合﹛15,0,﹣30,+20 ﹜;非负数集合﹛15,0,0.15,,+20 ﹜.【考点】有理数.【分析】根据有理数的分类填空即可.【解答】解:正数集合为:15,0.15,,+20;负数集合为:﹣,﹣30,﹣128,﹣2.6;整数集合为:15,0,﹣30,+20;非负数集合为:15,0,0.15,,+20.故答案为:15,0.15,,+20;﹣,﹣30,﹣128,﹣2.6;15,0,﹣30,+20;15,0,0.15,,+20.【点评】本题考查了有理数的分类,解题的关键是正确掌握分类的标准以及注意0既不是正数也不是负数.22.计算:23﹣37+3﹣52.【考点】有理数的加减混合运算.【分析】根据有理数加减混合运算法则计算即可.【解答】解:23﹣37+3﹣52=23+3﹣37﹣52=26﹣89=﹣63.【点评】本题考查的是有理数加减混合运算,掌握有理数加减混合运算的法则是解题的关键.23.计算:(﹣+)÷(﹣)【考点】有理数的除法.【分析】首先根据除以一个不为0的数等于乘以这个数的倒数可得(﹣+)×(﹣36),再用乘法分配律计算即可.【解答】解:原式=(﹣+)×(﹣36),=×(﹣36)﹣×(﹣36)+×(﹣36),=﹣8+9﹣2,=﹣1.【点评】此题主要考查了有理数的除法,关键是掌握有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数.24.【考点】有理数的混合运算.【分析】利用有理数的运算法则,注意有理数乘方的运算法则,即可求出.【解答】解:,=﹣1××﹣,=,=﹣.【点评】此题主要考查了有理数的运算,以及有理数乘方运算,题目比较简单.25.化简:3x2﹣3+x﹣2x2+5.【考点】合并同类项.【分析】首先找出同类项,进而合并同类项得出答案.【解答】解:3x2﹣3+x﹣2x2+5=(3x2﹣2x2)+x+(5﹣3)=x2+x+2.【点评】此题主要考查了合并同类项,正确找出同类项是解题关键.26.计算:﹣x+(2x﹣2)﹣(3x+5)【考点】整式的加减.【专题】计算题.【分析】原式去括号合并即可得到结果.【解答】解:原式=﹣x+2x﹣2﹣3x﹣5=﹣2x﹣7.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.27.定义新运算,规定运算*是a*b=ab﹣a+b,求(﹣3)*4的值.【考点】有理数的混合运算.【专题】新定义.【分析】根据新定义的运算规则:等于两个数的积﹣第一个数+第二个数,代入计算即可.【解答】解:(﹣3)*4=(﹣3)×4﹣(﹣3)+4=﹣12+3+4=﹣5.【点评】此题主要考察新定义的运算,理清运算规则并准确代入计算是解题的关键.四、综合应用(共计22分)28.画出数轴,在数轴上表示下列各数,并用“<”连接:﹣3.5,,﹣1,4,0,2.5.【考点】有理数大小比较;数轴.【分析】先在数轴上表示出来,再根据数轴上表示的数,右边的数总比左边的数大比较即可.【解答】解:如图所示:用“<”连接为:﹣3.5<﹣1<0<<2.5<4.【点评】本题考查了数轴和有理数的大小比较的应用,注意:在数轴上表示的数,右边的数总比左边的数大,难度不是很大.29.先化简,再求值:5(3a2b﹣ab2)﹣3(ab2+5a2b),其中a=,b=﹣.【考点】整式的加减—化简求值.【分析】首先根据整式的加减运算法则将原式化简,然后把给定的值代入求值.注意去括号时,如果括号前是负号,那么括号中的每一项都要变号;合并同类项时,只把系数相加减,字母与字母的指数不变.【解答】解:原式=15a2b﹣5ab2﹣3ab2﹣15a2b=﹣8ab2,当a=,b=﹣时,原式=﹣8××=﹣.【点评】熟练地进行整式的加减运算,并能运用加减运算进行整式的化简求值.30.有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:回答下列问题:(1)这8筐白菜中最接近标准重量的这筐白菜重24.5 千克;(2)这8筐白菜一共重多少千克?【考点】正数和负数.【专题】应用题;图表型.【分析】(1)绝对值最小的数,就是最接近标准重量的数;(2)用25乘以8的积,加上图中八个数的和即可求得.【解答】解:(1)最接近的是:绝对值最小的数,因而是25﹣0.5=24.5千克;(2)由题意可得:25×8+1.5﹣3+2﹣0.5+1﹣2﹣2.5﹣2=200+4.5﹣10=194.5kg.∴这8筐白菜共重194.5kg.【点评】用正数表示其中一种意义的量,另一种量用负数表示;特别地,在用正负数表示向指定方向变化的量时,通常把向指定方向变化的量规定为正数,而把向指定方向的相反方向变化的量规定为负数.31.已知有理数a,b,c在数轴上的位置如图所示,(1)用<,>,=填空:a+c <0,c﹣b >0,b+a <0,abc >0;(2)化简:|a+c|+|c﹣b|﹣|b+a|.【考点】有理数大小比较;数轴;绝对值.【分析】(1)根据数轴,判断出a,b,c的取值范围,进而求解;(2)根据绝对值的性质,去绝对值号,合并同类项即可.【解答】解:(1)根据数轴可知:a<b<0<c,且|c|<|b|<|a|,∴a+c<0,c﹣b>0,b+a<0,abc>0,故答案为:<,>,<,>;(2)原式=﹣(a+c)+(c﹣b)+(b+a)=﹣a﹣c+c﹣b+b+a=0.【点评】本题主要考查数轴、绝对值、整式的加减等知识的综合运用,解决此题的关键是能够根据数轴上的信息,判断出a,b,c等字母的取值范围,同时解决此题时也要注意绝对值性质的运用.五、附加题32.(2015秋•西城区校级期中)观察下列各式: =1﹣, =﹣, =﹣,…(1)请根据以上的式子填写下列各题:①= ﹣;②= ﹣.(n是正整数)(2)由以上的几个式子及你找到的规律计算:.【考点】有理数的混合运算.【专题】规律型.【分析】(1)由于: =1﹣, =﹣, =﹣,…,利用题目规律即可求出结果;(2)根据=﹣,可得原式=1﹣+﹣+﹣+…+﹣,然后利用有理数的加减混合运算法则计算即可求解.【解答】解:(1)①=﹣;②=﹣(n是正整数).故答案为﹣,﹣;(2)原式=1﹣+﹣+﹣+…+﹣=1﹣=.【点评】此题主要考查了有理数的混合运算,解题时首先正确理解题目中隐含的规律,然后利用规律把题目变形,从而使计算变得比较简便.33.(2011•凉山州)我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等.(1)根据上面的规律,写出(a+b)5的展开式.(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.【考点】规律型:数字的变化类.【专题】压轴题;规律型.【分析】(1)由(a+b)=a+b,(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3可得(a+b)n的各项展开式的系数除首尾两项都是1外,其余各项系数都等于(a+b)n﹣1的相邻两个系数的和,由此可得(a+b)4的各项系数依次为1、4、6、4、1;因此(a+b)5的各项系数依次为1、5、10、10、5、1.(2)将25﹣5×24+10×23﹣10×22+5×2﹣1写成“杨辉三角”的展开式形式,逆推可得结果.【解答】解:(1)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;(2)原式=25+5×24×(﹣1)+10×23×(﹣1)2+10×22×(﹣1)3+5×2×(﹣1)4+(﹣1)5=(2﹣1)5=1注:不用以上规律计算不给分.【点评】本题考查了完全平方公式,学生的观察分析逻辑推理能力,读懂题意并根据所给的式子寻找规律,是快速解题的关键.。
北京市 七年级(上)期中数学试卷 (含答案)

七年级(上)期中数学试卷一、选择题(本大题共10小题,共30.0分)1.-2的相反数是()A. B. C. D. 22.在-,0,,-1这四个数中,最小的数是()A. B. 0 C. D.3.有理数a,b在数轴上的对应点如图所示,则下面式子中正确的是()A. B. C. D.4.A、B两地相距6980000m,用科学记数法表示为()m.A. B. C. D.5.下面各式中,与-2xy2是同类项的是()A. B. C. D.6.一个长方形的一边长是2a+3b,另一边的长是a+b,则这个长方形的周长是()A. B. C. D.7.下列代数式书写规范的是()A. B. C. ax3 D.8.关于多项式x5-3x2-7,下列说法正确的是()A. 最高次项是5B. 二次项系数是3C. 常数项是7D. 是五次三项式9.在代数式:,3m-3,-22,-,2πb2中,单项式的个数有()A. 1个B. 2个C. 3个D. 4个10.如果x是最大的负整数,y绝对值最小的整数,则-x2016+y的值是()A. B. C. 1 D. 2016二、填空题(本大题共10小题,共20.0分)11.的绝对值是______ ,的倒数是______ .12.在数轴上,若点P表示-2,则距P点3个单位长的点表示的数是______ .13.单项式-5πab2的系数是______ ,次数是______ .14.如图是一数值转换机,若输入的x为-1,则输出的结果为______ .15.绝对值小于3的所有整数的和是______ .16.数轴上表示数-5和表示-14的两点之间的距离是______ .17.在数4.3,-,|0|,-(-),-|-3|,-(+5)中,______ 是正数.18.已知|a|=2,|b|=5,且ab<0,那么a+b的值为______ .19.如果有|x-3|+(y+4)2=0,则x= ______ ,y x= ______ .20.现规定一种新的运算“*”:a*b=a b,如3*2=32=9,则()*3= ______ .三、解答题(本大题共13小题,共66.0分)21.把下面的有理数填在相应的大括号里:(★友情提示:将各数用逗号分开)15,,0,-30,0.15,-128,,+20,-2.6正数集合﹛______﹜负数集合﹛______﹜整数集合﹛______﹜分数集合﹛______﹜22.计算:28-37-3+52.23.计算:(-+)÷(-)24.计算(-4)×(-9)+(-)-23.25.化简:3x2-3+x-2x2+5.26.化简(5a-3a2+1)-(4a3-3a2).27.观察图形,写出一个与阴影面积有关的代数恒等式.28.(1)在数轴上表示下列各数,(2)用“<”连接:-3.5,,-1,4,0,2.5.29.先化简,再求值:5(a2b-ab2)-(ab2+5a2b),其中a=1,b=-2.30.10盒火柴如果以每盒100根为准,超过的根数记作正数,不足的根数记作负数,每盒数据记录如下:+3,+2,0,-1,-2,-3,-2,+3,-2,-2.求:这10盒火柴共有多少根.31.已知有理数a,b,c在数轴上的位置如图所示,(1)用<,>,=填空:a+c ______ 0,c-b ______ 0,b+a ______ 0,abc ______ 0;(2)化简:|a+c|+|c-b|-|b+a|.32.阅读下列解题过程,然后答题:已知如果两个数互为相反数,则这两个数的和为0,例如,若x和y互为相反数,则必有x+y=0.(1)已知:|a|+a=0,求a的取值范围.(2)已知:|a-1|+(a-1)=0,求a的取值范围.33.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等.(1)根据上面的规律,写出(a+b)5的展开式.(2)利用上面的规律计算:25-5×24+10×23-10×22+5×2-1.答案和解析1.【答案】D【解析】解:-2的相反数是2,故选:D.根据相反数的定义:只有符号不同的两个数叫做互为相反数即可得到答案.此题主要考查了相反数,关键是掌握相反数的定义.2.【答案】D【解析】解:根据有理数大小比较的法则,可得-1<-,所以在-,0,,-1这四个数中,最小的数是-1.故选:D.有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.3.【答案】D【解析】解:∵从数轴可知:b<0<a,|b|>|a|,∴A错误;B错误;∵a>0,b<0,∴ab<0,∴C错误;∵b<0<a,|b|>|a|,∴a-b>0,a+b<0,∴a-b>a+b,∴D正确;故选D.数轴可知b<0<a,|b|>|a|,求出ab<0,a-b>0,a+b<0,根据以上结论判断即可.本题考查了数轴,有理数的乘法、加法、减法等知识点的应用,关键是能根据数轴得出b<0<a,|b|>|a|.4.【答案】D【解析】解:6980000=6.98×106,故选:D.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.【答案】A【解析】解:由题意,得y2x与-2xy2是同类项,故选:A.根据同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,可得答案.本题考查同类项的定义,同类项定义中的两个“相同”:所含字母相同;相同字母的指数相同,是易混点,还有注意同类项定义中隐含的两个“无关”:①与字母的顺序无关;②与系数无关.6.【答案】B【解析】解:周长=2(2a+3b+a+b)=6a+8b.故选B.长方形的周长等于四边之和,由此可得出答案.本题考查有理数的加减运算,比较简单,注意长方形的周长可表示为2(长加宽).7.【答案】A【解析】解:选项A正确,B正确的书写格式是b,C正确的书写格式是3ax,D正确的书写格式是.故选A.根据代数式的书写要求判断各项即可得出正确答案.代数式的书写要求:(1)在代数式中出现的乘号,通常简写成“•”或者省略不写;(2)数字与字母相乘时,数字要写在字母的前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.8.【答案】D【解析】解:A、多项式x5-3x2-7的最高次项是x5,故本选项错误;B、多项式x5-3x2-7的二次项系数是-3,故本选项错误;C、多项式x5-3x2-7的常数项是-7,故本选项错误;D、多项式x5-3x2-7是五次三项式,故本选项正确.故选:D.根据多项式的项和次数的定义,确定各个项和各个项的系数,注意要带有符号.本题考查与多项式相关的概念,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.9.【答案】C【解析】解:-22,-,2πb2中是单项式;是分式;3m-3是多项式.故选C.根据单项式的定义进行解答即可.本题考查的是单项式,熟知数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式是解答此题的关键.10.【答案】B【解析】解:∵x是最大的负整数,y绝对值最小的整数,∴x=-1,y=0,∴-x2016+y=-(-1)2016=-1.故选B.由于x是最大的负整数,y绝对值最小的整数,由此可以分别确定x=-1,y=0,把它们代入所求代数式计算即可求解.此题主要考查了有理数的混合运算,解题的关键是根据最大的负整数,绝对值最小的整数的性质确定x、y的值,然后代入所求代数式即可解决问题.11.【答案】;【解析】解:-的绝对值为,1的倒数为.故答案为:,.根据绝对值、倒数,即可解答.本题考查了绝对值、倒数,解决本题的关键是熟记绝对值、倒数的定义.12.【答案】-5或1【解析】解:设距P点3个单位长的点表示的数是x,则|x+2|=3,当x+2≥0时,原式可化为:x+2=3,解得x=1;当x+2<0时,原式可化为:-x-2=3,解得x=-5.故答案为:-5或1.设距P点3个单位长的点表示的数是x,则|x+2|=3,求出x的值即可.本题考查的是数轴,熟知数轴上两点间的距离公式是解答此题的关键.13.【答案】-5π;3【解析】解:单项式-5πab2的系数是-5π,次数是3.故答案为:-5π,3.根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.此题考查了单项式,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.14.【答案】9【解析】解:(-1-2)×(-3)=(-3)×(-3)=9.故答案为:9.根据运算规则:先-2,再×(-3),进行计算即可求解.此题主要考察根据运算规则列式计算,读懂题中的运算规则,并准确代入求值是解题的关键.15.【答案】0【解析】解:根据绝对值的意义得绝对值小于3的所有整数为0,±1,±2.所以0+1-1+2-2=0.故答案为:0.绝对值的意义:一个数的绝对值表示数轴上对应的点到原点的距离.互为相反数的两个数的和为0.依此即可求解.此题考查了绝对值的意义,并能熟练运用到实际当中.16.【答案】9【解析】解:|-5-(-14)|=9.数轴上两点之间的距离等于这两点的数的差的绝对值,即较大的数减去较小的数.考查了数轴上两点之间的距离的计算方法.17.【答案】4.3,-(-)【解析】解:在数4.3,-,|0|,-(-)=,-|-3|=-3,-(+5)=-5中,4.3,-(-)是正数.故答案为:4.3,-(-).首先将各数化简,再根据正数的定义可得结果.本题主要考查了有理数的定义,熟练掌握有理数的分类是解答此题的关键.18.【答案】3或-3【解析】解:①a>0,b<0,则a=2,b=-5,a+b=-3;②a<0,b>0,则a=-2,b=5,a+b=3.故填3或-3.根据题意可得a和b异号,分情况讨论①a>0,b<0;②a<0,b>0.本题考查有理数的加法,注意讨论a和b的取值范围得出a和b的值是关键.19.【答案】3;-64【解析】解:由题意得,x-3=0,y+4=0,解得,x=3,y=-4,则y x=-64,故答案为:3;-64.根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.20.【答案】【解析】解:∵a*b=a b,3*2=32=9,∴()*3=(-)3=-.故答案为:-.根据题中所给出的运算方法列出乘方的式子,再根据乘方的运算法则进行计算即可.本题考查的是有理数的混合运算,熟知数的乘方法则是解答此题的关键.21.【答案】15,0.15,,+20;,-30,-128,-2.6;15,0,-30,-128,+20;,0.15,,-2.6【解析】解:正数集合﹛15,0.15,,+20,﹜负数集合﹛,-30,-128,-2.6,﹜整数集合﹛15,0,-30,-128,+20,﹜分数集合﹛,0.15,,-2.6,﹜按照有理数的分类填写:有理数.认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.注意整数和正数的区别,注意0是整数,但不是正数.22.【答案】解:28-37-3+52,=28+52-37-3,=80-40,=40.【解析】先根据加法交换律将同号数相加,再把两个异号数相加.本题是有理数的加减混合运算,可以看作是省略加号的加法,注意运用简便算法进行计算.23.【答案】解:原式=(-+)×(-36),=×(-36)-×(-36)+×(-36),=-8+9-2,=-1.【解析】首先根据除以一个不为0的数等于乘以这个数的倒数可得(-+)×(-36),再用乘法分配律计算即可.此题主要考查了有理数的除法,关键是掌握有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数.24.【答案】解:(-4)×(-9)+(-)-23=36+(-)-8=27.【解析】根据有理数的乘法和加减法可以解答本题.本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.25.【答案】解:3x2-3+x-2x2+5=(3x2-2x2)+x+(5-3)=x2+x+2.【解析】首先找出同类项,进而合并同类项得出答案.此题主要考查了合并同类项,正确找出同类项是解题关键.26.【答案】解:(5a-3a2+1)-(4a3-3a2)=5a-3a2+1-4a3+3a2=-4a3+5a+1.【解析】先去括号,然后合并同类项即可解答本题.本题考查整式的加减,解题的关键是明确整式的加减的计算方法,注意去括号后,各项内的符号是否变号.27.【答案】解:阴影部分的面积可表示为:a2-b2或(a+b)(a-b),∴a2-b2=(a+b)(a-b).【解析】分别利用不同的方法表示出阴影部分的面积,得到恒等式.本题考查的是平方差公式的几何背景,掌握平方差公式、矩形的面积公式是解题的关键.28.【答案】解:(1)如图所示:(2)-3.5<-1<0<<2.5<4【解析】在数轴上表示各数,数轴上各数从左往右的顺序,就是各数从小到大的顺序.本题考查了用数轴表示有理数和有理数的大小比较.数轴上各数从左往右的顺序就是各数从小到大的顺序.29.【答案】解:原式=5a2b-5ab2-ab2-5a2b=-6ab2,∴当a=1,b=-2时,∴原式=-6×1×4=-24【解析】先将原式化简,然后将a与b的值代入即可求出答案.本题考查整式运算,涉及代入求值.30.【答案】解:先求超过的根数:(+3)+(+2)+0+(-1)+(-2)+(-3)+(-2)+(+3)+(-2)+(-2)=-4;则10盒火柴的总数量为:100×10-4=996(根).答:10盒火柴共有996根.【解析】首先审清题意,明确“正”和“负”所表示的意义;然后根据每盒的数据记录求出超过的根数,进而可求得10盒火柴的总数量.解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.31.【答案】<;>;<;>【解析】解:(1)根据数轴可知:a<b<0<c,且|c|<|b|<|a|,∴a+c<0,c-b>0,b+a<0,abc>0,故答案为:<,>,<,>;(2)原式=-(a+c)+(c-b)+(b+a)=-a-c+c-b+b+a=0.(1)根据数轴,判断出a,b,c的取值范围,进而求解;(2)根据绝对值的性质,去绝对值号,合并同类项即可.本题主要考查数轴、绝对值、整式的加减等知识的综合运用,解决此题的关键是能够根据数轴上的信息,判断出a,b,c等字母的取值范围,同时解决此题时也要注意绝对值性质的运用.32.【答案】解:(1)∵|a|≥0,|a|+a=0,∴a≤0;(2)∵|a-1|≥0,∴a-1≤0,解得a≤1.【解析】(1)根据绝对值的性质可得出|a|≥0,再由相反数的定义即可得出结论;(2)根据绝对值的性质可得出|a-1|≥0,再由相反数的定义即可得出结论.本题考查的是有理数的加法,熟知相反数的定义是解答此题的关键.33.【答案】解:(1)如图,则(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;(2)25-5×24+10×23-10×22+5×2-1.=25+5×24×(-1)+10×23×(-1)2+10×22×(-1)3+5×2×(-1)4+(-1)5.=(2-1)5,=1.【解析】(1)直接根据图示规律写出图中的数字,再写出(a+b)5的展开式;(2)发现这一组式子中是2与-1的和的5次幂,由(1)中的结论得:25-5×24+10×23-10×22+5×2-1=(2-1)5,计算出结果.本题考查了完全式的n次方,也是数字类的规律题,首先根据图形中数字找出对应的规律,再表示展开式:对应(a+b)n中,相同字母a的指数是从高到低,相同字母b的指数是从低到高.。
新北师大版七年级(上)期中考试数学试题(含答案) (61)

2015—2016学年度第一学期七年级数学期中试卷(满分120分,考试时间120分钟)一、选择题(每题3分,共30分。
)1、-3的相反数是( ) A 、31 B 、3 C 、31- D 、-32、如图绕虚线旋转得到的几何体是( )3、下列说法正确的是 ( ) A 、一个数前面加上“-”号这个数就是负数; B 、正数和负数统称为有理数 C 、0既不是正数也不是负数; D 、非负数就是正数;4、在()2--,7--,012001⨯-,()31--,⎪⎭⎫ ⎝⎛+-25,42-中,非正数有 ( )A 、1个B 、2个C 、3个D 、4个 5、用平面去截五棱柱,在所得的截面中,不可能出现的是( )A 、八边形B 、四边形C 、六边形D 、三角形 6、 下列计算正确的是 ( )A 、2733-=- B 、(-4)2=-16 C 、(-34)31(D 1251)5143-=-=、 7、小新准备用如图的纸片做一个礼品盒,为了美观,他想在六个正方形纸片上画上图案,使做成后三组对面的图案分别相同,那么画上图案后正确的是 ( )8、铅笔的单价是a 元,圆珠笔的单价是铅笔单价的3倍,则圆珠笔的单价是( )元. A 、a 3 B 、a +3 C 、3-a D 、3a9、在下列各式子22223)(121b ab a y x bR s mn ab ++-=,, , ,, π中,代数式有( )A .2个B .3个C .4个D .5个10、如图,A 、B 两点在数轴上表示的数分别为a 、b ,下列式子不成立的是 ( )A. a b b a -=- B .-1<<a C .b a < D .0<+a b二、填空题(每题4分,共32分。
)11、如果向东走6米记作+6米,那么向西走10米记作 。
12、一个边长为1的正方形,第一次截去正方形的一半,第二次截去剩下的一半,如此截15.若032=-++y x ,则y x -的值为 。
2015-2016年西城区鲁迅中学七年级上期中数学试卷含解析

【考点】合并同类项. 【分析】本题考查同类项的概念,含有相同的字母,并且相同字母的指数相同,是同类项的两项可 以合并,否则不能合并.合并同类项的法则是系数相加作为系数,字母和字母的指数不变. 【解答】解:A、3a 与 b 不是同类项,不能合并.错误; B、3a﹣ a=2a.错误; C、2a3 与 3a2 不是同类项,不能合并.错误; D、﹣ a2b+2a2b=a2b.正确. 故选 D. 【点评】同类项的概念是所含字母相同,相同字母的指数也相同的项是同类项;注意不是同类项的 一定不能合并.
2.下列各式中,等号成立的是(
A.|﹣ a|=a B.﹣ 32=(﹣ 3)2 【考点】有理2数)的3 乘方.
) C.﹣ 27=(﹣ 2)7
D.﹣ (﹣ 3)2=﹣ (﹣
【分析】根据绝对值的性质,有理数乘方的定义对各选项分析判断后利用排除法求解.
【解答】解:A、只有 a≥0 时,|﹣ a|=a 成立,故本选项错误; B、﹣ 32=﹣ 9,(﹣ 3)2=9,故本选项错误; C、(﹣ 2)7=﹣ 27,故本选项正确;
23.已知﹣ 5x3y|a|﹣ (a﹣ 4)x﹣ 6 是关于 x、y 的七次三项式,求 a2﹣ 2a+1 的值.
24.(4﹣ n2)x2﹣ (n﹣ 2)x﹣ 8=0 是关于 x 的一元一次方程, (1)试求 x 值; (2)求关于 y 方程 n+|y|=x 的解.
25.已知:有理数 a、b 满足 ab>0,当 y﹣ 2x+z 的值.
2)3
3.光年是天文学中的距离单位,1 光年大约是 9500 000 000 000km,这个数据用科学记数法表示是 () A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km
2016-2017学年北京市鲁迅中学七年级第二学期期中数学试卷(含答案)

北京市鲁迅中学2016—2017学年第二学期 2017年4月班级 ,姓名 ,学号 密 封 装 订 线北京市鲁迅中学初一年级数学期中测试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)二部分,其中第Ⅰ卷(选择题)和第Ⅱ卷共100分。
另附加题20分。
考试时间100分钟。
第Ⅰ卷(共 30分)选择题:本大题共10小题,每小题3分,共30分. 在每小题的4个选项中,只有一项是符合题目要求的.1.以下列各组线段为边,能组成三角形的是( ) A .2cm ,3cm ,5cm B .5cm ,6cm ,10cm C .1cm ,1cm ,3cm D .3cm ,4cm ,9cm2.如果点A (x ,y )在第三象限,则点B (-x ,y -1)在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.-8的立方根与4的平方根的和是 ( ) A 、0 B 、0或4 C 、4 D 、0或-44.下列各式中,正确的是( )A.±34 B.±34; C.±38±345.下列说法正确的是: ( ) A .5-是25的平方根 B .25的平方根是5- C .5-是2(5)-的算术平方根D .5±是2(5)-的算术平方根6.点P(a,b)在第四象限,则点P 到x 轴的距离是( )A.aB.bC.│a │D.│b │ 7.若一个多边形的每个外角都等于60°,则它的内角和等于( ) A .180° B .720° C .1080° D .540°8.一个三角形的两边长分别是3和7,且第三边长为整数,这样的三角形周长最大的值为( ) A .15 B .16 C .18 D .199.同一平面内的四条直线满足a ⊥b ,b ⊥c ,c ⊥d ,则下列式子成立的是( ). A .a ∥b B .b ⊥d C .a ⊥d D .b ∥c10.两架编队飞行(即平行飞行)的两架飞机A 、B 在坐标系中的坐标分别为A (-1,2)、B (-2,3),当飞机A 飞到指定位置的坐标是(2,-1)时,飞机B 的坐标是( ) .A.(l ,5)B.(-4,5) C .(1,0) D.(-5,6)第Ⅱ卷(共70分)一、 填空题:本大题共10小题,每空2分,共20分.把答案填在题中横线上. 1.36的平方根是___________,81的算术平方根是______, 2. 387-1=________ 3.若2-a + | b 2-9 | = 0,则ab = ____________4.已知a ,b ,c 是△ABC 的三边,化简:|a +b -c |+|b -a -c |-|c +b -a |=________.215.如图,折叠宽度相等的长方形纸条,若∠1=630,则∠2=______ .6.在数轴上离原点的距离为35的点表示的数_______________7.在平面直角坐标系中,点A 的坐标为(-1,3),线段AB ∥X 轴,且AB=4,则点B 的坐标为 .8.如果一个多边形的边数增加1倍,它的内角和就为2160°,那么原来那个多边形是______边形. 9.如右图,AB ∥CD ,∠A=34°,∠C=70°,则∠F=_____°第5题10.如图,直角△ABC 的周长为2017,在其内部有5个小直角三角形,且这5个小直角三角形都有一条边与BC 平行,则这5个小直角三角形的周长之和是 。
2017-2018学年北京市鲁迅中学七年级第一学期期中数学试题.docx

北京市鲁迅中学初一年级数学期中测试题本试卷分第Ⅰ卷(选择题、填空)和第Ⅱ卷(计算、解答 题)两部分,其中第Ⅰ卷 20 分和第Ⅱ卷 80 分共 100 分。
第 Ⅲ 卷 20 分为附加题。
考试时间100 分钟。
第Ⅰ卷(共 20 分)一.选择题(每题 2 分,共 20 分). 1的相反数是 --------------------------------------------------------------------------()12A .1B .1C .2D . 22 22. 若家用电冰箱冷藏室的温度是4 C, 冷冻室的温度比冷藏室的温度低 22 C,则冷冻室的温度是 --------------------------------------------------------------------()A .18 CB . 26C C . 22 CD . 18 C3. 已知 a, b, c 在数轴上的位置如下图所示 ,则下列结论正确的是 -------------().b 0 a cA .b 表示负数, a, c 表示正数, 且 a bB . b 表示负数, a, c 表示正数,且 b a cC .b 表示负数, a, c 表示正数, 且 abcD .b 表示负数, a, c 表示正数, 且 ab4.下列各对算式中,结果相等的是 ---------------------------------------------------B .—32和(—3)2()A . —(— 8)和 +(— 8)5D . — 3 和—(— 3)C . — 2.5 和25. 下面结论中正确的是 ----------------------------------------------------------------()A .2 比 1 大 B . 31的倒数是2C .最小的负整数是 1D . 0.5 >17 32726.下列代数式中单项式共有------------------------------------------------------------()个 .x 2 5 3 ,xy 3 ,0.5,a , 1 , a,ab3x5A .2B . 3C . 4D . 57. 下列说法中 ,正确的是 ----------------------------------------------------------------() . 单项式 2x 2 y的系数是-2, 次数是 3 B .3 2 y4 x 1 是三次三项式 常数项是 1A 3x ,32ab 的次数是 2, 系数为 9. 单项式 a 的系数是 0, 次数是 0 D .单项式C228. 下列各组式子中 ,为同类项的是 ------------------------------------------------()A . 3x 2y 与 3xy 2B . 3xy 与 2yxC .2x 与 2x 2D . 5xy 与 5yz()..当式子(- )2+2 取最小值时, x 等于-------------------------------A. -0.5B. 0.5C. -2D. 210. 当 x > 1时, | x1| + 2 |1 x | + | x | 的值为 --------------------------------------------()A .3 4xB . 4x 3C .3 2xD .1第Ⅱ卷( 80 分)二.填空题(每空 2 分,共 26 分)11.地球到太阳的距离大约是 150000000000米,用科学记数法表示为 ________米. 12.用四舍五入法求 0.1287 精确到百分位的近似数为 . 13.若 |x|=5,则 x= .14.单项式 ab 2c 4 的系数是,次数是,多项式 3x 2 y 8x 2 y 2 9 的最高次3项为.15.若多项式 x 2 3kxy 3 y 26xy 8不含 xy 项,则 k =________.16.已知 (a 3)x |a| 2+6=0 是关于 x 的一元一次方程,则 a=____.17.若 a 、 b 互为相反数, c 、 d 互为倒数,则 2 (a+b ) +( 3cd ) = .18.定义计算“ ”,对于两个有理数 a ,b ,有 a b= a +b - ab ,则- 3 2=__________. 19.有理数 a 、b 、 在数轴上的对应点的位置如图所示, 化简: ac c ba b.cc b 0 a20.将一列有理数- 1,2,- 3, 4,- 5,6, ,, ,如图所示有序排列.根据图中的排列规律可知,“峰 1”中峰顶的位置 (C 的位置)是有理数 4,那么,“峰 6”中 C 的位置是有理数 ,-2017 应排在 A 、B 、C 、 D 、E 中的位置. .4-9C-3-58 10BD-126-7-11,,AE峰 1峰 2峰 n三 . 计算题 : (每小题 4 分,共 40 分 )21. -6-7-822. 3×(- 4) + (-28)÷723.1 48 (53 1 ) 24.2×(-2)÷ (- 1 1)2416 65442241 2 ( 3)225. -2 +(3― 7)― |―2|×(― 1)26. 1(1 0.5)327.化简:2(2a3b) 3(2b 3a)28. 化简 :5m2 n 4mn22mn 6m2 n3mn 29、解方程:x+12=4x-1530、解方程:4x﹣3(5﹣x)=2;四.解答题 ( 每题 4+4+3+3 分,共 14 分)31.先化简下式,再求值:63(3x 21) (92x3),其中 x1.x x332 、李明在计算一个多项式减去 2x 2 4 x 5 时,误认为加上此式,计算出错误结果为2x2x 1 ,试求出正确答案.33、有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:1.5320.51222.5回答下列问题:(1)这8筐白菜中,最接近25 千克的那筐白菜为_________千克;(2)以每筐25千克为标准,这8 筐白菜总计超过多少千克或不足多少千克?( 3)若白菜每千克售价 2.6 元,则出售这 8 筐白菜可卖多少元?.34、有理数 a,b,c 在数轴上的位置如图所示,化简: 3 a b a b c a 2 b c .第Ⅲ卷( 20 分)五、附加题(每题 5 分,共计 20 分)35、某服装厂生产一种西装和领带,西装每套定价 200 元,领带每条定价 40 元。
北京市鲁迅中学2015—2016学年第一学期初一年级数学期中测试题答案

x=4
长为 13 cm,宽为 11 cm,面积为 143 ㎝ 2 .
第2页共2页
第1页共2页
,姓名
封
班级
密
四 解答题 22. ab+4a,1
23. 解: ∵ − 5x3 y a − (a − 4)x − 6 是关于 x、y 的七次三项式
∴| a |=4,且 a≠4
3;1=25
24. x=2,y=-4,4 25. 解: ∵有理数 a、b 满足 ab>0,
鲁迅中学试卷
2015 年 11 月
线
订
,学号
装
北京市鲁迅中学 2012—2013 学年第一学期初一年级 数学期中测试题答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)第Ⅲ卷(附加题)三部分, 其中第Ⅰ卷(选择题)和第Ⅱ卷共 100 分,第Ⅲ卷 10 分。考试时间 100 分钟。 一、 选择题:在每小题的四个选项中,只有一项是符合题目要求的. 1. C. 2. C. 3. D. 4. C. 5. B. 6. D. 7. C. 8. A. 9. C. 10. C. 二 填空题 11. 0, -4. 12. 两;3 和-3 13. ,2/3x-1/4y 14. -1/3,3 15. 四,四 16. m<-n<n<-m 17. 13 18. 3,6 19. 2b-2c 20. -32x^6y,(-1)^n+1 2^(n-1)(x^ny 三 计算题 21. (1)-21,(2)1/6,(3)-x^2y+xy^2,(4)-x^2+13x-7,(5)9,(6)11/7
组成的,已知中间最小的正方形的边长是 1 cm,则这块长方形色块图的总面积是 多少?
解:设第二个正方形的边长为 x cm,第三个正方形的边长为 5
北京市鲁迅中学2011~2012学年度第一学期期中测试数学试卷及答案

( ) ( ) (6) x − 31− 2x + x2 + 2 − 2 + 3x + x2
(7)解方程 x+12=4x-15
(8)解方程 3(x-2)- 2=x-(2x-2)
第3页
(9)化简求值:当 x = −1, y = −2 时, 求 1 x − − 3 x + 1 y 2 − x + 2 y 2 的值. 2 2 3 3
四、解答题:本大题共 3 小题,每小题 4 分,共 12 分. 28. 若 a = 3, b = 6,且a >b, 求 a+b
29. 已知 − 5x3 y a − (a − 4)x − 6 是关于 x、y 的七次三项式, 求 a2 − 2a +1的值。
30. 已知:有理数 a、b、c 满足 abc<0,且 a+b+c>0,当 x = a + b + c 时, abc
,
6577123=
(保留 3 个有效数字)
21. m 与 n 互为相反数,p 与 q 互为倒数,则 m-pq+n=
22. 百位数字是 a,十位数字是 b,个位数字是 c 的三位数是
23+y2=
24. 若式子 4x2 − 2x + 5 = 7 ,则式子 2x2 − x +10=_________
A.
a = 2, b = −1.
B.
a = 0, b = 2.
C.
a = 1, b = 2.
D.
a = 1, b = 1.
D.不确定 ).
7. 下列式子计算正确的是( )
A. 5m2 − 3m2 = 2 B. 5x3 + 6x5 = 11x8 C.3a+2b=5ab D.-3a-2a=-5a
北京市西城区鲁迅中学七年级数学上学期期中试题(含解析)

七一、选择题:在每小题的四个选项中,只有一项是符合题目要求的.(每小题3分,共30分.)1.﹣5的绝对值等于()A.﹣5 B. C.5 D.2.下列各式中,等号成立的是()A.|﹣a|=a B.﹣32=(﹣3)2 C.﹣27=(﹣2)7 D.﹣(﹣3)2=﹣(﹣2)33.光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是()A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km4.若>0,则一定有()A.a>0且b>0 B.a<0且b<0C.a,b同正或同负D.不确定5.已知关于x的方程2x+m=5的解是x=﹣1,则m的值为()A.3 B.7 C.﹣7 D.﹣36.下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b7.若﹣1<m<0,则m、m2、的大小关系是()A.m<m2< B.m2<m< C.<m<m2 D.m<<m28.下列说法正确的个数有()①若|a|=|b|,则a=b;②若a≠b,则a2≠b2;③若a>b,则a2>b2;④a2>a.A.0个B.1个C.2个D.3个9.当式子(2x﹣1)2+2取最小值时,x等于()A.2 B.﹣2 C.0.5 D.﹣0.510.数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d ﹣2a=10,则数轴上原点应是()A.A点B.B点C.C点D.D点二、填空题:把答案填在题中横线上.(每题2分,共20分.)11.0的相反数为,的倒数为.12.数轴上与原点相距3个单位长度的点有个,它们表示的数各是.13.甲数x的与乙数y的的差可以表示为.14.单项式的系数是,次数是.15.m2﹣n4+3mn+2是次项式.16.m、n两数在数轴上的位置如图,请按从小到大的顺序排列m、n、﹣m、﹣n .17.已知:|x﹣2|+(y+3)2=0,则x2+y2= .18.若2a2m b4和﹣a6b n﹣2是同类项,则m= 、n= .19.有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|﹣|c﹣b|﹣|b+a|= .20.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…(1)按此规律写出第6个单项式;(2)试猜想第n个单项式为.三、计算题.(每小题30分,共30分.)21.(1)﹣6﹣7﹣8(2)(3)﹣3x2y+2x2y+3xy2﹣2xy2(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)(5)解方程 x+12=4x﹣15(6)解方程:y﹣=2﹣.四、解答题:(本大题共4小题,每小题5分,共20分.)22.求3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab的值,已知4|a﹣1|+8(b+3)2=0.23.已知﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,求a2﹣2a+1的值.24.(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,(1)试求x值;(2)求关于y方程n+|y|=x的解.25.已知:有理数a、b满足ab>0,当时,|y﹣4|=2,3a3z﹣1b与7ba5能够合并,求y ﹣2x+z的值.五、解答题26.(2007•湘潭)为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n27.(2015秋•西城区校级期中)如果a2+a﹣1=0,求a3+2a2+2的值.28.(2015秋•西城区校级期中)如图是一块在电脑屏幕上出现的长方形色块图,它是由6个不同颜色的正方形组成的,已知中间最小的正方形的边长是1cm,则这块长方形色块图的总面积是多少?2015-2016学年北京市西城区鲁迅中学七年级(上)期中数学试卷参考答案与试题解析一、选择题:在每小题的四个选项中,只有一项是符合题目要求的.(每小题3分,共30分.)1.﹣5的绝对值等于()A.﹣5 B. C.5 D.【考点】绝对值.【专题】常规题型.【分析】根据负数的绝对值等于它的相反数解答.【解答】解:﹣5的绝对值|﹣5|=5.故选C.【点评】本题考查了绝对值的性质,熟记一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0是解题的关键.2.下列各式中,等号成立的是()A.|﹣a|=a B.﹣32=(﹣3)2 C.﹣27=(﹣2)7 D.﹣(﹣3)2=﹣(﹣2)3【考点】有理数的乘方.【分析】根据绝对值的性质,有理数乘方的定义对各选项分析判断后利用排除法求解.【解答】解:A、只有a≥0时,|﹣a|=a成立,故本选项错误;B、﹣32=﹣9,(﹣3)2=9,故本选项错误;C、(﹣2)7=﹣27,故本选项正确;D、﹣(﹣3)2=﹣9,﹣(﹣2)3=8,﹣9≠8,故本选项错误.故选C.【点评】本题考查了有理数的乘方,负数的奇数次幂是负数,负数的偶数次幂是正数,要特别注意﹣32和(﹣2)2的区别.3.光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是()A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将9500 000 000 000km用科学记数法表示为:9.5×1012km.故选:B.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.若>0,则一定有()A.a>0且b>0 B.a<0且b<0C.a,b同正或同负D.不确定【考点】有理数的除法.【分析】根据有理数的除法运算法则,同号得正,异号得负解答.【解答】解:∵>0,∴a>0,b>0或a<0,b<0.故选C.【点评】本题考查了有理数的除法运算,熟记运算符合法则“同号得正,异号得负”是解题的关键.5.已知关于x的方程2x+m=5的解是x=﹣1,则m的值为()A.3 B.7 C.﹣7 D.﹣3【考点】一元一次方程的解.【分析】直接把x=﹣1代入2x+m=5可得关于m的方程,再解即可.【解答】解:把x=﹣1代入2x+m=5得:﹣2+m=5,m=7.故选:B.【点评】此题主要考查了一元一次方程的解,关键是掌握把方程的解代入原方程,等式左右两边相等.6.下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b【考点】合并同类项.【分析】本题考查同类项的概念,含有相同的字母,并且相同字母的指数相同,是同类项的两项可以合并,否则不能合并.合并同类项的法则是系数相加作为系数,字母和字母的指数不变.【解答】解:A、3a与b不是同类项,不能合并.错误;B、3a﹣a=2a.错误;C、2a3与3a2不是同类项,不能合并.错误;D、﹣a2b+2a2b=a2b.正确.故选D.【点评】同类项的概念是所含字母相同,相同字母的指数也相同的项是同类项;注意不是同类项的一定不能合并.7.若﹣1<m<0,则m、m2、的大小关系是()A.m<m2< B.m2<m< C.<m<m2 D.m<<m2【考点】有理数大小比较.【分析】本题可采用取特殊值的方法.由于﹣1<m<0,可设m=﹣,然后代入m、m2、中分别计算,然后进行比较即可.【解答】解:根据分析,可设m为﹣,代入可得m=﹣,m2=, =﹣2.即可得.故选C.【点评】本题为简单的有理数比较大小的题目,将满足条件的数字代入即可.8.下列说法正确的个数有()①若|a|=|b|,则a=b;②若a≠b,则a2≠b2;③若a>b,则a2>b2;④a2>a.A.0个B.1个C.2个D.3个【考点】有理数大小比较.【分析】根据绝对值相等的两个数可能相等也可能是相反数可得①错误;根据乘方的计算可得②③④的正误,并且找出错误命题的反例.【解答】解:①若|a|=|b|,则a=b,说法错误,例如:|﹣1|=|1|,但是﹣1≠1;②若a≠b,则a2≠b2,说法正确;③若a>b,则a2>b2;说法错误,例如2>﹣4,但是a2<b2;④a2>a,说法错误,例如0.12<0.1.正确的有1个,故选:B.【点评】此题主要考查了有理数的比较大小,以及绝对值和乘方,关键是错误的命题要正确找出反例.9.当式子(2x﹣1)2+2取最小值时,x等于()A.2 B.﹣2 C.0.5 D.﹣0.5【考点】非负数的性质:偶次方.【分析】根据非负数的性质解答即可.【解答】解:∵(2x﹣1)2,≥0,∴2x﹣1=0时,式子(2x﹣1)2+2取最小值,∴x=0.5.故选:C.【点评】本题考查的是非负数的性质,掌握一个数的偶次方是非负数是解题的关键.10.数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d ﹣2a=10,则数轴上原点应是()A.A点B.B点C.C点D.D点【考点】数轴.【分析】直接利用数轴得出a=d﹣7,再代入已知关系式求出答案.【解答】解:由数轴可得:a=d﹣7,则d﹣2a=d﹣2(d﹣7)=14﹣d=10,解得:d=4.故数轴上原点应是4.故选:C.【点评】此题主要考查了数轴,根据题意得出a=d﹣7是解题关键.二、填空题:把答案填在题中横线上.(每题2分,共20分.)11.0的相反数为0 ,的倒数为﹣4 .【考点】倒数;相反数.【分析】根据相反数、倒数,即可解答.【解答】解:0的相反数是0,﹣的倒数为﹣4,故答案为:0,﹣4.【点评】本题考查了相反数、倒数,解决本题的关键是熟记相反数、倒数的定义.12.数轴上与原点相距3个单位长度的点有 2 个,它们表示的数各是±3.【考点】数轴.【专题】探究型.【分析】设数轴上与原点相距3个单位长度的点所表示的数为a,再根据数轴上两点间的距离公式求出a的值即可得出结论.【解答】解:设数轴上与原点相距3个单位长度的点所表示的数为a,故|a|=3,解得a=±3.故答案为:2,±3.【点评】本题考查的是数轴的特点,即在数轴上到原点距离相等的点有两个,这两个数互为相反数.13.甲数x的与乙数y的的差可以表示为x﹣y .【考点】列代数式.【分析】被减式为x的,减式为y的,让它们相减即可.【解答】解:所求的关系式为: x﹣y.【点评】求两个式子的差的关键是找到被减式和减式.14.单项式的系数是,次数是 3 .【考点】单项式.【分析】根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.【解答】解:根据单项式系数、次数的定义可知:单项式的系数是,次数是1+2=3.【点评】确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.15.m2﹣n4+3mn+2是 4 次 4 项式.【考点】多项式.【分析】多项式中次数最高的项的次数叫做多项式的次数,多项式的每一项都是一个单项式,单项式的个数就是多项式的项数,进而可得出答案.【解答】解:多项式的最高次数项为:﹣n4,故次数为4;多项式有4个单项式组成,故项数是4.即m2﹣n4+3mn+2是4次4项式.故答案为:4、4.【点评】此题考查了多项式的知识,属于基础题,解答本题的关键是掌握多项式次数及项数的判断方法.16.m、n两数在数轴上的位置如图,请按从小到大的顺序排列m、n、﹣m、﹣n m<﹣n<n<﹣m..【考点】有理数大小比较;数轴.【专题】计算题.【分析】根据数轴表示数的方法得到m<0<n,且|m|>n,则﹣m>n,﹣n>m,即可得到m、n、﹣m、﹣n的大小关系.【解答】解:∵m<0<n,且|m|>n,∴﹣m>n,﹣n>m,∴m、n、﹣m、﹣n的大小关系为m<﹣n<n<﹣m.故答案为m<﹣n<n<﹣m.【点评】本题考查了有理数的大小比较:正数大于零,负数小于零;负数的绝对值越大,这个数反而越小.也考查了数轴.17.已知:|x﹣2|+(y+3)2=0,则x2+y2= 13 .【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:由题意得,x﹣2=0,y+3=0,解得,x=2,y=﹣3,则x2+y2=13,故答案为:13.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.18.若2a2m b4和﹣a6b n﹣2是同类项,则m= 3 、n= 6 .【考点】同类项.【分析】根据同类项的概念求解.【解答】解:∵2a2m b4和﹣a6b n﹣2是同类项,∴2m=6,n﹣2=4,解得:m=3,n=6.故答案为:3,6.【点评】本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.19.有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|﹣|c﹣b|﹣|b+a|= 2b﹣2c .【考点】整式的加减;数轴;绝对值.【分析】根据数轴,可得出a+c、c﹣b、a+b的符号,再去绝对值即可.【解答】解:由数轴得,a<b<c,且|a|>|b|>|c|,∴a+c<0,c﹣b>0,b+a<0,∴原式=﹣a﹣c﹣c+b+b+a=2b﹣2c.故答案为2b﹣2c.【点评】本题考查了整式的加减,以及绝对值、数轴,掌握正数的绝对正等于本身,负数的绝对值等于它的相反数,0的绝对值是0是解题的关键.20.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…(1)按此规律写出第6个单项式﹣32x6y ;(2)试猜想第n个单项式为(﹣1)n+12n﹣1x n y .【考点】单项式.【专题】规律型.【分析】(1)通过观察题意可得:6为偶数,单项式为负数.x的指数为6时,2的指数为5,由此可解出本题;(2)通过观察题意可得:n为偶数时,单项式为负数.x的指数为n时,2的指数为(n﹣1),由此可解出本题.【解答】解:(1)∵当n=1时,xy,当n=2时,﹣2x2y,当n=3时,4x3y,当n=4时,﹣8x4y,当n=5时,16x5y,∴第6个单项式是﹣26﹣1x6y,即﹣32x6y.故答案为:﹣32x6y.(2)∴n为偶数时,单项式为负数.x的指数为n时,2的指数为n﹣1,∴当n为奇数时的单项式为2n﹣1x n y,该单项式为(﹣1)n+12n﹣1x n y.故答案为:(﹣1)n+12n﹣1x n y.【点评】本题考查的是单项式,根据题意找出各式子的规律是解答此题的关键.三、计算题.(每小题30分,共30分.)21.(1)﹣6﹣7﹣8(2)(3)﹣3x2y+2x2y+3xy2﹣2xy2(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)(5)解方程 x+12=4x﹣15(6)解方程:y﹣=2﹣.【考点】有理数的混合运算;解一元一次方程.【分析】(1)根据有理数的减法计算即可;(2)根据有理数的混合计算解答即可;(3)根据合并同类项进行计算即可;(4)根据整式的混合计算即可;(5)利用一元一次方程进行解答即可;(6)利用一元一次方程进行解答即可.【解答】解:(1)﹣6﹣7﹣8=﹣21;(2)=﹣1﹣=﹣1+=;(3)﹣3x2y+2x2y+3xy2﹣2xy2=﹣x2y+xy2;(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)=x﹣3+6x﹣3x2﹣4+6x+2x2=12x﹣7;(5)x+12=4x﹣154x﹣x=27,3x=27,x=9;(6)y﹣=2﹣,10y﹣5(y﹣1)=20﹣2(y+2)10y﹣5y+5=20﹣2y﹣47y=11y=【点评】此题考查有理数混合计算,关键是根据有理数的混合计算顺序、整式的混合计算和解方程计算解答.四、解答题:(本大题共4小题,每小题5分,共20分.)22.求3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab的值,已知4|a﹣1|+8(b+3)2=0.【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【分析】先求出a、b的值,再去小括号,去中括号,合并同类项,最后代入求出即可.【解答】解:∵4|a﹣1|+8(b+3)2=0,∴a﹣1=0,b+3=0,∴a=1,b=﹣3,∴3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab=3a2b﹣[2a2b﹣2ab+a2b﹣4a2]﹣ab=3a2b﹣2a2b+2ab﹣a2b+4a2﹣ab=ab+4a2=1×(﹣3)+4×12=1.【点评】本题考查了整式的加减和求值的应用,解此题的关键是能根据整式的加减法则进行化简,难度不是很大.23.已知﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,求a2﹣2a+1的值.【考点】多项式.【分析】根据多项式的次数为7,项数为3,可得出a的值,继而可得出代数式的值.【解答】解:∵﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,∴3+|a|=7,a﹣4≠0,解得:a=﹣4,故a2﹣2a+1=(a﹣1)2=25.【点评】本题考查了多项式的知识,用到的知识点为:多项式的次数由组成多项式的单项式的最高次数决定;组成多项式的单项式叫做多项式的项,有几项就是几项式.24.(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,(1)试求x值;(2)求关于y方程n+|y|=x的解.【考点】一元一次方程的定义;解一元一次方程.【分析】(1)根据二次项系数为零且一次项系数不为零是一元一次方程,可得n的值,根据解方程,可得方程的解;(2)根据互为相反数的绝对值相等,可得方程的解.【解答】解:(1)由(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,得4﹣n2=0且n﹣2≠0.解得n=﹣2.原方程等价于4x﹣8=0.解得x=2;(2)将n,x的值代入关于y方程n+|y|=x,得﹣2+|y|=2.化简,得|y|=4.解得y=4或y=﹣4.【点评】本题考查了一元一次方程的定义,利用二次项系数为零且一次项系数不为零是一元一次方程得出n的值是解题关键.25.已知:有理数a、b满足ab>0,当时,|y﹣4|=2,3a3z﹣1b与7ba5能够合并,求y﹣2x+z的值.【考点】代数式求值;绝对值;同类项.【分析】先根据ab>0可得出x的值,再由|y﹣4|=2求出y的值,3a3z﹣1b与7ba5能够合并求出z的值,代入代数式进行计算即可.【解答】解:∵ab>0,∴ab同号.当a>0,b>0时,x=2;当a<0,b<0时,x=﹣2.∵|y﹣4|=2,∴y=6或y=2;∵3a3z﹣1b与7ba5能够合并,∴3z﹣1=5,解得z=2.∴当x=2,y=6,z=2时,y﹣2x+z=6﹣4+2=4;当x=2,y=2,z=2时,y﹣2x+z=2﹣4+2=0;当x=﹣2,y=6,z=2时,y﹣2x+z=6+4+2=12;当x=﹣2,y=2,z=2时,y﹣2x+z=2+4+2=8.综上所述,代数式的值为4,0,12或8.【点评】本题考查的是代数式求值,在解答此题时要注意进行分类讨论.五、解答题26.(2007•湘潭)为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n【考点】规律型:图形的变化类.【专题】压轴题;规律型.【分析】观察给出的3个例图,注意火柴棒根数的变化是图②的火柴棒比图①的多6根,图③的火柴棒比图②的多6根,而图①的火柴棒的根数为2+6.【解答】解:第n条小鱼需要(2+6n)根,故选A.【点评】本题考查列代数式,本题的解答体现了由特殊到一般的数学方法(归纳法),先观察特例,找到火柴棒根数的变化规律,然后猜想第n条小鱼所需要的火柴棒的根数.27.(2015秋•西城区校级期中)如果a2+a﹣1=0,求a3+2a2+2的值.【考点】因式分解的应用.【分析】由已知条件得出a2+a=1,通过式子变形和因式分解得出a3+2a2=1,即可得出结果.【解答】解:∵a2+a﹣1=0,∴a2+a=1,∴a3+2a2=a3+a2+a2=a(a2+a)+a2=a+a2=1,∴a3+2a2+2=1+2=3.【点评】本题考查了因式分解的应用、等式变形、代数式的求值;熟练掌握因式分解和等式变形是解决问题的关键.28.(2015秋•西城区校级期中)如图是一块在电脑屏幕上出现的长方形色块图,它是由6个不同颜色的正方形组成的,已知中间最小的正方形的边长是1cm,则这块长方形色块图的总面积是多少?【考点】一元一次方程的应用.【专题】几何图形问题;方程思想.【分析】若设第二小的正方形的边长为xcm.则有两种不同的方法可以表示出长方形的长:根据正方形的边长相等,可得:第一种表示方法为x+x+(x+1);第二种表示方法为(x+2)+(x+3),即可列出方程.【解答】解:设第二小的正方形的边长为xcm,则有:x+x+(x+1)=(x+2)+(x+3),解之得:x=4,所以长方形的长为13cm,宽为11cm,面积=13×11=143cm2.【点评】注意要会由设第二小的正方形的边长,从两个不同的角度去表示长方形的长,从而列出方程.。
2018-2019年西城区鲁迅中学七年级上期中数学试卷含解析

2018-2019年西城区鲁迅中学七年级上期中数学试卷含解析-2019学年西鲁迅中学七年级(上)期中数学试卷一、选择题:在每小题的四个选项中,只有一项是符合题目要求的.(每小题3分,共30分.)1.﹣5的绝对值等于()A.﹣5 B. C.5 D.2.下列各式中,等号成立的是()A.|﹣a|=a B.﹣32=(﹣3)2C.﹣27=(﹣2)7D.﹣(﹣3)2=﹣(﹣2)33.光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是()A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km4.若>0,则一定有()A.a>0且b>0 B.a<0且b<0C.a,b同正或同负D.不确定5.已知关于x的方程2x+m=5的解是x=﹣1,则m的值为()A.3 B.7 C.﹣7 D.﹣36.下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b7.若﹣1<m<0,则m、m2、的大小关系是()A.m<m2<B.m2<m<C.<m<m2D.m<<m28.下列说法正确的个数有()①若|a|=|b|,则a=b;②若a≠b,则a2≠b2;③若a>b,则a2>b2;④a2>a.A.0个B.1个C.2个D.3个9.当式子(2x﹣1)2+2取最小值时,x等于()A.2 B.﹣2 C.0.5 D.﹣0.510.数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d﹣2a=10,则数轴上原点应是()A.A点 B.B点C.C点D.D点二、填空题:把答案填在题中横线上.(每题2分,共20分.)11.0的相反数为,的倒数为.12.数轴上与原点相距3个单位长度的点有个,它们表示的数各是.13.甲数x的与乙数y的的差可以表示为.14.单项式的系数是,次数是.15.m2﹣n4+3mn+2是次项式.16.m、n两数在数轴上的位置如图,请按从小到大的顺序排列m、n、﹣m、﹣n.17.已知:|x﹣2|+(y+3)2=0,则x2+y2=.18.若2a2m b4和﹣a6b n﹣2是同类项,则m=、n=.19.有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|﹣|c﹣b|﹣|b+a|=.20.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…(1)按此规律写出第6个单项式;(2)试猜想第n个单项式为.三、计算题.(每小题30分,共30分.)21.(1)﹣6﹣7﹣8(2)(3)﹣3x2y+2x2y+3xy2﹣2xy2(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)(5)解方程x+12=4x﹣15(6)解方程:y﹣=2﹣.四、解答题:(本大题共4小题,每小题5分,共20分.)22.求3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab的值,已知4|a﹣1|+8(b+3)2=0.23.已知﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,求a2﹣2a+1的值.24.(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,(1)试求x值;(2)求关于y方程n+|y|=x的解.25.已知:有理数a、b满足ab>0,当时,|y﹣4|=2,3a3z﹣1b与7ba5能够合并,求y ﹣2x+z的值.五、解答题26.(2007•湘潭)为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n27.(2018秋•西校级期中)如果a2+a﹣1=0,求a3+2a2+2的值.28.(2018秋•西校级期中)如图是一块在电脑屏幕上出现的长方形色块图,它是由6个不同颜色的正方形组成的,已知中间最小的正方形的边长是1cm,则这块长方形色块图的总面积是多少?2018-2019学年西鲁迅中学七年级(上)期中数学试卷参考答案与试题解析一、选择题:在每小题的四个选项中,只有一项是符合题目要求的.(每小题3分,共30分.)1.﹣5的绝对值等于()A.﹣5 B. C.5 D.【考点】绝对值.【专题】常规题型.【分析】根据负数的绝对值等于它的相反数解答.【解答】解:﹣5的绝对值|﹣5|=5.故选C.【点评】本题考查了绝对值的性质,熟记一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0是解题的关键.2.下列各式中,等号成立的是()A.|﹣a|=a B.﹣32=(﹣3)2C.﹣27=(﹣2)7D.﹣(﹣3)2=﹣(﹣2)3【考点】有理数的乘方.【分析】根据绝对值的性质,有理数乘方的定义对各选项分析判断后利用排除法求解.【解答】解:A、只有a≥0时,|﹣a|=a成立,故本选项错误;B、﹣32=﹣9,(﹣3)2=9,故本选项错误;C、(﹣2)7=﹣27,故本选项正确;D、﹣(﹣3)2=﹣9,﹣(﹣2)3=8,﹣9≠8,故本选项错误.故选C.【点评】本题考查了有理数的乘方,负数的奇数次幂是负数,负数的偶数次幂是正数,要特别注意﹣32和(﹣2)2的区别.3.光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是()A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将9500 000 000 000km用科学记数法表示为:9.5×1012km.故选:B.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.若>0,则一定有()A.a>0且b>0 B.a<0且b<0C.a,b同正或同负D.不确定【考点】有理数的除法.【分析】根据有理数的除法运算法则,同号得正,异号得负解答.【解答】解:∵>0,∴a>0,b>0或a<0,b<0.故选C.【点评】本题考查了有理数的除法运算,熟记运算符合法则“同号得正,异号得负”是解题的关键.5.已知关于x的方程2x+m=5的解是x=﹣1,则m的值为()A.3 B.7 C.﹣7 D.﹣3【考点】一元一次方程的解.【分析】直接把x=﹣1代入2x+m=5可得关于m的方程,再解即可.【解答】解:把x=﹣1代入2x+m=5得:﹣2+m=5,m=7.故选:B.【点评】此题主要考查了一元一次方程的解,关键是掌握把方程的解代入原方程,等式左右两边相等.6.下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b【考点】合并同类项.【分析】本题考查同类项的概念,含有相同的字母,并且相同字母的指数相同,是同类项的两项可以合并,否则不能合并.合并同类项的法则是系数相加作为系数,字母和字母的指数不变.【解答】解:A、3a与b不是同类项,不能合并.错误;B、3a﹣a=2a.错误;C、2a3与3a2不是同类项,不能合并.错误;D、﹣a2b+2a2b=a2b.正确.故选D.【点评】同类项的概念是所含字母相同,相同字母的指数也相同的项是同类项;注意不是同类项的一定不能合并.7.若﹣1<m<0,则m、m2、的大小关系是()A.m<m2<B.m2<m<C.<m<m2D.m<<m2【考点】有理数大小比较.【分析】本题可采用取特殊值的方法.由于﹣1<m<0,可设m=﹣,然后代入m、m2、中分别计算,然后进行比较即可.【解答】解:根据分析,可设m为﹣,代入可得m=﹣,m2=,=﹣2.即可得.故选C.【点评】本题为简单的有理数比较大小的题目,将满足条件的数字代入即可.8.下列说法正确的个数有()①若|a|=|b|,则a=b;②若a≠b,则a2≠b2;③若a>b,则a2>b2;④a2>a.A.0个B.1个C.2个D.3个【考点】有理数大小比较.【分析】根据绝对值相等的两个数可能相等也可能是相反数可得①错误;根据乘方的计算可得②③④的正误,并且找出错误命题的反例.【解答】解:①若|a|=|b|,则a=b,说法错误,例如:|﹣1|=|1|,但是﹣1≠1;②若a≠b,则a2≠b2,说法正确;③若a>b,则a2>b2;说法错误,例如2>﹣4,但是a2<b2;④a2>a,说法错误,例如0.12<0.1.正确的有1个,故选:B.【点评】此题主要考查了有理数的比较大小,以及绝对值和乘方,关键是错误的命题要正确找出反例.9.当式子(2x﹣1)2+2取最小值时,x等于()A.2 B.﹣2 C.0.5 D.﹣0.5【考点】非负数的性质:偶次方.【分析】根据非负数的性质解答即可.【解答】解:∵(2x﹣1)2,≥0,∴2x﹣1=0时,式子(2x﹣1)2+2取最小值,∴x=0.5.故选:C.【点评】本题考查的是非负数的性质,掌握一个数的偶次方是非负数是解题的关键.10.数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d﹣2a=10,则数轴上原点应是()A.A点 B.B点C.C点D.D点【考点】数轴.【分析】直接利用数轴得出a=d﹣7,再代入已知关系式求出答案.【解答】解:由数轴可得:a=d﹣7,则d﹣2a=d﹣2(d﹣7)=14﹣d=10,解得:d=4.故数轴上原点应是4.故选:C.【点评】此题主要考查了数轴,根据题意得出a=d﹣7是解题关键.二、填空题:把答案填在题中横线上.(每题2分,共20分.)11.0的相反数为0,的倒数为﹣4.【考点】倒数;相反数.【分析】根据相反数、倒数,即可解答.【解答】解:0的相反数是0,﹣的倒数为﹣4,故答案为:0,﹣4.【点评】本题考查了相反数、倒数,解决本题的关键是熟记相反数、倒数的定义.12.数轴上与原点相距3个单位长度的点有2个,它们表示的数各是±3.【考点】数轴.【专题】探究型.【分析】设数轴上与原点相距3个单位长度的点所表示的数为a,再根据数轴上两点间的距离公式求出a的值即可得出结论.【解答】解:设数轴上与原点相距3个单位长度的点所表示的数为a,故|a|=3,解得a=±3.故答案为:2,±3.【点评】本题考查的是数轴的特点,即在数轴上到原点距离相等的点有两个,这两个数互为相反数.13.甲数x的与乙数y的的差可以表示为x﹣y.【考点】列代数式.【分析】被减式为x的,减式为y的,让它们相减即可.【解答】解:所求的关系式为:x﹣y.【点评】求两个式子的差的关键是找到被减式和减式.14.单项式的系数是,次数是3.【考点】单项式.【分析】根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.【解答】解:根据单项式系数、次数的定义可知:单项式的系数是,次数是1+2=3.【点评】确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.15.m2﹣n4+3mn+2是4次4项式.【考点】多项式.【分析】多项式中次数最高的项的次数叫做多项式的次数,多项式的每一项都是一个单项式,单项式的个数就是多项式的项数,进而可得出答案.【解答】解:多项式的最高次数项为:﹣n4,故次数为4;多项式有4个单项式组成,故项数是4.即m2﹣n4+3mn+2是4次4项式.故答案为:4、4.【点评】此题考查了多项式的知识,属于基础题,解答本题的关键是掌握多项式次数及项数的判断方法.16.m、n两数在数轴上的位置如图,请按从小到大的顺序排列m、n、﹣m、﹣n m<﹣n<n<﹣m..【考点】有理数大小比较;数轴.【专题】计算题.【分析】根据数轴表示数的方法得到m<0<n,且|m|>n,则﹣m>n,﹣n>m,即可得到m、n、﹣m、﹣n的大小关系.【解答】解:∵m<0<n,且|m|>n,∴﹣m>n,﹣n>m,∴m、n、﹣m、﹣n的大小关系为m<﹣n<n<﹣m.故答案为m<﹣n<n<﹣m.【点评】本题考查了有理数的大小比较:正数大于零,负数小于零;负数的绝对值越大,这个数反而越小.也考查了数轴.17.已知:|x﹣2|+(y+3)2=0,则x2+y2=13.【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.【解答】解:由题意得,x﹣2=0,y+3=0,解得,x=2,y=﹣3,则x2+y2=13,故答案为:13.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.18.若2a2m b4和﹣a6b n﹣2是同类项,则m=3、n=6.【考点】同类项.【分析】根据同类项的概念求解.【解答】解:∵2a2m b4和﹣a6b n﹣2是同类项,∴2m=6,n﹣2=4,解得:m=3,n=6.故答案为:3,6.【点评】本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.19.有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|﹣|c﹣b|﹣|b+a|=2b﹣2c.【考点】整式的加减;数轴;绝对值.【分析】根据数轴,可得出a+c、c﹣b、a+b的符号,再去绝对值即可.【解答】解:由数轴得,a<b<c,且|a|>|b|>|c|,∴a+c<0,c﹣b>0,b+a<0,∴原式=﹣a﹣c﹣c+b+b+a=2b﹣2c.故答案为2b﹣2c.【点评】本题考查了整式的加减,以及绝对值、数轴,掌握正数的绝对正等于本身,负数的绝对值等于它的相反数,0的绝对值是0是解题的关键.20.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…(1)按此规律写出第6个单项式﹣32x6y;(2)试猜想第n个单项式为(﹣1)n+12n﹣1x n y.【考点】单项式.【专题】规律型.【分析】(1)通过观察题意可得:6为偶数,单项式为负数.x的指数为6时,2的指数为5,由此可解出本题;(2)通过观察题意可得:n为偶数时,单项式为负数.x的指数为n时,2的指数为(n﹣1),由此可解出本题.【解答】解:(1)∵当n=1时,xy,当n=2时,﹣2x2y,当n=3时,4x3y,当n=4时,﹣8x4y,当n=5时,16x5y,∴第6个单项式是﹣26﹣1x6y,即﹣32x6y.故答案为:﹣32x6y.(2)∴n为偶数时,单项式为负数.x的指数为n时,2的指数为n﹣1,∴当n为奇数时的单项式为2n﹣1x n y,该单项式为(﹣1)n+12n﹣1x n y.故答案为:(﹣1)n+12n﹣1x n y.【点评】本题考查的是单项式,根据题意找出各式子的规律是解答此题的关键.三、计算题.(每小题30分,共30分.)21.(1)﹣6﹣7﹣8(2)(3)﹣3x2y+2x2y+3xy2﹣2xy2(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)(5)解方程x+12=4x﹣15(6)解方程:y﹣=2﹣.【考点】有理数的混合运算;解一元一次方程.【分析】(1)根据有理数的减法计算即可;(2)根据有理数的混合计算解答即可;(3)根据合并同类项进行计算即可;(4)根据整式的混合计算即可;(5)利用一元一次方程进行解答即可;(6)利用一元一次方程进行解答即可.【解答】解:(1)﹣6﹣7﹣8=﹣21;(2)=﹣1﹣=﹣1+=;(3)﹣3x2y+2x2y+3xy2﹣2xy2=﹣x2y+xy2;(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)=x﹣3+6x﹣3x2﹣4+6x+2x2=12x﹣7;(5)x+12=4x﹣154x﹣x=27,3x=27,x=9;(6)y﹣=2﹣,10y﹣5(y﹣1)=20﹣2(y+2)10y﹣5y+5=20﹣2y﹣47y=11y=【点评】此题考查有理数混合计算,关键是根据有理数的混合计算顺序、整式的混合计算和解方程计算解答.四、解答题:(本大题共4小题,每小题5分,共20分.)22.求3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab的值,已知4|a﹣1|+8(b+3)2=0.【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【分析】先求出a、b的值,再去小括号,去中括号,合并同类项,最后代入求出即可.【解答】解:∵4|a﹣1|+8(b+3)2=0,∴a﹣1=0,b+3=0,∴a=1,b=﹣3,∴3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab=3a2b﹣[2a2b﹣2ab+a2b﹣4a2]﹣ab=3a2b﹣2a2b+2ab﹣a2b+4a2﹣ab=ab+4a2=1×(﹣3)+4×12=1.【点评】本题考查了整式的加减和求值的应用,解此题的关键是能根据整式的加减法则进行化简,难度不是很大.23.已知﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,求a2﹣2a+1的值.【考点】多项式.【分析】根据多项式的次数为7,项数为3,可得出a的值,继而可得出代数式的值.【解答】解:∵﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,∴3+|a|=7,a﹣4≠0,解得:a=﹣4,故a2﹣2a+1=(a﹣1)2=25.【点评】本题考查了多项式的知识,用到的知识点为:多项式的次数由组成多项式的单项式的最高次数决定;组成多项式的单项式叫做多项式的项,有几项就是几项式.24.(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,(1)试求x值;(2)求关于y方程n+|y|=x的解.【考点】一元一次方程的定义;解一元一次方程.【分析】(1)根据二次项系数为零且一次项系数不为零是一元一次方程,可得n的值,根据解方程,可得方程的解;(2)根据互为相反数的绝对值相等,可得方程的解.【解答】解:(1)由(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,得4﹣n2=0且n﹣2≠0.解得n=﹣2.原方程等价于4x﹣8=0.解得x=2;(2)将n,x的值代入关于y方程n+|y|=x,得﹣2+|y|=2.化简,得|y|=4.解得y=4或y=﹣4.【点评】本题考查了一元一次方程的定义,利用二次项系数为零且一次项系数不为零是一元一次方程得出n的值是解题关键.25.已知:有理数a、b满足ab>0,当时,|y﹣4|=2,3a3z﹣1b与7ba5能够合并,求y﹣2x+z的值.【考点】代数式求值;绝对值;同类项.【分析】先根据ab>0可得出x的值,再由|y﹣4|=2求出y的值,3a3z﹣1b与7ba5能够合并求出z的值,代入代数式进行计算即可.【解答】解:∵ab>0,∴ab同号.当a>0,b>0时,x=2;当a<0,b<0时,x=﹣2.∵|y﹣4|=2,∴y=6或y=2;∵3a3z﹣1b与7ba5能够合并,∴3z﹣1=5,解得z=2.∴当x=2,y=6,z=2时,y﹣2x+z=6﹣4+2=4;当x=2,y=2,z=2时,y﹣2x+z=2﹣4+2=0;当x=﹣2,y=6,z=2时,y﹣2x+z=6+4+2=12;当x=﹣2,y=2,z=2时,y﹣2x+z=2+4+2=8.综上所述,代数式的值为4,0,12或8.【点评】本题考查的是代数式求值,在解答此题时要注意进行分类讨论.五、解答题26.(2007•湘潭)为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n【考点】规律型:图形的变化类.【专题】压轴题;规律型.【分析】观察给出的3个例图,注意火柴棒根数的变化是图②的火柴棒比图①的多6根,图③的火柴棒比图②的多6根,而图①的火柴棒的根数为2+6.【解答】解:第n条小鱼需要(2+6n)根,故选A.【点评】本题考查列代数式,本题的解答体现了由特殊到一般的数学方法(归纳法),先观察特例,找到火柴棒根数的变化规律,然后猜想第n条小鱼所需要的火柴棒的根数.27.(2018秋•西校级期中)如果a2+a﹣1=0,求a3+2a2+2的值.【考点】因式分解的应用.【分析】由已知条件得出a2+a=1,通过式子变形和因式分解得出a3+2a2=1,即可得出结果.【解答】解:∵a2+a﹣1=0,∴a2+a=1,∴a3+2a2=a3+a2+a2=a(a2+a)+a2=a+a2=1,∴a3+2a2+2=1+2=3.【点评】本题考查了因式分解的应用、等式变形、代数式的求值;熟练掌握因式分解和等式变形是解决问题的关键.28.(2018秋•西校级期中)如图是一块在电脑屏幕上出现的长方形色块图,它是由6个不同颜色的正方形组成的,已知中间最小的正方形的边长是1cm,则这块长方形色块图的总面积是多少?【考点】一元一次方程的应用.【专题】几何图形问题;方程思想.【分析】若设第二小的正方形的边长为xcm.则有两种不同的方法可以表示出长方形的长:根据正方形的边长相等,可得:第一种表示方法为x+x+(x+1);第二种表示方法为(x+2)+(x+3),即可列出方程.【解答】解:设第二小的正方形的边长为xcm,则有:x+x+(x+1)=(x+2)+(x+3),解之得:x=4,所以长方形的长为13cm,宽为11cm,面积=13×11=143cm2.【点评】注意要会由设第二小的正方形的边长,从两个不同的角度去表示长方形的长,从而列出方程.。
新北师大版七年级(上)期中考试数学试题(含答案) (60)
2015—2016学年度第一学期七年级数学期中试卷(满分120分,考试时间120分钟)一、选择题(每题3分,共30分。
)1、-3的相反数是( ) A 、31 B 、3 C 、31- D 、-3 2、如图绕虚线旋转得到的几何体是( )3、下列说法正确的是 ( )A 、一个数前面加上“-”号这个数就是负数;B 、正数和负数统称为有理数C 、0既不是正数也不是负数;D 、非负数就是正数; 4、在()2--,7--,012001⨯-,()31--,⎪⎭⎫ ⎝⎛+-25,42-中,非正数有 ( )A 、1个B 、2个C 、3个D 、4个 5、用平面去截五棱柱,在所得的截面中,不可能出现的是( ) A 、八边形 B 、四边形 C 、六边形 D 、三角形 6、 下列计算正确的是 ( )A 、2733-=- B 、(-4)2=-16 C 、(-34)31(D 1251)5143-=-=、 7、小新准备用如图的纸片做一个礼品盒,为了美观,他想在六个正方形纸片上画上图案,使做成后三组对面的图案分别相同,那么画上图案后正确的是 ( )8、铅笔的单价是a 元,圆珠笔的单价是铅笔单价的3倍,则圆珠笔的单价是( )元. A 、a 3 B 、a +3 C 、3-a D 、3a9、在下列各式子22223)(121b ab a y x bR s mn ab ++-=,, , ,, π中,代数式有( )A .2个B .3个C .4个D .5个10、如图,A 、B 两点在数轴上表示的数分别为a 、b ,下列式子不成立的是 ( )A. a b b a -=- B .-01<<a C .b a < D .0<+a b二、填空题(每题4分,共32分。
)11、如果向东走6米记作+6米,那么向西走10米记作 。
12、一个边长为1的正方形,第一次截去正方形的一半,第二次截去剩下的一半,如此截下去,第六次后剩下的面积为 米.. 13、最大的负整数是 。
北师大二附中西城实验学校初一上期中数学(含解析)

2015-2016年北师大二附中西城实验学校初一上学期数学期中试卷一、选择题(本大题共10小题,每小题只有唯一正确答案.每小题3分,共30分) 1.5-的绝对值是( ). A .5B .5-C .15D .15-【答案】A【解析】|5|5-=.2.十八大报告指出:“建设生态文明,是关系人民福祉、关乎民族未来的长远大计”,这些年党和政府在生态文明的发展进程上持续推进,在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( ). A .714610⨯ B .71.4610⨯C .91.4610⨯D .101.4610⨯【答案】C【解析】91 460 000 000 1.4610=⨯.3.下列各式中运算正确的是( ). A .43m m -= B .220a b ab -=C .33323a a a -=D .2xy xy xy -=-【答案】D【解析】43m m m -=,22()a b ab ab a b -=-,33323a a a -=-,故正确的为D .4.已知代数式165m a b --和212n ab 是同类项,则m n -的值是( ).A .1B .1-C .2-D .3-【答案】B【解析】根据同类型的定义可有1162m n -=⎧⎨=⎩,即23m n =⎧⎨=⎩,所以1m n -=-.5.下列各式中去括号正确的是( ). A .22(22)22x x y x x y --+=--+ B .(1)()1mn m n mn m n --+-=--+- C .(5)5ab ab --+=- D .(53)(2)22x x y x y x y --+-=-+【答案】D【解析】A ,22(22)22x x y x x y --+=-+-,故本选项错误; B ,(1)()1mn m n mn m n --+-=-++-,故本选项错误; C ,(5)25ab ab ab --+=-,故本选项错误;D ,(53)(2)22x x y x y x y --+-=-+,故本选项正确.6.下列方程中,解为4x =的方程是( ). A .14x -= B .41x = C .4133x x -=+D .1(1)15x -=【答案】C【解析】将4x =代入各方程中,等式两边相等的只有C .7.下列说法正确的是( ).A .若ac bc =,则a b =B .若a bc c =,则a b = C .若22a b =,则a b = D .若163x -=,则2x =-【答案】B【解析】A ,当0c =时,即使a b ≠,等式也成立,故本选项错误; B ,若a bc c=,不存在0c =的情况,故恒成立,故本选项正确; C ,若22a b =,则a b =±,故本选项错误;D ,若163x -=,则18x =-,故本选项错误.8.有理数23-,2(3)-,3||3-,13-按从小到大的顺序排列是( ).A .223()|13|333<-<--<-B .322||()13333-<<-<--C .22313333()||<-<---<D .232||(13)333<-<--<-【答案】C 【解析】293-=-,2(93)-=,3|23|7-=,∴22313333()||<-<---<.9.实数a 、b 在数轴上的位置如图所示,则化简||a b a -+的结果为( ).obaA .2a b -+B .b -C .bD .2a b --【答案】C【解析】根据数轴的定义可有:0a b <<,∴||a b a a b a b -+=-++=.10.下面是按一定规律排列的一列数:第1个数:11122-⎛⎫-+ ⎪⎝⎭; 第2个数:2311(1)(1)1113234⎛⎫⎛⎫---⎛⎫-+++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭;第3个数:234511(1)(1)(1)(1)11111423456⎛⎫⎛⎫⎛⎫⎛⎫-----⎛⎫-+++++ ⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭;……第n 个数:232111(1)(1)(1)111112342n n n -⎛⎫⎛⎫⎛⎫----⎛⎫-++++ ⎪⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭L .那么,在第8个数、第9个数、第10个数、第11个数中,最大的数是( ). A .第8个数 B .第9个数 C .第10个数 D .第11个数【答案】A【解析】第n 个数:232111(1)(1)(1)111112342n n n -⎛⎫⎛⎫⎛⎫----⎛⎫-++++ ⎪⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭L1143652211112345621212n n n n n n -=-⋅⋅⋅⋅⋅⋅=-+-+L , 故在第8个数、第9个数、第10个数、第11个数中,最大的数是第8个数.二、填空题(每空2分,共20分.请将答案写在题目的横线上)11.2-的倒数是__________.【答案】12-【解析】1122=--.12.有理数3.645精确到百分位的近似数为__________. 【答案】3.65【解析】有理数3.645精确到百分位的近似数为3.65.13.列式表示“a 的3倍与b 的相反数的和”:__________. 【答案】3a b - 【解析】见答案.14.已知2是关于x 的方程21x a -=的解,则a =__________. 【答案】3【解析】将2x =代入方程中,解得3a =.15.如果2(2)|1|0a b ++-=,那么2015()a b +=__________. 【答案】1-【解析】根据完全平方式为零的条件可得21a b =-⎧⎨=⎩,故20152015()(1)1a b +=-=-.16.已知整式2x y -的值是2-,则整式32x y -+的值是__________. 【答案】5【解析】323(2)5x y x y -+=--=.17.已知整式2x y -的值是2-,则整式32x y -+的值是__________. 【答案】5【解析】323(2)5x y x y -+=--=.18.关于x 的二次三项式的一次项系数为5,二次项系数是3-,常数项是4-.按照x 的次数逐渐降低排列,这个二次三项式为__________. 【答案】2354x x -+-【解析】见答案.19.若x 、y 都是有理数,且使得四个两两不相等的数4x +、2x 、27y -、y 能分成两组,每组的两个数是互为相反数,则x y +的值等于__________. 【答案】1【解析】若4227x x y y +=-⎧⎨-=-⎩,则4373x y ⎧=-⎪⎪⎨⎪=⎪⎩,此时843x +=,823x =-,7273y -=-,73y =,满足条件,故1x y +=;若4272x y x y +=-⎧⎨=-⎩,则115225x y ⎧=-⎪⎪⎨⎪=⎪⎩,此时945x +=,2225x =-,22275y -=-,225y =,不满足条件,故舍去;若4227x y x y +=-⎧⎨=-⎩,则15414x y ⎧=-⎪⎪⎨⎪=-⎪⎩,此时144x +=,1522x =-,15272y -=-,14y =-,不满足条件,故舍去.故答案为1.20.有一列式子,按一定规律排列成23a -,59a ,1027a -,1781a ,26243a -,….@(1)当1a =时,其中三个相邻数的和是63,则位于这三个数中间的数是__________. 【答案】27-【解析】当1a =时,排列的式子为3-,9,27-,81,243-.三个相邻数的和是63,可知9278163-+=,故位于这三个数中间的数是27-. @(2)上列式子中第n 个式子为__________(n 为正整数). 【答案】31(3)n n a -- 【解析】见答案.三.用心算一算(共4个小题,每小题4分,共16分) 21.计算:91121-+-.【答案】19- 【解析】原式19=-.22.计算:311(2)|3|3-+-+-÷.【答案】0【解析】原式18330=--+⋅=.23.3212(3)4()23-÷⨯-.【答案】43【解析】原式22427()993=-⨯⨯-=.24.计算:22323223⎡⎤⎛⎫-⨯-⨯--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦. 【答案】9【解析】原式349229⎛⎫=-⨯-⨯- ⎪⎝⎭()3422=-⨯--()3692=-⨯-=.四.认真解一解下列方程(共2个小题,每小题4分,共8分)25.解方程:52652x x -=-.【答案】2x =-【解析】合并同类项,得:112x -=,系数化1,得:2x =-.26.解方程:353(1)(4)22y y -+=---.【答案】3y =-【解析】合并同类项,得:3y -= 系数化1,得:3y =-.五.化简或求值(本题5分+5分+5分+5分=20分) 27.化简:321325x y y x -++--.【答案】4x y +-【解析】原式3223154x x y y x y =--++-=+-.28.化简:221524()2x y xy x y xy ---.【答案】2x y【解析】原式2225242x y xy x y xy x y =--+=.29.已知13a =-,求整式()226213a a a a +-+-的值.【答案】53-【解析】原式232a =-,代入原式53=-.30.先化简,再求值:2224(25)2(3)xy x xy y x xy -+-++,其中2x =-,1y =.【答案】9-【解析】原式2222425265xy x xy y x xy xy y =--+++=+, 当2x =-,1y =时,原式25(2)111019=⨯-⨯+=-+=-.六.解答下列问题(2分+2分+2分=6分)31.首届中国国际魔术邀请赛、魔术论坛2012年11月30日至12月2日在北京昌平区体育馆举办刘谦的魔术表演风靡全世界.很多同学非常感兴趣,也学起了魔术.请看刘凯同学把任意有理数对(,)x y 放进装有计算装置的魔术盒,会得到一个新的有理数21x y +-.例如把(3,)2-放入其中,就会得到23(2)16+--=.现将有理数对(4,5)--放入其中,得到的有理数是__________.若将正整数对放入其中,得到的值都为5,则满足条件的所有的正整数对(,)x y 为__________.【答案】10;(1,5),(2,2)【解析】将有理数对(4,5)--放入,得到2(4)(5)110-+--=; 满足值都为5条件:215x y +-=,即26x y +=. 由于(,)x y 都为正整数,故15x y =⎧⎨=⎩或22x y =⎧⎨=⎩,故满足条件的所有正整数对为(1,5),(2,2).32.如果210a a +-=,求3222a a ++的值.【答案】3【解析】解法1:∵210a a +-=,∴21a a +=,∴3222a a ++3222a a a =+++22()2a a a a =+++22123a a =++=+=. 解法2: ∵210a a +-=, ∴21a a =-,∴3222a a ++2222aa a =++2(1)22a a a =-++2222a a a =-++22123a a =++=+=.33.国强同学喜欢用黑色棋子摆放在正多边形的边上来研究数的规律.请你观察下面表格中棋子的摆放规律,并回答下面问题:@(1)通过观察、归纳发现可以分别用含字母n (1n ≥的整数)的代数式表示P 、Q 、M .三角形……第n 个三角形棋子个数 3 6 9 …… P正方形……第n 个正方形棋子个数 4 8 12 …… Q正多边形第n 个正多边形棋子个数 3 8 15 24 M则P =__________,Q =__________,M =__________. 【答案】3n ,4n ,(2)n n + 【解析】见答案.@(2)下列数中既是三角形中的棋子数又是正方形中的棋子数的是__________. A .2013 B .2014C .2015D .2016【答案】D【解析】既是三角形中的棋子数又是正方形中的棋子数只需满足条件:34n m =, 故只需要为3和4的公倍数即可. 可知,2016符合条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年北京市西城区鲁迅中学七年级(上)期中数学试卷一、选择题:在每小题的四个选项中,只有一项是符合题目要求的.(每小题3分,共30分.)1.(3分)﹣5的绝对值等于()A.﹣5 B.C.5 D.2.(3分)下列各式中,等号成立的是()A.|﹣a|=a B.﹣32=(﹣3)2C.﹣27=(﹣2)7D.﹣(﹣3)2=﹣(﹣2)3 3.(3分)光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是()A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km4.(3分)若>0,则一定有()A.a>0且b>0 B.a<0且b<0C.a,b同正或同负D.不确定5.(3分)已知关于x的方程2x+m=5的解是x=﹣1,则m的值为()A.3 B.7 C.﹣7 D.﹣36.(3分)下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b7.(3分)若﹣1<m<0,则m、m2、的大小关系是()A.m<m2<B.m2<m<C.<m<m2D.m<<m28.(3分)下列说法正确的个数有()①若|a|=|b|,则a=b;②若a≠b,则a2≠b2;③若a>b,则a2>b2;④a2>a.A.0个 B.1个 C.2个 D.3个9.(3分)当式子(2x﹣1)2+2取最小值时,x等于()A.2 B.﹣2 C.0.5 D.﹣0.510.(3分)数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d﹣2a=10,则数轴上原点应是()A.A点B.B点 C.C点 D.D点二、填空题:把答案填在题中横线上.(每题2分,共20分.)11.(2分)0的相反数为,的倒数为.12.(2分)数轴上与原点相距3个单位长度的点有个,它们表示的数各是.13.(2分)甲数x的与乙数y的的差可以表示为.14.(2分)单项式的系数是,次数是.15.(2分)m2﹣n4+3mn+2是次项式.16.(2分)m、n两数在数轴上的位置如图,请按从小到大的顺序排列m、n、﹣m、﹣n.17.(2分)已知:|x﹣2|+(y+3)2=0,则x2+y2=.18.(2分)若2a2m b4和﹣a6b n﹣2是同类项,则m=、n=.19.(2分)有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|﹣|c﹣b|﹣|b+a|=.20.(2分)观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…(1)按此规律写出第6个单项式;(2)试猜想第n个单项式为.三、计算题.(每小题30分,共30分.)21.(30分)(1)﹣6﹣7﹣8(2)(3)﹣3x2y+2x2y+3xy2﹣2xy2(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)(5)解方程x+12=4x﹣15(6)解方程:y﹣=2﹣.四、解答题:(本大题共4小题,每小题5分,共20分.)22.(5分)求3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab的值,已知4|a﹣1|+8(b+3)2=0.23.(5分)已知﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,求a2﹣2a+1的值.24.(5分)(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,(1)试求x值;(2)求关于y方程n+|y|=x的解.25.(5分)已知:有理数a、b满足ab>0,当时,|y﹣4|=2,3a3z ﹣1b与7ba5能够合并,求y﹣2x+z的值.五、解答题26.为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n27.如果a2+a﹣1=0,求a3+2a2+2的值.28.如图是一块在电脑屏幕上出现的长方形色块图,它是由6个不同颜色的正方形组成的,已知中间最小的正方形的边长是1cm,则这块长方形色块图的总面积是多少?2015-2016学年北京市西城区鲁迅中学七年级(上)期中数学试卷参考答案与试题解析一、选择题:在每小题的四个选项中,只有一项是符合题目要求的.(每小题3分,共30分.)1.(3分)﹣5的绝对值等于()A.﹣5 B.C.5 D.【解答】解:﹣5的绝对值|﹣5|=5.故选:C.2.(3分)下列各式中,等号成立的是()A.|﹣a|=a B.﹣32=(﹣3)2C.﹣27=(﹣2)7D.﹣(﹣3)2=﹣(﹣2)3【解答】解:A、只有a≥0时,|﹣a|=a成立,故本选项错误;B、﹣32=﹣9,(﹣3)2=9,故本选项错误;C、(﹣2)7=﹣27,故本选项正确;D、﹣(﹣3)2=﹣9,﹣(﹣2)3=8,﹣9≠8,故本选项错误.故选:C.3.(3分)光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学记数法表示是()A.0.95×1013km B.9.5×1012km C.95×1011km D.950×1010km【解答】解:将9500 000 000 000km用科学记数法表示为:9.5×1012km.故选:B.4.(3分)若>0,则一定有()A.a>0且b>0 B.a<0且b<0C.a,b同正或同负D.不确定【解答】解:∵>0,∴a>0,b>0或a<0,b<0.故选:C.5.(3分)已知关于x的方程2x+m=5的解是x=﹣1,则m的值为()A.3 B.7 C.﹣7 D.﹣3【解答】解:把x=﹣1代入2x+m=5得:﹣2+m=5,m=7.故选:B.6.(3分)下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b【解答】解:A、3a与b不是同类项,不能合并.错误;B、3a﹣a=2a.错误;C、2a3与3a2不是同类项,不能合并.错误;D、﹣a2b+2a2b=a2b.正确.故选:D.7.(3分)若﹣1<m<0,则m、m2、的大小关系是()A.m<m2<B.m2<m<C.<m<m2D.m<<m2【解答】解:根据分析,可设m为﹣,代入可得m=﹣,m2=,=﹣2.即可得.故选:C.8.(3分)下列说法正确的个数有()①若|a|=|b|,则a=b;②若a≠b,则a2≠b2;③若a>b,则a2>b2;④a2>a.A.0个 B.1个 C.2个 D.3个【解答】解:①若|a|=|b|,则a=b,说法错误,例如:|﹣1|=|1|,但是﹣1≠1;②若a≠b,则a2≠b2,说法错误;③若a>b,则a2>b2;说法错误,例如2>﹣4,但是a2<b2;④a2>a,说法错误,例如0.12<0.1.正确的有0个,故选:A.9.(3分)当式子(2x﹣1)2+2取最小值时,x等于()A.2 B.﹣2 C.0.5 D.﹣0.5【解答】解:∵(2x﹣1)2,≥0,∴2x﹣1=0时,式子(2x﹣1)2+2取最小值,∴x=0.5.故选:C.10.(3分)数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d﹣2a=10,则数轴上原点应是()A.A点B.B点 C.C点 D.D点【解答】解:由数轴可得:a=d﹣7,则d﹣2a=d﹣2(d﹣7)=14﹣d=10,解得:d=4.故数轴上原点应是4.故选:C.二、填空题:把答案填在题中横线上.(每题2分,共20分.)11.(2分)0的相反数为0,的倒数为﹣4.【解答】解:0的相反数是0,﹣的倒数为﹣4,故答案为:0,﹣4.12.(2分)数轴上与原点相距3个单位长度的点有2个,它们表示的数各是±3.【解答】解:设数轴上与原点相距3个单位长度的点所表示的数为a,故|a|=3,解得a=±3.故答案为:2,±3.13.(2分)甲数x的与乙数y的的差可以表示为x﹣y.【解答】解:所求的关系式为:x﹣y.14.(2分)单项式的系数是,次数是3.【解答】解:根据单项式系数、次数的定义可知:单项式的系数是,次数是1+2=3.15.(2分)m2﹣n4+3mn+2是4次4项式.【解答】解:多项式的最高次数项为:﹣n4,故次数为4;多项式有4个单项式组成,故项数是4.即m2﹣n4+3mn+2是4次4项式.故答案为:4、4.16.(2分)m、n两数在数轴上的位置如图,请按从小到大的顺序排列m、n、﹣m、﹣n m<﹣n<n<﹣m..【解答】解:∵m<0<n,且|m|>n,∴﹣m>n,﹣n>m,∴m、n、﹣m、﹣n的大小关系为m<﹣n<n<﹣m.故答案为m<﹣n<n<﹣m.17.(2分)已知:|x﹣2|+(y+3)2=0,则x2+y2=13.【解答】解:由题意得,x﹣2=0,y+3=0,解得,x=2,y=﹣3,则x2+y2=13,故答案为:13.18.(2分)若2a2m b4和﹣a6b n﹣2是同类项,则m=3、n=6.【解答】解:∵2a2m b4和﹣a6b n﹣2是同类项,∴2m=6,n﹣2=4,解得:m=3,n=6.故答案为:3,6.19.(2分)有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|﹣|c﹣b|﹣|b+a|=2b﹣2c.【解答】解:由数轴得,a<b<c,且|a|>|b|>|c|,∴a+c<0,c﹣b>0,b+a<0,∴原式=﹣a﹣c﹣c+b+b+a=2b﹣2c.故答案为2b﹣2c.20.(2分)观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…(1)按此规律写出第6个单项式﹣32x6y;(2)试猜想第n个单项式为(﹣1)n+12n﹣1x n y.【解答】解:(1)∵当n=1时,xy,当n=2时,﹣2x2y,当n=3时,4x3y,当n=4时,﹣8x4y,当n=5时,16x5y,∴第6个单项式是﹣26﹣1x6y,即﹣32x6y.故答案为:﹣32x6y.(2)∴n为偶数时,单项式为负数.x的指数为n时,2的指数为n﹣1,∴当n为奇数时的单项式为2n﹣1x n y,该单项式为(﹣1)n+12n﹣1x n y.故答案为:(﹣1)n+12n﹣1x n y.三、计算题.(每小题30分,共30分.)21.(30分)(1)﹣6﹣7﹣8(2)(3)﹣3x2y+2x2y+3xy2﹣2xy2(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)(5)解方程x+12=4x﹣15(6)解方程:y﹣=2﹣.【解答】解:(1)﹣6﹣7﹣8=﹣21;(2)=﹣1﹣=﹣1+=;(3)﹣3x2y+2x2y+3xy2﹣2xy2=﹣x2y+xy2;(4)x﹣3(1﹣2x+x2)+2(﹣2+3x+x2)=x﹣3+6x﹣3x2﹣4+6x+2x2=12x﹣7;(5)x+12=4x﹣154x﹣x=27,3x=27,x=9;(6)y﹣=2﹣,10y﹣5(y﹣1)=20﹣2(y+2)10y﹣5y+5=20﹣2y﹣47y=11y=四、解答题:(本大题共4小题,每小题5分,共20分.)22.(5分)求3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab的值,已知4|a﹣1|+8(b+3)2=0.【解答】解:∵4|a﹣1|+8(b+3)2=0,∴a﹣1=0,b+3=0,∴a=1,b=﹣3,∴3a2b﹣[2a2b﹣(2ab﹣a2b)﹣4a2]﹣ab=3a2b﹣[2a2b﹣2ab+a2b﹣4a2]﹣ab=3a2b﹣2a2b+2ab﹣a2b+4a2﹣ab=ab+4a2=1×(﹣3)+4×12=1.23.(5分)已知﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,求a2﹣2a+1的值.【解答】解:∵﹣5x3y|a|﹣(a﹣4)x﹣6是关于x、y的七次三项式,∴3+|a|=7,a﹣4≠0,解得:a=﹣4,故a2﹣2a+1=(a﹣1)2=25.24.(5分)(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,(1)试求x值;(2)求关于y方程n+|y|=x的解.【解答】解:(1)由(4﹣n2)x2﹣(n﹣2)x﹣8=0是关于x的一元一次方程,得4﹣n2=0且n﹣2≠0.解得n=﹣2.原方程等价于4x﹣8=0.解得x=2;(2)将n,x的值代入关于y方程n+|y|=x,得﹣2+|y|=2.化简,得|y|=4.解得y=4或y=﹣4.25.(5分)已知:有理数a、b满足ab>0,当时,|y﹣4|=2,3a3z ﹣1b与7ba5能够合并,求y﹣2x+z的值.【解答】解:∵ab>0,∴ab同号.当a>0,b>0时,x=2;当a<0,b<0时,x=﹣2.∵|y﹣4|=2,∴y=6或y=2;∵3a3z﹣1b与7ba5能够合并,∴3z﹣1=5,解得z=2.∴当x=2,y=6,z=2时,y﹣2x+z=6﹣4+2=4;当x=2,y=2,z=2时,y﹣2x+z=2﹣4+2=0;当x=﹣2,y=6,z=2时,y﹣2x+z=6+4+2=12;当x=﹣2,y=2,z=2时,y﹣2x+z=2+4+2=8.综上所述,代数式的值为4,0,12或8.五、解答题26.为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n【解答】解:第n条小鱼需要(2+6n)根,故选A.27.如果a2+a﹣1=0,求a3+2a2+2的值.【解答】解:∵a2+a﹣1=0,∴a2+a=1,∴a3+2a2=a3+a2+a2=a(a2+a)+a2=a+a2=1,∴a3+2a2+2=1+2=3.28.如图是一块在电脑屏幕上出现的长方形色块图,它是由6个不同颜色的正方形组成的,已知中间最小的正方形的边长是1cm,则这块长方形色块图的总面积是多少?【解答】解:设第二小的正方形的边长为xcm,则有:x+x+(x+1)=(x+2)+(x+3),解之得:x=4,所以长方形的长为13cm,宽为11cm,面积=13×11=143cm2.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.2.如图,已知四边形ABCD 内接于⊙O ,对角线AC ⊥BD 于P ,设⊙O 的半径是2。
