德阳中考填空题专练
2022年四川中考复习冲刺德阳中考全真模拟试卷(含答案一)

2022年四川省德阳市中考数学全真模拟试卷(一)(满分:150分 考试时间:120分钟)第Ⅰ卷(选择题,共48分)一、选择题(本大题共12个小题,每小题4分,共48分)在每小题给出的四个选项中,有且仅有一项是符合题目要求的.1.13的相反数是( ) A .3 B .-3 C .13D .-132.下列运算正确的是( ) A .a 2·a 3=a 6 B .-2(a -b )=-2a -2b C .2x 2+3x 2=5x 4D .⎝⎛⎭⎫-12-2=4 3.如图,已知AD 与BC 相交于点O ,AB ∥CD ,如果∠B =20°,∠D =40°,那么∠BOD 为( )第3题A .40°B .50°C .60°D .70°4.某销售公司有营销人员15人,销售部为了制定某种商品的月销售量定额,统计了这15人某月的销售量,如下表所示:每人销售件数 1800 510 250 210 150 120 人 数113532那么这A .320,210,230 B .320,210,210 C .206,210,210D .206,210,2305.一个多边形的内角和比外角和的3倍多180°,则它的边数是( ) A .八 B .九 C .十D .十一6.下列调查中不适合抽样调查的是( ) A .调查某景区一年内的客流量 B .了解全国食盐加碘情况C .调查某小麦新品种的发芽率D .调查某班学生的数学成绩7.如图是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )第7题A .12π cm 2B .15π cm 2C .24π cm 2D .30π cm 28.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC 中,∠ACB =90°,AC +AB =10,BC =3,求AC 的长.在这个问题中,AC 的长为( )第8题A .4尺B .4.5尺C .4.55尺D .5尺9.分式方程x x -1-1x 2-x =1的解是( )A .x =-1B .x =-3C .x =1D .原分式方程无解 10.如图,△PQR 是⊙O 的内接正三角形,四边形ABCD 是⊙O 的内接正方形,且BC ∥QR ,则∠AOQ 的度数为( )第10题A .45°B .60°C .75°D .90°11.如图,一次函数y1=kx+b与二次函数y2=ax2交于A(-1,1)和B(2,4)两点,则当y1<y2时,x的取值范围是()第11题A.x<-1 B.x>2C.-1<x<2 D.x<-1或x>212.如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE 把它分成的四部分的面积分别为S1、S2、S3、S4,下面结论:①只有一对相似三角形;②EF∶ED=1∶2;③S1∶S2∶S3∶S4=1∶2∶4∶5,其中正确的结论是()第12题A.①③B.③C.①D.①②第Ⅱ卷(非选择题,共102分)二、填空题(本大题共6个小题,每小题4分,共24分)将答案填在答题卡对应的题号后的横线上.13.截至2021年1月3日,我国“天问一号”火星探测器已经在轨飞行163天,飞行里程突破4亿公里,距离地球约1.3亿公里,距离火星约830万公里.将1.3亿用科学记数法表示应为________.14.为了考察甲、乙两种小麦的长势,分别从中抽出20株测得其高度,并求得它们的方差分别为S2甲=3.6,S2乙=15.8,则________种小麦的长势比较整齐.15.把直线y=-x+2向上平移a个单位后,与直线y=2x+3的交点在第二象限,则a 的取值范围是________.16.如图,半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与⊙O相切时,该直角三角板平移的距离为________.第16题17.若实数x 、y 满足2x 2+3y 2=1,S =3x 2-2y 2,则S 的取值范围是________. 18.如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00测得小岛C 在轮船A 的北偏东45°方向上;上午10:00测得小岛C 在轮船B 的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为________海里.(精确到1海里,参考数据2≈1.414,3≈1.732)第18题三、解答题(本大题共7小题,共78分)答案应写出文字说明、证明过程或推演步骤. 19.(7分)计算:|1-3|-⎝⎛⎭⎫-13-1+(π-2021)0-2sin 60°.20.(8分)如图,在Rt △ABC 中,∠ACB =90°,D 是AB 边上任意一点,E 是BC 边上的中点,过点C 作CF ∥AB 交DE 的延长线于点F ,连接BF 、CD .(1)求证:四边形CDBF 是平行四边形;(2)若D 为AB 中点,求证:四边形CDBF 是菱形;(3)若∠FDB =30°,∠ABC =45°,BE =4,求△BDE 的面积.第20题21.(13分)在九年级综合素质评定结束后,为了了解年级的评定情况,现对九年级某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.第21题(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有________名学生; (2)补全女生等级评定的折线统计图;(3)根据调查情况,该班班主任从评定等级为合格和A 的学生中各选1名学生进行交流,请用树状图或表格求出刚好选中一名男生和一名女生的概率.22.(11分)我国汽车保有量的持续攀升,不仅给能源带来了危机,同时也给环境带来了巨大的危害.节能成为新世纪全球的主题,日益短缺的能源要求出现新的动力技术,混合动力可以比较好的解决燃油消耗问题和污染问题.节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶.则费用为60元;若完全用电做动力行驶,则费用为20元,已知汽车行驶中每千米用油费用比用电费用多0.5元.(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米? (2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过40元,则至少需要用电行驶多少千米?23.(12分)如图,反比例函数y =kx (x >0)的图象与直线OP 相交于点A (1,3),点C 为反比例函数图象上一点,且AC =2OA ,分别过点A 、C 作x 轴和y 轴的平行线,四线相交于点B 、D ,直线AB 、CD 分别交x 轴于点E 、F ,连接OD 交AC 于点G .(1)求k 的值;(2)证明:点B 在直线OD 上; (3)求∠DOF 的度数.第23题24.(13分)如图,P A 为⊙O 的切线,A 为切点,直线PO 交⊙O 于点E 、F ,过点A 作PO 的垂线AB ,垂足为点D ,交⊙O 于点B ,延长BO 与⊙O 交于点C ,连接AC 、BF .(1)求证:PB 与⊙O 相切;(2)试探究线段EF 、OD 、OP 之间的数量关系,并加以证明; (3)若tan F =12,求cos ∠ACB 的值.第24题25.(14分)如图,二次函数y =-x 2+bx +c 的图象与x 轴交于A 、B 两点,与y 轴交于点C ,OB =OC ,点D 在函数图象上,CD ∥x 轴且CD =2,直线l 是抛物线的对称轴,E 是抛物线的顶点.(1)求b 、c 的值;(2)如图1,连接BE ,线段OC 上的点F 关于直线l 的对称点F ′恰好在线段BE 上,求点F 的坐标;(3)如图2,动点P 在线段OB 上,过点P 作x 轴的垂线分别与BC 交于点M 、与抛物线交于点N .试问:抛物线上是否存在点Q ,使得△PQN 与△APM 的面积相等,且线段NQ 的长度最小?若存在,求出点Q 的坐标;若不存在,说明理由.图1图2 第25题参考答案一、1.D 2.D 3.C 4.B 5.B 6.D 7.B 8.C 9.D10.C 11.D 12.B二、13.1.3×108 14.甲 15.-72<a <1 16.2 317.-23≤S ≤3218.38三、19.解:原式=3-1+3+1-2×32=3-1+3+1-3=3 20.(1)证明:∵CF ∥AB ,∴∠ECF =∠EBD . ∵E 是BC 中点, ∴CE =BE .∵∠CEF =∠BED , ∴△CEF ≌△BED (ASA), ∴CF =BD ,且CF ∥AB , ∴四边形CDBF 是平行四边形.(2)证明:∵D 为AB 中点,∠ACB =90°, ∴AD =CD =BD ,且四边形CDBF 是平行四边形, ∴四边形CDBF 是菱形. (3)解:如图,作EM ⊥DB 于点M . 在Rt △EMB 中,∵∠ABC =45°, ∴BM =EM =BE ·sin ∠ABC =2 2. 在Rt △EMD 中, ∵∠EDM =30°, ∴DM =3EM =26, ∴BD =26+2 2.∴△BDE 的面积=12×BD ×EM =12×22×(26+22)=4+4 3.21.解:(1)50(2)根据题意可得,女生评级3A 的学生有50×16%-3=8-3=5(人),女生评级4A 的学生有50×50%-10=25-10=15(人),补全女生等级评定的折线统计图如下.(3)根据题意列表如下: 评级为“A ”评级为“合格”男 女 女 女 男 (男,男) (男,女) (男,女) (男,女) 男 (男,男) (男,女) (男,女) (男,女) 女(女,男)(女,女)(女,女)(女,女)∵共有12种等可能的结果数,其中一名男生和一名女生的共有7种, ∴P (一名男生和一名女生)=712,即选中一名男生和一名女生的概率为712. 22.解:(1)设汽车行驶中每千米用电费用是x 元,则每千米用油费用是(x +0.5)元, 由题意得:60x +0.5=20x ,解得:x =0.25,经检验,x =0.25是原方程的解. 200.25=80(千米), 答:汽车行驶中每千米用电费用是0.25元,甲、乙两地的距离是80千米;(2)汽车行驶中每千米用油费为:0.25+0.5=0.75(元),设汽车用电行驶y 千米,则汽车用油行驶(80-y )千米;由题意得:0.25y +0.75(80-y )≤40, 解得:y ≥40,答:至少需要用电行驶40千米.23.(1)解:∵点A (1,3)在反比例函数y =kx (x >0)的图象上,∴k =1×3= 3.(2)证明:∵分别过点A 、C 作x 轴和y 轴的平行线, ∴设点B (1,a ),则点C (3a,a ), ∴点D (3a,3). 又∵点O (0,0),∴直线OD 解析式为y =ax . 当x =1时,y =a , ∴点B 在直线OD 上; (3)解:设∠DOF 的度数为x , ∵过点A 、C 作x 轴和y 轴的平行线, ∴四边形ABCD 是平行四边形, ∴BC ∥AD ∥EF ,∴∠ABC =∠AEF =90°,∠ADO =∠DOF =x , ∴四边形ABCD 是矩形, ∴AC =BD ,AG =GD =BG =GC , ∴∠ADG =∠DAG =x , ∴∠AGO =2x . ∵AC =2OA ,∴AO =AG ,∴∠AOG =∠AGO =2x . ∵tan ∠AOE =AE OE =31=3,∴∠AOE =60°,∴∠AOG +∠DOF =60°, ∴2x +x =60°, ∴x =20°,∴∠DOF 的度数为20°. 24.(1)证明:连接OA . ∵AB ⊥PD , ∴OP 垂直平分AB , ∴P A =PB ,OA =OB , ∴△OAP ≌△OBP , ∴∠OAP =∠OBP . ∵P A 为⊙O 的切线, ∴∠OAP =90°, ∴∠OBP =90°. ∵点B 在⊙O 上, ∴PB 与⊙O 相切.(2)解:EF 、OD 、OP 间的数量关系为EF 2=4OD ·OP .理由: ∵∠OAP =90°,AD ⊥OP , ∴OA 2=OD ·OP . ∵OA =12EF ,∴OD ·OP =14EF 2,∴EF 2=4OD ·OP .(3)解:∵tan F =12,设BD =a ,∴FD =2a ,AD =a ,DE =12a ,EF =52a ,∴OD =34a ,∴AC =32a ,∴cos ∠ACB =35.25.解:(1)∵CD ∥x 轴,CD =2,∴二次函数y =-x 2+bx +c 的对称轴为直线x =1, ∴-b 2×(-1)=1,解得b =2. ∵OB =OC ,C (0,c ),∴点B 的坐标为(c,0),∴0=-c 2+2c +c ,解得c =3或c =0(舍去),∴c =3.(2)设点F 的坐标为(0,m ).∵对称轴为直线x =1,∴点F 关于直线l 的对称点F ′的坐标为(2,m ).由(1)可知抛物线解析式为y =-x 2+2x +3=-(x -1)2+4,∴E (1,4).∵直线BE 经过点B (3,0),E (1,4), ∴利用待定系数法可得直线BE 的解析式为y =-2x +6.∵点F ′在BE 上,∴m =-2×2+6=2,即点F 的坐标为(0,2).(3)存在点Q 满足题意.设点P 的坐标为(n,0),则P A =n +1,PB =PM =3-n ,PN =-n 2+2n +3. 作QR ⊥PN ,垂足为点R .∵S △PQN =S △APM ,∴12(-n 2+2n +3)·QR =12(n +1)(3-n ), ∴QR =1.当点Q 在直线PN 的左侧时,点Q 的坐标为(n -1,-n 2+4n ),点R 的坐标为(n ,-n 2+4n ),点N 的坐标为(n ,-n 2+2n +3),∴在Rt △QRN 中,NQ 2=1+(2n -3)2,∴n =32时,NQ 取最小值1,此时点Q 的坐标为⎝⎛⎭⎫12,154;当点Q 在直线PN 的右侧时,点Q 的坐标为(n +1,n 2-4).同理,NQ 2=1+(2n -1)2,∴n =12时,NQ 取最小值1,此时点Q 的坐标为⎝⎛⎭⎫32,154. 综上可知存在满足题意的点Q ,其坐标为⎝⎛⎭⎫12,154或⎝⎛⎭⎫32,154.。
四川省德阳市中考物理试卷

的电路中,则甲乙两电阻两端的电压之比为
;将它们并联接入同样的电路中,通
过甲乙两电阻的电流之比为
。
11.(4 分)某建筑工地用如图所示的滑轮组提升重物,工人对绳的拉力 F 为 400N,并能用
10s 的时间将 96kg 的重物匀速提升 2m,则拉力 F 的功率为
W,此时滑轮组的机
械效率为
%.(不计绳重和摩擦,取 g=10N/kg)
功率为
W.(不考虑灯丝电阻的变化)
第3页(共7页)
13.(4 分)如图甲所示,完全相同的 A、B 两物块叠放在水平桌面上,用 F1=30N 的水平
力作用在 B 物块上,AB 一起做匀速直线运动,此时 B 物块所受的摩擦力为
N;
若将 F2=50N 的水平力按如图乙所示作用在 A 物块上,它们仍一起做直线运动,则地面
四川省德阳市中考物理试卷
一、选择题 1.(3 分)下列与声现象有关的说法中不正确的是( )
A.宇航员之间在太空中不能直接对话,是因为真空不能传声 B.汽车安装的倒车雷达是利用超声波工作的 C.看电视时调节音量是为了改变声音的响度 D.高速公路两旁的隔音板可防止噪声的产生 2.(3 分)下列有关运动和力的说法中,正确的是( ) A.力是维持物体运动的原因 B.物体受到平衡力作用,它一定是静止的 C.力是改变物体运动状态的原因 D.物体运动的速度越大,受到的力也越大 3.(3 分)下列数据中,最接近实际情况的是( ) A.普通家用照明灯的工作电流约为 2A B.家用手电筒的额定功率约为 200W C.一节新干电池的电压约为 1.5V D.电饭锅加热煮饭时的功率约为 100W 4.(3 分)下列有关光学知识说法正确的是( ) A.近视眼的矫正是佩戴合适的凸透镜 B.用照相机照相时,景物在照相机镜头的二倍焦距以外 C.人站在穿衣镜前看到自己在镜中的像是实像 D.人通过放大镜看到的是物体正立放大的实像 5.(3 分)在如图所示的电路中,闭合开关 S 后,两灯都不亮,电压表有示数,电流表无示 数,则该电路故障可能是( )
德阳中考地理试题及答案

德阳中考地理试题及答案一、选择题(每题2分,共20分)1. 地球的自转周期是多久?A. 24小时B. 12小时C. 1个月D. 1年2. 以下哪个国家位于亚洲?A. 巴西B. 美国C. 中国D. 澳大利亚3. 长江是中国的第几大河?A. 第一大河B. 第二大河C. 第三大河D. 第四大河4. 以下哪个是世界四大渔场之一?A. 长江口B. 黄海C. 秘鲁渔场D. 地中海5. 以下哪个国家是世界上最大的石油生产国?A. 俄罗斯B. 沙特阿拉伯C. 美国D. 伊朗二、填空题(每题2分,共20分)6. 我国的首都是______。
7. 中国最大的淡水湖是______。
8. 我国最大的沙漠是______。
9. 我国的国花是______。
10. 我国的陆地面积是______平方千米。
三、简答题(每题10分,共20分)11. 请简述中国的地理位置。
12. 请简述中国的气候特点。
四、材料分析题(每题15分,共30分)13. 阅读以下材料,分析中国的地形特点。
材料:中国地形复杂多样,有高原、盆地、山地、丘陵和平原等地貌类型。
14. 阅读以下材料,分析中国的河流特点。
材料:中国的河流众多,其中长江和黄河是中国的母亲河,对中国的历史发展有着深远的影响。
五、综合题(10分)15. 请结合地理知识,谈谈如何保护我们的生态环境。
答案:一、选择题1. A2. C3. A4. C5. B二、填空题6. 北京7. 鄱阳湖8. 塔克拉玛干沙漠9. 牡丹10. 960万三、简答题11. 中国位于亚洲东部,东临太平洋,北接俄罗斯,西邻中亚国家,南濒东南亚国家,地理位置优越,具有丰富的自然资源和多样的气候类型。
12. 中国的气候特点为季风气候显著,雨热同期,气候类型多样,从南到北有热带、亚热带、温带、寒带等多种气候类型。
四、材料分析题13. 中国的地形特点是多样而复杂,高原、盆地、山地、丘陵和平原等地貌类型丰富,这为我国的生态环境和经济发展提供了多样化的条件。
德阳历年中考语文试题及答案

德阳历年中考语文试题及答案一、选择题(每题3分,共30分)1. 下列词语中,读音全部正确的一项是:A. 霎时(shàshí)B. 瞠目结舌(chēngmùjiéshé)C. 恣意(zìyì)D. 蹑手蹑脚(nièshǒunièjiǎo)答案:B2. 根据题目所给的语境,下列句子中没有语病的一项是:A. 经过老师耐心的教导,小明的学习成绩有了明显的提高。
B. 他虽然年纪不大,但已经担任了公司的高级职位。
C. 这篇文章的内容丰富,语言优美,受到了读者的广泛欢迎。
D. 我们一定要克服困难,努力完成今年的生产任务。
答案:D3. 下列句子中,使用了拟人修辞手法的一项是:A. 春风又绿江南岸。
B. 明月几时有,把酒问青天。
C. 桃花潭水深千尺,不及汪伦送我情。
D. 独在异乡为异客,每逢佳节倍思亲。
答案:A4. 根据题目所给的语境,下列句子中使用了反问修辞手法的一项是:A. 难道我们不应该珍惜时间吗?B. 你难道不知道这是违法的吗?C. 你真的不知道这是违法的吗?D. 这是违法的,难道你不知道吗?答案:A5. 下列句子中,使用了排比修辞手法的一项是:A. 他勤奋学习,刻苦钻研,成绩优异。
B. 春天的花开了,夏天的果实成熟了,秋天的落叶飘了,冬天的雪花飞了。
C. 他不仅学习好,而且品德高尚。
D. 我们要学好语文,学好数学,学好英语。
答案:B6. 下列句子中,使用了夸张修辞手法的一项是:A. 他跑得比兔子还快。
B. 他学习非常刻苦。
C. 他的成绩一直名列前茅。
D. 他对待工作一丝不苟。
答案:A7. 下列句子中,使用了设问修辞手法的一项是:A. 我们为什么要学习语文?因为语文是我们的母语。
B. 他为什么总是那么乐观?因为他有一颗积极向上的心。
C. 他为什么总是那么乐观,因为他有一颗积极向上的心。
D. 他为什么总是那么乐观?答案:A8. 下列句子中,使用了对偶修辞手法的一项是:A. 风声雨声读书声,声声入耳。
(word完整版)四川省德阳市中考模拟试卷(一)

四川省德阳市中考模拟试卷·数学(一)第Ⅰ卷(选择,共36分)一、选择题(本大题共12小题,每小题3分,共36分)下列各题给出的四个选项中,只有一个是正确的,请将正确的答案的字母代号填在下面的表格中.题序1 2 3 4 5 6 7 8 9 10 11 12 答案 1. —2016的相反数是( )A .-2016B .20161C .2016D .20161-2。
为了了解某校九年级400名学生的体重情况,从中抽查了50名学生的体重进行统计分析,在这个问题中,总体是( )A .400名学生的体重B .被抽取的50名学生C .400名学生D .被抽取的50名学生的体重 3.如图,AB ∥CD ,DE ⊥CE,∠1=34°,则∠DCE 的度数为( ) A .34° B .56° C .66° D .54°第3题图 第4题图 第9题图 4。
如图是由5个相同的立方块所搭成的几何体,其俯视图是( )A .B .C .D .5.下列各式计算正确的是( )A .123=-B .a 6÷a 2=a 3C .(x+y )2=x 2+y 2D .(—x 2)3=—x 66。
某彩票的中奖机会是1%,下列说法正确的是( ) A .买一张一定不会中奖 B .买10000张一定会中奖C .买1000张一定有10张中奖D .买1张有可能中奖7.的正整数解有( ) A .1个B .2个C .3个D .4个8.⊙O 的半径r=5cm ,圆心到直线l 的距离OM=4cm,在直线l 上有一点P,且PM=3cm ,则点P( ) A .在⊙O 内 B .在⊙O 上 C .在⊙O 外 D .可能在⊙O 上或在⊙O 内 9。
如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB 于点D ,∠ACD=3∠BCD ,E 是斜边AB 的中点,则A .22.5°B .30°C .36°D .45°10。
德阳中考英语试题及答案2024

德阳中考英语试题及答案2024一、听力理解(共20分)1. 根据所听对话,选择正确的图片。
(每题1分,共5分)A) [图片1] B) [图片2] C) [图片3] D) [图片4][听力材料1][听力材料2][听力答案] 1-5 ABCDE2. 根据所听短文,回答下列问题。
(每题2分,共10分)A. [问题1]B. [问题2]C. [问题3]D. [问题4]E. [问题5][听力材料3][听力答案] 6-10 ABCDE3. 根据所听对话或独白,完成下列句子。
每空填一词。
(每题1分,共5分)A. [句子1] _______ _______ _______ _______B. [句子2] _______ _______ _______ _______C. [句子3] _______ _______ _______ _______D. [句子4] _______ _______ _______ _______E. [句子5] _______ _______ _______ _______[听力材料4][听力答案] 11-15 one possible answer: A. meet B. book C. late D. important E. visit二、阅读理解(共30分)1. 阅读下列短文,选择最佳答案。
(每题2分,共10分)A. [问题1]B. [问题2]C. [问题3]D. [问题4]E. [问题5][短文1][阅读答案] 16-20 ABCDE2. 阅读下列短文,判断正误。
(每题1分,共5分)A. [陈述1]B. [陈述2]C. [陈述3]D. [陈述4]E. [陈述5][短文2][阅读答案] 21-25 TFFTF3. 阅读下列短文,回答问题。
(每题2分,共15分)A. [问题1]B. [问题2]C. [问题3]D. [问题4]E. [问题5][短文3][阅读答案] 26-30 ABCDE三、完形填空(共15分)[短文4]41. A. although B. because C. if D. when42. A. happy B. sad C. angry D. excited43. A. decided B. forgot C. remembered D. tried44. A. quickly B. slowly C. carefully D. nervously45. A. success B. failure C. achievement D. progress[完形填空答案] 41-45 B D A C A四、语法填空(共15分)[短文5]46. [空格1] _______47. [空格2] _______48. [空格3] _______49. [空格4] _______50. [空格5] _______51. [空格6] _______52. [空格7] _______53. [空格8] _______54. [空格9] _______55. [空格10] _______[语法填空答案] 46-55 one possible answer: 46. is 47. to 48. her 49. with 50. for 51. at 52. but 53. were 54. an 55. on五、书面表达(共20分)根据题目要求,写一篇不少于80词的短文。
2022年四川中考复习冲刺德阳中考全真模拟试卷(含答案二)

2022年四川省德阳市中考数学全真模拟试卷(二)(满分:150分 考试时间:120分钟)第Ⅰ卷(选择题,共48分)一、选择题(本大题共12个小题,每小题4分,共48分)在每小题给出的四个选项中,有且仅有一项是符合题目要求的.1.-223的倒数是( )A .223B .-312C .-38D .382.截至2020年8月底,中华骨髓库库容已超过281万人份.累计为临床提供造血干细胞10125例.干细胞是一种嗜碱性独核细胞.其大小约为8 μm ,呈圆形.已知1 μm 相当于1 m 的一百万分之一.则“8 μm ”用科学记数法表示正确的是( )A .800×104 mB .8×106 mC .800×10-4 mD .8×10-6 m3.将一个长方体内部挖去一个圆柱(如图所示),它的主视图是( )第3题4.已知直线AB ∥CD ,直线EF 与AB 相交于点O ,且∠BOE =140°,直线l 平分∠BOE 交CD 于点G ,那么∠CGO =( )A .110°B .105°C .100°D .70°5.如图,△ABC 绕点A 顺时针旋转80°得到△AEF ,若∠B =100°,∠F =50°,则∠α的度数是( )第5题A .40°B .50°C .60°D .70°6.下列说法正确的是( )A .为了了解全国中学生每天体育锻炼的时间,应采用普查的方式B .若甲组数据的方差是s 2甲=0.03,乙组数据的方差是s 2乙=0.2,则乙组数据比甲组数据稳定C .德阳市明天一定会下雨D .一组数据4,5,6,5,2,8的众数是57.关于x 的不等式组⎩⎪⎨⎪⎧2x <3(x -3)+1,3x +24>x +a 有四个整数解,则a 的取值范围是( )A .-114<a ≤-52B .-114≤a <-52C .-114≤a ≤-52D .-114<a <-528.如果圆柱的母线长为5 cm ,底面半径为2 cm ,那么这个圆柱的侧面积是( ) A .10 cm 2 B .10π cm 2 C .20 cm 2D .20π cm 29.如图,边长为1的小正方形网格中,⊙O 的圆心在格点上,则∠AED 的正弦值是( )第9题A .12B .13C .55D .3210.如图,反比例函数y 1=k 1x 的图象和正比例函数y 2=k 2x 的图象交于点A (-1,-2)、B (1,2),若y 1>y 2,则x 的取值范围是( )第10题A .-1<x <0B .-1<x <1C .x <-1或0<x <1D .-1<x <0或x >111.一个长为4 cm ,宽为3 cm 的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板点A 位置的变化为A →A 1→A 2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°的角,则点A 滚到A 2位置时共走过的路径长为( )第11题A .72π cmB .236π cmC .43π cmD .52π cm12.已知二次函数y =ax 2+bx +c 的y 与x 的部分对应值如下表:x -1 0 1 3 y-3131x =1;③当x <2时,函数值y 随x 的增大而增大;④方程ax 2+bx +c =0有一个根大于4.其中正确的结论有( )A .1个B .2个C .3个D .4个第Ⅱ卷 (非选择题,共102分)二、填空题(本大题共6个小题,每小题4分,共24分)将答案填在答题卡对应的题号后的横线上.13.已知x 2-3x +1=0,则x 3-x 2-5x +2021的值为________.14.某县进行教学质量抽测,有2千多名学生参加考试,为了解这些学生的抽测学科成绩,便于质量分析,从中抽取了200名考生的抽测学科成绩进行统计分析.这个问题中,有下列说法:①这2千多名学生的抽测成绩的全体是总体;②每个学生是个体;③200名考生是总体的一个样本;④样本容量是200.请你写出正确说法的序号________.15.对于任意的正数m 、n ,定义运算※为:m ※n =⎩⎨⎧m -n (m >n ),m +n (m <n ).计算(3※2)×(8※12)的结果为________.16.数字游戏.第一步:取一个自然数n 1=5,计算n 21+1得a 1;第二步:算出a 1的各位数字之和得n 2,计算n 22+1得a 2;第三步,算出a 2的各位数字之和得n 3,计算n 23+1得a 3……以此类推,则a 2021=__________.17.如图,矩形OABC 的顶点O 与原点重合,点A 、C 分别在x 轴、y 轴上,点B 的坐标为(-5,4),点D 为边BC 上一动点,连接OD ,若线段OD 绕点D 顺时针旋转90°后,点O 恰好落在AB 边上的点E 处,则点E 的坐标为________.第17题18.如图,边长为4的正方形ABCD 内接于⊙O ,点E 是AB ︵上的一动点(不与A 、B 重合),点F 是BC ︵上的一点,连接OE 、OF ,分别与AB 、BC 交于点G 、H ,且∠EOF =90°,有以下结论:①AE ︵ =BF ︵;②△OGH 是等腰直角三角形;③四边形OGBH 的面积随着点E 位置的变化而变化;④△OGH 周长的最小值为4+ 2.其中正确的是________.(填序号)第18题三、解答题(本大题共7小题,共78分)答案应写出文字说明、证明过程或推演步骤. 19.(7分)计算:(3-2)0+⎝⎛⎭⎫13-1+4cos 30°-|3-27|.20.(8分)将宽为6 cm ,长足够的两张矩形纸条叠放在一起,如图所示. (1)说出重叠部分即四边形ABCD 的形状,并说明理由; (2)当∠BCD =45°,求四边形ABCD 的面积.第20题21.(13分)在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档:t<8;B档:8≤t<9;C档:9≤t<10;D档:t≥10.根据调查情况,给出了部分数据信息:①A档和D档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;②图1和图2是两幅不完整的统计图.第21题根据以上信息,解答问题:(1)求本次调查的学生人数,并将图2补充完整;(2)已知全校共1200名学生,请你估计全校B档的人数;(3)学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.22.(11分)某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.(1)求甲、乙两条生产线每天的产能各是多少?(2)若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?(3)正式开工满负荷生产3天后,通过技术革新,甲生产线的日产能提高了50%,乙生产线的日产能翻了一番.再满负荷生产13天能否完成任务?23.(12分)如图,一次函数的图象与反比例函数y 1=-3x (x <0)的图象相交于点A ,与y轴、x 轴分别相交于B 、C 两点,且C (2,0).当x <-1时,一次函数值大于反比例函数值;当x >-1时,一次函数值小于反比例函数值.(1)求一次函数的解析式;(2)设函数y 2=a x (x >0)的图象与y 1=-3x (x <0)的图象关于y 轴对称.在y 2=ax (x >0)的图象上取一点P (点P 的横坐标大于2),过点P 作PQ ⊥x 轴,垂足为点Q .若四边形BCQP 的面积等于2,求点P 的坐标.第23题24.(13分)如图,已知BC ⊥AC ,圆心O 在AC 上,点M 与点C 分别是AC 与⊙O 的交点,点D 是MB 与⊙O 的交点,点P 是AD 延长线与BC 的交点,且AD ·AO =AM ·AP .(1)连接OP ,证明△ADM ∽△APO ; (2)证明:PD 是⊙O 的切线;(3)若AD =12,AM =MC ,求PB 和DM 的长.第24题25.(14分)如图,抛物线y =-x 2+bx +c 交x 轴于A 、B 两点,其中点A 坐标为(-3,0),与y 轴交于点C (0,3).(1)求抛物线的函数解析式;(2)点M 为抛物线y =-x 2+bx +c 上异于点C 的一个点,且S △OMC =12S △ABC ,求点M 的坐标;(3)若点P 为x 轴上方抛物线上任意一点,点D 是抛物线对称轴与x 轴的交点,直线AP 、BP 分别交抛物线的对称轴于点E 、F .请问DE +DF 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.第25题参考答案一、1.C 2.D 3.A 4.D 5.B 6.D 7.B 8.D9.C 10.C 11.B 12.A二、13.2019 14.①④ 15.2 16.65 17.(-5,3) 18.①② 解析:如图,连接OC 、OB 、CF 、BE . ∵∠BOE +∠BOF =90°,∠COF +∠BOF =90°, ∴∠BOE =∠COF , ∴BE ︵ =CF ︵ . ∵AB ︵ =CB ︵ ,∴AE ︵ =BF ︵,故①正确.在△BOG 与△COH 中,⎩⎪⎨⎪⎧∠BOG =∠COH ,OB =OC ,∠OBG =∠OCH ,∴△BOG ≌△COH (ASA), ∴OG =OH . ∵∠HOG =90°,∴△OGH 是等腰直角三角形,故②正确. ∵S △OBG =S △OCH ,∴S 四边形OGBH =S △BOC =14S 正方形ABCD =定值,故③错误.∵△OGH 是等腰直角三角形,∴当OH ⊥BC 时,OH 的值最小,即△OHG 的周长最小,此时OG =OH =2,GH =22, ∴△OGH 的周长的最小值为4+22,故④错误. ∴①②正确.三、19.解:原式=1+3+4×32-23=4. 20.解:(1)四边形ABCD 为菱形,理由如下:∵两张纸条都是矩形, ∴AB ∥CD ,BC ∥AD , ∴四边形ABCD 是平行四边形.分别过点B 、D 作BE ⊥CD 于点E ,DF ⊥CB 于点F . ∵两纸条宽为6 cm , ∴BE =DF =6 cm , ∵BC ·DF =CD ·BE , ∴BC =CD ,∴平行四边形ABCD 是菱形.(2)∵∠BEC =∠DFC =90°,BE =DF =6 cm ,∠BCD =45°, ∴△CDF 是等腰直角三角形,∴CF =DF =6 cm , ∴CD =62+62=62(cm),∴S 菱形ABCD =CD ×BE =62×6=362(cm 2). ∴四边形ABCD 的面积是36 2 cm 2.21.解:(1)∵A 档和D 档共有12个数据,而D 档有4个数据, ∴A 档共有12-4=8(人),∴本次调查的学生有8÷20%=40(人). 补全频数直方图如图所示.(2)1200×1640=480(人),即估计全校B 档的人数为480人.(3)用a 表示七年级学生,用b 表示八年级学生,用c 和d 分别表示九年级学生,画树状图如下:∵共有12种等可能的情况数,其中抽到的2名学生来自不同年级的情况有10种, ∴P (抽到2名学生来自不同年级)=1012=56.22.解:(1)设乙生产线每天的产能是x 万个,则甲生产线每天的产能是2x 万个. 依题意,得80x -802x =2.解得x =20.经检验,x =20是所列方程的解. 2x =2×20=40.故甲生产线每天的产能是40万个,乙生产线每天的产能是20万个. (2)设安排乙生产线生产y 天.依题意,得0.5y +1.2×1440-20y40≤40.解得y ≥32.故至少应安排乙生产线生产32天.(3)(40+20)×3+[40×(1+50%)+20×2]×13=1480(万个). ∵1440<1480,∴故再满负荷生产13天能完成任务.23.解:(1)∵当x <-1时,一次函数值大于反比例函数值;当x >-1时,一次函数值小于反比例函数值,∴点A 的横坐标是-1,∴A (-1,3).设一次函数解析式为y =kx +b .由直线过A 、C 两点,得⎩⎪⎨⎪⎧-k +b =3,2k +b =0,解得⎩⎪⎨⎪⎧k =-1,b =2.∴一次函数的解析式为y =-x +2.(2)∵y 2=a x (x >0)的图象与y 1=-3x (x <0)的图象关于y 轴对称,∴y 2=3x(x >0).∵点B 是直线y =-x +2与y 轴的交点, ∴B (0,2).设P ⎝⎛⎭⎫n ,3n ,n >2. 由S 四边形BCQP =S 梯形BOQP -S △BOC =2, 得12n ⎝⎛⎭⎫2+3n -12×2×2=2,解得n =52. ∴点P 的坐标为⎝⎛⎭⎫52,65.24.(1)证明:如图1,连接OD 、OP 、CD . ∵AD ·AO =AM ·AP , ∴AD AP =AMAO. ∵∠A =∠A , ∴△ADM ∽△APO .图1(2)证明:∵△ADM ∽△APO , ∴∠ADM =∠APO , ∴MD ∥PO ,∴∠DOP =∠MDO ,∠POC =∠DMO . ∵OD =OM , ∴∠DMO =∠MDO , ∴∠DOP =∠POC .在△ODP 和△OCP 中,∵⎩⎪⎨⎪⎧ OD =OC ,∠DOP =∠COP ,OP =OP ,∴△ODP ≌△OCP (SAS),∴∠ODP =∠OCP .∵BC ⊥AC ,∴∠OCP =90°,∴∠ODP =90°,∴OD ⊥AP ,∴PD 是⊙O 的切线.(3)解:如图2,连接CD 、OD .由切线长定理可知:PC =PD .设圆O 的半径为R . ∵AM =MC ,∴AM =2MO =2R .在Rt △AOD 中,OD 2+AD 2=OA 2,∴R 2+122=9R 2,∴R =32,∴OD =3 2 ,MC =6 2.∵AD AP =AM AO =23, ∴12AP =23,∴AP =18, ∴DP =AP -AD =18-12=6.∵O 是MC 的中点,∴CO MC =CP CB =12, ∴点P 是BC 的中点.∵MC 是⊙O 的直径,∴∠BDC =∠CDM =90°,∴PB =CP =DP =6.在Rt △BCM 中,∵BC =2DP =12,MC =62,∴BM =BC 2+MC 2=122+(62)2=66,易证△MDC ∽△MCB , ∴MD MC =MC MB ,即DM 62=6266, ∴DM =2 6.图225.解:(1)将点A 、C 的坐标代入抛物线解析式,得⎩⎪⎨⎪⎧0=-(-3)2+(-3)b +c ,3=c , 解得⎩⎪⎨⎪⎧b =-2,c =3. 故抛物线的解析式为y =-x 2-2x +3.(2)对于抛物线y =-x 2-2x +3,令y =0,则x =-3或1, 故点B (1,0), ∴12S △ABC =12×12×AB ×OC =14×4×3=3. ∵S △OMC =12×OC ×|x M |=32|x M |=3, 解得x M =±2,故点M 的坐标为(2,-5)或(-2,3).(3)DE +DF 是定值.理由如下:设点P 的坐标为(m ,-m 2-2m +3).设直线AP 的解析式为y =kx +t ,则⎩⎪⎨⎪⎧ 0=-3k +t ,-m 2-2m +3=mk +t , 解得⎩⎪⎨⎪⎧k =1-m ,t =3-3m . 故直线AP 的解析式为y =-(m -1)(x +3).当x =-b 2a=-1时,y =2-2m , 即点E (-1,2-2m ),即DE =2-2m .同理可得,直线BP 的解析式为y =-(m +3)(x -1). 当x =-1时,y =2m +6,故点F (-1,2m +6),即DF=2m+6.∴DE+DF=2-2m+2m+6=8,为定值.。
2022年四川中考复习冲刺德阳中考全真模拟试卷(含答案三)
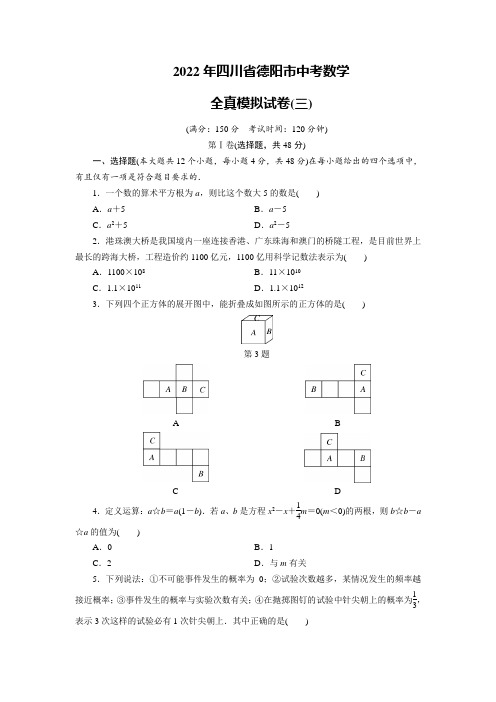
2022年四川省德阳市中考数学全真模拟试卷(三)(满分:150分 考试时间:120分钟)第Ⅰ卷(选择题,共48分)一、选择题(本大题共12个小题,每小题4分,共48分)在每小题给出的四个选项中,有且仅有一项是符合题目要求的.1.一个数的算术平方根为a ,则比这个数大5的数是( ) A .a +5 B .a -5 C .a 2+5D .a 2-52.港珠澳大桥是我国境内一座连接香港、广东珠海和澳门的桥隧工程,是目前世界上最长的跨海大桥,工程造价约1100亿元,1100亿用科学记数法表示为( )A .1100×108B .11×1010C .1.1×1011D .1.1×10123.下列四个正方体的展开图中,能折叠成如图所示的正方体的是( )第3题ABCD4.定义运算:a ☆b =a (1-b ).若a 、b 是方程x 2-x +14m =0(m <0)的两根,则b ☆b -a☆a 的值为( )A .0B .1C .2D .与m 有关5.下列说法:①不可能事件发生的概率为0;②试验次数越多,某情况发生的频率越接近概率;③事件发生的概率与实验次数有关;④在抛掷图钉的试验中针尖朝上的概率为13,表示3次这样的试验必有1次针尖朝上.其中正确的是( )A .①②B .②③C .①③D .①④6.自然数4,5,5,x ,y 从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么,所有满足条件的x ,y 中,x +y 的最大值是( )A .3B .4C .5D .67.已知正多边形的边心距与边长的比为12,则此正多边形为( )A .正三角形B .正方形C .正六边形D .正十二边形8.如图,线段AB 是⊙O 的直径,弦CD ⊥AB ,垂足为H ,点MCBD ︵是上任意一点,AH =2,CH =4,则cos ∠CMD 的值为( )第8题A .12B .34C .45D .359.若点P (x ,y )是第一象限内的点,且到两坐标轴的距离相等.并满足方程组⎩⎪⎨⎪⎧2x -y =3,mx +y =6,则m 的值是( ) A .-1 B .0 C .1D .210.如图,在矩形ABCD 中,AB =8,BC =16,将矩形ABCD 沿EF 折叠,使点C 与点A 重合,则折痕EF 的长为( )第10题A .6B .12C .2 5D .4 511.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,点E 为边CD 的中点,若菱形ABCD 的周长为16,∠BAD =60°,则△OCE 的面积为( )第11题A. 3 B.2C.2 3 D.412.如图,抛物线y=x2-2x-3与y轴交于点C,点D的坐标为(0,-1),在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,则点P的横坐标为()第12题A.1+ 2 B.1- 2C.2-1 D.1-2或1+ 2第Ⅱ卷(非选择题,共102分)二、填空题(本大题共6个小题,每小题4分,共24分)将答案填在答题卡对应的题号后的横线上.13.分解因式:3x2-18x+27=__________.14.在实数范围内定义新运算:m☆n=m-2n;若不等式k☆x>2的解集是x<-3,则k的值是________.15.如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,则∠ABD=________°.第15题16.若一次函数y=(-3a+1)x+a的图象不经过第四象限,则a的取值范围是________.17.如图,某景区门口的柱子上方挂着一块景点宣传牌CD,宣传牌的一侧用绳子AD 和BC牵引着两排小风车,经过测量得到如下数据:AM=2米,AB=4米,∠MAD=45°,∠MBC=30°,则CD的长度约为________米.(3≈1.73,结果精确到0.1米)第17题18.如图1所示,E 为矩形ABCD 的边AD 上一点,动点P 、Q 同时从点B 出发,点P 沿折线BE -ED -DC 运动到点C 时停止,点Q 沿BC 运动到点C 时停止,它们运动的速度都是1 cm/秒.设点P 、Q 同时出发t 秒,△BPQ 的面积为y cm 2.已知y 与t 的函数关系图象如图2(曲线OM 为抛物线的一部分),则下列结论:①AD =BE =5;②cos ∠ABE =35;③当0<t ≤5时,y =25t 2;④当t =294时,△ABE ∽△QBP ,其中正确的结论是____________.(填序号)图1图2 第18题三、解答题(本大题共7小题,共78分)答案应写出文字说明、证明过程或推演步骤. 19.(7分)计算:|-tan 45°|+(-3)2+(6-π)0-⎝⎛⎭⎫12-1.20.(8分)如图1,四边形ABCD 是矩形,将矩形ABCD 绕点C 顺时针旋转α(0°<α<180°),得到矩形CGFE ,连接AF 、BG .(1)当α=90°时,BG 的延长线交EF 的延长线于点H ,求证:AF 与BH 互相平分. (2)如图2,当90°<α<180°时,过点F 作FH ∥AB ,FH 交BG 延长线于点H ,(1)中的结论还成立吗?说明理由.图1图2第20题21.(13分)某校对八年级学生进行一次垃圾分类知识竞赛,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90≤x≤100,B等级:80≤x<90,C等级:60≤x<80,D等级:0≤x<60.该校随机抽取了一部分学生的成绩进行调查,并绘制不完整的统计图表.第21题等级频数(人数)频率A a 20%B 1640%C b mD 410%(1)上表中的a=________,b=________,m=________.(2)本次调查共抽取了________名学生.请补全条形图.(3)若从D 等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.22.(11分)现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地.已知这列货车挂有A 、B 两种不同规格的货车厢共40节,使用A 型车厢每节费用为6000元,使用B 型车厢每节费用为8000元.(1)设运送这批货物的总费用为y 万元,这列货车挂A 型车厢x 节,试写出y 与x 之间的函数解析式;(2)如果每节A 型车厢最多可装甲种货物35吨和乙种货物15吨,每节B 型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A 、B 两种车厢的节数,那么共有哪几种安排车厢的方案?(3)在上述方案中,哪个方案运费最省,最少运费为多少元?23.(12分)如图,一次函数y =ax +b (a ≠0)的图象交y 轴于点A (0,2),且与反比例函数y =kx(k ≠0)的图象在第一象限交于点B (m,4),连接 OB ,若S △AOB =2. (1)求反比例函数与一次函数的解析式;(2)若一次函数与x 轴交于C 点,求△OBC 的面积.第23题24.(13分)如图,AB 是⊙O 的弦,半径OC ⊥AB 交AB 于点D ,点P 是⊙O 上AB 上方的一个动点(点P 不与点A 、B 重合),已知∠APB =60°,∠OCB =2∠BCM .(1)设∠A =α,当圆心O 在∠APB 内部时,写出α的取值范围; (2)求证:CM 是⊙O 的切线;(3)若OC =4,PB =42,求PC 的长.第24题25.(14分)如图,在平面直角坐标系xOy 中,已知二次函数y =-12x 2+bx 的图象过点A (4,0),顶点为B ,连接AB 、BO .(1)求二次函数的解析式;(2)若C 是BO 的中点,点Q 在线段AB 上,设点B 关于直线CQ 的对称点为B ′,当△OCB ′为等边三角形时,求BQ 的长度;(3)若点D 在线段BO 上,OD =2DB ,点E 、F 在△OAB 的边上,且满足△DOF 与△DEF 全等,求点E 的坐标.第25题参考答案一、1.C 2.C 3.B 4.A 5.A 6.C 7.B 8.D 9.C10.D 11.A12.A 解析:令x =0,则y =-3, ∴点C 的坐标为(0,-3). ∵点D 的坐标为(0,-1), ∴线段CD 的中点坐标是(0,-2). ∵△PCD 是以CD 为底边的等腰三角形,∴点P 的纵坐标为-2.令x 2-2x -3=-2,解得x 1=1-2,x 2=1+ 2. ∵点P 在第四象限, ∴点P 的横坐标为1+ 2.二、13.3()x -32 14.-4 15.30 16.0≤a <1317.1.518.①③④ 解析:根据图2,得当点P 到达点E 时点Q 到达点C .又点P 、Q 的运动速度相同,∴AD =BC =BE =5 cm ,故①正确; 根据图2,易得ED =2 cm , ∴AE =AD -ED =3 cm ,∴在Rt △ABE 中,AB =BE 2-AE 2=4 cm , ∴cos ∠ABE =AB BE =45,故②错误;过点P 作PF ⊥BC 于点F . ∵AD ∥BC , ∴∠AEB =∠PBF ,∴sin ∠PBF =sin ∠AEB =AB BE =45,∴PF =45t cm ,∴当0<t ≤5时,y =12BQ ·PF =12t ·45t =25t 2,故③正确;当t =294时,点P 在CD 上,点Q 与点C 重合,此时PD =294-BE -ED =14 cm ,PQ =CD -PD =154 cm.∵AB AE =43,BQ PQ =5154=43,∠A =∠Q =90°, ∴△ABE ∽△QBP ,故④正确.综上所述,正确的有①③④. 三、19.解:原式=1+9+1-2=9. 20.解:(1)证明:连接BF 、AH .∵将矩形ABCD 绕点C 顺时针旋转α(0°<α<180°),得到矩形CGFE , ∴BC =CG ,CD =CE .∵四边形ABCD 和四边形CGFE 是矩形, ∴AB =CD ,CE =GF ,∠ABC =∠CEF =90°, ∴AB =GF ,HF ∥AB . ∵∠BCG =90°,BC =CG , ∴∠CBG =45°,∴∠HGF =∠GHF =45°, ∴GF =HF , ∴AB =HF ,∴四边形ABFH 是平行四边形, ∴AF 与BH 互相平分. (2)解:(1)中的结论还成立. 理由如下: 连接BF 、AH .图2∵将矩形ABCD 绕点C 顺时针旋转α(90°<α<180°),得到矩形CGFE ,∴BC =CG ,CD =CE , ∴∠CBG =∠BGC .∵四边形ABCD 和四边形CGFE 是矩形, ∴∠ABC =∠CGF =90°,AB =CD ,CE =GF ,∴∠ABH +∠CBG =90°,∠BGC +∠HGF =90°,AB =GF , ∴∠ABH =∠HGF . ∵AB ∥FH , ∴∠ABH =∠GHF , ∴GF =HF , ∴AB =HF ,∴四边形ABFH 为平行四边形, ∴AF 与BH 互相平分.21.解:(1)本次调查共抽取的学生人数为:4÷10%=40(人),∴a =40×20%=8,b =8+4=12,m =1-20%-40%-10%=30%;故答案为:8,12,30%;(2)由(1)得:本次调查共抽取了40名学生,故答案为:40, 补全条形图如图所示:(3)画树状图如图:共有12种等可能的结果,其中抽取的两名学生恰好是一男一女的结果有8种, ∴抽取的两名学生恰好是一男一女的概率为812=2322.解:(1)6000元=0.6万元,8000元=0.8万元.依题意,得y =0.6x +0.8(40-x )=-0.2x +32.(2)依题意,得⎩⎪⎨⎪⎧35x +25(40-x )≥1240,15x +35(40-x )≥880.即⎩⎪⎨⎪⎧x ≥24,x ≤26,∴24≤x ≤26.∵x 取整数,故A 型车厢可用24节或25节或26节,相应有三种装车方案:①24节A 型车厢和16节B 型车厢;②25节A 型车厢和15节B 型车厢;③26节A 型车厢和14节B 型车厢.(3)由函数y =-0.2x +32知,x 越大,y 越小,故当x =26时,运费最省,这时y =-0.2×26+32=26.8(万元).即安排A 型车厢26节、B 型车厢14节运费最省,最少运费为26.8万元.23.解:(1)由反比例函数过点B (m .4),得4m =k .由S △AOB =2,得12×2×m =2,解得m=2,故k =8,则反比例函数的解析式为y =8x .由一次函数过点A (0,2)、B (2,4),得⎩⎪⎨⎪⎧b =2,2a +b =4,解得⎩⎪⎨⎪⎧a =1,b =2,则一次函数的解析式为y =x +2. (2)由直线y =x +2可知,C (-2,0), ∴OC =2,∴S △OBC =12OC ·|y B |=12×2×4=4.24.(1)解:当点O 在P A 上,即AP 为直径,则∠PBA =90°. ∵∠APB =60°, ∴∠A =30°.当点O 在PB 上,即BP 为直径,则∠A =90°.∴当圆心O 在∠APB 内部时,α的取值范围为30°<α<90°. (2)证明:如图,连接OB .∵OC ⊥AB , ∴AC ︵ =BC ︵, ∴∠APC =∠BPC . ∵∠APB =60°, ∴∠BPC =30°,∴∠BOC =2∠BPC =60°, ∴△OBC 为等边三角形, ∴∠OCB =60°. ∵∠OCB =2∠BCM , ∴∠MCB =30°,∴∠OCM =∠OCB +∠MCB =90°, ∴OC ⊥MC , ∴CM 与⊙O 相切.(3)解:如图,作BE ⊥PC 于点E .在Rt △PBE 中,∠BPE =30°,PB =42, ∴BE =12PB =22,PE =3BE =2 6.∵△OBC 为等边三角形, ∴BC =OC =4.在Rt △BEC 中,CE =BC 2-BE 2=22, ∴PC =PE +CE =26+2 2.25.解:(1)将点A (4,0)的坐标代入二次函数的解析式,得-12×42+4b =0,解得b =2,∴二次函数的解析式为y =-12x 2+2x .(2)∵y =-12x 2+2x =-12(x -2)2+2,∴B (2,2),抛物线的对称轴为x =2.如图1,由两点间的距离公式,得OB =22+22=22,BA =(4-2)2+(2-0)2=2 2. ∵C 是OB 的中点, ∴OC =BC = 2.∵△OCB ′为等边三角形, ∴∠OCB ′=60°.又∵点B 与点B ′关于CQ 对称, ∴∠B ′CQ =∠BCQ =60°. ∵OA =4,OB =22,AB =22, ∴OB 2+AB 2=OA 2, ∴∠OBA =90°.在Rt △CBQ 中,∠CBQ =90°,∠BCQ =60°,BC =2, ∴tan 60°=BQBC,∴BQ =3CB =3×2= 6.图1(3)分两种情况:当F 在边OA 上时, ①如图2,过点D 作DF ⊥x 轴,垂足为点F . ∵△DOF ≌△DEF ,且E 在线段OA 上, ∴OF =FE . 由(2),得OB =2 2.∵点D 在线段BO 上,OD =2DB , ∴OD =23OB =423.∵∠BOA =45°, ∴cos 45°=OFOD ,∴OF =OD ·cos 45°=423×22=43, ∴OE =2OF =83,∴点E 的坐标为⎝⎛⎭⎫83,0.图2②如图3,过点D 作DF ⊥x 轴于点F ,过点D 作DE ∥x 轴,交AB 于点E ,连接EF ,过点E 作EG ⊥x 轴于G ,∴△BDE ∽△BOA , ∴BD OB =DE OA =13. ∵OA =4, ∴DE =43.∵DE ∥OA ,∴∠OFD =∠FDE =90°. ∵DE =OF =43,DF =DF ,∴△OFD ≌△EDF . 同理可得△EDF ≌△FGE , ∴△OFD ≌△EDF ≌△FGE ,∴OG =OF +FG =OF +DE =43+43=83,EG =DF =OD ·sin 45°=43,∴E 的坐标为⎝⎛⎭⎫83,43.图3③如图4,将△DOF 沿边DF 翻折,使得O 恰好落在AB 边上,记为点E , 过点B 作BM ⊥x 轴于点M ,过点E 作EN ⊥BM 于点N .图4由翻折的性质,得△DOF ≌△DEF , ∴OD =DE =423.∵BD =12OD =223,∴在Rt △DBE 中,由勾股定理,得BE =DE 2-BD 2=263, 则BN =NE =BE ·cos 45°=263×22=233,OM +NE =2+233,BM -BN =2-233,∴点E 的坐标为⎝⎛⎭⎫2+233,2-233. 当点F 在AB 上时,①如图5,过点D 作DF ∥x 轴,交AB 于点F ,连接OF 与DA . ∵DF ∥x 轴, ∴△BDF ∽△BOA , ∴BD BO =BFBA. 由抛物线的对称性,得OB =BA , ∴BD =BF ,则∠BDF =∠BFD ,∠ODF =∠AFD , ∴OD =OB -BD =BA -BF =AF , 则△DOF ≌△DAF ,∴E 和A 重合,则点E 的坐标为(4,0).图5②如图6,由①可知:当E 与O 重合时,△DOF 与△DEF 重合,此时点E (0,0).图6综上所述,点E 的坐标为⎝⎛⎭⎫83,0或⎝⎛⎭⎫83,43或⎝⎛⎭⎫2+233,2-233或(4,0)或(0,0).。
【精选试卷】四川德阳市中考数学填空题专项练习测试卷(答案解析)

一、填空题1.某品牌旗舰店平日将某商品按进价提高40%后标价,在某次电商购物节中,为促销该商品,按标价8折销售,售价为2240元,则这种商品的进价是______元.2.从﹣2,﹣1,1,2四个数中,随机抽取两个数相乘,积为大于﹣4小于2的概率是_____.3.一批货物准备运往某地,有甲、乙、丙三辆卡车可雇用.已知甲、乙、丙三辆车每次运货量不变,且甲、乙两车单独运完这批货物分别用2, a a 次;甲、丙两车合运相同次数,运完这批货物,甲车共运180吨;乙、丙两车合运相同次数,运完这批货物乙车共运270吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费20元计算)4.等腰三角形一腰上的高与另一腰的夹角的度数为20°,则顶角的度数是 . 5.如图,正方形ABCD 的边长为2,点E 为边BC 的中点,点P 在对角线BD 上移动,则PE+PC 的最小值是 .6.使分式x 2−1x+1的值为0,这时x=_____.7.甲、乙两人在1200米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进,已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y (米)表示甲、乙两人之间的距离,x (秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y 与x 函数关系,那么,乙到达终点后_____秒与甲相遇.8.如图,边长为2的正方形ABCD 的顶点A ,B 在x 轴正半轴上,反比例函数k y x在第一象限的图象经过点D ,交BC 于E ,若点E 是BC 的中点,则OD 的长为_____.9.如图,在△ABC 中E 是BC 上的一点,EC=2BE ,点D 是AC 的中点,设△ABC 、△ADF 、△BEF 的面积分别为S △ABC ,S △ADF ,S △BEF ,且S △ABC =12,则S △ADF -S △BEF =_________.10.已知圆锥的底面圆半径为3cm ,高为4cm ,则圆锥的侧面积是________cm 2.11.如图,反比例函数y=k x的图象经过▱ABCD 对角线的交点P ,已知点A ,C ,D 在坐标轴上,BD ⊥DC ,▱ABCD 的面积为6,则k=_____.12.不等式组0125x a x x ->⎧⎨->-⎩有3个整数解,则a 的取值范围是_____. 13.如图,已知AB ∥CD ,F 为CD 上一点,∠EFD=60°,∠AEC=2∠CEF ,若6°<∠BAE <15°,∠C 的度数为整数,则∠C 的度数为_____.14.关于x 的一元二次方程2310ax x --=的两个不相等的实数根都在-1和0之间(不包括-1和0),则a 的取值范围是___________15.如图,直线l x ⊥轴于点P ,且与反比例函数11k y x=(0x >)及22k y x =(0x >)的图象分别交于A 、B 两点,连接OA 、OB ,已知OAB ∆的面积为4,则12k k =﹣________.16.已知a ,b ,c 是△ABC 的三边长,a ,b 满足|a ﹣7|+(b ﹣1)2=0,c 为奇数,则c=_____.17.色盲是伴X 染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表: 抽取的体检表数n50 100 200 400 500 800 1000 1200 1500 2000 色盲患者的频数m3 7 13 29 37 55 69 85 105 138 色盲患者的频率m/n 0.060 0.070 0.065 0.073 0.074 0.069 0.069 0.071 0.070 0.069根据表中数据,估计在男性中,男性患色盲的概率为______(结果精确到0.01).18.如果a 是不为1的有理数,我们把11a -称为a 的差倒数如:2的差倒数是1112=--,-1的差倒数是111(1)2=--,已知14a =,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数,…,依此类推,则 2019a =___________ .19.如图,⊙O 是△ABC 的外接圆,∠A =45°,则cos ∠OCB 的值是________.20.已知关于x 的方程3x n 22x 1+=+的解是负数,则n 的取值范围为 . 21.分解因式:x 3﹣4xy 2=_____.22.如图,添加一个条件: ,使△ADE ∽△ACB ,(写出一个即可)23.如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=kx的图象上,则k的值为________.24.如图,直线a、b被直线l所截,a∥b,∠1=70°,则∠2= .25.如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A在反比例函数y=2x的图像上,则菱形的面积为_______.26.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为______.27.关于x的一元二次方程(a+1)x2-2x+3=0有实数根,则整数a的最大值是_____. 28.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是_____.29.如图,点A在双曲线y=4x上,点B在双曲线y=kx(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为____.30.3x x的取值范围是_____.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、填空题1.2000【解析】【分析】设这种商品的进价是x元根据提价之后打八折售价为2240元列方程解答即可【详解】设这种商品的进价是x元由题意得(1+40)x×08=2240解得:x=2000故答案为:20002.【解析】【分析】列表得出所有等可能结果从中找到积为大于-4小于2的结果数根据概率公式计算可得【详解】列表如下:-2-112-22-2-4-12-1-21-2-3.【解析】【分析】根据甲乙两车单独运这批货物分别用2a次a次能运完甲的效率应该为乙的效率应该为那么可知乙车每次货运量是甲车的2倍根据若甲丙两车合运相同次数运完这批货物时甲车共运了180吨;若乙丙两车合4.110°或70°【解析】试题分析:此题要分情况讨论:当等腰三角形的顶角是钝角时腰上的高在外部根据三角形的一个外角等于与它不相邻的两个内角的和即可求得顶角是90°+20°=110°;当等腰三角形的顶角5.【解析】试题分析:要求PE+PC的最小值PEPC不能直接求可考虑通过作辅助线转化PEPC的值从而找出其最小值求解试题解析:如图连接AE∵点C关于BD的对称点为点A∴PE+PC=PE+AP根据两点之间6.1【解析】试题分析:根据题意可知这是分式方程x2-1x+1=0然后根据分式方程的解法分解因式后约分可得x-1=0解之得x=1经检验可知x=1是分式方程的解答案为1考点:分式方程的解法7.30【解析】【分析】由图象可以V甲=9030=3m/sV追=90120-30=1m/s故V乙=1+3=4m/s由此可求得乙走完全程所用的时间为:12004=300s则可以求得此时乙与甲的距离即可求出8.【解析】【分析】设D(x2)则E(x+21)由反比例函数经过点DE列出关于x的方程求得x的值即可得出答案【详解】解:设D(x2)则E(x+21)∵反比例函数在第一象限的图象经过点D点E∴2x=x+29.2【解析】由D是AC的中点且S△ABC=12可得;同理EC=2BE即EC=可得又等量代换可知S△ADF-S△BEF=210.15π【解析】【分析】设圆锥母线长为l根据勾股定理求出母线长再根据圆锥侧面积公式即可得出答案【详解】设圆锥母线长为l∵r=3h=4∴母线l=∴S侧=×2πr×5=×2π×3×5=15π故答案为15π11.-3【解析】分析:由平行四边形面积转化为矩形BDOA面积在得到矩形PDOE面积应用反比例函数比例系数k的意义即可详解:过点P做PE⊥y轴于点E∵四边形ABCD为平行四边形∴AB=CD又∵BD⊥x轴∴12.﹣2≤a<﹣1【解析】【分析】先解不等式组确定不等式组的解集(利用含a的式子表示)根据整数解的个数就可以确定有哪些整数解根据解的情况可以得到关于a的不等式从而求出a的范围【详解】解不等式x﹣a>0得13.36°或37°【解析】分析:先过E作EG∥AB根据平行线的性质可得∠AEF=∠BAE+∠DFE再设∠CEF=x则∠AEC=2x根据6°<∠BAE<15°即可得到6°<3x-60°<15°解得22°<14.<a<-2【解析】【分析】【详解】解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根∴△=(-3)2-4×a×(-1)>0解得:a>−设f(x)=ax2-3x-1如图∵实数根都在-115.【解析】【分析】根据反比例函数的几何意义可知:的面积为的面积为然后两个三角形面积作差即可求出结果【详解】解:根据反比例函数的几何意义可知:的面积为的面积为∴的面积为∴∴故答案为8【点睛】本题考查反比16.7【解析】【分析】根据非负数的性质列式求出ab的值再根据三角形的任意两边之和大于第三边两边之差小于第三边求出c的取值范围再根据c是奇数求出c的值【详解】∵ab满足|a﹣7|+(b﹣1)2=0∴a﹣717.07【解析】【分析】随着实验次数的增多频率逐渐稳定到的常数即可表示男性患色盲的概率【详解】解:观察表格发现随着实验人数的增多男性患色盲的频率逐渐稳定在常数007左右故男性中男性患色盲的概率为007故18.【解析】【分析】利用规定的运算方法分别算得a1a2a3a4…找出运算结果的循环规律利用规律解决问题【详解】∵a1=4a2=a3=a4=…数列以4−三个数依次不断循环∵2019÷3=673∴a201919.【解析】【分析】根据圆周角定理可得∠BOC=90°易求BC=OC从而可得cos∠OCB的值【详解】∵∠A=45°∴∠BOC=90°∵OB=OC由勾股定理得BC=OC∴cos∠OCB=故答案为【点睛】20.n<2且【解析】分析:解方程得:x=n﹣2∵关于x的方程的解是负数∴n﹣2<0解得:n<2又∵原方程有意义的条件为:∴即∴n的取值范围为n<2且21.x(x+2y)(x﹣2y)【解析】分析:原式提取x再利用平方差公式分解即可详解:原式=x(x2-4y2)=x(x+2y)(x-2y)故答案为x(x+2y)(x-2y)点睛:此题考查了提公因式法与公式22.∠ADE=∠ACB(答案不唯一)【解析】【分析】【详解】相似三角形的判定有三种方法:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;23.-6【解析】因为四边形OABC是菱形所以对角线互相垂直平分则点A和点C关于y轴对称点C在反比例函数上设点C的坐标为(x)则点A的坐标为(-x)点B的坐标为(0)因此AC=-2xOB=根据菱形的面积等24.110°【解析】∵a∥b∴∠3=∠1=70°∵∠2+∠3=180°∴∠2=110°25.4【解析】【分析】【详解】解:连接AC交OB于D∵四边形OABC是菱形∴AC⊥OB∵点A在反比例函数y=的图象上∴△AOD的面积=×2=1∴菱形OABC的面积=4×△AOD的面积=4故答案为:426.5【解析】【分析】【详解】试题解析:∵∠AFB=90°D为AB的中点∴DF=AB=25∵DE 为△ABC的中位线∴DE=BC=4∴EF=DE-DF=15故答案为15【点睛】直角三角形斜边上的中线性质:27.-2【解析】【分析】若一元二次方程有实数根则根的判别式△=b2-4ac≥0建立关于a 的不等式求出a的取值范围还要注意二次项系数不为0【详解】∵关于x的一元二次方程(a+1)x2-2x+3=0有实数根28.【解析】【分析】根据概率的求法找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率【详解】共个数大于的数有个(大于);故答案为【点睛】本题考查概率的求法:如果一个事件有n种可29.12【解析】【详解】解:设点A的坐标为(a)则点B的坐标为()∵AB∥x轴AC=2CD∴∠BAC=∠ODC∵∠ACB=∠DCO∴△ACB∽△DCO∴∵OD=a则AB=2a∴点B的横坐标是3a∴3a=30.x≥﹣3【解析】【分析】直接利用二次根式的定义求出x的取值范围【详解】解:若式子在实数范围内有意义则x+3≥0解得:x≥﹣3则x的取值范围是:x≥﹣3故答案为:x≥﹣3【点睛】此题主要考查了二次根式2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、填空题1.2000【解析】【分析】设这种商品的进价是x元根据提价之后打八折售价为2240元列方程解答即可【详解】设这种商品的进价是x元由题意得(1+40)x×08=2240解得:x=2000故答案为:2000解析:2000,【解析】【分析】设这种商品的进价是x元,根据提价之后打八折,售价为2240元,列方程解答即可.【详解】设这种商品的进价是x元,由题意得,(1+40%)x×0.8=2240,解得:x=2000,故答案为:2000.【点睛】本题考查了一元一次方程的应用——销售问题,弄清题意,熟练掌握标价、折扣、实际售价间的关系是解题的关键.2.【解析】【分析】列表得出所有等可能结果从中找到积为大于-4小于2的结果数根据概率公式计算可得【详解】列表如下:-2-112-22-2-4-12-1-21-2-解析:1 2【解析】【分析】列表得出所有等可能结果,从中找到积为大于-4小于2的结果数,根据概率公式计算可得.【详解】列表如下:∴积为大于-4小于2的概率为612=12,故答案为12.【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.3.【解析】【分析】根据甲乙两车单独运这批货物分别用2a次a次能运完甲的效率应该为乙的效率应该为那么可知乙车每次货运量是甲车的2倍根据若甲丙两车合运相同次数运完这批货物时甲车共运了180吨;若乙丙两车合解析:2160【解析】【分析】根据“甲、乙两车单独运这批货物分别用2a次、a次能运完”甲的效率应该为1 2a ,乙的效率应该为1a,那么可知乙车每次货运量是甲车的2倍根据“若甲、丙两车合运相同次数运完这批货物时,甲车共运了180吨;若乙、丙两车合运相同次数运完这批货物时,乙车共运了270吨.”这两个等量关系来列方程.【详解】设这批货物共有T吨,甲车每次运t甲吨,乙车每次运t乙吨,∵2a⋅t甲=T,a⋅t乙=T,∴t甲:t乙=1:2,由题意列方程:180270 180270T Tt t--=甲乙,t乙=2t甲,∴180270180135T T--=,解得T=540.∵甲车运180吨,丙车运540−180=360吨,∴丙车每次运货量也是甲车的2倍,∴甲车车主应得运费15402021605⨯⨯= (元),故答案为:2160.【点睛】考查分式方程的应用,读懂题目,找出题目中的等量关系是解题的关键.4.110°或70°【解析】试题分析:此题要分情况讨论:当等腰三角形的顶角是钝角时腰上的高在外部根据三角形的一个外角等于与它不相邻的两个内角的和即可求得顶角是90°+20°=110°;当等腰三角形的顶角解析:110°或70°.【解析】试题分析:此题要分情况讨论:当等腰三角形的顶角是钝角时,腰上的高在外部.根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+20°=110°;当等腰三角形的顶角是锐角时,腰上的高在其内部,故顶角是90°﹣20°=70°.故答案为110°或70°.考点:1.等腰三角形的性质;2.分类讨论.5.【解析】试题分析:要求PE+PC的最小值PEPC不能直接求可考虑通过作辅助线转化PEPC的值从而找出其最小值求解试题解析:如图连接AE∵点C关于BD的对称点为点A∴PE+PC=PE+AP根据两点之间5【解析】试题分析:要求PE+PC的最小值,PE,PC不能直接求,可考虑通过作辅助线转化PE,PC 的值,从而找出其最小值求解.试题解析:如图,连接AE,∵点C 关于BD 的对称点为点A ,∴PE+PC=PE+AP ,根据两点之间线段最短可得AE 就是AP+PE 的最小值,∵正方形ABCD 的边长为2,E 是BC 边的中点,∴BE=1,∴22125+考点:1.轴对称-最短路线问题;2.正方形的性质.6.1【解析】试题分析:根据题意可知这是分式方程x2-1x+1=0然后根据分式方程的解法分解因式后约分可得x-1=0解之得x=1经检验可知x=1是分式方程的解答案为1考点:分式方程的解法解析:1【解析】试题分析:根据题意可知这是分式方程,x 2−1x+1=0,然后根据分式方程的解法分解因式后约分可得x-1=0,解之得x=1,经检验可知x=1是分式方程的解.答案为1.考点:分式方程的解法7.30【解析】【分析】由图象可以V 甲=9030=3m/sV 追=90120-30=1m/s 故V 乙=1+3=4m/s 由此可求得乙走完全程所用的时间为:12004=300s 则可以求得此时乙与甲的距离即可求出解析:30【解析】【分析】由图象可以V 甲=9030=3m/s ,V 追=90120−30=1m/s ,故V 乙=1+3=4m/s ,由此可求得乙走完全程所用的时间为:12004=300s ,则可以求得此时乙与甲的距离,即可求出最后与甲相遇的时间.【详解】由图象可得V 甲=9030=3m/s ,V 追=90120−30=1m/s , ∴V 乙=1+3=4m/s ,∴乙走完全程所用的时间为:12004=300s ,此时甲所走的路程为:(300+30)×3=990m . 此时甲乙相距:1200﹣990=210m则最后相遇的时间为:2103+4=30s故答案为:30【点睛】 此题主要考查一次函数图象的应用,利用函数图象解决行程问题.此时就要求掌握函数图象中数据表示的含义.8.【解析】【分析】设D (x2)则E (x+21)由反比例函数经过点DE 列出关于x 的方程求得x 的值即可得出答案【详解】解:设D (x2)则E (x+21)∵反比例函数在第一象限的图象经过点D 点E∴2x=x+2 解析:12x x 【解析】【分析】设D (x ,2)则E (x+2,1),由反比例函数经过点D 、E 列出关于x 的方程,求得x 的值即可得出答案.【详解】解:设D (x ,2)则E (x+2,1), ∵反比例函数k y x=在第一象限的图象经过点D 、点E , ∴2x =x+2,解得x =2,∴D (2,2),∴OA =AD =2,∴OD ==故答案为:【点睛】本题主要考查反比例函数图象上点的坐标特征,解题的关键是根据题意表示出点D 、E 的坐标及反比例函数图象上点的横纵坐标乘积都等于反比例系数k . 9.2【解析】由D 是AC 的中点且S△ABC=12可得;同理EC=2BE 即EC=可得又等量代换可知S△ADF-S△BEF=2解析:2【解析】由D 是AC 的中点且S △ABC =12,可得1112622ABD ABC S S ∆∆==⨯=;同理EC=2BE 即EC=13BC ,可得11243ABE S ∆=⨯=,又,ABE ABF BEF ABD ABF ADF S S S S S S ∆∆∆∆∆∆-=-=等量代换可知S △ADF -S △BEF =210.15π【解析】【分析】设圆锥母线长为l 根据勾股定理求出母线长再根据圆锥侧面积公式即可得出答案【详解】设圆锥母线长为l∵r=3h=4∴母线l=∴S侧=×2πr×5=×2π×3×5=15π故答案为15π解析:15π【解析】【分析】设圆锥母线长为l,根据勾股定理求出母线长,再根据圆锥侧面积公式即可得出答案.【详解】设圆锥母线长为l,∵r=3,h=4,∴母线l=225r h+=,∴S侧=12×2πr×5=12×2π×3×5=15π,故答案为15π.【点睛】本题考查了圆锥的侧面积,熟知圆锥的母线长、底面半径、圆锥的高以及圆锥的侧面积公式是解题的关键.11.-3【解析】分析:由平行四边形面积转化为矩形BDOA面积在得到矩形PDOE面积应用反比例函数比例系数k的意义即可详解:过点P做PE⊥y轴于点E∵四边形ABC D为平行四边形∴AB=CD又∵BD⊥x轴∴解析:-3【解析】分析:由平行四边形面积转化为矩形BDOA面积,在得到矩形PDOE面积,应用反比例函数比例系数k的意义即可.详解:过点P做PE⊥y轴于点E,∵四边形ABCD为平行四边形∴AB=CD又∵BD⊥x轴∴ABDO为矩形∴AB=DO∴S矩形ABDO=S▱ABCD=6∵P为对角线交点,PE⊥y轴∴四边形PDOE为矩形面积为3即DO•EO=3∴设P点坐标为(x,y)k=xy=﹣3故答案为:﹣3点睛:本题考查了反比例函数比例系数k的几何意义以及平行四边形的性质.12.﹣2≤a<﹣1【解析】【分析】先解不等式组确定不等式组的解集(利用含a的式子表示)根据整数解的个数就可以确定有哪些整数解根据解的情况可以得到关于a的不等式从而求出a的范围【详解】解不等式x﹣a>0得解析:﹣2≤a<﹣1.【解析】【分析】先解不等式组确定不等式组的解集(利用含a的式子表示),根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a的不等式,从而求出a的范围.【详解】解不等式x﹣a>0,得:x>a,解不等式1﹣x>2x﹣5,得:x<2,∵不等式组有3个整数解,∴不等式组的整数解为﹣1、 0、1,则﹣2≤a<﹣1,故答案为:﹣2≤a<﹣1.【点睛】本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.13.36°或37°【解析】分析:先过E作EG∥AB根据平行线的性质可得∠AEF=∠BAE+∠DFE再设∠CEF=x则∠AEC=2x根据6°<∠BAE<15°即可得到6°<3x-60°<15°解得22°<解析:36°或37°.【解析】分析:先过E作EG∥AB,根据平行线的性质可得∠AEF=∠BAE+∠DFE,再设∠CEF=x,则∠AEC=2x,根据6°<∠BAE<15°,即可得到6°<3x-60°<15°,解得22°<x <25°,进而得到∠C的度数.详解:如图,过E作EG∥AB,∵AB∥CD,∴GE∥CD,∴∠BAE=∠AEG,∠DFE=∠GEF,∴∠AEF=∠BAE+∠DFE,设∠CEF=x,则∠AEC=2x,∴x+2x=∠BAE+60°,∴∠BAE=3x-60°,又∵6°<∠BAE<15°,∴6°<3x-60°<15°,解得22°<x<25°,又∵∠DFE是△CEF的外角,∠C的度数为整数,∴∠C=60°-23°=37°或∠C=60°-24°=36°,故答案为:36°或37°.点睛:本题主要考查了平行线的性质以及三角形外角性质的运用,解决问题的关键是作平行线,解题时注意:两直线平行,内错角相等.14.<a<-2【解析】【分析】【详解】解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根∴△=(-3)2-4×a×(-1)>0解得:a>−设f (x)=ax2-3x-1如图∵实数根都在-1解析:94-<a<-2【解析】【分析】【详解】解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根∴△=(-3)2-4×a×(-1)>0,解得:a>−9 4设f(x)=ax2-3x-1,如图,∵实数根都在-1和0之间,∴-1<−32a-<0,∴a<−32,且有f(-1)<0,f(0)<0,即f(-1)=a×(-1)2-3×(-1)-1<0,f(0)=-1<0,解得:a<-2,∴−94<a <-2, 故答案为−94<a <-2. 15.【解析】【分析】根据反比例函数的几何意义可知:的面积为的面积为然后两个三角形面积作差即可求出结果【详解】解:根据反比例函数的几何意义可知:的面积为的面积为∴的面积为∴∴故答案为8【点睛】本题考查反比 解析:【解析】【分析】根据反比例函数k 的几何意义可知:AOP ∆的面积为112k ,BOP ∆的面积为212k ,然后两个三角形面积作差即可求出结果.【详解】解:根据反比例函数k 的几何意义可知:AOP ∆的面积为112k ,BOP ∆的面积为212k , ∴AOB ∆的面积为121122k k -,∴1211422k k -=,∴128k k -=. 故答案为8.【点睛】本题考查反比例函数k 的几何意义,解题的关键是正确理解k 的几何意义,本题属于基础题型. 16.7【解析】【分析】根据非负数的性质列式求出ab 的值再根据三角形的任意两边之和大于第三边两边之差小于第三边求出c 的取值范围再根据c 是奇数求出c 的值【详解】∵ab 满足|a ﹣7|+(b ﹣1)2=0∴a﹣7解析:7【解析】【分析】根据非负数的性质列式求出a 、b 的值,再根据三角形的任意两边之和大于第三边,两边之差小于第三边求出c 的取值范围,再根据c 是奇数求出c 的值.【详解】∵a ,b 满足|a ﹣7|+(b ﹣1)2=0,∴a ﹣7=0,b ﹣1=0,解得a=7,b=1,∵7﹣1=6,7+1=8,∴68c <<,又∵c 为奇数,∴c=7,故答案为7.【点睛】本题考查非负数的性质:偶次方,解题的关键是明确题意,明确三角形三边的关系. 17.07【解析】【分析】随着实验次数的增多频率逐渐稳定到的常数即可表示男性患色盲的概率【详解】解:观察表格发现随着实验人数的增多男性患色盲的频率逐渐稳定在常数007左右故男性中男性患色盲的概率为007故 解析:07【解析】【分析】随着实验次数的增多,频率逐渐稳定到的常数即可表示男性患色盲的概率.【详解】解: 观察表格发现,随着实验人数的增多,男性患色盲的频率逐渐稳定在常数0.07左右, 故男性中,男性患色盲的概率为0.07故答案为:0.07.【点睛】本题考查利用频率估计概率.18.【解析】【分析】利用规定的运算方法分别算得a1a2a3a4…找出运算结果的循环规律利用规律解决问题【详解】∵a1=4a2=a3=a4=…数列以4−三个数依次不断循环∵2019÷3=673∴a2019 解析:34. 【解析】【分析】 利用规定的运算方法,分别算得a 1,a 2,a 3,a 4…找出运算结果的循环规律,利用规律解决问题.【详解】∵a 1=4a 2=11111143a ==---, a 3=211311413a ⎛⎫ ⎪⎝=⎭=---, a 4=31143114a ==--, …数列以4,−1334,三个数依次不断循环, ∵2019÷3=673, ∴a 2019=a 3=34,故答案为:34. 【点睛】 此题考查规律型:数字的变化类,倒数,解题关键在于掌握运算法则找到规律.19.【解析】【分析】根据圆周角定理可得∠BOC=90°易求BC=OC 从而可得cos ∠OCB 的值【详解】∵∠A=45°∴∠BOC=90°∵OB=OC 由勾股定理得BC=OC ∴cos ∠OCB=故答案为【点睛】解析:2【解析】【分析】根据圆周角定理可得∠BOC=90°,易求OC ,从而可得cos ∠OCB 的值.【详解】∵∠A =45°,∴∠BOC=90°∵OB=OC ,由勾股定理得,OC ,∴cos ∠OCB =2OC BC ==.故答案为2. 【点睛】 本题考查的是圆周角定理、等腰直角三角形的判定及锐角三角函数的定义,属较简单题目题目.20.n <2且【解析】分析:解方程得:x=n ﹣2∵关于x 的方程的解是负数∴n ﹣2<0解得:n <2又∵原方程有意义的条件为:∴即∴n 的取值范围为n <2且解析:n <2且3n 2≠-【解析】 分析:解方程3x n 22x 1+=+得:x=n ﹣2, ∵关于x 的方程3x n 22x 1+=+的解是负数,∴n ﹣2<0,解得:n <2. 又∵原方程有意义的条件为:1x 2≠-,∴1n 22-≠-,即3n 2≠-. ∴n 的取值范围为n <2且3n 2≠-.21.x (x+2y )(x ﹣2y )【解析】分析:原式提取x 再利用平方差公式分解即可详解:原式=x (x2-4y2)=x (x+2y )(x-2y )故答案为x (x+2y )(x-2y )点睛:此题考查了提公因式法与公式解析:x (x+2y )(x ﹣2y )【解析】分析:原式提取x ,再利用平方差公式分解即可.详解:原式=x (x 2-4y 2)=x (x+2y )(x-2y ),故答案为x (x+2y )(x-2y )点睛:此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.22.∠ADE=∠ACB(答案不唯一)【解析】【分析】【详解】相似三角形的判定有三种方法:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似; 解析:∠ADE=∠ACB (答案不唯一)【解析】【分析】【详解】相似三角形的判定有三种方法:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.由此可得出可添加的条件:由题意得,∠A=∠A (公共角),则添加:∠ADE=∠ACB 或∠AED=∠ABC ,利用两角法可判定△ADE ∽△ACB ; 添加:AD AE AC AB=,利用两边及其夹角法可判定△ADE ∽△ACB. 23.-6【解析】因为四边形OABC 是菱形所以对角线互相垂直平分则点A 和点C 关于y 轴对称点C 在反比例函数上设点C 的坐标为(x)则点A 的坐标为(-x)点B 的坐标为(0)因此AC=-2xOB=根据菱形的面积等解析:-6【解析】因为四边形OABC 是菱形,所以对角线互相垂直平分,则点A 和点C 关于y 轴对称,点C 在反比例函数上,设点C 的坐标为(x ,k x ),则点A 的坐标为(-x ,k x ),点B 的坐标为(0,2k x ),因此AC=-2x,OB=2K X,根据菱形的面积等于对角线乘积的一半得: ()OABC 122122k S x x=⨯-⨯=菱形,解得 6.k =- 24.110°【解析】∵a∥b∴∠3=∠1=70°∵∠2+∠3=180°∴∠2=110°解析:110°【解析】∵a∥b,∴∠3=∠1=70°,∵∠2+∠3=180°,∴∠2=110°25.4【解析】【分析】【详解】解:连接AC交OB于D∵四边形OABC是菱形∴AC⊥OB∵点A在反比例函数y=的图象上∴△AOD的面积=×2=1∴菱形OABC 的面积=4×△AOD的面积=4故答案为:4解析:4【解析】【分析】【详解】解:连接AC交OB于D.∵四边形OABC是菱形,∴AC⊥OB.∵点A在反比例函数y=2x的图象上,∴△AOD的面积=12×2=1,∴菱形OABC的面积=4×△AOD的面积=4故答案为:426.5【解析】【分析】【详解】试题解析:∵∠AFB=90°D为AB的中点∴DF=AB =25∵DE为△ABC的中位线∴DE=BC=4∴EF=DE-DF=15故答案为15【点睛】直角三角形斜边上的中线性质:解析:5【解析】【分析】【详解】试题解析:∵∠AFB=90°,D为AB的中点,∴DF=12AB=2.5,∵DE为△ABC的中位线,∴DE=12BC=4,∴EF=DE-DF=1.5,故答案为1.5.【点睛】直角三角形斜边上的中线性质:在直角三角形中,斜边上的中线等于斜边的一半和三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.27.-2【解析】【分析】若一元二次方程有实数根则根的判别式△=b2-4ac≥0建立关于a的不等式求出a的取值范围还要注意二次项系数不为0【详解】∵关于x的一元二次方程(a+1)x2-2x+3=0有实数根解析:-2【解析】【分析】若一元二次方程有实数根,则根的判别式△=b2-4ac≥0,建立关于a的不等式,求出a的取值范围.还要注意二次项系数不为0.【详解】∵关于x的一元二次方程(a+1)x2-2x+3=0有实数根,∴△=4-4(a+1)×3≥0,且a+1≠0,解得a≤-23,且a≠-1,则a的最大整数值是-2.故答案为:-2.【点睛】本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的实数根;②当△=0时,方程有两个相等的实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.也考查了一元二次方程的定义.28.【解析】【分析】根据概率的求法找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率【详解】共个数大于的数有个(大于);故答案为【点睛】本题考查概率的求法:如果一个事件有n种可解析:12.【解析】【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【详解】共6个数,大于3的数有3个,P∴(大于3)31 62 ==;。
德阳市中考英语英语 完形填空专题练习(及答案)

德阳市中考英语英语完形填空专题练习(及答案)一、英语完形填空1.完形填空Rich or poor, young or old, we all have problems. We can easily become unhappy 1 we solve our problems. 2 about our problems can affect how we do things at school or at home. So how do we deal with our problems?Most of us have probably been angry 3 our friends, parents or teachers. Perhaps they said something you didn't like, or you felt they were unfair. Sometimes, people can stay angry for years about a small problem. Time goes by, and good friendships may 4 .When we are angry, however, we are usually the ones affected. Have you ever seen young children playing together? But they fight very soon, and decide not to talk to each other. However, this usually doesn't 5 for long. They become good friends again. This is an important 6 for us, we can solve a problem by learning to forget.Many students often complain about school. They might feel they have too much work to do sometimes, or think the rules are too 7 . We must learn how to change these "problems" into "challenges(挑战)". As young adults, it is our duty to 8 our best to deal with each challenge with the help of our teachers.By comparing yourself to other people, you will find your problems are not so 9 , Think about Stephen Hawking, for example, a very clever scientist. He can't walk or even speak, but he considers his many physical problems unimportant. Now he is known 10 a great scientistin the world. We are probably quite healthy and smart. Let's not worry about our problems. Let's face the challenges instead.1. A. unless B. if C. when D. as2. A. Worry B. Worrying C. Worried D. To worry3. A. of B. to C. with D. in4. A. lose B. be lost C. keep D. be kept5. A. last B. do C. produce D. make6. A. program B. tool C. class D. lesson7. A. kind B. strict C. weak D. free8. A. try B. have C. put D. keep9. A. terrible B. pleasant C. painless D. useful10. A. about B. for C. with D. as【答案】(1)A;(2)B;(3)C;(4)B;(5)A;(6)D;(7)B;(8)A;(9)A;(10)D;【解析】【分析】文章大意:本文介绍了怎么解决问题才能让我们更快乐。
德阳市初三中考练习题

德阳市初三中考练习题一、选择题1. 下列哪个数是4的倍数?A、 23B、 11C、 36D、 172. 以下哪个城市被称为“川南明珠”?A、成都B、德阳C、自贡D、南充3. 某比例尺为1:5000的地图上两地的实际距离为4km,那么这两地在地图上距离是多少厘米?A、 2B、 4C、 8D、 164. 把25提高20%后再降低20%,最后的数是多少?A、 21B、 23C、 24D、 255. 请找出下列单词中拼写错误的选项:A、降雨B、领导C、笑话D、天马行空二、填空题6. 中国的首都是______。
7. 2的平方根是______。
8. 一年有______个季节。
9. 世界上最长的河流是______。
10. 若m=3, n=5,则m的2次方加n的2次方等于______。
三、解答题11. 如果a + 2b = 7,3a - b = 11,求解a和b的值。
12. 一个长方形的长是5cm,宽是3cm,求该长方形的面积和周长。
13. 垂直于地面的杆子倾斜15°,杆子的倾斜边长为20米,求杆子与地面的夹角的正切值。
14. 请解释一下什么是化学反应,并举例说明。
15. 请写出你认为对环境保护很重要的措施,并解释原因。
四、写作题请根据你对德阳市的了解,写一篇文章,介绍德阳市的地理位置、历史文化、著名景点等内容。
文章需包含开头、主体和结尾部分。
(以下为示例文段)德阳市位于中国四川省中部,北纬30°26′,东经104°20′,地处成渝经济区腹地。
德阳市地理位置优越,交通发达,是四川省的重要城市之一。
德阳是一座拥有悠久历史文化的城市。
在汉代,德阳作为巴蜀的政治、军事和文化重镇,曾经是著名的丹阳郡。
古老的历史赋予了德阳丰富的文化底蕴,形成了独特的德阳文化特色。
德阳市拥有众多著名景点,其中最知名的是李白故居。
李白是唐代著名的浪漫主义诗人,他在德阳度过了一段重要的创作时光。
李白故居保存完好,游客可以近距离感受这位文学巨匠的生活氛围。
2023年四川省德阳市中考英语真题(含解析)

2023年四川省德阳市中考英语真题学校:___________姓名:___________班级:___________考号:___________kindness and I think people like her make the world a better place.6.A.trees B.animals C.flowers D.people 7.A.sitting B.jumping C.walking D.shouting 8.A.minutes B.hours C.days D.weeks 9.A.run B.listen C.ask D.cry 10.A.look after B.look at C.look for D.look up 11.A.got B.caught C.took D.found 12.A.teacher B.doctor C.nurse D.farmer 13.A.hospital B.school C.garden D.park 14.A.politely B.happily C.badly D.sadly 15.A.beats B.encourages C.wins D.toucheswill he pay?A.40 yuan.B.60 yuan.C.90 yuan.D.120 yuan. 17.Which bus will you take from Liuyangmingyuan Bus Stop to Sanxingdui Museum Station?A.No. 1 bus.B.No. 4 bus.C.No. 7 bus.D.No. 10 bus. 18.What can we learn from the text?A.Tourists can’t bring pets to the museum.B.Tourists can take photos in the museum.C.Tourists can enter the First Hall at 8:00.D.Tourists can enter the Second Hall at 19:00.A primary school in the southwest of China has become popular recently. In this school students and teachers can have free meals. There are more than 1, 000 students and teachers in this school. With enough farmland, students and teachers plant vegetables and keep pigs, sheep and chickens. Some of what is produced is sold at the market. The rest will be used to feed students and teachers. And this school has fed itself for 15 years.Each class has a piece of land to plant vegetables or keep animals. Students do farm work twice a week with the help of teachers. There is also a zoo in the school. It helps students get on with animals. The school has set up a greenhouse (温室) with fruit trees for students to learn about nature, instead of just listening to teachers in the classroom.“This is not simply a farm. This is connected with what the whole school can eat and also the quality of life of students and teachers,” said the school’s headmaster.He also said, “Children who have not kissed the land will not have a complete childhood. The labor (劳动) class helps students build excellent characters and better understand life and nature.”19.What does the primary school provide for the students?A.Free computers.B.Free clothes.C.Free meals.D.Free bikes.20.How often do the students do farm work?A.Once a week.B.Twice a week.C.Three times a week.D.Four times a week.21.What’s the purpose of setting up a greenhouse?A.To help students learn about nature.B.To take the place of all the teachers.C.To provide students with enough food.D.To help students to get on with animals.26.What are called dragons’ ears on this festival?A.Dumplings.B.Spring rolls.C.Noodles.D.Fried beans.In the near future, the doctors who treat our illness might be tiny machines that swim through our bodies. Some movies have played with the idea of making machines the size of a cell (细胞). Today robot technology has brought the idea closer to the real life. In my laboratory, I’m just trying to build such intelligent, or smart, tiny robots.Tiny living things, such as bacteria (细菌), have many intelligent actions. If we can make robots copy some of them, it’s very exciting. The way bacteria travel across their environment is unbelievable. At first, they move around without purpose, but when they start sensing food, like an amino acid (氨基酸), they will move gradually in that direction. As an expert making robots, I think it is great to make tiny robots that can do the same thing.For example, look at something like E. coli (大肠杆菌). It can sense amino acids around it. It can change how it’s moving. It can rebuild or repair itself. In fact, E. coli does all these so well that some researchers are using it as part of their tiny machines. They are making their tiny robots get free rides from E. coli. And E. coli does all the sensing for tiny robots and directs their movements.We’re already using smaller and smaller medical tools, like catheters (导管) that can travel deep into your brain to treat a blood clot (血块). Next, we will put tiny robots into the body that can travel into even smaller spaces and treat illness at an early time. Imagine a tiny robot that can treat a blood clot deep in your brain that can’t be reached with the catheters we are using today.We may not actually need something as powerful as artificial intelligence (AI) in these cases. We can still build a very useful tiny robot with a low degree of intelligence. For example, if a tiny robot notices a blood clot, it can slowly move in that direction, and carry medicine directly to that part. It might only have the intelligence of bacteria but could still work.27.What can we learn about the writer?A.The writer is a middle school teacher.B.The writer is a dentist from a hospital.C.The writer is an expert making robots.D.The writer is an expert makingmedicine.28.What are some researchers doing according to Paragraph 3?A.Using tiny robots to sense E. coli.B.Letting E. coli work for their tiny robots.C.Changing tiny robots into E. coli’s drivers.D.Telling tiny robots to direct E. coli’s movements.29.What does the writer think of the catheters today?A.They will be widely used by doctors in the future.B.They are not able to get to tinier areas in the body.C.They will be smarter than tiny robots in the future.D.They can help doctors take care of patients on time.30.What’s the last paragraph mainly about?A.AI plays an important role in developing tiny robots.B.Tiny robots can run fast and treat a blood clot easily.C.Tiny robots with a low degree of intelligence are still useful.D.We still need very powerful artificial intelligence to treat illness.三、阅读还原6选5A.Smile is a good way.B.Have good sleeping habits.C.Go to bed as early as possible.D.We can also get close to nature.E.There are different kinds of sports.F.In this way, we can fall asleep quickly.四、根据首字母填空六、材料作文56.德阳环境越来越好,请以Beautiful Jinghu Lake为题,用英语写一篇短文,投稿给某英文杂志。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
德阳中考填空题专练
16.(3分)如图,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DE的度数为.
17.(3分)如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是.18.(3分)在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的是.(填番号)①AC⊥DE;②=;③CD=2DH;④=.
16.如图,在直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三
,P2,P3,…,P n,
角形,射线OC⊥AB,在OC上依次截取点P
使OP1=1,P1P2=3,P2P3=5,…,P n﹣1P n=2n﹣1(n为正整数),
分别过点P1,P2,P3,…,P n向射线OA作垂线段,垂足分别为
点Q1,Q2,Q3,…,Q n,则点Q n的坐标为.
17.下列四个命题中,正确的是(填写正确命题的序号)
①三角形的外心是三角形三边垂直平分线的交点;
②函数y=(1﹣a )x 2
﹣4x+6与x 轴只有一个交点,则a=;
③半径分别为1和2的两圆相切,则两圆的圆心距为3;
④若对于任意x >1的实数,都有ax >1成立,则a 的取值范围是a ≥1.
16、如图所示,已知∠AOB =600,⊙O 1与∠AOB 的两边都相切,沿OO 1方向作⊙O 2与∠AOB 的
两边相切,且与⊙O 1外切,再作⊙O 3与∠AOB 的两边相切,且与⊙O 2外切,…,如此作下去,⊙O n 与∠AOB 的两边相切,县与⊙O n-1外切,设⊙O n 的半径为r n ,已知r 1=1,则r 2016= 。
17、如图,在△ABC 中,BC =AC =5,∠B =450,则下面结论正确的是 (填番号)。
①∠C 一定是钝角;②△ABC 外接圆半径为3;③sinA=35
;④△ABC 外接圆的外切
正六边形的边长是
3。
16.对于反比例函数y=,下列说法:①点(﹣2,﹣1)在它的图象上;②它的图象在第
一、三象限;③当x >0时,y 随x 的增大而增大;④当x <0时,y 随x 的增大而减小.上述说法中,正确的序号是 .(填上所有你认为正确的序号)
17.观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…………………….
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间
具有相同规律,我们称这类等式为“数字对称等式”.
根据上述规律填空:27×_________=_______×_________.
18.(2012•德阳)在平面直角坐标系xOy中,已知点A(0,2),⊙A的半径是2,⊙P 的半径是1,满足与⊙A及x轴都相切的⊙P有——————个.。
