习题5答案
北师大《无机化学》第四版习题答案5

北师大《无机化学》第四版习题答案5第五章化学热力学基础5-1 从手册中查出常用试剂浓硫酸、浓盐酸、浓硝酸、浓氨水的密度和质量分数计算它们的(体积)物质的量浓度和质量摩尔浓度。
解:经查阅: p(HCl)=1.19g/ml w(HCl)=37.23%p(H2SO4)=1.83g/ml w(H2SO4)=98%p(HNO3)=1.42g/ml w(HNO3)=69.80%p(NH3.H2O)=0.9g/ml w(NH3.H2O)=26%由公式c=pw/M可得:c(HCl)=12 mol·L–1c(H2SO4)=18.3mol·L–1c(HNO3)=15.7 mol·L–1 c (NH3.H2O)=13.8 mol·L–1设1㎏水中含溶质n mol,则由w=m/(m+1000)(m为溶质质量)可得:m (HCl)=16.2 mol/㎏m(H2SO4)=500 mol/㎏m(HNO3)=36.69 mol/㎏m (NH3.H2O)= 20.67 mol/㎏5-2 从手册查出常温下的饱和水蒸气压,计算当时相对湿度为40%时,水蒸气压多大。
解:在298K下,P(饱和水蒸气压)=3.167Kpa,P(不饱和)/P(饱和)=40%,则P(不饱和)/P(饱和)=40%×P(饱和)=0.4×3.167=1.2668 Kpa答:水蒸气压为1.2668 Kpa.5-3化学实验中经常用蒸馏水冲洗已用自来水洗净的烧杯。
设洗净烧杯残留“水”为1mL,试计算,用30mL蒸馏水洗1次和2次,烧杯中残留的“自来水的浓度”分别多大?解:再用自来水洗之后,烧杯中自来水为1ml之后,加入30ml 蒸馏水,一共为31ml 水,自来水占1/31,倒掉后又倒1ml,故自来水浓度为1/31。
若第一次加入的蒸馏水倒掉之后,1ml中含1/31ml的自来水;再加入30ml蒸馏水,一共为31ml水,自来水占1/312=1/963 所以倒掉后自来水占1/312=1/9635-4 计算15℃,97kPa下15g氯气的体积。
电力电子课后习题答案 5

第五章 直流—直流交流电路1.简述图5-1a 所示的降压斩波电路工作原理.答:降压斩波器的原理是:在一个控制周期中,让V 导通一段时间t on ,由电源E 向L 、R 、M 供电,在此期间,u o =E 。
然后使V 关断一段时间t off ,此时电感L 通过二极管VD 向R 和M 供电,u o =0.一个周期内的平均电压U o =E t t t ⨯+offon on。
输出电压小于电源电压,起到降压的作用。
2.在图5-1a 所示的降压斩波电路中,已知E =200V ,R =10Ω,L 值极大,E M =30V ,T =50μs ,t on =20μs ,计算输出电压平均值U o ,输出电流平均值I o 。
解:由于L 值极大,故负载电流连续,于是输出电压平均值为U o =E T t on =5020020⨯=80(V)输出电流平均值为I o =R E U M o -=103080-=5(A)3.在图5-1a 所示的降压斩波电路中,E =100V , L =1mH,R =0。
5Ω,E M =10V ,采用脉宽调制控制方式,T =20μs ,当t on =5μs 时,计算输出电压平均值U o ,输出电流平均值I o ,计算输出电流的最大和最小值瞬时值并判断负载电流是否连续。
当t on =3μs 时,重新进行上述计算。
解:由题目已知条件可得:m =E E M =10010=0。
1τ=RL =5.0001.0=0.002 当t on =5μs 时,有ρ=τT =0。
01αρ=τont =0。
0025由于11--ραρe e =1101.00025.0--e e =0.249>m 所以输出电流连续。
此时输出平均电压为U o =E T t on =205100⨯=25(V) 输出平均电流为I o =R E U M o -=5.01025-=30(A) 输出电流的最大和最小值瞬时值分别为I max =R E m e e ⎪⎪⎭⎫ ⎝⎛-----ραρ11=5.01001.01101.00025.0⎪⎪⎭⎫ ⎝⎛-----e e =30.19(A )I min =R E m e e ⎪⎪⎭⎫ ⎝⎛---11ραρ=5.01001.01101.00025.0⎪⎪⎭⎫ ⎝⎛---e e =29。
大学物理 习 题 5答案

P习 题 55-2.如习题5-2图所示的直角三角形ABC 的A 点上有电荷q 1=1.8×10-9 C ,B点上有电荷q 2=-4.8×10-9 C ,试求C 点的电场强度(设BC=0.04m ,AC=0.03m )。
解:设CB 为x 轴,AC 为y 轴,则C N E x/107.204.04108.44209⨯=⨯⨯=-πε,C N E /108.103.04108.14209y ⨯=⨯⨯=-πε,C N E E E y x /102.3422⨯=+=,电场方向和CB 的夹角为︒==7.33arctanxy E E ϕ5-3.用绝缘细线弯成的半圆环,半径为R ,其上均匀地带有正电荷Q ,试求圆心处的电场强度。
[解] 将半圆环分成无穷多小段,取一小段dl ,带电量l RQ q d d π=dq 在O 点的电场强度20204d 4d d R lR Q R q E πεππε== 从对称性分析,y 方向的电场强度相互抵消,只存在x l R Q E E d sin 4sin d d 302x ⋅=⋅=θεπθ θd d R l =θεπθd 4sin d 202x RQ E =2020202x x 2d 4sin d R QR Q E E E επθεπθπ====⎰⎰ 方向沿x 轴正方向5-4.如习题5-4图所示,真空中一长为L 的均匀带电细直杆,总电量为q ,试求在直杆延长线上到杆的一端距离为d 的点P 的电场强度。
[解] 建立如图所示坐标系ox ,在带电直导线上距O 点为x 处取电荷元x Lqq d d =,它在P 点产生的电电场强度度为 ()x x d L Lq x d L qE d 41d 41d 2020-+=-+=πεπε则整个带电直导线在P 点产生的电电场强度度为()d L d qx x d L Lq E L+=-+=⎰002041d 41πεπε故()iE d L d q+=04πε5-5.一厚度为d 的“无限大”均匀带电平板,电荷体密度为ρ。
《抽样技术》练习题5及答案

《抽样技术》练习题5及答案习题⼀1.请列举⼀些你所了解的以及被接受的抽样调查。
2.抽样调查基础理论及其意义;3.抽样调查的特点。
4.样本可能数⽬及其意义;5.影响抽样误差的因素;6.某个总体抽取⼀个n=50的独⽴同分布样本,样本数据如下:567 601 665 732 366 937 462 619 279 287690 520 502 312 452 562 557 574 350 875834 203 593 980 172 287 753 259 276 876692 371 887 641 399 442 927 442 918 11178 416 405 210 58 797 746 153 644 4761)计算样本均值y与样本⽅差s2;2)若⽤y估计总体均值,按数理统计结果,y是否⽆偏,并写出它的⽅差表达式;3)根据上述样本数据,如何估计v(y)?4)假定y的分布是近似正态的,试分别给出总体均值µ的置信度为80%,90%,95%,99%的(近似)置信区间。
习题⼆⼀判断题1 普查是对总体的所有单元进⾏调查,⽽抽样调查仅对总体的部分单元进⾏调查。
2 概率抽样就是随机抽样,即要求按⼀定的概率以随机原则抽取样本,同时每个单元被抽中的概率是可以计算出来的。
3 抽样单元与总体单元是⼀致的。
4 偏倚是由于系统性因素产⽣的。
5 在没有偏倚的情况下,⽤样本统计量对⽬标量进⾏估计,要求估计量的⽅差越⼩越好。
6 偏倚与抽样误差⼀样都是由于抽样的随机性产⽣的。
7 偏倚与抽样误差⼀样都随样本量的增⼤⽽减⼩。
8 抽样单元是构成抽样框的基本要素,抽样单元只包含⼀个个体。
9 抽样单元可以分级,但在抽样调查中却没有与之相对应的不同级的抽样框。
10 总体⽬标量与样本统计量有不同的意义,但样本统计量它是样本的函数,是随机变量。
11 ⼀个抽样设计⽅案⽐另⼀个抽样设计⽅案好,是因为它的估计量⽅差⼩。
12 抽样误差在概率抽样中可以对其进⾏计量并加以控制,随着样本量的增⼤抽样误差会越来越⼩,随着n越来越接近N,抽样误差⼏乎可以消除。
通信原理教程樊昌信习题答案第五章
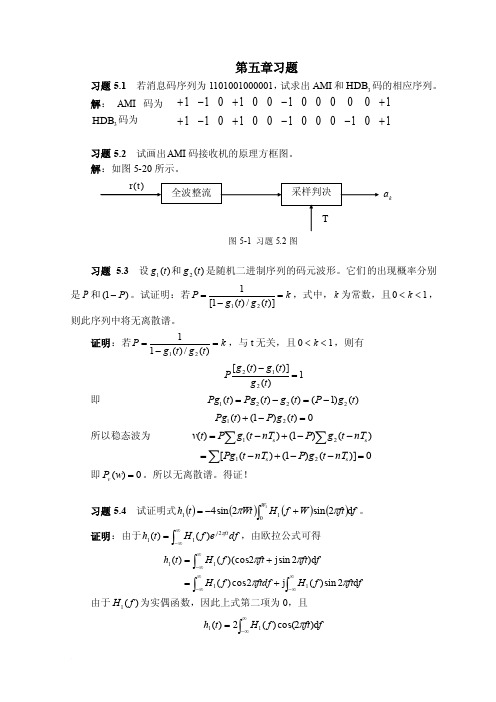
第五章习题习题5.1 若消息码序列为1101001000001,试求出AMI 和3HDB 码的相应序列。
解: AMI 码为 3HDB 码为习题5.2 试画出AMI 码接收机的原理方框图。
解:如图5-20所示。
图5-1 习题5.2图习题 5.3 设)(1t g 和)(2t g 是随机二进制序列的码元波形。
它们的出现概率分别是P 和)1(P -。
试证明:若k t g t g P =-=)](/)(1[121,式中,k 为常数,且10<<k ,则此序列中将无离散谱。
证明:若k t g t g P =-=)(/)(1121,与t 无关,且10<<k ,则有1)()]()([212=-t g t g t g P即 )()1()()()(2221t g P t g t Pg t Pg -=-=0)()1()(21=-+t g P t Pg所以稳态波为 ∑∑--+-=)()1()()(s 2s 1nT t g P nT t g P t v0)]()1()([s 2s 1=--+-=∑nT t g P nT t g P即0)(=w P v 。
所以无离散谱。
得证!习题5.4 试证明式()()()()⎰+-=1011d 2sin 2sin 4W f ft W f H Wt t h ππ。
证明:由于⎰∞∞-=df e f H t h ft j π211)()(,由欧拉公式可得⎰⎰⎰∞∞-∞∞-∞∞-+=+=fft f H ftdf f H fft ft f H t h d 2sin )(j 2cos )(d )2sin j 2)(cos ()(1111ππππ由于)(1f H 为实偶函数,因此上式第二项为0,且⎰∞∞-=f ft f H t h d )2cos()(2)(11π10100010010111000001001011+--+-++-+-+k a《通信原理》习题第五章令,'d d ,'f f W f f =+=,代入上式得⎰⎰⎰∞-∞-∞-+++=++=WWW fWt ft W f H f Wt ft W f H f t W f W f H t h d 2sin 2sin )(2d 2cos 2cos )(2'd ])'(2cos[)'(2)(1111πππππ由于)(1f H 单边为奇对称,故上式第一项为0,因此⎰⎰+=+=∞-WW fftt W f H W fftt W f H W t h 0111d 2sin )(2sin 4d 2sin )(2sin 2)(ππππ习题5.5 设一个二进制单极性基带信号序列中的“1”和“0”分别用脉冲)(t g [见图5-2的有无表示,并且它们出现的概率相等,码元持续时间等于T 。
习题5参考答案

习题5参考答案
一、简答题
1.参考答案:
异常(Exception)是程序运行过程中,由于环境变化、用户操作失误以及其它方面的原因而产生的运行时不正常的情况,它要求程序立即进行处理,否则将会引起程序错误甚至崩溃的现象。
当某个catch块捕捉到异常后,它就根据事先制定的策略对异常进行处理,这就是处理异常。
2.参考答案:
C++的异常处理机制就是将抛出异常与捕捉异常、处理异常分离开来。
抛出异常的模块并不负责异常的处理,它只是报告某个地方存在错误,这个报告可以帮助异常处理器解决这个错误。
而异常处理器则根据抛出异常模块的报告来处理异常。
C++引入了3个关键字try,throw和catch,用于进行异常处理。
这3个关键字也是C++异常处理机制的核心。
3.参考答案:
在C++中,如果出现未被捕捉的异常,就会调用函数terminate(),终止本程序的运行。
4.参考答案:
异常信号传递方式有三种:传值方式、引用方式和指针方式,他们的优缺点如下表
5.参考答案:
throw()表示函数不会抛出任何类型的异常;如果没有异常规范表示函数有可能抛出任何类型的异常。
6.参考答案:
标准C++库中的异常类及其继承关系如下图所示。
《树木学》习题5—被子植物3(橄榄科-竹亚科) - 参考答案 (1)

《树木学》习题5—被子植物3(橄榄科-竹亚科)(参考答案)学院年级专业班级学号姓名成绩一、名词解释:1.双翅果:干果中闭果的一种,花的雌蕊具离生的2心皮,各发育为一枚翅状果皮形成,各具一种子,为槭树属的典型特征。
2.唇形花冠:是合瓣花冠之一种,花冠呈对称的二唇形。
即上面由二裂片合生为上唇,下面三裂片多少结合构成下唇。
3.二强雄蕊:植物的花有雄蕊4枚,其中2枚较长,2枚较短。
4.肉穗花序:无限花序的一种,无柄单性小花生于肉质膨大的花序轴上,有的外面有一枚大的苞片,称为佛焰苞。
5.颖果:干果中闭果的一种,果中有且仅有一枚种子,果实发育成熟后,果皮不开裂且与种皮高度愈合,难以分离,是禾本科特有的果实类型。
6.合轴丛生:竹类地下茎类型的一种。
秆基的芽长笋,笋长竹,秆柄短,地上竹秆密集丛生。
7.叶鞘:叶片或叶柄的基部较宽或扩大成片状,形成一圆筒体的鞘而将茎的一部分或全部紧密包围,开裂或闭合。
8.箨:竹类植物笋或主秆的节上所生的,包被笋或主秆的片状物,属于变形叶。
具箨鞘、箨叶、箨舌、箨耳、繸毛等构造。
二、填空题:1.香椿是楝科树种,叶为一回偶数羽状复叶,是优良用材树种,有“中国的桃花心木”之称。
2.无患子科具聚伞圆锥花序,其中栾树属是蒴果,无患子属是核果。
3.写出下列树种的学名:龙眼Dimocarpus longan、桂花Osmanthus fragrans,写出下列树种的中名:Phyllostachys edulis毛竹、Acer palmatum鸡爪楲。
4.盐肤木的主要特征是奇数羽状复叶,叶轴有翅,花序生于枝顶,枝叶形成的虫瘿即五倍子。
5.槭树属典型特征是叶对生,无托叶,花柱2裂,柱头反卷,果为双翅果。
6.桂花属木犀科,花簇生于叶腋,花萼和花冠均为4裂,雄蕊生于花冠上,2枚。
7.(小粒)咖啡原产于埃塞俄比亚,是世界三大饮料之一,单叶,对生,托叶阔三角形。
8.泡桐属具唇形花冠,子房上位,果为蒴果。
9.棕榈树干具环状叶痕、残存叶基,叶柄基部具纤维质叶鞘,叶掌状分裂。
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
计算机操作系统习题5参考答案

计算机操作系统习题5参考答案习题5参考答案Ⅰ问答题1. 存储管理的主要功能是什么?答:(1)主存空间的分配与回收。
系统按照一定的算法把某一空闲的存储空间分配给作业或进程;用户不需要时,及时回收,以供其它用户程序使用。
(2)地址转换(地址重定位)。
把作业地址空间中使用的逻辑地址转换成内存空间中的物理地址。
(3)主存空间的共享和保护。
可用的主存空间可由两个或多个进程共享。
同时要保护系统程序区不被用户有意或无意的侵犯,不允许用户程序读写不属于自己地址空间的数据,避免各道程序间相互干扰。
特别是当一道程序发生错误时,不至于影响其它程序的运行。
(4)主存空间的扩充。
使用虚拟存储或自动覆盖技术提供比实际内存更大的空间。
2. 指出逻辑地址与物理地址的不同点。
答:用户的源程序一旦编译之后,每个目标模块都以0为基地址进行编址,这种地址称为逻辑地址或相对地址。
为了便于CPU访问,内存中的每个物理存储单元都有一个编号,这个编号称为内存地址,即物理地址(也称绝对地址)。
3. 何谓地址转换(重定位)?有哪些方法可以实现地址转换?答:当作业运行时,不能用逻辑地址在内存中读取信息,必须把作业地址空间中使用的逻辑地址转换成内存空间中的物理地址,这种转换称为地址转换。
实现地址转换的方法有:静态地址转换和动态地址转换。
4. 简述什么是覆盖?什么是交换?覆盖和交换的区别是什么?答:覆盖技术主要是指同一主存区可以被不同的程序段重复使用。
交换,就是系统根据需要把主存中暂时不运行的某个(或某些)作业部分或全部移到外存,而把外存中的某个(或某些)作业移到相应的主存区,并使其投入运行。
交换是由操作系统完成,用户并不知道。
操作系统按一定的策略采用“强占”和“礼让”的方法,把内存部分内容暂时放到硬盘交换区中。
覆盖是由用户控制,操作系统提供覆盖机制,用户给出该程序的覆盖结构。
覆盖机构将整个作业分为常驻和覆盖两部分。
子程序不会同时调入内存。
用户只要将最大的子程序作为覆盖区告诉系统即可。
第5章思考题及习题5参考答案

第5章思考题及习题5参考答案一、填空1.如果采用晶振的频率为3MHz,定时器/计数器T x(x=0,1)工作在方式0、1、2下,其方式0的最大定时时间为,方式1的最大定时时间为,方式2的最大定时时间为。
答:32.768ms,262.144ms,1024µs2.定时器/计数器用作计数器模式时,外部输入的计数脉冲的最高频率为系统时钟频率的。
答:1/243.定时器/计数器用作定时器模式时,其计数脉冲由提供,定时时间与有关。
答:系统时钟信号12分频后,定时器初值4.定时器/计数器T1测量某正单脉冲的宽度,采用方式可得到最大量程?若时钟频率为6MHz,求允许测量的最大脉冲宽度为。
答:方式1定时,131.072ms。
5. 定时器T2 有3种工作方式:、和,可通过对寄存器中的相关位进行软件设置来选择。
答:捕捉,重新装载(增计数或减计数),波特率发生器,T2CON6. AT89S52单片机的晶振为6MHz,若利用定时器T1的方式1定时2ms,则(TH1)= ,(TL1)= 。
答:FCH,18H。
二、单选1.定时器T0工作在方式3时,定时器T1有种工作方式。
A.1种B.2种 C.3种D.4种答:C2. 定时器T0、T1工作于方式1时,其计数器为位。
A.8位B.16位C.14位D.13位答:B3. 定时器T0、T1的GATE x=1时,其计数器是否计数的条件。
A. 仅取决于TR x状态B. 仅取决于GATE位状态C. 是由TR x和INT x两个条件来共同控制D. 仅取决于INT x的状态答:C4. 定时器T2工作在自动重装载方式时,其计数器为位。
A.8位B. 13位C.14位D. 16位答:D5. 要想测量INT0引脚上的正单脉冲的宽度,特殊功能寄存器TMOD的内容应为。
A.87HB. 09HC.80HD. 00H答:B三、判断对错1.下列关于T0、T1的哪些说法是正确的。
A.特殊功能寄存器SCON,与定时器/计数器的控制无关。
计算机组成习题5,6,8,9章答案

0002H:000AH0007H:000AH
0003H:0002H0008H:0002H
0004H:0007H0009H:0003H
0005H:0004H000AH:0009H
0006H:0005H000BH:0008H
指令为双字长指令,格式如下:
操作码,寻址方式码,寄存器号(16位)
10.什么是中断嵌套?它解决了什么问题?如何才能实现中断嵌套?
略
11.中断源可以分为哪几类?各自有何特点?
略
12.有哪几种中断优先级排队方法?比较它们的优缺点。
略
13.解释下列名词:
(1)中断向量(2)中断隐指令(3)DMA(4)通道
(5)多重中断(6)单重中断(7)中断类型号(8)菊花链电路
略
14.假设有4个中断源A、B、C、D,硬件排队后,中断优先级从高到低依次为A→B→C→D。现在需要将4个中断源得到CPU响应的次序更改为C→A→D→B,写出各个中断源的中断服务程序中应该设置的中断屏蔽字。
答:EBH, 0AH.
6.13某机器内共有16个32位的通用寄存器,设计一种有60种操作,8种寻址方式的指令系统。假设指令字长等于机器字长,机器字长为32位,请回答:
(1)若主存可直接寻址或间接寻址,采用“寄存器-存储器”型指令,能寻址最大存储空间是多少?画出指令格式并说明各字段的含意。
(2)若采用通用寄存器作基址寄存器,则“寄存器-存储器”型指令的指令格式是怎样? 能寻址最大存储空间是多少?
答:B
6.10某机16位字长指令格式如下:
OP
M
D
其中:D是形式地址,采用补码表示(包括一位符号位);
M是寻址方式
M=0立即寻址;
化工原理第二版两册答案(习题5 附图主编)

第一章 流体流动4.某储油罐中盛有密度为960 kg/m 3的重油(如附图所示),油面最高时离罐底9.5 m ,油面上方与大气相通。
在罐侧壁的下部有一直径为760 mm 的孔,其中心距罐底1000 mm ,孔盖用14 mm 的钢制螺钉紧固。
若螺钉材料的工作压力为39.5×106 Pa ,问至少需要几个螺钉(大气压力为101.3×103 Pa )? 解:由流体静力学方程,距罐底1000 mm 处的流体压力为[](绝压)Pa 10813.1Pa )0.15.9(81.9960103.10133⨯=-⨯⨯+⨯=+=gh p p ρ 作用在孔盖上的总力为N 10627.3N 76.04π103.10110813.1)(4233a ⨯⨯⨯⨯⨯-==)-=(A p p F每个螺钉所受力为N 10093.6N 014.04π105.39321⨯=÷⨯⨯=F因此()(个)695.5N 10093.610627.3341≈=⨯⨯==F F n5.如本题附图所示,流化床反应器上装有两个U 管压差计。
读数分别为R 1=500 mm ,R 2=80 mm ,指示液为水银。
为防止水银蒸气向空间扩散,于右侧的U 管与大气连通的玻璃管内灌入一段水,其高度R 3=100 mm 。
试求A 、B 两点的表压力。
解:(1)A 点的压力()(表)Pa 101.165Pa 08.081.9136001.081.9100042汞3水A ⨯=⨯⨯+⨯⨯=+=gR gR p ρρ(2)B 点的压力()(表)Pa 107.836Pa 5.081.91360010165.1441汞A B ⨯=⨯⨯+⨯=+=gR p p ρ 7.某工厂为了控制乙炔发生炉内的压力不超过13.3 kPa (表压),在炉外装一安全液封管(又称水封)装置,如本题附图所示。
液封的作用是,当炉内压力超过规定值时,气体便从液封管排出。
试求此炉的安全液封管应插入槽内水面下的深度h 。
数据结构习题五(答案)

数据结构习题(5)学号________ 姓名_______ 课堂号(___________)1.选择题1)对N个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为( A )A.(N+1)/2 B. N/2 C. N D. [(1+N)*N ]/22)下面关于二分查找的叙述正确的是 ( D )A. 表必须有序,表可以顺序方式存储,也可以链表方式存储B. 表必须有序且表中数据必须是整型,实型或字符型C. 表必须有序,而且只能从小到大排列D. 表必须有序,且表只能以顺序方式存储3)折半查找的时间复杂性为(D)A. O(n2)B. O(n)C. O(nlog(n))D. O(log(n))4)概率不同的有序表,最适合的查找算法是( C )A.顺序查找B.折半查找C.静态树表查找 D.索引顺序表查找5)平均查找长度最短的查找方法是____C________。
A.折半查找 B.顺序查找 C.哈希查找 4.其他6)折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
若查找表中元素58,则它将依次与表中A比较大小,查找结果是失败。
A.20,70,30,50 B.30,88,70,50 C.20,50 D.30,88,507)当采用分快查找时,数据的组织方式为 ( B )A.数据分成若干块,每块内数据有序B.数据分成若干块,每块内数据不必有序,但块间必须有序,每块内最大(或最小)的数据组成索引块C. 数据分成若干块,每块内数据有序,每块内最大(或最小)的数据组成索引块D. 数据分成若干块,每块(除最后一块外)中数据个数需相同8)分别以下列序列构造二叉排序树,与用其它三个序列所构造的结果不同的是( C )A.(100,80, 90, 60, 120,110,130) B.(100,120,110,130,80, 60, 90)C.(100,60, 80, 90, 120,110,130)D. (100,80, 60, 90, 120,130,110)9)设有一组记录的关键字为{19,14,23,1,68,20,84,27,55,11,10,79},用链地址法构造散列表,散列函数为H(key)=key MOD 13,散列地址为1的链中有( D )个记录。
数学物理方程第5章习题及答案

11.设 {(x, y) | x2 y2 R2, y 0}, 考虑半圆域狄利克雷问题
u 0, x
u(x, y) (x, y),(x, y)
应用对称法求区域 上的格林函数。
解:该问题所求格林函数应满足
G (P, P0 ), P
G(P, P0 ) 0, P B(圆周) G(P, P0 ) 0, P L(x轴上的边界)
C1
1
4
解为 u 1
4 r
方法二: 本题中u只与r有关,则
所以
uxx
u yy
+uzz
=
1 r
(2ur
rurr )
2ur rurr 0 2rur r 2urr 0 (r 2ur )r 0 r 2ur C
ur
C r2
u
C1
1 r
C2
随后求解过程与方法一相同。
注:在球面坐标系中
uxx
记 G \ B ,则 G B ,在格林第二公式
(uv vu)d
(u
v n
v
u )ds n
中,令 v (P, P0 ),注意到 0 ,则有
ud
G
(u
G
n
u )ds n
或
ud (u u )ds (u u )ds
G
n n
B n n
在圆周B 上有
( 1
随后求解过程与方法一相同。
(3)uxx uyy +uzz =0,r 0
解:方法一: 三维拉普拉斯方程的基本解表示通解
1 u C1 r C2
lim u(r)=0
r
C2
0
u n |B(0, )
u n
B(0, )
习题5-答案

武夷学院课程作业(11 级生物工程专业2011~2012学年度第一学期)课程名称《生物化学》习题五核酸化学一、填空题1.核酸可分为脱氧核糖核苷酸和核糖核苷酸两大类。
2.核酸完全水解的产物是戊糖、碱基和磷酸。
3.体内的嘌呤碱主要有 A 和G ,嘧啶碱主要有 C 、T 和U 。
某些RNA 分子中还含有微量的其它碱基,称为稀有碱基。
4.嘌呤环上第9 位氮原子与戊糖的第1 位碳原子相连形成糖苷键,通过这种键相连而形成的化合物叫嘌呤核苷。
5.嘧啶环上第 1 位氮原子与戊糖的第1 位碳原子相连形成糖苷键,通过这种键相连而形成的化合物叫嘧啶核苷。
6.核酸的基本组成单位是单核苷酸,它们之间是通过3’,5’-磷酸二酯键键相连的。
7.DNA双螺旋的两股链的顺序是反向平行、互补的关系。
8.DNA二级结构的重要特点是形成双螺旋结构,此结构的外部结构是由磷酸和戊糖(脱氧核糖)形成骨架,内部是由碱基通过氢键相连而成的碱基对平面。
9.由于含氮碱基具有共轭双键,所以核苷酸或核酸在260 nm处有最大紫外吸收值。
10.DNA分子双螺旋结构中A-T之间有 2 个氢键,而C-G之间有3 个氢键。
11.RNA主要分为tRNA ,rRNA 和mRNA 三类。
12.tRNA的二级结构是三叶草型,三级结构是倒L型。
tRNA的二级结构中反密码环环识别密码子,携带氨基酸的部位是氨基酸接受臂(3'端CCA—OH)。
13.在含DNA和RNA的试管中加入稀的NaOH溶液,室温放置24小时后,DNA 被水解了。
14.DNA热变性260nm紫外吸收显著升高,称为增色效应;吸光度增幅中点所对应的温度叫做解链温度,用符号T m表示;其值的大小与DNA中G+C 碱基对含量呈正相关。
15.提纯的结核分枝杆菌DNA,其腺嘌呤含量为15.1%,则鸟嘌呤、胞嘧啶、胸腺嘧啶的含量依次是34.9 %、34.9 %、15.1 % 。
16.大肠杆菌DNA分子量2.78×109,设核苷酸残基的平均分子量为309,该DNA含有 4.5⨯105 nm 圈螺旋,其长度为 1.53⨯106nm 。
结构力学课后习题答案

结构力学课后习题答案(总23页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lf y )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
信号与线性系统课后习题答案5

1 −( s+1) 1 1 ,∴ LT [ε (t − 1)] = e − s ,∴ LT [e −t ε (t − 1)] = e s s +1 s
d 1 −( s+1) s + 2 −( s − 2 ) [ ]= e e ds s + 1 ( s + 1) 2
∴ LT [te −(t −3)ε (t − 1)] = −e3
1 [sin(2t ) − cos(2t )]ε (t ) 2 2 1 s ( 2 ) − 2 2 s +4 s +4
, ∫ sin(πx)dx = ∫ sin(πx)ε ( x)dx
0
∴ LT [sin(2t − π / 4)ε (t )] =
(9) Q LT [sin(πt )ε (t )] =
∞ 1 2 1 ∴F ( s ) = ∫ f (t )e −st dt = − e −s + e −2 s 0− s s s
(e)
Q f (t ) =
2 2 t[ε (t ) − ε (t − T / 2)] − (t − T )[(ε (t − T / 2) − ε (t − T )] T T
∞
∴F ( s ) = ∫
5
sy (0−) + y′(0−) + 3 y (0−) s+4 + 2 F (s) , 2 s + 3s + 2 s + 3s + 2 1 1 1 sy (0−) + y′(0−) + 3 y (0−) Yx ( s ) = , = 2 = − 2 s + 3s + 2 s + 3s + 2 s + 1 s + 2 1 2 3 1 s+4 s+4 , Y f ( s) = 2 F ( s) = 2 × = − + s + 3s + 2 s + 3s + 2 s s s + 1 s + 2 Y (s) =t2 Nhomakorabeaπ
微积分课后习题答案 第五章

第五章习题5-11.求下列不定积分:(1)25)x -d x ;(2) 2⎰x ; (3)3e x x⎰d x ; (4) 2cos 2x⎰d x ; (5) 23523x xx⋅-⋅⎰d x ; (6) 22cos 2d cos sin xx x x ⎰.解5151732222222210(1)5)(5)573d d d d x x x x x x x x x x C -=-=-=-+⎰⎰⎰113222221132223522(2)(2)24235d d d d x x x x x xx x x x x x x x C--==-+=-+=++⎰⎰⎰⎰213(3)3(3)(3)ln(3)1ln 31cos 1111(4)cos cos sin 222222235222(5)[25()]25()333125225()223(ln 2ln 3)3ln()3e e d e d e e d d d d d d d d x x xxxxx x x xx xx xx x C Cx x x x x x x x x Cx x x x x C x C ==+=+++==+=++⋅-⋅=-⋅=-⋅=-⋅+=-+-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰2222222222cos 2cos sin (6)(csc sec )cos sin cos sin csc sec cot tan d d d d d x x x x x x x x x x x xx x x x x x C-==-=-=--+⎰⎰⎰⎰⎰2. 解答下列各题:(1) 一平面曲线经过点(1,0),且曲线上任一点(x ,y )处的切线斜率为2x -2,求该曲线方程; (2) 设sin x 为f (x )的一个原函数,求()f x '⎰d x ;(3) 已知f (x )的导数是sin x ,求f (x )的一个原函数;(4) 某商品的需求量Q 是价格P 的函数,该商品的最大需求量为1000(即P=0时,Q =1000),已知需求量的变化率(边际需求)为Q ′(P )=-10001()3Pln3,求需求量与价格的函数关系. 解 (1)设所求曲线方程为y =f (x ),由题设有f′(x )=2x -2,2()(22)2d f x x x x x C ∴=-=-+⎰又曲线过点(1,0),故f (1)=0代入上式有1-2+C =0得C =1,所以,所求曲线方程为2()21f x x x =-+.(2)由题意有(sin )()x f x '=,即()cos f x x =, 故 ()sin f x x '=-, 所以()sin sin cos d d d f x x x x x x x C '=-=-=+⎰⎰⎰.(3)由题意有()sin f x x '=,则1()sin cos d f x x x x C ==-+⎰于是12()(cos )sin d d f x x x C x x C x C=-+=-++⎰⎰.其中12,C C 为任意常数,取120C C ==,得()f x 的一个原函数为sin x -.注意 此题答案不唯一.如若取121,0C C ==得()f x 的一个原函数为sin x x --. (4)由1()1000()ln 33PQ P '=-得111()[1000()ln 3]1000ln 3()1000().333d d P P P Q P x x C =-=-⋅=⋅+⎰⎰将P =0时,Q =1000代入上式得C =0所以需求量与价格的函数关系是1()1000()3PQ P =.习题5-21.在下列各式等号右端的空白处填入适当的系数,使等式成立: (1) d x = d(ax +b )(a ≠0); (2) d x = d(7x -3); (3) x d x = d(52x ); (4) x d x = d(1-2x ); (5) 3x d x = d(3x 4-2); (6) 2e xd x = d(2e x); (7) 2ex -d x = d(1+2ex -); (8)d xx= d(5ln |x |);(9)= d(1-arcsin x ); (10)= d(11)2d 19x x += d(arctan3x ); (12) 2d 12xx +=d(arctan );(13) (32x -2)d x = d(2x -3x ); (14) cos(23x -1)d x = dsin(23x -1).解 1(1)()(0)()d d d d ax b a x a x ax b a +=≠∴=+22224334222221(2)(73)7(73)71(3)(5)10(5)101(4)(1)2(1)21(5)(32)12(32)121(6)()2()2(7)(1)d dd d d dd d d d d d d d d d de e d e d d e d e e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ---=∴=-=∴=-=-∴=---=∴=-=⋅∴=+=222221()2(1)251(8)(5ln )(5ln )5(9)(1arcsin )(1arcsin )(10)1(2)3(11)(arctan 3)19d e d d e d d d d d d d d d d d x x x x x x x x x x x x x x x x x x x x x --⋅-∴=-+=∴=-==---=-==-=+222322231(arctan 3)193(12)))1212(13)(2)(23)(32)(32)(2)222232(14)sin(1)cos(1)cos(1)sin(1)333323d d d d d d d d d d d dd x x x x x x x x x x x x x x x xx x x x x x ∴=+=∴=++-=-=--∴-=---=-∴-=- 2.求下列不定积分: (1)5e d t t ⎰; (2) 3(32)x -⎰d x ; (3)d 12xx -⎰; (4)(5)t ; (6)d ln ln ln xx x x ⎰;(7)102tan sec d x x x ⎰; (8) 2e d x x x -⎰;(9)dsin cos x x x ⎰; (10) ⎰; (11)de e x x x-+⎰; (12)x ;(13) 343d 1x x x-⎰; (14) 3sin d cos xx x ⎰;(15)x ; (16) 32d 9x x x +⎰; (17)2d 21xx -⎰; (18) d (1)(2)xx x +-⎰;(19 2cos ()d t t ωϕ+⎰); (20) 2cos ()sin()d t t t ωϕωϕ++⎰; (21) sin2cos3d x x x ⎰; (22) cos cos d 2x x x ⎰; (23)sin5sin 7d x x x ⎰; (24) 3tansec d x x x ⎰;(25)x ; (26);(27)ln tan d cos sin xx x x ⎰; (28)21ln d (ln )xx x x +⎰;(29)2,0x a >; (30)(31)d xx⎰; (32)(33); (34),0x a >;(35)x ; (36) x ; (37)2sec ()d 1tan x x x +⎰; (38) (1)d (1e )x x x x x ++⎰(提示:令xt e =). 解 5555111(1)5(5)555e d e d e d e tt t tt t t C =⋅==+⎰⎰⎰33411(2)(32)(32)(32)(32)28d d x x x x x -=---=--⎰⎰122333111(3)(12)ln 121221221131(4)(23)(23)()(23)(23)3322(5)22sin 111(6)(ln ln )ln ln l ln ln ln ln ln ln ln ln d d d d d d d d x x C x x x x x x C x Ct t C x x x x x x x x x x-=--=-+---=---=--+=--+===-=⋅==⎰⎰⎰⎰⎰⎰⎰222210210112n 1(7)tan sec tan (tan )tan 11111(8)(2))222(9)22csc 22sin cos 2sin cos sin 2ln ln csc 2cot 2tan sin c d d e d e d e d(-e d d d d d 或x x x x Cx x x x x x x Cx x x x x Cx x xx xx x x x x C C x x x x x ----+⋅==+=-⋅-=-=-+===⋅⋅=+=+-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰2cos 1tan ln tan os sin cos tan d d x x x Cx x x x x=⋅==+⎰⎰⎰22234(10)ln 1(11)()arctan 11()11(12)631333(13)14d d e d d e e e e e e d x x xx xx x Cx x C x x xCx x x -==-+===++++'=-=-=-==--⎰⎰⎰⎰⎰⎰⎰3444432334313(1)ln 11414sin sin 1(14)cos cos cos cos cos 2(15)1218)23812d d d d d d d x x x C x x x x x x x x x x C x x x x xx x x---=--=-+----=-=-=+=-=+-=⎰⎰⎰⎰⎰122221(94)(94)38)d x x x -+--⎰12arcsin 23x C =3322222222999(16)()9999119(9)ln(9)2922111(17)212221)1)x x x x xx x x x x x xx x x x x C x x x x xx +-==-+++=-+=-+++==--=-+⎰⎰⎰⎰⎰⎰⎰d d d d d d d2111111111(18)()(2)(1)(1)(2)32132311112ln ln ln 2133311cos(22)11(19)cos ()cos(22224C Cx x x x x x x x x x x C Cx x x t t t t t t ωϕωϕωω=-+=+++=-=--++--+-+-=-+=+-+++++==++⎰⎰⎰⎰⎰⎰ d d d d d d d 223)(2)11cos(22)(22)2411sin(22)241(20)cos ()sin()cos ()cos()1cos ()3(21)sin 2cos3t t t t t t Ct t t t t t C x x ϕωωϕωϕωωϕωωϕωϕωϕωϕωωϕω⋅=+++=+++++=-++=-++⎰⎰⎰⎰⎰d d d d 111(sin 5sin )sin 55sin 210211cos5cos 10213133(22)cos cos (cos cos )cos ()cos ()22223222213sin sin 3221(23)sin 5sin 7(cos12x x x x x x x xx x Cx x x x x x xx x x x xCx x x =-=-=-++=+=+=++=-⎰⎰⎰⎰⎰⎰⎰⎰d d d d d d d d d 2cos 2)11cos12(12)cos 2(2)24411sin12sin 2244x x xx x x x x x C-=-+=-++⎰⎰⎰⎰d d d322322(24)tan sec tan(sec)(sec1)sec1sec sec3(25)2arctan2(arctan1(26)(arcsin)d d ddddx x x x x x xx x Cx x xCx==-=-+===+=⎰⎰⎰⎰⎰1(arcsin)arcsinx Cx=-+⎰2222222ln tan1(27)ln tan seccos sin tan1ln tan(ln tan)(ln tan)21ln111(28)(1ln)(ln)(ln)ln(ln)ln(29)d ddd d ddxx x x xx x xx x x Cxx x x x x C x x x x x x x xx a=⋅⋅==++=+==-+==-⎰⎰⎰⎰⎰⎰⎰x⎰利用教材§5.2例16及公式(20)可得:原式=22211arcsin arcsin arcsin2222x a x a xa C Ca a a--=-.(30)令tan,(,)22ππx t t=∈-,则2secd dx t t=.所以2sec cos sinsecd dd dtt t t t t Ct====+⎰⎰tan,sin原式x t t C=∴=∴=+.(31)令3sec,(0,)2πx t t=∈,可求得被积函数在x>3上的不定积分,此时3sec tan3tand dx t t t t=⋅=故223tan3sec tan3tan3(sec1)3secd d dtx t t t t t t tt=⋅⋅==-⎰⎰⎰3tan3t t C=-+.由3sec,(0,)2πx t t=∈得tan3t=,又由3secx t=得33sec,cos,arccos3xt t tx x===,333arccos 3arccos )x C C x x∴=+=+ 又令x =3sec t ,类似地可得被积函数在x <-3上的不定积分.11333arccos 3(arccos )33arccos d π x C C x x x Cx=+=-+=+⎰综上所述有33arccos x C x=+. (32)令sin ,(,)22ππx t t =∈-,则cos d d x t t =. 11cos sin cos sin cos sin cos 2sin cos 11111(sin cos )ln sin cos 22sin cos 2211arcsin ln .22d d d d d t t t tt t tt t t tt t t t C t t t t x C x ++-=⋅=++=++=++++=++⎰⎰⎰⎰ (33)令sin ,(,)22ππx t t =∈-,则cos ,d d x t t =2cos 1(1)sec ()1cos 1cos 22tan arcsin .2d d d d t t tt t t t t t t C x C ∴==-=-++=-+=-⎰⎰⎰(34)21(2d d x a x x a =+=+⎰arcsinxa C a=⋅. (35)令2sin ,(,),2cos 22ππd d x t t x t t =∈-=,所以2222cos 2cos cot csc 4sin d d d d tx t t t t t t t t=⋅==-⎰⎰⎰⎰cot arcsin 2x t t C C x =--+=--+.(36)2d x x x ==12(1)ln12d xx Cxx=+=+++⎰由被积函数知x≤-2或x>0,令1xt=,当x>0时,(此时t>0)221222211222(12)(12)2.d dddx t tt ttt t CC C Cxx--==-=-=-++=-=-=-+=-+⎰当x≤-2时,此时12t-≤<221233311222(12)(12).d ddx t tt ttt t t CC C Cx--==-==++===+=+⎰综上所述:原式= ln1Cx+.(37)2222sec sec11()(1tan)1tan(1tan)(1tan)1tand d dx xx x x C x x x x==+=-+ ++++⎰⎰⎰.(38)令e x=t,则x=ln t,d x=1td t.11ln1111(ln)(ln)(1)ln(1ln)ln(1ln)ln1ln11(ln)(1ln)ln lnln1lnln1lnln ln ln ln ln ln111d d d ded dee e ee xxx x xx x tx t t t t t x x t t t t t t t t t t t tt t t t Ct t t tt t t txC C x Cxx x xx ++⎡⎤=⋅==-⎢⎥++++⎣⎦=-+=-+++=-+=+-+=+++++⎰⎰⎰⎰⎰⎰习题5-31.求下列不定积分:(1) sin dx x x⎰; (2) e d x x x-⎰;(3) arcsin d x x ⎰; (4) ecos d xx x -⎰;(5) 2e sin d 2xx x -⎰; (6) 2tan d x x x ⎰; (7) 2e d t t t -⎰; (8)2(arcsin )d x x ⎰; (9)2e sin d x x x ⎰;(10) x ⎰;(11)cos(ln )d x x ⎰; (12)2(1)sin 2d x x x -⎰;(13)ln(1)d x x x -⎰; (14)22cosd 2x x x ⎰; (15)32ln d xx x⎰; (16)sin cos d x x x x ⎰;(17)2cot csc d x x x x ⎰; (18)22(1)e d xx x x +⎰; (19)1(ln ln )d ln x x x+⎰; (20)e ln(1e )d x x x +⎰; (21) 23sin d cos x x x ⎰;(22)22ln(d (1)x x x x +⎰; (23)2e d (1)x x x x +⎰; (24)arctan 322e d (1)xx x x +⎰. 解 (1)sin cos cos cos cos sin d d d x x x x x x x x x x x x C =-=-+=-++⎰⎰⎰(2)()(1)e d de e e d e e d e e e x x x x x x xxxx x x x x x x x C x C---------=-=-+=---=--+=-++⎰⎰⎰⎰21(3)arcsin arcsin arcsin (1)2arcsin d x x x x x x x x x x x C=-=+-=+⎰⎰⎰(4)cos cos cos (sin )cos sin cos sin cos e d de e e d e de e e e d x x x x x x x x x x x x x x x x x x x x x---------=-=-+-=-+=-+-⎰⎰⎰⎰⎰12cos (sin cos )(sin cos )cos 2e d e e e d x x x xx x x x C x x x x C----∴=-+-∴=+⎰⎰22221111(5)sin sin sin cos 22222222e d de e e d x x x x x x x xx x ----=-=-+⋅⎰⎰⎰2222222211sin cos 22821111sin cos (sin )2282822111sin cos sin 2282162e de e e e d e e e d x xx x x x x x x xx x x x x x x x--------=--=--+-=---⎰⎰⎰2221221711sin sin cos 16222822sin (cos 4sin )21722e d e e e d e x x x x x x x xx C x x xx C-----∴=--+∴=-++⎰⎰222222222222221(6)tan (sec )sec 211(tan )tan tan 221tan ln cos 2111(7)2221111(2)2424d d d d de d de e e d e e d e t t t t t t t x x x x x x x x x x x x x x x x x x x x x x Cx t t t t tt t t -------=-=-=-=--=+-+=-=-+=---=--⎰⎰⎰⎰⎰⎰⎰⎰222222(8)(arcsin )(arcsin )2arcsin (arcsin )2arcsin (arcsin )2(arcsin )2e d d t Cx x x x x x xx x x x x x xx x x x -+=-⋅=+=+-=+-⎰⎰⎰⎰⎰22(arcsin )21cos 211(9)sin cos 222211cos 222e d e d e d e d e e d x x x x x x x x x x Cx x x x x x xx x=+-+-==-=-⎰⎰⎰⎰⎰而cos 2cos 2cos 22sin 2cos 22sin 2e d de e e d e de x x x x x xx x x x x x x x ==+=+⎰⎰⎰⎰cos 22sin 24cos 2e e e d x x x x x x x =+-⎰11cos 2(cos 22sin 2),511111(cos 22sin 2)(sin 2cos 2).2102510e d e 原式e e e x x x x x x x x x C x x C x x C ∴=++∴=-++=--+⎰(10)t =,则32,3d d x t x t t ==22222223336363663663(22)32)e d de e e d e de e e e d e e e e t t t t t t t t t t t t t x t t t t t tt t t t t t t C t t C C===-=-=-+=-++=-++=+⎰⎰⎰⎰⎰⎰(11)令ln x =t ,则,e d e d ttx x t ==,cos(ln )cos cos de e cos e sin e cos sin e e cos e sin e cos cos(ln )sin(ln )cos(ln )cos(ln )[cos(ln )sin(ln )]2d e d d d d d d t t t ttttttx x t t t t t t t t t t t tx x x x x xxx x x x C===+=+=+-=+-∴=++⎰⎰⎰⎰⎰⎰⎰⎰22222211(12)(1)sin 2sin 2sin 2cos 2sin 2(2)2211cos 2cos 2cos 222111cos 2cos 2sin 222211cos 2cos 2sin 222d d d d d d d x x x x x x x x x x x x x x x x x xx x x x xx x x x -=-=--=-++=-++=-++⎰⎰⎰⎰⎰⎰⎰2212sin 22111cos 2cos 2sin 2cos 2222413()cos 2sin 2222d x x xx x x x x x Cxx x x C-=-++++=--++⎰2222222221(13)ln(1)ln(1)()ln(1)2221111111ln(1)ln(1)(1)2212221111ln(1)()ln 122221(1)ln(1)2d d d d d d x x x x x x x x xx x x x x x x x x xx x x x x x Cx x x -=-=----+=--=--+---=--+-+-=--⎰⎰⎰⎰⎰⎰211.42x x C --+ 2222232321cos 11(14)cos cos 22221111sin sin sin 6262d d d d d d x x x x x x x x x x xx x x x x x x x x+=⋅=+=+=+-⎰⎰⎰⎰⎰⎰3232321111sin cos sin cos cos 626211sin cos sin .62d d x x x x x x x x x x x x x x x x x x C =++=++-=++-+⎰⎰333222323223232232ln 111(15)ln ()ln 3ln 11131ln 3ln ()ln ln 6ln 131ln ln 6ln ()1361ln ln ln 613ln ln d d d d d d d x x x x x xx x x xx x x x x xx x x x x x x x x x x x x x xx x x x x x x =-=-+=--=--+=---=---+=--⎰⎰⎰⎰⎰⎰⎰3266ln 1(ln 3ln 6ln 6) x x Cx x x x x Cx --+=-++++ 11(16)sin cos sin 2cos 22411cos 2cos 2cos 2cos 2244481cos 2sin 248d d d d d x x x x x x x x x x x x x x x x x x x x C==-=-+=-+=-++⎰⎰⎰⎰⎰()222221(17)cot csc csc csc csc 211csc csc csc cot 2222d d d d x x x x x x x x x x x x x x x x C=-=-=-+=--+⎰⎰⎰⎰222222222222222222211(18)(1)(1)(1)221111(1)2(1)()2222111(1)222e d e d de e e d e e d e e e x x x x x x x x x x x x x x x x x x x x x x C x C+=+=+=+-⋅=+-=+-+=+⎰⎰⎰⎰⎰11111(19)(ln ln )ln ln ln ln ln ln ln ln 11ln ln ln ln ln ln d d d d d d d x x x x x x x x x x x x x x xx x x x x x Cx x+=+=-⋅⋅+=-+=+⎰⎰⎰⎰⎰⎰⎰(20)ln(1)ln(1)(1)(1)ln(1)(1)1(1)ln(1)(1)ln(1)e e e d e d e e e e d e e e e d e e e xxxxxxxxxx x x x x x x x x C +=++=++-+⋅+=++-=++-+⎰⎰⎰⎰2233sin (21)tan sec tan (sec )tan sec sec cos d d d d x x x x x x x x x x x x=⋅==-⎰⎰⎰⎰ 2223323cos sin sin tan sec tan sec sec cos cos sin tan sec ln sec tan cos d d d d x x xx x x x x x x x x xxx x xx x x+=-=--=--+⎰⎰⎰⎰ 于是 213sin 2tan sec ln sec tan cos d xx x x C x x x =-++⎰, 所以 23sin 11tan sec ln sec tan cos 22d x x x x C x x x =-++⎰. 22211(22)ln(()211121ln(12(1)2d d d x x x x x x x =-++=+++=-++⎰⎰⎰令x =tan t , (,)22ππt ∈-,则d x =sec 2t dt21131sec cos sin sec d d d t t t t t C C t =⋅==+=+⎰⎰ ∴原式=2ln(2(1)x C x +. 211(23)()(1)111111e e d e d e e d e e ee d e x x x x xxxxx x x x x x x x x x x x x x x C C x x x=-=-+⋅+++++=-+=-++=++++⎰⎰⎰⎰arctan arctan arctan arctan 322(24)(1)e e d e xx xx x x x x ==+⎰⎰arctan arctan arctan arctan arctan 322(1)e 1e e e x x x x xx x =-=+⎰于是arctan arctan 13222(1)e e d x xx x C x =++⎰,所以arctan arctan 322(1)e e d x x x x C x =++⎰.习题5-4求下列不定积分:(1) 21d 1x x +⎰; (2)5438d x x x x x +--⎰;(3)sin d 1sin xx x +⎰; (4) cot d sin cos 1xx x x ++⎰.解 (1)令322111(1)(1)11A Bx Cx x x x x x x +==+++-++-+ 则 2331()()()11A B x B C A x A C x x +++-++=++ 从而 001A B B C A A C +=⎧⎪+-=⎨⎪+=⎩ 解得 131323A B C ⎧=⎪⎪⎪=-⎨⎪⎪=⎪⎩于是2322222123(1)3(1)1112111331612()2411ln ln 11361(1)ln 61d d d d d x x x x x x x x x x x x x x x Cx x x x Cx x -⎡⎤-=⎢⎥+-++⎣⎦-=-++-+-+=-++-++=-+⎰⎰⎰⎰⎰542233323323288(2)(1)11832111111ln 8()13221218ln 3ln 4ln 1132d d d d d x x x x x x x x x x x xx x x x xx x xx x x xx x x x x x x Cx x x +-+-=+++--=+++---=+++--++⋅--+=+++--+-+⎰⎰⎰⎰⎰ 222sin sin (1sin )1(3)cos (sec 1)1sin cos cos 1tan sec tan cos d d d d x x x x x x x x x x xx x C x x x Cx-==---+=-++=-++⎰⎰⎰⎰注 本题亦可用万能代换法(4)令tan2xt =,则 222222112sin ,cos ,cot ,2arctan ,1121d d t t t x x x x t x t t t t t--=====+++ 则222221cot 21111221sin cos 112221111111ln ln tan tan 222222d d d d d t x t t x t t t t t t x x t t t t t x x t C Ct --=⋅==--+++++++=-+=-+⎰⎰⎰⎰⎰。
化工原理第二版两册答案(习题5 附图主编)

第一章 流体流动4.某储油罐中盛有密度为960 kg/m 3的重油(如附图所示),油面最高时离罐底9.5 m ,油面上方与大气相通。
在罐侧壁的下部有一直径为760 mm 的孔,其中心距罐底1000 mm ,孔盖用14 mm 的钢制螺钉紧固。
若螺钉材料的工作压力为39.5×106 Pa ,问至少需要几个螺钉(大气压力为101.3×103 Pa )? 解:由流体静力学方程,距罐底1000 mm 处的流体压力为[](绝压)Pa 10813.1Pa )0.15.9(81.9960103.10133⨯=-⨯⨯+⨯=+=gh p p ρ 作用在孔盖上的总力为N 10627.3N 76.04π103.10110813.1)(4233a ⨯⨯⨯⨯⨯-==)-=(A p p F每个螺钉所受力为N 10093.6N 014.04π105.39321⨯=÷⨯⨯=F因此()(个)695.5N 10093.610627.3341≈=⨯⨯==F F n5.如本题附图所示,流化床反应器上装有两个U 管压差计。
读数分别为R 1=500 mm ,R 2=80 mm ,指示液为水银。
为防止水银蒸气向空间扩散,于右侧的U 管与大气连通的玻璃管内灌入一段水,其高度R 3=100 mm 。
试求A 、B 两点的表压力。
解:(1)A 点的压力()(表)Pa 101.165Pa 08.081.9136001.081.9100042汞3水A ⨯=⨯⨯+⨯⨯=+=gR gR p ρρ(2)B 点的压力()(表)Pa 107.836Pa 5.081.91360010165.1441汞A B ⨯=⨯⨯+⨯=+=gR p p ρ 7.某工厂为了控制乙炔发生炉内的压力不超过13.3 kPa (表压),在炉外装一安全液封管(又称水封)装置,如本题附图所示。
液封的作用是,当炉内压力超过规定值时,气体便从液封管排出。
试求此炉的安全液封管应插入槽内水面下的深度h 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题五(A )1. 用施密特方法把向量组123(1,1,1),(1,2,3),(1,4,9)T T T ===ααα正交化. 解:利用施密特正交化方法 ,可得11111⎛⎫ ⎪== ⎪ ⎪⎝⎭βα,1222121111[,]20[,]1-⎛⎫⎪=-=-= ⎪ ⎪⎝⎭βαβαβαβββ13233312312112,213[,][,]1424[,][]3313⎛⎫⎪ ⎪⎪=--=--=- ⎪ ⎪ ⎪ ⎪⎝⎭βαβαβαββαββββββ 再单位化得到单位正交组111111⎛⎫⎪==⎪⎪⎭ββe222101-⎛⎫⎪==⎪⎪⎭ββe333132313⎛⎫⎪⎪⎪==-⎪ ⎪ ⎪ ⎪⎝⎭ββe2. 下列矩阵是不是正交矩阵,并说明理由(1) 11123111;2211132⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭ (2). 184999814.999447999⎛⎫-- ⎪ ⎪ ⎪-- ⎪⎪ ⎪--⎪⎝⎭解:(1)矩阵111231112211132⎛⎫-⎪ ⎪⎪- ⎪ ⎪ ⎪- ⎪⎝⎭不是正交矩阵.因为令111231112211132⎛⎫-⎪ ⎪⎪=- ⎪ ⎪ ⎪- ⎪⎝⎭A ,且假设A 的列向量为 1231113211,1,2211123⎛⎫⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪ ⎪⎪ ⎪ ⎪=-== ⎪ ⎪ ⎪⎪ ⎪ ⎪- ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭ααα125[,]06=-≠αα,故123,,ααα不是单位正交组,即A 不是正交矩阵. (2).矩阵184999814999447999⎛⎫-- ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪-- ⎪⎝⎭是正交矩阵. 因为令184999814999447999⎛⎫-- ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪-- ⎪⎝⎭B =,且假设B 的列向量为123184999814,999447999⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪=-- ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭βββ=,=经验证1231,1,1===βββ,且121323[,]0,[,]0,[,]0===ββββββ 故123,,βββ是单位正交组,所以B 是正交矩阵.3. 求矩阵123213336⎛⎫ ⎪⎪ ⎪⎝⎭的特征值和特征向量,并问它的特征向量是否两两正交?解:令123213336⎛⎫ ⎪= ⎪ ⎪⎝⎭A ,且特征多项式123213336----λλλλA E =A 的特征值为1230,1,9==-=λλλ当10=λ时,方程(0)-A E X =0的系数矩阵123123123213033011336033000⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=→--→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭A基础解系1111⎛⎫⎪= ⎪ ⎪-⎝⎭P ,从而特征值10=λ对应的全部特征向量为111(0)≠k P k当21=-λ时,方程()A+E X =0的系数矩阵223223223000337001⎛⎫⎛⎫ ⎪ ⎪=→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A+E基础解系2110-⎛⎫⎪= ⎪ ⎪⎝⎭P ,从而特征值21=-λ对应的全部特征向量为222(0)≠k P k当39=λ时,方程(9)-A E X =0的系数矩阵8231119283021333000--⎛⎫⎛⎫ ⎪ ⎪-=-→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭A E基础解系3112⎛⎫⎪= ⎪ ⎪⎝⎭P ,从而特征值31=-λ对应的全部特征向量为333(0)≠k P k又因为121323[]0,[]0,[]0===P ,P P ,P P ,P ,故A 的特征向量两两相交.4. 设n 阶可逆矩阵A 有特征值λ,对应的特征向量为α.求1*1---A ,A ,E A 的一个特征值和对应的特征向量. 解: 因为αλαA =,则111---αλαλαA A =A =A ,故11-ααλA =所以1-A 的特征值为1λ,对应的特征向量为α.又由于αλαA =,*AA =A E ,*ααAA =A E则*1-αααλAA =A A =所以*A 的特征值为λA,对应的特征向量为α.而 111()(1)---=--ααααλE A A =故1--E A 的特征值为11-λ,对应的特征向量为α.5. 设3阶方阵A 的特征值为1231,0,1===-λλλ;对应的特征向量依次为1231222,2,1,212P P P -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪==-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭求A .解:由于1231,0,1===-λλλ,则123≠≠λλλ故A 可对角化.又令123()P =P ,P ,P ,有1100000001-⎛⎫⎪⎪ ⎪-⎝⎭P AP = 故1100000001-⎛⎫⎪ ⎪ ⎪-⎝⎭A =P P (*)122221212-⎛⎫ ⎪-- ⎪ ⎪⎝⎭P =,则1122999221999212999-⎛⎫ ⎪⎪⎪- ⎪ ⎪ ⎪--⎪⎝⎭P = 把1-P,P 代入(*)式有120331203322033⎛⎫- ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭A =6. 设方阵12422421x --⎛⎫ ⎪-- ⎪ ⎪--⎝⎭A =与50000004y ⎛⎫⎪Λ ⎪ ⎪-⎝⎭=相似,求,x y .解:因为A 与Λ相似,则208Λ=-A = 故348x y -=-再由4-λ=是A 的特征值知40--=E A 由此得9360x -+=,故4x = 把4x =代入(*)式得5y = 所以 4,5x y ==7. 设20131405x ⎛⎫⎪= ⎪ ⎪⎝⎭A ,问:(1)当x 为何值时, A 能相似对角化? (2)当x 为何值时, A 不能相似对角化?(3)当A 可相似对角化时,求出相似变换矩阵P 和对应的对角矩阵Λ. 解: A 的特征多项式220131(1)(6)45x ----------λλλλλλE A == A 的特征值为1231,6==λλλ=当121=λλ=时,方程()0-=E A X 的系数矩阵10110130003404000x x ----⎛⎫⎛⎫ ⎪ ⎪-=--→- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭E A(1).由上述计算可知,当3x =时,A 能相似对角化. (2).当3x ≠时,A 不能相似对角化.(3).当3x =时,易知当121λλ==时,方程()X 0-=E A而系数矩阵101101303000404000----⎛⎫⎛⎫ ⎪ ⎪-=--→ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭E A基础解系: 12100110⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭P =,P =当36λ=时,方程(6)0-=E A X 的系数矩阵4014016353043401000--⎛⎫⎛⎫⎪ ⎪-=--→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭E A基础解系 3134⎛⎫⎪⎪ ⎪⎝⎭P =故相似变换矩阵为101013104⎛⎫ ⎪⎪ ⎪-⎝⎭P =相应的对角矩阵100010006⎛⎫ ⎪Λ= ⎪ ⎪⎝⎭.8. 试求一个正交的相似变换矩阵,使下列对称阵相似于对角阵,220212.020-⎛⎫ ⎪-- ⎪ ⎪-⎝⎭解:令220212020-⎛⎫⎪-- ⎪ ⎪-⎝⎭A =,则特征方程为:220212(1)(2)(4)02-------++---λλλλλλλA E == A 的特征值为1232,1,4=-=λλλ=当12-λ=时,方程(2)0=A+E X 的系数矩阵4202102232022022000--⎛⎫⎛⎫ ⎪ ⎪=--→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭A+E基础解系: 1122⎛⎫⎪⎪ ⎪⎝⎭α=当21λ=时,方程()0-=A E X 的系数矩阵120120120202042021021021000---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-=--→--→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭A E基础解系: 2212⎛⎫ ⎪⎪ ⎪-⎝⎭α=当34λ=时,方程(4)0-=A E X 的系数矩阵2201104232012024000--⎛⎫⎛⎫ ⎪ ⎪-=---→-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭A E基础解系: 3221⎛⎫ ⎪- ⎪ ⎪⎝⎭α=因为A 的特征值各不相同,故只需将123,,ααα单位化.3121231231221112,1,2333221⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ααααααP ==P ==P ==令123122333212()333221333⎛⎫ ⎪ ⎪ ⎪=- ⎪ ⎪ ⎪- ⎪⎝⎭P =P ,P ,P ,则P 为一个正交的相似变换矩阵.9. 用矩阵记号表示下列二次型(1) 2227244;f x y z xy xz yz =+----(2) 22221234121314232424264.f x x x x x x x x x x x x x x =+++-+-+-解:(1) ()2221127244,,112227x f x y z xy xz yz x y z y z --⎛⎫⎛⎫⎪⎪=+----=-- ⎪⎪ ⎪⎪---⎝⎭⎝⎭(2) 22221234121314232424264.f x x x x x x x x x x x x x x =+++-++-+-()1212343411211132,,,23101201x x x x x x x x --⎛⎫⎛⎫ ⎪⎪-- ⎪⎪= ⎪⎪ ⎪⎪--⎝⎭⎝⎭10. 求一个正交变换化二次型222123232334f x x x x x =+++为标准型,并求正惯性指数和负惯性指数.解: ()122212323123232002334,,032023x f x x x x x x x x x x ⎛⎫⎛⎫⎪⎪=+++= ⎪⎪ ⎪⎪⎝⎭⎝⎭令123x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭X ,200032023⎛⎫⎪= ⎪ ⎪⎝⎭A ,故T f =X AX特征多项式200032(2)(1)(5)023-------λλλλλλλA E == A 的特征值: 1231,2,5==λλλ=当11λ=时,方程()0-=A E X 的系数矩阵100100022011022000⎛⎫⎛⎫ ⎪ ⎪-=→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A E基础解系: 1011⎛⎫⎪⎪ ⎪-⎝⎭α=当22λ=时,方程(2)0-=A E X 的系数矩阵0000002012012021003⎛⎫⎛⎫ ⎪ ⎪-=→ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭A E基础解系: 2100⎛⎫⎪⎪ ⎪⎝⎭α=当35λ=时,方程(5)0-=A E X 的系数矩阵3003005022011022000--⎛⎫⎛⎫ ⎪ ⎪-=-→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭A E基础解系: 3011⎛⎫⎪⎪ ⎪⎝⎭α=因为A 的特征值各不相同,故只需将123,,ααα单位化:3121231230101,0,1101⎛⎫⎛⎫⎛⎫⎪ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪-⎭⎝⎭⎭ααααααP ==P ==P ==令123010()0022⎛⎫ ⎪ =- ⎝⎭P =P ,P ,P123(y (y ,y ,y ))T =其中X =PY所以22212325f y y y =++,且f 的正惯性指数为3,负惯性指数为0.11. 判别下列二次型的正定型.(1) 222123121326422f x x x x x x x =---++(2) 2222123412131424343919242612f x x x x x x x x x x x x x x =+++-++--解:(1)由已知得:f 的矩阵为: 211160104-⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A211160104--⎛⎫⎪-=- ⎪ ⎪-⎝⎭A-A 的一阶主子式20>,二阶主子式2111016-=>-,三阶主子式380A -=>故-A 正定,则A 负定.所以f 是负定二次型. (2)由已知得f 的矩阵为: 11211303209613619-⎛⎫ ⎪--⎪ ⎪- ⎪--⎝⎭A = A 的一阶主子式10>,二阶主子式112013-=>-,三阶主子式11213026029--=>,四阶主子式240A => 故A 正定,所以A 是正定二次型.12.设U 为可逆矩阵, TA U U =,证明T f X AX =为正定二次型.证明:因为(U U)T T T T A U U A ===,则A 为实对称矩阵,且对应的二次型为2(U U)X (UX)T T T Tf X AX X UX UX====而u 为可逆矩阵,若0x ≠,则20UX >即20f UX =>,所以f 为正定二次型.习题五(B )填空题1. 已知,αβ为正交阵A 的两个相异的列向量,则内积[,]αβ______.=解:由已知,αβ为正交阵,则[,]0=αβ.2. 若P 是n 阶正交阵,则TP P =_____.解:因为P 是正交阵,则1T -P =P ,所以1TP P =.3. 实二次型221231223(,,)2f x x x x x x x =++相应的实对称矩阵有__个特征值大于0. 解: f 的实对称矩阵010110001A ⎛⎫⎪= ⎪ ⎪⎝⎭,且特征多项式为2(1)(1)E A λλλλ-=---则特征值为1231,λλλ===其中有两个特征值大于0.4. 设A 是n 阶方阵, *A 是A 的伴随矩阵, 2=A ,则方阵*B =AA 的特征值是___,特征向量是___.解: 因为*2==B =AA A E E ,则(2)0n E B -=-=λλ,特征值2(n )=重λ,故方程(22)X 0E E -=,所以特征向量x 为任意n 维非零向量.5. 三阶方阵A 的特征值为1,-1,2,则323-B =2A A 的特征值为____.解:A 的特征方程为()(1)(1)(2)f λλλλ=-+- 则B 的特征方程为32()2()3()g f f λλλ=- 所以B 的特征值为1,5,4--.6. 设1λ和2λ是3阶实对称矩阵A 的两个不同的特征值, 12(1,1,3),(4,5,)T T a ==ξξ依次是A 的对应于特征值12,λλ的特征向量,则实数___.a = 解:因为实对称不同特征值对应的特征向量正交,则12,0<>=ξξ 所以141530a ⨯+⨯+⨯=,即 3.a =-7. 已知A ,B 均为n 阶方阵, A 与B 相似,且方程组Ax =b 仅有一个解,则(B)___.R = 解:因为A 与B 相似,则秩(A )=秩(B )由于Ax =b 有唯一解,所以秩(A )=秩(B )=n8. 若n 阶方阵A 与B 相似,且a =A ,则___.=AB 解:因为方阵A 与B 相似,则存在一个可逆矩阵P ,使得1-A =P BP ,11--=A =P BP P B P ,所以a =A =B ,即2a =AB =A B9. 矩阵124221413⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A 对应的二次型是_____.解:由已知得 ()112323124,,221413x x x x x x ⎛⎫⎛⎫⎪⎪- ⎪⎪ ⎪⎪-⎝⎭⎝⎭=()11231231232324,22,43x x x x x x x x x x x x ⎛⎫⎪+++--+ ⎪ ⎪⎝⎭=22212312132323482x x x x x x x x x ++++-所以22212312132323482f x x x x x x x x x =++++-10. 已知二次型22212312323(,,)2332,(0)f x x x x x x ax x a =+++>通过正交变换化成标准型22212325f y y y =++,则___.a = 解:由已知得原二次型对应的实对称矩阵的特征值为1,2,5,而原二次型对应的矩阵为2000303a a ⎛⎫⎪= ⎪⎪⎝⎭A且123200303212510303aa a a ==⨯==⨯⨯=λλλA 所以295a -= 2a =± 又0a > 故2a =二.解答题1.设A 是3阶矩阵,它的3个特征值为1231,1,2==-=λλλ,设325-B =A A ,求B 及5.-A E解:由题意可知325-B =A A 的特征值为: 4,6,12---,故 (4)(6)(12)288=-⨯-⨯-=-B而5-A E 的特征值为: 4,6,3---,所以5(4)(6)(3)72-=-⨯-⨯-=-A E2.用正交变换化二次型为2123132(,,)2f x x x x x x =+标准型,并写出标准型及所用的正交变换.解: 已知2123132(,,)2f x x x x x x =+,设二次型的矩阵为A ,且001010100⎛⎫⎪= ⎪⎪⎝⎭AA 特征多项式为 20110(1)(1)1----+--λλλλλλA E == A 的特征值: 1231,1=-=λλλ=当11-λ=时,方程()0=A+E X 的系数矩阵101101020010101000⎛⎫⎛⎫ ⎪ ⎪=→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A+E基础解系: 1101⎛⎫⎪⎪ ⎪-⎝⎭α=当231=λλ=时,方程()0-=A E X 的系数矩阵101101000000101000--⎛⎫⎛⎫ ⎪ ⎪-=→ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭A E基础解系: 23100,110⎛⎫⎛⎫⎪ ⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭αα==因为11-λ=仅对应一个线性无关的特征向量,故只需要单位化.111202⎛⎫ ⎪⎪ ⎪- ⎝⎭ααP == 当231=λλ=对应的特征向量23,αα用施密特方法正交化,得22101⎛⎫ ⎪== ⎪ ⎪⎝⎭βα323323220[,]1[,]0⎛⎫⎪=-== ⎪ ⎪⎝⎭αββαβαββ再单位化322323020,102⎛ ⎛⎫ ⎪⎪⎪ ⎪⎪⎝⎭ ⎝⎭ββββP ==P ==令1230()0010⎛⎫ ⎪ ⎪= ⎪⎪ ⎪ ⎪⎝⎭P =P ,P ,PP 为正交阵,且1100010001--⎛⎫ ⎪⎪ ⎪⎝⎭P AP =作正交变换123123((,,),y (y ,y ,y ))T T x x x x ==其中X =PY所以标准型222123f y y y =-++.3.已知二次曲面方程2222224x ay z bxy xz yz +++++=可以经正交变换x y z ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ςηξP化为椭圆柱面方程2244+=ηξ,求,a b 的值及正交矩阵P . 解:令222222f x ay z bxy xz yz =+++++,故二次型矩阵为: 111111b b a ⎛⎫⎪ ⎪ ⎪⎝⎭A =,且A 经正交变换后224f =+ηξ 所以A 特征值为: 0,1,4,即A 0=,由此得: 1b =,代入A11111111a ⎛⎫⎪⎪⎪⎝⎭A =再有1=λ是A 的特征值知: 0-=E A ,故3a =即111131,:0,1,4111⎛⎫⎪ ⎪ ⎪⎝⎭其特征值为A =当10λ=时,方程0=AX 的系数矩阵 111131111⎛⎫⎪= ⎪ ⎪⎝⎭A特征向量: 1101⎛⎫ ⎪⎪ ⎪-⎝⎭α=当21λ=时,方程()0-=A E X 的系数矩阵011121110⎛⎫ ⎪-= ⎪ ⎪⎝⎭A E特征向量: 2111⎛⎫⎪- ⎪ ⎪⎝⎭α=当34λ=时,方程(4)0-=A E X 的系数矩阵3114111113-⎛⎫ ⎪-=- ⎪ ⎪-⎝⎭A E特征向量: 3121⎛⎫⎪⎪ ⎪⎝⎭α=因为A 的特征值各不相同,故只需将123,,ααα单位化:31212312320,,33⎛⎫⎛⎫ ⎪ ⎪ ⎪ - ⎪ ⎪ ⎪ ⎪⎝ ⎪⎝⎭⎝⎭ααααααP ==P ==P == 所以123236()0236⎛= - ⎝⎭P =P ,P ,P4.设A 为三阶实对称阵,且满足220+A A =,已知A 的秩()2r A =,(1).求A 的特征值;(2). k +A E 为正定阵,求k 的范围.解:(1)假设A 的特征值为λ,则有题意有: 220λλ+=解得A 的特征值122,0.λλ=-= (2)由(1)得k +A E 的特征值为2,k k -因为k +A E 是正定的,故k +A E 的所有特征值为正的.即 020k k >⎧⎨->⎩所以 2k >5.设2112-⎛⎫⎪-⎝⎭A =,求nA解:由于2112-⎛⎫⎪-⎝⎭A =特征多项式21(1)(3)12--=---λλλλλE A =A 的特征值: 121,3==λλ当11λ=时,方程()0-=A E X 的系数矩阵 1111-⎛⎫-=⎪-⎝⎭A E特征向量: 111⎛⎫ ⎪⎝⎭α=当23λ=时,方程(3)0-=A E X 的系数矩阵 11311--⎛⎫-=⎪--⎝⎭A E特征向量: 211⎛⎫⎪-⎝⎭α= 因为A 的特征值各不相同,故只需将12,αα单位化:12121222,22⎛⎛⎫⎪- ⎝⎭⎝⎭ααααP ==P ==令12()22⎫⎪= - ⎝⎭P =P ,P11003-⎛⎫⎪⎝⎭P AP =1111111003n n n ------⎛⎫∙∙∙∙= ⎪⎝⎭个相乘P AP P AP P AP P AP P AP P A P = 故11003n n -⎛⎫⎪⎝⎭A =P P由于P 是正交阵,故12222T-⎛⎫⎪= ⎝⎭P =P所以10222203nn ⎛⎫⎛⎫⎪ ⎪⎛⎫= ⎪⎝⎭A 111133131312222111121313332222nn n n n n n n ⎛⎫+- ⎪⎛⎫+-==⎪ ⎪-+ ⎪⎝⎭-+⎪⎝⎭三.证明题1.设λ是n 阶正交阵P 的特征值,证明1λ也是P 的特征值.证明:(1)先证TP 的特征值等于P 的特征值, 考虑的特征多项式-=λE P将上式两边转置()()0T T -=-=λλE P E P det()det()T-=-λλE P E P故有 0T -=-=λλE P E P所以P 与TP 有相同的特征值.P 为正交阵,故1T -P =P ,所以1λ是TP的特征值,再由(1)知1λ也是P的特征值.2.设x为n维列向量x T x=E,令H = E- 2x T x,求证:H对称的正交阵。
