Kaluza-Klein Holography

合集下载

五维轴对称Kaluza—Klein时空解

０引言
五维Ｋａｕａ１ｎ理论统一引力场和电磁场。ｌｚ —Ｋｅｉ在这个理论中，五维是一个紧致的空间维，第电磁四矢被第五维和其它空间维的交叉项来表示。标准的五维Ｋｌｚ－Ｋｌｎ理论也可从下面有ａａｕｅｉ
这里变量一（，，ｆ．Ｐ２，）Ａｐ是电磁四矢量，是ｇ
作者简舟：魏盏焕（９２）男．１６＋，酎教授．师大博士研究生．北从事引力理论研究
＊此课题为省教委资助砸目．目编号为９０１１８项８８１０４
维普资讯
对于ｎ一３情形，用量（）等价于下面的作１
五维Ｅｎｔｉｉｓｅｎ— Ｈｉｂｒ作用量ｌｅｔｌ
Ｓ孟
收藕日期：０１１９２０ — ０２．
／Ｒ，＝ｃ ”
（３）
一
“ ｇ
这里Ｇ — Ｇ／是四维引为常数，是相应的２Ｇ
Ｖｏ．２１３Ｎ０．２
Ｊｍ２００２
五维轴对称Ｋａｚ－Ｋｌｎ时空解ｌａｕｅｉ
魏益焕，国权陈维石祁，
（州师范学院物理系，宁锦州１１０；．京师范大学物理系，京ｉ０５）１锦辽２００２北北０８９
－１ｑＭａｏ给Ｓ— Ｉｖ［ｄ／二一Ｒ＋２ＶＯ－Ｃ，解能够在文献１７一ｚ中被发现。ｔｓ出了一（）＋ｅＺＦ］，
（）１

用于生成射线跟踪图像的可视化的技术[发明专利]

专利名称：用于生成射线跟踪图像的可视化的技术
专利类型：发明专利
发明人：A·N·金罗斯,S·L·哈格里维斯,A·帕特尔,T·L·戴维松申请号：CN201980016496.2
申请日：20190221
公开号：CN111801713A
公开日：
20201020
专利内容由知识产权出版社提供
摘要：本文中描述的示例总体上涉及生成图像的可视化。

从图形处理单元(GPU)或图形驱动器拦截指定用于使用射线跟踪来生成图像的射线跟踪指令的专有结构。

可以基于辅助信息来将专有结构转换为用于生成图像的可视化的可视化结构。

可以从可视化结构来生成图像的可视化。

申请人：微软技术许可有限责任公司
地址：美国华盛顿州
国籍：US
代理机构：北京市金杜律师事务所
代理人：彭梦晔
更多信息请下载全文后查看。

外文翻译---基于离散混沌映射的图像加密并行算法

这种并行图像加密框架下，我们提出了一种新的算法，这是基于四个基本的转换。因此，我们将描述我们的算法之前，先介绍这些转换。
3.转换
3.1.A-转换
在A转换中，A代表加，能被形式化的定义如下：
a+b=c(1)
加法被定义为按位与操作
转换A有三个基本性质：
(2.1)a+a=0
(2.2)a+b=b+a(2)
(2.3)(a+b)+c=a+(b+c)
在并行模式计算时，许多的PE可以同时读取或写入相同的内存区域（即临界区），
这往往会导致意想不到的执行程序。因此，有必要在关键区域使用一些并行技术管理。
2.2.并行图像的加密框架
为了满足上述要求，我们提出了一个并行图像加密的框架，这是一个四个步骤的过程：
步骤1：整个图像被划分成若干块。
步骤2：每个PE负责确定数量块。一个区域内的像素可以充分使用有效的混乱和扩散进行操作加密。
附件C：译文
基于离散混沌映射的图像加密并行算法
摘要：
最近，针对图像加密提出了多种基于混沌的算法。然而，它们都无法在并行计算环境中有效工作。在本文中，我们提出了一个并行图像加密的框架。基于此框架内，一个使用离散柯尔莫哥洛夫流映射的新算法被提出。它符合所有并行图像加密算法的要求。此外，它是安全、快速的。这些特性使得它是一个很好的基于并行计算平台上的图像加密选择。
这个框架可以非常有效的实现整个图像的扩散。但是，它是不适合在并行计算环境中运行。这是因为当前像素的处理无法启动直到前一个像素已加密。即使有多个处理元素（PE），这种计算仍然是在一个串行模式下工作。此限制了其应用平台，因为许多基于FPGA / CPLD或者数字电路的设备可以支持并行处理。随着并行计算技术的应用，加密速度可以大大加快。

马尔可夫链蒙特卡洛方法在医学影像分析中的应用案例解析(七)

马尔可夫链蒙特卡洛方法在医学影像分析中的应用案例解析引言医学影像分析是医学图像处理领域的重要研究方向，它主要利用计算机技术对医学影像进行处理和分析，以辅助医生进行诊断和治疗。

马尔可夫链蒙特卡洛方法是一种常用的概率计算方法，在医学影像分析中有着广泛的应用。

本文将结合实际案例，对马尔可夫链蒙特卡洛方法在医学影像分析中的应用进行解析。

马尔可夫链蒙特卡洛方法简介马尔可夫链蒙特卡洛方法（MCMC）是一种用于从复杂概率分布中抽样的统计方法。

它基于马尔可夫链的概念，通过模拟从目标概率分布中抽样，从而实现对该分布的近似推断。

MCMC方法在众多领域都有着广泛的应用，包括金融、生物学、物理学等领域。

医学影像分析中的应用案例在医学影像分析中，MCMC方法被广泛应用于图像分割、图像重建、图像配准等方面。

以图像分割为例，医学影像中常常需要将感兴趣的组织或器官从背景中分割出来，这对于疾病的诊断和治疗至关重要。

MCMC方法可以利用图像的灰度、纹理等特征，实现对医学影像的自动分割，从而辅助医生进行诊断。

在图像重建方面，MCMC方法可以利用患者的多个医学影像数据，通过概率模型推断出患者的三维图像，从而实现对患者的个性化治疗。

此外，MCMC方法还可以用于医学影像的配准，即将多个医学影像进行空间上的对齐，以便医生进行多模态影像的融合分析。

案例分析以医学影像分割为例，研究人员利用MCMC方法对乳腺X射线照片进行分割。

乳腺癌是女性常见的恶性肿瘤，早期诊断对于提高治愈率至关重要。

然而，乳腺X射线照片的解读需要经验丰富的医生，而且容易受主观因素的影响。

利用MCMC方法，研究人员可以构建乳腺X射线照片的概率模型，通过抽样得到乳腺组织的分割结果，从而辅助医生进行乳腺癌的早期筛查。

在图像重建方面，MCMC方法也有着重要的应用。

研究人员利用MCMC方法对患者的多个MRI影像数据进行处理，通过概率模型得到患者的三维图像，从而实现对患者的个性化治疗。

这种方法可以更好地指导手术，提高手术的成功率，减少对患者的伤害。

Brane世界中的宇宙学方程

文章编号：1000-2375（2004）02-0119-03Brane 世界中的宇宙学方程胡永红，林树渊，刘鑫，靳海芹，张多（湖北大学物理学与电子技术学院，湖北武汉430062）摘要：首先介绍了相关概念———外赋曲率，引入Brane 世界宇宙模型.然后由Brane 度规和五维能动张量推得五维爱因斯坦方程，积分得到Brane 边界条件，应用到爱因斯坦方程得到与Friedmann 类似的方程.由爱因斯坦方程和能动张量守恒方程得到Brane 宇宙标度因子的演化规律.最后，在将Brane 张量和体宇宙学常数进行微调后，分别在高能和低能范围里讨论修正了的Friedmann 方程的解及其中各项的意义.关键词：Brane 世界；外赋曲率；~ubble 常数；标度因子中图分类号：0412.1文献标志码：A收稿日期：2003-12-10作者简介：胡永红（1978-），男，硕士生1引言我们的目的是提供一个新的处理附加维的方法，即Brane 世界梗概，其中通常的物质局限于一个嵌图1嵌入五维时空中的Brane于高维时空（Bulk ）的三维曲面（Brane ）上.这个方法必须与Kaluza-Klein 相比较.在Kaluza -Klein 方法里，物质场可以存在于紧附加维的任何地方，而且能通过傅立叶展开描述为四维场的无穷叠加.所谓的Kaluza -Klein 模只有在能量超过质量时，特别是与附加维尺度（R ）成反比时才能被激发，这意味着在Kaluza -Klein 图景里，附加维尺度R 小于或等于1TeV -1.在Brane 世界里，只有引力在高维时空中传播，由于四维引力只能在大约1mm 的尺度上图2矢量沿平面曲线平移检测到，所以附加维的尺寸可能比以前想象的大很多.这个新的维数减少的方法源自近来弦和M 理论的新进展，尤其是认为Brane 是开弦闭合的子空间的观点和规范场的定义.这个模型的宇宙学现象已经从各方面得到了研究，这里我们为了得到一个方便处理的模型，舍弃一些高能现象，仅考虑嵌入五维空体（Bulk ）时空的自引力Brane 世界［1~4］.如图1所示，B 代表体时空，b 代表三维曲面，附加维坐标为y.t 为时间坐标，X 为三维最图3矢量沿球面曲线平移和外赋曲线概念大对称空间坐标.为了更好地理解这个模型，我们需要了解外赋曲率，下面介绍此概念.如图2所示，平面P 上有一条曲线C ，从p 点引任意矢量，将它沿曲线C 移动，当它回到p 点时，它的方向仍和开始一样.然而如图3所示，如果P 是一三维球面，C 是P 上的闭合曲线，从p 点引出的任意矢量沿曲线C 平移一圈回到p 点时，它的方向将与初始方向不一致.这两个例子给了我们一个曲率的概念.二维曲面是一个平面，而三维曲面是弯曲的.从图2和图3（a ），我第26卷第2期2004年6月湖北大学学报（自然科学版）JOurnal Of ~ubei University （Natural Science EditiOn ）VOl.26NO.2June ，!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!2004们可以看出只有在初始平行的测地线不能保持平行时，才能说这个空间弯曲了.测地线是一个曲线，它的切矢量在其上平移，它是一条最短的曲线.我们用切矢量t a、偏导数算符!a来定义矢量平行移动的概念.如果沿曲线满足方程t a!a16=0时，则可以说曲线上每一点给定的矢量1a在沿曲线移动时，是平行移动的.如图3（b），考虑曲面M上一点g的法矢量!，如果将它平移到p点，它将与虚线一致，很显然，它不与p点的法线一致是因为嵌入时空里的曲面M是弯曲的.那么这个不一致可以用如下定义的外赋曲率来表示.K a6=h c a!c I6（1）其中ha6是曲面M上的度规.2五维爱因斯坦方程假设沿三维空间维（在Brane中与我们平常所在的空间各维相对应），各向同性且均匀，时空度规（至少在Brane附近）可写为d S2=-I（t，y）2d t2+a（t，y）2Y ij d x j d x j+d y2（2）其中Y ij是最大对称三维度规，空间曲率可为正、零和负（I=-1，0，1）.在这些坐标系中，Brane世界总位于y=0处，且Brane上的观测者测到的宇宙标度因子为a（t）" a（t，0）.我们通常可以重新标度时间坐标以让它与Brane宇宙时一致，即I0（t）"I（t，0）=1.总的能动张量可以分解成体能动张量和Brane能动张量，前者在这里假设为零，后者取以下形式：T A B=S A B S（y）=｛P6，p B，p B，p B，0｝S（y）（3）这里S函数表示物质存在于Brane位置y=0处.物理量P B和p B是Brane上只依耐于时间的总的能量密度和压强.允许体中存在一个宇宙常数A，那么五维爱因斯坦方程为G AB+A g AB=K2T AB（4）其中K2为引力耦合.3Brane世界里的Friedmann方程我们不直接解具有分散物质源的爱因斯坦方程，而是首先求得一个整体解，然后在Brane上应用边界条件.这个条件可以通过在Brane附近积分爱因斯坦方程得到.根据连接条件，度规必须连续且外赋曲率张量KAB的跃变只依耐于物质分布的能动张量，即［K A B-K S A B］=K2S A B（5）其中方括号代表在Brane上的跃变，外赋曲率如前述定义为KAB=h C A!C I B，I A为与Brane正交的单位矢，外赋曲率的跃变值为Brane一边的值的两倍.将度规（2）式代入（5）式得到两个连接条件（I'I）0+=K26（3pB+2P B），（a'a）0+=-K26P B（6）在度规（2）式下解爱因斯坦方程（4）式，得到一个控制Brane世界里的几何的方程［2］H20"'a2a20=K436P2B+A6-Ka20+ca40（7）其中c是积分常数.这个方程与第一个Friedmann方程类似.由于它将哈勃常数与能量密度联系在一起，但它与通常的Friedmann方程不同.此方程的一个特别引人注意的特点是方程右边的能量密度项为二次项，这与标准的四维Friedmann方程不同.标准的四维Friedmann方程与能量密度线性相关.由五维爱因斯坦方程（4）式得到的另一个结果是能量守恒方程没有变化，仍然为'P B+3H（P B+p B）=0（8）在c=0且A=0的简单情况下，取理想流体状态方程p B=O P B，解方程（7）式和（8）式可得到标度因子的演化a0#t13（1+O）（9）修正了的Friedmann规律（7）式中有一个P2B项而没有体宇宙常数和c项，随后RandaII和Sundrum提出了021湖北大学学报（自然科学版）第26卷一个描述带有一维附加维的平直世界的新模型［5］.这一模型的新成分赋予Brane 一个张量（常能量密度）和五维体（BuIk ）一个负的宇宙常数.这两项间的微调可致使有效四维哈勃参数在（7）式里为零（即c=0）.可以证明除在非常小的能量范围里以外，这样一个假设给出一个常见的四维引力［5，6］.此引力的发现暗示RandaII and Sundrum 模型的推广应该与标准模型在小能量范围内一致.这一点很快被证实［7，8］.4Brane 宇宙学为了绕过Minkowski 几何且考虑一个有重要意义的Brane 宇宙，我们必须假设Brane 中总的能量密度P B 包含两部分，即P B =O +P（10）其中张量O 是不随时间变化的常量.P 为通常的宇宙学能量密度.将上式带入（7）式得到H 2=（K 436O 2+A 6）+K 418P 2-K a 2+c a4（11）将Brane 张量和体宇宙学常数进行微调，让圆括号中的项为零或很小.当P ＜O 时，下一项主导着P 2项，这样就回到了通常的低能范围处的Friedmann 方程.这时有等式8!G =K 46O（12）这个式子与由实验物质的引力相互作用推得的牛顿常数一致.（11）式右边的第三项为能量密度的平方项，它提供了Friedmann 方程的高能修正，这个修正在能量密度值接近张量O 值且在高能密度处为主时，变得特别有意义.在非常高的能量范围内，P ＜O ，由于体宇宙常数变得可以忽略，我们发现（9）式的不同寻常.取状态方程p =W P ，守恒方程（8）式给出通常形式P =P 兴a -g ，g E 3（1+W ）（13）将上式带入方程（11）式得到a （t ）=［gm 兴t （1+g 2P t ）］1/g （14）式中引入了两个质量标度m 兴E K 26P 兴，P E -A /＼6（15）我们看到标度因子的演化介于高能和低能范围之间，且变换时与P -1同数量级.而P -1为宇宙常数的特征标度.方程（11）的最后一项源自积分常数c ，且类似辐射项.常数c 与SchwarzschiId 质量类似.且它与体WeyI 张量相联系.常数c 为零时，Weyl 张量也为零.参考文献：［1］Binettruy P ，Deffayet C ，LangIois D.Non -conventionaI cosmoIogy from a Brane -universe ［J ］.NucI Phys B ，2000，565：269~278.［2］Binettruy P ，Deffayet C ，EIIwanger U ，et aI.Brane cosmoIogicaI evoIution in a buIk with cosmoIogicaI constant ［J ］.Phys Lett B ，2000，477：285~296.［3］FIanagan E E ，Tye S H ，Wasserman I.CosmoIogicaI expansion in the RandaII -Sundrum Brane worId scenario ［J ］.Phys Rev D ，2000，62：1641~1655.［4］Shiromizu T ，Maeda K ，Sasaki I M.The Einstein eguations on the 3-Brane worId ［J ］.Phys Rev D ，2000，62：349~356.［5］RandaII L ，Sundrum R.An aIternative to compactification ［J ］.Phys Rev Lett ，1999，83：4690~4693.［6］Garriga J ，Tanaka T.Gravity in the RandaII -Sundrum Brane worId ［J ］.Phys Rev Lett ，2000，84：2778~2785.［7］Csaki C ，Graesser M ，KoIda J ，et aI.CosmoIogy of one extra dimension with IocaIized gravity ［J ］.Phys Lett B ，1999，462：34~40.［8］CIine J M ，Grogean C ，Servant G.CosmoIogicaI expansion in the presence of an extra dimension ［J ］.Phys Rev Lett ，1999，83：4245~4248.121第2期胡永红等：Brane 世界中的宇宙学方程Cosmological dynamic eguation in the Brane-worldHU Yong-hong，LIN Shu-yuan，LIU Xin，JIN Hai-gin，ZHANG Duo（School of Physics and Electronic Technology，Hubei University，Wuhan430062，China）Abstract：Introduced a model of Brane world and an important conception———extrinsic curvature.Then ob-tained the five-dimensional Einstein eguation from Brane metric and five-dimensional energy-momentum tensor. Integrate it，got two Brane junction conditions.Applied to the Einstein eguation，found an eguation analogous to Friedmann eguation.Then got the evolution of the Brane world scale factor from the Einstein eguation and the ener-gy-momentum conservation eguation.At last，after the fine-tuning of the Brane tensor and the bulk cosmological constant，discussed the solution of the corrected Friedmann eguation in high and low energy scale cases and the physical meaning of each term of the corrected Friedmann eguation.Key words：Brane world；extrinsic curvature；Hubble constant；scale factor（责任编辑严家利）（上接第118页）式中^!'、^!~由（7）式给出，而d2V（^!）d^!2=dd u［d V（^!）d^!］/^!'亦可借助（9）式和（7）式求出.若进一步考虑到标度因子的幂次律：a（t）=（tt0）S，相应地："（u）=（uu0）S1-S，u0=t0/（1-S）.则单圈抵消项（24）式可表示为时间的明显表达式：!c=1#（-51.3S4+63.3S3-11.25S2-S+1）u-4（1-S）4（25a）或!c =1#（-51.3S4+63.3S3-11.25S2-S+1）t3S-4/t3S0（25b）（24）或（25）式的结果表明，在背景场展开方案下，平直Robertson-Walker宇宙背景下的量子引力是单圈可重整的，且发散抵消项是时间的函数.在宇宙的不同时期，发散抵消项与时间的函数关系有所不同.例如：（1）辐射为主的时期：S=12，!c!t-52；（2）物质为主的时期：S=23，!c!t-2.参考文献：［1］陈中秋，邵常贵，林树渊，等.平直Robertson-Walker宇宙背景的场方程［J］.湖北大学学报（自然科学版），2003，25（4）：312~315.［2］温伯格S.引力论和宇宙论［M］.邹振隆.北京：科学出版社，1980.474~478.［3］陈中秋，张祖全，马为川，等.外引力背景下标量场的抵消拉氏量的计算［J］.湖北大学学报（自然科学版），1996，18（2）：103~108.［4］陈中秋，邵常贵.含耦合标量场的量子引力发散抵消项的计算［J］.湖北大学学报（自然科学学版），1997，19（1）：30~35.One-loop counter Lagrangian of gravity on the flat universe backgroundCHEN Zhong-giu，SHAO Chang-gui，CHEN Yi-han，LIN Shu-yuan，MA Wei-chuan（School of Physics and Electronic.Technology，Hubei University，Wuhan430062，China）Abstract：Using the background field method，find the one-loop divergence counter term of guantum gravity coupling scalar field in the framework of covariant guantization.The results show that the aforementioned counter term is a power law in time coordinates.Key words：Robertson-Walker metric；backgroud field；guantum gravity；1-loop counter term（责任编辑严家利）221湖北大学学报（自然科学版）第26卷。

Glueballs and Their Kaluza-Klein Cousins

a r X i v :h e p -t h /9806171v 1 19 J u n 1998UCB-PTH-98/35,LBNL-41948,NSF-ITP-98-070hep-th/9806171Glueballs and Their Kaluza-Klein CousinsHirosi Ooguri,Harlan Robins and Jonathan Tannenhauser Department of Physics,University of California at Berkeley,Berkeley,CA 94720Theoretical Physics Group,Mail Stop 50A-5101,Lawrence Berkeley National Laboratory,Berkeley,CA 94720Institute for Theoretical Physics,University of California,Santa Barbara,CA 93106Abstract Spectra of glueball masses in non-supersymmetric Yang-Mills theory in three and four dimensions have recently been computed using the conjectured duality between superstring theory and large N gauge theory.The Kaluza-Klein states of supergravity do not correspond to any states in the Yang-Mills theory and therefore should decouple in the continuum limit.On the otherhand,in the supergravity limit g 2Y M N →∞,we ﬁnd that the masses of theKaluza-Klein states are comparable to those of the glueballs.We also showthat the leading (g 2Y M N )−1corrections do not make these states heavier than the glueballs.Therefore,the decoupling of the Kaluza-Klein states is not evident to this order.1IntroductionSpectra of glueball masses in non-supersymmetric Yang-Mills theory in three and four dimensions have recently been calculated[1]using the conjectured duality between string theory and large N gauge theory[2–5].The results are apparently in good numerical agreement with available lattice gauge theory data,although a direct comparison may be somewhat subtle,since the supergravity computation is expected to be valid for large ultraviolet couplingλ=g2Y M N,whereas we expect that QCD in the continuum limit is realized forλ→0[5,6].As explained in[6,1],the supergravity computation atλ≫1 gives the glueball masses in units of theﬁxed ultraviolet cutoﬀΛUV.Forﬁniteλ,the glueball mass M is expected to be a function of the formM2=F(λ)Λ2UV.(1.1)In the continuum limitΛUV→∞,M should remainﬁnite and of orderΛQCD.This would require F(λ)→0asλ→0.In[1],the leading string theory corrections to the masses were computed and shown to be negative and of orderλ−3/2,in accordance with expectation.Witten has proposed[5]that three-dimensional pure QCD is dual to type IIB string theory on the product of an AdS5black hole and S5.This proposal requires that certain states in string theory decouple in the continuum limitλ→0.One class of such states are Kaluza-Klein excitations on S5.The supergravityﬁelds on the AdS5black hole×S5 can be classiﬁed by decomposing them into spherical harmonics(the Kaluza-Klein modes) on S5[7,8].They fall into irreducible representations of the isometry group SO(6)of S5, which is the R-symmetry of the four-dimensional N=4supersymmetric gauge theory from which QCD3is obtained by compactiﬁcation on a circle.Consequently,only SO(6) singlet states should correspond to physical states in QCD3in the continuum limit.These are the glueball states studied in[1].However,weﬁnd that,in the supergravity limit, masses of the SO(6)non-singlet states are of the same order as the SO(6)singlet states. Since these states should decouple in the limitλ→0,it was speculated in[1]that the string theory corrections should make the non-singlet states heavier than the singlet states.The purpose of this paper is to test this idea.We compute the masses of the SO(6)non-singlet states coming from the Kaluza-Klein excitations of the dilaton in ten dimensions. Weﬁnd the masses in the supergravity limit to be of the same order as those of the SO(6) singlet states.We then calculate the leading string theory corrections to the masses.We ﬁnd that the leading corrections do not make the Kaluza-Klein states heavier than theglueballs.Therefore,the decoupling of the Kaluza-Klein states is not evident to this order.This suggests that the quantitative agreement between the glueball masses from supergravity and the lattice gauge theory data should be taken with a grain of salt.2The Supergravity LimitWe calculate the masses of the Kaluza-Klein states following the analysis of[1].Ac-cording to[5],QCD3is dual to type IIB superstring theory on the AdS5black hole×S5 geometry given bydx24πg2Y M N =dρ2ρ2 +ρ2−b4dρ (ρ4−1)ρd f0this shooting method can be used to compute k 20and the wavefunction f 0(ρ)to arbitrarilyhigh precision.The results of the numerical work are listed in Table 1.As expected,the masses are all of the order of the ultraviolet cutoﬀΛUV =b .l135711.5929.2654.9388.6034.5363.60100.6145.668.98109.5157.9214.3l 2sρ2−b 4ρ2 dτ2+ρ23 i =1dx 2i +d Ω25,(3.1)where δ1=+15γ 5b 4ρ8−19b 12ρ4+5b 8ρ12 ,(3.2)and γ=18γ b 42ρ8+b 1216πG 10 d 10x √2g µν∂µΦ∂νΦ+γe −3periodicity2πR ofτis also modiﬁed toR= 1−152b.(3.5) It is the inverse radius R−1that serves as the ultraviolet cutoﬀof QCD3.To solve the dilaton wave equation in theα′-corrected geometry(3.1),we writeΦ=Φ0+f(ρ)e ikx Y l(Ω5),(3.6) whereΦ0is the dilaton background given by(3.3),and expand f(ρ)and k2inγasf(ρ)=f0(ρ)+γh(ρ),k2=k20+γδk2.(3.7) Here f0(ρ)obeys the lowest order equation(2.3)and is a numerically given function,and k20is likewise determined from(2.3).The second-order diﬀerential equation obtained from the action(3.4)in the background metric(3.1)and dilatonﬁeld(3.3)is,in units in which b=1,ρ−1ddρ −(k20+l(l+4)ρ2)h==(75−240ρ−8+165ρ−12)d2f0dρ+(δk2−120(k20+l(l+4)ρ2)ρ−12−405ρ−14)f0(ρ).(3.8) With f0(ρ)and k20given,one may regard this as an inhomogeneous version of the equation (2.3).We solve this equation for h(ρ)andδk2.We are now ready to present our results.Let us denote the lowest mass of the l-th Kaluza-Klein state by M l.In units of the ultraviolet cutoﬀΛUV=(2R)−1,with R given by(3.5),weﬁndM20=11.59×(1−2.78ζ(3)α′3+···)Λ2UVM21=19.43×(1−2.66ζ(3)α′3+···)Λ2UVM22=29.26×(1−2.62ζ(3)α′3+···)Λ2UVM23=41.10×(1−2.61ζ(3)α′3+···)Λ2UVM24=54.93×(1−2.63ζ(3)α′3+···)Λ2UVM25=70.76×(1−2.66ζ(3)α′3+···)Λ2UVM26=88.60×(1−2.69ζ(3)α′3+···)Λ2UVM27=108.4×(1−2.72ζ(3)α′3+···)Λ2UV.(3.9)Similar behavior is observed for the excited levels of each Kaluza-Klein state.Thus the corrections do not make the Kaluza-Klein states heavier than the glueballs, and the decoupling of the Kaluza-Klein states is not evident to this order.According to Maldacena’s duality,theλ−1/2expansion of the gauge theory corresponds to theα′-expansion of the two-dimensional sigma model with the AdS5black hole×S5as its target space.It is possible that the decoupling of the Kaluza-Klein states takes place only non-perturbatively in the sigma model.AcknowledgmentsWe thank Csaba Cs´a ki,Aki Hashimoto,Yaron Oz,John Terning,and especially David Gross for useful discussions.We thank the Institute for Theoretical Physics at Santa Barbara for its hospitality.This work was supported in part by the NSF grant PHY-95-14797and the DOE grant DE-AC03-76SF00098,and in part by the NSF grant PHY-94-07194through ITP.H.R. and J.T.gratefully acknowledge the support of the A.Carl Helmholz Fellowship in the Department of Physics at the University of California,Berkeley.Appendix:The Boundary Condition at the HorizonIn this appendix,we show that the boundary condition at the horizonρ=b used in the shooting method[1]is consistent,and that the eigenvalue k2and the wavefunction f(ρ)can be evaluated to an arbitrarily high precision using this method.In the neighborhood ofρ=b,the dilaton wave equation takes the form∂ρ(ρ−b)∂ρf(ρ)+···=0.(3.10) Its general solution is of the formf(ρ)=c1[1+α(ρ−b)+···]+c2[log(ρ−b)+···](3.11)with arbitrary coeﬃcients c1,2(the constantαis determined by the wave equation and is in general non-zero).The regularity of the dilatonﬁeld requires c2=0.In the shooting method,we numerically integrate the diﬀerential equation starting from a suﬃciently large value ofρdown to the horizon.For generic k2,the function thus obtained,when expanded as in(3.11),would have c2=0.The task is to adjust k2so that c2=0.Since f(ρ)is divergent atρ=b for generic k2,it is numerically diﬃcult to impose the boundary condition directly atρ=b.Instead,in[1]and in this paper,we required f′=0 atρ=b+ǫfor a given smallǫ(for example,ǫ=0.0000001b in this paper).By(3.11), this condition impliesc2=−c1αǫ+···.(3.12)Therefore,c2can be made arbitrarily small by adjustingǫ.This justiﬁes the numerical method used in[1]and in this paper.We thank Aki Hashimoto for discussions on the numerical method.References[1]C.Cs´a ki,H.Ooguri,Y.Oz and J.Terning,“Glueball Mass Spectrum from Supergravity,”hep-th/9806021.[2]J.M.Maldacena,“The Large N Limit of Superconformal Field Theories and Supergravity,”hep-th/9711200.[3]S.S.Gubser,I.R.Klebanov and A.M.Polyakov,“Gauge Theory Correlators from Non-Critical String Theory,”hep-th/9802109.[4]E.Witten,“Anti-de Sitter Space and Holography,”hep-th/9802150.[5]E.Witten,“Anti-de Sitter Space,Thermal Phase Transition,And Conﬁnement in GaugeTheories,”hep-th/9803131.[6]D.J.Gross and H.Ooguri,“Aspects of Large N Gauge Theory Dynamics as Seen by StringTheory,”hep-th/9805129.[7]H.J.Kim,L.J.Romans and P.Van Nieuwenhuizen,“Mass Spectrum of Chiral Ten-Dimensional N=2Supergravity on S5,”Phys.Rev.D32(1985)389.[8]M.G¨u naydin and N.Marcus,“The Spectrum of The S5Compactiﬁcation of Chiral N=2,D=10Supergravity and The Unitary Supermultiplets of U(2,2/4),”Class.Quant.Grav.2(1985)L11.[9]S.S.Gubser,I.R.Klebanov and A.A.Tseytlin,“Coupling Constant Dependence in theThermodynamics of N=4Supersymmetric Yang-Mills Theory,”hep-th/9805156.[10]M.T.Grisaru,A.E.M.van de Ven and D.Zanon,“Four-Loop Beta Function for theN=1and N=2Supersymmetric Nonlinear Sigma-Model in Two Dimensions,”Phys.Lett.B173(1986)423;M.T.Grisaru and D.Zanon,“Sigma-Model Superstring Corrections to the Einstein-Hilbert Action,”Phys.Lett.B177(1986)347.[11] D.J.Gross and E.Witten,“Superstring Modiﬁcations of Einstein Equation,”Nucl.Phys.B277(1986)1.。

利用Krawtchouk矩不变量实现基于形状的图像检索

（ｏｌｅｆＩｏｍｔｎＳｉｃａｄＴｃｎｌｙＮａｊｇＵｉｒｉｆＣｌｇｎｒａｉｃｎｅｎｅｈｏｏ，ｎｉｎｖｓｔｅｏｆｏｅｇｎｅｙｏ
ＡｒｎｕｉｎＡｔｎｕｉ，ｍｉ１０６ＣｉａｅｏａｔｓｄｓｒａｔｓＮａｎ２０１，ｈｎ）ｃａｏｃｇ
ｗｅｅｒｔｅｅｎｍａｅｒｔｉｖｌｗａｏｌｔｄｏｃ．Ｅｘｅｍｅｔｌｒｓｌｒｉｅ．ＡｏａｉｎｗａｄｒｅｒｖｄａｄｉｇｅｒａｓｃｍｐｅｅｎｅｉｅｐｒｉｎａｅｕｔｗｅｅｇｖｎｓｃｍｐｒｓｓｍａｅｏｂｔｅｈｒｐｓｄｍｅｈｄａｄｔｅｉｇｅｒｅａｔｏｓｎｅｍｅｒｍｅｔｉｖｒａｔｒＺｅｎｋｍｅｔｅｗｅｎｔｅｐｏｏｅｔｏｎｈｍａｅｒｔｖｌｉｍｅｈｄｕｉｇｇｏｔｉｍｏｎｎａｉｎｓｏｒｉｅｍｏｎｃｉｖｒａｔ．ｈｘｅｍｅｔｌｅｕｔｈｗａｅｐｏｏｅｔｏｒｆｃｉｅｉｍａｅｒｔｅａｎｄｉｒｖｓｉｎａｉｎｓＴｅｅｐｒｉｎａｓｌｓｏｔｔｔｒｐｓｄｍｅｈｄｉｍｏｅｅｅｔｎｉｇｅｒｖｌｒｓｈｈｓｖｉａｍｐｏｅｔｓ
ｍｅｓｒｅｗｅｎｆａｕｅｖｃｏｓａｏｔｄＥｕｌｅｎｄｓａｃｕｃｉｎＡｃｏｄｎｏｔｅｓｍｉｒｔｅｒｅｓｍｉｒｉｇｓａｕｅｂｔｅｅｔｅｔｒｄｐｅｃｉａｉｎｅｆｎｔ．ｃｒｉｇｔｉｌｉｄｇｅ，ｉｌｒｄｔｏｈａｙａｍａｅ

卡拉西奥多里实变函数论参考文献

卡拉西奥多里实变函数论参考文献在深入探讨卡拉西奥多里和实变函数论之前，我们应该先了解这两个主题的基本概念。

卡拉西奥多里（Carathéodory）是20世纪著名的希腊数学家，他在实变函数论领域做出了重要贡献。

实变函数论是数学分析中的一个重要领域，研究的是实数域上的函数的性质和性质。

在本文中，我们将以从简到繁、由浅入深的方式来探讨卡拉西奥多里和实变函数论这两个主题。

我们将介绍卡拉西奥多里的生平和学术成就，然后深入探讨实变函数论的基本概念和重要定理。

我们将分析卡拉西奥多里对实变函数论的影响，探讨他对该领域的重要贡献。

我们将总结和回顾本文的内容，共享个人对这两个主题的理解和观点。

一、卡拉西奥多里简介卡拉西奥多里（1873-1950）是一位具有希腊和德国血统的数学家，他在数学分析、复变函数论和实变函数论等领域做出了杰出的贡献。

他曾在德国、俄罗斯和希腊等国家任教，是一位颇具国际影响力的学者。

他对复变函数论和实变函数论的研究成果为这两个领域的发展做出了重要贡献。

二、实变函数论基本概念实变函数论是数学分析中研究实数域上的函数的性质和性质的一个重要分支。

它涉及到实数域上的函数序列、级数、连续性、导数、积分等内容。

实变函数论的基本概念包括实数、实函数、集合论、度量空间、拓扑空间、测度论等知识。

在实变函数论中，有一些重要的定理，如连续映射的性质、一致收敛的性质、傅里叶级数的收敛性等。

三、卡拉西奥多里对实变函数论的贡献卡拉西奥多里在实变函数论领域进行了深入的研究，他提出了许多重要的理论和定理。

其中，卡拉西奥多里收敛定理是他最为著名的成果之一。

这个定理在实变函数论和复变函数论中都有重要的应用。

卡拉西奥多里还对测度论、拓扑空间、可测函数等问题做出了深刻的研究，为实变函数论的发展做出了重要贡献。

四、总结和回顾通过对卡拉西奥多里和实变函数论的深入探讨，我们对这两个主题有了更加全面、深刻和灵活的理解。

卡拉西奥多里作为一位杰出的数学家，在实变函数论领域做出了重要贡献，他的成果对后人的研究产生了深远的影响。

英吉苏凹陷碎屑锆石测年及其对沉积物源的指示

试点的同位索比值和Ｕ．ｂ年龄由专，加权平均年龄及谐和图ＩＴＲｖｒ４０）的绘制采用Ｉｏｌｔ．９ｓｐｏ４成．２ａ完
２测年结果
测年数据较多，品２３１１共分析了３数样（１ｍ）０个
维普资讯
第２卷５
第４期
新
疆
地
质
中图分类号：６２Ｐ３
２００７年１２月
Ｄｅ．（７ｃ２）０
、１２Ｎｏ４ｒ．５０．
ＸＩＩＮＪＡＮＧＧＥ０ＬＯＧＹ
文童编号：１０．８５２０）．５．５００８４（０７０３１０４
３，）同时在白垩系下部选取１个细砂岩样品进行对比据点，品３３３２３ｍ）分析了３样（５．共５个数据点，品样分析（品１．石的分选工作在河北区调队（坊）样）锆廊完１白垩系２５．ｍ）（１共分析２数据点（１，６３４个表）满足统
塔里木盆地英吉苏凹陷侏罗系油气成藏条件优岩浆环带，晶型完整，具有暗色增生边．石多遭少数锆
越，由于侏罗系河流．但扇三角洲陆相沉积变化大，中低孔．中低渗储层复杂，利储盖组合分布规律不明有晰，重影响该区油气勘探的进程【Ｊ严Ｊ．由于该区位于库鲁克塔格山与阿尔金山的交汇部位，深入了解该区沉积物来源方向，沉积相研究与储层预测及油气成对

Constraining theories of low-scale quantum gravity by non-observation of the bulk vector bo

a r X i v :0804.1659v 1 [h e p -p h ] 10 A p r 2008Constraining theories of low-scale quantum gravity bynon-observation of the bulk vector boson signal from the SunR.Horvat,D.Kekez,Z.Kreˇc ak and A.Ljubiˇc i´cRudjer Boˇs kovi´c Institute,P.O.B.180,10002Zagreb,CroatiaAbstract We aim to detect Kaluza-Klein (KK)excitations of the bulk gauge ﬁeld,emitted in a bremsstrahlung process on solar plasma constituents,by looking at a process analogous to the photoelectric eﬀect inside the HPGe ing a generic feature of the underlying eﬀective theory that the unknown 4-dimensional gauge coupling is independent of the number of extra large dimensions δ,we show that the expected number of events in the detector is insensitive to the true scale of quantum gravity for δ=2.With the entire data collection time of 202days in the energy interval 1.7-3.8keV,the number of events detected was as low as 1.1·106,compared to 2.7·106from the expected high multiplicity of the solar KK excitations for δ=2.Hence,our bound from the presumed existence of new forces associated with additional gauge bosons actually conforms with very stringent bounds set from various astrophysical considerations,ruling thereby out the possibility of observing any signal at the LHC for δ=2.Although a dependence on the funda-mental scale referring to (4+δ)-dimensional gravity turns on again for δ=3,the experimental sensitivity of the present setup proves insuﬃcient to draw any constraint for δ>2.In a remarkable proposal of Arkani-Hamed,Dimopoulos and Dvali(ADD)[1],the sce-nario of large extra dimensions has been advocated as an alternative viewpoint capable to shed some light on the gauge hierarchy problem.The radical revision from the standard description of physics beyond SM lies in the fact that low-scale(right above the weak scale) Planck mass M∗and Newton’s constant M−2P l do peacefully coexist,if gravity is allowed to propagate inδextra large compact dimensions.By applying Gauss’law,the simple case of the original Kaluza-Klein(KK)theory[2]can be generalized toδextra dimensions asM2P l=M2+δVδ,(1)∗where,considering aδ-dimensional torus of radius R,Vδ=(2πR)δ.Although the ADD proposal is considered only as a reformulation of the hierarchy problem and not a full solution1,it is still of non-ceasing interest nowadays due to its remarkable phenomenological implications[4].Besides bulk gravitons,the same scenario,in which heavy mass scales in four dimensions are replaced by lighter mass scales in higher dimensions,can be applied to other non-SMﬁelds as well.Examples cover successful application to neutrino [5]as well as axion phenomenology[6].Since the SM has been tested down to distances 10−16cm,much shorter than the compactiﬁcation radius R,such class of higher-dimensional theories is nowadays conventionally considered in the context of the brane paradigm,where all the SM degrees of freedom are localized on a3-brane.The realization of the ADD proposal is possible in type I string theory[7],for example,with the SM degrees of freedom localized on a D-brane.On the observational side,there are two main classes of laboratory tests for the ADD proposal.Theﬁrst searches for possible deviations from Newton’s inverse-squared law in table top experiments[8].Typically,we have M∗>2TeV forδ=2,although model-dependent eﬀects can substantially aﬀect these predictions.The second class deals with the collider bounds,giving M∗>1.45(0.65)TeV forδ=2(6)for the combined LEP-Tevatron data[9],with an extra possibility to study the so-called transplanckian regime at the LHC [10].Much more stringent bounds on gravity inﬂat extra dimensions comes from variety of astrophysical considerations.The most restrictive limits on large extra dimensions comesfrom low measured luminosity of some pulsars,giving M∗>750(35)TeV forδ=2(3)[11]. However,contrary to the collider bounds,these bounds are quite sensitive to the infrared part of the KK graviton spectrum.Yet another possibility is to have gaugeﬁelds in the bulk,gauging B−L(or either B or L separately),for example[4].The limited impact of additional gauge bosons at low energy,due to decoupling of heavy-particle species,may not be the case any more if the new bosons are allowed to propagate freely in the bulk.The one-loop correction of a bulk gauge boson to the muon magnetic moment has already been calculated[12].In the present paper,we aim to observe gauge-boson KK excitations coming from the Sun and emitted in a bremsstrahlung process,e+X→e′+X+b,where X is a proton orαparticle and “b”stands for the KK gauge boson.Our experimental setup has been designed such as to capture KK modes from the Sun in the HPGe detector,in a process analogous to the ordinary photoelectric eﬀect,b+A→e+A′,where now A(A′)refers to the germanium atom.Due to the expected high multiplicity of the solar KK modes,we expect a clear signal above background forδ=2.The important point in testing higher-dimensional eﬀective theory lies in the fact that the relevant combination of the4-dimensional coupling g4and the total number of KK modes in the kinematically allowed interval N tot,g44N tot,turns out to be independent of M∗forδ=2(see below).This means that non-observation of the KK signal would rule out2extra dimensions.Unfortunately,our present experimental setup has no potential to catch a signal above the background forδ>2modes.Considering U(1)gaugeﬁeld propagating in the bulk,the eﬀective4-dimensional coupling, representing a universal coupling of each KK mode to fermions,can be estimated as[4,12] asg24>∼M2∗By plugging(2),we get m A0∼R−1δ=2∼10−4eV,and considering the kinematical cutoﬀ(essentially given by thermal energies of electrons in the Sun of order∼keV),we see that only the far-infrared part of the KK spectrum is aﬀected by m A0.So we can safely disregard m A0in our considerations.With the above preliminaries,we are ready to write down the expected number of event in the detector,diﬀerential with regard to the gauge boson energy E,asdN bdEσb+A→e+A′N Ge t,(3) where N Ge is the number of germanium atoms in the detector,and t is the data collection time.The diﬀerentialﬂux of gauge bosons at Earth in(3),integrated over a standard solar model[13],can be found to bedΦbd2⊙ Sun(n H+4n He)r2dr +∞0dT e dσe+p→e′+p+b(T e)2T e T e n eβ3/2exp(−βT e)π ,(4) where dσe+p→e′+p+b(T e)/dE represents a diﬀerential cross section for the bremsstrahlung process in the Sun,and is given bydσe+p→e′+p+b(T e)πσThm eEln (√T e−E)2δM2P l0246810E keV 10201022102410261028d b d E c m 2s e c 1k e V 1 FIG.1:Energy dependence of the solar ﬂux of KK gauge bosons at Earth,assuming M ∗=1TeV and g 4=10−16.calculating cross section for the production of an individual mode with mass m ,and then integrating over m ’s)in order to show manifestly that by Eqs.(2)and (6)g 44N tot (T e )∼T δeM 2−δ∗ασγ+A →e +A ′,(8)with the data for σγ+A →e +A ′taken from Ref.[15].In Fig.1we display the ﬂux of KK gauge-bosons at Earth as a function of their energy using the typical values for M ∗and g 4.In a bremsstrahlung proces in the Sun most of the gauge bosons will be emitted in the low energy region,as is evident from Fig.1.For energies of a few keV we estimate that the most sensitive process for detection of gauge bosons will be the boson-electric eﬀect on L,M and N electrons,respectively,of germanium atoms.After being ejected from the germanium atoms,their energies,together with subsequently emitted X-rays,will be completely absorbed in our large 1.5kg HPGe crystal.Detector eﬃciency relative to 3”×3”NaI crystal at 30cm was 65%,peak-to-Compton ratio at 1.33MeV was 60:1,and the FWHM at 5.9keV20406080100channels 2 1054 105c o u n t s c h a n n e l 123456keV FIG.2:Number of events in our detector in diﬀerent energy channels.The expected contribution of KK gauge bosons for M ∗=1TeV and g 4=10−16(thick line),the experimental data (full circles)and the interpolation through the experimental data points (thin line)are shown.The 27th channel corresponds to 1.7keV and the 60th channel to 3.8keV.was ∼800eV.Energy calibration was obtained with a set of calibrated radioactive sources.Possible instabilities were controlled on a daily basis,and were less than 1channel,which is equivalent to 0.0634keV.Detector was placed inside an iron box with internal dimensions 54×33×33cm 3and with wall thickness ranging from 16to 23cm.The iron was more than 70years old and was essentially free of 60Co impurities.The box was lined outside with 1cm thick lead and background events were reduced by a faxtor of ∼5.The energy spectra accumulated for ∼202days are shown with full circles in Fig.2.In the low energy region a huge electronic noise dominates,and only spectra above 1.7keV were analyzed.The full line represents the expected KK gauge boson events superimposed on the background.In the energy interval 1.7-3.8keV number of counts of 1.1·106was detected,while for the same energy interval the expected number of detected KK gauge bosons was 2.7·106.Given the smallness of g 4,and the highest mass of the KK excitations in the keV range,in explaining our ﬁnding we can safely ignore the possibility of strong attenuation of the gauge bosons in the Sun as well as the possibility that some particles do not not survive the journey from the Sun.This means that when this experimental result is interpretedin the context of higher-dimensional low-scale gravity and the ADD proposal,two extra dimensions are deﬁnitely ruled out,since by Eq.(7)the eﬀect is expected not to depend on the fundamental scale M∗.Our result actually supersedes the existing stringent astrophysical bounds forδ=2,which had already been considered to excludeδ=2,if the ADD proposal had something to do with the hierarchy problem.Finally,we explore a potential of our detector to observeδ=3KK modes.In this case we see from(7)that a dependence on the fundamental scale shows up,but the eﬀect is additionally suppressed by a factor of T e/M∗compared with theδ=2case.In the same time/energy interval as above we have found the expected number of events to be several orders of magnitude below the background.Since this is far below the background, we conclude that the present experimental setup has no potential to exploreδ>2extra dimensions.In conclusion,we have used a HPGe detector to detect electrons and gammas produced in a U(1)-electric eﬀect when the presumed massive KK modes of the bulk vectorﬁeld hit the detector from the Sun.Our calculation of the expected number of events assumes that massive KK modes were produced in a bremsstrahlung process in the Sun.With no signal detected above background,and a theoretical prediction that for two extra dimensions the expected number of events in the detector is practically independent of the fundamental scale of gravity,we can deﬁnitely rule out the said number of extra dimensions.With the existence of new gauge bosons our result therefore conclusively conﬁrms what a variety of(more model-dependent and thus more uncertain)astrophysical bounds had indicated earlier.In searching for the KK signal from more than two dimensions,we conclude that the limited experimental sensitivity of the present setup has no potential to uncover this possibility.Acknowledgments.The authors acknowledge the support of the Croatian MSES project No.098-0982887-2872.[1]N.Arkani-Hamed,S.Dimopoulos and G.Dvali,Phys.Lett.B429(1998)263.[2]T.Kaluza,Sitzungdber.Press Akad.Wiss.Berlin(Math.Phys.)1921(1921)966;O.Klein,Z.Phys.37(1926)895.[3]N.Arkani-Hamed,L.J.Hall,D.R.Smith and N.Weiner,Phys.Rev.D62(2000)105002.[4]N.Arkani-Hamed,S.Dimopoulos and G.Dvali,Phys.Rev.D59(1999)086004.[5]K.R.Dines,E.Dudas and T.Gherghetta,Nucl.Phys.B557(1999)25;N.Arkani-Hamed,S.Dimopoulos,G.Dvali and J.March-Russell,Phys.Rev.D65(2002)024032.[6]K.R.Dines,E.Dudas and T.Gherghetta,Phys.Rev.D62(2000)105023.[7]I.Antoniadis,N.Arkani-Hamed,S.Dimopoulos and G.Dvali,Phys.Lett.B436(1998)257.[8]For a review,see E.G.Adelberger et al.,Ann.Rev.Nucl.and Part.Sci.53(2003)77.[9]G.F.Giudice and A.Sturmia,Nucl.Phys.B663(2003)377.[10]S.B.Giddings and S.Thomas,Phys.Rev.D65(2002)056010;S.Dimopoulos and nds-berg,Phys.Rev.Lett.87(2001)161602.[11]S.Hannestad and G.G.Raﬀelt,Phys.Rev.Lett.88(2002)071301.[12]M.L.Graesser,Phys.Rev.D61(2000)074019.[13]Solar model BS05(OP)described by J.N.Bahcall,A.M.Serenelli,and S.Basu,Astrophys.J.621(2005)L85.[14] C.Csaki,TASI lectures on extra dimensions and branes,arXiv:hep-ph/0404096.[15]Berger,M.J.,Hubbell,J.H.,Seltzer,S.M.,Chang,J.,Coursey,J.S.,Sukumar,R.,andZucker,D.S.(2005),XCOM:Photon Cross Section Database(version1.3).[Online]Avail-able:/xcom[2008,February29].National Institute of Standards and Technology,Gaithersburg,MD.。

【国家自然科学基金】_条纹分析_基金支持热词逐年推荐_【万方软件创新助手】_20140801

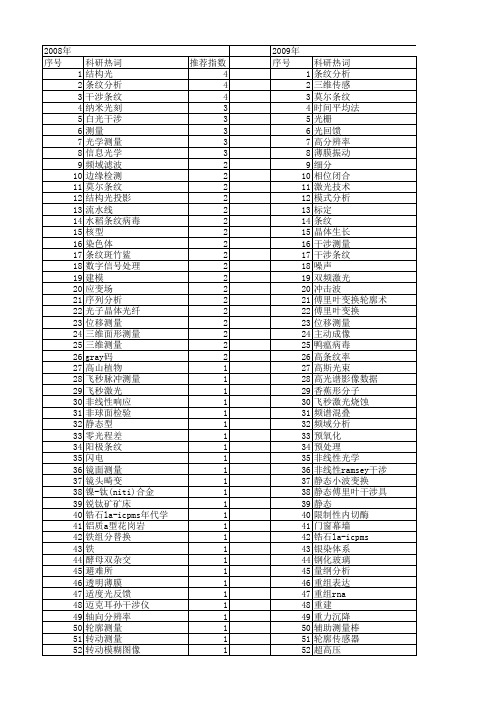
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 1干涉条纹纳米光刻白光干涉测量光学测量信息光学频域滤波边缘检测莫尔条纹结构光投影流水线水稻条纹病毒核型染色体条纹斑竹鲨数字信号处理建模应变场序列分析光子晶体光纤位移测量三维面形测量三维测量 gray码高山植物飞秒脉冲测量飞秒激光非线性响应非球面检验静态型零光程差阳极条纹闪电镜面测量镜头畸变镍-钛(niti)合金锐钛矿矿床锆石la-icpms年代学铝质a型花岗岩铁组分替换铁酵母双杂交避难所透明薄膜适度光反馈迈克耳孙干涉仪轴向分辨率轮廓测量转动测量转动模糊图像
超快时间分辨超定非线性方程组贴片机贝叶斯估计调频回馈误差分析设计计算机层析成像裂纹群裂纹扩展速率表面质量表面等离子体共振表面周期性条纹补偿衍射花样螺旋自旋序蛋白质芯片蛋白质组学蛋白质组致病性自组装脊波变换脉冲数字全息缺陷结构光经验模态分解细分电路线结构光线宽展宽因子纳米级位移红花红外分析系统学意义精度标定精密测量等离子体空间相关方法空间相位调制空间滤波移相器离焦打靶离散小波变换磨料水射流磁交换作用碱性岩相干编码成像相位轮廓术相位检测相位标靶相位疲劳断口电离层总电子含量电子结构甚长基线干涉测量:全球定位系统

多标量场产生的膜世界

多标量场产生的膜世界膜世界理论在解决层次问题，宇宙学常数，暗物质暗能量等问题上取得了巨大的进展。

本文首先回顾了额外维和膜世界理论的发展历史。

然后我们从高维弯曲时空中多标量场产生的膜中得到了新的解，在这个解中有一个参数 b 它可以决定能量密度T 00 的分布。

只有当0<b≤1时，才能生成膜世界。

我们考虑物质场在这个膜上的局域化，对于自由标量场和自由矢量场而言，我们发现零模可以局域化到膜上。

在我们引入了矢量场与背景标量场的耦合e τΨF MN F MN 后，发现耦合参数3b ->τ时，零模也能局域化到膜上。

然而自由的Kalb-Ramond 场的零模一般是不能局域化到膜上的，但是在引入KR 场与背景标量场的耦合 e ζΨH MNL H MNL 之后，在()b b 3/2->ζ时，KR 场也可以局域化到膜上。

研究几种重要的物质场在膜上的局域化成功验证了这个新厚膜解的理论合理性。

关键词：额外维，膜世界，KK 模式第一章绪论1.1 额外维理论浩瀚的宇宙中有着说不尽的秘密，维度之谜或许就是其中之一。

我们的世界真的是三维空间吗？是否有额外的维度存在？如果真的有额外的空间维度存在，那为什么我们从来没有察觉到它们的存在？在从婴儿时代起各种常识就不断的加深我们三维世界的固有认识，而不去怀疑是否存在额外的维度。

然后细细想来，千百年来人类所总结出的物理学的基本原理中没有一条是依赖于世界的三维空间性的，这不仅不能否认额外维的存在，反而说明我们对额外维度的存在性一无所知。

取得巨大成功的广义相对论并没有对空间的维度做出限制，这一点提示我们构建一个高维引力理论的可行性。

其实早在1914年1,Gunnar Nordström就提出了五维形式的标量引力理论[1,2]，试图将引力统一到Maxwell理论之中。

之后由于广义相对论的巨大成功，该理论很快就被人们所遗忘，但这一突破性地引入额外维的实践却启示了后来者：额外维度在物理学的统一之路上将占据及其重要的位置。

北京大学科技成果——拉普拉斯域光学乳腺影像系统(LD-DOT)

北京大学科技成果——拉普拉斯域光学乳腺影像系
统（LD-DOT）
项目概述
拉普拉斯域光学乳腺影像系统（LD-DOT）是一种基于漫反射光成像原理的功能成像手段。

有别于基于形态学进行诊断的传统医学成像手段，它利用不同病变的乳腺组织对光的漫反射程度的不同，通过得到双乳全局血管微循环特征参数的定量分布来诊断组织病理属性（正常/良性/恶性）以及分布范围，探测深度可达6厘米以上，扫描过程安全快速，结果直接客观，是一种经济高效的诊断乳腺病变的无创方法。

应用范围
本系统可用于例行的乳腺检查、乳腺癌筛查，提供定量的生理信息可帮助医生对患者进行早期的乳腺癌诊断，准确区分正常组织与良性、恶性肿瘤。

由于该系统便携程度高，不仅适用于医院、体检中心筛查，也适用于流动医疗工作站。

另外，系统技术也可扩展到脑血管相关研究，如中风监控、脑活动跟踪等。

技术优势
系统技术先进性主要体现在：
（1）成本低廉成像质量高
DOT领域的自主技术创新（美国专利8649010），克服传统DOT 技术以及常用影像学手段无法兼顾成像质量和成本的局限；
（2）准确性高
由定量生理信息的检测来形成诊断依据，灵敏度，特异性均高于其他影像学方法，不存在读图差异；
（3）无创且无放射性
使用对人体无害的低能量近红外光，适用不同年龄段广大人群密集跟踪检查；
（4）便携度高，对环境无特殊要求。

研究阶段
该技术前期已在新加坡国家肿瘤中心进行了临床验证，目前正在制造第二代样机，并与相关三甲医院达成人体实验合作意向，处于中试早期阶段。

设备目标市场定位于体检机构、高端美容院、社区医院等。

克里雅河下游丹丹乌里克遗址区沉积物光释光年龄的计算

克里雅河下游丹丹乌里克遗址区的沉积物光释光年龄计算是一种用于确定沉积物年龄的方法，通常是用于考古学和地质学研究中。

这种方法利用沉积物中的矿物颗粒中所含的光释光材料，来估算这些沉积物的年代。

下面是大致的步骤：
1. 样本采集：首先，需要采集沉积物样本，通常是从遗址区域的深层中获取的。

这些样本需要精心标记和记录，以确保后续分析的准确性。

2. 样本制备：采集的样本需要进行样品制备，通常是将沉积物中的颗粒分离出来，并且精细研磨以准备进行分析。

3. 光释光测量：样本中的石英或长石等矿物颗粒含有捕获电子的能力。

当这些颗粒受到自然辐射（如太阳光或自然辐射）时，它们会捕获一些电子。

然后，当这些颗粒受到激发光源（通常是激光或红外光）时，它们会释放先前捕获的电子，产生可测量的光释光信号。

这个信号的大小与沉积物中颗粒所暴露于自然辐射的时间长短有关。

4. 建立光释光剂量-深度曲线：为了确定沉积物年龄，研究人员需要建立一个光释光剂量-深度曲线。

这个曲线描述了光释光信号与沉积物深度之间的关系。

通常，这需要对不同深度的样本进行光释光测量。

5. 计算年龄：一旦建立了光释光剂量-深度曲线，就可以使用它来计算样本的光释光年龄。

这通常涉及到比较样本的光释光信号与曲线上的标准信号，以确定沉积物的年代。

需要注意的是，光释光年龄计算的准确性取决于许多因素，包括样本制备的质量、实验条件的准确性以及曲线的建立过程。

因此，这是一个需要高度专业知识和经验的技术，通常由专门的实验室和科学家来执行。

Klein瓶上达到最大因子临界度的图的刻画（英文）

Klein瓶上达到最大因子临界度的图的刻画（英文）
李秋丽
【期刊名称】《兰州大学学报：自然科学版》
【年(卷),期】2017(53)2
【摘要】若从一个阶数为n的图中任意删除p(p<n)个点之后都有完美匹配,则称此图是p-因子临界的.给定曲面Σ,令p(Σ)为最小的正整数满足此曲面上的图都不是p(Σ)-因子临界的.文献[9]证明了p(N_2)=6,其中N_2代表曲面Klein瓶.即Klein 瓶上的图最多是5-因子临界的.刻画了Klein瓶上所有5-因子临界图.
【总页数】4页(P241-243)
【作者】李秋丽
【作者单位】兰州大学数学与统计学院
【正文语种】中文
【中图分类】O157;O158
【相关文献】
1.独立集可削去因子临界图和无爪的独立集可削去因子临界图的度条件
2.关于临界h棱连通图的最大棱数及最大图的结构（Ⅱ）：临界h棱连通图的性质...
3.一类项链图在Klein瓶上的嵌入
4.具有最大控制数的连通图的刻画(英文)
5.广义指数达到最大值的竞赛图的刻画
因版权原因，仅展示原文概要，查看原文内容请购买。

印度Karnataka克拉通元古代Kaladgi石英砂岩中的微型剪切带

印度Karnataka克拉通元古代Kaladgi石英砂岩中的微型剪切带Jadh.,PB;刘永江【期刊名称】《世界地质》【年(卷),期】1991(010)001【摘要】在印度Karnataka北部Lokapur地区的玻璃状石英岩中,可以观察到石英集合体在增加和连续应变环境中对变形作用的异常反应。

细粒石英岩是斑状灰岩、石英岩和泥质岩多层序列中最强干的岩性单位,这一序列组成了双倾伏向斜构造,轴向为西-北西-东-南东,褶皱的幅度高波长短。

与向斜轴向相切的异常层面破裂,可以清楚地在航空照片上识别出来。

然而,石英集合体异常行为的表而显示在露头上是非常微弱的,因此,这儿应用了“微型剪切带”的概念。

石英残斑显示的大量显微构造说明,在局部域中存在着复杂的变形作用环境。

在显微薄片中识别出两组主要剪切面,其所夹锐角为65～70°,与优选定向方位的夹角为20°。

沿剪切面分布的残斑显示出对变形作用反应的不一致性。

【总页数】2页(P118-119)【作者】Jadh.,PB;刘永江【作者单位】不详;不详【正文语种】中文【中图分类】P588.341【相关文献】1.克拉通和古生代造山带中的韧性剪切带型金矿:金矿成矿条件与成矿环境分析 [J], 朱永峰2.印度Karnataka克拉通元古代Kaladgi石英岩的共轴变形作用 [J], Jadh.,PB;刘永江3.南印度克拉通地质:太古代和元古代构造背景之间对比 [J], Naqvi,SM;徐学纯4.华北克拉通孔兹岩带古元古代凉城石榴石花岗岩成因机制及其岩石学意义 [J], 王洛娟;郭敬辉;彭澎5.华北克拉通中北部古元古代碰撞造山时限:来自强过铝花岗岩和韧性剪切时代的制约 [J], 张华锋;罗志波;周志广;柳长峰因版权原因，仅展示原文概要，查看原文内容请购买。

布拉舍实验报告

一、实验目的通过布拉格衍射实验，了解布拉格衍射的基本原理，掌握X射线衍射的基本方法，学会利用X射线衍射分析晶体结构，并加深对晶体学知识的理解。

二、实验原理布拉格衍射是指当X射线照射到晶体上时，由于晶体中原子排列的周期性，X射线会发生衍射现象。

根据布拉格定律，衍射条件可以表示为：\[ 2d\sin\theta = n\lambda \]其中，\( d \) 为晶面间距，\( \theta \) 为入射角，\( n \) 为衍射级数，\( \lambda \) 为X射线的波长。

通过测量衍射角 \( \theta \) 和已知波长 \( \lambda \)，可以计算出晶面间距\( d \)，从而推断出晶体的结构。

三、实验器材1. X射线衍射仪2. 晶体样品3. 计算器4. 测量尺5. 数据记录表四、实验步骤1. 将晶体样品固定在X射线衍射仪的样品架上。

2. 调整X射线衍射仪，使X射线束垂直照射到晶体样品上。

3. 打开X射线衍射仪，记录衍射图谱。

4. 根据衍射图谱，测量各个衍射峰的衍射角 \( \theta \)。

5. 利用布拉格定律，计算出晶面间距 \( d \)。

6. 根据晶面间距 \( d \)，推断出晶体的结构。

五、实验结果与分析1. 实验数据：| 衍射峰 | 衍射角 \( \theta \) (°) | 晶面间距 \( d \) (Å) || ------ | ------------------------ | --------------------- || 1 | 15.0 | 2.3 || 2 | 25.0 | 1.8 || 3 | 35.0 | 1.5 |2. 分析：根据实验数据，我们可以计算出晶体的晶面间距。

通过对比标准晶体数据，我们可以推断出实验晶体的结构。

例如，若实验晶体的晶面间距与立方晶系中某晶体的晶面间距相匹配，则可判断实验晶体为立方晶系。

六、实验结论通过布拉格衍射实验，我们成功了解了布拉格衍射的基本原理，掌握了X射线衍射的基本方法，并利用实验数据推断出晶体的结构。

荧光靶历史图像数据存储系统设计与实现

荧光靶历史图像数据存储系统设计与实现
吴汉楠;岳敏;马涛;张玮;张洁
【期刊名称】《强激光与粒子束》
【年(卷),期】2024(36)7
【摘要】针对兰州重离子研究装置(HHIRFL)荧光靶历史图像数据存储系统所产生的数据不断递增和历史数据检索速度慢的问题,构建了基于MongoDB数据库的荧光靶历史图像数据存储系统。

为了能够保存和观测分析荧光靶束流图像,搭建了基于EPICS的历史数据归档系统获取荧光靶图像过程变量(PV)数据,用MongoDB数据库分片技术对所得数据进行存储,通过Django框架完成图像的转化和Web页面的实现,并在系统中应用了图像分类算法,提高了数据读写的速率。

该系统在HIRFL 上可以稳定获取、存储、观测荧光靶束流历史图像,为束流分析、调束工作提供了便利。

【总页数】7页(P69-75)
【作者】吴汉楠;岳敏;马涛;张玮;张洁
【作者单位】西北师范大学物理与电子工程学院;中国科学院近代物理研究所【正文语种】中文
【中图分类】TL507
【相关文献】
1.基于图像处理技术的自动报靶系统设计和实现
2.基于LVDS的高速图像数据存储器的设计与实现
3.基于SD卡的BMS海量历史数据存储系统设计
4.基于LVDS的高速图像数据存储系统设计
5.基于USB芯片的图像数据存储与回读系统设计
因版权原因，仅展示原文概要，查看原文内容请购买。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Contents
1 Introduction 2 N = 4 SYM on the Coulomb branch 3 KK reduction with gauge invariant variables 3.1 3.2 Gauge invariance at linear order . . . . . . . . . . . . . . . . . . . . . . . . Gauge invariance at quadratic order . . . . . . . . . . . . . . . . . . . . . . 2 6 8 10 11 14 14 15 18 18 21 22 23 26 26 27 31 33 37 38 38 41 42 43
1/2 dx2 ds2 = H (x⊥ )−1/2 dx2 ⊥ || + H (x⊥ )
monic function in transverse directions. For a distribution σ (y ) of D3 branes, the harmonic function reads H (x⊥ ) = d6 y Q0 σ (y ) = 4 4 |x⊥ − y| r 1+
ABSTRACT
We construct a holographic map between asymptotically AdS5 × S 5 solutions of 10d supergravity and vacuum expectation values of gauge invariant operators of the dual QFT. The ingredients that enter in the construction are (i) gauge invariant variables so that the KK reduction is independent of any choice of gauge ﬁxing; (ii) the non-linear KK reduction map from 10 to 5 dimensions (constructed perturbatively in the number of ﬁelds); (iii) application of holographic renormalization. A non-trivial role in the last step is played by extremal couplings. This map allows one to reliably compute vevs of operators dual to any KK ﬁelds. As an application we consider a Coulomb branch solution and compute the ﬁrst two non-trivial vevs, involving operators of dimension 2 and 4, and reproduce the ﬁeld theory result, in agreement with non-renormalization theorems. This constitutes the ﬁrst quantitative test of the gravity/gauge theory duality away from the conformal point involving a vev of an operator dual to a KK ﬁeld (which is not one of the gauged supergravity ﬁelds).
5 Holographic 1-point functions 5.1 5.2 5.3 5.4 Generalities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5d supergravity ﬁelds . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . KK modes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Extremal couplings . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
hep-th/0603016 ITFA-2006-04
Kaluza-Klein Holography
arXiv:hep-th/0603016v2 9 May 2006
Kostas Skenderis and Marika Taylor Institute for Theoretical Physics, University of Amsterdam, Valckenierstraat 65, 1018XE Amsterdam, The Netherlands skenderi,taylor@science.uva.nl
7 Conclusions A Harmonic expansion of the antisymmetric tensor B Spherical harmonics B.1 Spherical harmonics with SO(4) symmetry . . . . . . . . . . . . . . . . . . C Field equations up to second order C.1 Scalar ﬁelds . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C.2 Tensor ﬁelds . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 Field equations 4.1 4.2 Linear order . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Quadratic order . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1
Introduction
Gravity/gauge theory dualities relate string theory on spacetimes that asymptote to AdSm × X , where X is a compact manifold and gauge theory residing on the conformal boundary of the AdS part of the geometry. In the initial work [1] the dual theory was a conformal ﬁeld theory (CFT) and the bulk spacetime AdSm × X (rather than asymptotic to it), but it was soon recognized that the duality can be extended to describe quantum ﬁeld theories that can be obtained from the CFT by either adding new terms in the action or considering vacua where the conformal symmetry is spontaneously broken. Both of these cases are described gravitationally by a solution that is asymptotic to AdSm × X . Despite much work however basic questions still remain. One such question that will be the subject of this paper is: Given a ten dimensional solution that is asymptotic to AdSm × X how does one compute the vacuum expectation values of gauge invariant operators? Roughly speaking vevs of chiral primary operators should appear in the radial expansion of the bulk solution. However making this precise proves to be a lot more subtle that one might have anticipated, and even qualitative features are not reproduced correctly by naive methods. The answer to this question should follow from the basic AdS/CFT dictionary [2, 3]. This is indeed the case but in order to implement the idea one has to sharpen existing methods and overcome several technical issues. To illustrate the issues involved it is instructive to consider a simple example where the physics of the solution is well understood. A class of such examples is provided by multicenter D3-brane solutions, which in the near-horizon limit correspond to the Coulomb branch of N = 4 SYM [4]. These examples are particularly interesting because the QFT vevs are protected by a non-renormalization theorem, and the gravitational results must therefore agree exactly with those computed at weak coupling. The metric is of the wellknown form