数字信号实验1
数字信号处理实验

数字信号处理实验实验一信号、系统及系统响应1、实验目的认真复习采样理论、离散信号与系统、线性卷积、序列的z 变换及性质等有关内容;掌握离散时间序列的产生与基本运算,理解离散时间系统的时域特性与差分方程的求解方法,掌握离散信号的绘图方法;熟悉序列的z 变换及性质,理解理想采样前后信号频谱的变化。
2、实验内容a. 产生长度为500 的在[0,1]之间均匀分布的随机序列,产生长度为500 的均值为0 单位方差的高斯分布序列。
b. 线性时不变系统单位脉冲响应为h(n)=(0.9)nu(n),当系统输入为x(n)=R10(n)时,求系统的零状态响应,并绘制波形图。
c. 描述系统的差分方程为:y(n)-y(n-1)+0.9y(n-2)=x(n),其中x(n)为激励,y(n)为响应。
计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位脉冲响应h(n);计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位阶跃响应s(n);由h(n)表征的这个系统是稳定系统吗?d. 序列x(n)=(0.8)nu(n),求DTFT[x(n)],并画出它幅度、相位,实部、虚部的波形图。
观察它是否具有周期性?e. 线性时不变系统的差分方程为y(n)=0.7y(n-1)+x(n),求系统的频率响应H(ejω),如果系统输入为x(n)=cos(0.05πn)u(n),求系统的稳态响应并绘图。
f. 设连续时间信号x(t)=e-1000|t|,计算并绘制它的傅立叶变换;如果用采样频率为每秒5000 样本对x(t)进行采样得到x1(n),计算并绘制X1(ejω),用x1(n)重建连续信号x(t),并对结果进行讨论;如果用采样频率为每秒1000 样本对x(t)进行采样得到x2(n),计算并绘制X2(ejω),用x2(n)重建连续信号x(t),并对结果进行讨论。
加深对采样定理的理解。
g. 设X1(z)=z+2+3z-1,X2(z)=2z2+4z+3+5z-1,用卷积方法计算X1(z)X2(z)。
数字信号处理上机实验1

数字信号处理实验信息252120502123赵梦然实验一快速傅里叶变换与信号频谱分析一.实验目的1. 在理论学习的基础上,通过本实验加深对离散傅里叶变换的理解。
2. 熟悉并掌握按时间抽取编写快速傅里叶变换(FFT)算法的程序。
3. 了解应用FFT 进行信号频谱分析过程中可能出现的问题,例如频谱混淆、泄漏、栅栏效应等,以便在实际中正确使用FFT 算法进行信号处理。
二.实验内容1. 仔细分析教材第六章“时间抽取法FFT 的FORTRAN 程序”,编写出相应的使用FFT 进行信号频谱分析的Matlab 程序。
2. 用FFT 程序分析正弦信号,分别在以下情况进行分析,并讨论所得的结果:a) 信号频率F=50Hz,采样点数N=32,采样间隔T=0.000625s;b) 信号频率F=50Hz,采样点数N=32,采样间隔T=0.005s;c) 信号频率F=50Hz,采样点数N=32,采样间隔T=0.0046875s;d) 信号频率F=50Hz,采样点数N=32,采样间隔T=0.004s;e) 信号频率F=50Hz,采样点数N=64,采样间隔T=0.000625s;f) 信号频率F=250Hz,采样点数N=32,采样间隔T=0.005s;g) 将c)中信号后补32 个0,做64 点FFT,并与直接采样64 个点做FFT 的结果进行对比。
3. 思考题:1) 在实验a)、b)、c)和d)中,正弦信号的初始相位对频谱图中的幅度特性是否有影响?为什么?信号补零后做FFT 是否可以提高信号频谱的分辨率?为什么?三.实验程序function pushbutton1_Callback(hObject, eventdata, handles)F=str2double(get(handles.f,'string'));N=str2double(get(handles.n,'string'));T=str2double(get(handles.t,'string'));fai=str2double(get(handles.fai,'string'));zero=get(handles.zero,'value');%进行采样t=0:T:(N-1)*T;x=cos(2*pi*F*t+fai);%进行fft运算if zeroy=abs(fft(x,N+32));y=y/max(y);elsey=abs(fft(x));y=y/max(y);end%画图axes(handles.axes2);stem((0:N-1),x,'*');axes(handles.axes1);if zerostem((0:N+31),y,'.');elsestem((0:N-1),y);endxlabel('频率/Hz');ylabel('振幅');grid on;四.实验结果实验数据记录:(a)输入信号频率:50输入采样点数:32输入间隔时间:0.000625是否增加零点?否信号频率F=50Hz,采样长N=32,采样周期T=0.000625s,fs=1/T=1600Hz,基频为fs/N=50Hz,50/50=1.故此在频谱图上的第1个点和第31个点有值。
实验一 数字信号源实验(1)

实验一数字信号源实验一、实验目的1、了解单极性码、双极性码、归零码、不归零码等基带信号波形特点。
2、掌握集中插入帧同步码时分复用信号的帧结构特点。
3、掌握数字信号源电路组成原理。
二、实验内容1、用示波器观察单极性非归零码(NRZ)、帧同步信号(FS)、位同步时钟(BS)。
2、用示波器观察NRZ、FS、BS三信号的对应关系。
3、学习电路原理图。
三、基本原理本模块是实验系统中数字信号源,即发送端,其原理方框图如图1-1所示。
本单元产生NRZ信号,信号码速率约为170.5KB,帧结构如图1-2所示。
帧长为24位,其中首位无定义,第2位到第8位是帧同步码(7位巴克码1110010),另外16位为2路数据信号,每路8位。
此NRZ信号为集中插入帧同步码时分复用信号。
发光二极管亮状态表示‘1’码,熄状态表示‘0’码。
本模块有以下测试点及输入输出点:∙ CLK-OUT 时钟信号测试点,输出信号频率为4.433619MHz ∙ BS-OUT 信源位同步信号输出点/测试点,频率为170.5KHz ∙ FS 信源帧同步信号输出点/测试点,频率为7.1KHz∙ NRZ-OUT NRZ信号输出点/测试点图1-3为数字信源模块的电原理图。
图1-1中各单元与图1-3中的元器件对应关系如下:∙晶振CRY:晶体;U1:反相器7404∙分频器US2:计数器74161;US3:计数器74193;US4:计数器40160∙并行码产生器KS1、KS2、KS3:8位手动开关,从左到右依次与帧同步码、数据1、数据2相对应;发光二极管左起分别与一帧中的24位代码相对应∙八选一US5、US6、US7:8位数据选择器4512∙三选一US8:8位数据选择器4512∙倒相器US10:非门74HC04∙抽样US9:D触发器74HC74图1-1 数字信源方框图图1-2 帧结构下面对分频器,八选一及三选一等单元作进一步说明。
(1)分频器74161进行13分频,输出信号频率为341kHz。
实验一 数字信号处理 实验报告

1.已知系统的差分方程如下式:y1(n)=0.9y1(n-1)+x(n)程序编写如下:(1)输入信号x(n)=R10 (n),初始条件y1(-1)=1,试用递推法求解输出y1(n);a=0.9; ys=1; %设差分方程系数a=0.9,初始状态: y(-1)=1xn=ones(1,10); %矩型序列R10(n)=u(n)-u(n-10),定义其宽度为0~9n=1:35; %设差分方程系数a=0.9,初始状态: y(-1)=1xn=sign(sign(10-n)+1);B=1;A=[1,-a]; %差分方程系数xi=filtic(B,A,ys); %由初始条件计算等效初始条件输入序列xiyn=filter(B,A,xn,xi); %调用filter解差分方程,求系统输出y(n)n=0:length(yn)-1;subplot(2,1,1);stem(n,yn,'linewidth',2); axis([-5,15,0,8]); grid ontitle('图(a) y1(n)=0.9y1(n-1)+x(n) 初始条件y1(-1)=1 ');xlabel('n');ylabel('y(n)')(2) 输入信号x(n)=R10 (n),初始条件y1(-1)=0,试用递推法求解输出y1(n)。
a=0.9; ys=0; %设差分方程系数a=0.9,初始状态: y(-1)=1xn=ones(1,10); %矩型序列R10(n)=u(n)-u(n-10)B=1;A=[1,-a]; %差分方程系数xi=filtic(B,A,ys); %由初始条件计算等效初始条件输入序列xiyn=filter(B,A,xn,xi); %调用filter解差分方程,求系统输出y(n)n=0:length(yn)-1;subplot(2,1,2);stem(n,yn, 'linewidth',2); axis([-5,15,0,8]); grid ontitle('图(b) y1(n)=0.9y1(n-1)+x(n) 初始条件y1(-1)=0 ');xlabel('n');ylabel('y(n)') 图形输出如下:-505101502468图(a) y1(n)=0.9y1(n-1)+x(n) 初始条件y1(-1)=1ny (n )-55101502468图(b) y1(n)=0.9y1(n-1)+x(n) 初始条件y1(-1)=0ny (n )2. 已知系统差分方程为: y 1(n )=0.9y 1(n -1)+x (n ) 用递推法求解系统的单位脉冲响应h (n ),要求写出h (n )的封闭公式,并打印h (n )~n 曲线。
数字信号处理实验报告1-5

实验一时域离散信号的产生及时域处理实验目的:了解Matlab软件数字信号处理工具箱的初步使用方法。
掌握其简单的Matlab语言进行简单的时域信号分析。
实验内容:[1.1]已知两序列x1=[0,1,2,3,4,3,2,1,0];n1=[-2:6];x2=[2,2,0,0,0,-2,-2],n2=[2:8].求他们的和ya及乘积yp. 程序如下:x1=[0,1,2,3,4,3,2,1,0];ns1=-2;x2=[2,2,0,0,0,-2,-2];ns2=2;nf1=ns1+length(x1)-1;nf2=ns2+length(x2)-1;ny=min(ns1,ns2):max(nf1,nf2);xa1=zeros(1,length(ny));xa2=xa1;xa1(find((ny>=ns1)&(ny<=nf1)==1))=x1;xa2(find((ny>=ns2)&(ny<=nf2)==1))=x2;ya=xa1+xa2yp=xa1.*xa2subplot(4,4,1),stem(ny,xa1,'.')subplot(4,1,2),stem(ny,xa2,'.')line([ny(1),ny(end)],[0,0])subplot(4,1,3),stem(ny,ya,'.')line([ny(1),ny(end)],[0,0])subplot(4,1,4),stem(ny,yp,'.')line([ny(1),ny(end)],[0,0])[1.2]编写产生矩形序列的程序。
并用它截取一个复正弦序列,最后画出波形。
程序如下:clear;close alln0=input('输入序列起点:n0=');N=input('输入序列长度:N=');n1=input('输入位移:n1=');n=n0:n1+N+5;u=[(n-n1)>=0];x1=[(n-n1)>=0]-[(n-n1-N)>=0];x2=[(n>=n1)&(n<(N+n1))];x3=exp(j*n*pi/8).*x2;subplot(2,2,1);stem(n,x1,'.');xlabel('n');ylabel('x1(n)');axis([n0,max(n),0,1]);subplot(2,2,3);stem(n,x2,'.');xlabel('n');ylabel('x2(n)');axis([n0,max(n),0,1]);subplot(2,2,2);stem(n,real(x3),'.'); xlabel('n');ylabel('x3(n)的实部');line([n0,max(n)],[0,0]);axis([n0,max(n),-1,1]);subplot(2,2,4);stem(n,imag(x3),'.'); xlabel('n');ylabel('x3(n)的虚部');line([n0,max(n)],[0,0]);axis([n0,max(n),-1,1]);[1.3]利用已知条件,利用MATLAB生成图形。
实验1常见数字信号的产生和显示

信息工程学院实验报告课程名称:数字信号处理实验项目名称:实验1常见数字信号的产生与显示 实验时间:班级: 姓名: 学号:一、实验目的复习MATLAB 的使用方法和基本功能;熟悉单位冲激序列、单位阶跃序列、矩形序列和指数序列等常用序列的产生;掌握利用MATLAB 画图函数显示信号波形的方法。
二、实验设备与软件MATLAB 2008软件。
三、实验内容及结果分析3.1 分别给出模拟信号1()sin(10)2cos(20)x t t t ππ=+在采样周期T1=1/100s 和模拟信号42()sin(5000)2cos(10)x t t t ππ=+在采样周期T2=1/50 000s 下得到的离散时间信号,作出波形图。
指令语句如下:t=-20:20;x=sin(10*pi*t/100)+2*cos(20*pi*t/100); y=sin(5000*pi*t/50000)+2*cos(10.^4*pi*t/50000); close all ; subplot(1,2,1); stem(t,x); title('x1'); subplot(1,2,2); stem(t,y); title('x2');执行结果如图3-1所示:图3-13.2 作出实指数序列在a 分别等于 -0.5 和 -1.5时候的信号波形图。
指令语句如下:N=10; n=0:N-1; a=-0.5; b=-1.5; x=a.^n; y=b.^n; close all ; subplot(1,2,1); stem(n,x);title('a 为-0.5的实指数序列'); subplot(1,2,2); stem(n,y);title('a 为-1.5的实指数序列');执行结果如图3-2所示:x1x20510a 为-1.5的实指数序列图3-23.3 某正弦信号的幅值为1,初始初始相位为0,频率为10Hz ,作出其在0.5s 内的波形图;若在正弦信号上叠加范围在0~ 0.2之间的均匀分布的白噪声,试作出0.5s 内的新的波形图。
实验一__信号、系统及系统响应lx

北华大学数字信号实验实验项目:信号、系统及系统响应班级:信息10-1姓名:张慧学号:36实验一 信号、系统及系统响应一.实验目的1.熟悉理想采样的性质,了解信号采用前后的频谱变化,加深对采样定理的理解。
2.熟悉离散信号和系统的时域特性。
3.熟悉线性卷积的计算编程方法:利用卷积的方法,观察、分析系统响应的时域特性。
4.掌握序列傅氏变换的计算机实现方法,利用序列的傅氏变换对离散信号、系统及系统响应进行频域分析。
二.实验原理1.连续时间信号的采样)()()(ˆt M t x t xa a = 其中)(ˆt xa 是连续信号)(t x a 的理想采样,)(t M 是周期冲激脉冲 ∑+∞-∞=-=n nT t t M )()(δ它也可以用傅立叶级数表示为:∑+∞-∞=Ω=n tjm s e T t M 1)(其中T 为采样周期,T s /2π=Ω是采样角频率。
设)(s X a 是连续时间信号)(t x a 的双边拉氏变换,即有:⎰+∞∞--=dt e t x s X sta a )()( 此时理想采样信号)(ˆt x a 的拉氏变换为 ∑⎰+∞-∞=+∞∞--Ω-===m s a sta ajm s X T dt e t x s X )(1)(ˆ)(ˆ作为拉氏变换的一种特例,信号理想采样的傅立叶变换[]∑+∞-∞=Ω-Ω=Ωm s a a m j X T j X )(1)(ˆ∑+∞-∞=-=n nzn x z X )()(以ωj e 代替上式中的z ,就可以得到序列)(n x 的傅立叶变换 ∑+∞-∞=-=n nj j en x e X ωω)()(具有如下关系:Tj a e X j X Ω==Ωωω)()(ˆ信号卷积∑+∞-∞=-=*=m m n h m x n h n x n y )()()()()()()()(z H z X z Y =)()()(ωωωj j j e H e X e Y =三.实验内容及步骤1, 分析理想采样的特性。
数字信号处理实验一

实验一 离散时间信号分析一、实验目的1.熟悉MATLAB 应用环境,常用窗口的功能和使用方法。
2.掌握各种常用的序列,理解其数学表达式和波形表示。
3.掌握在计算机中生成及绘制数字信号波形的方法。
4.掌握序列的相加、相乘、移位、反褶、卷积等基本运算及计算机实现。
5.通过编程,上机调试程序,进一步增强使用计算机解决问题的能力。
二、实验原理1.序列的基本概念离散时间信号是指在离散时刻才有定义的信号,简称离散信号,或者序列。
离散时间信号在数学上可用时间序列)}({n x 来表示,其中)(n x 代表序列的第n 个数字,n 代表时间的序列,n 的取值范围为∞<<∞-n 的整数,n 取其它值)(n x 没有意义。
离散时间信号可以是由模拟信号通过采样得到,例如对模拟信号)(t a x 进行等间隔采样,采样间隔为T ,得到一个有序的数字序列)}({nT x a 就是离散时间信号,简称序列。
2.常用序列常用序列有:单位脉冲序列(单位抽样))(n δ、单位阶跃序列)(n u 、矩形序列)(n R N 、实指数序列、复指数序列、正弦型序列等。
3.序列的基本运算序列的运算包括移位、反褶、和、积、点乘、累加、差分运算、卷积等。
4.序列的卷积运算)()()()()(n h n x m n h m x n y m *=-=∑∞-∞=上式的运算关系称为卷积运算,式中*代表两个序列卷积运算。
两个序列的卷积是一个序列与另一个序列反褶后逐次移位乘积之和,故称为离散卷积,也称两序列的线性卷积。
其计算的过程包括以下4个步骤(1)反褶:先将)(n x 和)(n h 的变量n 换成m ,变成)(m x 和)(m h ,再将)(m h 以纵轴为对称轴反褶成)(m h -。
(2)移位:将)(m h -移位n ,得)(m n h -。
当n 为正数时,右移n 位;当n 为负数时,左移n 位。
(3)相乘:将)(m n h -和)(m x 的对应点的值相乘。
数字信号处理实验报告

数字信号处理实验报告通信0303 汪勇 学号:实验一:信号、系统及系统响应 1、实验目的:(1) 熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解. (2) 熟悉时域离散系统的时域特性(3) 利用卷积方法观察分析系统的时域特性.(4) 掌握序列傅立叶变换的计算机实现方法,利用序列的傅立叶变换对连续信号,离散信号及系统响应进行频域分析.2、实验原理简述:对一个连续信号)(t xa 进行理想采样的过程可用下式表示:^x a(t)= )(t xa p(t)其中^x a(t)为)(t xa 的理想采样,p(t)为周期冲激脉冲,即p(t)=∑∞-∞=n δ(t-nT )^x a(t)的傅立叶变换^X a(j Ω)为^X a(j Ω)=[])(1s m Tn aX Ω-Ω∑∞-∞=上式表明^X a(j Ω)为)(Ωj Xa 的周期延拓,其周期延拓为采样角频率(T s π2=Ω).采样前后信号的频谱示意图见图.只有满足采样定理时,才不会发生频率混叠失真.离散信号和系统在时域均可用序列来表示。
为了在数字计算机上观察分析各种序列的频域特性,通常对()e j X ω在[]π2,0上进行M 点采样来观察分析。
对长度为N 的有限长序列x(n)有()()ee nj N n kj k m x Xωω--=∑=10其中,1,0,2==k k Mkπω,M-1 一个时域离散线性非移变系统的输入/输出关系为y(n)=x(n)*h(n)=()()m n h m x m -∑∞-∞=如果x(n)和h(n)的长度分别为M 和N ,则y(n)的长度为L=N+M-1。
上述卷积运算也可在频域实现()()()e e e j j j H X Yωωω=3、实验内容及步骤首先认真复习采样理论.离散信号与系统.线性卷积.序列的傅立叶变换及性质等有关内容,了解本实验原理与方法.1>编制实验用主程序及相应子程序.①信号产生子程序,用于产生实验中要用的下列信号序列: a) 采样信号序列:对下面连续信号:()()()t u t A t ex ataΩ-=0sin进行采样,可得到采样序列()()()()500,sin 0<≤==Ω=n n u nT A nT n e x x anTa a其中A 为幅度因子,a 为衰减因子,是模拟角频率,T 为采样间隔.这些参数都要在实验过程中由键盘输入,产生不同的x(t)和x(n)b) 单位脉冲序列:()[]n n x bδ=c) 矩形序列:()()10,==N n n R x Nc②系统单位脉冲响应序列产生子程序.本实验要用到两种FIR 系统.()()()()()()()325.215.210-+-+-+==n n n n n n n hR h baδδδδ ③有限长序列线性卷积子程序,用于完成两个给定长度的序列的卷积.可以直接调用MATLAB 语言中的卷积函数conv 。
数字信号处理实验1--5含代码

数字信号处理实验1--5含代码实验一离散时间信号的时域分析 1. 在MATLAB中利用逻辑关系式n,,0来实现序列,显示范围。
(产生如下,,,n,nn,n,n012图所示的单位脉冲信号的函数为impseq(n0,n1,n2),程序如示例所示),3,n,10并利用impseq函数实现序列:; ,,,,,,yn,2,n,3,,n,6,,xn1nnnn120源代码:impseq.mfunction y=impseq(n0,n1,n2)n=[n1:n2]y=[(n-n0)==0]exp01-1.mfunction impseq(n0,n1,n2)n=-3:1:10y=2*impseq(3,-3,10)+impseq(6,-3,10);stem(n,y)n,,0,,2. 在MATLAB中利用逻辑关系式来实现序列,显示范围。
(自己编写un,nn,n,n012产生单位阶跃信号的函数,函数命名为stepseq(n0,n1,n2)) 并利用编写的stepseq函数实现序列: ,,,,,,yn,un,2,un,2,5,n,10源代码:stepseq.mfunction y=stepseq(n0,n1,n2)n=n1:1:n2y=[(n-n0)>=0]exp01-2.mfunction stepseq(n0,n1,n2)n=-5:1:20y=stepseq(-2,-5,20)+stepseq(2,-5,20)stem(n,y)3. 在MATLAB中利用数组运算符“.^”来实现一个实指数序列。
如: n ,,,,xn,0.30,n,15源代码:n=0:1:15;x=0.3.^nstem(n,x)4. 在MATLAB中调用函数sin或cos产生正余弦序列,如:π,, ,,,,xn,3sin0.4πn,,5cos0.3πn0,n,20,,5,,源代码:n=0:1:20x=11*sin(0.3*pi*n+pi/5)+5*cos(0.3*pi*n)stem(n,x)思考题:1.在MATLAB环境下产生单位脉冲序列和单位阶跃序列各有几种方法,如何使用,2.在MATLAB环境下进行序列的相乘运算时应注意什么问题,实验二离散时间系统的时域分析1. 在MATLAB中利用内部函数conv来计算两个有限长序列的卷积。
数字信号处理实验1

k1r xk2r x yk2r y x桂林理工大学实验报告1.实验目的(1)掌握信号表示方法。
(2)掌握离散信号的延迟、相加、相乘及平移、反折变换 2.实验原理与方法首先,在用MATLAB 表示离散序列并将其可视化时,我们还应注意以下几点: 第一、离散时间序列无法用符号运算来表示,要用矩阵的形式;第二、由于在MATLAB 中矩阵的元素个数有限,因此,MATLAB 无法表示无限长的序列;第三、在绘制离散信号波形的函数stem 命令,而不是plot 命令。
习题1-2 计算卷积(2)x[k=g[k]={k+1;0<=k<=3} 实验程序为 x=[1,2,3,4]; kx=0:3; g=[1,2,3,4]; kg=0:3; y1 = conv(x, g); xf=fliplr(x) y2 = conv(xf,g);k1=kx(1)+kg(1):kx(end)+kg(end); stem(k1,y1);xlabel('k1'); ylabel('y1'); 习题1-3 (1)已知序列想x[k]={1,2,3,4;k=0,1,2,3},y[k]={-1,1,-2,3;k=0,1,2,3},试计算序列x[k]的自相关函数rx[n],以及序列x[k]与y[k]的互相关函数rxy[k]和ryx[k]。
(2)若某两个序列的自相关函数rx[k]相同,则该两个序列之间存在何种关系?(3)若信号s[k]=x[k]+n[k],x[k]与n[k]相关性很小,如何判断s[k]中存在x[k]?x=[1,2,3,4]; kx=0:3;y=[-1,1,-2,3]; ky=0:3; xf=fliplr(x);rx = conv(x, x+1);rxy = conv(xf,y);ryx=conv(y,xf); k1=kx(1)+ky(1):kx(end)+ky(end); kxf=-fliplr(kx); k2=kxf(1)+ky(1):kxf(end)+ky(end);subplot(1,3,1)stem(k1,rx);xlabel('k1'); ylabel('rx');subplot(1,3,2) stem(k2,rxy); xlabel('k2'); ylabel('rxy'); subplot(1,3,3); stem(k2,ryx);xlabel('k2'); ylabel('ryx');(2)因为rx[n]=x[n]*x[-n],所以这两个序列相等或互为翻转序列。
数字信号处理实验一报告

实验一:用FFT 对信号作频谱分析1.实验目的学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析 误差及其原因,以便正确应用FFT 。
2. 实验原理用FFT 对信号作频谱分析是学习数字信号处理的重要内容。
经常需要进行谱分析的信号是模拟信号和时域离散信号。
对信号进行谱分析的重要问题是频谱分辨率D 和分析误差。
频谱分辨率直接和FFT 的变换区间N 有关,因为FFT 能够实现的频率分辨率是N /2π,因此要求D N ≤/2π。
可以根据此式选择FFT 的变换区间N 。
误差主要来自于用FFT 作频谱分析时,得到的是离散谱,而信号(周期信号除外)是连续谱,只有当N 较大时离散谱的包络才能逼近于连续谱,因此N 要适当选择大一些。
周期信号的频谱是离散谱,只有用整数倍周期的长度作FFT ,得到的离散谱才能代表周期信号的频谱。
如果不知道信号周期,可以尽量选择信号的观察时间长一些。
对模拟信号进行谱分析时,首先要按照采样定理将其变成时域离散信号。
如果是模拟周期信号,也应该选取整数倍周期的长度,经过采样后形成周期序列,按照周期序列的谱分析进行。
3.实验步骤及内容(1)对以下序列进行谱分析。
⎪⎩⎪⎨⎧≤≤-≤≤-=⎪⎩⎪⎨⎧≤≤-≤≤+==其它nn n n n n x 其它nn n n n n x n R n x ,074,330,4)(,074,830,1)()()(3241选择FFT 的变换区间N 为8和16 两种情况进行频谱分析。
分别打印其幅频特性曲线。
并进行对比、分析和讨论。
(2)对以下周期序列进行谱分析。
4()cos4x n n π=5()cos(/4)cos(/8)x n n n ππ=+选择FFT 的变换区间N 为8和16 两种情况分别对以上序列进行频谱分析。
分别打印其幅频特性曲线。
并进行对比、分析和讨论。
(3)对模拟周期信号进行谱分析6()cos8cos16cos20x t t t t πππ=++选择 采样频率Hz F s 64=,变换区间N=16,32,64 三种情况进行谱分析。
实验一 数字信号处理

实验一系统响应及系统稳定性一、实验目的(1)掌握求系统响应的方法。
(2)掌握时域离散系统的时域特性。
(3)分析、观察及检验系统的稳定性。
二实验内容及步骤1、给定一个低通滤波器的差分方程为y(n)=0.05x(n)+0.05x(n-1)+0.9y(n-1),输入信号x1(n)=R8(n)x2(n)=u(n)a)分别求出系统对x1(n)=R8(n)和x2(n)=u(n)的响应序列,并画出其波形。
b)求出系统的单位冲响应,画出其波形。
xn1=[1 1 1 1 1 1 1 1 zeros(1,50)];xn2=ones(1,128);xn3=[1,zeros(1,50)];B=[0.05,0.05];A=[1,-0.9];yn1=filter(B,A,xn1);yn2=filter(B,A,xn2);yn3=filter(B,A,xn3);figure(1);n1=0:length(yn1)-1;subplot(2,2,1);stem(n1,yn1,'.');xlabel('n');ylabel('yn1');title('yn1');n2=0:length(yn2)-1;subplot(2,2,2);stem(n2,yn2,'.');xlabel('n');ylabel('yn2');title('yn2');n3=0:length(yn3)-1;subplot(2,2,3);stem(n3,yn3,'.');xlabel('n');ylabel('yn3');title('yn3');2、给定系统的单位脉冲响应为h1(n)=R10(n),h2(n)=δ(n)+2.5δ(n-1)+δ(n-2)+δ(n-3)用线性卷积法分别求系统h1(n)和h2(n)对x1(n)=R8(n)的输出响应,并画出波形。
数字信号处理实验一

DSP 实验一 报告(1)编写程序产生下列离散序列: ①()()(),34f n n n δ=-≤≤Matlab 程序如下: n1 = -3; n2 = 4; n0 = 0; n = n1:n2;x = [n==n0]; % x 在n=n0时为1,其余为0 stem(n,x,'filled'); %filled:序列圆心处用实心圆表示 axis([n1,n2,0,1.1*max(x)]) title('单位抽样序列') xlabel('time(n)')ylabel('Amplitude:x(n)')② ,55f n u n n =-≤≤Matlab 程序如下: n1 = -5; n2 = 5; n0 = 0; n = n1:n2;x = [n>=n0]; % x 在n>=n0时为1,其余为0 stem(n,x,'filled');axis([n1,n2,0,1.1*max(x)])title('单位阶跃序列') xlabel('time(n)')ylabel('Amplitude:x(n)')运行结果如下:③ ()()()0.1 1.6*,016j nf n e n π+=≤≤Matlab 程序如下: sigma = 0.1; omega = 1.6; n = 0:16;x = exp((sigma+i*omega)*n); subplot(2,2,1),plot(n,real(x)); title('复指数信号的实部')subplot(2,2,3),stem(n,real(x),'filled'); title('复指数序列的实部') subplot(2,2,2),plot(n,imag(x)); title('复指数信号的虚部')subplot(2,2,4),stem(n,imag(x),'filled'); title('复指数序列的虚部')运行结果如下:④ ()()3sin,0204n f n n π=≤≤Matlab 程序如下: n=0:20;y=3*sin(n*pi/4); stem(n,y)运行结果如下:⑤()()() sin5,2020 5nf n nn=-≤≤Matlab程序如下:n = -20:20;f = sinc(n/5);subplot(2,1,1),plot(n,f);title('sinc信号')subplot(2,1,2),stem(n,f);title('sinc序列')运行结果如下:(2)一个连续的周期性三角波信号频率为50Hz,信号幅度在0~+2V之间,在窗口上显示2个周期的信号波形,对信号的一个周期进行16点采样来获得离散信号。
数字信号处理实验 (云南大学)实验报告一

《数字信号处理》·实验一实验题目:离散时间信号的时域分析教师:杨鉴专业:电子信息科学与技术学号:姓名:Q1.29 运行程序P 1.5,以产生所有相关的信号MATLAB 程序代码如下:%程序 p1.5 通过平均的信号平滑 clf; R=51;d=0.8*(rand(R,1)-0.5); m=0:R-1;s=2*m.*(0.9.^m); x=s+d';subplot(2,1,1);plot(m,d','r-',m,s,'g--',m,x,'b-.'); xlabel('时间序号n'); ylabel('振幅'); legend('d[n]','s[n]','x[n]');x1=[0 0 x]; x2=[0 x 0]; x3=[x 0 0]; y=(x1+x2+x3)/3; subplot(2,1,2);plot(m,y(2:R+1),'r-',m,s,'g--'); legend('y[n]','s[n]');xlabel('时间序号n'); ylabel('振幅');5101520253035404550-50510时间序号n振幅d[n]s[n]x[n]051015202530354045502468时间序号n振幅y[n]s[n]Q 1.30 未污染的信号s[n]是什么样的形式?加性噪声d[n] 是什么样的形式? 信号s[n] 的MATLAB 程序代码如下:clf; R=51; m=0:R-1;s=2*m.*(0.9.^m); plot(m,s,'b-.'); xlabel('时间序号n'); ylabel('振幅');legend('未污染信号s[n]');510152025303540455001234567时间序号n振幅未污染信号s[n]信号d[n]的MATLAB 程序代码如下: clf; R=51;d=0.8*(rand(R,1)-0.5); m=0:R-1;plot(m,d','r-'); xlabel('时间序号n'); ylabel('振幅');legend('加性噪声d[n]');05101520253035404550-0.4-0.3-0.2-0.100.10.20.30.4时间序号n振幅加性噪声d[n]Q 1.31使用语句x=s+d 能产生被噪声污染的信号吗?若不能,为什么?答:不能,因为s 和d 均是 矩阵,d 与s 要想相加必须匹配,而矩阵d 本身与矩阵s 不匹配,必须把d 转置变为d'才能与s 进行相加。
数字信号处理实验一 实验报告
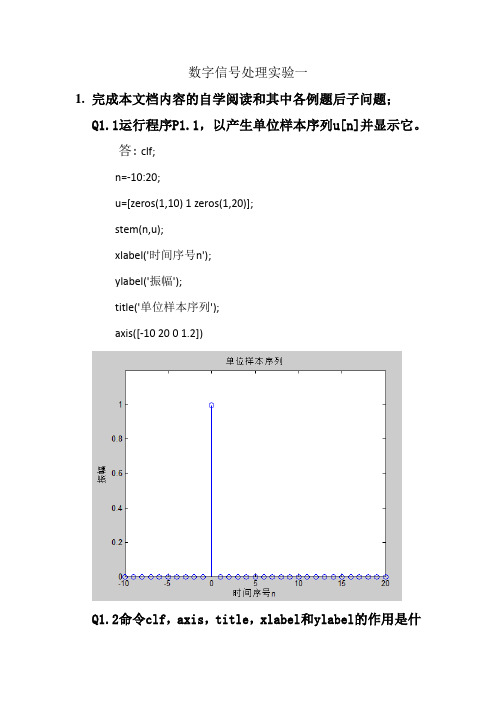
数字信号处理实验一1.完成本文档内容的自学阅读和其中各例题后子问题;Q1.1运行程序P1.1,以产生单位样本序列u[n]并显示它。
答: clf;n=-10:20;u=[zeros(1,10) 1 zeros(1,20)];stem(n,u);xlabel('时间序号n');ylabel('振幅');title('单位样本序列');axis([-10 20 0 1.2])Q1.2命令clf,axis,title,xlabel和ylabel的作用是什么?答:clf清除图对象,axis 控制轴刻度和风格的高层指令,title 设置图名,xlabel和ylabel设置横纵坐标轴名称。
Q1.3修改程序P1.1以产生带有延时11个单位样本的延迟单位样本序列ud[n]。
运行修改的程序并显示产生的序列。
答:clf;n=0:30;ud=[zeros(1,11) 1 zeros(1,19)];stem(n,ud);xlabel('时间序号n');ylabel('振幅');title('单位样本序列');axis([0 30 0 1.2])Q1.4修改程序P1.1以产生单位步长序列s[n].运行修改后程序并显示产生的序列。
答:clf;n = 0:30;u = [1.*n];stem(n,u);title('Unit Sample Sequence');axis([0 30 0 30])Q1.5修改程序P1.1,以产生带有超前7个样本的延时单位阶跃序列sd[n]。
运行修改后的程序并显示产生的序列。
答:clf;n = -15:30;s=[zeros(1,8) ones(1,38)];stem(n,s);xlabel('Time index n');ylabel('Amplitude'); title('Unit Sample Sequence');axis([-15 30 0 1.2]);Q1.6 运行程序P1.2,以产生复数值的指数序列。
数字信号实验1

实验一 FFT 及其应用学号: K031541822 姓名: 黄蕾蕾 评分:一、实验目的1.加深对FFT 的理解,熟悉MATLAB 中的有关函数。
2.应用FFT 对典型信号进行频谱分析的方法。
3.熟悉应用FFT 实现两个序列的线性卷积的方法。
二、实验原理长度为N 的序列()x n 的离散傅立叶变换()X k 为:∑-=-==101,....,0,)()(N n nkN N k W n x k X序列()X k 的离散傅立叶反变换为x n NX k Wn N Nnk k N ()(),,....,==--=-∑1011离散傅立叶反变换与正变换的区别在于N W 变为1N W -,并多了一个1N 的运算。
因为N W 和1NW -对于推导按时间抽取的快速傅立叶变换算法并无实质性区别,因此可将FFT 和快速傅立叶反变换(IFFT )算法合并在同一个程序中。
在MATLAB 中,可以用函数X=fft (x ,N )和x=ifft (X ,N )计算N 点序列的DFT 正、反变换,其中点数N 可以缺省。
因为DFT 是DTFT 在一个周期上的等间隔采样,因此可以借助DFT 近似分析信号的频谱;同样因为其循环卷积定理并且在满足一定条件下循环卷积与线性卷积是相等的,因此可以借助DFT 进行卷积运算。
(一) 连续信号的谱分析连续信号首先经过采样转换为离散信号,后经截断得到有限长序列,再进行DFT 即可得到其近似的离散谱。
这一过程通过简短的M 程序就可以实现,例如下列程序: k=8;n1=[0:1:19];xa1=sin(2*pi*n1/k); subplot(2,2,1) plot(n1,xa1)xlabel('t/T');ylabel('x(n)');xk1=fft(xa1);xk1=abs(xk1); subplot(2,2,2) stem(n1,xk1) xlabel('k');ylabel('X(k)'); n2=[0:1:15]; xa2=sin(2*pi*n2/k); subplot(2,2,3) plot(n2,xa2) xlabel('t/T');ylabel('x(n)'); xk2=fft(xa2);xk2=abs(xk2); subplot(2,2,4) stem(n2,xk2) xlabel('k');ylabel('X(k)');对于连续信号的谱分析,主要在于误差分析,通过选择合适的参数把误差降低到最低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Doc convDescriptionLet m = length(u) and n = length(v) . Then w is the vector of length m+n-1 whose kth element isThe sum is over all the values of j which lead to legal subscripts for u(j) and v(k+1-j), specifically j = max(1,k+1-n): min(k,m). When m = n, this givesw(1) = u(1)*v(1)w(2) = u(1)*v(2)+u(2)*v(1)w(3) = u(1)*v(3)+u(2)*v(2)+u(3)*v(1)...w(n) = u(1)*v(n)+u(2)*v(n-1)+ ... +u(n)*v(1)...w(2*n-1) = u(n)*v(n)翻译:让m =长度(u)和n =(v)。
那么w是向量的长度m + n - 1 k元素是结束所有的值求和j导致法律下标u(j)和v(k + 1-j),特别是j = max(k +其它):min(k、m)。
当m = n,这给了w(1)= u(1)*(1)w(2)= u(1)*(2)+ u(2)*(1)w(3)= u(1)*(3)+ u(2)*(2)+ u(3)*(1)…w(n)= u(1)* v(n)+ u(2)*(n - 1)+…+ u(n)*(1)…w(2 * n - 1)= u v(n)*(n)doc num2strThe num2str function converts numbers to their string representations. This function is useful for labeling and titling plots with numeric values.str = num2str(A) converts array A into a string representation str. Converted floating-point values have a maximum of four digits of precision, and an exponent if required. For integer values, num2str returns the exact string representation of the value.str = num2str(A, precision) converts the array A into a string representation str with the maximum number of digits specified by precision.str = num2str(A, format) converts array A using the supplied format, as described on the fprintf function reference page. By default, num2str displays floating point values using the '%11.4g' format (four significant digits in exponential or fixed-point notation, whichever is shorter).翻译:num2str函数将数字转换为字符串表示。
这个函数是用于标签和标题的情节与数值。
str = num2str(A)将一个数组转换成一个字符串str。
转换精度浮点值有最大的四个数字,和一个指数如果需要。
为整数值,num2str返回的字符串表示的值。
str = num2str(精度)的数组转换成字符串表示str由精密数字指定的最大数量。
str = num2str(格式)转换数组使用提供的格式,如流函数参考网页上的描述。
默认情况下,num2str显示浮点值使用“% 11.4 g”格式(四个有效数字在指数或定点表示法,哪个更短)。
Doc filterThe filter function filters a data sequence using a digital filter which works for both real and complex inputs. The filter is a direct form II transposed implementation of the standard difference equation (see "Algorithm").y = filter(b,a,X) filters the data in vector X with the filter described by numerator coefficient vector b and denominator coefficient vector a. If a(1) is not equal to 1, filter normalizes the filter coefficients by a(1). If a(1) equals 0, filter returns an error.If X is a matrix, filter operates on the columns of X. If X is a multidimensional array, filter operates on the first nonsingleton dimension.[y,zf] = filter(b,a,X) returns the final conditions, zf, of the filter delays. If X is a row or column vector, output zf is a column vector of max(length(a),length(b))-1. If X is a matrix, zf is an array of such vectors, one for each column of X, and similarly for multidimensional arrays.[y,zf] = filter(b,a,X,zi) accepts initial conditions, zi, and returns the final conditions, zf, of the filter delays. Input zi is a vector of length max(length(a),length(b))-1, or an array with the leading dimension of size max(length(a),length(b))-1 and with remaining dimensions matching those of X.y = filter(b,a,X,zi,dim) and [...] = filter(b,a,X,[],dim) operate across the dimension dim.翻译:过滤函数过滤数据序列使用数字滤波器工作实际和复杂的输入。
过滤器是一种直接二转置实现标准的差分方程(见“算法”)。
y =过滤器(b,a,X)过滤器过滤的数据向量X描述分子系数向量b和分母系数向量a。
如果一个(1)不等于1,滤波器可实现滤波器系数(1)。
如果(1)= 0,过滤器返回一个错误。
如果X是一个矩阵,过滤操作的列X如果X是一个多维数组,过滤作用于第一nonsingleton维度。
[y,zf]=过滤器(b,a,X)返回最后一个条件,过滤器的zf延迟。
如果X是一个行或列向量,输出zf是一个列向量的最大长度(长度(a)、(b))1。
如果X 是一个矩阵,zf这样的向量是一个数组,一个用于每一列(X)和类似的多维数组。
[y,zf]=过滤器(b,a,X,zi)接受初始条件,子,并返回最终的条件,过滤器的zf延迟。
输入子是一个向量的最大长度(长度(a)、(b))1,或数组大小的主要维度最大长度(长度(a)、(b))1和剩余的尺寸匹配的X。
y =过滤器(b,a,X,子,暗)和[…)=过滤器(b,a,X,[],昏暗的)跨维度的操作。
Doc impzThe next sections describe common impz operation with adaptive, discrete-time, and multirate filters. For more input options, refer to impz in Signal Processing Toolbox documentation.翻译:下一小节将描述常见impz操作与自适应离散,多重速率的过滤器。
更多的输入选项,请参阅impz信号处理工具箱中的文档。
3.doc stemDoc convnum2str(pi) is 3.142.num2str(eps) is 2.22e-16.num2str(randn(2,2),3) produces the following string matrix:num2str(randn(2,2),3)ans =0.538 -2.261.83 0.862num2str with a format of %10.5e\n returns a matrix of strings in exponential format, having 5 decimal places, with each element separated by a newline character:x = rand(2,3) * 9999; % Create a 2-by-3 matrix.A = num2str(x, '%10.5e\n') % Convert to string array.6.87255e+0031.55597e+0038.55890e+0033.46077e+0031.91097e+0034.90201e+003Doc filterdata = [1:0.2:4]';windowSize = 5;filter(ones(1,windowSize)/windowSize,1,data)ans=0.20000.44000.72001.04001.40001.60001.80002.00002.20002.40002.60002.80003.00003.20003.40003.6000Q2.2clf;n = 0:100;s1 = cos(2*pi*0.5*n);s2 = cos(2*pi*0.7*n);x = s1+s2;M = 2;num = ones(1,M);y = filter(num,1,x)/M;subplot(2,2,1);plot(n, s1);axis([0, 100, -2, 2]);xlabel('时间序号 n'); ylabel('振幅'); title('信号 #1');subplot(2,2,2);plot(n, s2);axis([0, 100, -2, 2]);xlabel('时间序号 n'); ylabel('振幅'); title('信号 #2');subplot(2,2,3);plot(n, x);axis([0, 100, -2, 2]);xlabel('时间序号 n'); ylabel('振幅'); title('输入信号');subplot(2,2,4);plot(n, y);axis([0, 100, -2, 2]);xlabel('时间序号 n'); ylabel('振幅'); title('输出信号');axis;Q2.4Q2.5 Q2.6 Q2.7Q2.12。
