最大熵阈值分割

基于最大模糊熵和微粒群的双阈值图像分割

基于最大模糊熵和微粒群的双阈值图像分割
周鲜成，中群太王俊年，
（湖南商学院计算机与电子工程系，湖南长沙４００；１．１２５２．中南大学信息科学与工程学院，湖南长沙４０８）１０３
摘要：于最大模糊熵准则和微粒群算法，出了一种新的双闽值图像分割方法。该方法通过定义３种模糊隶属度函数，基提将图像模糊划分为暗、灰和亮３个不同的区域。同时采用微粒群算法搜索最大模糊准则下模糊参数的最优组合，而确定图进像的两个最佳分割阈值。仿真结果表明，算法具有良好的分割效果和较强的实时处理能力。该
０引言
图像分割是图像处理和分析中的重要问题，是计算机也视觉研究中的一个经典难题。阈值分割是图像分割中应用最
关键词：大模糊熵；微粒群；阈值；模糊划分；二维灰度直方图；图像分割最
Hale Waihona Puke 中图法分类号：Ｐ９．１Ｔ３１４
文献标识码：Ａ
文章编号：００７２２０）２３８—３１０ —０４（０８１—１８０
Ｄｏｂｅｔｒｓｏｄｎｌｏｉｍｒｉｇｅｍｅｔｔｎｂｓｄｏｘｍｕｆｚｙｕｌｅｈｌｉｇａｇｒｈｆｈｔｏｍａｅｓｇｎａｉａｅｎｍａｉｍｚｏｕ
ＡｂｔａｔＡｏｂｅｔｒｓｏｄｎｌｏｔｍｒｍａｅｓｇｅｔｔｎｂｓｄｏｘｍｕｆｚｙｅｔｏｙａｄｐｒｉｌｌ１ｏｔｉａｉｎｓｒｃ：ｄｕｌｅｈｌｉｇａｇｒｈｆｇｅｍｎａｉａｅｎｍａｉｍｕｚｎｒｐｎａｔｅｓＴｐｉｚｔｈｉｏｉｏｃＷａＩｍｏｉｒｓｎｅ．Ｔｈｇａｔｎｔｒｅｐｒｚｉｒｕｈｄｆｉｇｔｒｅｆｚｙｍｅｅｓｉｎｔｎ，ｉｃｕｉｇｄｒ，ｇａｄｓｐｅｅｔｄｅｉｍａｅｉｐｒｉｔｅａｔｆｚｌｔｏｇｅｉｎｅｕｚｍｂｒｈｐｆｃｉｓｎｌｄｎａｋｓｏｏｈｓｕｙｈｎｈｕｏｒｙａｎｗｈｔａｔＡｃｏｄｎｏｔｅｍａｉｍｆｚｙｅｔｏｙｐｎｉｌ，ｔｅｏｔｌｏｉａｉｎｏｔｅｆｚｙｐｒｍｅｅｓｉｅｃｅ，ａｄｔｅｉｅｐｒ．ｃｒｉｇｔｈｘｍｕｕｚｎｐｒｃｐｅｈｒｉｐｍａｍｂｔｏｆｉｃｎｈｕｚａａｔｒｓａｈｄｎｈｓｒｏｔｌｈｅｈｌｓｉｅｅｍｉｅｙｐｒｉｌＷａＩｏｔｚｔｏｌｏｔｍ．Ｅｘｅｍｅｔｌｅｕｔｓｏｔａｅｐｏｏｅｔｏｉｅｐｉｒｓｏｄｓｄｔｒｎｄｂａｔｅｓｌ１ｐｉａｎａｇｒｈｍａｔｃＴｍｉｉｉｐｒｎａｓｌｈｗｔｒｐｓｍｅｄｇｖｓｉｒｓｈｔｈｄｈｂｔｒｅｆｒａｃ，ａｄｓｅｄｓｍｅｅｔｒｏｎｅｎｎｓｌｓｉ．ｅｐｍｐｅｔＫｅｒｓｍａｉｍｚｙｅｔｏｙｐｒｉｌｌＩｏｔｚｔｎｔｒｓｏｄｎ；ｕｚａｔｔｎ２ｇａｓｏｒｍ；ｍａｅｓｇｎａｉｎｙｗｏｄ：ｘｍｕｆｚｒｐ；ａｔｅｓＴ１ｐｉａｉ；ｈｅｈｌｉｇｆｚｙｐｒｉｏ；ＤｒｙｈｉｇａｉｇｅｍｅｔｔｕｎｃＷａｍｉｏｉｔｏ

python最大熵阈值分割

python最大熵阈值分割摘要：1.最大熵阈值分割简介2.最大熵阈值分割原理3.最大熵阈值分割在Python 中的实现4.结论正文：1.最大熵阈值分割简介最大熵阈值分割是一种基于熵的图像分割方法。

熵是信息论中的一个重要概念，用于衡量一个事件的不确定性。

在图像分割中，最大熵阈值分割算法通过计算图像的熵来确定最佳阈值，使得分割后的前景和背景两部分熵之和最大。

这种方法可以用于二值图像、灰度图像和彩色图像的分割。

2.最大熵阈值分割原理最大熵阈值分割的原理如下：(1) 计算图像的直方图，得到像素值的概率分布。

(2) 计算图像的熵，表示为各像素值概率分布的加权熵之和。

(3) 设定一个阈值，将图像分为前景和背景两部分。

(4) 计算分割后前景和背景的熵之和。

(5) 求解使熵之和最大的阈值，即为最佳阈值。

3.最大熵阈值分割在Python 中的实现在Python 中，可以使用OpenCV 库实现最大熵阈值分割。

以下是一个简单的示例代码：```pythonimport cv2# 读取图像image = cv2.imread("image.jpg", cv2.IMREAD_GRAYSCALE)# 计算直方图hist, _ = cv2.calcHist([image], [0], None, [256], cv2.HIST_GRAYSCALE) # 计算熵entropy = -np.sum(hist * np.log2(hist + 1e-5))# 设定阈值threshold = 128# 进行最大熵阈值分割_, binary_image = cv2.threshold(image, threshold, 255,cv2.THRESH_BINARY)# 显示结果cv2.imshow("Original Image", image)cv2.imshow("Binary Image", binary_image)cv2.waitKey(0)cv2.destroyAllWindows()```4.结论最大熵阈值分割是一种基于熵的图像分割方法，可以用于二值图像、灰度图像和彩色图像的分割。

基于熵的图像二值化算法设计-二维最大熵分割

1设计目的与要求1.1 设计目的(1)熟悉和掌握MATLAB程序设计方法。

(2)学习和掌握MATLAB图像处理工具箱。

(2)了解图像分割和图像二值化的原理。

(3)掌握图像二值化技术阈值的选取。

(4)将原彩色图像变为二值化后的图像，通过二维最大熵图像分割法对图像进行分割达到预期目的。

1.2 设计要求(1)了解图像变换的意义和手段。

(2)熟悉最大熵和二值化的基本性质。

(3)通过本实验掌握利用MATLAB编程实现数字图像处理。

(4)理解图像分割的原理，了解其应用，掌握最大熵和二值化分割的方法。

2 设计方案2.1 图像二值化图像二值化是数字图像处理技术中的一项基本技术，二值化图像的显示与打印十分方便，存储与传输也非常容易，在目标识别、图像分析、文本增强、字符识别等领域得到广泛应用。

图像二值化是将灰度图像转化为只有黑白两类像素的图像，大多采用阈值化算法处理。

在不同的应用中，阈值的选取决定着图像特。

征信息的保留。

因此，图像二值化技术的关键在于如何选取阈值。

2.2 最大熵原理最大熵原理：最大熵原理是在1957 年由E.T.Jaynes 提出的，其主要思想是，在只掌握关于未知分布的部分知识时，应该选取符合这些知识但熵值最大的概率分布。

因为在这种情况下，符合已知知识的概率分布可能不止一个。

我们知道，熵定义的实际上是一个随机变量的不确定性，熵最大的时候，说明随机变量最不确定，换句话说，也就是随机变量最随机，对其行为做准确预测最困难。

图像分割中最大熵的引入：在图像分割中若假定以灰度级T 分割图像，则图像中低于灰度级T 的像素点构成目标物体,高于灰度级T 的像素点构成背景那么各个灰度级在图像分割后的两区域中的概率如下：O ：ti N N (0<=i<=t) （3.2.1）B ：ti N N N - (t+1<=i<=255) （3.2.2）其中Ni 为图像中灰度级为i 的像素点个数，Nt 为灰度级从0～t 的像素点总和，N 为图像总像素点，t 为假定灰度阈值T 。

快速最大熵多阈值图像分割算法

ｓｎｆａｔｍｐｏｅｏａｅｔｏｖｎｉｎｌｍａｉｍｎｒｐｔｏｎｓａｌｃｏｉｉｃｎｌｉｒｖｄｃｍｐｒｄｗｉｃｎｅｔａｘｍｕｅｔｏｙｍｅｈｄａｄｉｅｔａｃｍｍｏａｅｇｎｒｌ印ｐｉａｉｎｒｑｉｍｅｔ．ｇｉｙｈｏｂｏｄｔｅｅａｌｔｅｕｒｃｏｅｎｓ
０引言
图像分割就是依据图像的性质，将一幅图像划分不同区域
大小的影响小，可用于小目标分割。但因为传统的最大熵算法是使用穷举法选取使目标函数取得最大值的阈值，并且目标
的过程。图像分割是图像处理和计算机视觉中的基本技术，是图像分析、理解和描述的关键步骤。阈值方法是一种重要的图像分割方法，由于其算法简单和易于执行，图像分割中得到了在广泛的应用。如果只是将图像分为目标和背景两类，么就只那需要选取一个阈值，图像中每个像素的灰度值与阈值比较，将灰度值大于阈值的像素为一类，度值小于阈值的像素则为另一灰类。如果要将图像分为多个目标，就需要选取多个阚值，图像将中每个像素的灰度值与阈值比较，得到分割结果。
推公式提出了快速选取阈值的方法；文献［］７提出了一种利用
粒子群优化算法提高选取阈值速度的方法；文献［］出了一８提种利用增量学习法（Ｌ提高选取阈值速度的方法。本文的研Ｒ）
究目的就是要提高最大熵算法的运算速度。文献［］２针对Ｏｓｔｕ算法利用代数运算的递推公式，出了一种快速Ｏｓ法。受提ｔｕ算其思想启发，本文针对选取阈值的最大熵算法，出了一种基于提最大熵算法的快速阙值选取算法，能够实现对图像的多阈值快

基于最大熵分割和区域生长的水岸线快速提取方法

基于最大熵分割和区域生长的水岸线快速提取方法Rapid extraction of waterline based on maximumentropy segmentation and regional growth 刘秀峰1，庹先国1,2，陆景1，刘婷婷1LIU Xiu-feng 1, TUO Xian-guo 1,2, LU Jing 1, LIU Ting-ting 1（1.西南科技大学信息工程学院，绵阳 621010；2.四川轻化工大学，自贡 643000）摘要：针对传统区域生长算法在水岸图像水岸线提取上时间开销大，鲁棒性不高的问题，提出一种基于最大熵分割和区域生长相结合的水岸线提取方法。

首先，将水岸图像转换为Lab颜色空间，并对其L分量进行最大熵分割；然后，通过形态学腐蚀和膨胀相结合的方法，消除水岸线附近部分前景像素过分割的影响，从二值图像水面区域提取得到初始生长区域；最后，在此基础上执行区域生长算法，提取最终生长区域轮廓得到水岸线。

通过对三组不同环境下采集到的水岸图像进行水岸线提取实验表明，该方法能有效提取到水岸图像的水岸线，并且鲁棒性较好，平均误差在5像素左右，时间开销平均仅为34ms。

关键词：水岸线提取；区域生长法；最大熵分割；无人艇中图分类号：TP391 文献标识码：A 文章编号：1009-0134(2021)06-0095-05收稿日期：2020-03-12基金项目：国家自然科学基金青年科学基金（41704175）；四川省科技厅重点研发（2019YFG0294）作者简介：刘秀峰（1993 -），男，四川成都人，硕士，研究方向为先进传感器与仪器仪表。

0 引言随着机器视觉的发展，越来越多的研究人员尝试将视觉传感器应用到无人艇的环境感知系统中[1]，利用视觉实现无人艇的目标检测与导航[2～4]。

在不同的应用方向对图像区域的关注点常常不同，例如，水面目标检测则更加关注水面情况。

基于分形理论的改进型二维最大熵红外图像分割算法

ｐｉｅｐｅｉｓｄｔｅｅｍｉｅａｐｉａｗｏｄｍｅｓｏａｅｍｅｔｔｏｔｒｓｏｄａｄｈｎｅｔｂａｎｒｎｉｌＳｕｅｏｄｔｒｎｎｏｔｍｌｔ－ｉｎｉｎｌｓｇｎａｉｎｈｅｈｌｎｅｃｏｏｔｉｔｎｌｅｍｅｔｔｏｅｕｔｈｅｆａｇｉｓｎａｉｎｒｓｌ．Ｔｈｘｅｉｎａｅｕｔｓｏｈｔｔｅｉｒｖｄａｇｒｔｍｓｂｅｔｒｔａｅｅｐｒｍｅｔｌｓｌｈｗｓｔａｈｍｐｏｅｌｏｉｈｉｔｅｈｎｒｔｅｔａｉｉｎｌｔ．ｉｅｓｏａａｉｕｅｔｏｙｓｇｈｒｄｔｏａｗｏ．ｍｎｉｎｌｄｍｘｍｍｎｒｐｅｍｅｔｔｏｌｏｉｈｉｅｍｅｔｔｏｆｅｔｖｎｓ．ｎａｉｎａｇｒｔｍｎｓｇｎａｉｎｅｃｉｅｅｓ
文章编号：１７—７５２１）８０２－５６２８８（２０—０７００
基于分形理论的改进型二维最大熵红外图像分割算法
陈洪科杨晓玲
（闽南理工学院电子与电气工程系，福建石狮３２０）６７０
ａｄｃｎｔｕｔｉｓｊｉｔｐｒｂｂｌｙｄｓｒｂｉｎＯｎｔａａｉ，ｔｗｏｄｉｅｓｏａａｉｍｎｒｐｎｏｓｒｃｔｏｎｏａｉｔｉｔｉｕｔｏ．ｉｈｔｂｓｓｈｅｔ — ｍｎｉｎｌｍｘｍｕｅｔｏｙ

粒子群算法在图像分割中的应用

t max [(t )]
0t L 1
图像分割方式流程
开始
以任意的位置和速度来初始化粒子
计算各个粒子的适应值更新 Pid与Pgd 值更新各个粒子位置及速度
否
满足终止条件
是结束
最大信息熵图像分割的效果
最大信息熵算法通过编程可以迅速得到计算结果，但对大小不同尺寸的图像，运行速度会受到影响。总体来看，经过最大信息熵图像分割处理，照片画面清晰，图像信息得到最大的保留。
粒子群算法在图像分割的应用
Particle Swarm Algorithm and Its Applications in Image Segmentation
电气信息工程学院霍凤财
引言
粒子群算法，是一种以群体为基础 (Populationbased) 的最优化启发式算法；由
James Kennedy 和 Russell Eberhart 两位学者于1995年时所提出。
PSO 目标式
速度：vid(t +1)= wxvid(t)+
c1xrand()x[pid(t)- xid(t)(t)]+ c2xrand()x[Pgd(t)-xid(t)(t)]
目前的区域最佳解pbest 新位置 xid(t+1) 过去自身经验
v-速度 w-惯性权重 C-加速因子 pid-局部最优解 Pgd-全局最优解
f ( x, y) T f ( x, y) T
这样得到的g (x, y)是一幅二值图像。
直方图阈值化后的二值图像
直方图阈值双峰法的图像分割程序序 clear I=imread('细胞.png') % 读入灰度图像并显示 imshow(I); figure;imhist(I); % 显示灰度图像直方图 Inew=im2bw(I,140/255); % 图像二值化，根据140/255 %确定的阈值，划分目标与背景 figure;imshow(Inew); % 显示分割后的二值图像

【转】七种常见阈值分割代码（Otsu、最大熵、迭代法、自适应阀值、手动、迭代法、基本全局阈值法）

【转】七种常见阈值分割代码（Otsu、最⼤熵、迭代法、⾃适应阀值、⼿动、迭代法、基本全局阈值法）⼀、⼯具：VC+OpenCV⼆、语⾔：C++三、原理otsu法（最⼤类间⽅差法，有时也称之为⼤津算法）使⽤的是聚类的思想，把图像的灰度数按灰度级分成2个部分，使得两个部分之间的灰度值差异最⼤，每个部分之间的灰度差异最⼩，通过⽅差的计算来寻找⼀个合适的灰度级别来划分。

所以可以在⼆值化的时候采⽤otsu 算法来⾃动选取阈值进⾏⼆值化。

otsu算法被认为是图像分割中阈值选取的最佳算法，计算简单，不受图像亮度和对⽐度的影响。

因此,使类间⽅差最⼤的分割意味着错分概率最⼩。

设t为设定的阈值。

wo：分开后前景像素点数占图像的⽐例uo：分开后前景像素点的平均灰度w1：分开后被景像素点数占图像的⽐例u1：分开后被景像素点的平均灰度u=w0*u0 + w1*u1 :图像总平均灰度从L个灰度级遍历t，使得t为某个值的时候，前景和背景的⽅差最⼤，则这个 t 值便是我们要求得的阈值。

其中，⽅差的计算公式如下：g=wo * (uo - u) * (uo - u) + w1 * (u1 - u) * (u1 - u)[ 此公式计算量较⼤，可以采⽤： g = wo * w1 * (uo - u1) * (uo - u1) ]由于otsu算法是对图像的灰度级进⾏聚类，so 在执⾏otsu算法之前，需要计算该图像的灰度直⽅图。

迭代法原理：迭代选择法是⾸先猜测⼀个初始阈值，然后再通过对图像的多趟计算对阈值进⾏改进的过程。

重复地对图像进⾏阈值操作，将图像分割为对象类和背景类，然后来利⽤每⼀个类中的灰阶级别对阈值进⾏改进。

图像阈值分割---迭代算法1 .处理流程：1.为全局阈值选择⼀个初始估计值T(图像的平均灰度)。

2.⽤T分割图像。

产⽣两组像素：G1有灰度值⼤于T的像素组成，G2有⼩于等于T像素组成。

3.计算G1和G2像素的平均灰度值m1和m2；4.计算⼀个新的阈值:T = (m1 + m2) / 2;5.重复步骤2和4,直到连续迭代中的T值间的差⼩于⼀个预定义参数为⽌。

基于最大熵的模糊核聚类图像分割方法

３模糊核聚类算法
假设输入空间的样本向量Ｘ∈Ｒ，＝，，ｎ，被某一非ｉ１ …，２线性映射映射到某一特征空间Ｒ，从而得到Ｏ（．ｘ），（，Ｏ（） …，ｘ）。模糊核聚类算法的目标函数为：
２研究背景
近几年来，随着核方法构造的支持向量机理论的飞跃发展，学者们尝试着把核方法应用到聚类算法中来Ｊ。通过引入Ｍｅｃｒｒｅ核函数，使得复杂的模式分类问题映射到高维空间后，比在低维空间里更容易线性可分。输入空间映射到特征
用最大熵算法对原始图像进行初步分割，求得初始聚类中心；引入Ｍｅｅ核函数，把输入空间的样本映射到高维特征空间，并在特征空ｒｒｃ间中进行图像分割。实验结果表明，该方法能减少迭代次数，使分类结果更稳定，从而较好地把目标从背景中分割出来。
关健诃：糊核聚类；最大熵；特征空间；图像分割模
ｌ８８
计
算
机
工
程
２１年５月２日０１０
的隶属度。，需要满足如下约束条件：
域中心为ｔ背景所在的区域中心为＋一１２，这里￡为／２，Ｌ）／图像的灰度级；然后把（２＠＋ —１２作为基于最大熵的模ｔ，Ｌ））／／
糊核聚类图像分割方法的初始聚类中心 “ 。 ” （）３选择核函数及其参数。本文采用可以将有限维样本宅
（，・（）ｖ）
其中，为高斯核函数的宽度。（）４根据式（）５，利用聚类中心矩阵 “ “ 更新隶属度矩阵，
得到ｕ“）。

图像二值化阈值选取常用方法汇总

图像二值化阈值选取常用方法最近在公司搞车牌识别的项目，车牌定位后，发现对车牌区域二值化的好坏直接影响后面字符切分的过程，所以就想把常用阈值选取方法做一个总结。

图像二值化阈值选取常用方法：1.双峰法。

2.P 参数法。

3.最大类间方差法（Otsu 、大津法）。

4.最大熵阈值法。

5.迭代法(最佳阈值法)。

1.双峰法在一些简单的图像中，物体的灰度分布比较有规律，背景与目标在图像的直方图各自形成一个波峰，即区域与波峰一一对应，每两个波峰之间形成一个波谷。

那么，选择双峰之间的波谷所代表的灰度值T 作为阈值，即可实现两个区域的分割。

如图1所示。

2.P 参数法当目标与背景的直方图分布有一定重叠时，两个波峰之间的波谷很不明显。

若采用双峰法，效果很差。

如果预先知道目标占整个图像的比例P ，可以采用P 参数法。

P 参数法具体步骤如下：假设预先知道目标占整个图像的比例为P ，且目标偏暗，背景偏亮。

1）、计算图像的直方图分布P(t)，t=0,1,.....255。

2）、计算阈值T ，使其满足0()*Tt p t Pm n =-∑最小。

P 参数法一般用于固定分辨率下，目标所占整个图像比例已知的情况。

3.最大类间方差法(Otsu)最大类间方差法是由Otsu 于1979年提出的，是基于整幅图像的统计特性实现阈值的自动选取的，是全局二值化最杰出的代表。

Otsu 算法的基本思想是用某一假定的灰度值t 将图像的灰度分成两组，当两组的类间方差最大时，此灰度值t 就是图像二值化的最佳阈值。

设图像有L 个灰度值，取值范围在0～L-1，在此范围内选取灰度值T ，将图像分成两组G0和G1，G0包含的像素的灰度值在0～T ，G1的灰度值在T+1～L-1，用N 表示图像像素总数，i n 表示灰度值为i 的像素的个数。

已知：每一个灰度值i 出现的概率为/i i p n N =；假设G0和G1两组像素的个数在整体图像中所占百分比为01ϖϖ、，两组平均灰度值为01μμ、，可得概率：00=T ii p ϖ=∑11011L i i T p ωω-=+==-∑平均灰度值：00T i i ipμ==∑111L ii T i p μ-=+=∑图像总的平均灰度值：0011μϖμϖμ=+类间方差：()()()22200110101()g t ωμμωμμωωμμ=-+-=-最佳阈值为：T=argmax(g(t))使得间类方差最大时所对应的t 值。

融合视觉模型和最大熵的阈值分割算法

受到噪声的干扰。针对一维阈值算法抗噪性差的缺点，人们ｌ３提出了二维阈值算法。二维阈值算
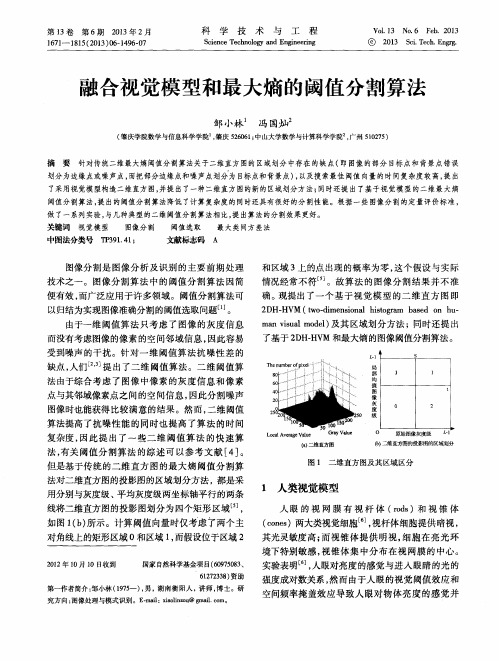
了基于２ＤＨ — ＨＶＭ和最大熵的图像阈值分割算法。
法由于综合考虑了图像中像素的灰度信息和像素点与其邻域像素点之间的空间信息，因此分割噪声图像时也能获得比较满意的结果。然而，二维阈值
划分为边缘点或噪声点，而把部分边缘点和噪声点划分为目标点和背景点），以及搜索最佳阈值向量的时间复杂度较高，提出
了采用视觉模型构造二维直方图，并提出了一种二维直方图的新的区域划分方法；同时还提出了基于视觉模型的二维最大熵
阚值分割算法，提出的阈值分割算法降低了计算复杂度的同时还具有很好的分割性能。根据一些图像分割的定量评价标准，
究方向：图像处理与模式识别。Ｅ — ｍａｉｌ：ｘｉａｏｌｉｎｚｏｕ＠ｇｍａｉｌ．ＣＯｎｒ。
６期
邹小林，等：融合视觉模型和最大熵的阈值分割算法
一鲁ｐ。一，ａ目昌一茸三ｐ１０暑０，１
法对二维直方图的投影图的区域划分方法，都是采用分别与灰度级、平均灰度级两坐标轴平行的两条
图１二维直方图及其区域区分
１人类视觉模型
人眼的视网膜有视杆体（ｒｏｄｓ）和视锥体
线将二维直方图的投影图划分为四个矩形区域Ｌ５Ｊ，对角线上的矩形区域０和区域１，而假设位于区域２
算法提高了抗噪性能的同时也提高了算法的时间
复杂度，因此提出了一些二维阈值算法的快速算法，有关阈值分割算法的综述可以参考文献［４］。

最大熵阈值分割一、背景介绍最大熵阈值分割是一种基于信息论的图像分割方法，其主要思想是在保持图像局部均匀性的前提下，寻找最优的阈值来将图像分成两部分。

二、原理解析1.信息熵信息熵是度量随机变量不确定性的一种指标，定义为：H(X)=-Σp(x)log2p(x)其中p(x)表示随机变量X在取值x时的概率。

当p(x)越大时，H(X)越小，表示随机变量X越确定；当p(x)越小时，H(X)越大，表示随机变量X越不确定。

2.最大熵原理最大熵原理认为，在未知条件下，应该假设随机变量的不确定性最大。

因此，在求解问题时应该选择使得信息熵最大的方案。

3.最大熵阈值分割在图像分割中，我们可以将图像看作一个随机变量X，并将其灰度级别作为取值。

我们需要找到一个阈值T来将图像分成两个部分：灰度级别小于等于T的部分和灰度级别大于T的部分。

我们需要选择一个合适的阈值T来实现这个目标。

首先计算整幅图像的灰度直方图，并将其归一化，得到每个灰度级别出现的概率。

然后，我们可以根据最大熵原理来求解最优的阈值T。

具体来说，我们需要将整幅图像分成两部分，并计算每部分的信息熵。

然后，我们可以通过最大化两部分信息熵之和来选择最优的阈值T。

4.实现步骤最大熵阈值分割的实现步骤如下：（1）计算整幅图像的灰度直方图，并将其归一化；（2）选择一个初始阈值T；（3）将整幅图像分成两部分：灰度级别小于等于T的部分和灰度级别大于T的部分；（4）计算两部分的信息熵；（5）根据最大熵原理选择新的阈值T；（6）重复步骤（3）至（5），直到满足停止条件。

三、优缺点1.优点最大熵阈值分割方法不需要任何先验知识，适用于各种类型的图像。

同时，该方法可以保证在保持图像局部均匀性的前提下，寻找到最优的阈值。

2.缺点最大熵阈值分割方法对噪声比较敏感，且计算量较大。

同时，该方法只能将图像分成两部分，对于多目标分割不太适用。

四、应用场景最大熵阈值分割方法可以应用于各种类型的图像分割任务，如目标检测、边缘检测、纹理分析等。

基于Sobel算子的图像快速二维最大熵阈值分割算法

ＭｏｄｉｆｉｃａｔｉｏｎｖｉａＤｉｆｆｅｒｅｎｔｉａｌ
［５］Ｓａｐｉｒｏ
Ｇ，ＣａｓｅｌｌｅｓＶ．Ｈｉｓｔｏｇｒａｍｏｆ
法［Ｊ］．计算机科学，２００８，３５（１２）：２１４—２１５［１０］Ｇｒｉｇｏｒｙａｎ
Ａ
ｏｎ
ｆａｓｔｔｈｒｅｓｈｏｌｄｒｅｃｕｒｓｉｏｎａｌｇｏｒｉｔｈｍ，ａｔ
ｍｅｔｈｏｄＷ３Ｓｐｒｏｐｏｓｅｄｂａｓｅｄｔｈｅ
ｓａｉＹｌｅ
ｔｈｅｓｔａｎｄａｒｄｔｗｏ－ｄｉｍｅｎｓｉｏｎａｌｍａ）【ｉｍｕｍｅｎｔｒｏｐｙｔｈｒｅｓｈｏｌｄ
ｓｅｇｍｅｎｔａｔｉｏｎ
ｔｉｍｅ，ｔｈｅｔｈｒｅｓｈｏｌｄｏｂｔａｉｎｅｄｂｙＳｏｂｅｌｏｐｅｒａｔｏｒｅｄｇｅｄｉｃｔｉｏｎｗａｓａｐｐｌｉｅｄｔＯｔｈｅｆａｓｔｔｈｒｅｓｈｏｌｄｓｅｇｍｅｎｔａｔｉｏｎａｌ—
能够提高运算速度，减少重复的操作，必须对二维最大熵进行进一步优化。
当计算Ｈ（ｓ，汁１）时，必须先计算只。（ｓ，￡＋１）和Ｈ。（ｓ，
￡＋１），如果每次都从ｉ一１，ｊ＝ｌ开始计算，会造成大量的重复运算。而只，（ｓ，￡＋１）和Ｈ。（ｓ，ｆ＋１）也存在以下的递推公式［９］：
＋１）一∑∑户。＝∑互户＋善Ａ，』只，（ｓ，ｔ＋１）一喜蓦纯，＝ｉ竞＝１壹户ｉ，ｊ＋姜ｓ九』
５
（１２）
Ｓｏｂｅｌ算子的快速二维熵分割算法
Ｓｏｂｅｌ算子能够检测出图像真正的边缘，将Ｓｏｂｅｌ算子边
缘检测获取的阈值应用到快速二维最大熵分割算法中。由于用二维最大熵阈值分割算法进行分割，获得的是图像的整体阈值，分割出来的效果不好。所以，我们根据图像的边缘信
图１二维灰度直方图
息，在对它大部分背景进行整体阈值分割后，对分割效果不好的图像再进行局部阈值分割，使得整体阈值和局部阈值结合起来。不管是图像的灰度值存在差别，还是图像的亮度或明或暗，总有一些目标在灰度不连续的位置上，而目标边缘可以通过边缘检测算子获得。因此，可以使用Ｓｏｂｅｌ算子检测出图像的边缘，然后进行非极大值抑制噪声，最后结合快速二维最大熵分割算法进行图像分割【１０３。下面给出算法步骤：（１）首先用快速二维最大熵阈值分割算法计算出图像的

最大熵阈值分割

最大熵阈值分割最大熵阈值分割是一种常用的图像分割方法，其目标是将一幅图像分割成多个具有相似特征的区域。

该方法通过选择合适的阈值对图像进行二值化处理，从而实现图像的分割。

通过最大熵原理，可以求解出最佳阈值，从而获取最优的分割结果。

1. 最大熵原理最大熵原理是一种概率模型的学习原理，它保守地学习未知模型的分布函数。

最大熵原理的核心思想是，在已知的条件下，选择熵最大的模型分布。

最大熵原理应用于图像分割中，可以用来寻找合适的阈值进行图像二值化，从而实现图像的分割。

2. 最大熵阈值分割步骤最大熵阈值分割方法的实现步骤如下：2.1 图像灰度化首先，将彩色图像转换为灰度图像。

灰度图像只保留一个通道，使得后续的计算更加简洁高效。

2.2 直方图统计对灰度图像进行直方图统计，获得每个灰度级别的像素个数。

可以得到图像的灰度分布情况。

2.3 求解最大熵阈值以直方图的灰度级别为横坐标，像素个数为纵坐标，绘制出直方图。

然后，通过最大熵原理，求解出最佳阈值，使得图像在该阈值下的熵最大。

2.4 图像二值化将图像根据最佳阈值进行二值化处理，得到分割后的图像。

根据像素的灰度值和最佳阈值的大小关系，将像素赋予不同的值或者像素被赋予不同的颜色，以实现区域的分割。

3. 最大熵阈值分割算法实例下面是一个最大熵阈值分割算法的实例，用于将一幅灰度图像分割成黑白两个区域。

import cv2import numpy as np# 图像灰度化def gray_scale(img):return cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)# 直方图统计def histogram(img):hist = np.zeros(256)for i in range(img.shape[0]):for j in range(img.shape[1]):hist[img[i, j]] += 1return hist# 求解最大熵阈值def find_threshold(hist):total_pixels = np.sum(hist)max_entropy = -1threshold = -1for t in range(256):w0 = np.sum(hist[:t+1]) / total_pixelsw1 = np.sum(hist[t+1:]) / total_pixelsif w0 == 0 or w1 == 0:continueentropy = -w0 * np.log2(w0) - w1 * np.log2(w1)if entropy > max_entropy:max_entropy = entropythreshold = treturn threshold# 图像二值化def binary_thresholding(img, threshold):binary_img = np.zeros_like(img)binary_img[img > threshold] = 255return binary_img# 主函数def main():# 读取图像img = cv2.imread('image.jpg')# 图像灰度化gray_img = gray_scale(img)# 直方图统计hist = histogram(gray_img)# 求解最大熵阈值threshold = find_threshold(hist)# 图像二值化binary_img = binary_thresholding(gray_img, threshold)# 保存结果cv2.imwrite('binary_image.jpg', binary_img)# 调用主函数main()4. 结果展示最终的分割结果将被保存为一副二值图像，其中黑色像素表示分割后的目标区域，白色像素表示分割后的背景区域。

基于遗传算法的最大熵阈值的图像分割_宋家慧

基于遗传算法的最大熵阈值的图像分割宋家慧(东南大学自动控制系,江苏省南京市210096)摘要图像阈值分割技术在图像分析和图像识别中具有重要的意义。

最大熵方法具有很多优点,但同时也存在弱点:需要大量的运算时间,特别是在计算多阈值时。

因此需要引入优化算法。

文中将遗传算法用于最大熵阈值的图像分割方法中,分别对一维及二维阈值分割的情况进行讨论,并提出了一种基于改进型遗传算法的最大熵阈值图像分割方法。

通过对几幅经典图像的分割结果对比,表明了基于遗传算法的最大熵阈值的图像分割方法可以有效地提高最大熵图像分割的计算速度,提高图像处理的实时性。

关键词:图像分割,遗传算法,阈值中图分类号:TN911.73收稿日期:2004 11 01;修回日期:2004 12 11。

0 引言图像分割是图像处理和计算机视觉中基本而且关键的技术之一,其目的是将目标和背景分离,为后续的分类、识别和检索提供依据。

图像分割法包括阈值法、边缘检测法和区域跟踪法等。

其中图像阈值分割是一种广泛使用的图像分割方法。

目前,已有很多阈值分割方法,例如直方图阈值分割、类间方差阈值分割、最大熵阈值分割等。

最大熵阈值分割方法不需要先验知识,而且对于非理想双峰直方图的图像也可以进行分割。

但是在确定阈值时,尤其是确定多阈值时,计算量很大。

遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律演化而来的随机化搜索算法,是一种具有鲁棒性、并行性和自适应性的优化算法。

本文将以一维最大熵阈值法和二维最大熵阈值法为例,探讨如何利用遗传算法和改进型遗传算法进行最大熵阈值的选取。

1 最大熵阈值分割1.1 一维最大熵阈值分割将Shannon 熵概念应用于图像分割时,依据是使图像中目标与背景分布的信息量最大,通过分析图像灰度直方图的熵,找到最佳阈值。

对于灰度范围为{0,1, ,L -1}的图像,假设图中灰度级低于t 的像素点构成目标区域(O),灰度级高于t 的像素点构成背景区域(B),那么各概率在其本区域的分布分别为:O 区:p i /p t ,i =0,1, ,t ;B 区:p i /(1-p t ),i =t +1,t +2, ,L -1。

复杂背景下的最大熵阈值红外目标分割算法

复杂背景下的最大熵阈值红外目标分割算法温凯峰;叶仕通;万智萍【摘要】为了有效地分割出实际拍摄中的红外目标信号,提出了一种适用于复杂背景下的最大熵阈值红外目标分割算法;该算法根据图像中信号的相关性,对图像的干扰信号的预处理,随后对所得的图像信号进行熵值的求取;接着根据目标与背景信号的分布特性,对所获得的目标信号与背景信号进行深入提纯处理,最终获得更为理想的红外目标信号.实验结果表明,该算法能够在不同背景下始终保持较好的红外目标分割效果,且具有耗时低、清晰度高的分割优势.【期刊名称】《激光与红外》【年(卷),期】2016(046)001【总页数】6页(P103-108)【关键词】红外图像;分割算法;阈值;相关性;目标提纯【作者】温凯峰;叶仕通;万智萍【作者单位】嘉应学院,广东梅州514015;广东工业大学华立学院,广东增城511325;中山大学新华学院,广东广州510520【正文语种】中文【中图分类】TP391红外图像根据目标与背景的温度分布情况来进行获取,使采集回来的图像摆脱了光照条件的约束而被广泛地运用在军事与医疗等领域。

但在实际的红外图像采集过程中,往往图像容易受到自身成像系统以及目标背景的温度分布的影响,使得采集回来的红外图像存在噪声大、目标模糊等问题,这无疑给后续的工作带来了很多不便；因此,为了便于观察与分析,适当地增强红外目标、削弱与去除不需要的信息,显得十分重要,这时便需要采用图像的分割技术[1-2]。

现有具有代表性的分割算法有迭代分割算法[3-4]、最大类间方差分割算法(Otsu算法)[5-6]以及最大熵阈值分割算法[7]。

其中最大熵阈值分割算法颇受关注,该算法凭借其实现简单、性能稳定的特点,被广泛地运用于图像处理中。

但由于实际的红外图像中其低分辨率与噪声大等特点,使最大熵阈值分割算法所分割出来的红外目标图像并非理想。

为此,提出了一种有效红外目标分割的分割算法。

针对实际采集回来的红外图像中含有较多的噪声信号这样问题,根据红外图像中有效信号的相关性[8],对图像进行了噪声信号进行了预处理；然后对所得的图像信号根据传统的最大熵阈值分割算法对图像的熵值进行初步确定。

二维最大熵阈值分割

二维最大熵阈值分割
二维最大熵阈值分割算法
若一幅图像的灰度级数为L，总的象素点数为N（m×n），设f i，j 为图像中点灰度为i及其区域灰度均值为j的象素点数，p i，j为点灰度－区域灰度均值对（i，j）发生的概率，即：p i，j＝f i，j／N，其中N （m×n）为图像的总象素数，则｛p i，j，i，j＝1，2，…，L｝是该图像关于点灰度－区域灰度均值的二维直方图。

图1为二维直方图的xoy平面图。

沿对角线分布的A区和B区分别代表目标和背景，远离对角线的C区和D区代表边界和噪声，所以应该在A区和B区上利用点灰度－区域灰度均值二维最大熵法确定最佳阈值，可使真正代表目标和背景的信息量最大。

于是，定义离散二维熵为：
3 二维最大熵阈值分割递推算法
在上述二维阈值化方法中，对于每个（s，t）对，都要从头开始计算P A（s，t）和H A（s，t），运算过程是一个4重循环，计算复杂性为，计算比较耗时。

实际应用中，为了提高运算速度，减少重复计算，必须对二维最大熵进行进一步优化。

对于一个固定的s，当t取1-L时，计算Φ（s，t）已经不存在重复计算，但同样s也要从1取到L，这样
这样通过优化，该递推算法可将计算的复杂性减至O（L2），大大减少了计算的复杂性，提高了计算速度。

具体算法实现如下：（1）计算原始图像中各个象素点的灰度值以及各个象素点的4邻域平均灰度值，并计算统计灰度信息P［i］［j］；
（2）相关计算
（3）求出最佳阈值（s＊，t＊），分割图像。

(5)(b)图像处理-图像的二值化---最大熵

基于最大熵的阈值选取及图像分割在讲基于最大熵的阈值选取的具体算法之前先来简要介绍下相关原理。

熵：用来描述体系混乱度的物理量。

最大熵原理①：最大熵原理是在1957 年由E.T.Jaynes提出的，其主要思想是，在只掌握关于未知分布的部分知识时，应该选取符合这些知识但熵值最大的概率分布。

因为在这种情况下，符合已知知识的概率分布可能不止一个。

我们知道，熵定义的实际上是一个随机变量的不确定性，熵最大的时候，说明随机变量最不确定，换句话说，也就是随机变量最随机，对其行为做准确预测最困难。

下面简单解释下最大熵原理：例：一个盒子中有三种小球，白球重量10g/个，红球重量20g/个，黑球30g/个，且三种球的重量占总重的比例分别为p1，p2，p3，盒子中球的平均重量为15g/个。

此时有约束条件为显而易见的是：在上述问题中有三个变量却只有两个约束条件。

此时必有无穷多组解满足已知约束，这些解就构成了一个随机变量的集合，而这个随机变量往往可以用一个概率密度分布函数来表示（显然这样的概率密度分布函数也有多个）。

而我们应该怎么选取呢？若假设满足已知约束条件的集合为A，在已知约束上再增加一个约束后，满足增加后的约束的集合为B，则必有B⊆A，即A出现的概率必然大于B。

这表明熵越大的决策在已知约束条件下出现的概率越大受到的其他位置约束条件越少。

这就是最大熵理论：熵值最大的理论即为最合理决策。

图像分割中最大熵的引入②：在图像分割中若假定以灰度级T分割图像，则图像中低于灰度级T的像素点构成目标物体（o）,高于灰度级T的像素点构成背景（B）那么各个灰度级在图像分割后的两区域中的概率如下：O： (0<=i<=t) B：(t+1<=i<=255) 其中ni为图像中灰度级为i的像素点个数，nt为灰度级从0~t的像素点总和，N为图像总像素点，t为假定灰度阈值T。

此时O区熵： (0<=i<=t)B区熵： (t+1<=i<=255)令H=HB+Ho则根据最大信息熵理论在已知条件下要对图像做出分割的最佳决策即为最接近实际图像分割的理想决策。

二维最大熵阈值分割法

二维最大熵阈值分割算法[引用]杜峰，施文康，邓勇等：《一种快速红外图像分割方法》1. 二维最大熵阈值分割熵是平均信息量的表征。

二维最大熵法是基于图像二维直方图。

图像二维直方图定义如下：NM n P j i j i ⨯=,,其中N M ⨯表示图像大小，j i n ,表示图像灰度值为i ，邻域灰度平均值为j 的像素个数。

通常二维直方图的平面示意图可以用下图1表示：其中区域1和2表示背景和目标像素，区域3和4通常表示边界和噪声信息。

阈值向量(t ,s )，t 表示灰度值，s 表示像素邻域均值（通常是8邻域）。

对于L 个灰度级的图像，设在阈值(t,s)定义区域1和2的概率P1，P2：∑∑-=-==101,1s i t j ji PP ，∑∑-=-==11,2L s i L tj j i P P定义二维离散熵H 的一般表示：∑∑-=ijji ji P PH ,,lg对各区域概率j i P ,进行归一化处理可得区域1的二维熵：11)1lg(1lg 1)1(101,,P H P P P P P H s i t j j i ji +=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=∑∑-=-= 同理区域2的二维熵：22)2lg()2(P H P H +=其中，H 1，H 2为：∑∑-=-=-=101,,lg 1s i t j ji ji P PH ，∑∑-=-=-=11,,lg 2L s i L tj j i j i P P H那么整个图像中目标和背景熵之和的函数)2()1(),(H H t s +=φ根据最大熵原则，存在最佳的阈值向量满足条件：图1 二维直方图平面示意图灰阶)},(max{),(t s t s φφ=**图2显示了一幅图像的二维直方图说明了背景和目标的主要分布情况，其中图2(b)横坐标表示邻域的均值，纵坐标表示灰度值分布：2. 微粒群寻优算法（PSO ）PSO 最早由Kenredy 和Eberhart 于1995年提出。