罗三中重难点训练题
(整理)八级数学秋季提高班第4讲等腰三角形综合提高拔高练习(人教版)
八年级数学秋季提高班第4讲等腰三角形综合提高拔高练习(人教版)试卷简介:<p> 本卷共10题,2道选择题,4道填空题,3道证明题,1道解答题。
本卷共100分,时间为60分钟。
本卷是视频课的预习讲义,希望大家独立完成。
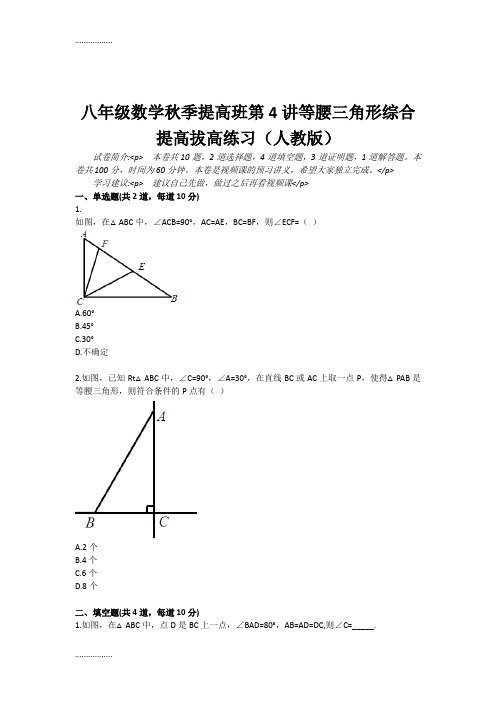
</p>学习建议:<p> 建议自己先做,做过之后再看视频课</p>一、单选题(共2道,每道10分)1.如图,在△ABC中,∠ACB=90°,AC=AE,BC=BF,则∠ECF=()A.60°B.45°C.30°D.不确定2.如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有()A.2个B.4个C.6个D.8个二、填空题(共4道,每道10分)1.如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C=_____.2.在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为am,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面墙上,此时梯子顶端距地面的垂直距离NB为bm,梯子的倾斜角为45°,则这间房子的宽AB是_______m.3.如图,在等边△ABC中,DE分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE的度数是_______.4.如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数是________.三、解答题(共1道,每道10分)1.两个全等的含30°,60°角的三角板ADE和三角板ABC,如图所示放置,E、A、C三点在一条直线上,连结BD,取BD的中点M,连结ME、MC,试判断△EMC的形状,并说明理由四、证明题(共3道,每道10分)1.已知:如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、CA上的点,且BD=CE,∠DEF=∠B.证明:△DEF是等腰三角形2.如图,延长△ABC各边,使得BF=AC,AE=CD=AB,顺次连接D、E、F,得到△DEF为等边三角形.求证:(1)△AEF≌△CDE;(2)△ABC为等边三角形.3.如图,△ABC为等边三角形,E是BC延长线上一点,CD平分∠ACE,CD=BE.求证:△ADE 为等边三角形.八年级数学秋季提高班第4讲等腰三角形综合提高(人教版)。
专题06 八年级数学上册期中考试重难点题型(举一反三)(原卷版)

专题06八年级数学上册期中考试重难点题型【举一反三】【人教版】【知识点1】三角形1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边.3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.钝角三角形三条高的交点在三角形外,直角三角形的三条高的交点在三角形上,锐角三角形的三条高的交点在三角形内,三条高线的交点叫做三角形的垂心4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.(三条中线的交点叫重心)5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.(三角形三条角平分线的交点到三边距离相等,三条角平分线的交点叫做内心6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.(例如自行车的三角形车架利用了三角形具有稳定性)7.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角:多边形相邻两边组成的角叫做它的内角.9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面,13.公式与性质:⑴三角形的内角和:三角形的内角和为180°⑵三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和.性质2:三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式:n 边形的内角和等于(2)n -·180°⑷多边形的外角和:多边形的外角和为360°.⑸多边形对角线的条数:①从n 边形的一个顶点出发可以引(3)n -条对角线,把多边形分成(2)n -个三角形.②n 边形共有(3)2n n -条对角线.【知识点2】全等三角形1.基本定义:⑴全等形:能够完全重合的两个图形叫做全等形.⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边.⑸对应角:全等三角形中互相重合的角叫做对应角.2.基本性质:⑴三角形的稳定性:三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.3.全等三角形的判定定理:⑴边边边(SSS ):三边对应相等的两个三角形全等.⑵边角边(SAS ):两边和它们的夹角对应相等的两个三角形全等.⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等.⑸斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形全等.4.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上.(三角形三条角平分线的交点到三边距离相等)【知识点3】轴对称1.基本概念:⑴轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.⑵两个图形成轴对称:把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.⑶线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.⑷等腰三角形:有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.⑸等边三角形:三条边都相等的三角形叫做等边三角形.2.基本性质:⑴对称的性质:①不管是轴对称图形还是两个图形关于某条直线对称,对称轴都是任何一对对应点所连线段的垂直平分线.②对称的图形都全等.⑵线段垂直平分线的性质:①线段垂直平分线上的点与这条线段两个端点的距离相等.②与一条线段两个端点距离相等的点在这条线段的垂直平分线上.⑷等腰三角形的性质:①等腰三角形两腰相等.②等腰三角形两底角相等(等边对等角).③等腰三角形的顶角角平分线、底边上的中线,底边上的高相互重合.④等腰三角形是轴对称图形,对称轴是三线合一(1条).⑸等边三角形的性质:①等边三角形三边都相等.②等边三角形三个内角都相等,都等于60°③等边三角形每条边上都存在三线合一.④等边三角形是轴对称图形,对称轴是三线合一(3条).3.基本判定:⑴等腰三角形的判定:①有两条边相等的三角形是等腰三角形.②如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边).⑵等边三角形的判定:①三条边都相等的三角形是等边三角形.②三个角都相等的三角形是等边三角形.③有一个角是60°的等腰三角形是等边三角形.4.基本方法:⑴做已知直线的垂线:⑵做已知线段的垂直平分线:⑶作对称轴:连接两个对应点,作所连线段的垂直平分线.⑷作已知图形关于某直线的对称图形:⑸在直线上做一点,使它到该直线同侧的两个已知点的距离之和最短.【考点1灵活运用三角形三边关系】【例1】(2019秋•洛龙区校级期中)已知△ABC的三边长为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是()A.2b﹣2c B.﹣2b C.2a+2b D.2a【变式1-1】(2019秋•濉溪县期中)设三角形三边之长分别为3,8,1﹣2a,则a的取值范围为()A.﹣6<a<﹣3B.﹣5<a<﹣2C.﹣2<a<5D.a<﹣5或a>2【变式1-2】(2019秋•宁都县期中)如图,在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是()A.2<AD<8B.0<AD<8C.1<AD<4D.3<AD<5【变式1-3】(2019•防城港期中)在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是()A.1cm<AB<4cm B.5cm<AB<10cmC.4cm<AB<8cm D.4cm<AB<10cm【考点2角平分线与多边形内角和】【例2】(2019春•沛县期中)如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是()A.90°+αB.﹣90°C.D.540°【变式2-1】(2019春•西湖区校级期中)如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=210°,则∠P=()A.10°B.15°C.30°D.40°【变式2-2】(2019秋•香洲区期中)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD 的平分线交于点P,则∠P=()A.90°﹣αB.αC.90°+αD.360°﹣α【变式2-3】(2018秋•遵义期中)如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=()A.∠A+∠D﹣45°B.(∠A+∠D)+45°C.180°﹣(∠A+∠D)D.∠A+∠D【考点3多边形内角和与外角和】【例3】(2019秋•岳池县期中)一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是()A.6条B.7条C.8条D.9条【变式3-1】(2019春•内江期中)马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830°,则该多边形的边数是()A.7B.8C.7或8D.无法确定【变式3-2】(2019春•诸城市期中)过多边形的一个顶点可以作7条对角线,则此多边形的内角和是外角和的()A.4倍B.5倍C.6倍D.3倍【变式3-3】(2019•凉山州期中)一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为()A.7B.7或8C.8或9D.7或8或9【考点4三角形全等的条件判断】【例4】(2018秋•利津县期中)如图,AB∥CD,BC∥AD,AB=CD,AE=CF,其中全等三角形的对数是()A.4B.3C.2D.1【变式4-1】(2018秋•思明区校级期中)如图,已知,∠CAB=∠DAE,AC=AD,增加下列条件:①AB =AE;②BC=ED;③∠C=∠D;④∠B=∠E;⑤∠1=∠2.其中能使△ABC≌△AED的条件有()A.2个B.3个C.4个D.5个【变式4-2】(2018秋•东台市期中)根据下列已知条件,能够画出唯一△ABC的是()A.AB=6,BC=5,∠A=50°B.AB=5,BC=6,AC=13C.∠A=50°,∠B=80°,AB=8D.∠A=40°,∠B=50°,∠C=90°【变式4-3】(2018秋•东台市期中)如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,BC=EF,∠B=∠E;③∠B=∠E,∠C=∠F,BC=EF;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有()A.1组B.2组C.3组D.4组【考点5等腰三角形中的分类讨论思想】【例5】(2018春•鄄城县期中)等腰三角形的周长为15cm,其中一边长为3cm,则该等腰三角形的腰长为()A.3cm B.6cm C.3cm或6cm D.8cm【变式5-1】(2018春•金水区校级期中)已知等腰三角形一腰的垂直平分线与另一腰所在的直线的夹角为40°,则此等腰三角形的顶角是()A.50°B.130°C.50°或140°D.50°或130°【变式5-2】(2019秋•绥棱县期中)已知一个等腰三角形底边的长为5cm,一腰上的中线把其周长分成的两部分的差为3cm,则腰长为()A.2cm B.8cm C.2cm或8cm D.10cm【变式5-3】(2018秋•沙依巴克区校级期中)等腰三角形一腰上的高等于该三角形某一条边的长度的一半,则其顶角等于()A.30°B.30°或150°C.120°或150°D.30°或120°或150°【考点6三种双角平分线应用】【例6】(2018春•翠屏区校级期中)已知△ABC,下列说法正确的是(只填序号).①如图(1),若点P是∠ABC和∠ACB的角平分线的交点,则∠P=90°+∠A;②如图(2),若点P是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣∠A;③如图(3),若点P是∠ABC和外角∠ACE的角平分线的交点,则∠P=∠A.【变式6-1】(2019秋•新洲区期中)如图,△ABC中,∠BAC=70°,∠ABC的平分线与∠ACB的外角平分线交于点O,则∠BOC=度.【变式6-2】(2019秋•高密市期中)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BD的平分线与∠A1CD的平分线交于点A2,若∠A=60°,则∠A2的度数为.【变式6-3】(2018秋•江汉区校级期中)如图,△ABC中,∠C=104°,BF平分∠ABC与△ABC的外角平分线AE所在的直线交于点F,则∠F=.【考点7线段垂直平分线的应用】【例7】(2018春•叶县期中)如图所示,在△ABC中,AB=AC,∠BAC为钝角,BC=6,AB、AC的垂直平分线分别交BC于点D、E,连接AD、AE,那么△ADE的周长为.【变式7-1】(2018秋•江都区期中)如图,在△ABC中,DM、EN分别垂直平分AC和BC交AB于M、N,∠ACB=118°,则∠MCN的度数为.【变式7-2】(2019秋•新乡期中)如图,在△DAE中,∠DAE=30°,线段AE,AD的中垂线分别交直线DE于B和C两点,则∠BAC的大小是.【变式7-3】(2018秋•老河口市期中)如图,△ABC的边AB,AC的垂直平分线相交于点P,连接PB,PC,若∠A=70°,则∠BPC的度数是.【考点8利用轴对称变换求最值】【例8】(2017秋•襄州区期中)如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是【变式8-1】(2018秋•洛龙区校级期中)如图,等腰三角形ABC的面积是16,且底边BC长为4,腰AC 的垂直平分线EF分别交边AC,AB于点EF,若点D为边BC的中点,点M为线段EF上一动点,则△CMD 周长的最小值是.【变式8-2】(2019秋•北塘区期中)如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为.【变式8-3】(2019•黄冈期中)如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是.【考点9全等三角形的判定与性质】【例9】(2019秋•吉县期中)如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD =AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何,请说明理由.【变式9-1】(2019•内江期中)如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE 交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.【变式9-2】(2019秋•九龙坡区校级期中)如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长交AC于点F,AF=EF,求证:AC=BE.【变式9-3】(2019秋•吴兴区校级期中)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=DAE =90°,线段BD,CE有怎样的数量关系和位置关系?请说明理由.【考点10灵活运用30°直角三角形】【例10】(2018秋•天台县期中)如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1.(1)求∠B的度数;(2)求CN的长.【变式10-1】(2019秋•江津区校级期中)已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm.求BC的长.【变式10-2】(2019秋•重庆校级期中)如图,已知△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F,且CF=3.求BF.【变式10-3】(2018春•槐荫区期中)如图所示,在等边△ABC中,点D,E分别在边BC,AC上,且DE ∥AB,过点E作EF⊥DE,交BC的延长线于点F.(1)求∠F的大小;(2)若CD=3,求DF的长.【考点11灵活运用“三线合一”】【例11】(2018秋•思明区校级期中)如图,已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点.【变式11-1】(2018秋•湖里区校级期中)如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB.【变式11-2】(2019春•广饶县期中)已知△ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图,若E、F分别是AB、AC上的点,且BE=AF.求证:△DEF为等腰直角三角形;(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.【变式11-3】(2018秋•硚口区期中)如图,在等边△ABC中,D是AB上一点,E是BC延长线上一点,AD=CE,DE交AC于点F.(1)求证:DF=EF;(2)过点D作DH⊥AC于点H,求.【考点12复杂的尺规作图】【例12】(2019秋•罗平县期中)作图题,求作一点P,使PM=PN,且到∠AOB的两边距离也相等.【变式12-1】(2019春•东阳市期中)如图,已知△ABC.(1)用尺规作△ABC的角平分线BD(保留痕迹,不写作法);(2)画BC边上的高AE;(3)画AB边上中线CF;(4)在AC边上找点P,使得点P到点B与点C的距离相等.【变式12-2】(2019春•雁塔区校级期中)请用直尺、圆规作图,不写作法,但要保留作图痕迹:已知:如图,∠ABC,射线BC上一点D.求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,点P到∠ABC两边的距离相等.【变式12-3】(2018•惠山区二模)如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):(1)在边BC上确定一点P,使得PA+PC=BC;(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.【考点13三角形内角和与等腰三角形】【例13】(2018秋•杭州期中)如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,求∠EFC 的度数.【变式13-1】(2019秋•沛县期中)如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC 上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=115°时,∠BAD=°,∠EDC=°,∠DEC=°;点D从B 向C的运动过程中,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由.【变式13-2】(2018秋•泗阳县期中)已知,在△ABC中,点D在BC上,点E在BC的延长线上,且BD =BA,CE=CA.(1)如图1,若∠BAC=90°,∠B=45°,试求∠DAE的度数;(2)若∠BAC=90°,∠B=60°,则∠DAE的度数为(直接写出结果);(3)如图2,若∠BAC>90°,其余条件不变,探究∠DAE与∠BAC之间有怎样的数量关系?【变式13-3】(2019秋•越秀区期中)在△ABC中,AB=AC,点D在底边BC上,AE=AD,连结DE.(1)如图①,已知∠BAC=90°,∠BAD=60°,求∠CDE的度数.(2)如图①,已知∠BAC=90°,当点D在BC(点B、C除外)上运动时,试探究∠BAD与∠CDE的数量关系;(3)如图②,若∠BAC≠90°,试探究∠BAD与∠CDE的数量关系.【考点14等腰三角形中的新定义问题】【例14】(2019秋•椒江区校级期中)定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的“三阶等腰线”.(1)请你在图1,图2中用两种不同的方法画出顶角为36°的等腰三角形的“三阶等腰线”,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种).(2)如图3,△ABC中,∠B=36°,AD和DE是△ABC的“三阶等腰线”,点D在BC边上,点E 在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.【变式14-1】(2019春•市北区期中)(本题画图时,直接用直尺画出相关线段即可,不需尺规作图,直接标注等腰三角形顶角度数即可,不需写出求解过程)把一张顶角为36°的等腰三角形纸片折叠两次,得到3个等腰三角形,你能办到吗?图1是其中的一种方法(虚线表示折痕)定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线(1)请你在图1后面用另一种不同的方法画出顶角为36°的等腰三角形的三分线①标注折痕(折痕用虚线表示)②标注得到的每个等腰三角形顶角的度数;(若两种方法分得的三角形形成3对全等三角形,则视为同一种)(2)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(不必标注折痕,若两种方法分得的三角形成3对全等三角形,则视为同一种)【变式14-2】(2019春•顺德区期中)如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.(1)如图1,△ABC是等腰锐角三角形,AB=AC(AB>BC),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=度;(2)如图2,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE 是△ABC的一条特异线;(3)如图3,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数(如有需要,可在答题卡相应位置另外画图).【变式14-3】(2018秋•滨湖区期中)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.【理解】如图①,在△ABC中,∠A =36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.【应用】(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值;(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB 边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.【考点15翻折变换中的角度问题】【例15】(2019春•东台市校级期中)△ABC,直线DE交AB于D,交AC于E,将△ADE沿DE折叠,使A落在同一平面上的A′处,∠A′的两边与BD、CE的夹角分别记为∠1,∠2.(1)如图①,当A′落在四边形BDEC内部时,探索∠A与∠1+∠2之间的数量关系,并说明理由.(2)如图②,当A′落在AC右侧时,探索∠A与∠1,∠2之间的数量关系,并说明理由.【变式15-1】(2019春•淮阴区期中)如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是.研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.【变式15-2】(2019秋•李沧区期中)图形在折叠过程中会形成相等的边和相等的角,下面是同学们在数学课上所做的三角形、四边形折叠实验,请根据实验过程解决问题:问题(一)如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′和∠A的数量关系是;研究(2):如果折成图②的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是;研究(3):如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.问题(二)研究(4):将问题(一)推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD 的内部时,∠1+∠2与∠A、∠B之间的数量关系是.(直接写出结论)【变式15-3】(2019春•广陵区校级期中)发现(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A有何数量关系,直接写出你的结论,不必说明理由思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=100°,求∠BIC的度数;拓展(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC 折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.【考点16三角形中的动点问题】【例16】(2019秋•全椒县期中)已知△ABC中,AC=BC,∠C=120°,点D为AB边的中点,∠EDF =60°,DE、DF分别交AC、BC于E、F点.(1)如图1,若EF∥AB.求证:DE=DF.(2)如图2,若EF与AB不平行.则问题(1)的结论是否成立?说明理由.【变式16-1】(2018秋•开州区期中)在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.(1)如图①,若∠BAC=60°,则按边分类:△CEF是三角形;(2)若∠BAC<60°.①如图②,当点D在线段CB上移动时,判断△CEF的形状并证明;②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请在图③中画出相应的图形并直接写出结论(不必证明).【变式16-2】(2018秋•十堰期中)在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE=.(2)设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.21【变式16-3】(2019秋•洪山区期中)(1)如图1,已知△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .求证:DE =BD +CE .(2)如图2,将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC ,求证:DE =BD +CE(3)拓展与应用:如图3,D 、E 是D 、A 、E 三点所在直线m 上的两动点(D 、A 、E 三点互不重合),点F 为∠BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形,连接BD 、CE ,若∠BDA =∠AEC =∠BAC ,求证:△DEF为等边三角形。
深圳罗湖区文锦中学数学初中九年级二次根式选择题易错题压轴难题专项综合训练

深圳罗湖区文锦中学数学初中九年级二次根式选择题易错题压轴难题专项综合训练一、易错压轴选择题精选:二次根式选择题1.有意义,那么直角坐标系中点A(a,b)在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.下列计算正确的是( )A =B .2-=C .22=D 3=3.使式子214x -x 的取值范围是( ) A .x≥﹣2 B .x >﹣2 C .x >﹣2,且x ≠2 D .x≥﹣2,且x ≠24.是同类二次根式,那么a 的值是( ) A .﹣2 B .﹣1 C .1 D .25.设0a >,0b >=的值是( )A .2B .14C .12D .31586.若|x 2﹣4x+4|x+y 的值为( )A .3B .4C .6D .97.下面有四个命题:①两条直线被第三条直线所截,同位角相等;②0.1的算术平方根是0.01)=5;④如果点P (3-2n ,1)到两坐标轴的距离相等,那么n =1,其中假命题的有( )A .1个B .2个C .3个D .4个 8.下列计算正确的是( )A =B =C 6=-D 1= 9.下列运算错误的是( )A B2 C .D 1=10.如果a ,那么a 的取值范围是( )A .a 0=B .a 1=C .a 1≤D .a=0a=1或11.已知m 、n 是正整数,若2m +5n 是整数,则满足条件的有序数对(m ,n )为( )A .(2,5)B .(8,20)C .(2,5),(8,20)D .以上都不是 12.若化简1682+-x x -1x -的结果为5-2x ,则x 的取值范围是( )A .为任意实数B .1≤x≤4C .x≥1D .x≤4 13.若ab <0,则代数式可化简为( ) A .a B .a C .﹣a D .﹣a14.如图直线a ,b 都与直线m 垂直,垂足分别为M 、N ,MN =1,等腰直角△ABC 的斜边,AB 在直线m 上,AB =2,且点B 位于点M 处,将等腰直角△ABC 沿直线m 向右平移,直到点A 与点N 重合为止,记点B 平移平移的距离为x ,等腰直角△ABC 的边位于直线a ,b 之间部分的长度和为y ,则y 关于x 的函数图象大致为( )A .B .C .D .15.设,n k 为正整数,()()1314A n n =+-+()2154A n A =++()3274A n A =++()4394A n A =++…()1214k k A n k A -=+++….,已知1002005A =,则n =( ). A .1806B .2005C .3612D .4011 16.“分母有理化”是我们常用的一种化简的方法,如:33)(23)74323(23)(23)==+--+3535+-3535x =+-3535+>-,故0x >,由22(3535)35352(35)(35)2x =+--=++--+-=,解得2x =,即35352+--=.根据以上方法,化简3263363332-+--++后的结果为( )A .536+B .56+C .56-D .536- 17.已知,那么满足上述条件的整数的个数是( ). A .4 B .5 C .6 D .718.下列计算正确的是( ) A .531883+=B .()322326a b a b -=-C .222()a b a b -=-D .2422a ab a a b a -+⋅=-++ 19.给出下列结论:①101+在3和4之间;②1x +中x 的取值范围是1x ≥-;③81的平方根是3;④31255--=-;⑤51528->.其中正确的个数为( ) A .1个B .2个C .3个D .4个 20.若a 、b 、c 为有理数,且等式成立,则2a +999b +1001c 的值是( )A .1999B .2000C .2001D .不能确定【参考答案】***试卷处理标记,请不要删除一、易错压轴选择题精选:二次根式选择题1.A【解析】试题分析:根据二次根式的概念,可知a≥0,ab >0,解得a >0,b >0,因此可知A (a ,b )在第一象限.故选A解析:A【解析】试题分析:根据二次根式的概念,可知a≥0,ab >0,解得a >0,b >0,因此可知A (a ,b )在第一象限.故选A2.C【分析】根据立方根、二次根式的加减乘除运算法则计算.【详解】A、非同类二次根式,不能合并,故错误;B、,故原结果错误;C、,正确;D、开不出有理数,故原结果错误;故选C.【点睛】解析:C【分析】根据立方根、二次根式的加减乘除运算法则计算.【详解】A、非同类二次根式,不能合并,故错误;B、=C、22=,正确;D故选C.【点睛】本题考查二次根式、立方根的运算法则,熟练掌握基本法则是关键.3.C【分析】根据分式和二次根式有意义的条件(分式的分母不为零,二次根式的被开方数为非负数)即可得到结果.【详解】解:由题意得:-4,,又∵,∴x≥-2.∴x的取值范围是:x>-2且.解析:C【分析】根据分式和二次根式有意义的条件(分式的分母不为零,二次根式的被开方数为非负数)即可得到结果.【详解】解:由题意得:2x-40≠,x+≥,又∵20∴x≥-2.x≠.∴x的取值范围是:x>-2且2故选C.【点睛】本题考查了分式和二次根式有意义的条件,解不等式,是基础题.4.D【分析】根据最简二次根式与同类二次根式的定义列方程组求解.【详解】=2.由题意,得7-2a=3,解得a=2,故选D.【点睛】此题主要考查了同类二次根式的定义,即:二次根式化成最简解析:D【分析】根据最简二次根式与同类二次根式的定义列方程组求解.【详解】由题意,得7-2a=3,解得a=2,故选D.【点睛】此题主要考查了同类二次根式的定义,即:二次根式化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.5.C【分析】将变形后可分解为:(−5)(+3)=0,从而根据a>0,b>0可得出a和b 的关系,代入即可得出答案.【详解】由题意得:a+=3+15b,∴(−5)(+3)=0,故可得:=5,解析:C=变形后可分解为:)=0,从而根据a>0,b>0可得出a和b的关系,代入即可得出答案.【详解】由题意得:a=+15b,∴+)=0,=,a=25b,12.故选C.【点睛】本题考查二次根式的化简求值,有一定难度,根据题意得出a和b的关系是关键.6.A【解析】根据题意得:|x2–4x+4|+=0,所以|x2–4x+4|=0,=0,即(x–2)2=0,2x–y–3=0,所以x=2,y=1,所以x+y=3.故选A.解析:A【解析】根据题意得:|x2–4x,所以|x2–4x+4|=0,即(x–2)2=0,2x–y–3=0,所以x=2,y=1,所以x+y=3.故选A.7.D【分析】利用平行线的性质、算术平方根的定义、实数的运算及点的坐标的性质分别判断后即可确定正确的选项.【详解】解:①两条平行线直线被第三条直线所截,同位角相等,故错误;②0.01的算术平方解析:D【分析】利用平行线的性质、算术平方根的定义、实数的运算及点的坐标的性质分别判断后即可确定正确的选项.【详解】解:①两条平行线直线被第三条直线所截,同位角相等,故错误;②0.01的算术平方根是0.1,故错误;)=17322+=,故错误;④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1或n=2,故错误,故选D.【点睛】本题考查了命题与定理的知识,解题的关键是熟悉平行线的性质、算术平方根的定义、实数的运算及点的坐标的性质,难度一般.8.B【分析】根据二次根式加减运算和二次根式的性质逐项排除即可.【详解】与不能合并,所以A选项错误;,所以B选项正确;,所以C选项错误;与不能合并,所以D选项错误;故选答案为B.【点睛解析:B【分析】根据二次根式加减运算和二次根式的性质逐项排除即可.【详解】与A选项错误;===B选项正确;321=-=,所以C选项错误;与D选项错误;故选答案为B.【点睛】本题考查了二次根式加减运算和二次根式的性质,掌握同类二次根式的定义和二次根式的性质是解答本题的关键.9.D【分析】根据二次根式的乘法法则对A进行判断;根据分母有理化对B进行判断;根据二次根式的加减法对C进行判断;根据二次根式的性质对D进行判断.【详解】A、计算正确,不符合题意;B、计算正确,解析:D【分析】根据二次根式的乘法法则对A进行判断;根据分母有理化对B进行判断;根据二次根式的加减法对C进行判断;根据二次根式的性质对D进行判断.【详解】AB计算正确,不符合题意;C、计算正确,不符合题意;D11=≠符合题意;故选:D.【点睛】本题考查了二次根式的混合运算,正确掌握相关运算法则是解题关键.10.C【解析】试题解析:∵a+=1,∵∴1-a≥0,a≤1,故选C.解析:C【解析】试题解析:∵a1,a∴1-a≥0,a≤1,故选C.11.C【分析】根据二次根式的性质分析即可得出答案.【详解】解:∵+是整数,m、n是正整数,∴m=2,n=5或m=8,n=20,当m=2,n=5时,原式=2是整数;当m=8,n=20时,原式解析:C【分析】根据二次根式的性质分析即可得出答案.【详解】解:∵m、n是正整数,∴m=2,n=5或m=8,n=20,当m=2,n=5时,原式=2是整数;当m=8,n=20时,原式=1是整数;即满足条件的有序数对(m,n)为(2,5)或(8,20),故选:C.【点睛】本题考查了二次根式的性质和二次根式的运算,估算无理数的大小的应用,题目比较好,有一定的难度.12.B【解析】【分析】根据完全平方公式和=|a|,先把多项式化简为|x-4|-|1-x|,然后根据x的取值范围分别讨论,求出符合题意的x的值即可.【详解】解:原式=-=|x-4|-|1-x|,解析:B【解析】【分析】先把多项式化简为|x-4|-|1-x|,然后根据x的取值范围分别讨论,求出符合题意的x的值即可.【详解】-=|x-4|-|1-x|,解:原式1x当x≤1时,此时1-x≥0,x-4<0,∴(4-x)-(1-x)=3,不符合题意,当1≤x≤4时,此时1-x≤0,x-4≤0,∴(4-x)-(x-1)=5-2x,符合题意,当x≥4时,此时x-4≥0,1-x<0,∴(x-4)-(x-1)=-3,不符合题意,∴x的取值范围为:1≤x≤4故选B.【点睛】本题主要考查绝对值及二次根式的化简,要注意正负号的变化,分类讨论.13.C【解析】【分析】二次根式有意义,就隐含条件b<0,由ab<0,先判断出a、b的符号,再进行化简即可.【详解】解:若ab<0,且代数式a2b有意义;故由b>0,a<0;则代数式a2b=解析:C【解析】【分析】二次根式有意义,就隐含条件b<0,由ab<0,先判断出a、b的符号,再进行化简即可.【详解】解:若ab<0,且代数式有意义;故由b>0,a<0;则代数式故选:C.【点睛】本题主要考查二次根式的化简方法与运用:当a>0时,,当a<0时,,当a=0时,.14.D【解析】【分析】根据等腰直角△ABC被直线a和b所截的图形分为三种情况讨论:①当0≤x≤1时,y是BM+BD;②当1<x≤2时,y是CP+CQ+MN;当2<x≤3时,y=AN+AF,分别用x解析:D【解析】【分析】根据等腰直角△ABC被直线a和b所截的图形分为三种情况讨论:①当0≤x≤1时,y是BM+BD;②当1<x≤2时,y是CP+CQ+MN;当2<x≤3时,y=AN+AF,分别用x表示出这三种情况下y的函数式,然后对照选项进行选择.【详解】①当0≤x≤1时,如图1所示.此时BM=x,则DM=x,在Rt△BMD中,利用勾股定理得BD=2x,所以等腰直角△ABC的边位于直线a,b之间部分的长度和为y=BM+BD=(2+1)x,是一次函数,当x=1时,B点到达N点,y=2+1;②当1<x≤2时,如图2所示,△CPQ是直角三角形,此时y=CP+CQ+MN=2+1.即当1<x≤2时,y的值不变是2+1.③当2<x≤3时,如图3所示,此时△AFN是等腰直角三角形,AN=3﹣x,则AF=2(3﹣x),y=AN+AF=(﹣1﹣2)x+3+32,是一次函数,当x=3时,y=0.综上所述只有D答案符合要求.故选:D.【点睛】本题主要考查动点问题的函数图象,解题的方法是动中找静,在不同的情况下找到y与x的函数式.15.A【解析】【分析】利用多项式的乘法把各数开方进行计算,然后求出A1,A2,A3的值,从而找出规律并写出规律表达式,再把k=100代入进行计算即可求解.【详解】∵(n+3)(n -1)+4=n解析:A【解析】【分析】利用多项式的乘法把各数开方进行计算,然后求出A 1,A 2,A 3的值,从而找出规律并写出规律表达式,再把k=100代入进行计算即可求解.【详解】∵(n+3)(n-1)+4=n 2+2n-3+4=n 2+2n+1=(n+1)2,∴A 11n =+∵(n+5)A 1+4=(n+5)(n+1)+4=n 2+6n+5+4=n 2+6n+9=(n+3)2,∴A 23n =+∵(n+7)A 2+4=(n+7)(n+3)+4=n 2+10n+21+4=n 2+10n+25=(n+5)2,∴A 35n =+⋯⋯依此类推,A k =n+(2k-1)∴A 100=n+(2×100-1)=2005解得,n=1806.故选A.【点睛】本题是对数字变化规律的考查,对被开方数整理,求出A 1,A 2,A 3,从而找出规律写出规律的表达式是解题的关键.16.D【分析】根据题中给的方法分别对和进行化简,然后再进行合并即可.【详解】设,且,∴,∴,∴,∴,∵,∴原式,故选D.【点睛】本题考查了二次根式的混合运算,涉及了分母有理化等解析:D【分析】进行化简,然后再进行合并即可.【详解】设x=<x<,∴0∴266x=-+,∴212236x=-⨯=,∴x=∵5=-,∴原式5=-5=-故选D.【点睛】本题考查了二次根式的混合运算,涉及了分母有理化等方法,弄清题意,理解和掌握题中介绍的方法是解题的关键.17.C【解析】【分析】利用分母有理化进行计算即可.【详解】由原式得: 4(3-2)(3+2)(3-2)<x<4(5+3)(5-3)(5+3)所以4(3-2)<x<2(5+3),因为1<4(解析:C【解析】【分析】利用分母有理化进行计算即可.【详解】由原式得:所以,因为,, 所以. 故选:C【点睛】 此题考查解一元一次不等式的整数解,解题关键在于分母有理化.18.D【分析】分别运用二次根式、整式的运算、分式的运算法则逐项排除即可.【详解】解:A. ,故A 选项错误;B. ,故B 选项错误;C. ,故C 选项错误;D. ,故D 选项正确.故答案解析:D【分析】分别运用二次根式、整式的运算、分式的运算法则逐项排除即可.【详解】解:A. 53183253=A 选项错误;B. ()()()33322363228a b a b a b -=-=-,故B 选项错误; C. 222()2a b a ab b -=-+,故C 选项错误; D. ()()2224222a a a ab a b a a b a a b a +--++⋅=⋅=-++++,故D 选项正确. 故答案为D .【点睛】本题考查了二次根式、整式的运算、分式的运算,掌握相关运算法则是解答本题的关键.19.A【分析】根据估算出的大小、二次根式的意义、算术平方根、无理数比较大小方法,即可解答.【详解】解:①,,故①错误;②因为二次根式中的取值范围是,故②正确;③,9的平方根是,故③错误;解析:A【分析】 根据估算出10的大小、二次根式的意义、算术平方根、无理数比较大小方法,即可解答. 【详解】 解:①3104<<,41015∴<+<,故①错误;②因为二次根式1x +中x 的取值范围是1x ≥-,故②正确;③819=,9的平方根是3±,故③错误;④31255--=,故④错误;⑤∵5154598---=,()22459<,∴51508--<,即51528-<,故⑤错误; 综上所述:正确的有②,共1个,故选:A .【点睛】本题考查了故算无理数的大小,解决本题的关键是掌握估算平方法比较无理数大小.20.B【解析】因5+26=(2)2+2×2×3+(3)2=(2+3)2=2+3 =a+b2+c3,所以a=0,b=1,c=1,即可得2a +999b +1001c=999+1001=2000,故选B.点解析:B【解析】因=,所以a =0,b =1,c =1,即可得2a +999b +1001c =999+1001=2000,故选B. 点睛:本题考查了二次根式的性质与化简,将复合二次根式根据完全平方公式化简并比较系数是解题的关键.。
上海娄山中学运动和力中考综合专项复习训练

上海娄山中学运动和力中考综合专项复习训练一、选择题1.现有3块相同的砖,每块砖重为10N,一人用竖直的两板将三块砖如图所示夹起,则“2号”砖左侧和右侧各自所受摩擦力大小分别为()A.5N 5N B.5N 10N C.10N 5N D.10N 10N2.一个竖直固定在水平地面上的管道如图甲所示,利用拉力F将一木块从管道的左端竖直拉进,右端竖直拉出。
已知管道中的竖直管口对木块的挤压作用相同,并测得拉动全过程中拉力和木块移动速度随时间变化的图像如图乙所示。
则下列说法正确的是()A.木块受到的重力为2NB.4~6秒,木块受到的摩擦力为8NC.0~2秒,木块受到的合力为7ND.2~4秒,木块受到的摩擦力最大3.如图,轻质弹簧竖直放置,下端固定于地面,上端位于O点时弹簧恰好不发生形变.现将一小球放在弹簧上端,再用力向下把小球压至图中A位置后由静止释放,小球将竖直向上运动并脱离弹簧,不计空气阻力,则小球()A.运动至最高点时,受平衡力作用B.被释放瞬间,所受重力大于弹簧弹力C.从A点向上运动过程中,速度先增大后减小D.从O点向上运动过程中,重力势能转化为动能4.如图甲所示,小球从某高度处由静止下落到竖直放置的轻弹簧上并压缩弹簧.从小球刚接触弹簧到将弹簧压缩到最短的过程中,得到小球的速度和弹簧被压缩的长度△L之间的关系图像,如图乙所示,其中b为曲线最高点.不计空气阻力,弹簧在整个过程中始终发生弹性形变,则小球()A.在a处弹簧的弹力最大B.在b处弹簧的弹性势能最大C.从a到c过程中,小球的速度逐渐减小D.在b处小球受到的弹力与它所受的重力满足二力平衡的条件5.如图甲所示,水平地面上的一物体,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物体的速度v与时间t的关系如图乙所示,以下说法不正确的是()A.0~2秒,物体没有推动,是因为推力小于摩擦力B.2~4秒物体受到的摩擦力是2NC.4~6秒物体受到的摩擦力是2ND.4~6秒,物体受到的摩擦力与水平推力是一对平衡力6.如图所示,甲、乙两位同学做如图所示的“拔河”游戏,两人分别用伸平的手掌托起长凳的一端,保持凳子水平,然后各自向两侧“拉”,若凳子下表面各处的粗糙程度相同,且在乙端的凳面上放四块砖,则下列判断正确的是()A.凳子向甲方移动B.凳子向乙方移动C.凳子原处不动D.凳子向体重大的同学一方移动7.如图所示,用大小为F的垂直于墙面的力挤压黑板擦,黑板擦静止于墙面上,此时黑板擦受到的摩擦力为f1;改变F的大小使其变成13F,黑板擦恰好匀速下滑,此时黑板擦受到的摩擦力为f2,请问f1和f2的大小关系是()A.f1<f2B.f1=f2C.f1>f2D.无法判断8.如图所示,水平地面上静置着A、B两个物体,下列说法正确的是()A.B物体对A物体的支持力与A物体对B物体的压力是一对平衡力B.A物体受到的重力与A物体受到B物体的支持力是一对相互作用力C.B物体受到的重力与水平地面对B物体的支持力是一对相互作用力D.B物体对水平地面的压力与水平地面对B物体的支持力是一对相互作用力9.用弹簧测力计拉着重8N的物体在水平面上以2.5m/s的速度做匀速直线运动,弹簧测力计的示数为2N.当绳子突然断开时,则:()A.物体速度保持不变,受到的摩擦力等于2N B.物体速度逐渐减小,受到的摩擦力等于2NC.物体速度逐渐不变,受到的摩擦力等于8N D.物体立即停止,受到的摩擦力为零10.若物体不受任何外力作用,则该物体()A.一定做匀速直线运动B.运动状态可能改变C.一定静止D.可能做匀速直线运动二、填空题11.物体在流体(气体或液体)中运动时,会受到阻力作用,该阻力叫做流体阻力。
上海民办浦东交中初级中学九年级数学上册第三单元《旋转》测试(有答案解析)

一、选择题1.下面四个图案是常用的交通标志,其中为中心对称图形的是( )A .B .C .D . 2.如图,在等边△ABC 中,AC=8,点O 在AC 上,且AO=3,点P 是边AB 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD ,要使点D 恰好落在BC 上,则AP 的长是( ).A .4B .5C .6D .83.以下四幅图案,其中图案是中心对称图形的是( )A .B .C .D .4.直线26y x =-+与x 轴交于A 点,与y 轴交于B 点,将AOB 绕点A 顺时针旋转90°得到AO B ''△,则点B '的坐标是( )A .()9,9B .()3,9-C .()9,3D .()3,9 5.如图,正方形ABCD 内一点P ,5AB =,2BP =,把ABP △绕点B 顺时针旋转90°得到CBP ',则PP '的长为( )A .22B .23C .3D .32 6.如图,在ABC ∆中,30,8,5BAC AB AC ∠===,将ABC ∆绕点A 顺时针旋转30得到ADE ∆连接CD ,则CD 的长是( )A .7B .8C .12D .137.如图,在平面直角坐标系中,将正方形OABC 绕点O 逆时针旋转45°后得到正方形111OA B C ,依此方式,绕点O 连续旋转2020次得到正方形202020202020OA B C ,如果点A 的坐标为(1,0),那么点2020B 的坐标为( )A .(﹣1,1)B .(2,C .(﹣1,﹣1)D .(02)-, 8.如图:在△ABC 中,∠ACB=90°,∠ABC=30°,AC=1,现将△ABC 绕点C 逆时针旋转至△EFC ,使点E 恰巧落在AB 上,连接BF ,则BF 的长度为( )A .3B .2C .1D .2 9.下列图形中,既是轴对称图形又是中心对称图形的是( ) A .等边三角形 B .平行四边形 C .正五边形 D .菱形 10.下列图标中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D . 11.如图,把△ABC 绕着点A 逆时针旋转40°得到△ADE ,∠1=30°,则∠BAE =( )A .10°B .30°C .40°D .70°12.如图①,正方形A 的一个顶点与正方形B 的对称中心重合,重叠部分面积是正方形A 面积的12,如图②,移动正方形A 的位置,使正方形B 的一个顶点与正方形A 的对称中心重合,则重叠部分面积是正方形B 面积的( )A .12B .14C .16D .18二、填空题13.如图,将矩形ABCD 绕点A 顺时针旋转90︒后,得到矩形AB C D ''',若8CD =,6DA =,那么AC '=______.14.如图.面积为8的正方形ABCD 的顶点A 在数轴上,点A 表示实数2-,正方形ABCD 绕点A 旋转时,顶点B 的运动轨迹与数轴的交点表示的数为______________15.如图,将AOB 绕点O 按逆时针方向旋转45°后得到COD △,若15AOB ∠=︒,则BOC ∠=______度.16.已知点(,2)A m m 在直线3y x 上,则点A 关于原点对称点B 的坐标为______. 17.已知点()2,3A x -与点()4,5B y -关于原点对称,则xy 的值等于______. 18.如图,在平面直角坐标系中,将正方形OABC 绕点O 逆时针旋转45︒后得到正方形111OA B C ,依此方式,绕点O 连续旋转2019次得到正方形201920192019OA B C ,如果点A 的坐标为(1,0),那么点2019B 的坐标为________.19.矩形是中心对称图形,对矩形ABCD 而言,点A 的对称点是点____.20.一副直角三角尺叠放,如图①所示,现将含45°角的三角尺ADE 固定不动,将含30°角的三角尺ABC 绕顶点A 顺时针转动(旋转角不超过180度),使两个三角尺有一组边互相平行.例如图②,当∠BAD =15°时,BC ∥DE ,当90°<∠BAD <180°时,∠BAD 的度数为___.三、解答题21.在下列网格图中,每个小正方形的边长均为1个单位.在Rt △ABC 中,∠C=90°,AC=3,BC=4.(1)试在图中作出△ABC 以A 为旋转中心,沿顺时针方向旋转90°后的图形△AB 1C 1; (2)若点B 的坐标为(-3,5),试在图中画出平面直角坐标系,并标出A ,C 两点的坐标. 22.点O 为直线AB 上一点,过点O 作射线OC ,使65BOC ∠=︒,将一直角三角板的直角顶点放在点O 处.(1)如图1,将三角板MON 的一边ON 与射线OB 重合时,求MOC ∠的度数;(2)如图2,将三角板MON 绕点O 逆时针旋转一定角度,此时OC 是MOB ∠的角平分线,求旋转角BON ∠的度数,CON ∠的度数;(3)将三角板MON 绕点O 逆时针旋转至图3时,5NOC ∠=︒,求AOM ∠.23.如图,△ABC 在平面直角坐标系中,每个小正方形网格的边长都是1个单位长度. (1)画出ABC 关于x 轴的对称图形111A B C △,并写出点1A 的坐标;(2)将△ABC 绕点O 顺时针旋转90°,请画出旋转后的222A B C △,并写出A 2的坐标. (3)直接写出12B B 的长度.24.实践与探究已知:△ABC 和△DOE 都是等腰三角形,∠CAB=∠DOE=90°,点O 是BC 的中点,发现结论:(1)如图1,当OE 经过点A ,OD 经过点C 时,线段AE 和CD 的数量关系是 ,位置关系是 .(2)在图1的基础上,将△DOE 绕点O 顺时针旋转α(090α︒<<︒)得到图2,则问题(1)中的结论是否成立?请说明理由.(3)如图3在(2)的基础上,当AE=CE 时,请求出α的度数.(4)在(2)的基础上,△DOE 在旋转的过程中设AC 与OE 相交于点F ,当△OFC 为等腰三角形时,请直接写出α的度数.25.如图1,AC ⊥CH 于点C ,点B 是射线CH 上一动点,将△ABC 绕点A 逆时针旋转60°得到△ADE (点D 对应点C ).(1)延长ED 交CH 于点F ,求证:FA 平分∠CFE ;(2)如图2,当∠CAB >60°时,点M 为AB 的中点,连接DM ,请判断DM 与DA 、DE 的数量关系,并证明.26.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;(2)请画出△ABC关于点(1,0)成中心对称的图形△A2B2C2;(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标;(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据中心对称图形的概念进行判断即可;【详解】A、图形旋转180度之后不能与原图形重合,故不是中心对称图形;B、图形旋转180度之后不能与原图形重合,故不是中心对称图形;C、图形旋转180度之后能与原图形重合,故是中心对称图形;D、图形旋转180度之后不能与原图形重合,故不是中心对称图形;故选:C.【点睛】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合;2.B解析:B【分析】连接DP ,根据题意,得OP OD =,=60DOP ∠,从而得到120AOP COD ∠+∠=;再根据等边三角形和三角形内角和性质,得120AOP OPA ∠+∠=,从而得COD OPA ∠=∠,通过全等三角形判定,即可得到答案.【详解】如图,点D 落在BC 上,连接DP∵线段OP 绕点O 逆时针旋转60°得到线段OD∴OP OD =,=60DOP ∠∴180120AOP COD DOP ∠+∠=-∠=∵等边△ABC∴180120AOP OPA A ∠+∠=-∠=∴COD OPA ∠=∠即:OP OD COD OPA A C =⎧⎪∠=∠⎨⎪∠=∠⎩∴AOP CDO △≌△∴AP OC =∵AC=8,AO=3∴5OC AC AO =-=∴5AP OC ==故选:B .【点睛】本题考查了等边三角形、全等三角形、旋转、三角形内角和的知识;解题的关键是熟练掌握等边三角形、全等三角形、旋转、三角形内角和的性质,从而完成求解.3.A解析:A【分析】根据中心对称图形的定义逐一分析即可.【详解】解:A 、是中心对称图形,故此选项符合题意;B、不是中心对称图形,故此选项不合题意;C、不是中心对称图形,故此选项不合题意;D、不是中心对称图形,故此选项不合题意.故选:A.【点睛】本题考查中心对称图形的识别,掌握中心对称图形的定义是解题的关键.4.C解析:C【分析】由题意可求点A(3,0),点B(0,6),根据旋转的性质可得OA=O'A=3,BO=B'O'=6,B'O'∥OA,即可求点B'坐标.【详解】解:如图:∵直线y=-2x+6与x轴交于A点,与y轴交于B点,∴当x=0时,y=6;当y=0时,x=3.∴点A(3,0),点B(0,6)∴OA=3,OB=6∵将△AOB绕点A顺时针旋转90°得到△AO′B′,∴OA=O'A=3,BO=B'O'=6,∠OAO'=∠B'O'A=90°∴B'O'∥OA∴点B'(9,3)故选:C.【点睛】本题考查了一次函数图象上点的坐标特征,旋转的性质,熟练运用旋转的性质是本题的关键.5.A解析:A【分析】由△ABP绕点B顺时针旋转90°得到△CBP',根据旋转的性质得BP=BP′,∠PBP′=90,则△BPP′为等腰直角三角形,由此得到2BP,即可得到答案..【详解】解:解:∵△ABP 绕点B 顺时针旋转90°得到△CBP',而四边形ABCD 为正方形,BA=BC ,∴BP=BP′,∠PBP′=90,∴△BPP′为等腰直角三角形,而BP=2,∴PP′=2BP=22.故选:A .【点睛】本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了正方形和等腰直角三角形的性质. 6.A解析:A【分析】过点D 作DF AC ⊥与F ,由旋转的性质可得AD=AB=8,30BAC DAB ∠=∠=︒,由直角三角形的性质可得AF=4,DF=3AF=43,由勾股定理可求解.【详解】解:过点D 作DF AC ⊥与F ,将ABC ∆绕点A 顺时针旋转30得到ADE ∆,830AD AB BAC DAB ∴==∠=∠=︒,,60CAD ∴∠=︒,且DF AC ⊥,AD=84343AF DF AF ∴===,,1CF ∴=,224817CD DF CF ∴=+=+=故选A ..【点睛】本题考查了旋转的性质、勾股定理,添加合适的辅助线构造直角三角形是解题的关键. 7.C解析:C【分析】根据图形可知:点B在以O为圆心,以OB为半径的圆上运动,由旋转可知:将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,可得对应点B的坐标,根据规律发现是8次一循环,可得结论.【详解】解:如图,∵四边形OABC是正方形,且OA=1,∴B(1,1),连接OB,由勾股定理得:2,由旋转得:OB=OB1=OB2=OB32,∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,∴B1(02),B2(-1,1),B3(20),B4(-1,-1),…,发现是8次一循环,所以2020÷8=252…4,∴点B2020的坐标为(-1,-1)故选:C.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.也考查了坐标与图形的变化、规律型:点的坐标等知识,解题的关键是学会从特殊到一般的探究规律的方法,属于中考常考题型.8.A解析:A【解析】试题分析:由题意可知:∠A=60°,AC=EC,所以△ACE是等边三角形,所以∠CEA=∠ECA=60°,由旋转可知,∠CEF=∠A=60°,所以∠FEB=60°,因为∠ECF=∠ACB=90°,所以∠BCF=∠ACE=60°,因为CB=CF,所以△CBF是等边三角形,所以∠CBF=60°,∠FBE=60°+30°=90°,△BEF是30度角直角三角形,因为AE=AC=1,AB=2AC=2,所以BE=1,EF=2,21213-=A.考点:1.旋转性质;2.直角三角形性质.9.D解析:D【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A、是轴对称图形,不是中心对称图形.故不符合题意;B、不是轴对称图形,是中心对称图形.故不符合题意;C、是轴对称图形,不是中心对称图形.故不符合题意;D、是轴对称图形,也是中心对称图形.故符合题意.故选:D.【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.10.D解析:D【解析】试题分析:根据轴对称图形和中心对称图形的概念,可知:A既不是轴对称图形,也不是中心对称图形,故不正确;B不是轴对称图形,但是中心对称图形,故不正确;C是轴对称图形,但不是中心对称图形,故不正确;D即是轴对称图形,也是中心对称图形,故正确.故选D.考点:轴对称图形和中心对称图形识别11.D解析:D【分析】先找到旋转角,根据∠BAE=∠1+∠CAE进行计算.【详解】解:根据题意可知旋转角∠CAE=40°,所以∠BAE=30°+40°=70°.故选D.【点睛】本题主要考查了旋转的性质,解题的关键是找准旋转角.12.D解析:D【分析】设正方形B的面积为S,正方形B对角线的交点为O,标注字母并过点O作边的垂线,根据正方形的性质可得OE=OM,∠EOM=90°,再根据同角的余角相等求出∠EOF=∠MON,然后利用“角边角”证明△OEF和△OMN全等,根据全等三角形的面积相等可得阴影部分的面积等于正方形B的面积的1 4,再求出正方形B的面积=2正方形A的面积,即可得出答案.【详解】解:设正方形B对角线的交点为O,如图1,设正方过点O作边的垂线,则OE=OM,∠EOM=90°,∵∠EOF+∠EON=90°,∠MON+∠EON=90°,∴∠EOF=∠MON,在△OEF和△OMN中EOF MONOE0MOEF OMN90︒∠=∠⎧⎪=⎨⎪∠=∠=⎩,∴△OEF≌△OMN(ASA),∴阴影部分的面积=S四边形NOEP+S△OEF=S四边形NOEP+S△OMN=S四边形MOEP=14S正方形CTKW,即图1中阴影部分的面积=正方形B的面积的四分之一,同理图2中阴影部分烦人面积=正方形A的面积的四分之一,∵图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的12,∴正方形B的面积=正方形A的面积的2倍,∴图2中重叠部分面积是正方形B面积的18,故选D.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.二、填空题13.10【分析】根据旋转的性质可得在中利用勾股定理即可求解【详解】ABCD 为矩形CD=8DA=6由旋转的性质可得:在中由勾股定理得:即故答案为:10【点睛】本题考查旋转性质及勾股定理的综合应用根据旋转性解析:10【分析】根据旋转的性质可得8CD C D ''==,6DA D A '==,在Rt ''△AD C 中利用勾股定理即可求解.【详解】ABCD 为矩形,CD=8,DA=6由旋转的性质可得:8CD C D ''==,6DA D A ='=,90CDA C D A ''∠=∠=︒∴在Rt ''△AD C 中由勾股定理得:AC '=10AC '== 故答案为:10.【点睛】本题考查旋转性质及勾股定理的综合应用,根据旋转性质得到直角三角形的基础上应用勾股定理求出边的长度是解题关键.14.或﹣【分析】先由正方形的面积公式求出AB=再根据点A 表示实数即可求出顶点B 的运动轨迹与数轴的交点表示的数【详解】解:∵正方形ABCD 的面积为8∴AB=∵点A 表示实数∴顶点B 的运动轨迹与数轴的交点表示或﹣【分析】先由正方形的面积公式求出AB=A 表示实数,即可求出顶点B 的运动轨迹与数轴的交点表示的数.【详解】解:∵正方形ABCD 的面积为8,∴AB=∵点A 表示实数,∴顶点B 的运动轨迹与数轴的交点表示的数为+或﹣﹣【点睛】本题考查了正方形的面积、实数和数轴、旋转的性质、算术平方根、二次根式的加减运算,理解实数与数轴的关系是解答的关键.15.60【分析】根据旋转的性质得到∠BOD=45°且∠COD=∠AOB 再用∠BOD 加∠COD 即可【详解】∵将△AOB 绕点O 按逆时针方向旋转45°后得到△COD ∴∠BOD=45°∠COD=∠AOB 又∵∠A解析:60【分析】根据旋转的性质得到∠BOD=45°,且∠COD=∠AOB ,再用∠BOD 加∠COD 即可.【详解】∵将△AOB 绕点O 按逆时针方向旋转45°后,得到△COD ,∴∠BOD=45°,∠COD=∠AOB ,又∵∠AOB=15°,∴∠BOC=∠BOD+∠COD=45°+15°=60°,故答案为60°.【点睛】本题考查了旋转的定义和性质,解题的关键是找准旋转角以及对应的边.16.【分析】先由点在直线上求出m 的值然后根据关于原点对称的点的坐标特点:横纵坐标均互为相反数解答即可【详解】解:∵点在直线上∴2m=m+3∴m=3∴点A 坐标是(36)∴点(36)关于原点对称的点的坐标为 解析:(3,6)--【分析】先由点(,2)A m m 在直线3y x 上求出m 的值,然后根据关于原点对称的点的坐标特点:横纵坐标均互为相反数解答即可. 【详解】解:∵点(,2)A m m 在直线3y x 上,∴2m =m +3,∴m =3,∴点A 坐标是(3,6),∴点A (3,6)关于原点对称的点B 的坐标为(﹣3,﹣6).故答案为:(﹣3,﹣6).【点睛】本题考查了一次函数图象上点的坐标特点和关于原点对称的点的坐标特征,属于基本题型,熟练掌握基本知识是解题的关键. 17.-4【分析】利用关于原点对称点的性质求出xy 的值进而求出答案【详解】解:∵点与点关于原点对称∴x-2=-4y-5=-3∴x=-2y=2∴xy=(-2)×2=-4故答案为:-4【点睛】本题考查了关于原解析:-4【分析】利用关于原点对称点的性质求出x ,y 的值,进而求出答案.【详解】解:∵点()2,3A x -与点()4,5B y -关于原点对称,∴x-2=-4,y-5=-3,∴x=-2,y=2,∴xy=(-2)×2=-4.故答案为:-4【点睛】本题考查了关于原点对称点的性质,根据与原点对称的点的坐标特点(纵坐标,横坐标都互为相反数)得出x,y的值是解题关键.18.【分析】根据图形可知:点B在以O为圆心以OB为半径的圆上运动由旋转可知:将正方形OABC绕点O逆时针旋转45∘后得到正方形OA1B1C1相当于将线段OB绕点O逆时针旋转45∘可得对应点B的坐标根据规解析:(2,0)【分析】根据图形可知:点B在以O为圆心,以OB为半径的圆上运动,由旋转可知:将正方形OABC 绕点O逆时针旋转45∘后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45∘,可得对应点B的坐标,根据规律发现是8次一循环,可得结论.【详解】∵四边形OABC是正方形,且OA=1,∴B(1,1),连接OB,由勾股定理得:2,由旋转得:OB=OB1=OB2=OB32,∵将正方形OABC绕点O逆时针旋转45∘后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45∘,依次得到∠AOB=∠BOB1=∠B1OB2=…=45∘,∴B12),B2(−1,1),B32,…,发现是8次一循环,所以2019÷8=252…3,∴点B2019的坐标为2【点睛】本题考查了旋转的性质,对应点到旋转中心的距离相等;对应点与旋转中心所连接线段的夹角等于旋转角,也考查了坐标与图形的变化、规律型、点的坐标等知识,解题的关键是学会从特殊到一般的探究规律的方法.19.C【分析】根据把一个图形绕某一点旋转180°如果旋转后的图形能够与原来的图形重合那么这个图形就叫做中心对称图形这个点叫做对称中心可得答案【详解】解:矩形是中心对称图形对称中心是对角线的交点点A的对称解析:C【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心可得答案.【详解】解:矩形是中心对称图形,对称中心是对角线的交点,点A的对称点是点C,故答案为C.【点睛】本题考查了中心对称图形,关键是掌握中心对称图形的性质.20.105°或135°【分析】根据题意画出图形再由平行线的判定定理即可得出结论【详解】解:如图(1)当AC∥DE时∠BAD=∠DAE=45°;如图(2)当BC∥AD时∠DAB=∠B=60°;如图(3)当解析:105°或135°【分析】根据题意画出图形,再由平行线的判定定理即可得出结论.【详解】解:如图(1),当AC∥DE时,∠BAD=∠DAE=45°;如图(2),当BC∥AD时,∠DAB=∠B=60°;如图(3),当BC∥AE时,∵∠EAB=∠B=60°,∴∠BAD=∠DAE+∠EAB=45°+60°=105°;如图(4),当AB∥DE时,∵∠E=∠EAB=90°,∴∠BAD=∠DAE+∠EAB=45°+90°=135°.∴当90°<∠BAD<180°时,∠BAD=105°或135°.故答案为:105°或135°.【点睛】本题考查的是旋转的性质,平行线的判定与性质,根据题意画出图形,利用平行线的性质及直角三角板的性质求解是解答此题的关键.三、解答题21.(1)见解析;(2)见解析;A(0,1),C(-3,1)【分析】(1)根据图形旋转的性质画出△AB1C1即可;(2)根据B点坐标,作出平面直角坐标系,即可写出各点坐标.【详解】(1)解:旋转后图形如图所示(2)解:由B点坐标,建立坐标系如图所示,则A(0,1),C(-3,1).【点睛】本题考查的是作图-旋转变换,熟知图形旋转的性质是解答此题的关键.22.(1)25° (2)40°,25° (3)20°.【分析】(1)直接利用角的和差计算即可;(2)先根据角平分线的性质求得∠MOB=130°,再根据旋转角的定义BON ∠,然后∠BOC-∠BON 即可求得CON ∠;(3)先求出∠BON ,然后利用平角的性质和角的和差即可解答.【详解】(1)906525MOC MON BOC ∠=∠-∠=︒-︒=︒,故答案为25°;(2)∵OC 是MOB ∠的角平分线,∴2265130MOB BOC ∠=∠=⨯︒=︒,∴旋转角1309040BON MOB MON ∠=∠-∠=︒-︒=︒,654025CON BOC BON ∠=∠-∠=︒-︒=︒,故答案为40°,25°;(3)∵5NOC ∠=︒,65BOC ∠=︒,∴70BON NOC BOC ∠=∠+∠=︒,∵点O 为直线AB 上一点,∴180AOB ∠=︒,∵90MON ∠=︒,∴180907020AOM AOB MON BON ∠=∠-∠-∠=︒-︒-︒=︒.【点睛】本题主要考查了角平分线的定义、旋转角的性质、直角的性质和角的和差等知识点,考查知识点较多,灵活运用所学知识成为解答本题的关键.23.(1)图见详解,A 1(-3,-5);(2)图见详解;A 2(5,3);(3)B 1B 2=32.【分析】(1)找到A 、B 、C 关于x 轴的对称点A 1、B 1、C 1连接各点即可得到结果,同时得到点A 1的坐标;(2)找到A 、B 、C 绕着O 点旋转90°后的对应点A 2、B 2、C 2连接各点即可得到结果,同时得到点A 2的坐标;(3)利用勾股定理求出B 1B 2的长.【详解】解:(1)如图所示,△A 1B 1C 1即为所求,A 1(-3,-5);(2)如图所示,△A 2B 2C 2即为所求,A 2(5,3);(3)B 1B 22233+2.【点睛】本题考查利用轴对称变换和旋转变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.24.(1)AE=CD AE ⊥CD ;(2)成立,理由见解析;(3)45°;(4)45°或22.5°【分析】(1)证明△AOC 是等腰直角三角形即可得到结论;(2)连接AO ,延长DC 交AE 于点M ,设OE ,MD 相交于点N ,证明△AOE ≌△COD 可得AE=CD ,证明∠DME=90°可得AE ⊥CD ;(3)证明OE 是AC 的垂直平分线即可得到结论;(4)分OF=FC和OC=CF两种情况求解即可.【详解】解:(1)∵△ABC是等腰三角形,∠CAB =90°,∴∠ACB=45°∵点O是BC的中点,∴AO⊥BC∴△AOC是等腰直角三角形,∴AO=CO∵△DOE是等腰三角形,∠DOE=90°,∴EO=DO∴EO-AO=DO-CO即AE=CD∵OE经过点A,OD经过点C,∴AE⊥CD故答案为:AE=CD AE⊥CD(2)(1)中的结论仍然成立理由如下:连接AO,延长DC交AE于点M,设OE,MD相交于点N∵△ABC是等腰直角三角形,O是BC的中点∴AO=CO,AO⊥BC∴∠AOC=∠EOD=90°∴∠AOE=∠COD∵OE=OD∴△AOE≌△COD(SAS)∴AE=CD,∠AEO=∠CDO∵∠CDO+∠OND=90°,且∠OND=∠MNE∴∠AEO+∠MNE=90°∴∠DME=90°∴DM⊥AE即DC⊥AE(3)连接OA,如图3,∵AE=CE,OA=OC∴OE是AC的垂直平分线∴∠AOE=∠COE=45°∴α=45°(4)①若OF=FC时,如图4,∵△ABC是等腰直角三角形,∠BAC=90°,∴∠ACB=45°∴∠FOC=45°∵AO⊥BC∴∠AOC=90°∴∠AOF=90°-45°=45°,即α=45°;②当OC=FC时,如图5,∵△ABC是等腰直角三角形,∠BAC=90°,∴∠ACB=45°∴∠FOC=1804567.52︒-︒=︒ ∵AO ⊥BC∴∠AOC=90°∴∠AOF=90°-67.5°=22.5°,即α=22.5°;综上所述,α的度数为45°或22.5°. 【点睛】本题是几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,添加恰当辅助线构造全等三角形是本题的关键.25.(1)见解析;(2)2DM +3AD =DE ,证明见解析.【分析】(1)根据直角三角形全等判定,得到对应角相等,根据角分线定义证明.(2)延长AD 交BC 于F ,连接CD ;利用旋转的到特殊值三角形,运用三角形的中位线定理,将DE 解转化到CB 决问题即可.【详解】(1)如图1中,∵△ADE 由△ABC 旋转得到,∴AC =AD ,∠ACF =∠ADE =∠ADF =90°,AF=AF∴ACF ADF ≌(HL),AFC AFD ∴∠=∠, FA 平分∠CFE ; (2)结论:23DM AD DE +=,理由如下:如图2中,延长AD 交BC 于F ,连接CD ,∵AC =AD ,∠CAD =60°,∴△ACD 为等边三角形,∴AD =CD =AC ,∵∠ACF =90°,∠CAF =60°,∴∠AFC =30°,∴AD=AC=1AF,2∴AD=DF,∴D为AF的中点,又∵M为AB的中点,∴DM=1FB,即FB=2DM2在Rt△AFC中,FC=3AC=3AD,==+,DE CB FB FC∴+=+23FB FC DM AD∴23+=.DM AD DE【点睛】本题考查图形旋转、30°直角三角形性质及三角形中位线定理,综合运用所学知识,将DE 解转化为CB是解题关键.26.(1)见解;(2)见解析;(3)M的坐标为(-1,0);(4)P的坐标为(2,0)【分析】(1)分别作出A,B,C的对应点A1,B1,C1即可.(2)分别作出A,B,C关于点(1,0)的对称点A2,B2,C2即可.(3)连接A1A2,B1B2交于点M,点M即为所求.(4)连接BA2交x轴于点P,点P即为所求.【详解】解:(1)如图,△A1B1C1即为所求.(2)如图,△A2B2C2即为所求.(3)如图,点M即为所求,点M的坐标为(-1,0).(4)如图,点P即为所求,点P的坐标为(2,0).【点睛】本题考查作图——旋转变换,平移变换,轴对称最短问题等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.。
深圳罗湖区罗芳中学人教版七年级下册数学期末压轴难题试卷及答案-百度文库

深圳罗湖区罗芳中学人教版七年级下册数学期末压轴难题试卷及答案-百度文库一、选择题1.如图,下列结论中错误的是( )A .∠1与∠2是同旁内角B .∠1与∠4是内错角C .∠5与∠6是内错角D .∠3与∠5是同位角2.在下列图形中,不能..通过其中一个三角形平移得到的是( ) A . B . C .D .3.平面直角坐标系中,点()1,0A -在( )A .x 轴的正半轴B .x 轴的负半轴C .y 轴的正半轴D .y 轴的负半轴 4.以下命题是真命题的是( )A .相等的两个角一定是对顶角B .过直线外一点有且只有一条直线与已知直线平行C .两条平行线被第三条直线所截,内错角互补D .在同一平面内,垂直于同一条直线的两条直线互相垂直5.如图,小明课间把老师的三角板的直角顶点放在黑板的两条平行线a ,b 中的直线b 上,已知155∠=︒,则2∠的度数为( )A .45︒B .35︒C .55︒D .25︒6.小雪在作业本上做了四道题目:327-3;164;3819;2(6)--6,她做对了的题目有( )A .1道B .2道C .3道D .4道 7.如图,//AB CD ,EF 交AB 于点G ,EM 平分CEF ∠,80FGB ∠=︒,则GME ∠的度数为( ).A .60°B .55°C .50°D .45°8.如图,在平面直角坐标系中,一动点从原点O 出发,向右平移3个单位长度到达点1A ,再向上平移6个单位长度到达点2A ,再向左平移9个单位长度到达点3A ,再向下平移12个单位长度到达点4A ,再向右平移15个单位长度到达点5A ……按此规律进行下去,该动点到达的点2021A 的坐标是( )A .(3030,3030)--B .(3030,3033)-C .(3033,3030)-D .(3030,3033)二、填空题9.9的算术平方根是 .10.已知点A (2a +3b ,﹣2)和点B (8,3a +1)关于y 轴对称,那么a +b =_____. 11.如图.已知点C 为两条相互平行的直线,AB ED 之间一动点,ABC ∠和CDE ∠的角平分线相交于F ,若3304BCD BFD ∠=∠+︒,则BCD ∠的度数为________.12.如图,把一把直尺放在含30度角的直角三角板上,量得154∠=︒,则2∠的度数是_______.13.如图所示,一个四边形纸片ABCD ,B D 90︒∠=∠=,把纸片按如图所示折叠,使点B 落在AD 边上的B '点,AE 是折痕,C 130︒∠=,则AEB ∠=________度.14.如图,按照程序图计算,当输入正整数x 时,输出的结果是161,则输入的x 的值可能是__________.15.()2260a b ++-=,则(),a b 在第_____象限. 16.如图,一只跳蚤在第一象限及x 轴、y 轴上跳动,第一秒它从原点跳动到点(0,1),第二秒它从点(0,1)跳到点(1,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],每秒跳动一个单位长度,那么43秒后跳蚤所在位置的坐标是________.三、解答题17.计算:(1)|23-|+22;(2)22312127(6)(5)+----18.求下列各式中x 的值:(1)()24264x -=;(2)3338x -=. 19.如图,已知3A ∠=∠,DE BC ⊥,AB BC ⊥,求证:DE 平分CDB ∠.证明:DE BC ⊥,AB BC ⊥ (已知)90DEC ABC ∴∠=∠=︒(垂直的定义)//DE AB ∴( ) 23∴∠=∠( ) 1∠= (两直线平行,同位角相等)又3A ∠=∠(已知)∴ ( )DE ∴平分CDB ∠(角平分线的定义)20.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A 处出发去看望B 、C 、D 处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A 到B 记为:A →B (+1,+4),从B 到A 记为:A →B (﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中(1)A →C ( , ),B →D ( , ),C → (+1, );(2)若这只甲虫从A 处去甲虫P 处的行走路线依次为(+2,+2),(+1,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P 的位置.21.在学习《实数》内容时,我们通过“逐步逼近”的方法可以计算出2的近似值,得出1.4<2<1.5.利用“逐步逼近“法,请回答下列问题:(1)17介于连续的两个整数a 和b 之间,且a <b ,那么a = ,b = . (2)x 是17+2的小数部分,y 是17﹣1的整数部分,求x = ,y = . (3)(17﹣x )y 的平方根.二十二、解答题22.如图,在3×3的方格中,有一阴影正方形,设每一个小方格的边长为1个单位.请解决下面的问题.(1)阴影正方形的面积是________?(可利用割补法求面积)(2)阴影正方形的边长是________?(3)阴影正方形的边长介于哪两个整数之间?请说明理由.二十三、解答题23.问题情境:(1)如图1,//AB CD ,128PAB ∠=︒,119PCD ∠=︒.求APC ∠度数.小颖同学的解题思路是:如图2,过点P 作//PE AB ,请你接着完成解答.问题迁移:(2)如图3,//AD BC ,点P 在射线OM 上运动,当点P 在A 、B 两点之间运动时,ADP α∠=∠,PCE β∠=∠.试判断CPD ∠、α∠、β∠之间有何数量关系?(提示:过点P 作//PF AD ),请说明理由;(3)在(2)的条件下,如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你猜想CPD ∠、α∠、β∠之间的数量关系并证明.24.已知两条直线l 1,l 2,l 1∥l 2,点A ,B 在直线l 1上,点A 在点B 的左边,点C ,D 在直线l 2上,且满足115ADC ABC ∠=∠=o .(1)如图①,求证:AD ∥BC ;(2)点M ,N 在线段CD 上,点M 在点N 的左边且满足MAC BAC ∠=∠,且AN 平分∠CAD ;(Ⅰ)如图②,当30ACD ∠=o 时,求∠DAM 的度数;(Ⅱ)如图③,当8CAD MAN ∠=∠时,求∠ACD 的度数.25.模型与应用.(模型)(1)如图①,已知AB ∥CD ,求证∠1+∠MEN +∠2=360°.(应用)(2)如图②,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6的度数为.如图③,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为.(3)如图④,已知AB∥CD,∠AM1M2的角平分线M1 O与∠CM n M n-1的角平分线M n O交于点O,若∠M1OM n=m°.在(2)的基础上,求∠2+∠3+∠4+∠5+∠6+……+∠n-1的度数.(用含m、n的代数式表示)26.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动,A、B不与点O重合,如图1,已知AC、BC分别是∠BAP和∠ABM角的平分线,(1)点A、B在运动的过程中,∠ACB的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的大小.(2)如图2,将△ABC沿直线AB折叠,若点C落在直线PQ上,则∠ABO=________,如图3,将△ABC沿直线AB折叠,若点C落在直线MN上,则∠ABO=________(3)如图4,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其反向延长线交于E、F,则∠EAF=;在△AEF中,如果有一个角是另一个角的32倍,求∠ABO的度数.【参考答案】一、选择题1.B解析:B【分析】根据同位角、内错角、同旁内角的定义结合图形进行判断即可.【详解】解:如图,∠1与∠2是直线a与直线b被直线c所截的同旁内角,因此选项A不符合题意;∠1与∠6是直线a与直线b被直线c所截的内错角,而∠6与∠4是邻补角,所以∠1与∠4不是内错角,因此选项B符合题意;∠5与∠6是直线c与直线d被直线b所截的内错角,因此选项C不符合题意;∠3与∠5是直线c与直线d被直线b所截的同位角,因此选项D不符合题意;故选:B.【点睛】本题主要考查同位角、内错角、同旁内角,掌握同位角、内错角、同旁内角的定义是关键.2.D【分析】根据平移的性质即可得出结论.【详解】解:A、能通过其中一个三角形平移得到,不合题意;B、能通过其中一个三角形平移得到,不合题意;C、能通过其中一个三角形平移得到,不合题意;D解析:D【分析】根据平移的性质即可得出结论.【详解】解:A、能通过其中一个三角形平移得到,不合题意;B、能通过其中一个三角形平移得到,不合题意;C、能通过其中一个三角形平移得到,不合题意;D、不能通过其中一个三角形平移得到,上面的三角形需要由下面的三角形旋转才能得到,符合题意.故选:D.【点睛】本题考查的是利用平移设计图案,熟知图形的平移只改变图形的位置,而不改变图形的形状和大小是解答此题的关键.3.B【分析】根据坐标轴上点的坐标特征对点A(-1,0)进行判断.【详解】解:∵点A的纵坐标为0,∴点A在x轴上,∵点A的横坐标为-1,∴点A在x轴负半轴上.故选:B.【点睛】本题考查了点的坐标:直角坐标系中点与有序实数对一一对应;在x轴上点的纵坐标为0,在y轴上点的横坐标为0;记住各象限点的坐标特点.4.B【分析】利用对顶角的定义、平行线的性质等知识分别判断后即可确定正确的选项.【详解】解:A、相等的两个角不一定是对顶角,故原命题错误,是假命题,不符合题意;B、过直线外一点有且只有一条直线与已知直线平行,正确,是真命题,符合题意;C、两条平行线被第三条直线所截,内错角相等,故原命题错误,是假命题,不符合题意;D、在同一平面内,垂直于同一条直线的两条直线互相平行,故原命题错误,是假命题,不符合题意,故选:B.【点睛】本题考查了命题与定理的知识,解题的关键是了解对顶角的定义、平行线的性质等知识,难度不大.5.B【分析】先根据平行线的性质求出∠1的同位角,再由两角互余的性质求出∠2的度数即可;【详解】∵直线a∥b,∠1=55°,∴∠1=∠3=55°,∵三角板的直角顶点放在b上,∴∠3+∠2=90°,∴∠2=90°-55°=35°,故选:B.【点睛】本题考查了平行线的性质,即两直线平行,同位角相等以及互余的两角,正确掌握知识点是解题的关键;6.A【分析】依据立方根、平方根算术平方根的定义求解即可【详解】327=-3,故①正确16故②错误;③错误故④错误.故选:A.【点睛】此题考查立方根,算术平方根和平方根,掌握运算法则是解题关键7.C【分析】根据两直线平行的性质定理,进行角的转换,再根据平角求得CEF ∠,进而求得GME ∠.【详解】//AB CD ,FED FGB ∴∠=∠,CEM GME ∠=∠又∵80FGB ∠=︒80FED ∴∠=︒18080100CEF ∴∠=-︒=︒, EM 平分CEF ∠,1502CEM CEF ∴∠=∠=︒, 50GME ∴∠=︒故选:C .【点睛】本题主要考查的是平行线的性质,角平分线的定义等知识点,根据条件数形结合是解题切入点.8.C【分析】求出A1(3,0),A5(9,-6),A9(15,-12),A13(21,-18),•••,探究规律可得A2021(3033,-3030),从而求解.【详解】解:由题意A1(3,0解析:C【分析】求出A 1(3,0),A 5(9,-6),A 9(15,-12),A 13(21,-18),•••,探究规律可得A 2021(3033,-3030),从而求解.【详解】解:由题意A 1(3,0),A 5(9,-6),A 9(15,-12),A 13(21,-18),•••, 可以看出,9=1532+,15=2732+,21=3932+, 得到规律:点A 2n +1的横坐标为()32136622n n +++=,其中0n ≥的偶数, 点A 2n +1的纵坐标等于横坐标的相反数+3,2021210101=⨯+,即1010n=,故A2021的横坐标为61010630332⨯+=,A2021的纵坐标为303333030-+=-,∴A2021(3033,-3030),故选:C.【点睛】本题考查了坐标与图形变化-平移,规律型问题,解题的关键是学会探究规律的方法,属于中考常考题型.二、填空题9.【分析】根据一个正数的算术平方根就是其正的平方根即可得出.【详解】∵,∴9算术平方根为3.故答案为3.【点睛】本题考查了算术平方根,熟练掌握算术平方根的概念是解题的关键.解析:【分析】根据一个正数的算术平方根就是其正的平方根即可得出.【详解】∵239=,∴9算术平方根为3.故答案为3.【点睛】本题考查了算术平方根,熟练掌握算术平方根的概念是解题的关键.10.-3.【分析】关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.据此可得a,b 的值.【详解】解:∵点A(2a+3b,﹣2)和点B(8,3a+1)关于y轴对称,∴,解得,∴a+b=解析:-3.【分析】关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.据此可得a,b的值.【详解】解:∵点A (2a +3b ,﹣2)和点B (8,3a +1)关于y 轴对称,∴238312a b a +=-⎧⎨+=-⎩, 解得12a b =-⎧⎨=-⎩, ∴a +b =﹣3,故答案为:﹣3.【点睛】本题考查的是关于y 轴对称的两个点的坐标关系,掌握以上知识是解题的关键. 11.120°【分析】由角平分线的定义可得,,又由,得,;设,,则;再根据四边形内角和定理得到,最后根据即可求解.【详解】解:和的角平分线相交于,,,又,,,设,,,在四边形中,,,,解析:120°【分析】由角平分线的定义可得EDA ADC ∠=∠,CBE ABE ∠=∠,又由//AB ED ,得EDF DAB ∠=∠,DFE ABF ∠=∠;设EDF DAB x ∠=∠=,DFE ABF y ∠=∠=,则DFB x y ∠=+;再根据四边形内角和定理得到3602()BCD x y ∠=︒-+,最后根据3304BCD BFD ∠=∠+︒即可求解. 【详解】解:ABC ∠和CDE ∠的角平分线相交于F ,EDA ADC ∴∠=∠,CBE ABE ∠=∠,又//AB ED ,EDF DAB ∴∠=∠,DEF ABF ∠=∠,设EDF DAB x ∠=∠=,DEF ABF y ∠=∠=,BFD EDA ADE x y ∴∠=∠+∠=+,在四边形BCDF 中,FBC x ∠=,ADC y ∠=,BFD x y ∠=+,3602()BCD x y ∴∠=︒-+,0433BCD BFD ∠=∠+︒, 120BFD x y ∴∠=+=︒,3602()120BCD x y ∴∠=︒-+=︒,故答案为:120︒.【点睛】本题考查了平行线的判定和性质,正确的识别图形是解题的关键.12.【分析】由已知可知,由平行可知,根据三角形外角的性质可知从而求得的答案.【详解】已知可知直尺的两边平行故答案为:114°【点睛】本题考查了平行线的性质,三角形的外角性质,掌握三解析:114︒【分析】由已知可知460∠=︒,由平行可知13∠=∠,根据三角形外角的性质可知234∠=∠+∠从而求得的答案.【详解】已知可知460∠=︒直尺的两边平行∴13∠=∠∴234145460114∠=∠+∠=∠+∠=︒+︒=︒故答案为:114°【点睛】本题考查了平行线的性质,三角形的外角性质,掌握三角形的外角性质是解题的关键. 13.【分析】根据四边形的内角和等于求出,根据翻折的性质可得,然后求出 ,再根据直角三角形两锐角互余列式计算即可得解.【详解】,由翻折的性质得,,,,.故答案为:.【点睛】解析:【分析】根据四边形的内角和等于360︒求出BAD ∠,根据翻折的性质可得BAE DAE ∠=∠,然后求出 BAE ∠,再根据直角三角形两锐角互余列式计算即可得解.【详解】解:90B D ∠=∠=︒,130C ∠=︒,360909013050BAD ,由翻折的性质得,BAE DAE ∠=∠, 11502522BAE BAD ,90B ∠=︒,902565AEB .故答案为:65.【点睛】本题考查了翻折变换的性质,四边形的内角和定理,直角三角形两锐角互余的性质. 14.、、、.【详解】解:∵y=3x+2,如果直接输出结果,则3x+2=161,解得:x=53;如果两次才输出结果:则x=(53-2)÷3=17;如果三次才输出结果:则x=(17-2)÷3=5;解析:53、17、5、1.【详解】解:∵y =3x +2,如果直接输出结果,则3x +2=161,解得:x =53;如果两次才输出结果:则x =(53-2)÷3=17;如果三次才输出结果:则x =(17-2)÷3=5;如果四次才输出结果:则x =(5-2)÷3=1;则满足条件的整数值是:53、17、5、1.故答案为53、17、5、1.点睛:此题的关键是要逆向思维.它和一般的程序题正好是相反的.15.二根据非负数的性质列方程求出a、b的值,再根据各象限内点的坐标特征解答.【详解】解:由题意得,a+2=0,b-6=0,解得a=-2,b=6,所以,点(-2,6)在第二象限;故答解析:二【分析】根据非负数的性质列方程求出a、b的值,再根据各象限内点的坐标特征解答.【详解】解:由题意得,a+2=0,b-6=0,解得a=-2,b=6,所以,点(-2,6)在第二象限;故答案为:二【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).16.(5,6)【分析】根据题意判断出跳蚤跳到(n,n)位置用时n(n+1)秒,然后根据43秒时n 是偶数,即可判断出所在位置的坐标.【详解】解:跳蚤跳到(1,1)位置用时1×2=2秒,下一步向下跳解析:(5,6)【分析】根据题意判断出跳蚤跳到(n,n)位置用时n(n+1)秒,然后根据43秒时n是偶数,即可判断出所在位置的坐标.【详解】解:跳蚤跳到(1,1)位置用时1×2=2秒,下一步向下跳动;跳到(2,2)位置用时2×3=6秒,下一步向左跳动;跳到(3,3)位置用时3×4=12秒,下一步向下跳动;跳到(4,4)位置用时4×5=20秒,下一步向左跳动;…由以上规律可知,跳蚤跳到(n,n)位置用时n(n+1)秒,当n为奇数时,下一步向下跳动;当n为偶数时,下一步向左跳动;∴第6×7=42秒时跳蚤位于(6,6)位置,下一步向左跳动,则第43秒时,跳蚤需从(6,6)向左跳动1个单位到(5,6),故答案为:(5,6).【点睛】此题考查了点的坐标问题,解题的关键是读懂题意,能够正确确定点运动的规律,从而可以得到到达每个点所用的时间.三、解答题17.(1)(2)3【分析】(1)根据二次根式的运算法即可求解;(2)根据实数的性质化简,故可求解.【详解】(1)||+2==(2)==3.【点睛】此题主要考查实数与二次根式的运算解析:(12)3【分析】(1)根据二次根式的运算法即可求解;(2)根据实数的性质化简,故可求解.【详解】(1)-+(22(+--=11365=3.【点睛】此题主要考查实数与二次根式的运算,解题的关键是熟知其运算法则.18.(1)或;(2)【分析】(1)根据平方根的性质求解即可;(2)根据立方根的性质求解即可;【详解】(1),,,或,∴或;(2),,;【点睛】本题主要考查了平方根的性质应用和解析:(1)6x =或2x =-;(2)32x =【分析】(1)根据平方根的性质求解即可;(2)根据立方根的性质求解即可;【详解】(1)()24264x -=, ()2216x -=,24x -=±,24x -=或24-=-x ,∴6x =或2x =-;(2)3338x -=, 3278x , 32x =; 【点睛】本题主要考查了平方根的性质应用和立方根的性质应用,准确计算是解题的关键. 19.见解析【分析】应用平行线的判定与性质进行求解即可得出答案.【详解】解:证明:∵DE ⊥BC ,AB ⊥BC (已知),∴∠DEC=∠ABC=90°(垂直的定义).∴DE∥AB(同位角相等,两直线解析:见解析【分析】应用平行线的判定与性质进行求解即可得出答案.【详解】解:证明:∵DE⊥BC,AB⊥BC(已知),∴∠DEC=∠ABC=90°(垂直的定义).∴DE∥AB(同位角相等,两直线平行).∴∠2=∠3(两直线平行,内错角相等),∠1=∠A(两直线平行,同位角相等).又∵∠A=∠3(已知),∴∠1=∠2(等量代换).∴DE平分∠CDB(角平分线的定义).【点睛】本题主要考查了平行线的判定与性质,熟练应用平行线的判定与性质进行求解是解决本题的关键.20.(1)3,4,3,﹣2,D,﹣2;(2)见解析【分析】(1)根据向上向右走为正,向下向左走为负,可得答案;(2)根据向上向右走为正,向下向左走为负,可得答案.【详解】解:(1)A→C( 3解析:(1)3,4,3,﹣2,D,﹣2;(2)见解析【分析】(1)根据向上向右走为正,向下向左走为负,可得答案;(2)根据向上向右走为正,向下向左走为负,可得答案.【详解】解:(1)A→C( 3,4),B→D(3﹣2),C→D(+1,﹣2);故答案为3,4;3,﹣2;D,﹣2;(2)这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置,如图【点睛】本题主要考查了用有序实数对表示路线.读懂题目信息,正确理解行走路线的记录方法是解题的关键.21.(1)4;5;(2);3;(3)±8.【分析】(1)首先估算出的取值范围,即可得出结论;(2)根据 (1)的结论,得到,即可求得答案;(3)根据(2)的结论代入计算即可求得答案.【详解】解析:(1)4;5;(2174;3;(3)±8.【分析】(117的取值范围,即可得出结论;(2)根据 (1)的结论4175<<,得到61727<<,即可求得答案;(3)根据(2)的结论代入计算即可求得答案.【详解】解:(1)∵16<17<25, ∴4175<,∴a =4,b =5.故答案为:4;5(2)∵4175<<, ∴61727<<, 172的整数部分为6174, ∴174x =,3y =. 174;3(3)当174x ,3y =时,代入,()33(17)17174464y x ⎡⎤===⎣⎦﹣.∴64的平方根为:8±.【点睛】本题考查了平方和平方根估算无理数大小应用,正确计算是解题的关键,注意平方根是一对互为相反数的两个数.二十二、解答题22.(1)5;(2);(3)2与3两个整数之间,见解析【分析】(1)通过割补法即可求出阴影正方形的面积;(2)根据实数的性质即可求解;(3)根据实数的估算即可求解.【详解】(1)阴影正方形的解析:(1)5;(23)2与3两个整数之间,见解析【分析】(1)通过割补法即可求出阴影正方形的面积;(2)根据实数的性质即可求解;(3)根据实数的估算即可求解.【详解】(1)阴影正方形的面积是3×3-4×1212⨯⨯=5 故答案为:5;(2)设阴影正方形的边长为x ,则x 2=5∴x(3)∵ ∴23<<∴阴影正方形的边长介于2与3两个整数之间.【点睛】本题考查了无理数的估算能力和不规则图形的面积的求解方法:割补法.通过观察可知阴影部分的面积是5个小正方形的面积和.会利用估算的方法比较无理数的大小. 二十三、解答题23.(1)见解析;(2),理由见解析;(3)①当在延长线时(点不与点重合),;②当在之间时(点不与点,重合),.理由见解析【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC= 解析:(1)见解析;(2)180CPD αβ∠=∠+︒-∠,理由见解析;(3)①当P 在BA 延长线时(点P 不与点A 重合),180CPD βα∠=︒-∠-∠;②当P 在BO 之间时(点P 不与点B ,O 重合),180CPD αβ∠=∠-︒+∠.理由见解析【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC =113°;(2)过过P 作//PF AD 交CD 于F ,,推出////AD PF BC ,根据平行线的性质得出180BCP ,即可得出答案;(3)画出图形(分两种情况:①点P 在BA 的延长线上,②当P 在BO 之间时(点P 不与点B ,O 重合)),根据平行线的性质即可得出答案.【详解】解:(1)过P 作//PE AB ,//AB CD ,////PE AB CD ∴,=180APE PAB ,180CPE PCD ∠+∠=︒,128PAB ∠=︒,119PCD ∠=︒52APE ∴∠=︒,61CPE ∠=︒,5261113APC ∴∠=︒+︒=︒;(2)180CPD αβ∠=∠+︒-∠,理由如下:如图3,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠又ADP α∠=∠=180CPD DPF CPF ;(3)①当P 在BA 延长线时(点P 不与点A 重合),180CPD βα∠=︒-∠-∠; 理由:如图4,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠,又ADP α∠=∠,180CPD CPF DPF αβ∴∠=∠-∠=︒-∠-∠;②当P 在BO 之间时(点P 不与点B ,O 重合),180CPD αβ∠=∠-︒+∠.理由:如图5,过P 作//PF AD 交CD 于F ,//AD BC ,////AD PF BC ∴,ADP DPF ∴∠=∠,BCP CPF ∠=∠,180BCP PCE ∠+∠=︒,PCE β∠=∠,180BCP β∴∠=︒-∠,又ADP α∠=∠180CPD DPF CPF αβ∴∠=∠-∠=∠+∠-︒.【点睛】本题考查了平行线的性质的应用,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.24.(1)证明见解析;(2)(Ⅰ);(Ⅱ).【分析】(1)先根据平行线的性质可得,再根据角的和差可得,然后根据平行线的判定即可得证;(2)(Ⅰ)先根据平行线的性质可得,从而可得,再根据角的和差可得 解析:(1)证明见解析;(2)(Ⅰ)5DAM ∠=︒;(Ⅱ)25ACD ∠=︒.【分析】(1)先根据平行线的性质可得65BAD ∠=︒,再根据角的和差可得180BAD ABC ∠+∠=︒,然后根据平行线的判定即可得证;(2)(Ⅰ)先根据平行线的性质可得30BAC ACD ∠=∠=︒,从而可得30MAC ∠=︒,再根据角的和差可得35DAC ∠=︒,然后根据DAM DAC MAC ∠=∠-∠即可得;(Ⅱ)设MAN x ∠=,从而可得8CAD x ∠=,先根据角平分线的定义可得142CAN CAD x ∠=∠=,再根据角的和差可得5BAC MAC x ∠=∠=,然后根据65CAD BAC BAD ∠+∠=∠=︒建立方程可求出x 的值,从而可得BAC ∠的度数,最后根据平行线的性质即可得.【详解】(1)12//,115l l ADC ∠=︒,18065BAD ADC ∴∠=︒-∠=︒,又115ABC ∠=︒,180BAD ABC ∴∠+∠=︒,//AD BC ∴;(2)(Ⅰ)12//,30l l ACD ∠=︒,30BAC ACD ∴∠=∠=︒,MAC BAC ∠=∠,30MAC ∴∠=︒,由(1)已得:65BAD ∠=︒,35DAC BAD BAC ∴∠=∠-∠=︒,35305DAM DAC MAC ∴∠=∠-∠=︒-︒=︒;(Ⅱ)设MAN x ∠=,则8CAD x ∠=, AN 平分CAD ∠,142CAN CAD x ∴∠=∠=, 5MAC CAN MAN x ∴∠=∠+∠=,MAC BAC ∠=∠,5BAC x ∴∠=,由(1)已得:65BAD ∠=︒,65CAD BAC BAD ∴∠+∠=∠=︒,即8565x x +=︒,解得5x =︒,525BAC x ∴∠==︒,又12//l l ,25ACD BAC ∴∠=∠=︒.【点睛】本题考查了平行线的判定与性质、角的和差、角平分线的定义、一元一次方程的几何应用等知识点,熟练掌握平行线的判定与性质是解题关键.25.(1)证明见解析;(2)900° ,180°(n -1);(3)(180n -180-2m)°【详解】【模型】(1)证明:过点E 作EF ∥CD ,∴EF∥AB,∴∠1+∠MEF解析:(1)证明见解析;(2)900°,180°(n-1);(3)(180n-180-2m)°【详解】【模型】(1)证明:过点E作EF∥CD,∵AB∥CD,∴EF∥AB,∴∠1+∠MEF=180°,同理∠2+∠NEF=180°∴∠1+∠2+∠MEN=360°【应用】(2)分别过E点,F点,G点,H点作L1,L2,L3,L4平行于AB,利用(1)的方法可得∠1+∠2+∠3+∠4+∠5+∠6=180×5=900°;由上面的解题方法可得:∠1+∠2+∠3+∠4+∠5+∠6+…+∠n=180°(n-1),故答案是:900°, 180°(n-1);(3)过点O作SR∥AB,∴SR∥CD,∴∠AM1O=∠M1OR同理∠C M n O=∠M n OR∴∠A M1O+∠CM n O=∠M1OR+∠M n OR,∴∠A M1O+∠CM n O=∠M1OM n=m°,∵M1O平分∠AM1M2,∴∠AM1M2=2∠A M1O,同理∠CM n M n-1=2∠CM n O,∴∠AM1M2+∠CM n M n-1=2∠AM1O+2∠CM n O=2∠M1OM n=2m°,又∵∠A M1M2+∠2+∠3+∠4+∠5+∠6+……+∠n-1+∠CM n M n-1=180°(n-1),∴∠2+∠3+∠4+∠5+∠6+…+∠n-1=(180n-180-2m)°点睛:本题考查了平行线的性质,角平分线的定义,解决此类题目,过拐点作平行线是解题的关键,准确识图理清图中各角度之间的关系也很重要.26.(1)∠AEB的大小不会发生变化,∠ACB=45°;(2)30°,60°;(3)60°或72°.【分析】(1)由直线MN与直线PQ垂直相交于O,得到∠AOB=90°,根据三角形的外角的性质得到∠解析:(1)∠AEB的大小不会发生变化,∠ACB=45°;(2)30°,60°;(3)60°或72°.【分析】(1)由直线MN与直线PQ垂直相交于O,得到∠AOB=90°,根据三角形的外角的性质得到∠PAB+∠ABM=270°,根据角平分线的定义得到∠BAC=12∠PAB,∠ABC=12∠ABM,于是得到结论;(2)由于将△ABC沿直线AB折叠,若点C落在直线PQ上,得到∠CAB=∠BAQ,由角平分线的定义得到∠PAC=∠CAB,即可得到结论;根据将△ABC沿直线AB折叠,若点C落在直线MN上,得到∠ABC=∠ABN,由于BC平分∠ABM,得到∠ABC=∠MBC,于是得到结论;(3)由∠BAO与∠BOQ的角平分线相交于E可得出∠E与∠ABO的关系,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的32倍分情况进行分类讨论即可.【详解】解:(1)∠ACB的大小不变,∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,∴∠OAB+∠OBA=90°,∴∠PAB+∠ABM=270°,∵AC、BC分别是∠BAP和∠ABM角的平分线,∴∠BAC=12∠PAB,∠ABC=12∠ABM,∴∠BAC+∠ABC=12(∠PAB+∠ABM)=135°,∴∠ACB=45°;(2)∵将△ABC沿直线AB折叠,若点C落在直线PQ上,∴∠CAB=∠BAQ,∵AC平分∠PAB,∴∠PAC=∠CAB,∴∠PAC=∠CAB=∠BAO=60°,∵∠AOB=90°,∴∠ABO=30°,∵将△ABC沿直线AB折叠,若点C落在直线MN上,∴∠ABC=∠ABN,∵BC平分∠ABM,∴∠ABC=∠MBC,∴∠MBC=∠ABC=∠ABN,∴∠ABO=60°,故答案为:30°,60°;(3)∵AE、AF分别是∠BAO与∠GAO的平分线,∴∠EAO=12∠BAO,∠FAO=12∠GAO,∴∠E=∠EOQ﹣∠EAO=12(∠BOQ﹣∠BAO)=12∠ABO,∵AE、AF分别是∠BAO和∠OAG的角平分线,∴∠EAF=∠EAO+∠FAO=12(∠BAO+∠GAO)=90°.在△AEF中,∵∠BAO与∠BOQ的角平分线相交于E,∴∠EAO= 12∠BAO,∠EOQ=12∠BOQ,∴∠E=∠EOQ-∠EAO=12(∠BOQ-∠BAO)=12∠ABO,∵有一个角是另一个角的32倍,故有:①∠EAF=32∠F,∠E=30°,∠ABO=60°;②∠F=32∠E,∠E=36°,∠ABO=72°;③∠EAF=32∠E,∠E=60°,∠ABO=120°(舍去);④∠E=32∠F,∠E=54°,∠ABO=108°(舍去);∴∠ABO为60°或72°.【点睛】本题主要考查的是角平分线的性质以及三角形内角和定理的应用.解决这个问题的关键就是要能根据角平分线的性质将外角的度数与三角形的内角联系起来,然后再根据内角和定理进行求解.另外需要分类讨论的时候一定要注意分类讨论的思想.。
深圳罗湖中学九年级数学上册第二十三章《旋转》经典测试卷(含答案解析)

一、选择题1.如图,将△ABC 绕点A 旋转,得到△AEF ,下列结论正确的个数是( ) ①△ABC ≌△AEF ;②AC=AE ;③∠FAB=∠EAB ;④∠EAB=∠FAC .A .1B .2C .3D .42.如图,在ABC 中,,90AB AC BAC =∠=︒,直角EPF ∠的顶点P 是BC 的中点,两边PE 、PF 分别交AB 、AC 于点E 、F ,当EPF ∠在ABC 内绕点P 旋转时,下列结论错误的是( )A .AE CF =B .EPF 为等腰直角三角形C .EP AP =D .2ABC AEPF S S =四边形3.如图,在Rt ABC 中,90ACB ∠=︒,60B ∠=︒,1BC =,A B C ''由ABC 绕点C 顺时针旋转得到,其中点A '与点A 、点B '与点B 是对应点,连接AB ',且点A 、B '、A '在同一条直线上,则AA '的长为( )A .3B .3C .4D .454.“保护生态,人人有责”.下列生态环保标志中,是中心对称图形的是( )A .B .C .D .5.如图,在ABC ∆中,30,8,5BAC AB AC ∠===,将ABC ∆绕点A 顺时针旋转30得到ADE ∆连接CD ,则CD 的长是( )A .7B .8C .12D .136.如图,将一个含30角的直角三角尺AOB 放在平面直角坐标系中,两条直角边分别与坐标轴重叠.已知30OAB ∠=︒,12AB =,点D 为斜边AB 的中点,现将三角尺AOB 绕点O 顺时针旋转90︒,则点D 的对应点D 的坐标为( )A .(33,3)B .3,6)-C .(3,33)-D .(33,3)- 7.如图,等边△OAB 的边OB 在x 轴上,点B 坐标为(2,0),以点O 为旋转中心,把△OAB 逆时针转90︒,则旋转后点A 的对应点A '的坐标是( )A .(-1,3)B .(3,-1)C .(31-,)D .(-2,1) 8.下列图形中,既是轴对称又是中心对称图形的是( )A .B .C .D .9.下列图形中,是轴对称图形,但不是中心对称图形的是( )A .B .C .D . 10.如图,在平面直角坐标系中Rt △ABC 的斜边BC 在x 轴上,点B 坐标为(1,0),AC=2,∠ABC=30°,把Rt △ABC 先绕B 点顺时针旋转180°,然后再向下平移2个单位,则A 点的对应点A′的坐标为( )A .(﹣4,﹣2﹣3)B .(﹣4,﹣2+3)C .(﹣2,﹣2+3)D .(﹣2,﹣2﹣3)11.如图,Rt OCB ∆的斜边在y 轴上,3OC =,含30︒角的顶点与原点重合,直角顶点C 在第二象限,将Rt OCB ∆绕原点顺时针旋转120︒后得到'OC B ∆',则B 点的对应点B ′的坐标是( )A .3,1)-B .(1,3)C .(2,0)D .(3,0)12.把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB 绕点B 逆时针旋转45°得到△D′E′B ,则点A 在△D′E′B 的( )A .内部B .外部C .边上D .以上都有可能 13.下列图形中,既是轴对称图形又是中心对称图形的是( )A .等边三角形B .平行四边形C .正五边形D .菱形 14.如图,点O 是矩形ABCD 的对称中心,点E 在AB 边上,连接CE .若点B 与点O 关于CE 对称,则CB :AB 为( )A .12B .512-C .33D .3215.如图,在△ABC 中,AB =2.2,BC =3.6,∠B =60°,将△ABC 绕点A 按逆时针方向旋转得到△ADE ,若点B 的对应点D 恰好落在BC 边上时,则CD 的长为( )A .1.5B .1.4C .1.3D .1.2二、填空题16.如图.面积为8的正方形ABCD 的顶点A 在数轴上,点A 表示实数2-,正方形ABCD 绕点A 旋转时,顶点B 的运动轨迹与数轴的交点表示的数为______________17.如图,在AOB 中,90AOB ∠=︒,30B ∠=︒,A OB ''△是由AOB 绕点O 顺时针旋转1(8)0αα<︒角度得到的,若点A '在AB 上,则旋转角α=___︒.18.已知点(,2)A m m 在直线3y x 上,则点A 关于原点对称点B 的坐标为______. 19.在平面直角坐标系中,点()4,6P -与点()4,1Q m -+关于原点对称,那么m =______.20.如图,在边长为1的正方形ABCD 中,将射线AC 绕点A 按顺时针方向旋转α度(0<α≤360°),得到射线AE ,点M 是点D 关于射线AE 的对称点,则线段CM 长度的最小值和最大值的和为_____.21.在Rt ABC △中,90ACB ∠=︒,将ABC 绕顶点C 顺时针旋转得到A B C '',点M 是BC 的中点,点P 是A B ''的中点,连接PM .若4BC =,30A ∠=︒,则在旋转一周的过程中线段PM 长度的最大值等于_____.22.一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA 与边FE 叠合,顶点B 、C 、D 在一条直线上).将三角尺DEF 绕着点F 按顺时针方向旋转n°后(0<n <180),如果EF ⊥AB ,那么n 的值是_______.23.将边长为1的正方形ABCD 绕点C 按顺时针方向旋转到FECG 的位置(如图),使得点D 落在对角线CF 上,EF 与AD 相交于点H ,则HD =_________.(结果保留根号)24.在平面直角坐标系中,点A (-5,b)关于原点对称的点为B (a ,6),则(a+b)2019=____.25.如图,把Rt △ABC 绕顶点C 顺时针旋转90°得到Rt △DFC ,若直线DF 垂直平分AB ,垂足为点E ,连接BF ,CE ,且BC =2.下面四个结论:①BF =22②∠CBF =45°;③∠CED =30°;④△ECD 的面积为223,其中正确的结论有_____.(填番号)参考答案26.若点()3,5B n +与点()4,A m 关于原点O 中心对称,则m n +=______________.三、解答题27.如图,已知正方形ABCD 的边长为3,E 、F 分别是AB 、BC 边上的点,且∠EDF=45°,将△DAE 绕点D 逆时针旋转90°,得到△DCM .若AE=1,求FM 的长.28.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1)、B(-3,1)、C(-1,4).(1)画出△ABC绕点C顺时针旋转90°后得到的△A1B1C;(2)画出△ABC关于点P(1,0)对称的△A2B2C2.29.阅读理解并解决问题:一般地,如果把一个图形绕着一个定点旋转一定角度α(α小于360°)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心,α叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:(1)请写出一个旋转对称图形,这个图形有一个旋转角是90°,这个图形可以是______;(2)为了美化环境,某中学需要在一块正六边形空地上分别种植六种不同的花草,现将这块空地按下列要求分成六块:①分割后的整个图形必须既是轴对称图形又是旋转对称图形;②六块图形的面积相同;请你按上述两个要求,分别在图中的两个正六边形中画出两种不同的分割方法(只要求画图正确,不写作法).30.如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:(1)将△ABC以x轴为对称轴,画出对称后的△A1B1C1;(2)将△ABC绕点C逆时针旋转90°,画出旋转后的△A2B2C2.。
深圳罗芳中学人教版初中物理八年级上册第三章综合经典测试题(含答案解析)

一、选择题1.对甲、乙两种物质同时持续加热,其温度随时间变化的图象如图所示,下列说法正确的是()A.甲物质的沸点一定是°80CB.乙物质的熔点一定是°60CC.甲物质在4-6min内一定持续吸收热量D.乙物质在6-10min内一定是固液共存态C解析:CAB.甲乙两种物质不能确定其本身的状态,不知道是晶体的熔化还是液体的沸腾,故不能确定是熔点还是沸点,故AB错误;C.由图知甲物质在4-6min内温度升高,内能增加,是持续吸收热量的结果,故C正确;D.由于不能确定是晶体的熔化还是液体的沸腾,故不能确定乙物质在6-10min内的状态,故D错误。
故选C。
2.盛一盆水,在盆里放两块高出水面的砖,砖上搁一只比盆小点的篮子,篮子里装上熟食,再把一个纱布袋罩在篮子上,并使袋口的边缘浸入水里(如图),就做成了一个简易冰箱,针对这个装置下列说法中不正确...的是()A.简易冰箱能制冷是因为水蒸发吸热B.将该装置放在通风的地方,制冷效果更好C.篮子上罩着纱布袋是为了增大蒸发面积D.简易冰箱与电冰箱的工作原理一样,在工作时都有汽化和液化现象D解析:DA.简易冰箱能制冷是因为水蒸发时需要吸热,降低篮子里的温度,故A正确,A不符合题意;B.将该装置放在通风的地方,蒸发效果更加明显,则制冷效果更好,故B正确,B不符合题意;C.加大表面积可以加快蒸发,因此篮子上罩着纱布袋是为了增大蒸发面积,加快蒸发,故C正确,C不符合题意;D.简易冰箱的工作原理与冰箱的工作原理相同都是利用了汽化吸热的原理,但简易冰箱没用到液化放热,故D错误,D符合题意。
故选D。
3.夏季,小李打开冰箱的冷冻室看见一股“白气”向下飘出,联想到了烧开水时壶嘴里向上冒“白气”的情景,下列说法中正确的是()A.两股“白气”本质是相同的,都是空气中的水蒸气液化形成的小水珠B.两股“白气”本质是相同的,他们都是汽化成的水蒸气C.两股“白气”本质是不同的,前者是液化形成的,后者是汽化形成的D.两股“白气”形成的过程都要放热D解析:D打开冰箱的冷冻室看见一股“白气”,是由于空气中的水蒸气遇冷液化成的小水滴;烧开水时壶嘴里向上冒“白气”,是由于高温水蒸气遇冷液化成的小水滴,二者物态变化相同,都会放热。
骆店中学初三数学上册期中重点考试题(含答案解析)

骆店中学初三数学上册期中重点考试题(含答案解析)骆店中学2021初三数学上册期中重点考试题(含答案解析)一、选择题〔3×10=30〕1.m是方程x2﹣x﹣1=0的一个根,那么代数式m2﹣m的值等于〔〕A. 1 B. 0 C.﹣1 D. 22.方程x2=3x的解是〔〕A. x=3 B. x=0 C. x1=3,x2=0 D. x1=﹣3,x2=0 3.一元二次方程x2+x﹣1=0的根的状况是( )A.有两个不相等的实数根 B.有两个相等的实数根C.没有实数根 D.无法判别4.假定a+b+c=0,那么关于x的一元二次方程ax2+bx+c=0〔a≠0〕有一根是( )A.1 B.﹣1 C.0 D.无法判别5.二次函数y=x2﹣3x+m〔m为常数〕的图象与x轴的一个交点为〔1,0〕,那么关于x的一元二次方程x2﹣3x+m=0的两实数根是( )A.x1=1,x2=﹣1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=36.以下二次函数中,图象以直线x=2为对称轴、且经过点〔0,1〕的是( )A.y=〔x﹣2〕2+1 B.y=〔x+2〕2+1 C.y=〔x﹣2〕2﹣3 D.y=〔x+2〕2﹣37.二次函数y=x2﹣2x+3的图象的顶点坐标是〔〕A.〔1,-4〕 B.〔-1,2〕 C.〔1,2〕 D.〔0,3〕8.把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,那么平移后抛物线的解析式为〔〕A. y=﹣〔x﹣1〕2﹣3B. y=﹣〔x+1〕2﹣3C.y=-〔x﹣1〕2+3D. y=﹣〔x+1〕2+39.在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象能够是〔〕A. B. C. D.10.〔3分〕如图,二次函数y=ax2+bx+c〔a≠0〕的图象的顶点在第一象限,且过点〔0,1〕和〔﹣1,0〕.以下结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是〔〕A.5个 B.4个 C.3个 D. 2个二、填空题:〔3×6=18〕11.假定抛物线y=(m-1) 启齿向下,那么m=___ .12.抛物线y=x2+2与y轴的交点坐标为.13.一元二次方程kx2+x+4=0有两个实数根,那么k的取值范围是________.14.设a,b是方程x2+x﹣2021=0的两个实数根,那么a2+2a+b的值为__________.15.假定抛物线y=x2﹣bx+9的顶点在x轴上,那么b的值为.16. 二次函数,当x>1时,y随x的增大而增大,而m的取值范围是。
深圳罗湖区笋岗中学浮力单元专项综合训练

深圳罗湖区笋岗中学浮力单元专项综合训练一、选择题1.如图所示,在三个相同的容器中装有质量相同的水,将木块 A、金属块 B 按不同的方式放入水中,待 A、B 静止时,三个容器中木块 A 所受浮力和水对容器底部的压强相比较,正确的是()A.F甲=F乙=F 丙p甲=p 乙=p 丙B.F甲<F乙<F丙p甲=p乙>p丙C.F甲>F乙>F丙p甲=p乙=p丙D.F 甲>F乙>F丙p甲=p乙>p丙2.如图所示,底面积为50cm2、高为13cm、质量为100g的平底圆柱形容器(厚度不计),将一个质量为250g、体积为200cm3的实心小球置于水平桌面上,放入小球之前容器内水的深度为10cm,将小球放入水中静止后,下列说法正确的是()A.水对容器底部的压强为1400Pa B.小球受到的浮力为2.5NC.水对容器底部的压力为5N D.容器对桌面的压强为1600Pa3.如图所示,在两个完全相同的容器中装有甲、乙两种不同的液体,将体积相等的实心小球1、2、3 分别放入两个容器中,放入小球后两个容器中的液面高度相同,且 1、3 两球排开液体体积相同,2 球在甲液体中悬浮,在乙液体中下沉。
则下列选项正确的是()A.1、3 两球所受的浮力相等B.甲液体比乙液体对容器底的压强大C.三个小球中密度最小的是 2 球D.把 1、3 两球对调,1 球在乙液体中不会下沉4.春天到了,农村还有人让老母鸡来孵小鸡。
逐渐发育的小鸡会把鸡蛋内的营养成分消耗掉,总质量变小,来实现自己的成长。
利用这个原理,孵过一段时间后,人们会把鸡蛋拿出来放入盆中加水,来检验孵化是否成功,这时会发现有的鸡蛋沉底,有的鸡蛋则浮出水面,假设最初挑选的是大小完全相同的鸡蛋,那么()A.浮出水面的鸡蛋受到的浮力大B.下沉的鸡蛋是孵化成功的鸡蛋C.无论哪种,鸡蛋的密度都不变D.上浮鸡蛋孵化成功,密度变小5.在水平桌面上有一个盛有水的容器,将木块用细线系住没入水中时,情景如图甲所示;将细绳剪断,木块最终漂浮在水面上,且有五分之二的体积露出水面,如图乙所示。
2021学年九年级数学专题1.4 解直角三角形章末重难点题型(举一反三)(沪科版)(解析版)

专题1.4 解直角三角形章末重难点题型【沪科版】【考点1 锐角三角函数的定义】【方法点拨】锐角角A的正弦(sin),余弦(cos)和正切(tan),都叫做角A的锐角三角函数。
正弦(sin)等于对边比斜边,余弦(cos)等于邻边比斜边正切(tan)等于对边比邻边.【例1】(2020•平房区二模)在Rt△ABC中,∠C=90°,∠B=α,若BC=m,则AB的长为()A.mcosαB.m•cosαC.m•sinαD.m•tanα【分析】根据解直角三角形的三角函数解答即可.【解答】解:如图所示:∵cosα=BC AB,∴AB =m cosα, 故选:A .【点评】本题考查了锐角三角函数的定义的应用,关键是根据学生的理解能力和计算能力解答. 【变式1-1】(2019秋•沈河区校级期中)如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D ,下列各组线段的比不能表示sin ∠BCD 的( )A .BD BCB .BCABC .CD BCD .CD AC【分析】根据三角形内角和定理求出∠BCD =∠A ,再解直角三角形得出即可. 【解答】解:∵CD ⊥AB , ∴∠CDA =∠CDB =90°, ∵∠ACB =90°,∴∠BCD +∠ACD =90°,∠A +∠ACD =90°, ∴∠BCD =∠A , ∴sin ∠BCD =sin A =BC AB =CD AC =BDBC, 即只有选项C 错误,选项A 、B 、D 都正确, 故选:C .【点评】本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义的内容是解此题的关键,注意:在Rt △ACB 中,∠C =90°,则sin A =BC AB ,cos A =AC AB ,tan A =BC AC ,cot A =AC BC. 【变式1-2】(2019秋•包河区期末)如图,BD ⊥AC 于D ,CE ⊥AB 于E ,BD 与CE 相交于O ,则图中线段的比不能表示sin A 的式子为( )A .BD ABB .CD OCC .AEADD .BEOB【分析】根据BD ⊥AC 于D ,CE ⊥AB 于E ,利用锐角三角函数的定义进行求解即可.【解答】解:A、∵BD⊥AC于D,CE⊥AB于E,∴sin A=BDAB=EC AC,故A不合题意;B、∵∠A+∠ACE=90°,∠ACE+∠COD=90°,∴∠A=∠COD,∴sin A=sin∠COD=CDOC,故B不合题意;C、无法得出sin A=AEAD,符合题意;D、∵∠BOE=∠COD,∴∠A=∠BOE,∴sin A=sin∠BOE=BEBO,故D不合题意;故选:C.【点评】本题主要考查的是锐角三角函数的定义的有关知识,正确掌握边角关系是解题关键.【变式1-3】(2020•下城区模拟)如图,△ACB中,∠ACB=Rt∠,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为()A.a•(cosα﹣cosβ)B.atanβ−tanαC.a cosα−a⋅sinαtanβD.a•cosα﹣a sinα•a•tanβ【分析】利用锐角三角函数关系分别表示出BC,DC的长进而得出答案.【解答】解:∵∠C=90°,∠B=α,∠ADC=β,AB=a,∴cos B=cosα=BCAB=BC a,则BC=a•cosα,sin B=sinα=ACAB=AC a,故AC=a•sinα,则tanβ=AC DC,故DC =AC tanβ=a⋅sinαtanβ, 则BD =BC ﹣DC =a •cos α−a⋅sinαtanβ. 故选:C .【点评】此题主要考查了锐角三角函数的定义,正确表示出DC 的长是解题关键. 【考点2 网格中的锐角三角函数值计算】【方法点拨】解决此类问题的关键在于构造直角三角形,利用勾股定理求解各边的长度,有时还会运用面积法来求解关键边的长度.【例2】(2020•岳麓区模拟)如图,在6×6的正方形网格中,△ABC 的顶点都在小正方形的顶点上,则tan ∠BAC 的值是( )A .45B .43C .34D .35【分析】过点B 作BD ⊥AC ,交AC 延长线于点D ,利用正切函数的定义求解可得. 【解答】解:如图,过点B 作BD ⊥AC ,交AC 延长线于点D ,则tan ∠BAC =BDAD =34, 故选:C .【点评】本题主要考查三角函数的定义,解题的关键是掌握正切函数的定义:锐角A 的对边a 与邻边b 的比叫做∠A 的正切.【变式2-1】(2020•南海区一模)如图,在网格中,小正方形的边长均为1,点A 、B 、O 都在格点上,则∠OAB 的正弦值是 .【分析】过点O 作OC ⊥AB 的延长线于点C ,构建直角三角形ACO ,利用勾股定理求出斜边OA 的长,即可解答.【解答】解:如图,过点O 作OC ⊥AB 的延长线于点C ,则AC =4,OC =2,在Rt △ACO 中,AO =√AC 2+OC 2=√42+22=√20=2√5, ∴sin ∠OAB =OCOA =225=√55. 故答案为:√55.【点评】本题考查了解直角三角形,锐角三角函数的定义和勾股定理,作出辅助线并利用网格构造直角三角形是解题的关键.【变式2-2】(2020•铁东区三模)如图,将∠BAC 放置在5×5的正方形网格中,如果顶点A 、B 、C 均在格点上,那么∠BAC 的正切值为 .【分析】连接BC ,先利用勾股定理逆定理证△ABC 是等腰直角三角形,再根据正切函数的定义可得. 【解答】解:如图所示,连接BC ,则AB =BC =√12+32=√10,AC =√22+42=2√5, ∴AB 2+BC 2=10+10=20=AC 2,∴△ABC 是等腰直角三角形,且∠ABC =90°, ∴∠BAC =45°, 则tan ∠BAC =1, 故答案为:1.【点评】本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理及其逆定理和三角函数的定义. 【变式2-3】(2020•泰兴市一模)如图,△ABC 的三个顶点都在正方形网格的格点上,则sin ∠ACB 的值为 .【分析】根据勾股定理,可得BC 、AC 的长,求出△ABC 的面积,求出高AN ,解直角三角形求出即可.【解答】解:设小正方形的边长为1,则由勾股定理得:BC =√32+42=5,AC =√12+22=√5, ∵S △ABC =S △BDC ﹣S 正方形EAFD ﹣S △AFC ﹣S △BEA =12×4×3−1×1−12×1×2−12×3×1=52, ∴12×BC ×AN =52,∴AN =1, ∴sin ∠ACB =AN AC =1√5=√55, 故答案为:√55. 【点评】本题考查了锐角三角函数的定义和勾股定理,能构造直角三角形是解此题的关键,注意:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边. 【考点3 锐角三角函数的增减性】【方法点拨】解决此类问题的关键在于掌握锐角三角函数的增减性,当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)【例3】(2019秋•新乐市期中)sin58°、cos58°、cos28°的大小关系是()A.cos28°<cos58°<sin58°B.sin58°<cos28°<cos58°C.cos58°<sin58°<cos28°D.sin58°<cos58°<cos28°【分析】先把正弦化成余弦,然后根据锐角三角函数值的变化规律:锐角余弦值随着角度的增大而减小进行排列大小.【解答】解:sin58°=cos32°.∵58°>32°>28°,∴cos58°<cos32°<cos28°,∴cos58°<sin58°<cos28°.故选:C.【点评】本题考查了锐角三角形的增减性,当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).也考查了互余两角的三角函数之间的关系.【变式3-1】(2020春•兴庆区校级月考)比较大小:(1)cos35°cos45°,tan50°tan60°;(2)若sinα=0.3276,sinβ=0.3274,则αβ.【分析】(1)根据余弦值随角度的增大余弦值越小,正切值随角度的增增大而增大,进而得出答案;(2)利用正弦值随角度的增大而增大,进而得出答案.【解答】解:(1)cos35°>cos45°,tan50°<tan60°;故答案为:>,<;(2)∵sinα=0.3276,sinβ=0.3274,则α>β.故答案为:>.【点评】此题主要考查了锐角三角函数的增减性,熟练记忆锐角三角函数增减性是解题关键.【变式3-2】(2020•高邮市一模)比较大小:sin81°tan47°(填“<”、“=”或“>”).【分析】根据sin81°<1,tan47°>1即可求解.【解答】解:∵sin81°<sin90°=1,tan47°>tan45°=1,∴sin81°<1<tan47°,∴sin81°<tan47°.故答案为<.【点评】本题考查了锐角三角函数值的增减性:当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).也考查了不等式的传递性.【变式3-3】(2019•丰台区模拟)如图所示的网格是正方形网格,∠AOB∠COD.(填“>“,“=”或“<“)【分析】连接CD,则CD⊥OD,过B作BE⊥OA于E,在Rt△OBE与Rt△OCD中,分别求∠AOB、∠COD的正切,根据锐角的正切值随着角度的增大而增大作判断即可.【解答】解:连接CD,则CD⊥OD,过B作BE⊥OA于E,在Rt△OBE中,tan∠AOB=BEOE=2,在Rt△OCD中,tan∠COD=CDOD=33=1,∵锐角的正切值随着角度的增大而增大,∴∠AOB>∠COD,故答案为:>.【点评】本题考查了锐角三角函数的增减性,构建直角三角形求角的三角函数值进行判断,熟练掌握锐角三角函数的增减性是关键. 【考点4 同角三角函数的关系】【方法点拨】解决此类问题的关键在于掌握同角三角函数的关系:平方关系:sin2A+cos2A =1;(2)正余弦与正切之间的关系(积的关系):一个角的正切值等于这个角的正弦与余弦的比,即tanA =sinA cosA或sinA=tanA •cosA .【例4】(2019•东明县一模)如图,P 是∠α的边OA 上一点,且点P 的横坐标为3,sin α=45,则tan α=( )A .35B .34C .43D .45【分析】先由sin α=PQOP =45求得PQ =4,OP =5,再根据正切函数的定义求解可得. 【解答】解:如图,由sin α=PQOP =45可设PQ =4a ,OP =5a , ∵OQ =3,∴由OQ 2+PQ 2=OP 2可得32+(4a )2=(5a )2, 解得:a =1(负值舍去),∴PQ =4,OP =5, 则tan α=PQ OQ =43, 故选:C .【点评】本题考查了锐角三角函数的定义,勾股定理的应用,能求出PQ 、OP 的长是解此题的关键. 【变式4-1】(2020春•西湖区校级月考)若∠a 为锐角,且tan a 是方程x 2﹣2x ﹣3=0的一个根,则sin α等于( ) A .1B .√22C .√1010D .3√1010【分析】运用因式分解法解方程,根据锐角三角函数值都大于0,确定tan α的值,再根据锐角三角函数的定义求解.【解答】解:解方程x 2﹣2x ﹣3=0,得 x =﹣1或x =3. ∵tan a >0, ∴tan a =3.设α所在的直角三角形的对边是3,则邻边是1. 根据勾股定理,得斜边是√10. 所以sin α=3√1010. 故选:D .【点评】此题综合考查了一元二次方程的解法和锐角三角函数的知识.【变式4-2】(2020秋•丰泽区校级月考)在Rt △ABC 中,∠C =90°,下列式子正确的是( ) A .sin A +cos A <1 B .sin A +cos A =1C .sin A +cos A >1D .sin A +cos A ≥1【分析】根据三角函数的定义得到sin A =ac ,cos A =bc ,则sin A +cos A =a+bc ,然后根据三角形三边的关系可判断sin A +cos A >1.【解答】解:∵sin A =a c ,cos A =bc , ∴sin A +cos A =a+bc , ∵a +b >c , ∴sin A +cos A >1.故选:C .【点评】本题考查了同角三角函数的关系:平方关系:sin 2A +cos 2A =1;(2)正余弦与正切之间的关系(积的关系):一个角的正切值等于这个角的正弦与余弦的比,即tan A =sinAcosA 或sin A =tan A •cos A . 【变式4-3】(2019秋•肥西县期末)已知sin αcos α=18,且0°<α<45°,则sin α﹣cos α的值为( ) A .√32B .−√32C .34D .±√32【分析】把已知条件两边都乘以2,再根据sin 2α+cos 2α=1,进行配方,然后根据锐角三角函数值求出cos α与sin α的取值范围,从而得到sin α﹣cos α<0,最后开方即可得解. 【解答】解:∵sin αcos α=18, ∴2sin α•cos α=14,∴sin 2α+cos 2α﹣2sin α•cos α=1−14, 即(sin α﹣cos α)2=34, ∵0°<α<45°,∴√22<cos α<1,0<sin α<√22, ∴sin α﹣cos α<0, ∴sin α﹣cos α=−√32.故选:B .【点评】本题考查了同角的三角函数的关系,利用好sin 2α+cos 2α=1,并求出sin α﹣cos α<0是解题的关键.【考点5 互余两角三角函数的关系】【方法点拨】解决此类问题的关键在于掌握互余角的三角函数间的关系:sin (90°-α)=cos α, cos(90°-α)=sinα,【例5】如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC ,垂足为D .给出下列四个结论:①sin α=sin B ;②sin β=sin C ;③sin B =cos C ;④sin α=cos β.其中正确的结论有 .【分析】本题主要考查锐角三角函数的定义,根据∠A=90°,AD⊥BC,可得∠α=∠B,∠β=∠C,再利用锐角三角函数的定义可列式进行逐项判断.【解答】解:∵∠BAC=90°,AD⊥BC,∴∠α+∠β=90°,∠B+∠β=90°,∠B+∠C=90°,∴∠α=∠B,∠β=∠C,∴sinα=sin B,故①正确;sinβ=sin C,故②正确;∵在Rt△ABC中sin B=ACBC,cos C=ACBC,∴sin B=cos C,故③正确;∵sinα=sin B,cos∠β=cos C,∴sinα=cos∠β,故④正确;故答案为①②③④.【点评】本题主要考查锐角的三角函数,解题的关键是熟练掌握互余两角的三角函数间的关系.【变式5-1】已知α为锐角,sinα+cos(90°﹣α)=√3,则α=.【分析】求出sinα的值即可解决问题;【解答】解:∵sinα+cos(90°﹣α)=√3,∴2sinα=√3,∴sinα=√3 2,∴α=60°,故答案为60°.【点评】本题考查互余两角三角函数的关系,特殊角的三角函数值等知识,记住sin A=cos(90°﹣∠A),cos A=sin(90°﹣∠A)是解题的关键;【变式5-2】若a<60°,且sin(60°﹣a)=1215,则cos(30°+a)=.【分析】由于60°﹣α+30°+α=90°,且α<60°,即60°﹣α和30°+α互余,根据互余两角的三角函数的关系即可得到cos (30°+α)=sin (60°﹣a )=45. 【解答】解:∵60°﹣α+30°+α=90°,且α<60°, ∴cos (30°+α)=sin (60°﹣a )=45. 故答案为45.【点评】本题考查了互余两角的三角函数的关系:若∠A +∠B =90°,则sin A =cos B ,cos A =sin B . 【变式5-3】化简:√(1−sin57°37′)2−|cos32°23′−1|= .【分析】先化简二次根式和去绝对值符号,再根据互余两角三角函数的关系计算即可求解. 【解答】解:√(1−sin57°37′)2−|cos32°23′−1| =1﹣sin57°37′+cos32°23′﹣1 =1﹣sin57°37′+sin57°37′﹣1 =0. 故答案为:0.【点评】考查了互余两角三角函数的关系,若∠A +∠B =90°,那么sin A =cos B 或sin B =cos A . 【考点6 特殊角的三角函数值的计算】【方法点拨】解决此类问题的关键在于熟记特殊角三角函数值:【例6】(2020•灌云县模拟)计算: (1)2sin30°+3cos60°﹣4tan45° (2)cos 230°1+sin30°+tan 260°【分析】(1)直接利用特殊角的三角函数值进而分别代入求出答案; (2)直接利用特殊角的三角函数值进而分别代入求出答案. 【解答】解:(1)原式=2×12+3×12−4×1=1+32−4 =−32;(2)原式=(√32)1+122+(√3)2=3432+3=72.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.【变式6-1】(2020•青浦区一模)计算:3tan30°−1cos60°+√8cos45°+√(1−tan60°)2【分析】代入特殊角的三角函数值即可.【解答】解:原式=3×√33−112+√8×√22+√(1−√3)2=√3−2+2+√3−1=2√3−1.【点评】考查了特殊角的三角函数值,属于只记内容,熟练掌握特殊角的三角函数值,代入求值即可.【变式6-2】(2020•涡阳县模拟)计算:2sin260°−cos60°tan260°+4cos45°【分析】直接利用特殊角的三角函数值代入进而得出答案.【解答】解:原式=2×(√32)2−12 (√3)2+4×√22=13+2√2=√2(3+22)(3−22)=3﹣2√2.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.【变式6-3】(2019秋•碑林区校级期中)计算(1)3tan60°﹣tan245°﹣2cos30°.(2)√1−2tan30°+tan230°+2sin230°−sin45°cos45°.【分析】(1)直接利用特殊角的三角函数值分别代入化简得出答案;(2)直接利用特殊角的三角函数值分别代入化简得出答案.【解答】解:(1)原式=3√3−1﹣2×√32=3√3−1−√3 =2√3−1;(2)原式=(1−33)2+2×(12)2√22√22=1−√33+12−1 =−√33+12.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键. 【考点7 特殊角的三角函数值中的新定义问题】【例7】(2020•丛台区校级一模)嘉琪在某次作业中得到如下结果:sin 27°+sin 283°≈0.122+0.992=0.9945,sin 222°+sin 268°≈0.372+0.932=1.0018,sin 229°+sin 261°≈0.482+0.872=0.9873,sin 237°+sin 253°≈0.602+0.802=1.0000,sin 245°+sin 245°=(√22)2+(√22)2=1.据此,嘉琪猜想:在Rt △ABC 中,∠C =90°,设∠A =α,有sin 2α+sin 2(90°﹣α)=1. (1)当α=30°时,验证sin 2α+sin 2(90°﹣α)=1是否成立. (2)请你对嘉琪的猜想进行证明.【分析】(1)将α=30°代入,根据三角函数值计算可得;(2)设∠A =α,则∠B =90°﹣α,根据正弦函数的定义及勾股定理即可验证. 【解答】解:(1)当α=30°时, sin 2α+sin 2(90°﹣α) =sin 230°+sin 260° =(12)2+(√32)2=14+34=1;(2)嘉琪的猜想成立,证明如下: 如图,在△ABC 中,∠C =90°,设∠A =α,则∠B =90°﹣α, ∴sin 2α+sin 2(90°﹣α) =(BCAB)2+(ACAB)2=BC 2+AC 2AB 2=AB 2AB2 =1.【点评】本题主要考查特殊锐角的三角函数值及正弦函数的定义,熟练掌握三角函数的定义及勾股定理是解题的关键.【变式7-1】阅读下列材料,并完成相应的任务.初中阶段,我们所学的锐角三角函数反映了直角三角形中的边角关系: sin α=BC AC cos α=AB AC tan α=BC AB一般地,当α、β为任意角时,sin (α+β)与sin (α﹣β)的值可以用下面的公式求得: sin (α+β)=sin αcos β+cos αsin β sin (α﹣β)=sin αcos β﹣cos αsin β例如sin15°=sin (45°﹣30°)=sin45°cos30°﹣cos45°sin30° =√22×√32−√22×12=√6−√24根据上述材料内容,解决下列问题: (1)计算:sin75°=√2+√64; (2)在Rt △ABC 中,∠A =75°,∠C =90°,AB =4,请你求出AC 和BC 的长.【分析】(1)根据公式可求.(2)根据锐角的三角函数值,求AC 和BC 的值. 【解答】解:(1)sin75°=sin (30°+45°) =sin30°cos45°+cos30°sin45° =12×√22+√32×√22 =√2+√64,故答案为:√2+√64. (2)Rt △ABC 中,∵sin ∠A =sin75°=BCAB =√2+√64∴BC =AB ×√2+√64=4×√2+√64=√2+√6∵∠B =90﹣∠A ∴∠B =15°∵sin ∠B =sin15°=AC AB =√6−√24∴AC =AB ×√6−√24=√6−√2【点评】本题考查了同角三角函数关系,利用特殊的三角函数值求线段的长度是本题的关键. 【变式7-2】规定:sin (﹣x )=﹣sin x ,cos (﹣x )=cos x ,sin (x +y )=sin x •cos y +cos x •sin y .据此 (1)判断下列等式成立的是 (填序号).①cos (﹣60°)=−12;②sin2x =2sin x •cos x ;③sin (x ﹣y )=sin x •cos y ﹣cos x •sin y . (2)利用上面的规定求①sin75° ②sin15°. 【分析】(1)根据已知中的定义以及特殊角的三角函数值即可判断; (2)利用已知进而将原式变形求出答案.【解答】解:(1)①cos (﹣60°)=cos60°=12,命题错误; ②sin2x =sin x •cos x +cos x •sin x =2sin x •cos x ,命题正确;③sin (x ﹣y )=sin x •cos (﹣y )+cos x •sin (﹣y )=sin x •cos y ﹣cos x •sin y ,命题正确. 故答案为:②③;(2)①sin75°=sin (30°+45°)=sin30°•cos45°+cos30°•sin45°=12×√22+√32×√22=√24+√64=√6+√24;②sin15°=sin (45°﹣30°)=sin45°•cos30°﹣cos45°•sin30° =√22×√32−√22×12=√6−√24.【点评】本题考查锐角三角函数以及特殊角的三角函数值,正确理解三角函数的定义是关键. 【变式7-3】对于钝角α,定义它的三角函数值如下: sin α=sin (180°﹣α),cos α=﹣cos (180°﹣α) (1)求sin120°,cos120°,sin150°的值;(2)若一个三角形的三个内角的比是1:1:4,A ,B 是这个三角形的两个顶点,sin A ,cos B 是方程4x 2﹣mx ﹣1=0的两个不相等的实数根,求m 的值及∠A 和∠B 的大小. 【分析】(1)按照题目所给的信息求解即可;(2)分三种情况进行分析:①当∠A =30°,∠B =120°时;②当∠A =120°,∠B =30°时;③当∠A =30°,∠B =30°时,根据题意分别求出m 的值即可. 【解答】解:(1)由题意得,sin120°=sin (180°﹣120°)=sin60°=√32, cos120°=﹣cos (180°﹣120°)=﹣cos60°=−12, sin150°=sin (180°﹣150°)=sin30°=12;(2)∵三角形的三个内角的比是1:1:4, ∴三个内角分别为30°,30°,120°,①当∠A =30°,∠B =120°时,方程的两根为12,−12,将12代入方程得:4×(12)2﹣m ×12−1=0,解得:m =0,经检验−12是方程4x 2﹣1=0的根, ∴m =0符合题意;②当∠A =120°,∠B =30°时,两根为√32,√32,不符合题意; ③当∠A =30°,∠B =30°时,两根为12,√32,将12代入方程得:4×(12)2﹣m ×12−1=0,解得:m =0, 经检验√32不是方程4x 2﹣1=0的根. 综上所述:m =0,∠A =30°,∠B =120°.【点评】本题考查了特殊角的三角函数值,解答本题的关键是按照题目所给的运算法则求出三角函数的值和运用分类讨论的思想解题,难度一般. 【考点8 解直角三角形】【方法点拨】解决此类问题的关键在于解直角三角形(Rt△ABC,∠C=90°)①三边之间的关系:a 2+b 2=c 2;②两锐角之间的关系:∠A+∠B=90°;③边角之间的关系;正弦(sin )等于对边比斜边, 余弦(cos )等于邻边比斜边 正切(tan )等于对边比邻边.;④解直角三角形中常见类型:①已知一边一锐角.②已知两边.【例8】(2020秋•沙坪坝区校级月考)如图,在△ABC 中,AD 是BC 边上的高,BC =14,AD =12,sin B =45. (1)求线段CD 的长度; (2)求cos ∠C 的值.【分析】根据sin B =45,求得AB =15,由勾股定理得BD =9,从而计算出CD ,再利用三角函数,求出cos ∠C 的值即可.【解答】解:(1)∵AD 是BC 上的高, ∴∠ADB =∠ADC =90°. ∵sin B =45,AD =12, ∴AB =15,∴BD =√AB 2−AD 2=√152−122=9, ∵BC =14,∴DC =BC ﹣BD =14﹣9=5;(2)由(1)知,CD=5,AD=12,∴AC=√AD2+CD2=√122+52=13,cos C=CDAC=513.【点评】本题考查了解直角三角形中三角函数的应用,熟练掌握好三角形边角之间的关系是解题的关键.【变式8-1】(2020•浦城县一模)如图,在Rt△ABC中,设a,b,c分别为∠A,∠B,∠C的对边,∠C=90°,b=8,∠A的平分线AD=163√3,求∠B,a,c的值.【分析】根据锐角三角函数,可以求得∠CAD的度数,从而可以得到∠CAB的度数,然后即可得到∠B 的度数,再根据锐角三角函数即可得到a、c的值.【解答】解:∵∠C=90°,b=8,∠A的平分线AD=163√3,∴cos∠CAD=ACAD=1633=√32,∴∠CAD=30°,∴∠CAB=60°,∴∠B=30°,∴c=2b=16,a=btan30°=√33=8√3,即∠B=30°,a=8√3,c=16.【点评】本题考查解直角三角形,解答本题的关键是明确题意,利用锐角三角函数解答.【变式8-2】(2020秋•东明县期末)如图,Rt△ABC中,∠A=90°,AD、AE分别是BC边的中线和高,若cos B=35,BC=10.(1)求AB的长;(2)求AE的长;(3)求sin∠ADB的值.【分析】(1)在Rt △ABC 中,通过解直角三角形可求出AB 的长;(2)在Rt △ABC 中,利用勾股定理可求出AC 的长,再利用面积法可求出AE 的长;(3)利用直角三角形斜边上的中线等于斜边的一半可求出AD 的长,在Rt △AED 中,利用正弦的定义可求出sin ∠ADB 的值.【解答】解:(1)在Rt △ABC 中,∠A =90°,cos B =AB BC,BC =10, ∴AB =BC •cos B =10×35=6.(2)在Rt △ABC 中,∠A =90°,BC =10,AB =6,∴AC =√BC 2−AB 2=√102−62=8.∵AE 是BC 边的高,∴12AC •AB =12BC •AE ,即12×8×6=12×10AE , ∴AE =245.(3)Rt △ABC 中,AD 是BC 边的中线,BC =10,∴AD =12BC =5.在Rt △AED 中,∠AED =90°,AD =5,AE =245,∴sin ∠ADB =AE AD =2455=2425.【点评】本题考查了解直角三角形以及勾股定理,解题的关键是:(1)利用余弦的定义,找出AB =BC •cos B ;(2)利用面积法,求出AE 的长;(3)利用正弦的定义,求出sin ∠ADB 的值.【变式8-3】(2019秋•解放区校级期中)如图,在△ABC 中,∠ACB =90°,cos A =35,BC =12,D 是AB 的中点,过点B 作直线CD 的垂线,垂足为点E .求:(1)线段CD 的长;(2)cos ∠ABE 的值.【分析】(1)在△ABC 中根据正弦的定义得到cos A =AC AB =35,则可计算出AB =15,然后根据直角三角形斜边上的中线性质即可得到CD =12AB =152.(2)在Rt △ABC 中先利用勾股定理计算出AC =6,在根据三角形面积公式得到S △BDC =S △ADC ,则S △BDC =12S △ABC ,即12CD •BE =12•12AC •BC ,于是可计算出BE =365,然后在Rt △BDE 中利用余弦的定义求解. 【解答】解:(1)在△ABC 中,∵∠ACB =90°,∴cos A =AC AB =35, ∴可以假设AC =3k ,AB =5k ,则BC =4k ,而BC =12,∴k =3,∴AB =15∵D 是AB 中点,∴CD =12AB =152.(2)在Rt △ABC 中,∵AB =15,BC =12,AC =9,∵D 是AB 中点,∴BD =152,S △BDC =S △ADC ,∴S △BDC =12S △ABC ,即12CD •BE =12•12AC •BC ,∴BE =9×122×152=365, 在Rt △BDE 中,cos ∠ABE =BE BD =365152=2425, 即cos ∠ABE 的值为2425.【点评】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了直角三角形斜边上的中线性质和三角形面积公式.【考点9 解斜三角形】【方法点拨】解决此类问题的关键在于作垂线将斜三角形分割成两个直角三角形,进而通过解直角三角形进行求解.【例9】(2020春•牡丹江期末)如图,在△ABC 中,∠BAC =120°,AC =6,AB =4,则BC 的长是( )A .6√2B .2√19C .2√13D .9【分析】作CD ⊥AB ,根据直角三角形的性质求出AD ,根据勾股定理求出CD ,根据勾股定理计算,得到答案.【解答】解:过点C 作CD ⊥AB ,交BA 的延长线于点D ,∵∠BAC =120°,∴∠DAC =180°﹣120°=60°,∴∠ACD =30°,∴AD =12AC =3,∴BD =AB +AD =7,由勾股定理得,CD =√AC 2−AD 2=3√3,在Rt △BCD 中,BC =√BD 2+CD 2=2√19,故选:B .【点评】本题考查的是解直角三角形,掌握含30°的直角三角形的性质、勾股定理是解题的关键.【变式9-1】(2020春•东城区校级期末)如图,在△ABC中,∠A=30°,tan B=34,AC=6√3,求AB的长.【分析】过点C作CD⊥AB于点D,根据∠A=30°,tan B=34,AC=6√3可求出AD与BD的长度.【解答】解:如图,过点C作CD⊥AB于点D.∵在Rt△CDA中,∠A=30°,∴CD=AC•sin30°=3√3,AD=AC×cos30°=9,在Rt△CDB中,∵tan B=3 4∴CDBD =34∴BD=4√3,∴AB=AD+DB=9+4√3.【点评】本题考查解直角三角形,解题的关键是熟练运用锐角三角函数的定义,本题属于中等题型.【变式9-2】已知.在△ABC中,BC=√2AC,∠BCA=135°,求tan A的值.【分析】过B点作BD⊥AC交AC的延长线于D点,根据等腰直角三角形的性质得到BD=CD=√22BC,根据正切的定义计算即可.【解答】解:过B点作BD⊥AC交AC的延长线于D点,则∠BCD=45,∴BD=CD=√22BC,设AC=k,则BD=CD=k,AD=2k,tan A=BDAD=12.【点评】本题考查的是解直角三角形,掌握等腰直角三角形的性质、正切的定义是解题的关键.【变式9-3】(2019秋•抚州期末)如图,在△ABC中,∠B=45°,∠C=75°,夹边BC的长为6.求△ABC的面积.【分析】如图,作CD⊥AB于点D.解直角三角形求出CD,AB即可解决问题.【解答】解:如图,作CD⊥AB于点D.∵∠B=45°,CD⊥AB,∴∠BCD=45°,∵BC=6,∴CD=3√2,在Rt△ACD中,∠ACD=75°﹣45°=30°,∴tan30°=AD3√2,∴AD=3√2×√33=√6,∴S=12×(3√2+√6)×3√2=9+3√3,∴△ABC的面积是9+3√3.【点评】本题考查解直角三角形,解题的关键是学会添加常用辅助线,构造特殊三角形解决问题.【考点10 解直角三角形(作垂线)】【例10】(2019•包头模拟)如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠BCD=120°,∠ADC+∠ABC=180°.(1)求△BCD的面积;(2)求cos∠ADB.【分析】(1)在Rt△DEC中,∠E=90°,sin∠DCE=DECD,求出DE的长度,即可求解;(2)在Rt△DEB中,由勾股定理知:DE2+BE2=BD2,求出BD的长度;同理在Rt△DFB中,求出DF 的长度,即可求解.【解答】解:(1)过点D作DE⊥BC交BC的延长线于E,∵∠BCD=120°,∴∠DCE=60°,在Rt△DEC中,∠E=90°,sin∠DCE=DECD,cos∠DCE=CECD,CD=5,∴DE=CD⋅sin∠DCE=5×sin60°=5√32,CE=CD⋅cos∠DCE=5×cos60°=52,∵BC=3,∴S△BCD=12BC⋅DE=12×3×5√32=15√34;(2)过点B作BF⊥AD于F,∵∠BCD=120°,∠ADC+∠ABC=180°,∴∠A=60°,∵在Rt△AFB中,∠AFB=90°,sin∠A=BFAB,AB=8,∴BF=AB⋅sin∠A=8×sin60°=4√3,∵BE=BC+CE=3+52=112;∵在Rt△DEB中,∠E=90°,由勾股定理知:DE2+BE2=BD2,∴BD=√DE2+BE2=(532)2+(112)2=7,∵在Rt△DFB中,∠DFB=90°,由勾股定理知:DF2+BF2=BD2,∴DF=√BD2−BF2=√72−(4√3)2=1,∴在Rt△DFB中,∠DFB=90°,cos∠ADB=DFAB=17.【点评】此题是一个综合性很强的题目,主要考查勾股定理的运用、三角形面积计算、解直角三角形等知识点,难度很大,有利于培养同学们钻研和探索问题的精神.【变式10-1】(2019秋•锦江区校级期中)已知:BD是四边形ABCD的对角线,AB⊥BC,∠C=60°,AB =1,BC=3+√3,CD=2√3(1)求∠ABD的值;(2)求AD的长.【分析】(1)过点D作DE⊥BC于点E,根据∠C=60°求出CE、DE,再求出BE,从而得到DE=BE,然后求出∠EDB=∠EBD=45°,再求出∠ABD=45°,然后根据特殊角的三角函数值解答;(2)过点A作AF⊥BD于点F,求出BF=AF=√22,再求出BD,然后求出DF,在Rt△ADF中,利用勾股定理列式计算即可得解.【解答】解:(1)过点D作DE⊥BC于点E,∵在Rt△CDE中,∠C=60°,CD=2√3,∴CE=√3,DE=3,∵BC=3+√3,∴BE=BC﹣CE=3+√3−√3=3,∴DE=BE=3,∴在Rt△BDE中,∠EDB=∠EBD=45°,∵AB⊥BC,∠ABC=90°,∴∠ABD=∠ABC﹣∠EBD=45°;(2)过点A作AF⊥BD于点F.在Rt△ABF中,∠ABF=45°,AB=1,∴BF=AF=√2 2,∵在Rt△BDE中,DE=BE=3,∴BD=3√2,∴DF=BD﹣BF=3√2−√22=5√22,∴在Rt△AFD中,AD=√DF2+AF2=(5√22)2+(√22)2=√13.【点评】本题考查了勾股定理,解直角三角形,根据边的长度得到等腰直角三角形是解题的关键,难点在于作辅助线构造成直角三角形.【变式10-2】(2020•福建模拟)已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,DE⊥BC于E,连接BD,设AD=m,DC=n,BE=p,DE=q.(1)若tan C=2,BE=3,CE=2,求点B到CD的距离;(2)若m=n,BD=3√2,求四边形ABCD的面积.【分析】(1)要求点B 到CD 的距离,于是作垂线构造直角三角形,又知tan C =2,BE =3,CE =2,可以得到BF =2FC ,设未知数根据勾股定理列方程可以求解.(2)m =n ,即AD =DC ,通过作垂线,构造全等三角形将问题转化为求正方形BEDG 的面积即可.【解答】解:(1)过点B 作BF ⊥CD ,垂足为F ,则∠BFC =90°∵DE ⊥BC ,∴∠DEC =∠DEB =90°,在Rt △DEC 中,∵tan C =2,EC =2,∴DE =4,在Rt △BFC 中,∵tan C =2,∴BF =2FC ,设BF =x ,则FC =12x ,∵BF 2+FC 2=BC 2,∴x 2+(12x )2=(3+2)2, 解得:x =2√5,即:BF =2√5,答:点B 到CD 的距离是2√5.(2)过点D 作DG ⊥AB ,交BA 的延长线相交于点G ,∵四边形ABCD 的内角和是360°,∠ABC =∠ADC =90°,∴∠C +∠BAD =180°,又∵∠BAD +∠GAD =180°,∴∠C =∠GAD ,∵∠DEC =∠G =90°,AD =CD∴△DEC ≌△DGA ,(AAS )∴DE =DG ,∴四边形BEDG 是正方形,∴S 四边形ABCD =S 正方形BEDG =12BD 2=9.答:四边形ABCD 的面积是9.【点评】考查解直角三角形,勾股定理、和全等三角形等知识,作垂线构造直角三角形是常用的辅助线作法,通过作辅助线将问题转化求正方形的面积.【变式10-3】如图,在四边形ABCD中,∠DAB=60°,AD:AB=2:3,BD=√7,AB⊥BC.(1)求sin∠ABD的值.(2)若∠BCD=120°,求CD的长.【分析】(1)作DE⊥AB于E,CF⊥DE于F.设AE=a.在Rt△BDE中,利用勾股定理构建方程求出a,即可解决问题;(2)作CF⊥DE于F.首先证明四边形CFEB是矩形,解直角三角形△CFB即可解决问题;【解答】解:(1)作DE⊥AB于E,设AE=a.在Rt△ADE中,∵∠A=60°,AE=a,∴∠ADE=30°,∴AD=2a,DE=√3a,∵AD:AB=2:3,∴AB=3a,EB=2a,在Rt△DEB中,(√3a)2+(2a)2=(√7)2,解得a=1,∴DE=√3,BE=2,∴sin∠ABD=DEBD=√3√7=√217.(2)CF⊥DE于F.∵CB⊥AB,CF⊥DE,∴∠CFE=∠FEB=∠CBE=90°,∴四边形CFEB是矩形,∴CF=EB=2,BC=EF,∵∠DCB=120°,∠FCB=90°,∴∠DCF=30°,∴DF=CF•tan30°=2√3 3,∴CD=2DF=4√3 3.【点评】本题考查解直角三角形,矩形的判定和性质,直角三角形30度角性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.【考点11 解直角三角形的应用(实物建模问题)】【例11】(2020•芝罘区一模)如图1,图2分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆DE、箱长BC、拉杆AB的长度都相等,即DE=BC=AB,点B、F在线段AC上,点C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°.请根据以上信息,解决下列问题;(1)求AC的长度(结果保留根号);(2)求拉杆端点A到水平滑杆ED的距离(结果保留到1cm).参考数据:√2≈1.41,√3≈1.73,√6≈2.45.【分析】(1)过F作FH⊥DE于H,解直角三角形即可得到结论;(2)过A作AG⊥ED交ED的延长线于G,根据等腰直角三角形的性质即可得到结论.【解答】解:(1)过F作FH⊥DE于H.∴∠FHC=∠FHD=90°.∵∠FDC=30°,DF=30,∴FH=12DF=15,DH=√32DF=15√3,∵∠FCH=45°,∴CH=FH=15,∴CD=CH+DH=15+15√3,∵CE:CD=1:3,∴DE=43CD=20+20√3,∵AB=BC=DE,∴AC=(40+40√3)cm;(2)过A作AG⊥ED交ED的延长线于G,∵∠ACG=45°,∴AG=√22AC=20√2+20√6,=20×1.41+20×2.45=77.2≈77(cm)答:拉杆端点A到水平滑杆ED的距离为77cm.【点评】此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键是用数学知识解决实际问题.【变式11-1】(2020•柯桥区模拟)目前,各大城市都在积极推进公共自行车建设,努力为人们绿色出行带来方便.图(1)所示的是一辆自行车的实物图.图(2)是自行车的车架示意图.CE=30cm,DE=20cm,AD=25cm,DE⊥AC于点E,座杆CF的长为15cm,点A,E,C,F在同一直线上,且∠CAB=75°,公共自行车车轮的半径约为30cm,且AB与地面平行.(1)求车架中AE的长;(2)求车座点F到地面的距离.(结果精确到1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)【分析】(1)由DE⊥AC及DE,AD的长,利用勾股定理即可求出AE的长;(2)作FG⊥AB于G,延长FG交地平线于点Q,由AE,CE,CF的长可得出F A的长,通过解直角三角形可求出FG的长,再结合FQ=FG+GQ即可求出结论.【解答】解:(1)∵DE⊥AC,DE=20,AD=25,∴AE=2−DE2=√252−202=15(cm);(2)在图(2)中,作FG⊥AB于G,延长FG交地平线于点Q.∵AE=15,CE=30,CF=15,∴F A=FC+CE+EA=15+30+15=60.∵sin∠CAB=FG FA,∴FG=F A•sin∠CAB≈60×0.97=58.2(cm),∴FQ=FG+GQ=58.2+30=88.2≈88(cm).答:车座点F到地面的距离约为88cm.【点评】本题考查了勾股定理以及解直角三角形,解题的关键是:(1)利用勾股定理求出AE的长;(2)通过解直角三角形求出FG的长.【变式11-2】(2020•东胜区二模)如图是一种简易台灯的结构图,灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.(1)求DE与水平桌面(AB所在直线)所成的角;(2)当E点到水平桌面(AB所在直线)的距离为45cm﹣46cm时,视线最佳,通过计算说明此时光线是否为最佳.(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,√3=1.73.)【分析】(1)过点D作DN⊥AB于点N,过E作EM⊥AB于点M,过点D作DF∥AB,交EM于F,得到四边形DNMF是矩形,进而得出∠EDF的值;(2)利用锐角三角函数关系得出DN以及EF的值,进而得出答案.【解答】解:(1)如图所示:过点D作DN⊥AB于点N,过E作EM⊥AB于点M,过点D作DF∥AB,交EM于F,故四边形DNMF是矩形,则∠NDF=90°,∵∠A=60°,∠AND=90°,∴∠ADN=30°,∴∠EDF=135°﹣90°﹣30°=15°,即DE与水平桌面(AB所在直线)所成的角为15°;(2)如图所示:∵∠ACB=90°,∠A=60°,AB=16cm,∴∠ABC=30°,。
2021年广东省深圳市罗湖区中考数学三模试卷(解析版)

2021年广东省深圳市罗湖区中考数学三模试卷一.选择题(共10小题).1.如图,数轴上点A所表示的数的绝对值是()A.2B.C.D.﹣22.下列图形中,既不是中心对称图形,也不是轴对称图形的是()A.B.C.D.3.据统计,某城市去年接待旅游人数约为89 000 000人,89 000 000这个数据用科学记数法表示为()A.8.9×106B.8.9×105C.8.9×107D.8.9×1084.如图是由四个相同的小正方体组成的几何体,若从正面观察该几何体,得到的形状图是()A.B.C.D.5.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好是9.4环,方差分别是S甲2=0.90,S乙2=1.22,S丙2=0.45,S丁2=1.9,在本次射击测试中,成绩最稳定的是()A.甲B.乙C.丙D.丁6.下列运算正确的是()A.x3+x3=x6B.a12÷a4=a3C.(a3)2=a5D.a7•a5=a127.如图,已知l1∥l2,将一个含45°角的三角尺按图中方式放置,∠1=24°,则∠2的大小是()A.21°B.24°C.30°D.66°8.如图,用尺规作角平分线,根据作图步骤,在说明射线AN是∠BAC的平分线过程中,以下说法错误的是()A.由作弧可知AE=AF B.由作弧可知FP=EPC.由SAS证明△AFP≌△AEP D.由SSS证明△AFP≌△AEP9.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为()A.1B.2C.3D.410.如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=()A.B.C.D.二.填空题(每小题3分共15分)11.因式分解:2x2+xy=.12.一个不透明的袋子中装有除颜色外完全相同的球共10个,从中随机摸出一个球,若摸到红色球的概率为,则袋子中红色球的个数是.13.如图,在△ACB中,∠ACB=90°,点D为AB的中点,将△ACB绕点C按顺时针方向旋转,当CB经过点D时得到△A1CB1.若AC=6,BC=8,则DB1的长为.14.如图,已知等边三角形ABC的顶点A,B分别在反比例函数y=图象的两个分支上,点C在反比例函数y=(k≠0)的图象上,当△ABC的面积最小时,k的值为.15.如图,在正方形ABCD中,E是对角线AC上的动点,以DE为边作正方形DEFG,H 是CD的中点.连接GH,若GH的最小值是1,则正方形ABCD的边长为.三、解答题(本大题共7小题,其中第16题5分,第17题6分,第18题8分,第19题8分,第20题8分,第21题10分,第22题10分,共55分)16.计算:2﹣1+sin30°+﹣(﹣tan60°)0.17.解方程:(1)=;(2)x2+6x﹣2=0.18.为弘扬中华优秀传统文化,某校开展了“经典雅韵”诵读比赛活动,现随机抽取部分同学的成绩进行统计,并绘制如下两个不完整的统计图,请结合图中提供的信息,解答下列各题:(1)直接写出a的值,a=,并把频数分布直方图补充完整.(2)求扇形B的圆心角度数.(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?.19.如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD =CB,连接DO并延长交CB的延长线于点E.(1)判断直线CD与⊙O的位置关系,并说明理由;(2)若BE=4,DE=8,求AC的长.20.某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋兴趣小组使用,其中购买象棋用了210元,购买围棋用了378元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共50副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?21.如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.(1)直接写出抛物线的解析式:;(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F 作BC的垂线与抛物线的对称轴和y轴交于点G、H,设点D的横坐标为m.①求DF+HF的最大值;②连接EG,若∠GEH=45°时,求m的值.22.在平面直角坐标系中,O为原点,四边形ABCD是矩形,点A(0,2),C(2,0),点D是对角线AC上一点(不与A、C重合),连接BD,作DE⊥BD,交x轴于点E,以线段DE、DB为邻边作矩形BDEF.(1)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长;若不存在,请说明理由;(2)求证:;(3)设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式,并求出当x取何值时,y有最小值?参考答案一.选择题(每小题3分共30分)1.如图,数轴上点A所表示的数的绝对值是()A.2B.C.D.﹣2【分析】观察数轴易知点A表示的数为﹣2,找到﹣2的绝对值即可.解:由题易知点A表示的数为﹣2,∵|﹣2|=2,故选:A.2.下列图形中,既不是中心对称图形,也不是轴对称图形的是()A.B.C.D.【分析】结合选项根据轴对称图形与中心对称图形的概念求解即可.解:A、既是轴对称图形,也是中心对称图形,不合题意;B、是轴对称图形,不是中心对称图形,不合题意;C、不是轴对称图形,是中心对称图形,不合题意;D、既不是轴对称图形,也不是中心对称图形,符合题意.故选:D.3.据统计,某城市去年接待旅游人数约为89 000 000人,89 000 000这个数据用科学记数法表示为()A.8.9×106B.8.9×105C.8.9×107D.8.9×108【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.解:89 000 000这个数据用科学记数法表示为8.9×107.故选:C.4.如图是由四个相同的小正方体组成的几何体,若从正面观察该几何体,得到的形状图是()A.B.C.D.【分析】根据主视图是从物体正面看所得到的图形解答即可.解:从正面看有两层,底层是三个正方形,上层右边是一个正方形,右齐.故选:D.5.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好是9.4环,方差分别是S甲2=0.90,S乙2=1.22,S丙2=0.45,S丁2=1.9,在本次射击测试中,成绩最稳定的是()A.甲B.乙C.丙D.丁【分析】根据方差的意义求解即可.解:∵S甲2=0.90,S乙2=1.22,S丙2=0.45,S丁2=1.9,∴S丙2<S甲2<S乙2<S丁2,∴在本次射击测试中,成绩最稳定的是丙,故选:C.6.下列运算正确的是()A.x3+x3=x6B.a12÷a4=a3C.(a3)2=a5D.a7•a5=a12【分析】分别计算各选项即可.解:A.x3+x3=2x3,该选项不正确,不符合题意;B.a12÷a4=a8,该选项错误,不符合题意;C.(a3)2=a6,该选项错误,不符合题意;D.a7•a5=a12,该选项正确,符合题意.故选:D.7.如图,已知l1∥l2,将一个含45°角的三角尺按图中方式放置,∠1=24°,则∠2的大小是()A.21°B.24°C.30°D.66°【分析】过B作BD∥l1得到BD∥l1∥l2,根据平行线的性质证得∠ABD=∠1,∠2=∠CBD,由含45°角的三角尺锐角的度数求出∠CBD的度数,即可得到∠2的大小.解:过B作BD∥l1,∵l1∥l2,∴BD∥l1∥l2,∴∠ABD=∠1,∠2=∠CBD,∵∠1=24°,∴∠ABD=24°,∵∠ABC=45°,∴∠ABD+∠CBD=45°,∴∠CBD=∠ABC﹣∠ABD=21°,∴∠2=21°,故选:A.8.如图,用尺规作角平分线,根据作图步骤,在说明射线AN是∠BAC的平分线过程中,以下说法错误的是()A.由作弧可知AE=AF B.由作弧可知FP=EPC.由SAS证明△AFP≌△AEP D.由SSS证明△AFP≌△AEP【分析】由作图可知,AF=AE,PF=PE结合全等三角形的判定可得结论.解:连接PF,PE.由作图可知,AF=AE,PF=PE,∵AP=AP,∴△APF≌△APE(SSS),故选项A,B,D正确,故选:C.9.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为()A.1B.2C.3D.4【分析】由函数y=x2+bx+c与x轴无交点,可得b2﹣4c<0;当x=1时,y=1+b+c=1;当x=3时,y=9+3b+c=3;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c <x,继而可求得答案.解:∵函数y=x2+bx+c与x轴无交点,∴b2﹣4c<0;故①错误;当x=1时,y=1+b+c=1,故②错误;∵当x=3时,y=9+3b+c=3,∴3b+c+6=0;③正确;∵当1<x<3时,二次函数值小于一次函数值,∴x2+bx+c<x,∴x2+(b﹣1)x+c<0.故④正确.故选:B.10.如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=()A.B.C.D.【分析】连接CF、GF,由△AFD∽△EAD可得正方形边长,再由△AFG∽△DFC即可得到答案.解:连接CF、GF,如图:∵正方形ABCDA中,∠EAD=∠ADC=90°,AF⊥DE,∴△AFD∽△EAD,∴=,又∵DF=5EF=5,∴AD====CD,在Rt△AFD中,AF===,∵∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,∴∠DAF=∠CDF,∵四边形GFCD是⊙OO的内接四边形,∴∠FCD+∠DGF=180°,∵∠FGA+∠DGF=180°∴∠FGA=∠FCD,∴△AFG∽△DFC∴=,∴=,∴AG=,∴DG=AD﹣AG=﹣,故选:D.二.填空题(每小题3分共15分)11.因式分解:2x2+xy=x(2x+y).【分析】直接提取公因式y,进而分解因式即可.解:2x2+xy=x(2x+y).故答案为:x(2x+y).12.一个不透明的袋子中装有除颜色外完全相同的球共10个,从中随机摸出一个球,若摸到红色球的概率为,则袋子中红色球的个数是6.【分析】首先设袋子中红球有x个,利用概率公式求即可得方程,进而解答即可.解:设袋子中红球有x个,根据题意可得:,解得:x=6,故答案为:6.13.如图,在△ACB中,∠ACB=90°,点D为AB的中点,将△ACB绕点C按顺时针方向旋转,当CB经过点D时得到△A1CB1.若AC=6,BC=8,则DB1的长为3.【分析】根据勾股定理得到AB===10,由直角三角形的性质的CD=AB=5,由旋转的性质得到CB1=BC=8,于是得到结论.解:∵在△ACB中,∠ACB=90°,AC=6,BC=8,∴AB===10,∵点D为AB的中点,∴CD=AB=5,∵将△ACB绕点C按顺时针方向旋转,当CB经过点D时得到△A1CB1.∴CB1=BC=8,∴DB1=8﹣5=3,故答案为:3.14.如图,已知等边三角形ABC的顶点A,B分别在反比例函数y=图象的两个分支上,点C在反比例函数y=(k≠0)的图象上,当△ABC的面积最小时,k的值为﹣3.【分析】当等边三角形ABC的边长最小时,△ABC的面积最小,点A,B分别在反比例函数y=图象的两个分支上,则当A、B在直线y=x上时最短,即此时△ABC的面积最小,根据反比例函数图象的对称性可得OA=OB,设OA=x,则AC=2x,OC=x,根据等边三角形三线合一可证明△AOE∽△OCF,根据相似三角形面积比等于相似比的平方可得结论.解:根据题意当A、B在直线y=x上时,△ABC的面积最小,函数y=图象关于原点对称,∴OA=OB,连接OC,过A作AE⊥y轴于E,过C作CF⊥y轴于F,∵△ABC是等边三角形,∴AO⊥OC,∴∠AOC=90°,∠ACO=30°,∴∠AOE+∠COF=90°,设OA=x,则AC=2x,OC=x,∵AE⊥y轴,CF⊥y轴,∴∠AEO=∠OFC=∠AOE+∠OAE=90°,∴∠COF=∠OAE,∴△AOE∽△OCF,∴=()2=()2=,∵顶点A在函数y=图象的分支上,∴S△AOE=,∴S△OCF=,∵点C在反比例函数y=(k≠0)的图象上,∴k=﹣3,故答案为﹣3.15.如图,在正方形ABCD中,E是对角线AC上的动点,以DE为边作正方形DEFG,H 是CD的中点.连接GH,若GH的最小值是1,则正方形ABCD的边长为2.【分析】连接CG.证明△ADE≌△CDG(SAS),推出∠DCG=∠DAE=45°,推出点G的运动轨迹是射线CG,根据垂线段最短可知,当GH⊥CG时,GH的值最小,再解直角三角形求得CH,便可得正方形ABCD的边长.解:连接CG.∵四边形ABCD是正方形,四边形DECG是正方形,∴DA=DC,DE=DG,∠ADC=∠EDG=90°,∠DAC=45°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴∠DCG=∠DAE=45°,∴点G的运动轨迹是射线CG,根据垂线段最短可知,当GH⊥CG时,GH的值最小为1,∴CH=.∴CD=2CH=2,故答案为:2.三、解答题(本大题共7小题,其中第16题5分,第17题6分,第18题8分,第19题8分,第20题8分,第21题10分,第22题10分,共55分)16.计算:2﹣1+sin30°+﹣(﹣tan60°)0.【分析】利用零指数幂、负整数指数幂法则以及二次根式的性质计算即可得到结果.解:原式==.17.解方程:(1)=;(2)x2+6x﹣2=0.【分析】(1)先把分式方程整理成整式方程,再按照解整式方程的步骤进行计算,最后再进行检验,即可得出答案.(2)根据配方法的步骤先把﹣2移到等号的右边配方,再进行配方,求出x的值.解:(1)=,5(x﹣1)=6x,5x﹣6x=5,﹣x=5,x=﹣5,经检验x=﹣5是原方程的根,则原方程的解是x=﹣5;(2)x2+6x﹣2=0x2+6x=2,x2+6x+9=2+9,(x+3)2=11,x+3=,x1=﹣3﹣,x2=﹣3+;18.为弘扬中华优秀传统文化,某校开展了“经典雅韵”诵读比赛活动,现随机抽取部分同学的成绩进行统计,并绘制如下两个不完整的统计图,请结合图中提供的信息,解答下列各题:(1)直接写出a的值,a=30,并把频数分布直方图补充完整.(2)求扇形B的圆心角度数.(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?.【分析】(1)先根据E等级人数及其占总人数的比例可得总人数,再用D等级人数除以总人数可得a的值,用总人数减去其他各等级人数求得C等级人数可补全图形;(2)用360°乘以A等级人数所占比例可得;(3)用总人数乘以样本中E等级人数所占比例.解:(1)∵被调查的总人数为10÷=50(人),∴D等级人数所占百分比a%=×100%=30%,即a=30,C等级人数为50﹣(5+7+15+10)=13人,补全图形如下:故答案为:30;(2)扇形B的圆心角度数为360°×=50.4°;(3)估计获得优秀奖的学生有2000×=400人.19.如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD =CB,连接DO并延长交CB的延长线于点E.(1)判断直线CD与⊙O的位置关系,并说明理由;(2)若BE=4,DE=8,求AC的长.【分析】(1)欲证明CD是切线,只要证明OD⊥CD,利用全等三角形的性质即可证明;(2)设⊙O的半径为r.在Rt△OBE中,根据OE2=EB2+OB2,可得(8﹣r)2=r2+42,推出r=3,由tan∠E==,推出=,可得CD=BC=6,再利用勾股定理即可解决问题;【解答】(1)证明:连接OC.∵CB=CD,CO=CO,OB=OD,∴△OCB≌△OCD,∴∠ODC=∠OBC=90°,∴OD⊥DC,∴DC是⊙O的切线.(2)解:设⊙O的半径为r.在Rt△OBE中,∵OE2=EB2+OB2,∴(8﹣r)2=r2+42,∴r=3,∵tan∠E==,∴=,∴CD=BC=6,在Rt△ABC中,AC===6.20.某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋兴趣小组使用,其中购买象棋用了210元,购买围棋用了378元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共50副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?【分析】(1)设每副围棋x元,则每副象棋(x﹣8)元,根据210元购买象棋数量=378元购买围棋数量列出方程并解答;(2)设购买围棋m副,则购买象棋(50﹣m)副,根据题意列出不等式并解答.解:(1)设每副围棋x元,则每副象棋(x﹣8)元,根据题意,得.解得x=18.经检验x=18是所列方程的根.所以x﹣8=10.答:每副围棋18元,每副象棋10元;(2)设再次购买围棋m副,则购买象棋(50﹣m)副,根据题意,得18m+10(50﹣m)≤600.解得m≤12.5.因m只能取整数,故m最大值是12.答:该校最多可再购买12副围棋.21.如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.(1)直接写出抛物线的解析式:y=﹣x2+2x+3;(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F 作BC的垂线与抛物线的对称轴和y轴交于点G、H,设点D的横坐标为m.①求DF+HF的最大值;②连接EG,若∠GEH=45°时,求m的值.【分析】(1)用待定系数法即可求解;(2)①设D(m,﹣m2+2m+3),F(m,﹣m+3),则=(﹣m2+2m+3)﹣(﹣m+3)+2m,进而求解;②由∠GEH=∠EFH,∠EHF是公共角得到△EHG∽△FHE,则,得到,进而求解.解:(1)设抛物线的表达式为y=a(x﹣x1)(x﹣x2),将点A、B的坐标代入上式得:y=﹣(x+1)(x﹣3)=﹣x2+2x+3,故答案为:y=﹣x2+2x+3;(2)①当x=0时,y=﹣x2+2x+3=3,∴点C(0,3).设直线BC的解析式为y=mx+n,把B(3,0),C(0,3)代入,得,解得,∴BC的解析式为:y=﹣x+3.∵OB=OC=3,∴∠OBC=∠OCB=45°.作FK⊥y轴于点K,又∵FH⊥BC,∴∠KFH=∠KHF=45°,∴.设D(m,﹣m2+2m+3),F(m,﹣m+3),∴=(﹣m2+2m+3)﹣(﹣m+3)+2m,整理得:.由题意有0<m<3,且,﹣1<0,当时,取最大值,的最大值为;②作GM⊥y轴于点M,记直线FH与x轴交于点N.∵FK⊥y轴,DE⊥x轴,∠KFH=45°,∴∠EFH=∠ENF=45°,∴EF=EN.∵∠KHF=∠ONH=45°,∴OH=ON.∵y=﹣x2+2x+3的对称轴为x=1,∴MG=1,∵∠KHF=45°,∴.∵∠GEH=45°,∴∠GEH=∠EFH.又∵∠EHF是公共角,∴△EHG∽△FHE,∴,∴,在Rt△ONH中,OH=ON=|OE﹣EN|=|OE﹣EF|=|m﹣(﹣m+3)|=|2m﹣3|,OE=m,在Rt△OEH中,∵HE2=OE2+OH2=m2+(2m﹣3)2=5m2﹣12m+9,∴5m2﹣12m+9=2m,解得m1=1,.22.在平面直角坐标系中,O为原点,四边形ABCD是矩形,点A(0,2),C(2,0),点D是对角线AC上一点(不与A、C重合),连接BD,作DE⊥BD,交x轴于点E,以线段DE、DB为邻边作矩形BDEF.(1)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长;若不存在,请说明理由;(2)求证:;(3)设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式,并求出当x取何值时,y有最小值?【分析】(1)由锐角三角函数可求∠ACO=30°,∠ACB=60°,分两种情况讨论,由等腰三角形的性质可求解;(2)通过证明△BMD∽△DNE,可得结论;(3)由勾股定理可求BD2的值,由面积公式可求解析式,即可求解.解:(1)存在;理由如下:∵点A(0,2),C(2,0),∴OA=2,OC=2,∵tan∠ACO=,∴∠ACO=30°,∠ACB=60°,分两种情况:①当E在线段CO上时,△DEC是等腰三角形,观察图像可知,只有ED=EC,如图1所示:∴∠DCE=∠EDC=30°,∴∠DBC=∠BCD=60°,∴△DBC是等边三角形,∴DC=BC=2,在Rt△AOC中,∠ACO=30°,OA=2,∴AC=2AO=4,∴AD=AC﹣CD=4﹣2=2,∴当AD=2时,△DEC是等腰三角形;②当E在OC的延长线上时,△DCE是等腰三角形,只有CD=CE,∠DBC=∠DEC=∠CDE=15°,如图2所示:∴∠ABD=∠ADB=75°,∴AB=AD=2,综上所述,满足条件的AD的值为2或2;(2)证明:过点D作MN⊥AB交AB于M,交OC于N,如图3所示:设DN=a,∵∠ACO=30°,∴,∵∠BDE=90°,∴∠BDM+∠NDE=90°,∠BDM+∠DBM=90°,∴∠DBM=∠EDN,∵∠BMD=∠DNE=90°,∴△BMD∽△DNE,∴;(3)作DH⊥AB于H,如图4所示:在Rt△ADH中,AD=x,∠DAH=∠ACO=30°,∴DH=AD=x,,∴BH=2﹣x,在Rt△BDH中,BD2=,由(2)得,∴,∴矩形BDEF的面积为,∴,∵>0,∴x=3时,y有最小值为,即当点D运动到距A点的距离为3时,y有最小值.。
重难点题型巩固(应用题)- 三年级上册数学 人教版

三年级数学上册人教版《重难点题型巩固与复习》1.古代有孔融让梨的佳话,淘气的涛涛也要学他们,但是是在七个装有梨的盘子中取梨,每个盘子中分别装有1个、2个、3个、5个、6个、7个和9个梨.妈妈允许他从这些盘子中取出15个梨,但要求每个盘子中的梨要么都拿,要么都不拿.共有多少种不同的拿法?2.小明、小华和小光三个人都是少先队的干部。
他们中一个是大队长,一个是中队长,一个是小队长。
在一次体育比赛中,他们的一百米赛跑的结果是:小光比大队长的成绩好;小明和中队长的成绩不相同;中队长比小华的成绩差。
根据以上情况,你能知道小明、小华、小光三个人中,谁是大队长吗?3.兴华小学某班有60人,在收看"邓小平同志追悼大会"实况时,他们着装白色或黑色上衣,黑色或蓝色裤子。
其中有12人穿白上衣蓝裤子,有34人穿黑裤子,29人穿黑上衣,那么穿黑上衣黑裤子的有多少人?4.100个和尚分100个馒头,大和尚每人分3个馒头,小和尚3人分1个馒头,恰好分完,问大和尚、小和尚各有多少人?5.甲乙丙三人同锯同样粗细的木棍,分别领取8米,10米,6米的木棍,要求都按2米规格锯开,劳动结束后,甲乙丙分别锯了 24段,25 段,27 段,那么锯木棍速度最快的比速度最慢的多聚几次?6.一辆旅行车,当车子开过全程的一半路时,一位旅客开始睡觉.当他醒来时,剩下的路程是他睡觉中走过路程的2分之1,他在睡觉中走过的路程是全程的几分之几?7.陈爷爷去年在自家屋后面的山坡上种下90棵小树,过了一段时间发现枯死了9棵,于是又补种10棵,结果全部成活,陈爷爷去年植树的成活率是多少?8.甲、乙两筐苹果,甲筐比乙筐多19千克,从甲筐取出多少千克放入乙筐,就可以使乙筐中的苹果比甲筐的多3千克?9.老师拿来一批树苗,分给一些同学去栽,每人每次分给一棵,一轮一轮往下分,当分剩下12棵时不够每人分一棵了,如果再拿来8棵,那么每个同学正好栽10棵。
问参加栽树的有多少名同学?原有树苗多少棵?10.甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
深圳罗湖区罗芳中学数学几何模型压轴题单元测试卷 (word版,含解析)

深圳罗湖区罗芳中学数学几何模型压轴题单元测试卷(word版,含解析)一、初三数学旋转易错题压轴题(难)1.如图,四边形ABCD为正方形,△AEF为等腰直角三角形,∠AEF=90°,连接FC,G 为FC的中点,连接GD,ED.(1)如图①,E在AB上,直接写出ED,GD的数量关系.(2)将图①中的△AEF绕点A逆时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.(3)若AB=5,AE=1,将图①中的△AEF绕点A逆时针旋转一周,当E,F,C三点共线时,直接写出ED的长.【答案】(1)DE=2DG;(2)成立,理由见解析;(3)DE的长为42或32.【解析】【分析】(1)根据题意结论:DE=2DG,如图1中,连接EG,延长EG交BC的延长线于M,连接DM,证明△CMG≌△FEG(AAS),推出EF=CM,GM=GE,再证明△DCM≌△DAE (SAS)即可解决问题;(2)如图2中,结论成立.连接EG,延长EG到M,使得GM=GE,连接CM,DM,延长EF交CD于R,其证明方法类似;(3)由题意分两种情形:①如图3-1中,当E,F,C共线时.②如图3-3中,当E,F,C 共线时,分别求解即可.【详解】解:(1)结论:DE=2DG.理由:如图1中,连接EG,延长EG交BC的延长线于M,连接DM.∵四边形ABCD是正方形,∴AD=CD,∠B=∠ADC=∠DAE=∠DCB=∠DCM=90°,∵∠AEF=∠B=90°,∴EF∥CM,∴∠CMG=∠FEG,∵∠CGM=∠EGF,GC=GF,∴△CMG≌△FEG(AAS),∴EF=CM,GM=GE,∵AE=EF,∴AE=CM,∴△DCM≌△DAE(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∴DG⊥EM,DG=GE=GM,∴△EGD是等腰直角三角形,∴DE=2DG.(2)如图2中,结论成立.理由:连接EG,延长EG到M,使得GM=GE,连接CM,DM,延长EF交CD于R.∵EG=GM,FG=GC,∠EGF=∠CGM,∴△CGM≌△FGE(SAS),∴CM=EF,∠CMG=∠GEF,∴CM∥ER,∴∠DCM=∠ERC,∵∠AER+∠ADR=180°,∴∠EAD+∠ERD=180°,∵∠ERD+∠ERC=180°,∴∠DCM=∠EAD,∵AE=EF,∴AE=CM,∴△DAE≌△DCM(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∵EG=GM,∴DG=EG=GM,∴△EDG 是等腰直角三角形, ∴DE =2DG .(3)①如图3﹣1中,当E ,F ,C 共线时,在Rt △ADC 中,AC =22AD CD +=2255+=52,在Rt △AEC 中,EC =22A AE C -=22(52)1-=7,∴CF =CE ﹣EF =6,∴CG =12CF =3, ∵∠DGC =90°, ∴DG =22CD CG -=2253-=4,∴DE =2DG =42.②如图3﹣3中,当E ,F ,C 共线时,同法可得DE =32.综上所述,DE 的长为2或2.【点睛】本题属于四边形综合题,考查正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.2.已知抛物线y=ax 2+bx-3a-5经过点A(2,5)(1)求出a 和b 之间的数量关系.(2)已知抛物线的顶点为D 点,直线AD 与y 轴交于(0,-7)①求出此时抛物线的解析式;②点B 为y 轴上任意一点且在直线y=5和直线y=-13之间,连接BD 绕点B 逆时针旋转90°,得到线段BC ,连接AB 、AC ,将AB 绕点B 顺时针旋转90°,得到线段BH .截取BC 的中点F 和DH 的中点G .当点D 、点H 、点C 三点共线时,分别求出点F 和点G 的坐标.【答案】(1)a+2b=10;(2)①y= 2x 2+4x-11,②G 1,),F 1(,,G 2,F 2,) 【解析】【分析】(1)把点A 坐标代入抛物线y=ax 2+bx-3a-5即可得到a 和b 之间的数量关系;(2)①求出直线AD 的解析式,与抛物线y=ax 2+bx-3a-5联立方程组,根据直线与抛物线有两个交点,结合韦达定理求出a ,b ,即可求出解析式;②作AI ⊥y 轴于点I ,HJ ⊥y 轴于点J.设B (0,t ),根据旋转性质表示粗H 、D 、C 坐标,应含t 式子表示直线AD 的解析式,根据D 、H 、C 三点共线,把点C 坐标代入求出1t =,2t =,分两类讨论,分别求出G 、F 坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
罗三中训练题
1.从化学角度分析,下列叙述不正确的是
A .利用太阳能蒸馏海水是海水淡化的方法之一
B .将地沟油回收再加工为食用油,以减缓水体富营养化
C .研制开发燃料电池汽车,降低机动车尾气污染,可以减少PM2.5污染
D .绿色化学的核心是利用化学原理从源头上减少和消除工农业生产等对环境的污染 2.下列有关化学用语,表达正确的是
A .Na 2S 的电子式:Na S Na ∙
∙∙
∙∙
∙∙∙
B .铯—137:137Cs
A .NH 3溶于水后显碱性,在FeC13饱和溶液中通入适量NH 3可制取Fe (OH )3胶体
B .金属有导热性,铝、钠熔点不高,核反应堆内使用液体铝钠合金作载热介质
C .碳酸钠溶液显碱性,用热的饱和碳酸钠溶液可除去金属表面的矿物油污
D .次氯酸钠具有强还原性,可用于配制“84”消毒液 4.室温下,下列各组离子在指定溶液中一定能大量共存的是
A .饱和氯水中:Cl -、NO 3-、Na + 、SO 32-
B .c (H +
)=
w K 的溶液中:K +、Fe
3+
、Cl -
、SO 4
2-
C .澄清透明的溶液中:Cu 2+、NH 4+、NO 3—、ClO 4—
D .使红色石蕊试纸变蓝的溶液中:CH 3COO -、HCO 3-、Na +、K +
5.短周期主族元素A 、B 、C 、D ,原子序数依次增大。
A 、C 原子序数相差8,A 、B 、C 三种元
素原子的最外层电子数之和为15,B 原子最外层电子数等于A 原子最外层电子数的一半。
下列叙述正确的是
A .原子半径:A <D <C <B
B .B 、
C 、
D 分别与A 形成的化合物一定含有相同的化学键 C .最高价氧化物对应水化物的酸性:D <C D .常温下,单质B 能大量溶于浓硝酸中 6.下列离子方程式与所述事实相符且正确的是
A .向稀氨水中逐滴加入稀硝酸银溶液配制银氨溶液:
Ag +
+2NH 3·H 2O=[ Ag (NH 3)2] +
+2 H 2O
B .用双氧水和稀硫酸可以雕刻印刷电路板:Cu+H 2O 2+2H +
=Cu 2+
+2H 2O
C .硫化钾晶体溶于水:S 2-
+ 2H 2 O 2OH -
+ H 2S
D .澄清石灰水与过量苏打溶液混合:Ca 2+
+2OH -
+2HCO 3-
=CaCO 3↓ +CO 32-
+2H 2O
7.下列图示实验合理的是
A .图1为证明非金属性强弱:S C S i >>
B .图2为制备少量氧气
C .图3为配制一定浓度硫酸溶液
D .图4制备并收集少量NO 2气体 8.设N A 为阿伏加德罗常数的值。
下列说法正确的是
A .0.1mol AlCl 3完全水解转化为氢氧化铝胶体,生成0.1 N A 个胶粒
B .1molCu 与足量的硫固体反应转移的电子数为N A
C .标准状况下,2.24 L 三氧化硫所含分子数为0.1 N A
D .只有在标准状况下,N A 个氧气分子所占的体积才是22.4 L
9.下列关系图中,A 是一种正盐,B 是气态氢化物,C 是单质,F 是强酸。
当X 无论是强酸还
是强碱时都有如下转化关系(其他产物及反应所需条件均已略去)。
当X 是强碱时,过量B 跟Cl2反应除生成C 外,另一产物是盐酸盐。
下列说法不正确的是
A .当X 是强酸时,A 、
B 、
C 、
D 、
E 、
F 均含同一种元素,F 是H 2SO 4
B .当X 是强碱时,A 、B 、
C 、
D 、
E 、
F 均含同一种元素,F 是HNO 3 C .当X 是强碱时,C 在常温下是固态单质 D .B 也可在O 2作用下直接转化为D
10.关于下列各图的叙述,正确的是
A .甲表示H 2与O 2发生反应过程中的能量变化,则H 2的燃烧热为241.8 kJ·mol -1
图1 图2 图3 图4
B.乙表示恒温恒容条件下,2NO2(g)N2O4(g)中,各物质的浓度与其消耗速率之间的关系,其中交点A对应的状态为化学平衡状态
C.丙表示A、B两物质的溶解度随温度变化情况,将t l℃时A、B的饱和溶液分别升温至t2℃时,溶质的质量分数B>A
D.丁表示常温下,稀释HA、HB两种酸的稀溶液时,溶液pH随加水量的变化,则NaA溶液的pH小于同浓度的NaB溶液的pH
11.下列说法正确的是
A.常温下,向饱和Na2CO3溶液中加入少量BaSO4粉末,过滤,向洗净的沉淀中加稀盐酸,有气泡产生,则常温下K sp (BaCO3)<K sp (BaSO4)
B.常温下,向纯水中加入钠或氢氧化钠都能使水的电离平衡逆向移动,水的离子积不变C.常温下,反应4Fe(OH)2(s)+ O2(g) +2H2O(l) =4Fe(OH)3(s)的△H<0、△S<0
D.铅蓄电池在工作过程中,负极质量减少,阳极质量增加
12.(15分)斑螯素能抑制肝癌的发展,去掉斑螯素中的两个甲基制得的化合物——去甲基斑螯素仍具有相应的疗效,其合成路线如下:
O C HO
−
−
−→
−NaOH
浓
O
C O O Na
−
−→
−HCl
O
CO O H
−→
−∆
①②③
O
O
O
O
O
H
④⑤(去甲基斑螯素)
CH3OH+HCOONa
已知:①2HCHO+NaOH
(Diels-Alder 反应)
②
③当每个1,3-丁二烯分子与一分子氯气发生加成反应时,有两种产物:
CH2ClCH=CHCH2Cl;CH2ClCHClCH=CH2。
请回答下列问题:
(1)物质A中含有的含氧官能团名称分别为;第①步反应中还生成另一产物,此产物的结构简式为。
(2)写出H的结构简式;第⑤步反应的反应类型是。
(3)去甲基斑螯素与X互为同分异构体。
X能与FeCl3溶液发生显色反应,能与Na2CO3溶液反应生成气体,且其核磁共振氢谱有4个吸收峰。
写出满足上述条件的X的一种结构简
式。
(4)结合题中有关信息,写出由制备丁烯二酸酐
O
O
O的合成路线流程图(无机试剂任选)。
合成路线流程图示例如下:
13(15分)无水硫酸铜在强热下会发生分解反应:
CuSO4CuO + SO3↑2SO3
△
2SO2↑+ O2↑
用下图所示装置(夹持仪器已略去),根据D管在反应前后的质量差计算出分解了的无水硫酸铜的质量。
实验步骤:
①称量反应前D管的质量。
②连接好装置,关闭K,加热硬质玻璃管A一段时间后,停止加热。
③待硬质玻璃管A冷却后,打开K,通入一段时间的已除去二氧化碳等酸性气体的空气。
④再称量D管,得其反应前后的质量差为m。
回答下列问题:
(1) 2SO3(g)
△
2SO2(g)+ O2(g)该反应的平衡常数表达式为K=。
(2) B管中除温度明显升高外,还可看到的现象是,而温度明显升高的主要原因
是;B管中发生的有关离子方程式是。
(3)步骤③中通一段时间已除去二氧化碳等酸性气体的空气的目的是。
(4)按上述方法实验,假设B、C、D对气体的吸收均完全,并忽略空气中CO2的影响,能否
根据m计算出分解了的无水CuSO4的质量?(任选其一回答)
①如果能,则分解的无水CuSO4的质量为(用m表示)。
②如果不能,则原因是。
为了能测得分解了的无水硫酸铜的质量,你的简单实验方案是。
强热
A
选择题(本题包括10小题,每小题2分,共20分,每小题只有一个....选项符合题意) 1.B 2.D 3.B 4.C 5.A 6.B 7.A 8.B 9.C 10.D 11.C 12.(共15分)(1)醛基、醚键 (2分
)
(2分)
(2)
O O
O
O
(2分) 加成反应或还原反应(2分)
(3) (2
分)
(4)(5分)
13.(15分)
(1) K =c (O 2)·c 2
(SO 2) / c 2
(SO 3) (2分)
(2) 有气泡冒出,产生白色沉淀(2分) SO 3溶于水放热(2分)
SO 3 + H 2O + Ba 2+= BaSO 4↓+ 2H +
或SO 3 + H 2O = 2H ++ SO 42-和Ba 2++ SO 42-= BaSO 4↓(2分) (3)使残留在装置中的SO 2、SO 3被充分吸收(2分)
(4) ②SO 3不能完全分解为SO 2和O 2;SO 2会部分溶解在溶液中(2分)
称量装有无水硫酸铜的A 管质量,强热一段时间后,冷却后再称量A 管质量,根据A 管在反应前后的质量差计算出分解了的无水硫酸铜的质量(3分)。
