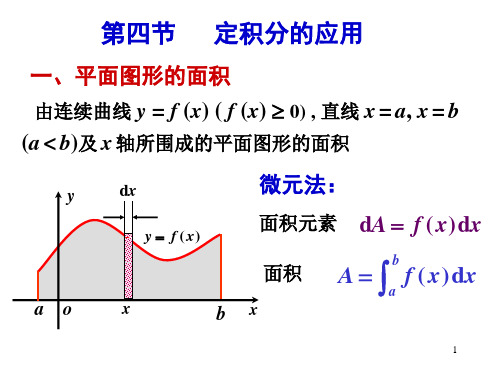
定积分的元素法,平面图形的面积

•P(r, )
令
a

v
r .

r0

v

,

••
OM
x
特别地，当 r0 0 时，等速螺线的极坐标方程为 r a .
注：附录Ⅱ中常用的曲线的极坐标方程。
18
3．极坐标与直角坐标的关系
x r cos y r sin
r2 x2 y2
tan y
x
y
r
•
O

x
x, y

x
r ( )
d
O
21
例4 计算阿基米德螺线
r a (a 0)
上相应于 从0 变到2π的一段弧与极轴所围成的图形的面积。
解：积分变量为 , 积分区间为
0,2 , 在此区间上任取小区间
2a
, d , 面积元素为

O
x
dA 1 (a )2 d
2
2
所以曲边扇形的面积为：
d


O
r ( )
x
圆扇形面积公式为 A 1 R2 2
A



1 (
2
)2
d
20
极 点 在 图 形 外 （ 曲 边 环扇 形 ）
面 积 元 素: 面积:
dA

1 2
出 (
)2 d

1 2
入
(
)2 d
A
1 2
0
0
3
9
例２ 计算抛物线 y2 2x与直线 y x 4 所围成的
图形的面积。
y
解（1） 解方程组

y2
2x
y dy
y x 4
y
得交点(2,2), 8,4 ，
以y为积分变量，积分区间为[-2,4]， o
x 1 y2 2
(8,4)
x y4
x
(2,2)
在[-2,4]上任取小区间[y,y+dy],面积元素为
设由曲线 r ( ) 及射线 ,
围成一图形（称为曲边扇形）。
d
假设 ( )在 , 上连续，且
( ) 0 。
求这个曲边扇形的面积:
取极角 为积分变量，积分区间为
, , 任取小区间 , d 。
面积元素为：dA 1 ( )2 d
一个极坐标系。其中，定点 O叫做极点，射线 Ox叫做极轴。
r • P(r, )
• • • O
•
x
在极坐标系下，平面上任一点 P 的位置就可以用线段 OP 的长度 r 及从 Ox 到 OP的角度 来确定。有序实数对 (r, ) 就称为 P 点的极坐标，记为 P(r, ) 。其中 r 叫做极径， 叫做极角。极点 O 的极径为 0 ，极角可取任何值。
• P(r, ) y
x
以极点O为圆心，以 a为半径的的圆的极坐标方程: r a.
x2 y2 a2
以点(a,0) 为圆心，以 a 为半径的的圆的极坐标方程 r 2a cos r 2a cos r 2 2a r cos x 2 y 2 2ax
19
二. 极坐标情形
（3）以 f ( i )xi 近似代替部分量 Ai 时，它们只相差一比 n x i高阶的无穷小， 因此和式 f ( i )xi 的极限就是A的 i 1
精确值，即：
b
A a f ( x)dx;
4
求A的积分表达式的步骤可简化如下：
（1）确定积分变量x及积分区间[a，b]；
（2）在 [a,b]上任取小区间 x, x dxy

出2
(
)

入
2
(
)
d
极 点 在 图 形 内 部 ， 可 以想 象 沿
着 极 轴 把 图 形 剪 开 到 极点 。
于是可以看出：
O
面 积 元 素 为 ：dA 1 2 ( )d
2
面积:
A 1 2 2 ( )d
20
d

r 出( )
d

r
入 ( )
则椭圆的面积为
a
A 4A1 4 0 ydx
A1
o x x dx x
利用椭圆的参数方程
x

y
a cos t b si Nhomakorabea t应用定积分换元法，令 x a cost, 则：
y bsint, dx a sintdt , x 0t ; x a, t 0.
d
于是所求面积为:
A
2 0
a2 2

2 d

a2 2
3

3
2
0
4 a 2 3
3
22
补充例题： 计算心形线r 1 cos与圆r 3cos
所围成的图形阴影部分的面积。
解 如图所示，这个图形关于极轴对称， 设极轴以上部分图形

y2 2
4 y3 4
4y 2


6
2
18
10
注：如果取x为积分变量
X型 在 0,8 上任取小区间x, x dx,
则 dA 2 x 1 xdx

A

8
0

2
x



1
x
dx
y穿出 y穿入
y
dA
o (2,2)
dA

y

4
1 2
y2
dy
所求面积为：A

4
2

y

4

1 2
y
2
dy


y2 2
4y
y3 4
6
2
18
注：若将所求图形的面积看成两个曲边梯形的面积之差：则
A
4 2
y 4 dy
4 2
1 2
y2d y

(8,4)
不好！
x
11
补充例题：求曲线 y =ln x, x =2及 x 轴，
所
围成的平面图形的面积y。
解：按照X型，Y型计算都可以。
y=lnx x=2
按X型：
有关的曲线写成y ( x)型
O
1
2x
A

2
1
ln
x

0dx

x
ln
x
2 1

2
1
xd
ln
x

2ln 2

1.
y
按Y型：
ln 2
1
t 1 t dt
y
d
Y型：
y+dy
d
d
d
c x出 x入 dy c x出dy c x入 dy
y

2
2
2
t

2
t
dt
1 1 1
t

1
t
dt
c
L1
L2
x14
补充：极坐标
1．极坐标系
在平面内任取一定点 O，过 O点引射线Ox ，再规定一个长 度单位及角度的正方向（通常取逆时针方向），这样就确定了
以极点O为圆心，以 a为半径的的圆的极坐标方程: r a.
P(r, )
P(r, )
r
•
O
(a,0) x O• (a•,0)
x

P(r, )

3
•3
O
x
以点(a,0) 为圆心，以 a 为半径的的圆的极坐标方程 r 2a cos
过极点O，且与极轴的夹角为 的直线方程 .
面积A须经过以下四个步骤：
（1）分割: 把 a,b 分成n个小区间， 设第i个小曲边梯形的
面积为 Ai , 则：
n
A Ai i 1
（2）近似替代：
y
y f (x)
Ai f ( i )xi ( xi1 i xi );
n
（3）求和： A f ( i )xi
（1）U是与一个变量x的变化区间[a，b]有关的量； （2）U对于区间[a，b]具有可加性；
（3）部分量 Ui的近似值可表为 f i xi 那么这个量就
可以用积分来表示。 具体步骤是：
（1）确定积分变量，和它的变化区间[a,b]； （2）写出积分元素
U dU f xdx
（3）写出 U 的积分表达式，即：
在 [0,1]上任取小区间 x, x dx ， o x x dx 1 x
面积元素为 dA ( x x 2 )dx.
故所求面积为 A 1 0
x

x2
dx

2

3
3
x2

x3 3

1 0

1. 3
注：所求的面积可以看作是两个曲边梯形面积的差，即
A 1 xdx 1 x 2dx 1 .
15
r
• •
O
• P(r, )
•• x
• P(r, )
• •
O
•
•
x
•P(r, ) 对于给定的极坐标 (r, )，平面上有唯一的点与之对应；但 对于平面上的点 P(r, )，则 (r, 2n ), (r, (2n 1) ) (n Z ) 都可以作为它的极坐标。 因此，平面上的点与有序实数对 (r, )
右脑思维的核心是形象思维， 在大脑中多出现形象的东西，在 各项思维活动中，多借助形象， 就训练了右脑。