完整版2018初三数学中考复习直角三角形的性质专项复习练习题含答案
【中考专题】2018年九年级数学 中考专题复习--解直角三角形实际问题 培优练习卷(含答案)

2018年九年级数学中考专题复习--解直角三角形实际问题培优练习卷1.如图,在△ABC中,∠C=60°,AC=2,BC=3.求tanB的值.2.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)3.如图,在△ABC中,AD是BC上的高,tan B=cos ∠DAC.(1)求证;AC=BD;(2)若sin C=,BC=12,求AD的长.4.如图,长方形广告牌加载楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75,,1.732,结果精确到0.1m)5.某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.(1)求建筑物CD的高度;(2)求建筑物AB的高度.(参考数据:≈1.73,sin37°≈0.6,cos37°≈0.6,tan37°≈0.75)6.如图1,某同学家的一面窗户上安装有遮阳篷,图2和图3是截面示意图,CD是遮阳篷,窗户AB为1.5米,BC为0.5米.该遮阳篷有伸缩功能.如图2,该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为60°,遮阳篷CD正好将进入窗户AB的阳光挡住;如图3,该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为30°,将遮阳篷收缩成CD′时,遮阳篷正好完全不挡进入窗户AB的阳光.(1)计算图3中CD′的长度比图2中CD的长度收缩了多少米;(结果保留根号)(2)如果图3中遮阳篷的长度为图2中CD的长度,请计算该遮阳落在窗户AB上的阴影长度为多少米?(请在图3中画图并标出相应字母,然后再计算)7.如图,天星山山脚下西端A处与东端B处相距800(1+)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?8.如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.(1)求出此时点A到岛礁C的距离;(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)9.如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积。
天津市河西区2018届中考《三角形》专项强化练习(含答案)
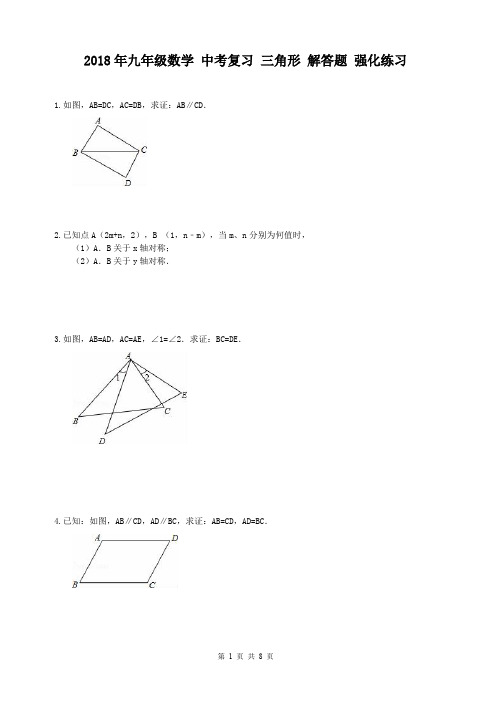
2018年九年级数学中考复习三角形解答题强化练习1.如图,AB=DC,AC=DB,求证:AB∥CD.2.已知点A(2m+n,2),B (1,n﹣m),当m、n分别为何值时,(1)A.B关于x轴对称;(2)A.B关于y轴对称.3.如图,AB=AD,AC=AE,∠1=∠2.求证:BC=DE.4.已知:如图,AB∥CD,AD∥BC,求证:AB=CD,AD=BC.5.如图,已知点B、E、C、F在同一条直线上,BE=CF,AB∥DE,∠A=∠D.求证:AB=DE.6.如图,已知△ABC,AB=AC,AD是△ABC角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,O,F.若∠CAD=20°,求∠OCD的度数.7.如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.求证:(1)AD=AG;(2)AD与AG的位置关系如何?并证明你的结论.8.如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,BN和CM有什么数量关系?请说明理由.9.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.求证:直线AD是线段CE的垂直平分线.10.如图:AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD。
求证:BE⊥AC。
11.如图、已知∠AOB=30°,OC平分∠AOB,P为OC上任意一点,PD∥OA交OB于D,PE⊥OA于E.如果OD=4cm,求PE的长.12.如图,△ABC中,AD是∠CAB的平分线,且AB=AC+CD,求证:∠C=2∠B13.如图,在等边三角形ABC中,点M是BC边上的任意一点(不与端点重合),连接AM,以AM为边作等边三角形AMN,连接CN.(1)求∠ACN的度数.(2)若点M在△ABC的边BC的延长线上,其他条件不变,则∠ACN的度数是否发生变化?(直接写出结论即可)14.如图,∠BAD=∠CAE=90o,AB=AD,AE=AC,AF⊥CF,垂足为F.(1)若AC=10,求四边形ABCD的面积;(2)求证:AC平分∠ECF;(3)求证:CE=2AF .15.在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,求∠BCE的度数;(2)设∠BAC=α,∠BCE=β.①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.参考答案1.证明:∵在△ABC和△DCB中,,∴△ABC≌△DCB(SSS).∴∠ABC=∠DCB(全等三角形的对应角相等).∴AB∥CD(内错角相等,两直线平行).2.解:(1)∵点A(2m+n,2),B (1,n﹣m),A.B关于x轴对称,∴,解得;(2)∵点A(2m+n,2),B (1,n﹣m),A.B关于y轴对称,∴,解得:.3.证明:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC.即:∠BAC=∠DAE.在△ABC与又△ADE中,,∴△ABC≌△ADE.∴BC=DE.4.解:如图,∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∴AB=CD,AD=BC.5.证明:∵BE=CF,∴BC=EF.∵AB∥DE,∴∠B=∠DEF.在△ABC与△DEF中,,∴△ABC≌△DEF(AAS),∴AB=DE.6.50°7. (1)证明:∵BE⊥AC∴∠AEB=90∴∠ABE+∠BAC=90∵CF⊥AB∴∠AFC=∠AFG=90∴∠ACF+∠BAC=90,∠G+∠BAG=90∴∠ABE=∠ACF∵BD=AC,CG=AB∴△ABD≌△GCA(SAS)∴AG=AD2、AG⊥AD证明:∵△ABD≌△GCA∴∠BAD=∠G∴∠GAD=∠BAD+∠BAG=∠G+∠BAG=90∴AG⊥AD8.证明:如图,连接PB,PC,∵AP是∠BAC的平分线,PN⊥AB,PM⊥AC,∴PM=PN,∠PMC=∠PNB=90°,∵P在BC的垂直平分线上,∴PC=PB,在Rt△PMC和Rt△PNB中,,∴Rt△PMC≌Rt△PNB(HL),∴BN=CM.9.证明:∵DE⊥AB,∴∠AED=90°=∠ACB,又∵AD平分∠BAC,∴∠DAE=∠DAC,∵AD=AD,∴△AED≌△ACD,∴AE=AC,∵AD平分∠BAC,∴AD⊥CE,即直线AD是线段CE的垂直平分线.10.证明:(1) AD为△ABC上的高,∴BDA=ADC =90.∵BF=AC,FD=CD.∴Rt△BDF≌Rt△ADC.(2)由①知∠C=∠BFD,∠CAD=∠DBF.∠BFD=∠AFE,又∠CBE=∠CAD,∴∠AEF=∠BDF.∠BDF= 90,∴BE⊥AC.11.解:过P作PF⊥OB于F,∵∠AOB=30°,OC平分∠AOB,∴∠AOC=∠BOC=15°,∵PD∥OA,∴∠DPO=∠AOP=15°,∴∠BOC=∠DPO,∴PD=OD=4cm,∵∠AOB=30°,PD∥OA,∴∠BDP=30°,∴在Rt△PDF中,PF=PD=2cm,∵OC为角平分线,PE⊥OA,PF⊥OB,∴PE=PF,∴PE=PF=2cm.12.证明:延长AC至E,使CE=CD,连接ED∵AB=AC+CD∴AE=AB∵AD平分∠CAB∴∠EAD=∠BAD∴AE=AB∠EAD=∠BAD AD=AD ∴△ADE≌△ADB∴∠E=∠B且∠ACD=∠E+∠CDE,CE=CD∴∠ACD=∠E+∠CDE=2∠E=2∠B即∠C=2∠B13.14.(1)解:∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=∠EAD+∠CAD∴∠BAC=∠EAD,在△ABC和△ADE中,∴△ABC≌△ADE(SAS),∵S四边形ABCD=S△ABC+S△ACD,(2)证明:∵△ACE是等腰直角三角形,∴∠ACE=∠AEC=45°,由△ABC≌△ADE得:∠ACB=∠AEC=45°,∴∠ACB=∠ACE,∴AC平分∠ECF;(3)证明:过点A作AG⊥CG,垂足为点G,∵AC平分∠ECF,AF⊥CB,∴AF=AG,又∵AC=AE,∴∠CAG=∠EAG=45°,∴∠CAG=∠EAG=∠ACE=∠AEC=45°,∴CG=AG=GE,∴CE=2AG,∴CE=2AF.15.。
中考数学真题分类汇编(第三期)专题28 解直角三角形试题(含解析)-人教版初中九年级全册数学试题

解直角三角形一.选择题1.(2018·某某市B卷)5.坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)()【分析】作BM⊥ED交ED的延长线于M,⊥DM于N.首先解直角三角形Rt△CDN,求出,DN,再根据tan24°=,构建方程即可解决问题;【解答】解:作BM⊥ED交ED的延长线于M,⊥DM于N.在Rt△CDN中,∵==,设=4k,DN=3k,∴CD=10,∴(3k)2+(4k)2=100,∴k=2,∴=8,DN=6,∵四边形BMNC是矩形,∴BM==8,BC=MN=20,EM=MN+DN+DE=66,在Rt△AEM中,tan24°=,∴0.45=,∴AB=21.7(米),故选:A.【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.2.(2018·某某某某·3分)如图,某地修建高速公路,要从A地向B地修一条隧道(点A.B在同一水平面上).为了测量A.B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A.B两地之间的距离为()A.800sinα米B.800tanα米C.米D.米【分析】在Rt△ABC中,∠CAB=90°,∠B=α,AC=800米,根据tanα=,即可解决问题;【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米,∴tanα=,∴AB==.故选:D.【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是熟练掌握基本知识,属于中考常考题型.3.(2018·某某某某·2分)某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是()A.B.C.D.【分析】如图,连接AD.只要证明∠AOB=∠ADO,可得sin∠AOB=sin∠ADO==;【解答】解:如图,连接AD.∵OD是直径,∴∠OAD=90°,∵∠AOB+∠AOD=90°,∠AOD+∠ADO=90°,∴∠AOB=∠ADO,∴sin∠AOB=sin∠ADO==,故选:D.【点评】本题考查圆周角定理、直径的性质、锐角三角函数等知识,解题的关键是学会用转化的思想思考问题,属于中考创新题目.二.填空题1. (2018·某某江汉·3分)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)n mile 处,则海岛A,C之间的距离为18n mile.【分析】作AD⊥BC于D,根据正弦的定义、正切的定义分别求出BD.CD,根据题意列式计算即可.【解答】解:作AD⊥BC于D,设AC=x海里,在Rt△ACD中,AD=AC×sin∠ACD=x,则CD=x,在Rt△ABD中,BD=x,则x+x=18(1+),解得,x=18,答:A,C之间的距离为18海里.故答案为:182. (2018·某某荆州·3分)荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为米(≈1.73,结果精确到0.1).【解答】解:如图,设CD为塔身的高,延长AB交CD于E,则CD=40,DE=7,∴CE=33,∵∠CBE=45°=∠BCE,∠CAE=30°,∴BE=CE=33,∴AE=a+33,∵tanA=,∴tan30°=,即33=a+33,解得a=33(﹣1)≈24.1,∴a的值约为24.1米,故答案为:24.1.3.(2018·某某省某某市) 如图,某景区的两个景点A.B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C 处时、测得景点A的俯角为45°,景点B的俯角为知30°,此时C到地面的距离CD为100米,则两景点A.B间的距离为100+100米(结果保留根号).【解答】解:∵∠MCA=45°,∠NCB=30°,∴∠ACD=45°,∠DCB=60°,∠B=30°.∵CD=100米,∴AD=CD=100米,D B=米,∴AB=AD+DB=100+100(米).故答案为:100+100.4. (2018·某某某某·3分)如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为_____m(结果保留整数,≈1.73).【答案】300【解析】【分析】在Rt△ABD中,根据正切函数求得BD=AD•tan∠BAD,在Rt△ACD中,求得CD=AD•tan∠CAD,再根据BC=BD+CD,代入数据计算即可.【详解】如图,∵在Rt△ABD中,AD=110,∠BAD=45°,∴BD= AD•tan45° =110(m),∵在Rt△ACD中,∠CAD=60°,∴CD=AD•tan60°=110×≈190(m),∴BC=BD+CD=110+190=300(m),即该建筑物的高度BC约为300米,故答案为:300.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,熟练应用锐角三角函数关系是解题关键.5.(2018·某某某某·3分)如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5m,则旗杆AB的高度约为m.(精确到0.1m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)解:过D作DE⊥AB,∵在D处测得旗杆顶端A的仰角为53°,∴∠ADE=53°.∵BC=DE=6m,∴AE=DE•tan53°≈6×1.33≈7.98m,∴AB=AE+BE=AE+CD=7.98+1.5=9.48m≈9.5m.故答案为:9.5.三.解答题1. (2018·某某贺州·8分)如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:≈1.41,≈1.73)【解答】解:过点C作CM⊥AB,垂足为M,在Rt△ACM中,∠MAC=90°﹣45°=45°,则∠MCA=45°,∴AM=MC,由勾股定理得:AM2+MC2=AC2=(20×2)2,解得:AM=CM=40,∵∠ECB=15°,∴∠BCF=90°﹣15°=75°,∴∠B=∠BCF﹣∠MAC=75°﹣45°=30°,在Rt△BCM中,tanB=tan30°=,即=,∴BM=40,∴AB=AM+BM=40+40≈40+40×1.73≈109(海里),答:A处与灯塔B相距109海里.2. (2018·某某某某·8分)随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测量人员在瀑布的对面山上D点处测得瀑布顶端A点的仰角是30°,测得瀑布底端B点的俯角是10°,AB与水平面垂直.又在瀑布下的水平面测得CG=27m,GF=17.6m(注:C.G、F三点在同一直线上,CF⊥AB于点F).斜坡CD=20m,坡角∠ECD=40°.求瀑布AB的高度.(参考数据:≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)【分析】过点D作DM⊥CE,交CE于点M,作DN⊥AB,交AB于点N,在Rt△CMD中,通过解直角三角形可求出CM的长度,进而可得出MF、DN的长度,再在Rt△BDN、Rt△ADN中,利用解直角三角形求出BN、AN的长度,结合AB=AN+BN即可求出瀑布AB的高度.【解答】解:过点D作DM⊥CE,交CE于点M,作DN⊥AB,交AB于点N,如图所示.在Rt△CMD中,CD=20m,∠DCM=40°,∠CMD=90°,∴CM=CD•cos40°≈15.4m,DM=CD•sin40°≈12.8m,∴DN=MF=CM+CG+GF=60m.在Rt△BDN中,∠BDN=10°,∠BND=90°,DN=60m,∴BN=DN•tan10°≈10.8m.在Rt△ADN中,∠ADN=30°,∠AND=90°,DN=60m,∴AN=DN•tan30°≈34.6m.∴AB=AN+BN=45.4m.答:瀑布AB的高度约为45.4米.【点评】本题考查了解直角三角形的应用中的仰角俯角问题及坡度坡角问题,通过解直角三角形求出AN、BN的长度是解题的关键.3. (2018·某某某某·7分)如图,一艘海轮位于灯塔C的北偏东45方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时船距灯塔的距离(参考数据:≈1.414,≈1.732,结果取整数).【分析】过C作CD垂直于AB,根据题意求出AD与BD的长,由AD+DB求出AB的长即可.【解答】解:过C作CD⊥AB,在Rt△ACD中,∠A=45°,∴△ACD为等腰直角三角形,∴AD=CD=AC=50海里,在Rt△BCD中,∠B=30°,∴BC=2CD=100海里,根据勾股定理得:BD=50海里,则AB=AD+BD=50+50≈193海里,则此时船锯灯塔的距离为193海里.【点评】此题考查了解直角三角形﹣方向角问题,熟练掌握各自的性质是解本题的关键.4.(2018·某某省某某·7分)小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,≈1.73)【分析】如图作AE⊥BD于E.分别求出BE.DE,可得BD的长,再根据CD=BD﹣BC计算即可;【解答】解:如图作AE⊥BD于E.在Rt△AEB中,∵∠EAB=30°,AB=10m,∴BE=AB=5(m),AE=5(m),在Rt△ADE中,DE=AE•tan42°=7.79(m),∴BD=DE+BE=12.79(m),∴CD=BD﹣BC=12.79﹣6.5≈6.3(m),答:标语牌CD的长为6.3m.【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助线面构造直角三角形解决问题.5.(2018·某某省某某·8分)图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,X角∠HAC 为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)【分析】作CE⊥BD于F,AF⊥CE于F,如图2,易得四边形AHEF为矩形,则EF=AH=3.4m,∠HAF=90°,再计算出∠CAF=28°,则在Rt△ACF中利用正弦可计算出CF,然后计算CF+EF 即可.【解答】解:作CE⊥BD于F,AF⊥CE于F,如图2,易得四边形AHEF为矩形,∴EF=AH=3.4m,∠HAF=90°,∴∠CAF=∠CAH﹣∠HAF=118°﹣90°=28°,在Rt△ACF中,∵sin∠CAF=,∴CF=9sin28°=9×0.47=4.23,∴CE=CF+EF=4.23+3.4≈7.6(m),答:操作平台C离地面的高度为7.6m.【点评】本题考查了解直角三角形的应用:先将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题),然后利用勾股定理和三角函数的定义进行几何计算.6.(2018·某某省某某市)两栋居民楼之间的距离CD=30米,楼AC和B D均为10层,每层楼高3米.(1)上午某时刻,太阳光线GB与水平面的夹角为30°,此刻B楼的影子落在A楼的第几层?(2)当太阳光线与水平面的夹角为多少度时,B楼的影子刚好落在A楼的底部.【解答】解:(1)延长BG,交AC于点F,过F作FH⊥BD于H,由图可知,FH=CD=30m.∵∠BFH=∠α=30°.在Rt△BFH中,BH=,,答:此刻B楼的影子落在A楼的第5层;(2)连接BC\1BD=3×10=30=CD,∴∠BCD=45°,答:当太阳光线与水平面的夹角为45度时,B楼的影子刚好落在A楼的底部.7.(2018·某某省某某市)(12.00分)如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A.B.C.D.M、N均在同一平面内,CM∥AN).(1)求灯杆CD的高度;(2)求AB的长度(结果精确到0.1米).(参考数据:=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)【分析】(1)延长DC交AN于H.只要证明BC=CD即可;(2)在Rt△BCH中,求出BH、CH,在Rt△ADH中求出AH即可解决问题;【解答】解:(1)延长DC交AN于H.∵∠DBH=60°,∠DHB=90°,∴∠BDH=30°,∵∠CBH=30°,∴∠CBD=∠BDC=30°,∴BC=CD=10(米).(2)在Rt△BCH中,CH=BC=5,BH=5≈8.65,∴DH=15,在Rt△ADH中,AH===20,∴AB=AH﹣BH=20﹣8.65=11.4(米).【点评】本题考查解直角三角形的应用﹣坡度坡角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.8. (2018•呼和浩特•8分)如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为33°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)解:作DH⊥BC于H.设AE=x.∵DH:BH=1:3,在Rt△BDH中,DH2+(3DH)2=6002,∴DH=60,BH=180,在Rt△ADE中,∵∠ADE=45°,∴DE=AE=x,∵又HC=ED,EC=DH,∴HC=x,EC=60,在Rt△ABC中,tan33°=,∴x=,∴AC=AE+EC=+60=.答:山顶A到地面BC的高度AC是米9. (2018•某某•8分)据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据:≈1.41,≈1.73)【分析】根据直角三角形的性质和三角函数得出DB,DA,进而解答即可.【解答】解:由题意得:∠DCA=60°,∠DCB=45°,在Rt△CDB中,tan∠DCB=,解得:DB=200,在Rt△CDA中,tan∠DCA=,解得:DA=200,∴AB=DA﹣DB=200﹣200≈146米,轿车速度,答:此车没有超过了该路段16m/s的限制速度.【点评】本题考查了解直角三角形的应用﹣方向角问题,解答本题的关键是利用三角函数求出AD与BD的长度,难度一般.10. (2018•莱芜•9分)在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C.E.D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)【分析】过点B作BF⊥AC于F,BG⊥CD于G,根据三角函数和直角三角形的性质解答即可.【解答】解:过点B作BF⊥AC于F,BG⊥CD于G,在Rt△BAF中,∠BAF=65°,BF=AB•sin∠×0.9=0.72,AF=AB•cos∠×0.4=0.32,∴FC=AF+AC=4.32,∵四边形FCGB是矩形,∴BG=FC=4.32,CG=BF=0.72,∵∠BDG=45°,∴∠BDG=∠GBD,∴GD=GB=4.32,∴CD=CG+GD=5.04,在Rt△ACE中,∠AEC=50°,CE=,∴≈1.7,答:小水池的宽DE为1.7米.【点评】此题考查的知识点是解直角三角形的应用﹣仰角俯角问题,关键是本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.11.(2018·某某某某·6分)如图,校园内有两幢高度相同的教学楼AB,CD,大楼的底部B,D在同一平面上,两幢楼之间的距离BD长为24米,小明在点E(B,E,D在一条直线上)处测得教学楼AB顶部的仰角为45°,然后沿EB方向前进8米到达点G处,测得教学楼CD 顶部的仰角为30°.已知小明的两个观测点F,H距离地面的高度均为1.6米,求教学楼AB 的高度AB长.(精确到0.1米)参考值:≈1.41,≈1.73.【解答】解:延长HF交CD于点N,延长FH交AB于点M,如右图所示,由题意可得,MB=HG=FE=ND=1.6m,HF=GE=8m,MF=BE,HN=GD,MN=BD=24m,设AM=xm,则=xm,在Rt△AFM中,MF=,在Rt△H中,HN=,∴HF=MF+HN﹣MN=x+x﹣24,即8=x+x﹣24,解得,x≈11.7,∴AB=11.7+1.6=13.3m,答:教学楼AB的高度AB长13.3m.12.(2018·某某某某·8分)京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A.B和点C.D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH 的长).【分析】过D作DE⊥AB,可得四边形CHED为矩形,由矩形的对边相等得到两对对边相等,分别在直角三角形ACH与直角三角形BDE中,设CH=DE=xm,利用锐角三角函数定义表示出AH与BE,由AH+HE+EB=AB列出方程,求出方程的解即可得到结果.【解答】解:过D作DE⊥AB,可得四边形CHED为矩形,∴HE=CD=40m,设CH=DE=xm,在Rt△BDE中,∠DBA=60°,∴BE=xm,在Rt△ACH中,∠BAC=30°,∴AH=xm,由AH+HE+EB=AB=160m,得到x+40+x=160,解得:x=30,即CH=30m,则该段运河的河宽为30m.【点评】此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.。
【中考刷题本】2018年九年级数学中考小题刷题本24--解直角三角形(含答案)

2018年九年级数学中考小题刷题本--解直角三角形一、选择题:1.的值等于().A.B.C.D.2.在△ABC中,∠C=90°,∠A=50°,BC=4,则AC为( )A.4tan50°B.4tan40°C.4sin50°D.4sin40°3.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=()A. B. C. D.4.在△ABC中,若cosA=,tanB=,则这个三角形一定是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形5.在Rt△ABC中,∠C=90°,sinB=,则tanA的值为( )A.B.C.D.6.如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )A.0.75 B.4/3 C.0.6 D.0.87.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中错误的是( )A.sinα=cosαB.tanC=2 C.sinβ=cosβD.tanα=18.数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为ɑ,已知sinɑ=0.6,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为()m.A.7.4 B.7.2 C.7 D.6.89.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底端G为BC的中点,则矮建筑物的高CD 为( )A.20米B.10 米C.15 米D.5 米10.若一个三角形三个内角度数的比为1:2:3,那么这个三角形最小角的正切值为()A.B.C.D.11.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是()A.B.4 C.8D.412.一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为()A.10海里/小时B.30海里/小时C.20海里/小时 D.30海里/小时二、填空题:13.若∠A为锐角,且tan2A+2tanA-3=0,则∠A=___________.14.如图,已知在△ABC中,∠C=90°,tanB=,AC=2.线段AB的长为.15.如图,在矩形ABCD中,AB=10,BC=8,E为AD边上的一点,沿CE将△CDE对折,点D正好落在AB边上,则tan∠AFE=________.16.如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为 cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).17.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)18.在△ABC 中,∠A .∠B 都是锐角,若sinA=23,cosB=21,则∠C=________. 19.如图,菱形ABCD 的边长为10cm,DE ⊥AB,sinA=,则这个菱形的面积= cm 2.20.如图,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为 .21.如图,在边长为1的正方形格点图中,B 、D 、E 为格点,则∠BAC 的正切值为 .22.如图,∠BAC 位于6×6的方格纸中,其中A ,B ,C 均为格点,则tan ∠BAC= .23.在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF ∥MN,小聪在河岸MN 上点A 处用测角仪测得河对岸小树C 位于东北方向,然后沿河岸走了30米,到达B 处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为米.(结果保留根号)24.如图,在边长相同的小正方形组成的网格中,点A.B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是.参考答案1.答案为:D2.答案为:C.3.答案为:D4.答案为:A5.答案为:C.6.答案为:D7.答案为:D8.答案为:C9.答案为:B10.答案为:A11.答案为:D12.答案为:D13.答案为:45°14.答案为:2.15.答案为:0.75.16.答案为:14.1.17.答案为:(5+5).18.答案为:60°.19.菱形的面积=DE•AB=6×10=60(cm2).20.答案为:.21.答案为:0.75.22.答案为:1.5.23.解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,∵∠CKA=90°,∠CAK=45°,∴∠CAK=∠ACK=45°,∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,∴HD=x﹣30+10=x﹣20,在RT△BHD中,∵∠BHD=30°,∠HBD=30°,∴tan30°=,∴=,解得x=30+10.∴河的宽度为(30+10)米.24.答案为:2.。
中考数学总复习《直角三角形》专项测试卷带答案

中考数学总复习《直角三角形》专项测试卷带答案学校:___________班级:___________姓名:___________考号:___________【A层·基础过关】1.如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF则∠1=( )A.30°B.45°C.60°D.75°2.如图,在数轴上,以原点O为圆心,OB的长为半径画弧,交数轴正半轴于点A,则点A对应的数是( )A.1.5B.1.4C.√2D.-√23.小华想用老师提供的三条线段首尾相连围成一个直角三角形,则他应该选择的三条线段长度是( )A.2,3,4B.3,4,5C.4,5,6D.5,6,74.一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A,B对应的刻度为1,7,则CD=( )A.3.5 cmB.3 cmC.4.5 cmD.6 cm5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则EF的长为( )A.9B.9√2C.3√2D.36.如图,在Rt△ABC中,∠A=90°,点D是AB上一点,且BD=CD=6,∠DBC=15°,则△BCD的面积为( )A.9B.12C.18D.67.如图,图中所有四边形都是正方形,三角形是直角三角形,若正方形A,B的面积分别为18,10,则正方形C的面积是.【B层·能力提升】8.在如图的方格中,△ABC的顶点A,B,C都是方格线的交点,则三角形ABC的外角∠ACD的度数等于( )A.130°B.140°C.135°D.145°9.如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB 交于点D,再分别以A,D为圆心,大于12AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为( )A.52B.3 C.2√2 D.10310.(2024·凯里模拟)如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC=2,∠AOB=30°,则OC的长为( )A.√5B.2√5C.4D.211.(2024·凯里模拟)如图,在平面直角坐标系中,点B的坐标为(0,2),点A在x轴负半轴上,AB=2√2,以点B为圆心,BA长为半径作弧,交x轴正半轴于点C,则点C的坐标为.12.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为km.【C层·素养挑战】13.如图,在四边形ABCD中,∠ABC=∠BAD=90°,AB=5,AD=4,AD<BC,点E在线段BC上运动,点F在线段AE上,∠ADF=∠BAE,求线段BF的最小值.参考答案【A层·基础过关】1.如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF则∠1=(C)A.30°B.45°C.60°D.75°2.如图,在数轴上,以原点O为圆心,OB的长为半径画弧,交数轴正半轴于点A,则点A对应的数是(C)A.1.5B.1.4C.√2D.-√23.小华想用老师提供的三条线段首尾相连围成一个直角三角形,则他应该选择的三条线段长度是(B)A.2,3,4B.3,4,5C.4,5,6D.5,6,74.一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A,B对应的刻度为1,7,则CD=(B)A.3.5 cmB.3 cmC.4.5 cmD.6 cm5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则EF的长为(C)A.9B.9√2C.3√2D.36.如图,在Rt△ABC中,∠A=90°,点D是AB上一点,且BD=CD=6,∠DBC=15°,则△BCD的面积为(A)A.9B.12C.18D.67.如图,图中所有四边形都是正方形,三角形是直角三角形,若正方形A,B的面积分别为18,10,则正方形C的面积是28.【B层·能力提升】8.在如图的方格中,△ABC的顶点A,B,C都是方格线的交点,则三角形ABC的外角∠ACD的度数等于(C)A.130°B.140°C.135°D.145°9.如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB 交于点D,再分别以A,D为圆心,大于12AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为(A)A.52B.3 C.2√2 D.10310.(2024·凯里模拟)如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC=2,∠AOB=30°,则OC的长为(B)A.√5B.2√5C.4D.211.(2024·凯里模拟)如图,在平面直角坐标系中,点B的坐标为(0,2),点A在x轴负半轴上,AB=2√2,以点B为圆心,BA长为半径作弧,交x轴正半轴于点C,则点C的坐标为(2,0).12.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为50km.【C层·素养挑战】13.如图,在四边形ABCD中,∠ABC=∠BAD=90°,AB=5,AD=4,AD<BC,点E在线段BC上运动,点F在线段AE上,∠ADF=∠BAE,求线段BF的最小值.【解析】设AD的中点为O,以AD为直径画圆,连接OB交☉O于F'∵∠ABC=∠BAD=90°∴AD∥BC∴∠DAE=∠AEB∵∠ADF=∠BAE∴∠DFA=∠ABE=90°∴点F在以AD为直径的半圆上运动,当点F运动到OB与☉O的交点F'时,线段BF有最小值∵AD=4AD=2∴AO=OF'=12∴BO=√52+22=√29∴线段BF的最小值为√29-2.。
2018年中考数学真题分类汇编(第一期)专题23 直角三角形与勾股定理试题(含解析)

直角三角形与勾股定理一、选择题1.(2018•山西•3分)“算经十书”是指汉唐一千多年间的十部著名数学著作,它们曾经是隋唐时期国子监算学科的教科书,这些流传下来的古算书中凝聚着历代数学家的劳动成果.下列四部著作中,不属于我国古代数学著作的是()A.《九章算术》B. 《几何原本》C. 《海岛算经》D. 《周髀算经》【答案】B【考点】数学文化【解析】《几何原本》的作者是欧几里得2.(2018•山东滨州•3分)在直角三角形中,若勾为3,股为4,则弦为()A.5 B.6 C.7 D.8【分析】直接根据勾股定理求解即可.【解答】解:∵在直角三角形中,勾为3,股为4,∴弦为=5.故选:A.【点评】本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.3. (2018·湖北省孝感·3分)如图,菱形ABCD的对角线AC,BD相交于点O,AC=10,BD=24,则菱形ABCD的周长为()A.52 B.48 C.40 D.20【分析】由勾股定理即可求得AB的长,继而求得菱形ABCD的周长.【解答】解:∵菱形ABCD中,BD=24,AC=10,∴OB=12,OA=5,在Rt△ABO中,AB==13,∴菱形ABCD的周长=4AB=52,故选:A.【点评】此题考查了菱形的性质、勾股定理等知识,解题的关键是熟练掌握菱形的性质,属于中考常考题型.4. (2018·山东青岛·3分)如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点.沿过点E的直线折叠,使点B与点A重合,折痕现交于点F.已知EF=,则BC的长是()A.B.C.3 D.【分析】由折叠的性质可知∠B=∠EAF=45°,所以可求出∠AFB=90°,再直角三角形的性质可知EF=AB,所以AB=AC的长可求,再利用勾股定理即可求出BC的长.【解答】解:∵沿过点E的直线折叠,使点B与点A重合,∴∠B=∠EAF=45°,∴∠AFB=90°,∵点E为AB中点,∴EF=AB,EF=,∴AB=AC=3,∵∠BAC=90°,∴BC==3,故选:B.【点评】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用,求出∠AFB=90°是解题的关键.5. (2018·四川自贡·4分)如图,若△ABC内接于半径为R的⊙O,且∠A=60°,连接OB、OC,则边BC的长为()A.B.C.D.【分析】延长BO交圆于D,连接CD,则∠BCD=90°,∠D=∠A=60°;又BD=2R,根据锐角三角函数的定义得BC=R.【解答】解:延长BO交⊙O于D,连接CD,则∠BCD=90°,∠D=∠A=60°,∴∠CBD=30°,∵BD=2R,∴DC=R,∴BC=R,故选:D.【点评】此题综合运用了圆周角定理、直角三角形30°角的性质、勾股定理,注意:作直径构造直角三角形是解决本题的关键.6. (2018·台湾·分)如图1的矩形ABCD中,有一点E在AD上,今以BE为折线将A点往右折,如图2所示,再作过A点且与CD垂直的直线,交CD于F点,如图3所示,若AB=6,BC=13,∠BEA=60°,则图3中AF的长度为何?()A.2 B.4 C.2 D.4【分析】作AH⊥BC于H.则四边形AFCH是矩形,AF=CH,AH=CF=3.在Rt△ABH中,解直角三角形即可解决问题;【解答】解:作AH⊥BC于H.则四边形AFCH是矩形,AF=CH,AH=CF=3.在Rt△AHB中,∠ABH=30°,∴BH=AB•cos30°=9,∴CH=BC﹣BH=13﹣9=4,∴AF=CH=4,故选:B.【点评】本题考查翻折变换、矩形的性质、勾股定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.7. (2018·台湾·分)如图,坐标平面上,A、B两点分别为圆P与x轴、y轴的交点,有一直线L通过P点且与AB垂直,C点为L与y轴的交点.若A、B、C的坐标分别为(a,0),(0,4),(0,﹣5),其中a<0,则a的值为何?()A.﹣2B.﹣2C.﹣8 D.﹣7【分析】连接AC,根据线段垂直平分线的性质得到AC=BC,根据勾股定理求出OA,得到答案.【解答】解:连接AC,由题意得,BC=OB+OC=9,∵直线L通过P点且与AB垂直,∴直线L是线段AB的垂直平分线,∴AC=BC=9,在Rt△AOC中,AO==2,∵a<0,∴a=﹣2,故选:A.【点评】本题考查的是垂径定理、坐标与图形的性质以及勾股定理,掌握垂径定理的推论是解题的关键.8.(2018•湖北黄冈•3分)如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB 边上的中线,AD=2,CE=5,则CD=A.2B.3C.4D.23(第5题图)【考点】直角三角形斜边上的中线的性质,勾股定理。
中考数学专题复习导学案直角三角形(含答案)

中考数学专题练习19《直角三角形》【知识归纳】1.直角三角形的定义有一个角是的三角形叫做直角三角形2.直角三角形的性质(1)直角三角形的两个锐角;(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的;(3)在直角三角形中,斜边上的中线等于斜边的3.直角三角形的判定(1)两个内角的三角形是直角三角形;(2)一边上的中线等于这条边的的三角形是直角三角形4.勾股定理及逆定理勾股定理:如果直角三角形两条直角边分别为a,b,斜边为c,那么逆定理:如果三角形三边长a,b,c满足a2+b2=c2,那么这个三角形是三角形【基础检测】1.(·广西百色·3分)如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=()A.6 B.6 C.6 D.122.(·贵州安顺·3分)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2 B. C. D.3.(广西南宁3分)如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是()A.5sin36°米 B.5cos36°米 C.5tan36°米 D.10tan36°米4.(海南3分)如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C 落在点E的位置.如果BC=6,那么线段BE的长度为()A.6 B.6C.2D.35.(·四川南充)如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC 的中点,则DE的长为()A.1 B.2 C.D.1+6. (·浙江省湖州市·4分)如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是.7. (·湖北随州·3分)如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=BD,连接DM、DN、MN.若AB=6,则DN= .8.(·湖北荆州·10分)如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.(1)求证:CD是半圆O的切线;(2)若DH=6﹣3,求EF和半径OA的长.【达标检测】一.选择题1.(•毕节市)(第5题)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是()A.,, B. 1,, C. 6,7,8 D. 2,3,42.(•青岛,第4题3分)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=()A. B. 2 C.3 D. +23. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有()A.2个 B.3个 C.4个 D.5个4.如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是A.5 B.10 C.12 D.135.(·湖北荆门·3分)如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为()A.5 B.6 C.8 D.106. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )A.120° B.90° C.60° D.30°7. 已知等腰三角形ABC中,腰AB=8,底BC=5,则这个三角形的周长为( )(第11题图)A. 21B. 20C. 19D. 188.(·四川宜宾)如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为()A. B.2 C.3 D.29.(·湖北荆州·3分)如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是()A.2 B. C. D.二.填空题10.(湖北省鄂州市,15,3分)著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为10 cm.11.(·四川宜宾)在平面直角坐标系内,以点P(1,1)为圆心、为半径作圆,则该圆与y轴的交点坐标是.12.(·四川内江)如图4,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=______.13. (·湖北武汉)如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA =55,则BD的长为_______.14. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果精确到0.1米,=1.73).15. (·江西·3分)如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是.DO CEBA图4三.解答题16.(江西,23,10分)某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:●操作发现:在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是(填序号即可)①AF=AG=AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.●数学思考:在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧..作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD和ME具有怎样的数量和位置关系?请给出证明过程;●类比探索:在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,试判断△MED的形状.答:.17.(·湖北咸宁)定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC=,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.【知识归纳答案】1.直角三角形的定义有一个角是 90°的三角形叫做直角三角形2.直角三角形的性质(1)直角三角形的两个锐角互余;(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;(3)在直角三角形中,斜边上的中线等于斜边的一半3.直角三角形的判定(1)两个内角和为90°的三角形是直角三角形;(2)一边上的中线等于这条边的一半的三角形是直角三角形4.勾股定理及逆定理勾股定理:如果直角三角形两条直角边分别为a,b,斜边为c,那么a2+b2=c2逆定理:如果三角形三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形【基础检测答案】1.(·广西百色·3分)如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=()A.6 B.6C.6D.12【考点】含30度角的直角三角形.【分析】根据30°所对的直角边等于斜边的一半求解.【解答】解:∵∠C=90°,∠A=30°,AB=12,∴BC=12sin30°=12×=6,故答选A.2.(·贵州安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2B. C. D.【分析】根据勾股定理,可得AC、AB的长,根据正切函数的定义,可得答案.【解答】解:如图:,由勾股定理,得AC=,AB=2,BC=,∴△ABC为直角三角形,∴tan∠B==,故选:D.【点评】本题考查了锐角三角函数的定义,先求出AC、AB的长,再求正切函数.3.(广西南宁3分)如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是()A.5sin36°米 B.5cos36°米 C.5tan36°米 D.10tan36°米【考点】解直角三角形的应用.【分析】根据等腰三角形的性质得到DC=BD=5米,在Rt△ABD中,利用∠B的正切进行计算即可得到AD的长度.【解答】解:∵AB=AC,AD⊥BC,BC=10米,∴DC=BD=5米,在Rt△ADC中,∠B=36°,∴tan36°=,即AD=BD•tan36°=5tan36°(米).故选:C.【点评】本题考查了解直角三角形的应用.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.4.(海南3分)如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C 落在点E的位置.如果BC=6,那么线段BE的长度为()A.6 B.6C.2D.3【考点】翻折变换(折叠问题).【分析】根据折叠的性质判定△EDB是等腰直角三角形,然后再求BE.【解答】解:根据折叠的性质知,CD=ED,∠CDA=∠ADE=45°,∴∠CDE=∠BDE=90°,∵BD=CD,BC=6,∴BD=ED=3,即△EDB是等腰直角三角形,∴BE=BD=×3=3,故选D.【点评】本题考查了翻折变换,还考查的知识点有两个:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、等腰直角三角形的性质求解.5.(四川南充)如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为()A.1 B.2 C.D.1+【分析】由“30度角所对的直角边等于斜边的一半”求得AB=2BC=2.然后根据三角形中位线定理求得DE=AB.【解答】解:如图,∵在Rt△ABC中,∠C=90°,∠A=30°,∴AB=2BC=2.又∵点D、E分别是AC、BC的中点,∴DE是△ACB的中位线,∴DE=0.5 AB=1.故选:A.【点评】此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.6. (浙江省湖州市·4分)如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是 5 .【考点】作图—基本作图;直角三角形斜边上的中线;勾股定理.【分析】首先说明AD=DB,利用直角三角形斜边中线等于斜边一半,即可解决问题.【解答】解:由题意EF是线段AB的垂直平分线,∴AD=DB,Rt△ABC中,∵∠ACB=90°,BC=6,AC=8,∴AB===10,∵AD=DB,∠ACB=90°,∴CD=AB=5.故答案为5.7. (湖北随州·3分)如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=BD,连接DM、DN、MN.若AB=6,则DN= 3 .【考点】三角形中位线定理;直角三角形斜边上的中线;平行四边形的判定与性质.【分析】连接CM,根据三角形中位线定理得到NM=CB,MN∥BC,证明四边形DCMN是平行四边形,得到DN=CM,根据直角三角形的性质得到CM=AB=3,等量代换即可.【解答】解:连接CM,∵M、N分别是AB、AC的中点,∴NM=CB,MN∥BC,又CD=BD,∴MN=CD,又MN∥BC,∴四边形DCMN是平行四边形,∴DN=CM,∵∠ACB=90°,M是AB的中点,∴CM=AB=3,∴DN=3,故答案为:3.8.(湖北荆州·10分)如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.(1)求证:CD是半圆O的切线;(2)若DH=6﹣3,求EF和半径OA的长.【分析】(1)连接OB,根据已知条件得到△AOB是等边三角形,得到∠AO B=60°,根据圆周角定理得到∠AOF=∠BOF=30°,根据平行线的性质得到OC⊥CD,由切线的判定定理即可得到结论;(2)根据平行线的性质得到∠DBC=∠EAO=60°,解直角三角形得到BD=BC=AB,推出AE= AD,根据相似三角形的性质得到,求得EF=2﹣,根据直角三角形的性质即可得到结论.【解答】解:(1)连接OB,∵OA=OB=OC,∵四边形OABC是平行四边形,∴AB=OC,∴△AOB是等边三角形,∴∠AOB=60°,∵∠FAD=15°,∴∠BOF=30°,∴∠AOF=∠BOF=30°,∴OF⊥AB,∵CD∥OF,∴CD⊥AD,∵AD∥OC,∴OC⊥CD,∴CD是半圆O的切线;(2)∵BC∥OA,∴∠DBC=∠EAO=60°,∴BD=BC=AB,∴AE=AD,∵EF∥DH,∴△AEF∽△ADH,∴,∵DH=6﹣3,∴EF=2﹣,∵OF=OA,∴OE=OA﹣(2﹣),∵∠AOE=30°,∴==,解得:OA=2.【点评】本题考查了切线的判定,平行四边形的性质,直角三角形的性质,等边三角形的判定和性质,连接OB构造等边三角形是解题的关键.【达标检测答案】一.选择题1.(•毕节市)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是() A.,, B. 1,, C. 6,7,8 D. 2,3,4【解析】勾股定理的逆定理..知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.【解答】解:A、()2+()2≠()2,不能构成直角三角形,故错误;B、12+()2=()2,能构成直角三角形,故正确;C、62+72≠82,不能构成直角三角形,故错误;D、22+32≠42,不能构成直角三角形,故错误.故选:B.【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.2.(•青岛)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=()A. B. 2 C.3 D. +2【解析】含30度角的直角三角形.根据角平分线的性质即可求得CD的长,然后在直角△BDE 中,根据30°的锐角所对的直角边等于斜边的一半,即可求得BD长,则BC即可求得.故选C .【点评】本题考查了角的平分线的性质以及直角三角形的性质,30°的锐角所对的直角边等于斜边的一半,理解性质定理是关键.3. 如图,在△ABC 中,∠A=36°,AB=AC ,BD 是△ABC 的角平分线,若在边AB 上截取BE=BC ,连接DE,则图中等腰三角形共有( )A .2个B .3个C .4个D .5个 【答案】D【解析】在△ABC 中,∠A=36°,AB=AC ,求得∠ABC=∠C=72°,且△ABC 是等腰三角形. 因为BD 是△ABC 的角平分线 所以∠ABD=∠DBC=36° 所以△ABD 是等腰三角形. 在△BDC 中有三角形的内角和求出∠BDC=72° 所以△BDC 是等腰三角形.所以BD=BC=BE 所以△BDE 是等腰三角形.所以∠BDE=72°, 所以∠ADE=36°, 所以△ADE 是等腰三角形.共5个. 故选D .4.如图,在△ABC 中,∠C=90°,AB 的垂直平分线交AB 于D ,交BC 于E ,连接AE ,若CE=5,AC=12,则BE 的长是 A .5B .10C .12D .13【解答】解:∵AD 是△ABC 的角平分线,DE ⊥AB ,∠C=90°, ∴CD=DE=1,又∵直角△BDE 中,∠B=30°, ∴BD=2DE=2, ∴BC=CD+BD=1+2=3.【答案】D.【解析】在Rt△CAE中,CE=5,AC=12,由勾股定理得:2213AE AC CE=+=又DE是AB的垂直平分线,∴BE=AE=13.故选D.5.(湖北荆门·3分)如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为()A.5 B.6 C.8 D.10【考点】勾股定理;等腰三角形的性质.【分析】根据等腰三角形的性质得到AD⊥BC,BD=CD,根据勾股定理即可得到结论.【解答】解:∵AB=AC,AD是∠BAC的平分线,∴AD⊥BC,BD=CD,∵AB=5,AD=3,∴BD==4,∴BC=2BD=8,故选C.6. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )A.120° B.90° C.60° D.30°【答案】D.【解析】根据直角三角形两锐角互余列式计算即可得解:(第11题图)∵直角三角形中,一个锐角等于60°,∴另一个锐角的度数=90°﹣60°=30°.故选D.7. 已知等腰三角形ABC中,腰AB=8,底BC=5,则这个三角形的周长为( )A. 21B. 20C. 19D. 18【答案】A.【解析】由于等腰三角形的两腰相等,题目给出了腰和底,根据周长的定义即可求解:∵8+8+5=21.∴这个三角形的周长为21.故选A.8.(四川宜宾)如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为()A. B.2C.3 D.2【考点】旋转的性质.【分析】通过勾股定理计算出AB长度,利用旋转性质求出各对应线段长度,利用勾股定理求出B、D两点间的距离.【解答】解:∵在△ABC中,∠C=90°,AC=4,BC=3,∴AB=5,∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,∴AE=4,DE=3,∴BE=1,在Rt△BED中,BD==.故选:A.9.(湖北荆州·3分)如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC 的顶点都在格点上,则图中∠ABC的余弦值是()A.2 B. C. D.【分析】先根据勾股定理的逆定理判断出△ABC的形状,再由锐角三角函数的定义即可得出结论.【解答】解:∵由图可知,AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,∴△ABC是直角三角形,且∠ACB=90°,∴cos∠ABC==.故选D.【点评】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.二.填空题10.(湖北省鄂州市,15,3分)著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为10 cm.【解析】直角三角形斜边上的中线.【解答】连接OP,根据直角三角形斜边上的中线等于斜边的一半可得OP的长,画出的圆的半径就是OP长.【点评】解:连接OP,∵△AOB是直角三角形,P为斜边AB的中点,∴OP=AB,∵AB=20cm,∴OP=10cm,故答案为:10.11.(四川宜宾)在平面直角坐标系内,以点P(1,1)为圆心、为半径作圆,则该圆与y轴的交点坐标是(0,3),(0,﹣1).【考点】坐标与图形性质.【分析】在平面直角坐标系中,根据勾股定理先求出直角三角形的另外一个直角边,再根据点P的坐标即可得出答案.【解答】解:以(1,1)为圆心,为半径画圆,与y轴相交,构成直角三角形,用勾股定理计算得另一直角边的长为2,则与y轴交点坐标为(0,3)或(0,﹣1).故答案为:(0,3),(0,﹣1).12.(四川内江)如图4,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE ⊥BC,垂足为点E,则OE=______.[答案]12 5[考点]菱形的性质,勾股定理,三角形面积公式。
2018年中考数学专题复习卷 三角形(含解析)

三角形一、选择题1.在直角三角形中,若勾为3,股为4,则弦为()A. 5B. 6C. 7D. 8【答案】A【解析】:∵在直角三角形中,勾为3,股为4,∴弦为故答案为:A.【分析】根据在直角三角形中,勾是最短的直角边,股是长的直角边,弦是斜边,知道勾和股利用勾股定理,即可得出答案。
2.在▱ABCD中,对角线AC,BD相交于点O,AC=8,BD=10,那么BC的取值范围是()A.8<BC<10B.2<BC<18C.1<BC<8D.1<BC<9【答案】D【解析】:如图∵▱ABCD,AC=8,BD=10,∴OB=BD=5,OC=AC=4∴5-4<BC<5+4,即1<BC<9故答案为:D【分析】根据平行四边形的性质求出OB、OC的长,再根据三角形三边关系定理,建立不等式组,求解即可。
3.如图所示,∠A=50°,∠B=20°,∠D=30°,则∠BCD的度数为()A. 80°B. 100°C. 120°D. 140°【答案】B【解析】如图,延长BC交AD于点E,∵∠BCD=∠D+∠DEC,∠DEC=∠A+∠B,∴∠BCD=∠A+∠B+∠D,∵∠A=50°,∠B=20°,∠D=30°,∴∠BCD=50°+20°+30°=100°,故答案为:B.【分析】延长BC交AD于点E,根据三角形的一个外角等于和它不相邻的两个内角的和可得∠BCD=∠D+∠DEC,∠DEC=∠A+∠B,所以∠BCD=∠A+∠B+∠D,由已知可得∠BCD=50°+20°+30°=100°。
4.如图,BE∥AF,点D是AB上一点,且DC⊥BE于点C,若∠A=35°,则∠ADC的度数()A. 105°B. 115°C. 125°D. 135°【答案】C【解析】:∵BE∥AF,∴∠B=∠A=35°.∵DC⊥BE,∴∠DCB=90°,∴∠ADC=90°+35°=125°.故答案为:C.【分析】由平行线的性质可得∠B=∠A=35°,根据三角形的一个外角等于和它不相邻的两个内角的和可得∠ADC=90°+35°=125°。
2018届中考全程演练《第24课时:直角三角形和勾股定理》含答案.doc

第24课时直角三角形和勾股定理屈练出高分(60 分)、选择题(每题5分,共25分)C = 90° AC= 9, BC= 12,则点C到AB的距离是(A)A36A-36【解析】在Rt^ABC中,AC= 9,BC= 12,根据勾股定理得AB= AC2 + BC21 1=15,过C作CD 丄AB,交AB 于点 D , 又&ABC=2AC• BC=• CD,••• CD二ACBC =普51冬36,则点C到AB的距离是36.故选A.3. [2017 •甘孜]如图24-2,点D在厶ABC的边AC上,将△ ABC沿BD翻折后,点A恰好与点C重合.若BC = 5, CD = 3,则BD的长为(D)1. [2016 •节]下列各组数据中的三个数作为三角形的边长,是A. 3, .4, 5C. 6, 7, 82.如图24- 1,在Rt其中能构成直角三角形的(B)B.D.1,2,2, 33, 4ABC中,c 12B-25D.3.34B. 2C. 3D. 44.将一个有45°角的三角板的直角顶点放在一张宽为3cm 的矩形纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一 边与纸带的一边所在的直线成30。
角,如图24- 3,则三角板最长边的长为(D)A . 3 cm C . 3 2 cm【解析】 如答图,过点C 作CD 丄AD 于点D , ••• CD = 3.在直角三角形 ADC 中,v/ CAD = 30°,•i AC = 2CD = 2 X 3= 6.又•••三角板是有45°角的三角板, 二 AB = AC = 6,••• BC 2= AB 2 + AC 2= g + 62 = 72, ••• BC = 6 .2,故选 D.5. 直角三角形纸片的两直角边长分别为 6, 8,现将△ ABC 如图24-4那样折叠,使点A 与点B 重合,折痕为DE ,贝Utan / CBE 的值是 B 近B 37 C.242 1 (8 - x)2=x【解析】:2+ &,解得 x = 7, B . 6 cm D. 6 2 cm(C)24 A.24tan / CBE =CE_4_Z BC= 6_ 24.二、填空题(每题5分,共25分)6. [2016 内江]在厶ABC中,/ B_30° AB_ 12,AC_6,则BC_ ^3 .7.[2017凉山]已知直角三角形两边的长分别是3和4,则第三边的长为5 或[78. 将一副三角尺按图24- 5所示叠放在一起,若AB_14 cm,贝U阴影部分的面积是—^—Cm2【解析】•••/ B_30°,1--AC_gAB_7 cm,易证AC_ CF,1 12 1 2 49 2•••S AACF_2AC • CF_2AC _2X7 _"^(cm ).9. [2017 •无锡]如图24-6, △ ABC中,CD 丄AB于D , E是AC的中点,若AD_ 6, DE_ 5,则CD 的长等于8 .【解析】TA ABC中,CD丄AB于D , E是AC的中点,DE _ 5,• DE _ 2AC_ 5,• AC_ 10.在直角△ ACD中,/ ADC_90°, AD_6, AC_ 10,则根据勾股定理,得CD _ ,AC2- AD2_ 102-62_ 8.10. [2016 •图24 - 6遵义]我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图24-7①).图24-7②由弦图变化得至叽它是由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1, S2, S B.若正方形EFGH的边长为2,则S+S3__工一.•••在Rt A CBD 中,CD = 5 cm, [来源:Z。
(完整版)2018初三数学中考复习直角三角形的性质专项复习练习题含答案

(完整版)2018初三数学中考复习直角三角形的性质专项复习练习题含答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN2018 初三数学中考复习直角三角形的性质专项复习练习题1. 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M、C两点间的距离为( )A.0.5km B.0.6km C.0.9km D.1.2km2.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=6,BC=15,则△EFM的周长是( )A.21 B.18 C.15 D.133.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )A.3.5 B.4.2 C.5.8 D.74.在等腰直角三角形ABC中,∠C=90°,点D为BC上一点,且∠BAD=15°,AD=8,则CD等于( )A.4 B.3 C.2 D.55. 如图所示,在△ABC中,BD、CE是高,G、F分别是BD、DE的中点,则下列结论中错误的是( )A.GE=GD B.GF⊥DE C.GF平分∠DGE D.∠DGE=60°6. 如图,在Rt△ABC中,∠BAC=90°,D、E分别为BC、AB的中点,且AC=6cm,AB=8cm,则△ADE的周长为( )A.10cm B.12cm C.14cm D.16cm7.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( )A.2cm B.4cm C.8cm D.16cm8. 如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC,若DE=10,AE=16,则BE的长度为( )A.10 B.11 C.12 D.139. △ABC中,∠ACB=90°,AB=10,AC=6,CD⊥AB于D,则CD=______.10. △ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为________.11. 在Rt△ABC中,∠C=90°,∠A=30°,AB=12cm,则BC=_____cm.12. 已知直角三角形的两边为3cm和4cm,则它们的第三边长为__________cm.13. 如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为______.14. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是_____.15.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD =12,则四边形ABOM的周长为______.16. 如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.求证:DE=EF.17. 如图,在Rt△ABC中,∠C=90°,∠B=30°,∠ADC=60°,BD=10.求CD的长.18. 如图,已知:△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE,G是垂足.求证:(1)G是CE的中点;(2)∠B=2∠BCE.参考答案:1---8 DBDBD BCC9. 4.810. 6.5cm11. 斜边的一半12. 5或713. 214. 215. 2016. 证明:∵在△ABC中,∠ACB=90°,点D为边AB的中点,∴DC=DA,∵DE∥BC,∴AE=CE,∴∠A=∠FCE,又∵∠AED=∠CEF,∴△AED≌△CEF,∴DE=EF.17. 解:∵∠B=30°,∠ADC=60°,∴∠BAD=∠ADC-∠B=30°,∴AD=BD=10,∵∠C=90°,∠DAC=60°-30°=30°,∴CD=12AD=5.18. 证明:(1)连接DE,∵AD⊥BC,E是AB的中点,∴DE是Rt△ABD斜边上的中线,即DE=BE=12AB,∴DC=DE=BE,又∵DG=DG,∴Rt△EDG≌Rt△CDG,∴GE=CG,∴G是CE的中点;(2)由(1)知:BE=DE=CD,∴∠B=∠BDE,∠DEC=∠DCE,∴∠B=∠BDE=2∠BCE.。
2018年全国中考数学真题分类 解直角三角形及其应用解析版(精品文档)

2018年全国中考数学真题分类 解直角三角形及其应用(三)一、选择题1. (2018吉林省长春市,6,3) 如图,某地修建高速公路,要从A 地向B 地修一条隧道(点A 、B 在同一水平面上).为了测量A 、B 两地之间的距离,一架直升飞机从A 地出发,垂直上升800米到达C 处,在C 处观察B 地的俯角为α,则A 、B 两地之间的距离为 (A )800sin α米 (B )800tan α米 (C )800sin α米 (D )800tan α米【答案】D【解析】由题中条件可知,在RT △ABC 中,∠ABC=α,AC=800米,建立数学模型tan α=ACAB,可得AB=800tan α米. 【知识点】解直角三角形,锐角三角函数,俯角问题.2. (2018江苏苏州,8,3分)如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A 处时,测得岛屿P 恰好在其正北方向,继续向东航行1小时到达B 处,测得岛屿P 在其北偏两30°方向,保持航向不变又航行2小时到达C 处,此时海监船与岛屿P 之问的距离(即PC 的长)为 A .40海里B .60海里C .D .αACB【答案】D【解析】 本题解答时要利用直角三角形的边角关键和勾股定理来进行计算.由题意可知AB =20,∠APB =30゜,∴PA,∵BC =2⨯20=40,∴AC =60,∴PC,故选D .二、填空题1. (2018湖北省江汉油田潜江天门仙桃市,15,3分)我国海域辽阔,渔业资源丰富.如图,现有渔船B 在海岛A ,C 附近捕鱼作业,已知海岛C 位于海岛A 的北偏东45°方向上.在渔船B 上测得海岛A 位于渔船B 的北偏西30°的方向上,此时海岛C 恰好位于渔船B的正北方向18(1n mile 处,则海岛A ,C 之间的距离为 n mile .【答案】218【解析】本题主要考察三角函数的应用.过A 作AD ⊥BC 于D .设x AD =,∵∠C 45°,∠B 30°,∴x xC AD CD ===︒45tan tan ,x xC AD AC 245sin sin ===︒,x xB AD BD 330tan tan ===︒.∵BD CD BC +=+=)31(18,∴x x 3)31(18+=+,解得18=x .∴218=AC . 【知识点】三角函数的应用==2. (湖北省咸宁市,13,3)如图,航拍无人机从A 处测得一幢建筑物顶部的仰角为45 °,测得底部C 的俯角为60°,此时航拍无人机与该建筑物的水平距离AD 为110m ,那么该建筑物的高度BC 约为_________m.(1.73≈)【答案】300【解析】在Rt △ABD 中,∠BAD =45°,∴BD =AD =110 m ,在Rt △ACD 中,∠CAD =60°,AD =110 m∴CD=AD tan 60⋅︒=BC =BD +CD=110+300 m 【知识点】解直角三角形的应用3. (2018辽宁葫芦岛,15,3分) 如图,某景区的两个景点A 、B 处于同一水平地面上,一架无人机在空中沿水平方向飞行进行航拍作业,M N 与A B 在同一铅直平面内,当无人机飞行至C 处时,测得景点A 的俯角为45°,景点B 为的俯角为30°,此时C 到地面的距离C D 为100米,则两景点A 、B 间的距离为__________米(结果保留根号).【答案】:100+100,【解析】∵MN ∥AB ,∴∠A =∠MCA =45°,∠B =∠NCB =30°. ∵CD =100,∴AD =tan 45CD ︒=100,DB =tan30CD︒. ∴AB =AD +DB =100+DC AB4. (2018广西南宁,16,3)如图,从甲楼底部A 处测得乙楼顶部C 处的仰角是30°,从甲楼顶部B 处测得乙楼底部D 处的俯角是45°.已知甲楼的高AB 是120m ,则乙楼的高CD 是m .(结果保留根号)【答案】403,【解析】∵俯角是45°,∴∠BDA =45°,∴AB =AD =120m ,又∵∠CAD =30°∴在Rt △ADC 中,tan ∠CDA =tan30°=CD AD =33. ∴CD = 403.5. (2018湖北黄石,14,3分)如图,无人机在空中C 处测得地面A 、B 两点的俯角分别为60°、45°,如果无人机距地面高度CD 为1003米,点A 、D 、E 在同一 水平直线上,则A 、B 两点间的距离是____________米.(结果保留根号)第14题图【答案】100(1+3)【解析】由题意可知∠A =30°,∠B =45°,∴AD =tan CDA=100米,BD =CD =1003米,∴AB =AD +BD =100+1003=100(1+3)米.6.(2018·宁夏,15,3)一艘货轮以182km/h 的速度在海面上沿正东方向航行,当行驶至A 处时,发现它的东南方向有一灯塔B ,货轮继续向东航行30分钟后到达C 处,发现灯塔B 在它的南偏东15°方向,则此时货轮与灯塔B 的距离为____________km .D C B A45°60°甲 楼ABCD乙 楼30°第16题图45°【答案】18.【解析】如下图,过点C作CD⊥AB于点D,则∠CAD=45°,∠ACB=105°,从而∠B=30°,AC=12×Rt△ACD中,sin∠CAD=CDAC,从而CD=AC sin∠CAD=sin45°=2=9.在Rt△BCD中,∵∠B=30°,∴BC=2CD=18(km),故填18.【知识点】解直角三角形;方向角7.(2018辽宁锦州,16,3分)如图,射线OM在第一象限,且与x轴正半轴的夹角为60°,过点D(6,0)作DA⊥OM于点A,作线段OD的垂直平分线BE交x轴于点E,交AD于点B,作射线OB,以AB为边的△AOB的外侧作正方形ABCA1,延长A1C交射线OB于点B1,以A1B1为边在△A1OB1的外侧作正方形A1B1C1A2,延长A2C1交射线OB于点B2,以AB为边在△A2OB2的外侧作正方形A2B2C2A3……按此规律进行下去,则正方式A2017B2017C2017A2018的周长为东CBAD东CBA【答案】4×()2017201613)33(+⨯,【解析】本题为规律探究题,先根据图形运用三角函数∠AOD=60°,OD=3,AD=33,BD=23,AB=,B 1C=1 ,A 1B 1=3+1, B 2C1=tan30°A 1B 1=33A 1B 1,A 2B 2=A 1B 1+33A 1B 1=33A 1B 1(3+1)=33(3+1)2B 3C 2=33A 2B 2,A 3B 3=A 2B 2+33A 2B 2=33A 2B 2(3+1)=(33)2(3+1)3 A 2017B 2017=(33)2016(3+1)2017 A 2017B 2017C 2017A 2018的周长4A 2017B 2017=4×(33)2016(3+1)2017 三、解答题1. (2018广西省桂林市,23,8分)如图所示,在某海域,一艘指挥船在C 处收到渔船在B 处位于C 处的南偏西45°方向上,且BC =60海里;指挥船搜索发现,在C 处的南偏西60°方向上有一艘海监船A ,恰好位于B 处的正西方向.于是命令海监船A 前往救援,已知海监船A 的航行速度为30海里/小时,问渔船在B 处需要等待多长时间才能得到海监船A≈1.41 1.73, 2.45,结果精确到0.1小时)【思路分析】过点B 作BD ⊥DC 于点D ,由题意可知,∠BCD =45°,∠ACD =60°,先根据BC =60,利用特殊角的三角函数值求出BD 的长,再求出AD 的长即可.【解题过程】解:如图(1),过点B 作BD ⊥DC 于点D ,由题意可知,∠BCD =45°,∠ACD =60°,DC =BD ,则在Rt △DEF 中,∵BC =60,∴sin ∠BCD =BD BC,即sin 45402BD =︒=,解得BD =DC =BD =则在Rt △ACD 中, tan ∠ACD =ADCD,tan 60=︒=解得AD =,∴AB =AD -BD =-≈30(2.45-1.41)=31.2(海里),∴渔船在B 处等待得到海监船A 的救援需要的时间为31.230=1.04≈1.0(小时),答:渔船在B 处等待得到海监船A 的救援需要约1.0小时. 【知识点】锐角三角函数的实际应用;二次根式的化简2. (2018海南省,22,8分)如图10,某数学兴趣小组为测量一棵古树BH 和教学楼CG 的高,先在A 处用高1.5米的测角仪测得古树顶端H 的仰角∠HDE 为45°,此时教学楼顶端G 恰好在视线DH 上,再向前走7米到达B 处,又测得教学楼顶端G 的仰角∠GEF 为60°,点A ,B ,C 三点在同一水平线上. (1)计算古树BH 的高;(2)计算教学楼CG 的高.(参考数据:412.≈,713.≈)【思路分析】(1)在Rt△DEH中,∠HDE=45°,∴HE=DE,BH=HE+BE,从而求出BH的长.(2)设EF=x米,在Rt△GEF中,∠GEF=60°,用x表示出GF的长,GF=3x,在Rt△GDF中,∠GDF=45°,∴DF=GF,7+x=3x,求解出x,从而得到GF的长,GC=GF+FC,故求得CG的长.【解题过程】(1)在Rt△DEH中,∵∠DEH=90°,∠HDE=45°,∴HE=DE=7米.∴BH=HE+BE=7+1.5=8.5米.(2)设EF=x米,在Rt△GEF中,∵∠GFE=90°,∠GEF=60°,∴GF=EF·tan60°=3x.在Rt△GDF中,∵∠GFD=90°,∠GDF=45°,∴DF=GF.∴7+x=3x.将7代入上式,解得x=10.GF=3x=17.3.1∴GC=GF+FC=18.5米.答:古树高为8.5米,教学楼高为18.5米.【知识点】解直角三角形,解直角三角形的应用3.如图,甲、乙两座建筑物的水平距离为,从甲的顶部处测得乙的顶部处的俯角为,测得底部处的俯角为,求甲、乙建筑物的高度和(结果取整数).参考数据:,.【答案】甲建筑物的高度约为,乙建筑物的高度约为.【解析】分析:首先分析图形:根据题意构造直角三角形;本题涉及两个直角三角形,应利用其公共边构造关系式,进而可求出答案.详解:如图,过点作,垂足为.则. 由题意可知,,,,,.可得四边形为矩形.∴,.在中,, ∴. 在中,,∴. ∴ .∴. 答:甲建筑物的高度约为,乙建筑物的高度约为.点睛:本题考查解直角三角形的应用--仰角俯角问题,首先构造直角三角形,再借助角边关系、三角函数的定义解题,难度一般.4. (2018甘肃省兰州市,23,7分) (7分)如图,斜坡BE ,坡顶B 到水平地面的距离AB 为3米,坡底AE 为18米,在B 处,E 处分别测得CD 顶部点D 的仰角为30°,60°.求CD 的高度.(结果保留根号)【思路分析】作BF ⊥CD 于F ,然后在两个直角三角形中分别表示出BF ,CE ,然后利用BF 和CE 相B A DCFE等即可求解.【解题过程】作BF⊥CD于F,设CE=x米,因为∠DEC=60°,所以DC米。DF-2)米,因为∠FBD=30°,所以BF x-2)米。因为BA⊥AC,DC⊥AC,所以四边形BACF为矩形,所以BF=AC,(x-2)=x+18,解得x答:CD的高度是米。【知识点】解直角三角形三角函数5. (2018黑龙江省齐齐哈尔市,题号23,分值12)折纸是一项有趣的活动,同学们小时候都玩过折纸,可能折过小动物、小花、飞机、小船等,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以通过研究图形的性质和运动、确定图形位置等,进一步发展空间观念,在经历借助图形思考问题的过程中,我们会初步建立几何直观.折纸往往从矩形纸片开始,今天,就让我们带着数学的眼光来玩一玩折纸,看看折叠矩形的对角线之后能得到哪呰数学结论.实践操作如图1,将矩形纸片ABCD沿对角线AC翻折,使点B’落在矩形所在平面内,B’C和AD相交于点E,连接B’D.解决问题(1)在图1中,①B’D和AC的位置关系为______________;②将△AEC剪下后展开,得到的图形是_________________;(2) 若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由;(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到的仍是轴对称图形.则小红折叠的矩形纸片的长宽之比为____________;拓展应用(4)在图2中,若∠B=30°,AB=43AB’D恰好为直角三角形时,BC的长度为__________. . 【思路分析】(1)由折叠的性质可知,∠ACB=∠ACE,再由四边形ABCD为矩形,AC为对角线可知,∠ACB=∠DAC,∴∠DAC=∠ACE,即AE=CE,∵BC=AD=B’C,∴B’E=DE,∴∠EB’D=∠EDB’,又∵∠B’ED=∠AEC 为对顶角,∴∠DAC=∠ACE=∠EB’D=∠EDB’,∴B’D∥AC,将△AEC剪下展开后,能得到四条边均相等的四边形,即菱形,故答案为①B’D∥AC,②菱形;(2)利用(1)的思路即可得出矩形变平行四边形时也可得到B’D∥AC和菱形的结论;(3)当矩形为正方形时符合题意,即长宽之比为1:1;当∠ACB=30°时符合题意,3 1;(4)由(2)可知,AE=CE,B’E=DE, AC∥B’D.当∠AB’D=90°,且点B’在AD上方时,可得出∠B’AC=∠AB’D=90°,∴BC='cos'ABAB C∠;当点B’在AD下方,∠ADB’=90°时,∠ADC=∠B=30°,得出BC=AD=cos∠ADC×CD.当∠B’AD=90°,且点B’在AD上方时,∵∠AB’C=30°,AE=CE,AB’3可得出BC=B’E+CE=B’E+AE='cos'ABAB C∠+tan∠AB’C×AB’. 当∠B’AD=90°,且点B’在AD下方时,∠ADC=30°,∵B’E=DE,∴AB’=AB=AE+B’E=AD×tan∠ADC+cos ADADC∠.【解题过程】解:(1)由折叠的性质可知,∠ACB=∠ACE.再由四边形ABCD为矩形,AC为对角线可知,∠ACB=∠DAC,∴∠DAC=∠ACE,即AE=CE,∵BC=AD=B’C,∴B’E=DE,∴∠EB’D=∠EDB’.又∵∠B’ED=∠AEC为对顶角,∴∠DAC=∠ACE=∠EB’D=∠EDB’.∴B’D∥AC.将△AEC剪下展开后,能得到四条边均相等的四边形,即菱形.故答案为①B’D∥AC,②菱形.(2)结论仍然成立.若选择结论①证明:∵B’C=AD,AE=CE,∴B’E=DE.∴∠CB’D=∠ADB’.∵∠AEC=∠B’ED,∠ACB’=∠CAD.∴∠ADB’=∠DAC.∴B’D∥AC.若选择结论②证明:如图所示,设点E的对应点为点F.∵四边形ABCD是平行四边形,∴CF∥AE.∴∠DAC=∠ACF.由折叠可得,∠ACE=∠ACF,CE=CF.∴∠DAC=∠ACE.∴AE=CE.∴AE=CF.∴四边形AECF是菱形.(3)当矩形为正方形时符合题意,即长宽之比为1:1;当∠ACB=30°时符合题意,:1.(答对一个得1分,写成“1(4)由(2)可知,AE=CE ,B ’E=DE, AC ∥B ’D.当∠AB ’D=90°,且点B ’在AD 上方时,可得出∠B ’AC=∠AB ’D=90°.∵∠B=∠AB ’C=30°, ∴在Rt △AB ’C 中,BC='cos 'AB AB C∠=8;当点B ’在AD 下方,∠ADB ’=90°时,∠ADC=∠B=30°,得出BC=AD=cos ∠ADC ×CD=6.当∠B ’AD=90°,且点B ’在AD 上方时,∵∠AB ’C=30°,AE=CE,AB ’可得出BC=B ’E+CE=B ’E+AE='cos 'AB AB C∠+tan ∠AB ’C ×AB ’=12.当∠B ’AD=90°,且点B ’在AD 下方时,∠ADC=30°,∵B ’E=DE,∴AB ’=AB=AE+B ’E=AD ×tan ∠ADC+cos ADADC∠AD=4.故答案为4或6或8或12.(答对一个得1分)【知识点】折叠的性质,平行线的判定与性质,锐角三角函数的应用,菱形的判定与性质,等腰三角形的性质.6.(2018湖南省怀化市,23,12分)已知:如图,在四边形ABCD 中,AD//BC ,点E 为CD 边上一点,AE 与BE 分别为∠DAB 和∠CBA 的平分线.(1)请你添加一个适当的条件________,使得四边形ABCD 是平行四边形,并证明你的结论; (2)作线段AB 的垂直平分线交AB 于点O ,并以AB 为直径作ʘ O (要求:尺规作图,保留作图痕迹,不写做法);(3)在(2)的条件下,ʘ O 交边AD 于点F ,连接BF ,交AE 于点G ,若AE =4,sin ∠AGF =54,求ʘ O 的半径.【思路分析】(1)在四边形中,一组对边平行且相等,那么这个四边形为平行四边形.(2)由AB 为圆的直径,根据直径所对的圆周角为直角得到︒=∠90AFG ,通过AE 为DAB ∠的角平分线,可知EAB FAG ∠=∠,所以在三角形AFG 和三角形AEB 中有两角对应相等,所以两三角形相似,所以sin ∠AGF =sin ∠ABE ,又已知AE =4,所以通过直角三角形的三角函数可求出直径AB 的值,继而求出半径的值.【解题过程】(1)令AD =BC ,又∵AD//BC ,根据平行四边行的判定定理,∴四边形ABCD 是平行四边形.(2)∵ʘ O 交边AD 于点F ,∴点F 为圆上一点,∴︒=∠90AFG ,因为AE 与BE 分别为∠DAB 和∠CBA 的平分线,AD//BC ,所以︒=∠+∠90EBA EAB ,即得,在AEB ∆中,︒=∠90AEB又∵AE 为DAB ∠的角平分线,∴EAB FAG ∠=∠,所以在三角形AFG 和三角形AEB 中,有AEB AFG ∠=∠,EAB FAG ∠=∠,∴AFG ∆∽EAB ∠,∴sin ∠AGF =AB AE =sin ABE ∠=54,已知AE =4,所以可得出直径AB =5,即半径等于2.5.【知识点】平行四边形的判定定理 尺规作图三角形相似的判定定理和相似三角形的性质 直角三角形的三角函数求值 圆周角的性质7. (2018年江苏省南京市,23,8分)如图,为了测量建筑物AB 的高度,在D 处树立标杆CD ,标杆的高是2m .在DB 上选取观测点E 、F ,从E 测得标杆和建筑物的顶部C 、A 的仰角分别为58、45,从F 测得C 、A 的仰角分别为22、70.求建筑物AB 的高度(精确到0.1m ) .(参考数据:tan 220.40≈,tan58 1.60≈,tan 70 2.75≈.)【思路分析】在△CED 中,得出DE ,在△CFD 中,得出DF ,进而得出EF ,列出方程即可得出建筑物AB 的高度。
中考数学复习 直角三角形 专项训练试题 含答案

中考数学复习直角三角形专项训练题1.如图,在平行线a、b之间放置一块直角三角板,三角板的顶点A、B分别在直线a、b上,则∠1+∠2的值为()A.90°B.85°C.80°D.60°2.如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于() A.70°B.80°C.90°D.100°3.下列四组线段中,能组成直角三角形的是()A.a=1,b=2,c=3B.a=2,b=3,c=4C.a=2,b=4,c=5D.a=3,b=4,c=54.由下列条件不能判定△ABC是直角三角形的是()A.∠A=37°,∠C=53°B.∠A-∠C=∠BC.∠A∶∠B∶∠C=3∶4∶5D.∠A∶∠B∶∠C=2∶3∶55.下列各组条件中,能判断两个直角三角形全等的是()A.一组边对应相等B.两组直角边对应相等C.两组锐角对应相等D.一组锐角对应相等6.如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是()A.AC=AD B.AB=ABC.∠ABC=∠ABD D.∠BAC=∠BAD7.如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长为()A.5B.6C.8D.108.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A 点与BC的中点D重合,折痕为MN,则线段BN的长为()55A.3B.2C.4D.59.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,如图,那么下列各条件中,不能使Rt△ABC≌Rt△A′B′C′的是()A.AB=A′B′=5,BC=B′C′=3B.AB=B′C′=5,∠A=∠B′=40°C.AC=A′C′=5,BC=B′C′=3D.AC=A′C′=5,∠A=∠A′=40°10.在两个直角三角形中,若有一对角(非直角)相等,一对边相等,则两个直角三角形()A.一定全等B.一定不全等C.不一定全等D.以上都不是11.直角三角形的两个锐角,有两个角的三角形是直角三角形.12.直角三角形的两条直角边的等于斜边的平方,用字母表示为a2+b2=c2.13.如果三角形两边的等于第三边的平方,那么这个三角形是直角三角形.14.如图,四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为.15.已知c-10+|a-6|+(b-8)2=0,则以a、b、c为三边的三角形是.16.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC 的面积为cm2.17.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为_____海里18.在等边△ABC中,点D、E分别在边BC、AC上,若CD=2,过点D 作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.19.如图,∠B=90°,AB=3,BC=4,CD=12,AD=13.求四边形ABCD的面积.ACB=∠DCE=90°,20.如图,△ABC、△CDE均为等腰直角三角形,∠点E在AB上.求证:△CDA≌△CEB.21.如图,在△ABC中,∠C=90°,D为BC上一点,且DE⊥AB于E,AC=AE.求证:AD平分∠BAC.22.如图所示,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=4,FC=3.求EF 长.23.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30°,求∠ACF的度数.24.如图,∠ABC=∠ADE=90°,AD=AB,AC=AE,BC与DE相交于点F,连接CD、EB.(1)图中共有几对全等三角形,请你一一列举;(2)求证:CF=EF.25.杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC、BD相匀于O,OD⊥CD垂足为D.已知AB=20米.请根据上述信息求标语CD的长度.参考答案:1---10 ACDCB ACCBC11.互余互余12.平方和13.平方和14.110°15.直角三角形16. 126或6617.30318.解:∵△ABC 是等边三角形,∴∠B=∠ACB=60°,∵DE∥AB,∴∠EDC=∠B=60°,∴△EDC 是等边三角形,∴DE=DC=2,在Rt△DEF 中,∵∠DEF=90°,DE=2,∴DF=2DE=4,∴EF=DF 2-DE 2=42-22=2 3.19.解:连接AC.∵∠B=90°,∴AC=AB 2+BC 2=32+42=5,在△ACD 中,AC 2+CD 2=52+122=169.AD 2=132=169,∴AC 2+CD 2=AD 2,∴∠ACD=90°,1111∴S 四边形ABCD =S △ABC +S △ACD =AB·BC+AC·CD=×3×4+×5×12=36.222220.证明:∵△ABC、△CDE 均为等腰直角三角形,∠BCA=∠ECD=90°,∴BC=AC,CE=CD,又∠BCE=90°-∠ACE=∠ACD,∴△CDA≌△CEB.21.证明:∵DE⊥AB,∴∠AED=90°.∵∠C=90°,∴∠AED=∠C=90°.⎧⎪AC=AE 在Rt△ACD 和Rt△AED 中,⎨⎪⎩AD=AD ,∴Rt△ACD≌Rt△AED(HL),∴∠CAD=∠EAD,∴AD 平分∠BAC.22.解:连接BD.∵△ABC 是等腰直角三角形,D 是AC 边上的中点,∴∠A =∠ABD=∠CBD=45°,∴AD=BD,∵AD=DC,∴BD⊥AC,∴∠ADB=90°,∵DE⊥DF,∴∠EDF=∠ADB=90°,∴∠ADE=∠BDF,∴△ADE≌△BDF,∴AE=BF=4,同理BE=CF=3,在Rt△BEF 中,EF=BE 2+BF 2=5.23.解:(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°,在Rt△ABE 和Rt△CBF 中,∵AE=CF,AB=BC,∴Rt△ABE≌Rt△CBF(HL);(2)∵AB=BC,∠ABC=90°,∴∠CAB=∠ACB=45°,∴∠BAE=∠CAB-∠CAE=45°-30°=15°.由(1)知Rt△ABE≌Rt△CBF,∴∠BCF=∠BAE=15°,∴∠ACF=∠BCF+∠ACB=15°+45°=60°.24.解:(1)Rt△ABC≌Rt△ADE,△ACD≌△AEB,△CDF≌△EBF中考数学复习直角三角形专项训练试题含答案(2)连接AF,∵∠ABC=∠ADE=90°,AB=AD,AC=AE,∴Rt△ABC≌Rt△ADE(HL),∴BC=DE.在Rt△ABF和Rt△ADF中,AB=AD,AF=AF,∴Rt△ABF ≌Rt△ADF(HL),∴BF=DF,BC-BF=DE-DF,即CF=EF.25.解:∵AB∥CD,∴∠ABO=∠CDO,又∵OD⊥CD,∴∠CDO=90°,∴∠ABO=90°,即OB⊥AB,∵相邻两平行线间的距离相等,∴OB=OD,在△⎧⎪∠ABO=∠CDO,∴△ABO≌△CDO,∴CD=AB=ABO与△CDO中,⎨OB=OD⎪⎩∠AOB=∠COD20(米),(也可利用“AAS”证△ABO≌△CDO,其它过程相同).11/11。
数学中考复习专题直角三角形

"2017-2018中考数学复习专题-直角三角形"一.选择题〔每题3分,共计36分〕1.直角三角形的两个锐角平分线的夹角是〔〕A.45°B.135°C.45°或135°D.由两个锐角的大小决定2.直角三角形三边的长分别为3、4、*,则*可能取的值为〔〕A.5 B.C.5或D.不能确定3.如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=4,则以下结论中不正确的选项是〔〕A.BC=2 B.BD=1 C.AD=3 D.CD=24.将一副三角板按如下图方式放置,则∠1与∠2的和是〔〕A.60°B.45°C.30°D.25°第3题图第4题图第5题图5.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,假设∠A=25°,则∠BDC等于〔〕A.44°B.60°C.67°D.70°6.如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为〔〕A.5 B.6 C.8 D.107.如图,△ABC是等腰直角三角形,点D是斜边AB上一点,DE⊥AC于点E,DF⊥BC于点F,AC=4,则EF的最小值是〔〕A.4B.4 C.2 D.2第6题图第7题图第8题图8.如图,△ABC中,AB=AC,∠BAC=90°,P为BC中点,∠EPF=90°,给出四个结论:①∠B=∠BAP;②AE=CF;③PE=PF;④S四边形AEPF=S△ABC,其中成立的有〔〕A.4个B.3个 C.2个 D.1个9.以下条件:〔1〕∠A+∠B=∠C,〔2〕∠A:∠B:∠C=1:2:3,〔3〕∠A=90°﹣∠B,〔4〕∠A=∠B=∠C中,其中能确定△ABC是直角三角形的条件有〔〕个.A.1 B.2 C.3 D.410.如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有〔〕A.1 B.2 C.3 D.411.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=A.B.C.D.12.如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为〔〕A.〔〕2013B.〔〕2014C.〔〕2013D.〔〕2014第11题图第12题图"2017-2018中考数学复习专题-直角三角形"题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二.填空题〔每题4分,共计24分〕13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,假设EC=2,则EF=.14.如图,△ABC中,AB=AC,D为AB中点,E在AC上,且BE⊥AC,假设DE=5,AE=8,则BC的长度为.第13题图第14题图第15题图15.如图,在△ABC中,AB=AC=10,BC=12,BD是高,则BD的长为.16.如下图的一块地,∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为m2.17.如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的外表从点A爬到点B,徐亚爬行的最短距离是cm.第16题图第17题图18.观察一下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出有以上规律的第⑤组勾股数:,第n〔n为正整数〕组勾股数:.三.解答题〔共7小题,共计60分〕19.〔8分〕如图,在△ABCC中,∠ACB=90°,CD⊥AB,AF是角平分线,交CD于点E.求证:∠1=∠2.20.〔8分〕:如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm.求AC的长.21.〔8分〕如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD 的中点,求证:〔1〕MD=MB;〔2〕MN平分∠DMB.22.〔8分〕如图,长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.23.〔8分〕如图,△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一点且BP=AC,Q是CF延长线上一点且CQ=AB,连接AP、AQ、QP,判断△APQ的形状.24.〔10分〕如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点.〔1〕如图1,假设E、F分别是AB、AC上的点,且AE=CF.求证:①△AED≌△CFD;②△DEF为等腰直角三角形.〔2〕如图2,点F、E分别D在CA、AB的延长线上,且AE=CF,猜测△DEF是否为等腰直角三角形?如果是请给出证明.25.〔10分〕∠MAN,AC平分∠MAN.〔1〕在图1中,假设∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;〔2〕在图2中,假设∠MAN=120°,∠ABC+∠ADC=180°,则〔1〕中的结论是否仍然成立?假设成立,请给出证明;假设不成立,请说明理由."中考专题---直角三角形"参考答案与试题解析一.选择题〔共12小题〕1.直角三角形的两个锐角平分线的夹角是〔〕A.45°B.135°C.45°或135°D.由两个锐角的大小决定【解答】解:如图,∠ACB=90°,OA、OB分别平分∠BAC和∠ABC,∵OA、OB分别平分∠BAC和∠ABC,∴∠OAB=BAC,∠OBA=∠ABC,∴∠OAB+∠OBA=〔∠BAC+∠ABC〕,∵∠C=90°,∴∠BAC+∠ABC=90°,∴∠OAB+∠OBA=45°,∴∠AOB=180°﹣45°=135°,∴直角三角形的两个锐角平分线的夹角是135°或45°.应选C.2.直角三角形三边的长分别为3、4、*,则*可能取的值为〔〕A.5 B.C.5或 D.不能确定【解答】解:当*为斜边时,*==5;当4为斜边时,*==.∴*的值为5或;应选:C.3.如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=4,则以下结论中不正确的选项是〔〕A.BC=2 B.BD=1 C.AD=3 D.CD=2【解答】解:∵∠ACB=90°,∠A=30°,∴BC=AB=2,∵CD⊥AB,∴CD<AB,即CD<2,则CD=2错误,应选:D.4.将一副三角板按如下图方式放置,则∠1与∠2的和是〔〕A.60°B.45°C.30°D.25°【解答】解:∵图中是一副直角三角板,∴∠B=∠ACB=45°,∠BAC=∠EDF=90°,∠E=30°,∠F=60°,∴∠BCA+∠BAC=45°+90°=135°.∵∠EDF=90°,∴∠DCA+∠DAC=90°,∴∠1+∠2=〔∠BCA+∠BAC〕﹣〔∠DCA+∠DAC〕=135°﹣90°=45°.应选B.5.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC 边上的点E处,假设∠A=25°,则∠BDC等于〔〕A.44°B.60°C.67°D.70°【解答】解:∵△ABC中,∠ACB=90°,∠A=25°,∴∠B=90°﹣∠A=65°,由折叠的性质可得:∠CED=∠B=65°,∠BDC=∠EDC,∴∠ADE=∠CED﹣∠A=40°,∴∠BDC=〔180°﹣∠ADE〕=70°.应选D.6.如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为〔〕A.5 B.6 C.8 D.10【解答】解:∵BD⊥AC于D,点E为AB的中点,∴AB=2DE=2×5=10,∴在Rt△ABD中,BD==8.应选C.7.如图,△ABC是等腰直角三角形,点D是斜边AB上一点,DE⊥AC于点E,DF⊥BC于点F,AC=4,则EF的最小值是〔〕A.4B.4 C.2D.2【解答】解:连接DC.∵DE⊥AC,DF⊥BC,∴∠DEC=∠DFC=∠C=90°;又∵∠ACB=90°,∴四边形ECFD是矩形,∴EF=DC,∴当DC最小时,EF也最小,即当CD⊥AB时,PC最小,∵AC=BC=4,∴AB=4,∴AC•BC=AB•DC,∴DC=2.∴线段EF长的最小值为2;应选C.8.如图,△ABC中,AB=AC,∠BAC=90°,P为BC中点,∠EPF=90°,给出四个结论:①∠B=∠BAP;②AE=CF;③PE=PF;④S四边形AEPF=S△ABC,其中成立的有〔〕A.4个B.3个C.2个D.1个【解答】解:∵AB=AC,∠BAC=90°,P为BC中点,∴①正确;∠B=∠PAC=45°∵∠BPE+∠EPA=90°,∠EPA+∠APF=90°∴∠BPE=∠APF,又AP为公共边,∴△PBE≌△PAF,∴BE=AF,又AB=AC,∴AE=CF,∴②正确;②中,△PBE≌△PAF,∴PE=PF,∴③正确,∵△PFC≌△PEA,△PBE≌△PAF,∴④也正确所以①②③④都正确,应选A.9.以下条件:〔1〕∠A+∠B=∠C,〔2〕∠A:∠B:∠C=1:2:3,〔3〕∠A=90°﹣∠B,〔4〕∠A=∠B=∠C中,其中能确定△ABC是直角三角形的条件有〔〕个.A.1 B.2 C.3 D.4【解答】解:A是,因为根据三角形角和定理可求出∠C=90°,所以是直角三角形;B是,因为根据三角形角和定理可求出三个角分别为30°,60°,90°,所以是直角三角形;C是,因为由题意得∠C=90°,所以是直角三角形;D是,因为根据三角形角和定理可求出∠C=90°,所以是直角三角形.应选D.10.如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有〔〕A.1 B.2 C.3 D.4【解答】解:〔1〕S1=a2,S2=b2,S3=c2,∵a2+b2=c2,∴a2+b2=c2,∴S1+S2=S3.〔2〕S1=a2,S2=b2,S3=c2,∵a2+b2=c2,∴a2+b2=c2,∴S1+S2=S3.〔3〕S1=a2,S2=b2,S3=c2,∵a2+b2=c2,∴a2+b2=c2,∴S1+S2=S3.〔4〕S1=a2,S2=b2,S3=c2,∵a2+b2=c2,123综上,可得面积关系满足S1+S2=S3图形有4个.应选:D.11.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=〔〕A.B.C.D.【解答】解:∵OP=1,OP1=,OP2=,OP3==2,∴OP4==,…,OP2017=.应选:D.12.如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为〔〕A.〔〕2013B.〔〕2014C.〔〕2013D.〔〕2014【解答】解:在图中标上字母E,如下图.∵正方形ABCD的边长为2,△CDE为等腰直角三角形,∴DE2+CE2=CD2,DE=CE,∴S2+S2=S1.观察,发现规律:S1=22=4,S2=S1=2,S3=S2=1,S4=S3=,…,n当n=2016时,S2016==.应选C.二.填空题〔共6小题〕13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,假设EC=2,则EF= 4 .【解答】解:作EG⊥OA于G,如下图:∵EF∥OB,∠AOE=∠BOE=15°∴∠OEF=∠COE=15°,EG=CE=2,∵∠AOE=15°,∴∠EFG=15°+15°=30°,∴EF=2EG=4.故答案为:4.14.如图,△ABC中,AB=AC,D为AB中点,E在AC上,且BE⊥AC,假设DE=5,AE=8,则BC的长度为2.【解答】解:∵BE⊥AC,∴∠AEB=90°,∵D为AB中点,∴AB=2DE=2×5=10,∵AE=8,∴BE==6.∴BC===2,故答案为:2.15.如图,在△ABC中,AB=AC=10,BC=12,BD是高,则BD的长为9.6 .【解答】解:设AD=*,由勾股定理得,AB2﹣AD2=BC2﹣CD2,即102﹣*2=122﹣〔10﹣*〕2,解得,*=2.8,BD==9.6,故答案为:9.6.16.如下图的一块地,∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为96 m2.【解答】解:如图,连接AC.在△ACD中,∵AD=12m,CD=9m,∠ADC=90°,∴AC=15m,又∵AC2+BC2=152+202=252=AB2,∴△ABC是直角三角形,∴这块地的面积=△ABC的面积﹣△ACD的面积=×15×20﹣×9×12=96〔平方米〕.故答案为:96.17.如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的外表从点A爬到点B,徐亚爬行的最短距离是25 cm.【解答】解:只要把长方体的右侧外表剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:∵长方体的宽为10,高为20,点B离点C的距离是5,∴BD=CD+BC=10+5=15,AD=20,在直角三角形ABD中,根据勾股定理得:∴AB=;只要把长方体的右侧外表剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:∵长方体的宽为10,高为20,点B离点C的距离是5,∴BD=CD+BC=20+5=25,AD=10,在直角三角形ABD中,根据勾股定理得:∴AB=;只要把长方体的上外表剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:∵长方体的宽为10,高为20,点B离点C的距离是5,∴AC=CD+AD=20+10=30,在直角三角形ABC中,根据勾股定理得:∴AB=;∵25<5,∴蚂蚁爬行的最短距离是25.故答案为:2518.观察一下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出有以上规律的第⑤组勾股数:11,60,61 ,第n〔n为正整数〕组勾股数:2n+1,2n〔n+1〕,2n〔n+1〕+1 .【解答】解:∵①3=2×1+1,4=2×1×〔1+1〕,5=2×1×〔1+1〕+1,②5=2×2+1,12=2×2×〔2+1〕,13=2×2×〔2+1〕+1,③7=2×3+1,24=2×3×〔3+1〕,25=2×3×〔3+1〕+1,…,∴第n组勾股数为:2n+1,2n〔n+1〕,2n〔n+1〕+1,∴第⑤组勾股数为2×5+1=11,2×5×〔5+1〕=60,2×5×〔5+1〕+1=61,即11,60,61.故答案为:11,60,61;2n+1,2n〔n+1〕,2n〔n+1〕+1.三.解答题〔共7小题〕19.如图,在△ABCC中,∠ACB=90°,CD⊥AB,AF是角平分线,交CD 于点E.求证:∠1=∠2.【解答】证明:∵AF是角平分线,∴∠CAF=∠BAF,∵∠ACB=90°,CD⊥AB,∴∠CAF+∠2=90°,∠BAF+∠AED=90°,∴∠2=∠AED,∵∠1=∠AED,∴∠1=∠2.20.:如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm.求AC的长.【解答】解:连接AD,∵ED是AB的垂直平分线,∴DB=DA=4cm,∵∠B=30°,∴∠ADC=2∠B=60°,∴∠DAC=30°,∴DC=2,∵在△ABC中,∠C=90°∴由勾股定理得:AC=2cm.21.如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:〔1〕MD=MB;〔2〕MN平分∠DMB.【解答】证明:〔1〕∵,∠ABC=∠ADC=90°,M是AC的中点,∴BM=AC,DM=AC,∴MD=MB;〔2〕∵MD=MB,N是BD的中点,∴MN平分∠DMB〔等腰三角形三线合一〕.22.如图,长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.【解答】解:∵四边形ABCD是矩形,∴AD=BC=10cm,CD=AB=8cm,根据题意得:Rt△ADE≌Rt△AFE,∴∠AFE=90°,AF=10cm,EF=DE,设CE=*cm,则DE=EF=CD﹣CE=8﹣*,在Rt△ABF中由勾股定理得:AB2+BF2=AF2,即82+BF2=102,∴BF=6cm,∴CF=BC﹣BF=10﹣6=4〔cm〕,在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,即〔8﹣*〕2=*2+42,∴64﹣16*+*2=*2+16,∴*=3〔cm〕,即CE=3cm.23.如图,△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一点且BP=AC,Q是CF延长线上一点且CQ=AB,连接AP、AQ、QP,判断△APQ 的形状.【解答】解:△APQ是等腰直角三角形.∵BE、CF都是△ABC的高,∴∠1+∠BAE=90°,∠2+∠CAF=90°〔同角〔可等角〕的余角相等〕∴∠1=∠2又∵AC=BP,CQ=AB,在△ACQ和△PBA中,∴△ACQ≌△PBA∴AQ=AP,∴∠CAQ=∠BPA=∠3+90°∴∠QAP=∠CAQ﹣∠3=90°∴AQ⊥AP∴△APQ是等腰直角三角形24.如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点.〔1〕如图1,假设E、F分别是AB、AC上的点,且AE=CF.求证:①△AED ≌△CFD;②△DEF为等腰直角三角形.〔2〕如图2,点F、E分别D在CA、AB的延长线上,且AE=CF,猜测△DEF 是否为等腰直角三角形?如果是请给出证明.【解答】〔1〕证明:①∵∠BAC=90°,AB=AC,D为BC中点,∴∠BAD=∠DAC=∠B=∠C=45°,∴AD=BD=DC,∵在△AED和△CFD中,,∴△AED≌△CFD〔SAS〕;②∵△AED≌△CFD,∴DE=DF,∠ADE=∠CDF,又∵∠CDF+∠ADF=90°,∴△DEF为等腰直角三角形;〔2〕△DEF为等腰直角三角形,理由:∵∠BAC=90° AB=AC,D为BC中点∴∠BAD=∠DAC=∠B=∠C=45°,∴AD=BD=DC,∵在△AED和△CFD中,,∴△AED≌△CFD〔SAS〕;∴DE=DF∠ADE=∠CDF,又∵∠CDF﹣∠ADF=90°,∴△DEF为等腰直角三角形.25.∠MAN,AC平分∠MAN.〔1〕在图1中,假设∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;〔2〕在图2中,假设∠MAN=120°,∠ABC+∠ADC=180°,则〔1〕中的结论是否仍然成立?假设成立,请给出证明;假设不成立,请说明理由.【解答】〔1〕证明:∵∠MAN=120°,AC平分∠MAN,∴∠CAD=∠CAB=60°.又∠ABC=∠ADC=90°,∴AD=AC,AB=AC,∴AB+AD=AC.〔2〕解:结论仍成立.理由如下:作CE⊥AM、CF⊥AN于E、F.则∠CED=∠CFB=90°,∵AC平分∠MAN,∴CE=CF.∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°∴∠CDE=∠ABC,在△CDE和△CBF中,,∴△CDE≌△CBF〔AAS〕,∴DE=BF.∵∠MAN=120°,AC平分∠MAN,∴∠MAC=∠NAC=60°,∴∠ECA=∠FCA=30°,在Rt△ACE与Rt△ACF中,则有AE=AC,AF=AC,则AD+AB=AD+AF+BF=AD+AF+DE=AE+AF=AC+AC=AC.∴AD+AB=AC.。
中考数学总复习《直角三角形》专项测试卷(含答案)

中考数学总复习《直角三角形》专项测试卷(含答案)(考试时间:90分钟;试卷满分:100分)学校:___________班级:___________姓名:___________考号:___________一、选择题(本题共10小题,每小题3分,共30分)。
1.在△ABC中,∠A=40°,∠C=90°,则∠B的度数为()A.40°B.50°C.60°D.70°2.一直角三角形的两直角边长为6和8,则斜边长为()A.10B.13C.7D.143.如图,在△ABC中,已知∠C=90°,AC=5cm,BC=12cm,则斜边AB上的高为()A.B.C.30cm D.cm4.如图,在Rt△ABC中,∠C=90°,CD为AB边上中线,过点D作DE⊥AB,连接AE,BE,若AE=1 0,CD=8,则DE的长为()A.3B.4C.5D.65.如图,在△ABC中,∠ABC为直角,∠A=30°,BD⊥AC于D,若CD=2,则AC的长为()A.8B.6C.4D.26.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件()A.∠BAC=∠BAD B.AC=AD或BC=BDC.∠ABC=∠ABD D.以上都不正确7.如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的依据是()A.HL B.ASA C.AAS D.SAS8.下列各组数是勾股数的是()A.1 B.0.6,0.8,1C.5,11,12D.8,15,179.如图,长为8cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C垂直向上拉升3cm到D点,则橡皮筋被拉长了()A.2cm B.3cm C.4cm D.1cm10.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=6,BC=10,点D,E,F,G,H,I都在长方形KLM J的边上,则长方形KLMJ的面积为()A.420B.440C.430D.410二、填空题(本题共6题,每小题2分,共12分)。
2018年中考数学专项复习 直角三角形综合训练题

直角三角形1.在Rt △ABC 中,∠C =90°,已知a =2,cos B =13,则b 的长为( ) A.2310 B .210 C .4 2 D.432 2. 如图,已知在Rt △ABC 中,∠C =90°,AB =5,BC =3,则cos B 的值是( )A.35B.45C.34D.433. 在Rt △ABC 中,∠C =90°,若sin A =35,则cos B 的值是( ) A.45 B.35 C.34 D.434. 在△ABC 中,∠C =90°,tan A =13,则cos A 的值为( ) A.1010 B.23 C.34 D.310105. 如图,点A 为∠α边上的任意一点,作AC⊥BC 于点C ,CD ⊥AB 于点D ,下列表示cos α的值,错误的是( )A.BD BCB.BC ABC.AD ACD.CD AC6. 如图,某飞机在空中A 处探测到它的正下方地平面上目标C ,此时飞行高度AC =1 200 m ,从飞机上看地平面指挥台B 的俯角α=30°,则飞机A 与指挥台B 的距离为( )A .1 200 mB .1 200 2 mC .1 200 3 mD .2 400 m7. 已知一个直角三角形中:①两条边的长度;②两个锐角的度数;③一个锐角的度数和一条边的长度.利用上述条件中的一个,能解这个直角三角形的是( )A .①②B .②③C .①③D .①②③8. 在△ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,且a =35,c =352,则∠B 为( )A .30°B .45°C .60°D .75°9. 如图,从山顶A 望地面C ,D ,测得它们的俯角分别为45°,30°,已知CD =100 m ,点C 在BD 上,则山高AB 等于( )A .100 mB .50 3 mC .50 2 mD .50(3+1) m10. 某楼梯的侧面如图所示,已测得BC 的长约为3.5米,∠BCA 约为29°,则该楼梯的高度AB 可表示为( )A .3.5sin 29°米B .3.5cos 29°米C .3.5tan 29°米 D. 3.5cos 29°米 11. 如图,在东西方向的海岸线上有A ,B 两个港口,甲货船从A 港沿北偏东60°的方向以20海里/时的速度出发,同时乙货船从B 港沿西北方向出发,2小时后相遇在点P 处,则乙货船每小时航行________海里.12. 如图,在Rt △ABC 中,∠C=90°,BC =2,AC =6,解此直角三角形.13. 如图,在△ABC 中,∠C=90°,∠B=30°,AD 是∠BAC 的角平分线,与BC 相交于点D ,且AB =4,求AD 的长.14. 如图,在△ABC 中,AD 是BC 边上的高,AE 是BC 边上的中线,∠C=45°,sin B =,AD =1.(1)求BC 的长;(2)求tan ∠DAE 的值.参考答案:1---10 CABDC DCBDA 11. 10 212. 在Rt △ABC 中,∵tan A =BC AC =2662=33,∴∠A =30°. ∴∠B =90°-30°=60°,AB =2BC =4 613. 在Rt △ABC 中,AC =AB·sin 30°=23,在Rt △ADC 中,AD =AC cos 30°=4 14. (1)在△ABC 中,∵AD 是BC 边上的高,∴∠ADB =∠ADC=90°.在△ADC 中,∵∠ADC =90°,∠C =45°,AD =1,∴DC =AD =1.在△ADB 中,∵∠ADB =90°,sin B =13,AD =1,∴AB =AD sin B=3,∴BD =AB 2-AD 2=2 2.∴BC =BD +DC =22+1(2)∵AE 是BC 边上的中线,∴CE =12BC =2+12,∴DE =CE -CD =2-12,∴tan ∠DAE =DE AD =2-12。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018 初三数学中考复习直角三角形的性质专项复习练习题
1. 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M、C两点间的距离为( )
A.0.5km B.0.6km C.0.9km D.1.2km ABCCFABFBEACEMBCEFBC,,为⊥=于2.如图,在△中,的中点,⊥,于6EFM的周长是,则△( )
=15
A.21 B.18 C.15 D.13
3.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
4.在等腰直角三角形ABC中,∠C=90°,点D为BC上一点,且∠BAD=15°,AD=8,则CD等于( )
A.4 B.3 C.2 D.5
5. 如图所示,在△ABC中,BD、CE是高,G、F分别是BD、DE的中点,则下列结论中错误的是( )
=60°DGE.∠DGE D平分∠GF.DE C⊥GF.GD B=GE.A.6. 如图,在Rt△ABC中,∠BAC=90°,D、E分别为BC、AB的中点,且AC=6cm,AB=8cm,则△ADE的周长为( )
A.10cm B.12cm C.14cm D.16cm
7.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB 的长度是( )
A.2cm B.4cm C.8cm D.16cm
8. 如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC,若DE=10,AE=16,则BE的长度为( )
A.10 B.11 C.12 D.13
9. △ABC中,∠ACB=90°,AB=10,AC=6,CD⊥AB于D,则CD=______.
10. △ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为________.
11. 在Rt△ABC中,∠C=90°,∠A=30°,AB=12cm,则BC=
_____cm.
12. 已知直角三角形的两边为3cm和4cm,则它们的第三边长为
__________cm.
13. 如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD 的长为______.
14. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC 于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是_____.
AD,5=AB的中点,若AD是M的中点,AC的对角线ABCD是矩形O.如图,15.
=12,则四边形ABOM的周长为______.
16. 如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.求证:DE=EF.
求10.=BD=60°,ADC=30°,∠B=90°,∠C中,∠ABC△Rt如图,在17.
CD的
18. 如图,已知:△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE,G是垂足.
求证:(1)G是CE的中点;(2)∠B=2∠BCE.
参考答案:1---8 DBDBD BCC
9. 4.8
10. 6.5cm
斜边的一半11.
或7 12. 5
13. 2
14. 2
15. 20
16. 证明:∵在△ABC中,∠ACB=90°,点D为边AB的中点,∴DC=DA,∵DE∥BC,∴AE=CE,∴∠A=∠FCE,又∵∠AED=∠CEF,∴△AED≌△CEF,∴DE=EF.
17. 解:∵∠B=30°,∠ADC=60°,∴∠BAD=∠ADC-∠B=30°,∴AD=1BD=10,∵∠C=90°,∠DAC=60°-30°=30°,∴CD=AD=5.
218. 证明:(1)连接DE,∵AD⊥BC,E是AB的中点,∴DE是Rt△ABD斜边上的1中线,即DE=BE=AB,∴DC=DE=BE,又∵DG=DG,∴Rt△EDG≌Rt△CDG,∴2GE=CG,∴G是CE的中点;
(2)由(1)知:BE=DE=CD,∴∠B=∠BDE,∠DEC=∠DCE,∴∠B=∠BDE=2∠BCE.。
