MATLAB作业6参考答案(修)

合集下载

控制系统仿真matlab第六章习题答案汇总

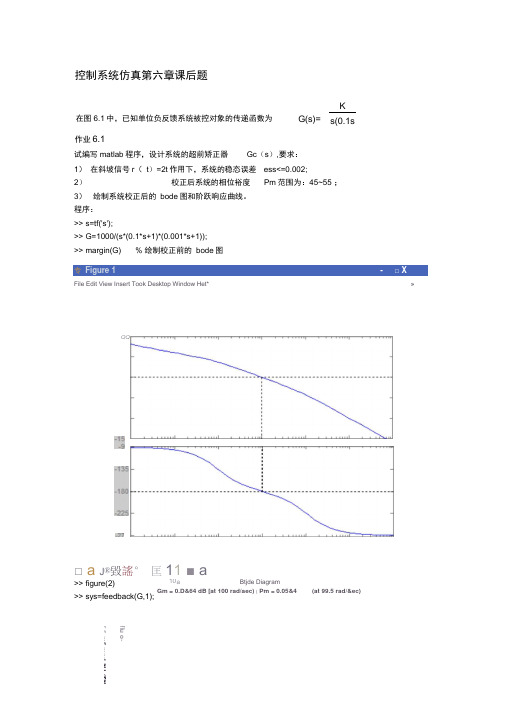
控制系统仿真第六章课后题作业6.1试编写matlab 程序，设计系统的超前矫正器 Gc （s ）,要求：1）在斜坡信号r （ t ）=2t 作用下，系统的稳态误差 ess<=0.002;2）校正后系统的相位裕度 Pm 范围为：45~55 ； 3）绘制系统校正后的 bode 图和阶跃响应曲线。

程序：>> s=tf('s');>> G=1000/(s*(0.1*s+1)*(0.001*s+1));>> margin(G)% 绘制校正前的 bode 图专 Figure 1 - □ X File Edit View Insert Took Desktop Window Het* »□ a J ®毀謠° 匡11 ■ a >> figure(2)>> sys=feedback(G,1); 在图6.1中，已知单位负反馈系统被控对象的传递函数为G(s)= Ks(0.1s 1)(0.0QQo oBtjde Diagram Gm = 0.D&64 dB [at 100 rad/aec) ( Pm = 0.05&4 (at 99.5 rad/&ec)flu o-5 5 mE mprl 左一6『左 a 10>> step(sys) %绘制校正前的单位阶跃响应曲线Figure 2File Edit 过ew Insert Tools Window Help□已鸟|罠4紗®悬乙| 口目| ■回Step Response1.3>> [Gm,Pm]=margin(G); %该句值计算bode图的增益裕量Gm和相位裕量Pm >> [mag,phase,w]=bode(G); %该句只计算bode图上多个频率点w对应的幅值和相位>> QWPm=50; %取矫正后的相位为50>> Flm=QWPm-Pm+5;>> Flm=Flm*pi/180;>> alfa=(1-si n(FIm))/(1+si n( FIm));>> adb=20*log10(mag);>> am=10*log10(alfa);>> wc=spli ne(adb,w,am);>> T=1/(wc*sqrt(alfa));>> alfat=alfa*T;>> Gc=tf([T 1],[alfat 1]) %校正器的传递函数Tran sfer function:0.01794 s + 1Time 330.00179 s + 1>> figure(3)>> margin(Gc*G) %系统矫正后的bode图Ffgure 3Filt gdit yisw ifisert Hcdt Mfimdcw title】I ■回Bode DiagramGm = 17.6 dB (st 69B rad/sec) s Pm = 4S.2 deg (at 176 rad/sec)"I 0 0 N -- 1 1 I I I ! 1 ! | ! ■' I I ' ' I J I I ........... | I I « i i i | i | i f ■ J !!|!|>> figure(4)>> step(feedback(Gc*G ,1)) % 校正后的单位阶跃响应曲线Figure 4n xl Fie Edit 辺足w Insert Tools Desktop Window HelpO t3 J -S □ S ■ Q1010°ID1 1 孑10Frequency (r&fh'see)作业6.2在图6.1中，已知单位负反馈系统被控对象的传递函数为试编写matlab 程序，设计系统的滞后校正器 Gc ( s ),要求:1) 在斜坡信号r(t)=t 作用下，系统的稳态误差ess 乞0.01 ； 2) 校正后系统的相位裕度 Pm 范围为：40~50 ；3) 绘制系统矫正前后的 bode 图和阶跃响应曲线。

数字图像处理及应用（MATLAB）第6章习题答案

第六章习题与思考题参考答案1. 简述飞机红外图像识别中用到的五个红外特征量各自的作用？1）长宽比：反应了目标的几何形状；2）复杂度：反应了红外目标轮廓的情况；3）紧凑度：反应了红外目标在其所在最小外接矩形中所占比重；4）均值对比度：反映了目标的物理特性与背景的物理特性之间的关系；5）部分最亮像素点数与目标总像素数的比值：反应了目标的明暗变化情况；2. 可视密码共享中,如果实现（4 , 5）门限的可视密码分享，程序将做如何编写？clear allclose allM=imread('0.jpg');ss=rgb2gray(M);figureimshow(ss);[m n]=size(ss);for i=1:m*nif ss(i)>250ss(i)=250;endends=double(ss)+1;x=[1 2 3 4 5];g1=zeros(m,n);g2=zeros(m,n);g3=zeros(m,n);g4=zeros(m,n);g5=zeros(m,n);yy1=zeros(m,n);yy2=zeros(m,n);yy3=zeros(m,n);yy4=zeros(m,n);yy5=zeros(m,n);y1=zeros(m,n);y2=zeros(m,n);y3=zeros(m,n);y4=zeros(m,n);y5=zeros(m,n);for j=1:m*na1=mod(2*j,251);a2=mod(3*j,251);a3=mod(5*j,251);f=[a1 a2 a3 s(j)];g1(j)=polyval(f,x(1));yy1(j)=mod(g1(j),251);g2(j)=polyval(f,x(2));yy2(j)=mod(g2(j),251);g3(j)=polyval(f,x(3));yy3(j)=mod(g3(j),251);g4(j)=polyval(f,x(4));yy4(j)=mod(g4(j),251);g5(j)=polyval(f,x(5));yy5(j)=mod(g5(j),251);endy1=uint8(yy1-1)y2=uint8(yy2-1);y3=uint8(yy3-1);y4=uint8(yy3-1);y5=uint8(yy3-1);figure,imshow(y1);figure,imshow(y2)figure,imshow(y3);figure,imshow(y4);figure,imshow(y5);l1=(x(2)*x(3)*x(4)*x(5))/[(x(1)-x(2))*(x(1)-x(3))*(x(1)-x(4))*(x(1)-x(5))];l2=(x(1)*x(3)*x(4)*x(5))/[(x(2)-x(1))*(x(2)-x(3))*(x(2)-x(4))*(x(2)-x(5))];l3=(x(1)*x(2)*x(4)*x(5))/[(x(3)-x(1))*(x(3)-x(2))*(x(3)-x(4))*(x(3)-x(5))];l4=(x(1)*x(2)*x(3)*x(5))/[(x(4)-x(1))*(x(4)-x(2))*(x(4)-x(3))*(x(4)-x(5))];l5=(x(1)*x(2)*x(3)*x(4))/[(x(5)-x(1))*(x(5)-x(2))*(x(5)-x(3))*(x(5)-x(4))];rr1=zeros(m,n);r=zeros(m,n);for j=1:m*nrr1(j)=mod(yy1(j)*l1+yy2(j)*l2+yy3(j)*l3+yy4(j)*l4+yy5(j)*l5,251);endr=uint8(rr1-1);figure,imshow(r);3. 已知图像⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=805020016821024015010017018013070901262068M 。

matlab课后习题及答案

第一章 5题已知a=4.96，b=8.11，计算)ln(b a eba +-的值。

解：clear clc a=4.96; b=8.11;exp(a-b)/log(a+b) ans =0.0167 6题已知三角形的三边a=9.6,b=13.7, c=19.4,求三角形的面积。

提示：利用海伦公式area =))()((c s b s a s s ---计算，其中S=(A+B+C)/2. 解：clear clc a=9.6; b=13.7; c=19.4; s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c)) s =21.3500 第二章 8题已知S=1+2+2^2+2^3+……+2^63,求S 的值解：clear clc S=0;for i=0:1:63 S=S+2^i; end S S =1.8447e+019 9题分别用for 和while 循环结构编写程序，计算∑=-1001n 1n 2）（的值。

解：clear clc s=0;for n=1:100 s=s+(2*n-1); end s s =10000 clear clc n=1; s=0;while n<=100 s=s+(2*n-1); n=n+1; end s s =10000 第三章 2题在同一坐标下绘制函数x ,,2x-,2x xsin(x)在()∏∈,0x 的曲线。

解：clear clcx=0:0.2:pi; y1=x; y2=x.^2; y3=-(x.^2); y4=x.*sin(x);plot(x,y1,'-' ,x,y2,'-' ,x,y3,'-' ,x,y4,'-')0.511.522.53-10-8-6-4-202468109题用不同的线型和颜色在同一坐标内绘制曲线y1=2ex5.0 、y2=sin(2∏x )的图形。

MATLAB习题及参考答案经典.doc

习题：1，计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

2，对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

3，已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。

4，角度[]604530=x ，求x 的正弦、余弦、正切和余切。

(应用sin,cos,tan.cot)5，将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵：（1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546，将(x -6)(x -3)(x -8)展开为系数多项式的形式。

(应用poly,polyvalm)7，求解多项式x 3-7x 2+2x +40的根。

(应用roots)8，求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

(应用poly,polyvalm)9，计算多项式9514124234++--x x x x 的微分和积分。

(应用polyder,polyint ，poly2sym)10，解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。

(应用x=a\b)11，求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。

(应用pinv) 12，矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。

(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。

matlab课后习题及答案详解

matlab课后习题及答案详解第1章练习题1.安装matlab时，在选择组件窗口中哪些部分必须勾选，没有勾选的部分以后如何补安装？在安装matlab时，安装内容由选择组件窗口中个复选框是否被勾选来决定，可以根据自己的需要选择安装内容，但基本平台（即matlab选项）必须安装。

第一次安装没有选择的内容在补安装时只需按照安装的过程进行，只是在选择组件时只勾选要补装的组件或工具箱即可。

2.matlab操作方式桌面存有几个窗口？如何并使某个窗口瓦解桌面沦为单一制窗口？又如何将瓦解过来的窗口再次置放至桌面上？与其他计算机语言相比较，matlab语言注重的特点就是什么？matlab系统由那些部分共同组成？在matlab操作桌面上有五个窗口，在每个窗口的右上角有两个小按钮，一个是关闭窗口的close按钮，一个是可以使窗口成为独立窗口的undock按钮，点击undock按钮就可以使该窗口脱离桌面成为独立窗口，在独立窗口的view菜单中选择dock……菜单项就可以将独立的窗口重新防止的桌面上。

matlab具备功能强大、使用方便、输出简便、库函数多样、开放性弱等特点。

matlab系统主要由开发环境、matlab数学函数库、matlab语言、图形功能和应用程序接口五个部分组成。

3.如何设置当前目录和搜寻路径，在当前目录上的文件和在搜寻路径上的文件存有什么区别？命令历史窗口除了可以观测前面键入的命令外，除了什么用途？当前目录可以在当前目录浏览器窗口左上方的输入栏中设置，搜索路径可以通过选择操作桌面的file菜单中的setpath菜单项来完成。

在没有特别说明的情况下，只有当前目录和搜索路径上的函数和文件能够被matlab运行和调用，如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件，如果没有特别说明，数据文件将存储在当前目录上。

命令历史窗口除了用作查阅以前键入的命令外，还可以轻易执行命令历史窗口中选取的内容、将选取的内容拷贝到剪贴板中、将选取内容轻易拷贝到m文件中。

matlab习题及答案

matlab习题及答案Matlab习题及答案Matlab是一种强大的数学计算软件，被广泛应用于科学计算、数据分析和工程设计等领域。

在学习和使用Matlab的过程中，习题是一种非常有效的学习方式。

本文将给出一些常见的Matlab习题及其答案，帮助读者更好地掌握Matlab的使用技巧。

一、基础习题1. 计算1到100之间所有奇数的和。

解答：```matlabsum = 0;for i = 1:2:100sum = sum + i;enddisp(sum);```2. 编写一个函数，计算任意两个数的最大公约数。

解答：```matlabfunction gcd = computeGCD(a, b)while b ~= 0temp = b;a = temp;endgcd = a;end```3. 编写一个程序，生成一个5×5的随机矩阵，并计算矩阵的行和列的平均值。

解答：```matlabmatrix = rand(5);row_average = mean(matrix, 2);col_average = mean(matrix);disp(row_average);disp(col_average);```二、进阶习题1. 编写一个程序，实现插入排序算法。

解答：```matlabfunction sorted_array = insertionSort(array)n = length(array);for i = 2:nj = i - 1;while j > 0 && array(j) > keyarray(j+1) = array(j);j = j - 1;endarray(j+1) = key;endsorted_array = array;end```2. 编写一个程序，实现矩阵的转置。

解答：```matlabfunction transposed_matrix = transposeMatrix(matrix) [m, n] = size(matrix);transposed_matrix = zeros(n, m);for i = 1:mfor j = 1:ntransposed_matrix(j, i) = matrix(i, j);endendend```3. 编写一个程序，实现二分查找算法。

matlab答案第六章

值
figure, plot(alpha3, tan_alpha3, 'k:p');
hold on; %绘精确正切曲线
alpha4=0:75;
tan_Y1=interp1(alpha3, tan_alpha3, alpha4,
'spline'); %3 次样条正切插值
plot(alpha4, tan_Y1,'r-*'); hold on; %绘 3
运行结果：
x=
-1.8060
-0.5373
3.0448
(2) 程序设计：
方法 1：矩阵求逆法
clear all; close all; clc;
A=[5, 1, -1, 0; 1, 0, 3, -1;-1,-1,0, 5; 0,
0, 2, 4];
b=[1; 2; 3; -1];
x=inv(A)*b
运行结果：
第六章
1. 利用 MATLAB 提供的 randn 函数生成符合正
态分布的 10×5 随机矩阵 A，进行如下操作：
(1) A 各列元素的均值和标准方差。
(2) A 的最大元素和最小元素。
(3) 求 A 每行元素的和以及全部元素之和。
(4) 分别对 A 的每列元素按升序、每行元素按
降序排列。
答：
clear all; close all; clc;
141
Yi 187 126 172 125 148 求它的线性拟合曲线。答：程序设计： clear all; close all; clc; x=[165, 123, 150, 123, 141]; y=[187, 126, 172, 125, 148]; P=polyfit(x, y, 3) 运行结果： P= 1.0e+003 * -0.0000 0.0013 -0.1779 8.4330 所以它的线性拟合曲线为： P(x)=1.3x2-177.9x+8433 4. 已知多项式 P1(x)=3x+2，P2(x)=5x2−x+2， P3(x)=x2−0.5，求： (1) P(x)=P1(x)P2(x)P3(x)。 (2) P(x)=0 的全部根。 (3) 计算 xi=0.2i (i=0,1,2,…,10)各点上的 P(xi)。答： (1) 程序设计： clear all; close all; clc; P1=[0, 3, 2]; P2=[5, -1, 2]; P3=[1, 0, -0.5]; P=conv(conv(P1, P2), P3) 运行结果： P= 0 15.0000 7.0000 -3.5000 0.5000 -2.0000 -2.0000 所以 P(x)=15x5+7x4-3.5x3+0.5x2-2x-2 (2) 程序设计： r=roots(P) 运行结果： r= 0.7071 0.1000 + 0.6245i 0.1000 - 0.6245i -0.7071 -0.6667 (3) 程序设计： i=0:10; xi=0.2*i; Pxi=polyval(P, xi) 运行结果： Pxi =

matlab教程习题答案

matlab教程习题答案MATLAB教程习题答案MATLAB是一种广泛应用于科学计算和工程领域的高级编程语言和环境。

它的强大功能和灵活性使得许多人对其感兴趣，但对于初学者来说，掌握MATLAB 可能会有一些困难。

为了帮助大家更好地理解和掌握MATLAB，下面将给出一些常见的MATLAB教程习题的答案，希望能对大家有所帮助。

1. 编写一个MATLAB程序，计算1到100之间所有偶数的和。

答案：```matlabsum = 0;for i = 2:2:100sum = sum + i;enddisp(sum);```2. 编写一个MATLAB程序，生成一个10行10列的随机矩阵，并计算该矩阵的行和列的和。

答案：```matlabmatrix = rand(10, 10);row_sum = sum(matrix, 2);col_sum = sum(matrix);disp(col_sum);```3. 编写一个MATLAB程序，计算斐波那契数列的前20个数。

答案：```matlabfibonacci = zeros(1, 20);fibonacci(1) = 1;fibonacci(2) = 1;for i = 3:20fibonacci(i) = fibonacci(i-1) + fibonacci(i-2);enddisp(fibonacci);```4. 编写一个MATLAB程序，计算一个正整数的阶乘。

答案：```matlabnum = input('请输入一个正整数：');factorial = 1;for i = 1:numfactorial = factorial * i;end```5. 编写一个MATLAB程序，求解一个二次方程的根。

假设二次方程的形式为ax^2 + bx + c = 0，其中a、b、c为用户输入的系数。

答案：```matlaba = input('请输入二次方程的系数a：');b = input('请输入二次方程的系数b：');c = input('请输入二次方程的系数c：');delta = b^2 - 4*a*c;if delta < 0disp('该二次方程无实根。

中南大学matlab课后答案-第六章

实验指导二1，（1）>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[,,]';x=A\B （2）>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[,,]';x=A\B （3）>> cond(A)2，（1）建立函数文件，命令如下;Function fx=funx(x)fx=x^41+x^3+1;$调用fzero函数求根，命令如下;>> z=fzero(@funx,-1)(2) 建立函数文件，命令如下;Function fx=sin(x)fx=x-(sin(x))/x;调用fzero函数求根，命令如下;>> z=fzero(@sin,(3) 建立函数文件，命令如下;function q=myfun(p)x=p(1);、y=p(2);z=p(3);q(1)=sin(x)+y^2+log(z)-7;q(2)=3*x+2^y-z^3+1;q(3)=x+y+z-5;调用fsolve函数求根，命令如下;>> options=optimset('Display','off');x=fsolve(@myfun,[1,1,1]',options) 3,(1) 建立函数文件,命令如下;function yp=funt(t,y)>yp=-y*+sin(10*t));求微分方程，程序如下：>> t0=0;tf=5;y0=1;[t,y]=ode23(@funt,[t0,tf],y0)(2) 建立函数文件,命令如下;function yp=funr(t,y)yp=cos(t)-(y)/(1+t^2);求微分方程，程序如下：>> t0=0;tf=5;y0=1;[t,y]=ode23(@funr,[t0,tf],y0)4,建立函数文件命令如下:{function fx=mymax(x)fx=-1*(1+x^2)/(1+x^4);求最大值，程序如下:>> [x,y]=fminbnd(@mymax,0,2)5,编写目标函数M文件，命令如下:function f=fop(x)f=-1*(x(1)^(1/2)+x(2)^(1/2)+x(3)^(1/2)+x(4)^(1/2));设定约束条件，并调用fmincon函数求解此约束最优化问题，程序如下：>>x0=[200,200,200,200];%A=[1,0,0,0;,1,0,0;,,1,0;,,,1];b=[400,440,484,];Ib=[0,0,0,0];options=optimset('Display','off');[x,y]=fmincon(@fop,x0,A,b,[],[],Ib,[],[],options)思考练习1,(1)矩阵求逆：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=inv(A)*b矩阵除法：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=A\b！矩阵分解：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';[L,U]=lu(A);x=U\(L\b) (2)矩阵求逆：>>A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]';x=inv(A)*b矩阵除法：>>A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]';x=A\b矩阵分解：>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]'; [L,U]=lu(A);x=U\(L\b)2,(1)建立函数文件，命令如下：function fx=fun1(x)fx=3*x+sin(x)-exp(x);调用fzero函数求根，命令如下;>> y=fzero(@fun1,、(2) 建立函数文件，命令如下：function fx=fun2(x)fx=1-(1/x)+5;调用fzero函数求根，命令如下;>> y=fzero(@fun2,1)(3) 建立函数文件，命令如下;function q=fun3(p)x=p(1);y=p(2);q(1)=x^2+y^2-9;'q(2)=x+y-1;调用fsolve函数求根，命令如下;>> options=optimset('Display','off');x=fsolve(@fun3,[1,1]',options) 3,(1)建立函数文件，命令如下：function ydot=fun5(t,y)ydot(1)=(2-3*y(2)-2*t*y(1))/(1+t^2);ydot(2)=y(1);ydot=ydot';求解微分方程，命令如下：'>> t0=0;tf=5;x0=[0,1];[t,y]=ode45(@fun5,[t0,tf],x0);[t,y](2) (1)建立函数文件，命令如下：function ydot=fun6(t,y)ydot(1)=cos(t)+(5*y(1)*cos(2*t))/(t+1)^2-y(2)-y(3)/(3+sin(t)); ydot(2)=y(1);ydot(3)=y(2);ydot=ydot';求解微分方程，命令如下：>> t0=0;tf=5;x0=[0,1];[t,y]=ode45(@fun5,[t0,tf],x0);[t,y]4,】建立函数文件命令如下:function fx=max(x)fx=-1*(sin(x)+cos(x^2));求最大值，程序如下:>> [x,y]=fminbnd(@mymax,0,pi)5,编写目标函数M文件，命令如下:function f=topm(x)f=-1*x*(3-2*x)^2;设定约束条件，并调用fmincon函数求解此约束最优化问题，程序如下：>>x0=[0];A=[1];b=[];Ib=[0];options=optimset('Display','off');[x,y]=fminco n(@top,x0,A,b,[],[],Ib,[],[],options)。

matlab习题与答案

matlab习题与答案
MATLAB习题与答案
MATLAB是一种强大的数学软件，广泛应用于工程、科学和金融等领域。

通过MATLAB，用户可以进行数据分析、图像处理、模拟建模等多种操作。

为了帮
助大家更好地掌握MATLAB的应用，我们为大家准备了一些习题与答案，希望
能够帮助大家更好地理解和掌握MATLAB的使用。

习题一：编写一个MATLAB程序，实现对给定矩阵的转置操作。

解答：可以使用MATLAB中的transpose函数来实现矩阵的转置操作。

例如，
对于一个3x3的矩阵A，可以使用以下代码实现转置操作：
A = [1 2 3; 4 5 6; 7 8 9];
B = transpose(A);
习题二：编写一个MATLAB程序，实现对给定矩阵的逆矩阵计算。

解答：可以使用MATLAB中的inv函数来实现对矩阵的逆矩阵计算。

例如，对
于一个3x3的矩阵A，可以使用以下代码实现逆矩阵计算：
A = [1 2 3; 4 5 6; 7 8 9];
B = inv(A);
习题三：编写一个MATLAB程序，实现对给定矩阵的特征值和特征向量计算。

解答：可以使用MATLAB中的eig函数来实现对矩阵的特征值和特征向量计算。

例如，对于一个3x3的矩阵A，可以使用以下代码实现特征值和特征向量计算：A = [1 2 3; 4 5 6; 7 8 9];
[V, D] = eig(A);
通过以上习题与答案的学习，相信大家对MATLAB的应用已经有了更深入的了
解。

希望大家能够多加练习，不断提升自己的MATLAB技能，为今后的工作和学习打下坚实的基础。

MATLAB作业6参考答案(修)

MATLAB 作业6参考答案（修）1、用图解的方式找到下面两个方程构成的联立方程的近似解。

（注：在图上可用局部放大的方法精确读出交点值）2223223,x y xy x x y y +=-=-【求解】这两个方程应该用隐式方程绘制函数ezplot() 来绘制，交点即方程的解。

>> ezplot('x^2+y^2-3*x*y^2');hold onezplot('x^3-x^2=y^2-y')可用局部放大的方法求出更精确的值。

从图上可以精确读出两个交点，(0:4012;¡0:8916)，(1:5894; 0:8185)。

试将这两个点分别代入原始方程进行验证。

2、在图形绘制语句中，若函数值为不定式NaN ，则相应的部分不绘制出来，试利用该规律绘制sin()z xy =的表面图，并剪切下2220.5x y +≤的部分。

【求解】给出下面命令可以得出矩形区域的函数值，再找出x 2 + y 2 <=0.5^2 区域的坐标，将其函数值设置成NaN ，最终得出所示的曲面。

>> [x,y]=meshgrid(-1:.1:1); z=sin(x.*y);ii=find(x.^2+y.^2<=0.5^2); z(ii)=NaN; surf(x,y,z)3、试用图解法求解下面的一元和二元方程，并验证得出的结果。

222(1)/2221)()sin(52),2)(,)()x x y xy f x e x f x y x y xy e π-++---=+=++【求解】①中给出的一元方程可以用曲线表示出来，这些曲线和y = 0 线的交点即为方程的解，可以用图形局部放大的方法读出这些交点的x 值，。

在本图中，xi 均为方程的解，若放大x 轴区域，则可能得出更多的解。

>> ezplot('exp(-(x+1)^2+pi/2)*sin(5*x+2)')②中的二元方程可以由下面的命令用图形的方式显示出来。

matlab简明教程第六章答案

m a t l a b简明教程第六章答案本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March第6章习题参考答案1. 假设x = [-3, 0, 0, 2, 5, 8]且y = [-5, -2,0, 3, 4, 10]。

通过手算得到以下运算的结果，并使用MATLAB检验计算的结果。

(1) z = y<~x(2)z = x&y(3) z = x|y(4) z = xor(x,y)参考答案： (1) z = [1, 1, 1, 0, 0, 0]；(2) z = [1, 0, 0, 1, 1, 1]；(3) z = [1, 1, 0, 1, 1, 1]；(4) z = [0, 1, 0, 0, 0, 0]2. 在MATLAB中使用一个循环确定：如果用户最初在一个银行帐户中存储$10000，并且在每年的年终再存储$10000(银行每年支付6%的利息)，那么账户上要积累$1000000要需要多长时间。

参考答案： 33年。

3.某个特定的公司生产和销售高尔夫手推车。

每周周末，公司都将那一周所生产的手推车转移到仓库(库存)之中。

卖出的所有手推车都是从库存中提取。

这个过程的一个简单模型为：I (k + 1) = P(k) + I (k) - S(k)其中：P(k) = 第k周所生产的手推车数量；I (k) = 第k周库存中的手推车数量；S(k) = 第k周所卖出的手推车数量；以下为10周计划中的每周销售额；假设每周的产量都基于前一周的销售额，所以有P(k) = S(k - 1)。

假设第一周的产量为50辆手推车：即，P(1) = 50。

编写一个MATLAB程序计算：10周之内每周库存之中的手推车数量或者计算手推车库存数量减少到0为止的时间，并同时绘制图形。

针对以下两种情况运行该程序：（1）初始库存为50辆手推车，所以I(1)= 50；（2）初始库存为30辆手推车，所以I (1) = 30。

MATLAB 课后部分答案

P77 第2章1、>> x=2;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)>> x=4;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)7、>> mat=rand(4,5);>> m=1;>> for i=1:2for j=1:5if mat(i,j)>0.3b(m)=mat(i,j);m=m+1;endendend>> b8、>> V=inv(A)>> A=rand(5,5);10、>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7]; >> C=A*B??? Error using ==> mtimesInner matrix dimensions must agree.>> C=A.*BC =5 16 24 -26-18 -12 -15 72-2 -21 108 -5611、>> x=linspace(0,2*pi,125);>> y=cos((x).*(0.5+3*sin(x)./(1+x.^2)));>> plot(x,y)13、>> x=-2:0.1:2;y=-2:0.1:2;>> [X,Y]=meshgrid(x,y);>> Z=X.^2.*exp(-X.^2-Y.^2);>> mesh(Z)建立一个M函数文件mycos.m，程序如下：function y=mycos(x)clear allx=input('请输入x的值')y=1./((x-2).^2+0.1)+1./((x-3).^3+0.01)在命令窗口输入：mycosP123 第3章1、>> x=[446 714 950 1422 1634];y=[7.04 4.28 3.40 2.54 2.13];>> xi=500:500:1500;>> yi=interp1(x,y,xi,'linear')4、>> p=[3 4 7 2 9 12];>> roots(p)8、>> a=[2 4 9;4 2 4;9 4 18];>> [V,D]=eig(a) %V的列向量是相应的特征向量,对角阵D的对角元素为a的特征值10、>> p1=[-1 4 0];p2=[-1 -4 0];>> A=polyder(p1);B=polyder(p2);>> A1=roots(A);B1=roots(B);>> y=4*A1-4*B1-A1.^2-B1.^213、>> syms x y>> Ex=int(int(x.*12.*y.^2,y,0,x),x,0,1)>> Ey=int(int(y.*12.*y.^2,x,y,1),y,0,1)>> Exy=Ex.*Ey14、>> A=rand(4,4);>> [L,U]=lu(A)>> [Q,R]=qr(A)P183 第4章1、>> n=-2*pi:0.01:2*pi;>> N=12;x=cos(n*pi./6);>> X=fft(x,N)>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> y=conv(xn,hn)4、>> n=0:11;h=0:5;>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> M=length(xn);N=length(hn);>> L=pow2(nextpow2(M+N-1));>> Xk=fft(xn,L);Hk=fft(hn,L);>> Yk=Xk.*Hk;>> yn=ifft(Yk,L)5、>> num=[2 3 0];den=[1 0.4 1];>> [z,p,k]=tf2zp(num,den)6、>> num=[4 15.6 6 2.4 -6.4];den=[3 2.4 6.3 -11.4 6]; >> [z,p,k]=tf2zp(num,den)>> zplane(z,p)7、>> num=[18 0 0 0];den=[18 3 -4 -1];>> [r,p,k]=residuez(num,den)9、建立一个M函数文件，程序如下：clear allN=10;[z,p,k]=buttap(N);[A,B,C,D]=zp2ss(z,p,k);wc1=100;wc2=200;[At,Bt,Ct,Dt]=lp2bp(A,B,C,D,wc1,wc2);[num1,den1]=ss2tf(At,Bt,Ct,Dt);[num2,den2]=impinvar(num1,den1);dimpulse(num2,den2)10、建立一个M函数文件，程序如下：clear allwp=100*2*pi;ws=200*2*pi;Rp=2;Rs=15;Fs=500;[N,Wc]=buttord(wp,ws,Rp,Rs,'s'); %选择滤波器的最小阶数[z,p,k]=buttap(N);[B,A]=zp2tf(z,p,k);[num,den]=bilinear(B,A,Fs); %模拟滤波器的传递函数转换为数字滤波器的传递函数freqz(num,den)11、建立一个M函数文件，程序如下：clear allN=48;w=[0.35,0.65];B=fir1(N,w,'bandpass'); %返回一个N阶的带通滤波器freqz(B) %绘制滤波器的频率响应曲线12、建立一个M函数文件，程序如下：clear allN=37;wc=0.3*pi;B=fir1(N,wc);freqz(B) %绘制滤波器的频率响应曲线13、建立一个M函数文件，程序如下：clear allN=55;F=[0:1/55:1];A=[ones(1,28),zeros(1,N-27)];B=fir2(N,F,A);freqz(B) %绘制滤波器的频率响应曲线15、建立一个M函数文件，程序如下：clear allwc=0.4*pi/(2*pi);N=12;[B,A]=butter(N,wc);%设计N阶截止频率为wc的Butterworth低通数字滤波器的传递函数模型m=dimpulse(B,A,101);stem(m,'.')P277 第6章2、建立一个M函数文件，程序如下：function [h,l]=huffmancode(P)if length(find(P<0))~=0,error('Not a prod.vector')endif abs(sum(P)-1)>10e-10error('Not a prod.vector')endn=length(P);for i=1:n-1for j=i:nif P(i)<=P(j)p=P(i);P(i)=P(j);P(j)=p;endendenddisp('概率分布'),PQ=P;m=zeros(n-1,n);for i=1:n-1[Q,l]=sort(Q);m(i,:)=[l(1:n-i+1),zeros(1,i-1)];Q=[Q(1)+Q(2),Q(3:n),1];endfor i=1:nc(i,:)=blanks(n*n);endc(n-1,n)='0';c(n-1,2*n)='1';for i=2:n-1c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))-(n-2):n*(find(m(n-i+1,:)==1)));c(n-1,n)='0';c(n-i,n+1:2*n-1)=c(n-i,1:n-1);c(n-i,2*n)='1';for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(m(n-i+1,:)==j+1)-1)+1:n*find(m(n-i+1,:)==j+1));endendfor i=1:nh(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32));endl=sum(P.*ll); %计算平均码长在命令窗口中输入：>> P=[0.20 0.15 0.13 0.12 0.1 0.09 0.08 0.07 0.06];>> [h,l]=huffmancode(P)3、建立一个M函数文件，程序如下：function[sqnr,a_quan,code]=u_pcm(a,n)% U_PCM 一个序列均匀的PCM编码.% n=量化级数的数目（偶数）.% sqnr=输入信号量化噪声比（偶数）。

matlab课后习题答案刘

matlab课后习题答案刘MATLAB课后习题答案刘在本学期的MATLAB课程中，我们学习了MATLAB的基础知识和一些高级功能。

为了帮助同学们更好地复习和巩固所学知识，以下是针对课后习题的一些参考答案。

1. 向量和矩阵的基本操作- 创建一个3x3的单位矩阵。

```matlabA = eye(3);```- 计算矩阵A和B的乘积，其中B是A的转置。

```matlabB = A';C = A * B;```2. 条件语句和循环- 编写一个循环，打印出1到10的所有奇数。

```matlabfor i = 1:2:10disp(i);end```- 编写一个条件语句，检查一个数是否为素数。

```matlabfunction isPrime(n)if n <= 1isPrime = false;elsefor i = 2:sqrt(n)if mod(n, i) == 0isPrime = false;return;endendisPrime = true;endend```3. 函数和脚本- 编写一个函数，计算给定半径的圆的面积。

```matlabfunction area = circleArea(radius)area = pi * radius^2;end```- 编写一个脚本来调用上述函数，并打印出半径为5的圆的面积。

```matlabradius = 5;disp(['Area of circle with radius ', num2str(radius), ' is ', num2str(circleArea(radius))]);```4. 数据结构和文件I/O- 读取一个文本文件中的数据到一个cell数组。

```matlabfilename = 'data.txt';fileID = fopen(filename, 'r');data = textscan(fileID, '%s');fclose(fileID);```- 将一个矩阵写入到一个CSV文件中。

matlab作业六参考答案

matlab作业六参考答案Matlab作业六参考答案在本次作业中，我们将探讨一些与Matlab相关的问题，并给出相应的参考答案。

希望这些答案能够帮助大家更好地理解和掌握Matlab的使用。

一、Matlab基础知识1. 什么是Matlab？Matlab是一种高级技术计算语言和环境，用于数值计算、数据分析和可视化。

它提供了丰富的函数库和工具箱，可以用于各种科学和工程计算任务。

2. 如何定义和访问矩阵？在Matlab中，可以使用方括号定义矩阵。

例如，A = [1 2 3; 4 5 6; 7 8 9]定义了一个3x3的矩阵A。

可以使用A(i, j)来访问矩阵中的元素，其中i和j分别表示行和列的索引。

3. 如何进行矩阵运算？Matlab提供了丰富的矩阵运算函数。

例如，可以使用*运算符进行矩阵乘法，A*B表示矩阵A和B的乘积。

还可以使用.+和.-运算符进行矩阵的逐元素相加和相减。

二、Matlab图形化界面1. 如何绘制函数图像？可以使用plot函数来绘制函数的图像。

例如，可以使用x = linspace(0, 2*pi, 100)生成一个包含100个点的从0到2π的等间距向量，然后使用y = sin(x)计算对应的正弦值，最后使用plot(x, y)绘制图像。

2. 如何设置图像的标题和坐标轴标签？可以使用title函数设置图像的标题，xlabel和ylabel函数设置坐标轴的标签。

例如，可以使用title('Sin Function')设置标题，xlabel('x')和ylabel('y')设置坐标轴的标签。

三、Matlab编程1. 如何定义函数？可以使用function关键字定义函数。

例如，可以使用以下语法定义一个计算两个数之和的函数：function sum = add(a, b)sum = a + b;end2. 如何调用函数？可以使用函数名和参数列表调用函数。

matlab课后习题参考答案

Matlab课后习题部分参考答案习题二2．student=struct('name',{'zhang','wang','li'},'age',{18,21,[] },'email',{['zh ang@','zhang@'],'',''})5、a=[1 0 0;1 1 0;0 0 1];b=[2 3 4;5 6 7;8 9 10];c=[a b]d=[a;b]c =1 0 023 41 1 0 5 6 70 0 1 8 9 10d =1 0 01 1 00 0 12 3 45 6 78 9 1010、reshape(c,2,9)1 0 1 0 1 5 3 9 71 0 0 02 8 6 4 10 reshape(d,2,9)ans =1 0 5 0 0 6 0 1 71 2 8 1 3 9 0 4 10 (注意：重新排列矩阵，是将原来的矩阵按列排序)11、a.’12、a+b a.*ba\b (即inv(a)*b，考试时，要求能自己手算出a的逆)ans =2 3 43 3 38 9 1013、c=4*ones(3);a>=cb>=c14．strcat('The picture is ','very good')a=['The picture is ','very good']18．double('very good')1．norm（A），det（A），rank（A）2．b=[1 1 1 1 1];c=b';a=[17,24,1,8,50;23,5,7,14,49;4,6,13,20,43;10,12,19,21,62;11,18,25,2,56]; x=a\c习题四1、a=14*rand(1,10)-5;for i=1:9max=i;for j=i+1:10if a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;enda将上述脚本保存为script41.m2、function y=function42(n)3*randn(1,n)+3;for i=1:n-1max=i;for j=i+1:nif a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;endy=a;将上述函数保存为function42.m 3、r=input(‘please input 1/2: ’);if r= =1script41;elsen=input(‘please input the length: ’);y=funtion42(n);end4．function f=function1(x,y)if y==1f=sin(x);elseif y==2f=cos(x);elsef=sin(x).*cos(x);end在命令窗口调用函数f=function1(1,3) 5．function result=function3(x,n)result=0;for i=1:nresult=result+sin(x.*i)+(-1).^i.*cos(i.*x); endfunction result=function4(n,t)result=0;A=[1 2 3;0 1 2;0 0 1];for i=1:nresult=result+A*i.*exp(A*i.*t);end习题五3．x1=-2:0.01:2;x2=-2:0.01:2;y1=x1.*sin(x2);y2=x2.*cos(x1);plot3(x1,x2,y 1,'-d',x1,x2,y2,'-d')14、x=8*rand(1,100)-2;y=reshape(x,10,10);save mydata.mat yclearclcload mydatak=y>ones(10);totel=0;for i=1:100if k(i)==1totel=totel+1;endend15、x=rand(5); %生成5*5均匀分布的随机矩阵（该处只作举例，未按题目要求）fid=fopen(‘text.txt’,’w’);count=fwrite(fid,x,’int32’); closestatus=fclose(fid);清除内存，关闭所有窗口fid=fopen(‘text.txt’,’r’);x=fread(fid,[5,5],’int32’); closestatus=fclose(fid); inv(x)16．随便生成一个矩阵，x1=-1:0.2:0.8;x2=-1:0.2:0.8;y1=x1.*sin(x2)；y2=x2.*cos(x1)；a=reshape([y1;y2],10,10)；fid=fopen('table.txt','w'); fprintf (fid,‘%f’，a); fclose(fid) ;清除内存，关闭所有窗口a=fscanf('table.txt','%f') ; exp(a) ;fclose(fid) ;习题六1.c=ploy2str(A)；B=[2,0,0,1,3,5]；2.x=1:10;B=ployval(A，x)；。

matlab习题6答案

matlab习题6答案Matlab习题6答案Matlab是一种广泛应用于科学计算和工程领域的高级编程语言和环境。

它以其强大的数值计算和数据可视化功能而闻名于世。

在Matlab的学习过程中，习题是提高编程技能和理解语言特性的重要方式。

在本文中，我将为大家提供Matlab习题6的答案，帮助大家更好地理解和掌握Matlab编程。

习题1：编写一个Matlab函数，计算给定向量的均值和标准差。

函数的输入参数为一个向量，输出为该向量的均值和标准差。

解答：```matlabfunction [mean_value, std_value] = calculate_stats(vector)mean_value = mean(vector);std_value = std(vector);end```习题2：编写一个Matlab函数，计算给定矩阵的特征值和特征向量。

函数的输入参数为一个矩阵，输出为该矩阵的特征值和特征向量。

解答：```matlabfunction [eigenvalues, eigenvectors] = calculate_eigen(matrix)[eigenvectors, eigenvalues] = eig(matrix);end```习题3：编写一个Matlab函数，计算给定矩阵的逆矩阵。

函数的输入参数为一个矩阵，输出为该矩阵的逆矩阵。

解答：```matlabfunction inverse_matrix = calculate_inverse(matrix)inverse_matrix = inv(matrix);end```习题4：编写一个Matlab函数，实现矩阵的转置操作。

函数的输入参数为一个矩阵，输出为该矩阵的转置矩阵。

解答：```matlabfunction transpose_matrix = calculate_transpose(matrix)transpose_matrix = matrix';end```习题5：编写一个Matlab函数，计算给定向量的累积和。

matlab课后练习习题及答案详解

matlab课后习题及答案详解第1章MATLAB概论与其余计算机语言对比较，MATLAB语言突出的特色是什么？MATLAB拥有功能强盛、使用方便、输入简捷、库函数丰富、开放性强等特色。

MATLAB系统由那些部分构成？MATLAB系统主要由开发环境、MATLAB数学函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。

安装MATLAB时，在选择组件窗口中哪些部分一定勾选，没有勾选的部分此后怎样补安装？在安装MATLAB时，安装内容由选择组件窗口中个复选框能否被勾选来决定，能够依据自己的需要选择安装内容，但基本平台（即MATLAB选项）一定安装。

第一次安装没有选择的内容在补安装时只要依据安装的过程进行，不过在选择组件时只勾选要补装的组件或工具箱即可。

MATLAB操作桌面有几个窗口？怎样使某个窗口离开桌面成为独立窗口？又怎样将离开出去的窗口从头搁置到桌面上？在MATLAB操作桌面上有五个窗口，在每个窗口的右上角有两个小按钮，一个是封闭窗口的Close按钮，一个是能够使窗口成为独立窗口的Undock 按钮，点击Undock按钮就能够使该窗口离开桌面成为独立窗口，在独立窗口的view菜单中选择Dock,,菜单项就能够将独立的窗口从头防备的桌面上。

怎样启动M文件编写/调试器？在操作桌面上选择“成立新文件”或“翻开文件”操作时，M文件编写/调试器将被启动。

在命令窗口中键入edit命令时也能够启动M文件编写/调试器。

储存在工作空间中的数组能编写吗？怎样操作？储存在工作空间的数组能够经过数组编写器进行编写：在工作空间阅读器中双击要编写的数组名翻开数组编写器，再选中要改正的数据单元，输入改正内容即可。

命令历史窗口除了能够察看前方键入的命令外，还有什么用途？命令历史窗口除了用于查问从前键入的命令外，还能够直接履行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中。

怎样设置目前目录和搜寻路径，在目前目录上的文件和在搜寻路径上的文件有什么差别？目前目录能够在目前目录阅读器窗口左上方的输入栏中设置，搜寻路径能够经过选择操作桌面的file菜单中的SetPath菜单项来达成。