吴淞至芜湖潮汐表
潮--汐

潮--汐潮汐地球上的海水受到月球、太阳的作用会发生有规律的升降运动。
这种海水周期性涨落运动的现象称为潮汐。
与潮汐现象同时发生的还有海水周期性的水平流动,叫做潮流。
尤其在靠近沿岸的岛屿、海峡和江河入海口附近,流向流速变化更为明显。
陆军船艇主要活动在岛礁区和浅水区,与潮汐有着十分密切的关系。
为了准确掌握时机通过浅水区、进出港湾、登退陆和利用潮流航行、靠离码头等,航海人员必须熟悉潮汐的变比规律及计算方法。
第一节潮汐成因及变化规律一、潮汐形成的原因潮汐现象主要是由于地球上的海水受到月球、太阳的共同作用而产生的。
其中由于月球距地球最近,作用也就最大。
我国劳动人民在长期的生产实践中早就发现潮汐现象和月球运行的密切关系,所谓“潮之兴也,与月盛衰”,“潮之涨落,皆系于月”的说法,就是对这种关系的认识。
下面着重讨论月球引潮力的作用。
(一)月球的吸引力万有引力定律指出:宇宙间任何两个物体之间都存在着相互吸引力,吸引力的大小和这两个物体质量的乘积成正比,和它们之间的距离的平方成反比。
由于万有引力的存在,所以月球对地球表面各点的海水都有吸引力,且引力的大小因距离的不同而不同。
距离近的地方比距离远的地方要大,但引力的方向都是指向月球球心的。
(2)月球绕月,地共有重心运动的离心力①向月处③地球表③指人们月球在一个太阴月(29.5天)内绕地球公转一周。
这一运动实际上是月球球心与地球球心都绕月,地共有重心旋转,月球转大圈,地球转小圈。
地共有重心位于距地心7/10地球半径处。
当地心绕g点运动时,地心与地球上任意一点的连线,都在作平行的移动。
也就是说,除地心外,地球上其它各点,都不是绕9运动,而是绕着各自的圆心以相同的半径运动。
地球表面各点的海水在绕各自的圆心旋转时受到一种离心力的作用,这种离心力的大小各处相等,方向都平行地背向月球。
(三)潮汐的形成月球的吸引力和地心绕月、地共有重心旋转的离心力的合力称为,月破己l潮力,地球各点引潮力的大小、方向是不同的,如图4-4所示。
吴淞VTS各航段报告频道
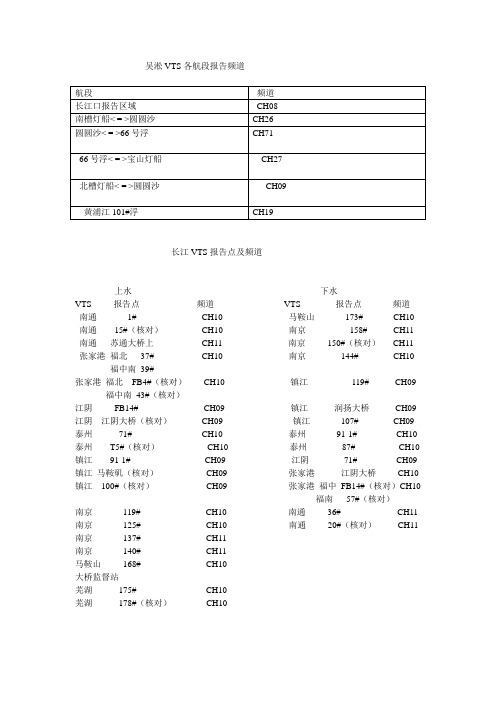
吴淞VTS各航段报告频道
航段频道
长江口报告区域CH08
南槽灯船< = >圆圆沙CH26
圆圆沙< = >66号浮CH71
66号浮< = >宝山灯船CH27
北槽灯船< = >圆圆沙CH09
黄浦江101#浮CH19
长江VTS报告点及频道
上水下水
VTS 报告点频道VTS 报告点频道
南通1# CH10 马鞍山173# CH10 南通15#(核对)CH10 南京158# CH11 南通苏通大桥上CH11 南京150#(核对)CH11 张家港福北37# CH10 南京144# CH10 福中南39#
张家港福北FB4#(核对)CH10 镇江119# CH09 福中南43#(核对)
江阴FB14# CH09 镇江润扬大桥CH09 江阴江阴大桥(核对)CH09 镇江107# CH09 泰州71# CH10 泰州91-1# CH10 泰州T5#(核对)CH10 泰州87# CH10 镇江91-1# CH09 江阴71# CH09 镇江马鞍矶(核对)CH09 张家港江阴大桥CH10 镇江100#(核对)CH09 张家港福中FB14#(核对)CH10
福南57#(核对)
南京119# CH10 南通36# CH11 南京125# CH10 南通20#(核对)CH11 南京137# CH11
南京140# CH11
马鞍山168# CH10
大桥监督站
芜湖175# CH10
芜湖178#(核对)CH10。
吴淞零点和吴淞高程系

吴淞与废黄河、黄海、八五基准点的关系:
1、吴淞=废黄河+1.763m;
2、吴淞=黄海+1.924m;
3、吴淞=八五基准+1.953m。
一、吴淞零点和吴淞高程系:清咸丰十年(1860年),海关巡工司在黄浦江西岸张华浜建立信号站,设置水尺,观测水位。
光绪九年(1883年)巡工司根据咸丰十年至光绪九年在张华浜信号站测得的最低水位作为水尺零点。
后又于光绪二十六年,根据同治十年至光绪二十六年(1871~1900年)在该站观测的水位资料,制定了比实测最低水位略低的高程作为水尺零点,并正式确定为吴淞零点(W.H.Z)。
以吴淞零点计算高程的称为吴淞高程系,上海历来采用这个系统。
民国11年(1922年),扬子江水利委员会技术委员会确定长江流域均采用吴淞高程系。
1951年,华东水利部规定,华东区水准测量暂时以吴淞零点为高程起算基准。
2:吴淞高程系与1956年黄海高程系的基面差。
江苏省水利厅于1953年以精密水准测量方法施测了佘苏线(佘山—苏州)、佘高线(佘山—金丝娘桥—高桥—张华浜)和佘张线(佘山—张华浜)等3条水准路线,观测高差纳入华东地区高程控制网,参加国家测绘总局主持的1957年中国东南部地区精密水准网平差。
平差后的水准点高程均为1956年黄海高程系,佘山水准基点既有黄海高程(44.4350米),又有吴淞高程(46.0647米),两者之差为1.6297米,即在上海地区吴淞高程系基面比1956年黄海高程系基面低1.6297米,远离上海的地区,同一点的两个高程值之差会略有不同。
3:1956黄海高程水准原点的高程是72.289米。
1985国家高程系统的水准原点的高程是72.260米。
长江下游镇江至吴淞段潮位相关途径预报方法
1 日平均 水 位 相 关 分 析
通 过分 析沿 江各 潮位 站 断面 日平 均水 位 的影 响因素 , 建立 日平 均水 位 的相 关方 程 .
1 1 日平均 水位 与大 通流 量 的相关 关 系 .
l 1 21 4l 6l 1 91 1 31 5l 7 81 5
要一定的传播时间才能影响本断面水位 )d为流量 与水 位之 间 不是线 性关 系 .
Da o g Sa o tn tt n i
收 稿 日期 : 0 10 — 7 2 1 —5 1
作者简 介:朱琰 (93 , , 16 一) 男 江苏无 锡人 , 副教 授 , 博士 , 主要从事工程水文及水资源研究 . -alhuy i 1 3. 0n Em i h z@vp 6 c r :
沿 江各 断 面整 点 潮位过 程 , 可取得 较 高的预 报 精度 .
关 键词 :潮位 预报 ; 差 因子 ; 潮 天文 潮位 ; 关分析 ; 相 长江 下游
中图分 类 号 :7 12 P 3 .3 文 献标 志码 : A 文章 编 号 :00 18 (0 10 一 67 0 10 —9 0 2 1 )6 O 0 — 5
D :0 3 7 / . s .0 0 18 .0 10 .0 OI 1 .8 6 ji n 10 —9 0 2 1 .6 0 3 s
长 江 下 游 镇 江 至 吴 淞 段 潮 位 相 关 途 径 预 报 方 法
朱 琰 , 水 艳 , 刚毅 , 林 程文辉
( 河海大学水文水资 源学 院 , 江苏 南京 209 ) 108
图 1 5个 站 的 日平 均 水 位 与 大 通 站 流量 过 程
F g Dal v r g t rlv l t i .1 i a e a e wa e e e a y i t t s a d ds h r eo f e sai n n ic a g f v o
2019年潮汐表

2019年潮汐表2019年的潮汐表预计将是复杂的,而潮汐之间的差别还会随着行星旋转带来变化。
以下是2019年潮汐表:1月份:1月1日,报潮时刻11:10,涨潮高度7.71米;1月16日,报潮时刻21:35,涨潮高度7.41米;1月31日,报潮时刻17:41,涨潮高度7.67米。
2月份:2月1日,报潮时刻00:23,涨潮高度7.89米;2月15日,报潮时刻10:37,涨潮高度7.67米;2月28日,报潮时刻19:50,涨潮高度7.66米。
3月份:3月1日,报潮时刻03:02,涨潮高度7.45米;3月15日,报潮时刻13:17,涨潮高度7.56米;3月30日,报潮时刻00:00,涨潮高度7.78米。
4月份:4月1日,报潮时刻04:48,涨潮高度7.64米;4月15日,报潮时刻14:55,涨潮高度7.72米;4月30日,报潮时刻02:04,涨潮高度7.81米。
5月份:5月1日,报潮时刻06:36,涨潮高度7.93米;5月15日,报潮时刻15:45,涨潮高度7.83米;5月31日,报潮时刻04:17,涨潮高度7.62米。
6月份:6月1日,报潮时刻08:26,涨潮高度7.39米;6月15日,报潮时刻17:41,涨潮高度7.62米;6月30日,报潮时刻05:22,涨潮高度7.77米。
7月份:7月1日,报潮时刻10:18,涨潮高度7.94米;7月15日,报潮时刻22:11,涨潮高度7.47米;7月31日,报潮时刻06:17,涨潮高度7.71米。
8月份:8月1日,报潮时刻12:10,涨潮高度7.78米;8月15日,报潮时刻00:01,涨潮高度7.45米;8月30日,报潮时刻08:38,涨潮高度7.74米。
9月份:9月1日,报潮时刻14:02,涨潮高度7.91米;9月15日,报潮时刻01:57,涨潮高度7.65米;9月30日,报潮时刻10:20,涨潮高度7.93米。
10月份:10月1日,报潮时刻15:56,涨潮高度7.74米;10月15日,报潮时刻03:50,涨潮高度7.70米;10月31日,报潮时刻12:07,涨潮高度7.84米。
85国家高程基准及高程系简介

85国家⾼程基准及⾼程系简介 85国家⾼程基准是指以青岛⽔准原点和青岛验潮站1952年到1979年的验潮数据确定的黄海平均海⽔⾯所定义的⾼程基准,其⽔准点起算⾼程为72.260⽶。
吴淞与废黄河、黄海、⼋五基准点的关系: 1、吴淞=废黄河+1.763m; 2、吴淞=黄海+1.924m; 3、吴淞=⼋五基准+1.953m。
⼀、吴淞零点和吴淞⾼程系:清咸丰⼗年(1860年),海关巡⼯司在黄浦江西岸张华浜建⽴信号站,设置⽔尺,观测⽔位。
光绪九年(1883年)巡⼯司根据咸丰⼗年⾄光绪九年在张华浜信号站测得的最低⽔位作为⽔尺零点。
后⼜于光绪⼆⼗六年,根据同治⼗年⾄光绪⼆⼗六年(1871~1900年)在该站观测的⽔位资料,制定了⽐实测最低⽔位略低的⾼程作为⽔尺零点,并正式确定为吴淞零点(W.H.Z)。
以吴淞零点计算⾼程的称为吴淞⾼程系,上海历来采⽤这个系统。
民国11年(1922年),扬⼦江⽔利委员会技术委员会确定长江流域均采⽤吴淞⾼程系。
1951年,华东⽔利部规定,华东区⽔准测量暂时以吴淞零点为⾼程起算基准。
⼆、吴淞⾼程系与1956年黄海⾼程系的基⾯差。
江苏省⽔利厅于1953年以精密⽔准测量⽅法施测了佘苏线(佘⼭—苏州)、佘⾼线(佘⼭—⾦丝娘桥—⾼桥—张华浜)和佘张线(佘⼭—张华浜)等3条⽔准路线,观测⾼差纳⼊华东地区⾼程控制⽹,参加国家测绘总局主持的1957年中国东南部地区精密⽔准⽹平差。
平差后的⽔准点⾼程均为1956年黄海⾼程系,佘⼭⽔准基点既有黄海⾼程(44.4350⽶),⼜有吴淞⾼程(46.0647⽶),两者之差为1.6297⽶,即在上海地区吴淞⾼程系基⾯⽐1956年黄海⾼程系基⾯低1.6297⽶,远离上海的地区,同⼀点的两个⾼程值之差会略有不同。
三、1956黄海⾼程⽔准原点的⾼程是72.289⽶。
1985国家⾼程系统的⽔准原点的⾼程是72.260⽶。
长江中下游干流吴淞高程系统概论

长江中下游干流吴淞高程系统概论高程控制是水利勘测、规划、设计以及工程建设的重要测绘基础工作,统一的高程系统和准确的高程成果尤其对堤防建设、水情测报、防汛调度至关重要。
吴淞高程系统自1900年建立以来,一直为长江的水位观测、防汛调度以及水利建设所采用。
1957年以青岛验潮站1950~1956年测定的平均海水面为基准面(零点),建立了“1956年黄海高程系统”。
1985年又以青岛验潮站1952~1979年潮汐观测计算的平均海水面为基准面,建立了“1985国家基准”以替代“1956年黄海高程系统”。
长江流域水利建设曾采用的高程系统繁多,但主要采用“吴淞高程系统”、“1956年黄海高程系统”和“1985国家高程基准”。
其中“1956年黄海高程系统”和“1985国家高程基准”为国家法定的高程系统,资料较为完善,但吴淞高程系统是长江流域所特有的,没有专门机构对其进行数据更新、维护。
考虑到吴淞高程系统在长江流域建设中起到的重要作用,有必要对吴淞高程系统建立、发展及目前存在的问题进行了解。
1 吴淞高程系统介绍采用上海吴淞口验潮站1871~1900年实测的最低潮位所确定的海面作为基准面,所建立的高程系统称为“吴淞高程系统”。
1.1 吴淞高程系统起源鸦片战争以后,1854年6月英、美、法驻沪公使、领事决定引进外国势力与征税机关,组织了关税管理委员会,由英、美、法三国领事与沪道缔结关于上海海关之约九条……于是就有了外国人管理我国海关之先河。
为了保证舰船安全通过吴淞内沙浅滩,旧海关就在长江口内东距海滨40余千米处的吴淞口设立了验潮站(又称测潮站),即吴淞口验潮站。
1871年或以前,旧海关(吴淞海关港务司署)设立吴淞零点水尺,供航行及测量之用,当时名“信号站”;自1871年起即有潮汛资料供给浚浦局,经长期记载定出1871~1900年之间出现的最低潮位为零点,当时称为“吴淞海关零点”简称“吴淞零点”,是吴淞零点高程系统的起算依据。
上海潮汐表

上海潮汐表(总3页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除上海潮汐表农历涨潮落潮涨潮落潮初九、二十四 07:12 13:24 19:36 01:48初十、二十五 08:00 14:12 20:24 02:36初十一、二十六 08:48 15:00 21:12 03:24初十二、二十七 09:36 15:48 22:00 04:12初十三、二十八 10:24 16:36 22:48 05:00初十四、二十九 11:12 17:24 23:36 05:48初十五、三十 12:00 18:12 00:24 06:36初一、十六 00:48 07:00 13:12 19:24初二、十七 01:36 07:48 14:00 20:12初三、十八 02:24 08:36 14:48 21:00初四、十九 03:12 09:24 15:36 21:48初五、二十 04:00 10:12 16:24 22:36初六、二十一 04:48 11:00 17:12 23:24初七、二十二 05:36 11:48 18:00 00:12初八、二十三 06:24 12:36 18:48 01:00以上数据会有些许误差,但基本准确,红色为最大潮时间(鱼进来机率最大),紫色为小潮时间(鱼进来机率最小)潮汐时间计算解析:1.地球各点地方时与太阳的关系:由于地球一刻不停地自西向东自转,一般来说,东边比西边先看到日出,也就是东边的时刻比西边时刻早。
古时候,各地都把当地太阳高度最大时刻定为12 点,因此各地的地方是不同的。
如右图,在此光照图上我们可以确定此图中任一点的地方时。
2.潮汐与太阳和月球的关系:海洋的潮汐现象是因月球和太阳的引力在地球上分布不均造成的。
引潮力是在地球朝向月球(或太阳)的一面和背向月球(或太阳)的一面同时发生的。
朝向月球和太阳一面形成的潮汐称顺潮,背向月球和太阳一面形成的潮汐称对潮。
长江下游镇江至吴淞段潮位相关途径预报方法

长江下游镇江至吴淞段潮位相关途径预报方法朱琰;水艳;林刚毅;程文辉【摘要】Base on the analysis of the factors that influence the daily average water level at the tidal stations along the Yangtze River, the correlation between the daily average water level at the tidal stations along the Yangtze River and the daily average discharge at Datong Station in upper Yangtze River was established by using the multiple linear regression equatipn. The Zhenjiang, Jiangyin, Xupu, Qipu, and Wusongkou tidal stations were selected for case study. The precision of the correlation equation was improved by adding the tidal range factor to the equation, considering that the daily average water level at the tidal stations along the Yangtze River was not only correlated with the daily average discharge at Datong Station in upper Yangtze River, but with the astronomical tide at Wusongkou Station. Based on the fact that there will be a decrease of the tidal range, phase delay, and tidal deformation when the tides at Wusongkou Station spread upstream, and the tidal ranges at the tidal stations along the Yangtze River are in close relation with the tidal range at Wusongkou Station and the discharge of the main stream of the Yangtze River, the correlation equation for the tidal range was established. The results show a high precision in forecasting the tidal level processes at the sections along the Yangtze River with the correlation analysis method.%选择镇江、江阴、浒浦、七浦、吴淞口等潮位站为研究对象,通过分析沿江各潮位站日平均水位的影响因素,利用多元线性回归建立了沿江各站日平均水位与上游大通站日平均流量过程的相关关系;在此基础上,考虑到沿江各站日平均水位除了与上游大通站流量有关外,还与吴淞口天文潮的大小有关,增加了能够反映潮差大小的相关因子,有效提高了相关方程的精度.由于吴淞口潮汐向上游传播时会产生潮差减小、相位后移、潮汐变形等水力现象,沿江各站的潮差大小与吴淞口潮差大小及长江干流的流量有密切关系,建立了相应的潮差相关方程.通过此相关途径方法来预报沿江各断面整点潮位过程,可取得较高的预报精度.【期刊名称】《河海大学学报(自然科学版)》【年(卷),期】2011(039)006【总页数】5页(P607-611)【关键词】潮位预报;潮差因子;天文潮位;相关分析;长江下游【作者】朱琰;水艳;林刚毅;程文辉【作者单位】河海大学水文水资源学院,江苏南京210098;河海大学水文水资源学院,江苏南京210098;河海大学水文水资源学院,江苏南京210098;河海大学水文水资源学院,江苏南京210098【正文语种】中文【中图分类】P731.23长江下游镇江至吴淞段潮位预报问题通常可以采用两种途径来解决:一是通过水动力学方法[1],即取大通断面流量作为长江下游干流的上边界条件,取吴淞口(南支)及三条巷(北支)潮位为下边界条件,并假定大通以下没有大支流汇入,除了与太湖流域有水量交换外,假定与其他地区无水量交换进行计算.该方法由于缺乏大量的长江下游干流实测大断面资料以及不考虑区间的水量交换,使得计算断面的水位精度较低[2].二是通过相关途径方法预报沿江潮位.为了使相关分析的物理概念比较清晰,将沿江潮位分解为两部分,一部分受上游大通流量影响[3],另一部分受下游吴淞口潮汐影响.本文利用吴淞口天文潮位预报结果[4-10]和大通站日平均流量,通过相关途径方法来预报沿江各站整点潮位过程.1 日平均水位相关分析通过分析沿江各潮位站断面日平均水位的影响因素,建立日平均水位的相关方程.1.1 日平均水位与大通流量的相关关系计算镇江至吴淞口沿江各潮位站断面的日平均水位,该水位基本上滤掉了吴淞口潮汐影响.1999年6月1日至8月31日镇江、江阴、浒浦、七浦和吴淞口沿江5个站的日平均水位及大通流量过程如图1所示.由图1可见,越是上游潮位站受长江上游来水影响越大.采用多元线性回归分析建立各断面日平均水位与大通流量的相关关系,则多元线性回归方程为式中:Z(t)——某站日平均水位,m;Q——大通站流量,m3/s;t——时间,d;ai(i=1,2,…,n)——系数;k——滞后时间(因为大通站流量需要一定的传播时间才能影响本断面水位),d;n——采用的相关天数,d;p——指数,因为流量与水位之间不是线性关系.图1 5个站的日平均水位与大通站流量过程Fig.1 Daily average water level at five stations and discharge of Datong Station经初步优化分析决定采用参数为:k=2d;n=4 d;p=0.05.相关方程式(1)中各站的相关系数如表1所示.1.2 相关方程式(1)的精度根据上述的参数和相关系数,计算沿江各站的日平均水位,并与实测日平均水位比较,如图2所示.各站的计算日平均水位与实测水位之间的均方差及相关系数分别为:镇江0.187m 和0.970,江阴0.170m和0.874,浒浦0.178m和0.666,七浦0.111m和0.789,吴淞口0.187m和0.762.表1 相关方程式(1)中各站的相关系数Tab le 1 Correlation coefficients in Eq.(1)for five stations镇江 -52.220 75.700 36.890 -17.850-40.750江阴 -19.990 37.200 14.830 -12.870-17.000浒浦 -8.481 25.850 5.194 -7.449-12.680七浦 -8.419 14.410 3.002 -4.069 -2.894吴淞口 -5.326 11.990 -0.951 -2.487 -1.184图2 沿江各站计算(式(1))与实测日平均水位过程Fig.2 Calculated(through Eq.(1))and measured daily average water levels at five stations1.3 影响日平均水位的其他因素从图2和各站的计算日平均水位与实测水位之间的均方差及相关系数可见,沿江各站日平均水位与大通流量的关系以镇江最为明显,相关系数亦最高,向下游相关系数逐渐减小,但浒浦站例外.特别值得注意的是吴淞口日平均水位与长江来水有一定的相关关系,吴淞口的水位不完全受天文潮[10-12]的影响.从七浦、浒浦、江阴日平均水位过程线可以发现有明显的周期约为14 d的波动,与大、小潮有关.为此,将上述3站潮位过程与日平均水位绘在同一图上,如图3所示.由图3可见,大潮期间日平均水位高,小潮期间日平均水位低.这是因为,大潮时潮流量大,落潮时水面比降大,潮位过程的低潮位区抬高而引起日平均水位抬高之故.吴淞口站主要受天文潮影响,镇江站潮流量已不大,因此大、小潮对日平均水位影响不明显.显然,沿江各站日平均水位除了与上游大通站流量有关外,还与吴淞口天文潮的大小有关.因此相关方程(1)中需要增加能反映潮差大小的相关因子,变为图3 各站潮位过程和日平均水位Fig.3 Tidal levels and daily average water levels at five stations式中,F(t)为能反映t时刻潮差大小的一个因子.由于潮汐自吴淞口传播到浒浦约3h,到江阴约4h,到镇江有8~10h,因此只取当天的潮差因子.可以取当天的潮差作为F(t),亦可以取其他类似的指标作为F(t),例如:式中:Zj——吴淞口整点潮位,m;Z0——吴淞口日平均水位,m.本文取方程(3)作为F(t)指标.相关方程式(2)中各站的相关系数如表2所示.1.4 相关方程式(2)的精度根据表2中的相关系数,计算沿江各站日平均水位,并与实测日平均水位比较,如图4所示.表2 相关方程式(2)中各站的相关系数Table 2 Correlation coefficients in Eq.(2)for five stations镇江 -52.203 70.556 41.135-14.790-43.247 0.415江阴 -20.003 31.716 18.186 -7.854-20.371 0.641浒浦 -8.507 20.443 8.210 -2.072-16.171 0.679七浦 -8.432 11.276 4.958 -1.188-4.859 0.355吴淞口 -5.332 10.025 0.437 -0.803-2.428 0.189图4 沿江各站计算(式(2))与实测日平均水位过程Fig.4 Calculated(through Eq.(2))and measured daily average water levels at five stations由图4可见,相关方程中增加反映潮差因子后精度有明显提高.从图4可以发现吴淞口日平均水位与长江干流的径流量及大小潮有关,并非纯粹的天文潮.各站的计算日平均水位与实测日平均水位之间的均方差及相关系数分别为:镇江0.161m和0.978,江阴0.085m和0.971,浒浦0.079m和0.944,七浦0.073m和0.915,吴淞口0.073m和0.834.2 潮差相关分析吴淞口潮汐向上游传播时,会产生潮差减小、位相后移、潮汐变形,即涨潮变陡、落潮变平缓等水力现象.上游某站的潮差大小,首先与吴淞口潮差大小有关,其次是长江干流的流量.显然,长江干流流量越大,潮差衰退越快.因此,上游某站的潮差可用以下相关方程表示:式中:F s(t)——上游某站潮差,m;F0(t)——吴淞口潮差,m.经初步优化分析,采用参数为:k=2d;n=4d;p=0.25.相关方程式(4)中各站的相关系数如表3所示.表3 相关方程(4)中各站的相关系数Tab le 3 Correlation coefficients inEq.(4)for five stations站名 a0 a1 a2 a3 a4 a5镇江 0.987 0.112 -1.379 -0.464 0.971 0.346江阴 0.032 0.181 -0.591 -0.267 0.571 0.768浒浦 -1.048 -0.783 0.121 -1.472 2.887 0.775七浦 -0.756 0.322 -0.413 0.115 0.466 0.918吴淞口 0 0 0 0 0 1根据上述的参数和系数,计算沿江各站潮差,并与实测日潮差比较,如图5所示.各站的计算潮差与实测潮差之间的均方差及相关系数分别为:镇江0.069m和0.964,江阴0.068m和0.996,浒浦0.127m和0.975,七浦0.057m和0.996.图5 沿江各站计算(式(4))与实测潮差过程Fig.5 Calculated(through Eq.(4))and measured tidal ranges at five stations3 潮汐传播时间分析潮汐向上游传播时高潮传播时间略短,低潮传播时间略长,因此引起潮汐变形,潮汐越向上游,涨潮历时越短,落潮历时越长.但对沿江口门引排水而言,重要的是平均水位和潮差.为了简单起见,不考虑潮汐变形,潮汐传播时间亦取整点值,潮汐传播时间分别为:吴淞口至七浦为1h,七浦至浒浦为1h,浒浦至江阴为2h,江阴至镇江为4h.4 沿江各站潮位过程预报综上所述,根据吴淞口天文潮调和常数计算出吴淞口整点天文潮位过程线.吴淞口日平均水位受长江来水和潮差影响,因此取反映海平面平均水位的常数项为零,仅计算潮汐过程.根据式(3)计算吴松口潮差指标F(t),根据相关方程式(2)计算沿江各潮位站日平均水位,根据相关方程式(4)计算沿江各潮位站潮差,过程线形状借用吴淞口天文潮位过程,得各潮位站“天文潮位”过程.将各潮位站平均水位与“天文潮位”过程叠加得沿江各潮位站整点潮位过程.根据传播时间将各潮位站的整点潮位过程向后推移,即得沿江各站的预报潮位过程线.5 结语由于长江下游镇江至吴淞段潮位受潮汐和长江上游径流量影响,对于沿江各站潮位预报问题,吴淞口潮位预报是关键的一环,因为黄浦江的泄流与吴淞口潮位密切相关,而且吴淞口上游沿江各断面潮位也由吴淞口潮位推算而得.吴淞口潮位站处于长江口和黄浦江口,除了天文潮外还受长江和黄浦江径流量的影响,但相对于天文潮而言,径流量的影响很微弱.通过计算结果与实测数据比较分析,采用的相关途径方法具有较高的模拟预报精度,可以用于预报沿江各断面潮位过程.该方法已在太湖流域洪水预报调度系统中得到了应用.参考文献:【相关文献】[1]严以新,刘均卫,吴德安,等.长江口综合整治工程前后潮汐特征分析[J].河海大学学报:自然科学版,2009,37(1):100-104.(YAN Yi-xin,LIU Jun-wei,WU De-an,et al.Analysis of tidal characteristics before and after construction of regulation projects in Yangtze River estuary[J].Journal of Hohai University:Natural Sciences,2009,37(1):100-104.(in Chinese)) [2]赵人俊.水文预报文集[M].北京:水利电力出版社,1994.[3]李国芳,谭亚,张秀菊.感潮河段上游流量对潮位预报的影响[J].河海大学学报:自然科学版,2006,34(2):144-147.(LI Guo-fang,TAN Ya,ZHANG Xiu-ju.Influence of upstream discharge in tidal level prediction for tidal reaches[J].Journal of Hohai University:Natural Sciences,2006,34(2):144-147.(in Chinese))[4]方国洪,郑文振,陈宗镛,等.潮汐和潮流的分析和预报[M].北京:海洋出版社,1986.[5]方国洪.潮汐分析和预报的准调和分潮方法:Ⅰ.准调和分潮[J].海洋科学集刊,1974,9:1-15.(FANG Guo-hong.Quasiharmonic constituent method for analysis and prediction oftides:Ⅰ.quasi-harmonic constituent[J].Studia Marina Sinica,1974,9:1-15.(in Chinese)) [6]方国洪.潮汐分析和预报的准调和分潮方法:Ⅱ.短期观测的分析[J].海洋科学集刊,1976,11:33-56.(FANG Guo-hong.Quasi-harmonic constituent method for analysis and prediction of tides:Ⅱ.analysis of short-term observationt[J].Studia Marina Sinica,1976,11:33-56.(in Chinese))[7]方国洪.潮汐分析和预报的准调和分潮方法:Ⅲ.潮流和潮汐分析的一个实际计算过程[J].海洋科学集刊,1981,18:19-39.(FANG Guo-hong.Quasi-harmonic constituent method for analysis and prediction of tides:Ⅲ.a calculational method of tidal current and tide analysis[J].Studia Marina Sinica,1981,18:19-39.(in Chinese))[8]王骥,方国洪.不完整逐时潮汐观测记录的分析[J].海洋学报:中文版,1981(2):193-210.(WANG Ji,FANG Guo-hong.An analysis of incomplete hourly tidal records[J].Acta Oceanologica Sinica,1981(2):193-210.(in Chinese))[9]陈宗镛.潮汐学[M].北京:科学出版社,1980.[10]王莹辉,谭亚.近17年福建沿海台风及风暴增水特性统计分析[J].河海大学学报:自然科学版,2008,36(3):384-389.(WANG Ying-hui,TAN Ya.Characteristic analysis of the typhoons and storm surgesin the Fujian coastal area over the past 17 years[J].Journal of Hohai University:Natural Sciences,2008,36(3):384-389.(in Chinese))[11]SMITH L H,CHEN R T.Tidal and tidally averged circulation characteristics of Suisun Bay,Califorlia[J].Water Resources Research,1987,23(1):143-155.[12]AMIN M.The fine resolution of tidal harmonics[J].Geophysical Journal of the Royal Astronomical Society,1976(2):293-310.。
吴淞高程

吴淞与废黄河、黄海、八五基准点的关系:1、吴淞=废黄河+1.763m;2、吴淞=黄海+1.924m;3、吴淞=八五基准+1.953m。
一、吴淞零点和吴淞高程系:清咸丰十年(1860年),海关巡工司在黄浦江西岸张华浜建立信号站,设置水尺,观测水位。
光绪九年(1883年)巡工司根据咸丰十年至光绪九年在张华浜信号站测得的最低水位作为水尺零点。
后又于光绪二十六年,根据同治十年至光绪二十六年(1871~1900年)在该站观测的水位资料,制定了比实测最低水位略低的高程作为水尺零点,并正式确定为吴淞零点(W.H.Z)。
以吴淞零点计算高程的称为吴淞高程系,上海历来采用这个系统。
民国11年(1922年),扬子江水利委员会技术委员会确定长江流域均采用吴淞高程系。
1951年,华东水利部规定,华东区水准测量暂时以吴淞零点为高程起算基准。
2:吴淞高程系与1956年黄海高程系的基面差。
江苏省水利厅于1953年以精密水准测量方法施测了佘苏线(佘山—苏州)、佘高线(佘山—金丝娘桥—高桥—张华浜)和佘张线(佘山—张华浜)等3条水准路线,观测高差纳入华东地区高程控制网,参加国家测绘总局主持的1957年中国东南部地区精密水准网平差。
平差后的水准点高程均为1956年黄海高程系,佘山水准基点既有黄海高程(44.4350米),又有吴淞高程(46.0647米),两者之差为1.6297米,即在上海地区吴淞高程系基面比1956年黄海高程系基面低1.6297米,远离上海的地区,同一点的两个高程值之差会略有不同。
3:1956黄海高程水准原点的高程是72.289米。
1985国家高程系统的水准原点的高程是72.260米。
关于56黄海高程、85国家高程、吴淞高程之间的关系85国家高程基准85国家高程基准是指以青岛水准原点和青岛验潮站1952年到1979年的验潮数据确定的黄海平均海水面所定义的高程基准,其水准点起算高程为72.260米。
54北京坐标系54北京坐标系即54国家坐标系,采用克拉索夫斯基椭球参数。
长江中下游干流吴淞高程系统概论

⾼程控制是⽔利勘测、规划、设计以及⼯程建设的重要测绘基础⼯作,统⼀的⾼程系统和准确的⾼程成果尤其对堤防建设、⽔情测报、防汛调度⾄关重要。
吴淞⾼程系统⾃1900年建⽴以来,⼀直为长江的⽔位观测、防汛调度以及⽔利建设所采⽤。
1957年以青岛验潮站1950~1956年测定的平均海⽔⾯为基准⾯(零点),建⽴了“1956年黄海⾼程系统”。
1985年⼜以青岛验潮站1952~1979年潮汐观测计算的平均海⽔⾯为基准⾯,建⽴了“1985国家基准”以替代“1956年黄海⾼程系统”。
长江流域⽔利建设曾采⽤的⾼程系统繁多,但主要采⽤“吴淞⾼程系统”、“1956年黄海⾼程系统”和“1985国家⾼程基准”。
其中“1956年黄海⾼程系统”和“1985国家⾼程基准”为国家法定的⾼程系统,资料较为完善,但吴淞⾼程系统是长江流域所特有的,没有专门机构对其进⾏数据更新、维护。
考虑到吴淞⾼程系统在长江流域建设中起到的重要作⽤,有必要对吴淞⾼程系统建⽴、发展及⽬前存在的问题进⾏了解。
1 吴淞⾼程系统介绍 采⽤上海吴淞⼝验潮站1871~1900年实测的最低潮位所确定的海⾯作为基准⾯,所建⽴的⾼程系统称为“吴淞⾼程系统”。
1.1 吴淞⾼程系统起源 鸦⽚战争以后,1854年6⽉英、美、法驻沪公使、领事决定引进外国势⼒与征税机关,组织了关税管理委员会,由英、美、法三国领事与沪道缔结关于上海海关之约九条……于是就有了外国⼈管理我国海关之先河。
为了保证舰船安全通过吴淞内沙浅滩,旧海关就在长江⼝内东距海滨40余千⽶处的吴淞⼝设⽴了验潮站(⼜称测潮站),即吴淞⼝验潮站。
1871年或以前,旧海关(吴淞海关港务司署)设⽴吴淞零点⽔尺,供航⾏及测量之⽤,当时名“信号站”;⾃1871年起即有潮汛资料供给浚浦局,经长期记载定出1871~1900年之间出现的最低潮位为零点,当时称为“吴淞海关零点”简称“吴淞零点”,是吴淞零点⾼程系统的起算依据。
约在1900年,在黄浦江⼝左岸附近的吴淞海关港务司署内设⽴⼀个⼟中⽯质⽔准基点,测定⽯质⽔准基点的吴淞零点⾼程作为基准。
吴淞高程

1.1 吴淞高程系统起源鸦片战争以后,1854年6月英、美、法驻沪公使、领事决定引进外国势力与征税机关,组织了关税管理委员会,由英、美、法三国领事与沪道缔结关于上海海关之约九条……于是就有了外国人管理我国海关之先河。
为了保证舰船安全通过吴淞内沙浅滩,旧海关就在长江口内东距海滨40余千米处的吴淞口设立了验潮站(又称测潮站),即吴淞口验潮站。
1871年或以前,旧海关(吴淞海关港务司署)设立吴淞零点水尺,供航行及测量之用,当时名“信号站”;自1871年起即有潮汛资料供给浚浦局,经长期记载定出1871~1900年之间出现的最低潮位为零点,当时称为“吴淞海关零点”简称“吴淞零点”,是吴淞零点高程系统的起算依据。
约在1900年,在黄浦江口左岸附近的吴淞海关港务司署内设立一个土中石质水准基点,测定石质水准基点的吴淞零点高程作为基准。
1.2 吴淞高程系统基准点的变迁每一个高程系统均须有一水准原点,并依据基准面决定水准原点高程,以作为高程控制网的起算点,为与国家高程系统的水准原点相区别,吴淞高程系统的水准原点改称为基准点(基点)。
基准点的点位须稳定,标志要能长期保存。
由于上海地区地面沉陷,致使吴淞高程系统几易基点,了解基点的变迁,对正确使用吴淞高程系统的高程资料是很有裨益的。
1.2.1 张华浜基点的设置1921年浚浦局在距海关吴淞信号站基准标石不到300m处,打入一根7.32m长的钢筋混凝土桩,桩顶嵌有铜头,地面筑成阴井,加水泥盖板。
测得高程为吴淞零点5.1054m。
该点称之为“张华浜基点”。
由于该点距离长江江岸较近,1922年扬子江技术委员会就从此点出发,引测而上直至宜昌,测程近1800km,成为长江流域普遍使用的吴淞高程系统。
这个“基点”一直使用到20世纪50年代初期。
由于确定该点已随上海陆地沉降而发生严重沉陷,因此失去作为水准“基点”的作用。
1.2.2 佘山基点的设测1922年6月,浚浦局在长江三角洲冲积平原外,离吴淞约60km的松江县西北面的佘山半坡天主教堂右侧天然岩石石壁上,用水泥镶嵌一个直径76.2mm、长约254mm 的铜棒(露出端部分为圆球状),作为永久性的吴淞水准基点,其上附设有铜牌,刻有“浚浦局佘山水准基点”文字,其顶部高程为吴淞零点上46.0647m。
85、黄海、吴淞高程之间的关系及由来

黄海高程系翁克勤2016年7月黄海高程系1,潮汐现象与海平面1.1,潮汐现象潮汐现象是沿海地区的一种自然现象,指海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动,习惯上把海面垂直方向涨落称为潮汐,而海水在水平方向的流动称为潮流。
古人把发生在早晨的高潮叫潮,发生在晚上的高潮叫汐。
这是潮汐的名称的由来。
图1 月光下的潮汐由于海潮现象十分明显,并且与人们的生活、经济活动、交通运输等关系密切,因而习惯上将潮汐(tide)一词狭义地理解为海洋潮汐。
日球、月球引潮力作用下引起的海面周期性的升降与海水的流动,称海洋潮汐,简称海潮。
图2 潮汐示意图1.2,潮汐类型按照涨落次数和潮高,一般将潮汐分为:半日潮、混合潮(含不规则半日潮和不规则日潮)、日潮。
半日潮型:一个太阴日内出现两次高潮和两次低潮,前一次高潮的潮高与后一次高潮的潮高大致相近,涨潮历时和落潮历时的时间也比较接近,约6小时12分钟。
一年内大约出现705个潮次。
一个太阴日指月球绕地球一周的时间,约24小时50分钟。
在我国渤海、黄海与东海沿岸,一般每日涨落两次,潮高比较接近,称为半日潮。
比如天津大沽、青岛、厦门等。
日潮型:一个太阴日内经常只出现一次高潮和一次低潮,出现半日潮的天数相对比较少。
比如在广西北部湾沿岸的北海港、龙门港,是世界上比较典型的全日潮海区。
混合潮型:细分为不规则半日潮与不规则日潮两类。
前者为一月内经常出现两次高潮和两次低潮,但两次高潮和低潮的潮差相差较大,涨潮历时和落潮历时也有长有短;后者为一月内有些日子出现两次高潮和两次低潮,又有些日子出现一次高潮和一次低潮。
我国南海地区多数属于型。
比如海口属于不规则日潮(F = 3.92),一年内全日潮天数约200天,其余约160天出现不规则半日潮,1980年时全年出现518个潮次。
湛江港(F = 0.82 )属于不规则半日潮。
潮汐研究中发现:潮波可以分解成很多半日分潮与日分潮之和,其中最主要的半日分潮为H M2,日分潮为H K1和H O1。
