人教版高中数学必修4课后习题答案
高中数学必修4习题和复习参考题对应答案
高中数学必修4习题和复习参考题及对应答案
A 组
1、在0°～360°范围内，找出与下列各角终边相同的角，并指出它们是哪个象限的角： （1）－265°；（2）－1000°；（3）－843°10′；（4）3900°． 答案：（1）95°，第二象限； （2）80°，第一象限； （3）236°50′，第三象限； （4）300°，第四象限．
说明：能在给定范围内找出与指定的角终边相同的角，并判定是第几象限角．
2、写出终边在x 轴上的角的集合． 答案：S={α|α=k ·180°，k ∈Z }．
说明：将终边相同的角用集合表示．
3、写出与下列各角终边相同的角的集合，并把集合中适合不等式－360°≤β＜360°的元素β写出来：
（1）60°；（2）－75°；（3）－824°30′；（4）475°；（5）90°；（6）270°；（7）180°；（8）0°．
答案：（1）{β|β=60°＋k ·360°，k ∈Z }，－300°，60°； （2）{β|β=－75°＋k ·360°，k ∈Z }，－75°，285°； （3）{β|β=－824°30′＋k ·360°，k ∈Z }，－104°30′，255°30′； （4）{β|β=475°＋k ·360°，k ∈Z }，－245°，115°； （5）{β|β=90°＋k ·360°，k ∈Z }，－270°，90°； （6）{β|β=270°＋k ·360°，k ∈Z }，－90°，270°； （7）{β|β=180°＋k ·360°，k ∈Z }，－180°，180°； （8）{β|β=k ·360°，k ∈Z }，－360°，0°． 说明：用集合表示法和符号语言写出与指定角终边相同的角的集合，并在给定范围内找出与指定的角终边相同的角．
人教版A版高中数学必修4课后习题解答
第一章 三角函数 1．1任意角和弧度制 练习（P5）
1、锐角是第一象限角，第一象限角不一定是锐角；直角不属于任何一个象限，不属于任何一个象限的角不一定是直角；钝角是第二象限角，第二象限角不一定是钝角.
2、三，三，五
说明：本题的目的是将终边相同的角的符号表示应用到其他周期性问题上. 题目联系实际，把教科书中的除数360换成每个星期的天数7，利用了“同余”（这里余数是3）来确定7k 天后、7k 天前也是星期三，这样的练习不难，可以口答. 3、（1）第一象限角； （2）第四象限角； （3）第二象限角； （4）第三象限角. 4、（1）305°42′第四象限角；（2）35°8′第一象限角；（3）249°30′第三象限角. 5、（1）{130318+360,}k k Z ββ'=︒⋅︒∈，49642'-︒，13642'-︒，22318'︒； （2）{225+360,}k k Z ββ=-︒⋅︒∈，585-︒，225-︒，135︒. 练习（P9）
1、（1）
8π
； （2）76π-
； （3）203
π
.
2、（1）15°；（2）240-︒； （3）54°.
3、（1）{,}k k Z ααπ=∈； （2）{,}k Z απ∈.
4、（1）cos0.75cos0.75︒>； （2）. 说明：体会同数值不同单位的角对应的三角函数值可能不同，并进一步认识两种单位制. 注意在用计算器求三角函数值之前，要先对计算器中角的模式进行设置. 如求cos0.75︒之前，要将角模式设置为DEG （角度制）；求cos0.75之前，要将角模式设置为RAD （弧度制）.
高中数学必修4习题和复习参考题及对应答案
高中数学必修4习题和复习参考题及对应答案
A组
1、在0°～360°范围内，找出与下列各角终边相同的角，并指出它们是哪个象限的角：
（1）－265°；（2）－1000°；（3）－843°10′；（4）3900°．
答案：（1）95°，第二象限；
（2）80°，第一象限；
（3）236°50′，第三象限；
（4）300°，第四象限．
说明：能在给定范围内找出与指定的角终边相同的角，并判定是第几象限角．
2、写出终边在x轴上的角的集合．
答案：S={α|α=k·180°，k∈Z}．
说明：将终边相同的角用集合表示．
3、写出与下列各角终边相同的角的集合，并把集合中适合不等式－360°≤β＜360°的元素β写出来：
（1）60°；（2）－75°；（3）－824°30′；（4）475°；（5）90°；（6）270°；（7）180°；（8）0°．
答案：（1）{β|β=60°＋k·360°，k∈Z}，－300°，60°；
（2）{β|β=－75°＋k·360°，k∈Z}，－75°，285°；
（3）{β|β=－824°30′＋k·360°，k∈Z}，－104°30′，255°30′；
（4）{β|β=475°＋k·360°，k∈Z}，－245°，115°；
（5）{β|β=90°＋k·360°，k∈Z}，－270°，90°；
（6）{β|β=270°＋k·360°，k∈Z}，－90°，270°；
（7）{β|β=180°＋k·360°，k∈Z}，－180°，180°；
（8）{β|β=k·360°，k∈Z}，－360°，0°．
说明：用集合表示法和符号语言写出与指定角终边相同的角的集合，并在给定范围内找出与指定的角终边相同的角．
人教版高中数学必修四课后习题答案详解
数学必修4课后习题答案
第二章平面向量
2．1平面向量的实际背景及基本概念
练习（P77）
1、略.
2、AB，BA. 这两个向量的长度相等，但它们不等.
3、2
AB =， 2.5
CD=，3
EF =，22
GH=
4、（1）它们的终点相同；（2）它们的终点不同.习题2.1 A组（P77）
1、
（2
）
.
3、与DE相等的向量有：,
AF FC；与EF相等的向量有：,
BD DA；
与FD相等的向量有：,
CE EB.
4、与a相等的向量有：,,
CO QP SR；与b相等的向量有：,
PM DO；
与c 相等的向量有：,,DC RQ ST
5、33AD =、（1）×； （2）√； （3）
√； （4）×.
习题2.1 B 组（P78） 1、海拔和高度都不是向量.
2、相等的向量共有24对. 模为1的向量有18对. 其中与AM 同向的共有6对，与AM 反向的也有6对；与
AD 同向的共有3对，与AD 反向的也有6对；的向量共有4对；模为2的向量有2对 2．2平面向量的线性运算 练习（P84）
1、图略.
2、图略.
3、（1）DA ； （2）
CB .
4、（1）c ； （2）f ； （3）f ； （4）g . 练习（P87）
1、图略.
2、DB ，CA ，AC ，AD ，BA .
3、图略.
练习（P90） 1、图略.
2、57
AC AB =，27
BC AB =-.
说明：本题可先画一个示意图，根据图形容易得出
水流方向
C
D
A B 正确答案. 值得注意的是BC 与AB 反向.
3、（1）2b a =； （2）74b a =-； （3）12b a =-； （4）8
人教版高中数学必修4课后习题答案详解
第二章平面向量
2．1 平面向量的实质背景及基本观点练习（P77）
1、略.
uuur uuur
这两个向量的长度相等，但它们不等 .
2、AB，BA .
uuur uuur uuur uuur
3、 AB2， CD 2.5 ， EF3，GH 2 2.
4、（ 1）它们的终点同样；（2）它们的终点不一样 .
习题 A 组（P77）
1、（ 2 ）
B
45°
O
30°
C
A
D
.
C
A B
uuur uuur uuuruuur uuur uuur
3、与 DE 相等的向量有：AF , FC ；与 EF 相等的向量有： BD , DA ；
uuur uuur uuur
与 FD 相等的向量有： CE , EB .
r uuur uuur uurr uuuur uuur
4、与 a 相等的向量有：CO , QP, SR；与 b 相等的向量有： PM , DO ；
r uuur uuur uuur
与 c 相等的向量有： DC , RQ, ST
uuur 3 3
6、（1）×；（2）√；（3）√；（4）× .
5、 AD.
2
习题 B 组（P78）
1、海拔和高度都不是向量 .
uuuur
2、相等的向量共有24 对.模为 1的向量有 18对 . 此中与 AM 同向的共有 6
uuuur uuur uuur
对，与 AM 反向的也有 6 对；与 AD 同向的共有 3 对，与 AD 反向的也有 6 对；模为 2 的向量共有 4 对；模为 2 的向量有 2 对
2．2 平面向量的线性运算 练习（P84）
1、图略 .
2、图略 .
uuur uuur
3、（1） DA ； （2） CB .
人教版高中数学必修4课后习题答案详解
第二章
平面向量
2．1平面向量的实际背景及基本概念练习（P77）1、略. 2、AB ，BA . 这两个向量的长度相等，但它们不等
.
3、2AB
， 2.5CD
，3EF ，22GH .
4、（1）它们的终点相同；（2）它们的终点不同.
习题2.1 A 组（P77）1
、
30°
45°
C
A
O
B
（
2
）
D C
B
A
. 3、与DE 相等的向量有：,AF FC ；与EF 相等的向量有：,BD DA ；
与FD 相等的向量有：,CE EB .
4、与a 相等的向量有：,,CO QP SR ；与b 相等的向量有：,PM DO ；
与c 相等的向量有：,,DC RQ ST
5、33
2
AD
. 6、（1）×；（2）√；（3）√；（4）×.
习题2.1 B 组（P78）1、海拔和高度都不是向量. 2、相等的向量共有24对.
模为1的向量有18对. 其中与AM 同向的共有6对，
与AM 反向的也有6对；与AD 同向的共有3对，与AD 反向的也有6对；模为2
的向量共有4对；模为2的向量有2对
水流方向
C
D
A
B
2．2平面向量的线性运算练习（P84）1、图略. 2、图略. 3、（1）DA ；（2）CB .
4、（1）c ；（2）f ；
（3）f ；
（4）g .
练习（P87）1、图略. 2、DB ，CA ，AC ，AD ，BA .
3、图略.
练习（P90）1、图略. 2、5
7AC
AB ，2
7
BC AB . 说明：本题可先画一个示意图，根据图形容易得出正确答案. 值得注意的是BC
与AB 反向. 3、（1）2b
a ；（2）7
4
b a ；（3）12
b
a ；（4）89
【人教A版】高中数学必修4第二章课后习题解答
新课程标准数学必修4第二章课后习题解答
第二章 平面向量
2．1平面向量的实际背景及基本概念 练习（P77）
1、略.
2、AB ，BA . 这两个向量的长度相等，但它们不等.
3、2AB =， 2.5CD =，3EF =，22GH =
4、（1）它们的终点相同； （2）它们的终点不同. 习题2.1 A 组（P77） 1、
（2
）
. 3、与DE 相等的向量有：,AF FC ；与EF 相等的向量有：,BD DA ； 与FD 相等的向量有：,CE EB .
4、与a 相等的向量有：,,CO QP SR ；与b 相等的向量有：,PM DO ； 与c 相等的向量有：,,DC RQ ST
5、33
2
AD =
. 6、（1）×； （2）√； （3）√； （4）×. 习题2.1 B 组（P78）
1、海拔和高度都不是向量.
2、相等的向量共有24对. 模为1的向量有18对. 其中与AM 同向的共有6对，与AM 反向的也有6对；与
AD 同向的共有3对，与AD 反向的也有64对；模为2的向量有2对
2．2平面向量的线性运算 练习（P84）
1、图略.
2、图略.
3、（1）DA ； （2）CB .
4、（1）c ； （2）f ； （3）f ； （4）g .
练习（P87）
1、图略.
2、DB ，CA ，AC ，AD ，BA .
3、图略. 练习（P90） 1、图略.
2、57AC AB =，2
7
BC AB =-.
说明：本题可先画一个示意图，根据图形容易得出正确答案. 值得注意的是BC 与AB 反向.
3、（1）2b a =； （2）74b a =-； （3）12b a =-； （4）8
人教版高中数学必修4课后习题答案详解
数学必修四答案详解
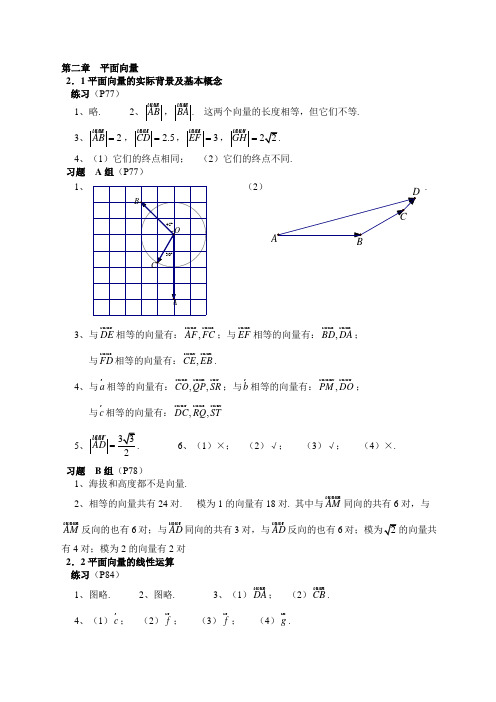
第二章 平面向量
2．1平面向量实际背景及基本概念 练习（P77）
1、略.
2、AB u u u r ，BA u u u r
. 这两个向量长度相等，但它们不等.
3、2AB =u u u r ， 2.5CD =u u u r ，3EF =u u u r
，GH =u u u r
4、（1）它们的终点相同； （2）它们的终点不同. 习题2.1 A 组（P77） 1
、
（2
）
. 3、与DE u u u r 相等的向量有：,AF FC u u u r u u u r ；与EF u u u r
相等的向量有：,BD DA u u u r u u u r ； 与FD u u u r
相等的向量有：,CE EB u u u r u u u r .
4、与a r 相等的向量有：,,CO QP SR u u u r u u u r u u r ；与b r 相等的向量有：,PM DO u u u u r u u u r
； 与c r 相等的向量有：,,DC RQ ST u u u r u u u r u
u u r
5、AD =u u u r .
6、（1）×； （2）√； （3）√； （4）×.
习题2.1 B 组（P78）
1、海拔和高度都不是向量.
2、相等的向量共有24对. 模为1的向量有18对. 其中与AM u u u u r
同向的共有6对，与AM u u u u r 反向的也有6对；与AD u u u r 同向的共有3
对，与AD u u u r
反向的也有6的向量共有4对；模为2的向量有2对
2．2平面向量的线性运算 练习（P84）
人教版高中数学必修4课后习题答案详解
人教版高中数学必修4课后习题答案详解
第二章 平面向量
2．1平面向量的实际背景及基本概念 练习（P77）
1、略.
2、AB ，BA . 这两个向量的长度相等，但它们不等.
3、2AB =， 2.5CD =，3EF =，22GH =
4、（1）它们的终点相同； （2）它们的终点不同. 习题2.1 A 组（P77） 1
、
（2
）
. 3、与DE 相等的向量有：,AF FC ；与EF 相等的向量有：,BD DA ； 与FD 相等的向量有：,CE EB .
4、与a 相等的向量有：,,CO QP SR ；与b 相等的向量有：,PM DO ； 与c 相等的向量有：,,DC RQ ST
5、33
2
AD =
. 6、（1）×； （2）√； （3）√； （4）×. 习题2.1 B 组（P78）
1、海拔和高度都不是向量.
2、相等的向量共有24对. 模为1的向量有18对. 其中与AM 同向的共有6对，与AM 反向的也有6对；与
AD 同向的共有3对，与AD 反向的也有6的向量共有4对；模为2的向量有2对
2．2平面向量的线性运算 练习（P84）
1、图略.
2、图略.
3、（1）DA ； （2）CB .
4、（1）c ； （2）f ； （3）f ； （4）g . 练习（P87）
1、图略.
2、DB ，CA ，AC ，AD ，BA .
3、图略. 练习（P90） 1、图略.
2、57AC AB =，2
7
BC AB =-.
说明：本题可先画一个示意图，根据图形容易得出正确答案. 值得注意的是BC 与AB 反向.
3、（1）2b a =； （2）74b a =-； （3）12
人教版A版高中数学必修4课后习题解答
第一章 三角函数 1．1任意角和弧度制 练习（P5）
1、锐角是第一象限角，第一象限角不一定是锐角；直角不属于任何一个象限，不属于任何一个象限的角不一定是直角；钝角是第二象限角，第二象限角不一定是钝角.
2、三，三，五
说明：本题的目的是将终边相同的角的符号表示应用到其他周期性问题上. 题目联系实际，把教科书中的除数360换成每个星期的天数7，利用了“同余”（这里余数是3）来确定7k 天后、7k 天前也是星期三，这样的练习不难，可以口答. 3、（1）第一象限角； （2）第四象限角； （3）第二象限角； （4）第三象限角. 4、（1）305°42′第四象限角；（2）35°8′第一象限角；（3）249°30′第三象限角. 5、（1）{130318+360,}k k Z ββ'=︒⋅︒∈，49642'-︒，13642'-︒，22318'︒； （2）{225+360,}k k Z ββ=-︒⋅︒∈，585-︒，225-︒，135︒. 练习（P9）
1、（1）
8π； （2）76π-； （3）203
π
. 2、（1）15°；（2）240-︒； （3）54°.
3、（1）{,}k k Z ααπ=∈； （2）{,}2
k k Z π
ααπ=
+∈.
4、（1）cos0.75cos0.75︒>； （2）tan1.2tan1.2︒<. 说明：体会同数值不同单位的角对应的三角函数值可能不同，并进一步认识两种单位制. 注意在用计算器求三角函数值之前，要先对计算器中角的模式进行设置. 如求cos0.75︒之前，要将角模式设置为DEG （角度制）；求cos0.75之前，要将角模式设置为RAD （弧度制）.
人教版高中数学必修4课后习题答案详解
: $ (
第二章 平面向量
2．1平面向量的实际背景及基本概念 练习（P77）
1、略.
2、AB ，BA . 这两个向量的长度相等，但它们不等.
3、2AB =， 2.5CD =，3EF =，22GH =
…
4、（1）它们的终点相同； （2）它们的终点不同. 习题 A 组（P77） 1
、
（2
）
. 3、与DE 相等的向量有：,AF FC ；与EF 相等的向量有：,BD DA ； 与FD 相等的向量有：,CE EB .
4、与a 相等的向量有：,,CO QP SR ；与b 相等的向量有：,PM DO ； 与c 相等的向量有：,,DC RQ ST
5、33
AD =
. 6、（1）×； （2）√； （3）√； （4）×. $
习题 B 组（P78）
1、海拔和高度都不是向量.
2、相等的向量共有24对. 模为1的向量有18对. 其中与AM 同向的共有6
对，与AM 反向的也有6对；与AD 同向的共有3对，与
AD 反向的也有6对；模的向量共有4对；模为2的向量有2对 2．2平面向量的线性运算 练习（P84）
1、图略.
2、图略.
3、（1）DA ； （2）CB .
4、（1）c ； （2）f ； （3）f ； （4）g . 练习（P87） …
1、图略.
2、DB ，CA ，AC ，AD ，BA .
3、图略. 练习（P90） 1、图略.
2、57AC AB =，2
7
BC AB =-.
说明：本题可先画一个示意图，根据图形容易得出正确答案. 值得注意的是BC 与AB 反向.
3、（1）2b a =； （2）74b a =-； （3）12b a =-； （4）8
人教版高中数学必修4课后习题答案详解
5、略
6、不一定构成三角形. 说明：结合向量加法的三角形法则，让学生理解，若三个非零向量的和为零向量，且这三个向量不共线时，则表示这三个向量的有向线段一定能构成三角形.
7、略. 8、（1）略； （2）当a b ⊥时，a b a b +=-
9、（1）22a b --； （2）102210a b c -+； （3）132
a b +； （4）2()x y b -. 10、14a b e +=，124a b e e -=-+，1232310a b e e -=-+. 11、如图所示，OC a =-，OD b =-，
DC b a =-，BC a b =--.
12、14AE b =，BC b a =-，1()4DE b a =-，34DB a =， 34EC b =，1()8DN b a =-，11()48
AN AM a b ==+. 13、证明：在ABC ∆中，,E F 分别是,AB BC 的中点， 所以EF AC //且12EF AC =， 即12
EF AC =； 同理，12
HG AC =， 所以EF HG =.
习题2.2 B 组（P92）
1、丙地在甲地的北偏东45°方向，距甲地1400 km.
2、不一定相等，可以验证在,a b 不共线时它们不相等.
3、证明：因为MN AN AM =-，而13AN AC =，13
AM AB =， 所以1111()3333
MN AC AB AC AB BC =-=-=. 4、（1）四边形ABCD 为平行四边形，证略
（2）四边形ABCD 为梯形.
证明：∵13
AD BC =， ∴AD BC //且AD BC ≠
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 平面向量
2．1平面向量的实际背景及基本概念
练习（P77） 1、略. 2、AB u u u r ，BA u u u r . 这两个向量的长度相等，但它们不等.
3、2AB =u u u r ， 2.5CD =u u u r ，3EF =u u u r ，GH =u u u r
4、（1）它们的终点相同； （2）它们的终点不同.
习题 A 组（P77）
1、 （2）.
3、与DE u u u r 相等的向量有：,AF FC u u u r u u u r ；与EF u u u r 相等的向量有：,BD DA u u u r u u u r ；
与FD u u u r 相等的向量有：,CE EB u u u r u u u r .
4、与a r 相等的向量有：,,CO QP SR u u u r u u u r u u r ；与b r 相等的向量有：,PM DO u u u u r u u u r ；
与c r 相等的向量有：,,DC RQ ST u u u r u u u r u u u r
5、AD =u u u r .
6、（1）×； （2）√； （3）√； （4）×.
习题 B 组（P78）
1、海拔和高度都不是向量.
2、相等的向量共有24对. 模为1的向量有18对. 其中与AM u u u u r 同向的共有6
对，与AM u u u u r 反向的也有6对；与AD u u u r 同向的共有3对，与AD u u u r 反向的也有6对；模
的向量共有4对；模为2的向量有2对
2．2平面向量的线性运算
练习（P84）
1、图略.
2、图略.
3、（1）DA u u u r ； （2）CB u u u r .
4、（1）c r ； （2）f u r ； （3）f u r ； （4）g u r .
练习（P87）
1、图略.
2、DB u u u r ，CA u u u r ，AC u u u r ，AD u u u r ，BA u u u r .
3、图略.
练习（P90）
1、图略.
2、57AC AB =u u u r u u u r ，27
BC AB =-u u u r u u u r . 说明：本题可先画一个示意图，根据图形容易得出正确答案. 值得注意的是BC
uuu r 与AB u u u r 反向.
3、（1）2b a =r r ； （2）74b a =-r r ； （3）12b a =-r r ； （4）89
b a =r r . 4、（1）共线； （2）共线.
5、（1）32a b -r r ； （2）111123
a b -+r r ； （3）2ya r . 6、图略. 习题 A 组（P91）
1、（1）向东走20 km ； （2）向东走5 km ； （3）向东北走km ；
（4）向西南走；（5）向西北走；（6）向东南走
2、飞机飞行的路程为700 km ；两次位移的合成是向北偏西53°方向飞行500 km.
3、解：如右图所示：AB u u u r 表示船速，AD u u u r 表示河水
的流速，以AB 、AD 为邻边作□ABCD ，则
AC u u u r 表示船实际航行的速度.
在Rt △ABC 中，8AB =u u u r ，2AD =u u u r ，
所以AC ===u u u r 因为tan 4CAD ∠=，由计算器得76CAD ∠≈︒
所以，
实际航行的速度是km/h ，船航行的方向与河岸的夹角约为76°.
4、（1）0r ； （2）AB u u u r ； （3）BA u u u r ； （4）0r ； （5）0r ； （6）CB u u u r ； （7）0r .
5、略
6、不一定构成三角形. 说明：结合向量加法的三角形法则，让学生理解，若三个非零向量的和为零向量，且这三个向量不共线时，则表示这三个向量的有向线段一定能构成三角形.
7、略.
8、（1）略； （2）当a b ⊥r r 时，a b a b +=-r r r r
9、（1）22a b --r r ； （2）102210a b c -+r r r ； （3）132a b +r r ； （4）2()x y b -r . 10、14a b e +=r r u r ，124a b e e -=-+r r u r u u r ，1232310a b e e -=-+r r u r u u r .
11、如图所示，OC a =-u u u r r ，OD b =-u u u r r ，
DC b a =-u u u r r r ，BC a b =--u u u r r r .
12、14AE b =u u u r r ，BC b a =-u u u r r r ，1()4DE b a =-u u u r r r ，34DB a =u u u r r ， 34EC b =u u u r r ，1()8DN b a =-u u u r r r ，11()48
AN AM a b ==+u u u r u u u u r r r . 13、证明：在ABC ∆中，,E F 分别是,AB BC 的中点，
所以EF AC //且12EF AC =， 即12EF AC =u u u r u u u r ； 同理，12
HG AC =u u u r u u u r ， 所以EF HG =u u u r u u u r .
习题 B 组（P92）
1、丙地在甲地的北偏东45°方向，距甲地1400 km.
2、不一定相等，可以验证在,a b r r 不共线时它们不相等.
3、证明：因为MN AN AM =-u u u u r u u u r u u u u r ，而13AN AC =u u u r u u u r ，13
AM AB =u u u u r u u u r ， （第11题） （第12题） （第13题）
（第1题）