用Origin计算CV积分面积
关于origin计算面积的详解

(一)一般步调计算曲线与坐标轴间的面积之袁州冬雪创作
操纵Analysis → mathematics →integrate饬令停止操纵:
Input:输入计算区域;
Row:也可以手动选择计算区间;
Area type: 停止积分的方式;
Plot integrated curve:是否画出积分曲线;
Result log output:成果是否显示;
例.计算下图中在区间[10,40]中,曲线与x轴形成的面积. Analysis → mathematics →integrate,选择行 From 10 To 40 ,点击ok,生成计算成果.
(二)峰面积的计算(曲线和基线形成的面积)
例求下图中的各峰面积.
解法1 可以采取多峰积分的方法
Analysis → Spectroscopy → Integrate Multiple Peaks 就会出现以下对话框,峰数选择3,就会出现3个黄色区域,baseline选择connect line,鼠标选中其中的黄色框便可以得到该区域中峰面积.
解法 2 可以采取基线和峰分析向导计算(Baseline and Peaks)
Analysis → Spectroscopy →Baseline and Peaks,出
现以下对话框
点击next,进入下一步
峰数选择3,会出现3个黄色框分别包含3个峰(注. 黄色框是可以移动和缩放的,作用是改变选择的区间),接下来的步调都是点击next,最后点击finish,完成.积分成果会在工作表中显示.如下.。
关于origin计算面积的详解

关于origin计算面积的详解
(一)一般步骤计算曲线与坐标轴间的面积
利用Analysis → mathematics →integrate 命令进行操作:
Input:输入计算区域;
Row:也可以手动选择计算区间;
Area type: 进行积分的方式;
Plot integrated curve:是否画出积分曲线;Result log output:结果是否显示;
例. 计算下图中在区间[10,40]中,曲线与x轴形成的面积。
Analysis → mathematics →integrate,选择行 From 10 To 40 ,点击ok,生成计算结果。
(二)峰面积的计算(曲线和基线形成的面积)例求下图中的各峰面积。
解法1 可以采用多峰积分的方法
Analysis →Spectroscopy →Integrate Multiple Peaks
就会出现以下对话框,峰数选择3,就会出现3个黄色区域,baseline选择connect line,鼠标选中其中的黄色框就可以得到该区域中峰面积。
解法 2 可以采用基线和峰分析向导计算(Baseline and Peaks)
Analysis → Spectroscopy →Baseline and Peaks,出现以下对话框
点击next,进入下一步
峰数选择3,会出现3个黄色框分别包含3个峰(注. 黄色框是可以移动和缩放的,作用是改变选择的区间),接下来的步骤都是点击
next,最后点击finish,完成。
积分结果会在工作表中显示。
如下。
CV数据用origin求积分面积
用origin计算CV积分面积
武汉科思特仪器股份有限公司
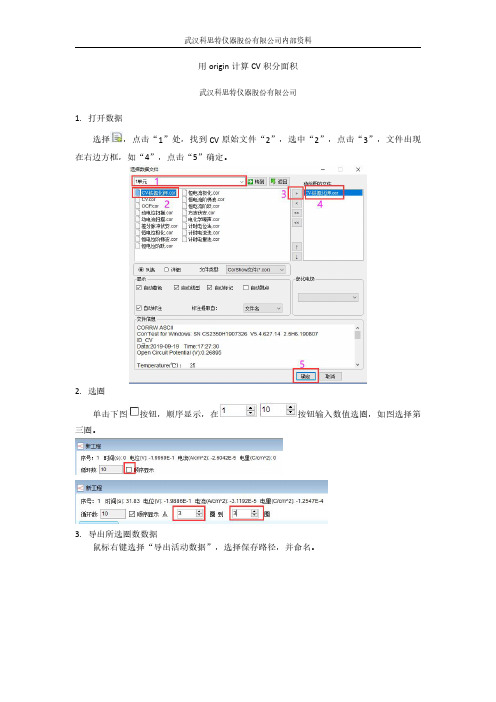
1.打开数据
选择,点击“1”处,找到CV原始文件“2”,选中“2”,点击“3”,文件出现在右边方框,如“4”,点击“5”确定。
2.选圈
单击下图按钮,顺序显示,在按钮输入数值选圈,如图选择第三圈。
3.导出所选圈数数据
鼠标右键选择“导出活动数据”,选择保存路径,并命名。
打开Origin,点击Import Single ASCII(如图所示)
导入需要计算的数据,注意文件类型选择All Files,点击打开。
选中C列,点右键进行删除,Delete。
选中X=0.16这个数据到X=0.55,点右键Plot―Line―Line,作图
依次点击Analysis—Peaks and Baseline—Peak Analyzer—Open Dialog
点击Next—Baseline Mode改成User Defined—Enable Auto Find(勾去掉),点击Add。
双击点击两点,点击done.
依次点击Next—Next—Next—Enable Auto Find(勾去掉)—Add.
双击最高峰—Done—Next
点击Finish,完成,Book1中的Area即为所求面积。
关于origin计算面积的详解
(一)一般步骤计算曲线与坐标轴间的面积
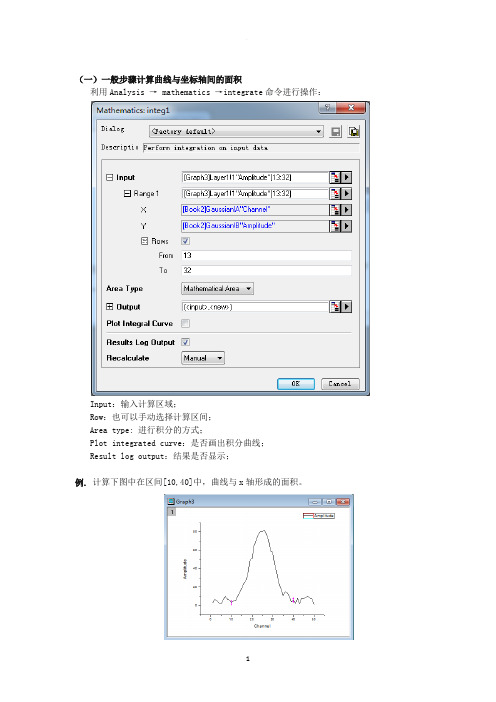
利用Analysis → mathematics →integrate命令进行操作:
Input:输入计算区域;
Row:也可以手动选择计算区间;
Area type: 进行积分的方式;
Plot integrated curve:是否画出积分曲线;
Result log output:结果是否显示;
例.计算下图中在区间[10,40]中,曲线与x轴形成的面积。
Analysis → mathematics →integrate,选择行 From 10 To 40 ,点击ok,生成计算结果。
(二)峰面积的计算(曲线和基线形成的面积)
例求下图中的各峰面积。
解法1 可以采用多峰积分的方法
Analysis → Spectroscopy → Integrate Multiple Peaks
就会出现以下对话框,峰数选择3,就会出现3个黄色区域,baseline选择connect line,鼠标选中其中的黄色框就可以得到该区域中峰面积。
解法2 可以采用基线和峰分析向导计算(Baseline and Peaks)
Analysis → Spectroscopy →Baseline and Peaks,出现以下对话框
点击next,进入下一步
峰数选择3,会出现3个黄色框分别包含3个峰(注. 黄色框是可以移动和缩放的,作用是改变选择的区间),接下来的步骤都是点击next,最后点击finish,完成。
积分结果会在工作表中显示。
如下。
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
关于origin计算面积的详解
(一)一般步骤计算曲线与坐标轴间得面积
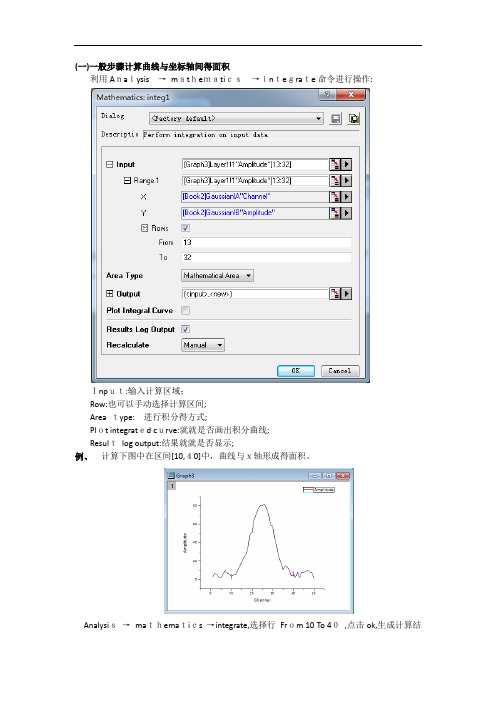
利用Analysis→mathematics→integrate命令进行操作:
Input:输入计算区域;
Row:也可以手动选择计算区间;
Area type:进行积分得方式;
Plot integrated curve:就就是否画出积分曲线;
Resultlog output:结果就就是否显示;
例、计算下图中在区间[10,40]中,曲线与x轴形成得面积。
Analysis→mathematics →integrate,选择行From 10 To 40,点击ok,生成计算结
果。
(二)峰面积得计算(曲线与基线形成得面积) 例求下图中得各峰面积。
解法1 可以采用多峰积分得方法
Analysis→Spectroscopy→IntegrateMultiple Peaks
就会出现以下对话框,峰数选择3,就会出现3个黄色区域,baseline选择connect line,鼠标选中其中得黄色框就可以得到该区域中峰面积。
解法2 可以采用基线与峰分析向导计算(Baseline and Peaks)
Analysis →Spectroscopy→Baseline and Peaks,出现以下对话框
点击next,进入下一步
峰数选择3,会出现3个黄色框分别包含3个峰(注、黄色框就就是可以移动与缩放得,作用就就是改变选择得区间),接下来得步骤都就就是点击next,最后点击finish,完成。
积分结果会在工作表中显示。
如下。
关于origin计算面积的详解

(一)一般步骤计算曲线与坐标轴间的面积
利用Analysis →mathematics →integrate命令进行操作:
Input:输入计算区域;
Row:也可以手动选择计算区间;
Area type: 进行积分的方式;
Plot integrated curve:是否画出积分曲线;
Result log output:结果是否显示;
例.计算下图中在区间[10,40]中,曲线与x轴形成的面积。
Analysis →mathematics →integrate,选择行From 10 To 40 ,点击ok,生成计算结果。
(二)峰面积的计算(曲线和基线形成的面积)
例求下图中的各峰面积。
解法1 可以采用多峰积分的方法
Analysis →Spectroscopy →Integrate Multiple Peaks
就会出现以下对话框,峰数选择3,就会出现3个黄色区域,baseline选择connect line,鼠标选中其中的黄色框就可以得到该区域中峰面积。
解法2 可以采用基线和峰分析向导计算(Baseline and Peaks)
Analysis →Spectroscopy →Baseline and Peaks,出现以下对话框
点击next,进入下一步
峰数选择3,会出现3个黄色框分别包含3个峰(注. 黄色框是可以移动和缩放的,作用是改变选择的区间),接下来的步骤都是点击next,最后点击finish,完成。
积分结果会在工作表中显示。
如下。
利用Origin9.0对曲线在指定区间进行积分求面积
如何对曲线在指定区间进行积分
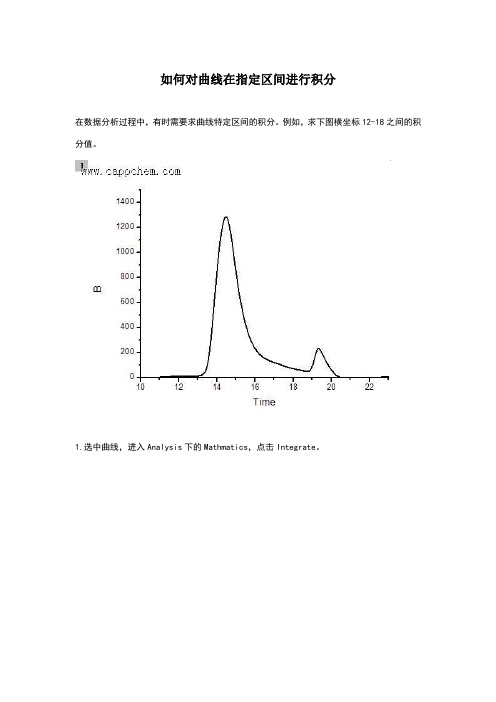
在数据分析过程中,有时需要求曲线特定区间的积分。
例如,求下图横坐标12-18之间的积分值。
1.选中曲线,进入Analysis下的Mathmatics,点击Integrate。
2.依次点开Input、Range前的+号,即可看到积分对应的数据(红色矩形框内)。
在此,是对X轴的指定段12-18求积分;因此点击Rows后面的下拉框,选择By X。
All指全段积分;
By Row指按照Workbook中指定行的范围积分;
By X指按照图中X轴的范围积分;
3.在Input-Range-Rows下的From和To中填写区间范围12-18。
点击OK按钮即可获取积分值。
4.积分结果会在Results Log中显示,约为2076;
对应的积分范围见下图。
注意:曲线在X值为12和18处的点不在同一基线上,如需要以12和18处两点的连线作基线计算积分,请按后面的方法操作。
5.同样选中曲线,进入Analysis下的Mathmatics,点击Integrate下的Open Dialog(以前使用过积分功能的话,则会出现Open Dialog)。
6.同上选择By X,填写区间12-18。
然后勾选“Use End Points Straight Line as Baseline”。
点击OK按钮即可。
7.积分结果约为1841,对应的范围见下图中的阴影部分。
关于origin计算面积的详解
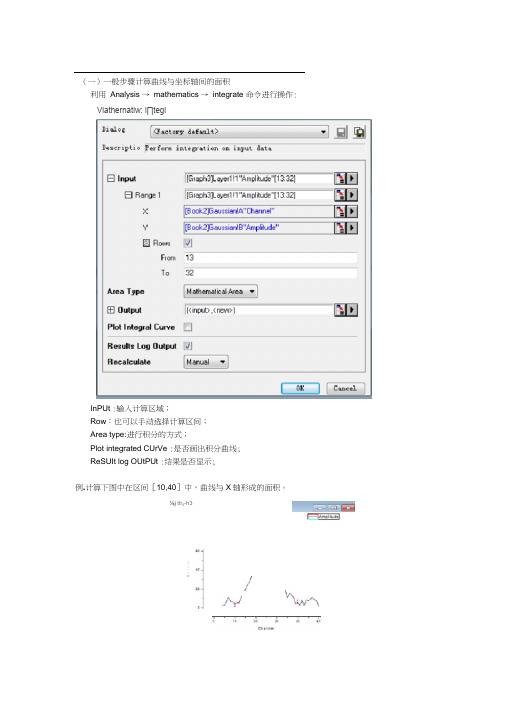
(一)一般步骤计算曲线与坐标轴间的面积利用Analysis → mathematics → integrate 命令进行操作:InPUt :输入计算区域;Row:也可以手动选择计算区间;Area type:进行积分的方式;Plot integrated CUrVe :是否画出积分曲线;ReSUIt log OUtPUt :结果是否显示;例.计算下图中在区间[10,40]中,曲线与X轴形成的面积。
⅛j tlr fl-h31二一二审Vlathernatiw: i∏teglAnalysis → mathematics → integrate ,选择行From 10 Ta 40 ,点击Ok ,生成计算结果。
(二)峰面积的计算(曲线和基线形成的面积)例求下图中的各峰面积。
解法1可以采用多峰积分的方法Analysis → SPeCtroSCoPy → Integrate MUItiPle PeakS就会出现以下对话框,峰数选择3,就会出现3个黄色区域,baseline选择Connect line ,鼠标选中其中的黄色框就可以得到该区域中峰面积。
解法2可以采用基线和峰分析向导计算( BaSeline and PeakS)Analysis → SPeCtroSCoPy →BaSeIine and PeakS,出现以下对话框3: Find PeakSInlVgrate点击next ,进入下一步Wl GrjpblTheme 4CtOry default>∣blr⅛ctCreate a b⅛seline ι≡ing d⅞t⅛ POiJktS OliItli d⅛ w indew 3,J*NUmber Of ReCt 3 审□COnneCtiOn TVPe Line TNO SUbtraCt ΞWiZald StePi31;Create baseliπe(Use WirIeh2BASeIine SuIbt½cl(oρtior∣al)3Frld PeakS4IntegrateT* LlFinish CloseFrev Jext峰数选择3,会出现3个黄色框分别包含3个峰(注.黄色框是可以移动和缩放的,作用是改变选择的区间),接下来的步骤都是点击next ,最后点击finish,完成。
origin积分曲线面积

origin积分曲线面积概述在数学中,积分是一种重要的数学工具,用于计算曲线下的面积、求解定积分等。
origin积分曲线面积是指在origin坐标系下,通过积分计算得到的曲线下的面积。
本文将详细探讨origin积分曲线面积的计算方法、应用场景以及相关的数学知识。
基本概念在开始讨论origin积分曲线面积之前,我们先来了解一些基本概念。
积分积分是微积分的重要概念之一,用于计算曲线下的面积、求解定积分等。
在数学中,积分可以看作是求和的一种推广。
通过将曲线划分成无穷多个微小的矩形,然后对这些矩形的面积进行求和,即可得到曲线下的面积。
曲线面积曲线面积是指在坐标系下,曲线与坐标轴之间的区域的面积。
对于简单的曲线,我们可以通过几何图形的面积公式进行计算。
但是对于复杂的曲线,几何方法往往不够有效,这时就需要借助积分来求解曲线面积。
计算方法origin积分曲线面积的计算方法与一般的积分计算方法相同,只是在计算过程中需要考虑坐标系的特点。
下面将介绍两种常用的计算方法。
定积分法定积分法是最常见的计算曲线面积的方法之一。
通过将曲线划分为无穷多个微小的矩形,然后对这些矩形的面积进行求和,即可得到曲线下的面积。
在origin坐标系下,可以通过积分公式来计算定积分。
例如,对于函数f(x)在区间[a, b]上的定积分,可以表示为:其中,f(x)为要计算的函数,a和b为积分的上下限。
数值积分法数值积分法是一种通过数值逼近的方法来计算曲线面积的方法。
它将曲线划分为若干个小区间,然后在每个小区间上选择若干个代表性点,计算这些点的函数值并进行加权求和,得到近似的曲线面积。
在origin坐标系下,可以使用数值积分法来计算曲线面积。
常见的数值积分方法包括梯形法则、辛普森法则等。
应用场景origin积分曲线面积在科学研究、工程设计等领域有着广泛的应用。
下面将介绍一些常见的应用场景。
物理学中的应用在物理学中,往往需要计算物体的质心、重心等物理量。
用Origin计算CV积分面积(学习资料)
用Origin计算CV积分面积,及计算电化学活性面积方法
蒋庆来
1.打开Origin,点击Import ASCII(如图所示)
2.导入需计算的数据,注意文件类型选择All Files,点击打开。
3.选中C列,点右键进行删除,Delete。
4.选中从第一个数据到X=0.2,点右键Plot――Line,作图。
5.最小化该图层,在数据栏中选Y(X=0.2)复制。
6.将图层最大化,在Tools中选Baseline,选中User Defined Equation,在Y=后粘贴上步复制得到的数据,点击Create Baseline。
7.得到基线后,选择Area,点击Use Baseline。
8.得到以下结果,其中Area下方对应的数值即所求积分面积S,该面积除以扫描速度(如0.02V/s)即得电量Q H。
9.Pt电催化剂的电化学活性表面积EAS(m2/gPt)可按下式计算:m(0.095mg)
EAS=Q H/(2.1*m)=5Q=5S/0.02=250000S
式中m为电极中Pt的量,单位为g;2.1C/m2是每平方厘米多晶铂表面可吸附1.3×1015个氢原子所对应的电量。
如何用Origin 8.0对曲线部分区域积分求面积教程
JIEER
如何对曲线部分区域积分求面积教程
1. 运行 Origin 8.0,将文本数据导入
2. 画出Байду номын сангаас线图
方法一
1. 选择 Analysis>Spectroscopy>Integrate Multiple Peaks>Open Dialog
2. 选择积分的峰数量和积分区域,再点击 Report,得到表中结果
运行origin80将文本数据导入画出直线图jieer方法一选择analysisspectroscopyintegratemultiplepeaksopendialog选择积分的峰数量和积分区域再点击report得到表中结果方法二peaksopendialog然后点击next设置积分区域数量选择积分区域再点击next直到图标变灰接着点击finish得到积分结果在表格中可将baseline表格中的数据复制粘贴到文档表格中选择abd列数据做fillarea
方法二
1. 选择 Analysis>Spectroscopy>Baseline and Peaks>Open Dialog
2. 然后点击 Next,设置积分区域数量,选择积分区域,再点击 Next 直到图标变灰,接着 点击 Finish,得到积分结果(在表格中)
3. 可将 Baseline 表格中的数据复制粘贴到文档表格中,选择 A、B、D 列数据,做 Fill Area 图。
origin面积积分步骤
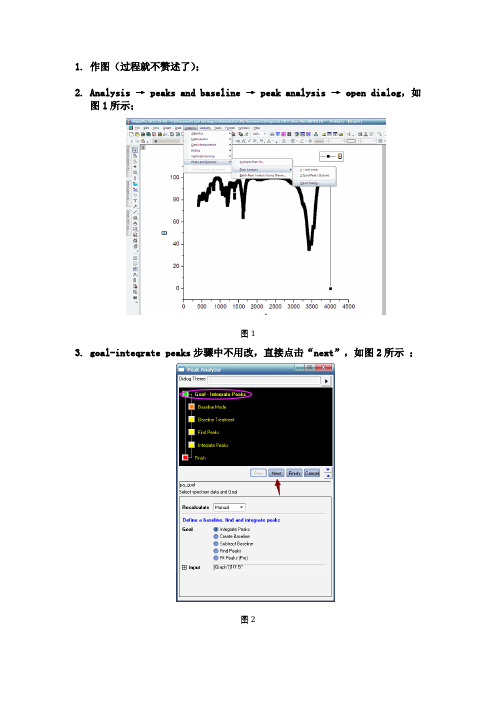
1.作图(过程就不赘述了);
2.Analysis → peaks and baseline → peak analysis → open dialog,如
图1所示;
图1
3.goal-inteqrate peaks步骤中不用改,直接点击“next”,如图2所示;
图2
4.baseline mode步骤中, 将Y下面改为“custom”,然后输入合适的Y值作为
基线值,然后点击“next” ,如图3所示;
图3
5.baseline treatment 步骤中不用改,直接点击“next” ,如图4所示;
图4
6.find peaks步骤中,如图5:去掉enable auto find 后面的勾选,点击“add”,
然后如图6:在峰的任一位置双击(求一个峰的面积就在一个位置双击一下,n个峰的各自面积就在不同的位置双击n下),接下来点击小对话框中的“done” , “next” ;
图5
图6
7.inteqrate peaks 步骤中,如图7所示,将“all peaks”取消勾选,integration
window width中选择“adjust preview graph” ,就会出现图8所示,拖动长方形阴影两侧使之刚好覆盖需求面积的峰,图中是以一个峰和所有峰为例,点击“finish”(图9),最小化当前窗口,就会出现如图10所示表格,其中“area”栏表示的就是面积,这样求面积比就很方便了。
图7
图8
图9
图10。
origin面积积分步骤

1.作图(过程就不赘述了);
2.Analysis → peaks and baseline → peak analysis → open dialog,如
图1所示;
图1
3.goal-inteqrate peaks步骤中不用改,直接点击“next”,如图2所示;
图2
4.baseline mode步骤中, 将Y下面改为“custom”,然后输入合适的Y值作为
基线值,然后点击“next” ,如图3所示;
图3
5.baseline treatment 步骤中不用改,直接点击“next” ,如图4所示;
图4
6.find peaks步骤中,如图5:去掉enable auto find 后面的勾选,点击“add”,
然后如图6:在峰的任一位置双击(求一个峰的面积就在一个位置双击一下,n个峰的各自面积就在不同的位置双击n下),接下来点击小对话框中的“done” , “next” ;
图5
图6
7.inteqrate peaks 步骤中,如图7所示,将“all peaks”取消勾选,integration
window width中选择“adjust preview graph” ,就会出现图8所示,拖动长方形阴影两侧使之刚好覆盖需求面积的峰,图中是以一个峰和所有峰为例,点击“finish”(图9),最小化当前窗口,就会出现如图10所示表格,其中“area”栏表示的就是面积,这样求面积比就很方便了。
图7
图8
图9
图10。
关于origin计算面积的详解

Analysis→mathematics→integrate,选择行From10To40,点击ok,生成计算结果。
(二)峰面积的计算(曲线和基线形成的面积)
例求下图中的各峰面积。
解法1可以采用多峰积分的方法
Analysis→Spectroscopy→IntegrateMultiplePeaks
点击next,进入下一步
峰数选择3,会出现3个黄色框分别包含3个峰(注.黄色框是可以移动和缩放的,作用是改变选择的区间),接下来的步骤都是点击next,最后点击finish,完成。积分结果会在工作表中显示。如下。
(一)一般步骤计算曲线与坐标轴间的面积
利用Analysis→mathemat输入计算区域;
Row:也可以手动选择计算区间;
Areatype:进行积分的方式;
Plotintegratedcurve:是否画出积分曲线;
Resultlogoutput:结果是否显示;
就会出现以下对话框,峰数选择3,就会出现3个黄色区域,baseline选择connectline,鼠标选中其中的黄色框就可以得到该区域中峰面积。
解法2可以采用基线和峰分析向导计算(BaselineandPeaks)
Analysis→Spectroscopy→BaselineandPeaks,出现以下对话框
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用Origin计算CV积分面积,及计算电化学活性面积方法
蒋庆来
1.打开Origin,点击Import ASCII(如图所示)
2.导入需计算的数据,注意文件类型选择All Files,点击打开。
3.选中C列,点右键进行删除,Delete。
4.选中从第一个数据到X=0.2,点右键Plot――Line,作图。
5.最小化该图层,在数据栏中选Y(X=0.2)复制。
6.将图层最大化,在Tools中选Baseline,选中User Defined Equation,在Y=后粘贴上步复制得到的数据,点击Create Baseline。
7.得到基线后,选择Area,点击Use Baseline。
8.得到以下结果,其中Area下方对应的数值即所求积分面积S,该面积除以扫描速度(如0.02V/s)即得电量Q H。
9.Pt电催化剂的电化学活性表面积EAS(m2/gPt)可按下式计算:m(0.095mg)
EAS=Q H/(2.1*m)=5Q=5S/0.02=250000S
式中m为电极中Pt的量,单位为g;2.1C/m2是每平方厘米多晶铂表面可吸附1.3×1015个氢原子所对应的电量。
感谢下载!
欢迎您的下载,资料仅供参考。
