人教版初中八年级数学暑期作业
人教版数学八年级暑假作业答案2021

⼈教版数学⼋年级暑假作业答案2021⼀提到暑假作业,⼤家⼀定都很发愁呢,影响我们快乐的⼼情了~但是⼤家还是要完成暑假作业的。
下⾯是⼩编为⼤家收集的关于⼈教版数学⼋年级暑假作业答案五篇2021。
希望可以帮助⼤家。
⼈教版数学⼋年级暑假作业答案篇⼀(⼀)基本概念:1、离散,2、极差,3、值,最⼩值,4、⼤,⼩,⼀致,作业:1、4973850,2、32,3、-8,4、-2或8,5、4,6、D,7、D,8、3040,9、13,10、16(⼆)⼀,知识回顾(1)平均数A:40.0B:40.0极差A.4B:0.4(2)不能⼆,基本概念,略三,例题分析:⽅差,A:0.012B:0.034标准差,略A更稳定四,作业:(1)B(2)B(3)C(4)8(5)200,10(6)100(7)⽅差:甲0.84⼄0.61所以⼄更稳定(三)1、12;2、①,②,③;3、2;4、;5、2,;6、100;7、⼄;8、⼄;9、4、3;10、0;11、C;12、C;13、C;14、D;15、B;16、A;17、B;18、C;19、C;20、C;21、(1)A:极差8,平均数99,⽅差6.6;B:极差9,平均数100,⽅差9;(2)A;22、(1)甲组及格率为0.3,⼄组及格率为0.5,⼄组的及格率⾼;(2)甲组⽅差为1,⼄组⽅差为1.8,甲组的成绩较稳定;23、(1)甲班的优秀率为60℅,⼄班的优秀率为40℅;(2)甲班的中位数为100,⼄班的中位数为97;(3)估计甲班的⽅差较⼩;(4)根据上述三个条件,应把冠军奖状发给甲班。
(四)⼀、选择题(本⼤题共10⼩题,每⼩题3分,共30分)题号12345678910答案CBAABDCCBD⼆、填空题(本⼤题共8⼩题,每题4分,共32分)11.212.13.14.6.1815.16.对⾓线互相平分的四边形是平⾏四边形17.318.⼈教版数学⼋年级暑假作业答案篇⼆《暑假乐园》(⼀)答案:1-8、DABDDDCA;9、1,2,3;10、a≤b;11、a<4且a≠0;12、a>-1;13、7;14、(1)x<2,(2)x<-3;15、a≤ ;16、1;17、18厘⽶;18、2121、18题;22、(1)a=0.6 ,b=0.4;(2)35%到50%之间(不含35%和50%)。
【暑假分层作业】第11练 一次函数的应用-2022年八年级数学(人教版)(原卷)

第11练 一次函数的应用一、单选题1.下表中列出的是一个一次函数的自变量x 与函数y 的几组对应值:x … -4 -3 -2 … y…-2-4…下列各选项中,正确的是( )A .y 随x 的增大而增大 B .该函数的图象不经过第四象限C .该函数图象与坐标轴围成的三角形的面积为16D .该函数图象关于x 轴对称的函数的表达式为24y x =+2.小张加工某种机器零件,工作一段时间后,提高了工作效率.小张加工的零件总数m (单位:个)与工作时间t (单位:时)之间的函数关系如图所示,则小张提高工作效率前每小时加工零件( )个A .3B .4C .5D .63.快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的距离y (km )与它们的行驶时间x (h )之间的函数关系.小欣同学结合图象得出如下结论: ①快车途中停留了0.5h ;②快车速度比慢车速度多20km/h ; ③图中a =340; ④快车先到达目的地. 其中正确的个数是( )A .1个B .2个C .3个D .4个4.暑期将至,某游冰俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次游泳费用按六折优惠;方案二:不购买学生暑期专享卡,每次游泳费用按八折优惠;按照方案一所需费用为y 1(元),且y =k 1x +b ;按照方案二所需费用为y 2(元),且y 2=k 2x ,其函数象如图所示.若小明打算办一张暑期专享卡使得游泳时费用更合算,则他去游泳的次数x 至少是( )A .5B .6C .7D .85.如图,正方形ABCD 的顶点A ,D 分别在x 轴,y 轴上,点(5,2)B 在直线:4l y kx =+上.直线l 分别交x 轴,y 轴于点E ,F .将正方形ABCD 沿y 轴向下平移m 个单位长度后,点C 恰好落在直线l 上.则m 的值为( )A .65B .115C .145D .26.如图1,在四边形ABCD 中,AD BC ∥,直线l AB ⊥,当直线l 沿射线BC 的方向从点B 开始向右平移时,直线l 与四边形ABCD 的边分别相交于点E ,F .设直线l 向右平移的距离为x ,线段EF 的长为y ,且y 与x 的函数关系如图2所示,则下列结论:①BC 的长为5;②AB 的长为32;③当45x ≤≤时,△BEF 的面积不变;④当6x =时,△BEF 的面积为332;其中正确的有( )个.A .1B .2C .3D .4二、填空题7.如图,已知点()2,3A -,()2,1B ,直线y kx k =+经过点()1,0P -.试探究:直线与线段AB 有交点时k 的变化情况,猜想k 的取值范围是______.8.某公司生产一种营养品,每日购进所需食材500千克,制成A ,B 两种包装的营养品,并恰好全部用完.信息如下表: 规格每包食材含量 每包售价A 包装 1千克 45元B 包装 0.25千克 12元已知生产的营养品当日全部售出.若A 包装的数量不少于B 包装的数量,则A 为__________包时,每日所获总售价最大,最大总售价为__________元.9.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为x (小时),两车之间的距离为y (千米),如图中的折线表示y 与x 之间的函数关系,根据图象可知,下列结论:①两车出发后4小时相遇;②动车的速度是普通列车速度的2倍;③两车相遇后,普通列车还需行驶6小时到达目的地;④C 点的坐标是()5,1000,其中正确的有__________.(填所有正确结论的序号)10.如图,在平面直角坐标系中,点O 为原点,点C 在x 轴正半轴上,以OC 为边在x 轴上方作矩形OABC ,若点B 坐标为(4,1),平面内有一条直线:2l y kx =+恰好将矩形OABC 分成面积相等的两部分,则k 的值为______.11.某公司以A 、B 两种材料,利用不同的搭配方式推出了两款产品,其中,甲产品每份含2克A 、2克B ;乙产品每份含2克A 、1克B ,甲乙两种产品每份成本价分别为A 、B 两种材料的成本之和,若甲产品每份成本为16元,公司在核算成本的时候把A 、B 两种材料单价看反了,实际成本比核算时的成本多760元,如果每天甲销量的4倍和乙销量的3倍之和不超过120份,那么公司每天的实际成本最多为______ 元.12.如图,直线443y x=-+与x轴和y轴分别交于A、B两点,把射线AB绕点A顺时针旋转90°得射线AC,点P是射线AC上一个动点,点Q是x轴上一个动点.若PQA△与AOB 全等,则点Q的横坐标是_________.13.如图1,在底面积为2100cm,高为20cm的长方体水槽内放入一个圆柱形烧杯,以恒定不变的速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不变,水槽中水面上升的高度h 与注水时间t之间的函数关系如图2,则烧杯的底面积是______2cm14.在平面直角坐标系xOy中,一次函数y = m(x + 3)- 1(m≠0)的图象为直线l,在下列结论中:①无论m取何值,直线l一定经过某个定点;②过点O作OH⊥l,垂足为H,则OH10;③若l与x轴交于点A,与y轴交于点B,△AOB为等腰三角形,则m = 1;④对于一次函数y1= a(x - 1)+ 2(a≠0),无论x取何值,始终有y1>y,则m< 0或0 <m<3? 4?.其中正确的是(填写所有正确结论的序号)______________.三、解答题15.陕西沿黄公路是一条全长800余公里的高颜值公路,它沿着黄河西岸串联陕西4市12县50多景点,其中一段48公里的公路串联府谷龙蛇湾景区和府州古城,甲、乙两人分别从府谷龙蛇湾景区、府州古城骑自行车出发相向而行,甲比乙先出发1小时,两人分别以各自的速度匀速行驶.甲、乙两人距府州古城的距离y(km)与甲出发时间x(h)的函数关系图象如图所示,结合图象信息回答下列问题:(1)甲的骑行速度为________km/h ,乙的骑行速度为________km/h ; (2)求线段2l 的函数表达式;(3)甲出发多长时间后两人第一次相距6km ?16.某超市经销某品牌的两种包装的产品,进价与售价如表: 类别 价格礼盒装独享装进价(元/袋) 40 aa 售价(元/袋) 7810已知购进50袋礼盒装的总价与购进300袋独享装的总价相同: (1)求礼盒装和独享装每袋的进价.(2)若超市用4000元购进了两种包装的该产品,其中礼盒装的数量不超过独享装的4倍,在两种包装的产品全部售完的情况下,求总利润的最大值.17.某校对校园操场进行绿化养护招标,现有甲、乙两公司进行竞标养护,两公司分别提出了自己的绿化养护收费方案.甲公司的方案:每月的养护费用y (元)与绿化面积x (平方米)的关系图象如图所示. 乙公司的方案:绿化面积不超过1000平方米时,每月收取费用5000元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.(1)分别求出甲、乙两公司的收费y (元)与绿化面积x (平方米)的关系式. (2)如果该学校目前的绿化面积是1100平方米,那么选择哪家公司的服务比较划算?18.在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.已知学生公寓、阅览室、超市依次在同一条直线上,阅览室离学生公寓1.2km ,超市离学生公寓2km ,小琪从学生公寓出发,匀速步行了12min 到阅览室;在阅览室停留70min 后,匀速步行了10min 到超市;在超市停留20min 后,匀速骑行了8min 返回学生公寓.给出的图象反映了这个过程中小琪离学生公寓的距离km y 与离开学生公寓的时间min x 之间的对应关系.请根据相关信息,解答下列问题: (1)填表:离开学生公寓的时间/min58 5087112离学生公寓的距离/km 0.5 1.6①阅览室到超市的距离为___________km ;②小琪从超市返回学生公寓的速度为___________km /min ;③当小琪离学生公寓的距离为1km 时,他离开学生公寓的时间为___________min .(3)当092≤≤时,请直接写出y关于x的函数解析式.x19.冰墩墩(BingDwenDwen)、雪容融(ShueyRhonRhon)分别是2022年北京冬奥会、冬残奥会的吉样物.冬奥会来临之际,冰墩墩、雪容融玩偶畅销全国.小雅在某网店选中两种玩偶,决定从该网店进货并销售,第一次小雅用1400元购进了冰墩墩玩偶15个和雪容融玩偶5个,已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元,销售时每个冰墩墩玩偶可获利28元,每个雪容融玩偶可获利20元.(1)求两种玩偶的进货价分别是多少?(2)第二次小雅进货时,网店规定冰墩墩玩偶进货数量不得超过雪容融玩偶进货数量的1.5倍.小雅计划购进两种玩偶共40个,应如何设计进货方案才能获得最大利润,最大利润是多少元?20.将一些相同规格的长方形纸按图①所示方法粘合起来,粘合部分的宽相等.某学校数学综合与实践小组从函数角度进行了如下探究:[观察测量]数学综合与实践小组通过观察测量,得到如表:长方形纸x(张) 1 2 3 4 5总长度y(厘米)15 25 35 45 55(1)[探究发现]建立平面直角坐标系,如图②,横轴表示长方形纸张数石纵轴表示粘合后的总长度y ,描出以表格中数据为坐标的各点(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如过不在同一条直线上,说明理由. (3)[结论应用]应用上述发现的规律让算 ①当x =20时,粘合后的纸条总长度y 为厘米.②粘合后内纸条总长度y 为505厘米时,需使用长方形纸张.1.如图(1),点P 从平行四边形ABCD 的顶点A 出发,以1cm /s 的速度沿A -B -C -D 路径匀速运动到D 点停止. 图(2)是△P AD 的面积S (cm 2)与运动时间t (s )之间的函数关系图象.下列说法:①平行四边形ABCD 是菱形;②250ABCD S cm =平行四边形;③BC 上的高10BC h cm =;④当24s t =时,216S cm =.其中正确的个数是( )A .1B .2C .3D .42.在一次趣味运动会中,“抢种抢收”的比赛规则如下:全程50米的直线跑道,在起点和终点之间,每隔10米放置一个小桶,共四个,参赛者用手托着放有4个乒乓球的盘子,在从起点跑到终点的过程中,将四个乒乓球依次放入4个小桶中(放入时间忽略不计),如果中途乒乓球掉出小桶,则需要返回将乒乓球放回桶中,率先到达终点者获胜.小明和小亮同时从起点出发,以各自的速度匀速跑步前进,小明在放入第二个乒乓球后,乒乓球跳出了小桶,落在了第二个桶的旁边,且落地后不再移动,但他并未发现,继续向前跑了一段距离,被裁判员提醒后立即原速返回捡球,并迅速放回桶中(捡球时间忽略不计),为了赶超小亮,小明将速度提高了1米/秒,小明和小亮之间的距离y (米)和出发时间x (秒)之间的函数关系如图所示,则小明在掉出乒乓球后又继续跑了______米后开始返回.3.如图,四边形ABCD 的顶点坐标分别为(4,0)A -,(2,1)B --,()3,0C ,()0,3D ,当过点B 的直线l 将四边形ABCD 的面积分成面积相等的两部分时,则直线l 的函数表达式为____________.4.某水果店经销甲、乙两种水果,两次购进水果的情况如下表所示:进货批次甲种水果质量(单位:千克)乙种水果质量(单位:千克) 总费用(单位:元)第一次 60 40 1520 第二次 30501360(1)求甲、乙两种水果的进价;(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲、乙两种水果共200千克,且投入的资金不超过3360元.将其中的m千克甲种水果和3m千克乙种水果按进价销售,剩余的甲种水果以每千克17元、乙种水果以每千克30元的价格销售.若第三次购进的200千克水果全部售出后,获得的最大..利润不低于800元,求正整数m 的最大值.。
2020年人教版 八年级上册数学国庆假期作业:第11章《三角形》练习题(含详解)
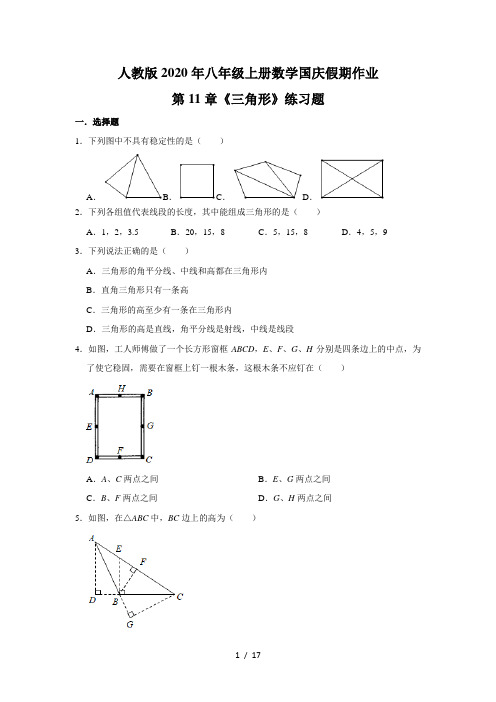
人教版2020年八年级上册数学国庆假期作业第11章《三角形》练习题一.选择题1.下列图中不具有稳定性的是()A.B.C.D.2.下列各组值代表线段的长度,其中能组成三角形的是()A.1,2,3.5B.20,15,8C.5,15,8D.4,5,93.下列说法正确的是()A.三角形的角平分线、中线和高都在三角形内B.直角三角形只有一条高C.三角形的高至少有一条在三角形内D.三角形的高是直线,角平分线是射线,中线是线段4.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在()A.A、C两点之间B.E、G两点之间C.B、F两点之间D.G、H两点之间5.如图,在△ABC中,BC边上的高为()A.AD B.BE C.BF D.CG6.适合条件∠A=∠B=∠C的△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形7.已知一个多边形的内角和是900°,则这个多边形是()A.五边形B.六边形C.七边形D.八边形8.已知,在△ABC中,∠B是∠A的3倍,∠C比∠A大30°,则∠A的度数是()A.30°B.50°C.70°D.90°9.如图,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是()A.64°B.32°C.30°D.40°10.如图,△ABC中,BO,CO分别是∠ABC,∠ACB的平分线,∠A=50°,则∠BOC等于()A.110°B.115°C.120°D.130°11.如图,△ABC中,∠A=110°,若图中沿虚线剪去∠A,则∠1+∠2等于()A.110°B.180°C.290°D.310°12.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=()A.90°B.100°C.130°D.180°13.如图,BP、CP是△ABC的外角角平分线,若∠P=60°,则∠A的大小为()A.30°B.60°C.90°D.120°14.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=()A.70°B.80°C.90°D.100°二.填空题15.若三角形三边长为3,2x+1,10,则x的取值范围是.16.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D.若∠A=32°,则∠BCD =°.17.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=.18.BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是.19.如图,共有个三角形.20.已知:如图所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为cm2.21.如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF,以下结论:①AD∥BC;②∠ACB=∠ADB;③∠ADC+∠ABD=90°;④,其中正确的结论有.三.解答题22.说出下列各图中∠1的度数.23.如图,O是△ABC内的一点,连结OB,OC,求证:AB+AC>OB+OC.24.已知:a、b、c为三角形的三边长化简:|b+c﹣a|+|b﹣c﹣a|﹣|c﹣a﹣b|﹣|a﹣b+c|25.若一个三角形的三边长分别是a,b,c,其中a和b满足方程,若这个三角形的周长为整数,求这个三角形的周长.26.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.27.如图,已知六边形ABCDEF的每个内角都相等,连接AD.(1)若∠1=48°,求∠2的度数;(2)求证:AB∥DE.28.如图,在三角形ABC中,AD⊥BC于点D,且AD平分∠BAC,点E是BA的延长线上任一点,过点E作EF⊥BC于点F,与AC交于点G.(1)求证:AD∥EF.(2)若∠CGF=36°,求∠B的度数.(3)猜想∠E与∠AGE的大小关系,并证明你的猜想.29.某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC =;(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并证明.30.平面内的两条直线有相交和平行两种位置关系.(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D 之间有何数量关系?请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.参考答案一.选择题1.解:因为三角形具有稳定性,四边形不具有稳定性,故选:B.2.解:A、1+2<3.5,不能组成三角形,故此选项错误;B、15+8>20,能组成三角形,故此选项正确;C、5+8<15,不能组成三角形,故此选项错误;D、4+5=9,不能组成三角形,故此选项错误;故选:B.3.解:A、错误.三角形的高不一定在三角形内.B、错误.直角三角形也有三条高.C、正确.D、错误.三角形的高,角平分线,中线都是线段.故选:C.4.解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.故选:B.5.解:由图可知,△ABC中,BC边上的高为AD,故选:A.6.解:∵∠A=∠B=∠C,∴∠B=2∠A,∠C=3∠A,∵∠A+∠B+∠C=180°,即6∠A=180°,∴∠A=30°,∴∠B=60°,∠C=90°,∴△ABC为直角三角形.故选:B.7.解:设这个多边形是n边形,则(n﹣2)•180°=900°,解得:n=7,即这个多边形为七边形.故选:C.8.解:由题意,解得,故选:A.9.解:∵AD∥BC,∴∠EAD=∠B=32°,∵AD是△ABC的外角∠EAC的平分线,∴∠EAC=2∠EAD=64°,∵∠EAC是△ABC的外角,∴∠C=∠EAC﹣∠B=64°﹣32°=32°,故选:B.10.解:∵∠A=50°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,∵BO,CO分别是∠ABC,∠ACB的平分线,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=×130°=65°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣65°=115°.故选:B.11.解:∵∠A=110°,∴∠B+∠C=70°,∵∠1+∠2+∠B+∠C=360°,∴∠1+∠2=290°.故选:C.12.解:法一:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,∠ABC=180°﹣60°﹣∠3=120°﹣∠3,∠ACB=180°﹣60°﹣∠2=120°﹣∠2,在△ABC中,∠BAC+∠ABC+∠ACB=180°,∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,∴∠1+∠2=150°﹣∠3,∵∠3=50°,∴∠1+∠2=150°﹣50°=100°.法二:图中∠1+∠2+∠3+小三角形的三个内角再加两个等边三角形的两个内角,再加正方形的一个内角,总和为180°*3=540°,减去三角形的三个内角之和180°,再减去两个三角形的内角60°*2=120°,再减去正方形的内角90°,则易得∠1+∠2+∠3=540°﹣120°﹣180°﹣90°=150°,而∠3=50°,所以∠1+∠2=100°.故选:B.13.证明:∵BP、CP是△ABC的外角的平分线,∴∠PCB=∠ECB,∠PBC=∠DBC,∵∠ECB=∠A+∠ABC,∠DBC=∠A+∠ACB,∴∠PCB+∠PBC=(∠A+∠ABC+∠A+∠ACB)=(180°+∠A)=90°+∠A,∴∠P=180°﹣(∠PCB+∠PBC)=180°﹣(90°+∠A)=90°﹣∠A=60°,∴∠A=60°,故选:B.14.解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∵∠ABP=20°,∠ACP=50°,∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,∴∠A=∠ACM﹣∠ABC=60°,∠ACB=180°﹣∠ACM=80°,∴∠BCP=∠ACB+∠ACP=130°,∵∠PBC=20°,∴∠P=180°﹣∠PBC﹣∠BCP=30°,∴∠A+∠P=90°,故选:C.二.填空题15.解:由三角形三边关系定理得:10﹣3<2x+1<10+3,且2x+1>0解得:3<x<6,即x的取值范围是3<x<6.故答案为:3<x<6.16.解:∵∠C=90°,∴∠BCD+∠ACD=90°,∵CD⊥AB,∴∠ADC=90°,∴∠A+∠ACD=90°,∴∠BCD=∠A=32°,故答案为:32.17.解:∵AE平分∠BAC,∴∠1=∠EAD+∠2,∴∠EAD=∠1﹣∠2=30°﹣20°=10°,Rt△ABD中,∠B=90°﹣∠BAD=90°﹣30°﹣10°=50°.故答案为50°.18.解:∵BD是△ABC的中线,∴AD=CD,∴△ABD和△BCD的周长的差=(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC,∵AB=5,BC=3,∴△ABD和△BCD的周长的差=5﹣3=2.故答案为:2.19.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.故答案为:620.解:∵D为BC中点,根据同底等高的三角形面积相等,∴S△ABD=S△ACD=S△ABC=×4=2,同理S△BDE=S△CDE=S△BCE=×2=1,∴S△BCE=2,∵F为EC中点,∴S△BEF=S△BCE=×2=1.故答案为1.21.解:①∵AD平分∠EAC,∴∠EAC=2∠EAD,∵∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,故①正确;②∵AD∥BC,∴∠ADB=∠DBC,∵BD平分∠ABC,∠ABC=∠ACB,∴∠ABC=∠ACB=2∠DBC,∴∠ACB=2∠ADB,故②错误;③在△ADC中,∠ADC+∠CAD+∠ACD=180°,∵CD平分△ABC的外角∠ACF,∴∠ACD=∠DCF,∵AD∥BC,∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,∴∠ADC+∠ABD=90°,故③正确;④∵BD平分∠ABC,∴∠ABD=∠DBC,∵AD∥BC,∴∠DCF=∠ADC,∵∠ADC+∠ABD=90°,∵∠DCF=90°﹣∠ABC=∠DBC+∠BDC,∴∠BDC=90°﹣2∠DBC,∴∠DBC=45°﹣∠BDC,故④正确;故答案是:①③④.三.解答题22.解:(1)∠1=180°﹣60°﹣30°=90°;(2)∠1=45°+50°=95°;(3)∠1=120°﹣35°=55°.23.证明:如图,延长BO交AC于点D,∵AB+AD>OB+OD,OD+CD>OC,∴AB+AD+CD>OB+OC,即:AB+AC>OB+OC.24.解:∵a、b、c为三角形三边的长,∴a+b>c,a+c>b,b+c>a,∴原式=|(b+c)﹣a|+|b﹣(c+a)|﹣|c﹣(a+b)|﹣|(a+c)﹣b|=b+c﹣a+a+c﹣b﹣a﹣b+c+b﹣a﹣c=2c﹣2a.25.解:由,解得,∴3<c<5,∵周长为整数,∴c=4,∴周长=4+4+1=9.26.解:∵∠CAB=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,又∵AD是高,∴∠ADC=90°,∴∠DAC=180°﹣90°﹣∠C=30°,∵AE、BF是角平分线,∴∠CBF=∠ABF=35°,∠EAF=25°,∴∠DAE=∠DAC﹣∠EAF=5°,∠AFB=∠C+∠CBF=60°+35°=95°,∴∠BOA=∠EAF+∠AFB=25°+95°=120°,∴∠DAC=30°,∠BOA=120°.故∠DAE=5°,∠BOA=120°.27.解:(1)∵六边形ABCDEF的各内角相等,∴一个内角的大小为,∴∠E=∠F=∠BAF=120°.∵∠F AB=120°,∠1=48°,∴∠F AD=∠F AB﹣∠DAB=120°﹣48°=72°.∵∠2+∠F AD+∠F+∠E=360°,∠F=∠E=120°,∴∠ADE=360°﹣∠F AD﹣∠F﹣∠E=360°﹣72°﹣120°﹣120°=48°.(2)证明:∵∠1=120°﹣∠DAF,∠2=360°﹣120°﹣120°﹣∠DAF=120°﹣∠DAF,∴∠1=∠2,∴AB∥DE.28.(1)证明:∵AD⊥BC,EF⊥BC,∴∠ADC=∠EFC=90°,∴AD∥EF;(2)∵AD∥EF,∠CGF=36°,∴∠CGF=∠CAD=36°,∵AD平分∠BAC,∴∠BAD=∠CAD=36°,∴∠B=180°﹣∠BAD﹣∠BDA=54°;(3)∠E=∠AGE,证明:理由是:∵AD∥EF,∴∠E=∠BAD,∠AGE=∠CAD,∵∠BAD=∠CAD,∴∠E=∠AGE.29.解:(1)∵BP、CP分别平分∠ABC和∠ACB,∴∠PBC=∠ABC,∠PCB=∠ACB,∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB),=180°﹣(∠ABC+∠ACB),=180°﹣(180°﹣∠A),=180°﹣90°+∠A,=90°+32°=122°,故答案为:122°;(2)∵CE和BE分别是∠ACB和∠ABD的角平分线,∴∠1=∠ACB,∠2=∠ABD,又∵∠ABD是△ABC的一外角,∴∠ABD=∠A+∠ACB,∴∠2=(∠A+∠ABC)=∠A+∠1,∵∠2是△BEC的一外角,∴∠BEC=∠2﹣∠1=∠A+∠1﹣∠1=∠A=;(3)∠QBC=(∠A+∠ACB),∠QCB=(∠A+∠ABC),∠BQC=180°﹣∠QBC﹣∠QCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BQC=90°﹣∠A.30.解:(1)不成立.结论是∠BPD=∠B+∠D延长BP交CD于点E,∵AB∥CD∴∠B=∠BED又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.(2)结论:∠BPD=∠BQD+∠B+∠D.(3)连接EG并延长,根据三角形的外角性质,∠AGB=∠A+∠B+∠E,又∵∠AGB=∠CGF,在四边形CDFG中,∠CGF+∠C+∠D+∠F=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.。
人教版八年级上册数学 八年级上册数学作业本参考答案

人教版八年级上册数学八年级上册数学作业本参考答案一、第一章实数1. 课前练习(1) 有理数的范围是整数、分数及其运算结果。
(2) 无理数是不能表示为有理数的数。
(3) 小数除了有限小数外,还有无限小数,无限小数有循环小数和非循环小数两种。
(4) √2、π、e等都是无理数。
2. 课后作业(1) 有理数是指整数、分数及其运算结果,如4、-5/6、√16等。
(2) 无理数是指不能表示为有理数的数,如√2、π、e等。
(3) 有限小数是指小数部分有限的小数,如0.5、-3.25等。
循环小数是指小数部分出现了一定规律循环的小数,如0.3(3)、0.25(25)等。
(4) 在实数轴上,0与正数、负数之间是有间隔的。
(5) 非负有理数和非负无理数都可以表示为不小于0的数,但有理数可以表示为x=a或a<x<b,而无理数不能表示为这样的形式。
3. 拓广探究(1) 设a是正整数,b是不为1的正整数,证明:如果a可整除b,则a和b的最大公约数是b的约数。
证:设d是a和b的最大公约数,因为a可整除b,所以a=k×b,其中k是正整数。
如果d≠b,那么d是b的真因数,d也是a的因数,这与d是a和b的最大公约数矛盾。
所以d=b,即a和b的最大公约数是b的约数。
(2) 设x和y都是有理数,证明:x+y和x-y都是有理数。
证:因为x和y都是有理数,所以可以表示为x=a/b,y=c/d,其中a、b、c、d都是整数。
则x+y=a/b+c/d=(ad+bc)/bd,其中ad+bc、bd都是整数,所以x+y也是有理数。
同理,x-y=a/b-c/d=(ad-bc)/bd,其中ad-bc、bd都是整数,所以x-y也是有理数。
(3) 设x和y都是无理数,是否有必要证明x+y和x-y都是无理数?答:不必要。
因为有理数和无理数的运算结果都是无理数,所以x+y和x-y一定都是无理数。
二、第二章代数式1. 课前练习(1) 代数式是由常数、变量及运算符号组成的式子。
暑假作业数学八年级(配人教版)答案

暑假作业㊀数学㊀八年级(配人教版)参考答案A 版㊀学习版练㊀习㊀一快乐基础屋一㊁选择题1.D ㊀2.B ㊀3.B ㊀4.C ㊀5.B ㊀6.D ㊀7.A ㊀8.B ㊀9.D ㊀10.C二㊁填空题11.3㊀-0.0212.<㊀=13.0.1m 14.2|a |c 2ab15.x x 2+y 216.1317.518.甲㊀被开方数是负数19.15320.当b >0时,a 2c 10c2b 当b <0时,-a 2c 10c2b三㊁解答题21.(1)解:原式=24ː3=8=22(2)解:原式=27ˑ33ˑ121=211(3)解:原式=12ː3=4=2(4)解:原式=273-123=9-4=3-2=1(5)解:原式=72ˑ-16117()ː14112=-16112ː14112=-23(6)解:原式=(2+26+3)(5-26)=25-(26)2=25-24=122.(1)解:原式=235=1155(2)解:原式=a 2(3)解:ȵxȡ0㊀ʑx+1>0ʑ(x+1)2=x+1(xȡ0) (4)解:原式=(|a+1|)2=(a+1)223.(1)解:原式=1(23)=3(23ˑ3) =36(2)解:原式=3210=(3ˑ10)(210ˑ10) =3020(3)解:原式=506=253=533(4)解:原式=15x35x=3x2=3x24.解:由题意可得2-xȡ0,x-2ȡ0ʑ可得x=2,y=5ʑx y=25欢乐提高吧1.解:原式=-23(m-n)2ˑa2ˑ1m-n =-a62.解:ȵa+1+b-1=0ʑa+1=0,b-1=0ʑa=-1,b=1ʑa2015+b2015=(-1)2015+12015=-1+ 1=0练㊀习㊀二快乐基础屋一㊁选择题1.C㊀2.C㊀3.B㊀4.C㊀5.A㊀6.A㊀7.D㊀8.D㊀㊀二㊁填空题9.010.-2211.29+125㊀66-36212.-24+4313.2+3314.-14215.-116.117.ʃ2318.219.42三㊁解答题20.(1)解:原式=7+27+97= 37+97=127(2)解:原式=32-22+3-33= 2-23(3)解:原式=22+32=52(4)解:原式=23-22+3+2= 33-2(5)解:原式=43+25+23-5 =63+5(6)解:原式=18-35-5=13-35(7)解:原式=22+33-32-2=-22-36(8)解:原式=62-22-2+342=154221.解:原式=2-1(2-1)(2+1)+3-2(3-2)(3+2)+2-3(2-3)(2+3)++10-3(10-3)(10+3)=2-1+3-2+2-3+ +10-3=-1+1022.(1)解:原式=43-(36)2+(3-3)3+33()=43-(36)2+2(2)解:原式=23ˑ3x +6ˑx 2-2x ˑx x=2x +3x -2x =3x23.解:原式=9a a -5a a +3aˑ2a 2a =9a a -5a a +6a a =10a a24.(1)解:ȵx =12(7+5),y =12(7-5)ʑx -y =5,xy =12ʑx 2-xy +y 2=(x -y )2+xy =112(2)解:ȵa =4+15,b =4-15ʑa +b =8,ab =1ʑa 2+5ab +b 2-3a -3b =(a +b )2-3(a +b )+3ab =4325.解:大正方形的边长为:4=2,小正方形的边长为2ʑ阴影部分的面积=(2-2)ˑ2=22-2欢乐提高吧1.解:原式=(25+1)2-12-1+3-23-2(+4-34-3+ +100-99100-99)=(25+1)[(2-1)+(3-2)+(4-3)+ +(100-99)]=(25+1)(100-1)=9(25+1)2.解:原式=(2x -1)2+(y -3)2=0要使两个数的平方和为0,只有使每项式为0,即:2x -1=0,y -3=0解得:x =12,y =323x9x-5x y x=23ˑ3x x-5xy=2x x-5xy=(2-56)2练㊀习㊀三快乐基础屋一㊁选择题1.D㊀2.A㊀3.C㊀4.B㊀5.C㊀6.D㊀7.D㊀8.A㊀9.B㊀10.C㊀11.D㊀12.B㊀13.C二㊁填空题14.13㊀15.20㊀16.11㊀17.24㊀18.601319.5㊀20.492㊀21.32㊀22.13或119㊀23.2㊁2㊁2㊀24.49㊀25.15三㊁解答题26.解:设矩形花池的长是a,宽是b根据题意得:ab=48①a2+b2=100②②+①ˑ2得:(a+b)2=196,即a+b =14ʑ矩形花池的周长是14ˑ2=28m27.解:设E站建在离A站x km处时, C㊁D两村到E站的距离相等㊂在RtәADE 中,DE2=AD2+AE2=152+x2,在RtәCBE 中,CE2=CB2+BE2=102+(25-x)2ȵDE=CE,ʑDE2=CE2,即152+x2= 102+(25-x)2,解得:x=10答:E站建在离A站10km处时,C㊁D 两村到E站的距离相等㊂28.解:设旗杆AB的高为x m,则绳子AC的长为(x+1)mABCȵ在RtәABC中,øABC=90ʎ,BC=5, AB=xAC=x+1,ʑx2+52=(x+1)2解得:x=12答:旗杆的高度为12m㊂欢乐提高吧1.解:连接BD,øA=90ʎ,BD=AB2+AD2 =5cmȵBD2+CD2=BC2ʑәBCD为直角三角形ʑәBCD面积=12ˑBDˑCD=30cm2әABD 的面积=12ˑAB ˑAD =6cm 2故四边形ABCD 的面积为36cm 22.解:过点D 作DE ʅAB 于点E ,ȵø1=ø2,øC =øDEA =90ʎ,AD =AD ,ʑәACD ɸәAED ,ʑCD =DE =1.5,AC =AE在RtәBED 中,BE =BD 2-DE 2=2在RtәABC 中,AC 2=AB 2-BC 2=(AC +BE )2-BC 2即AC 2=(AC +2)2-42ʑAC =33.解:如图所示,过点B 作纸条一边的垂线BDACBDȵ纸条的宽度为3cm ʑBD =3cm ȵøBAD =30ʎʑAB =2BD =2ˑ3=6cm ʑ根据勾股定理得:BC =2AB =2ˑ6=62cm练㊀习㊀四快乐基础屋一㊁选择题1.A ㊀2.C ㊀3.A ㊀4.D ㊀5.C ㊀6.C二㊁填空题7.80ʎ8.8cm 9.3cm 10.1211.12cm 12.12三㊁解答题13.解:ȵ四边形ABCD 为平行四边形ʑAD ʊBC ,ʑøADE =øDEC 又ȵDE 平分øADC ,ʑøADE =øCDEʑøDEC =øCDE ,ʑәCDE 为等腰三角形ʑCD =CE ,则BE =BC -CE =BC -CD=8-6=2(cm)14.证明:ȵ四边形ABCD 是平行四边形ʑAD ʊBC ,AD =BC ȵAE =12AD ,FC =12BC ʑAE =FC ,AE ʊFC ʑ四边形AECF 是平行四边形ʑGF ʊEH同理可证ED ʊBF 且ED =BF ʑ四边形BFDE 是平行四边形ʑGE ʊFHʑ四边形EGFH是平行四边形欢乐提高吧1.DE=BF证明:ȵ四边形ABCD是平行四边形ʑAEʊCF㊀AD=BCʑøE=øFȵO是AC的中点㊀AO=CO在әOCF和әOAE中øAOE=øCOF㊀øE=øF㊀AO=CO ʑәOCFɸәOAE㊀ʑAE=CFʑAE-AD=CF-BC㊀即DE=BF2.(1)证明:ȵ四边形ABCD是平行四边形ʑABʊCD㊀ADʊBC㊀AB=CD㊀AD= BCȵøDAB=60ʎʑøDAB=øDCB=60ʎȵABʊCD㊀ʑøEDA=øDAB㊀øDCB=øCBF ȵøDAB=øDCB=60ʎʑøEDA=øDAB=øDCB=øCBF= 60ʎȵøEDA=øCBF=60ʎ㊀AE=AD㊀CF=CBʑәAED和әCBF均为等边三角形ʑAD=DE㊀BC=BFȵAD=DE㊀BC=BF㊀AD=BCʑDE=BFȵDE=BF㊀AB=CDʑAF=CEȵAFʊCEʑ四边形AFCE是平行四边形(2)解:上述结论还成立,理由如下:ȵ四边形ABCD是平行四边形ʑøADC=øCBA㊀AB=CD㊀AD=BC ㊀ABʊCD㊀ADʊBCȵøADC=øCBA㊀ʑøADE=øCBF ȵAE=AD㊀CF=CB㊀ʑøADE=øAED㊀øCBF=øCFBʑøADE=øAED=øCBF=øCFB ȵøADE=øAED=øCBF=øCFB㊀AD=BCʑәADEɸәCBF㊀ʑDE=BFȵCD=AB㊀ʑAF=CEȵAF=CE㊀AFʊCEʑ四边形AFCE是平行四边形练㊀习㊀五快乐基础屋一㊁选择题1.A㊀2.D㊀3.C㊀4.A㊀5.C㊀6.C㊀7.C㊀二㊁填空题8.129.610.3㊀3㊀菱㊀矩㊀AB=AC且øA= 90ʎ11.8三㊁解答题12.解:ȵ四边形ABCD是平行四边形ʑBC=AD=8cm㊀OA=OCOB=OD=12BD=6cmȵBDʅAD㊀ʑøADO=90ʎʑOA=AD2+OD2=10cmʑAC=2OA=20cm13.证明:ȵBD㊁CE为әABC的中线ʑED为әABC的中位线ʑEDʊBC㊀DE=12CBȵF㊁G分别是BO㊁CO的中点ʑFG是әBOC的中位线ʑFGʊCB㊀FG=12BCʑED=FG㊀DEʊFGʑ四边形DEFG为平行四边形14.证明:ȵ四边形ABCD是平行四边形ʑADʊBC㊀AD=BCȵE㊁F分别是AD㊁BC的中点ʑAE=DE=12AD㊀CF=BF=12BC ʑAEʊCF㊀AE=CFʑ四边形AECF是平行四边形ʑCEʊAFʑEM是әDAN的中位线,FN是әBCM的中位线ʑDM=MN㊀BN=MNʑBN=MN=DM15.证明:ȵ四边形ABCD是平行四边形ʑAB=CD㊀OA=OCʑøBAF=øCEF㊀øABF=øECFȵCE=DC在▱ABCD中,CD=ABʑAB=CEʑ在әABF和әECF中øBAF=øCEFAB=CEøABF=øECFʑәABFɸECF(ASA)ʑBF=CFȵOA=OCʑOF是әABC的中位线ʑAB=2OF欢乐提高吧1.证明:ȵ四边形ABCD是平行四边形ʑADʊBCʑøCBE=øFȵDF=ADʑDF=BC在әBCE和әFDE中,øF=øCBE㊀øDEF=øCEBDF=BC㊀ʑәBCEɸәFDE(AAS)ʑBE=FE㊀DE=CE即点E是CD㊁BF的中点㊂AB CED F2.证明:过点M作MGʅAB连接DG,ADCBMEF G123ȵCFʅABʑMGʊCFȵAM平分øCAB㊀ʑø2=ø3ȵMCʅCA㊀MGʅAB㊀ʑCM=MG ȵøCDM=ø1+ø2㊀øCMD=ø3+øB ø2=ø3㊀ø1=øBʑøCDM=øCMDʑCM=CD㊀ʑCD=CM=MGȵCDʊMG㊀ʑ四边形CDGM是菱形ʑCM=DG㊀且CBʊDGȵDEʊAB㊀ʑ四边形DEBG是平行四边形ʑDG=EB㊀ʑCM=EB练㊀习㊀六快乐基础屋一㊁选择题1.C㊀2.C㊀3.A㊀4.C㊀5.C㊀6.A㊀7.B㊀8.B㊀9.A二㊁填空题10.5311.312.60ʎ13.AB=AC或øB=øC或AD是øBAC的平分线或BD=CD14.AC=BD或ABʅBC15.3三㊁解答题16.证明:ȵDEʊAC㊀DFʊABʑ四边形AEDF是平行四边形ʑøADE=øDAFȵAD平分øBAC㊀ʑøDAE=øDAF ʑøDAE=øADE㊀ʑAE=DEʑ平行四边形AEDF是菱形17.(1)证明:ȵ四边形ABCD是矩形ʑABʊCD㊀ʑøOAE=øOCF㊀øOEA=øOFCȵAE=CF㊀ʑәAEOɸCFO(ASA)ʑOE=OF(2)解:连接BOȵOE=OF㊀BE=BFʑBOʅEF且øEBO=øFBOʑøBOF=90ʎȵ四边形ABCD是矩形ʑøBCF=90ʎ又ȵøBEF=2øBAC㊀øBEF=øBAC+øEOAʑøBAC=øEOA㊀ʑAE=OEȵAE=CF㊀OE=OF㊀ʑOF=CF又ȵBF=BF㊀ʑәBOFɸәBCF(HL)ʑøOBF=øCBF㊀ʑøCBF=øFBO =øOBEȵøABC=90ʎ㊀øOBE=30ʎ㊀øBEO =60ʎʑøBAC=30ʎ㊀ʑAB=3BC=618.(1)证明:ȵ对角线BD平分øABC ʑøABD=øCBD又ȵAB=BC㊀BD=BDʑәABDɸәCBD(SAS)ʑøADB=øCDB(2)证明:ȵPMʅAD㊀PNʅCDʑøPMD=øPND=90ʎȵøADC=90ʎʑ四边形MPND是矩形由(1)知øADB=øCDB又ȵPMʅAD㊀PNʅCDʑPM=MDʑ四边形MPND是正方形欢乐提高吧1.(1)证明:ȵ四边形ABCD是矩形ʑAB=CD㊀AD=BC㊀øA=øC=90ʎȵ在矩形ABCD中,M㊁N分别是AD㊁BC的中点ʑAM=12AD㊀CN=12BCʑAM=CN在әMBA和әNDC中ȵAB=CD㊀øA=øC=90ʎ㊀AM= CNʑәMBAɸәNDC(2)四边形MPNQ是菱形证明:连接MN㊀ȵәMBAɸәNDC ʑMB=ND㊀ȵ四边形ABCD是矩形ʑADʊBC㊀øA=90ʎ㊀AD=BCȵM㊁N分别是AD㊁BC的中点ʑAM=BNʑ四边形AMNB是矩形ʑøMNB=90ʎ在RtәMNB中ȵP是BM的中点ʑPN=12BM=PM同理MQ=NQȵBM=ND㊀P㊁Q分别是BM㊁DN的中点ʑPM=NQ㊀ʑPM=PN=NQ=MQ ʑ四边形MPNQ是菱形2.(1)解:猜想结果,图2结论为BE+ CF=2AG图3结论为BE-CF=2AG (2)证明:连接CE,过D作DQʅl,垂足为点Q,交CE于点HȵøAGO=øDQO=90ʎ㊀øAOG=øDOQ(对顶角相等)且O为AD的中点即AO=DOʑәAOGɸәDOQ(AAS)即AG=DQ ȵBEʊDHʊFC㊀BD=DCʑCHʒEH=CDʒBD=FQʒEQʑQH是三角形EFC的中位线ʑBE=2DH㊀CF=2QHʑBE-CF=2(DQ+QH)-2QH=2DQ =2AGDQFlCH OE A G B练㊀习㊀七快乐基础屋一㊁选择题1.C ㊀2.B ㊀3.C ㊀4.C ㊀5.B ㊀6.B二㊁填空题7.y =100x -408.y =8x ㊀40㊀809.s =2n +110.S =2x 2-4x +411.y =0.25x +6(0ɤx ɤ10)三㊁解答题12.(1)解:由题意可得,甲㊁乙两条生产线投入生产后,甲生产线生产时对应的函数关系式是y 1=20x +200乙生产线生产时对应的函数关系式是y 2=30x(2)令20x +200=30x ㊀解得x =20故第20天结束时,两条生产线的产量相同ʑ甲生产线对应的函数图像一定经过点(0,200)和(20,600)画出函数图像,如下图所示:y x观察图像可知,当第10天结束时甲生产线的总产量高,当第30天结束时乙生产线的总产量高㊂13.(1)由图像得:出租车的起步价是8元,当x >3时,设y 与x 的函数关系式为y =kx +b (k ʂ0),将坐标(3,8)和(5,12)代入函数关系式得:3k +b =8①5k +b =12②{②-①得:2k =4㊀ʑk =2代入①得:b =2解得:k =2,b =2ʑy 与x 的函数关系式为y =2x +2(2)ȵ32元>8元,ʑ把y =32代入函数解析式y =2x +2,解得:x =15ʑ这位乘客乘车的里程是15km欢乐提高吧1.(1)解:设y 1=k 1x 1,将(10,600)代入上式得:k 1=60,ʑy 1=60x (0ɤx ɤ10)设y 2=k 2x 2+b ,将(0,600),(6,0)代入上式得:k 2=-100,b =600ʑy 2=-100x +600(0ɤx ɤ6)(2)根据题意可知当y 1=y 2时,x =154,故当0ɤx ɤ154时,S =600-160x当154ɤx<6时,S=160x-600当6ɤxɤ10时,S=y2=60x,即S关于x的函数关系式为:S=600-160x0ɤx<154() 160x-600154ɤx<6() 60x(6ɤxɤ10)ìîíïïïïïï(3)根据题意,当A加油站在甲地与B 加油站之间时,60x+200=-100x+600,解得:x=52,此时A加油站离甲地的距离为:60ˑ52 =150km,当B加油站在甲地与A加油站之间时, -100x+600+200=60x解得:x=5,此时A加油站离甲地的距离为:60ˑ5=300km综上所述,A加油站离甲地的距离为150km或300km㊂2.解:如图所示,过点B作BDʅOC于点D,则øO=øBDC设OC=x,根据光的反射原理,øACO=øBCD,故әAOCʐәBDC根据三角形的性质可得:OCʒDC= AOʒBD即xʒ(4-x)=2ʒ3解得:x=85故根据勾股定理得:AC=22+85()2 =2415BC=32+4-85()2=3415故这束光从点A到点B所经过的路径的长度为:AC+BC=41练㊀习㊀八快乐基础屋一㊁选择题1.D㊀2.D㊀3.C㊀4.D㊀5.A㊀6.A㊀二㊁填空题7.k<28.y=-2x9.y=x10.(2,0)㊀(0,4)11.6㊀-32三㊁解答题12.(1)解:设y=kx+b则40k+b=7537k+b=70{解得k=53㊀b=253ʑy=53x+253(2)当x=39时,y=53ˑ39+253ʂ78.2ʑ一把高39cm 的椅子和一张高78.2cm的课桌不配套13.如图所示:y 14.解:把(4,a )代入y =12x 得:a =12ˑ4=2ʑ一次函数y =kx +b 的图像经过点(-2,-4)和点(4,2)ʑ-2k +b =-44k +b =2{解得k =1,b =-2ʑ该一次函数的解析式为y =x -215.(1)解:把x =0,y =0代入y =(3-k )x -2k +18可得:k =9(2)解:把x =0,y =-2代入y =(3-k )x -2k +18可得:k =10欢乐提高吧1.解:ȵ一次函数y =-x +a 和一次函数y =x +b 的交点坐标为(m ,8)ʑ8=-m +a ①㊀8=m +b ②①+②得:16=a +b 即a +b =162.解:如图所示,由题意可知A 点坐标为(-1,2+m ),B 点坐标为(1,m -2)C 点坐标为(2,m -4),D 点坐标为(0,2+m ),E 点坐标为(0,m ),F 点坐标为(0,-2+m ),G 点坐标为(1,m -4)ʑDE =EF =BG =2又ȵAD =BF =GC =1ʑ图中阴影部分的面积和等于12ˑ2ˑ1ˑ3=3练㊀习㊀九快乐基础屋一㊁选择题1.B ㊀2.C ㊀3.C ㊀4.B ㊀5.A ㊀6.A ㊀7.A ㊀二㊁填空题8.56㊀80㊀156.89.y =10000+16x ㊀x ȡ110.a <b ㊀011.-212.-213.ʃ414.3<x <6三、解答题15.解:设这个一次函数的解析式为y =kx+bȵ该一次函数的图像经过点(2,3)和点(-1,4)ʑ2k+b=3-k+b=4{解得k=-13,b=113ʑ这个一次函数的解析式为y=-13x+ 11316.解:直线y=kx+b与直线y=5-4x 平行ʑk=-4直线y=-3(x-6)与y轴的交点是(0,18)将x=0,y=18代入y=-4x+b解得b=18ʑ直线的函数解析式是y=-4x+1817.解:设正比例函数的解析式为y= kx,则有-6=3k㊀ʑk=-2即正比例函数解析式为y=-2xȵA(a,a+3)是正比例函数图像上的点ʑa+3=-2a㊀ʑa=-1则平行该图像的一次函数y=kx+a的解析式为y=-2x-1欢乐提高吧1.(1)解:由题意得:x-2y=-k+6x+3y=4k+1{解得:x=k+4,y=k-1ʑ两直线的交点坐标为(k+4,k-1)又ȵ交点在第四象限内ʑk+4>0k-1<1{解得-4<k<1(2)解:由于k为非负整数且-4<k<1ʑk=0㊀ʑ直线方程x-2y=6,x+3y=1两直线相交,即x-2y=6x+3y=1{㊀解得:x=4,y=-1ʑ两直线的交点坐标为(4,-1)ȵ直线x-2y=6与y轴的交点为(0,-3)直线x+3y=1与y轴的交点为0,13()ʑ围成的三角形的面积=12ˑ3+13()ˑ4=2032.(1)解:直线y=-x+b交y轴于点P(0,b),由题意得:b>0,tȡ0,b=1+t,当t=3时,b=4ʑy=-x+4(2)解:当直线y=-x+b过点M(3,2)时,2=-3+b㊀解得:b=55=1+t㊀解得:t=4当直线y=-x+b过点N(4,4)时4=-4+b㊀解得:b=88=1+t㊀解得:t=7故若点M㊁N位于l的异侧,t的取值范围是4<t<7练㊀习㊀十快乐基础屋一㊁选择题1.C㊀2.A㊀3.C㊀4.C㊀5.C㊀6.D二㊁填空题7.29㊀298.769.乙10.711.甲12.87三㊁解答题13.(1)解:70ˑ10%+80ˑ40%+88ˑ50%=83(分)(2)解:80ˑ10%+75ˑ40%+50%㊃x >83ʑx>90ʑ小文同学的总成绩是83分,小明同学要在总成绩上超过小文同学,则他的普通话成绩应超过90分㊂14.解:甲:数据10.8出现2次,次数最多,所以众数是10.8平均数=(10.8+10.9+11+10.7+ 11.2+10.8)ː6=10.9中位数=(10.8+10.9)ː2=10.85乙:数据10.9出现3次,次数最多,所以众数是10.9平均数=(10.9+10.9+10.8+10.8+ 10.5+10.9)ː6=10.8中位数=(10.8+10.9)ː2=10.85所以从众数上看,乙的整体成绩大于甲的整体成绩从平均数上看,甲的平均成绩优于乙的平均成绩从中位数看,甲㊁乙的成绩一样好欢乐提高吧(1)解:观察表格,可知这组样本的平均数=(0ˑ3+1ˑ13+2ˑ16+3ˑ17+4ˑ1)ː50=2样本数据中,3出现17次,出现的次数最多,所以这组数据的众数是3ȵ将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2ʑ这组数据的中位数=(2+2)2=2 (2)解:ȵ在50名学生中,读书多于2册的学生有18名,则该校七年级300名学生在本次活动中读书多于2册的人数为: 300ˑ1850()=108(人)ʑ根据样本数据,可以估计该校八年级300名学生在本次活动中读书多于2册的有108人㊂假期总结测试题一㊁选择题1.B㊀2.D㊀3.D㊀4.D㊀5.C㊀6.B㊀7.D㊀8.A二㊁填空题9.83310.311.等腰直角三角形12.20cm13.y=-x14.4815.y=t-0.6(tȡ3)㊀2.4㊀6.4三㊁解答题16.(1)选①(答案不唯一,任选其一) (2)证明:ȵ四边形ABCD是正方形ʑAB=CD㊀øA=øC=90ʎ又ȵAE=CF,øA=øC,AB=CD ʑәAEBɸCFD(SAS)ʑBE=DF选②:ȵ四边形ABCD是正方形ʑADʊBC又ȵBEʊDFʑ四边形EBFD是平行四边形ʑBE=DF选③:ȵ四边形ABCD是正方形ʑAB=CD㊀øA=øC=90ʎ又ȵø1=ø2ʑәAEBɸәCFD(AAS)ʑBE=DF17.(1)甲:7.5㊀3.8乙:7㊀7.5㊀ 5.4(2)因为甲的方差小于乙的方差,甲的成绩比较稳定,故甲胜出㊂18.(1)解:ȵAD平分øCAB㊀DEʅAB ㊀øC=90ʎʑCD=DE㊀ȵCD=3㊀ʑDE=3 (2)解:在RtәABC中,由勾股定理得: AB=AC2+BC2=62+82=10ʑәADB的面积为:SәADB=12AB㊃DE=12ˑ10ˑ3=1519.解:设一次函数解析式为y=kx+ b,把x=4,y=9和x=6,y=-1,分别带入得:4k+b=9①6k+b=-1②{①-②得:-2k=10㊀ʑk=-5把k=-5代入①得:b=29ʑ一次函数解析式为:y=-5x+2920.(1)解:y=8000-500(x-60)即y=38000-500x(xȡ60) (2)解:当x=70时y=38000-500ˑ70=3000当价格为70元时,这种商品的需求量是3000件㊂。
八年级暑期数学作业及参考答案

八年级暑期数学作业及参考答案八年级暑期数学作业及参考答案选择题(共8小题,每小题3分,满分24分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列图形中,既是轴对称图形,又是中心对称图形是( )A.B.C.D.考点:中心对称图形;轴对称图形.分析:根据轴对称图形与中心对称图形的概念求解.解答:解:A、不是轴对称图形,不是中心对称图形.故错误;B、是轴对称图形,也是中心对称图形.故正确;C、不是轴对称图形,不是中心对称图形.故错误;D、是轴对称图形,不是中心对称图形.故错误.故选B.点评:此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.2.下列分式中是最简分式的是( )A.B.C.D.考点:最简分式.分析:最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.解答:解:A、的分子、分母都不能再分解,且不能约分,是最简分式;B、;C、=;D、;故选A.点评:分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.3.下列调查中,适合普查的是( )A.中学生最喜欢的电视节目B.某张试卷上的印刷错误C.质检部门对各厂家生产的电池使用寿命的调查D.中学生上网情况考点:全面调查与抽样调查.分析:由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.解答:解:A、中学生最喜欢的电视节目,适于用抽样调查,故此选项不合题意;B、某张试卷上的印刷错误,适于用全面调查,故此选项符合题意;C、质检部门对各厂家生产的电池使用寿命的调查,适于用抽样调查,故此选项不合题意;D、中学生上网情况,适于用抽样调查,故此选项不合题意;故选:B.点评:本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的.对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.4.下列各式中,与是同类二次根式的是( )A.B.C.D.考点:同类二次根式.专题:计算题.分析:原式各项化简得到结果,即可做出判断.解答:解:与是同类二次根式的是=.故选D点评:此题考查了同类二次根式,熟练掌握同类二次根式的定义是解本题的关键.5.在平面中,下列说法正确的是( )A.四边相等的四边形是正方形B.四个角相等的四边形是矩形C.对角线相等的四边形是菱形D.对角线互相垂直的四边形是平行四边形考点:多边形.分析:此题根据平行四边形的判定与性质,矩形的判定,菱形的判定以及正方形的判定来分析,也可以举出反例来判断选项的正误.解答:解:A、四边相等的四边形也可能是菱形,故错误;B、四个角相等的四边形是矩形,正确;C、对角线相等的四边形不是菱形,例如矩形,等腰梯形,故此选项错误;D、对角线互相平分的四边形是平行四边形,故错误;故选:B.点评:本题考查了正方形、平行四边形、矩形以及菱形的判定.注意正方形是菱形的一种特殊情况,且正方形还是一种特殊的矩形.6.已知点P(x1,﹣2)、Q(x2,2)、R(x3,3)三点都在反比例函数y=的图象上,则下列关系正确的是( )A.x1考点:反比例函数图象上点的坐标特征.专题:计算题.分析:根据反比例函数图象上点的坐标特征,把三个点的坐标分别代入解析式计算出x1、x3、x2的值,然后比较大小即可.解答:解:∵点P(x1,﹣2)、Q(x2,2)、R(x3,3)三点都在反比例函数y=的图象上,∴x1=﹣,x2=,x3=,∴x1故选A.点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.7.如图,菱形ABCD的边长为4,过点A、C作对角线AC的垂线,分别交CB和AD的延长线于点E、F,AE=3,则四边形AECF的周长为( )A.22B.18C.14D.11考点:菱形的性质;平行四边形的判定与性质.专题:几何图形问题.分析:根据菱形的对角线平分一组对角可得∠BAC=∠BCA,再根据等角的余角相等求出∠BAE=∠E,根据等角对等边可得BE=AB,然后求出EC,同理可得AF,然后判断出四边形AECF是平行四边形,再根据周长的定义列式计算即可得解.解答:解:在菱形ABCD中,∠BAC=∠BCA,∵AE⊥AC,∴∠BAC+∠BAE=∠BCA+∠E=90°,∴∠BAE=∠E,∴BE=AB=4,∴EC=BE+BC=4+4=8,同理可得AF=8,∵AD∥BC,∴四边形AECF是平行四边形,∴四边形AECF的周长=2(AE+EC)=2(3+8)=22.故选:A.点评:本题考查了菱形的对角线平分一组对角的性质,等角的余角相等的性质,平行四边形的判定与性质,熟记性质并求出EC的长度是解题的关键.8.如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为( )A.3B.6C.7D.9考点:平行四边形的判定.专题:新定义.分析:根据平行四边形的判定,两组对边边必须平行,可以得出上下各两个平行四边形符合要求,以及特殊四边形矩形与正方形即可得出答案.解答:解:如图所示:∵矩形AD4C1B,平行四边形ACDB,平行四边形AC1D1B,上下完全一样的各有3个,还有正方形ACBC3,还有两个以AB为对角线的平行四边形AD4BD2,平行四边形C2AC1B.∴一共有9个面积为2的阵点平行四边形.故选D.点评:此题主要考查了平行四边形的性质,以及正方形与矩形的有关知识,找出特殊正方形,是解决问题的关键.。
2020年人教版初中八年级数学暑假作业全套精品版

初中八年级数学(人教版)暑假作业(一)一、选一选,看完四个选项再做决定!(每小题5分,共25分) 1. 下列等式中成立的是( D ) A. (x -y )3=(-x -y )3 B. (a -b )4=-(b -a )4 C. (m -n )2=m 2-n 2D. (x +y )(x -y )=(-x -y )(-x +y ) 2. 下列分解因式正确的是( C ) A. 2x 2-xy -x =2x (x -y -1)B. -xy +2xy -3y =-y (xy -2x -3)C. x (x -y )-y (x -y )=(x -y )2D. x 2-x -3=x (x -1)-33. 因式分解(x -1)2-9的结果是( B ) A. (x +8)(x +1) B. (x +2)(x -4) C. (x -2)(x +4) D. (x -10)(x +8)4. 下列各式中,与(a -1)2相等的是( B ) A. a 2-1 B. a 2-2a +1 C. a 2-2a -1 D. a 2+15. 计算(-12)2007+(-12)2008的结果为( B )A. (-12)2008B. -(-12)2008C. 12D. -12二、填一填,要相信自己的能力!(每小题5分,共25分) 1.分解因式:a 2-9=____(a +3)(a -3)______.2.分解因式xy -x -y +1=_____(x -1)(y -1)_____.3.若m 、n 互为相反数,则5m +5n -5=____-5 ______.4.如果x +y =-4,x -y =8,那么代数式x 2-y 2的值是____-32____.5.一个长方形的面积是(x 2-9)平方米,其长为(x +3)米,用含有x 的整式表示它的宽为__ x -3__米.三、做一做,要注意认真审题!(每小题10分,共30分) 1. 判断下列各式分解因式的对错,对的打“”,错的打“”: (1)4x 3-8x 2+4x =4x (x -1)2 (√ )(2)9(x +y +z )2-(x -y -z )2=4(2x +y +z )(x +2y +2z )(√ ) (3)m 2-n 2+2m -2n =(m -n )(m +n +2)(√ )2. 利用因式分解计算:1-22+32-42+52-62+…+992-1002+1012= 5151 。
人教版八年级上册数学作业本答案完整版

参考答案第十一章 三角形11.1与三角形有关的线段11.1.1三角形的边1.(1)3;әA B C,әA B D,әA D C(2)A B,B D,A D;A,B,D(3)øA D C,øD C A,øC A D2.(1)3(2)123.(1)> (2)> (3)> (4)<4.(1)能.理由略(2)不能.理由略(3)能.理由略(4)不能.理由略5.a=5c m或7c m,周长为17c m或19c m6.35c m的长铁条合适,10c m的长铁条不合适.理由略11.1.2三角形的高㊁中线与角平分线11.1.3三角形的稳定性1.略2.(1)4c m2(2)30ʎ(3)2.4c m3.(1)D (2)B4.14c m5.(1)C D,B C(2)әA B C,әA B E,әA E C(3)әD B C,әD B E,әD E C6.25ʎ,25ʎ*7.(1)S1=S2.理由略(2)S3=S5,因为S3+S6=S5+S6=12S(3)S7=S8=S9=S10=S11=S1211.2与三角形有关的角11.2.1三角形的内角(1)1.(1)180ʎ,75ʎ(2)30ʎ,60ʎ,90ʎ2.(1)77ʎ(2)70ʎ3.33ʎ4.ø2=50ʎ,øB=50ʎ,øA C B=90ʎ5.(1)120ʎ(2)1256.øA B P=30ʎ+25ʎ=55ʎ,øB A P=80ʎ11.2.1三角形的内角(2)1.302.(1)3(2)43.D4.115ʎ5.42ʎ6.R tәA B D,R tәA C D,R tәA D E.理由略11.2.2三角形的外角1.C2.60ʎ3.145ʎ4.(1)øA B C=90ʎ,øC=45ʎ(2)40ʎ,50ʎ,90ʎ5.40ʎ.理由:ø3=ø2+180ʎ-140ʎ6.74ʎ*7.øC A D=30ʎ,øA E D=80ʎ,øE A D=10ʎ11.3多边形及其内角和11.3.1多边形1.(1)首尾顺次相接,n边形(2)顶点,对角线,n(n-3)2(3)相等,相等2.1;øB C D;2;øD C E,øB C F3.略4.①④5.(1)⑤ (2)①ˑ ②ˑ ③6.(1)图略,3,4(2)4,5,5,6(3)n-3,n-211.3.2多边形的内角和1.(1)720ʎ(2)八(3)45ʎ2.53.36ʎ,72ʎ,108ʎ,144ʎ4.1165.116.160ʎ复习题1.A B C,A D E2.①3.1,图略4.125.62ʎ,118ʎ6.(1)由A CʅB C,得ø1+øB C D=90ʎ,又因为ø1=øB,所以øB+øB C D=90ʎ,所以C D是әA B C的高(2)2c m7.118.øA E B=øC.理由略9.(1)26ʎ(2)略10.(1)øI=90ʎ+12øA,øO=12øA,øP=90ʎ-12øA.理由略(2)125ʎ,35ʎ,55ʎ11.(1)19,0(2)0<x<19第十二章 全等三角形12.1全等三角形1.(1) (2)ˑ (3)ˑ (4)2.C,øA,A C3.97,104.B C与D E,A C与A E,øB A C与øD A E,øC与øE5.直线B C,逆时针旋转180ʎ,平移B C长度6.(1)øE D C,E C(2)6,90ʎ12.2三角形全等的判定(1)1.S S S2.A B=B C,A B D,C B E3.提示:由әA B DɸәB A C(S S S),得øD=øC4.略5.øB A D=øC A D,理由略.提示:әA O EɸәA O F(S S S)6.(1)略(2)A BʊD E,A CʊD F,理由略*7.提示:由әA B DɸәA C D(S S S),可得A DʅB C,A D平分øB A C12.2三角形全等的判定(2)1.øB E D,D E,әB D E,S A S2.øE A D=øB A C或øE A B=øD A C或E D=B C3.B4.由әE DHɸәF DH,得E H=F H.还能得如下结论:øD E H=øD F H,øDH E=øDH F5.由әB C AɸәD E B(S A S),得B C=D E6.由әA B CɸәA B D(S A S),得øA B C=øA B D, ʑ øC B E=øD B E7.(1)A B=A C,A D=A D,øB=øC*(2)不全等.两边及一边的对角对应相等的两个三角形不一定全等12.2三角形全等的判定(3)1.C2.(1)øB C A=øE F D(2)øB=øE3.提示:由øC B A=øF E D,øB C A=øE F D,A B=D E,得әB A CɸәE D F(A A S)4.提示:由әA B CɸәE D C(A S A),得D E=A B5.提示:由әB C DɸәC B E(A S A),得B E=C D6.提示:可先证明әA O DɸәA O E,得出O D=O E;再证明әB O DɸәC O E,从而得出O B=O C12.2三角形全等的判定(4)1.D2.(1) (2)ˑ (3)ˑ (4)3.(1)A C=D C(2)øA=øD或øB=øE(3)A C=D C4.(1)提示:әA B CɸәA D C(A A S)(2)由(1)得C B=C D5.提示:әA O DɸәC O B(S A S),әA O EɸәC O F(A A S)6.全等三角形有әA B CɸәD C B(S A S),әA B OɸәD C O(A A S).理由略12.2三角形全等的判定(5)1.D2.A C=D F或B C=E F或øA=øD或øB=øE3.提示:由R tәA D EɸR tәA D F(H L),得øD A E=øD A F,即A D是øB A C的平分线4.(1)A E=D F,A BʊC D(2)略5.(1)ȵ A D=B D,A C=B E,øA D C=øB D E, ʑ әB E DɸәA C D(H L)(2)提示:由әB E DɸәA C D,得D E=D C6.当A P=A C=10c m,即点P与点C重合时,或A P=B C=5c m,即P是A C的中点时,әA B C与әA P Q全等*7.正确. ȵ R tәO C PɸR tәO D P, ʑ øC O P=øD O P,即O P平分øA O B12.2三角形全等的判定(6)1.(1)A A S(2)A S A (3)S A S(4)H L2.②④3.D4.提示:先证明әA B EɸәA C D,再证明әO B DɸәO C E5.提示:先证明әA O DɸәB O C,再证明әO C EɸәO D F6.提示:延长A M到点N,使MN=A M,连接B N.先证明әA C MɸәN B M,得到B N=A C,再由әA B N的三边关系得到A N<A B+B N, ʑ 2A M<A B+A C12.3角的平分线的性质(1)1.(1)略(2)5c m2.(1)B C,C D(2)A B,A D3.P B=P C,A B=A C4.提示:根据角平分线的性质可得A E=E F,D E=E F,故A E=D E5.提示:由әP DMɸәP E N(S A S),得P M=P N6.(1)提示:两个三角形的边A B,A C上的高相等(2)方法一:ȵ B D=C D,ʑ SәA B D=SәA C D. ʑ A B=A C方法二:过点D分别作A B,A C的垂线段,通过三角形全等证明12.3角的平分线的性质(2)1.A2.253.略4.21ʎ5.提示:可证明әC O EɸәB O D,得O E=O D6.(1)略(2)作图略,A DʅA E复习题1.A2.4对:әA F DɸәA F E,әB D FɸәC E F,әA F BɸәA F C,әA B EɸәA C D3.由әA B CɸәA'B'C',得B C=B'C',即影子一样长4.点P为øA和øB的平分线的交点,图略5.提示:由әB D FɸәC D E(S A S),得øF=øD E C,故B FʊC E6.3c m,37ʎ7.由R tәA B DɸR tәC B E(H L),得øB A D=øB C E.ȵøE+øB C E= 90ʎ, ʑ øE+øB A D=90ʎ, ʑ A FʅC E8.(1)提示:证明әC B DɸәE F C,D B=C F(2)2(3)2第十三章 轴对称13.1轴对称13.1.1轴对称1.B2.A DʅB C,中点,垂直平分线3.(1) (2)ˑ4.①和③是轴对称图形.对称轴及对称点略5.(1)点D ,E ,F (2)l 垂直平分线段A D (3)交点在直线l 上6.图略.正三㊁四㊁五㊁ n 边形分别有3,4,5, ,n 条对称轴13.1.2 线段的垂直平分线的性质(1)1.(1)B M (2)90 (3)2c m 2.A D +D E +A E =B D +D E +E C =B C =5c m3.ȵ A C =A D , ʑ 点A 在C D 的垂直平分线上.同理,点B 在C D 的垂直平分线上, ʑ AB 垂直平分CD 4.以点A 为圆心㊁适当长为半径作弧,交l 于点B 和C ,再分别以点B 和C 为圆心㊁大于12B C 的长为半径作弧,两弧交于点D ,连接D A ,直线D A 就是所求作的垂线5.ȵ A B =A C ,B D =D C , ʑ 直线A D 是线段B C 的垂直平分线.ȵ 点E 在A D 上, ʑ E B =E C6.A C =A E =12A B =3c m13.1.2 线段的垂直平分线的性质(2)1.对应点,垂直平分线2.连接A B ,分别以点A 和B 为圆心㊁大于12A B 的长为半径画弧,两弧交于点C 和D ,连接C D ,C D 就是所求作的直线3.①②③⑤是轴对称图形.图略 4.略5.提示:作出三角形任意一边的中线即可6.方案一:两组对边中点的连线;方案二:两条对角线13.2 画轴对称图形(1)1.(1)略 (2)A 'B 2.略 3.略 4.略 5.略 6.略13.2 画轴对称图形(2)1.C 2.点P 的坐标(2,3)(1,-4)(-2.5,-6)0,-72点P 关于x 轴对称的点的坐标(2,-3)(1,4)(-2.5,6)0,72 点P 关于y 轴对称的点的坐标(-2,3)(-1,-4)(2.5,-6)0,-723.1,24.略5.(1)图略.-3,5,-1,1,-3,3 (2)图略.-1,5,-3,1,-1,3 (3)是.图略6.A 2(1,-3),B 2(4,-1),C 2-12,-2.图略13.3 等腰三角形13.3.1 等腰三角形(1)1.(1)50ʎ (2)66ʎ 2.50 3.3,904.øB C D =25ʎ,øA D C =50ʎ,øA C B =90ʎ5.由әA B C ɸәA E D (S A S ),得A C =A D .又AM ʅC D , ʑ C M =MD .ʑ M 是C D 的中点6.提示:连接A P ,证明әA D P ɸәA E P 或әB D P ɸәC E P ,得P D =P E*7.(1)15ʎ (2)20ʎ (3)øE D C =12øB A D ,理由略13.3.1 等腰三角形(2)1.70,等腰 2.(1)30ʎ (2)30ʎ或75ʎ或120ʎ3.提示:由øD B C =øD C B ,得әB C D 是等腰三角形4.30海里5.øC =30ʎ,C D =3c m 6.ȵ øB =øC =12(180ʎ-øA ), ʑ A B =A C .ȵ B D =C E , ʑ A D =A E , ʑ øA D E =øA E D =12(180ʎ-øA ),ʑ øA D E =øB , ʑ D E ʊB C*7.(第7题)13.3.2 等边三角形(1)1.(1)0.5c m (2)3 2.D 3.90ʎ4.提示: ȵ әA D F ɸәB E D ɸәC F E , ʑ A D =B E =C F5.(1)ȵ әA B C 是等边三角形,ʑ AC =C B ,øA =øE C B =60ʎ.又AD =CE ,ʑ әA D C ɸәC E B (S A S ), ʑ øC B E =øA C D(2)øC F E =øC B E +øD C B =øA C D +øD C B =øA C B =60ʎ6.提示:可证明әA B D ɸәA C E (S A S ), ʑ A D =A E ,øD A E =øB A C =60ʎ,ʑ әA D E 是等边三角形13.3.2等边三角形(2)1.2402.30ʎ,4c m,2c m3.ȵ øA=90ʎ-60ʎ=30ʎ,øC=90ʎ, ʑ A B=2B C.又ȵ A B-B C=5c m, ʑ B C=5c m4.øB=15ʎ,øD A C=øB+øA C B=30ʎ,C D=12A C=12A B=25c m5.(1)略(2)(12+43)c m6.ȵ B'D=B'E, ʑ B B'平分øA B C, ʑ øB'B D=30ʎ,ʑ B B'=2B'D=5ˑ2=10c m7.根据әA B D的画法,有A B=A C=B C=C D,ʑәA B C是等边三角形, *øA B C=øA C B=60ʎ,øD=øC B D=12øA C B=30ʎ.ʑ øA B D=60ʎ+30ʎ=90ʎ, ʑ әA B D就是所要画的三角形13.3.2等边三角形(3)1.12.60,1203.74.әO D E是等边三角形.提示:证明øD O E=2øA O B=60ʎ,O D=O C=O E即可5.(1)15时30分(2)17时30分6.(1)连接A D,证明әA D FɸәB D E,得到D E=D F,øA D F=øB D E即可*(2)әD E F仍为等腰直角三角形.连接A D,证明әA D FɸәB D E,得到D E=D F,øA D F=øB D E即可13.4课题学习最短路径问题1.提示:作点O关于A B的对称点O',连接O'C,交A B于点P2.提示:作点O关于A B的对称点O',点M关于B C的对称点M',连接O'M',交A B,B C于点P和Q3.提示:利用平移,将点C移动到边C D上的点C'处,C C'=2c m,作点O关于A B对称点O',连接O'C',交A B于点P复习题1.C2.5c m,50ʎ3.18ʎ4.略5.ȵ E DʅB C, ʑ øE+øB=90ʎ,øD F C+øC=90ʎ.ȵ A B=A C, ʑ øB=øC.又øD F C=øA F E, ʑ øE=øA F E, ʑ A E=A F.ʑ әA E F是等腰三角形6.ȵ әA C E与әA D E关于直线A E对称, ʑ D E=E C,A D=A C=C B,ʑ D E+E B+D B=E C+E B+D B=C B+D B=10c m7.ȵ øA=60ʎ,A D=12A B=A C, ʑ әA C D是等边三角形,øD C B=90ʎ-øA C D=30ʎ.øA C E=90ʎ-øA=30ʎ,øE C D=30ʎ,ʑøA C E=øE C D =øD C B8.ȵ E B=E C, ʑ øE B C=øE C B. ȵ øA B E=øA C E,ʑ øA B C=øA C B, ʑ A B=A C.又ȵ E B=E C,ʑ 点A和E在B C的垂直平分线上. ʑ A DʅB C9.(1)a=2,b=3(2)(-6,-2)10.(第10题)11.(1)略(2)P(a,b)关于直线m对称的点的坐标为(-a-4,b);P(a,b)关于直线n对称的点的坐标为(b,a)12.(1)由әA B EɸәD B C(S A S),得A E=D C(2)成立(3)等边三角形第十四章 整式的乘法与因式分解14.1整式的乘法14.1.1同底数幂的乘法1.(1)不正确.a6(2)正确(3)不正确.-79(4)不正确.-2102.(1)108(2)1211(3)-127(4)5103.(1)m6(2)x2m+1(3)a6(4)-x54.1020次5.(1)(a+b)3(2)(x-y)7(3)b9(4)(a-b)56.1.2ˑ1011m 14.1.2幂的乘方14.1.3积的乘方1.B2.(1)26(2)b9(3)1012(4)-x153.(1)不正确.8x3(2)不正确.a3b6(3)不正确.9a6(4)不正确.-127x3y64.(1)-a6(2)9ˑ1010(3)a12b6(4)-8x6y35.54a2,27a36.5.14ˑ108k m214.1.4整式的乘法(1)1.(1)15a5(2)-72a3b6(3)6ˑ107(4)-3x5y42.(1)不正确.3x3y2(2)不正确.-2x2-2x y3.(1)2x2+2x(2)6x2-18x y(3)-2a+2b-2c(4)-15a4+43a34.a b-b25.3x3-5x2+6x,-146.(1)2x y,4x y-2y(2)15x y+y14.1.4整式的乘法(2)1.(1)x2+3x+2(2)2x2-x-12.(1)x2-4(2)6x2+x-1(3)x2+4x y-21y2(4)6x2+11x y-10y23.(1)x2-y2(2)4x2-9(3)x2+2x y+y2(4)4x2-12x+94.(1)3m2-m n-5m+2n-2(2)6x-9,35.(a-b)(a-2b)=a2-3a b+2b26.小丽说得对,理由略14.1.4整式的乘法(3)1.(1)a2(2)a2(3)a3b3(4)12.C3.(1)100(2)a6(3)-b3(4)-a b4.(1)1(2)-1(3)1(4)15.(1)a4(2)-m3(3)1(4)2a76.104s14.1.4整式的乘法(4)1.(1)2a(2)-5y2(3)-2ˑ103(4)r32.自上而下:-x3y,6x z,-12x3.D4.(1)-14a b(2)3x+1(3)3a+4(4)-6x+2y-15.(1)-y+2x y2(2)-2a2+4a+8,26.(8.47ˑ1010)ː(2.75ˑ103ˑ105)=308年14.2乘法公式14.2.1平方差公式1.(1)a2-1(2)y-32.(1) (2) (3) (4) (5)ˑ3.(1)a2-4(2)9a2-b2(3)y2-0.09x2(4)a2-14b24.(1)(100+3)(100-3)=9991(2)(60-0.2)(60+0.2)=3599.965.(1)二,去括号后未变号(2)略6.(1)-8a2(2)5x2-34y2(3)-2a2+7a+27.(1)a2-b2(2)a-b,a+b,(a-b)(a+b)(3)(a-b)(a+b)=a2-b2 *(4)略14.2.2 完全平方公式(1)1.D2.(1)9+6x +x 2(2)y 2-14y +49 (3)x 2-10x +25 (4)9+2t +19t 23.(1)10000 (2)38809 4.(1)14x 2-2x y +4y 2 (2)-4a 2-12a -95.(1)略 (2)(a -b )2+4a b =(a +b )2(3)69 ʃ11 6.8a b14.2.2 完全平方公式(2)1.D 2.(1)y +z (2)y -z (3)2b -c ,2b -c3.(1)4x 2+12x y +9y 2 (2)4x 2-4x +14.(1)4x 2+y 2+z 2-4x y +4x z -2y z (2)a 2-4b 2+4b -15.x 2-3,1 6.(1)a 5+5a 4b +10a 3b 2+10a 2b 3+5a b 4+b 5(2)24314.3 因式分解14.3.1 提公因式法1.C2.(1)3 (2)x (3)2a 2(4)a -b 3.(1)2x 2(x +3) (2)3p q (q 2+5p 2) (3)x y (x +y -1) (4)-2a b 3(4a -3c )4.(1)(a -b )(2a -2b -1) (2)(x -y )2(3-x +y )(3)(a -b )(7+a )5.-24 6.(1)998 (2)-1020197.2r h +12πr 2,分解因式得r 2h +12πr,64πm 214.3.2 公式法(1)1.B2.(1)2x ,3y ,(2x +3y )(2x -3y )(2)5b ,4a ,(5b +4a )(5b -4a )(3)x 2-y 2,x y (x +y )(x -y )3.(1)(x +1)(x -1) (2)3(2+a )(2-a ) (3)(a +b +c )(a +b -c )(4)(a 2+9b 2)(a +3b )(a -3b )4.(1)2013 (2)-15.a 2-4b 2=(a +2b )(a -2b )=128c m26.(1)34 (2)23 (3)58 (4)10120014.3.2 公式法(2)1.D 2.(1)3a +2 (2)9y 2,3y (3)-2m n 3.(1)(x -3)2 (2)(2a +b )2 (3)-(3x -2y )2 (4)a +12b24.(5x+y)2,4255.(1)-3x(x-1)2(2)(2a+b-4)2(3)(a+2b)2(a-2b)2(4)(a+2)(a-2)6.(1)1ˑ104(2)1ˑ1047.(1)(x+2y-1)2(2)(a+b-2)2*复习题1.D2.(1)3x4y4(2)-4a b3.a2+4a b+4b2,a2-4b2,4b2-a2,-a2-4a b-4b24.(1)2a3b3c3+12a3b c3(2)-3a b+8b(3)14x2-16a2(4)16m2+8m+15.②6.(1)(x+2)(x-2)(2)(8-a)2(3)(x-y)(2+a)(4)(0.7x+0.2y)(0.7x-0.2y)7.(1)2x5(2)-7x3y2+2x2(3)-4x-12(4)x-y8.(1)(x-y)(5x-4y)(2)-a2(b-1)2(3)4a(x+2y)(x-2y)(4)(x-2)(x-3)(x+3)9.吃亏了,少了25m2,理由略10.(1)(a+2b)(2a+b)=2a2+5a b+2b2(2)如图(3)答案不唯一.如图,(a+2b)(a+b)=a2+3a b+2b2[第10(2)题][第10(3)题]11.原式=(2-1)ˑ(2+1)ˑ(22+1)ˑ(24+1)ˑ(28+1)ˑ ˑ(22048+1)=(22-1)ˑ(22+1)ˑ(24+1)ˑ(28+1)ˑ ˑ(22048+1)=(22048-1)ˑ(22048+1)=24096-112.(1)C(2)(x-2)4(3)设x2-2x=y,原式=y(y+2)+1=(y+1)2=(x2-2x+1)2=(x-1)4第十五章 分式15.1 分式15.1.1 从分数到分式1.(1)3t (2)nm +12.m ,x 5,13a 2b ,23,5π整式集合 2a ,x x -3,x 2-x +1y,x +1x -1分式集合3.(1)x ʂ0 (2)x ʂ2 (3)x ʂ0且x ʂ1 (4)x ʂʃ34.(1)m +n x +y千克 (2)b45a 5.(1)x =43 (2)x =-12 (3)-3 6.x -5x 2-3615.1.2 分式的基本性质(1)1.(1)x (2)3a 2-3a b (3)y -2 (4)1 2.(1)ˑ (2) (3)ˑ (4)ˑ 3.(1)12x (2)-x 3y(3)2a5b 4.(1)相等.因为把第一个分式的分子㊁分母同乘以3x 就是第二个分式(2)相等.因为把第一个分式的分子㊁分母同乘以3b 2就是第二个分式5.(1)5x -103x +20 (2)x -23x -1 6.(1)A (2)3y (答案不唯一) 15.1.2 分式的基本性质(2)1.B 2.A 3.(1)c b (2)-4x 5y (3)34(x -y )4.(1)x +2x -2 (2)1m (m -2) (3)x +2x -25.(1)x +2y 4x ,34 (2)a +3a -3,46.答案不唯一,例如:x 2-1x 2+x=x -1x ,1215.1.2 分式的基本性质(3)1.(1)5a (2)a 2b 22.D3.(1)412x 2与5x 12x 2 (2)3b c a 2b 2与2a c a 2b 2 (3)5a 2c 21a c 与35c 21a c (4)3a b 23b 2与a 3b24.(1)a c +c (a -1)(a +1)与a c -c (a -1)(a +1) (2)2y 2x y (y +1)与3x 2x y (y +1)5.(1)a -2a 与a 2-2a a (2)x 2-y 2x +y 与2y 2x +y6.(1)c -a (a -b )(b -c )(c -a ),a -b (a -b )(b -c )(c -a )与c -b(a -b )(b -c )(c -a )(2)2a (a -3)(a +3)(a -3)2与3(a +3)(a +3)(a -3)215.2 分式的运算15.2.1 分式的乘除(1)1.C 2.(1)不正确.-3x (2)不正确.8x 23a 2 3.(1)1 (2)-5a14x 4.(1)-1a c (2)1a (a -2) (3)2x -2x +2 (4)-13m5.s a ːm s b =b a m6.300x ㊃2x m =600m 个15.2.1 分式的乘除(2)1.B2.(1)a b (2)a 2b 2 (3)(x -1)2(4)4a 2c 4 (5)4c 2d 2a 2b 6 (6)(2a +b )2(a -b )23.(1)3c a b (2)49x 2y 2 (3)m 2n 24.(1)1b (2)-y (x +y )5.32倍15.2.2 分式的加减(1)1.(1)3x (2)x -y a (3)1 (4)-b a2.C3.(1)5y -4x 6x 2y 2 (2)3b c 3+2a36a 2b 2c 24.(1)2 (2)a b a -b (3)3x +4 (4)4x +25.(1)2a a +2 (2)1m -1 (3)2a 2a -2 6.3000a -30003a =2000a时15.2.2 分式的加减(2)1.D 2.(1)2 (2)-1a 3.(1)b 2a3 (2)1a -2 (3)1x +1 (4)1x -14.aa -3,a 可选除0,2,3以外的任意数5.方法一:原式=2x (x +4)(x -2)(x +2)㊃x 2-4x =2x +8;方法二:原式=3x x -2㊃x 2-4x -x x +2㊃x 2-4x =2x +8*6.(1)100(x +y ),100x +100y ,x +y 2,2xy x +y(2)乙购买粮食的方式更合算,理由略15.2.3 整数指数幂(1)1.(1)25,1,125 (2)25,1,1252.(1)不正确.1 (2)不正确.-1 (3)不正确.19 (4)正确3.(1)1100 (2)127 (3)1000 (4)94 4.(1)6a2c 4 (2)y 2x 6z45.(1)8m 8n 7 (2)b 138a 8 6.原式=y -9x 3,8915.2.3 整数指数幂(2)1.C 2.A3.(1)1.0ˑ105 (2)1.0ˑ10-5 (3)-1.12ˑ105 (4)-1.12ˑ10-44.(1)75 (2)3.6ˑ10-135.(1)0.00001 (2)0.000236.3.1ˑ10-315.3 分式方程(1)1.C 2.(1)x =73(2)x =4 3.m =14 4.(1)x =12 (2)x =35.(1)x =1 (2)x =-1*6.设原分式为x -16x ,则x -15x +1=12,解得原分数为153115.3 分式方程(2)1.A 2.90x +6=60x 3.设乙单独做,x 天完成,则46+4x=1,解得x =124.120元5.设原计划每天铺设x m 管道,则3000x -3000(1+25%)x =30,解得x =20,(1+25%)x =25.实际每天铺设管道25m 6.(1)70m /m i n (2)李明能在联欢会开始前赶到学校15.3 分式方程(3)1.10 2.B 3.35.6mm4.设乙每分钟输入x 名学生的成绩,则26402x =2640x-2ˑ60,解得x =11,2x =22.乙每分钟输入11名学生的成绩,甲每分钟输入22名学生的成绩5.设货车的速度是x km /h ,由题意得14401.5x +6=1440x,解得x =80.货车的速度是80k m /h ,客车的速度是120k m /h *6.255p -1元 复习题1.B2.C3.C4.3ˑ10-4微米 5.(1)1.2ˑ104 (2)10-46.(1)y 29x 6 (2)x -5 7.(1)x =1 (2)无解 8.设甲的速度为x k m /h ,则8-0.5x x =122x,解得x =4,所以甲的速度是4k m /h ,乙的速度是8k m /h9.设该市去年居民用水的价格为x 元/米3,则今年居民用水的价格为(1+25%)x元/米3.根据题意,得36(1+25%)x -18x=6,解得x =1.8,(1+25%)x =2.25.该市今年居民用水的价格为2.25元/米310.王师傅这次运输所花时间为180v h ,180v ˑ29v +14+180v ˑ20=176,解得v =45.王师傅这次运输的平均速度为45k m /h 11.(1)取a =1,b =1,得M =N =1;取a =2,b =12,得M =N =1.猜想:M =N (2)M =a a +1+b b +1=a a +a b +b b +a b =1b +1+1a +1=N ,因此M =N 总复习题1.C2.C3.D4.B5.A6.1.83ˑ10-77.538.5409.所有图案都是轴对称图形,图略10.(1)3x2-20x+26(2)-111.(1)2x(3-2y)(2)y(y+2x)(y-2x)(3)(a+3)2(a-3)2(4)(a-b)(2a-2b+3)(2a-2b-3)12.(1)无解(2)x=-713.ȵ øA=50ʎ,øB D C=85ʎ,ʑøA B D=35ʎ.又ȵB D平分øA B C,D EʊB C,得øB D E=35ʎ, ʑ øBE D=110ʎ. ʑ әB D E各内角度数分别为35ʎ,35ʎ,110ʎ14.әA B C,әA B D,әA C D;øB=36ʎ15.B E=A B-A E=7c m,在әB E F中,øB E F=øG E F=øA E G=60ʎ,得E F=2B E=14c m16.øA B C=øA D C.提示:连接B D,证明øA D B=øA B D,øC D B=øC B D,得øA D B+øC D B=øA B D+øC B D,即øA D C=øA B C17.设甲公司单独完成需要x天,则12x+121.5x=1,解得x=20,1.5x=30.甲㊁乙两公司单独完成此项工程,分别需要20天和30天18.(1)在R tәA D B与R tәC E A中,A B=A C,øB A D=øA C E, ʑ әA D BɸәC E A, ʑ A D=C E,A E=B D. ʑ D E=B D+C E(2)D E=B D+C E(3)D E=C E-B D19.(1)øA+øD=øB+øC(2)6(3)øP=45ʎ(4)øP=øB+øD2,理由略20.(1)32(2)ʃ321.略期末综合练习1.D2.D3.A4.A5.B6.D7.B8.C9.C 10.A 11.4.2ˑ10-712.23b13.3x(x+2y)(x-2y)14.ʃ4 15.116.917.= 18.24ʎ19.20ʎ或35ʎ或80ʎ或50ʎ20.2 21.a+1,选取a=2,所求的值为322.略23.提示:(1)由әB O DɸәC O E可得(2)提示:证明A B=A C,得点A,O都在B C的垂直平分线上24.(1)甲工程队每月修建绿道1.5k m,乙工程队每月修建绿道1k m(2)甲工程队至少修建绿道8个月25.(1)①30 ②|60ʎ-2α|(2)①略 ②|8-2n|。
人教版八年级数学暑假作业参考答案

参考答案第1讲二次根式练一练巩固演练1.B2.C3.D4.A5.B6.67.1008.139.a ≤010.111.解:原式=[(22+3)(22-3)]2017·(22-3)=(-1)2017·(22-3)=3-22.12.解:∵x +1x =10,∴()x +1x 2=10,∴x 2+1x 2+2=10,∴x 2+1x2=8.13.解:∵x <2,∴x -2<0,3-x >0,∴(x -2)2=2-x ,|3-x |=3-x ,∴原式=2-x +3-x =5-2x.提高演练1.B2.A3.-24.75.解:a =681×2019-681×2018=681×(2019-2018)=681,b =6782+678+680+690+678=678×(678+1+1)+680+690=678×680+680+690=680×(678+1)+690=680×(680-1)+690=6802+10,a =(680+1)2=6802+1360+12,则b <a.赛一赛1.B2.C3.b <a <c4.解:∵{1-8x ≥0,8x -1≥0,∴8x -1=0,即x =18,∴y =0+12=12,=52-32=1.第1讲测试题1.C2.D3.B4.C5.B6.C7.B8.C9.B10.C11.112.<13.x >214.2015.016.52+2317.解:(=43-2-3+2=33;(2)原式3-96=8-9218.解:∵b <0<a <2,|b |>|a |,∴a +2>0,b -2<0,a +b <0,∴原式=a +2+(b -2)-a -b =a +2+b -2-a -b =0.∵-5无意义,∴过程错误.=4=2;(2)当a ≥0且b >0b.20.解:(1)原式=a 2-1+2a +1×1a 2+1=1a +1,将a =2-1代入上式得:1a +1=12-1+1(2)原式=x 2+2x +1-x 2-2xy -2x =1-2xy ,将x =3+1,y =3-1代入上式得:1-2xy =1-2(3+1)(3-121.解:(1)17+6=1×(-)7676=7-6;(2)原式=2-1+3-2+4-3+…+100-99=100-1=922.解:x 22(+1)22=3+221=3+22,y =2-12+1=(2-1)2(2+1)(2-1)=3-221=3-22,∴x 2-y 2=(x -y )(x +y )=(3+22-3+22)(3+22+3-22)=42×6=242.23.解法一:m 2=(2-1)2=3-22,1m2=13-22=3+22=3+22.∴=3-22+3+22-2=4=2.解法二:∵(m+1)2=2,∴m2+2m-1=0,∴m+2-1m=0,.24.解:x2+x+1=()x+12+34=)+122+34=54+34=2.第2讲勾股定理练一练巩固演练2.C3.C4.B5.B6.537.239.810.1311.解:∵AC=3,AB=8-3=5,∴BC=52-32=4(m).∴BC的长为4m.12.解:在Rt△ABC中,AC=AB2-BC2=52-42=3(km),∵30.3=10(天),∴10天能将隧道AC凿通.13.解:在△ADB中,∵AD2+AB2=42+32=25=52=BD2,∴∠A=90°.在△BDC中,∵BD2+BC2=52+122=169=132=DC2,∴∠DBC=90°,∴∠BDC<90°,∴该零件不符合要求.提高演练1.C2.A解析:答图2-1如答图2-1,作A点关于O B的对称点A',∵四边形O ABC为正方形.∴A'与C重合,CD为所求最小值,CD=62+22=210.3.6013解析:如答图2-2,作A H⊥BC,垂足为H,连接CD,答图2-2在Rt△AB H中,A H=132-52=12,∴S△ABC=12×10×12=60.∵D为AB的中点,∴S△ADC=S△DBC=30,∴12·AC·DE=30,即DE=6013.4.4解析:如答图2-3,E H=2,F H=8,D H⊥EF,ED⊥DF,答图2-3设D H=x,则由DE2+DF2=EF2,得x2+22+x2+82=(2+8)2,解得x=4.5.解:如答图2-4,连接DB,∵DC=BC,∠C=120°,∴∠1=30°,答图2-4∴∠2=120°-30°=90°.作C H⊥DB,垂足为H,在Rt△C H B中,C H=5,H B=53,AB=DB=103,∴S四边形ABCD=S△ABD+S△BDC=12×(103)2+12×103×5=(150+253)(m2).赛一赛1.D解析:如答图2-5,答图2-5∵AE=EB,DE⊥AB,∴AD=D B.设CD=x,则AD=BD=10-x.在Rt△ACD中,(10-x)2=x2+52,解得x=154,∴CD=154cm.2.解:∵∠BAC+∠ACB=∠ACB+∠ECD=90°,∴∠BAC=∠ECD,∴△ABC≌△CDE,∴AB=CD,BC=ED,∴AC2=3=AB2+BC2=S3+S4,即S3+S4=3.同理,2=S2+S3,S1+S2=1,∴S1+S2+S3+S4=1+3=4.3.解:若n=1,则a=0,不符合题意;n≠1时,∵n2+1>n2-1,c>a.又∵c-b=n2+1-2n=(n-1)2>0,∴c>b.又∵a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=(n2+1)2=c2,∴△ABC为直角三角形.第2讲测试题1.C解析:a可为直角边,也可为斜边.2.A解析:设AC=4x,则BC=3x,由(4x)2+(3x)2= 102,解得x=2,∴AC=8,BC=6,由AB·CD=AC·BC,得CD=8×610=245.3.D解析:由勾股定理可知AB=25m,即践踏绿地走25m,原来需要走24+7=31(m),所以少走31-25=6(m).4.B解析:连接BD,在Rt△ABD中,∵AB=3,AD=4,∴BD=5,又CD=12,BC=13,∴△BCD是直角三角形,∴S四边形ABCD=S△ABD+ S△BCD=12×3×4+12×5×12=36(cm2).5.C解析:设其余两边为a,b(a,b为自然数),则有112+a2=b2,∴112=121=b2-a2=(b+a)(b-a),∴b+a=121,b-a=1,∴b=61,a=60,∴三角形的周长为11+61+60=132.6.D解析:连接BE,交AD于O.作AF⊥BC,垂足为点F.答图Ⅱ-1∵∠BAC=90°,AB=3,AC=4,∴BC=5,∴12AB·AC=12BC·AF,∴AF=125.∵AB=AE,DE=DB=DC,∴AD垂直平分BE,△BEC是直角三角形.∴12AD·B O=12BD·AF.又∵AD=BD,∴B O=AF=125,BE=2B O=245.在Rt△BEC中,CE=BC2-BE2=75.7.B解析:连接AD,在Rt△AED中有:AE2= AD2-DE2,在Rt△EBD中有:BE2=BD2-DE2,又BD=CD,∴AE2-BE2=AD2-DE2-BD2+DE2=AD2-BD2=AD2-CD2=AC2.8.A解析:32+42+122=169=132.9.C解析:分三类,当点A处是直角时,有2个点;当点B处是直角时,有4个点;当点C处是直角时,有2个点,故共有2+4+2=8个点.10.B11.12m12.80解析:由a∶b∶c=15∶8∶17可知△ABC是直角三角形,∴设两条直角边为8x和15x.∵△ABC的面积为240,∴12×8x×15x=240,解得x=2,∴△ABC的三边长为16,30,34,∴△ABC的周长为80.13.12013解析:答图Ⅱ-2过点A作AE⊥BC,垂足为E,又AB=AC,∴E是BC的中点.∵在Rt△ABE中,有AE=AB2-BE2= 132-52=12,点D在AB上运动时,CD最短是当CD⊥AB时,此时CD是边AB上的高,∴S△ABC=12·CD·AB=12·AE·BC,即CD=12×1013=12013.14.45解析:根据图形可得四个三角形的面积+小正方形的面积=大正方形的面积,即4×12ab+4= 49,得2ab+4=49,∴2ab=49-4=45.15.30解析:O D2=O A2+AB2+BC2+CD2=16+1+4+ 9=30.16.直角三角形解析:∵a,b,c满足a2+|b-15|+(c-17)2+64=16a,∴a2-16a+64+|b-15|+(c-17)2=0,即:(a-8)2+|b-15|+(c-17)2=0,由非负性可知:a-8=0,b-15=0,c-17=0,∴a=8,b=15,c=17.又∵a2+b2=82+152=172=c2,∴△ABC是直角三角形.17.解:根据题意画出圆柱侧面展开图,连接AC,答图Ⅱ-3根据两点之间线段最短,蚂蚁从A出发沿圆柱侧面爬行到C的最短路程为A C.∵圆柱的底面周长为20cm,∴BC=AD=10cm.又∵AB=4cm,∴在Rt△ADC中,AC=AD2+DC2=229,则蚂蚁爬行的最短路程为229cm.18.解:过点A作AE⊥BC,垂足为E.答图Ⅱ-4∵AB=AC=20,BC=32,∴CE=BE=16,∴在Rt△AEC中,AE=AC2-EC2=12.∵AD⊥AC,设DE=x,∴在Rt△ADC中,有AD2= DC2-AC2=(x+16)2-202,在Rt△ADE中,有AD2=DE2+AE2=x2+122,∴(x+16)2-202=x2+122,解得:x=9,∴BD=BE-DE=16-9=7(cm).19.解:∵CD=DE=2,∴在Rt△CDE中,CE=CD2+DE2=22.∵直角三角形斜边上的中线等于斜边的一半,∴CE=12AB,∴AB=2CE=42.20.证明:如答图Ⅱ-5,过点A作A M∥BC,交FD 的延长线于点M,连接E M.答图Ⅱ-5∵A M∥BC,∴∠M AE=∠ACB=90°,∠M AD=∠B.∵AD=BD,∠ADM=∠BDF,∴△ADM≌△BDF,∴AM=BF,MD=DF.又∵DE⊥DF,∴EF=EM,∴AE2+BF2=AE2+AM2=EM2=EF2. 21.解:∵c2=a2+22a2=5a2,∴c=5a,∴a c=22.解:∵ìíîïïOB2+OA2=16,①OB2+OC2=9,②OA2+OD2=25,③∴②+③-①:OC2+OD2=25+9-16=18,∴DC2=18,∴DC=32.23.解:如答图Ⅱ-6,作AD关于AB的对称线AD',作D'F⊥AC,垂足为F,交AB于点E,则D'F为EF+DE的最小值.答图Ⅱ-6∵AD=AD'=6,∠D'AD=60°,AF=3,∴在Rt△AD'F中,D'F=D'A2-AF2=33.故DE+EF的最小值为33.24.解:在Rt△ABC中,AB=AC2+BC2=4.∵∠BAD=∠ADB ,∴BD=AB=4.∴CD=BC+BD=10+4.∴S △ADC =12AC ·CD =15+26.25.证明:(1)∵∠ACB=90°,CD ⊥AB ,垂足为点D ,∴S △ABC =12AB ·CD =12AC ·BC ,∴AB·CD=AC·BC ,即ch=ab.∴1a 2+1b 2=a 2+b 2a 2b 2=c 2c 2h 2=1h 2.(2)∵(c +h )-(a +b )=()c +abc-(a +b )=c 2+ab -ac -bc c=(c -a )(c -b )c ,又∵c >a ,c >b ,∴(c -a )(c -b )c>0.∴(c +h )-(a +b )>0.∴c +h >a +b ,即a +b <c +h.(3)∵c +h >a +b ,c +h >h ,∴(c +h )2=c 2+2ch +h 2=a 2+b 2+2ab +h 2=(a +b )2+h 2.∴以a +b ,h ,c +h 为边的三角形是直角三角形.第3讲平行四边形练一练巩固演练1.B2.C3.C4.D5.C6.BO=DO (答案不唯一)7.78.439.310.2411.证明:∵AB ∥CD ,∴∠DCA =∠BA C .∵DF ∥BE ,∴∠DFA =∠BEC ,∴∠AEB =∠DF C .在△AEB 和△CFD 中,{∠DCF =∠EAB,AE =CF,∠DFC =∠AEB,∴△AEB ≌△CFD (ASA ),∴AB =CD.∵AB ∥CD ,∴四边形ABCD 为平行四边形.12.解:∵四边形ABCD 是平行四边形,∴∠ADE =∠DE C .又∵∠DAF =62°,AF ⊥DE ,∴∠ADE =∠DEC =90°-62°=28°.∵∠BED +∠DEC =180°,∴∠BED =180°-28°=152°.13.(1)证明:∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥B C .∵DE =12AD ,F 是BC 边的中点,∴DE =FC ,DE ∥FC ,∴四边形CEDF 是平行四边形;(2)解:过点D 作D N ⊥BC ,垂足为点N ,∵四边形ABCD 是平行四边形,∠A =60°,∴∠BCD =∠A =60°.∵AB =3∴FC =2,N C =12DC =32,D N2∴F N =12,则DF =CE=DN 2+FN 2=7.答图3-1提高演练1.D2.D3.①②④5.解:设x s 后,四边形ABQP 是平行四边形.则AP=x ,CQ=2x ,∴BQ =6-2x.∵AD ∥BC ,∴当AP=BQ 时,四边形ABQP 是平行四边形.∴x =6-2x ,解得x =2.当x =2时,AP=BQ =2<BC<AD ,∴2s 后,四边形ABQP 是平行四边形.测一测1.B2.C3.C4.D5.D6.C7.B8.B 9.310.AF=CE ,答案不唯一11.3312.1<a <713.1014.415.证明:∵四边形ABCD 是平行四边形,∴AB ∥DC ,AB =DC ,∴∠BAE =∠DCF.在△AEB 和△CFD 中,{AB =CD,∠BAE =∠DCF,AE =CF,∴△AEB ≌△CFD (SAS ),∴BE=DF.16.(1)证明:∵O 是AC 的中点,∴OA=OC.∵AD ∥BC ,∴∠ADO=∠CBO.在△AOD 和△COB 中,{∠ADO =∠CBO,∠AOD =∠COB,OA =OC,∴△AOD ≌△COB ,∴OD=OB ,∴四边形ABCD 是平行四边形.(2)解:∵四边形ABCD 是平行四边形,AC ⊥BD ,∴四边形ABCD 是菱形,∴S ▱ABCD =12AC·BD =24.17.(1)证明:∵D ,E 分别是AB ,AC 边的中点,∴DE ∥BC ,且DE =12B C .同理,G F ∥BC ,且G F =12BC ,∴DE ∥GF 且DE=GF ,∴四边形DEFG 是平行四边形.(2)解:当OA=BC 时,▱DEFG 是菱形.18.(1)证明:∵四边形ABCD 是平行四边形,∴DC=AB ,DC ∥AB ,∴∠ODF=∠OBE.在△ODF 与△OBE 中,{∠ODF =∠OBE,∠DOF =∠BOE,DF =BE,∴△ODF ≌△OBE (AAS ),∴BO=DO.(2)解:∵BD ⊥AD ,∴∠ADB =90°.∵∠A=45°,∴∠DBA=∠A =45°.∵EF ⊥AB ,∴∠G =∠A =45°,∴△ODG 是等腰直角三角形.∵AB ∥CD ,EF ⊥AB ,∴DF ⊥OG ,∴OF=FG ,△DFG 是等腰直角三角形,∴DF=FG=1,∴DG=DF 2+FG 2=2.∵DG=DO=2,又∵DO=BO ,∴AD =2DO =22.19.解:(1)△ABC (或△CDA )与△FAE 全等.(下面仅对△ABC ≌△FAE 证明)∵∠FAB =∠EAD =90°,∴∠EAF +∠DAB =180°.∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∴∠DAB +∠CBA =180°,∴∠CBA=∠EAF.∵AE=AD ,∴BC=AE.又∵AB=AF ,∴△ABC ≌△FAE.(2)由(1)同理可得,△AEF ≌△DAC ≌△CIJ ,△BGH ≌△DKL ≌△CDB ,则四个三角形面积和为12×5×4=10.赛一赛解:如答图3-2,分别延长AC ,BD 交于点H ,连接HP.∵∠A =∠DPB =60°,∴AH ∥PD.∵∠B=∠CPA =60°,∴BH ∥PC ,∴四边形CPDH 为平行四边形.∴CD 与HP 互相平分,又∵G 为CD 的中点,∴G 正好为PH 的中点,即在P 运动过程中,G 始终为PH 的中点,所以G 的运动轨迹为△HAB 的中位线MN ,∴MN =12AB =5.答图3-2第4讲特殊的平行四边形练一练巩固演练1.C2.C3.D4.A5.D6.27.2458.139.7-110.511.证明:∵∠BAD=∠D =90°,BA=AD=DC ,又∵点M ,N 分别是AD ,CD 的中点,∴AM=DN =12AD ,∴△ABM ≌△DAN ,∴∠ABM=∠DAN.∵∠BAN+∠DAN =90°,∴∠BAN+∠ABM=90°,∴∠AEB =90°,即AN ⊥BM.12.(1)证明:∵∠OBC=∠OCB ,∴BO=CO.又∵在▱ABCD 中,∴AO=CO ,DO=BO ,∴2BO=2AO ,即BD=AC ,∴▱ABCD 为矩形.(2)解:AC ⊥BD 或AB=BC.13.证明:(1)∵四边形ABCD 是矩形,∴AD ∥BC ,AD=BC.∵E ,F 分别是AD ,BC 的中点,∴AE=12AD ,CF =12BC ,∴AE=CF ,∴四边形AFCE 是平行四边形.(2)∵四边形AFCE 是平行四边形,∴CE ∥AF ,∴∠DGE=∠AHD=∠BHF.∵AD ∥BC ,∴∠EDG=∠FBH.在△DEG 和△BFH 中,{∠DGE =∠BHF,∠EDG =∠FBH,DE =BF,∴△DEG ≌△BFH (AAS ),∴EG=FH.提高演练1.D2.C3.103-104.65.(1)解:猜想DM 与ME 的关系是:DM=ME.证明:如答图4-1,延长EM 交AD 于点H.∵四边形ABCD、四边形ECGF 都是矩形,答图4-1∴AD ∥BG ,EF ∥BG ,∠HDE =90°,∴AD ∥EF ,∴∠AHM=∠FEM.又∵AM=FM ,∠AMH=∠FME ,∴△AMH ≌△FME ,∴HM=EM.又∵∠HDE=90°,∴DM=EM.(2)DM=ME ,DM ⊥ME.(3)证明:如答图4-2,连接AC .答图4-2∵四边形ABCD 、四边形ECGF 都是正方形,∴∠DCA=∠DCE =45°,∴点E 在AC 上,∴∠AEF=∠FEC =90°.又∵M 是AF 的中点,∴ME=12AF.∵∠ADC =90°,M 是AF 的中点,∴DM=12AF ,∴DM=EM.∵ME =12AF=FM ,DM=12AF=FM ,∴∠DFM=12(180°-∠DMF ),∠MFE =12(180°-∠FME ),∴∠DFM+∠MFE =180°-12(∠DMF+∠FME )=180°-12∠DME.∵∠DFM+∠MFE=180°-∠CFE =180°-45°=135°,∴180°-12∠DME=135°,∴∠DME=90°,∴DM ⊥ME.测一测2.C3.A4.A5.A6.B7.D8.C 910.311.2-212.105cm 85cm13.4或814.(2,4)或(8,4)15.证明:∵四边形ABCD 是菱形,∴AB=BC ,∠A=∠C.∵在△ABF 和△CBE 中,{AF =CE,∠A =∠C,AB =CB,∴△ABF ≌△CBE (SAS ),∴∠ABF=∠CBE.16.解:线段AF ,BF ,EF 三者之间的数量关系为AF=BF+EF ,理由如下:∵四边形ABCD 是正方形,∴AB =AD ,∠DAB =∠ABC =90°.∵DE ⊥AG ,垂足为E ,BF ∥DE 交AG 于F ,∴∠AED =∠DEF =∠AFB =90°,∴∠ADE +∠DAE =90°,∠DAE+∠BAF =90°,∴∠ADE=∠BAF.在△ABF 和△DAE 中,{∠BAF =∠ADE,∠AFB =∠DEA,AB =AD,∴△ABF ≌△DAE (AAS ),∴BF=AE ,∴AF=AE+EF=BF+EF.17.解:(1)连接AC ,BD ,交于点O ,菱形ABCD 的周长是48cm ,答图4-3则AB=BC=CD=AD =12cm .∵∠A ∶∠B =1∶2,∴∠A =60°,∠B =120°,∴△ADB 是等边三角形,AD=BD =12cm ,在Rt△ADO 中,AO =AD 2-DO 2=63cm ,∴AC=2AO=123cm .(2)S 菱形ABCD =12AC·BD =723cm 2.18.证明:如答图4-4,连接AC ,答图4-4∵四边形ABCD 为菱形,∴AC ⊥BD ,AD =CD ,∴∠ADP =∠CDP.又∵DP =DP ,∴△APD ≌△CP D .∴PA =PC ,∠DAP =∠DCP.又∵∠AEP =∠DCP ,∴∠AEP =∠DAP.∴PA =PE.∴PC =PE.19.(1)解:如答图4-5,答图4-5利用邻边长分别为3和5的平行四边形进行3次操作,所剩四边形是边长为1的菱形,故邻边长分别为3和5的平行四边形是3阶准菱形;如答图4-6,答图4-6∵b =5r ,∴a =8b +r =40r +r =8×5r +r ,利用邻边长分别为41r 和5r 的平行四边形进行8+4=12次操作,所剩四边形是边长为r 的菱形,故邻边长分别为41r 和5r 的平行四边形是12阶准菱形.故答案为:3,12.(2)证明:由折叠知:∠ABE =∠FBE ,AB =BF ,∵四边形ABCD 是平行四边形,∴AE ∥BF ,∴∠AEB =∠FBE ,∴∠AEB =∠ABE ,∴AE =AB ,∴AE =BF ,∴四边形ABFE 是平行四边形,∴四边形ABFE 是菱形.赛一赛解:(1)等腰(2)如答图4-7①,连接BE ,作BE 的垂直平分线交BC 于点F ,连接EF ,△BEF 是矩形ABCD 的一个折痕三角形.∵折痕垂直平分BE ,AB =AE =2,∴点A 在BE 的垂直平分线上,即折痕经过点A ,∴四边形ABFE 为正方形,∴BF =AB =2,∴F 的坐标为(2,0).(3)矩形ABCD 存在面积最大的折痕△BEF ,其面积为4.理由如下:①当F 在边BC 上时,如答图4-7②所示,S △BEF ≤12S 矩形ABCD ,即当F 与C 重合时,△BEF 的面积最大为4.②当F 在边CD 上时,如答图4-7③所示,过F 作F H ∥BC 交AB 于点H ,交BE 于点K ,∵S △E K F =12K F ·A H ≤12H F ·A H =12S 矩形A H FD ,S △B K F =12K F ·B H ≤12H F ·B H =12S 矩形BCF H ,∴S △BEF ≤12S 矩形ABCD =4,即当F 为CD 的中点时,△BEF 的面积最大为4.下面求面积最大时,点E 的坐标:①当F 与点C 重合时,如答图4-7④所示,由折叠可知CE=CB =4,在Rt △CDE 中,ED =CE 2-CD 2=42-22=23,∴AE =4-23,∴E 的坐标为(4-23,2).②当F 在边DC 的中点时,点E 与点A 重合,如答图4-7⑤所示,此时E 的坐标为(0,2).综上所述,折痕△BEF 的最大面积为4时,点E的坐标为(0,2)或(4-23,2).答图4-7第3—4讲测试题1.D2.D3.C4.C5.D6.C7.B8.C9.D 10.D 11.BC=DF (答案不唯一)12.5∶113.60°14.715.75°16.2017.证明:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AB=CD ,∴∠BAC=∠DCA ,∴180°-∠BAC =180°-∠DCA ,∴∠EAB=∠DCF.∵BE ⊥AC ,DF ⊥AC ,∴∠BEA=∠DFC=90°.在△BEA 和△DFC 中,{∠BEA =∠DFC,∠EAB =∠DCF,AB =CD,∴△BEA ≌△DFC (AAS ),∴AE=CF.18.证明:∵四边形ABCD 是平行四边形,∴点O 是BD 的中点.又∵点E 是CD 的中点,∴OE 是△BCD 的中位线,∴OE ∥BC ,且OE =12BC.又∵CF=12BC ,∴OE=CF.又∵点F 在BC 的延长线上,∴OE ∥CF ,∴四边形OCFE 是平行四边形.19.证明:如答图Ⅲ-1,连接AF ,EC.答图Ⅲ-1∵四边形ABCD 是矩形,∴OB=OD.又∵AE ∥CF ,∴∠BEO=∠DFO ,∠OBE=∠ODF.∴△BOE ≌△DOF (AAS ),∴BE=DF.∵AB+BE=DC+DF ,∴AE=CF ,AE ∥CF ,∴四边形AECF 为平行四边形.20.证明:∵AB=CD ,AD=BC ,∴四边形ABCD 是平行四边形,∴AD ∥BC.又∵EF ⊥AD ,∴EF ⊥BC.21.证明:∵四边形ABCD 是正方形,∴AB=BC ,∠A=∠CBE =90°.∵BF ⊥CE ,∴∠BCE+∠CBG =90°.∵∠ABF+∠CBG =90°,∴∠BCE=∠ABF.在△BCE 和△ABF 中,{∠BCE =∠ABF,BC =AB,∠CBE =∠A,∴△BCE ≌△ABF (ASA ),∴BE=AF.22.(1)证明:∵四边形ABCD 是矩形,∴AB=DC ,AC=BD ,AD=BC ,∠ADC=∠ABC =90°.由平移的性质得:DE=AC ,CE=BC ,∠DCE=∠ABC=90°,DC=AB ,∴AD=EC.在△ACD 和△EDC 中,{AD =EC,∠ADC =∠DCE,CD =DC,∴△ACD ≌△EDC (SAS ).(2)解:△BDE 是等腰三角形.理由如下:∵AC=BD ,DE=AC ,∴BD=DE ,∴△BDE 是等腰三角形.23.证明:∵四边形ABCD 是菱形,∴AB=BC ,AD ∥BC ,∴∠A=∠CBF.又∵AE=BF ,∴△ABE ≌△BCF ,∴BE=CF.24.(1)证明:如答图Ⅲ-2,连接BD.答图Ⅲ-2∵点E ,H 分别为边AB ,DA 的中点,∴EH ∥BD ,EH =12B D .∵点F ,G 分别为边BC ,CD 的中点,∴FG ∥BD ,FG=12BD ,∴EH ∥FG ,EH=GF ,∴中点四边形EFGH 是平行四边形.(2)四边形EF GH 是菱形.证明:如答图Ⅲ-3,连接AC ,BD,交于点O.答图Ⅲ-3∵∠APB=∠CPD ,∴∠APB+∠APD=∠CPD+∠APD ,即∠APC=∠BPD.在△APC 和△BPD 中,{AP =PB,∠APC =∠BPD,PC =PD,∴△APC ≌△BPD ,∴AC=BD.∵点E ,F ,G 分别为边AB ,BC ,CD 的中点,∴EF =12AC ,FG=12BD ,∴EF=FG.∵四边形EFGH 是平行四边形,∴四边形EFGH 是菱形.(3)四边形EFGH 是正方形.证明:如答图Ⅲ-3,AC 与PD 交于点M ,AC 与EH 交于点N.∵△APC ≌△BPD ,∴∠ACP=∠BDP.∵∠DMO=∠CMP ,∴∠COD=∠CPD =90°.∵EH ∥BD ,AC ∥HG ,∴∠EHG=∠ENO=∠BOC=∠DOC =90°.∵四边形EFGH 是菱形,∴四边形EFGH 是正方形.25.解:(1)()2,32(2)设点D 的坐标为(x ,y ),当AB 为一条对角线时,AB 的中点坐标为()1,32,则ìíîïïïïx+12=1,y +42=32,解得{x =1,y =-1,此时点D 的坐标为(1,-1).当AC 为一条对角线时,AC 的中点坐标为(0,3),则ìíîïïïïx +32=0,y +12=3,解得{x =-3,y =5,此时点D 的坐标为(-3,5).当BC 为一条对角线时,BC 的中点坐标为()2,52,则ìíîïïïïx -12=2,y +22=52,解得{x =5,y =3,此时点D 的坐标为(5,3).综上所述,点D 的坐标为(1,-1)或(-3,5)或(5,3).第5讲一次函数练一练巩固演练1.B2.A解析:一次函数y =(m -2)x +3的图象经过第一、二、四象限,∴m -2<0,解得m <2.3.B解析:根据函数图象上加下减的平移法则,可得y =2x -3+8,即y =2x +5.4.C解析:由已知可得{n +3=km +k +1,①2n -1=k (m +1)+k +1,②②-①得k =n -4,又0<k <2,则有0<n -4<2,解得4<n <6,只有选项C 的数值符合条件,故选C .5.B6.1解析:由题意可得{y =kx +2,y =2x +k,解得{x =1,y =k +2,故答案为1.7.-40℃8.k =-1(答案不唯一)解析:正比例函数y =kx (k 是常数,k ≠0)的图象经过第二、四象限,根据正比例函数的性质可得k <0,只要符合条件的k 值都可以.9.y =x 或y =-x.解析:∵点A (m ,n )在直线y =kx (k ≠0)上,-1≤m ≤1时,-1≤n ≤1,∴图象过点(-1,-1)和(1,1)或者图象过点(-1,1)和(1,-1).∴k =-1或k =1,∴y =x 或y =-x ,故答案为:y =x 或y =-x.10.0.311.解:∵一次函数y =kx +2,当x =-1时,y =1,∴-k +2=1,∴k =1,∴y =x +2.函数图象如答图5-1所示.x y1324答图5-112.(1)l 23020解析:乙离A 地的距离越来越远,图象是l2;甲的速度60÷2=30(km/h);乙的速度60÷(3.5-0.5)=20(km/h);(2)解:设l1所表示的函数关系式为y1=k1x+b1(k1≠0),l2所表示的函数关系式为y2=k2x+b2(k2≠0),可得y1=-30x+60,y2=20x-10,由y1-y2=5得x=1.3;由y2-y1=5得x=1.5.答:甲出发后1.3h或者1.5h时,甲、乙相距5km.13.(1)1,3,1.2,3.3(2)解:y1=0.1x(x≥0);当0≤x≤20时,y2=0.12x,当x>20时,y2=0.12×20+0.09(x-20),即y2=0.09x+ 0.6.故y2关于x的函数解析式为y2={0.12x(0≤x≤20),0.09x+0.6(x>20).(3)解:顾客在乙复印店复印花费少.当x>70时,有y1=0.1x,y2=0.09x+0.6,∴y1-y2=0.1x-(0.09x+0.6)=0.01x-0.6,记y=0.01x-0.6,由于0.01>0,y随x的增大而增大,又x=70时,有y=0.1.∴x>70时,有y>0.1,即y>0,∴y1>y2,∴当x>70时,顾客在乙复印店复印花费少.提高演练1.A解析:∵一次函数y=kx-m-2x的图象与y 轴的负半轴相交,且函数值y随自变量x的增大而减小,∴k-2<0,-m<0,∴k<2,m>0.2.B解析:∵一次函数y=-2x+m的图象经过点P(-2,3),∴3=4+m,解得m=-1,∴y=-2x-1.∵当x=0时,y=-1,∴它的图象与y轴的交点为B(0,-1),∵当y=0时,x=-12,∴它的图象与x轴的交点为A()-12,0,∴S△A O B=12×1×12=14.3.an=bm解析:设交点为(x,0),ax+b=0①,mx+ n=0②,①×m-②×a得:mb-an=0,an=bm.4.-25解析:根据题意得y1+y2=3(x1+x2)-16=3×(-3)-16=-25.5.解:(1)观察函数图象可得当横坐标为18时,纵坐标为45,即应交水费为45元.(2)设当x>18时,y关于x的函数解析式为y=kx+ b(k≠0),将(18,45)和(28,75)代入可得{18k+b=45,28k+b=75,解得{k=3,b=-9,则当x>18时,y关于x的函数解析式为y=3x-9,当y=81时,3x-9=81,解得x=30.答:这个月的用水量为30m3.赛一赛解:(1)依据题意画图,如答图5-2.答图5-2∴S△O PA=12O A·PB=12·O A·y.∵点A的坐标为(6,0),∴S=12×6×y=3y.由题知:x+y=8,∴y=8-x,∴S=3(8-x)=24-3x(0<x<8).画图如答图5-3所示.答图5-3(2)当x=3时,S=24-3×3=15.∴当点P的横坐标为3时,△O PA的面积为15.第5讲测试题1.C2.B3.B4.A5.A6.A7.D8.D9.B10.B11.>12.14.-2或-515.七16.(2021217.解:∵直线y=2x+b经过点(3,5),∴5=2×3+b.∴b=-1.即不等式为2x-1≥0,解得x≥12.18.解:将点(0,2)代入y=kx+b(k≠0)中,得:b=2,则一次函数y=kx+b(k≠0)与x轴的交点横坐标为-bk=-2k,由题意可得:S=12×||||||-2k×2=2,解得k=±1,则一次函数的解析式为y=x+2或y=-x+2. 19.解:(1)设直线AB的解析式为y=kx+b.直线AB过点A(1,0),B(0,-2),∴{k+b=0,b=-2,解得{k=2,b=-2,∴直线AB的解析式为y=2x-2.(2)设点C的坐标为(x,y).∵S△B O C=2,∴12×2×x=2,解得x=2,代入y=2x-2中,∴y=2×2-2=2,∴点C的坐标是(2,2). 20.解:(1)直线y=-x+b交y轴于点P(0,b),由题意,得b>0,t≥0,∵b=1+t,当t=3时,b=4.∴y=-x+4.(2)当直线y=-x+b过点M(3,2)时,有2=-3+b,解得b=5.∵b=1+t,∴t=4.当直线y=-x+b过点N(4,4)时,有4=-4+b,解得b=8.∵b=1+t,∴t=7.故若点M,N位于l的异侧,t的取值范围是4<t<7.21.(1)将(1,0),(0,2)代入y=kx+b中,得{k+b=0,b=2,解得{k=-2, b=2,∴一次函数的解析式为y=-2x+2.把x=-2代入y=-2x+2,得y=6,把x=3代入y=-2x+2,得y=-4,∴y的取值范围是-4≤y<6.(2)∵点P(m,n)在该函数的图象上,∴n=-2m+2.∵m-n=4,∴m-(-2m+2)=4,解得m=2,n=-2,∴点P的坐标为(2,-2). 22.解:(1)3min16s=196(s),196+40=236(s).设y=kx+b,则(196,70),(236,80)在直线y=kx+b上,∴{196k+b=70,236k+b=80,解得{k=0.25, b=21,∴y与x之间的函数关系式为y=0.25x+21.(2)令y=100,得0.25x+21=100,解得x=316,令y=28,得0.25x+21=28,解得x=28,∴316-28=288(s),∴需加热288s. 23.解:(1)由题意可知y=60-5x+3x.∴y=60-2x(x≤30).(2)根据题意得60-2x≥40,∴x≤10.∴最迟应在下午6:00关闭两水管.24.解:(1)y1=280×0.8(x-10)+280×10=224x+560(x>10),y2=280×0.9x=252x(x>10).(2)y1-y2=-28x+560,令-28x+560=0,则x=20;①当x>20时,y1<y2,选甲旅行社的费用较低;②当x=20时,y1=y2,选甲、乙两家旅行社的费用相同;③10<x<20时,y1>y2.选乙旅行社的费用较低.25.解:(1)由题意:y=380x+280(62-x)=100x+ 17360,∵30x+20(62-x)≥1441,∴x≥20.1,∴x的取值范围为21≤x≤62.(2)由题意得100x+17360≤21940,∴x≤45.8.又∵x≥20.1,∴21≤x≤45,∴共有25种租车方案.∵y随x的增大而增大,∴x=21时,y取最小值.x=21时,y=100×21+17360=19460,即租A型号客车21辆,B型号客车41辆时最省钱,最少租车费为19460元.第6讲数据的分析练一练巩固演练1.B2.B3.C4.C5.C6.27.908.59.解:(1)由题意可得,调查的学生有:30÷25%= 120(人),选B的学生有:120-18-30-6=66(人),B所占的百分比是:66÷120×100%=55%,D所占的百分比是:6÷120×100%=5%,故补全条形统计图与扇形统计图如答图6-1所示,答图6-1(2)由(1)中补全的条形统计图知,所抽取学生对数学学习喜欢程度的众数是:比较喜欢,故答案为:比较喜欢.(3)由(1)中补全的扇形统计图可得,该年级学生中对数学学习“不太喜欢”的有:960×25%=240(人),即估计该年级学生中对数学学习“不太喜欢”的有240人.10.解:(1)-x 乙=(73+80+82+83)÷4=79.5,∵80.25>79.5,∴应选派甲.(2)-x 甲=(85×2+78×1+85×3+73×4)÷(2+1+3+4)=79.5,-x 乙=(73×2+80×1+82×3+83×4)÷(2+1+3+4)=80.4,∵79.5<80.4,∴应选派乙.提高演练1.C2.D3.84.96分,96.4分5.解:(1)甲的平均成绩为a =5×1+6×2+7×4+8×2+9×11+2+4+2+1=7(环),∵乙射击的成绩从小到大排列为:3,4,6,7,7,8,8,8,9,10,∴乙射击成绩的中位数b =7+82=7.5(环),乙射击成绩的方差为c =110×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]=110×(16+9+1+3+4+9)=4.2.(2)从平均成绩看,甲、乙二人的成绩相等,均为7环;从中位数看,甲射中7环以上的次数小于乙;从众数看,甲射中7环的次数最多;而乙射中8环的次数最多;从方差看甲的成绩比乙的成绩稳定.综合以上各因素,若选派一名队员参加比赛,可选择乙参赛,因为乙获得高分的可能更大.赛一赛解:(1)28-22=6(天),∴10盆花的花期最多相差6天.(2)由平均数公式得:-x 甲=15(25+23+28+22+27)=25,-x 乙=15(27+24+24+27+23)=25,∴-x 甲=-x 乙.故无论用哪种花肥,花的平均花期相等.(3)由方差公式得:s 甲2=15[(25-25)2+(23-25)2+(28-25)2+(22-25)2+(27-25)2]=5.2,s 乙2=15[(27-25)2+(24-25)2+(24-25)2+(27-25)2+(23-25)2]=2.8,得s 2乙<s 2甲,故施用乙种花肥效果更好.第6讲测试题1.B 2.C 3.B 4.C 5.B 6.D 7.C 8.C9.D 10.B 11.312.713.1514.4.8或5或5.215.2.516.18317.解:(1)根据题意得:30÷30%=100(人),∴劳动时间为“1.5h ”的人数为100-(12+30+18)=40(人),补全统计图,如答图Ⅵ-1所示:答图Ⅵ-1(2)根据题意得:40100×360°=144°,则扇形图中的“1.5h ”部分的圆心角是144°.(3)根据题意得:抽查的学生劳动时间的众数为1.5h ,中位数为1.5h .18.解:(1)由题意可得,甲组的平均成绩是:91+80+783=83(分),乙组的平均成绩是:81+74+853=80(分),丙组的平均成绩是:79+83+903=84(分),从高分到低分小组的排名顺序是:丙>甲>乙.(2)由题意可得,甲组的平均成绩是:91×40%+80×30%+78×30%40%+30%+30%=83.8(分),乙组的平均成绩是:81×40%+74×30%+85×30%40%+30%+30%=80.1(分),丙组的平均成绩是:79×40%+83×30%+90×30%40%+30%+30%=83.5(分),由上可得,甲组的成绩最高.19.解:(1)根据题意得:15×40+25×40+30×2040+40+20=22(元/千克).则该什锦糖的单价是22元/千克;(2)设加入丙种糖果x kg ,则加入甲种糖果(100-x )kg ,根据题意得:30x +15(100-x )+22×100200≤20,解得x ≤20.答:最多加入丙种糖果20kg .20.解:(1)由表格中的数据可以将折线统计图补充完整,如答图Ⅵ-2所示,答图Ⅵ-2(2)将乙的射击训练成绩按照从小到大排列是:6,7,7,7,7,8,9,9,10,10,故乙运动员射击训练成绩的众数是7,中位数是:7+82=7.5,故答案为:77.5;(3)由表格可得,-x 甲=8+9+7+9+8+6+7+8+10+810=8,s 甲2=110×[(8-8)2×4+(9-8)2×2+(7-8)2×2+(6-8)2+(10-8)2]=1.2,∵1.2<1.8,∴甲本次射击成绩的稳定性好.21.解:(6+12+16+10)÷4=44÷4=11,∴这四个小组回答正确题数的平均数是11题.22.解:(1)如答图Ⅵ-3所示:答图Ⅵ-3(2)由题意知,10+9+9+a +b5=9,∴a +b =17.23.解:(1)-x 甲=15×(7.2+9.6+9.6+7.8+9.3)=8.7(万元),把乙的销售额按照从小到大依次排列可得:5.8,5.8,9.7,9.8,9.9;则中位数为9.7.丙中出现次数最多的数为9.9.(2)我赞同甲的说法.甲的平均销售额比乙、丙都高.24.解:(1)由折线统计图可知,甲组成绩从小到大排列为3,6,6,6,6,6,7,9,9,10,∴甲组学生成绩的中位数a =6,乙组学生成绩的平均分b =5×2+6×1+7×2+8×3+9×210=7.2.(2)∵甲组的中位数为6,乙组的中位数为7.5,而小英的成绩位于全班中上游,∴小英属于甲组学生.(3)①乙组的平均分高于甲组,即乙组的总体平均水平高;②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定.25.解:(1)4030(2)观察条形统计图,∵-x =13×4+14×10+15×11+16×12+17×340=15,∴这组数据的平均数为15;∵在这组数据中,16出现了12次,出现的次数最多,∴这组数据的众数为16;∵将这组数据按照从小到大的顺序排列,其中处于中间的两个数都是15,有15+152=15,∴这组数据的中位数为15.综合测试题1.D2.C3.C4.C5.B6.D7.C8.A9.A 10.D11.三12.y =12x -513.x <114.751615.n -1416.517.解:(1)27+48=33-23+43=53;(2)原式=3+1-3+9+62+2=12+62.18.(1)点A 关于y 轴对称的点的坐标是(2,3).(2)点B对应点的坐标是(0,-6),画图略.(3)以A,B,C为顶点的平行四边形的第四个顶点D的坐标为(-7,3)或(-5,-3)或(3,3). 19.(1)∠ACB=90°;(2)S△ABC=16-12×2×4-12×2×1-12×4×3=5. 20.(1)解:AD=13BC,理由如下:∵AD∥BC,AB∥DE,AF∥DC,∴四边形ABED和四边形AFCD是平行四边形,∴AD=BE,AD=F C.又∵四边形AEFD是平行四边形,∴AD=EF,∴AD=BE=EF=FC,∴AD=13B C.(2)证明:∵四边形ABED和AFCD是平行四边形,∴DE=AB,AF=D C.∵AB=DC,∴DE=AF.又∵四边形AEFD是平行四边形,∴四边形AEFD是矩形.21.解:(1)由题意{17(a+0.8)+3(b+0.8)=66,①17(a+0.8)+8(b+0.8)=91,②②-①,得5(b+0.8)=25,解得b=4.2,把b=4.2代入①,得17(a+0.8)+3×5=66,得a=2.2,b=4.2.(2)当用水量为30m3时,水费为:17×3+13×5=116(元),9200×2%=184(元),∵116<184,∴小王家6月份用水超过30m3.设小王家6月份用水x m3,由题意,得17×3+13×5+6.8(x-30)≤184,6.8(x-30)≤68,解得x≤40.则小王家6月份最多能用水40m3.22.解:从成绩统计表看,甲组成绩高于90分的有20人,乙组成绩高于90分的有24人,乙组成绩集中在高分段的人数多,同时乙组得满分的人数比甲组得满分的人数多6人,从这一角度看乙组的成绩较好.当然还可以从其他角度来分析.(从不同的角度分析,可能会得到不同的结论)23.(1)证明:由折叠知AE=AD=E G,BC=C H,∵四边形ABCD是矩形,∴AD=BC,∴E G=C H.(2)解:∵∠ADE=45°,∠F G E=∠A=90°,AF=2,∴D G=G F=2,DF=DG2+GF2=2,∴AD=AF+DF=2+2.∵∠G EF=∠AEF,又∵∠BEC=∠H EC,∴2∠G EF+2∠H EC=180°,∴∠CEF=90°.∵∠CE H+∠H CE=90°,∠FE G+∠CE H=90°,∴∠G EF=∠H CE.在△F G E和△E H C中,{∠FGE=∠CHE,∠GEF=∠HCE,CH=EG,∴△F G E≌△E H C,∴F G=E H=AF=BE=2,∴AB=AE+BE=AD+AF=2+2+2=22+2. 24.解:(1)设直线l1的表达式为y=k1x,过B(18,6),得18k1=6,解得k1=13,∴直线l1的表达式为y=13x.设直线l2的表达式为y=k2x+b,过A(0,24),B(18,6),得{b=24,18k2+b=6,解得{k2=-1,b=24,∴直线l2的表达式为:y=-x+24.(2)∵点C在直线l1上,且点C的纵坐标为a,∴a=13x,则x=3a,∴点C的坐标为(3a,a).∵CD∥y轴,∴点D的横坐标为3a.∵点D在直线l2上,∴y=-3a+24,∴点D的坐标为(3a,-3a+24).25.证明:由图①知:S多边形ABCDEF=S正方形AB O F+S正方形C O ED+2S△B O C=a2+b2+ 2×12ab=a2+b2+ab.设BC=c,则B'C'=c.由图③知:S多边形A'B'C'D'E'F'=S△A'B'F'+S正方形B'C'E'F'+S△C'D'E'=12ab+ c2+12ab=c2+ab.∵S多边形ABCDEF=S多边形A'B'C'D'E'F',∴a2+b2+ab=c2+ab.∴a2+b2=c2.。
八年级数学下册暑假综合测试题附答案-人教版

八年级数学下册暑假综合测试题附答案-人教版(全卷三个大题,共24个小题;满分100分,考试用时120分钟)姓名班级学号成绩一、选择题(本大题共12小题.每小题只有一个正确选项,每小题3分,共36分)1.下列根式是二次根式的是()3C.√2x D.√−4A.√x2+1B.√72.下列各式计算正确的是()A.√2 + √3=√5B.4 √3﹣3 √3=1C.2 √3×2 √3=4 √3D.√27÷√3=33.已知a、b、c是三角形的三边长,如果满足(a−6)2+√b−8+|c−10|=0,则三角形的形状是()A.底与边不相等的等腰三角形B.等边三角形C.钝角三角形D.直角三角形4.如图,在长方形ABCD中CF⊥BD,垂足为E,CF交AD于点F,连接BF,则图中面积相等的三角形的对数为()A.3对B.4对C.5对D.6对5.在下列各图象中,y不是x函数的是()A.B.C.D.6.下列说法错误的是()A.如果一组数据的众数是5,那么这组数据出现的次数最多的是5B.一组数据的平均数一定大于其中每一个数据C.一组数据的平均数、众数、中位数有可能相同D.一组数据的中位数有且只有一个7.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是1,那么另一组数据3x1−2,3x2−2,3x3−2,3x4−2,3x5−2的平均数和方差分别是()A.0 -1 B.6 3 C.4 9 D.4 18.如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(4,8),则使y1<y2的x的取值范围为()A.x>4B.x>8C.x<4D.x<89.如图,在Rt△ABC中∠ACB=90°,BC=6,AC=8。
AP、BP分别平分∠BAC,∠ABC,则PC的长为()A.2√2B.4√2C.4 D.210.如图,在长方体ABCD−EFGH盒子中,已知AB=4cm,BC=3cm,CG=5cm,长为10cm的细直木棒IJ恰好从小孔G处插入,木棒的一端I与底面ABCD接触,当木棒的端点I在长方形ABCD内及边界运动时,GJ长度的最小值为()A.(10−5√2)cm B.3cm C.(10−4√2)cm D.5cm11.如图,将菱形ABCD沿AE折叠,点B的对应点为F,若E、F、D刚好在同一直线上,设∠ABE=α,∠BAE=β,∠C=γ则关系正确的是()A.γ=α+2β−180°B.3β+γ=180°C.3α+2β=360°D.2α+γ=180°12.在平行四边形ABCD中∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE, BF相交于H,BF与AD的延长线相交于点G,下面给出四个结论:①BD=√2BE;②∠A=∠BHE;③AB=BH;④ΔBCF≅ΔDCE,其中正确的结论是()A.①②③B.①②④C.②③④D.①②③④二、填空题(本大题共4小题,每小题2分,共8分)13.若1<x<2,则|x﹣1|+ √(x−2)2的值为.14.已知菱形的对角线的长分别是6和8,则这个菱形的面积是;15.学校组织一分钟跳绳比赛.八(1)班准备从甲、乙两人中挑选一名成绩比较稳定的同学参赛.两人最近四次的跳绳测试的成绩(单位:个)为:甲:197,213,209,196;乙:205,203,202,205,而这两人平均成绩相同,根据信息,应该选参加比赛.16.如图,已知在△ABC中AB=4,BC=5,∠ABC=60°在边AC上方作等边△ACD,则BD的长为.三、解答题(本答题共8小题,共56分)17.计算:3+|√3−2|;(1)√12−√8−(√5+√3)(√5−√3)(2)√27×√1318.在平面直角坐标系xOy中,直线y=2x+1与x轴交于点A,与y轴交于点B.求点A,B的坐标.19.学生的平时作业、期中考试、期末考试三项成绩分别按2:3:5的比例计入学期总评成绩.小明、小亮、小红的平时作业、期中考试、期末考试的数学成绩如下表,计算这学期谁的数学总评成绩最高?20.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)21.汉巴南高铁将打通巴中市第一条高铁大通道,全面助推巴中经济发展,实现“川陕渝边界地区中心城市”的定位.巴中东站是汉巴南铁路全线最大建设规模的高架式车站,建成后将成为巴中市未来全新的“城市门户”,目前,巴中东站站房项目正在如火如荼地建设中.某公司承包了该项目的部分绿化工程,总面积为2000m2,由甲、乙两个工程队来完成;已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍、并且在独立完成面积为240m2区域的绿化时,甲队比乙队少用3天.(1)求甲、乙两工程队每天能完成绿化的面积;(2)若甲队每天绿化费用是0.8万元,乙队每天绿化费用为0.3万元,且甲、乙两队施工的总天数不超过35天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.22.已知:如图,在△ABC中,AD⊥BC于点D,E为AC上一点,且BF=AC,DF=DC.(1)求证:△BDF≅△ADC;(2)已知AC=10√3,DF=6√3,求AF的长.23.如图,矩形ABCD,过点B作BE∥AC交DC的延长线于点E.过点D作DH⊥BE于H,G为AC 中点,连接GH.(1)求证:BE=AC.(2)判断GH与BE的数量关系并证明.24.如图,正方形ABCD中E,F分别为AB,BC中点CE,DF交于M,CE与DA 的延长线相交于点P .求证:(1)△EBC≅△FCD;(2)CP⊥DF;(3)AM=AD .参考答案:1.A 2.D 3.D 4.C 5.C 6.B 7.C 8.C 9.A 10.A 11.C 12.A 13.1 14.24 15.乙 16.√61 17.(1)解:原式= 2√3−2+2−√3=√3. 故答案为: √3 .(2)解:原式= 3√3×√3(5−3)=3−2=1 . 故答案为:118.解:将x =0代入y =2x +1得,y =1,则B(0,1) 将y =0代入y =2x +1得,x =−12,则A(−12,0)19.解:小明数学总评成绩:96×210+94×310+90×510=92.4,小亮数学总评成绩:90×210+96×310+93×510=93.3,小红数学总评成绩:90×210+90×310+96×510=93,∵93.3>93>92.4,∴小亮成绩最高.答:这学期小亮的数学总评成绩最高. 20.解:∵△ABD 是等边三角形∴∠B=60°∵∠BAC=90°∴∠C=180°﹣90°﹣60°=30°∵AB=2∴BC=2AB=4在Rt △ABC 中,由勾股定理得:AC= √BC 2−AB 2 = √42−22 =2 √3 ∴△ABC 的周长是AC+BC+AB=2 √3 +4+2=6+2 √3 . 答:△ABC 的周长是6+2 √3 .21.(1)解:设乙工程队每天能完成绿化的面积是am 2根据题意得:240a=2402a+3解得:a =40经检验,a =40是原方程的解,且符合题意则甲工程队每天能完成绿化的面积是40×2=80(m 2)答:甲工程队每天能完成绿化的面积是80m 2,乙工程队每天能完成绿化的面积是40m 2; (2)解:设安排甲工程队施工x 天,乙工程队施工y 天,施工总费用为w 元根据题意,得:80x +40y =2000整理得:y =50−2x ∵甲乙两队施工的总天数不超过35天∴x +y ≤35∴x +50−2x ≤35解得:x ≥15设施工总费用为w 元,根据题意得:w =0.8x +0.3y =0.8x +0.3(50−2x)=0.2x +15∵k =0.2>0∴w 随x 减小而减小∴当x =15时,w 有最小值,最小值为0.2×15+15=18(万元)此时y =50−2×15=20. ∴安排甲工程队施工15天,乙工程队施工20天,施工费用最少为18万元.22.(1)证明:∵AD ⊥BC 于点D ∴∠ADC =∠ADB =90°在Rt △BDF 与Rt △ADC 中∵{DF =DC BF =AC∴Rt △BDF ≅Rt △ADC(HL) (2)解:∵△BDF ≅△ADC ∴BF =AC =10√3,AD =BD 在Rt △BDF 中,BD =√BF 2−DF 2=√(10√3)2−(6√3)2=8√3∴AD =BD =8√3∴AF =AD −DF =8√3−6√3=2√3. 23.(1)证明:∵四边形ABCD 是矩形∴AB ∥CD ∵AC ∥BE ∴四边形ABEC 是平行四边形∴BE =AC (2)解:GH = 12 BE证明:连接BD∵四边形ABCD是矩形,G为AC的中点∴G为BD的中点,AC=BD∵DH⊥BE,即∠DHB=90°∴GH=12 BD∵AC=BD,AC═BE∴GH=12BE24.(1)解:∵四边形ABCD是正方形∴AB=BC=CD=AD,∠B=∠BCD=90°∵E,F分别为AB,BC中点∴AE=BE=CF=BF在△EBC和△FCD中{BC=CD∠B=∠BCDBE=CF∴△EBC≅△FCD(SAS);(2)解:∵△EBC≅△FCD∴∠BCE=∠CDF∵∠CDF+∠CFD=90°∴∠BCE+∠CFD= 90°∴∠CMF=90°∴CP⊥DF;(3)解:∵AD//BC∴∠P=∠BCE在△APE和△BCE中{∠P=∠BCE∠AEP=∠BECAE=BE∴△APE≅△BCE(AAS)∴AP=BC∴AP=AD=12PD∵DM⊥PM∴AM=12PD∴AM=AD。
《我的作业》八年级下册数学人教版 第120页

《我的作业》八年级下册数学人教版第120页摘要:一、作业的重要性1.巩固课堂所学知识2.培养自主学习能力3.提高解决问题的能力4.养成良好的学习习惯二、如何高效完成作业1.制定合理的学习计划2.遵循“四先四后”原则3.注重课堂知识的消化4.及时向老师请教问题三、面对难题时的应对策略1.保持冷静,分析问题2.尝试多种解题方法3.查阅相关资料,积累经验4.与同学讨论,共同进步四、作业与考试的关系1.作业是考试的基础2.作业与考试相互促进3.学会将作业经验运用到考试中正文:【我的作业】八年级下册数学人教版第120页一、作业的重要性作为学生,我们深知作业的重要性。
首先,作业能帮助我们巩固课堂所学知识,将理论知识转化为实际解题能力。
其次,通过完成作业,我们可以培养自主学习能力,提高自我管理、自我驱动的能力。
此外,作业中的问题多种多样,可以提高我们解决问题的能力,培养我们的发散性思维。
最后,按时完成作业,可以养成良好的学习习惯,为今后的学习生活打下坚实的基础。
二、如何高效完成作业想要高效完成作业,我们需要制定合理的学习计划。
每天晚上,可以先将当天的作业列成清单,然后根据难易程度和自己的掌握情况,分配好每个任务所需的时间。
遵循“四先四后”原则,即先复习后作业、先易后难、先独立后求助、先理解后记忆。
在做作业的过程中,注重课堂知识的消化,对不懂的问题及时查阅相关资料,或者向老师请教。
三、面对难题时的应对策略在做作业时,遇到难题是不可避免的。
这时,我们要保持冷静,分析问题,尝试从不同角度去理解问题。
同时,可以尝试多种解题方法,积累解题经验。
如果实在无法解决,可以与同学讨论,共同进步。
四、作业与考试的关系作业和考试是相辅相成的。
作业是我们对课堂知识的巩固和运用,而考试则是对我们知识掌握情况的检验。
我们要学会将作业中的经验运用到考试中,提高自己的应试能力。
同时,通过考试的反馈,我们可以发现自己在作业中的不足之处,从而调整学习方法,提高学习效果。
人教版初二数学暑期作业

人教版初二数学暑期作业一、选择题1.要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( ) A.调查全体女生 B.调查全体男生C.调查九年级全体学生D.调查七,八,九年级各100名学生2.为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是( ).A.某市八年级学生的肺活量B.从中抽取的500名学生的肺活量C.从中抽取的500名学生D.5003. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球.下列事件是必然事件的是( )A.摸出的三个球中至少有一个球是黑球.B.摸出的三个球中至少有一个球是白球.C.摸出的三个球中至少有两个球是黑球.D.摸出的三个球中至少有两个球是白球.4、下列约分,结果正确的是( )A、 B、 C、 D、5、若中的x和y都缩小一半,那么分式的值 ( )A、缩小为原来的B、不变C、扩大到原来的2倍D、扩大到原来的4倍6、在平行四边形ABCD中,对角线AC,BD相交于O,若AC=10,BD=6,则AB的长的取值范围是( ).A、27. 如图.在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )A.AB∥DCB.AC=BDC.AC⊥BDD.OA=OC8. 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( )A. 4B. 6C. 8D. 109. 如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是A.△AED≌△BFAB.DE-BF=EFC.AF-BF=EFD.DE-BG=FG第7题图第8题图第9题图10、如图,矩形ABCG(ABA.0B.1C.2D.3。
人教版初中八年级数学暑期作业

人教版初中八年级数学暑期作业丰厚的学习生活对自己的协助十分大,接上去就是查字典数学网为大家提供的初中八年级数学暑期作业,希望会对大家的学习带来协助!一、选择题(每题4分,共32分)1.以下语句是命题的是( ).A.延伸线段AB到C点B.同一平面内两条直线被第三条直线所截,同旁内角互补C.明天你上网了吗?D.求五边形的内角和2.一次数学活动课上,小聪将一副三角板按图中方式叠放,那么等于( ).A.30B.45C.60D.753.某商品的商标可以笼统为如下图的三条线段,其中AB∥CD,EAB=45,那么FDC的度数是( ).A.30B.45C.60D.754.如图,CD∥AB,1=120,2=80,那么E的度数是( ).A.4 0B.60C.80D.1205.如图,以下说法正确的选项是( ).A. B.DC.DD. 16.如图,AD=AB=BC,那么1和2之间的关系是( ).A.2B.22=180C.1+32=180D.32=1807. 如下图,CGE=,那么B+D+F等于( ).A.360B.270C.180D.28. 如下图,光线l照射到平面镜Ⅰ上,然后在平面镜Ⅰ、Ⅱ之间来回反射.=55,=75,那么为( ).A.50B.55C.60D.65二、填空题(每题4分,共16分)9.三条不同的直线a,b,c在同一平面内,以下四个命题:①假设a∥b,ac,那么b②假设b∥a,c∥a,那么b∥c;③假设ba,ca,那么b④假设ba,ca,那么b∥c.其中真命题是__________.(填写一切真命题的序号)10.将命题同角或等角的余角相等改写成假设那么的方式是:__________.11.如下图,AB∥DE,ABC=80,CDE=140,那么BCD=__________.12.把矩形纸片ABCD沿B E折叠,使得BA边与BC重合,然后再沿着BF折叠,使得BE也与BC边重合,展开后如下图,那么DFB=__________.查字典数学网为大家引荐的初中八年级数学暑期作业,还满意吗?置信大家都会细心阅读,加油哦!。
人教版八年级数学上册暑期课程跟踪——13.3.2等边三角形基础练习

13.3.2等边三角形基础练习一、选择题1.如图,在△ABC中,D,E是BC上两点,且BD=DE=AD=AE=EC.则∠BAC的度数是()A.90°B.108°C.120°D.135°2.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有()A.①②③B.①②④C.①③D.①②③④3.一个三角形具备下列条件仍不是等边三角形的是()A.一个角的平分线是对边的中线或高线B.两边相等,有一个内角是60°C.两角相等,且两角的和是第三个角的2倍D.三个内角都相等4.如图,△ABC 是等边三角形,点D 在AC 边上,∠DBC =35°,则∠ADB 的度数为( )A .25°B .60°C .85°D .95°5.在ABC ∆中,,60,6AB AC A BC =∠=︒=,则AB 的值是( )A.12B.8C.6D.3 6.如图,将边长为5个单位的等边△ABC 沿边BC 向右平移4个单位得到△A’B’C’,则四边形AA’C’B 的周长为( )A .22B .23C .24D .25 7.如图,△ABC 是等边三角形,D 是BC 边的中点,点E 在AC 的延长线上,且∠CDE=30°.若DE 的长( ).A B.C D.8.已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P 关于OA对称,则P1,O,P2三点所构成的三角形是( )A.直角三角形B.钝角三角形C.等腰三角形D.等边三角形9.如图,P为边长为2的等边三角形ABC内任意一点,连接PA、PB、PC,过P点分别作BC、AC、AB边的垂线,垂足分别为D、E、F,则PD+PE+PF 等于()A. B.C.2D.二、填空题10.如图,ABC ∆是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有______个等边三角形.11. 如图,在等边三角形ABC 中,点D 是边BC 的中点,则∠BAD =_____.12.已知在等边三角形ABC 中,点D 是边BC 的中点,AC=8,则BD=______________.13.如图,直线a b ∥,ABC ∆的顶点C 在直线b 上,边AB 与直线b 相交于点D .若BCD ∆是等边三角形,20A ∠=︒,则1∠=__°14.如图,△ABC 以点A 为旋转中心,按逆时针方向旋转60°得到△AB′C′,则△ABB′是________三角形.15.如图,已知等边△ABC中,BD=CE,AD与BE交于点P,则∠APE=________.16.如图,将边长为6 cm的等边三角形沿BC方向向右平移4 cm,得到△DEF,DE交AC于点G,则△EGC是_______三角形,DG=____cm.三、解答题17.如图,△ ABC 是等边三角形,D是AC边上一点,E是BC延长线上一点,连接BD和DE,若∠ABD=40°,BD=DE,求∠CDE的度数.18.如图,在等边△ABC中,DE分别是AB,AC上的点,且AD=CE.(1)求证:BE=CD;(2)求∠1+∠2的度数.19.如图1,△ACB 和△DCE 均为等边三角形,点A .D. E 在同一直线上,连接BE.填空:(1),①∠AEB 的度数为 ;②线段AD 、BE 之间的数量关系是 ;(2)拓展探究:如图2,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点A 、D 、E 在同一直线上,且交BC 于点F ,连接BE.若∠CAF=∠BAF ,BE=2,试求AF 的长.20. 如图,等边△ABC 中,D 是AC 的中点,E 是BC 延长线上的一点,且CE =CD ,DF ⊥BE ,垂足为F.求证:BF =EF.21.如图,E 是AOB ∠的平分线上一点,,EC OB ED OA ⊥⊥,C 、D 是垂足,连接CD 交OE 于点F ,若60AOB ︒∠=(1)求证: OCD ∆是等边三角形:(2)若EF=5,求线段OE 的长,22. 如图,△ABC 是等边三角形,D 是AB 边上一点,以CD 为边作等边三角形CDE ,使点E ,A 在直线DC 的同侧,连接AE.求证:AE ∥BC.答案1. C2. D3. A4. D5. C6.B7.A8.D9.B10.511. 30°12.413.4014.等边15.60°16.等边,417.解∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵∠ABD=40°,∴∠DBC=∠ABC-∠ABD=60°-40°=20°,∵BD=DE,∴∠E=∠DBC=20°,∴∠CDE=∠ACB-∠E=40°.18.(1)证明:∵△ABC是等边三角形,∴∠A=∠ACB=60°,AC=BC,在△ACD和△CBE中,AC=BC,∠A=∠BCE,AD=CE,∴△ACD ≌△CBE (SAS ), ∴BE=CD ;(2)解:∵△ACD ≌△CBE , ∴∠1=∠ACD ,∴∠1+∠2=∠ACD+∠2=∠ACB=60°. 19.解 (1)①如图1, ∵△ACB 和△DCE 均为等边三角形, ∴CA=CB,CD=CE,∠ACB=∠DCE=60°. ∴∠ACD=∠BCE.在△ACD 和△BCE 中, AC BC ACD BCE CD CE =⎧⎪∠=⎨⎪=⎩,∴△ACD ≌△BCE(SAS).∴∠ADC=∠BEC.∵△DCE 为等边三角形, ∴∠CDE=∠CED=60°.∵点A,D,E 在同一直线上, ∴∠ADC=120°.∴∠BEC=120°.∴∠AEB=∠BEC−∠CED=60°. 故答案为:60°.②∵△ACD ≌△BCE ,∴AD=BE.故答案为:AD=BE ;(2)∵△ACB 和△DCE 均为等腰直角三角形, ∴CA=CB,CD=CE,∠ACB=∠DCE=90°. ∴∠ACD=∠BCE.在△ACD 和△BCE 中, CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE(SAS).∴AD=BE ,∠ADC=∠BEC. ∵△DCE 为等腰直角三角形, ∴∠CDE=∠CED=45°.∵点A ,D ,E 在同一直线上, ∴∠ADC=135°.∴∠BEC=135°.∴∠AEB=∠BEC−∠CED=90°; 延长BE 交AC 的延长线于点G , 在△ACF 和△BCG 中,90CAD CBE AC BCACF BCG ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴△ACF ≌△BCG ,∴AF=BG ,∵∠CAF=∠BAF,∠AEB=90°, ∴E 是BG 的中点,∵BE=2,∴AF=4.20. 解:∵BD 是等边三角形ABC 的中线,∴BD 平分∠ABC ,∴∠DBE =12∠ABC =12∠ACB , 又∵CE =CD ,∴∠E =12∠ACB , ∴∠DBE =∠E ,∴DB =DE ,∵DF ⊥BE ,∴DF 为底边上的中线,∴BF =EF21. 解 (1)∵点E 是AOB ∠的平分线上一点,,EC OB ED OA ⊥⊥,垂足分别是C 、D , DE CE ∴=,在 Rt ODE ∆与Rt OCE ∆中,DE CE OE OE =⎧⎨=⎩, Rt ODE Rt OCE(HL)∴∆≅∆,OD OC ∴=,60AOB ︒∠=,OCD ∴∆是等边三角形;(2)OCD ∆是等边三角形,OF 是COD ∠的平分线,OE DC ∴⊥,60AOB ︒∠=,30AOE BOE ︒∴∠=∠=,60,ODF ED OA ︒∠=⊥,30EDF ︒∴∠=,210DE EF ∴==,220OE DE ∴==22. 解:∵△ABC 和△EDC 是等边三角形,∴∠BCA =∠DCE =60°, ∴∠BCD =∠ACE.在△DBC 和△EAC 中,BC =AC ,∠BCD =∠ACE ,DC =EC , ∴△DBC ≌△EAC(SAS),∴∠DBC =∠EAC ,又∵∠DBC =∠ACB =60°,∴∠ACB =∠EAC ,∴AE ∥BC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
丰富的学习生活对自己的帮助非常大,接下来就是查字典数学网为大家提供的初中八年级数学暑期作业,希望会对大家的学习带来帮助!一、选择题(每小题4分,共32分)1.下列语句是命题的是( ).A.延长线段AB到C点B.同一平面内两条直线被第三条直线所截,同旁内角互补C.今天你上网了吗?D.求五边形的内角和2.一次数学活动课上,小聪将一副三角板按图中方式叠放,则等于( ).A.30 B.45 C.60 D.753.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,EAB=45,则FDC的度数是( ).A.30 B.45C.60 D.754.如图,CD∥AB,1=120,2=80,则E的度数是( ).A.4 0 B.60 C.80 D.1205.如图,下列说法正确的是( ).A. B.DC.D D.
16.如图,AD=AB=BC,那么1和2之间的关系是( ).A.2 B.22=180C.1+32=180 D.32=1807. 如图所示,CGE=,则B+D+F等于( ).A.360B.270C.180D.28. 如图所示,光线l照射到平面镜Ⅰ上,然后在平面镜Ⅰ、Ⅱ之间来回反射.已知=55,=75,则为( ).A.50 B.55C.60 D.65二、填空题(每小题4分,共16分)9.已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果a∥b,ac,那么b②如果b∥a,c∥a,那么b∥c;③如果ba,ca,那么b④如果ba,ca,那么b∥c.其中真命题是__________.(填写所有真命题的序号)10.将命题同角或等角的余角相等改写成如果那么的形式是:__________.11.如图所示,已知AB∥DE,ABC=80,CDE=140,则BCD=__________.12.把矩形纸片ABCD沿B E折叠,使得BA边与BC重合,然后再沿着BF 折叠,使得BE也与BC边重合,展开后如图所示,则DFB=__________.查字典数学网为大家推荐的初中八年级数学暑期作业,还满意吗?相信大家都会仔细阅读,加油哦!。
