第三届华罗庚金杯少年数学邀请赛决赛第二试
六年级下册数学试题-小升初:第十讲 计数之加乘原理与技巧(解析版)全国通用

第十讲 计数之加乘原理与技巧1. 回顾分类枚举与排列组合; 2. 精讲计数问题的经典范例。
排列最简单的计数问题,只需一一列举就可以;复杂的计数问题则需要借助排列与组合的相关知识予以解决.一般地,从n 个不同的元素中,任取m(m≤n)个不同的元素,按照一定的顺序排成一列,叫做从n 个不同元素中任取m 个元素的一个排列.我们主要来研究满足某种条件的排列的个数.相同的排列应满足: 它们所含的元素均相同; 它们的顺序也一样.一般地,从n 个不同元素中取出m 个元素的排列的个数称为从n 个不同元素中取出m 个元素的排列数,记作:mn A (m ≤n).从n 个元素中取出m 个元素排成一排,有多少种排法,是从n 个元素中取出m 个元素的排列数.这个问题可以看成有m 个位置,从n 个元素中取m 个元素放到m 个位置中,可分m 个步骤:第①步:第1个位置有n 种选择; 第②步:第2个位置有n -1种选择; 第③步:第3个位置有n -2种选择; ……第m 步:第m 个位置有n -m+1种选择.由乘法原理:mn A = n ×(n - 1)×(n - 2)×…×(n -m+1).——乘积中共有m 项特别地,当m=n 时, ()1...21mnn n A A n n ==⨯-⨯⨯叫做n 个元素的全排列数.1×2×3×…×n 称为n 的阶乘,记作n!因此()!!mn n A n m =- (m≤n).排列数乘积形式的公式:mn A =n×(n - 1)×(n - 2)×…×(n -m+1).教学目标专题回顾本讲内容非常有趣,不过要在计数过程中达到“不重不漏”,必须掌握计数问题的原理与一些技巧才行。
在小升初的考试与其它的竞赛活动中,计数问题出现频率很高。
排列数阶乘形式的公式: ()!!mn n A n m =- (m≤n).组合有时我们只需从若干元素中取出一些就可以了,这种问题称为组合问题,组合问题与排列问题的区别就是:组合问题是将元素取出即可,不需排序,而排列问题是取出后要进行排序.一般地,从n 个不同元素中任取m(m≤n)个不同的元素并成一组,叫做从n 个不同元素中取出,n 个元素的组合.从n 个不同元素中,每次取出m 个元素的组合总数,叫做从n 个不同元素中取出m 个元素的组合数,记作mn C (m ≤n).从n 个元素中取出m 个元素的排列问题可以看成分两步完成: 第①步:从n 个元素中取出m 个元素,这时有多少种取法?实际上就是从n 个元素中取出m 个元素的组合数mn C ;第②步:对取出的m 个元素进行排列,排法数就是mm A .由乘法原理可知:mmmn nmA C A =,因此,mmn nm mA C A =. 将排列数公式代人得:()()().1...1.1...3.2.1mn n n n m C m m --+=-或 ()!!!mn n C n m m =-.分类枚举【例1】 ★★★(《小数报》数学竞赛决赛填空题第ll 题)方格纸上有一只小虫,从直线AB 上的一点O 出发,沿方格纸上的横线或竖线爬行.方格纸上每小段的长为1厘米.小虫爬过若干小段后仍然在直线AB 上,但不一定回到O 点.如果小虫一共爬过2厘米,那么小虫的爬行路线有____种;如果小虫一共爬过3厘米,那么小虫爬行的路线有___种.【解】为了方便,下面叙述省去“上、下、左、右”4个字前面的“向”. (1)小虫爬过2厘米,可有以下6种路线,分别是: 左,右;右,左; 上,下;下,上;左,左;右,右.(以上前4种路线均回到O点)(2)小虫爬过3厘米,可有20种路线,分别是:上,左,下;上,右,下;下,左,上;下,右,上;上,下,左;上,下,右;下,上,左;下,上,右.(以上8种都是先“上”或先“下”.)如果第一步为“左”或“右”,那么转化为第(1)题,各有6种路线,一共是8+6×2=20(种)答案是:(1)6;(2)20。
2019年香港华罗庚金杯少年数学邀请赛(决赛)初中二年级、初一年级组试题含答案

一小時三十分鐘完卷 (上午 10:00 至上午 11:30) 比賽須知:
1. 全卷共 10 題,滿分 100 分。包括填空題 6 道,每題 10 分;詳答題 4 道,每題 10 分。 2. 參賽學生必須全部作答,所有答案寫在答題紙上。 3. 填空題無需書寫步驟,只須填寫答案;詳答題要求寫出詳細過程。 4. 比賽時使用自備文具,例如鉛筆、原子筆及橡皮擦膠等。不准使用計算器。違規者將被
若 | x1-x2|=2 2,則 k 的值為
.
答案:1. 解:令 x+2=kxx2+2x-k=0,△=22+4k≥0k≥-1.
x1+x2=-2,x1x2=-k,|x1-x2|= (x1+x2)2-4x1x2= 4+4k=2 2 k=1.
9. 如圖,方格紙中的每個小正方形的邊長為 1.記圖中陰影部分的面積 A
中二組 F.2 (10 marks for each question)
1. (3x-1)2=0x=3,故3x+3x=2
2.
24+1=4( 2-1),3-4 5=3+ 5即滿足要求的 m 可以取 2,3,4,
5,共 4 個數
3. 取(0,2)關於直線 y=x 的對稱點(2,0),過(-4,-2),(2,0)的直線為 y= 13(x-2),與 y=x 交於點(-1,-1).即為周長最小時的點 C.故 a=-1
二、解答下列各題 (每小題 10 分,共 40 分,要求寫出詳細過程。)
7. 求 − 2 + 2 (− 2 )2 − 4 (− 2 )4 的值。
2
2
2
8. 設 k 為非零實數, 兩個函數 y = x + 2 與 y = k 的圖像相交於 A(x1,y1)、B(x2,y2) x
历届“华杯赛”初赛决赛试题汇编【小中组(附答案)】

二、简答题(每小题 15 分, 共 60 分, 要求写出简要过程)
9. 用 4 个数码 4 和一些加、减、乘、除号和小括号, 写出值分别等于 2、3、4、 5、6 的五个算式. 10. 右图是 U, V, W, X 四辆不同类型的汽车每百千米的耗油 量. 如果每辆车都有 50 升油, 那么这四辆车最多可行驶 的路程总计是多少千米? 11. 某商店卖出一支钢笔的利润是 9 元, 一个小熊玩具的进 价为 2 元. 一次, 商家采取 “买 4 支钢笔赠送一个小熊玩具”的打包促销, 共 获利润 1922 元. 问这次促销最多卖出了多少支钢笔? 12. 编号从 1 到 10 的 10 个白球排成一行, 现按照如下方法涂红色: 1)涂 2 个球; 2)被涂色的 2 个球的编号之差大于 2. 那么不同的涂色方法有多少种?
四百米比赛进入冲刺阶段,甲在乙前面 30 米,丙在丁后面 60 米,乙在丙前面 20 米. 这时,跑在最前面的两位同学相差( (A)10 (B)20 )米. (D)60
(C)50
5.
在右图所示的两位数的加法算式中, 已知 A B C D 22 , ). (B)4 (C)7 (D)13
一、选择题 (每小题 10 分, 满分 60 分. 以下每题的四个选项中, 仅 有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号 内.)
小学数学竞赛学习材料(五年级上期)

小学数学竞赛学习材料五年级上期第一讲速算与巧算(一)例1 计算72.19+6.48+27.81-1.38-5.48-0.62。
解:观察发现,有些加数可以凑整;有的加数和减数尾数相同,可以抵消。
于是:72.19+6.48+27.81-1.38-5.48-0.62=(72.19+27.81)+(6.48-5.48)-(1.38+0.62)=100+1-2=99例2用简便方法计算 1.25×67.875+125×6.7875+1250×0.053375。
解:观察发现:相加的三个乘积中分别有1.25、125、250,因此想到利用积不变的性质,使三个积有相同的因数。
于是:1.25×67.875+125×6.7875+1250×0.053375=1.25×67.875+1.25×678.75+1.25×53.375=1.25×(67.875+678.75+53.375)=1.25×800=1000例3 计算1999+199.9+19.99+1.999。
解法一:观察发现,构成这四个加数的数字和排列顺序完全相同,因此可以把它们都看作1999与某个数的积,于是:1999+199.9+19.99+1.999=1999×(1+0.1+0.01+0.001)=1999×1.111=(2000-1)×1.111=2222-1.111=2220.889解法二:观察发现这四个加数分别接近2000、200、20、2,于是1999+199.9+19.99+1.999=2000+200+20+2-1.111=2220.889例4 计算(1+0.33+0.44)×(0.33+0.44+0.55)-(1+0.33+0.44+0.55)×(0.33+0.44)。
解:观察发现这些因数中有一些相同的部分,可以进行代换。
第四届华罗庚金杯少年数学邀请赛-初中一年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷

第四届华罗庚金杯少年数学邀请赛-初中一年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载---------------------------------------第四届“华罗庚金杯”少年数学邀请赛初赛试题复赛试题决赛第一试决赛第二试团体决赛口试初赛(1)请将下面算式结果写成带分数:[分析] 这是每位小学生都会算的题目,但初赛要求在30秒内计算出正确的结果,就需要在平时锻炼快算的技巧。
注意0.5乘236之积为118,仅比分母小1。
抓住这个特点,算起来便很快了。
[注] 华罗庚爷爷在四十年代给他的孩子出了一道题:“全家九口人,每人每日食半两油,问全家一个月30天要食几斤油?”当时一斤等于16两。
快速心算的思路是:每人一月食15两油,即一斤少一两。
全家九口人,一月食9斤少9两,即8斤7两。
列成算式是本题便是根据华爷爷的问题改编而成的。
(2)一块木板上有13枚钉子(右图)。
用橡皮筋套住其中的几枚钉子,可以构成三角形,正方形,梯形,等等(下图)。
请回答:可以构成多少个正方形?[答案]共11个。
[分析]可以构成的正方形有好几种,大小和位置不一样。
要想无一遗漏地数出全部正方形,最好用分类法。
[解]依正方形的面积分类,设最小的正方形面积为1。
面积为1的正方形,有5个(图a);面积为2的正方形,有4个(图b);面积为4的正方形,有1个(图c);还有1个面积比4大的正方形(图d)。
[讨论]本题也可以按其他特征来分类。
例如按正方形各边的方向的特征,如果各边是水平和竖直方向的,有6个(图a和图c);各边都是倾斜的有5个(图b和图d)。
用分类法的关键是抓住事物的特征,给列举的类排序。
既要穷尽所有的可能性,以避免遗漏,又要注意每二类之间是否有共同的部分,如果有,则需要加以排除。
(3)这里有一个圆柱和一个圆锥(下图),它们的高和底面直径都标在图上,单位是厘米。
请回答:圆锥体积与面积的比是多少?[分析]这是一道普通的体积计算题。
第三届华杯赛全套试题

第三届华罗庚金杯赛少年数学邀请赛初赛试题(小学组)1.光的速度是每秒30万千米,太阳离地球1亿5千万千米.问:光从太阳到地球要用几分钟(得数保留一位小数)? 2.计算?712631351301=⨯⎪⎭⎫⎝⎛++3.有3个箱子,如果两箱两箱地称它们的重量,分别是83千克、85千克和86千克.问:其中最轻的箱子重多少千克?4.请将算式100.010.01.0 ++的结果写成最简分数.5.(如右图)将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.求这个物体的表面积(取π=3).6.一位少年短跑选手,顺风跑90米用了10秒钟.在同样的风速下,逆风跑70米,也用了10秒钟.问:在无风的时候,他跑100米要用多少秒?7.一个矩形分成4个不同的三角形(如右图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?8.有一对紧贴的传动胶轮,每个轮子上都画有一条通过轴心的标志线(如下图).主动轮的半径是105 厘米,从动轮的半径是90厘米.开始转动时,两个轮子上的标志线在一条直线上.问:主动轮至少转了几转后,两轮的标志线又在一条直线上?9.小明参加了四次语文测验,平均成绩是68分.他想在下一次语文测验后,将五次的平均成绩提高到70分以上,那么,在下次测验中,他至少要得多少分?10.如下图中共有7层小三角形,求白色小三角形的个数与黑色小三角形的个数之比.11.下面的算式里,每个方框代表一个数字.问:这6个方框中的数字的总和是多少?12.在所有的两位数中,十位数字比个位数字大的两位数有多少个?13.有甲、乙两个同样的杯子,甲杯中有半杯清水,乙杯中盛满了含50%酒精的溶液.先将乙杯中酒精溶液的一半倒入甲杯,搅匀后,再将甲杯中酒精溶液的一半倒入乙杯.问这时乙杯中的酒精是溶液的几分之几?14.射箭运动的箭靶是由10个同心圆组成,两个相邻的同心圆半径之差等于最里面的小圆半径.最里面的小圆叫做10环(如右图所示),最外面的圆环叫做1环.问:10环的面积是1环面积的几分之几?15.王师傅在某个特殊岗位上工作、他每上8天班后,就连续休息2天.如果这个星期六和星期天他休息,那么,至少再过几个星期后他才能又在星期天休息?第三届华罗庚金杯赛少年数学邀请复赛赛试题(小学组)1.计算:9819375.4121314532852÷⎪⎭⎫⎝⎛+⨯-2.某年的10月里有5个星期六,4个星期日.问:这年的10月1日是星期几?3. 电子跳蚤每跳一步,可从一个圆圈跳到相邻的圆圈.现在,一只红跳蚤从标有数字“0”的圆圈按顺时针方向跳了1991步,落在一个圆圈里.一只黑跳蚤也从标 有数字“0”的圆圈起跳,但它是沿着逆时针方向跳了1949步,落在另一个圆圈里.问:这两个圆圈里数字的乘积是多少?4.173□是个四位数字.数学老师说:“我在这个□中先后填入3个数字,所得到的3个四位数,依次可被9、11、6整除.”问:数学老师先后填入的3个数字的和是多少?5.我们知道:339⨯=,4416⨯=,这里,9、16叫做“完全平方数”,在前300个自然数中,去掉所有的“完全平方数”,剩下的自然数的和是多少?6.如图,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?7.在射箭运动中,每射一箭得到的环数或者是“0”(脱靶),或者是不超过10的自然数.甲、乙两名运动员各射了5箭,每人5箭得到的环数的积都是1764,但是甲的总环数比乙少4环.求甲、乙的总环数.8.下图中有6个点,9条线段.一只甲虫从A 点出发,要沿着某几条线段爬到F 点.行进中,同一个点或同一条线段只能经过1次.这只甲虫最多有多少种不同的走法?9.下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?10.已知:199111982119811198011++++=S ,求:S 的整数部分.11.今年,祖父的年龄是小明的年龄的6倍.几年后,祖父的年龄将是小明的年龄的5倍.又过几年以后,祖父的年龄将是小明的年龄的4倍.求:祖父今年是多少岁?12.某个班的全体学生进行了短跑、游泳、篮球三个项目的测试,有4名学生在这三个项目上都没有达到优秀,其余每人至少有一个项目达到优秀,这部分学生达到优秀的项目、人数如下表: 求这个班的学生数.13.恰好能被6、7、8、9整除的五位数有多少个?14.计算:200119991197531+--+-+-15.五环图由内圆直径为8,外圆直径为10的五个圆环组成,其中两两相交的小曲边四边形(阴影部分)的面积都相等.已知五个圆环盖住的总面积是112.5,求每个小曲边四边形的面积(圆周率π取3.14).16.下图中8个顶点处标注的数字:a 、b 、c 、d 、e 、f 、g 、h ,其中的每一个数都等于相邻三个顶点处数的和的31,求:()()h g f e d c b a +++-+++的值.第三届华罗庚金杯赛少年数学邀请赛决赛一试试题(小学组)1.计算:99163135115131++++2.说明:360这个数的约数有多少个?这些约数的和是多少?3.观察下面数表(横排为行):根据前5行数所表达的规律,说明19491991这个数位于由上而下的第几行?在这一行中,它位于由左向右的第几个?4.将一个圆形纸片用直线划分成大小不限的若干小纸片,如果要分成不少于50个小纸片,至少要画多少条直线?请说明.5.某校和某工厂之间有一条公路,该校下午2点钟派车去该厂接某劳模来校作报告,往返需用1小时.这位劳模在下午1点钟便离厂步行向学校走来,途中遇到接他的汽车,更立刻上车驶向学校,在下午2点40分到达.问:汽车速度是劳模步行速度的几倍?6.在一个圆周上放了1枚黑色的和1990枚白色的围棋子(如右图).一个同学进行这样的操作:从黑子开始,按顺时针方向,每隔一枚,取走一枚.当他取到黑子时,圆周上还剩下多少枚白子?第三届华罗庚金杯赛少年数学邀请赛二试试题(小学组)1.写出从360到630的自然数中有奇数个约数的数.2,四边形ABCD被AC和DB分成甲,乙,丙,丁4个三角形(如右图).已知:BE=80cm.CE=60cm,DE=40cm,AE=30cm.问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?3.已知:,问:a除以13所得余数是几?4.某班在一次数学考试中,平均成绩是78分,男、女生各自的平均成绩是75.5分、81分.问:这个班男、女生人数的比是多少?5.某玩具厂生产大小一样的正方体形状的积木,每个面分别涂上红、黄、蓝3种颜色中的1种,每色各涂2个面.当两个积木经过适当的翻动以后,能使各种颜色的面所在位置相同时,它们就被看作是同一种积木块.试说明:最多能涂成多少种不同的积木块?6.一条双向铁路上有11个车站,相邻两站都相距7千米.从早晨7点开始,有18列货车由第十一站顺次发出,每隔5分钟发出一列,都驶向第一站,速度都是每小时60千米.早晨8点,由第一站发出一列客车,向第十一站驶去,时速是100千米.在到达终点站前,货车与客车都不停靠任何一站.问:在哪两个相邻站之间,客车能与3列货车先后相遇?11。
一个整数的约数个数和约数和的计算方法

【內容概困一个整数的约数个数与约数和的讣算方法,两数的最大公约数与最小公倍数之间的关系,分数的最小公倍数•涉及一个整数的约数,以及若干整数最大公约数与最小公倍数的问题,其中质因数分解发挥着重要作用.f典型问题】第三届“华罗庚金杯”少年数学邀请赛•决赛一试第2题1.数360的约数有多少个?这些约数的和是多少?【分析与解】360分解质因数:360二2X2X2X3X3X5二2'X3'X5:360的约数可以且只能是2a X3b X5c,(其中a, b, c均是整数,且a为0〜3, 6为0〜2, c 为0-1).因为a、b、c的取值是相互独立的,由讣数问题的乘法原理知,约数的个数为(3+1) X (2+1)X(1+1)二24.我们先只改动关于质因数3的约数,可以是1, 3, 3‘,它们的和为(1+3+3=),所以所有360约数的和为(1+3+3') X2y X5w:我们再来确定关于质因数2的约数,可以是1, 2, 23,21它们的和为(1+2+23+29),所以所有360 约数的和为(1+3+3:) X (1+2+2:+25)X5W;最后确泄关于质因数5的约数,可以是1, 5,它们的和为(1+5),所以所有360的约数的和为(1+3+3') X (1+2+2=+28) X (1+5).于是,我们计算出{&:13X15X6=U70.所以,360所有约数的和为1170.评注:我们在本题中分析了约数个数、约数和的求法•下而我们给出一般结论:I•一个合数的约数的个数是在严格分解质因数之后,将每个质因数的指数(次数)加1后所得的乘积.如:1400严格分解质因数后为23X5:X7,所以它的约数有(3+1) X (2+1) X (1+1) =4X3X2=24 个.(包括1 和它自身)II.约数的和是在严格分解质因数后,将M的每个质因数最髙次幕的所有约数的和相乘所得到的积.如:21000二2'X3X5'X7,所以21000所有约数的和为(1+2+2=+23) X (1+3) X (1+5+55+53) X (1+7)=74880.匕T华罗庚金杯”少年数学邀请赛•决赛一试第6題豆克第二届“兴趣杯”少年数学邀请赛•预赛C 卷第4题2.一个数是5个2, 3个3, 6个5,1个7的连乘积•这个数有许多约数是两位数,那么在这些两位数的约数中,最大的是多少?【分析与解】设这个数为扎有A=25X 33X 56X 7, 99=3X 3X 11, 98=2 X 7X 7, 97均不是A 的约数,而96=25X3为A的约数,所以96为其最大的两位数约数.臺三届“华罗庚金杯”少年教学邀请赛•决赛二试第1题3.写出从360到630的自然数中有奇数个约数的数.【分析与解】一个合数的约数的个数是在严格分解质因数之后,将每个质因数的指数(次数) 加1后所得的乘积.如:1400严格分解质因数后为25X5:X7,所以它的约数有(3+1) X (2+1) X (1+1)二4X3X2二24个.(包括1和它自身)如果某个自然数有奇数个约数,那么这个数的所有质因子的个数均为偶数个•这样它们加1 后均是奇数,所得的乘枳才能是奇数.而所有质因数的个数均是偶数个的数为完全平方数.即完全平方数(除0外)有奇数个约数,反过来,有奇数个约数的数一定是完全平方数.由以上分析知,我们所求的为360〜630之间有多少个完全平方数?18 X 18=324,19 X19二361, 25 X 25=625, 26 X26=676,所以在360〜630 之间的完全平方数为19:, 20:, 211 22”, 23:, 24:, 25=.即360到630的自然数中有奇数个约数的数为361, 400, 441, 484, 529, 576, 625.觀㈱级数:冲北京市第二届“迎春杯”数学竟賽•决赛第一題第2题4.今有语文课本42册,数学课本112册,自然课本70册,平均分成若干堆,每堆中这3种课本的数量分别相等.那么最多可分多少堆?【分析与解】显然堆数是42的约数,是112的约数,是70的约数.即为42,112, 70的公约数,有(42,112, 70)=14.所以,最多可以分成14堆.觀越)级数:車;5.加工某种机器零件,要经过三道工序,第一道工序每名工人每小时可完成6个零件,第二道工序每名工人每小时可完成10个零件,第三道工序每名工人每小时可完成15个零件.要使加工生产均衡,三道工序最少共需要多少名工人?【分析与解】为了使生产均衡,则每道工序每小时生产的零件个数应相等,设第一、二、三道工序上分别有A、B、C个工人,有6A=10B=15C=k,那么k的最小值为6,10, 15的最小公倍数,即[6, 10, 15]二30.所以A二5, B二3, 02,则三道工序最少共需要5+3+2二10名工人.画级数:* * *6.有甲、乙、丙3人,甲每分钟行走120米,乙每分钟行走100米,丙每分钟行走70米.如果3个人同时同向,从同地出发,沿周长是300米的圆形跑道行走,那么多少分钟之后,3人又可以相聚?【分析与解】设在x分钟后3人再次相聚,甲走了120x米,乙泄了100x米,丙走了70x米, 他们3人之间的路程差均是跑道长度的整数倍.即120x-100x, 120x-70x, 100x-70x 均是300 的倍数,那么300 就是20x, 50x, 30x 的公约数.有(20x, 50x, 30x) : 300,而(20x, 50x, 30x)二x(20, 50, 30) =10x,所以x二30.即在30分钟后,3人又可以相聚.7. 3条圆形跑道,圆心都在操场中的旗杆处,甲、乙、内3人分别在里圈、中圈、外圈沿同样 的方向跑步•开始时,3人都在旗杆的正东方向,里圈跑道长丄千米,中圈跑道长丄千米,外圈 5 43 1 跑道长二千米.甲每小时跑3—千米,乙每小时跑4千米,丙每小时跑5千米•问他们同时出发, 8 2几小时后,3人第一次同时回到出发点?【分析与解】 甲跑完一圈需= —小时,乙跑一圈需丄一4 =丄小时,丙跑一圈需 5 2 35 4 163 3 2 1 3 --5 = 一则他们同时回到出发点时都跑了整数圈,所以经历的时间为一,一,一的倍数,即 8 40 35 16 40它们的公倍数.所以,6小时后,3人第一次同时回到出发点.评注:求一组分数的眾小公倍数,先将这些分数化为最简分数,将分子的最小公倍数作为 新分数的分子,将分母的灵大公约数作为新分数的分母,这样得到的新分数即为所求的置小 公倍数:求一组分数的最大公约数,先将这些分数化为最简分数,將分子的最大公约数作为新分 数的分子,将分母的灵小公倍数作为新分数的分母,这样得到的新分数即为所求的最大公约 数.&甲数和乙数的最大公约数是6最小公倍数是90.如果甲数是1&那么乙数是多少? [分析与解]有两个数的最大公约数与最小公倍数的乘积等于这两数的乘积.有它们的最 大公约数与最小公倍数的乘积为6X90二540,则乙数为540宁18二30.9. A, B 两数都仅含有质因数3和5,它们的最大公约数是75.已知数A 有12个约数,数B 有 10个约数,那么A,B 两数的和等于多少?【分析与解】方法一:由题意知A 可以写成3X5:Xa, B 可以写成3X5*6,英中a 、b 为 整数且只含质因子3、5.即A:3"x X5=B=3'+mX5=其中x 、Y 、m 、n 均为自然数(可以为0)由 A 有 12 个约数,所以[(l+x)+ll X [(2+y)+l]=(2+x) X (3+y)=12,3^X5^=46875:Hl = 0 由 B 有 10个约数,所以[(l+m)+l] X[(2+n)+l] = (2+m) X (3+n) : 10,所以< •对应 B n = 2而2,丄,235 16 40 [2,1,3] _6 (35,16,4) "T级数:卓x = l.y =1 或< [y = 4 对应 A 为 3也X 5匚675, 3^X5岀二1125,或为3^X5^=1875.只有(675,1875)=75,所以A二675, B二1875.那么A, B两数的和为675+1875=2550.方法二:由题中条件知A、B中有一个数质因数中岀现了两次5,多于一次3,那么,先假设它出现了N次3,则约数有:(2+1) X (N+1): 3X (N+1)个12与10其中只有12是3的倍数,所以3(N+1)=12,易知N二3,这个数是A,即A=3a X5=675.那么B的质数中岀现了一次3,多于两次5,则出现了M次5,则有:(1+1) X (M+l)=2(M+l)=10, M=4. B=3X5S=1875.那么A, B两数的和为675+1875=2550.10.有两个自然数,它们的和等于297,它们的最大公约数与最小公倍数之和等于693.这两个自然数的差等于多少?【分析与解】设这两数为a, b,记a二(a, b)ql, b二(a, b)q2.它们的和为:a+b= (a, b) ql+(a, b) q2= (a, b) (ql+q2) =297 ................ ①它们的最大公约数与最小公倍数的和为:[a, b]+(a, b) = (a, b) qlq2+ (a, b) = (a, b) (qlq2+l)=693>且(ql,q2)二1. ...................................................................................................... ②综合①、②知Qb)是297, 693的公约数,而(297, 693)二99,所以Q,b)可以是99, 33,11,9, 3,1・第一种情况:(a, b)二99,则(ql+q2)=3, (qlq2+l)=7,即qlq2=6=2X3,无满足条件的ql, q2;第二种情况:(a, b)二33,则(ql+q2)=9, (qlq2+l)=21,即qlq2=20=23X5>则ql=5, q2=4 时满足,a= (a, b) ql=33 X 5=165, b= (a, b) q2=33 X 4=132,则a-b二165-132二33:第三种情况:(a, b)=ll,则(ql+q2)=27, (qlq2+l)=63,即qq2=62=2X31,无满足条件的ql, q2;一一验证第四种情况,第五种情况,第六种情况没有满足条件的Q1Q2.所以,这个两个自然数的差为33・go壌数:*卓**11.两个不同自然数的和是60,它们的最大公约数与最小公倍数的和也是60.问这样的自然数共有多少组?【分析与解】设这两数为a, b,记a= (a, b) ql, b= (a, b) q2.它们的和为:a+b= (a, b)ql+(a, b) q2= (a, b) (ql+q2) =60 ...................... ①它们的最大公约数与最小公倍数的和为:[a, b] + (a, b) = (a, b)qlq2+ (a, b) = (a, b) (qlq2+l)=60,且(ql,q2)=l .............................................................................................................. ②联立①、②有(ql+q2) = (qlq2+l),即ql+q2-qlq2=l, (ql-1) (l-q2)=0,所以ql二1 或q2二1・即说明一个数是另一个数的倍数,不妨记a二kb(k为非零整数),a+ b = kb + h = 60有J r . ,即(k + \)b = 60确泄,则k确定,则kb即3确定(a,b) + [a,b] = b + a=b + kb = ()O ' 760 的约数有 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 这 11 个,b 可以等于 2, 3, 4, 5, 6, 10. 12, 15, 20, 30这10个数,除了 60,因为如果6=60,则(k+l)=l,而k 为非零 整数.对应的a 、b 有10组可能的值,即这样的自然数有10组.进一步,列出有(a, b)为(58, 2), (57,3), (56,4), (55,5), (54,6), (50, 10), (48,12), (45,15), (40, 20), (30, 30).评注:如果两个自然数的和等于这两个数最大公约数与最小公倍数的和,那么这两个数 存在倍数关系.蹴國级数:車車I 塑芳全国/学数学奧林匹克•预赛A 卷第4题12. 3个连续的自然数的最小公倍数是982&那么这3个自然数的和等于多少?【分析与解】若三个连续的自然数中存在两个偶数,那么它们的最小公倍数为三个数乘积 的一半;若三个连续的自然数中只存在一个偶数,那么它们的最小公倍数为三个数的乘积.则当 a, a+1, a+2 中有 2 个偶数时,a(a+l) (a+2) =9828X2,当 a, a+1, a+2 中有 1 个偶数时,a(a+l) (a+2) =9828.对9828分解质因数:9828=2X2X3X3X3X7X13,我们注意,13是其最大的质因数,验 证不存在3个连续的自然数的积为9828.则这三个自然数的积只能是9828X2,此时这三个数中存在两个偶数,有 9828X2=2X2X2X3X3X3X7X13.13X2二26,有26,27, 28三个数的积为9828X2,所以这三个连续的自然数为26, 27, 2& 其中有两个偶数,满足题意.所以,这三个数的和为26+27+28二81.评注:我们知道两个连续的自然数互质,而两个互质的数的公倍数等于它们的积,即 [0, b]二aXb.记这3个连续的自然数为a, a+1, a+2.冇[a, a+1, a+2] = _a, a+1, a+1, a+2]二[[a, a+1], [a+1, a+2]]二[aX (a+1) , (a+1) X (a+2)] = (a+l) X [a, a+2].因为a, a+2同奇同偶,当a, a+2均是偶数时,a, a+2的最大公约数为2,则它们的最小公倍数为f 珂:一?); 2 当a, a+2均是奇数时,a, a+2互质,则它们的最小公倍数为aX (a+2)・卄小呼1汹偶数 a +1) x a x (a + 2)a 为奇数 即[a, a+1, a+2]为 a (a+1) (a+2)或川"+ ")("-2)2若三个连续的自然数中存在两个偶数,那么它们的最小公倍数为三个数乘积的一半:若 三个连续的自然数中只存在一个偶数,那么它们的最小公倍数为三个数的乘积.所以(a+1) X [a, a+2J = <觀越)级数:車車車1995年全国小学数学奧林匹克•决賽B卷第4题13•甲、乙两数的最小公倍数是90,乙、丙两数的最小公倍数是105,甲、丙两数的最小公倍数是126,那么甲数是多少?【分析与解】对90分解质因数:90二2X3X3X5.因为5r 126,所以5片甲,即甲中不含因数5,于是乙必含因数5.因为2丫105,所以2/乙,即乙中不含因数2,于是甲必含2X2.因为9丫105,所以9r乙,即乙最多含有一个因数3.第一种情况:当乙只含一个因数3时,乙=3X5=15,由[甲,乙]=90=2X3s X5,则甲二2X35=18:第一种情况| :当乙不含因数3时,乙二5,由[甲,乙]二90二2X3* 5,则甲二2X3T8,综上所需,甲为18.评注:两个数的最小公倍数含有两数的所有质因子,并且这些质因数的个数为两数中此质因数的最大值.如a=2X33X53X7, b=23 X 33 X 5 X 7X 11,则A、B 的最小公倍数含有质因子2, 3, 5, 7,11> 并且它们的个数为a、b中含有此质因子较多的那个数的个数.即依次含有3个,3个,2个,1 个,1 个,即[a,b]=2"X3d X52X7Xll.觀娥)级数:*車*14. a>b>c是3个整数.a, b, c的最大公约数是15; a, b的最大公约数是75:a, b的最小公倍数是450; b, c的最小公倍数是1050.那么c是多少?【分析与解】由(a, b) =75=3 X 52, [a, b] =450=32X 2 X 52=75X 3 X 2,又a > b 所以a = 450 r或[b = 75(a = 225 r n,[b, c]二1050二2X3X5-X7.b = 15O最小公倍数的乘积等于这两个数的乘积,所以(75, c ) X [75, c]二75X (2=15X1050,得 c=210,但是c>b,不满足;条件的为一解. 那么c 是105.艇:级数:*拿車W 灼生舍国小学数学奥林匹克初赛•第18題 15.有4个不同的自然数,它们的和是1111,它们的最大公约数最大能是多少?【分析与解】 设这4个不同的自然数为A 、B 、C 、D,有A+B+C+D 二1111.将1111分解质因数:1111二11X101,显然A 、B 、C 、D 的最大公约数最大可能为101,记此时A=101a> B=101b, C 二 101c, D=101d,有 a+b+c+d=ll,当 a+b+c+d=l+2+3+5 时满足,即这 4 个数的 公约数可以取到101.综上所述,这4个不同的自然数,它们的最大公约数最大能是101.评注:我们把此题稍做改动:“有5个不同的自然数,它们的和是1111,它们的最大公约数最 大能是多少? 大家不妨自己试试.「“ = 450方=75 时有 (450,75,c) =(75,c) = 15 = [75,c] = 1050 因为两个数的最大公约数与a = 225b = 150时有< (225,150,c) = (75,c) = 15 [»c] = [150,c] = 1050(a = 225 ,则c=105, c < b,满足,即* = 150为满足 c = I05。
2011、2012年华罗庚金杯少年数学邀请赛决赛真题及详解

2011、2012年华罗庚金杯少年数学邀请赛决赛真题及详解第十六届华罗庚金杯少年数学邀请赛 决赛试题A (小学组) (时间: 2011年4月16日10:00~11:30) 一、填空题(每小题 10分, 共80分) 1. 135713572468+++= . 2. 工程队的8个人用30天完成了某项工程的31, 接着增加了4个人完成其余的工程, 那么完成这项工程共用了 天. 3. 甲乙两人骑自行车同时从A 地出发去B 地, 甲的车速是乙的车速的1.2倍. 乙骑了5千米后, 自行车出现故障, 耽误的时间可以骑全程的61. 排除故障后, 乙的速度提高了60%, 结果甲乙同时到达B 地. 那么A, B 两地之间的距离为 千米. 4. 在火车站的钟楼上装有一个电子报时钟, 在圆形钟面的边界, 每分钟的刻度处都有一个小彩灯. 晚上9时35分20秒时, 在分针与时针所夹的锐角内有 个小彩灯. 5. 在边长为1厘米的正方形ABCD 中, 分别以A , B , C , D 为圆心, 1厘米为半径画四分之一圆, 交点E , F , G , H , 如图所示. 则中间阴影部分的周长为 厘米.(取圆周率 3.141π=) 6. 用40元钱购买单价分别为2元、5元和11元的三种练习本, 每种至少买一本, 而且钱恰好花完. 则不同的购买方法有 种.7. 已知某个几何体的三视图如右图,根据图中标示的尺寸(单位: 厘米),这个几何体的体积是 (立方厘米).学校____________姓名_________参赛证号密封线内请勿答题8. 将自然数1~22分别填在下面的“□”内(每个“□”只能填一个数), 在形成的11个分数中, 分数值为整数的最多能有 个.二、解答下列各题(每题10分, 共40分, 要求写出简要过程)9. 长方形ABCD 的面积是2011平方厘米. 梯形AFGE的顶点F 在BC 上, D 是腰EG 的中点. 试求梯形AFGE 的面积.10. 公交车的线路号是由数字显示器显示的三位数,其中每个数字是由横竖放置的七支荧光管显示,如右图所示. 某公交车的数字显示器有两支坏了的荧光管不亮, 显示的线路号为“351”, 则该公交车的线路号有哪些可能?11. 设某年中有一个月里有三个星期日的日期为奇数, 则这个月的20日可能是星期几?12. 以[]x 表示不超过x 的最大整数, 设自然数n 满足201115151153152151>⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡n n , 则n 的最小值是多少?三、解答下列各题(每小题 15分,共30分,要求写出详细过程)13. 在右面的加法竖式中, 不同的汉字代表不同的数字. 问: 满足要求的不同算式共有多少种?14. 如图, 两只蜘蛛同处在一个正方体的顶点A , 而一只爬虫处在A 的体对顶点G . 假设蜘蛛和爬虫均以同样的速度沿正方体的棱移动, 任何时候它们都知道彼此的位置, 蜘蛛能预判爬虫的爬行方向. 试给出一个两只蜘蛛必定捉住爬虫的方案.2011年“华杯赛”复赛小学组试题及详解第16届华杯赛复赛小学组试题及详解1. 原式=(2+4+6+8)-(1/2+1/4+1/6+1/8)=20-(1+1/24)=18+23/24。
1987年第二届华罗庚金杯少年数学邀请赛初赛试题(小学组)及答案
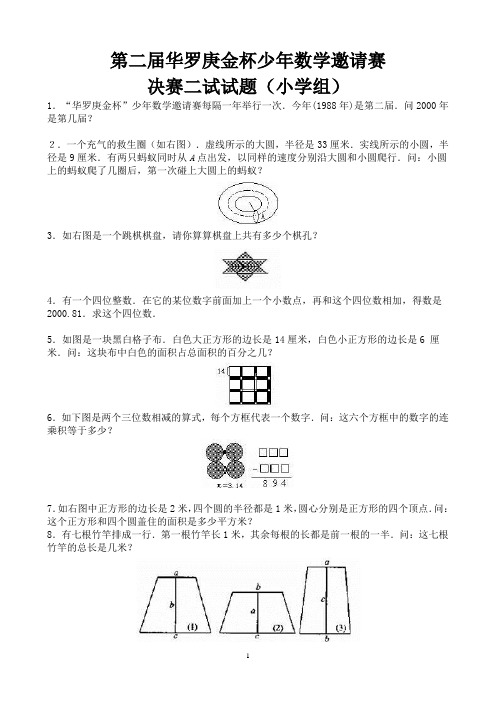
第二届华罗庚金杯少年数学邀请赛决赛二试试题(小学组)1.“华罗庚金杯”少年数学邀请赛每隔一年举行一次.今年(1988年)是第二届.问2000年是第几届?2.一个充气的救生圈(如右图).虚线所示的大圆,半径是33厘米.实线所示的小圆,半径是9厘米.有两只蚂蚁同时从A点出发,以同样的速度分别沿大圆和小圆爬行.问:小圆上的蚂蚁爬了几圈后,第一次碰上大圆上的蚂蚁?3.如右图是一个跳棋棋盘,请你算算棋盘上共有多少个棋孔?4.有一个四位整数.在它的某位数字前面加上一个小数点,再和这个四位数相加,得数是2000.81.求这个四位数.5.如图是一块黑白格子布.白色大正方形的边长是14厘米,白色小正方形的边长是6 厘米.问:这块布中白色的面积占总面积的百分之几?6.如下图是两个三位数相减的算式,每个方框代表一个数字.问:这六个方框中的数字的连乘积等于多少?7.如右图中正方形的边长是2米,四个圆的半径都是1米,圆心分别是正方形的四个顶点.问:这个正方形和四个圆盖住的面积是多少平方米?8.有七根竹竿排成一行.第一根竹竿长1米,其余每根的长都是前一根的一半.问:这七根竹竿的总长是几米?9.有三条线段A、B、C,a长2.12米,b长2.71米,c长3.53米,以它们作为上底、下底和高,可以作出三个不同的梯形.问:第几个梯形的面积最大(如下图)?10.有一个电子钟,每走9分钟亮一次灯,每到整点响一次铃.中午12点整,电子钟响铃又亮灯.问:下一次既响铃又亮灯是几点钟?11.一副扑克牌有四种花色,每种花色有13张,从中任意抽牌.问:最少要抽多少张牌,才能保证有4张牌是同一花色?12.有一个班的同学去划船.他们算了一下,如果增加一条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人.问:这个班共有多少同学?13.四个小动物换座位.一开始,小鼠坐在第1号位子,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子.第一次上下两排交换.第二次是在第一次交换后再左右两排交换.第三次再上下两排交换.第四次再左右两排交换……这样一直换下去.问:第十次交换位子后,小兔坐在第几号位子上?(参看下图)14.用1、9、8、8这四个数字能排成几个被11除余8的四位数?15.如下图是一个围棋盘,它由横竖各19条线组成.问:围棋盘上有多少个右图中的小正方形一样的正方形?参考答案1.第八届2.11 3.121 4.1981 5.58% 6.0 7.13.42 8.9.第三个10.3点钟11.13 12.36人13.第十次交换座位后,小兔坐在第2号位子14.能排成4个被11除余8的数15.100个1.【解】“每隔一年举行一次”的意思是每两年举行1次。
中考 初中竞赛项目

数学竞赛一、“华罗庚金杯”少年数学邀请赛“华杯赛”是由广东省惠州市人民政府、中国少年儿童新闻出版总社、中国优选法统筹法与经济数学研究会、中国教育学会、中央电视台青少中心、华罗庚实验室、中国教师报等单位联合主办的。
赛制为每年一届,每两年举办一次总决赛。
二、“希望杯”全国数学邀请赛“希望杯”全国数学邀请赛已经成为中学生中规模最大、影响最广的学科课外活动之一。
据介绍,该竞赛活动分两试进行。
第一试(每年三月进行)以各地 (省、市、县、〔区〕、学校)为单位组织参赛学生,在全国各参赛学校同时进行,各测试点按命题委员会下发的评分标准进行阅卷、评分,从中按七分之一的比例按成绩择优选拔参加第二试的选手。
第二试(每年四月进行)由当地《数理天地》编委分会或地、市级教研室或教育学院、教科所、教师进修学校统一组织,测试结束后,各测试点将试卷密封,向组委会挂号寄出,由命题委员会阅卷,从中按八分之一的比例按成绩评定一、二、三等奖,分别授予金、银、铜奖牌及获奖证书。
对组织工作做得出色的地区或学校,组委会颁发“希望杯”数学邀请赛组织奖。
三、全国初中数学联赛全国初中数学联赛每年4月举行,分为一试和二试。
成绩公布的时间各省市不尽相同,北京市公布时间大约在五月底至六月。
第一试着重基础知识和基本技能,题型为选择题6题、填空题4题,共70分。
第二试着重分析问题和解决问题的能力,题型为三道解答题,内容分为代数题、几何题、几何代数综合题或杂题,共70 分,两试合计共140分。
全国初中数学联合竞赛的意义:“全国初中数学联赛”是初中生初中阶段最为重要的竞赛之一,方式较为规范,也是许多高中入学考察的对象之一,因此,许多初中生为此而加紧培优,从某种意义上讲,这种为大众认可的竞赛提升了中国初中生的整体数学成绩。
在北京,全国数学联赛的获奖成绩常常被作为人大附中、四中等重点高中提前录取的一个重要参考。
四、迎春杯数学竞赛(北京)五、.数理化联赛,初三才有六、走美杯七、北京市中学生初二年级数学竞赛初中英语竞赛1、北京市中小学生“我能行”素质技能大赛海淀区选拔赛英语口语比赛2、新少年杯中小学生现场英语作文竞赛3、全国中学生英语能力竞赛11月16日4. 初中科普英语竞赛5、通讯杯中小学生英语听力竞赛12月7日6、希望之星全国英语风采大奖赛北京市中小学生科技英语创意大赛北京青少年科技创新大赛是一项大型的具有示范意义的科技活动,其根本宗旨在于推动青少年科技活动的蓬勃开展,培养青少年的创新精神和实践能力,提高青少年的科技素质,鼓励优秀人才的涌现。
第三届“华罗庚金杯”少年数学邀请赛(全套) 新人教版

第三届“华罗庚金杯”少年数学邀请赛初赛部分复赛部分决赛第一试决赛第二试团体决赛口试初赛试题与解答(1)光的速度是每秒30万千米,太阳离地球1亿5千万千米。
问:光从太阳到地球要用几分钟(得数保留一位小数)?[分析]知道距离和速度,求通过全程的时间,这是很容易做的一道题。
但是因为给出的数字很大,同学们在大数算术运算时一定要注意计量单位,不然便会出错。
[解法1] 将距离单位换为“万千米”,时间单位用“分”。
光速=30万千米/秒=1800万千米/分,距离=1亿5千万千米=15000万千米,时间=距离÷速度=15000÷1800[解法2]如果时间单位用“秒”,最后必须按题目要求换算为“分”.光速=30万千米/秒,距离=15000万千米,时间=15000÷30=500(秒),答:光从太阳到地球约需8.3分钟。
(2)计算[分析]这是一道很简单的分数四则运算题,但要在30秒钟内算出正确答案,需要平时养成简捷的思维习惯。
同学们可以比较一下后面的两种解法。
[解法1] 先求出30,35,63的最小公倍数。
30=2×3×5;35=5×7;63=3×3×7;所以公倍数是2×3×3×5×7=630。
原式通分,有〔解法2〕[注] 两种解法同样都用到通分和约分的技巧,只有一点小区别:解法2在通分时不急于把公分母算出来,而是边算边约分。
这一点小小的不同,却节省了求连乘积的运算,约分也简单些,使计算快了不少哩!(3)有3个箱子,如果两箱两箱地称它们的重量,分别是83公斤、85公斤和86公斤。
问:其中最轻的箱子重多少公斤?[分析]如果将3个箱子按重量区分为大、中、小,在草稿纸上可以这样写:83=中+小,85=大+小,86=大+中.这样分析后,便很容易想到简单的解法。
[解法1](83+85+86)是3箱重量之和的2倍,所以小箱重量是[解法2] (83+85)=中+大+2×小,所以小箱重量=(83+85-86)×答:最轻的箱子重41公斤。
2011-2016年第16-22届华罗庚杯少年数学邀请赛几何试题(小学高年级组)全解析

B
2011年第16届华罗庚杯少年数学邀请赛决赛C几何试题 长方形ABCD的面积为70,梯形AFGE的顶点F在BC上,D是EG的中点,则梯形AFGE的 的面积是()。
E A D
G
B
F
C
长方形ABCD的面积为70,梯形AFGE的顶点F在BC上,D是EG的中点,则梯形AFGE的 的面积是()。 解1:连接DF, E A D S△ADF= G
������ ������
利用蝴蝶模型,在梯形AFGE中, S□ AFGE
利用蝴蝶模型,在长方形ABCD中, S△ADF=
������ ������
S□ ABCD
B
F
C
故: S□ AFGE= S□ ABCD=70
长方形ABCD的面积为70,梯形AFGE的顶点F在BC上,D是EG的中点,则梯形AFGE的 的面积是()。
一个长40、宽25、高60的无盖长方体容器(厚度忽略不计)盛有水,深度为a,其中0 ˂a ≤60,现将棱长尾10的长方体铁块放在容器底面,问放入铁块后水深是()。
1
2
3
分析:无盖长方体容器盛有水情况有三种: 1、水很满;放入铁块后,水溢出; 2、水深很浅,放入铁块后,铁块一部分在水中,另一部分露出水面,水面也有升高。
A
由三角形AFC的面积和四边形DBEF的面积相等,得: S△AEC=S△BCD,则:������������ × ������������ = ������������ × ������������ 由于BD:AB=DM:AN=1:3,则:EC:BC=1:3
E
A
O C D
B
如图所示,AB∥CE,AC ∥ DE,且AB=AC=5,CE=DE=10。若
华罗庚金杯赛数学试题与答案[第1至15届]
![华罗庚金杯赛数学试题与答案[第1至15届]](https://img.taocdn.com/s3/m/be6d1522bb68a98271fefabf.png)
华罗庚金杯赛数学试题与答案[第1至15届]目录第1届华罗庚金杯赛数学试题与答案 (1)第2届华罗庚金杯赛数学试题与答案 (6)第3届华罗庚金杯赛数学试题与答案 (14)第4届华罗庚金杯赛数学试题与答案 (21)第5届华罗庚金杯赛数学试题与答案 (26)第6届华罗庚金杯赛数学试题与答案 (31)第7届华杯赛初赛试题及解答 (38)第8届华杯赛初赛试题及解答 (41)第9届华杯赛初赛试题及解答 (45)第10届华杯赛初赛试题及解答 (49)第11届华杯赛初赛试题及解答 (53)第12届华杯赛初赛试题及解答 (60)第13届华杯赛少年邀请赛初赛摸拟试卷 (64)第14届华罗庚金杯少年数学邀请赛 (66)第15届华杯赛决赛真题及答案解析 (68)第1届华罗庚金杯赛数学试题与答案1、甲班和乙班共83人,乙班和丙班共86人,丙班和丁班共88人。
问甲班和丁班共多少人?2、一笔奖金分一等奖、二等奖、三等奖,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍。
如果评一、二、三等奖各两人,那么每个一等奖的奖金是308元;如果一个一等奖,两个二等奖,三个三等奖,那么一等奖的奖金是多少元?3、一个长方形,被两条直线分成四个长方形,其中三个的面积是20亩、25亩和30亩。
问另一个长方形的面积是多少亩?4、在一条公路上,每隔一百公里有一个仓库,共有五个仓库。
一号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。
现在想把所有的货物集中存放在一个仓库里,如果每吨货物运输一公里需要0.5元的运费,那么最少要花多少运费才行?5、有一个数,除以3余数是2,除以4余数是1。
问这个数除以12余数是几?6、四个一样的长方形和一个小的正方形(如图)拼成了一个大正方形。
大正方形的面积是49平方米,小正方形的面积是4平方米。
问长方形的短边长度是几米?7、有两条纸带,一条长21厘米,一条长13厘米,把两条纸带剪下同样长的一段以后,发现短纸带剩下的长度是长纸带的长度的八分之十三。
华杯赛1-15届的真题和答案

=11111111110000000000-1111111111=111111111088888888889 于是有 10 个数字是奇数。 12.【解】10 根筷子,可能 8 根黑,1 根白,1 根黄,其中没有颜色不同的两双筷子。 如果取 11 根,那么由于 11>3,其中必有两根同色组成一双,不妨设这一双是黑色的,去掉 这两根,余下 9 根,其中黑色的至多 6(=8-2)根,因而白、黄两色的筷子至少有 3(=9-6) 根,3 根中必有 2 根同色组成一双。这样就得到颜色不同的两双筷子。所以至少要取 11 根。 13.【解】菜地的 3 倍和麦地的 2 倍是 13× 6 公顷。菜地的 2 倍和麦地的 3 倍是 12× 6 公顷, 因此菜地与麦地共:(13× 6+12× 6)÷ (3+2)=30(公顷), 菜地是 13× 6-30× 2=18(公顷)。 14. 【解】71427 被 7 除,余数是 6,19 被 7 除,余数是 5,所以 71427× 19 被 7 除,余数就 是 6× 5 被 7 除所得的余数 2。 15.【解】从第一次记录到第十二次记录,相隔十一次,共 5× 11=55(小时)。时针转一圈是 12 小时,55 除以 12 余数是 7,9-7=2 答:时针指向 2。 16.【解】因为电车每隔 5 分钟发出一辆,15 分钟走完全程。骑车人在乙站看到的电车是 15 分钟以前发出的,可以推算出,他从乙站出发的时候,第四辆电车正从甲站出发骑车人从乙 站到甲站的这段时间里,甲站发出的电车是从第 4 辆到第 12 辆。电车共发出 9 辆,共有 8 个 间隔。于是:5× 8=40(分) 。 17.【解】小数点后第 7 位应尽可能大,因此应将圈点点在 8 上,新的循环小数是 。
18.【解】三个背包分别装 8.5 千克、6 千克与 4 千克,4 千克、3 千克与 2 千克,这时最重 的背包装了 lO 千克。 另一方面最重的包放重量不少于 10 千克:8.5 千克必须单放(否则这一包的重量超过 10)6 千 克如果与 2 千克放在一起, 剩下的重量超过 10, 如果与 3 千克放在一起, 剩下的重量等于 10。 所以最重的背包装 10 千克。 19.【解】从第一排与第二排看,五个小纸片的长等于三个小纸片的长加三个小纸片的宽, 也就是说,二个小纸片的长等于三个小纸片的宽。 已知小纸片的宽是 12 厘米,于是小纸片的长是:12× 3÷ 2=18(厘米), 阴影部分是三个正方形,边长正好是小纸片的长与宽的差:18-12=6 于是,阴影部分的面积是:6× 6× 3=108(平方厘米)。
第11~14届全国华罗庚金杯少年数学邀请赛决赛试题

第十一届全国"华罗庚金杯"少年数学邀请赛决赛试题一、填空。
1.计算:2.图1a是一个长方形,其中阴影部分由一副面积为1的七巧板拼成(如图1b),那么这个长方形的面积是()。
3.有甲、乙、丙、丁四支球队参加的足球循环赛,每两队都要赛一场,胜者得3分,负者得0分,如果踢平,两队各得1分。
现在甲、乙和丙分别得7分、1分和6分,已知甲和乙踢平,那么丁得()分。
4.图2中,小黑格表示网络的结点,结点之间的连线表示它们有网线相联。
连线标注的数字表示该段网线单位时间内可以通过的最大信息量。
现在从结点A向结点B传递信息,那么单位时间内传递的最大信息量是()。
5.先写出一个两位数62,接着在62右端写这两个数字的和为8,得到628,再写末两位数字2和8的和10,得到62810,用上述方法得到一个有2006位的整数:628101123……,则这个整数的数字之和是()。
6.智慧老人到小明的年级访问,小明说他们年级共一百多同学。
老人请同学们按三人一行排队,结果多出一人,按五人一行排队,结果多出二人,按七人一行排队,结果多出一人,老人说我知道你们年级的人数应该是()人。
7.如图3所示,点B是线段AD的中点,由A,B,C,D四个点所构成的所有线段的长度均为整数,若这些线段的长度之和为10500,则线段AB的长度是()。
8.100个非0自然数的和等于2006,那么它们的最大公约数最大可能值是()。
二、解答下列各题,要求写出简要过程。
(每题10分,共40分)9.如图4,圆O中直径Ab与CD互相垂直,AB=10厘米。
以C为圆心,CA为半径画弧AEB。
求月牙形ADBEA(阴影部分)的面积?10.甲、乙和丙三只蚂蚁爬行的速度之比是8:6:5,它们沿一个圆圈从同一点同时同向爬行,当它们首次同时回到出发点时,就结束爬行。
问蚂蚁甲追上蚂蚁乙一共多少次?(包括结束时刻)。
11.如图5,ABCD是矩形,BC=6cm,AB=10cm,AC和BD是对角线。
初一数学历年“华罗庚杯”竞赛试题

初一数学试题集
初一数学
历年“华罗庚杯”竞赛试题
(由我爱我家整理)
二〇〇九年九月十六日
第一届全国“华罗庚金杯”少年数学邀请赛决赛一试试题(初一组)
[初一组]第一届“华杯赛”数学第2试答案
第二届全国“华罗庚金杯”少年数学邀请赛决赛一试试题(初一组)
第二届全国“华罗庚金杯”少年数学邀请赛决赛一试试题参考答案(初一组)
第二届全国“华罗庚金杯”少年数学邀请赛决赛二试试题(初一组)
第二届全国“华罗庚金杯”少年数学邀请赛决赛二试试题参考答案(初一组)
第三届全国“华罗庚金杯”少年数学邀请赛决赛一试试题参考答案(初一组)
[初一组]第三届“华杯赛”数学第1试答案
第三届全国“华罗庚金杯”少年数学邀请赛决赛二试试题(初一组)
第三届全国“华罗庚金杯”少年数学邀请赛决赛二试试题参考答案(初一组)
[初一组]第四届“华杯赛”数学第1试
第四届全国“华罗庚金杯”少年数学邀请赛决赛一试试题参考答案
第四届全国“华罗庚金杯”少年数学邀请赛决赛二试试题(初一组)
第四届全国“华罗庚金杯”少年数学邀请赛决赛二试试题参考答案(初一组)
第五届全国“华罗庚金杯”少年数学邀请赛决赛一试试题(初一组)
第五届全国“华罗庚金杯”少年数学邀请赛决赛一试试题参考答案(初一组)
[初一组]第五届“华杯赛”数学第2试
第五届全国“华罗庚金杯”少年数学邀请赛决赛二试试题参考答案(初一组)
[初一组]第六届“华杯赛”数学第1试答案
[初一组]第六届“华杯赛”数学第2试。
第10~16届全国华罗庚金杯少年数学邀请赛决赛试题详细解释答案

第十届全国"华罗庚金杯"少年数学邀请赛决赛试题一、填空(每题10分,共80分)1.下表中每一列为同一年在不同历法中的年号,请完成下表:第1小题:2.计算:① 18.3×0.25+5.3÷0.4-7.13 = ( ); ②= ( )。
答案:10.695;13.计算机中最小的存储单位称为“位”,每个“位”有两种状态:0和1。
一个字节由8个“位”组成,记为B。
常用KB,MB等记存储空间的大小,其中1KB=1024B, 1MB=1024KB。
现将240MB的教育软件从网上下载,已经下载了70%。
如果当前的下载速度为每秒72KB,则下载完毕还需要()分钟。
(精确到分钟)答案:174.a,b和c都是二位的自然数,a,b的个位分别是7与5,c的十位是1。
如果它们满足等式ab+c=2005,则a+b+c=( )。
答案:1025.一个正方体的每个顶点都有三条棱以其为端点,沿这三条棱的三个中点,从这个正方体切下一个角,这样一共切下八个角,则余下部分的体积(图1中的阴影部分)和正方体体积的比是()。
答案:6.某种长方体形的集装箱,它的长宽高的比是4∶3∶2,如果用甲等油漆喷涂它的表面,每平方米的费用是0.9元,如果改用乙等油漆,每平方米的费用降低为0.4元,一个集装箱可以节省6.5元,则集装箱总的表面积是()平方米,体积是()立方米。
答案:13:37.一列自然数0,1,2,3,…,2005,…,2004,第一个数是0,从第二个数开始,每一个都比它前一个大1,最后一个是2024。
现在将这列自然数排成以下数表:规定横排为行,竖排为列,则2005在数表中位于第()行和第()列。
答案:20;458.图2中,ABCD是长方形,E,F分别是AB,DA的中点,G是BF和DE的交点,四边形BCDG 的面积是40平方厘米,那么ABCD的面积是()平方厘米。
图2答案:60二、解答下列各题,要求写出简要过程(每题10分,共40分)9.图3是由风筝形和镖形两种不同的砖铺设而成。
小学生家长熟知的奥数四大杯赛

小学生家长熟知的奥数四大杯赛小学生家长熟知的奥数四大杯赛二年级开始就陆续的有各种可以参加的杯和赛了,三年级之后就更有扑面而来的感觉了。
被广大小学生家长熟知的奥数四大杯赛,简介如下:迎春杯数学解题能力大赛权威指数:五星迎春杯”是北京市的一项传统中小学赛事,开始于1984年,首届杯赛是由北京市教育局基础教育研究部主持,由北京市数学会协助,中小学数学教学报承办。
“迎春杯”数学竞赛对激发学生数学的兴起,发现优秀的数学特长生,推动北京中、小学数学教学改革等主面都起了很大的作用。
2001年,“迎春杯”数学竞赛更名为“迎春杯数学科普日”。
2002年,“迎春杯”增加了团体奖项,并于2003年新增了参与奖,这些变化使得“迎春杯”的获奖面大大地提高了,2003年达到了90%,但是由于增加了团体奖项,使得“迎春杯”的获奖者水平出现了参差不齐的局面。
(迎春杯现在已经更名为数学解题能力展示) 参赛对象:1、小学中年级(三、)学生。
2、小学高年级(五、六年级)的学生。
2009年大型数学赛事之一的"数学解题能力展示"(迎春杯)初赛已经于2008年12月6日进行。
初赛捷报传来,在整体30%的复赛入闱比例情况下,学而思学员以过半比例进入复赛的遥遥领先成绩证明了学而思培优教育的成功。
走进美妙数学花园竞赛权威指数:四星举办方:中国少年科学院;中国青少年发展服务中心;全国“青少年走进科学世界”科普活;动指导委员会办公室;走进美妙的数学花园”中国青少年数学论坛组委会。
参赛意义:按照国家教委提出的“以培养学生创新精神和实践能力”为核心的素质教育要求,通过开展“走进美妙数学花园”中国青少年数学论坛活动,使广大青少年在生动有趣的数学学习中感受到陈省身先生所说的“数学好玩”、“数学之美”和“数学是有用的”,使们自觉地成为数学的主人,实现从“学数学”到“用数学”过程的转变,从而进一步推动我国数学文化的`传播与普及。
“走美”始创于2003年(第一届没有笔试,仅仅是活动),现在已举行过5届,“走美”作为数学竞赛中的后起之秀,凭借其新颖的考试形式以及较高的竞赛难度取得了非常迅速的发展,近年来在重点中学选拔中引起了广泛的关注。
