2014高考汇编2

合集下载

高考语文常考成语分类汇编2

【成语】:涣然冰释【拼音】:huàn rán bīng shì【解释】:涣然：流散的样子；释：消散。

象冰遇热消融一般。

形容疑虑、误会、隔阂等完全消除。

【出处】:《老子》第十五章：“涣兮若冰之将释。

”【示例】:误解和偏见并不能随着时间的推移而～。

【近义词】:烟消云散、冰消瓦解、化为乌有【语法】:偏正式；作谓语、宾语；比喻相互间的嫌隙等消除【成语】感激涕零【拼音】gǎn jī tì líng【解释】涕：眼泪；零：落。

因感激而流泪。

形容极度感激。

【出处】唐·刘禹锡《平蔡行》诗：“路旁老人忆旧事，相与感激皆涕零。

”【示例】贾政听了，～，叩首不已。

◎清·曹雪芹《红楼梦》第一○七回【近义词】感恩图报、感激不尽【反义词】忘恩负义、恩将仇报【语法】偏正式；作谓语；形容极度感激【成语】：犯而不校【拼音】：fàn ér bù jiào【解释】：犯：触犯；校：计较。

受到别人的触犯或无礼也不计较。

【出处】：《论语·泰伯》：“以能问与不能，以多问于寡；有若无，实若虚，犯而不校。

”【示例】：惠养民道：“～，何以罚为？”大家微笑，各自散去。

◎清·李绿园《歧路灯》第五十五回【近义词】：唾面自干【反义词】：针锋相对、以眼还眼【语法】：复杂式；作谓语、宾语、定语；含贬义【成语】：点石成金【拼音】：diǎn shí chéng jīn【解释】：比喻修改文章时稍稍改动原来的文字，就使它变得很出色。

【出处】：汉·刘向《列仙传》：“许逊，南昌人。

晋初为旌阳令，点石化金，以足逋赋。

”【近义词】：点铁成金【反义词】：点金成铁【语法】：兼语式；作谓语、定语；含褒义【成语】铤而走险【拼音】tǐng ér zǒu xiǎn【解释】铤：急走的样子；走险：奔赴险处。

指在无路可走的时候采取冒险行动。

高考语文真题所考成语汇编(2014—2024)

高考语文真题所考成语汇编（2014—2024）A安之若素：（遇到不顺利情况或反常现象）像平常一样对待，毫不在意。

（2014·四川卷）安步当车：慢慢地步行，就当作是坐车。

（2016·全国卷II）按图索骥：按照图像寻找好马，比喻按照死规矩机械、呆板地做事，也泛指按照线索寻找目标。

（2016·全国卷III）（（2018·全国卷II）B不容置喙：不允许别人插嘴说话。

（2015·广东卷）不足为训：不能当作典范或法则。

（2011·北京卷）筚路蓝缕：形容创业艰难。

（2016·全国卷II）不期而遇：指没有约定而意外地相遇。

（2011·北京卷）不言而喻：不用说就可以明白，形容道理很明显。

（2017·山东卷）（2021·新高考卷II）不可名状：不能够用语言形容。

（2022·全国乙卷）笔走龙蛇：形容书法笔势雄健活泼。

（2016·全国卷III）博大精深：（思想、学说等）广博高深。

多用于形容理论、学识、思想、作品等广博丰富，深奥精深。

（2020·全国卷III）敝帚自珍：把破扫帚当成宝贝，比喻东西虽然不好，自己却很珍惜。

（2014·全国大纲卷）别无二致：指区分不出两者的差别。

（2010·安徽卷）不忍卒读：卒，尽，完。

不忍心读完，常用以形容文章内容悲惨动人。

（2013·浙江卷）变幻莫测：指事物变化多端，难以揣测。

（2013·福建卷）兵马未动，粮草先行：指出兵之前，先准备好粮食和草料，比喻在做某件事情之前，提前做好准备工作。

（2014北京卷）别树一帜：另外树起一面旗帜，指与众不同，另成一家。

（2014·江苏卷）别有洞天：另有一种境界，形容景物等引人入胜。

（2014·江苏卷）不寒而栗：指不寒冷而发抖，形容非常恐惧。

（2014·山东卷）不瘟不火：指表演既不沉闷也不过火。

单项选择-【中职专用】陕西省2014年-2019年对口高考英语真题分类汇编(原卷版) (2)

专题04 单项选择1. —Kate, why are you so happy?—Oh, you know, there ________ a football match.A. isB. areC. wasD. were2. —look, where you are sitting? Can't you see the sign?—Oh, sorry. I ________ it just now（刚才）.A. haven't found it.B. won't seeC. don't seeD. didn't see3. —Please don't laugh at others again.—________.A. Sorry, I won'tB. Sorry, I can'tC. Yes, I won'tD. OK, I didn't4. —What do you think ________ her speech?—Wonderful.A. atB. ofC. overD. about5. This is Lucy's coat. ________ is on the shelf.A. MyB. Your coatsC. MineD. My coats6. —When is Children's Day? —It is ________.A. on March 1stB. on July 1stC. on the first day of JuneD. on May lst7. —You look pale. What is wrong?—I failed in exam. ________ you help me?A. MustB. NeedC. CanD. Shall8. I am so hungry now ________ I want to eat something.A. thoughB. ifC. butD. and9. —How was your summer holiday?—It was boring. But I am glad to read ________ books during that holiday.A. manyB. muchC. littleD. lot10. Last Monday, we had a meeting. But you know it ________ me three hours to get ready for it.A. hadB. spentC. tookD. used11. —How ________ is it from here Hefei to Beijing?—It's about two hours' flight.A. longB. soonC. oftenD. far12. Can you tell me how to ________ English well?A. sayB. tellC. saidD. speak13. Today is my daughter's ________ birthday. I bought a toy car for her.A. fiveB. fifthC. the fifthD. the five14. My little daughter is looking for her book, but she can't find ________ anywhere.A. themB. anyC. itD. some15. —I feel tired now? Can I use you room for a ________?—Yes, go ahead and here is the key.A. playB. restC. walkD. run16. When you leave, please ________ all the lights.A. turn overB. turn onC. turn offD. turn down17. There is a man ________ is waiting for you at the school gate now.A. whoB. whichC. whomD. whose18. —You did not come to the cinema with me. Why?—My son is ill.—________.A. Don't worry.B. Are you going to look after her?C. I'm sorry to hear that.D. It doesn't matter.19. —How many people are there in Beijing?—There are about ________ people in Beijing.A.twelve millionsB. twelve million ofC. twelve millionD. twelve millions of20. My mother is a ________ teacher and she teaches us English well.A. badB. wellC. goodD. ill21. Thank you ________ your help.A. ofB. for C . to D. with22. How do you do? I don’t think we have met ________.A. afterB. sinceC. forD. before23. Alt, you must be Mary’s sister. Come in and ________ everyone.A. seeB. lookC. findD. meet24. Please give my regards to your family. And have a safe ________ home.A. journeyB. stayC. welcomeD. way25.—How are you?—________.A. Very bad. Thank you.B. Very well. Thank you. And you?C. I feel pain in my stomach.D. How are you?26.—You are really a good swimmer.—________.A. Thank you.B. It’s kind of you to say so.C. No, I can’t swim as well as you.D. Just so-so.27.—I’ m from Shaanxi V ocational School. How do you do?—________.A. How are you?B. How do you do?C. Fine.D. Are you ok?28. Hello, Mr. Zhang. I’m glad ________ you here.A. seeingB. to seeingC. to seeD. seen29. When you meet a new friend, be the first to say ________ and introduce yourself.A. goodbyeB. sorryC. helloD. nothing30. San is waiting for a chance ________ himself.A. to introduceB. introduceC. introducingD. introduced31. I saw your ruler is broken. You can use ________.A. IB. meC. myD. mine32. Wow! ________ heavy the snow is! Let’s make a snowman.A. WhatB. HowC. What aD. How a33.—Judy, be quiet! Your grandpa ________.—Sorry, mum.A. sleptB. sleepsC. is sleepingD. had slept34.—May I use your pen?—Sorry, there’s ________ with it.A.nothing wrongB. wrong nothingC. something wrongD. wrong something35.—Can you sing the song in English?—No, I ________.A.may notB. mustn’tC. needn’tD. can’t36.—What did you do last night?—I did my homework and ________ TV.A. watchB. watchedC. will watchD. am watching37. Most of the children enjoy ________ computer games.A. playB. playingC. playedD. to play38.—________ are your English books?—Eighteen Yuan.A. whatB. How manyC. How muchD. How long39.—________ you ________ your homework last evening?—Yes.A. Did; doB. Do; doC. Do; didD. Is; do40. Mary, Lucy misses you very much. She wants you to ________ to her soon.A. writeB. to writeC. wroteD. writing。

2014年全国高考英语试题分类汇编：改错题【Word版,含解析】

2014全国高考汇编改错一（2014大纲卷）第一节短文改错(共10小题；每小题1分，满分l0分)此题要求改正所给短文中的错误。

对标有题号的每一行作出判断:如无错误.在该行右边横线上画一个勾(√):如有错误(每行只有一个错误)，则按下列情况改正:此行多一个词:把多余的词用斜线(\)划掉。

在该行右边横线上写出该词，并也用斜线划掉。

此行缺一个词:在缺词处加一个肠字符号(A)，在该行右边横线上写出该加的词。

此行错一个词:在错的词下划一横线，在该行右边横线上写出改正后的词。

注意:原行没有错的不要改。

All of us need friendship. The understanding 76.______________between two friends mean both of them have similar 77.______________ideas and trusting each other. Otherwise, it is 78.______________impossible for him to help each other and to make 79.______________their friendship to last long. As an old saying goes, 80.______________“A friend in need is a friend indeed.” So really friendship 81.______________should able to stand all sorts of tests. And it is 82.______________wise to have as many good friends that we can. 83.______________The more friends we have, the more we can learn for 84.______________one another, but the more pleasure we can share together. 85.______________76. √77. 【答案】means【试题解析】本句的主语是the understanding…，这是单个的动名词定语，做主语的时候，谓语动词要使用单数形式。

2014高考语文试题分类汇编——诗歌鉴赏(含答案)

2014高考语文试题分类汇编——诗歌鉴赏目录一、全国新课标卷I二、全国新课标卷II三、四川卷四、安徽卷五、广东卷六、江西卷七、湖南卷八、山东卷九、湖北卷十、福建卷十一、重庆卷十二、辽宁卷十三、北京卷十四、天津卷十五、浙江卷十六、江苏卷十七、大纲全国卷一、（2014年新课标卷Ⅰ）阅读下面这首宋词，完成后面的试题。

阮郎归无名氏①春风吹雨绕残枝，落花无可飞。

小池寒渌欲生漪，雨晴还日西。

帘半卷，燕双归。

讳愁无奈眉②。

翻身整顿着残棋，沉吟应劫迟③。

[注]①作者一作秦观。

②讳愁：隐瞒内心的痛苦。

③劫：围棋术语。

（1）词上半阕的景物描写对全词的感情抒发起了什么作用？请结合内容分析。

(5分) 【试题答案】奠定了词的情感基调。

春风吹雨，残红满地，词一开始就给人以掩抑低回之感；接下来写风雨虽停，红日却已西沉，凄凉的氛围非但没有解除，反而又被抹上了一层暗淡的暮色。

【试题考点】鉴赏诗歌的表达技巧——结构作用【试题解析】词的上阕主要在写景，描写的是凄凉的景象场面：丝丝细雨被和暖的春风吹送着，飘洒在繁花落尽的树枝上。

满地落花被雨水浇湿，再也飞舞不起来了。

池塘里碧绿的水面上随风荡起微微的波纹。

雨晴了，一轮斜阳依旧出现在西方的天空上。

在“哀”的暮春景色中，抒发的是一种“哀”情，奠定了全词的感情基调。

（2）末尾两句表现了词中人物什么样的情绪？是如何表现的？请简要阐述。

(6分) 【试题答案】末尾两句表现了词中人物思绪纷乱、无法排遣的愁情。

是通过人物自身的动作来表现的。

回身整理残棋并想续下，借以转移愁情，可又因心事重重，以致犹豫不决，落子迟缓。

【试题考点】分析评价诗歌的思想内容【试题解析】下阕写当主人公在百无聊赖中卷起珠帘，恰恰看到燕子成双成对地飞来飞去。

这更加勾起了女主人公的一怀愁绪。

这种愁绪实在难以排遣，满心想加以掩饰，无奈却在紧蹙的双眉中显露出来。

于是只好强打精神，翻身起来，继续下那盘没有下完的棋。

岂料应劫之际，她竟然举棋不定，沉吟半晌，难以落子。

2014年高考英语完型填空试题汇编有解析

2014年高考英语完型填空试题汇编有解析十六（2014新课标II）阅读下面短文，从短文后各题所给的四个选项（A, B, C和D）中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

Joe Simpson and Simon Yates were the first people to climb the West Face of the Siula Grande in the Andes mountains. They reached the top __21_____, but on their way back conditions were very _22______. Joe fell and broke his leg. They both knew that if Simon __23_____ alone, he would probably get back _24______. But Simon decided to risk his __25_____ and try to lower Joe down the mountain on a rope（绳）.As they __26_____ down, the weather got worse. Then another ___27____ occurred. They couldn’t see or hear each other and, ___28____, Simon lowered his friend over the edge of a precipice（峭壁）. It was ___29____ for Joe to climb back or for Simon to pull him up. Joe’s __30_____ was pulling Simon slowly towards the precipice. ___31____, after more than an hour in the dark and the icy cold, Simon had to __32_____. In tears, he cut the rope. Joe __33_____ into a large crevasse（裂缝）in the ice below. He had no food or water and he was in terrible pain. He couldn’t walk, but he __34_____ to get out of the crevasse and started to ___35____ towards their camp, nearly ten kilometers __36_____.Simon had ___37____ the camp at the foot of the mountain. He thought that Joe must be __38_____, but he didn’t want to leave ___39____. Three days later, in the middle of the night, he heard Joe’s voice. He couldn’t ___40____ it. Joe was there, a few meters from their tent, still alive.21.A. hurriedly B. carefully .C. successfully D. early22. A. difficult B. similar C. special D. normal23. A. climbed B. worked C. rested . D. continued24. A. unwillingly B. safely C. slowly D. regretfully25. A. fortune B. time C. health D. life26. A. lay B. settled C. went D. looked27. A. damage B. storm C. change D. trouble28. A. by mistake B. by chance C. by chance D. by luck29. A. unnecessary B. practical C. important D. impossible30. A. height B. weight C. strength .D. equipment31. A. Finally B. Patiently .C. Surely D. Quickly32. A. stand back B. take a rest C. make a decision .D. hold on33. A. jumped B. fell C. escaped D. backed34. A. managed B. planned C. waited D. hoped35. A. run B. skate C. move D. march36. A. around B. away C. above D. along37. A. headed for B. travelled C. left for D. returned to38. A. dead B. hurt C. weak D. late39. A. secretly B. tiredly .C. immediately D. anxiously40. A. find B. believe C. make D. accept【考点】考察故事类完型填空【文章大意】本文讲述了一个生命的奇迹的故事，Simon和Joe一起攀登安第斯山脉的Siula Grande，Joe摔倒了腿，最后摔进了冰裂缝，最后他顽强地爬回到了几英里之外的营地。

全国高考汇编阅读之语法填空(附答案解析)

全国高考汇编阅读之语法填空一（2014福建卷）第一节短文填词（共10小题；每小题1分，满分10分）阅读下面短文，根据以下提示：1）汉语提示，2）首字母提示，3）语境提示，在每个空格内填人一个适当的英语单词，所填单词要求意义准确，拼写正确，并将该词完整地写在答题卡中相应的横线上。

Many of us were raised with the saying "Waste not, want not.” None of us, (76) _h , can completely avoid waste in our lives.Any kind of waste is thoughtless. Whether we waste our potential talents, our own time, our limited natural(77) （资源）,our money, or other people's time, each of us can become more aware and careful. The smallest good habits can make a big (78) _d . It's a good feeling to know in our hearts we are doing our(79)h in a world that is in serious trouble. By focusing on( 80) （节省）oil, water, paper, food, and clothing, we are playing a part (81) cutting down on waste.We must keep reminding (82) （白己）that it is easier to get into something (83) it is to get out of it. Actually, severe damage( 84)d ____to our land is fairly recent in the history of our evolution. It's time for us to( 85)____no to waste so that our grandchildren’s children will be able to develop well. We can't solve all the problems of waste, but we can encourage mindfulness.Waste not！76. 【答案】however【试题解析】很多人都知道：勤俭节约，吃穿不愁。

2014年高考真题化学解析分类汇编—专题04 氧化还原反应

2014年普通高等学校招生全国统一考试化学试题分类汇编专题四氧化还原反应1．（2014·上海单科化学卷，T19）下列反应与Na2O2＋SO2→Na2SO4相比较，Na2O2的作用相同的是A．2Na2O2＋CO2→2Na2CO3＋O2B．2Na2O2＋2SO3→2Na2SO4＋O2C．Na2O2＋H2SO4→Na2SO4＋H2O2D．3Na2O2＋Cr2O3→2Na2CrO4＋Na2O【答案】D【解析】氧化还原反应Na2O2＋SO2→Na2SO4中，Na2O2是氧化剂，SO2是还原剂；A、2Na2O2＋CO2→2Na2CO3＋O2反应中，Na2O2既是氧化剂也是还原剂，A不选；B、2Na2O2＋2SO3→2Na2SO4＋O2反应中，Na2O2既是氧化剂也是还原剂，B不选；C、Na2O2＋H2SO4→Na2SO4＋H2O2属于非氧化还原反应，C不选；D、3Na2O2＋Cr2O3→2Na2CrO4＋Na2O反应中，Na2O2是氧化剂，D选。

2．（2014·山东理综化学卷，T7）下表中对应关系正确的是2CH+HCl【答案】B【解析】A、CH2=CH2+HCl CH3CH2Cl为取代反应，A错误；B、由油脂得到甘油，属于酯类的水解反应。

由淀粉得到葡萄糖，属于糖类的水解反应，B正确；C、Zn+Cu2+=Zn2++Cu的单质Zn化合价升高，被氧化，C错误；D、Cl2+H2O=HCl+HClO反应中H2O既不是氧化剂也不是还原剂，D错误。

3．（2014·全国大纲版理综化学卷，T13）已知：将Cl2通人适量KOH溶液，产物中可能有KC1、KClO、KC1O3，且()()cc--C1C1O的值与温度高低有关。

当n(KOH)=amol时，下列有关说法错误的是A ．若某温度下，反应后()()c c --C1C1O ＝11，则溶液中()()c c --C1C1O ＝12B ．参加反应的氯气的物质的量等于12amol C ．改变温度，反应中转移电子的物质的量n e 的范围：12amol ≤n e ≤56amol D ．改变温度，产物中KC1O 3的最大理论产量为17amol 【答案】D【解析】A 、令n （ClO —）=1mol ，反应后()()c c --C1C1O =11，则n （Cl —）=11mol ，电子转移守恒，5×n （ClO 3—）+1×n （ClO —）=1×n （Cl —），即5×n （ClO 3—）+1×1mol=1×11mol ，解得n （ClO 3—）=2mol ，故溶液中()()c c --C1C1O =12，A 正确；B 、由Cl 原子守恒可知，2n （Cl 2）=n （KCl ）+n （KClO ）+n （KClO 3），由钾离子守恒可知n （KCl ）+n （KClO ）+n （KClO 3）=n （KOH ），故参加反应的氯气的物质的量=12n （NaOH ）=12amol ，B 正确；C 、氧化产物只有KClO 3时，转移电子最多，根据电子转移守恒5n （KCl ）=n （KClO 3），由钾离子守恒：n （KCl ）+n （KClO 3）=n （KOH ），故n （KClO 3）=16n （KOH ）=16a mol ，转移电子最大物质的量=16a mol×5=56a mol ，氧化产物只有KClO 时，转移电子最少，根据电子转移守恒n （KCl ）=n（KClO ），由钾离子守恒：n （KCl ）+n （KClO ）=n （KOH ），故n （KClO ）=12n （KOH ）= 12a mol ，，转移电子最小物质的量=12a mol×1=12a moll ，故反应中转移电子的物质的量ne 的范围：12a mol≤n e ≤56amol ，C 正确；D 、氧化产物只有KClO 3时，其物质的量最大，由C 中计算可知：n 最大（KClO 3）=16n （KOH ）=16a mol ，D 错误。

十年(2014-2023)高考数学真题分项汇编文科专题5 数列小题(文科)(解析版)

n 项和
Sn，公差
d≠0， a1 d
1 ．记
b1=S2，
bn+1=Sn+2–S2n， n N ，下列等式不可能成立的是
( )
A．2a4=a2+a6
B．2b4=b2+b6
C． a42 a2a8
D． b42 b2b8
【答案】D
解析：对于 A，因为数列an 为等差数列，所以根据等差数列的下标和性质，由 4 4 2 6 可得，
由 an
a1
n
1 d
0
可得 n
1
a1 d
，取
N0
1
a1 d
1 ，则当 n
N0
时， an
0，
所以，“an 是递增数列” “存在正整数 N0 ，当 n N0 时， an 0 ”；
若存在正整数 N0 ，当 n N0 时， an 0 ，取 k N 且 k N0 ， ak 0 ，
假设 d
0 ，令 an
Sn =
1 2
An An+1 ×tan q Bn Bn+1 ，都为定值，所以 Sn+1 - Sn 为定值．故选 A．
3．(2022 高考北京卷·第 15 题)己知数列an 各项均为正数，其前 n 项和 Sn 满足 an Sn 9(n 1, 2,) ．给
出下列四个结论：
①an 的第 2 项小于 3； ②an 为等比数列；
2a4 a2 a6 ，A 正确；
对于 B，由题意可知， bn1 S2n2 S2n a2n1 a2n2 ， b1 S2 a1 a2 ，
∴ b2 a3 a4 ， b4 a7 a8 ， b6 a11 a12 ， b8 a15 a16 ．
∴ 2b4 2 a7 a8 ， b2 b6 a3 a4 a11 a12 ．

水溶液中的平衡高考题汇编

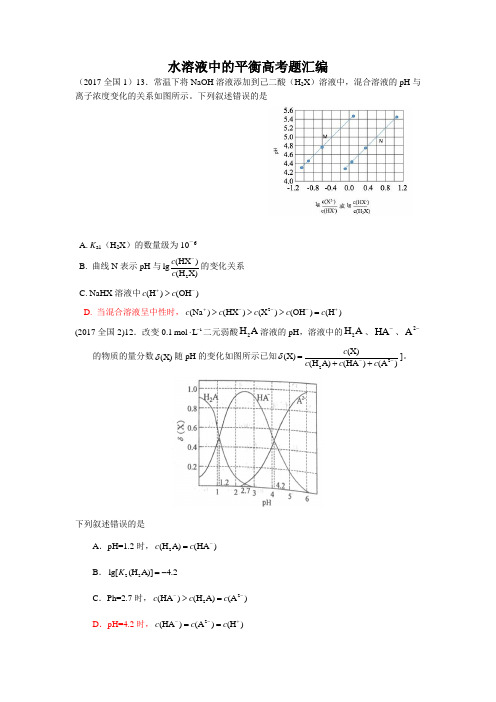
水溶液中的平衡高考题汇编（2017全国1）13．常温下将NaOH 溶液添加到己二酸（H 2X ）溶液中，混合溶液的pH 与离子浓度变化的关系如图所示。

下列叙述错误的是A. K a1（H 2X ）的数量级为10－6B. 曲线N 表示pH 与2(HX )lg (H X)c c -的变化关系C. NaHX 溶液中(H )(OH )c c +->D. 当混合溶液呈中性时，2(Na )(HX )(X )(OH )(H )c c c c c +---+>>>=(2017全国2)12．改变0.11mol L -⋅二元弱酸2H A 溶液的pH ，溶液中的2H A 、HA -、2A-的物质的量分数(X)δ随pH 的变化如图所示已知22(X)(X)(H A)(HA )(A )c c c c δ--=++]。

下列叙述错误的是A ．pH=1.2时，2(H A)(HA )c c -=B ．22lg[(H A)] 4.2K =-C ．Ph=2.7时，22(HA )(H A)(A )c c c -->=D ．pH=4.2时，2(HA )(A )(H )c c c --+==（2017浙江）23．25℃时，在含CH 3COOH 和CH 3COOˉ的溶液中，CH 3COOH 和CH 3COOˉ二者中各自所占的物质的量分数（α）随溶液pH 变化的关系如图所示．下列说法不正确的是（）A ．在pH ＜4.76的溶液中，c （CH 3COO ﹣）＜c （CH 3COOH ）B ．在pH=7的溶液中，α（CH 3COOH ）=0，α（CH 3COO ﹣）=1.0C ．在pH ＞4.76的溶液中，c （CH 3COO ﹣）与c （OH ﹣）之和可大于c （H +）D ．在pH=4.76的溶液中加盐酸，α（CH 3COOH ）与α（CH 3COO ﹣）之和保持不变（2016全国1）12.298K 时，在20.0mL 0.10mol 氨水中滴入0.10mol 的盐酸，溶液的pH 与所加盐酸的体积关系如图所示。

高考真题分类汇编

高考真题分类汇编一、语文题目1. 散文题2. 诗歌题3. 阅读题4. 改错题5. 审美题6. 文言文题7. 写作题8. 短文写作题二、数学题目1. 初等数学题2. 几何题3. 代数题4. 概率与统计题5.函数题6. 推理与证明题三、英语题目1. 词汇题2. 阅读理解题3. 完型填空题4. 语法题5. 写作题四、物理题目1. 力学题2. 光学题3. 电学题4. 热学题5. 声学题6. 直流电路题7. 交流电路题8. 波动题五、化学题目1. 元素与化合物题2. 离子反应题3. 化学方程式题4. 酸碱中和题5. 氧化还原题6. 有机化学题六、生物题目1. 动物学题2. 植物学题3. 生态学题4. 生物实验题5. 遗传学题6. 分子生物学题七、历史题目1. 战国时期问题2. 三国时期问题3. 隋唐时期问题4. 宋元明清问题5. 近代史问题6. 20世纪问题八、地理题目1. 中国地理题2. 世界地理题3. 物理地理题4. 人文地理题5. 地图题九、政治题目1. 政治理论问题2. 国际政治问题3. 共和社会主义问题4. 中华人民共和国政治问题5. 中央政府问题6. 地方政府问题十、经济题目1. 经济基本知识问题2. 经济体制改革问题3. 经济发展问题4. 财政与税收问题5. 市场经济与社会主义问题。

2014全国高考难题汇编---------函数

2014全国高考汇编---------函数选择填空：1、(2014年安徽∙理科6)设函数))((R x x f ∈满足()()sin f x f x x π+=+，当π<≤x 0时，0)(=x f ，则=)623(πf （） A ．12 B ．23C ．0D ．21-答案：A ，解析：231717()()sin 666111117()sin sin666551117()sin sin sin6666111102222f f f f ππππππππππ=+=++=+++=+-+=2、(2014年安徽∙理科9)若函数()12f x x x a =+++的最小值为3，则实数a 的值为（）A ．5或8B ．1-或5C ．1-或4-D ．4-或8答案：D ，解析：（1）当2a <时，12a-<-，此时31,11,1()2312x a x a x a x f x ax a x ---<-⎧⎪⎪--+-≤≤-=⎨⎪⎪++>-⎩；（2）当2a >时，12a->-，此时31,2()1,12311a x a x f x a x a x x a x ⎧---<-⎪⎪=⎨+--≤≤-⎪⎪++>-⎩在两种情况下，min ()()|1|322a af x f =-=-+=，解得4a =-或8a =。

注：此题也可以由绝对值的几何意义得min ()|1|32af x =-+=，从而得4a =-或8a =。

3、(2014年安徽∙文科15) 若直线l 与曲线C 满足下列两个条件：)(i 直线l 在点()00,y x P 处与曲线C 相切；)(ii 曲线C 在P 附近位于直线l 的两侧，则称直线l 在点P 处“切过”曲线C .下列命题正确的是__1、3、4_______(写出所有正确命题的编号) ①直线0:=y l 在点()0,0P 处“切过”曲线C ：2x y = ②直线1:-=x l 在点()0,1-P 处“切过”曲线C ：2)1(+=x y ③直线x y l =:在点()0,0P 处“切过”曲线C ：x y sin = ④直线x y l =:在点()0,0P 处“切过”曲线C ：x y tan = ⑤直线1:-=x y l 在点()0,1P 处“切过”曲线C ：x y ln =4、(2014年江苏∙文理科10)已知函数2()1f x x mx =+-，若对任意[1]x m m ∈+，，都有()0f x <成立，则实数m 的取值范围是．【答案】202⎛⎫-⎪⎝⎭， 5、(2014年江苏∙文理科13)已知()f x 是定义在R 上且周期为3的函数，当[03)x ∈，时，21()22f x x x =-+．若函数()y f x a =-在区间[34]-，上有10个零点(互不相同)，则实数a 的取值范围是．【答案】()102， 6、（14年天津∙理）已知函数()23f x x x =+，R x ∈.若方程()10f x a x --=恰有4个互异的实数根，则实数a 的取值范围为___01a <<或9a >_____. 解析：显然0a >.解1：（ⅰ）当()1y a x =--与23y x x =--相切时，1a =，此时()10f x a x --=恰有3个互异的实数根.（ⅱ）当直线()1y a x =-与函数23y x x =+相切时，9a =，xy13O此时()10f x a x --=恰有2个互异的实数根. 结合图象可知01a <<或9a >.解2：显然1a ¹，所以231x xa x +=-.令1t x =-，则45a t t =++.因为(][),,444t t ?? ++，所以(][)45,19,t t?ゥ+++.结合图象可得01a <<或9a >.7、(2014湖南∙ 理)已知函数f （x ）=2x1x +e -2（x<0）与g （x ）=2x +In x+a)（的图象在存在关于y 轴对称点，则a 的取值范围是A 、1-e ∞（，） B 、-e ∞（，）C 、1-e e （，）D 、1-e e（，）【答案】B【解析】由题可得存在()0,0x ∈-∞满足()()0220001ln 2xx e x x a +-=-+-+ ()001ln 2x e x a ⇒--+-0=,当0x 取决于负无穷小时,()001ln 2x e x a --+-趋近于-∞,因为函数()1ln 2xy e x a =--+-在定义域内是单调递增的,所以ln ln a e a e <⇒<,故选B.【考点定位】指对数函数方程8、(2014四川∙理科9)已知f （x ）=ln （1+x ）﹣ln （1﹣x ），x ∈（﹣1，1）．现有下列命题：①f（﹣x ）=﹣f （x ）；②f（）=2f （x ）③|f（x ）|≥2|x|其中的所有正确命题的序号是（ A ） A ． ①②③ B ． ②③ C ． ①③ D ． ①②解：∵f（x ）=ln （1+x ）﹣ln （1﹣x ），x ∈（﹣1，1）， ∴f（﹣x ）=ln （1﹣x ）﹣ln （1+x ）=﹣f （x ），即①正确；tyO91f（）=ln（1+）﹣ln（1﹣）=ln（）﹣ln（）=ln （）=ln[（）2]=2ln（）=2[ln（1+x）﹣ln（1﹣x）]=2f（x），故②正确；解：∵f（x）=ln（1+x）﹣ln（1﹣x），x∈（﹣1，1），∴f（﹣x）=ln（1﹣x）﹣ln（1+x）=﹣f（x），即①正确；f（）=ln（1+）﹣ln（1﹣）=ln（）﹣ln（）=ln （）=ln[（）2]=2ln（）=2[ln（1+x）﹣ln（1﹣x）]=2f（x），故②正确；当x∈[0，1）时，|f（x）|≥2|x|⇔f（x）﹣2x≥0，令g（x）=f（x）﹣2x=ln（1+x）﹣ln（1﹣x）﹣2x（x∈[0，1））∵g′（x）=+﹣2=≥0，∴g（x）在[0，1）单调递增，g（x）=f（x）﹣2x≥g（0）=0，又f（x）≥2x，又f（x）与y=2x为奇函数，所以丨f（x）丨≥2丨x丨成立，故③正确；故正确的命题有①②③，故选：A本题以命题的真假判断为载体，考查了对数的运算性质，代入法求函数的解析式等知识点，难度中档．9、(2014四川理科15)以A表示值域为R的函数组成的集合，B表示具有如下性质的函数φ（x）组成的集合：对于函数φ（x），存在一个正数M，使得函数φ（x）的值域包含于区间[﹣M，M]．例如，当φ1（x）=x3，φ2（x）=sinx时，φ1（x）∈A，φ2（x）∈B．现有如下命题：①设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”；②函数f（x）∈B的充要条件是f（x）有最大值和最小值；③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）+g（x）∉B．④若函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，则f（x）∈B．其中的真命题有_________ ．（写出所有真命题的序号）考点：命题的真假判断与应用；充要条件；函数的值域．专题：新定义；极限思想；函数的性质及应用；不等式的解法及应用．分析：根据题中的新定义，结合函数值域的概念，可判断出命题①②③是否正确，再利用导数研究命题④中函数的值域，可得到其真假情况，从而得到本题的结论．解答：解：（1）对于命题①“f（x）∈A”即函数f（x）值域为R，“∀b ∈R ，∃a ∈D ，f （a ）=b”表示的是函数可以在R 中任意取值，故有：设函数f （x ）的定义域为D ，则“f（x ）∈A”的充要条件是“∀b ∈R ，∃a ∈D ，f （a ）=b”∴命题①是真命题；（2）对于命题②若函数f （x ）∈B ，即存在一个正数M ，使得函数f （x ）的值域包含于区间[﹣M ，M]． ∴﹣M≤f（x ）≤M．例如：函数f （x ）满足﹣2＜f （x ）＜5，则有﹣5≤f （x ）≤5，此时，f （x ）无最大值，无最小值．∴命题②“函数f （x ）∈B 的充要条件是f （x ）有最大值和最小值．”是假命题；（3）对于命题③ 若函数f （x ），g （x ）的定义域相同，且f （x ）∈A ，g （x ）∈B ，则f （x ）值域为R ，f （x ）∈（﹣∞，+∞），并且存在一个正数M ，使得﹣M≤g（x ）≤M． ∴f（x ）+g （x ）∈R ．则f （x ）+g （x ）∉B ． ∴命题③是真命题．（4）对于命题④ ∵函数f （x ）=aln （x+2）+（x ＞﹣2，a ∈R ）有最大值，∴假设a ＞0，当x→+∞时，→0，ln （x+2）→+∞，∴aln（x+2）→+∞，则f（x ）→+∞．与题意不符；假设a ＜0，当x→﹣2时，→，ln （x+2）→﹣∞，∴aln（x+2）→+∞，则f （x ）→+∞．与题意不符． ∴a=0．即函数f （x ）=（x ＞﹣2）当x ＞0时，，∴，即；当x=0时，f （x ）=0；当x ＜0时，，∴，即．∴．即f （x ）∈B ．故命题④是真命题．故答案为①③④．点评：本题考查了函数值域的概念、基本不等式、充要条件，还考查了新定义概念的应用和极限思想．本题计算量较大，也有一定的思维难度，属于难题．10、（2014湖北∙ 理10).已知函数)(x f 是定义在R 上的奇函数，当0≥x 时，)3|2||(|21)(222a a x a x x f --+-=，若R ∈∀x ，)()1(x f x f ≤-，则实数a 的取值范围为（） A .]61,61[- B .]66,66[-C . ]31,31[-D . ]33,33[-【解题提示】考查函数的奇函数的性质、分段函数、最值及恒成立【解析】选B . 依题意，当0≥x 时，⎪⎩⎪⎨⎧≤≤-≤<->-=2222220,2,2,3)(a x x a x a a a x a x x f ，作图可知，)(x f 的最小值为2a -，因为函数)(x f 为奇函数，所以当0<x 时)(x f 的最大值为2a ，因为对任意实数x 都有，)()1(x f x f ≤-，所以，1)2(422≤--a a ，解得6666≤≤-a ，故实数a 的取值范围是]66,66[-. 11、（2014湖北∙文9）已知f （x ）是定义在R 上的奇函数，当x ≥0时，f （x ）=x 2﹣3x ，则函数g （x ）=f （x ）﹣x+3的零点的集合为（） A ． {1，3} B ． {﹣3，﹣1，1，3} C ． {2﹣，1，3} D ． {﹣2﹣，1，考点：函数奇偶性的性质．专题：函数的性质及应用．分析：首先根据f （x ）是定义在R 上的奇函数，求出函数在R 上的解析式，再求出g （的解析式，根据函数零点就是方程的解，问题得以解决．解答：解：∵f （x ）是定义在R 上的奇函数，当x ≥0时，f （x ）=x 2﹣3x ，令x ＜0，则﹣x ＞0，∴f （﹣x ）=x 2+3x=﹣f （x ）∴f （x ）=﹣x 2﹣3x ，∴∵g （x ）=f （x ）﹣x+3 ∴g （x ）=令g （x ）=0，当x ≥0时，x 2﹣4x+3=0，解得x=1，或x=3，当x ＜0时，﹣x 2﹣4x+3=0，解得x=﹣2﹣， ∴函数g （x ）=f （x ）﹣x+3的零点的集合为{﹣2﹣，1，3}故选：D ．12、（2014湖北∙文15）如图所示，函数y=f（x）的图象由两条射线和三条线段组成，若∀x∈R，f（x）＞f（x﹣1），则正实数a的取值范围为（0，）．考点：函数的图象．专题：函数的性质及应用．分析：由已知中的函数图象可得f（4a）=a，f（﹣4a）=﹣a，若∀x∈R，f（x）＞f（x﹣1），则，解不等式可得正实数a的取值范围．解答：解：由已知可得：a＞0，且f（4a）=a，f（﹣4a）=﹣a，若∀x∈R，f（x）＞f（x﹣1），则，解得a＞，故正实数a的取值范围为：（0，），故答案为：（0，）点评：本题考查的知识点是函数的图象，其中根据已知分析出，是解答的关键．13、（2014年全国大纲∙理科3)函数y=f（x）的图象与函数y=g（x）的图象关于直线x+y=0对称，则y=f（x）的反函数是（）A．y=g（x）B．y=g（﹣x）C．y=﹣g（x）D．y=﹣g（﹣x）解：设P（x，y）为y=f（x）的反函数图象上的任意一点，则P关于y=x的对称点P′（y，x）一点在y=f（x）的图象上，又∵函数y=f（x）的图象与函数y=g（x）的图象关于直线x+y=0对称，∴P′（y，x）关于直线x+y=0的对称点P″（﹣x，﹣y）在y=g（x）图象上，∴必有﹣y=g（﹣x），即y=﹣g（﹣x）∴y=f（x）的反函数为：y=﹣g（﹣x）故选：D14、（2014年全国大纲∙文科3)奇函数()f x 的定义域为R ，若(2)f x +为偶函数，且(1)1f =，则(8)(9)f f +=（）A ．-2B ．-1C ．0D ．1 答案：D15、（2014年山东∙理科)已知实数,x y 满足x y a a <（01a <<），则下列关系式恒成立的是（A ）221111x y >++（B ）22ln(1)ln(1)x y +>+ （C ）sin sin x y >（D ）22x y > 答案：D16、(2014年山东∙理科)已知函数()()y f x x R =∈.对函数()()y g x x I =∈，定义()g x 关于()f x 的“对称函数”为()()y h x x I =∈，()y h x =满足：对任意x I ∈，两个点(,())x h x ，(,())x g x 关于点(,())x f x 对称.若()h x 是2()4g x x =-关于()3f x x b =+的“对称函数”，且()()h x g x >恒成立，则实数b 的取值范围是 . 答案：17、（2014年山东文∙科)对于函数()f x ，若存在常数0a ≠，使得x 取定义域内的每一个值，都有()(2)f x f a x =-，则称()f x 为准偶函数，下列函数中是准偶函数的是( ) (A) ()f x x =(B) 3()f x x =(C) ()tan f x x =(D) ()cos(1)f x x =+答案：D18、【2014年辽宁卷∙理】已知定义在[0,1]上的函数()f x 满足： ①(0)(1)0f f ==；②对所有,[0,1]x y ∈，且x y ≠，有1|()()|||2f x f y x y -<-.若对所有,[0,1]x y ∈，|()()|f x f y k -<，则k 的最小值为（）A ．12 B ．14 C ．12πD ．18【答案】B【解析】依题意，定义在[0，1]上的函数y=f （x ）的斜率|k|＜，不妨令k ＞0，构造函数f （x ）=（0＜k ＜），满足f （0）=f （1）=0，|f （x ）﹣f （y ）|＜|x ﹣y|．当x ∈[0，]，且y ∈[0，]时，|f （x ）﹣f （y ）|=|kx ﹣ky|=k|x ﹣y| ≤k|﹣0|=k ×＜；当x ∈[0，]，且y ∈[，1]，|f （x ）﹣f （y ）|=|kx ﹣（k ﹣ky ）| =|k （x+y ）﹣k|≤|k （1+）﹣k|=＜；当y ∈[0，]，且y ∈[，1]时，同理可得，|f （x ）﹣f （y ）|＜；当x ∈[，1]，且y ∈[，1]时，|f （x ）﹣f （y ）|=|（k ﹣kx ）﹣（k ﹣ky ）|=k|x ﹣y|≤k ×（1﹣）=＜；综上所述，对所有x ，y ∈[0，1]，|f （x ）﹣f （y ）|＜， ∵对所有x ，y ∈[0，1]，|f （x ）﹣f （y ）|＜k 恒成立， ∴k ≥，即k 的最小值为．故选：B19、【2014年辽宁卷∙文10】（已知()f x 为偶函数，当0x ≥时，1cos ,[0,]2()121,(,)2x x f x x x π⎧∈⎪⎪=⎨⎪-∈+∞⎪⎩，则不等式1(1)2f x -≤的解集为（）A ．1247[,][,]4334B ．3112[,][,]4343-- C ．1347[,][,]3434D ．3113[,][,]4334-- 【答案】A 【解析】()⎥⎦⎤⎢⎣⎡∈≤⎥⎦⎤⎢⎣⎡∈≤21,31,21cos ,21,0,21x x x x f 解得则若π ()⎥⎦⎤⎝⎛∈≤-⎪⎭⎫ ⎝⎛+∞∈≤43,21,2112,,21,21x x x x f 解得则若()()⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡≤433131-43-21，，的解集是为偶函数， x f x f()⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-∴473432411，，的解集是 x f20、【2014年陕西卷∙文14】已知0,1)(≥+=x xxx f ，若++∈==N n x f f x f x f x f n n )),(()(),()(11，则)(2014x f 的表达式为________.【答案】 x x20141+【解析】.20141)(,31211,21)(,2111,1)(∴)),(()(,,1)()(,20143211xxx f x x xx x xx f x x x x x x x f x f f x f x x x f x f n n +=+=+++=+=+++==+==+经观察规律，可得21、(2014年重庆∙理科)若不等式2212122++≥++-a a x x 对任意实数x 恒成立，则实数a 的取值范围是____________.【答案】]211-[，【解析】]211-[∈1-2≥0221≥25221≥)(∴25)21f(|2||21-||21-|)(222，解得，，即恒成立，即有最小值由数轴可知，a a a a a a a x f x x x x f +++++=+++= 解答题：1、（2014•湖北∙文16）某项研究表明：在考虑行车安全的情况下，某路段车流量F （单位时间内经过测量点的车辆数，单位：辆/小时）与车流速度v （假设车辆以相同速度v 行驶，单位：米/秒）、平均车长l （单位：米）的值有关，其公式为F=．（Ⅰ）如果不限定车型，l=6.05，则最大车流量为 1900 辆/小时；（Ⅱ）如果限定车型，l=5，则最大车流量比（Ⅰ）中的最大车流量增加 100 辆/小时．解：（Ⅰ）F==，∵v+≥2=22，当v=11时取最小值， ∴F=≤1900，故最大车流量为：1900辆/小时；（Ⅱ）F===，∵v+≥2=20，∴F ≤2000，2000﹣1900=100（辆/小时）故最大车流量比（Ⅰ）中的最大车流量增加100辆/小时．故答案为：1900，1002、(2014四川∙理科21)．已知函数f （x ）=e x﹣ax 2﹣bx ﹣1，其中a ，b ∈R ，e=2.71828…为自然对数的底数．（1）设g （x ）是函数f （x ）的导函数，求函数g （x ）在区间[0，1]上的最小值；（2）若f （1）=0，函数f （x ）在区间（0，1）内有零点，求a 的取值范围．解：∵f（x ）=e x﹣ax 2﹣bx ﹣1，∴g（x ）=f′（x ）=e x﹣2ax ﹣b ，又g′（x ）=e x ﹣2a ，x ∈[0，1]，∴1≤e x≤e，∴①当时，则2a≤1，g′（x）=e x﹣2a≥0，∴函数g（x）在区间[0，1]上单调递增，g（x）min=g（0）=1﹣b；②当，则1＜2a＜e，∴当0＜x＜ln（2a）时，g′（x）=e x﹣2a＜0，当ln（2a）＜x＜1时，g′（x）=e x﹣2a＞0，∴函数g（x）在区间[0，ln（2a）]上单调递减，在区间[ln（2a），1]上单调递增，g（x）min=g[ln（2a）]=2a﹣2aln（2a）﹣b；③当时，则2a≥e，g′（x）=e x﹣2a≤0，∴函数g（x）在区间[0，1]上单调递减，g（x）min=g（1）=e﹣2a﹣b，综上：函数g（x）在区间[0，1]上的最小值为；（2）由f（1）=0，⇒e﹣a﹣b﹣1=0⇒b=e﹣a﹣1，又f（0）=0，若函数f（x）在区间（0，1）内有零点，则函数f（x）在区间（0，1）内至少有三个单调区间，由（1）知当a≤或a≥时，函数g（x）在区间[0，1]上单调，不可能满足“函数f（x）在区间（0，1）内至少有三个单调区间”这一要求．若，则g min（x）=2a﹣2aln（2a）﹣b=3a﹣2aln（2a）﹣e+1令h（x）=（1＜x＜e）则．由＞0⇒x＜∴h（x）在区间（1，）上单调递增，在区间（，e）上单调递减，=+＜0，即g min（x）＜0 恒成立，∴函数f（x）在区间（0，1）内至少有三个单调区间⇔⇒，又，所以e﹣2＜a＜1，综上得：e﹣2＜a＜1．3、（2014年江苏文理科23)已知函数0sin ()(0)x f x x x =>，设()n f x 为1()n f x -的导数，n *∈N ．（1）求()()122222f f πππ+的值；（2）证明：对任意的n *∈N ，等式()()124442n n nf f -πππ+=成立．(1)解：由已知，得102sin cos sin ()(),x x x f x f x x x x '⎛⎫'===- ⎪⎝⎭于是21223cos sin sin 2cos 2sin ()(),x x x x x f x f x x x x x x ''⎛⎫⎛⎫'==-=--+ ⎪ ⎪⎝⎭⎝⎭所以12234216(),(),22f f πππππ=-=-+ 故122()() 1.222f f πππ+=- (2)证明：由已知，得0()sin ,xf x x =等式两边分别对x 求导，得00()()cos f x xf x x '+=，即01()()cos sin()2f x xf x x x π+==+，类似可得122()()sin sin()f x xf x x x π+=-=+，2333()()cos sin()2f x xf x x x π+=-=+，344()()sin sin(2)f x xf x x x π+==+.下面用数学归纳法证明等式1()()sin()2n n n nf x xf x x π-+=+对所有的n ∈*N 都成立.(i)当n =1时，由上可知等式成立.(ii)假设当n =k 时等式成立, 即1()()sin()2k k k kf x xf x x π-+=+.因为111[()()]()()()(1)()(),k k k k k k k kf x xf x kf x f x xf x k f x f x --+'''+=++=++(1)[sin()]cos()()sin[]2222k k k k x x x x ππππ+''+=+⋅+=+，所以1(1)()()k k k f x f x +++(1)sin[]2k x π+=+. 所以当n=k +1时,等式也成立.综合(i),(ii)可知等式1()()sin()2n n n nf x xf x x π-+=+对所有的n ∈*N 都成立.令4x π=，可得1()()sin()44442n n n nf f πππππ-+=+(n ∈*N ).所以12()()4442n n nf f πππ-+=(n ∈*N ).4、(2014年辽宁卷∙理21)（本小题满分12分）已知函数8()(cos )(2)(sin 1)3f x x x x x π=-+-+，2()3()cos 4(1sin )ln(3)xg x x x x ππ=--+-.证明：（1）存在唯一0(0,)2x π∈，使0()0f x =；（2）存在唯一1(,)2x ππ∈，使1()0g x =，且对（1）中的x 0有01x x π+<.解：（Ⅰ）当(0,)2x π∈时，2'()(1sin )(2)2cos 03f x x x x x π=-++--<，函数()f x 在(0,)2π上为减函数，又2816(0)0,()0323f f πππ=->=--<，所以存在唯一0(0,)2x π∈，使0()0f x =.（Ⅱ）考虑函数3()cos 2()4ln(3),[,]1sin 2x x h x x x x ππππ-=--∈+，令t x π=-，则[,]2x ππ∈时，[0,]2t π∈，记3cos 2()()4ln(1)1sin t t u t h t t t ππ=-=-++，则3()'()(2)(1sin )f t u t t t π=++ ，由（Ⅰ）得，当0(0,)t x ∈时，'()0u t >，当0(,)2t x π∈时，'()0u t <.在0(0,)x 上()u t 是增函数，又(0)0u =，从而当0(0,]t x ∈时，()0u t >，所以()u t 在0(0,]x 上无零点. 在0(,)2x π上()u t 是减函数，由0()0,()4ln 202u x u π>=-<，存在唯一的10(,)2t x π∈ ，使1()0u t =.所以存在唯一的10(,)2t x π∈使1()0u t =.因此存在唯一的11(,)2x t πππ=-∈，使111()()()0h x h t u t π=-==.因为当(,)2x ππ∈时，1sin 0x +>，故()(1sin )()g x x h x =+与()h x 有相同的零点，所以存在唯一的1(,)2x ππ∈，使1()0g x =.因1110,x t t x π=->，所以01x x π+<5、【2014年辽宁卷∙理24】（本小题满分10分）选修4-5：不等式选讲设函数()2|1|1f x x x =-+-，2()1681g x x x =-+，记()1f x ≤的解集为M ，()4g x ≤的解集为N. （1）求M ；（2）当x M N ∈时，证明：221()[()]4x f x x f x +≤. 解：（Ⅰ）33,[1,)()1,(,1)x x f x x x -∈+∞⎧=⎨-∈-∞⎩当1x ≥时，由()331f x x =-≤得43x ≤，故413x ≤≤；当1x <时，由()11f x x =-≤得0x ≥，故01x ≤<；所以()1f x ≤的解集为4{|0}3M x x =≤≤.(Ⅱ)由2()16814g x x x =-+≤得2116()4,4x -≤解得1344x -≤≤，因此13{|}44N x x =-≤≤，故3{|0}4M N x x =≤≤.当x MN ∈时，()1f x x =-，于是22()[()]()[()]x f x x f x xf x x f x +⋅=+2111()(1)()424x f x x x x =⋅=-=--≤.。

2014高考化学名校试题汇编---有机物的合成和推断2

专题14 有机物的合成和推断2【江西省吉安市二中2013届高三上学期周测】（10分）已知：（1）2ROH →R-O-R+H 2O (R 为烃基，R-O-R 为醚)（2）RCH=CH 2+HOCl →RCHOH-CH 2Cl RCH=CH 2+HOCl →RCHCl-CH 2OH试根据下列回答下列问题(1)写出结构简式A ________________，C ________________。

(2)从结构上分析，可与A 互为同分异构体的结构简式有：________________。

(3)上述反应中属于取代反应的是________________________________(填反应序号①②⑧④⑤⑥)(4)写出方程式：D+E=F________________________________________________________六、(本题包括2d 、题，共16分)【答案】(1)CH 2Cl —CH 2OH ， (CH=CH)2O(2)CH 3CH(OH)C1， CH 3OCH 2C1 (每正确一个给1分) (3)②④⑥(少选一个或二个得1分，多选不给分) (4)2ClCH 2－COOH+HO-CH 2-OHClCH 2COOCH 2CH 2OOCCH 2Cl+2H 2O【陕西省汉中市中学2013届高三上学期模拟考试】已知：（1）该反应的生成物中含有的官能团的名称是_______________，该物质在一定条件下能发生___________（填序号）：①银镜反应 ②酯化反应 ③还原反应（2）已知HCHO 分子中所有原子都在同一平面内。

若要使R 1CHO 分子中所有原子都在同一平面内，R 1可以是_____________（填序号）；① —CH 3 ②③ —CH=CH 2（3）某氯代烃A 的分子式为C 6H 11Cl ，它可以发生如下转化：结构分析表明E 分子中含有两个甲基且没有支链。

试回答：①写出C 的分子式：__________________________________________； ②写出A 、E 的结构简式：A__________________________________________________________、 E__________________________________________________________。

【推荐】2014年高考历史模拟新题分类汇编：专题02 中国古代的农耕经济(解析版)

专题二中国古代的农耕经济1．（2014·湖北孝感一模）《淮南子·修务训》云：“神农乃始教民播百谷，相土地，宜燥湿肥硗高下，尝百草之滋味，水泉之甘苦，令民知所辟就，当此之时，一日而遇七十毒。

”材料说明()A．中国农业历史悠久B．神农最早发现百谷C．“播百谷，相土地”就是垄作法D．中国原始农业和医药学同时产生【考点】古代中国的经济——原始农业【解析】神农相传是远古时代农业的发明者，“乃始教民播百谷”，故A项正确；神农“尝百草之滋味”，但无法推测最早发现百谷，故B项错误；垄作法最早出现在春秋战国时期，原始农业不可能使用垄作法，故C项错误；“百草”泛指农作物，故D项错误。

【答案】A2．（2014·四川广元一模）观察下列图片，你从中获取的信息主要是()骨耜石犁铁锄A．中国传统农业生产经历了粗放到精耕细作的演变B．中国传统农业工具以石器为主C．中国传统农业政策是重农抑商政策D．铁器的广泛使用反映了我国科学技术高度发达【答案】A【解析】考查学生提取信息的能力。

从骨、石制农具到铁制农具的进步，是中国古代农业生产技术的进步，铁制农具锋利、坚固、灵活、耐用、大大提高了农耕的效率，使得农业由粗放到精耕细作发展，故A项正确；春秋之后，中国农具以贴器为主，故B项错误；重农抑商政策从在题中没有体现，故C项错误；铁器的广泛使用从“铁锄”的图片中不能读出，故D项错误。

3．（2014·山东日照校际联合检测）“权耙扫帚扬场掀，碌碡簸箕使牛鞭；筛子抬筐麻袋囤，胶轮条筐和车绊……锄镰锨镢样样有，各种农具要健全。

”该农谣反映出古代农耕经济怎样的特点()A．自给自足B．精耕细作 C．男耕女织D．家庭经营【答案】B【解析】该农谣介绍中国古代“各种农具要健全”，改进生产工具的目的在于提高粮食单位面积产量，符合“精耕细作”的特点，故B项正确；A项是古代农业生产的目的，C、D项是古代农业的组织形式，都与材料无关，故A、C、D项错误。

高考英语试题七选五汇编(二)(2014)

高考英语试题七选五汇编（二）（2014）根据短文内容，从短文后的七个选项中选出正确的填入空白处。

选项中有两项为多余选项。

一2014北京卷Evaluating Sources (来源) of health InformationMaking good choices about your own health requires reasonable evaluation. A key first step in bettering your evaluation ability is to look carefully at your sources of healthy information. Reasonable evaluation includes knowing where and how to fins relevant information, how to separate fact from opinions, how to recognize poor reasoning, and how to analyze information and the reliability of sources. 71Go to the original source. Media reports often simplify the results of medical research. Find out for yourself what a study really reported, and determine whether it was based on good science. Think about the type of study. 73Watch for misleading language. Some studies will find that a behavior ―contributes to‖ or is ―associated with‖ an outcome; this does not mean that a certain course must lead to a certain result. 73 Carefully read or listen to information in order to fully understand it.Use your common sense. If a report seems too good to be true, probably it is. Be especially careful of information contained in advertisements. 74 Evaluate ―scientific‖ statements carefully, and be aware of quackery(江湖骗术).75 Friends and family members can be a great source of ideas and inspiration, but each of us needs to find a healthy lifestyle that works for us.Developing the ability to evaluate reasonably and independently about the health problems will serve you well throughout your life.A. Make choice that are right for you.B. The goal of an ad is to sell you something.C. Be sure to work through the critical questions.D. And examine the findings of the original research.E. Distinguish between research reports and public health advice.F. Be aware that information may also be incorrectly explained by an author‘s point of view.G. The following suggestions can help you sort through the health information you receive from common sources.二2014辽宁卷Eyesight plays a very important role in our daily life. Every waking moment, the eyes are working to see the world around us. Over forty percent of Americans worry about losing eyesight, but it's easy to include steps into our daily life to ensure healthy eyes. Here are five suggestions for a lifetime of healthy eyesight:Schedule yearly exams. 36 Experts advise parents to bring babies 6 to 12 months of age to the doctor for a careful check. The good news is that millions of children now can have yearly eye exams and following treatment,including eyeglasses.•Protect against UV rays (紫外线). Long-term stay in the sun creates risk to your eyes. No matter what the season is, it's extremely important to wear sunglasses. 37•Give your eyes a break. Two-thirds of Americans spend up to seven hours a day using computers or other digital products. 38 Experts recommend that people practice the 20/20/20 rule: every 20 minutes, take a 20-second break and look at something 20 feet away.•39 As part of a healthy diet, eat more fruits and vegetables each day. Vitamins C and E help protect eyesight and promote eye health.•Practice safe wear and care of contact lenses (隐形眼镜). Many Americans use contact lenses to improve their eyesight. While some follow the medical guidance for wearing contact lenses, many are breaking the rules and putting their eyesight at risk. 40 Otherwise, you may have problems such as red eyes, pain in the eyes, or a more serious condition.A. Eat your greens.B. Eye care should begin early in life.C. They can properly protect your eyes.D. Stay in good shape by taking more vitamins.E. Parents usually don‘t care about their own eyesight.F. Always follow the docto r‘s advice for appropriate wear.G. This frequent eye activity increases the risk for eye tiredness.三2014 浙江卷下面文章中有5个段落需要添加首句（第61—65题）。

【2022高考必备】2012-2021十年全国高考数学真题分类汇编-01集合(精解精析)

2012-2021十年全国卷高考真题分类汇编集合（精解精析）1．(2021年高考全国乙卷理科)已知集合{}21,S s s n n ==+∈Z ,{}41,T t t n n ==+∈Z ,则S T Ç=( )A ．∅B ．SC ．TD ．Z【结果】C思路：任取t T ∈,则()41221t n n =+=⋅+,其中n Z ∈,所以,t S ∈,故T S ⊆,因此,S T T = ．故选：C ．2．(2021年高考全国甲卷理科)设集合{}104,53M x x N xx ⎧⎫=<<=≤≤⎨⎬⎩⎭,则M N = ( )A ．103x x ⎧⎫<≤⎨⎬⎩⎭B ．143xx ⎧⎫≤<⎨⎬⎩⎭C ．{}45x x ≤<D ．{}05x x <≤【结果】B思路：因为1{|04},{|5}3M x x N x x =<<=≤≤,所以1|43M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭,故选：B ．【点睛】本题考查集合地运算,属基础题,在高考中要求不高,掌握集合地交并补地基本概念即可求解．3．(2020年高考数学课标Ⅰ卷理科)设集合A ={x |x 2–4≤0},B ={x |2x +a ≤0},且A ∩B ={x |–2≤x ≤1},则a =( )A ．–4B ．–2C ．2D ．4【结果】B【思路】求解二次不等式240x -≤可得：{}2|2A x x -=≤≤,求解一次不等式20x a +≤可得：|2a B x x ⎧⎫=≤-⎨⎬⎩⎭．由于{}|21A B x x ⋂=-≤≤,故：12a-=,解得：2a =-．故选：B ．【点睛】本题主要考查交集地运算,不等式地解法等知识,意在考查学生地转化能力和计算求解能力．4．(2020年高考数学课标Ⅱ卷理科)已知集合U ={−2,−1,0,1,2,3},A ={−1,0,1},B ={1,2},则()U A B ⋃=ð( )A ．{−2,3}B ．{−2,2,3}C ．{−2,−1,0,3}D ．{−2,−1,0,2,3}【结果】A思路：由题意可得：{}1,0,1,2A B ⋃=-,则(){}U 2,3A B =- ð．故选：A【点睛】本题主要考查并集，补集地定义与应用,属于基础题．5．(2020年高考数学课标Ⅲ卷理科)已知集合{(,)|,,}A x y x y y x =∈≥*N ,{(,)|8}B x y x y =+=,则A B 中圆素地个数为( )A ．2B ．3C ．4D ．6【结果】C思路：由题意,A B 中地圆素满足8y xx y ≥⎧⎨+=⎩,且*,x y N ∈,由82x y x +=≥,得4x ≤,所以满足8x y +=地有(1,7),(2,6),(3,5),(4,4),故A B 中圆素地个数为4．故选：C ．【点晴】本题主要考查集合地交集运算,考查学生对交集定义地理解,是一道容易题．6．(2019年高考数学课标Ⅲ卷理科)已知集合{}1,0,1,2A =-,2{|1}B x x =≤,则A B =( )A ．{}1,0,1-B ．{}0,1C ．{}1,1-D ．{}0,1,2【结果】A 【思路】因为{}1,0,1,2A =-,{}11B x x =-≤≤,所以{}1,0,1A B =- ,故选A ．【点评】本题考查了集合交集地求法,是基础题．7．(2019年高考数学课标全国Ⅱ卷理科)设集合{}2560A x x x =-+>,{}10B x x =-<,则A B =( )A ．(),1-∞B ．()2,1-C ．()3,1--D ．()3,+∞【结果】A.【思路】{}{25602A x x x x x =-+>=≤或}3x ≥,{}{}101B x x x x =-<=<,故{}1A B x x =< ,故选A ．【点评】本题主要考查一圆二次不等式,一圆二次不等式地解法,集合地运算,属于基础题．本题考点为集合地运算,为基础题目,难度偏易．不能领会交集地含义易致误,区分交集与并集地不同,交集取公共部分,并集包括二者部分．8．(2019年高考数学课标全国Ⅰ卷理科)已知集合{42}M x =-<<,2{|60}N x x x =--<,则M N =( )A ．{|43}x x -<<B ．{|42}x x -<<-C ．{|22}x x -<<D ．{|23}x x <<【结果】C 思路：2{|60}{|(2)(3)0}{|23},{|22}N x x x x x x x x M N x x =--<=+-<=-<<∴=-<< ．9．(2018年高考数学课标Ⅲ卷（理）)已知集合{}|10A x x =-≥,{}0,1,2B =,则A B = ( )A ．{}0B ．{}1C ．{}1,2D ．{}0,1,2【结果】C思路：{}{}|10|1A x x x x =-≥=≥,{}0,1,2B =,故{}1,2A B = ,故选C ．10．(2018年高考数学课标Ⅱ卷（理）)已知集合(){}223A x y xy x y =+∈∈Z Z ，≤，，,则A 中圆素地个数为( )A ．9B ．8C ．5D ．4【结果】A 思路：(){}{}223(1,1),(1,0),(1,1),(0,1),(0,0),(0,1),(1,1),(1,0),(1,1)A x y xy x y =+∈∈=-------Z Z ,≤,,,故选A ．11．(2018年高考数学课标卷Ⅰ（理）)己知集合{}220A x x x =-->,则R A =ð( )A ．{}12x x -<<B ．{}12x x -≤≤C ．{}{}12x x x x <-> D ．{}{}12x x x x ≤-≥ 【结果】B思路：集合{}220A x x x =+->,可得{}12A x x x =<->或,则{}-12R A x x =≤≤ð,故选：B ．地．【思路】解法一：常规解法∵ ∴ 1是方程地一个根,即,∴ 故解法二：韦达定理法∵ ∴ 1是方程地一个根,∴ 利用伟大定理可知：,解得：,故解法三：排除法∵集合中地圆素必是方程方程地根,∴ ,从四个选项A ﹑B ﹑C ﹑D 看只有C 选项满足题意．【知识拓展】集合属于新课标必考点,属于函数范畴,常与解方程﹑求定义域和值域﹑数集意义相结合,集合考点有二：1．集合间地基本关系。