2013年9月花都区高三摸底考试成绩汇总

合集下载

广东省2013届高三下学期入学摸底考试理科综合试题 Word版含答案

广东省2013届高三下学期入学摸底考试理科综合试题 Word版含答案理科物理试题一、单项选择题：本大题共16小题，每小题4分，共64分。

在每小题给出的四个选项中，只有一个选项符合题目要求，选对的得4分，选错或不答的得0分。

13.家用封闭在贮气瓶中的石油气可近似看成理想气体，当温度升高时，下列说法中正确的是(容器的热膨胀忽略不计)________． A ．密度不变，压强增大，内能增大 B ．密度不变，压强减小，内能增大 C ．密度增大，压强不变，内能减小 D ．密度减小，压强不变，内能不变 14．右图为两分子系统的势能p E 与两分子间距离r 的关系曲线。

下列说法正确的是 A ．当r 大于r 1时，分子间的作用力表现为引力 B ．当r 小于r 1时，分子间的作用力表现为引力 C ．当r 等于r 2时，分子间的作用力为零 D ．当r 由r 1变到r 2的过程中，分子间的作用力做负功15.在某驾校的训练场地上，有一段圆弧形坡道，如图所示，若将同一辆车先后停放在a 点和b 点，下述分析和比较正确的是（）A ．车在a 点受坡道的支持力大于在b 点受的支持力B ．车在a 点受坡道的摩擦力大于在b 点受的摩擦力C ．车在a 点受到的合外力大于在b 点受的合外力 R BvD ．车在a 点受的重力的下滑分力大于在b 点受的重力的下滑分力 16.如图所示，在磁感应强度为B 的水平匀强磁场中，有两根竖直放置的平行金属导轨，顶端用一电阻R 相连，两导轨所在的竖直平面与磁场方向垂直．一根金属棒ab 以初速度v 0沿导轨竖直向上运动，到某一高度后又向下运动返回到原出发点．整个过程中金属棒与导轨保持垂直且接触良好，导轨与棒间的摩擦及它们的电阻均可忽略不计．则在金属棒整个上行与整个下行的两个过程中，下列说法不正确的是（） A ．上行的运动时间小于下行的运动时间 B ．上行过程中通过R 的电量等于下行过程中通过R 的电量 C ．上行过程中R 上产生的热量大于下行过程中R 上产生的热量 D ．回到出发点的速度v 等于初速度v 0 二、双项选择题：本大题共9小题，每小题6分，共54分。

2013年摸底考试成绩汇总

十九里中学五马中学颜集中学张店中学全区平均全区合计
100 8.00% 十九里中学 135 14.81% 五马中学 124 38.71% 颜集中学 177 11.86% 张店中学 260.32 6.00% 全区平均 13016 全区合计
100 0.00% 十九里中学 135 11.11% 五马中学 124 23.39% 颜集中学 177 8.47% 张店中学 260.32 7.09% 全区平均 13016 全区合计
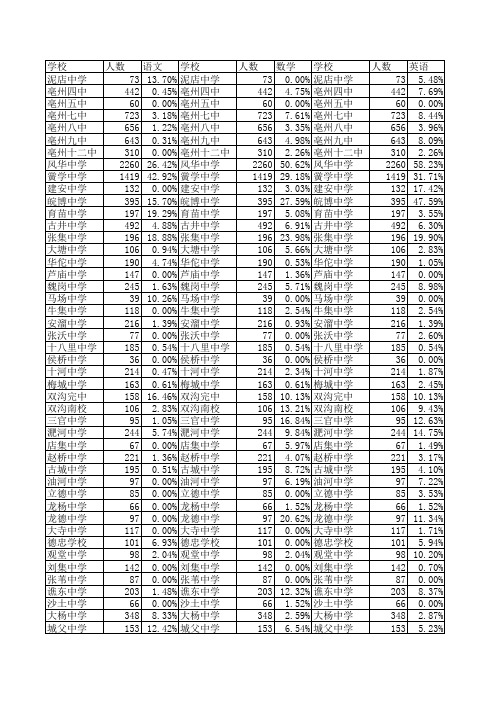
学校人数语文学校人数数学学校人数英语泥店中学 73 13.70% 泥店中学 73 0.00% 泥店中学 73 5.48% 亳州四中 442 0.45% 亳州四中 442 4.75% 亳州四中 442 7.69% 亳州五中 60 0.00% 亳州五中 60 0.00% 亳州五中 60 0.00% 亳州七中 723 3.18% 亳州七中 723 7.61% 亳州七中 723 8.44% 亳州八中 656 1.22% 亳州八中 656 3.35% 亳州八中 656 3.96% 亳州九中 643 0.31% 亳州九中 643 4.98% 亳州九中 643 8.09% 亳州十二中 310 0.00% 亳州十二中 310 2.26% 亳州十二中 310 2.26% 风华中学 2260 26.42% 风华中学 2260 50.62% 风华中学 2260 58.23% 黉学中学 1419 42.92% 黉学中学 1419 29.18% 黉学中学 1419 31.71% 建安中学 132 0.00% 建安中学 132 3.03% 建安中学 132 17.42% 皖博中学 395 15.70% 皖博中学 395 27.59% 皖博中学 395 47.59% 育苗中学 197 19.29% 育苗中学 197 5.08% 育苗中学 197 3.55% 古井中学 492 4.88% 古井中学 492 6.91% 古井中学 492 6.30% 张集中学 196 18.88% 张集中学 196 23.98% 张集中学 196 19.90% 大塘中学 106 0.94% 大塘中学 106 5.66% 大塘中学 106 2.83% 华佗中学 190 4.74% 华佗中学 190 0.53% 华佗中学 190 1.05% 芦庙中学 147 0.00% 芦庙中学 147 1.36% 芦庙中学 147 0.00% 魏岗中学 245 1.63% 魏岗中学 245 5.71% 魏岗中学 245 8.98% 马场中学 39 10.26% 马场中学 39 0.00% 马场中学 39 0.00% 牛集中学 118 0.00% 牛集中学 118 2.54% 牛集中学 118 2.54% 安溜中学 216 1.39% 安溜中学 216 0.93% 安溜中学 216 1.39% 张沃中学 77 0.00% 张沃中学 77 0.00% 张沃中学 77 2.60% 十八里中学 185 0.54% 十八里中学 185 0.54% 十八里中学 185 0.54% 侯桥中学 36 0.00% 侯桥中学 36 0.00% 侯桥中学 36 0.00% 十河中学 214 0.47% 十河中学 214 2.34% 十河中学 214 1.87% 梅城中学 163 0.61% 梅城中学 163 0.61% 梅城中学 163 2.45% 双沟完中 158 16.46% 双沟完中 158 10.13% 双沟完中 158 10.13% 双沟南校 106 2.83% 双沟南校 106 13.21% 双沟南校 106 9.43% 三官中学 95 1.05% 三官中学 95 16.84% 三官中学 95 12.63% 淝河中学 244 5.74% 淝河中学 244 9.84% 淝河中学 244 14.75% 店集中学 67 0.00% 店集中学 67 5.97% 店集中学 67 1.49% 赵桥中学 221 1.36% 赵桥中学 221 4.07% 赵桥中学 221 3.17% 古城中学 195 0.51% 古城中学 195 8.72% 古城中学 195 4.10% 油河中学 97 0.00% 油河中学 97 6.19% 油河中学 97 7.22% 立德中学 85 0.00% 立德中学 85 0.00% 立德中学 85 3.53% 龙杨中学 66 0.00% 龙杨中学 66 1.52% 龙杨中学 66 1.52% 龙德中学 97 0.00% 龙德中学 97 20.62% 龙德中学 97 11.34% 大寺中学 117 0.00% 大寺中学 117 0.00% 大寺中学 117 1.71% 德忠学校 101 6.93% 德忠学校 101 0.00% 德忠学校 101 5.94% 观堂中学 98 2.04% 观堂中学 98 2.04% 观堂中学 98 10.20% 刘集中学 142 0.00% 刘集中学 142 0.00% 刘集中学 142 0.70% 张苇中学 87 0.00% 张苇中学 87 0.00% 张苇中学 87 0.00% 谯东中学 203 1.48% 谯东中学 203 12.32% 谯东中学 203 8.37% 沙土中学 66 0.00% 沙土中学 66 1.52% 沙土中学 66 0.00% 大杨中学 348 8.33% 大杨中学 348 2.59% 大杨中学 348 2.87% 城父中学 153 12.42% 城父中学 153 6.54% 城父中学 153 5.23%

2013年广州市中考各批次录取分数线

2013年广州市高中阶段学校招生各批次录取最低控制分数线区、县普通高中中等职业学校提前批第一批第二批第三批优先公费择校民办优先公费择校民办优先公费择校民办优先公费择校民办老三区702645635645610595610595550520--465不设录取最低控制分数线，实行分段投档。

天河区645607580607592550--白云区625545540550485485--黄埔区625568558550513505--番禺区630530520550485485--花都区620530520550485485--南沙区630530520550485485--萝岗区625530520--------增城市625550525550490490465从化市610540530550480480--注：“老三区”指荔湾、越秀、海珠三区。

2013年广州市普通高中学校录取分数(提前批)2013年广州市普通高中提前批招生学校录取工作于7月9日进行，现将录取分数公布如下：序号学校名称录取类别招生区域最低分数最低分数末位同分序号末位考生志愿序号末位考生分数末位考生分数同分序号外区最低分数外区最低分数末位同分序号外区末位考生志愿序号外区末位考生分数外区末位考生分数同分序号1华南师范大学附属中学公费全市72831172831择校全市726712726712广东实验中学公费全市72072172072自筹全市7112152711215 3广东广雅中学公费全市71611171611择校全市71894271894 4广州市执信中学公费全市7201151720115择校全市72087272087 5广州市第二中学公费全市7101601710160择校全市71514271514 6广州市第六中学公费全市6951041695104择校全市7081642708164 7广东华侨中学公费全市6423803642162择校全市6503332650333 8广州市协和中学公费全市6561151656115择校全市68628726862879广州大学附属中学（黄华路校区）公费全市70026170026择校全市70212637153010广州大学附属中学（大学城校区）公费全市7023362705278择校全市7114427114411广州市铁一中学（亚运城校区）公费全市68292168292择校全市6988826988812广州市铁一中学(校本部)公费全市7012601701260择校全市692138269213813广州市第一中学公费全市64534626613206573981657398择校全市678272678276793732679373 14广州市第四中学公费全市6453122654226463012655231择校全市66236126623616662172666217 15广州市真光中学公费全市6806016806068060168060择校全市68829226882927012882701288 16广州市第三中学公费全市64536426723436453642673312择校全市6639326639317广州市第七中学公费全市66037716603776682481668248择校全市6938826938869632696318广州市第十六中学公费全市66235816623586643441664344择校全市688612688616886126886119广州市培正中学公费全市6547216547265472165472择校全市663472663476861882686188 20广州市育才中学公费全市645300267510064774267664择校全市65738826573886603932660393 21广州市第五中学公费全市6453422673107660442678139择校全市66012526601256772492677249 22广州市南武中学公费全市6394103644278640340365910择校全市6621052662105663414266341423广州市第四十七中学公费全市67829116782916782541678254择校全市6923602692360692360269236024广州市第八十九中学公费全市645250365119464934436574择校全市666186266618625广州市天河中学公费全市660381660386631061663106择校全市68620726862076873052687305 26广州市培英中学公费全市648851648856491181649118择校全市70082700827广州市第六十五中学(校本部)公费全市64534936452936502113650211择校全市679392267939228广州市第六十五中学（同德校区）公费全市648563648566511323651132择校全市649349264934929广州市第八十中学公费全市64534156751466501565675146择校全市66327626632766644726644730广州市第八十六中学公费全市6103043659301635716357择校全市6591412659141674120267412031广东仲元中学公费全市69216316921636952491695249择校全市7025427025470340270340 32广东番禺中学公费全市6605816605866195166195择校全市68662268662688273268827333广州市番禺区实验中学公费番禺和三镇645221265338834广州市番禺区象贤中学公费全市653141653146592631659263择校全市674156267415635广州市禺山高级中学公费全市63036346431076302624666278择校全市635365368213963835368213936广东第二师范学院番禺附属中学公费全市64535046462086553342655334择校全市63629636583546536826536837广州市花都区秀全中学公费全市66235316623536663101666310择校全市67421326742137035837035838广州市花都区邝维煜纪念中学公费全市626329363429643262365458择校全市6353573666118647293366814439广州市花都区新华中学公费全市602301360314160596360976择校全市6353714663271644210466630340广州市南沙第一中学公费全市65169165169择校全市661341266134141广州市玉岩中学公费全市6353153683256541651654165择校全市67624426762446761182676118 42增城市增城中学公费全市67135316713536863511686351择校全市67322526732256783322678332 43增城市新塘中学公费全市6453674648152择校全市63924736691056431582643158 44从化市从化中学公费全市63426836582116402563658211择校全市63725236461026391373646102 45从化市第六中学公费全市61232736172416122723618280择校全市65112336511236511233651123 46华师附中南海实验高中民办全市6583631658363说明：1.“最低分数末位同分序号”是指向该校投档考生最低分数的同分最大排位序号。

2013年普通高等学校招生全国统一模拟考试

2013年普通高等学校招生全国统一模拟考试（广东卷）语文参考答案及评分标准题号分值答案说明1 3 C A．léi／lèi，shè／niè，jī／jī；B．chù／chù，qiú／qiú，fāng／fáng；C．xiàng／hàng，zhé／zhì，xiè／jiě；D．qiǎn／qiǎn，zhēng／zhèng，jiān／qiān。

2 3 B 炙手可热：指手一挨近就感觉到热，比喻气焰很盛，权势很大。

贬义。

3 3 B A成分残缺，“表达”缺少主语，在“响起”后面加“的”；C关联词使用不当，把“而且”改为“但”；D“防止资金投向实体经济”有误，把“防止”改为“确保”。

4 3 D 第一步，确定首句。

比较⑥②两句，其中第⑥句中的“有兴趣”跟“国学热”在内容上紧密相联，故选⑥。

第二步，根据句子间的逻辑关系确定句序。

第⑥句中的“本是”与第③句的“但”构成转折关系；第③句中的“…轻浮‟的文化争论”与第⑤句中的“随便地进行谈判”在内容上紧密相联；而第①句是通过打比方的方法对第⑤句的解说；第①句与第④句构成递进关系。

5 3 A 滋：滋生、蔓延。

6 3 C A以：连词，表目的/连词，表原因；B焉：兼词，于此/疑问代词，什么；C均表修饰关系；D之：助词，用于主谓之间，取消句子独立性/助词，的。

7 3 A ①“其心洒然而醒”是“乐”的实质，虽然是“或醉且劳”者之乐，但是也是欧阳公之乐；②由“一山之隅，一泉之旁，岂公乐哉”可知这不是“公之乐”；③④由“天下之学者，皆为才且良，夷狄鸟兽草木之生者，皆得其宜，公乐也”可知均是“公之乐”；⑤是写同游者的“喜”与“幸”。

8 3 C “这种…乐‟就在于…一山之隅，一泉之旁‟的山水之乐”错。

原文已经说明，欧阳公的“乐”是建立一个“和谐的社会”：国君无为不治，百姓安居乐业，人才各显其能，万物自然生长。

2013秋季学期高三期末考试成绩

地理历史 41 41 1889 1582 46.07 38.59 86 73 12 16 7 3 17.07317 7.317073 1 0 2.439024 0 何军华卢少梅地理历史 41 41 1868 1430 45.56 34.88 68 61 19 12 6 2 14.63415 4.878049 0 0 0 0
英语 40 2557 63.93 106 26 4 10 0 0 周泉英语 30 1169 38.97 78 28 0 0 0 0 张月芳英语 41 1558 38.00 64 25 0 0 0 0 邹贤英英语 41 1492 36.39 54 22 0 0 0 0
政治 40 1793 44.83 75 16 4 10 0 0 冉孟永政治 35 1052 30.06 50 0 0 0 0 0 樊扬兴政治 41 1290 31.46 52 13 0 0 0 0 冉孟永政治 41 1132 27.61 50 6 0 0 0 0
5班语文人数 35 总分 2513 平均分 71.80 最高分 96 最低分 19 及格人数 2 及格率 5.714286 优秀人数 0 优秀率 0 任课教师廖崃利 6班语文人数 41 总分 2936 平均分 71.61 最高分 97 最低分 28 及格人数 1 及格率 2.439024 优秀人数 0 优秀率 0 任课教师廖崃利 7班语文人数 41 总分 2948 平均分 71.90 最高分 93 最低分 13 及格人数 4 及格率 9.756098 优秀人数 0 优秀率 0
4班人数总分平均分最高分最低分及格人数及格率优秀人数优秀率任课教师
语文 40 3764 94.10 109 78 28 70 0 0 杨威桢

2013年花都区一模及参考答案

2013年花都区九年级语文综合测试题（全卷满分150分，考试时间为120分钟）第一部分积累与运用（共34分）一、（6小题，19分）1．下列词语中，每对加点字的读音都相同的一项是（） (3分) A．迸．射/骈．进立刻．/恪．尽职守 B. 祈．祷/菜畦．悄悄．/惟妙惟肖．C. 猝．死/憔悴．诘．问/鳞次栉．比D. 诓．骗/竹筐．明显．/鲜．为人知2．下列词语中，没有．．错别字的一组是( ) (3分)A．混淆孤漏寡闻寒噤山崩地裂B．炫耀锋芒毕露挑衅黯然失色C．呵责不容置疑稀疏根深缔固D．销毁冥思暇想揣摩味同嚼蜡3. 下面语段中，加点的词语运用不恰当．．．的一项是（）（3分）2013年3月1日下午，在广州珠江边发生了一件英雄舍己救人．．．．的事。

一对夫妇在珠江西堤码头游玩。

那位先生在后退时不慎被铁链绊腿掉进珠江。

在这雷霆万钧．．．．地．．．．之际，途经此处的武警战士郑益龙毫不犹豫跳进江中救人。

由于江水湍急，当郑益龙把落水之人救上岸后，他却因体力不支被水流冲走了。

他牺牲了，但他的精神永垂不朽．．．．。

A. 舍己救人B. 雷霆万钧C. 毫不犹豫D. 永垂不朽4. 下面句子中没有语病的一项是（）（3分）A. 近段时间，H7N9禽流感肆虐，广州部分观鸟景点寥寥无人，人们更是谈鸡、谈鸟色变。

B. 今年2月23日，广东河源地区发生大约里氏4.8级左右的地震，我区也有震感。

C. 在身体虚弱和严重缺氧的情况下，登山运动员摸黑进行高山行军，这不仅相当危险，而且很困难。

D. 近几年，国产奶粉的质量问题频发，从客观上推进了我国消费者对“洋奶粉”的依赖心理，使得“洋奶粉”格外受宠。

5．罗董事长的三位朋友分别在今天过七十大寿、乔迁新居、分店开幕。

如果你是董事长的秘书，下面三副对联该如何送才恰当？（）（3分）（甲）祥云浮紫阁，喜气溢朱门（乙）交以道接以礼，近者悦远者来（丙）室有芝兰春自永，人如松柏岁长新A．甲送给过七十大寿者；乙送分店开幕者；丙送乔迁新居者。

2013年广州市高三第二次模拟考试试题答案

2013年广州市普通高中毕业班综合测试（二）数学（文科）试题参考答案及评分标准说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力对照评分标准给以相应的分数．2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，选择题和填空题不给中间分．一、选择题：本大题考查基本知识和基本运算．共10小题，每小题5分，满分50分．二、填空题：本大题查基本知识和基本运算，体现选择性．共5小题，每小题5分，满分20分．其中14~15题是选做题，考生只能选做一题．第13题第一个空2分，第二个空3分．11．14π- 12 13．36；3981 14．1415三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题主要考查随机抽样、平均数、古典概型等基础知识，考查数据处理能力，本小题满分12分）解：（1）高三文科（1）班抽取的8名学生视力的平均值为4.42 4.62 4.82 4.95.14.78⨯+⨯+⨯++=．据此估计高三文科（1）班学生视力的平均值约为4.7．……………………………3分（2）因为高三文科六个班学生视力的平均值分别为4.3、4.4、4.5、4.6、4.7、4.8，所以任意抽取两个文科班学生视力的平均值数对有()4.34.4，，()4.34.5，，()4.34.6，，()4.34.7，， ()4.34.8，，()4.44.5，，()4.44.6，，()4.44.7，，()4.44.8，，()4.54.6，，()4.54.7，，()4.54.8，，()4.64.7，，()4.64.8，，()4.74.8，，共15种情形．……………………………………7分其中抽取的两个班学生视力的平均值之差的绝对值不小于0.2的有()4.34.5，，()4.34.6，，()4.34.7，，()4.34.8，，()4.44.6，，()4.44.7，，()4.44.8，，()4.54.7，，()4.54.8，，()4.64.8，，共10种． ………10分所以抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率为102=153． ………………12分17．（本小题主要考查解三角形等基础知识，考查正弦定理与余弦定理的应用，本小题满分12分）解：（1）在△ABC 中，因为80AB =m ，70BC =m ，50CA =m ，由余弦定理得222cos 2AB AC BC BAC AB AC+-∠=⨯⨯ ………………………………………………………2分2228050701280502+-==⨯⨯． ………………………………………3分因为BAC ∠为△ABC 的内角，所以3BAC π∠=．…………………………………4分（2）方法1：因为发射点O 到A 、B 、C 三个工作点的距离相等，所以点O 为△ABC 外接圆的圆心．……………………………………………………5分设外接圆的半径为R ，在△ABC 中，由正弦定理得2sin BCR A=， ……………………………………………7分因为70BC =，由（1）知3A π=，所以sin A =．所以2R ==R =．………8分过点O 作边BC 的垂线，垂足为D ，……………9分在△OBD中，OB R ==，703522BC BD ===，所以OD ==………………………………………………………11分=．所以点O 到直线BCm ．………………12分方法2：因为发射点O 到A 、B 、C 三个工作点的距离相等，所以点O 为△ABC 外接圆的圆心．……5分连结OB ，OC ，过点O 作边BC 的垂线，垂足为D ， ………6分由（1）知3BAC π∠=，所以3BOC 2π∠=．所以3BOD π∠=．………………………………………………………………9分在Rt △BOD 中，703522BC BD ===，所以35tan tan 60BD OD BOD ===∠11分所以点O 到直线BCm ．…………………………………12分 18．（本小题主要考查空间直线与平面的位置关系和几何体的体积计算等基础知识，考查空间想象能力等，本小题满分14分）（1）证明：因为90PAB PAC ∠=∠=，所以PA AB ⊥，PA AC ⊥．……………1分因为ABAC A =，所以PA ⊥平面ABC ．…………………………………2分因为BC ⊂平面ABC ，所以BC PA ⊥．……………………3分因为90ACB ∠=，所以BC CA ⊥．……………………………………………4分因为PACA A =，所以BC ⊥平面PAC ．……………………………………5分因为BC ⊂平面PBC ，所以平面PBC ⊥平面PAC ．………………………6分（2）方法1：由已知及（1）所证可知，PA ⊥平面ABC ，BC CA ⊥，所以PA 是三棱锥P ABC -的高．………………7分因为1PA=，=2AB ，设BC x =()02x <<，…8分PAB所以AC===．…9分因为13P ABC ABCV S PA-=⨯△16=………………………………………………10分=()224162x x+-≤⨯………………………………………………11分13=．……………………………………………………………12分当且仅当224x x=-，即x=时等号成立．………………………13分所以当三棱锥P ABC-的体积最大时，2=BC．…………………………14分方法2：由已知及（1）所证可知，PA⊥平面ABC，所以PA是三棱锥P ABC-的高．…………………………………7分因为90ACB∠=，设ABCθ∠=02πθ⎛⎫<<⎪⎝⎭，……………………8分则cos2cosBC ABθθ==，sin2sinAC ABθθ==．………………9分所以112cos2sin sin222ABCS BC ACθθθ=⨯⨯=⨯⨯=△．………………10分所以13P ABC ABCV S PA-=⨯△1sin23θ=．…………………………………11分因为02πθ<<，所以当4πθ=，P ABCV-有最大值13．……………………………12分此时2cos4BCπ==．……………………………………………13分所以当三棱锥P ABC-的体积最大时，2=BC．…………………………14分19．（本小题主要考查等差数列、裂项法求和等基础知识，考查运算求解能力和推理论证能力等，本小题满分14分）解：（1）设等差数列{}n a的公差为d，因为1235,7.a a a +=⎧⎨=⎩即1125,27.a d a d +=⎧⎨+=⎩……………………………………2分解得11,3.a d =⎧⎨=⎩ ………………………………………………………3分所以()()1113132n a a n d n n =+-=+-=-．所以数列{}n a 的通项公式为32n a n =-*()n ∈N ． ………………………4分（2）因为()()111111323133231n n a a n n n n +⎛⎫==- ⎪-+-+⎝⎭， ……………………5分所以数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和1223341111111n n nn n S a a a a a a a a a a -+=+++++ 1111111111111113434737103353233231n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+- ⎪ ⎪ ⎪ ⎪ ⎪---+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭11133131nn n ⎛⎫=-= ⎪++⎝⎭．……………………………………………7分假设存在正整数m 、n ，且1m n <<，使得1S 、m S 、n S 成等比数列，则21m n S S S =．………………………………………………………8分即2131431m n mn ⎛⎫=⨯ ⎪++⎝⎭．………………………………………………9分所以224361m n m m =-++．因为0n >，所以23610m m -++>．即23610m m --<．因为1m >，所以113m <<<．因为*m ∈N ，所以2m =．……………………………………12分此时22416361m n m m ==-++．………………………………………………………13分所以存在满足题意的正整数m 、n ，且只有一组解，即2m =，16n =． ……14分20．（本小题主要考查函数的单调性和最值等基础知识，考查数形结合思想、分类讨论思想和运算求解能力等，本小题满分14分）解：（1）因为函数2()2ln f x x a x =-，所以函数()f x 的定义域为(0,)+∞．……………………………………1分且2()2af x x x'=-．………………………………………………………2分若()f x 在定义域上是增函数，则2()20af x x x'=-≥在(0,)+∞上恒成立．…………………………………3分即2a x ≤在(0,)+∞上恒成立，所以0a ≤． ………………………4分由已知0a ≠，所以实数a 的取值范围为(),0-∞．…………………………………………5分（2）①若0a <，由（1）知，函数2()2ln f x x a x =-在区间[1,2]上为增函数．所以函数()f x 在区间[1,2]上的最小值为(1)1f =．……………………………6分②若0a >，由于222()x a f x x -'==所以函数()f x 在区间(上为减函数，在区间)+∞上为增函数．…………7分1≤，即01a <≤时，)[1,2]⊂+∞，函数2()2ln f x x a x =-在区间[1,2]上为增函数，所以函数()f x 在[1,2]的最小值为(1)1f =．…………………………9分（ⅱ）若12<≤，即14a <≤时，函数2()2ln f x xa x =-在区间(为减函数，在)2上为增函数，所以函数()f x 在区间[1,2]上的最小值为ln f a a a =-．……………11分2>，即4a >时，([1,2]⊂，函数()f x 在区间[1,2]上为减函数，所以函数()f x 在[1,2]的最小值为(2)42ln 2f a =-． ………………………13分综上所述，当1a ≤且0a ≠时，函数()f x 在区间[1,2]上的最小值为(1)1f =．当14a <≤时，函数()f x 在区间[1,2]的最小值为ln fa a a =-．当4a >时，函数()f x 在区间[1,2]上的最小值为(2)42ln 2f a =-．……14分21．（本小题主要考查动点的轨迹和直线与圆锥曲线的位置关系、导数的几何意义等基础知识，考查运算求解能力和推理论证能力等，本小题满分14分）解：（1）方法1：设动圆圆心为(),x y1分整理，得24x y =．所以轨迹M 的方程为24x y =．…………………………2分方法2：设动圆圆心为P ，依题意得点P 到定点()0,1F 的距离和点P 到定直线1y =-的距离相等，根据………………1分且其中定点()0,1F 为焦点，定直线1y =-为准线．所以动圆圆心P 的轨迹M 的方程为24x y =．………2分（2）由（1）得24x y =，即214y x =，则12y x '=．设点2001,4D x x ⎛⎫⎪⎝⎭，由导数的几何意义知，直线的斜率为012BC k x =．…………………………3分由题意知点2001,4A x x ⎛⎫- ⎪⎝⎭．设点2111,4C x x ⎛⎫ ⎪⎝⎭，2221,4B x x ⎛⎫ ⎪⎝⎭，则2212120121114442BCx x x x k x x x -+===-，AB CDOxylE即1202x x x +=．…………………………4分因为2210101011444ACx x x x k x x --==+，2220202011444AB x x x x k x x --==+．……………5分由于()120102020444AC AB x x x x x x x k k +---+=+==，即AC AB k k =-．……6分所以BAD CAD ∠=∠．……………………………………………………7分（3）方法1：由点D 到ABBAD ∠45=．……………8分不妨设点C 在AD 上方（如图），即21x x <，直线AB 的方程为：()20014y x x x -=-+．由()20021,44.y x x x x y ⎧-=-+⎪⎨⎪=⎩解得点B 的坐标为()20014,44x x ⎛⎫-- ⎪⎝⎭．……………………………10分)()042x ---=-．由（2）知CAD BAD ∠=∠45=，同理可得2AC =+．…………11分所以△ABC的面积20122244202S x =⨯-⨯+=-=，解得03x =±．………………………………………………………………12分当03x =时，点B 的坐标为11,4⎛⎫- ⎪⎝⎭，32BC k =，直线BC 的方程为()13142y x -=+，即6470x y -+=．…………………………13分当03x =-时，点B 的坐标为497,4⎛⎫- ⎪⎝⎭，32BC k =-，直线BC 的方程为()493742y x -=-+，即6470x y +-=． …………………14分方法2：由点D 到ABBAD ∠45=．……………8分由（2）知CAD BAD ∠=∠45=，所以CAB ∠90=，即AC AB ⊥．由（2）知104AC x x k -=，204AB x x k -=．所以1020144AC ABx x x xk k --=⨯=-．即()()102016x x x x --=-． ① 由（2）知1202x x x +=． ②不妨设点C 在AD 上方（如图），即21x x <，由①、②解得10204,4.x x x x =+⎧⎨=-⎩………10分2=-，同理2AC =+． …………………………………………………11分以下同方法1．。

2013年度广州中考各高中录取分数线

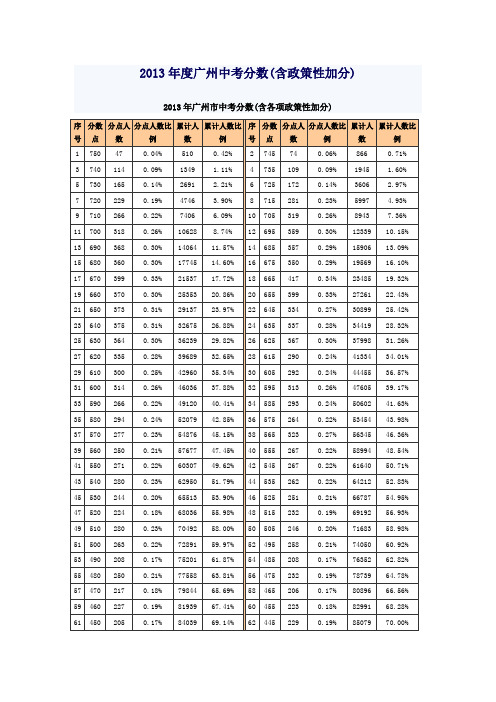
2013年度广州中考分数(含政策性加分) 2013年广州市中考分数(含各项政策性加分)序号分数点分点人数分点人数比例累计人数累计人数比例序号分数点分点人数分点人数比例累计人数累计人数比例1750470.04%5100.42%2745740.06%8660.71% 37401140.09%1349 1.11%47351090.09%1945 1.60% 57301650.14%2691 2.21%67251720.14%3606 2.97% 77202290.19%4746 3.90%87152810.23%5997 4.93% 97102660.22%7406 6.09%107053190.26%89437.36% 117003180.26%106288.74%126953590.30%1233910.15% 136903680.30%1406411.57%146853570.29%1590613.09% 156803600.30%1774514.60%166753500.29%1956916.10% 176703990.33%2153717.72%186654170.34%2348519.32% 196603700.30%2535320.86%206553990.33%2726122.43% 216503730.31%2913723.97%226453340.27%3089925.42% 236403750.31%3267526.88%246353370.28%3441928.32% 256303640.30%3623929.82%266253670.30%3799831.26% 276203350.28%3968932.65%286152900.24%4133434.01% 296103000.25%4296035.34%306052920.24%4445536.57% 316003140.26%4603637.88%325953130.26%4760539.17% 335902660.22%4912040.41%345852930.24%5060241.63% 355802940.24%5207942.85%365752640.22%5345443.98% 375702770.23%5487645.15%385653230.27%5634546.36% 395602500.21%5767747.45%405552670.22%5899448.54% 415502710.22%6030749.62%425452670.22%6164050.71% 435402800.23%6295051.79%445352620.22%6421252.83% 455302440.20%6551353.90%465252510.21%6678754.95% 475202240.18%6803655.98%485152320.19%6919256.93% 495102800.23%7049258.00%505052460.20%7168358.98% 515002630.22%7289159.97%524952580.21%7405060.92% 534902080.17%7520161.87%544852080.17%7635262.82% 554802500.21%7755863.81%564752320.19%7873964.78% 574702170.18%7984465.69%584652060.17%8089666.56% 594602270.19%8193967.41%604552230.18%8299168.28% 614502050.17%8403969.14%624452290.19%8507970.00%634402210.18%8615070.88%644352190.18%8719071.73% 654301950.16%8822672.59%664252010.17%8925673.43% 674201990.16%9021574.22%684151930.16%9116875.01% 694102090.17%9214275.81%704051830.15%9310476.60% 714001850.15%9402277.36%723951730.14%9493178.10% 733902280.19%9589178.89%743851690.14%9677379.62% 753801720.14%9766280.35%763751570.13%9853281.07% 773701770.15%9940481.78%783651780.15%10023882.47% 793601730.14%10110783.18%803551460.12%10191283.85% 813501660.14%10274884.53%823451420.12%10345685.12% 833401680.14%10424585.77%843351710.14%10500386.39% 853301510.12%10581187.06%863251690.14%10655987.67% 873201350.11%10724088.23%883151450.12%10794388.81% 893101310.11%10865689.40%903051450.12%10933189.95% 913001320.11%10996490.47%备注：1.分点人数：指中考成绩(含各项政策性加分)为该分数点的人数;2.分点人数比例：指中考成绩(含各项政策性加分)为该分数点的人数占考生总人数的比例;3.累计人数：指中考成绩(含各项政策性加分)在该分数点及以上的人数;4.累计人数比例：指中考成绩(含各项政策性加分)在该分数点及以上的人数占考生总人数的比例。

广州市2013届高三年级调研测试答案

广州市2013届高三年级调研测试理科综合参考答案一、单项选择题：本题包括16小题，每小题4分，共64分。

每小题给出的四个选项中，二、双项选择题：本题包括9小题，每小题6分，共54分。

每小题给出的四个选项中，有两个选项符合题目要求。

全选对得6分，只选1个且正确得3分，错选、不选得0分。

三、非选择题：本题包括11小题，共182分。

26.（16分，每空2分）（1）（2）植物Ⅰ主要在夜间吸收CO2，植物Ⅱ主要在白天吸收CO2Ⅰ自然选择（进化）（3）光照强度（光照）、温度、无机盐（矿质元素）（任答二项）（4）糖类中的化学能转化为ATP中的化学能和热能[H]和ATP ①②27.（16分，除说明外，每空2分）（1）Ⅰ（1分）（2）AaX b Y 6 (3)aaX B X B3/16（4）用aaX b Y个体对其测交（5）基因b突变成基因B（答基因突变1分）（6）构建含抗虫基因的基因表达载体（1分），将其导入紫花植株的体细胞中（1分），再利用植物组织培养出含抗虫基因的紫花品种（1分）（或答抗虫基因的检测与鉴定）。

28.（16分，每空2分）（1）胰岛素葡萄糖载体胰岛素（的浓度）、胰岛素受体（的数目）（2）胰高血糖素（肾上腺素）（3）Ⅰ型自身免疫Ⅱ型（4）核糖体、内质网、高尔基体29.（16分，每空2分）（1）C（2）丙产生（少量）甲醛（3）A 肝脏具有解除甲醛毒害的功能（4）②等量肝脏培养液染色体的形态和数目 ③B 30．（16分）（1）2 ； 2.5 （每空3分）（2）②和③ ； ①和② （每空2分）（3）0.010或1.0 ×10-2 （3分，0.01得2分）（4）如右图（3分。

标注1分，正确做图2分）31．（16分）（1）放热（2分）CH 4(g)+H 2O(g)=CO(g)+3H 2 (g) ΔH=+161.1kJ•mol -1 （4分）（化学方程式书写占2分，未配平不给分，未标注状态得1分；反应热计算占2分，漏“+”且数值正确，得1分）（2）①K ＝c(H 2O)/[c(CO 2) • c 2(NH 3)] （3分）；100 L 2•mol -2 （3分，未写单位不扣分）； ②AB （4分。

2013年广东省广州一模分数线

2013年广东省广州一模分数线
2013年广州“一模”分数线预计文科重点线为556分，理科重点线为563分。

2012年广州一模相关信息：
根据近5年广州考生在全省高考上线率的平均数划线，今年广州“一模”文科重点线为554分，理科重点线为559分;其中，超重点本科线的广州考生有6140人，超过25000人能读上本科。

■成绩公布
理科重点率比文科高两倍
事实上，在广州“一模”情况公布前几天，网上已流传出各种民间版本。

从昨日公布的官方数据来看，与民间预测版本基本一致：文科一本上线分数为554分，本A线为505分，本B线为469分;理科方面，一本上线分数为559分，本A线490分，本B线444分。

而要上大专，文科需要在424分以上，理科需要在376分以上。

2013年广州市普通高中学校录取分数(已排版)

661
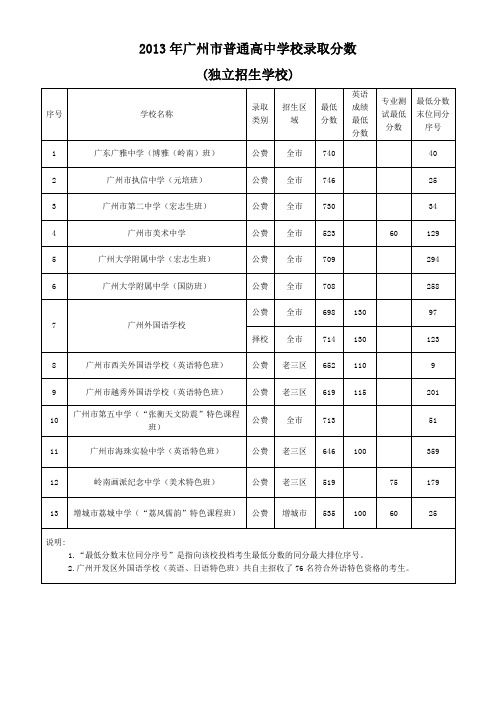
341
2
661
341
41
广州市玉岩中学
公费
全市
635
315
3
683
25
654
165
1
654
165
择校
全市
676
244
2
676
244
676
118
2
676
118
42
增城市增城中学
公费
全市
671
353
1
671
353
686
351
1
686
351
择校
全市
673
225
2
673
225
678
332
2
678
332
19
广州市培正中学
公费
全市
654
72
1
654
72
654
72
1
654
72
择校
全市
663
47
2
663
47
686
188
2
686
188
20
广州市育才中学
公费
全市
645
300
2
675
100
647
74
2
676
64
择校
全市
657
388
2
657
388
660
393
2
660
393
21
广州市第五中学
公费
全市
645
342
2
公费
番禺和三镇
645

2013届广州市调研测文科综合答案

松宝联考2013届高三年级调研测试文科综合参考答案、选择题：本题包括35小题，每小题4分，共140分。

每小题给出的四个选项中，只有一个选项符合题目要求。

多选、错选均不得分。

36. （26 分）评卷提示：依据本标准评卷，从一而终，宽严有度；踩点与踩意结合，其他表述，可酌情赋分。

（1）（5分）①该省的企业信用规模与GDP都在逐年增长，信用规模的增长快于GDP勺增长。

（2分）②企业信用规模的扩张对经济增长的拉动作用明显，两者呈正相关关系。

（3分）（2）（9分）①市场调节具有自发性。

（2分）政府运用法律手段和行政手段开展“三打两建”有利于调节和规范经济秩序，弥补市场调节的不足。

（1分）②只有具备公正、公平的市场秩序，形成统一开放、竞争有序的现代市场体系，市场才能合理配置资源。

（2分）“三打两建”有利于促进广东省各地加强市场监管，建立和规范良好的市场秩序，完善社会主义市场经济体系。

（1分）③诚实信用是现代市场经济正常运行必不可少的条件。

建立健全社会信用体系既是完善社会主义市场经济的一项重要制度建设，也是整顿和规范市场经济秩序的治本之策。

（2分。

只答前一句得1分，只答后一句得2分）“三打两建”有利于促进广东省尽快健全社会信用体系，尤其是加快建立信用监督和失信惩戒制度，促进信用规模的进一步发展。

（1分）评分说明：若考生从市场经济是法制经济的角度回答，且言之成理，加2分。

（3）（12分）①政府要坚持为人民服务的工作态度。

（2分）三打两建”要让人民群众得到实惠，对欺行霸市、制假售假等行为严厉打击，维护人民群众利益。

（2分）②树立求真务实的工作作风。

（2分）三打两建”要着力解决食品药品等市场经济发展中最突出的问题，切实整顿和规范市场秩序。

（2分）③坚持从群众中来到群众中去的工作方法。

（2分）“三打两建”要广泛宣传发动群众积极参与，举报违法犯罪。

（2分）37. （26 分）评卷提示：依据本标准评卷，从一而终，宽严有度；踩点与踩意结合，其他表述，可酌情赋分。

13年分数分布

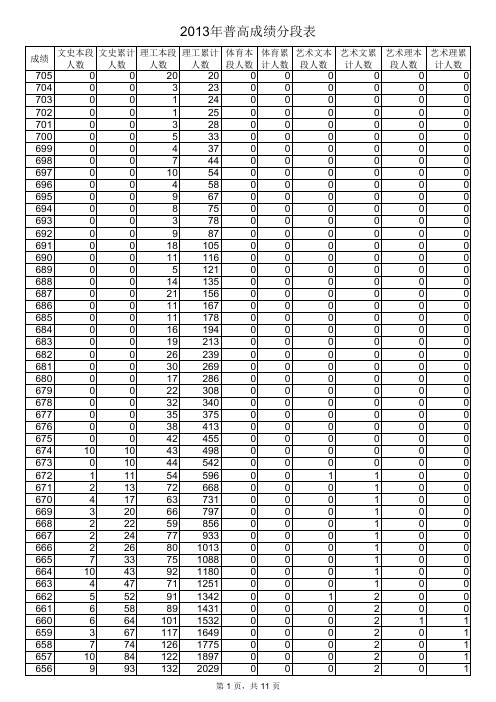
3187 3350 3513 3710 3883 4060 4254 4441 4647 4876 5081 5301 5540 5752 6000 6239 6498 6764 7014 7302 7614 7910 8204 8508 8847 9158 9487 9828 10167 10556 10904 11245 11617 11968 12322 12702 13129 13576 13964 14378 14766 15191 15566 15997 16419 16838 17280 17707 18169
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
93 102 111 133 137 150 172 195 212 231 250 266 288 313 347 367 391 422 450 483 517 559 591 643 692 749 809 872 938 1005 1075 1151 1244 1322 1405 1486 1592 1692 1782 1897 2002 2107 2223 2367 2483 2610 2748 2892 3046

2013年广州一模数据分析报告(参考)

（一）淡化单科均分，关注总分上线（二）尝试实施“包班”制度的建议
六、给学校的一模分析建议?????????????????9
（一）主要参考数据（二）操作模式（三）跟踪指导策略（四）班级分析示例
七、预测分数线?????????????????????11
4．成绩统计（考试质量指标、均分/标准差、文理各学科项目均分/通过率）
5．答题统计（试题难度/区分度、试题均分/标准差、选择题各选项选择率、得分点难度/区分度）
6．选做统计（选做题难度/区分度、选做题均分/标准差）
三、部分统计项目的说明???????????????????5
1．平均分 2．标准差 3．难度 4．区分度 5．信度
2013年广州市普通高中毕业班综合测试（一）
数据统计分析报告
Teaching Research Office of Guangzhou Education Bureau eaching Research Office of Guangzhou Education Bureau Teaching Research Office of Guangzhou Education Bureau Teaching Research Office of Guangzhou Education Bureau
四、关于“贡献率”和“命中率”指标的使用说明???????5
1．学科上线有效分 2．贡献率与命中率
3．运用指标进行评价的初步建议 4．贡献率与命中率两项指标之间的关系
5．评定学科贡献等级的试行方法
五、运用贡献率与命中率指标指导高考备考工作的建议??????8
4．文\理各学科命中率、贡献率、等级（表五～表十八） 5．各学科试卷信度、难度、区分度（表十九） 6．各学科分组平均分、标准差（表二十） 7．全市文\理科总分前百名（表二十一～表二十二） 8．全市单科分数前十名（表二十三～表三十四）

高2013级年级三诊成绩

姓名李梦玲周莹佘潇罗茗耀宋玉皓高月贺箫王浩左梦迪唐莉萍宦丁洋王倩成凤徐开洋魏嘉莉杨杰汪莹罗帅秦琴刘凤军万鹏李丹刘洁曾友联袁陈李燕廖凯周缘陈启阳兰林张莹李凤娇帅翔何巍李慧周文慧蒲君燕应隽爔林然吴豪伍建羽余林罗倩倩陈佳文周翔
52 50 44 58 53 35 56 53 53 51 51 50 49 49 47 45 41 68 57 38 65 49 48 31 67 63 57 55 54 50 49 48 47 42 76 57 55 54 54 41 62 59 54 48 46 68 63
58 61 55 30 56 63 62 67 61 53 51 45 60 39 35 54 45 61 57 43 66 59 49 50 64 62 50 53 38 27 67 59 54 48 57 47 41 60 41 71 61 49 64 56 43 58 65
130122060034 130122063022 130122060887 130122060411 130122060428 130122060358 130122060136 130122060710 130122060725 130122060210 130122061092 130122061128 130122060721 130122060148 130122060012 130122060853 130122060460 130122060245 130122063032 130122060404 130122060889 130122060970 130122060984 130122060761 130122060441 130122061027 130122063046 130122060398 130122060871 130122060112 130122060083 130122063065 130122060799 130122060602 130122060257 130122060695 130122060559 130122060915 130122060766 130122063021 130122060681 130122060421 130122063012 130122060223 130122060381 130122060941 130122060863

广州市2013届高三年级第一次调研测试(文)

广州市2013届高三年级调研测试（文）一．选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．复数1+i （i 为虚数单位）的模等于AB ．1 CD ．122．已知集合}4,3,2,1,0{=A ，集合},2|{A n n x x B ∈==，则=B AA ．}0{B ．}4,0{C ．}4,2{D ．}4,2,0{ 3．已知函数()2030x x x fx x log ,,⎧>=⎨≤⎩, 则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值是 A ．9 B ．19 C ．9- D ．19- 4．已知等差数列}{n a 的前n 项和为n S ，若34512a a a ++=，则7S 的值为A ．56B ．42C ．28D ．145．已知e 为自然对数的底数，函数y x =e x的单调递增区间是A . )1,⎡-+∞⎣B ．(1,⎤-∞-⎦C ．)1,⎡+∞⎣D ．(1,⎤-∞⎦ 6．设n m ,是两条不同的直线，γβα,,是三个不同的平面，下列命题正确的是A ．αα//,//,//n m n m 则若B ．βαγβγα//,,则若⊥⊥C ．n m n m //,//,//则若ααD ．n m n m ⊥⊥则若,//,αα7．如图1，程序结束输出s 的值是A ．30B ．55C ．91D ．140 8．已知函数()()212fx x x cos cos =-⋅，x ∈R ，则()f x 是A ．最小正周期为2π的奇函数 B ．最小正周期为π的奇函数 C ．最小正周期为2π的偶函数 D ．最小正周期为π的偶函数图29．在区间15,⎡⎤⎣⎦和24,⎡⎤⎣⎦分别取一个数,记为a b ,,则方程22221x y a b+=表示焦点在x椭圆的概率为 A ．12 B ．1532C ．1732D ．3132 10．在R 上定义运算).1(:y x y x -=⊗⊗若对任意2x >，不等式()2x a x a -⊗≤+ 都成立，则实数a 的取值范围是 A. 17,⎡⎤-⎣⎦ B. (3,⎤-∞⎦C. (7,⎤-∞⎦D. ()17,,⎤⎡-∞-+∞⎦⎣二．填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分. （一）必做题（11～13题） 11．已知()fx 是奇函数, ()()4g x f x =+, ()12g =, 则()1f -的值是 .12．已知向量a ，b 都是单位向量，且 a b 12=，则2-a b 的值为 . 13．设x x f cos )(1=，定义)(1x f n +为)(x f n 的导数，即)(' )(1x f x f n n =+，n ∈N *，若ABC ∆的内角A 满足1220130f A f A f A ()()()+++= ，则sin A 的值是 .（二）选做题（14～15题，考生只能从中选做一题） 14.（几何证明选讲选做题）如图2，已知AB 是⊙O 的一条弦，点P 为AB 上一点， PC OP ⊥，PC 交⊙O 于C ，若4AP =，2PB =，则PC 的长是 .15．（坐标系与参数方程选讲选做题）已知圆C 的参数方程为2x y cos ,sin ,θθ⎧=⎨=+⎩(θ为参数), 以原点为极点,x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为1sin cos ρθρθ+=, 则直线l 截圆C 所得的弦长是 .侧视D CBAP 图5图4图3625x 0611y 11988967乙甲三．解答题：本大题共6小题，满分80分．解答应写出文字说明、证明过程或演算步骤. 16．（本小题满分12分）已知函数2f x x x ()sin sin π⎛⎫=-+⎪⎝⎭. （1）求函数)(x f y =的单调递增区间；（2）若43f ()πα-=)42(πα+f 的值.17．（本小题满分12分）某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图3，其中甲班学生的平均分是85，乙班学生成绩的中位数是83. （1）求x 和y 的值；（2）计算甲班7位学生成绩的方差2s ；（3）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率.参考公式：方差()()()2222121n s x x x x x x n ⎡⎤=-+-+⋅⋅⋅+-⎢⎥⎣⎦，其中12nx x x x n+++=.18．(本小题满分14分)已知四棱锥P ABCD -的正视图是一个底边长为4、腰长为3的等腰三角形，图4、图5 分别是四棱锥P ABCD -的侧视图和俯视图. （1）求证：AD PC ⊥；（2）求四棱锥P ABCD -的侧面PAB 的面积.19．（本小题满分14分）已知数列}{n a 的前n 项和为n S ，数列}1{+n S 是公比为2的等比数列，2a 是1a 和3a 的等比中项.（1）求数列}{n a 的通项公式；（2）求数列{}n na 的前n 项和n T .20.（本小题满分14分）已知()fx 是二次函数，不等式()0f x <的解集是()05,，且()f x 在点()()11f ,处的切线与直线610x y ++=平行. （1）求()fx 的解析式；（2）是否存在t ∈N *，使得方程()370fx x+=在区间()1t t ,+内有两个不等的实数根？若存在，求出t 的值；若不存在，说明理由.21.（本小题满分14分）已知椭圆()22122:10x y C a b a b+=>>的右焦点与抛物线22:4C y x =的焦点F 重合,椭圆1C 与抛物线2C 在第一象限的交点为P ,53PF =. (1)求椭圆1C 的方程；(2) 若过点()1,0A -的直线与椭圆1C 相交于M 、N 两点，求使FM FN FR +=成立的动点R 的轨迹方程；(3) 若点R 满足条件（2），点T 是圆()2211x y -+=上的动点，求RT 的最大值.广州市2013届高三第一次调研测试参考答案一、选择题：本大题主要考查基本知识和基本运算．共10小题，每小题5分，满分50分.二、填空题：本大题主要考查基本知识和基本运算．本大题共5小题，考生作答4小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题．11．2 12.13. 1 14. 15. 三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤. 16．（本小题满分12分）(本小题主要考查三角函数性质、同角三角函数的基本关系、二倍角公式等知识, 考查化归与转化的数学思想方法和运算求解能力) （1）解：2f x x x ()sin sin π⎛⎫=-+⎪⎝⎭x x cos sin =+ …………… 1分22x x sin cos ⎛⎫=+ ⎪ ⎪⎝⎭4x sin π⎛⎫=+ ⎪⎝⎭. …………… 3分由22242k x k ,πππππ-+≤+≤+ …………… 4分解得32244k x k k ,ππππ-+≤≤+∈Z . …………… 5分 ∴)(x f y =的单调递增区间是32244k k k [,],ππππ-++∈Z . ………… 6分（2）解：由（1）可知)4sin(2 )(π+=x x f ，∴43f ()sin παα-==，得13sin α=. …………… 8分∴)42(πα+f =22sin πα⎛⎫+ ⎪⎝⎭ …………… 9分2cosα=…………… 10分()212sinα=-…………… 11分9=. …………… 12分17．（本小题满分12分）(本小题主要考查茎叶图、样本均值、样本方差、概率等知识, 考查或然与必然的数学思想方法，以及数据处理能力、运算求解能力和应用意识)（1）解：∵甲班学生的平均分是85，∴92968080857978857x+++++++=. …………… 1分∴5x=. …………… 2分∵乙班学生成绩的中位数是83，∴3y=. …………… 3分（2）解：甲班7位学生成绩的方差为2s()()()22222221675007117⎡⎤=-+-+-++++⎢⎥⎣⎦40=. …… 5分（3）解：甲班成绩在90分以上的学生有两名，分别记为,A B，…………… 6分乙班成绩在90分以上的学生有三名，分别记为,,C D E. …………… 7分从这五名学生任意抽取两名学生共有10种情况：()()(),,,,,,A B A C A D()()()()()()(),,,,,,,,,,,,,A EBC BD BE C D C E D E. …………… 9分其中甲班至少有一名学生共有7种情况：()()(),,,,,,A B A C A D()()()(),,,,,,,A EBC BD B E. ……………11分记“从成绩在90分以上的学生中随机抽取两名学生，甲班至少有一名学生”为事件M，则()710P M=.答：从成绩在90分以上的学生中随机抽取两名学生，甲校至少有一名学生的概率为710.……………12分18．（本小题满分14分）（本小题主要考查空间线面位置关系、三视图、几何体的侧面积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力）（1）证明：依题意，可知点P在平面ABCD上的正射影是线段CD的中点E，连接PE，则PE⊥平面ABCD. …………… 2分FE D CBAP∵AD ⊂平面ABCD ，∴AD PE ⊥. …………… 3分 ∵AD CD ⊥，CD PE E CD ,=⊂ 平面PCD ，PE ⊂平面PCD ， ∴AD ⊥平面PCD . …………… 5分 ∵PC ⊂平面PCD ，∴AD PC ⊥. …………… 6分（2）解：依题意，在等腰三角形PCD 中，3PC PD ==，2DE EC ==，在R t △PED中，PE ==，…………… 7分过E 作EF AB ⊥，垂足为F ，连接PF ，∵PE ⊥平面ABCD ，AB ⊂平面ABCD ，∴AB PE ⊥. …………… 8分∵EF ⊂平面PEF ，PE ⊂平面PEF ，EF PE E = ，∴AB ⊥平面PEF . …………… 9分 ∵PF ⊂平面PEF ，∴AB PF ⊥. …………… 10分依题意得2EF AD ==. …………… 11分在R t △PEF 中，3PF ==， …………… 12分∴△PAB 的面积为162S AB PF == . ∴四棱锥P ABCD -的侧面PAB 的面积为6. …………… 14分 19．（本小题满分14分）(本小题主要考查数列、数列求和等知识, 考查化归与转化、分类与整合的数学思想方法，以及抽象概括能力、推理论证能力、运算求解能力和创新意识) （1）解：∵}1{+n S 是公比为2的等比数列，∴11112)1(2)1(1--⋅+=⋅+=+n n n a S S . …………… 1分 ∴12)1(11-⋅+=-n n a S .从而11122+=-=a S S a ，221233+=-=a S S a . …………… 3分 ∵2a 是1a 和3a 的等比中项∴)22()1(1121+⋅=+a a a ，解得=1a 1或11-=a . …………… 4分当11-=a 时，11+S 0=，}1{+n S 不是等比数列， …………… 5分 ∴=1a 1.∴12-=n n S . …………… 6分当2n ≥时，112--=-=n n n n S S a . …………… 7分 ∵11=a 符合12-=n n a ，∴12-=n n a . …………… 8分（2）解：∵12n n na n -= ，∴1211122322n n T n -=⨯+⨯+⨯++ . ① …………… 9分 21231222322n n T n =⨯+⨯+⨯++ .② …………… 10分①-②得2112222n n n T n --=++++- …………… 11分12212nn n -=-- …………… 12分 =()121nn -- . …………… 13分∴()121nn T n =-+ . …………… 14分20.（本小题满分14分）(本小题主要考查二次函数、函数的性质、方程的根等知识, 考查函数与方程、分类与整合的数学思想方法，以及抽象概括能力、推理论证能力、运算求解能力和应用意识) （1）解法1：∵()f x 是二次函数，不等式()0f x <的解集是()05,，∴可设()()5fx ax x =-，0a >. …………… 1分∴25f x ax a /()=-. …………… 2分 ∵函数()fx 在点()()11f ,处的切线与直线610x y ++=平行，∴()16f /=-. …………… 3分∴256a a -=-，解得2a =. …………… 4分 ∴()()225210fx x x x x =-=-. …………… 5分解法2：设()2fx ax bx c =++， ∵不等式()0fx <的解集是()05,，∴方程20ax bx c ++=的两根为05,.∴02550c a b ,=+=. ① …………… 2分 ∵2f x ax b /()=+. 又函数()fx 在点()()11f ,处的切线与直线610x y ++=平行，∴()16f /=-.∴26a b +=-. ② …………… 3分由①②,解得2a =,10b =-. …………… 4分 ∴()2210fx x x =-. …………… 5分（2）解：由（1）知，方程()370fx x+=等价于方程32210370x x -+=.…………… 6分设()h x=3221037x x -+，则()()26202310hx x x x x /=-=-. …………… 7分当1003x ,⎛⎫∈ ⎪⎝⎭时，()0h x /<，函数()h x 在1003,⎛⎫ ⎪⎝⎭上单调递减； ……… 8分当103x ,⎛⎫∈+∞⎪⎝⎭时，()0h x />，函数()h x 在103,⎛⎫+∞ ⎪⎝⎭上单调递增. … 9分 ∵()()1013100450327h h h ,,⎛⎫=>=-<=>⎪⎝⎭， …………… 12分 ∴方程()0h x=在区间1033,⎛⎫ ⎪⎝⎭，1043,⎛⎫⎪⎝⎭内分别有唯一实数根，在区间()03,,()4,+∞内没有实数根. …………… 13分∴存在唯一的自然数3t =，使得方程()370fx x+=在区间()1t t ,+内有且只有两个不等的实数根. …………… 14分21.（本小题满分14分）(本小题主要考查求曲线的轨迹方程、直线、椭圆、抛物线等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法，以及推理论证能力、运算求解能力和创新意识) (1)解法1：抛物线22:4C y x =的焦点F 的坐标为()1,0，准线为1x =-，设点P 的坐标为()00,x y ，依据抛物线的定义，由53PF =，得01x +53=，解得023x =.…………… 1分∵ 点P 在抛物线2C 上，且在第一象限，∴ 2002443y x ==⨯，解得0y =.∴点P 的坐标为23⎛⎝⎭. …………… 2分 ∵点P 在椭圆22122:1x y C a b+=上， ∴2248193a b +=. …………… 3分又1c =，且22221a b c b =+=+， …………… 4分解得224,3a b ==.∴椭圆1C 的方程为22143x y +=. …………… 5分解法2: 抛物线22:4C y x =的焦点F 的坐标为()1,0，设点P 的坐标为()00x y ,,0000x y ,>>. ∵53PF =, ∴()22002519x y -+=. ① …………… 1分 ∵点P 在抛物线22:4C y x =上,∴2004y x =. ②解①②得023x =,0y =.∴点P 的坐标为23⎛ ⎝⎭. …………… 2分∵点P 在椭圆22122:1x y C a b+=上， ∴2248193a b +=. …………… 3分又1c =，且22221a b c b =+=+， …………… 4分解得224,3a b ==. ∴椭圆1C 的方程为22143x y +=. …………… 5分 (2)解法1：设点M ()11,x y 、()22,N x y 、(),R x y ，则()()()11221,,1,,1,FM x y FN x y FR x y =-=-=- .∴()12122,FM FN x x y y +=+-+ .∵ FM FN FR += ,∴121221,x x x y y y +-=-+=. ① …………… 6分∵M 、N 在椭圆1C 上， ∴222211221, 1.4343x y x y +=+= 上面两式相减得()()()()12121212043x x x x y y y y +-+-+=.②把①式代入②式得()()()12121043x x x y y y +--+=. 当12x x ≠时，得()1212314x y y x x y+-=--. ③ …………… 7分设FR 的中点为Q ，则Q 的坐标为1,22x y +⎛⎫⎪⎝⎭. ∵M 、N 、Q 、A 四点共线， ∴MN AQ k k =, 即121221312y y y y x x x x -==+-++. ④ …………… 8分把④式代入③式，得()3134x y x y+=-+，化简得()2243430y x x +++=. …………… 9分当12x x =时，可得点R 的坐标为()3,0-，经检验，点()3,0R -在曲线()2243430y x x +++=上.∴动点R 的轨迹方程为()2243430y x x +++=. …………… 10分解法2：当直线MN 的斜率存在时，设直线MN 的方程为()1y k x =+，由()221143y k x x y ,,⎧=+⎪⎨+=⎪⎩消去y ，得()22223484120k x k x k +++-=. 设点M ()11,x y 、()22,N x y 、(),R x y ，则2122834k x x k+=-+, ()()()1212122611234k y y k x k x k x x k +=+++=++=+.…6分 ∵()()()11221,,1,,1,FM x y FN x y FR x y =-=-=- .∴()12122,FM FN x x y y +=+-+ .∵ FM FN FR += ,∴121221,x x x y y y +-=-+=. ∴21228134k x x x k+=+=-+, ① 2634k y k=+. ② …………… 7分 ①÷②得()314x k y +=-， ③ …………… 8分把③代入②化简得()2243430y x x +++=. (*) …………… 9分当直线MN 的斜率不存在时，设直线MN 的方程为1x =-,依题意, 可得点R 的坐标为()3,0-，经检验，点()3,0R -在曲线()2243430y x x +++=上.∴动点R 的轨迹方程为()2243430y x x +++=. …………… 10分(3)解: 由(2)知点R ()x y ,的坐标满足()2243430y x x +++=, 即()224343y x x =-++, 由20y ≥,得()23430x x -++≥,解得31x -≤≤-. …………… 11分 ∵圆()2211x y -+=的圆心为()10F ,,半径1r =,∴RF ==12=. …………… 12分 ∴当3x =-时,4RFmax =, …………… 13分此时,415RTmax =+=. …………… 14分。

广东省广州市2013届高三毕业班综合测试(二)--数学理

广州市普通高中2013年毕业班综合测试（二）数学（理）试题本试卷共21小题，满分150分．考试用时120分钟注意事项：1．答卷前，考生务必用2B 铅笔在“考生号”处填涂考生号。

用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

5．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

参考公式：锥体的体积公式Sh V 31=，其中S 是锥体的底面积，h 是锥体的高．一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．对于任意向量a 、b 、c ，下列命题中正确的是 A ．|b ||a ||b a |=⋅ B ．+=+a b a bC ．)()(c b a c b a ⋅=⋅D ．2||a a a =⋅2．直线1y kx =+与圆2220x y y +-=的位置关系是A ．相交B ．相切C ．相离D ．取决于k 的值3．若1i -（i 是虚数单位）是关于x 的方程220x px q ++=（p q ∈R 、）的一个解，则p q +=A ．3-B ．1-C ．1D ．34．已知函数()y f x =的图象如图1所示，则其导函数()y f x '=的图象可能是图1A ．B ．C ．D ．5．若函数cos 6y x πω⎛⎫=+⎪⎝⎭()*ω∈N 的一个对称中心是06π⎛⎫⎪⎝⎭，，则ω的最小值为 A ．1 B ．2 C ．4D ．86．一个圆锥的正（主）视图及其尺寸如图2所示．若一个平行于圆锥底面的平面将此圆锥截成体积之比为1﹕7的上、下两部分，则截面的面积为 A ．14π B ．πC ．94πD ．4π7．某辆汽车购买时的费用是15万元，每年使用的保险费、路桥费、汽油费等约为1．5万元．年维修保养费用第一年3000元，以后逐年递增3000元，则这辆汽车报废的最佳年限（即使用多少年的年平均费用最少）是 A ．8年 B ．10年 C ．12年 D ．15年 8．记实数1x ，2x ，…，n x 中的最大数为{}12max ,,n x x x …,，最小数为{}12min ,,n x x x …,，则{}{}2max min 116x x x x +-+-+=，，A ．34B ．1C ．3D ．72二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（9～13题）9．某商场销售甲、乙、丙三种不同型号的钢笔，甲、乙、丙三种型号钢笔的数量之比依次为2﹕3﹕4．现用分层抽样的方法抽出一个容量为n 的样本，其中甲型钢笔有12支，则此样本容量n = ． 10．已知 α为锐角，且3cos 45απ⎛⎫+= ⎪⎝⎭，则 sin α= ． 11．用0，1，2，3，4，5这六个数字，可以组成个没有重复数字且能被5整除的五位数（结果用数值表示）． 12．已知函数()22f x x x =-，点集()()(){}M x y f x f y =+，≤2，()()(){}N x y f x f y =-，≥0，则M N 所构成平面区域的面积为．13．数列}{n a 的项是由1或2构成，且首项为1，在第k 个1和第1k +个1之间有21k -个2，即数列}{n a 为：1，2，1，2，2，2，1，2，2，2，2，2，1，…，记数列}{n a 的前n 项和为n S ，则20S = ；2013S = ．图2（二）选做题（14～15题，考生只能从中选做一题） 14．（几何证明选讲选做题）在△ABC 中，D 是边AC 的中点，点E 在线段BD 上，且满足13BE BD =，延长AE 交BC 于点F ，则BFFC的值为． 15．（坐标系与参数方程选做题）在极坐标系中，已知点1,2A π⎛⎫ ⎪⎝⎭，点P 是曲线2sin 4cos ρθθ=上任意一点，设点P 到直线 cos 10ρθ+=的距离为d ，则PA d +的最小值为．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）某单位有A 、B 、C 三个工作点，需要建立一个公共无线网络发射点O ，使得发射点到三个工作点的距离相等．已知这三个工作点之间的距离分别为80AB =m ，70BC =m ，50CA =m ．假定A 、B 、C 、O 四点在同一平面内．（1）求BAC ∠的大小；（2）求点O 到直线BC 的距离． 17．（本小题满分12分）已知正方形ABCD 的边长为2，E F G H 、、、分别是边AB BC CD DA 、、、的中点．（1）在正方形ABCD 内部随机取一点P，求满足||PH <（2）从A B C D E F G H 、、、、、、、这八个点中，随机选取两个点，记这两个点之间的距离为ξ，求随机变量ξ的分布列与数学期望E ξ．18．（本小题满分14分）等边三角形ABC 的边长为3，点D 、E 分别是边AB 、AC 上的点，且满足AD DB =12CE EA =（如图3）．将△ADE 沿DE 折起到△1A DE 的位置，使二面角1A DE B --成直二面角，连结1A B 、1A C （如图4）．（1）求证：1A D ⊥平面BCED ；（2）在线段BC 上是否存在点P ，使直线1PA 与平面1A BD 所成的角为60？若存在，求出PB的长，若不存在，请说明理由． 19．（本小题满分14分）已知0a >，设命题p ：函数()2212f x x ax a =-+-在区间[]0,1上与x 轴有两个不同的交点；命题q ：()g x x a ax =--在区间()0,+∞上有最小值．若()p q ⌝∧是真命题，求实数a 的取值范围．20．（本小题满分14分）经过点()0,1F 且与直线1y =-相切的动圆的圆心轨迹为M ．点A 、D 在轨迹M 上，且关于y 轴对称，过线段AD （两端点除外）上的任意一点作直线l ，使直线l 与轨迹M 在点D 处的切线平行，设直线l 与轨迹M 交于点B 、C ．（1）求轨迹M 的方程；（2）证明：BAD CAD ∠=∠；（3）若点D 到直线AB ，且△ABC 的面积为20，求直线BC 的方程． 21．（本小题满分14分）设n a 是函数()321f x x n x =+-()*n ∈N 的零点．（1）证明：01n a <<；（2）证明：1n n <+1232n a a a +++< ．参考答案说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力对照评分标准给以相应的分数．2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分． 3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数，选择题和填空题不给中间分．二、填空题：本大题查基本知识和基本运算，体现选择性．共7小题，每小题5分，满分30分．其中14~15题是选做题，考生只能选做一题．第13题第一个空2分，第二个空3分．9．54 10．10 11．216 12．2π 13．36；3981 14．1415三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题主要考查解三角形等基础知识，考查正弦定理与余弦定理的应用，本小题满分12分）解：（1）在△ABC 中，因为80AB =m ，70BC =m ，50CA =m ，由余弦定理得222cos 2AB AC BC BAC AB AC +-∠=⨯⨯ …………………………………2分2228050701280502+-==⨯⨯． ……………………………………………………3分因为BAC ∠为△ABC 的内角，所以3BAC π∠=．…………………………………4分（2）方法1：因为发射点O 到A 、B 、C 三个工作点的距离相等，所以点O 为△ABC 外接圆的圆心．……………………………………………………………………5分设外接圆的半径为R ，在△ABC 中，由正弦定理得2sin BCR A=， ……………………………………………7分因为70BC =，由（1）知3A π=，所以sin 2A =．所以2R==，即3R=．…………………8分过点O作边BC的垂线，垂足为D，…………………………9分在△OBD中，OB R==703522BCBD===，所以OD==…………………………………11分=所以点O到直线BC的距离为3m．………………………………………12分方法2：因为发射点O到A、B、C三个工作点的距离相等，所以点O为△ABC外接圆的圆心．……………………5分连结OB，OC，过点O作边BC的垂线，垂足为D，…………………6分由（1）知3BACπ∠=，所以3BOC2π∠=．所以3BODπ∠=．………………………………………9分在Rt△BOD中，703522BCBD===，所以35tan tan603BDODBOD===∠11分所以点O到直线BC的距离为3m．………………………………………12分17．（本小题主要考查几何概型、随机变量的分布列与数学期望等基础知识，考查运算求解能力与数据处理能力等，本小题满分12分）解：（1）这是一个几何概型．所有点P构成的平面区域是正方形ABCD的内部，其面积是224⨯=．………………………1分满足||PH<P构成的平面区域是以H为半径的圆的内部与正方形ABCD内部的公共部分，它可以看作是由一个以H为半径、所以满足||PH<112484π+π=+．………………………………………………………4分（2）从A B C D E F G H、、、、、、、这八个点中，任意选取两个点，共可构成28C28=条不同的线段．……………………………………5分其中长度为1的线段有8的线段有4条，长度为2的线段有6有8条，长度为2条．所以ξ所有可能的取值为12．…………………………………7分且()821287Pξ===，(41287Pξ===，()6322814Pξ===，(82287Pξ===，(212814Pξ===．………………………………………9分所以随机变量ξ的分布列为：随机变量ξ的数学期望为21321127714714Eξ=⨯+⨯+=12分18．（本小题主要考查空间直线与平面垂直、直线与平面所成角等基础知识，考查空间想象能力和运算求解能力等，本小题满分14分）证明：（1）因为等边△ABC的边长为3，且ADDB=12CEEA=，所以1AD=，2AE=．在△ADE中，60DAE∠= ，由余弦定理得DE==．……10分因为222AD DE AE+=，所以AD DE⊥．折叠后有1A D DE⊥．…………………………………………………………2分因为二面角1A DE B--是直二面角，所以平面1A DE⊥平面BCED．…………3分又平面1A DE 平面BCED DE=，1A D⊂平面1A DE，1A D DE⊥，所以1A D⊥平面BCED．……………………………………………………4分（2）解法1：假设在线段BC上存在点P，使直线1PA与平面1A BD所成的角为60 ．如图，作PH BD⊥于点H，连结1A H、1A P．…………5分由（1）有1A D⊥平面BCED，而PH⊂平面BCED，所以1A D⊥PH．……………………………6分又1A D BD D=，所以PH⊥平面1A BD．…………………………7分所以1PA H∠是直线1PA与平面1A BD所成的角．………………………………8分设PB x=()03x≤≤，则2xBH=，PH x=．……………………………9分在Rt△1PA H中，160PA H∠= ，所以112A H x=．………………………10分在Rt△1A DH中，11A D=，122DH x=-．…………………………………11分由22211A D DH A H+=，得222111222x x⎛⎫⎛⎫+-=⎪ ⎪⎝⎭⎝⎭．………………………………………………………12分解得52x=，满足03x≤≤，符合题意．……………………………………………………………13分所以在线段BC上存在点P，使直线1PA与平面1A BD所成的角为60 ，此时52PB=．……14分解法2：由（1）的证明，可知ED DB⊥，1A D⊥平面BCED．以D为坐标原点，以射线DB、DE、1DA分别为x轴、y轴、z轴的正半轴，建立空间直角坐标系D xyz -如图． ………………………………5分设2PB a =()023a ≤≤，则BH a =，PH =，2DH a =-． ……………………6分所以()10,0,1A，()2,0P a -，()E ．…………7分所以()12,,1PA a =- ．………………………………………………8分因为ED ⊥平面1A BD ，所以平面1A BD的一个法向量为()DE =．…………………9分因为直线1PA 与平面1A BD 所成的角为60，所以11sin 60PA DE PA DE =…………………………………………10分==，……………………………………………………………11分解得54a =． ……………………………………………………………………12分即522PB a ==，满足023a ≤≤，符合题意． …………………………………13分所以在线段BC 上存在点P ，使直线1PA 与平面1A BD 所成的角为60，此时52PB =．……14分19．（本小题主要考查二次函数的交点与分段函数的最值、常用逻辑用语等基础知识，考查数形结合思想、分类讨论思想和运算求解能力、抽象概括能力等，本小题满分14分）解：要使函数()2212f x x ax a =-+-在[]0,1上与x 轴有两个不同的交点，必须()()0101,0.f f a ⎧⎪⎪⎨<<⎪⎪∆>⎩≥0，≥0,…………………………………………………………………2分即()()2,1224012412a a a a a -⎧⎪-⎪⎨<<⎪⎪--->⎩≥0,≥0,0.………………………………………………4分112a<≤．112a<≤时，函数()2212f x x ax a=-+-在[]0,1上与x轴有两个不同的交点．……………………………5分下面求()g x x a ax=--在()0,+∞上有最小值时a的取值范围：方法1：因为()()()1,,1,.a x a x ag xa x a x a--⎧⎪=⎨-++<⎪⎩≥……………………………6分①当1a>时，()g x在()0,a和[),a+∞上单调递减，()g x在()0,+∞上无最小值；……………7分②当1a=时，()1,,21, 1.xg xx x-⎧=⎨-+<⎩≥1()g x在()0,+∞上有最小值1-；……………8分③当01a<<时，()g x在()0,a上单调递减，在[),a+∞上单调递增，()g x在()0,+∞上有最小值()2g a a=-．…………………………………………………………9分所以当01a<≤时，函数()g x在()0,+∞上有最小值．……………………………………………10分方法2：因为()()()1,,1,.a x a x ag xa x a x a--⎧⎪=⎨-++<⎪⎩≥……………………………6分因为0a>，所以()10a-+<．所以函数()()110y a x a x a=-++<<是单调递减的．…………………………7分要使()g x在()0,+∞上有最小值，必须使()21y a x a=--在[),a+∞上单调递增或为常数．……8分即10a-≥，即1a≤．………………………………………………………9分所以当01a<≤时，函数()g x在()0,+∞上有最小值．………………………………10分若()p q⌝∧是真命题，则p⌝是真命题且q是真命题，即p是假命题且q是真命题．………11分所以101,,20 1.a aa⎧<>⎪⎨⎪<⎩≤或……………………………………………12分解得01a<或112a<≤．……………………………………………13分故实数a的取值范围为(11,12⎛⎤⎤⎥⎦⎝⎦．…………………………………………14分20．（本小题主要考查动点的轨迹和直线与圆锥曲线的位置关系、导数的几何意义等基础知识，考查运算求解能力和推理论证能力等，本小题满分14分）解：（1）方法1：设动圆圆心为(),x y1y =+．……………1分整理，得24x y =．所以轨迹M 的方程为24x y =．……………………………2分方法2：设动圆圆心为P ，依题意得点P 到定点()0,1F 的距离和点P 到定直线1y =-的距离相等，根据抛物线的定义可知，动点P 的轨迹是抛物线．………………………………1分且其中定点()0,1F 为焦点，定直线1y =-为准线．所以动圆圆心P 的轨迹M 的方程为24x y =．………………………………………………………2分（2）由（1）得24x y =，即214y x =，则12y x '=．设点2001,4D x x ⎛⎫ ⎪⎝⎭，由导数的几何意义知，直线l 的斜率为012BC k x =．……………3分由题意知点2001,4A x x ⎛⎫- ⎪⎝⎭．设点2111,4C x x ⎛⎫ ⎪⎝⎭，2221,4B x x ⎛⎫⎪⎝⎭，则2212120121114442BCx x x x k x x x -+===-，即1202x x x +=．……4分因为2210101011444ACx x x x k x x --==+，2220202011444ABx x x x k x x --==+．……………………………5分由于()120102020444AC AB x x x x x x x k k +---+=+==，即AC AB k k =-．………………………6分所以BAD CAD ∠=∠．…………………………………………………………………………………7分（3）方法1：由点D 到AB，可知BAD ∠45= ．………………8分 A B CDOxylE不妨设点C 在AD 上方（如图），即21x x <，直线AB 的方程为：()20014y x x x -=-+．由()20021,44.y x x x x y ⎧-=-+⎪⎨⎪=⎩解得点B 的坐标为()20014,44x x ⎛⎫-- ⎪⎝⎭．…………………………………………10分所以)()00042AB x x =---=-．由（2）知CAD BAD ∠=∠45=，同理可得02AC =+．………………11分所以△ABC的面积200012244202S x =⨯-⨯+=-=，解得03x =±．…………………………………………………………………12分当03x =时，点B 的坐标为11,4⎛⎫- ⎪⎝⎭，32BC k =，直线BC 的方程为()13142y x -=+，即6470x y -+=．…………………………13分当03x =-时，点B 的坐标为497,4⎛⎫- ⎪⎝⎭，32BC k =-，直线BC 的方程为()493742y x -=-+，即6470x y +-=． ……………………14分方法2：由点D 到AB，可知BAD ∠45= ．…………………8分由（2）知CAD BAD ∠=∠45=，所以CAB ∠90=，即AC AB ⊥．由（2）知104AC x x k -=，204AB x x k -=．所以1020144AC ABx x x xk k --=⨯=-．即()()102016x x x x --=-． ① 由（2）知1202x x x +=． ②不妨设点C 在AD 上方（如图），即21x x <，由①、②解得10204,4.x x x x =+⎧⎨=-⎩……………10分因为02AB ==-，同理02AC =+． ……………………………………………………11分以下同方法1．21．（本小题主要考查函数的零点、函数的导数和不等式的证明等基础知识，考查运算求解能力和推理论证能力等，本小题满分14分）证明：（1）因为()010f =-<，()210f n =>，且()f x 在R 上的图像是一条连续曲线，所以函数()f x 在()01，内有零点．………………………………………1分因为()2230f x x n '=+>，所以函数()f x 在R 上单调递增．…………………………………2分所以函数()f x 在R 上只有一个零点，且零点在区间()01，内．而n a 是函数()f x 的零点，所以01n a <<．……………………………………………3分（2）先证明左边的不等式：因为3210n n a n a +-=，由（1）知01n a <<，所以3n n a a <．………………………………………………………4分即231n n n n a a a -=<．所以211n a n >+．……………………………………………………5分所以1222211111211n a a a n +++>++++++ ．……………………………6分以下证明222111112111nn n +++≥++++ ． ① 方法1（放缩法）：因为()21111111n a n n n n n >≥=-+++，………………………7分所以1211111111223341n a a a n n ⎛⎫⎛⎫⎛⎫⎛⎫+++>-+-+-++- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭1111nn n =-=++．…………………………………………………9分方法2（数学归纳法）：1）当1n =时，2111111=++，不等式①成立． 2）假设当n k =（*k ∈N ）时不等式①成立，即222111112111kk k +++≥++++ ．那么()222211111121111k k +++++++++ ()21111k k k ≥++++．以下证明()()()21111111k k k k k ++≥+++++． ② 即证()()()21111111k kk k k +≥-+++++．即证22112232k k k k ≥++++．由于上式显然成立，所以不等式②成立．即当1n k =+时不等式①也成立．根据1）和2），可知不等式①对任何*n ∈N 都成立．所以121n na a a n +++>+ ．…………………………………9分再证明右边的不等式：当1n =时，()31f x x x =+-．由于31113102228f ⎛⎫⎛⎫=+-=-< ⎪ ⎪⎝⎭⎝⎭，3333111044464f ⎛⎫⎛⎫=+-=> ⎪ ⎪⎝⎭⎝⎭，所以11324a <<．……………………………………………………10分由（1）知01n a <<，且3210n n a n a +-=，所以32211n n a a n n -=<． ……………11分因为当2n ≥时，()2111111n n n n n<=---，…………………………………12分所以当2n ≥时，12342311111114223341n a a a a a n n ⎛⎫⎛⎫⎛⎫+++++<++-+-++- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭113122n =+-<．所以当*n ∈N 时，都有1232n a a a +++< ．综上所述，1n n <+1232n a a a +++< ．…………………………14分。

2013年高三第二次次摸底考试

2014届高三第三次月考考务工作安排2014届第三次月考考试于10月25日-10月26日进行，参加考试的学生有，文科考生188人，理科考生624人，总共812人。

共有考室20个。

一、考点负责人主考：雷华清副主考：谢建军巡考：雷元花曾智生谢志雄二、考务：李昂雄三、发卷及收卷：汤素芳胡智勇四、保密及学生处分通告：胡智勇五、监控组：邝佳雄（包括司铃，放英语磁带）六、考试时间及考试科目安排：上午下午日期7:50-----9:20 9:40-----11:40 14:20----16:50 10月25日化学（地理）英语语文8:00----9:30 10:10---11:40 14:20---16:20 10月26日生物（政治）物理（历史）数学七、考室及监考人员安排：考室号考试科目考生人数化学（地理）、英语、语文生物(政治)、物理（历史）、数学监考老师主监考流动监考主监考流动监考42（理）01 袁旭刘海雄曾令华袁旭02 李建军刘海雄邝玉忠袁旭42（理）03 蒋海斌刘斌邝志忠袁旭42（理）04 黄进峰刘斌尹亮国袁旭40（理）05 李红丽胡华雄刘斌郭勇辉42（理）06 雷俊军胡华雄彭继勇郭勇辉42（理）07 雷光华欧阳文华肖成远郭勇辉42（理）08 李律欧阳文华曾凡华郭勇辉42（理）09 何瑞英邝玉忠谢源海郭勇辉42（理）10 曾轶邝玉忠胡华雄郭勇辉42（理）11 罗淑英邝井平王先勇李律42（理）12 李艳华邝井平邝井平李律41（理）13 郑四秀邝志忠彭艳梅雷光华21（文）14 胡扬兵周瑾周瑾罗淑英41（理）15 唐爱迪周瑾郑飘伶罗淑英41（理）16 王日凤邝志忠欧阳文华雷光华41（理）17 曾红仔王学文刘海雄李律42（文）18 郭勇辉王学文王学文李红丽42（文）19 李刚杰肖瑾罗静李红丽42（文）20 李志勇肖瑾肖瑾李红丽41（文）各位老师：本次考试为高三第三月考，请老师们认真，严格监考。

考出真实水平。

1、请全体文化老师于10月24日下午第三节课（16：00）到二楼会议室召开考务会。