高一不等式试题

合集下载

高一数学基本不等式试题

高一数学基本不等式试题1.设且,则的最小值为________．【答案】4【解析】由，当且仅当时等号成立．故答案为4．【考点】均值不等式的应用．2.当时，函数的最小值为 .【答案】6【解析】由于，所以函数【考点】基本不等式的应用.3.已知，，则的最小值为．【答案】4【解析】,由基本不等式得【考点】基本不等式的应用．4.设二次函数的值域为[0，+∞），则的最大值是（）A．B．2C．D．【答案】C【解析】由二次函数特点可知，在定义域R上其值域为，则,且,即. 欲求的最大值，利用前面关系，建立，由，故选C.【考点】（1）二次函数性质；（2）函数最值；（3）基本不等式.5.已知，则x + y的最小值为．【答案】【解析】，，由，可得，当且仅当时等号成立，故，故答案为.【考点】对数的性质运算；均值不等式的应用.6.若，则下列不等式正确的是（）.A．B．C．D．【答案】C【解析】由基本不等式得，则；又，.【考点】基本不等式.7.若,则的最小值是( )A．B．1C．2D．4【答案】C【解析】．【考点】基本不等式．8.已知等比数列，，则其前三项和的取值范围是（）A．B．C．D．【答案】D【解析】由已知得，当公比时，；当公比时，，.【考点】利用基本不等式求最值。

9.（1）阅读理解：①对于任意正实数，只有当时，等号成立．②结论：在（均为正实数）中，若为定值，则，只有当时，有最小值．（2）结论运用：根据上述内容，回答下列问题：（提示：在答题卡上作答）①若，只有当__________时，有最小值__________．②若，只有当__________时，有最小值__________．（3）探索应用：学校要建一个面积为392的长方形游泳池，并且在四周要修建出宽为2m和4 m的小路（如图所示）。

问游泳池的长和宽分别为多少米时，共占地面积最小？并求出占地面积的最小值。

【答案】（2）①1 ，2：②3，10（3）游泳池的长为28m，宽14m时，占地面积最小，占地面积的最小值是648【解析】（2）①利用阅读材料，可知当时，有最小值2，②，当时，有最小值10．（3）设游泳池的长为m，则游泳池的宽为m,又设占地面积为，依题意，得，整理运用所给结论，可求面积的最值．（2）①利用阅读材料，可知当时，有最小值2，②，当时，有最小值10．（3）设游泳池的长为m，则游泳池的宽为m,又设占地面积为，依题意，得，整理．当且仅当即取“=”．此时所以游泳池的长为28m，宽14m时，占地面积最小，占地面积的最小值是648【考点】基本不等式在最值问题中的应用；进行简单的合情推理10.在分别是角A、B、C的对边,若,则的周长的取值范围是（）A． B． C． D．【答案】C【解析】∵，∴，化简后可得：，∴，又∵，∴，即周长的范围为．【考点】1、余弦定理；2、基本不等式．11.若两个正实数x，y满足＋＝1，并且2x＋y＞m恒成立，则实数m的取值范围是．【答案】【解析】因为且，所以，当且仅当即时取。

高一数学不等式测试题

高一数学不等式测试题1. 不等式的基本性质题目：请证明对于任意实数a、b、c，不等式\( a < b \) 时，\( a + c < b + c \) 成立。

2. 解一元一次不等式题目：解不等式 \( 5x - 3 > 2x + 7 \)。

3. 解绝对值不等式题目：解绝对值不等式 \( |x - 4| < 3 \)。

4. 解二次不等式题目：解不等式 \( x^2 - 4x + 3 > 0 \)。

5. 不等式与函数题目：已知函数 \( f(x) = x^2 - 2x + 1 \)，求函数值大于0的x的取值范围。

6. 不等式组的解集题目：解不等式组 \( \begin{cases} x + 2 > 0 \\ 3x - 7 < 0 \end{cases} \)。

7. 不等式的变换题目：将不等式 \( x^2 - 4x + 4 \geq 0 \) 转化为标准形式，并找出其解集。

8. 不等式的应用题目：一个矩形的长为 \( 2x + 3 \)，宽为 \( x - 1 \)，当x取何值时，矩形的面积最大？9. 不等式与数列题目：若数列 \( \{a_n\} \) 满足 \( a_1 = 1 \) 且 \( a_{n+1} \leq 2a_n \) 对所有正整数 n 成立，证明数列 \( \{a_n\} \) 是递增的。

10. 不等式的证明题目：证明对于所有正实数 \( x \) 和 \( y \)，不等式\( \sqrt{xy} \leq \frac{x + y}{2} \) 成立。

11. 不等式与几何题目：在三角形ABC中，如果 \( a + b > c \)，证明三角形ABC 是锐角三角形。

12. 不等式的综合应用题目：若 \( x, y \) 为正实数，且 \( x^2 + y^2 = 1 \)，求\( x^2y + xy^2 \) 的最大值。

13. 不等式的解法题目：解不等式 \( \frac{2x}{x^2 - 1} < 1 \)。

不等式高考试题及答案

不等式高考试题及答案一、选择题1. 若不等式3x+2>7成立，则x的取值范围是：A. x < -1B. x > -1C. x < 1D. x > 1答案：D2. 已知不等式2(x-1) > 3(x+2)，则x的取值范围是：A. x < -7/5B. x > -7/5C. x < -1D. x > -1答案：C3. 若x<y，则对x+y，下列不等式成立的是：A. x + y < 2xB. x + y < 2yC. x + y > 2xD. x + y > 2y答案：C4. 若不等式5x+3y > 6成立，下列不等式中一定成立的是：A. 10x + 6y > 12B. 5x + 6y > 12C. 5x + 3y > 6D. 10x + 3y > 6答案：D5. 下列不等式组中，解集与其他三个不同的是：A. {x | -2 < x < 3}B. {x | 0 < x < 5}C. {x | 1 < x < 4}D. {x | -3 < x < 2}答案：B二、填空题1. 若不等式2x - 1 > 5成立，则x的取值范围为________。

答案：x > 32. 若不等式-3(x - 1) < 2(x + 3)成立，则x的取值范围为________。

答案：x < 13/53. 已知不等式2x - 3 < 5x + 4，则x的取值范围为________。

答案：x > -7/34. 若不等式x + 5 > 2x - 3成立，则x的取值范围为________。

答案：x < 85. 若不等式3x - 2 > 5成立，则x的取值范围为________。

答案：x > 7/3三、解答题1. 解不等式组{x | 2x + 3 > 5, x - 1 < 4}，并将解表示在数轴上。

高中数学最全《不等式》分类试题及答案

第1节一元二次不等式（1）0122≤-+x x （2）0122>-+x x 【解】 ]3,4[- 【解】),3()4,(+∞⋃--∞（3）01522≤-+x x （4）03652≤-+x x 【解】]3,5[- 【解】 ]4,9[-（5）02832≤-+-x x （6）02142>+--x x 【解】R x ∈ 【解】]3,7[-（7）06562≤-+x x （8）012522≤-+x x 【解】]32,23[- 【解】]23,4[-（9）03652≤--x x （10）0262>--x x 【解】]9,4[- 【解】),32()21,(+∞⋃--∞（11）0617122>++x x （12）06122≤--x x 【解】),32()43,(+∞-⋃--∞ 【解】]43,32[-（13）0110252>+-x x （14）01412≤+-x x 【解】),51()51,(+∞⋃-∞ 【解】 {2}（15）0107122≤+--x x （16）0)23)(2(≤--x x 【解】),32[]45,(+∞⋃--∞ 【解】]2,23[（17）06752>++-x x （18）0252042≤-+-x x 【解】)2,53(- 【解】R（19）035122≤--x x （20）0163212>-+x x 【解】]47,35[- 【解】),41()43,(+∞⋃--∞（21）02049302>++x x （22）01562≤-+x x 【解】),54()65,(+∞-⋃--∞ 【解】]12,13[-（23）06)32(2>++-x x （24）06222≤--x x【解】),3()2,(+∞⋃-∞ 【解】]23,2[-（25）03692≤--x x （26）08624≤+-x x 【解】]12,3[- 【解】]2,2[]2,2[⋃--（27）03212≤--y y （28）0261692≤+-y y 【解】 ),31[]1,(+∞⋃--∞ 【解】{13}（29）032<-+-x x （30）0)1()12(2≤-+-+a a x a x【解】 R 【解】]1,[a a --第2节分式不等式（1）52>x （2）32<-x【解】)52,0( 【解】),0()32,(+∞⋃--∞（3）235>-x （4）122>+x x 【解】)211,3( 【解】),2()2,(+∞⋃--∞（5）1113<+<-x （6）322≥-x 【解】),0()34,(+∞⋃--∞ 【解】]38,2(（7）16+<x x （8）321<<-x【解】),2()0,3(+∞⋃- 【解】),32()2,(+∞⋃--∞ （9）125+<+x x （10）2120<+-<x x【解】),2321()2,2321(+∞-⋃-+- 【解】),2()4,(+∞⋃--∞ （11）123->-+x x （12）224-≤-+x x【解】),2()21,(+∞⋃--∞ 【解】)2,0[（13）042>--x x （14）172>-+xx 【解】),4()2,(+∞⋃-∞ 【解】)7,25(（15）04332>-+x x （16）02312≥++x x【解】),34()23,(+∞⋃--∞ 【解】),21[)32,(+∞-⋃--∞（17）02354>--x x （18）2211<-+<-x x【解】)54,32( 【解】),5()21,(+∞⋃-∞（19）043)32(≥++x x x （20）01)32)(2(<---x x x【解】),0[)34,23[+∞⋃-- 【解】)2,23()1,(⋃-∞第3节不等式（1）1．实数大小顺序与运算性质之间的关系a －b ＞0⇔a >b ；a －b ＝0⇔a ＝b ；a －b ＜0⇔a b ⇔b <a ⇔ 传递性 a >b ，b >c ⇒a >c ⇒ 可加性a >b ⇒a ＋c >b ＋c⇒可乘性⎭⎬⎫a >bc >0⇒ac >bc c 的符号⎭⎬⎫a >bc <0⇒ac <bc 同向可加性 ⎭⎬⎫a >bc >d ⇒a ＋c >b ＋d ⇒同向同正可乘性⎭⎬⎫a >b >0c >d >0⇒ac >bd ⇒可乘方性a >b >0⇒a n >b n (n ∈N ，n ≥2)同正可开方性a >b >0⇒n a >nb (n ∈N ，n ≥2)1、（2004浙江）已知{0101)(≥<-=x x x f ，，，则不等式)2()2(+⋅++x f x x ≤5的解集是)23,(-∞2、不等式x lg(x ＋2)>lg(x ＋2)的解集是 ),1()1,2(+∞⋃--3、设f (x )= 1232,2,log (1),2,x e x x x -⎧<⎪⎨-≥⎪⎩ 则不等式f (x )>2的解集为（1,2）⋃（10,+∞） 4、关于x 的不等式(k 2－2k ＋25)x ＜(k 2－2k ＋25)1–x 的解集是 )21,(-∞5、已知函数y=log 21(3x )52+-ax 在[-1，+∞）上是减函数，则实数a 的取值范围]6,8(--6、已知函数f (x )＝⎩⎪⎨⎪⎧x ＋2， x ≤0－x ＋2， x >0，则不等式f (x )≥x 2的解集是 [－1,1]7、函数d cx bx ax x f +++=23)(的图象如图所示．（1）方程0)(=x f 的解集是________________}2,1,1{-_（2）不等式0)(<x f 的解集是____________ _)2,1()1,(⋃--∞（3）不等式0)(>x f 的解集是_______________),2()1,1(+∞⋃- 8、已知2log 3.6,a =4log 3.2,b =4log 3.6,c =则( B )A.a b c >>B. a c b >>C. b a c >>D. c a b >>9、已知数列}{n a 的通项公式902+=n na n ，+∈N n ，则数列中最大项是第____9或10项．10、若11<<<-βα，则下列不等式恒成立的是（ A ） A 、02<-<-βα B 、 12-<-<-βα C 、 01<-<-βα D 、11<-<-βα11、若不等式()y x a xy x +≤+22对一切正数y x ,恒成立，则正数a 的最小值为 112、已知b a b -<<2，则比值ba的取值范围是 )2,1(- 13、已知函数()(),1log 2+=x x f 且,0>>>c b a 则()()()cc f b b f a a f ,,的大小关系正确的是（ B ）A 、()()()c c f b b f a a f >>B 、()()()a a f b b f c c f >>C 、()()()c c f a a f bb f >> D 、()()()bb fc c f a a f >>14、设,,,0,022sin cosθθy x b y x a y x ⋅=+=>>则a 与b 的大小关系为b a >yx21O－115、二次函数()x f 的二次项系数为负，满足()()(),2R x x f x f ∈-=那么不等式()()[]x f x f -+>+1lg 1lg 1的解集为（ B ）A ，⎩⎨⎧⎭⎬⎫≤<121x xB ，⎩⎨⎧⎭⎬⎫<<121x xC ，⎩⎨⎧⎭⎬⎫<<-121x xD ，⎩⎨⎧⎭⎬⎫≤<-121x x16、设y 是实数，且06442=+++x xy y ，则x 的取值范围是),3[]2,(+∞⋃--∞17、设关于x 的方程23222---k x kx =0的两个实数根一个小于1，另一个大于1，则实数k 的取值范围是 ),0()4,(+∞⋃--∞18、如果实数x,y 满足x 2＋y 2=1，则(1－xy ) (1＋xy )有 ( B )A 、最小值21和最大值1 B 、最大值1和最小值43C 、最小值43而无最大值 D 、最大值1而无最小值19、设a ∈R ，若x ＞0时均有[(a －1)x －1]( x 2－ax －1)≥0，则a ＝______2________．20、下列命题中正确的是（ B ）A 、 x x 1+的最小值是2 B 、1222++x x 的最小值是2C 、 4522++x x 的最小值是2 D 、xx 432--的最小值是221、若关于x 的方程x 2＋mx ＋1＝0有两个不相等的实数根，则实数m 的取值范围是 (－∞，－2)∪(2，＋∞)22、若a ＝20.5，b ＝log 3，c ＝log sin52π，则( A )A 、a ＞b ＞cB 、b ＞a ＞cC 、c ＞a ＞bD 、b ＞c ＞a23、若A ＝(x ＋3)(x ＋7)，B ＝(x ＋4)(x ＋6)，则A 、B 的大小关系为________B A < 24、设函数⎩⎨⎧<->=0101)(x x x f ，，，则不等式xf (x )＋x ≤4的解集是____________]2,0()0,(⋃-∞25、若,02log 2log <<n m 则实数n m ,的关系是（ B ）A 、m n <<1B 、10<<<m nC 、n m <<1D 、10<<<n m26、设,10<<a 则不等式：()01log 2<--x x a a a 的解为 )2log ,(a -∞ 27、若()}{,,,0122Φ=∈=+++=+R A R x x m x x A 且则有（ D ） A 、2->m B 、0≥m C 、04<<-m D 、4->m28、方程0cos sin 2=++k x x 有解，则k 的范围是 ]1,45[-29、已知()x f 是定义在()+∞,0的等调递增函数，()()(),y f x f xy f +=且()12=f ，则不等式()()23≤-+x f x f 的解集为 ]4,3( 30、已知}01|{>+=x x M ，}011|{>-=xx N ，则=⋂N M ____________（－1,1） 31、不等式031>--x x 的解集是________________),3()1,(+∞⋃-∞_32、已知正数,,a b c 满足a b ab +=,a b c abc ++=，则c 的取值范围是___4(1,]3___ 【方法】分离变量33、已知00>>>x b a ，，那么x a x b ++的取值范围是_____________)1,(ab34、已知b a ，都是正数，4=ab ，则b a +的最小值是______________435、设实数x 、y 满足x 2＋2xy －1＝0，则x ＋y 的取值范围是____),1[]1,(+∞⋃--∞____36、设不等式1)11(log >-xa 的解集为D ，若D ∈-1，则=D 1(,0)1a -37、若实数y x ,满足02422=+++y y x x ，则y x +2的范围是 ]0,2[- 【方法】判别式法38、已知方程2(2)50x m x m ++++=有两个正实数根，则实数m 的取值范围是_____]45(--________．【方法】二次函数图像性质；【方法二】分离变量法39、已知函数]1)1()23lg[()(22+-++-=x m x m m x f 的定义域为R ，则实数m 的取值范围是 ),37(]1,(+∞⋃-∞40、函数f (x )＝x 2＋ax ＋3，当x ∈[－2, 2]时f (x )≥a 恒成立，则a 的取值范围是]2,7[-【方法】分类讨论；数形结合41、若函数21()2x x f x a+=-是奇函数，则使3f x >（）成立的x 的取值范围为 (0 , 1) .42、不等式1-x ax＜1的解集为{x |x ＜1或x ＞2},那么a 的值为____21______.【提示】原不等式等价于［(a －1)x +1］(x －1)＜0，所以x =2是方程(a －1)x +1=0的根. 43、设,x y 为实数，若2241,x y xy ++=则2x y +的最大值是5102 .。

高一数学不等式测试题(完整资料).doc

【最新整理，下载后即可编辑】高一数学不等式测试题一、选择题（本大题共10小题，每小题5分，共50分） 1．若a ＜b ＜0，则（）A ．b11<a B ． 0＜ba ＜1 C ． ab ＞b 2 D ．bb a a > 2．若|a ＋c|＜b ，则（）A ． |a |＜|b|－|c| B ． |a |＞|c|－|b| C ． |a |＞|b|－|c| D ． |a |＜|c|－|b|3．设a ＝26c ,37b ,2-=-=，则a ,b,c 的大小顺序是（） A ． a ＞b ＞c B ． a ＞c ＞b C ． c ＞a ＞b D ． b ＞c ＞a 4．设b ＜0＜a ,d ＜c ＜0，则下列各不等式中必成立的是（）A ． a c ＞bd B ．db >c a C ． a ＋c ＞b ＋d D ． a －c ＞b －d5．下列命题中正确的一个是（）A ．ba ab +≥2成立当且仅当a ,b 均为正数B ．2222ba b a +≥+成立当且仅当a ,b 均为正数C ．log a b ＋log a b ≥2成立当且仅当a ,b ∈(1,＋∞)D ．|a ＋a1|≥2成立当且仅当a ≠06．函数y ＝log ⎪⎭⎫⎝⎛-+⋅+-2134223x x x x 的定义域是（）A ．x ≤1或x ≥3B ．x ＜－2或x ＞1C ．x ＜－2或x ≥3D ．x <－2或x ＞37．已知x,y ∈R ，命题甲: |x －1|＜5,命题乙: ||x |－1|＜5，那么（）A ．甲是乙的充分条件，但不是乙的必要条件B ．甲是乙的必要条件，但不是乙的充要条件C ．甲是乙的充要条件D ．甲不是乙的充分条件，也不是乙的必要条件 8．已知实数x ,y 满足x 2＋y 2＝1，则代数式(1－x y)(1＋x y)有（） A ．最小值21和最大值1 B ．最小值43和最大值1C ．最小值21和最大值43D ．最小值19．关于x 的方程ax 2＋2x －1＝0至少有一个正的实根的充要条件是（） A ．a ≥0 B ．－1≤a ＜0C ．a ＞0或－1＜a ＜0D ．a ≥－110．函数y ＝x x x +++132(x ＞0)的最小值是（）A ．23B ．－1＋23C ．1＋23D ．－2＋23二、填空题（本大题共4小题，每小题6分，共24分）11．关于x 的不等式a x 2+b x +2>0的解集是}3121|{<<-x x ，则a +b=_____________。

高一数学不等式试题

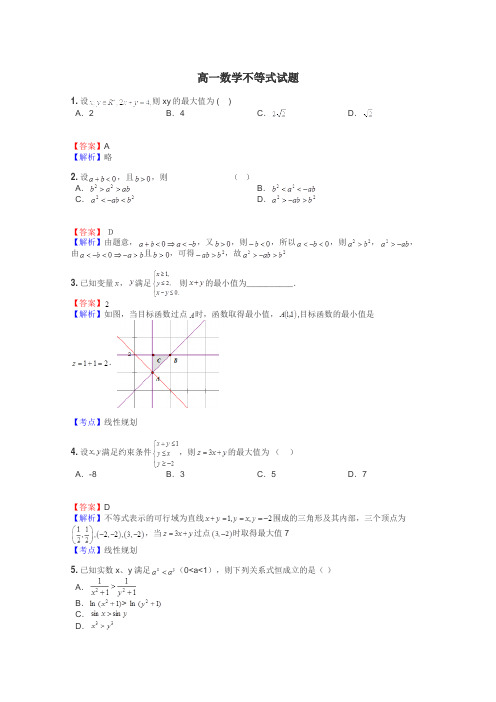
高一数学不等式试题1.设则xy的最大值为 ( )A．2B．4C．D．【答案】A【解析】略2.设，且，则（）A．B．C．D．【答案】Ｄ【解析】由题意，，又，则，所以，则，，由且，可得，故3.已知变量，满足则的最小值为__________．【答案】【解析】如图，当目标函数过点时，函数取得最小值，,目标函数的最小值是．【考点】线性规划4.设满足约束条件，则的最大值为（）A．-8B．3C．5D．7【答案】D【解析】不等式表示的可行域为直线围成的三角形及其内部，三个顶点为，当过点时取得最大值7【考点】线性规划5.已知实数x、y满足（0<a<1），则下列关系式恒成立的是（）A．B．>C．D．【答案】D【解析】，是减函数，所以当时，，所以当时，只有成立，而当时，不能确定与的大小，以及与的大小．【考点】不等式的性质6.若不等式对一切恒成立，则实数取值的集合为（）A．B．C．D．【答案】D【解析】当时，恒成立，当，解得，所以【考点】含参不等式恒成立问题7.若实数，满足，则的取值范围是（用区间表示）【答案】【解析】且，设，，则，所以且，所以且．所以的取值范围是．【考点】1．基本不等式；2．三角换元求取值范围．8.设的最小值为_________．【答案】【解析】正数满足，，当且仅当时取等号，所以所求的最小值为。

【考点】基本不等式9.下列选项中，使不等式成立的x的取值范围是A．（1，+∞）B．（0,1）C．（-1,0）D．（-∞，-1）【答案】D【解析】当时，不等式为显然无解，当时，不等式为，即，所以不等式解集为（-∞，-1），故选择D【考点】解不等式10.解关于的不等式：【答案】详见解析【解析】解含参的一元二次不等式，第一步先讨论二次项前的系数，此题为，所以先不讨论，第一步，先将式子分解因式，整理为，第二步，，，讨论两根的大小关系，从而写出解集的形式．试题解析：原不等式可化为：，（1）当－1＜a＜0时，，所以x＞－或x＜1。

高一数学具体的不等式试题

高一数学具体的不等式试题1.已知关于的不等式的解集是，则 .【答案】2【解析】化分式不等式为整式不等式，根据解集是得，,方程的两实根分别为，，所以=，a=2【考点】解分式不等式，二次方程与二次不等式之间的关系.2.不等式2x－x－1>0的解集是A．(，1)B．(1，+∞)C．(－∞，1)∪(2，+∞)D．(－∞，)∪(1，+∞)【答案】D【解析】不等式2x－x－1>0，即，所以，其解集为(－∞，)∪(1，+∞)，选D。

【考点】一元二次不等式的解法点评：简单题，一元二次不等式的解法应首先考虑“因式分解法”。

3.不等式的解集是 .【答案】【解析】根据题意，由于不等式，故可知不等式的解集为【考点】一元二次不等式点评：主要是考查了一元二次不等式的求解，属于基础题。

4.若，且，则下列不等式一定成立的是（）A．B．C．D．【答案】D【解析】根据题意，由于，且，那么根据不等式两边同时加上一个数不等式方向不变，不等式的可乘性可知，只有c>0选项B成立，对于C，只有c不为零时成立，对于A，由于c=0不成立，故选D.【考点】不等式的性质点评：主要是考查了不等式性质的运用，属于基础题。

5.已知是任意实数，且，则下列结论正确的是（）A．B．C．D．【答案】D【解析】根据题意，由于是任意实数，且，当a=0,b=-1,选项A不成立，对于B，由于a=3,b=2,不成立，对于C，由于,只有a-b>1不等式成立，故排除发选D.【考点】不等式的性质点评：主要是考查了对数函数性质以及不等式性质的运用，属于基础题。

6.不等式的解集是；【答案】【解析】根据题意，由于不等式，等价于当x> ,x-1<1, x<2，即当x,得到1-2x-x<1,x>0,故可知0<x,综上可知满足不等式的解集为【考点】绝对值不等式点评：主要是考查了绝对值不等式的求解，属于基础题。

7.当时，不等式恒成立，则m的取值范围是__ __.【答案】【解析】，设，当时，当时【考点】不等式恒成立点评：不等式恒成立求参数范围的题目常采用分离参数法，转化为求函数最值8.（1）解关于x的不等式；（2）若关于x的不等式的解集为，解关于x的不等式【答案】（1）（2）【解析】解：（1）因为方程的两个根为1和3所以不等式的解集为（2）因为不等式的解集为所以的两个根为1和2将跟代入方程得，解得所以不等式化为因为方程的两个为和1所以不等式的解集为【考点】一元二次不等式的解法点评：若方程有两根（），则一元二次不等式的解集是（），当不等式由等号时，解集也有等号。

高一数学不等式的性质试题

高一数学不等式的性质试题1.若则下列不等式成立的是（）A．B．C．D．【答案】D【解析】由题意可得又有基本不等式可得，且，对不四个选项可得.【考点】基本不等式；不等关系与不等式.2.已知且，则下列不等式恒成立的是（）A．B．C．D．【答案】C【解析】由题知，值不确定，，由于所以对，其它三项不一定对．【考点】判断不等式的大小关系．3.若，则下列不等式成立的是（）A．B．C．D．【答案】D.【解析】由条件可知：A：∵，∴A错误；B：，∴B错误；C：，∴C错误；D：，∴D正确.【考点】作差法证明不等式.4.下列不等式正确的是A．若，则B．若，则C．若，则D．若，则【答案】B【解析】A.若c<0，则不等号改变，若c=0，两式相等，故A错误；B. 若，则，故，故B正确；C.若b=0，则表达是不成立故C错误；D.c=0时错误.【考点】不等式的性质.5.已知a，b为非零实数，且a＜b，则下列命题一定成立的是（）A．B．C．D．【解析】A．中，例如当时不成立；B．中，例如时不成立；D．中，例如时不成立；C．中，不等式两边同乘以非零正实数，不等号方向不变，得到，所以C正确【考点】不等式的简单性质6.如果a＜b＜0，那么( )．A．a－b＞0B．ac＜bc C．＞D．a2＜b2【答案】C【解析】根据题意，由于a＜b＜0，则a－b<0 故错误，对于c=0时则不等式ac＜bc不成立，对于＞符合倒数性质可知，成立，对于a2＜b2，a=-3,b=-2不成立，故答案为C.【考点】不等式的性质点评：主要是考查了不等式的性质的运用，属于基础题。

7.设x > 0, y > 0,, ， a 与b的大小关系（）A．a >b B．a <b C．a b D．a b【答案】B【解析】由x＞0，y＞0，结合不等式的性质可得，解：∵x＞0，y＞0，∴x+y+1＞1+x＞0，1+x+y＞1+y＞0,则可知，，那么可知，故可知得到a <b，选B.【考点】不等式的性质点评：本题主要考查了不等式的性质的简单应用，解题的关键是熟练应用基本性质8.已知实数满足，，则的取值范围是．【答案】【解析】将代入，并化简，构造关于的一元二次方程：，该方程有解，则，解得【考点】不等式的运用点评：主要是考查了构造方程的思想，借助于判别式得到范围，属于中档题。

高中不等式试题及答案

高中不等式试题及答案1. 若不等式\(2x-1 > 5\)成立，求\(x\)的取值范围。

答案：首先将不等式\(2x-1 > 5\)进行移项，得到\(2x > 6\)。

然后将不等式两边同时除以2，得到\(x > 3\)。

因此，\(x\)的取值范围是\(x > 3\)。

2. 已知\(a > 0\)，求不等式\(\frac{1}{a} < \frac{1}{2}\)的解集。

答案：将不等式\(\frac{1}{a} < \frac{1}{2}\)进行交叉相乘，得到\(2 < a\)。

因为已知\(a > 0\)，所以解集为\(a > 2\)。

3. 已知\(x\)和\(y\)满足\(x + y = 10\)，且\(y > 0\)，求\(x\)的取值范围。

答案：由\(x + y = 10\)可得\(x = 10 - y\)。

因为\(y > 0\)，所以\(10 - y > 0\)，即\(y < 10\)。

因此，\(x\)的取值范围是\(0 < x< 10\)。

4. 已知不等式\(3x - 2 > 7\)，求\(x\)的取值范围。

答案：将不等式\(3x - 2 > 7\)进行移项，得到\(3x > 9\)。

然后将不等式两边同时除以3，得到\(x > 3\)。

因此，\(x\)的取值范围是\(x > 3\)。

5. 已知\(a\)和\(b\)满足\(a + b = 12\)，且\(a > 0\)和\(b > 0\)，求\(a\)的取值范围。

答案：由\(a + b = 12\)可得\(b = 12 - a\)。

因为\(a > 0\)和\(b > 0\)，所以\(12 - a > 0\)，即\(a < 12\)。

同时，\(a > 0\)。

因此，\(a\)的取值范围是\(0 < a < 12\)。

高一上数学不等式等综合测试题

高一上数学不等式等综合测试题一、单项选择题1.已知b<0<a,则下列不等式正确的是（）A.b2<a2B.1b >1aC.-b<-aD.a -b>a+b2.已知有理数a ，b ，c 在数轴上的位置如图所示，则下列式子正确的是（）A.cb>abB.ac>abC.cb<abD.c ＋b>a ＋b3.若点P 21,23a a ⎛⎫+-- ⎪⎝⎭在第三象限内，则a 的取值范围是（）A.⎝ ⎛⎭⎪⎫－12，6 B.（－∞，－6）∪1,2⎛⎫+∞⎪⎝⎭C.⎝ ⎛⎭⎪⎫－12，－6 D.⎝ ⎛⎭⎪⎫－6，－12 4.若A ＝（－2，5]，B ＝[－6，3]，则A∪B 等于（）A.[－6，5）B.[－2，3]C.（－2，3]D.[－6，5]5.不等式|1－3x|<2的解集是（） A.11,1133⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭ B.11,3⎛⎫- ⎪⎝⎭C.()－∞，－1∪1,3⎛⎫+∞ ⎪⎝⎭ D.1,3⎛⎫-∞- ⎪⎝⎭∪()1，＋∞6.设集合A ＝{x|2（x ＋3）>6}，B ＝{x|x2－3x ＋2≥0}，则A∪B 等于（） A.RB.{x|x ≥2}C.{x|x<1或x≥2}D.{x|x>0}7.如图所示，在数轴上表示的区间是下列哪个不等式的解集？（）A.x2－x －6≤0B.x2－x －6≥0C.⎪⎪⎪⎪⎪⎪x －12≥52D.x －3x ＋2≥08.已知log2x ＝－1，则x －2等于（）A.4B.2C.14D.129.若x∪R ，下列不等式一定成立的是（） A.x 5＜x 2B.5－x ＞2－xC.x2＞0D.（x ＋1）2＞x2＋x ＋110.已知x ＞0，则x ＋x －1的（）A.最小值为2B.最大值为2C.最小值为1D.最大值为111.｜3－2x ｜＜1的解集是（）A.（－1，1）B.（－1，2）C.（1，2）D.（－2，1）12.若3x2－2＝1，则x 的值是（）A.±2B.±3C.12D.1313.区间[－3，0）∪（1，＋∞）在数轴上表示正确的是（）14.已知a －b>0，则下列不等式正确的是（）A.a2>b2B.1a <1bC.a －2>b －3D.|a|>|b|15.已知a －b<0，a>0，那么a ，b ，－a ，－b 的大小关系是（） A.a>b>－b>－aB.b>a>－a>－bC.a>－b>－a>bD.a>－b>b>－a16.已知x>0，则x 2＋12x 有（）A.最大值1B.最小值1C.最大值12D.最小值1217.不等式|x|＋1<0的解集是（）A.∅B.RC.（－1，1）D.（－∞，－1）∪（1，＋∞）18.已知三角形的三边分别为a,b,c,则下列不等式关系错误的是（） A.a+b>cB.a<b+cC.c -b<aD.（a+b -c ）（b+c -a ）<019.集合A={x|x<2或x ≥5}用区间表示为（）A.（-∞,2）∪[5,+∞）B.（2,5]C.（-∞,2]∪[5,+α）D.（2,5）20.不等式组340,30x x ->⎧⎨-≥⎩的解集是（） A.4,33⎡⎫⎪⎢⎣⎭ B.4,3⎛⎫+∞ ⎪⎝⎭C.(,3]-∞D.4,33⎛⎤⎥⎝⎦二、填空题21.若x∪（－4，3]，则－2x ＋1的取值范围是 .22.比较大小：（x ＋5）（x ＋7）（x ＋6）2.23.结合二次函数性质，可得不等式x2＋4x ＋5＜0的解集是 .24.当x∪ 时，代数式x －53的值与代数式2x －72的值之差不小于2.25.已知x>1，则y ＝4x ＋x ＋3的最低点坐标为 .26.抗洪救灾，志愿小队向灾区运送物资，共有120 km 路程，需要1小时内送达，前半小时已经走了50 km 后，为保证及时送达，后半小时的平均速度至少为 km/h.27.比较大小：87 1211 .（用最恰当的不等号填空）28.已知xy=2,则x2＋4y2的最小值是 .三、解答题29.问：当x 取何值时，12（1－5x ）－23x 的值为非负数？30.已知关于x 的不等式{x|mx2＋nx ＋5≤0}的解集是512x x ⎧⎫≤≤⎨⎬⎩⎭，求m 和n 的值.31.解不等式：（1）|2x －3|≤4; （2）|4－3x|>2.32.比较2x2＋4x ＋9和（x ＋3）2＋（x －1）2的大小.33.解不等式.（1）（x－1）2－9<0;（2）x2＋2x＋3≥0.答案一、单项选择题1.B2.A3.D4.D5.A6.A7.D8.A9.B10.A【提示】利用均值定理变形公式a＋b≥2ab.11.C【分析】｜3－2x｜＜1，∴－1＜3－2x＜1，－4＜－2x＜－2，1＜x＜2.12.A【提示】由223x ＝1得x2－2＝0，x＝± 2.13.C【提示】选项的区别在于端点是否是空心．14.C15.B16.B【提示】∪x>0，∴x2＋12x≥214＝1.（当x2＝12x，即x＝1时，“＝”成立）17.A 【提示】∪|x|≥0，∪不等式|x|＋1<0的解集为∅.18.D 【解析】根据三角形三边中“两边之和大于第三边”可得.19.A20.D二、填空题21.[－5，9）【提示】根据区间的两个端点，当x ＝－4时，取值9，显然9是取不到的；当x ＝3时，取值－5，所以答案是半开半闭区间．22.<23.∅24.{x|x ≤－14}【提示】x －53－2x －72≥2⇒2（x －5）－3（2x －7）≥12⇒2x －10－6x ＋21≥12⇒－4x≥1⇒x ≤－14.25.（2，7）26.140【提示】设后半小时的平均速度为x km/h ，根据题意得50＋（1－0.5）x≥120，解得x≥140.27.>【提示】用作差比较法28.8三、解答题 29.319x x ⎧⎫≤⎨⎬⎩⎭30.解：由题意得⎩⎪⎨⎪⎧1×52＝5m ，1＋52＝－n m ，解得⎩⎪⎨⎪⎧m ＝2，n ＝－7. 31.解：（1）原不等式等价于－4≤2x －3≤4，∴－1≤2x≤7，解得－12≤x≤72， ∴原不等式的解集是1722x x ⎧⎫≤≤⎨⎬⎩⎭. （2）原不等式等价于4－3x>2或4－3x<－2，解得x<23或x>2， ∴原不等式的解集是223x x x ⎧⎫<>⎨⎬⎩⎭或. 32.解：∪2x2＋4x ＋9－[（x ＋3）2＋（x －1）2]＝－1<0， ∴2x2＋4x ＋9<[（x ＋3）2＋（x －1）2].33.解：(1)移项得(x －1)2<9，解得－2<x<4，故原不等式的解集为{x|－2<x<4}．(2)令x2＋2x ＋3＝0，易知Δ<0，方程没有实数根，故原不等式的解集为R.。

高一数学不等式试题

高一数学不等式试题1.下列命题不正确的是A．B．C．D．【答案】D【解析】略2.已知实数x，y满足，则z＝4x＋y的最大值为（）A．10B．8C．2D．0【答案】B【解析】根据条件，可知，因为，所以两不等式相减得到，所以最大值为8【考点】函数最大最小值3.已知，．（1）当时，①解关于的不等式；②若关于的不等式在上有解，求的取值范围；（2）若，证明不等式．【答案】（1）①时，时，，时，②（2）详见解析【解析】（1）代入转化为关于的一元二次不等式，结合二次不等式的解法求解时需要对参数分情况讨论，从而确定方程的两根大小关系；不等式在上有解中将不等式变形分离出，转化为的形式，转化为函数求值域；（2）首先将代入化简转化为用表示的函数式，利用求得的范围，进而求得函数的最小值试题解析：（1）①不等式代入整理为，当时，时，，时，；②整理得有解，当时最大值为5，取值范围是（2），所以，即【考点】1．一元二次不等式解法；2．不等式与函数的转化；3．函数求最值4.若是正实数，且则的最小值为．【答案】【解析】将化简得，令，则。

①，因为是正实数，所以，则对于①式当时有最小值．【考点】1．换元法；2．二次函数最值；5.关于x的不等式的解集是，则关于x的不等式的解集是（）A．B．C．D．【答案】D【解析】关于x的不等式的解集是，所以，所以不等式可化为，从而确定解集；【考点】1．一元二次不等式的解法；2．一元一次不等式的解集与系数的关系；6.已知变量，满足则的最小值为__________．【答案】【解析】如图，当目标函数过点时，函数取得最小值，,目标函数的最小值是．【考点】线性规划7.若实数x，y满足则z＝的取值范围是（）A．B．C．D．【答案】D【解析】作出可行域如图．，表示可行域内的点与点连线的斜率．图中，所以，由图分析可知或．所以或．故D正确．【考点】1线性规划；2直线的斜率．8.（8分）关于的不等式，（1）已知不等式的解集为，求a的值；（2）解关于的不等式．【答案】（1）；（2）时原不等式解集为；时原不等式解集为；时原不等式解集为；时原不等式解集为；时原不等式解集为．【解析】（1）由不等式的解集可知，2是方程的两根，由韦达定理可求得的值．（2）讨论二次项系数是否为0，由时的根为或，讨论两根的大小，并注意抛物线开口方向．结合一元二次函数图像解不等式．试题解析：解：因为的解集为，所以方程的两根为或，所以，解得．（2），当时原不等式变形为，解得；当时，的根为或．时，或，时，，时，，时，综上可得时原不等式解集为；时原不等式解集为；时原不等式解集为；时原不等式解集为；时原不等式解集为．【考点】一元二次不等式．9.（12分）已知函数，（1）当时，解不等式；（2）比较的大小；（3）解关于x的不等式．【答案】（1）；（2）详见解析；（3）详见解析【解析】（1）当时，将不等式分解因式，得到解集；（2）比较大小，可以做差，然后通分，分解因式，然后讨论的范围，比较两数的大小；（3）第一步，先分解因式，第二步，根据上一问的结果得到与的大小关系，得到解集．试题解析：解：（1）当时，有不等式，∴，∴不等式的解集为：；（2）∵且∴当时，有当时，有当时，；（3）∵不等式当时，有，∴不等式的解集为；当时，有，∴不等式的解集为；当时，不等式的解集为．【考点】1．解二次不等式；2．比较大小．10.已知不等式的解集为，那么=（）A．3B．C．-1D．1【答案】B【解析】因为不等式的解集为，所以，，故选B．【考点】分式不等式的解法11.如果，那么下面不等式一定成立的是（）A．B．C．D．【答案】D【解析】取a=-2,b=-1,c=1,代入选项进行逐一验证得选项D正确，故选D．【考点】不等式的基本性质12.已知，则_______【答案】23【解析】，两边平方得【考点】代数式求值13.已知实数满足,则的最大值是 .【答案】13【解析】作出二元一次不等式组所表示的可行域如图所示：根据图像可知当经过直线与直线的交点时，取最大值时，最大值为【考点】二元一次不等式的线性规划问题；14.（本小题满分16分）设函数f（x）＝x2－2tx＋2，其中t∈R．（1）若t＝1，求函数f（x）在区间[0，4]上的取值范围；（2）若t＝1，且对任意的x∈[a，a＋2]，都有f（x）≤5，求实数a的取值范围．（3）若对任意的x1，x2∈[0，4]，都有|f（x1）－f（x2）|≤8，求t的取值范围．【答案】（1） [1，10] （2） [－1，1] （3） [4－2 ，2 ]【解析】（1）若t=1，则f（x）＝x2－2tx＋2，根据二次函数在[0，4]上的单调性可求函数的值域（2）由题意可得函数在区间[a，a+2]上，[f（x）]max≤5，分别讨论对称轴x=t与区间[a，a+2]的位置关系，进而判断函数在该区间上的单调性，可求最大值，进而可求a的范围（3）设函数f（x）在区间[0，4]上的最大值为M，最小值为m，对任意的x1，x2∈[0，4]，都有|f（x1）－f（x2）|≤8等价于M-m≤8，结合二次函数的性质可求试题解析：因为f（x）＝x2－2tx＋2＝（x－t）2＋2－t2，所以f（x）在区间（－∞，t]上单调减，在区间[t，∞）上单调增，且对任意的x∈R，都有f（t＋x）＝f（t－x），（1）若t＝1，则f（x）＝（x－1）2＋1．①当x∈[0，1]时．f（x）单调减，从而最大值f（0）＝2，最小值f（1）＝1．所以f（x）的取值范围为[1，2]；②当x∈[1，4]时．f（x）单调增，从而最大值f（4）＝10，最小值f（1）＝1．所以f（x）的取值范围为[1，10]；所以f（x）在区间[0，4]上的取值范围为[1，10]．（2）“对任意的x∈[a，a＋2]，都有f（x）≤5”等价于“在区间[a，a＋2]上，[f（x）]max≤5”．若t＝1，则f（x）＝（x－1）2＋1，所以f（x）在区间（－∞，1]上单调减，在区间[1，∞）上单调增．当1≤a＋1，即a≥0时，由[f（x）]max＝f（a＋2）＝（a＋1）2＋1≤5，得－3≤a≤1，从而0≤a≤1．当1＞a＋1，即a＜0时，由[f（x）]max＝f（a）＝（a－1）2＋1≤5，得－1≤a≤3，从而－1≤a＜0．综上，a的取值范围为区间[－1，1]．（3）设函数f（x）在区间[0，4]上的最大值为M，最小值为m，所以“对任意的x1，x2∈[0，4]，都有|f（x1）－f（x2）|≤8”等价于“M－m≤8”．①当t≤0时，M＝f（4）＝18－8t，m＝f（0）＝2．由M－m＝18－8t－2＝16－8t≤8，得t≥1．从而t∈Æ．②当0＜t≤2时，M＝f（4）＝18－8t，m＝f（t）＝2－t2．由M－m＝18－8t－（2－t2）＝t2－8t＋16＝（t－4）2≤8，得4－2≤t≤4＋2．从而4－2≤t≤2．③当2＜t≤4时，M＝f（0）＝2，m＝f（t）＝2－t2．由M－m＝2－（2－t2）＝t2≤8，得－2≤t≤2．从而2＜t≤2．④当t＞4时，M＝f（0）＝2，m＝f（4）＝18－8t．由M－m＝2－（18－8t）＝8t－16≤8，得t≤3．从而t∈Æ．综上，a的取值范围为区间[4－2 ，2 ]．【考点】1．二次函数在闭区间上的最值；2．二次函数的性质15.已知，关于的一元二次不等式的解集中有且仅有个整数，则实数的取值范围为．【答案】【解析】二次函数的对称轴为，所以个整数为：，，．所以，解得．【考点】一元二次不等式整数解16.若关于的不等式在区间上恒成立，则实数的取值范围是．【答案】【解析】关于的不等式在区间上恒成立等价于在时，函数的图像恒在函数的图像的下方．从上图易知且，即，解得．【考点】恒成立问题求参数范围．【方法点睛】恒成立问题求参数范围，常常把参数移到一边转化为求最值，但是本题将参数移到一边比较困难，就是移到一边了，另一边的最值也难于计算，所以考虑数形结合．如上图，从图中能直接看出满足题意的条件且，从而求出参数范围．本题使我们感受到数形结合的魅力所在．17.（2015秋•宝山区期末）解不等式组：．【答案】原不等式组的解集为（1，2）．【解析】由条件利用分式不等式、绝对值不等式的解法，等价转化，求得x的范围．解：不等式组，即，即，求得 1＜x＜2，即原不等式组的解集为（1，2）．【考点】其他不等式的解法．，b=a sinα，c=a cosα，则（）18.（2015秋•黄山期末）已知α∈（0，），a=logaA．c＞a＞b B．b＞a＞c C．a＞c＞b D．b＞c＞a【答案】D【解析】根据指数函数对数函数三角图象和性质即可判断解：∵α∈（0，），∴0＜sinα＜cosα＜1，∴a=log＜0，a∵y=a x为减函数，∴a sinα＞a cosα＞0，∴b＞c＞a，故选：D【考点】指数函数的图象与性质．19.设实数，满足则的取值范围是．【答案】．【解析】作出可行域，令，则由的几何意义可知取点时，取得最大值，取点时，取得最小值，则，又，由及单调递增，可知单调递增，故，，所以的取值范围是．【考点】1、线性规划；2、函数单调性求最值．【思路点睛】本题主要考查目标函数求取最值（范围）问题，属困难题．由题给不等式组作出相应可行域，取目标函数中，由的几何意义：可行域中的点与原点的连线斜率，可知，取得最大值和最小值的最优解分别为点和点，从而，此时目标函数为，结合函数单调性可求．20.若关于x的不等式（2x－1）2<ax2的解集中整数恰好有3个，则实数a的取值范围是__________.【答案】【解析】关于x的不等式（2x－1）2<ax2等价于，其中且有，故有，不等式的解集为，所以解集中一定含有1,2,3，可得，所以，解得.【考点】含参数的一元二次方程的解法.21.下列四个不等式中，解集为的是（）A．B．C．D．【答案】B【解析】对于A．，得，判别式，所以此不等式的解集不为；对于B．，判别式，所以此不等式的解集为；对于C．，判别式，所以此不等式的解集为，不为；对于D．，得：判别式，所以此不等式的解集不为；故选B．【考点】一元二次不等式．22.对任意实数，不等式恒成立，则实数的取值范围是（）A．－24＜k＜0B．－24＜k≤0C．0＜k≤24D．k≥24【答案】B【解析】当时不等式即为，不等式恒成立，当时，若不等式恒成立，则，即，即，综合知，故选择B．【考点】二次函数与二次不等式.23.已知c＜d，a＞b＞0，下列不等式中必成立的一个是（）A．a+c＞b+d B．a﹣c＞b﹣d C．ad＜bc D．＞【答案】B【解析】由题意可得﹣c＞﹣d，且 a＞b，相加可得 a﹣c＞b﹣d，从而得出结论．解：∵c＜d，a＞b＞0，∴﹣c＞﹣d，且 a＞b，相加可得a﹣c＞b﹣d，故选：B24.若x＞0，y＞0，且＋＝1，则xy有（）A．最大值64B．最小值C．最小值D．最小值64【答案】D【解析】因为，所以（当且仅当，即时取等号），即；故选D．【考点】基本不等式．【方法点睛】本题考查利用基本不等式求最值，属于基础题；在利用基本不等式求最值时，要注意其适用条件（一正，二定，三相等）的验证，陪凑“定和或定积”的解题的关键，也是难点，而验证“相等”是学生易忽视的问题，如“由判定的最小值为2”是错误的，因为是不成立的.25.如果a＜b＜0，那么下面一定成立的是( )A．ac＜bc B．a﹣b＞0C．a2＞b2D．【答案】C【解析】利用不等式的性质即可得出．∵a＜b＜0，∴-a＞-b＞0，∴a2＞b2．故选C．【考点】不等式比较大小．26.已知，且，若恒成立，则实数的取值范围为__________．【答案】【解析】，∴∵恒成立，∴，求得-4＜m＜2【考点】函数恒成立问题27.以下列函数中，最小值为的是（）A．B．C．D．【答案】A【解析】由不等式性质可知，当且仅当即时等号成立，取得最小值2【考点】不等式性质28.已知，且，则的值是（）A．20B．C．D．400【答案】B【解析】由已知可得【考点】指数式对数式化简及化简29.解关于的不等式：.【答案】当时，原不等式的集为，当时，原不等式的集为，当时，原不等式的集为或，当时，原不等式的集为.【解析】不等式中含有参数，对分和两种情况讨论，当时，原不等式为，解得即可，当时，原不等式化为一元二次不等式，再对分和两种情况分别求解.试题解析：原不等式整理得.当时，原不等式为，∴；当时，原不等式为，∴当时，原不等式可化为，当时，原不等式可化为，当时，原不等式为，原不等式的集为或，若，则，原不等式的集为或，当时，原不等式的集为.综上，当时，原不等式的集为，当时，原不等式的集为，当时，原不等式的集为或，当时，原不等式的集为.【考点】不等式的解法.30.已知，，，则A．B．C．D．【答案】D【解析】【考点】比较大小31.已知函数满足，且．（Ⅰ）求实数，的值；（Ⅱ）若不等式的解集为，求实数的值．【答案】（Ⅰ），；（Ⅱ）【解析】（Ⅰ）由可得到关于的关系式，由可得到关于的另一关系式，解方程组得到的值；（Ⅱ）将不等式变形，从而得到关于的方程，求解其值试题解析：（Ⅰ）∵满足．∴，即，则=0，即，∵，∴，得，即实数，的值为，；…………6分（Ⅱ）∵，，∴不等式的解集为（0，2），则＞0，由得，由，得．…………12分【考点】抽象函数运算及不等式解法32.不等式对任意实数恒成立，则实数的取值范围是（）A．B．C．D．【答案】A【解析】因，故，解之得或，故选A.33.设，且b＞0，则下列不等式正确的是（）A．B．C．D．【答案】C【解析】解答：∵a+b<0，且b>0，∴−a>b>0，∴a2>b2.本题选择C选项.34.在平面直角坐标系xOy中，与原点位于直线3x+2y+5=0同一侧的点是（）A．（-3，4）B．（-3，-2）C．（-3，-4）D．（0，-3）【答案】A【解析】当时，，对于当时，，故满足，对于当时，，故不满足，对于，故不满足，对于时，，故不满足，故选A.35.若，则下列不等式正确的是（）A．B．C．D．【答案】B【解析】因为，所以，因此A错，B对；取，可得，故错误；.取，可得，故错误，故选B.36.不等式的解集是_____________.【答案】【解析】由，得，解得或，故不等式的解集是，故答案为.37.（2015年苏州B14）若，，，则的取值范围为________．【答案】【解析】因为，解得，当时等号成立。

高中数学必修一不等式试卷

必修一不等式一、单选题1．“06x π<<”是“1sin 2x <”的（） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件【答案】A【分析】根据充分必要条件的定义判断．【详解】06x π<<时，1sin 2x 成立，是充分的，但0x =时，1sin 02x =<，不满足6x π<<，必要性不满足，因此是充分不必要条件．故选：A ．2．命题“x R ∀∈，均有2cos 10x x ++<”的否定为（）A ．x R ∀∈，均有2cos 10x x ++≥B ．0x R ∃∈，使得200cos 10x x ++<C ．0x R ∃∈，使得200cos 10x x ++≥D ．x R ∀∈，均有2cos 10x x ++>【答案】C【分析】全称命题的否定是特称命题【详解】根据全称命题的否定是特称命题，所以命题“x R ∀∈，均有2cos 10x x ++<”的否定为“0x R ∃∈，使得200cos 10x x ++≥”故选：C3．若,a b ∈R ，且0ab >，则下列不等式中，恒成立的是A ．222a b ab +>B ．a b +≥C ．11a b +D ．2b a a b +≥ 【答案】D【详解】试题分析：，所以A 错；，只能说明两实数同号，同为正数，或同为负数，所以当时，B 错；同时C 错；或都是正数，根据基本不等式求最值，，故D 正确．考点：不等式的性质4．关于x 的不等式22280(0)x ax a a --<>的解集为12(,)x x ，且：2115x x -=，则a =（）A ．52B ．72C ．154D ．152【答案】A【详解】因为关于x 的不等式22280(0)x ax a a --<>的解集为12(,)x x ，所以212122,8x x a x x a +==-，又2115x x -=，所以2222212121()()43615x x x x x x a -=+-==，解得52a =±，因为0a >，所以52a =. 故选：A.5．若实数,a b 满足12a b+=ab 的最小值为A B ．2 C ．D ．4【答案】C【详解】12121002ab a b ab ab a ba b a +=∴=+≥⨯∴≥，＞，＞，（当且仅当2b a =时取等号），所以ab 的最小值为 C.考点：基本不等式【名师点睛】基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能，因此可以用在一些不等式的证明中，还可以用于求代数式的最值或取值范围．如果条件等式中，同时含有两个变量的和与积的形式，就可以直接利用基本不等式对两个正数的和与积进行转化，然后通过解不等式进行求解．6．若不等式220ax x c ++<的解集是121,,3⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭，则不等式220cx x a ++≤的解集是. A ．11,23⎡⎤-⎢⎥⎣⎦B ．11,32⎡⎤-⎢⎥⎣⎦C ．[-2，3]D ．[-3，2] 【答案】D【分析】先由题意求出,a c ，再代入不等式220cx x a ++≤，求解，即可得出结果.【详解】因为不等式220ax x c ++<的解集是121,,3⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭，所以021*******a a c a⎧⎪<⎪⎪-=-+⎨⎪⎪=-⨯⎪⎩，解得122a c =-⎧⎨=⎩，所以不等式220cx x a ++≤可化为222120x x +-≤，即260x x +-≤，解得32x -≤≤.故选D 【点睛】本题主要考查一元二次不等式的解法，熟记三个二次之间的关系即可，属于基础题型.7．若正实数,a b 满足1a b +=，则A ．11a b +有最大值4 B ．ab 有最小值14CD ．22a b +【答案】C【详解】试题分析：因为正实数，满足，所以112224a b a b b a a b a b a b +++=+=++≥+=，故11a b+有最小值4，故A 不正确；由基本不等式可得112,4a b ab ab +=≥∴≤，故有最大值14，故B 不正确；由于()22122,2a b a b ab ab a b +=++=+≤∴+≤，故+a b 由最大值为2，故C 正确；()22211212122a b a b ab ab +=+-=-≥-=，故22a b +由最小值12，故D 不正确．考点：基本不等式8．已知0a >，0b >，若44a b ab +=，则a b +的最小值是（）A ．2B 1C ．94D ．52【答案】C【分析】将44a b ab +=，转化为144b a +=，由()11414544a b a b a b b a b a ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭，利用基本不等式求解. 【详解】因为44a b ab +=，所以144b a+=，所以()11414544a b a b a b b a b a ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭，19544⎛≥+=⎝，当且仅当1444b a a b b a ⎧+=⎪⎪⎨⎪=⎪⎩，即3234a b ⎧=⎪⎪⎨⎪=⎪⎩时，等号成立，故选：C9．对x R ∀∈，不等式()()222240a x a x -+--<恒成立，则a 的取值范围是（）A ．22a -<≤B ．22a -≤≤C ．2a <-或2a ≥D ．2a ≤-或2a ≥【答案】A【分析】对a 讨论，结合二次函数的图象与性质，解不等式即可得到a 的取值范围.【详解】不等式()()222240a x a x -+--<对一切x ∈R 恒成立，当20a -=，即2a =时，40-<恒成立，满足题意；当20a -≠时，要使不等式恒成立，需200a -<⎧⎨∆<⎩，即有()()22421620a a a <⎧⎪⎨-+-<⎪⎩，解得22a -<<.综上可得，a 的取值范围为(]2,2-.故选：A.10．不等式(x ＋3)2＜1的解集是( )A ．{x |x ＞－2}B ．{x |x ＜－4}C ．{x |－4＜x ＜－2}D ．{x |－4≤x ≤－2}【答案】C【解析】原不等式可化为x 2＋6x ＋8＜0，解得－4＜x ＜－2.选C.11．不等式20ax x c -+>的解集为{21}x x -<<∣，则函数2y ax x c =++的图像大致为（）A ．B ．C ．D ．【答案】C【分析】根据不等式的解集求出参数，从而可得22y x x =-++，根据该形式可得正确的选项．【详解】因为不等式20ax x c -+>的解集为{21}xx -<<∣，故021121a c a a ⎧⎪<⎪⎪-⨯=⎨⎪⎪-+=⎪⎩，故1,2a c =-=，故222y ax x c x x =++=-++，令220x x -++=，解得1x =-或2x =，故抛物线开口向下，与x 轴的交点的横坐标为1,2-，故选：C ．12．若不等式220ax bx ++>的解集是1123x x ⎧⎫-<<⎨⎬⎩⎭，则a b +的值为（） A ．10-B ．14-C ．10D ．14【答案】B【分析】分析可知关于x 的二次方程220ax bx ++=的两根分别为12-、13，利用韦达定理可求得实数a 、b 的值，即可得解. 【详解】由题意可知，关于x 的二次方程220ax bx ++=的两根分别为12-、13，且有0a <，由韦达定理可得112231123a b a ⎧-⨯=⎪⎪⎨⎪-+=-⎪⎩，解得122a b =-⎧⎨=-⎩，因此，14a b +=-. 故选：B.13．若0a B ．11a b >C ．222a b ab +> D．a b +>-【答案】 D【分析】将0a ->a b ，利用不等式的基本性质判断A ，B 的正误，利用重要不等式判断C 的正误，利用特殊值判断D 的正误.【详解】因为0a ->a b 所以a b >，11a b -<-即11a b >，故A ，B 正确. 因为()20a b -≥，所以222a b ab +≥，所以222a b ab +>故C 正确.当 2,1a b =-=-时， +<-a b D 错误.故选：D【点睛】本题主要考查不等式的基本性质，基本不等式，还考查了理解辨析的能力，属于基础题.14．若两个正实数x ，y 满足141x y +=，且存在这样的x ，y 使不等式234y x m m +<+有解，则实数m 的取值范围是（）A ．(1,4)-B ．(4,1)-C ．()(),41,-∞-+∞ D ．()(),30,-∞-⋃+∞【答案】C【分析】利用基本不等式1的妙用，求4y x +的最小值，由题意可得2min 34y m m x ⎛⎫+>+ ⎪⎝⎭，解不等式即可求解. 【详解】因为正实数x ，y 满足141x y+=，所以144224444y y x y x x x y y x ⎛⎫⎛⎫+=++=++≥+ ⎪ ⎪⎝⎭⎝⎭，当且仅当44x y y x =且141x y+=，即2x =，8y =时取等号，所以min 44y x ⎛⎫+= ⎪⎝⎭，因为存在x ，y 使不等式234y x m m +<+有解，所以234m m +>，解得：1m 或4m <-，所以实数m 的取值范围是()(),41,-∞-+∞，故选：C ．15．已知a 、b 、c 满足c b a <<且0ac <，则下列选项中不一定能成立的是A ．ab ac >B ．()0c b a ->C ．22cb ca <D ．()0ac a c -<【答案】C【分析】由已知条件得出0a >，0c <且b 的符号不确定，利用不等式的性质以及特殊值法可判断各选项中不等式的正误.【详解】c b a <<且0ac <，0a ∴>，0c <且b 的符号不确定.对于A 选项，b c >，0a >，由不等式的基本性质可得ab ac >，A 选项中的不等式一定能成立；对于B 选项，a b >，则0b a -<，又0c <，()0c b a ∴->，B 选项中的不等式一定能成立；对于C 选项，取0b =，则22b a <，0c <，22cb ca ∴>；取3c =-，1b =-，2a =，则22cb ca >，C 选项中的不等式不一定成立；对于D 选项，0a >，0c <，则0ac <，0a c ->，()0ac a c ∴-<，D 选项中的不等式一定能成立. 故选：C.【点睛】本题以命题的真假判断与应用为载体，考查了不等式的基本性质，实数的性质，难度不大，属于基础题． 16．“1a >”是“11a<”的（） A ．充分非必要条件 B ．必要非充分条件C ．充要条件D ．非充分非必要条件【答案】A【分析】根据不等式的关系结合充分条件和必要条件的定义进行判断即可．【详解】当1a >时，11a<成立，即充分性成立，当1a =-时，满足11a <，但1a >不成立，即必要性不成立，则“1a >“是“11a<“的充分不必要条件，故选：A ． 17．“0a b >>”是“1a b >”的（） A ．充要条件 B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件【答案】B【分析】根据充分条件、必要条件的定义判断即可；【详解】解：由0a b >>，得1a b >，反之不成立，如2a =-，1b =-，满足1a b >，但是不满足0a b >>，故“0a b >>”是“1a b >”的充分不必要条件．故选：B18．已知a >1，b >1，记M ＝11a b +，N ，则M 与N 的大小关系为（） A ．M >N B ．M ＝NC ．M <ND ．不确定【答案】A【分析】利用基本不等式可得答案.【详解】因为1,1a b >>，所以11a bM a b ab +=+=≥11a b =取等号，N=>=，故选：A ．19．不等式111x ≥--的解集为（）A ．(],0-∞B ．(](),01,-∞+∞C ．[)()0,11,+∞D ．[)0,+∞【答案】B【分析】本题可将111x ≥--转化为01xx ≥-，通过解()1010x x x ⎧-≥⎨-≠⎩即可得出结果.【详解】111x ≥--，即1101x +≥-，01xx ≥-，则()1010x x x ⎧-≥⎨-≠⎩，解得0x ≤或1x >，故不等式111x ≥--的解集为(](),01,-∞+∞，故选：B. 20．若“﹣2<x <3”是“x 2+mx ﹣2m 2<0（m >0）”的充分不必要条件，则实数m 的取值范围是（） A ．m ≥1B ．m ≥2C ．m ≥3D ．m ≥4【答案】C【分析】x 2+mx ﹣2m 2<0（m >0），解得﹣2m <x <m .根据“﹣2<x <3”是“x 2+mx ﹣2m 2<0（m >0）”的充分不必要条件，可得﹣2m ≤﹣2，3≤m ，m >0.解出即可得出.【详解】解：x 2+mx ﹣2m 2<0（m >0），解得﹣2m <x <m .∵“﹣2<x <3”是“x 2+mx ﹣2m 2<0（m >0）”的充分不必要条件，∴﹣2m ≤﹣2，3≤m ，(两个等号不同时取)m >0.解得m ≥3.则实数m 的取值范围是[3，+∞）.故选：C.21．若,a b c d >>，则下列关系一定成立的是（）A ．ac bd >B ．ac bc >C ．a c b d +>+D ．a c b d ->- 【答案】C【分析】利用基本不等式的性质，对选项进行一一验证，即可得到答案；【详解】对A ，当0,0a b c d ac bd >>>>⇒>，故A 错误；对B ，当0c >时，ac bc >，故B 错误；对C ，同向不等式的可加性，故C 正确；对D ，若2,1,0,31,4a b c d a c b d ====-⇒-=-=，不等式显然不成立，故D 错误；故选：C. 22．当01x <<时，141x x+-的最小值为（） A ．0B ．9C ．41e e e +-D ．10【答案】B【分析】将代数式141x x +-与()1x x +-相乘，展开后利用基本不等式可求得141x x+-的最小值. 【详解】因为01x <<，则011x <-<，因此，()1414141559111x x x x x x x x x x -⎛⎫+=++-=++≥+⎡⎤ ⎪⎣⎦---⎝⎭，当且仅当13x =时，等号成立，故141x x+-的最小值为9. 故选：B.23．若命题“22103x x -+<”是命题“x a >”的充分不必要条件，则a 的取值范围是（） A ．1a ≥B ．12a ≥C ．12a ≤D ．1a ≤【答案】C【分析】解不等式22103x x -+<得112x <<，进而根据题意得集合1,12⎛⎫ ⎪⎝⎭是集合(),+∞a 的真子集，再根据集合关系求解即可. 【详解】解：解不等式22103x x -+<得112x <<，因为命题“22103x x -+<”是命题“x a >”的充分不必要条件，所以集合1,12⎛⎫ ⎪⎝⎭是集合(),+∞a 的真子集，所以12a ≤ 故选：C24．若0a <，则关于x 的不等式(1)(2)0ax x -->的解集为（）A ．12x x a ⎧⎫<<⎨⎬⎩⎭ B ．12x x a ⎧⎫<<⎨⎬⎩⎭ C ．1{x x a <或2}x > D ．{2x x <或1}x a> 【答案】B【分析】结合含参一元二次不等式的解法即可.【详解】解：方程(1)(2)0ax x --=的两个根为2x =和1x a=，因为0a <，所以12a <，故不等式(1)(2)0ax x -->的解集为1|2x x a ⎧⎫<<⎨⎬⎩⎭．故选：B ．二、多选题25．下列选项中，满足p 是q 的充分不必要条件的是（）A ．:1p x >，:0q x >B ．:2≠p x ，2:4≠q xC ．:0p x =，:0=q xyD ．:p x y >，22:q x y > 【答案】AC【分析】利用充分条件、必要条件的定义逐项判断即得.【详解】对于A ，∵:1p x >，:0q x >，∴由p 能推出q ，由q 推不出p ，即p 是q 的充分不必要条件，故A 正确；对于B ，∵:2≠p x 即2x ≠±，2:4≠q x 即2x ≠±，∴p 是q 的充要条件，故B 错误；对于C ，∵:0p x =，:0=q xy 即0x =或0y =，∴由p 能推出q ，由q 推不出p ，即p 是q 的充分不必要条件，故C 正确；对于D ，∵:p x y >，22:q x y >，取12x y =->=-，则2214x y =<=，由p 推不出q ；取2210,10x y x y =-<==>=，由q 推不出p ；故p 是q 的既不充分也不必要条件，故D 错误.故选：AC.26．已知,a b R +∈且1a b +=，那么下列不等式中，恒成立的有（）．A ．14abB ．1174ab ab +C 2bD ．11222a b+ 【答案】ABC【分析】利用基本不等式，逐个进行验证，即可得到结论．【详解】,,1a b R a b +∈+=，2124a b ab +⎛⎫∴= ⎪⎝⎭(当且仅当12a b ==时取得等号)．所以选项A 正确由选项A 有14ab ≤，设1y x x =+，则1y x x =+在104⎛⎤ ⎥⎝⎦，上单调递减. 所以1117444ab ab +≥+=，所以选项B 正确 2(2a b a b ab a b a b +=+++++=(当且仅当12a b ==时取得等号)，2b ．所以选项C 正确.113332222222a b a b b a b a b a b a ba +++=+=+++=+222ab =时等号成立），所以选项D 不正确．故A ，B ，C 正确故选：ABC 【点睛】本题考查基本不等式的运用，考查学生分析解决问题的能力，属于中档题27．若正实数a ，b 满足1a b +=则下列说法正确的是（）A ．ab 有最大值14B C ．11a b +有最小值2 D ．22a b +有最大值12【答案】AB【分析】对A,根据基本不等式求ab 的最大值；对B,对C,根据()1111a b a b a b ⎛⎫+=++ ⎪⎝⎭再展开求解最小值；对D,对1a b +=平方再根据基本不等式求最值.【详解】对A,2211224a b ab +⎛⎫⎛⎫≤== ⎪ ⎪⎝⎭⎝⎭,当且仅当12a b ==时取等号.故A 正确.对B, 22a b a b a b =+++++=,,当且仅当12a b ==时取等号.故B 正确.对C,()1111224b a a b a b a b a b ⎛⎫+=++=++≥+⎝= ⎪⎭.当且仅当12a b ==时取等号.所以11a b +有最小值4.故C 错误. 对D, ()()2222222121a b a ab b a a b b +=⇒++=≤+++,即2212a b +≥,故22a b +有最小值12.故D 错误. 故选：AB【点睛】本题主要考查了基本不等式求解最值的问题,需要根据所给形式进行合适的变形,再利用基本不等式.属于中档题. 28．解关于x 的不等式：2(24)80ax a x +-->，则下列说法中正确的是（）A ．当0a =时，不等式的解集为{}4x x >B ．当0a >时，不等式的解集为{|4x x >或2x a ⎫<-⎬⎭C ．当0a <时，不等式的解集为24x x a ⎧⎫-<<⎨⎬⎩⎭D ．当12a =-时，不等式的解集为∅ 【答案】ABD【分析】讨论参数a ，结合一元二次不等式的解法求解集即可判断各选项的正误.【详解】A ：0a =，则280x ->，可得解集为{}4x x >，正确；B ：0a >，则(2)(4)0ax x +->，可得解集为{|4x x >或2x a ⎫<-⎬⎭，正确； C ：0a <，当24a -<时解集为24x x a ⎧⎫-<<⎨⎬⎩⎭；当24a -=时无解；当24a ->时解集为24x x a ⎧⎫<<-⎨⎬⎩⎭，错误； D ：由C 知：12a =-，即24a -=，此时无解，正确. 故选：ABD29．若0a b <<，下列不等式中不成立的是（）A ．1a b b -D ．22b a >【答案】ABD【分析】根据不等式的性质判断各选项．【详解】A 选项，10a a b b b --=>，∴1a b>，不成立， B 选项，110b a a b ab--=>，不成立， C 选项，∵0a b <<，∴a a b -=>-，成立，D 选项，由0a b ->->，∴22()()a b ->-，即22a b >，不成立，故选：ABD.30．设正实数m 、n 满足2m n +=，则下列说法中正确的是（）A ．124m n ->B ．mn 的最大值为1C 的最小值为2D ．22m n +的最小值为2【答案】ABD【分析】利用不等式的性质以及指数函数的性质可判断A 选项的正误，利用基本不等式可判断BCD 选项的正误.【详解】对于A 选项，因为正实数m 、n 满足2m n +=，则02m <<，()()2222,2m n m m m -=--=-∈-，故21224m n -->=，A 对；对于B 选项，由基本不等式可得212m n mn +⎛⎫≤= ⎪⎝⎭，当且仅当1m n ==时，等号成立，B 对；对于C 选项，由基本不等式可得()222m n m n =+++=，02，当且仅当1m n ==时，等号成立，C 错；对于D 选项，()()()()222222222224m n m n m n m n mn m n +=+++≥++=+=，可得222m n +≥，当且仅当1m n ==时，等号成立，D 对.故选：ABD.31．已知,,,a b c d R ∈，则下列结论正确的是（）A ．若,a b c d >>，则ac bd >B ．若22ac bc >，则a b >C ．若0a b >>，则()0a b c ->D ．若,a b c d >>，则a d b c ->- 【答案】BD【分析】举反例可判断选项A 、C 不正确，由不等式的性质可判断选项B 、D 正确，即可得正确选项.【详解】对于选项A ：举反例：3a =-，4b =-，0c ，2d =-满足,a b c d >>，但ac bd <，故选项A 不正确；对于选项B ：因为22ac bc >，则20c >，所以 a b >，故选项B 正确；对于选项C ：因为2a =，1b =，1c =-，满足0a b >>，但()0a b c -<，故选项C 不正确；对于选项D ：因为c d >，所以d c ->-，因为a b >，所以a d b c ->-，故选项D 正确，故选：BD.32．设0a >，0b >，给出下列不等式恒成立的是（）A ．21a a +>B ．296a a +>C ．()114a b a b ⎛⎫++≥ ⎪⎝⎭D ．114a b a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭ 【答案】ACD【分析】选项A ，B 可用作差法比较大小；选项C ，D 可用基本不等式求范围.【详解】由()22131024a a a ⎛⎫+-=-+> ⎪⎝⎭可得21a a +>，故A 正确；由()()229630a a a +-=-≥可得296a a +≥，故B 错误；由()11224a b a b a b b a ⎛⎫++=++≥+= ⎪⎝⎭，当且仅当a b =时取等号，故C 正确；由1114a b a b ab a b ab b a ⎛⎫⎛⎫⎛⎫⎛⎫++=+++≥= ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，当且仅当1ab ab a b b a⎧=⎪⎪⎨⎪=⎪⎩，即1a b ==时取等号，故D 正确. 故选：ACD.三、填空题33．某公司一年购买某种货物600吨，每次购买x 吨，运费为6万元/次，一年的总存储费用为4x 万元．要使一年的总运费与总存储费用之和最小，则x 的值是__________．【答案】30【详解】总费用为600900464()4240x x x x +⨯=+≥⨯，当且仅当900x x=，即30x =时等号成立．故答案为30. 点睛:在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误． 34．函数y R ，则实数k 的取值范围为______．【答案】[]0,4【分析】函数y =R ，等价于2240kx kx -+≥恒成立，然后分 0k =和0k ≠两种情况讨论求解即可得答案【详解】函数y =R ，等价于2240kx kx -+≥恒成立，当 0k =时，显然成立；当0k ≠时，由2Δ(2)440k k =--⨯≤，得04k <≤．综上，实数k 的取值范围为[]0,4．故答案为：[]0,435．设0a >，1b >，若2a b +=，则911a b +-的最小值为__________．【答案】16【分析】把911a b +-乘以111a b =+-=得到()9191111a b a b a b ⎛⎫+=++-⎡⎤ ⎪⎣⎦--⎝⎭，后用均值定理【详解】解：0a >，1b >且210a b b +=⇒->且()11a b +-= ∴()()91919111010616111b a a b a b a b a b -⎛⎫+=++-=++≥+=⎡⎤ ⎪⎣⎦---⎝⎭ 当且仅当()911b a a a -=-取等号，又2a b +=，即34a =，54b =时取等号，故所求最小值为16．故答案为：16【点睛】考查均值定理的应用，基础题36．已知0x ≥,0y ≥,且1x y +=,则22x y +的取值范围是_____. 【答案】1[,1]2【详解】试题分析：22222(1)221,[0,1]x y x x x x x +=+-=-+∈，所以当01x =或时，取最大值1；当12x =时，取最小值12.因此22xy +的取值范围为1[,1]2.【名师点睛】本题考查了转化与化归的能力，除了像本题的方法，即转化为二次函数求取值范围，也可以转化为几何关系求取值范围，即0,0x y ≥≥，1x y +=表示线段，那么22xy +的几何意义就是线段上的点到原点距离的平方，这样会更加简单.37．不等式2320x x -++>的解集为____________．【答案】2,13⎛⎫- ⎪⎝⎭ 【分析】由题意结合一元二次不等式的解法即可得解.【详解】由2320x x -++>得()()2321320x x x x --=-+<，所以不等式2320x x -++>的解集为2,13⎛⎫- ⎪⎝⎭．故答案为：2,13⎛⎫- ⎪⎝⎭. 【点睛】本题考查了一元二次不等式的求解，考查了运算求解能力，属于基础题.38．若4x >，1y >，且124xy x y =++，则x y + 最小值是_____．【答案】13【分析】由题得124x y x +=- ，进而124x x y x x ++=+-，结合基本不等式求解即可【详解】由题得124x y x +=- ，故124x x y x x ++=+-又12164551344x x x x x ++=+-+≥=--，当且仅当x=8,y=5,等号成立故答案为13【点睛】本题考查基本不等式求最值，考查换元思想，准确计算变形是关键，是中档题39．已知x 、y 都是正数，且满足230x y xy ++=，则xy 的最大值为_________．【答案】18.【分析】根据基本不等式2x y +≥xy 的范围，求出答案.【详解】因为,0x y >，且230x y xy ++=，所以302xy x y -=+≥（当且仅当2x y =时，取等号）即2030≤+，解得≤≤-180xy ≤<，所以xy 的最大值是18.此时6x =，3y =.故答案为：18.【点睛】关键点点睛：本题的关键点是运用基本不等式把230x y xy ++=转化为2030≤+.40．已知0x >，则97x x --的最大值为________．【答案】1【分析】直接利用基本不等式求最大值.【详解】0x ，则997771x x x x ⎛⎫--=-+≤- ⎪⎝⎭，当且仅当9x x=即3x =时取等号．故答案为：141．不等式3442x x +≥-的解集是___________．【答案】(2,12]【分析】移项通分化简，等价转化为1202x x -≥-，进一步等价转化为二次不等式(组),注意分母不能为零，然后求解即得. 【详解】原不等式等价于34402x x +-≥-，化简得1202x x -≥-，又等价于()()122020x x x ⎧--≥⎨-≠⎩，解得：212x <≤，故答案为：(2,12].四、解答题42．()1已知3x >，求43y x x =+-的最小值，并求取到最小值时x 的值； ()2已知0x >，0y >，223x y +=，求xy 的最大值，并求取到最大值时x 、y 的值．【答案】()1当5x =时，y 的最小值为7．()2 2x =，3y =时，xy 的最大值为6．【分析】()1直接利用基本不等式的关系式的变换求出结果．()2直接利用基本不等式的关系式的变换求出结果．【详解】()1已知3x >，则：30x ->，故：44333733y x x x x =+=-++≥=--，当且仅当：433x x -=-，解得：5x =，即：当5x =时，y 的最小值为7．()2已知0x >，0y >，223x y +=，则：23x y +≥ 解得：6xy ≤，即：123x y ==，解得：2x =，3y =时，xy 的最大值为6．【点睛】在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.43．设函数()21f x mx mx =--（1）若对一切实数x ，()0f x <恒成立，求m 的取值范围；（2）若对于[]1,3x ∈，()5f x m <-+恒成立，求m 的取值范围：【答案】（1）(]4,0-.（2）6,7⎛⎫-∞ ⎪⎝⎭ 【分析】（1）对m 进行分类讨论，利用判别式进行求解；（2）利用参数分离得到261m x x <-+对[]1,3x ∈恒成立，利用二次函数的性质求得26()1g x x x =-+的值域即可. 【详解】（1）210mx mx --<对x ∈R 恒成立，若0m =，显然成立，若0m ≠，则00m <⎧⎨∆<⎩，解得40m -<<. 所以，(]4,0m ∈-.（2）对于[]1,3x ∈，()5f x m <-+恒成立，即2(1)6m x x -+<对[]1,3x ∈恒成立210x x -+>对[]1,3x ∈恒成立 ∴261m x x <-+对[]1,3x ∈恒成立，即求26()1g x x x =-+在[]1,3的最小值， 21y x x =-+的对称轴为12x =， ∴min 13()24y y ==，max (3)7y y ==，∴22]1146[,][,8173176x x x x ∈⇒∈-+-+，可得min 6(),7g x =即6,7m ⎛⎫∈-∞ ⎪⎝⎭. 【点睛】本题考查一元二次函数的图象与性质、不等式恒成立问题，考查逻辑推理能力、运算求解能力，求解时注意参变分离法的应用.44．已知函数2()()f x x ax a R =-∈.（1）若2a =，求不等式()3f x ≥的解集；（2）若[1,)x ∈+∞时，2()2f x x ≥--恒成立，求a 的取值范围.【答案】（1）{|1x x ≤-或3}x ≥；（2）(,4]-∞.【详解】试题分析：（1）先对不等式移项并因式分解得()()310x x -+≥，再根据不等号方向得不等式解集，（2）先化简不等式，并分离12a x x ⎛⎫≤+ ⎪⎝⎭，转化为求对应函数最值：()min a h x ≤，其中()12h x x x ⎛⎫=+ ⎪⎝⎭，再根据基本不等式求()h x 最值，即得a 的取值范围.试题解析：（1）若()2,3a f x =≥即()()2230,310x x x x --≥-+≥所以原不等式的解集为{|1x x ≤-或3}x ≥（2）()22f x x ≥--即12a x x ⎛⎫≤+ ⎪⎝⎭在[)1,x ∈+∞时恒成立，令()12h x x x ⎛⎫=+ ⎪⎝⎭，等价于()min a h x ≤在[)1,x ∈+∞时恒成立，又()124h x x x ⎛⎫=+≥ ⎪⎝⎭，当且仅当1x x =即1x =等号成立，所以4a ≤. 故所求a 的取值范围是(],4-∞.45．已知0,0x y >>，且41x y +=.（1）求xy 的最大值；试卷第21页，共21页（2）求1y x y+的最小值. 【答案】（1）最大值为116；（2）最小值为5. 【分析】（1）直接用基本不等式求解；（2）依题意，1441y y x y y x x y x y x y++=+=++，进而用基本不等式可求得结果. 【详解】（1）因为0,0,x y >>所以14x y =+≥ 即1.16xy ≤当且仅当4x y =取等号. 又41x y +=，所以当11,82x y ==时，xy 的最大值为1.16（2）因为0,0,x y >>且41x y +=.144115,y y x y y x x y x y x y ++=+=++≥= 当且仅当4y x x y =即2y x =取等号.又41x y +=，所以当11,63x y ==时，1y x y +的最小值为5.。

高一数学不等式试题

高一数学不等式试题1.（2014•重庆）若log4（3a+4b）=log2，则a+b的最小值是（）A．6+2B．7+2C．6+4D．7+4【答案】D【解析】利用对数的运算法则可得＞0，a＞4，再利用基本不等式即可得出解：∵3a+4b＞0，ab＞0，∴a＞0．b＞0∵log4（3a+4b）=log2，∴log4（3a+4b）=log4（ab）∴3a+4b=ab，a≠4，a＞0．b＞0∴＞0，∴a＞4，则a+b=a+=a+=（a﹣4）++7+7=4+7，当且仅当a=4+2取等号．故选：D．点评：本题考查了对数的运算法则、基本不等式的性质，属于中档题．2.（2014•榆林模拟）已知各项均为正数的等比数列{an }满足a7=a6+2a5，若存在两项am，an使得的最小值为（）A．B．C．D．【答案】A【解析】由a7=a6+2a5求得q=2，代入求得m+n=6，利用基本不等式求出它的最小值．解：由各项均为正数的等比数列{an }满足 a7=a6+2a5，可得，∴q2﹣q﹣2=0，∴q=2．∵，∴q m+n﹣2=16，∴2m+n﹣2=24，∴m+n=6，∴，当且仅当=时，等号成立．故的最小值等于，故选A．点评：本题主要考查等比数列的通项公式，基本不等式的应用，属于基础题．3.（2014•咸阳二模）若正实数a，b满足a+b=1，则（）A．有最大值4B．ab有最小值C．有最大值D．a2+b2有最小值【答案】C【解析】由于==2+≥4，故A不正确．由基本不等式可得a+b=1≥2，可得ab≤，故B不正确．由于=1+2≤2，故≤，故 C 正确．由a2+b2 =（a+b）2﹣2ab≥1﹣=，故D不正确．解：∵正实数a ，b 满足a+b=1， ∴==2+≥2+2=4，故有最小值4，故A 不正确．由基本不等式可得 a+b=1≥2，∴ab≤，故ab 有最大值，故B 不正确．由于=a+b+2=1+2≤2，∴≤，故有最大值为，故C 正确．∵a 2+b 2 =（a+b ）2﹣2ab=1﹣2ab≥1﹣=，故a 2+b 2有最小值，故D 不正确．故选：C ．点评：本题考查基本不等式的应用，注意检验等号成立的条件，式子的变形是解题的关键，属于基础题．4. （2014•鹤城区二模）已知a ，b 为正实数，函数y=2ae x +b 的图象经过点（O ，1），则的最小值为（） A ．3+2B ．3﹣2C ．4D ．2【答案】A【解析】将点（O ，1）的坐标代入y=2ae x +b ，得到a ，b 的关系式，再应用基本不等式即可．解：∵函数y=2ae x +b 的图象经过点（O ，1）， ∴1=2a•e 0+b ，即2a+b=1（a ＞0，b ＞0）． ∴=（）•1=（）•（2a+b ）=（2+1++）≥3+2（当且仅当b=a=﹣1时取到“=”）．故选A ．点评：本题考查基本不等式，将点（O ，1）的坐标代入y=2ae x +b ，得到a ，b 的关系式是关键，属于基础题．5. （2014•郑州模拟）已知正项等比数列{a n }满足：a 7=a 6+2a 5，若存在两项a m ，a n ，使得a m a n =16a 12，则+的最小值为（） A ．B ．C ．D ．不存在【答案】A【解析】应先从等比数列入手，利用通项公式求出公比q ，然后代入到a m a n =16a 12中，可得到关于m ，n 的关系式，再利用基本不等式的知识解决问题．解：设正项等比数列{a n }的公比为q ，易知q≠1，由a 7=a 6+2a 5得，解得q=﹣1（舍），或q=2，因为a m a n =16a 12，所以，所以m+n=6，（m ＞0，n ＞0），所以≥，当且仅当m+n=6，即m=2，n=4时等号成立．故选A点评：对等比数列的考查一定要突出基本量思想，常规思路一般利用同项、求和公式，利用首项，公比表示已知，进一步推出我们需要的隐含条件或结论；基本不等式要重视其适用条件的判断，这里容易在取“=”时出错．6. （2014•南昌模拟）若正数x ，y 满足x 2+3xy ﹣1=0，则x+y 的最小值是（） A ．B ．C ．D ．【解析】先根据题中等式将y用x表示出来，然后将x+y中的y消去，然后利用基本不等式可求出最值，注意等号成立的条件．解：∵正数x，y满足x2+3xy﹣1=0，∴3xy=1﹣x2，则y=，∴x+y=x+=+≥2=当且仅当=即x=时取等号，故x+y的最小值是．故选：B．点评：本题主要考查了消元法的应用，以及基本不等式的应用，同时考查了分析问题的能力和运算求解的能力，属于中档题．7.若x＜1，则y=的最大值．【答案】﹣1【解析】变形利用基本不等式的性质即可得出．解：∵x＜1，∴y===2x+=+3=﹣1．当且仅当x=0时取等号．故答案为﹣1．点评：熟练掌握基本不等式的性质是解题的关键．8.若实数x，y，z满足x+2y+3z=a（a为常数），则x2+y2+z2的最小值为．【答案】【解析】利用题中条件：“x+2y+3z=a”构造柯西不等式：（x2+y2+z2）（12+22+32）≥（x+2y+3z）2=a2这个条件进行计算即可．解：∵（x2+y2+z2）（12+22+32）≥（x+2y+3z）2=a2，…（5分）∴（x2+y2+z2）≥，当且仅当时取等号，…（8分）则x2+y2+z2的最小值为．…（10分）故答案为：．点评：本题考查用综合法证明不等式，关键是利用：（x2+y2+z2）（12+22+32）≥（x+2y+3z）29.设x＞3，则x= 时，的最小值是．【答案】3+2，．【解析】根据x+=（x﹣3）++3，注意x﹣3与的积为定值，利用基本不等式求出它的最小值及相应的x的值即可．解：∵x＞3，∴x+=（ x﹣3）++3≥2 +3=，当且仅当（ x﹣3）=即x=3+2时，等号成立，故答案为：3+2，．点评：本题考查基本不等式的应用，注意检验等号成立的条件，式子的变形使得x﹣3与的积为定值是解题的关键．10.已知二次函数f（x）=ax2﹣4x+c+1的值域是[1，+∞），则+的最小值是．【解析】由已知可得a＞0且，然后利用基本不等式即可求解最值解：∵f（x）=ax2﹣4x+c+1的值域是[1，+∞），∴a＞0且即ac=4∴c＞0∴=3当且仅当且ac=4，则a=时取等号∴的最小值为3故答案为：3点评：本题主要考查了二次函数的性质的应用，基本不等式求解函数的最值等知识的综合应用．。

高一数学具体的不等式试题

高一数学具体的不等式试题1.记关于x的不等式的解集为P，不等式的解集为Q.（1）若a=3,求P（2）若求正数a的取值范围【答案】（1）（2）【解析】思路分析：（1）解得（2）化简由得得到。

解：（1）由得（2）由得所以，即的取值范围是【考点】集合的概念，集合的运算，简单不等式的解法。

点评：中档题，为进行集合的运算，首先化简集合，明确集合中的元素是什么。

2.不等式ax2＋bx＋2＞0的解集是，则a＋b的值是()A．10B．－10C．－14D．14【答案】C【解析】根据题意，由于不等式ax2＋bx＋2＞0的解集是，那么说明了是ax2＋bx＋2=0的两个根，然后利用韦达定理可知则a＋b的值是-14，故选C.【考点】一元二次不等式的解集点评：主要是考查了二次不等式的解集的运用，属于基础题。

3.关于x的不等式：的解集为 .【答案】【解析】根据题意，由于等价于，故可知不等式的解集为。

【考点】不等式的求解点评：主要是考查了不等式的求解，属于基础题。

4.若,则下列不等式:①;②;③;④中,正确的有( )A．1个B．2个C．3个D．4个【答案】C【解析】取，可以验证①②③都是正确的，所以正确的有3个.【考点】本小题主要考查不等式的性质的应用.点评：遇到考查不等式性质的题目时，要注意特殊值法的应用，这种方法一般情况下简单有效.5.函数在上满足，则的取值范围是（）A．B．C．D．【答案】D【解析】根据题意，当a=0时，显然成立，故排除答案B,C，对于当时，函数为二次函数，那么使得在实数域上函数值小于零，则判别式小于零，开口向下可知得到,解得，综上可知为,选D.【考点】不等式点评：主要是考查了函数性质的运用，属于基础题。

6.不等式的解集是，【答案】【解析】根据题意，由于不等式，故可知答案为【考点】一元二次不等式的解法点评：本试题主要是考查了一元二次不等式的解集的求解，属于基础题。

7.已知关于的不等式的解集是，则 .【答案】【解析】因为，关于的不等式的解集是，所以，a=。

高一数学(不等式)试题及答案

试卷3 不等式专题一、选择题1、当1x >时，不等式11x a x +≥-恒成立，则实数a 的取值范围是（） A ．(,2]-∞ B ．[2,)+∞ C ．[3,)+∞ D ．(,3]-∞2、下列函数中，最小值为4的是（）A ．4y x x=+ B ．4sin sin y x x =+（0x π<<） C ．4x x y e e -=+ D ．3log 4log 3x y x =+3、若实数,a b满足12a b+=，则ab 的最小值为( ) A、2 C 、D 、44、设x ，y 满足约束条件2330233030x y x y y +-⎧⎪-+⎨⎪+⎩≤≥≥，则2z x y =+的最小值是( )A ．B ．C ．D ．5、若直线1(0,0)x y a b a b+=>>过点(1,1)，则a b +的最小值等于（） A ．2 B ．3 C ．4 D ．56、、若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为－4，则k 的值为( )A ．2B ．-2C ．12 D ．12-7、已知正项等比数列{}()n a n N +∈满足5432a a a =+，若存在两项,m n a a18a =，则19m n +的最小值为（）A. 1B. 2C. 3D. 48、若函数f (x )＝x ＋1x －2(x >2)在x ＝a 处取最小值，则a 等于( )A ．1＋ 2B ．1＋ 3C ．3D ．49、已知x ，y ＞0且x ＋4y ＝1，则1x ＋1y 的最小值为( )A ．8B ．9C ．10D ．1110、y x ,满足约束条件⎪⎩⎪⎨⎧≥+-≤--≤-+02202202y x y x y x ，若ax y z -=取得最大值的最优解不唯一．．．，则实数a 的值为（）A ．121-或B ．212或C ．2或1D ．12-或11、设变量y x y x y x 2,1||||,+≤+则满足的最大值和最小值分别为( )A ．1，－1B ．2，－2C ．1，－2D ．2，－112、若,x y 满足约束条件10040x x y x y -⎧⎪-⎨⎪+-⎩≥≤≤，则yx 的最大值为( )A ．2B ．3C ．4D ．5二、填空题13、函数42(0)y x x x =-->的最大值为________.14、已知，且，则的最小值为_____________.15、若,a b ∈R ，0ab >，则4441a b ab++的最小值为___________. 16、正数a ，b 满足ab ＝a ＋b ＋3，则ab 的取值范围是________．三、大题17、已知x >0，y >0，且2x ＋8y －xy ＝0，求：(1)xy 的最小值； (2)x ＋y 的最小值．18、已知. （1）当时，求不等式的解集；（2）若时不等式成立，求的取值范围.19、已知函数f (x )=-x 2+ax+4,g (x )=|x+1|+|x-1|.(1)当a=1时,求不等式f (x )≥g (x )的解集;(2)若不等式f (x )≥g (x )的解集包含[-1,1],求a 的取值范围.20、已知函数(1)解不等式.(2)若关于的不等式的解集为，求实数的取值范围.21、已知（为常数）.（1）若，求实数的取值范围；（2）若的值域为，且，求实数的取值范围.22、已知，，.若函数的最小值为2.(1)求的值；(2)证明：.答案1、 D2、C 44x x e e -+≥=，当且仅当4,ln 2x x e e x -==时等号成立，故选C. 3、C 12121002ab a b ab ab a b a ba +=∴=+≥⨯=≥，＞，＞，2b a =时取等号），所以ab 的最小值为，故选C.4、A结合目标函数的几何意义可得函数在点()6,3B --处取得最小值，最小值为min 12315z =--=-．故选A ．5、C6、D7、B8、C【解析】:当x>2时，x－2>0，f(x)＝(x－2)＋1x－2＋2≥2x－2×1x－2＋2＝4，当且仅当x－2＝1x－2(x>2)，即x＝3时取等号，即当f(x)取得最小值时，x＝3，即a＝3，选C．9、B【解析】:∵x ＋4y ＝1(x ，y ＞0)，∴1x ＋1y ＝x ＋4y x ＋x ＋4y y ＝5＋⎝ ⎛⎭⎪⎫4y x ＋x y ≥5＋24y x ·x y＝5＋4＝9⎝ ⎛⎭⎪⎫当且仅当x ＝2y ＝13时，取等号. 10、D11、B12、3 【解析】作出可行域（图略），可知在点(1,3)处，yx 取得最大值3． 13、-2【解析】44222y x x x x ⎛⎫=---+≤-- ⎪⎝⎭＝２，当且仅当4x x＝，即x ＝２时，“＝”成立 14、由可知，且：，因为对于任意x ，恒成立，结合均值不等式的结论可得：.当且仅当，即时等号成立.综上可得的最小值为. 15、4【解析】:44224141144a b a b ab ab ab ab +++≥=+≥= ，（前一个等号成立条件是222a b =，后一个等号成立的条件是12ab =，两个等号可以同时取得，则当且仅当22a b ==时取等号）. 16、[9，＋∞) 【解析】:∵a ，b 是正数，∴ab ＝a ＋b ＋3≥2ab ＋3，∴ab －2ab －3≥0，∴(ab ＋1)(ab －3)≥0，∴ab ≤－1(舍去)或ab ≥3. 即ab ≥9.17、【答案】(1) 64， (2)18【解析】: (1)由2x ＋8y －xy ＝0，得8x ＋2y ＝1，又x >0，y >0，则1＝8x ＋2y ≥2 8x ·2y ＝8xy，得xy ≥64，当且仅当x ＝16且y ＝4时，等号成立．所以xy 的最小值为64.18、19、20、解得或故实数的取值范围是或.21、22、所以得证.。

高一数学不等式试题

高一数学不等式试题1.（本题满分12分）已知函数（1）当时，求不等式的解集（2）若关于的不等式的解集为R，求实数的取值范围（3）当时，若在内恒成立，求实数b的取值范围。

【答案】，，【解析】2.（文）若，则的最大值为．【答案】文 -4【解析】（文），当且仅当时等号成立，所以最小值为【考点】1．线性规划；2．均值不等式求最值3.对于任意实数x，一元二次不等式恒成立，则实数a取值范围是（）A．B．C．（－2,2）D．【答案】C【解析】试题分析因为一元二次不等式，所以a-2≠0，a-2＜04(a-2)2+16(a-2)＜0解得-2＜a＜2。

故选C【考点】函数不等式的运用4.设满足约束条件，则的最大值为（）A．-8B．3C．5D．7【答案】D【解析】不等式表示的可行域为直线围成的三角形及其内部，三个顶点为，当过点时取得最大值7【考点】线性规划5.（本题满分10分）解关于的不等式【答案】当或时，不等式解集为；当或时，不等式的解集为；当或时, 不等式解集为．【解析】首先将原不等式通过十字相乘法分解因式得，然后得到两根与相同时参量的值，再根据与的大小分情况讨论进而借助一元二次函数解不等式．试题解析：原不等式可化为：，令，可得：∴当或时，，；当或时，,不等式无解；当或时, ,综上所述，当或时，不等式解集为；当或时，不等式的解集为；当或时, 不等式解集为．【考点】（1）含参量一元二次不等式的解法；（2）不等式的基本性质．6.设变量x，y满足约束条件则z＝3x－2y的最大值为A．0B．2C．4D．6【答案】C【解析】约束条件对应的可行域为直线围成的三角形区域，，当直线过交点时取得最大值4【考点】线性规划问题7.已知，则的最小值是（）A．10B．C．12D．20【解析】，，当且仅当时取得等号．【考点】基本不等式．8.不等式的解集是____________________．【答案】【解析】不等式变形为：，分解因式可得：，所以解集为【考点】解一元二次不等式9.在约束条件下，目标函数取最大值时的最优解为_______．【答案】【解析】根据约束条件画出可行域，再由目标函数可得，平移直线可知在点处目标函数取得最大值．【考点】线性规划问题．10.已知满足且，则下列选项中一定成立的是（）A．B．C．D．【答案】D【解析】因为满足，所以．又因为，所以，故选D．【考点】不等式的性质．【一题多解】根据题意令，代入A、B、C、D中，易知只有D成立，故选D．11.比较的大小关系是（）A．B．C．D．【答案】D【解析】∵，，又幂函数在上是增函数，，∴，故选D．【考点】1、指数式；2、比较大小.12.已知，，则下列不等式中成立的是（）A．B．C．D．【解析】,【考点】不等式的性质13.三个数的大小顺序是（）A．B．C．D．【答案】D【解析】由，，则大小顺序可知为：【考点】指数和对数函数性质的应用。

高一数学基本不等式试题

高一数学基本不等式试题1.已知x，y均为正数且x+2y=xy，则（）.A．xy+有最小值4B．xy+有最小值3C．x+2y+有最小值11D．xy﹣7+有最小值11【答案】C【解析】由，得，由得，则（当且仅当，即时取等号），；令，则在上为增函数，，排除A,B; 而选项D:;选项C：（当且仅当，即或时取等号;故选C.【考点】基本不等式.2.已知，则x + y的最小值为．【答案】【解析】，，由，可得，当且仅当时等号成立，故，故答案为.【考点】对数的性质运算；均值不等式的应用.3.若，则下列不等式正确的是（）.A．B．C．D．【答案】C【解析】由基本不等式得，则；又，.【考点】基本不等式.4.若正数满足，则的取值范围是________________.【答案】【解析】，；可化为，，即，，即.【考点】基本不等式.5.在下列函数中，最小值为2的是( )A．B．C．D．【答案】D【解析】A中不满足x＞0；B中，因为0＜sinx＜1，故“=”取不到；C中，因为0＜lgx＜1，故“=”取不到；D中 y=3x+3-x≥2，当且仅当 3x=3-x时取等号，此时x存在；故选D．【考点】基本不等式.6.对任意正数x，y不等式恒成立，则实数的最小值是 ()A．1B．2C．3D．4【答案】【解析】根据选项可知,所以此时不等式左边两项都是正数．根据基本不等式有,因为恒成立,所以,消掉,解得．所以．【考点】不等式恒成立;基本不等式．7.已知正数满足，则的最小值为．【答案】【解析】.【考点】基本不等式.8.在分别是角A、B、C的对边,若,则的周长的取值范围是（）A． B． C． D．【答案】C【解析】∵，∴，化简后可得：，∴，又∵，∴，即周长的范围为．【考点】1、余弦定理；2、基本不等式．9.设实数满足：,则取得最小值时，．【答案】121【解析】∵，∴，上述等号成立的条件依次为：，∴a=1，b=c=10，d=100，a+b+c+d=121．【考点】1、基本不等式；2、不等式的放缩．10.下列各函数中，最小值为2的是 ()．A．y＝x＋B．y＝sin x＋，x∈C．y＝D．y＝＋【答案】D【解析】（1）函数：当时，，当且仅当即时取；当时，，此时，即，当且仅当即时取。

高一数学不等式试题答案及解析

高一数学不等式试题答案及解析1.下列函数中，最小值为2的是----------------------------------------（）A．B．C．D．【答案】B【解析】略2.（本题满分10分）已知正数满足,求的最小值有如下解法：解：∵且.∴∴. 判断以上解法是否正确？说明理由；若不正确，请给出正确解法【答案】不正确【解析】∵且.∴∴. 判断以上解法是否正确？说明理由；若不正确，请给出正确解法解：以上解法错误------1分理由：∵，当且仅当x=y时取到等号，3.已知则的最小值为（）A．2B．C．4D．5【答案】C【解析】【考点】均值不等式求最值4.设常数,若对一切正实数成立,则的取值范围为 .【答案】【解析】【考点】1.不等式与函数的转化；2.均值不等式求最值5.已知点满足约束条件，为坐标原点，则的最小值为_______________．【答案】【解析】将约束条件中任意俩条件进行联立，若想满足三个不等式，则解出y=，将y值带入不等式，解出，所以的最小值为。

【考点】函数不等式6.如果，则下列不等式中成立的只有（）A．B．C．D．【答案】C【解析】令，可得，故不正确，正确．再根据，可得不正确，只有选项成立，故选．【考点】不等式关系与不等式7.如果，那么下列不等式成立的是（）A．B．C．D．【答案】A【解析】因为，则，所以，A正确；因为，则，B错；因为，则，所以，C错；因为，则，D错；【考点】不等式的基本性质；8.关于x的不等式的解集是，则关于x的不等式的解集是（）A．B．C．D．【答案】D【解析】关于x的不等式的解集是，所以，所以不等式可化为，从而确定解集；【考点】1．一元二次不等式的解法；2．一元一次不等式的解集与系数的关系；9.若，且，则的最小值等于_______．【答案】【解析】约束条件对应的平面区域如上图所示，当直线过点时取得最小值3．【考点】线性规划10.（本小题16分）已知函数（1）时，解关于的不等式；（2）当时，若对任意的，不等式恒成立，求实数的取值范围；（3）若，求的取值范围．【答案】（1）（2）（3）【解析】（1）将不等式系数整理可得到二次不等式，结合二次函数图像即可求解；（2）将不等式恒成立问题采用分离参数的方法转化为求函数最值问题，本题中首先将不等式变形为进而利用均值不等式求解的最小值；（3）将不等式化简得到关于的不等式，进而求得范围，将所求式子的绝对值去掉，结合值及线性规划求式子的范围试题解析：（1）化为因此解集为；（2）原不等式化为：，因为所以原不等式化为恒成立，，当且仅当时等号成立，所以（3）题目条件化为，作图可知，去绝一个绝对值z＝，对讨论再去掉一个绝对值．当时，由线性规划得；当时，，综上可得【考点】1．不等式解法；2．函数最值；3．线性规划问题11.不等式组所表示的平面区域的面积是 ____________．【答案】25【解析】由已知条件可计算出，不等式表示的平面区域为，易得【考点】线性规划不等式组表示的平面区域及三角形的面积计算12.二次不等式的解集是全体实数的条件是（）A．B．C．D．【答案】B【解析】当时，原不等式换位对任意的都成立，要使二次不等式的解集是全体实数，只需，综上，故选B。