江苏省宝应县画川高级中学2020届高考数学第二轮复习圆锥曲线导学案2(无答案)

合集下载

导数的复习2(学案)

课题导数的复习2 课型习题时间09/ 10 / 学习目标 1.能熟练地求解导数的概念、实际意义、应用等基本问题； 2.能综合运用导数的知识方法分析解决有关的综合问题与应用。

学习重点运用导数的知识方法分析解决有关的综合问题一．选择题1．已知函数(),()13f x x f x =在处的导数为则的解析式可能为（） A ．()()()2131f x x x =-+- B ．()()21f x x =- C ．()()221f x x =- D ．()1f x x =-2．设()f x '是函数()f x 的导函数,()y f x '=的图象如下左图,则()y f x =的图象最有可能的是（）3．已知命题p ：函数y=f(x)的导函数是常数函数，而命题p 是命题q 的必要不充分条件，则命题q 不可以是（）A ．f(x)=1B ．f(x)=x 2C ．f(x)=2xD ．f(x)=1-x 4．若函数1)(23+++=mx x x x f 是R 上的单调函数，则m 的取值范是（） A ．),31(+∞B ．)31,(-∞C ．),31[+∞D ．]31,(-∞5．下列结论正确的是（）A ．若0x 是)(x f 在],[b a 上的极大值点，则)(0x f 是)(x f 在],[b a 上的最大值B ．若0x 是)(x f 在),(b a 上的极大值点，则)(0x f 是)(x f 在],[b a 上的最大值C ．若0x 是)(x f 在),(b a 上唯一的极大值点，则)(0x f 是)(x f 在],[b a 上的最大值D ．若0x 是)(x f 在),(b a 上唯一的极大值点，且)(x f 在),(b a 上无极小值点，则)(0x f 是)(x f 在],[b a 上的最大值二．填空题6.已知函数y =x 3+ax 2+bx +27在x =－1处有极大值，在x =3处有极小值，则a +b =_____ ___.7.设函数f （x ）=x 3－22x －2x +5.若对任意x ∈［－1，2］，都有f （x ）>m ，则实数m 的取值范围是____ ____.学习反思：O 1 2 y xy=f/O1 2 yxO 1 2 y xO1 2 y xO 1 2 y xA B C D8.若函数f （x ）=x 3+x 2+mx +1是R 上的单调递增函数，则m 的取值范围是___________________________________.9．若函数x ax x f +=3)(恰有三个单调区间，则a 的取值范围是． 10．若函数21)(xx x f +=在（a ，3-a 2）上有最大值，则实数a 的取值范围是 11．函数y =2x 3-3x 2-12x +5在闭区间[0，3]上的最大值与最小值的和是12（2005年北京东城区模拟题）如果函数y =f （x ）的导函数的图象如下图所示,给出下列判断: x y 12345-1-2-3O 1-2-①函数y =f （x ）在区间（－3,－21）内单调递增;②函数y =f （x ）在区间（－21,3）内单调递减;③函数y =f （x ）在区间（4,5）内单调递增; ④当x =2时,函数y =f （x ）有极小值;⑤当x =－21时,函数y =f （x ）有极大值.则上述判断中正确的是_____________ 三．计算与证明13．（1）求函数f （x ）=x 3-x 2-40x +80的单调区间；（2）若函数y =x 3+b x 2+c x 在区间（-∞，0）及[2，+∞）是增函数，而在（0，2）是减函数，求此函数在[-1，4]上的值域．学习反思：过抛物线y =x 2-3x 上一点P 的切线的倾斜角为45°，它与两坐标轴交于A ，B 两点，则△AOB的面积是．学习反思：14．设函数f(x)=ax3+bx2+cx+d的图象与y轴的交点为P，且曲线f(x)在P点出处的切线方程为24x+y-12=0，又函数在x=2出处取得极值-16，求该函数的单调递减区间．15．若函数f(x)=ax3+x，(1) 求实数a的取值范围，使f(x)在R上是增函数．(2) 求实数a的取值范围，使f(x)恰好有三个单调区间．16 ．设函数f（x）=x3+mx2+nx+p在（－∞，0］上是增函数，在［0，2］上是减函数，x=2是方程f（x）=0的一个根.（1）求n的值；（2）求证：f（1）≥2.17．某工厂需要建一个面积为512 m2的矩形堆料场，一边可以利用原有的墙壁，问堆料场的长和宽各为多少时，才能使砌墙所用的材料最省？练习反思：学习反思：如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器．当这个正六棱柱容器的底面边长为_______时,其容积最大．。

江苏省扬州市宝应县高中数学第二章圆锥曲线与方程 2.1 曲线与方程(2)教案新人教A版选修21

曲线与方程（2）上课时间：上课班级：高二（）学时： 1课时教学目标：1. 求曲线的方程；2. 通过曲线的方程，研究曲线的性质．教学重难点：掌握相关点法求动点的轨迹方法导学过程学习体会任务1：预习课本6760P P -页，根据课本内容填空复习1：已知曲线C 的方程为 22y x = ，曲线C 上有点(1,2)A ，A 的坐标是不是22y x = 的解？点(0.5,)t 在曲线C 上,则t =___ ．复习2：曲线（包括直线）与其所对应的方程(,)0f x y =之间有哪些关系?探究:圆心C 的坐标为(6,0)，半径为4r =，求此圆的方程．问题：此圆有一半埋在地下，求其在地表面的部分的方程．探究：(1)若4AB =，如何建立坐标系求AB 的垂直平分线的方程．(2)若4=AB ，点A 与点B 分别在x 轴和y 轴上运动，求线段AB 中点的轨迹方程任务2：认真理解曲线的方程、方程的曲线的定义完成下列例题例1 有一曲线,曲线上的每一点到x 轴的距离等于这点到(0,3)A 的距离的2倍，试求曲线的方程．变式：现有一曲线在x 轴的下方，曲线上的每一点到x 轴的距离减去这点到点(0,2)A ，的距离的差是2，求曲线的方程．小结：点(,)P a b 到x 轴的距离是；点(,)P a b 到y 轴的距离是；点),(b a P 到直线10x y +-=的距离是．例2.求平面内到两个定点B A ,的距离之比等于2的动点M 的轨迹方程例 3.探照灯的截面是抛物线x y =2，平行于x 轴的光线照射到抛物线上的点)1,1(-P ,反射光线过焦点后又照射到抛物线上的Q 点，试求点Q 的坐标巩固练习：1．方程[]2(3412)log (2)30x y x y --+-=的曲线经过点(0,3)A -，(0,4)B ，(4,0)C ，57(,)34D -中的（）.A ．0个B ．1个C ．2个D ．3个2．已知(1,0)A ，(1,0)B -，动点满足：2MA MB -=,则点M 的轨迹方程是（）.A ．0(11)y x =-≤≤B ．0(1)y x =≥C ．0(1)y x =≤-D ．0(1)y x =≥3．曲线21y x =--与曲线0y x +=的交点个数一定是（）．A ．0个B ．2个C ．4个D ．3个4．若定点(1,2)A 与动点(,)P x y 满足4OP OA •=v v ,则点P 的轨迹方程是．5．由方程111x y -+-=确定的曲线所围成的图形的面积是．6．以O 为圆心，2为半径，上半圆弧的方程是什么？在第二象限的圆弧的方程是什么？7.求与圆0422=-+x y x 外切，且与y 轴相切的动圆圆心的轨迹方程8.双曲线1322=-y x 的左，右焦点分别为21,F F ，过1F 作倾斜角为6π的弦AB 。

江苏省宝应县画川高级中学高三数学迎二模填空题训练无答案

迎二模填空题训练11．设,a b R ∈，231a bii i+=+-，其中i 是虚数单位，则a b += ．2．已知集合{}P x x a =≤，{}sin ,Q y y R θθ==∈．若P Q ⊇，则实数a 的取值范围是．3．为了了解一片经济林的生长情况，随机测量了其中100株树木的底部周长（单位：cm )，所得数据如图．则在这100株树木中，底部周长不小于100cm 的有株．4．设向量(1,)a m =r ，(1,2)b m =-r ，且a b ≠r r ，若()a b a -⊥r r r ，则实数m = ．5．如图所示的流程图的运行结果是．6．将边长为a 的正方形ABCD 沿对角线AC 折起，使BD a =，则三棱锥D ABC -的体积为．7．设等差数列{}n a 的前n 项和为n S ，若19a =，462a a +=．当n S 取最大值时，n = ． 8．已知44ππθ-≤≤，且1cos45θ=，则44cos sin θθ-= ．9．若在区间(1,1)-内任取实数a ，在区间(0,1)内任取实数b ，则直线0ax by -=与圆22(1)(2)1x y -+-=相交的概率为．10．设函数()sin(2),[,]66f x x x a ππ=+∈-的值域是1[,1]2-，则实数a 的取值范围为．第5题图第3题图11．已知函数()f x 满足：当[]1,3x ∈时，()ln f x x =，当1[,1)3x ∈时，1()2()f x f x =．若在区间1[,3]3内，函数()()(0)g x f x ax a =->恰有一个零点，则实数a 的取值范围是．12．设椭圆2222:1(0)x y C a b a b+=>>和圆222:O x y b +=，若椭圆C 上存在点P ，使得过点P 引圆O 的两条切线，切点分别为A 、B ，满足60APB ∠=，则椭圆C 的离心率的取值范围是．13．设数列{}n a 的通项公式为13()2n n a -=，则满足不等式113n ni i i i a a ==>∑∑的正整数n 的集合为．14．设函数()332x x f x x -=--，则满足12(2)(log )0x f x -<的x 的取值范围是．迎二模填空题训练21．已知集合{1,1}A k =-，{2,3}B =，且{2}A B =，则实数k 的值为．2．设2(12)(,R)i a bi a b +=+∈，其中i 是虚数单位，则ab = ．0,1s n ←←第4题图3．已知函数()y f x =是奇函数，当0x <时，2()(R)f x x ax a =+∈，且(2)6f =，则a = ．4．右图是某算法流程图，则程序运行后输出的结果是．5．设点P ，A ，B ，C 是球O 表面上的四个点，PA ，PB ，PC 两两互相垂直，且1PA PB PC cm ===，则球的表面积为 2cm ．6．已知{(,)|6,0,0}x y x y x y Ω=+<>>，{(,)|4,0,20}A x y x y x y =<>->，若向区域Ω上随机投掷一点P ，则点P 落入区域A 的概率为．7．将参加夏令营的500名学生编号为：001,002,,500，采用系统抽样的方法抽取一个容量为50的样本，且随机抽得的号码为003，这500名学生分住在三个营区，从001到200在第一营区，从201到355在第二营区，从356到500在第三营区，则第三个营区被抽中的人数为．8．ABC ∆中，“角,,A B C 成等差数列”是“sin sin )cos C A A B =+”成立的的条件． (填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”之一)9．已知双曲线22221(0,0)x y a b a b-=>>，以右顶点为圆心，实半轴长为半径的圆被双曲线的一条渐近线分为弧长为1:2的两部分，则双曲线的离心率为．10．已知442cos sin ,(0,)32πααα-=∈，则2cos(2)3πα+= ．11．已知正数1234,,,a a a a 依次成等比数列，且公比1q ≠．将此数列删去一个数后得到的数列(按原来的顺序)是等差数列，则公比q 的取值集合是．12．如图，梯形ABCD 中，//AB CD ，6AB =，2AD DC ==，若12AC BD ⋅=-uu u r uu u r ，则AD BC ⋅=u u u r u u u r．第12题图13．设ABC ∆的内角,,A B C 所对的边,,a b c 成等比数列，则sin sin BA的取值范围是．14．设函数()f x 满足()(3)f x f x =，且当[1,3)x ∈时，()ln f x x =．若在区间[1,9)内，存在3个不同的实数123,,x x x ，使得312123()()()f x f x f x t x x x ===，则实数t 的取值范围为．迎二模填空题训练31．已知集合{}2|20M x x x =-≥,{}|1N x x =≤，则R M N （）ð= .2．如果1a bi -+与-b i +互为共轭复数（,a b ∈R ，i 为虚数单位），则||a bi += ．3．如右图，该程序运行后输出的结果为 .4．在△ABC 中，∠C ＝90°，M 是BC 的中点，1AC =．若sin B ＝13，则AM ＝________.5．某单位有,,A B C 三部门，其人数比例为3∶4∶5，现欲用分层抽样方法抽调n 名志愿者支援西部大开发．若在A 部门恰好选出了6名志愿者，那么n ＝________．6．函数()2sin()(0,f x x ωϕω=+>且||)2πϕ<的部分图像如图所示,则(0)f 的值为 .7．连续抛掷两颗骰子得到的点数分别是a ，b ，则函数2()f x ax bx =-在1x =处取得最值的概率是 .8．在等差数列{}n a 和等比数列{}n b 中，已知12128,2,1,2a a b b =-=-==，那么满足n n a b =的n 的所有取值构成的集合是 .9．已知如图所示的多面体EF ABCD -中，四边形ABCD 是菱形，四边形BDEF 是矩形，ED ⊥平面ABCD ，∠BAD ＝3π.若BF ＝BD ＝2，则多面体的体积．10．如果关于x 的方程23ax x+=有两个实数解，那么实数a 的值是．11．设()()2,0,1,0.x a x f x x a x x⎧-⎪=⎨++>⎪⎩… 若()0f 是()f x 的最小值，则实数a 的取值范围为 .12．已知椭圆2221(3x y a a +=>的中心、右焦点、右顶点依次为,,,O F G直线2x =x 轴交于H 点，则FG OH取得最大值时a 的值为 .FEDCBA13．在四边形ABCD 中， 2AB =，AD BC =，BA BC BABC+3BD BD=，则四边形ABCD 的面积是．14．()f x 是定义在R 上的奇函数，若当0x ≥时，[)[)12log (1),0,1()13,1,x x f x x x ⎧+∈⎪=⎨⎪--∈+∞⎩ ，则关于x 的函数()()(10)F x f x a a =+-<<的所有零点之和为（用a 表示）迎二模填空题训练41. 全集{}1,2,3,4,5U =，集合{}1,3,4A =，{}3,5B =，则()U C AB = ．2. 已知复数z 满足i z i 51)1(+-=+，(i 是虚数单位)，则复数z 的共轭复数z = .3. 已知4瓶饮料中有且仅有2瓶是果汁饮料，从这4瓶饮料中随机取2瓶，则所取两瓶中至少有一瓶是果汁饮料的概率是．4. 某鲜花店对一个月的鲜花销售数量(单位：支)进行统计，统计时间是4月1日至4月30日，5天一组分组统计，绘制了如图的鲜花销售数量频率分布直方图．已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1，且第二组的频数为180，那么该月共销售出的鲜花数(单位：支)为．(第4题图)5. 如图程序运行的结果是．6. 顶点在原点且以双曲线1322=-y x 的右准线为准线的抛物线方程是．7. 给出下列命题：（1）若两个平面平行，那么其中一个平面内的直线一定平行于另一个平面；（2）若两个平面平行，那么垂直于其中一个平面的直线一定垂直于另一个平面；（3）若两个平面垂直，那么垂直于其中一个平面的直线一定平行于另一个平面；（4）若两个平面垂直，那么其中一个平面内的直线一定垂直于另一个平面．则其中所有真命题的序号是．8. 已知π()3sin(2)6f x x =-，若存在π(0,)2α∈，使()()f x f x αα+=--对一切实数x 恒成立，则α= ．9. 设实数x ，y ，b 满足⎩⎪⎨⎪⎧2x －y ≥0，y ≥x ，y ≥－x ＋b，若z ＝2x ＋y 的最小值为3，则实数b 的值为．10. 若0,0,x y >>的最小值为．11. 在R t △ABC 中，CA ＝CB ＝2，M ，N 是斜边AB 上的两个动点，且MN ＝2，则CM →·CN →的取值范围为．12. 在平面直角坐标系xOy 中，圆C 的方程为(x －1)2＋y 2＝4，P 为圆C 上一点．若存在一个定圆M ，过P 作圆M 的两条切线PA ，PB ，切点分别为A ，B ，当P 在圆C 上运动时，使得∠APB 恒为60︒，则圆M 的方程为．13．三次函数)(x f y =的两个极值点为12,.x x 且11,())Px f x （与原点重合，22(,())Q x f x 又在曲线221x x y -+=上，则曲线)(x f y =的切线斜率的最大值的最小值为_________.14. 设各项均为正整数的无穷等差数列{a n }，满足a 54=2014，且存在正整数k ，使a 1，a 54，a k 成等比数列，则公差d 的所有可能取值之和为．迎二模填空题训练51．函数y ＝2sin(3x ＋π6)的最小正周期为．2. 设复数z 满足z (1+2i )=2－i ，则|z |＝．3．集合{x |－1≤log 1x10<－12，x ∈N *}的真子集的个数是．4．从{1，2，3，…，18}中任取两个不同的数，则其中一个数恰好是另一个数的3倍的概率为．5．运行如图的算法，则输出的结果是．6．某校从参加高三年级期中考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六段后得到如图的频率分布直方图，请你根据频率分布直方图中的信息，估计出本次考试数学成绩的平均分为． 7．如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，E ，F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1－EDF 的体积为．8．已知圆C 过点(1,0)，且圆心在x 轴的正半轴上．直线l ：y ＝x －1被圆C 所截得的弦长为22，则过圆心且与直线l 垂直的直线的方程为． 9．已知等比数列{a n }的前n 项和为S n ，并且对任意正整数n 均有S n +2＝4S n +3．则a 2= ．第5题10．已知集合A ={x |x 2+2x －8>0}，B ={x |x 2－2ax +4≤0}．若a >0，且A ∩B 中恰有1个整数，则a 的取值范围是．11．已知点A (1，-1)，B (4,0)，C (2,2)．平面区域D 由所有满足AP →＝λAB →＋μAC →(1＜λ≤a ，1＜μ≤b )的点P (x ，y )组成的区域．若区域D 的面积为8，则a +b 的最小值为．12．设函数f (x )＝ax +12sinx+32cos x 的图象上存在两条切线垂直，则a 的值是．13．实数x 、y 、z 满足0≤x ≤y ≤z ≤4．如果它们的平方成公差为2的等差数列，则 |x －y |+|y －z |的最小可能值．14．若实数x , y 满足x －4y ＝2x －y ，则x 的取值范围是．。

江苏省宝应县画川高级中学高考数学补丁专题5圆锥曲线小题(无答案)

补丁专题5——圆锥曲线小题一、考查离心率问题1．若一个正方形的四个顶点都在双曲线C 上，且其一边经过C 的焦点，则双曲线C 的离心率是．2. 已知B 为双曲线22221(0,0)x y a b a b-=>>的左准线与x 轴的交点，点(0,)A b ，若满足 2AP AB =的点P 在双曲线上，则该双曲线的离心率为 .3、若椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F 、2F ，线段12F F 被抛物线22y bx =的焦点分成53：两段，则此椭圆的离心率为．4．过双曲线22221(0,0)x y a b a b-=>>的左焦点(,0)(0)F c c ->，作圆：2224a x y +=的切线，切点为E ，直线FE 交双曲线右支于点P ，若1()2OE OF OP =+，则双曲线的离心率为．5.已知双曲线1222=-y ax 的一条渐近线方程为02=-y x ,则该双曲线的离心率e=_______6. 已知双曲线22221y x a b-=（00a b >>, ）的两个焦点为1F 、2F ，且12F F P 在双曲线第一象限的图象上，且12Sin PF F ∠=，21cos PF F ∠=，则双曲线的离心率为．7、已知A ，B ，P 是双曲线22221x y a b-=上不同的三点，且A ，B 连线经过坐标原点，若直线 PA ，PB 的斜率乘积23PA PB k k ⋅=，则该双曲线的离心率为．8．已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C 于点D ，且FD BF 2=，则C 的离心率为．9．在△ABC 中，1tan ,0,()022C AH BC AB CA CB =⋅=⋅+=，H 在BC 边上，则过点B 以A 、H 为两焦点的双曲线的离心率为10．椭圆2221(5x y a a +=为定值，且a >的左焦点为F ，直线x m =与椭圆相交于点A 、B ，FAB ∆的周长的最大值是12，则该椭圆的离心率是．。

江苏省宝应县画川高级中学届高考化学二轮复习微专题4信息方程式的书写导学案【精品教案】

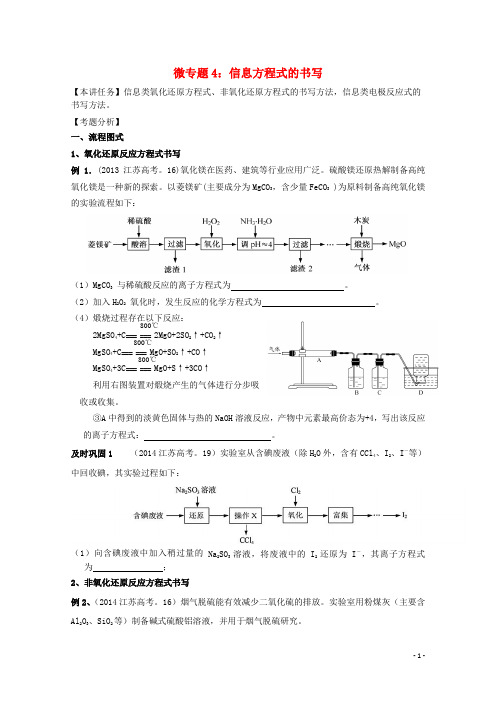
微专题4：信息方程式的书写【本讲任务】信息类氧化还原方程式、非氧化还原方程式的书写方法，信息类电极反应式的书写方法。

【考题分析】一、流程图式1、氧化还原反应方程式书写例1．(2013江苏高考。

16)氧化镁在医药、建筑等行业应用广泛。

硫酸镁还原热解制备高纯氧化镁是一种新的探索。

以菱镁矿(主要成分为MgCO 3，含少量FeCO 3 )为原料制备高纯氧化镁的实验流程如下：（1）MgCO 3 与稀硫酸反应的离子方程式为。

（2）加入H 2O 2 氧化时，发生反应的化学方程式为。

（4）煅烧过程存在以下反应：2MgSO 4+C === === 2MgO+2SO 2↑+CO 2↑MgSO 4+C === === MgO+SO 2↑+CO ↑MgSO 4+3C === === MgO+S ↑+3CO ↑利用右图装置对煅烧产生的气体进行分步吸收或收集。

③A 中得到的淡黄色固体与热的NaOH 溶液反应，产物中元素最高价态为+4，写出该反应的离子方程式：。

及时巩固1 （2014江苏高考。

19）实验室从含碘废液（除H 2O 外，含有CCl 4、I 2、I －等）中回收碘，其实验过程如下：（1）向含碘废液中加入稍过量的Na 2SO 3溶液，将废液中的I 2还原为I －，其离子方程式为； 2、非氧化还原反应方程式书写例2、（2014江苏高考。

16）烟气脱硫能有效减少二氧化硫的排放。

实验室用粉煤灰（主要含Al 2O 3、SiO 2等）制备碱式硫酸铝溶液，并用于烟气脱硫研究。

800℃800℃800℃（1）酸浸时反应的化学方程式为；滤渣Ⅰ的主要成分为（填化学式）。

（2）加CaCO 3调节溶液的pH 至3.6，其目的是中和溶液中的酸，并使Al 2 (SO 4)3转化为Al 2(SO 4)x (OH)6—2x 。

滤渣Ⅱ的主要成分为（填化学式）；若溶液的pH 偏高，将会导致溶液中铝元素的含量降低，其原因是（用离子方程式表示）。

江苏省宝应县画川高级中学高考数学自主整理清单2(无答案)

N MED CB A自主整理清单212.（1）如图，两射线,AM AN 互相垂直，在射线AN上取一点B 使AB 的长为定值2a ，在射线AN 的左侧以AB 为斜边作一等腰直角三角形ABC ．在射线,AM AN 上各有一个动点,D E 满足ADE ∆与ABC ∆的面积之比为3:2，则CD ED ⋅u u u r u u u r的取值范围为__________．（2）如右侧下图, 在等腰ABC ∆中, 底边EB AE DC AD BC 21,,2===, 若21-=⋅AC BD , 则=⋅AB CE __________.．（3）已知O 为ABC △的外心，若51213OA OB OC +-=0u u u r u u u r u u u r，则C ∠等于 ______- ．（4）已知向量a r ，b r ，满足1a =r ，()()02=-+b a b a ，则b r的最小值为．分析：向量问题一般可以采用两种方法处理，（1）（2）题图形比较特殊，故可以使用建系坐标法；（3）（4）题不能使用坐标法，故只能使用向量公式法。

答案：（1）[)+∞,52a ；（2）34-；（3）43π（4）21.13.（1）定义在R 上的函数()x f y =是减函数，且函数()1-=x f y 的图象关于()0,1成中心对称，若t s ,满足不等式()()2222t t f s s f --≤-，则当41≤≤s 时，st 的取值范围是 ___________（2）设实数6≤n ，若不等式()0822≥--+n x xm 对任意[]2,4-∈x 都成立，则nm n m 344-的最小值为_______________. （3）若动点P 在直线021=--y x l ：上，动点Q 在直线062=--y x l ：上，设线段PQ 的中点为()00,y x M ，且()()8222020≤-+-y x ，则2020y x +的取值范围是______________分析：这些问题实际要求考生对“00--=s t s t ”、“33441⎪⎭⎫⎝⎛-=-n m n m n m n m ”、“()()2020202000-+-=+y x y x ”等这些形式要具备一定的敏感度，这些就是在线性规划问题中提及的斜率问题、距离问题等。

江苏省宝应县画川高级中学2020届高三数学12月测试试题苏教版

D第12题图画川高级中学2020学年度高三B 部数学试题一、填空题：1.已知集合},1{},2,0{2a B A ==，若}4,2,1,0{=B A Y ，则实数a = . 2. 函数65cos2cos 6sin2sin )(ππx x x f -=的最小正周期为 . 3. 写出命题：“,sin x R x x ∀∈<”的否定： .4. 幂函数f(x)＝x α(α为常数)的图象经过，则f(x)的解析式是． 5. 已知函数)2(22)(>--+=x x a x x f 的图像过点(3,7)A ，则此函数的最小值是 __ ． 6. 已知点01=-+y x 若直线，平分圆04)1(22222=++--+y a ax y x 周长，则a = ．7. 已知偶函数f(x)在[0，＋∞)上是增函数，若f(lgx)＜f(1)，则x 的取值范围是．8. 过点)2,3(-M 作圆22:4240O x y x y ++-+=的切线方程是9. 若向量(,2),(3,2)a x x b x ==-r r ，且,a b r r的夹角为钝角，则x 的取值范围是 .10. 已知直线l 经过点(2,1)P ，且与直线2310x y ++=垂直，则l 的方程是____ ___. 11. 给出下列命题： ①存在实数x ，使得3cos sin π=+x x ；②函数x y 2sin =的图象向右平移4π个单位，得到)42sin(π+=x y 的图象； ③函数)2732sin(π-=x y 是偶函数； ④已知βα,是锐角三角形ABC 的两个内角，则βαcos sin >。

其中正确的命题的个数为 .12. 如图已知圆内接四边形ABCD 中，4,6,2====CD AD BC AB ，则四边形ABCD 的面积S= .13. 数列{}n a 中,()()111,()211n n n na a a n N n na *+==∈++，则数列{}n a 的前2012项的和为 .14. 已知定义在R 上的函数()f x 满足()12f =，()1f x '<，则不等式()221f x x <+的解集为_ . 二、解答：15. （本小题满分14分）在四面体ABCD 中，BD AD CD CB ⊥=,，且F E ,分别是BD AB ,的中点，求证：（1）直线⊥EF 面ACD（2）面⊥EFC 面BCD16. （本小题满分14分）设向量(4cos ,sin ),(sin ,4cos ),(cos ,4sin )ααββββ===-a b c（1）若a 与2-b c 垂直，求tan()αβ+的值；（2）求||+b c 的最大值;17.（满分14分）已知方程042:22=+--+m y x y x C ，(1)若方程C 表示圆，求实数m 的范围；(2)在方程表示圆时，该圆与直线042:=-+y x l 相交于M 、N两点，MN =求m 的值； (3)在(2）的条件下，定点)0,1(A ，P 在线段MN 上运动，求直线AP 的斜率取值范围。

江苏省扬州市宝应县画川高级中学2024届高三上学期第二次阶段性学情检测数学试题

江苏省扬州市宝应县画川高级中学2024届高三上学期第二
次阶段性学情检测数学试题
学校:___________姓名：___________班级：___________考号：___________一、单选题
99
二、多选题
A ．正四棱台111ABCD A
B
C
D -B ．正四棱台111ABCD A B C D -C ．A
E ∥平面1BC D D ．1A 到平面1BC D 的距离为
三、填空题
13．34(1)(2)x x +-展开式中3x 项的系数为
14．已知圆C 的圆心坐标是(0,)m (2,1)A --，则r =
15．若关于x 的不等式22ax x a -+16．已知点,,A B C 在圆221x y +=||FA FB FC ++
的最大值为
四、解答题
（1）证明：AB PM ⊥；
（2）求直线AN 与平面19．食品安全问题越来越受到人们的重视，某超市在某种蔬菜进货前，要求食品安检部门对每箱蔬菜进行三轮各项指标的综合检测，销售．已知每箱这种蔬菜第一轮检测不合格的概率为
第三轮检测合格的概率为格相互之间没有影响．
(1)求每箱这种蔬菜不能在该超市销售的概率；
(2)如果这种蔬菜能在该超市销售，箱亏损200元，现有4箱这种蔬菜，求这20．已知数列满足2n a +=(1)证明：{}12n n a a +-是等比数列，并求(2)已知数列{}n b 满足n b =21．已知椭圆22
1169
x y +=，
与椭圆交于M 、N 两点，且（1）若0b =，证明：直线（2）若3
4
k =
，求四边形22．已知函数()ln f x x =（1）讨论函数()f x 的单调性；（2）证明不等式2x e ax --。

江苏省宝应县画川高级中学2020届高考数学限时训练41-46(无答案)

高三下学期限时训练41 ——三角向量立体几何15．(本小题满分14分)在ABC ∆中，,,A B C 的对边分别是,,a b c ，已知向量(sin(),cos )m C C π=-u r，(sin(),sin )2n B B π=+r ，且sin 2m n A ⋅=u r r ．（1）求A ；（2）若4c bb c+=，求sinBsinC 的值.16．(本小题满分14分)如图，在四棱锥P －ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD ＝DC ，E 是PC 的中点. ⑴求证：PA ∥平面BDE ；⑵求证：平面BDE ⊥平面PBC.高三下学期限时训练42——三角向量、立体几何15．（本小题满分14分）已知△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且2a cos B ＝c cos B ＋b cos C ．（1）求角B 的大小；FMND BCA（2）设向量m =(cos A ，cos 2A )，n =(12，－5)，求当⋅m n 取最大值时，tan C 的值．16．（本小题满分14分）如图，直角梯形ABCD 中，AB ∥1,2CD AB CD =,AB BC ⊥,平面ABCD ⊥平面BCE ,BCE ∆为等边三角形，,M F 分别是,BE BC 的中点，14DN DC =．(1)证明EF ⊥AD ; (2)证明MN ∥平面ADE ;(3)若1,2AB BC ==,求几何体ABCDE 的体积．高三下学期限时训练43 ——三角向量、立体几何15．（本小题满分14分）在ABC ∆中，角A B C 、、的对边分别为a b c 、、，已知5sin 13B =，且a b c 、、成等比数列．(1)求11tan tan A C+的值； (2)若cos 12ac B =，求a c +的值．16．（本小题满分14分）如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，//AD BC ，ADC ∠=90°，12BC AD =，PA PD =，,M N 分别为AD 和PC 的中点．（1）求证：//PA 平面MNB ；（2）求证：平面PAD ⊥平面PMB ．高三下学期限时训练44 ——三角向量、立体几何15．（本小题满分14分）在四边形ABCD 中，CA ＝CD ＝12AB ＝1， AB AC ⋅u u u r u u u r ＝1，sin ∠BCD ＝35．（1）求BC 的长；（2）求三角形ACD 的面积．P AD MNC B (第16题图)AE DC B16．（本小题满分14分）如图，六面体ABCDE 中，面DBC ⊥面ABC ，AE ⊥面ABC ．（1）求证：AE //面DBC ；（2）若AB ⊥BC ，BD ⊥CD ，求证：AD ⊥DC ．高三下学期限时训练45 ——三角向量、立体几何15．(本题满分14分)已知∆ABC 的面积S 满足443S ≤≤，且AB AC ⋅u u r u u u r=—8．（Ⅰ）求角A 的取值范围；（Ⅱ）若函数22cos 2sin 33cos 4444()x x x x f x -+⋅=，求()f A 的最大值．16．(本题满分14分)如图，把长、宽分别为4、3的长方形ABCD 沿对角线AC 折成直二面角．（Ⅰ）求顶点B 和D 之间的距离；（Ⅱ）现发现BC 边上距点C 的31处有一缺口E ，请过点E 作一截面，将原三棱锥分割成一个三棱锥和一个棱台两部分，为使截去部分体积最小，如何作法？请证明你的结论．高三下学期限时训练45 ——三角向量、立体几何15．（本小题满分14分）已知函数f (x )＝3sin x 4cos x4＋cos 2x4．（1）若f (x )＝1，求cos(2π3－x )的值；（2）在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且满足a cos C ＋12c ＝b ，求f (B )的取值范围． 16．（本小题满分14分）如图，已知BC 是半径为1的半圆O 的直径，A 是半圆周AB CDE .ACE .DE AD上不同于B ，C 的点，F 为⌒AC 的中点．梯形ACDE 中，DE ∥AC ，且AC ＝2DE ，平面ACDE ⊥平面ABC ．求证：（1）平面ABE ⊥平面ACDE ；（2）平面OFD ∥平面BAE ．。

江苏省宝应县画川高级中学高考数学解析几何学案2(无答案)

在平面直角坐标系 xOy 中，已知对于任意实数 k，直线( 3k＋1)x＋(k－ 3)y－(3k＋ 3) ＝0 恒过定点 F.设椭圆 C 的中心在原点，一个焦点为 F，且椭圆 C 上的点到 F 的最大距离为 2＋ 3. (1)求椭圆 C 的方程； (2)设(m，n)是椭圆 C 上的任意一点，圆 O：x ＋y ＝r (r＞0)与椭圆 C 有 4 个相异公共点，试分别判断圆 O 与直线 l1：mx＋ny＝1 和 l2：mx＋ny＝4 的位置关系．
2 2 2
x2 y2 a b
5 、设椭圆 C ∶ 2 ＋ 2 ＝ 1(a ＞ b ＞ 0) 恒过定点 A(1,2) ，则椭圆的中心到准线的距离的最小值 ________．三．例题
x2 a
y2 b
1. 在平面直角坐标系 xOy 中，过点 A(－2，－1)椭圆 C∶ 2＋ 2＝1(a＞b＞0)的左焦点为 F，短 → → 2 轴端点为 B1、B2，FB1·FB2＝2b . (1)求 a、b 的值； (2)过点 A 的直线 l 与椭圆 C 的另一交点为 Q，与 y 轴的交点为 R.过原点 O 且平行于 l 的直线与椭圆的一个交点为 P.若 AQ·AR＝3OP ，求直线 l 的方程．
x2 y2 a b
3、已知双曲线 2－ 2＝1(a>0，b>0)的一个焦点与抛物线 y ＝4x 的焦点重合，且双曲线的离心率等于 5，则该双曲线的方程为________．
x2 y2 a b
2
4、设 F1，F2 是双曲线 C： 2－ 2＝1(a>0，b>0)的两个焦点，P 是 C 上一点，若|PF1|＋|PF2|＝6a 且△PF1F2 的最小内角为 30°，则双曲线 C 的离心率为________．
画川高级中学高三

江苏省宝应县画川高级中学高中数学等差数列的前n项和(2)导学案(无答案)新人教版必修5

课题：等差数列的前n 项和（2）上课时间：上课班级：高一（）学时： 1课时学习目标：能运用等差数列的前n 项和公式解决简单的问题；通过问题的解决培养学生观察、分析的能力由特殊到一般的归纳能力.学习重点：能运用等差数列的前n 项和公式解决简单的问题学习难点：能运用等差数列的前n 项和公式解决简单的问题导学过程学习体会一自主导航1．等差数列的前n 项和的公式：=n S _________________________；或 =n S _________________________．2．等差数列的前n 项和的有关公式：（1）等差数列{}n a 中，前m 项的和，次m 项的和，后m 项的和仍然为等差数列.（2）由=n S d n n na 2)1(1-+可知：在数列{}n a 的前n 项和=n S C Bn An ++2中，若0=C ，则{}n a 为等差数列．（3）等差数列{}n a 中， n 为奇数：21+=-n a S S 偶奇；11-+=n n S S 偶奇； n 为偶数：d n S S 2=-奇偶； 122-=n na a S S 偶奇．二、合作探究例1某剧场有20排座位，后一排比前一排多2个座位，最后一排有60个座位，这个剧场共有多少个座位？例2. 某种卷筒卫生纸绕在盘上，空盘时盘芯直径mm 40，满盘时直径mm 120，已知卫生纸的厚度为mm 10．，问：满盘时卫生纸的总长度大约是多少米（精确到m 1）？例3设等差数列{}n a 的前n 项的和为n S ，已知123=a ，012>S ，013<S ．（1）求公差d 的取值范围；（2）判断前几项的和最大．三、巩固练习 1．等差数列{}n a 的前n 项和为n S ，且164=a ，810=a ，则13S 等于（）Ａ．168 Ｂ．156 Ｃ．78 Ｄ．1522．设等差数列的通项公式n a n 420-=．则该数列的前多少项和最大（）Ａ．前三项Ｂ．前四项或前五项Ｃ．前五项Ｄ．前六项 3．等差数列{}n a 中，405=S ，1952=+a a ，则=1a ________．4．一个等差数列的前12项和为354，前12项中，偶数项和与奇数项和之比为2732∶，求公差d ．5．已知等差数列{}n a 的前n 项和为n n S n 352+=，写出它的前3项，并求这个数列的通项公式．。

江苏省宝应县画川高级中学高中数学苏教版必修二2.1.4两条直线的交点学案

2.1.4两条直线的交点学习目标：1．会求两条直线的交点．2．理解两条直线的三种位置关系（平行、相交、重合）与相应的直线方程所组成的二元一次方程组的解（无解、有惟一解、有无数个解）的对应关系．3．会应用这种对应关系通过方程判断两直线的位置关系，以及由已知两直线的位置关系求它们方程的系数所满足的条件．4．通过学习两直线的位置关系与它们所对应的方程组的解的对应关系，培养学生的转化思想．活动方案：活动一：探究两个二元一次方程所组成的方程组解的情况与两方程所表示的两条直线的位置之间的对应关系问题1：判断直线2x y +=与直线0x y -=的位置关系，若不平行，求出其交点坐标。

思考1：如何求两相交直线的交点坐标？思考2：如果直线1l 和2l 相交，那么交点的坐标是这两个方程组成的方程组的解，反之，以这两个方程组成的方程组的解为坐标的点是否为两直线的交点？问题2：如果方程组1112220A xB yC A x B y C ++=⎧⎨++=⎩只有一个公共解，那么对应的两条直线位置关系如何？如果方程组无解、有无数组解，两直线的位置关系又如何？结论1：利用求交点坐标的方法（即解方程组）可以判断两直线的位置关系。

结论2：两个二元一次方程所组成的方程组解的情况与两方程所表示的两条直线的位置之间的对应关系：活动二：掌握两直线的位置关系的判断例1：分别判断下列直线是否相交，若相交，求出它们的交点：（1）1l :72=-y x ，2l :0723=-+y x ；（2）1l :0462=+-y x ，2l :08124=+-y x ；（3）1l :0424=++y x ，2l :32+-=x y ．【解】（1）因为方程组⎩⎨⎧=-+=--0723072y x y x 的解为⎩⎨⎧-==13y x ,因此直线12l l 和相交，交点坐标为()13-，．（2）方程组⎩⎨⎧=+-=+-081240462y x y x 有无数组解，这表明直线21l l 和重合．（3）方程组⎩⎨⎧=-+=++0320424y x y x 无解，这表明直线21l l 和没有公共点，故1l ∥2l ．小结：研究两条直线21,l l 的位置关系（相交、重合、平行）可以转化为两条直线方程所得的方程组⎩⎨⎧=++=++00222111C y B x A C y B x A 的解的个数问题．例2：已知两条直线1:60l x my ++=，2:(2)320l m x y m -++=，当m 为何值时，直线1l 与2l ：(1)平行；(2)重合；(3)相交．答：()11,m =-()23,m =()31,3m ≠-小结：两条直线的位置关系活动三：会求直线方程例3：直线l 经过原点，且经过另外两条直线0832=++y x ，01=--y x 的交点，求直线l 的方程．思考3：如何求直线方程？需要哪些条件？分析：法一由两直线方程组成方程组⎩⎨⎧=--=++010832y x y x ，求出交点()2,1--，再过原点()0,0，由两点求直线方程．思考4：经过两条直线0832=++y x ，01=--y x 的交点的直线有多少条？它们的方程有什么共同特征？本题还有其它解法吗？法二设经过两条直线0832=++y x ，01=--y x 交点的直线方程为()()01832=--+++y x y x λ，又过原点，由()0,0代入可求λ的值．思考:方程238(1)0x y x y λ+++--=(λ为任意实数)表示的直线有什么特点?小结：已知直线1l :0111=++C y B x A ，2l :0222=++C y B x A 相交，那么过两直线的交点的直线方程可设为()()0222111=+++++C y B x A C y B x A λ()R ∈λ（不包括直线2l ）。

(江苏专用)2020年高考数学二轮复习专题14圆锥曲线学案

专题14圆锥曲线回顾2020〜2020年的高考题，在填空题中主要考查了椭圆的离心率和定义的运用，在解答题中2020、2020、2020年连续三年考查了直线与椭圆的综合问题，难度较高.在近四年的圆锥曲线的考查中抛物线和双曲线的考查较少且难度很小，这与考试说明中A 级要求相符合.预测在2020年的高考题中：(1) 填空题依然是以考查圆锥曲线的几何性质为主，三种圆锥曲线都有可能涉及.(2) 在解答题中可能会出现圆、直线、椭圆的综合问题，难度较高，还有可能涉及简单的轨迹方程的求解.答案：3或252. ____________________________________________________________________________________ 若抛物线y 2= 2x 上的一点M 到坐标原点 O 的距离为• .3,则M 到该抛物线焦点的距离为 _______________________1 3解析：设 M 的坐标为(x , 土 2x )( x >0)，则x 2 + 2x = 3,解得x = 1，所求距离为1 + ?=-. 3 答案：-3. ____________________________________________________________________________________ 双曲线2x 2-y 2 + 6 = 0上一个点P 到一个焦点的距离为 4,则它到另一个焦点的距离为 _________________________ .2 2解析：双曲线方程化为七-x 3 = 1.设P 到另一焦点的距离为 d,则由|4 - d | = 2 6得 d = 4 + 2.6,或d =4 - 2 .6（舍去）.■小题展础练请金取送讨融一分不能少2 2x y1. 若椭圆三+乞=1的离心率5 m .10 5，贝U m 的值是解析：当当n <5时, 10 5- m寸」.5，解得m= 3. n >5 时,答案：2 6 + 42 2X y4. (2020 •江苏高考)在平面直角坐标系 xOy 中，若双曲线--m ^4=1的离心率为• 5,贝U m 的值为解析：由题意得 m>0，二a = m b = m + 4,2 ,严, c J-Z0m+ m^ 4 L --c = ■ m + m^ 4，由 e = = 5得=5,arn解得m= 2. 答案：22 2x y5•已知椭圆r+ 2= 1(a >b >0)的左、右焦点分别为F l 、F 2,离心率为e ,若椭圆上存在点a be ,则该椭圆离心率 e 的取值范围是 __________ .解析：••• pg = e ,「. PF = ePF = e (2a -PF ),2ae 2ae 2e厂又 a -c w PF < a + c , a - c <i^-e < a + c, a (1 — e ) < I T -W a (1 + e) , 1 — e <i r ~仝 1 + e,解得 21 i e 1 i e 1 i e—1.又 0<e <1，二 2 — 1 w e < 1. 答案：［.2 — 1,1)p,使得pg =PF =2ae i T e .增分考点讲透■ ZENQFE h J K AOD>AF. JI AMQTOU［典例1］2 2X y(2020 •四川高考)(1)椭圆丁+%= 1的左焦点为F ,直线x = m 与椭圆相交于点 A B .当△ FAB 的周长4 3 最大时，△ FAB 的面积是 _________ •(2)(2020 •福建高考)设圆锥曲线r 的两个焦点分别为 F l , F 2.若曲线 r 上存在点 P 满足|PF | ：』F l F 2| : | PF 2| = 4： 3 : 2，则曲线 r 的离心率等于 _________ •［解析］ ⑴法一：依题意得知，点 F ( — 1,0)，不妨设点 A (2cos0 , .'3sin 0 )(sin 0 >0)，则有02cos 0,—念si n 0 ) , | FA | = | FB | =__2+ 3sin 2 0 = 2 + cos 0 , | AB = psi n 0 ,.— 冗 r n nI FA + I FB + |AB = 4 + 2cos 0 + ^/3sin 0 = 4 + 4sin 0 + w ，当 0 +〒=2k n + =, k € Z ,即卩 0 =* 6 6 2n312k n+ 3, k € Z , 2cos 0 = 1, '3sin 0 =，时，△ FAB 的周长最大，此时△ FAB 的面积等于 (1 + 1) X3=3.法二：椭圆右焦点为 F ' (1,0) •由椭圆定义 | AF + |AF | = | BF + |BF | = 2a . 则△ FAB 的周长 l = | AF + | BF + | AB =4a —(| F ' A | + | F ' B ) + | AB=4a —1| F ' A | + | F ' B — I AB I <4 a .所以△ FAB 周长最大时，直线 x = m 经过F ' (1,0)这时|AE | = 3, 1此时 S\ FAB = 22X 3= 3.⑵ 由题意可设：|PF | = 4m , I F 1F 2I = 3m , | PF a | = 2m ,当圆锥曲线是椭圆时，长轴长为 2a = | PF | + | P 冋= 4讨 2m= 61m 焦距为 2c = | F 1F 2| = 3m当圆锥曲线是双曲线时，实轴长为c 2c 3m 3 心率e =a = 2a = 2m 2.1 3 ［答案］(1)3(2) 或 2■ flfaCff “解决圆锥曲线上的点与焦点的距离问题，一般考虑用定义，在椭圆和双曲线的方程中要注意之间关系的区别.攻克更弗融分井都抓牢c 2c 所以离心率e =a = 2a 3m =16m =2a =ir | PF | — | PF | = 4m — 2m= 2m 焦距为 2c = | RF 2| = 3m,所以离a ,b , c1)与椭圆C 交于不同的两点 M N(1) 求椭圆C 的方程；(2) 当厶AMN 勺面积为~3^时，求k 的值. 3a = 2,［解］(1)由题意得C =,a 22. 22a =b +c ,2 2所以椭圆C 的方程为x + 2 = 1.解得b = ；2,y = k x — 1⑵由x 2x +2 2 2 2(1 + 2k )x — 4k x + 2k — 4= 0.设点M N 的坐标分别为(X 1, y 1) , (X 2, y 2)，则 y 1= k (x 1 — 1), 4k 2y 2= k (X 2— 1) , x 1+ X 2 = 1 + 2k 2, X 1X 2 = 2k 2— 4 21+ 2k ，[演练1]2 2⑴ 已知双曲线善■— y 2= 1的一个焦点坐标为(-、/3, 0)，则其渐近线方程为 ___________ ；(2)已知直线11： 4x — 3y + 6 = 0和直线I 2： x =- 1,抛物线y 2 = 4x 上一动点P 到直线I i 和直线l 2的距离之和的最小值是 _____________ .解析：(1)由a + 2 = 3，可得a = 1,2双曲线方程为x —2 = 1,距离.动点 P 到直线I 1和直线I 2的距离之和的最小值即为点 F (1,0)到直线11: 4x — 3y + 6 = 0的距离d =I 4 + 6|—22— 2・.'4 + 3答案：(1) y =± ;'2x (2)2［典例2］.••其渐近线方程为即 y =± '2x .⑵ 由y 2= 4x 可知12： x =— 1是抛物线的准线，所以P 到I 2的距离等于 P 到抛物线的焦点 ”1,0)的 (2020 •北京高考)已知椭圆2 2x yC ： a 2+ £ = 1( a >b >0)的一个顶点A (2,0)，离心率为舟.直线y = k (x —所以 MN= : X 2— x i 2+ y — y i =■' 1 + k 2 [ x i + X 22— 4x i X 2]2 弋 1 + k 2 4 + 6k 2=1 + 2k 2.又因为点A (2,0)到直线y = k (x — 1)的距离d = , k| 2,寸1 + k 所以△ AMN 勺面积为 1 | k | 4 + 6 k 2 S= 2处 d =1+ 2k 2 .由 1 k| 1+：+26k =¥，化简得 7k 4 — 2k 2— 5= 0,1 + 2k 3 解得k =± 1.• flfli 发牌""本题主要考查椭圆的标准方程、几何性质及直线与椭圆的位置关系•解决直线与圆锥曲线的位置关系的相关问题，一般是联立方程消元后转化为二次方程的问题.［演练2］已知过抛物线 y 2= 2px (p >0)的焦点，斜率为 2 : 2的直线交抛物线于 A (X 1, yj , B (X 2, y 2)( X 1<X 2)两点, 且AB= 9.求该抛物线的方程.解：直线AB 的方程是y = 2羽x — P ，与y 2= 2px 联立，从而有4x 2— 5px + p 2= 0，所以X 1 + X 2=扌. 由抛物线定乂得 AB= X 1 + X 2+ p = 9, 所以p = 4，从而抛物线方程是 y 2= 8x .［典例3］2(2020 •南师大信息卷)已知双曲线x 2— y 3 = 1，椭圆与该双曲线共焦过点(2,3).(1) 求椭圆方程；(2) 设椭圆的左、右顶点分别为A, B,右焦点为F ,直线I 为椭圆线，N 为I 上的一动点，且在 x 轴上方，直线 AN 与椭圆交于点 M①若AM= MN 求/ AMB 勺余弦值;②设过A, F , N 三点的圆与y 轴交于P, Q 两点，当线段PQ 的中点为(0,9)时，求这个圆的方程. ［解］(1)双曲线焦点为(土 2,0)，2 2x y设椭圆方程为—+ 2 = 1(a >b >0).a b点，且经的右准2 2a —b = 4,则 49 解得 a 2= 16, b 2 = 12.2+ 2= 1.a b2 2x y故椭圆方程为16+12= i.⑵①由已知，A — 4,0) , B (4,0) , F (2,0)，直线 I 的方程为 x = 8.设 N(8 , t )(t >0).•/ AM= MN ••• M 2, 2 .令 x = 0，得 y 2— t + 72 y — 8= 0. 设 P (0 , y 1) , Q 0, y 2),72由线段PQ 的中点为(0,9)，得y 1 + y 2= t + - = 18. 此时，所求圆的方程为 x 2 + y 2 + 2x — 18y — 8= 0.本题是直线、双曲线、椭圆、圆的综合问题，主要考查待定系数法求曲线方程.[演练3]2 2x y如图，在平面直角坐标系 xOy 中，椭圆C ： 2+ 2= 1(a >b >0)的离a b原点为圆心，椭圆 C 的短半轴长为半径的圆与直线x — y + 2= 0相切.(1) 求椭圆C 的方程；(2) 已知点P (0,1) , Q0,2).设M N 是椭圆C 上关于y 轴对称的不同两点，直线 PM 与 QN 相交于点由点 M 在椭圆上，得t = 6. M 的坐标为M 2,3).LUU LUITMA = ( — 6,— 3) , MB = (2 , — 3),UULT• MB =— 12 + 9 =— 3.UUU UULT r MA • MB — 3 J 65 / AMB=—uuur uuur ==— .| MA | •I MB | 736+ 9 ^/4+965故点所以 uur MA cos16— 4D + F = 0, 4+ 2D+ F = 0,64 +12+ 8D + Et + F = 0,D= 2, 72得 E =— t —-,圆的方程为 x 2+ y 2+ 2x —t + 72 y — 8= 0,T.求证：点T在椭圆C上.解：⑴由题意知椭圆C 的短半轴长为圆心到切线的距离，即所以a = 2 .'2设T 点的坐标为(x , y ).x3y — 4联立①②解得x o =时,y o =时.因为x l +yf = 1，所以1亠2+1心因为 8 + 2 '所以 8 2y — 3 + 2 2y — 32 2一 e x3y — 4 2整理得 8 + 2 = (2y —3),2 2 2 2x 9yox y所以孑+十一12y + 8= 4y 2— 12y + 9,即石+?= 1.8 2 8 2 所以点T 的坐标满足椭圆 C 的方程，即点T 在椭圆C 上.［典例4］2 2秸+誇=1的中心，焦点与该椭圆的右焦点重合.(1)求抛物线D 的方程;①若直线I 的斜率为1,求MN 的长;②是否存在垂直于 x 轴的直线m 被以MA 为直径的圆E 所截得的弦长为定值？如果存在，求出m 的方程；如果不存在，说明理由.［解］(1)由题意，可设抛物线方程为 y 2= 2px (p >0).由a 2— b 2= 16— 15= 1，得c = 1.•••抛物线的焦点为(1,0) ,••• p = 2.2•抛物线D 的方程为y = 4x . (2)设 Mx 1, y 1), N X 2, y 2).①直线I 的方程为：y = x — 4,联立［'y = 4x ,2整理得 x — 12x + 16= o. 则 X 1+ X 2= 12 , X 1X 2= 16,因为离心率e =|=今，所以a =1 —21=2.所以椭圆C 的方程为 2 2x y —I —=18 1 2 (2)证明：由题意可设M N 的坐标分别为 (x o , y o )，( — x o . y 。

江苏省扬州市宝应县高中数学第二章圆锥曲线与方程 2

双曲线（2）教学目标：1.掌握双曲线的标准方程；
2.掌握双曲线的定义
教学重点：掌握双曲线的标准方程
教学难点：掌握双曲线的标准方程
圆的哪些几何性质？
离心率：
的几何性质
长为
注意：实轴与虚轴等长的双曲线叫
曲线
率及渐近线的方程．
半轴长和虚半轴长、焦点坐标、
的焦点为顶点，以椭圆的顶点为焦点的双曲
练习：对称轴都在坐标轴上的等到轴双曲线的一个焦点是求它的标准方程和渐近线方程．
，虚轴长是
曲线
．双曲线
经过点并且对称轴都在坐标轴上的等轴双
上，焦距是。

江苏省扬州市宝应县高中数学第二章圆锥曲线与方程2.1.2圆锥曲线教案新人教A版选修2-1

2。

1 圆锥曲线教学目标：1。

理解三种圆锥曲线的定义。

2。

能根据圆锥曲线的定义判断轨迹的形状.教学重点：能根据圆锥曲线的定义判断轨迹的形状教学难点：能根据圆锥曲线的定义判断轨迹的形状导学过程学习体会一、创设情境某地区的居民生活用水来源有2处，一处是位于该地区内的一口深水井，另一处是位于该地区南端的一条河（河岸可以近似看成直线），已知井C到河岸AB的距离为4千米，请为该区域划一条分界线,并指出就如何取水最合理.二、活动尝试1．圆锥面可看成一条直线绕着与它相交的一条定直线l（两条直线不互相垂直）旋转一周所形成的__ __．其中直线l叫做圆锥面的轴．2．圆锥面的截线的形状在两个对顶的圆锥面中，若圆锥面的母线与轴所成的角为θ，不过圆锥顶点的截面与轴所成的角为α，则α＝错误!时，截线的形状是圆;当θ<α〈错误!时,截线的形状是椭圆；0≤α≤θ时，截线的形状是双曲线；当α＝θ时,截线的形状是抛物线．3．椭圆的定义平面内与________________________________等于常数（大于F 1F 2)的点的轨迹叫做椭圆,两个定点F 1，F 2叫做椭圆的________．两焦点间的距离叫做椭圆的________．4．双曲线的定义平面内与_________________________________等于常数（小于F 1F 2的正数）的点的轨迹叫做双曲线，两个定点F 1,F 2叫做双曲线的________，两焦点间的距离叫做双曲线的________．5．抛物线的定义平面内_________________________________________的轨迹叫做抛物线，________叫做抛物线的焦点，________叫做抛物线的准线．6．椭圆、双曲线、抛物线统称为____________．三、师生探究例1试用适当的方法作出以两个定点，1F 、2F 为焦点的一个椭圆练习：举出生活中一些椭圆、双曲线、抛物线的实例例2已知定点F 和定直线,l F 不在直线,l 上，动圆M 过点F 且与直线l 相切，求证：圆心M 的轨迹是一条抛物线例3（选用）已知两个定点坐标是),3,2(),3,8(21F F -动点P满足,221m PF PF =-当m 分别取3和5时，求点P 的轨迹四、思考题一束光线垂直于一个墙面，将一块圆形纸板置于光源与墙面之间，墙面上会出现纸板的影子，变化纸析与光线的角度，影子的形状也会发生变化，观察这些影子会出现哪些不同的形状五、巩固运用1、若动圆与定圆1)2(22=+-y x 外切，又与直线01=+x 相切,则动圆圆心的轨迹是2、设有两定点1F 、2F ，且,421=F F 动点M 满足,421=+MF MF 则动点M 的轨迹是3、若),(y x M 在运动过程中,总满足,10)3()3(2222=-++++y x y x 则M 的轨迹是4、已知A 、B 两地相距800m ，在A 地听到炮弹爆炸声比在B 地晚2s ,且声速是340s m /，则炮弹爆炸点的可能的轨迹是5、设MNP N M ∆-),0,5(),0,5(的周长为36，则顶点P 的轨迹为的距离大1，则点M 的轨迹为尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

江苏省宝应县画川高级中学2020届高考数学第二轮复习 圆锥曲线导学案2(无答案)

导数的复习2(学案)

江苏省扬州市宝应县高中数学 第二章 圆锥曲线与方程 2.1 曲线与方程(2)教案 新人教A版选修21