高三理科数学限时训练15之欧阳道创编
奥数题100道,奥数题大全之欧阳与创编

一、计算题。
( 共100题 )1.有一串珠子,第32颗是什么珠子?第49颗呢?2.20个小朋友排一队,从前面数学学排在第2个,思思排在学学后面第4个,那么思思从后往前数排第几个?3.森林里的小动物举行运动会,小猪排第13,小兔排第5,小猪要超过多少只小动物才能与小兔并列第5呢?4.有一个四位数,各位数字之和等于34。
符合这个条件的四位数有哪些?5.妈妈买来一些巧克力,送给邻居小妹妹2块后拿回了家,小亚先吃了其中的一半,又给弟弟吃了剩下的一半,这时还有1块巧克力,妈妈一共买了多少块巧克力?6.用0,5,6三张卡片可以构成多少个数?7.商店新进6盒小皮球,连续5天,每天都卖出8个。
服务员重新整理一下,剩下的小皮球正好装满2盒。
原来每盒有几个小皮球?8.小猴喜欢吃香蕉,猴王摘了30个,他送给小猴15个后,中猴为了讨好他又送给他8个,这时他们三个的香蕉一样多,算一算,小猴和中猴原来各摘了多少个香蕉?9.小明心中想到三个数,这三个数的和等于这三个数的积,你知道小明想的三个数都是什么吗?10.由2,5,0,7四个数字可以组成多少个不同的四位数?11.老奶奶家养了20只鸡,分别装在5个笼子里,每只笼子里鸡的只数都不相同。
老奶奶是怎样把20只鸡装进5只笼子的呢?12.一本小人书共100 页,排版时一个铅字只能排一位数字,请你算一下,排这本书的页码共用了多少个铅字?13.联欢会上,要把10个水果装在6个袋子里,要求每个袋子中装的水果都是双数,而且水果和袋子都不剩。
应该怎样装?14.新型电脑公司有87台电脑,上午卖出19台,下午卖出26台,还剩下多少台?(用两种方法解答)15.王师傅做了80个面包,第一次卖了17个,第二次卖了25个,还剩多少个?16.小朋友做操,第一队有15个同学,从第二队调3人到第一队以后,第二队的人数比第一队少6人。
第二队原来有多少人?17.王红到超市想买一个书包、一双球鞋和一个足球。
标价为:书包28元,球鞋35元,足球26元。
继续再教育考试及参考答案1之欧阳道创编

继续再教育考试返回上一级单选题(共30题,每题2分)1 .蒋大宗教授在生物医学工程领域做出了杰出贡献,2007年,他获选为(),也是获此殊荣的第二位中国人。
•A.美国电气与电子工程师协会终身会士(IEEE LifeFellow)•B.美国电气与电子工程师协会会士(IEEE Fellow)•C.英国电气与电子工程师协会终身会士(IEEE LifeFellow)•D.英国电气与电子工程师协会会士(IEEE Fellow)我的答案: A参考答案:A答案解析:暂无2 .蒋大宗(1922-2014),1944年毕业于西南联合大学电机系,西安交通大学教授,是中国()的创始人之一、西安交通大学生物医学工程专业的奠基人。
•A.生物医学工程•B.生物工程•C.医学工程•D.生命工程我的答案: A参考答案:A答案解析:暂无3 .李怀祖,我国管理学家,中国()的开拓者与倡导者之一。
•A.决策科学•B.计量科学•C.人口科学•D.统计科学我的答案: A参考答案:A答案解析:暂无4 .姚熹,西安交通大学教授,国际知名的材料科学家,他是国际陶瓷科学院院士,是我国在()研究方面的主要奠基人之一,并被国内外同行看成是我国在这一领域的学术带头人和代表。
•A.陶瓷•B.铁电陶瓷•C.电子瓷器•D.电子器件我的答案: B参考答案:B答案解析:暂无5 .俞茂宏,西安交通大学教授,长期从事材料强度理论和结构强度理论研究,他提出的()理论,是第一个被写入基础力学教科书的由中国人提出的理论。
•A.材料强度理论•B.结构强度理论•C.多维强度理论•D.统一强度理论我的答案: D参考答案:D答案解析:暂无6 .陈学俊教授出生在大变革时代,使得他的命运和祖国的命运紧紧联系在一起,他提出了()的呐喊。
•A.工程救国•B.工学救国•C.力学救国•D.热能救国我的答案: D参考答案:A答案解析:暂无7 .西安交通大学姚熹教授牵头成立了(),帮助日本、韩国、泰国、马来西亚等国的科研发展,力推俄罗斯、法国、德国等国家的国际合作,为电子陶瓷行业的发展做出很大贡献。
参照物专项练习(含答案)之欧阳道创编

运动的描述【课时训练】一、单选题1.有一首歌的歌词唱道:“月亮在白莲花般的云朵里穿行”,这里选取的参照物是A. 地面B. 云朵C. 人D. 月亮2.一人骑自行车由南向北行驶,这时有辆汽车也由南向北从他身旁疾驶而过,若以这辆汽车为参照物,此人A. 向北运动 B. 向南运动C. 静止D. 运动方向无法确定3.诗句“满眼风光多闪烁,看山恰似走来迎,仔细看山,山不动,是船行.”其中“看山恰似走来迎”和“是船行”所选的参照物依次是A. 船和山B. 山和船C. 山和水D. 水和山4.关于机械运动,下列说法正确的是A. 空气的流动不属于机械运动B. 运动路线是直的,运动路程是不变的运动才是机械运动C. 一个物体位置改变就是运动,位置没有改变就是静止D. 判断一个物体是否运动和怎样运动,离开了参照物就失去了意义5.一位勇敢的漂流者,坐橡皮船在湍急的河水中顺流而下,对此,下列说法正确的是A. 以岸边的树为参照物,人是静止的B. 以船为参照物,河水是流动的C. 以河水为参照物,人是静止的D. 以河水为参照物,人是运动的6.甲看路旁的树木向南运动,乙看甲静止不动,若以树木为参照物,则A. 甲、乙都向北运动B. 甲、乙都向南运动C. 甲向北运动,乙向南运动D. 甲向南运动,乙向北运动7.在平直轨道上行驶的一列火车,放在车厢小桌上的茶杯,相对下列哪个物体是运动的A. 这列火车B. 坐在车厢椅子上的乘客C. 关着的车门D.从旁边走过的列车员二、多选题8.下列两个物体可认为保持相对静止的是A. 地球和太阳B. 一列直线行驶的列车中 1 号车厢和 5 号车厢C. 人行走时左脚和右脚D. 火箭发射离开地面时,火箭和其运载的卫星9.下列说法中,正确的是A. 一个物体或物体的一部分,相对于参照物的位置的改变叫运动B. 乌云遮住了太阳,是以太阳为参照物的C. 研究某个物体的运动时,可同时选择几个物体做参照物D. 某同学站着感到没风,当他快跑时,立即感到有风迎面吹来,是以他做参照物的三、填空题10.整个宇宙都是由________ 的物质组成的,绝对____ 的物体是没有的,平常我们所说的运动或静止是__的,物理学中把______ 叫做机械运动.11.描述物体的运动情况时,首先要选择______,选择不同的______ 判断同一物体的运动,得到的结果不尽相同,所以说,运动和静止具有______ 性。
借助外物成功的名人事例之欧阳道创编

借助外物胜利的名人事例1、成吉思汗,就是善于借助他人力量。
铁木真昔时进攻蒙古蔑乞儿部时,军力不济,后来他联合草原雄鹰札木合,一举歼灭蔑乞儿部,比及他与札木合争雄时,又联合王罕,打败了札木合,奠定其草原霸主位置。
2、汉高祖刘邦共有八个皇子,生母不一,为了争夺太子之位,展开了子与子、母与母之间的明争冷战。
刘邦有位爱姬戚夫人,她想要刘邦拔除太子,改立自己的儿子如意为太子。
可吕后想保住自己的儿子刘盈的太子位置,于是她找张良辅佐。
张良献上一计:"皇上一直想招聘四个隐居的贤人出山,但他们始终不肯,若将他们迎为宾客,太子常请此四人赴宴,必会被皇上看见而问其原因。
"果然不出张良所料,高祖以为刘盈为人恭敬仁孝,天下名人慕名而来,终于撤销了废去太子的念头。
刘盈的胜利完全是因为借助了四年夜贤人的盛名,借助他们的欧阳道创编2021.03.06名望保住了太子的位置。
一个人的力量究竟是有限的,要想在事业上获告捷利,除靠自己的努力斗争之外,有时需要借助他人的力量,只有"好风凭借力",才干"送我上青云"。
3、“君子生非异也,善假于物也。
”善于借助他人的力量是一种能力,我们的老祖宗给我们留下了无穷的智慧,诚意、正心、格物、至知……其实,何必拘泥于“自我”……4、葡萄藤借助木竿,盘环而上,沐浴阳光;年夜海的浮游生物借助洋流,四处漂泊,一日千里;蒲公英借助徐徐轻风,随遇而安,繁衍生息。
孔明借以春风,火烧赤壁;曹聪不是借水浮之力,轻灵之船,那么即使有百斤之砣,百方之盘,百米之杆,又怎能称出年夜象的重量;鲲鹏借巨风以升万里,而行至南海;候鸟借气流以结队遨游翱翔,而南北迁徙;明月借日光以照亮黑夜,而皎辉如练,荀子《劝学》中所说:“登高而招,臂非加长也,而见者远;顺风而呼,声非加疾也,而闻者彰。
假舆马者,非利足也,而致千里;假舟楫者,非能水也,而绝江河,君子生非异也,善假于物也。
”善于利用外物的人是有智慧的人,而智者的胜利可能性是很年夜的。
最大公因数和最小公倍数练习题1之欧阳道创编

最大公因数和最小公倍数小练习一、写出下列各数的最大公因数和最小公倍数(1) 4和6的最大公因数是;最大公倍数是;(2) 9和3的最大公因数是;最大公倍数是;(3) 9和18的最大公因数是;最大公倍数是;(4) 11和44的最大公因数是;最大公倍数是;(5) 8和11的最大公因数是;最大公倍数是;(6) 1和9的最大公因数是;最大公倍数是;(7) 已知A=2×2×3×5,B=2×3×7,那么A、B的最大公因数是;最小公倍数是;(8)已知A=2×3×5×5,B=3×5×5×11,那么A、B的最大公因数是;最小公倍数是。
1.在17、18、15、20和30五个数中,能被2整除的数是();能被3整除的数是();能被5整除的数是();能同时被2、3整除的数是();能同时被3、5整除的数是();能同时被2、5整除的数是();能同时被2、3、5整除的数是()。
2.在20以内的质数中,()加上2还是质数。
3.如果有两个质数的和等于24,可以是()+(),()+()或()+()。
4.把330分解质因数是()。
5.一个能同时被 2、3、5整除的三位数,百位上的数比十位上的数大9,这个数是()。
6.在50以内的自然数中,最大的质数是(),最小的合数是()。
7.既是质数又是奇数的最小的一位数是()。
二、判断题1.两个质数相乘的积还是质数。
()2.成为互质数的两个数,必须都是质数。
()3.任何一个自然数,它的最大约数和最小倍数都是它本身。
()4.一个合数至少得有三个约数。
()5.在自然数列中,除2以外,所有的偶数都是合数。
()6.12是36与48的最大公约数。
()三、选择题1.15的最大约数是(),最小倍数是()。
①1 ②3 ③5 ④152.在14=2×7中,2和7都是14的()。
①质数②因数③质因数3.有一个数,它既是12的倍数,又是12的约数,这个数是()。
编程基础之顺序查找题之欧阳道创编

01:查找特定的值••查看•提交•统计•提问总时间限制:1000ms内存限制:65536kB描述在一个序列(下标从1开始)中查找一个给定的值,输出第一次出现的位置。
输入第一行包含一个正整数n,表示序列中元素个数。
1 <= n <= 10000。
第二行包含n个整数,依次给出序列的每个元素,相邻两个整数之间用单个空格隔开。
元素的绝对值不超过10000。
第三行包含一个整数x,为需要查找的特定值。
x的绝对值不超过10000。
输出若序列中存在x,输出x第一次出现的下标;否则输出-1。
样例输入样例输出02:输出最高分数的学生姓名•查看描述输入学生的人数,然后再输入每位学生的分数和姓名,求获得最高分数的学生的姓名。
输入第一行输入一个正整数N(N <= 100),表示学生人数。
接着输入N行,每行格式如下:分数姓名分数是一个非负整数,且小于等于100;姓名为一个连续的字符串,中间没有空格,长度不超过20。
数据保证最高分只有一位同学。
输出获得最高分数同学的姓名。
样例输入样例输出来源习题(13-1)03:不高兴的津津•查看描述津津上初中了。
妈妈认为津津应该更加用功学习,所以津津除了上学之外,还要参加妈妈为她报名的各科复习班。
另外每周妈妈还会送她去学习朗诵、舞蹈和钢琴。
但是津津如果一天上课超过八个小时就会不高兴,而且上得越久就会越不高兴。
假设津津不会因为其它事不高兴,并且她的不高兴不会持续到第二天。
请你帮忙检查一下津津下周的日程安排,看看下周她会不会不高兴;如果会的话,哪天最不高兴。
输入包括七行数据,分别表示周一到周日的日程安排。
每行包括两个小于10的非负整数,用空格隔开,分别表示津津在学校上课的时间和妈妈安排她上课的时间。
输出包括一行,这一行只包含一个数字。
如果不会不高兴则输出0,如果会则输出最不高兴的是周几(用1, 2, 3, 4, 5, 6, 7分别表示周一,周二,周三,周四,周五,周六,周日)。
高三数学限时训练15

高三数学限时训练(15)(时间:30分钟)1、若函数2()()a f x x a x=+∈R ,则下列结论正确的有 . ①a ∀∈R ,()f x 在(0,)+∞上是增函数 ②a ∀∈R ,()f x 在(0,)+∞上是减函数 ③a ∃∈R ,()f x 是偶函数 ④a ∃∈R ,()f x 是奇函数2、函数21)(++=x ax x f 在区间),2(+∞-上为单调增函数,则a 的取值范围是 .3、定义在[]2,2-上的偶函数()g x 满足:当0x ≥时,()g x递减.若(1)()g m g m -<,则m 的取值范围是4、阅读下面程序框图,则输出结果s 的值为5、设P 是双曲线2211620x y -=上一点,F 1,F 2分别是双曲线 左右两个焦点,若|PF 1|= 9,则|PF 2|=_________6、公比为4的等比数列{}n b 中,若n T 是数列{}n b 的前n 项积,则有304020301020,,T T T T T T 也成等比数列,且公比为1004;类比上述结论,相应的在公差为3的等差 数列{}n a 中,若n S 是{}n a 的前n 项和,则有一相应的等差数列,该等差数列的公差为_____. 7、已知向量)sin ,cos (αλαλ=OA (0≠λ),)c o s ,si n (ββ-=OB ,)0,1(=OC ,其中O 为坐标原点.(1)若2=λ,3πα=,),0(πβ∈,且OA BC ⊥,求β;(2)若2AB OB ≥对任意实数α,β都成立,求实数λ的取值范围.8、(理科做) 同时掷两颗质地均匀的骰子,观察朝上一面出现的点数.求两颗骰子中出现的最大点数X 的概率分布,并求X 大于2小于5的条件下,两颗骰子点数和为偶数的概率。
高三数学第十五次考试试题 理含解析 试题

一中2021年春期高三第15次考试数学试题〔理科〕本卷贰O贰贰年贰月捌日编写;出题人:令狐学复;欧阳化语;令狐理总。
第一卷〔一共60分〕一、选择题:本大题一一共12个小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的.,,那么〔〕A. B. C. D.【答案】B【解析】分析:先化简集合,,利用交集定义能求出详解:那么应选点睛:此题主要考察了集合的交集及其运算,利用指数、对数求出不等式解集得到集合,继而求出交集。
是虚数单位〕,那么复数在平面内对应〔〕A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】A【解析】试题分析:,对应点在第四象限,选D.考点:复数几何意义【名师点睛】此题重点考察复数的根本运算和复数的概念,属于基此题.首先对于复数的四那么运算,要实在掌握其运算技巧和常规思路,如. 其次要熟悉复数相关根本概念,如复数的实部为、虚部为、模为、对应点为,一共轭为假命题...的是〔〕A. 随机变量,假设,那么;B. 在三角形中,是的充要条件;C. 向量,,那么在的方向上的投影为2;D. 命题“或者为真命题〞是命题“为真命题且为假命题〞的必要不充分条件。
【答案】B【解析】【分析】根据正态分布的特征可判断A;根据正弦定理和三角形的性质可判断B;根据向量投影的定义可判断C;根据必要不充分条件的概念,可判断D.【详解】对于A,根据正态分布的对称性可得:假设,那么,故A正确;对于B,三角形中,大角对大边,大边对大角;所以假设那么,由正弦定理得;反之,也成立,故B正确;对于C,因为,,所以在的方向上的投影为,故C错误;对于D,假设“或者为真命题〞,那么,至少一个为真,不能推出“为真命题且为假命题〞;反之,假设“为真命题且为假命题〞那么“或者为真命题〞,能推出,故D正确;应选C【点睛】此题主要考察命题真假的判断,熟记相关知识点,逐项判断即可,属于根底题型.的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数的图象,那么〔〕A. 的图象关于直线对称 B. 的最小正周期为C. 的图象关于点对称D. 在单调递增【答案】D【解析】【分析】根据三角函数的平移变化规律,求解f〔x〕的解析式,结合三角函数的性质判断各选项即可.【详解】函数y=sin2x的图象上各点的横坐标伸长到原来的2倍,可得:y=sinx,即f〔x〕=sinx.根据正弦函数的图象及性质:可知:对称轴x=,∴A不对.周期T=2π,∴B不对.对称中心坐标为:〔kπ,0〕,∴C不对.单调递增区间为[],k∈Z,∴f〔x〕在单调递增.应选:D.【点睛】此题主要考察利用y=Asin〔ωx+φ〕的图象特征,平移变化的规律和性质的应用.属于根底题.5.我国古代数学名著?九章算术?里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤〔两〕.问玉、石重各几何?〞如下图的程序框图反映了对此题的一个求解算法,运行该程序框图,那么输出的,分别为〔〕A. ,B. ,C. ,D. ,【答案】C【解析】执行程序框图,;;;,完毕循环,输出的分别为,应选C.【方法点睛】此题主要考察程序框图的循环构造流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支构造还是循环构造;(3) 注意区分当型循环构造和直到型循环构造;(4) 处理循环构造的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,〔6〕在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到到达输出条件即可.的公差为2,且是与的等比中项,那么该数列的前项和取最小值时,那么的值是〔〕A. 7 B. 6 C. 5 D. 4【答案】B【解析】以为变量,得,,那么,所以最小,故,应选B.的图象大致是〔〕A. B.C. D.【答案】D【解析】【分析】利用奇偶性排除B,利用极值点及单调性排除A、C,即可得结论.【详解】∵,∴函数为偶函数,排除B,又x>0时,y=2xlnx,y′=2(1+lnx)=0时,x=,即函数在〔0,〕单减,在〔〕单增,排除A、C,应选D.【点睛】此题考察了函数图象的判断,考察了利用导数研究函数的极值、单调性及函数性质的应用,属于中档题.,满足时,目的函数的最大值等于5,那么实数的值是〔〕A. 2B. 3C. 4D. 5【答案】B【解析】由知故所求目的区域为如图,目的函数时,将向上平移得到最优点为B或者C,假设B为最优点,那么目的函数为,因为将向上平移最优点应该为C,这将产生矛盾,假设C为最优点,代入符合题意,选B.9.,那么〔〕A. 9B. 36C. 84D. 243【解析】【分析】等价变形为,然后利用二项式定理将其拆开,求出含有的项,便可得到。
高三理科数学限时训练15

高三理科数学限时训练15(2016年河南省六市高三第二次联科试题)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、集合2{|0},{|55}xA x x xB x =+≥=≥,则AB =A .{|01}x x x ≥≤-或B .{|1}x x ≥-C .{|1}x x ≥D .{|0}x x ≥ 2、已知2(,)a ib i a b R i+=+∈,其中i 为虚数单位,则a b += A .-1 B .2 C .2 D .33、下列函数中既是奇函数又在区间[]1,1-上单调递减的是 A .sin y x = B .1y x =-+ C .2ln 2x y x -=+ D .1(22)2x x y -=+ 4、下列说法错误的是A .自变量取值一定时,因变量的取值费油一定随机性的两个变量之间的关系叫做相关关系B .在线性回归分析中,相关系数r 越大,变量间的相关性越强C .{|1}x x ≥ 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高D .在回归分析中,2R 为0.98的模型比2R 为0.80的模型拟合的效果好5、在明朝大位《算法统宗》中有这样的一首歌谣:“远看魏巍七层,红光点点倍加增,共灯三百八十一,请问尖点几盏灯?”这首古诗描述的这个宝塔其古称浮屠,本题说它一共有7层,每次悬挂的红灯数是上一层的2倍,共有381盏灯,问塔顶有几盏灯? A .5 B .6 C .4 D .36、执行如右图程序框图,若输入2x =,则输出y 的值为 A .23 B .11 C .5 D .27、双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别是12,F F ,过1F 作倾斜角为45的直线交双曲线右支于M 点,若2MF 垂直x 轴,则双曲线的离心率为 A 2 B 3.12.138、已知实数,x y 满足401010x y y x +-≤⎧⎪-≥⎨⎪-≥⎩,则2y z x =的最大值是A .13B .1C .2D .9 9、已知某几何体的三视图如下图所示(图中数据单位:cm ),则这个几何体的体积为 A .320cm B .322cm C .324cm D .326cm 10、在ABC ∆中,1267,cos ,sin 57BC A C ===,若动点P 满足2(1)()3AB AB AC R λλλ=+-∈,则点P 的轨迹与直线AB 、所围成的封闭区域的面积为 A .36 B .46 C .66 D .12611、如图,在长方形ABCD 中,3,1,AB BC E ==为线段DC 上一动点,现将AED 沿AE 折起,使点D 在面ABC 上的射影K 在直线AE 上,当E 从D 运动到C ,则所形成的轨迹长度为 A .32 B .23 C .2π D .3π12、已知函数()21ln 2f x a x x =-存在极小值,且对于b 的所有可能取值,()f x 的极小值恒大于0,则a 的最小值为A .3e -B .2e -C .e -D .1e -班别 姓名学号 一、选择题二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。
梁平法标注资料之欧阳道创编

梁平法施工图的看图要点看结构设计说明中的有关内容;譬如记住各构件抗震等级,混凝土强度等级等看图要点:1 根据相应的建筑平面图,校对轴线网、轴线编号、轴线尺寸;2 根据相应的建筑平面图的房间分隔、墙柱布置,检查梁的平面布置是否合理,梁轴线定位尺寸是否齐全正确。
3 仔细检查每一根梁的编号、跨数、截面尺寸、配筋、箍筋、相对标高。
首先根据梁的支承情况、跨数分清主梁或次梁,检查跨数是否注写正确;同样的问题对梁,搭接处也必须要加密而且间距不是100,而是5d 纵向钢筋连接区域的箍筋加密,与抗震非抗震无关4 若为主梁时,检查附加横向钢筋有没有遗漏,截面尺寸、梁的标高是否满足次梁的支承要求。
5 检查梁的截面尺寸及梁的相对标高与建筑图洞口尺寸、洞顶标高、节点详图等有无矛盾。
检查集中标注的梁上部通长钢筋与原位标注的钢筋有无矛盾;6 检查集中标注的梁上部通长钢筋与原位标注的钢筋有无矛盾;问清楚往往某些图纸出现一些梁什么也没有标注8 检查楼梯间平台梁、平台板是否没有支座这是很普遍的设计通病楼梯间平台梁、平台板没有支座,是很普遍的设计通病因为楼梯梁、平台板一般搁置在后砌填充墙上在施工主题需要人员上下的时候,后砌填充墙还没实施,就需要先上楼梯,于是就有楼梯间平台梁、平台板没有支座的问题发生9 结合平法构造详图,确定箍筋加密区的长度、纵向钢筋切断点的位置、锚固长度、附加横向钢筋及梁侧构造钢筋的设置要求等10 非矩形截面梁,还得结合截面详图看图,且应看与建筑图中的详图有没有矛盾非矩形截面梁,如果没有剖面图,就得盯着设计要非矩形截面梁,如果没有剖面图,就得盯着设计要剖面详图——因为非矩形截面梁——平法写不到家——唯有画图,才可以看出那个角角落落有或者没有钢筋这主要是一些装饰线条等非矩形截面类梁构件11 初学者可以通过亲自翻样,画出梁的配筋立面图、剖面图、模板图、甚至画出各个钢筋的形状和尺寸动手画画,看图识图,用图来配合思考12 检查各设备专业的管道、设备安装与梁平法施工图有无矛盾,楼层较大设备基础下方,一般应设置梁。
层次分析法实例之欧阳道创编
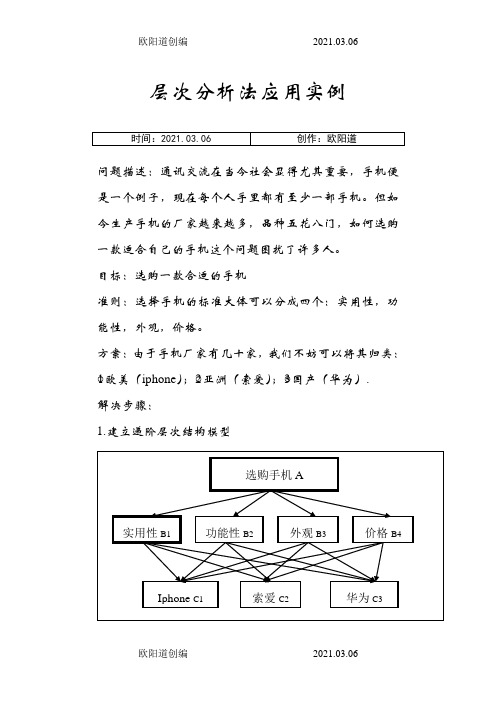
层次分析法应用实例问题描述:通讯交流在当今社会显得尤其重要,手机便是一个例子,现在每个人手里都有至少一部手机。
但如今生产手机的厂家越来越多,品种五花八门,如何选购一款适合自己的手机这个问题困扰了许多人。
目标:选购一款合适的手机准则:选择手机的标准大体可以分成四个:实用性,功能性,外观,价格。
方案:由于手机厂家有几十家,我们不妨可以将其归类:○1欧美(iphone);○2亚洲(索爱);○3国产(华为).解决步骤:1.建立递阶层次结构模型图1 选购手机层次结构图2.设置标度人们定性区分事物的能力习惯用5个属性来表示,即同样重要、稍微重要、较强重要、强烈重要、绝对重要,当需要较高精度时,可以取两个相邻属性之间的值,这样就得到9个数值,即9个标度。
为了便于将比较判断定量化,引入1~9比率标度方法,规定用1、3、5、7、9分别表示根据经验判断,要素i 与要素j相比:同样重要、稍微重要、较强重要、强烈重要、绝对重要,而2、4、6、8表示上述两判断级之间的折衷值。
注:aij表示要素i与要素j相对重要度之比,且有下述关系:aij=1/aji ;aii=1;i,j=1,2,…,n显然,比值越大,则要素i的重要度就越高。
3.构造判断矩阵A B1B2B3B4B11351B21/3131/3B31/51/311/5B41351表1 判断矩阵A—BB1C1C2C3C1 1 1/31/5C2 3 1 1/3C3 5 3 1表2 判断矩阵B1—CB2C1C2C3C1 1 3 3C21/3 1 1C31/3 1 1表3 判断矩阵B2—CB3C1C2C3C1 1 3 6C21/3 1 4C31/61/4 1表4 判断矩阵B3—CB4C1C2C3C1 1 1/41/6C2 4 1 1/3C3 6 3 1表5 判断矩阵B4—C4.计算各判断矩阵的特征值,特征向量和一致性检验 用求和发计算特征值:○1将判断矩阵A 按列归一化(即列元素之和为1):bij= aij /Σaij ;○2将归一化的矩阵按行求和:ci=Σbij (i=1,2,3….n ); ○3将ci 归一化:得到特征向量W=(w1,w2,…wn )T ,wi=ci /Σci ,W 即为A 的特征向量的近似值; ○4求特征向量W 对应的最大特征值:1).15311131513131311531=A ,按列归一化后为381514522938153831412213833851432235391514522938152).按行求和并归一化后得()T389.0069.0153.0389.0=W3).计算特征根:()TAW 389.0069.0153.0389.015315113113131311531=582.1389.0*1069.0*5153.0*3389.0*11=+++=AW ,同理有619.02=AW ,275.0AW 3=,582.1AW 4=4).计算最大特征根: 5).进行一致性检验:查同阶平均随机一致性指针(表6所示)知R.I=0.89,(一般认为CI<0.1、 CR<0.1时,判断矩阵的一致性可以接受,否则重新两两进行比较)。
数学建模大赛一等奖作品之欧阳道创编

数学建模论文高速公路道路交通事故分析预测摘要我国目前的道路交通安全状况相对于世界水平要差得多,高速公路道路交通事故所造成的损失非常高。
因此,改善交通安全状况、预防和减少高速公路交通事故具有重大的现实意义。
针对这样的现状,我们必须进行高速公路交通事故的预测,从而及早采取措施进行预防工作,从而减少事故发生次数及损失程度。
针对此次建模的要求,在对此问题的深入研究下,我们提出了合理的假设,将本问题归结为一个预测分析的问题,其基本思想是通过聚类分析、SPSS软件求解、GM(1,1)灰色预测模型、多元线性回归分析,组合模型等方法的运用得到最优的预测结果。
针对问题一,我们首先运用了聚类分析的思想,建立了基于聚类分析的模型Ⅰ,通过聚类分析方法对给定的信息的筛选、加工、延伸和扩展,从而将评价对象确定在某一范围内,通过了该方法,最终得到了各类评价等级方法,为科学预测交通事故提供了依据。
针对问题二,本文选取受伤人数这一单项指标作为预测的对象,首先运用了GM(1,1)灰色预测模型,建立模型Ⅱ,通过对给定的事故原始数据,通过MATLAB 软件预测了五年内的交通事故受伤人数;运用多元线性回归方法建立模型Ⅲ,在模型Ⅱ和模型Ⅲ的基础之上,通过基于组合模型思想的模型Ⅳ,求解得出了交通事故受伤人数在五年内的预测。
关键词:SPSS聚类分析GM(1,1)灰色预测模型组合预测模型 MATLAB目录一.问题重述错误!未定义书签。
二.问题的分析4三.模型假设与符号系统63.1模型假设63.2符号系统6四.模型的建立及求解84.1 问题一84.1.1建立模型Ⅰ84.1.2模型Ⅰ的求解及结果84.1.3实验结果的分析说明104.2 问题二134.2.1建立GM(1,1)模型Ⅱ134.2.2 用MATLAB求解模型Ⅱ194.2.3 建立模型Ⅲ214.2.4 建立优化模型Ⅳ224.2.5最优组合模型的求解23五.模型的评价25参考文献26附录27一.问题重述随着道路交通事业的发展,高速公路交通事故也在不断增加,对人类的生命和财产安全构成了极大的威胁。
鸡兔同笼练习题大全之欧阳与创编

鸡兔同笼练习题年夜全鸡兔同笼类练习题一1. 有鸡兔共20只,脚44只,鸡兔各几只?2、龟鹤共有100个头,350只脚.龟、鹤各几多?3、鸡兔共笼,兔比鸡多4只,共有脚76只,鸡、兔各几多只?4、鸡兔共200只,鸡的脚比兔的脚少56只,则鸡有几只,兔有几只?5、鸡、兔共笼,鸡比兔多26只,足数共274只,问鸡、兔各几只?6、鹤龟同池,鹤比龟多12只,鹤龟足共72只,求鹤龟各有几多只?鸡兔同笼类练习题二1、有钢笔和铅笔共27盒,共计300支.钢笔每盒10支,铅笔每盒12支,则钢笔有几多盒?铅笔有几多盒?2、年夜油瓶一瓶装4千克,小油瓶2瓶装1千克.现有100千克油装了共60个瓶子.问年夜、小油瓶各几多个?3、100个馒头100个和尚吃,年夜和尚每人吃4个,小和尚4人吃一个,则年夜和尚有几多个?小和尚有几多个?4、100个馒头100个和尚吃,年夜和尚每人吃3个,小和尚3人吃一个,则年夜和尚有几多个?小和尚有几多个?5、全班46人去划船,共乘12只船,其中年夜船每只坐5人,小船每只坐3人,求年夜船和小船各有几多只?6、停车场上停了35辆小轿车和两轮摩托车,空中上数一上共有10个轮子,请问小轿车和摩托车各有几多辆?7、一次植树活动,规定年夜树每人种2棵,小树每人种4棵,全班50人植树140棵,问种这两种树的各有几多人?8、幼儿园买来20张小桌和30张小凳共用去1860元,已知每张小桌比小凳贵8元,问小桌、小凳的价格各几多?9、一个年夜人一次吃两个苹果,两个小孩一次吃一个苹果,现在有年夜人和小孩供99人,共吃了99个苹果,年夜人小孩各几多人?10、现有年夜小油桶50个,每个年夜桶可装油4千克,每个小桶可装油2千克,年夜桶比小桶共多装油20千克,问年夜小桶各几多个?鸡兔同笼类练习题三1. 学校有象棋、跳棋共26副,恰好可供120个学生同时进行活动.象棋2人下一副棋,跳棋6人下一副.象棋和跳棋各有几副?2. 王老师带48名同学去公园划船,共租了10条船恰好坐满。
时分秒的练习题整理后之欧阳德创编

时分秒的练习题1一、在()里填上时间单位。
1. 一节数学课上了40()。
小红上午在校时间约4()。
2. 小芳跳绳20下用了15()。
课间休息10()。
3. 小明吃饭用了20()。
小明做20道口算题用了2()。
4. 爸爸每天工作约8()。
王艳跑 50米用了10()。
5. 南京乘火车去上海用了5()。
晚间新闻联播时间大约是30()。
6. 看一场电影用了90()。
做一次深呼吸大约7()。
7. 从教室前面走到后面用了5()。
夏天午睡大约1()。
8. 脉搏跳10次用了8()。
跑100米需要13()。
9. 小红下午在学校的时间是2()。
一集电视剧的播放时间是50()。
10. 小惠每天晚上睡觉9()。
小芳早晨起床穿衣服大约用了5()。
11. 学生一天在校时间大约是6( )。
爷爷每天晨练1()。
运动会上,小明跑60米用了12()。
二、填空12. 我们学过的时间单位有()、()和(),其中()是最小的时间单位。
13. 钟面上一共有()个大格,每个大格分成了()个小格,钟面上一共有()个小格。
时针走一大格的时间是();分针走一小格的时间是();秒针走一小格的时间是(),走一大格的时间是()。
14. 时针走一大格,分针走()小格,分针走了()分;秒针走一圈,分针走()小格,是()分。
15. 时针从数字3走到数字6,经过的时间是();分针从数字3走到数字6,经过的时间是();秒针从数字3走到数字6,经过的时间是()。
16. 8:30:25是()时()分()秒。
17. 一节课是()分钟,课间休息()分钟,再加上()分钟就是一小时。
18. ()时整,时针、分针重合。
19. 时针在钟面上走一圈是()时;分针在钟面上走一圈是()分,等于()时;秒针在钟面上走一圈是()秒,等于()分。
20. 分针走半圈是()分,时针走半圈是()时,秒针走半圈是()秒。
21. 时针从12走到1,分钟走了()小格,是()分;秒针走60小格,分钟走了()小格,是()分。
高三数列专题练习30道带答案之欧阳法创编

欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10 欧阳治创编 2021.03.10高三数列专题训练二学校:___________姓名:___________班级:___________考号:___________一、解答题1(1(22.已知等差数列的前项和为,公差.1,公比为3的等比数列,求3.(1(2)设,若对任意,不等式4.已知等差数列且等比数列(Ⅰ)求数列的通项公式和数列(Ⅱ)记数列5.设数列的前项和为,且满足(1(2的通项公式;(36(1(27欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10 欧阳治创编 2021.03.10(1(28.已知是各项均为正数的等比数列,且(1(29.10(Ⅱ)求数11(1(212.设公差不为01,且(1(2)na+13.(I(II n项和。
1412nn-+=(1(215.成等差数列.(1(2欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10 欧阳治创编 2021.03.1016(Ⅱ)求数17. (1(218(1(219满. (1(220(1n 项和; (2n 项和为Tn ,数m 的取值范围.21(1(222(1(223.(本小题满分14. (1(2欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10欧阳治创编 2021.03.10(3.24.(1(2(325.已知各项均不为零的数列满足:(1(2)26.项和且(1(227.在数列{an}中,a1=1,a4=7,an+2﹣2an+1+an=0(n∈N﹢)(1)求数列an 的通项公式;(2)若bn=)(n∈N+),求数列{bn}的前n项和Sn .28.已知数列{}n a 的前n 项和为n S ,且()()1n S n n n N *=+∈. (1)求数列{}n a 的通项公式; (2{}n b 满足31223 (31313131)n n n b b b ba =++++++++,求数列{}nb 的通项公式; (3)令()4n nn a b c n N *=∈,数列{}n c 的前n 项和为n T . 29.已知数列{}n a 的前n 项和2)1(+=n n S n . (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设)12()1(1nn a n n n a a a b n-+⋅-=+,求数列{}n b 的前n项和n T .30.设数列{}n a 满足:1113n n a a a +==,,*n N ∈.设n S 为数列{}n b 的前n 项和,已知10b ≠,112n n b b S S -=,*n N ∈. (1)求数列{}n a ,{}n b 的通项公式;(2)设3log n n n c b a =,求数列{}n c 的前n 项和n T .欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10 欧阳治创编 2021.03.10参考答案1.(12【解析】 试题分析:(1)求等差数列通项公式,基本方法为待定系数法,即根据条注意公差不为零,(2)先根据等差数列求和公式得,2231n n n ----⎪ ⎪ ⎪-⎭⎝⎭⎝⎭试题解析:①设{}a 的公差为d,依题意得.................3分........................5分∴............................6分..............................9分2231n n n ----⎪ ⎪ ⎪-⎭⎝⎭⎝⎭......12分考点:等差数列通项,裂项相消法求和【方法点睛】裂项相消法是指将数列的通项分成两个式子的代数和的形式,然后通过累加抵消中间若干项的方法,其c 为常数)的数列.裂项相消法求和,常见的有相邻两项的裂项求和(如本例),还有一类隔一项的裂项求和,如2.(ⅠⅡ【解析】 试题分析:(Ⅰ)将已知条件转化为首项和公差表示,解方程组可得到基本量,从而确定数列的通项公式;(Ⅱ试题解析:(Ⅰ)依题意得分 …………4分 (6)分欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10欧阳治创编 2021.03.10(Ⅱ分……………………9分∴分 考点:数列求通项公式及数列求和 3.(1(2【解析】试题分析:(1(2)由(1即可求试题解析:(1∵∴∴∵∴∴∴(2∴两式相减得, ∴欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10 欧阳治创编 2021.03.10∴∴∴∴考点:数列的综合问题.【方法点晴】本题主要考查了数列的综合问题,其中解答中涉及到等比数列的通项公式、等比数列的性质、数列的乘公比错位相减法求和、数列与函数的应用等知识点的综合考查,着重中考查了学生分析问题和解答问题的能力,以及学生转化与化归思想的应用,本题的解答中利用乘公比错位相减法求得数列的和,转化为利用函数的单调性是解答的关键,试题有一定的难度,属于中档试题. 4.(Ⅰ(Ⅱ【解析】试题分析:(Ⅰ)因为等差数列{}的公差,所以有,解之得,得比数列前n 项和公式即可求出结果.(Ⅱ)由(Ⅰ. 试题解析:解:(Ⅰ)因为等差数列(Ⅱ)由(Ⅰ因此(1n --3考点:1.等差数列与等比数列;2.数列求和.【方法点睛】裂项相消在使用过程中有一个很重要得特征,就是能把一个数列的每一项裂为两项的差,其本质就是两大类型类型一:型,通过拼凑法裂解成阶乘和组合数公式直接裂项型;该类型的特点是需要熟悉无理型的特征,对数的运算法则和阶乘和组合数公式。
水泥杆、拉盘、导线重量之欧阳道创编

11、钢芯铝绞线JL/G1A,70/10
275(kg)
12、钢绞线,1×7-7.8-1270-B,35,镀锌
318.2(Kg)
13、钢绞线,1×7-7.8-1270-B,50,镀锌
420(Kg)
14、钢绞线,1×7-7.8-1270-B,100,镀锌
859.4(Kg)
15、布电线,BV,铜,50,1
创作:欧阳道
531(kg)
6、架空绝缘导线,AC10kV,JKLYJ,95
440
Kg/Km
7、架空绝缘导线,AC10kV,JKLYJ,70
369
Kg/Km
8、钢芯铝绞线,AC10kV,LGJ,240/30
922.2(Kg)
9、钢芯铝绞线JL/G1A,150/20
617(kg)
10、钢芯铝绞线JL/G1A,120/20
名称
时间:2021.03.06
创作:欧阳道
描述
单位
备注
杆塔重量
1、锥形水泥杆,非预应力,整根杆,15m,190mm,M
1560(Kg)
2、锥形水泥杆,非预应力,整根杆,12m,190mm,M
1250(Kg)
3、锥形水泥杆,预应力,整根杆,12m,190mm,G
1160(Kg)
3、锥形水泥杆,预应力,整根杆,10m,190mm,G
900(Kg)
导线型号
1、架空绝缘导线,AC10kV,JKLGYJ,50/8
355(Kg)
2、架空绝缘导线,AC10kV,JKLYJ,50
291(Kg)
3、架空绝缘导线,AC10kV,JKLGYJ,150/25
851(Kg)
4、架空绝缘导线,AC10kV,JKLGYJ,120/20
2023届高考理科数学模拟试卷十五(含参考答案)

2023届高考理科数学模拟试卷十五(含参考答案)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24小题,共150分,考试时间120分钟。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内;2.选择题必须用2B 铅笔填涂;非选择题必须使用0.5毫米的黑色字迹的签字笔书写,字体工整、笔迹清楚;3.请按照题号顺序在各题的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效;4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑;5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷一、选择题:本大题共12题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U R =,集合{}|2A x x =≥,{|05}B x x =≤<,则集合)U C A B ⋂=(( ) A .{|02}x x <<B .{|02}x x <≤C .{|02}x x ≤<D.{|02}x x ≤≤2.命题“若1,x >则0x >”的否命题是 ( ) A .若1x >,则0x ≤ B .若1x ≤,则0x > C .若1x ≤,则0x ≤ D .若1x <,则0x < 3.已知是虚数单位,复数的共轭复数是,如果,那么等于( )A .B .C .D .4下图是用模拟方法估计圆周率π的程序框图,P 表示估计结果,则图中空白框内应填入( ) A. 1000N P = B. 41000N P =C. 1000MP =D. 41000M P = 5.以下四个命题中错误的是( )已知随机变量X~N (2,9),)1c X (P )1c X (P -<=+>则两个随机变量相关性越强,则相关系数的绝对值越接近于1在回归直线方程中,当解释变量每增加一个单位时,预报变量平均增加0.2个单位对分类变量与的随机变量的观测值,越小,“与有关系”的把握程度越大. 6.若n 的展开式中第四项为常数项,则n =( )i z z ||84z z i +=-z 34i --34i -+43i +34i +.A 2c =.B r .C ˆ0.212yx =+x ˆy .D X Y 2K k k XYA .4B .5C .6D .77.已知函数,为了得到函数的图象,只需要将的图象( )A.向右平移个单位长度 B.向左平移个单位长度 C.向右平移个单位长度 D.向左平移个单位长度 8.给四面体ABCD 的六条棱分别涂上红,黄,蓝,绿四种颜色中的一种,使得有公共顶点的棱所涂的颜色互不相同,则不同的涂色方法共有 ( )A .96B .144 C. 240 D. 3609.已知直线0x y k +-=(0)k >与圆224x y +=交于不同的两点A 、B ,O 是坐标原点,且有3||||3OA OB AB +≥,那么k 的取值范围是() A. )+∞B. )+∞C.D.10.把一个皮球放入如图所示的由8根长均为20 cm 的铁丝接成的正四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为( ) A .cm B .10 cm C ..30cm 11.已知函数xx x a x f +-+=1)1(2ln )((R a ∈)定义域为)1,0(,则)(x f 的图像不可能是( )(A ) (B ) (C ) (D )12. 如图,边长为1的正方形的顶点,分别在轴、轴正半轴上移动,则的最大值是( )A BC D 4第Ⅱ卷()cos f x x x =()sin 2cos 2g x x x =+()y f x =4π4π8π8πABCD A D x y OC OB ⋅2123O x y 1 O x y 1 O x y 1 O xy 1二、填空题:本大题共4个小题,每小题5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三理科数学限时训练15(2016年河南省六市高三第二次联科试题)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、集合
2{|0},{|55}x
A x x x
B x =+≥=≥,则A B = A .{|01}x x x ≥≤-或B .{|1}x x ≥-
C .{|1}x x ≥
D .{|0}x x ≥ 2、已知
2(,)a i
b i a b R i
+=+∈,其中i 为虚数单位,则
a b +=
A .-1
B .2
C .2
D .3
3、下列函数中既是奇函数又在区间[]1,1-上单调递减的是
A .sin y x =
B .1y x =-+
C .2ln
2x y x -=+D .1
(22)
2x x y -=+
4、下列说法错误的是
A .自变量取值一定时,因变量的取值费油一定随机性的两个变量之间的关系叫做相关关系
B .在线性回归分析中,相关系数r 越大,变量间的相关性越强
C .{|1}x x ≥ 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D .在回归分析中,2R 为0.98的模型比2R 为0.80的模型拟合的效果好
5、在明朝大位《算法统宗》中有这样的一首歌谣:“远看魏巍七层,红光点点倍加增,共灯三百八十一,请问尖点几盏灯?”这首古诗描述的这个宝塔其古称浮屠,本题说它一共有7层,每次悬挂的红灯数是上一层的2倍,共有381盏灯,问塔顶有几盏灯? A .5 B .6 C .4 D .3
6、执行如右图程序框图,若输入2x =,则输出y 的值为 A .23 B .11 C .5 D .2
7、双曲线
22
22
1(0,0)x y a b a b -=>>的左、右焦点分别是
12
,F F ,过1F 作倾斜角为45的直线交双曲线右支于M
点,若2MF 垂直x 轴,则双曲线的离心率为 A .2B .
3C .12+D .13+
8、已知实数,x y 满足401010
x y y x +-≤⎧⎪
-≥⎨⎪-≥⎩,则
2
y z x =的最
大值是
A .1
3B .1 C .2 D .9
9、已知某几何体的三视图如下图所示(图中数据单位:cm ), 则
这
个
几
何
体
的
体
积
为
A .320cm
B .322cm
C .324cm
D .3
26cm
10、在ABC ∆中,
126
7,cos ,sin 5BC A C ===
,若动点P 满
足
2(1)()3AB AB AC R λ
λλ=
+-∈,则点
P 的轨迹与直线AB 、
所围成的封闭区域的面积为 A .3
6B .46C .66D .126
11、如图,在长方形ABCD 中,3,1,AB BC E =
=为线段
DC 上一动点,现将AED 沿AE 折起,使点D 在面ABC 上的射影K 在直线AE 上,当E 从D 运动到C ,则所形成的轨迹长度为 A .
3.23C .2πD .3π
12、已知函数
()2
1
ln 2f x a x x =-存在极小值,且对于b 的所
有可能取值,()f x 的极小值恒大于0,则a 的最小值为
A .3e -
B .2
e -C .e -D .1e
-
班别姓名学号
一、
选择题
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。
. 13、将函数
()sin(2)()
2f x x π
ϕϕ=+<
的图象向左平移6
π
个单
位后的图形关于原点对称, 则函数()f x 在[0,]2π
上的最小值为
14、若321()()n y x n N x y *
+
∈的展开式中存在常数项,则常数
项为
15、已知等差数列{}n a 的公差0d ≠,且1313,,a a a 成等比数列,若11,n a S =为数列{}n a 的前n 项和,则216
3n n S a ++的最小
值为
16、已知抛物线24y x =,过焦点
F 作直线l 交抛物线于
A 、
B 两点,M 为抛物线的准线与x 轴的交点,
4
tan 3AMB ∠=
,则AB =
三、解答题:本大题共5小题,满分60分,选做题3
小题,考生任作一题,共10分 17、(本小题满分12分)
已知ABC ∆中,内角,,A B C 的对边分别为,,a b c 。
(1)若cos cos a b A B =且
221
sin (2cos )cos 2A C B -=+
,求角C 的大小;
(2)若ABC ∆为锐角三角形,且
,2
4
A a π
=
=,求ABC ∆面积的取值范围。
18、(本小题满分12分)
微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出边风靡全国,甚至涌现出一批子啊微信的朋友圈内销售商品的人(被称为微商),为了调查每天微信用户用微信的时间,就经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
(1)根据以上数据,能够有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5
人赠送营养面膜1份,求所抽取5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列与数学期望。
时间:2021.03.06 创作:欧阳道。
