江苏省南通市海安县海安高级中学2020届高三模拟考试数学试卷 Word版含答案
江苏省海安高级中学2020届高三第二次模拟考试数学试题及解析word

2020届高三年级阶段检测(二)数学Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上. 1.设集合{}1,3A =,{}2230B x x x =--<,则A B =I ____________.2.已知z i 12i ⋅=+(i 为虚数单位),则复数z =__________.3.命题“20210x x x ∃<-->,”的否定是______________.4.袋中有形状和大小都相同的4只球,其中1只白球,1只红球,2只黄球.现从中一次随机摸出两只球,则这两只球颜色不同的概率为____________.5.“sin cos 0αα+=”是“cos20α=”的__________条件.(填写“充分必要”、“充分不必要”、“必要不充分”、“既不充分也不必要”之一)6.设等比数列{}n a 的前n 项和为n S .若28365262a a a a S ==-,,则1a 的值为__________.7.若幂函数()a f x x =的图象经过点)12,则其单调递减区间为___________. 8.若函数()sin f x x x ωω= (x ∈R ,0ω>)满足()()02f f αβ==,,且||αβ-的最小值等于2π,则ω的值为___________. 9.已知函数()2241020ax x x f x x bx c x ⎧--≥⎪=⎨++<⎪⎩,,,是偶函数,直线y t =与函数()y f x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数t 的值为______________.10.设集合{}1 A a =-,,,2a e B e ⎧⎫=⎨⎬⎩⎭(其中e 是自然对数的底数),且A B ≠∅I ,则满足条件的实数a 的个数为_______________.11.已知过原点O 的直线与函数()3xf x =的图象交于A ,B 两点,点A 在点O ,B 之间,过A 作平行于y轴的直线交函数()9xg x =的图象于C 点,当BC ∥x 轴时,点A 的横坐标为_____________.12.设点P 在函数()1e 2xf x =的图象上,点Q 在函数()()ln 2g x x =的图象上,则线段PQ 长度的最小值为__________________.13.设()f x 为偶函数,且当(]20x ∈-,时,()()2f x x x =-+;当[)2x ∈+∞,时,()()()2f x a x x =--.关于函数()()g x f x m =-的零点,有下列三个命题:①当4a =时,存在实数m ,使函数()g x 恰有5个不同的零点; ②若[]01m ∀∈,,函数()g x 的零点不超过4个,则2a ≤;③对()1m ∀∈+∞,,()4a ∃∈+∞,,函数()g x 恰有4个不同的零点,且这4个零点可以组成等差数列. 其中,正确命题的序号是_________________.14.已知函数()2211x kx f x x x ++=++,若对于任意正实数123,,x x x ,均存在以()()()123,,f x f x f x 为三边边长的三角形,则实数k 的取值范围是_______________.二、解答题:本大题共6小题,共90分.解答时写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分14分)已知集合{}220A x x x =-->,集合(){}222550B x x k x k =+++<,k R ∈.(1)求集合B ;(2)记M A B =I ,且集合M 中有且仅有一个整数,求实数k 的取值范围. 16.(本小题满分14分) 已知π02α⎛⎫∈ ⎪⎝⎭,,ππ2β⎛⎫∈ ⎪⎝⎭,,1cos 3β=-,()7sin 9αβ+=.(1)求sin α的值; (2)求()tan +2βα的值.17.(本小题满分14分)设数列{}n a ,{}n b 的各项都是正数,n S 为数列{}n a 的前n 项和,且对任意N n *∈,都有22n n n a S a =-,1b e =,21n n b b +=,ln n n n c a b =⋅(e 是自然对数的底数).(1)求数列{}n a ,{}n b 的通项公式; (2)求数列{}n c 的前n 项和n T . 18.(本小题满分16分)已知矩形纸片ABCD 中,6,12AB AD ==,将矩形纸片的右下角沿线段MN 折叠,使矩形的顶点B 落在矩形的边AD 上,记该点为E ,且折痕MN 的两端点M ,N 分别在边,AB BC 上.设,MNB MN l θ∠==,EMN ∆的面积为S .(1)将l 表示成θ的函数,并确定θ的取值范围;(2)求l 的最小值及此时sin θ的值;(3)问当θ为何值时,EMN ∆的面积S 取得最小值?并求出这个最小值.19.(本小题满分16分)已知函数()y f x =.若在定义域内存在0x ,使得()()00f x f x -=-成立,则称0x 为函数()y f x =的局部对称点.(1)若a ,b ∈R 且a ≠0,证明:函数()2f x ax bx a =+-有局部对称点;(2)若函数()2xg x c =+在定义域[]1,1-内有局部对称点,求实数c 的取值范围;(3)若函数()12423xx h x m m +=-⋅+-在R 上有局部对称点,求实数m 的取值范围.20.(本小题满分16分) 已知函数()ln f x x =.(1)求函数()()1g x f x x =-+的零点; (2)设函数()f x 的图象与函数1ay x x=+-的图象交于()11A x y ,,()()1112B x y x x <,两点,求证:121a x x x <-;(3)若0k >,且不等式()()()2211x f x k x --≥对一切正实数x 恒成立,求k 的取值范围.数学Ⅱ21.本大题共两小题,每小题10分,共计20分.请在答题卡指定区域内........作答.解答应写出文字说明、证明过程或演算步骤.B.选修4—2:矩阵与变换 已知矩阵()001a k A k ⎡⎤=≠⎢⎥⎣⎦的一个特征向量为1k α⎡⎤=⎢⎥-⎣⎦,A 的逆矩阵1A -对应的变换将点()3,1变为点()1,1.求实数a ,k 的值.A MBNC DEC.(选修4—4:坐标系与参数方程)已知曲线C 的极坐标方程为4sin ρθ=.以极点为原点,极轴为x 轴的非负半轴建立平面直角坐标系,直线l的参数方程为1212x t y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),求直线l 被曲线C 截得的线段长度.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内........作答.解答应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)如图,在正四棱锥P ABCD -中,PA AB ==,点M ,N 分别在线段PA 和BD 上,13BN BD =.(1)若13PM PA =,求证:MN AD ⊥; (2)若二面角M BD A --的大小为π4,求线段MN 的长度.23.(本小题满分10分)在一次电视节目的答题游戏中,题型为选择题,只有“A ”和“B ”两种结果,其中某选手选择正确的概率为p ,选择错误的概率为q ,若选择正确则加1分,选择错误则减1分,现记“该选手答完n 道题后总得分为n S ”.(1)当12p q ==时,记3S ξ=,求ξ的分布列及数学期望; (2)当13p =,23q =时,求82S =且()01234i S i ≥=,,,的概率.江苏省海安高级中学2020届第二次学测参考答案数学Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分. 1.答案:{}1 2.答案:2z i =- 3.答案:20,210x x x ∀<--≤ 4.答案:565.答案:充分不必要6.答案:-27.答案:()0,+∞8.答案:19.答案:52-10.答案:2 1l.答案:3log 212.)1ln 2-13.答案:①②③14.答案:1,42⎡⎤-⎢⎥⎣⎦二、解答题:本大题共6小题,共90分. 15.(本小题满分14分)解:(1)因为22(25)50x k x k +++<,所以(25)()0x x k ++<. 当52k -<-即52k >时,5,2B k ⎛⎫=-- ⎪⎝⎭;………………………………………………………2分当52k -=-即52k =时,B =∅;………………………………………………………………4分 当52k ->-即52k <时,5,2B k ⎛⎫=-- ⎪⎝⎭.……………………………………………………6分 (2)由220x x -->得()(),12,x ∈-∞-+∞U ,…………………………………………8分 当52k -<-即52k >时,M 中仅有的整数为-3, 所以43k -≤-<-,即(]3,4k ∈;………………………………………………………………10分 当52k ->-即52k <时,M 中仅有的整数为-2, 所以23-<-≤时,即[)3,2k ∈-;………………………………………………………………12分 综上,满足题意的k 的范围为[)(]3,23,4-U ………………………………………………14分 16.(本小题满分14分) 解:(1)因为1,,cos 23πβπβ⎛⎫∈=-⎪⎝⎭,所以sin 3β===………………………………………………2分又0,2πα⎛⎫∈ ⎪⎝⎭,故3,22ππαβ⎛⎫+∈⎪⎝⎭,从而cos()αβ+===,………………………………4分所以sin sin[()]sin()cos cos()sin ααββαββαββ=+-=+-+711933⎛⎛⎫=⨯--= ⎪ ⎝⎭⎝⎭……………………………………………………………6分(2)由(1)得,1sin ,0,32παα⎛⎫=∈ ⎪⎝⎭,故cos 3α===,所以sin tan cos 4ααα==…………………………………………………………8分因为22222222cos sin 1tan 222cos cos sin 22cos sin 1tan 222βββββββββ--=-==++,且1cos 3β=-, 所以221tan 1231tan 2ββ-=-+,解得2tan 22β=, 因为,2πβπ⎛⎫∈ ⎪⎝⎭,所以,242βππ⎛⎫∈ ⎪⎝⎭,从而tan 02β>,所以tan2β=…………………………………………………………………………12分故tan tan24tan 121tan tan 122βαβαβα+⎛⎫+=== ⎪⎝⎭-⋅-………………………………14分17.(本小题满分14分)解:(1)因为0n a >,22n n n a S a =-,①当1n =时,21112a S a =-,解得11a =;……………………………………………………2分当2n ≥时,有21112n n n a S a ---=-,②由①-②得,()()2211112(2)n n n n n n n n a a S S a a a a n -----=---=+≥.而0n a >,所以11(2)n n a a n --=≥,…………………………………………………………4分 即数列{}n a 是公差为1的等差数列,故n a n =………………………………………………6分又因为21n n b b +=,且0n b >,取自然对数得1ln 2ln n n b b +=,又因为1ln ln 1b e ==,所以1ln 2ln n nb b +=, 所以{}ln n b 是1为首项,以2为公比的等比数列,所以1ln 2n n b -=,即12n n b e -=…………………………………………………………………………8分(2)由(1)知,1ln 2n n n n c a b n -==⨯,………………………………………………………10分 所以1221112(2)3(2)(1)(2)(2)n n n T n n --=⨯+⨯+⨯++-⨯+⨯L ,③123121(2)2(2)3(2)(1)(2)(2)n n n T n n -⨯=⨯+⨯+⨯++-⨯+⨯L ,④③减去④得:2112222n nn T n --=++++-⨯L ,所以(1)21nn T n =-⋅+…………………………………………………………………………14分18.(本小题满分16分)解:(1),2ENM MNB EMA θθ∠=∠=∠=.故cos ,sin ,cos 2sin cos 2NB l MB ME l AM ME l θθθθθ=====.因为6AM MB +=,所以sin cos2sin 6l l θθθ+=,…………………………………………2分 从而263sin (cos 21)sin cos l θθθθ==+………………………………………………………4分又12BN ≤,6BM ≤,所以124ππθ≤≤,所以23sin cos 124l ππθθθ⎛⎫=≤≤ ⎪⎝⎭…………………6分 (2)记()2sin cos ,124f ππθθθθ=≤≤,则224()sin cos f θθθ=.记22212cos ,()(1),,24x f x x x θθ⎡+==-∈⎢⎣⎦.记2()(1)g x x x =-,则2()23g x x x '=-,令212()0,,324g x x ⎡+'==∈⎢⎣⎦.所以()g x 在12,23⎡⎤⎢⎥⎣⎦上单调递增,在22,34⎡⎢⎣⎦上单调递减,………………………………8分故当22cos 3x θ==时l 取最小值,此时sin 3θ=,l .………………10分(3)EMN ∆的面积23191sin cos 22sin cos 124S l ππθθθθθ⎛⎫==⨯≤≤ ⎪⎝⎭,从而2268114sin cos S θθ=⨯设21cos ,1242t t ππθθ⎛⎫=≤≤≤≤ ⎪⎝⎭,………………12分 记323()(1),()34f t t t f t t t '=-=-令3()0,4f t t '==.()f t 在1,234⎡⎤⎢⎥⎣⎦上单调递增,在2,434⎡+⎢⎣⎦上单调递减,故当23cos 4t θ==,记6πθ=时,面积S 取最小值为15分 答:略…………………………………………………………………………………………16分19.(本小题满分16分)解:(1)由()2f x ax bx a =+-得()2f x ax bx a -=--,代入()()0f x f x -+=得,()()220ax bx a ax bx a +-+--=,………………………………2分 得到关于x 的方程20(0)ax a a -=≠,由于a R ∈且0a ≠,所以1x =±,所以函数()2(0)f x ax bx a a =+-≠必有局部对称点……………………………………………4分(2)方程2220x x c -++=在区间[]1,1-上有解,于是222x x c --=+,设12(11),22x t x t =-≤≤≤≤,所以12c t t-=+…………………………………………………6分 令11(),22s t t t t =+≤≤,则221(1)(1)()1t t s t t t -+'=-=,当1,12t ⎛⎫∈⎪⎝⎭时,()0s t '<,故函数()s t 在区间1,12⎛⎫⎪⎝⎭上单调递减, 同理函数()s t 在区间()1,2上单调递增,所以1522t t ≤+≤, 所以514c -≤≤-………………………………………………………………………………10分 (3)12()423xx h x m m --+-=-⋅+-,由于()()0h x h x -+=,所以()1212423423x x x x m m m m --++-⋅+-=--⋅+-于是()()()244222230x x x x m m --+-++-=(*)在R 上有解,……………………12分 令22(2)xxt t -+=≥,则2442x x t -+=-,所以方程(*)变为222280t mt m -+-=在区间[)2,+∞内有解, 需满足条件:()2248402m m ⎧∆=--≥≥即1m m ⎧-≤≤⎪⎨-≤≤⎪⎩得1m ≤≤16分 20.(本小题满分16分)解:(1)令()ln 1g x x x =-+,所以11()1xg x x x-'=-=. 当()0,1x ∈时,()0g x '>,()g x 在()0,1上单调递增;当()1,x ∈+∞时,()0g x '<,()g x 在()1,+∞上单调递减;所以max ()(1)0g x g ==,所以()g x 的零点为1x =………………………………………………2分(2)因为111222ln 1ln 1a x x x a x x x ⎧=+-⎪⎪⎨⎪=+-⎪⎩,所以211221ln ln 1x x a x x x x ⎛⎫-=⋅- ⎪-⎝⎭,………………………………4分要证121a x x x <-,即证211212121ln ln 1x x x x x x x x x ⎛⎫-⋅-<- ⎪-⎝⎭,即证2112ln 1x x x x ⎛⎫>-⎪⎝⎭,令2111,ln 1x t t x t =>>-……………………………………………………6分 由(1)知ln 1x x ≤-,当且仅当1x =取等,所以11ln 1t t<-,即1ln 1t t>-,所以原不等式成立.…………………………………………………………………8分 (3)不等式()221ln (1)x x k x -≥-对一切正实数x 恒成立. 因为()()222(1)1ln (1)1ln 1k x x x k x x x x -⎡⎤---=--⎢⎥+⎣⎦…………………………………………10分 设222(1)122(1)1()ln ,()1(1)(1)k x k x k x h x x h x x x x x x -+-+'=-=-=+++. 记22()2(1)1,4(1)44(2)x x k x k k k ϕ=+-+∆=--=-, ①当0∆≤,即02k <≤时,()0h x '≥恒成立,故()h x 单调递增.于是当01x <<时,()()10h x h <=,又210x -<,故()221ln (1)x x k x ->-, 当1x >时,()()10h x h >=,又210x ->,故()221ln (1)x x k x ->-, 又当1x =时,()221ln (1)x x k x -=-.因此当02k <≤时,()221ln (1)x x k x -≥-对一切正实数x 恒成立.…………………………12分 ②当0∆>,即2k >时,设22(1)10x k x +-+=的两个不等实根分别为()3434,x x x x <.又()1420k ϕ=-<,于是3411x k x <<-<.故当()1,1x k ∈-时,()0h x '<,从而()h x 在()1,1k -在单调递减;当()1,1x k ∈-时,()()10h x h <=,此时210x ->,于是()21()0x h x -<,即()221ln (1)x x k x -<-,舍去;…………………………………………………………15分 综上,k 的取值范围是02k <≤.…………………………………………………………16分数学Ⅱ21.本大题共两小题,每小题10分,共计20分. B.选修4-2:矩阵与变换 解:设特征向量为1k α⎡⎤=⎢⎥-⎣⎦对应的特征值为λ, 则0111a k k k λ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦,即1ak k k λλ-=⎧⎨=⎩, 因为0k ≠,所以2a =.………………………………………………………………………………5分 因为13111A -⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,所以1311A ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,即2130111k ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦, 所以23k +=,解得1k =,综上,2a =,1k =.……………………………………………………………………………………10分 C.(选修4-4:坐标系与参数方程)解:将曲线C 的极坐标方程化为直角坐标方程为2240x y y +-=,即22(2)4x y +-=,它表示以()0,2为圆心,2为半径的圆,…………………………………………4分直线方程l 的普通方程为1y =+,……………………………………………………………………6分 圆C 的圆心到直线l 的距离12d =,……………………………………………………………………8分故直线l 被曲线C 截得的线段长度为=…………………………………………10分【必做题】第22题、第23题,每题10分,共计20分. 22.(本小题满分10分)证明:连接,AC BD 交于点O ,以OA 为x 轴正方向,以OB 为y 轴正方向,OP 为z 轴建立空间直角坐标系.因为PA AB ==,则(1,0,0), (0,1,0), (0,1,0), (0,0,1)A B D P -.(1)由13BN BD =u u u r u u u r ,得10,,03N ⎛⎫ ⎪⎝⎭,由13PM PA =u u u u r u u u r ,得12,0,33M ⎛⎫ ⎪⎝⎭, 所以112,,,(1,1,0)333MN AD ⎛⎫=--=-- ⎪⎝⎭u u u u r u u u r . 因为0MN AD ⋅=u u u u r u u u r ,所以MN AD ⊥.…………………………………………………………4分(2)因为M 在PA 上,可设PM PA λ=u u u u r u u u r ,得(,0,1)M λλ-.所以(,1,1),(0,2,0)BM BD λλ=--=-u u u u r u u u r设平面MBD 的法向量(),,n x y z =r ,由00n BD n BM ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u u r ,得20(1)0y x y z λλ-=⎧⎨-+-=⎩, 其中一组解为1,0,x y z λλ=-==,所以可取(1,0,)n λλ=-r ………………………………………8分因为平面ABD 的法向量为()0,0,1OP =u u u r , 所以cos 4||||n OP n OP π⋅=r u u u r r u u u r,即2=,解得12λ=, 从而111,0,,0,,0223M N ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,所以6MN ==………………………………………………10分 23.(本小题满分10分)解:(1)ξ的取值为3,-1,1,3,又因为12p q ==;……………………………………………1分 故311(3)28P ξ⎛⎫=-== ⎪⎝⎭,311(3)28P ξ⎛⎫=== ⎪⎝⎭, 223113(1)228P C ξ⎛⎫=-=⨯⨯= ⎪⎝⎭;223113(1)228P C ξ⎛⎫==⨯⨯= ⎪⎝⎭,…………………………………3分 所以ξ的分布列为:所以1331()(3)(1)308888E ξ=-⨯+-⨯++⨯=;……………………………………………………5分 (2)当82S =时,即答完8题后,正确的题数为5题,错误的题数是3题,…………………6分 又已知0(1,2,3,4)i S i =≥,第一题答对,若第二题回答正确,则其余6题可任意答对3题;若第二题回答错误,第三题回答正确,则后5题可任意答对题,………………………………8分此时的概率为()5333658712308803333P C C ⨯⎛⎫⎛⎫=+⋅⋅== ⎪ ⎪⎝⎭⎝⎭(或802187).……………………10分。
2020届江苏省南通市海安高级中学高三阶段测试三数学试题(解析版)

2020届江苏省南通市海安高级中学高三阶段测试三数学试题一、填空题1.设全集{1,2,3,4,5}U =,若{1,2,4}U A =ð,则集合A =_________. 【答案】{3,5}.【解析】直接求根据{1,2,4}U A =ð求出集合A 即可. 【详解】解:因为全集{1,2,3,4,5}U =若{1,2,4}U A =ð, 则集合A ={3,5}. 故答案为:{3,5}. 【点睛】本题考查补集的运算,是基础题.2.已经复数z 满足(2)1z i i -=+(i 是虚数单位),则复数z 的模是________. 10 【解析】【详解】(2)1z i i -=+Q ,11323,i iz i i i++∴=+==- 10z =10.3.已知一组数据123,,a a a ,…,n a 的平均数为a ,极差为d ,方差为2S ,则数据121,a +221,a +321a +,…,21n a +的方差为___________.【答案】24S【解析】根据在一组数据的所有数字上都乘以同一个数字,得到的新数据的方差是原来数据的平方倍,得到结果. 【详解】解: ∵数据123,,a a a ,…,n a 的方差为2S ,∴数据121,a +221,a +321a +,…,21n a +的方差是22224S S ⨯=, 故答案为:24S . 【点睛】此题主要考查了方差,关键是掌握方差与数据的变化之间的关系. 4.如图是一个算法的伪代码,其输出的结果为_______.【答案】1011【解析】由题设提供的算法流程图可知:1111101122310111111S =++⋅⋅⋅+=-=⨯⨯⨯,应填答案1011. 5.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为______。
【答案】18【解析】试题分析:分类讨论:从0、2中选一个数字0,则0只能排在十位;从0、2中选一个数字2,则2排在十位或百位,由此可得结论.解:从0、2中选一个数字0,则0只能排在十位,从1、3、5中选两个数字排在个位与百位,共有23A =6种;从0、2中选一个数字2,则2排在十位,从1、3、5中选两个数字排在个位与百位,共有23A =6种; 2排在百位,从1、3、5中选两个数字排在个位与十位,共有23A =6种;故共有323A =18种,故答案为18. 【考点】计数原理点评:本题考查计数原理的运用,考查分类讨论的数学思想,正确分类是关键6.在平面直角坐标系xOy 中,若双曲线()2222:10,0x y C a b a b-=>>10,则双曲线C 的渐近线方程为_______. 【答案】3y x =±【解析】10,可以得到10ca=222a b c +=求出,a b 的关系,从而得出渐近线的方程. 【详解】解:因为双曲线()2222:10,0x y C a b a b-=>>10,所以10ca= 故2210c a=, 又因为222a b c +=,所以22210a b a +=,即229b a=,即3=b a , 所以双曲线的渐近线3y x =±. 【点睛】本题考查了双曲线渐近线的问题,解题的关键是由题意解析出,a b 的关系,从而解决问题. 7.将函数f(x)的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象,则()π4f 为 .【答案】4【解析】试题分析:将函数f(x)的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象,即将函数()π4sin 23y x =-的图象向左平移π6个单位得y=4sin[2(x+π6)π3-]=4sin2x ,所以()π4f =4sin 42π=. 故答案为:4.【考点】三角函数的图象平移.8.设定义在R 上的奇函数()f x 在区间[0,)+∞上是单调减函数,且()23(2)0f x x f -+>,则实数x的取值范围是_________ 【答案】(1,2)【解析】根据题意,由函数的奇偶性和单调性分析可得函数()f x 在R 上为减函数,则()23(2)0f x x f -+>可以转化为232x x -<-,解可得x 的取值范围,即可得答案.【详解】解:根据题意,()f x 是在R 上的奇函数,且在区间[0,)+∞上是单调减函数, 则其在区间(,0)-∞上递减, 则函数()f x 在R 上为减函数,()()22223(2)03(2)(3)(2)32f x x f f x x f f x x f x x -+>⇒->-⇒->-⇒-<-,解得:12x <<;即实数x 的取值范围是(1,2); 故答案为:(1,2). 【点睛】本题考查函数的单调性与奇偶性的综合应用,关键是分析函数在整个定义域上的单调性. 9.在锐角三角形ABC 中3sin 5A =,1tan()3A B -=-,则3tan C 的值为_________.【答案】79【解析】由题意可得tan A ,进而可得tan B ,而tan tan()C A B =-+,由两角和与差的正切公式可得. 【详解】解:∵在锐角三角形ABC 中3sin 5A =, 24cos 1sin 5A A ∴=-=, sin 3tan cos 4A A A ∴==, 31tan tan()1343tan tan[()]311tan tan()9143A A B B A A B A A B +--∴=--===+--⨯, 313tan tan 7949tan tan()3131tan tan 3149A B C A B A B ++∴=-+=-=-=--⨯, 3tan 79C ∴=故答案为:79. 【点睛】本题考查两角和与差的正切公式,属中档题.10.已知n S 为数列{}n a 的前n 项和3(1)(*)n n S na n n n N =--∈且211a =.则1a 的值________ 【答案】5【解析】由3(1)(*)n n S na n n n N =--∈,且211a =.取2n =即可得出. 【详解】解:∵3(1)(*)n n S na n n n N =--∈,且211a =.12226a a a ∴+=-,即1265a a =-=.故答案为:5. 【点睛】本题考查了递推式的简单应用,是基础题. 11.设正实数x ,y 满足x yxy x y+=-,则实数x 的最小值为______. 21.【解析】由正实数x ,y 满足x y xy x y +=-,化为()2210xy x y x +-+=,可得()222212121401010x x x y y x y y ⎧∆=--≥⎪⎪-⎪+=>⎨⎪=>⎪⎪⎩,计算即可. 【详解】解:由正实数x ,y 满足x yxy x y+=-, 化为()2210xy xy x +-+=,∴()222212121401010x x x y y x y y ⎧∆=--≥⎪⎪-⎪+=>⎨⎪=>⎪⎪⎩,化为426101x x x ⎧-+≥⎨>⎩, 解得21x ≥.因此实数x 21.故答案为:21+. 【点睛】本题考查了一元二次方程的实数根与判别式、根与系数的关系、一元二次不等式的解法,考查了推理能力和计算能力,属于中档题.12.如图正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点)且//EF BC ,则四棱锥1A AEFD -的体积为___________.【答案】9【解析】由11113A AED E A AD A AD V V S AB --∆==⋅,由此能求出四棱锥1A AEFD -的体积. 【详解】 解:连接DE ,∵正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点),且//EF BC ,11A AED A FED V V --∴=,1111111111193662A AED E A AD A AD A ADD ABCD A C D V V S AB S AB V --∆-∴==⋅=⋅==,∴四棱锥1A AEFD -的体积19A AEFD V -=.故答案为:9. 【点睛】本题考查四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、运算求解能力,是中档题.13.已知向量,,a b c r r r 满足0a b c ++=r r r 且a r 与b r 的夹角的正切为12-,b r 与c r 的夹角的正切为13-,||2b =r ,则a c ⋅r r的值为___________.【答案】45【解析】可设,,AB a BC b CA c ===u u u r u u u r u u u r r r r ,由题意可得11tan ,tan 23B C ==,由两角和的正切公式,可得tan A ,再由同角的基本关系式可得sin ,sin B C ,再由正弦定理可得AB ,AC ,由数量积的定义即可得到所求值. 【详解】解:可设,,AB a BC b CA c ===u u u r u u u r u u u r r r r,由题意可得11tan ,tan 23B C ==, 则11tan tan 23tan tan()1111tan tan 123B C A B C B C ++=-+=-=-=---⨯, 即为135A ︒=,又,B C 为锐角,22sin 1sin cos 1,cos 2B B B B +==, 可得5sin 5B =, 同理可得10sin C =, 由正弦定理可得2sin135510︒==r r,即有2102555c a ==r r ,则2102524||||cos 4525a c c a ︒⋅=⋅⋅==u u rr r r .故答案为:45. 【点睛】本题考查向量的数量积的定义,考查正弦定理和三角函数的化简和求值,以及运算求解能力,属于中档题.14.已知()(2)(3),()22x f x m x m x m g x =-++=-,若同时满足条件:①,()0x R f x ∀∈<或()0<g x ;②(,4),()()0x f x g x ∃∈-∞-<.则m 的取值范围是________________.【答案】()4,2m ∈--【解析】根据()220xg x =-<可解得x<1,由于题目中第一个条件的限制,导致f(x)在1x ≥是必须是()0f x <,当m=0时,()0f x =不能做到f(x)在1x ≥时()0f x <,所以舍掉,因此,f(x)作为二次函数开口只能向下,故m<0,且此时2个根为122,3x m x m ==--,为保证条件成立,只需1221{31x m x m =<=--<1{24m m <⇒>-,和大前提m<0取交集结果为40m -<<;又由于条件2的限制,可分析得出在(,4),()x f x ∃∈-∞-恒负,因此就需要在这个范围内g(x)有得正数的可能,即-4应该比12x x 两个根中较小的来的大,当(1,0)m ∈-时,34m --<-,解得交集为空,舍.当m=-1时,两个根同为24->-,舍.当(4,1)m ∈--时,24m <-,解得2m <-,综上所述,(4,2)m ∈--.【考点定位】本题考查学生函数的综合能力,涉及到二次函数的图像开口,根大小,涉及到指数函数的单调性,还涉及到简易逻辑中的“或”,还考查了分类讨论思想.二、解答题15.已知ABC ∆的面积为3()18AC AB CB ⋅-=u u u r u u u r u u u r ,向量(tan tan ,sin 2)m A B C =+u r和向量(1,cos cos )n A B =r是共线向量.(1)求角C ;(2)求ABC ∆的边长c .【答案】(1) 3C π=(2) 36【解析】(1)利用向量共线的条件,建立等式,再利用和角的正弦公式化简等式,即可求得角C ;(2)由()18AC AB CB ⋅-=u u u r u u u r u u u r 得:2()18AC AB BC AC ⋅+==u u u r u u u r u u u r u u u r ,进而利用ABC ∆的面积为93,及余弦定理可求ABC ∆的边长c . 【详解】(1)因为向量(tan tan ,sin 2)m A B C =+r 和(1,cos cos )n A B =r是共线向量, 所以cos cos (tan tan )sin 20A B A B C +-=, 即sin cos cos sin 2sin cos 0A B A B C C +-=, 化简sin 2sin cos 0C C C -=, 即sin (12cos )0C C -=.因为0C π<<,所以sin 0C >,从而1cos ,2C =3C π=.(2)()18AC AB CB ⋅-=u u u r u u u r u u u r Q ,18()AC AB CB ∴=⋅-u u u r u u u r u u u r 2||AC AC AC =⋅=u u u r u u u r u u u r 则||1832AC ==u u u r32AC =因为ABC V 的面积为93, 所以1sin 932CA CB C ⋅= 即132sin 9323CB π⨯=解得62CB =在ABC V 中,由余弦定理得2222cos AB CA CB CA CB C =+-⋅221(32)(62)232622=+-⨯54=,所以5436AB ==【点睛】本题重点考查正弦、余弦定理的运用,考查向量知识的运用,解题的关键是正确运用正弦、余弦定理求出三角形的边.16.如图,四棱锥P-ABCD的底面为矩形,且AB=2,BC=1,E,F分别为AB,PC中点.(1)求证:EF∥平面PAD;(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.【答案】证明:(1)方法一:取线段PD的中点M,连结FM,AM.因为F为PC的中点,所以FM∥CD,且FM=12 CD.因为四边形ABCD为矩形,E为AB的中点,所以EA∥CD,且EA=12 CD.所以FM∥EA,且FM=EA.所以四边形AEFM为平行四边形.所以EF∥AM.……………………… 5分又AM⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD.………7分方法二:连结CE并延长交DA的延长线于N,连结PN.因为四边形ABCD为矩形,所以AD∥BC,所以∠BCE=∠ANE,∠CBE=∠NAE.又AE=EB,所以△CEB≌△NEA.所以CE=NE.又F为PC的中点,所以EF∥NP.………… 5分又NP⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD.……………7分方法三:取CD的中点Q,连结FQ,EQ.在矩形ABCD中,E为AB的中点,所以AE=DQ,且AE∥DQ.所以四边形AEQD为平行四边形,所以EQ∥AD.又AD⊂平面PAD,EQ⊄平面PAD,所以EQ∥平面PAD.………………2分因为Q,F分别为CD,CP的中点,所以FQ∥PD.又PD⊂平面PAD,FQ⊄平面PAD,所以FQ∥平面PAD.又FQ,EQ⊂平面EQF,FQ∩EQ=Q,所以平面EQF∥平面PAD.…………… 5分因为EF⊂平面EQF,所以EF∥平面PAD.……………………………… 7分(2)设AC,DE相交于G.在矩形ABCD中,因为AB=2BC,E为AB的中点.所以DAAE=CDDA=2.又∠DAE=∠CDA,所以△DAE∽△CDA,所以∠ADE=∠DCA.又∠ADE+∠CDE=∠ADC=90°,所以∠DCA+∠CDE=90°.由△DGC的内角和为180°,得∠DGC=90°.即DE⊥AC.……………………… 10分因为平面PAC⊥平面ABCD 因为DE⊂平面ABCD,所以DE⊥平面PAC,又DE⊂平面PDE,所以平面PAC⊥平面PDE.………………………… 14分【解析】略17.如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知,,Q到海岸线OM,ON的距离分别为3 km,km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.(1)求水上旅游线AB的长;(2)若小岛正北方向距离小岛6 km处的海中有一个圆形强水波P,从水波生成t h时的半径为(a 为大于零的常数).强水波开始生成时,一游轮以km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.【答案】(1)(2)【解析】试题分析:(1)由条件建立直角坐标系较为方便表示:,直线的方程为.由Q到海岸线ON的距离为km,得,解得,再由两直线交点得,利用两点间距离公式得(2)由题意是一个不等式恒成立问题:设小时时,游轮在线段上的点处,而不等式恒成立问题往往利用变量分离将其转化为对应函数最值问题:试题解析:(1)以点为坐标原点,直线为轴,建立直角坐标系如图所示.则由题设得:,直线的方程为.由,及得,∴.∴直线的方程为,即,由得即,∴,即水上旅游线的长为.(2)设试验产生的强水波圆,由题意可得P(3,9),生成小时时,游轮在线段上的点处,则,∴.强水波不会波及游轮的航行即,当时 ,当.,,当且仅当时等号成立,所以,在时恒成立,亦即强水波不会波及游轮的航行.【考点】函数实际应用,不等式恒成立18.在平面直角坐标系xOy 中已知椭圆222:1(0)3x y E a b a +=>>过点61,2⎛ ⎝⎭,其左、右焦点分别为12F F 、,离心率为22.(1)求椭圆E 的方程;(2)若A ,B 分别为椭圆E 的左、右顶点,动点M 满足MB AB ⊥,且MA 交椭圆E 于点P . (i )求证:OP OM ⋅uu u r uuu r为定值;(ii )设PB 与以PM 为直径的圆的另一交点为Q ,问:直线MQ 是否过定点,并说明理由.【答案】(1) 22142x y += (2) (i )证明见解析,定值为4 (ii )直线MQ 过定点(0,0)O .【解析】(1)由题意得离心率公式和点满足的方程,结合椭圆的,,a b c 的关系,可得,a b ,进而得到椭圆方程;(2)(i )设()02,,M y ()11,P x y ,求得直线MA 的方程,代入椭圆方程,解得点P 的坐标,再由向量的数量积的坐标表示,计算即可得证;(ii )直线MQ 过定点O (0,0).先求得PB 的斜率,再由圆的性质可得MQ ⊥PB ,求出MQ 的斜率,再求直线MQ 的方程,即可得到定点. 【详解】解:(1)易得22312122a b c a⎧⎪+=⎪⎨⎪=⎪⎩,且222c a b =-, 解得2242a b ⎧=⎨=⎩,,所以椭圆E 的方程为22142x y +=(2)设()02,,M y ()11,P x y , ①易得直线MA 的方程为:0042y yy x =+, 代入椭圆22142x y +=得,2222000140822y y y x x ⎛⎫+++-= ⎪⎝⎭, 由()201204828y x y --=+得,()20120288y x y --=+,从而012088y y y =+, 所以示()()20002200288,2,88y y OP OM y y y ⎛⎫-- ⎪⋅=⋅ ⎪++⎝⎭u u u r u u u u r ()22002200488488y y y y --=+=++, ②直线MQ 过定点(0,0)O ,理由如下:依题意,()2020020882288PBy y k y y y +==---+, 由MQ PB ⊥得,02MQ y k =, 则MQ 的方程为:00(2)2y y y x -=-,即02yy x =,所以直线MQ 过定点(0,0)O . 【点睛】本题考查椭圆的方程和性质,主要考查椭圆的离心率公式和方程的运用,注意联立直线方程和椭圆方程,运用韦达定理,同时考查向量的数量积的坐标表示和直线和圆的位置关系,属于中档题. 19.已知数列{}n a 满足:123a a a k ===(常数0k >),111n n n n K a a a a -+-+=()*3,n n N ≥∈.数列{}n b 满足:21n n n n a a b a +++=()*n N ∈. (1)求1,b 2,b 3,b 4b 的值; (2)求出数列{}n b 的通项公式;(3)问:数列{}n a 的每一项能否均为整数?若能,求出k 的所有可能值;若不能,请说明理由.【答案】(1) 132b b ==,2421k b b k +==;(2) 41122nn k b k k+-=+(); (3) k 为1,2时数列{}n a 是整数列.【解析】(1)经过计算可知:45621,2,4a k a k a k k=+=+=++,由数列{}n b 满足:21n n n n a a b a +++=(n=1,2,3,4…),从而可求1,b 2,b 3,b 4b ;(2)由条件可知121n n n n a a k a a +--=+.得211n n n n a a k a a +-+=+,两式相减整理得2n n b b -=,从而可求数列{}n b 的通项公式;(3)假设存在正数k ,使得数列{}n a 的每一项均为整数,则由(2)可知:2122122222211n n n n n n a a a k a a a k +-+=-⎧⎪+⎨=+-⎪⎩,由1a k Z =∈,624Z a k k =++∈,可求得1,2k =.证明1,2k =时,满足题意,说明1,2k =时,数列{}n a 是整数列. 【详解】(1)由已知可知:45621,2,4a k a k a k k=+=+=++, 把数列{}n a 的项代入21n n n n b a a a =+++求得132b b ==,2421k b b k+==; (2)由121n n n n k a a a a --++=3,n n N ≥∈*() 可知:121n n n n a a k a a +--=+① 则:211n n n n a a k a a +-+=+② ①−②有:2211n n n nn n a a a a a a +-+-++=,即:2n n b b -=2123n n b b --∴==…13122a a b a +===,222n n b b -== (242321)a a kb a k++===,41122nn k b k k+-∴=+(); (3)假设存在正数k 使得数列{}n a 的每一项均为整数,则由(2)可知:2122122222211n n n n n n a a a k a a a k +-+=-⎧⎪+⎨=+-⎪⎩③, 由1a k Z =∈,624Z a k k=++∈,可知1k =,2. 当1k =时,213k k+=为整数,利用123,,a a a Z ∈结合③式可知{}n a 的每一项均为整数; 当2k =时,③变为2122122222512n n n n n n a a a a a a +-+=-⎧⎪⎨=+-⎪⎩④ 用数学归纳法证明21n a -为偶数,2n a 为整数.1n =时结论显然成立,假设n k =时结论成立,这时21n a -为偶数,2n a 为整数,故212212n n n a a a +-=-为偶数,22n a +为整数,1n k ∴=+时,命题成立.故数列{}n a 是整数列.综上所述k 为1,2时数列{}n a 是整数列. 【点睛】本题考查了等差数列的基本性质和数列的递推公式,考查了学生的计算能力和对数列的综合掌握,注意分类讨论思想和转化思想的运用,属于难题. 20.设函数()()ln ,f x x a x x a =--+a R ∈. (1)若0a =求函数()f x 的单调区间;(2)若0a <试判断函数()f x 在区间()22,e e -内的极值点的个数,并说明理由;(3)求证:对任意的正数a 都存在实数t 满足:对任意的(,)x t t a ∈+,()1f x a <-. 【答案】(1) 单调递减区间为(0,1)单调递增区间为(1,)+∞. (2) 见解析 (3)证明见解析【解析】(1)求解()ln f x x '=,利用()0,()0f x f x ''><,解不等式求解单调递增区间,单调递减区间;(2)'()ln af x x x=-,其中0x >, 再次构造函数令()ln g x x x a =-,分析()g x 的零点情况.()ln 1g x x '=+,令1()0,g x x e'==,列表分析得出()g x 单调性,求其最小值, 分类讨论求解①若1a e≤-,②若212a e e -<<-,③若220,()a f x e -≤<的单调性,()f x 最大值,最小值,确定有无零点问题;(3)先猜想(1,1),()1x a f x a ∈+<-恒成立.再运用导数判断证明.令'1()ln 1,1,()10G x x x x G x x=-+≥=-≤,求解最大值,得出()(1)0G x G <=即可. 【详解】(1)当0a =时,()ln f x x x x =-,()ln f x x '=, 令()0f x '=,1x =,列表分析x (0,1)1(1,)+∞()f x '− 0 + ()f x单调递减单调递增故()f x 的单调递减区间为(0,1)单调递增区间为(1,)+∞.(2)()()ln f x x a x x a =--+,()ln f x x ax '=-,其中0x >, 令()ln g x x x a =-,分析()g x 的零点情况.()ln 1g x x '=+ 令()0g x '=,1x e=,列表分析 x(0,1e)1e(1,)e +∞()g x '− 0 +()g x单调递减 单调递增min 11()()g x g a e e ==--,而11()1n 1f ae ae e e'=-=--,222()2(2)f e ae ae -'=--=-+22221()2(2)a f e e a e e '=-=-,①若1a e≤-则()ln 0af x x x '=-≥,故()f x 在22(,)e e -内没有极值点;②若212a e e -<<-,则11()1n 0f ae e e '=-<,22()(2)0f e ae -'=-+> 2221()(2)0f e e a e'=->因此()f x '在22(,)e e -有两个零点,()f x 在22(,)e e -内有两个极值点;③若220a e -≤<则11()10f n ae e e '=-<,22()(2)0f e ae -'=-+≤,2221()(2)0f e e a e'=->, 因此()f x '在22(,)e e -有一个零点,()f x 在22(,)e e -内有一个极值点;综上所述当1(,]a e∈-∞-时,()f x 在22(,)e e -内没有极值点;当212,a e e ⎛⎫∈--⎪⎝⎭时,()f x 在22(,)e e -内有两个极值点; 当22,0a e ⎡⎫∈-⎪⎢⎣⎭时,()f x 在22(,)e e -内有一个极值点. (3)猜想:(1,1)x a ∈+,()1f x a <-恒成立. 证明如下:由(2)得()g x 在1(,)e+∞上单调递增,且(1)0g a =-<,(1)(1)ln(1)g a a a a +=++-. 因为当1x >时,1ln 1(*)x x>-,所以1(1)(1)(1)01g a a a a +>+--=+ 故()g x 在(1,1)a +上存在唯一的零点,设为0x .由x 0(1,)x0x0(,1)x a +()f x '− 0 + ()f x单调递减单调递增知(1,1)x a ∈+,()max{(1),(1)}f x f f a <+.又(1)ln(1)1f a a +=+-,而1x >时,ln 1(**)x x <-, 所以(1)(1)111(1)f a a a f +<+--=-=. 即(1,1)x a ∈+,()1f x a <-.所以对任意的正数a ,都存在实数1t =, 使对任意的(,)x t t ∈+∞, 使()1f x a <-. 补充证明(*): 令1()1n 1F x x x =+-,1x ≥.22111()0x F x x x x-'=-=≥, 所以()F x 在[1,)+∞上单调递增.所以1x >时,()(1)0F x F >=,即1ln 1x x>-. 补充证明(**)令()ln 1G x x x =-+,1x ≥.1()10G x x'=-≤, 所以()G x 在[1,)+∞上单调递减.所以1x >时,()(1)0G x G <=,即ln 1x x <-. 【点睛】本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间,考查了不等式与导数的结合,难度较大. 21.已知二阶矩阵,矩阵属于特征值的一个特征向量为,属于特征值的一个特征向量为.求矩阵.【答案】【解析】运用矩阵定义列出方程组求解矩阵 【详解】由特征值、特征向量定义可知,,即,得 同理可得解得,,,.因此矩阵【点睛】本题考查了由矩阵特征值和特征向量求矩阵,只需运用定义得出方程组即可求出结果,较为简单 22.在极坐标系中,已知1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,线段AB 的垂直平分线l 与极轴交于点C ,求l 的极坐标方程及ABC ∆的面积.【答案】l 的极坐标方程及cos 53πρθ⎛⎫-= ⎪⎝⎭,203ABC ∆的面积. 【解析】将1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭转化为直角坐标系下的坐标形式,然后求出线段AB 的中点与直线AB 的斜率,进而求出直线l 在直角坐标系下的方程,再转化为极坐标方程;在直角坐标系下,求出点C 到直线AB 的距离、线段AB 的长度,从而得出ABC ∆的面积. 【详解】解:以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系xoy 在平面直角坐标系xoy 中,1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ 的坐标为13993(),(22A B线段AB 的中点为553(2A ,3AB k =故线段AB 中垂线的斜率为133AB k k --==, 所以AB 的中垂线方程为:5335)2y x --=- 化简得:3100x +-=, 所以极坐标方程为cos 3sin 100ρθρθ+-=, 即cos()53πρθ-=,令0y =,则10x =,故在平面直角坐标系xoy 中,C (10,0)点C 到直线AB :3y x =的距离为1035331d ==+ 线段8AB =,故ABC ∆的面积为15382032S =⨯=【点睛】本题考查了直线的极坐标方程问题,解题时可以将极坐标系下的问题转化为平面直角坐标系下的问题,从而转化为熟悉的问题.23.已知实数,a b 满足2a b +≤,求证:22224(2)a a b b a +-+≤+.【答案】证明见解析【解析】对2222a a b b +-+进行转化,转化为含有2a b +≤形式,然后通过不等关系得证.【详解】 解:因为2a b +≤, 所以2222a a b b +-+ 2222a b a b =-++()()()2a b a b a b =-+++2a b a b=+-+()22a b a a b=+-++22a b a a b≤++++()22222244242a a a a≤++=+=+≤+,得证.【点睛】本题考查了绝对值不等式问题,解决问题的关键是要将要证的形式转化为已知的条件,考查了学生转化与化归的能力.24.如图,在四棱锥P ABCD-中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2.若DC ABλ=u u u r u u u r (Rλ∈),且向量PCuuu r与BDu u u r夹角的余弦值为1515.(1)求λ的值;(2)求直线PB与平面PCD所成角的正弦值.【答案】(1)2λ=;(210.【解析】试题分析:(1)以A为坐标原点,AB、AD、AP分别为x、y、z轴建立空间直角坐标系A xyz-,写出,PCu u u r,BDu u u r的坐标,根据空间向量夹角余弦公式列出关于λ的方程可求;(2)设岀平面PCD的法向量为(),,n x y z=r,根据n PCn DC⎧⊥⎪⎨⊥⎪⎩r u rr u r,进而得到⎧⋅=⎪⎨⋅=⎪⎩r u rr u rn PCn DC,从而求出nr,向量PBu r的坐标可以求出,从而可根据向量夹角余弦的公式求出cos,n PB<>r u r,从而得PB和平面PCD所成角的正弦值.试题解析:(1)依题意,以A为坐标原点,AB、AD、AP分别为x、y、z轴建立空间直角坐标系A xyz-(1,0,0),(0,2,0),(0,0,2)B D P,因为DC ABλ=u u u r u u u r,所以(,2,0)Cλ,从而(,2,2)PCλ=-u u u r,则由15cos,15PC BD=u u u r u u u r,解得10λ=(舍去)或2λ=.(2)易得(2,2,2)PC=-u u u r,(0,2,2)PD=-u u u r,设平面PCD的法向量(,,)n x y z=r,则0⋅=r u u u rn PC,0⋅=r u u u rn PD,即0x y z+-=,且0y z-=,所以0x=,不妨取1y z==,则平面PCD 的一个法向量(0,1,1)n=r,又易得(1,0,2)PB=-u u u r,故10cos,5=⋅=-u u u r rPB n PB n,所以直线PB与平面PCD所成角的正弦值为105.考点: 1、空间两向量夹角余弦公式;2、利用向量求直线和平面说成角的正弦.25.已知数列{}n a的通项公式为1515225n nna⎡⎤⎛⎫⎛⎥=-⎪⎪ ⎥⎝⎭⎝⎭⎦,n N∈,记1212n n nS C a C a=++…nn nC a+.(1)求1,S2S的值;(2)求所有正整数n,使得n S能被8整除.【答案】(1) 11S=;23S=;(2) {}*|3,n n k k N=∈【解析】(1)运用二项式定理,化简整理,再代入计算即可得到所求值;(2)通过化简得到213n n nS S S++=-,再由不完全归纳找规律得到结论,即可得到所求结论.【详解】解:(1)1212n n n n n n S C a C a C a =++⋯+2121515225n n C C ⎡⎛⎛+ =⋅+⋅+ ⎝⎭⎝…212151515n n n n n C C C ⎫⎛+--⎪ +⋅-⋅+⎪ ⎝⎭⎝⎭⎭⎝…15n n n C ⎤⎫-⎥⎪+⋅⎥⎪⎝⎭⎭⎦1515115n n ⎡⎤⎛⎛+-⎥=-+ ⎥⎝⎭⎝⎭⎦ 3535225n n ⎡⎤⎛⎛+⎢⎥=- ⎢⎥⎝⎭⎝⎭⎣⎦, 即有1S 515==; 2S 3535==; (2)35355n n S n ⎡⎤+-⎢⎥=-⎢⎥⎝⎭⎝⎭⎣⎦, 23535225n S n n +⎡⎤+-=+-+⎥⎥⎝⎭⎝⎭⎦ 3535353535352222225n n n n ⎡⎤⎡⎤⎛⎛⎫⎛⎫⎛⎫⎛+⎢⎥⎢⎥-⋅+-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦13n n S S +=-,即213n n n S S S ++=-,*n N ∈,因此2n S +除以8的余数,完全由1,n n S S +除以8的余数确定,因为11,a =21a =,所以11111S C a ==,12221223S C a C a =+=,3213918S S S =-=-=,432324321,S S S =-=-=543363855S S S =-=-=,654316521144,S S S =-=-=7535643255377S S =-=-=,87631131144987,S S S =-=-=987329613772584S S S =-=-= 由以上计算及213n n n S S S ++=-可知,数列{}n S 各项除以8的余数依次是: 1,3,0,5,7,0,1,3,0,5,7,0,…,它是一个以6为周期的数列,从而n S 除以8的余数等价于n 除以3的余数, 所以3,n k =*k N ∈,即所求集合为:{}*|3,n n k k N=∈.【点睛】本题考查数列通项的运用,解决问题的关键是运用二项式定理,本题属于难题.。
江苏省海安高级中学2020届高三3月线上考试 数学试题(word含答案版)

+(xn - x +xn)B =β = nβ = n江苏省海安中学高三数学模拟考试数学试卷方差公式s2 = 1[(x- x)2 + (x- x)2 +数学1)2 ],其中x =1(x + x +.n 1 2 n 1 2一、填空题:本大题共14 小题,每小题5 分,共70 分.不需要写出解答过程,请把答案直接填在答.题.卡.相.应.位.置.上..1.已知集合A ={x 0 < x < 2} ,B ={x x >1} ,则A ▲.2.复数z = i(1- i) 的共轭复数在复平面内对应的点位于第▲象限.3.为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200 辆汽车的时速,所得数据均在区间[40,80]中,其频率分布直方图如图所示,则在抽测的200 辆汽车中,时速在区间[40,60]内的汽车有▲辆.4.袋中装有5 个大小相同的球,其中3 个黑球,2 个白球,从中一次摸出2 个球,则摸出1 个黑球和1 个白球的概率等于▲.5.在一次知识竞赛中,抽取5 名选手,答对的题数分布情况如下表,则这组样本的方差为▲.(第3 题图)答对题数 4 8 9 10人数分布 1 1 2 1(第5 题表)6.如右图所示的算法流程图中,最后输出值为▲.7.已知m ,n 是两条不同的直线,α ,β 是两个不同的平面.①若m⊂α,m⊥β,则α⊥β;②若m⊂α,α第6 题图,α⊥β,则m⊥n;③若m⊂α,n⊂β,α//β,则m//n;④若m//α,m⊂β,α,则m//n.上述命题中为真命题的是▲.(填写所有真命题的序号).FED8.公元五世纪张丘建所著《张丘建算经》卷 22 题为:“今有女善织,日益功疾,初日织五尺,今一月日织九匹三丈,问日益几何”.题目的意思是:有个女子善于织布,一天比一天 织得快(每天增加的数量相同),已知第一天织布 5 尺,一个月(30 天)共织布 9 匹 3 丈,则该女子每天织尺布的增加量为▲尺.(1 匹=4 丈,1 丈=10 尺) 9.若cos α = 2cos(α + π) ,则 tan(α + π) = ▲ .C4810.如图,已知 O 为矩形 ABCD 内的一点,且 OA = 2 , OC = 4 , AC = 5 ,则OOB ⋅ OD = ▲ .A B11.已知关于 x 的方程 x (x - a ) =1 在 (-2, +∞) 上有三个相异实根,则实数 a 的取值范围是 ▲ .12.已知 a > 0,b > 0 ,且 1 + 1 = 1 ,则 3a + 2b + b 的最小值等于▲ .(第 10 题图)a b a13.如图,已知 AC = 8 ,B 为 AC 的中点,分别以 AB, AC 为直径在 AC 的同侧作半圆, M, N 分别为两半圆上的动点(不含端点 A ,B ,C ),且BM ⊥ BN ,则 AM ⋅CN 的最大值为 ▲ .14.若关于 x 的不等式 x 3 - 3x 2 +ax + b < 0 对任意的实数 x ∈[1,3] 及任意的实数 b ∈[2, 4] 恒成立,则实数 a 的取值范围是 ▲ .二、解答题:本大题共 6 小题,共 90 分.请在答.题.卡.指.定.区.域.内作答,解答时应写出文字 说明、证明过程或演算步骤.15.已知△ABC 内接于单位圆(半径为 1 个单位长度的圆),且 (1+ tan A )(1+ tan B ) = 2 .(1)求角 C 的大小;(2)求△ABC 面积的最大值.16.如图,在四面体 ABCD 中, AB = AC = DB = DC ,点 E 是 BC 的中点,点 F 在线段 AC 上,且 A F = λ .AC(1)若 EF //平面 ABD ,求实数 λ 的值; B(2)求证:平面 BCD ⊥ 平面 AED .ADC(第 16 题图)3 θ P17. 如图,长方形材料 ABCD 中,已知 AB = 2 , AD = 4 .点 P 为材料 ABCD 内部一点,PE ⊥ AB 于 E , PF ⊥ AD 于 F ,且 PE =1,PF = .现要在长方形材料 ABCD 中裁剪出四边形材料 AMPN ,满足 ∠MPN =150︒ ,点 M ,N 分别在边 AB ,AD 上. (1)设 ∠FPN = θ ,试将四边形材料 AMPN 的面积 S 表示为 θ 的函数,并指明 θ 的取 值范围;(2)试确定点 N 在 AD 上的位置,使得四边形材料 AMPN 的面积 S 最小,并求出其最 小值.DCN F AB(第 17 题图)18.已知椭圆 E : x 2+ 9y 2= m 2( m > 0 ),直线 l 不过原点 O 且不平行于坐标轴, l 与 E有两个交点 A , B ,线段 AB 的中点为 M .(1)若 m = 3 ,点 K 在椭圆 E 上,F 1 、F 2 分别为椭圆的两个焦点,求 KF 1 ⋅ KF 2 的范围; (2)证明:直线 OM 的斜率与 l 的斜率的乘积为定值;(3)若 l 过点 (m , m ) ,射线 OM 与椭圆 E 交于点 P ,四边形 OAPB 能否为平行四边形?3若能,求此时直线 l 斜率;若不能,说明理由.3+ a n b 1 = n n n nn3 19.已知函数 f (x ) = a e x ,g (x ) = ln x -ln a ,其中 a 为常数,且曲线 y= f (x ) 在其与 y轴的交点处的切线记为l 1 ,曲线 y= g (x ) 在其与 x 轴的交点处的切线记为 l 2 ,且 l 1 / / l 2 .(1)求l 1,l 2 之间的距离;(2)若存在x 使不等式 x - m > f (x )成立,求实数 m 的取值范围;(3)对于函数 f (x ) 和g (x ) 的公共定义域中的任意实数 x 0 ,称 |f (x 0 ) - g (x 0 )| 的值为 两函数在x 0 处的偏差.求证:函数 f (x ) 和 g (x ) 在其公共定义域内的所有偏差都大于 2.20.设数列 {a }的前 n 项和为 S , 2S +a = 3 , n ∈ N * . (1)求数列 {a n }的通项公式;(2)设数列 {b }满足:对于任意的 n ∈ N *,都有a b + a b+ a b +⎛ 1 ⎫ n -1+ 3n - 3 成立.1 n2 n -13 n -2⎪⎝ ⎭①求数列 {b n }的通项公式;②设数列 c n = a n ⋅b n ,问:数列{c n }中是否存在三项,使得它们构成等差数列?若存在, 求出这三项;若不存在,请说明理由.x2 22数学(理科)附加题说明:1.以下题目的答案请直接填写在答卷上.2.本卷总分 40 分,考试时间 30 分钟.21.【选做题】本题包括 A 、B 、C 、D 四小题,请.选.定.其.中.两.小.题.,并.在.相.应.的.答.题.区.域. 内.作.答.,若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算 步骤.A .[选修 4—1:几何证明选讲](本小题满分10 分)如图,四边形 ABCD 内接于圆 O ,弧 AB 与弧 AD 长度相等,过 A 点的切线交 CB 的延长线于 E 点.求证: AB 2=BE ⋅CD .EAB· ODC(第 21-A 题)B .[选修 4-2:矩阵与变换](本小题满分 10 分)⎡2 1⎤ ⎡ x ⎤ ⎡4⎤已知矩阵 A = ⎢ ⎥ ,列向量X = ⎢ y ⎥ , B = ⎢7⎥ ,且 AX = B . ⎣3 2⎦⎣ ⎦ ⎣ ⎦(1)求矩阵 A 的逆矩阵 A -1; (2)求 x , y 的值.C .[选修 4-4:坐标系与参数方程](本小题满分 10 分)⎪⎧x =4cos θ⎧x =3+ t , 已知点 P 在曲线 C :⎨ ⎩⎪y =3sin θ (θ为参数)上,直线 l :⎨ ⎩y =-3+ 2 (t 为参数), t求 P 到直线 l 距离的最小值.D .[选修 4—5:不等式选讲](本小题满分 10 分)已知 x ,y ,z 均为正数.求证: x + y + z ≥ 1 + 1 + 1 .yz zx xy x y z22.如图所示,在直三棱柱ABC-A1B1C1 中,CA=4,CB=4,CC1=2,∠ACB=90°,点2M 在线段A1B1 上.(1)若A1M=3MB1,求异面直线AM 和A1C 所成角的余弦值;(2)若直线AM 与平面ABC1所成角为30°,试确定点M 的位置.23.在平面直角坐标系xOy 中,已知焦点为F 的抛物线x2 = 4 y上有两个动点A 、B ,且满足AF = λ FB , 过A 、B 两点分别作抛物线的切线,设两切线的交点为M .--→ --→(1)求:OA ⋅ OB 的值;(2)证明:FM ⋅ AB 为定值.44答案一、填空题:1. (1, 2)2.四; 3.80 4. 355.22 56.257.①④ 16 8.299.2 +1 ;3 10. - 5211. (- 5, -2)212.11 13. 4 14. (-∞, -2)二、解答题:本大题共 6 小题,共 90 分.请在答.题.卡.指.定.区.域.内作答,解答时应写出文字 说明、证明过程或演算步骤. 15.命题立意:本题主要考查两角和与差的正切公式与正、余弦定理等基础知识,考查运算 求解能力.(1)由 (1 + tan A )(1 + tan B ) = 2 得 tan A + tan B =1- tan A tan B ,所以 tan( A + B ) = tan A + tan B = 1 ,(4 分)1 - tan A tan B故△ABC 中, A + B = π , C = 3π (6 分)2 2 2 2DE = E 3 (2)由正弦定理得 c = 2 ,即 c = ,(8 分) sin 3π 4由余弦定理得 2 = a 2 + b 2 - 2ab c os 3π ,即 2 = a 2 + b 2 + 4ab ,(10 分)由 2 = a 2 + b 2 + ab ≥2ab + ab 得 ab ≤2 - ,(当且仅当 a = b 时取等号)(12分)所以 S = 1 ab sin 3π≤ 2 -1 .(14 分)2 4 216.命题立意:本题主要考查直线与平面、平面与平面的位置关系,考查空间想象与推理论 证能力.解:(1)因为 EF ∥平面 ABD ,易得 EF ⊂ 平面 ABC ,平面 ABC 平面 ABD = AB , 所以 EF // AB ,(5 分) 又点 E 是 BC 的中点,点 F 在线段 AC 上, 所以点 F 为 AC 的中点, 由 AF = λ 得 λ = 1 ;(7 分) AC 2(2)因为 AB = AC = DB = DC ,点 E 是 BC 的中点,所以 BC ⊥ AE , BC ⊥ DE ,(9 分) 又 AE , AE 、DE ⊂ 平面 AED , 所以 BC ⊥ 平面 AED ,(12 分) 而 BC ⊂ 平面BCD , 所以平面 BCD ⊥ 平面 AED .(14 分)17.解:(1)在直角△ NFP 中,因为 PF = , ∠FPN = θ ,所以NF = 所以 S ∆NAP tan θ , = 1 NA ⨯ PF = 1 (1 + 2 2 tan θ ) ⨯ . ……………………………2 分在直角△ MEP 中,因为 PE = 1 , ∠EPM = π- θ ,3所以 ME = tan( π- θ ) ,32 3 3 392 3 3 - tan θ 2(1 + 3 tan θ )32 3tt ⨯ 43t 所以 S= 1 AM ⨯ PE = 1 [+ tan( π- θ )]⨯1 . ………………………………4 分∆AMP22 3所以 S = S∆NAP+ S ∆AMP= 3 tan θ + 1 tan( π - θ ) + 2 2 3 ,θ ∈[0, π]. 3……………………………………………………………………………………6 分 (注:定义域错误扣 1 分)(2)因为 S = 3 tan θ + 1 tan( π - θ ) + 2 2 3 = 3 tan θ + + 2 . …8 分令t = 1 + tan θ ,由θ ∈[0, π] ,得 t ∈[1, 4] , 33t 2 - 4t + 4 所以 S = + = (t + 4 ) +≥ 3 ⨯ 2 ⨯ 2 3t+ 3 = 2 + 33.………………12 分2 3 3当且仅当 t =2 3 时,即 tan θ = 2 - 3 时等号成立. ………………13 分 3 3 此时, AN = 2 3 , S = 2 + 3.3 min 3答:当 AN = 2 3 时,四边形材料 AMPN 的面积 S 最小,最小值为 2 + 3.3 3……………………………………………………………………………………14 分18.解:(Ⅰ) m = 3 ,椭圆 E : x + y 2 = 1,两个焦点 F (-2, 0) , F (2 , 0) 设 K (x , y ), F 1K = (x + 2 9, y ) ,F 2 K = (x - 2 12, y ) , 222KF 1 ⨯ KF 2 = FK 1 ⨯ F 2 K =(x + 2 , y ) ⨯ (x - 2 , y ) = x + y - 8= - 8y +1, ∵-1 ≤ y ≤ 1,∴ KF 1 ⨯ KF 2 的范围是 [-7,1] (4 分) ⎧x 2 + 9 y 2 = m 2,⎪ 1 1( 2 ) 设 A , B 的 坐 标 分 别 为 (x 1 , y 1 ) , (x 2 , y 2 ) , 则 ⎨ 两 式 相 减 , 得 x 2 + 9 y 2 = m 2 . ⎩⎪ 2 2 1+ 9 ( y 1 + y 2 )( y 1 - y 2 ) = 0 (x 1 + x 2 )(x 1 - x 2 ) + 9( y 1 + y 2 )( y 1 - y 2 ) = 0, (x + x )(x , 即- x )11+ 9k OM ⨯ k l = 0 ,故 k OM ⨯ k l = - ;(8 分) 12122 2 2 2 23 3 33 33 24 ± 7 2 x x x 2 ⎝ x x 2 x x 2 2 ⎝ x 2 ⎝ x P ÷ ÷÷ (3)∵直线 l 过点(m , m) , 3∴直线 l 不过原点且与椭圆 E 有两个交点的充要条件是k > 0 且 k ≠ 1. 3m m 设P (x P , y P ) ,设直线 l : y = k (x - m ) + 31( m ≠ 0, k ≠ 0 ),即l : y = kx - km + ,39m 2k 2由(2)的结论可 知O M : y = - 9k x , 代入椭圆方程得, x 2 =9k 2 +1, (10 分)⎛k 2m - km km - m ⎫ 由 y = k (x - m ) + m 与 y = - 1 9 3 x ,联立得 M , - 3 ÷ .(12 分)3 9k 9k 2+19k 2 +1 ÷ ⎝ ⎭若四边形 OAPB 为平行四边形,那么M 也是 OP 的中点,所以 2x 0 = x P ,⎛ 9k 2 m - 3km ⎫ 即 4 ÷ =9m 2 k 2,整理得 9k 2 - 8k +1 = 0 解得, k = . ⎝ 9k 2 +1 ⎭ 9k 2+19 所以当 k =4 ± 97时,四边形 OAPB 为平行四边形.(16 分) 19. 解:(1)f ' (x ) = ae x ,g '(x ) = 1, y = f (x ) 的图像与坐标轴的交点为 (0 , a ) ,y = g (x ) x的图像与坐标轴的交点为 (a , 0) ,由题意得f '(0) =g '(a ) ,即 a = 1a 又∵ a > 0 ,∴ a = 1 . (2 分)∴ f ( x ) = e x , g (x ) = ln x ,∴函数 y = f (x ) 和 y = g (x ) 的图像在其坐标轴的交点处的切线方程分别为: x - y + 1 = 0 , x - y - 1 = 0 ∴两平行切线间的距离为 (4 分)(2)由 x - m > f (x ) 得 x - m > e x,故 m < x - e x 在 x ∈[0 , + ∞) 有解,令 h (x ) = x - e x ,则 m < hmax (x )。
江苏省海安高级中学2020届高三阶段测试数学试题含答案

江苏省海安高级中学2020届高三阶段性测试(三)数学Ⅰ参考公式:样本数据1x ,2x ,…,n x 的方差2211()ni i s x x n ==-∑,其中11ni i x x n ==∑.锥体的体积13V Sh =,其中S 为底面积,h 为高.一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位......置上... 1. 设全集U ={1,2,3,4,5}.若UA ={1,2,5},则集合A = ▲ .2. 已知复数z 满足(z 2)i 1i -=+(i 为虚数单位),则复数z 的实部是 ▲ .3. 已知样本数据1234a a a a ,,,的方差为2,则数据123421212121a a a a ++++,,,的方差为 ▲ .4. 右图是一个算法的伪代码,其输出的结果为 ▲ .5. 从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,则该三位数为奇数的概率为 ▲ .6. 在平面直角坐标系xOy 中,若双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为10,则双曲线C 的渐近线方程为 ▲ .7. 将函数f (x )的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象,则()π4f 的值为 ▲ .8. 设定义在R 上的奇函数()f x 在区间[0 )+∞,上是单调减函数,且2(3)f x x -(2)f +0>,则实数x 的取值范围是 ▲ .9. 在锐角三角形ABC 中,若3sin 5A =,1tan()3A B -=-,则3tan C 的值为 ▲ .(第4题)10. 设S n 为数列{}n a 的前n 项和.若S n =na n -3n (n -1)(n ∈N *),且211a =,则S 20的值为 ▲ . 11. 设正实数x ,y 满足x yxy x y+=-,则实数x 的最小值为 ▲ . 12. 如图,正四棱柱1111ABCD A B C D -的体积为27,点E ,F分别为棱1B B ,1C C 上的点(异于端点),且//EF BC , 则四棱锥1A AEFD -的体积为 ▲ .13.已知向量a ,b ,c 满足++=0a b c ,且a 与b 的夹角的正切为12-,b 与c 的夹角的正切为13-,2=b ,则⋅a c 的值为 ▲ .14.已知()()()23f x m x m x m =-++,()22x g x =-,若同时满足条件:①x ∀∈R ,()0f x <或()0g x <;②()4x ∃∈-∞-,,()()0f x g x ⋅<,则实数m 的取值范围是 ▲ . 二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)已知△ABC的面积为18AC AB CB ,向量(tan tan sin 2)A B C ,m 和(1cos cos )A B ,n是共线向量.(1)求角C 的大小; (2)求△ABC 的三边长.16.(本题满分14分)如图,在四棱锥P -ABCD 中,已知底面ABCD 为矩形,且 AB =2,BC =1,E ,F 分别是AB ,PC 的中点,P A ⊥DE . (1)求证:EF ∥平面P AD ; (2)求证:平面P AC ⊥平面PDE .C1(第12题)C(第16题)AOBPQMN (第17题)17.(本题满分14分)如图,OM ,ON 是某景区的两条道路(宽度忽略不计,OM 为东西方向),Q 为景区内一景点,A 为道路OM 上一游客休息区.已知tan ∠MON =-3,OA =6(百米),Q 到直线OM ,ON 的距离分别为3(百米),6105(百米).现新修一条自A 经过Q 的有轨观光直路并延伸至道路ON 于点B ,并在B 处修建一游客休息区. (1)求有轨观光直路AB 的长;(2)已知在景点Q 的正北方6 百米的P 处有一大型组合音乐喷泉,喷泉表演一次的时长为9 分钟.表演时,喷泉喷洒区域以P 为圆心,r 为半径变化,且t分钟时,r =百米)(0≤t ≤9,0<a <1).当喷泉表演开始时,一观光车S (大小忽略不计)正从休息区B 沿(1)中的轨道BA 以2(百米/分钟)的速度开往休息区A ,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.18.(本题满分16分)在平面直角坐标系xOy 中,已知椭圆E :22221(0)x y abab 过点(1,其离心率.(1)求椭圆E 的标准方程;(2)若A ,B 分别是椭圆E 的左,右顶点,动点M 满足MB AB ⊥,且MA 交椭圆E 于点P .①求证:OP OM ⋅为定值;②设PB 与以PM 为直径的圆的另一交点为Q ,求证:直线MQ 经过定点.19.(本题满分16分)已知数列{}n a 满足:123a a a k ===(常数k >0),112n n n n k a a a a -+-+=(n ≥3,*n ∈N ).数列{}n b 满足:21n n n n a a b a +++=(*n ∈N ). (1)求b 1,b 2的值; (2)求数列{}n b 的通项公式;(3)是否存在k ,使得数列{}n a 的每一项均为整数? 若存在,求出k 的所有可能值;若不存在,请说明理由.20.(本题满分16分)设函数f (x )=(x -a )ln x -x +a ,a ∈R . (1)若a =0,求函数f (x )的单调区间;(2)若a <0,且函数f (x )在区间()22e e -,内有两个极值点,求实数a 的取值范围; (3)求证:对任意的正数a ,都存在实数t ,满足:对任意的x ∈(t ,t +a ), f (x )<a -1.数学Ⅰ参考答案一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位......置上... 1. 【答案】{3,5}2. 【答案】33. 【答案】84. 【答案】10115. 【答案】35 6. 【答案】y =±3x 7. 【答案】48. 【答案】(1,2)9. 【答案】7910. 【答案】1 24011. 【答案112. 【答案】913.【答案】4514.【答案】()42--,二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)解:(1)因为向量(tan tan sin 2)AB C ,m和(1cos cos )A B ,n 是共线向量, 所以cos cos tan tan sin 20A B ABC, ……2分即sin A cos B +cos A sin B -2sin C cos C =0,化简得sin C -2sin C cos C =0,即sin C (1-2cos C )=0. ……4分 因为0πC ,所以sin C >0,从而1cos 2C,π.3C……6分 (2)218AC AB CB AC BCBAAC ,于是AC 32. ……8分因为△ABC 的面积为1sin 2CA CB C ,即1π32sin 23CB ,解得6 2.CB …… 11分在△ABC 中,由余弦定理得2222212cos 32622326254.2AB CA CB CA CB C所以3 6.AB…… 14分16.(本题满分14分)证明:(1)取PD 中点G ,连AG ,FG , 因为F ,G 分别为PC ,PD 的中点,所以FG ∥CD ,且FG =12C D . ……2分又因为E 为AB 中点,所以AE //CD ,且AE =12C D . ……4分所以AE //FG ,AE =FG .故四边形AEFG 为平行四边形. 所以EF //AG ,又EF ⊄平面P AD ,AG ⊂平面P AD ,故EF //平面P A D . ……6分(2)设AC ∩DE =H ,由△AEH ∽△CDH 及E 为AB 中点得AG CG =AE CD =12,又因为AB =2,BC =1,所以AC =3,AG =13AC =33.所以AG AE =AB AC =23,又∠BAD 为公共角,所以△GAE ∽△BA C .所以∠AGE =∠ABC =90︒,即DE ⊥A C . ……10分 又DE ⊥P A ,P A ∩AC =A ,所以DE ⊥平面P A C . ……12分 又DE ⊂平面PDE ,所以平面P AC ⊥平面PDE . ……14分17.(本题满分14分)解:(1)以点O 为坐标原点,直线OM 为x 轴,建立平面直角坐标系,如图所示.则由题设得:A (6,0),直线ON 的方程为()()003 30y x Q x x =->,,.03x =,所以()3 3Q ,. ……2分 故直线AQ 的方程为()6y x =--,由360y x x y =-⎧⎨+-=⎩,得39x y =-⎧⎨=⎩,,即()3 9B -,,故AB == …… 5分答:水上旅游线AB 的长为. ……6分 (2)将喷泉记为圆P ,由题意可得P (3,9),生成t 分钟时,观光车在线段AB 上的点C 处, 则BC =2t ,0≤t ≤9,所以C (-3+t ,9-t ).若喷泉不会洒到观光车上,则PC 2>r 2对t ∈[0,9]恒成立,即PC 2=(6-t )2+t 2=2t 2-12t +36>4at , ……10分 当t =0时,上式成立,当t ∈(0,9]时,2a <t +18t -6,(t +18t -6)min =62-6,当且仅当t =32时取等号,因为a ∈(0,1),所以r <PC 恒成立,即喷泉的水流不会洒到观光车上.……13分 答:喷泉的水流不会洒到观光车上. ……14分18.解:(1)设椭圆焦距为2c,所以223121 a b c a ⎧⎪+=⎪⎨⎪=⎪⎩,且222c a b =-, 解得224 2 a b ⎧=⎪⎨=⎪⎩,,所以椭圆E 的方程为22142x y ; ……4分(2)设0(2 )M y ,,11( )P x y ,, ①易得直线MA 的方程为:0042y y y x =+, 代入椭圆22142x y 得,()2222000140822y y y x x +++-=, 由()201204828y x y --=+得,()20120288y x y --=+,从而012088y y y =+, ……8分所以()20002200288 (2 )88y y OP OM y y y --⎛⎫⋅=⋅ ⎪++⎝⎭,, ()22002200488488y y y y --=+=++. ……10分 ②直线MQ 过定点(0 0)O ,,理由如下:依题意,()02020208822828PB y y k y y y +==----+,由MQ PB ⊥得,02MQ y k =, 则MQ 的方程为:00(2)2y y y x -=-,即02y y x =,所以直线MQ 过定点(0 0)O ,. ……16分 19.(本题满分16分)解:(1)由已知得,41a k =+,所以1312=2a a b a +=,2423121a a k k kb a k k ++++===. ……2分 (2)由条件可知:()1213n n n n a a k a a n +--=+≥,①所以()21+12n n n n a a k a a n +-=+≥.② ……4分 ①-②得122111n n n n n n n n a a a a a a a a +-+--+-=-. 即:121121n n n n n n n n a a a a a a a a +-+-+-+=+. 因此:2211n n n nn n a a a a a a +-+-++=, ……6分故()23n n b b n -=≥,又因为12b =,221k b k+=,所以221n n b k n k⎧⎪=⎨+⎪⎩,为奇数,为偶数. ……8分(3)假设存在k ,使得数列{}n a 的每一项均为整数,则k 为正整数. ……10分由(2)知21221222122(123)21n n n n n n a a a n k a a a k +-++=-⎧⎪=⎨+=-⎪⎩,,③ 由162Z 4Z a k a k k=∈=++∈,,所以k =1或2, ……12分检验:当1k =时,312=+kk 为整数, 利用123Z a a a ∈,,结合③,{a n }各项均为整数; ……14分 当2k =时③变为21221222122(123)52n n n n n n a a a n a a a +-++=-⎧⎪=⎨=-⎪⎩,, 消去2121n n a a +-,得:222223(2)n n n a a a n +-=-≥ 由24Z a a ∈,,所以偶数项均为整数,而2221252n n n a a a ++=-,所以21n a +为偶数,故12a k ==,故数列{}n a 是整数列. 综上所述,k 的取值集合是{}12,. ……16分 20.(本题满分16分)解:(1)当a =0时,f (x )=x ln x -x ,f’(x )=ln x ,令f’(x )=0,x =1,列表分析x(0,1)1(1,+∞)故f (x )的单调递减区间为(0,1),单调递增区间为(1,+∞). ……3分(2)f (x )=(x -a )ln x -x +a ,f’(x )=ln x -ax,其中x >0,令g (x )=x ln x -a ,分析g (x )的零点情况.g ’(x )=ln x +1,令g ’(x )=0,x =1e,列表分析g (x )min =g (1e )=-1e -a , ……5分而f’(1e )=ln 1e-a e =-1-a e ,()2e f -'=-2-a e 2=-(2+a e 2),f’(e 2)=2-a e 2=1e2(2e 2-a ),①若a ≤-1e ,则f’(x )=ln x -ax ≥0,故f (x )在()22e e -,内没有极值点,舍;②若-1e <a <-2e 2,则f’(1e )=ln 1e-a e <0,f’(e -2)=-(2+a e 2)>0,f’(e 2)=1e2(2e 2-a )>0,因此f’(x )在()22e e -,有两个零点,设为1x ,2x ,所以当()21e x x -∈,时,f (x )单调递增,当()12x x x ∈,时,f (x )单调递减, 当()22e x x ∈,时,f (x )单调递增,此时f (x )在()22e e -,内有两个极值点;③若-2e 2≤a <0,则f’(1e )=ln 1e -a e <0,f’(e -2)=-(2+a e 2)≤0,f ’(e 2)=1e2(2e 2-a )>0,因此f’(x )在()22e e -,有一个零点,f (x )在()22e e -,内有一个极值点;综上所述,实数a 的取值范围为(-1e ,-2e 2). ……10分(3)存在1t =:x ∈(1,1+a ),f (x )<a -1恒成立. ……11分证明如下:由(2)得g (x )在(1e ,+∞)上单调递增,且g (1)=-a <0,g(1+a )=(1+a )ln(1+a )-a .因为当x >1时,ln x >1-1x (*),所以g(1+a )>(1+a )(1-1a +1)-a =0.故g (x )在(1,1+a )上存在唯一的零点,设为x 0.由知,x ∈(1,1+a ),f (x )<max{f (1),f (1+a )}. ……13分又f (1+a )=ln(1+a )-1,而x >1时,ln x <x -1(**), 所以f (1+a )<(a +1)-1-1=a -1=f (1). 即x ∈(1,1+a ),f (x )<a -1.所以对任意的正数a ,都存在实数t =1,使对任意的x ∈(t ,t +a ),使 f (x )<a -1. ……15分补充证明(*):令F (x )=ln x +1x -1,x ≥1.F ’(x )=1x -1x 2=x -1x 2≥0,所以F (x )在[1,+∞)上单调递增.所以x >1时,F (x )>F (1)=0,即ln x >1-1x .补充证明(**)令G (x )=ln x -x +1,x ≥1.G ’(x )=1x -1≤0,所以G (x )在[1,+∞)上单调递减.所以x >1时,G (x )<G (1)=0,即ln x <x -1.……16分。
江苏省海安高级中学2020届高三3月线上考试数学试题及答案word

江苏省海安中学高三数学模拟考试数学试卷数学1方差公式()()()2222121n s x x x x x x n ⎡⎤=-+-++-⎢⎥⎣⎦L ,其中()121n x x x x n=+++L .一、填空题:本大题共14小题,每小题5分,共70分.不需要写出解答过程,请把答案直接填在答题卡相....应位置上..... 1. 已知集合{}|02A x x =<<,{}|1B x x =>,则A B =I ______. 2. 复数()1z i i =-的共轭复数在复平面内对应的点位于第______象限.3. 为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间[]40,80中,其频率分布直方图如图所示,则在抽测的200辆汽车中,时速在区间[]40,60内的汽车有______辆.4. 袋中装有5个大小相同的球,其中3个黑球,2个白球,从中一次摸出2个球,则摸出1个黑球和1个白球的概率等于______.5. 在一次知识竞赛中,抽取5名选手,答对的题数分布情况如下表,则这组样本的方差为______.6. 如图所示的算法流程图中,最后输出值为______.7. 已知m ,n 是两条不同的直线,α,β是两个不同的平面. ①若m α⊂,m β⊥,则αβ⊥; ②若m α⊂,n αβ=I ,αβ⊥,则m n ⊥; ③若m α⊂,n β⊂,//αβ,则//m n ;④若//m α,m β⊂,n αβ=I ,则//m n .上述命题中为真命题的是______.(填写所有真命题的序号).8. 公元五世纪张丘建所著《张丘建算经》卷22题为:“今有女善织,日益功疾,初日织五尺,今一月日织九匹三丈,问日益几何”.题目的意思是:有个女子善于织布,一天比一天织得快(每天增加的数量相同),已知第一天织布5尺,一个月(30天)共织布9匹3丈,则该女子每天织尺布的增加量为______尺.(1匹=4丈,1丈=10尺) 9. 若cos 2cos 4παα⎛⎫=+⎪⎝⎭,则tan 8πα⎛⎫+= ⎪⎝⎭______. 10. 如图,已知O 为矩形ABCD 内的一点,且2OA =,4OC =,5AC =,则OB OD ⋅=u u u r u u u r______.11. 已知关于x 的方程()1x x a -=在()2,-+∞上有三个相异实根,则实数a 的取值范围是______. 12. 已知0a >,0b >,且111a b +=,则32ba b a++上的最小值等于______. 13. 如图,已知8AC =,B 为AC 的中点,分别以AB ,AC 为直径在AC 的同侧作半圆,M ,N 分别为两半圆上的动点(不含端点A ,B ,C ),且BM BN ⊥,则AM CN ⋅u u u u r u u u r的最大值为______.14. 若关于x 的不等式3230x x ax b -++<对任意的实数[]1,3x ∈及任意的实数[]2,4b ∈恒成立,则实数a 的取值范围是______.二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15. 已知ABC ∆内接于单位圆(半径为1个单位长度的圆),且()()1tan 1tan 2A B ++=. (1)求角C 的大小; (2)求ABC ∆面积的最大值.16. 如图,在四面体ABCD 中,AB AC DB DC ===,点E 是BC 的中点,点F 在线段AC 上,且AFACλ=.(1)若//EF 平面ABD ,求实数λ的值; (2)求证:平面BCD ⊥平面AED .17. 如图,长方形材料ABCD 中,已知AB =4AD =.点P 为材料ABCD 内部一点,PE AB ⊥于E ,PF AD ⊥于F ,且1PE =,PF =现要在长方形材料ABCD 中裁剪出四边形材料AMPN ,满足150MPN ∠=︒,点M ,N 分别在边AB ,AD 上.(1)设FPN θ∠=,试将四边形材料AMPN 的面积S 表示为θ的函数,并指明θ的取值范围; (2)试确定点N 在AD 上的位置,使得四边形材料AMPN 的面积S 最小,并求出其最小值. 18. 已知椭圆E :()22290x y m m +=>,直线l 不过原点O 且不平行于坐标轴,l 与E 有两个交点A ,B ,线段AB 的中点为M .(1)若3m =,点K 在椭圆E 上,1F 、2F 分别为椭圆的两个焦点,求12KF KF ⋅u u u r u u u u r的范围;(2)证明:直线OM 的斜率与l 的斜率的乘积为定值; (3)若l 过点,3m m ⎛⎫⎪⎝⎭,射线OM 与椭圆E 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时直线l 斜率;若不能,说明理由.19. 已知函数()xf x ae =,()ln lng x x a =-,其中a 为常数,且曲线()y f x =在其与y 轴的交点处的切线记为1l ,曲线()y g x =在其与x 轴的交点处的切线记为2l ,且12//l l . (1)求1l ,2l 之间的距离;(2)若存在x 使不等式()x mf x ->m 的取值范围; (3)对于函数()f x 和()g x 的公共定义域中的任意实数0x ,称()()00f x g x -的值为两函数在0x 处的偏差.求证:函数()f x 和()g x 在其公共定义域内的所有偏差都大于2. 20. 设数列{}n a 的前n 项和为n S ,23n n S a +=,*n N ∈. (1)求数列{}n a 的通项公式;(2)设数列{}n b 满足:对于任意的*n N ∈,都有11213211333n n n n n a b a b a b a b n ---⎛⎫++++=+- ⎪⎝⎭L 成立.①求数列{}n b 的通项公式;②设数列n n n c a b =⋅,问:数列{}n c 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.数学(理科)附加题说明:1. 以下题目的答案请直接填写在答卷上.2. 本卷总分40分,考试时间30分钟.21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两小题........,并.在相应的答题区域内作答...........,若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤. A. [选修4—1:几何证明选讲]如图,四边形ABCD 内接于圆O ,弧AB 与弧AD 长度相等,过A 点的切线交CB 的延长线于E 点.求证:2AB BE CD =⋅.B. [选修4-2:矩阵与变换]已知矩阵2132A ⎡⎤=⎢⎥⎣⎦,列向量x X y ⎡⎤=⎢⎥⎣⎦,47B ⎡⎤=⎢⎥⎣⎦,且AX B =.(1)求矩阵A 的逆矩阵1A -; (2)求x ,y 的值.C. [选修4-4:坐标系与参数方程]已知点P 在曲线C :4cos 3sin x y θθ=⎧⎨=⎩(θ为参数)上,直线l:3232x t y ⎧=+⎪⎪⎨⎪=-+⎪⎩(t 为参数),求P 到直线l 距离的最小值.D. [选修4—5:不等式选讲] 已知x ,y ,z 均为正数.求证:111x y z yz zx xy x y z++≥++. 22. 如图所示,在直三棱柱111ABC A B C -中,4CA =,4CB =,1CC =90ACB ∠=︒,点M 在线段11A B 上.(1)若113A M MB =,求异面直线AM 和1A C 所成角的余弦值; (2)若直线AM 与平面1ABC 所成角为30︒,试确定点M 的位置.23. 在平面直角坐标系xOy 中,已知焦点为F 的抛物线24x y =上有两个动点A 、B ,且满足AF FB λ=u u u r u u u r,过A 、B 两点分别作抛物线的切线,设两切线的交点为M .(1)求:OA OB ⋅u u u r u u u r的值;(2)证明:FM AB ⋅u u u u r u u u r为定值.答案一、填空题:1. ()1,22. 四3. 804. 355. 2256. 257. ①④8.1629 9. 13 10. 52- 11. 5,22⎛⎫-- ⎪⎝⎭12. 11 13. 4 14. (),2-∞- 二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15. 命题立意:本题主要考查两角和与差的正切公式与正、余弦定理等基础知识,考查运算求解能力. (1)由()()1tan 1tan 2A B ++=得tan tan 1tan tan A B A B +=-, 所以()tan tan tan 11tan tan A B A B A B++==-, 故ABC ∆中,A B π+=4,C π3=4.(2)由正弦定理得2sin c π=34,即c =由余弦定理得2222cosa b ab π3=+-4,即222a b =+,由2222a b ab =++≥+得2ab ≤(当且仅当a b =时取等号)所以13sin 2S ab π=≤4.16. 命题立意:本题主要考查直线与平面、平面与平面的位置关系,考查空间想象与推理论证能力. 解:(1)因为//EF 平面ABD ,易得EF ⊂平面ABC , 平面ABC I 平面ABD AB =, 所以//EF AB ,又点E 是BC 的中点,点F 在线段AC 上, 所以点F 为AC 的中点, 由AF AC λ=得12λ=; (2)因为AB AC DB DC ===,点E 是BC 的中点, 所以BC AE ⊥,BC DE ⊥,又AE DE E =I ,AE DE ⊂、平面AED , 所以BC ⊥平面AED , 而BC ⊂平面BCD ,所以平面BCD ⊥平面AED .17. 解:(1)在直角NFP ∆中,因为PF =FPN θ∠=,所以NF θ=,所以()11122NAP S NA PF θ∆=⋅=+ 在直角MEP ∆中,因为1PE =,3EPM πθ∠=-,所以tan 3ME πθ⎛⎫=- ⎪⎝⎭,所以11tan 1223AMP S AM PE πθ∆⎤⎛⎫=⋅=-⨯ ⎪⎥⎝⎭⎦.所以31tan tan 223NAP AMP S S S πθθ∆∆⎛⎫=+=+-+ ⎪⎝⎭0,3πθ⎡⎤∈⎢⎥⎣⎦. (注:定义域错误扣1分)(2)因为313tan tan tan2232S πθθθ⎛⎫=+-=+ ⎪⎝⎭令1t θ=,由0,3πθ⎡⎤∈⎢⎥⎣⎦,得[]1,4t ∈,所以243S t t ⎫==++⎪⎝⎭22≥=.当且仅当3t =时,即2tan 3θ=时等号成立.此时,AN =,min 2S =+.答:当AN =时,四边形材料AMPN 的面积S 最小,最小值为2+.18. 解:(Ⅰ)3m =,椭圆E :2219x y +=,两个焦点()1F -,()2F ,设(),K x y ,()1F K x y =+u u u u r ,()2F K x y =-u u u u r,()()1212=KF KF FK F K x y x y ⋅=⋅+⋅-u u u r u u u u r u u u u r u u u u r2228=81x y y =+--+,∵11-≤≤y ,∴12KF KF ⋅u u u r u u u u r的范围是[]7,1-. (2)设A ,B 的坐标分别为()11,x y ,()22,x y ,则222112222299x y mx y m⎧+=⎪⎨+=⎪⎩,两式相减,得()()()()1212121290x x x x y y y y +-++-=,()()()()12121212190y y y y x x x x +-+=+-,即190+⋅=OM l k k ,故19⋅=-OM l k k ;(3)∵直线l 过点,3m m ⎛⎫ ⎪⎝⎭, ∴直线l 不过原点且与椭圆E 有两个交点的充要条件是0>k 且13≠k . 设(),P P P x y ,设直线l :()()0,03m y k x m m k =-+≠≠,即l :3m y kx km =-+, 由(2)的结论可知OM :19y x k =-,代入椭圆方程得,2222991=+P m k x k , 由()3m y k x m =-+与19=-y x k ,联立得222933,9191⎛⎫- ⎪-- ⎪++ ⎪⎝⎭m km k m km M k k . 若四边形OAPB 为平行四边形,那么M 也是OP 的中点,所以02P x x =,即22222293949191⎛⎫-= ⎪++⎝⎭k m km m k k k ,整理得29810-+=k k解得,k .所以当k 时,四边形OAPB 为平行四边形. 19. 解:(1)()'xf x ae =,()1'g x x=,()y f x =的图像与坐标轴的交点为()0,a ,()y g x =的图像与坐标轴的交点为(),0a ,由题意得()()'0'f g a =,即1a a=,又∵0a >,∴1a =.∴()xf x e =,()lng x x =,∴函数()y f x =和()y g x =的图像在其坐标轴的交点处的切线方程分别为:10x y -+=,10x y --=(2)由()x m f x ->x x me->x m x <在[)0,x ∈+∞有解, 令()xh x x =,则()max m h x <.当0x =时,0m <;当0x >时,∵()'11x x x h x e ⎫=-=-⎪⎭,∵0x >,=1x e >,∴x e >,故()'10x h x e =-<,即()x h x x =在区间[)0,+∞上单调递减,故()()max 00h x h ==,∴0m <. 即实数m 的取值范围为(),0-∞. (3)解法一:∵函数()y f x =和()y g x =的偏差为:()()()ln x F x f x g x e x =-=-,()0,x ∈+∞, ∴()1'x F x e x =-,设x t =为()1'0x f x e x=-=的解,则当()0,x t ∈,()'0F x <; 当(),x t ∈+∞,()'0F x >,∴()F x 在()0,t 单调递减,在(),t +∞单调递增, ∴()min 1ln ln t t tt F x e t e e t e=-=-=+,∵()'110f e =->,1'202f ⎛⎫=<⎪⎝⎭,∴112t <<,故()12min 1112222tF x e t e =+=+=>=. 即函数()y f x =和()y g x =在其公共定义域内的所有偏差都大于2. 解法二:由于函数()y f x =和()y g x =的偏差:()()()ln x F x f x g x e x =-=-,()0,x ∈+∞, 令()1xF x e x =-,()0,x ∈+∞;令()2ln F x x x =-,()0,x ∈+∞,∵()'11xF x e =-,()'2111xF x x x-=-=, ∴()1F x 在()0,+∞单调递增,()2F x 在()0,1单调递减,在()1,+∞单调递增, ∴()()1101F x F >=,()()2211F x F ≥=,∴()()()12ln 2xF x e x F x F x =-=+>,即函数()y f x =和()y g x =在其公共定义域内的所有偏差都大于2.20. 解:(1)由23n n S a +=,① 得()11232n n S a n --+=≥,② 由①–②得120n n n a a a -+-=,即()1123n n a a n -=≥. 对①取1n =得,110a =≠,所以0n a ≠,所以113n n a a -=为常数, 所以{}n a 为等比数列,首项为1,公比为13,即113n n a -⎛⎫= ⎪⎝⎭,*n N ∈.(2)①由113n n a -⎛⎫= ⎪⎝⎭,可得对于任意*n N ∈有2111121111333333n n n n n b b b b n ----⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+=+- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,③则()()2221231111131323333n n n n n b b b b n n -----⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+=+--≥ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,④则()23111231111112233333n n n n n b b b b n n -----⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+=+-≥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,⑤由③–⑤得()212n b n n =-≥. 对③取1n =得,11b =也适合上式, 因此21n b n =-,*n N ∈. ②由(1)(2)可知1213n n n n n c a b --==, 则()11412121333n n n n nn n n c c +--+--=-=, 所以当1n =时,1n n c c +=,即12c c =,当2n ≥时,1n n c c +<,即{}n c 在2n ≥且*n N ∈上单调递减, 故12345c c c c c =>>>>L .假设存在三项s c ,p c ,r c 成等差数列,其中*,,s p r N ∈,由于12345c c c c c =>>>>L ,可不妨设s p r <<,则2p s r c c c =+()*, 即()1112212121333p s r p s r ------=+.因为*,,s p r N ∈且s p r <<,则1s p ≤-且2p ≥,由数列{}n c 的单调性可知,1s p c c -≥,即12212333s p s p ----≥. 因为12103r r r c --=>,所以()11122212121233333p s r p p s r p --------=+>, 即()122212333p p p p ---->,化简得72p <, 又2p ≥且*p N ∈,所以2p =或3p =.当2p =时,1s =,即121c c ==,由3r ≥时,21r c c <=,此时1c ,2c ,r c 不构成等差数列,不合题意. 当3p =时,由题意1s =或2s =,即1s c =,又359p c c ==,代入()*式得19r c =. 因为数列{}n c 在2n ≥且*n N ∈上单调递减,且519c =,4r ≥,所以5r =. 综上所述,数列{}n c 中存在三项1c ,3c ,5c 或2c ,3c ,5c 构成等差数列.数学(理科)附加题说明:1. 以下题目的答案请直接填写在答卷上.2. 本卷总分40分,考试时间30分钟. 21. A. 连结AC ,因为EA 切圆O 于A ,所以EAB ACB ∠=∠.因为弧AB 与弧AD 长度相等,所以ACD ACB ∠=∠,AB AD =. 于是EAB ACD ∠=∠.又四边形ABCD 内接于圆O ,所以ABE D ∠=∠. 所以ABE CDA ∆∆:. 于是AB BECD DA=,即AB DA BE CD ⋅=⋅, 所以2AB BE CD =⋅.21. B. 解:由2132A ⎡⎤=⎢⎥⎣⎦,()det 223110A =⨯-⨯=≠,所以A 可逆,从而12132A --⎡⎤=⎢⎥-⎣⎦.由AX B =得到121413272X A B --⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦.12x y =⎧⎨=⎩, (也可由AX B =得到214327x y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即24327x y x y +=⎧⎨+=⎩,解得12x y =⎧⎨=⎩. C. 解:将直线l 化为普通方程为:60x y --=. 则()4cos ,3sin P θθ到直线l的距离d ==,其中3tan 4ϕ=. 所以当()cos1θϕ+=时,min 2d =,即点P 到直线l 的距离的最小值为2. D. 因为x ,y ,z 无为正数.所以12x y x y yz zx z y x z⎛⎫+=+≥ ⎪⎝⎭, 同理可得2y z zx xy x +≥,2z x xy yz y+≥, 当且仅当x y z ==时,以上三式等号都成立.将上述三个不等式两边分别相加,并除以2,得111x y z yz zx xy x y z++≥++. 22. 解:(1)以C 为坐标原点,分别以CA ,CB ,1CC 所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则()0,0,0C ,()4,0,0A ,(14,0,A ,(10,4,B . (1)因为113A M MB =,所以(M .所以(14,0,CA=u u u r ,(AM =-u u u u r.所以111cos ,CA AM CA AM CA AM⋅===u u u r u u u u ru u u r u u u u r u u u r u u u u r . 所以异面直线AM和1A C . (2)由()4,0,0A,()0,4,0B ,(10,0,C ,知()4,4,0AB =-u u u r,(1AC =-u u u u r .设平面1ABC 的法向量为(),,n a b c =r ,由100n AB n AC ⎧⋅=⎪⎨⋅=⎪⎩r u u u rr u u u u r得44040a b a -+=⎧⎪⎨-+=⎪⎩, 令1a =,则1b =,c =1ABC的一个法向量为(n =r.因为点M 在线段11A B上,所以可设(,4M x x -,所以(4,4AM x x =--u u u u r,因为直线AM 与平面1ABC 所成角为30︒,所以1cos ,sin 302n AM =︒=r u u u u r .由cos ,n AM n AM n AM ⋅=r u u u u r r u u u u r r u u u u r,得()()1141422x x ⋅-+⋅-+=, 解得2x =或6x =.因为点M 在线段11A B 上,所以2x =, 即点(2,2,M 是线段11A B 的中点.23.(1).解:设211,4x A x ⎛⎫ ⎪⎝⎭,222,4x B x ⎛⎫ ⎪⎝⎭,∵焦点()0,1F ,∴211,14x AF x ⎛⎫=-- ⎪⎝⎭u u u r ,222,14x FB x ⎛⎫=- ⎪⎝⎭u u u r ,∵AF FB λ=u u u r u u u r ,∴2212121144x x x x λλ⎛⎫-=- ⎪⎝⎭-=⎧⎪⎨⎪⎩消λ得22211211044x x x x ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,化简整理得()1212104x x x x ⎛⎫-+= ⎪⎝⎭,∵12x x ≠,∴124x x =-,∴221212144x x y y =⋅=. ∴12123OA OB x x y y ⋅=+=-u u u r u u u r(定值).(2)抛物线方程为214y x =,∴1'2y x =, ∴过抛物线A 、B 两点的切线方程分别为()2111124x y x x x =-+和()2222124x y x x x =-+,即211124x y x x =-和222124x y x x =-,联立解出两切线交点M 的坐标为12,12x x +⎛⎫-⎪⎝⎭,∴221221212,24x x x x FM AB x x ⎛⎫+-⎛⎫⋅=-- ⎪ ⎪⎝⎭⎝⎭u u u u r u u u r 22222121022x x x x -=--=(定值).。
江苏省南通市海安高级中学2020届高三下学期阶段考试数学试题含解析

2020届高三阶段性检测试题数学注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,包含填空题(共14题)、解答题(共6题),满分为160分,考试时间为120分钟.考试结束后,请将答题卡交回.2.答题前,请您务必将自己的姓名、考试证号等用书写黑色字迹的0.5毫米签字笔填写在答题卡上.3.作答试题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其它位置作答一律无效.如有作图需要,可用2B 铅笔作答,并请加黑、加粗,描写清楚. 参考公式:锥体的体积公式 13V Sh =锥体,其中S 为锥体的底面积,h 为高.球的体积公式343V R =π球,球的表面积公式24S R π=球,其中R 为球的半径. 一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上. 1.已知集合{}1,0,3A =-,{1,2,3}B =,则A B =_________.【答案】{3} 【解析】由交集的定义{3}A B ⋂=,应填答案{3}.2.已知复数z 满足()12i z i -=+,则复数z 的模为_______.【答案】102【解析】 【分析】由已知得21i z i+=-,将其整理成1322z i =+,即可求出模.【详解】解:由题意知, ()()()()2121313111222i i i i z i i i i ++++====+--+所以223211022z ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭. 故答案为:102. 【点睛】本题考查了复数的运算,考查了复数的模.本题的易错点在于化简时,错把2i 当成了1来计算.3.某人5次上班途中所用的时间(单位:分钟)分别为12,8,10,11,9.则这组数据的平均数为_______. 【答案】10 【解析】 【分析】代入求解平均数的公式计算即可. 【详解】解:平均数()112810119105=⨯++++=. 故答案为:10.【点睛】本题考查了平均数的计算.易错点为计算出错. 4.如图,是一个算法的流程图,则输出的b 的值为_______.【答案】4【解析】 【分析】根据流程框图进行循环计算,跳出循环时b 的值即为所求.【详解】解:第一次循环:2,2b a ==;第二次循环:4,3b a ==.此时3a < 不成立 故答案为:4.【点睛】本题考查了程序框图.对于循环结构是常考的题型,一般做法为根据框图,计算每次循环的结果,注意,临界即跳出循环时的计算结果.通常循环框图常和数列求和综合到一块.5.在平面直角坐标系xOy 中,已知双曲线221x y -=的右焦点与抛物线()220y px p =>的焦点重合,则p 的值为_______.【答案】【解析】 【分析】求出双曲线的右焦点),令2p=即可求出p 的值.【详解】解:双曲线2112c =+=,即右焦点为).即抛物线()220y px p =>的焦点为)所以2p=,解得p =.故答案为: 【点睛】本题考查了双曲线的标准方程,考查了抛物线的方程.易错点是误把p 当做了抛物线焦点的横坐标.6.已知一个口袋中有形状、大小都相同的5只球,其中3只白球,2只红球.从中一次随机摸出2只球,则这2只球颜色相同的概率为____. 【答案】0.4 【解析】 【分析】从中一次随机摸2只球,写出基本事件总数n 和这2只球颜色相同包含的基本事件数m ,由古典概型概率公式计算即可.【详解】一个口袋中有形状、大小都相同的5只球,其中3只白球,2只红球.从中一次随机摸出2只球,基本事件总数n =25C =10,这2只球颜色相同包含的基本事件个数m =2232C C +=4,∴这2只球颜色相同的概率为p =410m n ==0.4. 故答案为0.4.【点睛】本题考查古典概型概率的求法,考查运算求解能力,是基础题.7.现有一个橡皮泥制作的圆锥,底面半径为1,高为4.若将它制作成一个总体积不变的球,则该球的表面积为_______. 【答案】4π 【解析】 【分析】求出圆锥的体积,则由题意,设球的半径为r ,可得34433r π=π,求出球的半径,进而可求球的表面积.【详解】解:由题意知,圆锥的体积为2141433ππ⨯⨯⨯=.设球的半径为r 则34433r π=π,解得1r =.所以表面积244r ππ=.故答案为:4π.【点睛】本题考查了圆锥的体积,考查了球的体积,考查了球的表面积.结合方程的思想,根据题意求出球的半径.对于球的问题,一般都要首先明确半径的大小.8.已知等比数列{}n a 的前n 项的和为n S ,11a =,639S S =,则3a 的值为_______. 【答案】4 【解析】 【分析】由639S S =可得()33319S q S +=,进而可求出公比的值,即可求3a 的值.【详解】解:()3333612345612312331S a a a a a a a a a a q a q a q S q =+++++=+++++=+639S S = ()33319S q S ∴+= 解得,2q.所以2314a a q ==.故答案为:4.【点睛】本题考查了等比数列的通项公式,考查了等比数列的前n 项和.等比数列问题,一般可采用基本量法进行求解,但是这种方法计算量比较大.因此,对于等比数列的问题,一般首先考虑利用性质简化计算.9.已知1e ,2e 是夹角为60的两个单位向量,1232a e e =+,122b e ke =-()k R ∈,且a ⋅()8ab -=则k 的值为_______.【答案】67- 【解析】 【分析】由题意知()()()121212323228a a b e e e e e ke ⋅-=+⋅+-+=,进而可求k 的值.【详解】解:()()()()()121212121232322322a a b e e e e e ke e e e k e ⋅-=+⋅+-+=+⋅++⎡⎤⎣⎦()()()()221122733822+338cos60221182e k e e k e k k k =++⋅+=++++=+=. 解得67k =-. 故答案为:67-. 【点睛】本题考查了平面向量的数量积.对于向量的数量积问题,若题目中无向量的坐标,则在求数量积时,一般套用定义求解;若题目中已知了向量的坐标,求数量积时一般代入数量积的坐标公式.10.在平面直角坐标系xOy 中,已知圆22:280C x y x ++-=,直线():1,l y k x k R =-∈过定点A ,与圆C 交于点,B D ,过点A 作BC 的平行线交CD 于点E ,则AEC ∆的周长为_______. 【答案】5 【解析】 【分析】由题意得1,0A ,圆心为()1,0C -,半径为3r =,由平行可知EA EDCB CD=,化简后可得EA CE r +=,进而可求三角形的周长.【详解】解:当1x = 时,0y = 与k 无关,则1,0A .圆()2222:2819C x y x x y ++-=++=所以,圆的圆心为()1,0C -,半径为3r =.则由题意知,ED r CE =-EA 与CB 平行 EA ED CB CD ∴= 即 EA r CEr r-= EA CE r ∴+= 则AEC ∆的周长235AC AE CE AC r =++=+=+=. 故答案为:5.【点睛】本题考查了直线过定点的问题,考查了圆的标准方程.本题的关键在于,由平行得比例关系.若联立直线与圆的方程,求解各点的坐标,这种思路也可以求出最后答案,但计算量太大.11.如图,已知两座建筑物,AB CD 的高度分别为15m 和9m ,且AB BC CD >>,从建筑物AB 的顶部A 看建筑物CD 的张角为CAD ∠,测得6tan 13CAD ∠=,则,B C 间的距离_______m .【答案】12 【解析】 【分析】由()tan tan 6BC BAD DAC BAC ∠==∠+∠,可得613156611315BC BC BC +=-⨯,进而可求,B C 间的距离.【详解】解:由题意知()tan tan 6BC BCBAD DAC BAC AB CD ∠===∠+∠-6tan tan 1315661tan tan 11315BCBC DAC BACBCDAC BAC +∠+∠==-∠⨯∠-⨯,整理得22391800BC BC -+= ,解得12BC =或152BC =.9BC CD >=,12BC ∴=故答案为:12.【点睛】本题考查了三角恒等变换的应用.难点在于已知正切值的使用.有的同学可能由正切值求出正弦和余弦,结合正弦定理和余弦定理列出方程进行求解.由于本题所给的正切值求出的正弦余弦值数比较大,因此这种思路计算量较大,效率不高而且容易做错. 12.设曲线()0+1my m x =>在,1x t t =≠-处的切线为l ,则点()2,1P t -到l 的最大距离为_______.【解析】 【分析】求出切线方程为()2120mx t y mt m ++--=,从而则()2,1P t - 到l 的距离可用t 表示出来,结合基本不等式即可求解. 【详解】解:()2'1my x =-+ ()21l mk t ∴=-+ 则切线方程为()()211m m y x t t t -=--++ 整理得()2120mx t y mt m ++--=.则()2,1P t - 到l 的距离()()()()()242224222212121111t m m t m d m m t t t ++++===++++++ ()()222121m t m t ++≥+,当且仅当()()22211m t t +=+即1t =± 时等号成立2112d ∴≤+=即d ≤故答案为.【点睛】本题考查了切线的求解,考查了点到直线的距离,考查了基本不等式.求最值常见的思路有导数法、函数图像法、函数单调性法、基本不等式法.本题的难点是对距离进行变形整理. 13.已知函数3cos()2y x ππ=+,55,66x t t ⎡⎫⎛⎫∈>⎪⎪⎢⎣⎭⎝⎭既有最小值也有最大值,则实数t 的取值范围是_______. 【答案】31326t <≤或52t > 【解析】 【分析】由诱导公式可知3cos sin 2y x x πππ⎛⎫=+=⎪⎝⎭,令m x π=,结合函数图像,讨论最大值为12和1两种情况,进而求出t 的取值范围. 【详解】解:3cos sin 2y x x πππ⎛⎫=+=⎪⎝⎭ 令m x π=.则由55,66x t t ⎡⎫⎛⎫∈>⎪⎪⎢⎣⎭⎝⎭可得5,6m t ππ⎡⎫∈⎪⎢⎣⎭则5sin ,,6y m m t ππ⎡⎫=∈⎪⎢⎣⎭.要使其既有最小值又有最大值 若最大值为12 则31326t πππ<≤,解得31326t <≤若最大值为1,则52t ππ>,解得52t >.综上所述: 31326t <≤或52t >. 故答案为:31326t <≤或52t >. 【点睛】本题考查了诱导公式,考查了三角函数最值问题.本题的易错点是漏解,只考虑了最大值为1的情况.本题的难点是分界点能否取得的判断.14.已知函数1()1f x x =-,11()(())k k f x f f x +=,5k ≤,k *∈N .若函数()ln k y f x x =-恰有3个不同的零点,则k 的取值集合为_______. 【答案】{3,5} 【解析】 【分析】由题意写出12345(),(),(),(),()f x f x f x f x f x 的解析式,根据图像的平移变换,分别画出它们的图像,判断哪个函数图像与ln y x = 图像有三个交点,即为所求.【详解】解:由题意知1()1f x x =-,2()11f x x =--,3()111f x x =---,4()1111f x x =----,5()11111f x x =-----.则其函数图像为由图像可知,当3k =或5时, 函数()ln k y f x x =-恰有3个不同的零点. 故答案为: {3,5}.【点睛】本题考查了函数的图像变换,考查了函数的零点.若函数()()()f x g x h x =-,则函数()f x 的零点个数就等同于函数(),()g x h x 图像的交点个数.本题的难点是画含绝对值的函数图像.对于()y f x =,首先画出()y f x = 的图像,然后将x 轴下方的图像向上翻折即可;对于()y f x = 的图像,首先画出()y f x = 的图像,然后将y 轴右侧向左翻折. 二、解答题:本大题共6小题,共计90分. 15.在平面直角坐标系xOy 中,设向量()()[]3sin ,sin ,cos ,sin ,0,a x x b x x x π==∈.(1)若a b =,求x 的值;(2)求a b ⋅的最大值及取得最大值时x 的值. 【答案】(1)6π或56π;(2)最大值32,3x π=. 【解析】 【分析】(1)求出||,||a b ,由||||a b =可得1|sin |2x =,结合[0,]x π∈可求出所求. (2) 1sin 262a b x π⎛⎫⋅=-+ ⎪⎝⎭,结合[0,]x π∈和正弦函数的图像,即可分析出最值及取得最大值时x 的值.【详解】解:(1)因为(3sin ,sin ),(cos ,sin )a x x b x x == 所以2222||3sin sin 2|sin |,||cos sin 1a x x x b x x =+==+=因为||||a b =,所以1|sin |2x =.因为[0,]x π∈,所以1sin 2x =于是6x π=或56π. (2)23sin cos sin a b x x x ⋅=+311sin 2cos 222x x =-+1sin 262x π⎛⎫=-+ ⎪⎝⎭因为[0,]x π∈,所以112,666x πππ⎡⎤-∈-⎢⎥⎣⎦,于是113sin 22622x π⎛⎫-≤-+≤ ⎪⎝⎭. 所以当226x ππ-=,即3x π=时,a b ⋅取最大值32. 【点睛】本题考查了向量的模,考查了向量的数量积,考查了三角恒等变换,考查了三角函数的最值.对于()sin y A ωx φ=+ 型的函数,在求最值、对称轴、对称中心、单调区间时,一般都是采取整体的思想进行计算.16.如图,在正方体1111ABCD A B C D -中,E 是棱1A A 的中点.求证:(1)AC//平面1EDB ; (2)平面1EDB ⊥平面1B BD .【答案】(1)证明见解析;(2)证明见解析. 【解析】 【分析】(1)取1B D 的中点F ,连,OF EF ,通过证明//AC EF 从而证明线面平行.(2)通过AC BD ⊥,1B B AC ⊥推出1EF BB ⊥,EF BD ⊥,从而证明EF ⊥平面1B BD ,进而可证面面垂直.【详解】证明:(1)在正方体1111ABCD A B C D -中,设AC 与BD 相交于点O ,则O 为BD 的中点取1B D 的中点F ,连,OF EF .所以1OF//BB ,112OF BB =.在正方体1111ABCD A B C D -中,1111,//AA BB AA BB =.又点E 是1A A 的中点 所以,//AE OF AE OF =.于是四边形AEFO 是平行四边形,从而//AC EF . 又因为AC ⊄平面1EDB ,EF ⊂平面1EDB ,所以//AC 平面1EDB .(2)在正方体1111ABCD A B C D -中,1B B ⊥平面ABCD ,而AC ⊂平面ABCD , 所以1B B AC ⊥.又在正方体1111ABCD A B C D -中,四边形ABCD 正方形所以AC BD ⊥.由(1)知,//EF AC ,于是1EF BB ⊥,EF BD ⊥.又1B B ⊂平面1B BD ,BD ⊂平面1B BD ,1B B BD B ⋂=,所以EF ⊥平面1B BD . 又因为EF ⊂平面1EDB ,所以平面1EDB ⊥平面1B BD .【点睛】本题考查了线面平行的判定,考查了面面垂直的判定.线面平行或者面面平行的判定,一般都归结为证明线线平行;线面垂直或者面面垂直的判定,一般都归结为证明线线垂直.此类问题如果采用逻辑推理的方法无法证明,有时也可以建立空间直角坐标系,运用空间向量证明平行和垂直.17.如图,在平面直角坐标系xOy 中,已知,A B 两点分别为椭圆22221,0x y a b a b+=>>的右顶点和上顶点,且7AB =,右准线l 的方程为4x =.(1)求椭圆的标准方程;(2)过点A 的直线交椭圆于另一点P ,交l 于点Q .若以PQ 为直径的圆经过原点,求直线PQ的方程.【答案】(1)22143x y +=0y --=0y +-=.【解析】 【分析】(1)由右准线l 的方程为4x =以及AB =可列出方程组22224a c a b c ⎧=⎪⎪⎪=+⎨=⎩解得即可求出椭圆的方程.(2) 设PQ 的方程为(2)y k x =-,与椭圆方程联立,求出2228612,4343k k P k k ⎛⎫-- ⎪++⎝⎭;联立(2)4y k x x =-⎧⎨=⎩可得(4,2)Q k ,由OP OQ ⊥可知0OP OQ ⋅=,从而可求出k =进而可求直线的方程.【详解】解:(1)设椭圆的焦距为2(0)c c >.由题意得22224a c a b c ⎧=⎪⎪⎪=+⎨=⎩,解得224,3a b ==.所以椭圆的标准方程为:22143x y +=.(2)由题意得直线PQ 不垂直于x 轴,设PQ 的方程为(2)y k x =-联立22(2),1,43y k x x y =-⎧⎪⎨+=⎪⎩,消y 得()2222431616120k x k x k +-+-=.又直线PQ 过点(2,0)A ,则方程必有一根为2,则228643P k x k -=+. 代入直线(2)y k x =-,得点2228612,4343k k P k k ⎛⎫-- ⎪++⎝⎭.联立(2)4y k x x =-⎧⎨=⎩,所以(4,2)Q k .又以PQ 为直径的圆过原点,所以OPOQ ⊥.则222228612824420434343k k k OP OQ k k k k ---⋅=⋅+⋅==+++,解得23k =,所以3k =±. 所以直线PQ 的方程为3230x y --=或3230x y +-=.【点睛】本题考查了椭圆的准线方程,考查了椭圆的性质,考查了直线与椭圆相交问题,考查了向量的数量积.本题第二问的难点在于圆过原点这一条件得运用.一般若题目中已知圆过某点,则一般等量关系为:圆心到该点的距离为半径或者圆上两点与已知点的连线垂直.18.下图是一块平行四边形园地ABCD ,经测量,20,10,AB m BC m ==120ABC ∠=.拟过线段AB 上一点E 设计一条直路EF (点F 在四边形ABCD 的边上,不计直路的宽度),将该园地分为面积之比为3:1的左,右两部分分别种植不同花卉.设,EB x EF y ==(单位:m ).(1)当点F 与点C 重合时,试确定点E 的位置; (2)求y 关于x 的函数关系式;(3)试确定点,E F 的位置,使直路EF 的长度最短.【答案】(1)E 是AB 的中点;(2)2222525010100001001020x x x y x x x ⎧-+≤<⎪=⎨++≤≤⎪⎩;(3) 当2.5EB m =,7.5FC m =时,EF 最短,其长度为53.【解析】 【分析】 (1)由14BEC ABCD S S ∆=可知1124EB h AB h ⋅=⋅,从而证明E 是AB 的中点. (2)求出平行四边形的面积为1003ABCDS=,进而可求253EBF S ∆=从而用x 可将BF表示出来,利用余弦定理即可得到y 关于x 的函数关系式.(3)当 010x ≤<,由二次函数的性质可求最值;当1020x ≤≤时,由基本不等式可求最值. 【详解】解:(1)当点F 与点C 重合时,由题设知,14BEC ABCDS S ∆=.于是1124EB h AB h ⋅=⋅,其中h 为平行四边形AB 边上的高. 得12EB AB =,即点E 是AB 的中点.(2)因为点E 在线段AB 上,所以020x ≤≤.当1020x ≤≤时,由(1)知 点F 在线段BC 上.因为20,10,120AB m BC m ABC ︒==∠=所以sin 20102ABCDSAB BC ABC =⋅⋅∠=⨯⨯=.由1sin1202EBF S x BF ︒∆=⋅⋅=,100BF x=.所以EBF ∆中,由余弦定理得y EF ===当010x ≤<时,点F 在线段CD 上,由1()10sin 602EBCF S x CF ︒=+⨯⨯=四边形得10CF x =-.当BE CF ≥时,EF =当BE CF <时,EF =化简均为y EF ==综上,0101020x y x ⎧≤<=≤≤. (3)当010x ≤<时,y ==于是当52x =时,min y =,此时15102CF x =-=. 当1020x ≤≤时,y =≥=当且仅当22100=00x x ,即10x =时,取等号 综上: 当E 距点 2.5B m ,F 距点7.5C m 时,EF最短,其长度为.【点睛】本题考查了函数模型的应用,考查了余弦定理,考查了基本不等式.本题的易错点是没有讨论自变量的取值,从而造成了漏解.求最值时,常用的方法有:导数法、函数图像法、函数单调性法、基本不等式法.19.已知函数()y f x =的定义域为D ,若满足,()()x D x f x f x ∀∈⋅≥,则称函数()f x 为“L 型函数”.(1)判断函数xy e =和ln y x =是否为“L 型函数”,并说明理由;(2)设函数()(1)ln (1)ln ,0f x x x x a a =+-->,记()g x 为函数()f x 的导函数. ①若函数()g x 的最小值为1,求a 的值; ②若函数()f x 为“L 型函数”,求a 的取值范围.【答案】(1)xy e =不是,ln y x =是,理由见解析;(2)①a e =;②20a e <≤.【解析】 【分析】(1)分别求出两个函数的定义域,判断,()()x D x f x f x ∀∈⋅≥即可. (2) ①求出1()()ln 1ln ,(0,)g x f x x a x x'==++-∈+∞,再求()g x ',通过导数探究当x 取何值时,()g x 取最小值,令最小值为1,即可求出a 的值.②由题意(0,),(1)()(1)[(1)ln (1)ln ]0x x f x x x x x a ∀∈+∞-=-+--≥恒成立,分别讨论当20a e <≤和2a e >时,通过探究()f x 的单调性判断是否使得不等式恒成立,从而求出a 的取值范围.【详解】解:(1)对于函数xy e =,定义域为R ,显然000e e ⋅≥不成立,所以xy e =不是“L 型函数”;对于函数ln y x =,定义域为(0,)+∞.当01x <<时,ln 0x <,所以(1)ln 0x x ->,即ln ln x x x >; 当1x ≥时,ln 0x ≥,所以(1)ln 0x x -≥,即ln ln x x x ≥.所以(0,)x ∀∈+∞,都有ln ln x x x ≥.所以函数ln y x =是“L 型函数”. (2)①因为11()()ln ln ln 1ln ,(0,)x g x f x x a x a x x x+'==+-=++-∈+∞ 所以22111()x g x x x x-'=-=.当(0,1)x ∈时,()0g x '<,所以()g x 在(0,1)上为减函数;当(1,)x ∈+∞时,()0g x '>,所以()g x 在(1,)+∞上为增函数. 所以min ()(1)2ln g x g a ==-.所以2ln 1a -=,故a e =. ②因为函数()(1)ln (1)ln f x x x x a =+--为“L 型函数”,所以(0,),(1)()(1)[(1)ln (1)ln ]0x x f x x x x x a ∀∈+∞-=-+--≥(*). (ⅰ)当2ln 0a -≥,即20a e <≤时,由①得()0g x ≥,即()0f x '≥. 所以()f x 在(0,)+∞上增函数,又(1)0f =,当(0,1)x ∈时,()0f x <所以(1)()0x f x ->;当[1,)x ∈+∞时,()0f x ≥,所以(1)()0x f x -≥. 所以(0,)x ∀∈+∞,适合(*)式.(ⅱ)当2ln 0a -<,即2a e >时,(1)0g <,1()10g a a=+>. 所以由零点存在性定理得0(1,)x a ∃∈,使()00g x =,又()g x 在(1,)+∞上为增函数 所以当()01,x x ∈时,()0<g x ,所以()f x 在()01,x 上为减函数又(1)0f =,所以当()01,x x ∈时,()0f x <,所以(1)()0x f x -<,不适合(*)式. 综上得,实数a 的取值范围为20a e <≤.【点睛】本题考查了不等式的性质,考查了函数的最值,考查了不等式恒成立问题.本题的难点在于最后一问,学生往往想不起来通过函数的单调性等来判断函数在某一区间的正负问题. 20.已知数列{}n a 的首项为1,各项均为正数,其前n 项和为n S ,112n nn n na a S a a ++=-,n *∈N .(1)求2a ,3a 的值;(2)求证:数列{}n a 为等差数列;(3)设数列{}n b 满足11b =,1n n n b b a +=,求证:111ni ib =≥∑. 【答案】(1)22a =,33a =;(2)证明见解析;(3)证明见解析. 【解析】 【分析】(1)令1,2n n == 即可求出2a ,3a 的值; (2)由112n n n n na a S a a ++=-得1112(2)n n n n n a a S n a a ---=≥-两式相减进行整理可得11(2)n n n n a a a a n +--=-≥,即可证明{}n a 为等差数列.(3)由(2)可知1n n b b n +=,11(2)n n b b n n -=-≥两式相减整理得111(2)n n nb b n b +-=-≥,则当2n ≥时,12111231111111nn n i i n b b b b b b b b b b +==++++=--++∑,通过放缩即可证明; 当1n =时,111b ≥.从而可证.【详解】解:(1)令1n =得,211212a a S a a =-,又11a =,解得22a =;令2n =得,122322a a S a a =-,即()1123222a a a a +=-,从而33a =. (2)因为112n n n n na a S a a ++=- ①;所以1112(2)n n n n n a a S n a a ---=≥- ② ①-②得,11112n n n n n n n n n a a a aa a a a a +-+-=---.因为数列{}n a 的各项均为正数,所以0n a >.从而11112n n n n n n a a a a a a +-+-=---.去分母得,()()()()1111112n n n n n n n n n n a a a a a a a a a a +----+--=---化简并整理得,21120n n n n n a a a a a +--+=,即112(2)n n n a a a n --=+≥,所以11(2)n n n n a a a a n +--=-≥.所以数列{}n a 为等差数列.(3)由(2)知,1n n b b n += ③.当1n =时,211b b =,又11b =,所以21b =. 由③知,11(2)n n b b n n -=-≥ ④.③-④得,111(2)n n n n b b b b n +--=≥ 即()111(2)n n n b b b n +--=≥,依题意,0n b ≠,所以111(2)n n nb b n b +-=-≥.当2n ≥时,112311111ni inb b b b b ==++++∑ 31425321111n n n n b b b b b b b b b b b -+-=+-+-+-++-+-12111n n b b b b b +=--++ 121n n b b +≥-21n a =-,当1n =时,111b ≥,原不等式也成立.综上得,1121nn i ia b =≥-∑. 【点睛】本题考查了由递推公式求项,考查了等差数列的定义,考查了放缩法,考查了数列求和.本题难点在于整理出111(2)n n nb b n b +-=-≥,从而对所证式子进行化简.涉及到n S 和n a 的递推公式时,一般代入公式11,1,2n n n a n a S S n -=⎧=⎨-≥⎩ 进行求解.Ⅱ(附加题)注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共2页,均为非选择题(第21~23题).本卷满分为40分,考试时间为30分钟.考试结束后,请将答题卡交回.2.答题前,请您务必将自己的姓名、考试证号等用书写黑色字迹的0.5毫米签字笔填写在答题卡上,并用2B 铅笔正确填涂考试号.3.作答试题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其它位置作答一律无效.如有作图需要,可用2B 铅笔作答,并请加黑、加粗,描写清楚.21.已知a ,b R ∈,若M =13a b -⎡⎤⎢⎥⎣⎦所对应的变换T M 把直线2x-y=3变换成自身,试求实数a ,b . 【答案】【解析】 【详解】设则即此直线即为则..22.在极坐标系中,设P 为曲线C :2ρ=上任意一点,求点P 到直线l :sin 33πρθ⎛⎫-= ⎪⎝⎭的最大距离. 【答案】5 【解析】 【分析】将圆C 和直线l 的极坐标方程化为直角坐标方程,转化为求圆上的点到直线l 距离的最大值,求出圆心到直线l 距离,即可求出结论.【详解】曲线C :2ρ=化直角坐标方程为224x y +=表示圆,13sin 3,sin cos 332πρθρθθ⎛⎫-== ⎪⎝⎭, 360x y -+=,圆C 上点P 到直线l 2225(3)1+=+.【点睛】本题考查极坐标方程与直角坐标方程互化、圆上点到直线距离的最值,考查数形结合思想,属于基础题.23.设a,b,c 为正实数,6a b c ++=1233a b c ++. 【答案】证明见解析 【解析】 【分析】根据柯西不等式()()()2222222112233123123x y x y x y x x x y y y ++≤++++,将原式进行配凑并结合已知条件6a b c ++=加以计算,即可得证;【详解】证明:因为a,b,c 为正实数,6a b c ++=,所以)22111=+ ()()1211127a b c ≤++++++=33,当且仅当==,即3a =,2b =,1c =时取等号,33,得证;【点睛】本题考查利用柯西不等式证明不等式,属于中档题.【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.24.假定某篮球运动员每次投篮命中率均为(01)p p <<.现有3次投篮机会,并规定连续两次投篮均不中即终止投篮,已知该运动员不放弃任何一次投篮机会,且恰好用完3次投篮机会的概率是2125. (1)求p 的值;(2)设该运动员投篮命中次数为X ,求X 的概率分布及数学期望()E X .【答案】(1)35;(2)分布列见解析,期望为213125. 【解析】分析:(1)设事件A :“恰用完3次投篮机会”,则其对立事件A :“前两次投篮均不中”, 所以, ()()1P A P A =- ()2211125p =--=(2) X 的所有可能值为0,1,2,3,计算其对应概率即可.详解:(1)设事件A :“恰用完3次投篮机会”,则其对立事件A :“前两次投篮均不中”, 依题意, ()()1P A P A =- ()2211125p =--=, 解得35p =. (2)依题意, X 的所有可能值为0,1,2,3,且()()240125P X p ==-=, ()()211P X p p ==- ()()2411125p p p +--=, ()3273125P X p ===, 故()()210P X P X ==-= ()()5413125P X P X -=-==. X 的概率分布列为:数学期望()242125E X =+⨯ 54272133125125125+⨯=. 点睛:利用对立事件计算概率是概率问题中长用的方法,所以出现“至多”“至少”等其他关键字眼时要注意利用对立事件的思路解题,往往能够简化计算.25.设4124k k S a a a =+++(*N k ∈),其中{}0,1i a ∈(1,2,,4i k =).当4k S 除以4的余数是b (0,1,2,3b =)时,数列124,,,k a a a 的个数记为()m b . (1)当2k =时,求()1m 的值;(2)求()3m 关于k 的表达式,并化简.【答案】(1)64;(2)()2134k m -=【解析】分析】 (1)(1)根据定义,确定条件:8个数的和除以4的余数是1,因此有1个1或5个1,其余为0,从而158864m C C =+=;(2)个数的和除以4的余数是3,因此有3个1,或7个1,或11个1,…,或()41k -个1 ,其余为0,()37114144443k k k k k m C C C C -=++++,再根据组合数性质即可化简求值. 【详解】(1)当2k =时,数列123,,,,n a a a a 中有1个1或5个1,其余为0,所以158864m C C =+=. (2)依题意,数列124,,,k a a a 中有3个1,或7个1,或11个1,…,或()41k -个1 ,其余为0,所以()37114144443k k k k k m C C C C -=++++.同理,得()1594344441k k k k km C C C C -=++++. 因为()4443,7,11,,41i k i k k C C i k -==-,所以()()13m m =.又()()13943414144444132k k k k k k k km m C C C C C ---+=+++++=, 所以()4221324k k m --==【点睛】本题考查组合数的性质,组合数的运算,属中档题.。
2020届江苏省南通市海安高级中学高三下学期模拟考试数学试题解析版

2020届江苏省南通市海安高级中学高三下学期模拟考试数学试题一、填空题1.已知全集2,1,0,1,{}2U =﹣﹣,集合2,,}1,{1A =﹣﹣则UA =_____.【答案】{}0,2【解析】根据补集的定义求解即可. 【详解】解:2,1,0,1,2{}{,2,1,1,}U A =﹣﹣=﹣﹣ {}0,2U A ∴=.故答案为{}0,2. 【点睛】本题主要考查了补集的运算,属于基础题.2.已知复数()()1z i a i =⋅+-(i 为虚数单位)为纯虚数,则实数a 的值为_____. 【答案】1﹣【解析】利用复数的乘法求解z 再根据纯虚数的定义求解即可. 【详解】解:复数()()()111z i a i a a i ⋅+++=﹣=﹣为纯虚数, 10,10,a a ∴+≠=﹣解得1a =﹣. 故答案为:1﹣. 【点睛】本题主要考查了根据复数为纯虚数求解参数的问题,属于基础题. 3.数据1,3,5,7,9的标准差为_____.【答案】【解析】先计算平均数再求解方差与标准差即可. 【详解】解:样本的平均数1357955x ++++==,∴这组数据的方差是()()()()()222222115355575955S ⎡⎤=-+-+-+-+-⎣⎦ 28,S ∴=标准差22S =, 故答案为:22 【点睛】本题主要考查了标准差的计算,属于基础题. 4.函数()12x f x =-的定义域是__________. 【答案】(],0-∞【解析】由120x -≥,得21x ≤,所以0x ≤,所以原函数定义域为(],0-∞,故答案为(],0-∞.5.在一底面半径和高都是2m 的圆柱形容器中盛满小麦,有一粒带麦锈病的种子混入了其中.现从中随机取出的32m 种子,则取出了带麦锈病种子的概率是_____. 【答案】14π【解析】求解32m 占圆柱形容器的的总容积的比例求解即可. 【详解】解:由题意可得:取出了带麦锈病种子的概率221224ππ==⨯⨯.故答案为:14π. 【点睛】本题主要考查了体积类的几何概型问题,属于基础题.6.如图是一个算法伪代码,则输出的i 的值为_______________.【答案】5【解析】执行循环结构流程图,即得结果. 【详解】执行循环结构流程图得9123410S =----=-<,结束循环,输出415i =+=. 【点睛】本题考查循环结构流程图,考查基本分析与运算能力,属基础题.7.在平面直角坐标系xOy 中,若双曲线()22210y x b b-=>经过点(3,4),则该双曲线的准线方程为_____.【答案】3x ±= 【解析】代入()3,4求解得b ,再求准线方程即可. 【详解】解:双曲线()22210y x b b-=>经过点()3,4,221631b∴=﹣,解得22b =,即b .又1,a ∴=c ==故该双曲线的准线方程为:3x ±= .故答案为:3x ±=. 【点睛】本题主要考查了双曲线的准线方程求解,属于基础题.8.设n S 是等比数列{}n a 的前n 项的和,396,,S S S 成等差数列,则258a a a +的值为_____. 【答案】2【解析】设等比数列{}n a 的公比设为,q 再根据396,,S S S 成等差数列利用基本量法求解,q 再根据等比数列各项间的关系求解258a a a +即可. 【详解】解:等比数列{}n a 的公比设为,q396,,S S S 成等差数列,可得9362,S S S +=若1,q =则1111836,a a a += 显然不成立,故1,q ≠则()()()9361111112111a q a q a q qqq---⋅=+---,化为6321,q q +=解得312q =﹣,则43251176811112214a a a q a q qa a q q -+++====故答案为:2. 【点睛】本题主要考查了等比数列的基本量求解以及运用,属于中档题.9.给出下列四个命题,其中正确命题的序号是______.(写出所有正确命题的序号) ①因为当3x π=时,2sin sin 3x x π⎛⎫+≠⎪⎝⎭,所以23π不是函数sin y x =的周期; ②对于定义在R 上的函数()f x ,若()()22f f -≠,则函数()f x 不是偶函数; ③“M N >”是“22log log M N >”成立的充分必要条件; ④若实数a 满足24a <,则2a ≤. 【答案】①②④.【解析】由周期函数的定义判断①;由偶函数的概念判断②;由充分必要条件的判定判断③;求解一元二次不等式判断④. 【详解】 因为当3x π=时,2sin sin 3x x π⎛⎫+≠ ⎪⎝⎭,所以由周期函数的定义知23π不是函数sin y x =的周期,故①正确;对于定义在R 上的函数()f x ,若()()22f f -≠,由偶函数的定义知函数()f x 不是偶函数,故②正确;由M N >,不一定有22log log M N >,反之成立,则“M N >”是“22log log M N >”成立的必要不充分条件,故③错误;若实数a 满足24a <,则22a -≤≤,所以2a ≤成立,故④正确. ∴正确命题的序号是①②④. 故答案为:①②④. 【点睛】本题考查命题的真假判断与应用,考查逻辑思维能力与推理论证能力,是中档题. 10.如图,是一个四棱锥的平面展开图,其中间是边长为2的正方形,上面三角形是等边三角形,左、右三角形是等腰直角三角形,则此四棱锥的体积为_____.【答案】43【解析】画图直观图可得该几何体为棱锥,再计算高求解体积即可. 【详解】解:如图,是一个四棱锥的平面展开图,其中间是边长为2的正方形,上面三角形是等边三角形,左、右三角形是等腰直角三角形,∴此四棱锥S ABCD ﹣中,ABCD 是边长为2的正方形,SAD 是边长为2的等边三角形,故CD AD ⊥,又CD SD ⊥,AD SD D ⋂= 故平面SAD ⊥平面ABCD ,∴SAD 的高SE 是四棱锥S ABCD ﹣的高, ∴此四棱锥的体积为:112233ABCD V S SE ⨯=⨯⨯=正方形=故答案为:3. 【点睛】本题主要考查了四棱锥中的长度计算以及垂直的判定和体积计算等,需要根据题意11.在平面直角坐标系xOy 中,若函数()f x lnx ax =﹣在1x =处的切线与圆22210C x x y a ++:﹣﹣=存在公共点,则实数a 的取值范围为_____.【答案】(][)0,12,+∞【解析】利用导数的几何意义可求得函数()f x lnx ax =﹣在1x =处的切线,再根据切线与圆存在公共点,利用圆心到直线的距离满足的条件列式求解即可. 【详解】解:由条件得到()1'f x a x=- 又()()1,'11f a f a =-=-所以函数在1x =处的切线为()()()1111y a x a a x =﹣﹣-=﹣﹣, 即()110a x y ﹣﹣﹣= 圆C 方程整理可得:()221x y a -+= 即有圆心()1,0C 且0a > 所以圆心到直线的距离d ==≤,≤解得2a ≥或01≤<a , 故答案为:(][)0,12,+∞.【点睛】本题主要考查了导数的几何意义求解切线方程的问题,同时也考查了根据直线与圆的位置关系求解参数范围的问题,属于基础题.12.已知函数()32,f x ax bx cx ++=若关于x 的不等式()0f x <的解集是()(),10,2∞⋃﹣﹣,则b ca+的值为_____. 【答案】3-【解析】根据题意可知20ax bx c ++=的两根为1,2-,再根据解集的区间端点得出参数的关系,再求解b ca+即可. 【详解】解:因为函数()()322f x ax bx cx x ax bx c =++=++,关于x 的不等式()0f x <的解集是()(),10,2-∞-⋃20ax bx c ∴++=的两根为:1﹣和2;所以有:()12ba +﹣=-且()12c a⨯﹣=; b a ∴=﹣且2c a =﹣;23b c a aa a+--∴==-; 故答案为:3﹣ 【点睛】本题主要考查了不等式的解集与参数之间的关系,属于基础题.13.在边长为4的菱形ABCD 中,60,A ︒=点P 在菱形ABCD 所在的平面内.若3,PA PC =PB PD ⋅=_____.【答案】1-【解析】以菱形的中心为坐标原点建立平面直角坐标系,再设(),P x y ,根据3,PA PC =P 的坐标,进而求得PB PD ⋅即可.【详解】解:连接,,AC BD 设,AC BD 交于点,O 以点O 为原点, 分别以直线,OC OD 为,x y 轴,建立如图所示的平面直角坐标系,则:()23,23()0202()(),A C B D --,,,,,, 设(),P x y321,PA PC ==,((2222392321x y x y ⎧++=⎪∴⎨⎪-+=⎩①﹣②得,312,x =-解得3x =, 32y ∴=±, 332P ⎛⎫∴- ⎪ ⎪⎝⎭或332P ⎛⎫ ⎪ ⎪⎝⎭,显然得出的PB PD ⋅是定值,∴取332P ⎛⎫ ⎪ ⎪⎝⎭则3731,,,2222PB PD ⎛⎫⎛⎫-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 37144PB PD ∴⋅=-=-. 故答案为:1-. 【点睛】本题主要考查了建立平面直角坐标系求解向量数量积的有关问题,属于中档题.14.设函数()21722,04,k x x f x x x ⎧+⎛⎫-+≤⎪ ⎪=⎝⎭⎨⎪>⎩,()43g x k x ⎛⎫⎪⎝⎭=-,其中0k >.若存在唯一的整数,x 使得()()f x g x <,则实数k 的取值范围是_____. 【答案】17[3,6] 【解析】根据分段函数的解析式画出图像,再根据存在唯一的整数x 使得()()f x g x <数形结合列出临界条件满足的关系式求解即可. 【详解】解:函数()21722,04,0k x x f x x x ⎧+⎛⎫-+≤⎪ ⎪=⎝⎭⎨⎪>⎩,且0,k > 画出()f x 的图象如下:因为()43g x k x ⎛⎫=-⎪⎝⎭,且存在唯一的整数,x 使得()()f x g x <, 故()g x 与()f x 在0x <时无交点,174k k +∴≥,得173k ≥; 又()43g x k x ⎛⎫=-⎪⎝⎭,()g x ∴过定点4,03⎛⎫⎪⎝⎭又由图像可知,若存在唯一的整数x 使得()()f x g x <时43x >,所以2x ≥ ()()58533939g k f ≥≥==,∴存在唯一的整数3,x =使得()()f x g x <所以()()22243g k f =≤=6k ⇒≤ ()()844163g k f ∴≤==6k ⇒≤.根据图像可知,当4x ≥时, ()()f x g x >恒成立.综上所述, 存在唯一的整数3,x =使得()()f x g x <,此时1763k ≤≤ 故答案为:17[3,6] 【点睛】本题主要考查了数形结合分析参数范围的问题,需要根据题意分别分析定点4,03⎛⎫ ⎪⎝⎭右边的整数点中3x =为满足条件的唯一整数,再数形结合列出2,4x =时的不等式求k 的范围.属于难题.二、解答题15.如图,四棱锥P ABCD -中,底面ABCD 是菱形,对角线,AC BD 交于点,O M 为棱PD 的中点,MA MC =.求证:(1)//PB 平面AMC ; (2)平面PBD ⊥平面AMC . 【答案】(1)详见解析;(2)详见解析.【解析】(1) 连结,OM 根据中位线的性质证明//PB OM 即可. (2) 证明AC BD ⊥,AC PD ⊥再证明AC ⊥平面PBD 即可.【详解】解:()1证明:连结,OMO 是菱形ABCD 对角线AC BD 、的交点,O ∴为BD 的中点, M 是棱PD 的中点, //,OM PB ∴OM ⊂平面,AMC PB ⊄平面,AMC//PB ∴平面,AMC()2解:在菱形ABCD 中,,AC BD ⊥且O 为AC 的中点,,MA MC =AC OM ∴⊥, OM BD O ⋂=, AC ∴⊥平面,PBD AC ⊂平面AMC ,∴平面PBD ⊥平面AMC .【点睛】本题主要考查了线面平行与垂直的判定,属于基础题.16.在锐角三角形ABC 中,角,,A B C 的对边分别为,,a b c .已知tan ,tan ,tan A B C 成等差数列,cos cos ,cos A C B 成等比数列. (1)求A 的值;(2)若ABC 的面积为1,求c 的值. 【答案】(1)4A π=;(2)3c =【解析】(1)根据,,tanA tanB tanC 成等差数列与三角形内角和可知()tanC tan A B =-+,再利用两角和的正切公式,代入2,tanB tanA tanC +=化简可得22tan tan tan 3A B A -=,同理根据三角形内角和与余弦的两角和公式与等比数列的性质可求得2tanAtanB =,联立即可求解求A 的值.(2)由(1)可知2,tan 3tanB C ==,再根据同角三角函数的关系与正弦定理可求得b ,再结合ABC 的面积为1,利用面积公式求解即可. 【详解】解:()1,,tanA tanB tanC 成等差数列, 可得2,tanB tanA tanC += 而()1tanA tanB tanC tan A B tanAtanB +=-+-=,即tan tan 2tan tan tan tan 1A BB A A B +-=-,展开化简得222tan tan 2tan tan tan tan A B B A B B --=,因为tan 0B ≠,故 22tan tan tan 3A B A -=①又cosA cosB 成等比数列,可得()cosAcosB cosC cos A B sinAsinB cosAcosB +==-=-, 即2sinAsinB cosAcosB =, 可得2,tanAtanB =②联立①②解得1tanA =(负的舍去), 可得锐角4A π=;()2由()1可得2,3tanB tanC ==,由sin 2cos BtanB B ==22,1,sin B cos B B +=为锐角,解得5sinB =,因为sin 3cos C tanC C ==22,1,sin C cos C C +=为锐角,故可得sinC ,由正弦定理可得sin2253sin10c Bb c cC===,又ABC的面积为1,可得21122212232bcsinA c⋅⋅==,解得3c=.【点睛】本题主要考查了等差等比中项的运用以及正切的和差角公式以及同角三角函数关系等.同时也考查了正弦定理与面积公式在解三角形中的运用,属于中档题.17.某房地产开发商在其开发的某小区前修建了一个弓形景观湖.如图,该弓形所在的圆是以AB为直径的圆,且300AB=米,景观湖边界CD与AB平行且它们间的距离为502米.开发商计划从A点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作PQ.设2AOPθ∠=.(1)用θ表示线段,PQ并确定sin2θ的范围;(2)为了使小区居民可以充分地欣赏湖景,所以要将PQ的长度设计到最长,求PQ的最大值.【答案】(1)502300sincosPQθθ-=2sin21θ<≤;(2)6.【解析】(1)过点Q作QH AB⊥于点,H再在AOP中利用正弦定理求解AP,再根据sin2QHAQπθ⎛⎫-⎪⎝⎭=求解AQ,进而求得PQ.再根据0PQ>确定sin2θ的范围即可.(2)根据(1)有150232cosPQ sinθθ⎫=-⎪⎭,再设()132cosf sinθθθ=-,求导分析函数的单调性与最值即可. 【详解】 解:()1过点Q 作QH AB ⊥于点,H 则502QH =在AOP 中,150,2OA OP AOP θ∠===,2OAP πθ∴∠-=, 由正弦定理得:sin 2sin 2OP APπθθ=⎛⎫- ⎪⎝⎭,300AP sin θ∴=,502cos sin 2QH AQ πθθ∴=⎛⎫- ⎪⎝⎭=, 502==300cos PQ AP AQ sin θθ∴--, 5023000cos PQ sin θθ->=,因为cos 0θ>, 化简得2sin 213θ<≤ ()2502130050232cos PQ sin sin θθθ⎫=-⎪⎭=, 令()132cos fθθθ=-2sin 21θ<≤,且2(0,)θπ∈, ()22sin tan '32cos 32cos cos f θθθθθθθ⎛⎫=-= ⎪⎝⎭()222sin cos tancoscosθθθθθ⎛⎫+⎪=⎪⎝⎭()()23cos tan1tan cos tan tanθθθθθθ⎡⎤=+=-⎣⎦因为(0,)2πθ∈,故cos0θ>令'()0,fθ=即3tan tan0θθ+-=,230(,)tan tanθθθ∴+=记000,2tanθθπ⎛⎫∈ ⎪⎝⎭,当00θθ<<时,()()'0,f fθθ>单调递增;当02πθθ<<时,()()'0,f fθθ<单调递减,又233sinθ=>,∴当tanθ时,()fθ取最大值,此时33sin cosθθ,1c osPQθθ⎫=-=⎪⎭PQ∴的最大值为【点睛】本题主要考查了三角函数在实际中的应用,需要根据题意建立角度与长度间的关系,进而求导分析函数的单调性,根据三角函数值求解对应的最值即可.属于难题.18.在平面直角坐标系xOy中,已知椭圆C的中心为坐标原点,O焦点在x轴上,右顶点()2,0A到右焦点的距离与它到右准线的距离之比为12.(1)求椭圆C的标准方程;(2)若,M N是椭圆C上关于x轴对称的任意两点,设()4,0P-,连接PM交椭圆C 于另一点E.求证:直线NE过定点,B并求出点B的坐标;(3)在(2)的条件下,过点B的直线交椭圆C于,S T两点,求OS OT⋅的取值范围.【答案】(1)22143x y +=;(2)证明详见解析,()1,0B -;(3)54,4⎡⎤--⎢⎥⎣⎦. 【解析】(1)根据题意列出关于,,a b c 的等式求解即可.(2)先根据对称性,直线NE 过的定点B 一定在x 轴上,再设直线PM 的方程为(4)y k x +=,联立直线与椭圆的方程, 进而求得NE 的方程,并代入11(4)y k x +=,22(4)y k x +=化简分析即可.(3)先分析过点B 的直线ST 斜率不存在时OS OT ⋅的值,再分析存在时,设直线ST 的方程为(1)y m x +=,联立直线与椭圆的方程,得出韦达定理再代入3434OS OT x x y y ⋅=+求解出关于k 的解析式,再求解范围即可. 【详解】解:()1设椭圆C 的标准方程()222210,x y a b a b+=>>焦距为2c ,由题意得,2,a =由212a c c a a a c-==-,可得1,c =则2223b a c =﹣=,所以椭圆C 的标准方程为22143x y +=;()2证明:根据对称性,直线NE 过的定点B 一定在x 轴上,由题意可知直线PM 的斜率存在, 设直线PM 的方程为(4)y k x +=,联立22(4)143y k x x y +⎧⎪⎨+=⎪⎩=,消去y 得到()2222433264120k x k x k +++﹣=, 设点1122(,),(,)M x y E x y ,则11(,)N x y ﹣. 所以22121222326412,4343k k x x x x k k -+=-=++,所以NE 的方程为()212221y y y y x x x x +-=--,令0,y =得()221221y x x x x y y -==+,将11(4)y k x +=,22(4)y k x +=代入上式并整理,()121212248x x x x x x x ++=++,整理得()()2222128241281322432k k x k k --==--++,所以,直线NE 与x 轴相交于定点(1,0)B -.()3当过点B 的直线ST 的斜率不存在时,直线ST 的方程为1x =-331,1,22S T ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭,, 此时54OS OT ⋅=-, 当过点B 的直线ST 斜率存在时,设直线ST 的方程为(1)y m x =+,且3344(,),(,)S x y T x y 在椭圆C 上,联立方程组22(1)143y m x x y +⎧⎪⎨+=⎪⎩=,消去y ,整理得22224384120m x m x m +++()﹣=, 则()()()()22222844341214410mmm m ++=﹣﹣=>.所以223434228412,,4343m m x x x x m m -+=-=++ 所以()()()222343434324439111m y y m x x m x x x m x =++=++=-++, 所以()2342342451253344343m OS OT x x y m m y +⋅=+=-=-++-, 由20,m ≥得54,4OS OT ⎡⎫⋅∈--⎪⎢⎣⎭,综上可得,OS OT ⋅的取值范围是54,4⎡⎤--⎢⎥⎣⎦.【点睛】本题主要考查了椭圆的基本量求解以及定值和范围的问题,需要分析直线的斜率是否存在的情况,再联立直线与椭圆的方程,根据韦达定理以及所求的解析式,结合参数的范围进行求解.属于难题.19.已知函数()212ax f x bx+=,其中0,0a b >>.(1)①求函数()f x 的单调区间; ②若12,x x 满足)1,2i x i =>,且1220,0x x x >+>.求证:()()122f x f x b>+ . (2)函数()2ln 12g x ax x -=.若12,x x ⎛∈ ⎝对任意,12,x x ≠都有()()()()1212||||f x f x g x g x ->-,求b a -的最大值.【答案】(1)①单调递增区间⎛-∞ ⎝,⎫+∞⎪⎭,单调递减区间⎛ ⎝;②详见解析;(2)116. 【解析】(1)①求导可得()221,02ax f x x bx-'=≠,再分别求解()0f x '>与()0f x '<的解集,结合定义域分析函数的单调区间即可.②根据(1)中的结论,求出()()122f x f x +的表达式,再分10x <与1>0x 两种情况,结合函数的单调性分析()()122f x f x +的范围即可.(2)求导分析()2ln 12g x ax x -=的单调性,再结合()f x 单调性,设12,x x <去绝对值化简可得()()()()11220[]f x g x f x g x --->,再构造函数()()()M x f x g x =﹣,x⎛∈ ⎝,根据函数的单调性与恒成立问题可知10≥,再换元表达b a -求解最大值即可. 【详解】解:()()2211,02ax f x x bx -'=≠,由()0f x '>可得x>或x <由()0f x '<可得x<<故函数的单调递增区间⎛-∞ ⎝,⎫+∞⎪⎭,单调递减区间⎛ ⎝;1220,0x x x +②>>,10x ∴>或10x <,若10x >,因为i x ,故1x >2x由①知f x ()在⎫+∞⎪⎭上单调递增,()()1223f x f x f b b +=>>, 若10,x <由1x 可得1x <x 1, 因为1220,0x x x +>>, 所以21x x >﹣, 由f x ①()在⎫+∞⎪⎭上单调递增,()()()()()1211122f x f x f x f x f x ++-->>=综上()()122f x f x +. ()20x<时,()2110axg x ax x x -'=-=<,g x ()在⎛ ⎝上单调递减,不妨设12,x x < 由(1)()f x 在⎛ ⎝上单调递减,由()()()()1212f x f x g x g x ->-, 可得()()()()1212f x f x g x g x ->-, 所以()()()()11220[]f x g x f x g x --->,令()()()M x f x g x =﹣,x ⎛∈ ⎝, 可得M x ()单调递减, 所以()()()222211211022ax bx ax M x ax bx x bx---'=-+=≤在⎛ ⎝上恒成立, 即120bx ≥﹣在⎛ ⎝上恒成立,即10≥,所以b ≤,2111241616b a a ⎫≤-=-+≤⎪⎭﹣ ,所以b a ﹣的最大值116. 【点睛】本题主要考查了分类讨论分析函数单调性的问题,同时也考查了利用导数求解函数不等式以及构造函数分析函数的最值解决恒成立的问题.需要根据题意结合定义域与单调性分析函数的取值范围与最值等.属于难题.20.已知{}{}{},,n n n a b c 都是各项不为零的数列,且满足1122,*,n n n n a b a b a b c S n N ⋯+=++∈其中n S 是数列{}n a 的前n 项和,{}n c 是公差为()0d d ≠的等差数列.(1)若数列{}n a 是常数列,2d =,23c =,求数列{}n b 的通项公式; (2)若n a n λ=λ(是不为零的常数),求证:数列{}n b 是等差数列; (3)若11a c d k ===(k 为常数,*k N ∈),()2,*n n k b c n n N +≥∈=.求证:对任意112,*,n n n n b b n n N a a ++≥∈>的恒成立. 【答案】(1)43n b n -=;(2)详见解析;(3)详见解析. 【解析】(1)根据2d =,23c =可求得n c ,再根据{}n a 是常数列代入1122,*,n n n n a b a b a b c S n N ⋯+=++∈根据通项与前n 项和的关系求解{}n b 即可.(2)取1n =,并结合通项与前n 项和的关系可求得11,n n n n n n S c S c a b ﹣﹣﹣=再根据1n n n a S S -=-化简可得1n n n S d nc nb λλ+﹣=,代入()112n n n S λ--=化简即可知()1332n n b n b d --=≥,再证明2132b b d -=也成立即可. (3)由(2) 当2n ≥时,11()n nn n n n n S c c a c a b +﹣﹣﹣=,代入所给的条件化简可得1,n n S ka ﹣=()11n n n n S S a k a ++﹣==,进而证明可得11n n k a a k-+=,即数列{}n a 是等比数列.继而求得21n n k a k -+⎛⎫= ⎪⎝⎭,再根据作商法证明11n n n n b b a a ++>即可. 【详解】()1解:22,3,d c ==21n c n ∴=﹣.{}n a 是各项不为零的常数列,12,n a a a ∴⋯===则1n S na =,则由1122n n n n c S a b a b a b ++⋯+=,及21,n c n=﹣得()1221n n n b b b ++⋯+﹣=, 当2n ≥时,()()121123n n n b b b ++⋯+﹣﹣﹣=,两式作差,可得43n b n=﹣. 当1n =时,11b =满足上式,则43n b n=﹣; ()2证明:1122n n n n a b a b a b c S ++⋯+=,当2n ≥时,11221111n n n n a b a b a b c S ++⋯+﹣﹣﹣﹣=,两式相减得:11,n n n n n n S c S c a b ﹣﹣﹣= 即()()11111,n n n n n n n n n n n n n n S a c S c a b S c c a c a b ++﹣﹣﹣﹣﹣﹣=﹣=.即1n n n S d nc nb λλ+﹣=.又()112n n n S λ--=,()12n n n n d nc nb λλλ-∴+=,即12n n n d c b -+=. ∴当3n ≥时,1122n n n d c b ---+=,两式相减得:()1332n n b n b d --=≥.∴数列{}n b 从第二项起是公差为32d 的等差数列.又当1n =时,由1111,S c a b =得11c b =,当2n =时,由22112113222b d c d c d b d -=+=++=+,得2132b b d -=. 故数列{}n b 是公差为32d 的等差数列;()3证明:由()2,当2n ≥时,()11n n n n n n n S c c a c a b +﹣﹣﹣=,即()1n n nn S d a b c ﹣=﹣, n n k b c +=,n n b c kd ∴+=,即n n b c kd ﹣=, 1•,n n S d a kd ∴﹣=即1n n S ka ﹣=. ()11n n n n S S a k a ∴++﹣==,当3n ≥时,()111,n n n S k a ka +﹣﹣==即11n n k a a k-+=. 故从第二项起数列{}n a 是等比数列,∴当2n ≥时,221n n k a a k -+⎛⎫= ⎪⎝⎭.()()()22111n n k n b c c kd c n k k k n k k k n k +++-+=+-+=+===.另外,由已知条件可得()1221122a a c a b a b ++=, 又()2122,,2c k b k b k k +===,21a ∴=,因而21n n k a k -+⎛⎫= ⎪⎝⎭.令nn nb d a =, 则()()()()()11111111101n n n n n n n k k n k d b a nd a k k b n +++-=++-=-=-+++<+. 故对任意的2,*,n n N ≥∈11n n n n b b a a ++>恒成立. 【点睛】本题主要考查了等差等比数列的综合运用,需要熟练运用通项与前n 项和的关系分析数列的递推公式继而求解通项公式或证明等差数列等.同时也考查了数列中的不等式证明等,需要根据题意分析数列为等比数列并求出通项,再利用作商法证明.属于难题.21.已知二阶矩阵a b A c d ⎡⎤=⎢⎥⎣⎦,矩阵A 属于特征值11λ=-的一个特征向量为111α⎡-⎤=⎢⎥⎣⎦,属于特征值24λ=的一个特征向量为232α⎡⎤=⎢⎥⎣⎦.求矩阵A .【答案】2321A ⎡⎤=⎢⎥⎣⎦【解析】运用矩阵定义列出方程组求解矩阵A 【详解】由特征值、特征向量定义可知,111A αλα=,即11111a b c d ⎡⎤⎡⎤⎡⎤=-⨯⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦,得1,1.a b c d -=-⎧⎨-=⎩同理可得3212,328.a b c d +=⎧⎨+=⎩解得2a =,3b =,2c =,1d =.因此矩阵2321A ⎡⎤=⎢⎥⎣⎦ 【点睛】本题考查了由矩阵特征值和特征向量求矩阵,只需运用定义得出方程组即可求出结果,较为简单22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知曲线C 的参数方程为2cos {sin x y αα== (α为参数).以直角坐标系原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos()4πρθ-=P 为曲线C 上的动点,求点P 到直线l 距离的最大值.【答案】(1)2214x y +=,4x y +=(2)max 2d = 【解析】【详解】试题分析:利用cos ,sin x y ρθρθ==将极坐标方程化为直角坐标方程:cos()4πρθ-=ρcosθ+ρsinθ=4,即为x +y =4.再利用点到直线距离公式得:设点P 的坐标为(2cosα,sinα),得P 到直线l 的距离2d =≤试题解析:解:cos()4πρθ-=化简为ρcosθ+ρsinθ=4,则直线l 的直角坐标方程为x +y =4.设点P 的坐标为(2cosα,sinα),得P 到直线l 的距离2d =≤,d max =2. 【考点】极坐标方程化为直角坐标方程,点到直线距离公式 23.若正数,,a b c 满足1a b c ++=,求111323232a b c +++++的最小值.【答案】1【解析】试题分析:由柯西不等式得[]111(32)(32)(32)323232a b c a b c ⎛⎫+++++++ ⎪+++⎝⎭9≥=,所以1111323232a b c ++≥+++试题解析:因为,,a b c 均为正数,且1a b c ++=, 所以(32)(32)(32)9a b c +++++=.于是由均值不等式可知[]111(32)(32)(32)323232a b c a b c ⎛⎫+++++++⎪+++⎝⎭33133(32)(32)(32)9(32)(32)(32)a b c a b c ≥⋅+++=+++,当且仅当13a b c ===时,上式等号成立. 从而1111323232a b c ++≥+++. 故111323232a b c +++++的最小值为1.此时13a b c ===.【考点】柯西不等式24.如图,在正四棱锥P ABCD ﹣中,底面正方形的对角线,AC BD 交于点O 且12OP AB =.(1)求直线BP 与平面PCD 所成角的正弦值; (2)求锐二面角B PD C --的大小. 【答案】(16(2)60︒. 【解析】(1) 以,,OE OF OP 分别为x 轴,y 轴,z 轴,建立空间直角坐标系, 设底面正方形边长为2,再求解BP 与平面PCD 的法向量,继而求得直线BP 与平面PCD 所成角的正弦值即可.(2)分别求解平面BPD 与平面PDC 的法向量,再求二面角的余弦值判断二面角大小即可. 【详解】解:()1在正四棱锥P ABCD ﹣中,底面正方形的对角线,AC BD 交于点,O 所以OP ⊥平面,ABCD 取AB 的中点,E BC 的中点,F 所以,,OP OE OF 两两垂直,故以点O 为坐标原点,以,,OE OF OP 分别为x 轴,y 轴,z 轴,建立空间直角坐标系.设底面正方形边长为2, 因为1,2OP AB =所以1,OP =所以()()()()1,1,0,1,1,0,1,1,0,0,0,1B C D P ﹣﹣﹣, 所以()1,1,1BP =﹣﹣,设平面PCD 的法向量是(),,n x y z =,因为()0,2,0CD =-,()1,1,1CP =﹣, 所以20CD n y ⋅=-=,0CP n x y z ⋅+=﹣=,取1,x =则0,1y z ==﹣, 所以()1,0,1n =- 所以6,BP n cos BP n BP n⋅=<>=所以直线BP 与平面PCD 所成角的正弦值为63. ()2设平面BPD 的法向量是(),,n x y z =,因为()1,1,1BP =﹣﹣,()-2,-2,1BD =,所以0,BP n x y z ⋅+=﹣﹣=220BD n x y ⋅=﹣﹣=,取1,x =则1,0,y z =﹣= 所以()1,1,0n =-,由()1知平面PCD 的法向量是()1,0,1n =-,所以12m ncos m n m n ⋅<,>== 所以,60m n ︒<>=,所以锐二面角B PD C ﹣﹣的大小为60︒. 【点睛】本题主要考查了建立平面直角坐标系求解线面夹角以及二面角的问题,属于中档题.25.定义:若数列{}n a 满足所有的项均由1,1﹣构成且其中1﹣有m 个,1有p 个()3m p +≥,则称{}n a 为“(),m p ﹣数列”.(1)(),,i j k a a a i j k <<为“()3,4﹣数列”{}n a 中的任意三项,则使得1i j k a a a =的取法有多少种?(2)(),,i j k a a a i j k <<为“(),m p ﹣数列”{}n a 中的任意三项,则存在多少正整数(),m p 对使得1100,m p ≤≤≤且1i j k a a a =的概率为12. 【答案】(1)16;(2)115.【解析】(1)易得使得1i j k a a a =的情况只有“1,1,1﹣﹣”,“1,1,1”两种,再根据组合的方法求解两种情况分别的情况数再求和即可.(2)易得“1,1,1﹣﹣”共有21m p C C 种,“1,1,1”共有3P C 种.再根据古典概型的方法可知213312m p pm pC C C C ++=,利用组合数的计算公式可得()()2232320pm p p mp m m +﹣﹣﹣﹣﹣=,当p m =时根据题意有()(),,,2,3,4,{},100m p k k k ∈⋯=,共99个;当2232320p p mp mm +﹣﹣﹣﹣=时求得()232m p +=,再根据1100,m p ≤≤≤换元根据整除的方法求解满足的正整数对即可.【详解】解:(1)三个数乘积为1有两种情况:“1,1,1﹣﹣”,“1,1,1”, 其中“1,1,1﹣﹣”共有:213412C C =种, “1,1,1”共有:344C =种,利用分类计数原理得:(),,i j k a a a i j k <<为“()3,4﹣数列”{}n a 中的任意三项,则使得1i j k a a a =的取法有:12416+=种.(2)与(1)同理,“1,1,1﹣﹣”共有21m p C C 种, “1,1,1”共有3P C 种,而在“(),m p ﹣数列”中任取三项共有3m p C +种,根据古典概型有:213312m p pm pC C C C ++=, 再根据组合数的计算公式能得到:()()2232320pm p p mp m m +﹣﹣﹣﹣﹣=, p m ①=时,应满足11003m p m p p m ≤≤≤⎧⎪+≥⎨⎪=⎩,()(),,,2,3,{,}4,100m p k k k ∴∈⋯=,共99个,2232320p p mp m m +②﹣﹣﹣﹣=时,应满足221100332320m p m p p p mp m m <≤<⎧⎪+≥⎨⎪--+--=⎩,视m 为常数,可解得()232m p +±=,1,m ≥5≥,根据p m ≥可知,()232m p ++=,1m ≥,5≥,根据p m ≥可知,()232m p ++=,(否则1p m≤﹣),下设k则由于p 为正整数知k 必为正整数,1100m ≤≤, 549k ∴≤≤,化简上式关系式可以知道:()()21112424k k k m -+-==, 1,1k k ∴+﹣均为偶数, ∴设()*21,k t t N +∈=,则224,t ≤≤()211246t t k m +-∴==, 由于,1t t +中必存在偶数,∴只需,1t t +中存在数为3的倍数即可,2,3,5,6,8,9,11,,23,24t ∴⋯=, 5,11,13,,47,49k ∴⋯=.检验:()()()23114850100,22424m k k p ++-++=≤== 符合题意,∴共有16个,综上所述:共有115个数对(),m p 符合题意. 【点睛】本题主要考查了排列组合的基本方法,同时也考查了组合数的运算以及整数的分析方法等,需要根据题意。
江苏省海安高级中学2020届高三下学期期初模拟考试数学试卷含答案

(3)当 a 1时,若函数 f (x) 在区间 0,kπ(k N*) 上恰有 2015 个零点,求 k 的值.
20.(本小题满分 16 分)
已知正整数 , 为常数,且 1.无穷数列an 的各项均为正整数,其前 n 项和为 Sn ,且 Sn an ,n N* .记数列 an 中任意不同两项的和构成的集合为 A. (1)求证:数列 an 为等比数列,并求 的值;
14.设函数 f x ex 2x 1 ax a .若存在唯一的整数 x0 ,使得 f x0 0 ,则 a 的取值范围是 ▲ .
二、解答题:本大题共 6 小题,共计 90 分.请在答.题.纸.指.定.区.域.内.作答,解答时应写出 文字说明、证明过程或演算步骤.
5.答案:1110
6.答案: , 4
7.答案:12 8.答案: k 3,k 7 ,k Z
8
8
9.答案: 1, 3
10.答案:1240
11.答案: 6 2, 6 2
12.答案: 2,0 1,
13.答案:18 π
11.在平面四边形 ABCD 中,∠A=∠B=∠C=75°,BC=2,则 AB 的取值范围是 ▲ .
x
2,
x1 2
12.已知函数
f
x
x
1 , 2x
2 x ≤ 1 ,若 f t ≥f
2
2
1 t
,则实数 t 的取值范围是
▲
.
2,
x≤ 2 2
(1)若 λ=1,求异面直线 DE 与 CD1 所成角的余弦值; (2)若平面 CDE⊥平面 CD1O,求 λ 的值.
江苏省南通市海安高级中学2020届高三阶段测试三数学试题
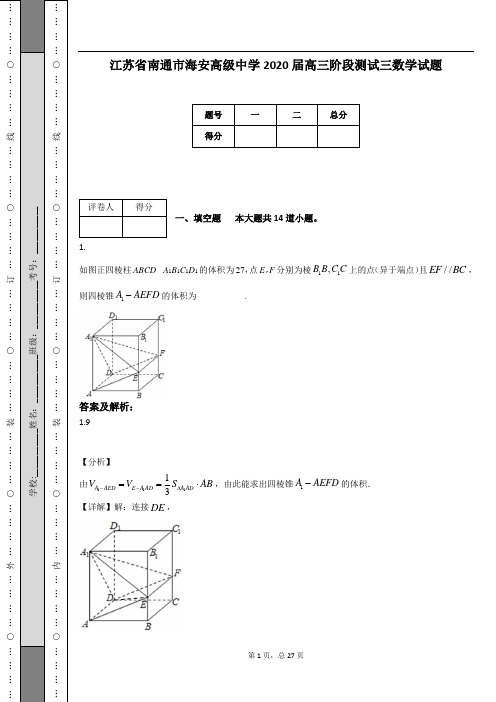
第1页,总27页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………江苏省南通市海安高级中学2020届高三阶段测试三数学试题题号 一 二 总分 得分评卷人 得分一、填空题 本大题共14道小题。
1.如图正四棱柱ABCD - A 1B 1C 1D 1的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点)且//EF BC ,则四棱锥1A AEFD -的体积为___________.答案及解析:1.9 【分析】由11113A AED E A AD A AD V V S AB --∆==⋅,由此能求出四棱锥1A AEFD -的体积. 【详解】解:连接DE ,答案第2页,总27页∵正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点),且//EF BC ,11A AED A FED V V --∴=,1111111111193662A AED E A AD A AD A ADD ABCD A C D V V S AB S AB V --∆-∴==⋅=⋅==,∴四棱锥1A AEFD -的体积19A AEFD V -=. 故答案为:9.【点睛】本题考查四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、运算求解能力,是中档题. 2.设全集{1,2,3,4,5}U =,若{1,2,4}U C A =,则集合A =_________.答案及解析:2.{3,5}. 【分析】 直接求根据{1,2,4}UA =求出集合A 即可.【详解】解:因为全集{1,2,3,4,5}U =若{1,2,4}UA =,则集合A ={3,5}. 故答案为:{3,5}.【点睛】本题考查补集的运算,是基础题. 3.已知S n 为数列{a n }的前n 项和3(1)(*)n n S na n n n N =--∈且211a =.则1a 的值________答案及解析:3.5 【分析】由3(1)(*)n n S na n n n N =--∈,且211a =.取2n =即可得出.。
江苏省南通市海安高级中学2020届高三上学期9月月考数学试题 Word版含解析

2020届高三学初学业质量监测试题数学注意事项:考生在答题前请认真阅读本注意事项及各题答题要求.1.本试卷共4页,包含填空题(共14题)、解答题(共6题),满分为160分,考试时间为120分钟.考试结束后,请将答题卡交回.2.答题前,请您务必将自己的姓名、考试证号等用书写黑色字迹的0.5毫米签字笔填写在答题卡上.3.作答试题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其它位置作答一律无效.如有作图需要,可用2B 铅笔作答,并请加黑、加粗,描写清楚. 参考公式: 锥体的体积公式13V Sh =,其中S 为锥体的底面积,h 为高. 一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.已知集合{}0,2,6,8A =,{}2,4,6B =-,则A B =______.【答案】{}6 【解析】 【分析】利用集合交集的定义可求出集合AB .【详解】因为集合{}0,2,6,8A =,{}2,4,6B =-, 所以{}6AB =,故答案为{}6.【点睛】本题考查集合的交集运算,考查计算能力,属于基础题. 2.已知复数()12z i i =-⋅,其中i 为虚数单位,则z 的模为______. 5【解析】 【分析】利用复数的乘法法则将复数z 表示为一般形式,然后利用复数的求模公式可计算出复数z 的模. 【详解】()21222z i i i i i =-⋅=-=+,因此,复数z的模为z ==,故答案【点睛】本题考查复数模的计算,对于复数问题,一般利用复数四则运算法则将复数表示为一般形式,再结合相关公式或知识求解,考查计算能力,属于基础题.3.某厂生产A 、B 、C 三种不同型号的产品,产品数量之比依次为2:3:5,现用分层抽样的方法抽取一个容量为n 的样本,其中A 型号产品有18件,则n 的值为_____. 【答案】90 【解析】分析】根据分层抽样总体和样本中,A 型号的产品所占的比例相等列等式求出n 的值. 【详解】由于在总体和样本中,A 型号的产品所占的比例相等,则有182235n =++,解得90n =,故答案为90.【点睛】本题考查分层抽样中的计算,解题时要根据分层抽样的特点列等式进行计算,考查运算求解能力,属于基础题. 4.函数y =的定义域是_____________【答案】[]2,3 【解析】 【分析】根据偶次方根被开方数为非负数列不等式,解不等式求得函数的定义域.【详解】依题意2560x x -+-≥,即()()256320x x x x -+=--≤,解得[]2,3x ∈. 【点睛】本小题主要考查具体函数定义域的求法,主要是偶次方根的被开方数为非负数,考查一元二次不等式的解法,属于基础题.5.已知长方体1111ABCD A B C D -的体积为72,则三棱锥1A BCD -的体积为______. 【答案】12 【解析】【分析】设长方体1111ABCD A B C D -的底面积为S ,高为h ,可得出72Sh =,则三棱锥1A BCD -的底面积为12S ,高为h ,再利用锥体的体积公式可计算出三棱锥1A BCD -的体积. 【详解】设长方体1111ABCD A B C D -的底面积为S ,高为h , 则长方体1111ABCD A B C D -的体积为72Sh =, 由题意可知,三棱锥1A BCD -的底面积为12S ,高为h , 因此,三棱锥1A BCD -的体积为1111172123266A BCDV S h Sh -=⨯⨯==⨯=,故答案为12. 【点睛】本题考查锥体体积的计算,解题的关键就是弄清楚锥体和长方体底面积以及高之间的等量关系,考查计算能力,属于基础题.6.如图是一个算法流程图,则输出的n 的值为______.【答案】9 【解析】 【分析】根据框图列出算法步骤,可得出输出结果. 【详解】由题意可得1024n =为偶数,则10245122n ==,922log 512log 29n ===,输出n 的值为9,故答案为9.【点睛】本题考查利用程序框图计算输出结果,考查条件结构框图的应用,一般根据算法框图列举出算法步骤,即可计算出输出结果,考查计算能力,属于中等题.7.在平面直角坐标系xOy 中,已知双曲线()222:10x C y a a-=>的右焦点的坐标为),则该双曲线的两条渐近线方程为______.【答案】2y x =± 【解析】 【分析】根据题意求出a 的值,即可得出双曲线的渐近线方程.【详解】由题意可得2212a =-=,则双曲线的方程为2212x y -=,因此,双曲线的渐近线方程为y x x ==,故答案为y x =.【点睛】本题考查双曲线渐近线方程的求解,解题的关键就是求出双曲线的方程,考查运算求解能力,属于基础题.8.某饮品店提供A 、B 两种口味的饮料,且每种饮料均有大杯、中杯、小杯三种容量.甲、乙二人各随机点一杯饮料,且甲只点大杯,乙点中杯或小杯,则甲、乙所点饮料的口味相同的概率为______. 【答案】12【解析】 【分析】记A 种口味饮料大杯、中杯、小杯分别记为1A 、2A 、3A ,B 种口味饮料大杯、中杯、小杯分别记为1B 、2B 、3B ,用列举法列出所有的基本事件,并确定事件“甲、乙所点饮料的口味相同”所包含的基本事件,然后利用古典概型的概率公式可求出所求事件的概率. 【详解】记A 种口味饮料大杯、中杯、小杯分别记为1A 、2A 、3A ,B 种口味饮料大杯、中杯、小杯分别记为1B 、2B 、3B ,事件“甲只点大杯,乙点中杯或小杯”所包含的基本事件有:()12,A A 、()13,A A 、()12,A B 、()13,A B 、()12,B A 、()13,B A 、()12,B B 、()13,B B ,共8个,其中事件“甲、乙所点饮料的口味相同”所包含的基本事件有:()12,A A 、()13,A A 、()12,B B 、()13,B B ,共4个,因此,所求事件的概率为4182=,故答案为12. 【点睛】本题考查利用古典概型概率公式计算事件的概率,解题的关键就是利用列举法列举出基本事件,并确定基本事件数目,考查计算能力,属于中等题. 9.已知函数()()sin 202f x x πϕϕ⎛⎫=+<< ⎪⎝⎭图象的一条对称轴方程为6x π=,则ϕ的值为______. 【答案】6π【解析】 【分析】 由题意得出()262k k Z ππϕπ⨯+=+∈,求出ϕ的表达式,再结合ϕ的取值范围,可得出ϕ的值.【详解】由题意得出()262k k Z ππϕπ⨯+=+∈,()6k k Z πϕπ∴=+∈,02πϕ<<,0k ∴=且6π=ϕ,故答案为6π.【点睛】本题考查利用正弦型函数对称轴方程求参数的值,解题时要结合正弦型函数的对称轴方程得出参数的表达式,并结合参数的取值范围得出参数的值,考查运算求解能力,属于中等题.10.设等比数列{}n a 的公比为()1q q >,前n 项和为n S .若存在m N *∈,使得2152m m m a a a +++=,且29m m S S =,则正整数m 的值为______. 【答案】3 【解析】 【分析】先利用条件2152m m m a a a +++=求出公比q 的值,然后利用等比数列求和公式以及29m m S S =可求出正整数m 的值. 【详解】2152m m m a a a +++=,252m m m a a q a q ∴+=,得25102q q -+=,1q >,解得2q .由29m m S S =,可得()()211121291212m m a a --=⨯--,所以,()212912mm -=-,即()()()1212912mmm-+=-,m N *∈,120m ∴-≠,129m ∴+=,解得3m =,故答案为3.【点睛】本题考查等比数列基本量的计算,同时也考查了等比数列求和公式,对于等比数列问题,通常利用首项和公比将等比数列中相关量表示出来,考查计算能力,属于中等题. 11.如图,在平面直角坐标系xOy 中,已知正方形OABC ,其中()1OA a a =>,函数23y x =交BC 于点P ,函数12y x -=交AB 于点Q ,则当AQ CP +最小时,a 的值为______.3【解析】 【分析】由题意得出直线AB 的方程为x a =,直线BC 的方程为y a =,求出点P 、Q 的坐标,可得出AQ 、CP 关于a 的表达式,然后利用基本不等式求出AQ CP +的最小值,并利用等号成立的条件求出对应的a 的值.【详解】由题意得出直线AB 的方程为x a =,直线BC 的方程为y a =,联立直线AB 的方程与函数12y x -=的解析式12x a y x -=⎧⎪⎨⎪=⎩,得1x a y a =⎧⎪⎨=⎪⎩, 所以点Q 的坐标为a a ⎛ ⎝,则AQ a =. 联立直线BC 的方程与函数23y x =的解析式()230y a y x x =⎧⎨=>⎩,得3ax y a⎧=⎪⎨⎪=⎩,所以点P 的坐标为,3a a ⎛⎫ ⎪ ⎪⎝⎭,则3aCP =. 由基本不等式得412333aa AQ CP a a +=+≥⋅=, 当且仅当3aa =,即当3a =时,等号成立,因此,3a =,故答案为3. 【点睛】本题考查利用基本不等式求最值,解题的关键就是结合条件建立关于a 的代数式,并结合基本不等式进行求解,考查分析问题和解决问题的能力,属于中等题.12.如图,在平面四边形ABCD 中,3AB =,1AD =,CB CD =,2ADB BCD π∠=∠=,则AC BD ⋅的值为______.【答案】4- 【解析】 【分析】以点D 为坐标原点,DB 、AD 所在直线分别为x 轴、y 轴建立平面直角坐标系,写出A 、B 、C 、D 四点的坐标,并求出向量AC 、BD 的坐标,利用坐标法来计算出AC BD ⋅的值.【详解】如下图所示,以点D 为坐标原点,DB 、AD 所在直线分别为x 轴、y 轴建立平面直角坐标系,3AB =,1AD =,2ADB π∠=,2222BD AB AD ∴=-=又CB CD =,且2BCD π∠=,BCD ∴∆是等腰直角三角形,则点()0,1A -、()B 、C 、()0,0D ,()2,1AC =,()BD =-,因此,()2104AC BD ⋅=⨯-+⨯=-,故答案为4-.【点睛】本题考查图形中向量数量积的计算,常利用基底向量法与坐标法来进行求解,考查数形结合思想的应用,属于中等题.13.在ABC ∆中,已知AB 边上的中线1CM =,且1tan A ,1tan C ,1tan B成等差数列,则AB 的长为________.【答案】3【解析】 【分析】 先由1tan A ,1tan C ,1tan B成等差数列,结合正弦定理与余弦定理,得到2222a b c +=,再由AB 边上的中线1CM =,()12CM CA CB =+,得到22224232c b a ab c ab=++⋅=,进而可求出结果.【详解】因为1tan A ,1tan C ,1tan B 成等差数列, 所以211tan tan tan C A B =+,即2cos cos cos sin()sin sin sin sin sin sin sin sin C A B A B CC A B A B A B+=+==, 所以2sin 2cos sin sin C C A B =,由正弦定理可得2cos 2c C ab=,又由余弦定理可得222cos 2a b c C ab +-=,所以222222a b c c ab ab+-=,故2222a b c +=, 又因为AB 边上的中线1CM =,所以1CM =,因为()12CM CA CB =+, 所以22222422cos CMCA CB CA CB CA CB CA CB C =++⋅=++,即22224232c b a ab c ab =++⋅=,解c =.即AB.故答案为3【点睛】本题主要考查解三角形与平面向量的应用,熟记正弦定理与余弦定理,以及向量数量积的运算即可,属于常考题型.14.在平面直角坐标系xOy 中,已知直线1:20l x y -+=与x 轴交于点A ,点B 在直线1l 上,直线2:310l x y +-=上有且仅有一点C 满足:AC BC ⊥(A 、B 、C 两两互不相同),则点B 的横坐标的所有可能值之积为______.【答案】19 【解析】 【分析】设点B 的坐标为(),2t t +,设点(),C x y ,根据AC BC ⊥转化为0AC BC ⋅=,可得出点C 的轨迹为圆,由题意得出点C 的轨迹圆与直线2l 相切,将直线2l 的方程与点C 的轨迹方程联立,利用0∆=得出关于t 的二次方程,利用韦达定理求出两根之积12t t 可得出结果. 【详解】设点B 的坐标为(),2t t +,直线1l 与x 轴的交点为点()2,0A -, 设点(),C x y ,()2,AC x y =+,(),2BC x t y t =---,AC BC ⊥,()()()220AC BC x x t y y t ∴⋅=+-+--=,联立()()()310220x y x x t y y t +-=⎧⎨+-+--=⎩,消去x 得()210214330y t y t +-+-=,()()2214410330t t ∆=--⨯⨯-=,化简得216190t t ++=,由韦达定理得1219t t =.当点B 为直线1l 与2l 的交点时5434x y ⎧=-⎪⎪⎨⎪=⎪⎩,要使0AC BC ⋅=,点C 与点B 重合,不合题意.因此,点B 的横坐标的所有可能值之积为1219t t =,故答案为19.【点睛】本题考查两直线垂直、直线与圆的位置关系的综合应用,解题的关键在于将点的个数问题转化为直线与圆的位置关系,并利用韦达定理进行求解,考查转化与化归思想以及方程思想,考查运算求解能力,属于难题.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15.在ABC ∆中,已知13,2,cos 2BC AC AB B =-==-. (1)求,AB AC 的值; (2)求sin()B C -的值.【答案】(1)5,7;(2)7【解析】 【分析】(1)运用余弦定理进行求解即可;(2)运用余弦定理,结合同角的三角函数关系式、两角差的正弦公式进行求解即可. 【详解】解:(1)设角,,A B C 的对边依次为,,a b c ,由余弦定理得,222cos 2a c b B ac+-=,又因为1cos ,3,22B a b c =-=-=,所以2223(2)1232c c c +-+=-⨯,解得5c =.所以,AB AC 的值分别为5,7;(2)在ABC ∆中,0B π<<,又1cos 2B =-,故23B π=. 由余弦定理得,222cos 2a b c C ab +-=,结合(1)知,22237511cos 23714C +-==⨯⨯,又0C π<<,由221153sin 1cos 114C C ⎛⎫=-=-= ⎪⎝⎭. 所以2sin()sin 3B C C π⎛⎫-=-⎪⎝⎭22sin cos cos sin 33C C ππ=- 311153214214=⨯+⨯437=. 【点睛】本题考查了余弦定理的应用,考查了两角差的正弦公式的应用,考查了数学运算能力.16.如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .【答案】(1)证明见解析;(2)证明见解析. 【解析】 【分析】(1)先证明出//AB 平面11A B D ,然后利用直线与平面平行的性质定理可得出//AB EF ; (2)由题意得出1111A B B C ⊥,由1BB ⊥平面111A B C ,可得出111A B BB ⊥,利用直线与平面垂直的判定定理证明出11A B ⊥平面11BB C C ,再利用平面与平面垂直的判定定理可证明出平面11A B D ⊥平面11B BCC .【详解】(1)在直三棱柱111ABC A B C -中,11//AB A B ,又AB ⊄平面11A B D ,11A B ⊂平面11A B D ,所以//AB 平面11A B D . 又AB平面1ABC ,平面11A B D平面1ABC EF =,所以//AB EF ;(2)在直三棱柱111ABC A B C -中,1B B ⊥平面111A B C , 又11A B ⊂平面111A B C ,故111B B A B ⊥ 又AB BC ⊥,故1111A B B C ⊥. 又因为1111B BB C B =,1B B ⊂平面11B BCC ,11B C ⊂平面11B BCC ,所以11A B ⊥平面11B BCC ,又11A B ⊂平面11A B D ,所以平面11A B D ⊥平面11B BCC .【点睛】本题考查直线与直线平行以及平面与平面垂直的证明,考查直线与平面平行的性质定理以及平面与平面垂直判定定理的应用,考查推理能力,属于中等题.17.现有一张半径为1m 的圆形铁皮,从中裁剪出一块扇形铁皮(如图1阴影部分),并卷成一个深度为hm 的圆锥筒,如图2.(1)若所裁剪的扇形铁皮的圆心角为23rad π,求圆锥筒的容积; (2)当h 为多少时,圆锥筒的容积最大?并求出容积的最大值. 【答案】(1)32281m π;(2)当3h 323π. 【解析】 【分析】(1)计算出扇形的弧长,利用扇形的弧长等于圆锥底面圆的周长可求出圆锥底面圆的半径,利用勾股定理计算出圆锥的高,再利用圆锥的体积公式可计算出圆锥的容积;(201h <<,利用圆锥的体积公式计算出圆锥的容积V 关于h 的函数,再利用导数可求出V 的最大值,并求出对应的h 的值. 【详解】设圆锥筒的半径为r ,容积为V .(1)由223r ππ=,得13r =,从而h ==所以)23111333V Sh m π⎛⎫==⨯= ⎪⎝⎭.答:圆锥筒的容积为381m ;(2)因为r 01h <<. 所以()()223111113333V Sh r h h h h h πππ===-⋅=-,即()313V h h π=-,01h <<.因为()21133V h π'=-,令0V '=得,3h =±(舍负值),列表如下:所以,当h 时,V 取极大值即最大值,且V .答:当h 时,圆锥筒3. 【点睛】本题考查圆锥体积的计算,同时也考查利用导数求函数的最值,解题的关键就是要结合题意求出函数解析式,考查分析问题和解决问题的能力,属于中等题.18.如图,在平面直角坐标系xOy 中,已知椭圆()2222:10x y C a b a b+=>>的右焦点为F ,左、右顶点分别为1A 、2A ,上、下顶点分别为1B 、2B ,连结2B F 并延长交椭圆于点P ,连结2PA ,12A B,记椭圆C的离心率为e.(1)若12e=,127A B=①求椭圆C的标准方程;②求21B A F∆和2PA F∆的面积之比.(2)若直线2PB和直线2PA的斜率之积为92-,求e的值.【答案】(1)①22143x y+=.②5;(2)12e=.【解析】【分析】(1)①设椭圆的焦距为2c,根据题意列出有关a、b、c的方程组,求出a、b的值,可得出椭圆的标准方程;②求出直线2B F的方程,将该直线方程与椭圆C的标准方程联立,求出点P的坐标,再利用三角形的面积公式可求出21B A F∆和2PA F∆的面积之比;(2)先利用截距式得出直线2PB的方程为1x yc b+=-,将该直线方程与椭圆C的方程联立,求出点P的坐标,利用斜率公式计算出直线2PA和2PB的斜率,然后由这两条直线的斜率之积为92-,得出关于a、c的齐次方程,由此可解出椭圆C的离心率e的值.【详解】(1)①设椭圆的焦距为2c,由题意,得22222127ceaa ba b c⎧==⎪⎪⎪+=⎨=+⎪⎪⎩2243ab⎧=⎨=⎩,所以椭圆的标准方程为22143x y +=;②由①知,()12,0A -、()22,0A ,()1,0F,(20,B , 所以直线2B F的方程为)1y x =-,将其代入椭圆的方程,得()22114x x +-=,即2580x x ,所以0x =或85x =,所以点P的坐标为8,55⎛⎫ ⎪ ⎪⎝⎭. 从而21B A F ∆和2PA F ∆的面积之比:212135B A F PA FS S ∆∆⨯==; (2)因为2B 、F 在直线2PB 上,所以直线2PB 的方程为1x yc b+=-. 解方程组22221,1,x yc bx y a b ⎧+=⎪⎪-⎨⎪+=⎪⎩,得()2122221222a c x a c b a c y a c ⎧=⎪+⎪⎨-⎪=⎪+⎩或220x y b =⎧⎨=-⎩, 所以点P 的坐标为()22222222,b a c a c a c a c ⎛⎫- ⎪ ⎪++⎝⎭. 因为直线2PB 的斜率()200PB b bk c c--==-,直线2PA 的斜率()()()()()222222222222222PA b a c b a c b a c a c k a c a a c a c a a c a a c ---++===---+-+, 又因为直线2PB 和直线2PA 的斜率之积为92-,所以()()()()()()()()222292a c a cb ac b a c a c b a a c c ac a c ac a c ac -++++-⨯=-=-=-=----, 即1922e e ++=,化简得22520e e -+=,01e <<,解得12e =.因此,椭圆C 的离心率为12e =. 【点睛】本题考查椭圆标准方程的求解、三角形面积的比值,以及椭圆离心率的求解,同时也考查了直线与椭圆交点坐标的求解,考查方程思想的应用,属于中等题.19.已知函数()2xx bx c f x e++=(e为自然对数的底数),()f x '为()f x 的导函数,且()10f '=.(1)求实数c 的值;(2)若函数()f x 在0x =处的切线经过点()1,0-,求函数()f x 的极值;(3)若关于x 的不等式()2f x ≤对于任意的[]0,2x ∈恒成立,求实数b 的取值范围. 【答案】(1)1;(2)函数()y f x =的极小值为0,极大值为4e;(3)(],22e -∞-. 【解析】 【分析】(1)求出函数()y f x =的导数()f x ',由()10f '=,可求出实数c 的值; (2)利用导数求出函数()y f x =在0x =处的切线方程,将点()1,0-代入切线方程,可求出实数b 的值,然后利用导数求出函数()y f x =的极值点,并列表分析函数()y f x =的单调性,由此可得出函数()y f x =的极小值和极大值;(3)方法1:由()2f x ≤,得()221xbx e x ≤-+,[]0,2x ∈,然后分0x =和02x <≤两种情况讨论,在0x =时可验证不等式成立,在(]0,2x ∈时,由参变量分离法得21x e b x x x ⎛⎫≤-+ ⎪⎝⎭,并构造函数()21x e g x x x x ⎛⎫=-+ ⎪⎝⎭,并利用导数求出函数()y g x =在区间(]0,2上的最小值,由此可得出实数b 的取值范围;方法2:解导数方程()0f x '=,得出11x b =-,21x =,然后分11b -=,10b -≤,011b <-<,12b -≥和112b <-<五种情况讨论,分析函数()y f x =在区间[]0,2上的单调性,求出函数()y f x =的最大值()max f x ,再解不等式()max 2f x ≤可得出实数b 的取值范围.【详解】(1)因为()2x x bx cf x e ++=,所以()()22xx b x b c f x e-+-+-'=, 又因为()10f '=,所以()120b b ce-+-+-=,解得1c =.(2)因为()2xx bx cf x e ++=,所以()01f =. 因为()()22xx b x b cf x e-+-+-'=,所以()01f b '=-. 因为,函数()y f x =在0x =处的切线方程为()11y b x -=-且过点()1,0-, 即()11b -=--,解得2b =. 因为()()()11xx x f x e -+'=-,令()0f x '=,得1x =±,列表如下:所以当1x =-时,函数()y f x =取得极小值()10f -=, 当1x =时,函数()y f x =取得极大值为()41f e=; (3)方法1:因为()212xx bx f x e++=≤在[]0,2x ∈上恒成立, 所以()221xbx e x ≤-+在[]0,2x ∈上恒成立. 当0x =时,01≤成立;当(]0,2x ∈时,21x e b x x x ⎛⎫≤-+ ⎪⎝⎭恒成立,记()21x e g x x x x ⎛⎫=-+ ⎪⎝⎭,(]0,2x ∈,则()()()()221212111xx x e x e x g x x x x ----⎛⎫'=--= ⎪⎝⎭. 令()21x h x e x =--,(]0,2x ∈,则()0212110xh x e e '=->-=>,所以函数()y h x =在区间(]0,2上单调递增,所以()()0020110h x h e >=--=>,即210x e x -->在区间(]0,2上恒成立.当(]0,2x ∈,令()0g x '=,得1x =,所以,函数()y g x =在区间()0,1上单调递减,在区间()1,2上单调递增, 所以()()min 122g x g e ==-,所以,22b e ≤-, 因此,实数b 的取值范围是(],22e -∞-;方法2:由(1)知,()21xx bx f x e++=, 所以()()()()22111x xx b x b x x b f x e e -+-+--+-'==-.令()0f x '=,得11x b =-,21x =.①当11b =-时,即0b =时,函数()y f x =在区间[]0,2上单调递减, 由题意可知()012f =≤,满足条件;②当10b -≤时,即1b ≥时,函数()y f x =在区间[]0,1上单调递增,在区间[]1,2上单调递减,由题意可知()212b f e+=≤,解得122b e ≤≤-; ③当011b <-<时,即01b <<时,函数()y f x =在[]0,1b -上单调递减,在[]1,1b -上单调递增,在[]1,2上单调递减, 由题意可知()212b f e+=≤,解得22b e ≤-,所以01b <<; ④当12b -≥时,即1b ≤-时,函数()y f x =在区间[]0,1上单调递减,在区间[]1,2上单调递增,由题意可知()22522b f e +=≤,解得252b e ≤-. 又因为1b ≤-,所以1b ≤-; ⑤当112b <-<时,即10b -<<时,函数()y f x =在[]0,1上单调递减,[]1,1b -上单调递增,在[]1,2b -上单调递减, 由题意可知()1212bb f b e ---=≤,即()12110be b ---+≥. 令1t b =-,则12t <<,设()2121tty e t e t =-+=--, 则210ty e '=->,所以,函数21ty e t =--区间()1,2上单调递增,又因为1t =时,220y e =->,所以0y ≥在区间()1,2上恒成立,所以10b -<<. 综上,22b e ≤-,因此,实数b 的取值范围是(],22e -∞-.【点睛】本题考查导数的计算、导数的几何意义、利用导数求函数的极值以及利用导数研究不等式恒成立问题,对于不等式恒成立问题,可以利用参变量分离法,也可以采用分类讨论法,转化为函数的最值来求解,考查分类讨论数学思想的应用,属于难题.20.若无穷数列{}n a 满足:只要*(,)p q a a p q N =∈,必有11p q a a ++=,则称{}n a 具有性质P .(1)若{}n a 具有性质P ,且12451,2,3,2a a a a ====,67821a a a ++=,求3a ; (2)若无穷数列{}n b 是等差数列,无穷数列{}n c 是公比为正数的等比数列,151b c ==,5181b c ==,n n n a b c =+判断{}n a 是否具有性质P ,并说明理由;(3)设{}n b 是无穷数列,已知*1sin ()n n n a b a n N +=+∈.求证:“对任意{}1,n a a 都具有性质P ”的充要条件为“{}n b 是常数列”.【答案】(1)316a =.(2){}n a 不具有性质P .(3)见解析. 【解析】试题分析:(1)根据已知条件,得到678332a a a a ++=++,结合67821a a a ++=求解即可.(2)根据{}n b 的公差为20,{}n c 的公比为13,写出通项公式,从而可得520193n n n n a b c n -=+=-+.通过计算1582a a ==,248a =,63043a =,26a a ≠,即知{}n a 不具有性质P . (3)从充分性、必要性两方面加以证明,其中必要性用反证法证明. 试题解析:(1)因为52a a =,所以63a a =,743a a ==,852a a ==. 于是678332a a a a ++=++,又因为67821a a a ++=,解得316a =. (2){}n b 的公差为20,{}n c 的公比为13, 所以()12012019n b n n =+-=-,1518133n n n c --⎛⎫=⋅= ⎪⎝⎭.520193n n n n a b c n -=+=-+.1582a a ==,但248a =,63043a =,26a a ≠, 所以{}n a 不具有性质P . [证](3)充分性:当{}n b 为常数列时,11sin n n a b a +=+.对任意给定的1a ,只要p q a a =,则由11sin sin p q b a b a +=+,必有11p q a a ++=. 充分性得证. 必要性:用反证法证明.假设{}n b 不是常数列,则存在k *∈N , 使得12k b b b b ==⋅⋅⋅==,而1k b b +≠.下面证明存在满足1sin n n n a b a +=+的{}n a ,使得121k a a a +==⋅⋅⋅=,但21k k a a ++≠. 设()sin f x x x b =--,取m *∈N ,使得πm b >,则()ππ0f m m b =->,()ππ0f m m b -=--<,故存在c 使得()0f c =.取1a c =,因为1sin n n a b a +=+(1n k ≤≤),所以21sin a b c c a =+==, 依此类推,得121k a a a c +==⋅⋅⋅==.但2111sin sin sin k k k k a b a b c b c ++++=+=+≠+,即21k k a a ++≠. 所以{}n a 不具有性质P ,矛盾.必要性得证.综上,“对任意1a ,{}n a 都具有性质P ”的充要条件为“{}n b 是常数列”. 【考点】等差数列、等比数列、充要条件的证明、反证法【名师点睛】本题对考生的逻辑推理能力要求较高,是一道难题.解答此类题目时,熟练掌握等差数列、等比数列的相关知识及反证法是基础,灵活应用已知条件进行推理是关键.本题易错主要有两个原因,一是不得法,二是对复杂式子的变形能力不足,导致错漏百出.本题能较好地考查考生的逻辑思维及推理能力、运算求解能力、分析问题解决问题的能力等.2020届高三学年初学业质量监测试题数学Ⅱ(附加题)注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共2页,均为解答题(第21-23题).本卷满分为40分,考试时间为30分钟. 考试结束后,请将答题卡交回.2.答题前,请您务必将自己的姓名、考试证号等用书写黑色字迹的0.5毫米签字笔填写在答题卡上,并用2B 铅笔正确填涂考试号.3.作答试题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其它位置作答一律无效.如有作图需要,可用2B 铅笔作答,并请加黑、加粗,描写清楚.【选做题】本题包括A 、B 、C 三小题,请选定其中两题,并在相应的答题区域内作答....................若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. [选修4-2:矩阵与变换]21.已知矩阵32x A y ⎡⎤=⎢⎥⎣⎦,41α⎡⎤=⎢⎥-⎣⎦,且94A α⎡⎤=⎢⎥⎣⎦.(1)求实数x 、y 的值; (2)求矩阵A 的特征值.【答案】(1)3x =,4y =;(2)特征值为1、6. 【解析】 【分析】(1)根据题中矩阵运算列出关于x 、y 的方程组,可解出x 、y 的值;(2)求出矩阵A 的特征方程,解出该方程可得出矩阵A 的特征值. 【详解】(1)因为32x A y ⎡⎤=⎢⎥⎣⎦,41α⎡⎤=⎢⎥-⎣⎦,94A α⎡⎤=⎢⎥⎣⎦,所以349214x y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦. 所以43984x y -=⎧⎨-=⎩,解得34x y =⎧⎨=⎩;(2)由(1)知,3324A ⎡⎤=⎢⎥⎣⎦,则矩阵A 的特征多项式()()()()()333461624fλλλλλλλ--==---=----,令()0f λ=,得1λ=,6λ=,因此,矩阵A 的特征值为1、6.【点睛】本题以矩阵计算以及矩阵特征值的计算,解题的关键在于写出矩阵的特征方程,并进行求和,考查方程思想的应用,属于中等题. [选修4-4:坐标系与参数方程]22.在极坐标系中,O 为极点,点()00,M ρθ在曲线:4sin C ρθ=上,直线l 过点()4,0A 且与OM 垂直,若03πθ=,求0ρ及l 的极坐标方程.【答案】0ρ=l 的极坐标方程为sin 26πρθ⎛⎫+= ⎪⎝⎭. 【解析】 【分析】 将点0,3M πρ⎛⎫⎪⎝⎭代入曲线C 的极坐标方程可得出0ρ的值,求出直线OM 的斜率,根据l OM ⊥求出直线l 的斜率,利用点斜式写出直线l 的方程,再将直线l 的普通方程化为极坐标方程.【详解】因为点()00,M ρθ在曲线:4sin C ρθ=上,所以004sin ρθ=.又03πθ=,故04sin3πρ==OM 的斜率为tan3π=l OM ⊥,设直线l 的斜率为k 1=-,解得k =.所以,直线l 的方程为)4y x =-,即40x +-=,所以,直线l 的极坐标方程为cos sin 40ρθθ+-=,即2sin 46πρθ⎛⎫+= ⎪⎝⎭, 因此,直线l 的极坐标方程为sin 26πρθ⎛⎫+= ⎪⎝⎭. 【点睛】本题考查极径的计算以及直线的极坐标方程的求解,一般要结合题意先写出直线的普通方程,再转化为极坐标方程,考查运算求解能力,属于中等题. [选修4-5:不等式选讲]23.对于正实数x 、y 满足11x -≤,21y -≤,求证:12x y -+≤. 【答案】证明见解析 【解析】 【分析】将代数式表示为()()112x y x y -+=---,再利用绝对值三角不等式可证出所证不等式成立.【详解】由绝对值三角不等式得()()112122x y x y x y -+=---≤-+-≤, 因此,原不等式成立.【点睛】本题考查利用绝对值三角不等式证明不等式成立,证明的关键在于对代数式进行配凑,考查推理能力,属于中等题.【必做题】第22题、第23题,每题10分,共计20分,请在答卷纸指定区域内作答.............解答应写出文字说明、证明过程或演算步骤.24.如图,在空间之间坐标系O xyz -中,四棱锥P ABCD -的底面ABCD 在平面xOy 上,其中点A 与坐标原点O 重合,点D 在y 轴上,CD AD ⊥,//BC AD ,顶点P 在z 轴上,且2PA AD CD ===,3BC =.(1)求直线PB 与平面PCD 所成角的大小; (2)设E 为PD 的中点,点F 在PC 上,且13PF PC =,求二面角F AE P --的正弦值. 【答案】(1)45;(26. 【解析】 【分析】(1)列出A 、B 、C 、D 、P 的坐标,计算出平面PCD 的一个法向量u ,利用空间向量法计算出直线PB 与平面PCD 所成角的正弦值,即可得出直线PB 与平面PCD 所成角的大小; (2)求出点E 、F 的坐标,计算出平面AEF 和AEP 的法向量m 、n ,利用空间向量法求出二面角F AE P --的余弦值的绝对值,由此可得出二面角F AE P --的正弦值. 【详解】因为四棱锥P ABCD -的底面ABCD 在平面xOy 上, 其中点A 与坐标原点O 重合,点D 在y 轴上,CD AD ⊥,//BC AD , 顶点P 在z 轴上,且2PA AD CD ===,3BC =, 所以()0,0,0A ,()2,1,0B -,()2,2,0C ,()0,2,0D,()002P ,,.(1)()2,1,2PB =--,()2,2,2PC =-,()0,2,2PD =-, 设平面PCD 的一个法向量为(),,u x y z =,则00u PC u PD ⎧⋅=⎨⋅=⎩,即2220220x y z y z +-=⎧⎨-=⎩,取1z =,则0x =,1y =,得()0,1,1u =.所以2cos ,232u PB u PB u PB⋅===-⨯⋅.所以直线PB 与平面PCD 所成角的大小为45;(2)因为E 为PD 的中点,点F 在PC 上,且13PF PC =,所以()0,1,1E ,224,,333F ⎛⎫⎪⎝⎭. 设平面AEF 的一个法向量为(),,m a b c =,则00m AE m AF ⎧⋅=⎨⋅=⎩,即02240333b c a b c +=⎧⎪⎨++=⎪⎩,取1b =,则1a =,1c =-,得()1,1,1m =-. 又平面AEP 的一个法向量为()1,0,0n =,所以cos ,33m n m n m n⋅===⨯⋅. 所以二面角F AE P --. 【点睛】本题考查利用空间向量法求直线与平面所成的角和二面角,解题的关键就是要列出问题所涉及的点的坐标,并计算出平面的法向量,考查运算求解能力,属于中等题. 25.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A 、B 两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A 、B 两种支付方式都不使用的有5人,样本中仅使用A 和仅使用B 的学生的支付金额分布情况如下:(1)从样本仅使用A 和仅使用B 的学生中各随机抽取1人,以X 表示这2人中上个月支付金额大于1000元的人数,求X 的分布列和数学期望;(2)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A 的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A 的学生中本月支付金额大于2000元的人数有变化?说明理由.【答案】(1)X 的分布列见解析,数学期望为1;(2)无法确定是否有变化,理由见解析. 【解析】 【分析】(1)根据表格中的数据确定仅使用A 支付方法或B 支付方法中,金额不大于1000和大于1000的人所占的频率,由题意得出随机变量X 的可能取值有0、1、2,再利用独立事件的概率乘法公式计算出随机变量X 在对应取值的概率,可列出随机变量X 的分布列,并利用数学期望公式可求出其数学期望;(2)计算出事件“从样本仅使用A 的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元”的概率,根据概率的意义得出结论. 【详解】(1)仅使用A 支付方法的30名学生中,金额不大于1000的人数占35,金额大于1000的人数占25, 仅使用B 支付方法的学生中,金额不大于1000的人数占25,金额大于1000的人数占35,且X 的所有可能值为0、1、2.则()32605525P X ==⨯=,()22321315525P X ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭,()32625525P X ==⨯=,所以X 分布列为:数学期望()61360121252525E X =⨯+⨯+⨯=; (2)无法确定是否有变化,理由如下:记事件:E “从样本仅使用A 的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.”假设样本仅使用A 的学生中,本月支付金额大于2000元的人数没有变化,则由上个月数据得,()3333014060C P E C ==.我们知道“小概率事件”的概率虽小,但还是有可能发生的,因此无法确定是否有变化. 【点睛】本题考查离散型随机变量分布列与数学期望,考查古典概型概率的计算以及概率的意义,解时要弄清事件的基本类型,结合相关公式计算事件的概率,考查推理能力与计算能力,属于中等题.。
江苏省南通市海安高级中学2020届高三下学期期初模拟考试数学试题(解析版)

江苏省南通市海安高级中学2020届高三下学期期初模拟考试数学试题一、填空题:本大题共14小题,每小题5分,共70分.1.已知集合A ={﹣1,0,2},B ={x |x =2n ﹣1,n ∈Z },则A ∩B 中元素的个数为_____. 『答案』1『解析』∵A ={﹣1,0,2},B ={x |x =2n ﹣1,n ∈Z }, ∴A ∩B ={﹣1},∴A ∩B 中元素的个数为1. 故答案为:1.2.已知复数z 1=1﹣2i ,z 2=a +2i (其中i 是虚数单位,a ∈R ),若z 1•z 2是纯虚数,则a 的值为_____. 『答案』-4『解析』∵z 1=1﹣2i ,z 2=a +2i ,∴12(12)(2)4(22)z z i a i a a i ⋅=-+=++-, 又z 1•z 2是纯虚数,∴40220a a +=⎧⎨-≠⎩,解得:a =﹣4.故答案为:﹣4.3.从集合{}1,2,3中随机取一个元素,记为a ,从集合{}2,3,4中随机取一个元素,记为b ,则a b ≤的概率为_______. 『答案』89『解析』从集合{}1,2,3中随机取一个元素,记为a ,从集合{}2,3,4中随机取一个元素,记为b ,则(,)a b 的事件数为9个,即为(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,2),(3,3),(3,4), 其中满足a b ≤的有(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,3),(3,4),共有8个, 故a b ≤的概率为89. 4.为了了解一批产品的长度(单位:毫米)情况,现抽取容量为400的样本进行检测,如图是检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为__________.『答案』100.『解析』由题意得,三等品的长度在区间[)10,15,[)15,,20和[]35,40内, 根据频率分布直方图可得三等品的频率为()0.01250.02500.012550.25++⨯=, ∴样本中三等品的件数为4000.25100⨯=.5.如图是一个算法的伪代码,其输出的结果为_______.『答案』1011『解析』由题设提供的算法流程图可知:1111101122310111111S =++⋅⋅⋅+=-=⨯⨯⨯,应填答案1011. 6.命题A :|x -1|<3,命题B :(x +2)(x +a )<0;若A 是B 的充分而不必要条件,则实数a 的取值范围是 . 『答案』(-∞,-4)『解析』对于命题A :∵|x -1|<3,∴-2<x <4,要使A 是B 的充分而不必要条件,则a <2,-a >4,即实数a 的取值范围是(-∞,-4)7.已知圆锥的母线长为5,侧面积为15π,则此圆锥的体积为________. 『答案』12π『解析』设圆锥的半径为r ,则侧面积为15215,32r r ππ⨯⨯==,4=,所以圆锥的体积为2134123ππ⨯⨯⨯=. 故答案为12π8.函数2()sin sin cos 1f x x x x =++的最小正周期是 ,单调递减区间是 . 『答案』,,.『解析』,故,由解得9.在平面直角坐标系xOy 中,已知A (0,﹣1),B (﹣3,﹣4)两点,若点C 在∠AOB 的平分线上,且10OC =C 的坐标是_____. 『答案』(﹣1,﹣3)『解析』由题意OA =(0,﹣1),是一个单位向量, 由于OB =(﹣3,﹣4),故OB 方向上的单位向量e =(35,45-),∵点C 在∠AOB 的平分线上,∴存在正实数λ使得OC = ()OA e λ+=34,155λ⎛⎫--- ⎪⎝⎭)=39,55λ⎛⎫-- ⎪⎝⎭,∵10OC =2981102525λ⎛⎫⋅+=⎪⎝⎭,解得53λ=代入得得()1,3OC =-- 故答案为:()1,3--.10.设S n 为数列{a n }的前n 项和,若S n =na n ﹣3n (n ﹣1)(n ∈N *),且a 2=11,则S 20的值为_____. 『答案』1240『解析』由S 2=a 1+a 2=2a 2﹣3×2(2﹣1),a 2=11,可得a 1=5. 当n ≥2时,由S n =na n ﹣3n (n ﹣1)=n (S n ﹣S n ﹣1)﹣3n (n ﹣1), 可得(n ﹣1)S n ﹣nS n ﹣1=3n (n ﹣1),∴131n n S S n n --=-,∴数列n S n ⎧⎫⎨⎬⎩⎭是首项151S =,公差为3的等差数列, ∴2020S =5+3×19=62, ∴S 20=1240. 故答案为:1240.11.如图在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是___________.『答案』『解析』如图所示,延长BA ,CD 交于E ,平移AD ,当A 与D 重合与E 点时,AB 最长,在△BCE 中,∠B =∠C =75°,∠E =30°,BC =2,由正弦定理可得sin sin BC BEE C=∠∠,即o o2sin 30sin 75BE=,解得BE ,平移AD ,当D 与C 重合时,AB 最短,此时与AB 交于F ,在△BCF 中,∠B =∠BFC =75°,∠FCB =30°,由正弦定理知,sin sin BF BCFCB BFC =∠∠,即o o2sin 30sin 75BF =,解得BF 所以AB 的取值范围.12.已知函数f(x)12211222x xx xxx⎧+-⎪⎪⎪=---≤-⎨⎪≤-,>,,,若f(t)≥f(1t),则实数t的取值范围是_____.『答案』)[)1⎡⋃+∞⎣,.『解析』根据函数f(x)的解析式作出其图象,如图所示.①当x>f(x)是增函数,若()1f t ft⎛⎫≥ ⎪⎝⎭,则112ttt⎧≥⎪⎪⎨⎪>-⎪⎩,解得:t≥1;②当x2≤-时,()f x=若()1f t ft⎛⎫≥ ⎪⎝⎭,则12t≤-,解得:0t≤<;综上①②所述,实数t的取值范围是)[)1⎡⋃+∞⎣,故答案为:)[)1⎡⋃+∞⎣,.13.在平面直角坐标系中,点集A={(x,y)|x2+y2≤1},B={(x,y)|x≤4,y≥0,3x﹣4y≥0},则点集Q={(x,y)|x=x1+x2,y=y1+y2,(x1,y1)∈A,(x2,y2)∈B}所表示的区域的面积为_____.『答案』18+π『解析』由x=x1+x2,y=y1+y2,得x1=x﹣x2,y1=y﹣y2,∵(x1,y1)∈A,∴把x1=x﹣x2,y1=y﹣y2,代入x2+y2≤1,∴(x﹣x2)2+(y﹣y2)2≤1点集Q所表示的区域是以集合B={(x,y)|x≤4,y≥0,3x﹣4y≥0}的区域的边界为圆心轨迹半径为1的圆内部分,如图,其面积为:5+6+4+3+π=18+π故答案为:18+π.14.设函数f(x)=(2x﹣1)e x﹣ax+a,若存在唯一的整数x0使得f(x0)<0,则实数a的取值范围是_____.『答案』『32e,1)∪23532e e⎛⎤⎥⎝⎦,『解析』令g (x )=(2x ﹣1)e x ,h (x )=a (x ﹣1),∵()(21)2(21)x x xg x x e e x e '=-+=+,∴当21x <-时,()0g x '<,则函数g (x )在(﹣∞,12-)上单调递减; 当12x >-时,()0g x '>,则函数g (x )在(12-,+∞)上单调递增; 而g (﹣1)=﹣3e ﹣1,g (0)=﹣1; 因为存在唯一的整数x 0使得f (x 0)<0. 即(2x 0﹣1)e x <a (x 0﹣1).所以结合图形知:()()()011100a g h h ⎧>⎪-≥-⎨⎪-<<⎩或()()()()2233h g h g ⎧>⎪⎨≤⎪⎩ 即:103210a e a a -⎧⎪-≥-⎨⎪--⎩><<或23325a e a e ⎧>⎨≤⎩解得32e ≤a <1或3e 2<a 352e ≤; 故答案为:『32e ,1)∪23532e e ⎛⎤⎥⎝⎦,.二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.已知函数()2222x x x f x cossin ⎫=-⎪⎭. (1)设θ∈『0,π』,且f (θ)=1,求θ的值;(2)在△ABC 中,AB =1,f (C )=1,且△ABC sin A +sin B 的值.解:(1)()2sin sin 2cos 26x f x x x x x π⎛⎫=-=-=++ ⎪⎝⎭由f (θ)1=,∴2cos 16πθ⎛⎫++= ⎪⎝⎭, ∴1cos 62πθ⎛⎫+= ⎪⎝⎭, ∵θ∈『0,π』,∴(θ6π+)∈『6π,76π』,∴θ6π=.(2)由f (C )=+1,C ∈(0,π),由(1)可得:C 6π=.由△ABC ,∴122=ab sin 6π,∴=ab由余弦定理可得:1=a 2+b 2﹣2ab cos6π,可得:a 2+b 2=7,联立解得:a =2,b =b =2,a =∴2+=a b . ∴12sinA sinB sinC a b c ===.∴sin A +sin B 12=(a +b )=1+. 16.如图,在多面体ABCDEF 中,四边形ABCD 是菱形,AC ,BD 相交于点O ,EF ∥AB ,EF 12=AB ,平面BCF ⊥平面ABCD ,BF =CF ,G 为BC 的中点,求证:(1)OG ∥平面ABFE ;(2)AC⊥平面BDE.证明:(1)∵四边形ABCD是菱形,AC,BD相交于点O,∴O是AC中点,∵G为BC的中点,∴OG∥AB,∵OG⊄平面ABFE,AB⊂平面ABFE,∴OG∥平面ABFE.(2)连接FG、EO,∵四边形ABCD菱形,AC,BD相交于点O,∴AC⊥BD,O是AC中点,∵G为BC的中点,∵EF∥AB,EF12=AB,平面BCF⊥平面ABCD,BF=CF,∴FG⊥平面ABCD,∴EO⊥平面ABCD,∴EO⊥AC,∵EO∩BD=O,∴AC⊥平面BDE.17.某生物探测器在水中逆流行进时,所消耗能量为E=cv n T,其中v为行进时相对于水的速度,T为行进时的时间(单位:h),c为常数,n为能量次级数,如果水的速度为4km/h,该生物探测器在水中逆流行进200km.(1)求T关于v的函数关系式;(2)①当能量次级数为2时,求探测器消耗的最少能量;②当能量次级数为3时,试确定v的大小,使该探测器消耗的能量最少.解:(1)由题意得,该探测器相对于河岸的速度为200T,又该探测器相对于河岸的速度比相对于水的速度小4km/h,即为v﹣4,则200T=v﹣4,即T2004v=-,(v>4);(2)①当能量次级数为2时,由(1)知2004Tv=-,v>4,是的22004v E c v =⋅=-()2[44]2004v c v -+⋅=-()16200484c v v ⎡⎤-++⎢⎥-⎣⎦ ≥200c 『8』=3200c ,当且仅当v ﹣4164v =-,即v =8km /h 时取等号, ②当能量次级数为3时,由(1)知32004v E c v =⋅-,v >4,则()2226200(4)v v E c v -'=⋅-,由0E '=,解得v =6,即当v <6时,0E '<,当v >6时,0E '>, 即当v =6时,函数E 取得最小值为E =21600c .18.在平面直角坐标系xOy 中,已知椭圆2222x y a b+=1(a >b >0)的焦距F 1F 2的长为2,经过第二象限内一点P (m ,n )的直线22mx nya b+=1与圆x 2+y 2=a 2交于A ,B 两点,且OA = (1)求PF 1+PF 2的值; (2)若AB •1283F F =,求m ,n 的值.解:(1)∵OA=a =∵把点P (m ,n )代入直线方程22mx ny a b +=1,可得:2222m n a b+=1,∴点P 在椭圆上, ∴PF 1+PF 2=2a =.(2)由a =c =1,∴b 2=a 2﹣c 2=1.设A (x 1,y 1),B (x 2,y 2).联立22212x y mx ny ⎧+=⎪⎨+=⎪⎩,化为:(4n 2+m 2)x 2﹣4mx +4﹣8n 2=0,∴x 1+x 22244m n m =+,x 1x 2222484n n m -=+.∵AB 1283F F ⋅=,∴(x 2﹣x 1,y 2﹣y 1)•(2,0)83=, 化为2(x 2﹣x 1)83=,即x 2﹣x 143=, ∴212()x x +-4x 1x 2169=, 代入可得:()22222224481616(4)49n m n m n m --=++, 化为:56n 4+10n 2m 2﹣36n 2﹣m 4=0, 又222m n +=1, 把m 2=2﹣2n 2代入化为8n 4﹣2n 2﹣1=0,解得m 2=1,n 212=. ∵点P 在第二象限,∴取m =﹣1,n 2=. 19.已知函数 f (x )=a (|sin x |+|cos x |)﹣sin2x ﹣1,a ∈R .(1)写出函数 f (x )的最小正周期(不必写出过程);(2)求函数 f (x )的最大值;(3)当a =1时,若函数 f (x )在区间(0,kπ)(k ∈N *)上恰有2015个零点,求k 的值. 解:(1)函数 f (x )的最小正周期为π.(2)∵f (x )=a (|sin x |+|cos x |)﹣sin2x ﹣1=sin2x ﹣1=(sin2x +1),令t =,t ∈『1』,当0,2x π⎡⎤∈⎢⎥⎣⎦时,()()(21f x t at t t μ==-≤≤,当,2x π⎛⎤∈π ⎥⎝⎦时,()()(221f x v t t at t ==+-≤≤, ∵()()()2222220t v t at t t at t μ-=--+-=-+≤即()()t v t μ≤.∴()()(){}max max max 1,f x v t v v==,∵()11v a =-,v =,∴当1a ≤-()f x 最大值为1a -;当1a >--()f x .(3)当a =1时,f (x )sin 21x =-,若f (x )=0sin 21x =+即22sin 22sin 2sin x x x =+,∴当且仅当sin2x =0时,f (x )=0,∴x ∈(0,π』时,f (x )有且仅有两个零点分别为2π,π, ∴2015=2×1007+1,∴k =1008.20.已知λ,μ为常数,且为正整数,λ≠1,无穷数列{a n }的各项均为正整数,其前n 项和为S n ,对任意的正整数n ,S n =λa n ﹣μ.记数列{a n }中任意两不同项的和构成的集合为A . (1)证明:无穷数列{a n }为等比数列,并求λ的值;(2)若2015∈A ,求μ的值;(3)对任意的n ∈N *,记集合B n ={x |3μ•2n ﹣1<x <3μ•2n ,x ∈A }中元素的个数为b n ,求数列{b n }的通项公式.(1)证明:∵S n =λa n ﹣μ.当n ≥2时,S n ﹣1=λa n ﹣1﹣μ,∴a n =λa n ﹣λa n ﹣1,λ≠1,∴, ∴数列{a n }为等比数列,∵各项均为正整数,则公比=为正整数,λ为正整数,∴λ=2.(2)解:由(1)可得:S n =2a n ﹣μ,当n =1时,a 1=μ,则a n =μ•2n ﹣1,∴A ={μ(2i ﹣1+2j ﹣1)|1≤i <j ,i ,j ∈N *}, ∵2015∈A ,∴2015=μ(2i ﹣1+2j ﹣1)=μ•2i ﹣1(1+2j ﹣i )=5×13×31,∵j ﹣i >0,则1+2j ﹣i 必为不小于3的奇数,∵2i ﹣1为偶数时,上式不成立,因此必有2i ﹣1=1,∴i =1,∴μ(1+2j ﹣1)=5×13×31,只有j =3,μ=403或j =7,μ=31时,上式才成立,∴μ=31或403.(3)解:当n ≥1时,集合B n ={x |3μ•2n ﹣1<x <3μ•2n ,x ∈A },即3μ•2n ﹣1<μ(2i ﹣1+2j ﹣1)<3μ•2n ,1≤i <j ,i ,j ∈N *.B n 中元素个数,等价于满足3×2n <2i +2j <3×2n +1的不同解(i ,j ),若j >n +2,则2i +2j ≥2i +2n +3=2i +4×2n +1>3×2n +1,矛盾.若j <n +2,则2i +2j ≤2i +2n +1≤2n +2n +1=3×2n ,矛盾.∴j =n +2,又∵(21+2n +2)﹣3×2n =2+4×2n ﹣3×2n =2+2n >0,∴3×2n <21+2n +2<22+2n +2<…<2n +1+2n +2=3×2n +1,即i =1,2,…,n 时,共有n 个不同的解(i ,j ),即共有n 个不同的x ∈B n ,∴b n =n (n ∈N *).『选做题』请选定其中两题,并在相应的答题区域内作答若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.『选修4-2:矩阵与变换』21.在平面直角坐标系xOy 中,先对曲线C 作矩阵()02cos sin A sin cos θθθπθθ-⎡⎤=<<⎢⎥⎣⎦所对应的变换,再将所得曲线作矩阵()10010B k k ⎡⎤=<<⎢⎥⎣⎦所对的变换.若连续实施两次变换所对应的矩阵为01102-⎡⎤⎢⎥⎢⎥⎣⎦,求,k θ的值. 解:先对曲线C 作矩阵()02cos sin A sin cos θθθπθθ-⎡⎤=<<⎢⎥⎣⎦所对应的变换,再将所得曲线作矩阵()10010B k k ⎡⎤=<<⎢⎥⎣⎦所对的变换, 故得到连续实施两次变换所得到的变换矩阵为:10cos sin cos sin 0sin cos sin cos BA k k k θθθθθθθθ--⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦因为连续实施两次变换所对应的矩阵为01102-⎡⎤⎢⎥⎢⎥⎣⎦, 所以01cos sin 1sin cos 02k k θθθθ-⎡⎤-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦, 根据矩阵相等定义得到,cos 0sin 11sin 2cos 0k k θθθθ=⎧⎪-=-⎪⎪⎨=⎪⎪=⎪⎩,解得212k πθ⎧=⎪⎪⎨⎪=⎪⎩. 『选修4-4:坐标系与参数方程』22.在极坐标系中,已知1,,9,33A B ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,线段AB 的垂直平分线l 与极轴交于点C ,求l 的极坐标方程及ABC ∆的面积.解:以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系xoy在平面直角坐标系xoy 中,1,,9,33A B ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的坐标为19(,(,)2222A B 线段AB的中点为5(2A,AB k =故线段AB中垂线的斜率为1AB k k -==, 所以AB的中垂线方程为:5)2y x -=-化简得:100x +-=,所以极坐标方程为cos sin 100ρθθ+-=, 即cos()53πρθ-=,令0y =,则10x =,故在平面直角坐标系xoy 中,C (10,0)点C 到直线AB :y =的距离为d == 线段8AB =,故ABC ∆的面积为182S =⨯= 『选修4-5:不等式选讲』23.已知实数,a b 满足2a b +≤,求证:22224(2)a a b b a +-+≤+. 证明:因为2a b +≤, 所以2222a a b b +-+ 2222a b a b =-++()()()2a b a b a b =-+++2a b a b =+-+()22a b a a b =+-++22a b a a b ≤++++()22222244242a a a a ≤++=+=+≤+,得证.24.在棱长为1的正方体1111ABCD A B C D -中,O 是AC 的中点,E 是线段D 1O 上一点,且D 1E =λEO .(1)若λ=1,求异面直线DE 与CD 1所成角的余弦值;(2)若平面CDE ⊥平面CD 1O ,求λ的值.解:(1)以1,,DA DC DD 为单位正交基底建立如图所示的空间直角坐标系D xyz -.则A (1,0,0),11022O ⎛⎫ ⎪⎝⎭,,,()010C ,,,D 1(0,0,1), E 111442⎛⎫⎪⎝⎭,,, 于是111442DE ⎛⎫= ⎪⎝⎭,,,()1011CD =-,,. 由cos 1DE CD 〈〉,=11||DECD DE CD ⋅⋅=6.所以异面直线AE 与CD 1所成角的余弦值为 (2)设平面CD 1O 的向量为m =(x 1,y 1,z 1),由m ·CO =0,m ·1CD =0得 1111110220x y y z ⎧-=⎪⎨⎪-+=⎩,,取x 1=1,得y 1=z 1=1,即m =(1,1,1) . ………8分 由D 1E =λEO ,则E ()()121211λλλλλ⎛⎫ ⎪ ⎪+++⎝⎭,,,DE =()()121211λλλλλ⎛⎫ ⎪ ⎪+++⎝⎭,,.10分又设平面CDE 的法向量为n =(x 2,y 2,z 2),由n ·CD =0,n ·DE =0.得 ()()22220021211y x y z λλλλλ=⎧⎪⎨++=⎪+++⎩,, 取x 2=2,得z 2=-λ,即n =(-2,0,λ) .12分 因为平面CDE ⊥平面CD 1F ,所以m ·n =0,得2λ= .25.一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分. (1)设抛掷5次的得分为ξ,求ξ的分布列和数学期望E ξ;(2)求恰好得到()*n n ∈N 分的概率.解:(1)所抛5次得分ξ的概率为5551()()(5,6,7,8,9,10)2i P i C i ξ-===, 其分布列如下105555115()22i i E iC ξ-===∑ (2)令n P 表示恰好得到n 分的概率,不出现n 分的唯一情况是得到1n -分以后再掷出一次反面.因为“不出现n 分”的概率是1n P -,“恰好得到1n -分”的概率是1n P -, 因为“掷一次出现反面”的概率是12,所以有1112n n P P --=, 即1212()323n n P P --=--. 于是23n P ⎧⎫-⎨⎬⎩⎭是以121213236P -=-=-为首项,以12-为公比的等比数列. 所以1211()362n n P --=--,即11[2()]32n n P =+-. 恰好得到n 分的概率是11[2()]32n +-.。
2020届江苏省南通市海安高级中学高三阶段测试三数学试题(解析版)

2020届江苏省南通市海安高级中学高三阶段测试三数学试题一、填空题1.设全集{1,2,3,4,5}U =,若{1,2,4}U A =ð,则集合A =_________. 【答案】{3,5}.【解析】直接求根据{1,2,4}U A =ð求出集合A 即可. 【详解】解:因为全集{1,2,3,4,5}U =若{1,2,4}U A =ð, 则集合A ={3,5}. 故答案为:{3,5}. 【点睛】本题考查补集的运算,是基础题.2.已经复数z 满足(2)1z i i -=+(i 是虚数单位),则复数z 的模是________.10【解析】【详解】(2)1z i i -=+Q ,11323,i iz i i i++∴=+==- 10z =10.3.已知一组数据123,,a a a ,…,n a 的平均数为a ,极差为d ,方差为2S ,则数据121,a +221,a +321a +,…,21n a +的方差为___________.【答案】24S【解析】根据在一组数据的所有数字上都乘以同一个数字,得到的新数据的方差是原来数据的平方倍,得到结果. 【详解】解: ∵数据123,,a a a ,…,n a 的方差为2S ,∴数据121,a +221,a +321a +,…,21n a +的方差是22224S S ⨯=, 故答案为:24S . 【点睛】此题主要考查了方差,关键是掌握方差与数据的变化之间的关系. 4.如图是一个算法的伪代码,其输出的结果为_______.【答案】1011【解析】由题设提供的算法流程图可知:1111101122310111111S =++⋅⋅⋅+=-=⨯⨯⨯,应填答案1011. 5.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为______。
【答案】18【解析】试题分析:分类讨论:从0、2中选一个数字0,则0只能排在十位;从0、2中选一个数字2,则2排在十位或百位,由此可得结论.解:从0、2中选一个数字0,则0只能排在十位,从1、3、5中选两个数字排在个位与百位,共有23A =6种;从0、2中选一个数字2,则2排在十位,从1、3、5中选两个数字排在个位与百位,共有23A =6种; 2排在百位,从1、3、5中选两个数字排在个位与十位,共有23A =6种;故共有323A =18种,故答案为18. 【考点】计数原理点评:本题考查计数原理的运用,考查分类讨论的数学思想,正确分类是关键6.在平面直角坐标系xOy 中,若双曲线()2222:10,0x y C a b a b-=>>10,则双曲线C 的渐近线方程为_______. 【答案】3y x =±【解析】10,可以得到10ca=222a b c +=求出,a b 的关系,从而得出渐近线的方程. 【详解】解:因为双曲线()2222:10,0x y C a b a b-=>>10,所以10ca= 故2210c a=, 又因为222a b c +=,所以22210a b a +=,即229b a=,即3=b a ,所以双曲线的渐近线3y x =±. 【点睛】本题考查了双曲线渐近线的问题,解题的关键是由题意解析出,a b 的关系,从而解决问题.7.将函数f(x)的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象,则()π4f 为 . 【答案】4【解析】试题分析:将函数f(x)的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象,即将函数(π4sin 23y x =-的图象向左平移π6个单位得y=4sin[2(x+π6)π3]=4sin2x ,所以()π4f =4sin 42π=.故答案为:4.【考点】三角函数的图象平移.8.设定义在R 上的奇函数()f x 在区间[0,)+∞上是单调减函数,且()23(2)0f x x f -+>,则实数x 的取值范围是_________【答案】(1,2)【解析】根据题意,由函数的奇偶性和单调性分析可得函数()f x 在R 上为减函数,则()23(2)0f x x f -+>可以转化为232x x -<-,解可得x 的取值范围,即可得答案.【详解】解:根据题意,()f x 是在R 上的奇函数,且在区间[0,)+∞上是单调减函数, 则其在区间(,0)-∞上递减, 则函数()f x 在R 上为减函数,()()22223(2)03(2)(3)(2)32f x x f f x x f f x x f x x -+>⇒->-⇒->-⇒-<-,解得:12x <<;即实数x 的取值范围是(1,2); 故答案为:(1,2). 【点睛】本题考查函数的单调性与奇偶性的综合应用,关键是分析函数在整个定义域上的单调性.9.在锐角三角形ABC 中3sin 5A =,1tan()3A B -=-,则3tan C 的值为_________.【答案】79【解析】由题意可得tan A ,进而可得tan B ,而tan tan()C A B =-+,由两角和与差的正切公式可得. 【详解】解:∵在锐角三角形ABC 中3sin 5A =, 24cos 1sin 5A A ∴=-=, sin 3tan cos 4A A A ∴==, 31tan tan()1343tan tan[()]311tan tan()9143A A B B A A B A A B +--∴=--===+--⨯,313tan tan 7949tan tan()3131tan tan 3149A B C A B A B ++∴=-+=-=-=--⨯,3tan 79C ∴=故答案为:79. 【点睛】本题考查两角和与差的正切公式,属中档题.10.已知n S 为数列{}n a 的前n 项和3(1)(*)n n S na n n n N =--∈且211a =.则1a 的值________ 【答案】5【解析】由3(1)(*)n n S na n n n N =--∈,且211a =.取2n =即可得出. 【详解】解:∵3(1)(*)n n S na n n n N =--∈,且211a =.12226a a a ∴+=-,即1265a a =-=.故答案为:5. 【点睛】本题考查了递推式的简单应用,是基础题.11.设正实数x ,y 满足x yxy x y+=-,则实数x 的最小值为______. 21.【解析】由正实数x ,y 满足x y xy x y+=-,化为()2210xy x y x +-+=,可得()222212121401010x x x y y x y y ⎧∆=--≥⎪⎪-⎪+=>⎨⎪=>⎪⎪⎩,计算即可. 【详解】解:由正实数x ,y 满足x yxy x y+=-, 化为()2210xy xy x +-+=,∴()22221212140110x xxy yxy y⎧∆=--≥⎪⎪-⎪+=>⎨⎪=>⎪⎪⎩,化为426101x xx⎧-+≥⎨>⎩,解得21x≥+.因此实数x的最小值为21+.故答案为:21+.【点睛】本题考查了一元二次方程的实数根与判别式、根与系数的关系、一元二次不等式的解法,考查了推理能力和计算能力,属于中档题.12.如图正四棱柱1111ABCD A B C D-的体积为27,点E,F分别为棱11,B BC C上的点(异于端点)且//EF BC,则四棱锥1A AEFD-的体积为___________.【答案】9【解析】由11113A AED E A AD A ADV V S AB--∆==⋅,由此能求出四棱锥1A AEFD-的体积.【详解】解:连接DE,∵正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点),且//EF BC ,11A AED A FED V V --∴=,1111111111193662A AED E A AD A AD A ADD ABCD A C D V V S AB S AB V --∆-∴==⋅=⋅==,∴四棱锥1A AEFD -的体积19A AEFD V -=. 故答案为:9. 【点睛】本题考查四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、运算求解能力,是中档题.13.已知向量,,a b c r r r 满足0a b c ++=r r r 且a r 与b r的夹角的正切为12-,b r 与c r的夹角的正切为13-,||2b =r ,则a c ⋅r r 的值为___________.【答案】45【解析】可设,,AB a BC b CA c ===u u u ru u ur u uu r r r r,由题意可得11tan ,tan 23B C ==,由两角和的正切公式,可得tan A ,再由同角的基本关系式可得sin ,sin B C ,再由正弦定理可得AB ,AC ,由数量积的定义即可得到所求值. 【详解】解:可设,,AB a BC b CA c ===u u u r u u u r u u u r r r r,由题意可得11tan ,tan 23B C ==, 则11tan tan 23tan tan()1111tan tan 123B CA B C B C ++=-+=-=-=---⨯, 即为135A ︒=,又,B C 为锐角,22sin 1sin cos 1,cos 2B B B B +==, 可得5sin 5B =, 同理可得10sin 10C =, 由正弦定理可得2sin135510︒==r r,即有2102555c a ==r r , 则2102524||||cos 455525a c c a ︒⋅=⋅⋅=⋅⋅=u u rr r r .故答案为:45. 【点睛】本题考查向量的数量积的定义,考查正弦定理和三角函数的化简和求值,以及运算求解能力,属于中档题.14.已知()(2)(3),()22x f x m x m x m g x =-++=-,若同时满足条件:①,()0x R f x ∀∈<或()0<g x ;②(,4),()()0x f x g x ∃∈-∞-<.则m 的取值范围是________________. 【答案】()4,2m ∈--【解析】根据()220xg x =-<可解得x<1,由于题目中第一个条件的限制,导致f(x)在1x ≥是必须是()0f x <,当m=0时,()0f x =不能做到f(x)在1x ≥时()0f x <,所以舍掉,因此,f(x)作为二次函数开口只能向下,故m<0,且此时2个根为122,3x m x m ==--,为保证条件成立,只需1221{31x m x m =<=--<1{24m m <⇒>-,和大前提m<0取交集结果为40m -<<;又由于条件2的限制,可分析得出在(,4),()x f x ∃∈-∞-恒负,因此就需要在这个范围内g(x)有得正数的可能,即-4应该比12x x 两个根中较小的来的大,当(1,0)m ∈-时,34m --<-,解得交集为空,舍.当m=-1时,两个根同为24->-,舍.当(4,1)m ∈--时,24m <-,解得2m <-,综上所述,(4,2)m ∈--.【考点定位】本题考查学生函数的综合能力,涉及到二次函数的图像开口,根大小,涉及到指数函数的单调性,还涉及到简易逻辑中的“或”,还考查了分类讨论思想.二、解答题15.已知ABC ∆的面积为3()18AC AB CB ⋅-=u u u r u u u r u u u r,向量(tan tan ,sin 2)m A B C =+u r 和向量(1,cos cos )n A B =r是共线向量.(1)求角C ;(2)求ABC ∆的边长c .【答案】(1) 3C π=(2) 36【解析】(1)利用向量共线的条件,建立等式,再利用和角的正弦公式化简等式,即可求得角C ;(2)由()18AC AB CB ⋅-=u u u r u u u r u u u r 得:2()18AC AB BC AC ⋅+==u u u r u u u r u u u r u u u r ,进而利用ABC ∆的面积为3,及余弦定理可求ABC ∆的边长c . 【详解】(1)因为向量(tan tan ,sin 2)m A B C =+r 和(1,cos cos )n A B =r是共线向量, 所以cos cos (tan tan )sin 20A B A B C +-=,即sin cos cos sin 2sin cos 0A B A B C C +-=, 化简sin 2sin cos 0C C C -=, 即sin (12cos )0C C -=.因为0C π<<,所以sin 0C >,从而1cos ,2C =3C π=. (2)()18AC AB CB ⋅-=u u u r u u u ru u u rQ ,18()AC AB CB ∴=⋅-u u u r u u u r u u u r 2||AC AC AC =⋅=u u u r u u u r u u u r 则||1832AC ==u u u r32AC =因为ABC V 的面积为3所以1sin 932CA CB C ⋅= 即132sin 9323CB π⨯=解得62CB =在ABC V 中,由余弦定理得2222cos AB CA CB CA CB C =+-⋅221(32)(62)232622=+-⨯54=,所以5436AB ==. 【点睛】本题重点考查正弦、余弦定理的运用,考查向量知识的运用,解题的关键是正确运用正弦、余弦定理求出三角形的边.16.如图,四棱锥P-ABCD的底面为矩形,且AB=2,BC=1,E,F分别为AB,PC中点.(1)求证:EF∥平面PAD;(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.【答案】证明:(1)方法一:取线段PD的中点M,连结FM,AM.因为F为PC的中点,所以FM∥CD,且FM=12 CD.因为四边形ABCD为矩形,E为AB的中点,所以EA∥CD,且EA=12 CD.所以FM∥EA,且FM=EA.所以四边形AEFM为平行四边形.所以EF∥AM.……………………… 5分又AM⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD.………7分方法二:连结CE并延长交DA的延长线于N,连结PN.因为四边形ABCD为矩形,所以AD∥BC,所以∠BCE=∠ANE,∠CBE=∠NAE.又AE=EB,所以△CEB≌△NEA.所以CE=NE.又F为PC的中点,所以EF∥NP.………… 5分又NP⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD. (7)分方法三:取CD的中点Q,连结FQ,EQ.在矩形ABCD中,E为AB的中点,所以AE=DQ,且AE∥DQ.所以四边形AEQD为平行四边形,所以EQ∥AD.又AD⊂平面PAD,EQ⊄平面PAD,所以EQ∥平面PAD. (2)分因为Q,F分别为CD,CP的中点,所以FQ∥PD.又PD⊂平面PAD,FQ⊄平面PAD,所以FQ∥平面PAD.又FQ,EQ⊂平面EQF,FQ∩EQ=Q,所以平面EQF∥平面PAD. (5)分因为EF⊂平面EQF,所以EF∥平面PAD.……………………………… 7分(2)设AC,DE相交于G.在矩形ABCD中,因为AB=2BC,E为AB的中点.所以DAAE=CDDA=2.又∠DAE=∠CDA,所以△DAE∽△CDA,所以∠ADE=∠DCA.又∠ADE+∠CDE=∠ADC=90°,所以∠DCA+∠CDE=90°.由△DGC的内角和为180°,得∠DGC=90°.即DE⊥AC. (10)分因为平面PAC⊥平面ABCD 因为DE⊂平面ABCD,所以DE⊥平面PAC,又DE⊂平面PDE,所以平面PAC⊥平面PDE.………………………… 14分【解析】略17.如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知,,Q到海岸线OM,ON的距离分别为3 km,km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.(1)求水上旅游线AB的长;(2)若小岛正北方向距离小岛6 km处的海中有一个圆形强水波P,从水波生成t h时的半径为(a为大于零的常数).强水波开始生成时,一游轮以km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.【答案】(1)(2)【解析】试题分析:(1)由条件建立直角坐标系较为方便表示:,直线的方程为.由Q到海岸线ON的距离为km,得,解得,再由两直线交点得,利用两点间距离公式得(2)由题意是一个不等式恒成立问题:设小时时,游轮在线段上的点处,而不等式恒成立问题往往利用变量分离将其转化为对应函数最值问题:试题解析:(1)以点为坐标原点,直线为轴,建立直角坐标系如图所示.则由题设得:,直线的方程为.由,及得,∴.∴直线的方程为,即,由得即,∴,即水上旅游线的长为.(2)设试验产生的强水波圆,由题意可得P(3,9),生成小时时,游轮在线段上的点处,则,∴.强水波不会波及游轮的航行即,当时,当.,,当且仅当时等号成立,所以,在时恒成立,亦即强水波不会波及游轮的航行.【考点】函数实际应用,不等式恒成立18.在平面直角坐标系xOy中已知椭圆222:1(0)3x yE a ba+=>>过点61,2⎛⎝⎭,其左、右焦点分别为12F F 、,离心率为22. (1)求椭圆E 的方程;(2)若A ,B 分别为椭圆E 的左、右顶点,动点M 满足MB AB ⊥,且MA 交椭圆E 于点P .(i )求证:OP OM ⋅uu u r uuu r为定值;(ii )设PB 与以PM 为直径的圆的另一交点为Q ,问:直线MQ 是否过定点,并说明理由.【答案】(1) 22142x y += (2) (i )证明见解析,定值为4 (ii )直线MQ 过定点(0,0)O . 【解析】(1)由题意得离心率公式和点满足的方程,结合椭圆的,,a b c 的关系,可得,a b ,进而得到椭圆方程;(2)(i )设()02,,M y ()11,P x y ,求得直线MA 的方程,代入椭圆方程,解得点P 的坐标,再由向量的数量积的坐标表示,计算即可得证;(ii )直线MQ 过定点O (0,0).先求得PB 的斜率,再由圆的性质可得MQ ⊥PB ,求出MQ 的斜率,再求直线MQ 的方程,即可得到定点. 【详解】解:(1)易得2231212a b c a⎧⎪+=⎪⎨⎪=⎪⎩,且222c a b =-, 解得2242a b ⎧=⎨=⎩,, 所以椭圆E 的方程为22142x y +=(2)设()02,,M y ()11,P x y ,①易得直线MA 的方程为:0042y y y x =+, 代入椭圆22142x y +=得,2222000140822y y y x x ⎛⎫+++-= ⎪⎝⎭, 由()201204828y x y --=+得,()20120288y x y --=+,从而012088y y y =+, 所以示()()20002200288,2,88y y OP OM y y y ⎛⎫-- ⎪⋅=⋅ ⎪++⎝⎭u u u r u u u u r ()22002200488488y y y y --=+=++, ②直线MQ 过定点(0,0)O ,理由如下:依题意,()2020020882288PBy y k y y y +==---+, 由MQ PB ⊥得,02MQ y k =, 则MQ 的方程为:00(2)2y y y x -=-,即02yy x =, 所以直线MQ 过定点(0,0)O . 【点睛】本题考查椭圆的方程和性质,主要考查椭圆的离心率公式和方程的运用,注意联立直线方程和椭圆方程,运用韦达定理,同时考查向量的数量积的坐标表示和直线和圆的位置关系,属于中档题.19.已知数列{}n a 满足:123a a a k ===(常数0k >),111n n n n K a a a a -+-+=()*3,n n N ≥∈.数列{}n b 满足:21n n n n a a b a +++=()*n N ∈. (1)求1,b 2,b 3,b 4b 的值;(2)求出数列{}n b 的通项公式;(3)问:数列{}n a 的每一项能否均为整数?若能,求出k 的所有可能值;若不能,请说明理由.【答案】(1) 132b b ==,2421k b b k +==;(2) 41122nn k b k k+-=+(); (3) k 为1,2时数列{}n a 是整数列.【解析】(1)经过计算可知:45621,2,4a k a k a k k=+=+=++,由数列{}n b 满足:21n n n n a a b a +++=(n =1,2,3,4…),从而可求1,b 2,b 3,b 4b ;(2)由条件可知121n n n n a a k a a +--=+.得211n n n n a a k a a +-+=+,两式相减整理得2n n b b -=,从而可求数列{}n b 的通项公式;(3)假设存在正数k ,使得数列{}n a 的每一项均为整数,则由(2)可知:2122122222211n n n n n n a a a k a a a k +-+=-⎧⎪+⎨=+-⎪⎩,由1a k Z =∈,624Z a k k =++∈,可求得1,2k =.证明1,2k =时,满足题意,说明1,2k =时,数列{}n a 是整数列. 【详解】(1)由已知可知:45621,2,4a k a k a k k=+=+=++, 把数列{}n a 的项代入21n n n n b a a a =+++求得132b b ==,2421k b b k+==; (2)由121n n n n k a a a a --++=3,n n N ≥∈*() 可知:121n n n n a a k a a +--=+① 则:211n n n n a a k a a +-+=+②①−②有:2211n n n nn n a a a a a a +-+-++=,即:2n n b b -=2123n n b b --∴==…13122a a b a +===,222n n b b -== (242321)a a kb a k++===, 41122nn k b k k+-∴=+(); (3)假设存在正数k 使得数列{}n a 的每一项均为整数,则由(2)可知:2122122222211n n n n n n a a a k a a a k +-+=-⎧⎪+⎨=+-⎪⎩③, 由1a k Z =∈,624Z a k k=++∈,可知1k =,2. 当1k =时,213k k+=为整数,利用123,,a a a Z ∈结合③式可知{}n a 的每一项均为整数;当2k =时,③变为2122122222512n n n n n n a a a a a a +-+=-⎧⎪⎨=+-⎪⎩④ 用数学归纳法证明21n a -为偶数,2n a 为整数.1n =时结论显然成立,假设n k =时结论成立,这时21n a -为偶数,2n a 为整数,故212212n n n a a a +-=-为偶数,22n a +为整数,1n k ∴=+时,命题成立.故数列{}n a 是整数列.综上所述k 为1,2时数列{}n a 是整数列. 【点睛】本题考查了等差数列的基本性质和数列的递推公式,考查了学生的计算能力和对数列的综合掌握,注意分类讨论思想和转化思想的运用,属于难题. 20.设函数()()ln ,f x x a x x a =--+a R ∈. (1)若0a =求函数()f x 的单调区间;(2)若0a <试判断函数()f x 在区间()22,e e -内的极值点的个数,并说明理由;(3)求证:对任意的正数a 都存在实数t 满足:对任意的(,)x t t a ∈+,()1f x a <-. 【答案】(1) 单调递减区间为(0,1)单调递增区间为(1,)+∞. (2) 见解析 (3)证明见解析【解析】(1)求解()ln f x x '=,利用()0,()0f x f x ''><,解不等式求解单调递增区间,单调递减区间; (2)'()ln af x x x=-,其中0x >, 再次构造函数令()ln g x x x a =-,分析()g x 的零点情况.()ln 1g x x '=+, 令1()0,g x x e'==,列表分析得出()g x 单调性,求其最小值, 分类讨论求解①若1a e≤-,②若212a e e -<<-,③若220,()a f x e-≤<的单调性,()f x 最大值,最小值,确定有无零点问题;(3)先猜想(1,1),()1x a f x a ∈+<-恒成立.再运用导数判断证明.令'1()ln 1,1,()10G x x x x G x x=-+≥=-≤,求解最大值,得出()(1)0G x G <=即可. 【详解】(1)当0a =时,()ln f x x x x =-,()ln f x x '=, 令()0f x '=,1x =,列表分析x (0,1)1(1,)+∞()f x '− 0 +()f x 单调递减 单调递增故()f x 的单调递减区间为(0,1)单调递增区间为(1,)+∞.(2)()()ln f x x a x x a =--+,()ln f x x ax '=-,其中0x >, 令()ln g x x x a =-,分析()g x 的零点情况.()ln 1g x x '=+令()0g x '=,1x e =,列表分析 x(0,1e)1e(1,)e +∞()g x '− 0 +()g x单调递减 单调递增min 11()()g x g a e e==--,而11()1n1f ae ae ee'=-=--,222()2(2)f e ae ae -'=--=-+ 22221()2(2)a f e e a e e'=-=-,①若1a e ≤-则()ln 0af x x x'=-≥, 故()f x 在22(,)e e -内没有极值点;②若212a e e -<<-,则11()1n 0f ae e e'=-<,22()(2)0f e ae -'=-+> 2221()(2)0f e e a e'=-> 因此()f x '在22(,)e e -有两个零点,()f x 在22(,)e e -内有两个极值点;③若220a e -≤<则11()10f n ae e e'=-<,22()(2)0f e ae -'=-+≤,2221()(2)0f e e a e'=->, 因此()f x '在22(,)e e -有一个零点,()f x 在22(,)e e -内有一个极值点;综上所述当1(,]a e∈-∞-时,()f x 在22(,)e e -内没有极值点;当212,a e e ⎛⎫∈-- ⎪⎝⎭时,()f x 在22(,)e e -内有两个极值点; 当22,0a e ⎡⎫∈-⎪⎢⎣⎭时,()f x 在22(,)e e -内有一个极值点. (3)猜想:(1,1)x a ∈+,()1f x a <-恒成立. 证明如下:由(2)得()g x 在1(,)e+∞上单调递增,且(1)0g a =-<,(1)(1)ln(1)g a a a a +=++-.因为当1x >时,1ln 1(*)x x>-, 所以1(1)(1)(1)01g a a a a +>+--=+故()g x 在(1,1)a +上存在唯一的零点,设为0x .由x0(1,)x0x0(,1)x a +()f x '− 0 +()f x 单调递减 单调递增知(1,1)x a ∈+,()max{(1),(1)}f x f f a <+.又(1)ln(1)1f a a +=+-,而1x >时,ln 1(**)x x <-, 所以(1)(1)111(1)f a a a f +<+--=-=. 即(1,1)x a ∈+,()1f x a <-.所以对任意的正数a ,都存在实数1t =, 使对任意的(,)x t t ∈+∞, 使()1f x a <-. 补充证明(*):令1()1n 1F x x x =+-,1x ≥.22111()0x F x x x x-'=-=≥, 所以()F x 在[1,)+∞上单调递增.所以1x >时,()(1)0F x F >=,即1ln 1x x>-. 补充证明(**)令()ln 1G x x x =-+,1x ≥.1()10G x x'=-≤, 所以()G x 在[1,)+∞上单调递减.所以1x >时,()(1)0G x G <=,即ln 1x x <-. 【点睛】本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间,考查了不等式与导数的结合,难度较大.21.已知二阶矩阵,矩阵属于特征值的一个特征向量为,属于特征值的一个特征向量为.求矩阵.【答案】【解析】运用矩阵定义列出方程组求解矩阵 【详解】由特征值、特征向量定义可知,,即,得同理可得解得,,,.因此矩阵【点睛】本题考查了由矩阵特征值和特征向量求矩阵,只需运用定义得出方程组即可求出结果,较为简单22.在极坐标系中,已知1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,线段AB 的垂直平分线l 与极轴交于点C ,求l 的极坐标方程及ABC ∆的面积.【答案】l 的极坐标方程及cos 53πρθ⎛⎫-= ⎪⎝⎭,203ABC ∆的面积. 【解析】将1,,9,33A B ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭转化为直角坐标系下的坐标形式,然后求出线段AB 的中点与直线AB 的斜率,进而求出直线l 在直角坐标系下的方程,再转化为极坐标方程;在直角坐标系下,求出点C 到直线AB 的距离、线段AB 的长度,从而得出ABC ∆的面积. 【详解】解:以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系xoy 在平面直角坐标系xoy 中,1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ 的坐标为13993((22A B 线段AB 的中点为553(,22A ,3AB k =故线段AB 中垂线的斜率为13AB k k --==, 所以AB 的中垂线方程为:5335)2y x --=- 化简得:3100x +-=,所以极坐标方程为cos 3sin 100ρθρθ+-=,即cos()53πρθ-=,令0y =,则10x =,故在平面直角坐标系xoy 中,C (10,0)点C 到直线AB :3y x =的距离为1035331d ==+线段8AB =,故ABC ∆的面积为15382032S =⨯=【点睛】本题考查了直线的极坐标方程问题,解题时可以将极坐标系下的问题转化为平面直角坐标系下的问题,从而转化为熟悉的问题.23.已知实数,a b 满足2a b +≤,求证:22224(2)a a b b a +-+≤+.【答案】证明见解析【解析】对2222a a b b +-+进行转化,转化为含有2a b +≤形式,然后通过不等关系得证. 【详解】解:因为2a b +≤,所以2222a a b b +-+2222a b a b =-++ ()()()2a b a b a b =-+++2a b a b =+-+()22a b a a b =+-++ 22a b a a b ≤++++()22222244242a a a a≤++=+=+≤+,得证.【点睛】本题考查了绝对值不等式问题,解决问题的关键是要将要证的形式转化为已知的条件,考查了学生转化与化归的能力.24.如图,在四棱锥P ABCD-中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2.若DC ABλ=u u u r u u u r(Rλ∈),且向量PCuuu r与BDu u u r夹角的余弦值为15.(1)求λ的值;(2)求直线PB与平面PCD所成角的正弦值.【答案】(1)2λ=;(2)105.【解析】试题分析:(1)以A为坐标原点,AB、AD、AP分别为x、y、z轴建立空间直角坐标系A xyz-,写出,PCu u u r,BDu u u r的坐标,根据空间向量夹角余弦公式列出关于λ的方程可求;(2)设岀平面PCD的法向量为(),,n x y z=r,根据n PCn DC⎧⊥⎪⎨⊥⎪⎩r u rr u r,进而得到⎧⋅=⎪⎨⋅=⎪⎩r u rr u rn PCn DC,从而求出nr,向量PBu r的坐标可以求出,从而可根据向量夹角余弦的公式求出cos,n PB<>r u r,从而得PB和平面PCD所成角的正弦值.试题解析:(1)依题意,以A为坐标原点,AB、AD、AP分别为x、y、z轴建立空间直角坐标系A xyz-读 万 卷 书 行万 里 路(1,0,0),(0,2,0),(0,0,2)B D P ,因为DC AB λ=u u u r u u u r,所以(,2,0)C λ,从而(,2,2)PC λ=-u u u r ,则由15cos ,15PC BD =u u u r u u u r ,解得10λ=(舍去)或2λ=.(2)易得(2,2,2)PC =-u u u r ,(0,2,2)PD =-u u u r ,设平面PCD 的法向量(,,)n x y z =r,则0⋅=r u u u r n PC ,0⋅=r u u u rn PD ,即0x y z +-=,且0y z -=,所以0x =,不妨取1y z ==,则平面PCD 的一个法向量(0,1,1)n =r ,又易得(1,0,2)PB =-u u u r,故10cos ,=⋅=-u u u r r PB n PB n ,所以直线PB 与平面PCD 所成角的正弦值为10.考点: 1、空间两向量夹角余弦公式;2、利用向量求直线和平面说成角的正弦.25.已知数列{}n a 的通项公式为15155n nn a ⎡⎤+-⎥=-⎥⎝⎭⎝⎭⎦,n N ∈,记1212n n n S C a C a =++…nn n C a +.(1)求1,S 2S 的值;(2)求所有正整数n ,使得n S 能被8整除.【答案】(1) 11S =;23S =; (2) {}*|3,n n k k N =∈【解析】(1)运用二项式定理,化简整理,再代入计算即可得到所求值;(2)通过化简得到213n n n S S S ++=-,再由不完全归纳找规律得到结论,即可得到所求结论.【详解】解:(1)1212nn n n n n S C a C a C a =++⋯+2121515225n n C C ⎡⎛⎛⎫+⎢ =⋅+⋅+ ⎪ ⎪⎢⎝⎭⎝⎣ (2)12151515222n n n n n C C C ⎫⎛⎛⎛⎪ +⋅-⋅+⋅+ ⎪ ⎝⎭⎝⎭⎭⎝…152n n n C ⎤⎫⎛⎫-⎥⎪+⋅⎪ ⎪⎥⎪⎝⎭⎭⎦ 1515115n n⎡⎤⎛⎛+-⎥=+-+ ⎥⎝⎭⎝⎭⎦3535225n n ⎡⎤⎛⎫⎛⎫⎥=- ⎪ ⎪ ⎪ ⎪⎥⎝⎭⎝⎭⎦, 即有1S 515==; 2S 3535==; (2)35355nn S n ⎡⎤+-⎥=-⎥⎝⎭⎝⎭⎦, 23535225n S n n +⎡⎤+-=+-+⎥⎥⎝⎭⎝⎭⎦3535353535352222225n n n n ⎡⎤⎡⎤⎛⎫⎛⎛⎛⎫⎛⎥⎢⎥-⋅+-- ⎪ ⎪ ⎪ ⎪ ⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎦⎣⎦13n n S S +=-,即213n n n S S S ++=-,*n N ∈, 因此2n S +除以8的余数,完全由1,n n S S +除以8的余数确定, 因为11,a =21a =,所以11111S C a ==,12221223S C a C a =+=,3213918S S S =-=-=,432324321,S S S =-=-=543363855S S S =-=-=, 654316521144,S S S =-=-=7535643255377S S =-=-=, 87631131144987,S S S =-=-=987329613772584S S S =-=-=由以上计算及213n n n S S S ++=-可知,数列{}n S 各项除以8的余数依次是: 1,3,0,5,7,0,1,3,0,5,7,0,…,它是一个以6为周期的数列,从而n S 除以8的余数等价于n 除以3的余数, 所以3,n k =*k N ∈,即所求集合为:{}*|3,n n k k N=∈.【点睛】本题考查数列通项的运用,解决问题的关键是运用二项式定理,本题属于难题.。
海安高级中学2020届高三数学模拟考试试题

(第6题)江苏省海安高级中学2020届高三数学模拟考试试题参考公式:样本数据1x ,2x ,…,nx 的标准差211()ni i s x x n ==-∑,其中11nii x x n ==∑;柱体的体积公式:V Sh =,其中S 为柱体的底面积,h 为柱体的高. 锥体的体积公式:13V Sh =,其中S 为锥体的底面积,h 为锥体的高. 一、填空题:本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上.1.已知全集{}21012U =--,,,,,集合{}2 1 1A =--,,,则UA =▲ .2.已知复数()()z 1i i a =-⋅+(i 为虚数单位)为纯虚数,则实数a 的值为 ▲ .3.数据1,3,5,7,9的标准差为 ▲ . 4.函数()12xf x =-的定义域是 ▲ .5.在一底面半径和高都是2m 的圆柱形容器中盛满小麦,有一粒带麦锈病的种子混入了其中.现从中随机取出23m 的种子,则取出了带麦锈病种子的概率是 ▲ .6.右图是一个算法的伪代码,则输出的i 的值为 ▲ . 7. 在平面直角坐标系xOy 中,若双曲线2221(0)y x b b-=>经过点()34,,则该双曲线的准线方程为 ▲ . 8。
设nS 是等比数列{}n a 的前n 项的和,396S S S ,,成等差数列,则258a a a +的值为 ▲ .(第15题)9.给出下列四个命题,其中正确命题的序号是 ▲ .(写出所有正确命题的序号)①因为当π3x =时,()2πsin sin 3x x +≠,所以2π3不是函数sin y x =的周期;②对于定义在R 上的函数()f x ,若()()22f f -≠,则函数()f x 不是偶函数; ③“M N >”是“22log log M N>"成立的充分必要条件;④若实数a 满足24a<,则2a ≤.10。
如图,是一个四棱锥的平面展开图,其中间是边长为2的正方形,上面三角形是等边三角形,左、右三角形是等腰直角三角形,则此四棱锥的体积为 ▲ .11.在平面直角坐标系xOy 中,若函数()ln f x x ax =-在1=x 处的切线与圆C :01222=-++-a y x x存在公共点,则实数a 的取值范围为 ▲ .12. 已知函数()32f x axbx cx=++,若关于x 的不等式()0f x <的解集是()()102-∞-,,,则b ca+的值为 ▲ .13.在边长为4的菱形ABCD 中,A =60°,点P 在菱形ABCD 所在的平面内.若3PA =,PC =PB PD ⋅= ▲ .14。
2020年江苏省南通市海安高中高考数学模拟试卷(5月份)(附答案详解)

2020年江苏省南通市海安高中高考数学模拟试卷(5月份)一、单空题(本大题共14小题,共70.0分)1.已知全集U={−2,−1,0,1,2},集合A={−2,−1,1},则∁U A=______.2.已知复数z=(1−i)⋅(a+i)(i为虚数单位)为纯虚数,则实数a的值为______.3.数据1,3,5,7,9的标准差为______.4.函数f(x)=√1−2x的定义域为______ .5.在一底面半径和高都是2m的圆柱形容器中盛满小麦,有一粒带麦锈病的种子混入了其中.现从中随机取出2m3的种子,则取出了带麦锈病种子的概率是______.6.如图是一个算法的伪代码,则输出的i的值为______.7.在平面直角坐标系xOy中,若双曲线x2−y2b2=1(b>0)经过点(3,4),则该双曲线的准线方程为______.8.设S n是等比数列{a n}的前n项的和,S3,S9,S6成等差数列,则a2+a5a8的值为______.9.给出下列四个命题,其中正确命题的序号是______.(写出所有正确命题的序号)①因为当x=π3时,sin(x+2π3)≠sinx,所以2π3不是函数y=sinx的周期;②对于定义在R上的函数f(x),若f(−2)≠f(2),则函数f(x)不是偶函数;③“M>N”是“log2M>log2N”成立的充分必要条件;④若实数a满足a2<4,则a≤2.10.如图,是一个四棱锥的平面展开图,其中间是边长为2的正方形,上面三角形是等边三角形,左、右三角形是等腰直角三角形,则此四棱锥的体积为______.11.在平面直角坐标系xOy中,若函数f(x)=lnx−ax在x=1处的切线与圆C:x2−2x+y2+1−a=0存在公共点,则实数a的取值范围为______.12. 已知函数f(x)=ax 3+bx 2+cx ,若关于x 的不等式f(x)<0的解集是(−∞,−1)∪(0,2),则b+c a的值为 .13. 在边长为4的菱形ABCD 中,A =60°,点P 在菱形ABCD 所在的平面内.若PA =3,PC =√21,则PB ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ =______. 14. 设函数f(x)={2−|(k+174)x +2|,x ≤0x 2,x >0,g(x)=k(x −43),其中k >0.若存在唯一的整数x ,使得f(x)<g(x),则实数k 的取值范围是______. 二、解答题(本大题共11小题,共142.0分)15. 如图,四棱锥P −ABCD 中,底面ABCD 是菱形,对角线AC ,BD 交于点O ,M 为棱PD的中点,MA =MC.求证: (1)PB//平面AMC ; (2)平面PBD ⊥平面AMC .16. 在锐角三角形ABC 中,角A ,B ,C 的对边分别为a ,b ,c.已知tanA ,tanB ,tanC 成等差数列,cosA ,√cosC ,cosB 成等比数列. (1)求A 的值;(2)若△ABC 的面积为1,求c 的值.17. 某房地产开发商在其开发的某小区前修建了一个弓形景观湖.如图,该弓形所在的圆是以AB 为直径的圆,且AB =300米,景观湖边界CD 与AB 平行且它们间的距离为50√2米.开发商计划从A 点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作PQ.设∠AOP =2θ. (1)用θ表示线段PQ ,并确定sin2θ的范围;(2)为了使小区居民可以充分地欣赏湖景,所以要将PQ 的长度设计到最长,求PQ 的最大值.18. 在平面直角坐标系xOy 中,已知椭圆C 的中心为坐标原点O ,焦点在x 轴上,右顶点A(2,0)到右焦点的距离与它到右准线的距离之比为12. (1)求椭圆C 的标准方程;(2)若M ,N 是椭圆C 上关于x 轴对称的任意两点,设P(−4,0),连接PM 交椭圆C 于另一点E.求证:直线NE 过定点B ,并求出点B 的坐标;(3)在(2)的条件下,过点B 的直线交椭圆C 于S ,T 两点,求OS ⃗⃗⃗⃗⃗ ⋅OT ⃗⃗⃗⃗⃗ 的取值范围.19.已知函数f(x)=ax2+12bx,其中a>0,b>0.(1)①求函数f(x)的单调区间;②若x1,x2满足|x i|>√a =1,2),且x1+x2>0,x2>0.求证:f(x1)+2f(x2)>√ab.(2)函数g(x)=12ax2−lnx.若对任意x1,x2∈√a),x1≠x2,都有|f(x1)−f(x2)|>|g(x1)−g(x2)|,求b−a的最大值.20.已知{a n},{b n},{c n}都是各项不为零的数列,且满足a1b1+a2b2+⋯+a n b n=c n S n,n∈N∗,其中S n是数列{a n}的前n项和,{c n}是公差为d(d≠0)的等差数列.(1)若数列{a n}是常数列,d=2,c2=3,求数列{b n}的通项公式;(2)若a n=λn(λ是不为零的常数),求证:数列{b n}是等差数列;(3)若a1=c1=d=k(k为常数,k∈N∗),b n=c n+k(n≥2,n∈N∗).求证:对任意的n≥2,n∈N∗,b na n>b n+1a n+1恒成立.21. 已知二阶矩阵A =[abc d ],矩阵A 属于特征值λ1=−1的一个特征向量为α1⃗⃗⃗⃗ =[1−1],属于特征值λ2=4的一个特征向量为α2⃗⃗⃗⃗ =[32].求矩阵A .22. 在平面直角坐标系xOy 中,已知曲线C 的参数方程为{x =2cosαy =sinα(α为参数).以直角坐标系原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为ρcos(θ−π4)=2√2.点P 为曲线C 上的动点,求点P 到直线l 距离的最大值.23. 若正数a ,b ,c 满足a +b +c =1,求13a+2+13b+2+13c+2的最小值.24. 如图,在正四棱锥P −ABCD 中,底面正方形的对角线AC ,BD 交于点O 且OP =12AB .(1)求直线BP 与平面PCD 所成角的正弦值;(2)求锐二面角B−PD−C的大小.25.定义:若数列{a n}满足所有的项均由−1,1构成且其中−1有m个,1有p个(m+p≥3),则称{a n}为“(m,p)−数列”.(1)a i,a j,a k(i<j<k)为“(3,4)−数列”{a n}中的任意三项,则使得a i a j a k=1的取法有多少种?(2)a i,a j,a k(i<j<k)为“(m,p)−数列”{a n}中的任意三项,则存在多少正整.数对(m,p)使得1≤m≤p≤100,且a i a j a k=1的概率为12答案和解析1.【答案】{0,2}【解析】解:∵U={−2,−1,0,1,2},A={−2,−1,1},∴∁U A={0,2}.故答案为:{0,2}.进行补集的运算即可.本题考查了列举法的定义,全集和补集的定义及补集的运算,考查了计算能力,属于基础题.2.【答案】−1【解析】解:复数z=(1−i)⋅(a+i)=a+1+(1−a)i为纯虚数,∴a+1=0,1−a≠0,解得a=−1.故答案为:−1.利用复数运算法则、纯虚数的定义即可得出.本题考查了复数运算法则、纯虚数的定义,考查了推理能力与计算能力,属于基础题.3.【答案】2√2【解析】【分析】首先做出这组数据的平均数,再利用方差的公式,代入数据做出这组数据的方差,最后把方差开方做出这组数据的标准差.本题考查一组数据的标准差,我们需要先求平均数,在求方差,最后开方做出标准差,属于基础题.【解答】=5,解:样本的平均数x=1+3+5+7+95[(1−5)2+(3−5)2+(5−5)2+(7−5)2+(9−5)2],∴这组数据的方差是S2=15∴S2=8,标准差S=2√2,故答案为:2√2,4.【答案】{x|x≤0}【解析】解:由1−2x≥0,即2x≤1=20,解得x≤0,定义域为{x|x≤0}.故答案为:{x|x≤0}.由1−2x≥0,结合指数函数的单调性,即可得到所求定义域.本题考查函数的定义域的求法,注意偶次根式和指数函数的性质,属于基础题.5.【答案】14π【解析】解:由题意可得:取出了带麦锈病种子的概率=2π×22×2=14π.故答案为:14π.利用几何概率计算公式即可得出.本题考查了几何概率计算公式,考查了推理能力与计算能力,属于基础题.6.【答案】5【解析】解:由算法语句知:算法的功能是求满足S=9−(1+2+3+⋯+i)<0的最小正整数i+1的值,∵S=9−(1+2+3)=3>0,S=9−(1+2+3+4)=−1<0,∴输出的i值为5.故答案为:5.算法的功能是求满足S=9−(1+2+3+⋯+i)<0的最大正整数i+1的值,计算S的值确定输出i的值.本题考查了当型循环结构的程序语句,根据算法的流程判断算法的功能是解题的关键.7.【答案】x=±√33【解析】解:∵双曲线x2−y2b2=1(b>0)经过点(3,4),∴32−16b2=1,解得b2=2,即b=√2.又a=1,∴该双曲线的准线方程为:x=±√33.故答案为:x=±√33.把已知点的坐标代入双曲线方程,求得b,则双曲线的渐近线方程可求.本题考查双曲线的标准方程,考查双曲线的简单性质,是基础题.8.【答案】2【解析】解:等比数列{a n}的公比设为q,S3,S9,S6成等差数列,可得2S9=S3+S6,若q=1,则18a1=3a1+6a1,显然不成立,故q≠1,则2⋅a1(1−q 9)1−q =a1(1−q3)1−q+a1(1−q6)1−q,化为2q6=1+q3,解得q3=−12,则a2+a5a8=a1q+a1q4a1q7=1+q3q6=1−1214=2,故答案为:2.等比数列{a n}的公比设为q,判断公比q不为1,由等比数列的求和公式和等差数列的通项公式,解方程可得q3=−12,再由等比数列的通项公式,计算可得所求值.本题考查等比数列的通项公式和求和公式,等差数列的中项性质,考查分类讨论思想和运算能力,属于中档题.9.【答案】①②④【解析】解:因为当x=π3时,sin(x+2π3)≠sinx,所以由周期函数的定义知2π3不是函数y=sinx的周期,故①正确;对于定义在R上的函数f(x),若f(−2)≠f(2),由偶函数的定义知函数f(x)不是偶函数,故②正确;由M>N,不一定有log2M>log2N,反之成立,则“M>N”是“log2M>log2N”成立的必要不充分条件,故③错误;若实数a满足a2<4,则−2≤a≤2,所以a≤2成立,故④正确.∴正确命题的序号是①②④.故答案为:①②④.由周期函数的定义判断①;由偶函数的概念判断②;由充分必要条件的判定判断③;求解一元二次不等式判断④.本题考查命题的真假判断与应用,考查逻辑思维能力与推理论证能力,是中档题.10.【答案】4√33【解析】解:如图,是一个四棱锥的平面展开图,其中间是边长为2的正方形,上面三角形是等边三角形,左、右三角形是等腰直角三角形,∴此四棱锥S−ABCD中,ABCD是边长为2的正方形,△SAD是边长为2的等边三角形,平面SAD⊥平面ABCD,∴△SAD的高AD是四棱锥S−ABCD的高,∴此四棱锥的体积为:V=13S正方形ABCD×SE=13×2×2×√4−1=4√33.故答案为:4√33.此四棱锥S−ABCD中,ABCD是边长为2的正方形,△SAD是边长为2的等边三角形,平面SAD⊥平面ABCD,△SAD的高AD是四棱锥S−ABCD的高,由此能求出此四棱锥的体积.本题考查四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理能力与计算能力,属于中档题.11.【答案】【解析】解:由条件得到f′(x)=1x−a,则当x=1时,f(1)=−a,f′(1)=1−a,所以函数在x=1处的切线为y=(1−a)(x−1)−a=(1−a)x−1,即(1−a)x−y−1=0圆C方程整理可得:(x−1)2+y2=a,即有圆心C(1,0),且a>0所以圆心到直线的距离d=√(1−a)<sup>2</sup>+1=√a2−2a+2≤√a,解得a≥2或0<a≤1,故答案为:(0,1]∪[2,+∞).利用导数可求出切线方程,则切线与圆存在公共点等价于圆心到直线的距离d小于等于半径,解出不等式即可本题考查曲线上某点的切线方程,考查直线与圆存在公共点问题,属于中档题.12.【答案】−3【解析】【分析】根据题意并结合一元二次不等式与一元二次方程的关系,可得方程ax2+bx+c=0的两根分别为−1和2,由此建立关于a、b,c的方程组并解之,即可得到实数a、b,c之间的关系,进而求出结论.本题给出三次函数,讨论不等式f(x)<0的解集并求参数的值,着重考查了一元二次不等式的应用、一元二次不等式与一元二方程的关系等知识.【解答】解:因为函数f(x)=ax3+bx2+cx=x(ax2+bx+c),∵关于x的不等式f(x)<0的解集是(−∞,−1)∪(0,2),∴ax2+bx+c=0的两根为:−1和2;所以有:(−1)+2=−ba 且(−1)×2=ca;∴b=−a且c=−2a;∴b+ca =−a−2aa=−3;故答案为:−3 13.【答案】−1【解析】解:连接AC ,BD ,设AC ,BD 交于点O ,以点O 为原点,分别以直线OC ,OD 为x ,y 轴,建立如图所示的平面直角坐标系,则:A(−2√3,0),C(2√3,0),B(0,−2),D(0,2),设P(x,y),∵PA =3,PC =√21,∴{(x +2√3)2+y 2=9①(x −2√3)2+y 2=21②, ①−②得,8√3x =−12,解得x =−√32,∴y =±32,∴P(−√32,−32)或P(−√32,32),显然得出的PB ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ 是定值,∴取P(−√32,32),则PB ⃗⃗⃗⃗⃗ =(√32,−72),PD ⃗⃗⃗⃗⃗ =(√32,12), ∴PB ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ =34−74=−1.故答案为:−1.可连接AC ,BD ,并设AC 与BD 交于点O ,然后以点O 为原点,OC ,OD 分别为x ,y 轴,建立平面直角坐标系,从而可求出A(−2√3,0),C(2√3,0),B(0,−2),D(0,2),并设P(x,y).根据PA =3,PC =√21即可求出P 点的坐标,进而可求出向量PB ⃗⃗⃗⃗⃗ ,PD ⃗⃗⃗⃗⃗ 的坐标,从而进行数量积的坐标运算即可求出PB ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ 的值.本题考查了通过建立平面直角坐标系,利用向量坐标解决向量问题的方法,两点间的距离公式,向量数量积的坐标运算,考查了计算能力,属于中档题.14.【答案】【解析】解:∵函数f(x)={2−|(k+174)x +2|,x ≤0x 2,x >0,且k >0, 画出f(x)的图象如下:∵g(x)=k(x −43),又∵存在唯一的整数x ,使得f(x)<g(x), ∴k ≥k+174,得k ≥173;又∵g(x)=k(x −43), ∴g(x)过定点(43,0), ∵g(2)=23k ≥349<f(2),g(3)=53k ≥859>f(3),∴存在唯一的整数x =3, ∴g(4)=83k ≤f(4)=16, ∴k ≤6. 故答案为:[173,6]本题利用f(x),g(x)的图象特点寻找整数x 的大致范围,再代入数字检验,确定k 的取值范围.本题考查了分段函数、带绝对值号函数的图象画法,以及数形结合思想,需要学生有较强的逻辑思维能力,分析出k 的范围.属于中档题.15.【答案】解:(1)证明:连结OM ,∵O 是菱形ABCD 对角线AC 、BD 的交点,∴O 为BD 的中点,∵M 是棱PD 的中点,∴OM//PB , ∵OM ⊂平面AMC ,PB ⊄平面AMC , ∴PB//平面AMC .(2)解:在菱形ABCD 中,AC ⊥BD ,且O 为AC 的中点,∵MA =MC ,∴AC ⊥OM , ∵OM ∩BD =O ,∴AC ⊥平面PBD , ∵AC ⊂平面AMC ,∴平面PBD ⊥平面AMC .【解析】(1)连结OM ,推导出OM//PB ,由此能证明PB//平面AMC . (2)推导出AC ⊥OM ,从而AC ⊥平面PBD ,由此能证明平面PBD ⊥平面AMC . 本题考查线面平行、面面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理能力与计算能力,属于中档题.16.【答案】解:(1)tanA ,tanB ,tanC 成等差数列,可得2tanB =tanA +tanC ,而tanC =−tan(A +B)=tanA−tanBtanAtanB−1,所以tanB =2tanA ,① 又cosA ,√cosC ,cosB 成等比数列,可得cosAcosB =cosC =−cos(A +B)=sinAsinB −cosAcosB , 即sinAsinB =2cosAcosB ,可得tanAtanB =2,② 联立①②解得tanA =1(负的舍去), 可得锐角A =π4;(2)由(1)可得tanB =2tanA =2,tanC =3, 由tanB =sinBcosB =2,sin 2B +cos 2B =1,B 为锐角, 解得sinB =2√55,同理可得sinC =3√1010,由正弦定理可得b =csinB sinC=2√53√10c =2√23c , 又△ABC 的面积为1,可得12bcsinA =12⋅2√23c 2⋅√22=1,解得c =√3.【解析】(1)运用等差数列和等比数列的中项性质,结合诱导公式、两角和的余弦公式、正切公式,化简计算可得tanA =1,进而得到所求角;(2)运用同角的基本关系式,求得sinB ,sinC ,再由正弦定理和面积公式,解方程可得所求值.本题考查等差数列和等比数列的中项性质,三角形的正弦定理、面积公式的运用,考查三角函数的同角公式、两角和的余弦、正切公式,考查化简运算能力,属于中档题.17.【答案】解:(1)过点Q 作QH ⊥AB 于点H ,则QH =50√2,在△AOP 中,∵OA =OP =150,∠AOP =2θ, ∴∠OAP =π2−θ, 由正弦定理得:OP sin(π2−θ)=APsin2θ,∴AP =300sinθ,∴AQ =QHsin(π2−θ)=50√2cosθ, ∴PQ =AP −AQ =300sinθ−50√2cosθ,∵PQ =300sinθ−50√2cosθ>0,即sin2θ>√23,且2θ∈(0,π);(2)∵PQ =300sinθ−50√2cosθ=50(6sinθ−√2cosθ), 令f(θ)=6sinθ−√2cosθ,sin2θ>√23,且2θ∈(0,π),∴f′(θ)=6cosθ−√2sinθcos 2θ=√2cosθ⋅(3√2−tanθ−tan 3θ),令f′(θ)=0,即tan 3θ+tanθ−3√2=0,∴(tanθ−√2)(tan 2θ+√2tanθ+3)=0, 记tanθ0=√2,θ0∈(0,π2),∴当0<θ<θ0时,f′(θ)>0,f(θ)单调递增;当θ0<θ<π2时,f′(θ)<0,f(θ)单调递减, 又∵sin2θ0=2√23>√23, ∴当tanθ=√2时,f(θ)取最大值,此时sinθ=√63,cosθ=√33,∴PQ 的最大值为50√6米.【解析】(1)过点Q 作QH ⊥AB 于点H ,则QH =50√2,所以∠OAP =π2−θ,由正弦定理求得AP =300sinθ,所以AQ QHsin(π2−θ)=50√2cosθ,所以PQ =300sinθ−50√2cosθ,又PQ =300sinθ−50√2cosθ>0,即sin2θ>√23,且2θ∈(0,π);(2)因为PQ =300sinθ−50√2cosθ=50(6sinθ−√2cosθ),令f(θ)=6sinθ−√2cosθ,利用导数得到当tanθ=√2时,f(θ)取最大值,此时sinθ=√63,cosθ=√33,所以PQ 的最大值为50√6米.本题主要考查了函数的实际运用,是中档题.18.【答案】解:(1)设椭圆C 的标准方程x 2a 2+y2b 2=1(a >b >0),焦距为2c , 由题意得,a =2,由a−c a 2c−a =c a =12,可得c =1,则b 2=a 2−c 2=3,所以椭圆C 的标准方程为x 24+y 23=1;(2)证明:根据对称性,直线NE 过的定点B 一定在x 轴上,由题意可知直线PM 的斜率存在,设直线PM 的方程为y =k(x +4), 联立{y =k(x +4)x 24+y 23=1,消去y 得到(4k 2+3)x 2+32k 2x +64k 2−12=0,设点M(x 1,y 1),E(x 2,y 2),则N(x 1,−y 1). 所以x 1+x 2=−32k 24k 2+3,x 1x 2=64k 2−124k 2+3,所以NE 的方程为y −y 2=y 2+y1x 2−x 1(x −x 2),令y =0,得x =x 2−y 2(x 2−x 1)y 2+y 1,将y 1=k(x 1+4).y 2=k(x 2+4)代入上式并整理,x =2x 1x 2+4(x 1+x 2)x 1+x 2+8,整理得x =(128k 2−24)−128k 2−32k 2+(24+32k 2)=−1,所以,直线NE 与x 轴相交于定点B(−1,0).(3)当过点M 的直线ST 的斜率不存在时,直线ST 的方程为x =−1,S(−1,32),T(−1,−32),此时OS ⃗⃗⃗⃗⃗ ⋅OT ⃗⃗⃗⃗⃗ =−54, 当过点B 的直线ST 斜率存在时,设直线ST 的方程为y =m(x +1),且S(x 3,y 3),T(x 4,y 4)在椭圆C 上,联立方程组{y =m(x +1)x 24+y 23=1,消去y ,整理得(4m 2+3)x 2+8m 2x +4m 2−12=0,则△=(8m 2)2−4(4m 2+3)(4m 2−12)=144(m 2+1)>0. 所以x 3+x 4=−8m 24m 2+3,x 3x 4=4m 2−124m 2+3,所以y 3y 4=m 2(x 3+1)(x 4+1)=m 2(x 3x 4+x 3+x 4+1)=−9m 24m 2+3,所以OS ⃗⃗⃗⃗⃗ ⋅OT ⃗⃗⃗⃗⃗ =x 3x 4+y 3y 4=−5m 2+124m 2+3=−54−334(4m 2+3), 由m 2≥0,得OS ⃗⃗⃗⃗⃗ ⋅OT ⃗⃗⃗⃗⃗ ∈[−4,−54), 综上可得,OS ⃗⃗⃗⃗⃗ ⋅OT ⃗⃗⃗⃗⃗ 的取值范围是[−4,−54].【解析】(1)根据题意,设椭圆方程,根据题意可知,a =2,c =1,即可求得b 的值,求得椭圆方程;(2)设直线PM 的方程.代入椭圆方程,根据直线点斜式方程结合韦达定理,即可求得B 点坐标;(3)分类讨论,当直线ST 的斜率存在,设直线ST 的方程,代入椭圆方程,根据韦达定理及向量的坐标运算,即可求得OS ⃗⃗⃗⃗⃗ ⋅OT ⃗⃗⃗⃗⃗ 的取值范围.本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,向量的坐标运算,考查转化思想,分类讨论思想,计算能力,属于难题.19.【答案】解:(1)f′(x)=ax 2−12bx 2,x ≠0, 由f′(x)>0可得x >√a 或x <√a ,由f′(x)<0可得√a <x <√a , 故函数的单调递增区间(−∞,√a ),(√a +∞),单调递减区间√a √a ); ②∵x 1+x 2>0,x 2>0, ∴x 1>0或x 1<0,若x 1>0因为|x i |>√a ,|x 1|>√a ,|x 2|>√a ,由①知f(x)在(√a +∞)上单调递增,f(x 1)+2f(x 2)>3f(√a)=3√a b>√ab, 若x 1<0,由|x 1|>√a 可得x 1<√a ,因为x 1+x 2>0,x 2>0,所以x 2>−x 1>√a ,由①f(x)在(√a +∞)上单调递增,f(x 1)+2f(x 2)>f(x 1)+2f(−x 1)=f(−x 1)>√ab综上f(x 1)+2f(x 2)>√ab .(2)0<x <√a 时,g′(x)=ax −1x=ax 2−1x<0,g(x)在√a )上单调递减,不妨设x 1<x 2,由(1)f(x)在√a )上单调递减,由|f(x 1)−f(x 2)|>|g(x 1)−g(x 2)|,可得f(x 1)−f(x 2)>g(x 1)−g(x 2), 所以f(x 1)−g(x 1)−[f(x 2)−g(x 2)]>0,令M(x)=f(x)−g(x),x ∈√a ),可得M(x)单调递减, 所以M′(x)=ax 2−12bx 2−ax +1x =(ax 2−1)(1−2bx)2bx 2≤0在√a )上恒成立,即1−2bx ≥0在√a )上恒成立,即1√a ≥0, 所以b ≤√a2,b −a ≤√a2−a =−(√a −14)2+116≤116,所以b −a 的最大值116.【解析】(1)①先对函数求导,然后结合导数与单调性的关系可求函数的单调区间; ②结合①的单调性及x 1,x 2的范围即可证明;(2)结合函数的单调性,把所要证明的不等式转化为同一函数的不同函数值的大小比较,进行合理的构造函数,结合单调性可求.本题综合考查了函数的性质及导数的综合应用,考查了考试分析及解决问题的能力,试题具有一定的难度.20.【答案】(1)解:∵d =2,c 2=3,∴c n =2n −1.∵{a n }是各项不为零的常数列,∴a 1=a 2=⋯=a n ,则S n =na 1,则由c n S n =a 1b 1+a 2b 2+⋯+a n b n ,及c n =2n −1,得n(2n −1)=b 1+b 2+⋯+b n , 当n ≥2时,(n −1)(2n −3)=b 1+b 2+⋯+b n−1, 两式作差,可得b n =4n −3.当n =1时,b 1=1满足上式,则b n =4n −3; (2)证明:∵a 1b 1+a 2b 2+⋯+a n b n =c n S n , 当n ≥2时,a 1b 1+a 2b 2+⋯+a n−1b n−1=c n−1S n−1, 两式相减得:S n c n −S n−1c n−1=a n b n ,即(S n−1+a n )c n −S n−1c n−1=a n b n ,S n−1(c n −c n−1)+a n c n =a n b n . 即S n−1d +λnc n =λnb n . 又S n−1=λn(n−1)2,∴λn(n−1)2d +λnc n =λnb n ,即n−12d +c n =b n .∴当n ≥3时,n−22d +c n−1=b n−1,两式相减得:b n −b n−1=32d(n ≥3).∴数列{b n}从第二项起是公差为32d的等差数列.又当n=1时,由S1c1=a1b1,得c1=b1,当n=2时,由b2=2−12d+c2=12d+c1+d=b1+32d,得b2−b1=32d.故数列{b n}是公差为32d的等差数列;(3)证明:由(2),当n≥2时,S n−1(c n−c n−1)+a n c n=a n b n,即S n−1d=a n(b n−c n),∵b n=c n+k,∴b n=c n+kd,即b n−c n=kd,∴S n−1d=a n⋅kd,即S n−1=ka n.∴S n=S n−1+a n=(k+1)a n,当n≥3时,S n−1=(k+1)a n−1=ka n,即a n=k+1ka n−1.故从第二项起数列{a n}是等比数列,∴当n≥2时,a n=a2(k+1k)n−2.b n=c n+k=c n+kd=c1+(n−1)k+k2=k+(n−1)k+k2=k(n+k).另外,由已知条件可得(a1+a2)c2=a1b1+a2b2,又c2=2k,b1=k,b2=k(2+k),∴a2=1,因而a n=(k+1k)n−2.令d n=b na n ,则d n+1d n−1=b n+1a na n+1b n−1=(n+k+1)k(n+1)(k+1)−1=−n(n+k)(k+1)<0.故对任意的n≥2,n∈N∗,b na n>b n+1a n+1恒成立.【解析】(1)由已知得c n=2n−1.由{a n}是各项不为零的常数列,得S n=na1,结合已知可得n(2n−1)=b1+b2+⋯+b n,则当n≥2时,(n−1)(2n−3)=b1+b2+⋯+b n−1,两式作差可得b n=4n−3.已知b1=1满足,得b n=4n−3;(2)由a1b1+a2b2+⋯+a n b n=c n S n,得n≥2时,a1b1+a2b2+⋯+a n−1b n−1=c n−1S n−1,两式相减得:S n−1d+λnc n=λnb n.进一步得到b n−b n−1=32d(n≥3).可得数列{b n}从第二项起是公差为32d的等差数列;(3)由(2),当n≥2时,S n−1(c n−c n−1)+a n c n=a n b n,即S n−1d=a n(b n−c n),结合b n=c n+k,得b n−c n=kd,进一步得到a n=k+1ka n−1.故从第二项起数列{a n}是等比数列,求得当n≥2时,a n=a2(k+1k )n−2.令d n=b na n,则d n+1d n−1=b n+1a na n+1b n−1=(n+k+1)k(n+1)(k+1)−1=−n(n+k)(k+1)<0.故对任意的n≥2,n∈N∗,b na n>b n+1a n+1恒成立.本题考查数列递推式,考查等差数列与等比数列的性质,考查逻辑思维能力与推理论证能力,考查运算能力,属难题.21.【答案】解:由特征值、特征向量定义可知,A α1⃗⃗⃗⃗ =λ1α1⃗⃗⃗⃗ ,A α2⃗⃗⃗⃗ =λ2α2⃗⃗⃗⃗ , ∵二阶矩阵A =[abcd ],矩阵A 属于特征值λ1=−1的一个特征向量为a 1⃗⃗⃗⃗ =[1−1], 属于特征值λ2=4的一个特征向量为a 2⃗⃗⃗⃗ =[32]. ∴[ab c d ][1−1]=−1×[1−1]=[−11],[ab cd ][32]=4[32]=[128],∴{a −b =−1c −d =1,且{3a +2b =123c +2d =8,解得a =2,b =3,c =2,d =1. ∴矩阵A =[2321].【解析】由特征值、特征向量定义可知,A α1⃗⃗⃗⃗ =λ1α1⃗⃗⃗⃗ ,A α2⃗⃗⃗⃗ =λ2α2⃗⃗⃗⃗ ,由此可建立方程组,从而可求矩阵A .本题考查待定系数法求矩阵,考查特征值、特征向量定、矩阵乘法法则等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.22.【答案】解:直线l 的极坐标方程为ρcos(θ−π4)=2√2.转换为直角坐标方程为x +y −4=0.设点P(2cosα,sinα)为曲线上任意一点, 则:点P 到直线的距离d =√2=√5sin(α+θ)−4|√2,当sin(α+θ)=−1时,d max =√5+4√2=√10+4√22.【解析】首先把极坐标方程转换为直角坐标方程,进一步利用点到直线的距离公式的应用和三角函数关系式的恒等变换和正弦型函数的性质的应用求出结果.本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,点到直线的距离公式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.23.【答案】解:∵正数a ,b ,c 满足a +b +c =1,∴(13a+2+13b+2+13c+2)[(3a +2)+(3b +2)+(3c +2)]≥(1+1+1)2, 即13a+2+13b+2+13c+2≥1,当且仅当a =b =c =13时,取等号, ∴当a =b =c =13时,13a+2+13b+2+13c+2的最小值为1.【解析】本题考查求最小值,解题的关键是利用柯西不等式进行求解,属于中档题. 利用柯西不等式,即可求得13a+2+13b+2+13c+2的最小值.24.【答案】解:(1)在正四棱锥P −ABCD 中,底面正方形的对角线AC ,BD 交于点O ,所以OP ⊥平面ABCD ,取AB 的中点E ,BC 的中点F ,所以OP ,OE ,OF 两两垂直,故以点O 为坐标原点,以OE ,OF ,OP 分别为x 轴,y 轴,z 轴,建立空间直角坐标系.设底面正方形边长为2,因为OP =12AB ,所以OP =1,所以B(1,1,0),C(−1,1,0),D(−1,−1,0),P(0,0,1),所以BP ⃗⃗⃗⃗⃗ =(−1,−1,1),设平面PCD 的法向量是n⃗ =(x,y,z), 因为CD ⃗⃗⃗⃗⃗ =(0,−2,0),CP⃗⃗⃗⃗⃗ =(1,−1,1), 所以CD ⃗⃗⃗⃗⃗ ⋅n ⃗ =−2y =0,CP ⃗⃗⃗⃗⃗ ⋅n ⃗ =x −y +z =0,取x =1,则y =0,z =−1,所以n⃗ =((1,0,−1), 所以cos <BP ⃗⃗⃗⃗⃗ ,n ⃗ >=BP ⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ |BP ⃗⃗⃗⃗⃗⃗ ||n ⃗⃗ |=−√63, 所以直线BP 与平面PCD 所成角的正弦值为√63. (2)设平面BPD 的法向量是m ⃗⃗⃗ =(x,y,z),因为BP ⃗⃗⃗⃗⃗ =(−1,−1,1),BD⃗⃗⃗⃗⃗⃗ =(−2,−2,0), 所以BP ⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ =−x −y +z =0,BD ⃗⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ =−2x −2y =0,取x =1,则y =−1,z =0,所以m⃗⃗⃗ =(1,−1,0), 由(1)知平面PCD 的法向量是n⃗ =(1,0,−1), 所以cos <m ⃗⃗⃗ ,n ⃗ >=m ⃗⃗⃗ ⋅n ⃗⃗ |m ⃗⃗⃗ ||n ⃗⃗ |=12,所以<m ⃗⃗⃗ ,n ⃗ >=60°, 所以锐二面角B −PD −C 的大小为60°.【解析】(1)取AB 的中点E ,BC 的中点F ,以点O 为坐标原点,以OE ,OF ,OP 分别为x 轴,y 轴,z 轴,建立空间直角坐标系.设底面正方形边长为2,求出平面PCD 的法向量,以及CP⃗⃗⃗⃗⃗ ,然后利用空间向量的数量积求解直线BP 与平面PCD 所成角的正弦值. (2)求出平面BPD 的法向量,平面PCD 的法向量,然后求解锐二面角B −PD −C 的大小. 本题考查直线与平面所成角的求法,二面角的求法,考查空间想象能力以及计算能力,是中档题.25.【答案】解:(1)三个数乘积为1有两种情况:“−1,−1,1”,“1,1,1”,其中“−1,−1,1”共有:C 32C 41=12种,“1,1,1”共有:C 43=4种,利用分类计数原理得:a i ,a j ,a k (i <j <k)为“(3,4)−数列”{a n }中的任意三项,则使得a i a j a k =1的取法有:12+4=16种.(2)与(1)基本同理,“−1,−1,1”共有C m 2C p 1种,“1,1,1”共有C p 3种,而在“(m,p)−数列”中任取三项共有C m+p 3种,根据古典概型有:C m 2C p 1+C p3C m+p 3=12, 再根据组合数的计算公式能得到:(p −m)(p 2−3p −2mp +m 2−3m −2)=0,①p =m 时,应满足{1≤m ≤p ≤100m +p ≥3p =m, ∴(m,p)=(k,k),k ∈{2,3,4,…,100},共99个,②p 2−3p −2mp +m 2−3m −2=0时,应满足{1≤m ≤p ≤100m +p ≥3p 2−3p −2mp +m 2−3m −2=0,视m 为常数,可解得p =(2m+3)±√24m+12, ∵m ≥1,∴√24m +1≥5,根据p ≥m 可知,p =(2m+3)+√24m+12,∵m ≥1,∴√24m +1≥5,根据p ≥m 可知,p =(2m+3)+√24m+12,(否则p ≤m −1),下设k =√24m +1,则由于p 为正整数知k 必为正整数,∵1≤m ≤100,∴5≤k ≤49,化简上式关系式可以知道:m =k 2−124=(k+1)(k+1)24,∴k −1,k +1均为偶数,∴设k =2t +1,(t ∈N ∗),则2≤t ≤24,∴m =k 2−124=t(t+1)6,由于t ,t +1中必存在偶数,∴只需t ,t +1中存在数为3的倍数即可,∴t =2,3,5,6,8,9,11,…,23,24,∴k =5,11,13,…,47,49.检验:p =(2m+3)+√24m+12=(k−1)(k+1)24≤48+5024=100,符合题意,∴共有16个,综上所述:共有115个数对(m,p)符合题意.【解析】(1)三个数乘积为1有两种情况:“−1,−1,1”,“1,1,1”,其中“−1,−1,1”共有:C 32C 41=12种,“1,1,1”共有:C 43=4种,利用分类计数原理能求出使得a i a j a k =1的取法种数.(2)“−1,−1,1”共有C m 2C p 1种,“1,1,1”共有C p 3种,而在“(m,p)−数列”中任取三项共有C m+p 3种,根据古典概型有:C m 2C p 1+C p 3C m+p 3=12,再根据组合数的计算公式能得到(p −m)(p 2−3p −2mp +m 2−3m −2)=0,利用p =m 和p 2−3p −2mp +m 2−3m −2=0分类讨论经,能求出存在多少正整数对(m,p)使得1≤m ≤p ≤100,且a i a j a k =1的概率为12. 本题考查不同的取法种数的求法,考查分类计数原理、古典概型等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是难题.。
江苏省海安中学2020届高三上学期阶段测试三数学试题 Word版含解析

海安中学2020届高三阶段测试三数 学 试 卷一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.设全集{1U =,2,3,4,5},若{1U A =ð,2,4},则集合A = . 解:全集{1U =,2,3,4,5}, 若{1U A =ð,2,4}, 则集合{3A =,5}. 故答案为:{3,5}.2.已知复数z 满足(2)1(z i i i -=+为虚数单位),则z 的模为 . 解:Q 复数z 满足(2)1(z i i i -=+为虚数单位),21()(1)22i i i z i i +-+∴=+=+- 213i i =+-=-,||9110z ∴=+=,故答案为:10.3.已知一组数据123,,,n a a a a L 的平均数为a ,极差为d ,方差为2S ,则数据12+1a ,22+1a ,32+1a ,L 2+1n a 的方差为_____.故答案为:24S4.如图是一个算法的伪代码,其输出的结果为 .解:模拟执行伪代码,可得:111111111100(1)()()11223101122310111111S =+++⋯+=-+-+⋯+-=-=⨯⨯⨯.故答案为:1011. 5.从0、2中选一个数字.从1、3、5中选两个数字,组成无重复数字的三位数.其中无重复的个数为 .解:从0、2中选一个数字0,则0不只能排在百位,从1、3、5中选两个数字之一排在百位,共有122312A A =种; 从0、2中选一个数字2,从1、3、5中选两个数字全排列,共有233318C A =种; 故共有121830+=种. 故答案为:30.6.在平面直角坐标系xoy 中,若双曲线2222:1(0,0)x y C a b a b-=>>线C 的渐近线方程为 .解:因为22()1()10c ba a =+=,所以3b a =,所以渐近线方程为3y x =±.故答案为:3y x =±. 7.将函数()f x 的图象向右平移6π个单位后得到函数4sin(2)3y x π=-的图象,则()4f π的值为 .解:由将函数()f x 的图象向右平移6π个单位后得到函数4sin(2)3y x π=-的图象, 可得把函数4sin(2)3y x π=-的图象向左平移6π个单位后得函数()f x 的图象,故()4sin(2)4sin 233f x x x ππ=+-=,则()4sin 442f ππ==,故答案为:4.8.设定义在R 上的奇函数()f x 在区间[0,)+∞上是单调减函数,且2(3)f x x f -+(2)0>,则实数x 的取值范围是 .解:根据题意,()f x 是在R 上的奇函数()f x ,且在区间[0,)+∞上是单调减函数, 则其在区间(,0])-∞上递减, 则函数()f x 在R 上为减函数,2(3)f x x f -+(2)20(3)f x x f >⇒->-(2)22(3)(2)32f x x f x x ⇒->-⇒-<-,解可得:12x <<;即实数x 的取值范围是(1,2);故答案为:(1,2).9.在锐角三角形ABC中,3sin5A=,1tan()3A B-=-,则3tan C的值为.解:锐角三角形ABC中,3sin5A=,1tan()3A B-=-,A B∴<,4cos5A=,sin3tancos4AAA==.3tan1tan tan4tan()331tan tan1tan4BA BA BA B B---=-==++Qg,13tan9B∴=.则tan tan3tan3tan()3791tan tanA BC A BA B+=-+=-=-g,故答案为:79.10.设nS为数列{}na的前n项和,若*3(1)()n nS na n n n N=--∈,且211a=,则20S的值为.解:由2122232(21)S a a a=+=-⨯-,211a=,可得15a=.解法1:当2n…时,由1n n na S S-=-,得13(1)[(1)3(1)(2)]n n na na n n n a n n-=-------,1(1)(1)6(1)n nn a n a n-∴---=-,即*16(2,)n na a n n N--=∈…,∴数列{}na是首项15a=,公差为6的等差数列,202019205612402S⨯∴=⨯+⨯=.解法2:当2n…时,由13(1)()3(1)n n n nS na n n n S S n n-=--=---,可得1(1)3(1)n nn S nS n n---=-,∴131n nS Sn n--=-,∴数列{}nSn是首项151S=,公差为3的等差数列,∴2053196220S=+⨯=,201240S∴=.11.设正实数x,y满足x yxyx y+=-,则实数x的最小值为.解:由正实数x,y满足x yxyx y+=-,化为22(1)0xy x y x +-+=,∴22221212(1)401010xx x y y x y y ⎧=--⎪-⎪+=>⎨⎪=>⎪⎩V …,化为426101x x x ⎧-+⎨>⎩…, 解得21x +….因此实数x 的最小值为21+. 故答案为:21+.12.如图,正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱1B B ,1C C 上的点(异于端点),且//EF BC ,则四棱锥1A AEFD -的体积为 .解:连接DE ,Q 正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱1B B ,1C C 上的点(异于端点),且//EF BC , ∴11A AED A FED V V --=,∴11113A AED E A AD A AD V V S AB --==V g111111119662A ADD ABCD A C D S AB V -===g , ∴四棱锥1A AEFD -的体积19A AEFD V -=.故答案为:9.13.已知向量a r ,b r ,c r 满足0a b c ++=r r r r ,且a r 与b r 的夹角的正切为12-,b r 与c r的夹角的正切为13-,||2b =r ,则a c r rg 的值为 .解:可设AB a =u u u r r ,BC b =u u u r r ,CA c =u u u r r,由题意可得1tan 2B =,1tan 3C =, 则11tan tan 23tan tan()1111tan tan 123B C A B C B C ++=-+=-=-=---⨯, 即为135A =︒,又B ,C 为锐角,22sin cos 1B B +=,sin 1cos 2B B =, 可得5sin B =, 同理可得10sin C =, 由正弦定理可得2sin135510==︒r r, 即有210||c =r ,25||a =r ,则2102524||||cos455a c c a =︒==r r r rg g g g g .故答案为:45.14.已知()(2)(3)f x m x m x m =-++,()22x g x =-,若同时满足条件: ①x R ∀∈,()0f x <或()0g x <; ②(,4)x ∃∈-∞-,()()0f x g x <. 则m 的取值范围是 .解:对于①()22x g x =-Q ,当1x <时,()0g x <, 又Q ①x R ∀∈,()0f x <或()0g x <()(2)(3)0f x m x m x m ∴=-++<在1x …时恒成立 则由二次函数的性质可知开口只能向下,且二次函数与x 轴交点都在(1,0)的左面则03121m m m <⎧⎪--<⎨⎪<⎩40m ∴-<<即①成立的范围为40m -<<又Q ②(,4)x ∈-∞-,()()0f x g x < ∴此时()220x g x =-<恒成立()(2)(3)0f x m x m x m ∴=-++>在(,4)x ∈-∞-有成立的可能,则只要4-比1x ,2x 中的较小的根大即可,()i 当10m -<<时,较小的根为3m --,34m --<-不成立, ()ii 当1m =-时,两个根同为24->-,不成立,()iii 当41m -<<-时,较小的根为2m ,24m <-即2m <-成立.综上可得①②成立时42m -<<-. 故答案为:(4,2)--.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字说明、证明过程或演算步骤 15.(本小题满分14分)已知ABC ∆的面积为93()18AC AB CB -=u u u r u u u r u u u r g ,向量(tan tan ,sin 2)m A B C =+r和向量(1,cos cos )n A B =r是共线向量.(1)求角C ;(2)求ABC ∆的边长c .解:(1)Q //m n r r,(tan tan )cos cos sin 2A B A B C ∴+=,即sin cos cos sin sin2A B A B C +=,sin()sin 2A B C ∴+=,sin 2sin cos C C C ∴= sin 0C ≠Q ,∴1cos 2C =,(0,)C π∈Q ∴3C π=(2)由()18AC AB CB -=u u u r u u u r u u u rg 得:2()18AC AB BC AC +==u u u r u u u r u u u r u u u r g ,∴11332sin 329322b S ab C a ====V g g , ∴62a =,2222cos 54c a b ab C ∴=+-=,∴36c =16.(本小题满分14分)如图,四棱锥P ABCD -的底面为矩形,且2AB =,1BC =,E ,F 分别为AB ,PC 中点.(1)求证://EF 平面PAD ;(2)若平面PAC ⊥平面ABCD ,求证:平面PAC ⊥平面PDE .证明:(1)方法一:取线段PD 的中点M ,连接FM ,AM .因为F 为PC 的中点,所以//FM CD ,且12FM CD =.因为四边形ABCD 为矩形,E 为AB 的中点,所以//EA CD ,且12EA CD =.所以//FM EA ,且FM EA =. 所以四边形AEFM 为平行四边形. 所以//EF AM .又AM ⊂平面PAD ,EF ⊂/平面PAD ,所以//EF 平面PAD . 方法二:连接CE 并延长交DA 的延长线于N ,连接PN . 因为四边形ABCD 为矩形,所以//AD BC , 所以BCE ANE ∠=∠,CBE NAE ∠=∠.又AE EB =,所以CEB NEA ∆≅∆.所以CE NE =. 又F 为PC 的中点,所以//EF NP .⋯(5分)又NP ⊂平面PAD ,EF ⊂/平面PAD ,所以//EF 平面PAD . 方法三:取CD 的中点Q ,连接FQ ,EQ .在矩形ABCD 中,E 为AB 的中点,所以AE DQ =,且//AE DQ . 所以四边形AEQD 为平行四边形,所以//EQ AD .又AD ⊂平面PAD ,EQ ⊂/平面PAD ,所以//EQ 平面PAD . 因为Q ,F 分别为CD ,CP 的中点,所以//FQ PD . 又PD ⊂平面PAD ,FQ ⊂/平面PAD ,所以//FQ 平面PAD .又FQ ,EQ ⊂平面EQF ,FQ EQ Q =I ,所以平面//EQF 平面PAD . 因为EF ⊂平面EQF ,所以//EF 平面PAD . (2)设AC ,DE 相交于G .在矩形ABCD 中,因为2AB BC =,E 为AB 的中点.所以2DA CDAE DA==. 又DAE CDA ∠=∠,所以DAE CDA ∆∆∽,所以ADE DCA ∠=∠. 又90ADE CDE ADC ∠+∠=∠=︒,所以90DCA CDE ∠+∠=︒. 由DGC ∆的内角和为180︒,得90DGC ∠=︒.即DE AC ⊥. 因为平面PAC ⊥平面ABCD因为DE ⊂平面ABCD ,所以DE ⊥平面PAC , 又DE ⊂平面PDE ,所以平面PAC ⊥平面PDE .17.(本小题满分14分)如图,OM ,ON 是两条海岸线,Q 为海中一个小岛,A 为海岸线OM 上的一个码头.已知tan 3MON ∠=-,6OA km =,Q 到海岸线OM ,ON 的距离分别为3km 610.现要在海岸线ON 上再建一个码头,使得在水上旅游直线AB 经过小岛Q .(1)求水上旅游线AB 的长;(2)若小岛正北方向距离小岛6km 处的海中有一个圆形强水波P ,从水波生成th 时的半径为3(r at a =为大于零的常数).强水波开始生成时,一游轮以182/km h 的速度自码头A 开往码头B ,问实数a 在什么范围取值时,强水波不会波及游轮的航行.解:(1)以点O 为坐标原点,直线OM 为x 轴,建立直角坐标系如图所示. 则由题设得:(6,0)A ,直线ON 的方程为3y x =-,0(Q x ,03)(0)x >. 061010=00x > 得03x =,(3,3)Q ∴. ∴直线AQ 的方程为(6)y x =--,即60x y +-=,由360y x x y =-⎧⎨+-=⎩ 得39x y =-⎧⎨=⎩ 即(3,9)B -,∴22(36)992AB =--+即水上旅游线AB 的长为92km . (2)设试验产生的强水波圆P ,由题意可得(3,9)P ,生成t 小时时,游轮在线段AB 上的点C 处,则 182AC t =,102t剟,(618,18)C t t ∴-. 强水波不会波及游轮的航行即2210,2PC r t ⎡⎤>∈⎢⎥⎣⎦对恒成立.2222(183)(189)9PC t t r at =-+->=,当0t = 时,上式恒成立,当10,0,2t t ⎛⎤≠∈ ⎥⎝⎦时即时,()101017248.7248,0,2a t g t t t t t ⎛⎤<+-=+-∈ ⎥⎝⎦令,10()724824548g t t t=+-…,当且仅当51(0,]2t 时等号成立, 所以,在024548a << 时r PC < 恒成立,亦即强水波不会波及游轮的航行.18.(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆2222:1(0)x y E a b a b+=>>过点6),其左、右焦点分别为1F 、2F ,离心率为22. (1)求椭圆E 的方程;(2)若A 、B 分别为椭圆E 的左、右顶点,动点M 满足MB AB ⊥,且MA 交椭圆E 于点P . ()i 求证:OP OM u u u r u u u u rg为定值; ()ii 设PB 与以PM 为直径的圆的另一交点为Q ,问:直线MQ 是否过定点,并说明理由. 解:(1)由题意可得22131222ab c a⎧+=⎪⎪⎨⎪=⎪⎩且222a b c -=,解得2a =,2b =,即有椭圆方程为22142x y +=; (2)()i 证明:由(2,0)A -,(2,0)B ,MB AB ⊥, 设0(2,)M y ,1(P x ,1)y , 可得00:42y yMA y x =+, 代入椭圆方程可得,2222000(1)40822y y y x x +++-=,由201204(8)28y x y --=+,可得201202(8)8y x y -=-+,00011208428y y yy x y ==+=+, 则200022004(8)8488y y OP OM y y y -=-+=++u u u r u u u u r gg 为定值;()ii 直线MQ 过定点(0,0)O .理由如下:由题意可得2001222100088282(8)2(8)PBy y y k x y y y +==-+---+g 02y =-, 由PB 与以PM 为直径的圆的另一交点为Q , 可得MQ PB ⊥,即有02MQ y k =. 则直线0:0(2)2y MQ y y x -=-, 即02y y x =, 故直线MQ 过定点(0,0)O . 19.(本小题满分16分)已知数列{}n a 满足:123a a a k ===(常数0)k >,*112(3,)n n n n k a a a n n N a -+-+=∈….数列{}n b 满足:*21()n n n n a a b n N a +++=∈. (1)求1b ,2b ,3b ,4b 的值; (2)求出数列{}n b 的通项公式;(3)问:数列{}n a 的每一项能否均为整数?若能,求出k 的所有可能值;若不能,请说明理由.解:(1)由已知可知:41a k =+,52a k =+,624a k k=++. 把数列{}n a 的项代入21n n n n a a b a +++=,求得132b b ==,2421k b b k+==;(2)由*112(3,)n n n n k a a a n n N a -+-+=∈…,可知:121n n n n a a k a a +--=+.⋯① 则:211n n n n a a k a a +-+=+.⋯② ①-②有:2211n n n nn n a a a a a a +-+-++=,即:2n n b b -= ∴132123122n n a a b b b a --+==⋯===,242222321n n a a k b b b a k -++==⋯===. ∴41(1)22nn k b k k+-=+;(3)假设存在正数k ,使得数列{}n a 的每一项均为整数,则由(2)可知:2122122212221n n n n n n a a a k a a a k +-++=-⎧⎪+⎨=-⎪⎩,⋯③ 由1a k Z =∈,624a k Z k =++∈,可知1k =,2.当1k =时,213k k+=为整数,利用1a ,2a ,3a Z ∈,结合③式,可知{}n a 的每一项均为整数;当2k =时,③变为2122122212252n n n n n n a a a a a a +-++=-⎧⎪⎨=-⎪⎩,⋯④ 用数学归纳法证明21n a -为偶数,2n a 为整数.1n =时,结论显然成立,假设n k =时结论成立,这时21n a -为偶数,2n a 为整数,故212212n n n a a a +-=-为偶数,22n a +为整数,1n k ∴=+时,命题成立. 故数列{}n a 是整数列.综上所述,k 为1,2时,数列{}n a 是整数列. 20.(本小题满分16分)设函数()()f x x a lnx x a =--+,a R ∈. (1)若0a =,求函数()f x 的单调区间;(2)若0a <,试判断函数()f x 在区间2(e -,2)e 内的极值点的个数,并说明理由; (3)求证:对任意的正数a ,都存在实数t ,满足:对任意的(,)x t t a ∈+,()1f x a <-. 解:(1)当0a =时,()f x xlnx x =-,()f x lnx '=, 令()0f x '=,1x =,列表分析故()f x 的单调递减区间为(0,1),单调递增区间为(1,)+∞.(2)()()f x x a lnx x a =--+,()af x lnx x'=-,其中0x >,令()g x xlnx a =-,分析()g x 的零点情况.()1g x lnx '=+,令()0g x '=,1x e=,列表分析11()()min g x g a e e==--,而11()1f ln ae ae e e '=-=--,222()2(2)f e ae ae -'=--=-+,221()2(2)22a f e e a e e '=-=-,①若1a e -„,则()0a f x lnx x '=-…,故()f x 在2(e -,2)e 内没有极值点;②若122a e e -<<-,则11()0f ln ae e e '=-<,22()(2)0f e ae -'=-+>,221()(2)02f e e a e '=->,因此()f x '在2(e -,2)e 有两个零点,()f x 在2(e -,2)e 内有两个极值点; ③若202a e -<„,则11()0f ln ae e e '=-<,22()(2)0f e ae -'=-+„,221()(2)02f e e a e '=->,因此()f x '在2(e -,2)e 有一个零点,()f x 在2(e -,2)e 内有一个极值点;综上所述,当(a ∈-∞,1]e-时,()f x 在2(e -,2)e 内没有极值点;当1(a e ∈-,2)2e -时,()f x 在2(e -,2)e 内有两个极值点;当2[2a e ∈-,0)时,()f x 在2(e -,2)e 内有一个极值点. (3)猜想:(1,1)x a ∈+,()1f x a <-恒成立. 证明如下:由(2)得()g x 在1(e ,)+∞上单调递增,且g (1)0a =-<,(1)(1)(1)g a a ln a a +=++-.因为当1x >时,11(*)lnx x >-,所以1(1)(1)(1)01g a a a a +>+--=+.故()g x 在(1,1)a +上存在唯一的零点,设为0x . 由知,(1,1)x a ∈+,(){f x max f <(1),(1)}f a +.又(1)(1)1f a ln a +=+-,而1x >时,1(**)lnx x <-, 所以(1)(1)111f a a a f +<+--=-=(1). 即(1,1)x a ∈+,()1f x a <-.所以对任意的正数a ,都存在实数1t =,使对任意的(,)x t t a ∈+,使()1f x a <-. 补充证明(*): 令1()1F x lnx x =+-,1x ….111()022x F x x x x -'=-=…,所以()F x 在[1,)+∞上单调递增.所以1x >时,()F x F >(1)0=,即11lnx x>-. 补充证明(**)令()1G x lnx x =-+,1x ….1()10G x x'=-„, 所以()G x 在[1,)+∞上单调递减.所以1x >时,()G x G <(1)0=,即1lnx x <-.海安中学2020届高三阶段测试三数学附加题21.[选做题,本题包括三小题,请选定其中两题,并在相应区域作答]A.已知二阶矩阵[]a b A c d =,矩阵A 属于特征值11λ=-的一个特征向量为11[]1a =-,属于特征值24λ=的一个特征向量为13[]2a =.求矩阵A .解:由特征值、特征向量定义可知,111A αλα=, 即1111111a b c d ⎡⎤⎡⎤⎡⎤⎡⎤=-⨯⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦,得11a b c d -=-⎧⎨-=⎩同理可得3212328a b c d +=⎧⎨+=⎩ 解得2a =,3b =,2c =,1d =.因此矩阵2321A ⎡⎤=⎢⎥⎣⎦. B .在极坐标系中,已知(A 1,3π ),(B 9,3π),线段AB 的垂直平分线l 与极轴交于点C ,求l 的极坐标方程及ABC ∆的面积. 解:由题意,线段AB 的中点坐标为(5,)3π,设点(,)P ρθ为直线l 上任意一点, 在直角三角形OMP 中,cos()53πρθ-=,所以,l 的极坐标方程为cos()53πρθ-=,令0θ=,得10ρ=,即(10,0)C .(8分)所以,ABC ∆的面积为:1(91)10sin 23π⨯-⨯⨯=22.已知实数a ,b 满足||2a b +„,求证:22|22|4(||2)a a b b a +-++„. 证明:由||||||2b a a b -+剟,可得||||2b a +„,22|22||()()2()|a a b b a b a b a b +-+=+-++|||2|2|2|a b a b a b =+-+-+g „,要证22|22|4(||2)a a b b a +-++„, 即证|2|2(||2)a b a -++„,由于|2|||||2a b a b -+++„, 即证||||22(||2)a b a +++„, 即为||||2b a +„,显然成立. 故原不等式成立.23.如图,在四棱锥P ABCD -中,已知棱AB ,AD ,AP 两两垂直,长度分别为1,2,2.若DC AB λ=u u u r u u u r ,且向量PC u u u r 与BD u u u r 夹角的余弦值为15.(1)求实数λ的值;(2)求直线PB 与平面PCD 所成角的正弦值.解:以A 为坐标原点,分别以AB ,AD ,AP 为x ,y ,z 轴建立如图所示空间直角坐标系; 则:(0A ,0,0),(1B ,0,0),(0D ,2,0),(0P ,0,2);DC AB λ=u u u r u u u r ,可得(C λ,2,0).(1)(PC λ=u u u r ,2,2)-,(1BD =-u u u r ,2,0),向量PC u u u r 与BD u u u r 15.215814λ=++g 10λ=(舍去)或2λ=.实数λ的值为2.;(2)(2PC =u u u r ,2,2)-,(0PD =u u u r ,2,2)-,平面PCD 的法向量(n x =r,y ,)z .则0n PC =u u u r r g 且0n PD =u u ur r g ,即:0x y z +-=,0y z -=,0x ∴=,不妨去1y z ==, 平面PCD 的法向量(0n =r,1,1).又(1PB =u u u r ,0,2).故10cos ,||||n PB n PB n PB <>==u u u r r u u u r g ru u u r r .直线PB 与平面PCD 10.24.已知数列{}n a 的通项公式为1515[(()]5n nn a +--,*n N ∈.记1212nn n n n n S C a C a C a =++⋯+.(1)求1S ,2S 的值;(2)求所有正整数n ,使得n S 能被8整除.解:(1)1212nn nn n n S C a C a C a =++⋯+ 122151515()()5nn n n n C C C +++=+⋯+-g g122151515((()]nn n n n C C C ---++⋯+g g1515(1]5n n+-=+-+ 3535[()(]5n n +-=-, 即有1515S ==g ;23535S =g ;(2)3535[((]5n nn S +-=-, 22235353535[((][()(]55n n n n n S ++++-+-=-=-g 135353535()[()(]3n nn n S S ++-+---=-,即213n n n S S S ++=-,*n N ∈,因此2n S +除以8的余数,完全由1n S +,n S 除以8的余数确定, 因为11a =,21a =,所以11111S C a ==,12221223S C a C a =+=,3213918S S S =-=-=, 432324321S S S =-=-=,543363855S S S =-=-=, 654316521144S S S =-=-=,765343255377S S S =-=-=, 87631131144987S S S =-=-=,987329613772584S S S =-=-=,由以上计算及213n n n S S S ++=-可知,数列{}n S 各项除以8的余数依次是: 1,3,0,5,7,0,1,3,0,5,7,0,⋯,它是一个以6为周期的数列,从而n S 除以8的余数等价于n 除以3的余数, 所以3n k =,*k N ∈,即所求集合为:{|3n n k =,*}k N ∈.。
江苏省海安高级中学2020届高三12月月考数学试题 Word版含答案

阶段性测试(三)数学Ⅰ参考公式:样本数据1x ,2x ,…,n x 的方差2211()ni i s x x n ==-∑,其中11ni i x x n ==∑.锥体的体积13V Sh =,其中S 为底面积,h 为高.一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1. 设全集U ={1,2,3,4,5}.若U A =ð{1,2,5},则集合A = ▲ . 2. 已知复数z 满足(z 2)i 1i -=+(i 为虚数单位),则复数z 的实部是 ▲ .3. 已知样本数据1234a a a a ,,,的方差为2,则数据123421212121a a a a ++++,,,的方差为 ▲ . 4. 右图是一个算法的伪代码,其输出的结果为 ▲ .5. 从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,则该三位数为奇数的概率为 ▲ .6. 在平面直角坐标系xOy 中,若双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为10,则双曲线C 的渐近线方程为 ▲ .S ←0For i From 1 To 10 Step 1 S ←S +1i (i +1)End For Print S(第4题)7. 将函数f(x)的图象向右平移π6个单位后得到函数()π4sin23y x=-的图象,则()π4f的值为▲ .8. 设定义在R上的奇函数()f x在区间[0)+∞,上是单调减函数,且2(3)f x x-(2)f+0>,则实数x的取值范围是▲.9. 在锐角三角形ABC中,若3sin5A=,1tan()3A B-=-,则3tan C的值为▲.10. 设S n为数列{}n a的前n项和.若S n=na n-3n(n-1)(n∈N*),且211a=,则S20的值为▲.11. 设正实数x,y满足x yxyx y+=-,则实数x的最小值为▲ .12. 如图,正四棱柱1111ABCD A B C D-的体积为27,点E,F分别为棱1B B,1C C上的点(异于端点),且//EF BC,则四棱锥1A AEFD-的体积为▲.13.已知向量a,b,c满足++=0a b c,且a与b的夹角的正切为12-,b与c的夹角的正切为13-,2=b,则⋅a c的值为▲.14.已知()()()23f x m x m x m=-++,()22xg x=-,若同时满足条件:①x∀∈R,()0f x<或()0g x<;②()4x∃∈-∞-,,()()0f xg x⋅<,则实数m的取值范围是▲.二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本题满分14分)已知△ABC的面积为93,且()18AC AB CB?=u u u r u u u r u u u r,向量(tan tan sin2)A B C=+,m和D1(第12题)BPN(1cos cos )A B =,n 是共线向量.(1)求角C 的大小; (2)求△ABC 的三边长.16.(本题满分14分)如图,在四棱锥P -ABCD 中,已知底面ABCD 为矩形,且AB =2,BC =1,E ,F 分别是AB ,PC 的中点,PA ⊥DE . (1)求证:EF ∥平面PAD ; (2)求证:平面PAC ⊥平面PDE .17.(本题满分14分)如图,OM ,ON 是某景区的两条道路(宽度忽略不计,OM 为东西方向),Q 为景区内一景点,A 为道路OM 上一游客休息区.已知tan ∠MON =-3,OA =6(百米),Q 到直线OM ,ON 的距离分别为3(百米),6105(百米).现新修一条自A 经过Q 的有轨观光直路并延伸至道路ON 于点B ,并在B 处修建一游客休息区. (1)求有轨观光直路AB 的长;(2)已知在景点Q 的正北方6 百米的P 处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟.表演时,喷泉喷洒区域以P 为圆心,r 为半径变化,且t 分钟时,2r at (百米)(0≤t ≤9,0<a <1).当喷泉表演开始时,一观光车S (大小忽略不计)正从休息区B 沿(1)中的轨道BA 以2(百米/分钟)的速度开往休息区A ,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.FABC D P(第1618.(本题满分16分)在平面直角坐标系xOy 中,已知椭圆E :22221(0)x y a b a b+=>>过点(1,. (1)求椭圆E 的标准方程;(2)若A ,B 分别是椭圆E 的左,右顶点,动点M 满足MB AB ⊥,且MA 交椭圆E 于点P .①求证:OP OM ⋅u u u r u u u u r为定值;②设PB 与以PM 为直径的圆的另一交点为Q ,求证:直线MQ 经过定点.19.(本题满分16分)已知数列{}n a 满足:123a a a k ===(常数k >0),112n n n n k a a a a -+-+=(n ≥3,*n ∈N ).数列{}n b 满足:21n n n n a a b a +++=(*n ∈N ). (1)求b 1,b 2的值; (2)求数列{}n b 的通项公式;(3)是否存在k ,使得数列{}n a 的每一项均为整数? 若存在,求出k 的所有可能值;若不存在,请说明理由.20.(本题满分16分)设函数f (x )=(x -a )ln x -x +a ,a ∈R . (1)若a =0,求函数f (x )的单调区间;(2)若a <0,且函数f (x )在区间()22e e -,内有两个极值点,求实数a 的取值范围;(3)求证:对任意的正数a ,都存在实数t ,满足:对任意的x ∈(t ,t +a ), f (x )<a -1.数学Ⅰ一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上.........1. 【答案】{3,5}2. 【答案】33. 【答案】84. 【答案】1011 5. 【答案】356. 【答案】y =±3x7. 【答案】48. 【答案】(1,2)9. 【答案】79 10. 【答案】1 24011. 【答案1 12. 【答案】9 13.【答案】4514.【答案】()42--,二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)解:(1)因为向量(tan tan sin 2)A B C =+,m 和(1cos cos )A B =,n 是共线向量,所以()cos cos tan tan sin 20A B A B C +-=, ……2分 即sin A cos B +cos A sin B -2sin C cos C =0,化简得sin C -2sin C cos C =0,即sin C (1-2cos C )=0. ……4分 因为0πC <<,所以sin C >0,从而1cos 2C =,π.3C = ……6分(2)()()218AC AB CB AC BC BA AC =?=?=u u u r u u u r u u u r u u u r u u u ru u u r u u u r ,于是AC =. ……8分因为△ABC 的面积为1sin 2CA CB C ?,即1πsin 23CB ,解得CB = …… 11分 在△ABC 中,由余弦定理得((2222212cos 254.2AB CA CB CA CB C=+-?+-创所以AB = …… 14分16.(本题满分14分)证明:(1)取PD 中点G ,连AG ,FG , 因为F ,G 分别为PC ,PD 的中点,所以FG ∥CD ,且FG =12C D . ……2分又因为E 为AB 中点,所以AE //CD ,且AE =12C D . ……4分所以AE //FG ,AE =FG .故四边形AEFG 为平行四边形. 所以EF //AG ,又EF ⊄平面PAD ,AG ⊂平面PAD ,故EF //平面PA D . ……6分(2)设AC ∩DE =H ,由△AEH ∽△CDH 及E 为AB 中点得AG CG =AE CD =12,又因为AB =2,BC =1,所以AC =3,AG =13AC =33.所以AG AE =AB AC =23,又∠BAD 为公共角,所以△GAE ∽△BA C .所以∠AGE =∠ABC =90︒,即DE ⊥A C . ……10分 又DE ⊥PA ,PA ∩AC =A ,所以DE ⊥平面PA C . ……12分 又DE ⊂平面PDE ,所以平面PAC ⊥平面PDE . ……14分17.(本题满分14分)解:(1)以点O 为坐标原点,直线OM 为x 轴,建立平面直角坐标系,如图所示.则由题设得:A (6,0),直线ON 的方程为()()003 30y x Q x x =->,,.3x=,所以()3 3Q,.……2分故直线AQ的方程为()6y x=--,由360y xx y=-⎧⎨+-=⎩,得39xy=-⎧⎨=⎩,,即()3 9B-,,故AB==……5分答:水上旅游线AB的长为.……6分(2)将喷泉记为圆P,由题意可得P(3,9),生成t分钟时,观光车在线段AB上的点C处,则BC=2t,0≤t≤9,所以C(-3+t,9-t).若喷泉不会洒到观光车上,则PC2>r2对t∈[0,9]恒成立,即PC2=(6-t)2+t2=2t2-12t+36>4at,……10分当t=0时,上式成立,当t∈(0,9]时,2a<t+18t-6,(t+18t-6)min=62-6,当且仅当t=32时取等号,因为a∈(0,1),所以r<PC恒成立,即喷泉的水流不会洒到观光车上.……13分答:喷泉的水流不会洒到观光车上.……14分18.解:(1)设椭圆焦距为2c,所以223121a bca⎧⎪+=⎪⎨⎪=⎪⎩,且222c a b=-,解得2242ab⎧=⎪⎨=⎪⎩,,所以椭圆E 的方程为22142x y +=; ……4分(2)设0(2 )M y ,,11( )P x y ,, ①易得直线MA 的方程为:0042y yy x =+, 代入椭圆22142x y +=得,()2222000140822y y y x x +++-=, 由()201204828y x y --=+得,()20120288y x y --=+,从而012088y y y =+, ……8分所以()20002200288 (2 )88y y OP OM y y y --⎛⎫⋅=⋅ ⎪++⎝⎭u u u r u u u u r ,, ()22002200488488y y y y --=+=++. ……10分 ②直线MQ 过定点(0 0)O ,,理由如下:依题意,()2020208822828PB y y k y y y +==----+,由MQ PB ⊥得,02MQ y k =, 则MQ 的方程为:00(2)2y y y x -=-,即02yy x =,所以直线MQ 过定点(0 0)O ,. ……16分 19.(本题满分16分)解:(1)由已知得,41a k =+,所以1312=2a a b a +=,2423121a a k k kb a k k ++++===. ……2分 (2)由条件可知:()1213n n n n a a k a a n +--=+≥,①所以()21+12n n n n a a k a a n +-=+≥.② ……4分 ①-②得. 即:.因此:, ……6分故()23n n b b n -=≥,又因为12b =,221k b k+=,所以221n n b k n k⎧⎪=⎨+⎪⎩,为奇数,为偶数. ……8分(3)假设存在k ,使得数列{}n a 的每一项均为整数,则k 为正整数. ……10分由(2)知21221222122(123)21n n n n n n a a a n k a a a k +-++=-⎧⎪=⎨+=-⎪⎩L ,,③ 由162Z 4Z a k a k k=∈=++∈,,所以k =1或2, ……12分检验:当1k =时,312=+kk 为整数, 利用123Z a a a ∈,,结合③,{a n }各项均为整数; ……14分 当2k =时③变为21221222122(123)52n n n n n n a a a n a a a +-++=-⎧⎪=⎨=-⎪⎩L ,, 122111n n n n n n n n a a a a a a a a +-+--+-=-121121n n n n n n n n a a a a a a a a +-+-+-+=+2211n n n nn n a a a a a a +-+-++=消去2121n n a a +-,得:222223(2)n n n a a a n +-=-≥ 由24Z a a ∈,,所以偶数项均为整数,而2221252n n n a a a ++=-,所以21n a +为偶数,故12a k ==,故数列是整数列.综上所述,的取值集合是{}12,. ……16分 20.(本题满分16分)解:(1)当a =0时,f (x )=x ln x -x ,f’(x )=ln x ,令f’(x )=0,x =1,列表分析3分(2)f (x )=(x -a )ln x -x +a ,f’(x )=ln x -ax ,其中x >0,令g (x )=x ln x -a ,分析g (x )的零点情况.g’(x )=ln x +1,令g’(x )=0,x =1e ,列表分析{}n a kg (x )min =g (1e )=-1e -a , ……5分而f’(1e )=ln 1e -a e =-1-a e ,()2e f -'=-2-a e 2=-(2+a e 2),f’(e 2)=2-a e 2=1e 2(2e 2-a ),①若a ≤-1e ,则f’(x )=ln x -ax ≥0,故f (x )在()22e e -,内没有极值点,舍;②若-1e <a <-2e 2,则f’(1e )=ln 1e -a e <0,f’(e -2)=-(2+a e 2)>0,f’(e 2)=1e 2(2e 2-a )>0,因此f’(x )在()22e e -,有两个零点,设为1x ,2x ,所以当()21e x x -∈,时,f (x )单调递增,当()12x x x ∈,时,f (x )单调递减,当()22e x x ∈,时,f (x )单调递增,此时f (x )在()22e e -,内有两个极值点;③若-2e 2≤a <0,则f’(1e )=ln 1e -a e <0,f’(e -2)=-(2+a e 2)≤0, f’(e 2)=1e 2(2e 2-a )>0,因此f’(x )在()22e e -,有一个零点,f (x )在()22e e -,内有一个极值点;综上所述,实数a 的取值范围为(-1e ,-2e 2). ……10分 (3)存在1t =:x ∈(1,1+a ),f (x )<a -1恒成立. ……11分证明如下:由(2)得g (x )在(1e ,+∞)上单调递增, 且g (1)=-a <0,g(1+a )=(1+a )ln(1+a )-a .因为当x >1时,ln x >1-1x (*),所以g(1+a )>(1+a )(1-1a +1)-a =0.故g (x )在(1,1+a )上存在唯一的零点,设为x 0.由知,x ∈(1,1+a ),f (x )<max{f (1),f (1+a )}. ……13分又f (1+a )=ln(1+a )-1,而x >1时,ln x <x -1(**), 所以f (1+a )<(a +1)-1-1=a -1=f (1). 即x ∈(1,1+a ),f (x )<a -1.所以对任意的正数a ,都存在实数t =1,使对任意的x ∈(t ,t +a ),使 f (x )<a -1. ……15分补充证明(*):令F (x )=ln x +1x -1,x ≥1.F’(x )=1x -1x 2=x -1x 2≥0,所以F (x )在[1,+∞)上单调递增.所以x >1时,F (x )>F (1)=0,即ln x >1-1x .补充证明(**)令G (x )=ln x -x +1,x ≥1.G’(x )=1x -1≤0,所以G (x )在[1,+∞)上单调递减.所以x >1时,G (x )<G (1)=0,即ln x <x -1.……16分数学Ⅱ(附加题)21.【选做题】本题包括A 、B 、C 三小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A . 选修4-2:矩阵与变换【解】由特征值、特征向量定义可知,A 1α1λ=1α,即11111 a b c d ⎡⎤⎡⎤⎡⎤=-⨯⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦,得11.a b c d -=-⎧⎨-=⎩,……5分 同理可得3212328a b c d +=⎧⎨+=⎩,, 解得2321, , , a b c d ====.因此矩阵A 2321 ⎡⎤=⎢⎥⎣⎦. ……10分B .解:因为A ( 1,π3 ),B ( 9,π3),所以线段AB 的中点坐标为(5,π3), ……2分设点P (ρ,θ)为直线l 上任意一点, 在直角三角形OMP 中,ρcos(θ-π3)=5,所以,l的极坐标方程为ρcos(θ-π3)=5,……6分令θ=0,得ρ=10,即C(10,0).……8分所以,△ABC的面积为:12×(9-1)×10×sinπ3=203.……10分C.证明:因为|a+b|≤2,所以|a2+2a-b2+2b|=|a+b||a-b+2|=|a+b||2a-(a+b)+2|≤|a+b|(|2a|+|a+b|+2)≤4(|a|+2).……10分22.解:依题意,以A为坐标原点,AB,AD,AP分别为x,y,z轴建立空间直角坐标系A-xyz则B(1,0,0),D(0,2,0),P(0,0,2),因为DC→=λAB→,所以C(λ,2,0),……2分(1)从而PC→=(λ,2,-2),BD→=(-1,2,0),则cos<PC→,BD→>=PC→·BD→|PC→|·|BD→|=4-λλ2+8×5=1515,解得λ=2;……5分(2)易得PC→=(2,2,-2),PD→=(0,2,-2),设平面PCD的法向量n=(x,y,z),则n·PC→=0,且n·PD→=0,(第22题)即x +y -z =0,且y -z =0, 所以x =0,不妨取y =z =1,则平面PCD 的一个法向量n =(0,1,1), …… 8分 又易得PB →=(1,0,-2),故cos <PB →,n >=PB →·n |PB →|·|n |=-22×5=-105,所以直线PB 与平面PCD 所成角的正弦值为105. ……10分 23.(本小题满分10分)解:(1)S 1=C 11a 1=1,S 2=C 12a 1+C 22a 2=3. ……2分(2)记α=1+52,β=1-52.则S n =15∑n i =1C i n (αi -βi )=15∑n i =0C i n (αi -βi )=15(∑n i =0C i n αi -∑n i =0C i n βi)=15[(1+α)n -(1+β)n ]=15[(3+52)n -(3-52)n ]. ……6分因为(3+52)×(3-52)=1.故S n +2=15{[(3+52)n +1-(3-52)n +1][ (3+52)+(3-52)]-[(3+52)n - (3-52)n]}=3S n +1-S n .所以存在=3λ,使得213n n n S S S +++=恒成立. ……10分。
江苏省海安中学2020届高三上学期阶段测试三数学试题 Word版含解析

海安中学2020届高三阶段测试三数 学 试 卷一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.设全集{1U =,2,3,4,5},若{1U A =ð,2,4},则集合A = . 解:全集{1U =,2,3,4,5}, 若{1U A =ð,2,4}, 则集合{3A =,5}. 故答案为:{3,5}.2.已知复数z 满足(2)1(z i i i -=+为虚数单位),则z 的模为 . 解:Q 复数z 满足(2)1(z i i i -=+为虚数单位),21()(1)22i i i z i i +-+∴=+=+- 213i i =+-=-,||9110z ∴=+=,故答案为:10.3.已知一组数据123,,,n a a a a L 的平均数为a ,极差为d ,方差为2S ,则数据12+1a ,22+1a ,32+1a ,L 2+1n a 的方差为_____.故答案为:24S4.如图是一个算法的伪代码,其输出的结果为 .解:模拟执行伪代码,可得:111111111100(1)()()11223101122310111111S =+++⋯+=-+-+⋯+-=-=⨯⨯⨯.故答案为:1011. 5.从0、2中选一个数字.从1、3、5中选两个数字,组成无重复数字的三位数.其中无重复的个数为 .解:从0、2中选一个数字0,则0不只能排在百位,从1、3、5中选两个数字之一排在百位,共有122312A A =种; 从0、2中选一个数字2,从1、3、5中选两个数字全排列,共有233318C A =种; 故共有121830+=种. 故答案为:30.6.在平面直角坐标系xoy 中,若双曲线2222:1(0,0)x y C a b a b-=>>线C 的渐近线方程为 .解:因为22()1()10c ba a =+=,所以3b a =,所以渐近线方程为3y x =±.故答案为:3y x =±. 7.将函数()f x 的图象向右平移6π个单位后得到函数4sin(2)3y x π=-的图象,则()4f π的值为 .解:由将函数()f x 的图象向右平移6π个单位后得到函数4sin(2)3y x π=-的图象, 可得把函数4sin(2)3y x π=-的图象向左平移6π个单位后得函数()f x 的图象,故()4sin(2)4sin 233f x x x ππ=+-=,则()4sin 442f ππ==,故答案为:4.8.设定义在R 上的奇函数()f x 在区间[0,)+∞上是单调减函数,且2(3)f x x f -+(2)0>,则实数x 的取值范围是 .解:根据题意,()f x 是在R 上的奇函数()f x ,且在区间[0,)+∞上是单调减函数, 则其在区间(,0])-∞上递减, 则函数()f x 在R 上为减函数,2(3)f x x f -+(2)20(3)f x x f >⇒->-(2)22(3)(2)32f x x f x x ⇒->-⇒-<-,解可得:12x <<;即实数x 的取值范围是(1,2);故答案为:(1,2).9.在锐角三角形ABC中,3sin5A=,1tan()3A B-=-,则3tan C的值为.解:锐角三角形ABC中,3sin5A=,1tan()3A B-=-,A B∴<,4cos5A=,sin3tancos4AAA==.3tan1tan tan4tan()331tan tan1tan4BA BA BA B B---=-==++Qg,13tan9B∴=.则tan tan3tan3tan()3791tan tanA BC A BA B+=-+=-=-g,故答案为:79.10.设nS为数列{}na的前n项和,若*3(1)()n nS na n n n N=--∈,且211a=,则20S的值为.解:由2122232(21)S a a a=+=-⨯-,211a=,可得15a=.解法1:当2n…时,由1n n na S S-=-,得13(1)[(1)3(1)(2)]n n na na n n n a n n-=-------,1(1)(1)6(1)n nn a n a n-∴---=-,即*16(2,)n na a n n N--=∈…,∴数列{}na是首项15a=,公差为6的等差数列,202019205612402S⨯∴=⨯+⨯=.解法2:当2n…时,由13(1)()3(1)n n n nS na n n n S S n n-=--=---,可得1(1)3(1)n nn S nS n n---=-,∴131n nS Sn n--=-,∴数列{}nSn是首项151S=,公差为3的等差数列,∴2053196220S=+⨯=,201240S∴=.11.设正实数x,y满足x yxyx y+=-,则实数x的最小值为.解:由正实数x,y满足x yxyx y+=-,化为22(1)0xy x y x +-+=,∴22221212(1)401010xx x y y x y y ⎧=--⎪-⎪+=>⎨⎪=>⎪⎩V …,化为426101x x x ⎧-+⎨>⎩…, 解得21x +….因此实数x 的最小值为21+. 故答案为:21+.12.如图,正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱1B B ,1C C 上的点(异于端点),且//EF BC ,则四棱锥1A AEFD -的体积为 .解:连接DE ,Q 正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱1B B ,1C C 上的点(异于端点),且//EF BC , ∴11A AED A FED V V --=,∴11113A AED E A AD A AD V V S AB --==V g111111119662A ADD ABCD A C D S AB V -===g , ∴四棱锥1A AEFD -的体积19A AEFD V -=.故答案为:9.13.已知向量a r ,b r ,c r 满足0a b c ++=r r r r ,且a r 与b r 的夹角的正切为12-,b r 与c r的夹角的正切为13-,||2b =r ,则a c r rg 的值为 .解:可设AB a =u u u r r ,BC b =u u u r r ,CA c =u u u r r,由题意可得1tan 2B =,1tan 3C =, 则11tan tan 23tan tan()1111tan tan 123B C A B C B C ++=-+=-=-=---⨯, 即为135A =︒,又B ,C 为锐角,22sin cos 1B B +=,sin 1cos 2B B =, 可得5sin B =, 同理可得10sin C =, 由正弦定理可得2sin135510==︒r r, 即有210||c =r ,25||a =r ,则2102524||||cos455a c c a =︒==r r r rg g g g g .故答案为:45.14.已知()(2)(3)f x m x m x m =-++,()22x g x =-,若同时满足条件: ①x R ∀∈,()0f x <或()0g x <; ②(,4)x ∃∈-∞-,()()0f x g x <. 则m 的取值范围是 .解:对于①()22x g x =-Q ,当1x <时,()0g x <, 又Q ①x R ∀∈,()0f x <或()0g x <()(2)(3)0f x m x m x m ∴=-++<在1x …时恒成立 则由二次函数的性质可知开口只能向下,且二次函数与x 轴交点都在(1,0)的左面则03121m m m <⎧⎪--<⎨⎪<⎩40m ∴-<<即①成立的范围为40m -<<又Q ②(,4)x ∈-∞-,()()0f x g x < ∴此时()220x g x =-<恒成立()(2)(3)0f x m x m x m ∴=-++>在(,4)x ∈-∞-有成立的可能,则只要4-比1x ,2x 中的较小的根大即可,()i 当10m -<<时,较小的根为3m --,34m --<-不成立, ()ii 当1m =-时,两个根同为24->-,不成立,()iii 当41m -<<-时,较小的根为2m ,24m <-即2m <-成立.综上可得①②成立时42m -<<-. 故答案为:(4,2)--.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字说明、证明过程或演算步骤 15.(本小题满分14分)已知ABC ∆的面积为93()18AC AB CB -=u u u r u u u r u u u r g ,向量(tan tan ,sin 2)m A B C =+r和向量(1,cos cos )n A B =r是共线向量.(1)求角C ;(2)求ABC ∆的边长c .解:(1)Q //m n r r,(tan tan )cos cos sin 2A B A B C ∴+=,即sin cos cos sin sin2A B A B C +=,sin()sin 2A B C ∴+=,sin 2sin cos C C C ∴= sin 0C ≠Q ,∴1cos 2C =,(0,)C π∈Q ∴3C π=(2)由()18AC AB CB -=u u u r u u u r u u u rg 得:2()18AC AB BC AC +==u u u r u u u r u u u r u u u r g ,∴11332sin 329322b S ab C a ====V g g , ∴62a =,2222cos 54c a b ab C ∴=+-=,∴36c =16.(本小题满分14分)如图,四棱锥P ABCD -的底面为矩形,且2AB =,1BC =,E ,F 分别为AB ,PC 中点.(1)求证://EF 平面PAD ;(2)若平面PAC ⊥平面ABCD ,求证:平面PAC ⊥平面PDE .证明:(1)方法一:取线段PD 的中点M ,连接FM ,AM .因为F 为PC 的中点,所以//FM CD ,且12FM CD =.因为四边形ABCD 为矩形,E 为AB 的中点,所以//EA CD ,且12EA CD =.所以//FM EA ,且FM EA =. 所以四边形AEFM 为平行四边形. 所以//EF AM .又AM ⊂平面PAD ,EF ⊂/平面PAD ,所以//EF 平面PAD . 方法二:连接CE 并延长交DA 的延长线于N ,连接PN . 因为四边形ABCD 为矩形,所以//AD BC , 所以BCE ANE ∠=∠,CBE NAE ∠=∠.又AE EB =,所以CEB NEA ∆≅∆.所以CE NE =. 又F 为PC 的中点,所以//EF NP .⋯(5分)又NP ⊂平面PAD ,EF ⊂/平面PAD ,所以//EF 平面PAD . 方法三:取CD 的中点Q ,连接FQ ,EQ .在矩形ABCD 中,E 为AB 的中点,所以AE DQ =,且//AE DQ . 所以四边形AEQD 为平行四边形,所以//EQ AD .又AD ⊂平面PAD ,EQ ⊂/平面PAD ,所以//EQ 平面PAD . 因为Q ,F 分别为CD ,CP 的中点,所以//FQ PD . 又PD ⊂平面PAD ,FQ ⊂/平面PAD ,所以//FQ 平面PAD .又FQ ,EQ ⊂平面EQF ,FQ EQ Q =I ,所以平面//EQF 平面PAD . 因为EF ⊂平面EQF ,所以//EF 平面PAD . (2)设AC ,DE 相交于G .在矩形ABCD 中,因为2AB BC =,E 为AB 的中点.所以2DA CDAE DA==. 又DAE CDA ∠=∠,所以DAE CDA ∆∆∽,所以ADE DCA ∠=∠. 又90ADE CDE ADC ∠+∠=∠=︒,所以90DCA CDE ∠+∠=︒. 由DGC ∆的内角和为180︒,得90DGC ∠=︒.即DE AC ⊥. 因为平面PAC ⊥平面ABCD因为DE ⊂平面ABCD ,所以DE ⊥平面PAC , 又DE ⊂平面PDE ,所以平面PAC ⊥平面PDE .17.(本小题满分14分)如图,OM ,ON 是两条海岸线,Q 为海中一个小岛,A 为海岸线OM 上的一个码头.已知tan 3MON ∠=-,6OA km =,Q 到海岸线OM ,ON 的距离分别为3km 610.现要在海岸线ON 上再建一个码头,使得在水上旅游直线AB 经过小岛Q .(1)求水上旅游线AB 的长;(2)若小岛正北方向距离小岛6km 处的海中有一个圆形强水波P ,从水波生成th 时的半径为3(r at a =为大于零的常数).强水波开始生成时,一游轮以182/km h 的速度自码头A 开往码头B ,问实数a 在什么范围取值时,强水波不会波及游轮的航行.解:(1)以点O 为坐标原点,直线OM 为x 轴,建立直角坐标系如图所示. 则由题设得:(6,0)A ,直线ON 的方程为3y x =-,0(Q x ,03)(0)x >. 061010=00x > 得03x =,(3,3)Q ∴. ∴直线AQ 的方程为(6)y x =--,即60x y +-=,由360y x x y =-⎧⎨+-=⎩ 得39x y =-⎧⎨=⎩ 即(3,9)B -,∴22(36)992AB =--+即水上旅游线AB 的长为92km . (2)设试验产生的强水波圆P ,由题意可得(3,9)P ,生成t 小时时,游轮在线段AB 上的点C 处,则 182AC t =,102t剟,(618,18)C t t ∴-. 强水波不会波及游轮的航行即2210,2PC r t ⎡⎤>∈⎢⎥⎣⎦对恒成立.2222(183)(189)9PC t t r at =-+->=,当0t = 时,上式恒成立,当10,0,2t t ⎛⎤≠∈ ⎥⎝⎦时即时,()101017248.7248,0,2a t g t t t t t ⎛⎤<+-=+-∈ ⎥⎝⎦令,10()724824548g t t t=+-…,当且仅当51(0,]2t 时等号成立, 所以,在024548a << 时r PC < 恒成立,亦即强水波不会波及游轮的航行.18.(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆2222:1(0)x y E a b a b+=>>过点6),其左、右焦点分别为1F 、2F ,离心率为22. (1)求椭圆E 的方程;(2)若A 、B 分别为椭圆E 的左、右顶点,动点M 满足MB AB ⊥,且MA 交椭圆E 于点P . ()i 求证:OP OM u u u r u u u u rg为定值; ()ii 设PB 与以PM 为直径的圆的另一交点为Q ,问:直线MQ 是否过定点,并说明理由. 解:(1)由题意可得22131222ab c a⎧+=⎪⎪⎨⎪=⎪⎩且222a b c -=,解得2a =,2b =,即有椭圆方程为22142x y +=; (2)()i 证明:由(2,0)A -,(2,0)B ,MB AB ⊥, 设0(2,)M y ,1(P x ,1)y , 可得00:42y y MA y x =+, 代入椭圆方程可得,2222000(1)40822y y y x x +++-=,由201204(8)28y x y --=+,可得201202(8)8y x y -=-+,00011208428y y yy x y ==+=+, 则200022004(8)8488y y OP OM y y y -=-+=++u u u r u u u u r gg 为定值;()ii 直线MQ 过定点(0,0)O .理由如下:由题意可得2001222100088282(8)2(8)PBy y y k x y y y +==-+---+g 02y =-, 由PB 与以PM 为直径的圆的另一交点为Q , 可得MQ PB ⊥,即有02MQ y k =. 则直线0:0(2)2y MQ y y x -=-, 即02y y x =, 故直线MQ 过定点(0,0)O . 19.(本小题满分16分)已知数列{}n a 满足:123a a a k ===(常数0)k >,*112(3,)n n n n k a a a n n N a -+-+=∈….数列{}n b 满足:*21()n n n n a a b n N a +++=∈. (1)求1b ,2b ,3b ,4b 的值; (2)求出数列{}n b 的通项公式;(3)问:数列{}n a 的每一项能否均为整数?若能,求出k 的所有可能值;若不能,请说明理由.解:(1)由已知可知:41a k =+,52a k =+,624a k k=++. 把数列{}n a 的项代入21n n n n a a b a +++=,求得132b b ==,2421k b b k+==;(2)由*112(3,)n n n n k a a a n n N a -+-+=∈…,可知:121n n n n a a k a a +--=+.⋯① 则:211n n n n a a k a a +-+=+.⋯② ①-②有:2211n n n nn n a a a a a a +-+-++=,即:2n n b b -= ∴132123122n n a a b b b a --+==⋯===,242222321n n a a k b b b a k -++==⋯===. ∴41(1)22nn k b k k+-=+;(3)假设存在正数k ,使得数列{}n a 的每一项均为整数,则由(2)可知:2122122212221n n n n n n a a a k a a a k +-++=-⎧⎪+⎨=-⎪⎩,⋯③ 由1a k Z =∈,624a k Z k =++∈,可知1k =,2.当1k =时,213k k+=为整数,利用1a ,2a ,3a Z ∈,结合③式,可知{}n a 的每一项均为整数;当2k =时,③变为2122122212252n n n n n n a a a a a a +-++=-⎧⎪⎨=-⎪⎩,⋯④ 用数学归纳法证明21n a -为偶数,2n a 为整数.1n =时,结论显然成立,假设n k =时结论成立,这时21n a -为偶数,2n a 为整数,故212212n n n a a a +-=-为偶数,22n a +为整数,1n k ∴=+时,命题成立. 故数列{}n a 是整数列.综上所述,k 为1,2时,数列{}n a 是整数列. 20.(本小题满分16分)设函数()()f x x a lnx x a =--+,a R ∈. (1)若0a =,求函数()f x 的单调区间;(2)若0a <,试判断函数()f x 在区间2(e -,2)e 内的极值点的个数,并说明理由; (3)求证:对任意的正数a ,都存在实数t ,满足:对任意的(,)x t t a ∈+,()1f x a <-. 解:(1)当0a =时,()f x xlnx x =-,()f x lnx '=, 令()0f x '=,1x =,列表分析故()f x 的单调递减区间为(0,1),单调递增区间为(1,)+∞.(2)()()f x x a lnx x a =--+,()af x lnx x'=-,其中0x >,令()g x xlnx a =-,分析()g x 的零点情况.()1g x lnx '=+,令()0g x '=,1x e=,列表分析11()()min g x g a e e==--,而11()1f ln ae ae e e '=-=--,222()2(2)f e ae ae -'=--=-+,221()2(2)22a f e e a e e '=-=-,①若1a e -„,则()0a f x lnx x '=-…,故()f x 在2(e -,2)e 内没有极值点;②若122a e e -<<-,则11()0f ln ae e e '=-<,22()(2)0f e ae -'=-+>,221()(2)02f e e a e '=->,因此()f x '在2(e -,2)e 有两个零点,()f x 在2(e -,2)e 内有两个极值点; ③若202a e -<„,则11()0f ln ae e e '=-<,22()(2)0f e ae -'=-+„,221()(2)02f e e a e '=->,因此()f x '在2(e -,2)e 有一个零点,()f x 在2(e -,2)e 内有一个极值点;综上所述,当(a ∈-∞,1]e-时,()f x 在2(e -,2)e 内没有极值点;当1(a e ∈-,2)2e -时,()f x 在2(e -,2)e 内有两个极值点;当2[2a e ∈-,0)时,()f x 在2(e -,2)e 内有一个极值点. (3)猜想:(1,1)x a ∈+,()1f x a <-恒成立. 证明如下:由(2)得()g x 在1(e ,)+∞上单调递增,且g (1)0a =-<,(1)(1)(1)g a a ln a a +=++-.因为当1x >时,11(*)lnx x >-,所以1(1)(1)(1)01g a a a a +>+--=+.故()g x 在(1,1)a +上存在唯一的零点,设为0x . 由知,(1,1)x a ∈+,(){f x max f <(1),(1)}f a +.又(1)(1)1f a ln a +=+-,而1x >时,1(**)lnx x <-, 所以(1)(1)111f a a a f +<+--=-=(1). 即(1,1)x a ∈+,()1f x a <-.所以对任意的正数a ,都存在实数1t =,使对任意的(,)x t t a ∈+,使()1f x a <-. 补充证明(*): 令1()1F x lnx x =+-,1x ….111()022x F x x x x -'=-=…,所以()F x 在[1,)+∞上单调递增.所以1x >时,()F x F >(1)0=,即11lnx x>-. 补充证明(**)令()1G x lnx x =-+,1x ….1()10G x x'=-„, 所以()G x 在[1,)+∞上单调递减.所以1x >时,()G x G <(1)0=,即1lnx x <-.海安中学2020届高三阶段测试三数学附加题21.[选做题,本题包括三小题,请选定其中两题,并在相应区域作答]A.已知二阶矩阵[]a b A c d =,矩阵A 属于特征值11λ=-的一个特征向量为11[]1a =-,属于特征值24λ=的一个特征向量为13[]2a =.求矩阵A .解:由特征值、特征向量定义可知,111A αλα=, 即1111111a b c d ⎡⎤⎡⎤⎡⎤⎡⎤=-⨯⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦,得11a b c d -=-⎧⎨-=⎩同理可得3212328a b c d +=⎧⎨+=⎩ 解得2a =,3b =,2c =,1d =.因此矩阵2321A ⎡⎤=⎢⎥⎣⎦. B .在极坐标系中,已知(A 1,3π ),(B 9,3π),线段AB 的垂直平分线l 与极轴交于点C ,求l 的极坐标方程及ABC ∆的面积. 解:由题意,线段AB 的中点坐标为(5,)3π,设点(,)P ρθ为直线l 上任意一点, 在直角三角形OMP 中,cos()53πρθ-=,所以,l 的极坐标方程为cos()53πρθ-=,令0θ=,得10ρ=,即(10,0)C .(8分)所以,ABC ∆的面积为:1(91)10sin 23π⨯-⨯⨯=22.已知实数a ,b 满足||2a b +„,求证:22|22|4(||2)a a b b a +-++„. 证明:由||||||2b a a b -+剟,可得||||2b a +„,22|22||()()2()|a a b b a b a b a b +-+=+-++|||2|2|2|a b a b a b =+-+-+g „,要证22|22|4(||2)a a b b a +-++„, 即证|2|2(||2)a b a -++„,由于|2|||||2a b a b -+++„, 即证||||22(||2)a b a +++„, 即为||||2b a +„,显然成立. 故原不等式成立.23.如图,在四棱锥P ABCD -中,已知棱AB ,AD ,AP 两两垂直,长度分别为1,2,2.若DC AB λ=u u u r u u u r ,且向量PC u u u r 与BD u u u r 夹角的余弦值为15.(1)求实数λ的值;(2)求直线PB 与平面PCD 所成角的正弦值.解:以A 为坐标原点,分别以AB ,AD ,AP 为x ,y ,z 轴建立如图所示空间直角坐标系; 则:(0A ,0,0),(1B ,0,0),(0D ,2,0),(0P ,0,2);DC AB λ=u u u r u u u r ,可得(C λ,2,0).(1)(PC λ=u u u r ,2,2)-,(1BD =-u u u r ,2,0),向量PC u u u r 与BD u u u r 15.215814λ=++g 10λ=(舍去)或2λ=.实数λ的值为2.;(2)(2PC =u u u r ,2,2)-,(0PD =u u u r ,2,2)-,平面PCD 的法向量(n x =r,y ,)z .则0n PC =u u u r r g 且0n PD =u u ur r g ,即:0x y z +-=,0y z -=,0x ∴=,不妨去1y z ==, 平面PCD 的法向量(0n =r,1,1).又(1PB =u u u r ,0,2).故10cos ,||||n PB n PB n PB <>==u u u r r u u u r g ru u u r r .直线PB 与平面PCD 10.24.已知数列{}n a 的通项公式为1515[(()]5n nn a +--,*n N ∈.记1212nn n n n n S C a C a C a =++⋯+.(1)求1S ,2S 的值;(2)求所有正整数n ,使得n S 能被8整除.解:(1)1212nn nn n n S C a C a C a =++⋯+ 122151515()()5nn n n n C C C +++=+⋯+-g g122151515((()]nn n n n C C C ---++⋯+g g1515(1]5n n+-=+-+ 3535[()(]5n n +-=-, 即有1515S ==g ;23535S =g ;(2)3535[((]5n nn S +-=-, 22235353535[((][()(]55n n n n n S ++++-+-=-=-g 135353535()[()(]3n nn n S S ++-+---=-,即213n n n S S S ++=-,*n N ∈,因此2n S +除以8的余数,完全由1n S +,n S 除以8的余数确定, 因为11a =,21a =,所以11111S C a ==,12221223S C a C a =+=,3213918S S S =-=-=, 432324321S S S =-=-=,543363855S S S =-=-=, 654316521144S S S =-=-=,765343255377S S S =-=-=, 87631131144987S S S =-=-=,987329613772584S S S =-=-=,由以上计算及213n n n S S S ++=-可知,数列{}n S 各项除以8的余数依次是: 1,3,0,5,7,0,1,3,0,5,7,0,⋯,它是一个以6为周期的数列,从而n S 除以8的余数等价于n 除以3的余数, 所以3n k =,*k N ∈,即所求集合为:{|3n n k =,*}k N ∈.。
2020届江苏省南通市海安高级中学高三阶段测试三数学试题(解析版)

2020届江苏省南通市海安高级中学高三阶段测试三数学试题一、填空题1.设全集{1,2,3,4,5}U =,若{1,2,4}U A =ð,则集合A =_________. 【答案】{3,5}.【解析】直接求根据{1,2,4}U A =ð求出集合A 即可. 【详解】解:因为全集{1,2,3,4,5}U =若{1,2,4}U A =ð, 则集合A ={3,5}. 故答案为:{3,5}. 【点睛】本题考查补集的运算,是基础题.2.已经复数z 满足(2)1z i i -=+(i 是虚数单位),则复数z 的模是________.【解析】【详解】(2)1z i i -=+Q ,11323,i iz i i i++∴=+==-z =.3.已知一组数据123,,a a a ,…,n a 的平均数为a ,极差为d ,方差为2S ,则数据121,a +221,a +321a +,…,21n a +的方差为___________.【答案】24S【解析】根据在一组数据的所有数字上都乘以同一个数字,得到的新数据的方差是原来数据的平方倍,得到结果. 【详解】解: ∵数据123,,a a a ,…,n a 的方差为2S ,∴数据121,a +221,a +321a +,…,21n a +的方差是22224S S ⨯=, 故答案为:24S . 【点睛】此题主要考查了方差,关键是掌握方差与数据的变化之间的关系. 4.如图是一个算法的伪代码,其输出的结果为_______.【答案】1011【解析】由题设提供的算法流程图可知:1111101122310111111S =++⋅⋅⋅+=-=⨯⨯⨯,应填答案1011. 5.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为______。
【答案】18【解析】试题分析:分类讨论:从0、2中选一个数字0,则0只能排在十位;从0、2中选一个数字2,则2排在十位或百位,由此可得结论.解:从0、2中选一个数字0,则0只能排在十位,从1、3、5中选两个数字排在个位与百位,共有23A =6种;从0、2中选一个数字2,则2排在十位,从1、3、5中选两个数字排在个位与百位,共有23A =6种; 2排在百位,从1、3、5中选两个数字排在个位与十位,共有23A =6种;故共有323A =18种,故答案为18. 【考点】计数原理点评:本题考查计数原理的运用,考查分类讨论的数学思想,正确分类是关键6.在平面直角坐标系xOy 中,若双曲线()2222:10,0x y C a b a b-=>>10,则双曲线C 的渐近线方程为_______. 【答案】3y x =±【解析】,可以得到ca=222a b c +=求出,a b 的关系,从而得出渐近线的方程. 【详解】解:因为双曲线()2222:10,0x y C a b a b-=>>,所以ca= 故2210c a=, 又因为222a b c +=,所以22210a b a +=,即229b a=,即3=b a , 所以双曲线的渐近线3y x =±. 【点睛】本题考查了双曲线渐近线的问题,解题的关键是由题意解析出,a b 的关系,从而解决问题.7.将函数f(x)的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象,则()π4f 为 . 【答案】4【解析】试题分析:将函数f(x)的图象向右平移π6个单位后得到函数()π4sin 23y x =-的(π23x -()π4f =4sin 42π=.故答案为:4.【考点】三角函数的图象平移.8.设定义在R 上的奇函数()f x 在区间[0,)+∞上是单调减函数,且()23(2)0f x x f -+>,则实数x 的取值范围是_________【答案】(1,2)【解析】根据题意,由函数的奇偶性和单调性分析可得函数()f x 在R 上为减函数,则()23(2)0f x x f -+>可以转化为232x x -<-,解可得x 的取值范围,即可得答案.【详解】解:根据题意,()f x 是在R 上的奇函数,且在区间[0,)+∞上是单调减函数, 则其在区间(,0)-∞上递减, 则函数()f x 在R 上为减函数,()()22223(2)03(2)(3)(2)32f x x f f x x f f x x f x x -+>⇒->-⇒->-⇒-<-,解得:12x <<;即实数x 的取值范围是(1,2); 故答案为:(1,2). 【点睛】本题考查函数的单调性与奇偶性的综合应用,关键是分析函数在整个定义域上的单调性.9.在锐角三角形ABC 中3sin 5A =,1tan()3A B -=-,则3tan C 的值为_________.【答案】79【解析】由题意可得tan A ,进而可得tan B ,而tan tan()C A B =-+,由两角和与差的正切公式可得. 【详解】解:∵在锐角三角形ABC 中3sin 5A =,4cos 5A ∴==, sin 3tan cos 4A A A ∴==, 31tan tan()1343tan tan[()]311tan tan()9143A A B B A A B A A B +--∴=--===+--⨯,313tan tan 7949tan tan()3131tan tan 3149A B C A B A B ++∴=-+=-=-=--⨯, 3tan 79C ∴=故答案为:79.【点睛】本题考查两角和与差的正切公式,属中档题.10.已知n S 为数列{}n a 的前n 项和3(1)(*)n n S na n n n N =--∈且211a =.则1a 的值________ 【答案】5【解析】由3(1)(*)n n S na n n n N =--∈,且211a =.取2n =即可得出. 【详解】解:∵3(1)(*)n n S na n n n N =--∈,且211a =.12226a a a ∴+=-,即1265a a =-=.故答案为:5. 【点睛】本题考查了递推式的简单应用,是基础题. 11.设正实数x ,y 满足x yxy x y+=-,则实数x 的最小值为______.1.【解析】由正实数x ,y 满足x y xy x y+=-,化为()2210xy x y x +-+=,可得()222212121401010x x x y y x y y ⎧∆=--≥⎪⎪-⎪+=>⎨⎪=>⎪⎪⎩,计算即可. 【详解】解:由正实数x ,y 满足x yxy x y+=-, 化为()2210xy xy x +-+=,∴()222212121401010x x x y y x y y ⎧∆=--≥⎪⎪-⎪+=>⎨⎪=>⎪⎪⎩,化为426101x x x ⎧-+≥⎨>⎩,解得1x ≥.因此实数x 的最小值为21+. 故答案为:21+. 【点睛】本题考查了一元二次方程的实数根与判别式、根与系数的关系、一元二次不等式的解法,考查了推理能力和计算能力,属于中档题.12.如图正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点)且//EF BC ,则四棱锥1A AEFD -的体积为___________.【答案】9【解析】由11113A AED E A AD A AD V V S AB --∆==⋅,由此能求出四棱锥1A AEFD -的体积.【详解】 解:连接DE ,∵正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点),且//EF BC ,11A AED A FED V V --∴=,1111111111193662A AED E A AD A AD A ADD ABCD A C D V V S AB S AB V --∆-∴==⋅=⋅==,∴四棱锥1A AEFD -的体积19A AEFD V -=. 故答案为:9.【点睛】本题考查四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、运算求解能力,是中档题.13.已知向量,,a b c r r r 满足0a b c ++=r r r 且a r 与b r 的夹角的正切为12-,b r 与c r的夹角的正切为13-,||2b =r ,则a c ⋅r r 的值为___________.【答案】45【解析】可设,,AB a BC b CA c ===u u u r u u u r u u u r r r r ,由题意可得11tan ,tan 23B C ==,由两角和的正切公式,可得tan A ,再由同角的基本关系式可得sin ,sin B C ,再由正弦定理可得AB ,AC ,由数量积的定义即可得到所求值. 【详解】解:可设,,AB a BC b CA c ===u u u r u u u r u u u r r r r,由题意可得11tan ,tan 23B C ==, 则11tan tan 23tan tan()1111tan tan 123B C A B C B C ++=-+=-=-=---⨯, 即为135A ︒=,又,B C 为锐角,22sin 1sin cos 1,cos 2B B B B +==,可得sin 5B =,同理可得sin 10C =,由正弦定理可得2sin135︒==r r,即有c a ==r r ,则4||||cos 455525a c c a ︒⋅=⋅⋅=⋅⋅=u u rr rr . 故答案为:45. 【点睛】本题考查向量的数量积的定义,考查正弦定理和三角函数的化简和求值,以及运算求解能力,属于中档题.14.已知()(2)(3),()22x f x m x m x m g x =-++=-,若同时满足条件:①,()0x R f x ∀∈<或()0<g x ;②(,4),()()0x f x g x ∃∈-∞-<.则m 的取值范围是________________. 【答案】()4,2m ∈--【解析】根据()220xg x =-<可解得x<1,由于题目中第一个条件的限制,导致f(x)在1x ≥是必须是()0f x <,当m=0时,()0f x =不能做到f(x)在1x ≥时()0f x <,所以舍掉,因此,f(x)作为二次函数开口只能向下,故m<0,且此时2个根为122,3x m x m ==--,为保证条件成立,只需1221{31x m x m =<=--<1{24m m <⇒>-,和大前提m<0取交集结果为40m -<<;又由于条件2的限制,可分析得出在(,4),()x f x ∃∈-∞-恒负,因此就需要在这个范围内g(x)有得正数的可能,即-4应该比12x x 两个根中较小的来的大,当(1,0)m ∈-时,34m --<-,解得交集为空,舍.当m=-1时,两个根同为24->-,舍.当(4,1)m ∈--时,24m <-,解得2m <-,综上所述,(4,2)m ∈--.【考点定位】本题考查学生函数的综合能力,涉及到二次函数的图像开口,根大小,涉及到指数函数的单调性,还涉及到简易逻辑中的“或”,还考查了分类讨论思想.二、解答题15.已知ABC ∆的面积为()18AC AB CB ⋅-=u u u r u u u r u u u r,向量(tan tan ,sin 2)m A B C =+u r 和向量(1,cos cos )n A B =r是共线向量.(1)求角C ;(2)求ABC ∆的边长c . 【答案】(1) 3C π=(2) 【解析】(1)利用向量共线的条件,建立等式,再利用和角的正弦公式化简等式,即可求得角C ;(2)由()18AC AB CB ⋅-=u u u r u u u r u u u r 得:2()18AC AB BC AC ⋅+==u u u r u u u r u u u r u u u r ,进而利用ABC ∆的面积为,及余弦定理可求ABC ∆的边长c . 【详解】(1)因为向量(tan tan ,sin 2)m A B C =+r 和(1,cos cos )n A B =r是共线向量, 所以cos cos (tan tan )sin 20A B A B C +-=, 即sin cos cos sin 2sin cos 0A B A B C C +-=, 化简sin 2sin cos 0C C C -=, 即sin (12cos )0C C -=.因为0C π<<,所以sin 0C >,从而1cos ,2C =3C π=.(2)()18AC AB CB ⋅-=u u u r u u u r u u u rQ ,18()AC AB CB ∴=⋅-u u u r u u u r u u u r 2||AC AC AC =⋅=u u u r u u u r u u u r则||AC ==u u u rAC =因为ABC V 的面积为,所以1sin 2CA CB C ⋅=即1sin 23π⨯=解得CB =在ABC V 中,由余弦定理得2222cos AB CA CB CA CB C =+-⋅22122=+-⨯54=,所以AB ==【点睛】本题重点考查正弦、余弦定理的运用,考查向量知识的运用,解题的关键是正确运用正弦、余弦定理求出三角形的边.16.如图,四棱锥P -ABCD 的底面为矩形,且AB ,BC =1,E ,F 分别为AB ,PC 中点.(1)求证:EF∥平面PAD;(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.【答案】证明:(1)方法一:取线段PD的中点M,连结FM,AM.因为F为PC的中点,所以FM∥CD,且FM=12 CD.因为四边形ABCD为矩形,E为AB的中点,所以EA∥CD,且EA=12 CD.所以FM∥EA,且FM=EA.所以四边形AEFM为平行四边形.所以EF∥AM.……………………… 5分又AM⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD.………7分方法二:连结CE并延长交DA的延长线于N,连结PN.因为四边形ABCD为矩形,所以AD∥BC,所以∠BCE=∠ANE,∠CBE=∠NAE.又AE=EB,所以△CEB≌△NEA.所以CE=NE.又F为PC的中点,所以EF∥NP.………… 5分又NP⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD. (7)分方法三:取CD的中点Q,连结FQ,EQ.在矩形ABCD中,E为AB的中点,所以AE=DQ,且AE∥DQ.所以四边形AEQD为平行四边形,所以EQ∥AD.又AD⊂平面PAD,EQ⊄平面PAD,所以EQ∥平面PAD. (2)分因为Q,F分别为CD,CP的中点,所以FQ∥PD.又PD⊂平面PAD,FQ⊄平面PAD,所以FQ∥平面PAD.又FQ,EQ⊂平面EQF,FQ∩EQ=Q,所以平面EQF∥平面PAD. (5)分因为EF⊂平面EQF,所以EF∥平面PAD.……………………………… 7分(2)设AC,DE相交于G.在矩形ABCD中,因为AB=2BC,E为AB的中点.所以DAAE=CDDA=2.又∠DAE=∠CDA,所以△DAE∽△CDA,所以∠ADE=∠DCA.又∠ADE+∠CDE=∠ADC=90°,所以∠DCA+∠CDE=90°.由△DGC的内角和为180°,得∠DGC=90°.即DE⊥AC. (10)分因为平面PAC⊥平面ABCD 因为DE⊂平面ABCD,所以DE⊥平面PAC,又DE⊂平面PDE,所以平面PAC⊥平面PDE.………………………… 14分【解析】略17.如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知,,Q到海岸线OM,ON的距离分别为3 km,km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.(1)求水上旅游线AB的长;(2)若小岛正北方向距离小岛6 km处的海中有一个圆形强水波P,从水波生成t h时的半径为(a为大于零的常数).强水波开始生成时,一游轮以km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.【答案】(1)(2)【解析】试题分析:(1)由条件建立直角坐标系较为方便表示:,直线的方程为.由Q到海岸线ON的距离为km,得,解得,再由两直线交点得,利用两点间距离公式得(2)由题意是一个不等式恒成立问题:设小时时,游轮在线段上的点处,而不等式恒成立问题往往利用变量分离将其转化为对应函数最值问题:试题解析:(1)以点为坐标原点,直线为轴,建立直角坐标系如图所示.则由题设得:,直线的方程为.由,及得,∴.∴直线的方程为,即,由得即,∴,即水上旅游线的长为.(2)设试验产生的强水波圆,由题意可得P(3,9),生成小时时,游轮在线段上的点处,则,∴.强水波不会波及游轮的航行即,当时,当.,,当且仅当时等号成立,所以,在时恒成立,亦即强水波不会波及游轮的航行.【考点】函数实际应用,不等式恒成立18.在平面直角坐标系xOy 中已知椭圆222:1(0)3x y E a b a +=>>过点61,2⎛ ⎝⎭,其左、右焦点分别为12F F 、,离心率为22. (1)求椭圆E 的方程;(2)若A ,B 分别为椭圆E 的左、右顶点,动点M 满足MB AB ⊥,且MA 交椭圆E 于点P .(i )求证:OP OM ⋅uu u r uuu r为定值;(ii )设PB 与以PM 为直径的圆的另一交点为Q ,问:直线MQ 是否过定点,并说明理由.【答案】(1) 22142x y += (2) (i )证明见解析,定值为4 (ii )直线MQ 过定点(0,0)O . 【解析】(1)由题意得离心率公式和点满足的方程,结合椭圆的,,a b c 的关系,可得,a b ,进而得到椭圆方程;(2)(i )设()02,,M y ()11,P x y ,求得直线MA 的方程,代入椭圆方程,解得点P 的坐标,再由向量的数量积的坐标表示,计算即可得证;(ii )直线MQ 过定点O (0,0).先求得PB 的斜率,再由圆的性质可得MQ ⊥PB ,求出MQ 的斜率,再求直线MQ 的方程,即可得到定点. 【详解】解:(1)易得22312122a b c a⎧⎪+=⎪⎨⎪=⎪⎩,且222c a b =-, 解得2242a b ⎧=⎨=⎩,,所以椭圆E 的方程为22142x y +=(2)设()02,,M y ()11,P x y , ①易得直线MA 的方程为:0042y y y x =+, 代入椭圆22142x y +=得,2222000140822y y y x x ⎛⎫+++-= ⎪⎝⎭, 由()201204828y x y --=+得,()20120288y x y --=+,从而012088y y y =+, 所以示()()20002200288,2,88y y OP OM y y y ⎛⎫-- ⎪⋅=⋅ ⎪++⎝⎭u u u r u u u u r ()22002200488488y y y y --=+=++, ②直线MQ 过定点(0,0)O ,理由如下:依题意,()2020020882288PBy y k y y y +==---+, 由MQ PB ⊥得,02MQ y k =, 则MQ 的方程为:00(2)2y y y x -=-,即02yy x =,所以直线MQ 过定点(0,0)O . 【点睛】本题考查椭圆的方程和性质,主要考查椭圆的离心率公式和方程的运用,注意联立直线方程和椭圆方程,运用韦达定理,同时考查向量的数量积的坐标表示和直线和圆的位置关系,属于中档题.19.已知数列{}n a 满足:123a a a k ===(常数0k >),111n n n n K a a a a -+-+=()*3,n n N ≥∈.数列{}n b 满足:21n n n n a a b a +++=()*n N ∈. (1)求1,b 2,b 3,b 4b 的值; (2)求出数列{}n b 的通项公式;(3)问:数列{}n a 的每一项能否均为整数?若能,求出k 的所有可能值;若不能,请说明理由.【答案】(1) 132b b ==,2421k b b k +==;(2) 41122nn k b k k+-=+(); (3) k 为1,2时数列{}n a 是整数列.【解析】(1)经过计算可知:45621,2,4a k a k a k k=+=+=++,由数列{}n b 满足:21n n n n a a b a +++=(n =1,2,3,4…),从而可求1,b 2,b 3,b 4b ; (2)由条件可知121n n n n a a k a a +--=+.得211n n n n a a k a a +-+=+,两式相减整理得2n n b b -=,从而可求数列{}n b 的通项公式;(3)假设存在正数k ,使得数列{}n a 的每一项均为整数,则由(2)可知:2122122222211n n n n n n a a a k a a a k +-+=-⎧⎪+⎨=+-⎪⎩,由1a k Z =∈,624Z a k k =++∈,可求得1,2k =.证明1,2k =时,满足题意,说明1,2k =时,数列{}n a 是整数列. 【详解】(1)由已知可知:45621,2,4a k a k a k k=+=+=++, 把数列{}n a 的项代入21n n n n b a a a =+++求得132b b ==,2421k b b k+==; (2)由121n n n n k a a a a --++=3,n n N ≥∈*() 可知:121n n n n a a k a a +--=+① 则:211n n n n a a k a a +-+=+② ①−②有:2211n n n nn n a a a a a a +-+-++=,即:2n n b b -=2123n n b b --∴==…13122a a b a +===,222n n b b -== (242321)a a kb a k++===, 41122nn k b k k+-∴=+(); (3)假设存在正数k 使得数列{}n a 的每一项均为整数,则由(2)可知:2122122222211n n n n n n a a a k a a a k +-+=-⎧⎪+⎨=+-⎪⎩③, 由1a k Z =∈,624Z a k k=++∈,可知1k =,2. 当1k =时,213k k+=为整数,利用123,,a a a Z ∈结合③式可知{}n a 的每一项均为整数;当2k =时,③变为2122122222512n n n n n n a a a a a a +-+=-⎧⎪⎨=+-⎪⎩④ 用数学归纳法证明21n a -为偶数,2n a 为整数.1n =时结论显然成立,假设n k =时结论成立,这时21n a -为偶数,2n a 为整数,故212212n n n a a a +-=-为偶数,22n a +为整数,1n k ∴=+时,命题成立.故数列{}n a 是整数列.综上所述k 为1,2时数列{}n a 是整数列. 【点睛】本题考查了等差数列的基本性质和数列的递推公式,考查了学生的计算能力和对数列的综合掌握,注意分类讨论思想和转化思想的运用,属于难题. 20.设函数()()ln ,f x x a x x a =--+a R ∈. (1)若0a =求函数()f x 的单调区间;(2)若0a <试判断函数()f x 在区间()22,e e -内的极值点的个数,并说明理由;(3)求证:对任意的正数a 都存在实数t 满足:对任意的(,)x t t a ∈+,()1f x a <-. 【答案】(1) 单调递减区间为(0,1)单调递增区间为(1,)+∞. (2) 见解析 (3)证明见解析【解析】(1)求解()ln f x x '=,利用()0,()0f x f x ''><,解不等式求解单调递增区间,单调递减区间; (2)'()ln af x x x=-,其中0x >, 再次构造函数令()ln g x x x a =-,分析()g x 的零点情况.()ln 1g x x '=+,令1()0,g x x e'==,列表分析得出()g x 单调性,求其最小值, 分类讨论求解①若1a e≤-,②若212a e e -<<-,③若220,()a f x e -≤<的单调性,()f x 最大值,最小值,确定有无零点问题;(3)先猜想(1,1),()1x a f x a ∈+<-恒成立.再运用导数判断证明.令'1()ln 1,1,()10G x x x x G x x=-+≥=-≤,求解最大值,得出()(1)0G x G <=即可. 【详解】(1)当0a =时,()ln f x x x x =-,()ln f x x '=, 令()0f x '=,1x =,列表分析故()f x 的单调递减区间为(0,1)单调递增区间为(1,)+∞.(2)()()ln f x x a x x a =--+,()ln f x x ax '=-,其中0x >, 令()ln g x x x a =-,分析()g x 的零点情况.()ln 1g x x '=+ 令()0g x '=,1x =,列表分析min 11()()g x g a e e==--,而11()1n1f ae ae ee '=-=--,222()2(2)f e ae ae -'=--=-+ 22221()2(2)a f e e a e e '=-=-,①若1a e≤-则()ln 0af x x x '=-≥,故()f x 在22(,)e e -内没有极值点;②若212a e e -<<-,则11()1n 0f ae e e '=-<,22()(2)0f e ae -'=-+> 2221()(2)0f e e a e'=->因此()f x '在22(,)e e -有两个零点,()f x 在22(,)e e -内有两个极值点;③若220a e -≤<则11()10f n ae e e '=-<,22()(2)0f e ae -'=-+≤,2221()(2)0f e e a e'=->,因此()f x '在22(,)e e -有一个零点,()f x 在22(,)e e -内有一个极值点;综上所述当1(,]a e∈-∞-时,()f x 在22(,)e e -内没有极值点;当212,a e e ⎛⎫∈--⎪⎝⎭时,()f x 在22(,)e e -内有两个极值点; 当22,0a e ⎡⎫∈-⎪⎢⎣⎭时,()f x 在22(,)e e -内有一个极值点. (3)猜想:(1,1)x a ∈+,()1f x a <-恒成立. 证明如下:由(2)得()g x 在1(,)e+∞上单调递增,且(1)0g a =-<,(1)(1)ln(1)g a a a a +=++-.因为当1x >时,1ln 1(*)x x >-, 所以1(1)(1)(1)01g a a a a +>+--=+ 故()g x 在(1,1)a +上存在唯一的零点,设为0x .由知(1,1)x a ∈+,()max{(1),(1)}f x f f a <+.又(1)ln(1)1f a a +=+-,而1x >时,ln 1(**)x x <-, 所以(1)(1)111(1)f a a a f +<+--=-=. 即(1,1)x a ∈+,()1f x a <-.所以对任意的正数a ,都存在实数1t =, 使对任意的(,)x t t ∈+∞, 使()1f x a <-. 补充证明(*): 令1()1n 1F x x x =+-,1x ≥.22111()0x F x x x x-'=-=≥, 所以()F x 在[1,)+∞上单调递增.所以1x >时,()(1)0F x F >=,即1ln 1x x>-. 补充证明(**)令()ln 1G x x x =-+,1x ≥.1()10G x x'=-≤, 所以()G x 在[1,)+∞上单调递减.所以1x >时,()(1)0G x G <=,即ln 1x x <-. 【点睛】本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间,考查了不等式与导数的结合,难度较大. 21.已知二阶矩阵,矩阵属于特征值的一个特征向量为,属于特征值的一个特征向量为.求矩阵.【答案】【解析】运用矩阵定义列出方程组求解矩阵 【详解】由特征值、特征向量定义可知,,即,得 同理可得解得,,,.因此矩阵【点睛】本题考查了由矩阵特征值和特征向量求矩阵,只需运用定义得出方程组即可求出结果,较为简单22.在极坐标系中,已知1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,线段AB 的垂直平分线l 与极轴交于点C ,求l 的极坐标方程及ABC ∆的面积. 【答案】l 的极坐标方程及cos 53πρθ⎛⎫-= ⎪⎝⎭,203ABC ∆的面积. 【解析】将1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭转化为直角坐标系下的坐标形式,然后求出线段AB 的中点与直线AB 的斜率,进而求出直线l 在直角坐标系下的方程,再转化为极坐标方程;在直角坐标系下,求出点C 到直线AB 的距离、线段AB 的长度,从而得出ABC ∆的面积. 【详解】解:以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系xoy 在平面直角坐标系xoy 中,1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ 的坐标为13993((22A B 线段AB 的中点为553(2A ,3AB k 故线段AB 中垂线的斜率为133AB k k --==, 所以AB 的中垂线方程为:5335()232y x -=- 化简得:3100x +-=,所以极坐标方程为cos 3sin 100ρθρθ+-=, 即cos()53πρθ-=,令0y =,则10x =,故在平面直角坐标系xoy 中,C (10,0)点C 到直线AB :y =的距离为d == 线段8AB =,故ABC ∆的面积为182S =⨯=【点睛】本题考查了直线的极坐标方程问题,解题时可以将极坐标系下的问题转化为平面直角坐标系下的问题,从而转化为熟悉的问题.23.已知实数,a b 满足2a b +≤,求证:22224(2)a a b b a +-+≤+.【答案】证明见解析【解析】对2222a a b b +-+进行转化,转化为含有2a b +≤形式,然后通过不等关系得证.【详解】 解:因为2a b +≤, 所以2222a a b b +-+ 2222a b a b =-++()()()2a b a b a b =-+++2a b a b =+-+()22a b a a b =+-++22a b a a b ≤++++()22222244242a a a a ≤++=+=+≤+,得证.【点睛】本题考查了绝对值不等式问题,解决问题的关键是要将要证的形式转化为已知的条件,考查了学生转化与化归的能力.24.如图,在四棱锥P ABCD -中,已知棱AB ,AD ,AP 两两垂直,长度分别为1,2,2.若DC AB λ=u u u r u u u r (R λ∈),且向量PC uuu r 与BD u u u r .(1)求λ的值;(2)求直线PB 与平面PCD 所成角的正弦值.【答案】(1)2λ=;(210【解析】试题分析:(1)以A 为坐标原点,AB 、AD 、AP 分别为x 、y 、z 轴建立空间直角坐标系A xyz -,写出,PC u u u r ,BD u u u r 的坐标,根据空间向量夹角余弦公式列出关于λ的方程可求;(2)设岀平面PCD 的法向量为(),,n x y z =r ,根据n PC n DC⎧⊥⎪⎨⊥⎪⎩r u r r u r ,进而得到00⎧⋅=⎪⎨⋅=⎪⎩r u r r u r n PC n DC ,从而求出n r ,向量PB u r 的坐标可以求出,从而可根据向量夹角余弦的公式求出cos ,n PB <>r u r ,从而得PB 和平面PCD 所成角的正弦值.试题解析:(1)依题意,以A 为坐标原点,AB 、AD 、AP 分别为x 、y 、z 轴建立空间直角坐标系A xyz -(1,0,0),(0,2,0),(0,0,2)B D P ,因为DC AB λ=u u u r u u u r ,所以(,2,0)C λ,从而(,2,2)PC λ=-u u u r ,则由15cos ,15PC BD =u u u r u u u r ,解得10λ=(舍去)或2λ=. (2)易得(2,2,2)PC =-u u u r ,(0,2,2)PD =-u u u r ,设平面PCD 的法向量(,,)n x y z =r ,则0⋅=r u u u r n PC ,0⋅=r u u u r n PD ,即0x y z +-=,且0y z -=,所以0x =,不妨取1y z ==,则平面PCD 的一个法向量(0,1,1)n =r ,又易得(1,0,2)PB =-u u u r ,故10cos ,=⋅=u u u r r PB n PB n ,所以直线PB 与平面PCD 10.考点: 1、空间两向量夹角余弦公式;2、利用向量求直线和平面说成角的正弦.25.已知数列{}n a 的通项公式为1515225n n n a ⎡⎤⎛⎫⎛⎫+⎥=- ⎪ ⎪ ⎪ ⎪⎥⎝⎭⎝⎭⎦,n N ∈,记1212n n n S C a C a =++…n n n C a +.(1)求1,S 2S 的值;(2)求所有正整数n ,使得n S 能被8整除.【答案】(1) 11S =;23S =; (2) {}*|3,n n k k N =∈ 【解析】(1)运用二项式定理,化简整理,再代入计算即可得到所求值; (2)通过化简得到213n n n S S S ++=-,再由不完全归纳找规律得到结论,即可得到所求结论.【详解】解:(1)1212n n n n n n S C a C a C a =++⋯+2121515225n n C C ⎡⎛⎛⎫+⎢ =⋅+⋅+ ⎪ ⎪⎢⎝⎭⎝⎣…212151515n n n n n C C C ⎫⎛+--⎪ +⋅-+⋅+⎪ ⎝⎭⎝⎭⎭⎝…15n n n C ⎤⎫-⎥⎪+⋅⎥⎪⎝⎭⎭⎦ 1515115n n ⎡⎤⎛⎛+-⎥=+-+ ⎥⎝⎭⎝⎭⎦ 35355n n ⎡⎤+-⎥=-⎥⎝⎭⎝⎭⎦,即有1S1==;2S33==;(2)3322nnS n⎡⎤⎛⎛-⎥=-⎥⎝⎭⎝⎭⎦,2332222nS n n+⎡⎤⎛⎛+-=+-+⎥⎥⎝⎭⎝⎭⎦333333222222n n n n ⎡⎤⎡⎤⎛⎫⎛⎛⎛⎛--⎥⎢⎥-⋅+-- ⎪⎪⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎦⎣⎦13n nS S+=-,即213n n nS S S++=-,*n N∈,因此2nS+除以8的余数,完全由1,n nS S+除以8的余数确定,因为11,a=21a=,所以11111S C a==,12221223S C a C a=+=,3213918S S S=-=-=,432324321,S S S=-=-=543363855S S S=-=-=,654316521144,S S S=-=-=7535643255377S S=-=-=,87631131144987,S S S=-=-=987329613772584S S S=-=-=由以上计算及213n n nS S S++=-可知,数列{}n S各项除以8的余数依次是:1,3,0,5,7,0,1,3,0,5,7,0,…,它是一个以6为周期的数列,从而n S除以8的余数等价于n除以3的余数,所以3,n k=*k N∈,即所求集合为:{}*|3,n n k k N=∈.【点睛】本题考查数列通项的运用,解决问题的关键是运用二项式定理,本题属于难题.。
2020届江苏省南通市海安高级中学高三阶段测试三数学试题(解析版)

2020届江苏省南通市海安高级中学高三阶段测试三数学试题一、填空题1.设全集{1,2,3,4,5}U =,若{1,2,4}U A =ð,则集合A =_________. 【答案】{3,5}.【解析】直接求根据{1,2,4}U A =ð求出集合A 即可. 【详解】解:因为全集{1,2,3,4,5}U =若{1,2,4}U A =ð, 则集合A ={3,5}. 故答案为:{3,5}. 【点睛】本题考查补集的运算,是基础题.2.已经复数z 满足(2)1z i i -=+(i 是虚数单位),则复数z 的模是________.【解析】【详解】(2)1z i i -=+Q ,11323,i iz i i i++∴=+==-z =.3.已知一组数据123,,a a a ,…,n a 的平均数为a ,极差为d ,方差为2S ,则数据121,a +221,a +321a +,…,21n a +的方差为___________.【答案】24S【解析】根据在一组数据的所有数字上都乘以同一个数字,得到的新数据的方差是原来数据的平方倍,得到结果. 【详解】解: ∵数据123,,a a a ,…,n a 的方差为2S ,∴数据121,a +221,a +321a +,…,21n a +的方差是22224S S ⨯=,故答案为:24S . 【点睛】此题主要考查了方差,关键是掌握方差与数据的变化之间的关系. 4.如图是一个算法的伪代码,其输出的结果为_______.【答案】1011【解析】由题设提供的算法流程图可知:1111101122310111111S =++⋅⋅⋅+=-=⨯⨯⨯,应填答案1011. 5.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为______。
【答案】18【解析】试题分析:分类讨论:从0、2中选一个数字0,则0只能排在十位;从0、2中选一个数字2,则2排在十位或百位,由此可得结论.解:从0、2中选一个数字0,则0只能排在十位,从1、3、5中选两个数字排在个位与百位,共有23A =6种;从0、2中选一个数字2,则2排在十位,从1、3、5中选两个数字排在个位与百位,共有23A =6种; 2排在百位,从1、3、5中选两个数字排在个位与十位,共有23A =6种;故共有323A =18种,故答案为18. 【考点】计数原理点评:本题考查计数原理的运用,考查分类讨论的数学思想,正确分类是关键6.在平面直角坐标系xOy 中,若双曲线()2222:10,0x y C a b a b-=>>10,则双曲线C 的渐近线方程为_______. 【答案】3y x =±【解析】10,可以得到10ca=222a b c +=求出,a b的关系,从而得出渐近线的方程. 【详解】解:因为双曲线()2222:10,0x y C a b a b-=>>,所以ca= 故2210c a=, 又因为222a b c +=,所以22210a b a +=,即229b a =,即3=b a , 所以双曲线的渐近线3y x =±. 【点睛】本题考查了双曲线渐近线的问题,解题的关键是由题意解析出,a b 的关系,从而解决问题.7.将函数f(x)的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象,则()π4f 为 . 【答案】4【解析】试题分析:将函数f(x)的图象向右平移π6个单位后得到函数()π4sin 23y x =-的(π23x -()π4f =4sin 42π=.故答案为:4.【考点】三角函数的图象平移.8.设定义在R 上的奇函数()f x 在区间[0,)+∞上是单调减函数,且()23(2)0f x x f -+>,则实数x 的取值范围是_________【答案】(1,2)【解析】根据题意,由函数的奇偶性和单调性分析可得函数()f x 在R 上为减函数,则()23(2)0f x x f -+>可以转化为232x x -<-,解可得x 的取值范围,即可得答案.【详解】解:根据题意,()f x 是在R 上的奇函数,且在区间[0,)+∞上是单调减函数, 则其在区间(,0)-∞上递减, 则函数()f x 在R 上为减函数,()()22223(2)03(2)(3)(2)32f x x f f x x f f x x f x x -+>⇒->-⇒->-⇒-<-,解得:12x <<;即实数x 的取值范围是(1,2); 故答案为:(1,2). 【点睛】本题考查函数的单调性与奇偶性的综合应用,关键是分析函数在整个定义域上的单调性.9.在锐角三角形ABC 中3sin 5A =,1tan()3A B -=-,则3tan C 的值为_________.【答案】79【解析】由题意可得tan A ,进而可得tan B ,而tan tan()C A B =-+,由两角和与差的正切公式可得. 【详解】解:∵在锐角三角形ABC 中3sin 5A =,4cos 5A ∴==, sin 3tan cos 4A A A ∴==, 31tan tan()1343tan tan[()]311tan tan()9143A A B B A A B A A B +--∴=--===+--⨯, 313tan tan 7949tan tan()3131tan tan 3149A B C A B A B ++∴=-+=-=-=--⨯,3tan 79C ∴=故答案为:79. 【点睛】本题考查两角和与差的正切公式,属中档题.10.已知n S 为数列{}n a 的前n 项和3(1)(*)n n S na n n n N =--∈且211a =.则1a 的值________ 【答案】5【解析】由3(1)(*)n n S na n n n N =--∈,且211a =.取2n =即可得出. 【详解】解:∵3(1)(*)n n S na n n n N =--∈,且211a =.12226a a a ∴+=-,即1265a a =-=.故答案为:5. 【点睛】本题考查了递推式的简单应用,是基础题. 11.设正实数x ,y 满足x yxy x y+=-,则实数x 的最小值为______.1.【解析】由正实数x ,y 满足x y xy x y+=-,化为()2210xy x y x +-+=,可得()222212121401010x x x y y x y y ⎧∆=--≥⎪⎪-⎪+=>⎨⎪=>⎪⎪⎩,计算即可. 【详解】解:由正实数x ,y 满足x yxy x y+=-, 化为()2210xy xy x +-+=,∴()222212121401010x x x y y x y y ⎧∆=--≥⎪⎪-⎪+=>⎨⎪=>⎪⎪⎩,化为426101x x x ⎧-+≥⎨>⎩,解得1x ≥.因此实数x1.故答案为:21+. 【点睛】本题考查了一元二次方程的实数根与判别式、根与系数的关系、一元二次不等式的解法,考查了推理能力和计算能力,属于中档题.12.如图正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点)且//EF BC ,则四棱锥1A AEFD -的体积为___________.【答案】9【解析】由11113A AED E A AD A AD V V S AB --∆==⋅,由此能求出四棱锥1A AEFD -的体积.【详解】 解:连接DE ,∵正四棱柱1111ABCD A B C D -的体积为27,点E ,F 分别为棱11,B B C C 上的点(异于端点),且//EF BC ,11A AED A FED V V --∴=,1111111111193662A AED E A AD A AD A ADD ABCD A C D V V S AB S AB V --∆-∴==⋅=⋅==,∴四棱锥1A AEFD -的体积19A AEFD V -=. 故答案为:9. 【点睛】本题考查四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、运算求解能力,是中档题.13.已知向量,,a b c r r r 满足0a b c ++=r r r 且a r 与b r 的夹角的正切为12-,b r 与c r的夹角的正切为13-,||2b =r ,则a c ⋅r r 的值为___________.【答案】45【解析】可设,,AB a BC b CA c ===u u u r u u u r u u u r r r r ,由题意可得11tan ,tan 23B C ==,由两角和的正切公式,可得tan A ,再由同角的基本关系式可得sin ,sin B C ,再由正弦定理可得AB ,AC ,由数量积的定义即可得到所求值. 【详解】解:可设,,AB a BC b CA c ===u u u ru u ur u uu r r r r, 由题意可得11tan ,tan 23B C ==, 则11tan tan 23tan tan()1111tan tan 123B CA B C B C ++=-+=-=-=---⨯, 即为135A ︒=,又,B C 为锐角,22sin 1sin cos 1,cos 2B B B B +==,可得sin 5B =,同理可得sin 10C =,由正弦定理可得2sin135︒==r r,即有c a ==r r ,则4||||cos 455525a c c a ︒⋅=⋅⋅=⋅⋅=u u rr r r .故答案为:45. 【点睛】本题考查向量的数量积的定义,考查正弦定理和三角函数的化简和求值,以及运算求解能力,属于中档题.14.已知()(2)(3),()22x f x m x m x m g x =-++=-,若同时满足条件:①,()0x R f x ∀∈<或()0<g x ;②(,4),()()0x f x g x ∃∈-∞-<.则m 的取值范围是________________. 【答案】()4,2m ∈--【解析】根据()220xg x =-<可解得x<1,由于题目中第一个条件的限制,导致f(x)在1x ≥是必须是()0f x <,当m=0时,()0f x =不能做到f(x)在1x ≥时()0f x <,所以舍掉,因此,f(x)作为二次函数开口只能向下,故m<0,且此时2个根为122,3x m x m ==--,为保证条件成立,只需1221{31x m x m =<=--<1{24m m <⇒>-,和大前提m<0取交集结果为40m -<<;又由于条件2的限制,可分析得出在(,4),()x f x ∃∈-∞-恒负,因此就需要在这个范围内g(x)有得正数的可能,即-4应该比12x x 两个根中较小的来的大,当(1,0)m ∈-时,34m --<-,解得交集为空,舍.当m=-1时,两个根同为24->-,舍.当(4,1)m ∈--时,24m <-,解得2m <-,综上所述,(4,2)m ∈--.【考点定位】本题考查学生函数的综合能力,涉及到二次函数的图像开口,根大小,涉及到指数函数的单调性,还涉及到简易逻辑中的“或”,还考查了分类讨论思想.二、解答题15.已知ABC ∆的面积为()18AC AB CB ⋅-=u u u r u u u r u u u r,向量(tan tan ,sin 2)m A B C =+u r 和向量(1,cos cos )n A B =r是共线向量.(1)求角C ;(2)求ABC ∆的边长c . 【答案】(1) 3C π=(2) 【解析】(1)利用向量共线的条件,建立等式,再利用和角的正弦公式化简等式,即可求得角C ;(2)由()18AC AB CB ⋅-=u u u r u u u r u u u r 得:2()18AC AB BC AC ⋅+==u u u r u u u r u u u r u u u r ,进而利用ABC ∆的面积为,及余弦定理可求ABC ∆的边长c . 【详解】(1)因为向量(tan tan ,sin 2)m A B C =+r 和(1,cos cos )n A B =r是共线向量, 所以cos cos (tan tan )sin 20A B A B C +-=, 即sin cos cos sin 2sin cos 0A B A B C C +-=, 化简sin 2sin cos 0C C C -=, 即sin (12cos )0C C -=.因为0C π<<,所以sin 0C >,从而1cos ,2C =3C π=.(2)()18AC AB CB ⋅-=u u u r u u u r u u u rQ ,18()AC AB CB ∴=⋅-u u u r u u u r u u u r 2||AC AC AC =⋅=u u u r u u u r u u u r则||AC ==u u u rAC =因为ABC V 的面积为,所以1sin 2CA CB C ⋅=即1sin 23π⨯=解得CB =在ABC V 中,由余弦定理得2222cos AB CA CB CA CB C =+-⋅22122=+-⨯54=,所以AB ==【点睛】本题重点考查正弦、余弦定理的运用,考查向量知识的运用,解题的关键是正确运用正弦、余弦定理求出三角形的边.16.如图,四棱锥P -ABCD 的底面为矩形,且AB ,BC =1,E ,F 分别为AB ,PC 中点.(1)求证:EF∥平面PAD;(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.【答案】证明:(1)方法一:取线段PD的中点M,连结FM,AM.因为F为PC的中点,所以FM∥CD,且FM=12 CD.因为四边形ABCD为矩形,E为AB的中点,所以EA∥CD,且EA=12 CD.所以FM∥EA,且FM=EA.所以四边形AEFM为平行四边形.所以EF∥AM.……………………… 5分又AM⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD.………7分方法二:连结CE并延长交DA的延长线于N,连结PN.因为四边形ABCD为矩形,所以AD∥BC,所以∠BCE=∠ANE,∠CBE=∠NAE.又AE=EB,所以△CEB≌△NEA.所以CE=NE.又F为PC的中点,所以EF∥NP.………… 5分又NP⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD. (7)分方法三:取CD的中点Q,连结FQ,EQ.在矩形ABCD中,E为AB的中点,所以AE=DQ,且AE∥DQ.所以四边形AEQD为平行四边形,所以EQ∥AD.又AD⊂平面PAD,EQ⊄平面PAD,所以EQ∥平面PAD. (2)分因为Q,F分别为CD,CP的中点,所以FQ∥PD.又PD⊂平面PAD,FQ⊄平面PAD,所以FQ∥平面PAD.又FQ,EQ⊂平面EQF,FQ∩EQ=Q,所以平面EQF∥平面PAD. (5)分因为EF⊂平面EQF,所以EF∥平面PAD.……………………………… 7分(2)设AC,DE相交于G.在矩形ABCD中,因为AB=2BC,E为AB的中点.所以DAAE=CDDA=2.又∠DAE=∠CDA,所以△DAE∽△CDA,所以∠ADE=∠DCA.又∠ADE+∠CDE=∠ADC=90°,所以∠DCA+∠CDE=90°.由△DGC的内角和为180°,得∠DGC=90°.即DE⊥AC. (10)分因为平面PAC⊥平面ABCD 因为DE⊂平面ABCD,所以DE⊥平面PAC,又DE⊂平面PDE,所以平面PAC⊥平面PDE.………………………… 14分【解析】略17.如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知,,Q到海岸线OM,ON的距离分别为3 km,km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.(1)求水上旅游线AB的长;(2)若小岛正北方向距离小岛6 km处的海中有一个圆形强水波P,从水波生成t h时的半径为(a为大于零的常数).强水波开始生成时,一游轮以km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.【答案】(1)(2)【解析】试题分析:(1)由条件建立直角坐标系较为方便表示:,直线的方程为.由Q到海岸线ON的距离为km,得,解得,再由两直线交点得,利用两点间距离公式得(2)由题意是一个不等式恒成立问题:设小时时,游轮在线段上的点处,而不等式恒成立问题往往利用变量分离将其转化为对应函数最值问题:试题解析:(1)以点为坐标原点,直线为轴,建立直角坐标系如图所示.则由题设得:,直线的方程为.由,及得,∴.∴直线的方程为,即,由得即,∴,即水上旅游线的长为.(2)设试验产生的强水波圆,由题意可得P(3,9),生成小时时,游轮在线段上的点处,则,∴.强水波不会波及游轮的航行即,当时,当.,,当且仅当时等号成立,所以,在时恒成立,亦即强水波不会波及游轮的航行.【考点】函数实际应用,不等式恒成立18.在平面直角坐标系xOy 中已知椭圆222:1(0)3x y E a b a +=>>过点6⎛ ⎝⎭,其左、右焦点分别为12F F 、,离心率为22. (1)求椭圆E 的方程;(2)若A ,B 分别为椭圆E 的左、右顶点,动点M 满足MB AB ⊥,且MA 交椭圆E 于点P .(i )求证:OP OM ⋅uu u r uuu r为定值;(ii )设PB 与以PM 为直径的圆的另一交点为Q ,问:直线MQ 是否过定点,并说明理由.【答案】(1) 22142x y += (2) (i )证明见解析,定值为4 (ii )直线MQ 过定点(0,0)O . 【解析】(1)由题意得离心率公式和点满足的方程,结合椭圆的,,a b c 的关系,可得,a b ,进而得到椭圆方程;(2)(i )设()02,,M y ()11,P x y ,求得直线MA 的方程,代入椭圆方程,解得点P 的坐标,再由向量的数量积的坐标表示,计算即可得证;(ii )直线MQ 过定点O (0,0).先求得PB 的斜率,再由圆的性质可得MQ ⊥PB ,求出MQ 的斜率,再求直线MQ 的方程,即可得到定点. 【详解】解:(1)易得22312122a b c a⎧⎪+=⎪⎨⎪=⎪⎩,且222c a b =-, 解得2242a b ⎧=⎨=⎩,, 所以椭圆E 的方程为22142x y +=(2)设()02,,M y ()11,P x y ,①易得直线MA 的方程为:0042y y y x =+, 代入椭圆22142x y +=得,2222000140822y y y x x ⎛⎫+++-= ⎪⎝⎭, 由()20124828y x y --=+得,()20120288y x y --=+,从而012088y y y =+, 所以示()()20002200288,2,88y y OP OM y y y ⎛⎫-- ⎪⋅=⋅ ⎪++⎝⎭u u u r u u u u r ()22002200488488y y y y --=+=++, ②直线MQ 过定点(0,0)O ,理由如下:依题意,()2020020882288PBy y k y y y +==---+, 由MQ PB ⊥得,02MQ y k =, 则MQ 的方程为:00(2)2y y y x -=-,即02yy x =,所以直线MQ 过定点(0,0)O . 【点睛】本题考查椭圆的方程和性质,主要考查椭圆的离心率公式和方程的运用,注意联立直线方程和椭圆方程,运用韦达定理,同时考查向量的数量积的坐标表示和直线和圆的位置关系,属于中档题.19.已知数列{}n a 满足:123a a a k ===(常数0k >),111n n n n K a a a a -+-+=()*3,n n N ≥∈.数列{}n b 满足:21n n n n a a b a +++=()*n N ∈. (1)求1,b 2,b 3,b 4b 的值; (2)求出数列{}n b 的通项公式;(3)问:数列{}n a 的每一项能否均为整数?若能,求出k 的所有可能值;若不能,请说明理由.【答案】(1) 132b b ==,2421k b b k +==;(2) 41122nn k b k k+-=+(); (3) k 为1,2时数列{}n a 是整数列.【解析】(1)经过计算可知:45621,2,4a k a k a k k=+=+=++,由数列{}n b 满足:21n n n n a a b a +++=(n =1,2,3,4…),从而可求1,b 2,b 3,b 4b ; (2)由条件可知121n n n n a a k a a +--=+.得211n n n n a a k a a +-+=+,两式相减整理得2n n b b -=,从而可求数列{}n b 的通项公式;(3)假设存在正数k ,使得数列{}n a 的每一项均为整数,则由(2)可知:2122122222211n n n n n n a a a k a a a k +-+=-⎧⎪+⎨=+-⎪⎩,由1a k Z =∈,624Z a k k =++∈,可求得1,2k =.证明1,2k =时,满足题意,说明1,2k =时,数列{}n a 是整数列. 【详解】(1)由已知可知:45621,2,4a k a k a k k=+=+=++, 把数列{}n a 的项代入21n n n n b a a a =+++求得132b b ==,2421k b b k+==; (2)由121n n n n k a a a a --++=3,n n N ≥∈*() 可知:121n n n n a a k a a +--=+① 则:211n n n n a a k a a +-+=+②①−②有:2211n n n nn n a a a a a a +-+-++=,即:2n n b b -=2123n n b b --∴==…13122a a b a +===,222n n b b -== (242321)a a kb a k++===, 41122nn k b k k+-∴=+(); (3)假设存在正数k 使得数列{}n a 的每一项均为整数,则由(2)可知:2122122222211n n n n n n a a a k a a a k +-+=-⎧⎪+⎨=+-⎪⎩③,由1a k Z =∈,624Z a k k=++∈,可知1k =,2. 当1k =时,213k k+=为整数,利用123,,a a a Z ∈结合③式可知{}n a 的每一项均为整数;当2k =时,③变为2122122222512n n n n n n a a a a a a +-+=-⎧⎪⎨=+-⎪⎩④ 用数学归纳法证明21n a -为偶数,2n a 为整数.1n =时结论显然成立,假设n k =时结论成立,这时21n a -为偶数,2n a 为整数,故212212n n n a a a +-=-为偶数,22n a +为整数,1n k ∴=+时,命题成立.故数列{}n a 是整数列.综上所述k 为1,2时数列{}n a 是整数列. 【点睛】本题考查了等差数列的基本性质和数列的递推公式,考查了学生的计算能力和对数列的综合掌握,注意分类讨论思想和转化思想的运用,属于难题. 20.设函数()()ln ,f x x a x x a =--+a R ∈. (1)若0a =求函数()f x 的单调区间;(2)若0a <试判断函数()f x 在区间()22,e e -内的极值点的个数,并说明理由;(3)求证:对任意的正数a 都存在实数t 满足:对任意的(,)x t t a ∈+,()1f x a <-. 【答案】(1) 单调递减区间为(0,1)单调递增区间为(1,)+∞. (2) 见解析 (3)证明见解析【解析】(1)求解()ln f x x '=,利用()0,()0f x f x ''><,解不等式求解单调递增区间,单调递减区间; (2)'()ln af x x x=-,其中0x >, 再次构造函数令()ln g x x x a =-,分析()g x 的零点情况.()ln 1g x x '=+,令1()0,g x x e'==,列表分析得出()g x 单调性,求其最小值, 分类讨论求解①若1a e≤-,②若212a e e -<<-,③若220,()a f x e -≤<的单调性,()f x 最大值,最小值,确定有无零点问题;(3)先猜想(1,1),()1x a f x a ∈+<-恒成立.再运用导数判断证明.令'1()ln 1,1,()10G x x x x G x x=-+≥=-≤,求解最大值,得出()(1)0G x G <=即可. 【详解】(1)当0a =时,()ln f x x x x =-,()ln f x x '=, 令()0f x '=,1x =,列表分析故()f x 的单调递减区间为(0,1)单调递增区间为(1,)+∞.(2)()()ln f x x a x x a =--+,()ln f x x ax '=-,其中0x >, 令()ln g x x x a =-,分析()g x 的零点情况.()ln 1g x x '=+ 令()0g x '=,1x =,列表分析min 11()()g x g a e e ==--,而11()1n 1f ae ae e e'=-=--,222()2(2)f e ae ae -'=--=-+22221()2(2)a f e e a e e'=-=-,①若1a e ≤-则()ln 0af x x x'=-≥, 故()f x 在22(,)e e -内没有极值点;②若212a e e -<<-,则11()1n 0f ae e e '=-<,22()(2)0f e ae -'=-+> 2221()(2)0f e e a e'=->因此()f x '在22(,)e e -有两个零点,()f x 在22(,)e e -内有两个极值点;③若220a e -≤<则11()10f n ae e e '=-<,22()(2)0f e ae -'=-+≤,2221()(2)0f e e a e'=->,因此()f x '在22(,)e e -有一个零点,()f x 在22(,)e e -内有一个极值点;综上所述当1(,]a e∈-∞-时,()f x 在22(,)e e -内没有极值点;当212,a e e ⎛⎫∈--⎪⎝⎭时,()f x 在22(,)e e -内有两个极值点; 当22,0a e ⎡⎫∈-⎪⎢⎣⎭时,()f x 在22(,)e e -内有一个极值点. (3)猜想:(1,1)x a ∈+,()1f x a <-恒成立. 证明如下:由(2)得()g x 在1(,)e+∞上单调递增,且(1)0g a =-<,(1)(1)ln(1)g a a a a +=++-.因为当1x >时,1ln 1(*)x x >-, 所以1(1)(1)(1)01g a a a a +>+--=+ 故()g x 在(1,1)a +上存在唯一的零点,设为0x .由知(1,1)x a ∈+,()max{(1),(1)}f x f f a <+.又(1)ln(1)1f a a +=+-,而1x >时,ln 1(**)x x <-, 所以(1)(1)111(1)f a a a f +<+--=-=. 即(1,1)x a ∈+,()1f x a <-.所以对任意的正数a ,都存在实数1t =, 使对任意的(,)x t t ∈+∞, 使()1f x a <-. 补充证明(*): 令1()1n 1F x x x =+-,1x ≥.22111()0x F x x x x-'=-=≥, 所以()F x 在[1,)+∞上单调递增.所以1x >时,()(1)0F x F >=,即1ln 1x x>-. 补充证明(**)令()ln 1G x x x =-+,1x ≥.1()10G x x'=-≤, 所以()G x 在[1,)+∞上单调递减.所以1x >时,()(1)0G x G <=,即ln 1x x <-. 【点睛】本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间,考查了不等式与导数的结合,难度较大. 21.已知二阶矩阵,矩阵属于特征值的一个特征向量为,属于特征值的一个特征向量为.求矩阵.【答案】【解析】运用矩阵定义列出方程组求解矩阵 【详解】由特征值、特征向量定义可知,,即,得 同理可得解得,,,.因此矩阵【点睛】本题考查了由矩阵特征值和特征向量求矩阵,只需运用定义得出方程组即可求出结果,较为简单22.在极坐标系中,已知1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,线段AB 的垂直平分线l 与极轴交于点C ,求l 的极坐标方程及ABC ∆的面积.【答案】l 的极坐标方程及cos 53πρθ⎛⎫-= ⎪⎝⎭,ABC ∆的面积. 【解析】将1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭转化为直角坐标系下的坐标形式,然后求出线段AB 的中点与直线AB 的斜率,进而求出直线l 在直角坐标系下的方程,再转化为极坐标方程;在直角坐标系下,求出点C 到直线AB 的距离、线段AB 的长度,从而得出ABC ∆的面积. 【详解】解:以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系xoy 在平面直角坐标系xoy 中,1,,9,33A B ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ 的坐标为19((22A B线段AB 的中点为5(,22A ,AB k故线段AB 中垂线的斜率为1AB k k -==,所以AB 的中垂线方程为:5)2y x =-化简得:100x +-=,所以极坐标方程为cos sin 100ρθθ+-=, 即cos()53πρθ-=,令0y =,则10x =,故在平面直角坐标系xoy 中,C (10,0)点C 到直线AB :y =的距离为d == 线段8AB =,故ABC ∆的面积为182S =⨯=【点睛】 本题考查了直线的极坐标方程问题,解题时可以将极坐标系下的问题转化为平面直角坐标系下的问题,从而转化为熟悉的问题.23.已知实数,a b 满足2a b +≤,求证:22224(2)a a b b a +-+≤+.【答案】证明见解析【解析】对2222a a b b +-+进行转化,转化为含有2a b +≤形式,然后通过不等关系得证.【详解】 解:因为2a b +≤, 所以2222a a b b +-+ 2222a b a b =-++()()()2a b a b a b =-+++2a b a b =+-+()22a b a a b =+-++22a b a a b ≤++++()22222244242a a a a ≤++=+=+≤+,得证.【点睛】本题考查了绝对值不等式问题,解决问题的关键是要将要证的形式转化为已知的条件,考查了学生转化与化归的能力.24.如图,在四棱锥P ABCD -中,已知棱AB ,AD ,AP 两两垂直,长度分别为1,2,2.若DC AB λ=u u u r u u u r (R λ∈),且向量PC uuu r 与BD u u u r .(1)求λ的值;(2)求直线PB 与平面PCD 所成角的正弦值.【答案】(1)2λ=;(210【解析】试题分析:(1)以A 为坐标原点,AB 、AD 、AP 分别为x 、y 、z 轴建立空间直角坐标系A xyz -,写出,PC u u u r ,BD u u u r 的坐标,根据空间向量夹角余弦公式列出关于λ的方程可求;(2)设岀平面PCD 的法向量为(),,n x y z =r ,根据n PC n DC⎧⊥⎪⎨⊥⎪⎩r u r r u r ,进而得到00⎧⋅=⎪⎨⋅=⎪⎩r u r r u r n PC n DC ,从而求出n r ,向量PB u r 的坐标可以求出,从而可根据向量夹角余弦的公式求出cos ,n PB <>r u r ,从而得PB 和平面PCD 所成角的正弦值.试题解析:(1)依题意,以A 为坐标原点,AB 、AD 、AP 分别为x 、y 、z 轴建立空间直角坐标系A xyz -(1,0,0),(0,2,0),(0,0,2)B D P ,因为DC AB λ=u u u r u u u r ,所以(,2,0)C λ,从而(,2,2)PC λ=-u u u r ,则由15cos ,15PC BD =u u u r u u u r ,解得10λ=(舍去)或2λ=. (2)易得(2,2,2)PC =-u u u r ,(0,2,2)PD =-u u u r ,设平面PCD 的法向量(,,)n x y z =r ,则0⋅=r u u u r n PC ,0⋅=r u u u r n PD ,即0x y z +-=,且0y z -=,所以0x =,不妨取1y z ==,则平面PCD 的一个法向量(0,1,1)n =r ,又易得(1,0,2)PB =-u u u r ,故10cos ,=⋅=u u u r r PB n PB n ,所以直线PB 与平面PCD 10.考点: 1、空间两向量夹角余弦公式;2、利用向量求直线和平面说成角的正弦.25.已知数列{}n a 的通项公式为1515225n n n a ⎡⎤⎛⎫⎛⎫+⎥=- ⎪ ⎪ ⎪ ⎪⎥⎝⎭⎝⎭⎦,n N ∈,记1212n n n S C a C a =++…n n n C a +.(1)求1,S 2S 的值;(2)求所有正整数n ,使得n S 能被8整除.【答案】(1) 11S =;23S =; (2) {}*|3,n n k k N =∈ 【解析】(1)运用二项式定理,化简整理,再代入计算即可得到所求值; (2)通过化简得到213n n n S S S ++=-,再由不完全归纳找规律得到结论,即可得到所求结论.【详解】解:(1)1212n n n n n n S C a C a C a =++⋯+2121515225n n C C ⎡⎛⎛⎫+⎢ =⋅+⋅+ ⎪ ⎪⎢⎝⎭⎝⎣…212151515n n n n n C C C ⎫⎛+--⎪ +⋅-+⋅+⎪ ⎝⎭⎝⎭⎭⎝…15n n n C ⎤⎫-⎥⎪+⋅⎥⎪⎝⎭⎭⎦ 1515115n n ⎡⎤⎛⎛+-⎥=+-+ ⎥⎝⎭⎝⎭⎦ 35355n n ⎡⎤+-⎥=-⎥⎝⎭⎝⎭⎦,即有1S1==;2S33==;(2)3322nnS n⎡⎤⎛⎛-⎥=-⎥⎝⎭⎝⎭⎦,2332222nS n n+⎡⎤⎛⎛+-=+-+⎥⎥⎝⎭⎝⎭⎦333333222222n n n n ⎡⎤⎡⎤⎛⎫⎛⎛⎛⎛--⎥⎢⎥-⋅+-- ⎪⎪⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎦⎣⎦13n nS S+=-,即213n n nS S S++=-,*n N∈,因此2nS+除以8的余数,完全由1,n nS S+除以8的余数确定,因为11,a=21a=,所以11111S C a==,12221223S C a C a=+=,3213918S S S=-=-=,432324321,S S S=-=-=543363855S S S=-=-=,654316521144,S S S=-=-=7535643255377S S=-=-=,87631131144987,S S S=-=-=987329613772584S S S=-=-=由以上计算及213n n nS S S++=-可知,数列{}n S各项除以8的余数依次是:1,3,0,5,7,0,1,3,0,5,7,0,…,它是一个以6为周期的数列,从而n S除以8的余数等价于n除以3的余数,所以3,n k=*k N∈,即所求集合为:{}*|3,n n k k N=∈.【点睛】本题考查数列通项的运用,解决问题的关键是运用二项式定理,本题属于难题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(第6题)数学参考公式:样本数据1x ,2x ,…,n x 的标准差211()ni i s x x n ==-∑11nii x x n ==∑;柱体的体积公式:V Sh =,其中S 为柱体的底面积,h 为柱体的高.锥体的体积公式:13V Sh=,其中S 为锥体的底面积,h 为锥体的高. 一、填空题:本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上. 1.已知全集{}21012U =--,,,,,集合{}2 1 1A =--,,,则UA = ▲ .2.已知复数()()z 1i i a =-⋅+(i 为虚数单位)为纯虚数,则实数a 的值为 ▲ .3.数据1,3,5,7,9的标准差为 ▲ . 4.函数()12xf x -的定义域是 ▲ .5.在一底面半径和高都是2m 的圆柱形容器中盛满小麦,有一粒带麦锈病的种子混入了其中.现从中随机取出23m 的种子,则取出了带麦锈病种子的概率是 ▲ . 6.右图是一个算法的伪代码,则输出的i 的值为 ▲ .7. 在平面直角坐标系xOy 中,若双曲线2221(0)y x b b -=>经过点()34,,则该双曲线的准线方程为 ▲ .8. 设n S 是等比数列{}n a 的前n 项的和,396S S S ,,成等差数列,则258a a a +的值为 ▲ . 9.给出下列四个命题,其中正确命题的序号是 ▲ .(写出所有正确命题的序号)①因为当π3x =时,()2πsin sin 3x x+≠,所以2π3不是函数sin y x =的周期;②对于定义在R 上的函数()f x ,若()()22f f -≠,则函数()f x 不是偶函数;③“M N >”是“22log log M N >”成立的充分必要条件;④若实数a 满足24a <,则2a ≤.(第15题)10. 如图,是一个四棱锥的平面展开图,其中间是边长为2的正方形,上面三角形是等边三角形,左、右三角形是等腰直角三角形,则此四棱锥的体积为 ▲ .11.在平面直角坐标系xOy 中,若函数()ln f x x ax =-在1=x 处的切线与圆C :01222=-++-a y x x 存在公共点,则实数a 的取值范围为 ▲ .12. 已知函数()32f x ax bx cx =++,若关于x 的不等式()0f x <的解集是()()102-∞-,,,则b ca+的值为 ▲ . 13.在边长为4的菱形ABCD 中,A =60°,点P 在菱形ABCD 所在的平面内.若3PA =,PC =则PB PD ⋅= ▲ .14.设函数()()21722040k x x f x x x ⎧+-+⎪=⎨⎪>⎩,,,,≤,()()43g x k x =-,其中0k >.若存在唯一的整数x ,使得()()f x g x <,则实数k 的取值范围是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)如图,四棱锥P -ABCD 中,底面ABCD 是菱形,对角线AC ,BD 交于点O ,M 为棱PD 的中点,MA =MC . 求证:(1)PB //平面AMC ;(2)平面PBD ⊥平面AMC .16.(本小题满分14分)在锐角三角形ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知tan A ,tan B ,tan C 成等差数列,cos Acos B 成等比数列. (1)求A 的值;(2)若△ABC 的面积为1,求c 的值.17.(本小题满分14分)某房地产开发商在其开发的某小区前修建了一个弓形景观湖.如图,该弓形所在的圆是以AB 为直径的圆,且300AB =米,景观湖边界CD 与AB平行且它们间的距离为米.开发商计划从A 点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作PQ .设2AOP θ∠=. (1)用θ表示线段PQ ,并确定sin 2θ的范围;(2)为了使小区居民可以充分地欣赏湖景,所以要将PQ 的长度设计到最长,求PQ 的最大值.18.(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C 的中心为坐标原点O ,焦点在x 轴上,右顶点A (2,0)到右焦点的距离与它到右准线的距离之比为12.(1)求椭圆C 的标准方程;(2)若M ,N 是椭圆C 上关于x 轴对称的任意两点,设P (-4,0),连接PM 交椭圆C 于另一点E .求证:直线NE 过定点B ,并求出点B 的坐标;(3)在(2)的条件下,过点B 的直线交椭圆C 于S ,T 两点,求OS OT ⋅的取值范围. 19.(本小题满分16分)已知函数()212ax f x bx +=,其中0a >,0b >. (1)①求函数()f x 的单调区间; ②若x 1,x 2满足)12i x i >=,,且120x x +>,20x >.求证:()()122f x f x +>.(2)函数()21ln 2g x ax x =-.若对任意(120x x ∈,,12x x ≠,都有|f (x 1)-f (x 2)|>|g (x 1)-g (x 2)|,求b a -的最大值.20.(本小题满分16分)已知{a n },{b n },{c n }都是各项不为零的数列,且满足*1122n n n n a b a b a b c S n +++=∈N ,,其中S n 是数列{a n }的前n 项和,{c n }是公差为()0d d ≠的等差数列.(1)若数列{a n }是常数列,d =2,c 2=3,求数列{b n }的通项公式; (2)若a n =λn (λ是不为零的常数),求证:数列{b n }是等差数列;(3)若11a c d k === (k 为常数,*k ∈N ),()*2n n kb c n n +=∈N ≥,. 求证:对任意的*2n n ∈N ≥,,11n n n n b b a a ++>恒成立.数学II (附加题)21. 【选做题】 在A ,B ,C 四小题中只能选做两题,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤. A. 选修4-2:矩阵与变换已知二阶矩阵A =⎣⎢⎡⎦⎥⎤a b c d ,矩阵A 属于特征值λ1=-1的一个特征向量为α1=⎣⎢⎡⎦⎥⎤1-1,属于特征值λ2=4的一个特征向量为α2=⎣⎢⎡⎦⎥⎤32.求矩阵A .B. 选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cos α,y =sin α(α为参数).以直角坐标系原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos 4πρθ⎛⎫-⎪⎝⎭=22.点P 为曲线C 上的动点,求点P 到直线l 距离的最大值.C. 选修4-5:不等式选讲若正数a 、b 、c 满足a +b +c =1,求13a +2+13b +2+13c +2的最小值.【必做题】第22题、第23题,每题10分,共计20分.请在答卷纸指定区域内........作答.解答应写出文字说明、证明过程或演算步骤.22. (本小题满分10分)如图,在正四棱锥P -ABCD 中,底面正方形的对角线AC ,BD 交于点O 且OP =12AB .(1)求直线BP 与平面PCD 所成角的正弦值; (2)求锐二面角B -PD -C 的大小.23. (本小题满分10分)(第22题)定义:若数列{}n a 满足所有的项均由11-,构成且其中1-有m 个,1有p 个()3m p +≥,则称{}n a 为“()m p -,数列”.(1)()i j k a a a i j k <<,,为“()34-,数列”{}n a 中的任意三项,则使得1i j k a a a =的取法有多少种?(2)()i j k a a a i j k <<,,为“()m p -,数列”{}n a 中的任意三项,则存在多少正整数对()m p ,使得1100m p ≤≤≤,且1i j k a a a =的概率为12?数学答案参考公式:样本数据1x ,2x ,…,n x 的标准差s =11nii x x n ==∑;柱体的体积公式:V Sh =,其中S 为柱体的底面积,h 为柱体的高.锥体的体积公式:13V Sh=,其中S 为锥体的底面积,h 为锥体的高. 二、填空题:本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上 1. 答案:{}02,2.答案:1- 3.答案:4.答案:(]0-∞,5.答案:14π6. 答案:5 7.答案:x =8.答案:2(必修五P.62第10题改编) 9.答案:①②④ 10.11.答案:(][)012+∞,,12. 答案:3- 13. 答案:-1 14.答案:1763⎡⎤⎢⎥⎣⎦, 三、解答题:本大题共6小题,共计90分.请在答题卡指定区域作答,解答时应写出文字说明、证明过程或演算步骤 15.(本小题满分14分)证明:(1)连结OM ,因为O 为菱形ABCD 对角线AC ,BD 的交点,所以O 为BD 的中点. …… 2分 又M 为棱PD 的中点,所以//OM PB , …… 4分 又OM ⊂平面AMC ,PB ⊄平面AMC ,所以PB //平面AMC ; …… 6分(2)在菱形ABCD 中,AC ⊥BD ,且O 为AC 的中点,又MA =MC ,故AC ⊥OM , …… 8分 而OMBD O =,OM ,BD ⊂平面PBD ,所以AC ⊥平面PBD , …… 11分 又AC ⊂平面AMC ,所以平面PBD ⊥平面AMC . …… 14分16. (本小题满分14分)解:(1)由题意知:tan tan 2tan cos cos cos A C B A B C +=⎧⎨⋅=⎩,,因为πA B C ++=,所以()cos cos cos cos sin sin cos cos C A B A B A B A B =-+=-+= 又因为△ABC 为锐角三角形,所以sin sin tan tan 2cos cos A BA B A B==①, …… 2分所以()tan tan tan tan tan tan tan tan 1A BC A B A B A B +=-+==+-,所以tan 2tan B A =,与①式联立,解得tan 1A =(负舍), …… 4分又()0,πA ∈,所以π4A =. …… 6分 (2)由(1)知,tan 1A =,tan 2tan 2B A ==,且tan 3C =,又22sin tan 2cos sin cos 1B B B B B ⎧==⎪⎨⎪+=⎩,结合()0πB ∈,解出sin B =, …… 8分同理解出sin C =…… 10分 在△ABC 中,由正弦定理知:sin sin b cB C=,因此sin 53sin 3B b c C =⋅==, …… 12分 又1sin 12bc A =,由此解出c =. …… 14分17.(本小题满分14分)解:(1)过点Q 作QH AB ⊥于点H,则QH =在三角形AOP 中,因为300AB =,2AOP θ∠=,所以π2OAP θ∠=-,300sin AP θ=,所以AQ =,故300sin PQ AP AQ θ=-=. …… 4分因为300sin 0cos PQ θθ=->,即sin 23θ>,且()20πθ∈,. …… 6分(2)因为(300sin 506sin PQ AP AQ θθ=-==-,令()6sin f θθ=,sin 2θ>,且()20πθ∈,. …… 8分所以()()36cos tan tan f θθθθθ'==⋅-,令()0f θ'=,即3tan tan 0θθ+-=,所以()2tan tan 30θθθ+=, …… 10分记0tan θ=()0π02θ∈,,所以当00θθ<<时,()0f θ'>,()f θ单调递增;所以当0π2θθ<<时,()0f θ'<,()f θ单调递减,又因为0sin 2θ=,所以当tan θ()f θ取最大值.此时sin cos 33θθ==,所以PQ 的最大值为答:湖上桥面PQ 长度的最大值为 …… 14分 18.解:(1)设椭圆C 的标准方程为x 2a 2+y 2b2=1(a >b >0),焦距为2c ,由题意得a =2,e =12, …… 2分即12c a =,所以c =1,2223b a c =-=. 所以椭圆C 的标准方程为x 24+y 23=1. …… 4分(2)证明:根据对称性,直线NE 过的定点B 一定在x 轴上.由题意可知直线PM 的斜率存在,设直线PM 的方程为y =k (x +4).由()224143y k x x y ⎧=+⎪⎨+=⎪⎩,消去y 得 (4k 2+3)x 2+32k 2x +64k 2-12=0.设点M (x 1,y 1),E (x 2,y 2),所以x 1+x 2=-32k 24k 2+3,x 1x 2=64k 2-124k 2+3, …… 6分又因为N (x 1,-y 1),所以直线NE 的方程为y -y 2=y 2+y 1x 2-x 1(x -x 2).令y =0,得x =x 2-y 2x 2-x 1y 2+y 1.将y 1=k (x 1+4),y 2=k (x 2+4)代入上式并整理, 得()121212248x x x x x x x ++=++.整理得()()2222128241281322432k k x k k --==--++.所以,直线NE 过x 轴上的定点B (-1,0). …… 10分 (3)当过点M 的直线ST 的斜率不存在时,直线ST 的方程为x =-1,S (-1,32),T (-1,-32),此时OS →·OT →=-54.…… 12分当过点B 的直线ST 的斜率存在时,设直线ST 的方程为y =m (x +1),且S (x S ,y S ),T (x T ,y T )在椭圆C 上, 由()221143y m x x y ⎧=+⎪⎨+=⎪⎩,,得(4m 2+3)x 2+8m 2x +4m 2-12=0,则Δ=(8m 2)2-4(4m 2+3)(4m 2-12)=144(m 2+1)>0.故有x S +x T =-8m 24m 2+3,x S x T =4m 2-124m 2+3, …… 14分从而y S y T =m 2(x S +1)(x T +1)=m 2[(x S +x T )+x S x T +1]=-9m 24m 2+3.所以OS →·OT →=x S x T +y S y T =-5m 2+124m 2+3=-54-334(4m 2+3).由20m ≥,得)544OS OT ⎡⋅∈--⎢⎣,. 综上,OS →·OT →的取值范围是544⎡⎤--⎢⎥⎣⎦,. …… 16分 19.(本小题满分16分)解:(1)①因为f ′ (x )=ax 2-12bx 2,0x .令f ′ (x )>0,得x <-1a 或x >1a, 所以f (x )的单调增区间为(-∞,-1a )和(1a,+∞). ……2分 令f ′ (x )<0,得-1a <x <0或0<x <1a, 所以f (x )的单调减区间为(-1a ,0)和(0,1a). ……4分 ②因为x 1+x 2>0,x 2>0,所以x 1>0,或x 1<0. 若x 1>0,因为|x i |>1a (i =1,2),所以x 1>1a ,x 2>1a, 由①,知f (x )在(1a,+∞)上是增函数, 所以f (x 1)+2f (x 2)>f (1a )+2f (1a)=3a b >a b . ……5分若x 1<0,由|x 1|>1a ,得x 1<-1a, 因为x 1+x 2>0,x 2>0,所以x 2>-x 1>1a, 由①,知f (x )在(1a,+∞)上是增函数,所以f (x 1)+2f (x 2)>f (x 1)+2f (-x 1)=f (-x 1)>a b .综上,f (x 1)+2f (x 2)>ab. ……8分 (2)g′ (x )=ax -1x =ax 2-1x ,x ∈(0,1a),所以g ′ (x )<0,所以函数g (x )在(0,1a)上是减函数. 不妨假设x 1<x 2. 由(1),知f (x ) 在(0,1a)上是减函数, 所以不等式|f (x 1)-f (x 2)|>|g (x 1)-g (x 2)|等价于f (x 1)-f (x 2)>g (x 1)-g (x 2), ……10分 即[f (x 1)-g (x 1)]-[f (x 2)-g (x 2)]>0. 令M (x )=f (x )-g (x ),x ∈(0,1a),则M (x )为减函数. 因为M ′ (x )=f ′ (x )-g′ (x )=ax 2-12bx 2-ax +1x =(ax 2-1)(1-2bx )2bx 2,所以(ax 2-1)(1-2bx )2bx 2≤0在区间(0,1a )上恒成立,即1-2bx ≥0在区间(0,1a)上恒成立,所以1-2b a≥0,即b ≤a2. ……14分所以b -a ≤a 2-a =-(a -14)2+116≤116. 所以b -a 的最大值为116. ……16分20.(本小题满分16分)解:(1)因为d =2,c 2=3,所以c n =2n -1.因为数列{a n }是各项不为零的常数列,所以a 1=a 2=…=a n ,S n =na 1,则由S n c n =a 1b 1+a 2b 2+…+a n b n 及c n =2n -1,得n (2n -1)=b 1+b 2+…+b n , 当n ≥2时,(n -1)(2n -3)=b 1+b 2+…+b n -1, 两式相减得b n =4n -3.当n =1时,b 1=1,也满足b n =4n -3,故b n =4n -3(n ∈N *). ……4分 (2)因为a 1b 1+a 2b 2+…+a n b n =S n c n ,当n ≥2时,S n -1c n -1=a 1b 1+a 2b 2+…+a n -1b n -1, 两式相减得S n c n -S n -1c n -1=a n b n ,即(S n -1+a n ) c n -S n -1c n -1=a n b n ,S n -1 (c n -c n -1)+a n c n =a n b n ,即S n -1d +λnc n =λnb n . ……7分 又S n -1=λn (n -1)2,所以λn (n -1)2d +λnc n =λnb n ,即n -12d +c n =b n ,所以当n ≥3时,n -22d +c n -1=b n -1,两式相减得b n -b n -1=32d (n ≥3),所以数列{b n }从第二项起是公差为32d 等差数列.又当n =1时,由S 1c 1=a 1b 1,得c 1=b 1,当n =2时,由b 2=2-12d +c 2=12d +c 1+d =b 1+32d ,得b 2-b 1=32d .故数列{b n }是公差为32d 等差数列. ……10分(3)由(2)得当n ≥2时,S n -1 (c n -c n -1)+a n c n =a n b n ,即S n -1d =a n (b n -c n ), 因为b n =c n +k ,所以b n =c n +kd ,即b n -c n =kd ,所以S n -1d =a n ·kd ,即S n -1=ka n . 所以S n =S n -1+a n =(k +1)a n . 当n ≥3时,S n -1=(k +1)a n -1=ka n ,即a n =k +1k a n -1,故从第二项起数列{a n }是等比数列.所以当n ≥2时,a n =a 2(k +1k )n -2. ……12分b n =c n +k =c n +kd =c 1+(n -1)k +k 2=k +(n -1)k +k 2=k (n +k ).另外由已知条件得,(a 1+a 2)c 2=a 1b 1+a 2b 2,又c 2=2k ,b 1=k ,b 2=k (2+k ), 所以a 2=1,因而a n =(k +1k)n -2.令d n =b n a n ,则d n +1d n -1=b n +1a n a n +1b n -1=(n +k +1)k (n +k )(k +1)-1=-n(n +k )(k +1)<0,对任意的*2n n ∈N ≥,,11n n n n b b a a ++>恒成立. ……16分数学II (附加题)21. 【选做题】 在A ,B ,C 四小题中只能选做两题,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤. A. 选修4-2:矩阵与变换解:由特征值、特征向量定义可知,Aα1=λ1α1,即⎣⎢⎡⎦⎥⎤a b cd ⎣⎢⎡⎦⎥⎤ 1-1=-1×⎣⎢⎡⎦⎥⎤1-1,得⎩⎪⎨⎪⎧a -b =-1,c -d =1. ……5分 同理可得⎩⎪⎨⎪⎧3a +2b =12,3c +2d =8,解得a =2,b =3,c =2,d =1. 因此矩阵A =⎣⎢⎡⎦⎥⎤2321. ……10分B. 选修4-4:坐标系与参数方程解:ρcos ⎝⎛⎭⎫θ-π4=22化简为ρcos θ+ρsin θ=4, 则直线l 的直角坐标方程为x +y =4. ……4分 设点P 的坐标为(2cos α,sin α),得P 到直线l 的距离d =|2cos α+sin α-4|2,即d =|5sin (α+φ)-4|2,其中cos φ=15,sin φ=25. ……8分当sin(α+φ)=-1时,d max =22+102. ……10分 C. 选修4-5:不等式选讲解:因为正数a 、b 、c 满足a +b +c =1,所以⎝⎛⎭⎫13a +2+13b +2+13c +2[(3a +2)+(3b +2)+(3c +2)]≥(1+1+1)2, ……5分即13a +2+13b +2+13c +2≥1, 当且仅当3a +2=3b +2=3c +2,即a =b =c =13时,原式取最小值1. ……10分【必做题】第22题、第23题,每题10分,共计20分.请在答卷纸指定区域内........作答.解答应写出文字说明、证明过程或演算步骤.22. (本小题满分10分)解:(1)在正四棱锥P -ABCD 中,底面正方形的对角线AC ,BD 交于点O ,所以OP ⊥平面ABCD ,取AB 的中点E ,BC 的中点F , 所以OP ,OE ,OF 两两垂直,故以点O 为坐标原点, 以OE ,OF ,OP 分别为x 轴,y 轴,z 轴,建立空间直角坐标系.设底面正方形边长为2,因为OP =12AB ,所以OP =1,所以B (1,1,0),C (-1,1,0),D (-1,-1,0),P (0,0,1),所以BP →=(-1,-1,1), ……2分 设平面PCD 的法向量是→n =(x ,y ,z ), 因为CD →=(0,-2,0),CP →=(1,-1,1), 所以CD →·→n =-2y =0,CP →·→n =x -y +z =0, 取x =1,则y =0,z =-1,所以→n =(1,0,-1), 所以cos<BP →,→n >=BP →·→n |BP →|·|→n |=-63,所以直线BP 与平面PCD 所成角的正弦值为63. ……5分 (2)设平面BPD 的法向量是→m =(x ,y ,z ),因为BP →=(-1,-1,1),BD →=(-2,-2,0), 所以BP →·→m =-x -y +z =0,BD →·→m =-2x -2y =0,取x =1,则y =-1,z =0,所以→m =(1,-1,0), ……7分 由(1)知平面PCD 的法向量是→n =(1,0,-1), 所以cos<→m ,→n >=→m ·→n|→m |·|→n |=12,所以<→m ,→n >=60°,所以锐二面角B -PD -C 的大小为60°. ……10分23. (本小题满分10分)解:(1)三个数乘积为1有两种情况:“1,1,1--”“1,1,1” ,“1,1,1--”:共有2134C C =12⋅种;“1,1,1”:共有34C =4种.利用分类计数原理,1i j k a a a =共有12416+=种取法. ……2分 (2)与(1)基本同理,“1,1,1--”共有21C C m p ⋅种;“1,1,1”:共有3C p 种.而在“(),m p -数列”中任取三项共有3C m p +种,所以根据古典概型有:2133C C C 12C m p pm p++=, ……4分 再根据组合数的计算公式能得到:()()2232320p m p p mp m m ---+--=,① p m =时,应满足11003m p m p p m ⎧⎪+⎨⎪=⎩≥≤≤≤,所以()(){},,,2,3,4,,100m p k k k =∈⋅⋅⋅,共有99个. ……6分② 2232320p p mp m m --+--= 时,应满足221100332320m p m p p p mp m m ⎧⎪+⎨⎪--+--=⎩≥≤≤≤,视m 为常数,可解得()232m p +±=.因为1m ≥5,根据p m ≥可知,()232m p ++=(否则1p m -≤)下设k =p 为正整数知k 必为正整数, 又因为1100m ≤≤,所以549k ≤≤.化简上述关系式可以知道:()()21112424k k k m -+-==, 所以1,1k k -+均为偶数,所以设()*21k t t =+∈N ,则224t ≤≤,所以()211246t t k m +-==,由于,1t t +中必存在偶数, 故只需,1t t +中存在数为3的倍数即可,所以2,3,5,6,8,9,11,,23,24t =⋅⋅⋅, 所以5,11,13,,47,49k =⋅⋅⋅, ……8分检验:()()()2311485010022424m k k p ++-+⨯===≤符合题意,所以共有16个.综上所述:共有115个数对(),m p 符合题意. ……10分。
