【教师版】2020年3月南海区2020届高三年级综合能力测试 理科数学
广东省佛山市南海区2020届3月高三年级综合能力测试文科综合试题Word版答案

2019~2020学年高三年级综合能力测试2020年03月文科综合(全国卷)参考答案1.C2.A3.C4.C5.D6.B7.C8.D9.D 10.C 11.B12. A 13.C 14.D 15.A 16.C 17.D 18.B 19.C 20.C 21.B 22.D 23.A24.D 25.D 26.C 27.B 28.D 29.C 30.B 31.A 32.B 33.D 34.C 35.A36.(1)(亚热带季风性湿润气候)夏季高温多雨,利于棉花生长;秋季降水少,光照充足,利于棉花的成熟和收获;平原面积广大,利于规模化生产;多条河流流经,灌溉水源充足。
(每要点2分,共6分)(2)传统产业本身处于衰落期,原材料、劳动力成本上升,导致生产效益低下;新技术和新兴产业的发展,吸引了更多的资金和劳动力转移;国内、外市场面临激烈的竞争。
(每要点2分,共6分)(3)被三所名校环绕,科研力量雄厚;工业活动少(或东北和西南各有一个湖泊),环境质量好;有多条道路通过,交通便利;政策支持力度大。
((每要点2分,共8分)(4)保持良好的研发和居住环境;为园区预留足够的发展空间。
(每要点2分,共4分)37.(1)春季气候干旱,降水少,空气湿度小;枯枝、落叶等松散、干燥的可燃物质较多树木较干燥;横断山区山高谷深,背风坡易发生焚风效应,加之春季气温普遍升高,局部温度较高;春季多风,横断山区地形复杂,风向多变。
(每要点2分,共8分)(2)山火导致火场气温升高,气流上升;近地面水平气流由四周流向火场,吸引“倒火”向火场方向燃烧;当两火相遇时,可燃物和氧气都已燃烧殆尽,山火自然熄灭。
(每要点2分,共6分)(3)原始森林下可燃物长期堆积,腐烂后产生大量可燃气体,遇火剧烈燃烧;风力、风向突变,带来充足氧气,火势迅速增强。
((每要点2分,共4分))(4)害:山火导致物种减少,破坏生物多样性;森林资源破坏,木材蓄积量减少。
益:增加土壤有机肥,加速优势树种的生长;杀灭害虫,降低森林虫害风险;促进物种更新,优化生态系统。
广东省佛山市南海区2019-2020学年高三下学期3月综合能力测试数学(文)试题(word无答案)

广东省佛山市南海区2019-2020学年高三下学期3月综合能力测试数学(文)试题一、单选题(★) 1 . 已知全集为,集合,,则等于()A.B.C.D.(★★) 2 . 复数满足,则复数在复平面内所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限(★) 3 . 下列函数中,既是偶函数又在区间上是减函数的是()A.B.C.D.(★) 4 . 抛物线的准线与轴交点为,过点与抛物线相切的直线方程为()A.或B.或C.或D.或(★) 5 . 函数的图象大致为()A.B.C.D.(★★) 6 . 已知数列的前项和(,),则“ ”是“数列为等比数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(★) 7 . 音乐,是用声音来展现美,给人以听觉上的享受,熔铸人们的美学趣味.著名数学家傅立叶研究了乐声的本质,他证明了所有的乐声都能用数学表达式来描述,它们是一些形如的简单正弦函数的和,其中频率最低的一项是基本音,其余的为泛音.由乐声的数学表达式可知,所有泛音的频率都是基本音频率的整数倍,称为基本音的谐波.下列函数中不能与函数构成乐音的是()A.B.C.D.(★) 8 . 把函数的图象向右平移个单位,得到函数的图象.给出以下四个命题① 的一个周期为;② 的值域为;③ 的一条对称轴是;④ 的一个对称中心是其中正确的命题个数是()A.1B.2C.3D.4(★) 9 . 窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一,它历史悠久,风格独特,神兽人们喜爱.下图即是一副窗花,是把一个边长为12的大正方形在四个角处都剪去边长为1的小正方形后剩余的部分,然后在剩余部分中的四个角处再剪出边长全为1的一些小正方形.若在这个窗花内部随机取一个点,则该点不落在任何一个小正方形内的概率是()A.B.C.D.(★★) 10 . 已知三棱锥且平面,其外接球体积为()A.B.C.D.(★★★★) 11 . 若的解集非空且最多有3个正整数根,则的取值范围为()A.B.C.D.(★★) 12 . 已知双曲线的焦距为,若的渐近线上存在点,使得经过点所作的圆的两条切线互相垂直,则双曲线的离心率的取值范围是()A.B.C.D.二、填空题(★) 13 . 已知向量,,且满足,则__________.(★) 14 . 在中,,,,则__________.三、双空题(★) 15 . 在棱长为1的正方体中,点是底面内的动点,,则动点的轨迹的面积为 __________ ,动线段的轨迹所形成几何体的体积是 __________ .四、填空题(★★★★) 16 . 点在曲线:上,过作轴垂线,设与曲线交于点,若,且点的纵坐标始终为0,则称点为曲线上的“水平黄金点”,则曲线上的“水平黄金点”的个数为__________.五、解答题(★★) 17 . 已知数列满足,.(1)求数列的通项公式;(2)设数列的前项和为,求证:.(★★) 18 . 在四棱锥中,,,,,平面平面.(1)求证:平面平面;(2)在棱上是否存在点,使平面,若存在,求的值;若不存在,说明理由.(★) 19 . 为了调查“双11”消费活动情况,某校统计小组分别走访了、两个小区各20户家庭,他们当日的消费额按,,,,,,分组,分别用频率分布直方图与茎叶图统计如下(单位:元):(1)分别计算两个小区这20户家庭当日消费额在的频率,并补全频率分布直方图;(2)分别从两个小区随机选取1户家庭,求这两户家庭当日消费额在的户数为1时的概率(频率当作概率使用);(3)运用所学统计知识分析比较两个小区的当日网购消费水平.(★★) 20 . 已知椭圆经过点,离心率为.(1)求椭圆的方程;(2)经过点且斜率存在的直线交椭圆于两点,点与点关于坐标原点对称.连接.求证:存在实数,使得成立.(★★★★) 21 . 已知(1)当时,判断函数的单调性;(2)记,若存在实数,使直线与函数的图象交于不同的两点,求证:.(★★) 22 . 已知曲线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)写出曲线的极坐标方程;(2)点是曲线上的一点,试判断点与曲线的位置关系.(★★) 23 . 已知,且.(1)请给出的一组值,使得成立;(2)证明不等式恒成立.。
广东省佛山市南海区2020届高三数学入学摸底考试试题 理 新人教A版

佛山市南海区2020届普通高中高三质量检测理科数学试题2020.8 一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是 符合题目要求的.第Ⅰ卷(选择题 共40分) 一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.设集合{}{}>1,|(2)0A x x B x x x ==-<,则B A I 等于( )(A ){|01}x x << (B ){}21<<x x (C ){}20<<x x (D ) {|2}x x > 2.已知a 是实数,i1ia +-是纯虚数,则a 等于( )(A ) 1 (B ) 1- (C ) (D )3.已知{}n a 为等差数列,其前n 项和为n S ,若36a =,312S =,则公差d 等于( )(A ) 1 (B )53(C ) 2 (D ) 3 4.用反证法证明命题:若整数系数的一元二次方程20(0)ax bx c a ++=≠ 有有理实数根,那么a ,b ,c 中至少有一个是偶数,下列假设中正确的是: (A )假设a ,b ,c 至多有一个是偶数 (B )假设a ,b ,c 至多有两个偶数 (C )假设a ,b ,c 都是偶数 (D )假设a ,b ,c 都不是偶数5.若a ,b 是两个非零向量,则“+=-a b a b ”是“⊥a b ”的( ) (A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件6.101x ⎫⎪⎭的展开式中含x 的正整数指数幂的项数是( )(A ) 0 (B ) 2 (C ) 4 (D ) 67.已知抛物线22y px =的焦点F 与双曲线22179x y -=的右焦点重合,抛物线的准线与x轴的交点为K ,点A 在抛物线上且|||AK AF =,则△AFK 的面积为( )(A ) 4 (B ) 8 (C ) 16 (D ) 328.给出下列命题:①在区间(0,)+∞上,函数1y x-=,12y x=,2(1)y x=-,3y x=中有三个是增函数;②若log3log30m n<<,则01n m<<<;③若函数()f x是奇函数,则(1)f x-的图象关于点(1,0)A对称;④已知函数233,2,()log(1),2,x xf xx x-⎧≤=⎨->⎩则方程1()2f x=有2个实数根,其中正确命题的个数为()(A)1(B)2(C)3(D)4第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
【试卷】2020年3月南海区2020届高三年级综合能力测试 理科数学 试卷及答案

知检查一个零件的成本为 10 元,而每个不合格零件流入市场带来的损失为 260 元.假设 n 充分大,为了
使损失尽量小,小张是否需要检查其余所有零件,试说明理由.
附:若随机变量ξ 服从正态分布 N (µ,σ 2 ) ,则
实用文档 用心整理
②直线 B1F 与直线 BC 所成角的正切值的取值范围是
2 4
,
1 2
;
③α 与平面 CDD1C1 所成锐二面角的正切值为 2 2 ;
④正方体 ABCD − A1B1C1D1 的各个侧面中,与α 所成的锐二面角相等的侧面共四个.
其中正确命题的序号是
.(写出所有正确命题的序号)
r2 a
=
r2 b ,从而
;若不等式 f (n) ≥ 0 恒成立,则 λ 的最大值为
.
16.正方体 ABCD − A1B1C1D1 中,E 是棱 DD1 的中点,F 是侧面 CDD1C1 上的动点,且 B1F / / 平面 A1BE ,
3 千里之行 始于足下
记 B1 与 F 的轨迹构成的平面为α . ① ∃F ,使得 B1F ⊥ CD1 ;
=(
)
A. (0, 2)
B. (1, 2]
C.[0,1]
D. (0,1]
2.复数满足 z + z = 4 + 8i ,则复数 z 在复平面内所对应的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.已知等差数列{an}的前 n 项和为 Sn ,且 a2 = −2, a8 = 10 ,则 S9 = (
① g(x) 的值域为 (0,1]
广东署山市南海区2020届高三数学统一调研测试试题一含解析

同.
故选:D.
【点睛】本题主要考查函数的定义,判断两函数是否相同的方法:看解析式和定义域是否都
相同,属于基础题.
3.
设等差数列
an
的前
n
项和为
S
n
,若
2
a5
a6
a3 ,则 S7
(
)
A. 28
B. 14
C. 7
D. 2
【答案】B 【解析】 【分析】
根据等差数列的性质 a6 a3 a4 a5 并结合已知可求出 a4 ,再利用等差数列性质可得
1 1 4
32 1 4n
=3
.
故选:D
【点睛】本题主要考查等比数列通项的求法和前 n 项和的计算,意在考查学生对这些知识的
理解掌握水平.
f x (1 cos x) cos x tan x
10. 关于函数
2 ,有下述四个结论:
①函数
f
x
在
4
, 4
上是增函数
② f x最小正周期为
f x
③
是奇函数
y
轴上的截距最小,
故 z y x 的最小值是 2 5 7 ,
故选:B.
【点睛】本题考查了简单线性规划,作图要细致认真,根据几何意义是解题的关键,属于基
础题.
6. 执行如图所示的程序框图,则输出 n 的值是( )
A. 2 【答案】D
B. 4
C. 5
D. 6
【解析】 【分析】 根据题意,利用程序框图循环结构计算求得 n 的值,可得答案.
12. 甲乙二队进行篮球比赛,若有一队胜 4 场,比赛就结束,假设甲,乙二队在每场比赛中
获胜的概率都是 0.5,则所需比赛的场数的数学期望为( )
2020届高三毕业班第一次综合质量检测数学(理)试题—附答案

5.
已知函数
f
(
x)
1
x x
2
sin x ,则函数 y
f (x) 的图像大致为
A.
B.
C.
D.
6.从区间 0,1随机抽取 2n 个数 x1, x2 ,, xn , y1, y2 ,, yn ,组成坐标平面上的 n 个点
(x1, y1 ) ,(x2 , y2 ) ,… (xn , yn ) ,其中到原点距离小于1的点有 m 个,用随机模拟的
A.20100
B.20200
C.40200
D.40400
12.在棱长为 4 的正方体 ABCD A1B1C1D1 中, E, F 分别为 AA1, BC 的中点,点 M 在
棱 B1C1 上, B1M
1 4
B1C1
,若平面
FEM
交
A1B1 于点 N
,四棱锥 N
BDD1B1 的五
个顶点都在球 O 的球面上,则球 O 半径为
A(3, 0, 0) , B(0, 3, 0) , S(0, 3 , 3 3 ) , C(1,0,0) , 22
上.
(1)求曲线 C 的普通方程及直线 l 的直角坐标方程. (2)求△PAB 面积的最大值.
23.(本小题满分 10 分)选修 4-5:不等式选讲
已知函数 f (x) | 2x t | ,若 f (x) 1的解集为 (1,0) . (1)求 t 并解不等式 f (x) x 2 ; (2)已知: a,b R ,若 f (x) 2a b | 2x 2 | ,对一切实数 x 都成立, 求证: a 2b 1 .
3
2
根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用
广东省佛山市南海区2020届高三统一调研测试卷(一)数学

广东省佛山市南海区2020届高三统一调研测试卷(一)数学一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{}|28x A x N =∈≤,{0,1,2,3,4}B =,则A B =I ()A.{}0,1,2,3B.{}1,2,3C.{}0,1,2D.{}0,1,2,3,4 2.下列函数中与函数y x =(0x >)相同的是()A.y x =B.lg y x =C.y x =D.lg 10x y =3.已知数列{}n a 为等差数列,n S 为其前n 项和,5632a a a +=+,则7S ()A.2B.7C.14 D .284.函数()1cos 1xx f e x ex -=+的图像大致是() A. B.C. D.5.若,x y 满足不等式组250205x y x y x +≥⎧⎪-≥⎨⎪≤⎩,则z y x =-的最小值是()A.8-B.7-C.0D.56.执行如图所示的程序框图,则输出n 的值是()A.2B.4C.5D.67.如图,四棱锥S ABCD -的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是()A.AC SB ⊥B.//AB 平面SCDC.SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角D.AB 与SC 所成的角等于DC 与SA 所成的角8.如图所示,ABC △中,2BD DC =u u u r u u u r ,点E 是线段AD 的中点,则AC =u u u r ()A.3142AC AD BE =+u u u r u u u r u u u rB.34AC AD BE =+u u u r u u u r u u u rC.5142AC AD BE =+u u u r u u u r u u u rD.54AC AD BE =+u u u r u u u r u u u r 9.已知{}n a 是等比数列,22a =,514a =,则1223341n n a a a a a a a a +++++=L () A.()1614n -- B.()1612n -- C.()32143n -- D.()32123n --10.关于函数()(1cos )cos tan2x x x f x =+,有下述四个结论: ①函数()f x 在,44ππ⎡⎤-⎢⎥⎣⎦上是增函数 ②()f x 最小正周期为π③()f x 是奇的数④()f x 的定义域|()2x x R x k k Z ππ⎧⎫∈≠+∈⎨⎬⎩⎭且 其中所有正确结论的编号是()A.①②③ B .②④ C.①④ D.①③11.已知,,,,P A B C D 是球O 的球面上的五个点,在四边形ABCD 中,//AD BC ,2AB DC AD ===,4BC PA ==,PA ⊥面ABCD ,则球O 的体积为()A.16π D. 12.甲乙二队进行篮球比赛,若有一队胜4场,比赛就结束,假设甲,乙二队在每场比赛中获胜的概率都是0.5,则所需比赛的场数的数学期望为()A.4B.5.8125C.6.8125D.7二、填空题:本大题共4小题,每小题5分,共20分.13.在复平面内,复数65i +与34i -+对应的向量分别是OA u u u r 与OB uuu r ,其中O 是原点,则向量AB u u u r 对应的复数为__________.14.已知ABC △中,5a =,8b =,60C =︒,则BC CA ⋅=u u u r u u u r __________.15.测量某一目标的距离时,所产生的随机误差X 服从正态分布()220,10N ,如果独立测量3次,至少一次测量误差在()0,30内的概率是__________.附参考数据: ()0.68P X μδμδ-<≤+=,()220.95P X μδμδ-<≤+=,()330.99P X μδμδ-<≤+= 20.1850.03=,30.1850.006=,20.8150.66=,30.8150.541=.16.已知F 是椭圆2212x y +=的右焦点,P 是椭圆上一动点,10,2A ⎛⎫ ⎪⎝⎭,则APF △周长的最大值为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.在ABC △中,,,a b c 分别为内角,,A B C 的对边,且满足5cos cos 4c a B b A ⎛⎫-=⎪⎝⎭. (1)若2sin 5A =,10a b +=,求a ;(2)若b =5a =,求ABC △的面积S .18.如图四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(1)证明//MN 平面PAB ;(2)求直线AN 与平面PMN 所成角的正弦值.19.如图,已知直线l 与抛物线22y px =(0p >)交于,A B 点,且OA OB ⊥,(1)若OD AB ⊥交AB 于点D ,求点D 的轨迹方程;(2)求AOB △面积的最小值.20.甲乙二人轮流抛一枚均匀的骰子,甲先掷,一直到掷了1点,交给乙掷,而到乙掷出1点,再交给甲掷,井如此一直下去,若第n 次由甲掷骰子的概率为n P .(1)求12,P P ;(2)写出n P 与1n P -的递推关系式,并判断数列12n P ⎧⎫-⎨⎬⎩⎭是什么数列,并求n P ; (3)当n 足够大时,n P 趋近什么数,它的统计意义是什么?21.已知函数()ln a x ax f x x=+-,其中a 为常数. (1)若()f x 的图像在1x =处的切线经过点()3,4,求实数a ;(2)若01a <<,求证:202a f ⎛⎫> ⎪⎝⎭; (3)当函数存在三个不同的零点时,求实数a 的取值范围.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程]已知极坐标系的极点在直角坐标系的原点O ,极轴与x 轴的正半轴重合,直线l的极坐标方程为cos 4πρθ⎛⎫-= ⎪⎝⎭,曲线C 的参数方程是12,12,x t t y t t ⎧⎛⎫=+ ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩(t 是参数) (1)求直线l 的直角坐标方程及曲线C 的普通方程;(2)若直线l 与曲线C 交于点M ,求以OM 为直径的圆的极坐标方程.23.[选修4-5:不等式选讲]已知定义在R 上的函数()()2121x x x f x =++-+-的最小值为s .(1)试求s 的值;(2)若,,a b c R +∈,且a b c s ++=.求证2223a b c ++≥.。
广东省佛山市南海区2020届高三统一调研测试(一)数学试题 Word版含解析

广东省佛山市南海区2020届高三统一调研测试卷(一)数学注意事项:1.答卷前,考生务必填写答题卡上的有关项目.2.选择题每小题选出答案后,用2B 铅笔把答案涂在答题卡的相应位置上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液,不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将答题卡交回.一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若集合{}{}|28,0,1,2,3,4x A x N B =∈≤=,则A B =( )A. {}0,1,2,3B. {}1,2,3C. {}0,1,2D. {}0,1,2,3,4【答案】A【解析】∵集合{}|28x A x N =∈≤∴集合{}0,1,2,3A =∵集合{}0,1,2,3,4B =∴{}0,1,2,3A B ⋂=故选A.2. 下列函数中与函数y x =(0x >)相同的是( )A. y x =B. lg y x =C. y x =D. lg 10x y = 【答案】D【解析】【分析】根据函数的定义对选项逐个进行分析即可得结果.【详解】y x =的定义域为R ,与y x =(0x >)的定义域不同,两函数不相同; lg y x =和y x =与y x =(0x >)解析式不同,两函数不相同;lg 10x y x ==的定义域为()0+∞,,与y x =(0x >)的解析式和定义域都相同,两函数相同.故选:D .【点睛】本题主要考查函数的定义,判断两函数是否相同的方法:看解析式和定义域是否都相同,属于基础题.3. 设等差数列{}n a 的前n 项和为n S ,若5632a a a +=+,则7S =( )A. 28B. 14C. 7D. 2 【答案】B【解析】【分析】根据等差数列的性质6345a a a a +=+并结合已知可求出4a ,再利用等差数列性质可得1774()772a a S a +==,即可求出结果. 【详解】因为6345a a a a +=+,所以5452a a a +=+,所以42a =,所以17747()7142a a S a +===, 故选:B【点睛】本题主要考查等差数列的性质及前n 项和公式,属于基础题. 4. 函数1()cos 1xx e f x x e-=+的图像大致是( ) A. B.C. D.【答案】A【解析】分析:利用函数的奇偶性排除选项,利用函数通过的特殊点,排除选项,即可推出结果.详解:函数()1cos 1xxe f x x e -=+, 可得()()()11cos cos 11x x x x e e f x x x f x e e -----=-==-++, ∴函数是奇函数,排除B ,2x π=时,02f ⎛⎫= ⎪⎝⎭π,排除D , 6x π=时,661061e f e πππ-⎛⎫=< ⎪⎝⎭+,对应点在第四象限,排除C. 故选:A.点睛:函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的周期性,判断图象的循环往复;(5)从函数的特征点,排除不合要求的图象. 5. 若,x y 满足不等式组250205x y x y x +≥⎧⎪-≥⎨⎪≤⎩,则z y x =-的最小值是( )A. 8-B. 7-C. 0D. 5【答案】B【解析】【分析】由题意作出其平面区域,将z y x =-化为y =x+z ,z 相当于直线y =x+z 的纵截距,由几何意义可得结果. 【详解】由题意作出不等式组250205x y x y x +≥⎧⎪-≥⎨⎪≤⎩所表示平面区域:将z y x =-化为y =x+z ,z 相当于直线y =x+z 的纵截距,则由2505x y x +=⎧⎨=⎩解得52x y =⎧⎨=-⎩, 由图可知,当直线y =x+z 过()5,2B -时,直线在y 轴上的截距最小,故z y x =-的最小值是257--=-,故选:B .【点睛】本题考查了简单线性规划,作图要细致认真,根据几何意义是解题的关键,属于基础题.6. 执行如图所示的程序框图,则输出n 的值是( )A. 2B. 4C. 5D. 6【答案】D【解析】【分析】 根据题意,利用程序框图循环结构计算求得n 的值,可得答案.【详解】初始值n=0,执行程序依次为:2,2420?n n ==>否;4,21620?nn ==>否;6,26420?n n ==>是,循环结束,输出n=6故选D【点睛】本题主要考查了程序框图的循环结构判断求值,属于基础题.7. 如图,四棱锥S-ABCD 的底面为正方形,SD⊥底面ABCD ,则下列结论中不正确的是( )A. AC⊥SBB. AB∥平面SCDC. SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角D. AB 与SC 所成的角等于DC 与SA 所成的角【答案】D【解析】试题分析:A 中由三垂线定理可知是正确的;B 中AB ,CD 平行,所以可得到线面平行;C 中设AC,BD 相交与O ,所以SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角分别为,ASO CSO∠∠ SA SC =所以两角相等,D 中由异面直线所成角的求法可知两角不等考点:1.线面平行垂直的判定;2.线面角,异面直线所成角8. 如图所示,ABC 中,BD 2DC =,点E 是线段AD 的中点,则AC (= )A. 31AC AD BE 42=+ B. 3AC AD BE 4=+ C. 51AC AD BE 42=+ D. 5AC AD BE 4=+ 【答案】C【解析】【分析】利用向量三角形法则、向量共线定理即可得出. 【详解】如图所示,AC AD DC =+,1DC BD 2=,BD BE ED =+,1ED AD 2=,51AC AD BE 42∴=+. 故选C . 【点睛】本题考查了向量三角形法则、向量共线定理,考查了推理能力与计算能力,属于基础题.9. 已知{}n a 是等比数列,22a =,514a =,则12231n n a a a a a a +++⋅⋅⋅+=( ) A. ()1614n -- B. ()1612n -- C.()32123n -- D.()32143n -- 【答案】D【解析】【分析】先求出31()2n n a -=,再求出2511()2n n n a a -+=,即得解.【详解】由题得35211,82a q q a ==∴=.所以2232112()()22n n n n a a q ---==⨯=, 所以32251111()()()222n n n n n a a ---+=⋅=. 所以1114n n n n a a a a +-=,所以数列1{}n n a a +是一个等比数列. 所以12231n n a a a a a a +++⋅⋅⋅+=18[1()]4114n --=()32143n --. 故选:D【点睛】本题主要考查等比数列通项的求法和前n 项和的计算,意在考查学生对这些知识的理解掌握水平.10. 关于函数()(1cos )cos tan2x x x f x =+,有下述四个结论: ①函数()f x 在,44ππ⎡⎤-⎢⎥⎣⎦上是增函数 ②()f x 最小正周期为π③()f x 是奇函数④()f x 的定义域|()2x x R x k k Z ππ⎧⎫∈≠+∈⎨⎬⎩⎭, 其中所有正确结论的编号是( )A. ①②③B. ②④C. ①④D. ①③ 【答案】D【解析】【分析】直接根据正切型函数的定义域可判断④,利用切化弦思想以及二倍角公式可将()f x 化简为()1sin 22f x x =,根据正弦型函数的性质可判断①②③. 【详解】要使()(1cos )cos tan 2x x x f x =+有意义,需满足,22x k k Z ππ≠+∈,解得2,x k k z ππ≠+∈,即函数的定义域为{}|2()x x R x k k Z ππ∈≠+∈,,故④错误; ∵()21(1cos )cos tan2cos cos tan 2sin cos cos sin 2222222x x x f x x x x x x x x =+===, ∵,44x ππ⎡⎤∈-⎢⎥⎣⎦,∴2,22x ππ⎡⎤∈-⎢⎥⎣⎦, 则可得()f x 在,44ππ⎡⎤-⎢⎥⎣⎦上是增函数,故①正确; ∴结合函数的定义域可得()f x 最小正周期为2T π=,故②错误;又∵定义域关于原点对称,()()()1sin 22x x x f f =-=--, ∴()f x 是奇函数,故③正确;故选:D .【点睛】本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题.11. 已知P ,A ,B ,C ,D 是球O 的球面上的五个点,四边形ABCD 为梯形,//AD BC ,2AB DC AD ===,4BC PA ==,PA ⊥面ABCD ,则球O 的体积为( )B. 3C.D. 16π【答案】A【解析】【分析】根据已知中的平行关系和长度关系可确定BC 中点E 为底面梯形的外接圆圆心,根据球的性质可知OE ⊥平面ABCD ,利用勾股定理构造出关于OE 和球的半径R 的方程,解方程求得R ,代入球的体积公式可求得结果.【详解】取BC 中点E ,连接,,AE DE BD//AD BC 且12AD BC EC == ∴四边形ADCE 为平行四边形 AE DC ∴=,又12DC BC = 12DE BC ∴= AE DE BE EC ∴===E ∴为四边形ABCD 的外接圆圆心设O 为外接球的球心,由球的性质可知OE ⊥平面ABCD作OF PA ⊥,垂足F ∴四边形AEOF 为矩形,2OF AE ==设AF x =,OP OA R ==则()22444x x +-=+,解得:2x = 4422R ∴=+=∴球O 的体积:346423V R π== 本题正确选项:A【点睛】本题考查棱锥外接球体积的求解问题,关键是能够明确外接球球心的位置,主要是根据球心与底面外接圆圆心连线垂直于底面的性质,通过勾股定理构造方程求得结果.12. 甲乙二队进行篮球比赛,若有一队胜4场,比赛就结束,假设甲,乙二队在每场比赛中获胜的概率都是0.5,则所需比赛的场数的数学期望为( )A. 4B. 5.8125C. 6.8125D. 7【答案】B【解析】【分析】先确定比赛需要的场数ξ的可能取值为4、5、6、7,求出相应的概率,即可求得数学期望..【详解】由题意可知,比赛需要的场数ξ的可能取值为4、5、6、7, ()441114228p ξ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭;()3341111522224p C ξ⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭;()323511156222216p C ξ⎛⎫⎛⎫==⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭; ()333611157222216p C ξ⎛⎫⎛⎫==⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭ ∴1155934567 5.812584161616E ξ=⨯+⨯+⨯+⨯==, 故选:B .【点睛】本题考查独立重复试验,理解n 次独立重复试验的模型与二项分布的区别, 能进行一些与n 次独立重复试验的模型及二项分布有关概率的计算,属于中档题.二、填空题:本大题共4小题,每小题5分,共20分.13. 在复平面内,复数65i +与34i -+对应的向量分别是OA 与OB ,其中O 是原点,则向量AB 对应的复数为__________.【答案】9i --【解析】【分析】根据所给的两个向量的代数形式,先求两个向量的差,求出AB ,得到向量的代数形式的表示式即可.【详解】∵复数65i +与34i -+对应的向量分别是OA 与OB ,∴ 34659OB OA i i AB i =-=-+--=--,故答案为:9i --.【点睛】本题主要考查复数的几何意义,向量的线性运算,属于基础题.14. 在ABC ∆中,5a =,8b =,60C =︒,则BC CA ⋅的值为________.【答案】-20【解析】分析】在ABC ∆中,5a =,8b =,60C =︒则,120BC CA ︒<>=然后用数量积求值即可.【详解】解:||||cos ,58cos12020BC CA BC CA BC CA ︒⋅=⋅<>=⨯⨯=-.故答案为:20-.【点睛】本题考查平面向量的数量积,多数同学错误认为,60BC CA C <>=∠=︒,从而出错. 15. 测量某一目标的距离时,所产生的随机误差X 服从正态分布()220,10N ,如果独立测量3次,至少一次测量误差在()0,30内的概率是__________.附参考数据:()0.68P X μδμδ-<≤+=,()220.95P X μδμδ-<≤+=,()330.99P X μδμδ-<≤+=,20.1850.03=,30.1850.006=,20.8150.66=,30.8150.541=.【答案】0.994 【解析】 【分析】根据正态分布的性质求出在一次测量中误差在()0,30内的概率,再求出测量3次,每次测量误差均不在()0,30内的概率,根据对立事件的性质可得结果.【详解】由题意可知在一次测量中误差在()0,30内满足2X μδμδ-<<+, 其概率为()()()111220.950.680.815222p p X p X μδμδμδμδ=-<≤++-<≤+=⨯+=, 测量3次,每次测量误差均不在()0,30内的概率为:()3310.8150.1850.006-==, ∴独立测量3次,至少一次测量误差在()0,30内的概率是10.0060.994-=, 故答案为:0.994.【点睛】本题主要考查正态分布概率的求法,n 次独立重复试验的模型,利用对立事件解决问题是解题的关键,属于中档题.16. 已知F 是椭圆2212x y +=的右焦点,P 是椭圆上一动点,10,2A ⎛⎫ ⎪⎝⎭,则APF 周长的最大值为__________.【解析】 【分析】根据椭圆的定义可将周长转化为|2AP a PF AF +-'+,当AP PF -'最大时,A 、P 、F '三点共线,即求出最大值. 【详解】∵APF 的周长为AP PF AF ++,而2PF a PF =-',∴APF 的周长为2AP a PF AF +-'+,当A P PF F A '-='最大时,A 、P 、F '三点共线,如图所示,由题意得2a =1c =,F 点坐标为()10,,F '坐标为()10-,, 则APF 的周长最大为:||2AF AF a '++222211(10)0(10)02222⎛⎫⎛⎫=--+--+- ⎪ ⎪⎝⎭⎝⎭522【点睛】本题考查了椭圆的定义标准方程及其性质、三角形三边大小关系,考查了数形结合方法、推理能力与计算能力,属于中档题.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:60分.17. 在ABC ∆中,,,a b c 分别为内角,,A B C 的对边,且满足5()cos cos 4c a B b A -=. (1)若2sin ,105A a b =+=,求a ; (2)若35,5b a ==,求ABC ∆的面积S . 【答案】(1)4a =;(2)15. 【解析】试题分析:本题是典型角正余弦定理解三角形问题,由于5c a cosB bcosA 4⎛⎫-=⎪⎝⎭是关于边的这里面次式,所以先统一角做.由(1)中知道a b 10+=,所以可以选择正弦定理,从而解出此三角形.由(2)b 35,a 5==及4cosB 5=.两边及一对角的题型,所以可以选择余弦定理. 试题解析: 因为5c a cosB bcosA 4⎛⎫-= ⎪⎝⎭,所以由正弦定理得5sinC sinA cosB sinBcosA 4⎛⎫-= ⎪⎝⎭,即有5sinCcosB sinAcosB cosAsinB 4=+ , 则5sinCcosB sinC 4=,因为sinC 0>,所以4cosB 5=. (1)由4cosB 5=,得3sinB 5=,因为2sinA 5=,所以a sinA 2b sinB 3==, 又a b 10+=,解得a 4=.(2)因为222b a c 2accosB,b 35,a 5=+-==,所以24525c 8c =+-, 即2c 8c 200--=,解得c 10=或c 2=-(舍去), 所以1S acsinB 152== 18. 如图,四棱锥P −ABCD 中,PA⊥底面ABCD ,AD∥BC,AB=AD=AC=3,PA=BC=4,M 为线段AD 上一点,AM=2MD ,N 为PC 的中点.(Ⅰ)证明MN∥平面PAB;(Ⅱ)求直线AN 与平面PMN 所成角的正弦值.【答案】(Ⅰ)详见解析;(Ⅱ)8525.【解析】 【详解】 【分析】 试题分析:(Ⅰ)取的中点T ,然后结合条件中的数据证明四边形 AMNT 为平行四边形,从而得到MN AT ∥,由此结合线面平行的判定定理可证;(Ⅱ)以 A 为坐标原点,AE 的方向为轴正方向,建立空间直角坐标系,然后通过求直线AN 的方向向量与平面 PMN 的法向量的夹角的余弦值来求解AN 与平面 PMN 所成角的正弦值. 试题解析:(Ⅰ)由已知得. 取的中点T ,连接,由为中点知,.又,故=TN AM ∥,四边形AMNT 为平行四边形,于是MN AT ∥.因为平面,平面,所以平面. (Ⅱ)取的中点,连结.由得,从而,且.以A 为坐标原点, AE 的方向为轴正方向,建立如图所示的空间直角坐标系.由题意知,,,,,(0,2,4)PM =-, 5(2)PN =-,5(,1,2)2AN =. 设(,,)x y z =n 为平面 PMN 的一个法向量,则0,{0,n PM n PN ⋅=⋅=即 240,{520,y z x y z -=+-=可取(0,2,1)n =.于是85cos,25n ANn ANn AN⋅〈〉==.【考点】空间线面间的平行关系,空间向量法求线面角.【技巧点拨】(1)证明立体几何中的平行关系,常常是通过线线平行来实现,而线线平行常常利用三角形的中位线、平行四边形与梯形的平行关系来推证;(2)求解空间中的角和距离常常可通过建立空间直角坐标系,利用空间向量中的夹角与距离来处理.19. 如图,已知直线l与抛物线22y px=(0p>)交于,A B点,且OA OB⊥,(1)若⊥OD AB交AB于点D,求点D的轨迹方程;(2)求AOB面积的最小值.【答案】(1)2220(0)x y px x+-=≠;(2)24p.【解析】【分析】(1)设点A 的坐标()11,x y ,点B 的坐标()22,x y ,点D 的坐标为()()000,0x y x ≠,由OA OB ⊥,得12120x x y y +=,由此入手能求出点D 的轨迹方程;(2)设出AO 的方程代入抛物线求得x 的值,进而表示出A 的坐标,同理可表示出B 的坐标,进而可表示出22||p OA k =,2||2OB pk =,利用面积公式求解即可. 【详解】(1)设点A 的坐标()11,x y ,点B 的坐标()22,x y ,点D 的坐标为()()000,0x y x ≠, 由OA OB ⊥,得12120x x y y +=,由已知,得直线l 的方程为220000y y x x x y =-++,又有2112y px =,2222y px =,()()22121222y y px px =,22121224y y x x p =,由12120x x y y +=得21240y y p +=,把220000y y x x x y =-++代入22y px =并消去x 得()2220000220x y py y p x y +-+=,得()22001202p x y y y x -+=,代入21240y y p +=,得()220000200x y px x +-=≠,故所求点D 的轨迹方程为2220(0)x y px x +-=≠. (2)设:OA y kx =,代入22y px =,得0x =,22p x k =,22||p OA k =,2||2OB pk =, AOB 面积2221241412k S OA OB p p k+==≥,当且仅当1k =±时,取等号, 所以AOB 面积的最小值为24p .【点睛】本题考查点的轨迹方程的求法,考查了面积的最值计算,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.20. 甲乙二人轮流抛一枚均匀的骰子,甲先掷,一直到掷了1点,交给乙掷,而到乙掷出1点,再交给甲掷,井如此一直下去,若第n 次由甲掷骰子的概率为n P .(1)求12,P P ;(2)写出n P 与1n P -的递推关系式,并判断数列12n P ⎧-⎫⎨⎬⎩⎭是什么数列,并求n P ; (3)当n 足够大时,n P 趋近什么数,它的统计意义是什么? 【答案】(1)11p =,216p =;(2)()112263n n n p p -=+≥,12n P ⎧-⎫⎨⎬⎩⎭是等比数列,1121232n n P -⎛⎫=+⎪⎝⎭;(3)12,意义见解析. 【解析】 【分析】(1)直接根据规则,可求1p ,2p ,的值;(2))第1n -()2n ≥次由甲投掷而第n 次仍由甲投掷的概率是1 56n p -,第1n -次由乙投掷而第n 次由甲投掷的概率是()11 16n p --,两者相加可得n P 与1n P -的递推关系式,构造即可得12n P ⎧-⎫⎨⎬⎩⎭为等比数列;(3)通过极限的思想可得n P 趋近12,其意义在于当n 足够大时,甲掷骰子和乙掷骰子的可能性基本相同 【详解】(1)由题意,11p =,256p =; (2)第1n -()2n ≥次由甲投掷而第n 次仍由甲投掷的概率是1 56n p -, 第1n -次由乙投掷而第n 次由甲投掷的概率是()11 16n p --于是()1111121+63566n n n n p p p p ----==+,()2n ≥所以1213231n n p p --=-,()2n ≥即1211232n n p p -⎛⎫=- ⎪⎝⎭-,()2n ≥, 故数列12n P ⎧-⎫⎨⎬⎩⎭是以12为首项,23为公比的等比数列; 所以1112223n n P -⎛⎫-= ⎪⎝⎭,故1121232n n P -⎛⎫=+ ⎪⎝⎭. (3)当n 足够大时,11223n -⎛⎫⎪⎝⎭趋于0,则1121232n n P -⎛⎫=+⎪⎝⎭趋于12, 它的统计意义在于当n 足够大时,甲掷骰子和乙掷骰子的可能性基本相同.【点睛】本题考查概率知识的运用,考查数列通项的确定,考查学生分析解决问题的能力,属于中档题.21. 已知函数()ln af x x ax x=-+,其中a 为常数. (1)若f (x )的图象在x =1处的切线经过点(3,4),求实数a 的值;(2)若0<a <1,求证:202a f ⎛⎫> ⎪⎝⎭;(3)当函数存在三个不同的零点时,求实数a 的取值范围 【答案】(1)12- ;(2)详见解析;(3)1(0,)2 .【解析】【详解】试题分析:(1)根据导数的几何意义可得:,再结合斜率公式进而得出a 的值;(2)表示出223322()ln 2ln ln 22222a a a af a a a =-+=+--,然后构造函数32()2ln ln 22x g x x x =+--通过讨论函数的单调性证明2()02a f >;(3)将函数零点的问题转化为函数图像与轴交点个数的问题,通过导数讨论函数的单调性来解决. 试题解析:由题知0x > (Ⅰ)211()(1)f x a x x =-+'(1)12f a '∴=- 4(1)(1)231f f 又-==-'11222a a ∴-=∴=-(Ⅱ)223322()ln 2ln ln 22222a a a a f a a a =-+=+--,令32()2ln ln 22x g x x x =+--,则242222334(1)()22x x x g x x x x -+-=--='∴(0,1x ∈)时,()0,()g x g x '<单调递减, 故(0,1x ∈)时,1()(1)2ln 202g x g >=-->, ∴当01a <<时,2()02a f >(Ⅲ)22211()(1)ax x af x a x x x -+=='--+ ①00()0,()a f x f x '≤+∞>当时,在(,)上,递增,∴()f x 至多只有一个零点,不合题意; ②10()0,()2a f x f x ≥+∞'≤当时,在(,)上,递减, ∴()f x 至多只有一个零点,不合题意;③10()0,2a f x <'<=当时,令得12x x == 此时,()f x 在1(0,)x 上递减,12(,)x x 上递增,2(,)x +∞上递减,所以,()f x 至多有三个零点.因为()f x 在1(,1)x 递增,所以1()(1)0f x f <=,又因为2()02a f >,所以201(,)2ax x ∃∈,使得0()0f x =,又001()()0,(1)0f f x f x =-==,所以恰有三个不同零点:0,011,x x ,所以函数()f x 存在三个不同的零点时,a 的取值范围是1(0,)2. 考点:函数与导数综合应用.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22. 已知极坐标系的极点在直角坐标系的原点O ,极轴与x 轴的正半轴重合,直线l 的极坐标方程为cos 4πρθ⎛⎫-= ⎪⎝⎭C 的参数方程是12,12,x t t y t t ⎧⎛⎫=+ ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩(t 是参数) (1)求直线l 的直角坐标方程及曲线C 的普通方程;(2)若直线l 与曲线C 交于点M ,求以OM 为直径的圆的极坐标方程.【答案】(1)60x y +-=,2211616x y -=;(2)313cos 5sin ρθθ=+ 【解析】 【分析】(1)直接利用转换关系式,把参数方程极坐标方程和直角坐标方程之间进行转换即可; (2)利用二元二次方程的解法求出M 的坐标,进一步求出圆的方程. 【详解】(1)直线l的极坐标方程为cos 4πρθ⎛⎫-= ⎪⎝⎭整理得cos cossin sin44ππρθρθ+=转换为直角坐标方程为22x y +=60x y +-=; 曲线C 的参数方程是1212x t t y t t ⎧⎛⎫=+ ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩(t 是参数).两式平方相减可转换为直角坐标方程为2211616x y -=.(2)直线l 与曲线C 交于点M ,所以2260 16x y x y +-=⎧⎨-=⎩,解得13353x y ⎧=⎪⎪⎨⎪=⎪⎩,即135,33M ⎛⎫ ⎪⎝⎭, 所以OM 的中点坐标为135,66M ⎛⎫⎪⎝⎭,半径6r =, 整理得22135976618x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,转换为极坐标方程为2213597cos sin 6618ρθρθ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,整理得:313cos 5sin ρθθ=+.【点睛】本题考查的知识要点:参数方程、极坐标方程和直角坐标方程之间的转换,二元二次方程组的解法及应用,主要考查学生的运算能力和转换能力及思维能力,属于中档型23. 已知定义在R 上的函数()()2121x x x f x =++-+-的最小值为s .(1)试求s 的值;(2)若,,a b c R +∈,且a b c s ++=.求证2223a b c ++≥.【答案】(1)3;(2)见解析【解析】【分析】(1)利用绝对值三角不等式可得当12x -≤≤时,12x x ++-的最小值为3,结合二次函数的性质即可得结果;(2)直接利用柯西不等式即可得结果.【详解】(1)由绝对值三角不等式可得:123x x ++-≥,当且仅当()()120x x +-≤,即12x -≤≤时取等号;由于()210x -≥,当且仅当1x =时取等号,故()()21213x x x f x =++--≥+,当且仅当1x =时取等号,故()3min f x =,即3s =.(2)由于3a b c ++=,由柯西不等式()()2222222111()9a b c a b c ++++≥++=, 即2223a b c ++≥,当且仅当1a b c ===取等号.【点睛】本题主要考查了绝对值不等式的性质,以及利用柯西不等式证明不等式,利用不等式求最值时注意取等号条件,属于中档题.。
广东省佛山市南海区2020届高三年级综合能力测试语文卷

南海区2020届高三年级综合能力测试语文2020.03本试卷共10页,22小题,满分150分。
考试用时150分钟。
注意事项:1.答卷前、考生务必将白己的姓名、准考证号、考场号(和座位号填写在试题卷和答题卡上。
用2B铅笔将试卷类型(B)项涂在答题卡相应位置上,将条形码粘贴在答题卡右上角“条形码粘贴处”。
2.作答选择题时、选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将答题卡交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
鲁迅说,《野草》里有我的哲学。
《野草》集中讨论的是个体生命深层困境的问题,展现了鲁迅人生哲学的精髓。
在《野草》里,鲁迅塑造了许多文学意象,以象征人类某些方面的深层困境。
如《死火》一篇,以被人遗弃在冰谷中的行将熄灭的“死火”,推出了“冻灭”与“烧完”两种选择。
“冻灭”就是留在原地“坐以待毙”;“烧完”就是随“我”走出,做“垂死挣扎”。
尽管最后等待它的都是死亡,但是“冻灭”和“烧完”是有区别的。
这个“冻灭”,他是什么事儿不干,他的生命没有光影,只是一个空壳。
这个烧完,虽然最后也是完,但他燃烧的那个瞬间是发出灿烂的光辉的,他的生命是充实的。
这就是一种人生哲学,生命的价值不在手结果,而在于过程。
人就是在冻灭和烧完之间作选择。
导师王瑶先生曾对我说,与其坐以待毙,不如垂死挣扎,因为垂死挣扎有--种挣扎之美。
《野草》里还有一篇《影的告别》,影子的物理特征是正午阳光直照或者完全黑暗的时候,影子就没有了,影子只能存在于明暗之间。
鲁迅就用影子的形象,来象征自己这样一种“历史中间物”的命运。
广东省佛山市南海区2020届3月高三年级综合能力测试文科综合地理试题 答案

2019~2020学年高三年级综合能力测试2020年03月文科综合(全国卷)参考答案1.C2.A3.C4.C5.D6.B7.C8.D9.D 10.C 11.B36.(1)(亚热带季风性湿润气候)夏季高温多雨,利于棉花生长;秋季降水少,光照充足,利于棉花的成熟和收获;平原面积广大,利于规模化生产;多条河流流经,灌溉水源充足。
(每要点2分,共6分)(2)传统产业本身处于衰落期,原材料、劳动力成本上升,导致生产效益低下;新技术和新兴产业的发展,吸引了更多的资金和劳动力转移;国内、外市场面临激烈的竞争。
(每要点2分,共6分)(3)被三所名校环绕,科研力量雄厚;工业活动少(或东北和西南各有一个湖泊),环境质量好;有多条道路通过,交通便利;政策支持力度大。
((每要点2分,共8分)(4)保持良好的研发和居住环境;为园区预留足够的发展空间。
(每要点2分,共4分)37.(1)春季气候干旱,降水少,空气湿度小;枯枝、落叶等松散、干燥的可燃物质较多树木较干燥;横断山区山高谷深,背风坡易发生焚风效应,加之春季气温普遍升高,局部温度较高;春季多风,横断山区地形复杂,风向多变。
(每要点2分,共8分)(2)山火导致火场气温升高,气流上升;近地面水平气流由四周流向火场,吸引“倒火”向火场方向燃烧;当两火相遇时,可燃物和氧气都已燃烧殆尽,山火自然熄灭。
(每要点2分,共6分)(3)原始森林下可燃物长期堆积,腐烂后产生大量可燃气体,遇火剧烈燃烧;风力、风向突变,带来充足氧气,火势迅速增强。
((每要点2分,共4分))(4)害:山火导致物种减少,破坏生物多样性;森林资源破坏,木材蓄积量减少。
益:增加土壤有机肥,加速优势树种的生长;杀灭害虫,降低森林虫害风险;促进物种更新,优化生态系统。
(每要点2分,共4分)43.变化:景区内部大部分耕地及居住用地转变成风景或旅游接待用地;景区边缘居住用地增加,并新增接待用地和交通用地。
((每要点2分,共4分))意义:古村、古建等景点增多,增加了旅游资源的数量;景区内耕地和居住用地减少,有利于改善改善景区生态环境;景区边缘居住用地、接待用地和交通用地增多,有利于提高景区接待能力。
2020年3月南海区2020届高三年级综合能力测试 理科数学

2020年3月南海区2020届高三年级综合能力测试理科数学参考答案1.答案:D 解析:12(1){|1},{|1}A x y x x y x x A x x -⎧⎫⎧⎫⎪⎪==-===>∴=⎨⎬⎨⎪⎪⎩⎩⎭R ≤ð, 2{|20}{|(2)0}{|02}B x x x x x x x x =-<=-<=<<,()(0,1]A B ∴=R I ð.2.答案:B 解析:设i (,)z a b a b =+∈R ,则i 48i z z a b +=++=+,64,68i 88a a zb b ⎧=-⎧⎪+=∴⇒∴=-+⎨⎨==⎩⎪⎩,所以复数z 在复平面内所对应的点在第二象限.3.答案:D 解析:192899()9()9(210)36222a a a a S ++⨯-+====.4.答案:A 解析:设()x x x f x e e -=+,则()()x xxf x f x e e ---==-+,所以函数()f x 是奇函数,其图象关于原点对称,排除B ,C ,且当x →+∞时,()0x xxf x e e-=→+,排除D ,选A . 5.答案:C 解析:由12f T ωπ==,可知若12()f nf n *=∈N ,则必有12()n n ωω*=∈N ,故选C .6.答案:B 解析:若22a b b a =r r r r 成立,则22a b b a =r r r r ,则向量a r 与b r的方向相同,且22a b b a =r r r r ,从而a b =r r ,所以a b =r r ;若a a b b =r r r r ,则向量a r 与b r的方向相同,且22a b =r r ,从而a b =r r ,所以a b =r r .所以“22a b b a =r r r r”为“a a b b =r r r r ”的充分必要条件.7.答案:C解析:2121cos 21cos 21112()sin ()cos 222262x x f x x g x x πππ⎛⎫-- ⎪-⎛⎫⎝⎭==−−−−−−→==--+ ⎪⎝⎭向右平移个单位, cos 2[1,1]6x π⎛⎫-∈- ⎪⎝⎭Q ,()g x ∴的值域为[0,1],①错误;当12x π=时,206x π-=,所以12x π=是函数()g x 的一条对称轴,②正确;当3x π=时,262x ππ-=,所以()g x 的一个对称中心是1,32π⎛⎫⎪⎝⎭,③正确; ()sin 2[1,1]6g x x π⎛⎫'=-∈- ⎪⎝⎭,则121212,,()1,()1,()()1x x g x g x g x g x ''''∃∈=-=⋅=-R ,则()g x 在1x x =和2x x =处的切线互相垂直,④正确.8.答案:D 解析:窗花的面积为21241140-⨯=,其中小正方形的面积为5420⨯=, 所以所求概率1402061407P -==.9.答案:A解析:AB =PB h =,则由2PA PB =2h =,解得1h =,可将三棱锥P ABC -还原成如图所示的长方体,则三棱锥P ABC -的外接球即为长方体的外接球,设外接球的半径为R,则22,1R R ===, 所以外接球的体积34433V R ππ==. 10.答案:C解析:所有可能的情况有3464=种,其中最大值不是4的情况 有3327=种,所以取得小球标号最大值是4的取法有642737-=种.11.答案:B解析:b a >Q ,所以离心率c e a ==>圆222()x c y a -+=是以(,0)F c 为圆心,半径r a =的圆,要使得经过点T所作的圆的两条切线互相垂直,必有TF =,而焦点(,0)F c 到双曲线渐近线的距离为b,所以TF b =≥,即ba所以c e a ==所以双曲线12.答案:解析:设M 设()ln 3g t t t =+,则22()33g t t t t '=-=,当03t <<时,()0,()g t g t '<单调递减,当3t >时, ()0,()g t g t '>单调递增,所以min 1()1ln 303g t g ⎛⎫==-< ⎪⎝⎭,且221120,(1)033e g g e ⎛⎫=-+>=> ⎪⎝⎭,1()ln 03g t t t∴=+=有两个不同的解,所以曲线G 上的“水平黄金点”的个数为2. 13.答案:2解析:设符合条件的点00(,)P x y ,则00015,4,4PF x x y =+=∴==±,所以符合条件的点有2个.14.答案:112n -⎛⎫- ⎪⎝⎭解析:当1n =时,1111221S a a a +==-⇒=-,由2n n S a +=-,可知当2n ≥时,112n n S a --+=-,两式相减,得120n n a a --=,即11(2)2n n a a n -=≥,所以数列{}n a 是首项为1-,公比为12的等比数列,所以112n n a -⎛⎫=- ⎪⎝⎭.15.答案:13,2⎛⎤-∞-⎥⎝⎦,132- 解析:由(2)1628210f λ=---≥,解得132λ-≤. 当n 为奇数时,cos 1n π=-,由32()2710f n n n n λ=+--≥,得2127n n nλ+-≤, 而函数21()27g n n n n=+-为单调递增函数,所以min ()(1)8g n g ==,所以8λ≤. 当n 为偶数时,cos 1n π=,由32()2710f n n n n λ=---≥,得2127n n nλ--≤,设21()27(2)h x x x x x =--≥,则212,()470x h x x x '∴=-+>Q ≥,()h x ∴单调递增,min 13()(2)2h x h ∴==-.所以132λ-≤,综上可知,若不等式()0f n ≥恒成立,则λ的最大值为132-.16.答案:①②③④解析:取CD 中点G ,连接EG ,则1//EG A B ,所以平面1A BE 即为平面1A BGE ,取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得111//,//B M BG B N A E ,从而平面1//B MN 平面1A BGE ,所以点F 的运动轨迹为线段MN ,平面1B MN 即为平面α.①取F 为MN 中点,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故①正确;②设正方体的棱长为2,当点F 为MN 中点时,直线1B F 与直线BC所成角最小,此时12C F =,11111tan C F C B F B C ∠==,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时111tan 2C B F ∠=,所以直线1B F 与直线BC所成角的正切值的取值范围是142⎤⎥⎣⎦,②正确; ③取F 为MN 中点,则1111,,MN C F MN B F B FC ⊥⊥∴∠即为α与平面11CDD C 所成的锐二面角,11111tan B CB FC C F∠==,所以③正确;④正方体1111ABCD A B C D -的各个侧面中, 平面ABCD ,平面1111A B C D ,平面11BCC B , 平面11ADD A 与平面α所成的角相等,所以④正确.17.解:(1)在ABC △,cos C =,所以2sin 3C ==.…………………………1分 所以 cos cos cos sin sin cos cos 4444A C C C C πππππ⎛⎫⎛⎫=--=-+=- ⎪ ⎪⎝⎭⎝⎭223236=-= (5)分 (2)由(1)可知cos 06A =<,所以2A π>.因为sin sin AD DC C DAC =∠,所以sin 2sin 3sin AD C DC DAC DACλ===∠∠.……………………8分 因为0DAC BAC <∠∠≤,所以 sin (0,1]DAC ∠∈.…………11分ABCDD 1A 1B 1C 1EGMNF CAB所以2,3λ⎡⎫∈+∞⎪⎢⎣⎭………………………………12分18.解析:(1)证明:取AD 中点为O ,连接PO . PAD △是等边三角形,所以PO AD ⊥. 因为PAD ABCD ⊥平面平面且相交于AD ,所以PO ⊥平面ABCD ,所以PO DC ⊥.因为//,AB CD AB PA ⊥,所以CD PA ⊥.因为PO PA P =I 在平面PAD 内,所以CD PAD ⊥平面. 所以PCD PAD ⊥平面平面.………… 3分(2)以O 为原点,过O 作AB 的平行线OF ,分别以OA , OF ,OP 分别为x 轴,y 轴,z 轴建立空间直角坐标系.设2AB AD ==,则(1,0,0)A ,(1,2,0)B ,(1,4,0)C -,P .………… 5分因为M 在棱PC上,可设[](1)(,4)),0,1OM t OP tOC t t t t =-+=--∈u u u u r u u u r u u u r,所以(1,4))AM t t t =---u u u u r.设平面PBC 的法向量为(,,)n x y z =r,因为(2,2,0),(1,4,BC PC =-=-u u u r u u u r,所以22040x y x y -+=⎧⎪⎨-+=⎪⎩ 令1x =,可得11x y z ⎧=⎪=⎨⎪=⎩,即n =r .设直线AM 与平面PBC 所成角为θ,所以sin cos ,AM n AM n AM n θ⋅===u u u u r ru u u u r r u u u u r r . 可知当110t =时, sin θ;…………8分(3)设2,AD DC m ==,则有(1,,0)P C m -,得(1,,PC m =-u u u r .设AN PMk AM PC==,那么,PM k PC AN k AM ==u u u u r u u u r u u u r u u u u r,所以(,,)PM k mk =-u u u u r.所以(,))M k mk k --.因为(1,0,0),(1,))A AM k mk k =---u u u u r所以.22,(,(1))AN k AM AN k k mk k ==---u u u r u u u u r u u u r因为所以.所以22(1,(1))N k k mk k --+-.又因为(1,0,0),1,,02m D B ⎛⎫- ⎪⎝⎭,所以22(2,(1))DN k k mk k =--+-u u u r .(1,0,2,,02m PD DB ⎛⎫=-= ⎪⎝⎭u u u r u u u r ,设平面PDB 的法向量为(,,)n x y z =r,有0202x m x y ⎧-=⎪⎨+=⎪⎩x =令1x y z ⎧=⎪⎪=⎨⎪=⎪⎩,1n m ⎛⎫= ⎪ ⎪⎝⎭r …………10分 因为N 在平面PDB 内,所以DN n ⊥u u u r r .所以0DN n ⋅=u u u r r.所以222)(1)0k k mk k m--++⋅-=.即2210k k +-=, 所以12k =或者1k =-(舍),即12AN AM =………………………………………………………12分19.解(1)1495050(2)1(1)(0)10.99870.00130.99870.003P X P X P X C =-=-==-⋅⋅-=≥,由于X 满足二项分布,故0.0013500.065EX =⨯= …………--5分(2)由题意可知不合格率为250,若不检查,损失的期望为252()2602020505E Y n n =⨯⨯-=-,若检查,成本为10n ,由于522()1020102055E Y n n n n -=--=-,当n 充分大时,2()102005E Y n n -=->所以为了使损失尽量小,小张需要检查其余所有零件. ………………………………12分 20.解:(1)由题意可知2b =,3c a =,又由222a c b -=,得a c == 所以椭圆M 的方程为22164x y +=;……………4分(2)证明:设直线l 的方程为为:1y kx =+,联立221164y kx x y =+⎧⎪⎨+=⎪⎩,消元可得:22(23)690k x kx ++-=,设1122(,),(,)Q x y N x y则有12122269,2323k x x x x k k+=-=-++ (8)因为121222,AQ AN y y k k x x ++==, 所以2222121212Q 1212223()92232A ANy y k x x k x x k k k k k x x x x +++++⋅=⋅==+--=-又因为点B 与点Q 关于原点对称,所以11(,)B x y --,即112AB y k x -+=-, 则有21112111224AQ ABy y y k k x x x +-+-⋅=⋅=--22所以23AQ ABk k ⋅=-,所以AQ AN AN AB AQ AB k k k k k k ⋅==⋅所以存在实数3λ=,使AN AB k k λ=(2)解法二:证明:设直线l 的方程为为:联立221164y kx x y =+⎧⎪⎨+=⎪⎩,消元可得:22(23)k x +则有12122269,2323k x x x x k k+=-=-++……………8分 121223x x k x x +∴=,12123()2x x kx x +=,222AN y k x +=,112AB y k x -=, 所以1212121121121221211221223()3(2)(3)393233()(2)(1)32AN ABx x x k y x kx x kx x x x x x x k x y x kx kx x x x x x +-++++======+---+-,所以存在实数3λ=,使AN AB k k λ=成立.………………12分 21.解析:(1)当12x >时,'()(2)kxf x k x e -=-,(())(2)0kx f x k ke -''=+>,所以()f x '在1,2⎛⎫+∞ ⎪⎝⎭递增.所以21()(1)02kf x f k e -⎛⎫''>=-> ⎪⎝⎭.所以()f x 在1,2⎛⎫+∞ ⎪⎝⎭递增,所以函数()f x 没有极值点;…………………………………4分(2)22()()ln (1)ln kxg x f x x m x k x m x e -=+-=+-+,存在实数t ,使直线y t =与函数()g x 的图象交于不同的两点12(,),(,)A x t B x t ,即存在121,,2x x ⎛⎫∈+∞⎪⎝⎭且12x x <,使12()()g x g x =.……… 6分由12()()g x g x =可得:21222121(ln ln )(1)()()kx kx m x x k x x ee ---=+-+-,12x x <,由(1)可知21()()f x f x >,可得:212221()kx kx e e k x x --->--.所以222121(ln ln )m x x x x->-,即22212122ln x x m x x ->.……………………8分 下面证明222112212ln x x x x x x ->,只需证明:221221112ln x x x x x x ⎛⎫- ⎪⎝⎭>. 令211x s x =>,则证:212ln s s s ->,即12ln 0s s s -->.……………………………………10分 设1()2ln h s s s s=--,那么22(1)()0s h s s -'=>. 所以()(1)0h s h >=.所以122mx x >,即122m x x >.………12分 22.解析:(1)曲线M 的极坐标方程是12ρ=.………………………………………4分(2)当3π4θ=时,线段OA 取得最小长度为22332sin(2π)4=-⨯.…………………………6分因为曲线M 是以原点为圆心,半径为12的圆,所以 12OA >. 所以点A 与曲线M 的位置关系是点A 在曲线M 外.………10分23.解析:(1)2,1,1,1a b c d ====-.(答案不唯一)………………………………4分(2)证明:由题意可知,0a ≠. 因为a c d ≥≥,所以()()0a c a d --≥. 所以2()0a c d a cd -++≥,即2()a cd c d a ++≥.……-7分 因为0a b >≥,所以cd a c d a ++≥.因为ab cd ≥,所以 cdb a≥. 所以cda b a c d a+++≥≥.………………10分。
广东省佛山市南海区2020届3月高三年级综合能力测试理科综合试题及答案

I-(mAg·sin α)·(t1+Δt)=mAv2-0 ④
(2 分)
说明∶如果分两段计算推力的冲量,0~v1 过程和 v1~v2 过程,算出每段过程推力的冲量,各占 1 分。
即∶I1=F1t1=4.8 N·S (1 分);I2-mAgΔt·sin α=mv2-mv1 I2=4.8 N·s (1 分)
⑤
(1 分)
(如果第②④⑤式的任意一处或多处 d 写成 L ,均只扣 1 分。)
(2)(共 7 分)
若(断开后认为板间电压等于电动势)断开 S 再立即撤去金属棒,板间电压为
U=E
⑥(1 分)
恒定速率,油滴做匀速圆周运动,有
mg=qU d
⑦(2 分)(含 mg=qE 电和 E 电=U两式,各 1 分) d
题 号 14
15
16
17
18
19
20
21
答案 B
C
A
B
D
AC BC
B
备注∶21 题修改为单选,分值仍为 6 分。
三、非选择题∶共 174 分,第 22~32 题为必考题,每个试题考生都必须作答。第 33~38 题为选考题,考生
根据要求作答。
(一)必考题:共 129 分
22.(5 分)
(1)2.5
(1 分)(2.50 不给分)
(4)小于,小于 (2 分)(各 1 分)(小、减小、<等不一致的均不给分)
第1页共6页
24.(12 分)如图所示,两正对的长为 2d 、间距为 d 的水平金属极板 M 、N ,处在垂直纸面向外的匀强 磁场中,磁感应强度大小为 B 。一电阻为 r 的光滑金属棒与极板垂直放置,有滑扣装置(图中无画出) 保证其能紧贴极板一侧无摩擦地运动,现在大小为 F 的水平恒力作用下加速向左运动,且与极板之间 无挤压。金属棒、金属极板与阻值为 R 的电阻构成闭合电路。重力加速度为 g 。不计金属极板电阻及 接触电阻。
2020年广东省佛山市南海区高考数学模拟试卷(理科)(3月份)(含答案解析)
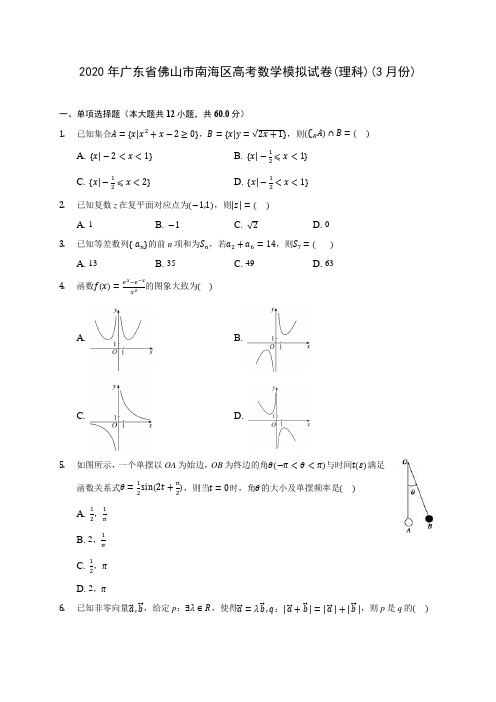
2020年广东省佛山市南海区高考数学模拟试卷(理科)(3月份)一、单项选择题(本大题共12小题,共60.0分)1. 已知集合A ={x|x 2+x −2≥0},B ={x|y =√2x +1},则(∁R A)∩B =( )A. {x|−2<x <1}B. {x|−12⩽x <1} C. {x|−12⩽x <2}D. {x|−12<x <1}2. 已知复数z 在复平面对应点为(−1,1),则|z |=( )A. 1B. −1C. √2D. 03. 已知等差数列{ a n }的前n 项和为S n ,若a 2+a 6=14,则S 7=( )A. 13B. 35C. 49D. 634. 函数f(x)=e x −e −xx 2的图象大致为( )A.B.C.D.5. 如图所示,一个单摆以OA 为始边,OB 为终边的角θ(−π<θ<π)与时间t(s)满足函数关系式θ=12sin(2t +π2),则当t =0时,角θ的大小及单摆频率是( )A. 12,1π B. 2,1π C. 12,π D. 2,π6. 已知非零向量a ⃗ ,b ⃗ ,给定p :∃λ∈R ,使得a⃗ =λb ⃗ ,q :|a ⃗ +b ⃗ |=|a ⃗ |+|b ⃗ |,则p 是q 的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件7.将函数的图象向右平移π12个单位,得到函数g(x)的图象,则下列说法不正确的是()A. g(5π12)=1B. g(x)在区间[5π12,3π4]上单调递减C. x=−π12是g(x)图象的一条对称轴D. (π8,0)是g(x)图象的一个对称中心8.如图,四个全等的直角三角形和一个小正方形组成一个大正方形,直角三角形两直角边的比为1:2,小正方形的边长为2,作出小正方形的内切圆,现在大正方形内随机取一点,则此点取自圆内部分的概率为()A. π8B. π12C. π20D. π259.如图所示,三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC,PA=AC=√2,则三棱锥P−ABC外接球的体积是()A.B.C.D. 2π10.4个不同的小球放入编号为1、2、3的3个盒子中,放法种数为()A. 4B. 24C. 64D. 8111.已知点P(1,2)在双曲线x2a2−y2b2=1(a>0,b>0)的渐近线上,则C的离心率是()A. √2B. √3C. √52D. √512.已知函数f(x)=x2−lnx (x≥√22),函数g(x)=x−1,直线y=t分别与函数f(x),g(x)的图象交于点A,B,则|AB|的最小值为()A. 12B. √22C. 1D. √2二、填空题(本大题共4小题,共20.0分)13.抛物线y=14x2上到焦点的距离等于6的点的坐标为______ .14.若S n为数列{a n}的前n项和,且S n=2a n−1(n∈N∗),则S6等于________.15.已知g(x)=λx+sinx在区间[−1,1]上是减函数,且g(x)≤t2+λt+1在x∈[−1,1]上恒成立,则实数t的取值范围是________。
2020届佛山市高三教学质量检测数学理科试题

2020年广东省佛山市高考数学一模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)在复平面内,复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【分析】利用复数代数形式的乘除运算化简,求出复数所对应点的坐标得答案.【解答】解:∵∴在复平面内,复数=,对应的点的坐标为(2,1),位于第一象限.故选:A.【点评】本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.2.(5分)已知集合A={x|x2﹣x﹣2<0},B={x||x|>1},则A∩B=()A.(﹣2,﹣1)B.(﹣1,1)C.(0,1)D.(1,2)【分析】可以求出集合A,B,然后进行交集的运算即可.【解答】解:A={x|﹣1<x<2},B={x|x<﹣1或x>1},∴A∩B=(1,2).故选:D.【点评】本题考查了描述法、区间的定义,一元二次不等式和绝对值不等式的解法,交集的运算,考查了计算能力,属于基础题.3.(5分)已知x,y∈R,且x>y>0,则()A.cos x﹣cos y>0B.cos x+cos y>0C.lnx﹣lny>0D.lnx+lny>0【分析】根据题意,结合函数的单调性分析选项A、C,可得A错误,C正确,对于B、D,利用特殊值分析可得其错误,综合即可得答案.【解答】解:根据题意,依次分析选项:对于A,y=cos x在(0,+∞)上不是单调函数,故cos x﹣cos y>0不一定成立,A错误;对于B,当x=π,y=时,cos x+cos y=﹣1<0,B不一定成立;对于C,y=lnx在(0,+∞)上为增函数,若x>y>0,则lnx>lny,必有lnx﹣lny>0,C正确;对于D,当x=1,y=时,lnx+lny=ln<0,D不一定成立;故选:C.【点评】本题考查函数单调性的应用,涉及实数大小的比较,属于基础题.4.(5分)函数f(x)的图象向左平移一个单位长度,所得图象与y=e x关于y轴对称,则f(x)=()A.e﹣x+1B.e﹣x﹣1C.e x﹣1D.e x+1【分析】根据函数图象变换关系,利用逆推法进行求解即可.【解答】解:y=e x关于y轴对称的函数为y=e﹣x,然后向右平移一个单位得到f(x),得y=e﹣(x﹣1),即f(x)=e﹣x+1,故选:A.【点评】本题主要考查函数图象变换,结合条件进行逆推法是解决本题的关键.比较基础.5.(5分)希尔宾斯基三角形是一种分形,由波兰数学家希尔宾斯基在1915年提出,先作一个正三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色代表挖去的面积,那么黑三角形为剩下的面积(我们称黑三角形为希尔宾斯基三角形).在如图第3个大正三角形中随机取点,则落在黑色区域的概率为(),A .B .C .D .【分析】我们要根据已知条件,求出第3 个大正三角形的面积,及黑色区域的面积,代入几何概型计算公式, 即可求出答案.【解答】解:由题意可知:每次挖去的面积为前一个三角形剩下面积的 ,不妨设第一个三角形的面积为 1.∴第三个三角形的面积为 1;则阴影部分的面积之为 :第 3 个大正三角形中随机取点,则落在黑色区域的概率:,故选:B .【点评】几何概型的概率估算公式中的“几何度量” 可以为线段长度、面积、体积等,而且这个“几何度量” 只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A 的基本事件对应的“几何度量”N (A ),再求出总的基本事件对应的“几何度量”N ,最后根据 P = 求解.6.(5 分)已知等比数列{a n }满足 a 1﹣a 2=36,a 1﹣a 3=24,则使得 a 1a 2…a n 取得最大值的 n 为( )A .3B .4C .5D .6【分析】结合等比数列的通项公式可求通项,然后结合项的正负及增减性可求. 【解答】解:∵等比数列{a n }满足 a 1﹣a 2=36,a 1﹣a 3=24,,解可得,q =∴a n =,a 1=27,,若使得 a 1a 2…a n 取得最大值,则 n 应该是偶数, 且 n >4 时,|a n |<1,故当 n =4 时,a 1a 2…a n 取得最大值. 故选:B .【点评】本题主要考查了等比数列的通项公式的简单应用,分析数列的项的特点是求解问题的关键.7.(5 分)已知α为锐角,cosα= ,则 tan (+ )=( )A .B .C .2D .3【分析】求出 tanα== ,从而 tan = ,由此能求出 tan ( + )的值.【解答】解:∵α为锐角,cosα= ,∴sinα= = ,tanα= = = ,解得 tan = ,或 tan =﹣2,∴tan(+)===3.故选:D.【点评】本题考查三角函数值的求法,考查诱导公式、正切函数的二倍角公式、正切加法定理等基础知识,考查运算求解能力,是基础题.8.(5分)已知双曲线C:,O为坐标原点,直线x=a与双曲线C的两条渐近线交于A,B两点,若△OAB是边长为2的等边三角形,则双曲线C的方程为()A.﹣y2=1B.x2=1C.=1D.=1【分析】求出双曲线的渐近线方程,令x=a,求得A,B的坐标,由等边三角形的性质可得a,b的值,进而得到双曲线的方程.【解答】解:双曲线C:的渐近线方程为bx﹣ay=0和bx+ay=0,由x=a与双曲线C的两条渐近线交于A(a,b),B(a,﹣b),△OAB是边长为2的等边三角形,即有2b=2,即b=1,且a=×2=,可得双曲线的方程为﹣y2=1.故选:A.【点评】本题考查双曲线的方程和性质,主要是渐近线方程的应用,考查等边三角形的性质,以及化简运算能力,属于基础题.9.(5分)地球上的风能取之不尽,用之不竭.风能是清洁能源,也是可再生能源.世界各国致力于发展风力发电,近10年来,全球风力发电累计装机容量连年攀升,中国更是发展迅猛,在2014年累计装机容量就突破了100GW,达到114.6GW,中国的风力发电技术也日臻成熟,在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图.根据以上信息,正确的统计结论是()A.截止到2015年中国累计装机容量达到峰值B.10年来全球新增装机容量连年攀升C.10年来中国新增装机容量平均超过20GWD.截止到2015年中国累计装机容量在全球累计装机容量中占比超过【分析】通过图结合选项分析.【解答】解:由图1知没有在截止到2015年中国累计装机容量达到峰值,A错;由图2知,10年来全球新增装机容量起伏,B错;由图1知,10年中国新增装机总容量为3.8+18.9+17.7+13+16.1+23.2+30.8+23.4+19.7+21.1=197.7,则10年来中国新增装机容量平均为19.77GW,C错;故选:D.【点评】本题考查频率直方图,属于基础题.10.(5分)已知函数f(x)=A.(﹣∞,﹣3)∪(1,+∞)C.(﹣2,0)+2x+1,且f(a2)+f(2a)>3,则a的取值范围是()B.(﹣∞,﹣2)∪(0,+∞)D.(﹣1,3)【分析】设F(x)=f(x)﹣=+2x+1﹣=+2x,分析函数F((x)的奇偶性,单调性,f(a2)+f(2a)>3,转化为F(a2)>﹣F(2a),即可解出答案.【解答】解:根据题意,设F(x)=f(x)﹣=则F(0)=f(0)﹣=0,+2x+1﹣=+2x,又由F(﹣x)=又由F′(x)=所以函数F(x)单调递增,若f(a2)+f(2a)>3,+2(﹣x)=﹣(=+2x)=﹣F(x),即函数F(x)为奇函数;=>0,则f(a2)﹣>,f(a2)﹣>﹣[f(2a)﹣],F(a2)>﹣F(2a),F(a2)>F(﹣2a),所以a2>﹣2a,解得,a<﹣2或a>0,故选:B.【点评】本题考查函数的奇偶性与单调性的综合应用,涉及构造法的应用,属于基础题.11.(5分)已知函数f(x)=sin x+sin(πx),现给出如下结论:①f(x)是奇函数;②f(x)是周期函数;③f(x)在区间(0,π)上有三个零点;④f(x)的最大值为2.其中正确结论的个数为()A.1B.2C.3D.4【分析】①根据函数奇偶性定义进行判断,②用反证法推出函数的函数无周期,③f(x)=sin x+sin(πx)=2sin cos,函数的零点为方程sin=0或cos=0,x=或x=,x∈(0,π),进而得出结论,④用反证法推出函数的函数最大值不是2.【解答】解:因为f(﹣x)=sin(﹣x)+sin(﹣πx)=﹣sin x﹣sin(πx)=﹣f(x),所以f(x)是奇函数,①正确.假设存在周期T,则sin(x+T)+sin(π(x+T))=sin x+sinπx,sin(x+T)﹣sin x=﹣[sin(π(x+T))﹣sinπx],所以sin•cos存在x0∈R,使得cos=﹣sin•cos=0,而cos①,≠0,将x∈R,﹣sin 由于•cos,=0,△1故﹣sin=0,所以 sin =0,sin=0,=k π,=m π,k ,m ∈Z,所以 k π=m ,矛盾,所以函数 f (x )=sin x +sin (πx ),没有周期,②错误.f (x )=sin x +sin (πx )=2sin函数的零点为方程 sin=0 或 coscos ,=0,x =x =或 x =, 或 ,x ∈(0,π),所以 f (x )在区间(0,π)上有三个零点;故③正确. 假设存在这样的 x 0 使得 f (x )最大值为 2,x 0=且πx 0=,(k ∈Z)即 x 0=所以且 x 0== ,,k =﹣ ,与 k ∈Z 矛盾,故④错误.故选:B .【点评】本题考查三角函数的图象和性质,属于难题. 12.(5 分)已知正三棱柱 ABC ﹣A 1B C 1 的侧棱长为 4,底面边长为 2,用一个平面截此棱柱,与侧棱AA 1,BB 1,CC 1分别交于点 M ,N ,△Q ,若 MNQ 为直角三角形,则 MNQ 面积的最大值为( ) A .3 B . C . D .3【分析】不妨设 N 在 B 处,AM =h ,CQ =m ,则有 MB 2=h 2+4,BQ 2=m 2+4,MQ 2=(h ﹣m )2+4 由 MB 2=BQ 2+MQ 2⇒ m 2 ﹣△h m +2=0. =h 2﹣8≥0⇒ h 2≥8,且 h ≤4, 可得 S 2=1+h 2,就可求出 S 最大值.【解答】解:解:如图,不妨设 N 在 B 处,AM =h ,CQ =m , 则有 MB 2=h 2+4,BQ 2=m 2+4,MQ 2=(h ﹣m )2+4由 MB 2=BQ 2+MQ 2⇒ m 2﹣hm +2=0.得 h =△=h 2﹣8≥0⇒ h 2≥8,且 h ≤4, 即 8≤h 2≤16,=m + ①S =,S 2= ×|MQ |2×|BQ |2=把①代入得[(h ﹣m )2+4]×(m 2+4)S 2= ×[(m + ﹣m )2+4]×(m 2+4)==5+( +m )2﹣4=1+( +m )2=1+h 2,所以 S 2=1+h 2∈[9,17], S 2max =17,S max = , 故选:C .[ +4]×(m 2+4)=5+( ( (• •(【点评】本题考查了空间线面位置关系,考查了转化思想,属于中档题. 二、填空题:本大题共 4 小题,每小题 5 分,满分 20 分. 13.5 分)从进入决赛的 6 名选手中决出 1 名一等奖,2 名二等奖,3 名三等奖,则可能的决赛结果共有 60 种.用数字作答)【分析】6 名选手中决出 1 名一等奖有 种方法,2 名二等奖, 种方法,利用分步计数原理即可得答案.【解答】解:依题意,可分三步,第一步从 6 名选手中决出 1 名一等奖有 种方法,第二步,再决出 2 名二等奖,有第三步,剩余三人为三等奖, 根据分步乘法计数原理得:共有种方法,• =60 种方法.故答案为:60.【点评】本题考查排列、组合及简单计数问题,掌握分步计数原理是解决问题的关键,属于中档题.14.(5 分)在△ABC 中,AB =2,AC =3,P 是边 BC 的垂直平分线上一点,则【分析】取 BC 的中点 D ,=( + )=( ( + )+ ), ⊥ 及向量的运算法则,可得结果. • = .,再利用两个向量垂直的性质【解答】解:取 BC 的中点 D ,由条件得 • =( + ) ﹣ )=( ( + )+ ) ﹣ )=﹣+ =﹣+•= +0= ,故答案为: .【点评】此题是基础题.本题考查两个向量的运算法则及其意义,两个向量垂直的性质.15.(5 分)函数 f (x )=lnx 和 g (x )=ax 2﹣x 的图象有公共点 P ,且在点 P 处的切线相同,则这条切线方程为 y =x ﹣1 .【分析】分别求得 f (x ),g (x )的导数,设 P (x 0,y 0),则 lnx 0=ax 02﹣x 0①,结合 f ′(x 0)=g ′(x 0), 联立消掉 a 可得关于 x 0 的方程,构造函数,根据函数单调性可求得唯一 x 0 值,进而可求 P 的坐标,以及切线 的斜率和切线方程.【解答】解:f (x )=lnx 的导数为 f ′(x )= ,g (x )=ax 2﹣x 的导数为 g ′(x )=2ax ﹣1,设 P (x 0,y 0),则 lnx 0=ax 02﹣x 0①,f ′(x 0)=g ′(x 0),即联立①②消 a 得,lnx 0==2ax 0﹣1,化简得 1=2ax 02﹣x 0②,,令φ(x )=lnx ﹣,φ′(x )= + >0,易知φ(x )在(0,+∞)上单调递增,又φ(1)=0, 所以φ(x )=lnx ﹣有唯一解 1,即 x 0=1,则 y 0=f (1)=0,a =1. 故 P (1,0),切线的斜率为 1,切线的方程为 y =x ﹣1.故答案为:y=x﹣1.【点评】本题考查利用导数研究函数的单调性及导数的几何意义,考查学生灵活运用所学知识分析问题解决问题的能力,属于中档题.16.(5分)在平面直角坐标系xOy中,对曲线C上任意一点P,P到直线x+1=0的距离与该点到点O的距离之和等于2,则曲线C与y轴的交点坐标是(0,±1);设点A(﹣,0),则|PO|+|PA|的最小值为.【分析】设P(x,y),P到直线x+1=0的距离与该点到点O的距离之和等于2,求出P的轨迹方程为抛物线,根据抛物线的性质,求出曲线C与y轴的交点坐标和|PO|+|PA|的最小值.【解答】解:设P(x,y),P到直线x+1=0的距离与该点到点O的距离之和等于2,则|x+1|=,化简得y2=2x+1,令x=0,y=1,故曲线C与y轴的交点为(0,1),(0,﹣1),A(﹣,0),根据题意,当O,P,A三点共线时,则|PO|+|PA|的最小,最小值长等于|OA|=,故答案为:(0,±1);.【点评】考查直线与抛物线的综合,求曲线的轨迹方程,中档题.三、解答题:本大题共5小题,共70分,解答须写出必要的文字说明、证明过程或演算步骤.17.(12分)绿水青山就是金山银山.近年来,祖国各地依托本地自然资源,打造旅游产业,旅游业正蓬勃发展.景区与游客都应树立尊重自然、顺应自然、保护自然的生态文明理念,合力使旅游市场走上规范有序且可持续的发展轨道.某景区有一个自愿消费的项目:在参观某特色景点入口处会为每位游客拍一张与景点的合影,参观后,在景点出口处会将刚拍下的照片打印出来,游客可自由选择是否带走照片,若带走照片则需支付20元,没有被带走的照片会收集起来统一销毁.该项目运营一段时间后,统计出平均只有三成的游客会选择带走照片.为改善运营状况,该项目组就照片收费与游客消费意愿关系作了市场调研,发现收费与消费意愿有较强的线性相关性,并统计出在原有的基础上,价格每下调1元,游客选择带走照片的可能性平均增加0.05,假设平均每天约有5000人参观该特色景点,每张照片的综合成本为5元,假设每个游客是否购买照片相互独立.(1)若调整为支付10元就可带走照片,该项目每天的平均利润比调整前多还是少?(2)要使每天的平均利润达到最大值,应如何定价?【分析】(1)当收费为20元时,照片被带走的可能性为0.3,不被带走的概率为0.7,设每个游客的利润为Y 1元,则Y1是随机变量,求出5000个游客的平均利润为5000元,当收费为10元时,照片被带走的可能性为0.3+0.05×10=0.8,不被带走的概率为0.2,设每个游客的利润为Y2,则Y2是随机变量,求出5000个游客的平均利润为15000元,由此能求出该项目每天的平均利润比调整前多10000元.(2)设降价x元,则0≤x<15,照片被带走的可能性为0.3+0.05x,不被带走的可能性为0.7﹣0.05x,设每个游客的利润为Y元,则Y是随机变量,求出其分布列,从而E(Y)=(15﹣x)×(0.3+0.05x)﹣5×(0.7﹣0.05x)=0.05[69﹣(x﹣7)2],由此求出当定价为13元时,日平均利润取最大值为17250元.【解答】解:(1)当收费为20元时,照片被带走的可能性为0.3,不被带走的概率为0.7,设每个游客的利润为Y1元,则Y1是随机变量,其分布列为:Y115﹣5P0.30.7E(Y1)=15×0.3﹣5×0.7=1(元),则5000个游客的平均利润为5000元,当收费为10元时,照片被带走的可能性为0.3+0.05×10=0.8,不被带走的概率为0.2,设每个游客的利润为Y2,则Y2是随机变量,其分布列为:Y25﹣5P0.80.2E(Y2)=5×0.8﹣5×0.2=3(元),则5000个游客的平均利润为5000×3=15000(元),该项目每天的平均利润比调整前多10000元.(2)设降价x元,则0≤x<15,照片被带走的可能性为0.3+0.05x,不被带走的可能性为0.7﹣0.05x,设每个游客的利润为Y元,则Y是随机变量,其分布列为:=Y P15﹣x ﹣5 0.3+0.05x 0.7﹣0.05xE (Y )=(15﹣x )×(0.3+0.05x )﹣5×(0.7﹣0.05x )=0.05[69﹣(x ﹣7)2], 当 x =7 时,E (Y )有最大值 3.45 元,∴当定价为 13 元时,日平均利润取最大值为 5000×3.45=17250 元.【点评】本题考查离散型随机变量的分布列和数学期望的求法,考查二项分布等基础知识,考查运算求解能 力,是中档题.18.(12 分)在△ABC 中,内角 A ,B ,C 的对边分别为 a ,b ,c ,已知 a sin B =b sin (A ﹣(1)求 A ;(2)D 是线段 BC 上的点,若 AD =BD =2,△C D =3,求 ADC 的面积. ).【分析】(1)由正弦定理,三角函数恒等变换的应用化简已知等式可得tan A =﹣ 可求 A 的值.(2)设∠B =θ, ,由题意可得∠BAD =θ,∠ADC =2θ,∠DAC =,结合范围 A ∈(0,π)﹣θ,∠ACD = ﹣θ,在△ADC 中,由正弦定理,三角函数恒等变换的应用可求 sinθ=cosθ,可求 sinθ,cosθ,利用二倍角的正弦函数公式可求 sin2θ,进而根据三角形的面积公式可求 △S ADC的值.【解答】解:(1)由正弦定理可得 a sin B =b sin A ,则有 b sin A =b ( sin A ﹣可得 tan A =﹣ , 因为 A ∈(0,π),所以 A = .(2)设∠B =θ,cos A ),化简可得 sin A =﹣ cos A ,,由题意可得∠BAD =θ,∠ADC =2θ,∠DAC = ﹣θ,∠ACD = ﹣θ,在△ADC 中,,则 = ,所以= ,可得 sinθ= cosθ,又因为 sin 2θ+cos 2θ=1,可得 sinθ=,cosθ= ,则 sin2θ=2sinθcosθ= ,所以 △S A DC sin∠ADC = = .【点评】本题主要考查了正弦定理,三角函数恒等变换的应用,三角形的面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.19.(12 分)已知椭圆 C :+=1(a >b >0)的离心率为 ,点 A (1, )在椭圆 C 上,直线 l 1 过椭圆 C的有交点与上顶点,动直线 l 2:y =kx 与椭圆 C 交于 M 、N 两点,交 l 1 于 P 点.(1)求椭圆 C 的方程;(2)已知 O 为坐标原点,若点 P 满足|OP |= |MN |,求此时|MN |的长度.【分析】(1)由离心率及过的点和 a ,b ,c 之间的关系求出椭圆的方程;(2)直线 l 2 的方程与椭圆联立求出点 M 的坐标,由|OP |= |MN |得 P 点坐标,P 的直线 l 1 上求出 k 值,进而求出 MN |的值.【解答】解:(1)由题意得:e==,+=1,b2=a2﹣c2,解得:a2=4,b2=3,所以椭圆的方程:=1;(2)由题意直线l2的方程:y=kx,代入椭圆中整理:(3+4k2)x2=12,解得x=,令M的坐标(,k∵|OP|=|MN|,由对称性可知,点P为OM的中点.)故P的坐标(,),由P在直线l1:所以x+y﹣+=0,﹣=0,解得:k=0或k=所以|OM|=2,或所以|MN|的长度为4或,故M的坐标为(2,0),或(,,.),【点评】考查直线与椭圆的综合,属于中难题.20.(12分)如图,三棱锥P﹣ABC中,平面PAB⊥平面ABC,PA=PB,∠APB=∠ACB=90°,点E,F分别是棱AB,PB的中点,点G是△BCE的重心.(1)证明:GF∥平面PAC;(2)若GF与平面ABC所成的角为60°,求二面角B﹣AP﹣C的余弦值.【分析】(1)连结EF,连结EG并延长,交BC于点D,由点D是BC的中点,推导出DE∥AC,EF∥AP,从而DE∥平面PAC,EF∥平面PAC,进而平面EFG∥平面PAC,由此能证明GF∥平面PAC.(2)连结PE,连结CG并延长交BE于点O,则O为BE的中点,连结OF,则OF∥PE,以O为原点,OC为x 轴,OB为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣AP﹣C的余弦值.【解答】解:(1)证明:连结EF,连结EG并延长,交BC于点D,由点D是BC的中点,∴D,E,F分别是棱CB,AB,PB的中点,∴DE∥AC,EF∥AP,∵DE,EF平面PAC,AC,AP⊂平面PAC,∴DE∥平面PAC,EF∥平面PAC,∵DE,EF⊂平面EFG,DE∩EF=E,∴平面EFG∥平面PAC,∵GF⊂平面EFG,∴GF∥平面PAC.(2)解:连结PE,∵PA=PB,E是AB的中点,∴PE⊥AB,∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PE⊂平面PAB,∴PE⊥平面ABC,连结CG并延长交BE于点O,则O为BE的中点,连结OF,则OF∥PE,∴OF⊥平面ABC,∴∠FGO是GF与平面ABC所成角,∴∠FGO=60°,在Rt△FGO中,设GF=2,则OG=1,OF=,∴OC=3,PE=2,∴AB=4,CE=2,OE=,∴OE2+OC2=CE2,∴OC⊥AB,以O为原点,OC为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,则A(0,﹣3,0),C(3,0,0),P(0,﹣,2),=(3,3,0),=(0,2),设平面PAC的一个法向量=(x,y,z),则,取z=1,得=(),平面PAB的法向量=(1,0,0),设二面角B﹣AP﹣C的平面角为θ,则cosθ===,∴二面角B﹣AP﹣C的余弦值为.【点评】本题考查线面平行的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.21.(12分)已知函数f(x)=1+x﹣2sin x,x>0.(1)求f(x)的最小值;(2)证明:f(x)>e﹣2x.【分析】(1)求导可知时f(x)单减,时f(x)单增,进而求得最小值;(2)即证x>0时,g(x)=(1+x﹣2sin x)e2x>1,利用导数容易得证.【解答】解:(1)f′(x)=1﹣2cos x,令f′(x)=0,得,故在区间[0,π]上,f′(x)的唯一零点是,当时,f′(x)<0,f(x)单调递减;当时,f′(x)>0,f(x)单调递增,故在区间[0,π]上,f(x)的极小值为,当x>π时,,∴f(x)的最小值为;(2)要证x>0时,f(x)>e﹣2x,即证x>0时,g(x)=(1+x﹣2sin x)e2x>1,g′(x)=2(1+x﹣2sin x)e2x+(1﹣2cos x)e2x=(3+2x﹣4sin x﹣2cos x)e2x,令h(x)=x﹣sin x,x>0,则h′(x)=1﹣cos x≥0,即h(x)是(0,+∞)上的增函数,∴h(x)>h(0)=0,即x>sin x,,∴3+2x﹣4sin x﹣2cos x>3+2sin x﹣4sin x﹣2cos x=3﹣2(sin x+cos x)=∴g′(x)=(3+2x﹣4sin x﹣2cos x)e2x>0,( 即 g (x )是(0,+∞)上的增函数,g (x )>g (0)=1,故当 x >0 时,f (x )>e ﹣2x ,即得证.【点评】本题考查利用导数研究函数的最值及证明不等式,考查推理论证及运算能力,属于中档题.请考生在第 22,23 题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清楚题号.[选修 4-4: 坐标系与参数方程选讲]22.(10 分)在直角坐标系 xOy 中,曲线 C 的参数方程为(m 为参数).(1)写出曲线 C 的普通方程,并说明它表示什么曲线;(2)已知倾斜角互补的两条直线 l 1,l 2,其中 l 1 与曲线 C 交于 A ,B 两点,l 2 与 C 交于 M ,N 两点,l 1 与 l 2 交于点 P (x 0,y 0),求证:|PA |•|PB |=|PM |•|PN |.【分析】(1)由 y =4m ,得 m = ,代入 x =4m 2,求出 C 的普通方程为 y 2=4x ,表示开口向右,焦点为 F (1,0)的抛物线.(2)设直线 l 1 的倾斜角为α,直线 l 2 的倾斜角为π﹣α,直线 l 1 的参数方程为, t 为参数), 与 y 2=4x 联立,得 t 2sin 2α+(2y 0sinα﹣4cosα)t +y 02﹣4x 0=0,由此能证明|PA |•|PB |=|PM |•|PN |.【解答】解:(1)解:由 y =4m ,得 m = ,代入 x =4m 2,得 y 2=4x ,∴曲线 C 的普通方程为 y 2=4x ,∴C 的普通方程为 y 2=4x ,表示开口向右,焦点为 F (1,0)的抛物线.(2)证明:设直线 l 1 的倾斜角为α,直线 l 2 的倾斜角为π﹣α,∴直线 l 1 的参数方程为,(t 为参数),与 y 2=4x 联立,得 t 2sin 2α+(2y 0sinα﹣4cosα)t +y 02﹣4x 0=0,设方程的两个解为 t 1,t 2,则 t 1t 2=,∴|PA |•|PB |=|t 1|•|t 2|=||,|PM |•|PN |=||=| |,∴|PA |•|PB |=|PM |•|PN |.【点评】本题考查曲线方程的求法,考查两组线段乘积相等的证明,考查直角坐标方程、极坐标方程、参数 方程的互化等基础知识,考查运算求解能力,是中档题.[选修 4-5:不等式选讲]23.已知函数 f (x )=|x ﹣a |+|x ﹣1|.(1)若 f (a )<2,求 a 的取值范围;(2)当 x ∈[a ,a +k ]时,函数 f (x )的值域为[1,3],求 k 的值.【分析】(1)f (a )=|a ﹣1|<2,即可得 a 的取值范围是(﹣1,3);(2)对 a 分类讨论,由单调性即可得 f (x )的单调性.【解答】解:(1)f (a )=|a ﹣1|<2,得﹣2<a ﹣1<2.即﹣1<a <3,所以 a 的取值范围是(﹣1,3).(2)当 a ≥1 时,函数 f (x )在区间[a ,a +k ]上单调递增.则[f (x )]min =f (a )=a ﹣1=1,得 a =2,[f (x )]max =f (a +k )=a +2k ﹣1=3,得 k =1.当 a <1 时,f (x )=则[f (x )]min =f (a )=1﹣a =1,得 a =0,[f(x)]max f(a+k)=a+2k﹣1=3,得k=2.=综上所述,k的值是1或2.【点评】本题考查了绝对值不等式,属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年3月南海区2020届高三年级综合能力测试理科数学一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集为R ,集合122(1),{|20}A x y x B x x x -⎧⎫⎪⎪==-=-<⎨⎬⎪⎪⎩⎭,则()A B =R I ð( )A .(0,2)B .(1,2]C .[0,1]D .(0,1]1.答案:D解析:12(1){|1},{|1}1A x y x x y x x A x x x -⎧⎫⎧⎪⎪==-===>∴=⎨⎬⎨⎬-⎪⎪⎩⎭⎩⎭R ≤ð, 2{|20}{|(2)0}{|02}B x x x x x x x x =-<=-<=<<,()(0,1]A B ∴=R I ð.2.复数满足48i z z +=+,则复数z 在复平面内所对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.答案:B解析:设i (,)z a b a b =+∈R ,则22i 48i z z a b a b +=+++=+,2264,68i 88a a ab z b b ⎧=-⎧⎪++=∴⇒∴=-+⎨⎨==⎩⎪⎩,所以复数z 在复平面内所对应的点在第二象限.3.已知等差数列{}n a 的前n 项和为n S ,且282,10a a =-=,则9S =( ) A .45 B .42C .25D .363.答案:D解析:192899()9()9(210)36222a a a a S ++⨯-+====. 4.函数x xxy e e-=+的图象大致为( )4.答案:A 解析:设()x x x f x e e -=+,则()()x xxf x f x e e ---==-+,所以函数()f x 是奇函数,其图象关于原点对称,排除B ,C ,且当x →+∞时,()0x xxf x e e -=→+,排除D ,选A .5.音乐,是用声音来展现美,给人以听觉上的享受,熔铸人们的美学趣味.著名数学家傅立叶研究了乐声的本质,他证明了所有的乐声都能用数学表达式来描述,它们是一些形如sin a bx 的简单正弦函数的和,其中频率最低的一项是基本音,其余的为泛音.由乐声的数学表达式可知,所有泛音的频率都是基本音频率的整数倍,称为基本音的谐波.下列函数中不能与函数0.06sin180000y t =构成乐音的是( )A .0.02sin 360000y t =B .0.03sin180000y t =C .0.02sin181800y t =D .0.05sin 540000y t =5.答案:C解析:由12f T ωπ==,可知若12()f nf n *=∈N ,则必有12()n n ωω*=∈N ,故选C . 6.已知,a b rr 为非零向量,“22a b b a =r r r r ”为“a a b b =r r r r ”的( )A .充分不必要条件B .充分必要条件C .必要不充分条件D .既不充分也不必要条件6.答案:B解析:若22a b b a =r r r r 成立,则22a b b a =r r r r ,则向量a r 与b r 的方向相同,且22a b b a =r r r r ,从而a b =r r , 所以a b =r r ;若a a b b =r r r r ,则向量a r 与b r的方向相同,且22a b =r r ,从而a b =r r ,所以a b =r r .所以“22a b b a =r r r r”为“a a b b =r r r r ”的充分必要条件.7.把函数2()sin f x x =的图象向右平移12π个单位,得到函数()g x 的图象.给出下列四个命题 ①()g x 的值域为(0,1]②()g x 的一个对称轴是12x π=③()g x 的一个对称中心是1,32π⎛⎫⎪⎝⎭④()g x 存在两条互相垂直的切线其中正确的命题个数是( ) A .1 B .2 C .3 D .47.答案:C解析:2121cos 21cos 21112()sin ()cos 222262x x f x x g x x πππ⎛⎫-- ⎪-⎛⎫⎝⎭==−−−−−−→==--+ ⎪⎝⎭向右平移个单位, cos 2[1,1]6x π⎛⎫-∈- ⎪⎝⎭Q ,()g x ∴的值域为[0,1],①错误;当12x π=时,206x π-=,所以12x π=是函数()g x 的一条对称轴,②正确;当3x π=时,262x ππ-=,所以()g x 的一个对称中心是1,32π⎛⎫⎪⎝⎭,③正确; ()sin 2[1,1]6g x x π⎛⎫'=-∈- ⎪⎝⎭,则121212,,()1,()1,()()1x x g x g x g x g x ''''∃∈=-=⋅=-R ,则()g x 在1x x =和2x x =处的切线互相垂直,④正确.8.窗花是贴在窗纸或窗户玻璃上的剪纸,是中国古老的传统民间艺术之一,它历史悠久,风格独特,神兽人们喜爱.右图即是一副窗花,是把一个边长为12的大正方形在四个角处都剪去边长为1的小正方形后剩余的部分,然后在剩余部分中的四个角处再剪出边长全为1部随机取一个点,则该点不落在任何一个小正方形内的概率是( )A .37B .47 C .57D .678.答案:D解析:窗花的面积为21241140-⨯=,其中小正方形的面积为5420⨯=, 所以所求概率1402061407P -==.9.已知三棱锥,2,1,P ABC AC BC AC BC -==⊥且2,PA PB PB =⊥平面ABC ,其外接球体积为( ) A .43πB .4πC .323πD .3π9.答案:A 解析:223AB AC BC =+PB h =,则由2PA PB =,可得232h h +=,解得1h =,可将三棱锥P ABC -还原成如图所示的长方体,则三棱锥P ABC -的外接球即为长方体的外接球,设外接球的半径为R ,则22221(2)12,1R R =++==,所以外接球的体积34433V R ππ==. AB 123h10.一个盒子里有4个分别标有号码为1,2,3,4的小球,每次取出一个,记下它的标号后再放回盒子中,共取3次,则取得小球标号最大值是4的取法有( ) A .17种 B .27种 C .37种 D .47种10.答案:C解析:所有可能的情况有3464=种,其中最大值不是4的情况有3327=种,所以取得小球标号最大值是4的取法有642737-=种.11.已知双曲线2222:1(0)x y M b a a b-=>>的焦距为2c ,若M 的渐近线上存在点T ,使得经过点T 所作的圆222()x c y a -+=的两条切线互相垂直,则双曲线M 的离心率的取值范围是( ) A .2] B .2,3]C .2,5]D .3,5]11.答案:B解析:b a >Q ,所以离心率212c b e a a ⎛⎫==+> ⎪⎝⎭222()x c y a -+=是以(,0)F c 为圆心,半径r a =的圆,要使得经过点T 所作的圆的两条切线互相垂直,必有2TF a =,而焦点(,0)F c 到双曲线渐近线的距离为b ,所以2TF a b =≥,即2b 213c b e a a ⎛⎫==+ ⎪⎝⎭,所以双曲线M 的离心率的取值范围是(2,3].bTFO1y x=交于点N ,3OM ON OP +=u u u u r u u u ru u u r ,,则曲线G 上的“水平黄金点”的个数为( ) A .0 B .1 C .2 D .3 12.答案:C解析:设(,3ln )M t t ,则1,N t t ⎛⎫⎪⎝⎭,所以21,ln 333OM ON t OP t t +⎛⎫==+ ⎪⎝⎭u u u u r u u u ru u u r ,依题意可得1ln 03t t +=,设1()ln 3g t t t =+,则221131()33t g t t t t -'=-=,当103t <<时,()0,()g t g t '<单调递减,当13t >时,()0,()g t g t '>单调递增,所以min 1()1ln 303g t g ⎛⎫==-< ⎪⎝⎭,且221120,(1)033e g g e ⎛⎫=-+>=> ⎪⎝⎭,1()ln 03g t t t∴=+=有两个不同的解,所以曲线G 上的“水平黄金点”的个数为2. 二、填空题:本题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13.抛物线24y x =上到其焦点F 距离为5的点有 个. 13.答案:2解析:设符合条件的点00(,)P x y ,则00015,4,4PF x x y =+=∴==±,所以符合条件的点有2个. 14.已知数列{}n a 的前n 项和为n S 且满足2n n S a +=-,则数列{}n a 的通项n a = .14.答案:112n -⎛⎫- ⎪⎝⎭解析:当1n =时,1111221S a a a +==-⇒=-,由2n n S a +=-,可知当2n ≥时,112n n S a --+=-,两式相减,得120n n a a --=,即11(2)2n n a a n -=≥,所以数列{}n a 是首项为1-,公比为12的等比数列,所以112n n a -⎛⎫=- ⎪⎝⎭.15.对任意正整数n ,函数32()27cos 1f n n n n n πλ=---,若(2)0f ≥,则λ的取值范围是 ;若不等式()0f n ≥恒成立,则λ的最大值为 . 15.答案:13,2⎛⎤-∞-⎥⎝⎦,132- 解析:由(2)1628210f λ=---≥,解得132λ-≤. 当n 为奇数时,cos 1n π=-,由32()2710f n n n n λ=+--≥,得2127n n nλ+-≤, 而函数21()27g n n n n=+-为单调递增函数,所以min ()(1)8g n g ==,所以8λ≤. 当n 为偶数时,cos 1n π=,由32()2710f n n n n λ=---≥,得2127n n nλ--≤,设21()27(2)h x x x x x =--≥,则212,()470x h x x x '∴=-+>Q ≥,()h x ∴单调递增,min 13()(2)2h x h ∴==-.所以132λ-≤,综上可知,若不等式()0f n ≥恒成立,则λ的最大值为132-.16.正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 是侧面11CDD C 上的动点,且1//B F 平面1A BE ,记1B 与F 的轨迹构成的平面为α.①F ∃,使得11B F CD ⊥;②直线1B F 与直线BC 所成角的正切值的取值范围是2142⎤⎥⎣⎦;③α与平面11CDD C 所成锐二面角的正切值为22④正方体1111ABCD A B C D -的各个侧面中,与α所成的锐二面角相等的侧面共四个. 其中正确命题的序号是 .(写出所有正确命题的序号)16.答案:①②③④解析:取CD 中点G ,连接EG ,则1//EG A B ,所以平面1A BE 即为平面1A BGE ,取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得111//,//B M BG B N A E ,从而平面1//B MN 平面1A BGE ,所以点F 的运动轨迹为线段MN ,平面1B MN 即为平面α.①取F 为MN 中点,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故①正确;②设正方体的棱长为2,当点F 为MN 中点时,直线1B F 与直线BC 所成角最小,此时122C F =, 111112tan 4C F C B F B C ∠==,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时111tan 2C B F ∠=,所以直线1B F 与直线BC 所成角的正切值的取值范围是2142⎤⎢⎥⎣⎦,②正确; ③取F 为MN 中点,则1111,,MN C F MN B F B FC ⊥⊥∴∠即为α与平面11CDD C 所成的锐二面角,11111tan 22B C B FC C F∠==,所以③正确; ④正方体1111ABCD A B C D -的各个侧面中,平面ABCD ,平面1111A B C D ,平面11BCC B ,平面11ADD A 与平面α所成的角相等,所以④正确.ABCDD 1A 1B 1C 1EGMNF三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(本小题满分12分) 在ABC △中,5,cos 43B C π∠==. (1)求cos A 的值;(2)点D 为边BC 上的动点(不与C 点重合),设AD DC λ=,求λ的取值范围. 17.解:(1)在ABC △,5cos 3C =,所以22sin 1cos 3C C =-=.…………………………1分 所以 cos cos cos sin sin cos cos 4444A C C C C πππππ⎛⎫⎛⎫=--=-+=- ⎪ ⎪⎝⎭⎝⎭222522103-==…………………………………………………………5分 (2)由(1)可知2210cos 0A -=<,所以2A π>.因为sin sin AD DC C DAC =∠,所以sin 2sin 3sin AD C DC DAC DACλ===∠∠.……………………8分 因为0DAC BAC <∠∠≤,所以 sin (0,1]DAC ∠∈.…………………………………………11分 所以2,3λ⎡⎫∈+∞⎪⎢⎣⎭.………………………………………………………………………………12分CAB D18.(本小题满分12分)在四棱锥P ABCD-中,1,//,,2AB PA AB CD AB CD PAD⊥=△是等边三角形,点M在棱PC上,平面PAD⊥平面ABCD.(1)求证:平面PCD⊥平面PAD;(2)若AB AD=,求直线AM与平面PBC所成角的正弦值的最大值;(3)设直线AM与平面PBD相交于点N,若AN PMAM PC=,求ANAM的值.18.解析:(1)证明:取AD中点为O,连接PO.PAD△是等边三角形,所以PO AD⊥.因为PAD ABCD⊥平面平面且相交于AD,所以PO⊥平面ABCD,所以PO DC⊥.因为//,AB CD AB PA⊥,所以CD PA⊥.因为PO PA P=I在平面PAD内,所以CD PAD⊥平面.所以PCD PAD⊥平面平面.…………3分(2)以O为原点,过O作AB的平行线OF,分别以OA, OF,OP分别为x轴,y轴,z轴建立空间直角坐标系.设2AB AD==,则(1,0,0)A,(1,2,0)B,(1,4,0)C-,3)P.…………5分因为M在棱PC上,可设[](1)(,43(1)),0,1OM t OP tOC t t t t=-+=--∈u u u u r u u u r u u u r,所以(1,43(1))AM t t t=---u u u u r.设平面PBC的法向量为(,,)n x y z=r,因为(2,2,0),(1,4,3)BC PC=-=-u u u r u u u r,PACDM所以220430x y x y z -+=⎧⎪⎨-+=⎪⎩ 令1x =,可得113x y z ⎧=⎪=⎨⎪=⎩,即3)n =r .设直线AM 与平面PBC 所成角为θ,所以2sin cos ,5(51)AM n AM n AM n t t θ⋅===-+u u u u r ru u u u r r u u u u r r . 可知当110t =时, sin θ219;…………8分(3)设2,AD DC m ==,则有3),(1,,0)P C m -,得(1,,3)PC m =-u u u r .设AN PMk AM PC==,那么,PM k PC AN k AM ==u u u u r u u u r u u u r u u u u r ,所以(,,3)PM k mk k =-u u u u r.所以(,3(1))M k mk k --. 因为(1,0,0),(1,3(1))A AM k mk k =---u u u u r所以.22,(,3(1))AN k AM AN k k mk k k ==---u u u r u u u u r u u u r因为所以.所以22(1,3(1))N k k mk k k --+-.又因为(1,0,0),1,,02m D B ⎛⎫- ⎪⎝⎭,所以22(2,3(1))DN k k mk k k =--+-u u u r .(1,0,3),2,,02m PD DB ⎛⎫=-= ⎪⎝⎭u u u r u u u r ,设平面PDB 的法向量为(,,)n x y z =r,有30202x z m x y ⎧-=⎪⎨+=⎪⎩3x =-令331x y m z ⎧=⎪⎪=⎨⎪=⎪⎩,即433,n ⎛⎫= ⎪ ⎪⎝⎭r …………10分 因为N 在平面PDB 内,所以DN n ⊥u u u r r .所以0DN n ⋅=u u u r r.所以22433(2)3(1)0k k mk k k --++-=.即2210k k +-=, 所以12k =或者1k =-(舍),即12AN AM =………………………………………………………12分PA BCDMxyz O F19.(本小题满分12分)某精密仪器生产车间每天生产n 个零件,质检员小张每天都会随机地从中抽取50个零件进行检查是否合格,若较多零件不合格,则需对其余所有零件进行检查.根据多年的生产数据和经验,这些零件的长度服从正态分布2(10,0.1)N (单位:微米m μ),且相互独立.若零件的长度d 满足9.710.3m d m μμ<<,则认为该零件是合格的,否则该零件不合格.(1)假设某一天小张抽查出不合格的零件数为X ,求(2)P X ≥及X 的数学期望EX ;(2)小张某天恰好从50个零件中检查出2个不合格的零件,若以此频率作为当天生产零件的不合格率.已知检查一个零件的成本为10元,而每个不合格零件流入市场带来的损失为260元.假设n 充分大,为了使损失尽量小,小张是否需要检查其余所有零件,试说明理由. 附:若随机变量ξ服从正态分布2(,)N μσ,则5049(33)0.9987,0.99870.9370,0.99870.00130.0012P μσξμσ-<<+==⨯=.19.解(1)1495050(2)1(1)(0)10.99870.00130.99870.003P X P X P X C =-=-==-⋅⋅-=≥,由于X 满足二项分布,故0.0013500.065EX =⨯= …………--5分(2)由题意可知不合格率为250,若不检查,损失的期望为252()2602020505E Y n n =⨯⨯-=-,若检查,成本为10n ,由于522()1020102055E Y n n n n -=--=-,当n 充分大时,2()102005E Y n n -=->所以为了使损失尽量小,小张需要检查其余所有零件. ……………………12分 20.(本小题满分12分)已知椭圆2222:1(0)x y M a b a b+=>>经过点(0,2)A -3.(1)求椭圆M 的方程;(2)经过点(0,1)E 且斜率存在的直线l 交椭圆于,Q N 两点,点B 与点Q 关于坐标原点对称.连接,AB AN .求证:存在实数λ,使得AN AB k k λ=成立.20.解:(1)由题意可知2b =,3c a =222a c b -=,得6,2a c == 所以椭圆M 的方程为22164x y +=;……………4分(2)证明:设直线l 的方程为为:1y kx =+,联立221164y kx x y =+⎧⎪⎨+=⎪⎩,消元可得:22(23)690k x kx ++-=,设1122(,),(,)Q x y N x y则有12122269,2323k x x x x k k +=-=-++……………-8分 因为121222,AQ AN y y k k x x ++==, 所以2222121212Q 1212223()92232A ANy y k x x k x x k k k k k x x x x +++++⋅=⋅==+--=-又因为点B 与点Q 关于原点对称,所以11(,)B x y --,即112AB y k x -+=-, 则有2111211224AQ ABy y y k k x x +-+-⋅=⋅=-,由点Q 在椭圆22:1x y C +=上,得2224y x -=, 所以23AQ AB k k ⋅=-,所以AN AB k k =所以存在实数3λ=,使AN k λ=(2)解法二:证明:设直线l 的方程为为:1y kx =+,联立221164y kx x y =+⎧⎪⎨+=⎪⎩,消元可得:22(23)690k x kx ++-=,设1122(,),(,)Q x y N x y ,则11(,)B x y --,则有12122269,2323k x x x x k k+=-=-++……………8分 121223x x k x x +∴=,12123()2x x kx x +=,222AN y k x +=,112AB y k x -=, 所以1212121121121221211221223()3(2)(3)393233()(2)(1)32AN ABx x x k y x kx x kx x x x x x x k x y x kx kx x x x x x +-++++======+---+-,所以存在实数3λ=,使AN AB k k λ=成立.………………12分 21.(本小题满分12分) 已知2()(0)kxf x kx e k -=+>(1)当12x >时,判断函数()f x 的极值点的个数; (2)记21()()ln 2g x f x x m x x ⎛⎫=+->⎪⎝⎭,若存在实数t ,使直线y t =与函数()g x 的图象交于不同的两点12(,),(,)A x t B x t ,求证:122m x x >. 21.解析:(1)当12x >时,'()(2)kxf x k x e -=-,(())(2)0kx f x k ke -''=+>,所以()f x '在1,2⎛⎫+∞ ⎪⎝⎭递增.所以21()(1)02kf x f k e -⎛⎫''>=-> ⎪⎝⎭.所以()f x 在1,2⎛⎫+∞ ⎪⎝⎭递增,所以函数()f x 没有极值点;…………………………………4分(2)22()()ln (1)ln kxg x f x x m x k x m x e -=+-=+-+,存在实数t ,使直线y t =与函数()g x 的图象交于不同的两点12(,),(,)A x t B x t ,即存在121,,2x x ⎛⎫∈+∞ ⎪⎝⎭且12x x <,使12()()g x g x =.……… 6分由12()()g x g x =可得:21222121(ln ln )(1)()()kx kx m x x k x x ee ---=+-+-,12x x <,由(1)可知21()()f x f x >,可得:212221()kx kx ee k x x --->--.所以222121(ln ln )m x x x x->-,即22212122ln x x m x x ->.……………………8分 下面证明222112212ln x x x x x x ->,只需证明:221221112ln x x x x x x ⎛⎫- ⎪⎝⎭>. 令211x s x =>,则证:212ln s s s ->,即12ln 0s s s -->.……………………………………10分 设1()2ln h s s s s=--,那么22(1)()0s h s s -'=>. 所以()(1)0h s h >=.所以122mx x >,即122m x x >.………12分 (二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所作的第一题计分. 22.【选修4—4:坐标系与参数方程】(本小题满分10分)已知曲线M 的参数方程为1cos 21sin 2x y αα⎧=⎪⎪⎨⎪=⎪⎩(α为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线N 的极坐标方程为22sin 2ρθ=-.(1)写出曲线M 的极坐标方程;(2)点A 是曲线N 上的一点,试判断点A 与曲线M 的位置关系. 22.解析:(1)曲线M 的极坐标方程是12ρ=.………………………………………4分 (2)当3π4θ=时,线段OA 取得最小长度为22332sin(2π)4=-⨯.…………………………6分因为曲线M 是以原点为圆心,半径为12的圆,所以 12OA >. 所以点A 与曲线M 的位置关系是点A 在曲线M 外.………10分 23.【选修4—5:不等式选讲】(本小题满分10分) 已知0,a b a c d >≥≥≥,且ab cd ≥.(1)请给出,,,a b c d 的一组值,使得2()a b c d ++≥成立; (2)证明不等式a b c d ++≥恒成立.23.解析:(1)2,1,1,1a b c d ====-.(答案不唯一)………………………………4分(2)证明:由题意可知,0a ≠. 因为a c d ≥≥,所以()()0a c a d --≥. 所以2()0a c d a cd -++≥,即2()a cd c d a ++≥.……-7分 因为0a b >≥,所以cd a c d a ++≥.因为ab cd ≥,所以 cdb a≥. 所以cda b a c d a+++≥≥.………………10分。
