北京市初二数学竞赛初赛试题(1992)
全国初中数学联赛试题-1992年

1992年全国初中数学联赛试题第一试一、选择题1.满足│a-b│+ab=1的非负整数对(a,b)的个数是( )A.1B.2C.3D.42.若x0是一元二次方程ax2+bx+c(a≠0)的根,则判别式△=b2-4ac 与平方式M=(2ax0+b)2的关系是( )A.△〉M B.△=M C.△〈M D.不确定3.若x2-13x+1=0,则x4+x-4的个位数字是( )A.1B.3C.5D.7─4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于√2,则这个多边形的边数必为( )A.7B.6C.5D.46.在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆。
若把圆周经过的所有小方格的圆内部分的面积之和记为S1,把圆周经过的所有S1小方格的圆外部分的面积之和记为S2,则─的整数部分是( )S2A.0B.1C.2D.38.设x1,x2,x3,...,x9均为正整数,且x1〈x2〈...〈x9,x1+x2+...+x9=220,则当x1+x2+...+x5的值最大时,x9-x1的最小值是( )A.8B.9C.10D.11二、填空题1.若一等腰三角形的底边上的高等于18cm,腰上的中线等于15cm,则这个等腰三角形的面积等于。
────────√1+x2+x4-√1+x42.若x≠0,则────────────的最大值是。
x3.在△ABC中,∠C=90°,∠A和∠B的平分线相交于P点,又PE⊥AB于E点,若BC=2,AC=3,则AE.EB=。
1 1 1 b 3 a 34.若a,b都是正实数,且─-─-──=0,则─+─=a b a+b a b第二试一、设等腰三角形的一腰与底边的长分别是方程x2-6x+a=0的两根,当这样的三角形只有一个时,试求a的取值范围。
三、某个信封上的两个邮政编吗M和N均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A:320651 B:105263 C:612305 D:316250已知编码A、B、C各恰有两个数字的位置与M和N相同,D恰有三个数字的位置与M和N相同,试求M和N。
数学竞赛试卷(初赛、决赛及答案)

2.下面五个图形中,有一个不是正方体的展开图:那么“不是的”图形的编号是 。
3.将60分成10个质数之和,要求最大的质数尽可能小,那么其中最大的质数是 。
4.34减去一个分数,513一个分数,两次计算结果相等,那么这个相等的结果是 。
5.右面残缺算式中已知三个“4”,那么补全后它的乘积是 。
6.有A 、B 两个整数,A 的各位数字之和为35,B 的各位数字之和为26,两数相加时进位三次,那么A+B 的各位数字之和是 。
7.苹果和梨各有若干只,如果5只苹果和3只梨装一袋,还多4只苹果,梨恰好装完;如果7只苹果和3只梨装一袋,苹果恰好装完,梨还多12只,那么苹果和梨共有______只。
8.甲班51人,乙班49人,某次考试两个班全体同学的平均成绩是81分,乙班的平均成绩要比甲班平均成绩高7分,那么乙班的平均成绩是______分。
9.在大于1000的整数中,找出所有被34除后商与余数相等的数,那么这些数的和是 。
10.高中学生的人数是初中学生的56,高中毕业生的人数是初中毕业生的1217,高、初中毕业生毕业后,高、初中留下的人数都是520人,那么高、初中毕业生共有 人。
11.如图,一个长方形的纸盒内,放着九个正方形的纸片,其中正方形A 和B 的边长分别为4和7,那么长方形(纸盒)的面积是 。
12.甲、乙两地相距100千米,张先骑摩托车从甲出发,1小时后李驾驶汽车从甲出发,两人同时到达乙地。
摩托车开始速度是50千米/d,时,中途减速为40千米/小时。
汽车速度是80千米/小时。
汽车曾在途中停驶10分钟,那么张驾驶的摩托车减速时在他出发后的_________小时。
。
3.下面五个图形中,有一个不是正方体的展开图:那么“不是的”图形的编号是_________。
4.34减去一个分数,513一个分数,两次计算结果相等,那么这个相等的结果是 。
5.规定:③=2×3×4,④=3×4×5,⑤=4×5×6,…,⑩=9×10×11,…如果,那么方框代表的数是________。
详解——1992全国初中数学联合竞赛试卷

1992全国初中数学联合竞赛试卷答案及详解第一试一、选择题1.(C) 由⎩⎨⎧==-01ab b a ⇒(1,0)(0,1). 又由⇒⎩⎨⎧==-1,0ab b a (1,1).∴共有3对.2.(B)设0x 是方程的根,则0020=++c bx ax .所以202022044)2(b abx x a b ax ++=+ac b c bx ax a 4)(42020-+++=ac b 42-=.3.(D)由01132-+-x x 知0≠x .所以131=+-x x ,167213222=-=+-x x .2167244-=+-x x ,从而42-+x x 的个位数字为9-2=7.4.(C)若满足条件的多边形的边数大于或等于6,则至少有一边所对的圆心角不大于60°.由余弦定理知该边长必不大于1;同理,若存在满足条件的四边形,则它至少有一边长不小于2.5.(B)设A 点的坐标为(11,y x ),C 点的坐标为(22,y x ),则k y x y x ==2211. ∴22211121212121S CD OD y x y x AB OB S =⋅===⋅=. 6.(B)据正方形的对称性,只需考虑它的41部分即可.记圆周经过的所有小方格的圆内部分的面积之和为1'S ,圆周经过的所有小方格的圆外部分的面积之和为2'S ,则841'-=πS ,π4152'-=S .∴ 44.256.44158444212'1'≈--==ππS S S S . 故21S S 的整数部分是1. 7.(B)8 (B )解:由题意:x1,x2,…,x9均为正整数得x9最小值为1∵当x1,x2,…,x8取到最小值时,x9取到最大值=220-(1+2+3+…+8)=220-36=184, ∴x9-x1的最大值为184-1=183, 又∵1+2+3+…+9=45,∴220-45=175,175除以9=19余4,在这种情况下:将4分配到九个数中,则只能在第六到九个上加,则最大的数必须加一以上,而第六到九同时加一则x9就大一了.∴x9-x1的最小值为9-1+1=9.故选B .二、填空题13 解:设Rt△ABC内切圆P的半径为r∴ FG是等腰三角形BFD顶角平分线,因而也是底边BD上的中线.即 BG=GD.所以BD=2BG=2DC.三、对于编码M,考虑编码A中恰有两个数位上的数字与M中相应数位上的数字相同.设这两位是x1,x2数位.由于B、C中该两数位上的数字均与A在这两数位上的数字不同,因此B,C中这两数位上的数字必与M中这两数位上的数字不同,于是B中与 M中数字相同的数位必异于x1,x2.不妨设为x3,x4;同理C中与 M中数字相同的数位只能是异于x1,x2,x3,x4的x5,x6两位.关于 N也有类似的结论.这就是说,在每个数位上,A,B,C分别在该数位上的数字中,必有一个与M在该数位上的数字相同;同样地,也必有一个与N在该数位上的数字相同.由此知,D中的6,0两数字必不是M,N在相应数位上的数字.于是D的3,1,2,5中只有一个数字与M在相应数位上的数字不同;与Ⅳ相比较也有类似的结果.(A)若3不对,则有610253,013256;(B)若1不对,则有360251,301256;(C)若2不对,则有312056,310652;(D)若5不对,则有310265,315206.经检验知:该信封上编码M,N或者同为610253,或者同为310265.或者一个是610253,另一个是310265.。
1992年全国初中数学竞赛试题及答案(修正版)

OAB CD x y1992年全国初中数学联合竞赛试题第一试一、选择题本题共有8个题,每小题都给出了(A),(B),(C),(D)四个结论,其中只有一个是正确的,请把正确结论的代表字母写在题后的圆括号内1.满足|a -b |+ab =1的非负整数(a ,b )的个数是()(A)1(B)2(C)3(D)42.若x 0是一元二次方程ax 2+bx +c =0(a ≠0)的根,则判别式δ=b 2-4ac 与平方式M =(2ax 0+b )2的关系是() (A)δ>M (B)δ=M (C)δ<M (D)不确定3.若x 2-13x +1=0,则x 4+x -4的个位数字是() (A)1(B)3(C)5(D)74.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为()(A)7(B)6(C)5(D)45.如图,正比例函数y =x 和y =ax (a >0)的图像与反比例函数y =(k >0)的图像分别相交于A 点和C 点,若Rt △AOB 和△COD 的面积 分别为S 1和S 2,则S 1与S 2的关系是()A B C D E F(A)S 1>S 2(B)S 1=S 2(C)S 1<S 2(D)不确定6.在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为S 1,把圆周经过的所有小方格的圆内部分的面积之和记为S 2,则21S S 的整数部分是()(A)0(B)1(C)2(D)37.如图,在等腰梯形ABCD 中,AB //CD ,AB =2CD ,∠A =60°,又E 是底边AB 上一点,且FE =FB =AC ,FA =AB ,则AE :EB 等于()(A)1:2(B)1:3(C)2:5(D)3:10 8.设x 1,x 2,x 3,……x 9均为正整数,且x 1<x 2<x 3<……<x 9,x 1+x 2+x 3+……+x 9=220则当x 1+x 2+x 3+x 4+x 5的值最大时,x 9-x 1的最小值是()(A)8(B)9(C)10(D)11二、填空题 1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________2.若x ≠0,则x x x x 44211+-++的最大值是__________.3.在△ABC 中,∠C =90°,∠A 和∠B 的平分线相交于P 点,又PE ⊥AB 于E 点,若BC =2,AC =3,则AE ?EB =.4.若a ,b 都是正实数,且0111=+--b a b a ,则=+33)()(ba ab .AB C D E第二试一、设等腰三角形的一腰与底边的长分别是方程x 2-6x +a =0的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在△ABC 中,AB =AC ,D 底边BC 上一点,E 是线段AD 上一点,且∠BED =2∠CED =∠A求证:BD =2CD三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250 已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同,D恰有三个数字的位置与M 和N 相同试求:M 和N 1992全国初中数学联合竞赛试卷答案第一试一.选择题1.(C)由⎩⎨⎧==-01ab b a ⇒(1,0)(0,1).又由⇒⎩⎨⎧==-1,0ab b a (1,1).∴共有3对.2.(B)设0x 是方程的根,则0020=++c bx ax .所以202022044)2(b abx x a b ax ++=+ac b 42-=.3.(D)由01132-+-x x 知0≠x .所以131=+-x x ,167213222=-=+-x x . 2167244-=+-x x ,从而42-+x x 的个位数字为9-2=7.4.(C)若满足条件的多边形的边数大于或等于6,则至少有一边所对的圆心角不大于60°.由余弦定理知该边长必不大于1;同理,若存在满足条件的四边形,则它至少有一边长不小于2. 5.(B)设A 点的坐标为(11,y x ),C 点的坐标为(22,y x ),则k y x y x ==2211. ∴22211121212121S CD OD y x y x AB OB S =⋅===⋅=.6.(B)据正方形的对称性,只需考虑它的41部分即可.记圆周经过的所有小方格的圆内部分的面积之和为1'S ,圆周经过的所有小方格的圆外部分的面积之和为2'S ,则841'-=πS ,π4152'-=S . ∴44.256.44158444212'1'≈--==ππS S S S .故21S S 的整数部分是1.7.(B)设1=CD ,则2==AB FA ,易证121==AB BC , 90=∠ABC ,3===AC FB FE . ∵△ABF ∽△FBE∴=,BE ==于是AE =,所以AE ∶EB =1∶38.(B )(1)先证x 1+x 2+x 3+x 4+x 5≤110,则x 5≥25从而x 6≥26,x 7≥27,x 8≥28,x 9≥29,于是x 1+x 2+x 3+……+x 9>220与假设矛盾.(2)若取x 1=20,x 2=21,x 3=22,x 4=23,x 5=24,则x 1+x 2+x 3+x 4+x 5=110.所以x 1+x 2+x 3+x 4+x 5当取得最大值时,x 1最大的值是20(3)若取x 6=26,x 7=27,x 8=28,x 9=29,则=110.所以x 1+x 2+x 3+x 4+x 5当取得最大值时,x 9最小的值是29因此x 9-x 1的最小值是29-20=9∴FG 是等腰三角形BFD 顶角平分线,因而也是底边BD 上的中线.即BG =GD .所以BD =2BG =2DC .三、对于编码M ,考虑编码A 中恰有两个数位上的数字与M 中相应数位上的数字相同.设这两位是x1,x2数位.由于B 、C 中该两数位上的数字均与A 在这两数位上的数字不同,因此B ,C中这两数位上的数字必与M中这两数位上的数字不同,于是B 中与M中数字相同的数位必异于x1,x2.不妨设为x3,x4;同理C中与M中数字相同的数位只能是异于x1,x2,x3,x4的x5,x6两位.关于N也有类似的结论.这就是说,在每个数位上,A,B,C分别在该数位上的数字中,必有一个与M在该数位上的数字相同;同样地,也必有一个与N在该数位上的数字相同.由此知,D中的6,0两数字必不是M,N在相应数位上的数字.于是D的3,1,2,5中只有一个数字与M在相应数位上的数字不同;与Ⅳ相比较也有类似的结果.(A)若3不对,则有610253,013256;(B)若1不对,则有360251,301256;(C)若2不对,则有312056,310652;(D)若5不对,则有310265,315206.经检验知:该信封上编码M,N或者同为610253,或者同为310265.或者一个是610253,另一个是310265.。
全国初中数学竞赛试题及答案(1992年)

1992年全国初中数学联合竞赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S =(C)21S S < (D)不确定 答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , F A=AB .则AE :EB 等于(A)1:2 (B)1:3(C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则xx x x 44211+-++的最大值是__________. 3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M和N均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A:320651 B:105263C:612305 D:316250已知编码A、B、C、D各恰有两个数字的位置与M和N相同.D恰有三个数字的位置与M和N相同.试求:M和N.。
1992年全国初中数学竞赛试题及答案(修正版)
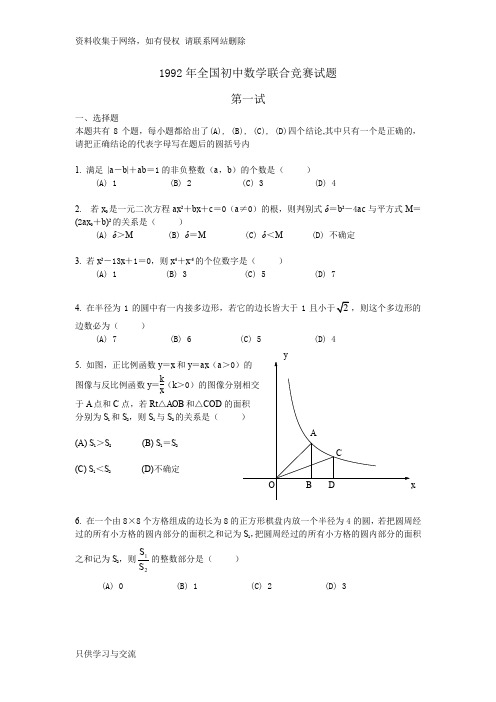
O AB C D x y1992年全国初中数学联合竞赛试题第一试一、选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的,请把正确结论的代表字母写在题后的圆括号内1. 满足 |a -b |+ab =1的非负整数(a ,b )的个数是( )(A) 1 (B) 2 (C) 3 (D) 42. 若x 0是一元二次方程ax 2+bx +c =0(a ≠0)的根,则判别式δ=b 2-4ac 与平方式M =(2ax 0+b )2的关系是( )(A) δ>M (B) δ=M (C) δ<M (D) 不确定3. 若x 2-13x +1=0,则x 4+x -4的个位数字是( )(A) 1 (B) 3 (C) 5 (D) 74. 在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为( )(A) 7 (B) 6 (C) 5 (D) 45. 如图,正比例函数y =x 和y =ax (a >0)的图像与反比例函数y =k x(k >0)的图像分别相交 于A 点和C 点,若Rt △AOB 和△COD 的面积分别为S 1和S 2,则S 1与S 2的关系是( )(A) S 1>S 2 (B) S 1=S 2(C) S 1<S 2 (D)不确定6. 在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为S 1,把圆周经过的所有小方格的圆内部分的面积之和记为S 2,则21S S 的整数部分是( ) (A) 0 (B) 1 (C) 2 (D) 3A B C D EF 7. 如图,在等腰梯形ABCD 中,AB //CD ,AB =2CD ,∠A =60°,又E 是底边AB 上一点,且FE =FB =AC ,F A =AB ,则AE :EB 等于( )(A) 1:2 (B) 1:3 (C) 2:5 (D) 3:108. 设x 1,x 2,x 3,…… x 9均为正整数,且x 1<x 2<x 3<……<x 9, x 1+x 2+x 3+……+x 9=220则当x 1+x 2+x 3+x 4+x 5的值最大时,x 9-x 1的最小值是( )(A) 8 (B) 9 (C) 10 (D) 11二、填空题1. 若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________2. 若x ≠0,则xx x x 44211+-++的最大值是__________.3. 在△ABC 中,∠C =90°,∠A 和∠B 的平分线相交于P 点,又PE ⊥AB 于E 点,若BC =2,AC =3,则AE •EB = .4. 若a ,b 都是正实数,且0111=+--b a b a ,则=+33)()(ba ab .A B C D E第二试一、设等腰三角形的一腰与底边的长分别是方程x 2-6x +a =0的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在△ABC 中,AB =AC ,D 底边BC 上一点,E 是线段AD 上一点,且∠BED =2∠CED =∠A求证:BD =2CD三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同,D 恰有三个数字的位置与M 和N 相同试求:M 和N1992全国初中数学联合竞赛试卷答案第一试一.选择题1.(C) 由⎩⎨⎧==-01ab b a ⇒(1,0)(0,1). 又由⇒⎩⎨⎧==-1,0ab b a (1,1).∴共有3对.2.(B)设0x 是方程的根,则0020=++c bx ax .所以202022044)2(b abx x a b ax ++=+ac b c bx ax a 4)(42020-+++=ac b 42-=.3.(D)由01132-+-x x 知0≠x .所以131=+-x x ,167213222=-=+-x x .2167244-=+-x x ,从而42-+x x 的个位数字为9-2=7.4.(C)若满足条件的多边形的边数大于或等于6,则至少有一边所对的圆心角不大于60°.由余弦定理知该边长必不大于1;同理,若存在满足条件的四边形,则它至少有一边长不小于2.5.(B)设A 点的坐标为(11,y x ),C 点的坐标为(22,y x ),则k y x y x ==2211. ∴22211121212121S CD OD y x y x AB OB S =⋅===⋅=.6.(B)据正方形的对称性,只需考虑它的41部分即可.记圆周经过的所有小方格的圆内部分的面积之和为1'S ,圆周经过的所有小方格的圆外部分的面积之和为2'S ,则841'-=πS ,π4152'-=S .∴ 44.256.44158444212'1'≈--==ππS S S S . 故21S S 的整数部分是1.7.(B)设1=CD ,则2==AB FA ,易证121==AB BC , 90=∠ABC , 3===AC FB FE .∵△ABF ∽△FBE∴AB BF =BF BE ,BE =BF 2AB =32于是AE =12,所以AE ∶EB =1∶38.(B )(1)先证x 1+x 2+x 3+x 4+x 5≤110,则x 5≥25从而x 6≥26,x 7≥27,x 8≥28,x 9≥29,于是x 1+x 2+x 3+……+x 9>220与假设矛盾.(2)若取x 1=20,x 2=21,x 3=22,x 4=23,x 5=24,则x 1+x 2+x 3+x 4+x 5=110.所以x 1+x 2+x 3+x 4+x 5当取得最大值时,x 1最大的值是20(3)若取x 6=26,x 7=27,x 8=28,x 9=29,则=110. 所以x 1+x 2+x 3+x 4+x 5当取得最大值时,x 9最小的值是29因此x 9-x 1的最小值是29-20=9∴ FG是等腰三角形BFD顶角平分线,因而也是底边BD上的中线.即BG=GD.所以BD=2BG=2DC.三、对于编码M,考虑编码A中恰有两个数位上的数字与M中相应数位上的数字相同.设这两位是x1,x2数位.由于B、C中该两数位上的数字均与A在这两数位上的数字不同,因此B,C中这两数位上的数字必与M中这两数位上的数字不同,于是B中与 M中数字相同的数位必异于x1,x2.不妨设为x3,x4;同理C中与 M中数字相同的数位只能是异于x1,x2,x3,x4的x5,x6两位.关于 N也有类似的结论.这就是说,在每个数位上,A,B,C分别在该数位上的数字中,必有一个与M在该数位上的数字相同;同样地,也必有一个与N在该数位上的数字相同.由此知,D中的6,0两数字必不是M,N在相应数位上的数字.于是D的3,1,2,5中只有一个数字与M在相应数位上的数字不同;与Ⅳ相比较也有类似的结果.(A)若3不对,则有610253,013256;(B)若1不对,则有360251,301256;(C)若2不对,则有312056,310652;(D)若5不对,则有310265,315206.经检验知:该信封上编码M,N或者同为610253,或者同为310265.或者一个是610253,另一个是310265.。
1992年全国初中数学竞赛试题及答案.doc

1992年全国初中数学联合竞赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S =(C)21S S < (D)不确定 答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , F A=AB .则AE :EB 等于(A)1:2 (B)1:3(C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则xx x x 44211+-++的最大值是__________. 3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M和N均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A:320651 B:105263C:612305 D:316250已知编码A、B、C、D各恰有两个数字的位置与M和N相同.D恰有三个数字的位置与M和N相同.试求:M和N.情感语录1.爱情合适就好,不要委屈将就,只要随意,彼此之间不要太大压力2.时间会把最正确的人带到你身边,在此之前,你要做的,是好好的照顾自己3.女人的眼泪是最无用的液体,但你让女人流泪说明你很无用4.总有一天,你会遇上那个人,陪你看日出,直到你的人生落幕5.最美的感动是我以为人去楼空的时候你依然在6.我莫名其妙的地笑了,原来只因为想到了你7.会离开的都是废品,能抢走的都是垃圾8.其实你不知道,如果可以,我愿意把整颗心都刻满你的名字9.女人谁不愿意青春永驻,但我愿意用来换一个疼我的你10.我们和好吧,我想和你拌嘴吵架,想闹小脾气,想为了你哭鼻子,我想你了11.如此情深,却难以启齿。
1991-1992全国初中数学联赛真题和详解

1991全国初中数学联合竞赛试卷一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内. 1.设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y是两两不同的实数,则22223yxy x y xy x +--+的值是( ) (A )3 ; (B )31; (C )2; (D )35. 2.如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是( )(A ) 10; (B )12; (C ) 16; (D )18. 3.方程012=--x x 的解是( )(A )251±; (B )251±-; (C )251±或251±-; (D )251±-±.4.已知:)19911991(2111n nx --=(n 是自然数).那么n x x )1(2+-,的值是( )(A)11991-; (B)11991--; (C)1991)1(n -; (D)11991)1(--n .5.若M n1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M( )(A)能被2整除,但不能被3整除;(B)能被3整除,但不能被2整除; (C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除.6.若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是( ) (A)1-;(B)5-;(C)0;(D)1.7.如图,正方形OPQR 内接于△ABC .已知△AOR 、△BOP 和△CRQ的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是( )(A)2;(B)3;(C)2 ;(D)3.11=S 3S =132=S8.在锐角△ABC 中,1=AC ,c AB =,60=∠A ,△ABC 的外接圆半径R ≤1,则( )(A)21< c < 2 ; (B)0< c ≤21; (C )c > 2; ( D )c = 2.二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果△BEG 的面积是1,则平行四边形ABCD 的面积是 .2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+acb 32 . 3.设m ,n ,p ,q 为非负数,且对一切x >0,qpnm x x x x )1(1)1(+=-+恒成立,则=++q p n m 22)2( .4.四边形ABCD 中,∠ ABC135=,∠BCD120=,AB 6=,BC 35-=,CD = 6,则AD = .三、解答题一、实数x 与y ,使得x + y , x - y , x y ,yx 四个数中的三个有相同的数值,求出所有具有这样性质的数对(x , y ).二、△ABC 中,AB <AC <BC ,D 点在BC 上,E 点在BA 的延长线上,且BD =BE =AC ,△BDE 的外接圆与△ABC 的外接圆交于F 点(如图).求证:BF =AF +CF三、将正方形ABCD 分割为 2n 个相等的小方格(n 是自然数),把相对的顶点A ,C 染成红色,把B ,D 染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.120135答案 1.(B )据算术根性质,由右端知y <a <x ,又由左端知a ≥0且a ≤0,故a =0. 由此得x=-y ,代入所求式算得值为312.(C )由平行截割定理,有①②①+②,得∴3.(D ) 设0x 是方程的解,则—0x 也是方程的解,排除(A )、(B );(D )的两值必是方程的解,否则方程的解也不是(C ). 将)51(21-代入方程,左边≠0,排除(C ). 4.(D ).(所以 原式, 112112221991)1()1991)19911991(21)199121991(4111-----=-=⎥⎦⎤⎢⎣⎡+=+-+=+n n nn n n n x5.(A )在1³2³3³…³100的质因数分解中,2的因子有所以,P P 21232100321484897⨯=⨯⨯=⨯⨯⨯⨯ ,其中2不整除P ,3不整除P ,因而M =2P .6.(B ) (a +b )+(c +d )=c +a , ∴b =-d .代入 b +c =d 得c =2d ,a =c +d =3d ,故a +b +c +d =2d +3d =5d =-5b ≤-5 (∵b ≥1). 故 a =-3,b =1,c =-2,d =-1. 7.(C ) 设正方形OPRQ 的边长为x ,即OP =PQ =QR =OR = x .作△ABC 的高AD ,交OR 于F ,在△AOR 中,xOR S AF 221==.如图.8.(A )作CD ⊥AB ,因△ABC 是锐角三角形,故D 在AB 内, 从而c = AB >AD = AC cos A = cos A =21. 又由正弦定理,得c = AB = 2R sin C <2R ≤2,所以21<c <2. 二、填空题1.12 由△BEG ∽△DAG ,得DG ∶GB =AD ∶BE =2∶1, ∴ DB =3GB .连接DE ,则2.6 设甲将a 看为a ′,由韦达定理得.于是 . , 438'6'-===-c b a ca b由于一次项系数b 的符号不改变判别式的值,因此,乙只能是看错a 或c 的符号.于是a ’ .4=ac由①②得3.9.-,即,则有再取 . 为奇数,因此 由于.,则有恒成立,取对一切由于q n n q n m p p m qpn m x m p x x xx x x -==-===-≠=-=>+=-+2232112321,012,0221210)1(1)1(若n >q ,则上式左边为奇数,右边为偶数,矛盾.若n <q ,则上式左边为整数,右边为真分数,矛盾. 所以,只能是n =q =1.于是93)2(222==++qp n m .4.192作AE ∥BC ,交CD 于E ,自B ,C 分别作AE 的垂直线BF 与CG ,F ,G 分别为垂足(如图).BCGF 为矩形,△AFB 为等腰直角三角形,32===AB AF BF ..,,所以 .2165)1610(21542222321==+=+++=+++=x x x xx x S S S S S OPRQ . .所以6126323=+-=+-=ac b ba1234222=⨯=⨯==E E ABCD S S S S在Rt △CEG 中,三、解答题 一.由于yx有意义,所以y ≠0,从而x + y ≠x -y . 因此x y =yx,即x (2y -1) = 0. 所以x = 0或y = ±1. (1)若x = 0,则由x y = x + y ,或x y = x -y ,得y = 0,这样yx无意义; (2)若y = 1,则由x y = x + y 得x = x +1, 或由x y = x -y 得x = x -1,都导致矛盾; (3)若y = -1,则由x y = x + y 得x =21, 由x y = x -y 得x =21-, 所以符合要求的数对只有 )121()121(---, 和 ,. 二、证法1 延长AF 到M ,使FM =CF .连CM 、DF ,在△EBD 与△FCM 中,由于BE =BD ,FM =CF ,因此△EBD 、△FCM 都是等腰三角形. ∵ ∠EBD =∠MFC , ∴ ∠BED =∠CMF , 又 ∠BED =∠BFD , ∴ ∠CMF =∠BFD , 在△BFD 与 △AMC 中,∠2=∠1,∠BFD =∠CMF ,BD =AC , ∴ △BFD ≌△AMC . ∴ BF =AM =AF +FM . 又∵ FM =CF , ∴ BF =AF +CF . 证法2 如图,连EF 、DF ∵ ∠1=∠2, ∠2=∠3, ∴ ∠1=∠3, ∵ ∠4=∠5, ∠5=∠6, ∴ ∠4=∠6.∴ △AFC ∽△EFD ..=== .== ==所以 .==,=,= 知=,由= 426613533521330--+-++-︒∠CE CD ED GE FG AF AE BC FG CE GE CGGCE .所以 .中应用余弦定理,有又 1927676241636120cos 2120222===++=︒⋅-+=︒=∠=∠AD ED AE ED AE AD BCD AED ²于是k CFDFAC DE AF EF ===, 即EF =k ²AF ,DE =k ²AC ,DF =k ²CF .由托勒密定理,知BF ²DE =BD ²EF +BE ²DF , 即BF ²k ²AC =BD ²k ²AF +BE ²k ²CF . 但是AC =BE =BD ≠0, 所以BF =AF +CF .一、证法1 用数代表颜色,将红色记为0,蓝色记为1,再将小方格编号,记为1,2,3,…,2n .又记第i 个小方格四个顶点数字之和为i A ,若恰有三个顶点同色,则i A =1或3为奇数,否则i A 为偶数.在221n A A A +++ 中,有如下事实:对正方形内部的交点,各加了4次; 原正方形边上非端点的交点,各加了2次(含两个0,两个1).因此221n A A A +++ =4(内部交点相应的数之和)+2³(边上非端点的交点相应的数之和)+2必为偶数.于是,在2,,,21n A A A 中必有偶数个奇数,这就是说,恰有三个顶点同色的小方格必有偶数个.证法2 用数代表颜色,红色记为l ,蓝色记为-1,将小方格编号,记为l ,2,…,2n . 记第 i 个小方格四顶点数字之乘积为i A ,若恰有三顶点同色,则1,1=-=i i A A 否则. 现在考虑乘积221n A A A ⨯⨯.对正方形内部交点,各点相应的数重复出现4次;A ,B ,C ,D 边上的不是端点的交点相应的数各出现2次;A ,B ,C ,D 四点相应的数的乘积为1³1³(-1)³(-1)=1.于是 221n A A A ⨯⨯=1.因此,221n A A A ⨯⨯中-1的个数必为偶数,即恰有三顶点同色的小方格必有偶数个. 证法3 考虑染了色之后,改变一个交点的染色方式,这时以此点为顶点的小方格,要么由三顶点同色变为非三顶点同色,要么由非三顶点同色变成三顶点同色.注意:除A ,B ,C ,D 之外,每一交点必是偶数个小方格的顶点,因此,改变一个交点的染色并不改变三顶点同色小方格数目的奇偶性. 当n =l 时,结论显然成立.当n >1时,每次改变一个交点的染色,最终总可以使B ,D 之外的点皆为红色,这时,三顶点同色的小方格只有两个,为偶数.因此,任意染色之下,三顶点同色的小方格有偶数个.1992年全国初中数学联赛试题一.选择题1.满足1=+-ab b a 的非负整数),(b a 的个数是( ) (A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是( )(A)∆>M (B)∆=M (C)∆>M ; (D)不确定. 3.若01132=+-x x ,则44-+x x 的个位数字是( ) (A)1; (B)3; (C)5; (D)7.4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为( )(A)7; (B)6; (C)5; (D)4.5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xky 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是( ) (A)21S S > (B)21S S = (C)21S S < (D)不确定6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是( )(A)0; (B)1; (C)2; (D)3.7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD , ︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , F A=AB .则AE :EB 等于( )(A)1:2 (B)1:3 (C)2:5 (D)3:108.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x , 则当54321x x x x x ++++的值最大时,19x x -的最小值是( ) (A)8; (B)9; (C)10; (D)11. 二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则xx x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 三.解答题一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.1.(C)由⎩⎨⎧==-01ab b a ⇒(1,0)(0,1). 又由⇒⎩⎨⎧==-1,0ab b a (1,1). ∴共有3对.2.(B)设0x 是方程的根,则0020=++c bx ax .所以202022044)2(b abx x a b ax ++=+ac b c bx ax a 4)(42020-+++=ac b 42-=.3.(D)由01132-+-x x 知0≠x .所以131=+-x x ,167213222=-=+-x x .2167244-=+-x x ,从而42-+x x 的个位数字为9-2=7.4.(C)若满足条件的多边形的边数大于或等于6,则至少有一边所对的圆心角不大于60°.由余弦定理知该边长必不大于1;同理,若存在满足条件的四边形,则它至少有一边长不小于2.5.(B)设A 点的坐标为(11,y x ),C 点的坐标为(22,y x ),则k y x y x ==2211. ∴22211121212121S CD OD y x y x AB OB S =⋅===⋅=. 6.(B)据正方形的对称性,只需考虑它的41部分即可.记圆周经过的所有小方格的圆内部分的面积之和为1'S ,圆周经过的所有小方格的圆外部分的面积之和为2'S ,则841'-=πS ,π4152'-=S . ∴44.256.44158444212'1'≈--==ππS S S S .故21S S 的整数部分是1. 7.(B) 设1=CD ,则2==AB FA ,易证121==AB BC ,90=∠ABC ,3===AC FB FE .∴ FG是等腰三角形BFD顶角平分线,因而也是底边BD上的中线.即 BG=GD.所以BD=2BG=2DC.三、对于编码M,考虑编码A中恰有两个数位上的数字与M中相应数位上的数字相同.设这两位是x1,x2数位.由于B、C中该两数位上的数字均与A在这两数位上的数字不同,因此B,C中这两数位上的数字必与M中这两数位上的数字不同,于是B中与 M中数字相同的数位必异于x1,x2.不妨设为x3,x4;同理C中与 M中数字相同的数位只能是异于x1,x2,x3,x4的x5,x6两位.关于 N也有类似的结论.这就是说,在每个数位上,A,B,C分别在该数位上的数字中,必有一个与M在该数位上的数字相同;同样地,也必有一个与N在该数位上的数字相同.由此知,D中的6,0两数字必不是M,N在相应数位上的数字.于是D的3,1,2,5中只有一个数字与M在相应数位上的数字不同;与Ⅳ相比较也有类似的结果.(A)若3不对,则有610253,013256;(B)若1不对,则有360251,301256;(C)若2不对,则有312056,310652;(D)若5不对,则有310265,315206.经检验知:该信封上编码M,N或者同为610253,或者同为310265.或者一个是610253,另一个是310265.。
1992年北京市初二数学竞赛初赛试题

1992年北京市初二数学竞赛初赛试题一、选择题:1.设x =y =z =x y 、、z 的大小关系是 ( )A .x y z ≤≤B .y z x ≤≤C .z x y ≤≤D .z y x ≤≤【解析】 D 0a ≤,于是991992993a a a ≥≥,因此x y z ≥≥.2.凸1992边形的内角中,非锐角的个数至少有( ). A .1988个 B .1989个 C .1990个 D .1991个 【解析】 B .因为凸n 边形的外角和为360︒,所以为钝角的外角至多有3个,也就是说至多只有3个锐角内角.因此凸1992边形非锐角的内角至少有1989个.3.若12x x 、是方程220x x k +-=的两个不等的实数根,则22122x x +-是( ). A .正数B .负数C .零D .不小于0的数【解析】 D .()22212121222242222x x x x x x k k +-=+--=+-=+.而440k =+△≥,∴1k -≥ ∴22122x x +-≥04.给出以下四个命题:(Ⅰ)若0a b <<,则4a b <-. (Ⅱ)若22a b <,则a b <.(1)a b =-,则0a ≥且1b ≥. (Ⅳ)若22x x +=--,则0x <. 其中正确命题的个数是( ). A .1个 B .2个 C .3个 D .4个【解析】 B .只有(I )(IV )正确.5.若1x <等于( ). A .1B .32x -C .23x -D .2-【解析】 B 1232x x x =-+-=-.6.设b 取1~11间的偶数,c 取任意正整数,则可以组成有两个不等的实数根的一元二次方程20x bx c ++=的个数是( ). A .50个 B .55个C .57个D .58个【解析】 A .方程20x bx c ++=有两个不等的实数根即240b c =->△,也即22b c ⎛⎫< ⎪⎝⎭.于是所有形如20x bx c ++=的方程有22222112131415150-+-+-+-+-=个.二、填空题:1.如图,在ABC △中,100ABC ∠=︒,AM AN CN CP ==,,求MNP ∠的度数. ABM NPC【解析】180MNP ANM PNC ∠=︒-∠-∠ ()()11180********A C =︒-︒-∠-︒-∠()12A C =∠+∠ ()11802B =︒-∠ 40=︒2.设x y z 、、都是实数,并且()()2111x a y a a a =-=---,,试求21x y a +++的值等于多少?【解析】 ∵()()210110a a a a -⎧⎪⎨---⎪⎩≥≥,而210a a --<,∴10a -=,1a = 于是0x =,0y =,1a =,212x y a +++=.3.若a b c 、、为非零实数,且0a b c ++=,试求a b b c c a a bb cc a++的值.【解析】 不妨设a b c ≥≥,则由303c a b c a ++=≤≤得0a >,0c <.因此11a b b c c a bb a b bc c a b b++=--=-4.在浓度为%x 的盐水中加入一定数量的水,则变为浓度是20%的新溶液,在此新溶液中再加入与前次所加入的水重量相等的盐,溶液浓度变为30%,求x =? 【解析】 设第一次加入水和第二次加入盐的相对重量为m ,则20100100301002100xm x m m ⎧=⎪⎪+⎨+⎪=⎪+⎩,解得x =7023.333≈.5.若x 、y 的值满足方程组3234571103177543897x y x y +=⎧⎨+=⎩,求4224199245x x y y ++=?【解析】 解得2x =,1y =,于是4224199245x x y y ++19921616531893=⨯++=.6.若0m >,0n >,实数a b c d 、、、满足a b c d +++=,2ac bd n ==,试求d a 的值(用m n ,表示).【解析】7.凸四边形ABCD 中,105ADB ABC ∠=∠=︒,45DAB DCB ∠=∠=︒,若A 点到直线BD 的距离为101,试求线段CD 的长度. 【解析】 ∵30ABD ∠=︒,∴202AB =在ABD △中,sin sin AB BDADB DAB =∠∠; 在BCD △中,sin sin BD CDBCD DBC=∠∠ ∴sin sin AB CD ADB DBC =∠∠,即202sin105sin 75CD =︒︒,∴202CD =.8.立方体的每个面上都写有一个自然数,并且相对的两个面上所写的二数之和都相等,若18的对面写的是质数a ,14的对面写的是质数b ,35的对面写的是质数c .试求222a b c ab bc ca ++---的值.183514【解析】181435a b c +=+=+, ∴222a b c ab bc ca ++---()()()22212a b b c c a ⎡⎤=-+-+-⎣⎦2221421173732⎡⎤=++=⎣⎦.。
1992年全国高中数学联合竞赛试题及解答.

★解析: ,即 ,
∴ 或 .
∴ .
1992*11、设数列 满足 , ,且对任何自然数 , 都有 ,又 ,则 的值是____.
◆答案:
★解析:由 ,得 ,
相减,得 ,由 ,得 .
又 , ,得 .
∴ 。
1992*12、函数 的最大值是_____.
◆答案:
★解析: ,表示点 与点 的距离及 距离差的最大值.由于此二点在抛物线两侧,故过此二点的直线必与抛物线交于两点.对于抛物线上任意一点,到此二点距离之差大于 .即所求最小值为 .
设 为圆 的内接四边形, 依次为 、 、 、 的垂心.求证: 四点在同一个圆上,并定出该圆的圆心位置.
★证明:连 ,取 的中点 ,连 ,由上证知 , , , ,从而 是平行四边形,故 , .
同理可知, , ;
, ;
, .
故 四边形 四边形 .
由四边形 有外接圆知,四边形 也有外接圆.取 的中点 ,作 ,且 ,则点 即为四边形 的外接圆圆心.
则这一曲线的方程是()
A.
B.
C.
D.
◆答案:D
★解析: 表示 轴右边的半圆, 表示 轴下方的半圆,故选D.
1992*3、设四面体四个面的面积分别为 ,它们的 最大值为 ,记 ,则 一定满足( )
A. B. C. D.
◆答案:A
★解析: ,故 ,又当与最大面相对的顶点向此面无限接近时, 接近 ,故选A.
★证明:⑴ 对于 的每个奇子集 ,当 时,取 ,当 时,取 ,则 为 的偶子集.反之,若 为 的偶子集,当 时,取 ,当 时,取 ,于是在 的奇子集与偶子集之间建立了一个一一对应,故 的奇子集与偶子集的个数相等.
⑵ 对于任一 , ,含 的 的子集共有 个,其中必有一半是奇子集,一半是偶子集,从而每个数 ,在奇子集的和与偶子集的和中, 所占的个数是一样的.
第七至十九届中国数学奥林匹克竞赛试题含答案

第七至十九届中国数学奥林匹克竞赛试题第七届中国数学奥林匹克 (1992年)1. 设方程x n +a n-1x n-1+a n-2x n-2+....+a 1x+a 0=0的系数都是实数,且适合条件0<a 0≦a 1≦a 2≦....≦a n-1≦1。
已知λ为方程的复数根且适合条件|λ|>1,试证:λn+1=1。
2. 设x 1, x 2, ... , x n 为非负实数,记 x n+1= x 1,a=min{x 1, x 2, ... , x n },试证:n Σ i=1 1+x i _ 1+x i+1 ≦n+ 1 (1+a)2nΣ i=1(x i -a)2 ,3. 且等式成立当且仅当 x 1 =x 2= ... =x n 。
4. 在平面上划上一个9x9的方格表,在这上小方格的每一格中都任意填入+1或-1。
下面一种改变填入数字的方式称为一次变动;对于任意一个小方格有一条公共边的所有小方格(不包含此格本身)中的数作连乘积,于是每取一个格,就算出一个数,在所有小格都取遍后,再将这些算出的数放入相应的小方格中。
试问是否总可以经过有限次变动,使得所有方小方格中的数都变为1?5. 凸四边形内接于圆O ,对角线AC 与BD 相交于P ,ΔABP 与ΔCDP 的外接圆相交于P 和另一点Q ,且O 、P 、Q 三点两两不重合。
试证∠OQP=90。
6. 在有8个顶点的简单图中,没有四边形的图的边数的是大值是多少?7. 已知整数序列{a 1, a 2, ...... }满足条件:1. a n+1=3a n -3a n-1+a n-2,n=2, 3, .....。
2. 2a 1= a 0+a 2-2。
3. 对任意的自然数m ,在序列{a 1, a 2, ...... }中必有相继的m 项a k , a k+1, ... , a k+m-1都为完全平方数。
试证:序列{a 1, a 2, ...... }的所有项都是完全平方数。
北京市中学生数学竞赛初二年级竞赛试题.doc

一、 ( 分 25 分,每小 只有一个正确答案,答 得5 分)1.当 m1,代数式21 5m m 9 mm 3的 是()6 m 2 9 m 2 m 3 m 3A. -1B.1C.1D.1222.一个正八 形中最 的 角 等于a ,最短的 角 等b , 个正八 形的面 ()A. a 2 b 2B. a 2b 2C.a bD. ab3. 111 1 16 11 26 26 1 1 的 是( ).6 11 16 2121 31 31 36A.1B.1C.1D.1183633664.若 n 是正整数, 1×2×3×⋯× n=n! ,比如 1!=1,4!=1×2×3×4=24,等等,若 M=1! ×2!×3!×4!×5!×6!×7!×8!×9!, M 的 数中是完全平方数的共有( )A.504 个B.672 个C.864 个D.936 个5.将 2009 表示成两个整数的平方差的形式, 不同的表示方法有()A.16 种B.14 种C.12 种D.10 种二、填空 ( 分 35 分,每小 7 分)1.45.12 13.9 2 45.1 13.9 的 等于.31.22.平行四 形 ABCD 中,AD= a ,CD=b , 点 B 分 作 AD 上的高h a 和 CD 上的高 h b ,已知 h a a , h b b , 角AC=20 厘米,平行四 形 ABCD的面 平方厘米 .3. 0 a 1 1 2 3 28 29,并且 a a a a a 18 ,已知30 30 30 30 30则 10a 等于.(其中x 表示不超过 x 的最大整数)4.已知△ ABC 中,∠A,∠B,∠C 的外角度数之比为α∶β∶γ(α,β,γ均为正数),则∠ A ∶∠ B∶∠ C 等于(.用含α,β,γ的式子之比表示)5.当1x 2 时,经化简x 2 x 1x 2 x 1 等于.三、(满分 10 分)已知 a b c 0 ,a2b2c21.(1)求ab bc ca的值(2)求a4b4c4的值四、(满分 15 分)如图所示,六边形ABCDEF 中, AB=BC=CD=DE=EF=FA ,并且∠ A+ ∠C+∠E=∠B+∠ D+∠ F,求证∠ A=∠ D,∠ B=∠E,∠ C=∠ F.五、(满分 15 分)BCA DF E(1)证明:由 2009 个 1 和任意个 0 组成的自然数不是完全平方数;(2)试说明,存在最左边 2009 位都是 1 的形如1111的自然数2009个1(其中 * 代表阿拉伯数码)是完全平方数.。
历年初中数学竞赛真题库(含答案)

1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1. 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不同的实数,则22223yxy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35.答( )2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是(A ) 10; (B )12; (C ) 16; (D )18. 答( )3. 方程012=--x x 的解是 (A )251±; (B )251±-; (C )251±或251±-; (D )251±-±. 答( ) 4.已知:)19911991(2111n nx --=(n 是自然数).那么n x x )1(2+-,的值是(A)11991-; (B)11991--; (C)1991)1(n -; (D)11991)1(--n . 答( )5. 若M n 1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M(A)能被2整除,但不能被3整除; (B)能被3整除,但不能被2整除; (C)能被4整除,但不能被3整除; (D)不能被3整除,也不能被2整除.答( )6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是 (A)1-;(B)5-;(C)0;(D)1. 答( )7. 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是(A)2;(B)3;(C)2 ;(D)3. 答( )8. 在锐角ΔABC 中,1=AC ,c AB =, 60=∠A ,ΔABC 的外接圆半径R ≤1,则(A)21< c < 2 ; (B)0< c ≤21;答( )(C )c > 2; (D )c = 2. 答( ) 二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 .2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+a cb 32 .3.设m ,n ,p ,q 为非负数,且对一切x >0,q pn m x x x x )1(1)1(+=-+恒成立,则 =++q p n m 22)2( .4.四边形ABCD 中,∠ ABC 135=,∠BCD 120=,AB 6=,BC 35-=,CD = 6,则AD = .第二试11=S 3S =132=S120135xx + y,x -y,x y,y四个数中的三个又相同的数值,求出所有具有这样性质的数对(x , y).二、ΔABC中,AB<AC<BC,D点在BC上,E点在BA的延长线上,且BD=BE=AC,ΔBDE的外接圆与ΔABC的外接圆交于F点(如图).求证:BF=AF+CF三、将正方形ABCD分割为2n个相等的小方格(n是自然数),把相对的顶点A,C染成红色,把B,D染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定. 3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7. 答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4. 答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xky 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S = (C)21S S < (D)不确定答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3. 答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD , ︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , FA=AB .则AE :EB 等于(A)1:2 (B)1:3 (C)2:5 (D)3:10 答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11. 答( ) 二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则xx x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ; 2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是 (A)Ⅰ,Ⅱ都对 (B)Ⅰ对,Ⅱ错 (C)Ⅰ错,Ⅱ对. (D)Ⅰ,Ⅱ都错. 3.设x 是实数,11++-=x x y .下列四个结论: Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值; Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A)Ⅰ (B)Ⅱ (C)Ⅲ (D)Ⅳ 4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x 其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是 (A)54321x x x x x >>>>; (B)53124x x x x x >>>>; (C)52413x x x x x >>>>; (D)24135x x x x x >>>>. 5.不等式73)1(12+<-<-x x x 的整数解的个解(A)等于4 (B)小于4 (C)大于5 (D)等于56.在ABC ∆中,BC AO O A =∠,,是垂心是钝角, 则)cos(OCB OBC ∠+∠的值是 (A)22-(B)22 (C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m ,n , p ,那么m :n :p 等于(A)cb a 1:1:1; (B)c b a ::(C)C B A cos :cos :cos (D)C B A sin :sin :sin . 答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+ 答( )二.填空题1. 当x 变化时,分式15632212++++x x x x 的最小值是___________.2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC 分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________.第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D ,E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8:30—9:30)考生注意:本试共两道大题,满分80分.一、选择题(本题满分48分,每小题6分)本题共有8个小题都给出了A,B、C,D,四个结论,其中只有一个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每小题选对得6分;不选、选错或选出的代表字母超过一个(不论是否写在圆括号内),一律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA.都不小于0 B.都不大于0C.至少有一个小0于D.至少有一个大于0 〔答〕( )3.如图1所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长A.等于4 B.等于5C.等于6 D.不能确定〔答〕( )A.1 B.-1 C.22001 D.-22001〔答〕( )5.若平行直线EF,MN与相交直线AB,CD相交成如图2所示的图形,则共得同旁内角A.4对B.8对C.12对D.16对〔答〕( )〔答〕( )7.设锐角三角形ABC的三条高AD,BE,CF相交于H。
1990年北京市初二数学竞赛初赛试题

1990年北京市初二数学竞赛初赛试题一、选择题(每小题7分,共56分) 1. a 是任意实数,则a a --的值为A. 必大于零B. 必小于零C. 必不大于零D. 必不小于零【解析】 若0a ≥,则0a a a a --=-=;若0a <,则2a a a a a --=--=-≥0,选D .2. a 表示一个两位数,b 表示一个四位数,把a 放在b 的左边组成一个六位数,那么这个六位数应表示成A. abB. 10000a b +C. 10010000a b +D. 100a b +【解析】a 作为前两位,b 作为后四位,应该写成0000a b +的形式,即为10000a b +,选B .3. 如图,在ABC △中,42A ∠=︒,B ∠和C ∠的三等分线分别交于D E ,,则BDC ∠的度数是A. 67︒B. 84︒C. 88︒D. 110︒ 【解析】 由“飞镖模型”可知:()13BDC A ABD ACD A ABC ACB ∠=∠+∠+∠=∠+∠+∠ ()121806033A A A =∠+︒-∠=∠+︒ 24260883=⨯︒+︒=︒,选C .4. 如图,在ABC △中,P 是AC 上一点,取BP 的中点Q ,过CQ 并延长与AB 交于D ,则ABP △的面积ABP S △与ACD △的面积ACD S △的大小关系是A. ABP ACD S S <△△B. ABP ACD S S =△△C. ABP ACD S S >△△D. 不能确定 【解析】 连接AQ ,记BDQ ADQ BCQ S a S b S c ===△△△,,,则由题意可知 APQ S a b =+△,CPQ S c =△,由“燕尾定理”得a b c bc a++=, ∴1c a b ca b++=>,∴c a >, ∴ABP ACD S S <△△,选A .5. 设0a b c d >>>>,且X =,YZ =,则X Y Z 、、的大小关系为A. X Z Y <<B. Y Z X <<C. X Y Z <<D. Z Y X << 【解析】22X ab cd ==++22Y ac bd ==++22Zad bc ==++,则()()220X Y ab cd ac bd a d b c -=+--=-->, ()()220Y Z ac bd ad bc a b c d -=+--=-->, ∴2220X Y Z >>>,∴0X Y Z >>>,选D .6. 在四个实数中,如果任意三个之和都不比另一个小,则下列说法中必定错误的是EDCB AQP DCBAc a+b cb aQP D CBAA. 非零的数不可能只有一个B. 四个数可以都是正数C. 负数有两个D. 如果有零就没有负数【解析】 由题意得a b c d ++≥,a b d c ++≥,a c d b ++≥,b c d a ++≥,则0a b c d +++≥,若这四个数中有两个负数,设为c d ,,则a b c d ++≥, 此时b c d a ++<,不合题意,选C .7. x y 、只能取A. 2553029464x y ==,B. 3761526855x y ==,C. 1512332477x y ==,D. 2832628614x y ==,【解析】 首先,奇数的平方被8除余1,那么两个奇数的平方和被8除余2,而偶数的平方一定能被4整除,则可以排除B 和C .其次,一个完全平方数的尾数只可能是0,1,4,5,6,9,而D 中22x y +的尾数为2,也不可能.所以选A .8. 已知实数a b 、分别满足424230a a--=和4230b b +-=,则代数式4444a b a +的值等于A. 175B. 55C. 13D. 7【解析】 根据题意,222b a -、是关于x 的一元二次方程230x x +-=的两个根,且222b a-≠,∴2221b a-+=-,2223b a -=-,()24422422442224422227a b b b b b a a a a a 2⎛⎫+⎛⎫⎛⎫=+=+-=-+--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,选D .二、填空题(前6个题,每题6分,第7个题8分,共44分)1. =_____________.【解析】 原式()()211111119901990119901==--⨯+.2. 设实数x y 、满足2242420x y x y ++-+=,则22y x +_____________. 【解析】 左边配方得()()221210x y ++-=,∴112x y =-=,,∴221y x +--3. 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形的底边的长为______________.【解析】 设腰长为2x ,底边长为y ,由题意得21221x x x y +=⎧⎨+=⎩或22112x x x y +=⎧⎨+=⎩,解得417x y =⎧⎨=⎩或75x y =⎧⎨=⎩, 检验发现第一组解无法构成三角形,不合题意舍去, 所以,等腰三角形的底边长为5cm .4._____________.【解析】2,2=10=5+5,而(22=24255<=,<5. 某厂二月份产量比一月份产量提高12.5%,三月份产量比二月份产量提高20%,那么三月份的产量比一月份产量提高的百分数为______________. 【解析】 设一月份的产量为x ,由题意可得二月份的产量为()112.5%x +,三月份的产量为()()27112.5%120%20x x ++=, 则三月份得产量比一月份产量提高了2735%20x x x ⎛⎫-÷= ⎪⎝⎭.6. 如图,AB BC CD ==,AD AE =,DE BE =,则C ∠的度数为_________. 【解析】 设BDE EBD x ∠=∠=,则2AED ADE x ∠=∠=, 在ADE △中,1804A x ∠=︒-, ∴1804C A x ∠=∠=︒-,又1801803CDB ADB x ∠=︒-∠=︒-, 则1803CBD CDB x ∠=∠=︒-,在BCD △中,180C CBD CDB ∠+∠+∠=︒, ∴180418031803180x x x ︒-+︒-+︒-=︒, ∴36x =︒,则180436C x ∠=︒-=︒.7. 如图1,我们规定在边长为1的正方形方格纸上,从格点O 到与它相邻的格点A 、B 、C 、D 、E 、F 、G 、H 的直线运动形成的线段分别记为数码0,1,2,3,4,5,6,7.如以点O 为始点,数码2代表线段OC ,数码7代表线段OH 等等.在图2中画出了从P 点出发,依次按数码001223355的轨线图形.请你在图3的边长为1的正方形方格纸上,从点M 出发,依次按数码006756442312画出相应的轨线图形,___________.图3图2图1【解析】 依题意画轨线图形如图所示:的正方形有5个,边长为2的正方形有3的正方形有4个,边EDCBA长为1个,共有534113+++=个.。
北京市初二数学竞赛初赛试题(1992)

初二初赛试题一、选择题(每小题6分,满分36分.)1.已知α是等边三角形的一个内角,β是顶角为30°的等腰三角形的一个底角,γ是等腰直角三角形的一个底角.则( ).(A)α<β<γ (B)γ<α<β (C)β<α<γ (D)α<γ<β2.(-2)4的平方根是( ).(A)-4 (B)±4 (C)2 (D)±23.下面有四个命题:①两个三角形有两边及一角对应相等,则这两个三角形全等;②两个三角形有两角及一边对应相等,则这两个三角形全等;③两个三角形的三条边分别对应相等,则这两个三角形全等;④两个三角形的三个角分别对应相等,则这两个三角形全等.其中真命题是( ).(A)②,③ (B)①,③ (C)③,④ (D)②,④-4.若P是两位的正整数,则可能成立的等式是( ),(A)x2+px+2001=(x-29)(x-69)(B)x2+px+2001=(x-23)(x-87)(C)x2+px+2001=(x+23)(x+87)(D)x2+px+2001=(x+29)(x+69)5.下面列举的平行四边形的判定条件中,不正确的一个是 ( )。
(A)两组对边分别相等(B)两组对角分别相等(C)一组对边平行,一组对角相等(D)一组对边平行,另一组对边相等6.在1 500年以前,我国古代伟大数学家祖冲之计算出圆周率π的七位小数值是3.1415926<π<3.1415927,并取113355为密率,722为约率,则,113355、π、722之间的正确关系是( ). (A) 722< 113355<π (B) 113355<π<722(C)π<113355<722 (D) 722<π<113355二、填空题(每小题8分,满分64分.)1.p 是负整数,且2001+P 是一个完全平方数,则P 的最大值为 2.如图,四边形ABCD 是正方形,△CDE 是正三角形,则∠AEB 的度数为3,若a 、b 都是正整数,且143a+500b =2001,则a+b 的值是 4.若有理数x ,y ,z 满足x +1-y +2-z =21(x+y+z),则(x-yz)3的值为 5.如图,将边长为12厘米的正方形ABCD 折叠,使得A 点落在边CD 上的E 点,然后压平得折痕FG ,若GF 的长为13厘米,则线段CE 的长为 . 6. 化简后=+++++++722-17562-15422-13302-11202-9122-762-522-37.将1~2001这2001个自然数依次写成一行,组成一个新的自然数,新的自然数除以9的余数为 8.已知实数x ,y 满足方程⎪⎩⎪⎨⎧=++=++6y x 232y xy x 22则|x+y+1|的值是参考答案1.B2.B3.A4.D5.D6.C1.-652.30°3. 94.-1255.76. 27. 68.3+22001年北京市初二年级数学竞赛复赛一、填空题(满分40分,每小题8分) 1.已知有理数x 满足方程200111x x 20011=--,则29x 2001x 43+-= 2.如图所示,正方形ABCD 的面积是64 cm 2,正方形CEFG 的面积是36 cm 2,DF 与BG相交于点O ,则△DBO 的面积等于 cm 2.3.已知a 2+b 2=6ab 且a>b>0,则ba ba -+= 4.化简表达式43333 |17160a 131a |17160a 131a 6 `⎥⎥⎦⎤⎢⎢⎣⎡-+--+-+,所得的结果等于 . 5.在边长为1cm 的正△ABC 中,P 0为BC 边上一点,作P 0 P 1⊥CA 于点 P 1,作P 1P 2⊥AB 于点P 2,作P 2P 3⊥BC于点P 3.如果点P 3恰与点P 0重合,则△P 1P 2P 3的面积是 cm 2.二、(15分)证明恒等式:a 4+b 4+(a+b)4=2(a 2+ab+b 2)2.三、(15分)在六张纸片的正面分别写上整数l 、2、3、4、5、6,打乱次序后,将纸片翻过来,在它们的反面也随意分别写上1~6这六个整数,然后计算每张纸片正面与反面所写数字之差的绝对值,得出六个数.请你证明:所得的六个数中至少有两个是相同的 四、(15分)如图所示,在等腰△ABC 中,延长边AB 到点D ,延长边CA 到点E ,连结DE ,恰有AD=BC=CE=DE .求证:∠BAC=100°五、(15分)l 与0交替排列,组成下面形成的一串数101,10101,1010101,101010101……请你回答,在这串数中有多少个质数?并请证明你的论断.2002年北京市初二数学竞赛初赛一、选择题(满分36分) 1.计算8008160061400413003120021-+-+( )A .60061 B .70073- c 80085 D .90097-2.2002年8月,将在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a ,较短直角边为b ,则a 3+b 4的值等于( ).A .35B .43C .89D .973.若20022002………200215(n 个2002)被15整除,则n 的最小值等于( ). A .2 15.5 C .4 D .54.两个边长为3,4,5的直角三角形纸片,可以拼成n 种不同的凸四边形,则n 的值等于( ). A .6 B .5 C4 D .35.已知三角形三个内角的度数都是质数,则这三个内角中必定有一个内角等于( ). A .2度 15.3度 C .5度D .7度6.a 4+4分解因式的结果是( ).A .(a 2+2a -2)(a 2—2a+2)B .(a 2+2a--2)(a 2-2a -2)C .(a 2+2a+2)(a 2—2a -2)D .(a 2+2a+2)(a 2—2a+2) 二、填空题(满分64分,每小题8分) 1.计算:(1+3 )2002—2(1+3)200l-2(1+3)20002.如图所示,AC=10,BC=l7,CD⊥AB 于点D ,CD=8,求△ABC 的面积.3.实数a ,b 满足ab≠O,且使得ba b a b b a a +++=+++111,求a+b 的值. 4.在梯形ABCD 中,下底BC=10 cm ,腰CD=5.5 cm ,如果∠ABC=50°,∠ADC=100°,求上底AD 的长.5.已知实数x ,y,z 满足1=+++++y x z x z y z y x ,求.yx z x z y z y x +++++222的值.6.如图所示,P 是边长为8的正方形ABCD 形外一点,PB=PC ,△PBD 的面积等于48,求△PBC 的面积.7.正数m ,n 满足m+4mn -2m -4n +4n=3,求2002282++-+n m n m 的值.8.一个正整数除以5,7,9及11的余数依次是1,2,3,4.求满足上述条件的最小的正整数.2002年北京市初二数学竞赛初赛 一、选择题1.C 2.B 3.B 4.C 5.A 6.D 二、填空题1.0 2.84 3.-2 4.4.5 5.0 6.32 7.4011-8.1731 2002年北京市中学生数学竞赛复赛一、填空题(满分40分,每小题8分)1.已知x 2+y 2+z 2-2x+4y-6z+14=O ,则(x-y-z)2002= .2.如图所示,A 在线段BG 上,四边形ABCD 和四边形DEFG 都是正方形,面积分别为7 cm 2和11 cm 2,则三角形CDE 的面积等于 cm 2. 3.化简: 3232-++== .4.如图所示,四边形ABCD 是正方形,E 为BF 上一点,四边形AEFC 恰是一个菱形,则∠EAB= .5.有6个学生,每人拥有的书中没有相同的,但每两个人都恰好有一本相同的书,每本书也恰好两个学生拥有,则这6个学生共有不同的书 本. 二、(满分15分)已知abc≠0,证明:四个数,)(,)(,)(,)(3333abcc b a abc b a c abc a c b abc c b a ------++中至少有一个不小于6.三、(满分15分)如图所示,△ABC 是正三角形,△A 1B 1 C 1的三条边A 1B 1、B l C 1、C 1 A 1交△ABC 各边分别于C 2、C 3,A 2、A 3,B 2、B 3.已知A 2C 3=C 2B 3=B 2 A 3,且C 2C 32+B 2B 32=A 2A 32。
北京市1982年中学生数学竞赛初中二年级试题

北京市1982年中学生数学竞赛初中二年级试题
佚名
【期刊名称】《数学教学通讯》
【年(卷),期】1983(000)001
【总页数】3页(P42-44)
【正文语种】中文
【中图分类】G6
【相关文献】
1.北京市1982年中学生数学竞赛初中三年级试题 [J], 苏炎;
2.北京市一九九○年中学生数学竞赛初中二年级初试试题 [J], 史树德
3.北京市1990年中学生数学竞赛初中二年级初试试题及答案 [J], 岳荫巍
4.1996年北京市中学生数学竞赛高一年级复试试题 [J], 周春荔
5.1991年北京市中学生数学竞赛高中一年级复试试题及解答 [J], 周春荔
因版权原因,仅展示原文概要,查看原文内容请购买。
边形竞赛试题

【例1】如图,四边形ABCD 有4个直角三角形拼凑而成,它们的公共顶点为O ,已知△AOB 、△BOC 、△COD 的面积分别为20、10、16,求△AOD 的面积。
(1992年北京市“迎春杯”竞赛题)【注释】求三角形的面积,通常需要求出底和高,当这两个值不易求出时,常把它们的积作为一个整体,设法求出它们的积。
【例2】如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数。
(1999年重庆市竞赛题)【注释】求凹多边形的内角和,常利用四边形和三角形的内角和进行计算,有事需要添加辅助线,将其转化为求一个凸多边形的和或一个凸多边形和一个三角形的内角和,如本题连接BF 、CE ,则所求的值等于四边形ABFG 的内角和加上△DCE 的内角和。
【例3】如图,在四边形ABCD 中,∠B=∠D=90°,∠A=60°,AB=4,AD=5,求CDBC的值。
(1993年“祖冲之杯”邀请赛试题)【注释】有些几何题,按原有的图形很难求解,可根据图形的特点,将原图形补成特殊图形,利用特殊图形的性质进行求解。
【例4】(1)是否存在这样的四边形,它的4条边依次是1、2、4、7?(2)是否存在这样的四边形,它的一组对角是直角,其中一个直角的两条边分别为3、4,另一个直角的边为6?【注释】探索存在型问题是指在一定条件下,判断是否存在某个结论。
解答这类问题,先假设结论存在,从假设出发,根据题设条件及有关性质进行推理论证,若推出矛盾,则不定假设,若推出合理的结果,则说明假设正确。
这种方法叫“假设法”。
【例5】如图,在四边形ABCD 中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD 的周长为32,求BC 和CD 的长。
【注释】对于四边形,作对角线是常用的辅助线。
【例6】如图,在四边形ABCD 中,AC 、BD 相交于O ,△DOC 的面积S 1=4,△AOB 的面积S 2=64,求四边形ABCD 的面积的最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二初赛试题一、选择题(每小题6分,满分36分.)1.已知α是等边三角形的一个内角,β是顶角为30°的等腰三角形的一个底角,γ是等腰直角三角形的一个底角.则( ).(A)α<β<γ (B)γ<α<β (C)β<α<γ (D)α<γ<β2.(-2)4的平方根是( ).(A)-4 (B)±4 (C)2 (D)±2 3.下面有四个命题:①两个三角形有两边及一角对应相等,则这两个三角形全等; ②两个三角形有两角及一边对应相等,则这两个三角形全等; ③两个三角形的三条边分别对应相等,则这两个三角形全等; ④两个三角形的三个角分别对应相等,则这两个三角形全等. 其中真命题是( ).(A)②,③ (B)①,③ (C)③,④ (D)②,④ -4.若P 是两位的正整数,则可能成立的等式是( ),(A)x 2+px+2001=(x-29)(x-69)(B)x 2+px+2001=(x-23)(x-87)(C)x 2+px+2001=(x+23)(x+87)(D)x 2+px+2001=(x+29)(x+69)5.下面列举的平行四边形的判定条件中,不正确的一个是 ( )。
(A)两组对边分别相等 (B)两组对角分别相等(C)一组对边平行,一组对角相等 (D)一组对边平行,另一组对边相等6.在1 500年以前,我国古代伟大数学家祖冲之计算出圆周率π的七位小数值是3.1415926<π<3.1415927,并取113355为密率,722为约率,则,113355、π、722之间的正确关系是( ). (A) 722< 113355<π (B) 113355<π<722(C)π<113355<722 (D) 722<π<113355二、填空题(每小题8分,满分64分.)1.p 是负整数,且2001+P 是一个完全平方数,则P 的最大值为 2.如图,四边形ABCD 是正方形,△CDE 是正三角形,则∠AEB 的度数为3,若a 、b 都是正整数,且143a+500b =2001,则a+b 的值是 4.若有理数x ,y ,z 满足x +1-y +2-z =21(x+y+z),则(x-yz)3的值为5.如图,将边长为12厘米的正方形ABCD 折叠,使得A 点落在边CD 上的E 点,然后压平得折痕FG ,若GF 的长为13厘米,则线段CE 的长为 . 6. 化简后=+++++++722-17562-15422-13302-11202-9122-762-522-37.将1~2001这2001个自然数依次写成一行,组成一个新的自然数,新的自然数除以9的余数为8.已知实数x ,y 满足方程⎪⎩⎪⎨⎧=++=++6y x 232y xy x 22则|x+y+1|的值是参考答案1.B2.B3.A4.D5.D6.C1.-652.30°3. 94.-1255.76. 27. 68.3+22001年北京市初二年级数学竞赛复赛一、填空题(满分40分,每小题8分) 1.已知有理数x 满足方程200111x 20011=--,则29x 2001x 43+-= 2.如图所示,正方形ABCD 的面积是64 cm 2,正方形CEFG 的面积是36cm 2,DF 与BG 相交于点O ,则△DBO 的面积等于 cm 2.3.已知a 2+b 2=6ab 且a>b>0,则ba ba -+= 4.化简表达式43333 |17160a 131a |17160a 131a 6 `⎥⎥⎦⎤⎢⎢⎣⎡-+--+-+,所得的结果等于 . 5.在边长为1cm 的正△ABC 中,P 0为BC 边上一点,作P 0 P 1⊥CA 于点 P 1,作P 1P 2⊥AB 于点P 2,作P 2P 3⊥BC 于点P 3.如果点P 3恰与点P 0重合,则△P 1P 2P 3的面积是 cm 2.二、(15分)证明恒等式:a 4+b 4+(a+b)4=2(a 2+ab+b 2)2.三、(15分)在六张纸片的正面分别写上整数l 、2、3、4、5、6,打乱次序后,将纸片翻过来,在它们的反面也随意分别写上1~6这六个整数,然后计算每张纸片正面与反面所写数字之差的绝对值,得出六个数.请你证明:所得的六个数中至少有两个是相同的四、(15分)如图所示,在等腰△ABC 中,延长边AB 到点D ,延长边CA 到点E ,连结DE ,恰有AD=BC=CE=DE .求证:∠BAC=100°五、(15分)l 与0交替排列,组成下面形成的一串数101,10101,1010101,101010101……请你回答,在这串数中有多少个质数?并请证明你的论断.2002年北京市初二数学竞赛初赛一、选择题(满分36分)1.计算8008160061400413003120021-+-+( ) A .60061 B .70073- c 80085 D .90097-2.2002年8月,将在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a ,较短直角边为b ,则a 3+b 4的值等于( ). A .35 B .43 C .89 D .973.若20022002………200215(n 个2002)被15整除,则n 的最小值等于( ). A .2 15.5 C .4 D .5 4.两个边长为3,4,5的直角三角形纸片,可以拼成n 种不同的凸四边形,则n 的值等于( ). A .6 B .5 C4 D .35.已知三角形三个内角的度数都是质数,则这三个内角中必定有一个内角等于( ). A .2度 15.3度 C .5度D .7度6.a 4+4分解因式的结果是( ).A .(a 2+2a -2)(a 2—2a+2)B .(a 2+2a--2)(a 2-2a -2)C .(a 2+2a+2)(a 2—2a -2)D .(a 2+2a+2)(a 2—2a+2) 二、填空题(满分64分,每小题8分) 1.计算:(1+3 )2002—2(1+3)200l-2(1+3)20002.如图所示,AC=10,BC=l7,CD⊥AB 于点D ,CD=8,求△ABC 的面积.3.实数a ,b 满足ab≠O,且使得ba b a b b a a +++=+++111,求a+b 的值. 4.在梯形ABCD 中,下底BC=10 cm ,腰CD=5.5 cm ,如果∠ABC=50°,∠ADC=100°,求上底AD 的长.5.已知实数x ,y,z 满足1=+++++y x z x z y z y x ,求.yx z x z y z y x +++++222的值. 6.如图所示,P 是边长为8的正方形ABCD 形外一点,PB=PC ,△PBD 的面积等于48,求△PBC的面积.7.正数m ,n 满足m+4mn -2m -4n +4n=3,求2002282++-+n m n m 的值.8.一个正整数除以5,7,9及11的余数依次是1,2,3,4.求满足上述条件的最小的正整数.2002年北京市初二数学竞赛初赛 一、选择题1.C 2.B 3.B 4.C 5.A 6.D 二、填空题1.0 2.84 3.-2 4.4.5 5.0 6.32 7.4011-8.1731 2002年北京市中学生数学竞赛复赛一、填空题(满分40分,每小题8分)1.已知x 2+y 2+z 2-2x+4y-6z+14=O ,则(x-y-z)2002= .2.如图所示,A 在线段BG 上,四边形ABCD 和四边形DEFG 都是正方形,面积分别为7 cm 2和11 cm 2,则三角形CDE 的面积等于 cm 2.3.化简: 3232-++== .4.如图所示,四边形ABCD 是正方形,E 为BF 上一点,四边形AEFC恰是一个菱形,则∠EAB= .5.有6个学生,每人拥有的书中没有相同的,但每两个人都恰好有一本相同的书,每本书也恰好两个学生拥有,则这6个学生共有不同的书 本.二、(满分15分)已知abc≠0,证明:四个数,)(,)(,)(,)(3333abcc b a abc b a c abc a c b abc c b a ------++中至少有一个不小于6.三、(满分15分)如图所示,△ABC 是正三角形,△A 1B 1 C 1的三条边A 1B 1、B l C 1、C 1 A 1交△ABC 各边分别于C 2、C 3,A 2、A 3,B 2、B 3.已知A 2C 3=C 2B 3=B 2 A 3,且C 2C 32+B 2B 32=A 2A 32。
请你证明: A l B 1⊥C 1A 1.四、(满分15分)从三位数100,101,102,…,499,500中任意取出n 个不同的数,使得总能找到其中三个数,它们的数字和相同.试确定n 的最小值,并说明理由。
五、(满分15分)能够找到这样的四个正整数,使得它们中任两个数的积与2002的和都是完全平方数吗?若能够,请举出一例;若不能够,请说明理由.四、在100,101,102,…,499,500这401个数中,数字和为1的只有100这一个数,数字和最大为22的只有499这一个数.其余的399个数的数字和都在2到2l之间.由抽屉原则,在这399个数,任取20×2+l=4 1个数,必存在三个数,它的数字和相同.考虑在100到500这401个整数中,任取43个数,必存在三个数,它们的数字和相同.最小值可能是43.下面说明,取如下的42个数:100;101,110;102,120;103,1 30;104,1 40;105,1 50;1 06,160,107,1 70;108,l 80;109,190;1 1 9,19 1;129,1 92;1 39,193;1 49,194;1 59,195;169,1 96;1 79、1 97; 1 89, l 98;469,4 96;479,497;489,498;499它们当中没有三个数的数字和相同,所以n的最小值是43.五、不能找到这样的四个正整数.使得它们中任两个数积与2002的和都是完全平方数.理由如下:偶数的平方能被4整除,奇数的平方被4除余1,也就是正整数的平方被4除余O或1.若存在正整数n l,n2,n3,满足n i n j+2002=m2;i.j=l,2,3,4. m是正整数;因为2002被4除余2,所以n i n j被4除应余2或3.(1)若正整数n l,n2,n3.n4中有两个是偶数,不妨设n1.n2是偶数,则n1n2+2002被4除余2.与正整数的平方被4除余O或1不符,所以正整数n1.n2,n3, n4中至多有一个是偶数,至少有三个是奇数.(2)在这三个奇数中,被4除的余数可分为余1或3两类,根据抽屉原则:,必有两个奇数属于同一类。
