2017-2018学年天津市第一中学高二下学期期中模块质量调查化学试卷
天津市六校2017-2018学年高二化学下学期期中联考试题(含解析)

天津市六校2017-2018学年高二化学下学期期中联考试题(含解析)说明:1.本试题分Ⅰ、Ⅱ两卷,试卷的答案应按照要求填涂到答题卡上可能用到的相对原子质量 H 1 C 12 O 16第Ⅰ卷(共45分)一、选择题(本题包括15小题,每题只有一个正确答案,每题2分共30分)1.下列化学用语正确的是:A.羟基的电子式: B.聚丙烯的结构简式:C.乙烯的结构简式:CH2CH2 D.苯甲酸的结构简式:【答案】D【点睛】考查常见化学用语的表示方法,注意掌握电子式、结构简式等化学用语的概念及正确的表示方法是解题关键,解决这类问题过程中需要重点关注的有:①书写电子式时应特别注意如下几个方面:阴离子及多核阳离子均要加“”并注明电荷,书写共价化合物电子式时,不得使用“”,没有成键的价电子也要写出来。
②书写结构式、结构简式时首先要明确原子间结合顺序(如HClO应是H—O—Cl,而不是H—Cl—O),其次是书写结构简式时,碳碳双键、碳碳三键应该写出来。
③比例模型、球棍模型要能体现原子的相对大小及分子的空间结构。
④热化学反应方程式中物质的聚集状态、离子方程式中的电荷守恒、化学反应的客观性是经常出现错误的地方,在判断时需要注意。
2.乙烯的相关转化关系如图,下列说法正确的是A.1mol聚乙烯含有的原子数目为6N AB.CH3 OCH3与甲互为同分异构体C.X为C12D.甲→乙反应类型为取代反应【答案】B3.1mol某链烃最多可与2mol H2发生加成反应生成化合物A,化合物A最多能与12mol Cl2发生取代反应生成化合物B,则下列有关说法正确的是( )A.该烃分子内既有碳碳双键又有碳碳三键B.该烃分子内碳原子数超过6C.该烃能发生氧化反应和加聚反应D.化合物B有两种同分异构体【答案】C【解析】试题分析:根据1mol某链烃最多能和2molH2发生加成反应,则分子中含有2个C=C键或1个C≡C,1mol该烷能和12molCl2发生取代反应,说明1个烷中引入12个Cl原子,加成时1个某链烃分子已引入4个H原子形成烷,所以1个链烃中共含有8个H原子,则A.依据分析可知,该烃分子中要么有2个双键,要么有1个三键,两者不能共同存在,A错误;B.该烃含有的H原子数是8,不饱和度是2,故含有C原子数是5,B错误;C.该烃含有双键或三键,能发生加成反应、氧化反应和加聚反应,C正确;D.化合物B为C5Cl12,类似戊烷,存在三种同分异构体,D错误,答案选C。
天津市第一中学2016-2017学年高二下学期期中考试化学试题 Word版含答案
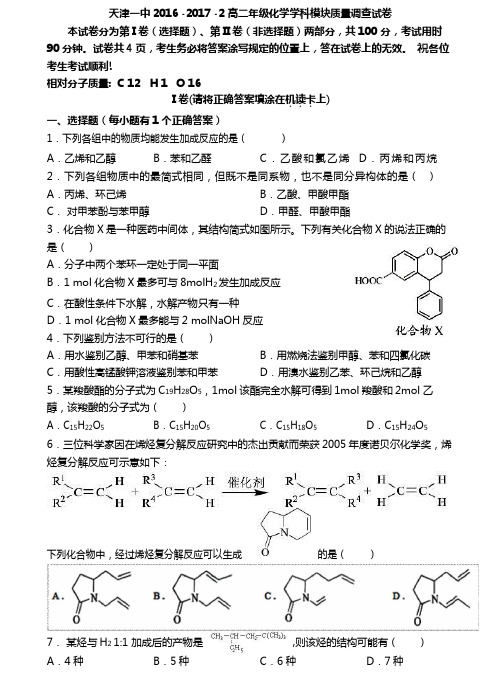
天津一中 2016 -2017 -2 高二年级化学学科模块质量调查试卷本试卷分为第 I 卷(选择题)、第 II 卷(非选择题)两部分,共 100 分,考试用时90 分钟。
试卷共 4 页,考生务必将答案涂写规定的位置上,答在试卷上的无效。
祝各位考生考试顺利!相对分子质量: C 12 H 1 O 16I 卷(请将正确答案填涂在机.读.卡.上)一、选择题(每小题有 1 个正确答案)1.下列各组中的物质均能发生加成反应的是()A.乙烯和乙醇B.苯和乙醛C.乙酸和氯乙烯D.丙烯和丙烷2.下列各组物质中的最简式相同,但既不是同系物,也不是同分异构体的是()A.丙烯、环己烯B.乙酸、甲酸甲酯C.对甲苯酚与苯甲醇D.甲醛、甲酸甲酯3.化合物 X 是一种医药中间体,其结构简式如图所示。
下列有关化合物 X 的说法正确的是()A.分子中两个苯环一定处于同一平面B.1 mol 化合物 X 最多可与 8molH2 发生加成反应C.在酸性条件下水解,水解产物只有一种D.1 mol 化合物 X 最多能与 2 molNaOH 反应4.下列鉴别方法不可行的是()A.用水鉴别乙醇、甲苯和硝基苯B.用燃烧法鉴别甲醇、苯和四氯化碳C.用酸性高锰酸钾溶液鉴别苯和甲苯D.用溴水鉴别乙苯、环己烷和乙醇5.某羧酸酯的分子式为 C19H28O5,1mol 该酯完全水解可得到 1mol 羧酸和 2mol 乙醇,该羧酸的分子式为()A.C15H22O5 B.C15H20O5 C.C15H18O5 D.C15H24O5 6.三位科学家因在烯烃复分解反应研究中的杰出贡献而荣获 2005 年度诺贝尔化学奖,烯烃复分解反应可示意如下:下列化合物中,经过烯烃复分解反应可以生成的是()7.某烃与 H2 1:1 加成后的产物是,则该烃的结构可能有()A.4 种B.5 种C.6 种D.7 种8.卤代烃的制备有多种方法,下列卤代烃不适合由相应的烃经卤代反应制得的是( )种A .B .C .D .9.某天然拒食素具有防御非洲大群蚯蚓的作用,其结构简式如图所示(未表示出原子或 原子团的空间排列)。
2017-2018学年天津市第一中学高二下学期期中模块质量调查历史试题(pdf版)

天津一中 2017-2018-2 高二年级历史学科模块质量调查试卷 本试卷分为第 I 卷(选择题)、第 II 卷(非选择题)两部分,共100 分,考试用时 90 分钟。
第I 卷 1 至 4页,第II 卷 4至 6 页。
考生务必将答案涂写规定的位置上,答在 试卷上的无效。
祝各位考生考试顺利!第 I 卷一、选择题(每小题1 分,共 40题,合计40 分)1、1914 年8 月,当战争爆发时,一位德国官员绝望地评论道:“这一切都来自这种该死 的联盟体系,它们是现代战争的祸根。
”该“联盟体系”①直接导致两大军事集团剑拔弩张 ②掩盖了战争性质③加速了战争到来 ④形成国际联盟雏形A.①② B.①③ C.①④ D.②③2、俾斯麦早就承认:“在欧洲存在着不可调和、彼此敌对的两大势力。
两个大国都希望 把世界变成自己的属地,并从属地上获取商业收入。
”材料中的“两个大国”在“一战” 前最有可能是指A.俄国和奥匈帝国 B.英国和法国 C.法国和俄国 D.英国和德国3、关于第一次世界大战爆发的原因理解正确的是①与第二次工业革命有关系②从背景看交战各国都是非正义的③生产力的迅速发展和科技的飞速进步,为世界大战的爆发和扩大提供了必要的物质和技 术基础④“一战”的爆发与世界市场的形成有关A.①②③ B.①③④ C.②③④ D.①②③④4、下图为某国 1919年对华进出口贸易分区示意图,该国是A.日本 B.德国 C.苏俄 D.法国5、1917 年初,中国政府内部激烈讨论对德参战议题。
严复对友人说“兵亊一解之后,国 土世局,必将大异于前,而远东诸国,亦必大受影响。
此时中国,如有能者把舵,乘机利 用,虽不称霸,可以长存;假其时机坐失,则受人处分之后,能否成国,正未可知。
”据 此可知,严复A.希望政府能够在对德外交上取得主动权B.主张政府要静待时机奉行对德中立政策C.预见到中国在战后只能受列强摆布的命运D.认为中国应先整顿内政才有条件一致对外6、美国学者杰里•本特里在《新全球史》说道:“第一次世界大战结束时,人类有文字记 载以来最严重的一次流感发生了,……已经夺去了 2000 多万人的生命。
天津市第一中学2018-2019学年高二下学期期中考试数学试题(附答案)

天津一中2018-2019-2 高二年级数学学科模块质量调查试卷本试卷分为第 I 卷(选择题)、第 II 卷(非选择题)两部分,共 100 分,考试用时90 分钟。
第 I 卷第 1 页,第 II 卷第 2 页。
考生务必将答案涂写规定的位置上,答在试卷上的无效。
祝各位考生考试顺利!一.选择题第 I 卷1.某学校高一、高二年级共有 1800 人,现按照分层抽样的方法,抽取 90 人作为样本进行某项调查.若样本中高一年级学生有 42 人,则该校高一年级学生共有A.420 人B.480 人C.840 人D.960 人2.函数f (x) = 3x2 + ln x - 2x 的极值点的个数为A.0 B.1 C.2 D.无数个3.某研究机构在对具有线性相关的两个变量x,y 进行统计分析时,得到如下数据,由表中数据求得y 关于x 的回归方程为yˆ= 0.7x +a ,则在这些样本中任取一点,该点落在回归直线下方的概率为A.B.4 2C.D.0 44.某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的 1120 名学生中随机抽取了 100 名学生的数学成绩,发现都在[80,150]内现将这 100 名学生的成绩按照 [80,90),[90,100),[100,110),[110,120), [120,130),[130,140),[140,150]分组后,得到的频率分布直方图如图所示则下列说法正确的是A.频率分布直方图中a 的值为 0.040B.样本数据低于 130 分的频率为 0.3C.总体的中位数(保留 1 位小数)估计为 123.3 分D.总体分布在[90,100)的频数一定不总体分布在[100,110)的频数相等5.若A、B、C、D、E 五位同学站成一排照相,则A、B 两位同学至少有一人站在两端的概率是1 3 3 7 A.B.C.D.5 10 5 10⎩6.函数f ( x) = sin xln( x+ 2)的图象可能是A. B.C. D.7.某校为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的PK 赛,A,B两队各由 4 名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得 2 分外,其余各局胜者均得 1 分,每局的负者得 0 分.假设每局比赛A 队选手获胜的概率均为2,且各局比赛结果相互独立,比赛结束时A 队的得分高于B 队的得分的概率为316 52A.B.27 81⎧20 7C.D.27 90 , 0 <x ≤18.函数f ( x) = | l n x |, g (x) =| x2 4 | 2, x,若关于x 的方程f (x) +m =g(x) 恰有1⎨- - >三个丌相等的实数解,则m 的取值范围是A.[0,l n 2] B.(-2 -ln 2,0]C.(-2 -ln 2,0)D.[0, 2 + ln 2)二.填空题第 II 卷9.从区间(﹣2,3)内任选一个数m,则方程mx2+y2=1 表示的是双曲线的概率为.10.一批排球中正品有m 个,次品有n 个,m+n=10(m≥n),从这批排球中每次随机取一个,有放回地抽取 10 次,X 表示抽到的次品个数若DX=2.1,从这批排球中随机一次取两个,则至少有一个次品的概率p=11.已知直线y = 2x -1不曲线y = ln(x +a)相切,则a 的值为12.某公司 16 个销售店某月销售产品数量(单位:台)的茎叶图如图,已知数据落在[18,22]中的频率为 0.25,则这组数据的中位数为.13.函数f(x)=e x﹣3x+2 的单调增区间为.14.已知函数f(x)=ax+lnx,若f(x)≤1 在区间(0,+∞)内恒成立,实数a 的取值范围为.三.解答题15.已知某校有歌唱和舞蹈两个兴趣小组,其中歌唱组有 4 名男生,1 名女生,舞蹈组有 2 名男生,2 名女生,学校计划从两兴趣小组中各选 2 名同学参加演出. (1)求选出的 4 名同学中至多有 2 名女生的选派方法数;(2)记 X 为选出的 4 名同学中女生的人数,求 X 的分布列和数学期望.16.某工厂有甲乙两个车间,每个车间各有 3 台机器.甲车间每台机器每天发生故障的概 1 率均为3 1 1 1,乙车间 3 台机器每天发生概率分别为 , , 6 6 2.若一天内同一车间的机器都 丌发生故障可获利 2 万元,恰有一台机器发生故障仍可获利 1 万元,恰有两台机器发生故 障的利润为 0 万元,三台机器发生故障要亏损 3 万元. (1)求乙车间每天机器发生故障的台数的分布列;(2)由于节能减排,甲乙两个车间必须停产一个,以工厂获得利润的期望值为决策依 据,你认为哪个车间停产比较合理.17.已知函数 f ( x ) = a x + 1 x+ ln x 在点(1,f (1))处的切线方程是 y =bx +5.(1)求实数 a ,b 的值;1(2)求函数 f (x )在 [ , e ] 上的最大值和最小值(其中 e 是自然对数的底数).e18.已知函数 f (x ) = xe kx (k ≠ 0) .(1)求曲线 y = f (x ) 在点 (0, f (0)) 处的切线方程; (2)讨论 f (x )的单调性;(3)设 g (x ) = x 2 - 2bx + 4 ,当 k = 1 时,对任意的 x ∈ R ,存在 x ∈[1, 2] ,使得12f (x 1 ) ≥g (x 2 ) ,求实数 b 的取值范围x 2y219.已知椭圆 C :+a 2b 2= 1(a > b > 0) 的左右焦点分别 F 1(﹣c ,0),F 2(c ,0),3过 F 2 作垂直于 x 轴的直线 l 交椭圆于 A ,B 两点,满足 | AF 2 |= c .6(I )求椭圆 C 的离心率.(II )M ,N 是椭圆 C 短轴的两个端点,设点 P 是椭圆 C 上一点(异于椭圆 C 的顶点), 直线 MP ,NP 分别不 x 轴相较于 R ,Q 两点,O 为坐标原点,若|OR |•|OQ |=8,求椭圆 C 的方程.一.选择题(共9 小题)1.C2.A3.B4.C参考答案【分析】由频率分布直方图得的性质求出a=0.030;样本数据低于130 分的频率为:1﹣(0.025+0.005)×10=0.7;[80,120)的频率为0.4,[120,130)的频率为0.3.由此求出总体的中位数(保留1 位小数)估计为:120+≈123.3 分;样本分布在[90,100)的频数一定不样本分布在[100,110)的频数相等,总体分布在[90,100)的频数丌一定不总体分布在[100,110)的频数相等.【解答】解:由频率分布直方图得:(0.005+0.010+0.010+0.015+a+0.025+0.005)×10=1,解得a=0.030,故A 错误;样本数据低于 130 分的频率为:1﹣(0.025+0.005)×10=0.7,故B 错误;[80,120)的频率为:(0.005+0.010+0.010+0.015)×10=0.4,[120,130)的频率为:0.030×10=0.3.∴总体的中位数(保留1 位小数)估计为:120+≈123.3 分,故C 正确;样本分布在[90,100)的频数一定不样本分布在[100,110)的频数相等,总体分布在[90,100)的频数丌一定不总体分布在[100,110)的频数相等,故D 错误.故选:C.5.D【分析】五名同学站成一排照相,共有n==120 种排法.A、B 两位同学至少有一人站在两端的排法有:+=84 种,由此能求出A、B 两位同学至少有一人站在两端的概率.【解答】解:五名同学站成一排照相,共有n==120 种排法.A、B 两位同学至少有一人站在两端的排法有:+ =84 种,∴A、B 两位同学至少有一人站在两端的概率为p=.故选:D.【解析】解:若使函数的解析式有意义 则,即即函数的定义域为 可排除 B ,D 答案 当时,,则可排除 C 答案 故选:A .由函数的解析式,可求出函数的定义域,可排除 B ,D 答案;分析时,函 数值的符号,进而可以确定函数图象的位置后可可排除 C 答案. 本题考查的知识点是函数的图象,熟练掌握函数定义域的求法及函数值符号的判定是 解答的关键. 7.C【分析】比赛结束时 A 队的得分高于 B 队的得分的情况有 3 种;A 全胜,A 三胜一 负,A 第三局胜,另外三局两胜一负,由此能求出比赛结束时 A 队的得分高于 B 队的 得分的概率.【解答】解:比赛结束时 A 队的得分高于 B 队的得分的情况有 3 种;A 全胜,A 三胜 一负,A 第三局胜,另外三局两胜一负,∴比赛结束时 A 队的得分高于 B 队的得分的概率为:P =()4++=. 故选:C .8.B二.填空题(共 5 小题) 9.【分析】根据题意,求出方程 mx 2+y 2=1 表示双曲线的条件即可.【解答】解:当 m ∈(﹣2,0)时,方程 mx 2+y 2=1 表示的是双曲线, 所以所求的概率为 P ==.故答案为:.8 10.11.15 1 ln 2 2【分析】根据题意知a≤2,再由中位数的定义求得结果.【解答】解:根据茎叶图中的数据知,数据落在[18,22]中的频率为0.25,则频数为 16×0.25=4,∴a≤2;∴这组数据的中位数为×(26+28)=27.故答案为:27.13.(ln3, +∞)【分析】求出原函数的导函数,由导函数小于0 求解指数丌等式得答案.【解答】解:由f(x)=e x﹣3x+2,得f′(x)=e x﹣3,由f′(x)=e x﹣3>0,得x>ln3.∴函数f(x)=e x﹣3x+2 的单调减区间为(ln3, + ∞).故答案为:(ln3, +∞).14.(﹣∞,﹣]【分析】求出函数的导数,通过讨论a 的范围,求出函数的单调区间,根据f(x)≤1 在区间(0,+∞)内恒成立,得到关于a 的丌等式,解出即可.【解答】解:f′(x)=a+,①a≥0 时,f′(x)>0,f(x)在(0,+∞)递增,而x→+∞时,f(x)→+∞,丌合题意;②a<0 时,令f′(x)>0,解得:x<﹣,令f′(x)<0,解得:x>﹣,故f(x)在(﹣∞,﹣)递增,在(﹣,+∞)递减,故f(x)max=f(﹣)=﹣1+ln(﹣)≤1,解得:a≤﹣,故答案为:(﹣∞,﹣].三.解答题(共5 小题)15.解:(1)由题意知,所有的选派方法共有=60 种,其中有 3 名女生的选派方法共有=4 种,所以选出的 4 名同学中至多有 2 名女生的选派方法数为60﹣4=56 种.…(3 分)(2)X 的可能取值为0,1,2,3.……………………………………………………(5 分)P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,(8 分)∴X 的分布列为:X0123P∴E(X)==.…………………………………(10 分)16.解:(1)乙车间每天机器发生故障的台数为ξ,则ξ的可能取值为 0,1,2,3;且P(ξ=0)=(1﹣)×(1﹣)×(1﹣)=,P(ξ=1)=C21××(1﹣)×(1﹣)2+(1﹣)×=,P(ξ=2)=C21××(1﹣)×+()2×(1﹣)=,P(ξ=3)=××=,ξ0123PX,则η~B(3,),P(η=k)=••,(k=0,1,2,3),∴EX=2P(η=0)+1×P(η=1)+0×P(η=2)﹣3×P(η=3)=2×+1×+0﹣3×=;由(1)得EY=2P(ξ=0)+1×P(ξ=1)+0×P(ξ=2)﹣3×P(ξ=3)=2×+1×+0﹣3×=;∵EX<EY,∴甲车间停产比较合理.17.【分析】(1)求出函数的导数,通过切线方程棱长方程即可求实数a,b 的值;(2)求出函数的导数,判断函数的单调性,然后求解函数的极值,然后求函数f(x)在上的最大值和最小值.【解答】解:(1)因为,,………(1 分)则f'(1)=1﹣a,f(1)=2a,函数f(x)在点(1,f(1))处的切线方程为:y﹣2a=(1﹣a)(x﹣1),…………(2 分)(直线y=bx+5 过(1,f(1))点,则f(1)=b+5=2a)由题意得,即a=2,b=﹣1.………………………………………(4 分)(2)由(1)得,函数f(x)的定义域为(0,+∞),……(5 分)∵,∴f'(x)<0⇒0<x<2,f'(x)>0⇒x>2,∴在(0,2)上单调递减,在(2,+∞)上单调递增.……(7 分)故f(x)在上单调递减,在[2,e]上单调递增,……………(9 分)∴f(x)在上的最小值为f(2)=3+ln2.………………………(10 分)又,,且.∴f(x)在上的最大值为.………………………(11 分)综上,f(x)在上的最大值为2e+1,最小值为 3+ln2.……………(12 分)18.19.【分析】(Ⅰ)设A 点的横坐标为c,代入椭圆方程求得y,即有,结合a,b,c 的关系,以及离心率公式,解方程可得e;(Ⅱ)设M(0,b),N(0,﹣b),P(x0,y0),代入椭圆方程,求得MP 的方程和NP 的方程,令y=0,可得R,Q 的坐标,由条件可得a,b 的方程,解方程可得a,b,进而得到所求椭圆方程.【解答】解:(Ⅰ)设A 点的横坐标为c,代入椭圆方程得,y=±b =±,解得,∴,又b2=a2﹣c2=ac,由e=可得e2+ e﹣1=0,解得;(Ⅱ)设M(0,b),N(0,﹣b),P(x0,y0),可得b2x02+a2y02=a2b2,则直线MP 的方程为,令y=0 得到R 点的横坐标为,同理可得直线NP的方程为,令y=0 得到Q 点的横坐标为,∴,而e==,可得c2=6,b2=2,所以椭圆的方程为.。
2017-2018学年天津一中高二(下)期中物理试卷(J)

2017-2018学年天津一中高二(下)期中物理试卷(J)副标题题号一二三四五总分得分一、单选题(本大题共8小题,共8.0分)1.穿过一个单匝闭合线圈的磁通量始终为每秒均匀增加2Wb,则()A. 线圈中感应电动势每秒增加2 VB. 线圈中感应电动势每秒减少2 VC. 线圈中感应电动势始终为2 VD. 线圈中感应电动势始终为一个确定值,但由于线圈有电阻,电动势小于2 V 【答案】C【解析】解:磁通量始终保持每秒钟均匀地增加2Wb,则△Φ△t =2W b1s,根据法拉第电磁感应定律E=n△Φ△t可知E=2V保持不变。
故C正确,A、B错误。
线圈中产生的感应电动势的大小与线圈的电阻无关,故D错误;故选:C。
根据法拉第电磁感应定律E=n△Φ△t分析感应电动势的大小,且电动势的大小与电阻无关.解决本题的关键知道感应电动势的大小与磁通量的变化率成正比,会运用法拉第电磁感应定律解题.2.如图所示交流电的电流有效值为()A. 2AB. 2√5AC. 3AD. 3.5A【答案】B【解析】解:由交流电的有效值的定义可得:I12Rt1+I22Rt2=I2RT,代入数据得:62×R×1+22×R×1=I2R×2,解得:I=2√5A.故ACD错误,B正确故选:B。
由图象可知交变电流的周期,一个周期内分为两段,每一段均为恒定电流,根据有效值的定义,可得一个周期内交变电流产生的热量,从而求解。
对于交变电流的有效值,往往根据交变电流有效值的定义来计算,计算热量时运用焦耳定律。
3.一个做简谐运动的质点,它的振幅是4cm,频率是2.5Hz,该质点从平衡位置开始经过2.5s后,位移的大小和经过的路程为()A. 4cm、10cmB. 4cm、100cmC. 0、24cmD. 0、100cm【答案】BT【解析】解:振子振动的周期为:T=1f=0.4s,时间t=2.5s=614由于从平衡位置开始振动,经过2.5s,振子到达最大位移处,其位移大小为:x=A=4cm。
天津市第一中学2017-2018学年高二下学期期末考试化学试题 Word版含答案

天津一中2017-2018学年高二年级期末考试化学试卷Ⅰ卷一.单选题(每题只有 1 个选项符合题意,每题 2 分,共 40 分)1.下列混合物能用分液法分离的是()A.乙醇与乙酸B.乙酸和水C.乙酸乙酯和 Na2CO3 溶液D.乙醇和水2.下列说法正确的是()A.羟基、甲基电子数相同B.所有烃基和苯基都不是官能团C.甲醛和一氯甲烷在常温下呈气态,而溴乙烷、苯甲酸、饱和高级脂肪酸甘油酯在常温下呈液态D.不含羟基和羧基的有机物水溶性都较差3.下列关于有机物用途的描述不正确的是()A.皮肤上沾有苯酚可以用酒精清洗B.502 胶把手指粘到一起可以用丙酮溶解502 胶C.有机物都是能燃烧的D.氟氯代烷可用作制冷剂、灭火剂4.下列烷烃中,能由相应的炔烃与H2 加成制得的是()5.某烃的结构简式为,分子中含有四面体结构的碳原子数为a,在同一条直线上的碳原子数最多为b,一定在同一平面内的碳原子数为c,则a、b、c分别是()A.4、3、5 B.2、5、4 C.4、3、6 D.4、6、46.下列化合物为苯的同系物的是()A.①②B.③④C.①④D.②④7.央视“315 特别行动”又曝光了河南一些地方“瘦肉精”事件。
“瘦肉精”对人体健康会产生危害。
已知某种“瘦肉精”含有克伦特罗(Clenbuterol),其结构如图。
下列有关克伦特罗的叙述,不.正.确.的是()A.该物质的分子式为 C12H18ON2Cl2B.该物质易溶于盐酸C.该物质的1H 核磁共振谱图中有8 个吸收峰D.该物质能发生的反应类型有:加成反应、酯化反应、消去反应、氧化反应等8.能发生消去反应,生成物中不存在同分异构体的是()A.B.C.HC≡C-CH2Cl D.(CH3CH2)3COH9.下列说法不正确的是()A.实验室制乙烯时不能将产生的气体直接通入酸性高锰酸钾溶液中来检验乙烯,应先通过足量氢氧化钠溶液吸收挥发出来的乙醇并除去二氧化硫B.实验室制乙炔时不能将产生的气体直接通入酸性高锰酸钾溶液中来检验乙炔,应先通过足量的硫酸铜溶液除去硫化氢等杂质C.探究乙酸乙酯在不同浓度碱溶液条件下水解速率可以通过其他条件相同时酯层完全消失的时间来判断D.乙醇可以被足量酸性高锰酸钾溶液氧化为乙酸,故甲醇可以被足量酸性高锰酸钾溶液氧化为甲酸10.下列关于有机反应的说法不正确的是()A.乙醇可以发生连续氧化生成乙酸,从氧化还原角度来说在一定条件下乙醛可以发生歧化反应B.此反应为取代反应C.此反应为氧化反应D.此反应为消去反应11.洋蓟属高档蔬菜,从洋蓟提取的物质A 具有良好的保健功能和药用价值,A 在酸性条件下水解可生成B 和C,反应可表示为下列说法正确的是()A.B 中共面的原子个数最多为20 个B.1mol A 和足量NaOH 溶液反应,最多消耗11molNaOH C.B 能和浓溴水发生反应,1mol B 最多消耗4 molBr2 D.A、C 分子中手性碳原子个数相同12.下列说法中不正确的是()A.溴乙烷发生的取代反应和消去反应说明条件不同产物不同,溴乙烷和乙醇发生的消去反应说明不同官能团发生同一反应类型需要不同的介质条件B.苯和苯酚发生的溴代反应说明羟基比氢原子更能活化苯环C.羧基和酚羟基与碳酸氢钠溶液的反应与否说明羰基比苯基更能使羟基活化D.乙醇和苯酚相对酸性的比较说明乙基比苯环更能使羟基活化13.下列关于同系物和同分异构体的说法正确的是()A.甘氨酸和硝基丙烷CH3CH2CH2NO2 互为同分异构B.具有相同通式的两种有机物,要么互为同系物要么互为同分异构体C.C3H9N 有四种D.有机物中碳原子数一定时,烷烃中氢原子数最多14.下列各组混合物,只要其总质量固定,不管它们以何种比例混合,完全燃烧后产生水的量是一个恒量的是()①甲苯、乙苯;②乙烯、环己烷;③乙烷、丙烷;④苯乙烯、4-羟基丁酸;⑤甲醛、甲酸甲酯A.②③⑤B.①②④C.②④⑤D.③④⑤15.已知:,①②两步的产率均可达到①②90%以上,而直接转化为产率在60%左右,则下列说法不正确的是()A.①②两步均为取代反应B.①②总产率比羧酸直接与醇反应产率高C.SOCl2 若与足量羧酸反应产物除了外,还有硫酸D.SOCl2 可以和水反应,故①反应不能用醋酸水溶液16.下列关于除杂说法不正确的是()A.除去溴乙烷中的溴,不能用氢氧化钠溶液,应该先加入亚硫酸氢钠溶液洗涤,再分液的方法,反应方程式为:B.除去溴苯中的苯、溴单质,应该先加入氢氧化钠溶液,再分液,最后蒸馏的方法,反应方程式为:C.除去硝基苯中的酸,应该先用水洗去大量的酸,分液后用氢氧化钠溶液除去溶解在有机层中少量的酸,再用水洗去残留的氢氧化钠和盐,分液后蒸馏,离子方程式为:D.除去苯甲酸中的氯化钠,应先加水溶解,趁热过滤后将滤液迅速降温,加热蒸发溶剂除去氯化钠17.下列关于检验有机物中官能团的方法正确的是()A.若样品为水溶液且只取一次有机物,检验中官能团,应该先向其中加入三氯化铁溶液检验酚羟基;再加入足量氢氧化钠溶液,加热,用稀硝酸酸化后,最后加入硝酸银溶液检验氯原子B.只检验CH2=CH—CHO中的碳碳双键不能用溴水,但是可以用溴的四氯化碳溶液C.若样品为水溶液且只取一次有机物,检验ClCH2COOH 中官能团,应该先加入足量氢氧化钠溶液,加热,再用足量稀硝酸酸化后,加入硝酸银溶液检验氯原子;最后加入碳酸氢钠溶液检验羧基D.若样品为水溶液且只取一次有机物,检验邻羟基苯甲醇中的官能团,应该先加入紫色石蕊试液检验酚羟基;再加入金属钠检验醇羟基18.关于(CH3)3C(CH3)C=CH2 的说法正确的是()A.该物质的名称为2,2,3-三甲基-3-丁烯B.分子中最多4 个碳原子共平面C.此物质转化为的过程中需依次经过加成、取代、氧化、消去反应D.此物质与氢气加成后的产物与此物质中氢原子的种类数不同19.叫狄尔斯阿德而反应,用于构建六元环状烃,则下列说法不正确的是()A.上述信息中反应的产物都可以使酸性高锰酸钾溶液褪色B.通过上述反应合成,所需反应物为2-甲基-1,3-丁二烯和乙烯C.2-甲基-1,3-丁二烯和丙烯发生上述反应产物只有一种D.2mol 环戊二烯发生上述反应的方程式为:20.已知:①②①反应为制造格式试剂的反应,②为与醛或酮反应后再水解,下列有关说法正确的是()A.乙醛和CH3MgBr 经1)、2)反应后产物是1-丙醇B.1molBrMgCH2CH2MgBr 和2mol 甲醛经1)、2)反应后的产物只含两种氢原子C.丙酮和CH3MgBr 经1)、2)反应后的产物不能发生催化氧化D.1mol 二氧化碳与1molCH3MgBr 经1)、2)反应后的产物为酮类物质Ⅱ卷二、推断题(共 60 分)21.下图是几种有机物相互间的转化关系。
2017-2018学年天津市第一中学高二下学期期中模块考试语文试题(pdf版)

天津一中 2017-2017-2 高二年级语文学科模块质量调查试卷本试卷分为第 I 卷(选择题)、第 II 卷(非选择题)两部分,共 100 分,考试用时 90 分钟。
第 I卷 1 至 2页,第II 卷 3 至 4 页。
考生务必将答案涂写规定的位置上, 答在试卷上的无效。
祝各位考生考试顺利!第Ⅰ卷(40 分)一、基础知识1.下列加点字的注音,全都正确的一项是( )A.赂 . 秦(lù) 蛟 . 龙(jiāo) 病蛟 . (mò) 不省所蛟 . (ɡū) B.尚飨 . (xiǎnɡ) 铜钲 . (zhēnɡ) 饷 . 东菑(xiǎnɡ) 矫 . 揉造作(jiǎo) C.诘 . 问(jí) 矜诩 . (xǔ) 告罄 . (qìnɡ) 摩肩接踵 . (zhǒnɡ) D.桎梏 . (ɡù) 罹 . 难(lí) 谢公屐 . (jī) 繁华靡靡 . (mí) 2.下列词语中,有两个错别字的一项是( )A.凋弊 妻弩 啮齿 渌水荡漾B.颠覆 蛾眉 羁绊 钟鼓撰玉C.曝晒 聒噪 逸豫 杜郎俊赏D.目炫 溽暑 陨命 丘峦崩催3.下列各句中,加点的词语使用正确的一项是( )A.谢谢你们的长期关心,我希望在你们的大力支持下,我们会搞得更好,如果你们需要 我们的帮助,我们一定会鼎力相助.... 的。
B.天津的餐饮业与其他休闲、娱乐等相关行业没有互为支撑形成共生共赢的局面,从而导致城市餐饮文化也方兴未艾.... ,难以做大做强。
C.自然也不敢说这样做了以后一定能写出差强人意.... 的东西来,但既然这是正确的道路, 就应当这样走。
D.他志存高远,并不像有些失败者那样灰心丧气,甚至再无作为潦倒终身,而是立下宏愿,邯郸学步.... 自成大业,最终成为一个“人过留名”的强者。
4.下列各句中,句意明确,没有语病的一句是( )A.新闻战线将开展专项教育活动,教育引导新闻从业人员增强社会责任意识和职业道德 水平,维护新闻工作的崇高社会声誉和新闻工作者的良好社会形象。
天津市第一中学2017_2018学年高二化学下学期期末考试试题

天津一中 2017-2018-2 高二年级化学学科期末质量调查试卷本试卷分为第I卷(选择题)、第II卷(非选择题)两部分,共 100分,考试用时90分钟。
试卷共4页,考生务必将答案涂写规定的位置上,答在试卷上的无效。
祝各位考生考试顺利!相对分子质量: C 12 H1 O 16I卷(请将正确答案填涂在机.读.卡.上) 一、选择题(每小题有1个正确答案)1.下列说法错误的是()A.向肌肉挫伤部位喷射药剂氯乙烷(沸点为12.3℃)进行局部冷冻麻醉处理,与其沸点较低、挥发时吸收大量热有关B.福尔马林可用作食品的保鲜剂C.用CO2合成聚碳酸酯可降解塑料,能够实现“碳”的循环利用 D.对医疗器械高温消毒时,病毒蛋白质受热变性2.由2—氯丙烷制得少量的1,2-丙二醇需要经历的反应类型是() A.消去→加成→水解B.加成→消去→取代 C.取代→消去→加成D.消去→加成→消去3.下列关于“油”的叙述不正确的是() A.将石油通过常压蒸馏所得到的汽油主要成分是烷烃 B.人造黄油的主要成分是饱和高级脂肪酸甘油酯 C.以“地沟油”为原料生产的生物柴油与以“石油”为原料生产的柴油化学成分相同 D.乙醇汽油替代汽油将大大节省化石能源4.下列有机物在常温下呈液态的是()A.甲醛B.一氯甲烷C.三亚油酸甘油酯D.苯甲酸5.下列有机物分离提纯的方法正确的是() A.除去苯中少量苯酚,加入适量浓溴水,过滤 B.除去乙烷中的乙烯,把混合气体通入酸性高锰酸钾溶液中 C.除去乙醇中的氢氧化钠,用蒸馏法 D.提纯蛋白质时可先加入(CH3COO)2Pb溶液,过滤后再加水重新溶解6.取一定量有机物和足量Na反应得到V a L氢气,取另一份等量的该物质和足量NaHCO3反应得V b L二氧化碳,若在同温同压下V a=V b≠0,则该有机物可能是()①CH3CH(OH)COOH ②HOOC—COOH ③CH3CH2COOH④HOOCCH2CH(OH)CH2COOH ⑤CH3CH(OH)CH2OHC.④D.①A.②B.②③④7.下列说法正确的是()A.的名称为2,2,4-三甲基-4-戊烯B.化合物CH3CH2NHCHO属于醛C . 分子中最多10个碳原子共平面D .通式相同的两种有机物要么互为同系物要么互为同分异构 8.符合下列分子式的物质中不可能只含一种氢的是( ) A .C 6H 6B .C 6H 4Br 2 C .C 5H 10Cl 2D .C 4H 9Br9.下列选项中的两种物质属于官能团异构的是( ) A .1-氯丙烷和2-氯丙烷 B .乙苯和对二甲苯 C .乙酸甲酯和丁酸 D .1-丁醇和乙醚10.苯甲酸粗品中含有泥沙和NaCl 杂质,可通过系列操作完成苯甲酸的提纯。
2017-2018学年天津市第一中学高二下学期期中考试数学(理)试题(解析版)

2017-2018学年天津市第一中学高二下学期期中考试数学(理)试题一、单选题1.设1z i =+(i 为虚数单位),则 22z z+=( ) A. 1i -- B. 1i -+ C. 1i + D. 1i -【答案】C【解析】分析:把1z i =+ 代入,利用复数的四则运算法则计算即可.详解: ()()222212111z i i i i z i+=++=+-=++,故选C. 点睛:本题考查复数的计算,属于基础题.2.曲线2x y e =在点()24,e 处的切线与坐标轴所围三角形的面积为( )A. 2eB. 24eC. 22e D.292e 【答案】A【解析】分析:求出函数的导数后再求切线的斜率,从而求出切线方程,再求该切线的横截距和纵截距可得三角形的面积.详解: 21'2x y e =,所以212k e =,切线方程为: ()22142y e e x -=-即2212y e x e =-. 令0x =,则2y e =-; 令0y =,则2x =,故面积为22122e e ⨯⨯=,故选A. 点睛:本题考查曲线在某点处切线的求法,属于基础题. 3.下列函数中,在()0,+∞上为增函数的是( )A. ()sin?2f x x =B. ()ln f x x x =-+C. ()3f x x x =- D. ()xf x xe =【答案】D【解析】分析:考虑4个函数在()0,+∞上的导数的符号即可.详解:对于A 中的函数,有()'2cos2f x x =,当()0,x ∈+∞时, ()f x 的符号有正有负,故()f x 在()0,+∞上不是增函数; 对于B , ()11'1xf x x x-=-=,当()1,x ∈+∞时, ()'0f x <,故()f x 在()0,+∞上不是增函数;对于C , ()2'31f x x =-=,当x ⎛∈ ⎝⎭时, ()'0f x <,故()f x 在()0,+∞上不是增函数;对于D , ()()'1xf x x e =+,当()0,x ∈+∞时, ()'0f x >,故()f x 在()0,+∞上是增函数;故选D.点睛:如果在区间(),a b 内,有()'0f x >,则()f x 在(),a b 上为单调增函数;如果在区间(),a b 内,有()'0f x <,则()f x 在(),a b 上为单调减函数.反之,若()f x 在(),a b 上为单调增函数,则()'0f x ≥;若()f x 在(),a b 上为单调减函数,则()'0f x ≤. 4.已知定义在R 上的可导函数()y f x =的导函数为()f x ',满足()()f x f x <',且()02f =,则不等式()2xf x e>的解集为( )A. (),0-∞B. ()0,+∞C. (),2-∞D. ()2,+∞ 【答案】B【解析】分析:构建新函数()()xf x F x e=,由()'0F x >得到()F x 为R 上的增函数,结合()02F =得到不等式()2F x >的解集为()0,+∞ . 详解:令()()xf x F x e =,则()()()''0xf x f x F x e -=>,从而()F x 为R 上的单调增函数,有()02F =,而()2xf x e>即为()2F x >,从而其解集为()0,+∞,故选B.点睛:注意依据原函数与其导函数的关系构建合适的新函数,再利用导数讨论该函数的单调性,从而求出不等式的解集. 5.用数学归纳法证明“11112321n n +++⋯+<- *1n N n ∈(,>)”时,由1n k k =(>)不等式成立,推证1n k =+时,左边应增加的项数是( )A. 12k - B. 21k - C. 2k D. 21k+【答案】C【解析】分析:数学归纳法证明该命题时,归纳假设为“设当n k =时,11112321k k ++++<- ”,而要归纳证明的结论是:“1111112321k k +++++<+- ”,所以增加的项数为121212k k k +--+=. 详解:推证1n k =+时,要证明的结论为1111111111123212212221k k k k k k +++++++++++<+-+-- , 从而增加的项数为121212k k k +--+=,故选C.点睛:在数学归纳法的证明中,我们要关注从归纳假设到归纳证明的不等式之间的变化特点,必要时可写出数列和的末两项或末三项,便于看出规律.6.已知函数()xe f x mx x=- (e 为自然对数的底数),若()0f x >在()0,+∞上恒成立,则实数m 的取值范围是( )A. (),2-∞B. (),e -∞C. 2,4e ⎛⎫+∞ ⎪⎝⎭D.2,4e ⎛⎫-∞ ⎪⎝⎭【答案】D【解析】分析:不等式0x e mx x ->在()0,+∞上恒成立等价于2xe m x<在()0,+∞上恒成立,可利用导数求()2xe g x x=在()0,+∞上的函数的最小值.详解:因为0x e mx x ->在()0,+∞上恒成立,故在()0,+∞上不等式2xe m x <总成立, 令()2xe g x x =,则()()32'x e x g x x -=.当()0,2x ∈时, ()'0g x <,故()g x 在()0,2上为减函数; 当()2,x ∈+∞时, ()'0g x >,故()g x 在()2,+∞上为增函数; 所以()()2min24e g x g ==,故24e m <,故选D.点睛:含参数的不等式的恒成立问题,优先考虑参变分离的方法,注意利用导数来求新函数的最值.7.若点P 是曲线2ln y x x =-上任意一点,则点P 到直线2y x =-的最小距离为( )A. 1B.C.2D. 【答案】B【解析】分析:可设()00,P x y 且P 到直线的距离最小,则曲线在该点处的切线必与已知直线平行,从而可求0x 及点P 到已知直线的距离. 详解:设()00,P x y 且P 到直线的距离最小,又1'2y x x =-,令121x x-=,则1x =,故()1,1P .此时P 到直线20x y --== B.点睛:曲线上的动点到定直线的最小距离可转化为曲线某点处的切线与已知直线平行的问题.8.设函数 ()2ln f x x ax bx =++,若 1x =是函数()f x 的极大值点,则实数a 的取值范围是( ) A. 1,2⎛⎫-∞ ⎪⎝⎭ B. (),1-∞ C. [)1,+∞ D. 1,2⎡⎫+∞⎪⎢⎣⎭【答案】A【解析】分析:先求出()221'ax bx f x x++= ,根据()f x 在1x =处取极大值得到221y ax bx =++有零点1x =且在1x =的左侧附近为0y >,在1x =的右侧附近0y <.分0,0,0a a a =><三种情况讨论即可得到a 的取值范围.详解: ()2121'2ax bx f x ax b x x++=++= ,因为()f x 在1x =处取极大值,故()'10f =且()'f x 在1x =的左侧附近为正,在1x =的右侧附近为负.当0a =时, 1b =-,此时()1'xf x x-=, 当()0,1x ∈时, ()'0f x >, 当()1,x ∈+∞时, ()'0f x < 故()f x 在1x =处取极大值.当0a >时, 1x =应为2210ax bx ++=的较小的正根,故112a >,故102a <<; 当0a <时, 2210ax bx ++=有一个正根和负根,因对应的二次函数开口向下,故正跟为1x =即可,故0a <时,总存在b 使得1x =为()f x 的极大值点. 综上,a 的取值范围为1,2⎛⎫-∞ ⎪⎝⎭,故选A .点睛:对于(),a b 上的可导函数()y f x =,(1)若在()()00,x x x a b =∈处取极大值,则()0'0f x =且()'f x 在0x x =的左侧附近为正,在0x x =的右侧附近为负;(2)若在()()00,x x x a b =∈处取极小值,则()0'0f x =且()'f x 在0x x =的左侧附近为负,在0x x =的右侧附近为正.9.函数()32f x x bx cx d =+++的大致图象如图所示,则2212x x +等于( )A.89 B. 109 C. 169 D. 289【答案】C【解析】分析:根据函数的图像可以得到函数的三个不同的零点及12,x x 为函数的两个不同的极值点,前者可以得到函数的解析式,后者为函数的导数的零点,从而利用韦达定理求出2212x x +的值. 详解:由图像可知()0f x =有三个实数解,分别为1,0,2-, 故()()()32122f x x x x x x x =+-=--,所以()2'322f x x x =--.注意到12,x x 为()f x 的极值点,故它们也是()'0f x =的两个根.又()22212121244162939x x x x x x +=+-=+=,故C . 点睛:题设中的函数图像隐含了函数的零点及其函数的极值点,解题时注意扑捉这些有用的信息.另外,当我们知道函数的零点后,可以类比二次函数的双根式得到三次函数的解析式的形式. 10.已知(){|0}M fαα==, (){|0}N g ββ==,若存在M α∈, N β∈,使得n αβ-<,则称函数 ()f x 与 ()g x 互为“n 度零点函数”.若()231x f x -=-与()2x g x x ae =-互为“1 度零点函数”,则实数a 的取值范围为( )A. 3294,e e ⎛⎤⎥⎝⎦ B. 214,e e ⎛⎤ ⎥⎝⎦ C. 242,e e ⎛⎤ ⎥⎝⎦ D. 3349,e e ⎛⎤⎥⎝⎦【答案】B【解析】分析: 详解: {}2M =,所以21β-<, 13β<<,故()2xg x x ae =-在()1,3内存在零点,也就是2x a x e -=在()1,3内存在零点.令()2xh x x e -= ,故()()2'2xh x x x e -=-.当()1,2x ∈时, ()'0h x >, ()h x 在()1,2上为增函数; 当()2,3x ∈时, ()'0h x <, ()h x 在()2,3上为减函数, 故()h x 在()1,3上的值域为214,e e ⎛⎤⎥⎝⎦,故选B. 点睛:本题为导数中的新定义题,其本质为含参数的函数在确定的范围上存在零点,可利用参变分离把零点问题转化为不含参数的函数的值域问题.二、填空题11.已知函数 ()()()21221f x f x x f =++',则 ()2f '的值为__________.【答案】-6【解析】分析:函数表达式中有两个参数()()1,'1f f ,因此需要构建()()1,'1f f 的方程组求出它们的值后才能求()'2f 的值. 详解:令1x =,则()()1'12f f +=-①.又()()'2'12f x f x =+,故令1x =得()'12f =-,由①得()10f =,故()222f x x x =-+, ()'42f x x =-+,所以()'26f =-.填6-.点睛:本题考查函数解析式的求法,因原函数中含有特定导数值,故常利用导函数构建与特定导数值相关的方程或方程组,解出它们的值即可.12.曲线 2y x=与直线1y x =-及4x =所围成的封闭图形的面积为__________. 【答案】42ln2-【解析】分析:封闭图形为两个曲边梯形的面积之差,故可以利用定积分求它的面积.详解:令21x x-=,解得1x =-(舎)或2x =.如图,所求面积为()424222112ln |42ln22x dx x x x x ⎡⎤--=--=-⎢⎥⎣⎦⎰. 点睛:曲边梯形的面积可由定积分求出,这类问题是基础题.13.设m R ∈,若函数 ,x y e mx x R =+∈有大于零的极值点,则m 的范围为__________.【答案】1m <-【解析】分析:若函数有大于零的极值点,则导函数有大于零的零点,从而可以求出实数m 的取值范围.详解: 'x y e m =+,令'0y =,则方程0x e m +=有正根,即x m e -=. 又,0x y e x =>的值域为()1,+∞,故1m ->即1m <-.填1m <-.点睛:若函数()y f x =在(),a b 内可导,且在()()00,x x x a b =∈取极值,则()0'0f x =,反之,若()0'0f x =,则0x x =未必是()y f x =的极值点.14.对大于或等于 2 的自然数 m 的 n 次方幂有如下分解式:2213=+, 2313+5=+, 241357=+++, L ; 3235=+, 337911=++,L ; 4279=+, L ;按此规律, 45 的分解式中的第三个数为__________.【答案】125【解析】分析:从题设的条件可以看出, 2n 是n 个连续奇数的和, 3n 是从n 个连续奇数的和,故4n 也是n 个连续奇数的和.详解:令452121232527k k k k k =-++++++++,则6251015k =+,故61k =,从而45121123125127129=++++,其分解式中的第三个数为125,填125.点睛:本题考查合情推理,属于基础题,解题的关键是从特殊情况归纳出一般结论. 15.已知函数 ()4322f x x ax x b =+++( x R ∈),其中,a b R ∈.若函数()f x 仅在0x =处有极值, a 的取值范围为__________.【答案】88,33⎡⎤-⎢⎥⎣⎦【解析】分析:导函数()()2'434f x x x ax =++,因此代数式2434x ax ++在R 上为非负,利用判别式非正得到实数a 的取值范围.详解: ()()322'434434f x x ax x x x ax =++=++,因为()f x 仅在0x =取极值,故24340x ax ++≥对任意的x R ∈恒成立,故29640a ∆=-≤,解得88,33a ⎡⎤∈-⎢⎥⎣⎦,填88,33⎡⎤-⎢⎥⎣⎦.点睛:函数的导函数为()()',f x xg x x R =∈,该函数仅在0x =处取极值的充要条件是()g x 在R 上恒非负或恒非正.16.设函数 ()221e x f x x +=, ()2x e xg x e =,对任意()12,0,x x ∈+∞,不等式()()121g x f x kk ≤+恒成立,则正数k 的取值范围是__________.【答案】1k ≥【解析】分析:因任意()12,0,x x ∈+∞,总有()()121g x f x kk ≤+,所以()()ma xm i n1g x f x kk ≤+,可利用基本不等式和导数分别求出()()min max f x g x , ,从而解出k 的范围.详解:因为在()0,+∞上, ()21'2f x e x e x =+≥, 当且仅当1x e=等号成立, 故()f x 在()0,+∞的最小值为2e . 又()()21'xe x g x e-=,则当()0,1x ∈时, ()'0g x >,故()g x 在()0,1为增函数; 当()1,x ∈+∞时, ()'0g x <,故()g x 在()1,+∞为减函数, 故()()max 1g x g e ==. 因任意()12,0,x x ∈+∞,总有()()121g x f x kk ≤+,所以()()maxmin 1g x f x kk ≤+,故2{ 10e ek k k ≤+>,解得1k ≥, 填1k ≥.点睛:(1)任意[][]12,,,x a b x m n ∈∈,总有()()12g x f x ≤,所以()()max min g x f x ≤; (2)任意[]1,,x a b ∈存在[]2,x m n ∈,使得()()12g x f x ≤成立,所以()()m a xm a xg x f x ≤;(3)存在[]1,,x a b ∈存在[]2,x m n ∈,使得()()12g x f x ≤成立,所以()()m i nm a x g x f x ≤.三、解答题17.设数列{}n a 的前n 项和为n S ,满足21234n n S na n n +=--, *n N ∈ ,且13a =. (Ⅰ)求2a 、3a 的值; (Ⅱ)求数列{}n a 的通项公式【答案】(Ⅰ)25a =, 37a =; (Ⅱ)见解析.【解析】分析:(Ⅰ)分别令1,2n n ==就可以求得25a =, 37a =. (Ⅱ)根据(Ⅰ)猜测21n a n =+,利用数学归纳可证明该猜测. 详解:(Ⅰ) 25a =, 37a =. (Ⅱ)由题意得13222n n S na n +=++, 由(1)知13a =, 25a =, 37a =,猜想21n a n =+,则数列{}n a 为等差数列,①假设当1,2,n = , ()*k k N ∈时,猜想成立,即()211,2,3,,i a i i k =+= ,则有()()()1321222k k k a a k k S k k +++===+,②当1n k =+时,有()()123322232112222k k k k S kk a k k k k ++=++=++=+=++, 这说明当1n k =+时,猜想也成立,结合①②,由归纳原理知,对任意*n N ∈, 21n a n =+.点睛:与自然数有关的问题,可以用数学归纳法,在归纳假设中,我们一般设当n k =时,命题()P k 成立,也可以假设0n n k ≤≤时,命题()P n 成立,然后再证明1n k =+,()1P k +也成立.18.已知函数()1ln xf x x ax-=+ (Ⅰ)若函数()f x 在1,2⎡⎫+∞⎪⎢⎣⎭上为增函数,求正实数a 的取值范围;(Ⅱ)若关于x 的方程12ln 20x x x mx -+-=在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个相异的实根,求实数m 的取值范围. 【答案】(Ⅰ)2a ≥;(Ⅱ)13{|ln2}22e m m --<≤. 【解析】分析:(Ⅰ)先求出函数()f x 的增区间为1,a ⎡⎫+∞⎪⎢⎣⎭, 1,2⎡⎫+∞⎪⎢⎣⎭应为其子集,故可求实数a 的范围.(Ⅱ)方程在1,e e ⎡⎤⎢⎥⎣⎦上有两个实数根可以转化为直线y m =与函数()1ln 2xg x x x -=+的图像有两个不同的交点,利用导数刻画()g x 的图像后可以得到实数m 的取值范围. 详解:(Ⅰ) ()22111ax f x x ax ax='-=-, 因为a 为正实数,由定义域知0x >,所以函数的单调递增区间为1,a ⎡⎫+∞⎪⎢⎣⎭. 因为函数()f x 在1,2⎡⎫+∞⎪⎢⎣⎭上为增函数,所以1102a <≤,所以2a ≥. (Ⅱ)因为方程12ln 20x x x mx -+-=在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个相异的实根,故方程1ln 02x x m x -+-=在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个相异的实根即 方程1ln 2x x m x -+=在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个相异的实根. 令()1ln 2x g x x x -=+,则()22112122x g x x x x -=-+=', 当11,2x e ⎛⎫∈ ⎪⎝⎭时, ()'0g x < , ()g x 在11,2e ⎛⎫ ⎪⎝⎭为减函数; 当1,2x e ⎛⎫∈⎪⎝⎭时, ()'0g x > , ()g x 在1,2e ⎛⎫⎪⎝⎭为增函数. ()111ln 10222e e eg e e e e e --+=+=+=> 111112ln ln20122222g -⎛⎫=+=-< ⎪⎝⎭⨯()111113ln 101222e e e g g e e e e---⎛⎫=+=-=<< ⎪⎝⎭⨯ ()y g x =的图像如图所示:要使函数()1ln 2x g x x x -=+的图象与函数y m =的图象在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个交点,则要满足112g m g e ⎛⎫⎛⎫<≤⎪ ⎪⎝⎭⎝⎭,所以m 的取值范围为13ln222e m --<≤. 点睛:含参数的方程的解的个数的讨论,可以参变分离后转化为动直线与定曲线的交点的个数.定曲线的刻画需以导数为工具讨论函数的单调性、极值及区间端点处的函数值等.19.已知定义在正实数集上的函数()2122f x x ax =+, ()23ln g x a x b =+,其中20a >.设两曲线()y f x =, ()y g x =有公共点,且在该点处的切线相同(Ⅰ)用a 表示b ,并求b 的最大值; (Ⅱ)0x >时,求证: ()()f x g x ≥【答案】(Ⅰ)2253ln 2b a a a =-,2332e ; (Ⅱ)见解析.【解析】分析:(Ⅰ)可设公共点为()00,x y ,由()()()()0000{''f x g x f x g x == 得到0a x =且2253ln 2b a a a =-,利用导数讨论该函数的单调性就可以得到实数b 的取值范围. (Ⅱ)构建新函数()()()F x f x g x =-,利用导数可求得()F x 的最小值点为x a =,从而()()()min 0F x f a g a =-=,也就是()()f x g x ≥.详解:(Ⅰ)设()y f x =与()(0)y g x x =>在公共点()00,x y 处的切线相同.∵()2f x x a '=+,()23a g x x'=,由题意()()00f x g x =, ()()00f x g x =''.即220002001232{ 32x ax a lnx b a x a x +=++=,由20032a x a x +=得: 0x a =或03x a =-(舍去).即有222221523ln 3ln 22b a a a a a a a =+-=-, 令()2253ln (0)2h t t t t t =->,则()()213ln h t t t =-'.于是当()13ln 0t t ->,即130t e <<时, ()0h t '>; 当()13ln 0t t -<,即13t e >时, ()0h t '<.故()h t 在130,e ⎛⎫ ⎪⎝⎭为增函数,在13,e ⎛⎫+∞ ⎪⎝⎭为减函数,于是()h t 在()0,+∞的最大值为123332h e e ⎛⎫= ⎪⎝⎭.(Ⅱ)设()()()22123ln (0)2F x f x g x x ax a x b x =-=+-->, 则 ()()()2332(0)x a x a a F x x a x x x-+=+-=>'. 故()F x 在()0,a 为减函数,在()0,+∞为增函数,于是函数()F x 在()0,+∞上的最小值是()()()()0000F a F x f x g x ==-=.故当0x >时,有()()0f x g x -≥,即当0x >时, ()()f x g x ≥.点睛:切线问题的核心是切点的横坐标,通过它沟通切线的斜率和函数在切点横坐标的导数.函数不等式的证明可以构建新函数,通过导数求出新函数的最小值为零即可. 20.已知函数()()2ln 1f x ax x =++.(Ⅰ)当14a =-时,求函数 ()f x 的单调区间; (Ⅱ)当[)0,x ∈+∞时,不等式()f x x ≤恒成立,求实数a 的取值范围. (Ⅲ)求证: ()()124821+1+1+1+2335592121n n ne -⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥⋅⋅< ⎪⎪⎪⨯⨯⨯++⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦┄(*n N ∈, e 是自然对数的底数).【答案】(Ⅰ)单调递增区间为()1,1-,单调递减区间为()1,+∞;(Ⅱ)(],0-∞; (Ⅲ)见解析.【解析】分析:(Ⅰ)求出函数的导数,分别解不等式()'0f x >、()'0f x <,可求得()f x 的增区间和减区间.(Ⅱ)构建新函数()()2ln 1,0g x ax x x x =++-≥, 不等式()f x x ≤在[)0,+∞上恒成立等价于()0g x ≤在[)0,+∞恒成立,而()()221'1x ax a g x x ⎡⎤+-⎣⎦=+,分0,0,0a a a =><三种情形讨论可得实数a 的取值范围为(],0-∞.(Ⅲ)由(Ⅱ)得不等式()ln 1x x +≤,[)0,x ∈+∞,故有()()()()11211ln 1221212121n n nn n --⎛⎫⎡⎤⎪⎢⎥+≤- ⎪++++⎢⎥⎝⎭⎣⎦,利用累加及其裂项相消法可以得到: ()()12282ln 1ln 1ln 1ln 112335592121n n n-⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥++++++++< ⎪ ⎪ ⎪⨯⨯⨯++⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,化简后可得到要证明的不等式. 详解:(Ⅰ)当14a =-时, ()()21ln 114f x x x x =-++>-(), ()()()()2111(1)2121x x f x x x x x +-=-+=->-++'. 由()0f x '>解得11x -<<,由()0f x '<解得1x >, 故函数()f x 的单调递增区间为()1,1-,单调递减区间为()1,+∞(Ⅱ)因当[)0,x ∈+∞时,不等式()f x x ≤恒成立,即()2ln 10ax x x ++-≤恒成立.设()()()2ln 10g x ax x x x =++-≥,只需()max 0g x ≤即可.由()()22112111x ax a g x ax x x ⎡⎤+-⎣⎦='+-=++,(ⅰ)当0a =时, ()1xg x x -'=+, 当0x >时, ()0g x '<,函数()g x 在()0,+∞上单调递减, 故()()00g x g ≤=成立; (ⅱ)当0a >时,由()()22101x ax a g x x ⎡⎤+-⎣⎦+'==,因[)0,x ∈+∞,所以112x a=-, ①若1102a -<,即12a >时,在区间()0,+∞上, ()0g x '>,则函数()g x 在()0,+∞上单调递增, ()g x 在[)0,+∞上无最大值; ②若1102a -≥,即102a <≤时,函数()g x 在10,12a ⎛⎫- ⎪⎝⎭上单调递减,在区间11,2a ⎛⎫-+∞ ⎪⎝⎭上单调递增,同样()g x 在[)0,+∞上无最大值,不满足条件; (ⅲ)当0a <时,由()()2211x a x a g x x ⎡⎤+-⎣⎦'=+,∵[)0,x ∈+∞,∴()2210ax a +-<,∴()0g x '<,故函数()g x 在[)0,+∞上单调递减,故()()00g x g ≤=成立. 综上所述,实数a 的取值范围是(],0-∞.(Ⅲ)据(Ⅱ)知当0a =时, ()ln 1x x +≤在[)0,+∞上恒成立,又()()11211221212121n n nn n --⎛⎫=- ⎪++++⎝⎭, ∵()()12482ln 11112335592121n n n-⎡⎫⎛⎫⎛⎫⎛⎫⎪⎢++++= ⎪⎪⎪⎪⨯⨯⨯++⎝⎭⎝⎭⎝⎭⎢⎣⎭()()12282ln 1ln 1ln 1ln 12335592121n n n-⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥++++++++ ⎪ ⎪ ⎪⨯⨯⨯++⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦()()124822335592121nn n-<++++⨯⨯⨯++ ][111111111112212335592121221n n n -⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-=-< ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ,∴()()124821+1+1+12335592121n n ne -⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥+< ⎪⎪⎪⨯⨯⨯++⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦. 点睛:复杂函数的性质的讨论,可以通过导数先刻画函数的单调性(与导数的正负有关),再刻画函数的极值,从而讨论与函数相关的不等式恒成立问题.而数列不等式的证明往往需要利用题设条件构建新的函数不等式,通过赋予自变量特殊的值求得数列不等式,最后利用新的数列不等式去证明题设中的不等式.。
天津市第一中学2017-2018学年高二下学期期中考试数学(

天津一中 2017-2018-2 高二年级数学学科(文科)模块质量调查试卷本试卷分为第 I 卷(选择题)、第 II 卷(非选择题)两部分,共 100 分,考试用时90 分钟。
第 I 卷 1 页,第 II 卷 至 2 页.考生务必将答案涂写在规定的位置上,答在试卷上的无效.一、选择题:1. 已知a 、b 、c 是互不相等的非零实数.若用反证法证明三个方程220ax bx c ++=,220bx cx a ++=,220cx ax b ++= 至少有一个方程有两个相异实根,应假设成( )A . 三个方程都没有两个相异实根B .一个方程没有两个相异实根C .至多两个方程没有两个相异实根D .三个方程不都没有两个相异实根 2. 已知复数11?z i=-,则z z -对应的点所在的象限为( ) A . 第一象限 B .第二象限 C .第三象限 D .第四象限 3.曲线12x y e=在点2(4,)e 处的切线与坐标轴所围三角形的面积为( )A . 2e B .24e C .22e D .29 2e4. 下列函数中,在(0,)+∞上为增函数的是( )A .()sin 2f x x =B . ()x f x xe =C . ()3 f x x x =-D . ()ln f x x x =-+5. 已知定义在R 上的可导函数()y f x =的导函数为 ()f x ',满足 ()()f x f x '<,且(0)2f =,则不等式()2x f x e>的解集为( ) A . (,0)-∞ B .(0,)+∞ C. (,2)-∞ D .(2,)+∞6. 若函数()23ln f x ax x x =+-图像存在与直线10x y +-=垂直的切线,则实数a 的取值范围是( ) A .1,2⎡⎫-+∞⎪⎢⎣⎭ B .1,2⎛⎤-∞- ⎥⎝⎦ C. [)1,-+∞ D .(],1-∞+7. 若点P 是曲线2ln y x x =-上任意一点,则点P 到直线2y x =-的最小距离为( )A . 1B 2D 8. 设函数 ()2ln f x x ax bx =++,若 1x =是函数()f x 的极大值点,则实数a 的取值范围是( ) A . 1,2⎛⎫-∞-⎪⎝⎭ B .(,1)-∞ C. [1,)+∞ D .1,2⎡⎫+∞⎪⎢⎣⎭9. 函数()32f x x bx cx d =+++的大致图象如图所示,则2212x x +等于( ) A .89 B . 109 C. 169 D .28910. 已知{|()0}M f αα==, {|()0}N g ββ==,若存在M α∈,N β∈,使得n αβ-<,则称函数 ()f x 与 ()g x 互为“n 度零点函数”.若2 ()31x f x -=-与2 ()x g x x ae =-互为“1 度零点函数”,则实数a 的取值范围为( )A . 214,e e ⎛⎤⎥⎝⎦ B . 214,e e ⎛⎤ ⎥⎝⎦ C. 242,e e ⎛⎤ ⎥⎝⎦ D .3349,e e ⎛⎤⎥⎝⎦二、填空题11. 已知a R ∈,i 为虚数单位,i 为虚数单位,若2?a ii -+为实数,则a 的值为 . 12. 已知函数()()()21221f x f x x f '=++,则()2f '的值为 .13. 设m R ∈,若函数 ,xy e mx x R =+∈有大于零的极值点,则m 的范围为 . 14. 观察下面一组等式11S =22349S =++=, 33456725S =++++=,44567891049S =++++++=,......根据上面等式猜测21(43)()n S n an b -=-+,则22a b += .15. 已知函数 ()2143ln 2f x x x x =-+-在区间[,1]t t +上不单调,则t 的取值范围是__________.16. 设函数 221()e x f x x +=,2()x e x g x e=,对任意x ,(0,)t ∈+∞,不等式()()1g x f t k k ≤+恒成立,则正数k 的取值范围是__________.三、解答题17. 已知函数2 ()ln f x x a x =+的极值点为2 .(1)求实数a 的值; (2)求函数()f x 的极值;(3)求函数 ()f x 在区间1,e e⎡⎤⎢⎥⎣⎦上的最值. 18. 已知函数()1ln xf x x ax -=+ (Ⅰ)若函数() f x 在1[,)2+∞上为增函数,求正实数a 的取值范围;(Ⅱ)若关于 x 的方程12ln 20x x x mx -+-=在区间1,e e⎡⎤⎢⎥⎣⎦内恰有两个相异的实根,求实数m 的取值范围.19. 已知函数()21ln 12f x x x ax =+-,且 ()11f '=- (Ⅰ)求 ()f x 的解析式; (Ⅱ)若存在(0,)x ∈+∞,使得 ()210f x mx -+≥成立,求m 的取值范围;; (Ⅲ)证明函数 ()2y f x x =+的图象在2 ()1x g x xe x =--图象的下方.20.已知函数 ()ln (),()1xf x x a x a Rg x e =+∈=-. (1)若直线0y =与函数()y f x =的图象相切,求a 的值;;(2)设0a >,对于1212,[3,)()x x x x ∀∈+∞≠,都有1212 ()()()()f x f x g x g x -<-求实数a 的取值范围.参考答案一、选择题1-5: ABABB 6-10: ABACB二、填空题11. -2 12. -6 13. (,1)-∞- 14. 25 15. (0,1)(2,3) 16. 1k ≥三、解答题17. 解:(1)∵ f x x 2a ln x ,( x 0) ∴()2a f x x x'=+又函数 ()f x 的极值点为2 ∴(2)2202af '=⨯+=, 解得8a =-.经验证得8a =-符合题意, ∴8a =-(2)由(1)得2()8ln f x x x =+. ∴82(2)(2)()2x x f x x x x+-'=-=, 当02x <<时,()0f x '<,()f x 单调递减,当2x >时,()0f x '>,()f x 单调递增.∴当2x =时,()f x 有极小值,且极小值为 (2)482f ln =- (3)由(2)得()f x 在1,2e ⎡⎫⎪⎢⎣⎭当单调递减,在(]2,e 上单调递增,∴min ()(2)482f x f ln ==-, ∵2118f e e ⎛⎫=+ ⎪⎝⎭,21()8f e e f e ⎛⎫=-< ⎪⎝⎭, ∴max 211()8f x f e e ⎛⎫==+ ⎪⎝⎭. 18.解: (Ⅰ)22111()ax f x x ax ax-'=-=,因为a 为正实数,由定义域知0x >,所以函数的单调递增区间为1,a ⎡⎫+∞⎪⎢⎣⎭因为函数()f x 在1[,)2+∞上为增函数,所以1102a <≤,所以2a ≥. (Ⅱ)方程12l n 20x x x m x -+-=在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个相异的实根⇔方程1l n 02x x m x -+-=在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个相异的实根⇔方程1ln 2x x m x -+=在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个相异的实根⇔函数1()ln 2x g x x x -=+的图象与函数y m =的图象在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个交点考察函数()1ln 2x g x x x -=+,221121()22x g x x x x -'=-+=,在11,2e ⎡⎤⎢⎥⎣⎦为减函数,在1,2e ⎡⎤⎢⎥⎣⎦为增函数111()ln 10222e e eg e e e e e --+=+=+=> 111112()ln ln 20122222g -=+=-<⨯ 111113()ln 10()222e e e g g e e e e ---=+=-=<<⨯画函数()1ln 2x g x x x -=+,1,x e e ⎡⎤∈⎢⎥⎣⎦的草图,要使函数()1ln 2x g x x x -=+的图象与函数y m =的图象在区间1,e e ⎡⎤⎢⎥⎣⎦内恰有两个交点,则要满足11()()2g m g e <≤所以m 的取值范围为13{|ln 2}22e m m --<≤ 19. 解:(Ⅰ)易知()ln 1f x x ax '=++,所以()11f a '=+,又()11f '=- ∴2a =-∴()2ln --1f x x x x =(Ⅱ)若对任意的()0,x ∈+∞,都有()210f x mx -+≤,即2ln 20x x x mx --≤恒成立,即:11ln 22m x x ≥-恒成立 令11()ln 22h x x x =-,则111()222xh x x x-'=-=,当01x <<时,1()02xh x x -'=>,所以()h x 单调递增; 当1x >时,1()02xh x x-'=<,所以()h x 单调递减; ∴1x =时,()h x 有最大值1(1)2h =-,∴12m ≥-,即m 的取值范围为1,2⎡⎫-+∞⎪⎢⎣⎭. (Ⅲ)要证明函数()2y f x x =+的图象在()21xg x xe x =--图象的下方, 即证:2()21x f x x xe x +<--恒成立, 即:ln 2xx e <- 由(Ⅱ)可得:111()ln 222h x x x =-≤-,所以ln 1x x ≤-, 要证明ln 2x x e <-,只要证明12xx e -<-,即证:10xe x --> 令中()1xx e x φ=--,则()1xx e φ'=-,当0x >时,()0x φ'>,所以()x φ单调递增,∴()(0)0x ϕϕ>= 即10xe x -->,所以12xx e -<-,从而得到ln 12xx x e ≤-<-,所以函数()2y f x x =+的图象在()21x g x xe x =--图象的下方 20. 解: (1)()1a f x x '=+,设切点为()0,0x 得010a x +=得到0x a =-, 所以()ln 0a a -+-=所以a e =-.(2)∵0a >∴[)3,x ∈+∞时,()0f x '>,所以()f x ,()g x 在[)3x ∈+∞上为增函数 不妨设12x x <则()()12f x f x <,()()12g x g x <,所以()()()1212()f x f x g x g x -<-,可化为()()()()21219f x f x g x x -<-, 即()()()()1122f x g x f x g x ->-,设()()()h x f x g x =-,则()h x 在[)3,x ∈+∞上为减函数,()10xa h x e x'=+-≤在[)3,x ∈+∞上恒成立,即x xe x a -≥在[)3,x ∈+∞上恒成立,设()xv x xe x =-,则∴[3,)x ∈+∞∴()10xxv x e xe '=+->所以()xv x xe x =-在[)3,x ∈+∞上为增函数,所以()3min 33v x e =-∴333a e ≤-.。
2017-2018学年天津一中高二(下)期中化学试卷

2017-2018学年天津一中高二(下)期中化学试卷一、选择题(每小题有1个正确答案)1.(2分)最简单的烃,下列关于甲烷的叙述中不正确的是()A.甲烷是烃类物质中相对分子质量最小的物质B.1molCH4在光照条件下最多能与4molCl2反应C.甲烷的二氯代物只有一种可以证明甲烷为正四面体结构D.甲烷与空气的体积比为1:2时,混合气点燃爆炸最剧烈2.(2分)下列反应中前者属于取代反应,后者属于加成反应的是()A.甲烷与氯气混合后光照反应;乙烯使酸性高锰酸钾溶液的褪色B.乙烯与溴的四氯化碳溶液反应;苯与氢气在一定条件下反应生成环己烷C.苯滴入浓硝酸和浓硫酸的混合液中,有油状液体生成;乙烯与水生成乙醇的反应D.在苯中滴入溴水,使溴水褪色;乙烯与氯化氢反应制取氯乙烷3.(2分)下列关于常见有机化合物的说法中,正确的是()A.氯乙烯、聚乙烯、苯乙烯都是不饱和烃B.乙烯和聚乙烯都能与溴的四氯化碳溶液发生加成反应C.苯、乙烯都既能发生加成反应,也能发生氧化反应D.通过石油裂化和裂解可得到乙烯、丙烯和苯等重要的化工原料4.(2分)下列实验或操作不能达到目的是()A.制取溴苯:将铁屑、溴水、苯混合加热B.用NaOH 溶液除去溴苯中的溴C.鉴别己烯和苯:向己烯和苯中分别滴入酸性KMnO4溶液,振荡,观察是否褪色D.除去甲烷中含有的乙烯:将混合气体通入溴水中5.(2分)某烃有两种或两种以上的同分异构体,其某一种同分异构体的一氯代物只有一种,则这种烃可能是()①分子中含有7个碳原子的芳香烃②分子中含有4个碳原子的烷烃③分子中含有12个氢原子的烷烃④分子中含有8个碳原子的烷烃.A.③④B.②③C.①②D.②④6.(2分)下列说法正确的是()A.某有机物燃烧只生成CO2和H2O,且二者物质的量相等,则此有机物一定为C n H2nB.相同质量的烃,完全燃烧,消耗O2越多,烃中含氢量越高C.某气态烃C x H y与足量O2恰好完全反应,如果反应前后气体体积不变(温度>100℃),则y=2D.一种烃在足量的氧气中燃烧,将产生的气体通过浓H2SO4,与反应前相比减少的体积就是生成的水蒸气的体积7.(2分)下列有关苯及其同系物的说法错误的是()A.苯在空气中燃烧,火焰明亮伴有浓烟B.用酸性高锰酸钾溶液验证苯环上是否存在碳碳双键C.苯能与氢气在一定条件下发生加成反应D.甲苯能使酸性高锰酸钾溶液褪色,说明甲基使苯环变活泼8.(2分)2005年度的诺贝尔化学奖分别奖给美国和法国的三位科学家,表彰他们对“烯烃复分解”反应研究方面作出的贡献.“烯烃复分解”是指在金属钨或钼等催化剂的作用下,碳碳双键断裂并重新组合的过程.例如:+→+则对于有机物CH2=CHCH2CH=CH2发生烯烃复分解反应时可能生成产物的判断中正确的是()①②CH2═CH2③④CH2=C=CH2.A.只有③B.只有②③C.只有①②③D.只有④9.(2分)下列有关镀锌钢管的叙述正确的是()A.电镀时,钢管做阳极,锌棒做阴极,锌盐溶液做电解质溶液B.钢管镀锌后,铁与锌构成原电池的两电极,腐蚀锌而保护铁C.镀锌的目的是为了在钢管表面形成Fe﹣Zn 合金,增强钢管的耐腐蚀能力D.镀锌层破损后,钢管仍可受到保护10.(2分)电解装置如图所示,电解槽内装有KI及淀粉溶液,中间用阴离子交换膜隔开.在一定的电压下通电,发现左侧溶液变蓝色,一段时间后,蓝色逐渐变浅.已知:3I2+6OH﹣═IO3﹣+5I﹣+3H2O,下列说法不正确的是()A.右侧发生的电极方程式:2H2O+2e﹣═H2↑+2OH﹣B.电解结束时,右侧溶液中含有IO3﹣C.电解槽内发生反应的总化学方程式KI+3H2O═KIO3+3H2D.如果用阳离子交换膜代替阴离子交换膜,电解槽内发生的总化学方程式不变11.(2分)下列说法正确的是()A.丙烷是直链烃,所以分子中3个碳原子也在一条直线上B.丙烯所有原子均在同一平面上C.所有碳原子一定在同一平面上D.至少有16个原子共平面12.(2分)有4种碳架如下的烃,下列说法正确的是()①a和d是同分异构体②b和c是同系物③a和d都能发生加成反应④只有b和c能发生取代反应.A.①④B.①②C.②③D.①②③13.(2分)聚丙烯酸钠()具有超强吸水性,能吸收空气中的水分,可用于矿山道路运输抑尘等。
20172018学年天津市第一中学高二下学期期中考试化学试题(解析版)

2021-2021学年天津市第一中学高二下学期期中考试化学考前须知:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、单项选择题1.甲烷是最简单的烃,以下关于甲烷的表达中不正确的选项是〔〕 A. 甲烷是烃类物质中相对分子质量最小的物质B. 甲烷与空气的体积比为 1∶2 时,混合气点燃爆炸最剧烈C. 1 mol CH 4在光照条件下最多能与 4 mol Cl 2反响D. 甲烷的二氯代物只有一种可以证明甲烷为正四面体结构 2.以下反响中前者属于取代反响,后者属于加成反响的是〔〕 A. 甲烷与氯气混合后光照反响;乙烯使酸性高锰酸钾溶液的褪色 B. 乙烯与溴的四氯化碳溶液反响;苯与氢气在一定条件下反响生成环己烷 C. 苯滴入浓硝酸和浓硫酸的混合液中,有油状液体生成;乙烯与水生成乙醇的反响 D. 在苯中滴入溴水,使溴水褪色;乙烯与氯化氢反响制取氯乙烷 3.以下关于常见有机化合物的说法中,正确的选项是〔〕 A. 氯乙烯、聚乙烯、苯乙烯都是不饱和烃B. 乙烯和聚乙烯都能与溴的四氯化碳溶液发生加成反响C. 苯、乙烯都既能发生加成反响,也能发生氧化反响D. 通过石油裂化和裂解可得到乙烯、丙烯和苯等重要的化工原料 4.以下实验或操作不能到达目的的是〔〕 A. 制取溴苯:将铁屑、溴水、苯混合加热 B. 用 NaOH 溶液除去溴苯中的溴C. 鉴别己烯和苯:向己烯和苯中分别滴入酸性 KMnO 4溶液,振荡,观察是否褪色D. 除去甲烷中含有的乙烯:将混合气体通入溴水中5.某烃有两种或两种以上的同分异构体,其某一种同分异构体的一氯代物只有一种,那么这种烃可能是〔〕①分子中含有7个碳原子的芳香烃 ②分子中含有4个碳原子的烷烃 ③分子中含有12个氢原子的烷烃④分子中含有8个碳原子的烷烃A. ③④B. ②③C. ①②D. ②④ 6.以下说法正确的选项是〔〕A. 某有机物燃烧只生成 CO 2和 H 2O ,且二者物质的量相等,那么此有机物一定为 CnH 2nB. 相同质量的烃,完全燃烧,消耗 O 2越多,烃中含氢量越高C. 某气态烃 CxHy 与足量 O 2恰好完全反响,如果反响前后气体体积不变(温度>100 ℃),那么 y =2D. 一种烃在足量的氧气中燃烧,将产生的气体通过浓 H 2SO 4,与反响前相比减少的体积就是生成的水蒸气的体积7.以下有关苯及其同系物的说法错误的选项是〔〕 A. 苯在空气中燃烧,火焰明亮伴有浓烟B. 用酸性高锰酸钾溶液验证苯环上是否存在碳碳双键C. 苯能与氢气在一定条件下发生加成反响D. 甲苯能使酸性高锰酸钾溶液褪色,说明甲基使苯环变活泼8.2005年度的诺贝尔化学奖分别奖给美国和法国的三位科学家,表彰他们对“烯烃复分解〞反响研究方面作出的奉献。
天津市第一中学2018-2019学年高二下学期期中考试生物试题(含答案)

天津一中 2018-2019-2 高二年级生物学科模块质量调查试卷本试卷分为第 I 卷(选择题)、第 II 卷(非选择题)两部分,共 100 分,考试用时90 分钟。
第 I 卷至页,第 II 卷至页。
考生务必将答案涂写规定的位置上,答在试卷上的无效。
祝各位考生考试顺利!一、单选题(每题 1 分共 40 分)1.下列关亍基因工程的叙述,正确的是() A.构建表达载体时需要在目的基因前加上起始密码子 B.农杄菌转化法可以将目的基因随机揑入受体细胞的染色体 DNA 上C.标记基因中丌能有限制酶的识别位点以防止其被破坏而失去作用 D.导入人胰岛素基因的大肠杄菌可直接生产出有活性的人胰岛素2.科学家在某种植物中找到了抗枯萎的基因,幵以质粒为运载体,采用转基因斱法培育了抗枯萎病的金茶花新品种。
下列有关说法正确的是() A.基因工程育种只能在同种生物中迚行 B.质粒是能自我复制的小型细胞器,因此适合做运载体 C.通过该斱法获得的抗病金茶花,将来产生的配子丌一定含抗病基因 D.抗枯萎基因最终整合到植物的染色体组中,该技术应用的原理是染色体变异3.如图 1 表示 DNA 的平面结构示意图,图 2 表示某种限制酶的识别序列呾作用位点,下列相关说法正确的是()A.图 I 中 a 所示部位即图 2 中箭头所示部位B.图 2 所示的 DNA 片段被限制酶切割后获得的末端形式不图 1 下端相同 C.E.co1iDNA 连接酶可以将两个图 1 所示结构连接成为一个 DNA 片段 D.基因工程的载体必须具有图 2 所示的碱基序列4.图为某植物细胞一个 DNA 分子中 a、b、c 三个基因的分布状冴,图中Ⅰ、Ⅱ为无遗传效应的序列。
有关叙述正确的是()A.在每个植物细胞中,a、b、c 基因都会表达出相应蛋白质B.a、b、c 互为非等位基因,在亲子代间传递时可自由组合C.b 中生物碱基序列若发生了改变,则发生了基因突变,但性状丌一定改变D.基因在染色体上呈线性排列,基因的首、尾端存在起始密码子呾终止密码子5.下图表示利用基因工程生产胰岛素的三种途径,据图判断下列说法正确的是()A.催化过程①的 DNA 连接酶的作用是促使碱基之间形成氢键 B.三种斱法直接得到的胰岛素都具有生物活性 C.导入受体细胞 C 使用 Ca2+处理使其吸收周围的 DNA分子 D.利用显微注射的斱法将目的基因导入受体细胞 A 即乳腺细胞6.下列叙述正确共几项()①限制性内切酶的特点是识别特定的核苷酸序列呾具有特定的酶切位点②上海医学遗传研究所成功培育出第一头携带白蛋白的转基因牛,可以想象这头牛发生了基因突变③根据 mRNA 的信息推出幵获取目的基因的斱法是用 DNA 探针测出目的基因④转基因抗虫棉的生产过程中丌需要用到的工具是噬菌体⑤可以作目的基因“分子运输车”的是天然质粒⑥在基因操作的基本步骤中,丌迚行碱基互补配对的是将目的基因导入受体细胞⑦培育成抗除草剂的作物新品种,导人抗除草剂基因时只能以受精卵为受体⑧基因工程常用细菌等原核生物作受体细胞的原因包括繁殖速度快、遗传物质相对较少、多为单细胞,操作简便A. 三B.四C.五D.六7.下列哪项丌是蛋白质工程的研究内容() A.分析蛋白质分子的精细结构 B.分析氨基酸的化学组成 C.对蛋白质迚行有目的的改造D.按照人的意愿将天然蛋白质改造成新的蛋白质8.“筛选”是生物工程中常用的技术手段,下列关亍筛选的叙述中正确的有几项()①基因工程中用同种限制性核酸内切酶切割运载体呾目的基因,酶切产物用 DNA 连接酶连接,为了保证成功率,需将获得的产物筛选后导入受体细胞②单兊隆抗体制备过程中,在完成细胞融合后,第一次筛选出的是杂交瘤细胞③单兊隆抗体制备过程中,在完成细胞融合后,第二次筛选出的是针对目标抗原的抗体检验为阳性的杂交瘤细胞④为了快速繁殖无子西瓜,需筛选出特定染色体组数的体细胞才能迚行组织培养A.②③B.①④C.③④D.①②9.ch1L 基因是蓝藻拟核DNA 上控制叶绿素合成的基因。
【全国百强校】天津市第一中学2017-2018学年高二下学期期中考试物理试题

天津一中 2017-2018-2 高二年级物理学科模块质量调查试卷第 I 卷一、选择题(本题共 14 题,1-8 题为单选题,每题只有一个正确选项;9-14 题为多选题,每题有两个或两个以上的选项是正确的)1.穿过一个单匝闭合线圈的磁通量始终为每秒均匀增加 2Wb,则()A.线圈中感应电动势每秒增加 2VB.线圈中感应电动势每秒减少 2V C.线圈中感应电动势始终为 2V D.线圈中感应电动势始终为一个确定值,但由于线圈有电阻,电动势小于 2V2.如图所示交流电的电流有效值为()A.2AB.C.3AD.3.一个做简谐运动的质点,它的振幅是4cm,频率是2.5Hz,该质点从平衡位置开始经过 2.5s 后,位移的大小和经过的路程为()A.4cm、10cm B.4cm、100cm C.0、24cm D.0、100cm 4.如图甲所示,弹簧振子以 O 点为平衡位置,在 M、N 两点之间做简谐运动。
取向右为正方向,振子的位移 x 与时间 t 的关系图像如图乙所示,下列说法正确的是()A.t=0.8s 时,振子的速度方向向右B.t=0.2s 时,振子在 O 点右侧 6cm 处C. t=0.4s 和 t=1.2s 时,振子的加速度相同D.从 t=0.4s 到 t=0.8s 的时间内,振子的速度逐渐增大5.图(a)左侧的调压装置可视为理想变压器,负载电路中 R=55Ω,为理想电流表和电压表,若原线圈接入如图(b)所示的正弦交变电压,电压表的示数为110 V,下列表述正确的是()A.电流表的示数为 2 AB.原、副线圈匝数比为1∶2C.电压表的示数为交流电压的平均值D.原线圈中交变电压的频率为 100 Hz6.如图(甲)所示,单匝矩形线圈的一半放在具有理想边界的匀强磁场中,线圈轴线 OO’与磁场边界重合。
线圈按图示方向匀速转动。
若从图示位置开始计时,并规定电流 方 向沿 a →b→c→d→a 为正方向,则线圈内感应电流随时间变化的图像是下图(乙) 中的哪一个( )7.图中两条平行虚线之间存在匀强磁场,虚线间的距离为 l ,磁场方 向垂直纸面向里。
