自由度计算举例1
3-3 平面机构自由度的计算

7
46
1
5
3 2
(avi)
8
F = 3n-2pL-pH = 3×7-2×6-0 = 9 ???
1. 复合铰链(Multiple Joint) 由两个以上构件在同一处构成的重合转动副,称为复合铰链。
(avi)
(avi)
1
21 2
12
1
2
3
3
3
3
由m个构件(m3)构成的复合铰链应包含(m-1)个转动副。
注意:机构中的虚约束都是在一定的几何条件下出现的,如 果这些几何条件不满足,则虚约束将变成实际有效的约束, 从而使机构不能运动。
例1: 计算图所示机构的自由度 (若存在局部自由度、复合铰链、
虚约束请标出)。
复合铰链
虚约束 局部自由度
F =3n-2PL-PH
=3×7-2×9-1 =2
例 2:如图所示,已知: DE=FG=HI,且相互平行;DF=EG,
3-3 平面机构自由度的计算
§3-3平面机构的自由度(Degrees of Freedom) 一、平面机构自由度的定义
1.定义:机构具有确定运动时所需的独立运动的数目称为机构 的自由度。也可理解为:为确定机构中所有活动构件的位置, 必须给定的独立广义坐标的数目。
C
2 B
1
A
1
4
3 D
什么是机构的独立运动?
F322214 2 即引入了两个虚约束。 未去掉虚约束时 F 3n2pLpH352516 1 去掉虚约束后 F 3n2pLpH3323121
6)若两构件在多处相接触构成平面高副,且各接触点处的公法线重合,
则只能算一个平面高副。若公法线方向不重合,将提供2个约束。
自由度计算例题

改进措施:
1、增加一个低副和一个活动构件; 2、用一个高副代替低副。
改进方案
改进方案
改进方案
改进方案
例 2 如图所示,已知: DE=FG=HI,且相互平行;DF=EG, 且相互平行;DH=EI,且相互平行。计算此机构的自由度 (若存在局部自由度、复合铰链、虚约束请标出)。
例 5 计算下图机构的自由度 (若存在局部自由度、复 合铰链、虚约束请标出)。
n7;
PL 9 ;
PH 1
F 3n 2 PL PH 3 7 2 9 1 2
I 8 J 9 11 10 C 2 K L E 4 F 5 3 D 1 A H 7 G 6 B
虚约束
I 8 J 9 11 10 H 7 G
复合铰链
局部自由度
6 C 2 D
B 1 A
K
L E 4 F 5
3
n 8 ; PL 11 ; PH 1 F 3n 2 PL PH 3 8 2 11 1 1
D 4 C 5 F 6 G B 1 2 3 E I A 7 H
D
虚约束
5 F 6 G H
局部自由度
C4B 12 Nhomakorabea3 E
7
I A
n 6 ; PL 8 ; PH 1 F 3n 2 PL PH 3 6 2 8 1 1
例 4 如图所示, 已知HG=IJ,且相互平行;GL=JK,且相 互平行。计算此机构的自由度 (若存在局部自由度、复 合铰链、虚约束请标出)。
机构自由度计算举例
例 1 图示牛头刨床 设计方案草图。设计 思路为:动力由曲柄1 输入,通过滑块2使摆 动导杆 3 作往复摆动, 并带动滑枕4作往复移 动 ,已达到刨削加工 目的。 试问图示的构 件组合是否能达到此 目的? 如果不能,该 如何修改?
自由度怎么计算

自由度怎么计算
自由度计算公式:
1、自由度:具有确定运动所必需要的独立运动参数为机构自由度。
2、自由度计算公式:F=3n-2pl-2ph
n:活动构件数pl:低副数ph:高副数
自由度(degree of freedom, df)指的是计算某一统计量时,取值不受限制的变量个数。
计算公式df=n-k。
其中n为样本数量,k为被限制的条件数或变量个数,或计算某一统计量时用到其它独立统计量的个数。
自由度通常用于抽样分布中。
物理学术语:自由度是指物理学当中描述一个物理状态,独立对物理状态结果产生影响的变量的数量。
如运动自由度是确定一个系统在空间中的位置所需要的最小坐标数。
例如火车车厢沿铁轨的运动,只需从某一起点站沿铁轨量出路程,就可完全确定车厢所在的位置,即其位置用一个量就可确定,我们说火车车厢的运动有一个自由度;
汽车能在地面上到处运动,自由程度比火车大些,需要用两个量(例如直角坐标x,y)才能确定其位置,我们说汽车的运动有两个自由度;飞机能在空中完全自由地运动,需要用三个量(例如直角坐标x,y,z)才能确定其位置,我们说飞机在空中的运动有三个自由度。
所谓自由度数就是确定物体在空间的位置所需独立坐标的数目。
第一章 机构自由度计算1

F=3N-2PL-Ph =33 -24=1 34 -26=0
B
2
E
C
B
2 5 4
F D CD
C
1
A AB CD
4
BC
3
F AD BE D AF
1
A
3
虚约束的本质是什么?
从运动的角度看,虚约束就是“重复的约束” 或者是“多余的约束”。
机构中为什么要使用虚约束? a.使受力状态更合理
b.使机构平衡
c.考虑机构在特殊位置的运动 使用虚约束时要注意什么问题? 保证满足虚约束存在的几何条件,在机械设计中 使用虚约束时,机械制造的精度要提高。
三、平面机构具有确定运动的条件
1. F≥1或F>0
2. F=原动件数目
判断图示机构能否运动?
C 3 A D 4 1
B
2
2 C 4 B 1 A E F 5 D 6 3
C 是构件 2、4、5组成的复合铰链,
D 是构件 3、5、6组成的复合铰链.
F=3n-2PL-Ph =35 -26 -2 =1
2 C 4 B 1 A E F 5 D 6 3
2. 局部自由度
不影响机构整体运动的自由度,称为局部自由度。
在计算机构自由度时,局部自由度应当舍弃不计。
带虚约束的行星轮系
(4) 当两构件在多处接触并构成平面高副, 且过各接触点的公法线方向彼此重合时
DOF=3N-2PL-Ph =32 -22 -1 =1 32 -23-2=-2
A 3 2 n
O
1
n
B
但是,当他们的公法线方向不重合 时,必须各自计算其高副数。
n n B A n n n A n n B n
计算自由度和体系构造分析例题
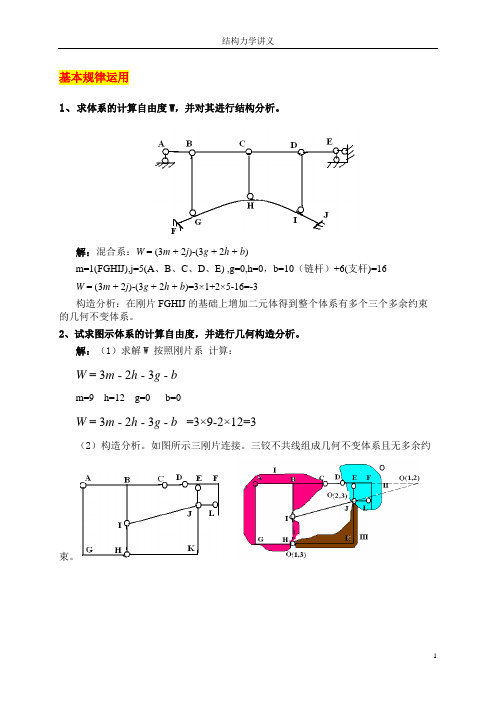
基本规律运用1、求体系的计算自由度W,并对其进行结构分析。
解:混合系:W = (3m + 2j)-(3g + 2h + b)m=1(FGHIJ),j=5(A、B、C、D、E) ,g=0,h=0,b=10(链杆)+6(支杆)=16W = (3m + 2j)-(3g + 2h + b)=3×1+2×5-16=-3构造分析:在刚片FGHIJ的基础上增加二元体得到整个体系有多个三个多余约束的几何不变体系。
2、试求图示体系的计算自由度,并进行几何构造分析。
解:(1)求解W 按照刚片系计算:W = 3m - 2h - 3g - bm=9 h=12 g=0 b=0W = 3m - 2h - 3g - b =3×9-2×12=3(2)构造分析。
如图所示三刚片连接。
三铰不共线组成几何不变体系且无多余约束。
3、试求图示体系的计算自由度,并进行几何构造分析。
解:(1)计算W:W = (3m + 2j)-(3g + 2h + b)m=1(FGHIJ),j=5(A、B、C、D、E) ,g=0,h=0,b=10(链杆)+6(支杆)=16W = (3m + 2j)-(3g + 2h + b)=3×1+2×5-16=-3(2)结构构造分析如图示体系内部(先撤除支座及地基)由三个刚片Ⅰ、Ⅱ、Ⅲ 用三个瞬铰两两相连,且三个瞬铰在一直线上,为几何瞬变体系。
4、如图所示为三角形ABC及其他链杆所组成体系,试考察BC边上G铰不同位置与体系整体几何特性的关系,给出简要分析过程。
(a) (b)(c) (d)解:(1)观察图(a)所示体系,△BEG直接与大地固定铰支,可以将B点看做铰结点,则BE,BG为链杆,因此,与大地直接相连的约束多余三根支杆,所以将大地必须看做是一个刚片。
BG和CD与GC相连,BE和A支座与△AEF相连,通过“找对家”的思路可以找到如图所示三刚片。
G铰位于BC中间时,三虚铰共线,组成瞬变体系。
第03讲自由度计算注意事项

1机械工程学院机械原理教研室第3讲 自由度计算注意事项2.6计算平面机构自由度时应注意的问题 计算图中圆盘锯机构的自由度 解:活动构件数n=7 低副数 F=3 n — 2PL — PH PL=6 =3 X 7 — 2 X 6 — 0 计算结果肯定不对! 1复合铰链一一两个以上的构件在同一处以转动副相联,如图所示。
计算时:m 个构件,有m — 1转动副。
上例中:在B 、C 、D 、E 四处应各有2个运动副。
所以圆盘锯机构的自由度计算为: 解:活动构件数 n=7 低副数 PL=10=9 高副数 PH=0 F=3 n — 2PL — PH=3 X 7 — 2X 10— 0=1 计算图中两种滚子凸轮机构的自由度。
解:左边机构 n=3, PL=3 , PH=1 F=3 n — 2PL — PH =3 X 3— 2X 3—仁2 对于右边的机构,有: F=3 X 2 — 2 X 2 —仁1事实上,两个机构的运动相同,且 2、局部自由度 定义:构件局部运动所产生的自由度。
本例中局部自由度 Fp=1 F=3 n — 2PL — PH — FP 或计算时去掉滚子和铰链:F=1出现在加装滚子的场合,计算时应去掉 =3 X 3-2 X 3 — 1—1=1Fp (局部自由度)F=3 X 2— 2 X 2 —仁1 滚子的作用:滑动摩擦变为滚动摩擦。
计算图中平行四边形机构的自由度 平行。
解:n=4, PL=6 , PH=O ,已知:AB 、 CD 、EF 互相 F=3 n — 2PL — PH 计算结果肯定不正确!3、虚约束 —— 对机构的运动实际不起作用的约束。
度时应去掉虚约束。
•/ FE = AB = CD ,故增加构件4前后E 点的轨迹都是圆弧。
增加的约束不起作用,应去掉构件 4。
如图2 — 27所示。
重新计算:n=3, PL=4, PH=0 =3 X 4— 2X 6 =0 计算自由 图 2— 26AF=3 n — 2PL — PH =3 X 3— 2X 4=1 特别注意:此例存在虚约束的几何条件是:2机械工程学院机械原理教研室AB 、CD 、EF 平行且相等。
机械工程基础-自由度计算例题(答案)

1.1.构件数n为7,低副p为9,高副pn为1,局部自由度为1,虚约束为0.E处为局部自由度,C处为复合铰链.F=3n-2p-pn=3*7-2*9-1=2(与原动件数目一致,运动确定)2.3.4.5.6.2. B处有复合铰链,有2个转动副。
无局部自由度。
B点左侧所有构件和运动副带入的约束为虚约束,属于与运动无关的对称部分。
n=5, PL=7, PH=0, F= 3n-2PL -PH=3×5-2×7-1×0=1。
运动链有确定运动,因为原动件数= 自由度数。
3.A处为复合铰链,因为有3个构件在此处组成成转动副,所以应算2个转动副。
B处为局部自由度,假设将滚子同构件CB固结。
无虚约束。
n=6, PL=8, PH=1, F= 3n-2PL -PH=3×6-2×8-1=1。
运动链有确定运动,因为原动件数= 自由度数。
4. 没有复合铰链、局部自由度、虚约束。
n=4, PL=5, PH=1, F= 3n-2PL -PH=3×4-2×5-1=1。
运动链有确定运动,因为原动件数= 自由度数。
5. 计算自由度:n=4, P L=6, P H=0, F= 3n-2P L -P H=3×4-2×6-1×0=0,运动链不能动。
修改参考方案如图所示。
6. F处为复合铰链,因为有3个构件在此处组成成转动副,所以应算2个转动副。
B处为局部自由度,假设将滚子同构件CB固结。
移动副M、N中有一个为虚约束,属于两构件在多处组成运动副。
n=7, PL=9, PH=1, F= 3n-2PL -PH=3×7-2×9-1=2。
运动链没有确定运动,因为原动件数< 自由度数。
自由度计算

1-10 冲压机构
解: B处为复合铰链 A处为局部自由度 C处为虚约束
F 3n 2 pl pH 3 4 - 2 4 - 2 2
原动件=机构自由度=2 故机构运动确定
F 3n 2 pl pH 3 8 - 2 11 - 1 1
原动件=机构自由度=1 故机构运动确定
故机构运动确定
1-7 加药泵加药机构
解:
1-8 测量仪表机构
解:
F 3n 2 pl pH 3 8 - 2 11 - 0 2
原动件=机构自由度=2 故机构运动确定
F 3n 2 pl pH 3 6 - 2 8 -1 1
原动件=机构自由度=1
故机构运动确定
1-9 缝纫机送布机构 解: A处为局部自由度
例:牛头刨床主体机构
解:
F 3n 2 pl pH 3 6 - 2 8 -1 1
原动件=机构自由度=1 故机构运动确定
例1-7 大筛机构
解: C处为复合铰链 F处为局部自由度 E’处为虚约束
F 3n 2 pl pH 3 7 - 2 9 -1 2
原动件=机构自由度=2
1-11 平炉渣口堵塞机构 解: A处为复合铰链
1-12 机械手
解:
F 3n 2 pl pH 3 4 - 2 4 - 2 2
原动件=机构自由度=2 故机构运动确定
F 3n 2 pl pH 3 3 - 2 3 - 0 3
原动件=机构自由度=3 故机构运动确定
1-5 平炉渣口堵塞机构 解: A处为局部自由度
1-6 据木机机构
解: A处为局部自由度
F 3n 2 pl pH 3 6 - 2 8 -1 1
第1章 平面机构的自由度计算

1处局部自由度 活动构件数为:n = 8 低副数为: P L = 11 高副数为: P H = 1 自由度数为: F = 3n - 2 P L - P H = 3 8 - 2 11 -1 = 1 一个原动件,运动确定
• • • • • • •
活动构件数为:n = 8 低副数为: P L = 11 高副数为: P H = 0 自由度数为: F = 3n - 2 P L - P H = 3 8 - 2 11 - 0 = 2 2个原动件,运动确定
测量仪表机构
• • • • • • • • 活动构件数为: n=6 低副数为: P L = 8 高副数为: P H = 1 自由度数为: F = 3n - 2 P L - P H = 3 6 -2 8 -1 = 1 一个原动件,运动确 定
练习
• 缝纫机送布机构
• • • • • • • • • • 注意事项: 1处局部自由度 2 处虚约束 活动构件数为:n = 4 低副数为: P L = 4 高副数为: P H = 2 自由度数为: F = 3n - 2 P L - P H = 3 4 -2 4 -2 = 2 2个原动件,运动确定。
其实,世上最温暖的语言,“ 不是我爱你,而是在一起。” 所以懂得才是最美的相遇!只有彼此以诚相待,彼此尊重 ,相互包容,相互懂得,才能走的更远。 相遇是缘,相守是爱。缘是多么的妙不可言,而懂得又是多么的难能可贵。否则就会错过一时,错过一世! 择一人深爱,陪一人到老。一路相扶相持,一路心手相牵,一路笑对风雨。在平凡的世界,不求爱的轰轰烈烈;不求誓 言多么美丽;唯愿简单的相处,真心地付出,平淡地相守,才不负最美的人生;不负善良的自己。 人海茫茫,不求人人都能刻骨铭心,但求对人对己问心无愧,无怨无悔足矣。大千世界,与万千人中遇见,只是相识的 开始,只有彼此真心付出,以心交心,以情换情,相知相惜,才能相伴美好的一生,一路同行。 然而,生活不仅是诗和远方,更要面对现实。如果曾经的拥有,不能天长地久,那么就要学会华丽地转身,学会忘记。 忘记该忘记的人,忘记该忘记的事儿,忘记苦乐年华的悲喜交集。 人有悲欢离合,月有阴晴圆缺。对于离开的人,不必折磨自己脆弱的生命,虚度了美好的朝夕;不必让心灵痛苦不堪, 弄丢了快乐的自己。擦汗眼泪,告诉自己,日子还得继续,谁都不是谁的唯一,相信最美的风景一直在路上。 人生,就是一场修行。你路过我,我忘记你;你有情,他无意。谁都希望在正确的时间遇见对的人,然而事与愿违时, 你越渴望的东西,也许越是无情无义地弃你而去。所以美好的愿望,就会像肥皂泡一样破灭,只能在错误的时间遇到错的人 。 岁月匆匆像一阵风,有多少故事留下感动。愿曾经的相遇,无论是锦上添花,还是追悔莫及;无论是青涩年华的懵懂赏 识,还是成长岁月无法躲避的经历……愿曾经的过往,依然如花芬芳四溢,永远无悔岁月赐予的美好相遇。 其实,人生之路的每一段相遇,都是一笔财富,尤其亲情、友情和爱情。在漫长的旅途上,他们都会丰富你的生命,使 你的生命更充实,更真实;丰盈你的内心,使你的内心更慈悲,更善良。所以生活的美好,缘于一颗善良的心,愿我们都能 善待自己和他人。 一路走来,愿相亲相爱的人,相濡以沫,同甘共苦,百年好合。愿有情有意的人,不离不弃,相惜相守,共度人生的每 一个朝夕……直到老得哪也去不了,依然是彼此手心里的宝,感恩一路有你!
算自由度的公式

算自由度的公式
1. 平面机构自由度计算公式。
- 对于平面机构,自由度计算公式为F = 3n - 2P_L-P_H。
- 其中n为活动构件数。
- P_L为低副(转动副和移动副)的数目。
- P_H为高副(例如齿轮副、凸轮副等)的数目。
2. 空间机构自由度计算公式(拓展)
- 空间机构自由度的计算相对复杂,常用的公式为F = 6n - 5P_5-4P_4-3P_3-2P_2-P_1。
- 这里n为活动构件数。
- P_5为五级副(相当于有5个相对运动自由度受到约束的运动副)的数目。
- P_4为四级副的数目,以此类推。
在人教版的机械原理相关教材中,平面机构自由度的计算是一个重要的基础内容,在分析机构的运动可能性和确定性方面有着关键的作用。
例如在分析平面连杆机构、凸轮机构等的运动时,通过计算自由度可以判断机构是否具有确定的运动等情况。
机械设计基础第1章平面机构的自由度和速度分析

§1 – 1 运动副及其分类
1.低 副 两构件通过面接触组成的运动副
①转 动 副(铰链): 组成运动副的两构件只能在平面内相对转动。
§1 – 1 运动副及其分类
②移 动 副: 组成运动副的两构件只能沿某一方向相对移动。
§1 – 1 运动副及其分类
2.高副:
F 3n2pLpH33241
§1 – 3 平面机构的自由度
⑷ 机构中对传递运动不起独立作用的对称部分
2B
3
4
1
A
DC
2 2
B
3 2
4
1
A
行星轮系
对称布置的两个行星轮2和2以及相应的两个转动副D、 C和4个平面高副提供的自由度
F322214 2 即引入了两个虚约束。 未去掉虚约束时 F 3n2pLpH352516 1 去掉虚约束后 F 3n2pLpH3323121
§1 – 3 平面机构的自由度 例
分析图c),可知: n=4,PL=6,PH=0 该平面机构的自由 度为:
F 3 n 2 P L P H 3 4 2 6 0 0
例:
复合
解: 1.如不考虑上述 2
3
因素,解得: 1
K=9, n=K-1=8
PL=10,PH=1,
虚 5局
6
7
8
4 9
§1 – 3 平面机构的自由度
机构具有确定运动的条件 (1)机构的自由度F >0。
(2)机构的原动件数等于机构的自由度F。
§1 – 3 平面机构的自由度
机构的自由度和原动件的数目与机构运动的关系
1)若机构自由度F≤0,则机构不能动; 2)若F>0且与原动件数相等,则机构各构件间
计算图示机构的自由度(如有复合铰链
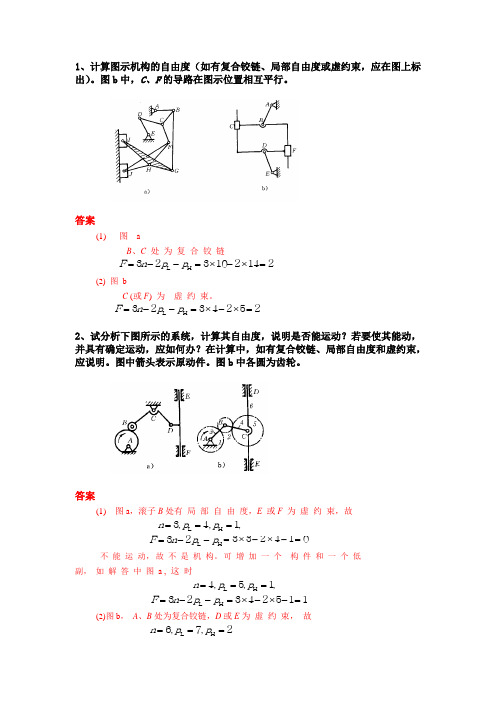
1、计算图示机构的自由度(如有复合铰链、局部自由度或虚约束,应在图上标出)。
图b中,C、F的导路在图示位置相互平行。
答案(1) 图 aB、C处为复合铰链F n p p=--=⨯-⨯=323102142L H(2) 图bC (或F) 为虚约束。
F n p p=--=⨯-⨯=3234252L H2、试分析下图所示的系统,计算其自由度,说明是否能运动?若要使其能动,并具有确定运动,应如何办?在计算中,如有复合铰链、局部自由度和虚约束,应说明。
图中箭头表示原动件。
图b中各圆为齿轮。
答案(1) 图a,滚子B处有局部自由度,E或F为虚约束,故n p p===341,,,L HF n p p =--32L H =⨯-⨯-= 332410不能运动,故不是机构。
可增加一个构件和一个低副,如解答中图a , 这时n p p===451,,,L HF n p p=--=⨯-⨯-=32342511L H(2)图b,A、B处为复合铰链,D或E为虚约束,故n p p===672,,L HF n p p =--32L H =⨯-⨯-=362722故 可 动, 但 因 只 有 一 个 原 动 件, 所 以 运 动 不 确 定。
修 改 方 法:(a) 可 增 加 一 个 原 动 件, 如 认 为 杆3 亦 为 原 动 件。
(b) 减 少 一 个构 件 和 一 个 低 副, 仍 用 一 个 原 动 件, 如 认 为 杆3 和 轮1 为 一 个 构 件 ( 图 b), 这 时n p p ===562,,,L HF n p p =--32L H =⨯-⨯-=352621注: 修 正 办 法 还 有 多 种。
3,计算下列机构的自由度。
如有复合铰链、局部自由度和虚约束,必须注明。
图b 中两圆为齿轮,导路F 垂直于AE 。
答案(1) 图aA 处 为 复 合 铰 链。
F n p p =--=⨯-⨯-=3231021402L H(2) 图bBC 杆 引 入 虚 约 束, 应 去 除。
自由度的计算

判断有无注意事项(复、局、虚) 确定构件数目,低副和高副各自的数目 运用公式计算机构自由度 检验机构是否具有确定运动
综合例题1:计算下图中大筛机构的自由度
复
虚
局
综合例题2:计算图示机构的自由度
1
复
2
4
3
虚
5
局
6
8 7
F= 3n-2PL -PH=3×8-2×11-1×1=1
课堂小结
(四个步骤缺一不可)
单击此处添加副标题
平面机构自由度的计算
单击此处添加正文,文字是您思想的提炼,请尽量言简意赅的阐述观 点。
构件的自由度
定义:构件所具有 的独立运动数目
二、机构的自由度
定义:机构中各构件相对于机架所具 有的独立运动数目 1、运动副与约束的关系 当构件组成运动副后,相对运动受到 约束,自由度减少
① 低副对自由度的 影响
副)数;
PH ——该机构中的高副数。
重点
记住上述公式,并能熟练应 用
F =3n 2PL PH
例
1
:
B 1 A
计算铰
C 2
链2C四3 D杆机B构2 C的3
自
F4 =33 Dn-2PL-BPH1A=4 3*3-2*4A1 -05=1
D4 E
由度
例2:计算内燃机内连杆机构的自
由度
C
C 2
3 C
D
2
1BF=34 n-32DPL-PHB=2 31A*4 3-2*4-0BA1 =15
课后思考:若在C 处增加一滑块呢?
2、机构自由度与原 动件数之间的关系 讨论
3
2
4
1
5
自由度F > 原动件数 原动件 F=3n-2PL-PH=3*4-2*5-0=2 运动不确定 原动件
计算自由度公式

计算自由度公式
计算自由度公式
一、自由度的基本概念
自由度(degree of freedom)是指统计分析中的独立变量总量,也称为独立自由变量量。
自由度是表示研究中可被用来分析的观测值的数目,自由度的大小可以反映研究的可靠性和研究的灵活性,是统计抽样检验中计算P 值和置信区间的重要指标。
二、计算公式
计算自由度的公式是:自由度=n-1,其中n表示样本的个数。
例如,样本的个数为50,那么自由度就是50-1=49。
三、应用实例
实验结果表明,有50个参与者参加研究,那么根据计算自由度的公式,此研究的自由度等于50-1=49。
用这49个样本做T检验时,会用到这49个自由度,用来计算P 值和置信度区间,从而得出检验结果,表明特定两组样本的均值是否有显著差异。
- 1 -。
自由度为什么是n-1

自由度为什么是n-1
因为在求离差平均和时, 只有 n-1 个数据可以自由取值, 所以
自由度为 n-1 . 样本方差的分母用 n-1 ,其原因可以从多方面来解释. 从实际应用的角度看,当我们用样本方差估计总体方差σ2 时, 是σ 2 的无偏估计量.
统计学上的自由度是指当以样本的统计量来估计总体的参数时,样本中独立或能自由变化的资料的个数,称为该统计量的自由度.
自由度计算公式:自由度=样本个数-样本数据受约束条件的个数,
即df = n - k(df 自由度,n样本个数,k约束条件个数)当样本数据的个数为n时,若样本平均数 x拔确定后,则附加给n个观测值的约束个数就是1个,一次只有n-1个数据可以自由取值,其中必有一个数据不能自由取值。
按照这一逻辑,如果对n个观测值附加的约束个数为k个,自由度则为n-k。
例如假设样本有3个值,即x1=2,x2=4,x3=9,则当 x拔 =5确定后,x1、x2、x3只有两个数据可以自由取值,另一个则不能自由取值,比如x1=6,x2=7,那么
x3必然取2,而不能取其他值。
样本方差自由度为什么为n-1呢,因为在计算离差平方和∑(xi -x)2 时,必须先求出样本平均数 x拔,而 x拔则是附加给∑(xi -x)2 的一个约束,因此,计算离差平方和时只有n-1个独立的观测值,而不是n个。
在估计总体的方差时,使用的是离差平方和。
只要n-1个数的离差平方和确定了,方差也就确定了;因为在均值确定后,如果知道了
其中n-1个数的值,第n个数的值也就确定了。
而在计算离差平方和∑(xi -x)2 时,必须先求出均值 x拔,均值就相当于一个限制条件,由于加了这个限制条件,估计总体方差的自由度为n-1。
算自由度公式

算自由度公式自由度这个概念在数学和物理学等领域中可有着重要的地位呢!咱先来说说啥是自由度。
比如说,一个在平面上自由运动的质点,它能往前后左右随便移动,那它的自由度就是 2。
为啥呢?因为它的位置可以用两个坐标来确定,一个是水平方向的,一个是垂直方向的。
再比如,有个刚体在空间里运动。
要是把它的质心固定住,那它还能绕着通过质心的三条互相垂直的轴转动,所以这个刚体的自由度就是 3。
咱来聊聊算自由度的公式。
一般来说,对于一个由 N 个质点组成的系统,如果存在 m 个完整约束条件,那这个系统的自由度 s 就可以用公式 s = 3N - m 来计算。
我记得有一次给学生讲这个知识点的时候,可有意思了。
有个学生特别调皮,他一开始听着听着就开始走神儿,我发现后就叫他起来回答问题。
我问他:“如果有 5 个质点,有 2 个完整约束条件,那自由度是多少?”这小家伙一脸懵,然后旁边的同学悄悄给他提示,被我发现了。
我就说:“自己好好想想,可别指望别人告诉你。
”他挠挠头,想了好一会儿,终于算对了。
从那以后,他上课再也不敢走神儿啦。
再来说说这个公式在实际中的应用。
比如在机械设计中,要确定一个机械结构的运动灵活性,就得算算自由度。
如果自由度不合适,那这个机械可能就没法正常工作。
还有在物理实验中,分析一些物体的运动状态也会用到自由度的计算。
比如研究一个多关节机器人的运动,通过计算自由度,就能更好地了解它能做出哪些动作。
其实啊,自由度的概念不仅仅在数学和物理中有用,在生活中也能找到它的影子。
就像我们规划自己的时间,每天能自由支配的时间也可以看作是一种“自由度”。
如果被各种琐事和任务占满了,那我们的“自由度”就低了,感觉就会很压抑。
相反,如果能合理安排,留出足够的自由时间做自己喜欢的事,那心情就会舒畅很多。
所以说,搞清楚自由度的计算,不仅能帮助我们解决学科里的难题,还能让我们更好地理解生活中的各种现象。
总之,自由度公式虽然看起来有点复杂,但只要多琢磨琢磨,多做几道题,就能掌握啦。
自由度计算举例1

例1:计算八杆机构的自由度(图1-15a )解:由于该机构中,AB 平行且等于CD ,AD 平行且等于BC ,因此ABCD 是平行四边形,则A 点与D 点或B 点与C 点之间的距离始终不变,故杆8(或4)与其相连的两个转动副产生一个虚约束,所以可将杆8(或4)去掉(图1-15b )。
如果去掉对称部分,则可简化成1-15c 和1-15d 的形式,其自由度计算分别为:(a) (b) (c) (d) 图1-15 八杆机构及其自由度计算b : 1011027323=⨯-⨯-⨯=--=h l P P n Fc : 101725323=⨯-⨯-⨯=--=h l P P n Fd : 101423323=⨯-⨯-⨯=--=h l P P n F例2、试计算图示机构的自由度。
(若有复合铰链、局部自由度或虚约束,必须明确指出。
)并指出杆组的数目与级别以及机构级别。
例3、试对图示机构:(本小题15分)(1)计算自由度;(3分)(2)分别取构件1和7 为原动件,拆出所有杆组,并确定机构的级别(必须画出各杆组)。
(8分)(3)求构件2、8和2、5之间的速度瞬心p和25p(4分)28例4、试对图示机构:(本小题11分)(1)计算自由度;(3分)(2)对图示机构进行高副低代和结构分析,并确定该机构的级别。
(8分)例5、计算图示机构的自由度,如有复合铰链、虚约束及局部自由度,直接在图中指出(本小题10 分)。
例6:计算如图所示机构的自由度并确定机构的级别解:例7、(本小题8分)计算图示机构的自由度,并在高副低代后判断机构的级别。
例8、已知图示机构的尺寸和位置(本小题10分):1、画出高副低代机构的运动简图,直接在图上作图(4分);2、拆分基本杆组,并判断机构的级别(6分)。
例9:计算如图所示的双缸曲柄滑块机构的自由度并确定机构的级别解:1011027323=⨯-⨯-⨯=--=h l P P n F 以4为原动件以2为原动件以8为原动件。
刚体自由度计算

刚体自由度计算
刚体自由度计算是一种重要的物理计算方法,它可以用来描述刚体在运动过程中的自由度。
刚体是指形状不变的物体,它的运动可以分解为平移和旋转两个部分。
而自由度则是指刚体在运动过程中可以自由变化的参数,例如位置、速度、角度等。
在刚体自由度计算中,我们需要考虑刚体的几何形状和运动状态。
对于一个刚体而言,它的自由度可以通过以下公式进行计算:
自由度 = 6 - 约束数
其中,6代表刚体在三维空间中的自由度,约束数则是指刚体在运动过程中受到的限制条件。
例如,一个固定在地面上的刚体就有3个约束,因为它不能在x、y、z三个方向上自由运动;而一个在空间中自由运动的刚体则没有约束,因此它的自由度为6。
在实际应用中,刚体自由度计算可以用来解决各种物理问题。
例如,在机械工程中,我们可以通过计算刚体的自由度来确定机械系统的运动状态和稳定性;在航空航天工程中,我们可以利用刚体自由度计算来设计飞行器的姿态控制系统。
刚体自由度计算是一种非常重要的物理计算方法,它可以帮助我们更好地理解和解决各种物理问题。
在未来的科学研究和工程设计中,刚体自由度计算将继续发挥重要作用,为人类创造更加美好的未来。
液压缸自由度计算

液压缸自由度计算液压缸是一种常见的液压传动装置,广泛应用于各个领域。
液压缸的自由度是指液压缸在空间中可以自由运动的方向数量。
了解液压缸的自由度有助于我们更好地理解和应用液压系统。
液压缸的自由度与其结构有关。
一般来说,液压缸的自由度取决于活塞和缸体的连接方式。
常见的液压缸结构有单作用液压缸和双作用液压缸两种。
单作用液压缸是指只能在一个方向上产生推力或拉力的液压缸。
它的结构比较简单,只有一个油腔,液压油只能从一个方向进入或排出。
因此,单作用液压缸的自由度较低,只有一个自由度。
它通常用于只需要单向运动的应用,如起重机械的升降装置。
双作用液压缸是指可以在两个方向上产生推力或拉力的液压缸。
它的结构比较复杂,有两个油腔,液压油可以从两个方向进入或排出。
因此,双作用液压缸的自由度较高,有两个自由度。
它通常用于需要双向运动的应用,如挖掘机的铲斗。
除了结构的不同,液压缸的自由度还受到其他因素的影响。
例如,液压缸的尺寸和工作压力也会影响其自由度。
一般来说,液压缸的尺寸越大,自由度越低。
这是因为大尺寸的液压缸需要更多的液压油来推动活塞,而液压油的流动速度有限,影响了液压缸的自由运动。
另外,工作压力越高,液压缸的自由度也会降低。
这是因为高压液体的流动速度更慢,同样影响了液压缸的自由运动。
在实际应用中,我们需要根据具体情况选择适合的液压缸结构和尺寸。
如果需要双向运动,就应选择双作用液压缸;如果只需要单向运动,就可以选择单作用液压缸。
同时,还应根据工作压力和空间限制等因素来选择液压缸的尺寸。
只有选择合适的液压缸,才能更好地满足工程需求。
液压缸的自由度是指其在空间中可以自由运动的方向数量。
液压缸的自由度与其结构、尺寸和工作压力等因素有关。
了解液压缸的自由度有助于我们更好地理解和应用液压系统。
在实际应用中,我们需要根据具体情况选择适合的液压缸结构和尺寸,以满足工程需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1:计算八杆机构的自由度(图1-15a )
解:由于该机构中,AB 平行且等于CD ,AD 平行且等于BC ,因此ABCD 是平行四边形,则A 点与D 点或B 点与C 点之间的距离始终不变,故杆8(或4)与其相连的两个转动副产生一个虚约束,所以可将杆8(或4)去掉(图1-15b )。
如果去掉对称部分,则可简化成1-15c 和1-15d 的形式,其自由度计算分别为:
(a) (b) (c) (d) 图1-15 八杆机构及其自由度计算
b : 1011027323=⨯-⨯-⨯=--=h l P P n F
c : 101725323=⨯-⨯-⨯=--=h l P P n F
d : 101423323=⨯-⨯-⨯=--=h l P P n F
例2、试计算图示机构的自由度。
(若有复合铰链、局部自由度或虚约束,必须明确指出。
)并指出杆组的数目与级别以及机构级别。
例3、试对图示机构:(本小题15分)
(1)计算自由度;(3分)
(2)分别取构件1和7 为原动件,拆出所有杆组,并确定机构的级别(必须画出各杆组)。
(8分)
(3)求构件2、8和2、5之间的速度瞬心
p和25p(4分)
28
例4、试对图示机构:(本小题11分)
(1)计算自由度;(3分)
(2)对图示机构进行高副低代和结构分析,并确定该机构的级别。
(8分)
例5、计算图示机构的自由度,如有复合铰链、虚约束及局部自由度,直接在图中指出(本小题10 分)。
例6:计算如图所示机构的自由度并确定机构的级别解:
例7、(本小题8分)
计算图示机构的自由度,并在高副低代后判断机构的级别。
例8、已知图示机构的尺寸和位置(本小题10分):
1、画出高副低代机构的运动简图,直接在图上作图(4分);
2、拆分基本杆组,并判断机构的级别(6分)。
例9:计算如图所示的双缸曲柄滑块机构的自由度并确定机构的级别
解:1011027323=⨯-⨯-⨯=--=h l P P n F 以4为原动件
以2为原动件
以8为原动件。
