微分方程例题
微分方程习题课例题解答

微分方程习题课例题解答例1.若微分方程的通解为x C y x +=e ,求该微分方程.解:对x C y x +=e 求导,有1e +='x C y ,消去C ,得1+-='x y y ,这就是所求的微分方程.例2.若函数x x x x y 21e e )(+=,x x x x y -+=e e )(2,x x x x x y -++=e e e )(23是二阶线性方程)()()(x f y x Q y x P y =+'+''的解,写出该方程的通解.解:根据非齐次线性微分方程两个解的差是相应齐次线性微分方程的解,得相应齐次线性 方程的两个线性无关的解x x y y y y 22313e e =-=--、,于是应齐次线性方程的通解为 x x C C Y 221e e +=-.取非齐次线性微分方程的一个特解为x x y y y y e 321*=-+=,所以原方程的通解为 x x x x C C y Y y e e e 221*++=+=-. (注:*y 也可以取321y y y 、、中的任何一个)例3.已知221,x y x y ==是二阶齐次线性微分方程0)()(=+'+''y x Q y x P y 的两个解,x y e *=是二阶非齐次线性微分方程)()()(x f y x Q y x P y =+'+''的一个特解,写出二阶非齐次线性微分方程)()()(x f y x Q y x P y =+'+''的通解,并写出此微分方程. 解:因为221,x y x y ==线性无关,根据线性微分方程解的结果,该方程的通解为 xx C x C y e 221++=.将221,x y x y ==分别代入到齐次线性微分方程0)()(=+'+''y x Q y x P y 之中,有⎩⎨⎧=++=+,,0)()(220)()(2x Q x x xP x xQ x P 解得x x P 2)(-=,22)(x x Q =. 将xy e *=代入到非齐次线性微分方程)(222x f y xy x y =+'-''之中,得 x x x xx x x x x f e )221(e 2e 2e )(22+-=+-=.所以该微分方程为xx x y xy x y e )221(2222+-=+'-'',或写为x x x y y x y x e )22(2222+-=+'-''.例4.求解下列微分方程:(1)求xy y y x 2=+'满足初始条件0)1(=y 的特解; 解:先求方程的通解. (方法1)化为齐次方程xyx y y 2=+',令u x y =,则u u u x u x 2d d =++,分离变量有xxu u u d )1(2d -=-,积分得x C u ln )1ln(=-,即x C u =-1,通解为C x xy =-.(方法2)看作伯努利方程y xx y y 2=+'(21=n ),令y y z n ==-1,则方程化为一阶线性方程xx z z 12=+',通解为)(1)d (1)d e 1(e2d 2d x C xx C x x x C z y x xxx+=+=⎰+⎰==⎰⎰-,即C x xy =-. (方法3)令u xy =,则方程化为u x u 2d d =,分离变量为x uud 2d =,积分得C x u +=,即通解为C x xy =-.再求满足初始条件的特解,由0)1(=y ,得1=C ,特解为1=-x xy ,或写作xx y 2)1(-=.(2)求)(ln 2d d x y y x y -=的通解; 解:(方法1)将方程改写为y x y y x )(ln 2d d -=,即yy x y y x ln 22d d =+,则方程通解为 )d ln (1)d ln 2(1)d e ln 2(e222d 2d y y y y C yy y y C y y y y C x y y tyt⎰⎰⎰-+=+=⎰+⎰=-)2ln (122y y y C yy-+=,或写作2ln 222y y y C xy -+=.(方法2)令u x y =-ln ,则xux y y d d 1d d 1=-,于是u x u 211d d =+,即u u x u 221d d -=, 分离变量有x u u d d )2111(-=--,积分得C x u u ln 21)21ln(21+-=-+,即 C u x u ln )21ln()(2=-++,化简为C x y y =+-)2ln 21(2,这就是原方程通解.(3)求y x x y ++-='221的通解;解:令u y x =+2,则u y x '='+2,于是u u +='1,分离变量为x uu d 1d =+.因为t tt t t t u uu d )111(2d 121d ⎰⎰⎰+-=+=+C u u C t t -+-=-+-=)]1ln([2)]1ln([2,所以方程通解为 x C u u =-+-)]1ln([2,即C x y x y x +=++-+)]1ln([222.(4)求)ln (ln x y y y x -''=''的通解;解:令)(x p y =',则p y '='',于是)ln (ln x p p p x -=',即xpx p x p ln d d =,这是齐次方程,再令u x p =,则u u u x u x ln d d =+,分离变量为xx u u u d )1(l n d =-,积分得x C u 1ln )1ln(ln =-,即x C x xu p y 11e +===',所以方程通解为21111111)1(e ]d e [e 1d e1111C C x C x C x x y x C x C x C xC +-=-==++++⎰⎰.(5)求012=+'-''y y y 的通解;解:令)(y p y =',则p p y '='',于是012=+-'p p yp ,分离变量为y yp p p d d 12=-,积分得y C p 12ln 1ln 21=-,即22121y C y =-'. 当1±='y 时,则C x y +±=; 当1>'y 时,有22121yC y =-',则1221+±='y C y ,分离变量有x C y C y C d 1d 12211±=+,积分得211arsh C x C y C +±=,原方程的通解为)(sh 1121x C C C y ±=; 当1<'y 时,有22121y C y ='-,则2211y C y -±=',分离变量有x C yC y C d 1d 12211±=-,积分得211arcsin C x C y C +±=,原方程的通解为)(sin 1121x C C C y ±=. (6)1)9(62='++''+'''y a y y (0>a ).解:这是三阶常系数非齐次线性方程,相应齐次线性方程为0)9(62='++''+'''y a y y ,特征方程为0)9(6223=+++r a r r ,特征根是ai a r r ±-=-±-==3246023,21、,相应齐次线性方程通解为x ax C ax C C Y 3321e )sin cos (-++=.对于原方程,0=λ是单重特征根,0=m ,为此设bx y =*,代入方程有1)9(2=+b a ,得291a b +=,所以2*9a x y +=.原方程通解为23321*9e )sin cos (a xax C ax C C y Y y x++++=+=-.例5.已知1)(=πϕ,试确定函数)(x ϕ使0d )(d )]([sin =+-y x x xyx x ϕϕ是全微分方程,并对所确定的)(x ϕ,求该方程满足1)(=πy 的特解. 解:设)()]([sin x Q x y x x P ϕϕ=-=、,由0d )(d )]([sin =+-y x x xyx x ϕϕ是全微分方程,有yPx Q ∂∂=∂∂,得)]([sin 1)(x x x x ϕϕ-=',即x x x x x sin )(1)(=+'ϕϕ,这是一阶线性方程,通解为)cos (1)d sin (1)d e sin (e)(d d x C x x x C x x x x C x x xxx-=+=⎰+⎰=⎰⎰-ϕ.由1)(=πϕ,有)1(11+=C π,得1-=πC ,所以)cos 1(1)(x xx --=πϕ.这时原方程为0d )cos 1(1d )]cos 1(1[sin =--+---y x xx x y x x x ππ, )cos 1(d )cos 1(1d 0d d )(01),()0,1(x x yy x x x y Q x P y x u y x y x --=--+=+=⎰⎰⎰ππ,,于是原方程通解为1)cos 1(C x xy=--π,由1)(=πy ,得11=C ,所以原方程的特解是1)cos 1(=--x x y π,或写作xx y cos 1--=π. (注:方程通解也可以用凑微分方法得到,方程左式凑微分得0)]cos 1([d =--x xyπ,于是原方程通解为1)cos 1(C x xy=--π)例6.若函数)(x f 连续,且满足⎰--+=x t t f t x x x x f 0d )()(cos sin )(,求)(x f .解:将所给式子改写为⎰⎰+-+=x x t t tf t t f xx x x f 0d )(d )(cos sin )(,有1)0(=f ,且⎰⎰--=+---='x xt t f x x x xf x xf t t f x x x f 0d )(sin cos )()(d )(sin cos )(,1)0(='f .)(cos sin )(x f x x x f ---='',即x x x f x f cos sin )()(--=+'',这是二阶常系数非齐次线性微分方程,相应齐次线性方程为0)()(=+''x f x f ,其特征方程是012=+r ,特征根为i r ±=,相应齐次线性方程通解为x C x C F sin cos 21+=.考虑方程ixx f x f e )()(-=+'',这里i =λ是特征根,0=m ,为此设ix ax fe **=,将ax x Q =)(代入到)()()()()2()(2x P x Q q p x Q p x Q m =+++'++''λλλ之中,有12-=ia ,得221i i a =-=,于是)cos (sin 2)sin (cos 2e 2**x i x xx i x x i x i f ix --=+==,则x x x f x f cos sin )()(--=+''的一个特解为)sin (cos 2)Re()Im(*****x x xf f f -=+=, 所以方程x x x f x f cos sin )()(--=+''的通解为)sin (cos 2sin cos )(21*x x xx C x C f F x f -++=+=. )cos (sin 2)sin (cos 21cos sin )(21x x xx x x C x C x f +--++-=',由初始条件1)0(=f 、1)0(='f ,得21121==C C 、,所以所求函数为=-++=)sin (cos 2sin 21cos )(x x xx x x f x x x x sin )221(cos )21(-++.例7.若二阶可导函数)(u f z =,其中y u xsin e =,满足方程x z yzx z 22222e =∂∂+∂∂,且0)0(=f ,2)0(='f ,试求函数)(u f .解:y u f x u u z x z x sin e )(d d '=∂∂=∂∂,y u f yuu z y z x cos e )(d d '=∂∂=∂∂, y u f y u f y u f x xz x x x sin e )()sin e )((]sin e )([222'+''='∂∂=∂∂, y u f y u f y u f y yz x x x sin e )()cos e )((]cos e )([222'-''='∂∂=∂∂, 由x z yz x z 22222e =∂∂+∂∂,有xx u f u f 22e )(e )(='',即0)()(=-''u f u f ,这是二阶常系数线性齐次微分方程,特征方程是012=-r ,特征根为1121-==r r 、,方程的通解是u u C C u f -+=e e )(21,u u C C u f --='e e )(21,由条件2)0(0)0(='=f f ,,有021=+C C , 221=-C C ,得1121-==C C 、,所所求函数是u u u f --=e e )(. 例8.求幂级数∑∞=-12!)!12(n nn x 的和函数.解:设∑∞=--=1121!)!12()(n n n x x s ,则0)0(1=s ,且)(1!)!12(1!)!32(1!)!32(1)(11122322221x xs n x x n x x n x x s n n n n n n +=-+=-+=-+='∑∑∑∞=-∞=-∞=-,即1)()(11=-'x xs x s ,这是一阶线性微分方程,通解为 )d e(e )d e (e )(x22xd d 122t C t C x s t x tt xx ⎰⎰--+=⎰+⎰=.由0)0(1=s ,得0=C ,所以幂级数∑∞=-12)!!12(n nn x 的和函数t x xs x s t x d ee)()(x 022122⎰-==.例9.设曲线位于xOy 面的第一象限,曲线上任一点)(y x M ,处的切线与y 轴交于A 点,=,且曲线过点2)323(,,求该曲线方程. 解:设所求曲线为)(x f y =,其在任一点)(y x M ,的切线方程为 ))(()(x X x f x f Y -'=-,令0=X ,得)()(x f x x f Y '-==,有222)]([Y x f Y x =-+,即)()()(2)()(222222x f x x f x xf x f x f x x '+'-='+,亦即yxx y y -='2,这是一阶齐次微分方程,令xu y =,则u x u x f '+=')(,于是u u u x u 1)(2-='+,即u u u x 212+-=',分离变量有x x u u u d d 122-=+,积分得x C u ln )1ln(2=+,即x C xy =+122.由初始条件23)23(=y ,有C 322=,得3=C ,所求曲线方程为x xy 3122=+,由曲线位于第一象限,于是)30(32≤≤-=x x x y .例10.一个质量为m 的物体,在海平面上由静止开始下沉,经过0t 秒后沉到海底,下沉过程中海水对物体的阻力与物体下沉速度成正比,求物体下沉运动的规律及海洋的深度h . 解:铅直向下取x 轴,原点在海平面,设时刻t 时,物体位于)(t x x =处,此时受力为t x k mg F d d -=(k 为比例系数),根据牛顿第二定律F ma =,有t xk mg tx m d d d d 22-=,即g tx m k t x =+d d d d 22(这是二阶常系数线性非齐次微分方程),初始条件为00==t x ,0d d 0==x t x.相应齐次微分方程为0d d d d 22=+t xm k tx ,特征方程为02=+r m k r ,特征根为01=r 、mkr -=2,相应齐次微分方程通解为t m kC C X -+=e 21.对原方程g t xm k tx =+d d d d 22,0=n 、0=λ是单重特征根,为此设at x =*,代入到方程之中,有g a m k =,得k mg a =,于是方程g t xm k tx =+d d d d 22的一个特解为t k mg x =*. 方程g t x m k tx =+d d d d 22的通解为=+=*x X x t k mg C C t m k++-e 21. kmg m k C t x t m k+-=-e d d 2,由初始条件00==t x ,0d d 0==x t x,有⎪⎩⎪⎨⎧=+-=+,,00221k m g mkC C C得222221k g m C k g m C =-=、,所以物体运动规律为t k mgk g m x t m k+-=-)1e (22.当0t t =时,得海洋深度为022)1e (0t k mgkg m h t m k+-=-.。
微分方程例题选解

微分方程例题选解1. 求解微分方程3ln (ln )0,|2x e x xdy y x dx y =+-==。
解:原方程化为x y x x dx dy 1ln 1=+, 通解为 ⎰+⎰⎰=-]1[ln 1ln 1C dx e xe y dx x x dx x x⎰+=]ln [ln 1C dx x x x ]ln 21[ln 12C x x += 由e x =,23=y ,得1=C ,所求特解为 11ln ln 2y x x =+。
2. 求解微分方程22'0x y xy y -+=。
解:令ux y =,u x u y '+=',原方程化为 2u u u x u -='+,分离变量得 dx x udu 12=-, 积分得C x u+=ln 1, 原方程的通解为 ln xy x C=+。
3. 求解微分方程dy y y x dx xy x )()(3223+=-。
解:此题为全微分方程。
下面利用“凑微分”的方法求解。
原方程化为 03223=---dy y ydy x dx xy dx x , 由 dy y ydy x dx xy dx x 3223---42222441)(2141dy dy x dx y dx -+-=)2(414224y y x x d --=, 得 0)2(4224=--y y x x d ,原方程的通解为 C y y x x =--42242。
注:此题也为齐次方程。
4. 求解微分方程2''1(')y y =+。
解:设y p '=,则dx dp y ='',原方程化为21p dxdp+=, 分离变量得dx p dp=+21,积分得 1arctan C x p +=,于是 )tan(1C x p y +==', 积分得通解为 12ln cos()y x C C =-++。
5. 求解微分方程''2'20y y y -+=。
微分方程习题

例6 解
1 求解方程 y′′ − 2 y′ + y = ( x + cos 2x). 2 特征方程 r 2 + 4 = 0,
特征根
r1, 2 = ±2i ,
对应的齐方的通解为 Y = C1 cos 2 x + C 2 sin 2 x .
则 ( y * )′ = [ax 3 + ( 3a + b ) x 2 + 2bx ]e x , ( y * )′′ = [ax 3 + (6a + b ) x 2 + (6a + 4b ) x + 2b]e x ,
将 y * , ( y * )′, ( y * )′′ 代入原方程比较系数得
1 1 a= , b=− , 6 2
1 y = C1 + C 2 x + . x
2
二、练习自测
1 求下列微分方程通解或特解 求下列微分方程通解或特解:
(1) (2) (3)
ydy + e
y2 +3 x
dx = 0;
dy 2 2 = 1 + x + y + xy ; dx
( y sin x − 1)dx − cos xdy = 0;
dy 1 cos y − sin y = e x sin 2 y; (4) dx x
dy = 1 + x + y 2 + xy 2 dx
原方程变为
dy = (1 + x )(1 + y 2 ), dx
微分方程习题

θ
Vs x a x 解:设所求曲线上一点M(x, y) M(x, y)
VS = {V x , V y } = {−VS cos θ, VS sin θ)
实际速效:
{−VS cos θ,V R − VS sin θ}
dx dy ⇒ = −VS cos θ, = VR − VS sin θ dt dt V R − V S sin θ dy ⇒ = dx − V S cos θ
b b
①
y ′ − 2 xy = 2 x → y
∫ p ( x ) dx [ Q ( x ) e ∫ p ( x ) dx dx + C ] =e ∫
−
= ce
x2
−1
(2)
② 由(1)分离变量后可得
dy 2 = 2 xdx → ln 1 + y = x + c 1 1+ y
⇒ y = ±e e
c1
x2
x f ′( x ) + f ( x ) = f ( x ) + 3 .
3 即 f ′( x ) = x
且
x =1 时
由
f (1) = 3
C =3
f ( x ) = ln x 3 + c
f (1) = 3 得
f ( x ) = 3 ln x 3 + 3 = 3 (ln x + 1) 故
2.设 f ( x ) = sin x −
微分方程习题课
一、解 问题1. 所有微分方程都有通解吗?
( y ′ ) 2 + 1 = 0,
( y ′) 2 + y 2 = 0
无(通)解. 只有0解(无通解)
问题2. 通解是否包含方程的所有解? ′) 2 − 4 y = 0 (y 有通解 y = ( x + c ) 2 , 但不含解
微分方程建模 个例

A1
C
C1
分析:1.追击开始后,大家将进入正方 A 形里面,距离将变小,由于追击的规则 及四个人速度和方向的假定,四人还是 在某个正方形的顶点上。 2.会不会出现四个人绕一个圆循环追? 不会!距离会不断缩小最后到一点,就 是正方形的中心。追击曲线是四条指向 D1 中心的螺旋线(可能绕中心几周) 3.坐标架怎么建? D O点在中心,直角坐标架。
2H g
2.二氧化碳的吸收
空气通过盛有CO2的吸收剂的圆柱形器皿,已知它吸收CO2的量与 CO2的浓度及吸收层的厚度成正比,今有含CO28%的空气通过厚度 为10cm的吸收层后浓度为2%,求: (1)若吸收层变为30cm厚,出口浓度是多少? (2)要使出口浓度为1%,应该设多厚的吸收层? 解: 记吸收层厚度为d,等分n份,每小层d/n厘米。入口浓 度为8%,在每小层看吸收量,第一层后被吸收量为: kd k8%d/n,含量变为: 8%(1)
v0t y x(0) 0 y , 就是曲线的切向量, 1 x y (0) 0
Q(1,v0t) 模型里y(t),x(t)都是t的函数,但是三个 变量不好处理,注意我们要求的是y(x)。 P(x,y) O 1 x
(1 x) y y v0t实现了变量t的分离
再建立一个y(t),x(t),t的关系:t时间里导弹已 飞行的距离是可求的。 x 1 y2 dx 5v0t (1 x) y y v0t , x0 0, y0 0
v r (0) 2 2 , (2r cos dx cos dr r sin d dx r sin cos d , , y r sin dy sin dr r cos d dy r cos sin dr d 1 sin cos dx dr r r cos r sin dy
质点的运动微分方程例题

质点的运动微分方程例题当涉及到质点的运动微分方程时,我们通常考虑质点在空间中的位置、速度和加速度之间的关系。
下面我将给出一个质点的运动微分方程的例题,并从多个角度进行回答。
例题,一个质点在直角坐标系中的运动满足以下条件,质点的位置矢量为r(t) = (3t^2, 2t, t^3),其中t为时间,求质点的速度和加速度。
从向量的角度回答:质点的速度可以通过对位置矢量求导得到。
对r(t) = (3t^2, 2t, t^3)关于时间t求导,得到速度矢量v(t) = (6t, 2, 3t^2)。
质点的加速度可以通过对速度矢量求导得到。
对v(t) = (6t, 2, 3t^2)关于时间t求导,得到加速度矢量a(t) = (6, 0, 6t)。
从微分方程的角度回答:质点的速度可以表示为位置矢量对时间的导数,即v(t) =dr(t)/dt。
根据给定的位置矢量r(t) = (3t^2, 2t, t^3),对其分别对时间求导,得到速度矢量v(t) = (6t, 2, 3t^2)。
质点的加速度可以表示为速度矢量对时间的导数,即a(t) = dv(t)/dt。
根据给定的速度矢量v(t) = (6t, 2, 3t^2),对其分别对时间求导,得到加速度矢量a(t) = (6, 0, 6t)。
从运动学的角度回答:根据质点的位置矢量r(t) = (3t^2, 2t, t^3),我们可以计算质点在各个方向上的速度和加速度。
在x方向上,质点的速度v_x(t) = d(3t^2)/dt = 6t,加速度a_x(t) = d(6t)/dt = 6。
在y方向上,质点的速度v_y(t) = d(2t)/dt = 2,加速度a_y(t) = d(2)/dt = 0。
在z方向上,质点的速度v_z(t) = d(t^3)/dt = 3t^2,加速度a_z(t) = d(3t^2)/dt = 6t。
从微分方程的角度回答:根据位置矢量r(t) = (3t^2, 2t, t^3),我们可以得到速度矢量v(t) = (6t, 2, 3t^2)和加速度矢量a(t) = (6, 0, 6t)。
第二节 可分离变量的微分方程

第二节 可分离变量的微分方程
一、可分离变量的微分方程 二、典型例题
一、可分离变量的微分方程
形如 y f ( x) g( y) 的方程,称为可分离变量
解 分离变量 , 得
dy 2xdx, y
两端积分 , 得
dy y
2
xdx,
解得 ln y x2 C1
即 y Ce x2 (C 为任意常数)
y Ce x2为所求通解.
例2 求解微分方程 ( y 1)2 y x3 0 的通解.
解 分离变量,得 ( y 1)2dy x3dx,
四、小船从河边点 0 处 出发驶向对岸(两岸为平行直线). 设船速为 a ,船行方向始终与河岸垂直,设河宽 为 h ,河中任意点处的水流速度与该点到两岸距离 的乘积成正比(比例系数为 k ).求小船的航行路 线.
练习题答案
一、1、tan x tan y C ; 2、(e x 1)(e y 1) C ; 3、4( y 1)3 3 x4 C .
正 比 , 已 知 M t0 M0 , 求 衰 变 过 程 中 铀 含 量
M (t )随时间 t 变化的规律.
解 根据题意,有
dM M ( 0)
dt M t0 M0 (初始条件)
对方程分离变量, 然后积分:
得 ln M t lnC, 即 M C e t
二、1、 2 cos y cos x ; 2、e x 1 2 2 cos y .
二阶常系数非齐次线性微分方程解法及例题

二阶常系数非齐次线性微分方程解法及例题在数学的领域中,二阶常系数非齐次线性微分方程是一个重要的研究对象。
它在物理学、工程学、经济学等众多学科中都有着广泛的应用。
接下来,让我们深入探讨一下二阶常系数非齐次线性微分方程的解法以及相关例题。
首先,我们来明确一下二阶常系数非齐次线性微分方程的一般形式:$y''+ py' + qy = f(x)$,其中$p$、$q$ 是常数,$f(x)$是一个已知的函数。
为了求解这个方程,我们通常分为两个步骤:第一步,先求解对应的齐次方程:$y''+ py' + qy = 0$ 。
对于这个齐次方程,我们假设它的解为$y = e^{rx}$,代入方程中得到特征方程:$r^2 + pr + q = 0$ 。
通过求解这个特征方程,可以得到两个根$r_1$ 和$r_2$ 。
当$r_1$ 和$r_2$ 是两个不相等的实根时,齐次方程的通解为$y_c = C_1e^{r_1x} + C_2e^{r_2x}$;当$r_1 = r_2$ 是相等的实根时,齐次方程的通解为$y_c =(C_1 + C_2x)e^{r_1x}$;当$r_1$ 和$r_2$ 是一对共轭复根$r_{1,2} =\alpha \pm \beta i$ 时,齐次方程的通解为$y_c = e^{\alpha x}(C_1\cos(\beta x) + C_2\sin(\beta x))$。
第二步,求出非齐次方程的一个特解$y_p$ 。
求特解的方法通常根据$f(x)$的形式来决定。
常见的形式有以下几种:1、当$f(x) = P_n(x)e^{\alpha x}$,其中$P_n(x)$是$n$ 次多项式。
如果$\alpha$ 不是特征根,设特解为$y_p = Q_n(x)e^{\alpha x}$,其中$Q_n(x)$是与$P_n(x)$同次的待定多项式;如果$\alpha$ 是特征方程的单根,设特解为$y_p = xQ_n(x)e^{\alpha x}$;如果$\alpha$ 是特征方程的重根,设特解为$y_p =x^2Q_n(x)e^{\alpha x}$。
微分方程例题范文

微分方程例题范文微分方程是描述物理学、化学、经济学、生物学等领域中变化规律的重要数学工具。
下面我将给出几个微分方程的例题,解析其求解过程。
例题1:一般线性微分方程已知其中一种细菌种群的个体数量N(t)随时间t的变化符合以下微分方程:dN(t)/dt = k*N(t)其中k为常数。
求解该微分方程,并给出其通解。
解析:思路:这是一个一阶线性微分方程,可以使用分离变量法进行求解。
将方程进行分离变量:dN(t)/N(t) = k*dt两边同时积分:∫ (1/N(t)) dN(t) = ∫ k dt得到:ln,N(t), = kt + C1其中C1为常数。
对上式两边取指数:N(t), = e^(kt+C1) = e^C1 * e^kt = C * e^kt其中C=e^C1为常数。
由于细菌数量N(t)永远为正数,所以可以去掉绝对值符号,得到通解:N(t) = C * e^kt其中C为常数。
例题2:二阶常系数齐次线性微分方程已知其中一振动系统满足以下微分方程:d²x(t)/dt² + 4dx(t)/dt + 5x(t) = 0求解该微分方程,并给出其通解。
解析:思路:这是一个二阶常系数齐次线性微分方程,可以使用特征根法进行求解。
将方程转化为特征方程:λ²+4λ+5=0求解特征方程的解,得到特征根:λ₁=(-4+√(-4²-4*5))/2=-2+iλ₂=(-4-√(-4²-4*5))/2=-2-i特征根为复数,分别为共轭复数对。
根据特征根的性质,解的形式为:x(t) = e^(-2t) (C₁cos(t) + C₂sin(t))其中C₁、C₂为常数。
例题3:二阶常系数非齐次线性微分方程已知其中一电路中的电流I(t)满足以下微分方程:d²I(t)/dt² + 3dI(t)/dt + 2I(t) = 6e²求解该微分方程,并给出其通解。
第六节微分方程的应用举例

第六节 微分方程的应用举例在学习了以上几节内容关于微分方程解法的基础上,本节将举例说明如何通过建立微分方程解决一些在几何上和物理上的实际问题。
例1 设曲线过(1,1),且其上任意点p 的切线在y 轴上的截距是切点纵坐标的三倍,求此曲线方程(图12-1)解:设所求的曲线方程为()()y x P x y y ,,=为其上任意点,则过点P 的切线方程为()x X y y Y -'=-. 其中()Y X ,是切线上动点,()y x ,是曲线上L令0=X ,的y x y Y '-=为切线在y 轴上的截距。
由x所给的条件得微分方程: 图12-1y y x y 3='-这是一阶线性齐次方程,易得其通解为2xCy =。
因曲线过点(1,1),代入上式,得1=C ,所以曲线方程为21x y =. 例2 设跳伞员开始跳伞后所受的空气阻力与他下落的速度成正比(比例系数为常数0>k ),起跳时的速度为0。
求下落的速度与时间之间的函数关系。
解:这是一个运动问题,我们可以利用牛顿第二定律ma F =建立微分方程。
首先,设下落速度为()t v ,则加速度()t v a '=。
再分析运动物体所受的外力。
在此,跳伞员只受重力和阻力这两个力的作用。
重力的大小为mg ,方向与速度方向一致;阻力大小为kv ,方向与速度方向相反。
因此,所受的外力为kv mg F -=,于是,由牛顿第二定律可得到速度()t v 应满足的微分方程为v m kv mg '=-,又因为假设起跳时的速度为0,所以,其初始条件为00==t v , 至此,我们已将这个运动问题化为一个初值问题()⎩⎨⎧=-='.00,v kv mg v m 解此初值问题。
这是一个一阶线性非齐次微分方程,但由于v v ',的系数及自由项均为常数,故也可按分离变量方程来解。
求出方程的通解为t mk Cekv mg -=-.将初始条件()00=v 代入,得mg C =。
微分方程例题

典型例题1、判断下列一阶微分方程的类型并求其通解(1)0)41(2=+−dy x ydx ;(2).0cos )cos (=+−dy x yx dx x y y x ;(3)0)sin (=−+dx x y xdy ;(4)0)4(3=+−dx y y x xdy ;(5)ydy dx y xydy dx +=+2;(6)0)12(23=−+dy xy dx y ;(7).0324223=−+dy y x y dx y x (8)231dy x x ydx x++=−+2、求一阶微分方程的特解(1)求解微分方程x yx ydx dytan +=满足初始条件61π==x y 的特解.(2)求微分方程,0)ln (ln =−+dx x y xdy x 满足所给初始条件.1==e x y 的特解3、求下列微分方程的通解(1)求x y xe ′′′=的通解(2)02)1(222=−+dx dyx dx y d x (3)求方程02=′−′′y y y 的通解4、求下列微分方程的特解(1)求方程x e y x cos 2−=′′满足1)0(,0)0(=′=y y 的特解.(2)求微分方程初值问题:,2)1(2y x y x ′=′′+,10==x y 30=′=x y (3)求微分方程)(22y y y y ′−′=′′满足初始条件,1)0(=y 2)0(=′y 的特解.5、求下列微分方程的通解(1)440y y y ′′′++=(2)340y y y ′′′−−=(3)250y y y ′′′++=(4)(5)(4)220y y y y y y ′′′′′′+++++=(5)(4)250y y y ′′′′′−+=6、求方程12360y y y′′′−+=满足条件:01x y ==,00x y =′=的特解。
7、求解下列微分方程(1)求方程22y y y x ′′′−+=的一个特解。
(2)求方程2x y y y e ′′′−+=的一个特解。
微分方程1-2-3

将y和y代入原方程 u(得 x)eP(x)dxQ (x),
积分得 u (x )Q (x )eP (x)dd x x C ,
一阶线性非齐次微分方程的通解为:
y [Q (x )e P (x )dd x x C ]e P (x )dx
C P (e x )d x e P (x )dxQ (x ) e P (x )dd x x
通解为 ln |x|u[f(u g)(u )g(u)d ] uC.
例3 衰变问题:衰变速度与未衰变原子含量 M成
正比,已知Mt0 M0,求衰变过程中铀含量M(t) 随时间t变化的规律.
解 衰变速d度 M, 由题设条件
dt
dM M dt
(0衰变)系dMM数 dt
dMMdt, lM n t lC n , 即 MC et,
u(u2)2
微分方程的解为 (y x )2 C (y y 2 x )3 .
例 3 抛物线的光学性质
实例: 车灯的反射镜面------旋转抛物面
解 如图 设旋转o轴 x轴 y T
光源(在 0,0), L:yy(x)
设M(x, y)为L上任一点M,
R
M为 T 切 , 斜 线率 y, 为 o
t (40h 3 0 2h 5)C , 0 .62 2g3 5
h|t010,0 C0.622g1 15 4 150,
所求规律为t (7 15 0 130 h 3 3h 5). 4 .65 2 g
一、齐次方程
1.定义 形如 dy f(y)的微分方程称为齐次方程. dx x
当 制 动 时 列 车 获 得 加 速 度 0.4米 /秒2,问 开 始 制 动
后 多 少 时 间 列 车 才 能 停 住 ? 以 及 列 车 在 这 段 时 间 内 行 驶 了 多 少 路 程 ?
微分方程应用举例
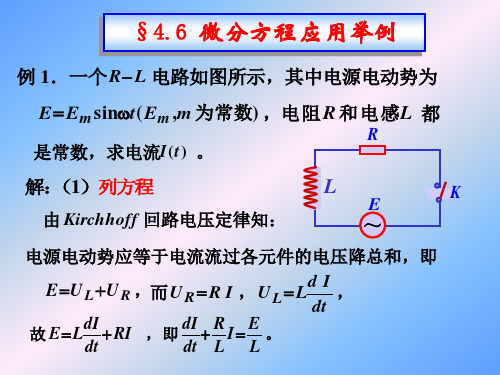
即 dx 2x 6 , dt 100t
通解为
x
e
2 100t
dt
[
6
e
2 100t
dt
dt
C
]
1 (100
t
)2
[2(100
t
)3
C
]
2(100
t
)
C (100
t
)2
.
把初始条件 x t0 50 代入通解,
得
50
2100
C 1002
,C 1002150
,
从而
x
2(100 t
)
1500000 (100 t )2
1 z2 z C1 , 1 x
代入初始条件 y(0)0 ,得C11 ,
从而 1 z2 z 1 ,即 1 x
1 y2 y 1 ,
①
1 x
亦即 1 y2 y 1 x ,
②
①- ②得 y 1 1 1 x ,
2 1 x 2
3
再积分得 y
1
x
1(1 3
x)2
C2
,
代入初始条件
y(0)0
,得C2
2 3
,
x t30 26015103000200171( g) 。
即 30 min后 容器内含盐 171g。
3.我缉私艇雷达发现,正东 1 海里处一艘走私船正以常 速 v向北方向逃窜,缉私艇立即以 2v 的速度追赶,借助 于雷达,缉私艇航行的方向始终对准走私船。试求缉私艇 的航行曲线方程,并问走私船航行多远时被我缉私艇追上。
解:如图建立坐标系。设缉私艇的航行曲线方程为y f ( x) ,
在时刻 t 缉私艇位于 P( x, y), y
rlc电路微分方程例题

rlc电路微分方程例题
好的,让我们来看一个简单的RLC电路。
假设我们有一个由电
阻(R)、电感(L)和电容(C)组成的串联RLC电路。
我们可以通
过基尔霍夫电压定律和基尔霍夫电流定律来建立微分方程。
首先,我们可以使用基尔霍夫电压定律来建立电路的微分方程。
假设电感两端的电压为v_L(t),电容两端的电压为v_C(t),电阻两
端的电压为v_R(t),电源电压为v_s(t)。
根据基尔霍夫电压定律,我们有:
L(di/dt) + v_R + v_C = v_s.
其中,di/dt是电感电流的变化率。
电阻两端的电压v_R等于
电阻R与电感电流i的乘积,即v_R = Ri。
电容两端的电压v_C等
于电容C与电压v_C的变化率的乘积,即v_C = (1/C)∫i dt。
代
入这些关系,我们可以得到RLC电路的微分方程。
另一种方法是使用基尔霍夫电流定律来建立微分方程。
根据基
尔霍夫电流定律,电路中的总电流等于电感电流i加上电容电流
i_C,即i = i_L + i_C。
根据电感和电容元件的特性,我们可以得
到i_L = L(di/dt)和i_C = C(dv_C/dt)。
将这些关系代入基尔霍夫电流定律,我们同样可以得到RLC电路的微分方程。
综上所述,建立RLC电路的微分方程可以通过基尔霍夫电压定律或者基尔霍夫电流定律来实现。
这些微分方程可以用来描述电路中电流和电压随时间变化的规律。
希望这个例子能帮助你理解RLC 电路微分方程的建立过程。
微分方程

一般形式为 : F( x, y , y ) 0
• (一)、可分离变量方程
• (二)、齐次方程
• (三)、一阶线性微分方程
一、可分离变量的微分方程
g( y )dy f ( x )dx 可分离变量的微分方程.
dy 例如 2 x 2 y y dy 2 x 2dx , dx
解法 设函数 g ( y )和 f ( x ) 是连续的,
Def9.1
微分方程:
凡含有未知函数的导数或微分的方程叫微分方程.
微分方程的阶: 微分方程中出现的未知函数的导 数的最高阶数. 常微分方程 偏微分方程 未知函数为一元函数的微分方程 未知函数为多元函数的微分方程
分类1: 常微分方程, 偏微分方程. 分类2: 一阶微分方程 F ( x , y , y ) 0, y f ( x , y ); 高阶微分方程 F ( x , y , y,, y ( n ) ) 0, (常见为二阶)y ( n ) f ( x , y , y,, y ( n1) ). 分类3:
形如
y?
py? qy = f ( x)
f ( x) = Pm ( x)ea x
特解形式:(1)当
y* = x k Qm ( x)ea x
ì 0, a 不是特征根 ï ï ï k = ï 1,a 是特征单根 í ï ï 2,a 是特征重根 ï ï î
特解形式:(2)当
f ( x) = Pm ( x)ea x [cos b x + sin b x]
三、一阶线性微分方程
一阶线性微分方程的标准形式:
dy P ( x ) y Q( x ) dx
当Q( x ) 0, 上面方程称为齐次的.
当Q( x ) 0, 上面方程称为非齐次的.
全微分方程例题

全微分方程例题
1. 求解微分方程dy/dx = 2x + 3y,且y(0) = 1。
解:因为dy/dx = 2x + 3y是一个一阶线性微分方程,可化为dy/dx - 3y = 2x,然后使用常系数齐次方程的解法得到通解为y = Ce^(3x) - (2/3)x - (1/9)。
将y(0) = 1代入可得C = 10/9,所以特解为y =
(10/9)e^(3x) - (2/3)x - (1/9)。
2. 求解微分方程(x^2 + y^2)dx - 2xydy = 0,且y(1) = 2。
解:将方程变形为(x^2 + y^2)dx = 2xydy,然后对两边同时求积分
得到x^3/3 + xy^2/2 = C,其中C为积分常数。
代入y(1) = 2可得C = 11/6,所以通解为x^3/3 + xy^2/2 = 11/6。
3. 求解微分方程dy/dx = e^(-x^2),且y(0) = 1。
解:因为dy/dx = e^(-x^2)不是一个线性微分方程,所以不能使用
常系数齐次方程的解法。
但是,我们可以利用求导的逆运算——积分来解
决它。
对两边同时积分得到y = ∫e^(-x^2)dx + C,其中C为积分常数。
但是,e^(-x^2)的不定积分无法用初等函数表示,因此这个方程的解是无
法用解析表达式表示的。
我们只能使用数值方法或者级数方法来近似求解。
如使用泰勒展开把积分函数近似为多项式形式,然后求和得到级数解。
微分方程例题

微分方程例题请问您需要什么类型的微分方程例题呢?以下是一些例题供您参考:1. 已知 $\frac{dy}{dx}+y=x$,且 $y(0)=1$,求 $y(x)$。
解:将 $\frac{dy}{dx}+y=x$ 化为 $\frac{dy}{dx}=x-y$,再利用一阶线性微分方程的通解公式 $y(x)=\mathrm{e}^{-\int1\mathrm{d}x}\left(\int\mathrm{e}^{\int1\mathrm{d}x}f(x)\mat hrm{d}x+C\right)$,其中 $f(x)=x$,则有。
$$。
y(x)=\mathrm{e}^{-x}\left(\int\mathrm{e}^{x}xf(x)\mathrm{d}x+C\right)=\mathrm{e}^{ -x}\left(\int\mathrm{e}^{x}x^2\mathrm{d}x+C\right)=\mathrm{e}^{-x}(x^2+x+C)。
$$。
代入 $y(0)=1$ 可得 $C=1$,因此 $y(x)=\mathrm{e}^{-x}(x^2+x+1)$。
2. 某物体的速度 $v$ 随时间 $t$ 的变化满足 $\frac{dv}{dt}=at-bv$,其中 $a$ 和 $b$ 为已知常数,且初始速度 $v_0=0$,求物体的速度 $v(t)$。
解:将 $\frac{dv}{dt}=at-bv$ 化为 $\frac{dv}{dt}+bv=at$,同样利用一阶线性微分方程的通解公式 $v(t)=\mathrm{e}^{-\intb\mathrm{d}t}\left(\int\mathrm{e}^{\intb\mathrm{d}t}f(t)\mathrm{d}t+C\right)$,其中 $f(t)=at$,则有。
$$。
v(t)=\mathrm{e}^{-bt}\left(\int\mathrm{e}^{bt}at\mathrm{d}t+C\right)=\mathrm{e}^{-bt}\left(\frac{a}{b}t^2+C_1t+C_2\right)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分离变量
积分得 即
代回原变量得通解
(C 为任意常数)
说明: 显然 x = 0 , y = 0 , y = x 也是原方程的解, 但 在 求解过程中丢失了.
例. 求方程 解: 注意 x, y 同号, 变形为 由一阶线性方程通解公式 , 得
这是以
的通解 . 故方程可
为因变量, y为
自变量的一阶线性方程
所求通解为
思考与练习
判别下列方程类型: 提示:
可分离 变量 方程
齐次方程
线性方程
线性方程
伯努利方 程
例. 求解
解: ∴ 这是一个全微分方程 .
用凑微分法求通解. 将方程改写为
即
故原方程的通解为
或
思考: 如何解方程 这不是一个全微分方程 , 但若在方程两边同乘
就化成上例 的方程 .
备用题 解方程
的解, 是任意
(89 考研 )
提示: 都是对应齐次方程的解,
二者线性无关 . (反证法可证)
例.
个解
已知微分方程
的特解 .
有三 求此方程满足初始条件 是对应齐次方程的解, 且 常数
解:
因而线性无关, 故原方程通解为 代入初始条件 故所求特解为
例. 已知齐次方程
求
解: 将所给方程化为:
的通解为 的通解.
解法1 积分因子法. 原方程变形为 取积分因子
故通解为 此外, y = 0 也是方程的解.
解法2 化为齐次方程. 原方程变形为
积分得 将 代入 , 得通解
此外, y = 0 也是方程的解.
解法3 化为线性方程. 原方程变形为
其通解为
即
此外, y = 0 也是方程的解.
例.
解:
例. 求解 解:
有根
思考与练习
1 . (填空) 设
时可设特解为
时可设特解为
提示:
2. 已知二阶常微分方程
求微分方程的通解 .
有特解
解: 将特解代入方程得恒等式
比较系数得
故原方程为
对应齐次方程通解: 原方程通解为
例1. 解:
则原方程化为
亦即 特征方程 其根
①
则①对应的齐次方程的通解为
设特解: 代入①确定系数, 得
分离变量
代入方程得
积分得
利用 于是有
两端再积分得 利用
因此所求特解为
对于
型方程(n≥2),可以令
得 如果能求出其通解 逐次积分n-1次,就可得到原方程的通解
其中C1,C2...,Cn为任意常数.
例. 解初值问题
解: 令 代入方程得
积分得
利用初始条件,
根据
得
积分得 故所求特解为
例.
解: 特征方程 因此原方程通解为 例. 解: 特征方程: 原方程通解: (不难看出, 原方程有特解
例. 解初值问题
解: 分离变量得
两边积分得
即 ( C 为任意常数 )
由初始条件得 C = 1, 故所求特解为
例. 求下述微分方程的通解:
解: 令 则
故有 即 解得 所求通解: ( C 为任意常数 )
例:
解法 1 分离变量 即 (C<0 )
解法 2
故有 积分
所求通解:
( C 为任意常数 )
例. 解微分方程
的一个特解.
代入方程 :
比较系数, 得
于是所求特解为
例2. 求解定解问题
解: 本题 特征方程为 其根为
故对应齐次方程通解为 设非齐次方程特解为 原方程通解为 代入方程得 故
由初始条件得
解得
于是所求解为
例4 解: 本题
特征方程
的一个特解 .
不是特征方程的根, 故设特解为 代入方程得
比较系数 , 得 于是求得一个特解
例5. 解: 特征方程为
对应齐次方程的通解为 其根为
的通解.
为特征方程的单根 , 因此设非齐次方程特解为 代入方程:
比较系数, 得 因此特解为 所求通解为
例6. 设下列高阶常系数线性非齐次方程的特解形式:
解: (1) 特征方程 有二重根 所以设非齐次方程特解为
(2) 特征方程 利用叠加原理 , 可设非齐次方程特解为
的通解. 特征根:
特征根 :
例.
解: 特征方程: 即 其根为 方程通解 :
备用题
为特解的 4 阶常系数线性齐次微分方程, 并求其通解 . 解: 根据给定的特解知特征方程有根 : 因此特征方程为 即 故所求方程为 其通解为
例. 设线性无关函数 性方程
常数, 则该方程的通解是 ( ).
都是二阶非齐次线
利用⑤,⑥建立方程组:
积分得 故所求通解为
例.
解: 对应齐次方程为
的通解. 由观察可知它有特解:
令
代入非齐次方程后化简得
(二阶常系数非齐次方程)
⑦
此题不需再作变换. 特征根:
设⑦的特解为 代入⑦可得: 于是得⑦的通解:
故原方程通解为
例1.
解: 本题 设所求特解为 而特征方程为 不是特征方程的根 .
① 的通解为
换回原变量, 得原方程通解为
例2.
解: 将征根: 设特解:
②
代入 ② 解得 A = 1, 所求通解为
