ODE45函数的使用翻译
ode45求解微分方程加入齿侧间隙函数的matlab程序_解释说明

ode45求解微分方程加入齿侧间隙函数的matlab程序解释说明1. 引言1.1 概述在科学和工程领域中,微分方程广泛应用于描述动态系统的行为。
针对复杂的微分方程,求解它们的解析解往往十分困难甚至不可行。
因此,数值求解方法成为研究者们探索问题背后物理现象的重要手段。
本文将重点介绍一种常用且高效的数值方法——ode45(一种ode系列函数),并结合齿侧间隙函数的应用来解决微分方程。
我们将使用MATLAB作为编程工具,并通过设计相应程序来进行仿真实验。
1.2 文章结构本篇文章总共包括五个部分:引言、ode45求解微分方程加入齿侧间隙函数的MATLAB程序、实验结果与讨论、结论以及结束语。
接下来,在引言部分中,我们将简要介绍文章的主题和内容,并概述每个章节所涉及到的问题。
1.3 目的本文旨在深入探讨如何使用ode45函数求解微分方程,并结合齿侧间隙函数进行更准确地建模和仿真。
通过详细说明MATLAB程序设计方法和实验结果与讨论,我们希望能够全面了解齿侧间隙函数在微分方程求解中的应用,并提供一种有效而可靠的数值方法。
最后,我们将总结ode45求解微分方程加入齿侧间隙函数的MATLAB程序的优势和限制,并对未来的研究和应用进行展望。
以上是“1. 引言”部分所包含的内容。
该部分主要介绍了本文的概述、结构和目的。
接下来,我们会详细展开介绍“2. ode45求解微分方程加入齿侧间隙函数的MATLAB程序”的相关内容。
2. ode45求解微分方程加入齿侧间隙函数的matlab程序2.1 ode45求解微分方程的介绍ode45是MATLAB中用于数值求解常微分方程(ODE)的函数之一。
它利用了Runge-Kutta法进行数值积分,具有较高的精度和适应性。
ode45可以处理非刚性和刚性系统,并且能够自动调整步长以确保结果的准确性。
2.2 齿侧间隙函数在微分方程中的应用齿侧间隙函数是一种描述啮合噪声产生机制的函数,常用于模拟和研究啮合传动系统中的振动和噪声特性。
matlab ode45 求解带积分的常微分方程

概述在工程和科学领域中,常微分方程是一种常见的数学建模工具。
其中,带积分的常微分方程更是一种需要特殊解法的方程形式。
MATLAB是一种功能强大的数学工具软件,而ode45是MATLAB中用于求解常微分方程的函数之一。
本文将详细介绍如何使用MATLAB中的ode45函数来求解带积分的常微分方程。
一、带积分的常微分方程简介带积分的常微分方程是指在微分方程中出现积分形式的项,通常表现为对某个函数进行积分。
这种形式的微分方程在工程和科学领域中有着广泛的应用,例如在电路分析、控制系统、生物学模型等领域中都能见到。
典型的带积分的常微分方程形式如下所示:y' = f(t,y) + ∫g(t,y)dt其中,y'表示y对自变量t的导数,f(t,y)为已知的函数,g(t,y)为未知的函数需要求解。
这种形式的微分方程要比普通的常微分方程更复杂,需要使用特定的求解方法来得到解析解或数值解。
二、MATLAB中的ode45函数介绍MATLAB是一种被广泛应用于科学计算和工程领域的数学软件工具,其中有丰富的数值计算函数库。
其中,用于求解常微分方程的ode45函数是应用较为广泛的函数之一。
ode45函数可以通过数值计算的方法来求解常微分方程的数值解,其基本调用格式如下:[t,y] = ode45(odefun,tspan,y0)其中,odefun是定义了微分方程的函数句柄,tspan是求解的时间范围,y0是初始条件。
ode45函数会返回微分方程在tspan范围内的数值解t和对应的y值。
三、使用MATLAB求解带积分的常微分方程对于带积分的常微分方程,我们需要将其转化为标准形式,然后利用MATLAB的ode45函数进行求解。
假设我们有如下形式的带积分的常微分方程:y' = f(t,y) + ∫g(t,y)dt我们将其转化为等价的无積分項的方程形式,例如∂F/∂t = f(t,y) + ∫g(t,y)dt我们可以利用MATLAB中的ode45函数来求解上述形式的微分方程。
Matlab中解常微分方程的ode45

Matlab 中解常微分方程的ode45ode 是专门用于解微分方程的功能函数,他有ode23,ode45,ode23s等等,采用的是Runge-Kutta 算法。
ode45 表示采用四阶,五阶runge-kutta单步算法,截断误差为(△x)A3。
解决的是Nonstiff(非刚性)的常微分方程•是解决数值解问题的首选方法,若长时间没结果,应该就是刚性的,换用ode23 来解.其他几个也是类似的用法使用方法[T,Y] = ode45(odefun,tspan,y0)odefun 是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名tspan 是区间[t0 tf] 或者一系列散点[t0,t1,...,tf]y0 是初始值向量T 返回列向量的时间点Y 返回对应T 的求解列向量[T,Y] = ode45(odefun,tspan,y0,options)options是求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等[T,Y,TE,YE,IE] =ode45(odefun,tspan,y0,options)每组(t,Y)之产生称为事件函数。
每次均会检查是否函数等于零。
并决定是否在零时终止运算。
这可以在函数中之特性上设定。
例如以events或@events产生一函数。
[value,isterminal,direction]=events(t,y) 其中,value(i) 为函数之值,isterminal(i)=1 时运算在等于零时停止,=0 时继续;direction(i)=0 时所有零时均需计算(默认值) ,+1 在事件函数增加时等于零,-1 在事件函数减少时等于零等状况。
此外,TE, YE, IE 则分别为事件发生之时间,事件发生时之答案及事件函数消失时之指针i。
sol =ode45(odefun,[t0 tf],y0...) sol 结构体输出结果应用举例1 求解一阶常微分方程程序:odefun=@(t,y) (y+3*t)/t A2; % 定义函数tspan=[1 4]; % 求解区间y0=-2; % 初值[t,y]=ode45(odefun,tspan,y0);plot(t,y) %作图title('tA2y''=y+3t,y(1)=-2,1<t<4') legend('tA2y''=y+3t') xlabel('t') ylabel('y') % 精确解% dsolve('tA2*Dy=y+3*t','y(1)=-2') % ans = % (3*Ei(1) - 2*exp(1))/exp(1/t) - (3*Ei(1/t))/exp(1/t)2 求解高阶常微分方程关键是将高阶转为一阶,odefun 的书写.F(y,y',y''...y(n-1),t)=0 用变量替换,y1=y,y2=y'... 注意odefun 方程定义为列向量dxdy=[y(1),y(2) ]程序: function Testode45 tspan=[3.9 4.0]; % 求解区间y0=[2 8]; % 初值[t,x]=ode45(@odefun,tspan,y0); plot(t,x(:,1),'-o',t,x(:,2),'-*') legend('y1','y2')title('y” ”=-t*y + e A t*y" +3sin2t') xlabel('t') ylabel('y') function y=odefun(t,x) y=zeros(2,1); % 列向量y(1)=x(2);y(2)=-t*x(1)+exp(t)*x(2)+3*sin(2*t);end end。
关于ode45函数的说明

n 1
0 cn1
(2)若微分方程的阶数(n阶)大于1,则作变量 替换:
y1 y, y2 y,..., yn1 y
n1
把高阶(大于2阶)的方程(组)写成一阶微分方 程组:
dy0 f 0 t , y0 , y1 , y2 ,..., yn 1 dt dy1 f1 t , y0 , y1 , y2 ,..., yn 1 dt dy2 f 2 t , y0 , y1 , y2 ,..., yn 1 dt dyn 1 f n 1 t , y0 , y1 , y2 ,..., yn 1 dt
[T,Y]=ode45(‘odefun’,tspan,y0)
tspan为求解区间 y0为初始条件
(1)根据问题所属学科中的规律、定律、公式, 用微分方程与初始条件进行描述。
F y , y , y ,..., y ,t 0 微分方程
n
初始条件 y 0 c0 , y 0 c1 ,..., y
dy0 f 0 t , y0 , y1 , y2 ,..., yn 1 dt dy1 f1 t , y0 , y1 , y2 ,..., yn 1 dt dy2 f 2 t , y0 , y1 , y2 ,..., yn 1 dt dyn 1 f n 1 t , y0 , y1 , y2 ,..., yn 1 dt
刚性ODE求解命令
求解器solver ode23t ode15s ode23s ode23tb 功能 梯形算法 说明 适度刚性情形
多步法;Gear’s反向数值微分; 若ode45失效时,可 精度中等 尝试使用 一步法;2阶Rosebrock算法; 当精度较低时,计算 精度低 时间比ode15s短 梯形算法;精度低 当精度较低时,计算 时间比ode15s短
matlab ode45函数用法

MATLAB ODE45函数用法在MATLAB中,ODE45函数是用于求解常微分方程(ODE)的一种常用工具。
它采用龙格-库塔法(Runge-Kutta)来数值求解微分方程,通常适用于非刚性的微分方程问题。
在本文中,我们将深入探讨ODE45函数的用法,并通过具体例子来演示它的实际应用。
1. ODE45函数概述ODE45函数的基本语法如下:```matlab[t, y] = ode45(@odefun, tspan, y0)```其中,@odefun是一个用户自定义的函数,用于定义微分方程的形式;tspan是时间范围;y0是初始条件。
这个函数返回两个参数:t是时间向量,y是对应时间点的解向量。
2. ODE45函数的详细用法2.1. 自定义微分方程函数在使用ODE45函数之前,我们需要先定义微分方程的形式。
通常,我们将微分方程表示为一个函数的形式,例如:```matlabfunction dydt = odefun(t, y)dydt = % 根据微分方程的具体形式对dydt进行计算end```在这个函数中,dydt表示微分方程的导数,t表示时间,y表示状态变量。
我们需要根据具体的微分方程形式来计算dydt的值。
2.2. 设定时间范围和初始条件在使用ODE45函数时,我们需要设定时间范围和初始条件。
时间范围可以用一个包含起始时间和结束时间的向量来表示,例如tspan = [0, 10];初始条件则是微分方程在起始时间点的状态变量值,例如y0 = 1。
2.3. 求解微分方程并获取结果一旦定义了ODE45函数的参数,我们就可以用它来求解微分方程了。
调用ODE45函数后,它将返回时间向量t和对应时间点的解向量y,我们可以利用这些结果来进行进一步的分析和应用。
3. ODE45函数的实际案例为了更好地理解ODE45函数的用法,让我们通过一个具体的案例来演示。
假设我们有一个简单的一阶微分方程:```matlabfunction dydt = odefun(t, y)dydt = -2*t*y;end```我们希望求解该微分方程在时间范围tspan = [0, 5],初始条件y0 = 1的情况下的解。
ode45 matlab 用法

在本文中,我将为您介细介绍MATLAB中的ode45函数的用法。
ode45函数是MATLAB中常用的求解常微分方程(ODE)的函数,可以对一阶或高阶ODE进行求解,并且能够处理刚体动力学、化学反应动力学、电路等各种领域的问题。
我将从ode45函数的基本用法、参数设定、示例应用以及个人理解这几个方面展开讨论。
1. ode45函数的基本用法ode45函数是MATLAB中常用的求解ODE的函数。
其基本用法为:[t, y] = ode45(odefun, tspan, y0)其中,odefun为自定义的求解函数,tspan为时间范围,y0为初值条件。
ode45函数通过自适应步长Runge-Kutta法对ODE进行求解,得到时间t与对应的解y。
2. 参数设定在使用ode45函数时,需要设定求解的ODE函数odefun、时间范围tspan和初值条件y0。
还可以设定相对误差容限RelTol和绝对误差容限AbsTol,以控制求解的精度。
还可以通过设定事件函数、输出函数等对求解过程进行控制和监测。
3. 示例应用下面通过一个简单的例子来说明ode45函数的应用。
考虑一个简单的一阶ODE问题:dy/dt = -y,y(0) = 1其MATLAB代码如下:```matlabodefun = @(t, y) -y;tspan = [0, 5];y0 = 1;[t, y] = ode45(odefun, tspan, y0);plot(t, y, '-o');```这段代码首先定义了ODE函数odefun,然后设定时间范围tspan和初值条件y0,最后利用ode45函数求解ODE并绘制解y随时间t的图像。
4. 个人观点和理解在我看来,ode45函数是MATLAB中非常强大且常用的求解ODE的工具。
它能够高效地对各种类型的ODE进行求解,并且通过设定参数和监控函数,可以实现对求解过程的精确控制。
在工程领域和科学研究中,ode45函数的灵活性和高效性使其成为了不可或缺的工具。
ODE_45使用方法

ode45 Solve non-stiff differential equations, medium order method.[TOUT,YOUT] = ode45(ODEFUN,TSPAN,Y0) with TSPAN = [T0 TFINAL] integrates the system of differential equations y' = f(t,y) from time T0 to TFINALwith initial conditions Y0. ODEFUN is a function handle. For a scalar Tand a vector Y, ODEFUN(T,Y) must return a column vector correspondingto f(t,y). Each row in the solution array YOUT corresponds to a timereturned in the column vector TOUT. To obtain solutions at specifictimes T0,T1,...,TFINAL (all increasing or all decreasing), use TSPAN =[T0 T1 ... TFINAL].[TOUT,YOUT] = ode45(ODEFUN,TSPAN,Y0,OPTIONS) solves as above with default integration properties replaced by values in OPTIONS, an argument createdwith the ODESET function. See ODESET for details. Commonly used optionsare scalar relative error tolerance 'RelTol' (1e-3 by default) and vectorof absolute error tolerances 'AbsTol' (all components 1e-6 by default).If certain components of the solution must be non-negative, useODESET to set the 'NonNegative' property to the indices of thesecomponents.ode45 can solve problems M(t,y)*y' = f(t,y) with mass matrix M that isnonsingular. Use ODESET to set the 'Mass' property to a function handleMASS if MASS(T,Y) returns the value of the mass matrix. If the mass matrixis constant, the matrix can be used as the value of the 'Mass' option. Ifthe mass matrix does not depend on the state variable Y and the functionMASS is to be called with one input argument T, set 'MStateDependence' to 'none'. ODE15S and ODE23T can solve problems with singular mass matrices.[TOUT,YOUT,TE,YE,IE] = ode45(ODEFUN,TSPAN,Y0,OPTIONS) with the 'Events'property in OPTIONS set to a function handle EVENTS, solves as abovewhile also finding where functions of (T,Y), called event functions,are zero. For each function you specify whether the integration isto terminate at a zero and whether the direction of the zero crossingmatters. These are the three column vectors returned by EVENTS:[VALUE,ISTERMINAL,DIRECTION] = EVENTS(T,Y). For the I-th event function:VALUE(I) is the value of the function, ISTERMINAL(I)=1 if the integrationis to terminate at a zero of this event function and 0 otherwise.DIRECTION(I)=0 if all zeros are to be computed (the default), +1 if onlyzeros where the event function is increasing, and -1 if only zeros wherethe event function is decreasing. Output TE is a column vector of timesat which events occur. Rows of YE are the corresponding solutions, andindices in vector IE specify which event occurred.SOL = ode45(ODEFUN,[T0 TFINAL],Y0...) returns a structure that can beused with DEVAL to evaluate the solution or its first derivative atany point between T0 and TFINAL. The steps chosen by ode45 are returned in a row vector SOL.x. For each I, the column SOL.y(:,I) containsthe solution at SOL.x(I). If events were detected, SOL.xe is a row vectorof points at which events occurred. Columns of SOL.ye are the corresponding solutions, and indices in vector SOL.ie specify which event occurred.Example[t,y]=ode45(@vdp1,[0 20],[2 0]);plot(t,y(:,1));solves the system y' = vdp1(t,y), using the default relative error tolerance 1e-3 and the default absolute tolerance of 1e-6 for each component, and plots the first component of the solution.Class support for inputs TSPAN, Y0, and the result of ODEFUN(T,Y):float: double, singleSee also ode23, ode113, ode15s, ode23s, ode23t, ode23tb, ode15i,odeset, odeplot, odephas2, odephas3, odeprint, deval,odeexamples, rigidode, ballode, orbitode, function_handle.Reference page in Help browserdoc ode45。
matlab中 ODE45的用法 英文资料

y
Values of the solution to the problem (array). Each column of y is a different
dependent variable. The size of the array is length(t)-by-length(y0)
Specific examples of using ode45 now follow. Mfiles for these examples are in the body of this document and should also be available in the folder that contains this document.
Contents:
Syntax for ode45 ....................................................................................................................... 2 Integrating a single, first-order equation...................................................................................... 3 Getting the solution at particular values of the independent variable........................................... 4 Integrating a set of coupled first-order equations......................................................................... 4 Integrating a second-order initial-value problem (IVP)................................................................ 7 Integrating an Nth-order initial-value problem............................................................................ 8 Changing model parameters........................................................................................................ 9 Integrating a second-order boundary-value problem (BVP)........................................................ 11 Setting options in ode45 .......................................................................................................... 12 Going beyond ode45................................................................................................................. 13
ODE45函数的使用——翻译

ODE45函数的使用——翻译
使用ODE45函数需要指定一个函数句柄,该函数句柄表示需要求解的微分方程。
另外,还需要提供初始条件和求解的时间段。
使用ODE45函数的一般步骤如下:
2.指定初始条件和时间段;
3.调用ODE45函数求解微分方程;
4.根据返回的时间向量t和解向量y进行后续处理。
需要注意的是,ODE45函数求解的是常微分方程初值问题,即已知初始条件,求解在一定时间段内的解。
如果需要求解的是边值问题,可以使用MATLAB中的其他函数,如bvp4c和bvp5c。
通过使用ODE45函数,可以方便地求解常微分方程初值问题,并得到准确而高效的结果。
ode45解微分方程组

ode45解微分方程组要解决微分方程组,我们可以使用MATLAB中的ODE45(常微分方程数值求解器)函数。
ode45可以求解形如dy/dt = f(t, y)的一阶常微分方程,其中t是自变量,y是因变量,f(t, y)是描述y在t上的变化率的函数。
对于多个变量的微分方程组,可以将其处理为向量形式并使用ode45以下是一个例子来说明如何使用ode45函数来解微分方程组。
假设我们要求解以下微分方程组:dy1/dt = y2dy2/dt = -2*y1 + 3*y2其中,y1和y2都是关于t的函数。
首先,我们需要将这个微分方程组转化为向量形式。
定义一个向量Y,其中Y(1)=y1,Y(2)=y2,我们可以将系统改写为:dY/dt = [Y(2); -2*Y(1) + 3*Y(2)]然后,在MATLAB中,我们可以定义一个函数来表示这个系统。
我们将其命名为"system",输入参数t和Y,输出参数是dY。
function dY = system(t, Y)dY(1,1)=Y(2);dY(2,1)=-2*Y(1)+3*Y(2);end接下来,我们可以使用ode45函数来求解该微分方程组。
首先,我们需要指定初始条件。
令t0为初始时间,Y0为初始向量,我们可以从初始条件中获得这些值。
在这个例子中,假设我们要从t=0开始,并且y1(0)=1,y2(0)=0。
因此,t0=0,Y0=[1;0]。
然后,我们可以调用ode45,将解密度'R'设置为1e-3(即0.001),并指定时间间隔[0 10]:tspan = [0 10];Y0=[1;0];R=1e-3;最后,我们得到了在时间间隔[010]上的数值解,通过't'和'Y'来表示。
t是时间向量,Y是与时间相对应的解向量。
我们可以绘制结果以获得更好的理解。
假设我们想绘制y1和y2的图像。
y1=Y(:,1);y2=Y(:,2);figure;plot(t, y1, 'r', t, y2, 'b')xlabel('t')ylabel('y')legend('y1', 'y2')title('Solution of the differential equations')以上就是求解微分方程组的一个例子。
ode45 matlab 例子

ode45 matlab 例子ode45 MATLAB 例子1. 简介ode45 是 MATLAB 中一个常用的求解常微分方程(ODE)的函数。
它使用了一个基于 Runge-Kutta 方法的算法来解决ODE问题。
2. 线性ODE的例子下面我们通过一个线性ODE的例子来说明 ode45 的基本用法。
线性ODE的定义:假设有一个一阶线性ODE,形式如下:dy/dt = a*y + b其中 a 和 b 是常数,y 是未知函数。
例子:考虑一个简单的线性ODE:dy/dt = 2*t*y + t^2为了使用 ode45 解决这个问题,我们需要定义一个 MATLAB 函数来表示这个方程:function dydt = myODE(t, y)dydt = 2*t*y + t^2;end然后,我们可以使用 ode45 来求解该问题:[t, y] = ode45(@myODE, [0 1], 1);上述代码中: - @myODE表示将myODE函数作为变量传递给ode45 函数。
- [0 1]表示求解的时间区间是 [0, 1]。
- 1表示初始条件。
3. 非线性ODE的例子除了线性ODE,ode45 也可以求解非线性ODE。
下面我们通过一个非线性ODE的例子来说明。
非线性ODE的定义:假设有一个二阶非线性ODE,形式如下:d^2y/dt^2 + a*dy/dt + b*y + c*y^2 = 0其中 a、b 和 c 是常数,y 是未知函数。
例子:考虑一个简单的非线性ODE:d^2y/dt^2 + 2*dy/dt + 3*y + 4*y^2 = 0为了使用 ode45 解决这个问题,我们需要将这个二阶ODE转化为两个一阶ODE。
令 z = dy/dt,我们可以得到以下一阶ODE系统:dz/dt = -2*z - 3*y - 4*y^2dy/dt = zfunction dydt = myODE(t, y)dydt = zeros(2,1);dydt(1) = -2*y(2) - 3*y(1) - 4*y(1)^2;dydt(2) = y(1);end然后,我们可以使用 ode45 来求解该问题:[t, y] = ode45(@myODE, [0 1], [1 0]);上述代码中,初始条件是[1 0],因为我们需要同时指定 y 和z 的初始值。
matlabode45函数用法

matlabode45函数用法Matlabode45函数是Matlab中一类重要的数值差分方法,其属于高级求解器,具有高精度、高可靠性和易于使用的特点。
Matlabode45函数主要用于求解微分方程的定常问题,也可用于求解离散事件系统的数值解。
的应用非常广泛,在科学研究、工程设计和生物建模等领域有着重要的作用。
Matlabode45函数的介绍Matlabode45函数是基于ODEPACK(Ordinary Differential Equation Package)的Fortran程序库,它提供一组算法来求解离散事件和常微分方程的数值解。
Matlabode45函数包括一系列基本功能,如选择步长控制、选择积分方法和选择初始值,可以自动调节步长,保证求解准确性和效率。
Matlabode45函数应用实例Matlabode45函数可以用于解决几何模型、动力学模型、可控模型、机器人运动模型等复杂的数学模型。
例如,我们可以用Matlabode45函数求解一个机器人的轨迹规划问题。
以机器人从起点A到终点B的运动模型为例,其中包括运动方程、限位函数及边界条件等。
们可以建立数值模型,使用Matlabode45函数求解机器人满足限位函数、边界条件等要求的路径。
Matlabode45函数使用方法Matlabode45函数使用非常简便,只需要几行Matlab代码即可完成数值求解。
先,我们要定义微分方程,实现遵循ODE45求解器规则的函数,将其记录在Matlab代码中,这可以用MATLAB的简单函数实现。
后,可以使用Matlabode45函数调用上述函数进行求解,并指定初值、步长大小和最大步长等参数,可以获得一组数值解。
Matlabode45函数的优势Matlabode45函数具有高精度和高可靠性的优点,可以自动调整步长,保证求解的准确性和效率。
起传统数值求解方法,它能够更有效地解决复杂的数学模型。
外,Matlabode45函数可以减少用户构建模型、指定初值和参数设置等操作量,具有较高的易用性。
ode45解随机微分方程

ode45解随机微分方程要使用MATLAB中的ode45函数来解随机微分方程,你需要使用MATLAB中的stochastic differential equations (SDEs)求解器。
ode45函数通常用于解决确定性微分方程,而不是随机微分方程。
对于随机微分方程,MATLAB提供了sde45函数来解决这个问题。
首先,你需要定义你的随机微分方程。
随机微分方程通常采用以下形式:dX(t) = f(t, X(t))dt + g(t, X(t))dW(t)。
其中,X(t)是随机过程,f(t, X(t))是确定性漂移项,g(t,X(t))是随机扩散项,dW(t)是随机过程的增量。
接下来,你可以使用MATLAB中的sde45函数来解决这个随机微分方程。
sde45函数的使用方式类似于ode45函数,但它专门用于解决随机微分方程。
你需要提供随机微分方程的漂移项和扩散项,以及初始条件和积分的时间范围。
以下是一个简单的示例,演示如何使用sde45函数解决随机微分方程:matlab.function SDEExample.% 定义随机微分方程的漂移项和扩散项。
f = @(t, X) -0.5X; % 漂移项。
g = @(t, X) 1; % 扩散项。
% 定义初始条件和积分的时间范围。
tspan = [0 1];X0 = 1;% 使用sde45函数解决随机微分方程。
[t, X] = sde45(@(t, X) f(t, X), @(t, X) g(t, X), tspan, X0);% 绘制结果。
plot(t, X);xlabel('Time');ylabel('X(t)');end.在这个示例中,我们定义了随机微分方程的漂移项f和扩散项g,并使用sde45函数解决了这个随机微分方程。
最后,我们绘制了结果以可视化随机过程X(t)随时间的变化。
总之,要使用MATLAB解决随机微分方程,你需要使用sde45函数而不是ode45函数,并提供随机微分方程的漂移项和扩散项。
ode45 riccati方程

ode45 riccati方程1. 简介ode45是MATLAB中的常用函数,用于求解常微分方程的数值解。
而riccati方程是一类特殊的微分方程,在控制理论和动力学系统等领域有着广泛的应用。
本文将介绍ode45函数与riccati方程的基本概念,并讨论如何利用ode45函数求解riccati方程。
2. ode45函数简介ode45函数是MATLAB中的一个常用函数,用于求解常微分方程的数值解。
其语法格式为:[t, y] = ode45(odefun, tspan, y0)其中,odefun是一个函数句柄,tspan是时间区间,y0是初始条件。
ode45函数会返回一个时间向量t和对应的解向量y,其中y是对应时间点t的微分方程的数值解。
3. riccati方程的定义riccati方程是一种特殊的微分方程,其一般形式为:dy/dx = A*x^2 + B*x + C - D*y^2 - E*y - F其中A、B、C、D、E、F都是常数,x和y是未知函数。
riccati方程在控制理论、动力学系统等领域有着重要的应用,因此求解riccati方程是一项重要的数值计算任务。
4. 如何利用ode45函数求解riccati方程要利用ode45函数求解riccati方程,首先需要将riccati方程化为一阶常微分方程的形式。
假设riccati方程为:dy/dx = A*x^2 + B*x + C - D*y^2 - E*y - F引入新的未知函数z,令y = z/x,将原方程化为一阶常微分方程:dz/dx = (A - D*z^2)*x^2 + (B - E*z)*x + C - F*z^2从而将riccati方程化为一阶常微分方程的形式,可以利用ode45函数求解得到z关于x的数值解。
5. 示例下面举一个简单的示例,说明如何利用ode45函数求解riccati方程。
假设riccati方程为:dy/dx = x^2 - y^2首先化为一阶常微分方程的形式:dz/dx = x^2 - z^2则可以利用ode45函数求解此一阶常微分方程,得到z关于x的数值解。
matlab中rungekutta方法的用法

matlab中rungekutta方法的用法在MATLAB中,Runge-Kutta方法可以通过ode45函数实现。
ode45函数是用于求解初值问题的常微分方程组的函数,它使用了4阶和5阶的Runge-Kutta方法来计算微分方程的数值解。
下面是在MATLAB中使用ode45函数的基本语法:[t,y] = ode45(odefun,tspan,y0)其中:* odefun:函数句柄,它描述了微分方程组。
odefun应该接受两个输入参数(t和y),并返回一个列向量,该列向量包含y的每个分量的导数。
* tspan:时间跨度,它是一个包含起始时间和结束时间的向量,例如[t0 tf]。
如果省略tf,则默认为Inf。
tspan也可以是一个包含多个时间点的向量,例如[t0,t1,...,tf]。
在这种情况下,ode45将在指定的时间点返回解。
* y0:初始条件向量,它包含了在tspan起始时间点的y的值。
ode45函数返回两个输出:* t:一个列向量,包含了ode45计算解的时间点。
* y:一个矩阵,每一行包含了对应时间点t的y的值。
例如,如果我们有一个简单的微分方程组 dy/dt = -2.3y,我们可以使用以下代码在MATLAB中使用ode45函数求解:首先定义odefun函数:function dy = odefun(t,y)dy = -2.3 * y;end然后在MATLAB命令窗口中输入以下代码:tspan = [0 10]; % 时间跨度为0到10y0 = 1; % 初始条件为1[t,y] = ode45(@odefun,tspan,y0); % 使用ode45函数求解微分方程组。
matlab function求解微分方程

matlab function求解微分方程Matlab是一种非常强大的数学计算软件,它可以用来求解各种数学问题,包括微分方程。
在Matlab中,我们可以使用函数ode45来求解微分方程。
ode45是Matlab中最常用的求解微分方程的函数之一。
它可以求解一阶或二阶微分方程,并且可以处理初值问题和边值问题。
使用ode45求解微分方程的步骤如下:1. 定义微分方程首先,我们需要定义要求解的微分方程。
在Matlab中,我们可以使用函数来表示微分方程。
例如,如果要求解dy/dx = x + y,我们可以定义一个函数f,使得f(x,y) = x + y。
这个函数可以写成Matlab代码:function dydx = f(x,y)dydx = x + y;2. 定义初值接下来,我们需要定义微分方程的初值。
也就是说,我们需要知道在某个点上y的值以及y的导数的值。
在Matlab中,我们可以使用一个向量来表示初值。
例如,如果y(0) = 1,y'(0) = 0,我们可以定义一个向量y0 = [1;0]。
3. 调用ode45函数现在,我们已经定义了微分方程和初值,可以调用ode45函数来求解微分方程。
ode45函数的语法如下:[t,y] = ode45(f,tspan,y0)其中,f是微分方程的函数句柄,tspan是一个包含起始时间和结束时间的向量,y0是初值向量。
函数的输出是一个包含时间和y值的矩阵。
t是时间向量,y是y值的矩阵。
例如,如果我们要求解dy/dx = x + y,y(0) = 1,y'(0) = 0,在时间范围[0,10]内的解,可以写成Matlab代码:function dydx = f(x,y)dydx = x + y;tspan = [0 10];y0 = [1;0];[t,y] = ode45(@f,tspan,y0);plot(t,y(:,1),'-o',t,y(:,2),'-o')legend('y','y''')这段代码会生成一个图形,显示y和y'随时间的变化。
关于ode45函数的说明

y0 y 1 x y2 ... yn 1
Dx是一个数组,其第一个元素Dx(1)表示dy0/dt 第二个元素Dx(2)表示dy1/dt 如此类推。
x也是一个数组,其第一个元素x(1)表示y0 第二个元素x(2)表示y1 如此类推。 根据这个关系,很容易可以把一阶微分方程组用 数组Dx与数组x的元素表示出来。例如(见下页)
dy0 f 0 t , y0 , y1 , y2 ,..., yn 1 dt dy1 f1 t , y0 , y1 , y2 ,..., yn 1 dt dy2 f 2 t , y0 , y1 , y2 ,..., yn 1 dt dyn 1 f n 1 t , y0 , y1 , y2 ,..., yn 1 dt
[T,Y]=ode45(‘odefun’,tspan,y0)
tspan为求解区间 y0为初始条件
(1)根据问题所属学科中的规律、定律、公式, 用微分方程与初始条件进行描述。
F y , y , y ,..., y ,t 0 微分方程
n
初始条件 y 0 c0 , y 0 c1 ,..., y
(3)根据(1)和(2)的结果,编写计算导数的 M函数文件。
(仅供参考)如何使用ODE45
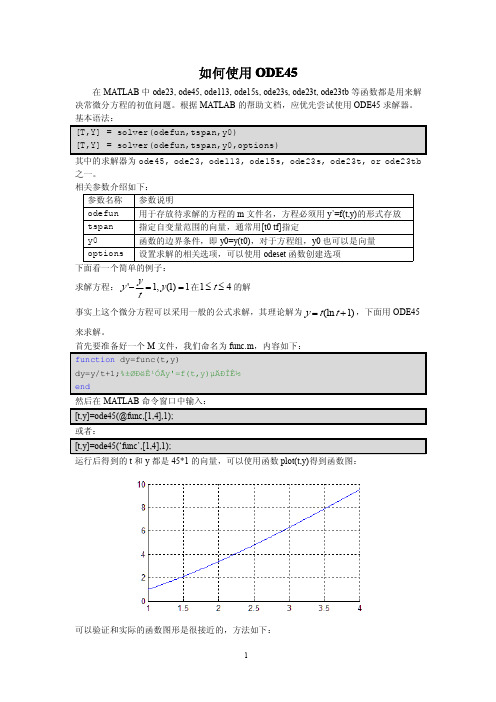
如何使用ODE45在MATLAB 中ode23,ode45,ode113,ode15s,ode23s,ode23t,ode23tb 等函数都是用来解决常微分方程的初值问题。
根据MATLAB 的帮助文档,应优先尝试使用ODE45求解器。
之一。
相关参数介绍如下:参数名称参数说明odefun 用于存放待求解的方程的m 文件名,方程必须用y’=f(t,y)的形式存放tspan指定自变量范围的向量,通常用[t0tf]指定y0函数的边界条件,即y0=y(t0),对于方程组,y0也可以是向量options 设置求解的相关选项,可以使用odeset 函数创建选项下面看一个简单的例子:求解方程:'1,(1)1y y y t−==在14t ≤≤的解事实上这个微分方程可以采用一般的公式求解,其理论解为(ln 1)y t t =+,下面用ODE45来求解。
可以验证和实际的函数图形是很接近的,方法如下:蓝色的线条是真实函数的曲线,而红色的点是数值计算的结果,可见两者符合的很好。
下面是一个比较复杂一点的方程,所谓的复杂是说用理论方法很难求解的:求微分方程232,(1)2y yt y t y t ′=+++=−在14t ≤≤时的数值解首先要将方程改写为:2232y y y t t t t ′=+++另外,也可以求微分方程组的问题,例如Matlab 帮助文档中提供的一个例子:求方程组'123'213'3220.51y y y y y y y y y ==−=−在满足初值条件123(0)0,(0)1,(0)1y y y ===时的数值解对于二阶微分方程,基本原理是一样的,但是M 文件却有很大的不同。
二阶常微分方程的一般形式为:0001''()'()(),(),'()y p t y q t y g t y t y y t y ++===下面的一个例子将做出说明。
求微分方程''''3sin 2,(0)1,(0)1t y ty e y t y y +−===−在02t ≤≤时的数值解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在Matlab 中使用ode45简介Matlab 中常微分方程常用的函数是ODE45,这个函数能够利用--龙哥库塔法--有效求解带时间变量步长的计算。
Ode45用于求解如下的一般问题:)(()00,,x t x x t f dtdx ==(1) 其中,时间t 是独立变量,x 为时间相关矢量,)(x t f ,是时间t 和x 的函数。
当(1)右边的)(x t f ,是固定的,且给定x 的初始值,那么问题的解是唯一的。
在ME175中,解法是不完整的,但是只要你解决了问题,就可以获得ODE 代表的系统运动趋势。
这有利于得到一个直观的印象,看起来很复杂的常微分方程,代表的质点运动轨迹确实简单明了的。
以下简要解释如何得到运动轨迹:第一步:对给定的ODE 方程进行降阶处理,得到一系列一阶方程这就是你要做的第一步,在一张草稿纸上处理。
例如,给定ODE 方程如下:1,3,5002-===-+⋅⋅⋅⋅y y y e y y m y (2)对本问题,矢量x 有两个组成分量:y 和⋅y ,或 ()()⋅==yx yx 21(3)且 ()()()()()()()()()()()211251221x e x m dt x d x dt x d x +-==(4) 其中,用(3)中的式子代表了y ,⋅y ,⋅⋅y ,于是把(2)改写为(4)。
如果求解的问题有更多阶数更多变量呢?例如,我们除了有上面的方程(2),同时还有以下的方程:().1,0,sin 002233===-+⋅z z t z dtz d dt z d (5) 那么,我们可以通过构造更大的矢量x 同时求解y ,z :()()()⋅⋅⋅===zx z x zx 543 (6)然后⎥⎦⎤⎢⎣⎡=⋅⋅⋅⋅z z z y y x ,,,, (7) 以及 [⎥⎦⎤==⋅⋅=⋅==⋅==000000,,,,t t t t t t z z z y y x (8) 其中,y 变量和z 变量的放置位置对求解不造成影响。
实际上,任意次序都是有效的,例如⎥⎦⎤⎢⎣⎡=⋅⋅⋅⋅z z y z y x ,,,, 和⎥⎥⎦⎤⎢⎣⎡=⋅⋅⋅⋅⋅⋅y y z z z x ,,,, 但是重要的是,在整个计算过程中,你使用的顺序都必须和一阶ODE 方程中定义的变量顺序相同。
之后,如果你使用的是(7)中给定的的式子,那么系统的一阶ODE 方程,由以下方程组组成。
(10)而涉及的表征变量⎥⎦⎤⎢⎣⎡=⋅⋅⋅⋅z z y z y x ,,,,结果如下:(11)基本上,可以处理任意数量的高阶ODE 方程。
重要的是把它们处理成多个一阶的ODE 方程,并且确保记住被求解的矢量X 中,不同变量所分配的顺序。
第二步 编写代码既然你已经有所求解问题的一阶格式,在你编程的主要代码中,将会用到以下的命令 []()options xinit tspan fname ode x t ,,,@45,=·fname 是函数的M 文件名用于求解方程(1)右边代数式的值。
这个函数将被输入一阶ODE 系统中,并且被积分(见(10),(11))。
后面,将会更详细的解释。
注:当然关于ODE45如何积分给定的方程有细微的差别,但是对于简单的问题,不分先后次序的积分,是可以接受的。
·tspan 是矢量定义了积分的起始点和终点,同时也定义了时间步长。
例如,我们需要积分t=0到t=10,希望步数是100步,那么tspan=[0:0.1:10]或者tspan=linspace (0,10,100). ·xinit 是初始条件矢量。
确保初始值的顺序和给定的x 中变量和它倒数的顺序是一致的。
同时注意如果x 有5个变量,那么同时要输入5个初始值。
·option 这个在matlab 的帮助文件中有很好的说明。
对于大部分的问题,使用默认值就可以满足计算要求。
·t 是独立变量,计算数组x 在时间点t 的数值。
这个矢量不必等于tspan ,ODE45自动调节步数以取得最大的效率和精确度。
(在快速变化部分采用小步长,在变化缓慢部分采用大步长)。
·x 相关内容如下。
X 是数组或矩阵,大小为length (t )*length (xinit )。
每一列x 代表不同的因变量。
例如,⎥⎦⎤⎢⎣⎡=⋅⋅⋅⋅z z z y y x ,,,,,为简单假定t=0,1,2....,10,将会计算函数在11个点的值。
(12)如果⋅z 是x 的第四个变量,那么()4,1x 得到了⋅z 在t=0时候的值,()4,7x 得到了⋅z 在t=6时候的值,()4,11x 得到了t=10时候的值。
简而言之,·()k x :,代表x 的第k 个变量,k=1与变量y 相关,k=2与变量⋅y 相关。
·():,j x 计算所有变量在某一时间点j 的数值 注:在产生hokey pokey 舞蹈前,史前儿童围坐在篝火前齐唱:You put your left foot inYou put your left foot out'You put your left foot inAnd you shake it all about当你使用matlab 函数ODE45及时完成作业时,x 就是要做得全部内容。
不幸的是由于缺乏matlab 软件,使得这本书过时了。
·()()时间,变量值x k j x ≡,命令[]()options xinit tspan fname ode x t ,,,@45,=的作用是重新定义变量。
、,然后,如果使用变量顺序为⎥⎦⎤⎢⎣⎡=⋅⋅⋅⋅z z z y y x ,,,,,应该这么写程序:[]()options xinit tspan fname ode x t ,,,@45,=()()()()()5:,4:,3:,2:,1:,x zdotdot x zdot x z x ydot x y =====当然,也不应该认为定义y ,ydot 麻烦。
直接表达为x 的形式(例如,使用()1:,x 代表y ),清晰的定义方式有利于后面的调试。
以下,你将以(或是被要求)绘图的形式描述感兴趣的轨迹:质点随时间运动轨迹,在平面中表示角度和径向关系等。
绘图和绘制子图的命令在matlab 帮助文件中有清晰的说明,这里不再详细说明。
记住如果你想在一张图中放多个图,应该使用子图的概念,当然在一张图片中画多个图,不是一个好主意。
别忘记给图加标签:包括标题,x 轴,y 轴的含义,如果多条曲线应该分别标明。
最后,请注意在[]()options xinit tspan fname ode x t ,,,@45,=中包含的仅仅是变量而已,依据自己的喜好使用字母,T 替换t ,x0替换xinit 都是可以的。
只有记住使用新变量名,之后的每个引用都用一样的名称。
另一个普遍的错误在于,同一变量的重复定义。
例如,定义()5:,x x =,如果足够幸运的话,会有错误警告;不幸的话,这种错误很难发现,要花数小时时间检查您的程序以解决问题。
此外,fname 是什么呢?回忆下,我们还没有告诉matlab 程序应该对什么函数进行积分,是吧?这就是为什么需要fname 文件,fname 文件含有所有之前在稿纸上重写的ODE 一阶函数。
你可以对这个文件起任意的名称,只要与[]()options xinit tspan fname ode x t ,,,@45,=中使用的fname 一致。
例如,你对fname 取名superman 那么[]()options xinit tspan erman ode x t ,,,sup @45,=是对的,而[]()options xinit tspan batman ode x t ,,,@45,=就不正确了。
更进一步说,函数不必须像在原始代码中写的在同一个m 文件中,一些人喜欢在程序末尾书写子程序,特别是代码不长,比较简单的时候。
例如,你的代码名称ME175example 文件,那么m 文件将如下:Function dxdt=ME175example(t,x)%这里 t,x 和 dxdt are 只是变量而已。
你可以起任意名称%只要 t 是独立变量,而X 是因变量%dxdt 是推到的一阶因变量% 定义常数m= 1;%定义变量使之清晰易懂%Recall that x = [y, ydot, z, zdot, zdotdot]y=x(1);ydot=x(2);z=x(3);zdot=x(4);zdotdot=x(5);%注意x仅仅是1列五行的数组%[t,x] = ode45(@fname, tspan, xinit, options)%数组dxdt与x的大小相同dxdt = zeros(size(x));dxdt(1) = ydot;dxdt(2) = 1/m(5 x(2)exp(y) +y2); %This is ydotdotdxdt(3) = zdot;dxdt(4) = zdotdot;dxdt(5) = t-zdotdot+sin(z); %This is zdotdotdot%Note that the input arguments must be t and x (in that order) even in the case where t is notexplicitly used in the function.基本模板以下是基本模板,当你想对一个高阶常微分方程进行积分时,把它复制黏贴到Matlab中Function 任何你想要的名字%定义起始时间tstat,终止时间tend,时间步数nTstart=?;Tend=?;N=?;Tspan=linspace(Tstart, Tend, N);%定义初始值,确保正确的顺序Xinit=[...; ...; ...; ...;...];%获得矢量x 。
把option 设置为默认值即可[]()x init tspan @45,,积分函数,ode t x =%定义输出变量()()2:,1:,x ydot x y ==... %所需要画图的函数 ()()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⋅⋅⋅⋅⋅y y y y t y t y ,,, Subplot (?, ?, ?)Plot(需要的图像)%plot3()画3D 图Title (' ')Xlabel(' ')Ylabel(' ')Zlabel(' ')-----------------------------------%积分函数,可以作为独立m 文件,或在本程序底部,语法如下Function dxdt=积分函数(t ,x )%定义积分中使用的常数%定义新变量;()() .21etcx ydotxy==%也可以不定义,这样的好处是,便于其他人阅读你的程序%写下你得到的一阶ODE方程dxdt=zeros(size(x))dxdt(1)=?;dxdt(2)=?;dxdt(3)=?;Etc.小结:如果所有的步骤都对了,方程也是正确的。
