数模 实验2
数学建模实验报告

湖南城市学院数学与计算科学学院《数学建模》实验报告专业:学号:姓名:指导教师:成绩:年月日目录实验一 初等模型........................................................................ 错误!未定义书签。
实验二 优化模型........................................................................ 错误!未定义书签。
实验三 微分方程模型................................................................ 错误!未定义书签。
实验四 稳定性模型.................................................................... 错误!未定义书签。
实验五 差分方程模型................................................................ 错误!未定义书签。
实验六 离散模型........................................................................ 错误!未定义书签。
实验七 数据处理........................................................................ 错误!未定义书签。
实验八 回归分析模型................................................................ 错误!未定义书签。
实验一 初等模型实验目的:掌握数学建模的基本步骤,会用初等数学知识分析和解决实际问题。
实验内容:A 、B 两题选作一题,撰写实验报告,包括问题分析、模型假设、模型构建、模型求解和结果分析与解释五个步骤。
数学建模实验2 - 副本

第八章一、线性规划1、圆钢原材料每根长5.5米,现需要A,B,C三种圆钢材料,长度分别为3.1m,2.1m, 1.2m 数量分别为100,200,400根,试安排下料方式,使所需圆钢原材料的总数最少。
设Xi为截取方式,共有五种截取方式。
Xi取值为1,表示截取,2,表示截取两段,取值为零表示不截取。
根据题目要求,A,B ,C型号钢管需要量为100 200 400,且要求使用的原材料最少,所以:X1+X2>=100X1+X3+2*X5>=2002*X2+2*X3+4*X4+X5>=400MIN=X1+x2+x3+x4+x5使用LINGO可得:第九章二、非线性规划2、住宅小区服务中心选址:某地新建一个生活住宅区,共有20栋住宅楼,小区内所有道路都是东西或南北走向,开发商拟在小区内修建一个服务中心,地址选在离所有楼房的总路程最小的地方。
为了保证建筑物之间有足够的空间,服务中心的位置与其它楼房位置之间的距离不能少于30米(已经考虑了所有建筑的占地面积),请你确定服务中心的位置。
设初始点x0=[20, 20], 设(ai,bi)(i=1,…20)为第i栋住宅楼的坐标:a=[29.74 4.9 69.32 65.0 98.3 55.27 40.0 19.8 62.5 73.3 37.58 0.98 41.98 75.37 79.38 92.0 84.47 36.77 62.08 73.13],b=[19.39 90.48 56.92 63.18 23.44 54.88 93.16 33.5 65.5 39.19 62.73 69.9 39.72 41.37 65.52 43.5 34.6 75.2 12.32 86.7].1、假设所有的建筑可以看做质点,那么服务中心词到其他楼房的距离不少于30米。
2、假设小区建筑道路按上北下南左西右东排列一、问题分析本问题的求解是求所有楼房的总路程最小值,也就是求一个最优化问题。
数学建模实验报告2

aij >0,
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
数学建模实验报告2

糖果问题题目:某糖果厂用原料A,B,C,加工成三种不同牌号的糖果甲,乙,丙。
已知各种糖果中A,B,C的含量、原料成本、各种原料的每月限制用量、三种牌号的单位加工费及销售如下表所示。
甲 乙 丙 原料成本/元kg 每月限制用量/kg A 》60% 》15% 2 2000 B 1.5 2500 C《20% 《60% 《50% 1 1200 加工费/元kg 0.5 0.4 0.3 售价3.42.852.25问该厂每月生产这三种牌号的糖果各多少千克,使该厂获利最大?是建立这个问题的先行规划模型。
问题分析:由于甲、乙、丙三种糖果中A,B,C 的含量是未知的,我们若只设生产三种牌号的糖果各x, y, z 千克,要解决问题还要设出A,B,C 三种原料在他们当中所占的百分比,如此下来,在建立线性规划模型列方程时,方程中会出现二次式,很不利于我们解决问题。
为此,我们就想怎么设变量才能把各个变量都统一起来,并且使方程都是线性的。
经过思考之后,我们可以假设每个品牌的糖果当中只含A,B,C 三种原料,设甲中A,B,C 的含量分别为x1,x2,x3 ,乙中A,B,C 的含量分别为y1,y2,y3 , 丙中A,B,C 的含量分别z1,z2,z3 ,那么由假设我们知道x=x1+x2+x3 ,y=y1+y2+y3 ,z=z1+z2+z3 ,在由表中的各个约束条件我们可列出如下方程:甲: 乙: 丙:60%20%aa b c ca b cX X X X X X X X ≥++≤++ 15%60%aa b cc a b c Y Y Y Y Y Y Y Y ≥++≤++ 50%a a b c Z Z Z Z ≤++有每月限制用量:200025001200a b c a b c a b c X X X Y Y Y Z Z Z ++≤++≤++≤利润函数:()()(,,)()(3.40.5)()(2.850.4)()(2.250.3)2.00,1.50,1.00,,,,13.40.5,2.250.4,2.250.3,,11,,a b c a b c a a c a a a b b b c c c Ta a a a ab b bc c c f X Y Z X X X Y Y Y Z Z Z X Y Z X Y Z X Y Z X Y Z X YX Y Z X Y Z =++-+++-+++--++⎛⎫ ⎪++ ⎪ ⎪++⎝⎭⎛⎫⎛⎫ ⎪ ⎪=---- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭()()()1,,1 2.00,1.50,1.001,,,,,,3.40.511,1,1,, 2.250.4,,1 2.00,1.50,1.002.250.31,,,,a b b b c c c a a a a a a b b b b b b c c c c c c Z X Y Z X Y Z X Y Z X Y Z X Y Z X Y Z X Y Z X Y Z ⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪=-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭程序源代码:clear; x=[];A=[-0.4,0.6,0.6,0,0,0,0,0,0 -0.2,-0.2,0.8,0,0,0,0,0,0 0,0,0,-0.85,0.15,0.15,0,0,0 0,0,0,-0.6,-0.6,0.4,0,0,0 0,0,0,0,0,0,-0.5,-0.5,0.5 1,0,0,1,0,0,1,0,00,1,0,0,1,0,0,1,00,0,1,0,0,1,0,0,1];B=[0;0;0;0;0;2000;2500;1200];C=[0.9,1.4,1.9,0.45,0.95,1.45,-0.05,0.45,0.95];xl=[0;0;0;0;0;0;0;0;0];xu=[2000;2500;1200;2000;2500;1200;2000;2500;1200];x=linprog(-C,A,B,A,B,xl,xu);x运行结果:x =1.0e+003 *2.00050.66680.66680.00020.00010.00000.00010.53400.5336问题结果有上述分析,通过matlab命令,我们求得最优解为甲乙丙使用总量A 2000.5 0.2 0.1 2000.8B 666.8 0.1 534 1200.9C 666.8 0 533.6 1200.4此时的利润为4748.5元。
数学模型实验报告2

教师签名:
实验小结: 本次试验主要让我们掌握线性方程组建模,利用 MATLAB 来计算线性方程,从而解决 实际问题,是一个非常实用的解决实际问题的方法。十分值得学习。
教师评语: 1. 实验结果及解释: ( 准确合理、 较准确、 不合理 ) ; 2. 实验步骤的完整度: ( 完整、 中等、 不完整 ) ; 3. 实验程序的正确性: ( 很好、 较好、 中等、 较差、 很差 ) ; 4. 卷面整洁度: ( 很好、 评定等级: ( ) 较好、 中等、 较差、 很差 ) ; 日期:
X4-X11+X12=500
X5+X8=310
Байду номын сангаас
X5-X6+X10=400
(2)使用 MATLAB 求线性方程组:
实验目的: 掌握线性方程组建模,并会用它解决一些实际问题;熟悉科学计算软件 MATLAB 求 线性方程组的命令。 实验仪器: 1、支持 Intel Pentium Ⅲ及其以上 CPU,内存 256MB 以上、硬盘 1GB 以上容量的 微机; 软件配有 Windows98/2000/XP 操作系统及 MATLAB 软件等。 2、了解 MATLAB 等软件的特点及系统组成,在电脑上操作 MATLAB 等软件。 实验内容、步骤及程序: 实验内容 问题一:某城市有下图所示的交通图, 每条道路都是单行线, 需要调查每条道路 每小时的车流量. 图中的数字表示该条路段的车流数. 如果每个交叉路口进入和 离开的车数相等, 整个图中进入和离开的车数相等 。
31 31
左上方框里填写学号后两位,学习委员按此顺号(报告展开排序)交给老师
数学模型实验报告
专业 姓名 实验时间 实验名称 信息与计算科学 史博强 2017 年 9 班级 同组人 月 23 日 初等模型 实验地点 k7-403 1班 组别 指导教师 许小芳
数学建模实验二初等模型实验

数学建模实验⼆初等模型实验集美⼤学计算机⼯程学院实验报告课程名称:数学模型班级:计算12 实验成绩:指导教师:付永钢姓名:实验项⽬名称:初等模型试验学号:上机实践⽇期:实验项⽬编号:实验⼆上机实践时间:2014.11⼀、实验⽬的掌握初等模型的建⽴的基本思路和⽅法,并了解其求解过程。
对给定的初等模型问题能够借助Matlab ⼯具进⾏求解。
⼆、实验内容实验 1 ⽤Matlab 验证划艇⽐赛成绩模型的结果,通过数值结果来检验你所得到的模型正确性。
(⾸先要阅读本⽬录中的Matlab 数据拟合和matlab 数据处理的相关材料)实验2 求解汽车刹车距离的模型,⽤Matlab 给出你的求解结果。
验证应该遵循的t 秒准则的标准。
实验3 从教材P56中的第7,13,14题,任选⼀题,建⽴相应的初等模型,并借助matlab 进⾏求解,并给出合理的模型解释。
三、实验使⽤环境WindowsXP 、Matlab6.1四、实验步骤1、划艇⽐赛成绩的模型检验根据推导出的模型公式和数据,对参数βα,进⾏求解βαn t =。
⾸先转换成对数形式:,log 'log n t βα+=其中ααlog '=然后对给定数据进⾏拟合。
代码:n=[1 2 4 8]t=[7.21 6.88 6.32 5.84]lgn=log(n);lgt=log(t);p=polyfit(lgn,lgt,1);alpha=exp(p(2));belta=p(1);x=1:20;y=alpha*x.^belta ;plot(x,y,’c*-‘) ;xlabel(‘Number of Athlete ’);ylabel(‘Time Cost ’);Matlab 拟合函数图像:结果分析:划艇⽐赛模型的结果为t∞n-(1/9).。
在matlab中检验得belta =-0.1035与-(1/9)接近。
因此,模型正确。
2、汽车刹车距离验证代码:function E=fun1(a,x,y)Y=a(1)*x.*x+0.75*x;E=y-Y;%M⽂件结束%⽤lsqnonlin调⽤解决:x=[29.3 44 58.7 73.3 88 102.7 117.3];y=[44 78 124 186 268 372 506];a0=[0.5];options=optimset('lsqnonlin');a=lsqnonlin(@fun1,a0,[],[],options,x,y)%绘图plot(x,y,'o');hold on;x=[0:200];y=a(1)*x.*x+0.75*x;plot(x,y,'-');hold off结果分析:汽车刹车距离求解结果在Matlab的模型如上所⽰。
数分数学建模实验报告2

实验报告(Mathematica)【实验名称】利用MATHEMATICA作图【实验目的】1. 掌握用MATHEMATICA作二维图形,熟练作图函数Plot、ParametricPlot 等应用,对图形中曲线能做简单的修饰。
2. 掌握用MATHEMATICA做三维图形,对于一些二元函数能做出其等高线图等,熟练函数Plot3D,ParametricPlot的用法。
【实验原理】1.二维绘图命令:二维曲线作图:Plot[fx,{x,xmin,xmax}],二维参数方程作图:ParametricPlot[{fx,fy},{t,tmin,tmax}] 2.三维绘图命令:三维作图plot3D[f,{x,xmin,xmax},{y,ymin,ymax}],三维参数方程作图:ParameticaPlot3D[{fx,fy,fz},{t,tmin,tmax}]【实验内容】(含基本步骤、主要程序清单及异常情况记录等)5.作出以下参数方程所描述的图形.x=4costy=3sint (0≤t≤2π);6.作出以下极坐标方程所描述的图形.r=4cos3θ7.作出函数z=sin(π x2+y2)的图形.8.作出以下三维图形椭球面x=R1cosu cosvy=R2cosu sinvz=R3sinu,u∈ −π2,π2, v∈0,2π,R1,R2,R3自行给定;【实验结果】5.6.7.8.的图分别如下。
【总结与思考】MATHEMATICA作图的常见错误:General::spell1: Possible spelling error。
因为在MATHEMATICA中作图函数大小写有区别,如例4中的ParametricPlot3D 函数中两个字母P都要大写,若将其中的一个写成小写p,则将提示以上拼写错误Possible spelling error。
数学建模计算实验2
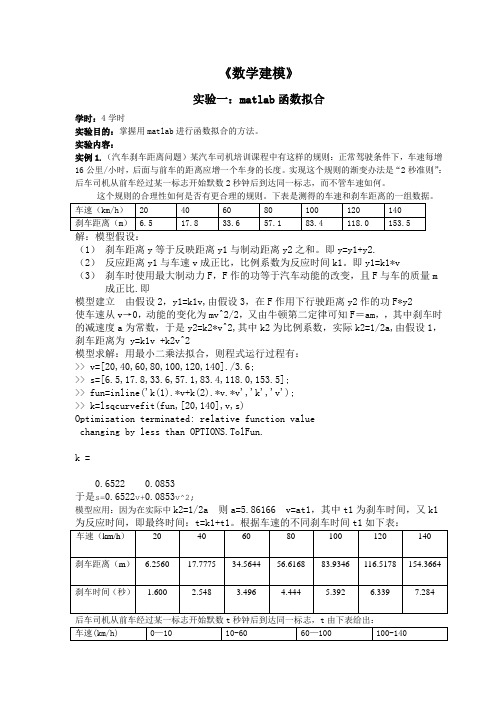
《数学建模》实验一:matlab函数拟合学时:4学时实验目的:掌握用matlab进行函数拟合的方法。
实验内容:实例1.(汽车刹车距离问题)某汽车司机培训课程中有这样的规则:正常驾驶条件下,车速每增16公里/小时,后面与前车的距离应增一个车身的长度。
实现这个规则的渐变办法是“2秒准则”:后车司机从前车经过某一标志开始默数2秒钟后到达同一标志,而不管车速如何。
这个规则的合理性如何是否有更合理的规则。
下表是测得的车速和刹车距离的一组数据。
车速(km/h)20 40 60 80 100 120 140刹车距离(m) 6.5 17.8 33.6 57.1 83.4 118.0 153.5解:模型假设:(1)刹车距离y等于反映距离y1与制动距离y2之和。
即y=y1+y2.(2)反应距离y1与车速v成正比,比例系数为反应时间k1。
即y1=k1*v(3)刹车时使用最大制动力F,F作的功等于汽车动能的改变,且F与车的质量m 成正比.即模型建立由假设2,y1=k1v,由假设3,在F作用下行驶距离y2作的功F*y2使车速从v→0,动能的变化为mv^2/2,又由牛顿第二定律可知F=am,,其中刹车时的减速度a为常数,于是y2=k2*v^2,其中k2为比例系数,实际k2=1/2a,由假设1,刹车距离为 y=k1v +k2v^2模型求解:用最小二乘法拟合,则程式运行过程有:>> v=[20,40,60,80,100,120,140]./3.6;>> s=[6.5,17.8,33.6,57.1,83.4,118.0,153.5];>> fun=inline('k(1).*v+k(2).*v.*v','k','v');>> k=lsqcurvefit(fun,[20,140],v,s)Optimization terminated: relative function valuechanging by less than OPTIONS.TolFun.k =0.6522 0.0853于是s=0.6522v+0.0853v^2;模型应用:因为在实际中k2=1/2a 则a=5.86166 v=at1,其中t1为刹车时间,又k1为反应时间,即最终时间:t=k1+t1。
数学建模实验报告2浙江万里学院
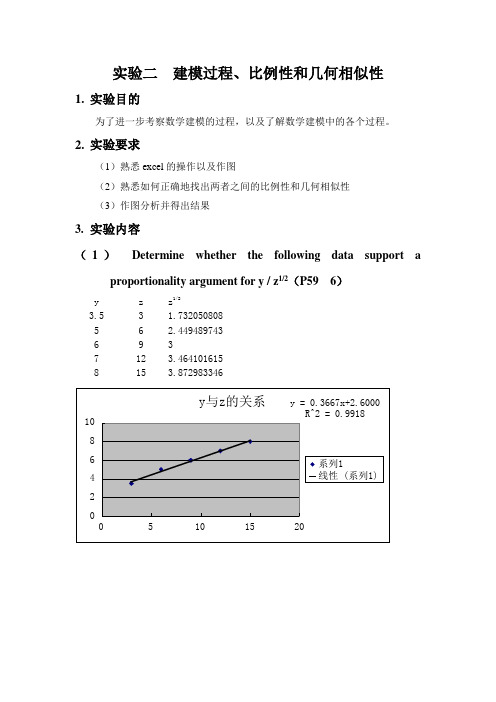
实验二 建模过程、比例性和几何相似性1. 实验目的为了进一步考察数学建模的过程,以及了解数学建模中的各个过程。
2. 实验要求(1)熟悉excel 的操作以及作图(2)熟悉如何正确地找出两者之间的比例性和几何相似性 (3)作图分析并得出结果3. 实验内容(1) Determine whether the following data support aproportionality argument for y / z 1/2(P59 6)y z z 1/23.5 3 1.732050808 5 6 2.449489743 6 9 37 12 3.464101615 8153.872983346024681005101520y与z的关系y = 0.3667x+2.6000R^2 = 0.9918系列1线性 (系列1)024681001234y与z^(1/2)的关系y = 2.0699x-0.1103R^2 = 0.9980系列1线性 (系列1)分别作出y 与z 和y 与z 1/2的关系图,可以得到以上两幅图形,并由此各自添加趋势线,得出公示和拟合值,可以看出y 与z 1/2的趋势线的拟合值更高,所以数据支持对y 与z 1/2的比例性论证。
斜率是2.0699。
(2)(P59 12)y x e x6 1 2.718281828 15 2 7.389056099 42 3 20.08553692 114 4 54.59815003 311 5 148.4131591 845 6 403.4287935 23007 1096.633158 6250 8 2980.957987 170009 8103.083928 462551022026.46579010000200003000040000500000500010000150002000025000y = 2.0999x-2.9002R^2 = 1.0000系列1线性 (系列1)通过上表就可以验证y 与e x 的关系成线性。
数学建模实验2

《数学建模与数学实验》实验报告实验二水道测量专业、班级信息1002 学号201010010213 姓名兰雪娇课程编号81010240 实验类型验证性学时 2实验(上机)地点教七楼数学实验中心完成时间2012-6-7任课教师谷根代评分一、实验目的及要求1.掌握数学软件Matlab的基本用法和一些常用的规则,能用该软件进行编程;2.能够借助数学软件进行二维和三维网格化数据绘图;3.理解数据生成的基本方法。
二、借助数学软件,研究、解答以下问题(一)依题“水道测量”所给数据和要求,讨论在下面假设情况下的模型。
假设:(1)海底光滑,无暗礁(因浅水海域);(2)每个给定的数据点对未知点的影响与它们之间距离的平方成反比。
【解】:由于是在考察水域内随机测量有限个数据点,因此所得的数据是散乱的,这就必须对这些散乱数据进行规则化处理。
散乱数据规则化处理的一般流程是:散乱数据的三角剖分→三角网格优化→构造插值曲面→生成规则网格数据1.1 三角剖分一般地,如果一组三维散乱数据点能够有效地投影到某个平面,就可以把空间三角剖分简化为平面问题处理。
曲面较为平坦时,用这样的方法处理效果比较好。
水道的水底面起伏较大,若将三维散乱数据投影到平面上进行三角剖分将明显改变相邻三角形之间的内角关系,也无法真实反映其空间的角度关系,从而影响剖分效果。
因此,这里采用曲面上散乱数据三角剖分的Choi算法。
1.2 三角网格优化这里采用光顺准则对三角网格进行优化,即当空间四边形严格凸时,选择一条对角线(即一对三角形)使得该四边形四条边上的两共边三角形(面)之间的最小夹角最大。
如图2所示,设空间中一个严格凸的四边形ABCD ,四边形由四边e 1,e 2,e 3,e 4界定。
该四边形可看作三角网格中的一个局部区域,我们的目标是利用光顺准则使该局部区域与周围的三角网格光滑的相连接,即对该四边形选择一种三角剖分,使得四条边上两条边三角形(面)之间的最小夹角最大。
数学建模实验答案_初等模型 (2)
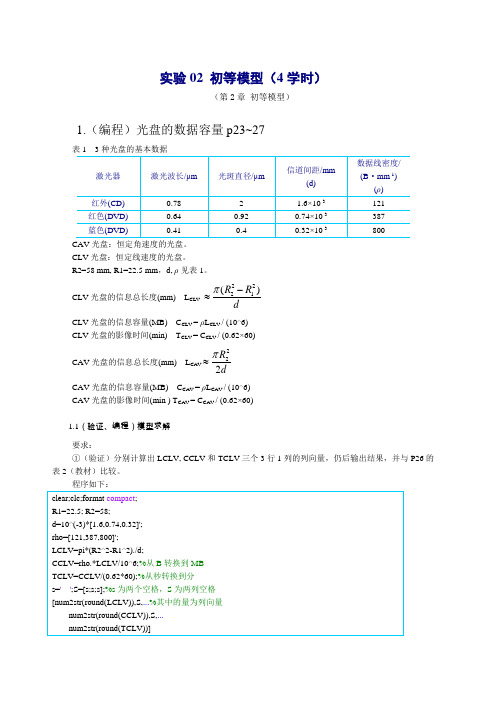
CAV光盘的信息容量(MB) CCAV=ρLCAV/ (10^6)
CAV光盘的影像时间(min ) TCAV= CCAV/ (0.62×60)
1.1(验证、编程)模型求解
要求:
①(验证)分别计算出LCLV, CCLV和TCLV三个3行1列的列向量,仍后输出结果,并与P26的表2(教材)比较。
t2=alfa*n.^beta;
[n,t,t2]
a=0:0.01:10;
t3=alfa*a.^beta;
plot(n,t,'x',a,t3);
数值结果:
图形结果:
3.(编程,验证)污水均流池的设计p34~37
表2 (p35)社区一天以小时为单位间隔的生活污水流量(单位:m3/h)
时间t(h)
0
1
2
3
functionM=tab()
%日期ABCD有雨=1/无雨=0
M=[1903090601;
2403050801;
3603080701;
bet较(数据比较和和拟合图形)
参考数据结果:
第1列为桨手人数,第2列为实际比赛平均成绩,第3列为计算比赛平均成绩。
参考图形结果:
要求:
①运行问题(1)中的程序。
②编程解决问题(2):实际值与计算值比较(数据比较和和拟合图形)。
★(验证)用数据拟合求参数α和β。给出α和β值和模型:
★编写的程序和运行结果:
程序:
R1=22.5;R2=58;
d=[1.6e-3,0.74e-3,0.32e-3]';
LCLV=zeros(3,1);
LCLV(1)=quad('2*pi/1.6e-3*sqrt(x.^2+(1.6e-3/(2*pi))^2)',R1,R2);
数学建模实验二

实验2实验报告2013326601054 夏海浜13信科1班一、完成教材(2013高教版)实验;P2131.求解线性规划问题clearf=[3,2,-8,5];A=[-3,6,-5,2;7,-3,-1,3];b=[-3,-1];Aeq=[1,8,1,-1];Beq=[-2];LB=[0;;0];[X,fval,exitflag,output,lambda]=linprog(f,A,b,Aeq,Beq,LB)2.某快餐店一周中每天需要不同数目的雇员,设周一至少a1员,周二至少a2人,周三至少a3人,周四至少a4员,周五至少a5人,周六至少a6人,周日至少a7人,有规定雇员连续工作五天,每人每天的工资为C元,问快餐店怎样雇佣才能满足条件,又能使总聘用费最少。
clearf=[100,100,100,100,100,100,100];A=[-1,0,0,-1,-1,-1,-1;-1,-1,0,0,-1,-1,-1;-1,-1,-1,0,0,-1,-1;-1,-1,-1,-1,0,0,-1;-1,-1,-1,-1,-1,0,0;0,-1,-1,-1,-1,-1,0;0,0,-1,-1,-1,-1,-1];b=[-16,-15,-16,-19,-14,-12,-18];[X,fval]=linprog(f,A,b)ans =1221P2183.求函数f(x)=x^2+4x+4的最小值。
clearfun='x^2+4*x+4'ezplot(fun,[-12,8])[X,fval,exitflag,output]=fminbnd(fun,-12,8)>> Untitled8 fun =x^2+4*x+4X =-2fval =exitflag =1output =iterations: 5funcCount: 6algorithm: 'golden section search, parabolic interpolation' message: '优化已终止:当前的 x 满足使用 1.000000e-04 的 OPTIONS.TolX 的终止条件'4.在区间【-10,10】上,求函数f(x)=(x-2)^4*sin(x)-(x-1)^2*cos(x)的最小值clearfun='(x-2)^4*sin(x)-(x-1)^2*cos(x)'ezplot(fun,[-10,10])[X,fval,exitflag,output]=fminbnd(fun,-10,10)>> Untitled9fun =(x-2)^4*sin(x)-(x-1)^2*cos(x) X =-2.2939fval =-247.6956exitflag =1output =iterations: 13funcCount: 14algorithm: 'golden section search, parabolic interpolation'message: '优化已终止:当前的x 满足使用1.000000e-04 的OPTIONS.TolX 的终止条件P2221.求有约束的线性优化问题:min f(x)=1/3*(x1+)^3+x2,约束条件为x1-1>=0,x2>=0.min=1/3*(x1+1)^3+x2;x1>=1;end运行结果:Local optimal solution found.Objective value: 2.666667Infeasibilities: 0.000000Extended solver steps: 5Total solver iterations: 44Variable Value Reduced CostX1 1.000000 0.000000X2 0.000000 1.000000Row Slack or Surplus Dual Price1 2.666667 -1.0000002 0.000000 -4.0000002.求有约束的非线性规划问题:minf(x)=2x1^2+2x2^2-2x1x2-4x1-6x2,约束条件为:x1+x2<=2,X1+5x2<=5,X1>=0,X2>=0,解:解:min=2*x1^2+2*x2^2-2*x1*x2-4*x1-6*x2;x1+x2<=2;x1+5*x2<=5;end运行结果:Local optimal solution found.Objective value: -7.161290 Infeasibilities: 0.4440892E-15Extended solver steps: 5Total solver iterations: 30Variable Value Reduced CostX1 1.129032 0.000000X2 0.7741935 0.000000Row Slack or Surplus Dual Price1 -7.161290 -1.0000002 0.9677419E-01 0.0000003 0.000000 1.032258二、lingo完成PPT上练习题;1.max=5*x1+8*x2;x1+x2<=6;5*x1+9*x2<=45;x1>=0;x2>=0;endGlobal optimal solution found.Objective value: 41.25000 Infeasibilities: 0.000000Total solver iterations: 2Variable Value Reduced CostX1 2.250000 0.000000X2 3.750000 0.000000Row Slack or Surplus Dual Price1 41.25000 1.0000002 0.000000 1.2500003 0.000000 0.75000004 2.250000 0.0000005 3.750000 0.0000002.min=3*x^2+2*y^2+z^2+2*x*y-y*z-0.8*y*z;x+y+z=1;1.3*x+1.2*y+1.08*z>=1.12;x>=0;x<=0.75;y>=0;y<=0.75;z>=0;z<=0.75;endGlobal optimal solution found.Objective value: 0.2479167Objective bound: 0.2479167 Infeasibilities: 0.000000Extended solver steps: 1Total solver iterations: 93Variable Value Reduced CostX 0.000000 0.000000Y 0.3958333 0.000000Z 0.6041667 0.000000Row Slack or Surplus Dual Price1 0.2479167 -1.0000002 0.000000 -0.49583333 0.7500000E-02 0.0000004 0.000000 -0.29583335 0.7500000 0.0000006 0.3958333 0.0000007 0.3541667 0.0000008 0.6041667 0.0000009 0.1458333 0.0000003.sets:D/1..7/:a;endsetsf=a(7);a(1)=1;a(2)=1;@for(D(i)|i#ge#3:a(i)=a(i-1)+a(i-2));endFeasible solution found.Total solver iterations: 0Variable ValueF 13.00000A( 1) 1.000000A( 2) 1.000000A( 3) 2.000000A( 4) 3.000000A( 5) 5.000000A( 6) 8.000000A( 7) 13.00000Row Slack or Surplus1 0.0000002 0.0000003 0.0000004 0.0000005 0.0000006 0.0000007 0.0000008 0.0000001.min=-x1-5*x2;x1-x2>=-2;5*x1+6*x2<=30;x1<=4;x1>=0;x2>=0;@gin(x1);@gin(x2);endGlobal optimal solution found.Objective value: -17.00000Objective bound: -17.00000 Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX1 2.000000 -1.000000X2 3.000000 -5.000000Row Slack or Surplus Dual Price1 -17.00000 -1.0000002 1.000000 0.0000003 2.000000 0.0000004 2.000000 0.0000005 2.000000 0.0000006 3.000000 0.0000002.max=3*x1-2*x2+5*x3;x1+2*x2-x3<=2;x1+4*x2+x3<=4;x1+x2<=3;4*x2+x3<=6;@bin(x1);@bin(x2);@bin(x3);endGlobal optimal solution found.Objective value: 8.000000Objective bound: 8.000000 Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX1 1.000000 -3.000000X2 0.000000 2.000000X3 1.000000 -5.000000Row Slack or Surplus Dual Price1 8.000000 1.0000002 2.000000 0.0000003 2.000000 0.0000004 2.000000 0.0000005 5.000000 0.0000003.min=13*x1+9*x2+10*x3+11*x4+12*x5+8*x6;x1+x4=400;x2+x5=600;x3+x6=500;0.4*x1+1.1*x2+x3<=800;0.5*x4+1.2*x5+1.3*x6<=900;@gin(x1);@gin(x2);@gin(x3);@gin(x4);@gin(x5);@gin(x6);endGlobal optimal solution found.Objective value: 13800.00Objective bound: 13800.00 Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX1 0.000000 13.00000X2 600.0000 9.000000X3 0.000000 10.00000X4 400.0000 11.00000X5 0.000000 12.00000X6 500.0000 8.000000Row Slack or Surplus Dual Price1 13800.00 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 140.0000 0.0000006 50.00000 0.0000004.sets:cities/s,a1,a2,a3,b1,b2,c1,c2,t/:l;roads(cities,cities)/s,a1 s,a2 s,a3a1,b1 a1,b2 a2,b1a2,b2 a3,b1 a3,b2b1,c1 b1,c2 b2,c1 b2,c2c1,t c2,t/:d;endsetsdata:d=6 3 36 5 8 67 46 7 8 95 6;enddatal(1)=0;@ for(cities(i ) |i#gt#@index(s ) :l(i )=@min(roads(j,i ) : l(j)+d(j,i )));endFeasible solution found.Total solver iterations: 0Variable ValueL( S) 0.000000L( A1) 6.000000L( A2) 3.000000L( A3) 3.000000L( B1) 10.00000L( B2) 7.000000L( C1) 15.00000L( C2) 16.00000L( T) 20.00000D( S, A1) 6.000000D( S, A2) 3.000000D( S, A3) 3.000000D( A1, B1) 6.000000D( A1, B2) 5.000000D( A2, B1) 8.000000D( A2, B2) 6.000000D( A3, B1) 7.000000D( A3, B2) 4.000000D( B1, C1) 6.000000D( B1, C2) 7.000000D( B2, C1) 8.000000D( B2, C2) 9.000000D( C1, T) 5.000000D( C2, T) 6.000000Row Slack or Surplus1 0.0000002 0.0000003 0.0000004 0.0000005 0.0000006 0.0000007 0.0000008 0.0000009 0.000000。
数学建模实验报告 (2)

3
结论 (结 果)
小结 (对 本次 实验 的思 考和 建 议) 指导教师评分(包括对实验的预习、操作和结果的综合评分) :
指导教师总评:
签名:
日期:
4
2
*表示红色的散点,蓝色表示原函数的曲线
for j=1:N Y(j+1)=Y(j)+h*feval('f',T(j),Y(j)); Y1(j+1)=Y(j)+h/2*feval('f',T(j+1),Y(j+1)); end
此处是双重迭代,根据下面这个式子迭代的,可以使得到的值更加精确
y (0) yn hf ( xn , yn ) n 1 ( k 1) h (k ) y n 1 y n [ f ( x n , y n ) f ( x n 1 , y n 1 ] 2 ( k 0 ,1, 2 , )
在命令窗输入 euler('f',0,1,1,10)得到: 把这个输入到命令窗 euler('f',0,1,1,10)就可以得到结果 euler('f',0,1,1,10) z= 1 z= 0.9182 z= 0.8562 z= 0.8077
数学建模实验二

基本实验1.微分方程稳定性分析绘出下列自治系统相应的轨线,并标出随t 增加的运动方向,确定平衡点,并按稳定的、渐近稳定的、或不稳定的进行分类:解答:(1)由平衡点的定义可得,f(x)=x=0,f(y)=y=0,因此平衡点为(0,0),系统的线性近似方程的系数矩阵为⎥⎦⎤⎢⎣⎡=1001A ,解得其特征值121==λλ.()0221<-=+-=λλp ,0121>=⋅=λλq .对照稳定性的情况表,可知平衡点(0, 0)是不稳定的。
自治系统相应轨线为:(2)由平衡点的定义可得,f(x)=-x=0,f(y)=2y=0,因此平衡点为(0,0),系统的线性近似方程的系数矩阵为⎥⎦⎤⎢⎣⎡-=2001A ,解得其特征值2;121=-=λλ.()0121<-=+-=λλp ,0221<-=⋅=λλq .对照稳定性的情况表,可知平衡点(0, 0)是不稳定的。
自治系统相应轨线为:(3)由平衡点的定义可得,f(x)=y=0,f(y)=-2x=0,因此平衡点为(0,0),系统的线性近似方程的系数矩阵为⎥⎦⎤⎢⎣⎡-=0210A ,解得其特征值i i 2;221-==λλ.()021=+-=λλp ,0221>=⋅=λλq .对照稳定性的情况表,可知平衡点(0, 0)是不稳定的。
自治系统相应轨线为:(4)由平衡点的定义可得,f(x)=-x=0,f(y)=-2y=0,因此平衡点为(0,0),系统的线性近似方程的系数矩阵为⎥⎦⎤⎢⎣⎡--=2001A ,解得其特征值2;121-=-=λλ.()0321>=+-=λλp ,0221>=⋅=λλq .对照稳定性的情况表,可知平衡点(0, 0)是稳定的。
自治系统相应轨线为:2.营养平衡问题营养以每单位时间R 个分子的常速流入一个细胞,并且以其内营养浓度成比例的速度离开,比例常数为K ,设N 为t 时刻的浓度,则上述营养变化速度的数学描述为:KN R dtdN-= 即N 的变化速度等于营养进入细胞的速度减去它们离开的速度,营养的浓度会达到平衡吗?如果能,平衡解是什么?它是稳定的吗?试用这个方程解的图示解释之。
数学实验与数学建模 实验二

数学实验与数学建模 实验二2.圆钢原材料每根长 5.5米,现需要A,B,C 三种圆钢材料,长度分别为3.1m,2.1m,1.2m,数量分别为100根,200根,400根,试安排下料方式,使所需圆钢原材料的总数最少。
解:可行的方案如下表所示: 材 料 料方 案ABCX11 1 0 X2 1 0 2 X3 0 1 2 X4 0 2 1 X54约束条件为: 4005442322200432110021≥+++≥++≥+x x x x x x x x x目标函数:54321minx x x x x ++++=则列lingo 程序如下: min =x1+x2+x3+x4+x5; x1+x2>=100;x1+x3+2*x4>=200;2*x2+2*x3+x4+4*x5>=400;@gin (x1);@gin (x2);@gin (x3);@gin (x4);@gin (x5); End运行结果如下:结合lingo 数据得出结论:方案一和三没有采用,方案二和四用去100跟原材料,方案五用去25跟原材料,一共用去225根原材料,即为最优。
3.住宅小区服务中心选址:某地新建一个生活住宅区,共有20栋住宅楼,小区内所有道路都是东西或南北走向,开发商拟在小区内修建一个服务中心,地址选在离所有楼房的总路程最小的地方。
为保证建筑物之间有足够的空间,服务中心的位置与其他楼房位置之间的距离不能少于30米(已经考虑了所有建筑的占地面积),请你确定服务中心的位置。
设初始点X0=[20,20],设(ai,bi )(i=1,......,20)为第i 栋住宅楼的坐标:a=[29.74 4.9 69.32 65.0 98.3 55.27 40.0 19.8 62.5 73.3 37.58 0.98 41.98 75.37 79.38 92.0 84.47 36.77 62.08 73.13],b=[19.39 90.48 56,92 63.18 23.44 54.88 93.16 33.5 65.5 39.19 62.73 69.9 39.72 41.37 65.52 43.5 34.6 75.2 12.32 86.7]。
工程数学建模试验2

(1)将问题建立成一个线性规划模型,确定最优的生产方案。(2)对于操作1,假定超过它当前每天430分钟能力的任何附加时间必须依靠每小时50美元的加班获得。每小时成本包括劳动力和机器运行费两个方面。对于操作1,使用加班在经济上有利吗?如果有利,最多增加多少时间?
(3)假定操作2的操作员已同意每天加班工作2小时,其加班费是45美元一小时。还有,操作自身的成本是一小时10美元。这项活动对于每天收入的实际结果是什么?(4)操作3需要加班时间吗
运行结果为:
由运行结果可知,选x1、x2、x3、x5、x7、x9。即微积分,线性代数,最优化方法,应用统计,计算机编程,数学实验。
题目
某公司拿出15百万美元,最多建造7个发射台来覆盖15个相邻社区中尽可能多的人口。表2.7给出了各个社区的人口数目,表2.8给出了每个发射台可以覆盖的社区及建造这个发射台的费用,确定出哪几个发射台需要建造?
Y4+Y5>=X6;
Y3+Y5+Y6>=X7;
Y4>=X8;
Y3+Y4+Y5>=X9;
Y3+Y6>=X10;
Y5>=X11;
Y6+Y7>=X12;
Y7>=X13;
Y6+Y7>=X14;
Y7>=X15;
Xi,Yj为整数。
目标函数最大值即为最优解。
LINGO程序:
运行结果
由运行结果可知:
需要建造的发射台为2,4,5,6,7,只有1社区无法覆盖,覆盖最多人口为129千人。
解答:
设i为饲料类型,i=1为颗粒饲料,i=2为粉状饲料。J为营养成分,j=1为蛋白质,j=2为脂肪,j=3为纤维素。
数学建模 -实验报告2

output =
iterations: 11 funcCount: 12 algorithm: 'golden section search, parabolic interpolation'
message: 'Optimization terminated: the current x satisfies the term...'
度AB,但是,当病床的长度一定时,要计算病床的宽度就比较麻烦,因此我们从定宽变长的角度来考虑
问题。这样就得到了这个问题的模型二。
假设:1、在转弯过程中我们的策略是转动与推进相结合;
2、在转弯的过程中,病床的宽度 h w 保持不变(显然 0 1 )。
记当病床的AB边与水平走廊的夹角为 时,恰好与走廊相抵的病床长度AB为 L( , w, ) (参看
的充分必要条件是:病床长度 L Lmin (w, ) 。因此,问题归结为求函数 L( , w, ) 关于变量 的最小值
Lmin (w, ) 。
令 t sin cos 得:1 t
2
, sin
cos
t2
1
,代入(6)式得
2
L( , w, ) f (t, w, )
图2
只要
L 2 h2 w2 2
0hw
化简得: L 2 w2 h2
0hw
(1)
即:当病床的长度 L 不超过走廊宽度 w 与病床宽度 h 的平方差的平方根
倍时,我们就可以把病床平推转过走廊拐角。 到此,我们似乎已经完全解决了这个问题。在下结论之前,我们来
Q B
O
F
D
the current x satisfies the term...' 即最小值在 x=0.2176 附近,为-1.1312。
《数学建模》实验报告二

《数学建模》实验报告二院系专业学号姓名指导教师二O一五年四月十六日第一部分:数学建模论文P135:11题有4名同学到一家公司参加三个阶段的面试:公司要求每个同学都必须首先找公司秘书初试,然后到部门主管处复试,最后到经理处参加面试,并且不允许插队(即在任何一个阶段4名同学的顺序是一样的),由于4名同学的专业背景不同,所以每人在三个阶段的面试时间也不同,如表1所示。
这4名同学约定他们全部面试完以后一起离开公司,假定现在时间是早晨8:00,请问他们最早何时能离开公司?表1 面试时间要求单位:min一:问题的提出本题问题是要合理安排4名同学的面试顺序,使完成全部面试所花费的时间最少。
二:模型假设定义数学符号如下tij:第i名同学参加第j阶段面试需要的时间;xij:第i名同学参加第j阶段面试的开始时刻(记早上8:00面试开始为0时刻)(i=1, 2, 3, 4;j=1, 2, 3);T:完成全部面试所花费的最少时间。
三:模型建立目标函数:Min T={Max i{xi3+ti3}}模型约束条件:①每个人只有参加完前一阶段的面试后才能进入下一个阶段,则xij+tij<=x(i,j+1) (i=1, 2, 3, 4,j=1, 2);②每个阶段j在同一时间只能面试1名同学,所以用0-1变量yik表示第k名同学是否排在第i名同学前面(1表示是,0表示否),则xij+ tij–xkj<=Tyik (i, k=1, 2, 3, 4; j=1, 2, 3; i<k)xkj+ tkj–xij<=T(1–yik) (i, k=1, 2, 3, 4; j=1, 2, 3; i<k) 线性优化目标:Min Ts.t. T >=x13+ t13T >=x23+ t23T >=x33+ t33T >=x43+ t43xij+ tij <=x(i, j+1) (i=1, 2, 3, 4;j=1, 2)xij+ tij–xkj<=Tyik (i, k=1, 2, 3, 4; j=1, 2, 3; i<k)xkj+ tkj–xij<=T(1–yik)(i, k=1, 2, 3, 4; j=1, 2, 3; i<k)xi3+ ti3<=T (i=1, 2, 3, 4)四:模型解法与结果程序:Model:min =T;T >= x13+ t13;T >= x23+ t23;T >= x33+ t33;T >= x43+ t43;x11+ t11 <= x12;x12+ t12 <= x13;x21+ t21 <= x22;x22+ t22 <= x23;x31+ t31 <= x32;x32+ t32 <= x33;x41+ t41 <= x42;x42+ t42 <= x43;x11+ t11 - x21<= T*y12;x21+ t21 - x11<= T*(1-y12); x12+ t12 - x22<= T*y12;x22+ t22 - x12<= T*(1-y12); x13+ t13 - x23<= T*y12;x23+ t23 - x13<= T*(1-y12); x11+ t11 - x31<= T*y13;x31+ t31 - x11<= T*(1-y13); x12+ t12 - x32<= T*y13;x32+ t32 - x12<= T*(1-y13); x13+ t13 - x33<= T*y13;x33+ t33 - x13<= T*(1-y13); x11+ t11 - x41<= T*y14;x41+ t41 - x11<= T*(1-y14); x12+ t12 - x42<= T*y14;x42+ t42 - x12<= T*(1-y14); x13+ t13 - x43<= T*y14;x43+ t43 - x13<= T*(1-y14); x21+ t21 - x31<= T*y23;x31+ t31 - x21<= T*(1-y23); x22+ t22 - x32<= T*y23;x32+ t32 - x32<= T*(1-y23); x23+ t23 - x33<= T*y23;x33+ t33 - x23<= T*(1-y23); x21+ t21 - x41<= T*y24;x41+ t41 - x21<= T*(1-y24);x22+ t22 - x42<= T*y24;x42+ t42 - x22<= T*(1-y24);x23+ t23 - x43<= T*y24;x43+ t43 - x23<= T*(1-y24);x31+ t31 - x41<= T*y34;x41+ t41 - x31<= T*(1-y34);x32+ t32 - x42<= T*y34;x42+ t42 - x32<= T*(1-y34);x33+ t33 - x43<= T*y34;x43+ t43 - x33<= T*(1-y34);t11=13;t12=15;t13=20;t21=10;t22=20;t23=18;t31=20;t32=16;t33=10;t41=8;t42=10;t43=15;@bin(y12);@bin(y13);@bin(y14);@bin(y23);@bin(y24);@bin(y34);End运行结果:Local optimal solution found.Objective value: 84.00000Extended solver steps: 35Total solver iterations: 975Variable Value Reduced Cost T 84.00000 0.000000 X13 36.00000 0.000000 T13 20.00000 0.000000 X23 56.00000 0.000000 T23 18.00000 0.000000X33 74.00000 0.000000T33 10.00000 0.000000X43 18.00000 0.000000T43 15.00000 0.000000X11 8.000000 0.000000T11 13.00000 0.000000X12 21.00000 0.000000T12 15.00000 0.000000X21 21.00000 0.000000T21 10.00000 0.000000X22 36.00000 0.000000T22 20.00000 0.000000X31 31.00000 0.000000T31 20.00000 0.000000X32 56.40000 0.000000T32 16.00000 0.000000X41 0.000000 0.9999970T41 8.000000 0.000000X42 8.000000 0.000000T42 10.00000 0.000000Y12 0.000000 -83.99950Y13 0.000000 0.000000Y14 1.000000 83.99950Y23 0.000000 -83.99950Y24 1.000000 0.000000Y34 1.000000 0.000000五:模型结果的分析所有面试完成至少需要84分钟,其面试顺序为4-1-2-3 (即丁-甲-乙-丙)。
091152024数模实验2

福建农林大学计算机与信息学院(数学类课程)实验报告课程名称:数学模型姓名:刘义江系:信息与计算科学专业:信息与计算科学年级:2009级学号:091152024指导教师:姜永职称:副教授2011年12月14日实验项目列表序号实验项目名称成绩指导教师1 数学规划模型建立及其软件求解姜永2 数据拟合与曲线拟合模型应用姜永3 统计回归模型应用姜永4567891011121314151617181920福建农林大学计算机与信息学院数学类实验报告(一)系: 信息与计算科学 专业: 信息与计算科学 年级: 2009级 姓名: 刘义江 学号: 091152024 实验课程: 数学模型 实验室号: 田C-507 实验设备号 24 实验时间: 2011/11/08 指导教师签字: 成绩:1.实验项目名称:数学规划模型建立及其软件求解 2.实验目的和要求:了解数学规划的的基本理论和方法,并用于建立实际问题的数学规划模型;会用LINDO 和LINGO 软件解数学规划问题并对结果加以分析应用。
3.实验使用的主要仪器设备和软件:惠普微机;1.6LINDO 和0.9LINGO 版本4.实验的基本理论和方法:数学规划模型的一般形式为x Min )(x f z = (1) ..t s g()m i x ,,2,1,0 =≤.(2)其中(1)式表示目标函数,(2)式为约束条件。
LINDO/LINGO 用于求解线性规划和二次规划问题,LINGO 除了具有LINDO 的全部功能外,还可以用于求解非线性规划问题,也可以用于一些和非线性方程(组)的求解,等等。
LINDO/LINGO 软件的最大特色在于可以允许优化模型中的决策变量是整数,而且执行速度很快。
线性优化求解程序通常使用单纯形算法,对LINDO/LINGO 软件,为了能解大规模问题,也可以使用内点算法。
非线性优化求解程序采用的是顺序线性规划法,即通过迭代法求解一系列线性规划来达到求解非线性规划的目的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆交通大学学生实验报告实验课程名称数学模型开课实验室数学实验室学院理学院年级09信息与计算科学专业班2班学生姓名张春晖学号09180203开课时间2011 至2012 学年第2 学期评分细则评分报告表述的清晰程度和完整性(20分)程序设计的正确性(40分)实验结果的分析(30分)实验方法的创新性(10分)总成绩教师签名韩逢庆钢管下料问题摘要本文是针对如何对钢管进行下料问题,根据题目要求以及下料时有关问题进行建立切割费用最少以及切割总根数最少两个目标函数通过结果分析需要使用何种切割模式。
生产方式所花费的成本价格或多或少有所不同,如何选取合理的生产方式以节约成本成为了很多厂家的急需解决的问题。
这不仅仅关系到厂家的利益,也影响到一个国家甚至整个人类星球的可利用资源,人们的生活水平不断提高对物资的需求量也不断上升,制定有效合理的生产方式不仅可以为生产者节约成本也可以为社会节约资源,以达到资源利用最大化。
本文以用于切割钢管花费最省及切割总根数最少为优化目标,通过构建多元函数和建立线性整数规划模型,利用数学及相关方面的知识对钢管的切割方式进行优化求解最佳方案。
本文最大的特色在于通过求解出切割钢管花费最省及切割总根数最少时分别得出两种目标函数取最小值时的切割模式。
通过结果发现两种目标函数取最小值时所需切割根数都一样。
于是选择切割钢管花费最省为目标函数,此时的切割模式达到最少,这样既满足了总根数最小有满足了切割费用最小。
关键词:切割模式, LINGO软件,线性整数一、问题的提出某钢管零售商从钢管厂进货,将钢管按照顾客的要求切割后出售。
从钢管厂进货时得到的原料钢管的长度都是1850mm。
现有一客户需要15根290mm、28根315mm、21根350mm和30根455mm的钢管。
为了简化生产过程,规定所使用的切割模式的种类不能超过4种,使用频率最高的一种切割模式按照一根原料钢管价值的1/10增加费用,使用频率次之的切割模式按照一根原料钢管价值的2/10增加费用,依次类推,且每种切割模式下的切割次数不能太多(一根钢管最多生产5根产品)。
此外,为了减少余料浪费,每种切割模式下的余料不能超过100mm。
为了使总费用最小,应如何下料?二、基本假设1、假设所研究的每根钢管的长度均为1850mm的钢管。
2、假设每次切割都准确无误。
3、假设切割费用短时间内不会波动为固定值。
5、假设钢管余料价值为0.6、假设一切运作基本正常不会产生意外事件。
7、每一根钢管的费用都一样,为一常值。
三、符号说明符号意义i )切割的原料钢管的根数i x表示按照第i种切割模式(1,2,3,4r第i种切割模式下每根原料钢管生产290mm钢管的数量1i2i r第i 种切割模式下每根原料钢管生产315mm 钢管的数量 3i r 第i 种切割模式下每根原料钢管生产350mm 钢管的数量4i r 第i 种切割模式下每根原料钢管生产455mm 钢管的数量P 生产钢管过程所需要增加的总费用N所需钢管的总根数四、问题分析和模型的建立与求解4.1、问题分析和模型的建立与求解4.1.1问题的分析结合题意,首先我们要确定应该选取哪些切割模式,生产15根290mm 、28根315mm 、21根350mm 和30根455mm 的钢管,每一种切割模式都要符合客户的需求在原料钢管上安排切割的一种组合,而且必须满足一根原料刚管只能生产5根钢管。
例如,我们可以将1850mm 的钢管切割成5根长350mm 的钢管,余料为100mm ;或者将长1850mm 的钢管切割成长315mm 、355mm 和455mm 的钢管2根、2根、1根,余料为65mm 。
显然,可行的切割模式是很多的。
于是问题化为在满足客户需要的条件下,按照哪几种合理的模式进行切割,每种模式切割多少根原料钢管最为节省。
而由于需求的钢管规格为4种,所以枚举法的工作量较大。
可以用xi 表示按照第i 种模式(i=1,2,3,4)切割的原料钢管的根数。
又设使用第i 种切割模式下每根原料钢管生产长290mm 、315mm 、355mm 和455mm 的钢管数量分别为1i r ,2i r ,3i r ,4i r 。
而所谓节省,这里有两种标准,一种切割后剩余的总余料量最小,二是切割原料钢管的总根数最少。
4.1.2模型的建立根据情况,我们忽略每根钢管的成本价,直接计算增加的总费用,即: 总根数最少:1234min 0.10.20.30.4p x x x x =+++1234min N x x x x =+++假设条件1234x x x x ≥≥≥ (4-1)满足客户需求的约束条件为:1111221331445r x r x r x r x +++≥ (4-2)21122223324428r x r x r x r x +++≥ (4-3)31132233334421r x r x r x r x +++≥ (4-4)41142243344430r x r x r x r x +++≥ (4-5)每一种切割模式必须可行、合理,所以每根原料钢管的成品量不能超过1850mm ,也不能少于1750mm (余料不能大于100mm ),于是112131411750152821301850r r r r ≤+++≤ (4-6)122232421750152821301850r r r r ≤+++≤ (4-7)132333431750152821301850r r r r ≤+++≤ (4-8)142434441750152821301850r r r r ≤+++≤ (4-9)最后,加上非负整数约束:i x ,ji r ∈ Z+ , i=1,2,3,4 j=1,2,3,4 (4-10)于是,问题归结为在在约束条件(4-2)~(4-10)下,求i x 和1,2,3,4i i i i r r r r (i=1,2,3)使目标(4-1)达到最小。
显然这是线性整数规划模型。
4.1.3模型的求解非线性整数规划模型(4-1)~(4-9)虽然用LINGO 软件可以直接求解,但为了减少运行时间,可以增加一些显然的约束条件,从而缩小可行解的搜索范围。
例如,由于4种切割模式的排列顺序是无关要紧的,所以不妨增加以下约束:1234x x x x ≥≥≥ (4-11)又如,注意到所需原料钢管的总根数有明显的上界和下界。
首先,原料钢管的根数不可能少于19185045530350213152829015=⎥⎥⎤⎢⎢⎡⨯+⨯+⨯+⨯ (4-12) (根)。
其次,考虑一种非常特殊的生产计划:第一种切割模式下只生产290mm钢管,一根原料钢管切割成6根290mm 钢管,为满足15根290mm 钢管的需求,需要3根原料钢管;第二种切割模式下只生产315mm 钢管,一根原料钢管切割成5根315mm 钢管为满足28根315mm 的需求,需要6根原料钢管;第三种切割模式下只生产350mm 钢管,一根原料钢管切割成5根350mm 钢管,为满足21根350mm 钢管的需求,需要5根原料钢管;第四种切割模式下只生产455mm 钢管,一根原料钢管切割成4根455mm 钢管,为满足30根455mm 钢管的需求,需要8根原料钢管。
于是满足要求的这种生产计划共需要3+6+5+8=22根原料钢管,这就得到了最优解的一个上界,所以可增加以下约束:12341922x x x x ≤+++≤ (4-13)将式(4-1)~(4-13)构成的模型输入LINGO 如下:model:1234min 0.1*0.2*0.3*0.4*x x x x =+++;11112213314415r x r x r x r x +++≥;21122223324428r x r x r x r x +++≥;31132233334421r x r x r x r x +++≥;41142243344430r x r x r x r x +++≥;11213141290*315*350*455*1850r r r r +++≤;12223242290*315*350*455*1850r r r r +++≤;132*********315*350*455*1850r r r r +++≤;14243444290*315*350*455*1850r r r r +++≤;11213141290*315*350*455*1750r r r r +++≥;12223242290*315*350*455*1750r r r r +++≥;132*********315*350*455*1750r r r r +++≥;14243444290*315*350*455*1750r r r r +++≥;123419x x x x +++≥;123422x x x x +++≤;12x x ≥;23x x ≥;34x x ≥;@gin(1x );@gin(2x );@gin(3x );@gin(4x );@gin(11r );@gin(12r );@gin(13r );@gin(14r );@gin(21r );@gin(22r );@gin(23r );@gin(24r );@gin(31r );@gin(32r );@gin(33r );@gin(34r );@gin(41r );@gin(42r );@gin(43r );@gin(44r );End当花费P 最少时,得到结果为:总共需要19根原料钢管。
分别为:模式一:一根原料可以切割成315mm 钢管2根,350mm 钢管2根,455mm 钢管1根,总共8根。
模式二:一根原料可以切割成290mm 钢管1根,315mm 钢管2根,455mm 钢管2根 总共6根。
模式三:一根原料可以切割成290mm 钢管2根,350mm 钢管1根,455mm 钢管2根,总共5根。
当总根数最少时,得到结果为:总共需要19根原料钢管。
分别为:模式一:一根原料可以切割成290mm 钢管1根,315mm 钢管2根, 455mm 钢管2根,总共7根。
模式二:一根原料可以切割成315mm 钢管1根,350mm 钢管3根,455mm 钢管1根 总共5根。
模式三:一根原料可以切割成290mm 钢管2根,315mm 钢管1根,455mm 钢管2根,总共4根。
模式四:一根原料可以切割成315mm 钢管2根,350mm 钢管2根,455mm 钢管1根,总共3根。
综合两种情况,当两个目标函数取最小值时,所需的总根数都为19。
如果选择总根数最小为目标函数,则切割模式增加一种,那么切割费用有所增加。
为此选择切割费用最小为目标函数,这样既满足了总根数最小有满足了切割费用最小。
五、评价与改进在本文中,对于如何下料是根据客户的需要建立了两个目标函数,通过求解模型发现,总根数最小为目标函数及切割费用最小为目标函数都取最小值时,所需原料都一样。
