中南大学硕士研究生考试题
中南大学历年真题简答题

中南⼤学历年真题简答题中南⼤学研究⽣⼊学考试简答题1、试⽐较极差、平均差和标准差三种变异指标的特点,并说明为什么标准差是最常⽤、最基本的变异指标?答:极差是数据最⼤值减去数据最⼩值之差,是数据离散或差异程度的最简单侧度值。
特点:数据的分散程度就越⼤,极差就越⼤。
极差计算简单,但它仅取决于极端标志值,不能全⾯反映各单位标志值变异的程度,也不能拿来评价平均指标的代表性。
平均差各标志值对其算术平均数的离差绝对值的平均数。
平均差通常采⽤算术平均法,有简单算术平均法和加权算术平均法两种:(未分组资料)(分组资料)特点:平均差愈⼤,标志变异程度愈⼤,平均数的代表性愈⼩;平均差愈⼩,标志变异程度愈⼩,平均数代表性愈⼤。
与极差相⽐,平均差计算也很简便,⽽且反映了总体各单位标志值差异的⼤⼩,但由于采⽤绝对值运算,不适于数理统计上的数学处理,因⽽在实际中受到很⼤限制。
标准差是总体各单位标志值与算术平均数的离差平⽅的算术平均数的平⽅根,⼜称均⽅差,是测定标志变异最主要的指标。
未分组资料计算标准差:δ=分组资料计算标准差:δ=特点:标准差越⼤标志变异程度越⼤,平均数的代表性越低;标准差越⼩,标志变异程度越⼩,平均数的代表性越⾼。
同平均差⼀样,标准差反映了总体各单位标志值的变异情况,但它克服了平均差的缺点,所以运⽤较⼴泛。
2、简要阐述平均指标与变异指标在说明同质总体特征⽅⾯的联系和区别?答:平均指标和变异指标是反映总体分布的两个重要特征值。
区别:平均指标反映总体单位的集中趋势,变异指标反映总体单位的离散趋势。
联系:为了全⾯描述总体分布的特征,必须将平均指标与变异指标结合使⽤,⽤变异指标衡量平均指标的代表性,说明平均指标反映总体⼀般⽔平的有效程度,使分析结论更确切、更可靠。
3、抽样推断时,为什么必须遵循随机原则抽样样本?我们在进⾏抽样的过程中时,会产⽣代表性误差,即⽤⾮全⾯的资料推算或代替总体指标时产⽣的误差。
代表性误差⼜分为系统性误差和偶然性误差两种。
中南大学公共管理考研905、721真题整理汇总

905公共管理综合考试√2020:一、名词解释二、简答题1.新公共服务理论行政程序的特性2.人事行政 2.公共选择学的“政府失效”理论3.弹性授权 3.人事行政4.管制 4.权力行使的程度的影响因素5.自由申辩权三、论述题1.领导与管理的区别与联系?2.行政行为的合法要件。
√2019:一、名词解释二、简答题1.ABC管理法 1.西方公务员制度特征2.行政责任 2.优秀领导者应具有的素质3.公共危机 3.行政决策程序的过程4.职位分类 4.“最多跑一趟”改革的内容5.精准扶贫6.行政执行三、论述题1.一些社会问题长期处于公众议程,无法进入政策议程,这是为什么?政府应该怎么做?2.政府始终做一些“低效率”的工作,如逢年过节走村过户送温暖,谈看法。
√2018:一、名词解释二、简答题1.政治行政二分法 1.新公共行政学的理论观点2.非正式授权 2.现代人事行政的发展方向3.行政效率 3.政府与社会团体相互作用的方式4.行政许可 4.行政责任的构成要件5.行政复议 5.政府职能的构成6.结构性权利 6.公共危机的构成要件三、论述题1.政府执行力2.结合当前我国主要矛盾的变化和矛盾理论论述公共服务供给改革√2017:一、名词解释(6*5)二、简答题(15*4)1.管理主义 1.古典行政学的四大信仰2.差序政府信任 2.整体治理理论对大部制改革的价值3.行政协调 3.公共危机预警机制的作用4.政党分肥制 4.公共物品为什么由政府提供5.公共利益三、论述题(30)改革开放对中国经济社会变迁的影响无疑是极为深刻的,请结合时代背景,阐述80年代以来中国“双向运动”的演化轨迹,进而阐释由此引发的政府治理的转型路径。
四、材料分析(30)材料内容主要是说如今的户籍改革在小城镇进行,专家学者们提出要在大城市进行。
(1)根据公共政策学多源流理论,分析为什么户籍改革要在大城市进行(2)根据府际关系,分析人口流入地和人口流出地怎样协调配合√2016:一、名词解释二、简答题1.新公共行政学派 1.我国公务员考核制度的内容2.政治与行政二分法 2.西蒙所谓的“行政谚语”是什么意思3.改革政府理论中的“掌舵而非划桨”原则4.民主行政 3.行政管理中的社会监督5.伍德罗*威尔逊 4.政策过程三、辨析题1.行政管理的生命力就是权力。
中南大学硕士研究生入学结构力学考试试题
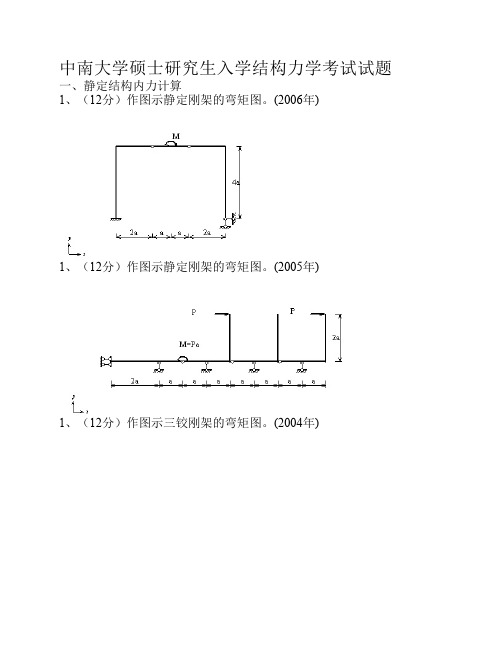
中南大学硕士研究生入学结构力学考试试题一、静定结构内力计算1、(12分)作图示静定刚架的弯矩图。
(2006年)1、(12分)作图示静定刚架的弯矩图。
(2005年)1、(12分)作图示三铰刚架的弯矩图。
(2004年)1、(13分)作图示结构的弯矩图。
(2003年)1、(9分)作图示结构的弯矩图。
(2002年)1、(12分)作图示结构的弯矩图。
(2001年)1、(10分)试作图示静定结构的M图。
(2000年)1、(10分)试作图示结构的弯矩图。
(1999年)1、(7分)试作图示结构的弯矩M图。
(1998年)1、(10分)作图示刚架的弯矩图。
(1997年)二、影响线分析2、(12分)作图示结构MEA、MCD、QF的影响线(P=1在DB段移动)。
(弯矩以下侧受拉为正)。
(2006年)3、(12分)作图示结构M E、Q F的影响线(P=1在CD段移动)。
(M E 弯矩以左侧受拉为正)。
(2005年)3、(12分)作图示结构M E、Q F的影响线(P=1在CD段移动)。
(弯矩以下侧受拉为正)。
(2004年)3、(13分)作图示结构M KA、Q K左、Q K右的影响线(P=1在CD段移动)。
(2003年)3、(10分)作图示结构中量值M K、Q F的影响线(P=1在CD段移动)。
(M E弯矩以右侧受拉为正)。
(2002年)2、(12分)作图示多跨静定梁M B、Q B右的影响线(P=1在AG段移动)。
(2001年)2、(12分)作图示多跨静定梁M B、Q B右的影响线(P=1在ABCDEF上移动)。
(2000年)3、(10分)作图示多跨静定梁R A、M E、Q F的影响线(P=1在CD上移动)。
(1999年)3、(分)作图示多跨静定梁R D、M E的影响线(P=1在ACF上移动)。
(1998年)3、(10分)作图示结构M F、Q F的影响线(P=1在AFCDE部分移动)。
(1997年)三、位移计算3、(12分)求图示结构最大挠度。
中南大学材基硕士研究生入学考试试题959

中南大学2013年硕士研究生入学考试试题959一、名词解释(10×3=30分)加工硬化沉淀强化交滑移上坡扩散调幅分解金属化合物临界分切应力珠光体 Orowan机制等强温度二、解答题(6×10=60分)1、判断下列位错反应能否进行:aaaaa(1)a[100][101][10];(2)[112][11][111] 223622、请指明下列五种结构分别属于什么布拉菲点阵。
注:a=b=c,α=β=γ=90°。
图省3、冷变形金属在回复和再结晶过程中,组织和性能分别有什么变化?4、试分别给出FCC,BCC及HOP的主要滑移系。
5、试分析液态金属凝固过程中形成中心等轴晶区的条件是什么?6、为什么空位是热力学稳定缺陷,而位错是非热力学稳定缺陷。
三、问答题(3×20=60分)1、绘出Fe-Fe3C相图,标出其中的关键成分和关键温度,并且回答:(1)分析碳含量对Fe-C合金室温组织和力学性能的影响。
(2)分析45钢的拉伸变形过程可分为哪几个阶段及其相应的特征和机理。
2、试解释为什么材料的理论强度远高于其实际强度。
随着现代科学技术的进步和国民经济的发展,材料的强韧化越来越重要,试举例说明材料强化或韧化的4种方法,并阐述相应的强化和韧化原理。
3、试分析下列材料科学过程是否与原子扩散有关,为什么?A 热弹性马氏体箱变B 脱溶分解C 成分均匀化D 高温蠕变E G.P形成中南大学2012年硕士研究生入学考试试题959一、名词解释(30分)配位数割阶硬化层错能滑移系体扩散凝固相律晶内偏析离异共晶直线定律二、分析计算题1、分析下列关于材料现象的描述是否正确。
(18分)a.空位和位错都是热力学稳定缺陷。
b.上坡扩散现象表明固体中原子扩散的驱动力是体系的化学势梯度。
c.冷变形是指材料室温下进行的变形过程。
d.液态金属凝固是需要过冷,那么固态金属融也需要过热。
e.在二元相图中,相邻相区的相数差永远为1。
2007-2013年中南大学967管理真题

2013年中南大学硕士研究生入学考试试题一、简答题(共60分,每小题12分)1、简述程序化决策的优缺点和在使用时需要注意的问题2、管理者在员工中建立信任的方式、方法有哪些3、简述矩阵型组织结构的优缺点4、什么是正式沟通及其分类5、根据控制时机、手段、来源,可以将控制分为那几种类型二、论述题(共40分,每小题20分)1、试根据管理理论,归纳总结激励的基本方法2、试举例说明组织目标及其在组织管理中的重要性三、案例分析题(共50分,每题25分)【案例一】某公司总经理为了使公司的供电设施规划尽快落实,并且把自己设想变为现实。
就把负责这一项目的设备工程师李工叫到总经办,在办公室里,总经理将自己想法和公司的供电设施规划一五一十的告诉了李工。
作为专业技术人员,李工对总经理要求一口应允。
突然有一天,总经理问李工所在的部门负责人王经理:“前段时间安排给李工去做的工作进展如何?一些项目为何没有按照要求去做。
”王经理被问得莫名其妙,委屈地说:我不知道有这回事,李工也没有向我汇报过这个情况。
结果工程未达到要求,也没有按时完成,为此王经理受到了总经理批评。
请问:总经理有无批评错?王经理有什么责任,李工应付什么责任?他们如何处理比较合理?【案例二】1998年8月8日是广东太阳神集团公司10周年大庆的日子。
而此时此刻,关于“太阳神”落山的说法却已是妇孺皆知的事了。
从1989年的年产值4300万元到1993年以13亿元的业绩傲视群雄,再到1997年的2亿元保健品销售和香港上市股票仅值9分钱,变化之大令人扼腕。
在此期间,其管理体制经历了四次大的“地震”:1990年董事长骆辉“杯酒释兵权”。
在保持待遇不变的情况下,原与骆辉一起闯天下的9位“开国元勋”基本退出高层管理。
他们中间没有一个是大学生。
与此同时,一批年轻的管理者脱颖而出,挑起了大梁。
1991年,企业的发展更见迅猛。
每天从各地汇往总部的现金收入达到二三百万,对企业内部的管理提出了更高的要求。
中南大学粉末冶金研究院 硕士研究生入学考试 粉末冶金原理 历年真题大题

2000四、问答1、压制一直径为38mm的圆柱体Fe基零件压坯,已知Fe粉的径向弹性后效为0.2%,烧结径向收缩率为0.3%,试计算阴模内径尺寸为多少?D(1+0.2%)(1-0.3%)=38D=38.04mm2、简述烧结机械零件与材料的分类,说明其中各类材料的基体类型及适用场合有哪些?烧结机械零件与材料的分类:烧结结构材料、烧结减摩材料、烧结摩擦材料烧结结构零件:烧结铁基材料:烧结铁,碳钢,合金钢,不锈钢烧结铜基材料:烧结青铜,黄铜,Cu-Ni合金,弥散强化烧结铝基材料:烧结铝合金,弥散强化铝烧结镍基材料:烧结钛基材料:烧结减摩零件:多孔轴承:铁基,铜基,铝基,不锈钢基固体自润滑材料:铁基,铜基,银基,双金属烧结摩擦零件:铜基摩擦零件:铁基摩擦零件:碳-碳复合材料:陶瓷基复合摩擦材料;用于干摩擦式离合器和制动器的关键材料.??3、欲制造Cu基结构零件、Cu基电工触头和Cu基过滤器三种粉末冶金零件,其原料Cu粉应分别采用哪种制粉方法?为什么?Cu基结构零件:雾化法(水雾化);颗粒形状不规则,颗粒间机械啮合,压坯强度也大。
Cu基电工触头:电解法;纯度高,导电性能好。
Cu基过滤器:雾化法(气雾化);颗粒近球形,粒子尺寸均匀,高输出体积4、说明粉末注射成形的工艺流程,它对原料粉末有何要求?流程中的关键工序及注意事项是什么?工艺流程:粉末(金属或陶瓷) + 粘结剂及添加剂↓↓原料↓↓↓粉末零件粉末注射成形常用的粉末颗粒一般在2-8um,一般小于30um,粉末形状多为球形,颗粒外形比最好在1-1.5之间,具有相当宽或窄的粒度分布,填充密度较高。
注射成型是整个工艺流程的关键工序,注射成形时,对可能产生缺陷的控制应从两个方面进行考虑:(1)注射温度、压力、时间等工艺参数的设定;(2)填充是喂料在模腔中的流动控制。
??5、运用挥发-沉淀长大机理,说明H2还原WO3制取细W粉时应如何控制工艺条件?(1)原料:A 粒度:当采用WO3时,其粒度与还原钨粉粒度间的依赖性不太明显,而主要取决于WO2的粒度。
中南大学2019年硕士研究生入学考试试题

中南大学2019年硕士研究生入学考试试题考试科目代码及名称:353卫生综合注意:1、所有答案(含选择题、填空题、判断题、作图题等)一律答在专用答题纸上,写在试题纸上或其他地点一律不给分。
2、作图题可以在原试题图上作答,然后将“图”剪切下来贴在答题纸上相应位置。
3、考试时限:3小时,总分:300分。
一、名词解释(每题5分,共100分)1、可耐受最高摄入量2、膳食指南3、食品安全4、食品腐败变质5、acid rain6、environment response gene7、iodine deficiency disorders8、涉水产品9、Occupational hazards 10、矽肺11、热射病12、放射病13、疫源地14、流行15、生态学研究16、患病率17、Randomized block design 18、Sample size19、Parameter estimation 20、偏回归系数二、单选题(每小题2分,共50分)1.蛋白质生物学价值是表示()A.蛋白质在体内的吸收量B.蛋白质在体内的消化率C.摄入蛋白质增加体重的克数D.蛋白质被机体消化酶分解的程度E.蛋白质吸收后在体内被利用的程度2.中国居民膳食中膳食纤维的重要来源是()A.肉类B.蛋类C.奶制品D.水果蔬菜E.精制米面3.关于老年人营养叙述正确的是()A.易出现维生素摄入不足B.宜多吃蜂蜜等含果糖丰富的食物C.因肝肾功能下降,应降低蛋白质的供能比D.为防止超重和肥胖,老年人应保持能量负平衡E.由于消化吸收率降低,蛋白质的摄入量应高于中年人的RNI值4.黄曲霉毒素具有特殊亲和性的器官是()A.脑B.肺C,胃D.肝脏E.心脏5.最容易污染海产食品的细菌是()A.沙门氏菌B.变形杆菌C.副溶血性弧菌D.大肠埃希氏菌E.金黄色葡萄球菌6.下列砷化物中,毒性最强的是()A.单甲基砷酸B.单甲基亚砷酸C.三甲基砷酸D.三氧化二砷E.砷酸钠7.下列常见的环境污染物中,不属于致癌物的是()A.多环芳烃B.二噁英C.氯化消毒副产物D.藻毒素E.镉8.大气污染对健康的间接危害不包括()A.臭氧层破坏B.酸雨C.温室效应D.大气能见度降低E.机体免疫力降低9.土壤污染的来源不包括()A.大气污染物B.工业废水和生活废水C.固体废弃物D.化肥及农药的使用E.地质环境中区域性差异导致土壤中某些元素过高10.一般认为痛痛病是慢性镉中毒,镉进入人体的主要途径是()A.饮水B.吃鱼C.蔬菜D.粮食E.空气11.手臂振动病的典型临床表现是()A.皮肤大理石样斑纹B菌性骨坏死C.一过性手指变白D.多发性周围神经炎E.冷水复温试验阳性12.土法炼金可致()A.铅中毒B.汞中毒C.砷中毒D.锰中毒E.砷化氢中毒13.驱汞治疗的首选药物是()A.依地酸二钠钙B.二巯基丙璜酸钠C.二疏基丁二酸钠D.巯乙胺B.美篮14.有机磷农药中毒的机制,通常认为是因其抑制()A.乙酰胆碱酯酶活性B.丁酰胆碱酯酶活性C .直接作用于胆碱能受体D .神经病靶酯酶活性E .神经-肌接头传导15.依法认定为呼吸系统职业性肿瘤的致癌物是( ) A .砷及其化合物 B .苯及其同系物 C .镍及其化合物D .氯乙烯E .联苯胺16.开展实验流行病学研究最好采用“双育法”,目的是为了尽可能减少( ) A .选择偏倚B .失访偏倚C .观察偏倚D .混杂偏倚17.并联试验可以提高( ) A 真实性B 阳性预测值C .特异度D 可花性E 敏感度18.下列哪一项属于第三级预防措施( ) A .遗传咨询 B .产前检查C .普查D .即预E .康复治疗19.流行病学研究的对象是( ) A .疾病B .病人C .人群D .健康人E .亚临床型病人20.以下哪一个不是流行病学的特征( ) A .群体特征 B .以分布为起点的特征 C .以治疗疾病为主的特征 D .对比的特征E .预防为主的特征21.正态性检验,按0.10α=水准,认为总体服从正态分布,此时若推断有错。
中南大学研究生考试专业真题

中南大学研究生考试专业真题中南大学资源加工与生物工程学院钢铁冶金原理、矿物加工学真题中南大学无机材料科学基础、无机化学、生物化学、化工原理真题中南大学资源与安全工程学院安全系统工程历年真题中南大学资源与安全工程学院经济学概论、工程力学、岩石力学真题中南大学勘探地球物理基础、测量平差基础、电路基础历年真题中南大学地球科学与信息物理学院土力学与地基基础历年真题中南大学地球科学与信息物理学院地质学基础、测量平差基础真题中南大学地球科学与信息物理学院地理信息系统原理历年真题中南大学土木工程学院材料力学、结构力学历年真题中南大学软件学院944软件工程历年真题中南大学信息科学与工程学院计算机网络基础、数据结构历年真题中南大学信息科学与工程学院计算机学科专业基础综合历年真题中南大学信息科学与工程学院940电路理论历年真题中南大学交通运输工程学院运筹学、车辆工程历年真题中南大学能源科学与工程学院传热学、工程热力学历年真题中南大学机电工程学院971机械设计历年真题中南大学冶金科学与工程学院环境工程原理、环境化学历年真题中南大学冶金科学与工程学院无机化学、冶金原理历年真题中南大学粉末冶金研究院材料科学基础、粉末冶金历年真题中南大学材料科学与工程学院材料科学与工程基础历年真题中南大学生物科学与技术学院细胞生物学历年真题中南大学生物科学与技术学院植物生理学与生物化学历年真题中南大学生物科学与技术学院生物综合、检验综合、基础医学真题中南大学化学化工学院有机化学、无机化学、化工原理历年真题中南大学物理与电子学院普通物理、量子力学、信号与系统历年真题中南大学数学与统计学院数学分析、高等代数历年真题中南大学数学与统计学院统计学基础、数量经济学基础历年真题中南大学商学院西方经济学、运筹学、管理学历年真题中南大学外国语学院基础英语、英语综合考试历年真题中南大学外国语学院日德法俄语、基础英语、英美文学史及作品真题中南大学外国语学院教育学专业基础综合历年真题中南大学文学院新闻与传播学理论、文化产业概论历年真题中南大学文学院古代汉语与现代汉语、语言学综合历年真题中南大学文学院美学原理、文学理论与写作、中外文学史历年真题中南大学法学院法理学、法学综合历年真题中南大学公共管理学院公共管理学基础、公共管理综合考试历年真题中南大学马克思主义学院政治学基础、世界政治与国际关系历年真题。
中南大学研究生入学考试数学分析试题

2002年一、(共18分,每小题6分)求下列极限(1)lim ,(0)n n n n n x x x x x --→+∞->+; (2)1lim ()1x x x x →+∞+-;(3)01lim sin AA xdx A→∞⎰。
二、(共16分,每小题8分)设函数()sin f x xπ=,(0,1)x ∈(1)证明()f x 连续;(2)()f x 是否一致连续?(请说明理由)。
三、(共16分,每小题8分) (1)设ax by u e +=,求n 阶全微分n d u ;(2)设cos u x e θ=,sin u y e θ=,变换以下方程22220z zx y ∂∂+=∂∂。
四、(共20分,每小题10分)(1)求积分101ln 1dx x-⎰;(2)求曲面22az x y =+ (0)a >,和z =所围成的体积。
五、(共12分,每小题6分)设1cos 21p qn n n I nπ∞==+∑,(0)q > (1)求I 的条件收敛域; (2)求I 的绝对收敛域。
六、证明:积分2()0()x a F a e dx +∞--=⎰是参数a 的连续函数。
七、(8分)设定义于(,)-∞+∞上的函数()f x 存在三阶的导函数(3)()f x ,且(1)0f -=,(1)1f =,(1)(0)0f =证明:(3)(1,1)sup ()3x f x ∈-≥。
2003年一、(共27分,每小题9分)求下列极限(1)lim n →+∞; (2)12200lim[3(cos )]xxxx t dt →+⎰;(3)设()f x 在[0,1]上可积,且1()1f x dx =⎰,求1121lim ()2n n k k f n n →+∞=-∑。
二、(共24分,每小题12分)设函数()f x 在[,)a +∞上连续, (1)证明:若lim ()x f x →+∞存在,则()f x 在[,)a +∞上一致连续;(2)上述逆命题是否成立?(请给出证明或举出反例)。
中南大学00-12无机化学考研真题及部分年份答案-96无机化学

1996年攻读硕士学位研究生入学考试试题考试科目:无机化学专业:无机化学、分析化学、有机化学、物理化学研究方向:以上各专业所有方向一、选择题(请将正确的选择填在括号内):(共10分)1、任意温度下都是“非自发过程”的是A.△H<0, △S<0;B.△H>0, △S<0;C.△H>0, △S>0;D.△H<0, △S>0;2、元素的第一电子亲合能大小正确的顺序是A.C<N<O<F;B.C>N>O>F;C.C>N<O<F;D.C>N<O>F;3、偶极矩不为零的分子是A.PCl5(g);B.NF3;C.SF6;D.BeCl2(g);4、按“MO”法,键级最大的是A.O2;B.O2+;C.O2-;D.CO5、不存在分子间或分子内氢键的分子是A.NH3;B.对羟基苯甲酸;C.CF3H;D.HNO36、路易斯酸性强弱正确的顺序是A.BF3<BCl3<BBr3;B.BF3>BCl3>BBr3;C.BF3<BCl3>BBr3;D.BF3>BCl3<BBr3;7、晶体熔点高低正确的顺序是A.NaCl>SiO2>HCl>HF;B.SiO2>NaCl>HCl>HF;C.NaCl>SiO2>HF>HCl;D.SiO2>NaCl>HF>HCl8、路易斯碱性强弱正确的顺序是A.NH3<N2H4<NH2OH;B.NH3>N2H4<NH2OH;C.NH3<N2H4>NH2OH;D.NH3>N2H4>NH2OH;9、不属于二元质子酸的是A.H3PO3;B.H2SO4;C.H3PO2;D.NaH2PO410、氧化性强弱正确的顺序是A. HClO4<HbrO4<H5IO6;B. H2SO4<H2SeO4>H2TeO4;C. HClO4<H2SO4<H3PO4;D. HNO3<H3PO4<H3AsO4二、填空题:(每空1分,共16分)1、H2(g)+I2(g)=2HI(g),Kθ=50.3(713k).某状态下,P氢气=P碘=5.379×105Pa,P碘化氢=62.59×105Pa.则自发进行的方向是______________,原因是________________。
中南大学矩阵论考试试题及参考答案

中南大学2010年秋季硕士研究生《矩阵论》考试试题考试形式:开卷 时间:120分钟 总分100分姓名 学号一、 (16分) 已知3阶Hermite 矩阵A 的特征值为1,2,2,且()(),0,1, 1,0,TTi i ξη==是A 的属于特征值2的两个相互正交的特征向量. 1.(10分) 求A ;2.(6分) 求A 的不变因子与最小多项式.二、(20分) 对任何()C ij n nA a ⨯=∈,定义111n nij m i j Aa ===∑∑.1.(8分) 证明1m ⋅是Cn n⨯上一种矩阵范数;2.(6分) 证明1m ⋅与向量∞-范数相容; 3.(6分) 证明1m ⋅与矩阵范数m ∞⋅等价,其中1,max ij m i j nAn a ∞≤≤=⋅.三、(20分) 设020i A i ⎛⎫⎪= ⎪⎝⎭. 1.(6分) 验证A 是否为收敛矩阵; 2.(6分) 判断矩阵幂级数()1012kk kk ∞+=-∑的敛散性;3.(8分) 求Ate .四、(14分) 设113242212A -⎛⎫ ⎪=- ⎪ ⎪⎝⎭.求A 的QR 分解.五、(15分) 设1211141111A -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭.利用特征值隔离法和盖尔圆定理证明:A 的三个特征值全为实数,且分别位于实数区间()()0.5, 2.5, 2.5, 5.5 -和[]10, 14内.六、(15分)设1121, 1101A b -⎛⎫⎛⎫==⎪ ⎪-⎝⎭⎝⎭.1. (8分)求A 的全部{}1逆;2. (7分)利用{}1逆判断Ax b =是否有解,并在有解时求其通解.2010年矩阵论试题参考答案一、解. 1.因为A 为3阶Hermite 矩阵,所以有3个相互正交的特征向量,且酉相似于对角形122⎛⎫⎪⎪ ⎪⎝⎭ . 设A 的属于特征值1的特征向量为()123,,T x x x x =,则, ,x x ξη⊥⊥ 即 131300ix x x ix -+=⎧⎨-=⎩,解得 ()0,1,0, 0Tx k k =≠任意. 将, , x ξη单位化得12301,0, 00p p p ⎛⎫⎪=== ⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭.令()12301000,,U p p p ⎛⎪ ⎪ ⎝==,则U 是酉矩阵且122H U AU ⎛⎫ ⎪= ⎪ ⎪⎝⎭从而0010112100202200212HU UA ⎛⎫⎛ ⎪ ⎪⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎝⎛⎫ ⎪=⎪⎪⎝⎭. 2.由A 相似于对角形122⎛⎫⎪⎪ ⎪⎝⎭知,A 的初等因子为 1, 2,2λλλ---,从而得A 的不变因子为 ()() 123()1,()2, ()12d d d λλλλλλ==-=--, 最小多项式为 ()()3()()12A m d λλλλ==--.二、1.证明. 1)()ij n nA a ⨯∀=∈C,显然有0A =时,10m A=,0A ≠时10m A>.2)(), n nij A a λ⨯∀∈∀=∈C C,111111nnnnij ji j m j m i i Aa aAλλλλ====⋅===∑∑∑∑.3)()(), ij ij n nA aB b ⨯∀==∈C,()11111111111nnnnn n n nij ij ij ij ij ij i j i j i j i m j m m a b a b a A BAb B=========++=≤+++=∑∑∑∑∑∑∑∑.4)()(), ij ij n nA aB b ⨯∀==∈C,1111111nnnnnnik kj ik kji j k i j m k a b a b AB=======≤⋅∑∑∑∑∑∑1111111111nnn n n nn nik kj ikkj i j k k i k j k m m a b a b AB========⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪⎪ ⎪⎝⎭⎝⋅⎝⎭⎝≤⎭⎭∑∑∑∑∑∑∑∑.由定义知1m A是n n⨯C上的矩阵范数.2.证明.()()12, ,,,Tn nn n ij A a x ξξξ⨯∀=∀=∈∈CC ,()11111111111111maxmax max m ma ax max m x x a n nnijnnnij ij jij ij i ni ni n j j j j j j m ni nj i j jj j nj na a AxAa xa a ξξξξξ≤≤≤≤≤≤===≤≤≤∞≤≤≤≤∞=≤===≤⋅≤⋅=⋅≤⋅⋅=∑∑∑∑∑∑所以矩阵范数1m ⋅与向量∞-范数相容.3.对任何()n nij A a ⨯=∈C,121,1,11ax x 1m ma m m nnij ij ij i j ni j nm i j n a A n a AAna ∞∞≤≤≤≤===≤=≤=∑∑所以矩阵范数1m ⋅与m ∞⋅等价.三、解. 1.2222122ii I A iλλλλλ--===+--,故A()A ρ=1()A ρ<,所以A 为收敛矩阵. 2.矩阵幂级数对应的复变量幂级数的收敛半径为()()1112lim212kk k kk r ++→+∞-⋅-==,而()A r ρ=<,故题中的矩阵幂级数绝对收敛.3.设()()()2101,2tet q t t b b λλλλ⎛⎫=++ ⎪⎝+⎭(()(()1010sin sin i b t b t e i b t b t ⎧==+⎪⎪⎨⎪=-=-⎪⎩解得()()01 b t b t ==. ()()10c 100.2010Ate b t A b i i t I ⎛⎫⎛=+⎫⎪=+=⎪⎪⎭⎪⎪⎭⎭四、解.记1231132, 4, 2,212a a a -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪===- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 先将A 的第一列1a 用Householder 变换化为与1100e ⎛⎫⎪= ⎪ ⎪⎝⎭共线.易得123a =, 11111211232-30=2202a a e a e -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-=-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.令1111213131a e u a e -⎛⎫-⎪==⎪-⎪⎭,31122121232212HI u H u ⎛⎫ ⎪- ⎪ ⎪-⎝⎭=-=,则 ()()11311111132221111222103212210H H a I uu a --⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=-=--=-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,()1211132411114031113H a ---⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪=--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭,()1333221121112210314H a -⎛⎫⎛⎫⎪ ⎪=--= ⎪⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝ ⎪ ⎪⎝⎭⎝⎭⎭,从而()()112311112133********H a a a H a H a H a H A ⎛⎫⎪=== ⎪ ⎝⎭-⎪.再记103b ⎛⎫= ⎪-⎝⎭.则123b =, 113303b -⎛⎫⎛⎫-= ⎪ ⎪-⎝⎭⎝⎭.令11213101130b v b ⎛⎫- ⎪-⎫⎝⎭==⎪-⎛⎫⎭- ⎪⎝⎭, 221011012011110H H I vv -⎛⎫⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭, 22101011H H ⎛⎫⎪-⎛⎫== ⎪⎝ ⎝⎭⎪⎪-⎭, 有2133103433100001010003140H H A R ⎛⎫⎛⎛⎫ ⎪-⎫ ⎪⎪=-= ⎪⎪ ⎪⎪-⎝ ⎪ ⎪⎝⎭⎭⎝-⎭ .令()1122121221121201322110HH HQ H H H H H H ⎛⎫⎛⎫⎪⎪====-- ⎪⎪ ⎪⎪--⎝⎭⎝⎭12233312221321221332123233123--⎛⎫ ⎪---⎛⎫⎪⎪-== ⎪ ⎪- ⎪⎝⎭⎭⎪⎝-⎪, 则Q 为酉矩阵,且A 的QR 分解为122333221331034333212030303QR A --⎛⎫⎪ ==⎪- ⎪⎛⎫⎪-⎪ ⎪⎝ ⎪⎪⎭⎭- ⎝.五、证明.A 的三个行盖尔圆和列盖尔圆都为:{}{}{}123 122, 42 1 ,2 n n n z G z G z z z G z =∈=∈=-≤-≤≤∈-C C C . 1G 为孤立的盖尔圆,而2G 与3G 相交.由盖尔圆定理知1G 中有A 的一个特征值,2G 与3G 的并中有A 的两个特征值.对任何0ε>,取 1232, 1d d d ε=+==.令2113,12221412112 1 B DAD d D d d εεεε-⎛⎫ ⎪+-- ⎪⎪==- ⎪+ ⎪⎪-+⎝⎛⎫ ⎪=⎭⎪ ⎪⎝⎭,则B 与A 相似,从而与A 有相同的特征值.B 的三个盖尔圆为:{}12 1242 41, 1, 2n n G z G z z z εε⎧⎫=∈=∈⎨⎬+-≤+-≤+⎩⎭C C 3 1121n z z G ε-≤⎧⎫=∈⎨+⎬+⎩⎭C .它们是三个孤立的盖尔圆,故由盖尔圆定理知,B 的三个特征值中分别位于这三个盖尔圆中.由于B 为实矩阵,其特征多项式为实系数多项式,从而其特征值如为复数,则必共轭成对出现.注意到 123, , G G G 的圆心都在实轴上, 123, , G G G都关于实轴对称,如果含有复特征值,则其共轭的特征值也在同一个盖尔圆中,与每个孤立盖尔圆中只有一个特征值矛盾.因此,B 的特征值,从而A 的特征值都为实数.综上,A 的特征值分别位于孤立的盖尔圆1G , 2G和 3G 的实轴上,即位于实数区间 []10, 14,113,522εε⎡⎤-+⎢⎥++⎣⎦ 和11, 2 22εε⎡⎤-+⎢⎥++⎣⎦中.注意到0ε>知,A 的特征值分别位于[]10, 14,()2.5, 5.5 和 ()0.5, 2.5 -中.六、解.1.11221122232100100000000000000110101111110112010000000001010S T I I AI --⎛⎫⎛⎫⎪⎪ ⎪ ⎪⎛⎫⎛⎫ ⎪ ⎪=→⎪ ⎪⎪⎪⎝⎭⎝⎭ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭- ,11112222111122221011001101001a ab T S ab ab b a b --++⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪⎪=-=-- ⎪ ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 故A 的全部{}1逆为{}11221122 1 , ab A ab aa b b -++⎛⎫⎪-- ⎧⎫⎪⎪=⎨⎬⎪⎪⎪⎝⎭⎪⎩⎭任意. 2.取A 的一个{}1逆()11221112200A -⎛⎫⎪= ⎪ ⎪⎝⎭.由 ()112211221111211121011011101000AA b b --⎛⎫⎛⎫--⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭⎪ ⎪⎝⎭⎝⎭知Ax b =有解,其通解为()()()111122221111222121100111201011100000100A b I A A y x y -⎡-⎤⎛⎫⎛⎫⎛⎫-⎛⎫⎛⎫⎢⎥⎪ ⎪ ⎪==+- ⎪ ⎪⎢⎥ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦+- 110010100100110001000y -⎡-⎤⎛⎫⎛⎫⎛⎫⎢⎥⎪ ⎪ ⎪=+-⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦1233100100011010110001y y y y -⎛⎫⎛⎫⎛-⎛⎫⎛⎫⎪ ⎪+- ⎪ ⎪ ⎪ ⎪⎝⎫ ⎪ ⎪⎪=+-= ⎪ ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎝⎝⎭⎭⎭⎭,3y 任意,或写成110101x k -⎛⎫⎛⎫⎪ ⎪=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, k 任意.中南大学2011年秋季硕士研究生《矩阵论》考试试题考试形式:开卷 时间:120分钟 总分:100分姓名 学号一、 (18分) 已知3阶方阵A 的不变因子为()()()()1231, ,6.d d d λλλλλλ===- 1.(6分) 求A 的谱半径()A ρ;2.(6分) 求()lim kk A A →+∞⎛⎫⎪ ⎪⎝⎭ρ;3.(6分) 判断矩阵幂级数()()012kkkk A A ρ∞=⎛⎫- ⎪ ⎪⎝⎭∑的收敛性.二、(20分) 设a ⋅和b ⋅是n n ⨯C 上的任意两种矩阵范数. 对任何()n n ij A a ⨯=∈C ,定义A =.1.(8分) 证明⋅也是n n ⨯C 上一种矩阵范数;2.(6分) 若v ⋅是n C 上一种向量范数,且a ⋅和b ⋅都与v ⋅相容,证明⋅也与v ⋅相容;3.(6分) 若n n A ⨯∈C 且20A A =≠,证明1a A ≥.三、(20分) 设4332A ⎛⎫=⎪--⎝⎭.1.(6分) 求()TdF x dx ,其中12x x x ⎛⎫= ⎪⎝⎭,()T F x x A =; 2.(8分) 求sin At ; 3.(6分) 求1cos Atdt ⎰.四、(16分) 设222112222243333644A ⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪⎝⎭. 利用Gerschgorin 定理,1.(8分) 证明A 可逆且有3个线性无关的特征向量;2.(8分) 证明A 的特征值全为实数,并求它们所在的实数区间.五、(26分)设101, 1001i A i b ⎛⎫⎛⎫ ⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭.1.(10分)求A 的奇异值分解;2.(8分)求A 的加号逆A +;3.(8分)利用A +判断Ax b =是否有解,并在有解时求其极小范数解,无解时求其极小范数最小二乘解.2011年矩阵论试题参考答案一、 (18分) 已知3阶方阵A 的不变因子为()()()()1231, , 6.d d d λλλλλλ===- 1.(6分) 求A 的谱半径()A ρ;2.(6分) 求()lim ;kk A A →+∞⎛⎫ ⎪ ⎪⎝⎭ρ3.(6分) 判断矩阵幂级数()()012kkkk A A ρ∞=⎛⎫- ⎪ ⎪⎝⎭∑的收敛性. 解. 1.A 的特征多项式为:()()()()12326I A d d d λλλλλλ==--,故A 的特征值为0, 0, 6, 从而()6A ρ=.2.因为A 的最小多项式()()()36A m d ==-λλλλ无重根(或者A 的初等因子均为一次的,它们是:, , 6-λλλ),从而A 可对角化, 故存在可逆矩阵P 使1006A P P -⎛⎫ ⎪= ⎪ ⎪⎝⎭,()10061A A P P A -⎛⎫ ⎪== ⎪ ⎪⎝⎭ρ, 从而()1100lim lim 00.611kkk k A A P P P P A --→+∞→+∞⎛⎫⎛⎫⎛⎫⎪ ⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭ρ 3.解法1. 记()AB A =ρ. 则 ()()()01122kkkk k k k k A B A ρ∞∞==⎛⎫--= ⎪ ⎪⎝⎭∑∑. ()() 166A A B ⎛⎫=== ⎪⎝⎭ρρρ,复变量幂级数()12kk kk ∞=-∑的收敛半径 ()()1112lim212kkk k k r +→+∞+-==-, ()B r <ρ, 故矩阵幂级数 ()()012kkkk A A ρ∞=⎛⎫- ⎪ ⎪⎝⎭∑绝对收敛. 解法2. 记()2AB A =ρ. 则 ()()()0112kkk kk k k A B A ρ∞∞==⎛⎫-=- ⎪ ⎪⎝⎭∑∑. ()()112122A A B ρρρ⎛⎫=== ⎪⎝⎭,复变量幂级数 ()01k kk z ∞=-∑的收敛半径 ()()11lim 11kk k r +→+∞-==-, ()B r <ρ, 故矩阵幂级数()()012kkkk A A ρ∞=⎛⎫- ⎪ ⎪⎝⎭∑绝对收敛. 解法3. ()()()0011 212kkkk k k k k A A A ρ∞∞==⎛⎫--= ⎪ ⎪⎝⎭∑∑ ,复变量幂级数()112kk k k ∞=-∑的收敛半径 ()()11112lim 12112kkk k k r +→+∞+-==-, ()A r <ρ, 故矩阵幂级数 ()()012kkk k A A ρ∞=⎛⎫- ⎪ ⎪⎝⎭∑ 绝对收敛.二、(20分) 设a ⋅和b ⋅是n n ⨯C 上的任意两种矩阵范数. 对任何()n n ij A a ⨯=∈C ,定义A =.1.(8分) 证明⋅也是n n ⨯C 上一种矩阵范数;2.(6分) 若v ⋅是n C 上一种向量范数,且a ⋅和b ⋅都与v ⋅相容,证明⋅也与v ⋅相容;3.(6分) 若n n A ⨯∈C 且20A A =≠,证明1a A ≥.1.证明. 1)当0A =时,0a b A A ==,故0A =;当 0A ≠时,0, 0,a b A A >>故0A >. 2), n nA ⨯∀∈∀∈C C λ,A A λλ===⋅.3), n nA B ⨯∀∈C,记 , ,a a b b x y A B A B ⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭则 22, ,x A B y ==222 .A B x y x y A B +=≤=++≤=+4), n nA B ⨯∀∈C,.AB A B =≤≤=⋅由定义知A 是n n⨯C上的矩阵范数.2.证明., ,n nn A x ⨯∀∈∀∈C C 由已知条件有, ,v a v v b v Ax A x Ax A x ≤⋅≤⋅故,v v Ax A x ≤≤=⋅ 即⋅与v ⋅相容.3.证法1. 2aa a aAA A A =≤⋅,而0A ≠,故 0a A >,从而 1a A ≥.证法2. 2, A A A =∴ 的特征值只能为0或1,而0A ≠,故A 的特征值不全为0,从而 ()()1, 1a A A A ρρ=≥=.证法3.由 2A A = 可得:1k ∀≥ 有 k A A =,故 lim 0kk A A →+∞=≠,因而A 不是收敛矩阵,从而()()1, 1a A A A ρρ≥≥≥. 三、(20分) 设4332A ⎛⎫=⎪--⎝⎭.1.(6分) 求()TdF x dx ,其中12x x x ⎛⎫= ⎪⎝⎭,()TF x x A =; 2.(8分) 求sin At ; 3.(6分) 求1cos Atdt ⎰.解. 1.()()121243,32F x x x x x =--,()()()()124, 3, 3, 2,F x F x x x ∂∂==--∂∂ 故()()()()12, 4, 3, 3, 2TdF x F x F x dx x x ∂∂⎛⎫==-- ⎪∂∂⎝⎭. 2.()243312I A λλλλ--=+--=,A 的特征值为121==λλ. 设 ()()()()210sin 1t g b t b t λλλλ=-++,则()()()101111 sin sint b t b t d tb t d λλλλλλλ===⎧=+⎡⎤⎣⎦⎪⎨=⎪⎩, 即()()()101 sin cost b t b t t t b t =+⎧⎪⎨=⎪⎩, 解得()()01 sincos cosb t t t t b t t t =-⎧⎪⎨=⎪⎩. 故()()()104310sin cos sin cos 3201sin 3cos 3cos .3cos sin 3cos At b t A b t I t t t t t t t tt t t tt t t ⎛⎫⎛⎫=+=+- ⎪ ⎪--⎝⎭⎝⎭+⎛⎫= ⎪--⎝⎭3.解法1. 43132A ==--,A 可逆且12334A ---⎛⎫= ⎪⎝⎭. 由2知sin13cos13cos1sin 3cos1sin13cos1A +⎛⎫= ⎪--⎝⎭.又 1sin cos d AtAt Adt-=,故 111111000sin cos sin sin 23sin13cos13cos12sin13cos13sin13cos1.343cos1sin13cos13sin13cos14sin13cos1d At Atdt A dt A At A A dt---===--+-+-+⎛⎫⎛⎫⎛⎫== ⎪⎪ ⎪----⎝⎭⎝⎭⎝⎭⎰⎰解法2. 用2中同样的方法可算得()43103sin cos 3sin cos sin sin cos ,32013sin 3sin cos t t tt t At t t t t t t t t t t -+-⎛⎫⎛⎫⎛⎫=-++= ⎪ ⎪ ⎪--+⎝⎭⎝⎭⎝⎭从而11003sin cos 3sin 2sin13cos13sin13cos1cos .3sin 3sin cos 3sin13cos14sin13cos1t t t t t Atdt dt t t t t t -+--+-+⎛⎫⎛⎫== ⎪ ⎪+--⎝⎭⎝⎭⎰⎰四、(16分) 设222112222243333644A ⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪⎝⎭. 利用Gerschgorin 定理,1.(8分) 证明A 可逆且有3个线性无关的特征向量;2.(8分) 证明A 的特征值全为实数,并求它们所在的实数区间.解.1.A 的3个盖尔圆{}()123 2, , , 1, 2, 3C i i G G z i R G G z i =∈-≤=的半径依次为1232221132283315, , 2243394416R R R =+==+==+=. 显然 310kk G=∉,由Gerschgorin 定理1知,A 的3个特征值都不等于0, A A =的3个特征值的乘积0≠,从而A 可逆.因为A 的任意两个相邻盖尔圆圆心的距离为2,而每个盖尔圆的半径都小于1,故A 的3个盖尔圆互不相交,由Gerschgorin 定理2知,A 有3个互异的特征值,从而有3个线性无关的特征向量.2.因为A 为实矩阵,其盖尔圆圆心都在实轴上,故A 的所有盖尔圆都关于实轴对称. 又实矩阵A 的复特征值必共轭成对出现,它们同时位于或同时不位于A 的某一个盖尔圆. 而由1知A 的每个盖尔圆中只有A 的一个特征值,从而A 只有实特征值,它们分别位于A 的3个盖尔圆的实轴上,由此得到A 的3个特征值所在的3个实数区间分别为338815152, 2, 4, 4, 6, 6, 44991616⎡⎤⎡⎤⎡⎤-+-+-+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即 511284481111, , , , , . 44991616⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦同理,A 的3个实特征值也分别位于A 的3个列盖尔圆{}()123 2,, ''''i 'i z G G i G G z R -=∈≤C的实轴上,123, , '''G G G 的半径依次为123222231713111217, , 341224162336'''R R R =+==+==+=. 综合前面的结论可知A 的3个特征值所在的3个实数区间分别为33111117172, 2, 4, 4, 6, 6, 4416163636⎡⎤⎡⎤⎡⎤-+-+-+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 即 5115375199233, , , , , . 441683636⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦五、(26分)设101, 1001i A i b ⎛⎫⎛⎫⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭.1.(12分)求A 的奇异值分解;2.(6分)求A 的加号逆A +;3.(8分)利用A +判断Ax b =是否有解,并在有解时求其极小范数解,无解时求其极小范数最小二乘解.解.1.110221102200Hi i i A A i i i ⎛⎫-⎛⎫⎛⎫ ⎪=-= ⎪ ⎪ ⎪---⎝⎭⎝⎭ ⎪⎝⎭, ()22422H iI A A i ---==--λλλλλ, H A A 的特征值为:4, 0, A 的奇异值为:2,()2∑=.由 ()40HI A A x -= 求得HA A 的属于特征值4的特征向量为:1i ⎛⎫ ⎪⎝⎭,由 ()00HI A A x -= 求得HA A 的属于特征值0的特征向量为:1i -⎛⎫⎪⎝⎭,将这两个特征向量单位化后组成矩阵V得:11i i V -⎫==⎪⎪⎭⎪⎭.取11i V ⎫=⎪⎭,令11111112000i i U AV i -⎛⎫ ⎪ ⎪⎛⎫⎫⎛⎫ =∑=-=⎪⎪ ⎝⎭⎭ ⎝ ⎪ ⎪⎝⎭,00001U ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭. 由奇异值分解定理知,A 的奇异值分解为02000000000001HA U V⎛⎫ ⎪⎪⎛⎫∑⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭. 2.解法1. 由1得A 的加号逆为1010*******000001H i i A V U -+⎫⎪⎪⎛⎫-⎛⎫∑⎫⎪ ⎪==⎪⎪⎪ ⎪⎭⎝⎭⎪⎝⎭ ⎪ ⎪⎝⎭101.104i i -⎛⎫= ⎪--⎝⎭解法2. 用初等行变换将A 化成行最简形111000000i i A i ⎛⎫⎛⎫ ⎪ ⎪=-→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,取 ()1, 10F i G i ⎛⎫ ⎪== ⎪ ⎪⎝⎭得A 的满秩分解为 A FG =.A 的加号逆为()()()()()1111111110100H H H H A G GG F F F i i i i i i ----+⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪⎪==-- ⎪ ⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭⎝⎭()()()1111012210104i i i i ---⎛⎫⎛⎫=-= ⎪ ⎪---⎝⎭⎝⎭. 3.由10101111110420010i i i AA b i b i +-⎛⎫⎛⎫⎛⎫-⎛⎫ ⎪ ⎪ ⎪=-=≠ ⎪ ⎪ ⎪ ⎪--⎝⎭ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭知Ax b =无解,其极小范数最小二乘解为0010111101441i i x A b i +⎛⎫--⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪---⎝⎭⎝⎭⎪-⎝⎭.中南大学2012年秋季硕士研究生《矩阵论》考试试题考试形式:开卷 时间:120分钟 总分:100分姓名 学号一、 (16分) 已知4阶方阵A 的特征值为1, 2, 2, 2,且其一阶和二阶行列式因子分别为()()121, 2.D D λλλ==-1.(6分) 求A 的不变因子和最小多项式;2.(4分) 求A 的Jordan 标准形;3.(6分) 求实数t 的取值范围,使cos At 为收敛矩阵.二、(16分) 设a⋅和b ⋅分别是m C 和n C 上的向量范数. 对任何()11, , , , , Tm n m m m n x +++=∈C ξξξξ,定义 a b x u v =+,其中()1, , Tm u = ξξ,()1, , Tm m n v ++= ξξ.1.(10分) 证明⋅是m n +C 上的一种向量范数;2.(6分) 若11122122, , , ,m m m n n m n n A A A A ⨯⨯⨯⨯∀∈∈∈∈C C C C 及, m n u v ∀∈∈C C 有11111111121221212222, , , ,a m a a mb b m a b m b A u A u A v A v A u A u A v A v ≤⋅≤⋅≤⋅≤⋅其中1m ⋅是矩阵1m 范数.证明()()m n m n +⨯+C 上的矩阵1m 范数与上面定义的向量范数⋅相容.三、(18分) 1.(8分)设()ijn nX x ⨯=是矩阵变量,且det 0X ≠.求()1det TdX dX-; 2.(10分)设1011A ⎛⎫= ⎪⎝⎭.求矩阵幂级数()()12211121!k k k k A t k --+∞=--∑的和.四、(14分) 设112010232A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭.1.(8分)求矩阵A 的Crout 分解;2. (6分)利用Crout 分解求方程Ax b =的解,其中()1, 1, 1Tb =-.五、(14分) 利用Gerschgorin 定理及特征值的隔离方法判断矩阵1211621111A -⎛⎫⎪= ⎪ ⎪⎝⎭是否有小于零的特征值,并估计A 的每个特征值的分布范围.六、(22分)设101101, 102112A D ⎛⎫⎛⎫ ⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭.1.(8分)求A 的全部{}1逆;2.(8分)求A 的加号逆A +;3.(6分)判断矩阵方程AX D =是否有解.2012年矩阵论试题参考答案一、(16分) 已知4阶方阵A 的特征值为1, 2, 2, 2,且其一阶和二阶行列式因子分别为()()121, 2.D D λλλ==-1.(6分) 求A 的不变因子和最小多项式;2.(4分) 求A 的Jordan 标准形;3.(6分) 求实数t 的取值范围,使cos At 为收敛矩阵.解. 1.因为()4D λ即为A 的特征多项式,且A 的特征值为1, 2, 2, 2,故()()()3412D λλλ=--. 再由行列式因子与不变因子的性质与相互关系知()()232D λλ=-,从而A 的不变因子为()()()()()()123412, , 2,12 d d d d λλλλλλλλ====----,A 的最小多项式为 ()()()()412A m d λλλλ==--.2.由A 的不变因子知,A 的初等因子为, , 12 2,2λλλλ----,故A 的Jordan 标准形为 1222J ⎛⎫⎪⎪= ⎪ ⎪⎝⎭. 3. cos At 的特征值为 cos , cos 2, cos 2, cos 2t t t t ,谱半径为(){cos max cos ,At t ρ= }cos 2t . cos At 为收敛矩阵当且仅当其谱半径小于1,即cos 1, cos 21t t ≠≠,故实数t 的取值范围是:,2k k t ππ≠.二、(16分) 设a⋅和b ⋅分别是m C 和n C 上的向量范数. 对任何()11, , , , , Tm n m m m n x +++=∈C ξξξξ,定义 a b x u v =+,其中()1, , Tm u = ξξ,()1, , Tm m n v ++= ξξ.1.(10分) 证明⋅是m n +C 上的一种向量范数;2.(6分) 若11122122, , , ,m m m n n m n n A A A A ⨯⨯⨯⨯∀∈∈∈∈C C C C 及, m n u v ∀∈∈C C 有11111111121221212222, , , ,a m a a mb b m a b m b A u A u A v A v A u A u A v A v ≤⋅≤⋅≤⋅≤⋅其中1m ⋅是矩阵1m 范数.证明()()m n m n +⨯+C 上的矩阵1m 范数与上面定义的向量范数⋅相容.证明.1. 1)非负性. 当()11,, , , , 0Tm m m n x ++== ξξξξ时,()1, , 0Tm u == ξξ,()1, , 0T m m n v ++== ξξ,故0a b x u v =+=. 当()11, , , , , 0Tm m m n x ++≠= ξξξξ时,0u ≠或0v ≠,故0au>或0b v >,从而0a b x u v =+>.2)齐次性. ()11, , , ,, , Tm m m n m nx λξξξξ+++∀∈∀=∈ C C,()a b a b a bx u v u v u vx λλλλλλλ=+=+=+⋅=⋅⋅⋅.3)三角不等式.()()1111, , , , , , , , , , , TTm m m n m m m n m n x y ξξξξηηηη+++++∀==∈ C ,记()()()()11112121, , , , , , , , , , , TTTTm m m n m m m n u v u v ξξξξηηηη++++==== ,则12121212aba ab bu u v v u v x y u y v x =+++++++=≤+.由定义知⋅是m n +C 上的一种向量范数. 2.()()()11, , , , , , m n Tm m n m n m m n A x ξξξξ+⨯++++∀∀∈=∈ CC ,将A 和x 分块为11122122A A A A A ⎛⎫=⎪⎝⎭及u x v ⎛⎫= ⎪⎝⎭,其中11122122, , , ,m m m n n m n n A A A A ⨯⨯⨯⨯∈∈∈∈C C C C mu ∈C ,n v ∈C ,则1112111221222122A A A u A v u Ax A A A u A v v +⎛⎫⎛⎫⎛⎫==⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭, 1112212211122122a b a a b b A u A v A u A v A u A v A u v A A x =+++≤+++111111122122m m m m a b ba u u A v vA A A ⋅+⋅+⋅+⋅≤()()11111111211222aa m m m m bbm m AA u u vA vA AA⋅+⋅⋅+=+⋅+≤()11,bm m a v u x AA=+=⋅⋅所以()()m n m n +⨯+C 上的矩阵范数1m ⋅与上面定义的向量范数⋅相容.三、(18分) 1.(8分)设()ijn nX x ⨯=是矩阵变量,且det 0X ≠.求()1det TdX dX-; 2.(10分)设1011A ⎛⎫= ⎪⎝⎭.求矩阵幂级数()()12211121!k k k k A t k --+∞=--∑的和. 解. 1.()111det , det det n nik ik ij ij ik ik k k jX X x X x X x X X -=≠===+∑∑,其中ik X 是ik x 的代数余子式,()det ij ijX X x ∂=∂,从而()()()()122det 11det det det det ij ijij ijX X X x x Xx X X -∂∂∂⎛⎫==-⋅=-⎪∂∂∂⎝⎭, ()()()()111*22de 1det de t 1de det t t TTij i Tj d X X dX X X X X x X X ---⎛⎫⎛⎫∂ ⎪==-=-= ⎪ ⎪- ⎪∂⎝⎭⎝⎭. 2.()()()()11221221111si 1121!!n 21k k k k k k k k A t A t A A At k k ----+∞+∞==---==--∑∑.()210111I A λλλλ--==---. 设()()()()120sin ,1b t b q t t t λλλλ=-++.在该式及对其两边关于λ求导后的式子中,将1λ=代入得()()()101sin ,cos ,t b t b t t t b t =+⎧⎪⎨=⎪⎩ 解得()()01sin cos co s , b t t t t b t t t =-=. 从而()()()101010cos sin cos .110sin 0sin cos sin 1t t t t tAt b t A b t I t t t t ⎛⎫=+⎛⎫⎛⎫=+-= ⎪ ⎝⎭⎝⎪⎭⎪⎭⎝()()()()112212211111011sin 1121!21!sin 0cos sin k k k k k k k k A t A t A A At k k t t t t ----+∞+∞=-=--⎛⎫===⎪-⎛-⎝⎭⎫⎪⎝⎭∑∑ sin 0sin cos sin t t t t t +=⎛⎫ ⎪⎝⎭.四、(14分) 设112010232A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭.1.(8分)求矩阵A 的Crout 分解;2. (6分)利用Crout 分解求方程Ax b =的解,其中()1, 1, 1Tb =-.解.1.设111213212223313233001001001l r r A l l r ll l ⎛⎫⎛⎫⎪⎪= ⎪⎪ ⎪⎪⎝⎭⎝⎭. 由Crout 分解的紧凑计算格式得 11111l a ==, 212131310, 2l a l a ====, 1312121311111, 2,a a r r l l ==== 222221121,l a l r =-=- 323231121,l a l r =-= ()232321132210,r a l r l =-= 3333311332232,l a l r l r =--=-故A 的Crout 分解为111201102120010000A ⎛⎫⎛⎫ ⎪⎪= ⎪⎪ ⎪⎝⎝-⎭-⎪⎭.2. 由 123101212001011y y y ⎛⎫⎛⎫⎛⎫⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎭--⎝ 解得123111y y y ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎝-⎪⎝⎭⎭, 再由 123101*********x x x ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪=- ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭解得123011x x x ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎝-⎪⎝⎭⎭, 即方程Ax b =的解的解为 011x ⎛⎫ =-⎪⎪ ⎪⎝⎭.五、(14分) 利用Gerschgorin 定理及特征值的隔离方法判断矩阵1211621111A -⎛⎫ ⎪= ⎪ ⎪⎝⎭是否有小于零的特征值,并估计A 的每个特征值的分布范围.证明.1. A 有小于零的特征值.A 的三个行盖尔圆为{}{}{}123 , 136,311 2 n n n G z G z z z z G z +-=∈=∈-≤=∈≤≤C C C ,三个列盖尔圆为{} {} {}123 , 126,311 3 n n n Gz G z z z z G z +-=∈=∈-≤=∈≤≤C C C . 1G 与 1G 均为孤立的盖尔圆,且 11G G ⊂,而2G 与3G 相交, 2G 与 3G 也相交.由盖尔圆定理知 1G 中有A 的一个特征值,() ()2323G G G G 中有A 的两个特征值. 令111115522251611521, 1215B D D AD -⎛⎫ ⎪ ⎪===⎛⎫ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎪, 则1B 与A 相似,从而与A 有相同的特征值.1B 的三个列盖尔圆为{}1112, ,41665 n B n B z z G z G z ⎧⎫=∈=∈⎨⎬⎩⎭-≤+≤C C139 2 11n B z z G -⎧⎫=∈⎨⎩⎭≤⎬C . 11B G仍为孤立的盖尔圆.由盖尔圆定理知 11B G 中仍有且仅有1B 的一个特征值. 由于1B 为实矩阵,其特征多项式为实系数多项式,从而其特征值如为复数,则必共轭成对出现.注意到 11B G的圆心为()1, 0-,在实轴上, 11B G 关于实轴对称,如果含有复特征值,则其共轭的特征值也在 11B G 中,与每个孤立盖尔圆中只有一个特征值矛盾.因此,含于 11B G中的该特征值必为实数,即位于实轴上.再注意到 11B G 的半径为45知,该特征值位于闭区间91, 55⎡⎤--⎢⎥⎣⎦中,故1B ,从而A ,有一个小于零的特征值.2. 令122228433324351, 31161114B D D AD -⎛⎫ ⎪ ⎪===⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭⎪,则2B 与A 相似,从而与A 有相同的特征值.2B 的三个行盖尔圆为{}123117146114, , 4 n n n G z G z G z z z z ⎧⎫⎧⎫=∈=∈=∈⎨⎬⎨⎬⎩⎭≤≤+-⎭-≤⎩C C C , 它们是3个孤立的盖尔圆,从而每个盖尔圆中各有2B ,即A 的一个特征值.由与上面相同的推理知,每个特征值均为实数,都位于实轴上,故A 的特征值分别位于[]5, 3-,1335, 44⎡⎤⎢⎥⎣⎦和 3751, 44⎡⎤⎢⎥⎣⎦中.综合1.的结果知,A 的3个特征值分别位于91, 55⎡⎤--⎢⎥⎣⎦,1335, 44⎡⎤⎢⎥⎣⎦ 和 3751, 44⎡⎤⎢⎥⎣⎦中.六、(22分)设101101, 102102A D ⎛⎫⎛⎫⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭.1.(8分)求A 的全部{}1逆;2.(8分)求A 的加号逆A +;3.(6分)判断矩阵方程AX D =是否有解.解.1.3221010101210111111111100002000001000000000000000000000AI TI I S ⎛⎫⎛⎫⎪⎪⎛⎫ ⎪ ⎪⎛⎫⎪ ⎪ ⎪=→⎪ ⎪⎪⎪⎝⎭ ⎪⎝⎭⎪ ⎪ ⎪ ⎪⎝⎭⎝--⎭- , 1001010101201001010121211a a a a a T S b b b b b ⎛⎫-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪=-= ⎪ ⎪⎪ ⎪ ⎪--+⎝⎭⎝⎭⎝⎭⎝⎭ ⎪-⎝⎭,故A 的全部{}1逆为{}12 , 112a a a b a A b b b ⎧⎫-⎛⎫⎪⎪=⎨⎬ ⎪--+⎝⎭⎪⎪⎩⎭任意. 2.A 为列满秩矩阵,故A 的加号逆为111010210252102010110112201121A --+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥ ⎪=-= ⎪ ⎪ ⎪ ⎪⎢⎥ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭ ⎪⎢⎥⎝⎭⎣⎦ 22212221021250116516-⎛⎫⎛⎛⎫⎪-⎫== ⎪⎪--⎝⎝-⎝⎭⎭⎭. 3. 在A 的{}1逆的集合{}1A 中取A 的一个{}1逆()1A =100010⎛⎫⎪-⎝⎭.由教材定理 6.5知AX D =有解的充要条件是()1AA D D =.计算得()1101110011110110010101021022100212100010AA D D ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪=-== ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎛⎫⎭⎝⎭⎝⎭⎪⎝⎭≠-, 故矩阵方程AX D =无解.中南大学2013年秋季硕士研究生《矩阵论》考试试题考试形式:开卷 时间:120分钟 总分:100分姓名 学号一、 (16分) 设A 为3阶Hermite 矩阵,||12A =−, ()1tr A =,且()1, 0, 2T i 为()40A I x ∗−=的一个解,其中I 为单位矩阵, A ∗为A 的伴随矩阵.1. (8分) 确定t 的取值范围,使ln()I At +有定义;2. (8分) 求A .二、(16分) 记所有形如00A M B =的矩阵(其中,A B 分别为m 和n 阶方阵)的集合为Ω.对每个00A MB Ω=∈(其中()ij m m A a ×=,()pq n n B b ×=),定义 1,11||||||max ||m mijpq p q ni j M an b ≤≤===+⋅∑∑.1.(10分) 证明M 是Ω上的一种矩阵范数;2.(6分) 证明M 与C m n +上的向量1范数相容.三、(18分) 1.(8分) 设()ijm nA a ×=是给定的矩阵,()ijn mX x ×=是矩阵变量,且()()f X tr XA =.求()Tdf X dX; 2.(10分)设2102A − =.求||A e 及AtAe .四、(14分) 设313010431A=−−.求矩阵A 的QR 分解.五、(16分) 利用Gerschgorin 定理及特征值的隔离方法判断矩阵1.511121219A −=是否可逆,并估计A 的每个特征值的分布范围.六、(20分)设1001010, 02100A b=−=.1.(12分)求A 的加号逆A +;2.(8分)利用加号逆判断方程Ax b =是否有解,并在有解时求其极小范数解,无解时求其极小范数最小二乘解.2013年矩阵论试题参考答案一、 (16分) 设A 为3阶Hermite 矩阵,||12A =−, ()1tr A =,且()1, 0, 2Ti为()40AI x ∗−=的一个解,其中I 为单位矩阵, A ∗为A 的伴随矩阵. 1. (8分) 确定t 的取值范围,使ln()I At +有定义; 2. (8分) 求A . 解 1. 设A 的三个特征值为123,,λλλ.依题意有12312312,,1λλλλλλ=−++=.记()11, 0, 2,T iξ= 则()140A E ξ∗−=,()11240E A ξ−−=,即()130E A ξ−−=,从而3−是A 的一个特征值,1ξ是对应的特征向量.代入前面的式子可算得A 的另两个特征值为2, 2. 所以()3,()3||A At t ρρ==. 故使ln()I At +有定义的t 须满足()3||1At t ρ=<, 即1||3t <. 2. 由Hermite 矩阵的不同特征值所对应的特征向量正交知,特征值2所对应的特征向量与1ξ正交,从而满足方程1320z iz −=,由此解得特征向量()()230, 1, 0, 2, 0, 1T Ti ξξ==. 将三个特征向量正交化单位化得酉矩阵00100U =, 满足322H U AU − =,从而0033102201020100202220200H i A U U i −−===−−.二、(16分) 记所有形如00A M B= 的矩阵(其中,A B 分别为m 和n 阶方阵)的集合为Ω.对每个00A M B Ω=∈(其中()ijm mA a ×=,()pqn nB b ×=),定义1,11||||||max ||m mijpq p q ni j M an b ≤≤===+⋅∑∑.1.(10分) 证明M 是Ω上的一种矩阵范数;2.(6分) 证明M 与C m n +上的向量1范数相容.证明 1.易知1||||||||||||m m M A B ∞=+,1||||,||||m m A B ∞都是矩阵范数.1)非负性. 当0M =时,必有0,0A B ==,从而1||||||0||||0||0m m M ∞=+=. 当0M ≠时,必有0A ≠或0B ≠,从而1||||0m A >或||||0m A ∞>, 1||||||||m M A =||||0m B ∞+>.2)齐次性. 0 0,C A M B λ∀∈∀=∈Ω,有00A M B λλλ = ,()111m m m m m m M A BA BA BMλλλλλλλ∞∞∞=+=⋅+⋅=⋅+=⋅.3)三角不等式. 12121200,00A A M M B B ∀==∈,12121200A A M M B B ++= +,111121212121212m m m m m m M M A A B B A A B B M M ∞∞∞+=+++≤+++=+.4)乘积不等式. 12121200,00A A M M B B ∀==∈,12121200A A M M B B=, 1111212121212m m m m m m M M A A B B A A B B ∞∞∞=+≤+()()11112212m m m m A B AB MM ∞∞≤++=⋅.由定义知M 是Ω上的一种矩阵范数.2.00A M B ∀=∈ Ω,12C m n x x x + = ∈ ,其中12,C C m nx x ∈∈, 12Ax Mx Bx =.由1||||,||||m m A B ∞都与向量1范数相容得1112121111111m m m m Mx Ax Bx A x Bx A x Bx ∞∞=+≤+≤+()111m m A BxM x ∞=+=⋅,所以Ω上的矩阵范数M 与C m n +上的向量1范数相容.三、(18分) 1.(8分) 设()ijm nA a ×=是给定的矩阵,()ijn mX x ×=是矩阵变量,且()()f X tr XA =.求()Tdf X dX; 2.(10分)设2102A − =.求||A e 及AtAe . 解 1.()1111()n mn m kl lk ij ji kl lkij ji k l k l f X tr XA x a x a x a x a =======+− ∑∑∑∑,()ji ij f X a x ∂=∂,故 ()()()()TT ji ijTij df X f X a a A dX x∂====∂.2. ()221202I A λλλλ−−==−−,故A 的特征值为2,2,A e 的特征值为22,e e ,故224||.A e e e e ==再设()()()()210,2te q t b t b t λλλλ=−++.在该式及对其两边关于λ求导后的式子中,将2λ=代入得()()()210212,,tteb t b t te b t =+ = 解得 ()()222012, tttb t e te b t te =−=.从而()()()2222210221102.02010t t Att t t t e te e b t A b t I te e te e −− =+=+−=2222222212202002t t tt t At t t e te e te e Ae e e −−−− ==.四、(14分) 设313010431A=−−.求矩阵A 的QR 分解.解 用Givens 变换求A 的QR 分解.A 的第一列为304,取 133405501043055T = −得 133403135315501001001043431013055T A=−=− −− −. 13T A 的右下角的2阶矩阵第一列为11− ,再取2310000T=得23131005315310010*******T T A R=−= −3. 令132333410005550100043040555H HQ T T−===, 则Q 为酉矩阵,且A 的QR 分解为35315004005A QR== .五、(16分)利用Gerschgorin定理及特征值的隔离方法判断矩阵1.511121219A−=是否可逆,并估计A的每个特征值的分布范围.解A的三个行盖尔圆为:{}{}{} 1231.52,,2293 n n nzG z G z zz G z=∈=∈=+≤−≤≤∈−C C C.三个列盖尔圆为:{}{}{} 1231.5,,32292 n n nG z Gz z z G z z′′′=∈=∈+≤−≤−≤=∈C C C.3G与3G′都为孤立的盖尔圆,且33G G′⊂,而1G与2G相交,1G′与2G′也相交.由盖尔圆定理知3G′中有A的一个特征值,1G与2G的并中有A的两个特征值.取12391,,4d d d===.令112341.5194,12999924dD d B DADd−−===,则B与A相似,从而与A有相同的特征值.B的三个行盖尔圆为:1231313271.52, 99,94 n n nG z G zz z G z z+≤−=∈=∈=∈≤−≤C C C1G是一个孤立的盖尔圆, 2G与 3G相交,由盖尔圆定理知, 1G中有A的一个特征值,2G与 3G的并中有B的两个特征值.而 1G及 2G与 3G的并都不包含原点,故B的三个特征值中都不等于零,B可逆,从而A也可逆.由于A,B都为实矩阵,其特征多项式都为实系数多项式,从而其特征值如为复数,则必共轭成对出现.注意到123,,G G G 及 123, , G G G 的圆心都在实轴上,123,,G G G 及 123, , G G G都关于实轴对称,如果含有复特征值,则其共轭的特征值也在同一个盖尔圆中,与每个孤立盖尔圆中只有一个特征值矛盾.因此,B 的特征值,从而A 的特征值都为实数.综上,A 有两个特征值分别位于孤立的盖尔圆 1G 和3G ′的实轴上,即位于实数区间 531, 1818 −− 和[]7, 11中.而另一个特征值位于 () ()123123\\G GG G G G G G 的实轴上,即位于155, 2, 6, 21899 −=中.所以,A 的特征值分别位于区间531, 1818 −− ,5, 29 和 []7, 11中.六、(20分)设1001010, 02100A b=−=.1.(12分)求A 的加号逆A +;2.(8分)利用加号逆判断方程Ax b =是否有解,并在有解时求其极小范数解,无解时求其极小范数最小二乘解.解 1. 100100010010, 210000A=−→A 的满秩分解为101000101021A=−,1101010100100100010101010010010212121HH HH HA −+ −−− 1110101052102221021010101220112501160000−−− = −−−。
中南大学粉末冶金研究院硕士研究生入学历考试粉末冶金原理真题详解

中南⼤学粉末冶⾦研究院硕⼠研究⽣⼊学历考试粉末冶⾦原理真题详解名词解释<2000年)1、氢损值---⽤氢还原,计算粉末还原前后的重量变化。
2、还原终点:浮斯体还原成海绵铁和海绵铁开始渗碳过程之间的转折点。
3、活化烧结:系指能降低烧结活化能,使体系的烧结在较低的温度下以较快的速度进⾏、烧结体性能得以提⾼的烧结⽅法。
4、拱桥效应<搭桥):颗粒间由于摩擦⼒的作⽤⽽相互搭架形成拱桥孔洞的现象5机械合⾦化:⽤⾼能研磨机或球磨机实现固态合⾦化的过程。
机械合⾦化是⼀个通过⾼能球磨使粉末经受反复的变形、冷焊、破碎,从⽽达到元素间原⼦⽔平合⾦化的复杂物理化学过程。
⼀种⾼能球磨法,可制造具有可控细显微组织的复合⾦属粉末,它是在⾼速搅拌球磨的条件下,利⽤⾦属粉末混合物的重复冷焊和断裂进⾏的机械和进化。
(2001>1、压缩性:表⽰粉末在指定的压制条件下,粉末被压紧的能⼒。
2、还原终点<2)3、露点:在标准⼤⽓压下,⽓氛中⽔蒸汽开始凝结的温度,⽓氛中含⽔量愈多,露点愈⾼。
4、瞬时液相烧结:在烧结中、初期存在液相,后期液相消失的烧结过程<2002)1、露点<2)2、瞬时液相烧结<2)3、挥发-沉积:氢中⽔分⼦与钨氧化物反应⽣成挥发性的⽔合物,WOX +H2O→WOX.nH2O(g> ↑,⽓相中的钨氧化物被氢还原沉积在钨颗粒上,导致W颗粒长⼤。
4、松装密度:粉末⾃由充满规定的容积内所具有的粉末重量成为松装密度5、粉末克⽐表⾯:1克质量的粉末所具有的总表⾯积,m2/g。
6、显微硬度:不同⽅法⽣产同⼀种⾦属的粉末,显微硬度是不同。
⼀般来讲,指的是采⽤普遍的显微硬度计测量⾦刚⽯⾓锥压头的压痕对⾓线长,经计算得到的。
颗粒的显微硬度值,在很⼤程度上取决于粉末中各种杂质与合⾦组元的含量以及晶格缺陷的多少,因此代表了粉末的塑性。
<2003)1、松装密度<2)2、压缩性<2)3、体积⽐表⾯:单位体积粉末所具有的总表⾯积4、弹性后效:粉末经模压推出模腔后,由于压坯内应⼒驰豫,压坯尺⼨增⼤的现象称作弹性后效。
(整理)中南大学年自然辩证法概论硕士研究生.

中南大学2010年硕士研究生《自然辩证法概论》课程结束考试题说明:1、开卷考试,独立完成。
2、考试时间为120分钟。
3、本试卷为全日制研究生和非全日制研究生(高校教师班研究生)公用试卷。
非全日制研究生在第3道答题中有不同要求。
其余各题的答题要求完全相同。
一、请在所给定的备选答案a、b、c、d中做出唯一性选择。
(每小题2分,满分共计40分)1、以下哪一个问题可以在科学技术学的学科范围内研究?a、探索创造新医术的可能性b、评价新医术的安全性c、比较新医术与传统医术之间的差异d、为新医术的使用立法2、以下哪一项思想建设是“自然辩证法概论”责无旁贷的教学责任?a、遵纪守法b、尊重科学,反击伪科学、迷信和神秘主义c、决策民主化d、政治和经济生活中廉洁自律3、按照英国哲学家卡尔·皮尔逊的观点,科学家的主要职责是a、严格而公正地认定事实b、严格而公正地表述事实c、严格而公正地分析事实d、严格而公正地收集事实4、以下哪一种科学是按照几何学规范(亦称“几何学传统”)建立的?a、电磁学b、化学c、病理学d、生物学5、最早通过实验证明的方式对外部世界做出判断的哲学家是:a、恩培多克勒b、苏格拉底c、柏拉图d、亚里士多德6、以下哪一种追求真理的方式属于信仰主义真理观?a、通过坚定地相信解决充分地理解问题b、通过充分地理解解决坚定地相信问题c、对于不理解的东西采取不相信的态度d、对于尚未明确是非的问题采取回避态度7、以下哪一个陈述是正确的?a、正确的就是科学的b、有效即真理c、经验证明就是一切d、科学性伴随着可错性8、以下哪一个思维过程不可能在经验主义的思维框架下完成?a、概括同类事物的共性b、把不同事物之间的相关性整理成“秩序”c、对经验过程不可企及的事物做出真理性判断d、以上三者9、以下哪一种技术演化现象属于“技术的异化”?a、把一种技术转化为另一种技术b、技术进步为道德败坏开启了方便之门c、采用先进的技术不能确保取得相应的商业利益d、将一种技术嫁接到另一种技术上10、以下哪一种判断属于依据“立木经济”的经济观做出的判断?a、这棵树长大以后可以做切菜的垫板b、这棵树可以为鸟类动物提供栖息场所c、这棵树具有可观的药用价值d、这是一棵材质难得的树11、以下哪一种经济模式属于“用后即弃”模式?a、资源——产品——垃圾b、资源——生产资料——消费资料c、垃圾——资源——产品d、废品——翻新产品——商品12、以下哪一个陈述可以作为科学研究的经验基础使用a、一个患者对医生说:“我自从使用手机以来就感到头晕。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中南大学2010年硕士研究生《自然辩证法概论》课程结束考试题
说明:1、开卷考试,独立完成。
2、考试时间为120分钟。
3、本试卷为全日制研究生和非全日制研究生(高校教
师班研究生)公用试卷。
非全日制研究生在第3道答
题中有不同要求。
其余各题的答题要求完全相同。
一、请在所给定的备选答案a、b、c、d中做出唯一性选择。
(每小题2分,满分共计40分)
1、以下哪一个问题可以在科学技术学的学科范围内研究?
a、探索创造新医术的可能性
b、评价新医术的安全性
c、比较新医术与传统医术之间的差异
d、为新医术的使用立法
2、以下哪一项思想建设是“自然辩证法概论”责无旁贷的教学责任?
a、遵纪守法
b、尊重科学,反击伪科学、迷信和神秘主义
c、决策民主化
d、政治和经济生活中廉洁自律
3、按照英国哲学家卡尔·皮尔逊的观点,科学家的主要职责是
a、严格而公正地认定事实
b、严格而公正地表述事实
c、严格而公正地分析事实
d、严格而公正地收集事实
4、以下哪一种科学是按照几何学规范(亦称“几何学传统”)建立的?
a、电磁学
b、化学
c、病理学
d、生物学
5、最早通过实验证明的方式对外部世界做出判断的哲学家是:
a、恩培多克勒
b、苏格拉底
c、柏拉图
d、亚里士多德
6、以下哪一种追求真理的方式属于信仰主义真理观?
a、通过坚定地相信解决充分地理解问题
b、通过充分地理解解决坚定地相信问题
c、对于不理解的东西采取不相信的态度
d、对于尚未明确是非的问题采取回避态度
7、以下哪一个陈述是正确的?
a、正确的就是科学的
b、有效即真理
c、经验证明就是一切
d、科学性伴随着可错性
8、以下哪一个思维过程不可能在经验主义的思维框架下完成?
a、概括同类事物的共性
b、把不同事物之间的相关性整理成“秩序”
c、对经验过程不可企及的事物做出真理性判断
d、以上三者
9、以下哪一种技术演化现象属于“技术的异化”?
a、把一种技术转化为另一种技术
b、技术进步为道德败坏开启了方便之门
c、采用先进的技术不能确保取得相应的商业利益
d、将一种技术嫁接到另一种技术上
10、以下哪一种判断属于依据“立木经济”的经济观做出的判断?
a、这棵树长大以后可以做切菜的垫板
b、这棵树可以为鸟类动物提供栖息场所
c、这棵树具有可观的药用价值
d、这是一棵材质难得的树
11、以下哪一种经济模式属于“用后即弃”模式?
a、资源——产品——垃圾
b、资源——生产资料——消费资料
c、垃圾——资源——产品
d、废品——翻新产品——商品
12、以下哪一个陈述可以作为科学研究的经验基础使用
a、一个患者对医生说:“我自从使用手机以来就感到头晕。
”
b、一个医生对接受治疗以后的患者说:“我看你今天的气色比昨天好多了。
”
c、一个尸检人员报告说:“在这位死者的肺部发现了一种新型的病毒。
”
d、一个哲学家说:“患者坚强的意志帮助他战胜了顽疾。
”
13、脑筋急转弯这种语言恶作剧犯了什么逻辑错误?
a、概念蕴含关系不一致
b、概念的时间指称混乱
c、概念的构造违背排中律
d、给出概念不符合简单性原则
14、以下哪一种与科学对立的东西完全蔑视科学方法?
a、原生科学
b、伪科学
c、在科学研究中犯错误
d、在科学研究中作弊
15、以下哪一种技术属于知识形态的技术
a、开车
b、勾兑白酒
c、改进合金工艺
d、进口的生产流水线
16、下列哪两个概念具有交叉关系
a、物理学和化学
b、男人和女人
c、老人和教师
d、动物和猫
17、早晨看到的太阳显得比中午看到的太阳大。
它最可能是以下哪一种原因造成的?
a、早晨的太阳以太阳赤道面对着地球,中午的太阳以太阳极地面对着地球
b、早晨的太阳与中午的太阳具有不同的观察环境。
c、早晨的太阳光线弱些,中午的太阳光线强些
d、早晨的太阳离地球近些,中午的太阳离地球远些
18、以下哪一个判断无意义?
a、绝对零度是达不到的
b、辩证唯物主义是最高意义上的科学
c、明天可能下雨也可能不下雨
d、假若今夜起东风,则明天清晨会下雨
19、以下哪一种创新属于反求创新?
a、把古老的陶瓷生产技术开发为工业陶瓷
b、在消化引进的基础上优化引进技术
c、通过工业间谍窃取他人新技术
d、把业已成熟的技术做一次“反过来”的研究尝试。
20、以下不属于研究工作的是?
a、为产品全面进入市场做试销调研
b、法医解剖不明原因死亡的尸体
c、为产品销售编写和翻译产品说明书
d、以上三者
二、简单回答下列问题。
(每小题6分,满分共计30分)
1、穆勒总结了五种析因方法。
请选择其中一种析因方法举例说明之。
(说明:多举例不多给分;照抄书本不给分。
)
2、当我们被暗示一尊石头“像猴子”之后,会出现“越看越像”的观察后果,这是什么原因造成的?试予以解释。
3、某企业在亏损300万元之后,国家拨给该企业400万元解困专款,运行两年以后,企业
不但没有解困,反而在原来亏损300万元的基础上再增加亏损了80万元。
这是为什么?试用复杂性系统演化的理论给以定性解释。
4、某统计学家,依据某市住院病人的死亡率西医医院高于中医医院做出判断说,中医比西医优越。
这样的判断合理吗?为什么?
5、可以通过对氢和氧的研究来研究水的物理性质和化学性质吗?为什么?
三、阅读下列科学史例,然后简单回答所附的问题。
(高校教师进修班的同学可以选做其中两道题,每小题15分。
其它各班要求三题全做,每小题10分。
)
热学在18世纪曾经经历了一次重大的变革。
瓦特和布莱克曾经非常相信“热质说”。
依据这个学说,“热”被理解为能使物体产生热感的流体,即热质;这种流体具有渗透一切物体使温度升高的能力;热质既不能被创造,也不能被消灭;它不能由别的东西来转化或合成,也不能转化或合成其他的东西。
热质说的实验检验曾经非常成功。
比如,把1000克的铅块、铁块和铝块分别加热到100摄氏度,然后取出,立即同时分别放在纯水结的冰块上,三块金属疙瘩所能溶化的冰的量不同。
这种现象完全符合热质说的预言:相同质量的不同物质被加热到相同温度时,它们含的热质不同。
不同物质具有不同的热容量,而且不同物质升高相同温度所需要的热量不同。
瓦特依据这个原理,利用不同材质的吸热特点,改进了纽可门蒸汽机的气缸,提高了热效率,最后引发了席卷世界的工业革命。
可是,到18世纪末,汉弗莱·戴维爵士(Sir Humphry Davy)在真空的实验器皿里,用一架钟表机件,使两块冰相互摩擦,摩擦实验的环境温度始终保持在冰点,以保证在实验过程中不受外界传热的影响。
实验的结果是,两块冰在摩擦一段时间之后全部融化了。
这个实验暗示人们,热质并不一定需要外部引入,运动本身就可以产生热质。
以后,又有焦耳在运动和热之间建立了“当量关系”。
从那以后,热被认为是由物体的运动造成的,而不是由物体蕴含的热质造成的。
依据这个科学史实,请你回答以下问题:
问题一:热质说是否属于伪科学?为什么?
问题二:既然热质说指导瓦特成功地改良了纽可门蒸汽机,并由此引发了工业革命,为什么我们还要放弃热质说?
问题三:依据科学理论建设的自洽性原则,热动说应该完满解释已经被热质说成功解释过的热学现象。
在以上史料中,哪一个热学现象需要热动说做出新的解释?。
