控制工程-第二次课
第二次课 水质与水体自净

混
沉
过
消
供
水
凝
淀
滤
毒
水
二、废水处理基本方法:
非持久性污染物的稀释扩散和降解
河断面达到充分混合后,污染物浓度受到纵向分散作用和 污染物的自身分解作用不断减小。根据质量守恒原理,其变化 过程可用下式描述:
c
c0
exp
vx 2M
x
1
1
4KM x v2
式中:v——河水流速;
x——初始点至下游x断面处的距离;
Mx——纵向分散系数; K——污染物分解速度常数;
有
在950℃高温下,以铂作为催化剂,使水样气化燃烧,然后测定气体 中的CO2含量,从而确定水样中碳元素总量。
测定中应该去除无机碳的含量。
机
TOD: total oxygen demand 在900~950℃高温下,将污水中能被氧化的物质(主要是有机物,
包括难分解的有机物及部分无机还原物质),燃烧氧化成稳定的氧
化学性指标
过多的氮、磷进入天然水体,易导致
植物营
富营养化,使水生植物尤其是藻类大量繁
无
养元素
殖,造成水中溶解氧急剧变化,影响鱼类
生存,并可能使某些湖泊由贫营养湖发展
为沼泽和干地。
机
一般要求处理后污水的pH在6~9之
性
pH和碱度
间。当天然水体遭受酸碱污染时,pH发 生变化,消灭或抑制水体中生物的生长,
机
酚浓度低时,能影响鱼类的洄游繁殖。 酚浓度达0.1~0.2mg/L时,鱼肉有酚味。
酚浓度高会引起鱼类大量死亡,甚至绝迹。
酚的毒性可抑制水中微生物的自然生长速度,有时甚
物 至使其停止生长。
酚能与饮用水消毒氯产生氯酚,具有强烈异臭(0.001
《控制工程理论基础》课后答案

目录第一章自动控制系统的基本原理第一节控制系统的工作原理和基本要求第二节控制系统的基本类型第三节典型控制信号第四节控制理论的内容和方法第二章控制系统的数学模型第一节机械系统的数学模型第二节液压系统的数学模型第三节电气系统的数学模型第四节线性控制系统的卷积关系式第三章拉氏变换第一节傅氏变换第二节拉普拉斯变换第三节拉普拉斯变换的基本定理第四节拉普拉斯逆变换第四章传递函数第一节传递函数的概念与性质第二节线性控制系统的典型环节第三节系统框图及其运算第四节多变量系统的传递函数第五章时间响应分析第一节概述第二节单位脉冲输入的时间响应第三节单位阶跃输入的时间响应第四节高阶系统时间响应第六章频率响应分析第一节谐和输入系统的定态响应第二节频率特性极坐标图第三节频率特性的对数坐标图第四节由频率特性的实验曲线求系统传递函数第七章控制系统的稳定性第一节稳定性概念第二节劳斯判据第三节乃奎斯特判据第四节对数坐标图的稳定性判据第八章控制系统的偏差第一节控制系统的偏差概念第二节输入引起的定态偏差第三节输入引起的动态偏差第九章控制系统的设计和校正第一节综述第二节希望对数幅频特性曲线的绘制第三节校正方法与校正环节第四节 控制系统的增益调整 第五节 控制系统的串联校正 第六节 控制系统的局部反馈校正 第七节 控制系统的顺馈校正第一章 自动控制系统的基本原理定义:在没有人的直接参与下,利用控制器使控制对象的某一物理量准确地按照预期的规律运行。
第一节 控制系统的工作原理和基本要求 一、 控制系统举例与结构方框图例1. 一个人工控制的恒温箱,希望的炉水温度为100C °,利用 表示函数功能的方块、信号线,画出结构方块图。
图1人通过眼睛观察温度计来获得炉内实际温度,通过大脑分析、比较,利用手和锹上煤炭助燃。
煤炭给定的温度100 C手和锹眼睛实际的炉水温度比较图2例2. 图示为液面高度控制系统原理图。
试画出控制系统方块图 和相应的人工操纵的液面控制系统方块图。
过程控制工程课程设计

过程控制工程 课程设计一、课程目标知识目标:1. 让学生掌握过程控制工程的基本概念,理解控制系统的结构、原理及分类。
2. 使学生了解过程控制系统中各环节的作用,掌握主要参数的测定与调整方法。
3. 帮助学生理解过程控制系统的数学模型,并学会运用相关理论分析控制系统的性能。
技能目标:1. 培养学生运用所学理论知识,分析实际过程控制工程问题的能力。
2. 培养学生设计简单的过程控制系统方案,并进行模拟与优化的能力。
3. 培养学生团队协作、沟通表达和动手实践的能力。
情感态度价值观目标:1. 培养学生对过程控制工程的兴趣,激发他们探究未知、解决问题的热情。
2. 培养学生严谨、务实的科学态度,使他们具备良好的工程素养。
3. 引导学生关注过程控制工程在国民经济和生活中的应用,提高他们的社会责任感。
本课程针对高年级学生,结合过程控制工程学科特点,注重理论与实践相结合,旨在提高学生的专业知识水平、实际操作能力和综合素养。
课程目标明确、具体,便于教师进行教学设计和评估,同时有利于学生明确学习方向,提高学习效果。
二、教学内容1. 过程控制工程基本概念:控制系统定义、分类、性能指标。
教材章节:第一章第一节2. 控制系统数学模型:传递函数、方框图、信号流图。
教材章节:第一章第二节3. 控制系统元件及环节:传感器、执行器、控制器、滤波器等。
教材章节:第二章4. 过程控制系统设计:系统建模、控制器设计、系统仿真。
教材章节:第三章5. 常见过程控制系统分析:PID控制、模糊控制、自适应控制。
教材章节:第四章6. 过程控制系统应用实例:化工、热工、电力等领域。
教材章节:第五章教学内容安排和进度:第一周:过程控制工程基本概念第二周:控制系统数学模型第三周:控制系统元件及环节第四周:过程控制系统设计第五周:常见过程控制系统分析第六周:过程控制系统应用实例教学内容根据课程目标进行选择和组织,确保科学性和系统性。
通过制定详细的教学大纲,明确教材章节和内容,有助于教师按计划进行教学,同时便于学生跟进学习进度。
控制工程基础课后答案

第二章2.1求下列函数的拉氏变换 (1)ss s s F 232)(23++=(2)4310)(2+-=s s s F(3)1)(!)(+-=n a s n s F (4)36)2(6)(2++=s s F(5) 22222)()(a s a s s F +-= (6))14(21)(2s s s s F ++= (7)521)(+-=s s F 2.2 (1)由终值定理:10)(lim )(lim )(0===∞→∞→s t s sF t f f (2)11010)1(10)(+-=+=s s s s s F 由拉斯反变换:t e s F L t f ---==1010)]([)(1 所以 10)(lim =∞→t f t2.3(1)0)2()(lim )(lim )0(2=+===∞→→s ss sF t f f s t )0()0()()()](['2''0''f sf s F s dt e t f t f L st --==-+∞⎰)0()0()(lim )(lim'2''0f sf s F s dt e t f s st s --=+∞→-+∞+∞→⎰1)2()(lim )0(222'=+==+∞→s s s F s f s (2)2)2(1)(+=s s F , t te s F L t f 21)]([)(--==∴ ,0)0(2)(22'=-=--f te et f tt又,1)0('=∴f2.4解:dt e t f et f L s F st s --⎰-==202)(11)]([)( ⎰⎰------+-=2121021111dt e edt e e sts st s)11(11)11(11222s s s s se s e s e e s s e -------+--=22)1(111s s e se ---∙-=2.5求下列函数的拉氏反变换(1)t t f 2sin 21)(= (2)t e t t f -=361)((3)t t e e t f 32321)(+-=- (4)t t e e t f 235352)(+=-(5)t e t e t f t t 3sin 313cos 2)(22--+= (6)t t t e e te t f 222)(----+-=2.6(1)0)()()(22=--dtt y d m t ky t f(2)0)()()(222121=-+-dtt y d m t y k k k k t f 2.7(1)14312)(23++++=s s s s s G(2)210)(22++=-s s e s G s2.8 解 水的流量Q1由调节控制阀的开度控制,流出量Q2则根据需要可通过负载阀来改变,被调量H 反映了。
控制科学与工程研究生专业基础课程-2

)
§2 状态转移矩阵的求解
4)化矩阵A为约当标准型
若A为一个 m m 的约当块,其重复的特征值为 1
1 1
0
1 1
A
..
.
1
0
1 mm
(2-22)
§2 状态转移矩阵的求解
则
1 t
(m
1
1)
!
t
m1
e At e1t
1t
.
.
(m
1
2)
!
t
m1
...
.
..
.
整理有
X (s) (sI A)1 x(0)
(2-15)
取拉普拉斯反变换,可得齐次状态方程的解为
§2 状态转移矩阵的求解
x(t) L1 (sI A)1 x(0)
(2-16)
比较式(2-16)与式(2-6),且根据定常微分方程组解的唯一性,有
(t) eAt L1( SI A)-1
(2-17)
e(AB)t eAteBt
§2 状态转移矩阵的求解
2-1状态转移矩阵的求解方法
状态转移矩阵可以通过以下五种方法计算得到 1)直接级数展开法 根据矩阵指数的定义直接计算
(t) eAt I At 1 A2t2 …… 1 Aktk n 1 Aktk
2!
k!
K0 k !
例2-1
已知
A
0 2
1 3
k!
§1 自由运动
则齐次方程的解可表示为
x(t) eAt x(0)
(2-7)
若初始时刻 t0 0 ,对应的初始状态为 x(t0 ),则齐次方程
的解可表示为
x(t) eAtt0x(t0 )
中国石油大学北京12春《控制工程基础》第二次在线作业 复习

第4题
您的答案:C
题目分数:0.5
此题得分:0.5
批注:控制对象的定义
第5题
您的答案:B
题目分数:0.5
此题得分:0.5
批注:干扰的定义
第6题
您的答案:B
题目分数:0.5
此题得分:0.5
批注:利用负反馈的定义
第38题
您的答案:正确
题目分数:0.5
此题得分:0.5
批注:利用劳斯判据
第39题
您的答案:正确
题目分数:0.5
此题得分:0.5
批注:利用劳斯判据
第40题
您的答案:正确
题目分数:0.5
此题得分:0.5
批注:考虑传递函数形式
此题得分:0.5
批注:先写出原函数之后进行拉氏变换
第28题
您的答案:B
题目分数:0.5
此题得分:0.5
批注:先写出原函数,之后进行拉氏变换求得
第29题
您的答案:B
题目分数:0.5
此题得分:0.5
批注:拉氏反变换
第30题
第35题
您的答案:C
题目分数:0.5
此题得分:0.5
批注:采用化简法
第36题
您的答案:错误
题目分数:0.5
此题得分:0.5
批注:注意初始条件
第37题
您的答案:正确
题目分数:0.5
此题得分:0.5
批注:结合定义
您的答案:A
题目分数:0.5
此题得分:0.5
批注:采用部分分式法中多重极点及不同极点的拉氏反变换
控制工程基础课后习题答案

详细描述
通过调整系统的传递函数,可以改变系统的 频率响应特性。在设计控制系统时,我们需 要根据实际需求,调整传递函数,使得系统 的频率响应满足要求。例如,如果需要提高 系统的动态性能,可以减小传递函数在高频 段的增益。
06 第五章 控制系统的稳定性 分析
习题答案5-
习题答案
• 习题1答案:该题考查了控制系统的基本概念和组成。控制系统的基本组成包 括被控对象、传感器、控制器和执行器等部分。被控对象是实际需要控制的物 理系统或设备;传感器用于检测被控对象的输出状态,并将检测到的信号转换 为可处理的电信号;控制器根据输入的指令信号和传感器的输出信号,按照一 定的控制规律进行运算处理,并输出控制信号给执行器;执行器根据控制信号 对被控对象进行控制操作,使其达到预定的状态或性能要求。
控制工程基础课后习题答案
目 录
• 引言 • 第一章 控制系统概述 • 第二章 控制系统的数学模型 • 第三章 控制系统的时域分析 • 第四章 控制系统的频域分析 • 第五章 控制系统的稳定性分析 • 第六章 控制系统的校正与设计
01 引言
课程简介
01
控制工程基础是自动化和电气工 程学科中的一门重要课程,主要 涉及控制系统的基本原理、分析 和设计方法。
总结词
控制系统校正的概念
详细描述
控制系统校正是指在系统原有基础上,通过加入适当的 装置或元件,改变系统的传递函数或动态特性,以满足 性能指标的要求。常见的校正方法有串联校正、并联校 正和反馈校正等。校正装置通常安装在系统的某一环节 ,以减小对系统其他部分的影响。
习题答案6-
总结词
控制系统设计的一般步骤
习题答案5-
总结词
《控制工程基础》王积伟第二_课后习题解答完整
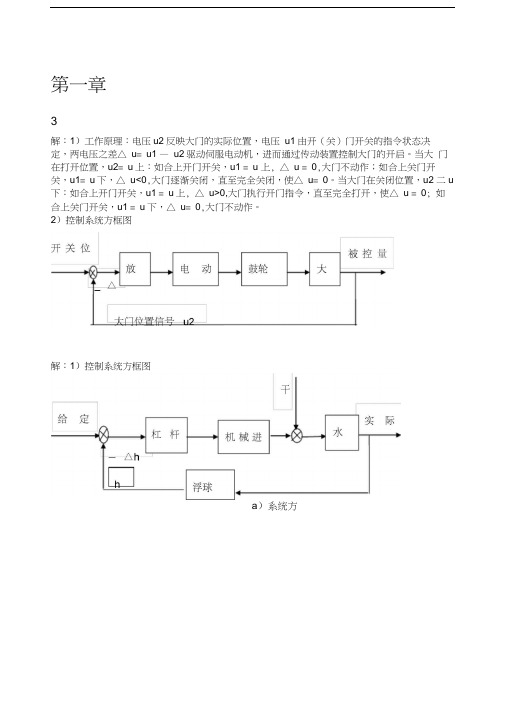
第一章3解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△ u= u1 —u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2= u上:如合上开门开关,u1 = u 上, △ u = 0,大门不动作;如合上关门开关,u1= u下,△ u<0,大门逐渐关闭,直至完全关闭,使△ u= 0。
当大门在关闭位置,u2 二u 下:如合上开门开关,u1 = u上, △ u>0,大门执行开门指令,直至完全打开,使△ u = 0; 如合上关门开关,u1 = u下,△ u= 0,大门不动作。
2)控制系统方框图解:1)控制系统方框图a)系统方a )水箱是控制对象,水箱的水位是被控量,水位的给定值 h '由浮球顶杆的长度给定,杠 杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水 压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是 进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随 之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制 系统。
b )水箱是控制对象,水箱的水位是被控量,水位的给定值 h '由浮球拉杆的长度给定。
杠 杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水 压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后, 在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水 位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离 散控制系统。
2-1 解:(c )确定输入输出变量(u1,u2)得到:CR 2dU 1(1 匹)u 2 =CR 2dU 1-R2u 1 dt R 1 dt R一阶微分方程(e )确定输入输出变量(u1,u2)消去i 得到:(& R 埒汁2牛亡 一阶微分方程第二章2- 2解:1)确定输入、输出变量f (t ) 、X 2□2)工作原理:b )系统方框图干f(t)-fK1⑴-fB 1⑴-fBMF^d^- - 1 -(s 2) (s 1) (s 1)2M(s)=0, 4) D(s)=0,得到极点:一1, M(s)=0, 得到零点:2) 对各元件列微分方程:2f f f _ d X 2(t)fB3 ~'T K2-'T B 2= m 2K1B3 dt 2=K 1X 1; f B1 = B 1 -- -dt B d (x 1 - x2) =B 3 甬;fK2 = K 2X23)4) 5) 拉氏变换.F(s)—KX(s)—B 1SX1G)—B3$(X 1(s) —X 2(s)] = gs 2X 1(s) 叉'B 3S[X 1(s) -X 2(s)] -K 2X2G)-B 2SX2G ) = m 2S 2X 2(s) 消去中间变量: 拉氏反变换:mi|m 2 d 4X d 3X d 2X$ (B 1m 2 七2口1 B s mh B s mJ $(B 1B 3 B 1B 2 B s B ?心口2 ^心)/dt dt dt 2_3(K 1B 2 K 1B 3 K 2B 1 K 2B 3)等 K 1g 弋詈解:(2) (4)1 1 11 1 1 — 29 s 49 s 13 (s 1)(5)(6)-0.25 2s 0.5 2 22 2.5 s2- 5解:1)D(s)=0, M(s)=0,2) D(s)=0, M(s)=0,得到极点:0,0,-2,-5得到零点:一 1 , ' 得到极点:一 2, — 1, —2 得到零点:0 , 0 , — 1+ □0 +oci3) D(s)=O, 得到极点:0,得到零点:一2,2- 8解:1) a )建立微分方程b) 拉氏变换 c) 画单元框图(略) d) 画系统框图mx o (t) = f k (t) f Bl (t) - f B2(t) f k (t)二 k(X i (t) —x °(t))ms 2X o (s) = F k (s) F BI (S ) -F B 2(S )b) 拉氏变换:F k (s )=k (X i (s )-X o (s))F Bi (s)=B i S (X j (s)—X o (s))F B 2(S )工 B 2S X O (S )c) 绘制单元方框图(略)4)绘制系统框图Fi ( s )2)a)建立微分方程:f B1(t) B id (N (t)-")) dtf B2 (t)=B 2 dX o (t) dt由于扰动产生的输出为:要消除扰动对输出的影响,必须使 X o2(S )=0 得到:QK 2K 3G o (s) -K 3K 4S =0第三章3- 1解:1)法一:一阶惯性环节的调整时间为 4T ,输出达稳态值的98%故: 4T = 1min ,得到:T = 15s法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
现代控制工程 第2章

L [
t
0
L [ f (t )] f (t )dt ] s
L [
t
0
L [ f (t )] f (t )dt ] s
5 复微分定理
若f(t) 可进行拉氏变换,则除了在F(s)的极点以外,有
L[tf (t )]
d F (s) ds
2.3 拉普拉斯变换定理
5 复微分定理
0
L[ f (t )1(t )] f (t )1(t )e st dt e s F (s)
0
2.2 拉普拉斯变换
2、常用函数的拉氏变换
(7)脉动函数
A A A L[ f (t )] L[ 1(t )] L[ 1(t t0 )] (1 e st0 ) t0 t0 t0 s
t t0 t t0
(t t0 )dt 1
2.2 拉普拉斯变换
2、常用函数的拉氏变换
(9)f(t)与e-at相乘
L[e
at
f (t )] e at f (t )e st dt F (s a)
0
应用举例
e at sin t
e at cos t
st 0 0
拉普拉斯反变换(拉氏反变换)
L [ F ( s)] f (t )
2、拉普拉斯变换的存在
(1)拉氏变换存在
1
2 j
1
c j
c j
F ( s)e st dt
(t 0)
C为收敛横坐标,是实常量。
若拉氏积分收敛,则函数f(t)的拉氏变换存在
自动控制第二次

学习内容和目的
学习内容
时域分析法,频域分析法为主线 数学模型的建立 系统性能(稳定性,稳态性能和动态性能)的分析 系统性能的改善(系统的校正) MATLAB软件的应用
目的
对自控系统的工作原理,数学模型,性能分析,系 统校正等有一个相对完整的认识。
培养“系统”的思想!
3
学习内容和目的
实验内容(8个学时)
23
第二节 自动控制的基本方式
被控对象:水池 被控量:实际水位 给定量:希望水位设定值 扰动量:出水量Q2 测量元件:浮子 比较元件:电位计 连杆 放大元件:放大器 执行元件:电动机、减速器、进水阀门 关键:理清H的变化与Q1 、 Q2变化的关系。
24
第二节 自动控制的基本方式
系统的结构方框图
25
结构
自动控制系统的组成 自动控制的基本方式 自动控制系统的分类 对控制系统的性能要求
重点
自动控制系统的组成(框图) 闭环控制方式 反映控制中共同规律的性能指标
6
第一节 自动控制系统的组成
一、系统的组成
被控对象 控制装置 测量元件 计算元件(比较、放大) ( ) 执行元件 校正元件
7Hale Waihona Puke 第一节 自动控制系统的组成
第二节 自动控制的基本方式
教与学系统方框图
预习
学生应掌 大纲与 握内容 学生实 际掌握 程度 成绩
教材
老师
学生 复习
考试
课堂回答问题 作业
结束 26
第三节 控制系统的分类
分类角度不同
按控制方式:开环控制和闭环控制系统 按执行元件物理特性的不同:机械、电气、液 压和气动控制系统 按数学模型是否满足叠加原理:线性和非线性 系统 按系统中输入、输出信号是否是时间的连续函 数:连续和离散系统 按系统结构参数是否是时间的函数:定常和时 变系统
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二次课
第一章 系统的数学模型
数学模型:所谓系统的数学模型就是描述系统输入输出关系的数学表达式。
§2.1 引言
一、系统的数学模型 微分方程 传递函数 状态方程 二、线性系统
如果系统的数学模型是线性的,这种系统称为线性系统。
判断下列系统是否为线性系统 1) 423+=x y
2)
x dt dx
y dt dy dt y d 36222+=++ 3) x y dt
dy
dt y d dt y d 46552
233=+++ 4) x xy x y ++=332
5)
x y dt
dy dt y d =++2
22)(线性系统最重要特性:满足叠加原理。
三、非线性系统
非线性系统最重要特性:不能应用叠加原理。
§2.2 线性微分方程式的建立
一、 步骤
1. 划分环节,确定每一环节的输入输出;
2. 列各环节微分方程;
3. 消中间变量;
4. 整理,化标准型。
(输出左,输入右,各阶导数降幂排列) 二、 举例
1. 机械系统(牛顿、胡克) 1)平移系统
x(t):外力;y(t):位移
1)旋转系统
J :转动惯量;f :阻尼系数;k :弹簧系数
1. 电气系统(基尔霍夫/克希霍夫、电磁感应)
)(t u i -输入电压;)(t u o -输出电压
消去中间变量1i ,2i ,3i ,得:
y(t)
)
t
)()()()()()(2212
1221t u R t u R R dt
t du L C R R dt t u d LC R i o o o =++++ 课堂练习:
某机械系统,x(t)为输入力,y(t)为输出位移,试列些该系统运动微分方程。
y(t)
§2.3 非线性系统的线性化(本节自学)
严格地说,一切系统都存在非线性因素,因而都是非线性系统。
对于非线性函数的线性化方法有两种。
忽略非线性因素 切线法(微小偏差法)。
