工程控制基础-课后习题答案-田作华(PDF)
控制工程基础课后作业解答(新)
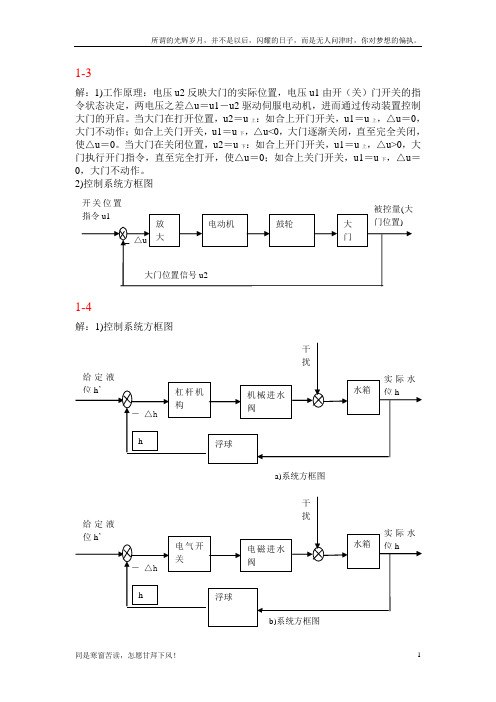
1-3解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u =u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u 上:如合上开门开关,u1=u 上,△u =0,大门不动作;如合上关门开关,u1=u 下,△u<0,大门逐渐关闭,直至完全关闭,使△u =0。
当大门在关闭位置,u2=u 下:如合上开门开关,u1=u 上,△u>0,大门执行开门指令,直至完全打开,使△u =0;如合上关门开关,u1=u 下,△u =0,大门不动作。
2)控制系统方框图1-4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h ’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构使进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h ’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:b) 确定输入输出变量x1,x2 )(212dtdx dt dx B kx -= 得到一阶微分方程:dtdxB kx dt dx B122=+ (c )确定输入输出变量(u1,u2) 22111R i R i u += 222R i u = ⎰-=-dt i i C u u )(11221 得到一阶微分方程:1121221222)1(u R Rdt du CR u R R dt du CR +=++d)确定输入输出变量x1,x2 )()(2112122x x k dtdx dt dx B x k -+-= 得到一阶微分方程:1112212)(x k dtdxB x k k dt dx B+=++ (e )确定输入输出变量(u1,u2)⎰++=idt CiR iR u 1211121Ruui-=消去i得到一阶微分方程:CudtduRCudtduRR1122221)(+=++f) 确定输入输出变量x1,x2)()(211322xxkxxk-=-)(3223xxkdtdxB-=消去x3得到一阶微分方程:1112121221)1(xkdtdxkkBxkdtdxkkB+=++得到一阶微分方程:1112212)(xkdtdxBxkkdtdxB+=++2-2解:1)确定输入、输出变量f(t)、x22)对各元件列微分方程:222213311111122222232121311;)(;)()()()()()(xKfdtxxdBfdtdxBfxKfdttxdmfffdttxdmtftftftfKBBKBKBBBK=-====--=---3)拉氏变换:)()()()]()([)()]()([)()()(22222222131212131111sXsmssXBsXKsXsXsBsXsmsXsXsBssXBsXKsF=---=----4)消去中间变量:)()()()(23223232131123sXsBsmsBKsBsmsBKsBssXBsF++++++=+5)拉氏反变换:dtdfB x K K dt dx B K B K B K B K dtx d K m m K B B B B B B dt x d m B m B m B m B dt x d m m s s 3221232123121222212122131323132122142421)()()(=++++++++++++++2-3解:(2)2112+-+s s t t e e 22--- (4)2)1(13111914191+++-+s s st t t te e e ---+-3191914 (5)2)1(1)1(2)2(2+-+++-s s s t t t te e e ----+-222 (6)s s s s s 5.2124225.04225.022++-+⨯⨯-+⨯- 5.222sin 2cos 5.0+----t e t t2-5解:1)D(s)=0,得到极点:0,0,-2,-5M(s)=0,得到零点:-1,∞+,∞+,∞+ 2) D(s)=0,得到极点:-2,-1,-2 M(s)=0,得到零点:0,0,-1 3) D(s)=0,得到极点:0,231j +-,231j -- M(s)=0,得到零点:-2,∞+,∞+4) D(s)=0,得到极点:-1,-2,∞- M(s)=0,得到零点:∞+ 2-6解:确定2-8解:1)a )建立微分方程dtt dx Bt f t f t x t x k t f t x k t f t f bat f t f t f t f t x m B k k k i k k )()()())()(()()()()()()()()()(202201121==-===--=••b)拉氏变换)()())()(()()()()()()()()()(20220112102s BsX s F s X s X k s F s X k s F s F bas F s F s F s F s X ms k k k i k k =-===--=c)画单元框图(略) d)画系统框图2)a)建立微分方程:dt t dx B t f dt t x t x d B t f t x t x k t f t f t f t f t x m oB o i B i k B B k )()())()(()())()(()()()()()(22110210=-=-=-+=••b)拉氏变换:)()())()(()())()(()()()()()(02211212s sX B s F s X s X s B s F s X s X k s F s F s F s F s X ms B o i B o i k B B k o =-=-=-+=c)绘制单元方框图(略) 4)绘制系统框图2-11解:a)1212321232141H G G H G G H G G G G G -+++(要有具体变换过程)b)))((1)(214321214321H G G G G H G G G G G G -++++ (要有具体变换过程)2-14解:(1)321232132132101111)()(K K K s Ts K K K TsK s K K Ts K s K K s X s X i i ++=+++==φ 321243032132132103402)(111)(1)()()(K K K s Ts s K K s G K K K TsK s K K Ts K s K K s G Ts K K s N s X s n ++-=+++++-==φ(2)由于扰动产生的输出为:)()()()()(321243032102s N K K K s Ts sK K s G K K K s N s s X n ++-==φ 要消除扰动对输出的影响,必须使0)(02=s X 得到:0)(430321=-s K K s G K K K 得到:2140)(K K sK s G =3-1解:1)法一:一阶惯性环节的调整时间为4T ,输出达稳态值的98%,故: 4T =1min ,得到:T =15s法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
(工程控制田作华版)第五章答案

频率响应法习题答案
A5-1 绘制下列系统的对数幅频特性图和相频特性图,并求增益剪切角频率 c 和相位剪切角频率 g : 增益剪切角频率 c :系统对数幅频特性穿越 0dB 的角频率,即 G ( j ) 1 ,或 L( ) 0dB 时的角频率
相位剪切角频率 g :系统相频特性曲线穿越 180 的角频率,即 ( ) 180 时的角频率
20dB / dec
5
1
10
?
60dB / dec
Matlab 画图结果如下:
g =10
c = 6.42
⑸ G( s)
40( s 10) s ( s 10)( s 20)
极点: 1 =0, 2 =10, 3 =20 零点: 1 =10
G ( s) 40( s 10) 2( s /10 1) s( s 10)( s 20) s ( s /10 1)( s / 20 1)
图(2):G(s)=
1 s 1) w1 1 1 ( s 1)( s 1) 2 w2 w3 K(
20lgK=25, K=17.78
L(1) L( w1 ) 20 , w1 =0.7 lg1 lg w1 L( w2 ) L(1) 20 , w2 =1.26 lg w2 lg1
20 lg K 20 lg(5) 14
积分因子 =1,所以其幅频特性图低频段是一条经过 =1,L(1)=14dB,斜率为-20dB/dec 的直线, 图像在 =10 处折线斜率增加到-60dB/dec,具体如下图: 从图中我们可以得到 c = 5。
L(? )(dB)
20 14 0 20
L ( ) dB
控制工程基础_课后答案
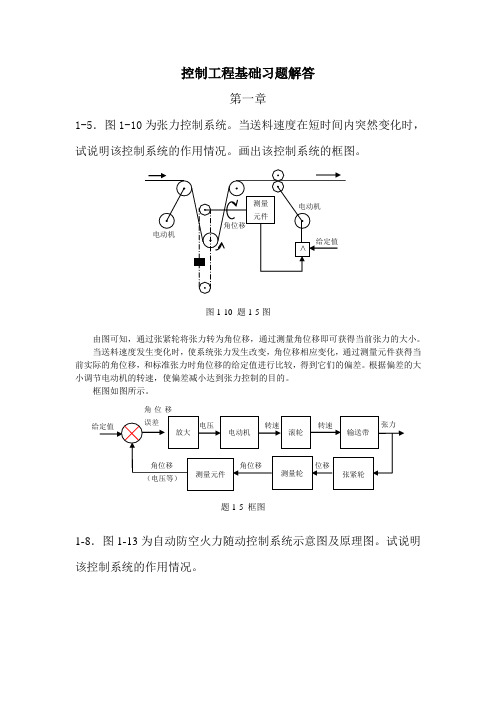
控制工程基础习题解答第一章1-5.图1-10为张力控制系统。
当送料速度在短时间内突然变化时,试说明该控制系统的作用情况。
画出该控制系统的框图。
由图可知,通过张紧轮将张力转为角位移,通过测量角位移即可获得当前张力的大小。
当送料速度发生变化时,使系统张力发生改变,角位移相应变化,通过测量元件获得当前实际的角位移,和标准张力时角位移的给定值进行比较,得到它们的偏差。
根据偏差的大小调节电动机的转速,使偏差减小达到张力控制的目的。
框图如图所示。
1-8.图1-13为自动防空火力随动控制系统示意图及原理图。
试说明该控制系统的作用情况。
题1-5 框图电动机给定值角位移误差张力-转速位移张紧轮滚轮输送带转速测量轮测量元件角位移角位移(电压等)放大电压测量 元件>电动机角位移给定值电动机图1-10 题1-5图该系统由两个自动控制系统串联而成:跟踪控制系统和瞄准控制系统,由跟踪控制系统获得目标的方位角和仰角,经过计算机进行弹道计算后给出火炮瞄准命令作为瞄准系统的给定值,瞄准系统控制火炮的水平旋转和垂直旋转实现瞄准。
跟踪控制系统根据敏感元件的输出获得对目标的跟踪误差,由此调整视线方向,保持敏感元件的最大输出,使视线始终对准目标,实现自动跟踪的功能。
瞄准系统分别由仰角伺服控制系统和方向角伺服控制系统并联组成,根据计算机给出的火炮瞄准命令,和仰角测量装置或水平方向角测量装置获得的火炮实际方位角比较,获得瞄准误差,通过定位伺服机构调整火炮瞄准的角度,实现火炮自动瞄准的功能。
控制工程基础习题解答第二章2-2.试求下列函数的拉氏变换,假定当t<0时,f(t)=0。
(3). ()t et f t10cos 5.0-=解:()[][]()1005.05.010cos 25.0+++==-s s t e L t f L t(5). ()⎪⎭⎫⎝⎛+=35sin πt t f 图1-13 题1-8图敏感 元件定位伺服机构 (方位和仰角)计算机指挥仪目标 方向跟踪环路跟踪 误差瞄准环路火炮方向火炮瞄准命令--视线瞄准 误差伺服机构(控制绕垂直轴转动)伺服机构(控制仰角)视线敏感元件计算机指挥仪解:()[]()252355cos 235sin 2135sin 2++=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=s s t t L t L t f L π2-6.试求下列函数的拉氏反变换。
《控制工程基础》第3版 课后答案

15 2 15 2 ) 2
8 15 4 15 F (s) 1 2 15 1 (s ) (s ) 2 ( 2 4 2
8 15 2 15 f (t ) e sin t 1(t ) 15 2
t
2-2(7)
F (s)
1 3 解: s 3 F ( s) 2 s 32 s 2 32
X o1 ( s) G1G2G3 (1 G4 ) X i1 ( s) 1 G1G2 G4 G1G4G5 H1 H 2 G1G2G4
同理可推得:
X o1 (s) G1G2G3 (1 G4 ) X i1 (s) 1 G1G2 G4 G1G4G5 H1H 2 G1G2G4
U o ( s) R2 R4 U i ( s) R1
R2 R4 R R Cs 1 4 2
、
2-12(b)
列写机械系统的方程组: 其中
A (t )
T1 (t ) 分别为 J 1
所在杆的转角和转矩, T2 (t ) 为 J 2 所在杆的转矩。
解:
对其进行拉氏变换,得:
E ( s) 1 X i (s) 1 G( s)
当 xi (t ) (10 2t ) 1(t ) 时,输入引起的稳态误差
ess1
1 lim e(t ) lim sE ( s) lim s X i ( s) s 0 s 0 s 0 1 G( s)
化简可得:
T1 ( s) k1[ i ( s) A ( s)] 2 T ( s ) T ( s ) J s 1 2 1 A ( s ) D1 s A ( s ) T2 ( s) k 2 [ A ( s) o ( s)] T (t ) J s 2 ( s) D s ( s) 2 o 2 o 2
控制工程基础第三版课后答案

控制工程基础第三版课后答案第一章简介1.1 控制工程概述控制工程是通过对物理过程或系统进行测量和调整,以实现期望的状态或行为。
它涉及到多个学科,包括数学、物理学、计算机科学等。
控制工程的目标是通过设计和实现反馈系统,使物理过程或系统达到期望的状态或行为。
1.2 控制系统的基本概念控制系统由输入、处理和输出三个基本要素组成。
输入是系统接收的信息或指令,处理是对输入信息进行处理和计算,输出是系统对处理结果产生的响应。
控制系统还包括传感器、执行器和控制器等组件。
1.3 控制系统的分类根据控制系统的特性和实现方式,控制系统可分为开环控制系统和闭环控制系统。
开环控制系统的输出不受系统状态的影响,闭环控制系统则通过测量系统状态并与期望状态进行比较,控制系统的输入来调整系统的行为。
第二章数学基础2.1 线性代数线性代数是控制工程的基础,它涉及到向量、矩阵、线性方程组等概念和运算。
控制系统的建模和分析中经常使用线性代数的方法进行求解和分析。
2.2 微积分微积分是控制工程的另一个基础,它涉及到函数、极限、导数和积分等概念和运算。
控制系统的建模和分析中经常使用微积分的方法进行求解和分析。
2.3 概率统计概率统计是控制工程中用来描述不确定性和随机性的工具。
控制系统的建模和分析中经常使用概率统计的方法进行不确定性的建模和分析。
第三章控制系统的数学表示3.1 传递函数表示法传递函数是描述控制系统输入和输出关系的一种表示方法。
传递函数可以通过对系统进行建模和实验来获得。
3.2 状态空间表示法状态空间表示是描述控制系统状态和动力学行为的一种表示方法。
状态空间表示可以通过系统的状态方程和输出方程来获得。
第四章控制系统的分析方法4.1 频域分析频域分析是通过对控制系统的输入和输出信号进行频率分析来获得系统的频率响应和稳定性等性能指标。
4.2 时域分析时域分析是通过对控制系统的输入和输出信号进行时域分析来获得系统的时域响应和稳定性等性能指标。
控制工程基础第2章答案

第2章系统的数学模型(习题答案)2.1什么是系统的数学模型?常用的数学模型有哪些?解:数学模型就是根据系统运动过程的物理、化学等规律,所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。
常用的数学模型有微分方程、传递函数、状态空间模型等。
2.2 什么是线性系统?其最重要的特性是什么?解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要的特性就是它满足叠加原理。
2.3 图( 题2.3) 中三图分别表示了三个机械系统。
求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。
题图2.3解:①图(a):由牛顿第二运动定律,在不计重力时,可得整理得将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[]于是传递函数为②图(b):其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并记其初始条件为零,得系统传递函数为③图(c):以的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2.4试建立下图(题图2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电压)(t u r 和位移)(t x r 为输入量;电压)(t u c 和位移)(t x c 为输出量;1,k k 和2k 为弹簧弹性系数;f 为阻尼系数。
+-+-u )tfC)+-+-f)(a )(b )(c )(d R题图2.4【解】:)(a方法一:设回路电流为i ,根据克希霍夫定律,可写出下列方程组:⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量,整理得:dtdu RC u dt du RCrc c =+方法二:dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量,各受力点任何时刻均满足∑=0F ,则有:cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ,根据牛顿运动定律,可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论:)(a 、)(b 互为相似系统,)(c 、)(d 互为相似系统。
《控制工程基础》课后作业解答
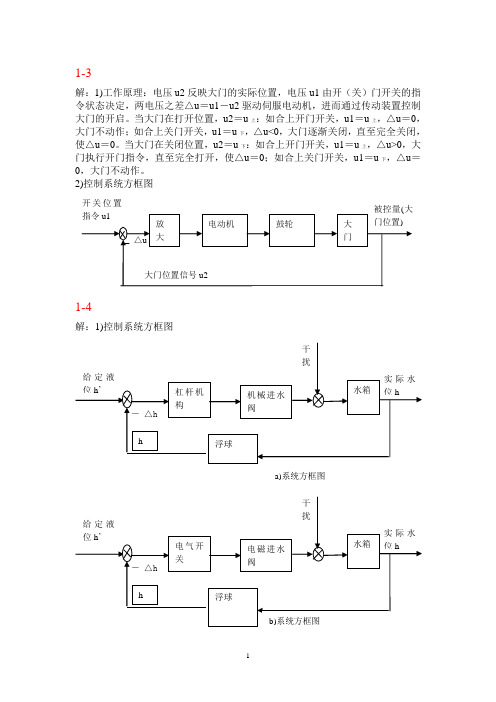
1-3解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u =u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u 上:如合上开门开关,u1=u 上,△u =0,大门不动作;如合上关门开关,u1=u 下,△u<0,大门逐渐关闭,直至完全关闭,使△u =0。
当大门在关闭位置,u2=u 下:如合上开门开关,u1=u 上,△u>0,大门执行开门指令,直至完全打开,使△u =0;如合上关门开关,u1=u 下,△u =0,大门不动作。
2)控制系统方框图1-4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h ’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构使进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h ’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:b) 确定输入输出变量x1,x2 )(212dtdx dt dx B kx -= 得到一阶微分方程:dtdxB kx dt dx B122=+ (c )确定输入输出变量(u1,u2) 22111R i R i u += 222R i u = ⎰-=-dt i i C u u )(11221 得到一阶微分方程:1121221222)1(u R Rdt du CR u R R dt du CR +=++d)确定输入输出变量x1,x2 )()(2112122x x k dtdx dt dx B x k -+-= 得到一阶微分方程:1112212)(x k dtdxB x k k dt dx B+=++ (e )确定输入输出变量(u1,u2)⎰++=i d t CiR iR u 1211121R u u i -=消去i 得到一阶微分方程:Cudt du R C u dt du R R 1122221)(+=++f) 确定输入输出变量x1,x2 )()(211322x x k x x k -=- )(3223x x k dtdx B-= 消去x3得到一阶微分方程:1112121221)1(x k dtdx k k B x k dt dx k k B +=++得到一阶微分方程:1112212)(x k dtdxB x k k dt dx B +=++2-2解:1)确定输入、输出变量f(t)、x 22)对各元件列微分方程:222213311111122222232121311;)(;)()()()()()(x K f dt x x d B f dtdxB f x K f dt t x d m f f f dt t x d m t f t f t f t f K B B K B K B B B K =-====--=--- 3)拉氏变换:)()()()]()([)()]()([)()()(22222222131212131111s X s m s sX B s X K s X s X s B s X s m s X s X s B s sX B s X K s F =---=----4)消去中间变量:)()()()(23223232131123s X sB s m s B K s B s m s B K s B s sX B s F ++++++=+5)拉氏反变换:dtdfB x K K dt dx B K B K B K B K dtx d K m m K B B B B B B dt x d m B m B m B m B dt x d m m s s 3221232123121222212122131323132122142421)()()(=++++++++++++++2-3解:(2)2112+-+s s t t e e 22--- (4)2)1(13111914191+++-+s s st t t te e e ---+-3191914 (5)2)1(1)1(2)2(2+-+++-s s s t t t te e e ----+-222 (6)s s s s s 5.2124225.04225.022++-+⨯⨯-+⨯- 5.222s i n 2c o s 5.0+----t e t t 2-5解:1)D(s)=0,得到极点:0,0,-2,-5M(s)=0,得到零点:-1,∞+,∞+,∞+ 2) D(s)=0,得到极点:-2,-1,-2 M(s)=0,得到零点:0,0,-1 3) D(s)=0,得到极点:0,231j +-,231j -- M(s)=0,得到零点:-2,∞+,∞+4) D(s)=0,得到极点:-1,-2,∞- M(s)=0,得到零点:∞+ 2-6解:确定2-8解:1)a )建立微分方程dtt dx Bt f t f t x t x k t f t x k t f t f bat f t f t f t f t x m B k k k i k k )()()())()(()()()()()()()()()(202201121==-===--=∙∙b)拉氏变换)()())()(()()()()()()()()()(20220112102s BsX s F s X s X k s F s X k s F s F bas F s F s F s F s X ms k k k i k k =-===--=c)画单元框图(略) d)画系统框图2)a)建立微分方程:dt t dx B t f dt t x t x d B t f t x t x k t f t f t f t f t x m oB o i B i k B B k )()())()(()())()(()()()()()(22110210=-=-=-+=∙∙b)拉氏变换:)()())()(()())()(()()()()()(02211212s sX B s F s X s X s B s F s X s X k s F s F s F s F s X ms B o i B o i k B B k o =-=-=-+=c)绘制单元方框图(略) 4)绘制系统框图2-11解:a)1212321232141H G G H G G H G G G G G -+++(要有具体变换过程)b)))((1)(214321214321H G G G G H G G G G G G -++++ (要有具体变换过程)2-14解:(1)321232132132101111)()(K K K s Ts K K K TsK s K K Ts K s K K s X s X i i ++=+++==φ 321243032132132103402)(111)(1)()()(K K K s Ts s K K s G K K K TsK s K K Ts K s K K s G Ts K K s N s X s n ++-=+++++-==φ(2)由于扰动产生的输出为:)()()()()(321243032102s N K K K s Ts sK K s G K K K s N s s X n ++-==φ 要消除扰动对输出的影响,必须使0)(02=s X 得到:0)(430321=-s K K s G K K K 得到:2140)(K K sK s G =3-1解:1)法一:一阶惯性环节的调整时间为4T ,输出达稳态值的98%,故: 4T =1min ,得到:T =15s法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
《控制工程基础》第三版课后答案

控制工程基础习题解答第一章1-1.控制论的中心思想是什么?简述其发展过程。
维纳(N.Wiener)在“控制论——关于在动物和机器中控制和通讯的科学”中提出了控制论所具有的信息、反馈与控制三个要素,这就是控制论的中心思想控制论的发展经历了控制论的起步、经典控制理论发展和成熟、现代控制理论的发展、大系统理论和智能控制理论的发展等阶段。
具体表现为:1.1765年瓦特(Jams Watt)发明了蒸汽机,1788年发明了蒸汽机离心式飞球调速器,2.1868年麦克斯威尔(J.C.Maxwell)发表“论调速器”文章;从理论上加以提高,并首先提出了“反馈控制”的概念;3.劳斯(E.J.Routh)等提出了有关线性系统稳定性的判据4.20世纪30年代奈奎斯特(H.Nyquist)的稳定性判据,伯德(H.W.Bode)的负反馈放大器;5.二次世界大仗期间不断改进的飞机、火炮及雷达等,工业生产自动化程度也得到提高;6.1948年维纳(N.Wiener)通过研究火炮自动控制系统,发表了著名的“控制论—关于在动物和机器中控制和通讯的科学”一文,奠定了控制论这门学科的基础,提出了控制论所具有的信息、反馈与控制三要素;7.1954年钱学森发表“工程控制论”8.50年代末开始由于技术的进步和发展需要,并随着计算机技术的快速发展,使得现代控制理论发展很快,并逐渐形成了一些体系和新的分支。
9.当前现代控制理论正向智能化方向发展,同时正向非工程领域扩展(如生物系统、医学系统、经济系统、社会系统等),1-2.试述控制系统的工作原理。
控制系统就是使系统中的某些参量能按照要求保持恒定或按一定规律变化。
它可分为人工控制系统(一般为开环控制系统)和自动控制系统(反馈控制系统)。
人工控制系统就是由人来对参量进行控制和调整的系统。
自动控制系统就是能根据要求自动控制和调整参量的系统,系统在受到干扰时还能自动保持正确的输出。
它们的基本工作原理就是测量输出、求出偏差、再用偏差去纠正偏差。
《控制工程基础》第二版课后习题答案
第一章习题解笞U]>U2 U\ U2第二章习题解答2-1a) b)d)f)L^f| 忙d)f\ — fl =^2X O严(f)=$(M+E ⑴虑 如(f) =iQ)RRC^-u o (t)^u o (t) = RC^-u^t) at at fs (r)=B 低[xi (f) -曲(幼 j/B (t)=fK (t) = KXo(t) B dB d 『八10602斤不%()+%©二斤击可()占dR^c —% (0+ (*i + 心)% ⑴=邛应 ~u i (0+ R 2u t (0 atati =i R +,C u o =IR?:R R 严冃3宙 % =gR\ +u oa)=K ](旳一兀)+」:dx o ](J?l + J?2)C —«c (!)+ %("■ R Q C — Wj(O + tti (Oat at(K[ + K2)B — x o (t)+ K\K2X o (t)= K\R 〒曲(f)+ 琦心再(f)dt at10602a) b) c) Q © f)U Q —1/?2 + — j icit— Z/?| + iR-f H —J idte)dxK\% K i (兀 _ %) = K 》(兀)—x)=号二dtoB 2+ (®K° ++ B'B? + 场*3 + 水2〃?)& 2+ (K }B 2+K }B 3 + 心汝 + KM 巴2 + K }K 2X 2 dt3J S + 2用 + 8S-丘($ + 2)($戈+2$十4)广、■炉+ 5,2+9用+7E ($+恥 + 2)乡一rn\fU2K 2rdx { dx 2< dt dt ;/(O™-坷罕~_叭 dtdxj … 一 —- - K?x^ = m dtdx l dx 2dt dt护d 2x 2 2~d^ k,用典2+ (的+创坷+用2创+加2*3);?7皿乔对)13173 G($)= --------------- —(£+。
控制工程基础课后习题答案

控制工程基础课后习题答案控制工程是一门涉及自动控制系统设计和分析的学科,它广泛应用于工业、交通、航空航天等领域。
作为控制工程学习的基础,掌握相关课后习题的答案对于学生来说至关重要。
本文将探讨控制工程基础课后习题的答案,帮助学生更好地理解和应用相关知识。
一、理论基础习题答案控制工程基础的理论基础包括线性系统、传递函数、稳定性等内容。
在课后习题中,学生常常会遇到一些理论性问题。
例如,“什么是传递函数?”、“什么是稳定性?”等。
对于这类问题,学生可以参考教材中的相关章节进行查阅和思考,并结合实例进行解答。
二、计算题答案除了理论性的问题,控制工程基础的习题中还包括一些计算题。
例如,给定一个系统的传递函数,要求计算其阶跃响应或频率响应等。
对于这类计算题,学生需要掌握传递函数的计算方法和相关的数学工具,如拉普拉斯变换、频域分析等。
在解答习题时,学生可以根据给定的传递函数,按照计算步骤逐步进行推导和计算,最终得到答案。
三、设计题答案控制工程基础的习题中还包括一些设计题,要求学生设计一个满足特定要求的控制系统。
例如,给定一个系统的传递函数和性能指标,要求设计一个闭环控制系统,使得系统具有良好的稳定性和快速的响应速度。
对于这类设计题,学生需要综合运用所学的知识和方法,如根轨迹法、频域分析等。
在解答习题时,学生可以根据给定的要求,选择合适的控制策略和参数,进行系统设计和分析,最终得到满足要求的控制系统。
四、实践应用题答案控制工程基础的习题中还包括一些实践应用题,要求学生将所学的知识应用于实际问题的解决。
例如,给定一个物理系统的数学模型,要求设计一个控制系统,使得系统能够实现特定的功能。
对于这类应用题,学生需要将所学的控制方法和技巧应用到实际问题中,进行系统建模、参数调节等。
在解答习题时,学生可以根据实际问题的要求,选择合适的控制策略和参数,进行系统设计和仿真,最终得到满足要求的控制系统。
总结:控制工程基础课后习题的答案涉及理论基础、计算题、设计题和实践应用题等多个方面。
控制工程基础课后答案

For personal use only in study and research;not for commercial use第二章2.1求下列函数的拉氏变换 (1)ss s s F 232)(23++=(2)4310)(2+-=s s s F(3)1)(!)(+-=n a s n s F (4)36)2(6)(2++=s s F(5) 22222)()(a s a s s F +-= (6))14(21)(2s s s s F ++= (7)521)(+-=s s F 2.2 (1)由终值定理:10)(lim )(lim )(0===∞→∞→s t s sF t f f (2)11010)1(10)(+-=+=s s s s s F 由拉斯反变换:t e s F L t f ---==1010)]([)(1 所以10)(lim =∞→t f t2.3(1)0)2()(lim )(lim )0(2=+===∞→→s ss sF t f f s t )0()0()()()](['2''0''f sf s F s dt e t f t f L st --==-+∞⎰)0()0()(lim )(lim '2''0f sf s F s dt e t f s st s --=+∞→-+∞+∞→⎰1)2()(lim )0(222'=+==+∞→s s s F s f s (2)2)2(1)(+=s s F , tte s F L t f 21)]([)(--==∴,0)0(2)(22'=-=--f te et f tt又,1)0('=∴f2.4解:dt e t f e t f L s F st s--⎰-==22)(11)]([)(⎰⎰------+-=212121111dt e e dt e e st s st s)11(11)11(11222s s s s se s e s e e s s e -------+--=22)1(111s s e se ---∙-=2.5求下列函数的拉氏反变换(1)t t f 2sin 21)(= (2)t e t t f -=361)((3)t t e e t f 32321)(+-=- (4)t t e e t f 235352)(+=-(5)t e t e t f t t 3sin 313cos 2)(22--+= (6)t t t e e te t f 222)(----+-=2.6(1)0)()()(22=--dtt y d m t ky t f(2)0)()()(222121=-+-dtt y d m t y k k k k t f 2.7(1)14312)(23++++=s s s s s G(2)210)(22++=-s s e s G s2.8 解 水的流量Q1由调节控制阀的开度控制,流出量Q2则根据需要可通过负载阀来改变,被调量H 反映了。
控制工程基础课后习题答案

详细描述
通过调整系统的传递函数,可以改变系统的 频率响应特性。在设计控制系统时,我们需 要根据实际需求,调整传递函数,使得系统 的频率响应满足要求。例如,如果需要提高 系统的动态性能,可以减小传递函数在高频 段的增益。
06 第五章 控制系统的稳定性 分析
习题答案5-
习题答案
• 习题1答案:该题考查了控制系统的基本概念和组成。控制系统的基本组成包 括被控对象、传感器、控制器和执行器等部分。被控对象是实际需要控制的物 理系统或设备;传感器用于检测被控对象的输出状态,并将检测到的信号转换 为可处理的电信号;控制器根据输入的指令信号和传感器的输出信号,按照一 定的控制规律进行运算处理,并输出控制信号给执行器;执行器根据控制信号 对被控对象进行控制操作,使其达到预定的状态或性能要求。
控制工程基础课后习题答案
目 录
• 引言 • 第一章 控制系统概述 • 第二章 控制系统的数学模型 • 第三章 控制系统的时域分析 • 第四章 控制系统的频域分析 • 第五章 控制系统的稳定性分析 • 第六章 控制系统的校正与设计
01 引言
课程简介
01
控制工程基础是自动化和电气工 程学科中的一门重要课程,主要 涉及控制系统的基本原理、分析 和设计方法。
总结词
控制系统校正的概念
详细描述
控制系统校正是指在系统原有基础上,通过加入适当的 装置或元件,改变系统的传递函数或动态特性,以满足 性能指标的要求。常见的校正方法有串联校正、并联校 正和反馈校正等。校正装置通常安装在系统的某一环节 ,以减小对系统其他部分的影响。
习题答案6-
总结词
控制系统设计的一般步骤
习题答案5-
总结词
工程控制基础-课后习题答案-田作华(PDF)

L1
=
−
5 s(T1s +1)
L2
=
−
8 s(T2s
+ 1)
L3
=
−
s2 (T1s
40 + 1)(T2 s
+ 1)
L4
=
s2 (T1s
40 + 1)(T2 s
+ 1)
L5
=
−
s2 (T1s
40 + 1)(T2 s
+ 1)
∆ = 1 − (L1 + L2 + L3 + L4 + L5 )
前向通路有四条:
前向通路有四条:
P1 = G1(s)G2 (s)
∆1 = 1
P2 = G1(s)G3 (s)
∆1 = 1
P3 = −G1(s)G3 (s)G4 (s)H3 (s), ∆3 = 1
P4 = −G1(s)G2 (s)G4 (s)H3 (s), ∆4 = 1
所以
C(s) = R(s)
G1(s)G2 (s) + G1(s)G3 (s) − G1(s)G3 (s)G4 (s)H3 (s) − G1(s)G2 (s)G4 (s)H3 (s) 1− G3 (s)H 1(s) − G2 (s)H 1(s) − G1(s)G3 (s)H2 (s)H3 (s)
+
+ R(s) +
−
− +
1 T1s +1
1 T2s +1
5 s
+
+ 8 s
C(s)
R(s) + −
(a)
+ + G1 ( s)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P2 = G1(s)G4 (s)G5 (s), ∆1 = 1
C2 (s) = G1(s)G2 (s)G3(s)G4 (s)G6 (s) + G1(s)G4 (s)G5 (s) R1(s) 1− G1(s)G2 (s) − G3 (s)G4 (s) + G1(s)G2 (s)G3(s)G4 (s)
④从 R2 到 C2 有一个前向通道
= G1(s)G2 (s)
R1(s) 1− G1(s)G2 (s) − G3(s)G4 (s) + G1(s)G2 (s)G3(s)G4 (s) 1− G1(s)G2 (s)
②从 R2 到 C1 没有前向通道,因此
C1(s) = 0 R2 (s)
③从 R1 到 C2 有两条前向通道
P1 = G1(s)G2 (s)G3 (s)G4 (s)G6 (s), ∆1 = 1
H 2 (s)
C(s) G3 (s)
H 3 (s)
C(s) =
G1G2G3 + G1G3H1
R(s) 1+ G2H2 + G2G3H3 + G1G2G3 + G1G3H1 + G3H1H3
B2-2 图 B2-2 是某个消除扰动影响的前馈控制系统的方块图。 N (s)
K1 − R(s) +
−
+ + K2
m k
b xo
P xi
(a)
(b)
图 A2-3 题 A2-7 汽车悬浮系统模型
解:由牛顿定理可得
k ( xi
−
xo )
+
b
d (xi − dt
xo
)
=
m
d 2 xo dt
X o = k + bs X i ms2 + bs + k
A2-9 试求图 A2-5 所示电路的传递函数 Eo (s) / Ei (s) 。 解:由电路学定律可得
系统的劳斯表为:
s3
2
-3
s2
1
10
s1
-23
s0
10
从劳斯表上可以看出首列元素变号两次,所以闭环系统不稳定,有两个根在 S 右半平
面。
解(2):
已知: G(s) = 1 , H (s) = s −1
(s −1)
s +1
系统的闭环传递函数为:
G(s) =
s +1 ,
s2 + s − 2
系统的闭环特征方程: s 2 + s − 2 = 0
第二章习题答案
A2-3 求图 A2-1 信号流图的传递函数 C(s) R(s)
− H1 (s)
R(s)
1
K
1
G1(s) G2 (s)
−H 3 (s)
−H 2 (s) −1
图 A2-1 题 A2-3 信号流图
1
s
C(s)
解: 这个系统只有一个前向通道,而有四个回路 L1 、 L2 、 L3 和 L4 ,没有两个及两个以
(b)其上半部弹簧与阻尼器之间,取辅助点 A,并设 A 点位移为 x,方向朝下;而在其下 半部 xo 引出点取为辅助点 B。则由弹簧力与阻尼力平衡的原则,从 A 和 B 两点可以分 别列出如下原始方程:
K1(xi − x) = b(x − xo ) K2 xo = b(x − xo )
消去中间变量 x,可得系统微分方程
第三章习题答案
A3-1 如图 A3-1 系统,用劳斯判据判别系统的稳定性。若不稳定,确定有几个根在右半 s 平 面。
R(s) + −
C(s) G(s)
H (s)
图 A3-1 题 A3-1 的系统方块图
⑴ G(s) =
10
, H (s) = 1
s(s −1)(2s + 3)
⑵ G(s) = 1 , H (s) = s −1
解: (a)设系统开始是平衡的。由牛顿第二运动定律,可得
b1(xi − xo ) − b2 xo = mxo
将上式进行垃氏变换,并整理(初始条件全部为零)得
[ms2 + (b1 + b2 )s]X o (s) = b1sXi (s)
于是传递函数为
Xo(s) =
b1
X i (s) ms + b1 + b2
∆ = 1− G1(s)G2 (s) − G3(s)G4 (s) + G1(s)G2 (s)G3 (s)G4 (s)
①从 R1 到 C1 只有一条前向通道
P1 = G1(s)G2 (s) , ∆1 = 1− G3 (s)G4 (s)
根据梅森增益公式,可得
C1(s) =
G1(s)G2 (s)(1− G3 (s)G4 (s))
+
+ R(s) +
−
− +
1 T1s +1
1 T2s +1
5 s
+
+ 8 s
C(s)
R(s) + −
(a)
+ + G1 ( s)
H 3 (s) G4 (s)
− +
(b)
图 A2-2 题 A2-4 图
H1(s) G2 (s) G3 (s) H 2 (s)
++
C (s)
解: (a) 这个系统有四条前向通道,五个回路,没有两个及以上互不接触回路。回路有:
C(s) = 0 . 所以当 R(s)=0 时, C(s) = 0 N (s)
B2-3 试求图 B2-3 所示各系统的传递函数 X o (s) / X i (s) ,xi 为系统的输入位移,xo 为系统的 输出位移。
(a)
(b)
(c )
b1 m
b2
xi
k1
b
xo k2
xi
xi
k1 b
xo
k2
xo
图 B2-3 题 B2-3 机械系统
Eo Ei
=
R2 +
R2
+
1 sC2
1 sC2
+
R1
+
1 sC1
=
sC1R2C2 + C1 sC1C(2 R2 + R1)+ C1 + C2
B2-1 将图 B2-1 的方块图简化, 并计算系统的传递函数 C(s) / R(s) 。 解:
R(s) + −
G1 ( s)
+ −
+ −
H1(s) +
+ G2 (s)
框图,指出输入量、输出量、被测量和控制器。 解:首先,系统要求液位有一个设定值,仪表测得液位的实际值,操作员将实际值与设定值 相比较,如果实际值比设定值大,操作员就减小阀门的开度,从而使得液位下降,如果实际 值比设定值小,操作员就增大阀门的开度,从而使得液位上升。其框图如下:
+
−
其中测量装置为仪表,执行装置为阀门。(应该将操作员放在比较器的位置上) (2)略
对上式进行拉氏变换,初始条件为零,得系统传递函数为
X o (s) = bs + K1 Xi (s) bs + (K1 + K2 )
B2-5 求图 B2-5 信号流图所示系统的下列传递函数:
⑴
W1 (s) =
C1 (s) R1 (s)
⑵
W1 (s)
=
C1 (s) R2 (s)
⑶
W1 (s)
=
C2 (s) R1 (s)
上互不接触回路。回路是:
L1
=
−
KG1(s)G2 s
(s)
L2 = −G1(s)G2 (s)H 2(s)
L3 = −G1 (s)H 3 (s)
L4 = −G1 (s)G2 (s)H1 (s)
∆
=
1−
(L1
+
L2
+
L3
+
L4
)
=
1+
KG1 (s)G2 s
(s)
+
G1 (s)G2
(s)H
2(s)
+ G1 (s)H 3 (s) + G1 (s)G2 (s)H1 (s)
R(s) s2 (T1s +1)(T2s +1) + 5s(T2s +1) + 8s(T1s +1) + 40
(b) 这个系统有三个回路,没有两个及以上互不接触回路:
L1 = G3 (s)H1(s)
L2 = G2 (s)H1(s) L3 = G1(s)G3 (s)H2 (s)H3 (s) ∆ = 1− G3(s)H 1(s) − G2 (s)H 1(s) − G1(s)G3 (s)H2 (s)H3(s)
(s −1)
s +1
⑶ G(s) = 12 , H (s) = 1
s(s +1)
s+3
解(1):
已知; G(s) =
10
, H (s) = 1
s(s −1)(2s + 3)
系统的闭环传递函数为:
G(s) =
10
,
2s3 + s 2 − 3s + 10
系统的闭环特征方程: 2s3 + s 2 − 3s + 10 = 0
C(s) G(s)
图 B2-2 前馈系统方块图
设 R(s) = 0 ,通过适当选择 K1 和 K 2 ,便可使由扰动引起的输出为零。假设扰动为单位
阶跃函数
N
(s)
=
1 s
,选择
