2017联合杯决赛(数学)试题及答案
2017年全国初中数学联合竞赛(初二年级)试题参考答案及

在 Rt △ EAD 中,有 422 (98 x)2 x2 ,解得 x 58 .
2017 年全国初中数学联合竞赛试题(初二年级)参考答案及评分标准 第 2 页(共 5 页)
二、填空题:(本题满分 28 分,每小题 7 分)
1.使得等式 1 1 a 3 a 成立的实数 a 的值为_______. 【答】 8 . 由所给等式可得 (1 1 a)3 a2 .令 x 1 a ,则 x 0 ,且 a x2 1,于是有 (1 x)3 (x2 1)2 ,
4.已知正整数 a,b, c 满足 a2 6b 3c 9 0 , 6a b2 c 0 ,则 a2 b2 c2 = ( )
A. 424. 【答】C.
B. 430.
C. 441.
D. 460.
由已知等式消去 c 整理得 (a 9)2 3(b 1)2 75 ,所以 3(b 1)2 75 ,又 b 为正整数,解得1 b 6 .
2
2
Байду номын сангаас
3
A
D
F
所以梯形的面积为 1 (1 4) 4 2 10 2 .
2
3
3
E
6.如图,梯形 ABCD 中, AD // BC , A 90 ,点 E 在 AB 上,若 AE 42 ,
BE 28, BC 70 , DCE 45 ,则 DE =
()
B
C
A. 56.
B. 58.
C.60.
D. 62.
为 A. 4. 【答】B.
B.3.
C.2.
D.1.
()
若 (a,b, c) 为好数组,则 abc 2(a b c) 6c ,所以 ab 6 .显然, a 只能为 1 或 2.
2017年全国初中数学联赛试题-含详细解析

2017年全国初中数学联合竞赛试题说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试(A)一、选择题(本题满分42分,每小题7分)1. 已知实数a b c ,,满足2133903972a b c a b c ++=++= ,,则32b ca b+=+ ( ) A .2 B .1 C .0 D .1− 2. 已知△ABC 的三边长分别是a ,b ,c ,有以下三个结论:(1) (2)以a 2,b 2,c 2为边长的三角形一定存在;(3)以|a -b |+1,|b -c |+1,|c -a |+1为边长的三角形一定存在. 其中正确结论的个数为( )A .0B .1C .2D .33. 若正整数a ,b ,c 满足a b c ≤≤且()2abc a b c =++,则称(a ,b ,c )为好数组.那么,好数组的个数为( )A .1B .2C .3D .44. 设O 是四边形ABCD 的对角线AC ,BD 的交点,若∠BAD +∠ACB =180︒,且BC =3,AD =4,AC =5,AB =6,则DOOB=( ) A .109 B .87 C .65 D .435. 设A 是以BC 为直径的圆上的一点,AD ⊥BC 于点D ,点E 在线段DC 上,点F 在CB的延长线上,满足∠BAF =∠CAE .已知BC =15,BF =6,BD =3,则AE =( ) A .43 B .213 C .214 D .2156. 对于正整数n ,设a n 是最接近n 的整数,则1a 1+1a 2+1a 3+…+1a 200=( )A .1917B .1927C .1937D .1947二、填空题(本题满分28分,每小题7分)7.成立的实数a 的值为______.8. 如图,平行四边形ABCD 中,∠ABC =72︒,AF ⊥BC 于点F ,AF 交BD 于点E ,若DE =2AB ,则∠AED =______.9. 设m ,n 是正整数,且m >n .若9m 与9n 的末两位数字相同,则m -n 的最小值为____.10. 若实数x ,y 满足x 3+y 3+3xy =1,则x 2+ y 2的最小值为______.第一试(B)一、选择题(本题满分42分,每小题7分)1.已知二次函数y =ax 2+bx +c (c ≠0)的图象与x 轴有唯一交点,则二次函数y =a 3x 2+b 3x +c 3的图象与x 轴的交点个数为( )A .0B .1C .2D .不确定 2.题目与(A )卷第1题相同. 3.题目与(A )卷第3题相同.4.已知正整数a ,b ,c 满足a 2-6b -3c +9=0,-6a +b 2+c =0,则a 2+b 2+c 2=( ) A .424. B .430. C .441. D .460.5.设O 是四边形ABCD 的对角线AC ,BD 的交点,若∠BAD +∠ACB =180,且BC =3,AD =4,AC =5,AB =6,DOOB=( )A .43B .65C .87D .1096.题目与(A )卷第5题相同.二、填空题(本题满分28分,每小题7分) 1.题目与(A )卷第1题相同.2.设O 是锐角三角形ABC 的外心,D ,E 分别为线段BC ,OA 的中点,∠ACB =7∠OED ,∠ABC =5∠OED ,则∠OED =______. 3.题目与(A )卷第3题相同. 4.题目与(A )卷第4题相同.第二试(A)一、(本题满分20分)已知实数x ,y 满足x + y =3,1x +y 2+1x 2+y =12,求x 5+y 5的值.二、(本题满分25分)如图,△ABC 中,AB >AC ,∠BAC =45︒,E 是∠BAC 的外角平分线与△ABC 的外接圆的交点,点F 在AB 上且EF ⊥AB .已知AF =1,BF =5,求△ABC 的面积.三、(本题满分25分)求所有的正整数数对(a ,b ),使得a 3=49×3b +8.第二试(B)一、(本题满分20分)已知实数a ,b ,c 满足a ≤b ≤c ,a +b +c =16,a 2+b 2+c 2+14abc = ,求c 的值.二、(本题满分25分)求所有的正整数m ,使得22m -1-2m +1是完全平方数.三、(本题满分25分)如图,O 为四边形ABCD 内一点,∠OAD =∠OCB ,OA ⊥OD ,OB ⊥OC .求证:AB 2+CD 2=AD 2+BC 2.7。
2017年全国高中数学联合竞赛试题和解答(A卷)

2017年全国高中数学联赛A卷一试一、填空题1•设f(x)是定义在R上的函数,对任意实数x有f(x 3) f(x_4) = -1 .又当0辽X ::: 7时,f (x) =log2(9 —x),则f(—100)的值为______________2•若实数x, y满足x2+2cosy =1,贝U x — cosy的取值范围是___________2 23.在平面直角坐标系xOy中,椭圆C的方程为:x y 1 , F为C的上焦点,A为C的9 10右顶点,P是C上位于第一象限内的动点,则四边形OAPF的面积的最大值为 _____________ . 4•若一个三位数中任意两个相邻数码的差不超过1,则称其为“平稳数”.平稳数的个数是5•正三棱锥P - ABC中,AB =1 , AP =2,过AB的平面:将其体积平分,则棱PC与平面a所成角的余弦值为___________ .6•在平面直角坐标系xOy中,点集K =〈x,y)x, y - -1,0,1】在K中随机取出三个点,贝U这三点中存在两点之间距离为J5的概率为______________7•在ABC中,M是边BC的中点,N是线段BM的中点若.A ABC的面积为3J3,则AM AN的最小值为______________ •8•设两个严格递增的正整数数列也Jb n 1满足:a®:::2017,对任意正整数n,有a n^ =a n* +a n,b n+ =2b n,则a 的所有可能值为___________ •二、解答题9•设k,m为实数,不等式x2—kx —m兰1对所有la,b】成立证明:b—a兰2应.10•设/必必是非负实数,满足x1 x2 X3 =1,求(x1 3x2 5X3)(X1 •—-)的最3 5小值和最大值•11.设复数Z1,Z2满足Re(z1) 0, ReZ) 0,且Re(才)=Re(z;) = 2(其中Re(z)表示复数z的实部)•(1)求Re⑵Z2)的最小值;(2)求N +2 + Z2 + 2 —乙—Z2的最小值•2017年全国高中数学联赛 A 卷二试.如图,在:ABC 中,AB=AC , I 为:ABC 的内心,以A 为圆心,AB 为半径作圆 M , 以I 为圆心,IB 为半径作圆 『2,过点B , I 的圆r 3与】1,丨2分别交于点P,Q (不同于点B ).设IP 与BQ 交于 点R .证明:BR_CR 二.设数列^aj 定义为 Q =1 ,a + nQ 兰 n,a n + = Jn =1,2,….求满足an- n,a n A n,a r ::: r < 32的正整数r 的个数•三•将33 33方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等 •若相邻连个小方格的颜色不同,则称它们的公共边为“分隔边”•试求分隔边条数的最小值•四•设m,n 均是大于1的整数,m_n , a 1,a 2/' ,a n 是n 个不超过 m 的互不相同的正整数, 且a 「a 2,…,a .互素•证明:对任意实数x ,均存在一个i (1 一 i 一 n ),使得2017年全国高中数学联赛A 卷一试答案1.答案:丄解:由黃件知*广(工+[4) = _—-——=r 所以dA-100)= <(-100 + 14x7)= === ~/(5) log-422a i x2 m(m 1)II X ,这里| y 表示实数y到与它最近的整数的距离答案:[-1*若+1] *解:由于 v'-1-2cosr^[-1. 3J* 故[-点间.由cw r --— 可知» v -cos v-x --------------- ----- -(.V - U : - 1.阖此当 r =[时,1- 7 'A g 和有最小值|(这时$可以S1-):当V - V'时 * A cos r 有最大值Jj I (这时F 可以取 2由于+的值域是[7 巧+ 1]・从而x-eosy 的取值范围是[-1, V3 + IL3.答第芈.£r解:易知卫⑶0)} F(0, 1). i 殳P 的坐标是(3cos<9, J?6审询,W 0冷・则盈>S — s 叫州F 屮 」辺神|——(vTOcosf/ I .sin//)= —^―sin(^ + ip) *2 2arctati ^1" 当/y-ardanVlO 时・四边形Oz 尸尸面积的最大值为芒叵. 10 24.答案:75. _解;考虑平稳数赢*若b = 0,则□ = ), c 怎{01}「有2个平稳数.若B=l ・JWX 仏2},虫{0丄2"有2x3 = 6个平稳数・, ^r2<6<8,则口,匚€少一1",占+ 1八 有7x3x3 = 63个平稳数.若b = 9、则{8,9} 1有2x2 = 4个平稳数.综上可知,平橈数的个数是2 + 6 +利+ 4=方・5.-丄 j.Jiihim 11WTT …答案:看解:设血PC 的中点分別为H ,则易证平而卫&灯就是平面口.由中线 长公式知5 I gg 」"土 %—; 2KMMC 石 故棱PC 与平面任所戒角的余弦值为婕.106.解:易知K 中有9个点,故在K 中粗机取出三个点的 方式数为C : = 84种.将K 中的点按右图标记为其中有8 对点之问的葩奥为J?.由对称性,考虑取厶局两点的情 况.则剩下的一个点有7种取法,这样有7x8 = 56个三点 组(不计每组中三点的次序人对每个4G = U,--S 8). K中恰有4宀4乜两点与之距證为{这里下标按模8理解).因而恰有 卩,心/』(心kN …⑻这$个三点组被计了两次.从而满足条件的三点组个 数为56-8 = 48・进而所求概率为—=-.S4 77.答案土 C 卜I 解:由条件知f AMACt AN故2'?斗 4I ,-?—-1' ][ ( I —' I TAM AN - -{Jfi + ^C]*| -.4B + - JC - - 3|AB^ +|^C| -4JS-Jtj.由于 ^3 = S 曲北=|jC | ■ sin J = |^45||/1C| r 所以 AB AC — 4* 进2 4步可得 AH AC — .4( I €0> .4 — 2* 从而IV/r所以 KM = JIC')- -PC --(2^= ---- T2文易知直线/<在平滴。
2017年全国初中数学联合竞赛试题及详细解答(含一试二试)

2. 设 O是 锐 角 三 角 形 ABC的 外 心 , D,E分 别 为 线 段 BC,OA的 中 点 ,
,
,则
_________.
3.题目与(A)卷第 3题相同. 4.题目与(A)卷第 4题相同
第二试 (A)
一、(本题满分 20分)已知实数 x,y满足 x+y=3,
,求
的值.
二、(本题满分25分)如图,△ABC中,AB AC, BAC 45,E是 BAC的 外角平分线与△ABC 的外接圆的交点,点F在AB 上且EF AB.已知AF 1,BF
1.已知二次函数 y ax2 bx c(c 0)的图象与x轴有唯一交点,则二次函
数
y a3x2 b3x c3 的图象与x轴的交点个数为 ( )
A.0
B.1
C.2
D.不确定.
2.题目与(A)卷第1 题相同.
3.题目与(A)卷第3 题相同.
4.已知正整数a,b,c满足 a2 6b 3c 9 0, 6a b2 c 0,则a2 b2 c2
CB的延长线上, 满足
.已知BC=15,BF=6,BD=3,则AE= ( )
A.
B.
C.
D.
6.对于正整数 n,设 an是最接近 的整数,则
A.191/7
B.192/7
C.193/7
() D.194/7
二、填空题(本题满分 28分,每小题 7分) (本题共有 4个小题,要求直接将答案写在横线上.)
1.使得等式
2017 年全国初中数学联合竞赛试题
2017年3月26日(星期日)上午8:30-11:30
第一试(A)
一、选择题(本题满分 42分,每小题 7分) (本题共有 6个小题,每题均给出了代号为 A,B,C,D的四个答案,其中有且仅
2017全国初中数学联赛初二卷及详解

2017年全国初中数学联合竞赛试题 初二卷第一试一、选择题:(本题满分 42 分,每小题 7 分) 1.已知实数a,b,c 满足2a+13b+3c=90,3a+9b+c=72,则32b ca b++的值为( ). A.2 B.1 C.0 D.-1 2.已知实数a,b,c 满足a+b+c=1,1110135a b c ++=+++,则(a+1)2+(b+3)2+(c+5)2的值为( ). A.125 B.120 C.100 D.813.若正整数a,b,c 满足a ≤b ≤c 且abc=2(a+b+c),则称(a,b,c)为好数组.那么好数组的个数为( ). A.4 B.3 C.2 D.14.已知正整数a,b,c 满足a 2-6b-3c+9=0,-6a+b 2+c=0,则a 2+b 2+c 2的值为( ). A.424 B.430 C.441 D.4605.梯形ABCD 中,AD ∥BC ,AB=3,BC=4,CD=2,AD=1,则梯形的面积为( ). A.102 B.103C.32D.33 6.如图,梯形ABCD 中,AD ∥BC ,∠A=90°,点E 在AB 上,若AE=42,BE=28,BC=70,∠DCE=45°,则DE 的值为( ).A.56B.58C.60D.62二、填空题:(本题满分 28 分,每小题 7 分)7.311a a ++=a 的值为________.8.已知△ABC 的三个内角满足A <B <C <100°.用θ表示100°-C,C-B,B-A 中的最小者,则θ的最大值为________.9.设a,b 是两个互质的正整数,且38ab p a b=+为质数.则p 的值为________.10.20个都不等于7的正整数排成一行,若其中任意连续若干个数之和都不等于7,则这20个数之和的最小值为________.第二试一、(本题满分20分)设A,B是两个不同的两位数,且B是由A交换个位数字和十位数字所得,如果A2-B2是完全平方数,求A的值.二、(本题满分25分)如图,△ABC中,D为BC的中点,DE平分∠ADB,DF平分∠ADC,BE⊥DE,CF⊥DF,P为AD与EF的交点.证明:EF=2PD.三、(本题满分25分)已知a,b,c 55a bb c++为有理数,求222a b ca b c++++的最小值.2017年全国初中数学联合竞赛试题初二卷参考答案第一试一、选择题:(本题满分42 分,每小题7 分)1.已知实数a,b,c满足2a+13b+3c=90,3a+9b+c=72,则32b ca b++的值为().A.2B.1C.0D.-1答案:B对应讲次:所属知识点:方程思路:因为所求分式的特点可以想到把a+2b,3b+c看成一个整体变量求解方程.解析:已知等式可变形为2(a+2b)+3(3b+c)=90,3(a+2b)+(3b+c)=72,解得a+2b=18,3b+c=18,所以312b ca b+=+.2.已知实数a,b,c满足a+b+c=1,111135a b c++=+++,则(a+1)2+(b+3)2+(c+5)2的值为().A.125B.120C.100D.81答案:C对应讲次:所属知识点:方程思路:可以想到换元法.解析:设x=a+1,y=b+3,z=c+5,则x+y+z=10,111x y z++=,∴xy+xz+yz=0,由x2+y2+z2=(x+y+z)2-2(xy+xz+yz)=100.则(a+1)2+(b+3)2+(c+5)2 =100.3. 若正整数a,b,c满足a≤b≤c且abc=2(a+b+c),则称(a,b,c)为好数组.那么好数组的个数为().A.4B.3C.2D.1答案:B对应讲次:所属知识点:数论思路:先通过a≤b≤c且abc=2(a+b+c)的限定关系确定可能的种类,再通过枚举法一一验证. 解析:若(a,b,c)为好数组,则abc=2(a+b+c)≤6c,即ab≤6,显然a=1或2.若a=1,则bc=2(1+b+c),即(b-2)(c-2)=6,可得(a,b,c)=(1,3,8)或(1,4,5),共2个好数组.若a=2,则b=2或3,可得b=2,c=4;b=3,c=52,不是整数舍去,共1个好数组.共3个好数组(a,b,c)=(1,3,8) (1,4,5) (2,2,4).4. 已知正整数a,b,c满足a2-6b-3c+9=0,-6a+b2+c=0,则a2+b2+c2的值为().A.424B.430C.441D.460答案:C对应讲次:所属知识点:方程思路:由已知等式消去c整理后,通过a,b是正整数的限制,枚举出所有可能,并一一代入原方程验证,最终确定结果.解析:联立方程可得(a-9)2+3(b-1)2=75,则3(b-1)2≤75,即1≤b≤6.当b=1,2,3,4,5时,均无与之对应的正整数a;当b=6时,a=9,符合要求,此时c=18,代入验证满足原方程.因此,a=9,b=6,c=18,则a2+b2+c2=441.5. 梯形ABCD中,AD∥BC,AB=3,BC=4,CD=2,AD=1,则梯形的面积为().A.102B.103C.32D.33答案:A对应讲次:所属知识点:平面几何思路:通过作平行四边形把边长关系转化到一个三角形中来.解析:作AE∥DC,AH⊥BC,则ADCE是平行四边形,则BE=BC-CE=BC-AD=3=AB,则△ABE 是等腰三角形,BE=AB=3,AE=2,经计算可得42AH =. 所以梯形ABCD 的面积为()142102142⨯+⨯=.6. 如图,梯形ABCD 中,AD ∥BC ,∠A=90°,点E 在AB 上,若AE=42,BE=28,BC=70,∠DCE=45°,则DE 的值为( ).A.56B.58C.60D.62 答案:B 对应讲次:所属知识点:平面几何思路:补形法,把直角梯形先补成正方形,再利用旋转把边长关系转化到同一个三角形Rt △EAD 中去,利用勾股定理求解.解析:作CF ⊥AD ,交AD 的延长线于点F ,将△CDF 绕点C 逆时针旋转90°至△CGB ,则ABCF 为正方形,可得△ECG ≌△ECD ,∴EG=ED. 设DE=x ,则DF=BG=x-28,AD=98-x.在Rt △EAD 中,有422+(98-x)2=x 2,解得x=58.二、填空题:(本题满分 28 分,每小题 7 分)7.311a a ++=a 的值为________.答案:8 对应讲次: 所属知识点:方程思路:通过等式两边都6次方可以去掉最外面根式,再用换元法化简等式,最后要验证结果是否满足最初的等式.解析:易得(321a =.令x ,则x ≥0,代入整理可得x(x-3)(x+1)2=0,解得x 1=0, x 2=3, x 3=-1,舍负,即a=-1或8,验证可得a=8.8. 已知△ABC 的三个内角满足A <B <C <100°.用θ表示100°-C,C-B,B-A 中的最小者,则θ的最大值为________. 答案:20° 对应讲次: 所属知识点:代数思路:一般来说,求几个中最小者的最大值时,就是考虑这几个都相等的情况. 解析:∵θ≤100°-C ,θ≤C-B ,θ≤B-A ∴θ≤16[3(100°-C )+2(C-B)+(B-A)]=20°又当A=40°,B=60°,C=80°时,θ=20°可以取到. 则θ的最大值为20°.9. 设a,b 是两个互质的正整数,且38ab p a b=+为质数.则p 的值为________.答案:7 对应讲次: 所属知识点:数论思路:因为p 是质数,只能拆成1和p ,另一方面通过a+b 、a 、b 两两互质来拆分38ab a b+的可能种类,最后分类讨论,要么与条件矛盾,要么得出结果.解析:因为a,b 互质,所以a+b 、a 、b 两两互质,因为38ab a b +质数,所以318ab p a b⎧=⎪⎨=⎪+⎩可得a=b=1,p=4,不是质数舍;381ab p a b⎧=⎪⎨=⎪+⎩可得a=7,b=1,p=7,符合题意.则p=7.10.20个都不等于7的正整数排成一行,若其中任意连续若干个数之和都不等于7,则这20个数之和的最小值为________. 答案:34 对应讲次: 所属知识点:数论思路:考虑1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1满足题设要求,其和为34,接下来只需要考虑该数列是否为和最小的数列.解析:设该正整数列为()20,*n a n n N ≤∈,考虑()16,,,14,*k k k i i i ki ka a a k k N ++==≤∈∑∑L ,依抽屉原理必然有两项模7的余数相同,则该两项的差是7的倍数,于是任意连续7项之中必有连续子列之和为7的倍数,又不能为7,则最小为14.于是20个数中至少有2组这样的子列其总和不小于28,剩下6个数之和不小于6,于是该数列之和不小于34.由1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1可知,存在数列和为34的情况.第二试一、(本题满分 20 分)设A,B 是两个不同的两位数,且B 是由A 交换个位数字和十位数字所得,如果A 2-B 2是完全平方数,求A 的值. 答案:65 对应讲次: 所属知识点:数论思路:对于需要考虑不同位数上数字的情况,可以把一个两位数ab 设为10a+b ,转为为代数问题,再利用完全平方数的质因数分解式也是以完全平方数对的形式出现,综合分析所有限定下可能性,最终确定结果. 解析:设A=10a+b(1≤a,b ≤9,a,b ∈N),则B=10b+a ,由A,B 不同得a ≠b ,A 2-B 2=(10a+b )2-(10b+a)2=9×11×(a+b )(a-b).………5分由A 2-B 2是完全平方数,则a >b ,()()11|a b a b +-,可得a+b=11, ………10分 a-b 也是完全平方数,所以a-b=1或4.………15分若a-b=1,则a=6,b=5; 若a-b=4,则没有正整数解. 因此a=6,b=5,A=65.………20分二、(本题满分 25 分)如图,△ABC 中,D 为BC 的中点,DE 平分∠ADB ,DF 平分∠ADC ,BE ⊥DE ,CF ⊥DF ,P 为AD 与EF 的交点.证明:EF=2PD.对应讲次:所属知识点:平面几何思路:因为EF 、PD 都在△DEF 中,所以想办法推出其性质,比较容易得出∠EDF=90°,此时若能得出EF=PD ,则自然可以得到结论.解析:由DE 平分∠ADB ,DF 平分∠ADC ,可得∠EDF=90°.………5分由BE ⊥DE 得BE ∥DF ,则∠EBD=∠FDC. ………10分又BD=DC ,∠BED=∠DFC=90°,则△BED ≌△DFC ,BE=DF . ………15分 得四边形BDFE 是平行四边形,∠PED=∠EDB=∠EDP ,EP=PD. ………20分 又△EDF 是直角三角形,∴EF=2PD.………25分三、(本题满分 25 分)已知a,b,c 为有理数,求222a b c a b c ++++的最小值.答案:3 对应讲次: 所属知识点:数论思路:通过a,b,c 是正整数,可以把有理部分和无理部分分离考虑.0c -≠,可以通过分母有理化来实现分离,再利用a,b,c 互不相等,从最小正整数开始讨论即可得出最小值.0c -≠)()22222555bcab bc bac b cb c +--+-==--b 2=ac. …10分()()22222a c ba b c a c b a b c a c b +-++==+-++++.………15分不妨设a <c ,若a=1,c=b 2,因为a ≠b ,则a+c-b=1+b(b-1)≥3,取等号当且仅当b=2时. ………20分 若a ≥2,因为c ≠b ≠1,则a+c-b=a+b(b-1)≥a+2≥4>3.所以222a b c a b c++++的最小值为3,当a=1,b=2,c=4时.………25分。
2017年全国初中数学联赛初二试题及参考答案(详解版)

2017年全国初中数学联合竞赛试题(初二)第一试一、选择题(本题满分 42 分,每小题 7 分)1.已知实数,,a b c 满足213390a b c ++=,3972a b c ++=,则32b ca b++的值为( ) A .2 B . 1 C . 0 D .1- 2.已知实数,,a b c 满足1a b c ++=,1110135a b c ++=+++,则()()()222135a b c +++++的值为( )A . 125B . 120C . 100D . 813.若正整数,,a b c 满足a b c ≤≤且()2abc a b c =++,则称(),,a b c 为好数组.那么好数组的个数为( )A . 4B . 3C . 2D . 14.已知正整数,,a b c 满足26390a b c --+=,260a b c -++=,则222a b c ++的值为( ) A .424 B . 430 C . 441 D . 4605.梯形ABCD 中,AD ∥BC ,3AB =,4BC =,2CD =,1AD =,则梯形的面积为( ) ABC. D.6.如图,梯形ABCD 中,AD ∥BC ,90A ∠=︒,点E 在AB 上,若42AE =,28BE =,70BC =,45DCE ∠=︒,则DE 的值为( )A . 56B . 58C . 60D . 62二、填空题:(本题满分 28 分,每小题 7 分)7.=a 的值为________.8.已知ABC 的三个内角满足100A B C <<<︒.用θ表示100,,C C B B A ︒---中的最小者,则θ的最大值为________.9.设,a b 是两个互质的正整数,且38ab p a b=+为质数.则p 的值为________.10.20个都不等于7的正整数排成一行,若其中任意连续若干个数之和都不等于7,则这20个数之和的最小值为________.第二试一、(本题满分 20 分)设,A B 是两个不同的两位数,且B 是由A 交换个位数字和十位数字所得,如果22A B -是完全平方数,求A 的值.二、(本题满分 25 分)如图,△ABC 中,D 为BC 的中点,DE 平分ADB ∠,DF 平分ADC ∠,BE DE ⊥,CF DF ⊥,P 为AD 与EF 的交点.证明:2EF PD =.三、(本题满分 25 分)已知,,a b c 是不全相等的正整数,求222a b c a b c ++++的最小值.2017年全国初中数学联合竞赛试题 初二卷参考答案第一试一、选择题(本题满分 42 分,每小题 7 分)1.已知实数,,a b c 满足213390a b c ++=,3972a b c ++=,则32b ca b++的值为( ) A .2 B . 1 C . 0 D .1- 【答案】B【思路】因为所求分式的特点可以想到把2a b +,3b c +看成一个整体变量求解方程. 【解析】已知等式可变形为()()223390a b b c +++=,()()32372a b b c +++=,解得218a b +=,318b c +=,所以312b ca b+=+. 2.已知实数,,a b c 满足1a b c ++=,1110135a b c ++=+++,则()()()222135a b c +++++的值为( )A . 125B . 120C . 100D . 81 【答案】C 【思路】换元法【解析】设1x a =+,3y b =+,5z c =+,则10x y z ++=,1110x y z++=, 0xy xz yz ∴++=,由()()22222100x y z x y z xy xz yz ++=++-++=.则()()()222135100a b c +++++=.3.若正整数,,a b c 满足a b c ≤≤且()2abc a b c =++,则称(),,a b c 为好数组.那么好数组的个数为( )A . 4B . 3C . 2D . 1 【答案】B【思路】先通过a b c ≤≤且()2abc a b c =++的限定关系确定可能的种类,再通过枚举法一一验证.【解析】若(),,a b c 为好数组,则()26abc a b c c =++≤,即6ab ≤,显然1a =或2. 若1a =,则()21bc b c =++,即()()226b c --=,可得()(),,1,3,8a b c =或()1,4,5,共2个好数组.若2a =,则2b =或3,可得2,4b c ==;53,2b c ==,不是整数舍去,共1个好数组. 共3个好数组()()()(),,1,3,8,1,4,5,2,2,4a b c =.4.已知正整数,,a b c 满足26390a b c --+=,260a b c -++=,则222a b c ++的值为( ) A .424 B . 430 C . 441 D . 460 【答案】C【思路】由已知等式消去c 整理后,通过,a b 是正整数的限制,枚举出所有可能,并一一代入原方程验证,最终确定结果.【解析】联立方程可得()()2293175a b -+-=,则()23175b -≤,即16b ≤≤. 当1,2,3,4,5b =时,均无与之对应的正整数a ;当6b =时,9a =,符合要求,此时18c =,代入验证满足原方程. 因此,9a =,6b =,18c =,则222441a b c ++=.5.梯形ABCD 中,AD ∥BC ,3AB =,4BC =,2CD =,1AD =,则梯形的面积为( ) ABC. D.【答案】A【思路】通过作平行四边形把边长关系转化到一个三角形中来.【解析】作AE ∥DC ,AH ⊥BC ,则ADCE 是平行四边形,则3BE BC CE BC AD AB =-=-==, 则ABE 是等腰三角形,3BE AB ==,2AE =,经计算可得AH =. 所以梯形ABCD 的面积为()1142⨯+. 6.如图,梯形ABCD 中,AD ∥BC ,90A ∠=︒,点E 在AB 上,若42AE =,28BE =,70BC =,45DCE ∠=︒,则DE 的值为( )A . 56B . 58C . 60D . 62【答案】B【思路】补形法,把直角梯形先补成正方形,再利用旋转把边长关系转化到同一个三角形Rt △EAD 中去,利用勾股定理求解.【解析】作CF △AD ,交AD 的延长线于点F ,将CDF 绕点C 逆时针旋转90︒至CGB ,则ABCF 为正方形,可得ECG △ECD ,EG ED ∴=. 设DE x =,则28DF BG x ==-,98AD x =-. 在RtEAD 中,有()2224298x x +-=,解得58x =.二、填空题:(本题满分 28 分,每小题 7 分) 7.=a 的值为________. 【答案】8【思路】通过等式两边都6次方可以去掉最外面根式,再用换元法化简等式,最后要验证结果是否满足最初的等式.【解析】易得(321a =.令x ,则0x ≥,代入整理可得()()2310x x x -+=,解得1230,3,1x x x ===-,舍负,即1a =-或8,验证可得8a =.8.已知△ABC 的三个内角满足100A B C <<<︒.用θ表示100,,C C B B A ︒---中的最小者,则θ的最大值为________. 【答案】20︒【思路】一般来说,求几个中最小者的最大值时,就是考虑这几个都相等的情况.【解析】100C θ≤︒-,C B θ≤-,B A θ≤-()()()131002206C C B B A θ∴≤︒-+-+-=︒⎡⎤⎣⎦ 又当40,60,80A B C =︒=︒=︒时,20θ=︒可以取到. 则θ的最大值为20︒.9.设,a b 是两个互质的正整数,且38ab p a b=+为质数.则p 的值为________.【答案】7【思路】因为p 是质数,只能拆成1和p ,另一方面通过a b +、a 、b 两两互质来拆分38ab a b+的可能种类,最后分类讨论,要么与条件矛盾,要么得出结果.【解析】因为,a b 互质,所以a b +、a 、b 两两互质,因为38ab a b +质数,所以318ab p a b⎧=⎪⎨=⎪+⎩可得1a b ==,4p =,不是质数舍; 381ab p a b⎧=⎪⎨=⎪+⎩可得7a =,1b =,7p =,符合题意. 则7p =.10.20个都不等于7的正整数排成一行,若其中任意连续若干个数之和都不等于7,则这20个数之和的最小值为________. 【答案】34【思路】考虑1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1满足题设要求,其和为34,接下来只需要考虑该数列是否为和最小的数列.【解析】设该正整数列为()20,*n a n n N ≤∈,考虑()16,,,14,*k k k i i i k i ka a a k k N ++==≤∈∑∑,依抽屉原理必然有两项模7的余数相同,则该两项的差是7的倍数,于是任意连续7项之中必有连续子列之和为7的倍数,又不能为7,则最小为14.于是20个数中至少有2组这样的子列其总和不小于28,剩下6个数之和不小于6,于是该数列之和不小于34. 由1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1可知,存在数列和为34的情况.第二试一、(本题满分 20 分)设,A B 是两个不同的两位数,且B 是由A 交换个位数字和十位数字所得,如果22A B -是完全平方数,求A 的值.【思路】对于需要考虑不同位数上数字的情况,可以把一个两位数ab 设为10a b +,转为为代数问题,再利用完全平方数的质因数分解式也是以完全平方数对的形式出现,综合分析所有限定下可能性,最终确定结果.【解析】设()101,9,,A a b a b a b N =+≤≤∈,则10B b a =+,由,A B 不同得a b ≠,()()()()22221010911A B a b b a a b a b -=+-+=⨯⨯+-.由22A B -是完全平方数,则a b >,()()11|a b a b +-,可得11a b +=,a b -也是完全平方数,所以1a b -=或4.若1a b -=,则6a =,5b =; 若4a b -=,则没有正整数解. 因此6a =,5b =,65A =.二、(本题满分 25 分)如图,△ABC 中,D 为BC 的中点,DE 平分ADB ∠,DF 平分ADC ∠,BE DE ⊥,CF DF ⊥,P 为AD 与EF 的交点.证明:2EF PD =.【思路】因为EF 、PD 都在DEF 中,所以想办法推出其性质,比较容易得出90EDF ∠=︒,此时若能得出EP PD =,则自然可以得到结论.【解析】由DE 平分ADB ∠,DF 平分ADC ∠,可得90EDF ∠=︒. 由BE DE ⊥得BE △DF ,则EBD FDC ∠=∠.又BD DC =,90BED DFC ∠=∠=︒,则BED △DFC ,BE DF =. 得四边形BDFE 是平行四边形,PED EDB EDP ∠=∠=∠,EP PD =. 又△EDF 是直角三角形,2EF PD ∴=.三、(本题满分 25 分)已知,,a b c 是不全相等的正整数,求222a b c a b c ++++的最小值.【思路】通过,,a b c 是正整数,可以把有理部分和无理部分分离考虑.0c -≠,可以通过分母有理化来实现分离,再利用,,a b c 互不相等,从最小正整数开始讨论即可得出最小值.0c -≠)()22222555bcab bc bac b c b c +--+-==--可得2b ac =.()()22222a c ba b c a c b a b c a c b+-++==+-++++.不妨设a c <,若1a =,2c b =,因为a b ≠,则()113a c b b b +-=+-≥,取等号当且仅当2b =时.若2a ≥,因为1c b ≠≠,则()1243a c b a b b a +-=+-≥+≥>.所以222a b c a b c++++的最小值为3,当1a =,2b =,4c =时.。
2017年全国初中数学联合竞赛试题含答案

2017 年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设 7 分和 0 分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试(A)一、选择题:(本题满分 42 分,每小题 7 分)1.已知实数a,b,c满足2a+13b+3c=90,3a+9b+c=72,则3b+c=()a +2bA. 2.B. 1.C. 0.D.-1.【答】B.已知等式可变形为 2( a+ 2b) + 3(3b+c ) = 90 , 3( a+ 2b) + (3b+c ) = 72 ,解得a+2b=18,3b+c=18 ,所以3b+c=1.a +2b2.已知△ABC的三边长分别是a,b,c,有以下三个结论:(1)以a,b,c为边长的三角形一定存在;(2)以 a 2, b 2, c2为边长的三角形一定存在;(3)以 | a-b | +1,| b-c | +1,| c-a | +1 为边长的三角形一定存在.其中正确结论的个数为()A.0.B.1.C.2.D.3.【答】C.不妨设 a ≥ b ≥ c ,则有 b + c > a .(1)因为 b + c > a ,所以 b + c +222b +c > a ,故以a,b,c为bc > a ,即( b + c ) >( a),即边长的三角形一定存在;(2)以 a =2, b =3, c =4为边长可以构成三角形,但以 a 2= 4, b2= 9, c2=16 为边长的三角形不存在;(3)因为 a ≥ b ≥ c ,所以| a - b |+1= a - b +1,| b - c |+1= b - c +1,| c - a |+1= a - c +1,故三条边中| c - a |+1大于或等于其余两边,而(| a-b | +1)+(| b-c | +1)=(a-b+ 1)+(b-c+1)=a-c+ 1 + 1 >a -c+ 1 =| c-a | +1 ,故以 | a-b | +1 , | b-c | +1 , | c-a | +1 为边长的三角形一定存在.3.若正整数a,b,c满足a≤b≤c且abc=2(a+b+c),则称(a,b,c)为好数组.那么,好数组的个数为()A. 1.B.2.C.3.D.4.【答】C.若( a, b, c) 为好数组,则abc= 2( a+b+c ) ≤ 6c,所以ab≤6.显然,a只能为1或2.若a =2,由ab≤6可得b=2或3,b=2时可得c=4,b=3时可得c=52(不是整数);若a =1,则bc=2(1+b+c),于是可得(b-2)(c-2)=6,可求得(a,b,c)=(1,3,8)或(1,4,5).综合可知:共有 3 个好数组,分别为(2,2,4),(1,3,8)和(1,4,5).4.设 O 是四边形 ABCD 的对角线 AC 、BD 的交点,若 ∠BAD + ∠ACB = 180︒,且 BC = 3,AD = 4 ,AC = 5 , AB = 6 ,则 DO = ( )OB10 8 64A..B..C..D..D9 7 5 3E【答】A.C过 B 作 BE // AD ,交 AC 的延长线于点 E ,则 ∠ABE = 180︒ - ∠BAD= ∠ACB ,所以△ ABC ∽△ AEB ,所以AC = BC ,所以4O3AB EBAB ⋅ BC6 ⨯318BEB = = = .A6AC 5 5再由 BE // AD ,得 DO = AD = 4 = 10 .BEOB 18 955.设 A 是以 BC 为直径的圆上的一点,AD ⊥ BC 于点 D ,点 E 在线段 DC 上,点 F 在 CB 的延长线上,满足 ∠BAF = ∠CAE .已知 BC =15 , BF = 6 , BD = 3 ,则 AE = ( )AA. 4 3 .B. 2 13 .C. 2 14 .D. 2 15 .【答】B.FBDEC如图,因为 ∠BAF = ∠CAE ,所以 ∠BAF + ∠BAE = ∠CAE + ∠BAE ,即 6 3∠FAE = ∠BAC = 90︒ .又因为 AD ⊥ BC ,故 AD 2 = DE ⋅ DF = DB ⋅ DC .而 DF = BF + BD = 6 + 3 = 9 ,DC = BC - BD = 15 - 3 =12 ,所以 AD 2 = DE ⋅ 9 = 3 ⋅ 12 ,所以 AD = 6 ,DE= 4 . 从而 AE = AD 2 + DE 2 = 62 + 42 = 213 .6.对于正整数 n ,设 a 是最接近的整数,则 1 + 1 + 1 + +1 = ( n)na 1 a 2 a 3a200A. 191 .B. 192 .C. 193 .D. 194 .777 7 【答】A.对于任意自然数 k , ( k +1 )2 = k 2 + k + 1不是整数,所以,对于正整数 n ,- 1 一定不是整数.n24 2的整数,则| m - |< 1 , m ≥1.设 m 是最接近 nn2易知:当 m ≥1时,| m - |< 1 ⇔ ( m - 1 ) 2 < n < ( m + 1 )2⇔ m 2 - m + 1 < n < m 2 + m + 1 .n 2 2 24 4 于是可知:对确定的正整数 m ,当正整数 n 满足 m 2 - m + 1 ≤ n ≤ m 2+ m 时,m 是最接近的整数,n 即 a n = m .所以,使得 a n = m 的正整数 n 的个数为 2m .注意到132 + 13 = 182 < 200 < 14 2 + 14 = 210 ,因此, a , a , ,8 个 4,……,26 个 13,18 个 14.所以1+1+1+ +1= 2 ⨯1+ 4 ⨯1+ 6 ⨯1+ + 26 ⨯1+ 18⨯1=191.a a a a12313147 123200二、填空题:(本题满分 28 分,每小题 7 分)1.使得等式 1 + 1+a=3a 成立的实数 a 的值为_______.【答】 8 .由所给等式可得 (1 + 1 +a )3=a2.令 x =1+a,则 x ≥0,且a=x2-1,于是有(1+ x )3=( x2-1)2,整理后因式分解得x ( x -3)( x +1)2=0,解得 x= 0 ,x= 3 ,x= -1 (舍去),所以a= -1或a=8.123验证可知: a = -1是原方程的增根, a =8是原方程的根.所以, a =8.2.如图,平行四边形ABCD中,∠ABC=72︒,AF⊥BC于点F, AFM交 BD 于点 E ,若 DE =2AB ,则∠AED =_______.【答】 66︒.BE 取 DE 的中点 M ,在Rt△ ADE中,有 AM = EM =1DE = AB .2设∠AED =α,则∠AME =180︒ -2α,∠ABM =α-18︒.又∠ABM = ∠AMB ,所以180︒ -2α=α-18︒,解得α=66︒.3.设m,n是正整数,且m>n.若9m与9n的末两位数字相同,则m-n的最小值为.【答】10.由题意知,9m- 9n= 9n⋅ (9m-n-1) 是100的倍数,所以9m-n-1是100的倍数,所以9m-n的末两位数字是 01,显然,m-n是偶数,设m-n=2t(t是正整数),则9m-n=92t=81t .计算可知: 812的末两位数字是61, 813的末两位数字是41, 814的末两位数字是21, 815的末两位数字是 01.所以 t 的最小值为5,从而可得 m - n 的最小值为10.4.若实数 x, y 满足 x 3+ y 3+3 xy =1,则 x 2+ y2的最小值为.1【答】2 .因为0= x 3+ y 3+3 xy -1=( x + y )3+(-1)3-3 x 2 y -3 xy 2+3xy=( x+y- 1)( x2+y2-xy+x+y+1) =12(x+y-1)[(x-y)2+(x+1)2+(y+1)2],所以 x = y = -1或x+y=1.若x = y = -1,则 x 2+ y2=2.若x + y =1,则x2+y2=12[(x+y)2+(x-y)2]=12[1+(x-y)2]≥12,当且仅当x=y=12时等号成立.所以, x 2+ y2的最小值为12.第一试(B)一、选择题:(本题满分 42 分,每小题 7 分)1.已知二次函数y=ax2+bx+c(c≠0)的图象与x轴有唯一交点,则二次函数y=a3x2+b3x+c3的图象与 x 轴的交点个数为()A.0.B.1.C.2.D.不确定.【答】C.因为二次函数 y = ax 2+ bx + c 的图象与 x 轴有唯一交点,所以∆1=b2-4ac=0,所以b2=4ac≠0.故二次函数 y = a 3 x 2+ b3 x + c3的判别式∆2=(b3)2-4a3c3=b6-161(4ac)3=b6-161(b2)3=1615b6>0 ,所以,二次函数y=a3x2+b3x+c3的图象与x轴有两个交点.2.题目和解答与(A)卷第 1 题相同.3.题目和解答与(A)卷第 3 题相同.4.已知正整数a,b,c满足a2-6b-3c+9=0,-6a+b2+c=0,则a2+b2+c2=()A. 424.B. 430.C. 441.D. 460.【答】C.由已知等式消去 c 整理得( a -9)2+3(b -1)2=75,所以3(b -1)2≤75,又b为正整数,所以1≤b≤6.若b =1,则( a -9)2=75,无正整数解;若b =2,则( a -9)2=72,无正整数解;若b =3,则( a -9)2=63,无正整数解;若b =4,则( a -9)2=48,无正整数解;若b =5,则( a -9)2=27,无正整数解;若b =6,则( a -9)2=0,解得a=9,此时c=18.因此, a =9,b=6, c =18,故a2+b2+c2==441.5.设O是四边形ABCD的对角线AC、BD的交点,若∠BAD+ ∠ACB=180︒,且BC=3,AD=4,AC =5, AB =6,则DO=()OBA.4.B.6.C.8.D.10.3579【答】D.解答过程与(A)卷第 4 题相同.6.题目和解答与(A)卷第 5 题相同.二、填空题:(本题满分 28 分,每小题 7 分)1.题目和解答与(A)卷第 1 题相同.2 .设O是锐角三角形ABC的外心,D,E分别为线段BC,OA的中点,∠ACB=7∠OED,∠ABC =5∠OED ,则∠OED =_________.A 【答】10︒.如图,设∠OED = x ,则∠A B =C5,x ∠ACB =7x ,∠DOC= ∠BAC =180︒ -12x ,∠AOC =10x ,所以∠AOD =180︒ -2x ,∠ODE =180︒ - x -(180︒ -2 x)= x ,所以OD=OE=1OA =1OC ,所22B 以∠DOC =60︒,从而可得 x =10︒.3.题目和解答与(A)卷第 3 题相同.4.题目和解答与(A)卷第 4 题相同.EODC第二试(A)一、(本题满分20分)已知实数 x, y 满足x+y=3,1+1=1,求 x 5+ y5的值. x+ y 2x 2+ y2解由1+1=1可得 2( x+y+x2+ y 2)= x 3+ y 3+ x 2 y 2+ xy . x + y 2x 2+ y2设xy = t ,则 x 2+ y 2=( x + y )2-2xy =9-2t , x 3+ y 3=( x + y )[( x + y )2-3 xy ]=3(9-3t ),代入上式可得 2(3 + 9 - 2t ) = 3(9 - 3t ) +t2+t,解得t=1或t=3.……………………10分当 t =3时,xy=3,又x+y=3,故x,y是一元二次方程m2-3m+3=0的两实数根,但易知此方程没有实数根,不合题意.……………………15分当 t =1时,xy=1,又x+y=3,故x,y是一元二次方程m2-3m+1=0的两实数根,符合题意.此时x 5+ y 5=( x 2+ y 2)( x 3+ y 3)-( x + y ) x 2 y 2=(9-2t )⋅[3(9-3t )]-3t 2=123.……………………20分二(、本题满分 25 分)如图,△ ABC 中,AB > AC ,∠BAC = 45︒ ,E 是 ∠BAC的外角平分线与 △ ABC 的外接圆的交点,点 F 在 AB 上且 EF ⊥ AB . 已知 AF =1, BF = 5,求△ ABC 的面积.解 在 FB 上取点 D ,使 FD =AF ,连接 ED 并延长,交△ ABC 的外接圆于点 G.由 EF ⊥AD ,AF =FD 知△AED 是等腰三角形,所以∠AED =180︒ - 2 ∠EAD =∠BAC , ……………………10 分EAFDCGB……………………15 分 所以 AG = BC ,所以 AC = BG ,所以 AC =BG. 又∠BGE =∠BAE =∠ADE =∠BDG ,所以 BG =BD ,所以 AC =BD =5-1=4, ……………………20 分△ ABC 的 AB 边上的高 h = AC sin 45︒ = 2 2 .所以,△ ABC 的面积 S = 1 ⋅ AB ⋅ h = 1 ⨯ 6 ⨯ 2 = 6 .2 2 ……………………25 分22三、(本题满分 25 分)求所有的正整数数对 ( a , b ) ,使得 a 3 = 49 ⨯ 3b +8 . 解 显然, 49 ⨯ 3b +8 为奇数,所以 a 为奇数.又因为 a 3 = 49 ⨯ 3b + 8 ≥ 49 ⨯ 3 + 8 > 53 ,所以 a > 5 .……………………5 分由 a 3 = 49 ⨯ 3b +8 可得 a 3 - 8 = 49 ⨯3b ,即 ( a - 2)( a 2 + 2a + 4) = 7 2 ⨯3b . ……………………10 分设 ( a - 2, a 2 + 2a + 4) = d ,则 d 为奇数.注意到 a 2 + 2a + 4 = ( a - 2)( a + 4) +12 ,所以 d | 12 ,所以 d=1 或 3. ……………………15 分⎧a - 2 = 7 2,⎧a - 2 = 3b,均无正整数解.……………………20 分若 d =1,则有 ⎨a 2 + 2 a + 4 或 ⎨a 2 + 2 a + 4 = 7 2 ⎪ = 3b ,⎪ , ⎩⎩⎧a - 2 = 3 ⨯7 2, ⎧a - 2 = 3b -1,解得 a =11, b = 3 . 若 d =3,则有 ⎨ 2 + 2 a + 4 b -1或 ⎨ 2 + 2 a + 4 = 3 ⨯7 2 ⎪ a = 3 , ⎪ a ,⎩⎩所以,满足条件的正整数对只有一个,为(11,3).……………………25 分第二试 (B )一、(本题满分 20 分)已知实数 a , b , c 满足 a ≤ b ≤ c , a + b + c =16 , a 2 + b 2 + c 2 +14 abc =128 ,求 c 的值.解 设 a + b = x , ab = y ,依题意有 x 2 - 2 y + (16 - x ) 2 +14 y (16 - x ) =128 ,整理得( x - 8) 2 = 1y ( x -8) ,8所以 x = 8 或 y = 8( x -8) .……………………10 分(1)若 x =8,则 a + b =8,此时 c =8.(2)若 y =8( x -8),即 ab =8( a + b -8),则( a -8)(b -8)=0,所以a=8或b=8.当a =8时,结合 a ≤ b ≤ c 可得 a + b + c ≥24,与 a + b + c =16矛盾.当b =8时,结合 a ≤ b ≤ c 及 a + b + c =16可得 a =0, c =8.综合可知: c =8.……………………20分二、(本题满分 25 分)求所有的正整数m,使得22m-1-2m+1是完全平方数.解当 m =1时,22m-1-2m+1=1是完全平方数.……………………5分当 m >1时,设22m-1-2m+1=n2( n 为正整数).注意到 22m-1- 2m+ 1 = 2 ⋅ (2m-1 ) 2- 2 ⋅ 2 m-1+ 1 = (2 m-1- 1) 2+ (2 m-1 )2,故可得(2 m-1- 1) 2+ (2 m-1 )2=n2,……………………10分所以 22m-2=n2- (2m-1- 1) 2= ( n+ 2 m-1- 1)( n- 2 m-1+1) .……………………15分设 x = n -2m-1+1, y = n +2m-1-1,则x<y, xy =22m-2,所以x,y均为2的方幂.……………………20分又 y - x =2m-2被4除余数为2,所以,只可能x=2, y =2m,故2⨯2m=22m-2,解得m=3.综上可知:满足条件的正整数 m 有两个,分别为1和3.……………………25分三、(本题满分 25 分)如图,O为四边形ABCD内一点,∠OAD= ∠OCB,DOA ⊥ OD , OB ⊥ OC .求证:AB2+CD2=AD2+BC2.AOP 证明由题设条件可知∠AOD = ∠BOC =90︒,又∠OAD =∠OCB,所以△ AOD ∽△ COB ,……………………5分OD AO OC AOB所以OB=CO,从而OB=OD .……………………10分C 又∠AOC = ∠AOB + ∠BOC = ∠AOB + ∠AOD = ∠DOB ,所以△ AOC ∽ △ DOB ,所以∠OAC = ∠ODB .……………………15分设AC 和BD交于点P,则∠APD = ∠AOD =90︒,所以 AC ⊥ DB ,……………………20分所以 AB 2+ CD 2=( AP 2+ PB 2)+( PD 2+ PC 2)=( AP 2+ PD 2)+( PB 2+ PC 2)= AD 2+ BC2.……………………25分。
2017年初中数学联合竞赛试题(含答案)

【答】 B.
F
B
D
E
C
如图,因为 BAF CAE ,所以 BAF BAE CAE BAE ,即
FAE BAC 90 . 又因为 AD BC ,故 AD 2 DE DF DB DC . 而 DF BF BD 6 3 9 ,DC BC BD 15 3 12 ,所以 AD 2 DE 9 3 12 ,所以 AD 6 ,DE 4 .
数字是 01.
所以 t 的最小值为 5,从而可得 m n 的最小值为 10.
4. 若实数 x, y 满足 x3 y3 3xy 1,则 x2 y2 的最小值为 1
【答】 .
2
因为
0 x3 y3 3xy 1 ( x y)3 ( 1)3 3x2 y 3xy2 3xy
( x y 1)[( x y)2 ( x y) ( 1) ( 1)2 ] 3xy( x y 1)
A. 424 . 【答】 C.
B. 430 .
C. 441 .
D. 460 .
由已知等式消去 c 整理得 (a 9)2 3(b 1)2 75 ,所以 3(b 1)2 75 ,又 b 为正整数, 所以 1 b 6 .
若 b = 1,则 ( a 9)2 75,无正整数解;
若 b = 2,则 ( a 9)2 72,无正整数解;
【答】 66 . 取 DE 的中点 M ,在 Rt △ ADE 中,有 AM EM 设 AED ,则 AME 180 2 , ABM
1 DE AB . 2
18 .
E BF
又 ABM AMB ,所以 180 2
18 ,解得
66 .
M C
3. 设 m, n 是正整数,且 m n .若 9 m 与 9 n 的末两位数字相同,则 m n 的最小值为
2017年全国高中数学联合竞赛广东赛区选拔赛试卷参考答案

m1 cos
2k
m1
i sin
2k
0, n1 cos 2k
n1
i sin
2k
0
k 0
m
ቤተ መጻሕፍቲ ባይዱ
k 0
m
k 0
n
k 0
n
所以 m1 cos 2k 0, n1 sin 2k 0 ,故: m1 cos 2k n1 sin 2k 0 .
k 0
m
k 0
n
k 0
m k0
n
而当 m
1 时 m 1 cos 2k
(x1, x2, x3, x4) (0,1,2,7),(0,1,3,6),(0,1,4,5),(0,2,3,5),(1,2,3,4) ,因此符合条件的四位数恰有:
4C31 3!4!
96 (个),故所求概率为
C915 C926
1 48
.
8. 已知 S 是正整数集合的无穷子集,满足对任何 a,b,c S, abc S ,将 S 中的元素按 照 由 小 到 大 的 顺 序 排 列 成 的 数 列 记 为 {an} , 且 已 知 a1 2, a2031 24061 , 则 a2017 _____ .
68
x
1 2
(
x1
x2 )
1 2
b 34
25 b
25
代入③式可得弦中点纵坐标恰好为点 Q( 25 , 9) 的纵坐标,即 bb
y 25 34 9 b bb
4
这就是说,点 Q( 25 , 9) 平分线段 MN . bb
--------------------------------------- 16 分
b3
|
11 11
2017年全国高中数学联合竞赛试题及解答.(A卷)

2 2 1 AM AN 3 AB AC 4 AB AC , 8
由 3 S ABC
1 3 AB AC sin A AB AC 得 AB AC 4 2 4
2
所以 AB AC 2 ,所以 3 AB
AC 8 3 ,当且仅当 AB
x x1 3x 2 5 x3 x1 2 3
★解析:由柯西不等式
x3 的最小值和最大值。 5 x2 5 x3 3 x3 5 1
2
x x x1 3x 2 5 x3 x1 x1 3 x 2 x1 2 3 3 5
当 x1 1 , x 2 0 , x 3 0 时取等号,故所求的最小值为 1 ; 又 x1 3 x 2 5 x 3 x1
x 2 x3 1 5x x1 3 x 2 5 x 3 5 x1 2 x 3 3 5 5 3
2
512 b1 ② 55
★证明:记 f ( x ) x kx m , x a, b ,则 f ( x ) 1,1 。于是
2
f (a ) a 2 ka m 1 ①; f (b) b 2 kb m 1 ② ab ab 2 ab )( ) k( ) m 1 ③ 2 2 2 ①+②- 2 ③知 f(
2017 年全国高中数学联合竞赛一试(A 卷)
一、填空题:本大题共 8 个小题,每小题 8 分,共 64 分。 2017A1、设 f ( x ) 是定义在 R 上函数,对任意的实数 x 有 f ( x 3) f ( x 4) 1 ,又当 0 x 7 时, f ( x ) log 2 (9 x ) ,则 f ( 100) 的值为 ◆答案:
2017年全国初中数学联赛初二卷和详解

2017年全国初中数学联合竞赛试题初二卷第一试一、选择题:(本题满分42 分,每小题7 分)1.已知实数a,b,c满足2a+13b+3c=90,3a+9b+c=72,则32b ca b++的值为().A.2B.1C.0D.-12.已知实数a,b,c满足a+b+c=1,111135a b c++=+++,则(a+1)2+(b+3)2+(c+5)2的值为().A.125B.120C.100D.813.若正整数a,b,c满足a≤b≤c且abc=2(a+b+c),则称(a,b,c)为好数组.那么好数组的个数为().A.4B.3C.2D.14.已知正整数a,b,c满足a2-6b-3c+9=0,-6a+b2+c=0,则a2+b2+c2的值为().A.424B.430C.441D.4605.梯形ABCD中,AD∥BC,AB=3,BC=4,CD=2,AD=1,则梯形的面积为().C. D.6.如图,梯形ABCD中,AD∥BC,∠A=90°,点E在AB上,若AE=42,BE=28,BC=70,∠DCE=45°,则DE的值为().A.56B.58C.60D.62二、填空题:(本题满分28分,每小题7分)7.=a的值为________.8.已知△ABC的三个内角满足A<B<C<100°.用θ表示100°-C,C-B,B-A中的最小者,则θ的最大值为________.9.设a,b是两个互质的正整数,且38abpa b=+为质数.则p的值为________.10.20个都不等于7的正整数排成一行,若其中任意连续若干个数之和都不等于7,则这20个数之和的最小值为________.第二试一、(本题满分20分)设A,B是两个不同的两位数,且B是由A交换个位数字和十位数字所得,如果A2-B2是完全平方数,求A的值.二、(本题满分25分)如图,△ABC中,D为BC的中点,DE平分∠ADB,DF平分∠ADC,BE⊥DE,CF⊥DF,P为AD与EF的交点.证明:EF=2PD.三、(本题满分25分)已知a,b,c为有理数,求222a b ca b c++++的最小值.2017年全国初中数学联合竞赛试题初二卷参考答案第一试一、选择题:(本题满分42 分,每小题7 分)1.已知实数a,b,c满足2a+13b+3c=90,3a+9b+c=72,则32b ca b++的值为().A.2B.1C.0D.-1答案:B对应讲次:所属知识点:方程思路:因为所求分式的特点可以想到把a+2b,3b+c看成一个整体变量求解方程.解析:已知等式可变形为2(a+2b)+3(3b+c)=90,3(a+2b)+(3b+c)=72,解得a+2b=18,3b+c=18,所以312b ca b+=+.2.已知实数a,b,c满足a+b+c=1,111135a b c++=+++,则(a+1)2+(b+3)2+(c+5)2的值为().A.125B.120C.100D.81答案:C对应讲次:所属知识点:方程思路:可以想到换元法.解析:设x=a+1,y=b+3,z=c+5,则x+y+z=10,111x y z++=,∴xy+xz+yz=0,由x2+y2+z2=(x+y+z)2-2(xy+xz+yz)=100.则(a+1)2+(b+3)2+(c+5)2 =100.3. 若正整数a,b,c满足a≤b≤c且abc=2(a+b+c),则称(a,b,c)为好数组.那么好数组的个数为().A.4B.3C.2D.1答案:B对应讲次:所属知识点:数论思路:先通过a≤b≤c且abc=2(a+b+c)的限定关系确定可能的种类,再通过枚举法一一验证. 解析:若(a,b,c)为好数组,则abc=2(a+b+c)≤6c,即ab≤6,显然a=1或2.若a=1,则bc=2(1+b+c),即(b-2)(c-2)=6,可得(a,b,c)=(1,3,8)或(1,4,5),共2个好数组.若a=2,则b=2或3,可得b=2,c=4;b=3,c=52,不是整数舍去,共1个好数组.共3个好数组(a,b,c)=(1,3,8) (1,4,5) (2,2,4).4. 已知正整数a,b,c满足a2-6b-3c+9=0,-6a+b2+c=0,则a2+b2+c2的值为().A.424B.430C.441D.460答案:C对应讲次:所属知识点:方程思路:由已知等式消去c整理后,通过a,b是正整数的限制,枚举出所有可能,并一一代入原方程验证,最终确定结果.解析:联立方程可得(a-9)2+3(b-1)2=75,则3(b-1)2≤75,即1≤b≤6.当b=1,2,3,4,5时,均无与之对应的正整数a;当b=6时,a=9,符合要求,此时c=18,代入验证满足原方程.因此,a=9,b=6,c=18,则a2+b2+c2=441.5. 梯形ABCD中,AD∥BC,AB=3,BC=4,CD=2,AD=1,则梯形的面积为().C. D.答案:A对应讲次:所属知识点:平面几何思路:通过作平行四边形把边长关系转化到一个三角形中来.解析:作AE∥DC,AH⊥BC,则ADCE是平行四边形,则BE=BC-CE=BC-AD=3=AB,则△ABE 是等腰三角形,BE=AB=3,AE=2,经计算可得AH =所以梯形ABCD 的面积为()1142⨯+=.6. 如图,梯形ABCD 中,AD ∥BC ,∠A=90°,点E 在AB 上,若AE=42,BE=28,BC=70,∠DCE=45°,则DE 的值为( ).A.56B.58C.60D.62 答案:B 对应讲次:所属知识点:平面几何思路:补形法,把直角梯形先补成正方形,再利用旋转把边长关系转化到同一个三角形Rt △EAD 中去,利用勾股定理求解.解析:作CF ⊥AD ,交AD 的延长线于点F ,将△CDF 绕点C 逆时针旋转90°至△CGB ,则ABCF 为正方形,可得△ECG ≌△ECD ,∴EG=ED. 设DE=x ,则DF=BG=x-28,AD=98-x.在Rt △EAD 中,有422+(98-x)2=x 2,解得x=58.二、填空题:(本题满分 28 分,每小题 7 分)7.=a 的值为________.答案:8 对应讲次: 所属知识点:方程思路:通过等式两边都6次方可以去掉最外面根式,再用换元法化简等式,最后要验证结果是否满足最初的等式.解析:易得(321a =.令x ,则x ≥0,代入整理可得x(x-3)(x+1)2=0,解得x 1=0, x 2=3, x 3=-1,舍负,即a=-1或8,验证可得a=8.8. 已知△ABC 的三个内角满足A <B <C <100°.用θ表示100°-C,C-B,B-A 中的最小者,则θ的最大值为________. 答案:20° 对应讲次: 所属知识点:代数思路:一般来说,求几个中最小者的最大值时,就是考虑这几个都相等的情况. 解析:∵θ≤100°-C ,θ≤C-B ,θ≤B-A ∴θ≤16[3(100°-C )+2(C-B)+(B-A)]=20°又当A=40°,B=60°,C=80°时,θ=20°可以取到. 则θ的最大值为20°.9. 设a,b 是两个互质的正整数,且38ab p a b=+为质数.则p 的值为________.答案:7 对应讲次: 所属知识点:数论思路:因为p 是质数,只能拆成1和p ,另一方面通过a+b 、a 、b 两两互质来拆分38ab a b+的可能种类,最后分类讨论,要么与条件矛盾,要么得出结果.解析:因为a,b 互质,所以a+b 、a 、b 两两互质,因为38ab a b +质数,所以318ab p a b⎧=⎪⎨=⎪+⎩可得a=b=1,p=4,不是质数舍;381ab p a b⎧=⎪⎨=⎪+⎩可得a=7,b=1,p=7,符合题意.则p=7.10.20个都不等于7的正整数排成一行,若其中任意连续若干个数之和都不等于7,则这20个数之和的最小值为________. 答案:34 对应讲次: 所属知识点:数论思路:考虑1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1满足题设要求,其和为34,接下来只需要考虑该数列是否为和最小的数列.解析:设该正整数列为()20,*n a n n N ≤∈,考虑()16,,,14,*k k k i i i k i ka a a k k N ++==≤∈∑∑,依抽屉原理必然有两项模7的余数相同,则该两项的差是7的倍数,于是任意连续7项之中必有连续子列之和为7的倍数,又不能为7,则最小为14.于是20个数中至少有2组这样的子列其总和不小于28,剩下6个数之和不小于6,于是该数列之和不小于34.由1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1可知,存在数列和为34的情况.第二试一、(本题满分 20 分)设A,B 是两个不同的两位数,且B 是由A 交换个位数字和十位数字所得,如果A 2-B 2是完全平方数,求A 的值. 答案:65 对应讲次: 所属知识点:数论思路:对于需要考虑不同位数上数字的情况,可以把一个两位数ab 设为10a+b ,转为为代数问题,再利用完全平方数的质因数分解式也是以完全平方数对的形式出现,综合分析所有限定下可能性,最终确定结果. 解析:设A=10a+b(1≤a,b ≤9,a,b ∈N),则B=10b+a ,由A,B 不同得a ≠b ,A 2-B 2=(10a+b )2-(10b+a)2=9×11×(a+b )(a-b).………5分由A 2-B 2是完全平方数,则a >b ,()()11|a b a b +-,可得a+b=11, ………10分 a-b 也是完全平方数,所以a-b=1或4.………15分若a-b=1,则a=6,b=5; 若a-b=4,则没有正整数解. 因此a=6,b=5,A=65.………20分二、(本题满分 25 分)如图,△ABC 中,D 为BC 的中点,DE 平分∠ADB ,DF 平分∠ADC ,BE ⊥DE ,CF ⊥DF ,P 为AD 与EF 的交点.证明:EF=2PD.对应讲次:所属知识点:平面几何思路:因为EF 、PD 都在△DEF 中,所以想办法推出其性质,比较容易得出∠EDF=90°,此时若能得出EF=PD ,则自然可以得到结论.解析:由DE 平分∠ADB ,DF 平分∠ADC ,可得∠EDF=90°.………5分由BE ⊥DE 得BE ∥DF ,则∠EBD=∠FDC. ………10分又BD=DC ,∠BED=∠DFC=90°,则△BED ≌△DFC ,BE=DF . ………15分 得四边形BDFE 是平行四边形,∠PED=∠EDB=∠EDP ,EP=PD. ………20分 又△EDF 是直角三角形,∴EF=2PD.………25分三、(本题满分 25 分)已知a,b,c 为有理数,求222a b c a b c ++++的最小值.答案:3 对应讲次: 所属知识点:数论思路:通过a,b,c 是正整数,可以把有理部分和无理部分分离考虑.0c -≠,可以通过分母有理化来实现分离,再利用a,b,c 互不相等,从最小正整数开始讨论即可得出最小值.0c -≠)()22222555bcab bc bac b cb c +--+-==--b 2=ac. …10分()()22222a c ba b c a c b a b c a c b +-++==+-++++.………15分不妨设a <c ,若a=1,c=b 2,因为a ≠b ,则a+c-b=1+b(b-1)≥3,取等号当且仅当b=2时. ………20分 若a ≥2,因为c ≠b ≠1,则a+c-b=a+b(b-1)≥a+2≥4>3.所以222a b c a b c++++的最小值为3,当a=1,b=2,c=4时.………25分。
2017全国初中数学联赛初二卷及详解

2017年全国初中数学联合竞赛试题初二卷第一试一、选择题:(本题满分42 分,每小题7 分)1.已知实数a,b,c满足2a+13b+3c=90,3a+9b+c=72,则32b ca b++的值为().A.2B.1C.0D.-12.已知实数a,b,c满足a+b+c=1,111135a b c++=+++,则(a+1)2+(b+3)2+(c+5)2的值为().A.125B.120C.100D.813.若正整数a,b,c满足a≤b≤c且abc=2(a+b+c),则称(a,b,c)为好数组.那么好数组的个数为().A.4B.3C.2D.14.已知正整数a,b,c满足a2-6b-3c+9=0,-6a+b2+c=0,则a2+b2+c2的值为().A.424B.430C.441D.4605.梯形ABCD中,AD∥BC,AB=3,BC=4,CD=2,AD=1,则梯形的面积为().C. D.6.如图,梯形ABCD中,AD∥BC,∠A=90°,点E在AB上,若AE=42,BE=28,BC=70,∠DCE=45°,则DE的值为().A.56B.58C.60D.62二、填空题:(本题满分28分,每小题7分)7.=a的值为________.8.已知△ABC的三个内角满足A<B<C<100°.用θ表示100°-C,C-B,B-A中的最小者,则θ的最大值为________.9.设a,b是两个互质的正整数,且38abpa b=+为质数.则p的值为________.10.20个都不等于7的正整数排成一行,若其中任意连续若干个数之和都不等于7,则这20个数之和的最小值为________.第二试一、(本题满分20分)设A,B是两个不同的两位数,且B是由A交换个位数字和十位数字所得,如果A2-B2是完全平方数,求A的值.二、(本题满分25分)如图,△ABC中,D为BC的中点,DE平分∠ADB,DF平分∠ADC,BE⊥DE,CF⊥DF,P为AD与EF的交点.证明:EF=2PD.三、(本题满分25分)已知a,b,c为有理数,求222a b ca b c++++的最小值.2017年全国初中数学联合竞赛试题初二卷参考答案第一试一、选择题:(本题满分42 分,每小题7 分)1.已知实数a,b,c满足2a+13b+3c=90,3a+9b+c=72,则32b ca b++的值为().A.2B.1C.0D.-1答案:B对应讲次:所属知识点:方程思路:因为所求分式的特点可以想到把a+2b,3b+c看成一个整体变量求解方程.解析:已知等式可变形为2(a+2b)+3(3b+c)=90,3(a+2b)+(3b+c)=72,解得a+2b=18,3b+c=18,所以312b ca b+=+.2.已知实数a,b,c满足a+b+c=1,111135a b c++=+++,则(a+1)2+(b+3)2+(c+5)2的值为().A.125B.120C.100D.81答案:C对应讲次:所属知识点:方程思路:可以想到换元法.解析:设x=a+1,y=b+3,z=c+5,则x+y+z=10,111x y z++=,∴xy+xz+yz=0,由x2+y2+z2=(x+y+z)2-2(xy+xz+yz)=100.则(a+1)2+(b+3)2+(c+5)2 =100.3. 若正整数a,b,c满足a≤b≤c且abc=2(a+b+c),则称(a,b,c)为好数组.那么好数组的个数为().A.4B.3C.2D.1答案:B对应讲次:所属知识点:数论思路:先通过a ≤b ≤c 且abc=2(a+b+c)的限定关系确定可能的种类,再通过枚举法一一验证. 解析:若(a,b,c)为好数组,则abc=2(a+b+c)≤6c ,即ab ≤6,显然a=1或2.若a=1,则bc=2(1+b+c),即(b-2)(c-2)=6,可得(a,b,c)=(1,3,8)或(1,4,5),共2个好数组. 若a=2,则b=2或3,可得b=2,c=4;b=3,c=52,不是整数舍去,共1个好数组. 共3个好数组(a,b,c)=(1,3,8) (1,4,5) (2,2,4).4. 已知正整数a,b,c 满足a 2-6b-3c+9=0,-6a+b 2+c=0,则a 2+b 2+c 2的值为( ). A.424 B.430 C.441 D.460 答案:C 对应讲次: 所属知识点:方程思路:由已知等式消去c 整理后,通过a,b 是正整数的限制,枚举出所有可能,并一一代入原方程验证,最终确定结果.解析:联立方程可得(a-9)2+3(b-1)2=75,则3(b-1)2≤75,即1≤b ≤6. 当b=1,2,3,4,5时,均无与之对应的正整数a ;当b=6时,a=9,符合要求,此时c=18,代入验证满足原方程. 因此,a=9,b=6,c=18,则a 2+b 2+c 2=441.5. 梯形ABCD 中,AD ∥BC ,AB=3,BC=4,CD=2,AD=1,则梯形的面积为( ).C. D.答案:A 对应讲次:所属知识点:平面几何思路:通过作平行四边形把边长关系转化到一个三角形中来.解析:作AE ∥DC ,AH ⊥BC ,则ADCE 是平行四边形,则BE=BC-CE=BC-AD=3=AB ,则△ABE 是等腰三角形,BE=AB=3,AE=2,经计算可得AH =所以梯形ABCD 的面积为()114233⨯+⨯=.6. 如图,梯形ABCD 中,AD ∥BC ,∠A=90°,点E 在AB 上,若AE=42,BE=28,BC=70,∠DCE=45°,则DE 的值为( ).A.56B.58C.60D.62 答案:B 对应讲次:所属知识点:平面几何思路:补形法,把直角梯形先补成正方形,再利用旋转把边长关系转化到同一个三角形Rt △EAD 中去,利用勾股定理求解.解析:作CF ⊥AD ,交AD 的延长线于点F ,将△CDF 绕点C 逆时针旋转90°至△CGB ,则ABCF 为正方形,可得△ECG ≌△ECD ,∴EG=ED. 设DE=x ,则DF=BG=x-28,AD=98-x.在Rt △EAD 中,有422+(98-x)2=x 2,解得x=58. 二、填空题:(本题满分 28 分,每小题 7 分)7.=a 的值为________.答案:8 对应讲次: 所属知识点:方程思路:通过等式两边都6次方可以去掉最外面根式,再用换元法化简等式,最后要验证结果是否满足最初的等式.解析:易得(321a =.令x ,则x ≥0,代入整理可得x(x-3)(x+1)2=0,解得x 1=0, x 2=3, x 3=-1,舍负,即a=-1或8,验证可得a=8.8. 已知△ABC 的三个内角满足A <B <C <100°.用θ表示100°-C,C-B,B-A 中的最小者,则θ的最大值为________. 答案:20° 对应讲次: 所属知识点:代数思路:一般来说,求几个中最小者的最大值时,就是考虑这几个都相等的情况. 解析:∵θ≤100°-C ,θ≤C-B ,θ≤B-A ∴θ≤16[3(100°-C )+2(C-B)+(B-A)]=20°又当A=40°,B=60°,C=80°时,θ=20°可以取到. 则θ的最大值为20°.9. 设a,b 是两个互质的正整数,且38ab p a b=+为质数.则p 的值为________.答案:7 对应讲次: 所属知识点:数论思路:因为p 是质数,只能拆成1和p ,另一方面通过a+b 、a 、b 两两互质来拆分38ab a b+的可能种类,最后分类讨论,要么与条件矛盾,要么得出结果.解析:因为a,b 互质,所以a+b 、a 、b 两两互质,因为38ab a b +质数,所以318ab p a b⎧=⎪⎨=⎪+⎩可得a=b=1,p=4,不是质数舍;381ab p a b⎧=⎪⎨=⎪+⎩可得a=7,b=1,p=7,符合题意.则p=7.10.20个都不等于7的正整数排成一行,若其中任意连续若干个数之和都不等于7,则这20个数之和的最小值为________. 答案:34 对应讲次: 所属知识点:数论思路:考虑1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1满足题设要求,其和为34,接下来只需要考虑该数列是否为和最小的数列.解析:设该正整数列为()20,*n a n n N ≤∈,考虑()16,,,14,*k k k i i i k i ka a a k k N ++==≤∈∑∑,依抽屉原理必然有两项模7的余数相同,则该两项的差是7的倍数,于是任意连续7项之中必有连续子列之和为7的倍数,又不能为7,则最小为14.于是20个数中至少有2组这样的子列其总和不小于28,剩下6个数之和不小于6,于是该数列之和不小于34.由1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1可知,存在数列和为34的情况.第二试一、(本题满分 20 分)设A,B 是两个不同的两位数,且B 是由A 交换个位数字和十位数字所得,如果A 2-B 2是完全平方数,求A 的值. 答案:65对应讲次: 所属知识点:数论思路:对于需要考虑不同位数上数字的情况,可以把一个两位数ab 设为10a+b ,转为为代数问题,再利用完全平方数的质因数分解式也是以完全平方数对的形式出现,综合分析所有限定下可能性,最终确定结果. 解析:设A=10a+b(1≤a,b ≤9,a,b ∈N),则B=10b+a ,由A,B 不同得a ≠b ,A 2-B 2=(10a+b )2-(10b+a)2=9×11×(a+b )(a-b).………5分由A 2-B 2是完全平方数,则a >b ,()()11|a b a b +-,可得a+b=11, ………10分 a-b 也是完全平方数,所以a-b=1或4.………15分若a-b=1,则a=6,b=5; 若a-b=4,则没有正整数解. 因此a=6,b=5,A=65.………20分二、(本题满分 25 分)如图,△ABC 中,D 为BC 的中点,DE 平分∠ADB ,DF 平分∠ADC ,BE ⊥DE ,CF ⊥DF ,P 为AD 与EF 的交点.证明:EF=2PD. 对应讲次:所属知识点:平面几何思路:因为EF 、PD 都在△DEF 中,所以想办法推出其性质,比较容易得出∠EDF=90°,此时若能得出EF=PD ,则自然可以得到结论.解析:由DE 平分∠ADB ,DF 平分∠ADC ,可得∠EDF=90°. ………5分 由BE ⊥DE 得BE ∥DF ,则∠EBD=∠FDC.………10分又BD=DC ,∠BED=∠DFC=90°,则△BED ≌△DFC ,BE=DF . ………15分 得四边形BDFE 是平行四边形,∠PED=∠EDB=∠EDP ,EP=PD. ………20分 又△EDF 是直角三角形,∴EF=2PD.………25分三、(本题满分 25 分)已知a,b,c 为有理数,求222a b c a b c ++++的最小值.答案:3 对应讲次: 所属知识点:数论思路:通过a,b,c 是正整数,可以把有理部分和无理部分分离考虑.0c -≠,可以通过分母有理化来实现分离,再利用a,b,c 互不相等,从最小正整数开始讨论即可得出最小值.0c -≠)()22222555bcab bc bac b c b c +--+-==--b 2=ac. …10分()()22222a c ba b c a c b a b c a c b+-++==+-++++.………15分不妨设a <c ,若a=1,c=b 2,因为a ≠b ,则a+c-b=1+b(b-1)≥3,取等号当且仅当b=2时. ………20分 若a ≥2,因为c ≠b ≠1,则a+c-b=a+b(b-1)≥a+2≥4>3.所以222a b c a b c++++的最小值为3,当a=1,b=2,c=4时.………25分。
2017联合杯决赛(数学)试题及答案
决赛试卷 数学(试卷共四大题 满分:90分)一.选择题(共12小题,每题2分,共24分)1.中央电视台晚上少儿节目“动画梦工场”开始,用24小时计时法表示是( ) A .07:00B .19:00C .晚上7:00D .19小时2.下面物品中( )的重量最接近一千克. A .1立方米的水B .3个易拉罐可乐C .3个鸡蛋3.最大的九位数比最小的十位数小 ( )A .1B .2C .10000000004.如果长方形的宽增加1分米,面积就增加3平方分米,并且正好称为正方形,那么原来这个长方形的面积是( )平方分米. A .27B .9C .65.当9:30时,钟面上时针和分针所组成的角是( ) A .直角 B .锐角 C .钝角 D .平角6.小红买售价4.4元的钢笔一支,根据你的生活经验,结合人民币币值的特点,下列付钱方式不合理的是( )A .付出4.5元,找回0.1元B .付出4.7元,找回0.3元C .付出5.4元,找回1.0元D .付出10元,找回5.6元7.从第( )个口袋里任意摸出一个球,摸出黑球的可能性是50%.A .B .C .8.要使是假分数,是真分数,a 应是( )A .5B .6C .7D .89.如图 所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD .取AB 的中点M 和BC 的中点N ,剪掉AMBN 得五边形AMNCD .则将折叠的五边形AMNCD 纸片展开铺平后的图形是( )A .B .C .D .10.一列数1,2,2,3,3,3,4,4,4,4,….中的第35个数为( ) A .6B .7C .8D .无答案11.如图中的正方体、圆柱和圆锥底面积相等,高也相等.下面哪句话是正确的?( )A .圆柱的体积比正方体的体积小一些B .圆锥的体积是正方体的C .圆柱体积与圆锥体积相等12.在任意的37个人中,至少有( )人的属相相同. A .2B .4C .6二.填空题(共10小题,每空1分,共10分)13.如图中,两个小正方形的周长和是8分米,则大正方形的边长是 分米.14.图中的饮料需要 瓶才正好是2升.15.小胖、小丁丁、小巧、小亚四人组成一个学习小组,要在四人中选一名组长和副组长,总共有 种不同的选法.16.如图可以折成一个正方体,面1与面 相对;面2与面 相对.姓名__________ 准考证号__________ 联系电话__________ 考场___________密 封 线 内 不 准 答 题17.爷爷患了感冒,医生给他开了感冒药,如图是该药品的部分说明,请根据说明书回答问题:(1)爷爷一天最多可服药克.(2)这种药片的保质期是年.18.如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是平方厘米.(18题图)(19题图)(20题图)19.如图,围绕礼品盒绳子的长度是厘米.20.小明统计了自己装有125个硬币的储蓄罐的情况如图,则储蓄罐内共有元钱.21.如图,甲、乙、丙三个图形面积的比是.22.一群人开舞会,每人头上都戴着一顶帽子.帽子只有黑白两种,黑的至少有一顶.每个人都能看到其它人帽子的颜色,却看不到自己的.主持人先让大家看看别人头上戴的是什么帽子,然后关灯,如果有人认为自己戴的是黑帽子,就拍手.第一次关灯,没有声音.于是再开灯,大家再看一遍,关灯时仍然鸦雀无声.一直到第三次关灯,才有劈劈啪啪手的声音响起.则有人戴着黑帽子.三.计算题(共2小题,23、24题各12分,共24分)23.直接写出下面各题的得数.+=×=﹣= ÷=24.能简算的要简算(1)2.5×12.5×32 =(2)1375+450÷18×25=(3)=(4)=四.解答题(共5题,25题7分,26、27题各8分,28题9分)25.王大娘家菜地里的西红柿获得了丰收,收下全部的时,装满了5筐还多48千克,收完其余的部分时,又刚好装满10筐,求王大娘共收获西红柿多少千克?26.图形计算(1)如图1,计算图形的体积.(得数保留两位小数,单位:米)(2)如图2,求阴影部分的面积.(单位:米)27.甲、乙和丙同时由东、西两城出发,甲、乙两人由东城到西城,甲步行每小时走5千米,乙骑自行车每小时行15千米,丙也骑自行车每小时20千米,已知丙在途中遇到乙后,又经过1小时才遇到甲,求东、西城相距多少千米?28.期六下午,城关二小王明同学骑自行车到6千米远的六郎镇姥姥家去玩,请根据下面折线统计图回答下列问题:(1)王明在姥姥家玩了多少时间?(2)如果王明从出发起一直骑自行车走不休息,下午几时几分可到达姥姥家?(3)求出王明骑自行车的往返的平均速度?2017年小升初学业水平测试数学试卷参考答案与试题解析一.选择题(共12小题)1-5 B.B.A.C.C.6-10 B.B.B.D.C.11-12 B.B.二.填空题(共12小题)13. 2.14. 8.15. 12.16. 6,4.17. 2.4,2.18. 6419. 340.20. 67.5.21. 1:5:4.22. 3三.计算题(共2小题)23.+==0.6 =7﹣=÷=(2.5×4)×(12.5×8),=10×100,=1000;(2)1375+450÷18×25=1375+25×25,=1375+625,=2000;(3)×0.25+×=0.25×(+),=0.25;(4)×[(+0.75)÷]=×[÷+÷],=×[1+],=×,=.四.解答题(共2小题)25. 【解答】解:48÷[1﹣÷10×(5+10)]=48÷[1﹣×15]=48÷[1﹣]=48=288(千克)答:王大娘共收获西红柿288千克.26.【解答】解:(1) 3.14×102×10+4.14×102×10=≈1046.67+3140=4186.67(立方米);答:它的体积是4186.67立方米.(2)8÷2=4(米),3.14×42×4×4÷2=3.14×16÷2=12.56﹣8=4.56(平方米);答:阴影部分的面积是4.56平方米.27.【解答】解:乙丙经过x小时相遇,根据总路程相等列出方程:(15+20)x=(5+20)(x+1)35x=25x+25x=2.5总路程:(15+20)×2.5=35×2.5=87.5(千米)答:东、西城相距87.5千米.28.【解答】解:(1)王明在姥姥家是从下午2时到2时30分;2时30分﹣2时=30分;答:王明在姥姥家玩了30分.(2)王明中间休息了20分钟;否则他会提前20分钟到姥姥家.2时﹣20分=1时40分;答:下午1时40分可到达姥姥家.(3)20+20=40(分);3时﹣2时30分=30分;40+30=70(分);70分=时;6×2÷,=12÷,=(千米/时);答:王明骑自行车的往返的平均速度是千米/时.。
2017年全国高中数学联合竞赛试题与解答(B卷)_PDF压缩

2017年全国高中数学联合竞赛一试(B 卷)一、填空题:本大题共8个小题,每小题8分,共64分.1.在等比数列{}n a中,2a =,3a =1201172017a a a a ++的值为 .2.设复数z 满足91022z z i +=+,则||z 的值为 .3.设()f x 是定义在R 上的函数,若2()f x x +是奇函数,()2x f x +是偶函数,则(1)f 的值为 .4.在ABC ∆中,若sin 2sin A C =,且三条边,,a b c 成等比数列,则cos A 的值为 .5.在正四面体ABCD 中,,E F 分别在棱,AB AC 上,满足3BE =,4EF =,且EF 与平面BCD 平行,则DEF ∆的面积为 .6.在平面直角坐标系xOy 中,点集{(,)|,1,0,1}K x y x y ==-,在K 中随机取出三个点,则这三个点两两之间距离均不超过2的概率为 .7.设a 为非零实数,在平面直角坐标系xOy 中,二次曲线2220x ay a ++=的焦距为4,则a 的值为 .8.若正整数,,a b c 满足2017101001000a b c ≥≥≥,则数组(,,)a b c 的个数为 .二、解答题 (本大题共3小题,共56分.解答应写出文字说明、证明过程或演算步骤.)9.设不等式|2||52|xxa -<-对所有[1,2]x ∈成立,求实数a 的取值范围.10.设数列{}n a 是等差数列,数列{}n b 满足212n n n n b a a a ++=-,1,2,n =.(1)证明:数列{}n b 也是等差数列;(2)设数列{}n a 、{}n b 的公差均是0d ≠,并且存在正整数,s t ,使得s t a b +是整数,求1||a 的最小值.11.在平面直角坐标系xOy 中,曲线21:4C y x =,曲线222:(4)8C x y -+=,经过1C 上一点P 作一条倾斜角为45的直线l ,与2C 交于两个不同的点,Q R ,求||||PQ PR ⋅的取值范围.2017年全国高中数学联合竞赛加试(B 卷)一、(本题满分40分)设实数,,a b c 满足0a b c ++=,令max{,,}d a b c =,证明:2(1)(1)(1)1a b c d +++≥-二、(本题满分40分)给定正整数m ,证明:存在正整数k ,使得可将正整数集N +分拆为k 个互不相交的子集12,,,k A A A ,每个子集i A 中均不存在4个数,,,a b c d (可以相同),满足ab cd m -=.三、(本题满分50分)如图,点D 是锐角ABC ∆的外接圆ω上弧BC 的中点,直线DA 与圆ω过点,B C 的切线分别相交于点,P Q ,BQ 与AC 的交点为X ,CP 与AB 的交点为Y ,BQ 与CP 的交点为T ,求证:AT 平分线段XY .四、(本题满分50分)设1220,,,{1,2,,5}a a a ∈,1220,,,{1,2,,10}b b b ∈,集合{(,)120,()()0}i j i j X i j i j a a b b =≤<≤--<,求X 的元素个数的最大值.。
2017年湖南省高中数学联合竞赛试题 (PDF版)

A1
P
K
D
1 1 1 3 1 3 ,选 A 因此,VD-ABC= ×S△ABC×AD= ( 1 1 ) 3 3 2 2 4 48
3、已知椭圆 C:ALx2 y 2 1 ,对于任意实数 k,椭圆 C 被下列直线中所截得弦长,与被直线 l: 8 4 y=kx+1 所截得的弦长不可能相等的是 A.kx+y+k=0 B. kx-y-1=0 C. kx+y-k=0 D. kx+y-2=0 x2 y 2 1 是关于原点 O 对称的中心对称图形,也是关于 x 轴、y 轴对称的轴对 8 4 称图形,∴只要两条直线关于原点成中心对称或者关于 x 轴、y 轴成轴对称,那么它们被椭圆所 截的弦一定是等长的。选 D n 4、对任意正整数 n 与 k(k≤n),用 f(n,k)表示不超过[ ] 且与 n 互质的正整数的个数(其中[x]表示 k
3 48
B.
3 24
C.
3 16
D.
3 12
解:取 B1C1 的中点 K,BC 的中点 L,在矩形 A1KLA 中(如图),
3 3 2 ,故 A1P= A1K= 。 ∵AB=BC=CA=1,∴AL=A1K= 2 3 3
又 AA1=2,由△ALD∽△AA1P 知 AD A1P AL 1 , AA1 4
( S n 1) 2 2S 1 , 2 2 an1 S n1 S n ,∴-(Sn-1) =Sn+1Sn-Sn ,即 S n 1 n Sn Sn
S 1 因此 S n 1 1 S n 1 ,故 1 n 1, Sn S n 1 1 S n 1 S n 1
12、设函数 f(x)是定义在(-,0)上的可导函数,其导数为 f(x),且有 2f(x)+xf(x)>x2,则不等式 (x+2017)2f(x+2017)-f(-1)>0 的解集为__________。 解:∵x<0,2f(x)+xf(x)>x2,∴2xf(x)+x2f(x)<x3<0,故 x2f(x)为(-,0)上的减函数。 不等式(x+2017)2f(x+2017)-f(-1)>0 即(x+2017)2f(x+2017)>(-1)2f(-1), 因此,x+2017<0 且 x+2017<-1,故 x<-2018。 三、解答题(本大题共 4 个小题,满分 72 分。解答需要有完整的推理过程或演算步骤。) 13、(本小题满分 16 分) 在锐角△ABC 中,sinA= (1)求 sin2(B+C)+ sin 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
决赛试卷数学
(试卷共四大题满分:90分)
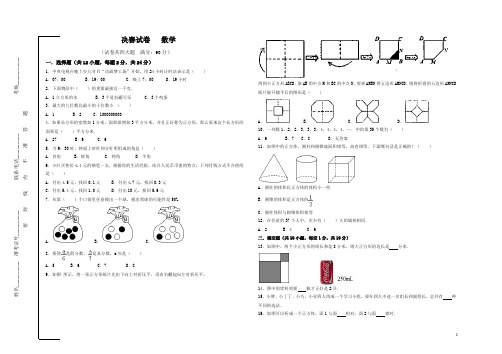
一.选择题(共12小题,每题2分,共24分)
1.中央电视台晚上少儿节目“动画梦工场”开始,用24小时计时法表示是()
A.07:00 B.19:00 C.晚上7:00 D.19小时
2.下面物品中()的重量最接近一千克.
A.1立方米的水 B.3个易拉罐可乐 C.3个鸡蛋
3.最大的九位数比最小的十位数小()
A.1 B.2 C.1000000000
4.如果长方形的宽增加1分米,面积就增加3平方分米,并且正好称为正方形,那么原来这个长方形的
面积是()平方分米.
A.27 B.9 C.6
5.当9:30时,钟面上时针和分针所组成的角是()
A.直角 B.锐角C.钝角D.平角
6.小红买售价4.4元的钢笔一支,根据你的生活经验,结合人民币币值的特点,下列付钱方式不合理的
是()
A.付出4.5元,找回0.1元 B.付出4.7元,找回0.3元
C.付出5.4元,找回1.0元 D.付出10元,找回5.6元
7.从第()个口袋里任意摸出一个球,摸出黑球的可能性是50%.
A. B.C.
8.要使是假分数,是真分数,a应是()
A.5 B.6 C.7 D.8
9.如图所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,
得到小正方形ABCD.取AB的中点M和BC的中点N,剪掉AMBN得五边形AMNCD.则将折叠的五边形AMNCD
纸片展开铺平后的图形是()
A. B.C. D.
10.一列数1,2,2,3,3,3,4,4,4,4,….中的第35个数为()
A.6 B.7 C.8 D.无答案
11.如图中的正方体、圆柱和圆锥底面积相等,高也相等.下面哪句话是正确的?()
A.圆柱的体积比正方体的体积小一些
B.圆锥的体积是正方体的
C.圆柱体积与圆锥体积相等
12.在任意的37个人中,至少有()人的属相相同.
A.2 B.4 C.6
二.填空题(共10小题,每空1分,共10分)
13.如图中,两个小正方形的周长和是8分米,则大正方形的边长是分米.
14.图中的饮料需要瓶才正好是2升.
15.小胖、小丁丁、小巧、小亚四人组成一个学习小组,要在四人中选一名组长和副组长,总共有种
不同的选法.
16.如图可以折成一个正方体,面1与面相对;面2与面相对.
17.爷爷患了感冒,医生给他开了感冒药,如图是该
药品的部分说明,请根据说明书回答问题:
(1)爷爷一天最多可服药克.
(2)这种药片的保质期是年.
18.如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是平方厘米.
(18题图)(19题图)(20题图)
19.如图,围绕礼品盒绳子的长度是厘米.
20.小明统计了自己装有125个硬币的储蓄罐的情况如图,则储蓄罐内共有元钱.
21.如图,甲、乙、丙三个图形面积的比是.
感冒清片
每片重0.2克
口服,一次3~4片,一日三次
生产日期:2009年1月1日
有效期:至2010年12月31日
姓
名
_
_
_
_
_
_
_
_
_
_
准
考
证
号
_
_
_
_
_
_
_
_
_
_
联
系
电
话
_
_
_
_
_
_
_
_
_
_
考
场
_
_
_
_
_
_
_
_
_
_
_
密
封
线
内
不
准
答
题
座号
22.一群人开舞会,每人头上都戴着一顶帽子.帽子只有黑白两种,黑的至少有一顶.每个人都能看到其它人帽子的颜色,却看不到自己的.主持人先让大家看看别人头上戴的是什么帽子,然后关灯,如果有人认为自己戴的是黑帽子,就拍手.第一次关灯,没有声音.于是再开灯,大家再看一遍,关灯时仍然鸦雀无声.一直到第三次关灯,才有劈劈啪啪手的声音响起.则有
人戴着黑帽子.
三.计算题(共2小题,23、24题各12分,共24分)
+=
×﹣
﹣= ÷
=
24.能简算的要简算
(1)2.5×12.5×
32 =
(2)1375+450÷18×25=
(3)
=
(4)=
四.解答题(共5题,25题7分,26、27题各8分,28题9分)
25.王大娘家菜地里的西红柿获得了丰收,收下全部的时,装满了5筐还多48千克,收完其余的部分时,又刚好装满10筐,求王大娘共收获西红柿多少千克?
26.图形计算
(1)如图1,计算图形的体积.(得数保留两位小数,单位:米)
(2)如图2,求阴影部分的面积.(单位:米)27.甲、乙和丙同时由东、西两城出发,甲、乙两人由东城到西城,甲步行每小时走5千米,乙骑自行车每小时行15千米,丙也骑自行车每小时20千米,已知丙在途中遇到乙后,又经过1小时才遇到甲,求东、西城相距多少千米?
28.期六下午,城关二小王明同学骑自行车到6千米远的六郎镇姥姥家去玩,请根据下面折线统计图回答下列问题:
(1)王明在姥姥家玩了多少时间?
(2)如果王明从出发起一直骑自行车走不休息,下午几时几分可到达姥姥家?
(3)求出王明骑自行车的往返的平均速度?
2017年小升初学业水平测试数学试卷
参考答案与试题解析
一.选择题(共12小题)
1-5 B.B.A.C.C.
6-10 B.B.B.D.C.
11-12 B.B.
二.填空题(共12小题)
13. 2.
14. 8.
15. 12.
16. 6,4.
17. 2.4,2.
18. 64
19. 340.
20. 67.5.
21. 1:5:4.
22. 3
三.计算题(共2小题)
+=
=7﹣÷
=
=(2.5×4)×(12.5×8),
=10×100,
=1000;
(2)1375+450÷18×25
=1375+25×25,
=1375+625,
=2000;
(3)×0.25+×
=0.25×(+),
=0.25;(4)×[(+0.75)÷]
=×[÷+÷],
=×[1+],
=×,
=.
四.解答题(共2小题)
25. 【解答】解:48÷[1﹣÷10×(5+10)]
=48÷[1﹣×15]
=48÷[1﹣]
=48
=288(千克)
答:王大娘共收获西红柿288千克.
26.【解答】解:(1) 3.14×102×10+4.14×102×10
=
≈1046.67+3140
=4186.67(立方米);
答:它的体积是4186.67立方米.
(2)8÷2=4(米),
3.14×42×4×4÷2
=3.14×16÷2
=12.56﹣8
=4.56(平方米);
答:阴影部分的面积是4.56平方米.
27.【解答】解:乙丙经过x小时相遇,根据总路程相等列出方程:(15+20)x=(5+20)(x+1)
35x=25x+25
x=2.5
总路程:(15+20)×2.5
=35×2.5
=87.5(千米)
答:东、西城相距87.5千米.
28.【解答】解:(1)王明在姥姥家是从下午2时到2时30分;
2时30分﹣2时=30分;
答:王明在姥姥家玩了30分.
(2)王明中间休息了20分钟;否则他会提前20分钟到姥姥家.2时﹣20分=1时40分;
答:下午1时40分可到达姥姥家.
(3)20+20=40(分);
3时﹣2时30分=30分;
40+30=70(分);
70分=时;
6×2÷,
=12÷,
=(千米/时);
答:王明骑自行车的往返的平均速度是千米/时.。
