高中数学必修三经典练习100例
高中必修三数学练习题

高中必修三数学练习题1. 已知一个等腰三角形,底边长为12cm,高为9cm,求等腰三角形的面积。
解析:等腰三角形的面积可通过底边长与高的乘积除以2来求得。
面积 = (底边长 ×高) / 2面积 = (12 × 9) / 2面积 = 54 cm²2. 一架飞机以每小时400km的速度飞行,飞行了5小时后加速到每小时450km的速度飞行,求这段航程的平均速度。
解析:航程的平均速度可以通过总距离除以总时间来求得。
总距离 = 400km × 5小时 + 450km × (总时间 - 5小时)总时间 = 5小时 + (总距离 - 400km × 5小时) / 450km总时间 = 5小时 + (总距离 - 2000km) / 450km平均速度 = 总距离 / 总时间平均速度 = [400km × 5小时 + 450km × (总时间 - 5小时)] / 总时间3. 已知一个等差数列的首项是3,公差是4,求第10项的值。
解析:等差数列的通项公式为:an = a1 + (n - 1)d,其中a1为首项,d为公差,n为项数。
第10项的值 = 3 + (10 - 1) × 4第10项的值 = 3 + 9 × 4第10项的值 = 3 + 36第10项的值 = 394. 已知一个等比数列的第1项是5,公比是2,求前5项的和。
解析:等比数列的前n项和公式为:Sn = a1(1 - q^n) / (1 - q),其中a1为第1项,q为公比,n为项数。
前5项的和 = 5(1 - 2^5) / (1 - 2)前5项的和 = 5(1 - 32) / (1 - 2)前5项的和 = 5(-31) / (-1)前5项的和 = 1555. 已知一个正方形的边长为8cm,求该正方形的对角线长度。
解析:正方形的对角线长度可以通过边长乘以√2来求得。
高中数学必修三练习题

高中数学必修三练习题在高中数学必修三中,我们将学习许多重要的数学概念和技巧。
为了巩固所学知识并提高解题能力,我们需要进行大量的练习。
本文将提供一些高中数学必修三的练习题,帮助你加深对数学知识的理解和掌握。
1. 函数与方程(1) 求解方程组:⎧ 2x + y = 5⎪⎪ 3x - y = 7(2) 已知函数 f(x) = 2x^2 - 3x + 1,求 f(3) 的值。
(3) 求方程 2x^2 - 5x + 3 = 0 的根。
2. 三角函数(1) 计算sin(π/6) - cos(π/4) + tan(π/3) 的值。
(2) 求解方程sin(x) = √3/2 在区间[0, 2π] 内的解。
(3) 已知sinα = 1/2,sinβ = -1/2,求sin(α + β) 的值。
3. 概率与统计(1) 有六个小球,其中两个是红色的,四个是蓝色的。
从中随机选择两个,求选出的两个小球都是红色的概率。
(2) 一次考试的及格率为80%,某班级有35人参加考试,求至少有33人及格的概率。
(3) 某班级的学生身高如下:150cm、155cm、160cm、165cm、170cm。
求身高的中位数和众数。
4. 平面向量(1) 已知向量 a = (3, 4),向量 b = (-1, 2),求 a + b 和 a - b。
(2) 已知向量 a = (2, -3),向量 b = (4, 1),求向量 a·b 的值(即点乘)。
(3) 已知向量 a = (1, 2),向量 b = (3, 4),求向量 a 与向量 b 的夹角的余弦值。
5. 解析几何(1) 求过点 A(2, 3) 且与直线 y = -2x + 1 平行的直线的方程。
(2) 已知三角形 ABC 的顶点分别是 A(1, 2),B(4, -1),C(-2, -3),求三角形 ABC 的周长和面积。
(3) 已知直线 L1 的方程为 2x + y - 4 = 0,直线 L2 的方程为 3x - 2y + 7 = 0,求 L1 和 L2 的交点坐标。
高中高一数学必修三练习试题.docx

高一数学必修三练习题一、选择题1. 下面一段程序执行后输出结果是( )程序:A=2A=A*2A=A+6PRINT AA. 2B. 8C. 10D. 182. 从学号为0~ 50的高一某班 50 名学生中随机选取5 名同学参加数学测试, 采用系统抽样的方法 ,则所选 5名学生的学号可能是()A. 1,2,3,4,5B.5,16,27,38,49 C.2,4,6,8,10D.4,13,22,31,403. 给出下列四个命题: ①“三个球全部放入两个盒子 , 其中必有一个盒子有一个以上的球”是必然事件②“当 x 为某一实数时可使x 20 ”是不可能事件③“明天福安要下雨”是必然事件④“从 100个灯泡中取出 5 个 ,5 个都是次品”是随机事件 . 其中正确命题的个数是( )A. 0B. 1C.2D.34. 下列各组事 件 中 , 不 是 互 斥 事 件 的 是( )A. 一个射手进行一次射击, 命中环数大于 8 与命中环数小于6B. 统计一个班数学期中考试成绩 , 平均分数低于 90分与平均分数不高于80 分C.播种菜籽100 粒 , 发芽 90 粒与发芽80 粒D. 检查某种产品, 合格率高于 70% 与合格率为 70%5. 某住宅小区有居民 2 万户 , 从中随机抽取200户, 调查是否安装电话, 调查的结果如表所示 ,则该小区已安装电话的户数估计有()电话动迁户原住户A. 6500 户B. 300户C. 19000户D. 9500已安装6530户4065未安装6.在样本的频率分布直方图中, 共有 11 个小长方形 , 若中间一个小长立形的面积等于其他110 个小长方形的面积的和的, 且样本容量为160, 则中间一组有频数为4( )A. 32B. 0.2C. 40D. 0.257. 袋中装有 6 个白球 ,5只黄球,4个红球,从中任取 1 球 , 抽到的不是白球的概率为()第 1 页共 12 页A.2B.4C.3D.非以上答案51558. x1, x2,..., x n的平均数是x, 方差是s 2, 则另一组数3x12, 3x 22,..., 3x n2的平均数和方差分别是()A.3x, s 2B.3x 2, s2C.3x2,3 s2D.3x2,3 s 2 2 6s 29.如下图所示 ,程序执行后的输出结果为了( )开始n 5s 0n n1nos 15?s s nyes输出 n第 9 题图结束A. -1B. 0C. 1D. 210.从 1,2,3,4,5中任取两个不同的数字, 构成一个两位数, 则这个数字大于40 的概率是()2413A. B. C. D.555511. 小强和小华两位同学约定下午在福安二中门口见面, 约定谁先到后必须等10 分钟 , 这时若另一人还没有来就可以离开. 如果小强是1: 40 分到达的 , 假设小华在 1 点到 2 点内到达, 且小华在1点到 2 点之间何时到达是等可能的, 则他们会面的概率是( )1B.1C.11A. D.624312.在两个袋内, 分别写着装有1,2,3,4,5,6六个数字的 6张卡片 , 今从每个袋中各取一张卡片,则两数之和等于9的概率为第 2 页共 12 页1111 ()A. B. C. D.36912二、填空题:13. 口袋内装有100 个大小相同的红球、白球和黑球, 其中有45 个红球 , 从中摸出 1 个球 , 摸出白球的概率为0.23, 则摸出黑球的概率为_______.14.用辗转相除法求出153 和 119 的最大公约数是______________.15.设有以下两个程序:程序 (1) A=-6程序 (2) x=1/3B=2i=1If A<0 then while i<3A=-A x=1/(1+x)END if i=i+1B=B^2wendA=A+B print xC=A-2*B endA=A/CB=B*C+1Print A,B,C程序( 1 )的输出结果是______,________,_________.程序( 2 )的输出结果是__________.16. 有 5 条长度分别为1,3,5,7,9的线段, 从中任意取出 3 条 , 则所取 3 条线段可构成三角形的概率是 ___________.三、解答题17.从一箱产品中随机地抽取一件产品 , 设事件 A= “抽到的一等品” , 事件 B= “抽到的二等品” ,事件 C= “抽到的三等品”, 且已知P A 0.7 , P B0.1, P C 0.05 ,求下列事件的概率:⑴事件 D= “抽到的是一等品或二等品”;⑵事件E=“抽到的是二等品或三等品”第 3 页共 12 页18. 一组数据按从小到大顺序排列, 得到 -1,0,4,x,7,14中位数为5, 求这组数据的平均数和方差 .19. 五个学生的数学与物理成绩如下表:⑴作出散点图;⑵求出回归方程 .学生A B C D E数学8075706560物理706668646220.铁路部门托运行李的收费方法如下: y 是收费额 ( 单位:元 ),x 是行李重量 ( 单位:㎏ ),当 0 x 20 时,按0.35/㎏收费,当 x20 ㎏时,20㎏的部分按0.35元/㎏,超出20㎏的部分 , 则按 0.65 元 / ㎏收费 . ⑴请根据上述收费方法求出Y 关于 X 的函数式;⑵画出流程图 .第 4 页共 12 页21. 某次数学考试中, 其中一个小组的成绩是:55, 89, 69, 73, 81, 56, 90, 74, 82.试画一个程序框图:程序中用S(i) 表示第i 个学生的成绩, 先逐个输入S(i)( i=1,2,,), 然后从这些成绩中搜索出小于75 的成绩 .( 注意:要求程序中必须含有循环结构)第 5 页共 12 页22 对某种电子元件的使用寿命进行调查, 抽样 200个检验结果如表:⑴列出频率分布表;⑵ 画出频率分布直方图以及频率分布折线图;⑶估计电子元件寿命在100h ~ 400h 以内的频率;⑷估计电子元件寿命在400h以上的频率 .寿命 (h)100,200200,300300,400400,500500,600个数20308040301. 下面一段程序执行后输出结果是( C )程序:A=2第 6 页共 12 页A=A*2A=A+6PRINT AA.2B.8C.10D.182. 从学号为0~ 50 的高一某班 50 名学生中随机选取5 名同学参加数学测试, 采用系统抽样的方 法 ,则所选5名学生的 学号可 能 是( B )A.1,2,3,4,5 B.5,16,27,38,49 C.2,4,6,8,10D.4,13,22,31,403. 给出下列四个命题: ①“三个球全部放入两个盒子 , 其中必有一个盒子有一个以上的球”是必然事件②“当 x 为某一实数时可使x 20 ”是不可能事件③“明天福安要下雨”是必然事件④“从 100个灯泡中取出 5 个 ,5 个都是次品”是随机事件 . 其中正确命题的个数是( D )A. 0B. 1C.2D.34.下列各组事 件 中 , 不 是 互 斥 事 件 的 是( B)A.一个射手进行一次射击, 命中环数大于 8 与命中环数小于6B.统计一个班数学期中考试成绩 , 平均分数低于 90分与平均分数不高于80 分C.播种菜籽100 粒 , 发芽 90 粒与发芽80 粒D. 检查某种产品, 合格率高于 70% 与合格率为 70%5. 某住宅小区有居民2 万户 , 从中随机抽取200 户 , 调查是否安装电话, 调查的结果如表所电话 动迁户示 , 则该小已安装 65区已安装电话的户数估计有( D )未安装40A. 6500 户B. 300户C. 19000户 D. 9500 户6.在样本的频率分布直方图中, 共有 11 个小长方形 , 若中间一个小长立形的面积等于其他110 个小长方形的面积的和的, 且样本容量为 160, 则中间一组有频数为4( A )A. 32B. 0.2C. 40D. 0.257.袋中装有 6 个白球 ,5只黄球 ,4 个红球 , 从中任取 1 球 , 抽到的不是白球的概率为( C )243A. B. C. D.非以上答案51558.x1 , x2 ,..., x n的平均数是x, 方差是s 2, 则另一组数3x12, 3x 22,..., 3x n2第7 页共 12 页的平均数和方差分别是( C )A.3x, s 2B.3x2, s2C.3x2,3 s2D.3x2,3 s 2 2 6s29.如下图所示,程序执行后的输出结果为了( B)开始n 5s 0n n1nos 15?s s nyes输出 n第 9 题图结束A.-1B.0C.1D.210.从 1,2,3,4,5中任取两个不同的数字, 构成一个两位数, 则这个数字大于40的概率是( A)A.2B.4C.1D.3555511. 小强和小华两位同学约定下午在福安二中门口见面, 约定谁先到后必须等10分钟 ,这时若另一人还没有来就可以离开. 如果小强是1:40分到达的 , 假设小华在 1 点到 2 点内到达,且小华在 1点到 2点之间何时到达是等可能的 , 则他们会面的概率是( D)A.1B.1C.1D.1 624312.在两个袋内 , 分别写着装有1,2,3,4,5,6六个数字的 6 张卡片 , 今从每个袋中各取一张卡片,则两数之和等于9的概率为1111(C) A. B. C. D.36912二、填空题:0.32第8 页共 12 页13. 口袋内装有100 个大小相同的红球、白球和黑球, 其中有45 个红球 , 从中摸出 1 个球 , 摸出白球的概率为0.23,则摸出黑球的概率为_______.14.用辗转相除法求出 153 和 119 的最大公约数是 ______________. 1715.设有以下两个程序:程序 (1) A=-6程序 (2)x=1/3B=2i=1If A<0 then while i<3A=-A x=1/(1+x)END if i=i+1B=B^2wendA=A+B print xC=A-2*B endA=A/CB=B*C+1Print A,B,C程序( 1)的输出结果是______,________,_________.程序( 2 )的输出结果是4__________.( 1) 5、9、 2;( 2 )716. 有 5 条长度分别为1,3,5,7,9的线段,从中任意取出 3 条 , 则所取 3 条线段可构成三角形的概率是 ___________.310三、解答题17.从一箱产品中随机地抽取一件产品 , 设事件 A= “抽到的一等品” , 事件 B= “抽到的二等品” ,事件 C= “抽到的三等品”, 且已知P A0.7 , P B0.1 , P C0.05 ,求下列事件的概率:⑴事件 D= “抽到的是一等品或二等品”;⑵事件 E= “抽到的是二等品或三等品”解:⑴ P D P A B P A P B =0.7+0.1=0.8⑵P E = P B C P B P C=0.1+0.05=0.1518. 一组数据按从小到大顺序排列, 得到 -1,0,4,x,7,14中位数为5, 求这组数据的平均数和方差 .解:排列式:-1,0,4,x,7,14第9 页共 12 页∵中位数是5, 且有偶数个数∴4 x5∴ x6 2∴这组数为-1,0,4,6,7,14∴x 519.五个学生的数学与物理成绩如下表:学生A B C D E数学8075706560物理7066686462⑴ 作出散点图;⑵求出回归方程 .解:1物理2()70()y0.36 x 40.8?60607080数学20.铁路部门托运行李的收费方法如下: y 是收费额 ( 单位:元 ),x 是行李重量 ( 单位:㎏ ),当 0 x 20 时,按0.35/㎏收费,当 x20 ㎏时,20㎏的部分按0.35元/㎏,超出20㎏的部分 , 则按 0.65 元 / ㎏收费 . ⑴请根据上述收费方法求出Y 关于 X 的函数式;⑵画出流程图 .0.35x0 x 20解: y0.35*20 0.65 x20x 20程序如下 :INPUT “请输入行李的重量”;xIF x>20 THENy= 0.35*20 0.65* x20ELSEy= 0.35* xEND IFPRINT “金额为”;yEND21. 某次数学考试中, 其中一个小组的成绩是:55, 89, 69, 73, 81, 56, 90, 74, 82.试画一个程序框图:程序中用S(i)表示第i 个学生的成绩, 先逐个输入S(i)( i=1,2,, ), 然第 10 页共 12 页后从这些成绩中搜索出小于75 的成绩 .( 注意:要求程序中必须含有循环结构)开始i 1Y i 9N输入 S ii i1i 1i9NS i75Y输出 S ii i1结束22 对某种电子元件的使用寿命进行调查, 抽样 200 个检验结果如表:寿命 (h)100,200200,300300,400400,500500,600个数2030804030⑴列出频率分布表;⑵画出频率分布直方图以及频率分布折线图;⑶估计电子元件寿命在 100h ~400h 以内的频率;⑷估计电子元件寿命在 400h以上的频率 .解 : (1)( 2)略第 11 页共 12 页区间频数频率频率 / 组距100,200200.10.001 200,300300.150.0015 300,400800.40.004 400,500400.20.002 500,600300.150.0015(3)P100 h ,400h=0.65( 4)P400 h ,600h=0.35第 12 页共 12 页。
高中数学必修三《事件与概率》课后练习(含答案)

事件与概率课后练习题一:袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是(球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是( )A .摸出的三个球中至少有一个球是黑球.摸出的三个球中至少有一个球是黑球B .摸出的三个球中至少有一个球是白球.摸出的三个球中至少有一个球是白球C .摸出的三个球中至少有两个球是黑球.摸出的三个球中至少有两个球是黑球D .摸出的三个球中至少有两个球是白球.摸出的三个球中至少有两个球是白球题二:下列事件中,必然事件是题二:下列事件中,必然事件是 ,不可能事件是,不可能事件是 ,随机事件是,随机事件是 .(1)某射击运动员射击1次,命中靶心;次,命中靶心;(2)从一只装着白球和黑球的袋中摸球,摸出红球;)从一只装着白球和黑球的袋中摸球,摸出红球;(3)13人中至少2个人的生日是同一个月;个人的生日是同一个月;(4)任意摸1张体育彩票会中奖;张体育彩票会中奖;(5)天上下雨,马路潮湿;)天上下雨,马路潮湿;(6)随意翻开一本有400页的书,正好翻到第100页;页;(7)你能长高到4m ;(8)抛掷1枚骰子得到的点数小于8.题三:一个射手进行一次射击,则事件“命中环数小于6环”的对立事件是(的对立事件是( )A .命中环数为7、8、9、10环B .命中环数为1、2、3、4、5、6环C .命中环数至少为6环D .命中环数至多为6环题四:某人连续投篮投3次,那么下列各组事件中是互斥且不对立的事件的组数为(次,那么下列各组事件中是互斥且不对立的事件的组数为( ) (1)事件A :至少有一个命中,事件B :都命中;:都命中;(2)事件A :至少有一次命中,事件B :至多有一次命中;:至多有一次命中;(3)事件A :恰有一次命中,事件B :恰有2次命中;次命中;(4)事件A :至少有一次命中,事件B :都没命中.:都没命中.A .0 B .1 C .2 D .3 题五:为了防控输入性甲型H1N1流感,某市医院成立隔离治疗发热流涕病人防控小组,决定从内科5位骨干医师中(含有甲)抽调3人组成,则甲一定抽调到防控小组的概率是人组成,则甲一定抽调到防控小组的概率是 .题六:小明将1枚质地均匀的硬币连续抛掷3次.次.(1)按3次抛掷结果出现的先后顺序,下列三种情况:次抛掷结果出现的先后顺序,下列三种情况:①正面朝上、正面朝上、正面朝上;①正面朝上、正面朝上、正面朝上;②正面朝上、反面朝上、反面朝上;②正面朝上、反面朝上、反面朝上;③正面朝上、反面朝上、正面朝上,③正面朝上、反面朝上、正面朝上,其中出现的概率(其中出现的概率( )A .①最小.①最小B .②最小.②最小C .③最小.③最小D .①②③均相同.①②③均相同(2)请用树状图说明:小明在3次抛掷中,硬币出现1次正面向上、2次反面向上的概率是多少多少题七:掷两个面上分别记有数字1至6的正方体玩具,设事件A 为“点数之和恰好为6”,则A 所有基本事件个数为(有基本事件个数为( )A .2个B .3个C .4个D .5个题八:从1,2,3,5中任取2个数字作为直线Ax +By =0中的A 、B .(1)求这个试验的基本事件总数;)求这个试验的基本事件总数;(2)写出“这条直线的斜率大于-1”这一事件所包含的基本事件.这一事件所包含的基本事件.题九:袋内装有红、白、黑球分别为3、2、1个,从中任取两个,则互斥而不对立的事件是( )A .至少一个白球;都是白球.至少一个白球;都是白球B .至少一个白球;至少一个黑球.至少一个白球;至少一个黑球C .至少一个白球;一个白球一个黑球.至少一个白球;一个白球一个黑球D .至少一个白球;红球、黑球各一个.至少一个白球;红球、黑球各一个题十:掷两颗相同的均匀骰子(各个面分别标有1,2,3,4,5,6),记录朝上一面的两个数,那么互斥而不对立的两个事件是(那么互斥而不对立的两个事件是( )A .“至少有一个奇数”与“都是奇数”B .“至少有一个奇数”与“至少有一个偶数”C .“至少有一个奇数”与“都是偶数”D .“恰好有一个奇数”与“恰好有两个奇数”题十一:下列说法中正确的是题十一:下列说法中正确的是 ..(1)事件A 、B 中至少有一个发生的概率一定比A 、B 中恰有一个发生的概率大;中恰有一个发生的概率大; (2)事件A 、B 同时发生的概率一定比A 、B 中恰有一个发生的概率小;中恰有一个发生的概率小;(3)互斥事件一定是对立事件,对立事件不一定是互斥事件;)互斥事件一定是对立事件,对立事件不一定是互斥事件;(4)互斥事件不一定是对立事件,对立事件一定是互斥事件.)互斥事件不一定是对立事件,对立事件一定是互斥事件.题十二:从一堆产品(其中正品与次品都多于2件)中任取2件,观察正品件数与次品件数,判断下列每件事件是不是互斥事件,如果是,再判断它们是不是对立事件.判断下列每件事件是不是互斥事件,如果是,再判断它们是不是对立事件.(1)恰好有1件次品和恰好有2件次品;件次品;(2)至少有1件次品和全是次品;件次品和全是次品;(3)至少有1件正品和至少有1件次品.件次品.题十三:经临床验证,一种新药对某种疾病的治愈率为49%,显效率28%,有效率12%,其余为无效.则某人患该病使用此药后无效的概率是余为无效.则某人患该病使用此药后无效的概率是 .题十四:我国西部一个地区的年降水量(题十四:我国西部一个地区的年降水量( 单位:mm )在下列区间内的概率如下表:)在下列区间内的概率如下表:年降水量水量[600,800) [800,1000) [1000,1200) [1200,1400) [1400,1600) 概率 0.12 0.26 0.38 0.16 0.08 (1)求年降水量在)求年降水量在事件与概率课后练习参考答案题一:题一: A .详解:必然事件就是一定发生的事件,随机事件是可能发生也可能不发生的事件.A 、是必然事件;B 、是随机事件,选项错误;C 、是随机事件,选项错误;、是随机事件,选项错误;D 、是随机事件,选项错误.故选A .题二:题二: (3)、(5)、(8);(2)、(7);(1)、(4)、(6). 详解:在一定条件下,可能发生也可能不发生的事件,称为随机事件.一定发生的事件称为必然事件;一定不发生的事件称为不可能事件.(1)某射击运动员射击1次,命中靶心;(随机事件)(随机事件)(2)从一只装着白球和黑球的袋中摸球,摸出红球;(不可能事件)(不可能事件)(3)13人中至少2个人的生日是同一个月;(必然事件)(必然事件)(4)任意摸1张体育彩票会中奖;(随机事件);(5)天上下雨,马路潮湿;(必然事件)(必然事件)(6)随意翻开一本有400页的书,正好翻到第100页;(随机事件);(7)你能长高到4m ;(不可能事件)(不可能事件)(8)抛掷1枚骰子得到的点数小于8.(必然事件).题三:题三: C .详解:根据对立事件的定义可得,一个射手进行一次射击,则事件“命中环数小于6环”的对立事件是:“命中环数至少为6环”,故选C .题四:题四: B .详解:利用互斥事件、对立事件的定义,即可得到结论.互斥事件:事件A 与事件B 不可能同时发生,强调的是“不同时发生”.对立事件:事件A 、B 中必定而且只有一个发生。
高中数学必修三练习题(含解析)

五一作业1.tan(﹣345°)=()A.2+B.﹣2+C.﹣2﹣D.2﹣【解答】解:∵tan30°=tan(2×15°)==,∴可得tan215°+6tan15°﹣=0,∴解得tan15°=2﹣,负值舍去,∴tan(﹣345°)=﹣tan(360°﹣15°)=tan15°=2﹣.故选:D.2.已知tan(π﹣α)=2,则=()A.±B.C.﹣D.﹣【解答】解:∵tan(π﹣α)=﹣tanα=2,∴tanα=﹣2,∴==4sinαcosα====﹣.故选:C.【点评】本题主要考查了二倍角公式,诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.3.将函数y=sin x cos x﹣cos2x+的图象向右平移个单位长度得到函数g(x)的图象,下列结论正确的是()A.g(x)是最小正周期为2π的偶函数B.g(x)是最小正周期为4π的奇函数C.g(x)在(π,2π)上单调递减D.g(x)在[0,]上的最大值为【解答】解:令f(x)=sin x cos x﹣cos2x+=sin2x﹣cos2x﹣=sin(2x﹣)﹣;∵f(x)向右平移个单位∴g(x)=sin[2(x﹣﹣)]﹣=sin(2x﹣)﹣=﹣cos2x﹣,A答案:T===π,所以A错.B答案:此函数为偶函数,所以B错误.C答案:增区间为kπ≤x≤kπ+,所以C错误.D答案:正确.故选:D.4.设当x=θ时,函数f(x)=sin x﹣2cos x取得最大值,则sinθ=()A.B.C.D.【解答】解:函数f(x)=sin x﹣2cos x=(sin x﹣cos x)=sin(x﹣φ),其中cosφ=,sinφ=.当x﹣φ=2kπ+(k∈Z)时,取的最大值.∴θ=φ+2kπ+(k∈Z)时,取得最大值,则sinθ=sin(φ+2kπ+)=cosφ=,故选:D.5.下列关于函数f(x)=sin|x|和函数g(x)=|sin x|的结论,正确的是()A.g(x)值域是[﹣1,1]B.f(x)≥0C.f(x+2π)=f(x)D.g(x+π)=g(x)【分析】结合f(x)和g(x)的解析式,分别进行判断即可.【解答】解:f(x)=sin|x|=,函数f(x)∈[﹣1,1],f(x)是偶函数,不具备周期性,故C,B错误,g(x)=|sin x|≥0,即函数g(x)的值域是[0,1],故A错误,g(x+π)=|sin(x+π)|=|﹣sin x|=|sin x|=g(x),故D正确,故选:D.【点评】本题主要考查命题的真假判断,涉及三角函数的周期性,值域的判断,结合绝对值的意义是解决本题的关键.6.函数f(x)=cosωx(ω>0)在区间上是单调函数,且f(x)的图象关于点对称,则ω=()A.或B.或2C.或2D.或【解答】解:f(x)的图象关于点对称,则ω=,整理得:ω=(k∈Z),当k=0时,ω=,所以函数f(x)=,函数的最小正周期为3π,所以函数f (x)在区间上是单调递减函数.当k=1时,ω=2,所以函数f(x)=cos2x,函数的最小正周期为π,所以函数f(x)在区间上是单调递减函数.当k=2时,ω=,所以函数f(x)=cos x,函数的最小正周期为,所以函数f(x)在区间上是不是单调递减函数,函数的单调性先减后增,故错误.故选:B.【点评】本题考查的知识要点:三角函数关系式的恒等变换,余弦型函数性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.7.设函数f(x)=cos(ωx+φ)(x∈R)(ω>0,﹣π<φ<0)的部分图象如图所示,如果,x1≠x2,且f(x1)=f(x2),则f(x1+x2)=()A.B.C.D.【解答】解:根据函数f(x)=cos(ωx+φ)(x∈R)(ω>0,﹣π<φ<0)的部分图象,可得=﹣,∴ω=2.再根据五点法作图可得2•+φ=﹣,∴φ=﹣,∴f(x)=cos(2x﹣).如果,x1≠x2,则2x1﹣∈(﹣,),2x2﹣∈(﹣,),∵f(x1)=f(x2),∴2x1﹣+(2x2﹣)=0,∴x1+x2=,则f(x1+x2)=cos(﹣)=cos=﹣cos=﹣,故选:B.8.已知tanα+=4(α∈(π,π)),则sinα+cosα=()A.B.﹣C.D.﹣【解答】解:∵tanα+=4,∴tan2α﹣4tanα+1=0,解得,又∵α∈(π,π),∴tan,sinα<0,cosα<0,∴sinαcosα=,∴,∴sinα+cosα=﹣,故选:B.【点评】本题主要考查了同角三角函数间的基本关系,是中档题.9.已知函数f(x)=2cos(ωx+φ)﹣1(ω>0,|φ|<π)的一个零点是,当时函数f(x)取最大值,则当ω取最小值时,函数f(x)在上的最大值为()A.﹣2B.C.D.0【解答】解:∵f()=2cos(+φ)﹣1=0,∴cos(+φ)=,∴+φ=2kπ±,k∈Z,①∵f()=2cos(+φ)﹣1=1,∴cos(+φ)=1,∴+φ=2mπ,m∈Z,②由①②可得φ=8kπ﹣6mπ±,由于|φ|<π,可取k=1,m=1,解得φ=(舍去),则ω=6m﹣2,m∈Z,可得正数ω的最小值为4,即有f(x)=2cos(4x+)﹣1,由x∈,可得4x+∈[,π],可得f(x)在上递减,则f(x)的最大值为f(﹣)=2cos﹣1=2×﹣1=0,故选:D.10.在锐角△ABC中,角A,B,C的对边分别为a,b,c,△ABC的面积为S,若sin(A+C)=,则tan C+的最小值为()A.B.2C.1D.【分析】利用正弦定理和余弦定理化简,求出sin(B﹣C)=sin C,可得tan(B﹣C)=tan C,利用基本不等式的性质即可得出.【解答】解:由sin(A+C)=,得sin B==,所以b2=c2+ac,由b2=a2+c2﹣2ac cos B,得a﹣2c cos B=c,利用正弦定理sin A﹣2sin C cos B=sin C,sin B cos C+cos B sin C﹣2sin C cos B=sin B cos C﹣cos B sin C=sin C,即sin(B﹣C)=sin C,∵锐角△ABC中,∴tan(B﹣C)=tan C,∴tan C+=tan C+≥2=,当且仅当tan C=时取等号.故选:A.【点评】本题考查了三角形面积的计算公式、正弦定理、和差公式、基本不等式的性质.,考查了推理能力与计算能力,属于中档题.11.已知A(x A,y A)是圆心为坐标原点O,半径为1的圆上的任意一点,将射线OA绕点O逆时针旋转到OB交圆于点B(x B,y B),则2y A+y B的最大值为()A.3B.2C.D.【解答】解:设A(cosθ,sinθ),则B(,),∴2y A+y B=2sinθ+=2sinθ+sinθcos+cosθsin===,∴2y A+y B的最大值为,故选:C.【点评】本题主要考查了任意角的三角函数的定义,考查了两角和与差的三角函数,是中档题.12.已知函数,过点,当的最大值为9,则m的值为()A.2B.C.2和D.±2【解答】解:由题意T=,故ω=2,将A的坐标代入f(x)得φ)=0,故φ=2kπ,k∈Z,∵|φ|<,∴φ=﹣.故,∴+[1﹣2]令t=∈[0,1],故g(x)可化为:y=﹣2t2+4mt+1,t∈[0,1]对称轴为:t=m,开口向下.①当m≤0时,t=0时,y max=1≠9②当m≥1时,t=1时,y max=4m﹣1=9,∴符合题意;③当0<m<1时,t=m时,y max=2m2+1=9,∴m=±2(舍)综上,当m的值为时,原函数取得最大值9.故选:B.【点评】本题考查了倍角公式、三角函数的图象与性质以及利用换元法求函数的最值等问题.本题的难点一是难以发现角之间的倍数关系,二是换元之后的分类讨论忽视了讨论的范围.13.已知α,β∈(,π),sinα=,cos(α+β)=,则β=【分析】利用两角和差的三角公式进行转化,先求出cosβ的值即可.【解答】解:由于α,β∈(,π),∴α+β∈(π,2π),∵cos(α+β)=,∴sin(α+β)=﹣,cosα=﹣,∴cosβ=cos[(α+β﹣α)]=cos(α+β)cosα)+sin(α+β)sinα=×(﹣)+(﹣)×==﹣,∴β=.【点评】本题主要考查三角函数值的计算,结合两角和差的余弦公式进行转化是解决本题的关键,难度不大.14.设,若f(x)在上为增函数,则ω的取值范围是【解答】解:设,在上,ωx﹣∈[﹣﹣,﹣],由于f(x)为增函数,∴,即,求得0<ω≤,【点评】本题主要考查正弦函数的单调增区间,属于基础题.15.如图,在平行四边形ABCD中,∠BAD=,AB=2,AD=1,若M,N分别是边AD,CD上的点,且满足,其中λ∈[0,1],则•的取值范围是[﹣3,﹣1].【解答】解:由题意=2,=1,•=••cos∠BAD=2×1×cos=1.∵=λ,=λ=λ.∴=(1﹣λ),=(1﹣λ)=(1﹣λ).结合图形,有=+=+(1﹣λ),=(1﹣λ)﹣.∴•=[+(1﹣λ)]•[(1﹣λ)﹣]=(1﹣λ)2﹣•+(1﹣λ)2•﹣(1﹣λ)2=1﹣λ﹣1+(1﹣λ)2﹣4(1﹣λ)=λ2+λ﹣3,∵λ∈[0,1],∴由二次函数知识,可知λ2+λ﹣3=(λ+)2﹣∈[﹣3,﹣1].∴•的取值范围为[﹣3,﹣1].故答案为:[﹣3,﹣1].16.如图,在等腰直角三角形ABC中,∠CAB=90°,AB=2,以AB为直径在△ABC外作半圆O,P为半圆弧AB上的动点,点Q在斜边BC上,若=,则的最小值为.【解答】解:如图,以O为原点建立直角坐标系,可得A(﹣1,0),B(1,0),C(﹣1,﹣2),即有直线BC的方程为y=x﹣1,可设Q(m,m﹣1),=,即为(2,0)•(m+1,m﹣1)=2(m+1)=,解得m=,即Q(,﹣),设P(cosα,sinα),0≤α≤π,可得=(,﹣)•(cosα+1,sinα+2)=cosα+﹣sinα﹣=(2cosα﹣sinα)=cos(α+θ),θ∈(0,),当cos(α+θ)=﹣1即α+θ=π,可得的最小值为﹣.故答案为:﹣.17.已知α∈(0,),β∈(0,),sinα=,cos(α+β)=﹣.(1)求tan2α的值;(2)求cosβ的值.【分析】(1)利用同角三角函数基本关系式可求cosα,tanα的值,进而根据二倍角的正切函数公式可求tan2α的值.(2)利用同角三角函数基本关系式可求sin(α+β)的值,根据两角差的余弦函数公式可求cosβ的值.【解答】解:(1)∵α∈(0,),sinα=,∴cosα==,tanα==4,∴tan2α===﹣.(2)∵α∈(0,),β∈(0,),sinα=,cos(α+β)=﹣,∴α+β∈(0,π),sin(α+β)==,∴cosβ=cos[(α+β)﹣α]=cos(α+β)cosα+sin(α+β)sinα=(﹣)×+×=.【点评】本题主要考查了同角三角函数基本关系式,二倍角的正切函数公式,两角差的余弦函数公式在三角函数化简求值中的应用,属于基础题.18.设函数,其中0<ω<3.若.(1)求ω;(2)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在上的最小值.【分析】(1)将代入,结合0<ω<3构造一个关于ω的不等式、方程的混合组,解出ω即可.(2)先根据图象的平移变换与伸缩变换的规律,求出y=g(x)的解析式,再利用“整体思想”结合正弦函数的性质求解即可.【解答】解:(1)因为f(x)=sin,且=0,所以﹣=kπ,k∈Z.故ω=6k+2,k∈Z.又0<ω<3,所以ω=2.(2)由(1)得f(x)=sin.所以g(x)=sin(),因为x∈,所以x﹣,所以,当x﹣=﹣,即x=﹣时,g(x)取得最小值﹣.【点评】本题通过对三角函数的图象和性质以及图象变换知识与方法的考查,考查了学生的数学运算、直观想象以及逻辑推理等数学核心素养,本题属于一道中档题.19.已知a,b,c分别是△ABC三个内角A,B,C的对边,a cos C+c sin A=b+c.(1)求A;(2)若a=,b+c=3,求b,c.【分析】(1)由已知结合正弦定理及和差角公式进行化简,然后结合辅助角公式即可求解;(2)由已知结合余弦定理即可求解.【解答】解:(1)因为a cos C+c sin A=b+c.由正弦定理可得,sin A cos C+sin C sin A=sin B+sin C=sin(A+C)+sin C,展开可得,sin A cos C+sin C sin A=sin A cos C+sin C cos A+sin C,因为sin C≠0,所以,即sin(A﹣)=,∴A﹣=或A﹣=(舍),故A=;(2)因为a=,b+c=3,由余弦定理可得,===,解可得,bc=2,所以或.【点评】本题主要考查了正弦定理、余弦定理和差角公式在求解三角形中的应用,属于中档试题.20.已知函数.(Ⅰ)求f(x)的单调递增区间;(Ⅱ)若,求cos2x0的值.【分析】(Ⅰ)先由二倍角公式及辅助角公式化简可得,然后根据正弦函数的性质令,解出即可得到增区间;(Ⅱ)先根据题意化简得,由x0的范围结合平方关系计算可得,再通过配角,利用余弦的和角公式计算得答案.【解答】解:(Ⅰ)=,令,解得,∴f(x)的单调递增区间为;(Ⅱ),则,由于,则,故,∴==.【点评】本题考查三角恒等变换以及三角函数的图象及性质,考查化简计算能力,属于基础题.21.在三角形ABC中,AB=2,AC=1,∠ACB=,D是线段BC上一点,且=,F为线段AB上一点.(1)设=,=,设=x+y,求x﹣y;(2)求•的取值范围;(3)若F为线段AB的中点,直线CF与AD相交于点M,求•.【解答】解:(1)∵=+=+=+(﹣)=+=+,∴x=,y=,∴x﹣y=(2)设=λ,(0≤λ≤1)因为在三角形ABC中,AB=2,AC=1,∠ACB=,∴∠CAB=60°,∴•=(﹣)•(﹣)=(λ﹣)(﹣λ)=﹣4λ2+λ•1×2×=﹣4λ2+λ=﹣4(λ﹣)2+∈[﹣3,](3)∵A,M,D三点共线,∴可设=x+(1﹣x)=x+(1﹣x)•,∵F为AB的中点,∴=+,又C,M,F三点共线,∴存在t∈R使得=t,∴x+(1﹣x)=+,∴,解得,•=(+)•=(++)•=•+2=×1×2×(﹣)+×4=22.已知,2sin x),=(sin,,函数.(1)求函数f(x)的零点;(2)已知在△ABC中,角A,B,C所对的边分别为a,b,c,且f(A)=2,△ABC的外接圆半径为,求△ABC周长的最大值.【分析】(1)根据向量数量积的定义求出f(x),结合零点的定义进行求解即可.(2)根据条件先求出A和a的大小,结合余弦定理,以及基本不等式的性质进行转化求解即可.【解答】解:(1)f(x)==2cos x sin(x﹣)+2sin x cos(x﹣)=2sin(2x﹣),由f(x)=0得2x﹣=kπ,k∈Z,得x=+,即函数的零点为x=+,k∈Z.(2)∵f(A)=2,∴f(A)=2sin(2A﹣)=2,得sin(2A﹣)=1,即2A﹣=2kπ+,即A=kπ+,在三角形中,当k=0时,A=,满足条件,∵△ABC的外接圆半径为,∴=2,即a=2×=3,由余弦定理得a2=b2+c2﹣2bc cos A=b2+c2﹣bc=(b+c)2﹣3bc≥=(b+c)2﹣(b+c)2=(b+c)2,即(b+c)2≤4×9=36,即b+c≤6当且仅当b=c时取等号,则a+b+c≤9,即三角形周长的最大值为9.。
高中数学《统计》单元练习题人教版必修三

必修3《统计》单元练习题一、选择题(每小题5分,共10小题,共50分)1、要完成下列两项调查,①从某社区125户高收入家庭、280户中等收入家庭、95户低收入家庭中选出100户调查社会购买力的某项指标;②从某中学的15名艺术特长生中选出3人调查学习负担情况,宜采用的抽样方法依次为( )A .①用随机抽样法,②用系统抽样法B .①用分层抽样法,②用简单随机抽样法C .①用系统抽样法,②用分层抽样法D .①②都用分层抽样法2、100个个体分成10组,编号后分别为第1组:00,01,02,…,09;第2组:10,11,12,…,19;…;第10组:90,91,92,…,99.现在从第k 组中抽取其号码的个位数与()1k m +-的个位数相同的个体,其中m 是第1组随机抽取的号码的个位数,则当5m =时,从第7组中抽取的号码是( )A .71B .61C .75D .65 3、某校对高三年级的学生进行体检,现将高三男生的体重()kg 数据进行整理后分成5组,并绘制频率分布直方图(如图1所示).根据一般标准,高三男生体重超过65kg 属于偏胖,低于55kg 属于偏瘦.已知图中从左到右第一,第三,第四,第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频数为400,则该校高三年级的男生总数和体重正常的概率分别为( )A .1000,0.60B .1000,0.50C .800,0.60D .800,0.50 4、对于一组数据ix (i =1,2,3,…,n ),如果将它们改变为ic x +(i =1,2,3,…,n ),其中0c ≠,则下列结论中正确的是( ) A .平均数与方差均不变 B .平均数不变,而方差变了C .平均数变了,而方差保持不变D .平均数与方差均发生了变化 5、下列说法中,正确的是( ) A .数据5,4,4,3,5,2的众数是4B .一组数据的标准差是这组数据的方差的平方C .数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半D .频率分布直方图中各小长方形的面积等于相应各组的频数 6、对于给定的两个变量的统计数据,下列说法正确的是( )A .都可以分析出两个变量的关系B .都可以用一条直线近似地表示两者的关系C .都可以作出散点图D .都可以用确定的表达式表示两者的关系 7、观察新生婴儿的体重,其频率分布直方图如图2所示,则新生婴儿体重(单位:g )在(]2700,3000的概率为( )A .0.001B .0.1C .0.2D .0.38、在一次数学测验中,某小组14名学生分别与全班的平均分85分的差是:2,3,3,5,12,12,8,2,1,4,10,2,5,5-----,那么这个小组的平均分是( )A .97.2分B .87.29分C .92.32分D .82.86分 A .0037.0 B .0020.2 C .0分 D .1分 10、下列说法正确的是( )A .根据样本估计总体,其误差与所选择的样本容量无关B .方差和标准差具有相同的单位C .从总体中可以抽取不同的几个样本D .如果容量相同的两个样本的方差满足2212s s <,那么推得总体也满足2212s s <是错的 二、填空题(每小题5分,共5小题,共25分)11、一个公司共有240名员工,下设一些部门,要采用分层抽样方法从全体员工中抽取一个容量为20的样本.已知某部门有60名员工,那么从这一部门抽取的员工人数是________. 12、常用的统计图表有:_________________________________________________________. 13、常用的抽样方法有:_________________________________________________________. 14、期中考试后,班长算出了全班40人的数学平均成绩为M ,如果把M 当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为N ,那么M :N 为______. 15、设几个实数1x ,2x ,…,n x 的算术平方数是x ,若a x ≠,设()()2212p x x x x =-+-+…()2n x x +-,()()2212q x a x a =-+-+…()2n x a +-,则一定有p __________q .三、解答题(共75分)16、(12分)某展览馆22天中每天进馆参观的人数如下:180 158 170 185 189 180 184 185 140 179 192 185 190 165 182 170 190 188 175 180 185 148计算参观人数的中位数、众数、平均数、标准差. 17、(12分)某校为了研究学生的数学成绩x 与物理成绩y 之间的关系,随机抽取了10名学生的成绩(),i i x y ,i =1,2,…,10,且计算出102158732ii x==∑,101758i i x ==∑,101774i i y ==∑,10159686i ii x y==∑.试求当90x =时,y 的线性回归估计值.18、(12分)假设关于某设备的使用年限x (年)和所支出的维修费用y (万元)有如下统计资料:(1)回归直线方程;(2)估计使用年限为10年时,维修费用约是多少?19、(12分)(1)将n 个数1x ,2x ,…,n x 分成两组,第1组数为1x ,2x ,…,k x ,第2组数为1k x +,2k x +,…,n x ,两组数据的均值与方差分别记为12,x x 与2212,s s .试用221212,,,x x s s 表示几个数据的均值x 与方差2s .(2)设i i y ax b =+(,a b 为常数,i =1,2,…,n )并记11n i i x x n ==∑,2211()n x i i s x x n ==-∑,11n i i y y n ==∑,2211()n y i i s y y n ==-∑.试证:222,y xy ax b s a s =+=.20、(13分)有同一型号的汽车100辆.为了解这种汽车每耗油1L所行路程的情况,现从中随机抽出10辆在同一条件下进行耗油1L所行程试验,得到如下样本数据(单位:km)(1)完成上面频率分布表;(2)根据上表,在图3给定坐标系中画出频率分布直方图,并根据样本估计总体数据落在[)12.95,13.95中的概率;(3)根据样本,对总体的平均值进行估计.(2)画出频率分布直方图和频率折线图;10.95,11.35范围内的可能性是百分之几?(3)据上述图表,估计数据落在[)(4)数据小于11.20的可能性是百分之几?。
数学必修三习题答案

数学必修三习题答案【篇一:高一数学必修3全册各章节课堂同步习题(详解答案)】概念班次姓名[自我认知]:1.下面的结论正确的是( ).a. 一个程序的算法步骤是可逆的b. 一个算法可以无止境地运算下去的 c. 完成一件事情的算法有且只有一种 d. 设计算法要本着简单方便的原则 2.下面对算法描述正确的一项是 ( ). a.算法只能用自然语言来描述 b.算法只能用图形方式来表示 c.同一问题可以有不同的算法d.同一问题的算法不同,结果必然不同3.下面哪个不是算法的特征( ) a.抽象性 b.精确性 c.有穷性 d.唯一性4.算法的有穷性是指( )a.算法必须包含输出b.算法中每个操作步骤都是可执行的c.算法的步骤必须有限d.以上说法均不正确5.早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(10min)、听广播(8min)几个步骤,从下列选项中选最好的一种算法() a.s1洗脸刷牙、s2刷水壶、s3烧水、s4泡面、s5吃饭、s6听广播 b.s1刷水壶、s2烧水同时洗脸刷牙、s3泡面、s4吃饭、s5听广播 c. s1刷水壶、s2烧水同时洗脸刷牙、s3泡面、s4吃饭同时听广播 d.s1吃饭同时听广播、s2泡面;s3烧水同时洗脸刷牙;s4刷水壶6.看下面的四段话,其中不是解决问题的算法是( )a.从济南到北京旅游,先坐火车,再坐飞机抵达b.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1c.方程x2?1?0有两个实根d.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15 7.已知直角三角形两直角边长为a,b,求斜边长c的一个算法分下列三步:①计算c?a,b的值;③输出斜边长c的值,其中正确的顺序是 ( ) a.①②③ b.②③①c.①③②d.②①③[课后练习]:8.若f?x?在区间?a,b?内单调,且f?a??f?b??0,则f?x?在区间?a,b?内( )a.至多有一个根 b.至少有一个根c.恰好有一个根 d.不确定9.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均成绩的一个算法为:第一步:取a=89 ,b=96 ,c=99;第二步:____①______;第三步:_____②_____;第四步:输出计算的结果.10.写出求1+2+3+4+5+6+?+100的一个算法.可运用公式1+2+3+?+n= 第一步______①_______;第二步_______②________;第三步输出计算的结果.12.写出按从小到大的顺序重新排列x,y,z三个数值的算法.n(n?1)直接计算. 21.1.2程序框图[自我认知]: 1.算法的三种基本结构是()A.顺序结构、条件结构、循环结构B.顺序结构、流程结构、循环结构C.顺序结构、分支结构、流程结构D.流程结构、循环结构、分支结构2.程序框图中表示判断框的是()A.矩形框B.菱形框 d.圆形框 d.椭圆形框3.如图(1)、(2),它们都表示的是输出所有立方小于1000的正整数的程序框图,那么应分别补充的条件为( )⑴333⑵3a.⑴n≥1000 ? ⑵n<1000 ?b. ⑴n≤1000 ?⑵n≥1000 ?c. ⑴n<1000 ? ⑵n≥1000 ?d. ⑴n<1000 ?⑵n<1000 ?4.算法共有三种逻辑结构,即顺序逻辑结构,条件逻辑结构和循环逻辑结构,下列说法正确的是 ( ) a.一个算法只能含有一种逻辑结构 b.一个算法最多可以包含两种逻辑结构 c.一个算法必须含有上述三种逻辑结构d.一个算法可以含有上述三种逻辑结构的任意组合 [课后练习]:5.给出以下一个算法的程序框图(如下图所示),该程序框图的功能是( ) a.求输出a,b,c三数的最大数 b.求输出a,b,c三数的最小数3333c.将a,b,c按从小到大排列d.将a,b,c按从大到小排列第5题图第6题图6.右边的程序框图(如上图所示),能判断任意输入的数x的奇偶性:其中判断框内的条件是( )a.m?0?b.x?0 ?c.x?1 ?d.m?1?7.在算法的逻辑结构中,要求进行逻辑判断,并根据结果进行不同处理的是哪种结构 ( ) a.顺序结构 b.条件结构和循环结构 c.顺序结构和条件结构 d.没有任何结构?x2?1(x?0)8.已知函数f?x??? ,设计一个求函数值的算法,并画出其程序框图(x?0)?2x?11.1.2程序框图(第二课时)[课后练习]:班次姓名1.如图⑴的算法的功能是____________________________.输出结果i=___,i+2=_____.2.如图⑵程序框图箭头a指向①处时,输出 s=__________. 箭头a指向②处时,输出 s=__________.3.如图⑷所示程序的输出结果为s=132, 则判断中应填a、i≥10?b、i≥11?c、i≤11? d、i≥12?4.如图(3)程序框图箭头b指向①处时,输出 s=__________. 箭头b指向②处时,输出 s=__________5、如图(5)是为求1~1000的所有偶数的和而设计的一个程序空白框图,将空白处补上。
高中数学必修三同步练习题库:算法案例(填空题:容易)

算法案例(填空题:容易)1、372和684的最大公约数是2、用秦九韶算法计算多项式当的值时,乘法运算的次数为________.3、七进制数1234转换成十进制数是__________.4、下列各数、、、中最小的数是____________。
5、__________.6、用“秦九韶算法”计算多项式,当时的值的过程中,要经过____________次乘法运算和_________次加法运算.7、用辗转相除法求240和288的最大公约数时,需要做____次除法;利用更相减损术求36和48的最大公约数时,需要进行______次减法。
8、将二进制数化为十进制数,结果为______.9、生活中常用的十二进位制,如一年有12个月,时针转一周为12个小时,等等,就是逢12进1的计算制,现采用数字0~9和字母A、B共12个计数符号,这些符号与十进制的数的对应关系如下表:例如用十二进位制表示A+B=19,照此算法在十二进位制中运算A×B= .10、用辗转相除法求两个数102、238的最大公约数是_________.11、用辗转相除法求得459和357的最大公约数是_________ .[12、把89化成二进制数为 .13、不超过2012的只有三个正因数的正整数个数为14、三个数72,120,168的最大公约数是_______________.15、用秦九韶算法计算时的值时,需要运算次16、设为正整数,若和除以的余数相同,则称和对同余.记,已知,,则的值可以是(写出以下所有满足条件的序号)①1007;②2013;③3003;④600217、用辗转相除法求得228和1995的最大公约数是 .18、阅读右侧程序框图,输出的结果的值为___ _____.19、 2012年1月20日上午,财政部公布2011年全国公共财政收入为103740亿元,将103740亿元用科学记数法表示为元.(保留3个有效数字)20、把二进制数110 011化为十进制数为;21、两个正整数840与1764的最大公约数为____ __.22、程序框图如图,将输出的的值依次记为,数列{}的通项公式为=__________。
高中数学人教B版必修第三册《8.2.3 倍角公式》练习题(2)

人教B版必修第三册《8.2.3 倍角公式》练习题(2) 一、单选题(本大题共12小题,共60.0分)1.在△ABC中,角A、B、C所对的边分别为a、b、c,若a=6,c=4,sin B2=√33,则b=()A. 9B. 36C. 6√2D. 62.若z∈C且z=cosα+isinα,α∈R,则|z−3−4i|的最大值是()A. 3B. 4C. 5D. 63.在平面直角坐标系xOy中,角α与角β的始边为x轴正半轴,顶点为坐标原点,终边关于x轴对称,已知sinα=35,则cosβ=()A. 35B. −45C. ±35D. ±454.给出下列四个命题:①映射不一定是函数,但函数一定是其定义域到值域的映射;②函数f(x)的反函数是y=log5x,则f(log515)=−1;③函数f(x)=sin(ωx+π4) (ω>0)在(π2,π)上递减,则ω的范围为[12,54];④若α是第一象限的角,则α2也是第一象限的角.其中所有正确命题的序号是()A. ①③B. ②③C. ①④D. ②④5.在△ABC中,A,B,C为三个内角,f(B)=4cosB⋅sin2(π4+B2)+√3cos2B−2cosB,若f(B)=2,则角B为()A. π12B. π6C. π4D. π36.已知π4<α<3π4,0<β<π4,cos(π4−α)=35,sin(3π4+β)=513,则sin(α+β)=()A. −5665B. 5665C. −1665D. 16657.函数的最小正周期为()A. 4B. 2C.D.8.下列函数中,在区间(0,)上为增函数且以为周期的函数是()A. B. C. D.9.已知:,则A. 4B.C. 5D. 310.若点在函数的图像上,则=()A. 2B. 4C. 6D. 811.若α为第三象限角,则√1−sinα2的结果为()A. sinαB. −sinαC. cosαD. −cosα12.已知α,β∈(0,π),tanα,tanβ是方程x2+4x+2=0的两根,则cos(α+β)的值是()A. √1717B. −√1717C. 45D. −45二、解答题(本大题共3小题,共36.0分)13.求值:(1)sin6°sin42°sin66°sin78°;(2)sin220°+cos250°+sin20°cos50°.14.在△ABC中,角A,B,C所对的边分别为a,b,c,且8sin2(A+B2)+3cos2C=3.(1)求cos C;(2)若B=π2,2AM⃗⃗⃗⃗⃗⃗ =MC⃗⃗⃗⃗⃗⃗ ,求tan∠ABM.15.在△ABC中,角A、B、C的对边分别为a、b、c,且a≥b,sinA+√3cosA=2sinB.(Ⅰ)求角C的大小;(Ⅱ)若c=√3,求a+b的最大值.【答案与解析】1.答案:D解析:解:∵a =6,c =4,sin B2=√33,∴cosB =1−2sin 2B2=1−2×(√33)2=13,∴由余弦定理可得:b =√a 2+c 2−2accosB =√36+16−2×6×4×13=6.故选:D .由已知利用二倍角的余弦函数公式可求cos B 的值,根据余弦定理即可计算得解b 的值.本题主要考查了二倍角公式以及余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.2.答案:D解析:解:∵z =cosα+isinα,α∈R , ∴|z −3−4i|=|(cosα−3)+(sinα−4)i| =√(cosα−3)2+(sinα−4)2 =√26−10sin(α+θ),∴|z −3−4i|的最大值是√26+10=6, 故选D .把z =cosα+isinα代入|z −3−4i|,利用三角恒等变换可求. 该题考查复数的模、三角恒等变换,属基础题.3.答案:D解析:解:由sinα=35,可得α的终边在第一或第二象限,β的终边在第三或第四象限,且cosβ=cosα. 若α的终边在第一象限,则β的终边在第四象限, ∵cosα=√1−sin 2α=45,∴cosβ=cosα=45.若α的终边在第二象限,则β的终边在第三象限, ∵cosα=−√1−sin 2α=−45,∴cosβ=cosα=−45. 综上可得,cosβ=cosα=±45, 故选:D .根据同角三角函数的基本关系,以及三角函数在各个象限中的符号,分类讨论求得cosβ的值. 本题主要考查同角三角函数的基本关系,以及三角函数在各个象限中的符号,属于基础题.4.答案:A解析:解:对于选项:①映射不一定是函数,但函数一定是其定义域到值域的映射;正确. 对于选项②:函数f(x)的反函数是y =log 5x ,则:f(x)=5x ,则f(log 515)=15;故错误. 对于选项③:函数f(x)=sin(ωx +π4) (ω>0)在(π2,π)上递减, 故π2+2kπ≤ωx +π4≤3π2+2kπ,(k ∈Z) 整理得π4ω+2kπω≤x ≤5π4ω+2kπω,(k ∈Z)由于函数在(π2,π)上递减,故π4ω+2kπω≤π2<x <π≤5π4ω+2kπω,即:{π≤5π4ω+2kπωπ4ω+2kπω≤π2,解得ω的范围为[12,54];故正确.对于选项④若α是第一象限的角,故则α2也是第一或第三象限的角,故错误. 故选:A .直接利用函数的定义的应用,反函数的应用,正弦型函数的性质的应用,象限角的应用求出结果. 本题考查的知识要点:函数的定义的应用,反函数的应用,正弦型函数的性质的应用,象限角的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.5.答案:A解析:解:∵f(B)=4cosB1−cos(π2+B)2+√3cos2B −2cosB =2cosB(1+sinB)+√3cos2B −2cosB =sin2B +√3cos2B =2sin(2B +π3)=2, ∴sin(2B +π3)=1, ∵B ∈(0,π),2B +π3∈(π3,7π3),∴2B +π3=π2,∴B =π12. 故选:A .先利用三角函数的和角公式、二倍角公式将原函数化成一个三角函数的形式,由f(B)=2得到sin(2B+π3)=1,结合B的范围,利用正弦函数的性质即可求解B的值.本题主要考查了二倍角公式,两角和的正弦函数公式以及正弦函数的性质的综合应用,考查了转化思想和函数思想,属于基础题.6.答案:B解析:解:∵π4<α<3π4,0<β<π4,cos(π4−α)=35,sin(3π4+β)=513,∴π4−α∈(−π2,0),3π4+β∈(π2,π),∴sin(π4−α)=√1−cos2(π4−α)=−45,cos(3π4+β)=−√1−sin2(3π4+β)=−1213,则sin(α+β)=sin[(3π4+β)−(π4−α)−π2]=−cos[(3π4+β)−(π4−α)]=−cos(3π4+β)cos(π4−α)−sin(3π4+β)sin(π4−α)=−1213⋅35−513⋅(−45)=−1665,故选:B.利用同角三角函数的基本关系、诱导公式、两角差的余弦公式,求得sin(α+β)的值.本题主要考查同角三角函数的基本关系、诱导公式、两角差的余弦公式的应用,属于基础题.7.答案:C解析:试题分析:;;则,函数的周期.所以本题答案选.考点:1.诱导公式;2.正弦二倍角公式;3.三角函数的周期.8.答案:D解析:试题分析:A项的周期为;B项周期;C项在上是减函数;D项满足在区间(0,)上为增函数且以为周期考点:三角函数周期性单调性点评:函数,的周期为,的周期为9.答案:A解析:解析:本题考查同角三角函数的基本关系。
数学必修三习题答案

数学必修三习题答案【篇一:高一数学必修3全册各章节课堂同步习题(详解答案)】概念班次姓名[自我认知]:1.下面的结论正确的是( ).a. 一个程序的算法步骤是可逆的b. 一个算法可以无止境地运算下去的 c. 完成一件事情的算法有且只有一种 d. 设计算法要本着简单方便的原则 2.下面对算法描述正确的一项是 ( ). a.算法只能用自然语言来描述 b.算法只能用图形方式来表示 c.同一问题可以有不同的算法d.同一问题的算法不同,结果必然不同3.下面哪个不是算法的特征( ) a.抽象性 b.精确性 c.有穷性 d.唯一性4.算法的有穷性是指( )a.算法必须包含输出b.算法中每个操作步骤都是可执行的c.算法的步骤必须有限d.以上说法均不正确5.早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(10min)、听广播(8min)几个步骤,从下列选项中选最好的一种算法() a.s1洗脸刷牙、s2刷水壶、s3烧水、s4泡面、s5吃饭、s6听广播 b.s1刷水壶、s2烧水同时洗脸刷牙、s3泡面、s4吃饭、s5听广播 c. s1刷水壶、s2烧水同时洗脸刷牙、s3泡面、s4吃饭同时听广播 d.s1吃饭同时听广播、s2泡面;s3烧水同时洗脸刷牙;s4刷水壶6.看下面的四段话,其中不是解决问题的算法是( )a.从济南到北京旅游,先坐火车,再坐飞机抵达b.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1c.方程x2?1?0有两个实根d.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15 7.已知直角三角形两直角边长为a,b,求斜边长c的一个算法分下列三步:①计算c?a,b的值;③输出斜边长c的值,其中正确的顺序是 ( ) a.①②③ b.②③①c.①③②d.②①③[课后练习]:8.若f?x?在区间?a,b?内单调,且f?a??f?b??0,则f?x?在区间?a,b?内( )a.至多有一个根 b.至少有一个根c.恰好有一个根 d.不确定9.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均成绩的一个算法为:第一步:取a=89 ,b=96 ,c=99;第二步:____①______;第三步:_____②_____;第四步:输出计算的结果.10.写出求1+2+3+4+5+6+?+100的一个算法.可运用公式1+2+3+?+n= 第一步______①_______;第二步_______②________;第三步输出计算的结果.12.写出按从小到大的顺序重新排列x,y,z三个数值的算法.n(n?1)直接计算. 21.1.2程序框图[自我认知]: 1.算法的三种基本结构是()A.顺序结构、条件结构、循环结构B.顺序结构、流程结构、循环结构C.顺序结构、分支结构、流程结构D.流程结构、循环结构、分支结构2.程序框图中表示判断框的是()A.矩形框B.菱形框 d.圆形框 d.椭圆形框3.如图(1)、(2),它们都表示的是输出所有立方小于1000的正整数的程序框图,那么应分别补充的条件为( )⑴333⑵3a.⑴n≥1000 ? ⑵n<1000 ?b. ⑴n≤1000 ?⑵n≥1000 ?c. ⑴n<1000 ? ⑵n≥1000 ?d. ⑴n<1000 ?⑵n<1000 ?4.算法共有三种逻辑结构,即顺序逻辑结构,条件逻辑结构和循环逻辑结构,下列说法正确的是 ( ) a.一个算法只能含有一种逻辑结构 b.一个算法最多可以包含两种逻辑结构 c.一个算法必须含有上述三种逻辑结构d.一个算法可以含有上述三种逻辑结构的任意组合 [课后练习]:5.给出以下一个算法的程序框图(如下图所示),该程序框图的功能是( ) a.求输出a,b,c三数的最大数 b.求输出a,b,c三数的最小数3333c.将a,b,c按从小到大排列d.将a,b,c按从大到小排列第5题图第6题图6.右边的程序框图(如上图所示),能判断任意输入的数x的奇偶性:其中判断框内的条件是( )a.m?0?b.x?0 ?c.x?1 ?d.m?1?7.在算法的逻辑结构中,要求进行逻辑判断,并根据结果进行不同处理的是哪种结构 ( ) a.顺序结构 b.条件结构和循环结构 c.顺序结构和条件结构 d.没有任何结构?x2?1(x?0)8.已知函数f?x??? ,设计一个求函数值的算法,并画出其程序框图(x?0)?2x?11.1.2程序框图(第二课时)[课后练习]:班次姓名1.如图⑴的算法的功能是____________________________.输出结果i=___,i+2=_____.2.如图⑵程序框图箭头a指向①处时,输出 s=__________. 箭头a指向②处时,输出 s=__________.3.如图⑷所示程序的输出结果为s=132, 则判断中应填a、i≥10?b、i≥11?c、i≤11? d、i≥12?4.如图(3)程序框图箭头b指向①处时,输出 s=__________. 箭头b指向②处时,输出 s=__________5、如图(5)是为求1~1000的所有偶数的和而设计的一个程序空白框图,将空白处补上。
高中数学必修三同步练习题库:古典概型(填空题:较难22,困难23)

古典概型(填空题:较难22,困难23)1、设有关于的一元二次方程.(Ⅰ)是从四个数中任取的一个数,是从三个数中任取的一个数,求上述方程有实根的概率;(Ⅱ)若是从区间任取的一个数,是从区间任取的一个数,求上述方程有实根的概率.2、在三张奖券中有一、二等奖各一张,另一张无奖,甲乙两人各抽取一张(不放回),两人都中奖的概率为.3、将4名大学生分配到A、B、C三个乡镇去当村官,每个乡镇至少分配一名,则大学生甲分配到乡镇A 的概率为(用数字作答)4、设函数是从1,2,3三个数中任意取一个数,是从2,3,4,5四个数中任意取一个数,则的概率是__________.5、已知集合,则满足条件的事件的概率为__________;集合的元素中含奇数个数的期望为_________.6、已知随机变量服从正态分布,,则.7、公共汽车车门高度是按男子与车门碰头机会不高于0.0228来设计的.设男子身高服从正态分布(单位:),参考以下概率,,,则车门的高度(单位:)至少应设计为______.8、若随机变量服从两点分布,且,令,则.9、在棱长为的正方体中,在正方体内随机取一点,则点到点的距离大于的概率为________.10、甲乙二人玩猜字游戏,先由甲在心中想好一个数字,记作,然后再由乙猜甲刚才所想到的数字,并把乙猜到的数字记为,二人约定:、,且当时乙为胜方,否则甲为胜方.则甲取胜的概率是______.11、一盒子装有只产品,其中有只一等品,只二等品.从中取产品两次,每次任取一只,作不放回抽样.设事件为“第一次取到的是一等品”,事件为“第二次取到的是一等品”,则条件概率.12、从,,,这四个数中一次随机地取两个数,则其中一个数是另一个数的两倍的概率是.13、已知菱形ABCD的边长为2,,则该菱形内的点到点A、B的距离均不小于1的概率是。
14、无重复数字的五位数a1a2a3a4a5,当a1<a2, a2>a3, a3<a4, a4>a5时称为波形数,则由1,2,3,4,5任意组成的一个没有重复数字的五位数是波形数的概率为 .15、为了庆祝六一儿童节,某食品厂制作了3种不同的精美卡片,每袋食品随机装入一张卡片,集齐3种卡片可获奖,现购买该种食品5袋,能获奖的概率为________.16、有一批种子的发芽率为,每粒种子能成长为幼苗的概率为,则在这批种子中,出芽后的幼苗成活率为。
高中数学必修三各章节同步练习题(附答案解析)

高中数学必修三 1.1.1算法的概念练习新人教A版基础巩固一、选择题1.以下关于算法的说法正确的是( )A.描述算法可以有不同的方式,可用形式语言也可用其它语言B.算法可以看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或序列只能解决当前问题C.算法过程要一步一步执行,每一步执行的操作必须确切,不能含混不清,而且经过有限步或无限步后能得出结果D.算法要求按部就班地做,每一步可以有不同的结果[答案] A[解析] 算法可以看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或计算序列能够解决一类问题.算法过程要求一步一步执行,每一步执行的操作,必须确切,只能有唯一结果,而且经过有限步后,必须有结果输出后终止,描述算法可以有不同的语言形式,如自然语言、框图语言及形式语言等.2.下列对算法的理解不正确的是( )A.一个算法应包含有限的步骤,而不能是无限的B.算法中的每一个步骤都应当是确定的,而不应当是含糊的、模棱两可的C.算法中的每一个步骤都应当有效地执行,并得到确定的结果D.一个问题只能设计出一种算法[答案] D[解析] 依据算法的概念及特征逐项排除验证.解:算法的有限性是指包含的步骤是有限的,故A正确;算法的确定性是指每一步都是确定的,故B正确;算法的每一步都是确定的,且每一步都应有确定的结果,故C正确;对于同一个问题可以有不同的算法,故D错误.[点评] 解决有关算法的概念判断题应根据算法的特征进行判断,特别注意能在有限步内求解某类问题,其中的每条规则必须是明确可行的,不能是模棱两可的,对同一个问题可设计不同的算法.3.下列语句中是算法的有( )①从广州到北京旅游,先坐火车,再坐飞机抵达;②解一元一次方程的步骤是去分母、去括号、移项、合并同类顼、系数化为1;③方程x2-1=0有两个实根;④求1+2+3+4的值,先计算1+2=3,再由3+3=6,6+4=10得最终结果是10.A.1个B.2个C.3个D.4个[答案] C[解析] ①中说明了从广州到北京的行程安排,完成任务;②中给出了一元一次方程这一类问题的解决方式;④中给出了求1+2+3+4的一个过程,最终得出结果;对于③,并没有说明如何去算,故①②④是算法,③不是算法.4.计算下列各式中S的值,能设计算法求解的是( )①S=1+2+3+ (100)②S=1+2+3+…+100+…;③S=1+2+3+…+n(n∈N+).A.①②B.①③C.②③D.①②③[答案] B5.阅读下面的算法:第一步,输入两个实数a,b.第二步:若a<b,则交换a,b的值,否则执行第三步.第三步,输出a.这个算法输出的是( )A.a,b中的较大数B.a,b中的较小数C.原来的a的值D.原来的b的值[答案] A[解析] 第二步中,若a<b,则交换a,b的值,那么a是a,b中的较大数;否则a<b不成立,即a≥b,那么a也是a,b中的较大数.6.阅读下面的四段话,其中不是解决问题的算法的是( )A.求1×2×3的值,先计算1×2=2,再计算2×3=6,最终结果为6B.解一元一次不等的步骤是化标准式、移项、合并同类项、系数化为1C.今天,我上了8节课,真累D.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15[答案] C[解析] A,B,D项中,都是解决问题的步骤,则A,B,D项中所叙述的是算法,C项中是说明一个事实,不是算法.二、填空题7.给出下列表述:①利用△ABC 的面积公式S =12ab sin C 计算a =2、b =1、C =60°时三角形的面积;②从江苏昆山到九寨沟旅游可以先乘汽车到上海,再乘飞机到成都,再乘汽车抵达; ③求过M (1,2)与N (-3,5)两点的连线所在的直线方程,可先求直线MN 的斜率,再利用点斜式方程求得;④求三点A (2,2)、B (2,6)、C (4,4)所确定的△ABC 的面积,可先算AB 的长a ,再求AB 的直线方程及点C 到直线AB 的距离h ,最后利用S =12ah 来进行计算.其中是算法的是________.[答案] ②③④[解析] 由算法的含义及特性知②③④是算法,①没有说明计算的步骤,所以①不是算法.8.完成解不等式2x +2<4x -1的算法: 第一步,移项并合并同类项,得________.第二步,在不等式的两边同时除以x 的系数,得________. [答案] -2x <-3 x >32三、解答题9.(2015·江西南昌期末)已知一个等边三角形的周长为a ,求这个三角形的面积.设计一个算法解决这个问题.[探究] 利用正三角形面积公式S =34l 2(l 为正三角形边长)求值设计. [解析] 第一步,输入a 的值. 第二步,计算l =a3的值.第三步,计算S =34×l 2的值. 第四步,输出S 的值. 10.下面给出一个问题的算法: 第一步,输入x ;第二步,若x ≥4,则执行第三步,否则执行第四步; 第三步,输出2x -1结束; 第四步,输出x 2-2x +3结束. 问:(1)这个算法解决的问题是什么?(2)当输入的x 的值为多少时,输出的数值最小?[解析] (1)这个算法解决的问题是求分段函数y =⎩⎪⎨⎪⎧2x -1x ≥4x 2-2x +3 x <4的函数值的问题.(2)本问的实质是求分段函数最小值的问题. 当x ≥4时,y =2x -1≥7;当x <4时,y =x 2-2x +3=(x -1)2+2≥2. ∴函数最小值为2,当x =1时取到最小值. ∴当输入x 的值为1时,输出的数值最小.能力提升一、选择题1.结合下面的算法: 第一步,输入x .第二步,判断x 是否小于0,若是,则输出x +2,否则执行第三步. 第三步,输出x -1.当输入的x 的值为-1,0,1时,输出的结果分别为( ) A .-1,0,1 B .-1,1,0 C .1,-1,0 D .0,-1,1[答案] C[解析] 根据x 值与0的关系,选择执行不同的步骤,当x 的值为-1,0,1时,输出的结果应分别为1,-1,0,故选C.2.给出下列算法:第一步,输入正整数n (n >1).第二步,判断n 是否等于2,若n =2,则输出n ;若n >2,则执行第三步.第三步,依次从2到n -1检验能不能整除n ,若不能整除n ,则执行第四步;若能整除n ,则执行第一步.第四步,输出n . 则输出的n 的值是( ) A .奇数 B .偶数 C .质数 D .合数[答案] C[解析] 根据算法可知n =2时,输出n 的值2;若n =3,输出n 的值3;若n =4,2能整除4,则重新输入n 的值……,故输出的n 的值为质数.3.小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用的分钟数为( )A .13B .14C .15D .23[答案] C[解析] ①洗锅盛水2分钟、②用锅把水烧开10分钟(同时②洗菜6分钟、③准备面条及佐料2分钟)、⑤煮面条3分钟,共为15分钟.4.已知两个单元分别存放了变量x 和y ,下面描述交换这两个变量的值的算法中正确的为( )A .第一步 把x 的值给y ;第二步 把y 的值给x .B .第一步 把x 的值给t ;第二步 把t 的值给y ;第三步 把y 的值给x .C .第一步 把x 的值给t ;第二步 把y 的值给x ;第三步 把t 的值给y .D .第一步 把y 的值给x ;第二步 把x 的值给t ;第三步 把t 的值给y . [答案] C[解析] 为了达到交换的目的,需要一个中间变量t ,通过t 使两个变量来交换. 第一步 先将x 的值赋给t (这时存放x 的单元可以再利用); 第二步 再将y 的值赋给x (这时存放y 的单元可以再利用); 第三步 最后把t 的值赋给y ,两个变量x 和y 的值便完成了交换.[点评] 这好比有一碗酱油和一碗醋.我们要把这两碗盛装的物品交换过来,需要一个空碗(即t );先把醋(或酱油)倒入空碗,再把酱油(或醋)倒入原来盛醋(或酱油)的碗,最后把倒入空碗中的醋(或酱油)倒入原来盛酱油(或醋)的碗,就完成了交换.二、填空题 5.给出下列算法: 第一步,输入x 的值.第二步,当x >4时,计算y =x +2;否则执行下一步. 第三步,计算y =4-x . 第四步,输出y .当输入x =0时,输出y =________. [答案] 2[解析] 由于x =0>4不成立,故计算y =4-x =2,输出y =2.6.已知点P (x 0,y 0)和直线l :Ax +By +C =0,写出求点到直线距离的一个算法. 有如下步骤:①输入点的坐标x 0,y 0.②计算z 1=Ax 0+By 0+C .③计算z 2=A 2+B 2.④输入直线方程的系数A ,B 和常数C .⑤计算d =|z 1|z 2.⑥输出d 的值.其中正确的顺序为__________________.[答案] ①④②③⑤⑥[解析] (1)算法步骤应先输入相关信息最后输出结果;(2)d =|Ax 0+By 0+C |A 2+B 2,应先将分子、分母求出,再代入公式.三、解答题7.设计一个算法,找出闭区间[20,25]上所有能被3整除的整数. [解析] 第一步,用20除以3,余数不为0,故20不能被3整除; 第二步,用21除以3,余数为0,故21能被3整除; 第三步,用22除以3,余数不为0,故22不能被3整除; 第四步,用23除以3,余数不为0,故23不能被3整除; 第五步,用24除以3,余数为0,故24能被3整除; 第六步,用25除以3,余数不为0,故25不能被3整除; 第七步,指出在闭区间[20,25]上能被3整除的整数为21和24.8.某人带着一只狼和一只羊及一捆青菜过河,只有一条船,船仅可载重此人和狼、羊及青菜中的一种,没有人在的时候,狼会吃羊,羊会吃青菜.设计安全过河的算法.[解析] 第一步,人带羊过河. 第二步,人自己返回. 第三步,人带青菜过河. 第四步,人带羊反回. 第五步,人带狼过河. 第六步,人自己返回. 第七步,人带羊过河.高中数学必修三 1.1.2第1课时程序框图、顺序结构练习 新人教A 版基础巩固一、选择题1.程序框图是算法思想的重要表现形式,程序框图中不含( ) A .流程线 B .判断框 C .循环框 D .执行框[答案] C[解析] 程序框图是由程序框和流程线组成.其中程序框包括起止框、、输入输出框、执行框、判断框.这里并没有循环框.2.在程序框图中,算法中间要处理数据或计算,可分别写在不同的( )A.处理框内B.判断框内C.输入、输出框内D.终端框内[答案] A[解析] 由处理框的意义可知,对变量进行赋值,执行计算语句,处理数据,结果的传送都可以放在处理框内,∴选A.3.下列关于程序框的功能描述正确的是( )A.(1)是处理框;(2)是判断框;(3)是终端框;(4)是输入、输出框B.(1)是终端框;(2)是输入、输出框;(3)是处理框;(4)是判断框C.(1)和(3)都是处理框;(2)是判断框;(4)是输入、输出框D.(1)和(3)的功能相同;(2)和(4)的功能相同[答案] B[解析] 根据程序框图的规定,(1)是终端框,(2)是输入、输出框,(3)是处理框,(4)是判断框.4.如图所示程序框图中,其中不含有的程序框是( )A.终端框B.输入、输出框C.判断框D.处理框[答案] C[解析] 含有终端框,输入、输出框和处理框,不含有判断框.5.如图,若输入a=10,则输出a=________( )A.2 B.8C.10 D.6[答案] 8[解析] b=10-8=2,a=10-2=8.6.如图所示的程序框图中,要想使输入的值与输出的值相等,输入的a值应为( )A.1 B.3C.1或3 D.0或3[答案] D[解析] 本题实质是解方程a=-a2+4a,解得a=0或a=3.二、填空题7.下面程序框图执行的功能是输入矩形的边长求它的面积,其中执行框中应填的是________.[答案] S=a×b8.如图所示的程序框图,若输出的结果是2,则输入的m=________.[答案] 100[解析] 由于输出的结果是2,则x=2,则lg m=2,故m=100.三、解答题9.如图,是解决某个问题而绘制的程序框图,仔细分析各框内的内容及图框之间的关系,回答下面的问题:(1)图框①中x=2的含义是什么?(2)图框②中y1=ax+b的含义是什么?(3)图框④中y2=ax+b的含义是什么?(4)该程序框图解决的是怎样的问题?(5)当最终输出的结果是y1=3,y2=-2时,求y=f(x)的解析式.[解析] (1)图框①中x=2表示把2赋值给变量x.(2)图框②中y1=ax+b的含义是:该图框在执行①的前提下,即当x=2时,计算ax+b的值,并把这个值赋给y1.(3)图框④中y2=ax+b的含义是:该图框在执行③的前提下,即当x=-3时,计算ax +b的值,并把这个值赋给y2.(4)该程序框图解决的是求函数y=ax+b的函数值的问题,其中输入的是自变量x的值,输出的是对应x的函数值.(5)y1=3,即2a+b=3.⑤y2=-2,即-3a+b=-2.⑥由⑤⑥,得a=1,b=1,所以f(x)=x+1.10.已知一个圆柱的底面半径为R,高为h,求圆柱的体积.设计解决该问题的一个算法,并画出相应的程序框图.[分析] 此题只要将半径R、高h代入圆柱的体积公式V=πR2h,最后输出结果即可,所以只用顺序结构就能表达出来.[解析]算法如下:第一步,输入R,h,第二步,计算V=πR2h.第三步,输出V.程序框图如图所示.能力提升一、选择题1.对终端框叙述正确的是( )A.表示一个算法的起始和结束,程序框是B.表示一个算法输入和输出的信息,程序框是C.表示一个算法的起始和结束,程序框是D.表示一个算法输入和输出的信息,程序框是[答案] C2.阅读右图所示程序框图.若输入的x=3,则输出的y的值为( )A.24 B.25C.30 D.40[答案] D3.如图所示的程序框图是已知直角三角形两直角边a,b求斜边c的算法,其中正确的是( )[答案] C[解析] A项中,没有终端框,所以A项不正确;B项中,输入a,b和c=a2+b2顺序颠倒,且程序框错误,所以B项不正确;D项中,赋值框中a2+b2=c错误,应为c=a2+b2,左右两边不能互换,所以D项不正确;很明显C项正确.4.阅读如图所示的程序框图,若输入的a,b,c的值分别是21,32,75,则输出的a,b,c分别是( )A.75,21,32 B.21,32,75C.32,21,75 D.75,32,21[答案] A[解析] 输入21,32,75后,该程序框图的执行过程是:输入21,32,75.x=21.a=75.c=32.b=21.输出75,21,32.二、填空题5.如下图是求长方体的体积和表面积的一个程序框图,补充完整,横线处应填________.[答案][解析] 变量在计算时应先赋值,这里的a、b,c的值是通过输入语句得到.根据题意,长方体的长、宽、高应从键盘输入,故横线处应填写输入框.6.图1是计算图2中阴影部分面积的一个程序框图,则图1中①处应填________.[答案] S =4-π4a 2[解析] 图2中,正方形的面积为S 1=a 2,扇形的面积为S 2=14πa 2,则阴影部分的面积为S =S 1-S 2=a 2-π4a 2=4-π4a 2.因此图1中①处应填入S =4-π4a 2.三、解答题7.已知x =10,y =2,画出计算w =5x +8y 值的程序框图.[解析] 算法如下: 第一步,令x =10,y =2. 第二步,计算w =5x +8y . 第三步,输出w 的值. 其程序框图如图所示.[特别提醒] (1)程序框图中的每一种图形符号都有特定的含义,在画程序框图时不能混用.(2)流程线上不要忘记加方向箭头.如果不画,就难以判断各程序框间的执行次序. 8.已知一个直角三角形的两条直角边长为a 、b ,斜边长为c ,写出它的外接圆和内切圆面积的算法,并画出程序框图.[解析] 算法步骤如下: 第一步,输入a ,b .第二步,计算c =a 2+b 2.第三步,计算r =12(a +b -c ),R =c2.第四步,计算内切圆面积S 1=πr 2,外接圆面积S 2=πR 2. 第五步,输出S 1、S 2,结束. 程序框图如图.高中数学必修三 1.1.2第2课时条件结构练习 新人教A 版基础巩固一、选择题1.下列关于条件结构的描述,正确的是( )A .条件结构的出口有两个,这两个出口有时可以同时执行B .条件结构的判断框内的条件是惟一的C .条件结构根据条件是否成立选择不同的分支执行D .在条件结构的任何一个分支中,只能执行一个语句,而不能是多个 [答案] C2.给出以下四个问题:①输入一个数x ,输出它的绝对值;②求面积为6的正方形的周长;③求三个数a ,b ,c 中的最大数;④求函数f (x )=⎩⎪⎨⎪⎧3x -1,x ≤0,x 2+1,x >0的函数值.其中需要用条件结构来描述算法的有( )A .1个B .2个C .3个D .4个[答案] C[解析] 其中①③④都需要对条件作出判断,都需要用条件结构,②用顺序结构即可. 3.如图所示的程序框图中,输入x =2,则输出的结果是( )A .1B .2C .3D .4[答案] B[解析] 输入x =2后,该程序框图的执行过程是: 输入x =2,x =2>1成立, y =2+2=2,输出y =2.4.已知a =212 ,b =log33,运算原理如图所示,则输出的值为( )A.22B. 2C.2-12D.2+12[答案] D[解析] 由a =2<b =log33=lg3lg3=2,知a >b 不成立,故输出a +1b =2+12. 5.如下图所示的程序框图,其功能是( ) A .输入a ,b 的值,按从小到大的顺序输出它们的值 B .输入a ,b 的值,按从大到小的顺序输出它们的值 C .求a ,b 的最大值 D .求a ,b 的最小值 [答案] C[解析] 输入a=1,b=2,运行程序框图可得输出2.根据执行过程可知该程序框图的功能是输入a,b的值,输出它们的最大值,即求a,b的最大值.第5题图第6题图6.在佛山市禅城区和南海区打的士收费办法如下:不超过2千米收7元,超过2千米的里程每千米收2.6元,另每车次超过2千米收燃油附加费1元(其他因素不考虑).相应收费系统的程序框图如图所示,则①处应填( )A.y=7+2.6x B.y=8+2.6xC.y=7+2.6(x-2) D.y=8+2.6(x-2)[答案] D[解析] 当行车里程x>2时,费用y=[7+2.6(x-2)]+1=8+2.6(x-2).二、填空题7.读下列流程图填空:(1)流程图(1)的算法功能是________________.(2)流程图(2)的算法功能是________________. (3)流程图(3)的算法功能是________________. (4)流程图(4)的算法功能是________________. [答案] (1)求输入的两个实数a 与b 的和(2)求以输入的两个正数a ,b 为直角边长的直角三角形斜边的长 (3)求输入两数a ,b 的差的绝对值 (4)求函数f (x )=|x -3|+1,即分段函数f (x )=⎩⎪⎨⎪⎧x -2x >34-xx ≤3的函数值8.(2015·广州市)某算法的程序框图如图所示,若输出结果为12,则输入的实数x 的值是________.[答案]2[解析] 当x ≤1时,y =x -1≤0,∵输出结果为12,∴x >1,∴log 2x =12,∴x = 2.三、解答题9.“特快专递”是目前人们经常使用的异地邮寄信函或托运物品的一种快捷方式,某快递公司规定甲、乙两地之间物品的托运费用根据下列方法运算:y =⎩⎪⎨⎪⎧0.53x ,x ≤50,50×0.53+x -50×0.85,x >50,其中y (单位:元)为托运费用,x (单位:千克)为托运物品的重量,试画出计算托运费用y 的程序框图.[解析] 算法程序框图如图所示:10.(2015·聊城高一检测)已知函数y =⎩⎪⎨⎪⎧1+x ,x >0,0,x =0,-x -3,x <0,设计一个算法,输入自变量x 的值,输出对应的函数值.请写出算法步骤,并画出程序框图.[探究] 该函数是分段函数,当x 取不同范围内的值时,函数表达式不同,因此当给出一个自变量x 的值时,也必须先判断x 的范围,然后确定利用哪一段的解析式求函数值,因此函数解析式分为三段,所以判断框需要两个,即进行两次判断.[解析] 算法如下: 第一步,输入自变量x 的值.第二步,判断x >0是否成立,若成立,计算y =1+x ,否则,执行下一步. 第三步,判断x =0是否成立,若成立,令y =0,否则,计算y =-x -3. 第四步,输入y . 程序框图如下图所示.能力提升一、选择题1.(2011·陕西高考)如图中,x 1,x 2,x 3为某次考试三个评阅人对同一道题的独立评分,p 为该题的最终得分.当x 1=6,x 2=9,p =8.5时,x 3等于( )A .10B .7C .8D .11[答案] C[解析] ∵x 1=6,x 2=9, ∴|x 2-x 1|=3>2,输入x 3, 假设|x 3-x 1|<|x 3-x 2|成立, 即|x 3-6|<|x 3-9|, 解得x 3<7.5, 把x 3赋值给x 2,p =x 1+x 22=x 1+x 32=8.5,解得x 3=11,与x 3<7.5矛盾,舍去; 假设|x 3-x 1|≥|x 3-x 2|成立, 即|x 3-6|≥|x 3-9|, 解得x 3≥7.5, 把x 3赋值给x 1,p =x 1+x 22=x 2+x 32=8.5,解得x 3=8,符合要求.2.(2013·新课标全国Ⅰ)执行如图所示的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( )A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5][答案] A[解析] 由程序框图得分段函数s =⎩⎪⎨⎪⎧3t ,t <14t -t 2,t ≥1.所以当-1≤t <1时,s =3t ∈[-3,3);当1≤t ≤3时,s =4t -t 2=-(t -2)2+4,所以此时3≤s ≤4.综上,函数的值域为[-3,4],即输出的s 属于[-3,4].3.(2015·中山高一检测)执行如图所示的程序框图,若输出的结果是8,则输入的数是( )A .2或-2 2B .22或-2 2C .-2或-2 2D .2或2 2[答案] A[解析] 当x 3=8时x =2,a =4,b =8,b >a ,输出8 当x 2=8时,x =±22,a =8,b =±62,又a >b ,输出8, 所以x =-22,故选A.4.2008年3月1日开始实施的《个人所得税法》规定:全月总收入不超过2000元的免征个人工资、薪金所得税,超过2000元部分需征税.设全月总收入金额为x 元,前三级税率如下表所示:级数全月应纳税金额x-2000税率1不超过500元的部分5%2超过500至2000元部分10%3超过2000至5000元部分15%………当工资薪金所得不超过4000元,计算个人所得税的一个算法框图如图,则输出①、输出②分别为( )A.0.05x;0.1xB.0.05x;0.15x-250C.0.05x-100;0.1x-200D.0.05x-100;0.1x-225[答案] D[解析] 当2000<x≤2500时,税收y=(x-2000)×5%=0.05x-100,当2500<x≤4000时,税收y=500×5%+(x-2500)×10%=0.1x-225.二、填空题5.(2015·北京东城二模)已知某程序的框图如图,若分别输入的x的值为0,1,2,执行该程序后,输出的y的值分别为a,b,c,则a+b+c=________.[答案] 6[解析] 该程序框图的功能是输入自变量x 的值,输出函数y =⎩⎪⎨⎪⎧x 2,x >1,1,x =1,4x ,x <1对应的函数值,记y =f (x ),则a =f (0)=40=1,b =f (1)=1,c =f (2)=22=4,则a +b +c =6.6.阅读程序框图,如果输出的函数值在区间[1,3]上,则输入的实数x 的取值范围是________.[答案] {x ∈R |0≤x ≤log 23,或x =2}[解析] 由题意及框图,得⎩⎪⎨⎪⎧-2<x <2,1≤2x≤3或⎩⎪⎨⎪⎧|x |≥2,1≤x +1≤3.解之,得0≤x ≤log 23或x =2.三、解答题7.下面给出了一个算法框图,如图所示.根据该算法框图回答以下问题:(1)该算法框图是为什么问题而设计的?(2)若输入的四个数为5,2,7,22,则最后输出的结果是什么?[解析] (1)“a <b 且a <c 且a <d ”是判断a 是否为最小的数,若成立,则输出a ,此时输出了a ,b ,c ,d 中最小的数;如果不成立,也就是a 不是最小数,从而进入“b <c 且b <d ”,它是判断当a 不是最小数时,b 是否为最小数,若成立,则输出b ,说明此时也是输出了a ,b ,c ,d 中最小的数;如果 不成立,就说明a 与b 都不是最小的数,从而进行“c <d ”,它是判断当a ,b 都不是最小数时,c 是否为最小数,若成立,则输出c ,说明此时输出的是a ,b ,c ,d 中最小的数;若不成立,则输出d ,此时d 是a ,b ,c ,d 中最小的数.故算法的流程图是为“求a ,b ,c ,d 四个数中的最小数并进行输出”而设计的.(2)当输入的四个数分别为5,2,7,22时,最后输出的结果是2.8.(2015·福建厦门模拟)某专家称,中国的通货膨胀率保持在3%左右对中国经济的稳定有利无害,所谓通货膨胀率为3%,指的是每年消费品的价格增长率为3%.在这种情形下,某种品牌的钢琴2010年的价格是10000元,请用程序框图描述这种钢琴今后4年的价格变化情况,并输出4年后钢琴的价格.[解析] 程序框图如下图所示.高中数学必修三 1.1.2第3课时循环结构、程序框图的画法练习新人教A版基础巩固一、选择题1.在循环结构中,每次执行循环体前对控制循环的条件进行判断,当条件满足时执行循环体,不满足则停止,这样的循环结构是( )A.分支型循环B.直到型循环C.条件型循环D.当型循环[答案] D2.下面关于当型循环结构和直到型循环结构的说法,不正确的是( )A.当型循环结构是先判断后循环,条件成立时执行循环体,条件不成立时结束循环B.直到型循环结构要先执行循环体再判断条件,条件成立时结束循环,条件不成立时执行循环体C.设计程序框图时,两种循环结构可以任选其中的一个,两种结构也可以相互转化D.设计循环结构的程序框图时只能选择这两种结构中的一种,除这两种结构外,再无其他循环结构[答案] D3.阅读如图所示的程序框图,运行相应的程序,输出的s值等于( )A.-3 B.-10C.0 D.-2[解析] 开始:k =1,s =1;1<4,是,s =2×1-1=1;k =2,2<4,是,s =2×1-2=0;k =3,3<4,是,s =2×0-3=-3;k =4,4<4,否,输出s =-3,故选 A.4.执行如图所示的程序框图,则输出的S 值是( ) A .4 B.32 C.23 D .-1[答案] D[解析] S =22-4=-1,i =2;S =22+1=23;i =3;S =22-23=32,i =4,S =22-32=4,i =5;S =22-4=-1,i =6. 5.(2015·北京卷)执行如图所示的程序框图,输出的结果为( ) A .(-2,2) B .(-4,0) C .(-4,-4)D .(0,-8)[解析] 运行程序:x =1,y =1,k =0;s =1-1=0,t =1+1=2,x =0,y =2,k =0+1=1,因为1≥3不满足,s =-2,t =2,x =-2,y =2,k =2,因为2≥3不满足,s =-4,t =0,x =-4,y =0,k =3,因为3≥3满足,输出(-4,0).6.(2014·重庆,理5)执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .s >12B .s >35C .s >710D .s >45[答案] C[解析] 该程序框图为循环结构.k =9,s =1时,经判断执行“是”,计算1×99+1=910赋值给s ,然后k 减少1变为8;k =8,s =910时,经判断执行“是”,计算910×88+1=810赋值给s ,然后k 减少1变为7;k =7,s =810时,经判断执行“是”,计算810×77+1=710赋值给s ,然后k 减少1变为6;k =6,s =710,根据输出k 为6,此时应执行“否”.结合选项可知,判断框内应填s >710,故选C.二、填空题7.(2013·湖南高考)执行如图所示的程序框图,如果输入a =1,b =2,则输出的a 的值为________.[答案] 98.(2015·温州高一检测)若如图所示的程序框图运行结果为S =90,那么判断框中应填入的关于k的条件是________.[答案] k>8?三、解答题9.画出求满足12+22+32+…+n2>20152的最小正整数n的程序框图.[分析] 题中要求满足条件的不等式的最小正整数n,不等式左侧是连续自然数的平方和,故可采用循环结构完成.[解析]10.运行如图所示的程序框图.(1)若输入x的值为2,根据该程序的运行过程完成下面的表格,并求输出的i与x的值.第i次i=1i=2i=3i=4i=5x=2×3i(2)若输出i的值为2,求输入x的取值范围.[解析] (1)第i次i=1i=2i=3i=4i=5x=2×3i61854162486因为162<(2)由输出i的值为2,则程序执行了循环体2次,即⎩⎪⎨⎪⎧3x ≤168,9x >168,解得563<x ≤56,所以输入x 的取值范围是563<x ≤56.能力提升一、选择题1.(2014·福建,理5)阅读如图所示的程序框图,运行相应的程序,输出的S 的值等于( )A .18B .20C .21D .40[答案] B[解析] 该程序框图为循环结构,由S =0,n =1得S =0+21+1=3,n =1+1=2,判断S =3≥15不成立,执行第二次循环,S =3+22+2=9,n =2+1=3,判断S =9≥15不成立,执行第三次循环,S =9+23+3=20,n =3+1=4,判断S =20≥15成立,输出S =20.故选B.2.(2013·浙江)某程序框图如图所示,若该程序运行后输出的值是95,则( )A .a =4B .a =5C .a =6D .a =7[答案] A[解析] k =1,S =1+1-12=32;k =2,S =1+1-13=53;k =3,S =1+1-14=74;k =4,S =1+1-15=95.输出结果是95,这时k =5>a ,故a =4.3.以下给出的是计算12+14+16+…+120的值的一个程序框图,其中判断框内应填入的条件是( )A .i <20?B .i >10?C .i <10?D .i ≤10?[答案] D[解析] i =1,S =12;i =2,S =12+14;i =3,S =12+14+16;依次下去:i =10,S =12+14+…+120,故选D. 4.(2015·陕西卷)根据下边的图,当输入x 为2006时,输出的y =( ) A .28 B .10 C .4D .2[答案] B[解析] 初始条件:x =2006;第1次运行:x =2004;第2次运行:x =2002;第3次运行:x =2000;……;第1003次运行:x =0;第1004次运行:x =-2,不满足条件x ≥0?,停止运行,所以输出的y =32+1=10,故选B.二、填空题5.(2014·辽宁,理13)执行下面的程序框图,若输入x =9,则输出y =________.[答案]299[解析] 输入x =9,则y =5,|y -x |=4>1,执行否,x =5,y =113,|y -x |=43>1,执行否,x =113,y =299,|y -x |=49<1,执行是,输出y =299.6.(2014·湖北,理13)设a 是一个各位数都不是0且没有重复数字的三位数,将组成a 的3个数字按从小到大排成的三位数记为I (a ),按从大到小排成的三位数记为D (a )(例如a =815,则I (a )=158,D (a )=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a ,输出的结果b =________.[答案] 495[解析] 不妨取a =815,则I (a )=158,D (a )=851,b =693; 则取a =693,则I (a )=369,D (a )=963,b =594; 则取a =594,则I (a )=459,D (a )=954,b =495; 则取a =495,则I (a )=459,D (a )=954,b =495. 故输出结果b =495. 三、解答题7.以下是某次考试中某班15名同学的数学必修三成绩:72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来并画出程序框图.[分析] 用条件分支结构来判断成绩是否高于80分,用循环结构控制输入的次数,同。
高中数学必修3《排列组合问题经典题型与通用方法》

排列组合问题经典题型与通用方法1.相邻问题捆绑法:题目中规定相邻的几个元素捆绑成一个组,当作一个大元素参与排列.例1.,,,,A B C D E五人并排站成一排,如果,A B必须相邻且B在A的右边,则不同的排法有()A、60种B、48种C、36种D、24种2.相离问题插空排:元素相离(即不相邻)问题,可先把无位置要求的几个元素全排列,再把规定的相离的几个元素插入上述几个元素的空位和两端.例2.七人并排站成一行,如果甲乙两个必须不相邻,那么不同的排法种数是()A、1440种B、3600种C、4820种D、4800种3.定序问题缩倍法:在排列问题中限制某几个元素必须保持一定的顺序,可用缩小倍数的方法.例3.A,B,C,D,E五人并排站成一排,如果B必须站在A的右边(,A B可以不相邻)那么不同的排法有()A、24种 B、60种 C、90种 D、120种4.标号排位问题分步法:把元素排到指定位置上,可先把某个元素按规定排入,第二步再排另一个元素,如此继续下去,依次即可完成.例4.将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有() A、6种 B、9种 C、11种 D、23种5.有序分配问题逐分法:有序分配问题指把元素分成若干组,可用逐步下量分组法.例5.(1)有甲乙丙三项任务,甲需2人承担,乙丙各需一人承担,从10人中选出4人承担这三项任务,不同的选法种数是() A、1260种 B、2025种 C、2520种 D、5040种(2)12名同学分别到三个不同的路口进行流量的调查,若每个路口4人,则不同的分配方案有()A、4441284C C C种 B、44412843C C C种 C、4431283C C A种 D、444128433C C CA种6.全员分配问题分组法:例6.(1)4名优秀学生全部保送到3所学校去,每所学校至少去一名,则不同的保送方案有多少种?(2)5本不同的书,全部分给4个学生,每个学生至少一本,不同的分法种数为()A、480种B、240种C、120种D、96种7.名额分配问题隔板法:例7:10个三好学生名额分到7个班级,每个班级至少一个名额,有多少种不同分配方案?8.限制条件的分配问题分类法:例8.某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设,其中甲同学不到银川,乙不到西宁,共有多少种不同派遣方案?9.多元问题分类法:元素多,取出的情况也多种,可按结果要求分成不相容的几类情况分别计数再相加。
高中数学必修三同步练习题库:用样本估计总体(填空题:较易)
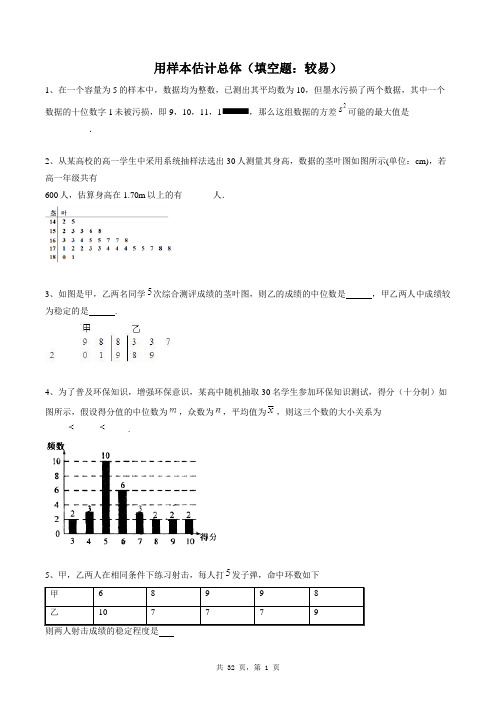
用样本估计总体(填空题:较易)1、在一个容量为5的样本中,数据均为整数,已测出其平均数为10,但墨水污损了两个数据,其中一个数据的十位数字1未被污损,即9,10,11,1,那么这组数据的方差可能的最大值是__________.2、从某高校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图所示(单位:cm),若高一年级共有600人,估算身高在1.70m以上的有_______人.3、如图是甲,乙两名同学次综合测评成绩的茎叶图,则乙的成绩的中位数是,甲乙两人中成绩较为稳定的是 .4、为了普及环保知识,增强环保意识,某高中随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为,众数为,平均值为,则这三个数的大小关系为_______________.5、甲,乙两人在相同条件下练习射击,每人打发子弹,命中环数如下则两人射击成绩的稳定程度是6、下图是甲、乙两市领导干部年龄的茎叶图,对于这两市领导干部的平均年龄给出的以下说法正确的是________.①甲市领导干部的年龄的分布主要集中在40~60之间;②乙市领导干部的年龄分布大致对称;③甲市领导干部的平均年龄比乙市领导干部的平均年龄大;④平均年龄都是50.7、从某高校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图所示(单位:cm),若高一年级共有600人,估算身高在1.70m以上的有_______人.8、某市为了了解居民家庭网购消费情况,调查了10000户家庭的月消费金额(单位:元),所有数据均有区间上,其频率分布直方图如图所示,则被调查的10000户家庭中,月消费金额在1000元以下的有__________户.9、一所中学共有4 000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有________人.10、某人连续五周内收到的包裹数分别为3,2,5,1,4,则这5个数据的标准差为________.11、下列四个命题①样本方差反映的是所有样本数据与样本平均值的偏离程度;②从含有2008个个体的总体中抽取一个容量为100的样本,现采用系统抽样方法应先剔除8人,则每个个体被抽到的概率均为;③从总体中抽取的样本数据共有m个a,n个b,p个c,则总体的平均数的估计值为;④某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497--512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.其中真命题的个数是_____个12、某校在市统测后,从高三年级的1000名学生中随机抽出100名学生的数学成绩作为样本进行分析,得到样本频率分布直方图,如图所示,则估计该校高三学生中数学成绩在之间的人数为__________.13、某植树小组测量了一批新采购的树苗的高度,所得数据如茎叶图所示(单位:),则这批树苗高度的中位数为__________.14、某人5次上班途中所花的时间(单位:分钟)分别为.已知这组数据的平均数为10,方差为2,则的值为___.15、若1,2,3,4,这五个数的平均数为3,则这五个数的方差为__________.16、某学院的三个专业共有1200名学生,为了调查这些学生勤工俭学的情况,拟采用分层抽样的方法抽取一个容量为120的样本.已知该学院的专业有380名学生,专业有420名学生,则在该学院的专业应抽取____________名学生.17、在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,则该35名运动员成绩的中位数为__________.18、为了解学生答卷情况,某市教育部门在高三某次测试后抽取了名同学的试卷进行调查,并根据所得数据画出了样本的频率分布直方图(如图),该样本的中位数是__________.19、已知一组数据,,,,,则该组数据的方差是____.20、气象意义上从春季进入夏季的标志为:“连续5天的日平均温度均不低于22℃.”现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数,单位:℃):①甲地:5个数据的中位数为24,众数为22;②乙地:5个数据的中位数为27,总体均值为24;③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.2.则肯定进入夏季的地区有____个.21、交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为,其中甲社区有驾驶员人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为,,,,则这四个社区驾驶员的总人数为.22、已知一组数据的方差是S,那么另一组数据的方差是。
高中数学必修三第三章《概率》章节练习题(含答案)

高中数学必修三第三章《概率》章节练习题(含答案)高中数学必修三第三章《概率》章节练题一、选择题(每小题3分,共18分)1.下列试验属于古典概型的有()。
A.1个B.2个C.3个D.4个2.任取两个不同的1位正整数,它们的和是8的概率是()。
A。
B。
C。
D。
补偿训练】一袋中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为()。
A。
B。
C。
D。
3.在全运会火炬传递活动中,有编号为1,2,3,4,5的5名火炬手。
若从中任选3人,则选出的火炬手的编号相连的概率为()。
A。
B。
C。
D。
4.任意抛掷两颗骰子,得到的点数分别为a,b,则点P(a,b)落在区域|x|+|y|≤3中的概率为()。
A。
B。
C。
D。
5.在棱长为a的正方体ABCD-A1B1C1D1中随机地取一点P,则点P与正方体各表面的距离都大于的概率为()。
A。
B。
C。
D。
6.如图,两个正方形的边长均为2a,左边正方形内四个半径为的圆依次相切,右边正方形内有一个半径为a的内切圆,在这两个图形上各随机撒一粒黄豆,落在阴影内的概率分别为P1,P2,则P1,P2的大小关系是()。
A。
P1=P2 B。
P1>P2 C。
P1<P2 D。
无法比较二、填空题(每小题4分,共12分)7.一颗骰子抛掷2次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,则a+b能被3整除的概率为()。
8.已知函数f(x)=log2x,x∈R。
在区间[1,8]上任取一点x,使f(x)≥-2的概率为()。
补偿训练】已知直线y=x+b,b∈[-2,3],则该直线在y轴上的截距大于1的概率是()。
A。
B。
C。
D。
9.如图,利用随机模拟的方法可以估计图中由曲线y=√(x)与两直线x=2及y=0所围成的阴影部分的面积S:①先产生两组[0,1]的均匀随机数,a=RAND,b=RAND;②做变换,令x=4a,y=√(b);③判断(x,y)是否在阴影部分中,若是则计数器加1;④重复上述步骤n次,估计S≈n×计数器/.则利用上述方法,当n=时,估计得到的阴影部分的面积S≈()。
(经典)高中数学必修三单元测试题附答案解析

(数学3必修)第二章:统计 [基础训练A 组] 一、选择题1.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ,则有( )A . c b a >>B .a c b >>C .b a c >>D .a b c >>2.下列说法错误的是 ( )A .在统计里,把所需考察对象的全体叫作总体B .一组数据的平均数一定大于这组数据中的每个数据C .平均数、众数与中位数从不同的角度描述了一组数据的集中趋势D .一组数据的方差越大,说明这组数据的波动越大3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( ) A .3.5 B .3- C .3 D .5.0- 4. 要了解全市高一学生身高在某一范围的学生所占比例的大小,需知道相应样本的( )A . 平均数B . 方差C . 众数D . 频率分布5.要从已编号(160)的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是( )A .5,10,15,20,25,30B .3,13,23,33,43,53C .1,2,3,4,5,6D .2,4,8,16,32,48 6.容量为100的样本数据,按从小到大的顺序分为8组,如下表:组号 1 2 3 4 5 6 7 8 频数 10 13 x 14 15 13 12 9第三组的频数和频率分别是 ( )A .14和0.14B .0.14和14C .141和0.14 D . 31和141二、填空题1.为了了解参加运动会的2000名运动员的年龄情况,从中抽取100名运动员;就这个问题,下列说法中正确的有 ;① 2000名运动员是总体;②每个运动员是个体;③所抽取的100名运动员是一个样本;④样本容量为100;⑤这个抽样方法可采用按年龄进行分层抽样;⑥每个运动员被抽到的概率相等。
高中数学必修三练习题(精编)

高中数学必修三练习题(精编)必修三第三章测试卷一、选择题:1.从甲、乙、丙三人中任选两名代表,甲被选中的概率是( 1/3 )。
2.将骰子向桌面上先后抛掷2次,其中向上的数之积为12的结果有( 2 )种。
3.在面积为S的△ABC的内部任取一点P,则△PBC的面积小于△ABC面积的概率为( 1/3 )。
4.从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论正确的是( A )A与C互斥。
5.如图,是由一个圆、一个三角形和一个长方形构成的组合图形,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则三个形状颜色不全相同的概率为( 3/8 )。
6.给甲、乙、丙三人打电话,若打电话的顺序是任意的,则第一个打电话给甲的概率是( 1/3 )。
7.在区间[-π,π]内随机取两个数分别记为a,b,则使得函数f(x)=x2+2ax-b2+π2有零点的概率为( 1/2 )。
8.如图所示,茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中有一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是( 27/49 )。
9.节日前夕,XXX在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒内间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( 1/3 )。
10.一个数学兴趣小组有女同学2名,男同学3名,现从这个数学兴趣小组中任选2名同学参加数学竞赛,则参加数学竞赛的2名同学中,女同学人数不少于男同学人数的概率为( 3/10 )。
11.掷一枚均匀的正六面体骰子,设A表示事件“出现2点”,B表示“出现奇数点”,则P(A∪B)等于( 1/2 )。
12.如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆,在扇形OAB内随机取一点,则此点取自阴影部分的概率是(1/2π )。
高中数学必修三《古典概型》课后练习(含答案)

高中数学必修三《古典概型》课后练习(含答案)古典概型课后练习(1)列出所有可能结果.题三:从1、2、3、4中任取两个不同的数字构成一个两位数,则这个两位数大于20的概率为.题四:一个不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片和三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.(1)从中任意抽取一张卡片,求该卡片上写有数字1的概率;(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率.求:(1)题七:在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.求取出的两个球上标号为相邻整数的概率.题八:在甲、乙两个盒子中分别装有标号为1,2,3,4,5的五个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.求事件“取出的两个球上标号之和能被3整除”的概率.题九:从1,3,5,7这四个数中随机地取两个数组成一个两位数,则组成的两位数是5的倍数的概率为.题十:已知:a、b、c为集合A={1,2,3,4,5,6}中三个不同的数,通过如下框图给出的一个算法输出一个整数a,则输出的数a=5的概率是.据此估计,该运动员两次掷镖恰有一次正中靶心的概率为.题十二:从某小组的2名女生和3名男生中任选2人去参加一项公益活动.(1)求所选2人中恰有一名男生的概率;(2)求所选2人中至少有一名女生的概率.题十三:已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.(1)求甲射击一次,命中不足8环的概率;(2)求甲射击一次,至少命中7环的概率.题十四:有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为()1123A.B.CD.3234题十五:设集合A={1,2},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线某+y=n上”为事件Cn(2≤n≤5,n∈N),若事件Cn的概率最大,则n的所有可能值为()A.3B.4C.2和5D.3和4题十六:已知关于某的一元二次函数f(某)=a某2b某+1,设集合P={1,2,3},Q={1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b.(1)求函数y=f(某)有零点的概率;(2)求函数y=f (某)在区间题一:312种结果,两位数大于20的为:题三:(1)0.56;(2)0.74.详解:记事件A为“不派出医生”,事件B为“派出1名医生”,事件C为“派出2名医生”,事件D为“派出3名医生”,事件E为“派出4名医生”,事件F为“派出不少于5名医生”.则事件A、B、C、D、E、F彼此互斥,且P(A)=0.1,P(B)=0.16,P(C)=0.3,P(D)=0.2,P(E)=0.2,P(F)=0.04.(1)“派出医生至多2人”的概率为P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.(2)“派出医生至少2人”的概率为P(C+D+E+F)=P(C)+P(D)+P(E)+P(F)=0.3+0.2+0.2+0.04=0.74,或1-P(A+B)=1-0.1-0.16=0.74.题四:111,,.364详解:记“任取一球,得到红球,得到黑球,得到黄球,得到白球”分别为事件A、B、C、D,则由题意可得。
同步人教B版高中数学必修第三册练习:第八章 8.2.3 倍角公式

[A 基础达标]1.若sin α-cos α=2,则sin 2α等于( ) A .2 B.12 C .1D .-1解析:选D.因为sin α-cos α=2,所以(sin α-cos α)2=1-sin 2α=2,所以sin 2α=-1. 2.2sin 2α1+cos 2α·cos 2αcos 2α等于( ) A .tan α B .tan 2α C .1D.12 解析:选B.原式=4sin αcos α2cos 2α·cos 2αcos 2α=sin 2αcos 2α=tan 2α.3.若θ∈⎣⎡⎦⎤π4,π2,sin 2θ=378,则sin θ等于( )A.35 B.45 C.74D.34解析:选D.因为θ∈⎣⎡⎦⎤π4,π2,所以2θ∈⎣⎡⎦⎤π2,π.所以cos 2θ=-1-sin 22θ=-18,所以sin θ=1-cos 2θ2=34. 4.若sin x ·tan x <0,则1+cos 2x 等于( ) A.2cos x B .-2cos x C.2sin xD .-2sin x解析:选B.因为sin x ·tan x <0,所以x 为第二、三象限角,所以cos x <0, 所以1+cos 2x =2cos 2 x =2|cos x |=-2cos x . 5.已知cos 2x2cos ⎝⎛⎭⎫x +π4=15,则sin 2x =( ) A .-2425B .-45C.2425D.255解析:选A.因为cos 2x2cos ⎝⎛⎭⎫x +π4=15, 所以cos 2x -sin 2x cos x -sin x =15,所以cos x +sin x =15,所以1+sin 2x =125,所以sin 2x =-2425.6.已知sin ⎝⎛⎭⎫π4-x =35,则sin 2x 的值等于________.解析:法一:因为sin ⎝⎛⎭⎫π4-x =35,所以cos ⎝⎛⎭⎫π2-2x =1-2sin 2⎝⎛⎭⎫π4-x =1-2×⎝⎛⎭⎫352=725, 所以sin 2x =cos ⎝⎛⎭⎫π2-2x =725. 法二:由sin ⎝⎛⎭⎫π4-x =35,得22(sin x -cos x )=-35, 所以sin x -cos x =-325,两边平方得1-sin 2x =1825,所以sin 2x =725.答案:7257.已知sin 2α=14,α∈⎝⎛⎭⎫π4,π2,则cos α-sin α=________.解析:因为α∈⎝⎛⎭⎫π4,π2,所以sin α>cos α即cos α-sin α<0,又sin 2α=14,则有cos α-sin α=-(cos α-sin α)2=-1-sin 2α=-1-14=-32. 答案:-328.已知2cos 2x +sin 2x =A sin(ωx +φ)+b (A >0),则A =________,b =________.解析:因为2cos 2x +sin 2x =1+cos 2x +sin 2x =1+2sin ⎝⎛⎭⎫2x +π4,所以1+2sin ⎝⎛⎭⎫2x +π4=A sin(ωx +φ)+b ,所以A =2,b =1.答案:2 19.化简2cos 2α-12tan ⎝⎛⎭⎫π4-αsin2⎝⎛⎭⎫π4+α.解:原式=cos 2α2tan ⎝⎛⎭⎫π4-αcos 2⎝⎛⎭⎫π4-α=cos 2α2sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α=cos 2αsin ⎝⎛⎭⎫π2-2α=cos 2αcos 2α=1.10.(1)已知sin α+cos α=33⎝⎛⎭⎫π2<α<π,求cos 2α,tan 2α的值; (2)已知sin ⎝⎛⎭⎫π4-αsin ⎝⎛⎭⎫π4+α=26⎝⎛⎭⎫0<α<π2,求sin 2α的值.解:(1)因为(sin α+cos α)2=13,所以1+2sin αcos α=13,所以2sin αcos α=sin2α=-23,所以(sin α-cos α)2=1-2sin αcos α=1+23=53.又π2<α<π,所以sin α>0,cos α<0,所以sin α-cos α=153,所以cos 2α=cos 2α-sin 2α=(cos α+sin α)·(cos α-sin α)=33×⎝⎛⎭⎫-153=-53, 所以tan 2α=sin 2αcos 2α=-23-53=255.(2)因为sin ⎝⎛⎭⎫π4-α=sin ⎣⎡⎦⎤π2-⎝⎛⎭⎫π4+α=cos ⎝⎛⎭⎫π4+α.所以sin ⎝⎛⎭⎫π4-αsin ⎝⎛⎭⎫π4+α=sin ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+α=12sin ⎣⎡⎦⎤2×⎝⎛⎭⎫π4+α=12sin ⎝⎛⎭⎫π2+2α=12cos 2α=26,所以cos 2α=23. 又因为0<α<π2,所以0<2α<π,所以sin 2α=73.[B 能力提升]11.已知tan x =2,则tan ⎣⎡⎦⎤2⎝⎛⎭⎫x -π4等于( )A.43 B .-43 C.34 D .-34 解析:选C.tan ⎣⎡⎦⎤2⎝⎛⎭⎫x -π4=tan ⎝⎛⎭⎫2x -π2=sin ⎝⎛⎭⎫2x -π2cos ⎝⎛⎭⎫2x -π2=-cos 2x sin 2x =-1tan 2x=-1-tan 2x 2tan x =4-12×2=34.12.已知θ∈⎝⎛⎭⎫π2,π,1sin θ+1cos θ=22,则sin ⎝⎛⎭⎫2θ+π3=________.解析:1sin θ+1cos θ=22⇒sin θ+cos θsin θcos θ=22 ⇒sin θ+cos θ=22sin θcos θ⇒1+sin 2θ=2sin 22θ, 因为θ∈⎝⎛⎭⎫π2,π,所以2θ∈(π,2π),所以sin 2θ=-12,所以sin θ+cos θ<0,所以θ∈⎝⎛⎭⎫3π4,π,所以2θ∈⎝⎛⎭⎫3π2,2π, 所以cos 2θ=32,所以sin ⎝⎛⎭⎫2θ+π3=sin 2θcos π3+sin π3cos 2θ=12. 答案:1213.已知cos ⎝⎛⎭⎫α+π4=35,π2≤α<3π2,求cos(2α+π4)的值.解:因为π2≤α<3π2,所以3π4≤α+π4<7π4.因为cos ⎝⎛⎭⎫α+π4>0,所以3π2<α+π4<7π4.所以sin ⎝⎛⎭⎫α+π4=-1-cos 2⎝⎛⎭⎫α+π4=-1-⎝⎛⎭⎫352=-45. 所以cos 2α=sin ⎝⎛⎭⎫2α+π2=2sin ⎝⎛⎭⎫α+π4cos ⎝⎛⎭⎫α+π4=2×⎝⎛⎭⎫-45×35=-2425, sin 2α=-cos ⎝⎛⎭⎫2α+π2=1-2cos 2⎝⎛⎭⎫α+π4=1-2×⎝⎛⎭⎫352=725.所以cos ⎝⎛⎭⎫2α+π4=22cos 2α-22sin 2α=22×⎝⎛⎭⎫-2425-725=-31250. 14.已知sin x 2-2cos x2 =0.(1)求tan x 的值; (2)求cos 2xcos ⎝⎛⎭⎫5π4+x sin (π+x )的值.解:(1)由sin x 2-2cos x2=0,知cos x 2≠0,所以tan x2=2,所以tan x =2tanx21-tan 2x2=2×21-22=-43.(2)由(1)知tan x =-43,所以cos 2xcos⎝⎛⎭⎫5π4+x sin (π+x )=cos 2x-cos ⎝⎛⎭⎫π4+x (-sin x )=cos 2x -sin 2x⎝⎛⎭⎫22cos x -22sin x sin x=(cos x -sin x )(cos x +sin x )22(cos x -sin x )sin x=2×cos x +sin xsin x=2×1+tan x tan x =24.[C 拓展探究]15.已知函数f (x )=1+sin x -cos x 1+sin x +cos x +1+sin x +cos x1+sin x -cos x .(1)化简f (x ),并求f (x )的最小正周期; (2)若f (α)=8,求cos 2α; (3)求f (x )的单调递增区间. 解:(1)因为f (x )=2sin 2x 2+2sin x 2cos x 22cos 2x 2+2sin x 2cos x 2+2cos 2x 2+2sin x 2cosx 22sin 2x 2+2sin x 2cosx 2=sinx 2cos x 2+cos x 2sin x 2=2sin x ,所以最小正周期T =2π.(2)因为f (α)=8,所以sin α=14,所以cos 2α=1-2sin 2α=78.(3)设u =sin x ,因为函数y =2u在(-∞,0),(0,+∞)上为减函数,所以要求f (x )的单调递增区间,即求u =sin x (x ≠k π,且x ≠-π2+2k π,k ∈Z )的单调递减区间,所以f (x )的单调递增区间为⎝⎛⎭⎫2k π-π,2k π-π2(k ∈Z )和⎝⎛⎭⎫2k π+π2,2k π+π(k ∈Z ).由Ruize收集整理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修三第一章 算法初步1.如果输入2=n ,那么执行下图中算法后的输出结果是( ) A.3 B.4 C.5 D.62.某同学设计下面的程序框图计算和式222220321++++ 的值,则判断框中应填写( )A.19i ≤?B.19i ≥?C.20i ≤?D.21i ≤?3.下列程序语言中,哪一个是输入语句( ) A. PRINT B. INPUT C. THEN D. END4.把89化成五进制数的末位数字为( ) A.1 B.2 C.3 D.45.把(4)1010化为十进制数为( ) A .60 B .68C .70D .746.计算机执行下面的程序段后,输出的结果是 ( )A .4,-2B .4,1C .1,4D .-2,47.当输入x=﹣4时,如图的程序运行的结果是( )A .7B .8C .9D .151=a ;3=b ;b a a +=;b a b -=;print(a ,b )8.执行如图所示程序框图所表达的算法,若输出的x 值为48,则输入的x 值为( ) A .3B .6C .8D .129.某程序框图如图所示,该程序运行后输出的k 的值是 ( ) A .4 B .5 C .6 D .7第9题10.在下列各数中,最大的数是( )A .)9(85 B.(5)210 C.(8)68 D.)2(11111 11.下列对算法的理解不正确的是( ) A. 一个算法包含的步骤是有限的B. 一个算法中每一步都是明确可操作的,而不是模棱两可的C. 算法在执行后,结果应是明确的D. 一个问题只可以有一个算法12.如图所示的程序框图表示求算式“2×3×5×9×17”之值,则判断框内可以填入( ) A . k≤10B . k≤16C . k≤22D . k≤3413.如图给出的是计算1+13+15+17+19的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句分别是( )A .2,5?n n i =+>B . 2,5?n n i =+=C .1,5?n n i =+=D .1,5?n n i =+>第12题第13题第8题IF 10a < THEN2y a =*els e y a a =*14.下列给出的赋值语句中正确的是( )A.A =3B.M M -=C.2==B AD.0=+y x 15.当3=a 时,下面的程序段输出的结果是( )A .9B .3C .10D .6 16.某程序框图如图所示,则该程序运行后输出的值是( ) A .3- B .3-C .3D .3 第16题17.用“除k 取余法”将十进制数259转化为五进制数是( )A .(5)2012B .(5)2013C .(5)2014D .(5)201518.对如图1所示的两个程序和输出结果判断正确的是( )图A.程序不同,结果不同B.程序不同,结果相同C.程序相同,结果不同D.程序相同,结果相同i=1S=0WHILE i<=1000 S=S+i i=i+1 WENDPRINT S ENDi=1000 S=0 DO S=S+i i=i-1LOOP UNTIL i<1 PRINT S END19.如图所示的程序框图是计算12+14+16+…+120的值,其中判断框内应填入的条件是( )A .i >8B .i >9C .i >10D .i >1120.执行如图所示的程序框图,若输出的S =88,则判断框内应填入的条件是( ) A .?7>k B .?6>k C .?5>k D .?4>k19题 第20题21.定义某种运算b a M ⊗=,运算原理如图所示,则式子11(2tan )sin (4cos )()4233πππ-⊗+⊗的值为( )A .4B .8C .11D .13 22.以下说法错误的是( ) A .最简单的算法结构是顺序结构B .输入框和输出框可用在算法中任何需要输入,输出的位置C .判断框是具有超过一个退出点的唯一符号D .可以利用赋值语句进行代数式的演算 23.如图程序框图输出的结果为( ) (A )511 (B )513 (C )49 (D )613第21题第23题24.如图,程序框图的运算结果为( ) A .6 B .24 C .20 D .12025. 如果上述程序运行的结果为S =132,那么判断框中应填入( ) A 、10?k ≤ B 、10?k ≥ C 、11?k ≤ D 、11?k ≥第24题 第25题26.执行如图所示的程序框图,若输入的x 的值为3,则输出的n 的值为( ) A . 4 B . 5 C . 6 D . 727.给出一个如图所示的流程图,若要使输入的x 值与输出的y 值相等, 则这样的x 值的个数是( )A .1B .2C .3D .4第26题第27题28.如图所示,该程序运行后,为使输出的b 值为16,则循环体的判断框内①处应填 ( )(A )3?a > (B )3?a ≥ (C )3?a ≤ (D )3?a <29.若如下框图所给的程序运行结果为35S =,那么判断框中应填入的关于k 的条件是( ) A .7=k B .6≤k C .6<k D .6>k第28题 第29题30.执行如图所示的程序框图,若输入n 的值为2,则输出s 的值是( ) A .1 B .2 C .4 D .731.执行如图所示的程序框图,若输入x 的值为2+log 23,则输出y 的值为( ) A .38B .8C .12D .24 第30题 第31题32.阅读下图的程序框图.若输入1n =, 则输出k 的值为( ) A .3 B .4 C .5 D .633.执行如图所示的程序框图,若输出结果为63,则M 处的条件为( ) (A )64?k < (B )64?k ≥ (C )32?k < (D )32?k ≥第32题 第33题34.如图是计算函数2x ,x 1y 0,1x 2x ,x 2⎧-≤-⎪=-<≤⎨⎪>⎩的值的程序框图,则在①、②、③处应分别填入的是A .y x =-,y 0=,2y x =B .y x =-,2y x =,y 0=C .y 0=,2y x =,y x =-D .y 0=,y x =-, 2y x = 35.阅读程序框图,为使输出的数据为31,则①处应填的数字为( ) (A )4 (B )5 (C )6 (D )734题第35题36.若右边的程序框图输出的S 是126,则条件①可为( ) (A )5n ≤ (B )6n ≤ (C )7n ≤ (D )8n ≤37.执行如图所示的程序框图,若输出x 的值为23,则输入的x 值为 ( ) A .0 B .1 C .2 D .11开始是否i <输出S结2iS S =+1i i =+①1,1S i ==开始x输入x 1>-x 2>y输出结束①②③否是否是第36题37题38.如图所示的程序框图,运行相应的程序,若输入x 的值为-5,则输出的y 值是( ) A .41B .1C .2D .-1 39.执行如图所示的程序框图,若输入2x =,则输出y 的值为( ) A .23 B .11 C .5 D .2第38题 第39题40.某班有24名男生和26名女生,数据1a ,2,a …50,a 是该班50名学生在一次数学学业水平模拟考试中的成绩(成绩不为0),如图所示的程序用来同时统计全班成绩的平均数:A ,男生平均分:M ,女生平均分:W .为了便于区别性别,输入时,男生的成绩用正数,女生的成绩用其相反数,那么在图中空白的判断框和处理框中,应分别填入( ) A .0,50M W T A +>=? B .0?,50M WT A +<= C .0?,50M W T A -<=D .0?,50M WT A ->= 41.某程序框图如图所示,则该程序运行后输出的值是( ) A .3- B 13+ C 13- D 321x x =+是否3n ≤1n n =+x输入开始1n =x输出结束第40题 第41题42.将二进制数)2(11100转化为四进制数,正确的是( ) A .)4(120 B .)4(130 C .)4(200 D .)4(20243.当输入1-=x ,20=y 时,图中程序运行后输出的结果为( )A .3; 43B .43;3 C.-18;16 D .16;-18 44.如果执行如图的程序框图,那么输出的值是( ) A .2010 B .-1C .21D .2INPUT x INPUT y IF x<0 THEN x=y+3 ELSE y=y-3 END IF开始s=0,n=n<=25? s=s+sin3n πn=n+输出s结束是 否45.执行如图所示的框图,如果输入的⎥⎦⎤⎢⎣⎡∈2,0πx ,则输出的y 值属于() A .[]0,1 B .20,2⎡⎤⎢⎥⎣⎦ C .3,12⎡⎤⎢⎥⎣⎦ D .2,12⎡⎤⎢⎥⎣⎦第44题 第45题46.给出以下四个问题:①输入一个数x ,输出它的相反数; ②求面积为6的正方形的周长; ③求三个数,,a b c 中的最大数;④求函数1,0()2,0x x f x x x -≥⎧=⎨+<⎩的函数值.其中不需要用条件语句来描述其算法的有( )A .1个B .2个C .3个D .4个 47.下列给出的赋值语句中正确的是( )A .1s a =+B .1a s +=C .1s a -=D .1s a -=48.算法共有三种逻辑结构,即顺序结构、条件结构和循环结构,下列说法正确的是( ) A .一个算法只含有一种逻辑结构 B .一个算法最多可以包含两种逻辑结构 C .一个算法必须含有上述三种逻辑结构 D .一个算法可以含有上述三种逻辑结构49.执行如图所示的程序框图,如果输入1,3a b ==,则输出的a 的值为( ) A .7 B .9 C .10 D .1350.阅读如图所示的程序框图,运行相应的程序,则输出的s 的值为( ) A .-1 B .1 C .0 D .3第49题第50题51.用秦九韶算法计算函数532()2323f x x x x x =-++-的值,若2x =,则3V 的值是( ) A .28- B .29 C .55 D .47 52.计算机执行右边的程序段后,输出的结果是( ) A .3,1 B .1,4 C .2,4- D .2,1-53.执行如图所示的程序框图,如果输入的N 是10,那么输出的S 是( )A .2B .101-C .111-D .231-1)3(+-⋅=i S S结束开始1,1==i S1+=i i?4>i 输出S 是 否a >8开始 输入a,b a =a+b 输出a 结束否 是开始S=0,k=1 S=S+输出S 结束k<N11k k++N输入1k k =+是否54.执行如图程序框图,如果输入的N 的值是6,那么输出的p 的值是( )A .105B .115C .120D .720 55.执行如图所示的程序框图,如果输出132=S ,则判断框中应填( ) A .?10≥i B .?11≥i C .?12≥i D .?11≤i56.执行如图所示的程序框图,若“否”箭头分别指向①和②,则输出的结果分别是( ) A .55,53 B .51,49 C .55,49 D .53,51第55题 第56题57.下面关于算法的说法正确的是( ) A .秦九韶算法是求两个数的最大公约数的方法 B .更相减损术是求多项式的值的方法C .割圆术是采用正多边形面积逐渐逼近圆面积的算法计算圆周率πD .以上结论皆错58.执行如图所示的程序框图,则输出S 的值是( )A .45B .95C .56D .11659.如下框图输出的S为()A.15 B.17 C.26 D.40 60.下列程序框图中,输出的B是()A.3- B.33- C.0 D.361.下边程序运行后输出的结果为()A.50 B.5 C.25 D.062.将两个数2010,2011a b==交换使得2011,2010a b==,下面语64.运行下图所示的程序,如果输出结果为sum=1320,那么判断框中应填()A.i≥9 B.i≥10 C.i≤9 D.i≤10tanB A=是开始,13A iπ==结束输出B1i i=+3A Aπ=+2015i≤否a=0j=1WHILE j<=5a=(a + j) MOD 5j=j+1WENDPRINT aEND65.将两个数20,37a b ==交换,使37,20a b ==,下面语句正确一组是 ( )66.如图所示程序框图中,输出S =( )A .45B .66C .66-D .55- 67.阅读下面的程序框图,输出结果s 的值为( ) A .12 B .316C .116D .18第66题 第67题68.当3n =时,执行如右图所示的程序框图,输出的S 值为( ) A .30 B.14 C.8 D .669.阅读下图程序框图,运行相应的程序,则程序运行后输出的结果为( ) A .7 B .9 C .11 D .13第68题 第69题70.执行如图所示的程序框图,输出的i值为()A.2 B.3 C.4 D.571.执行如图所示的程序框图,则输出的k的值为()A.4 B.5 C.6 D.7i =1, S = 01 S>输出ii = i + 1 S = S + lg i开始结束否是第70题第71题72.某程序框图如图所示,该程序运行后输出的k的值是()A.6 B.8 C.5 D.773.执行如图的程序框图,输出的T=()A.30 B.25 C.20 D.12第72题第73题74.执行下图所示的程序框图,若要使输入的x值与输出的y值相等,则这样的x值的个数是A.1 B.2 C.3 D.475.执行如图所示的程序框图,则输出的S=()(A)32(B)53(C)85(D)127第74题75题76.某程序框图(如上图)所示,该程序运行后输出的k 的值是 ( ) A .6 B .7 C .4 D .577.某程序框图如图所示,若输出的S=57,则判断框内为( ) A 、k >4? B 、k >5? C 、k >6? D 、k >7?第76题第77题78.如图给出的是计算11112462014++++的值的一个程序框图,则判断框内应填入的条件是( )A .1006i ≤B .1007i ≤C .1007i >D .1006i > 79.执行下边的程序框图,则输出的S 是( ) A .5040 B .4850 C .2550 D .2450第78题第79题开始结束0,1,1S A i ===1S S A=+1i i =+ 5?i >是 输出S否A A i=+80.用辗转相除法求得数98与63的最大公约数是____________; 81.执行如图所示的程序框图,若输入x =10,则输出y 的值为_____.82.设1234518,19,20,21,22x x x x x =====,将这五个数据依次输入下面程序框进行计算,则输出的S 值_______83.已知532()31f x x x x x =-+-+,应用秦九韶算法计算3x =时的值时,3v 的值为________.84.已知函数532)(2345-+-++=x x x x x x f ,用秦九韶算法计算=)5(f __________; 85.二进制数1101(2)化为五进制数为_________ 86.右边框图表示的程序所输出的结果是 . 87.执行如图所示的程序框图,若输入如下四个函数:①y =2x;②y =-2x; ③f(x)=x +x -1;④f(x)=x -x -1.则输出函数的序号为________.第86题第87题88.如图所示的算法中,3a e =,3b π=,c e π=,其中π是圆周率, 2.71828e =…是自然对数的底数,则输出的结果是 . 89.执行下图所示的程序框图,若输入2x =, 则输出y 的值为 .90.下图是一个算法的流程图,当n是 时运算结束.91.程序框图如下图所示,若该程序输出的结果为,则判断框中应填入的条件是__ __.92.程序:M=1 M=M+1 M=M+2 PRINT M END M 的最后输出值为 . 93.运行如图所示的程序框图,则输出的S 值是________. 94.如图,该程序运行后输出的结果为 。
